- Преподавателю
- Математика
- Олимпиадные задания 7 - 11 классы
Олимпиадные задания 7 - 11 классы
| Раздел | Математика |
| Класс | 11 класс |
| Тип | Другие методич. материалы |
| Автор | Черных А.Н. |
| Дата | 17.11.2015 |
| Формат | doc |
| Изображения | Есть |
Задания олимпиады
по математике
7 (VIII´) класс
-
Найдите наименьшее число, которое
при делении на 2 дает остаток 1,
при делении на 3 дает остаток 2,
при делении на 4 дает остаток 3,
при делении на 5 дает остаток 4,
при делении на 6 дает остаток 5,
при делении на 7 дает остаток 6,
при делении на 8 дает остаток 7,
при делении на 9 дает остаток 8.
(6 баллов)
-
В двух седьмых классах 70 учеников.
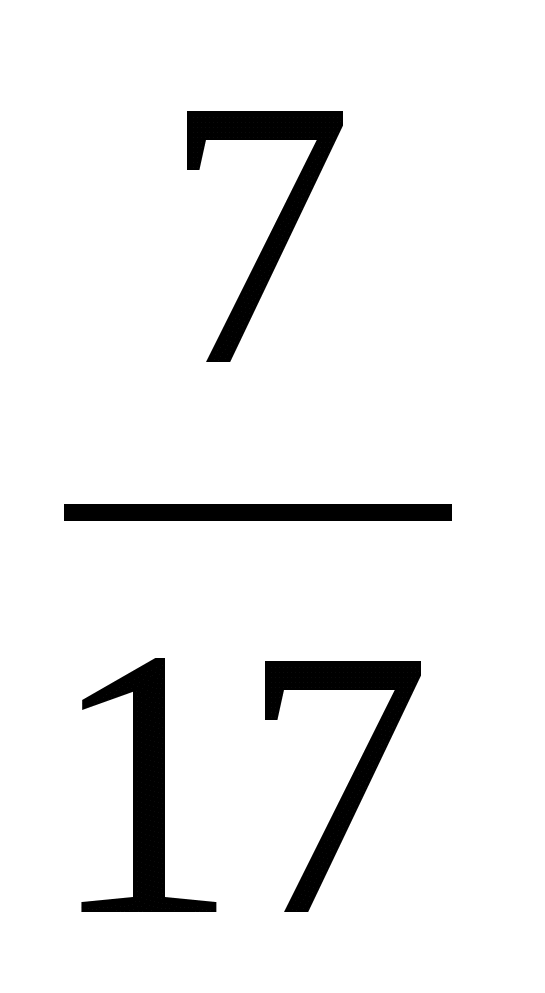 учеников одного класса и
учеников одного класса и 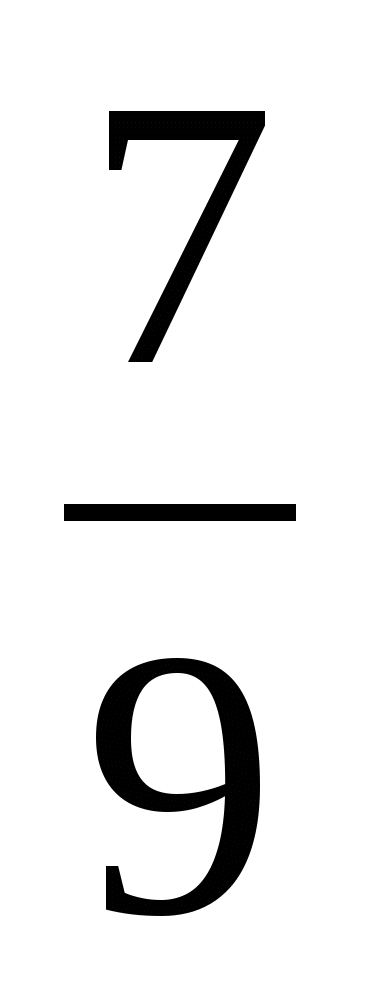 учеников другого посещают различные кружки и факультативы. Сколько учеников в каждом классе?
учеников другого посещают различные кружки и факультативы. Сколько учеников в каждом классе?
(7 баллов)
-
Сумма четырех чисел равна 100. Если первое число увеличить на 4, второе - в 4 раза, третье число уменьшить на 4, а четвертое - в 4 раза, получатся равные результаты. Найдите эти числа.
(8 баллов)
-
На полоске клетчатой бумаги двое играющих по очереди закрашивают клетки: первый всегда закрашивает пять любых подряд идущих клеток, второй - четыре клетки подряд. Причем, уже закрашенную клетку второй раз красить нельзя. Проигрывает тот, кто не может сделать очередной ход. Кто выигрывает при правильной игре - первый или второй, если по длине полоски размещено 2004 клетки? (Рис. 1)
Рис. 1
(9 баллов)
-
Отрезок AB длиной 2004 мм разбит на n равных отрезков, на каждом из которых, как на диаметре, построена окружность (на рисунке 2 изображено в качестве примера разбиение на 7 равных отрезков).







 A B
A B
Рис. 2
Определите значения, которые может принимать сумма длин всех этих окружностей.
(10 баллов)
Задания олимпиады
по математике
8 класс
-
Установите количество пятизначных чисел, кратных числу 1000, но не кратных числу 2000.
(7 баллов)
-
У Наташи
4005-3992 · (4003+2 · 4002+3·400+4) рублей.
Мороженое стоит 2004 рубля. Хватит ли у Наташи денег на мороженое?
(6 баллов)
-
В классе 33 человека. У каждого ученика спросили, сколько у него в классе тёзок и сколько однофамильцев (включая и родственников). Среди ответов учащихся встретились все целые числа от 0 до 10. Докажите, что в классе есть два ученика с одинаковыми фамилией и именем.
(8 баллов)
-
На 100-клеточной квадратной белой доске два игрока закрашивают ее клетки в черный цвет: первый всегда закрашивает квадрат 2х2, а второй - уголок, образованный тремя клетками. Уже закрашенную клетку второй раз красить нельзя. Какой игрок - первый или второй - выиграет при правильной игре?
(9 баллов)
-
Дан равносторонний треугольник АВС. На продолжении стороны СВ за точку В отмечена точка D, а на продолжение стороны AB за точку В - точка М так, что CD = ВМ. Докажите, что AD = DМ.
(10 баллов)
Задания олимпиады
по математике
9 класс
-
У трех сестер Веры, Надежды и Любови дни и месяцы рождения совпадают - 30 сентября. В день совершеннолетия - 18 лет - старшей сестры Веры оказалось, что сумма возрастов всех сестер делится на 18. В день 18-летия Надежды ситуация повторилась. Определите, сколько лет будет каждой сестре, когда младшая - Любовь - станет совершеннолетней.
(7 баллов)
-
На доске записали три числа. После того, как нашли их произведение, сумму и сумму попарных произведений оказалось, что получили три записанных на доске числа. Какие числа записаны на доске?
(7 баллов)
-
Вовочка рвет листок с результатами неудачного тестирования. За одну секунду он может разорвать какой-то один из клочков на 2 части или разорвать на две части каждый клочок. Может ли Вовочка через 16 секунд получить ровно 2004 клочка?
(9 баллов)
-
Докажите, что любой треугольник можно разрезать на три части так, что из них можно сложить прямоугольный треугольник.
(9 баллов)
-
Население острова состоит из рыцарей, которые всегда говорят правду, и лжецов, которые всегда лгут.
Троим островитянам, шедшим вместе, встретился турист, который каждому задал вопрос: «Сколько рыцарей среди Ваших спутников?».
Первый ответил: «Один».
Второй сказал: «Ни одного».
Что сказал третий островитянин?
(8 баллов)
Задания олимпиады
по математике
10 класс
-
Бригада землекопов должна была начать работу в 8 ч. Но, простояв в очереди за лопатами, землекопы начали работу позже: первый на 5 минут, второй - на 10 минут, третий - на 15 минут и т.д. До обеда бригада вырыла траншею, в 12 часов землекопы ушли на обед. После обеда землекопы работали с 13 до 16 часов и вырыли вторую траншею. Сколько землекопов было в бригаде?
(7 баллов)
-
Докажите, что число
9+99+999+…+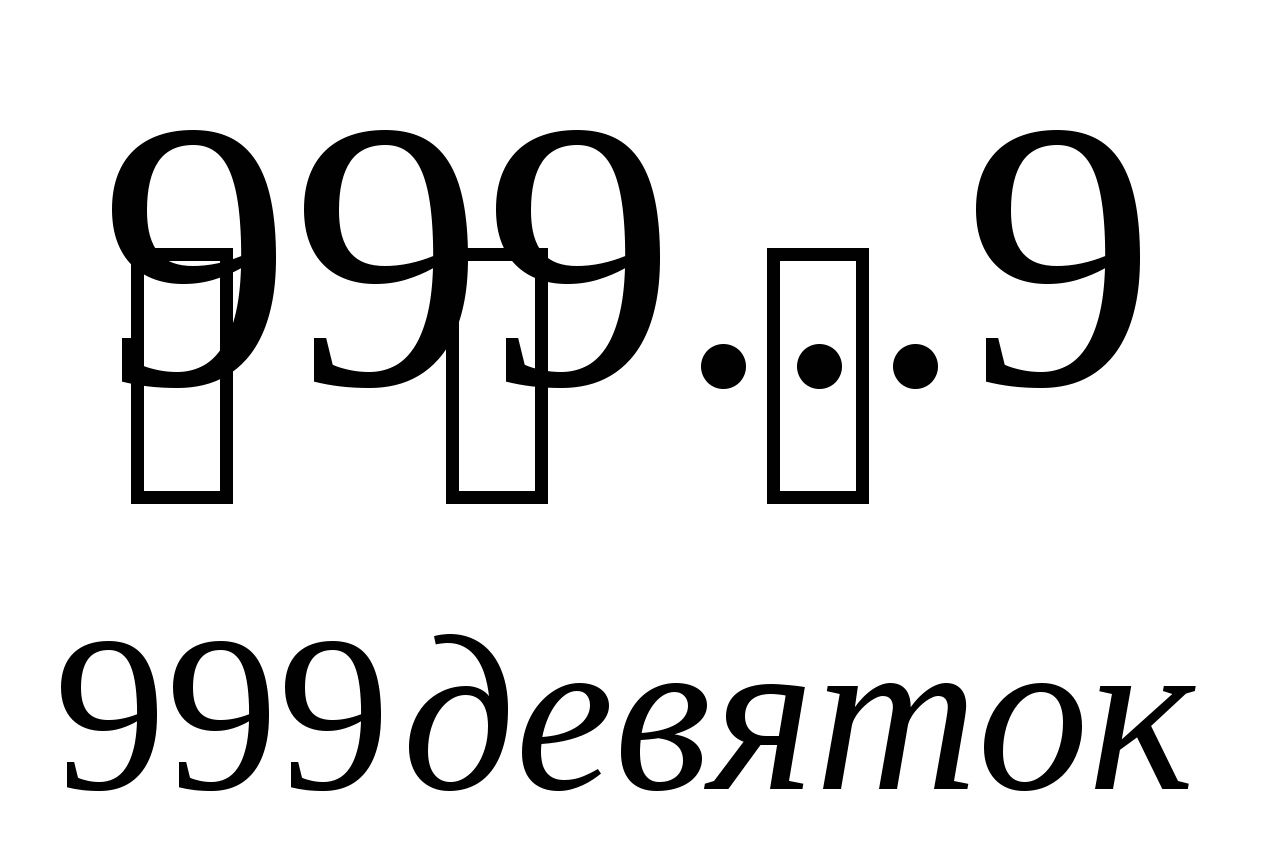
делится на 999.
(8 баллов)
-
Решите уравнение
2004[х]-2005{х}=0.
(6 баллов)
-
В трапеции ABCD боковая сторона CD перпендикулярна основанию AD, AD=8, AB=4. Окружность, которая проходит через вершины А, В и С содержит трапецию внутри и пересекает продолжение диагонали BD в точке К, такой, что ВК=9. Найдите длину диагонали BD.
(10 баллов)
-
Тестирование по математике проходили 100 учеников, среди которых были математики, которые всегда правдиво и правильно отвечают на любой вопрос, и математики, которые всегда лгут, разговаривая на нематематические темы. Первые 60 учеников, выходя после тестирования, заявили: «Среди оставшихся в аудитории учеников лжецов больше, чем правдивых». Можно ли определить, сколько всего лжецов принимало участие в тестировании?
(9 баллов)
Задания олимпиады
по математике
11 класс
-
Абитуриент принял участие в тестировании. Тестирование проводилось по трем предметам с равным количеством тестовых заданий по каждому предмету. С математикой абитуриент справился довольно успешно, выполнив 19 заданий, по физике удалось верно ответить ровно на 30% предложенных вопросов, а по русскому языку результат оказался хуже, чем по физике. Но в общей сложности абитуриент правильно выполнил ровно половину от общего количества тестовых заданий. Определите, из скольки заданий был составлен тест по каждому предмету.
(8 баллов)
-
Найдите наименьшее натуральное число такое, что для любой цифры 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 число имеет делитель, оканчивающийся этой цифрой.
(6 баллов)
-
Найдите все функции f, удовлетворяющие при любых действительных х и у уравнению
f (x-y) = f (x) + f (y) - 2xy.
(7 баллов)
-
Докажите, что высота прямоугольного треугольника, у которого все вершины лежат на параболе у = х2 и гипотенуза параллельна оси абсцисс, равна 1.
(10 баллов)
-
Определите стороны треугольника АВС, если известно, что из отрезков, длины которых равны cosA, cosB, cosC можно составить треугольник, равный треугольнику АВС.
(9 баллов)
Указания, решения и комментарии
7 (VIII´)класс
-
Ответ: 2519.
Решение. Найдём число, которое на 1 больше искомого. Если искомое число А, то число А+1 делится на 2, 3, 4, 5, 6, 7, 8, 9 без остатка. Наименьшим число, которое кратно каждому из чисел 2, 3, 4, 5, 6, 7, 8, 9 является число, которое равно произведению
5 · 7 · 8 · 9 = 2520.
Действительно, число 2520 делится на 8, а, следовательно, на 2 и на 4; это число делится на 9, а, следовательно, и на 3; поскольку число 2520 делится на 2 и на 3, то оно делится и на 6. Таким образом, число 2520 делится на все числа без остатка. Тогда число
2520 - 1 = 2519
делится на каждое данное число с наибольшим остатком.
-
Ответ: 34 ученика, 36 учеников.
Решение. Поскольку количество учащихся в каждом классе натуральное, и числитель и знаменатель каждой дроби 
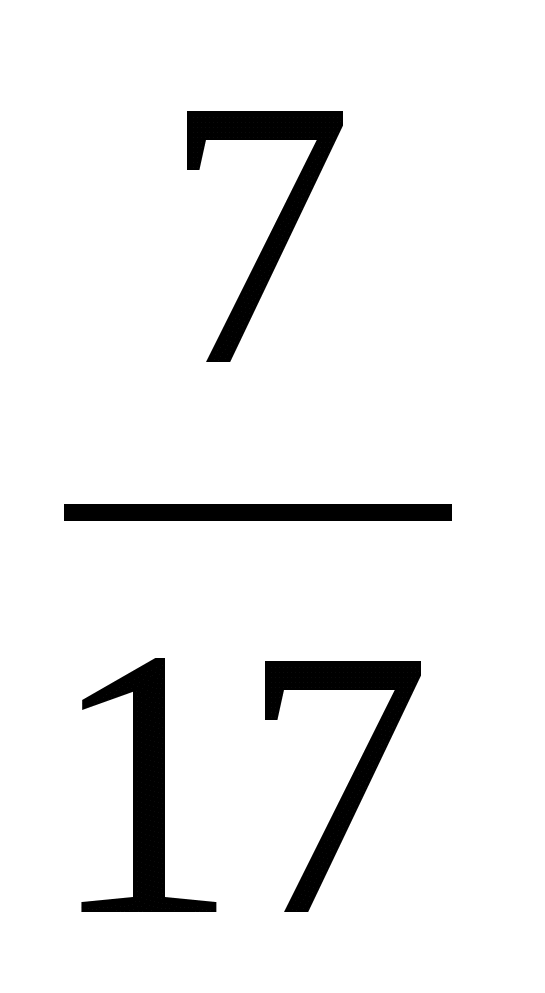 и
и 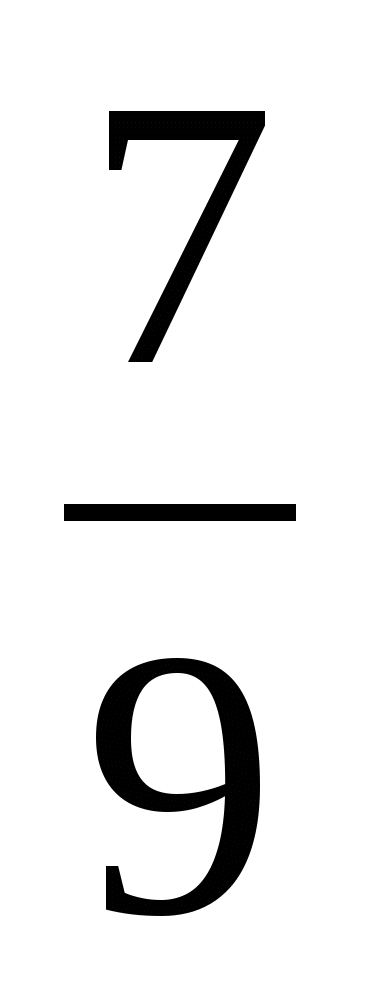 - взаимно простые числа, то число учащихся первого класса кратно 17, а второго класса - кратно 9. Составим таблицу возможных значений учащихся в каждом классе в зависимости от числа учащихся первого класса, обозначив это количество буквой а:
- взаимно простые числа, то число учащихся первого класса кратно 17, а второго класса - кратно 9. Составим таблицу возможных значений учащихся в каждом классе в зависимости от числа учащихся первого класса, обозначив это количество буквой а:
а
17
34
51
68
70-а
53
36
29
2
Только одна пара чисел - 34 и 36 - удовлетворяет утверждению задачи: 34 кратно 17, а 36 кратно 9.
-
Ответ: 12, 4, 20, 64.
Решение. Обозначим данные числа буквами а, b, с и d. По условию задачи:
a + b + с + d = 100,
a + 4 = b - 4 = 4 c = 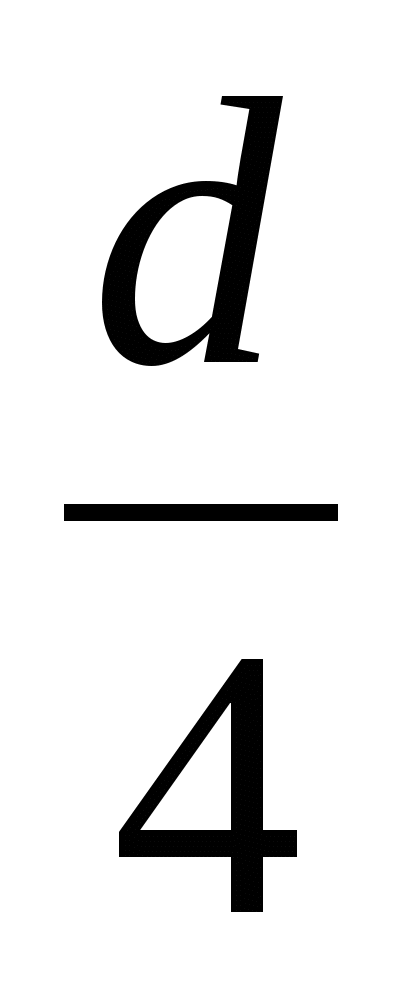 .
.
Выражая из второго равенства a, b и с через d и, подставляя полученные выражения в первое равенство, находим d=64, a=12, b=4, c=20.
-
Ответ: при правильной игре всегда выигрывает второй игрок.
Решение. Своим первым ходом первый игрок закрашивает 5 подряд идущих клеток,
414
Рис. 1
второй, отступив на 4 клетки от одного из краев полоски, закрашивает 4 клетки подряд (Рис. 1). В дальнейшем второй игрок делает любые ответные ходы, сохраняя незакрашенными 4 крайние клетки на одном из краев полоски. Когда других ходов не остается, второй игрок закрашивает эти клетки. У первого игрока ответного хода нет.
-
Ответ: 2004 мм.
Решение. Длина диаметра каждой окружности равна
D = 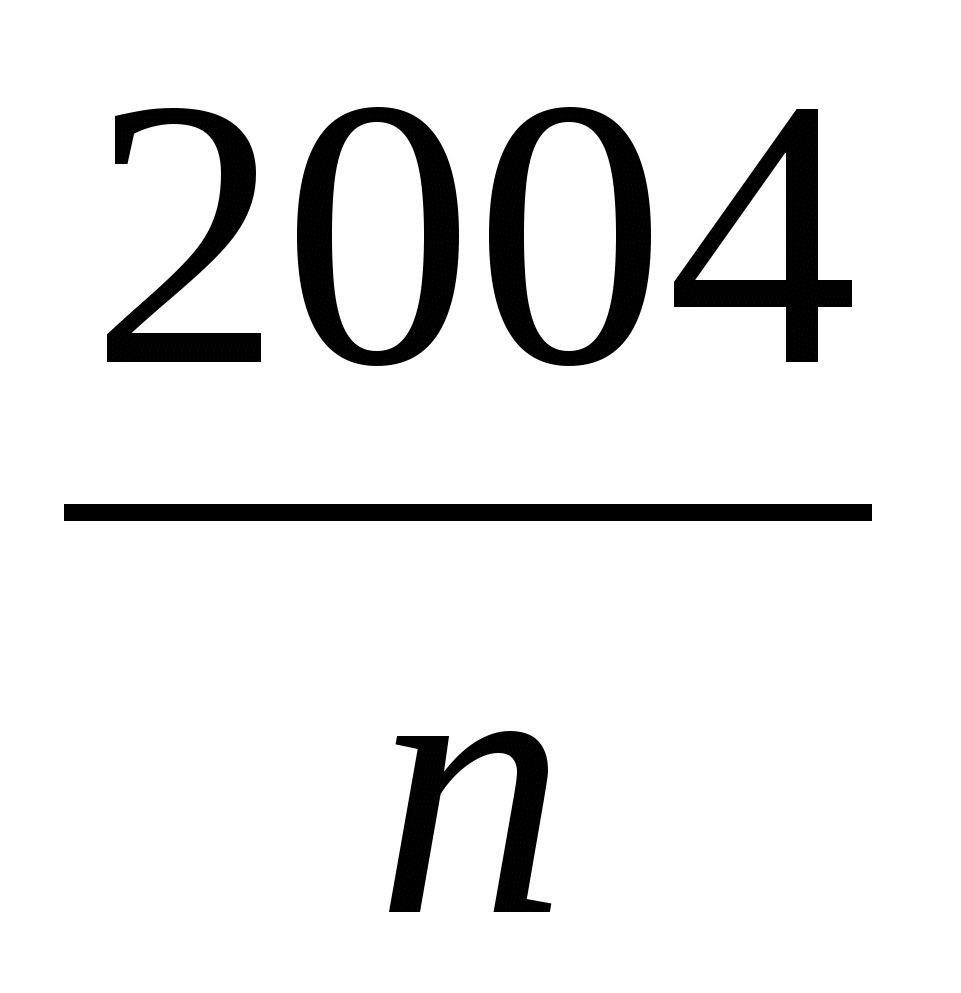 мм;
мм;
длина каждой окружности равна
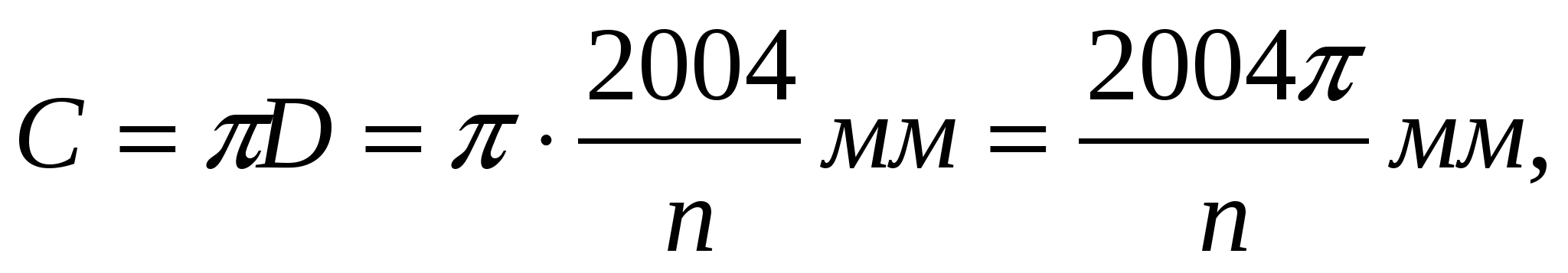
а длина n таких окружностей -
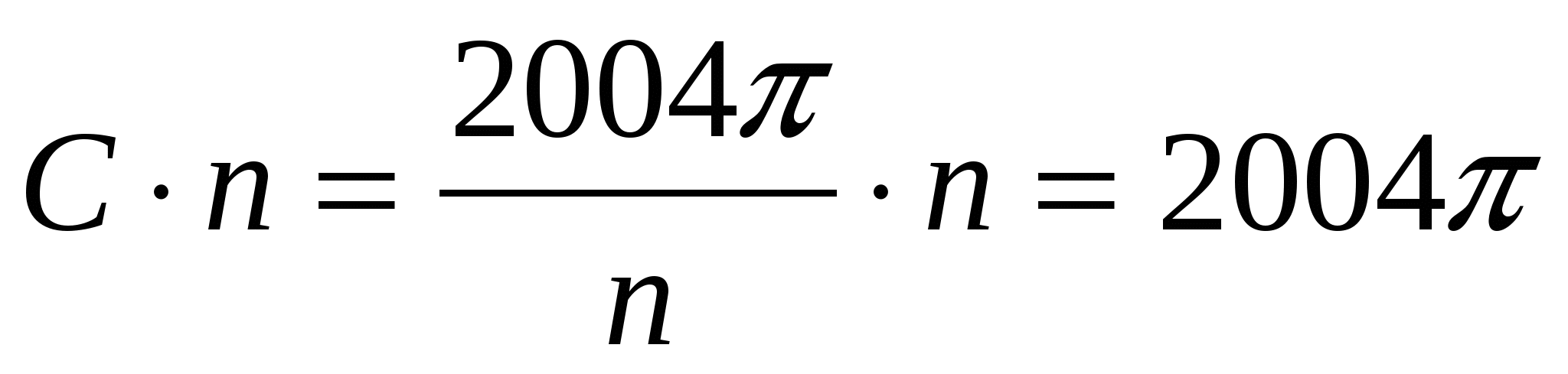 (мм).
(мм).
Указания, решения и комментарии
8 класс
-
Ответ: 45.
Решение. Первая цифра пятизначного числа может быть любой из девяти -
1, 2, 3, 4, 5, 6, 7, 8, 9; третья, четвертая и пятая - 0. Вторая цифра числа, кратного 1000 - любая из десяти 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, а числа, кратного 2000 - любая из пяти - 0, 2, 4, 6, 8. Поэтому пятизначных чисел, кратных 1000
9 · 10 · 1 · 1 · 1 = 90,
а кратных 2000
9 · 5 · 1 · 1 · 1 = 45.
Значит, чисел, удовлетворяющих условию задачи:
90 - 45 = 45.
-
Ответ: не хватит.
Решение. Обозначая n = 400, получаем:
n5-(n-1)2 (n3+2n2+3n+4) =
= n5-(n-1) (n4+n3+n2+n-4) =
= n5-(n5-5n+4) = 5n-4 =
= 5 · 400-4 = 1996 (рублей).
Т.к. 19962004, то денег на мороженое не хватает.
-
Доказательство.
Если объединить учеников в группы по фамилиям, то каждый войдет в одну группу по фамилии и вторую - по имени; причем, группа может состоять и из одного человека, если у ученика, например, нет тёзки или однофамильца. Всего в классе образуется 11 групп: есть группы из 1, 2, 3, 4, 5, …, 11 человек. Поскольку
1+2+3+…+11 = 66 = 2 · 33, то каждый ученик уже учтен дважды, а, следовательно, групп равно 11.
Рассмотрим группу из 11 человек - допустим, однофамильцев. В других группах меньше 11 человек. Групп тёзок не более десяти. Значит, два однофамильца из 11 обязательно входят в одну группу тёзок, т.е. у них одинаковы и имя и фамилия.
-
Ответ: второй.
Решение. После первого хода первого игрока второму игроку надо первым ходом закрасить в любом из свободных углов доски три клетки уголком так, что оставить незакрашенными три клетки (Рис. 1),
Рис. 1
которые образуют уголок. В дальнейшем второй игрок делает любые ходы, не закрашивая эти три клетки. Когда других возможных ходов не остается, второй игрок закрашивает этот уголок. Ответного хода у первого игрока нет.
-
Доказательство.



 А
А
С В D
N
M
На отрезке ВМ отметим точку N так, что 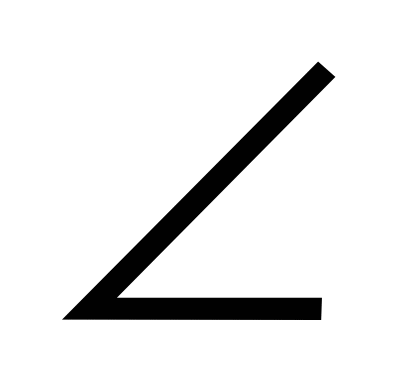 BDN = 60°. Тогда в треугольнике BDN:
BDN = 60°. Тогда в треугольнике BDN: 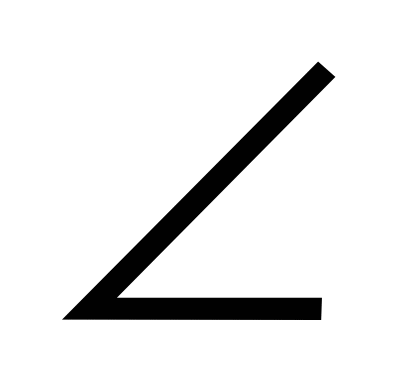 В = 60° как угол, вертикальный углу равностороннего треугольника,
В = 60° как угол, вертикальный углу равностороннего треугольника, 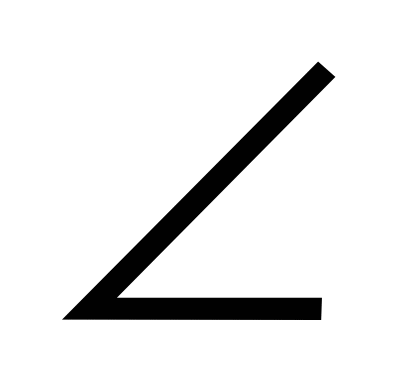 D = 60° - по построению. Следовательно, по теореме о сумме углов треугольника
D = 60° - по построению. Следовательно, по теореме о сумме углов треугольника 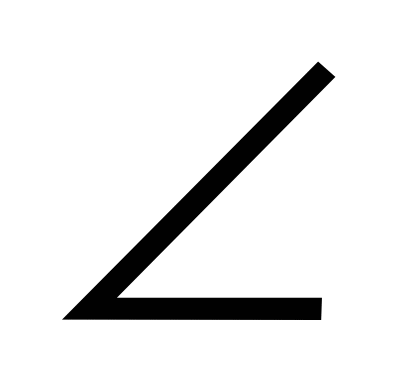 BDN=60°. Значит, треу-гольник BDN - равносторон-ний. Поэтому BD = BN = DN.
BDN=60°. Значит, треу-гольник BDN - равносторон-ний. Поэтому BD = BN = DN.
Получаем: MN = BM - BN = CD - BD = CB = AB.
Рассмотрим треугольники ADB и MDN:
AB = NM, BD = DN и 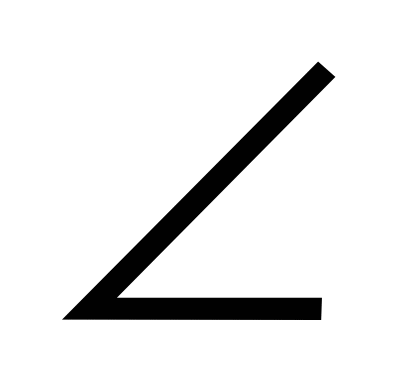 ABD =
ABD = 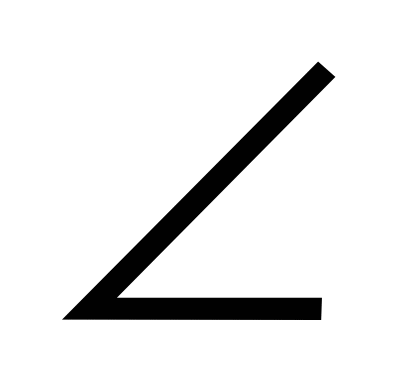 MND как внешние углы равносторонних треугольников. Значит, треугольники ADB и MDN равны по двум сторонам и углу между ними. Поэтому AD = DM.
MND как внешние углы равносторонних треугольников. Значит, треугольники ADB и MDN равны по двум сторонам и углу между ними. Поэтому AD = DM.
Указания, решения и комментарии
9 класс
1. Ответ: 30 лет, 24 года, 18 лет.
Решение. Предположим, что в день 18-летия Веры Надежде исполнилось а лет, Любови - b лет. Так как Вера старшая из сестер и сумма 18+а+b делится на 18, то 18+а+b<54, т.е. а+b<36. Получаем: а+b=18.
В день совершеннолетия Надежды - через b лет - Вере исполнится (18+b) лет, а Любови 2b лет; причем сумма 18+b+18+2b=36+3b кратна 18. Значит, 3b кратно 18, а b кратно 6. Учитывая, что a+b=18, получаем возможные значения b: 0, 6, 12, 18. Составим таблицу возможных возрастов сестер на момент совершеннолетия Веры:
Возможные значения b
b=0
b=6
b=12
b=18
Вера
18
18
18
18
Надежда
18
12
6
0
Любовь
0
6
12
18
Вывод
-
+
-
-
Ситуация при b=0 означает, что Любовь родилась в день совершеннолетия Веры, а Надежда и Вера - в один день. Это противоречит утверждению: Вера - старшая сестра.
В ситуациях при b=12 и b=18 возникает противоречие с утверждением: Любовь - младшая сестра.
В ситуации при b=6 выполняются все утверждения задачи.
Поэтому Любовь достигнет совершеннолетия через 12 лет после совершеннолетия Веры. Сестрам в этот день исполнится: Вере - 30 лет, Надежде - 24 года, Любови - 18 лет.
2. Ответ: -1, -1 и 1; 0, 0 и n.
Решение. Обозначим записанные на доске числа а, b, c; найдем их произведение abc, сумму a+b+c и сумму попарных произведений ab+bc+ac. Не теряя общности, можно считать что
a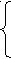 bc = a,
bc = a,
a+b+c=b,
ab+bc+ac=c.
Из первого равенства получаем:
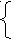 a ≠ 0, или a = 0.
a ≠ 0, или a = 0.
bc = 1;
При а ≠ 0 имеем 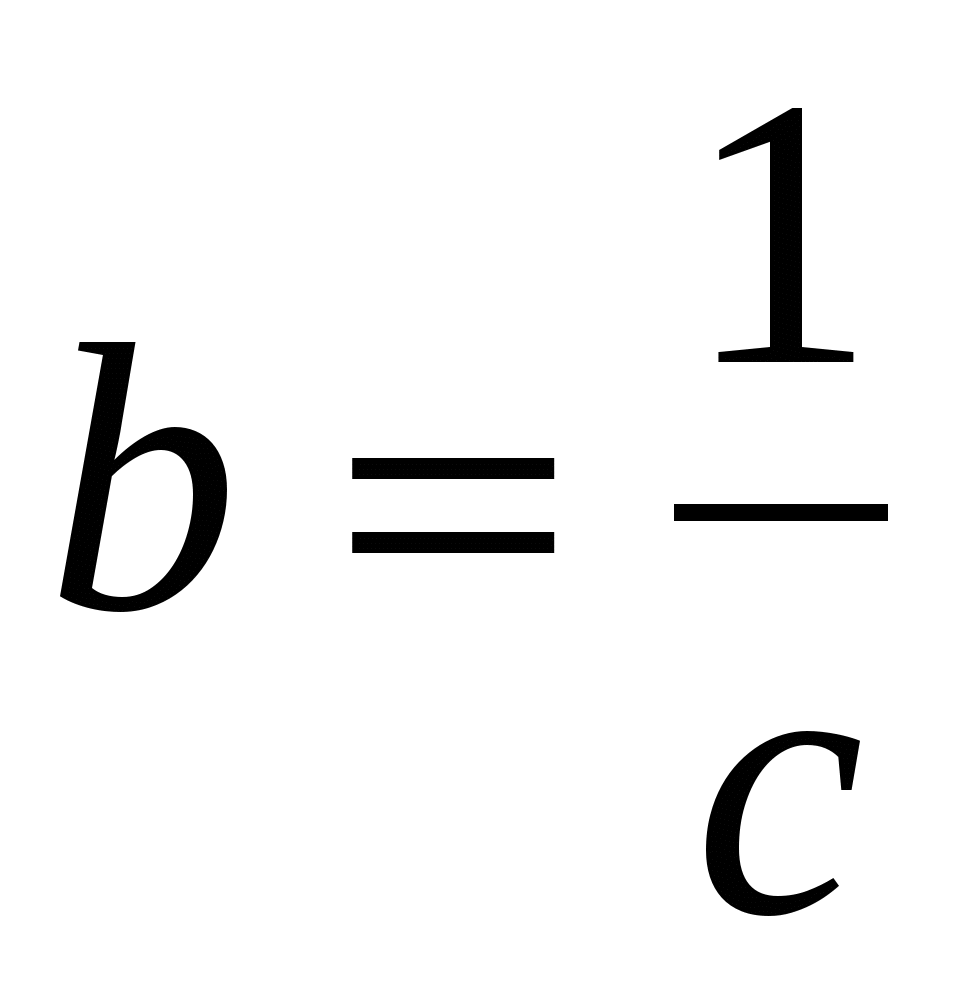 .
.
Второе равенство системы принимает вид:
а+с = 0, т.е.
а = -с.
Третье равенство -
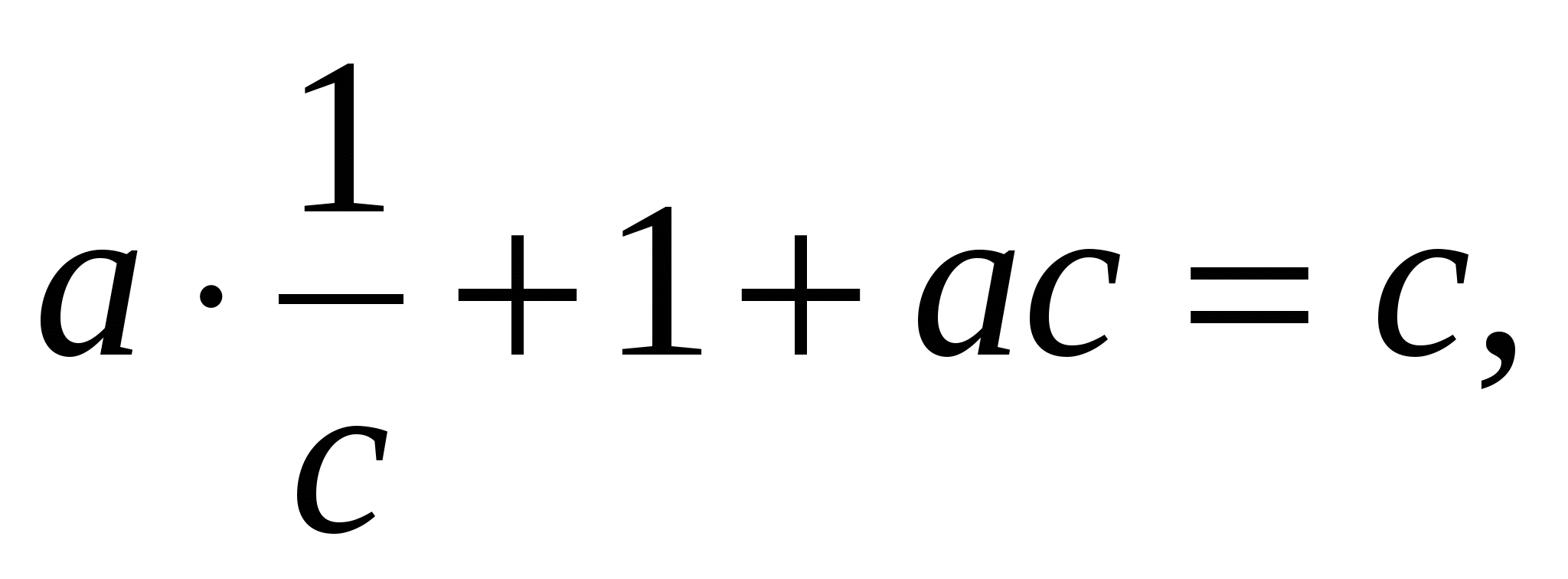
-1+1-с2 = с,
с2+с = 0,
с (с+1) = 0.
Поскольку условие bc=1 выполняется при с≠0, получаем с = -1, а, следовательно, а=1, b= -1.
При а = 0 из второго равенства системы получаем с = 0. Все равенства в этом случае выполняются при любом значении b.
3. Ответ: может.
Решение. «Восстановим» листок из 2004 клочков:
2004=2∙1002;
1002=2∙501;
501=500+1;
500=2∙250;
250=2∙125;
125=124+1;
124=2∙62;
62=2∙31;
31=30+1;
30=2∙15;
15=14+1;
14=2∙7;
7=6+1;
6=2∙3;
3=2+1;
2=2∙1.
Запись m=2∙n показывает, что Вовочка разорвал все имеющиеся клочки на две части; запись p=q+1 - разорвал на две части только один клочок (m, n, p, q - натуральные числа).
Поскольку каждой записи соответствует время, равное 1 секунде, то на получение 2004 клочков требуется 16 секунд.
4. Доказательство.





 P B R
P B R
M N
A K C
Рассмотрим треугольник АВС. Пусть M и N - середины сторон AB и ВС соответственно. Проведем перпендикуляр МК к стороне АС. Продолжим отрезок МК за точку M так, что МР=МК, соединим точки Р и В. Треугольники АМК и ВМР равны по двум сторонам и углу между ними.
Поэтому МРВ = МКА = 90°.
Поскольку МРВ и МКА - внутренние накрест лежащие углы, образованные пересечением РВ и АС прямой КР, то РВ || АС.
Продлим отрезок РВ за точку В до пересечения с прямой, проходящей через точки К и N, в точке R.
Треугольники BRN и CKN равны по стороне и двум прилежащим к ней углам.
Таким образом, треугольник KPR прямоугольный и может быть составлен из трех частей треугольника АВС.
5. Ответ: «Один».
Решение. Предположим, что первый ответивший оказался лжецом. В этом случае оба его спутника либо лжецы, либо рыцари. Если оба спутника лжецы, то второй ответивший - тоже лжец - сказал правду. Противоречие. Если оба спутника рыцари, то второй ответивший - рыцарь - солгал. Противоречие.
Поэтому первый ответивший сказал правду, т.е. он рыцарь. Второй - солгал, а третий - рыцарь - должен дать правдивый ответ: «Один».
Указания, решения и комментарии
10 класс
1. Ответ: 23 землекопа.
Решение. Землекоп, получивший лопату первым, работал
60 ∙ (12-8)-5 = 235 (минут),
вторым -
60 ∙ (12-8)-5 ∙ 2 = 230 (минут),
последним -
60 ∙ (12-8) - 5n = 240-5n (минут),
где n - количество землекопов.
Среднее время работы одного землекопа до обеда составило
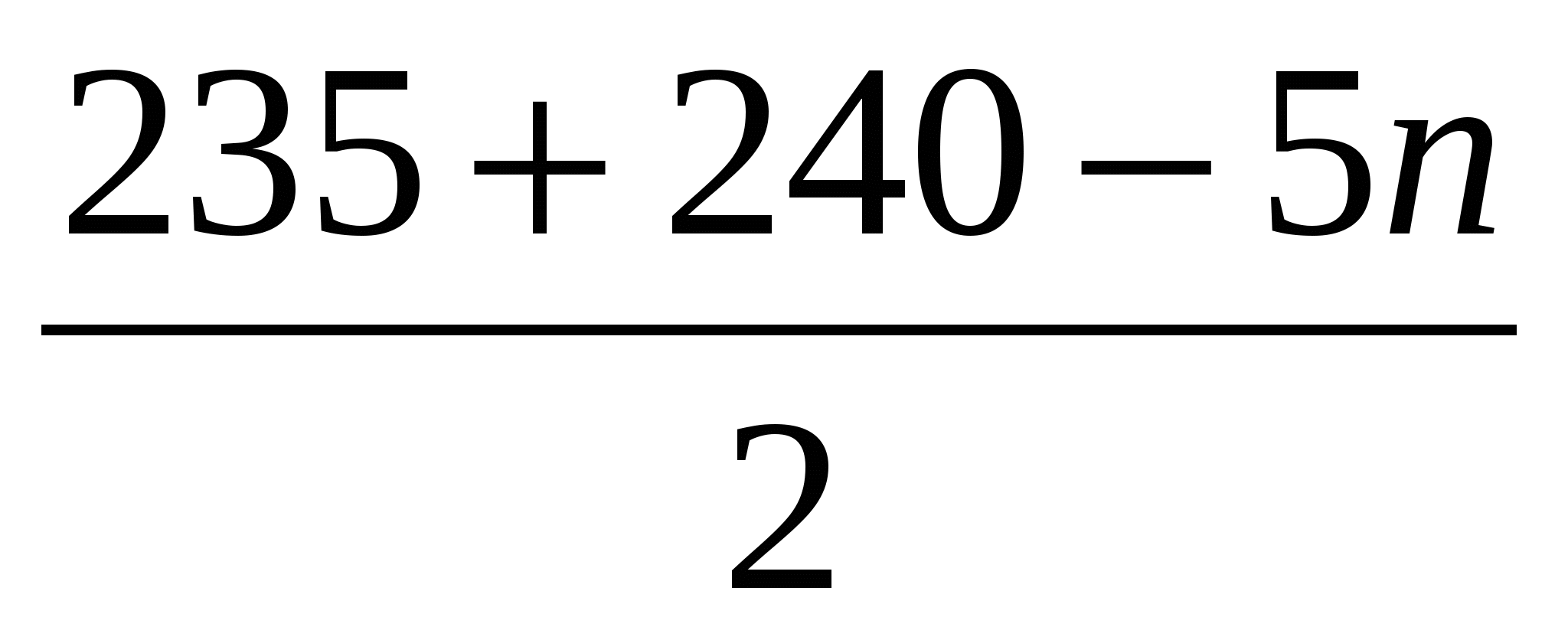 минут.
минут.
После обеда на рытье такой же траншеи каждый потратил
60 ∙ (16-13) = 180 (минут).
Получаем равенство
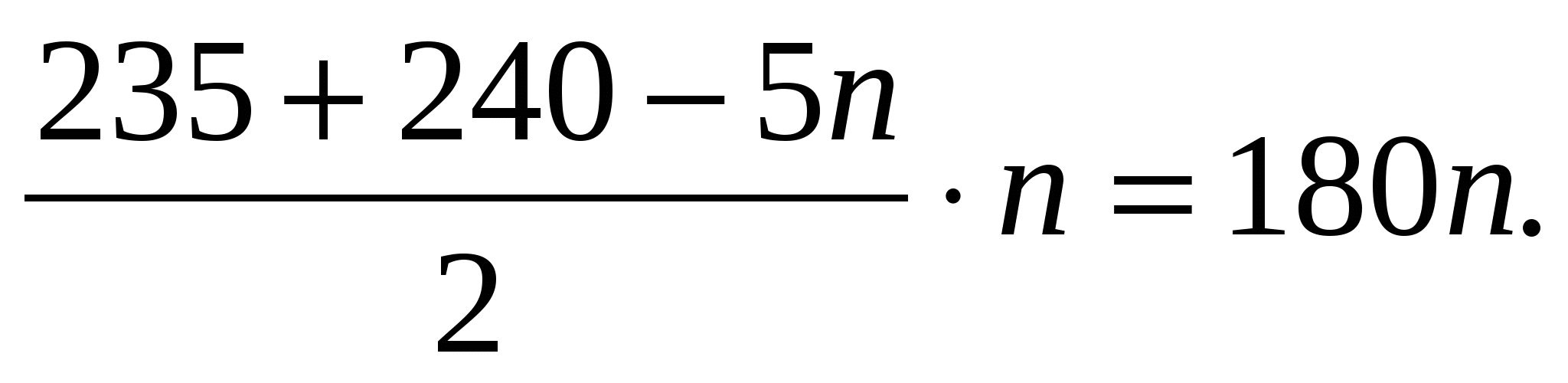
Поскольку n ≠ 0, 475-5n = 360; откуда n = 23.
2. Доказательство.
Преобразуем сумму:
9+99+999+…+![]() =
=
= ((9+1)-1)+((99+1)-1)+((999+1)-1)+…+((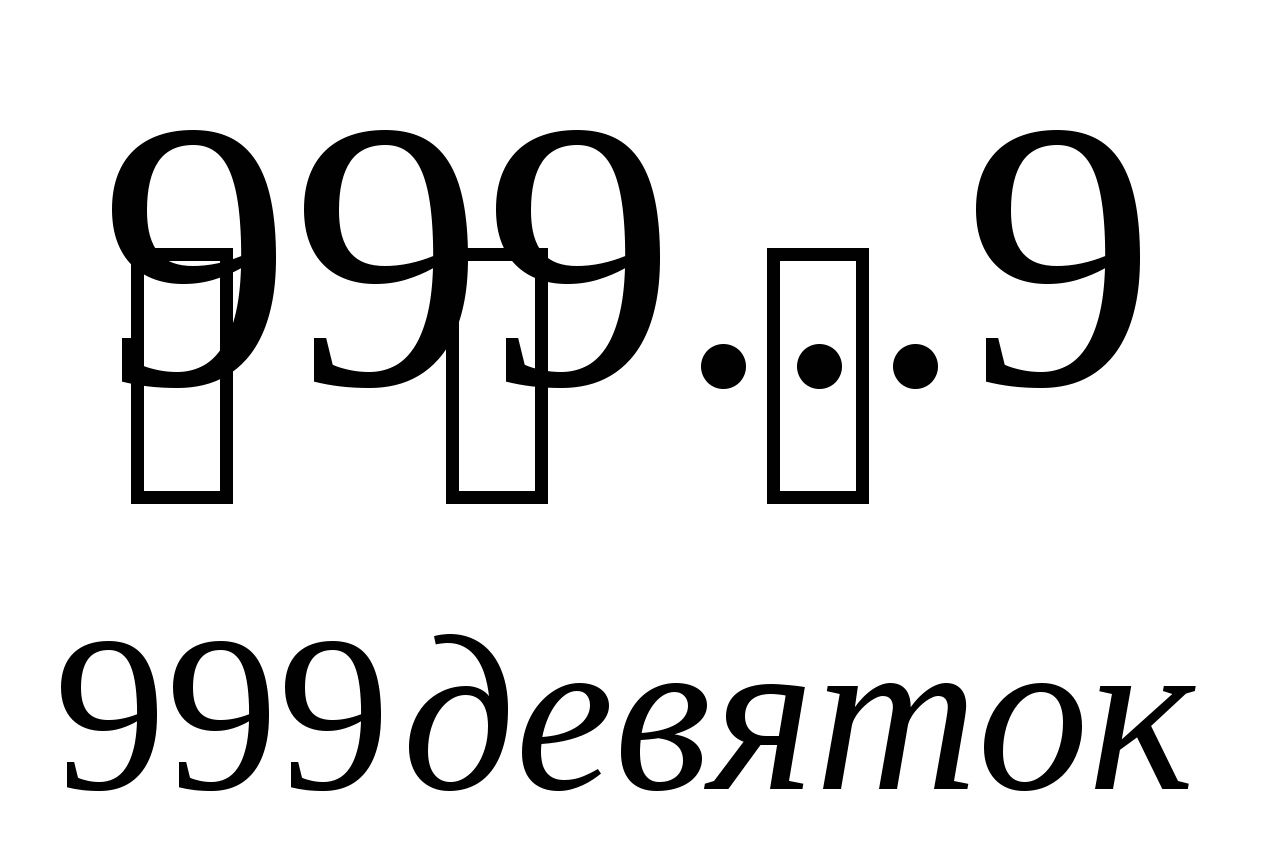 +1)-1) =
+1)-1) =
= 10+100+1000+…+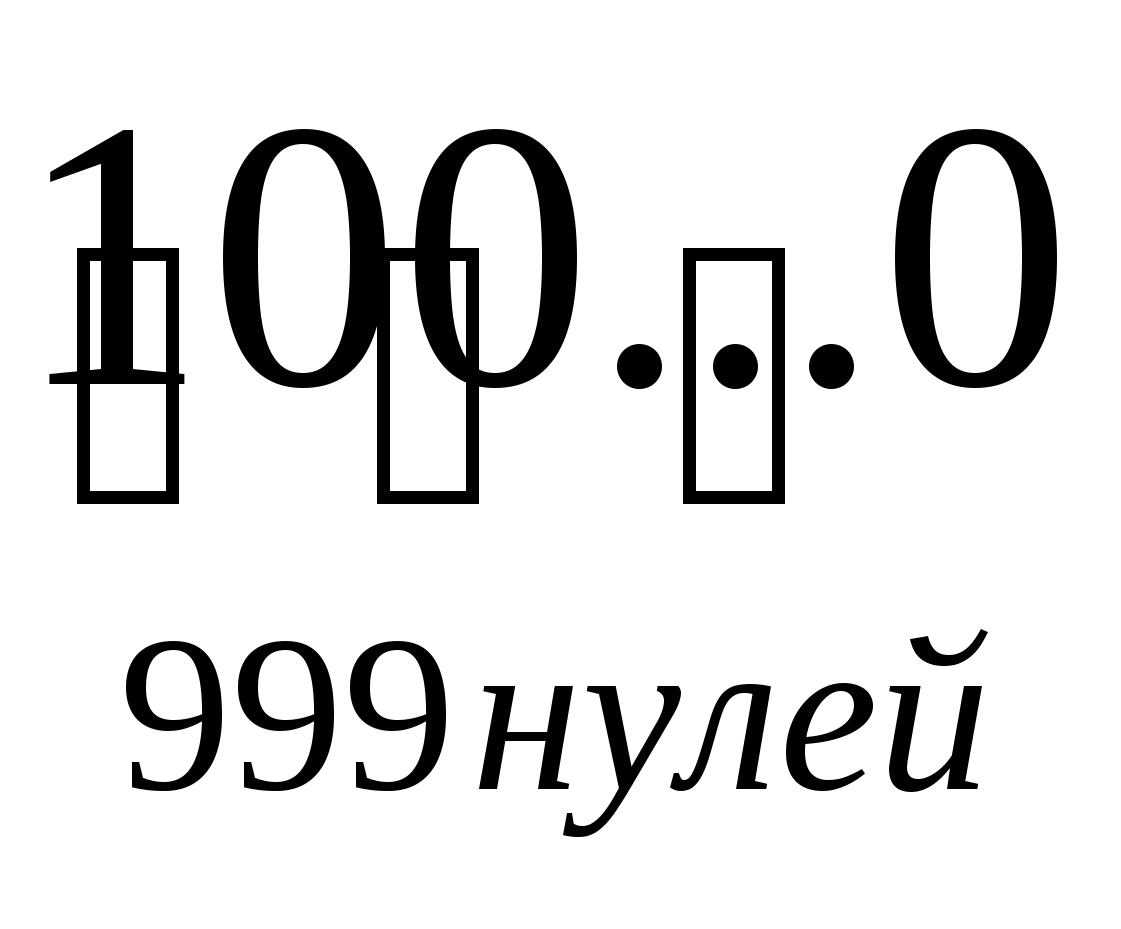 - 999 =
- 999 =
= 10(1+10+100+…+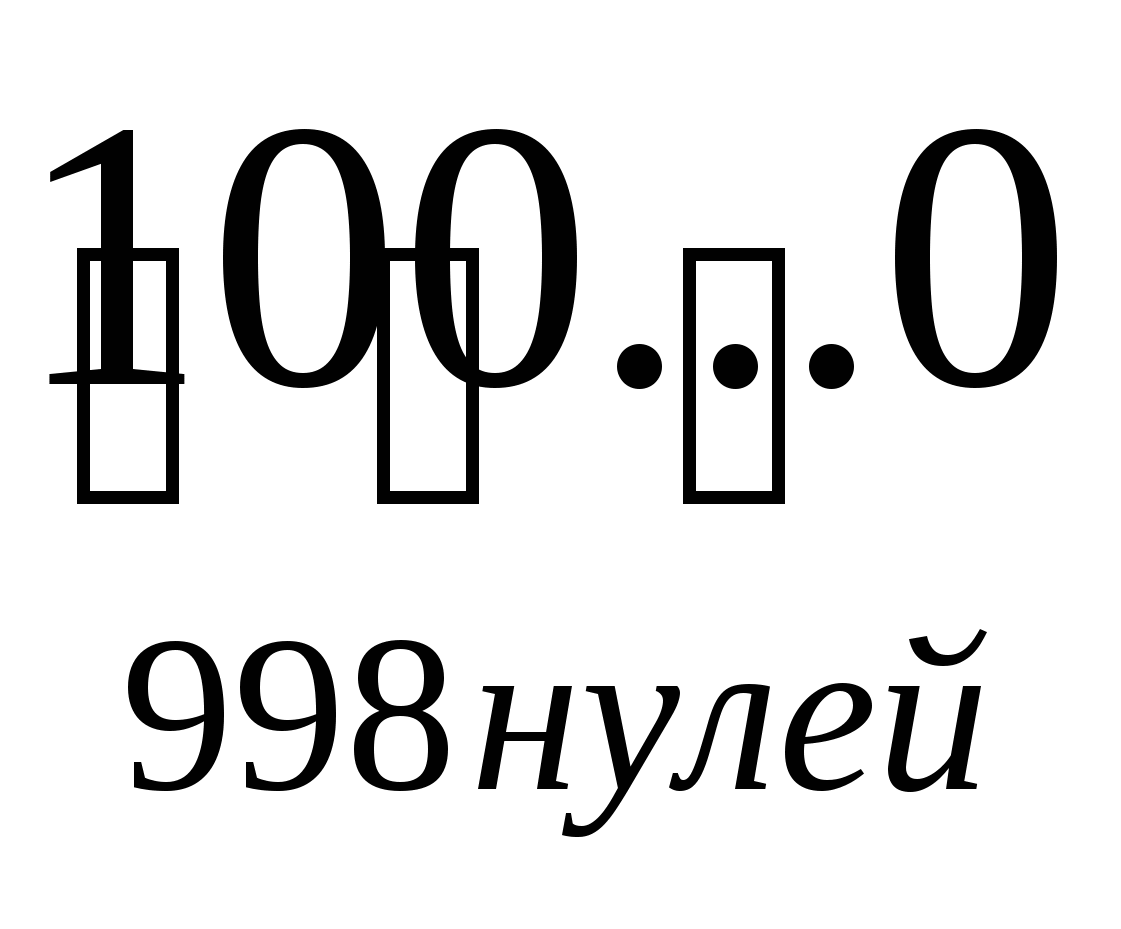 ) -999 =
) -999 =
= 10∙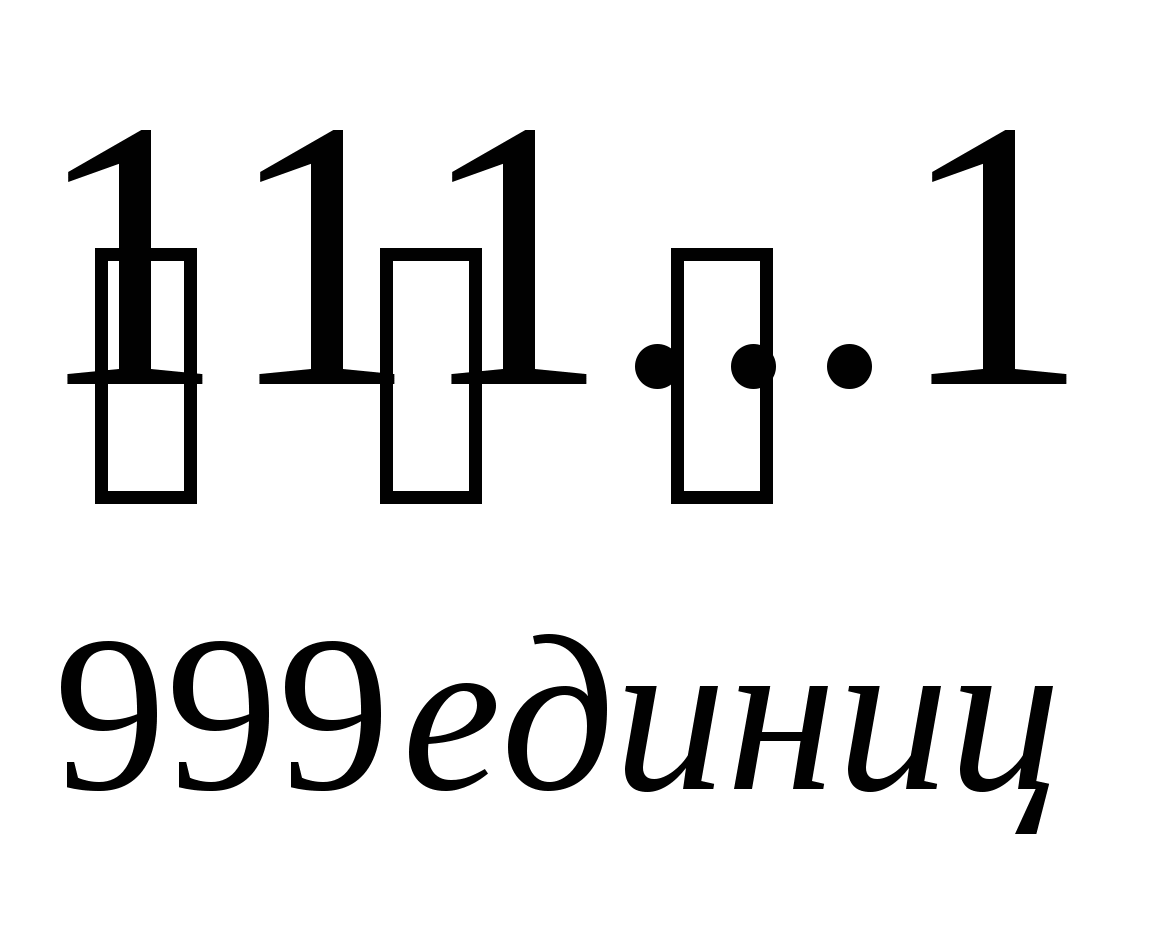 -999.
-999.
Число 111…1, записанное с помощью 999 единиц делится на 111:
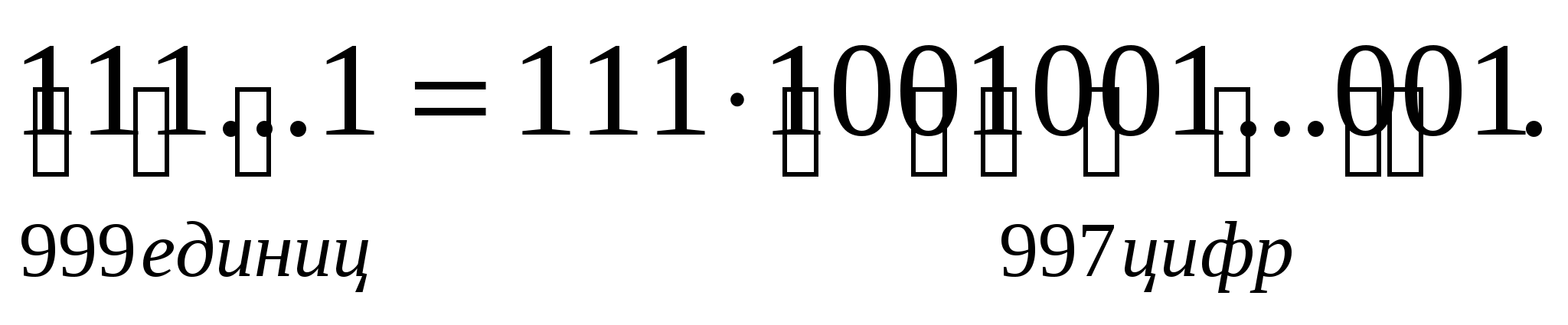
Второй множитель произведения содержит 333 единицы и 664 нуля, т.е. сумма цифр этого числа кратна 9, поэтому число делится на 9, а, следовательно, число 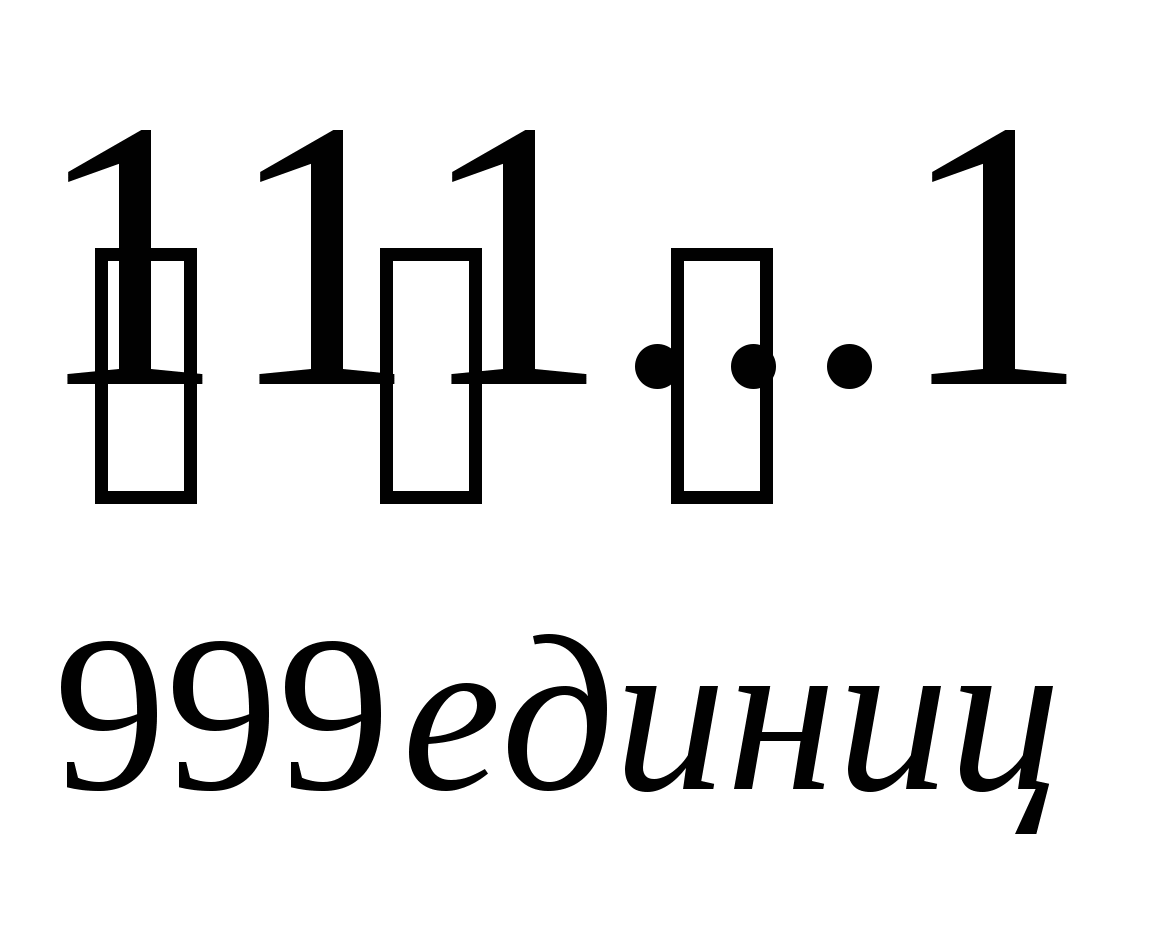 делится на 999.
делится на 999.
Т.к. уменьшаемое и вычитаемое разности 10∙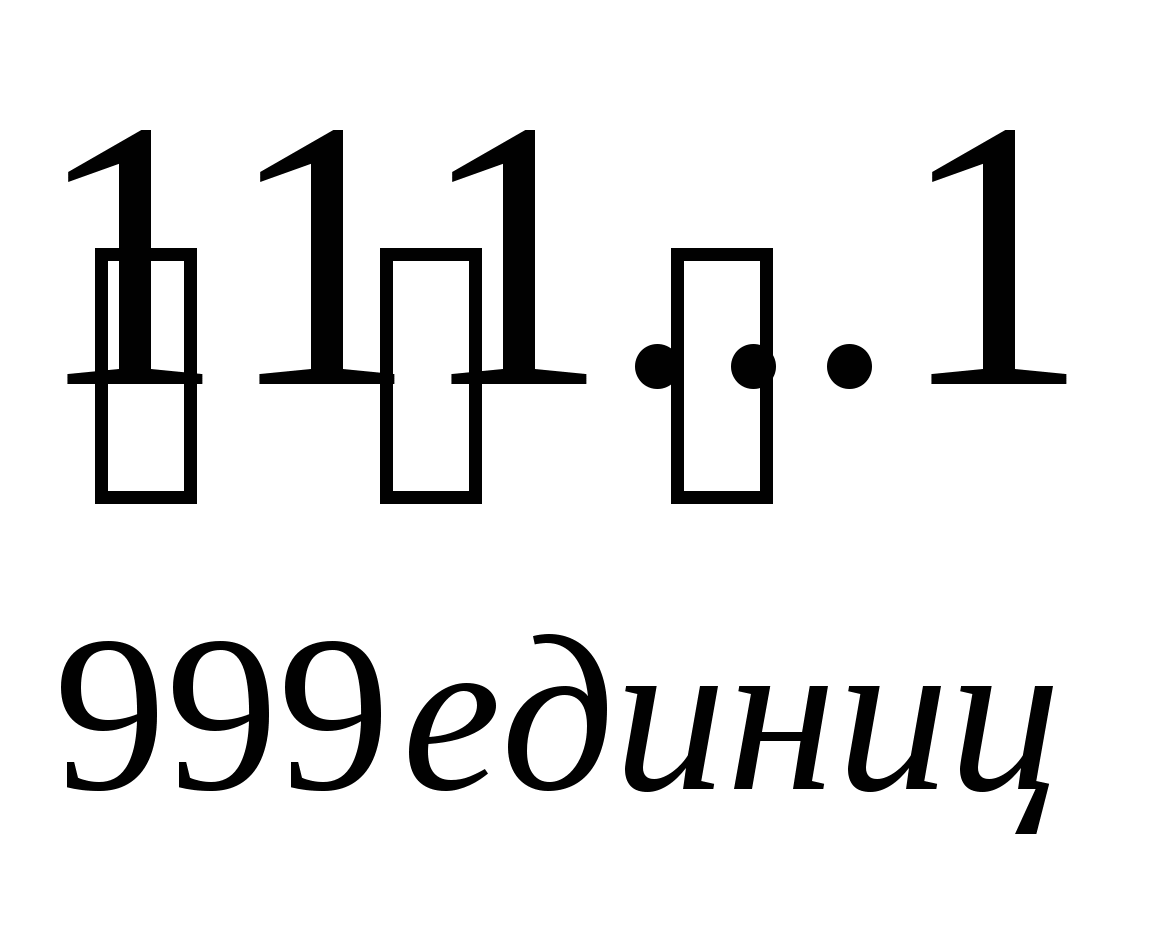 - 999
- 999
делятся на 999, то и разность делится на 999.
3. Ответ: 0; 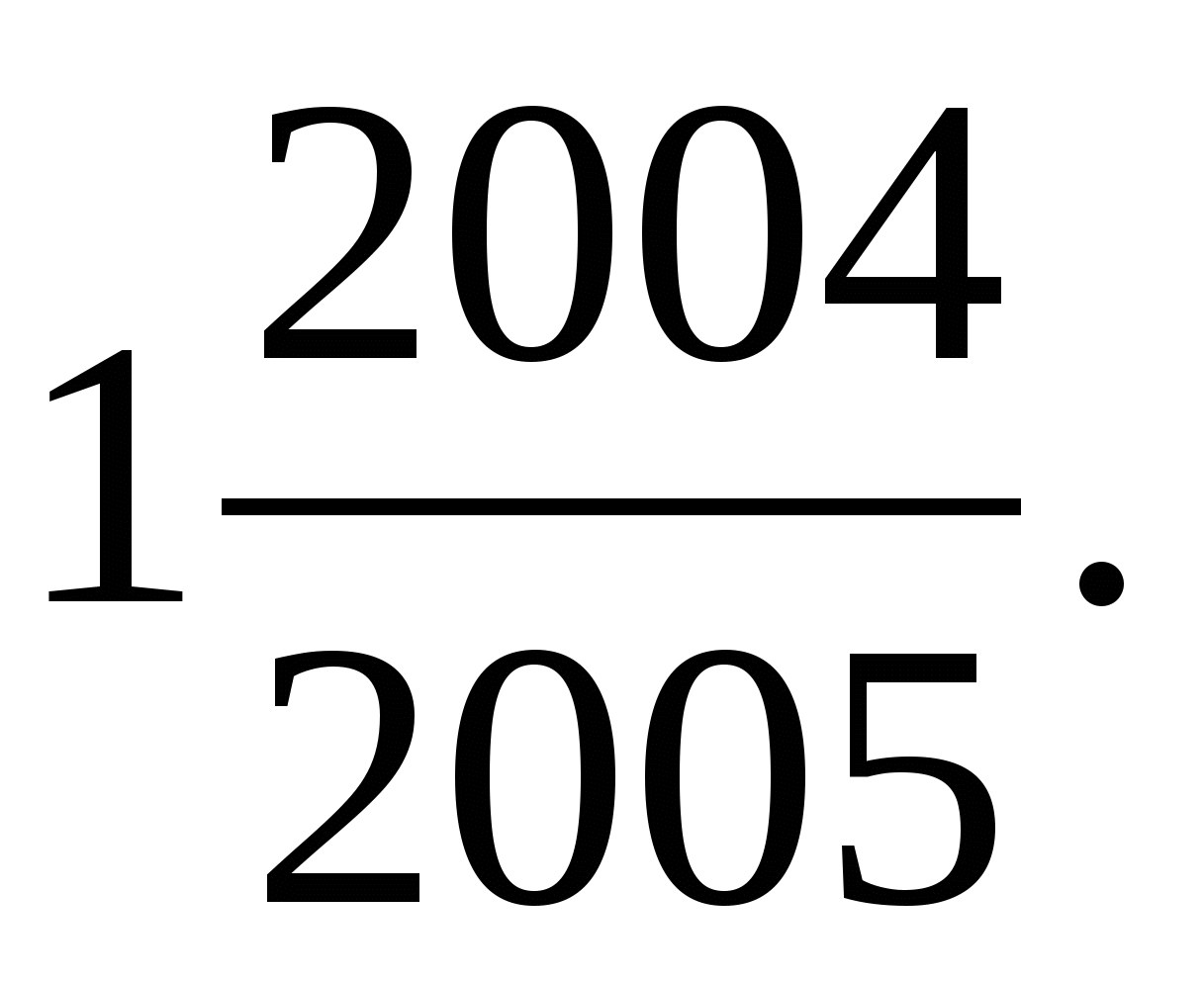
Решение. Перепишем уравнение в виде
2004[х]=2005{х}.
Поскольку {х}[0; 1), то 2005{х}[0; 2005), т.е. 2004[х][0; 2005).
Значит, [х][0; 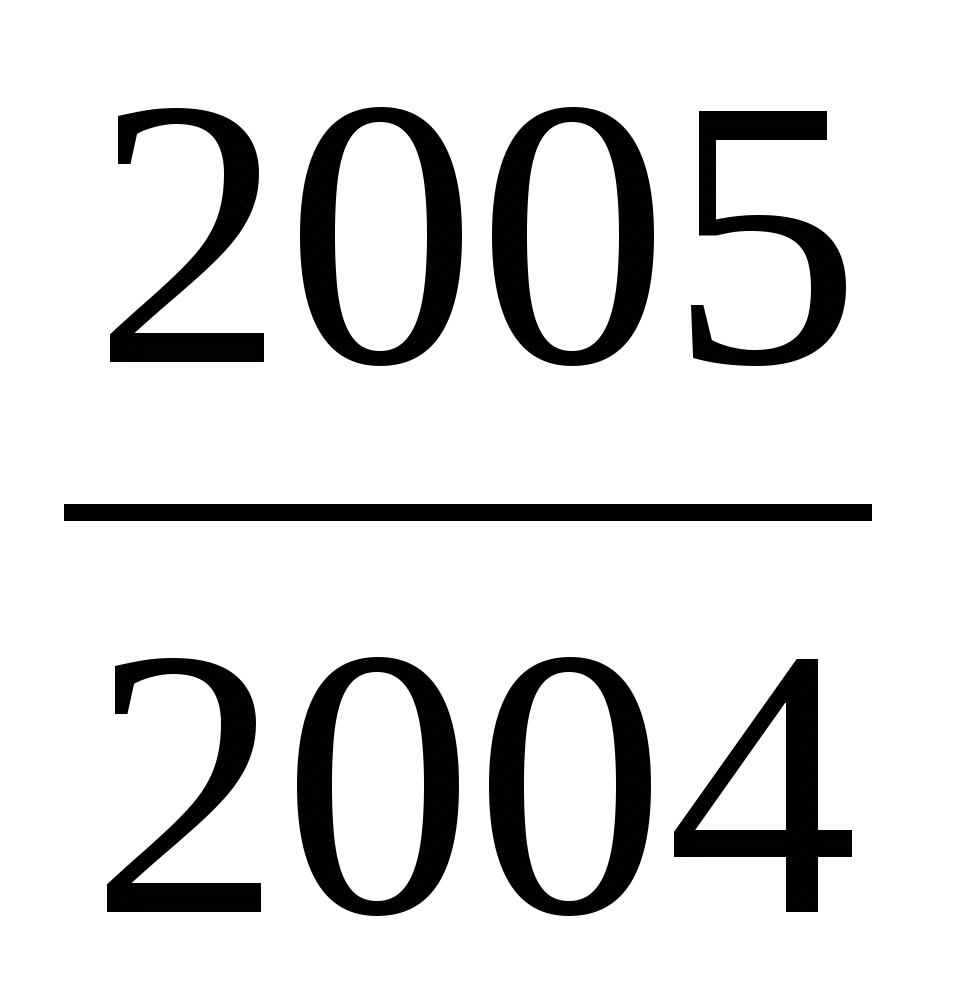 );
);
откуда
[х] = 0 или [х] = 1.
Если [х] = 0, то 2005{х}=0, т.е.
{х}=0.
Получаем х = 0.
Если [х] = 1, то 2005{х}=2004,
{х}=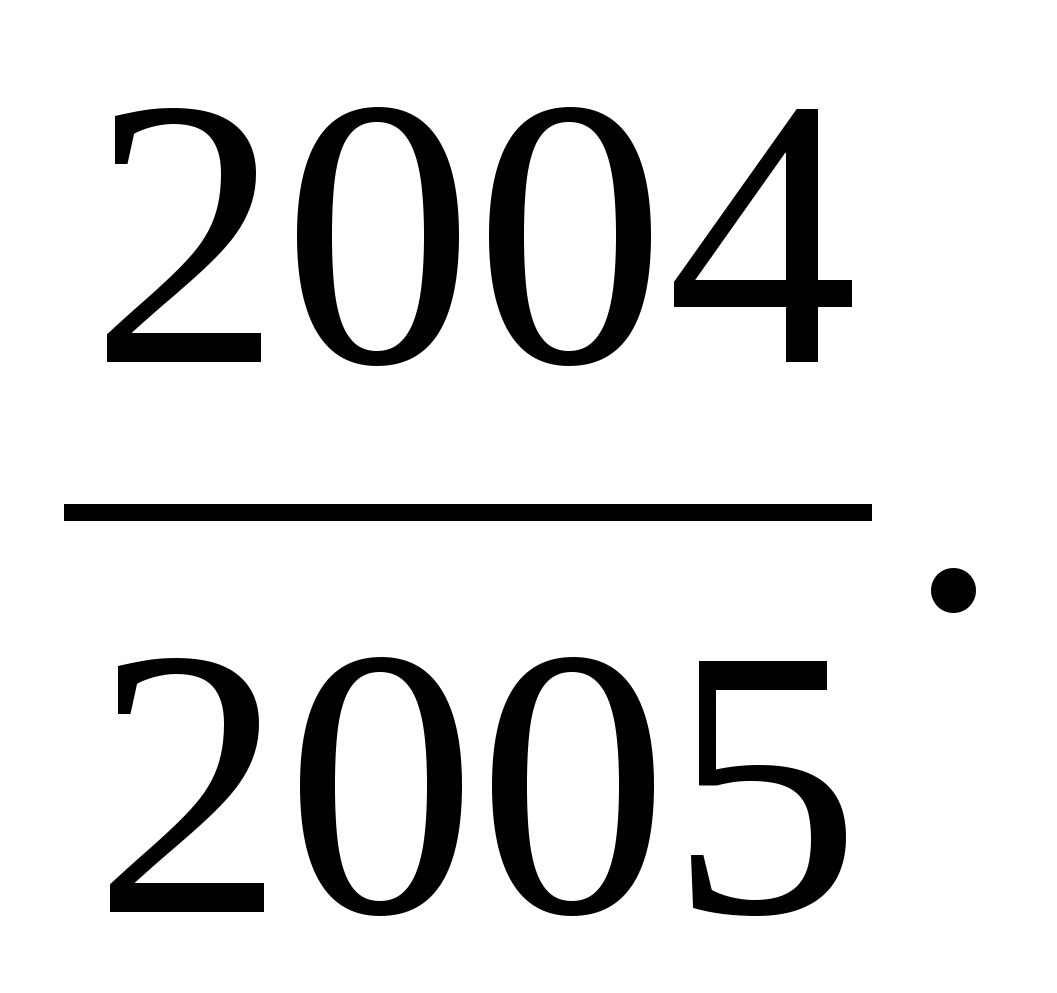
Получаем 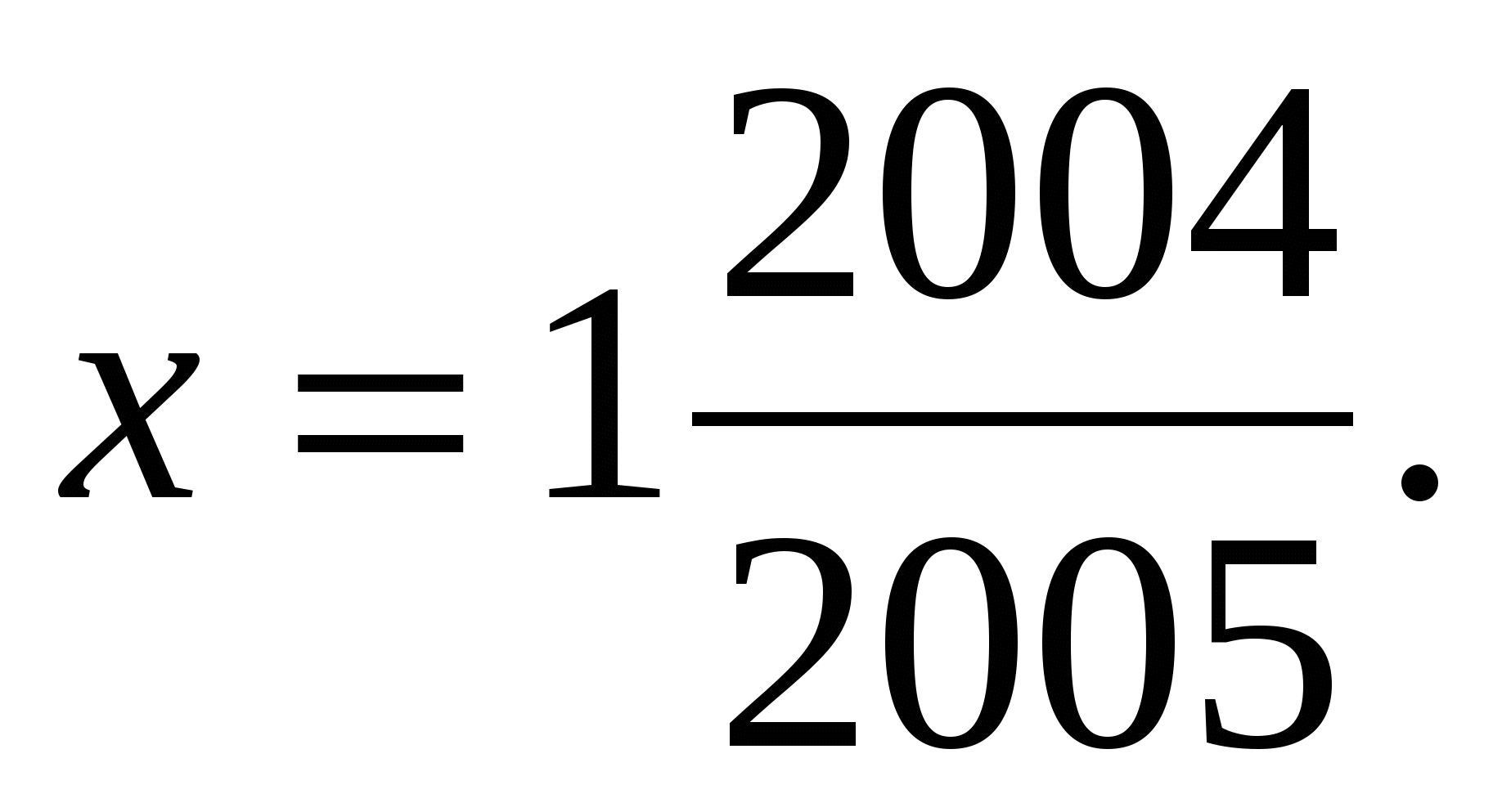
4. Ответ: 8.
Решение. Продолжим сторону AD за точку D до пересечения с окружностью в

точке М, соединим отрезком точки С и М. Трапеция МСВА - равнобокая, т.к. вписана в окружность. По свойству пересекающихся хорд окружности
AD∙DM=BD∙DK.
Обозначим BD=x, BAD=. По теореме косинусов для треугольника ABD получаем:

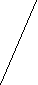
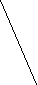

 C B
C B
 M A
M A
D
K
BD2=AB2+AD2 - 2ABADcos, т.е.
x2=16+64-64 cos,
x2=80-64 cos.
По свойству равнобокой трапеции
CM=AB=4, CMD=BAD=.
Поскольку CDAM, определим MD через гипотенузу СМ и угол :
MD = CM cos=4 cos.
Т.к. BK = BD+DK, DK = BK - BD = 9-x.
Получаем:
x (9-x) = 84 cos,
9x-x2 = 32 cos.
Исключая из равенств 1 и 2 cos, получаем:
х2-80=18х-2х2;
х2-18х+80 = 0,
откуда х=8 или х=10. Значение х=10 не подходит, т.к. 109, т.е. BDBK, что противоречит условию задачи.
5. Ответ: 50.
Решение. Если предположить, что лжецов было больше, чем правдивых, то первый лжец, который покинул аудиторию, сказал правду, заявляя, что в аудитории лжецов осталось больше, чем правдивых. Значит, в этом случае возникает противоречие.
Если предположить, что правдивых было больше, то первый, покинувший аудиторию правдивый математик, не прав, заявляя, что в аудитории лжецов больше чем правдивых. Значит, и в этом случае возникает противоречие.
Если предположить, что лжецов и правдивых было поровну - 50 лжецов и 50 правдивых, то и в этом случае возникает противоречие. Например, первыми вышли двое правдивых, после чего в аудитории осталось 48 правдивых и 50 лжецов. Если третьим вышедшим после тестирования был лжец, в аудитории осталось 48 правдивых и 49 лжецов, а, следовательно, ответ лжеца - правдивый. Противоречие. Значит, однозначно определить количество лжецов нельзя.
Указания, решения и комментарии
11 класс
1. Ответ: 20 заданий.
Решение. Пусть каждый тест содержал а тестовых заданий. Тогда по физике абитуриент ответил правильно на 0,3а вопросов. Поскольку 0,3а - целое число, то а кратно 10, т.е. а=10n, nN. Так как а≥19, то n≥2. Полагая, что по русскому языку абитуриент ответил правильно на b вопросов, определяем общее число правильных ответов:
19+3n+b,
что по условию равно 0,5∙3а, или 15n. Получаем уравнение:
19+3n+b=15n, т.е.
b=12n-19.
Т.к. результат по русскому языку оказался хуже, чем по физике, получаем:
12n-19<3n,
n<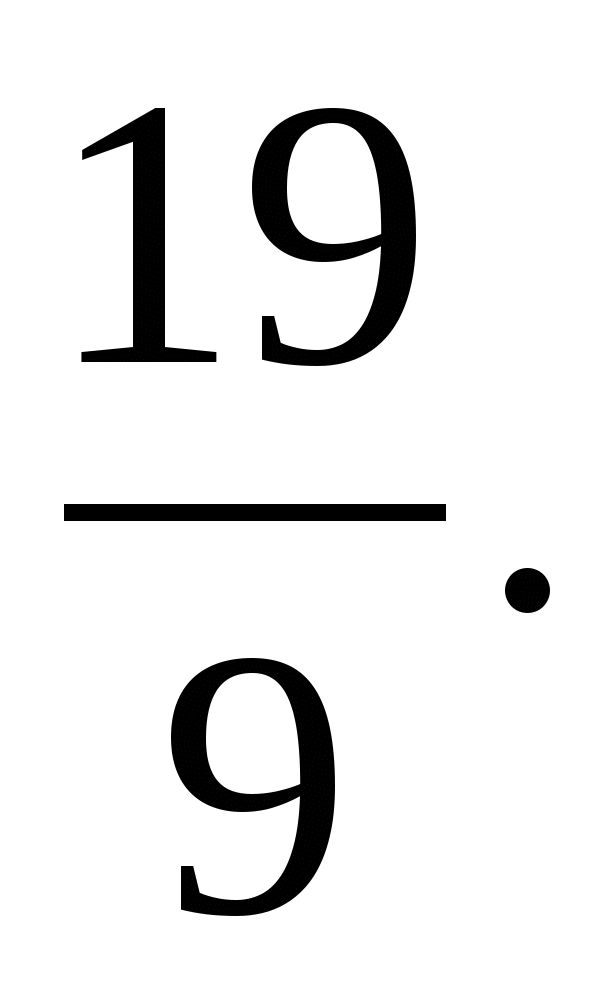
Получаем:
![]() 2 ≤ n < 2
2 ≤ n < 2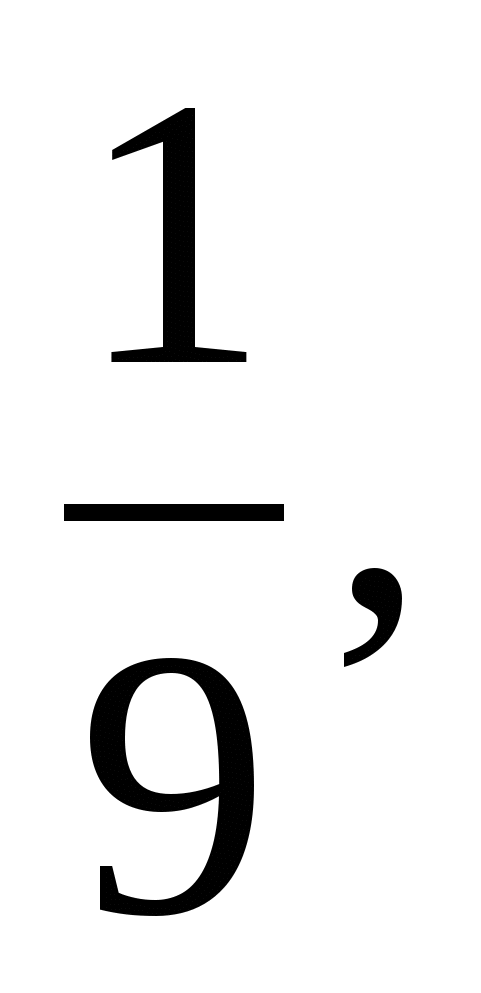
n = 2.
Значит, каждый тест содержал 20 заданий.
2. Ответ: 270.
Решение. Искомое число кратно 10, т.е. имеет натуральный делитель, оканчивающийся цифрой 0.
Допустим , что искомое число имеет делителем число 9. Поскольку числа 9 и 10 взаимно простые, то в рассматриваемом случае искомое число кратно 90:
90, 180, 270, …
Среди делителей чисел 90 и 180 нет оканчивающихся цифрой 7; среди делителей числа 270 есть оканчивающиеся всеми цифрами от 0 до 9:
10, 1, 2, 3, 54, 5, 6, 27, 18, 9.
Покажем, что 270 - наименьшее натуральное число с таким свойством. Представим число 270 в виде произведения двух взаимно простых множителей:
270 = 10∙27.
Чисел, оканчивающихся цифрой 9 и меньших 27 - два: 9 и 19.
Если искомое число имеет делителем число 19, то это число кратно 190. Среди чисел, кратных 190, меньше 270 только само число 190. Выписав делители числа 190:
1, 2, 5, 10, 19, 38, 95, 190, -
замечаем, что среди них нет оканчивающихся цифрами 3, 4, 6, 7.
Значит, число 270 - наименьшее натуральное число, которое удовлетворяет условию задачи.
3. Ответ: f (x)=x2.
Решение. При х=у имеем:
f (0)=f (x)+f (x) - 2x2;
f (x)=x2+
При х=у=0 получаем:
f (0) = f (0) + f (0) - 0;
f (0) = 0.
Значит, f (x) = x2.
4. Доказательство.
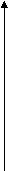

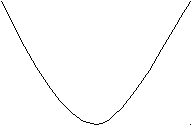






 y
y
y=x2
A a2 D B
h
a2-h C
-a 0 a x
Рассмотрим треугольник АВС с прямым углом С, гипотенуза AB которого параллельна оси Ох, а высота, проведенная к гипотенузе - CD. Точки пересечения прямой параллельной оси Ох, с параболой у=х2 симметричны относительно оси ординат.
Поэтому, предполагая, что а>0, определяем координаты вершин А и В треугольника АВС:
А (-а; а2), В (а; а2);
тогда AB=2а.
Обозначим высоту CD буквой h. Найдем координаты точки С:
C (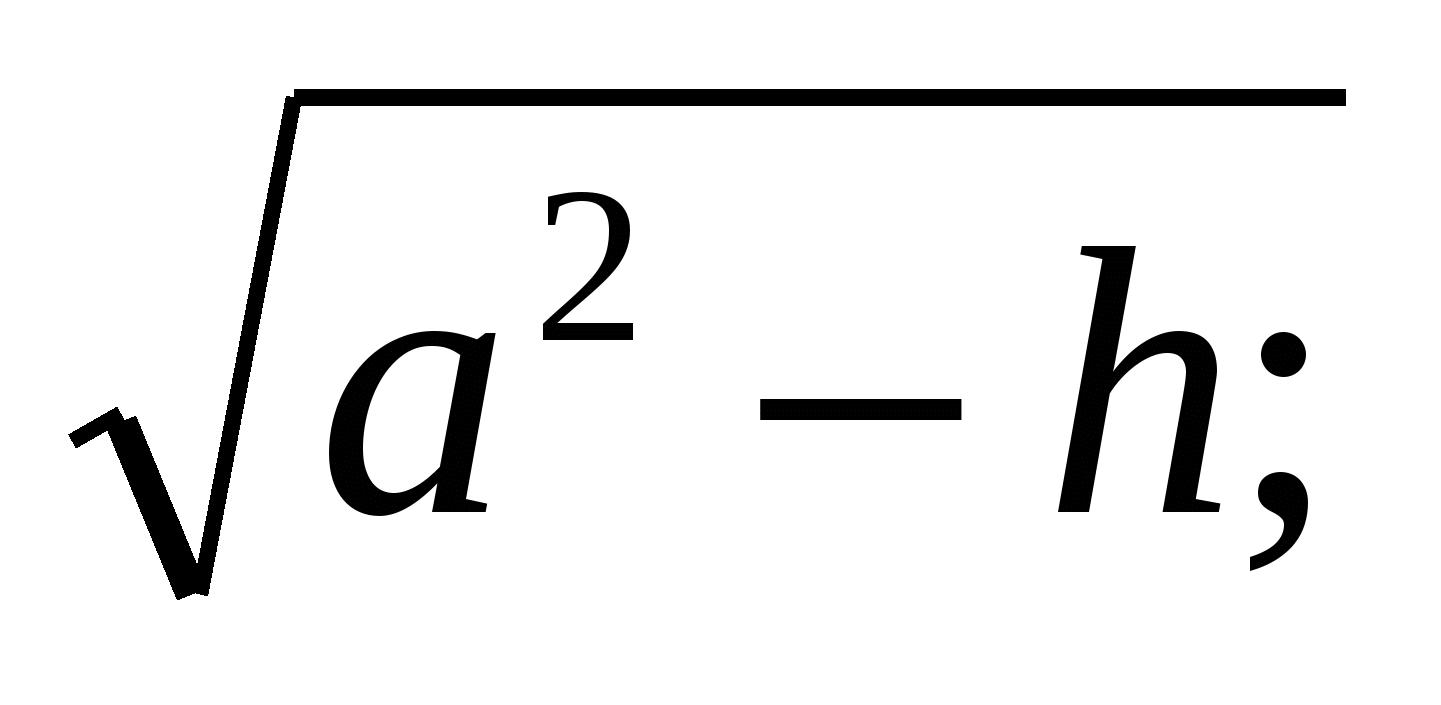 a2-h)
a2-h)
Поскольку С=90, то угол между векторами  и
и  прямой, а, следовательно, скалярное произведение векторов
прямой, а, следовательно, скалярное произведение векторов  и
и  равно 0, т.е.:
равно 0, т.е.:

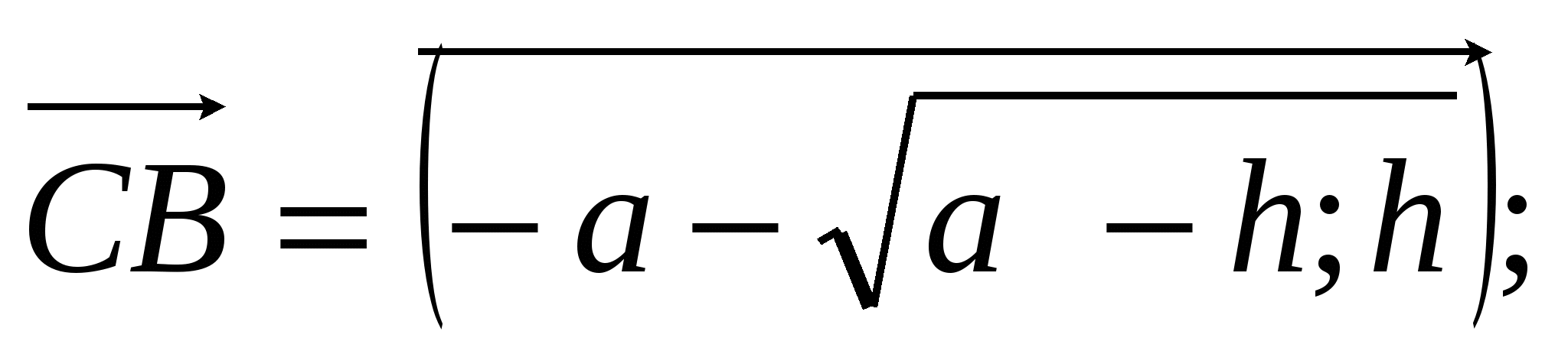
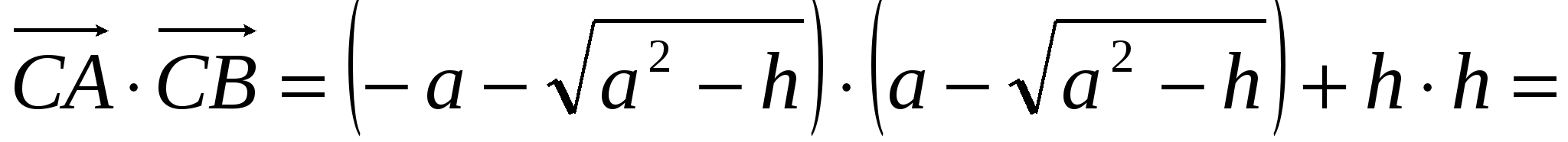
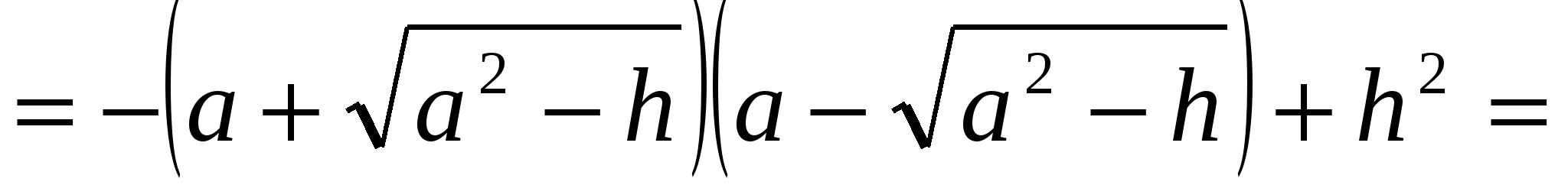
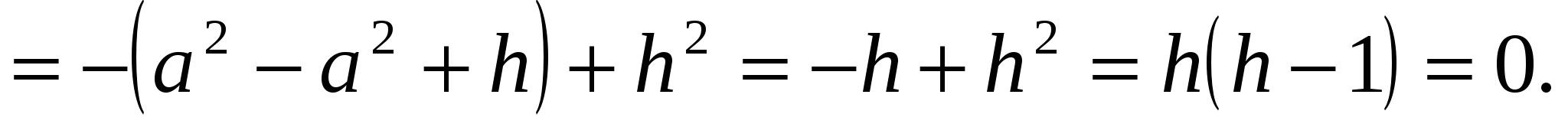
По смыслу задачи h0, поэтому h=1.
5. Ответ: 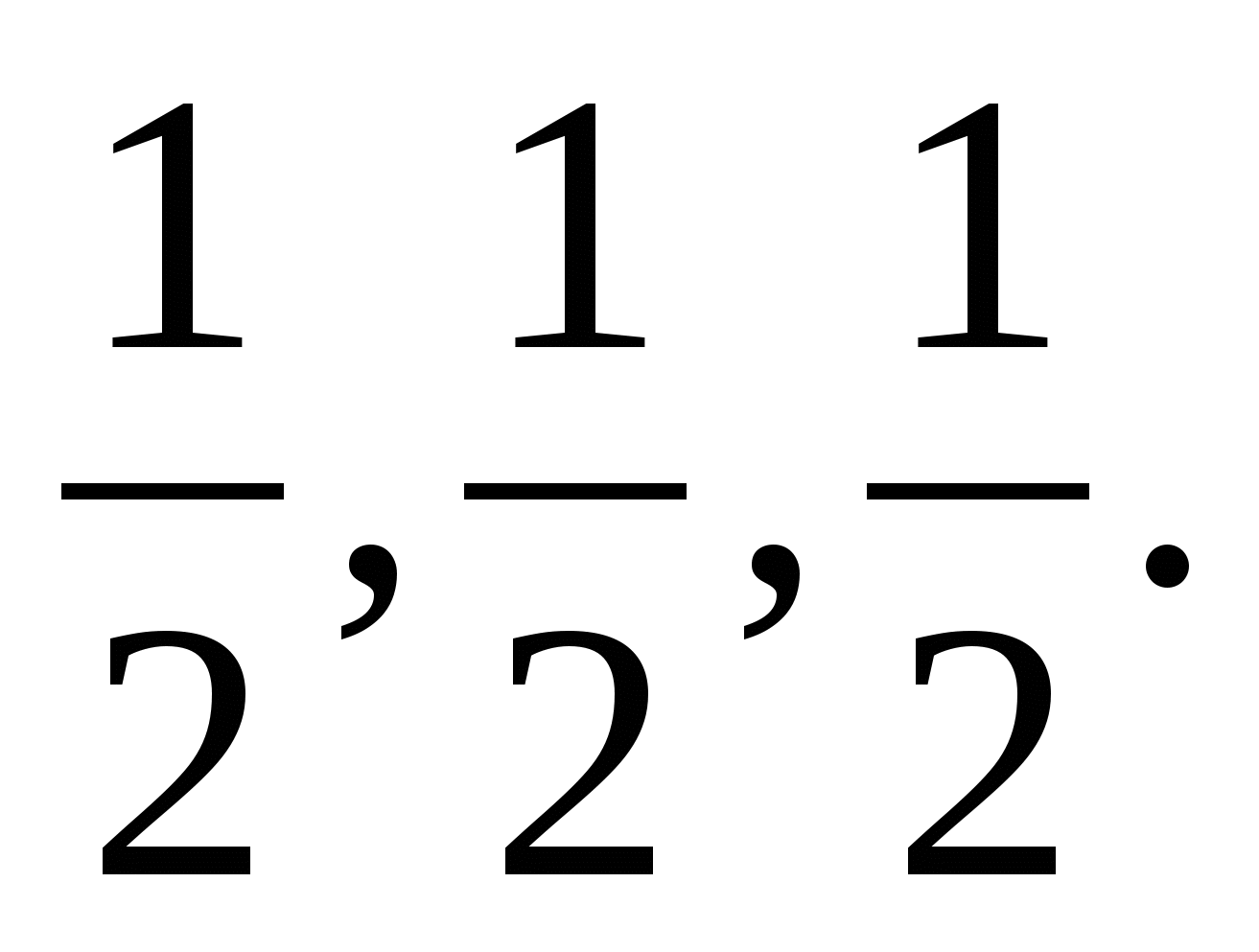
Решение. Обозначим длины сторон треугольника, противолежащие углам А, В, С буквами а, b, с соответственно; А=, В=, С=. Из условия задачи следует, что cos 0, cos 0, cos 0, т.е. АВС - остроугольный.
Без ограничения общности можно положить, что a b c, тогда . Поскольку на промежутке 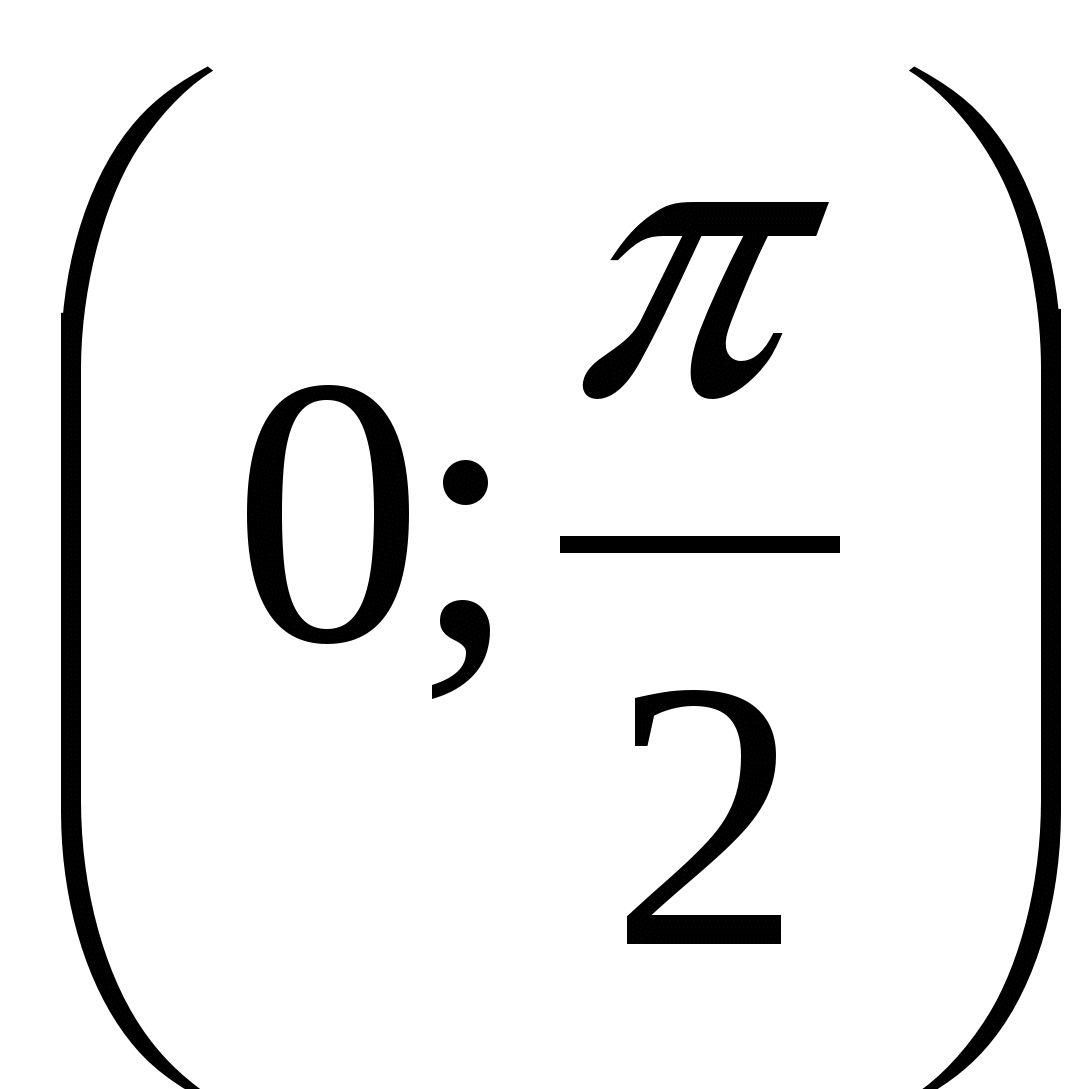 функция y = cos x убывает, получаем:
функция y = cos x убывает, получаем:
cos cos cos . Значит, a= cos , b= cos , c= cos .
По теореме синусов
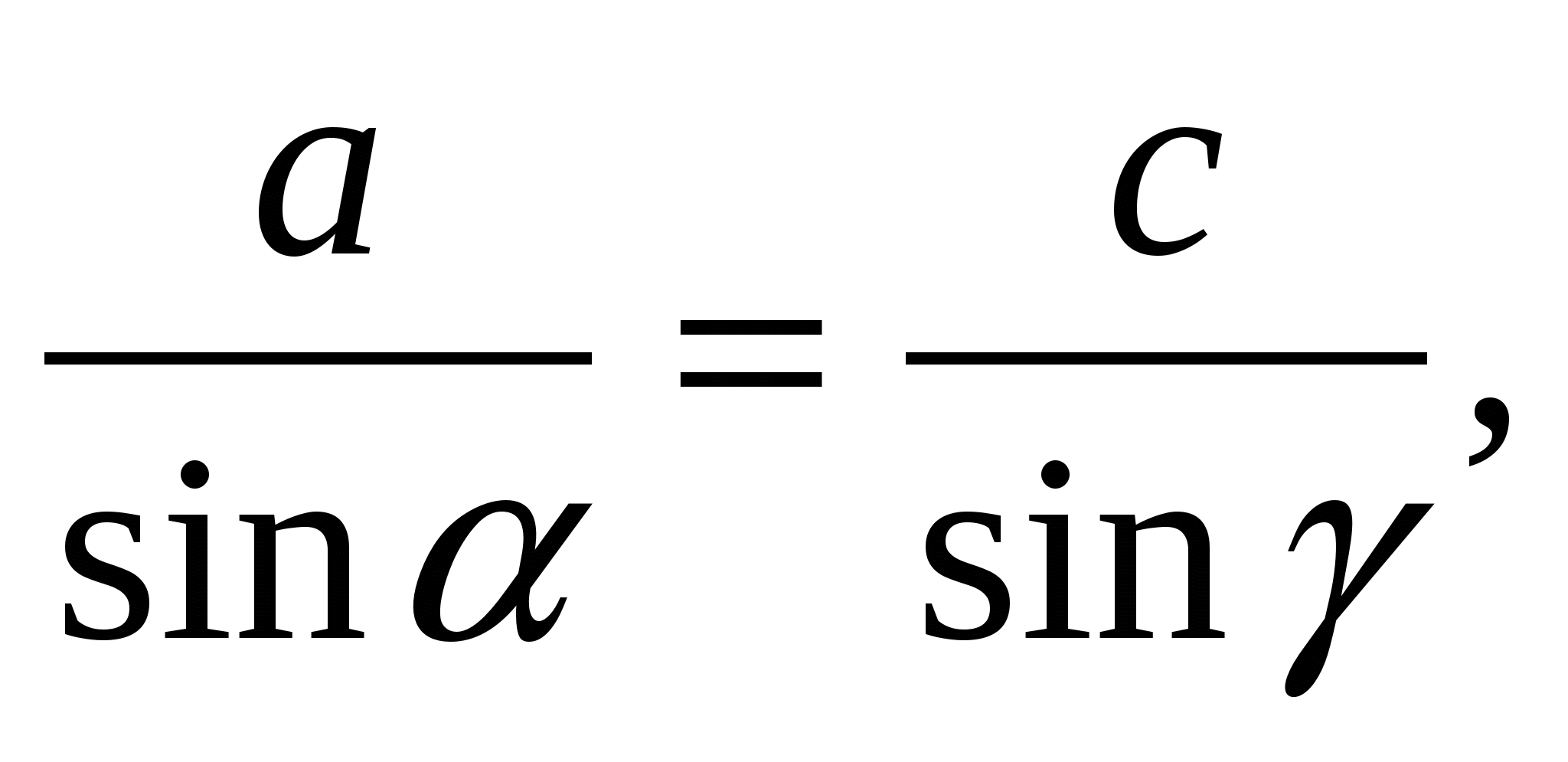 т.е.
т.е.
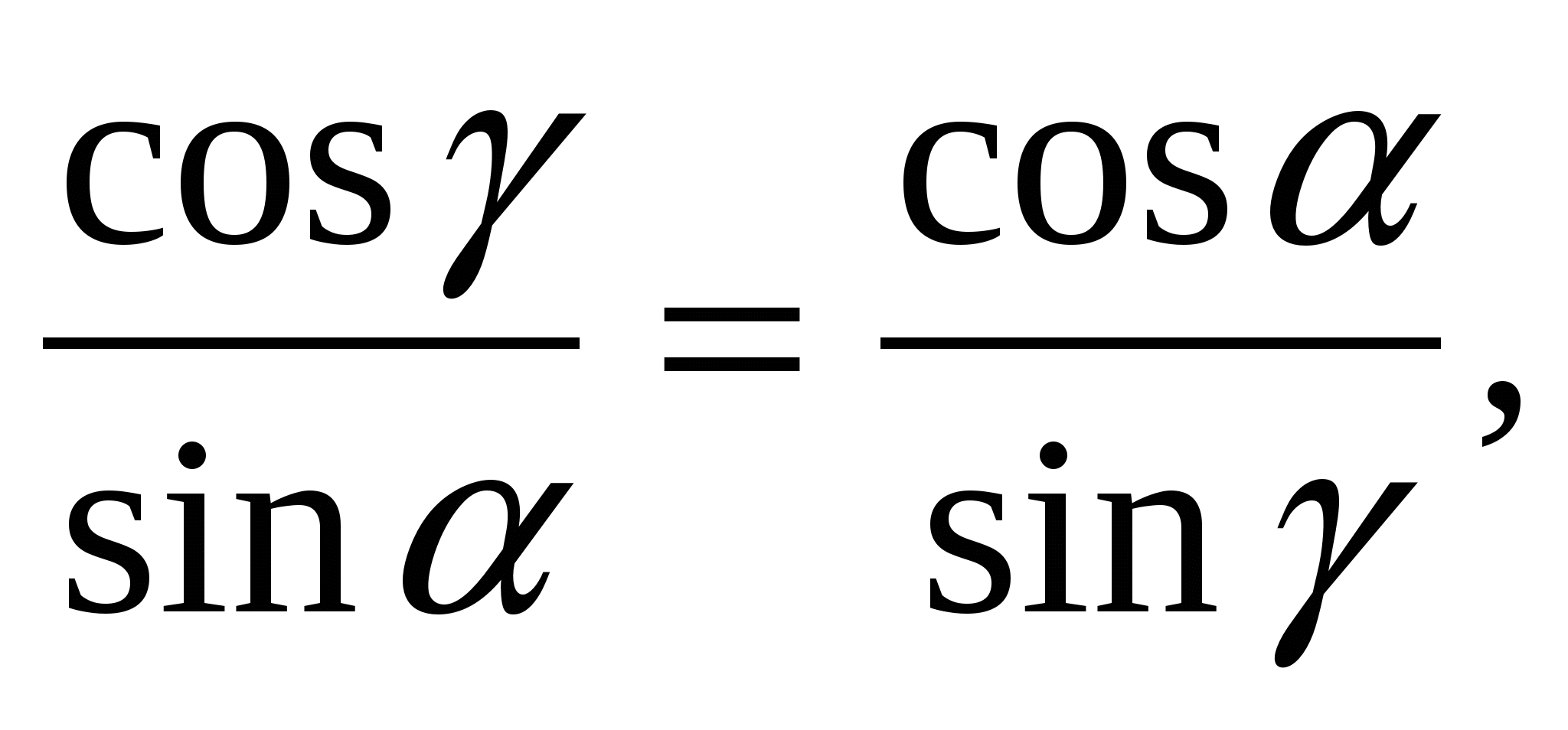
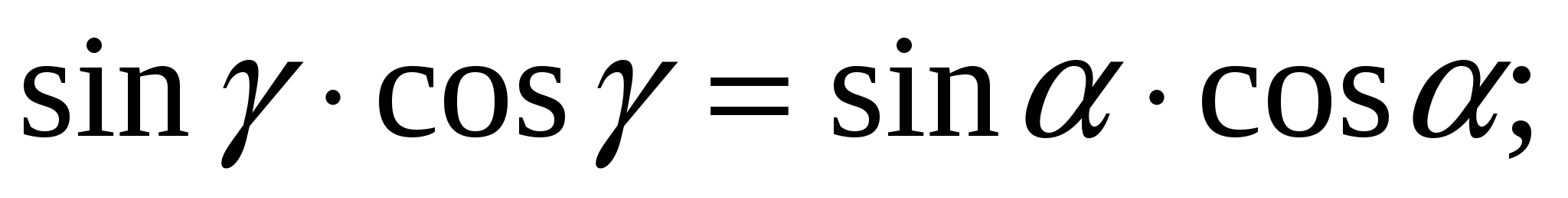
откуда
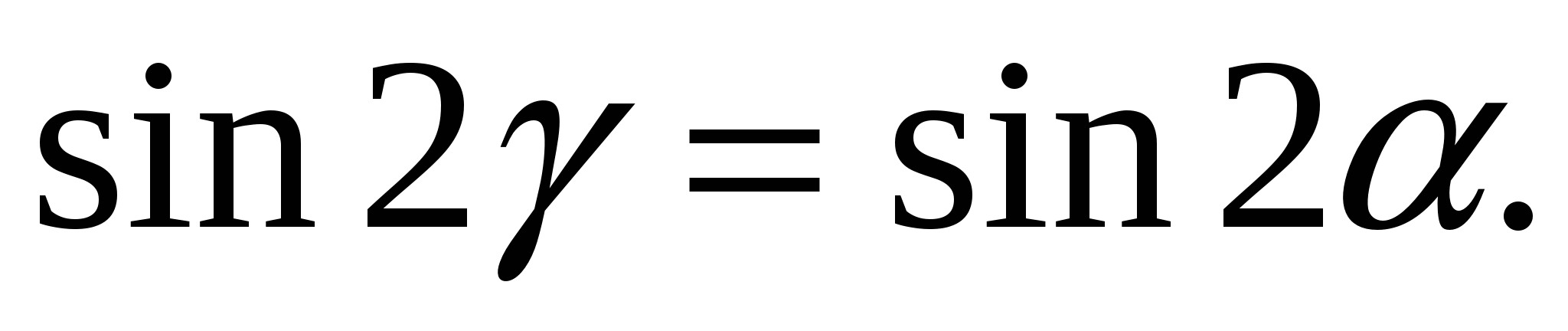
Получаем: 2=2 или 2+2=.
Если , то Значит, АВС - равносторонний со сторонами, равными 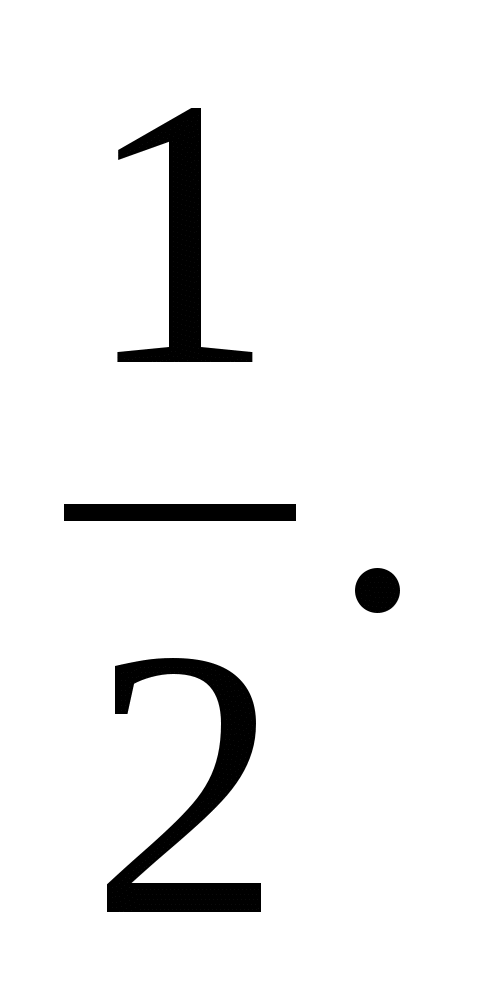 Если
Если 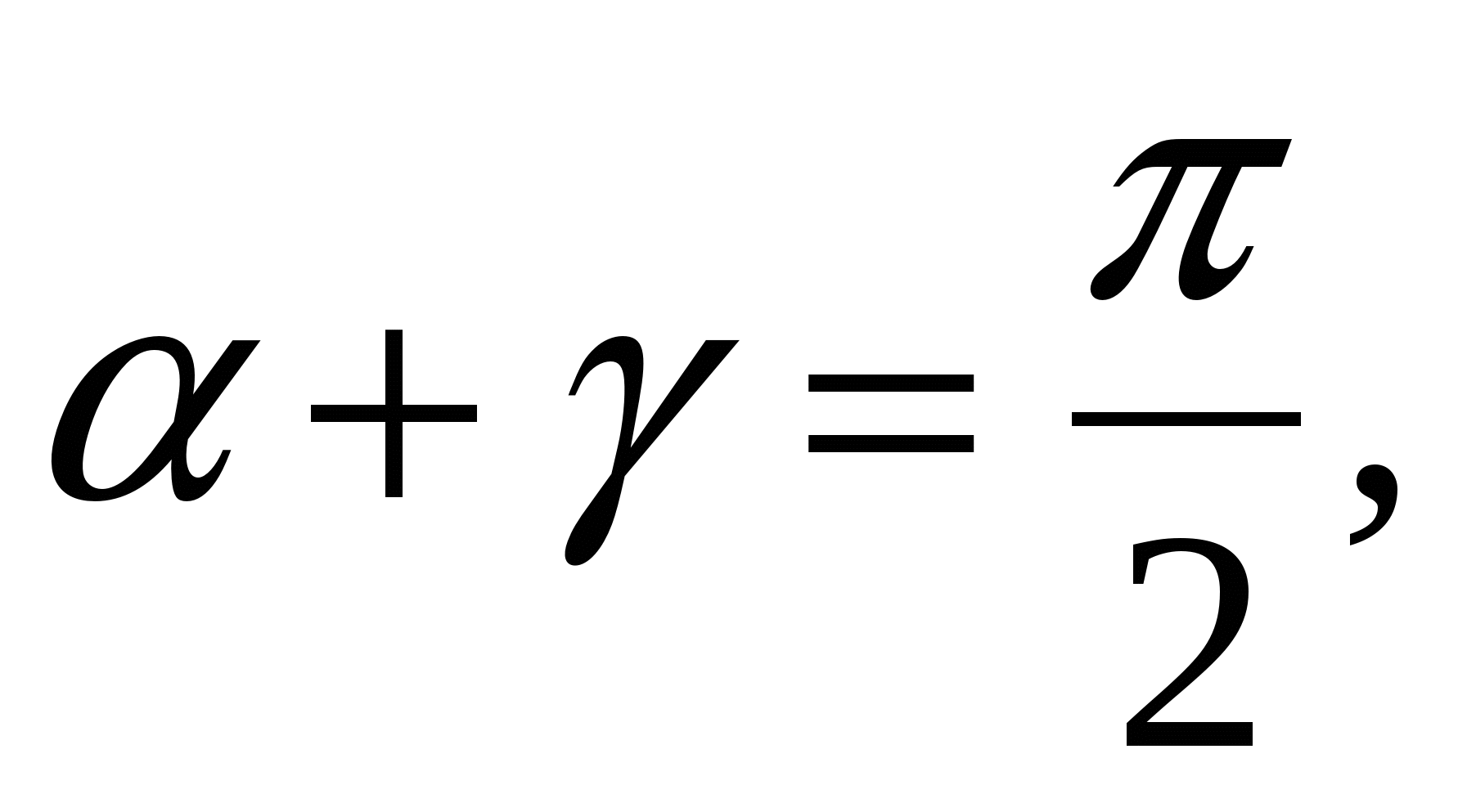 то
то 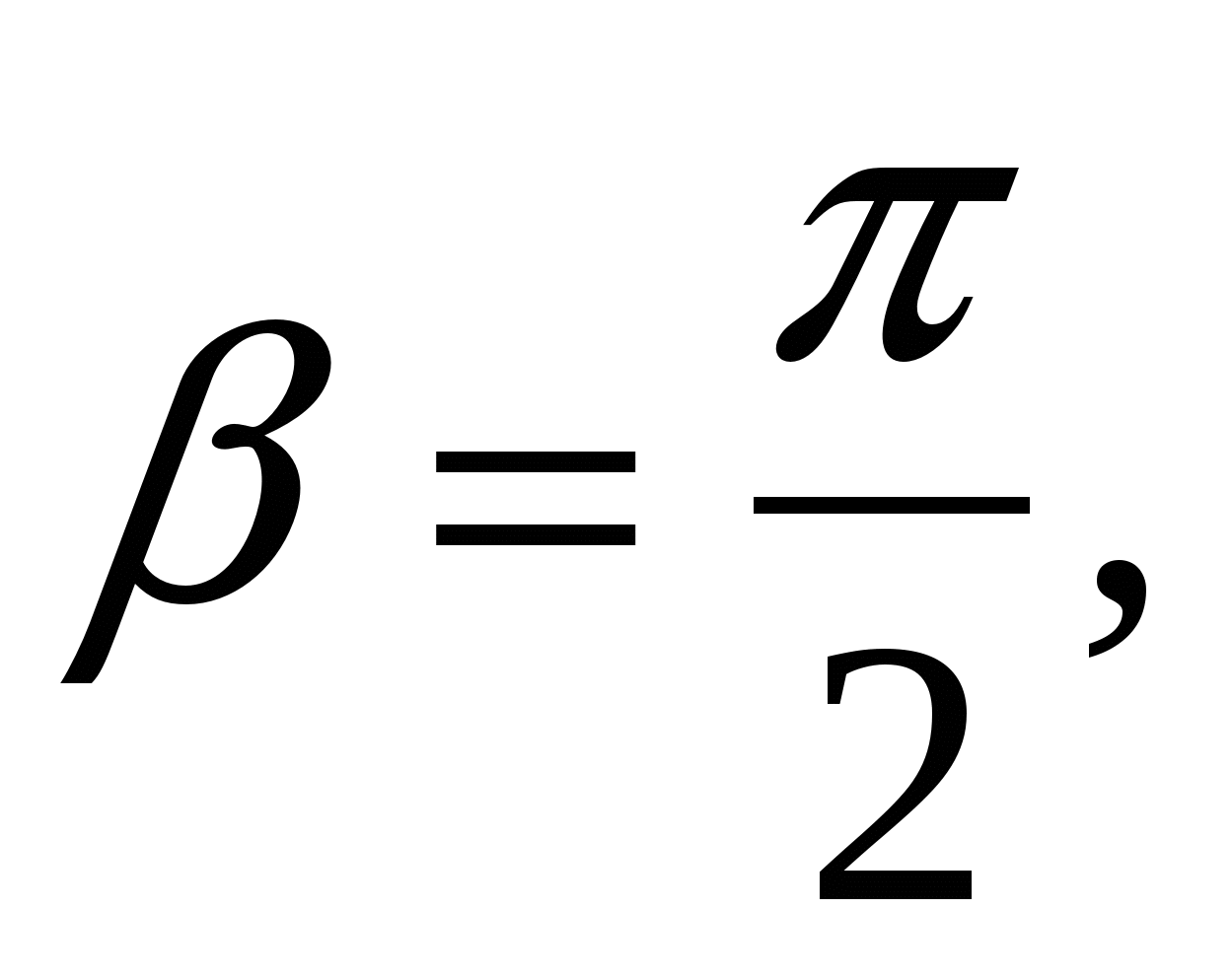 что невозможно.
что невозможно.


