- Преподавателю
- Математика
- Исследовательская работа Построение монад
Исследовательская работа Построение монад
| Раздел | Математика |
| Класс | - |
| Тип | Другие методич. материалы |
| Автор | Черданцева О.П. |
| Дата | 03.10.2015 |
| Формат | doc |
| Изображения | Есть |
Научная конференция
Малой академии наук школьников городского округа город Уфа
Секция: Математика
Номинация: Алгебра
Исследовательская работа
ПРИМЕНЕНИЕ «МОНАД»
Научный руководитель:
Черданцева Ольга Павловна, учитель математики, МБОУ СОШ № 137
Уфа 2013
Оглавление:
-
Введение………………………………………………………………….....3
-
Построение монады………………………………………………………...4
-
Применение теории монад………………………………………………...16
-
Основные теоремы…………………………………………………………21
-
Заключение ………………………………………………………………...22
-
Использованная литература……………………………………….............23
Введение.
В последнее время исследования в областях, традиционно относящихся к дискретной математике, занимают все более заметное место. Наряду с такими классическими разделами математики, как математический анализ, дифференциальные уравнения, в учебных планах специальности "Прикладная математика" и многих других специальностей появились разделы по математической логике, алгебре, комбинаторике и теории графов. Причины этого нетрудно понять, просто обозначив круг задач, решаемых на базе этого математического аппарата.
Пусть имеется конечное множество М. И пусть имеется отображение этого конечного множества в себя. Каждой точке этого конечного множества сопоставляется новая точка. Это и есть монада. Значит, оказывается, существует теория этих монад, и из этой теории вытекают совершенно нетривиальные математические и физические следствия. И некоторые из этих теорий и следствий мы сейчас разберем.
В своей работе мы изучаем доклад «Топология и статистика арифметических и алгебраических формул», сделанный В.И. Арнольдом в Московском математическом обществе. В нем показано как с помощью простейших экспериментов можно открывать новые и неожиданные законы природы.
Дирак учил, как создавать Новую Физику, следующими словами:
«Прежде всего, нужно отбросить все так называемые "физические представления", ибо они - не что иное, как термин для обозначения устаревших предрассудков предшествующих поколений».
Начинать, по его словам, следует с красивой математической теории. «Если она действительно красива,- говорит Дирак, - то она обязательно окажется прекрасной моделью важных физических явлений. Вот и нужно искать эти явления, развивать приложения красивой математической теории и интерпретировать их как предсказания новых законов физики», - так строится, по словам Дирака, вся новая физика.
Построение монады.
Во-первых. Чтобы понять монаду, мы будем ее изображать в виде графа - картинки. Граф монады строится таким образом: берется конечное множество точек. Это множество монада отображает в себя, то есть для каждой точки x из этого множества монада переводит ее в какую-то другую точку y -y, которое есть А от x, отображение в себя. Соединим каждую точку x стрелочкой с той точкой, в которую она отображается. Вот y, например, вот эта точка, тоже куда-то отображается. Например, сама в себя. А эта точка отображается, например, вот в эту. Ну, еще осталось тут указать, куда эта точка, ну, например, вот сюда.
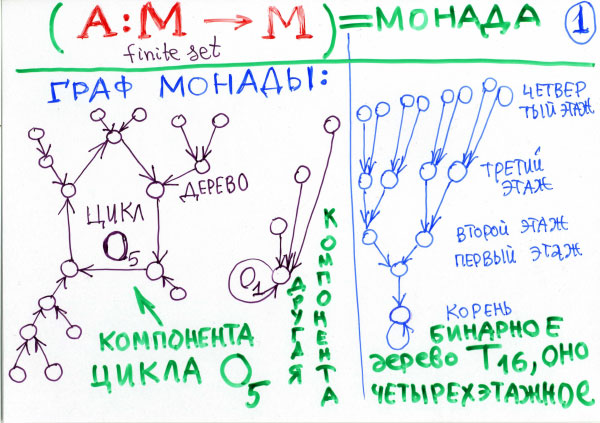
Теперь рассмотрим теорему первую, простейшую. Теорема: «Каждая монада - граф каждой монады - разбивается на связные компоненты». Вот эта монада связная - одна компонента только. А может быть, тут рядом имеются еще какие-то точки - в этом же множестве М - и монада их тоже переводит друг в друга. Тогда будет несколько компонент связности.
Теорема: «В каждой компоненте связности монады обязательно имеется цикл». Компоненты без цикла не бывает. Доказательство: множество точек конечное, поэтому, если мы выйдем и пойдем по стрелочкам, будем идти и когда-нибудь вернемся в точку, где уже были раньше. Потому что их конечное число. Тогда от первого посещения этой точки до второго будет цикл. Конец доказательства.
Второе утверждение: «В компоненте не может быть двух циклов». Доказательство: если бы в какой-нибудь компоненте было два цикла - тут где-то точки стоят в каком-то количестве, так как это в одной компоненте, между ними была бы связь, тоже из стрелок как-то состоящая. И тогда где-то посередине была бы точка, из которой можно идти по стрелкам и к одному циклу, и к другому. Но тут отображение: из каждой точки выходит только одна стрелка - приходить может много, а выходит только одна. Поэтому связь между двумя циклами невозможна. Не бывает связи между двумя циклами. Цикл только один.
Итак, как же устроена монада? Монада устроена так всегда: имеется цикл, у него имеются вершины, и в каждой из этих вершин имеется аттрактор - что-то, что к нему притягивается. А то, что к нему притягивается, - это дерево, это уже кусок без цикла. Деревья могут быть разные - некоторые деревья большие, некоторые маленькие, у некоторых вершин даже пустые деревья, может и не быть никакого дерева, такое тоже бывает. Но, во всяком случае, всякая монада имеет геометрическое строение, которое весьма просто.
Перед нами стоит задача. Эта задача такая: вот у нас имеется какая-то деятельность, мы что-то решаем, какие-то задачи, какие-то объекты исследуем. Среди этих объектов бывают объекты простые, а бывают объекты сложные. Задача, которую я хочу обсудить, - это такая: как различать, какие объекты простые, а какие сложные? Что такое сложность объекта?
Задача. Мы брали последовательность нулей и единиц при n от 2 до 6 и построили монады.
n=2
X
0
1
2
3
xi
00
01
10
11
yj
00
11
11
00
Ax
0
3
3
0
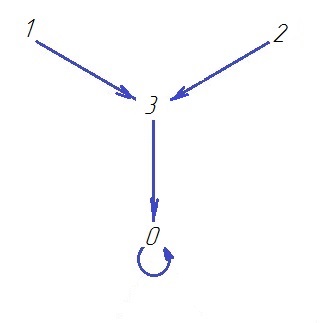
(О1*Т4)
n=3
X
0
1
2
3
4
5
6
7
xi
000
001
010
011
100
101
110
111
yj
000
011
110
101
101
110
011
000
Ax
0
3
6
5
5
6
3
0
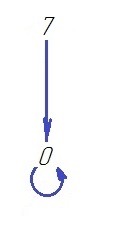
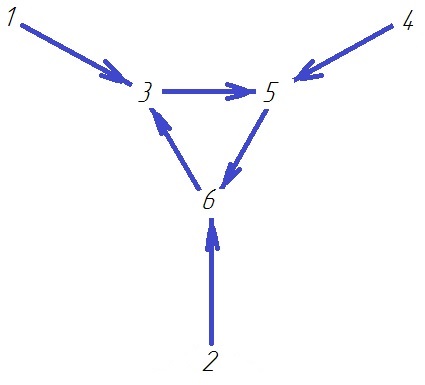
(О1*Т2)
(О3*Т2)
n=4
X
0
1
2
3
4
5
6
7
xi
0000
0001
0010
0011
0100
0101
0110
0111
yj
0000
0011
0110
0101
1100
1111
1010
1001
Ax
0
3
6
5
12
15
10
9
8
9
10
11
12
13
14
15
1000
1001
1010
1011
1100
1101
1110
1111
1001
1010
1111
1100
0101
0110
0011
0000
9
10
15
12
5
6
3
0
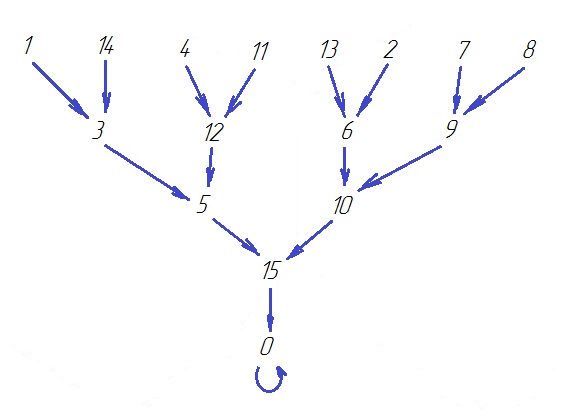
(О1*Т16)
n=5
![]()
0
1
2
3
4
5
6
7
8
![]()
00000
00001
00010
00011
00100
00101
00110
00111
01000
![]()
00000
00011
00110
00101
01100
01111
01010
01001
11000
![]()
0
3
6
5
12
15
10
9
24
9
10
11
12
13
14
15
16
17
18
01001
01010
01011
01100
01101
01110
01111
10000
10001
10010
11011
11110
11101
10100
10111
10010
10001
10001
10010
10111
27
30
29
20
23
18
17
17
18
23
19
20
21
22
23
24
25
26
27
28
10011
10100
10101
10110
10111
11000
11001
11010
11011
11100
10100
11101
11110
11011
11000
01001
01010
01111
01100
00101
20
29
30
27
24
9
10
15
12
5
29
30
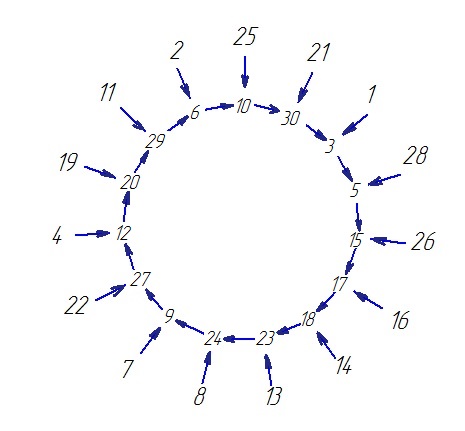 31
31
11101
11110
11111
00110
00011
00000
6
3
0
 (О15*Т2)
(О15*Т2)
(О1*Т2)
n=6
![]()
0
1
2
3
4
5
6
7
![]()
000000
000001
000010
000011
000100
000101
000110
000111
![]()
000000
000011
000110
000101
001100
001111
001010
001001
![]()
0
3
6
5
12
15
10
9
9
10
11
12
13
14
15
16
17
001001
001010
001011
001100
001101
001110
001111
010000
010001
011011
011110
011101
010100
010111
010010
010001
110000
110011
27
30
29
20
23
18
17
48
51
18
19
20
21
22
23
24
25
26
010010
010011
010100
010101
010110
010111
011000
011001
011010
110110
110101
111100
111111
111010
111001
101000
101011
101110
54
53
60
63
58
57
40
43
46
27
28
29
30
31
32
33
34
35
011011
011100
011101
011110
011111
100000
100001
100010
100011
101101
100100
100111
100010
100001
100001
100010
100111
100100
45
36
39
34
33
33
34
39
36
36
37
38
39
40
41
42
43
44
100100
100101
100110
100111
101000
101001
101010
101011
101100
101101
101110
101011
101000
111001
111010
111111
111100
110101
45
46
43
40
57
58
63
60
53
45
46
47
48
49
50
51
52
53
101101
101110
101111
110000
110001
110010
110011
110100
110101
110110
110011
110000
010001
010010
010111
010100
011101
011110
54
51
48
17
18
23
20
29
30
54
55
56
57
58
59
60
61
62
63
110110
110111
111000
111001
111010
111011
111100
111101
111110
111111
011011
011000
001001
001010
001111
001100
000101
000110
000011
000000
27
24
9
10
15
12
5
6
3
0
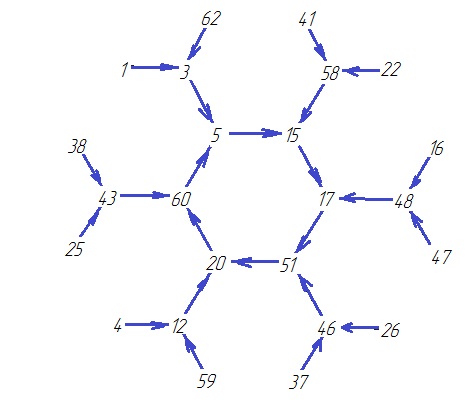
(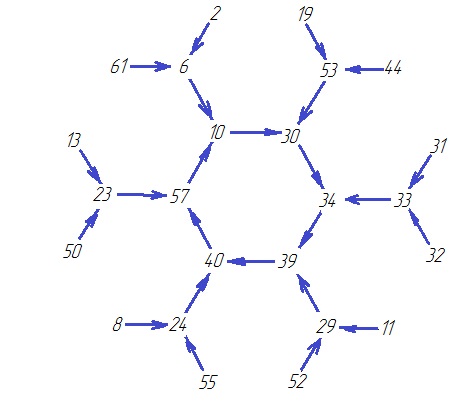 О6*Т4)
О6*Т4)
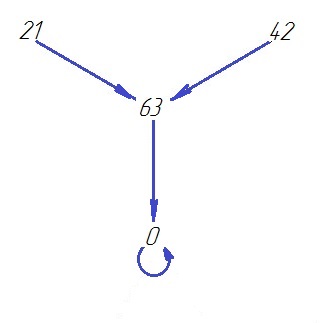
(О1*Т4)
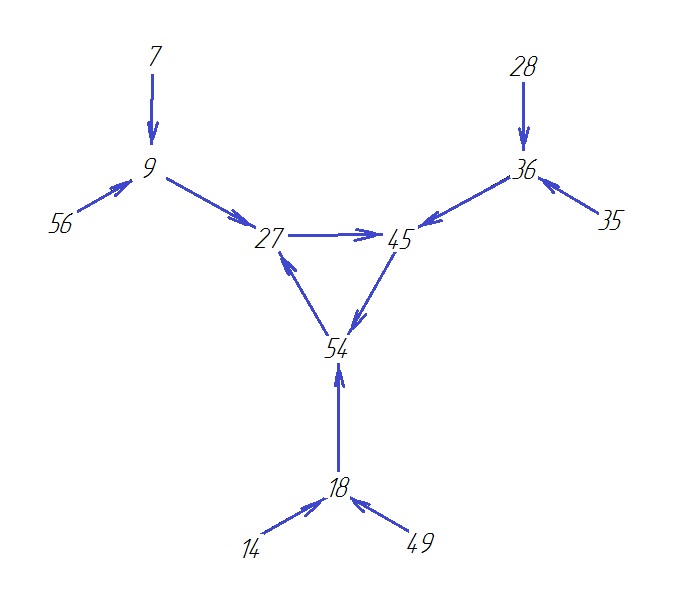
(О6*Т4)
(О3*Т4)
Последовательность 001 001 001 001 проще, чем последовательность 01 001 0111 001. Ниже описана формальная математическая теория, придающая этому интуитивно понятному утверждению точный смысл.
Пусть x - последовательность из n нулей и единиц, x = (x1, ..., xn), xj 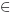
 . Множество M всех 2n таких последовательностей есть множество вершин n-мерного куба. Оно является также n-мерным векторным пространством над полем
. Множество M всех 2n таких последовательностей есть множество вершин n-мерного куба. Оно является также n-мерным векторным пространством над полем  из двух элементов: M =
из двух элементов: M = 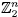 .
.
Н апример, при n=2 множество М является двухмерным векторным пространством, т.е. квадратом, а при n=3 - трехмерным, т.е. кубом с 8 вершинами.
апример, при n=2 множество М является двухмерным векторным пространством, т.е. квадратом, а при n=3 - трехмерным, т.е. кубом с 8 вершинами.
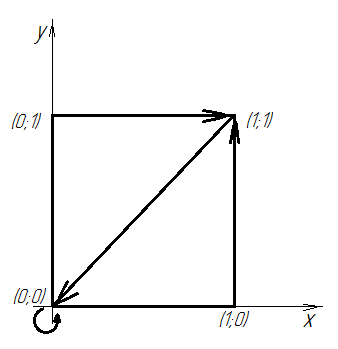
Для анализа сложности функции x 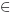 M мы последуем идее Ньютона и рассмотрим ее первые разности, определив линейный оператор
M мы последуем идее Ньютона и рассмотрим ее первые разности, определив линейный оператор
A : M → M, y = Ax
формулой yj = xj+1 - xj. Чтобы разностей получилось n, мы определим xn+1 как x1, т. е. будем считать нашу последовательность x циклической (так, что функция x со значениями xj в точках j будет периодической, с периодом n). Изложенная ниже геометрическая теория доставляет информацию о жордановой нормальной форме этого оператора A над полем  .
.
Отображение A конечного множества M в себя задается графом с 2n вершинами x. Из каждой вершины x в этом графе выходит ровно одно ребро, оно ведет в Ax.
ПРИМЕР. При n = 3 граф имеет 8 вершин и 8 ребер, A(0, 0, 0) = (0, 0, 0), A(1, 1, 1) = (0, 0, 0), A(1, 0, 0) = (1, 0, 1), A(0, 1, 0) = (1, 1, 0), A(0, 0, 1) = (0, 1, 1), A(1, 1, 0) = (0, 1, 1), A(1, 0, 1) = (1, 1, 0), A(0, 1, 1) = (1, 0, 1).
Обозначая последовательность x = (x1, ..., xn) числом в двоичной записи
X = x12n-1 + x22n-2 + ... + xn · 1,
мы записываем предыдущий граф в виде графа с вершинами
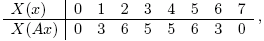
являющимися вычетами по модулю 2n = 8. При n = 3 этот граф состоит из двух компонент связности,
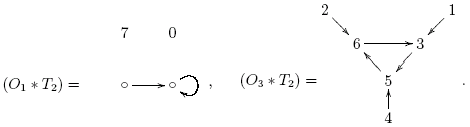
Мы будем обозначать символом Om цикл из m циклически соединенных вершин. Знаком T2n будет обозначаться бинарное дерево из 2n вершин:
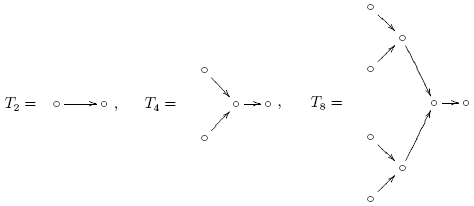
Знаком (Om 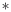 T) будем обозначать цикл из m вершин, оснащенный лесом из m корневых деревьев T, корнями которых являются вершины цикла Om (эти корневые деревья предполагаются состоящими из ориентированных направлениями к корням ребер):
T) будем обозначать цикл из m вершин, оснащенный лесом из m корневых деревьев T, корнями которых являются вершины цикла Om (эти корневые деревья предполагаются состоящими из ориентированных направлениями к корням ребер):
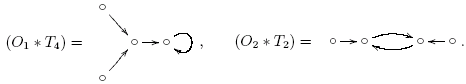
Граф (Om 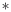 T2n) имеет, таким образом, m2n вершин.
T2n) имеет, таким образом, m2n вершин.
Граф оператора взятия разностей A : M → M разбивается на компоненты связности. Например, для n = 3 он состоит из двух компонент, (O1 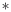 T2) и (O3
T2) и (O3 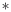 T2), изображенных выше.
T2), изображенных выше.
Прямые вычисления графов операторов взятия разностей A : ![]() →
→ ![]() при n ≤ 12 приводит к следующим ответам (в наиболее сложном случае n = 12 приходится соединять всего 4096 вершин, и рисунок умещается на одной странице):
при n ≤ 12 приводит к следующим ответам (в наиболее сложном случае n = 12 приходится соединять всего 4096 вершин, и рисунок умещается на одной странице):

Общее число вершин компонент графа, например, при n = 11 есть (3 · 341 + 1)2 = 211.
Применение теории монад.
Использовать теорию монад можно в различных областях.
Например, в теории алгоритмов имеются алгоритмически разрешимые проблемы и алгоритмически неразрешимые, имеется понятие алгоритмической сложности. Но дело в том, что во всех этих теориях рассматриваются бесконечные наборы и рассматривается сложность задач, у которых бесконечное число возможностей. И говорится, что какая-нибудь такая задача, скажем, проблема Ферма (xn + yn = zn)... Вот можно поставить вопрос: разрешима ли она алгоритмически, есть ли алгоритм, который будет решением. Так это значит вот что: ведь если n фиксированное, если x, y, z фиксированные, то проверить, так это или не так, всегда можно, это легко. Задача возникает из-за того, что нет ограничения, что система не ограниченная - бывают очень большие x, y и z, и узнать надо про все сразу, про всё бесконечное множество надо сразу узнать.
Например, составление программ в машине. Сложная она или простая?
Ньютон исследовал функции, как он исследовал, например, многочлен - функция или нет, - как он это делал? Он предложил: надо рассмотреть разности у этой функции. Задача у него была такая: дана функция, и нужно определить, простая она или сложная, как написать формулу для этой функции.
Например, теория монад связана с криптографией.
Криптография - (в переводе с греческого означает «тайнопись») - наука о методах преобразования (шифрования) информации с целью ее защиты от незаконных пользователей.
Начало криптографии, в своем современном понимании, связано с Юлием Цезарем.
«Шифр Цезаря» - способ, которым Юлий Цезарь прятал свои записи от чужих глаз. С современной точки зрения, шифр Цезаря кажется примитивным: в нем каждая буква заменяется на следующую за ней по алфавиту. Однако для того времени, когда умение читать и писать было редким исключением, использование такого шифра решало проблему секретной передачи сообщения, а проблема его подлинности решалась практически сама собой.
Вскрытие (взламывание) шифра - процесс получения защищаемой информации (открытого текста) из шифрованного сообщения (шифртекста) без знания примененного шифра.
Шифрование - процесс применения шифра к защищаемой информации.
Дешифрование - процесс, обратный шифрованию.
Шифр с помощью ЭВМ.
В ЭВМ преобразование открытого текста в числа происходит естественным путем, так как каждый символ кодируется двоичным числом. Вид этого преобразования зависит от используемой операционной системы. Для определенности будем считать, что сообщение в ЭВМ кодируется с помощью кодовых таблиц CP-1251.
Таблица CP-1251.
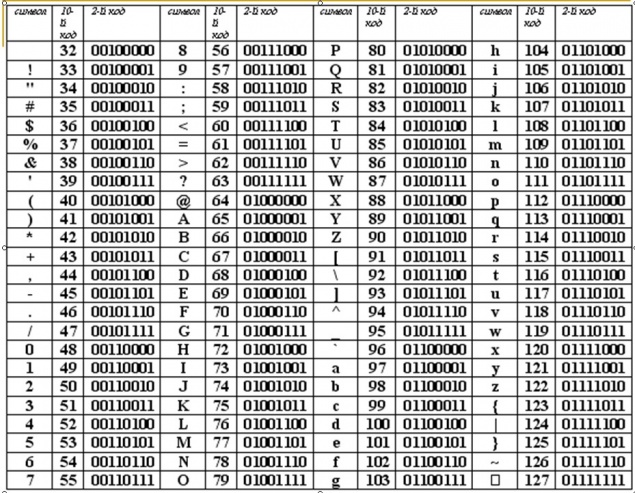
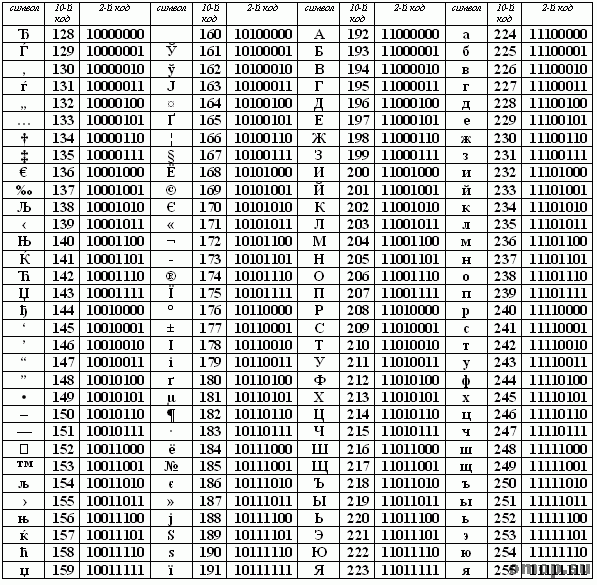
Пример шифрования при помощи данных таблиц:
Открытый текст
Г
Д
Е
А
Б
Б
А
Десятичное число
195
196
197
192
193
193
192
Двоичное число
11000011
11000100
11000101
11000000
11000001
11000001
11000000
Гамма (десятич.)
32
18
36
11
61
23
3
Гамма (двоичн.)
00100000
00010010
00100100
00001011
00111101
00010111
00000011
Криптогр. (двоичн.)
11100011
11010110
11100001
11001011
11111100
11010110
11000011
Криптогр. (десятич.)
227
214
225
203
252
214
195
Криптограмма
г
Ц
б
Л
ь
Ц
Г
Основные теоремы.
-
Каждая компонента связности графа любого отображения конечного множества в себя имеет цикл, и притом только один.
-
Граф «многочленов» периода n = 2k(2a + 1) является корневым бинарным деревом с 2k этажами, так что содержащая x = 0 компонента графа оператора взятия разностей есть
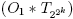 .
. -
Дерево, притягиваемое каждой точкой каждого цикла графа оператора взятия разностей A :
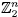 →
→ 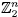 , изоморфно дереву, притягиваемому точкой x = 0 (т. е. бинарному дереву
, изоморфно дереву, притягиваемому точкой x = 0 (т. е. бинарному дереву 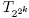 компоненты
компоненты теоремы 2).
теоремы 2).
ЛЕММА. Если 2k-1 ≤ j < 2k, то наименьший период функции 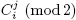 по i равен 2k.
по i равен 2k.
Заключение.
В ходе проведения исследований, были выяснены способы построения графов «Монады», понятия, с ними связанные, и их применение.
В дальнейшем мы планируем изучить остальные теоремы, а также роль криптографии в теории монад.
Использованная литература.
1. В. И. Арнольд, Топология и статистика арифметических и алгебраических формул, Успехи математических наук 58 (2003), № 4, 3-28 (особенно §6, с. 15-18).
22


