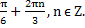- Преподавателю
- Математика
- Тригонометрические уравнения с параметром
Тригонометрические уравнения с параметром
| Раздел | Математика |
| Класс | - |
| Тип | Презентации |
| Автор | Хоружая Н.А. |
| Дата | 16.03.2015 |
| Формат | doc |
| Изображения | Есть |
Тригонометрические уравнения с параметром.
1. Найдите все значения параметра а, при каждом из которых уравнение COS4 x - (a + 2)COS2x - (a + 3) = 0 имеет решение.
Решение.
Введем новую переменную: t =COS2x, t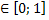 . Тогда данное уравнение принимает вид t2 - (а + 2)t - (a + 3) = 0.
. Тогда данное уравнение принимает вид t2 - (а + 2)t - (a + 3) = 0.
Чтобы решить получившееся квадратное уравнение с переменной t, найдем его дискриминант: D = a2 + 4a + 4 + 4a + 12 = a2 + 8a + 16 = (a + 4)2.
Так как D≥0, квадратное уравнение имеет решение
t1,2 = 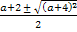 =
= 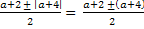 ;
;
t1=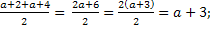
t2 =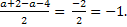
Число -1 не принадлежит промежутку 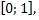 таким образом, заданное нам тригонометрическое уравнение с параметром имеет решение при условии
таким образом, заданное нам тригонометрическое уравнение с параметром имеет решение при условии
0 ≤ а +3 ≤ 1,
-3 ≤ а ≤ -2.
Ответ. Уравнение COS4 x - (a + 2)COS2x - (a + 3) = 0 имеет решение при а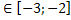 .
.
2. Найдите все значения параметра р, при которых уравнение 6Sin3x = p - 10Cos2x не имеет корней.
Решение.
6Sin3x = p - 10Cos2x;
6Sin3x + 10Cos2x = p;
6Sin3x + 10(1 - 2Sin2x) = p;
6Sin3x - 20Sin2x + 10 = p.
Введем новую переменную: t = Sinx, t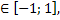 тогда тригонометрическое уравнение примет вид 6t3 - 20t2 + 10 = p.
тогда тригонометрическое уравнение примет вид 6t3 - 20t2 + 10 = p.
Рассмотрим функцию у = 6t3 - 20t2 + 10 и исследуем ее на наибольшее и наименьшее значения на отрезке 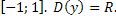
Находим производную: у| = 18t2 - 40t = 18t(t - ![]() D(y|)=R.
D(y|)=R.
Определяем критические точки функции: у|=0, 18t(t - 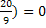 , t1=0, t2=
, t1=0, t2=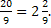
Число 2![]() не принадлежит промежутку
не принадлежит промежутку 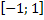 , поэтому вычисляем значения функции в точке 0 и на концах отрезка:
, поэтому вычисляем значения функции в точке 0 и на концах отрезка:
у(0) = 0 - 0 + 10 = 10,
у(-1) = -6 - 20 + 10 = -16,
у(1) = 6 - 20 + 10 = -4.
max y(t) = 10, min y(t) = -16 на отрезке 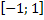 .
.
Значит, при р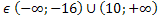 исходное уравнение не имеет корней.
исходное уравнение не имеет корней.
Ответ. Уравнение 6Sin3x = p - 10Cos2x не имеет корней при р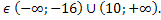
3. При каких значениях параметра а выражение 2 + Cosx(3Cosx + aSinx) не равно нулю ни при каких значениях х?
Решение.
Другими словами, необходимо найти все значения параметра а, при которых уравнение 2 + Cosx(3Cosx + aSinx) = 0 не имеет корней.
2 + Cosx(3Cosx + aSinx) = 0;
2(Cos2x + Sin2x) + Cosx(3Cosx + aSinx) = 0;
2Cos2x + 2Sin2x + 3Cos2x + aSinxCosx = 0;
2Sin2x + aSinxCosx + 5Cos2x = 0 - однородное уравнение второй степени.
Если бы Cosx = 0, то и Sinx = 0, что невозможно, так как Cos2x + Sin2х = 1, поэтому разделим левую и правую часть однородного уравнения на Cosx.
Получим уравнение вида 2tg2x + atgx + 5 = 0. Для решения этого уравнения введем новую переменную: t = tgx, t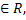 тогда 2t2 + at + 5 = 0.
тогда 2t2 + at + 5 = 0.
Далее можно проводить рассуждения двумя способами.
Способ 1.
Найдем сначала множество всех значений параметра а, при которых полученное квадратное уравнение разрешимо. Дополнение этого множества до R и будет искомым ответом.
Квадратное уравнение имеет корни тогда и только тогда, когда D≥0.
D = а2 - 40,
а2 - 40 ≥ 0,
а2 ≥ 40,
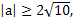
а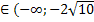 ]
]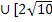 ;
;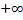 ).
).
Дополнением этого множества до R является промежуток (-2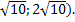
Способ 2.
Квадратное уравнение не имеет действительных корней тогда и только тогда, когда D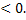
D = a2 - 40,
a2 - 40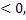
а2 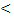 40,
40,
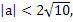
-2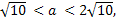
a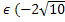 ;
;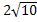 ).
).
Ответ. Выражение 2 + Cosx(3Cosx + aSinx) не равно нулю ни при каких значениях х, если a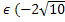 ;
;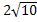 ).
).
4. Найдите все значения параметра р, при которых уравнение pCtg2x + 2Sinx + p = 3 имеет хотя бы один корень.
Решение.
ОДЗ: х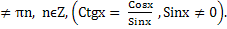
Преобразуем данное уравнение:
p (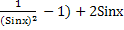 + p = 3.
+ p = 3.
Обозначим t = Sinx, t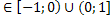 , тогда тригонометрическое уравнение примет вид
, тогда тригонометрическое уравнение примет вид
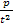 - p + 2t + p = 3,
- p + 2t + p = 3,
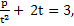
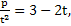
P = 3t2 - 2t3.
Рассмотрим функцию f(t) = 3t2 - 2t3 (D(f) = R) и найдем множество ее значений при t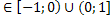 .
.
Находим производную: f|(t) = 6t - 6t2.
Определяем критические точки: f|(t) = 0, 6t - 6t2 = 0, t - t2 = 0, t(1 - t) = 0, t1=0, t2=1.
f(-1) = 3 + 2 = 5, f(t) 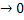 при t
при t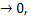 функция f(t) непрерывна на промежутке [-1;0), следовательно, E(f) = (0;5] при t
функция f(t) непрерывна на промежутке [-1;0), следовательно, E(f) = (0;5] при t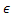 [-1;0).
[-1;0).
f(1) = 3 - 2 = 1, f(t) 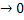 при t
при t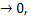 функция f(t) непрерывна на промежутке (0;1], следовательно,
функция f(t) непрерывна на промежутке (0;1], следовательно,
E(f) = (0;1] при t 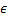 (0;1].
(0;1].
Значит, E(f) = (0;5] при t 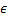 [-1;0)
[-1;0) 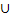 (0;1].
(0;1].
Чтобы алгебраическое уравнение относительно t, а следовательно, и исходное тригонометрическое уравнение имело хотя бы один корень, необходимо и достаточно, чтобы р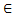 E(f), т.е. р
E(f), т.е. р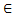 (0;5].
(0;5].
Ответ. Уравнение pCtg2x + 2Sinx + p = 3 имеет хотя бы один корень при р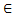 (0;5].
(0;5].
5. При каких значениях параметра а графики функций y = Sin2x + aCosx и y = 3a - 2a2 не имеют общих точек?
Решение.
Другими словами, нужно найти такие значения параметра а, при которых уравнение
Sin2x + aCosx = 3a - 2a2 не имеет корней.
1 - Cos2x + aCosx + 2a2 - 3a = 0;
Cos2x - aCosx - (2a2 - 3a + 1) = 0.
Введем новую переменную: t = Cosx, t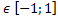 , тогда тригонометрическое уравнение примет вид t2 - at - (2a2 - 3a + 1) = 0. Получили квадратное уравнение с параметром а.
, тогда тригонометрическое уравнение примет вид t2 - at - (2a2 - 3a + 1) = 0. Получили квадратное уравнение с параметром а.
D = a2 + 4(2a2 - 3a + 1) = a2 + 8a2 - 12a + 4 = 9a2 - 12a + 4 = (3a - 2)2,
t1,2 = 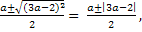 t1 =
t1 = 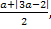 t2 =
t2 = 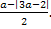
Так как 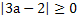 , то t1
, то t1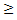 t2.
t2.
Случай 1.
t1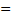 t2 , тогда
t2 , тогда 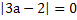 , а =
, а =  и t1
и t1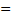 t2 =
t2 = 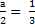 . В этом случае уравнение Cosx =
. В этом случае уравнение Cosx =  имеет корни.
имеет корни.
Случай 2.
t1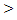 t2. Чтобы уравнения Cosx = t1 и Cosx = t2 не имели корней необходимо и достаточно выполнения одного из трех условий: t1 < -1, t2 > 1, t2 < -1 и t1 > 1. Рассмотрим каждое из этих условий.
t2. Чтобы уравнения Cosx = t1 и Cosx = t2 не имели корней необходимо и достаточно выполнения одного из трех условий: t1 < -1, t2 > 1, t2 < -1 и t1 > 1. Рассмотрим каждое из этих условий.
Условие 1. t1 < -1.
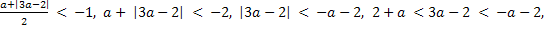
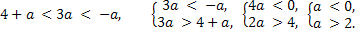
Система решений не имеет, значит, не существует таких значений а, при которых выполняется условие t1 < -1.
Условие 2. t2 > 1.
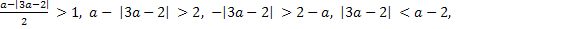
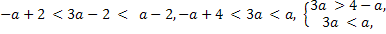
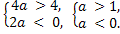
Система решений не имеет, следовательно, не существует таких значений а, при которых выполняется условие t2 > 1.
Условие 3. t2 < -1 и t1 > 1.
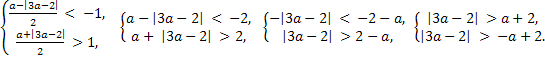
-
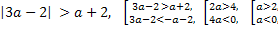 a
a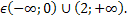
-
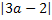
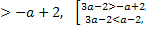
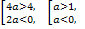 a
a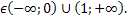
Таким образом, 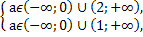 a
a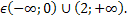
Ответ. Графики функций y = Sin2x + aCosx и y = 3a - 2a2 не имеют общих точек, если
a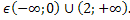
Тригонометрические уравнения с модулем и радикалом.
-
Sin2x +
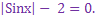
Решение.
Раскроем модуль.
Случай 1. Sinx 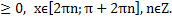
Sin2x + Sinx - 2 = 0.
Введем новую переменную: t = Sinx, t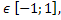 тогда t2 + t - 2 = 0 - приведенное квадратное уравнение. Решим его по теореме Виета: t1 + t2 =
тогда t2 + t - 2 = 0 - приведенное квадратное уравнение. Решим его по теореме Виета: t1 + t2 =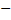 1, t1t2 =
1, t1t2 = 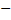 2, значит, t1 =
2, значит, t1 =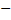 2, t2 = 1.
2, t2 = 1.
Число ![]() 2 не принадлежит промежутку
2 не принадлежит промежутку 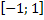 .
.
Sinx = 1 (особый случай),
x = 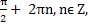 (
(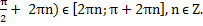
Случай 2. Sinx 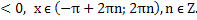
Sin2x - Sinx - 2 = 0.
Введем новую переменную: t = Sinx, t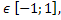 тогда t2
тогда t2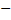 t - 2 = 0 - приведенное квадратное уравнение. Решим его по теореме Виета: t1 + t2 = 1, t1t2 =
t - 2 = 0 - приведенное квадратное уравнение. Решим его по теореме Виета: t1 + t2 = 1, t1t2 =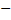 2, значит, t1 = 2, t2 =
2, значит, t1 = 2, t2 =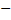 1.
1.
Число 2 не принадлежит промежутку 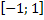 .
.
Sinx = ![]() 1 (особый случай),
1 (особый случай),
x = ![]()
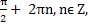 (
(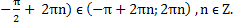
Объединяя две серии решений, получаем, что x = 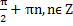
Ответ. x = 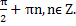
2. 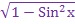 = 2Sin2x - 1.
= 2Sin2x - 1.
Решение.
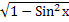 = 2Sin2x - 1,
= 2Sin2x - 1,
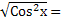 2Sin2x - 1,
2Sin2x - 1,
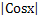 = 2Sin2x - 1,
= 2Sin2x - 1,
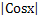
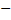 2Sin2x + 1 = 0,
2Sin2x + 1 = 0,

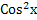 ) + 1 = 0,
) + 1 = 0,
2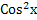 +
+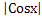
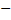 1 = 0.
1 = 0.
Раскроем модуль.
Случай 1. Cosx 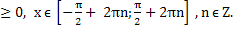
2Cos2x + Cosx - 1 = 0.
Введем новую переменную: t = Cosx, t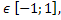 тогда 2t2 + t - 1 = 0 - квадратное уравнение.
тогда 2t2 + t - 1 = 0 - квадратное уравнение.
D = 1 + 8 = 9,
t1 =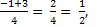 t2 =
t2 = 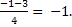
Cosx =![]() , Cosx =
, Cosx =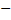 1 (особый случай)
1 (особый случай)
x =  x =
x = 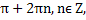
(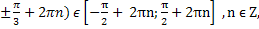 (
(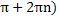 не принадлежит промежутку
не принадлежит промежутку
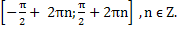
Случай 2. Cosx 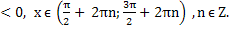
2Cos2x - Cosx - 1 = 0,
Введем новую переменную: t = Cosx, t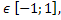 тогда 2t2 -t - 1 = 0 - квадратное уравнение.
тогда 2t2 -t - 1 = 0 - квадратное уравнение.
D = 1 + 8 = 9,
t1 =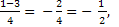 t2 =
t2 = 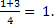
Cosx =![]() , Cosx = 1 (особый случай)
, Cosx = 1 (особый случай)
x = 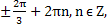 x =
x = 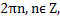
(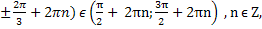 (
(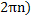 не принадлежит промежутку
не принадлежит промежутку
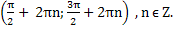
Объединяя две серии решений, получаем, что x = 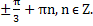
Ответ. x = 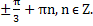
3. 
Решение.
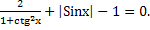
ОДЗ: x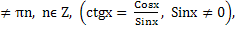
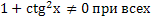 x
x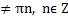 .
.
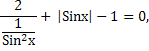
2Sin2x + 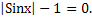
Раскроем модуль.
Случай 1. Sinx 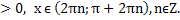
2Sin2x + Sinx - 1 = 0.
Введем новую переменную: t = Sinx, t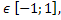 тогда 2t2 + t -1 = 0 -квадратное уравнение.
тогда 2t2 + t -1 = 0 -квадратное уравнение.
D = 1 + 8 = 9,
t1 =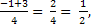 t2 =
t2 = 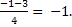
Sinx = ![]() Sinx =
Sinx = 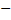 1 (особый случай),
1 (особый случай),
x = (![]() 1)n
1)n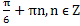 , x =
, x =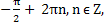
(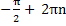 ) не принадлежит промежутку
) не принадлежит промежутку
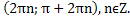
Случай 2. Sinx 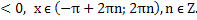
2Sin2x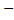 Sinx - 1 = 0.
Sinx - 1 = 0.
Введем новую переменную: t = Sinx, t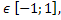 тогда 2t2
тогда 2t2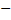 t - 1 = 0 -квадратное уравнение.
t - 1 = 0 -квадратное уравнение.
D = 1 + 8 = 9,
t1 =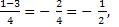 t2 =
t2 = 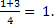
Sinx =![]()
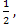 Sinx = 1 (особый случай)
Sinx = 1 (особый случай)
x = (![]() 1)n+1
1)n+1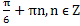 , x =
, x =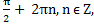
(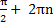 ) не принадлежит промежутку
) не принадлежит промежутку
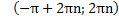
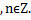
Объединяя две серии решений, получаем, что x = 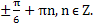
Ответ. x = 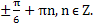
4. 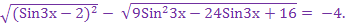
Решение.
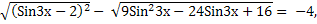
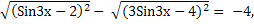
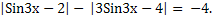
Оценим знаки подмодульных выражений:
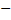 1
1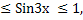
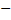 3
3 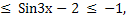
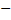 3
3 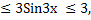
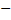 7
7 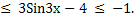
Раскроем модули:
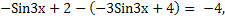
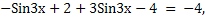
2Sin3x - 2 = 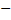 4,
4,
2Sin3x = 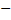 2,
2,
Sin3x = 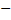 1 (особый случай),
1 (особый случай),
3x =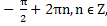
x = ![]()
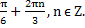
Ответ. x =