Добавить в избранное

КЕРІ ТРИГОНОМЕТРИЯЛЫҚ ФУНКЦИЯ ЖӘНЕ ИНТЕГРАЛ

Раздел Математика
Класс -
Тип Другие методич. материалы
Автор
Дата
Формат doc
Изображения Есть
For-Teacher.ru - все для учителя
Поделитесь с коллегами:

КЕРІ ТРИГОНОМЕТРИЯЛЫҚ ФУНКЦИЯ ЖӘНЕ ИНТЕГРАЛ


Кері тригонометриялық 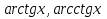КЕРІ ТРИГОНОМЕТРИЯЛЫҚ ФУНКЦИЯ ЖӘНЕ ИНТЕГРАЛ функцияларды 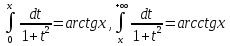КЕРІ ТРИГОНОМЕТРИЯЛЫҚ ФУНКЦИЯ ЖӘНЕ ИНТЕГРАЛ -шектерінің бірі айнымалы анықталған (меншіксіз) интеграл арқылы енгізіп, ол функциялардың барлық қасиеттерін, негізгі тепе-теңдікті тек қана интегралдың қасиеттерінен толық шығарып алуға болатындығы белгілі [1]. Осы тақырыпты ары қарай жалғастырып 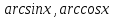КЕРІ ТРИГОНОМЕТРИЯЛЫҚ ФУНКЦИЯ ЖӘНЕ ИНТЕГРАЛ функцияларында сол тұрғыдан енгізіп, негізгі қасиеттерінің дәлелдеулерін келтіріп, соңында кері тригонометриялық функциялармен байланысты бірнеше есептердің шешімдерін береміз. Жалпы айта кету керек, ондай есептер әдетте оқушыларға жеткілікті дәрежеде қиындықтар туғызады. Себебі, негізгі оқулықтар мен оқу құралдарында кері тригонометриялық функциялармен байланысты есептерге жеткілікті түрде көңіл бөлмейді, тура тригонометриялық функцияларға кері ретінде енгізіп, бірнеше қарапайым мысалдар мен араларындағы қатынастарды келтірумен шектеледі.

Айта кетейік, біз келтірген әдіс кері тригонометриялық функцияларды енгізудің бір нұсқасы, бұрыннан белгілі тәсілдердің бірі болып, функциялардың табиғатын тереңірек түсінуге жол салатыны анық.

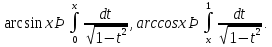
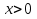КЕРІ ТРИГОНОМЕТРИЯЛЫҚ ФУНКЦИЯ ЖӘНЕ ИНТЕГРАЛ

КЕРІ ТРИГОНОМЕТРИЯЛЫҚ ФУНКЦИЯ ЖӘНЕ ИНТЕГРАЛболғанда 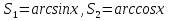КЕРІ ТРИГОНОМЕТРИЯЛЫҚ ФУНКЦИЯ ЖӘНЕ ИНТЕГРАЛ (анықтамалардың геометриялық мағынасы 1суретте көрсетілген).

X

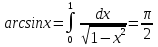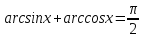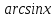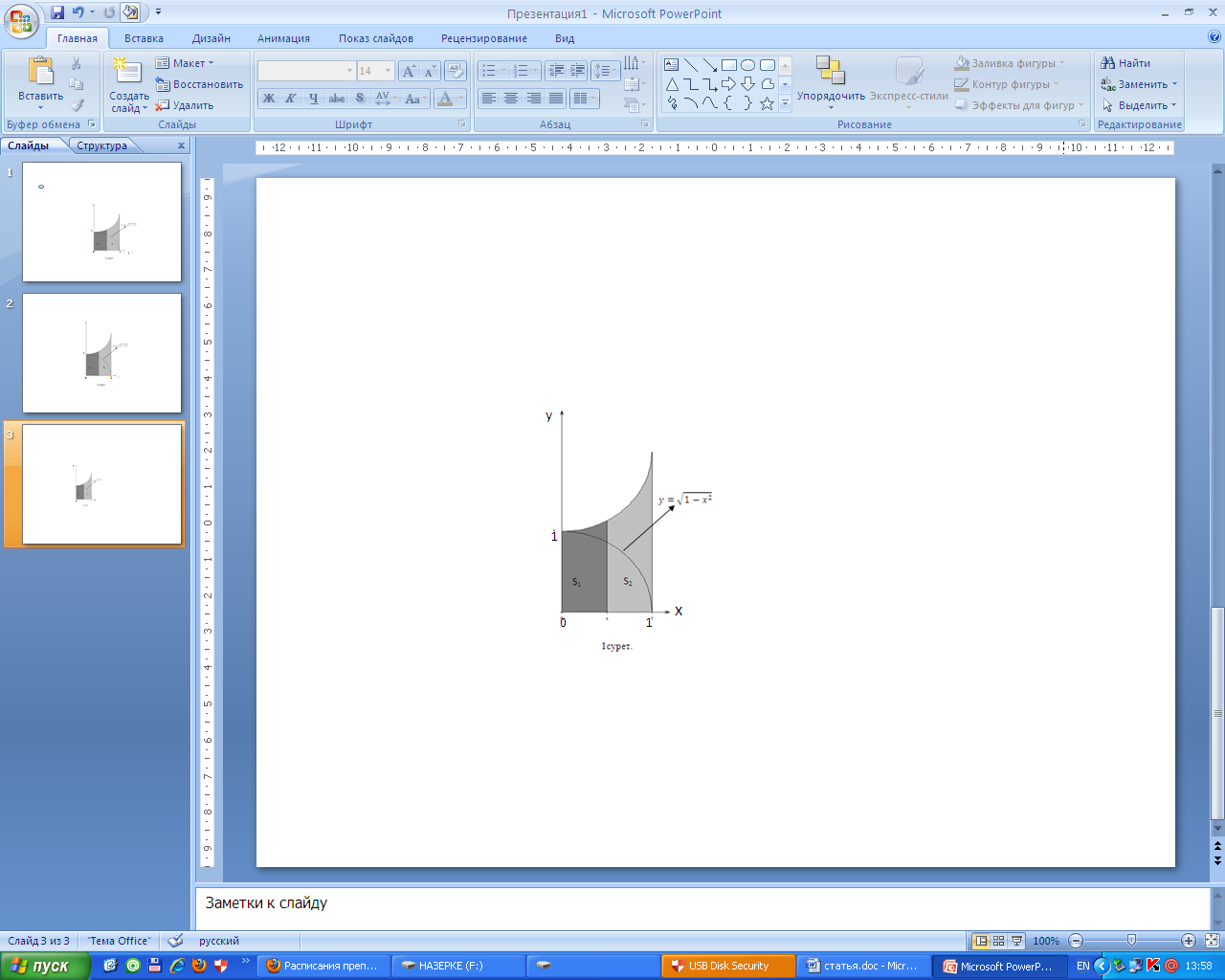
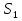Келтірілген анықтамалармен КЕРІ ТРИГОНОМЕТРИЯЛЫҚ ФУНКЦИЯ ЖӘНЕ ИНТЕГРАЛ теңдігінен КЕРІ ТРИГОНОМЕТРИЯЛЫҚ ФУНКЦИЯ ЖӘНЕ ИНТЕГРАЛ негізгі қатынастардың бірі шығатынын көреміз. Бұдан тек қана КЕРІ ТРИГОНОМЕТРИЯЛЫҚ ФУНКЦИЯ ЖӘНЕ ИНТЕГРАЛ функциясын зерттесек жеткілікті болатынын көреміз.КЕРІ ТРИГОНОМЕТРИЯЛЫҚ ФУНКЦИЯ ЖӘНЕ ИНТЕГРАЛ

  1. КЕРІ ТРИГОНОМЕТРИЯЛЫҚ ФУНКЦИЯ ЖӘНЕ ИНТЕГРАЛинтегралының бар болуынан 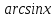КЕРІ ТРИГОНОМЕТРИЯЛЫҚ ФУНКЦИЯ ЖӘНЕ ИНТЕГРАЛ функциясының анықталу облысы болып [-1;1] сегменті табылатынын көреміз.

  2. Үзіліссіздігі. Анықталу облысының ішкі нүктелерінде қисық сызықты трапецияның ауданының үзіліссіз болатындығынан , ал ұштарында интегралдың бар болуынан шығады.

  3. Тақ, жұптығы. Егер жұп функцияның графигі координаталар бас нүктесінен өтетін болса, оның алғашқы функциясы тақ екендігі жалпы теориядан белгілі. Біздің жағдайда екі шарт та орындалып тұр, сондықтан 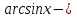КЕРІ ТРИГОНОМЕТРИЯЛЫҚ ФУНКЦИЯ ЖӘНЕ ИНТЕГРАЛ тақ функция.

  4. Монотондылығы. 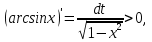КЕРІ ТРИГОНОМЕТРИЯЛЫҚ ФУНКЦИЯ ЖӘНЕ ИНТЕГРАЛ немесе (0,1) аралықта геометриялық мағынасы аудан болғандықтан, аргумент 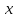КЕРІ ТРИГОНОМЕТРИЯЛЫҚ ФУНКЦИЯ ЖӘНЕ ИНТЕГРАЛ- өскенде ол да өскендіктен 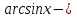КЕРІ ТРИГОНОМЕТРИЯЛЫҚ ФУНКЦИЯ ЖӘНЕ ИНТЕГРАЛөспелі функция, ал 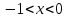КЕРІ ТРИГОНОМЕТРИЯЛЫҚ ФУНКЦИЯ ЖӘНЕ ИНТЕГРАЛ өсетіндігі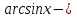КЕРІ ТРИГОНОМЕТРИЯЛЫҚ ФУНКЦИЯ ЖӘНЕ ИНТЕГРАЛ тақ екендігінен, тұтас [-1;1] анықталу облысында монотондылығы 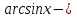КЕРІ ТРИГОНОМЕТРИЯЛЫҚ ФУНКЦИЯ ЖӘНЕ ИНТЕГРАЛтің үзіліссіздігінен шығады.

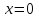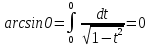  5. Функцияның нөлі. КЕРІ ТРИГОНОМЕТРИЯЛЫҚ ФУНКЦИЯ ЖӘНЕ ИНТЕГРАЛ болса КЕРІ ТРИГОНОМЕТРИЯЛЫҚ ФУНКЦИЯ ЖӘНЕ ИНТЕГРАЛ интегралдың қасиетінен, ал қатаң монотондылығынан 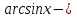КЕРІ ТРИГОНОМЕТРИЯЛЫҚ ФУНКЦИЯ ЖӘНЕ ИНТЕГРАЛтің басқа нөлдерінің болмайтынын көреміз.

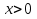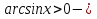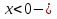  6. Функцияның таңбалары. КЕРІ ТРИГОНОМЕТРИЯЛЫҚ ФУНКЦИЯ ЖӘНЕ ИНТЕГРАЛ болса КЕРІ ТРИГОНОМЕТРИЯЛЫҚ ФУНКЦИЯ ЖӘНЕ ИНТЕГРАЛ тек оң, ал КЕРІ ТРИГОНОМЕТРИЯЛЫҚ ФУНКЦИЯ ЖӘНЕ ИНТЕГРАЛтек теріс мәндерге ие болатындығы 4-5 қасиеттерден шығады.

  7. Дөңес, ойыстығы. 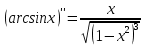КЕРІ ТРИГОНОМЕТРИЯЛЫҚ ФУНКЦИЯ ЖӘНЕ ИНТЕГРАЛ болғандықтан 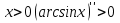КЕРІ ТРИГОНОМЕТРИЯЛЫҚ ФУНКЦИЯ ЖӘНЕ ИНТЕГРАЛ => [0;1] аралықта 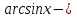КЕРІ ТРИГОНОМЕТРИЯЛЫҚ ФУНКЦИЯ ЖӘНЕ ИНТЕГРАЛойыс, ал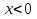 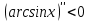КЕРІ ТРИГОНОМЕТРИЯЛЫҚ ФУНКЦИЯ ЖӘНЕ ИНТЕГРАЛ КЕРІ ТРИГОНОМЕТРИЯЛЫҚ ФУНКЦИЯ ЖӘНЕ ИНТЕГРАЛ => [-1;0] сегментінде дөңес, олай болса 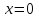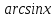КЕРІ ТРИГОНОМЕТРИЯЛЫҚ ФУНКЦИЯ ЖӘНЕ ИНТЕГРАЛ - КЕРІ ТРИГОНОМЕТРИЯЛЫҚ ФУНКЦИЯ ЖӘНЕ ИНТЕГРАЛ функциясының графигінің иілу нүктесі болып табылатынын көреміз.

[-1;1] кесіндісінде функцияның үзіліссіздігі мен монотондылығынан 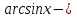КЕРІ ТРИГОНОМЕТРИЯЛЫҚ ФУНКЦИЯ ЖӘНЕ ИНТЕГРАЛтің мәндерінің жиыны 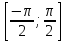КЕРІ ТРИГОНОМЕТРИЯЛЫҚ ФУНКЦИЯ ЖӘНЕ ИНТЕГРАЛ кесіндісі болып табылады.

Ал 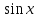КЕРІ ТРИГОНОМЕТРИЯЛЫҚ ФУНКЦИЯ ЖӘНЕ ИНТЕГРАЛ функциясын төмендегідей анықтауға болады. Синустың негізгі тармағы деп 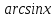КЕРІ ТРИГОНОМЕТРИЯЛЫҚ ФУНКЦИЯ ЖӘНЕ ИНТЕГРАЛ кері функцияны атаймызда, пайда болған қисықты 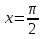КЕРІ ТРИГОНОМЕТРИЯЛЫҚ ФУНКЦИЯ ЖӘНЕ ИНТЕГРАЛ түзуіне қарағанда симметриялы бейнелейміз де, бүкіл 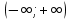КЕРІ ТРИГОНОМЕТРИЯЛЫҚ ФУНКЦИЯ ЖӘНЕ ИНТЕГРАЛ сан осіне 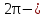КЕРІ ТРИГОНОМЕТРИЯЛЫҚ ФУНКЦИЯ ЖӘНЕ ИНТЕГРАЛпериодты жалғастырамыз. Осыған ұқсас 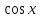КЕРІ ТРИГОНОМЕТРИЯЛЫҚ ФУНКЦИЯ ЖӘНЕ ИНТЕГРАЛ функциясыда енгізіледі, тек ғана негізгі тармақты Оу осіне қарағанда симметриялы бейнелеп 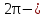КЕРІ ТРИГОНОМЕТРИЯЛЫҚ ФУНКЦИЯ ЖӘНЕ ИНТЕГРАЛпериодты жалғастырсақ (созсақ) жеткілікті.

Тригонометрия курсындағы негізгі қатынас 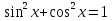КЕРІ ТРИГОНОМЕТРИЯЛЫҚ ФУНКЦИЯ ЖӘНЕ ИНТЕГРАЛ бірлік шеңбердің координаталары 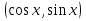КЕРІ ТРИГОНОМЕТРИЯЛЫҚ ФУНКЦИЯ ЖӘНЕ ИНТЕГРАЛ екенін ескерсек 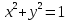КЕРІ ТРИГОНОМЕТРИЯЛЫҚ ФУНКЦИЯ ЖӘНЕ ИНТЕГРАЛ теңдеуінен бірден шығатынын көреміз.

Енді 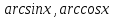КЕРІ ТРИГОНОМЕТРИЯЛЫҚ ФУНКЦИЯ ЖӘНЕ ИНТЕГРАЛ функцияларымен байланысты мысалдарға тоқталайық.

1 мысал. 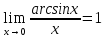КЕРІ ТРИГОНОМЕТРИЯЛЫҚ ФУНКЦИЯ ЖӘНЕ ИНТЕГРАЛ

Шешуі.
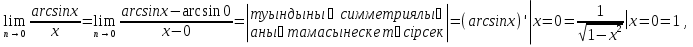
КЕРІ ТРИГОНОМЕТРИЯЛЫҚ ФУНКЦИЯ ЖӘНЕ ИНТЕГРАЛ

дәлелдеген қатынастан I тамаша шек 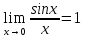КЕРІ ТРИГОНОМЕТРИЯЛЫҚ ФУНКЦИЯ ЖӘНЕ ИНТЕГРАЛ шығатыны көрініп тұр.

Кері тригонометриялық функциялар арқылы пайда болған теңдеулерді шешкенде негізгі тәсілдердің бірі - қатынастың екі жағынан қандай да бір тригонометриялық функцияларды табу болып табылады( функциялар монотондық аралықта жатса болғаны).

2 мысал. 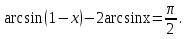КЕРІ ТРИГОНОМЕТРИЯЛЫҚ ФУНКЦИЯ ЖӘНЕ ИНТЕГРАЛ

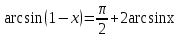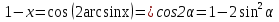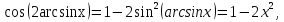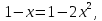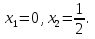
Шешуі:КЕРІ ТРИГОНОМЕТРИЯЛЫҚ ФУНКЦИЯ ЖӘНЕ ИНТЕГРАЛ деп жазып, келтіру формуласын ескеріп екі жағынан синусты тапсақ КЕРІ ТРИГОНОМЕТРИЯЛЫҚ ФУНКЦИЯ ЖӘНЕ ИНТЕГРАЛ болғандықтан КЕРІ ТРИГОНОМЕТРИЯЛЫҚ ФУНКЦИЯ ЖӘНЕ ИНТЕГРАЛ сол себепті КЕРІ ТРИГОНОМЕТРИЯЛЫҚ ФУНКЦИЯ ЖӘНЕ ИНТЕГРАЛяғни КЕРІ ТРИГОНОМЕТРИЯЛЫҚ ФУНКЦИЯ ЖӘНЕ ИНТЕГРАЛ

Пайда болған түбірлердің әрқайсысын жеке-жеке зерттейміз:

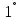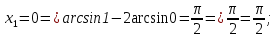
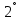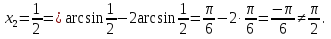
КЕРІ ТРИГОНОМЕТРИЯЛЫҚ ФУНКЦИЯ ЖӘНЕ ИНТЕГРАЛ. КЕРІ ТРИГОНОМЕТРИЯЛЫҚ ФУНКЦИЯ ЖӘНЕ ИНТЕГРАЛ

КЕРІ ТРИГОНОМЕТРИЯЛЫҚ ФУНКЦИЯ ЖӘНЕ ИНТЕГРАЛ.КЕРІ ТРИГОНОМЕТРИЯЛЫҚ ФУНКЦИЯ ЖӘНЕ ИНТЕГРАЛ

Нәтижесінде тек ғана біріншісі шешім болатынын көреміз.

Жауабы: х=0.

3 мысал. 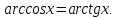КЕРІ ТРИГОНОМЕТРИЯЛЫҚ ФУНКЦИЯ ЖӘНЕ ИНТЕГРАЛ

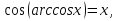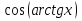Шешуі: Кері тригонометриялық функцияның анықтамасынан КЕРІ ТРИГОНОМЕТРИЯЛЫҚ ФУНКЦИЯ ЖӘНЕ ИНТЕГРАЛ енді

КЕРІ ТРИГОНОМЕТРИЯЛЫҚ ФУНКЦИЯ ЖӘНЕ ИНТЕГРАЛанықтайық, басқаша айтқанда, егер 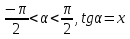КЕРІ ТРИГОНОМЕТРИЯЛЫҚ ФУНКЦИЯ ЖӘНЕ ИНТЕГРАЛ болса, 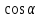КЕРІ ТРИГОНОМЕТРИЯЛЫҚ ФУНКЦИЯ ЖӘНЕ ИНТЕГРАЛ неге тең?

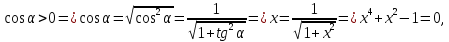
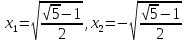КЕРІ ТРИГОНОМЕТРИЯЛЫҚ ФУНКЦИЯ ЖӘНЕ ИНТЕГРАЛКЕРІ ТРИГОНОМЕТРИЯЛЫҚ ФУНКЦИЯ ЖӘНЕ ИНТЕГРАЛ. Пайда болған x- тің екі мәнінен 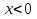КЕРІ ТРИГОНОМЕТРИЯЛЫҚ ФУНКЦИЯ ЖӘНЕ ИНТЕГРАЛ болғандықтан 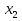КЕРІ ТРИГОНОМЕТРИЯЛЫҚ ФУНКЦИЯ ЖӘНЕ ИНТЕГРАЛ түбір бола алмайтынын көреміз.

Жауабы: 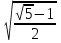КЕРІ ТРИГОНОМЕТРИЯЛЫҚ ФУНКЦИЯ ЖӘНЕ ИНТЕГРАЛ.

4 мысал. Параметр а- ның қандай мәндерінде 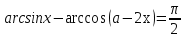КЕРІ ТРИГОНОМЕТРИЯЛЫҚ ФУНКЦИЯ ЖӘНЕ ИНТЕГРАЛ теңдеуінің шешімінің бар болатынын анықтайық.

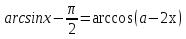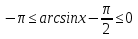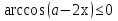Шешуі: Берілген теңдеуден КЕРІ ТРИГОНОМЕТРИЯЛЫҚ ФУНКЦИЯ ЖӘНЕ ИНТЕГРАЛ, ал КЕРІ ТРИГОНОМЕТРИЯЛЫҚ ФУНКЦИЯ ЖӘНЕ ИНТЕГРАЛ болғандықтан КЕРІ ТРИГОНОМЕТРИЯЛЫҚ ФУНКЦИЯ ЖӘНЕ ИНТЕГРАЛ, яғни КЕРІ ТРИГОНОМЕТРИЯЛЫҚ ФУНКЦИЯ ЖӘНЕ ИНТЕГРАЛ болатыны шығады. Ал екінші жағынан, 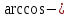КЕРІ ТРИГОНОМЕТРИЯЛЫҚ ФУНКЦИЯ ЖӘНЕ ИНТЕГРАЛтың анықтамасынан 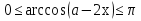КЕРІ ТРИГОНОМЕТРИЯЛЫҚ ФУНКЦИЯ ЖӘНЕ ИНТЕГРАЛ, сол себепті теңдеу <=> орынды, егер 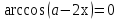КЕРІ ТРИГОНОМЕТРИЯЛЫҚ ФУНКЦИЯ ЖӘНЕ ИНТЕГРАЛ немесе 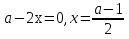КЕРІ ТРИГОНОМЕТРИЯЛЫҚ ФУНКЦИЯ ЖӘНЕ ИНТЕГРАЛ, олай болса берілген теңдеуден 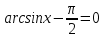КЕРІ ТРИГОНОМЕТРИЯЛЫҚ ФУНКЦИЯ ЖӘНЕ ИНТЕГРАЛ, яғни 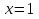КЕРІ ТРИГОНОМЕТРИЯЛЫҚ ФУНКЦИЯ ЖӘНЕ ИНТЕГРАЛ болатынын, ең соңында 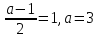КЕРІ ТРИГОНОМЕТРИЯЛЫҚ ФУНКЦИЯ ЖӘНЕ ИНТЕГРАЛ аламыз.

Жауабы: параметр 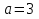КЕРІ ТРИГОНОМЕТРИЯЛЫҚ ФУНКЦИЯ ЖӘНЕ ИНТЕГРАЛ болған жағдайда ғана берілген теңдеудің шешімі бар.

Енді стандартты емес әдіс арқылы шығатын бір теңдеуге тоқталайық.

5-мысал. 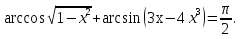КЕРІ ТРИГОНОМЕТРИЯЛЫҚ ФУНКЦИЯ ЖӘНЕ ИНТЕГРАЛ

Шешуі: Берілген теңдеуді 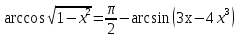КЕРІ ТРИГОНОМЕТРИЯЛЫҚ ФУНКЦИЯ ЖӘНЕ ИНТЕГРАЛтүрінде жазып алып, екі жағынан да косинусын табайық. Екі бөлігіндегі бұрыштар 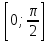КЕРІ ТРИГОНОМЕТРИЯЛЫҚ ФУНКЦИЯ ЖӘНЕ ИНТЕГРАЛ-де жататындықтан (косинустың қатаң монотондық аралығы болғандықтан), косинусты алғаннан бөгде түбірлер пайда болмайды, сонымен, 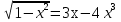КЕРІ ТРИГОНОМЕТРИЯЛЫҚ ФУНКЦИЯ ЖӘНЕ ИНТЕГРАЛ. Осы теңдеуді шешу үшін 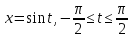КЕРІ ТРИГОНОМЕТРИЯЛЫҚ ФУНКЦИЯ ЖӘНЕ ИНТЕГРАЛ тригонометриялық ауыстырманы қолданамыз.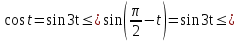 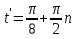КЕРІ ТРИГОНОМЕТРИЯЛЫҚ ФУНКЦИЯ ЖӘНЕ ИНТЕГРАЛ

КЕРІ ТРИГОНОМЕТРИЯЛЫҚ ФУНКЦИЯ ЖӘНЕ ИНТЕГРАЛнемесе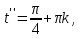 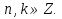КЕРІ ТРИГОНОМЕТРИЯЛЫҚ ФУНКЦИЯ ЖӘНЕ ИНТЕГРАЛ КЕРІ ТРИГОНОМЕТРИЯЛЫҚ ФУНКЦИЯ ЖӘНЕ ИНТЕГРАЛ Бұлардың ішінде 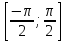КЕРІ ТРИГОНОМЕТРИЯЛЫҚ ФУНКЦИЯ ЖӘНЕ ИНТЕГРАЛ сегментінде тек қана 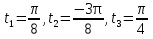КЕРІ ТРИГОНОМЕТРИЯЛЫҚ ФУНКЦИЯ ЖӘНЕ ИНТЕГРАЛ немесе 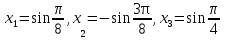КЕРІ ТРИГОНОМЕТРИЯЛЫҚ ФУНКЦИЯ ЖӘНЕ ИНТЕГРАЛ шешімдері жатады. Енді берілген теңдеуге қойып, тексеру жүргізейік.

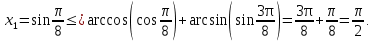
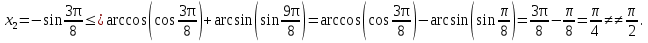
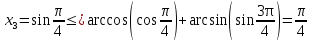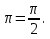
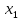  1. КЕРІ ТРИГОНОМЕТРИЯЛЫҚ ФУНКЦИЯ ЖӘНЕ ИНТЕГРАЛ

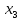  2. КЕРІ ТРИГОНОМЕТРИЯЛЫҚ ФУНКЦИЯ ЖӘНЕ ИНТЕГРАЛ

  3. КЕРІ ТРИГОНОМЕТРИЯЛЫҚ ФУНКЦИЯ ЖӘНЕ ИНТЕГРАЛ+КЕРІ ТРИГОНОМЕТРИЯЛЫҚ ФУНКЦИЯ ЖӘНЕ ИНТЕГРАЛ

КЕРІ ТРИГОНОМЕТРИЯЛЫҚ ФУНКЦИЯ ЖӘНЕ ИНТЕГРАЛмен КЕРІ ТРИГОНОМЕТРИЯЛЫҚ ФУНКЦИЯ ЖӘНЕ ИНТЕГРАЛ берілген теңдеуді қанағаттандыратынын көрдік.

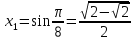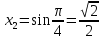Жауабы: КЕРІ ТРИГОНОМЕТРИЯЛЫҚ ФУНКЦИЯ ЖӘНЕ ИНТЕГРАЛ; КЕРІ ТРИГОНОМЕТРИЯЛЫҚ ФУНКЦИЯ ЖӘНЕ ИНТЕГРАЛ.

Сонымен, кері тригонометриялық 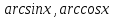КЕРІ ТРИГОНОМЕТРИЯЛЫҚ ФУНКЦИЯ ЖӘНЕ ИНТЕГРАЛ мектеп курсынан өзгеше жолмен енгізіп, барлық қасиеттерін аналитикалық жолмен толық шығарып алатын тәсілдің бар екенін көрдік, әдебиеттер тізімінде көрсетілген [1] мақалада басқа да әдістердің бар екеніне тоқталғанбыз (жинақты дәрежелік қатардың қосындысы, функционалдық теңдеулердің үзіліссіз функциялар класындағы шешімі т.с.с ). Кері тригонометриялық функциялармен байланысты теңсіздіктерге өзіндік ерекшеліктері бар болғандықтан келешекте жеке-дара тоқталамыз.

Әдебиеттер.


  1. Серікболқызы Н, Апышев О.Д. Интеграл және тригонометриялық функциялар. «Ғылым мен бизнестің кооперациясы: мәселелері мен болашағы» атты жас ғалымдар мен студенттердің ІІІ Республикалық ғылыми-тәжірибелік конференция. 2013, 3-5 сәуір. Өскемен. С. Аманжолов атындағы ШҚМУ баспасы, 1 бөлім, 105-109 б.

  2. Черкасов О.Ю, Якушев А.Г, Математика М. Изд.МГУ им М.В.Ломоносова, 1994, 253с.

  3. Васильева В.А и др.Методическое пособие математике для поступающих в вузы. М.Изд. МАИ, 1992, 304c.


загрузить
Пользовательское соглашениеО проектеОбратная связьАрхивные статьи
© 2010-2022