- Преподавателю
- Математика
- Сообщение по математике на тему Существование и гладкость решений уравнений Навье-Стокса
Сообщение по математике на тему Существование и гладкость решений уравнений Навье-Стокса
| Раздел | Математика |
| Класс | - |
| Тип | Другие методич. материалы |
| Автор | Уильямс М.(. |
| Дата | 05.01.2016 |
| Формат | docx |
| Изображения | Есть |
Существование и гладкость решений уравнений Навье - Стокса
Существование и гладкость решений уравнений Навье - Стокса - одна из семи математических задач тысячелетия, сформулированных в 2000 году Математическим институтом Клэя.
Уравнения Навье - Стокса описывают движение вязкой ньютоновской жидкости и являются основой гидродинамики. Численные решения уравнений Навье - Стокса используются во многих практических приложениях и научных работах. Однако в аналитическом виде решения этих уравнений найдены лишь в некоторых частных случаях, поэтому нет полного понимания свойств уравнений Навье - Стокса. В частности, решения уравнений Навье - Стокса часто включают в себя турбулентность, которая остаётся одной из важнейших нерешённых проблем в физике, несмотря на её огромную важность для науки и техники.
Уравнения Навье - Стокса
В математике это система нелинейных дифференциальных уравнений в частных производных для абстрактных векторных полей любой размерности. В физике это система уравнений, которая в рамках механики сплошных сред описывает движение жидкостей или неразреженных газов.
Пусть 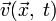 - трёхмерный вектор скорости жидкости,
- трёхмерный вектор скорости жидкости, 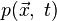 - давление. Тогда уравнения Навье - Стокса записываются так:
- давление. Тогда уравнения Навье - Стокса записываются так:
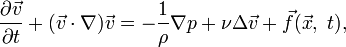
где 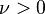 - это кинематическая вязкость,
- это кинематическая вязкость, 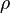 - плотность,
- плотность, 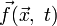 - внешняя сила,
- внешняя сила,  - оператор набла и
- оператор набла и 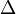 - оператор Лапласа (лапласиан), который также обозначается, как
- оператор Лапласа (лапласиан), который также обозначается, как 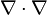 или
или 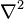 . Это векторное уравнение, которое в трёхмерном случае может быть представлено как три скалярных уравнения. Если обозначить компоненты векторов скорости и внешней силы, как
. Это векторное уравнение, которое в трёхмерном случае может быть представлено как три скалярных уравнения. Если обозначить компоненты векторов скорости и внешней силы, как

то для каждого значения 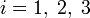 получается соответствующее скалярное уравнение:
получается соответствующее скалярное уравнение:
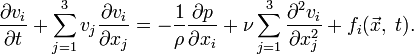
Неизвестными величинами являются скорость 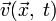 и давление
и давление 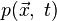 . Поскольку в трёхмерном случае получается три уравнения и четыре неизвестных (три компоненты скорости и давление), то необходимо ещё одно уравнение. Дополнительным уравнением является закон сохранения массы - уравнение неразрывности, которое в случае несжимаемой среды преобразуется в условие несжимаемости жидкости:
. Поскольку в трёхмерном случае получается три уравнения и четыре неизвестных (три компоненты скорости и давление), то необходимо ещё одно уравнение. Дополнительным уравнением является закон сохранения массы - уравнение неразрывности, которое в случае несжимаемой среды преобразуется в условие несжимаемости жидкости:
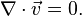
Начальные условия
Начальные условия к уравнениям Навье-Стокса задаются в виде
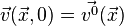 ,
,
где 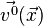 - заданная гладкая вектор-функция, удовлетворяющая уравнению неразрывности
- заданная гладкая вектор-функция, удовлетворяющая уравнению неразрывности 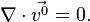
Варианты постановки задачи
Институт Клэя сформулировал два основных варианта постановки задачи о существовании и гладкости решений уравнений Навье - Стокса. В первом варианте уравнения рассматриваются во всём трёхмерном пространстве 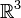 с некоторыми ограничениями на скорость роста решения на бесконечности. Во втором варианте уравнения рассматриваются на трёхмерном торе
с некоторыми ограничениями на скорость роста решения на бесконечности. Во втором варианте уравнения рассматриваются на трёхмерном торе 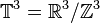 с периодическими граничными условиями. Для получения премии достаточно доказать или опровергнуть существование и гладкость решения в любом из двух вариантов.
с периодическими граничными условиями. Для получения премии достаточно доказать или опровергнуть существование и гладкость решения в любом из двух вариантов.
В трёхмерном пространстве
Пусть начальная скорость 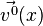 - произвольная гладкая функция, удовлетворяющая уравнению неразрывности и такая, что для любого мультииндекса
- произвольная гладкая функция, удовлетворяющая уравнению неразрывности и такая, что для любого мультииндекса 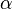 и любого
и любого 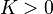 , существует постоянная
, существует постоянная 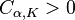 (зависящая только от
(зависящая только от 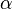 и K), такая, что
и K), такая, что
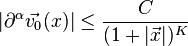 для всех
для всех 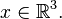
Пусть внешняя сила 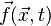 - также гладкая функция, удовлетворяющая аналогичному неравенству (здесь мультииндекс включает также производные по времени):
- также гладкая функция, удовлетворяющая аналогичному неравенству (здесь мультииндекс включает также производные по времени):
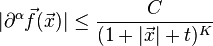 для всех
для всех 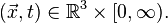
Решения должны быть гладкими функциями, которые не возрастают неограниченно при 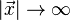 . Требуется выполнение следующих условий:
. Требуется выполнение следующих условий:
-
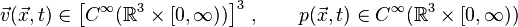
-
Существует постоянная
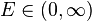 такая, что
такая, что 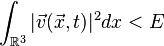 для всех
для всех 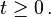
Первое условие означает, что функции глобально определены и являются гладкими; второе - что кинетическая энергия глобально ограничена.
Требуется доказать одно из двух утверждений:
(A) Существование и гладкость решений уравнений Навье - Стокса в 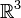 . Положим
. Положим 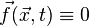 . Для любого начального условия
. Для любого начального условия 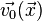 , удовлетворяющего вышеописанным условиям, существует глобальное гладкое решение уравнений Навье - Стокса, то есть вектор скорости
, удовлетворяющего вышеописанным условиям, существует глобальное гладкое решение уравнений Навье - Стокса, то есть вектор скорости 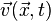 и поле давления
и поле давления 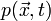 , удовлетворяющее условиям 1 и 2.
, удовлетворяющее условиям 1 и 2.
(B) Несуществование или негладкость решений уравнений Навье - Стокса в 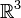 . Существует такое начальное условие
. Существует такое начальное условие 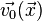 и внешняя сила
и внешняя сила 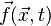 , такие, что не существует решений
, такие, что не существует решений 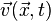 and
and 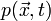 удовлетворяющих условиям 1 и 2.
удовлетворяющих условиям 1 и 2.
Попытки решения
10 января 2014 года казахстанский математик Мухтарбай Отелбаев опубликовал статью, в которой утверждает, что дал полное решение проблемы, проверка результата осложнена тем, что работа написана на русском языке. В сообществах математиков обсуждаются контрпримеры к основным утверждениям.


