- Преподавателю
- Математика
- Конспект урока Введение в комбинаторику
Конспект урока Введение в комбинаторику
| Раздел | Математика |
| Класс | 7 класс |
| Тип | Конспекты |
| Автор | Гаврикова Т.А. |
| Дата | 08.05.2015 |
| Формат | docx |
| Изображения | Есть |
Гаврикова Татьяна Анатольевна, ГБОУ школа № 353 Московского р-на СПб.
Урок 1. Введение в комбинаторику
Цели: дать понятие «Комбинаторика», «Комбинаторные задачи»; познакомить учащихся с историей данной науки; привести примеры нескольких комбинаторных задач с решениями для привития интереса учащихся к данной науке.
Ход урока
Сообщение темы и целей
Работа по теме
Комбинаторикой называется область математики, в которой изучаются задачи о том, сколько различных комбинаций (или выборок), подчиненных тем или иным условиям, можно составить из элементов, принадлежащих заданному множеству.
С задачами, в которых приходилось выбирать те или иные предметы, располагать их в определенном порядке и отыскивать среди разных расположений наилучшие, люди столкнулись еще в доисторическую эпоху, выбирая наилучшее положение охотников во время охоты, воинов - во время битвы, инструментов - во время работы.
Принято считать, что комбинаторика возникла в XVI веке, когда в жизни привилегированных слоев общества большое распространение получили азартные игры и всевозможные лотереи. К азартным играм относили карты и кости (бросание шестигранных игральных кубиков). Слово «азар» по-арабски означает «трудный». Арабы называли азартной игрой комбинацию очков, которая при бросании нескольких костей могла появиться лишь единственным образом. Например, при бросании двух костей трудным («азар») считалось появление в сумме двух или двенадцати очков. Первоначально комбинаторные задачи касались в основном азартных игр. Решались вопросы, сколькими способами можно получить некоторый набор карт в карточной игре, как часто выпадает выигрыш в той или иной лотерее. Эти и другие проблемы азартных игр и явились движущей силой в развитии комбинаторики.
Одним из первых занимался подсчетом числа различных комбинаций при игре в кости итальянский математик Тарталья (1500-1557). В XVII веке изучением теоретических вопросов комбинаторики занимались французские ученые Б. Паскаль (1623-1662) и П. Ферма (1601-1665). Исходным пунктом их исследований тоже были проблемы азартных игр. Дальнейшее развитие комбинаторики связано с именами Я. Бернулли (1654-705), Г. Лейбница (1646-1716) и Л. Эйлера (1707-1783). Однако и в работах этих математиков в основном рассматривались приложения к различным играм (лото, пасьянсы и т.д.). В дальнейшем комбинаторные методы играли значительную роль в развитии алгебры и геометрии.
В последние десятилетия комбинаторика активно развивается, она тесно связана с проблемами дискретной математики, линейного программирования, статистики. Ее методы широко используются при решении транспортных задач, для планирования производства и реализации продукции, для составления и декодирования шифров. Комбинаторику можно рассматривать как введение в теорию вероятностей, она помогает при решении задач этой теории осуществить подсчет числа возможных исходов и числа благоприятных исходов опыта или эксперимента в различных случаях.
Представителям самых различных специальностей приходится решать задачи, в которых рассматриваются те или иные комбинации, составленные из букв, цифр или иных объектов. Начальнику надо распределить несколько видов работ между подчиненными, завучу школы - составить расписание уроков, ученому-химику - рассмотреть возможные связи между атомами и молекулами, филологу - учесть различные варианты значений букв незнакомого языка и т.д. При решении подобных задач мы каким-либо образом выбираем m элементов из общего числа n элементов некоторого множества E, при этом в постановке задачи четко оговариваем, каким способом составляется выборка.
сначала мы рассмотрим два общих правила, с помощью которых решаются задачи комбинаторики - правило суммы и правило произведения.
С задачами, в которых приходилось выбирать те или иные предметы, располагать их в определенном порядке и отыскивать среди разных расположений наилучшие, люди столкнулись еще в доисторическую эпоху, выбирая наилучшее положение охотников во время охоты, воинов - во время битвы, инструментов - во время работы.
Комбинаторные навыки оказались полезными и в часы досуга. Нельзя точно сказать, когда наряду с состязаниями в беге, метании диска, прыжках появились игры, требовавшие, в первую очередь, умения рассчитывать, составлять планы и опровергать планы противника.
Со временем появились различные игры (нарды, карты, шашки, шахматы и т.д.). В каждой из этих игр приходилось рассматривать различные сочетания фигур, и выигрывал тот, кто их лучше изучил, знал выигрышные комбинации и умел избегать проигрышных.
Не только азартные игры давали пищу для комбинаторных размышлений математиков. Еще с давних пор дипломаты, стремясь к тайне переписки, изобретали сложные шифры, а секретные службы других государств пытались эти шифры разгадать. Стали применять шифры, основанные на комбинаторных принципах, например, на различных перестановках букв, заменах букв с использованием ключевых слов и т.д.
Задачи, в которых идет речь о тех или иных комбинациях объектов, называются комбинаторными. Область математики, в которой изучаются комбинаторные задачи, называется комбинаторикой. Комбинаторику можно рассматривать как часть теории множеств - любую комбинаторную задачу можно свести к задаче о конечных множествах и их отображениях
Раздел комбинаторики, в котором рассматривается лишь вопрос о подсчете числа решений комбинаторной задачи, теорией перечислений.
Комбинаторика как наука стала развиваться в XIII веке параллельно с возникновением теории вероятностей, так как для решения вероятностных задач необходимо было подсчитать число различных комбинаций элементов. Первые научные исследования по комбинаторике принадлежат итальянским ученым Дж. Кардано, Н. Тарталье (1499-1557), Г. Галилею (1564-1642) и французским ученым Б. Паскалю (1623-1662) и П. Ферма. Комбинаторику как самостоятельный раздел математики первым стал рассматривать немецкий ученый Г. Лейбниц в своей работе «Об искусстве комбинаторики», опубликованной в 1666 году. Он также впервые ввел термин «комбинаторика». Значительный вклад в развитие комбинаторики внес Л.Эйлер.
Перечень тем докладов
1) Дж. Кардано
2) Н. Тарталье
3) Бином Ньютона
4) Б. Паскаль
5) П. Ферма
6) Треугольник Паскаля
7) Л.Эйлер
8) Г. Галилею
9) Г. Лейбниц
10) Некоторые свойства числа сочетаний
11) Правила решения комбинаторных задач
12) Комбинаторная геометрия
13) Историческая справка о науке «Комбинаторике»
14) Магические квадраты
4. Итог урока
Урок 2. Поиск закономерностей
Цели: рассмотреть некоторые виды закономерностей.
Оборудование: мультимедийный проектор, жетоны.
Ход урока
Сообщение темы и целей.
Домашнее задание.
1. Выявить закономерности и записать еще 4 числа:
1) 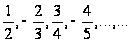
562
(26)
652
369
(__)
963
2) ответ: 36 - сумма цифр в числе
3. Разминка
Итак, начнем наш урок с разминки. Сегодня она будет в другой форме - в виде соревнования. Я задаю вопросы, и кто быстрее поднимет руку, тот и будет отвечать. За каждый правильный ответ даются жетоны.
1) Портной имеет кусок сукна в 16 м, от которого он ежедневно отрезает по 2 метра. По истечении скольких дней он отрежет последний кусок? (7 дней)
2) Разделить 5 яблок между пятью лицами так, чтобы каждый получил по яблоку, и одно осталось в корзине? (Один берет корзину вместе с яблоком)
3) Четыре коровы черной масти и три - рыжей масти за пять дней дали такой же надой молока, как 3 коровы черной масти и 5 рыжей за 4 дня. Какие коровы молочнее: черной или рыжей масти? (рыжей)
4) Как представить цифру 4 тремя пятерками? (4=5-5:5)
5) Шесть ног, а бежит не быстрее, чем на четырех. (всадник на коне)
6) Какие часы показывают верное время только два раза в сутки? (которые остановились)
7) В известной сказке «Поди туда - не знаю куда, принеси то - не знаю что» царь послал стрелка Андрея за «тридевять земель». Тридевять - это сколько? (27)
8) Шел Кондрат в Ленинград, а навстречу 12 ребят.
У каждого по 3 лукошка, в каждом лукошке - кошка.
У каждой кошки - 12 котят. У каждого котенка
В зубах по 4 мышонка. И задумался старый Кондрат:
«Сколько мышат и котят ребята несут в Ленинград?»
Как бы вы ответили на этот вопрос? (Один Кондрат шел в Ленинград)
9) В мешке лежат шарики белого и черного цвета. Сколько нужно взять шариков, чтобы 2 было одинакового цвета? (3)
10) Поехал мужик зимой на ярмарку, а базар далеко. Вот едет он лесом-полем, лесом-полем, лесом-полем. Встречает Бабу-Ягу и спрашивает: «Куда ехать?» Она ему показывает направо. И вот он снова едет лесом-полем, лесом-полем, лесом-полем, встречает Лешего. Спрашивает: «Как доехать до базара?» Он показывает налево. Вот он снова едет лесом-полем, лесом-полем, лесом-полем и выезжает к реке. А за рекой - базар. Как ему перебраться на тот берег, учитывая, что лодки нет и надо переправить весь груз? (Дело было зимой). Молодцы!
4. Работа по теме.
Объяснение материала.
Кто знает, что такое закономерность? Это закон, правило, по которому записаны числа, расположены фигуры.
Решение примеров.
Сейчас мы будем выявлять закономерности в расположении фигур.
1) Вставить недостающую картинку.
Ну, что, поняли, как выявляют закономерности в расположении фигур?
Теперь давайте попробуем выявлять закономерности в числовых рядах. Тот, кто ответит первым, получит жетон.
2) Вставить пропущенные числа:
24, 21, 19, 18, 15, 13, _ , _ , 7,6 (12, 9);
1, 4, 9, 16, _ , _ , 49, 64, 81, 100 (25, 36);
16, 17, 15, 18, 14, 19, _ , _ (13, 20);
1, 3, 6, 8, 16, 18, _ , _ , 76, 78 (36, 38);
7 26 19; 5 21 16; 9 _ 4 (13);
2 4 8 10 20 22 _ _ 92 94 (44, 48);
24 22 19 15 _ _ (10, 4).
3) Продолжить ряд:
15 16 18 21 25 _ (30);
2 5 8 11 _ (14);
6 9 12 15 18 _ (21);
16 12 15 11 14 10 _ _ (13, 9);
3 7 11 15 18 _ (22).
4) Вставить пропущенное число
2 5 9 (2+4):2=3
4 7 5 (5+7):2=6
3 6 ? (9+5):2=7
7 9 5 11 7+9-5=11
4 15 12 7 4+15-12=7
13 8 11 ? 13+8-11=10
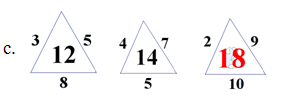
(3*5*8)/10=12
148 (220) 368 368-148=220
243 (___) 397 397-243=154
12 (56) 16 (12+16)∙2=56
17 (__) 21 (21+17) ∙2=76
Итог урока.
Урок 3. Перебор возможных вариантов. Дерево возможных вариантов
Цели:
- дать понятия: комбинаторика, комбинаторные задачи;
- изучить способы решения комбинаторных задач: перебор возможных вариантов, дерево возможных вариантов;
Оборудование: мультимедийный проектор, задачи на карточках.
Ход урока
1. Сообщение темы и целей
2. Подготовительная работа
Давайте с вами решим задания, которые подведут нас к теме.
2.1. Решение ребусов

Выявление закономерности

Решение задач
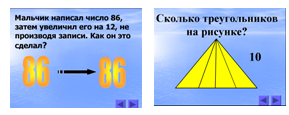
Изучение новой темы. Разбор задач
Давайте рассмотрим такую задачу: сколько двузначных чисел можно составить, используя цифры 1, 4 и 7?
Решение: для того, чтобы не пропустить и не повторить ни одно из чисел, будем записывать их в порядке возрастания. Сначала запишем числа, начинающиеся с цифры 1, затем с цифры 4, и, наконец, с цифры 7:
11, 14, 17, 41, 44, 47, 71, 74, 77.
Этот метод называется перебором вариантов. Таким образом, их трех данных цифр можно составить всего 9 различных двузначных чисел.
Эту задачу можно решить и другим способом. Его название - дерево возможных вариантов. Для этой задачи построена специальная схема.
Ставим звездочку. Она будет обозначать количество возможных вариантов.
Далее отводим от звездочки 3 отрезка. А почему? Как вы думаете? Так как в условии задачи даны 3 цифры - 1, 4, 7.
Ставим эти цифры на концах отрезков. Они будут обозначать число десятков в данном числе.
Далее от каждой цифры проводим по 3 отрезка. Почему? От цифры 1 три отрезка, от цифры 4 три отрезка и от цифры 7 также проводим три отрезка.
На концах этих отрезков записываем также цифры 1, 4, 7. Они будут обозначать число единиц.
рассмотрим, какие числа получились: 11, 14, 17, 41, 44, 47, 71, 74, 77. То есть всего получилось 9 чисел.
Эта схема действительно похожа на дерево, правда «вверх ногами» и без ствола.
Решение задач.
Итак, давайте решим несколько задач.
Сколько трехзначных чисел можно составить, используя цифры 3 и 5?
Ответ: всего 8 чисел.
В четверг в первом классе должно быть 3 урока: русский язык, математика и физкультура. Сколько различных вариантов расписания можно составить на этот день?
Ответ: всего можно составить 6 вариантов расписания.
Запишите все трехзначные числа, которые можно составить из цифр 0, 5, 9, используя при записи числа каждую цифру только один раз. Сколько всего таких чисел можно составить?
Ответ: всего 4 числа.
А теперь давайте сделаем так: мальчики решают задачу: Данила, Андрей и Коля собрались потренироваться в бросании мяча в баскетбольную корзину. У них только один мяч, и им надо договориться, кто за кем будет бросать мяч в корзину. Сколькими способами они могут занять очередь?
Девочки решают задачу: в костюмерной танцевального кружка имеются зелёные и жёлтые кофты, а также синие, красные и чёрные юбки. Сколько можно из них составить различных костюмов?
Домашнее задание
Откройте дневники и запишите домашнее задание. Решить задачи на карточках.
Сколько всего четырехзначных чисел можно составить из цифр 0 и 3?
В палатке имеется 3 сорта мороженого: рожок, брикет и эскимо? Наташа и Данил решили купить по одной порции каждого сорта мороженого. Сколько существует вариантов такой покупки?
Итог урока
Урок 4. Правило суммы и правило произведения
Цели:
познакомить учащихся с правилами произведения и суммы в комбинаторике;
закрепить правила с помощью решения задач;
Оборудование:
Ход урока
Сообщение темы и целей
Домашнее задание на карточках
Сколькими способами можно выбрать гласную и согласную буквы из слова «ЗДАНИЕ»? (в слове «здание» 3 согласных и 3 гласных буквы. По правилу произведения получаем 3*3=9 способами)
Сколькими способами можно указать на шахматной доске два квадрата - белый и черный? Решите эту же задачу, если нет ограничений на цвет квадратов; если надо выбрать два белых квадрата. (На шахматной доске 64 клетки: 32 белых квадрата, 32 черных квадрата. По правилу произведения получаем число выбора двух квадратов: одного черного и одного белого: 32*32=1024.
Если нет ограничений на цвет, то первый квадрат можно выбрать 64 способами, а второй - 63 способами (один квадрат уже выбран), следовательно, 64*63=4032
Если надо выбрать два белых квадрата, то первый квадрат можно выбрать 32 способами, а второй квадрат - 31 способом, поэтому, 32*31=992.
Повторение
Решить задачу: сколько трехзначных чисел можно составить из цифр 0, 5, 8?
Ответ: 18 чисел
Работа по новой теме
Правило сложения: если некоторый объект А можно выбрать m способами, а другой объект В можно выбрать n способами, то выбор «либо А, либо В» можно осуществить m+n способами.
Например: на тарелке лежат 5 яблок и 4 апельсина. Сколькими способами можно выбрать один плод?
По условию задачи яблоко можно выбрать пятью способами, апельсин - четырьмя. Так как в задаче речь идет о выборе «либо яблоко, либо апельсин», то его, согласно правилу сложения, можно осуществить 5+4=9 способами.
Задача 1: сколько трехзначных чисел можно составить из цифр 1,3,5,7, используя в записи числа каждую из них не более одного раза?
Решение: составим дерево возможных вариантов.
Эту задачу можно решить по-другому и намного быстрее, не строя дерева возможных вариантов. Рассуждать будем так. Первую цифру трехзначного числа можно выбрать четырьмя способами. Так как после выбора первой цифры останутся три, то вторую цифру можно выбрать из оставшихся цифр уже тремя способами. Наконец, третью цифру можно выбрать (из оставшихся двух) двумя способами. Следовательно, общее число искомых трехзначных чисел равно произведению 4∙3∙2, т.е. 24.
Сформулируем правило умножения: если объект А можно выбрать m способами и если после каждого такого выбора объект В можно выбрать п способами, то выбор пары (А, В) в указанном порядке можно осуществить m∙п способами.
Например, решите задачу с помощью правила умножения: сколько пятизначных чисел можно составить из цифр 5, 9, 0, 6?
По правилу умножения получаем: 4∙4∙4∙4=256 чисел.
Правило умножения можно также проиллюстрировать.
Задача 2: из города А в город В ведут две дороги, из города В в город С - три дороги, из города С до пристани - две дороги. Туристы хотят проехать из города А через города В и С к пристани. Сколькими способами они могут выбрать маршрут?
Решение: Пусть из города А в В туристы могут выбрать двумя способами. Далее в каждом случае они могут проехать из В в С тремя способами. Значит, имеется 2∙3 вариантов маршрута из А в С. Так как из города С на пристань можно попасть двумя способами, то всего существует 2∙3∙2=12 способов выбора туристами маршрута из города А к пристани.
Например: из пункта А в пункт В можно попасть десятью путями, а из пункта В в пункт С - девятью путями. Сколько имеется маршрутов из пункта А в пункт С через пункт В?
Решение: 10∙9=90 маршрутов
Задача 3: В кафе имеются три первых блюда, пять вторых блюд и два третьих. Сколькими способами посетитель кафе может выбрать обед, состоящий из первого, второго и третьего блюд?
Решение: первое блюдо можно выбрать тремя способами, второе - пятью и третье - двумя, отсюда, по правилу умножения получаем 3∙5∙2=30 способами.
Первичное закрепление знаний
Сколько различных пятизначных чисел, делящихся на 10 можно составить из цифр 0, 1, 2, 3, 4? Каждую цифру можно использовать в записи только один раз.
Сколько пятизначных чисел, делящихся на три, можно составить из цифр 3, 4, 6, 7, 9 если каждое число не содержит одинаковых цифр?
Сколько шестизначных чисел можно составить из цифр 4, 5, 6, 7, 8, 9 так, чтобы каждое из них начиналось с комбинации «567»?
Сколько пятизначных чисел можно составить из цифр 1, 2, 3, 4, 5, 6 так, чтобы каждое из них начиналось с комбинации «45»?
Сколько чётных положительных пятизначных чисел можно получить из цифр 5, 9, 6, 0, так, чтобы цифры в числе не повторялись?
Сколько чётных положительных пятизначных чисел можно получить из цифр 1, 2, 3, 4?
6. Итог урока


