- Преподавателю
- Математика
- Метафоры как инструмент изучения математических понятий
Метафоры как инструмент изучения математических понятий
| Раздел | Математика |
| Класс | - |
| Тип | Статьи |
| Автор | Стоян И.Б. |
| Дата | 28.01.2016 |
| Формат | doc |
| Изображения | Есть |
Метафоры как инструмент изучения математических понятий
Выяснилось также, что метафора - самая плодотворная вещь в науке.
Г.Хазакеров
Подобно тому, как само педагогическое мастерство признается формой творчества на грани науки и искусства, так мало-помалу возникает и поэтикоматематика, но уже скорее в творческом взаимодействии трёх дарований: математического, поэтического и педагогического.
Б.А.Кордемский
Формирование математических понятий, глубокое и осознанное владение ими учащимися - одна из важнейших задач математики. Необходимо четко разграничить вопрос об определении понятия с точки зрения формальной логики и с точки зрения задач формирования его в сознании ученика. Познание действительности осуществляется в диалектическом единстве чувственной (ощущения, восприятия, представления) и рациональной (понятия, суждения и умозаключения) форм мышления. Ощущения и восприятия - первые сигналы действительности. На их основе образуются общие представления, а от них в результате сложной умственной деятельности мы переходим к понятиям - форме мышления, в которой отражаются существенные признаки объектов реального мира. Всемирно известный исследователь творчества Роджер ван Оих называет эти типы мышления «мягким» и «жестким».1 «Мягкое» мышление метафорично, фантастично, юмористично, игриво и, возможно, противоречиво. «Жесткое» мышление отличается тенденцией к большей логичности, критичности, точности, конкретности и строгости. Автор рекомендует добрую порцию «мягкого» мышления в образной фазе творческого процесса и любезную помощь «жесткого» мышления в его практической стадии. Согласно данным нейрофизиологии эмоционально-образное восприятие окружающего мира гораздо древнее, чем понятийно-логическое. Следовательно, «истоки» всех форм познания нужно искать именно там. Глубоко и осознанно владеть большим количеством математических понятий, постоянно придерживаясь академического стиля строгих определений, нелегко. «Дело в том, - разъясняет известная писательница (профессор математики по основному роду занятий) И. Грекова, - что … живое содержание понятия, как правило, шире и богаче словесного определения - ведь оно формируется не определением, а всем опытом общественной жизни и практической деятельности людей, всей системой ассоциаций, образов, аналогий, даже эмоций, связанных с данным предметом, явлением». Эту систему И.Грекова называет ассоциативной базой понятия.2 Знаки, образы, символы и метафоры являются тем самым «источником», который дает возможность (тому, кто в состоянии «пить из самого источника») понять сущность явлений и процессов, происходящих в человеке и обществе. С завидным постоянством переходят они из эпохи в эпоху, из культуры в культуру, являясь необходимым элементом мира. Слово «метафора» употребляется в нейролингвистическом программировании в общем случае для обозначения истории или риторической фигуры, заключающей в себе сравнение. Она включает в себя простые сравнения и более длинные истории, аллегории и притчи.3 Метафоричность представляет собой лишь одну из стадий развития на пути к высшему виду мышления - абстрактно-логическому. Но может ли абстрактно-логическое мышление по-настоящему продуктивно работать без метафорических составляющих? Оперирование абстракциями всегда опирается на некую метафорическую модель. Это относится даже к тем абстракциям, которыми занимается такая точная наука как математика. «Ключевым моментом метафорического мышления является сходство. Фактически в нем отражается процесс развития мышления вообще: мы постигаем неизвестное через сходство с тем, что нам хорошо знакомо…Метафора - превосходный инструмент, который поможет вам «думать несколько иначе». Чувствуйте себя поэтом и ищите сходство и подобие в окружающем мире. Если у вас есть какая-то проблема, придумайте для нее метафору. Она даст вам возможность взглянуть на проблему свежим взглядом, под новым углом зрения. Помните: наш мир нелогичен по своей природе. Книжный червь вовсе не червяк, морской заяц совсем не заяц (а моллюск), английский рожок совсем не английский (а французский) и не рог (а деревянный духовой инструмент). Мы называем вещи или обозначаем их, не стремясь к точности, главное для нас - ухватить суть», - пишет американский психолог Роджер ван Оих4.
Метафора - не только языковое средство выражения сходства или подобия, метафора - специфический способ познания, без которого не обходится ни одно научное открытие. Внимание к метафоре как важному дидактическому и гносеологическому компоненту образовательной деятельности обусловлено стремлением ответить на вопрос: как человек добывает знания, приобретает навыки, как он мыслит? Каким образом в мозгу рождаются мысли и накапливаются знания, которые сопровождают нас всю жизнь? Несмотря на продолжающие попытки определять метафору лишь как троп, нельзя отрицать ее когнитивные способности.
Мир, состоящий из разнородных, не соотнесенных друг с другом предметов, называется хаосом. Сравнение - первый шаг навстречу гармонии. Мышление традиционно рассматривают как рождающееся из действия движение от хаоса к порядку и обратно. Известно, что предметы и явления находятся в различных связях и отношениях. Ассоциативное мышление позволяет ученику понять пространственные и временные отношения, осмыслить причинно-следственные связи. Прием образного, метафоричного сравнения, когда сложный процесс или явление сравнивается с более простым или наиболее известным, стимулирует творческую деятельность, позволяет избежать шаблонного повторения и запоминания. Век двадцатый был рациональным, и эта рациональность уже порядком всем наскучила и стала раздражать, поскольку она скрыла под своей серой, монолитной, неэстетичной глыбой огромный, богатый и очень древний слой совершенно иных способов познания мира - способов, построенных на интуиции, на сакральных значениях образов и символов. Применение этих древних способов поможет вернуть человеку утраченную гармонию существования.
Математика выражает стройные, системные, логические зависимости и оснащена техническими средствами для отображения таких зависимостей. Но велика и роль эмпирий живого созерцания в усвоении учебного материала, который дают художественные образы. Они напоминают о гармониях, недосягаемых для логического анализа. Опора на метафору как на механизм формирования художественного образа - это успешная форма занятий с детьми, которые относятся к правополушарной группе и воспринимают информацию через образный ряд. Гемиосферология (наука о деятельности левого и правого полушарий головного мозга) утверждает, что полушария имеют различные, но дополняющие друг друга функции. «Правый ум» отвечает за цветовую чувствительность, музыкальный слух, артистизм, эмоции. «Левый ум» обеспечивает четкость, логичность, последовательность. Использование правополушарных, то есть образных подходов и обучающих материалов, приводит к тому, что длительный процесс получения соответствующей информации сочетается с эмоциональным восприятием. Человек наиболее успешен, когда в его деятельность включаются оба полушария. При такой работе дети подключают, с одной стороны, ассоциативное творческое мышление и логическое - с другой. Подобная организация учебного процесса позволяет реализовать пространство собственно субъектного опыта при усвоении конкретных знаний. «Возможно, любая наука начинается с метафоры и завершается алгеброй; и вполне возможно, что без метафоры наука никогда не достигла бы никакой алгебры» [Black, цит.]5
В пятом классе при изучении темы «Свойства сложения и умножения» ребятам были процитированы слова Галилея о том, что «природа написана языком математики» и предложено творческое задание: математическим законам дать новые имена. Таким образом, мы вышли на понятие «метафора». Были разобраны удачные сравнения, находки, обсудили ошибки и неточности. Классы были разбиты на группы, при формировании которых учитывалось желание ребят работать вместе. Каждая группа работала со «своим» законом, над своим проектом. Результаты работы были заслушаны на уроке творческого отчета. Дальнейшая работа по изучению свойств действий с помощью метафор была продолжена в шестом и седьмом классах. Детская фантазия «черно-белые» законы раскрасила цветными красками, придумав различные метафоры для каждого свойства.
Приведу примеры ярких, выразительных сравнений, иногда носящих философский, иногда парадоксальный, но всегда творческий и оригинальный характер:
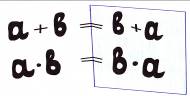
1.Переместительный (коммутативный) закон сложения и умножения: а + b = b + а,
а  b = b
b = b  а
а
- закон зеркала (Тишаков И.)
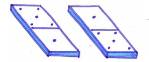
-закон домино (Сапрыкин Е.)
-закон смешивания красок (Агафонова А.)
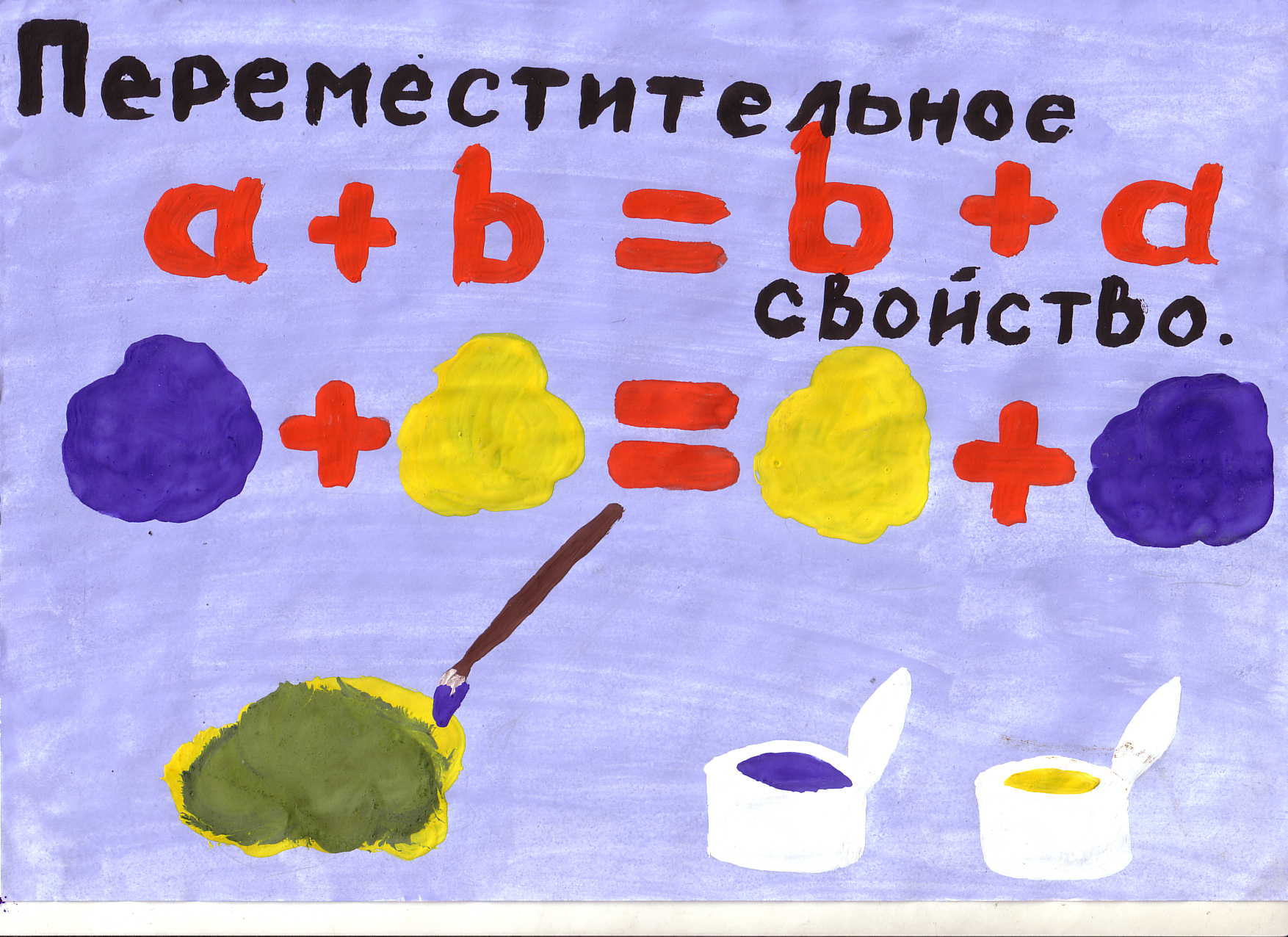
-закон игры.

-закон невезения «В обоих случаях червячку не повезло» (Кораблев А.)

-закон варенья (Мосина А.)
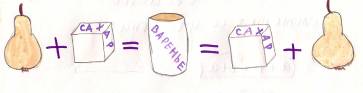
-закон плохих музыкантов (Мартьянова Е.)
«А вы, друзья, как не садитесь - все в музыканты не годитесь!» (басня И.Крылова «Квартет»)
-игра «догонялки» (Казакова И.)

-закон красоты «Колючее и красное - все равно прекрасное» (Власова Е.)

2.Сочетательный (ассоциативный) закон сложения и умножения :
а + (b + c) = (a + b) + c, a (b
(b c) = (a
c) = (a b)
b) c
c
-закон ядовитой поганки (Руденко Н.)

- закон дружной семьи (Лут Ю.)

-закон «некрепкой дружбы» (Репей С.)
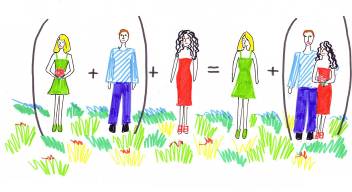
Закон мозаики (Агафонова Настя) иллюстрирует одновременность использования двух законов математики. Так как для упрощения вычислений в одном примере мы меняем и порядок действий, и порядок слагаемых, то переместительное и сочетательное свойства применяются одновременно.
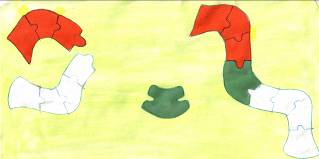
3.Распределительный (дистрибутивный) закон умножения относительно сложения а (b + c) = a
(b + c) = a b + a
b + a c.
c.
- закон справедливости «Всем - поровну».
«Каждой собачке по косточке» (Фролова Ирина, 6 «Д»)
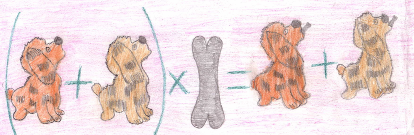
- пчела, собирающая нектар.

- «Солнце - одно на всех» (Кравченко М.)
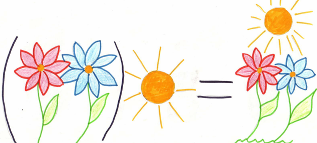
4.Свойство нуля при сложении :а + 0 = а, 0 + а = а
- закон копилки: сколько положишь - столько и возьмешь.
- закон пустых мечтаний: пустые мечты не сбываются (Рожкова И.) .
5.Свойство нуля при умножении а 0 = 0, 0
0 = 0, 0 а = 0
а = 0
- «Ноль стараний - ноль и знаний!» (Петуховская О.)
- закон дырявой бочки: сколько в дырявую бочку не лей - все равно все выльется (Байдин Э.).

- закон джунглей: «Сильный поедает слабого» (Сенькин А.)
- Ноль-проглот (так как при умножении числа на ноль, в результате получается ноль, назовем число ноль - проглотом. Ноль такой толстый, потому что съедает все числа).
- закон Бермудского треугольника.

6.Свойство единицы при умножении: а 1 = а, 1
1 = а, 1 а = а
а = а
-закон одиночества (Бабаева Д.).

7.Свойства деления, связанные с нулем: 0 : а = 0
-ничем можно поделиться со всеми (Кравченко А.)
8.Свойство суммы противоположных чисел : а - а = 0.
-закон войны «На войне нет победителей».


-закон свечи (Кравченко М.)

Интересные ассоциации вызвали метафоры, придуманные ребятами на правила действия со степенями (7 класс). Подростковый возраст - возраст первой любви. Познание себя, человеческих взаимоотношений, видимо, сыграло роль при создании этих метафорических законов.
З акон бракосочетания:
акон бракосочетания: 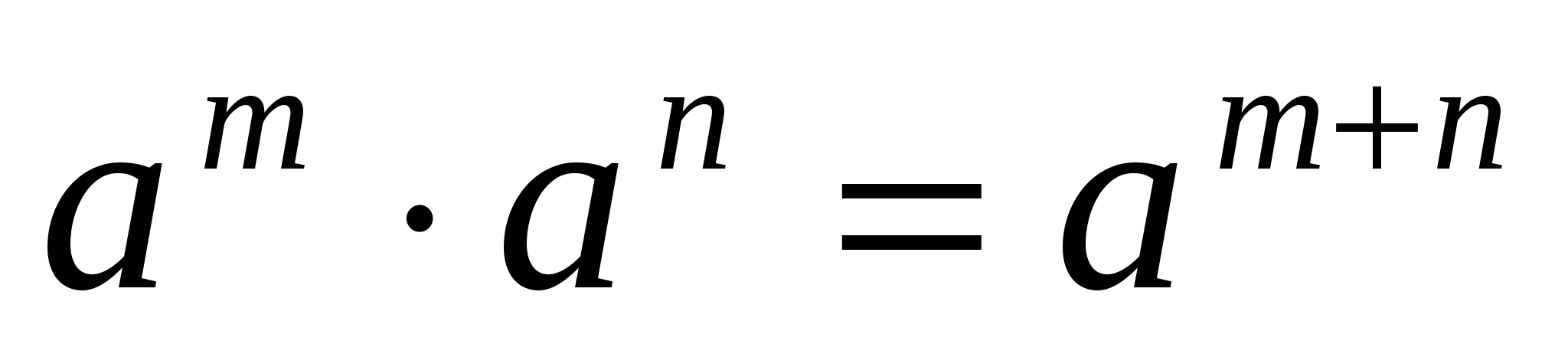
Закон развода: ![]()
Законы дружной семьи:
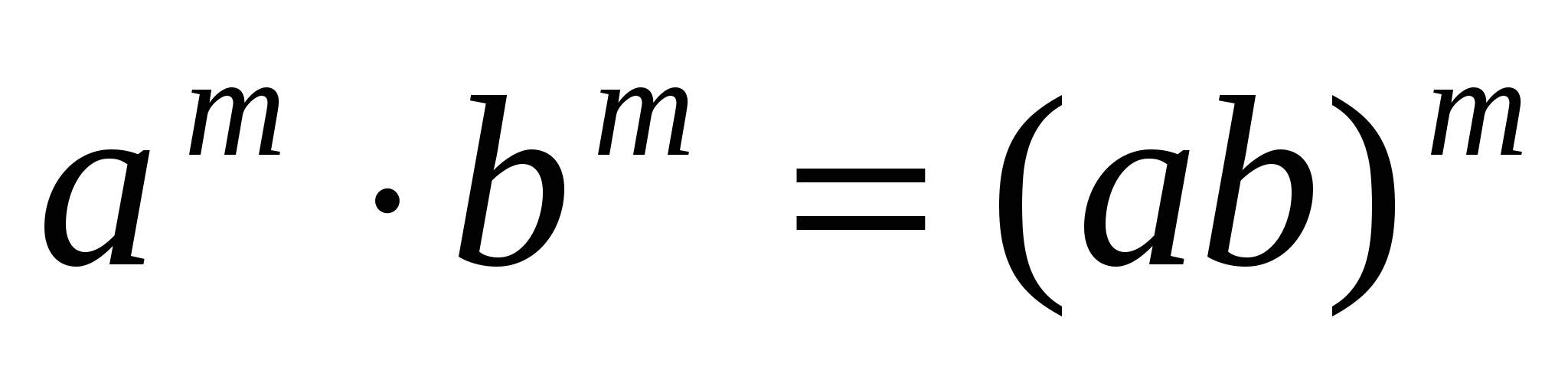 («твое горе - мое горе, твои радости - мои радости»)
(«твое горе - мое горе, твои радости - мои радости»)
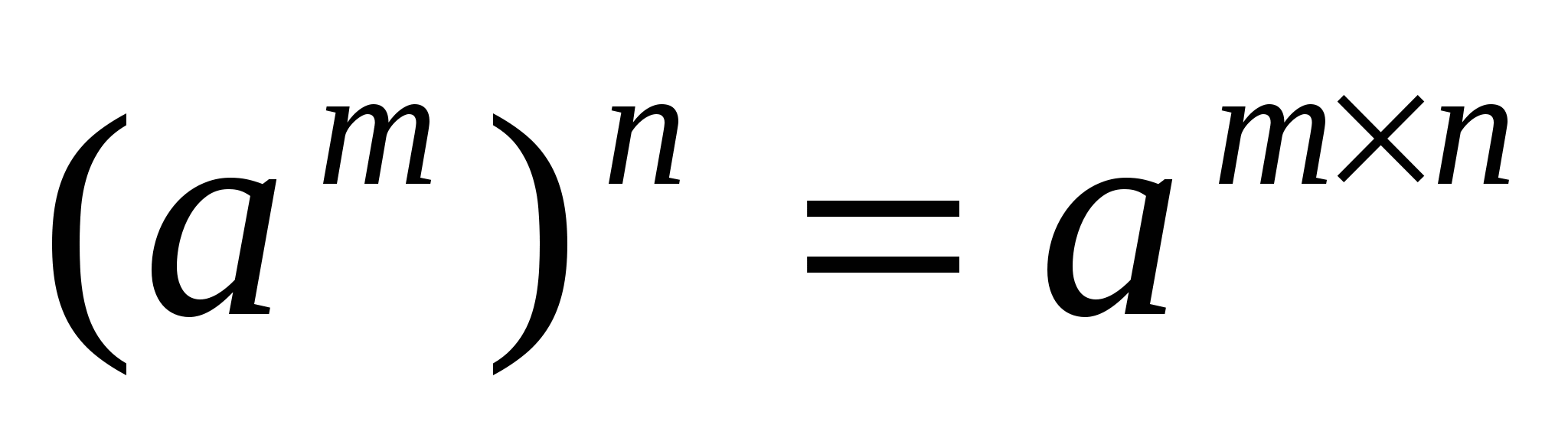 («если муж и жена - одно целое, то благополучие семьи множится»)
(«если муж и жена - одно целое, то благополучие семьи множится»)
Законы одиночества: 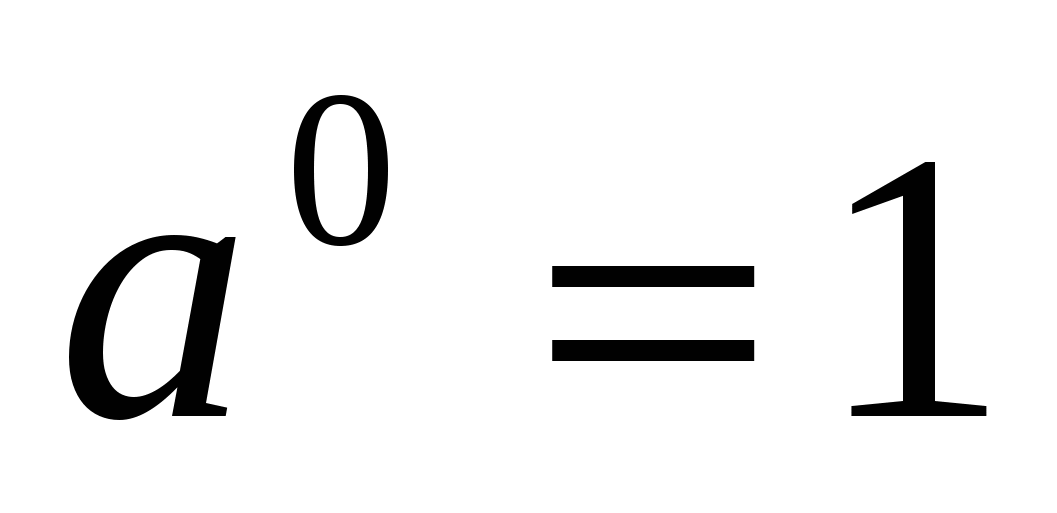 ,
,  («одинокий человек не может быть счастливым»).
(«одинокий человек не может быть счастливым»).
Оказалось, что метафоры не только инструмент изучения математических понятий, но и хороший инструмент обнаружения незнания. Как правило, при обсуждении неудачной метафоры выяснялось, что ребенок не понял суть закона. Дальнейшая работа помогала ликвидировать этот пробел. В седьмом классе при отработке алгоритма решения уравнения часто приходится сталкиваться с ошибками при переносе слагаемых из одной части уравнения в другую: то забудут знак поменять, то поменяют у слагаемых, которые «стоят на месте». Помощь пришла неожиданно: Климова Алина (ученица 7 «В» класса) принесла метафорический рисунок, на котором фломастеры и карандаши перемещались из одного стаканчика в другой так, чтобы в каждом из них оставались только карандаши или только фломастеры. Метафора, по ее мнению, демонстрировала один из этапов решения уравнения: собираем неизвестные в левой части уравнения, а числа - в правой. На вопрос учителя к классу: «А что еще мы при этом переносе должны помнить?» - ответ последовал мгновенно: «Точить карандаши, которые переставляем!» Осталась проблема, что же делать с фломастерами? Можно, конечно снять колпачок, но сошлись на следующем: поместить в стаканчики карандаши двух цветов, а при переносе карандаши чинить. Идея, которая родилась в голове одноклассника, помогла и Алине, и другим ребятам. Теперь при неправильном переносе мы повторяем эту фразу «точить карандаши», напоминая правило изменения знака на противоположный.
Образ, придуманный для одного математического понятия, иногда работал на другое, совершенно отличное от него. При изучении темы «Раскрытие скобок» сложные примеры с двойными, тройными скобками мы решали, разыскивая «смерть Кощея». Раскрывая скобку за скобкой, мы добираемся до «иглы» (работа Романичевой В., 7 класс)
2с - (3с + (2с - (с + 1)) + 7) = 2с - 3с - (2с - (с + 1)) - 7) = 2с - 3с -2с + (с + 1) + 7
кабан заяц яйцо

У других ребят эти правила ассоциировались с «Киндер Сюрпризом», цыпленком в скорлупе, набором матрешек..



Как же пригодились эти метафоры в десятом и одиннадцатых классах при работе со сложными функциями и композициями функций. Нахождение области определения функции, взятие производной, решение логарифмических неравенств и уравнений зависят от умения разбить сложную функцию на внутреннюю и внешнюю (умения анализировать), и работа по созданию образа сложной функции была продолжена.

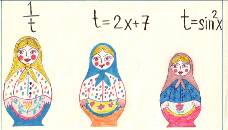

Рисунок Антуана де Сент-Экзюпери «Удав, проглотивший слона».
Цепь питания в экосистеме: дождевого червя поедает карась, который сам служит пищей сому.

Модель сложной функции от композиции трех, например,
y = tg (x2 + sin x + 5x).

Для конструирования сложной функции и последующего взятия производной ребятами была придумана игра в кости. Кубики, на гранях которых написаны различные функции: линейные, степенные, тригонометрические, логарифмические и другие. Выкидывая эти кубики по очереди, ученики составляли функцию, производную которой надо было найти.
Математические понятия отличаются высокой степенью абстракции, и нахождение образов, ассоциаций, метафор связанных с ними, - задача не из легких. Но насколько труден, настолько и увлекателен творческий процесс создания метафорических интерпретаций строгих математических определений и законов. У творческого процесса есть две стороны: игра позволяет ему опробовать различные подходы, работа - облечь идею в удобную и полезную для других форму. Создание метафоры - увлекательная и интересная игра, которая позволяет думать «иначе», развивает умения находить нестандартные решения не только при решении математических задач, но и при поиске выхода из различных жизненных ситуаций, способствует развитию творческих и нравственных способностей школьников. И если ученик войдет во вкус, - он потом возьмется и за учебники, за формулы и строгие доказательства. «Подобно тому, как рою бесчисленных пчел, поражающему наперебой своими жалами, не удается отогнать упивающегося медведя, если он хоть немного вкусил приятность скрытого в дереве меда, так нет, разумеется, никого, кто, хоть краем губ постигнув сладость математических доказательств (какая бы масса величайших трудностей, которыми эти доказательства сопровождаются, ни отталкивала его, точно частыми уколами жал), не стремился бы всеми своими силами освоить их вполне, до полного насыщения» (Бонавентура Кавальери, трактат «Геометрия»).6
Библиографический список
1. Роджер ван Оих. Психологические отмычки. - СПб: Питер Паблишинг, 1997.
2. Кордемский Б.А..Увлечь школьников математикой: (Материал для клас. и внеклас. занятий). М.: Просвещение, 1981. - 112 с., ил.
3. Джозеф О'Коннор, Джон Сеймор. Введение в нейролингвистическое программирование. Новейшая психология личного мастерства. - СПб: Питер, 1999.
4. Кулиев Г.Г. Метафоры и научное познание. Баку,1987.
5. Попов Ю.П,, Пухначев Ю.В. Математика в образах. - М. Знание,1989, - 208с. - (Нар.У-т . Естественных наук)
6. George Lakоff. Mark Jоhnsоn. Metaphors We Live By. Chicago, University of Chicago Press, 1980.
7. M. Black. Models and Metaphor. Studies in language and Philosophy. Ithaca- London, Cornell University Press, 1962, p. 25-47.
8. Пригожий И., Стенгерс И. Порядок из хаоса// Интернет ресурсы
dr-gng.dp.ua/library/хаос/ ОО.html
1 Роджер ван Оих. Психологические отмычки. - СПб: Питер Паблишинг, 1997.
2 Кордемский Б.А..Увлечь школьников математикой: (Материал для клас. и внеклас. занятий). М.: Просвещение, 1981. - 112 с., ил.
3 Джозеф О'Коннор, Джон Сеймор. Введение в нейролингвистическое программирование. Новейшая психология личного мастерства. - СПб: Питер, 1999.
4 Роджер ван Оих. Психологические отмычки. - СПб: Питер Паблишинг, 1997.
5 Кулиев Г.Г. Метафоры и научное познание. Баку,1987.
6 Попов Ю.П,, Пухначев Ю.В. Математика в образах. - М. Знание,1989, - 208с. - (Нар.У-т . Естественных наук)


