- Преподавателю
- Математика
- Мановская работа Логарифмические неравенства в ЕГЭ
Мановская работа Логарифмические неравенства в ЕГЭ
| Раздел | Математика |
| Класс | 11 класс |
| Тип | Другие методич. материалы |
| Автор | Гунько Л.Д. |
| Дата | 11.09.2015 |
| Формат | doc |
| Изображения | Есть |
33
ЛОГАРИФМИЧЕСКИЕ НЕРАВЕНСТВА В ЕГЭ
Сечин Михаил Александрович
Малая академия наук учащейся молодежи РК «Искатель»
МБОУ « Советская СШ №1», 11 класс, пгт. Советский Советского района
Гунько Людмила Дмитриевна, учитель МБОУ « Советская СШ №1»
Советского района
Цель работы: исследование механизма решения логарифмических неравенств С3 при помощи нестандартных методов, выявление интересных фактов логарифма.
Предмет исследования:
1)Найти необходимые сведения о нестандартных методах решения логарифмических неравенств.
2)Найти дополнительные сведения о логарифмах.
3)Научиться решать конкретные логарифмические неравенства С3 с помощью нестандартных методов.
Результаты:
Практическая значимость заключается в расширении аппарата для решения задач С3. Данный материал можно будет использовать на некоторых уроках, для проведения кружков, факультативных занятий по математике.
Проектным продуктом станет сборник «Логарифмические неравенства С3 с решениями».
Содержание
Введение………………………………………………………………………….4
Глава 1. История вопроса……………………………………………………...5
Глава 2. Сборник логарифмических неравенств ………………………… 7
2.1. Равносильные переходы и обобщенный метод интервалов…………… 7
2.2. Метод рационализации ………………………………………………… 15
2.3. Нестандартная подстановка………………............................................... 22
2.4. Задания с ловушками…………………………………………………… 27
Заключение…………………………………………………………………… 30
Литература……………………………………………………………………. 31
Введение
Я учусь в 11 классе и планирую поступить в ВУЗ, где профильным предметом является математика. А поэтому много работаю с задачами части С. В задании С3 нужно решить нестандартное неравенство или систему неравенств, как правило, связанное с логарифмами. При подготовке к экзамену я столкнулся с проблемой дефицита методов и приёмов решения экзаменационных логарифмических неравенств, предлагаемых в С3. Методы, которые изучаются в школьной программе по этой теме, не дают базу для решения заданий С3. Учитель по математике предложила мне поработать с заданиями С3 самостоятельно под её руководством. Кроме этого, меня заинтересовал вопрос: а в жизни нашей встречаются логарифмы?
С учетом этого и была выбрана тема:
«Логарифмические неравенства в ЕГЭ»
Цель работы: исследование механизма решения задач С3 при помощи нестандартных методов, выявление интересных фактов логарифма.
Предмет исследования:
1)Найти необходимые сведения о нестандартных методах решения логарифмических неравенств.
2)Найти дополнительные сведения о логарифмах.
3)Научиться решать конкретные задачи С3 с помощью нестандартных методов.
Результаты:
Практическая значимость заключается в расширении аппарата для решения задач С3. Данный материал можно будет использовать на некоторых уроках, для проведения кружков, факультативных занятий по математике.
Проектным продуктом станет сборник «Логарифмические неравенства С3 с решениями».
Глава 1. История вопроса
На протяжении 16 века быстро возрастало количество приближённых вычислений, прежде всего, в астрономии. Совершенствование инструментов, исследование планетных движений и другие работы потребовали колоссальных, иногда многолетних, расчетов. Астрономии грозила реальная опасность утонуть в невыполненных расчётах. Трудности возникали и в других областях, например, в страховом деле нужны были таблицы сложных процентов для различных значений процента. Главную трудность представляли умножение, деление многозначных чисел, особенно тригонометрических величин.
Открытие логарифмов опиралось на хорошо известные к концу 16 века свойства прогрессий. О связи между членами геометрической прогрессии q, q2, q3, ... и арифметической прогрессией их показателей 1, 2, 3,... говорил еще в "Псалмите" Архимед. Другой предпосылкой было распространение понятия степени на отрицательные и дробные показатели. Многие авторы указывали, что умножению, делению, возведению в степень и извлечению корня в геометрической прогрессии соответствуют в арифметической - в том же порядке - сложение, вычитание, умножение и деление.
Здесь скрывалась идея логарифма как показателя степени.
В истории развития учения о логарифмах прошло несколько этапов.
1 этап

Логарифмы были изобретены не позднее 1594 года независимо друг от друга шотландским бароном Непером (1550-1617) и через десять лет швейцарским механиком Бюрги (1552-1632). Оба хотели дать новое удобное средство арифметических вычислений, хотя подошли они к этой задаче по-разному. Непер кинематически выразил логарифмическую функцию и, тем самым, вступил в новую область теории функции. Бюрги остался на почве рассмотрения дискретных прогрессий. Впрочем, определение логарифма у обоих не похоже на современное. Термин "логарифм" (logarithmus) принадлежит Неперу. Он возник из сочетания греческих слов: logos - "отношение" и ariqmo - "число", которое означало "число отношений". Первоначально Непер пользовался другим термином: numeri artificiales- "искусственные числа", в противоположность numeri naturalts -"числам естественным".
В 1615 году в беседе с профессором математики Грешем Колледжа в Лондоне Генри Бригсом (1561-1631) Непер предложил принять за логарифм единицы нуль, а за логарифм десяти - 100, или, что сводится к тому же, просто 1. Так появились десятичные логарифмы и были напечатаны первые логарифмические таблицы. Позже таблицы Бригса дополнил голландский книготорговец и любитель математики Андриан Флакк (1600-1667). Непер и Бригс, хотя пришли к логарифмам раньше всех, опубликовали свои таблицы позже других - в 1620 году. Знаки log и Log были введены в 1624 году И. Кеплером. Термин "натуральный логарифм" ввели Менголи в 1659 г. и вслед за ним Н. Меркатор в 1668 г., а издал таблицы натуральных логарифмов чисел от 1 до 1000 под названием "Новые логарифмы" лондонский учитель Джон Спейдел.
На русском языке первые логарифмические таблицы были изданы в 1703 году. Но во всех логарифмических таблицах были допущены ошибки при вычислении. Первые безошибочные таблицы вышли в 1857 году в Берлине в обработке немецкого математика К. Бремикера (1804-1877).
2 этап
Дальнейшее развитие теории логарифмов связано с более широким применением аналитической геометрии и исчисления бесконечно малых. К тому времени относится установление связи между квадратурой равносторонней гиперболы и натуральным логарифмом. Теория логарифмов этого периода связана с именами целого ряда математиков.
Немецкий математик, астроном и инженер Николаус Меркатор в сочинении
"Логарифмотехника" (1668) приводит ряд, дающий разложение ln(x+1) по
степеням х:
Это выражение в точности соответствует ходу его мысли, хотя он, конечно, пользовался не знаками d, , ... , а более громоздкой символикой. С открытием логарифмического ряда изменилась техника вычисления логарифмов: они стали определяться с помощью бесконечных рядов. В своих лекциях "Элементарная математика с высшей точки зрения", прочитанных в 1907-1908 годах, Ф. Клейн предложил использовать формулу в качестве исходного пункта построения теории логарифмов.
3 этап
Определение логарифмической функции как функции обратной
показательной, логарифма как показателя степени данного основания
было сформулировано не сразу. Сочинение Леонарда Эйлера (1707-1783)
"Введение в анализ бесконечно малых" (1748 г.) послужило дальнейшему
развитию теории логарифмической функции. Таким образом,
прошло 134 года с тех пор, как логарифмы впервые были введены
(считая с 1614 г.), прежде чем математики пришли к определению
понятия логарифма, которое положено теперь в основу школьного курса.
Глава 2. Сборник логарифмических неравенств
2.1. Равносильные переходы и обобщенный метод интервалов.
Равносильные переходы
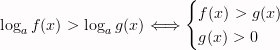 , если а > 1
, если а > 1
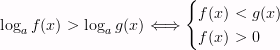 , если 0 < а < 1
, если 0 < а < 1
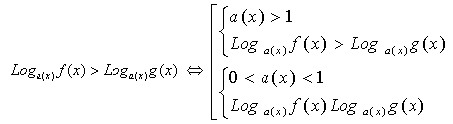
Обобщённый метод интервалов
Данный способ наиболее универсален при решении неравенств практически любого типа. Схема решения выглядит следующим образом:
1. Привести неравенство к такому виду, где в левой части находится функция 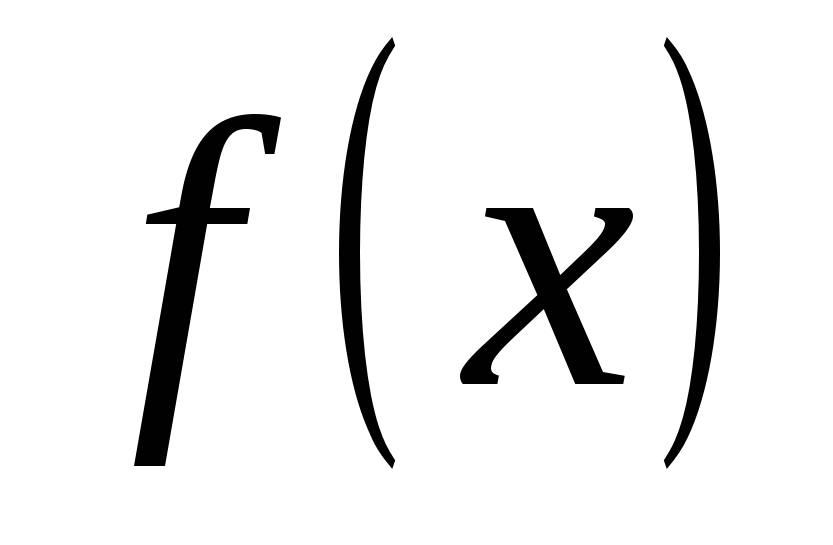 , а в правой 0.
, а в правой 0.
2. Найти область определения функции 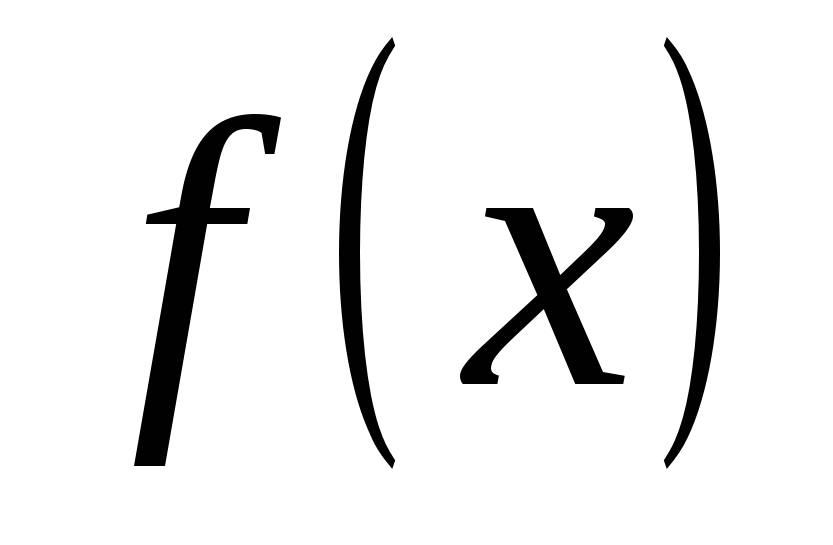 .
.
3. Найти нули функции 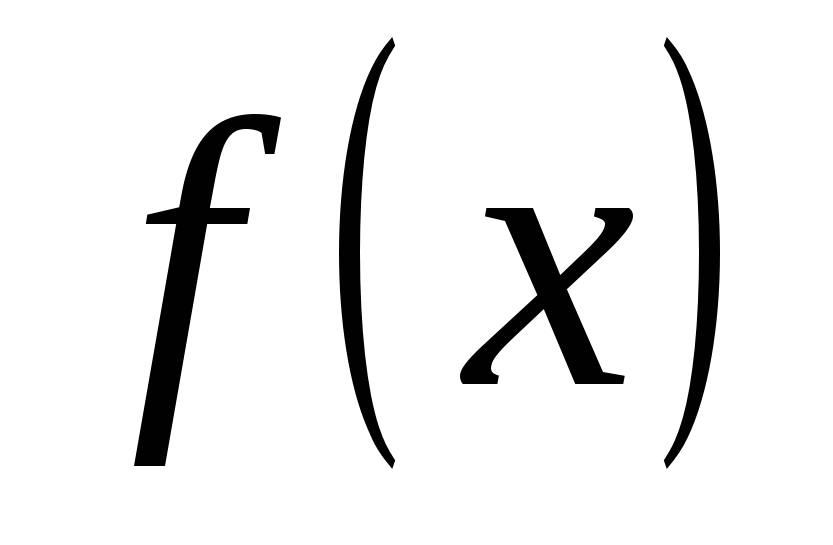 , то есть - решить уравнение
, то есть - решить уравнение 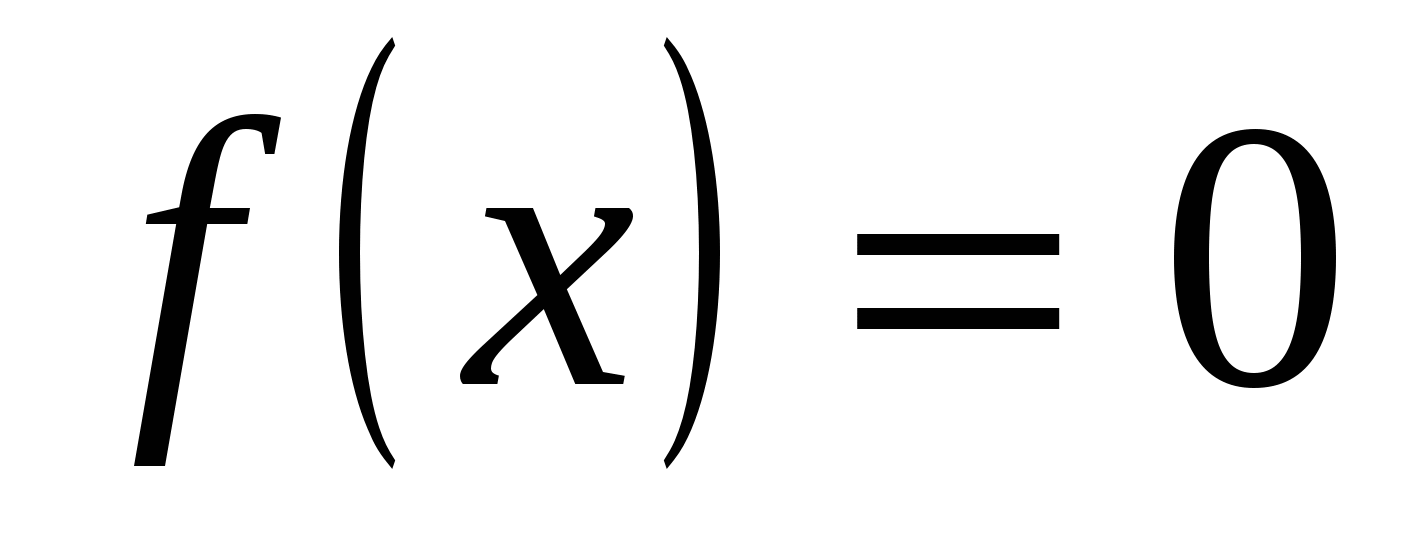 (а решать уравнение обычно проще, чем решать неравенство).
(а решать уравнение обычно проще, чем решать неравенство).
4. Изобразить на числовой прямой область определения и нули функции.
5. Определить знаки функции 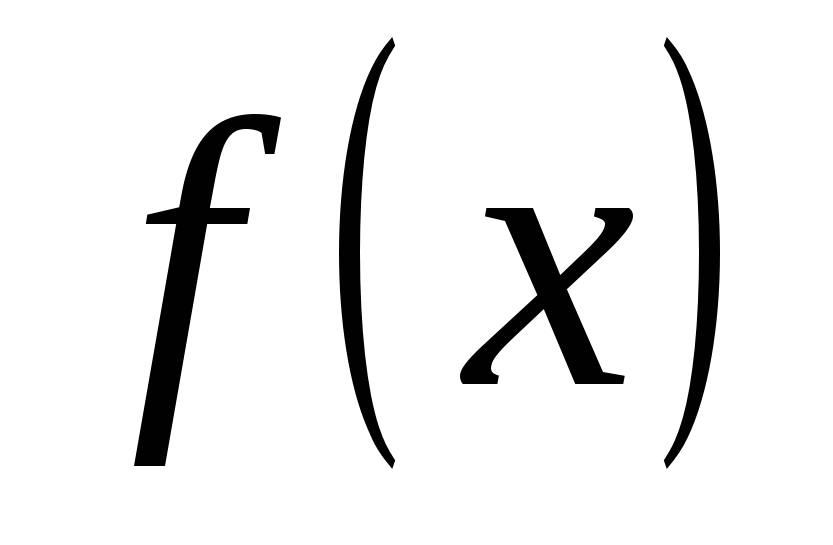 на полученных интервалах.
на полученных интервалах.
6. Выбрать интервалы, где функция принимает необходимые значения, и записать ответ.
Пример 1.
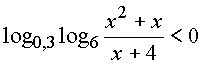
Решение:
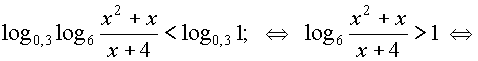
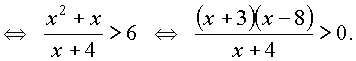
Применим метод интервалов
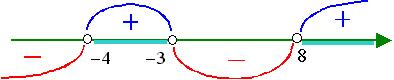
откуда
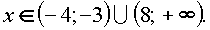
При этих значениях  все выражения, стоящие под знаками логарифмов, положительны.
все выражения, стоящие под знаками логарифмов, положительны.
Ответ:
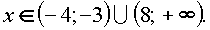
Пример 2.
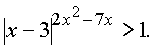
Решение:
1-й способ. ОДЗ определяется неравенством x > 3. Логарифмируя при таких x по основанию 10, получаем
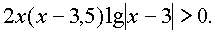
Последнее неравенство можно было бы решать, применяя правила разложения, т.е. сравнивая с нулём сомножители. Однако в данном случае легко определить интервалы знакопостоянства функции
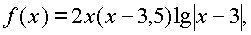
поэтому можно применить метод интервалов.
Функция f(x) = 2x(x - 3,5)lgǀ x - 3ǀ непрерывна при x > 3 и обращается в ноль в точках x1 = 0, x2 = 3,5, x3 = 2, x4 = 4. Таким образом, определяем интервалы знакопостоянства функции f(x):
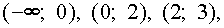
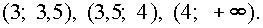

Ответ:
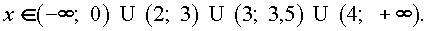
2-й способ. Применим непосредственно к исходному неравенству идеи метода интервалов.
Для этого напомним, что выражения ab - ac и (a - 1)(b - 1) имеют один знак. Тогда наше неравенство при x > 3 равносильно неравенству
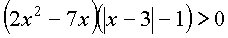
или
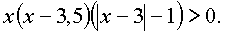
Поcледнее неравенство решается методом интервалов

Ответ:
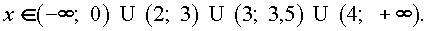
Пример 3.
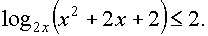
Решение:
Неравенство равносильно совокупности систем
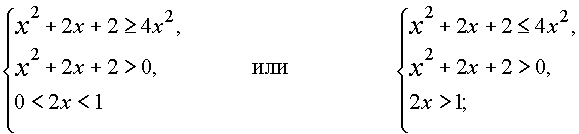
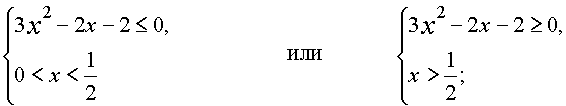
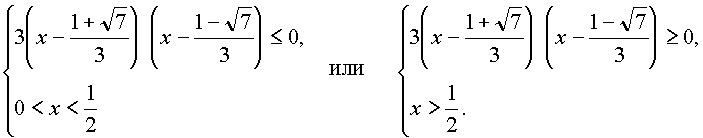
Применим метод интервалов
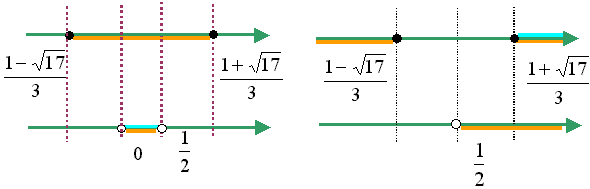
Ответ:
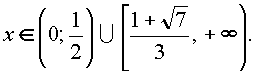
Пример 4.
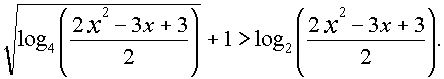
Решение:
Так как 2x2 - 3x + 3 > 0 при всех действительных x, то неравенство равносильно системе
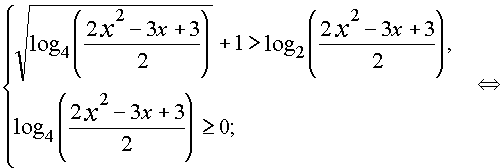
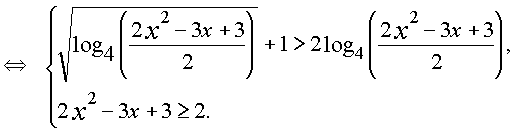
Для решения второго неравенства воспользуемся методом интервалов
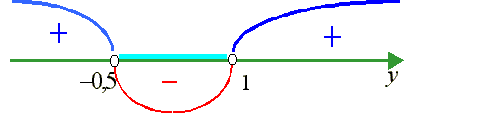
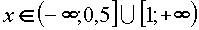
В первом неравенстве сделаем замену
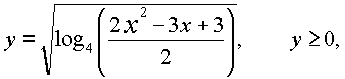
тогда приходим к неравенству 2y2 - y - 1 < 0 и, применив метод интервалов, получаем, что решениями будут те y, которые удовлетворяют неравенству -0,5 < y < 1.

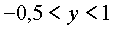
Откуда, так как
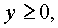
получаем неравенство
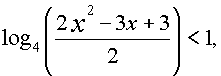
которое выполняется при тех x, для которых 2x2 - 3x - 5 < 0. Вновь применим метод интервалов

Теперь с учетом решения второго неравенства системы окончательно получаем

Ответ:
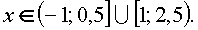
Пример 5.
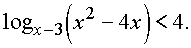
Решение:
Неравенство равносильно совокупности систем
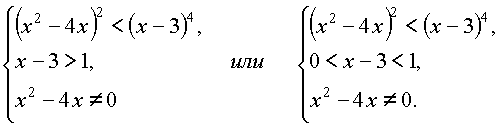
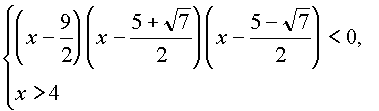
или
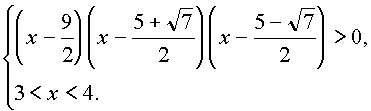
Применим метод интервалов или
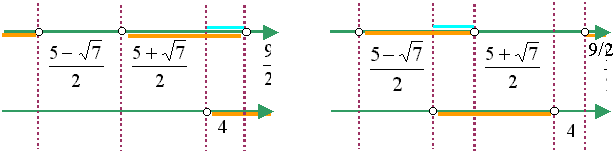
Ответ:
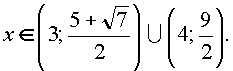
Пример 6.
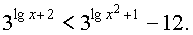
Решение:
Неравенство равносильно системе
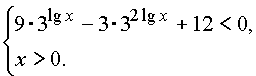
Пусть
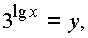
тогда y > 0,
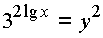
и первое неравенство
системы принимает вид
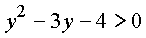
или, раскладывая
квадратный трехчлен на множители,
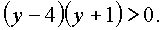
Применяя к последнему неравенству метод интервалов,
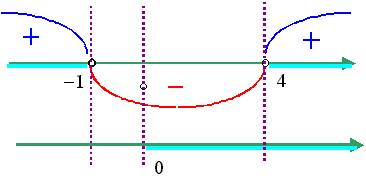
видим, что его решениями, удовлетворяющими условию y > 0 будут все y > 4.
Таким образом исходное неравенство эквивалентно системе:
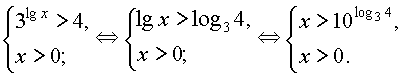
Итак, решениями неравенства являются все
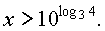
2.2. Метод рационализации.
Раньше методом рационализации неравенства не решали, его не знали. Это "новый современный эффективный метод решения показательных и логарифмических неравенств" (цитата из книжки Колесниковой С.И.)
И даже, если педагог его знал, была опаска - а знает ли его эксперт ЕГЭ, а почему в школе его не дают? Были ситуации, когда учитель говорил ученику: "Где взял? Садись - 2."
Сейчас метод повсеместно продвигается. И для экспертов есть методические указания, связанные с этим методом, и в "Самых полных изданиях типовых вариантов ..." в решении С3 используется этот метод.
МЕТОД ЧУДЕСНЫЙ!
«Волшебная таблица»

В других источниках
если a>1 и b>1, то logab>0 и (a-1)(b-1)>0;
если a>1 и 0<b<1, то logab<0 и (a-1)(b-1)<0;
если 0<a<1 и b>1, то logab<0 и (a-1)(b-1)<0;
если 0<a<1 и 0<b<1, то logab>0 и (a-1)(b-1)>0.
Проведенные рассуждения несложные, но заметно упрощающие решение логарифмических неравенств.





Пример 4.
logx(x2-3)<0
Решение: 
Пример 5.
log2x(2x2-4x+6)≤log2x(x2+x)
Решение: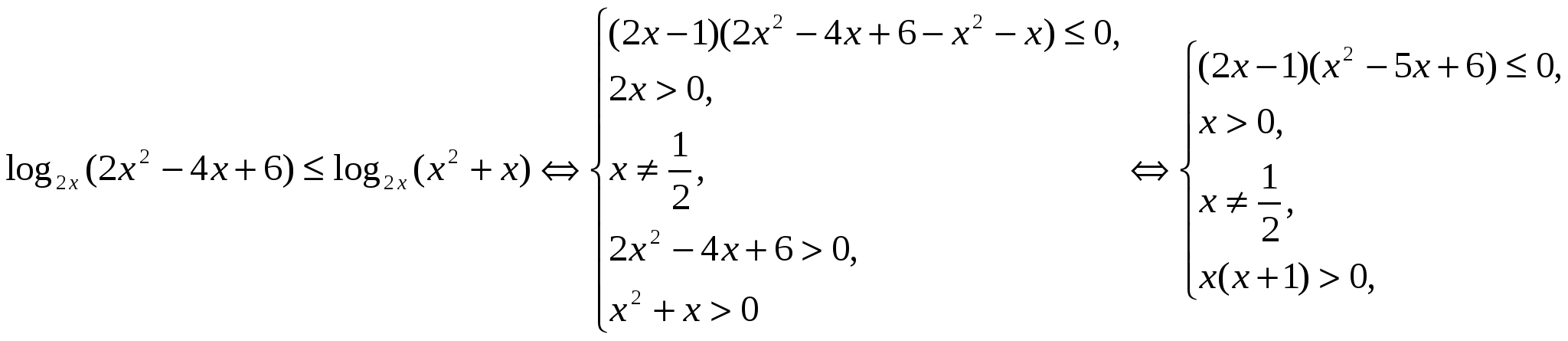
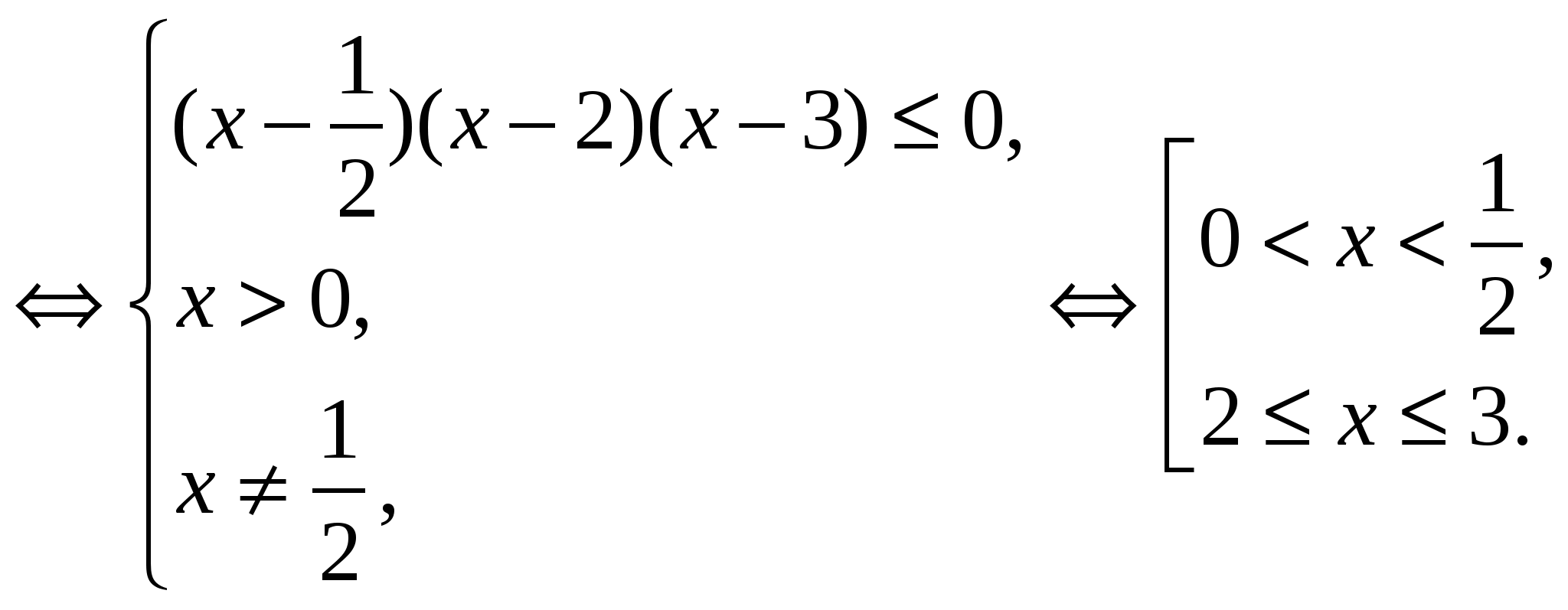 Ответ. (0; 0,5)U[2; 3].
Ответ. (0; 0,5)U[2; 3].

 Пример 6.
Пример 6.
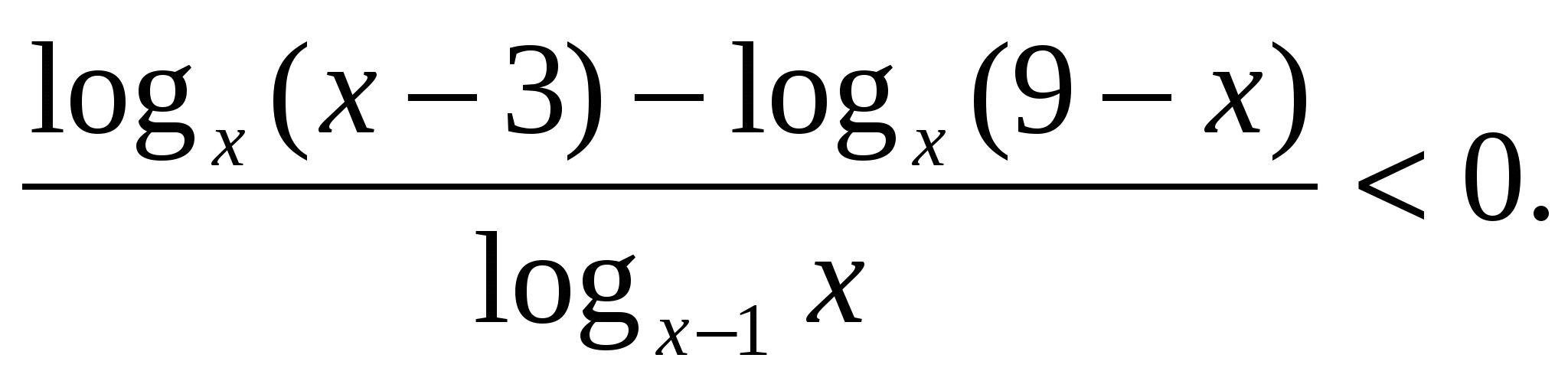
Для решения этого неравенства вместо знаменателя запишем (х-1-1)(х-1), а вместо числителя - произведение (х-1)(х-3-9+х).
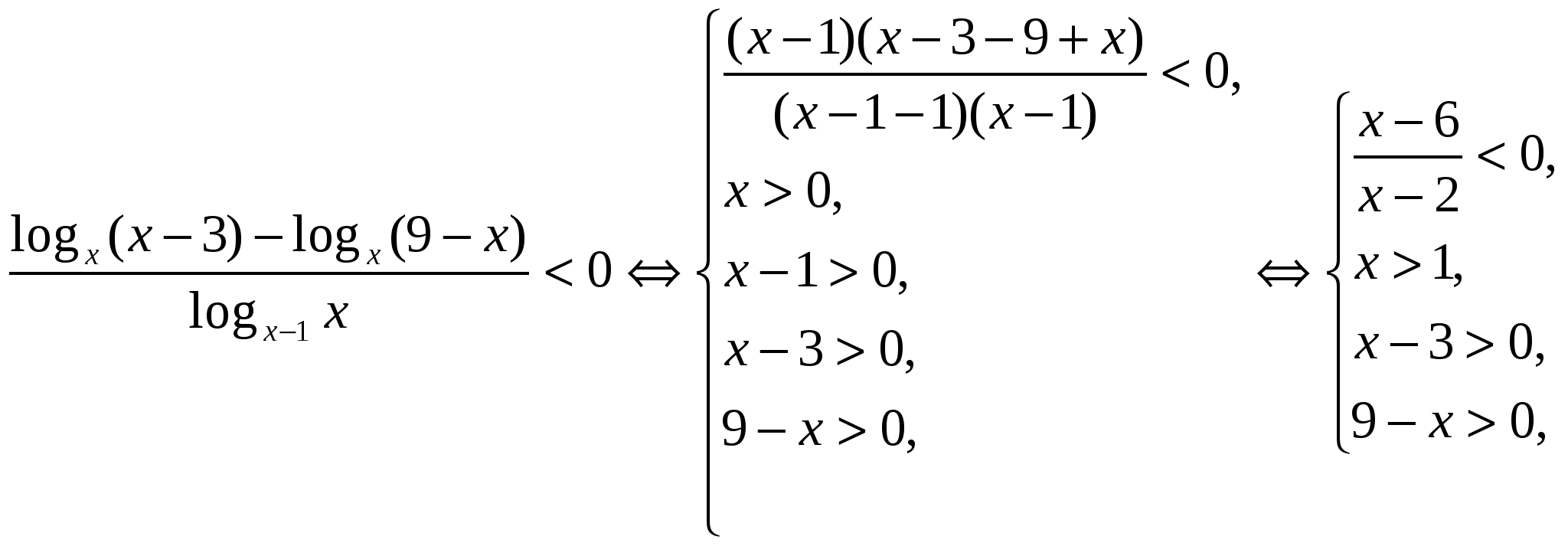

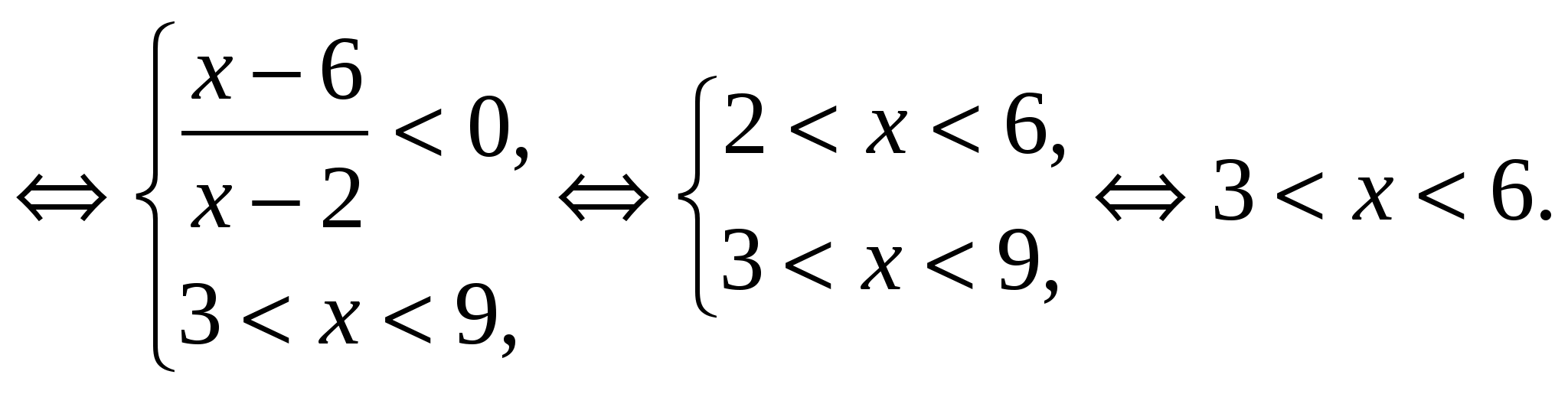 Ответ: (3;6)
Ответ: (3;6)
Пример 7.

Пример 8.

2.3. Нестандартная подстановка.
Пример 1.

Пример 2.
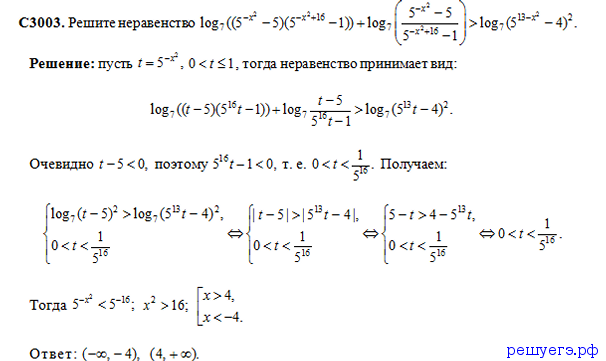
Пример 3.

Пример 4.

Пример 5.
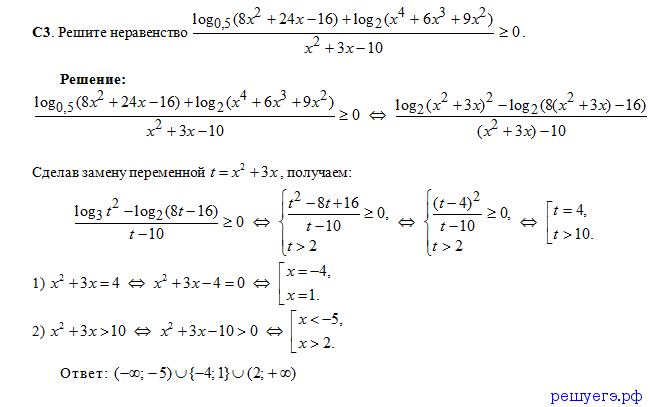
Пример 6.
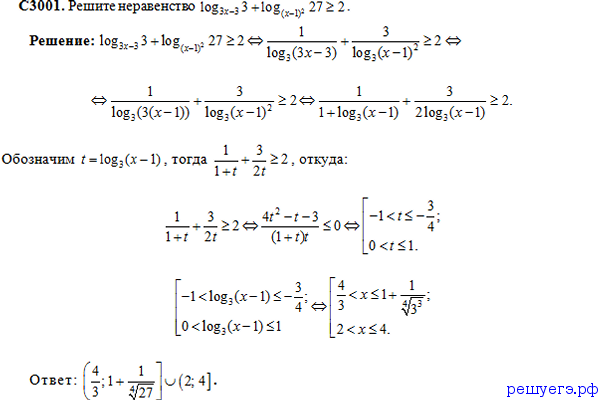
Пример 7.
log4(3x-1)log0,25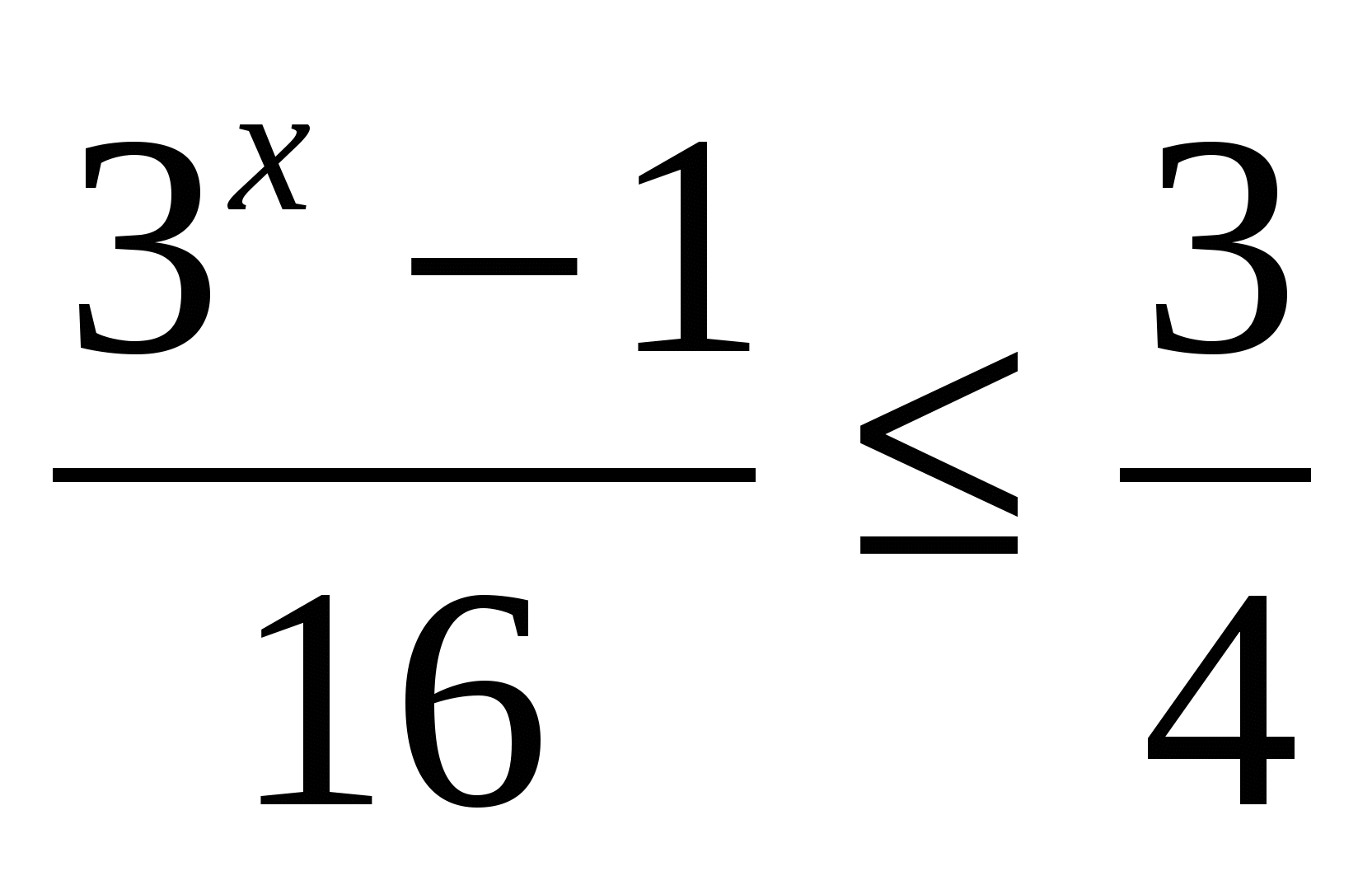
Сделаем замену у=3х-1; тогда данное неравенство примет вид
Log4log0,25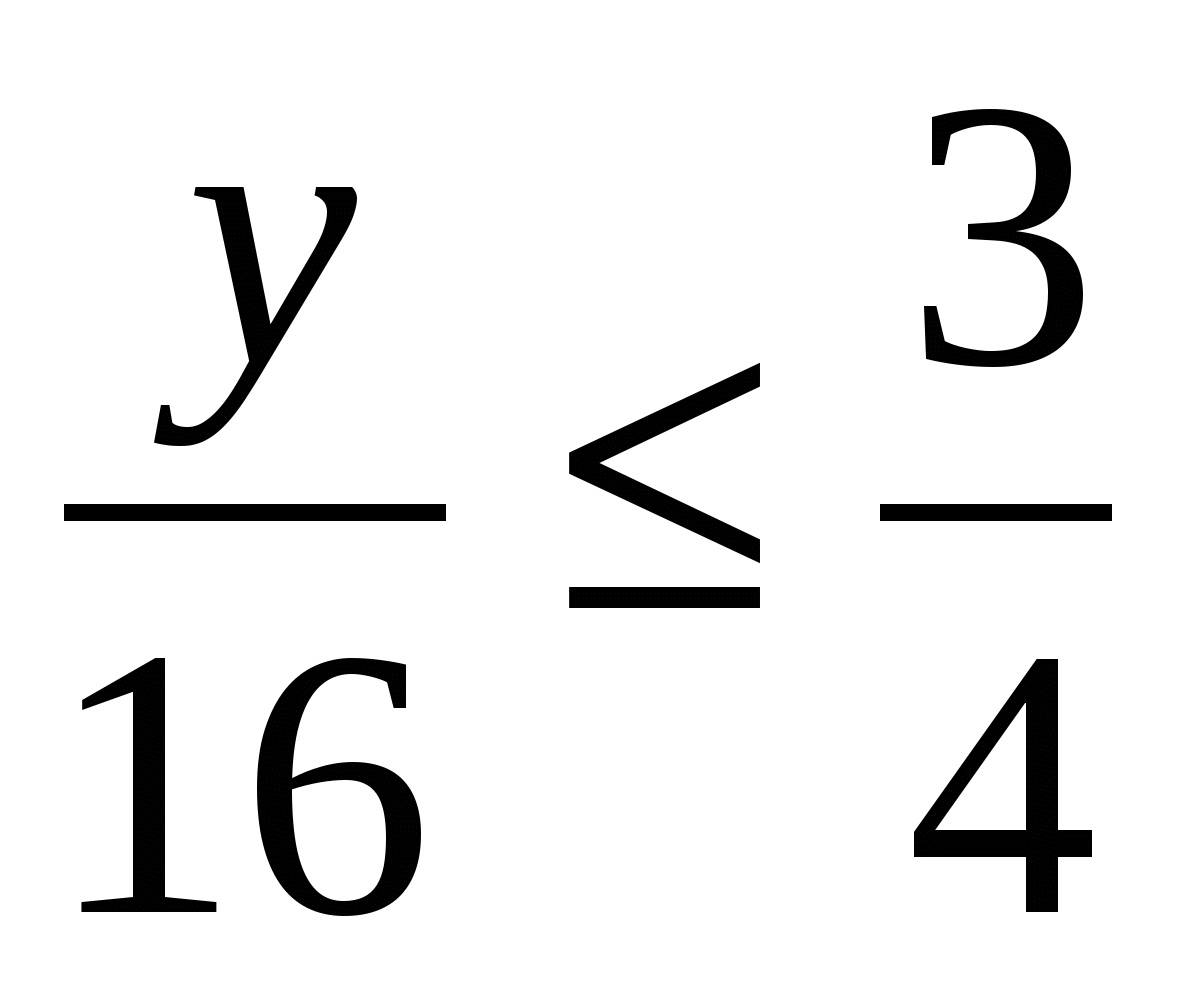 .
.
Так как log0,25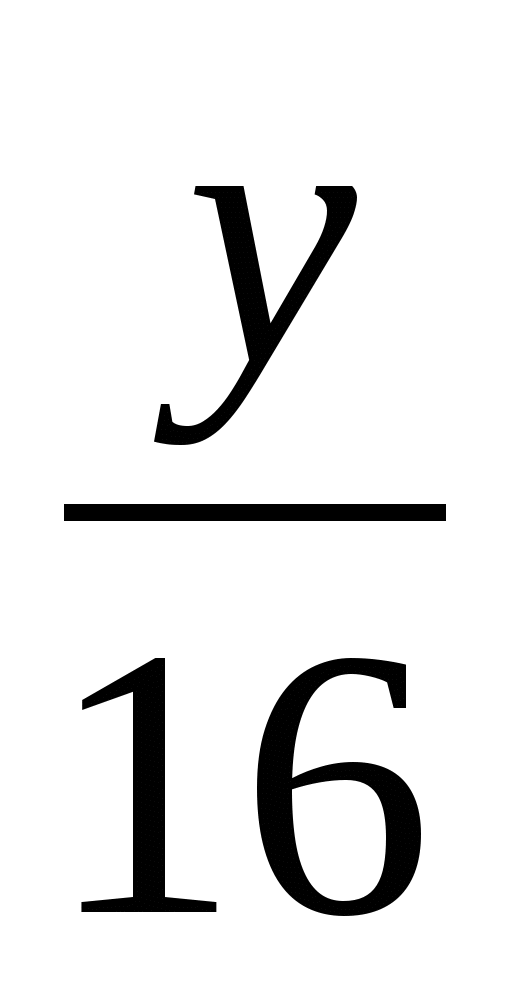 = -log4
= -log4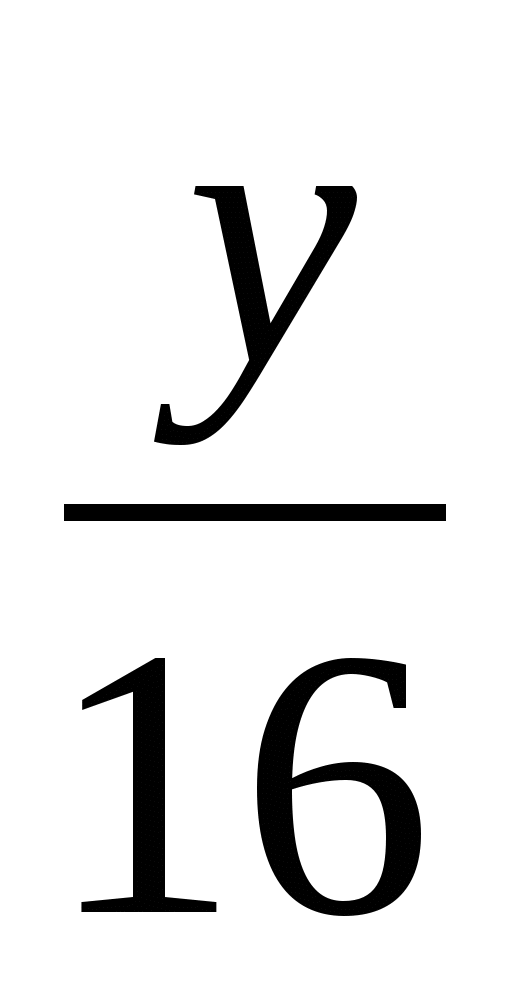 = -(log4y-log416)=2-log4y, то перепишем последнее неравенство в виде 2log4y-log42y≤
= -(log4y-log416)=2-log4y, то перепишем последнее неравенство в виде 2log4y-log42y≤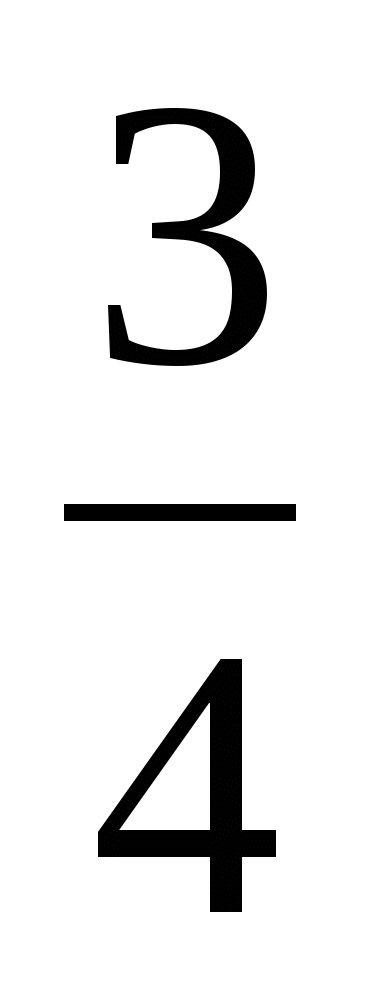 .
.
Сделаем замену t=log4y и получим неравенство t2-2t+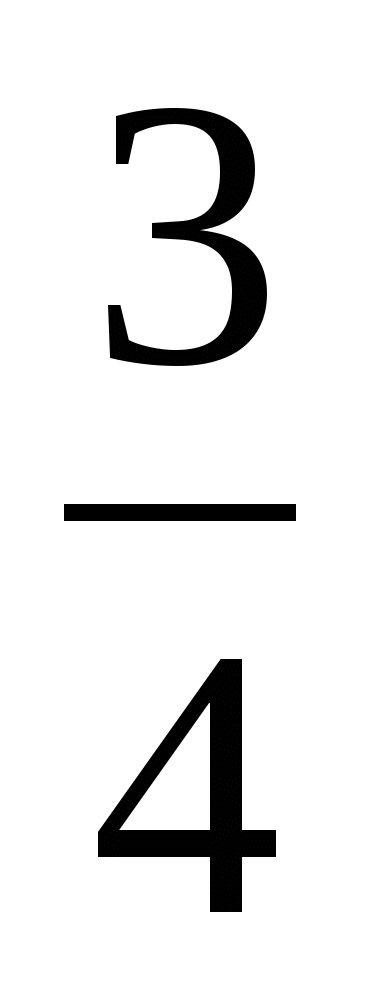 ≥0, решением которого являются промежутки -
≥0, решением которого являются промежутки -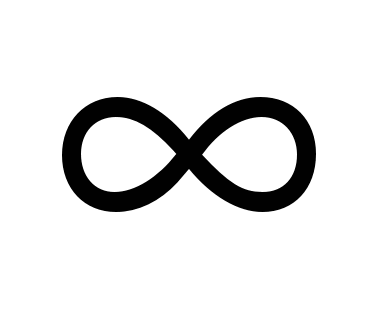 <t≤
<t≤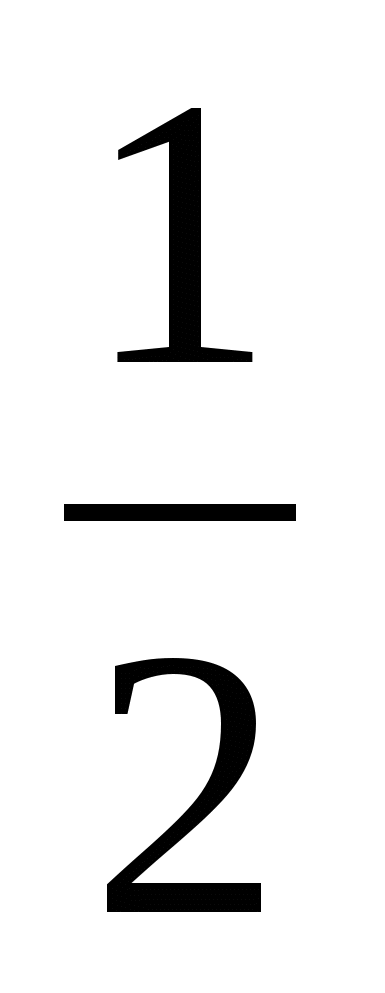 и
и 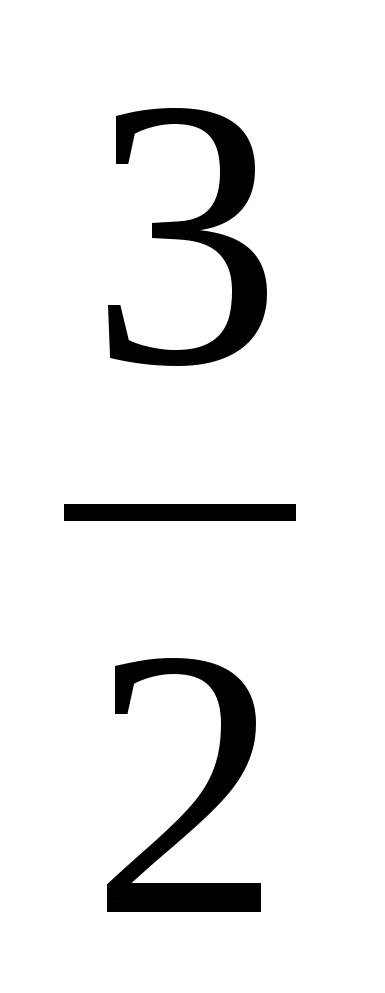 ≤t<+
≤t<+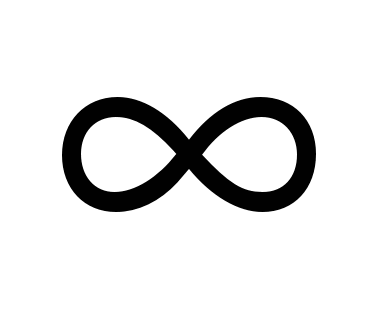 .
.
Таким образом, для нахождения значений у имеем совокупность двух простейших неравенств 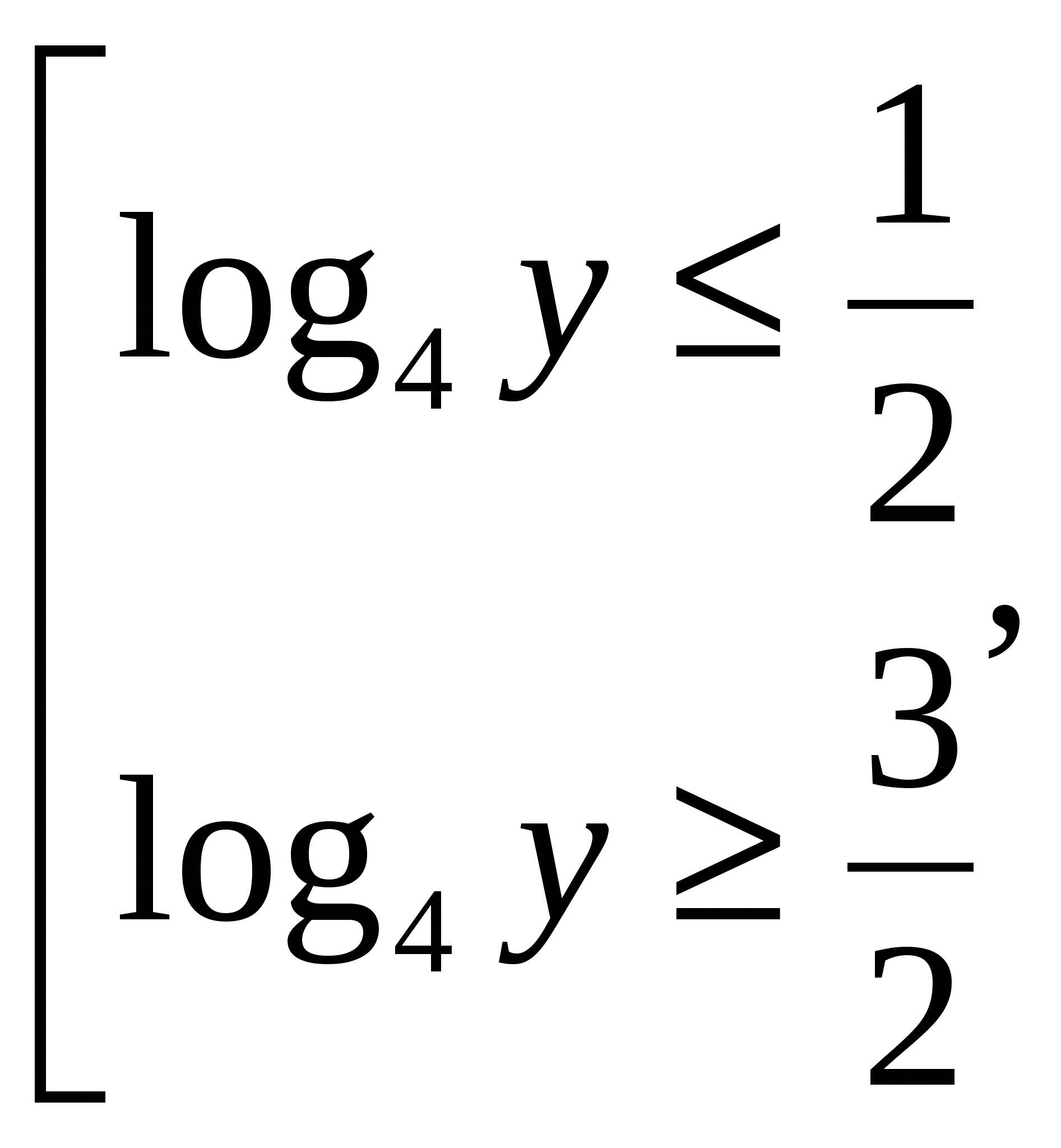 Решение этой совокупности есть промежутки 0<у≤2 и 8≤у<+
Решение этой совокупности есть промежутки 0<у≤2 и 8≤у<+ .
.
Следовательно, исходное неравенство равносильно совокупности двух показательных неравенств, 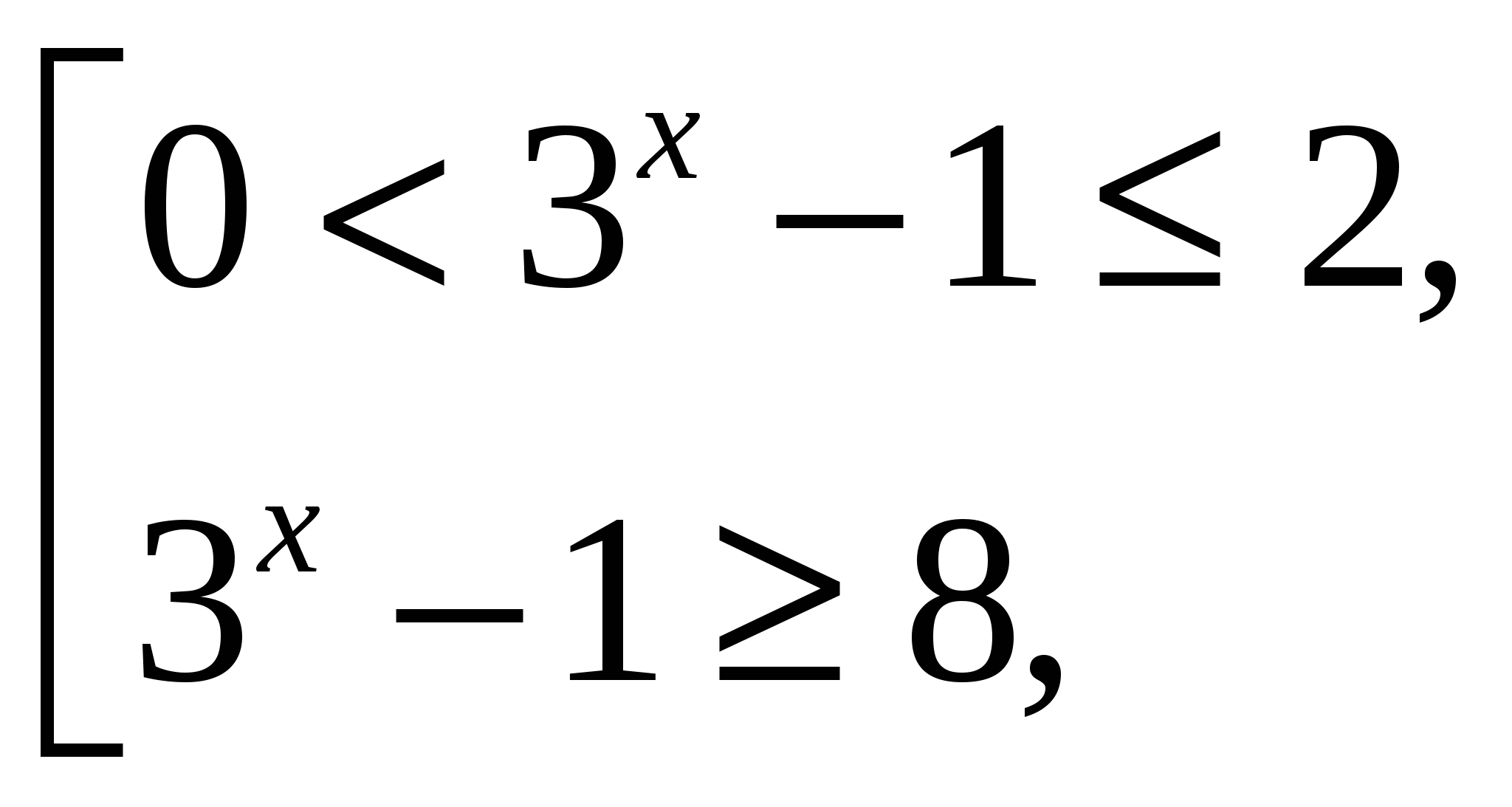 то есть совокупности
то есть совокупности 
Решением первого неравенства этой совокупности является промежуток 0<х≤1, решением второго - промежуток 2≤х<+ . Таким образом, исходное неравенство выполняется для всех значений х из промежутков 0<х≤1 и 2≤х<+
. Таким образом, исходное неравенство выполняется для всех значений х из промежутков 0<х≤1 и 2≤х<+ .
.
Пример 8.
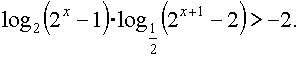
Решение:
Неравенство равносильно системе
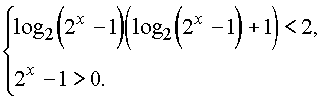
Решением второго неравенства, определяющего ОДЗ, будет множество тех x,
для которых x > 0.
Для решения первого неравенства сделаем замену
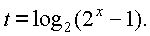
Тогда получаем неравенство
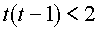
или
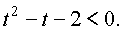
Множество решений последнего неравенства находится методом
интервалов: -1 < t < 2. Откуда, возвращаясь к переменной x, получаем

или
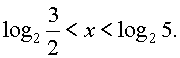
Множество тех x, которые удовлетворяют последнему неравенству
принадлежит ОДЗ (x > 0), следовательно, является решением системы,
а значит, и исходного неравенства.
Ответ:
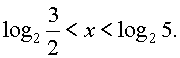
2.4. Задания с ловушками.
Пример 1.
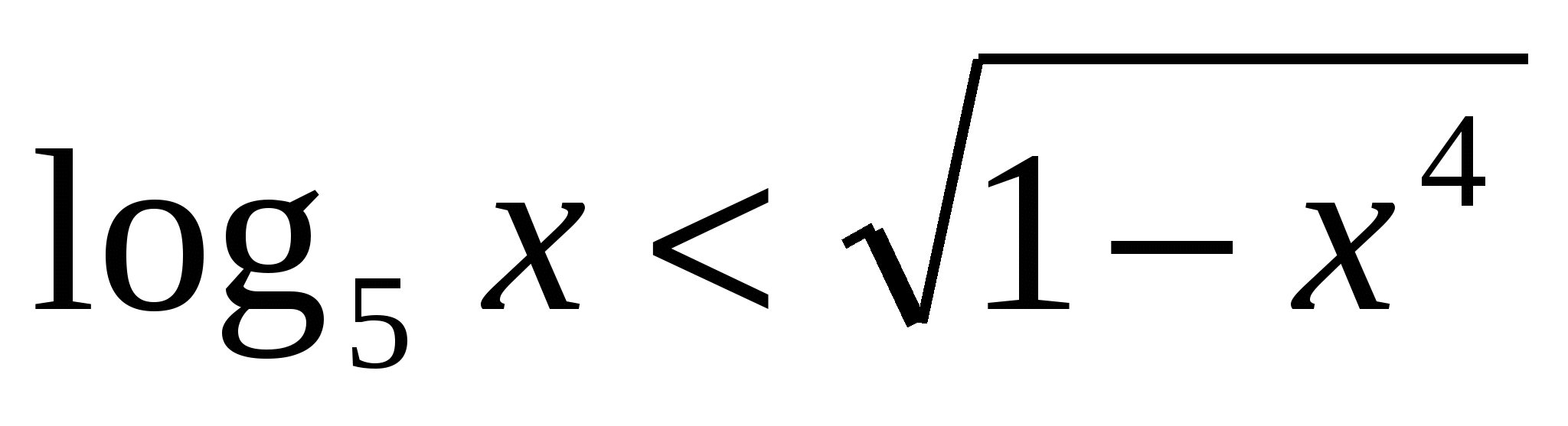 .
.
Решение. ОДЗ неравенства есть все х, удовлетворяющие условию 0<x≤1. Х=1 не является решением исходного неравенства. Для всех х из промежутка 0<x<1 имеем log5x<0, а 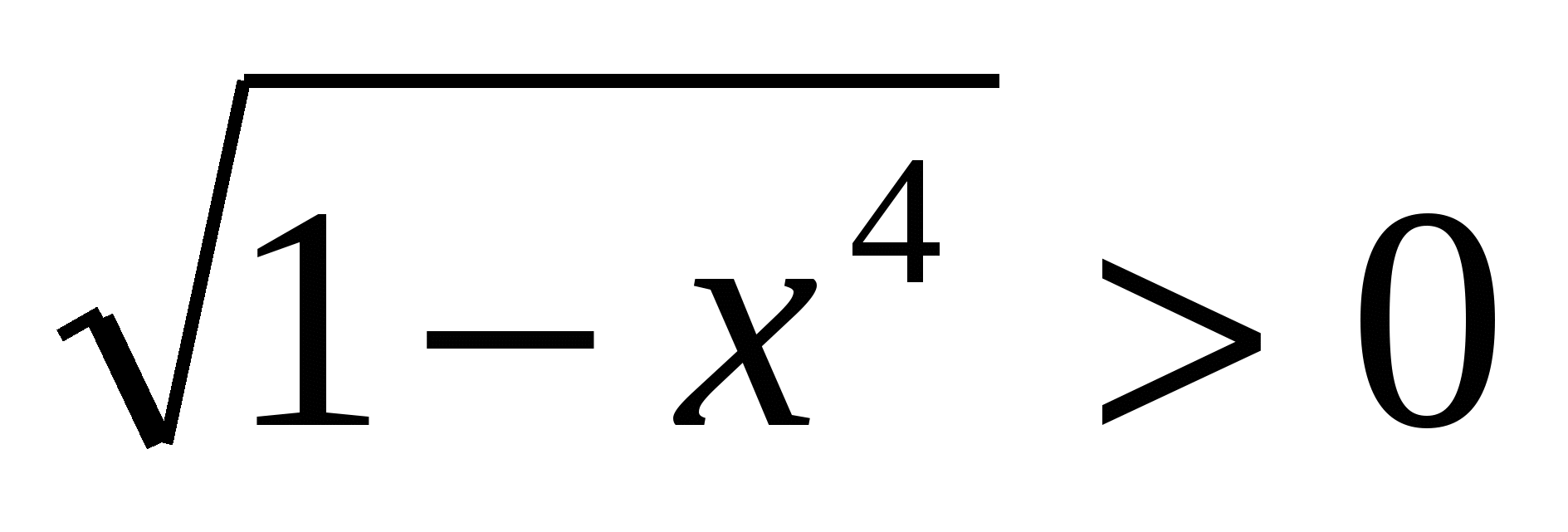 . Следовательно, все х из промежутка 0<x<1 являются решениями исходного неравенства.
. Следовательно, все х из промежутка 0<x<1 являются решениями исходного неравенства.
Пример 2.
log2(2x+1-x2)>log2(2x-1+1-x)+1.
Решение. Отыскание ОДЗ в данном случае - непростая задача, поэтому поступим иначе. Исходное неравенство равносильно системе неравенств
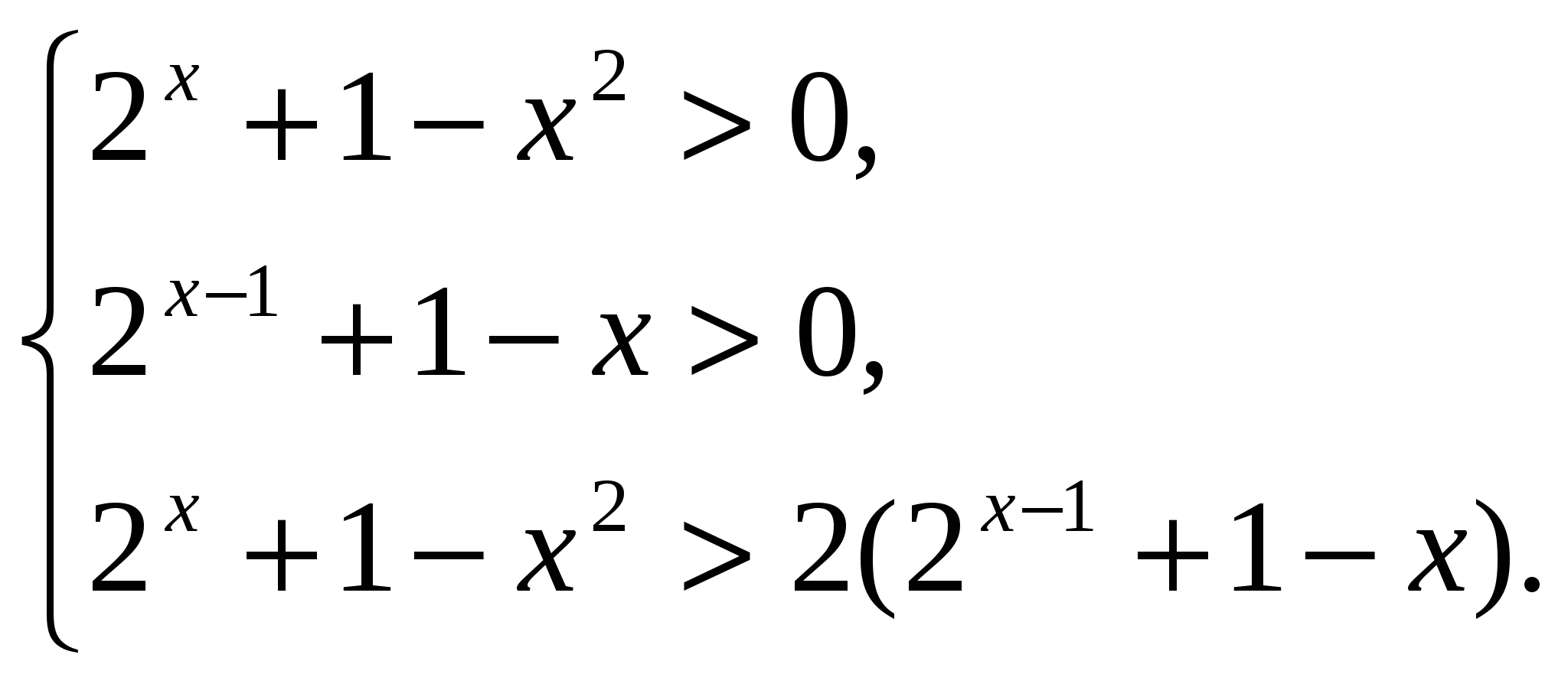
Последнее неравенство системы равносильно неравенству х2-2х+1<0, не имеющему решений. Следовательно, рассмотренная система неравенств не имеет решений, значит, и исходное неравенство не имеет решений.
Пример 3.
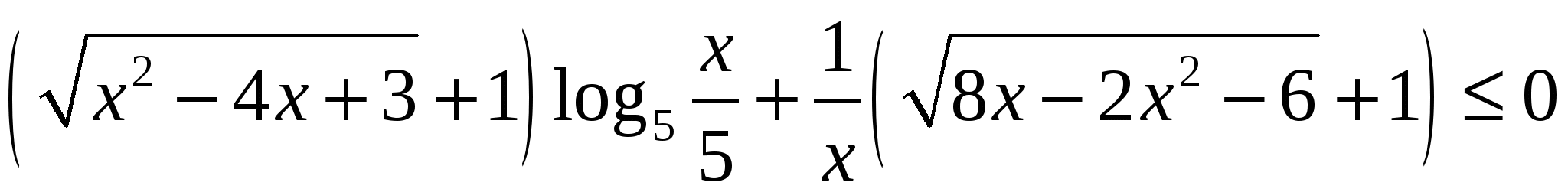 .
.
Ключевым моментом в решении данного неравенства является поиск его области определения.
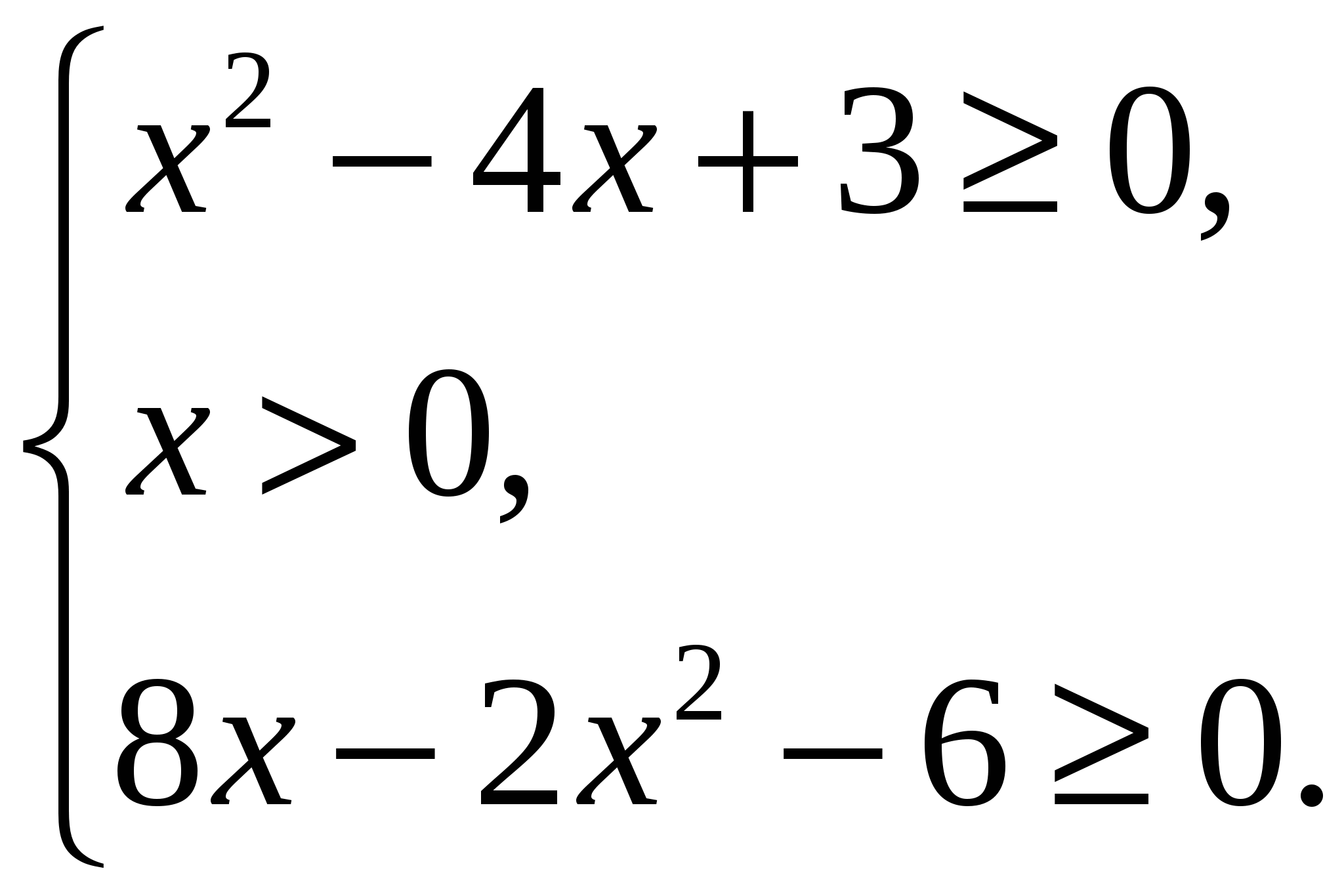
Решением данной системы являются два числа, ![]() и
и ![]() . Осталось подстановкой выяснить, какие из этих чисел удовлетворяют неравенству.
. Осталось подстановкой выяснить, какие из этих чисел удовлетворяют неравенству.
1. При 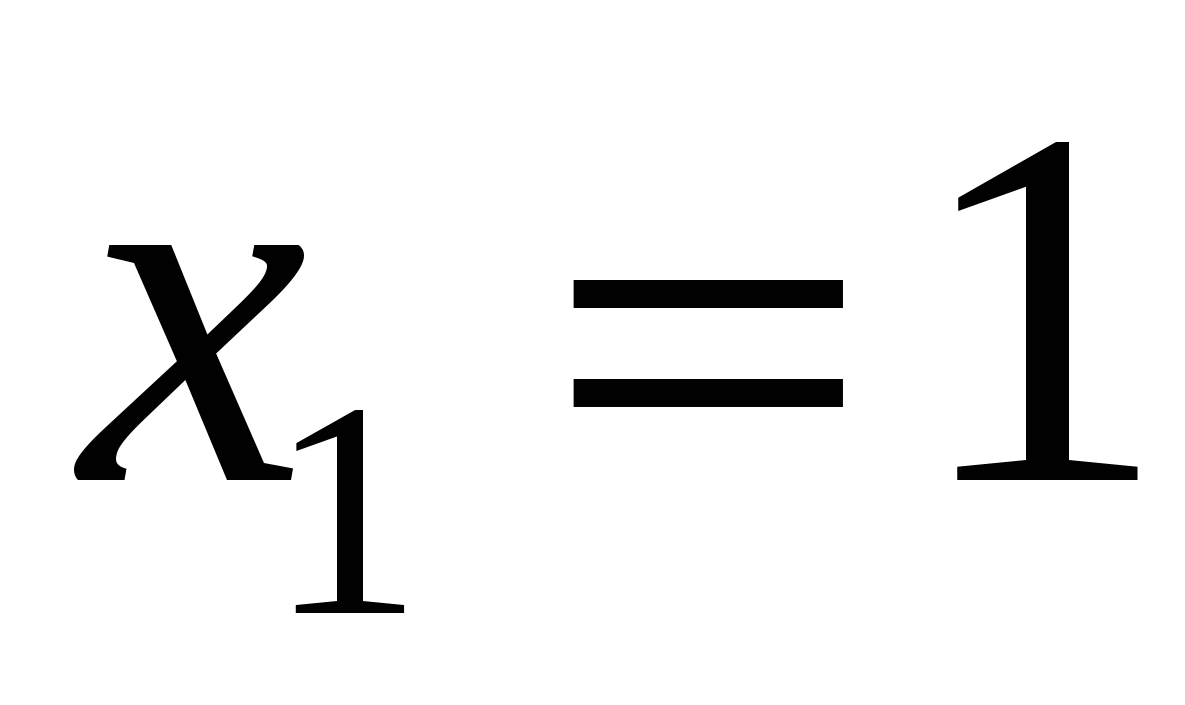 неравенство принимает вид:
неравенство принимает вид: 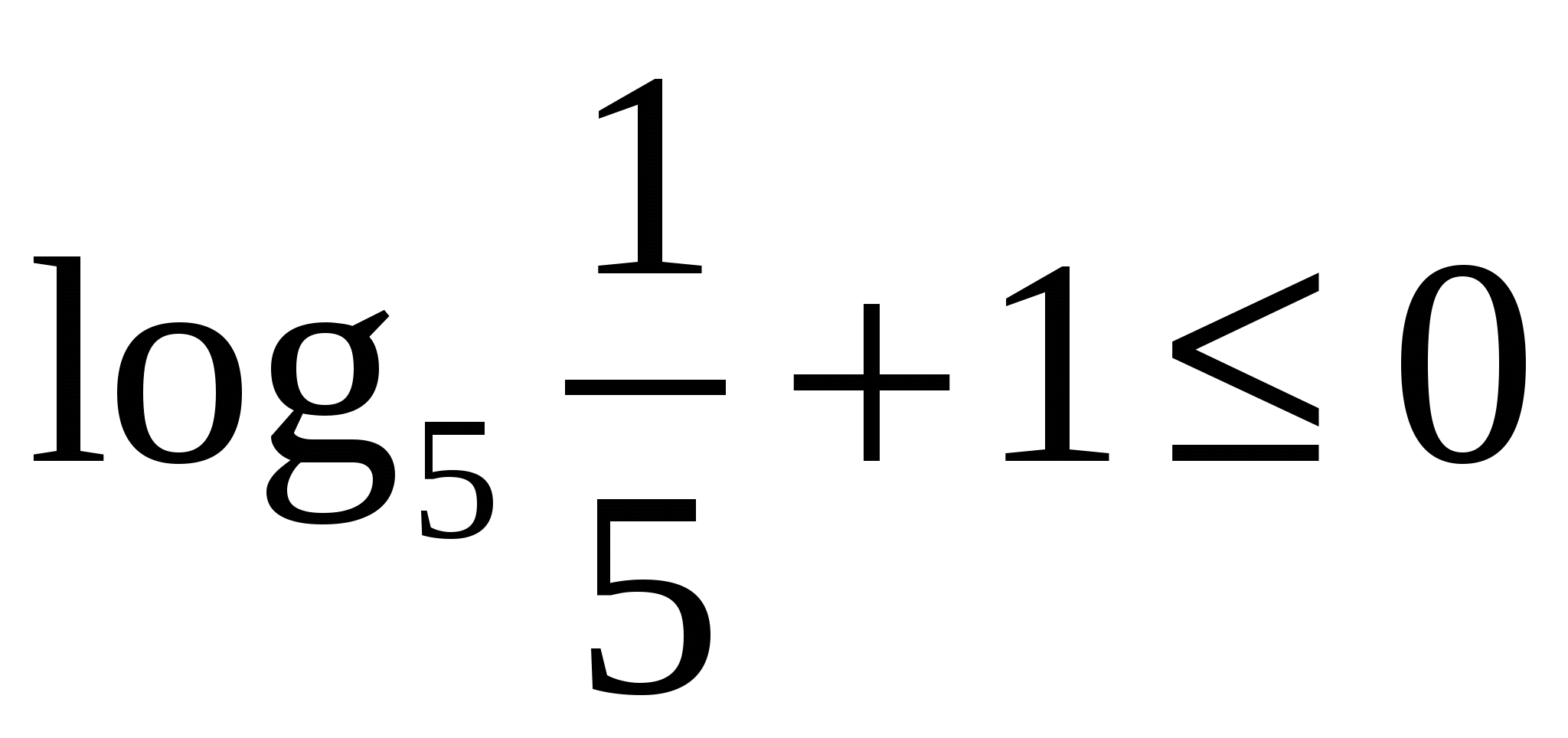 - истинно.
- истинно.
2. При 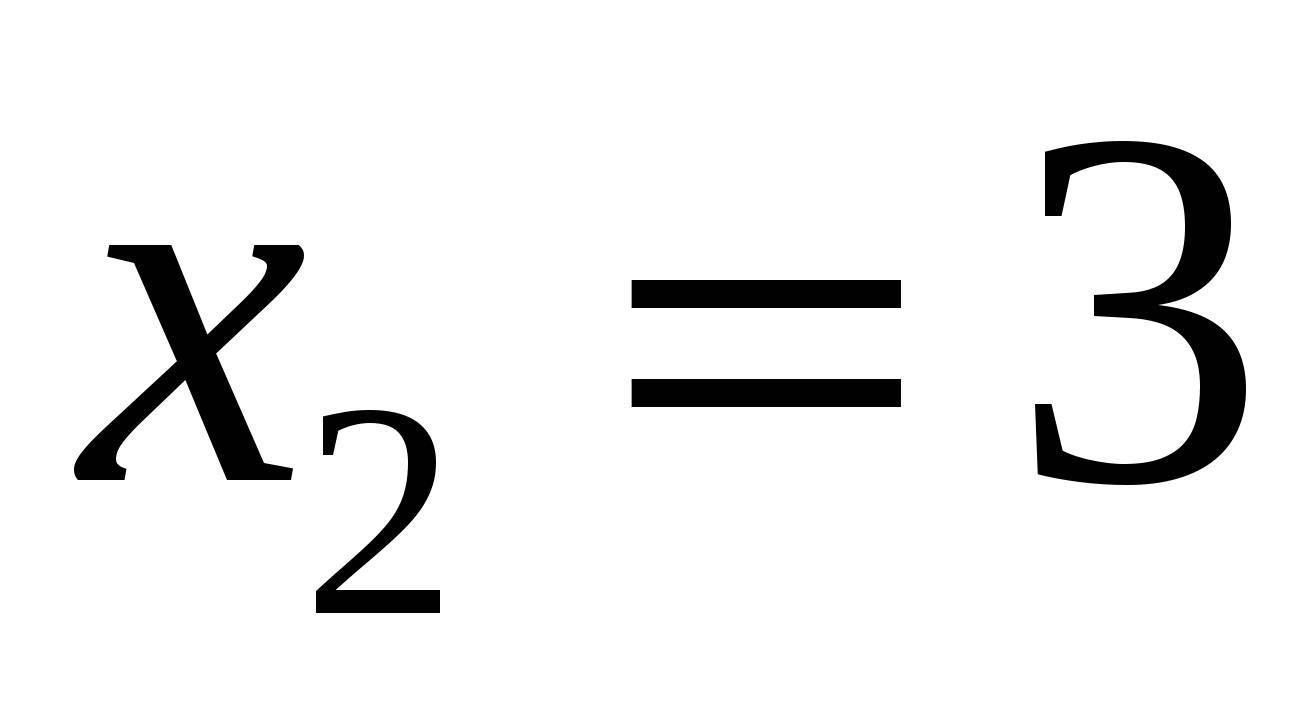 неравенство принимает вид:
неравенство принимает вид:  . Для установления истинности или ложности этого неравенства сделаем ряд преобразований:
. Для установления истинности или ложности этого неравенства сделаем ряд преобразований: 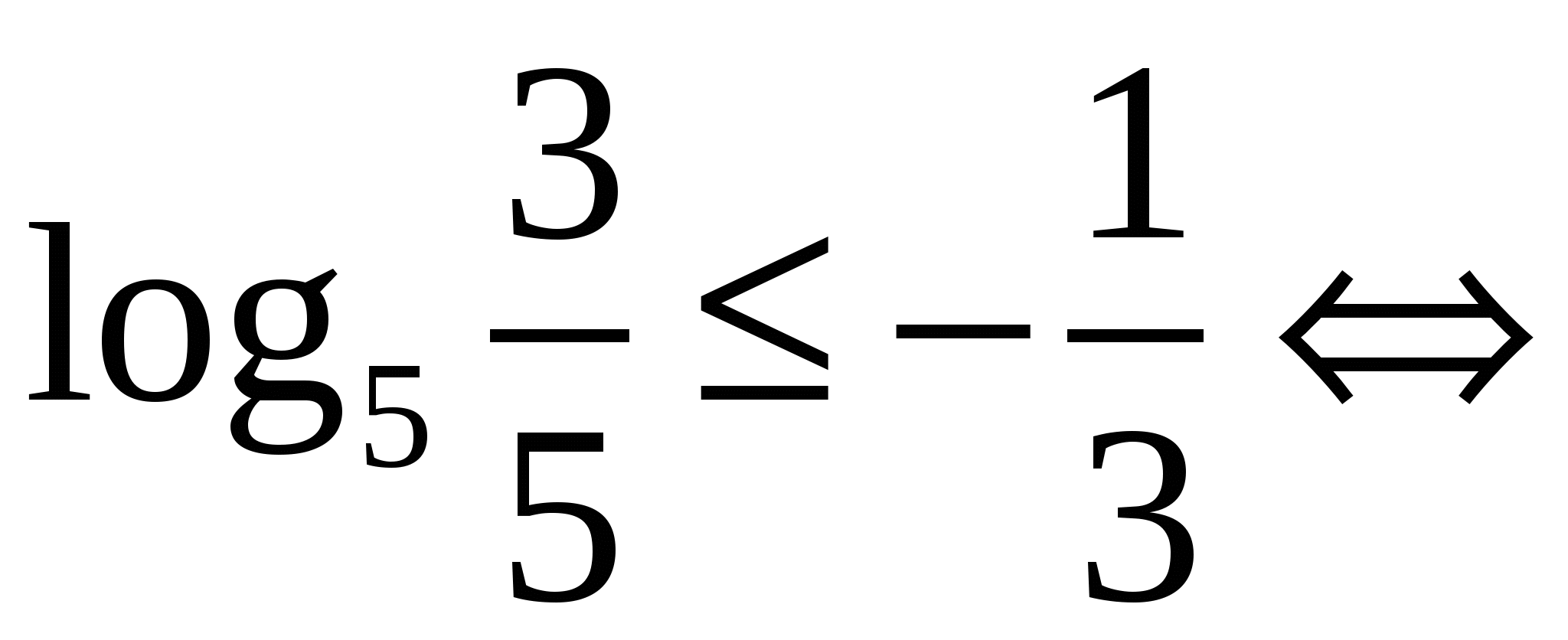
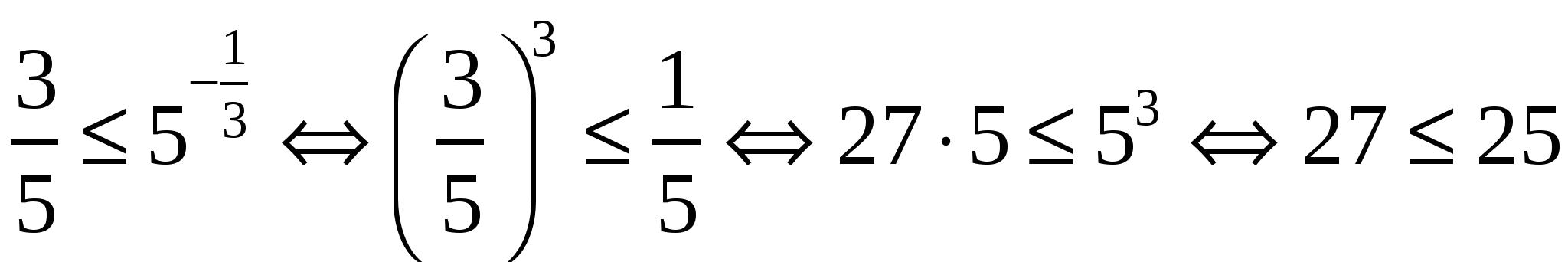 - ложно.
- ложно.
Ответ: 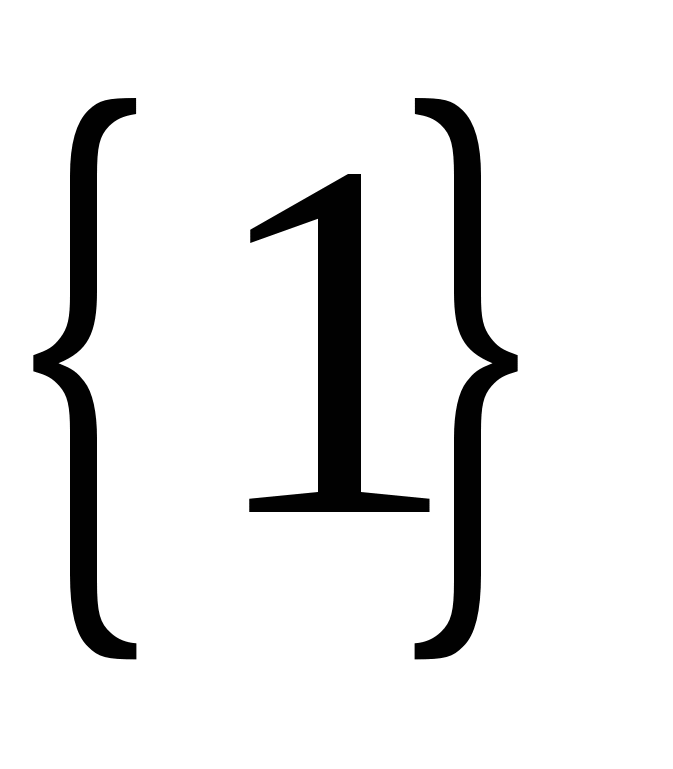 .
.
Пример 4.
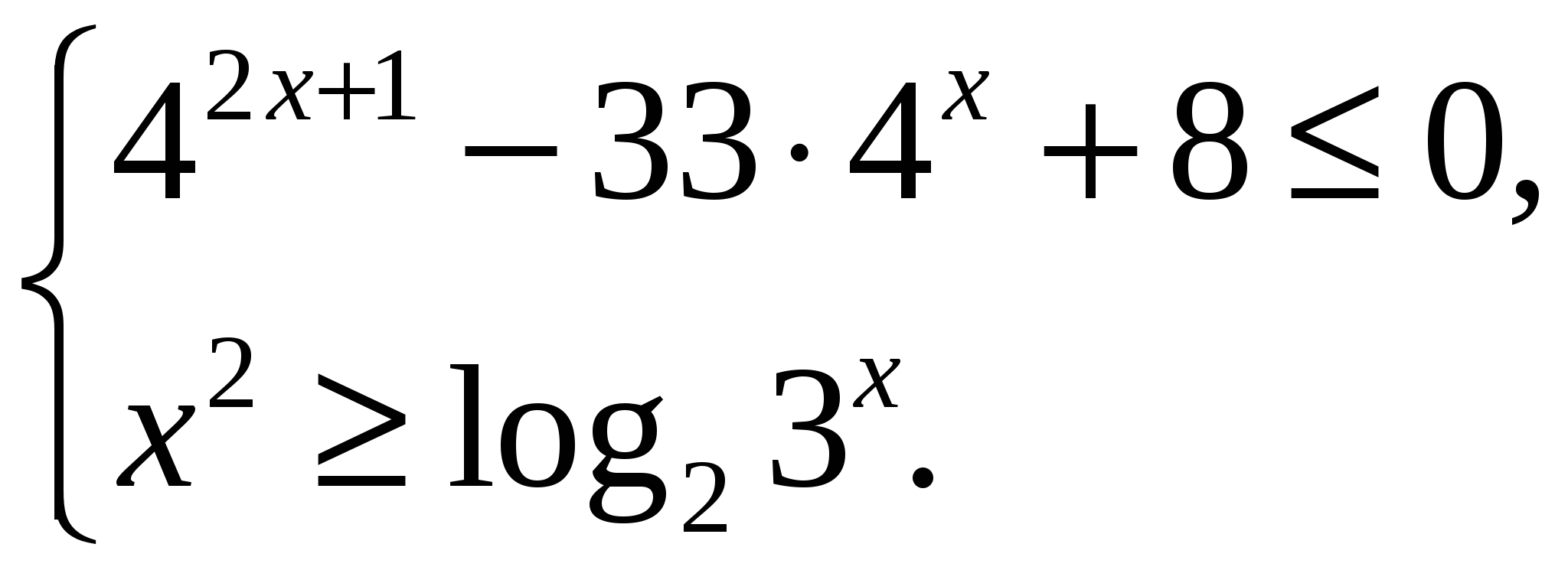
Решение систем по технике решения не отличается от решения неравенств. Однако иногда возникают трудности с ответом, основанные на сравнении чисел.
Опустив решение каждого из неравенств, приведем только множества их решений. Первое  , второе
, второе ![]() . Для нахождения пересечения этих множеств надо сравнить два числа
. Для нахождения пересечения этих множеств надо сравнить два числа ![]() и
и ![]() .
.
При затруднениях в сравнении двух чисел обычно используют два приема. Во-первых, можно составить разность этих чисел и преобразовать ее до вида, из которого очевиден ее знак. Во-вторых, иногда можно найти граничное число такое, что одно из чисел больше граничного, а другое меньше.
Воспользуемся первым вариантом. Разность  . Заметим, что число
. Заметим, что число 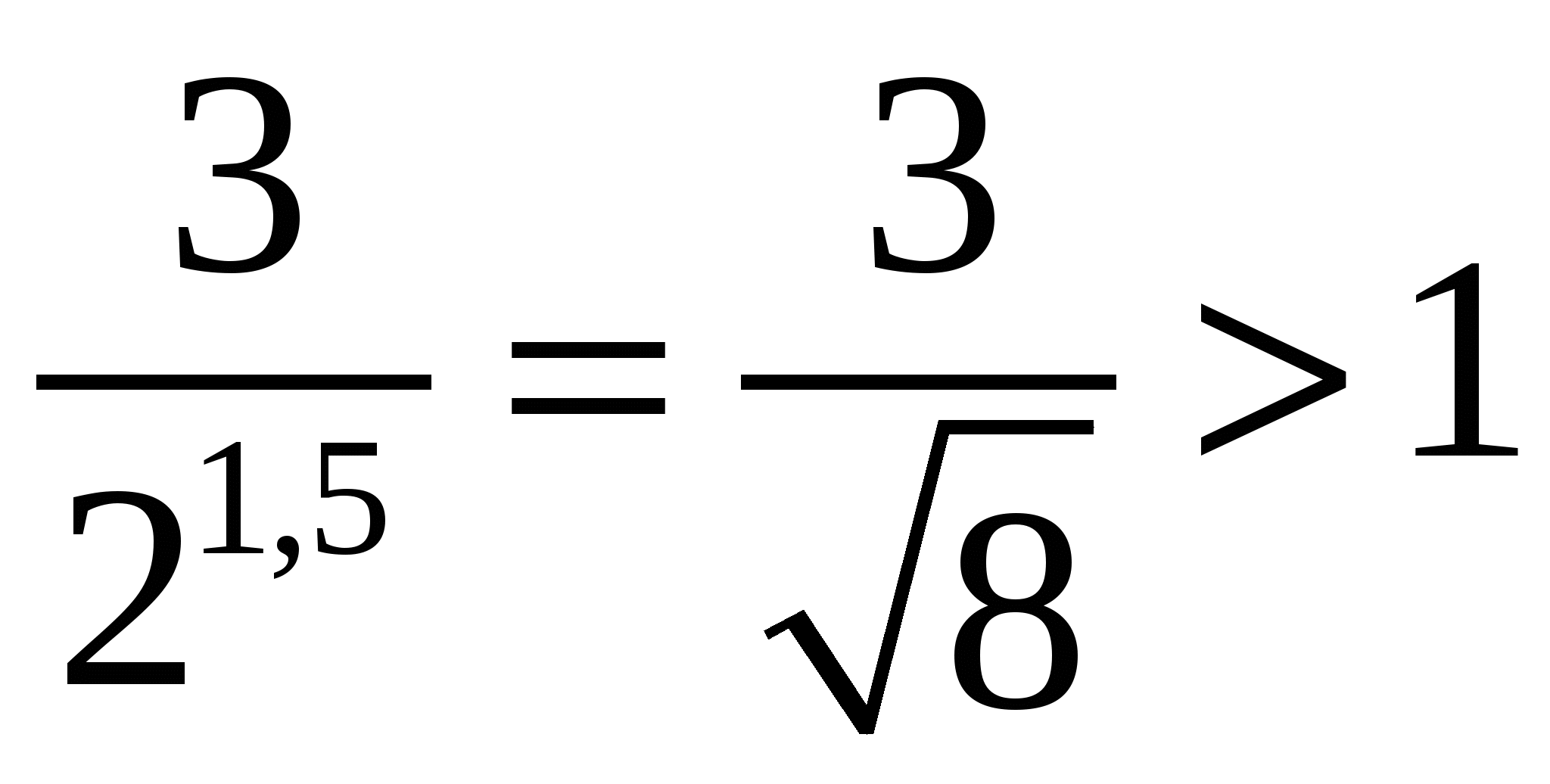 , следовательно,
, следовательно, 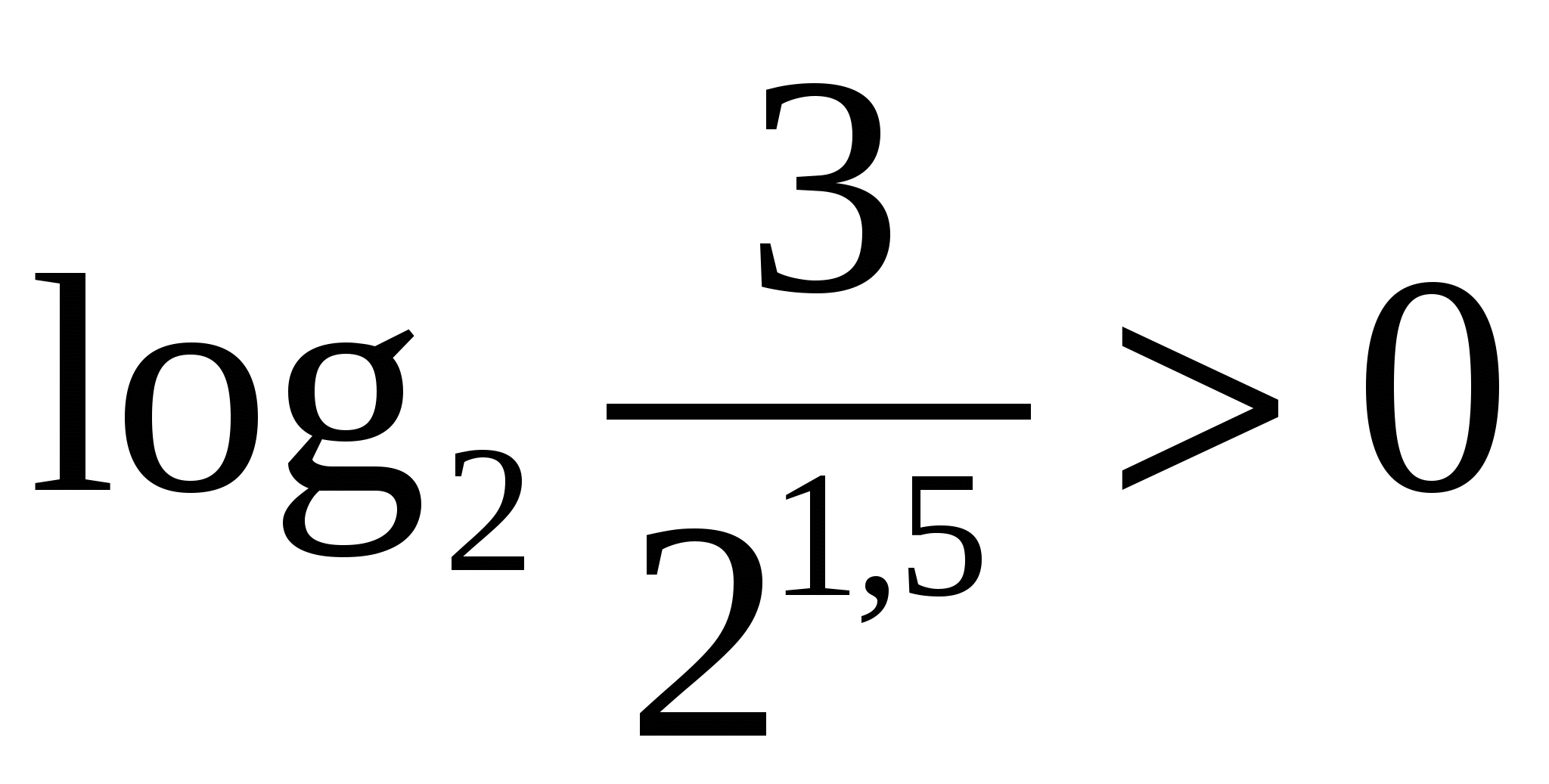 и
и 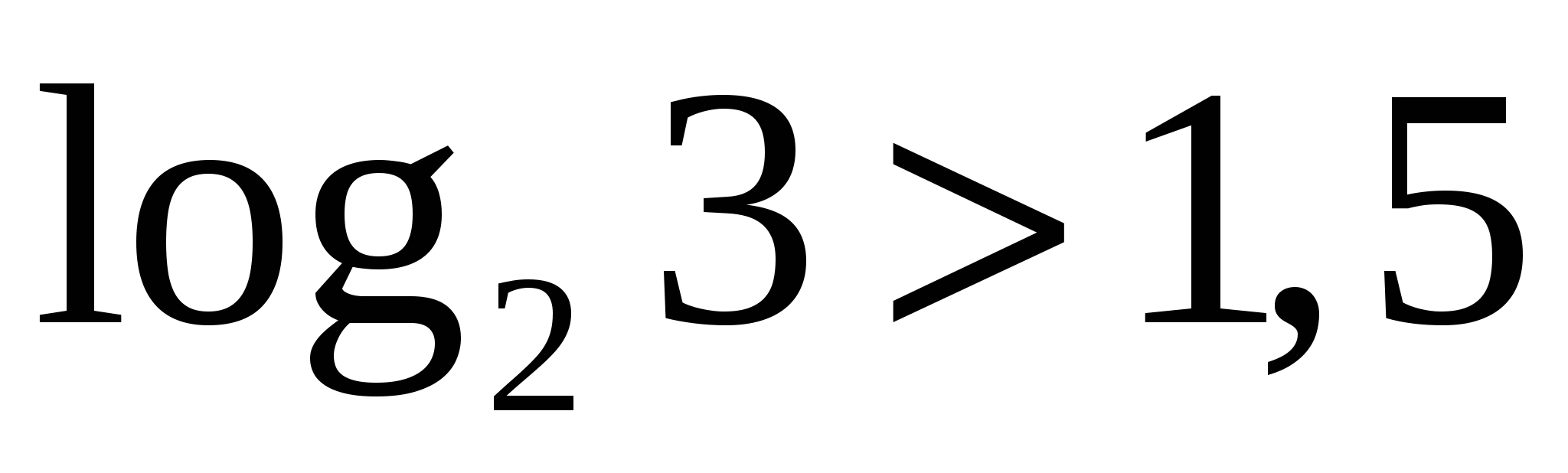 .
.
Ответ: 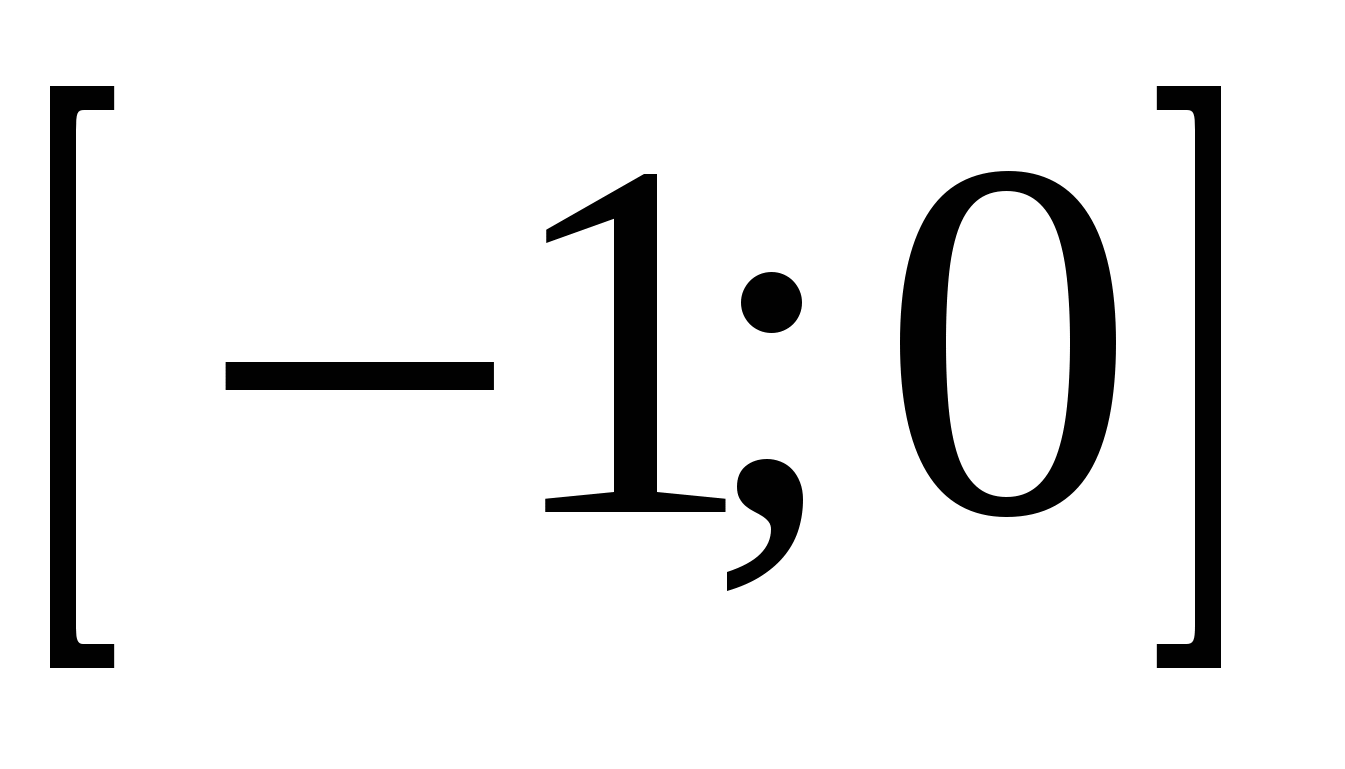 .
.
Пример 5.
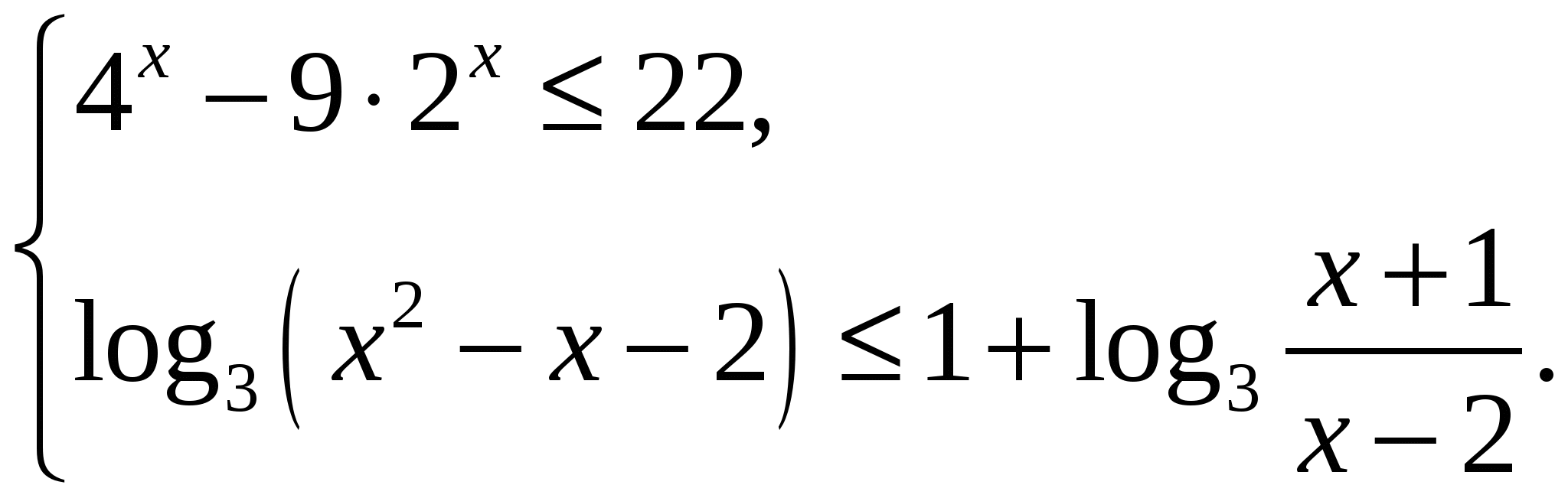
Решением первого неравенства является множество ![]() . Второе неравенство сводится к виду
. Второе неравенство сводится к виду  . Решение неравенства с учетом ОДЗ
. Решение неравенства с учетом ОДЗ 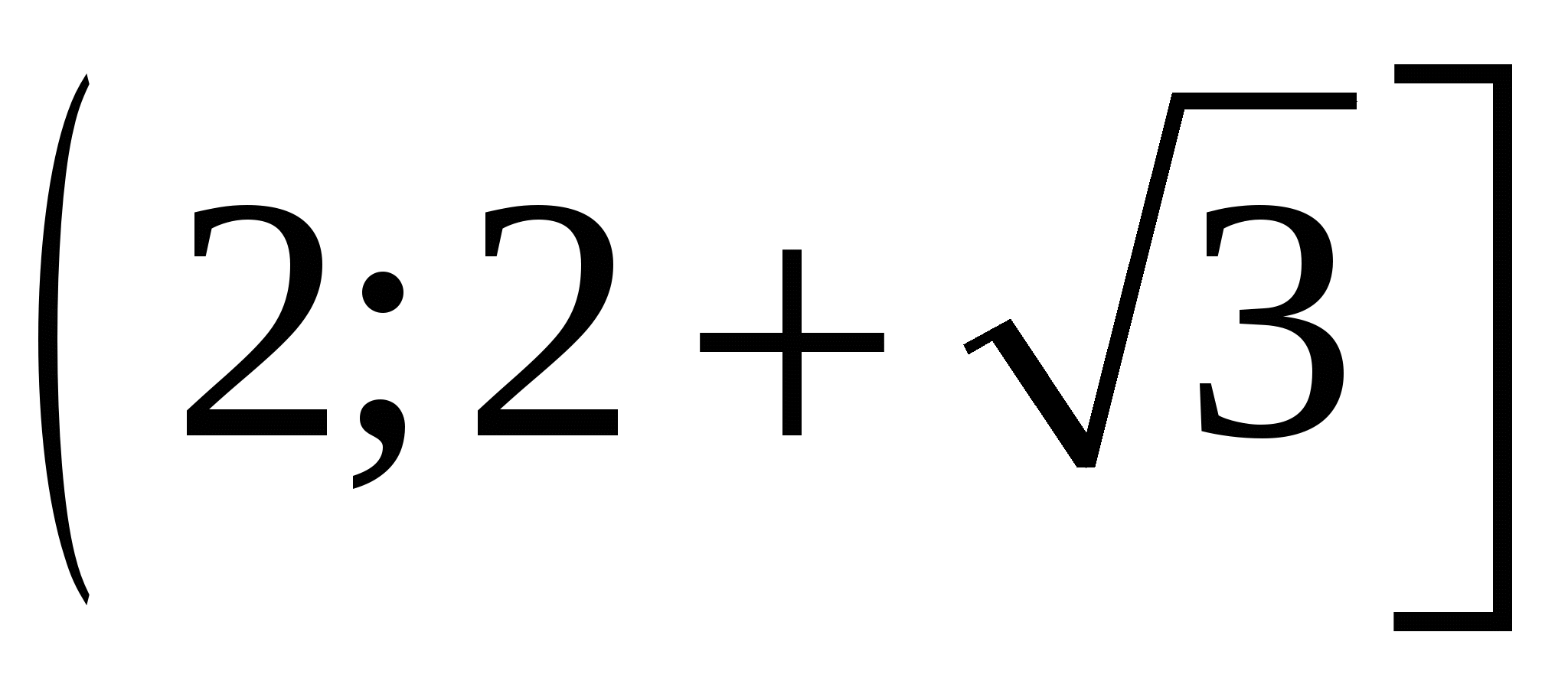 . Чтобы найти пересечение множеств необходимо сравнить два числа
. Чтобы найти пересечение множеств необходимо сравнить два числа 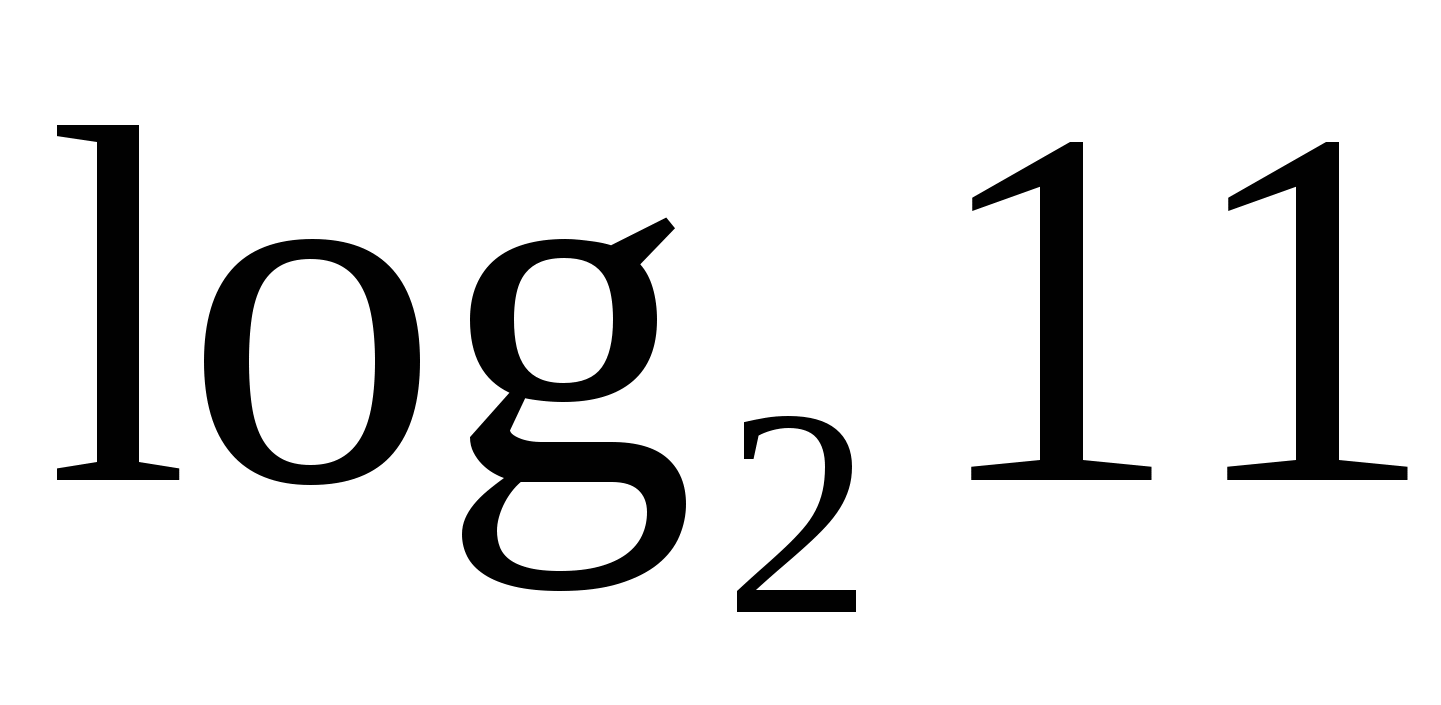 и
и 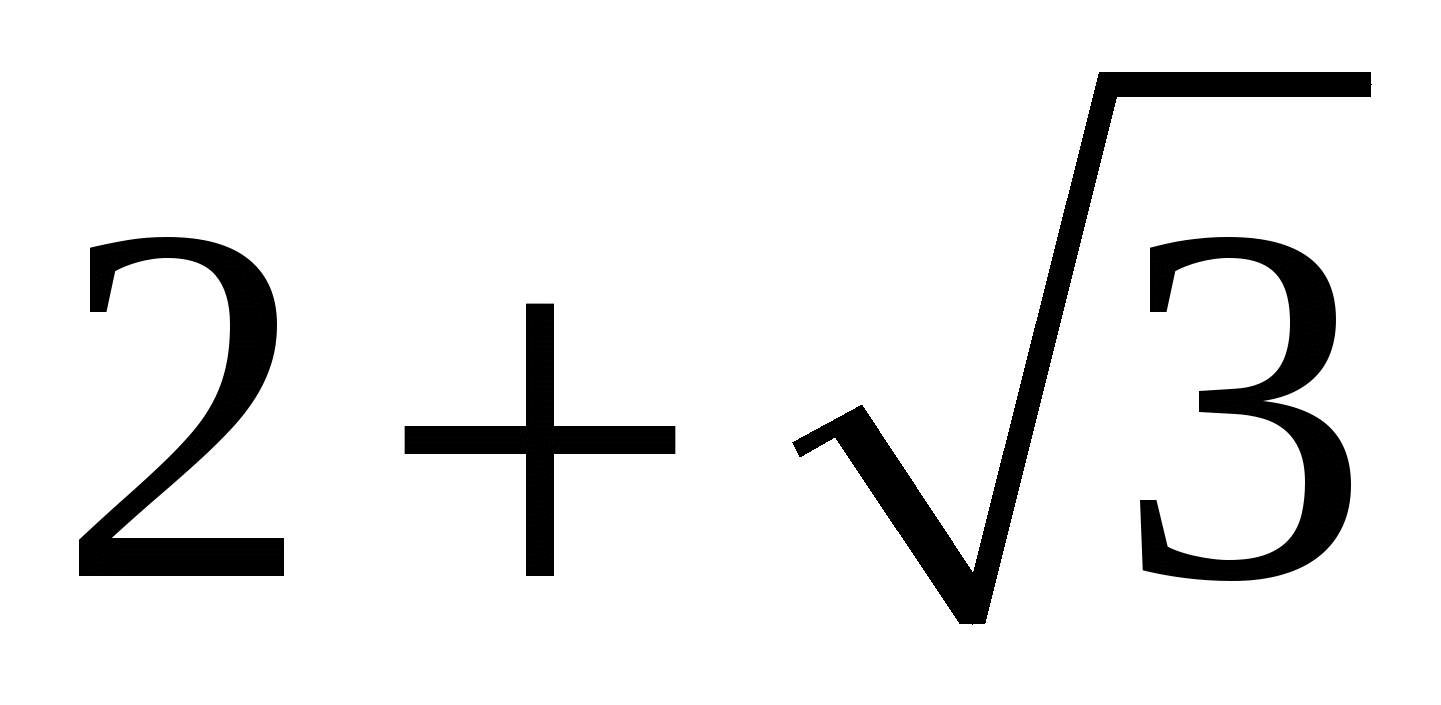 . В данном случае можно заметить, что число
. В данном случае можно заметить, что число 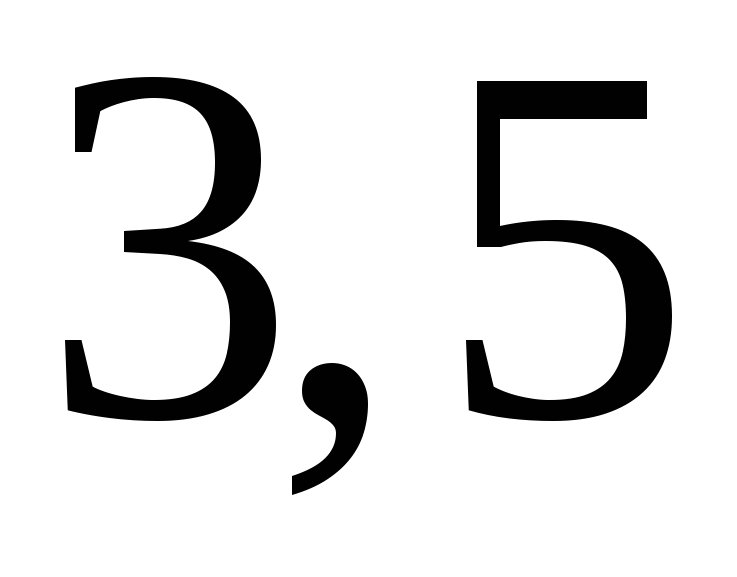 находится между этими числами. Почему именно
находится между этими числами. Почему именно 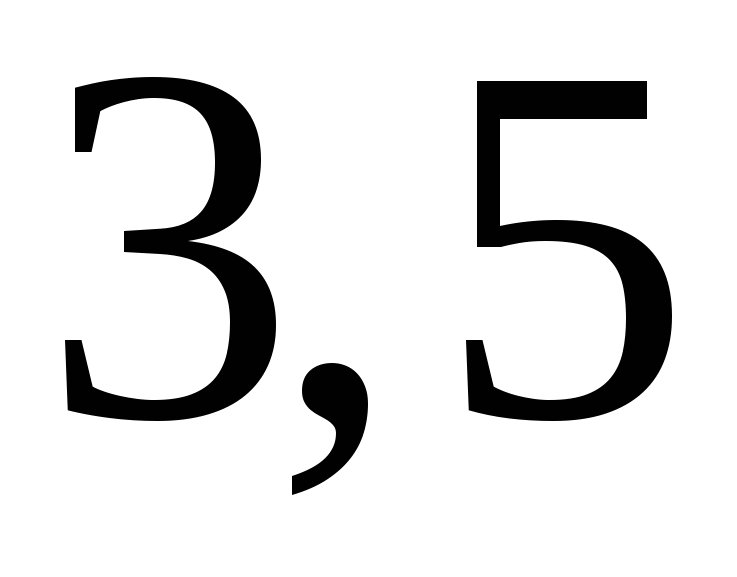 ? Дело в том, что второе число с очевидностью больше чем
? Дело в том, что второе число с очевидностью больше чем 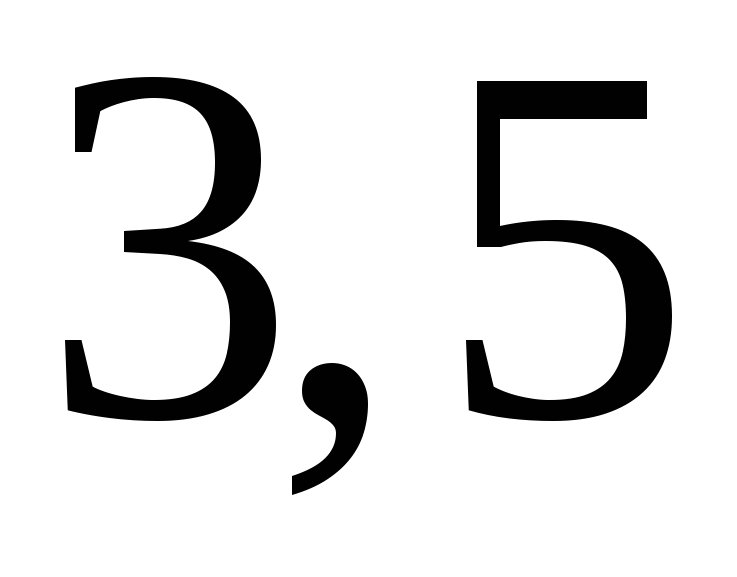 , т.к.
, т.к. ![]() . Первое число находится между
. Первое число находится между 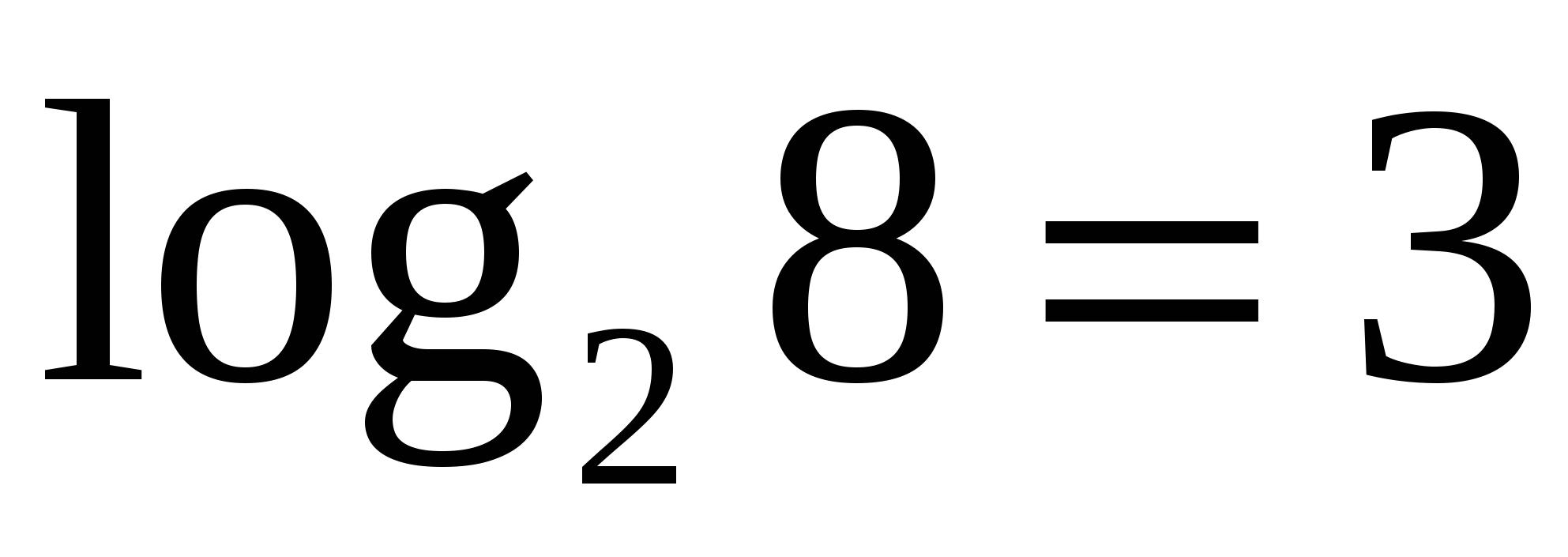 и
и 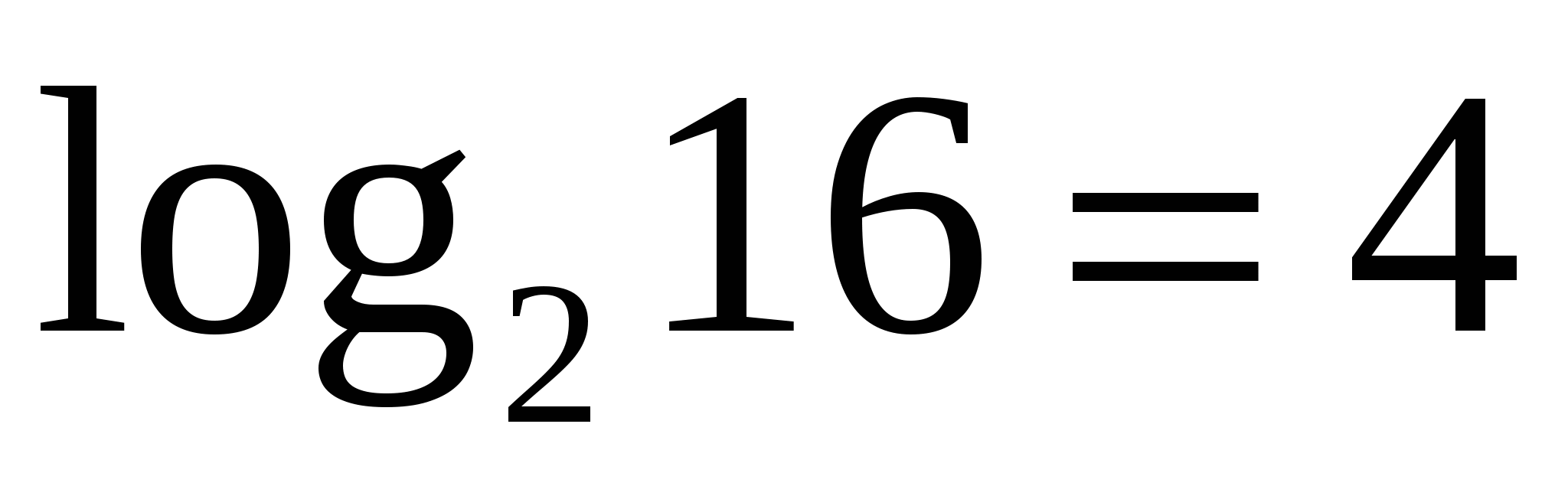 , но ближе к
, но ближе к ![]() . Строго доказать, что
. Строго доказать, что 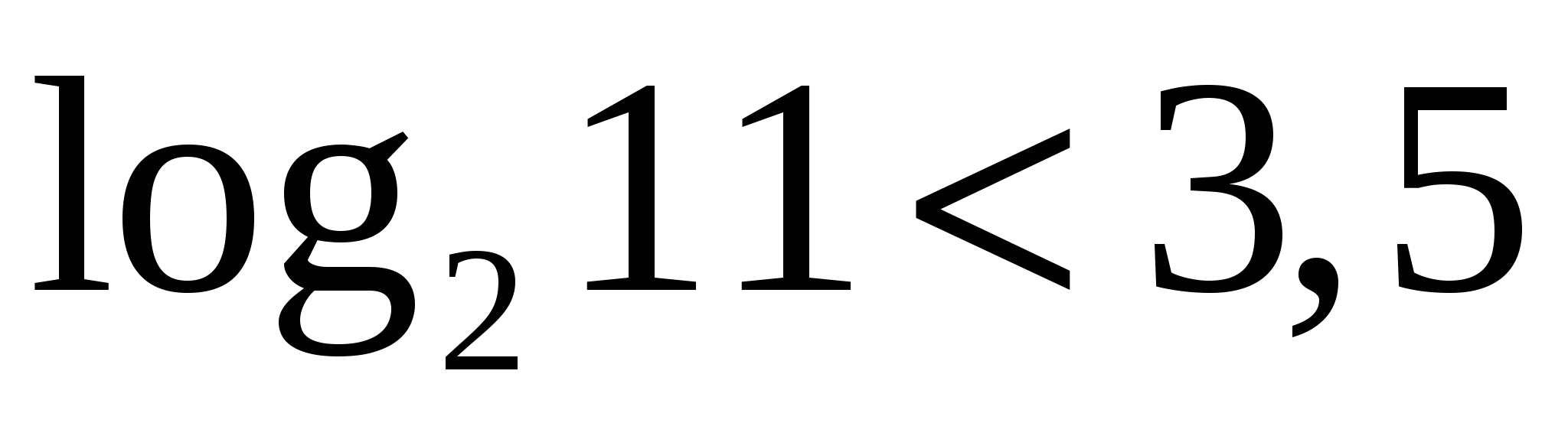 , можно составив разность
, можно составив разность 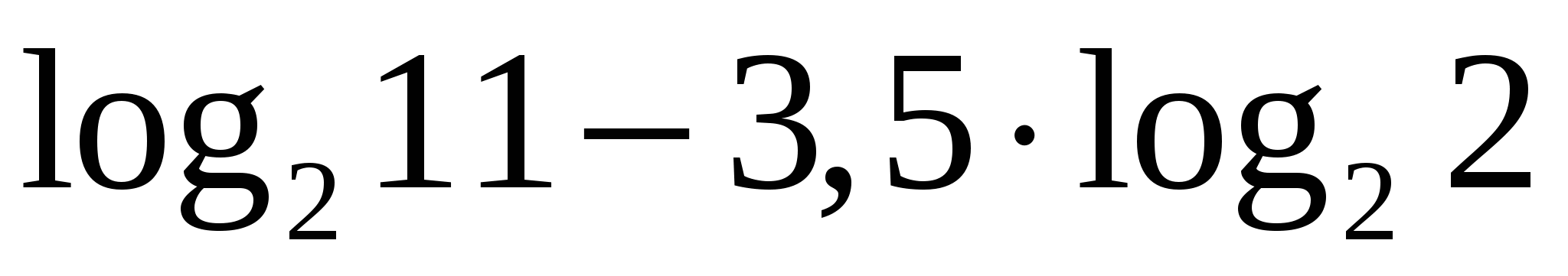 и преобразовав ее к виду
и преобразовав ее к виду 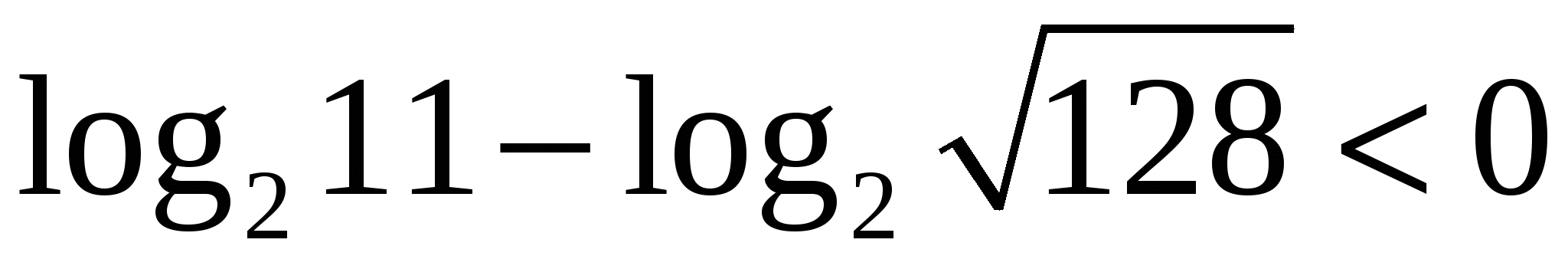 . Ответ:
. Ответ: ![]()
Заключение
Было не просто найти из большого обилия разных учебных источников особые методы решения задач С3. В ходе проделанной работы мне удалось изучить нестандартные методы решения сложных логарифмических неравенств. Это: равносильные переходы и обобщённый метод интервалов, метод рационализации, нестандартная подстановка, задания с ловушками на ОДЗ. В школьной программе эти методы отсутствуют.
Разными методами я решил 27 неравенств, предлагаемых на ЕГЭ в части С, а именно С3. Эти неравенства с решениями по методам легли в основу сборника «Логарифмические неравенства С3 с решениями», который стал проектным продуктом моей деятельности. Гипотеза, поставленная мною вначале проекта, подтвердилась: задачи С3 можно эффективно решать, зная эти методы.
Кроме этого, я выявил интересные факты логарифмов. Мне это было интересно делать. Мои проектные продукты будут полезны как для учащихся, так и для учителей.
Выводы:
Таким образом, поставленная цель проекта достигнута, проблема решена. А я получил наиболее полный и разносторонний опыт проектной деятельности на всех этапах работы. В ходе работы над проектом у меня основное развивающее воздействие было оказано на мыслительную компетентность, деятельность, связанную с логическими мыслительными операциями, развитие творческой компетентности, личной инициативы, ответственности, настойчивости, активности.
Гарантией успеха при создании исследовательского проекта для меня стали: значительный школьный опыт, умение добывать информацию из различных источников, проверять ее достоверность, ранжировать ее по значимости.
Кроме непосредственно предметных знаний по математике, расширил свои практические навыки в области информатики, получил новые знания и опыт в области психологии, наладил контакты с одноклассниками, научился сотрудничать с взрослыми людьми. В ходе проектной деятельности развивались организационные, интеллектуальные и коммуникативные общеучебные умения и навыки.
Литература
1. Корянов А. Г. ,Прокофьев А. А. Системы неравенств с одной переменной (типовые задания С3).
2. Малкова А. Г. Подготовка к ЕГЭ по математике.
3. Самарова С. С. Решение логарифмических неравенств.
4. Математика. Сборник тренировочных работ под редакцией А.Л. Семёнова и И.В. Ященко. -М.: МЦНМО, 2009. - 72 с.-
5. Математика . Тематические тесты. Часть 2. Подготовка к ЕГЭ -2010.10-11 классы /
Ф. Ф. Лысенко. - Ростов-на-Дону: Легион, 2009. - 176 с. - (Готовимся к ЕГЭ )
6.Самое полное издание типовых вариантов реальных заданий ЕГЭ : 2010: Математика /авт.-сост. И.Р. Высоцкий, Д.Д. Гущин, П.И. Захаров и др.;
7.ЯщенкоИ.В.,ШестаковС.А.,ЗахаровП.И.Подготовка к ЕГЭ по математике в 2010 году. Методические рекомендации.
8.Универсальные материалы для подготовки учащихся / ФИПИ - М: Интеллект-Центр, 2010. - 96 с. (Под редакцией А. Л. Семенова и И. В. Ященко).
9. Сайт Дмитрия Гущина «РЕШУ ЕГЭ».


