- Преподавателю
- Математика
- Методические указания Приложения определенного интеграла
Методические указания Приложения определенного интеграла
| Раздел | Математика |
| Класс | - |
| Тип | Другие методич. материалы |
| Автор | Лещенко М.Ю. |
| Дата | 27.10.2014 |
| Формат | doc |
| Изображения | Есть |
Математика
Приложения определённого интеграла
Учебно-методическое пособие
Содержание
Введение……………………………………………………………………………...3
1. Приложение определённого интеграла к геометрическим задачам…………...4
1.1. Вычисление площадей плоских фигур………………………………………...4
1.2. Вычисление объёмов тел вращения…………………………………………..11
2. Применения определенного интеграла к решению физических и технических задач…………………………………………………………………………………16
2.1. Путь, пройденный телом……………………………………………………...16
2.2. Работа переменной силы……………………………………………………....16
2.3. Вычисление силы давления жидкости……………………………………….17
Ответы………………………………………………………………………………22
Литература…………………………………………………………………………..23
Введение
Дифференциальное и интегральное исчисления были созданы в XVII столетии Исааком Ньютоном и И.В. Лейбницем. Толчком к их созданию послужили проблемы механики, физики, астрономии и других разделов естествознания того времени.
Создание интегрального и дифференциального исчислений открыло новую эпоху в развитии математики, дало возможность изучать процессы и явления, которые невозможно было рассматривать раньше. Значение этого открытия трудно преувеличить: без него не было бы ни современной физики, ни механики, ни современной техники. Во всех отраслях современной науки и техники, где нужны точные методы исследования, используются производные и интегралы.
Настоящее учебно-методическое пособие посвящено изучению приложений определённого интеграла - одного из важнейших и эффективнейших орудий математики в решении практических проблем.
Цель этого пособия - сформировать у учащихся умение решать задачи прикладного характера.
Методические пособие состоит из двух разделов:
-
Приложение определенного интеграла к геометрическим задачам.
-
Применения определенного интеграла к решению физических и технических задач.
Каждый из разделов содержит теоретические сведения по рассматриваемому вопросу, образцы решения задач и упражнения для самостоятельной работы с ответами. Задачи повышенной сложности помечены звездочками.
Нумерация формул, примеров, рисунков и упражнений двойная. Первое число показывает номер раздела, а второе номер формулы, примера, рисунка и упражнения в данном разделе.
Например: формула (2.3) - это третья формула второго раздела.
Методическое пособие содержит задачи для индивидуальной работы по вариантам двух уровней сложности: А, Б (для дифференцированного контроля знаний). Уровень А включает задачи среднего уровня сложности, уровень Б - более сложные задачи.
Данное учебно-методическое пособие предназначено для учащихся 11 классов, интересующихся математикой и собирающихся продолжить свое обучение в вузах.
1.Приложение определённого интеграла к геометрическим задачам
1.1. Вычисление площадей плоских фигур
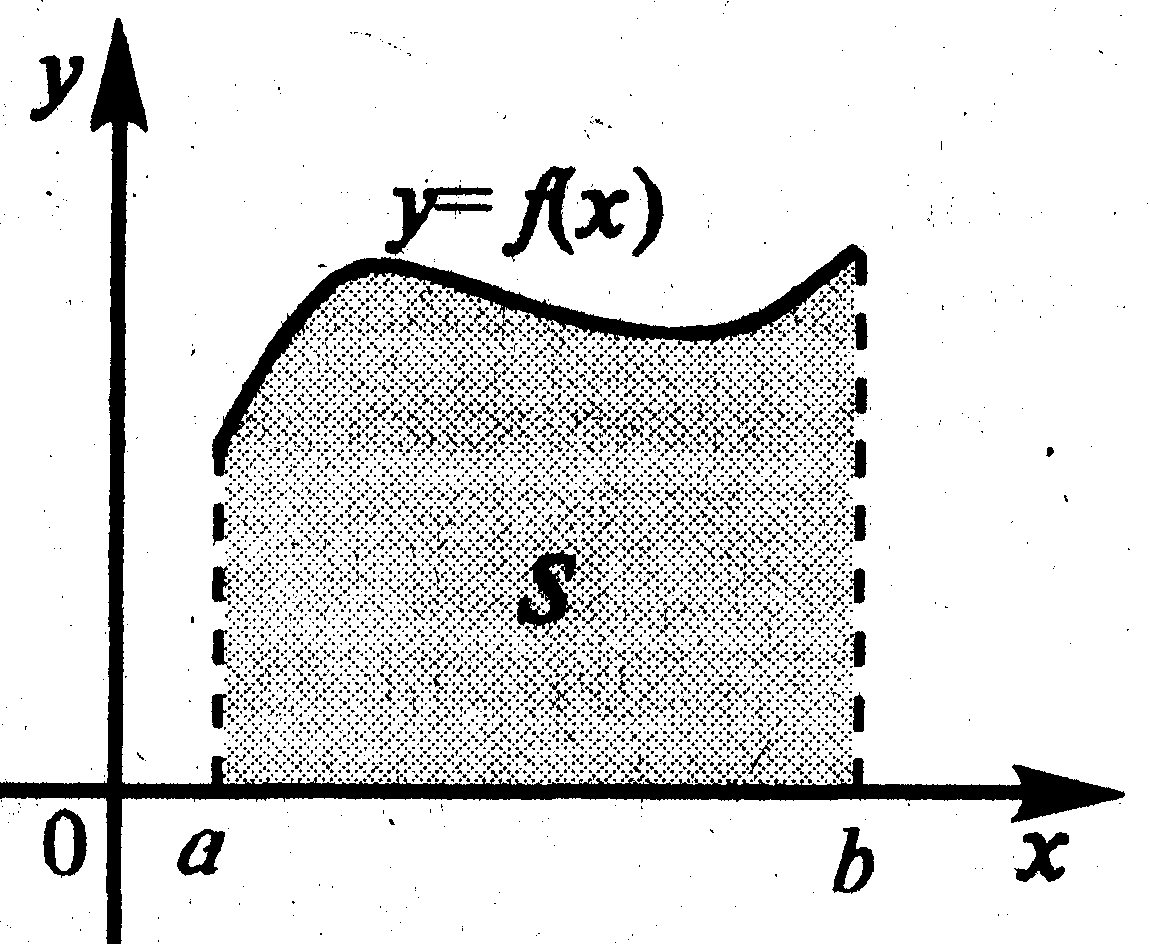
1. Пусть функция ![]() неотрицательна и непрерывна на отрезке
неотрицательна и непрерывна на отрезке 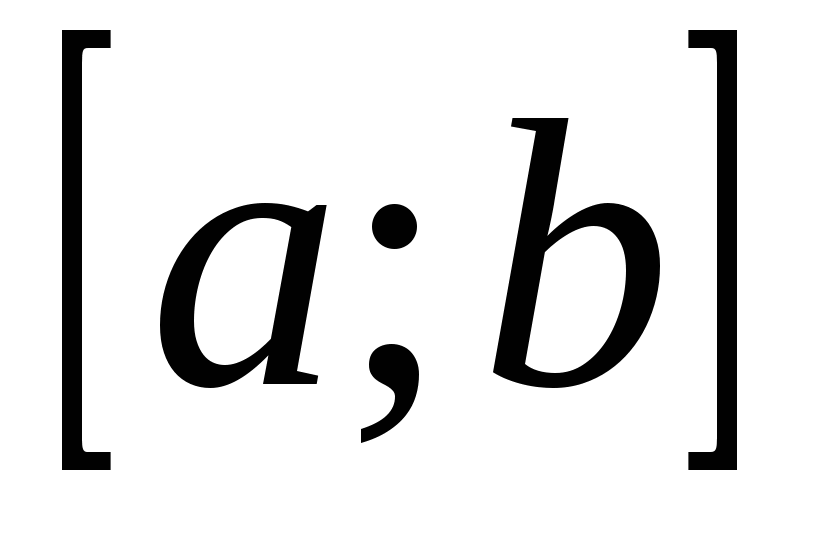 . Тогда по геометрическому смыслу определённого интеграла площадь S под кривой
. Тогда по геометрическому смыслу определённого интеграла площадь S под кривой 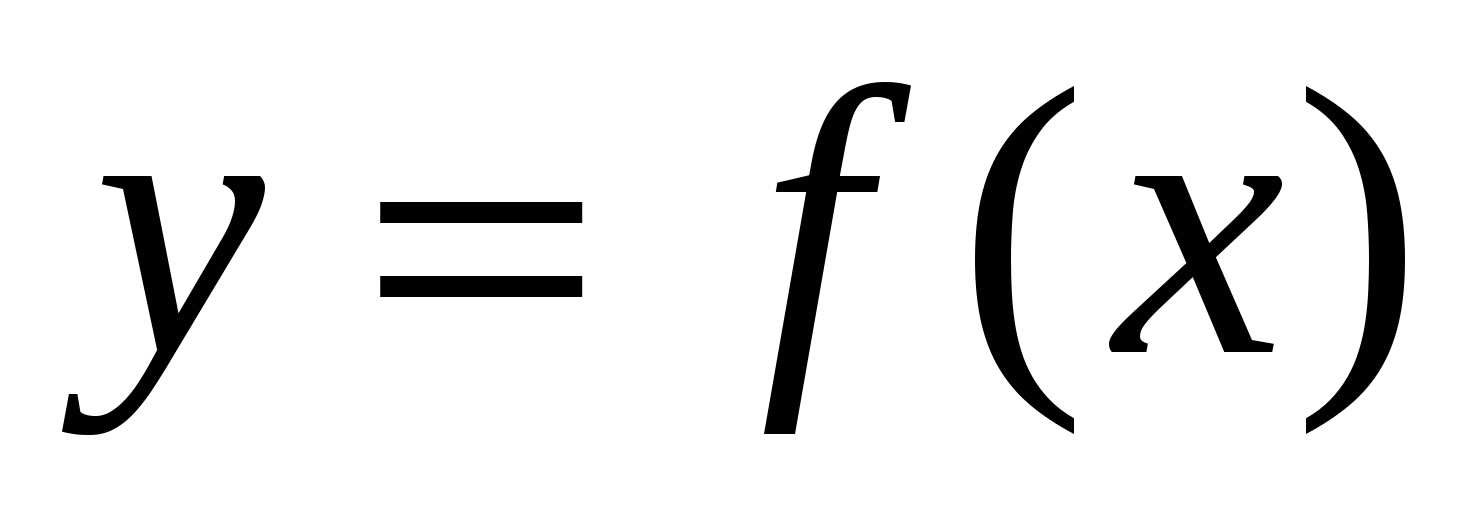 на
на 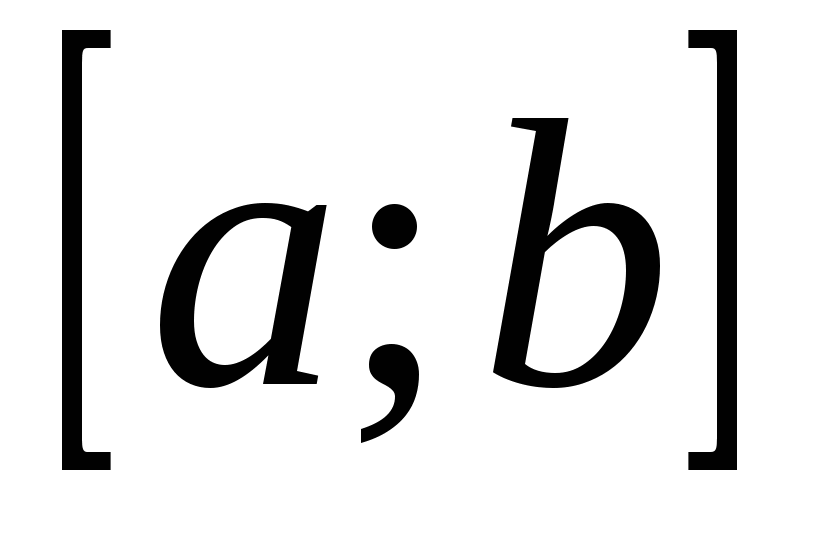 (см. рис 1.1) численно равна определённому интегралу
(см. рис 1.1) численно равна определённому интегралу 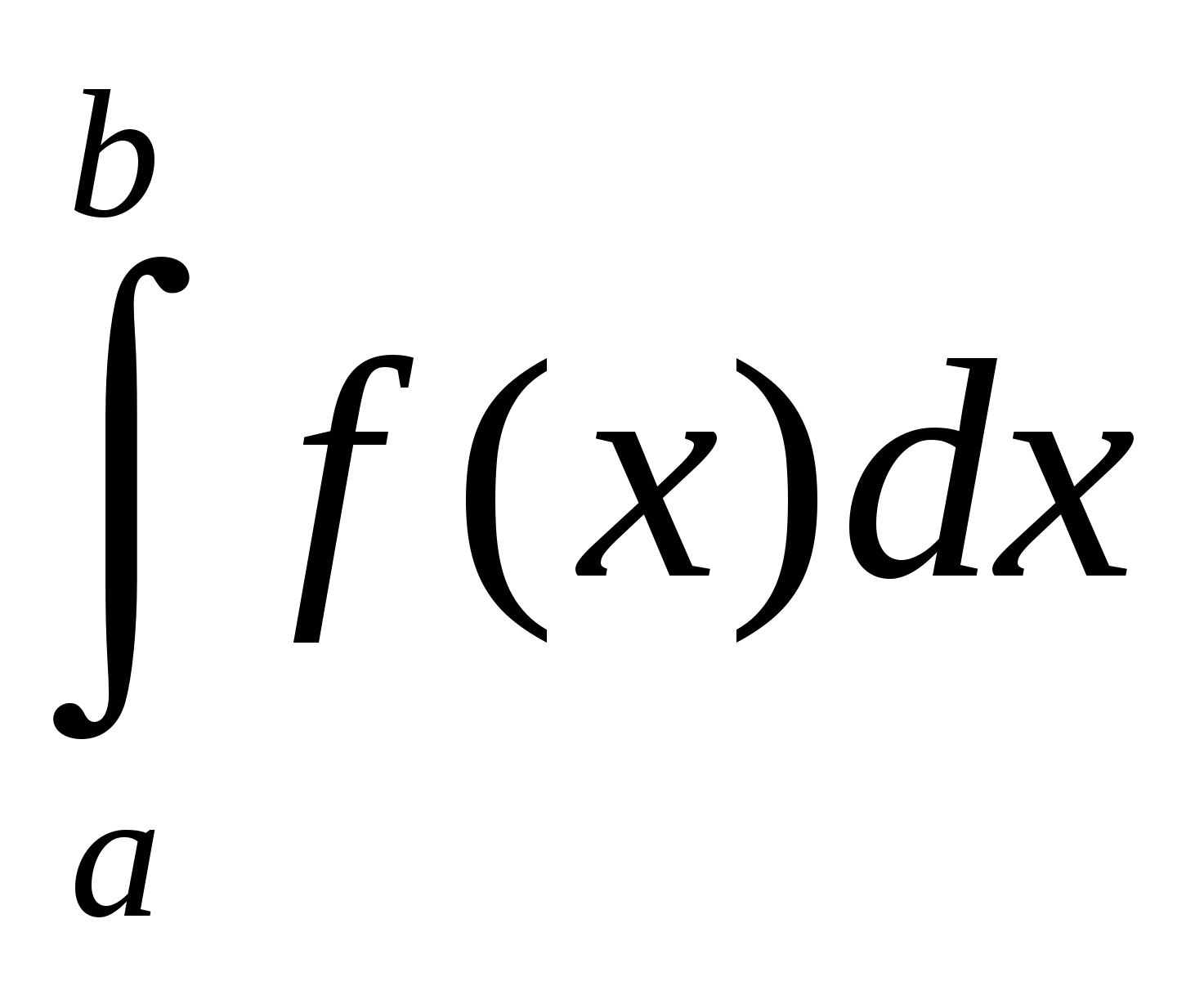 , т. е.
, т. е. 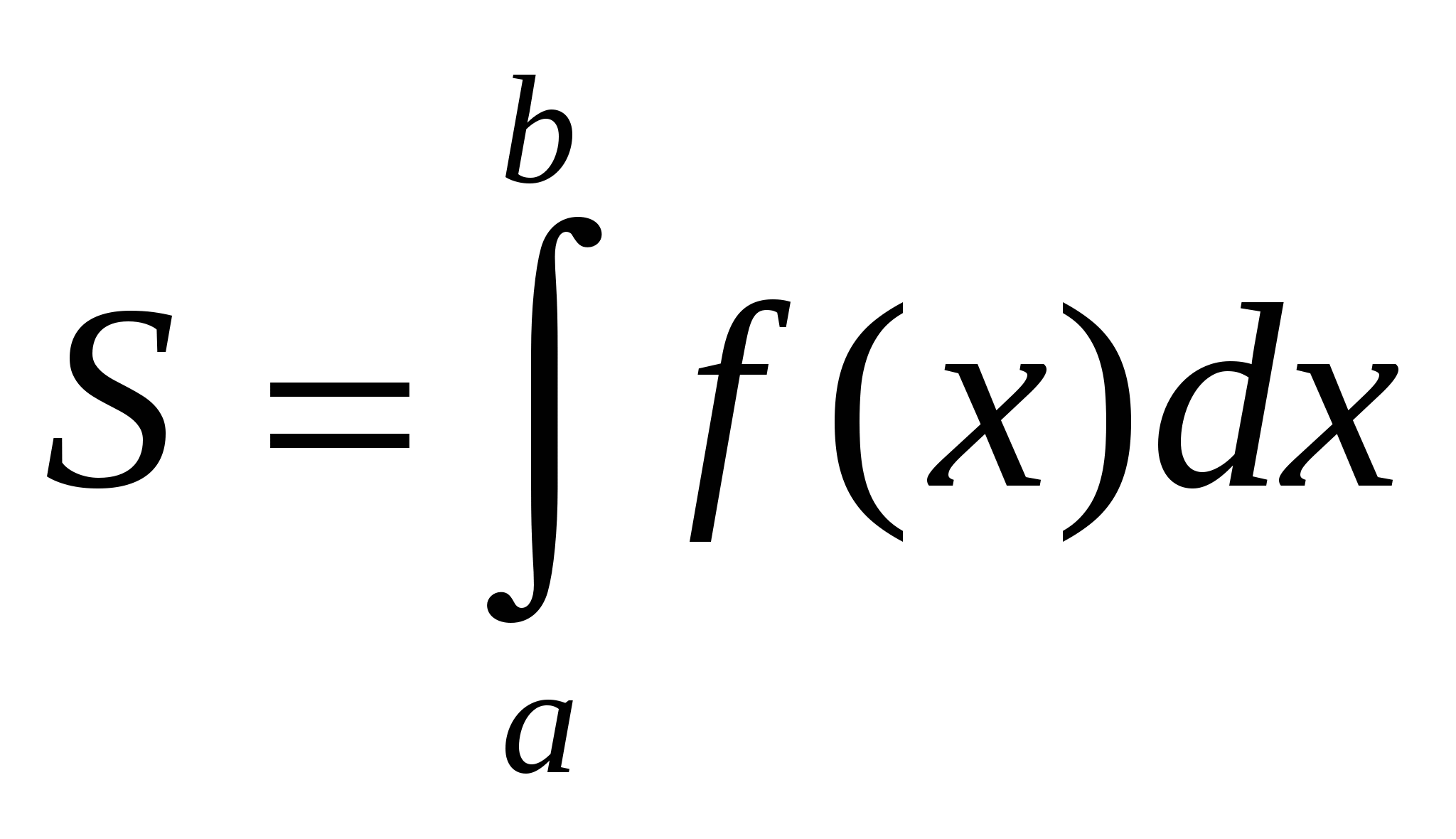 . (1.1)
. (1.1)
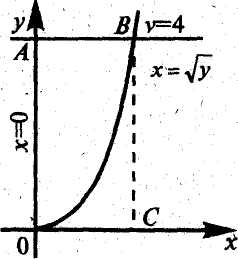
Рис. 1.1. Рис. 1.2.
Пример 1.1. Найти площадь фигуры, ограниченной линиями 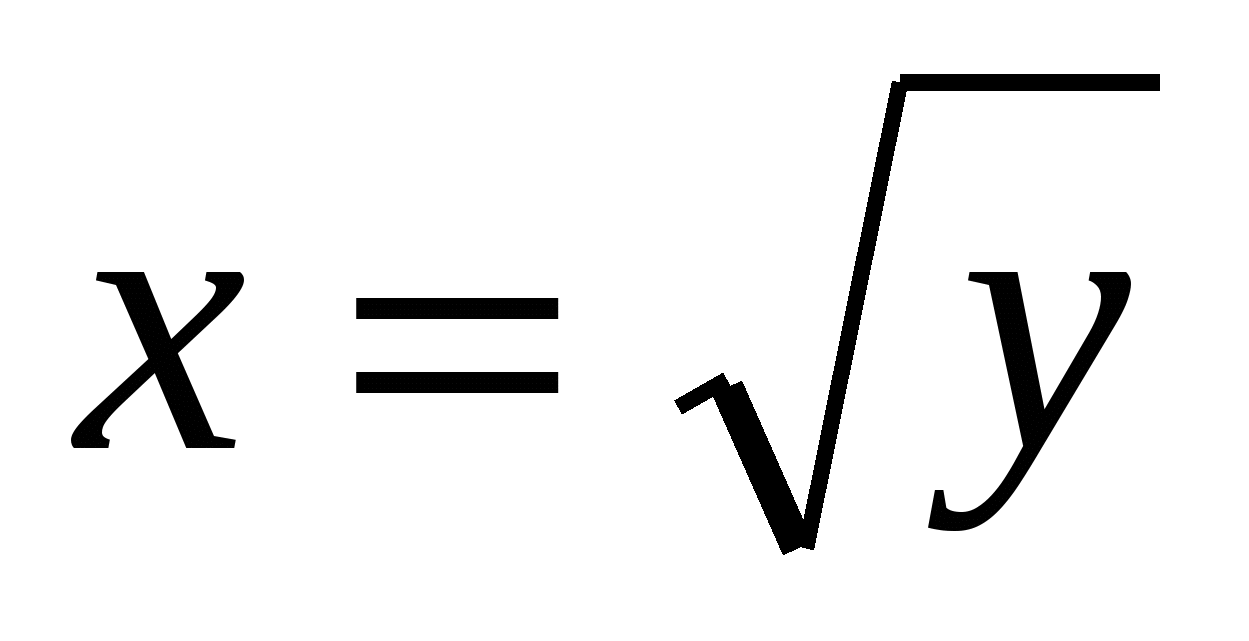 ,
, 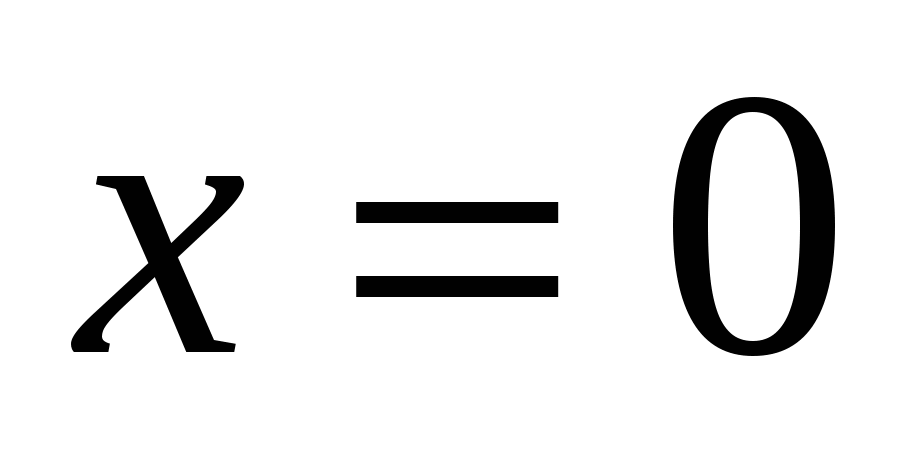 ,
, 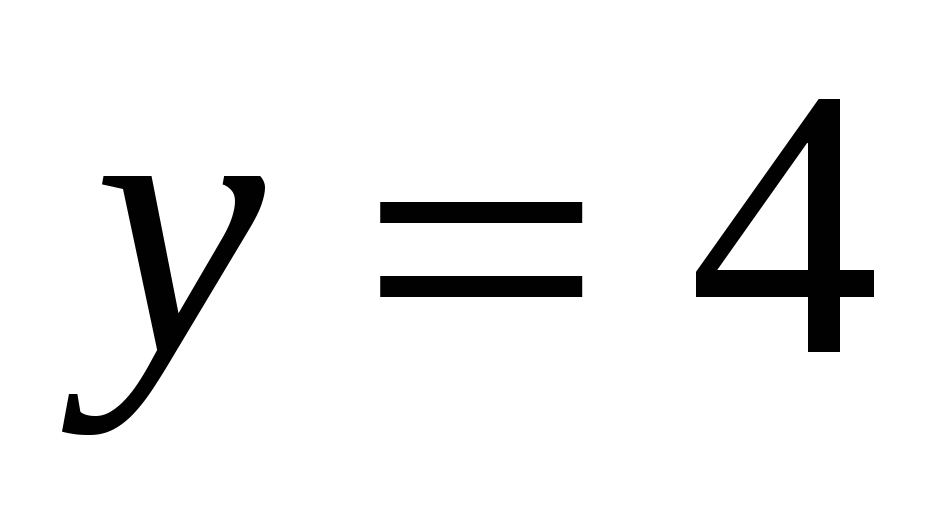 .
.
Решение:
Из чертежа видно, что искомая площадь S криволинейного треугольника OAB равна разности двух площадей:
S=SOABC -SOBC,
каждая, из которых находится по геометрическому смыслу определённого интеграла. Решая систему 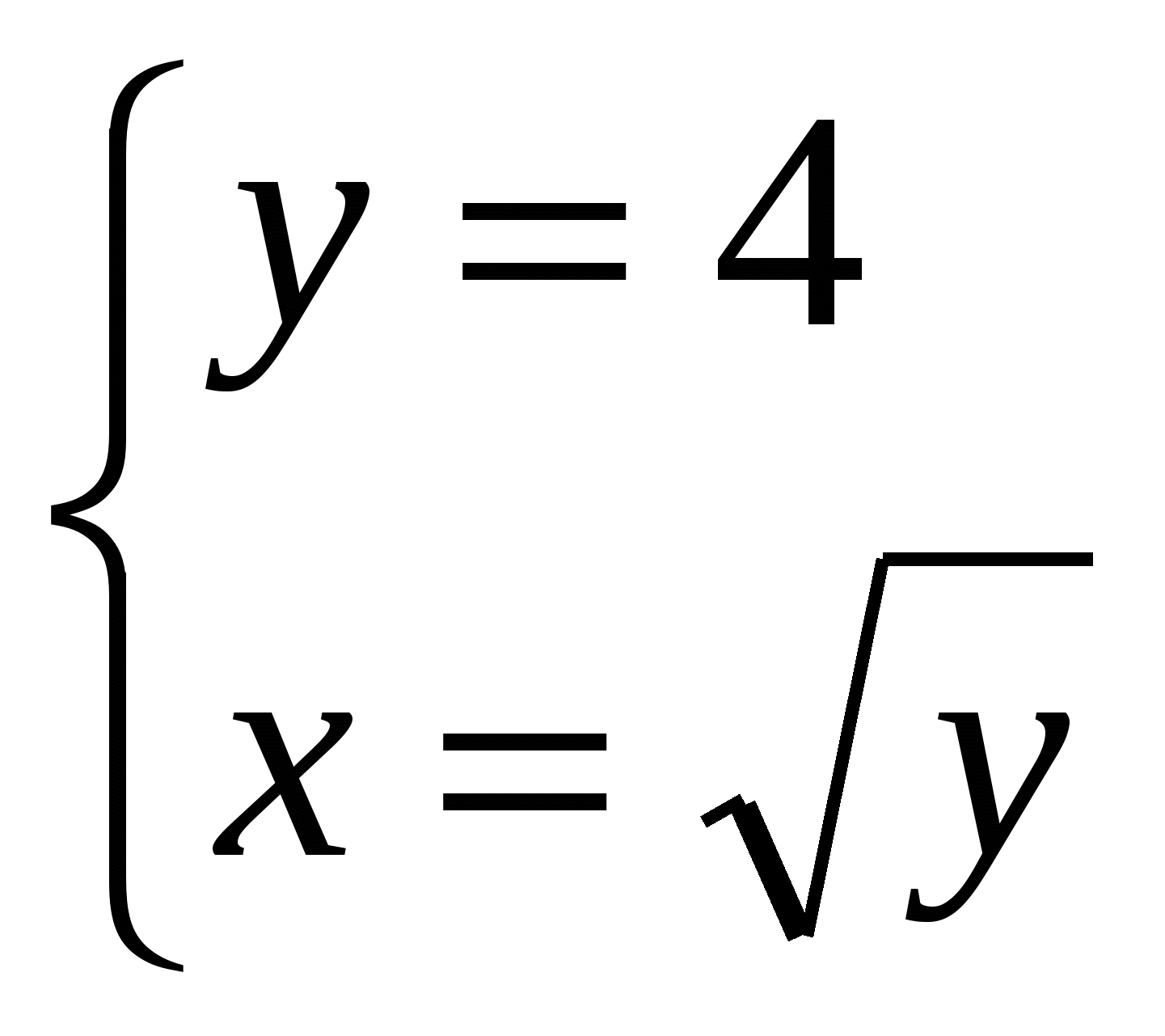 ,
,
получаем, что точка B пересечения прямой y=4 и кривой x=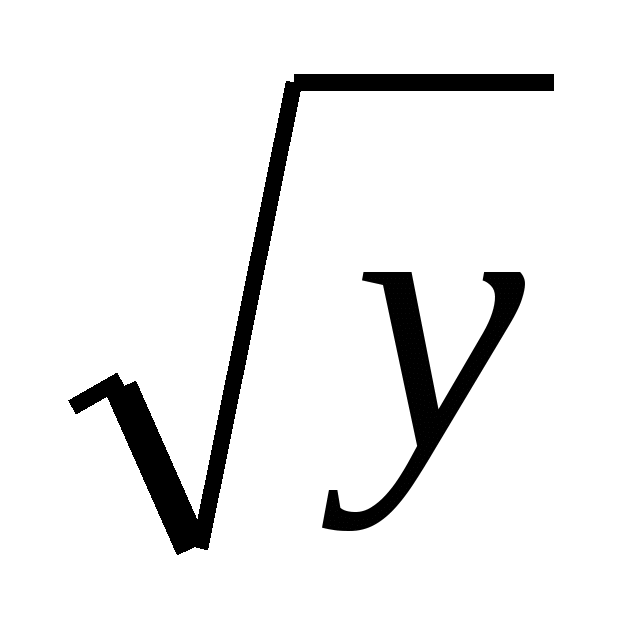 имеет координаты (2;4). Тогда SOABC=
имеет координаты (2;4). Тогда SOABC= ,
,
SOBC=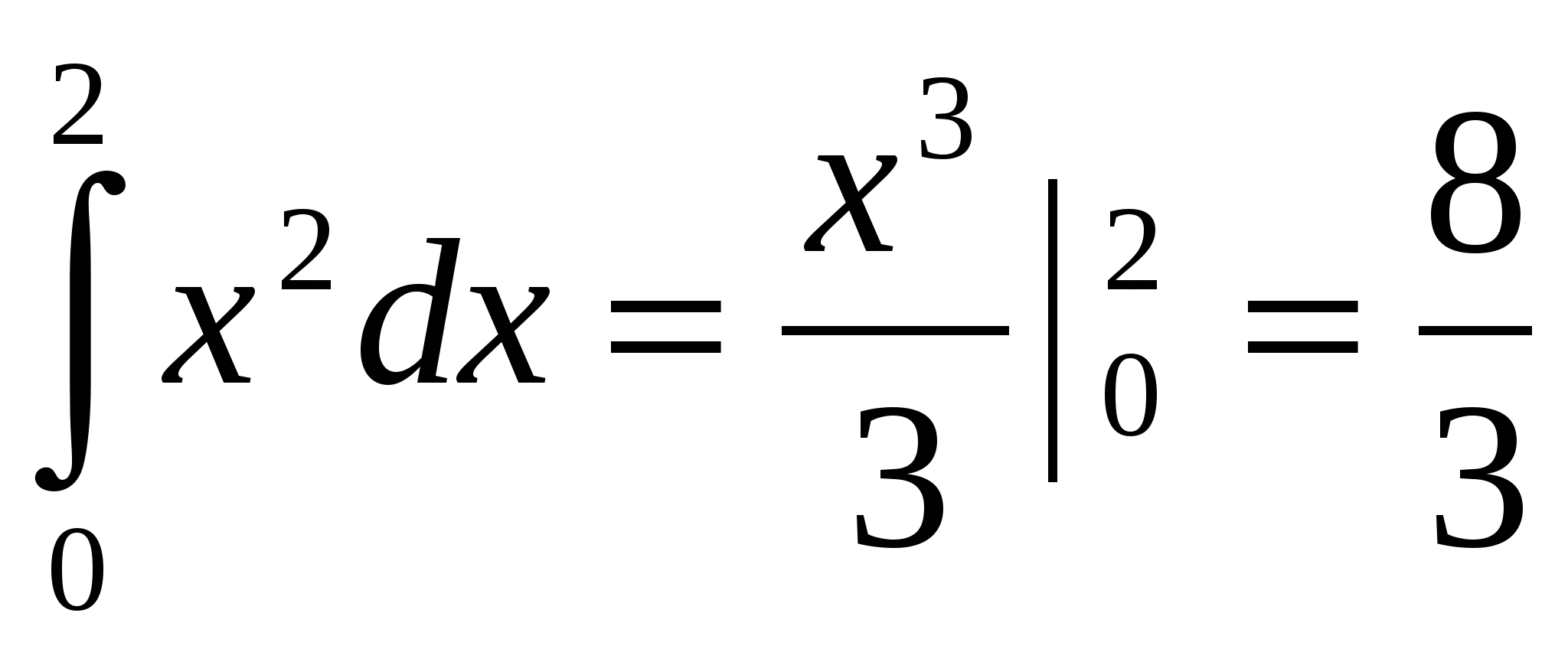 .
. 
Окончательно 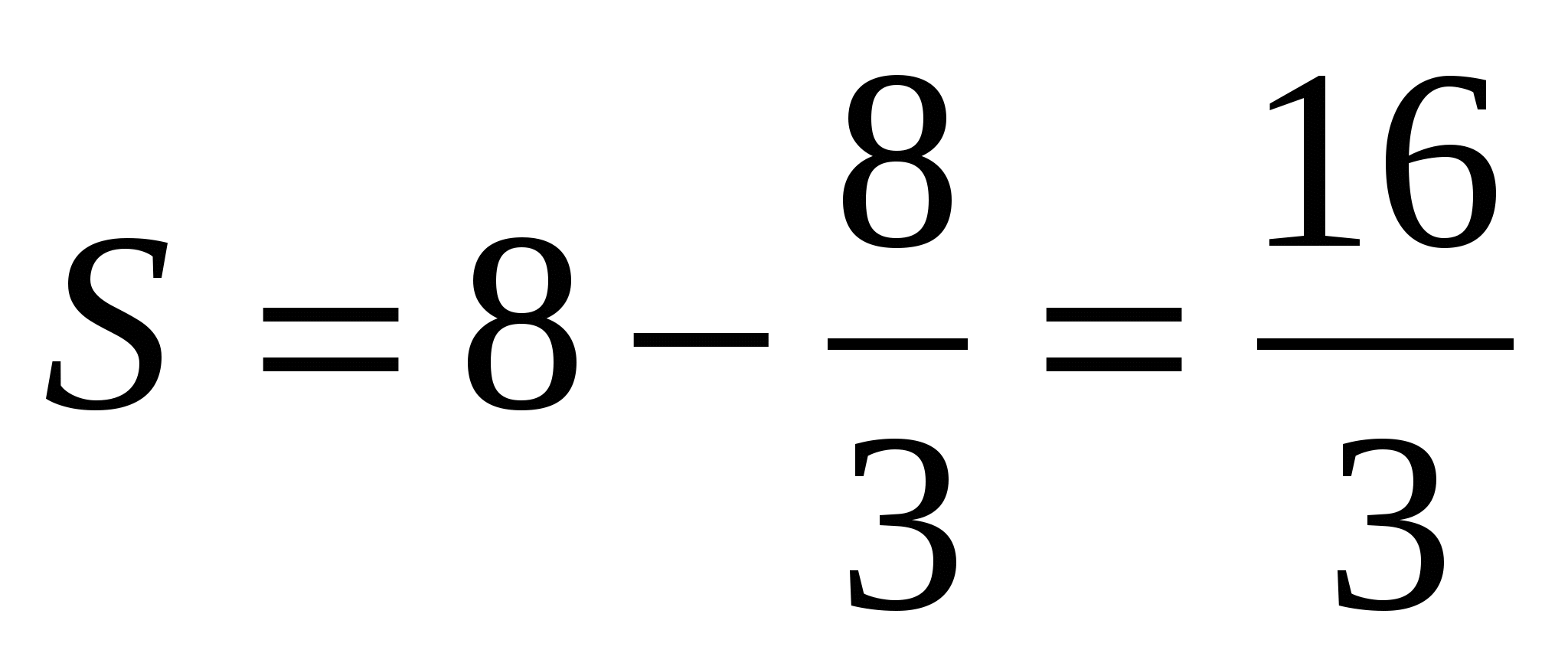 (ед.2)
(ед.2)
2. Пусть функция 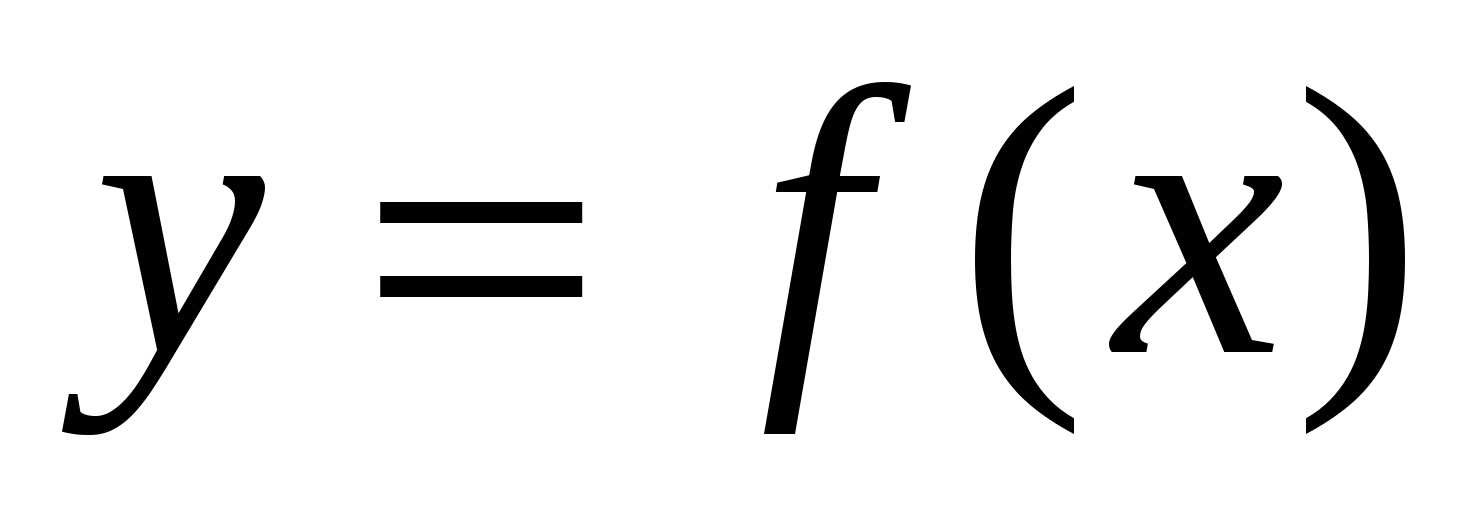 неположительна и непрерывна на
неположительна и непрерывна на  (см. рис. 1.3).
(см. рис. 1.3).
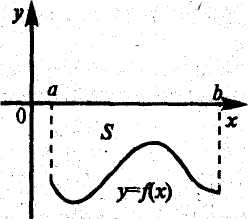
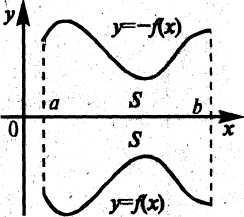
Рис. 1.3. Рис. 1.4.
Выясним, какая связь в этом случае существует между площадью S криволинейной трапеции «над кривой» 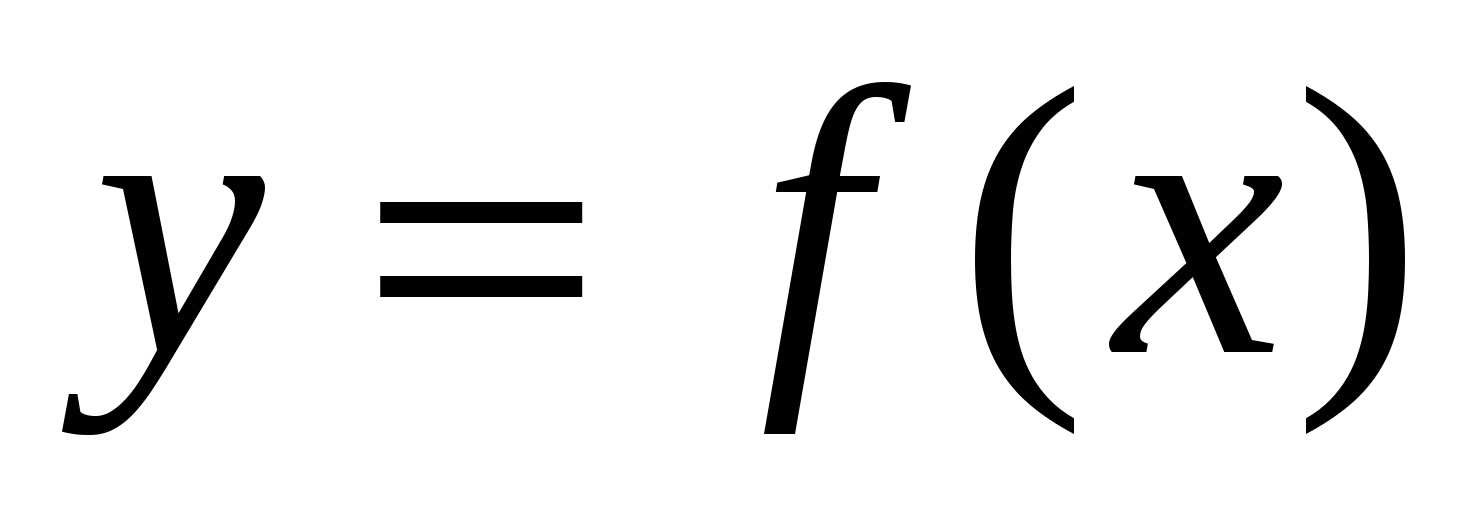 на
на  и интегралом
и интегралом 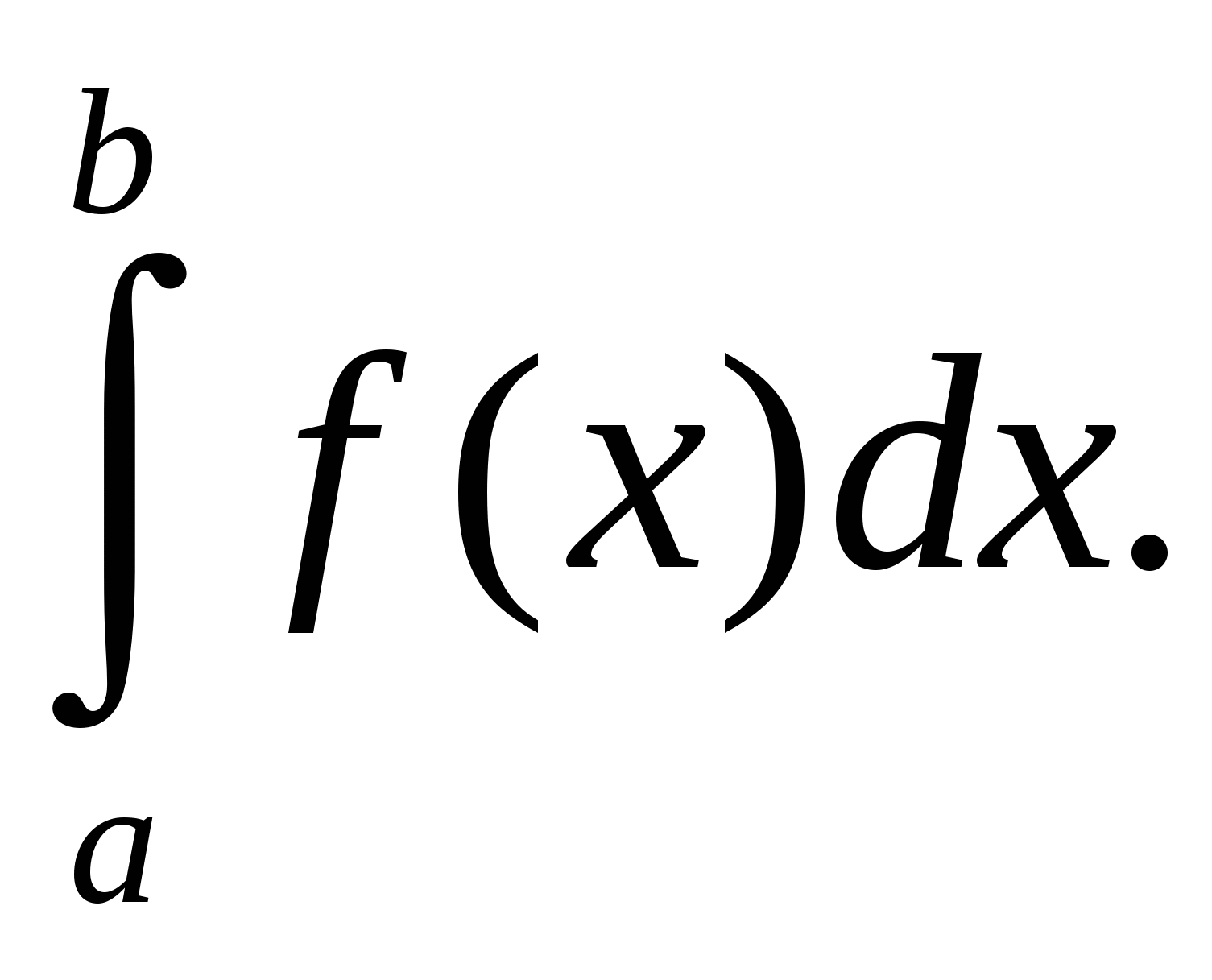 Отражая кривую
Отражая кривую ![]() относительно оси абсцисс, получаем кривую с уравнением
относительно оси абсцисс, получаем кривую с уравнением  . Функция
. Функция 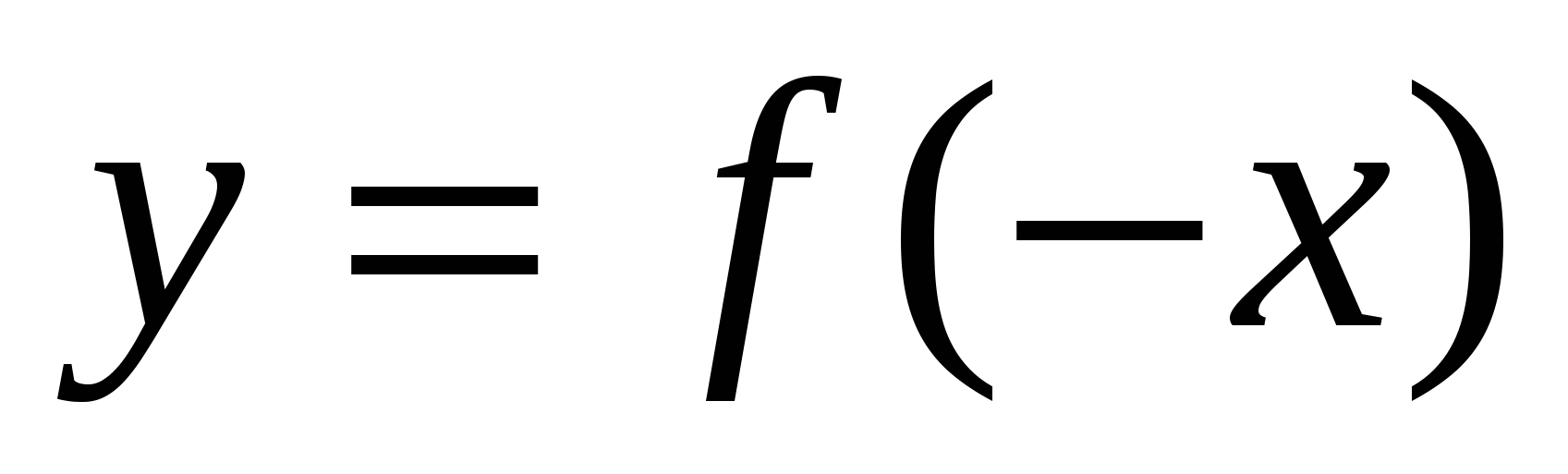 уже неотрицательна на
уже неотрицательна на ![]() , а площадь под этой кривой на
, а площадь под этой кривой на ![]() из соображений симметрии равна площади
из соображений симметрии равна площади (см. рис.1.4) .Тогда
(см. рис.1.4) .Тогда ![]() , т.е.
, т.е.  (1.2)
(1.2)
Таким образом, если функция 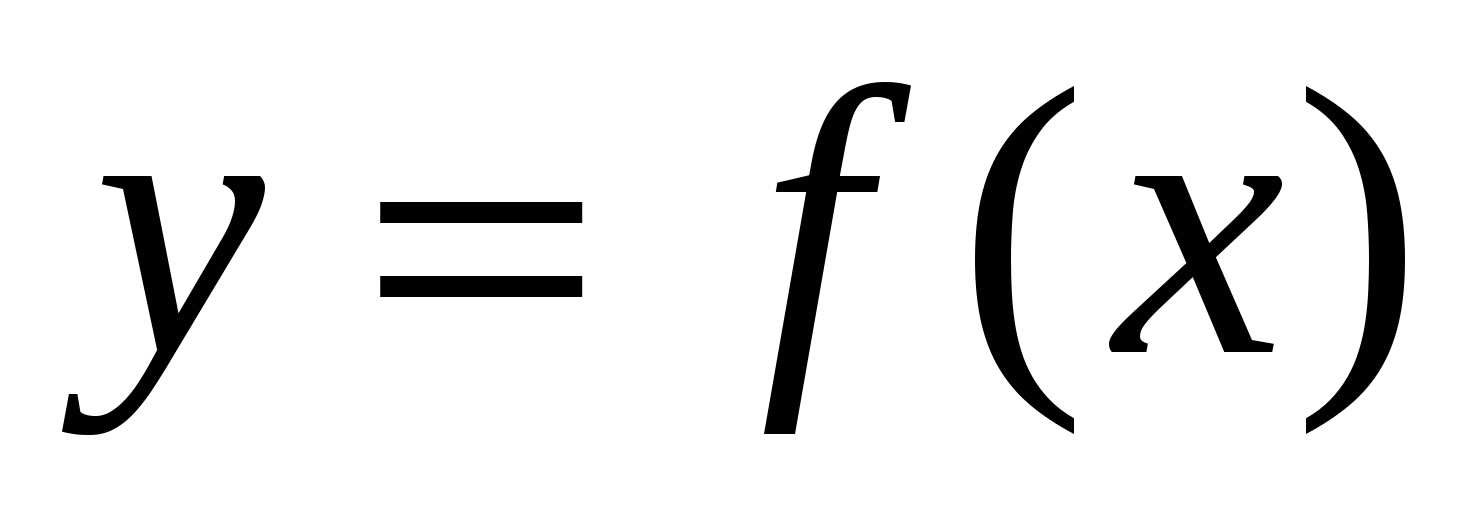 неположительна на
неположительна на![]() ,то площадь
,то площадь  над кривой
над кривой 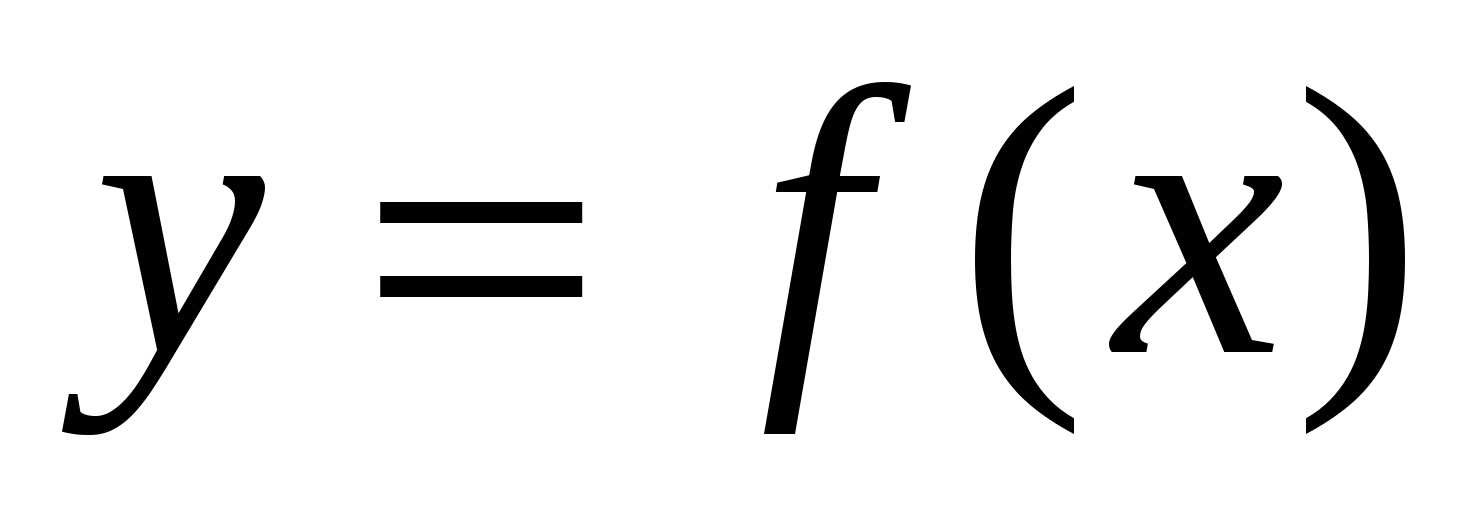 на
на  отличается знаком от определённого интеграла
отличается знаком от определённого интеграла 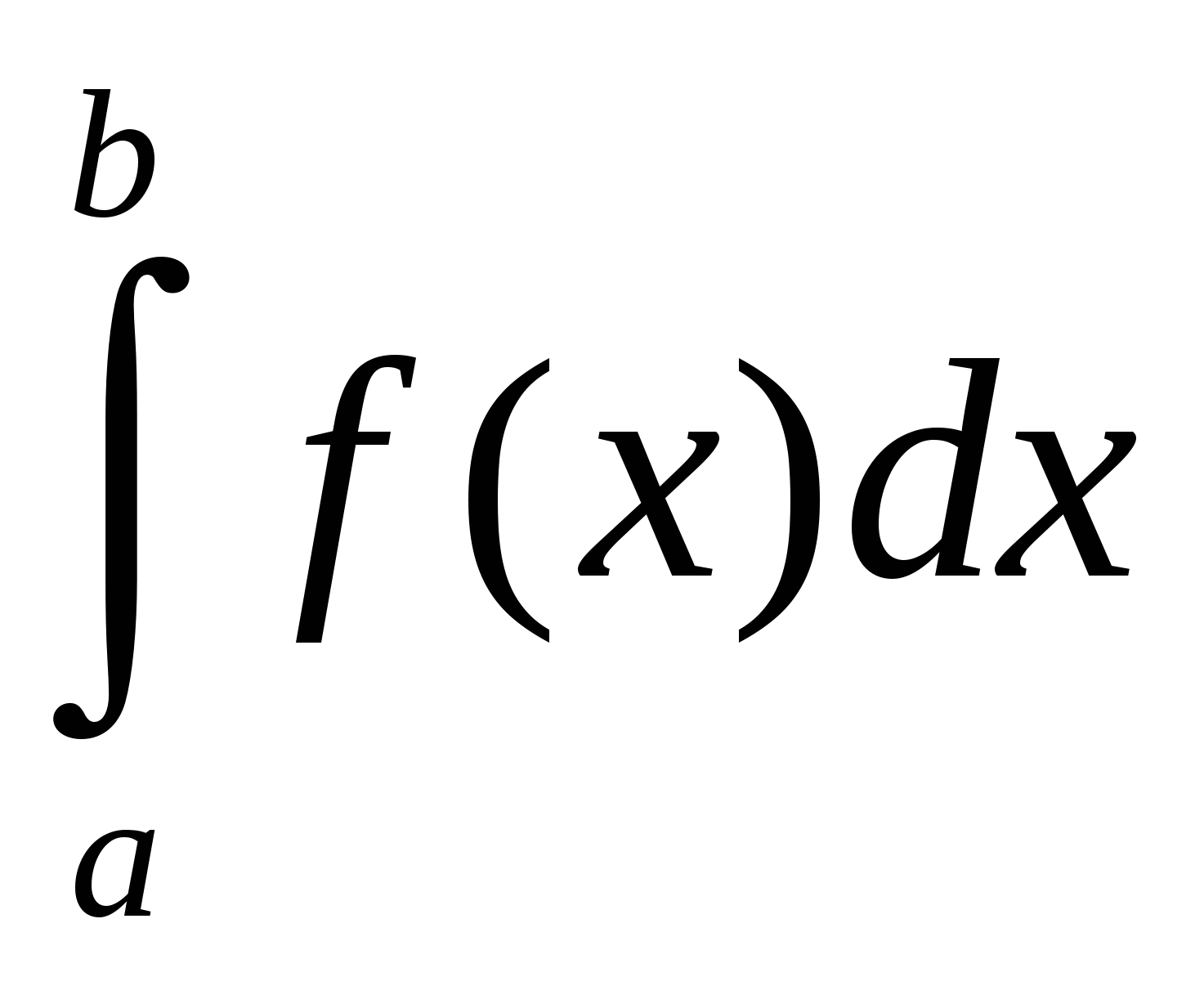 .
.
Пример 1.2. Найти площадь фигуры, ограниченной линиями 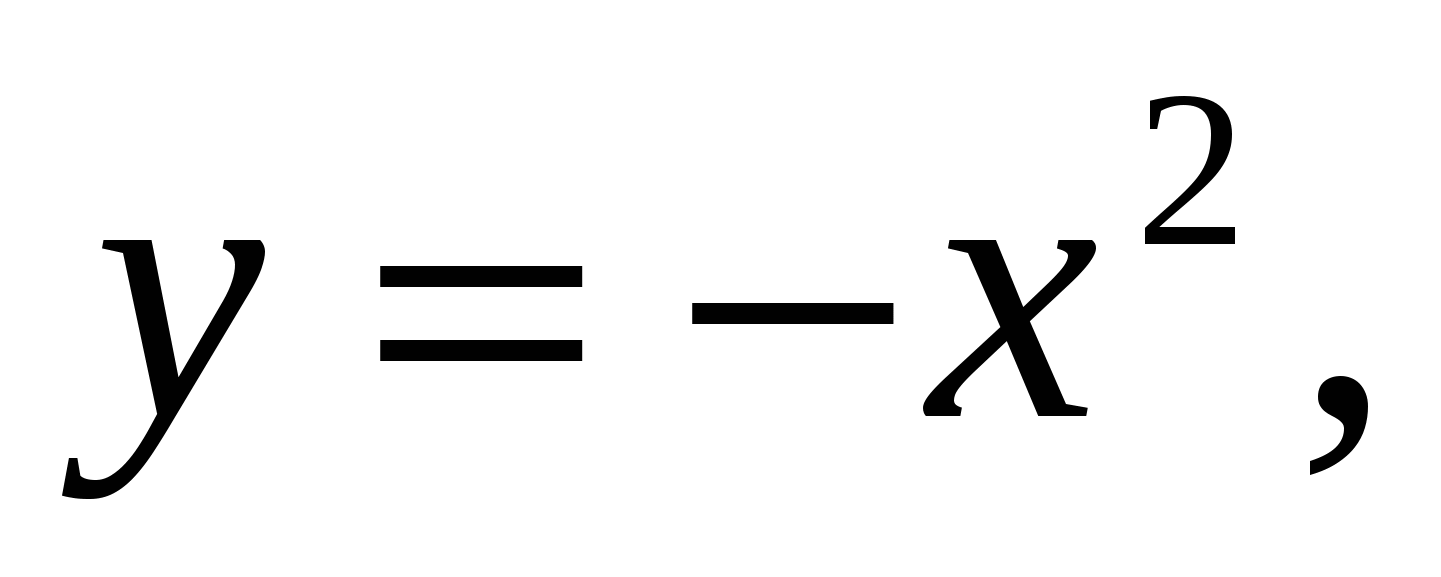
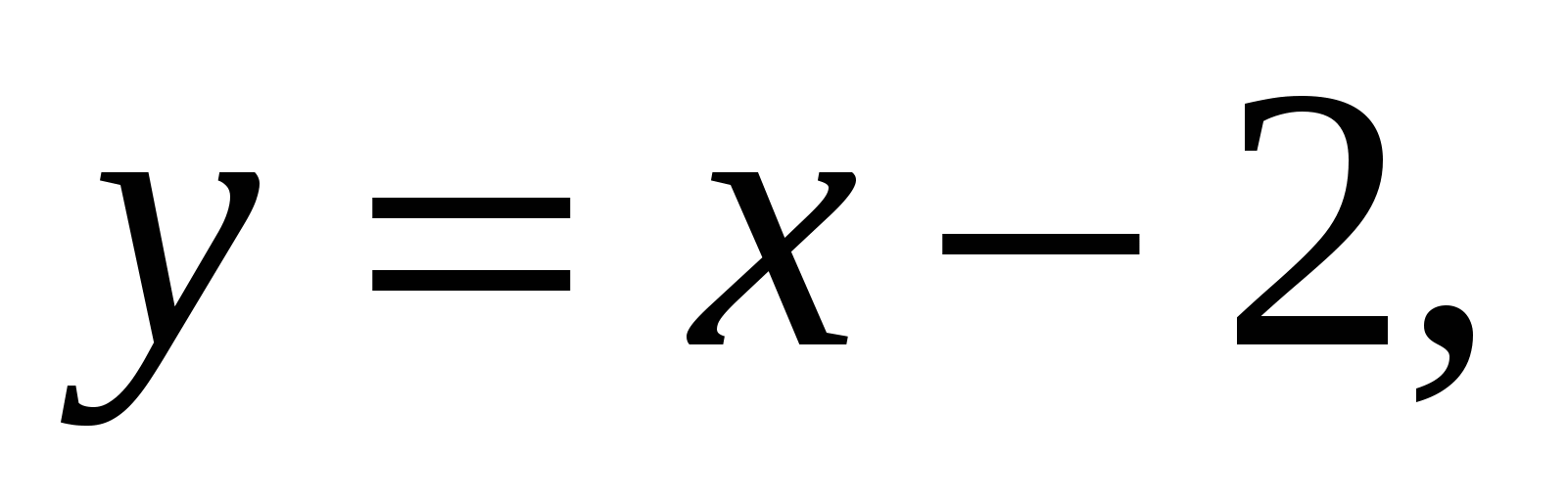
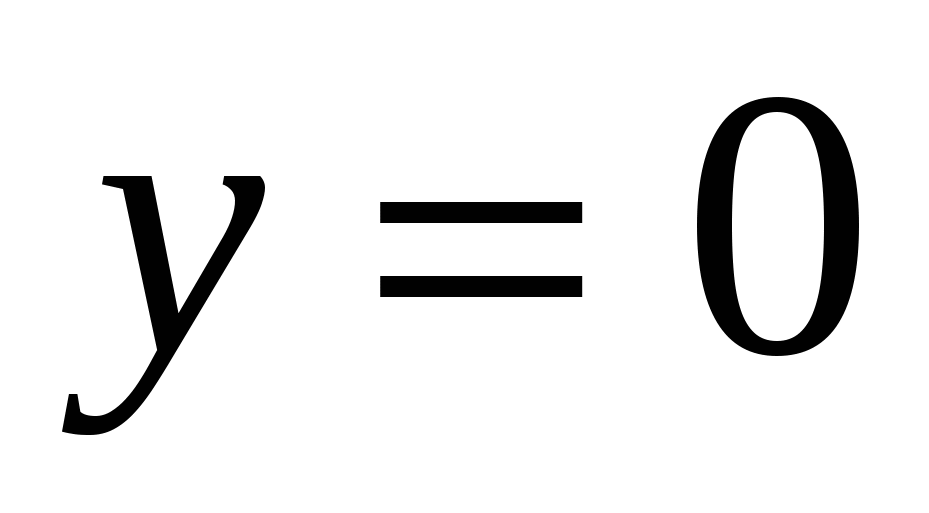 .
.
Решение:
Из рис. 1.5 видно, что искомая площадь 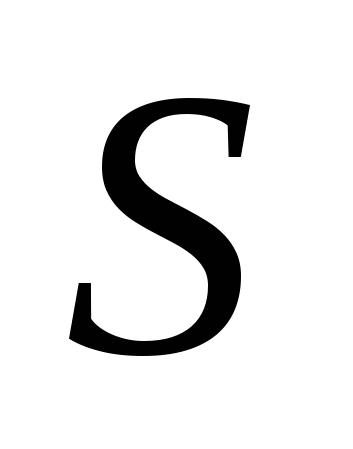 криволинейного треугольника OAB может рассматриваться как площадь над кривой OAB на отрезке
криволинейного треугольника OAB может рассматриваться как площадь над кривой OAB на отрезке  . Однако указанная кривая (ломаная) не задаётся одним уравнением. Поэтому для нахождения
. Однако указанная кривая (ломаная) не задаётся одним уравнением. Поэтому для нахождения ![]() разобьём криволинейный треугольник
разобьём криволинейный треугольник 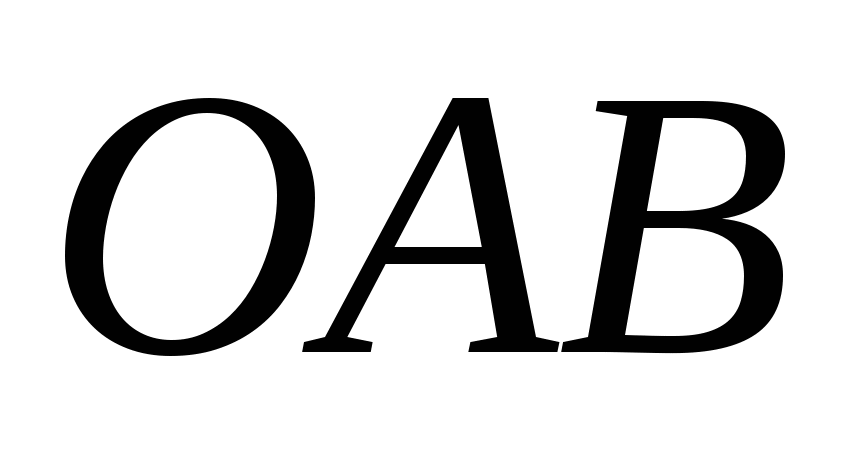 на части, проецируя точку
на части, проецируя точку  излома на ось абсцисс. Тогда
излома на ось абсцисс. Тогда  (см. рис. 1.5). Абсциссы точек
(см. рис. 1.5). Абсциссы точек 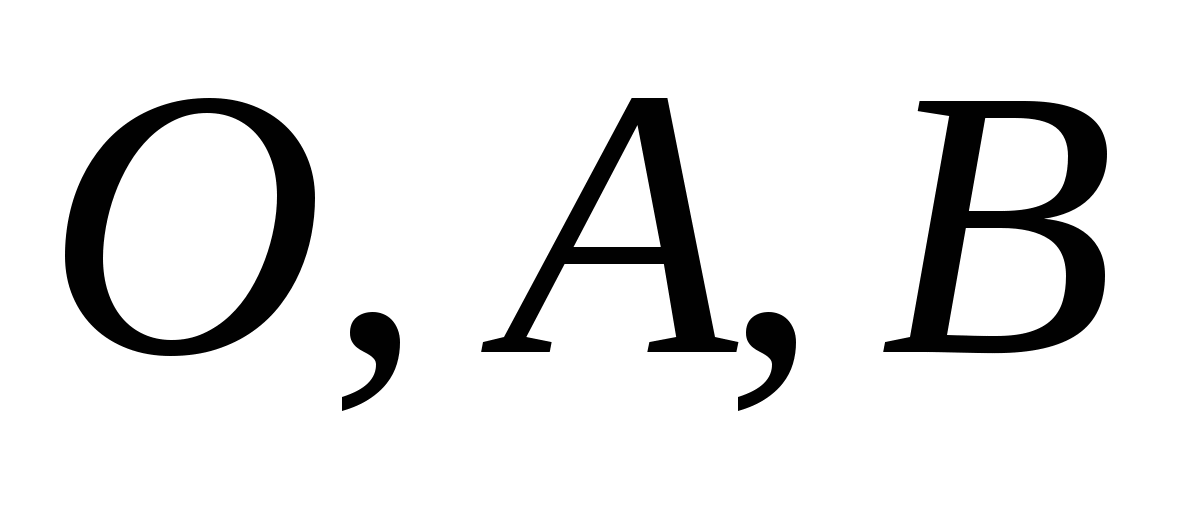 задают пределы интегрирования
задают пределы интегрирования 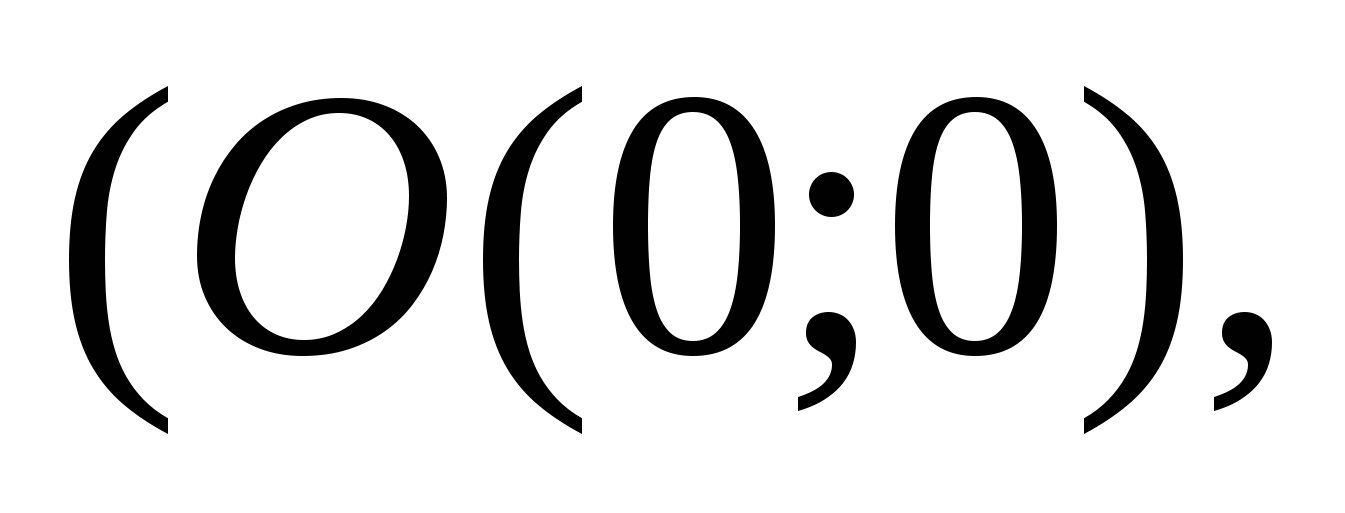
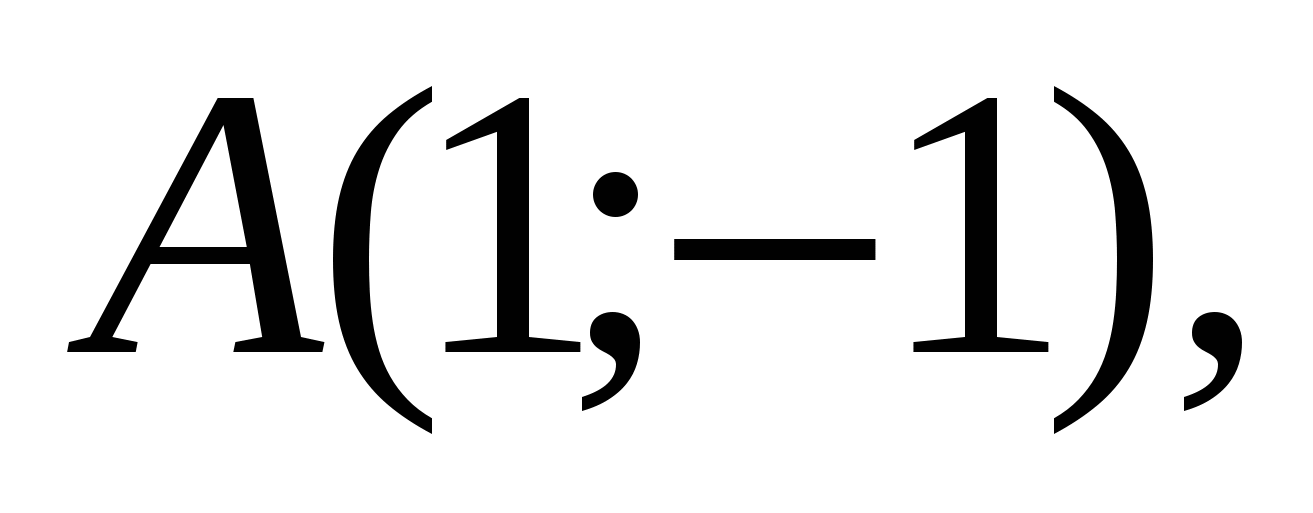
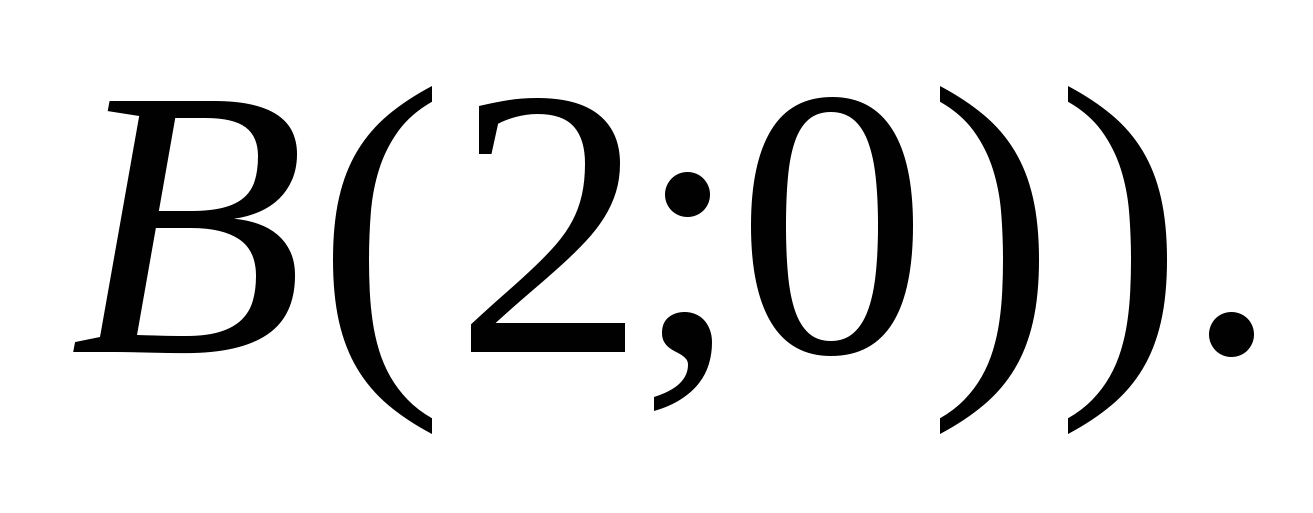
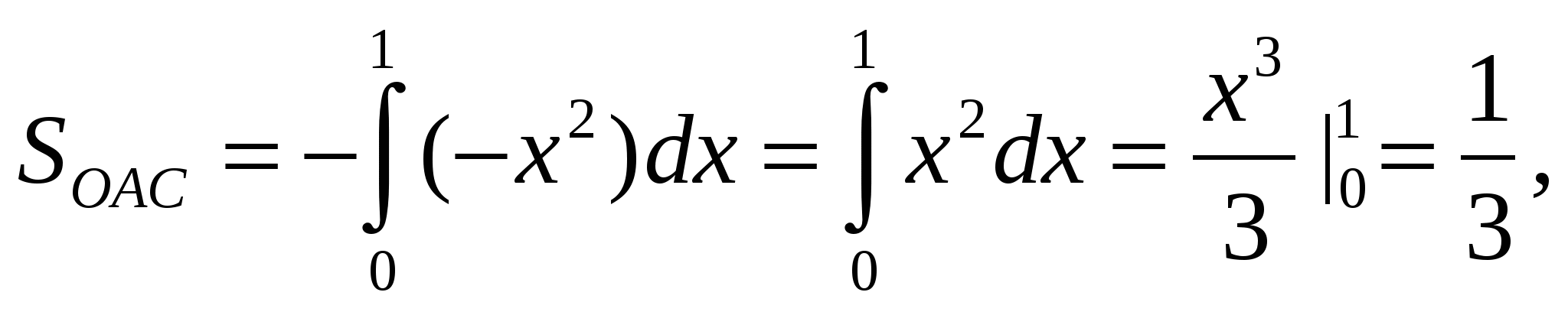
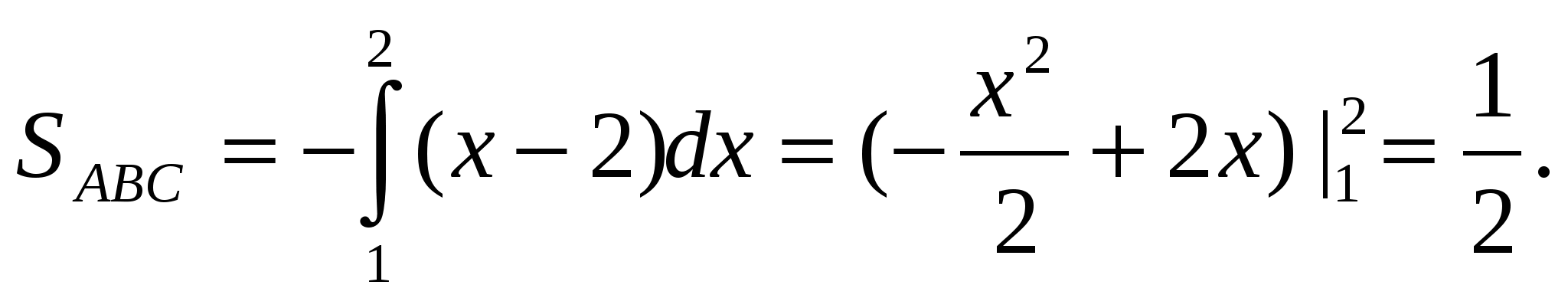
Окончательно 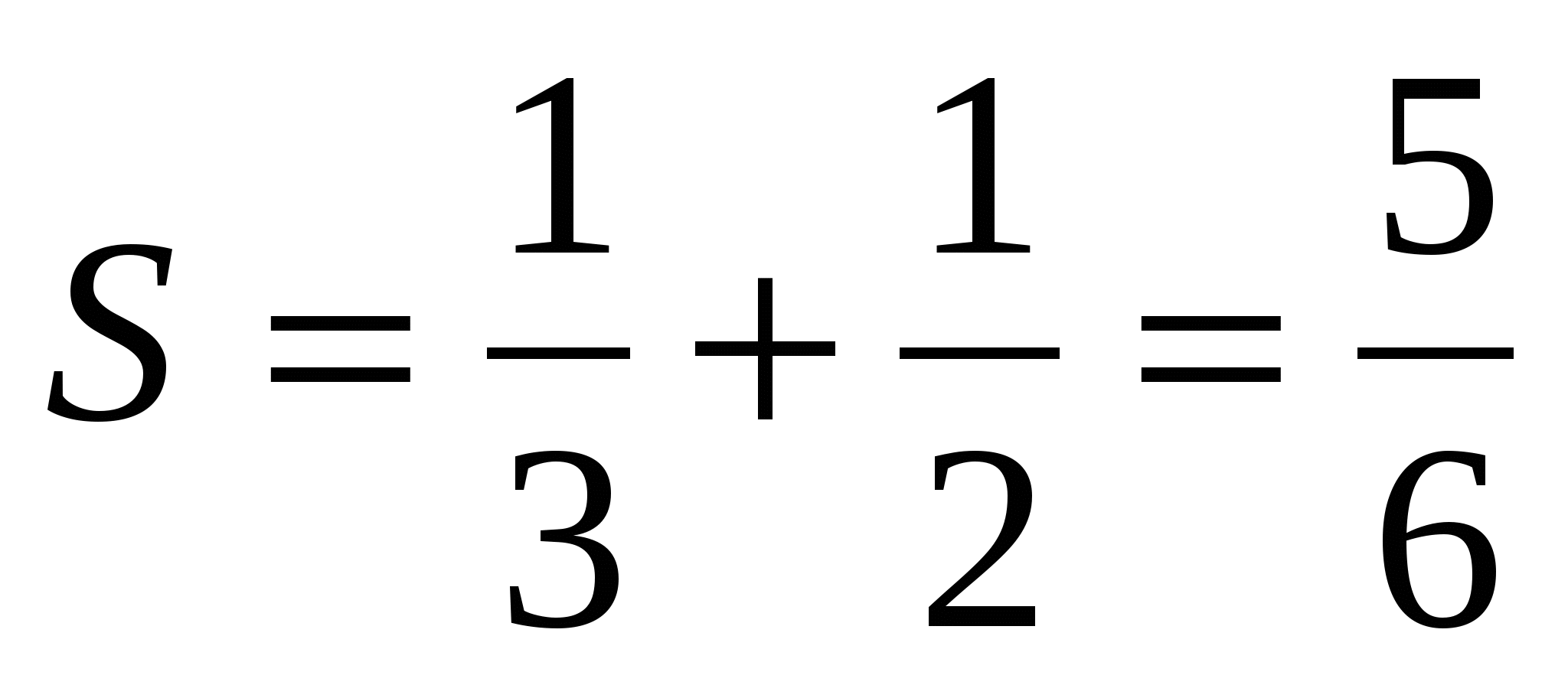 (ед.2).
(ед.2).

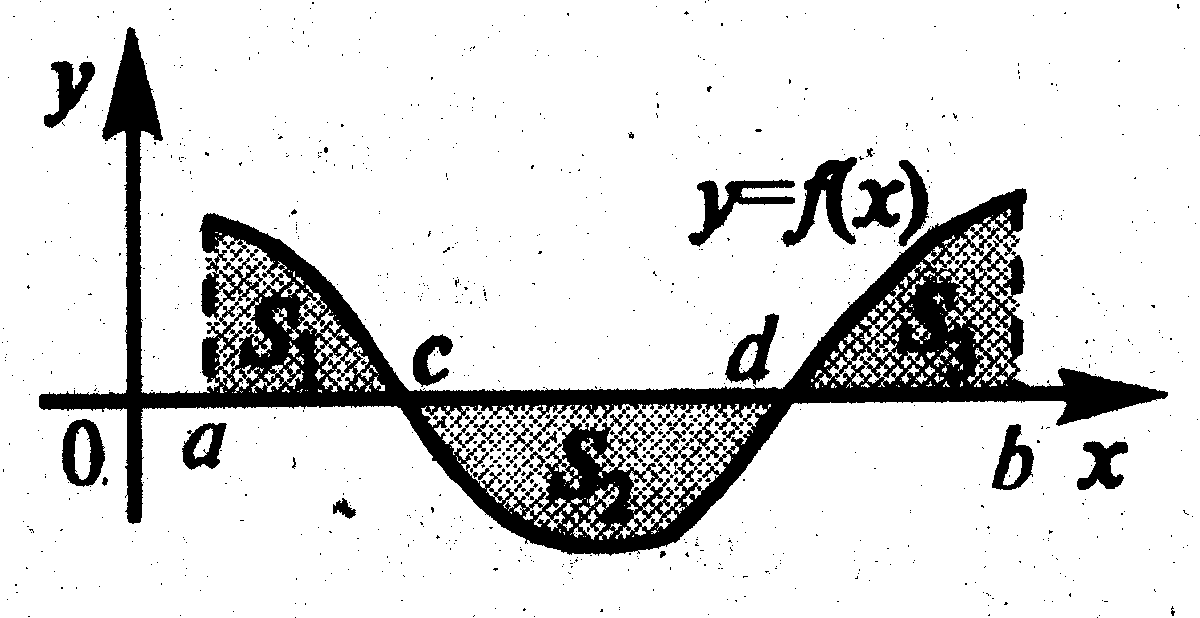
Рис. 1.5. Рис. 1.6.
3. Пусть на отрезке  задана непрерывная функция
задана непрерывная функция 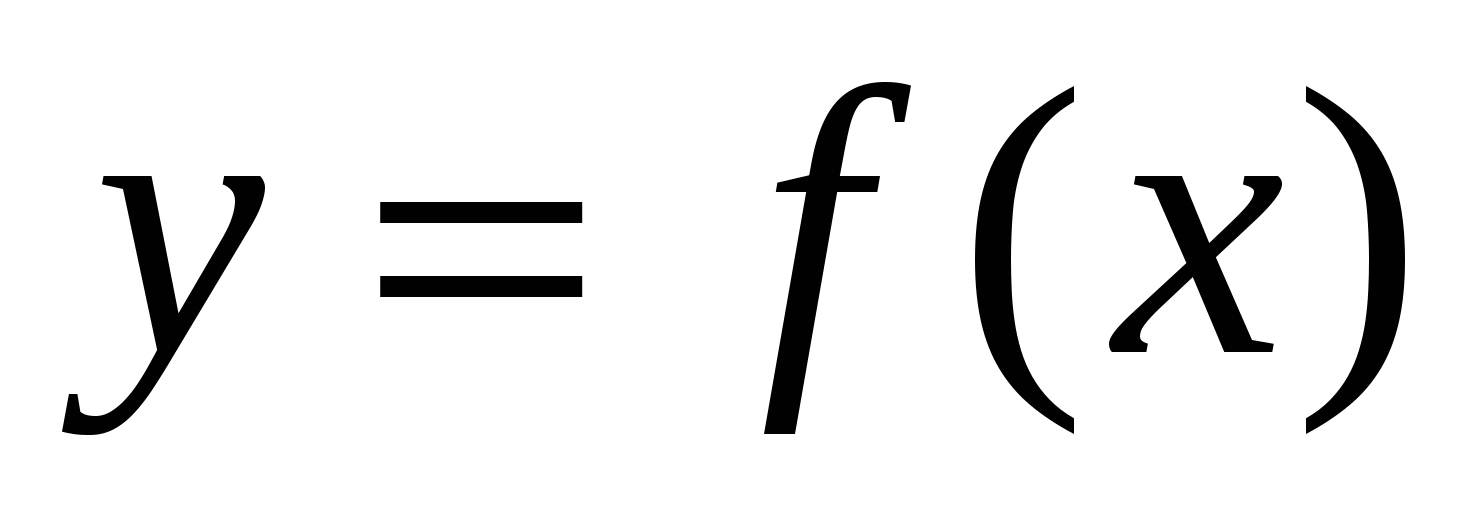 общего вида. Предположим также, что исходный отрезок можно разбить точками на конечное число интервалов так, что на каждом из них функция
общего вида. Предположим также, что исходный отрезок можно разбить точками на конечное число интервалов так, что на каждом из них функция 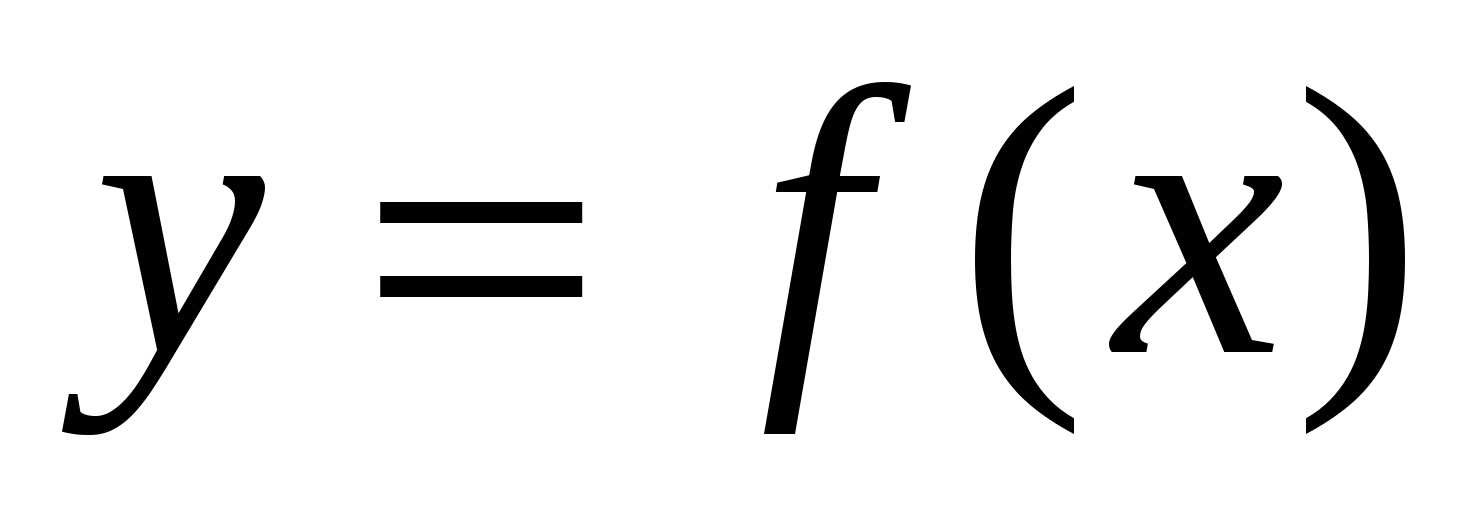 будет знакопостоянна или равна нулю. Рассмотрим, например, случай функции, изображенной на рис. 1.6. Площадь заштрихованной фигуры
будет знакопостоянна или равна нулю. Рассмотрим, например, случай функции, изображенной на рис. 1.6. Площадь заштрихованной фигуры 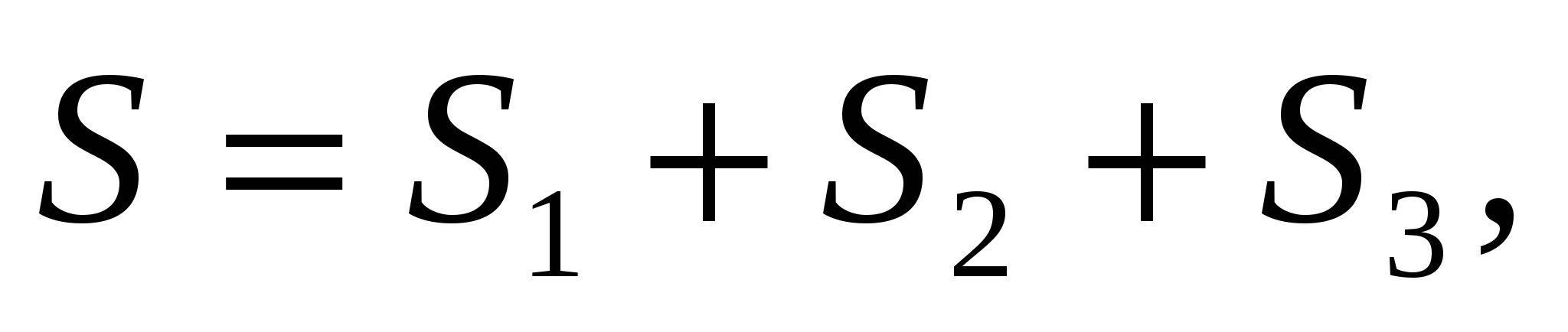
т.е. равна алгебраической сумме соответствующих определённых интегралов: 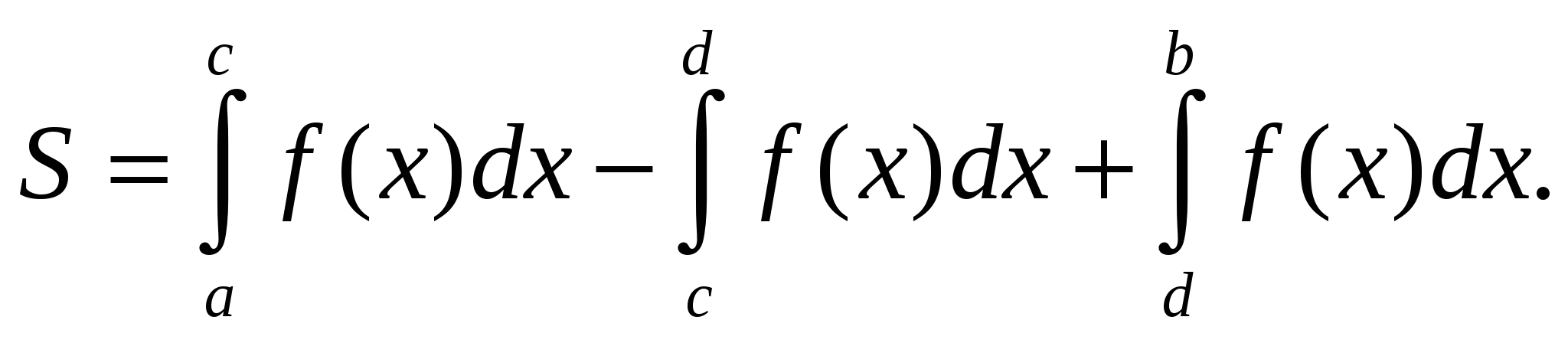
4. Приведём формулу, применение которой часто упрощает решение задач на вычисление площадей плоских фигур.
Теорема. Пусть на отрезке 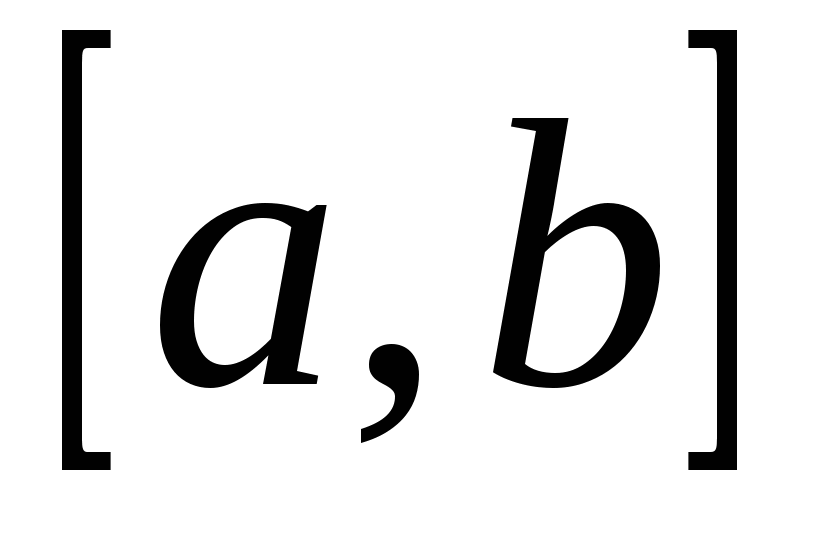 заданы непрерывные функции
заданы непрерывные функции 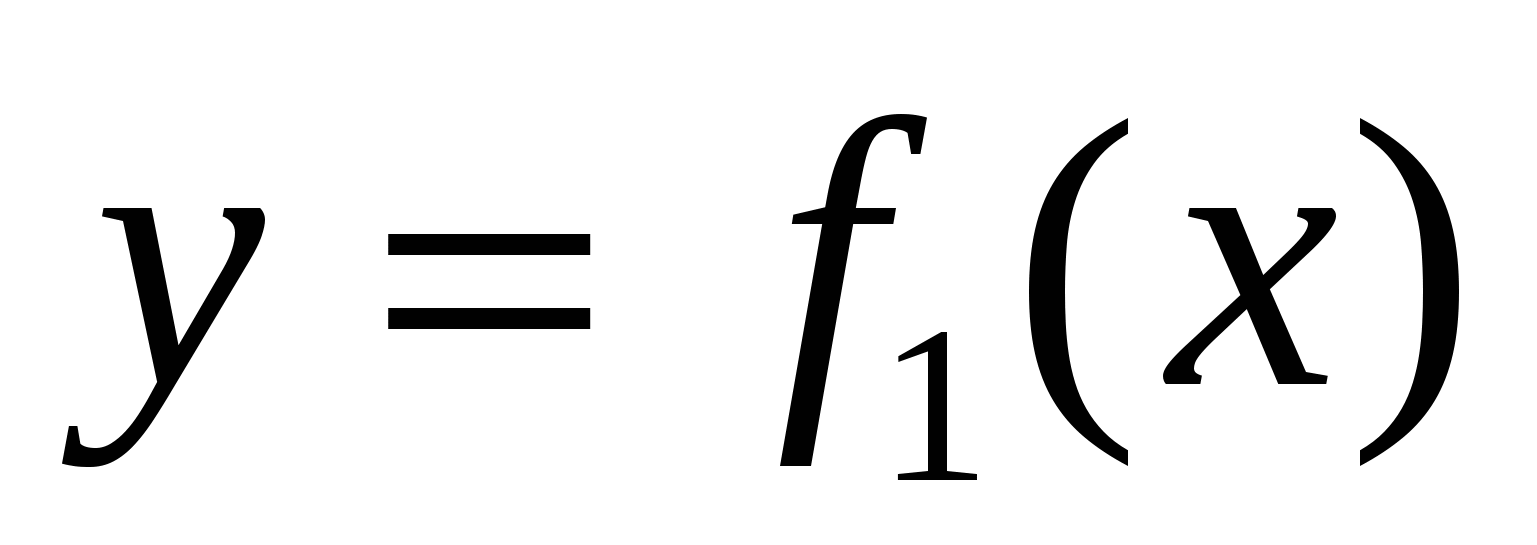 и
и 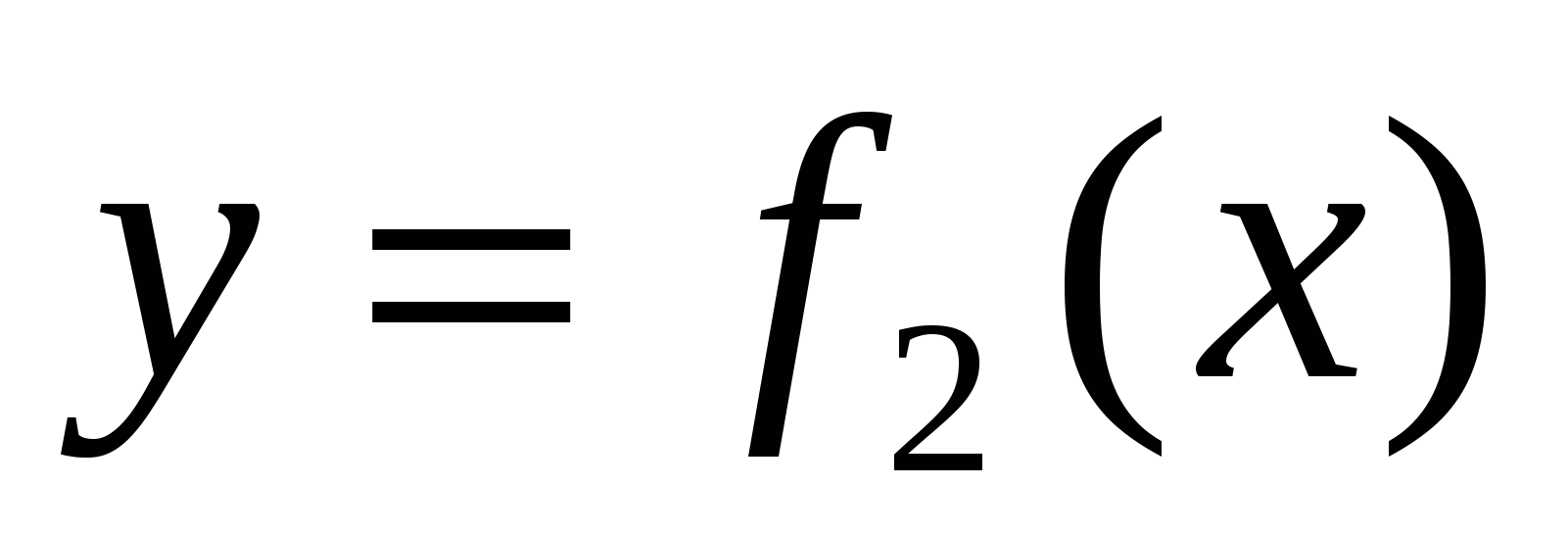 такие, что
такие, что 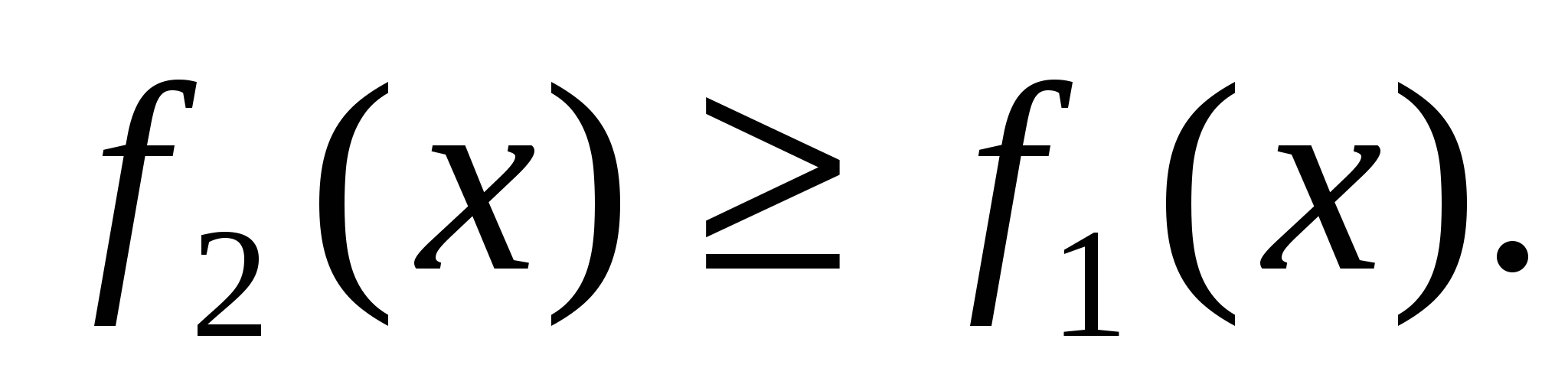 Тогда площадь
Тогда площадь 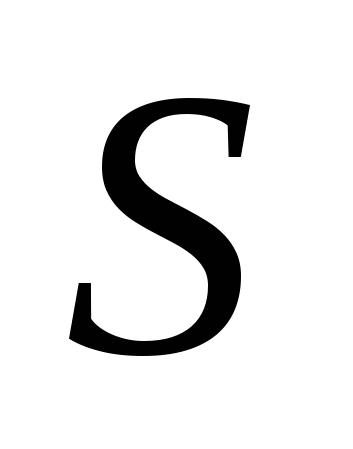 фигуры, заключённой между кривыми
фигуры, заключённой между кривыми 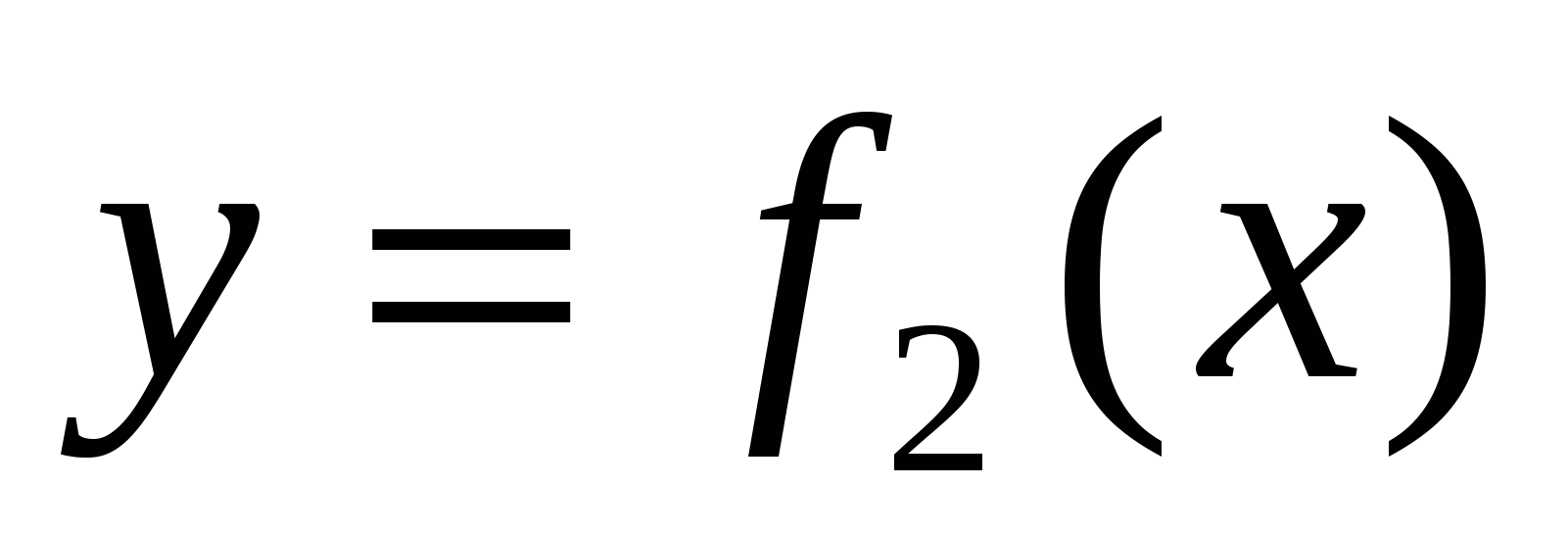 и
и 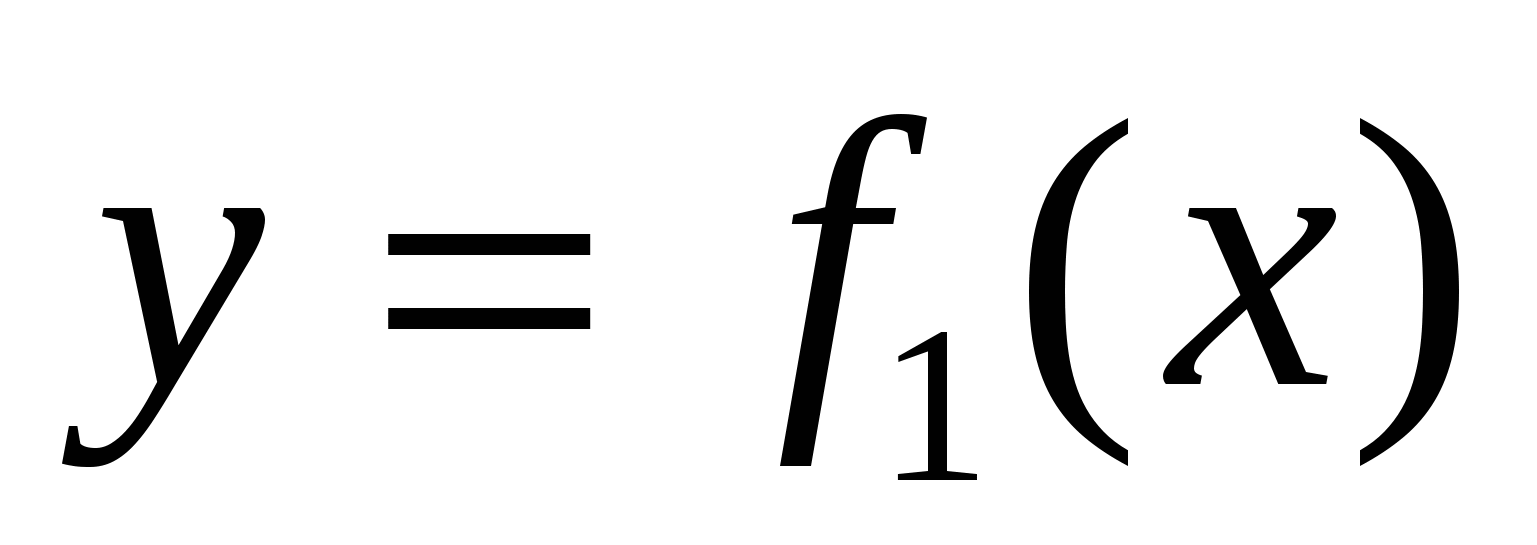 , на отрезке
, на отрезке 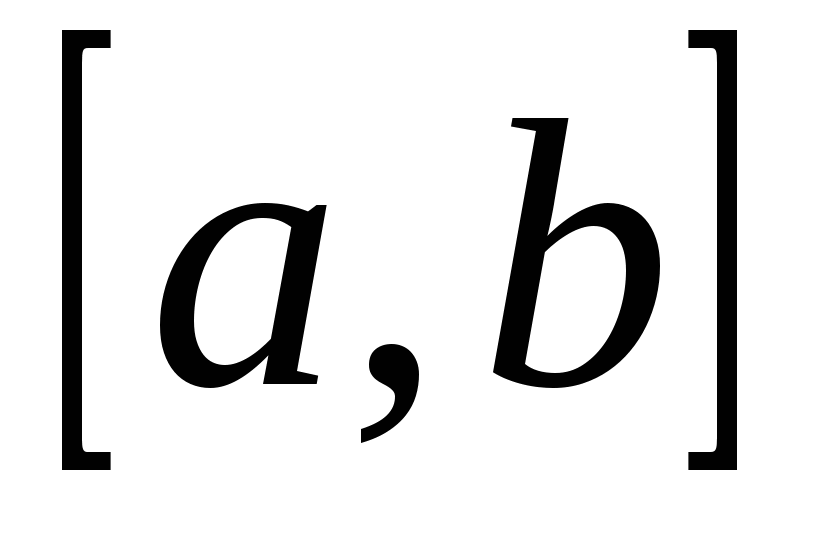 вычисляется по формуле
вычисляется по формуле
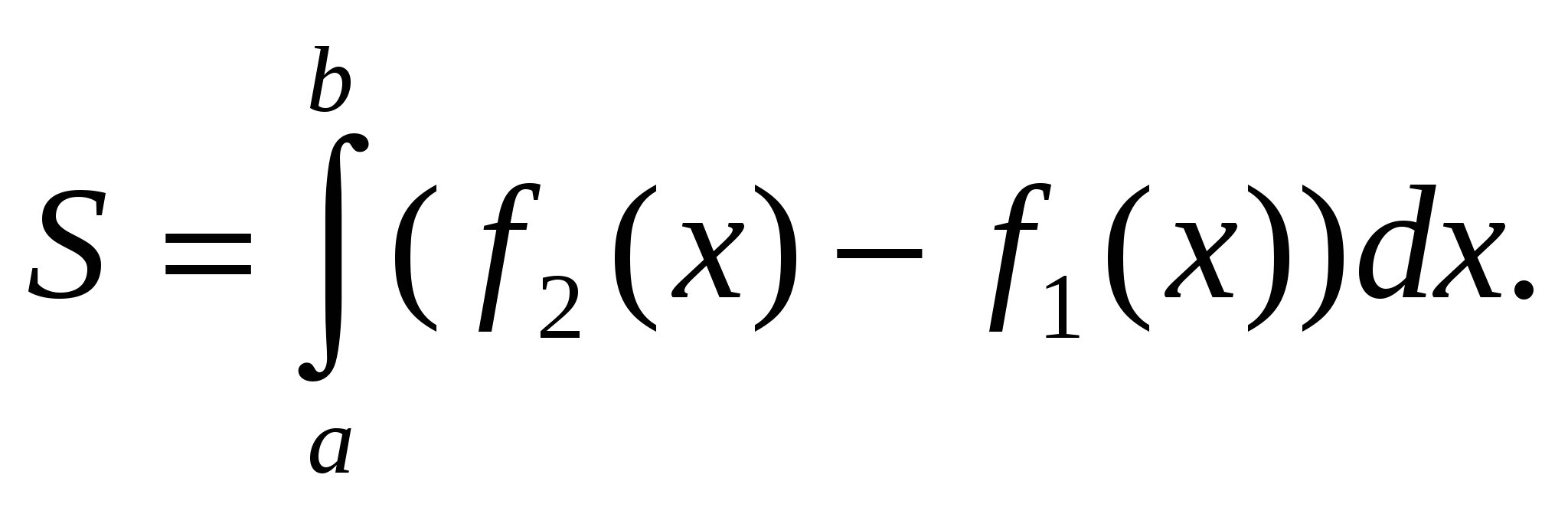 (1.3)
(1.3)
Проиллюстрируем теорему графически (см. рис. 1.7).
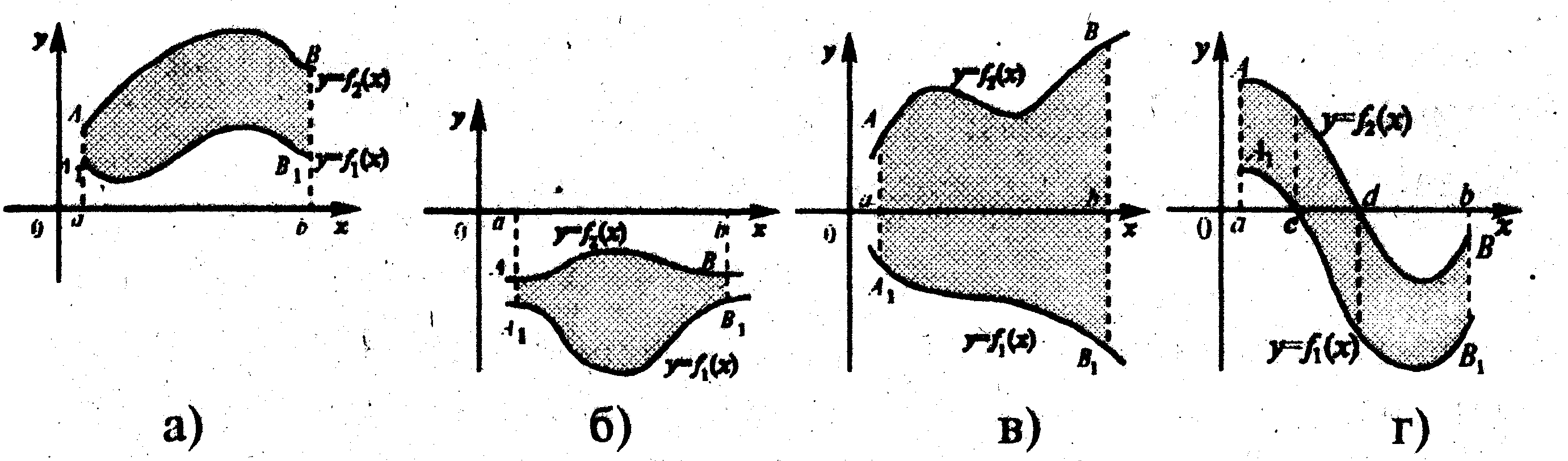
Рис. 1.7
Возможны несколько случаев расположения кривых на отрезке 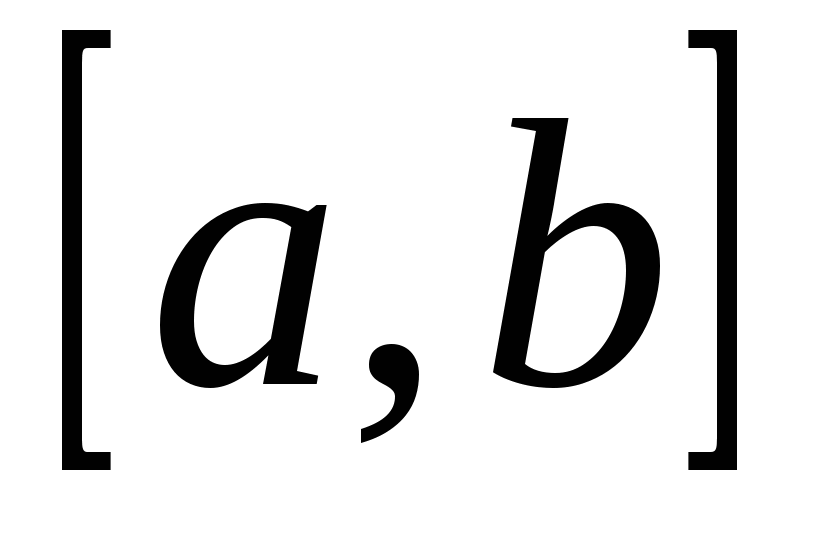 .
.
1) 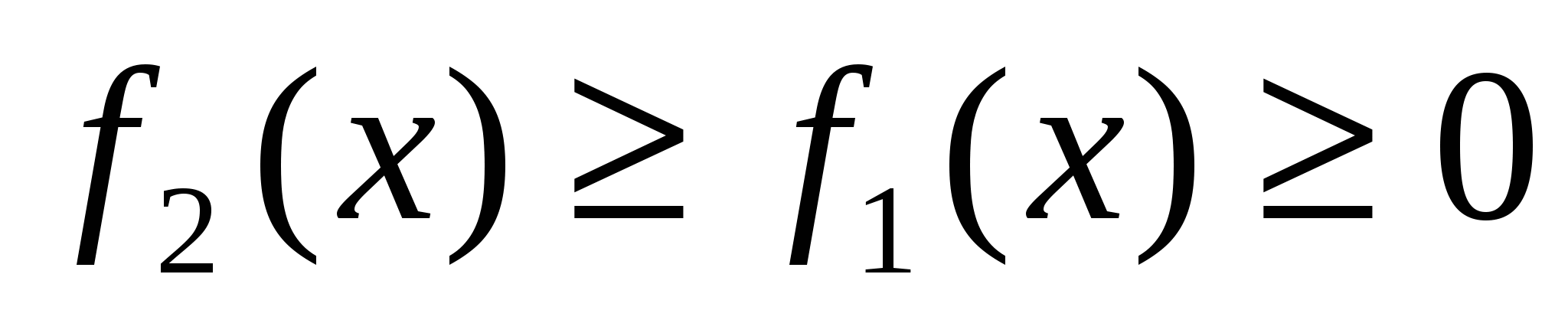 . (см. рис 1.7 а)
. (см. рис 1.7 а) 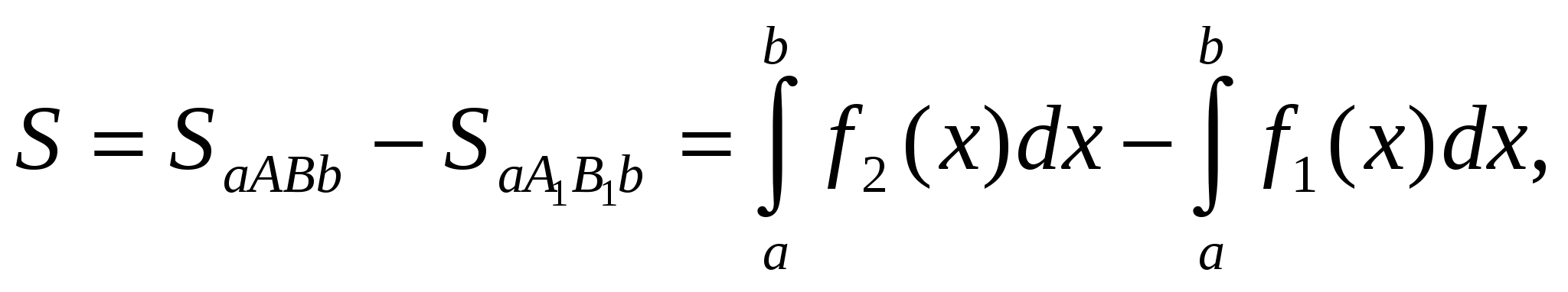 откуда следует формула (1.3).
откуда следует формула (1.3).
2) 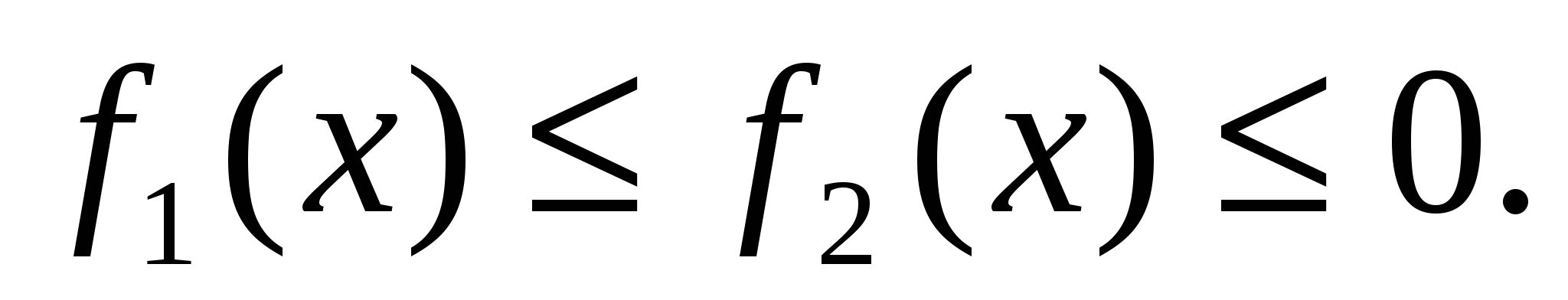 (см. рис. 1.7.б)
(см. рис. 1.7.б)
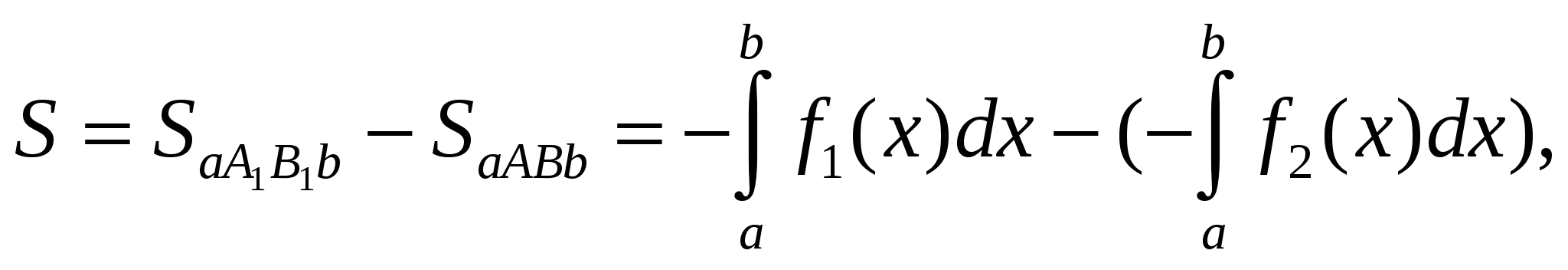 откуда следует (1.3).
откуда следует (1.3).
3) 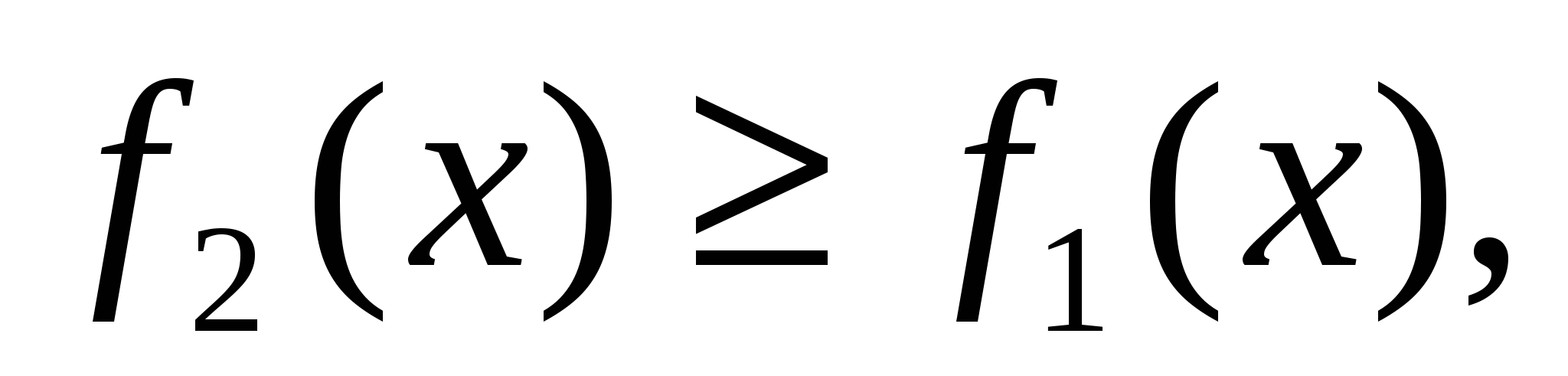
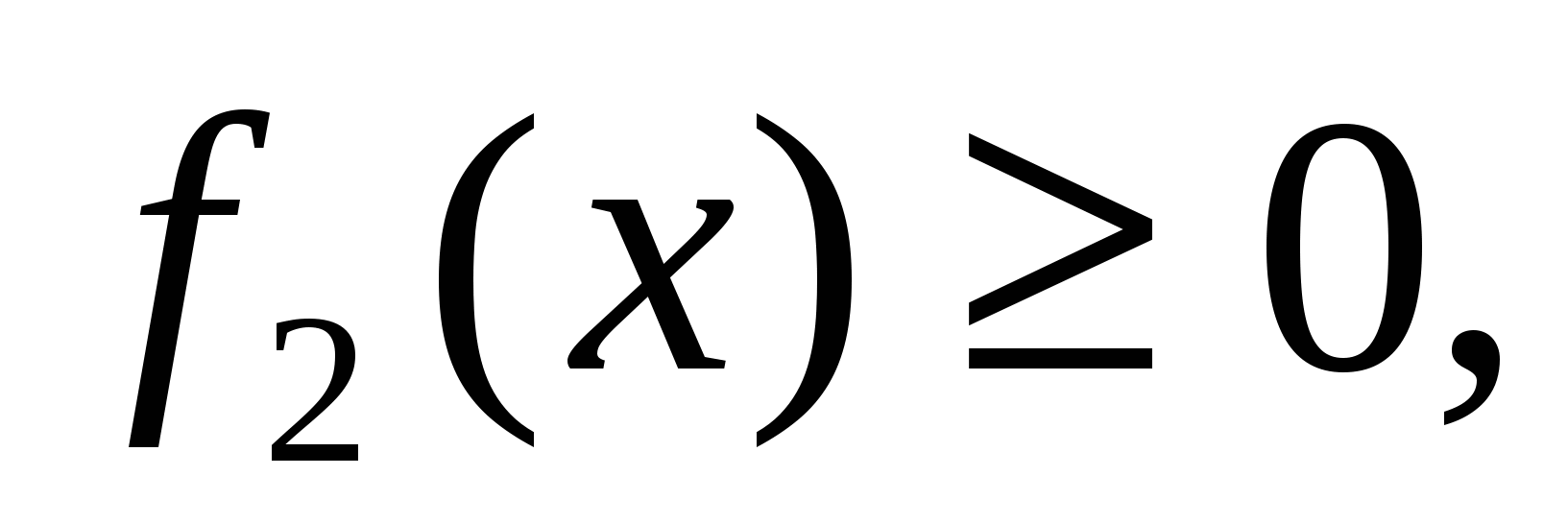
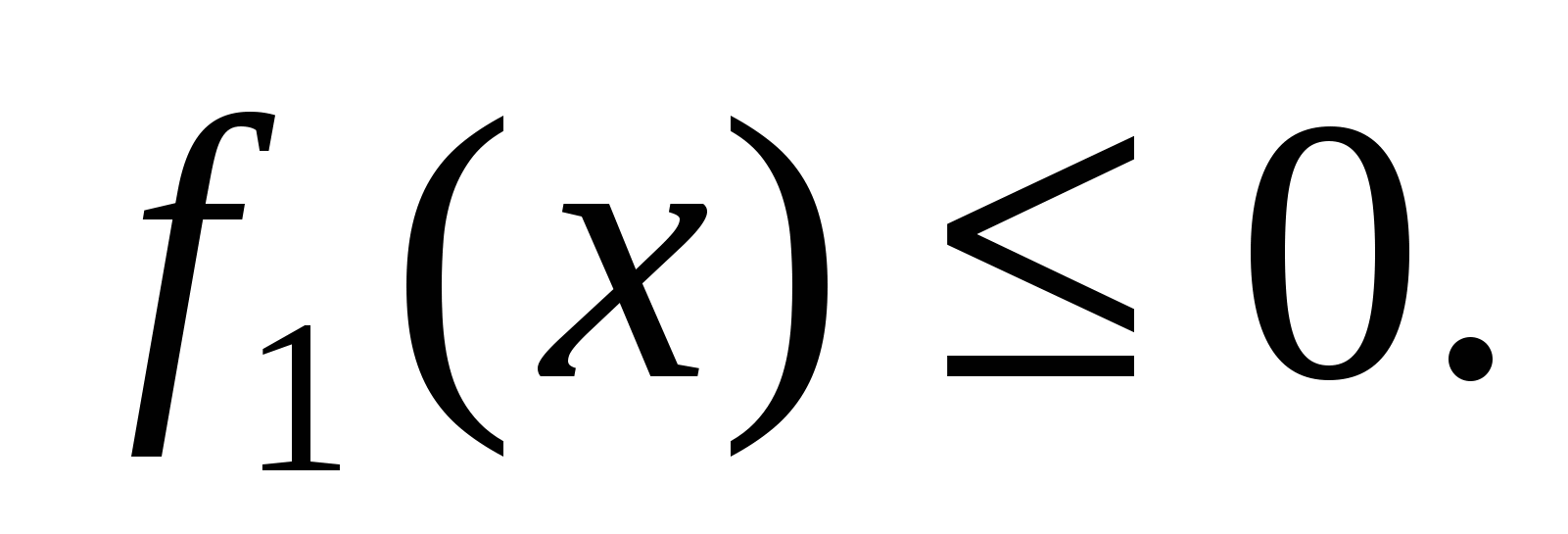 (см. рис. 1.7 в)
(см. рис. 1.7 в)
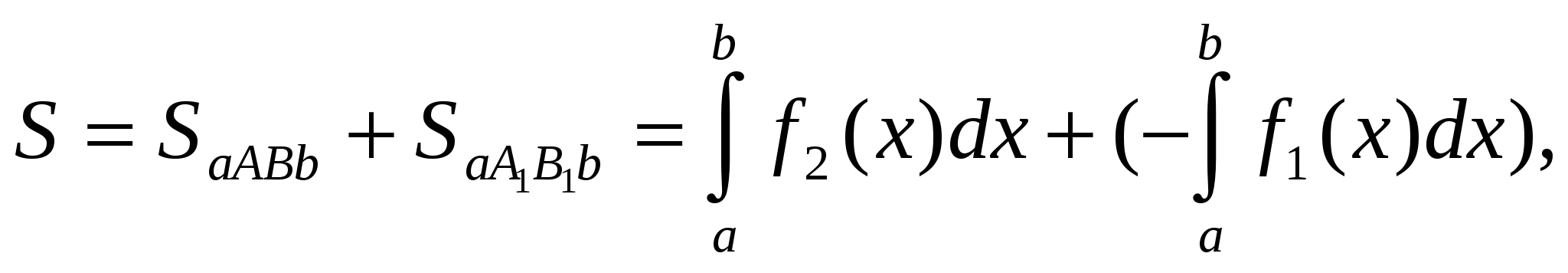 откуда следует (1.3).
откуда следует (1.3).
4) Общий случай (см. рис. 1.7 г) сводится к частным случаям, рассмотренным выше, если разбить отрезок 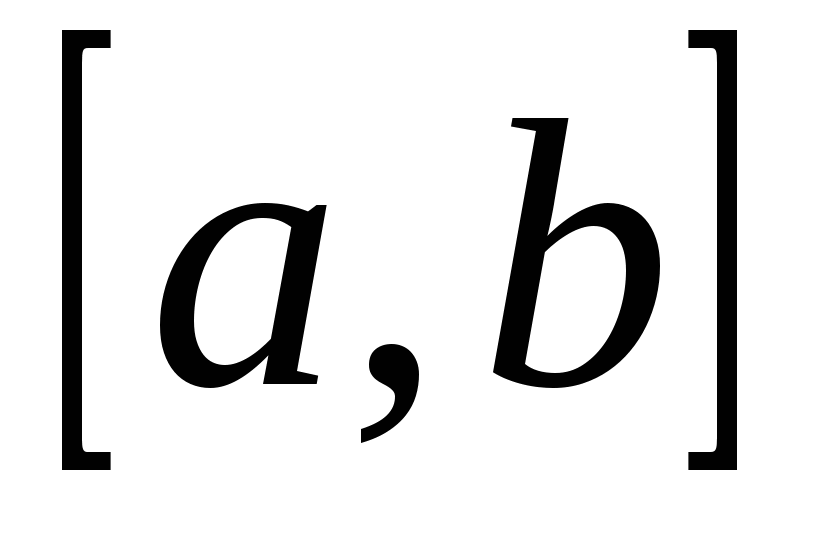 на отдельные отрезки
на отдельные отрезки ![]() ,
, 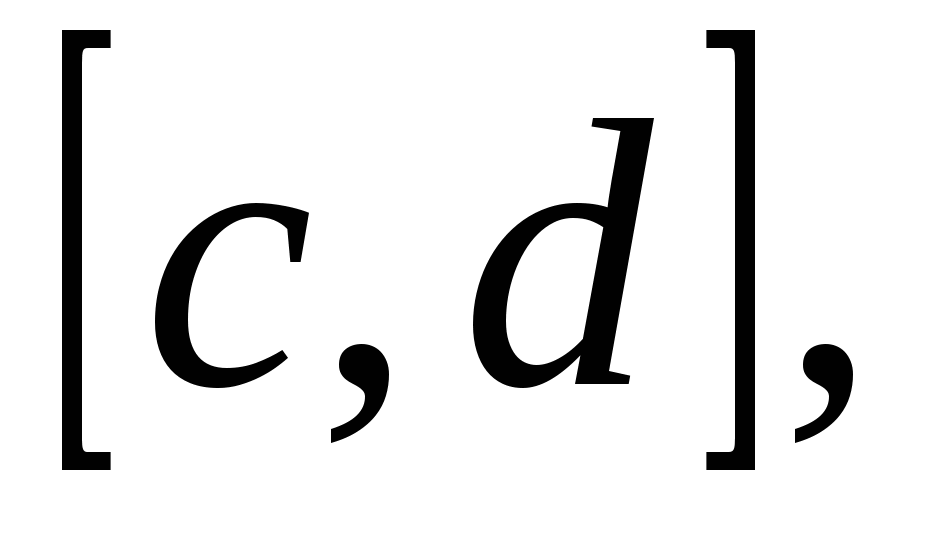
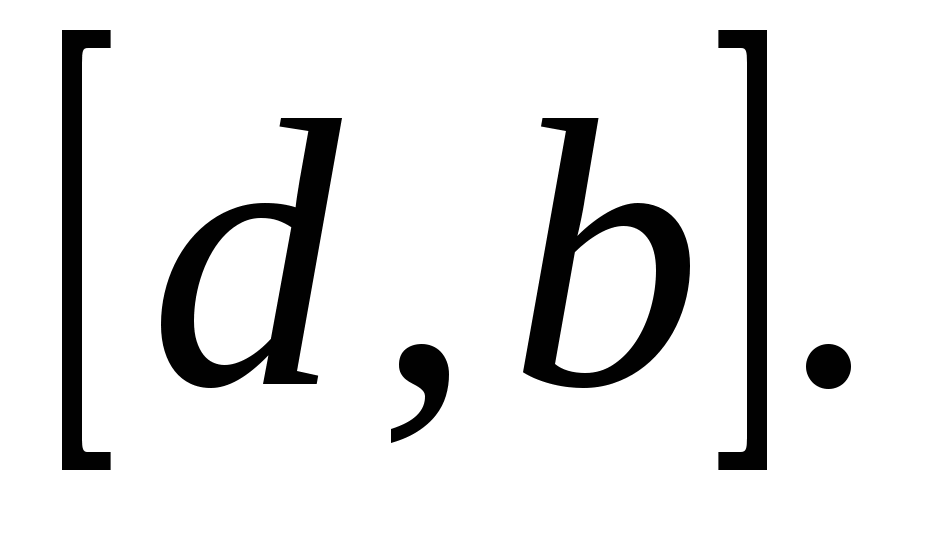
Пример 1.3. Найти площадь фигуры, ограниченной линиями 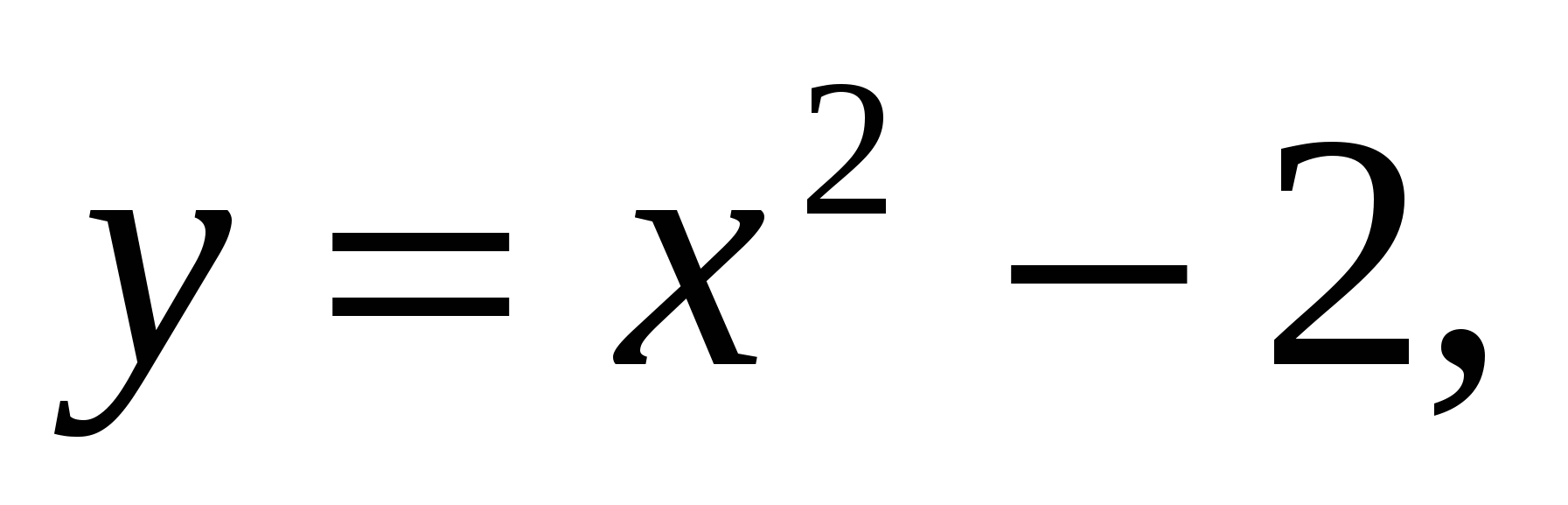
 (см. рис. 1.8).
(см. рис. 1.8).

Рис. 1.8
Решение:
Найдём координаты точек пересечения параболы 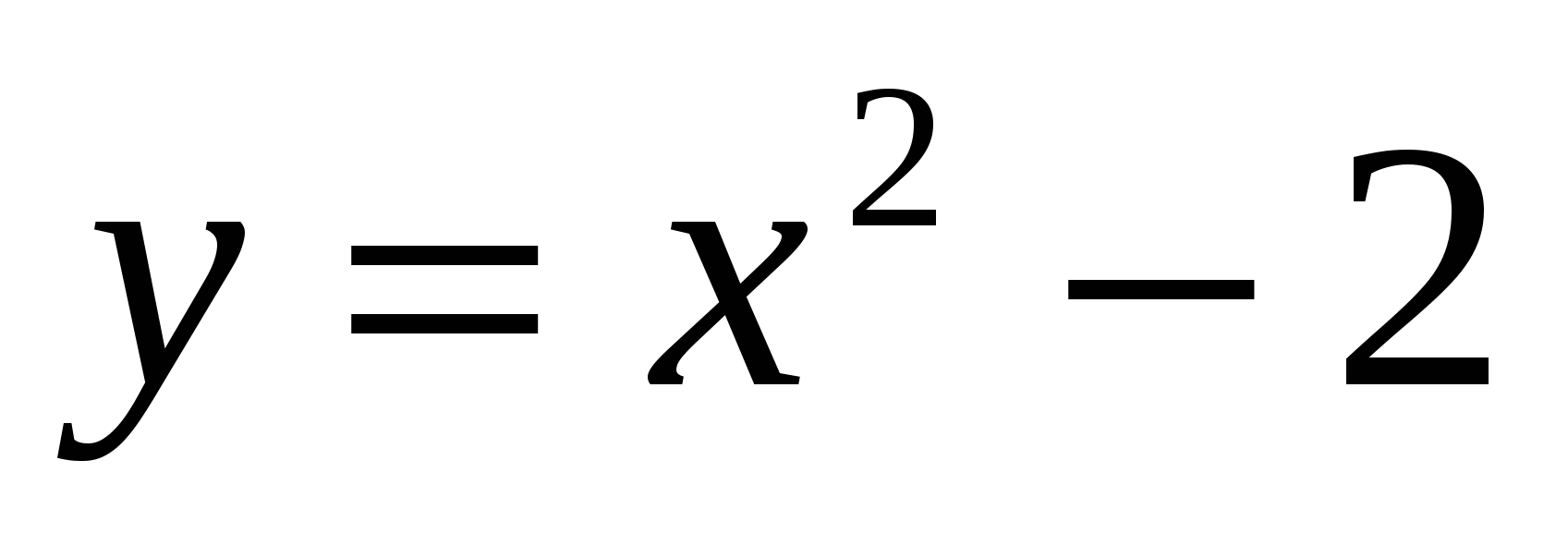 и прямой
и прямой 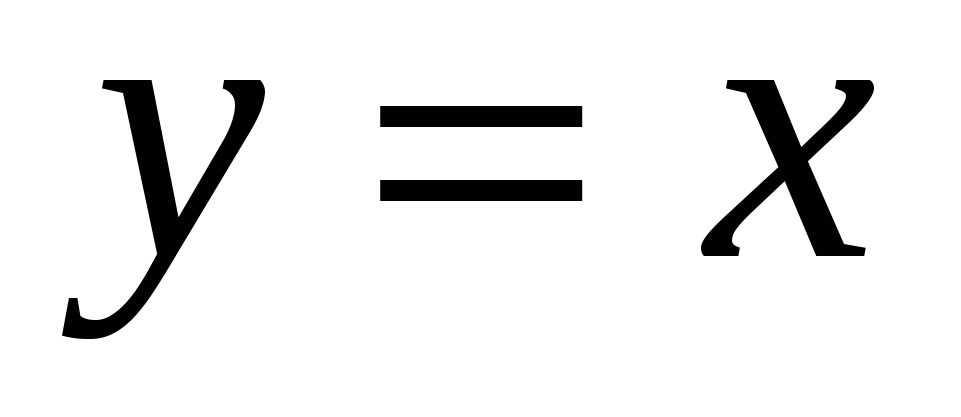 , решив систему этих уравнений: (-1;-1) и (2;2). На отрезке
, решив систему этих уравнений: (-1;-1) и (2;2). На отрезке 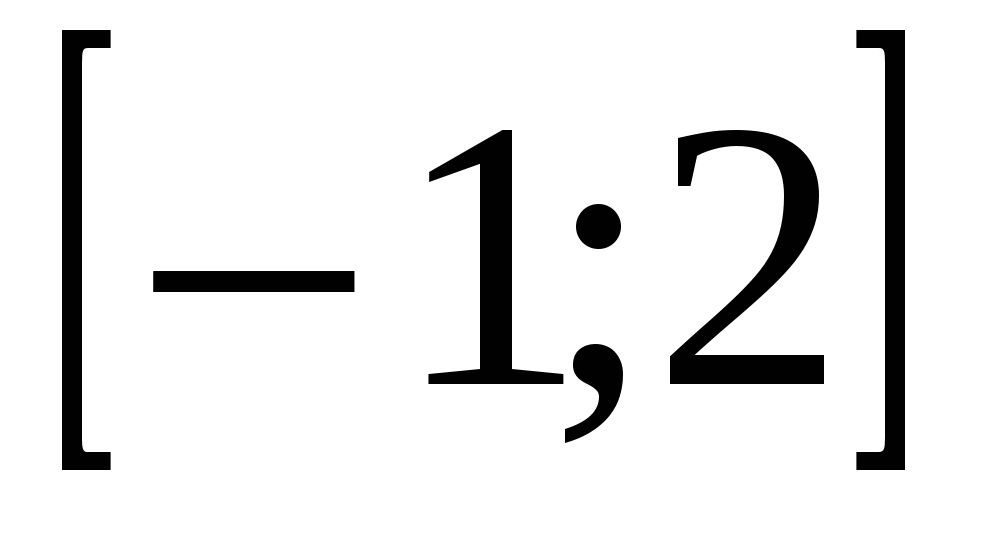

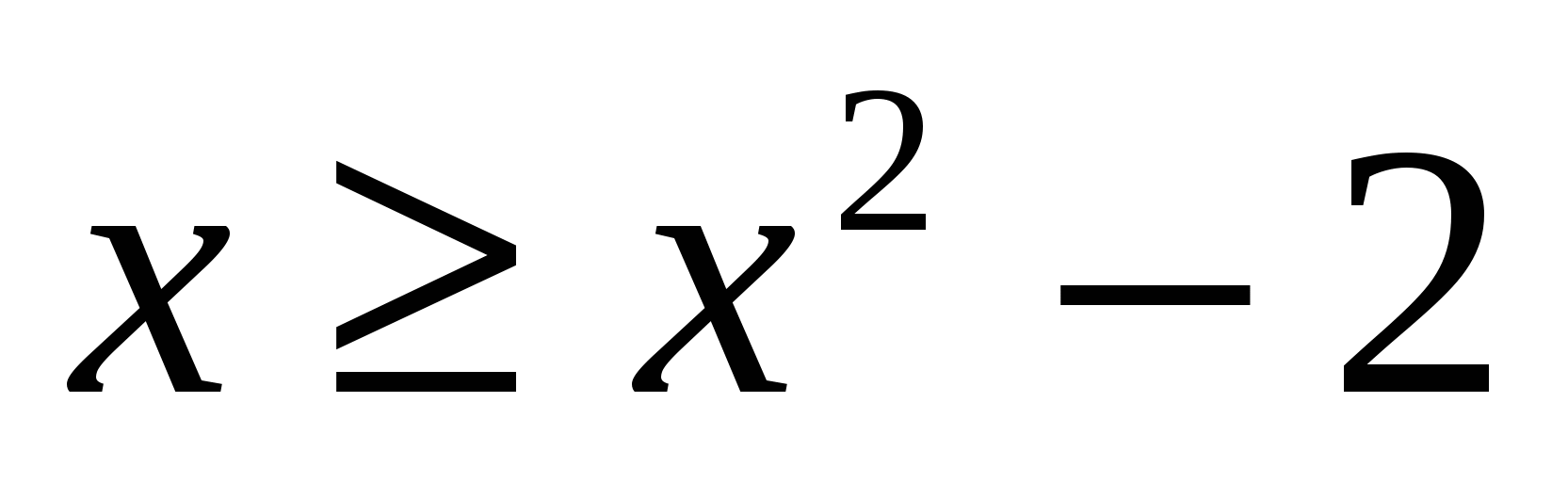 . Воспользуемся формулой (1.3), полагая
. Воспользуемся формулой (1.3), полагая 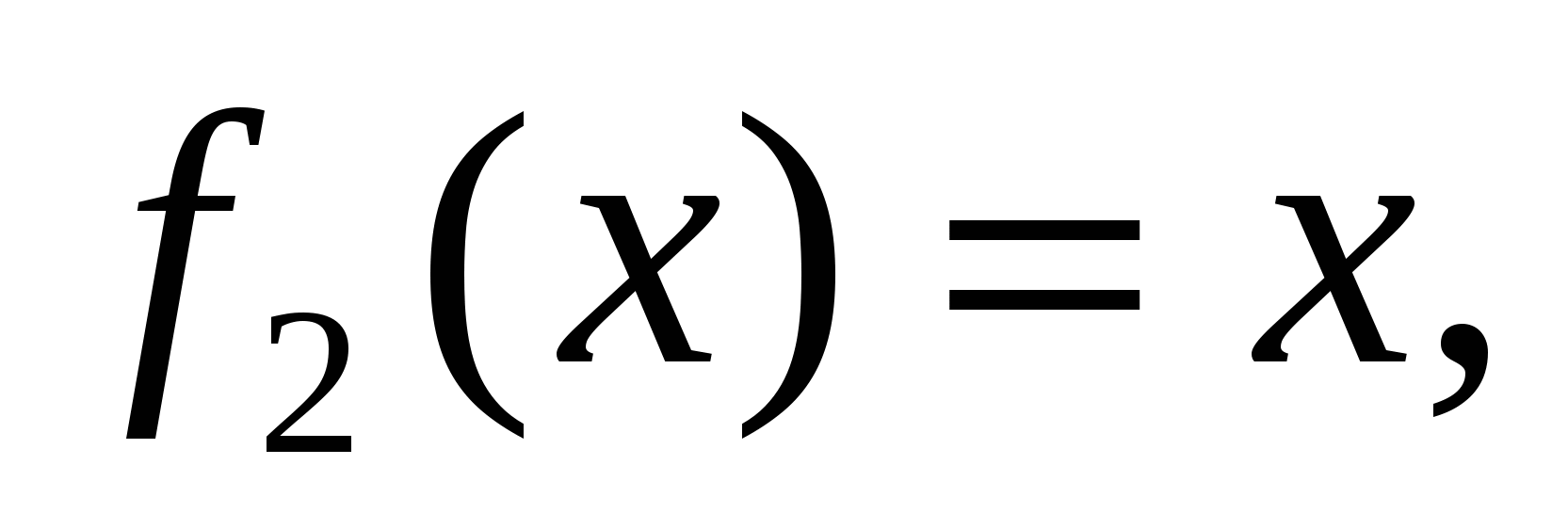
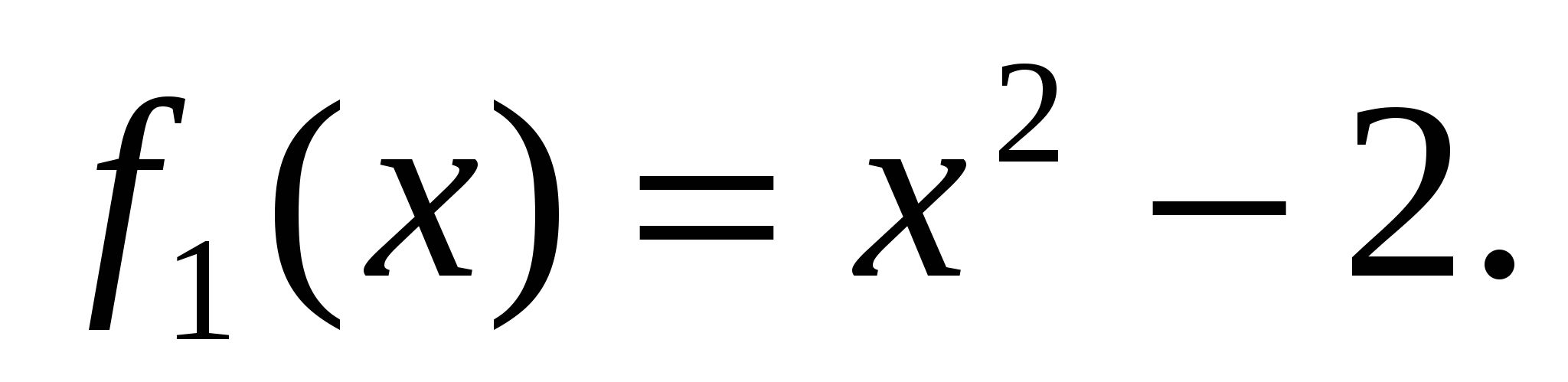
Абсциссы точек  и
и 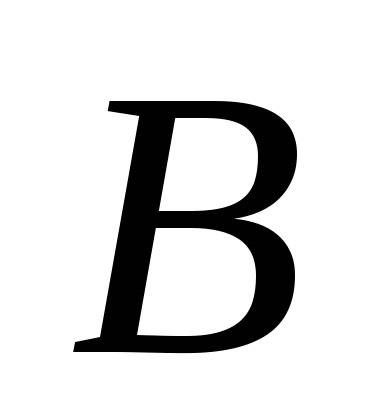 пересечения наших линий зададут пределы интегрирования:
пересечения наших линий зададут пределы интегрирования:
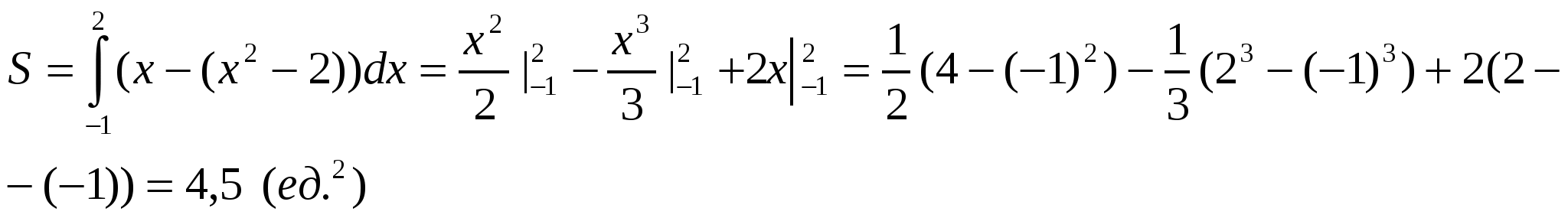
Упражнения для самостоятельной работы
Найти площадь фигуры, ограниченной линиями:
1.1. 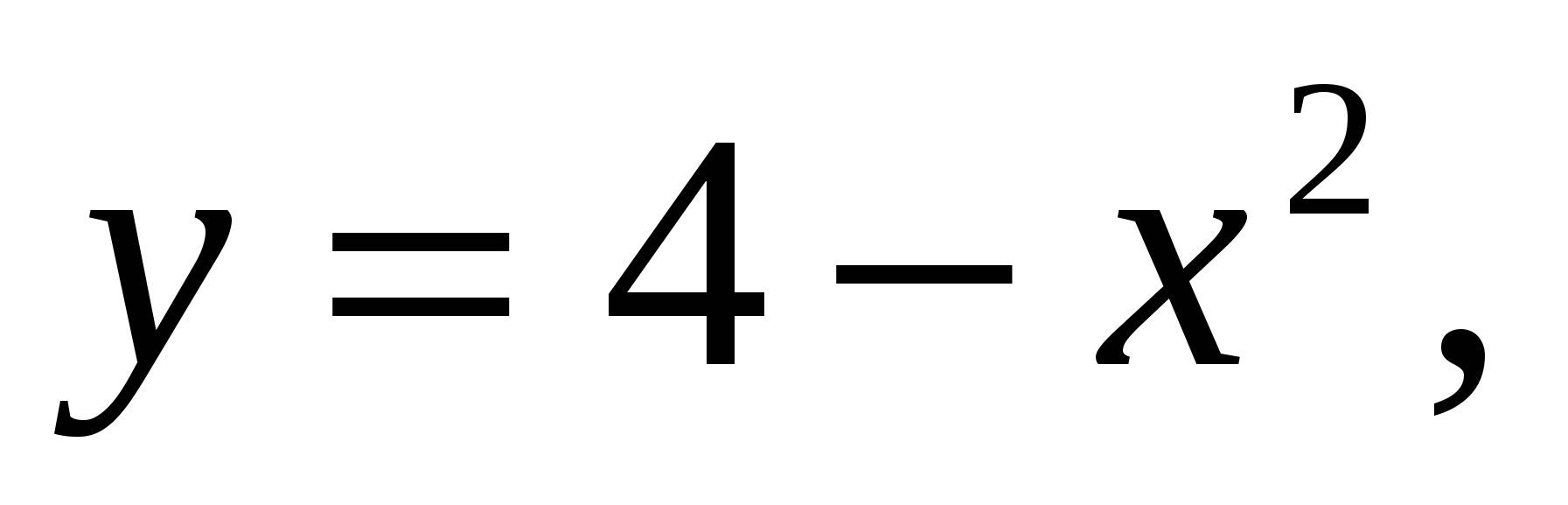
 1.2.
1.2. 
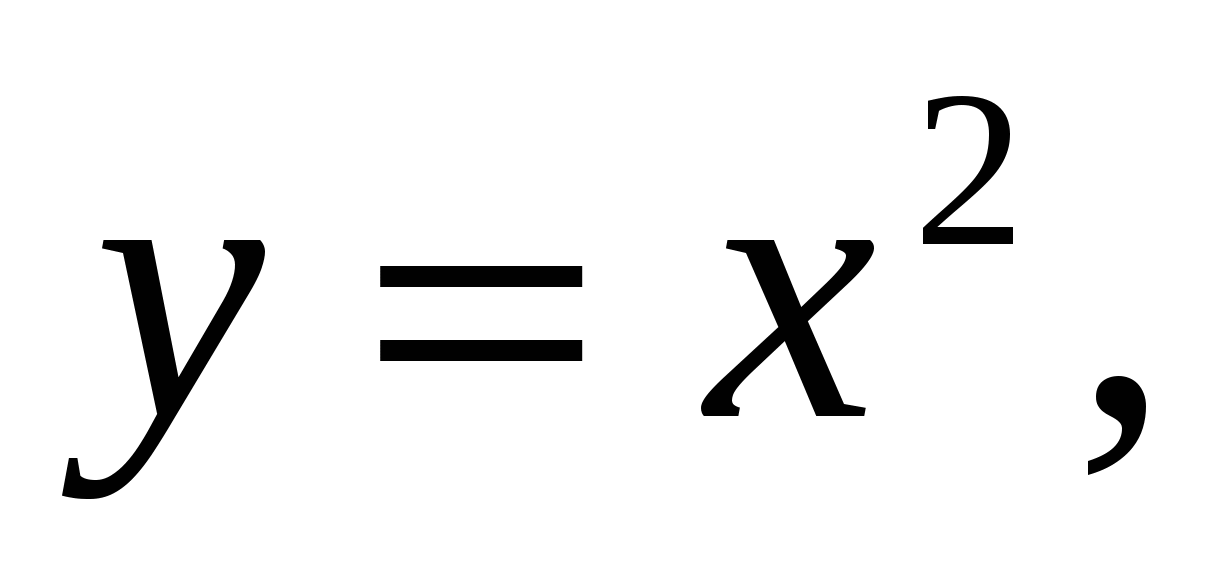
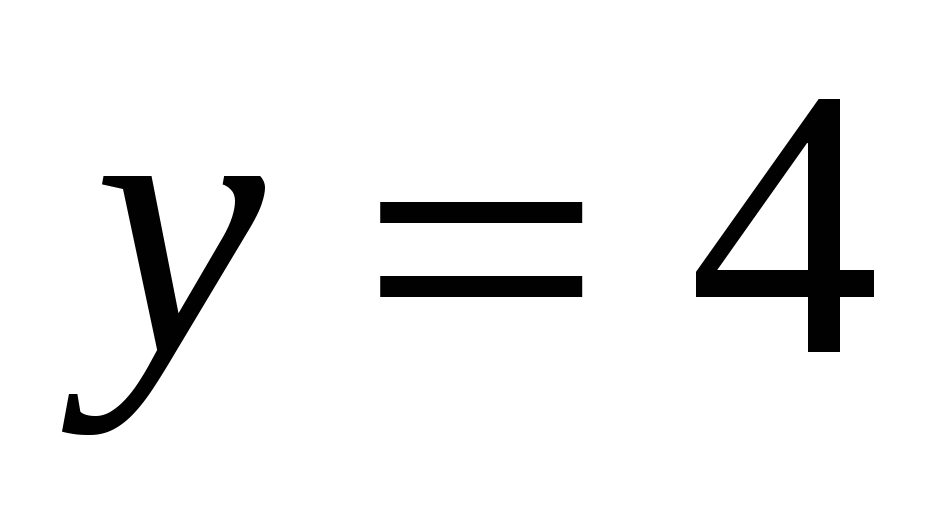 и
и
расположенной в I четверти.
1.3.
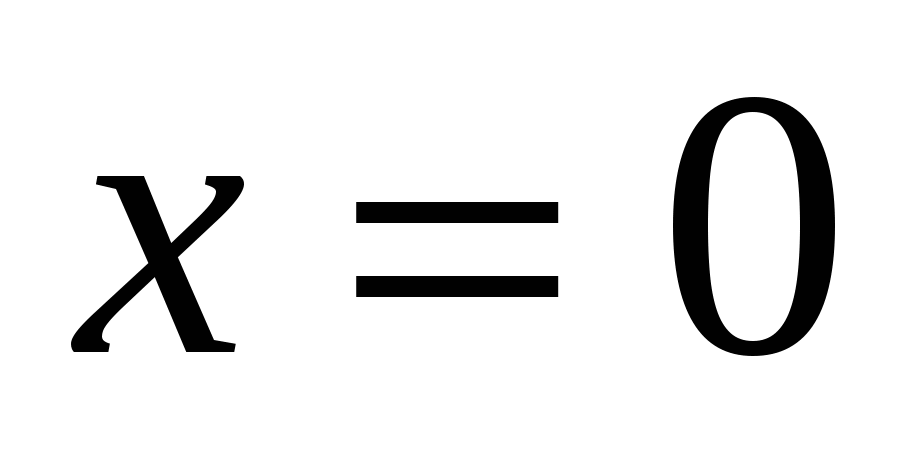 ,
,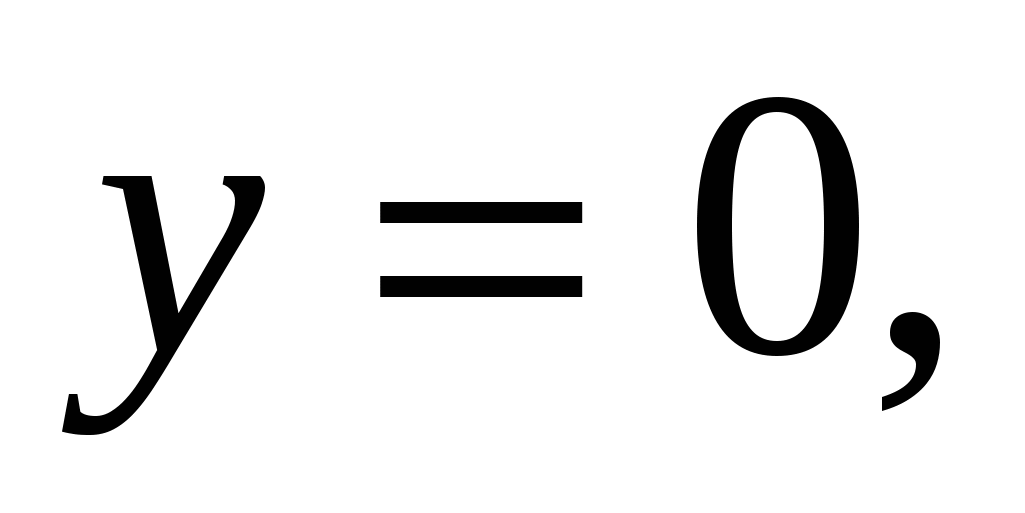
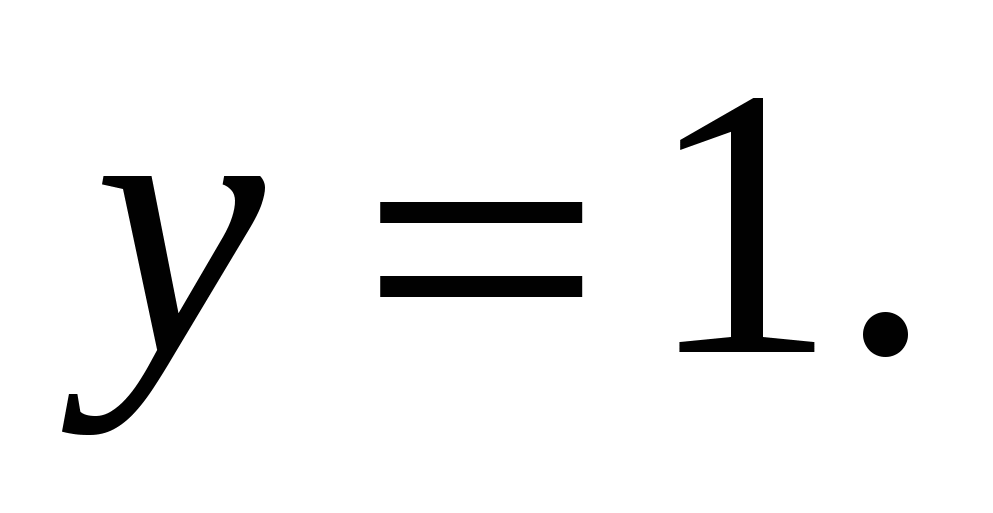 1.4.
1.4. 

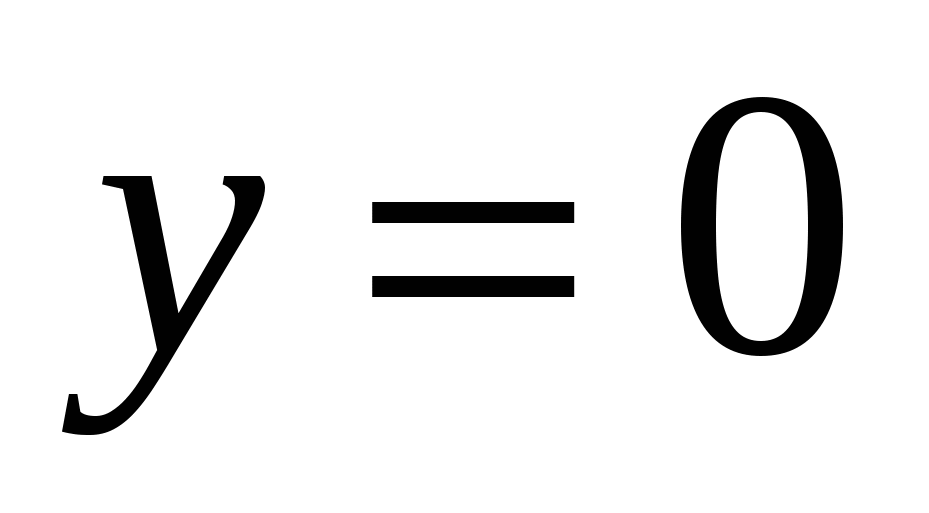
1.5. 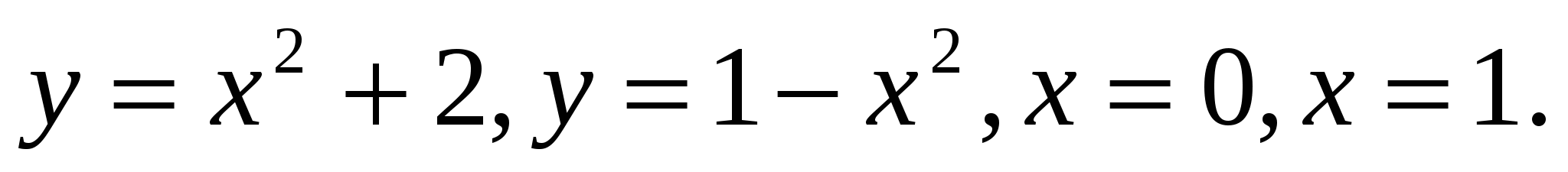 1.6.
1.6. 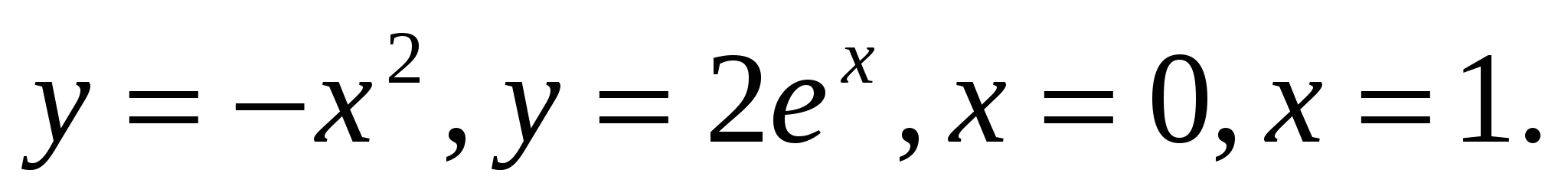
1.7. 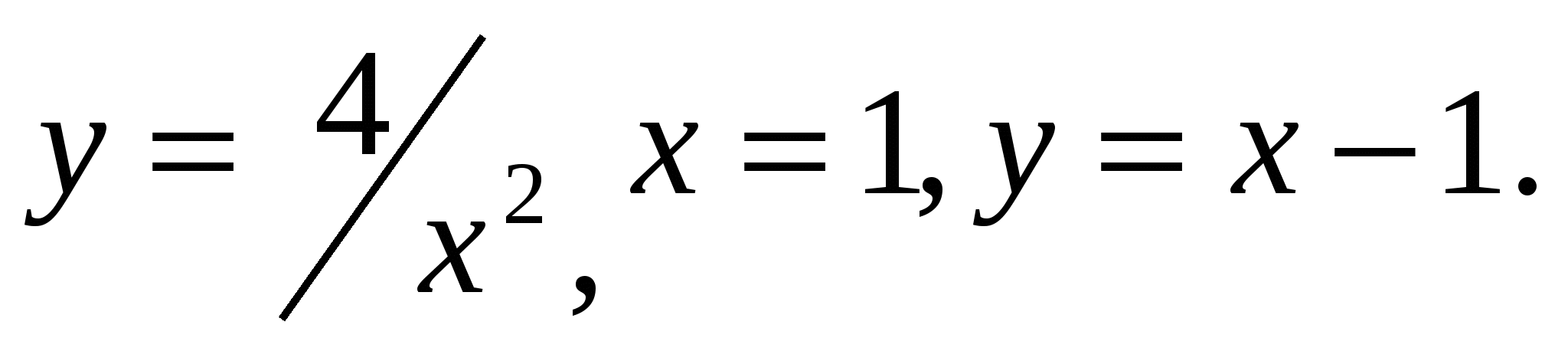 1.8.
1.8. 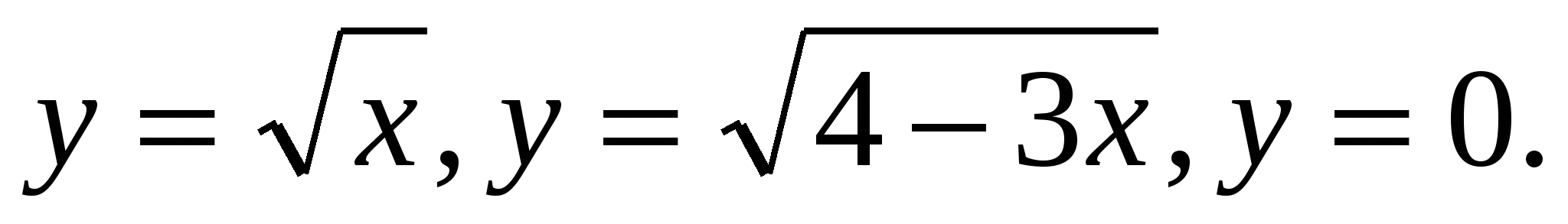
1.9. 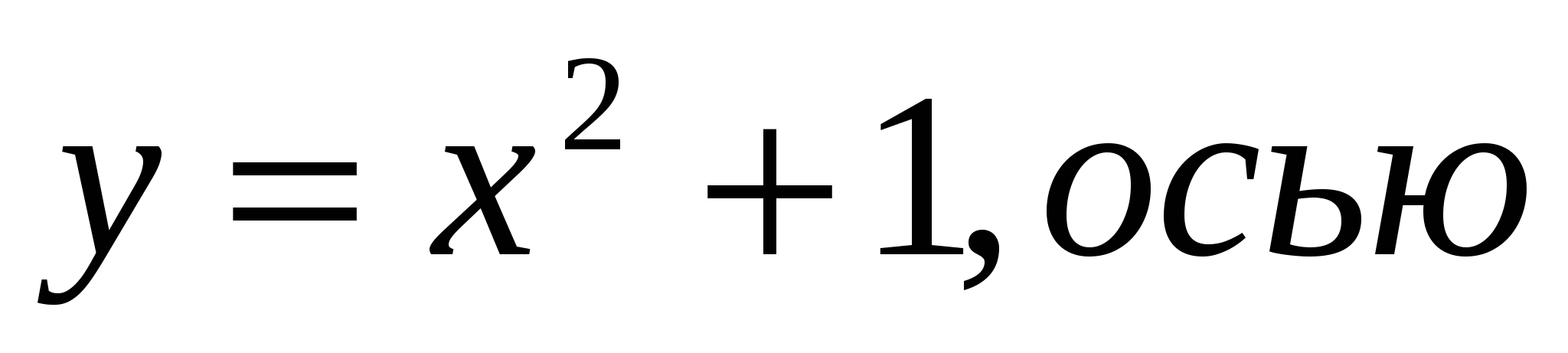
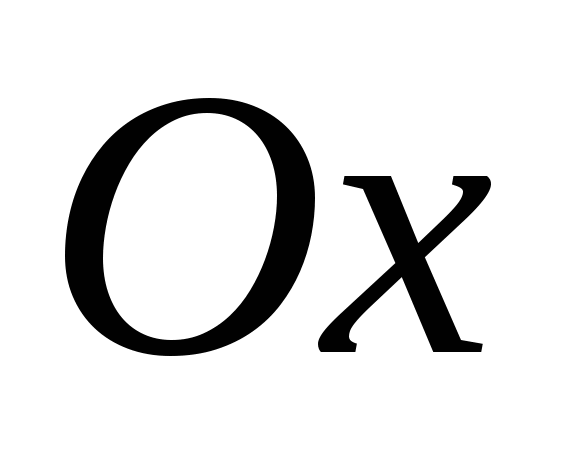 и
и 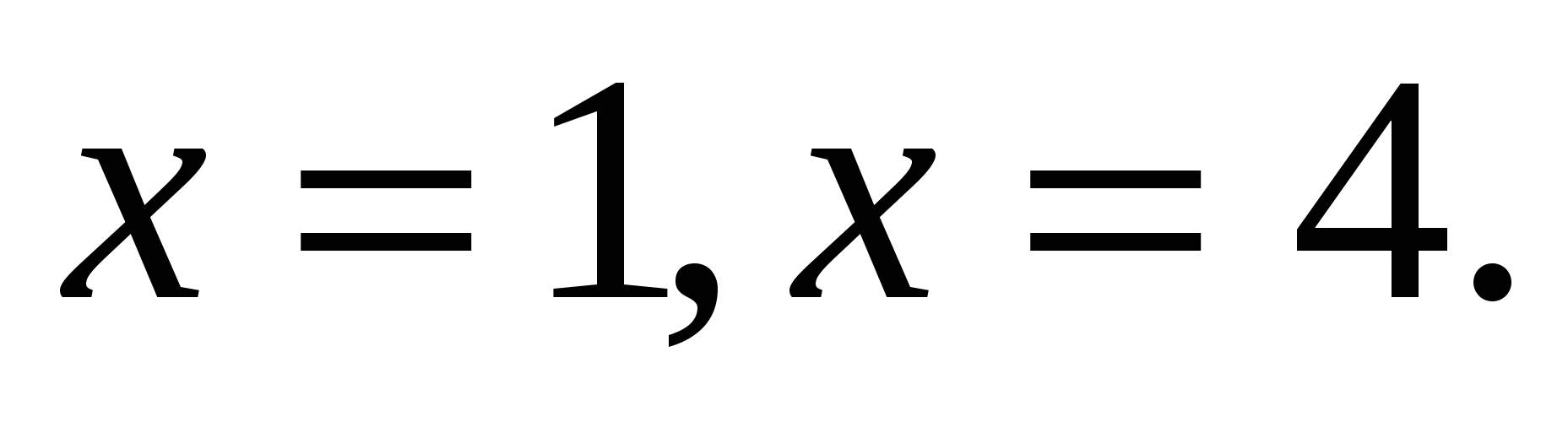 1.10.
1.10. 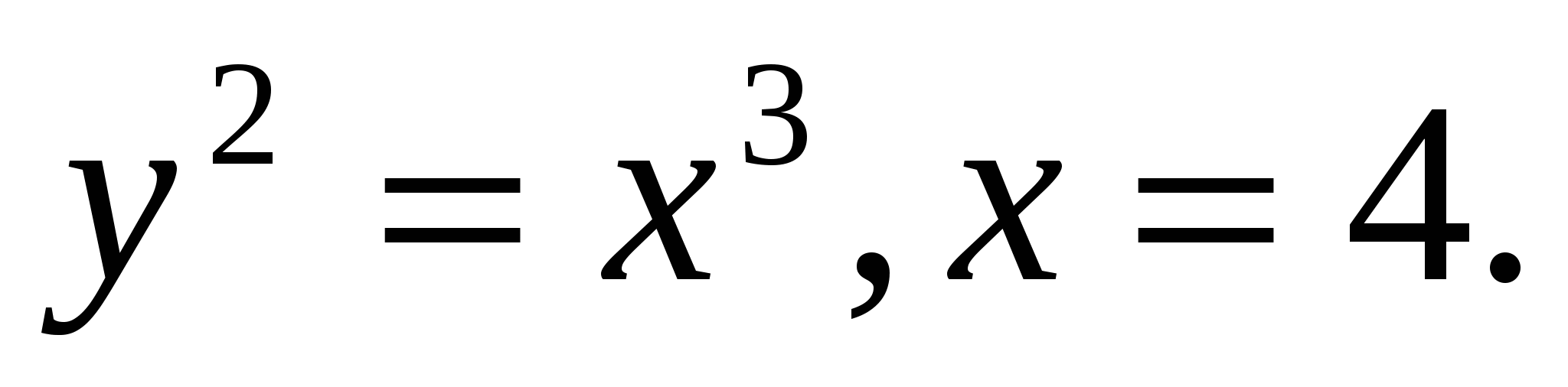
1.11. 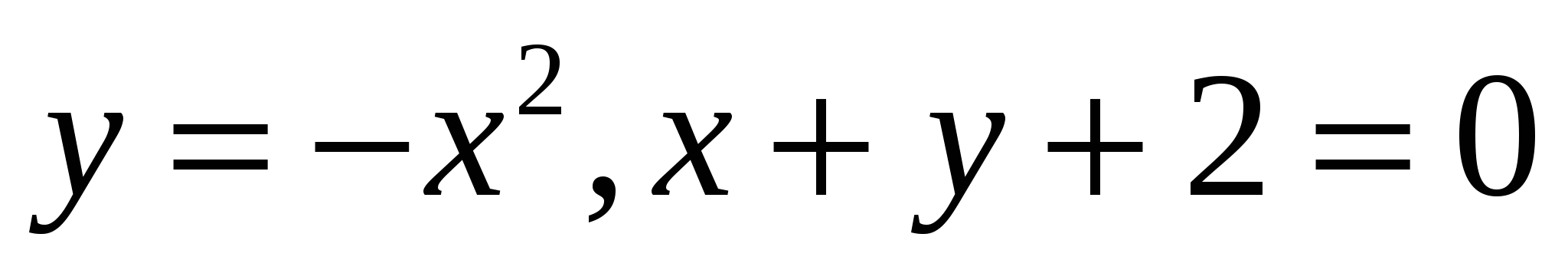 1.12.
1.12. 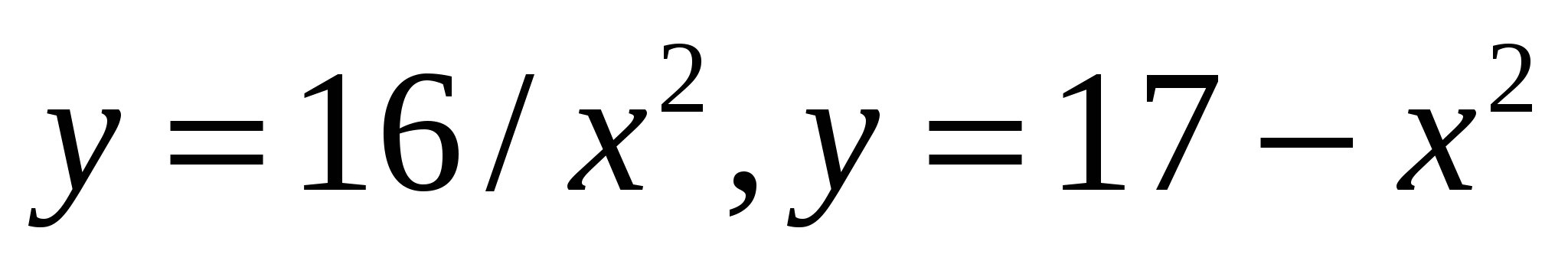 (I четверть)
(I четверть)
1.13. 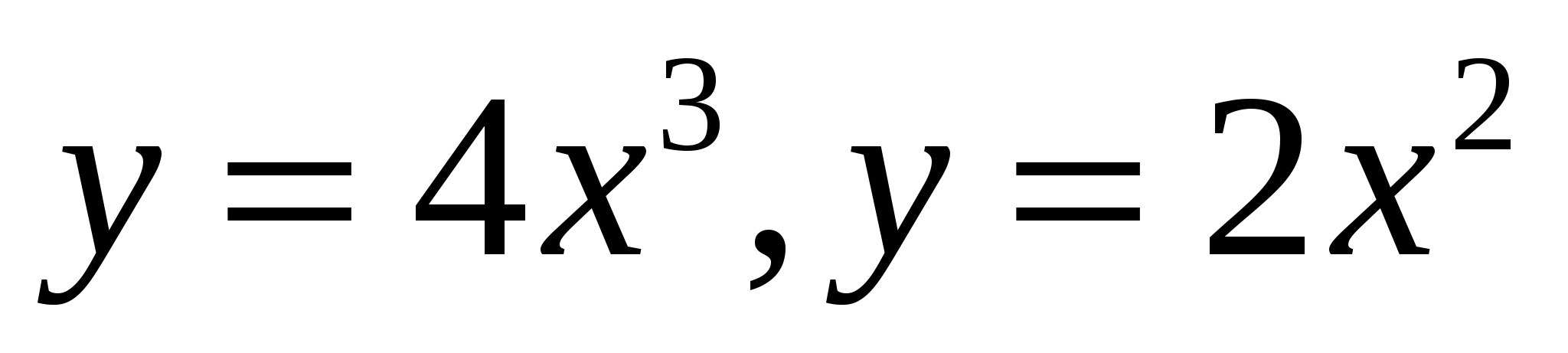 1.14*.
1.14*. 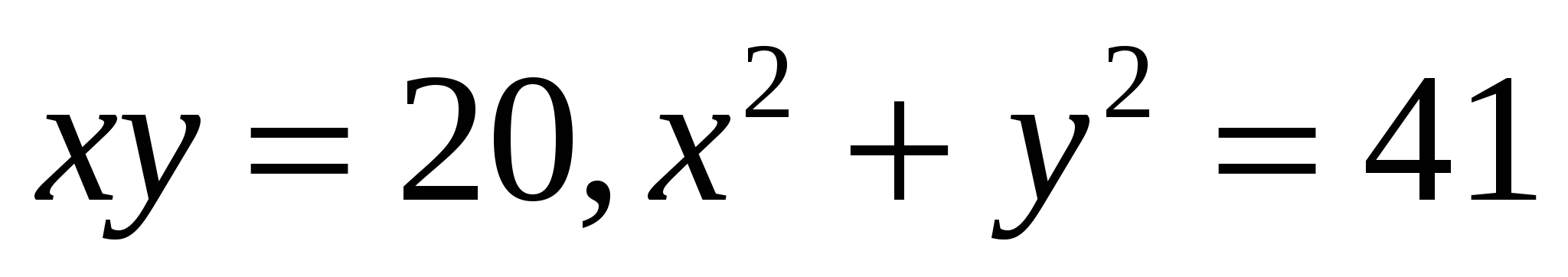 (I четверть)
(I четверть)
1.15. 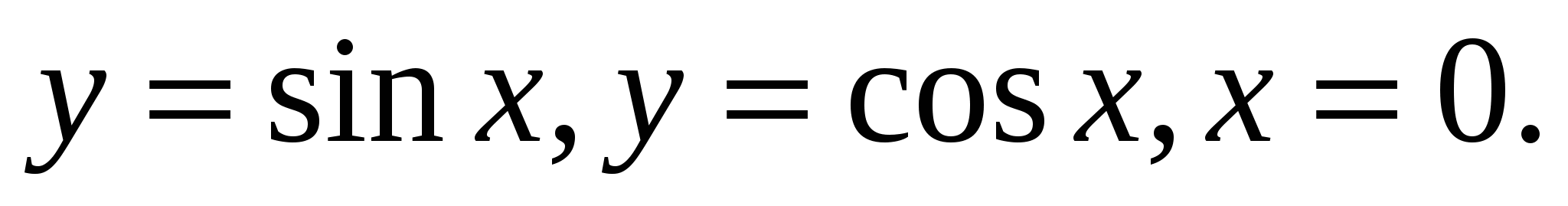 1.16.
1.16.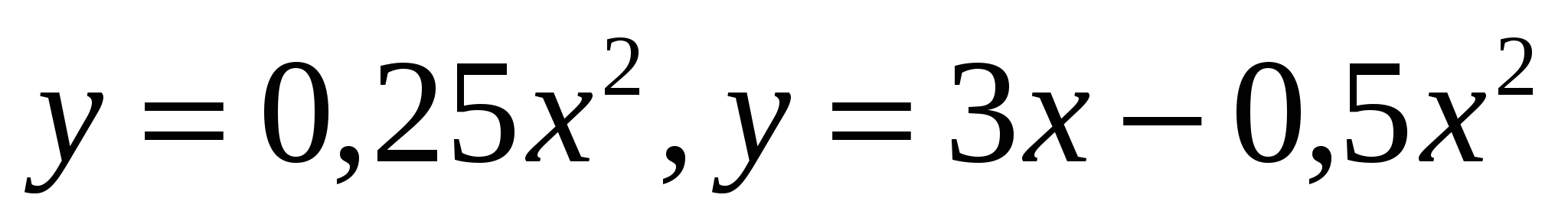
1.17*.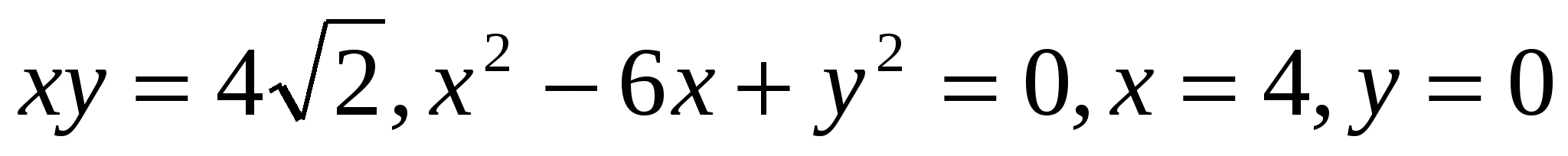
Индивидуальные задания
Раздел А
Задача 1. Вычислить площадь криволинейной трапеции, ограниченной
графиком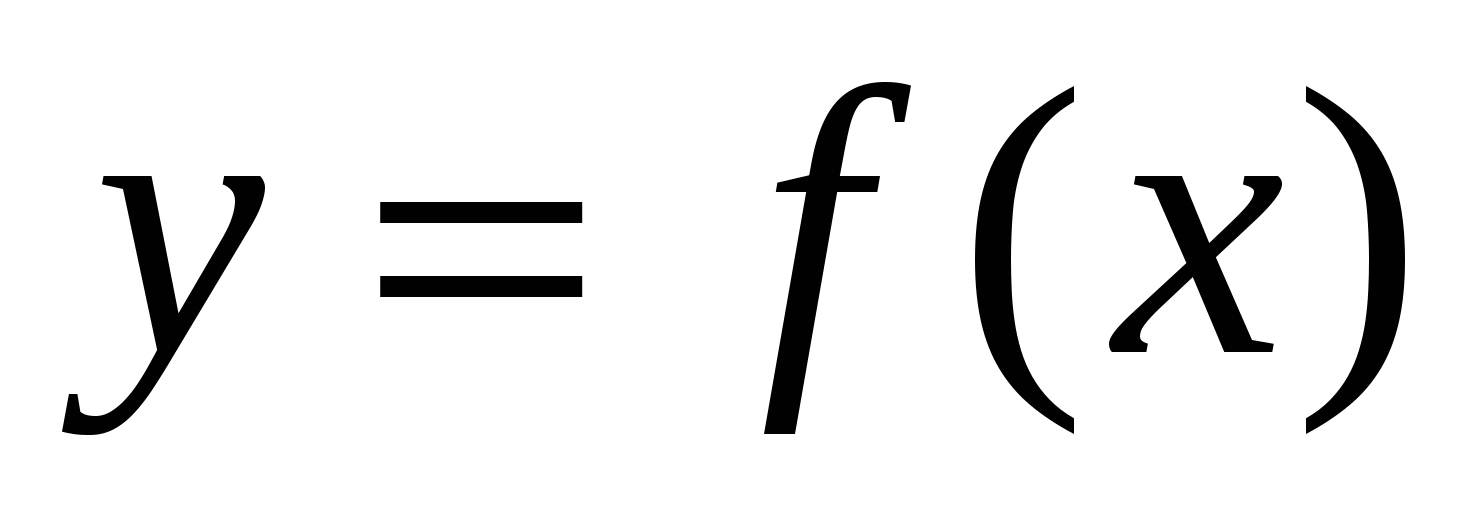 , осью Ox и прямыми
, осью Ox и прямыми  и
и 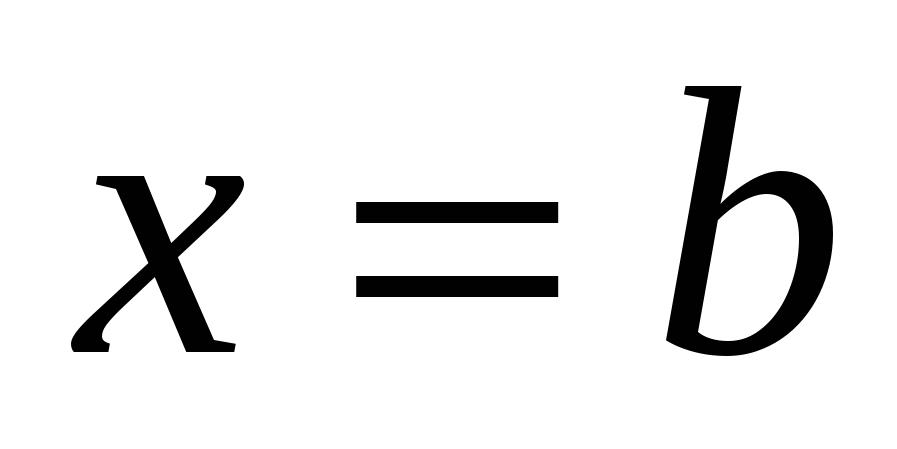 . Функция
. Функция 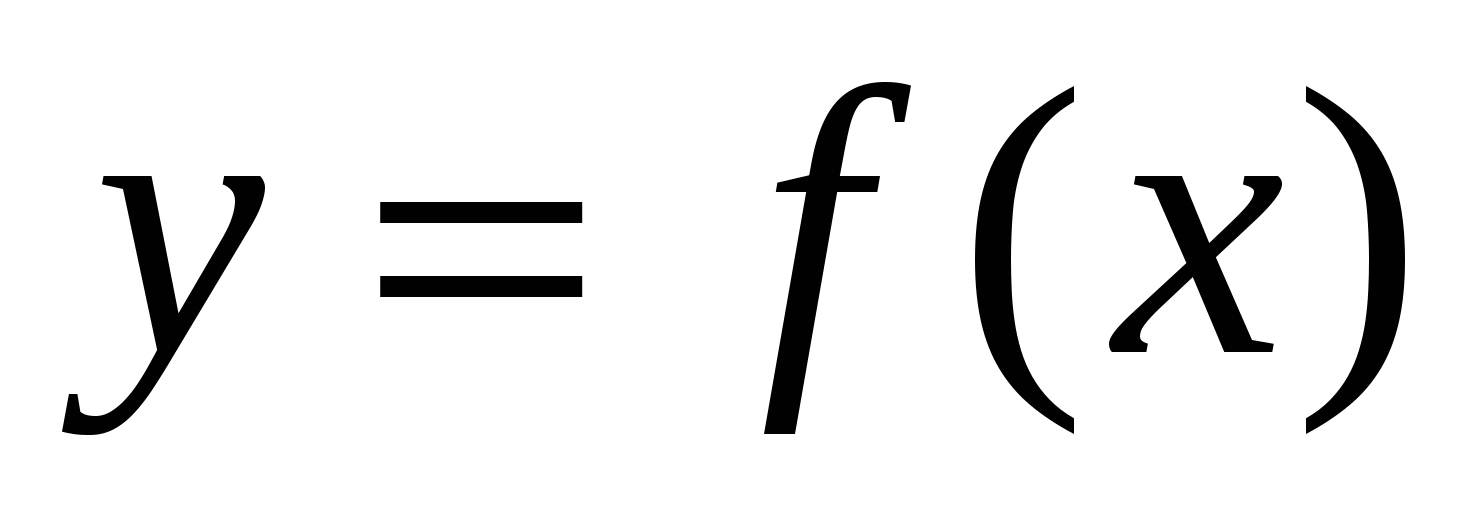 , отрезок
, отрезок 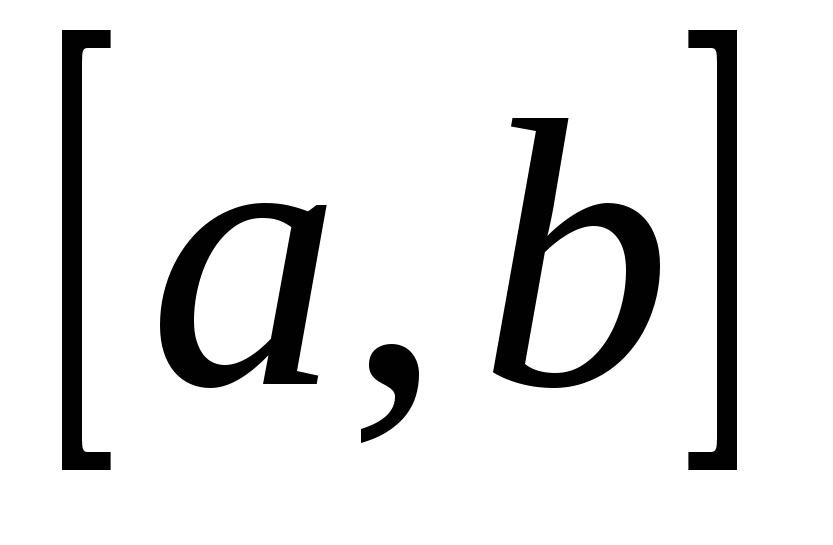 даны в таблице 1.
даны в таблице 1.
Таблица 1
№ вари-
анта
Функция
![]() .
.
Пределы интегрирования.
a
b
1
![]()
1
5
2
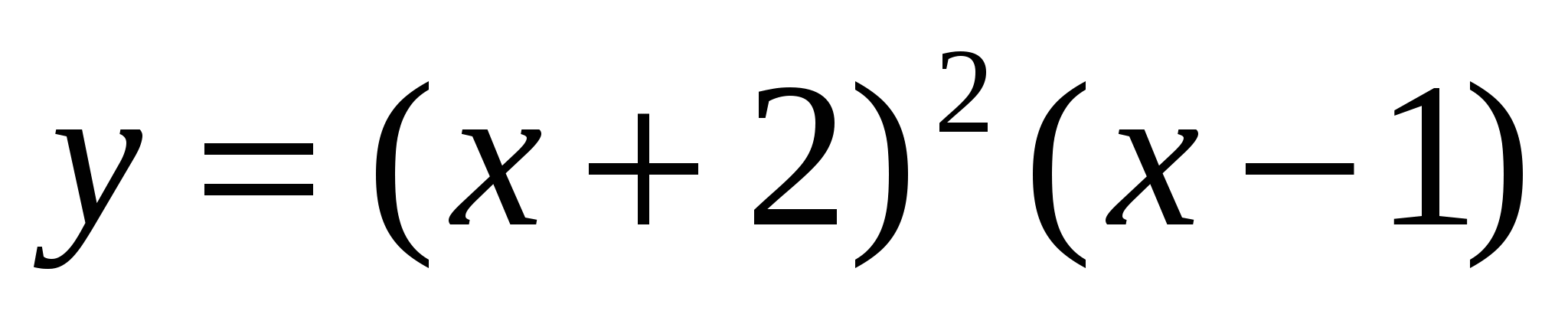
-2
1
3
![]()
-3
3
4
![]()
-1
1
5
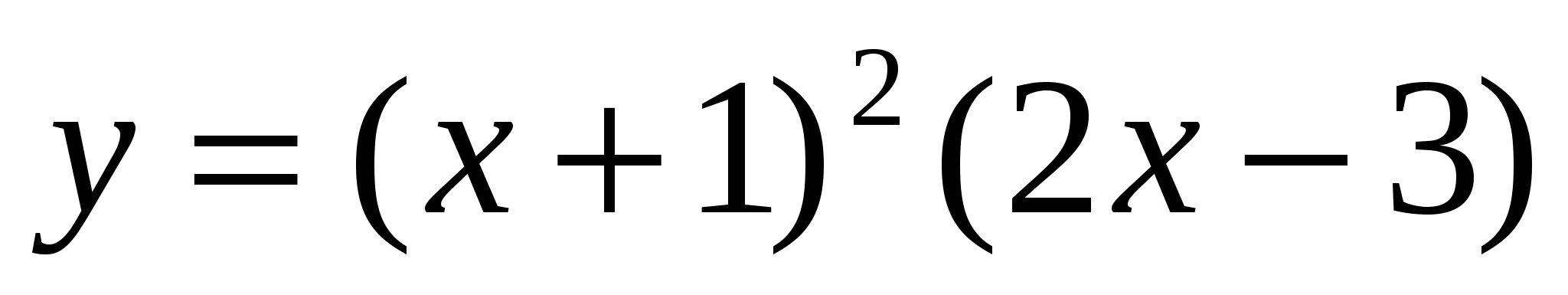
0
1
6
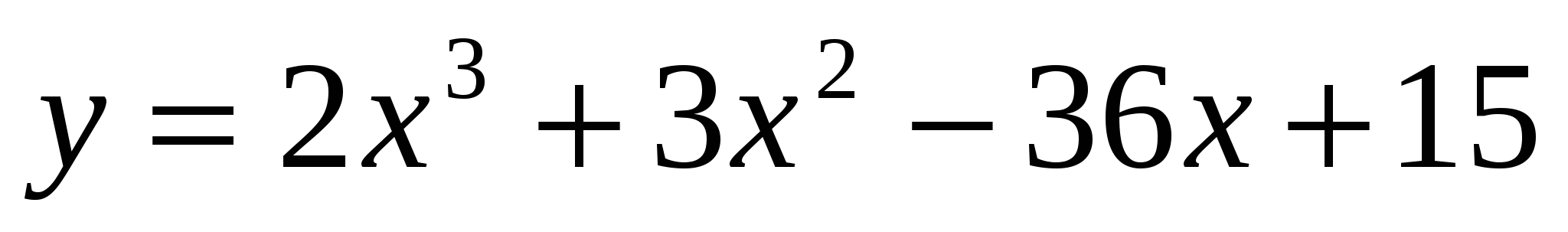
-3
0
7
![]()
0
1
8
![]()
-2
2
9

-1
0
10
![]()
0
2
11
![]()
0
1
12
![]()
0
2
13
![]()
1
2
14
![]()
-2
0
15
![]()
-1
1
16
![]()
1
5
17
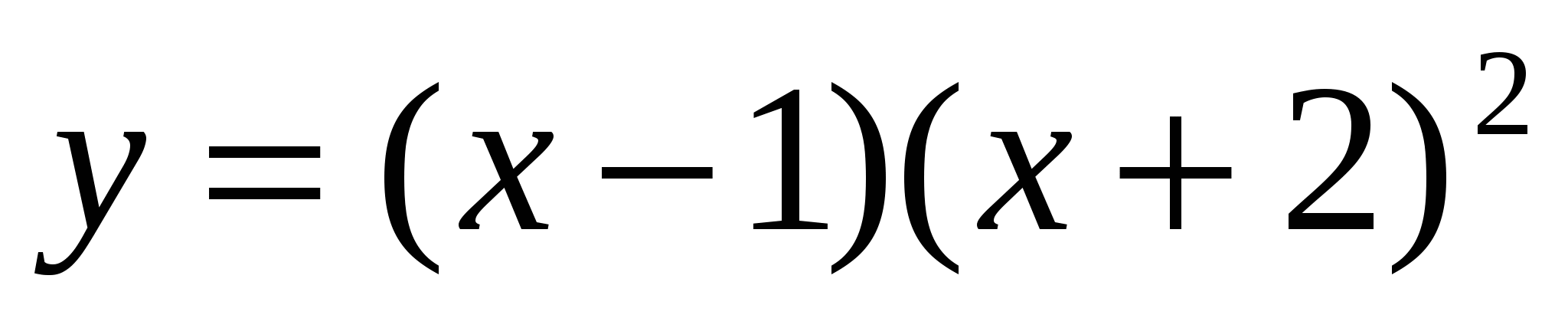
-2
1
18
![]()
-3
3
19
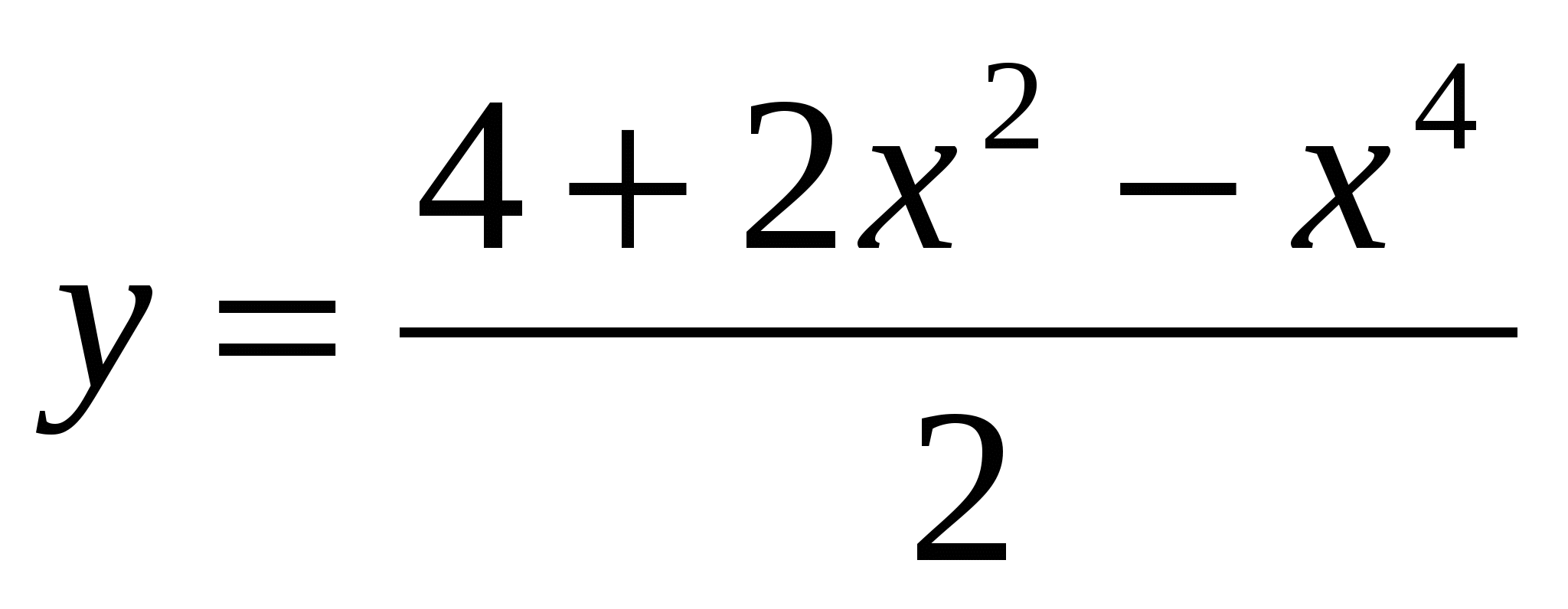
-1
1
20
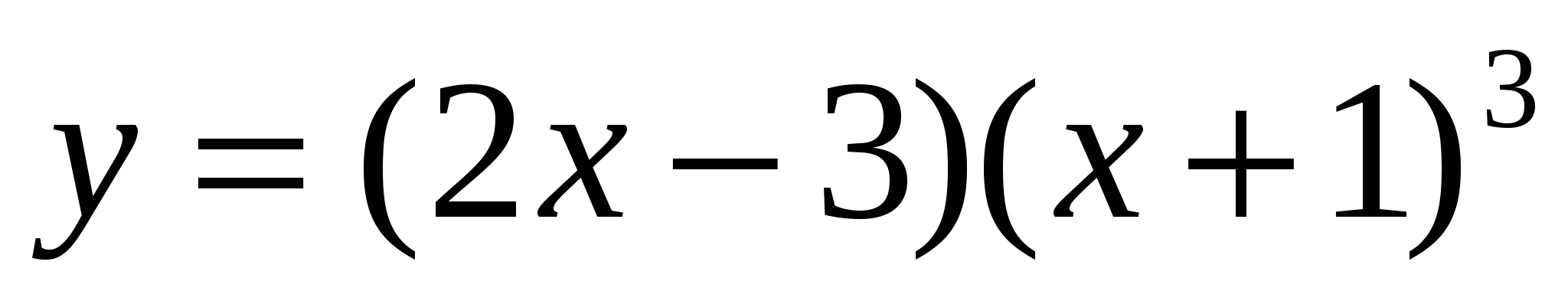
0
1
21
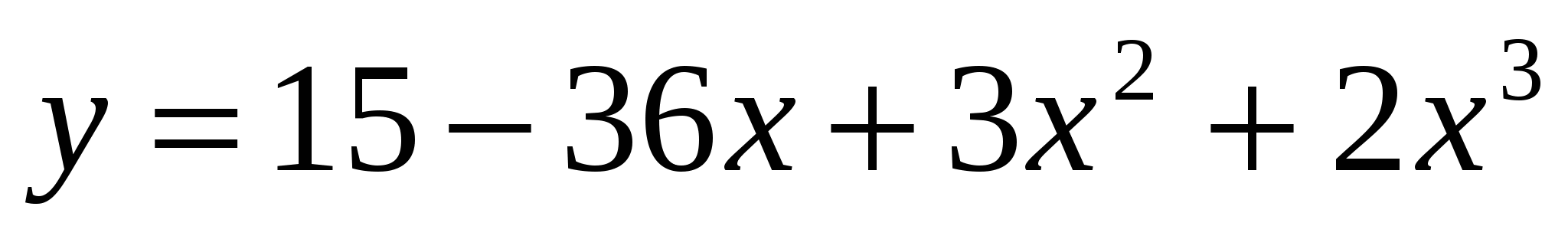
-3
0
22
![]()
0
1
23
![]()
-2
2
24

-1
0
25
![]()
0
2
26
![]()
0
1
27
![]()
0
2
28
![]()
1
2
29
![]()
-2
0
30
![]()
-1
1
Задача 2.
Вычислить площадь фигуры, ограниченной линиями (таблица 2).
Таблица 2
№
вари-
анта.
Уравнения линий.
№
вари-
анта.
Уравнения линий.
1
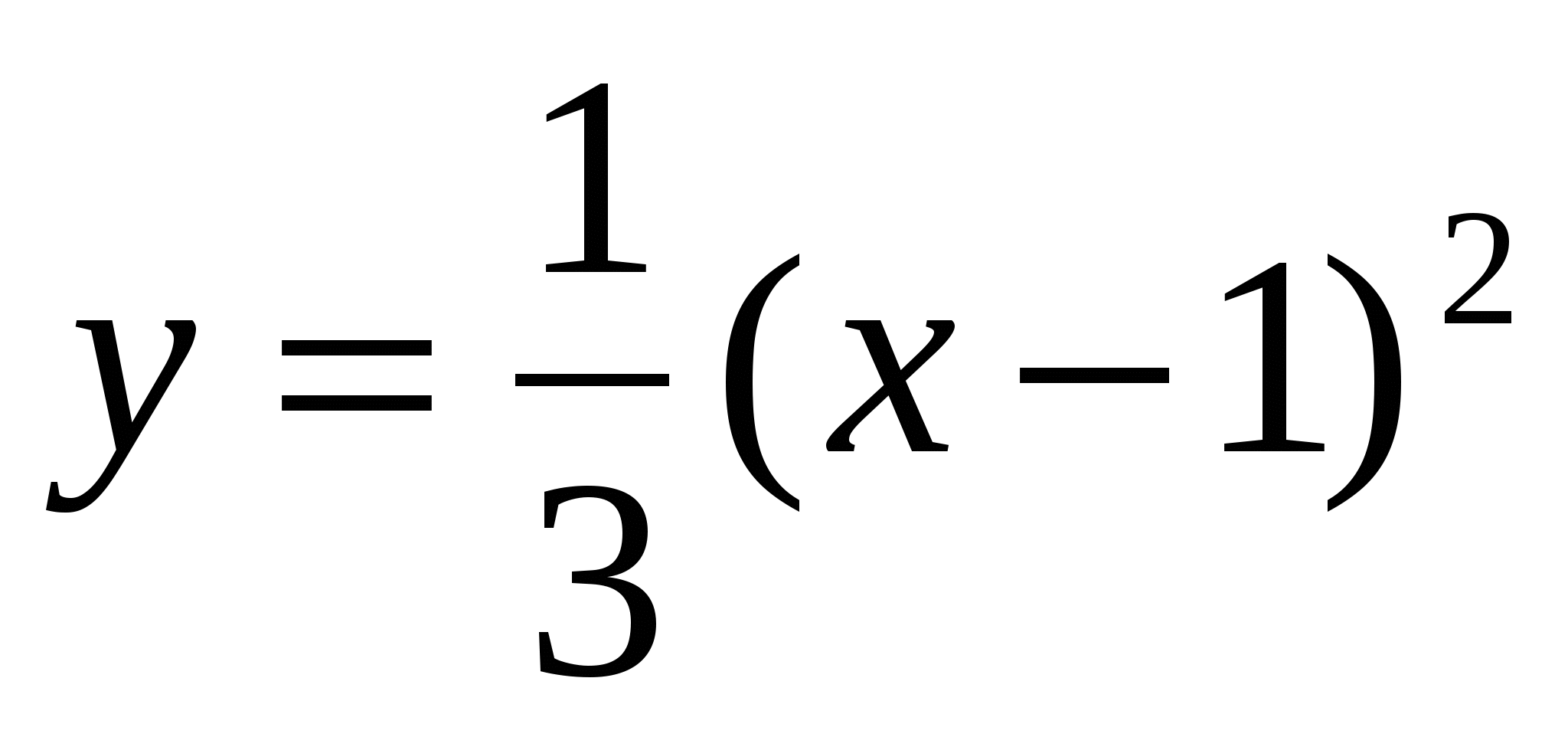 ,
, 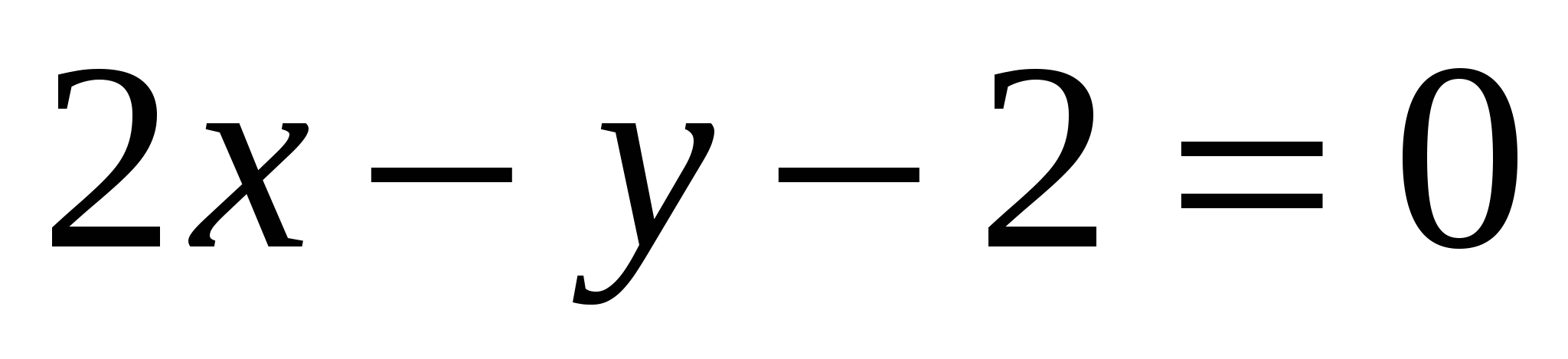
16
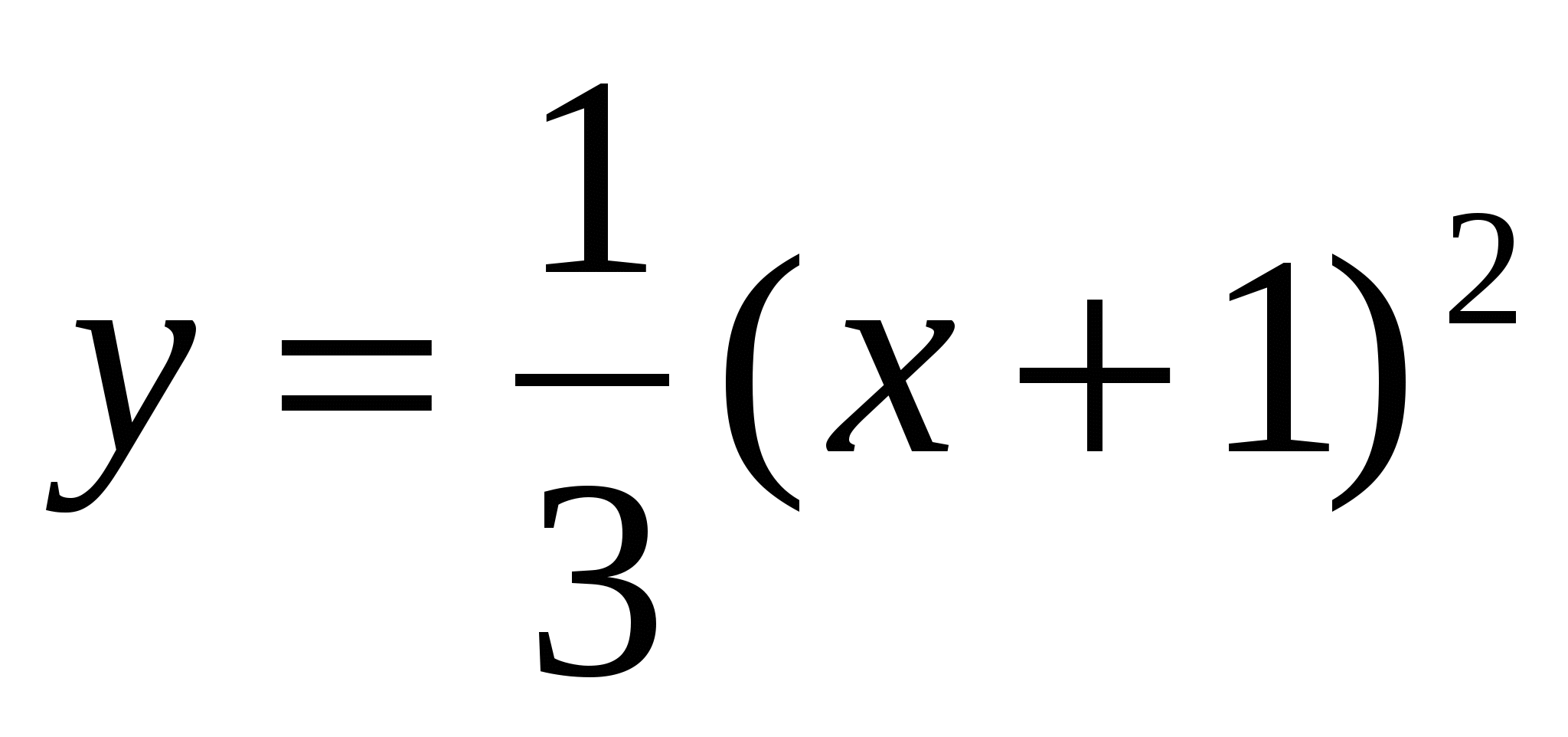 ,
, 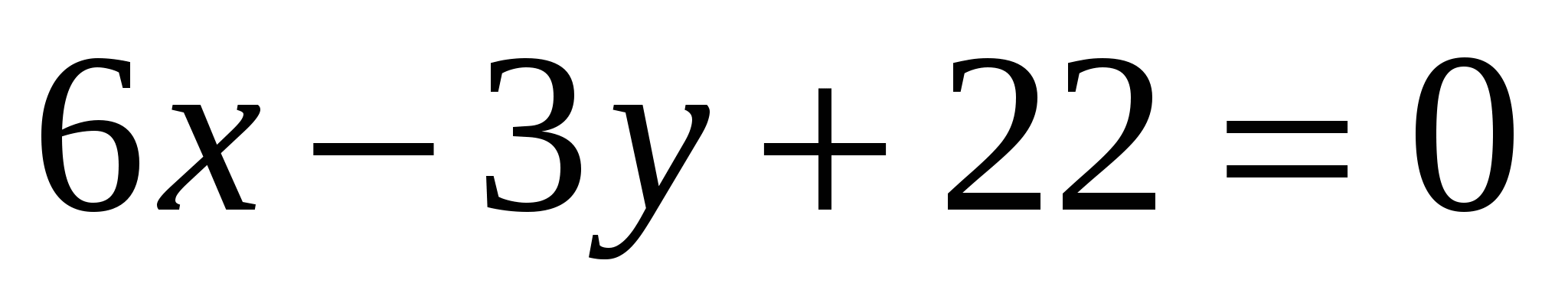
2
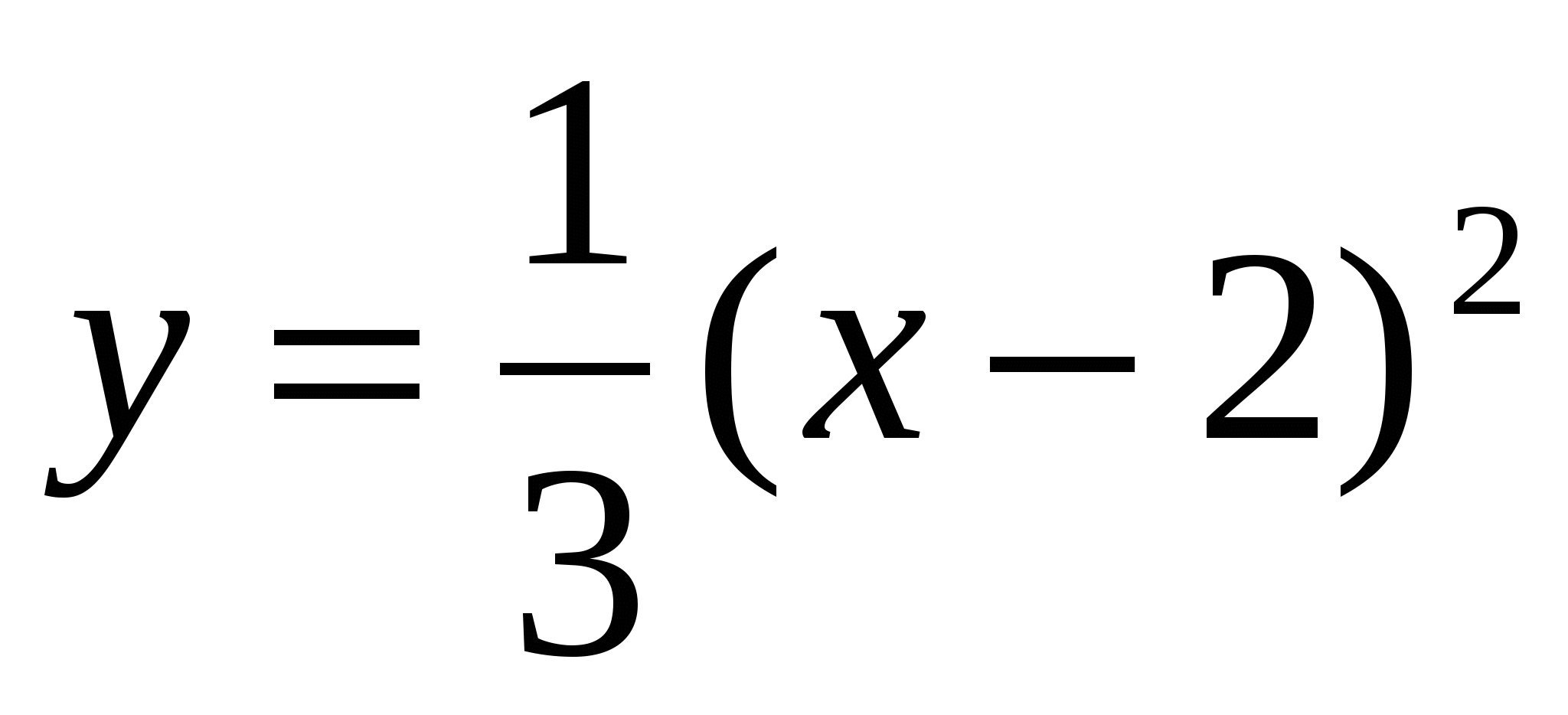 ,
, 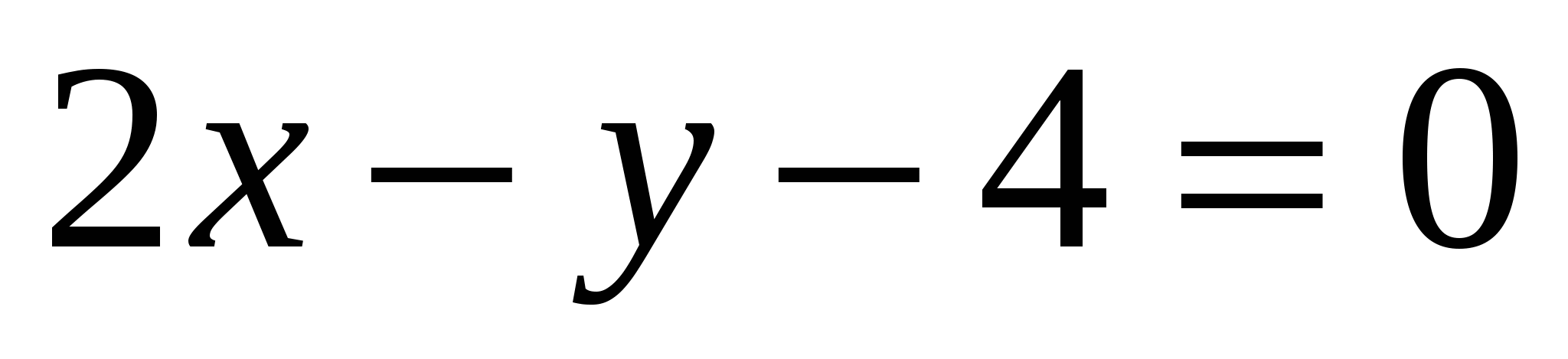
17
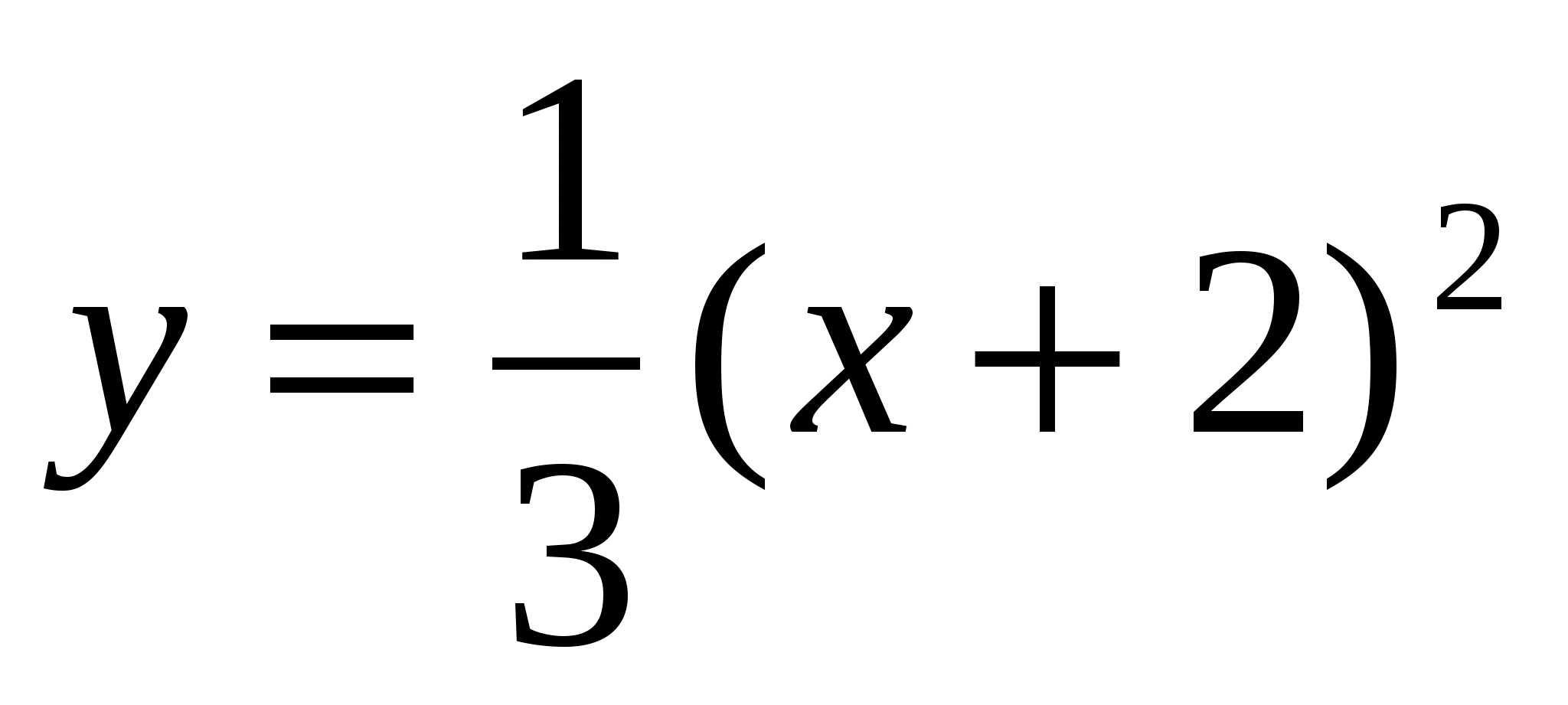 ,
, 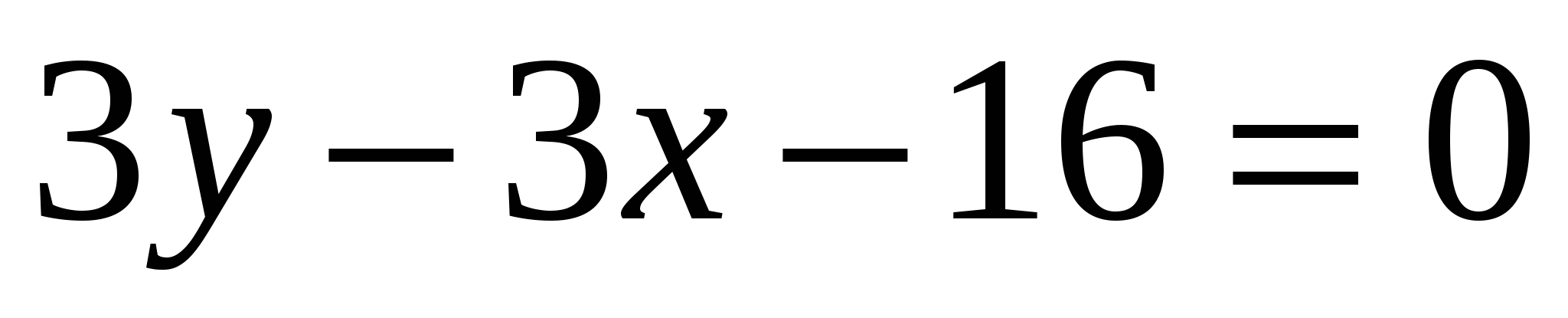
3
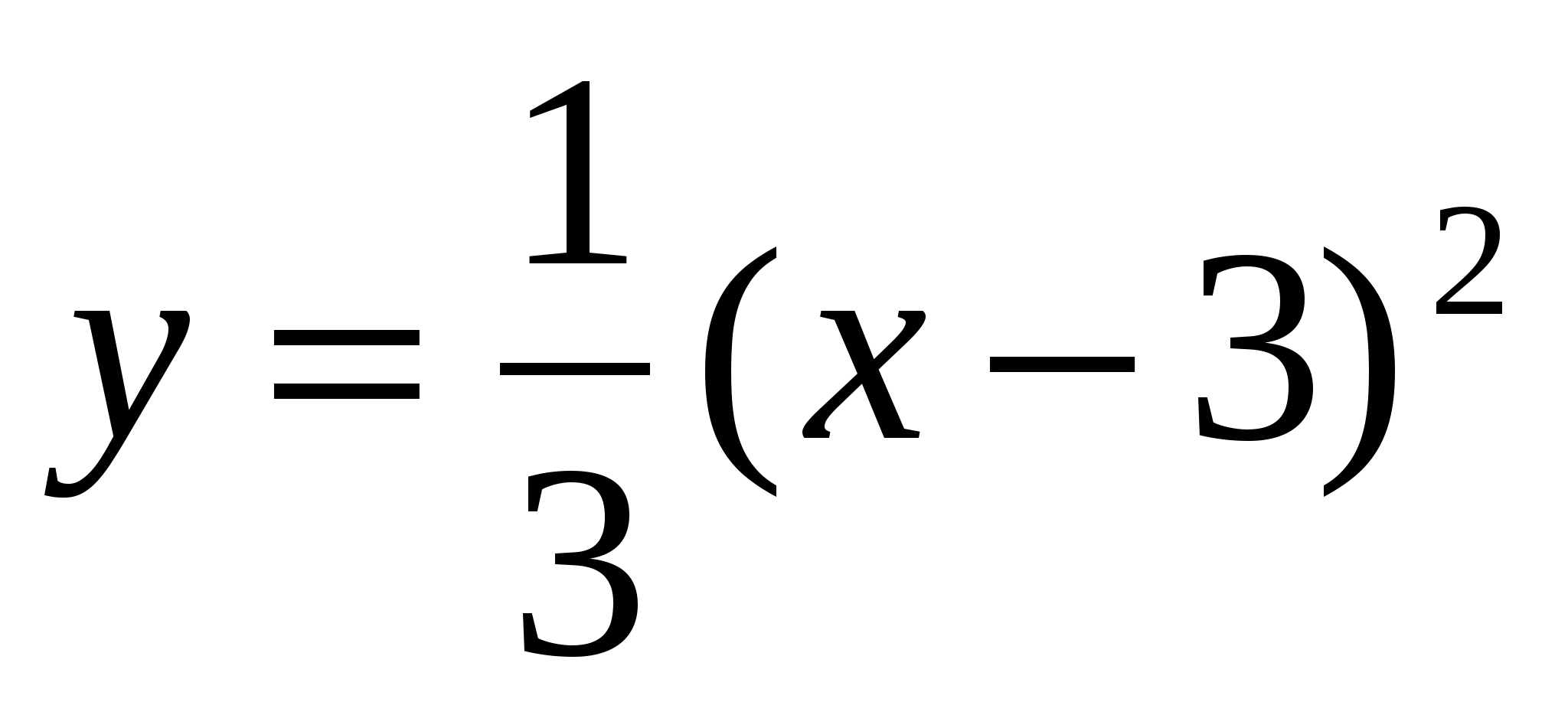 ,
, 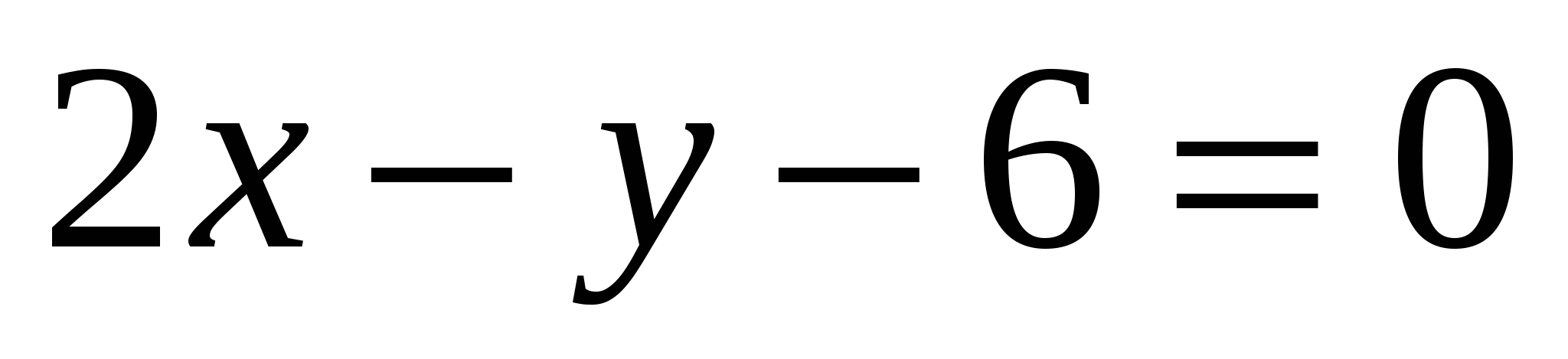
18
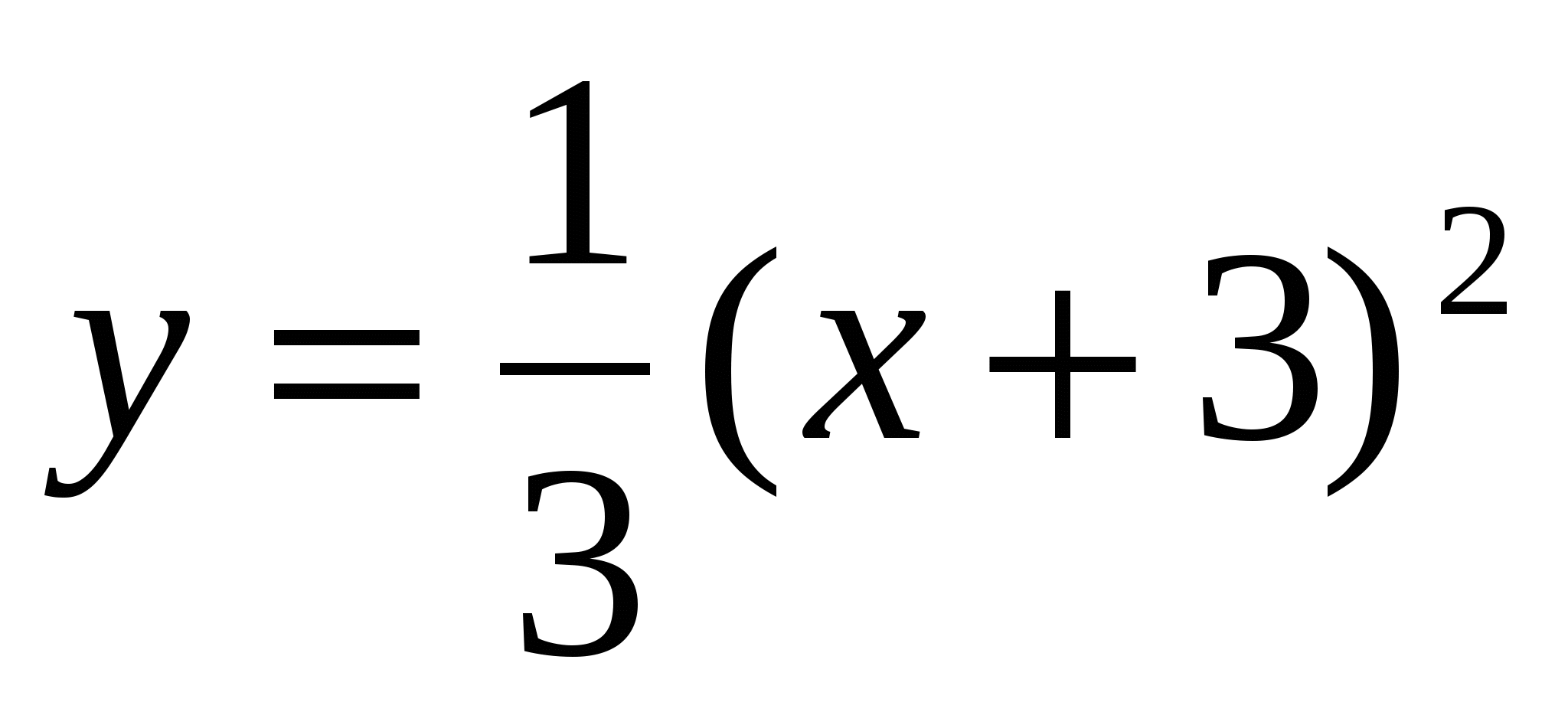 ,
, 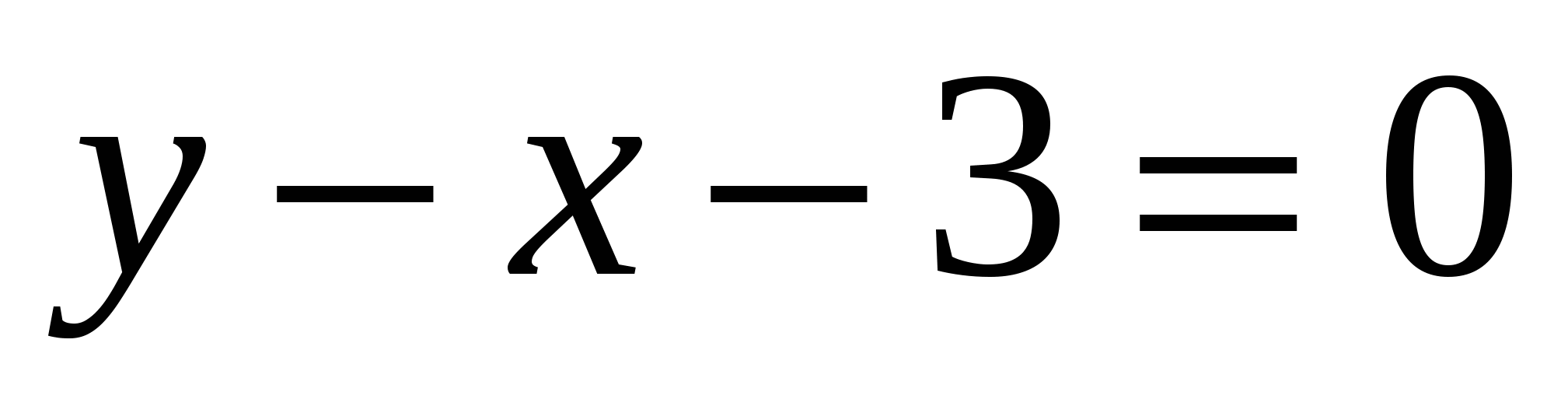
4
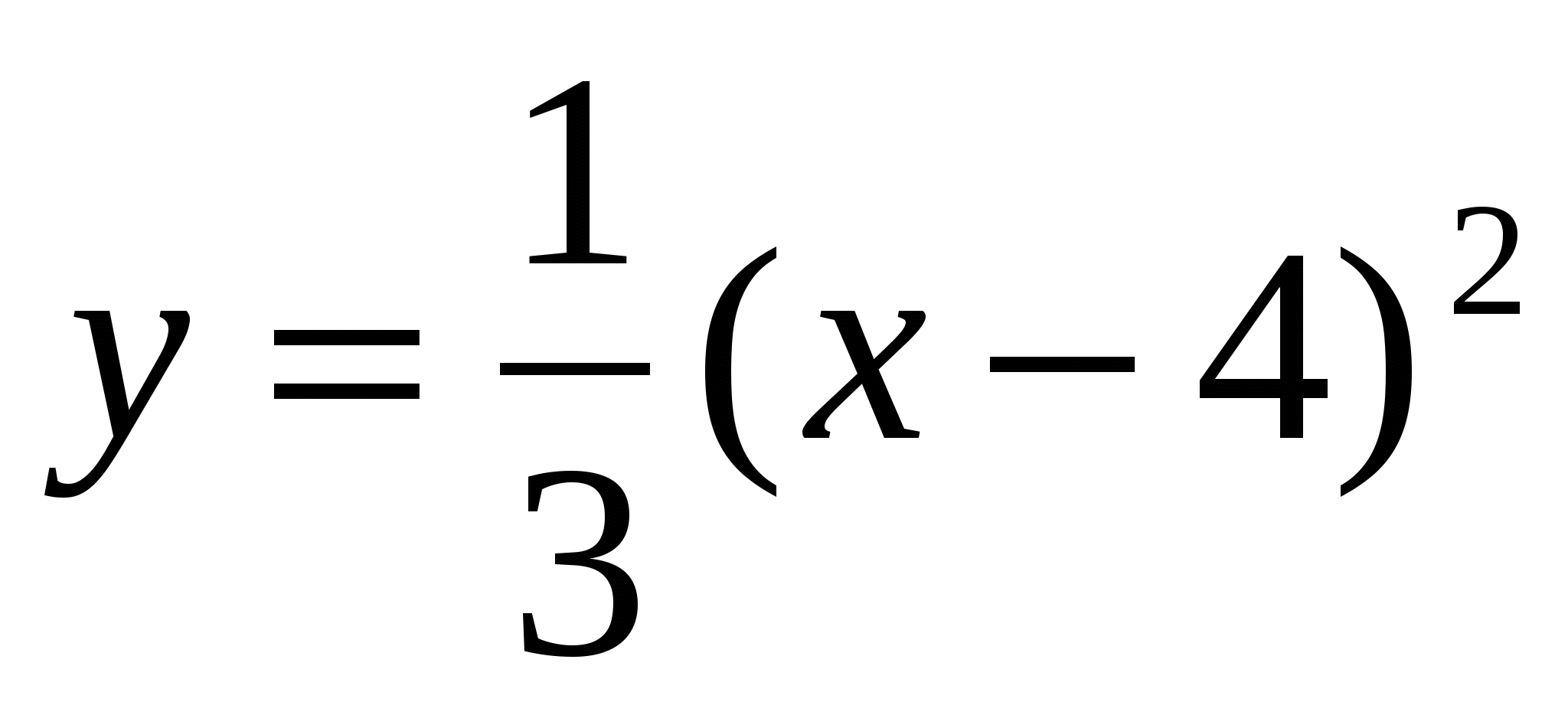 ,
, 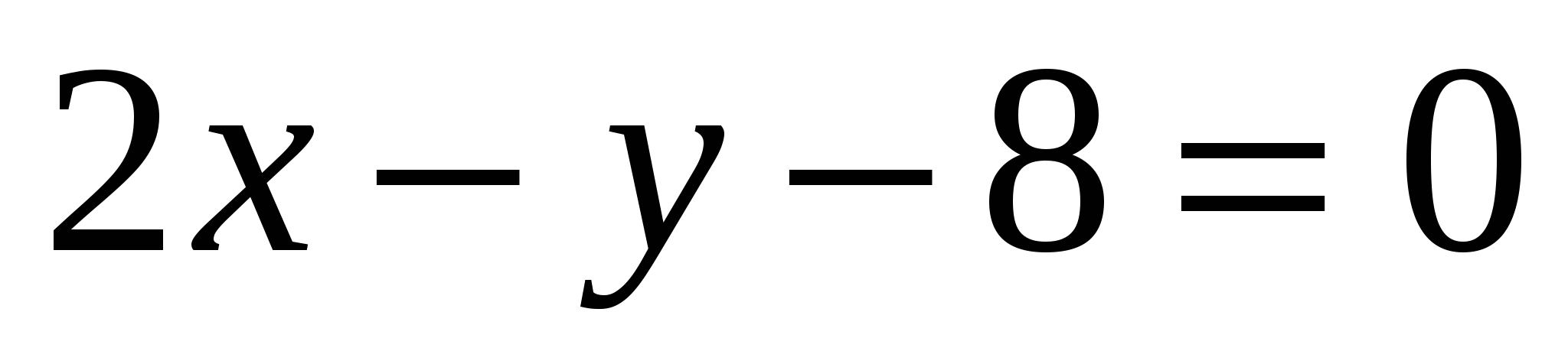
19
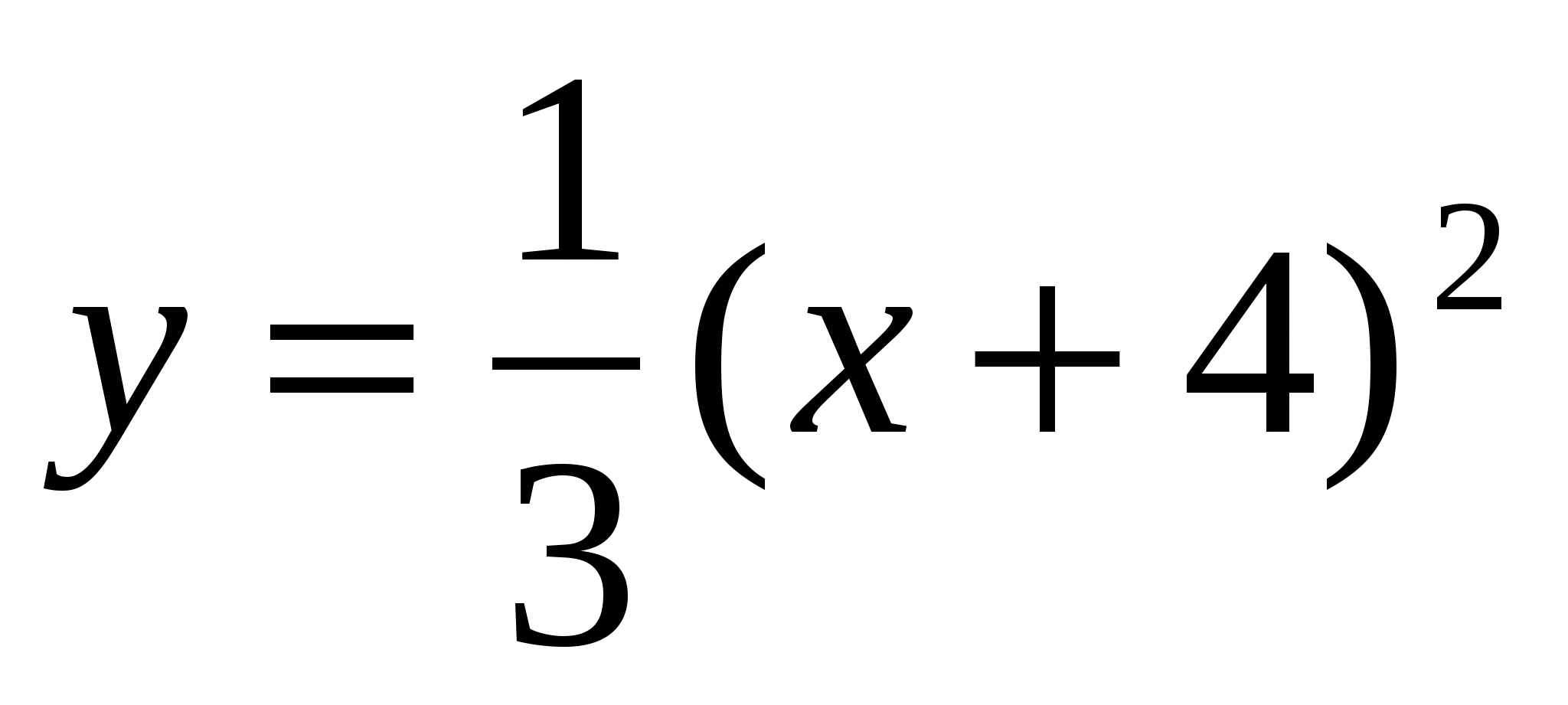 ,
, 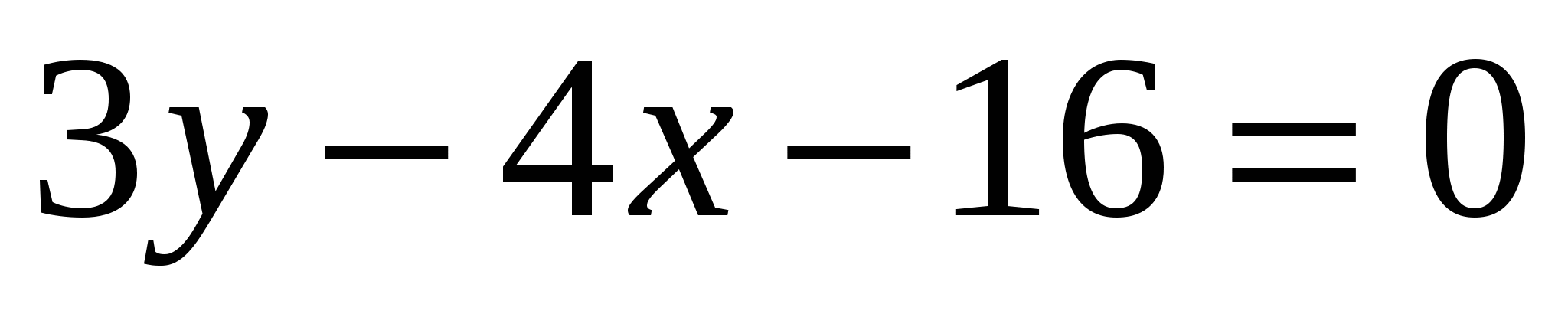
5
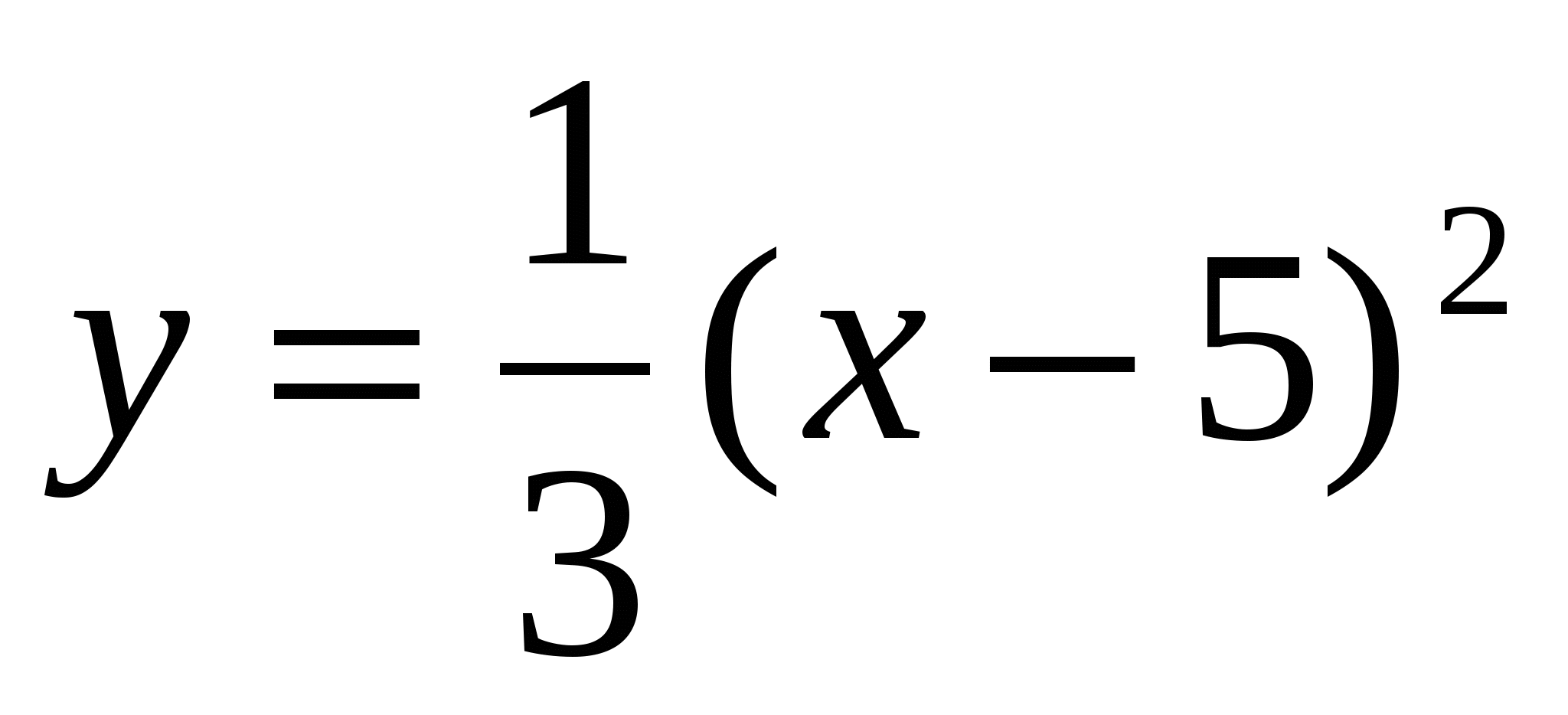 ,
, 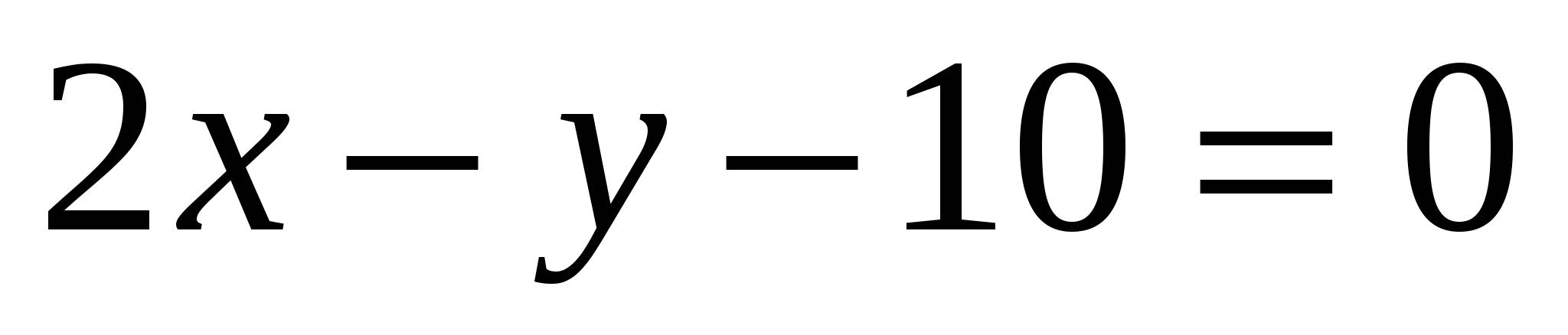
20
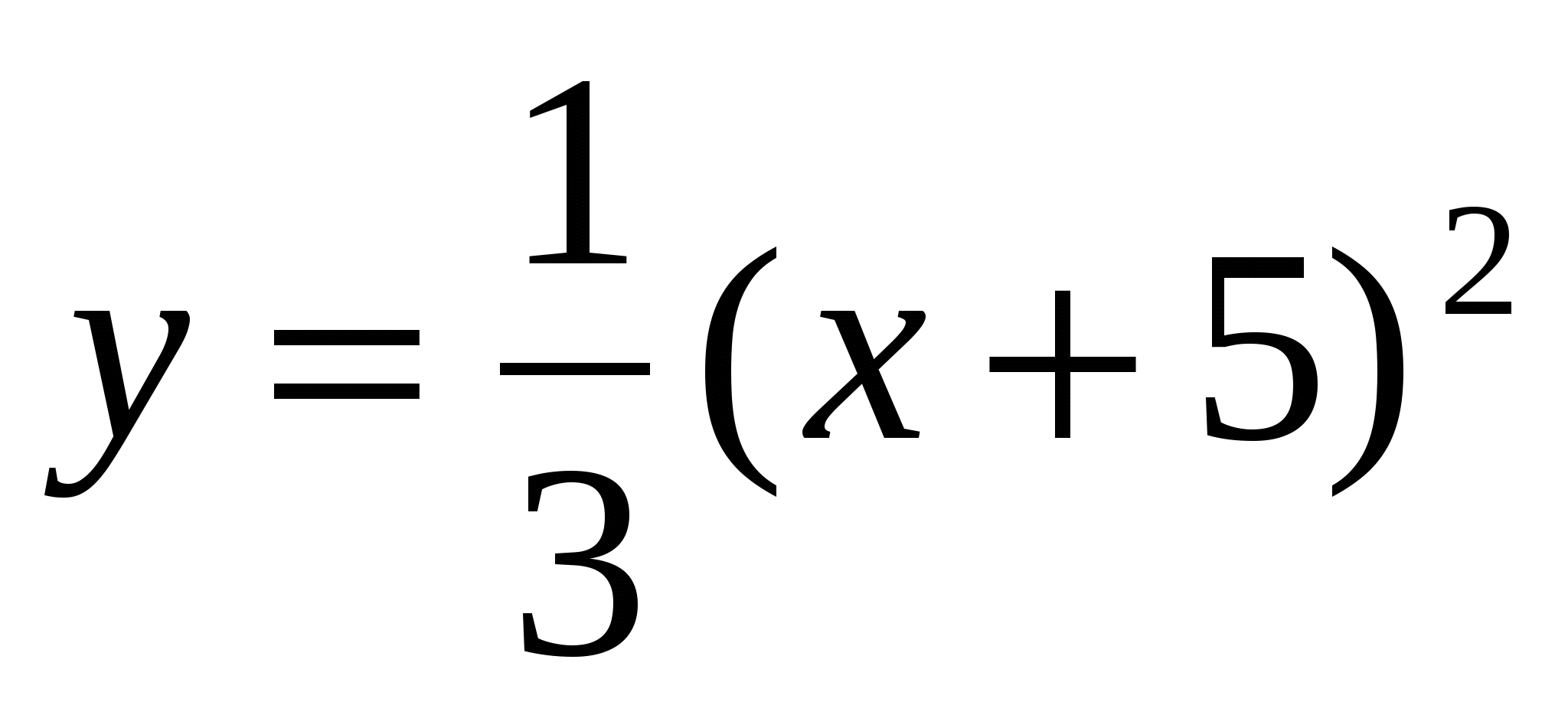 ,
, 
6
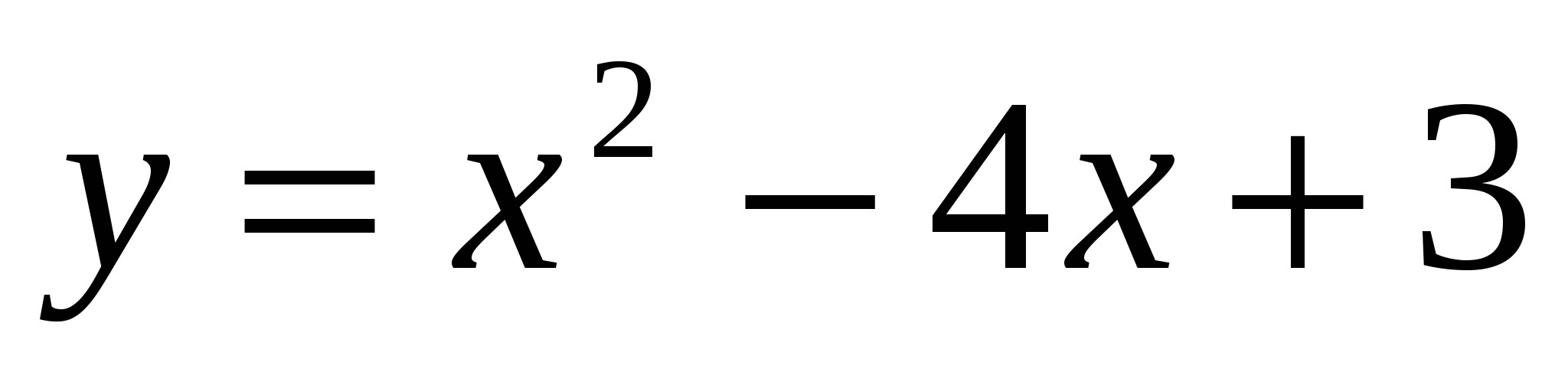 ,
, 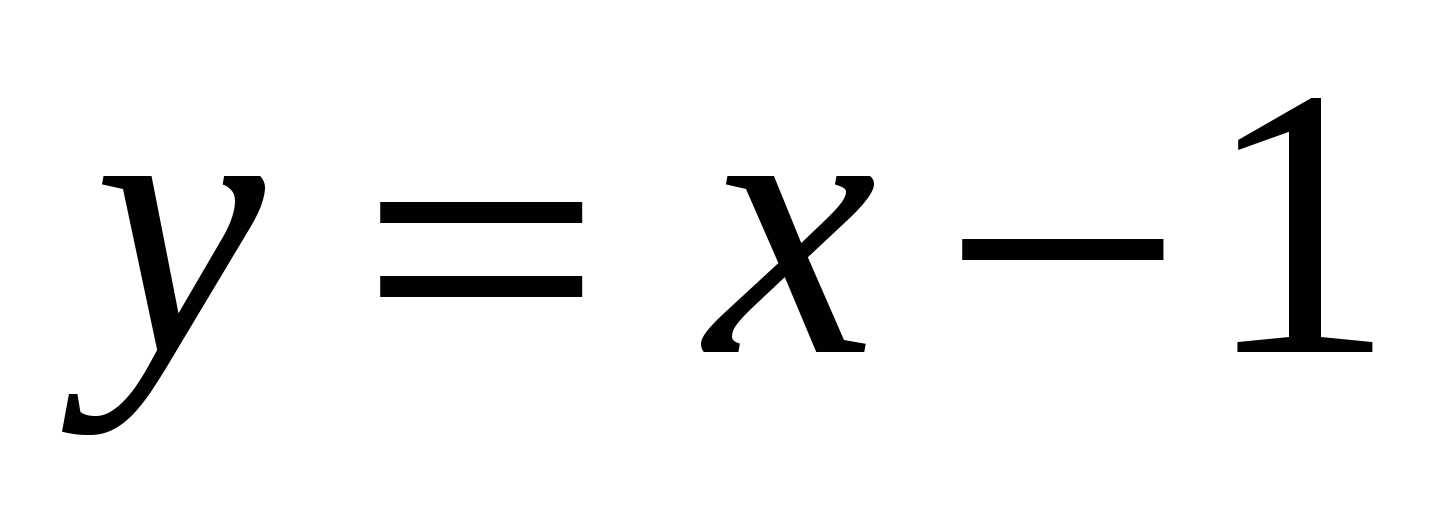
21
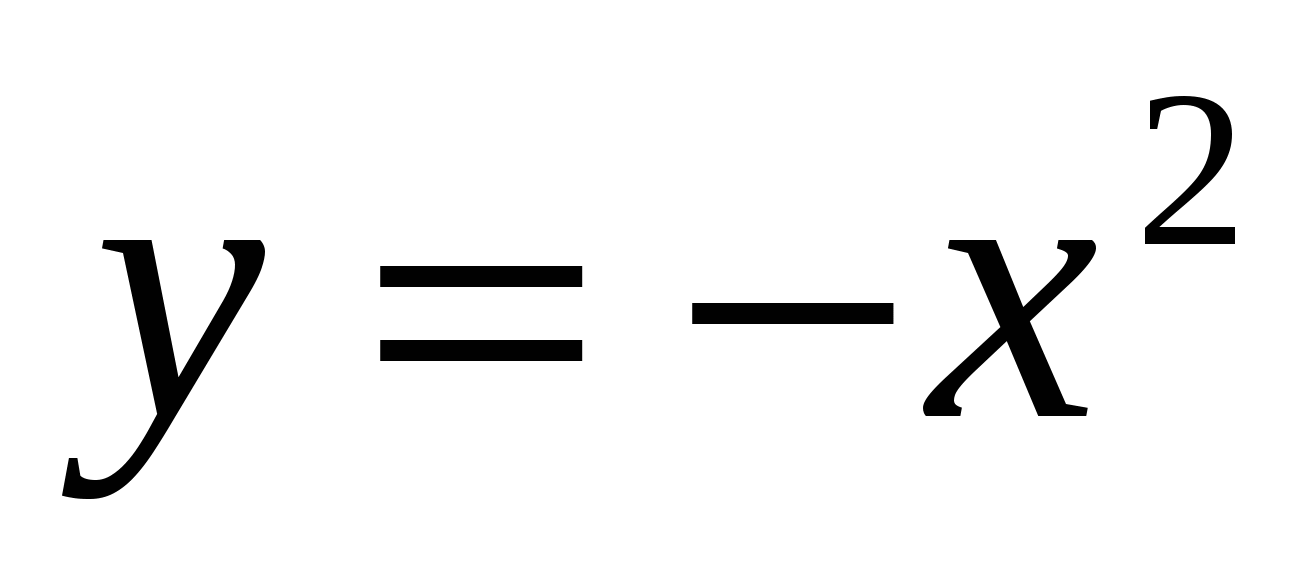 ,
, 
7
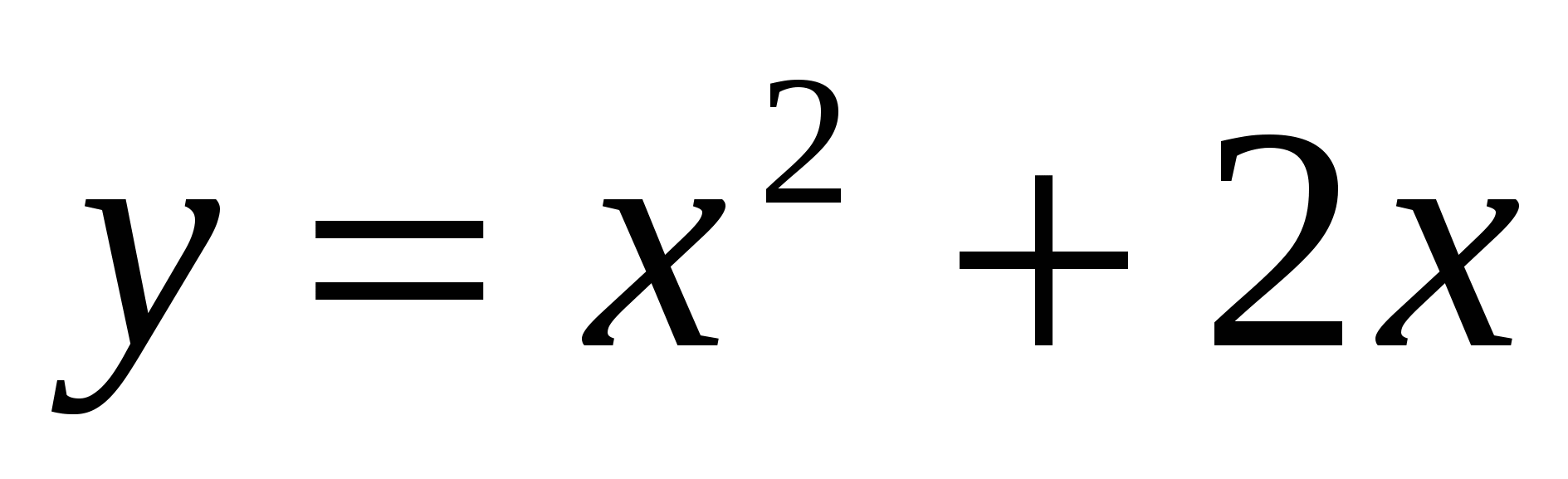 ,
, 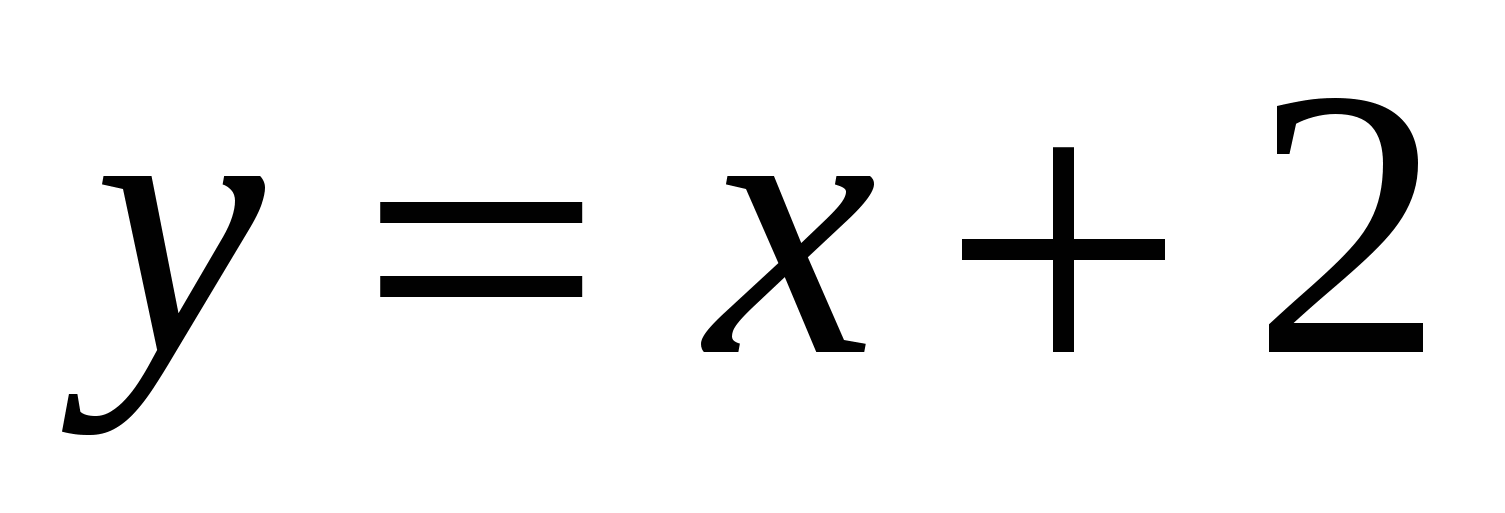
22
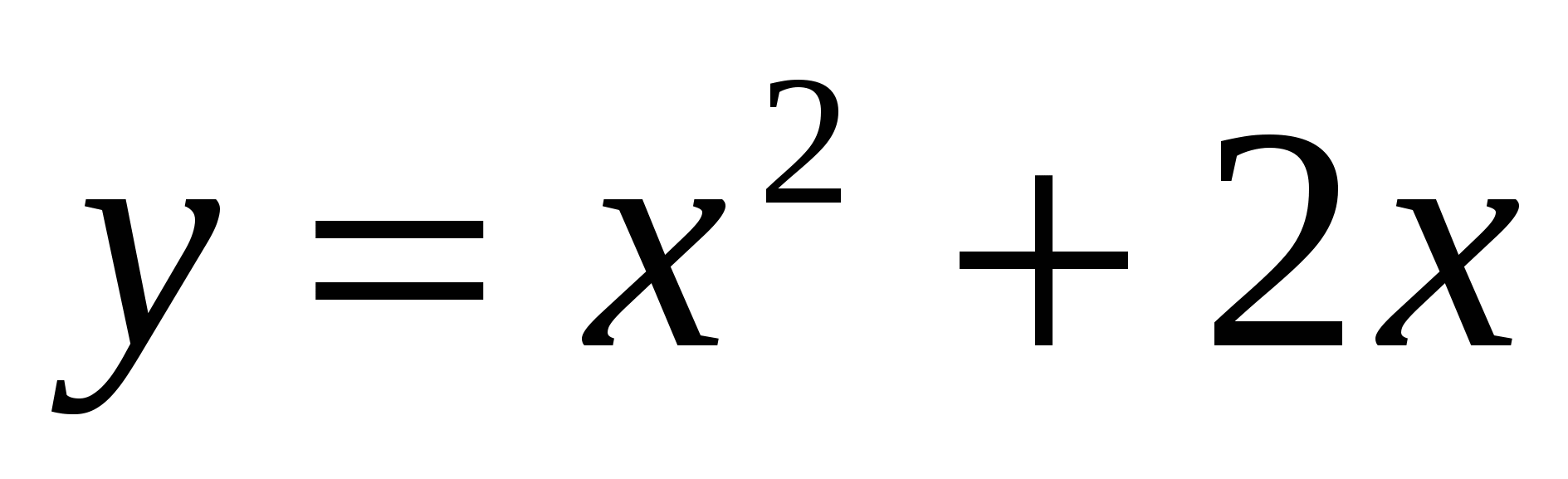 ,
, 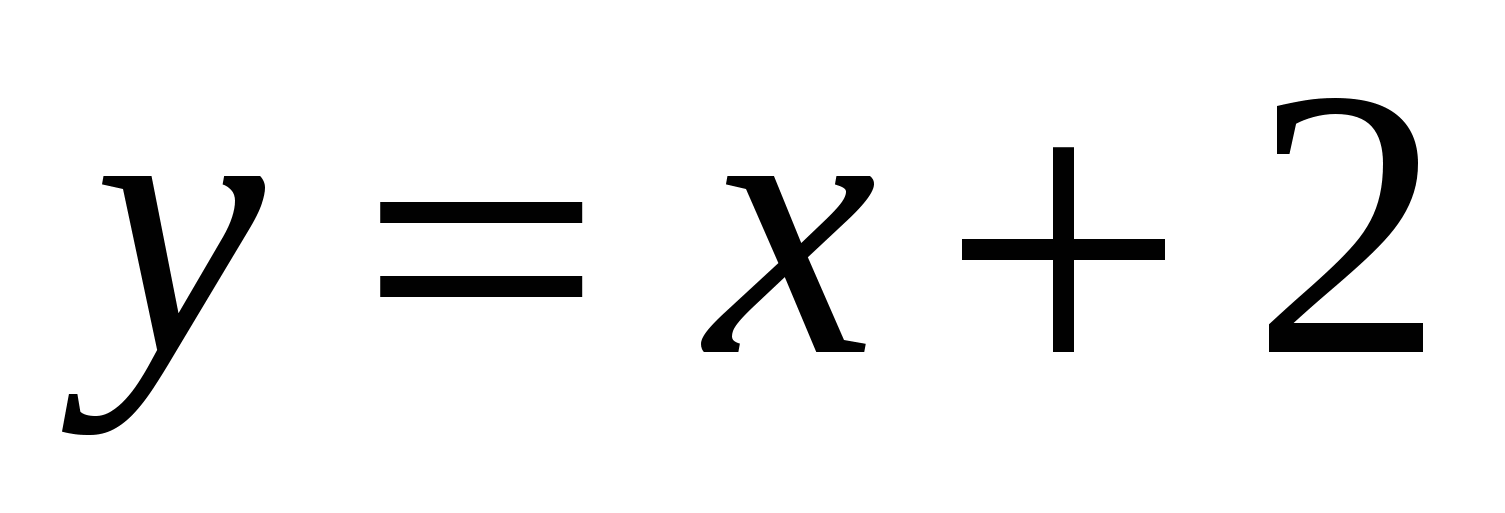
8
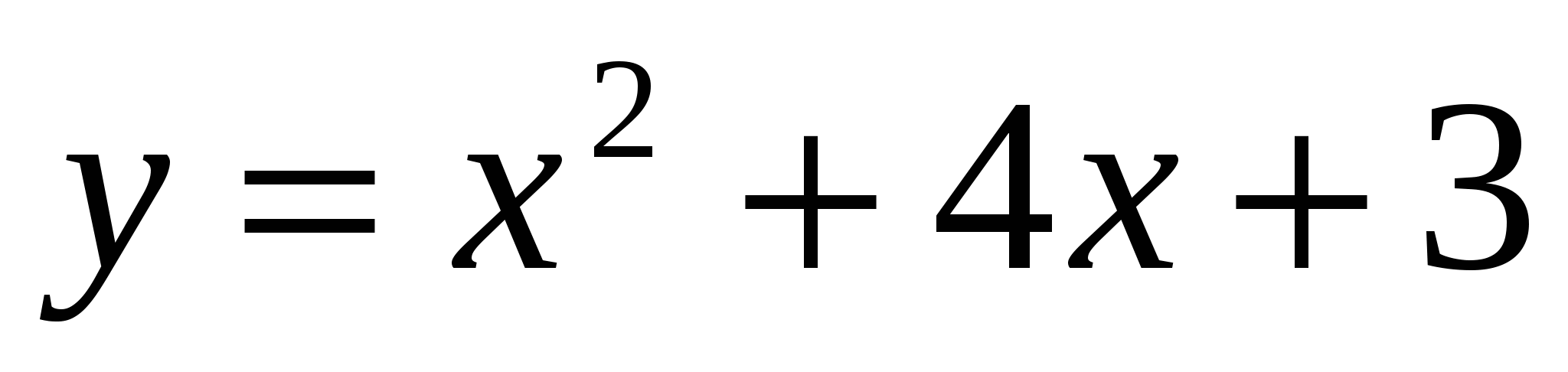 ,
, 
23
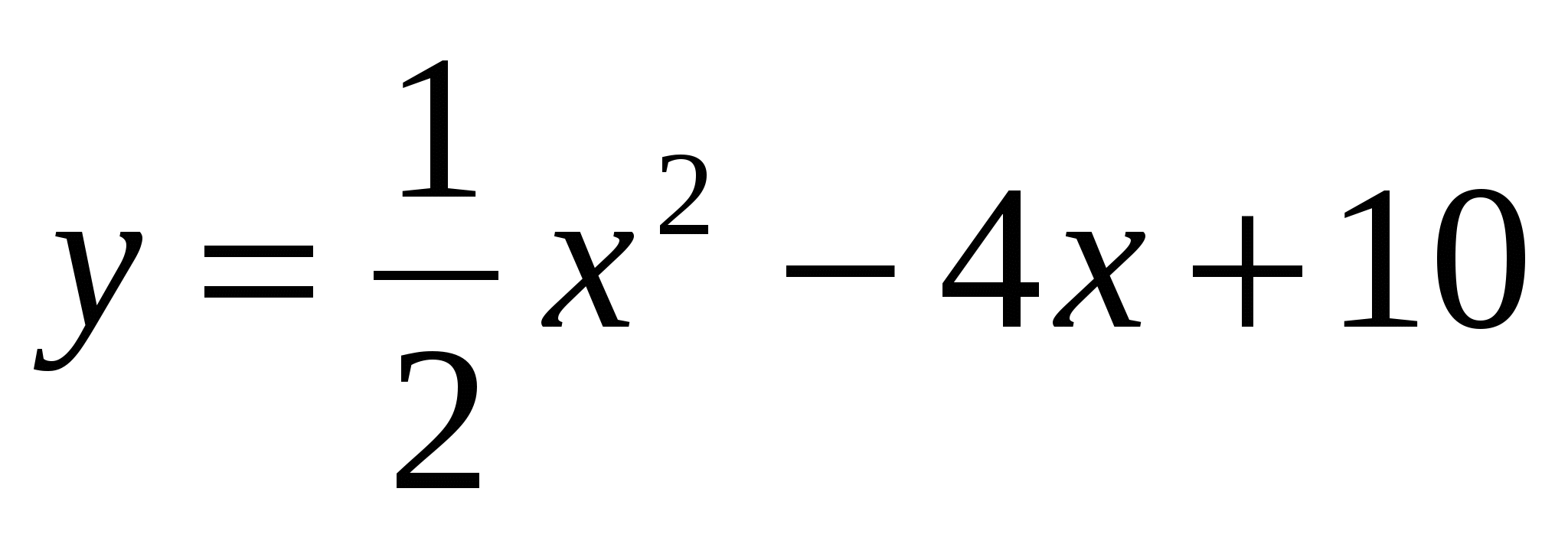 ,
, 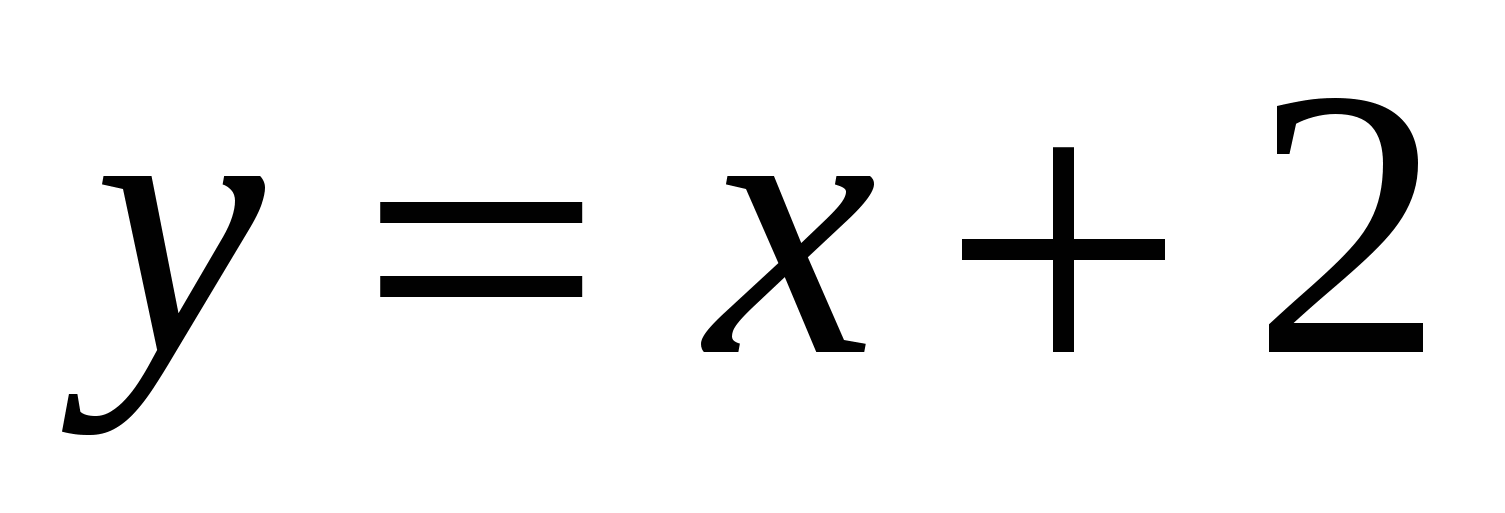
9
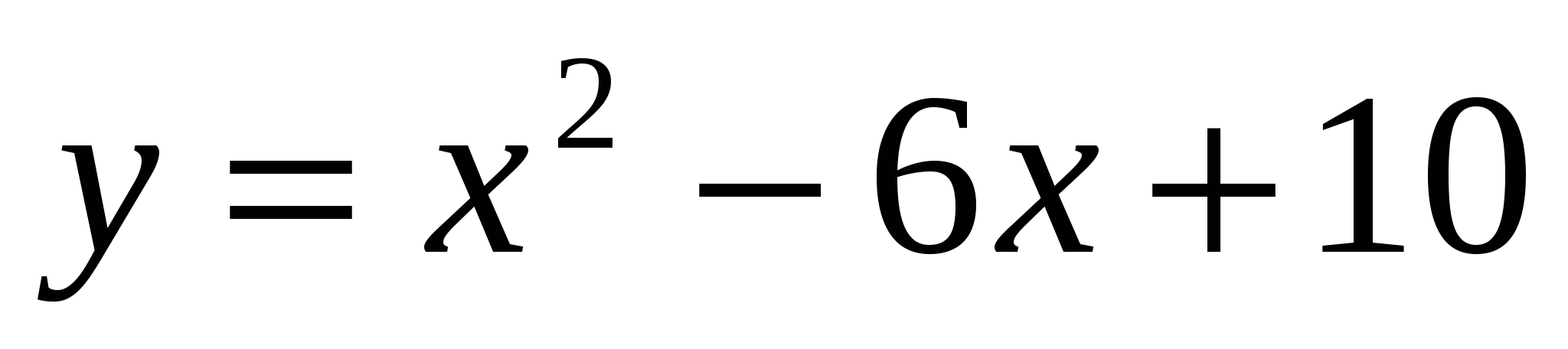 ,
, 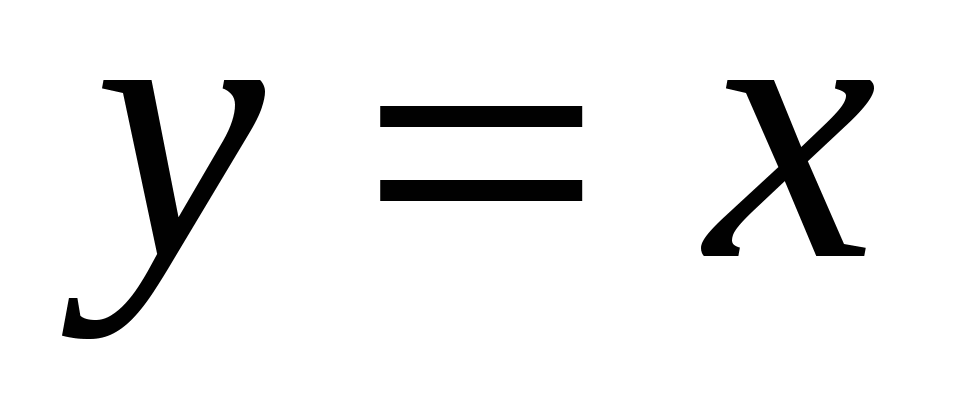
24
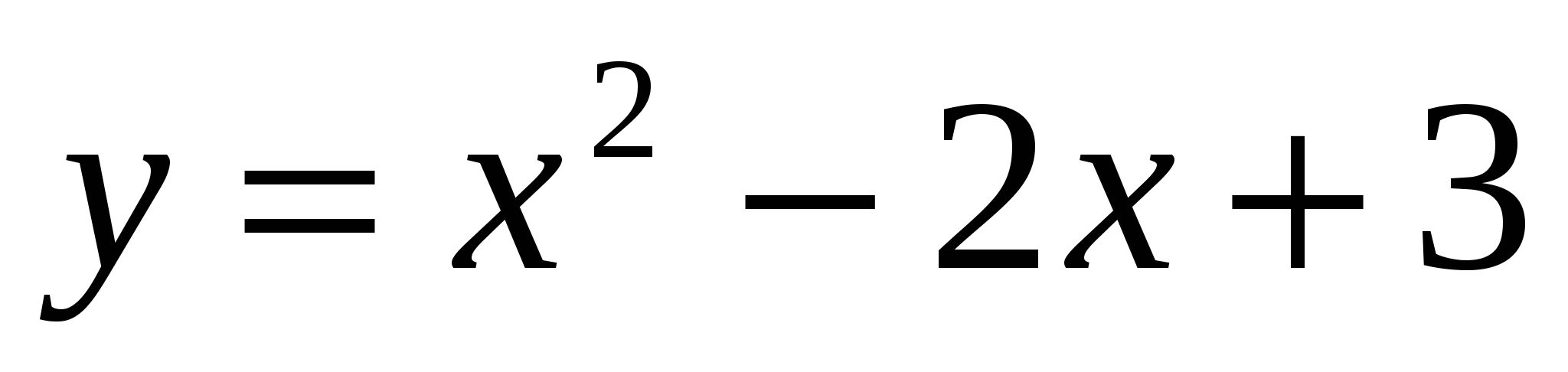 ,
, 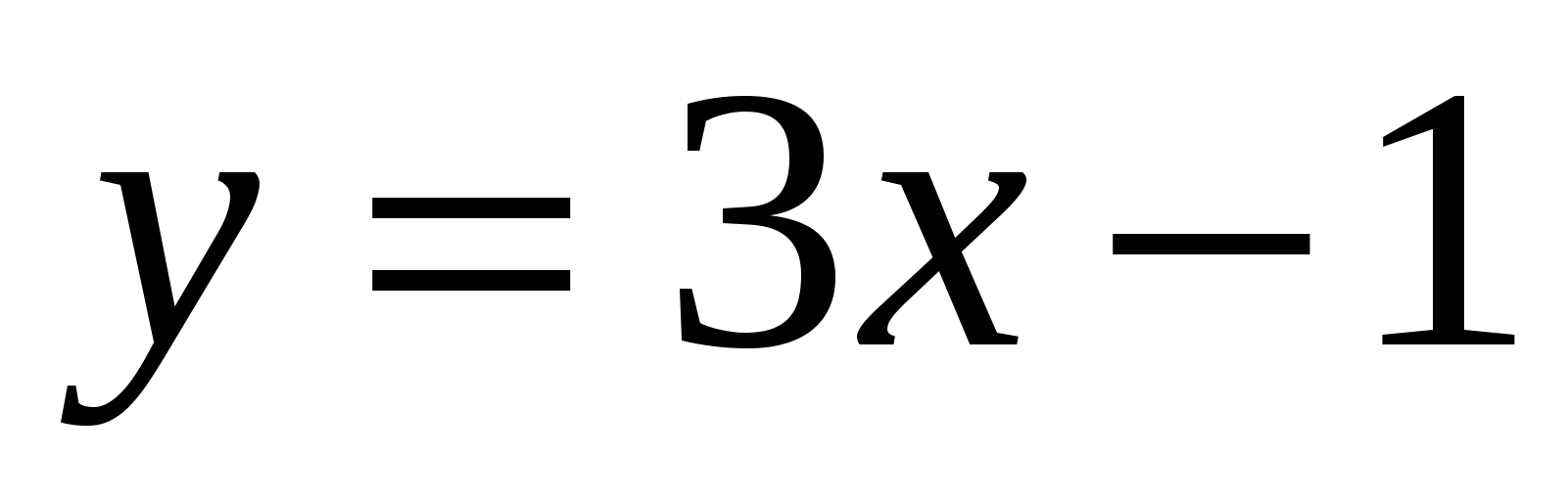
10
 ,
, 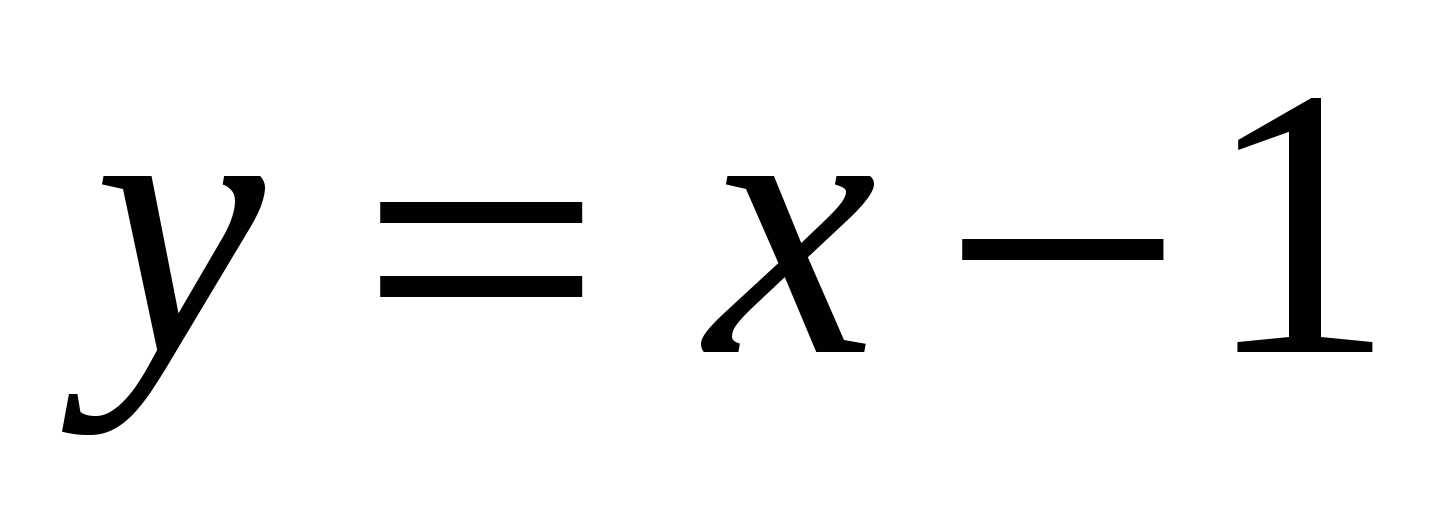
25
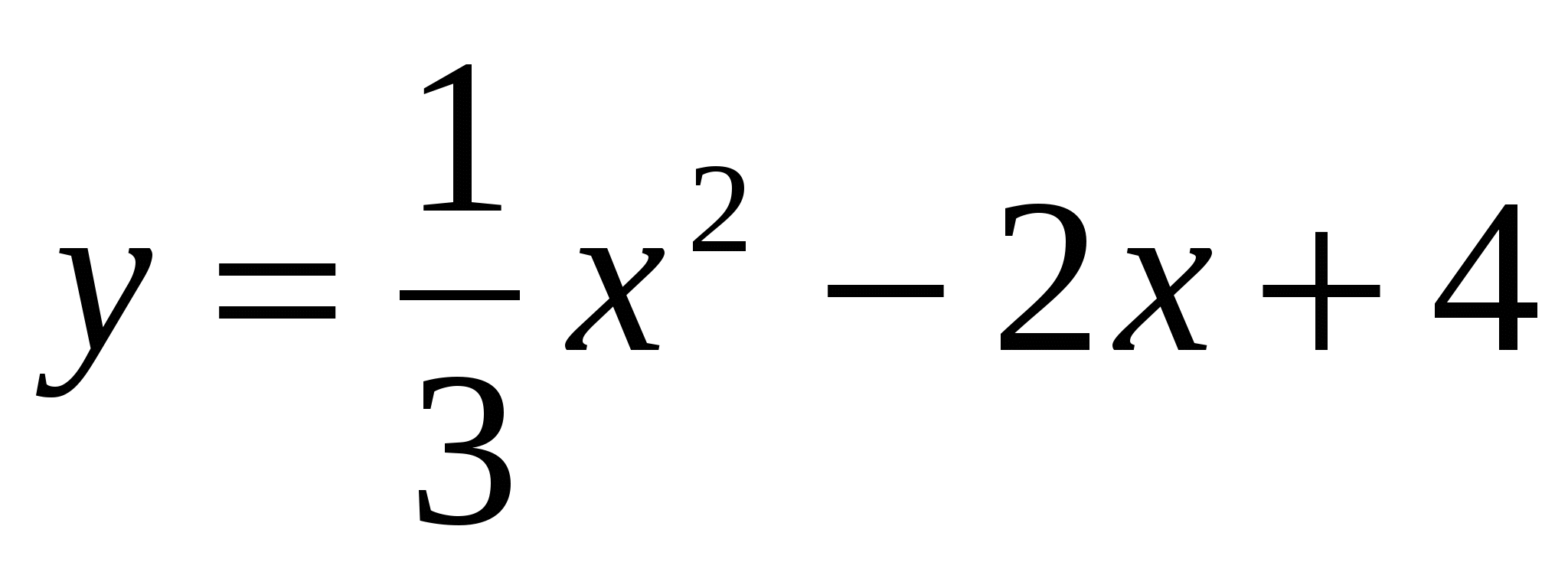 ,
, 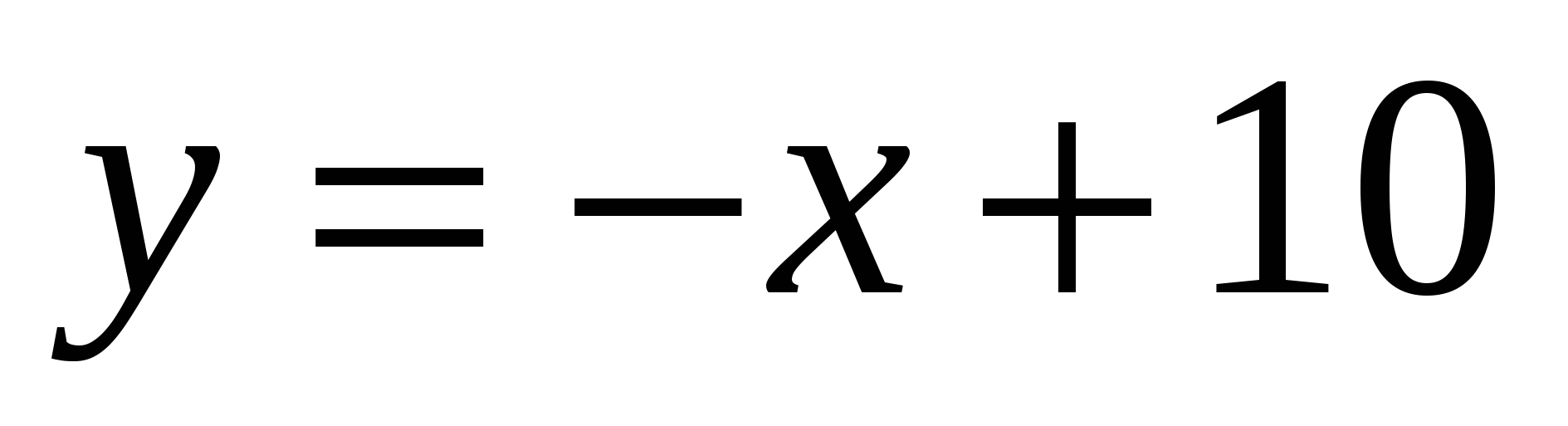
11
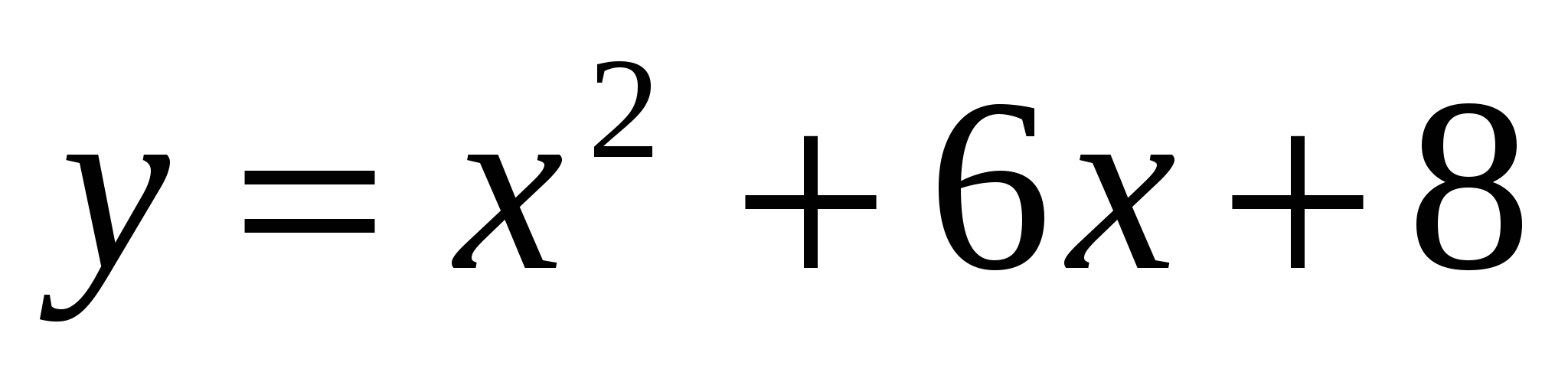 ,
, 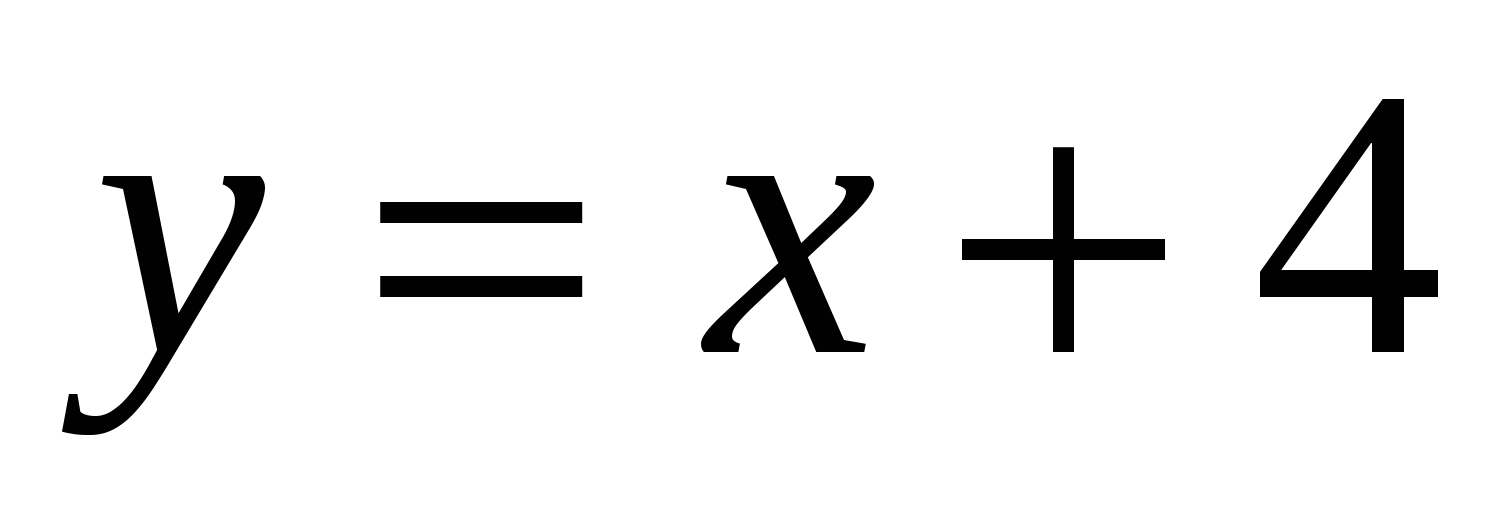
26
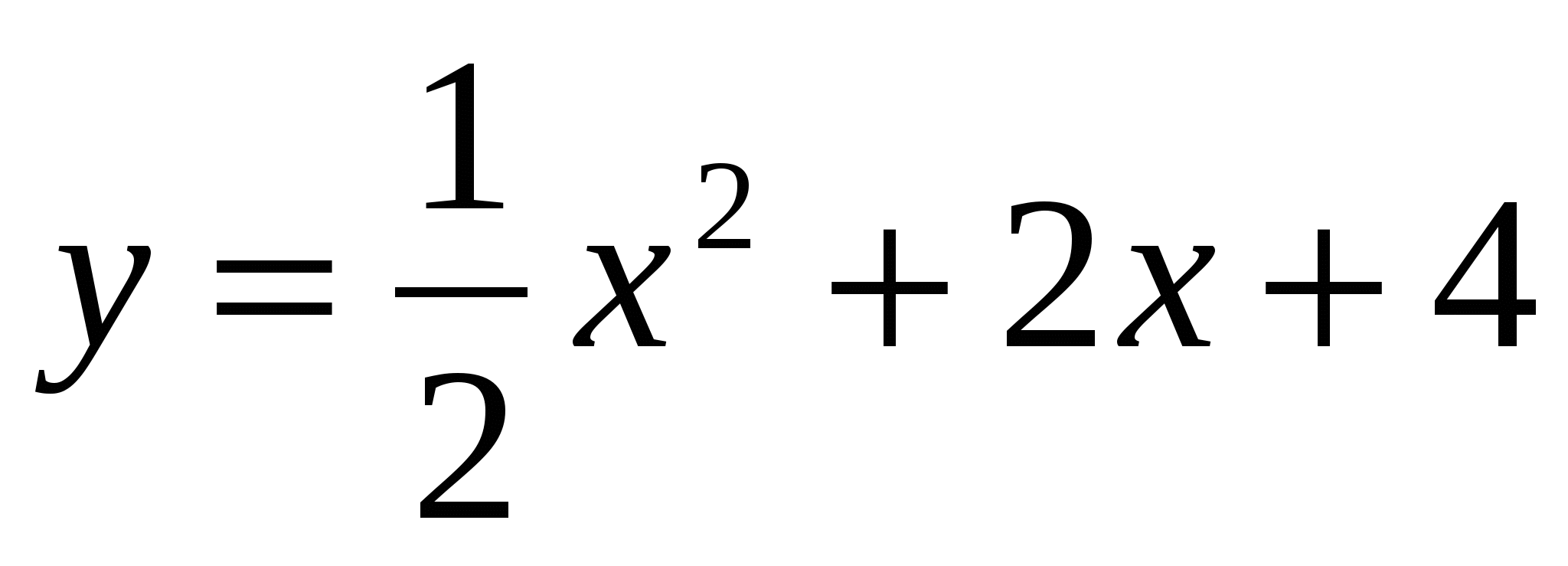 ,
, 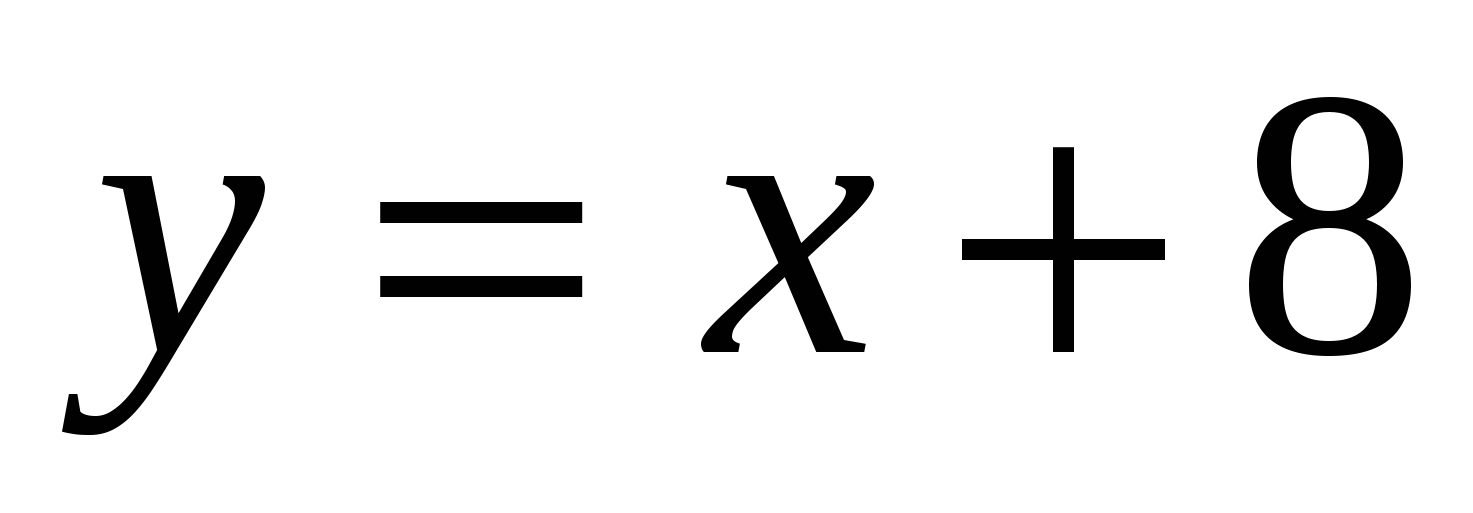
12
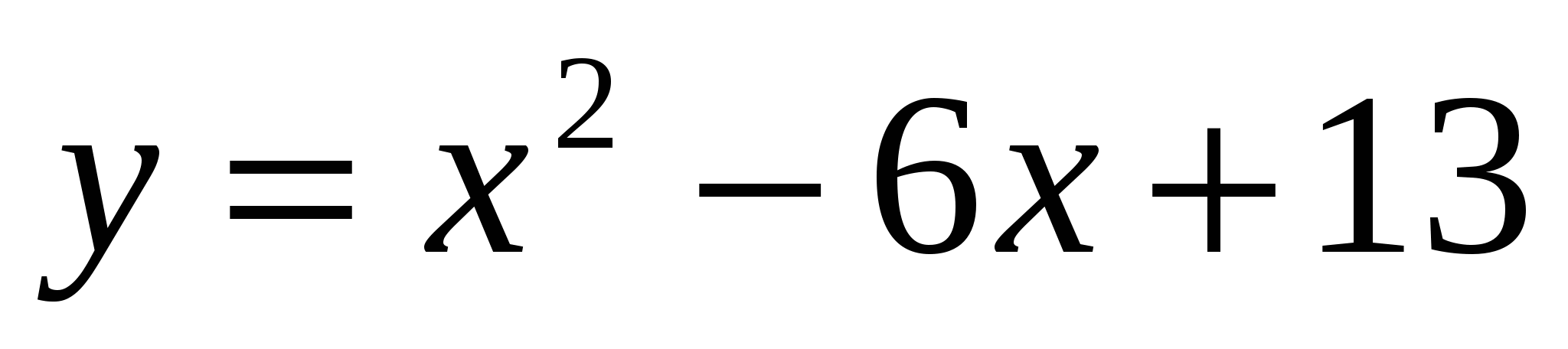 ,
, 
27
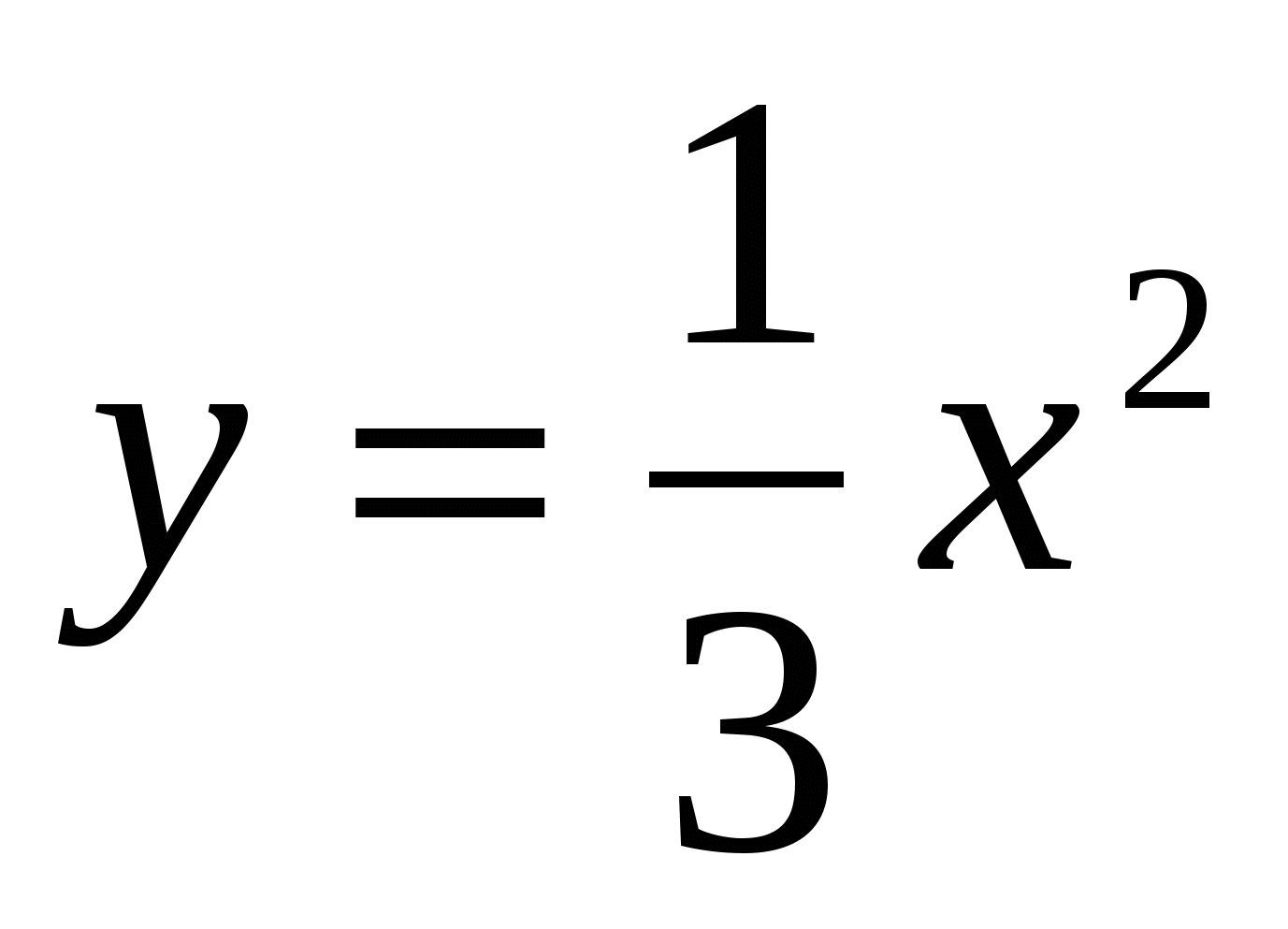 ,
, 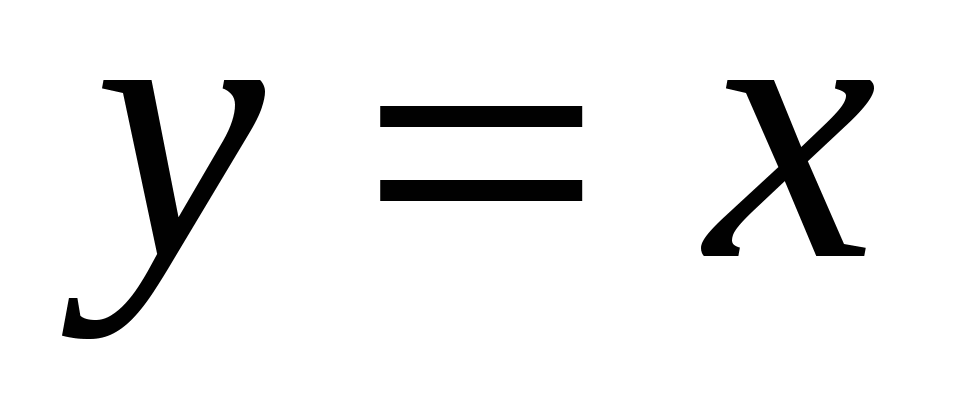
13
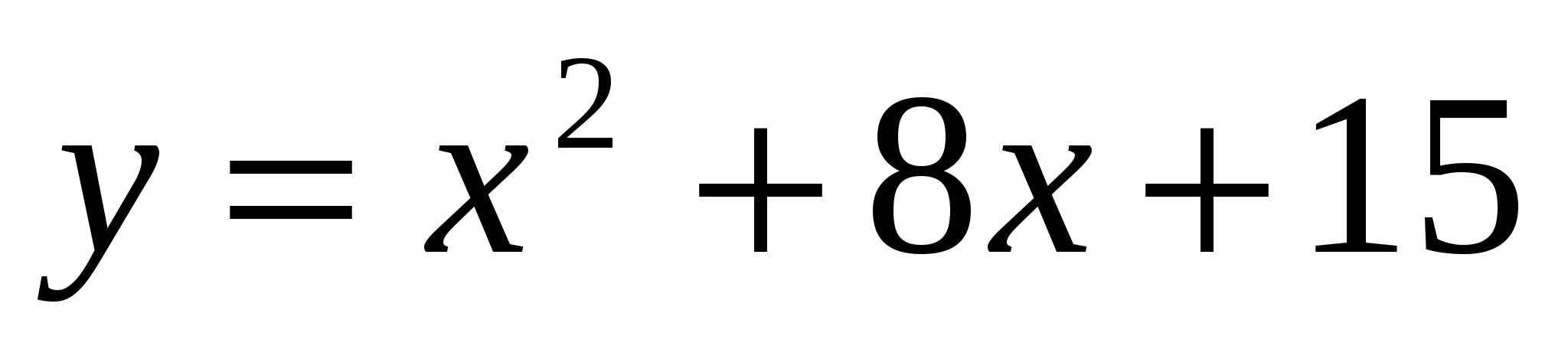 ,
, 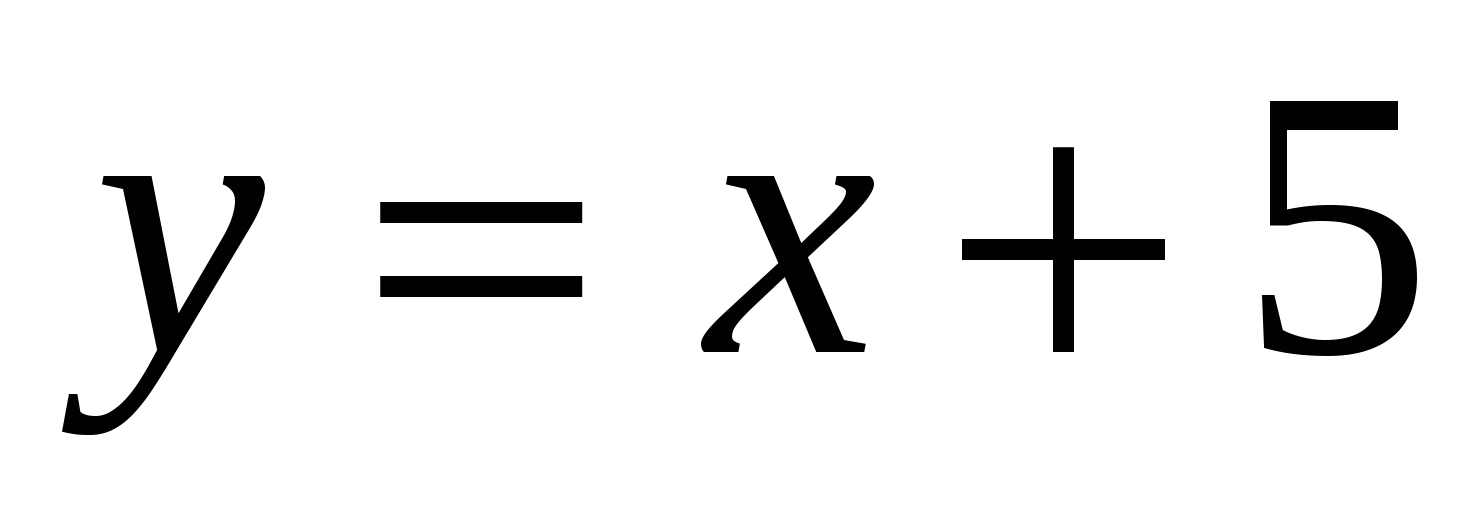
28
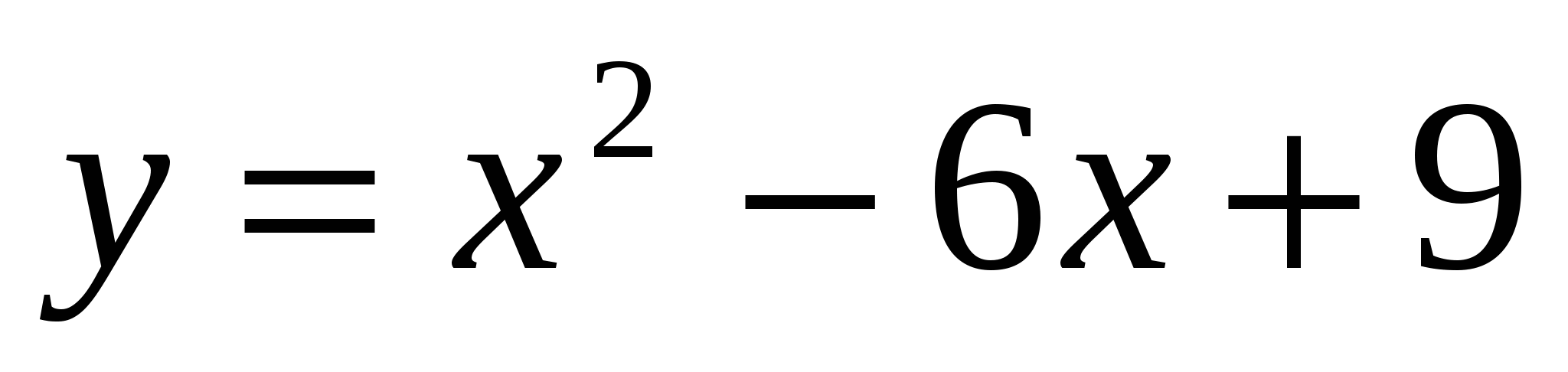 ,
, 
14
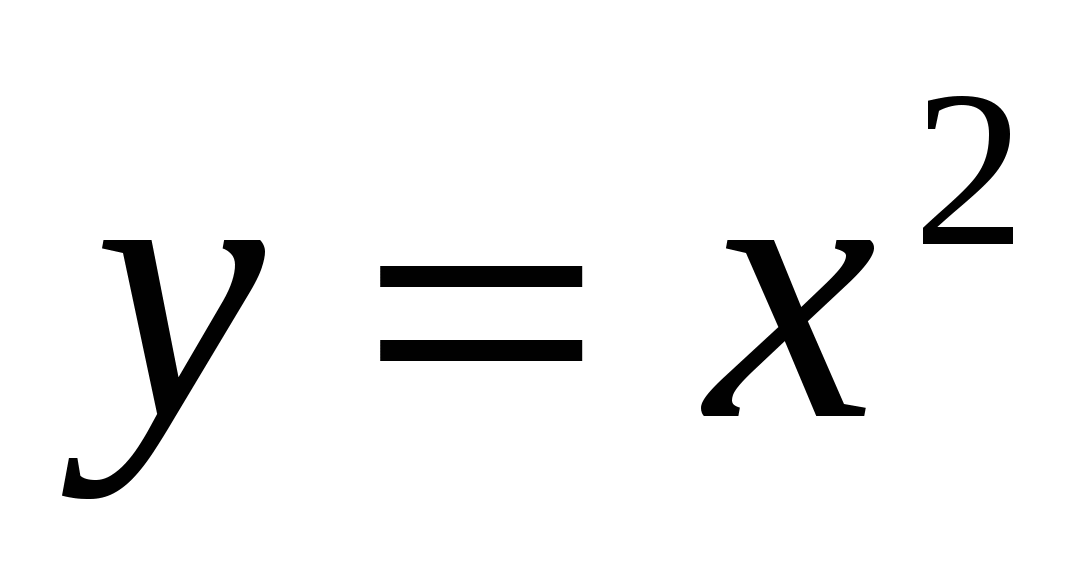 ,
, 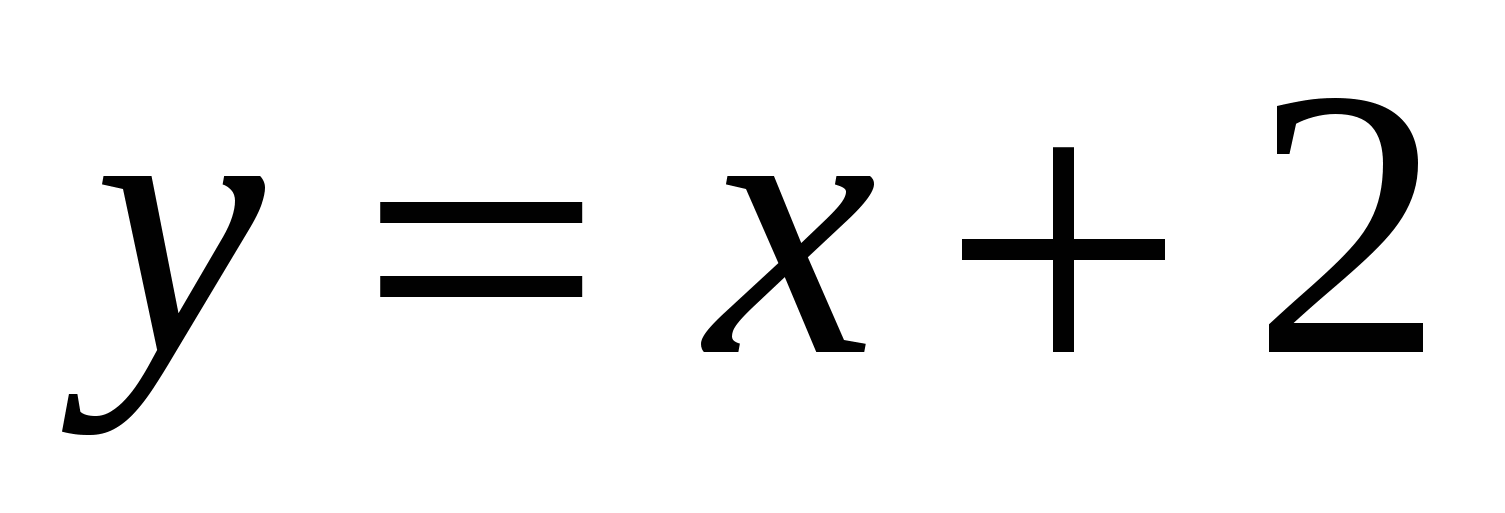
29
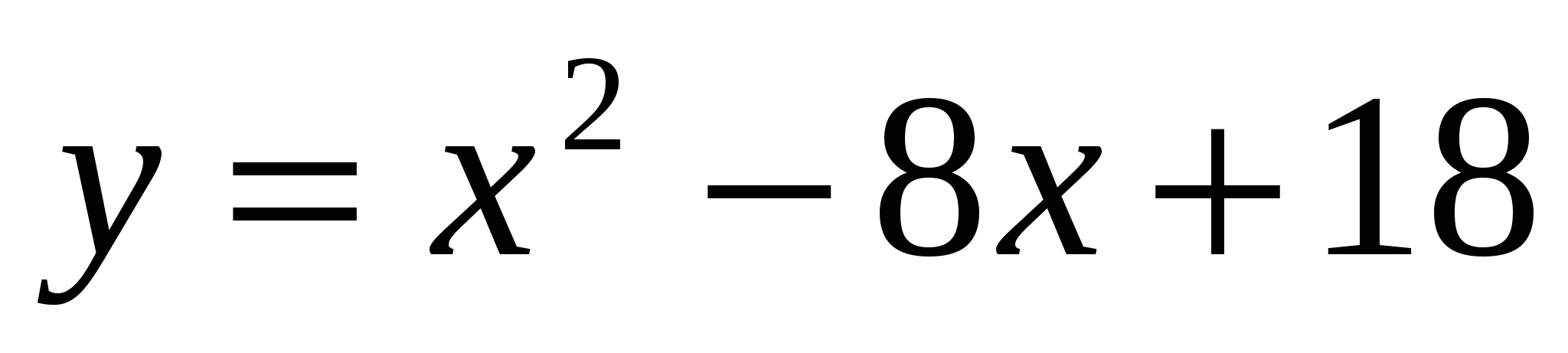 ,
, 
15
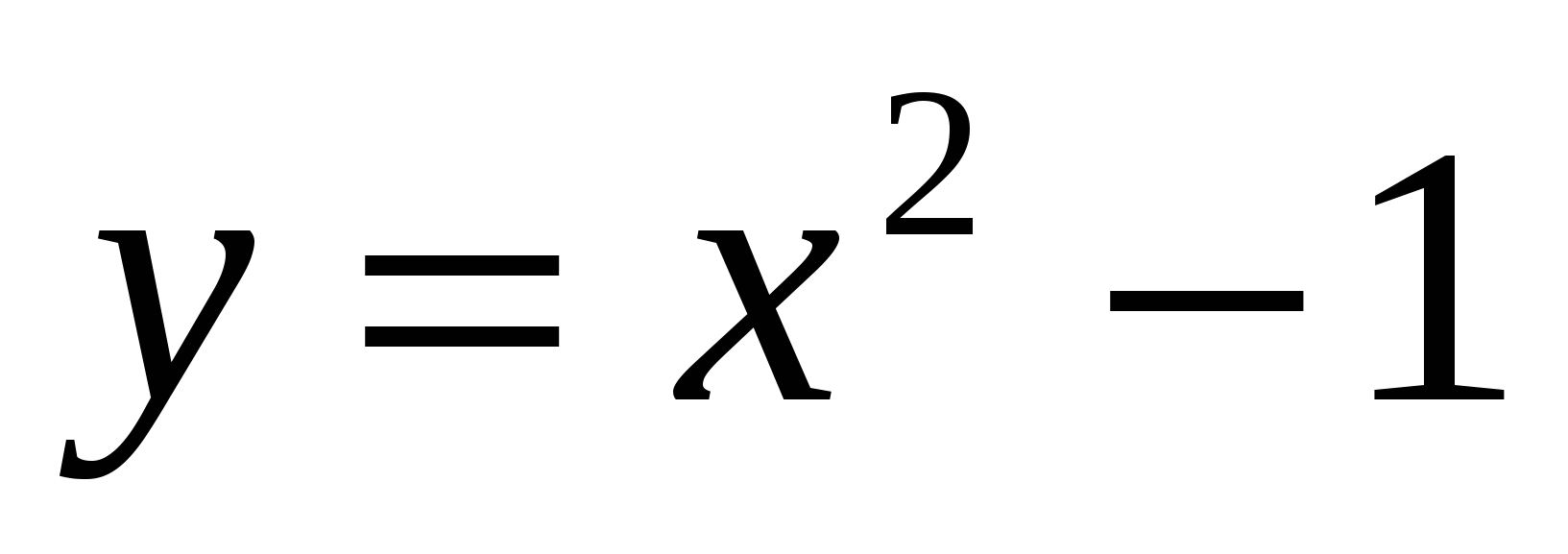 ,
, 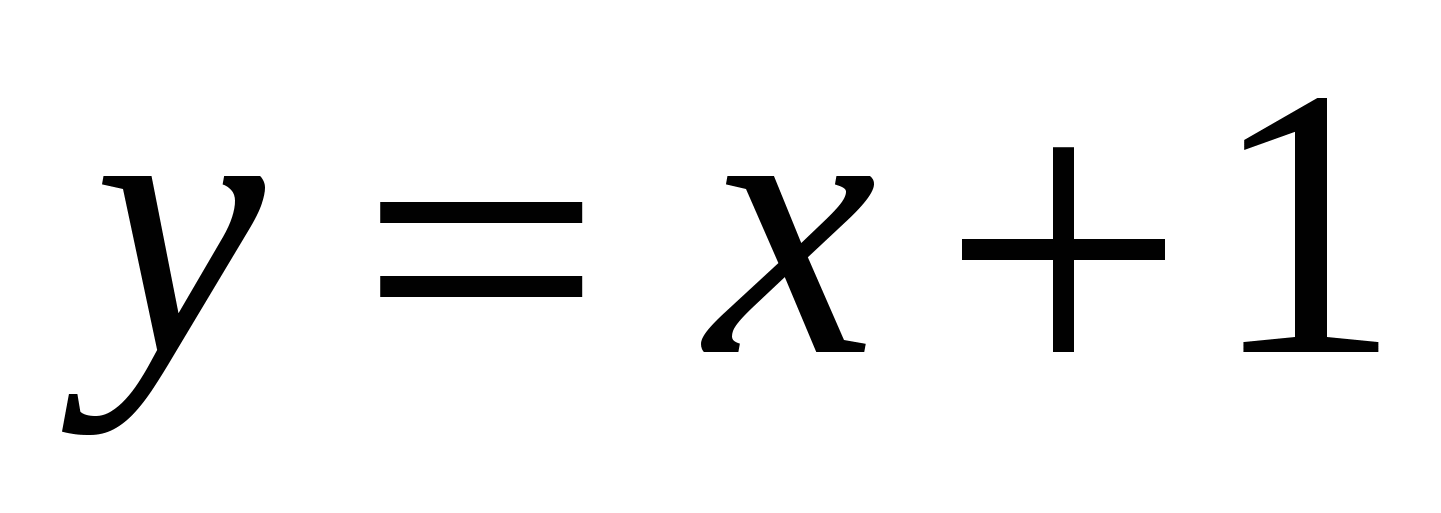
30
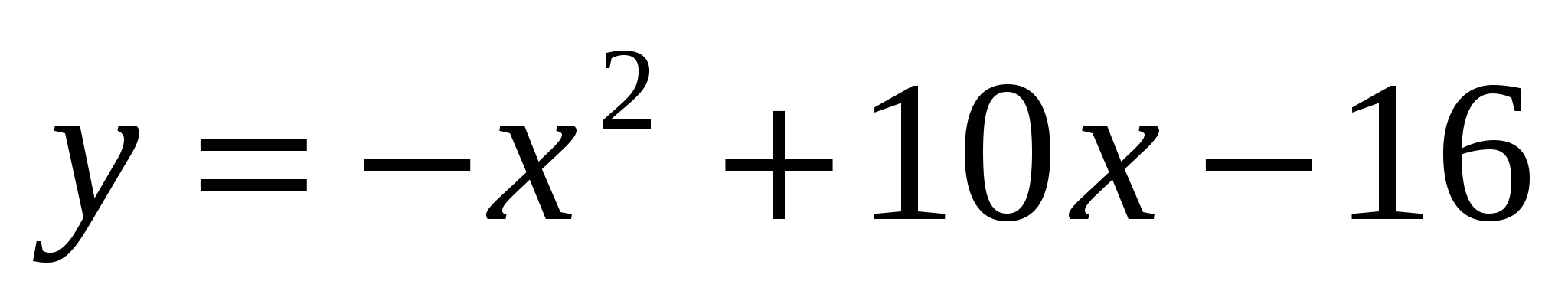 ,
, 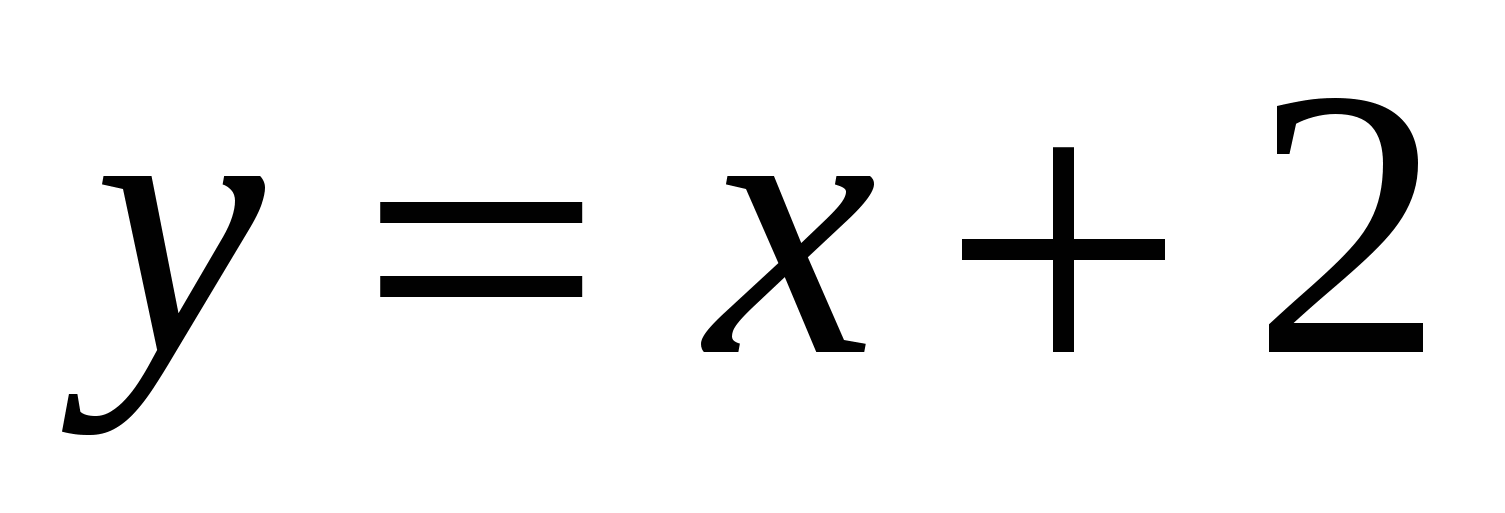
Раздел Б
Задача.
Вычислить площадь фигуры, ограниченной линиями (таблица 3).
Таблица 3
№
вари-
анта.
Уравнения линий.
№
вари-
анта.
Уравнения линий.
1
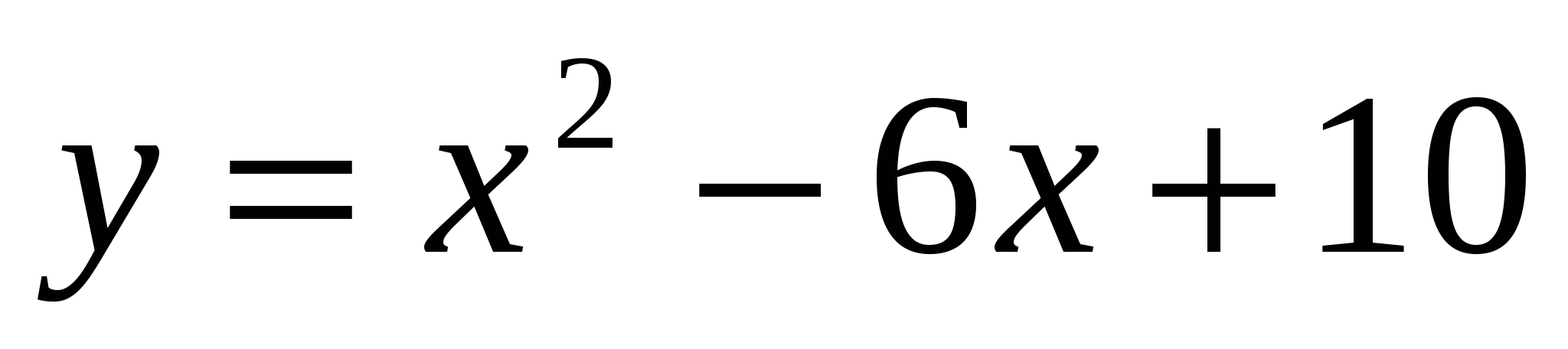 ,
,  ,
, 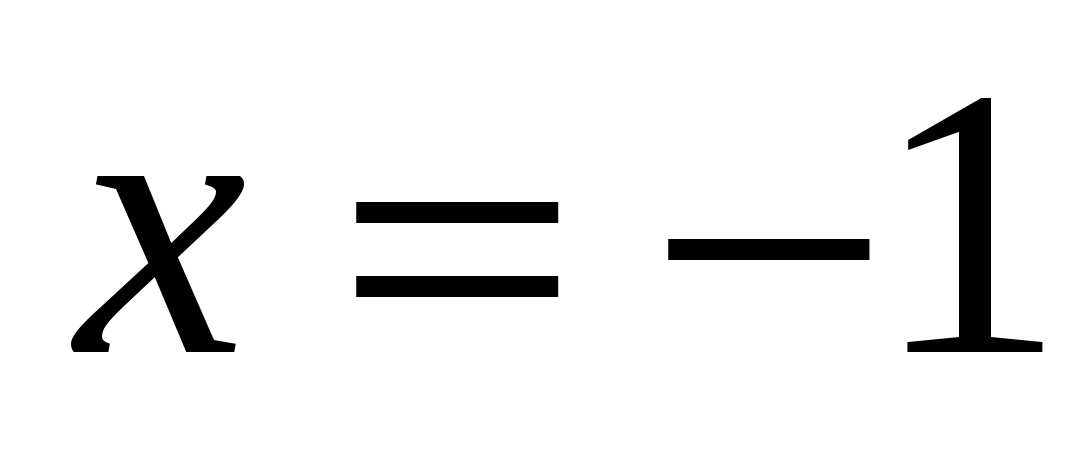
16
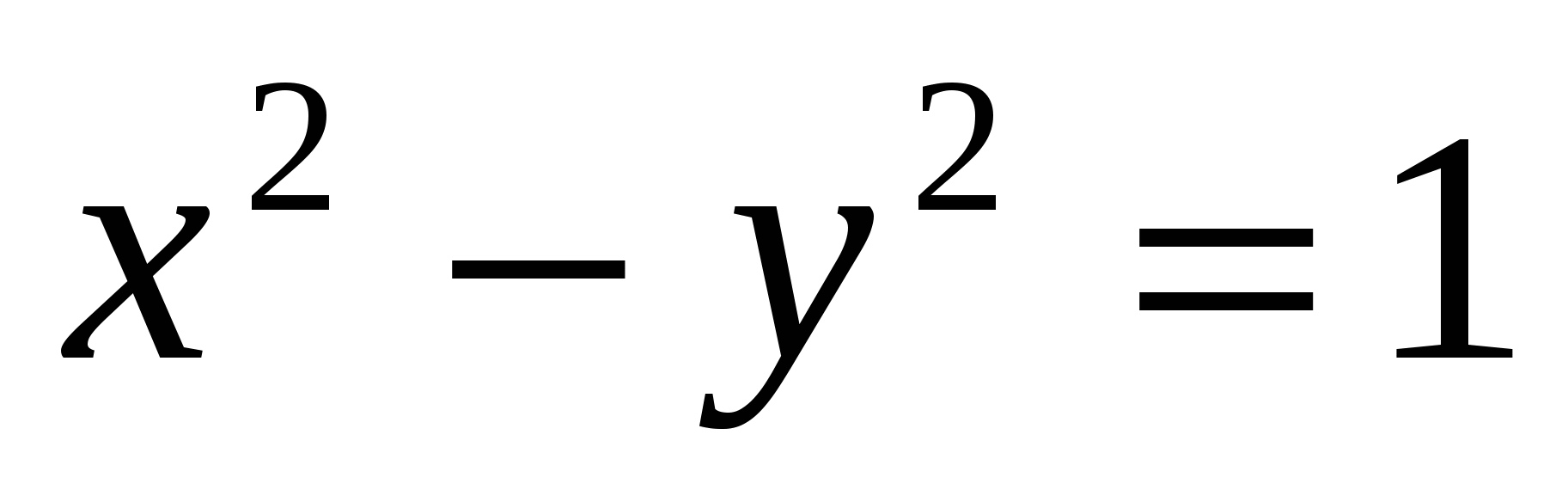 ,
, 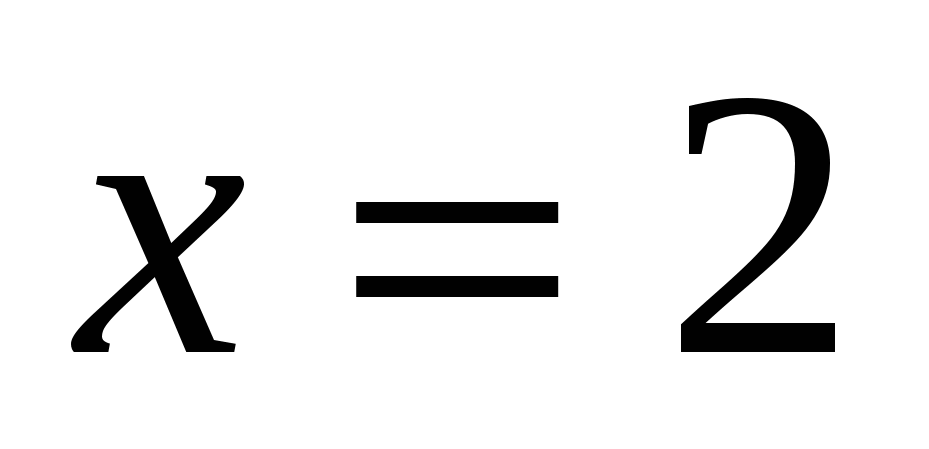
2
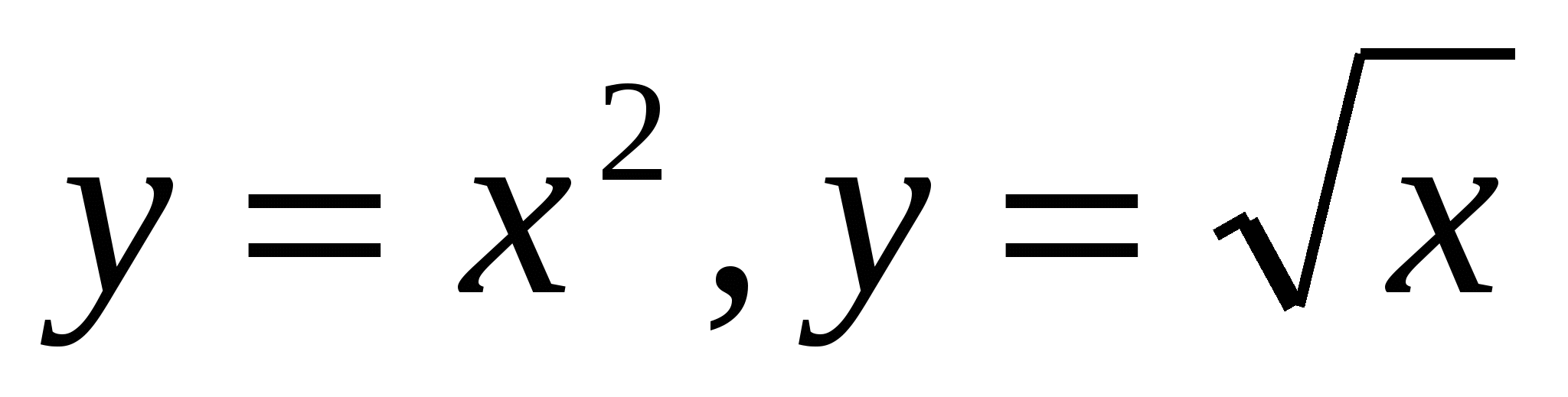
17
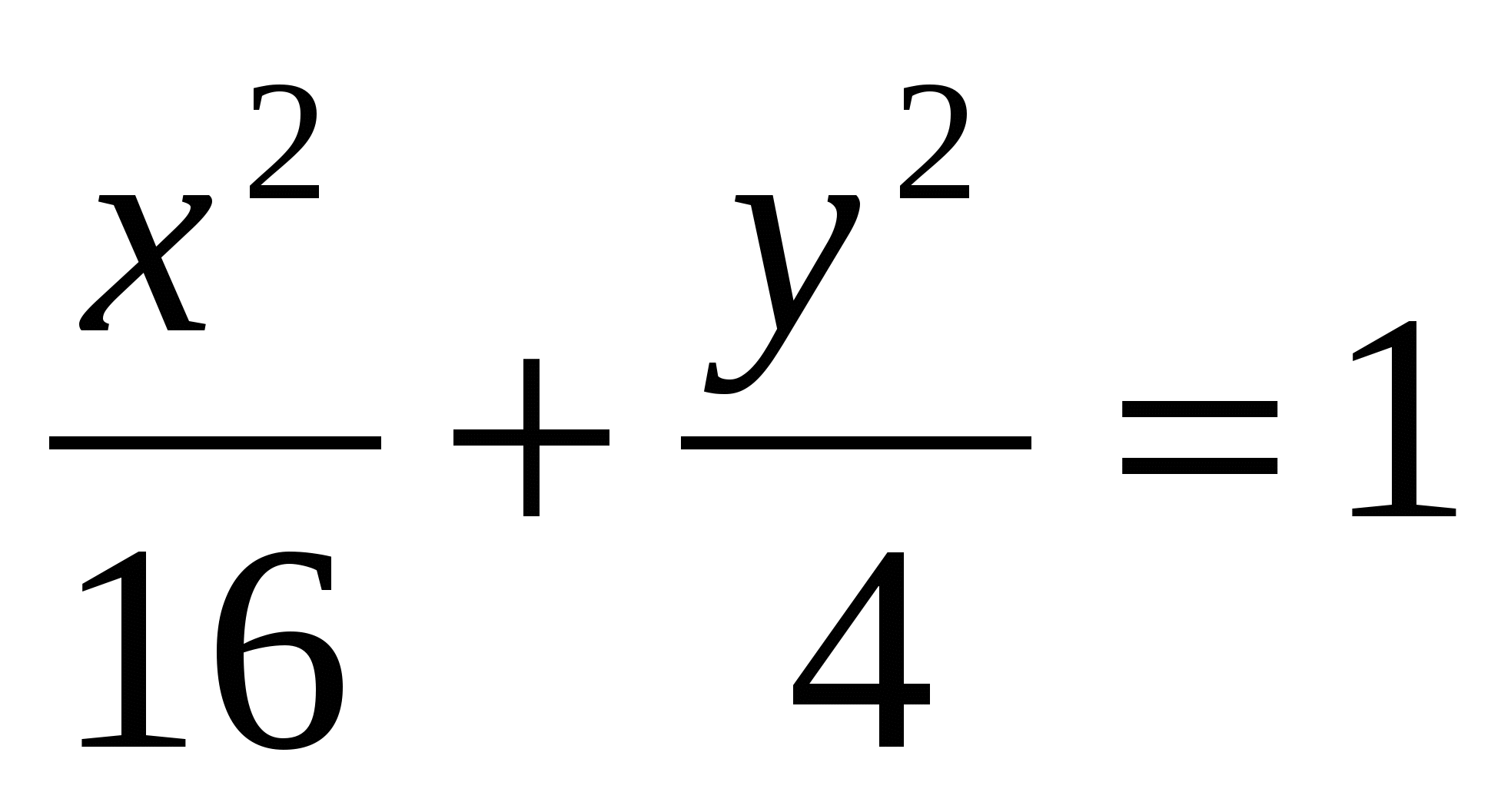
3
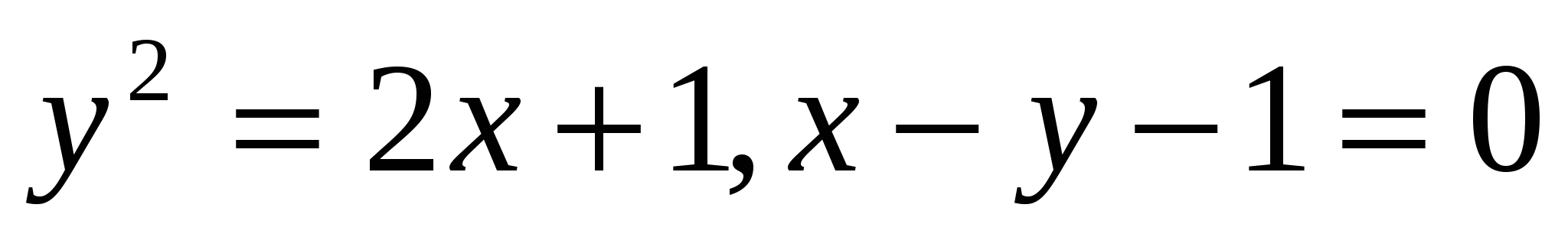
18
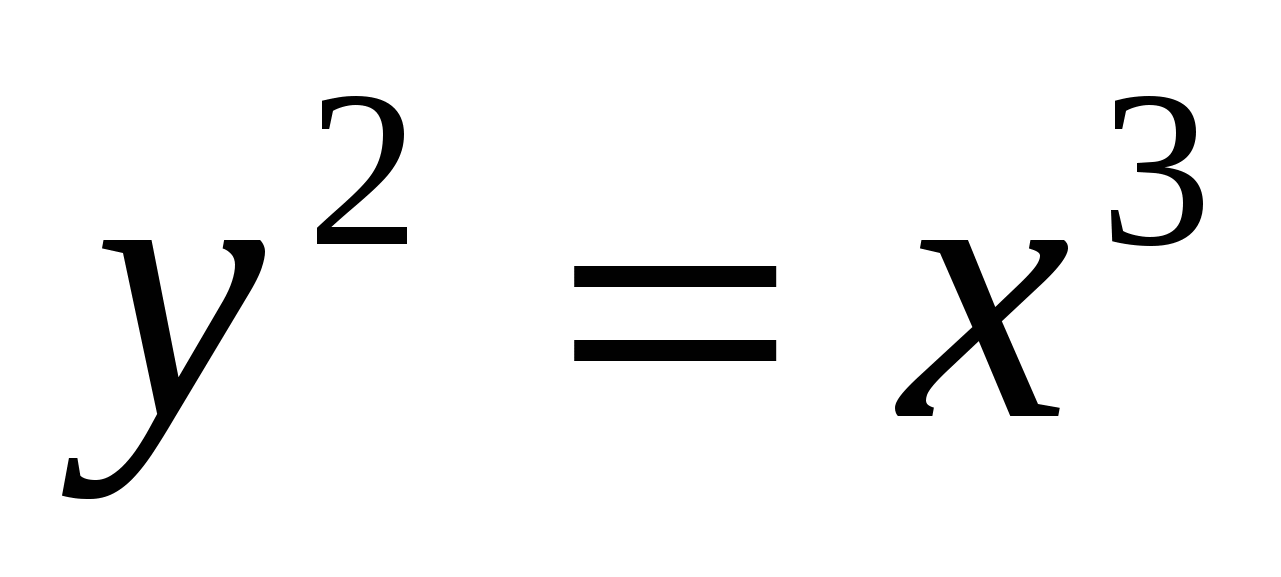 ,
, 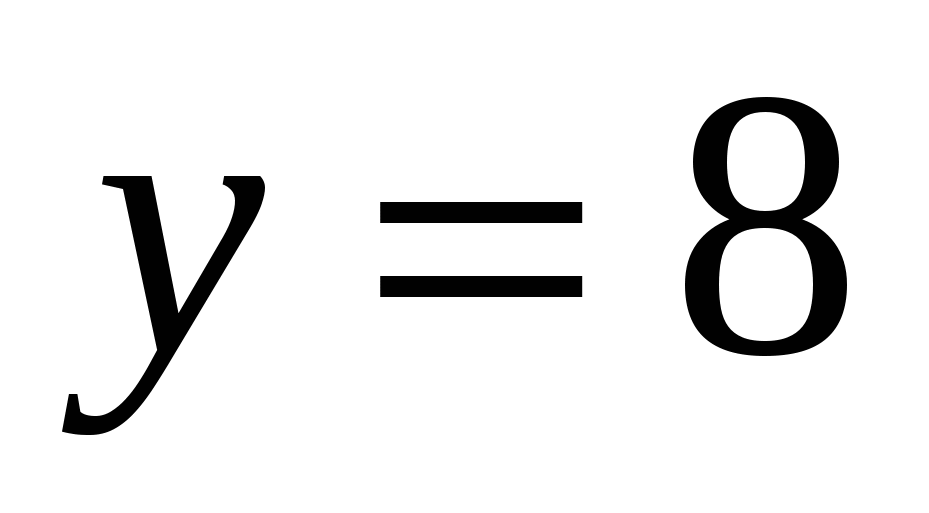 ,
, 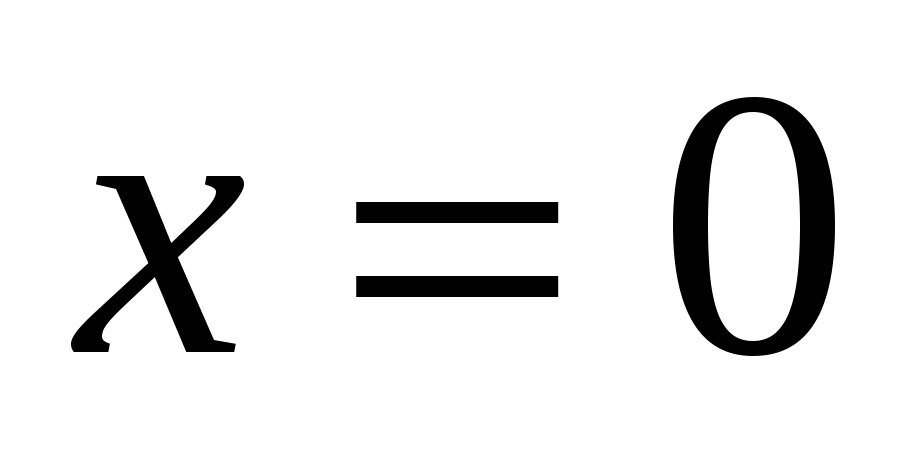
4
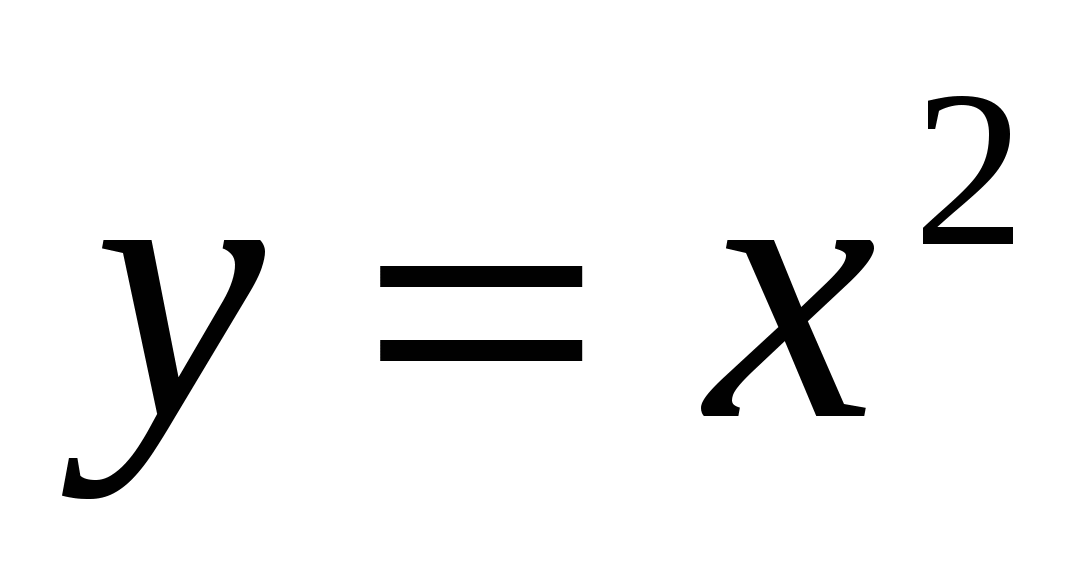 ,
, 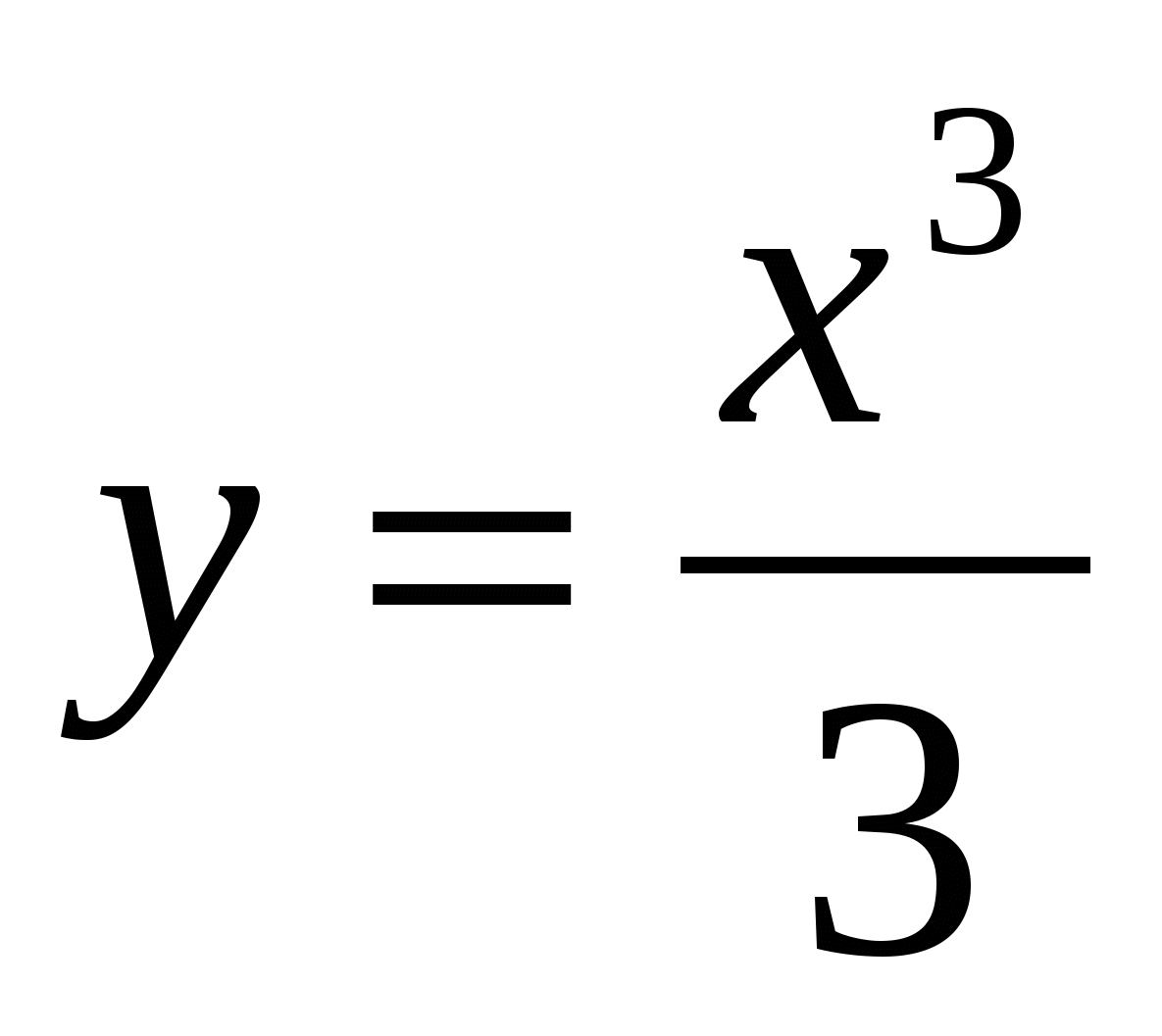
19
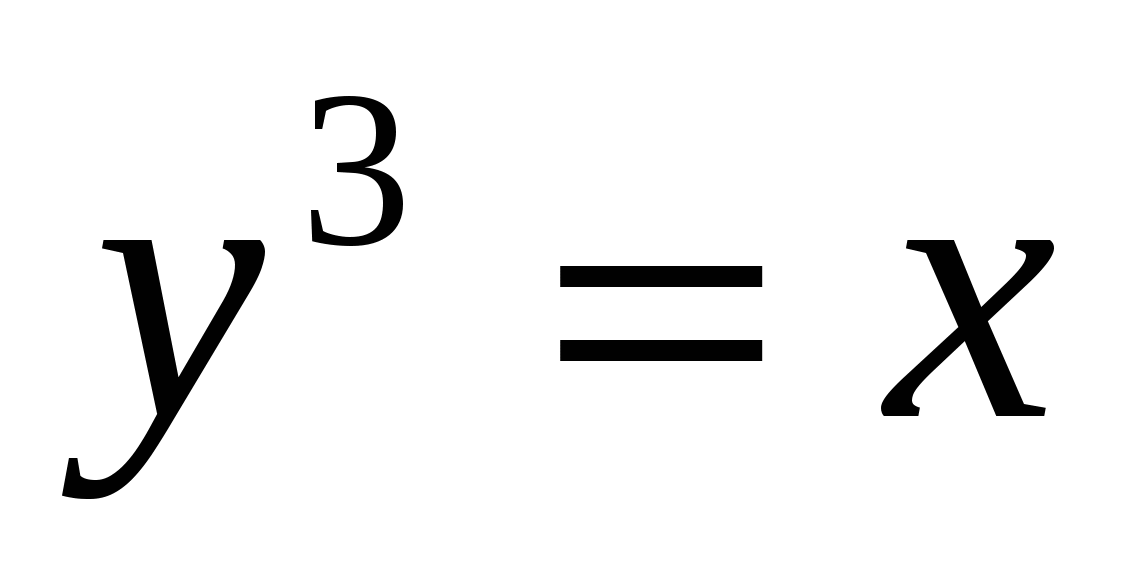 ,
, 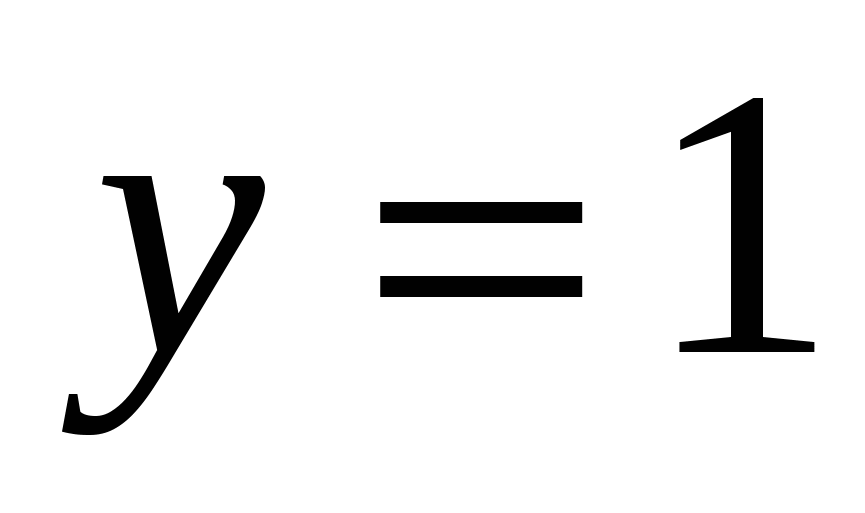 ,
, 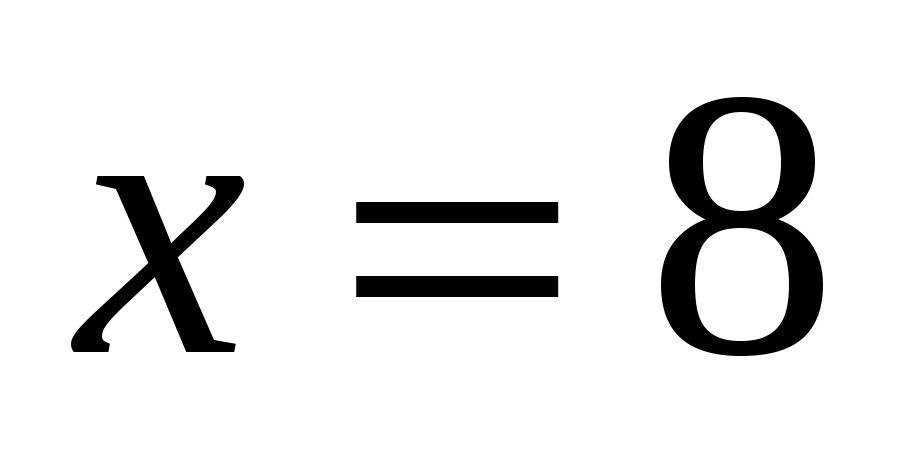
5
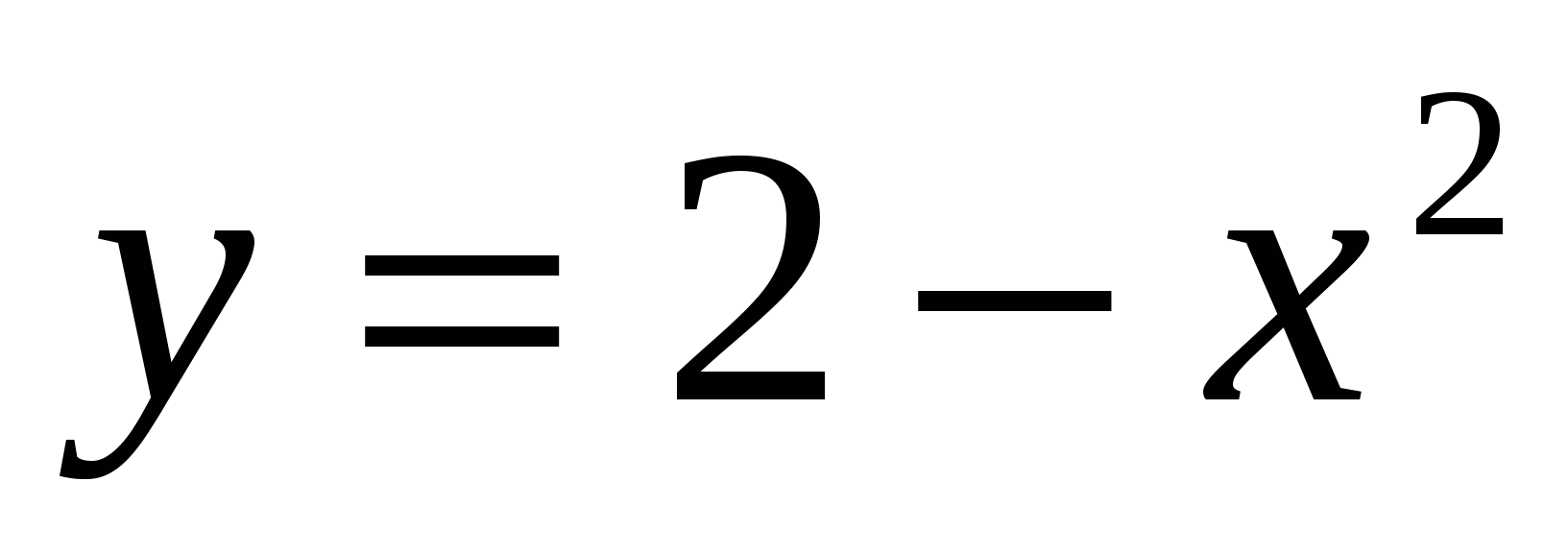 ,
, 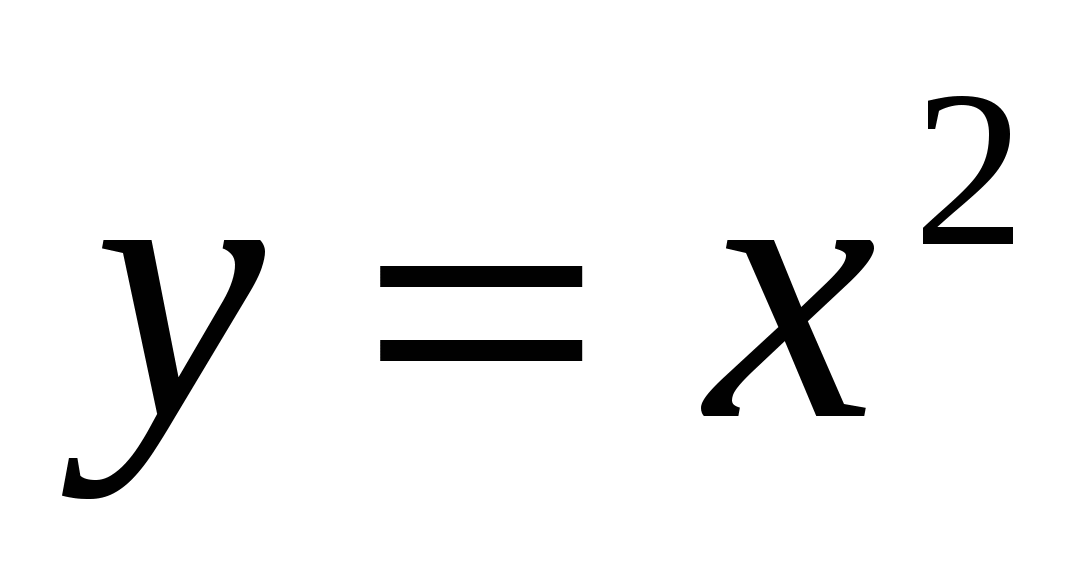
20
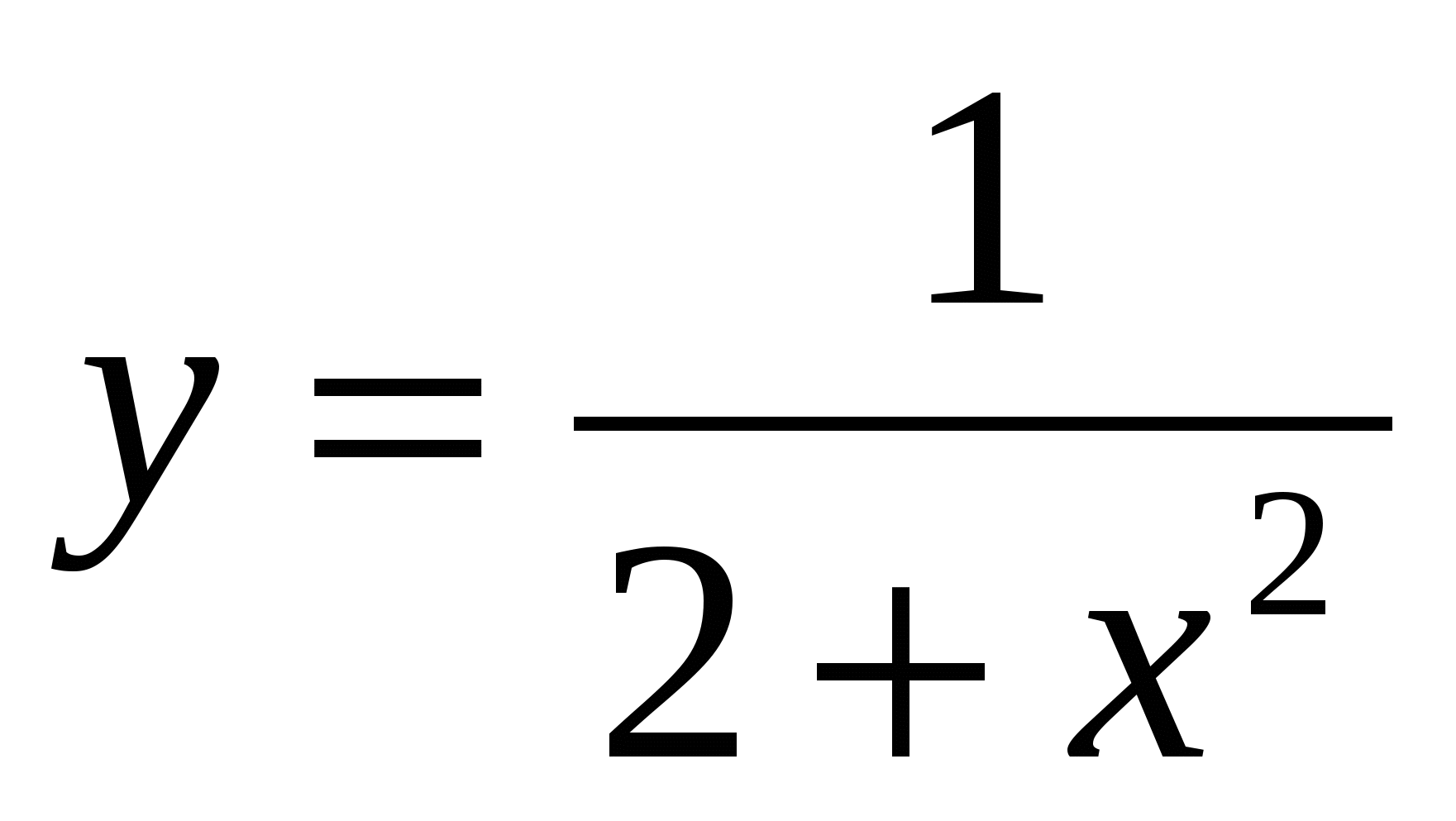 ,
, 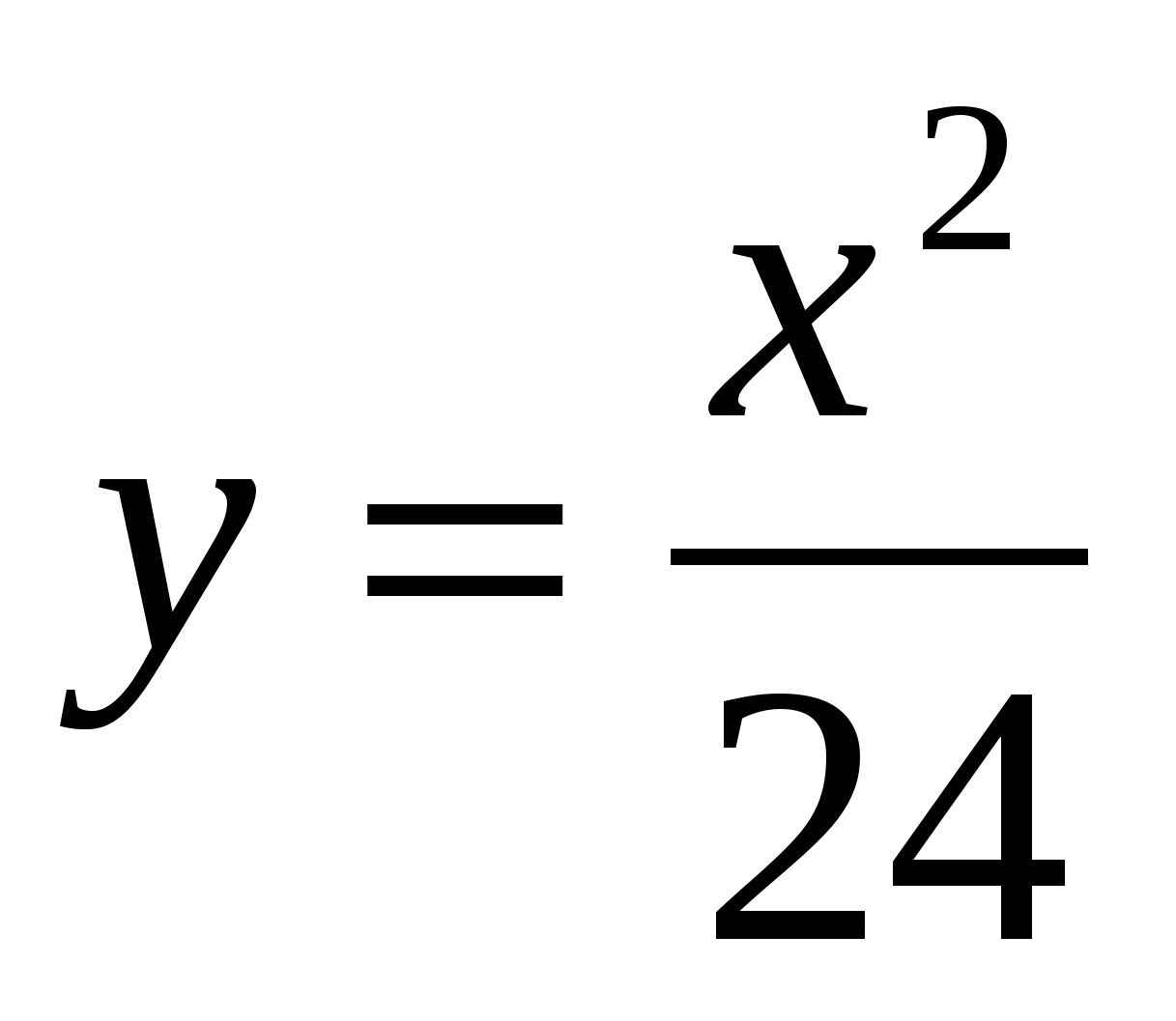
6
 ,
, 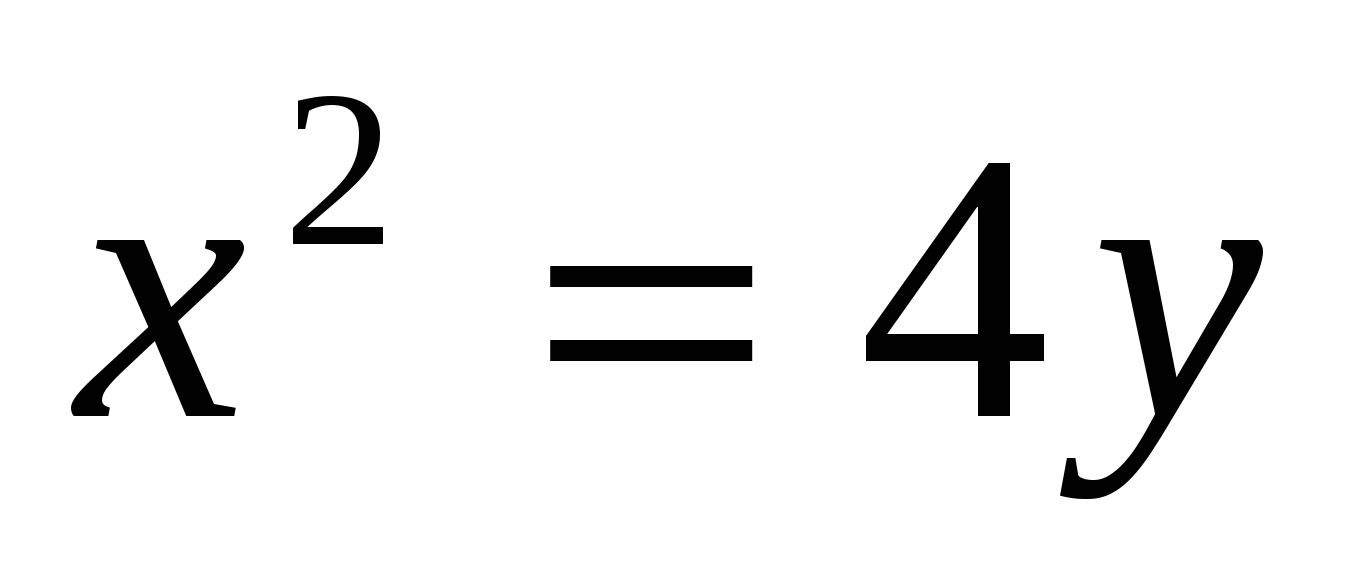
21
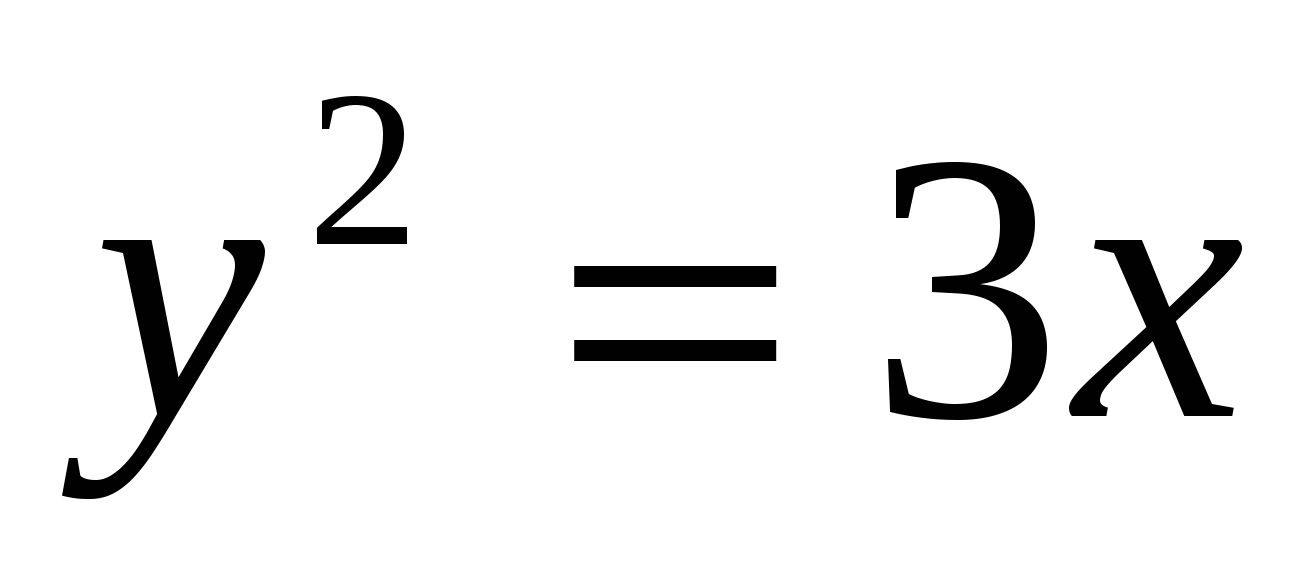 ,
, 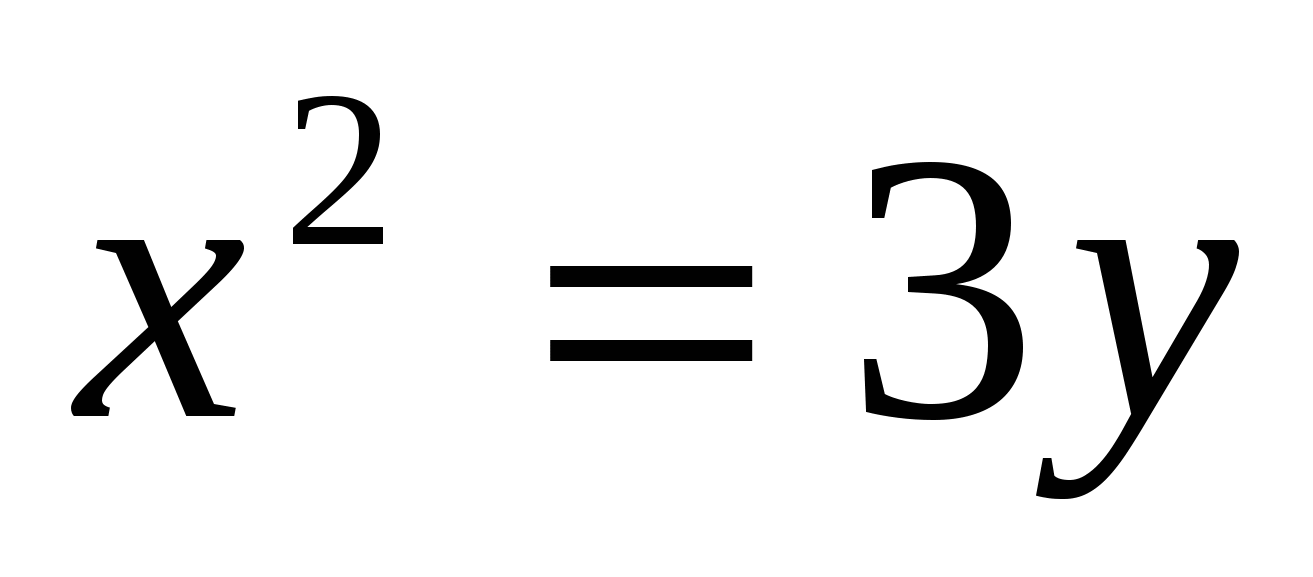
7
 ,
, 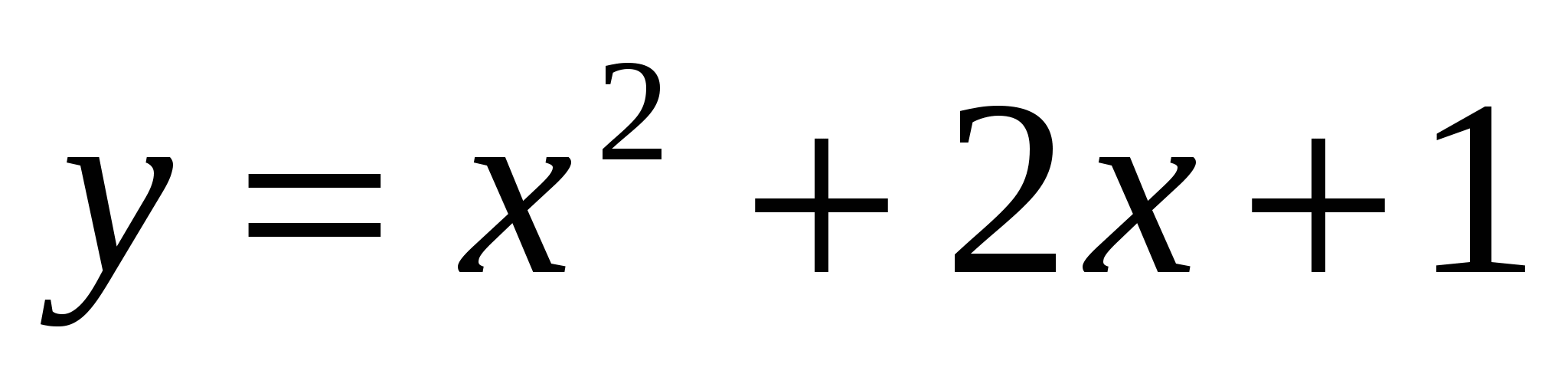
22
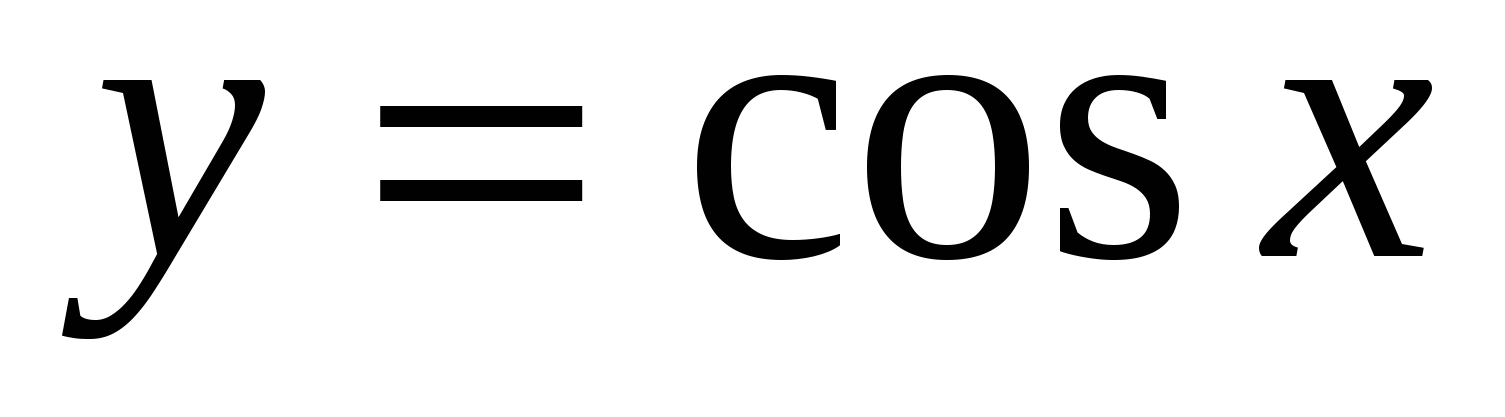 ,
, 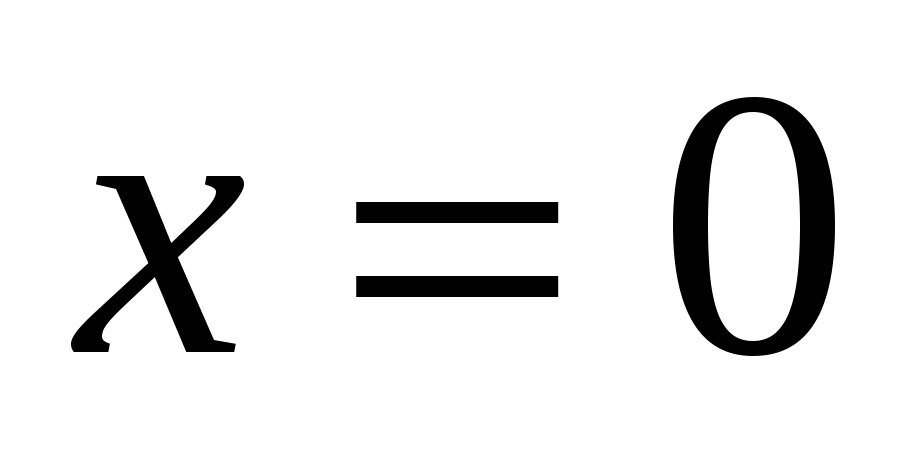 ,
, 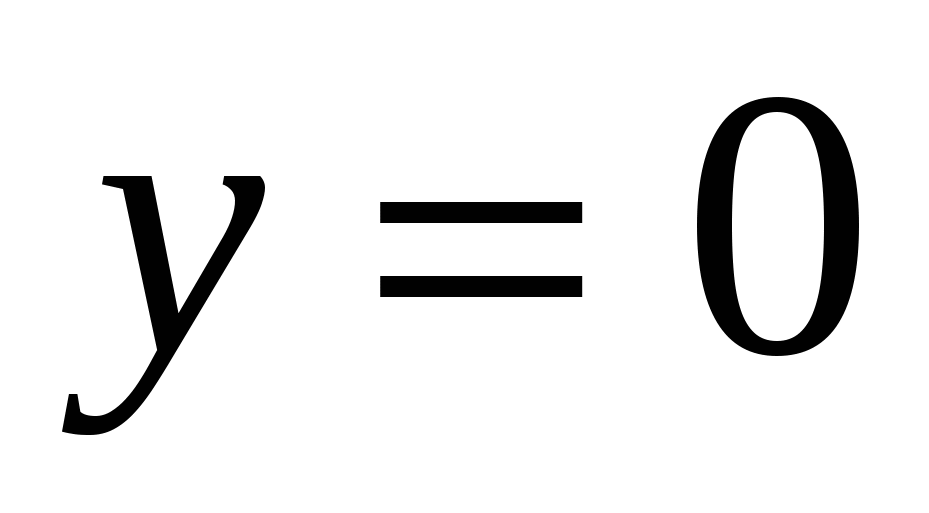
8
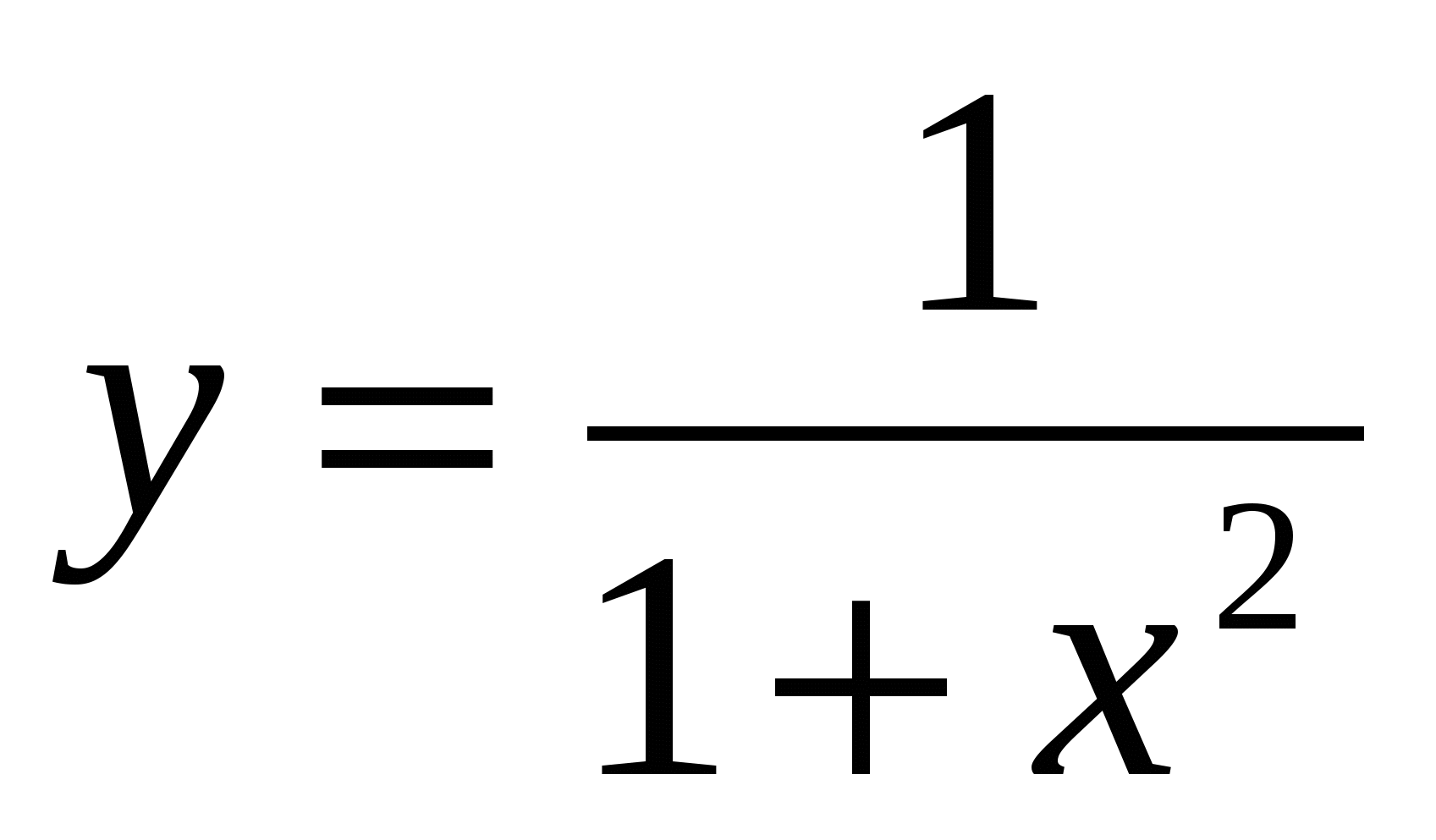 ,
, 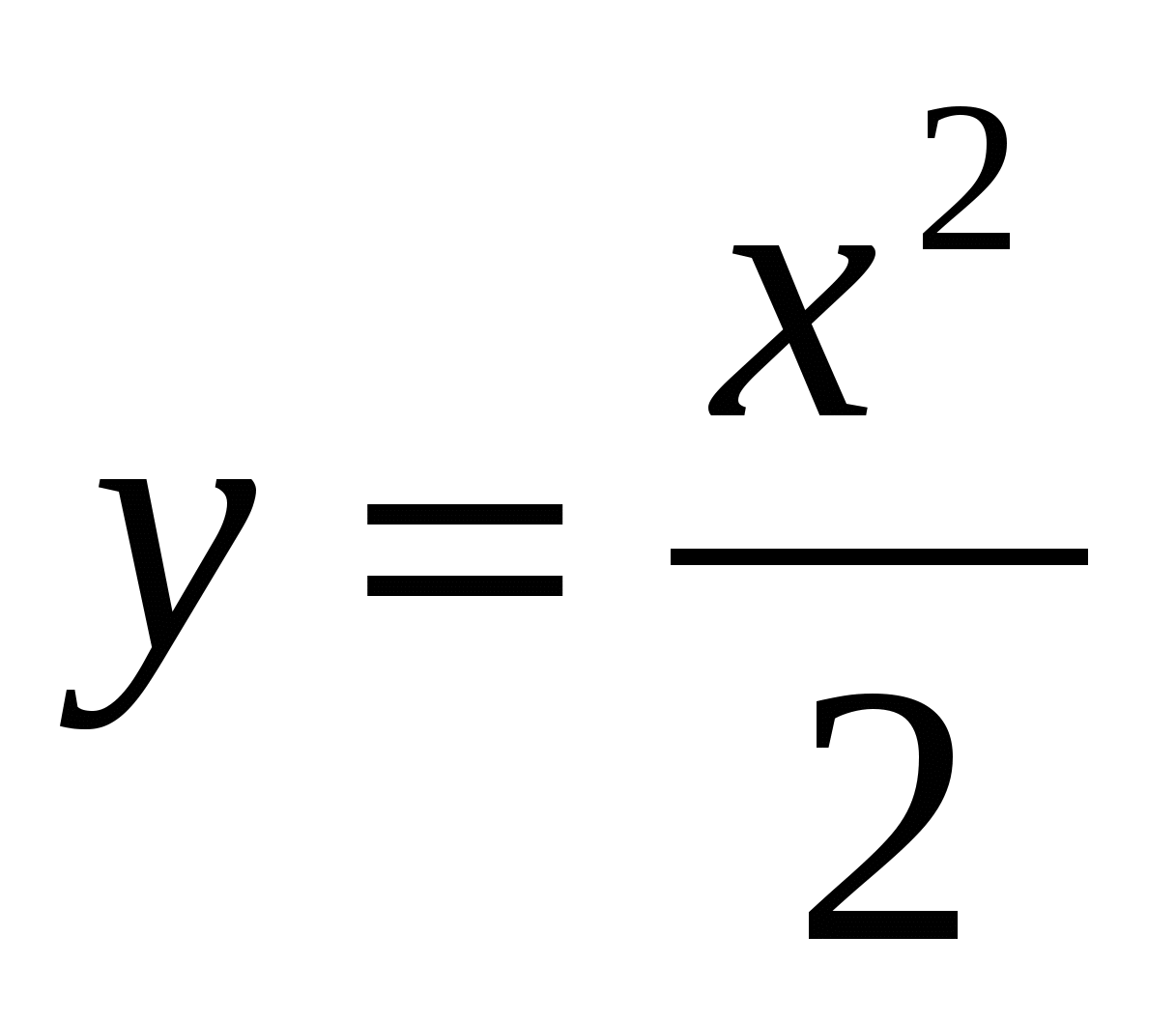
23
 ,
,  ,
, 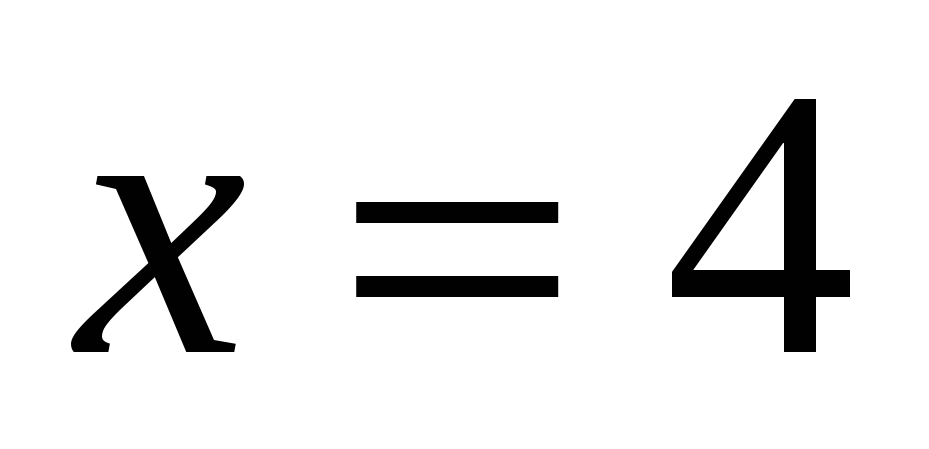
9
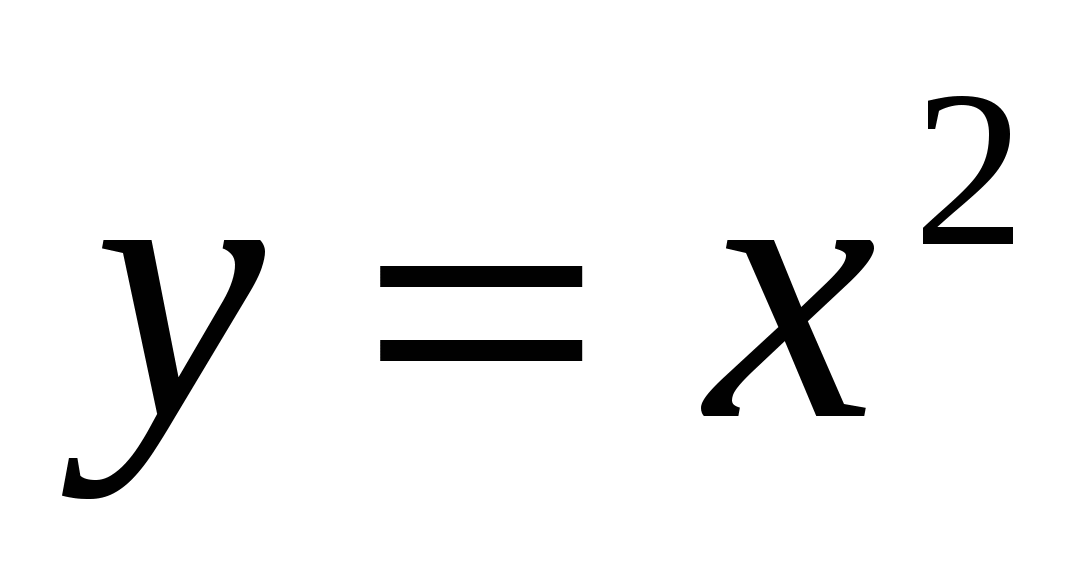 ,
, 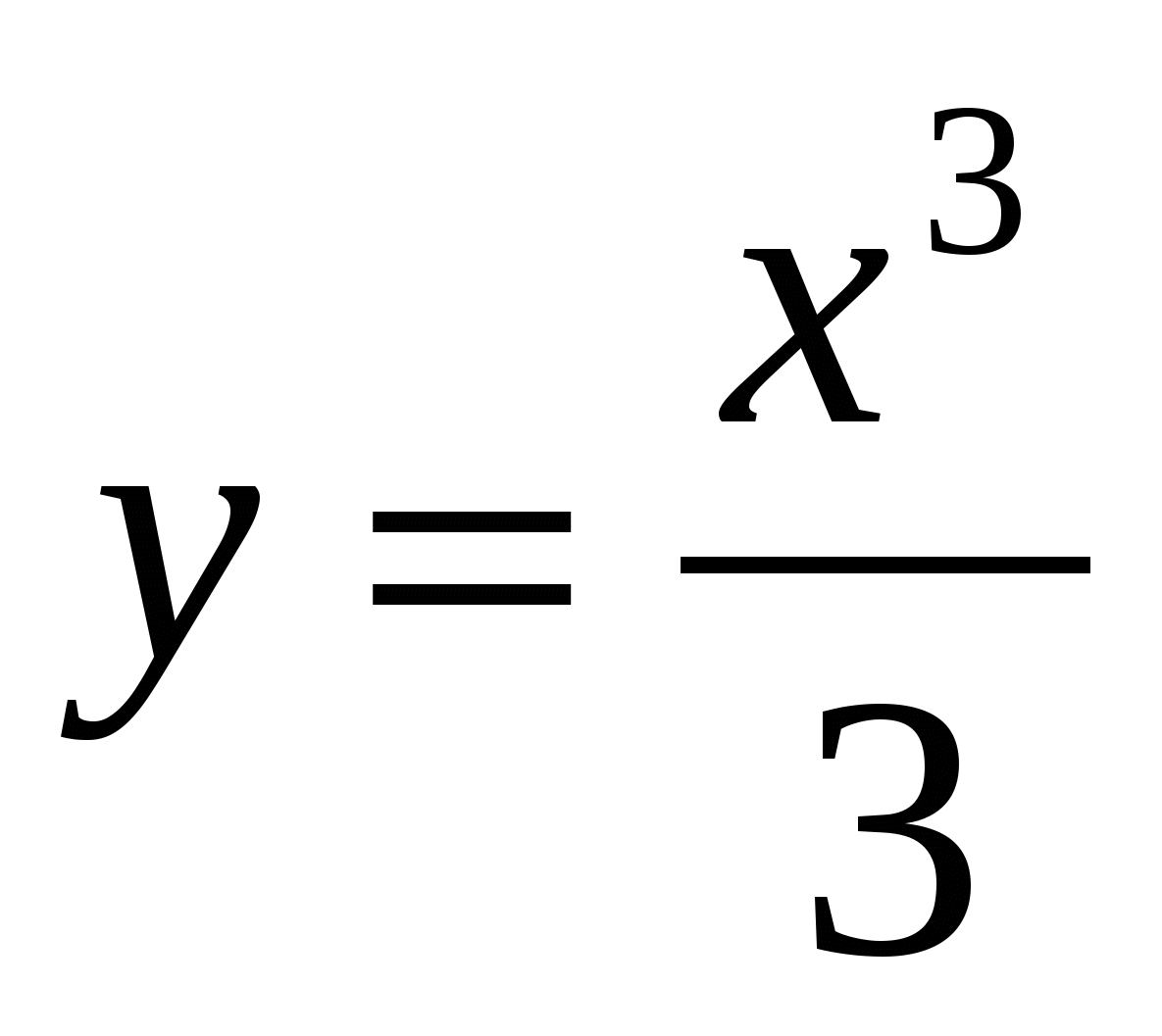
24
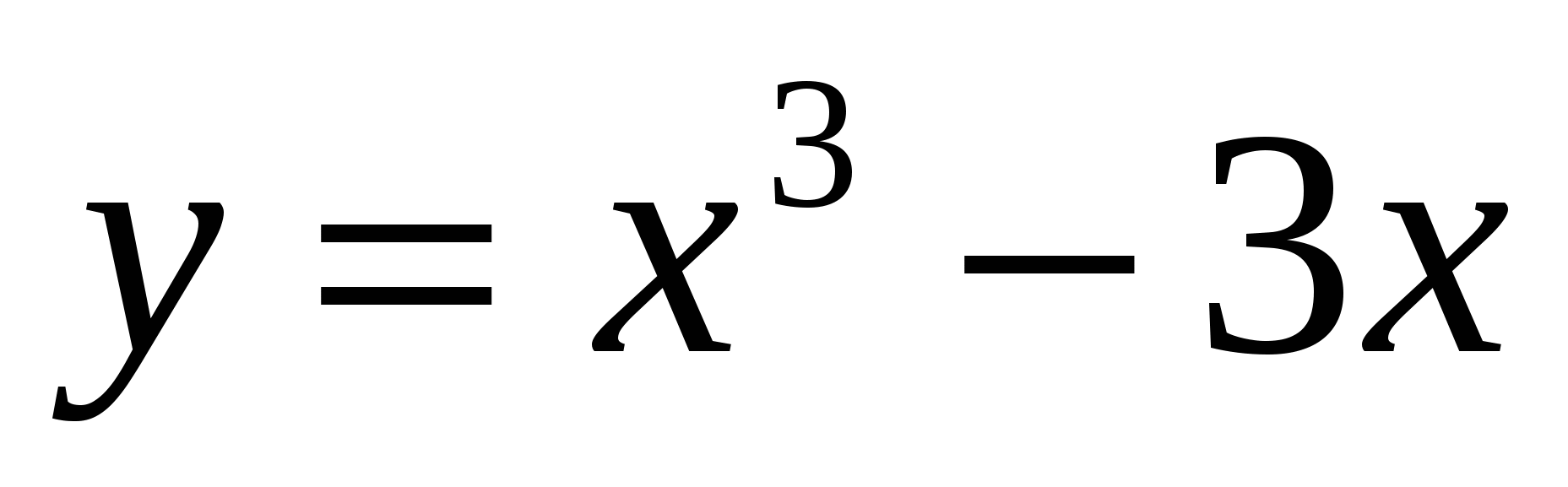 ,
, 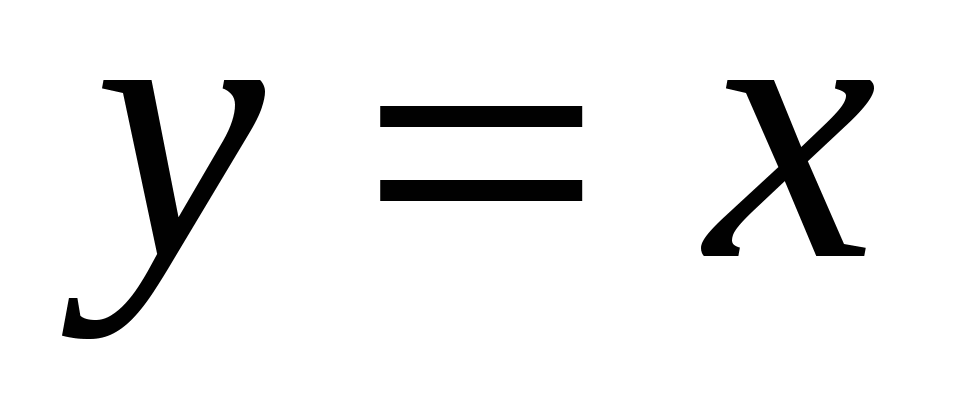
10
 ,
, 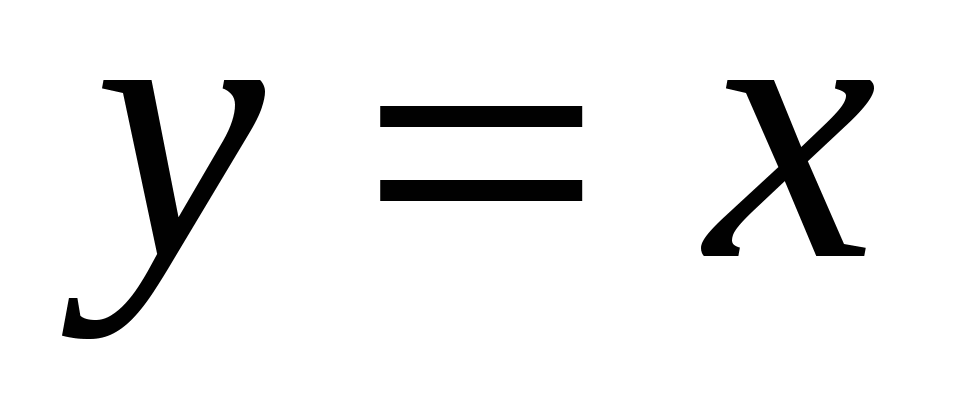 ,
, 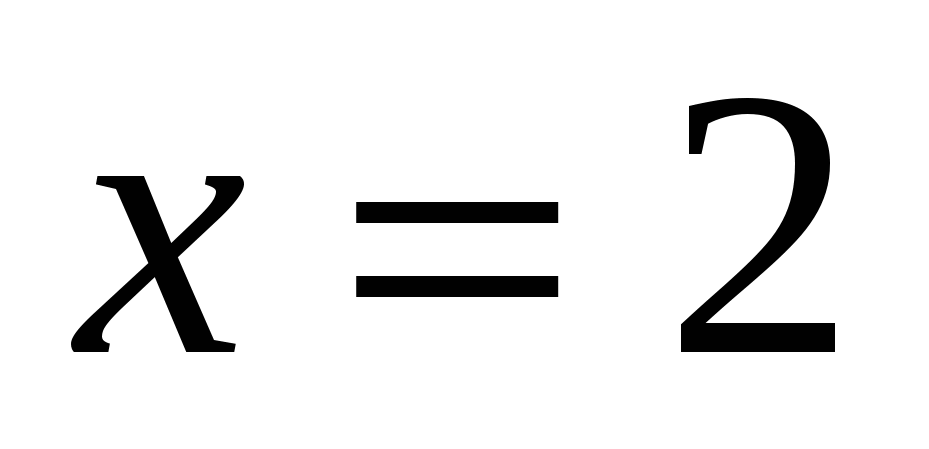
25
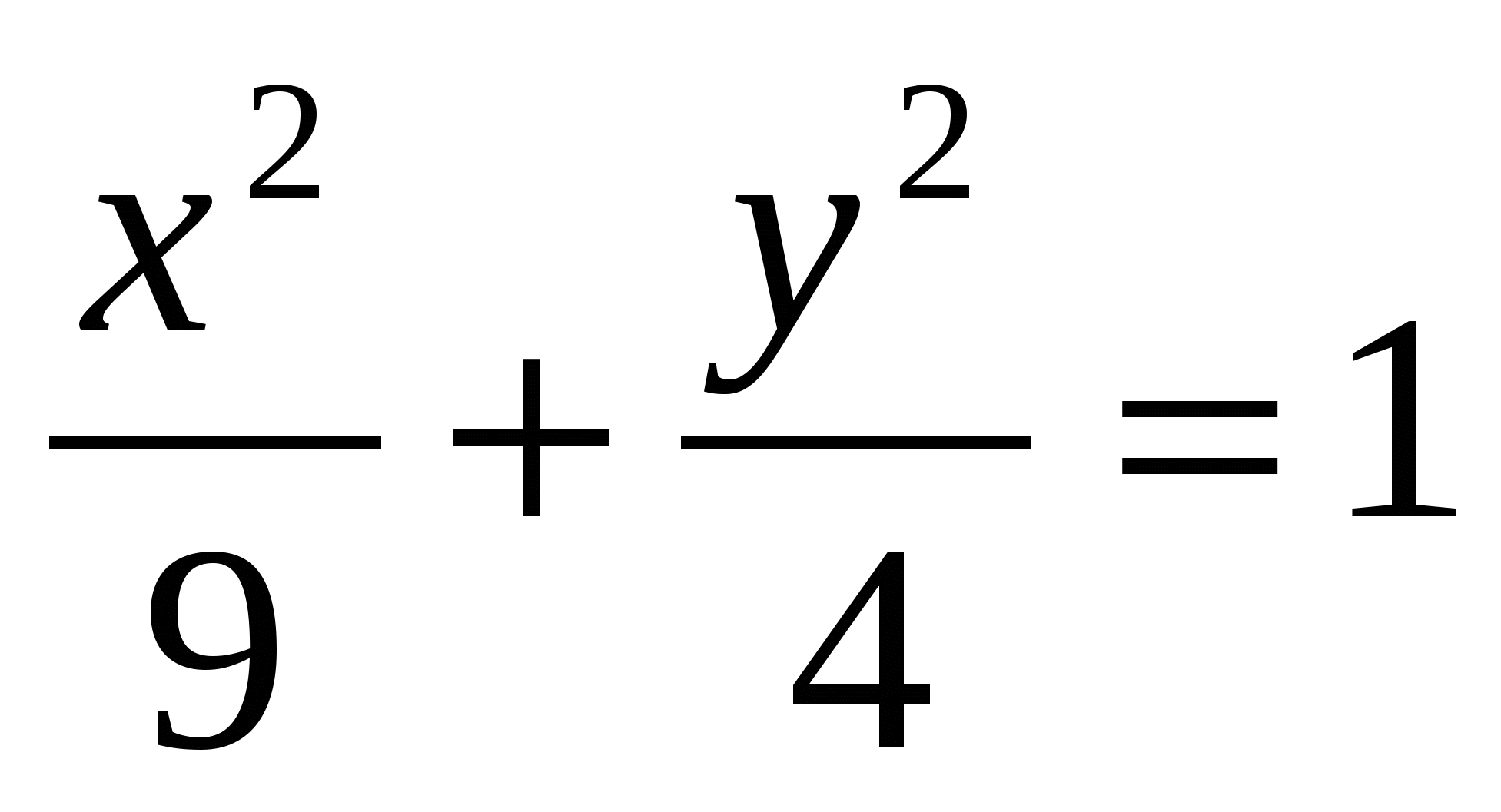
11
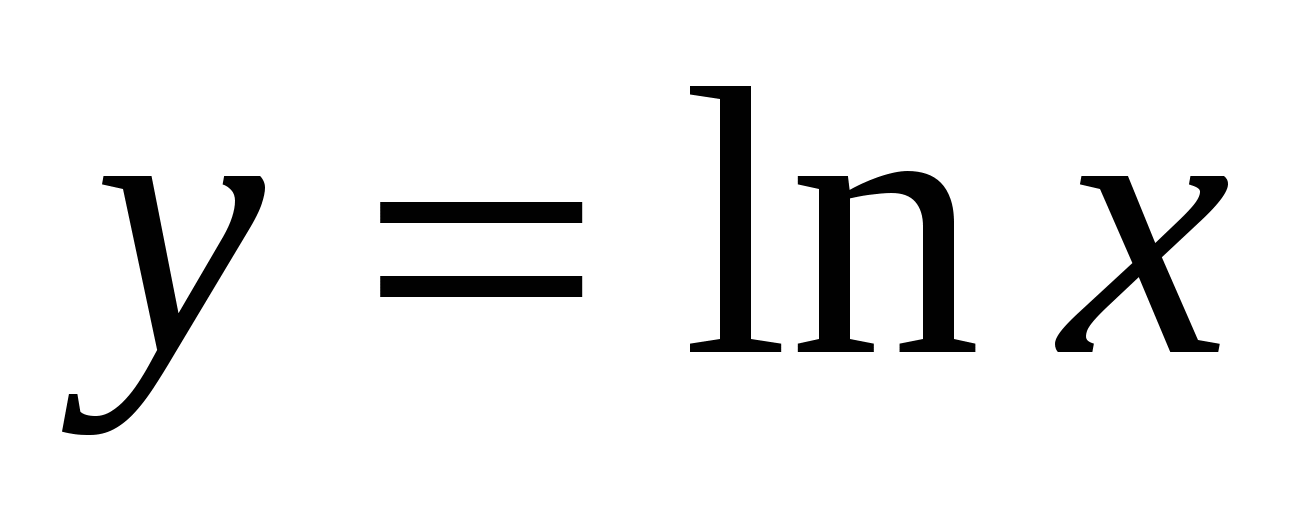 ,
, 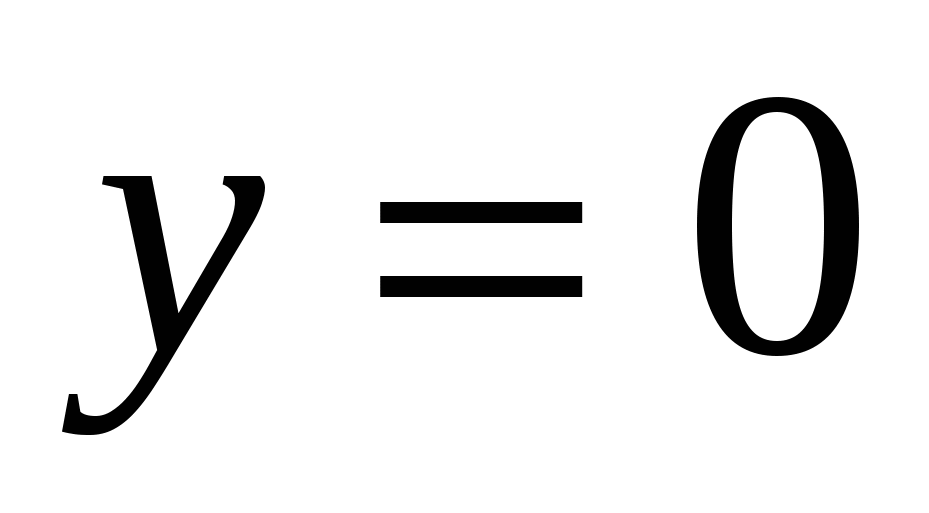 ,
, 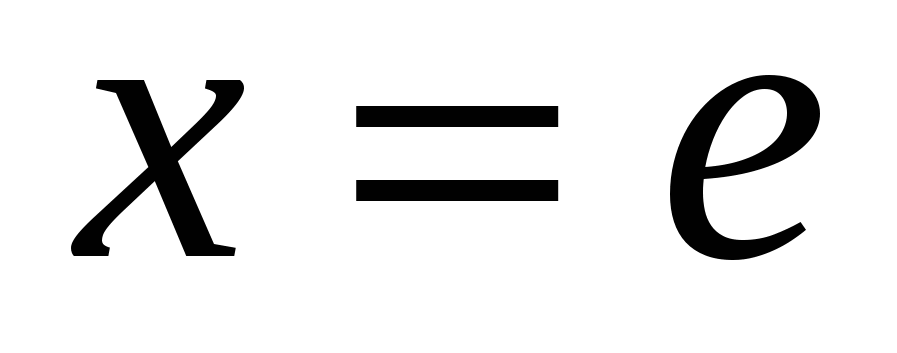
26
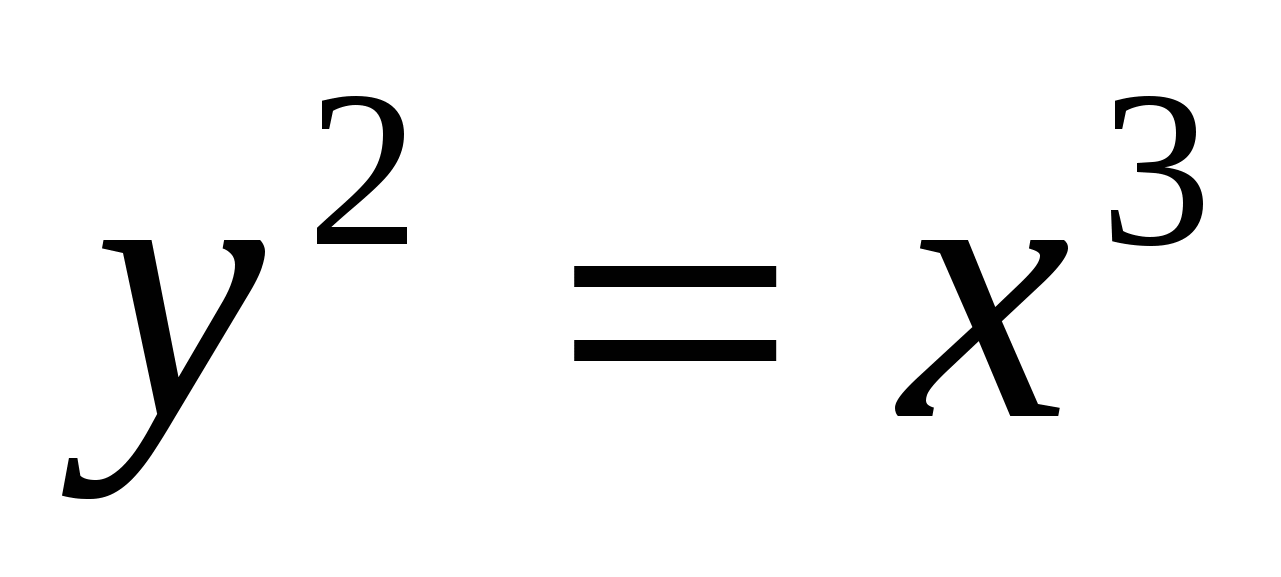 ,
, 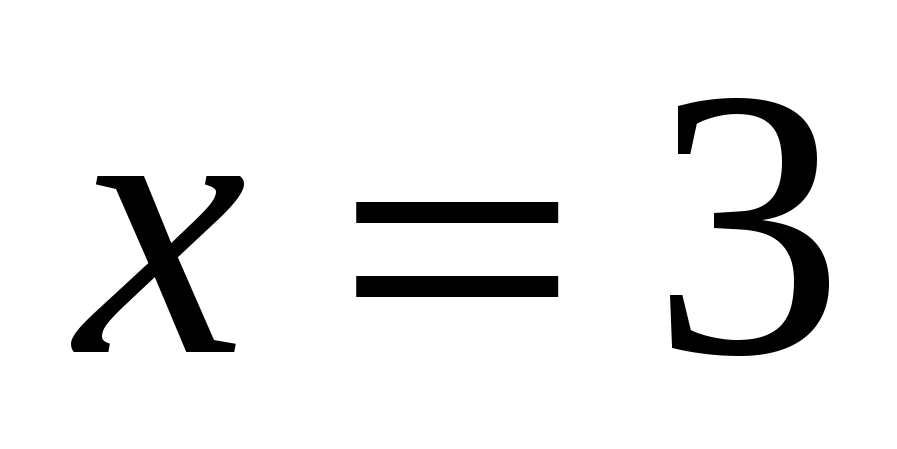
12
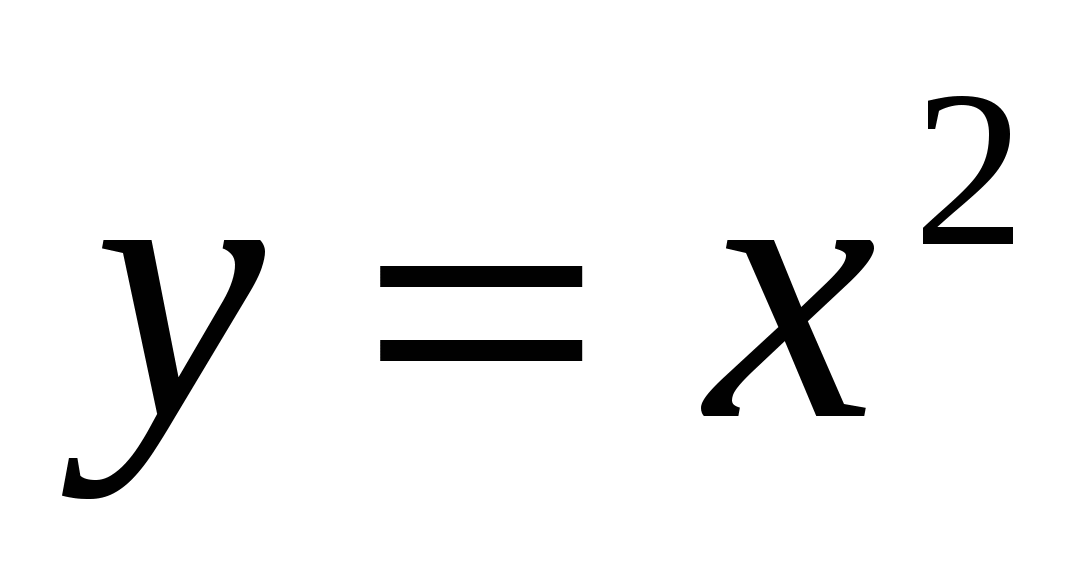 ,
, 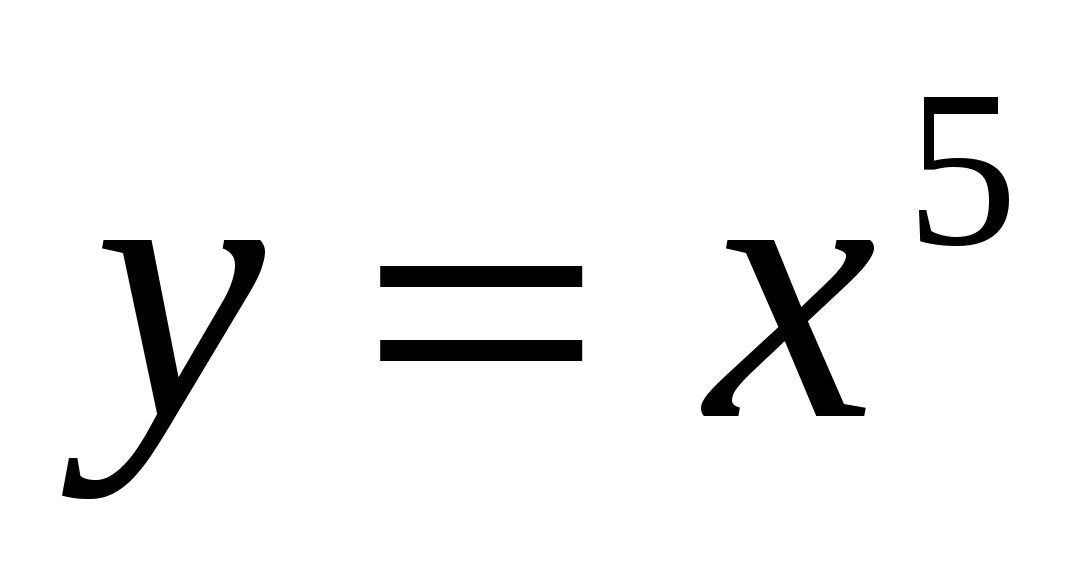
27
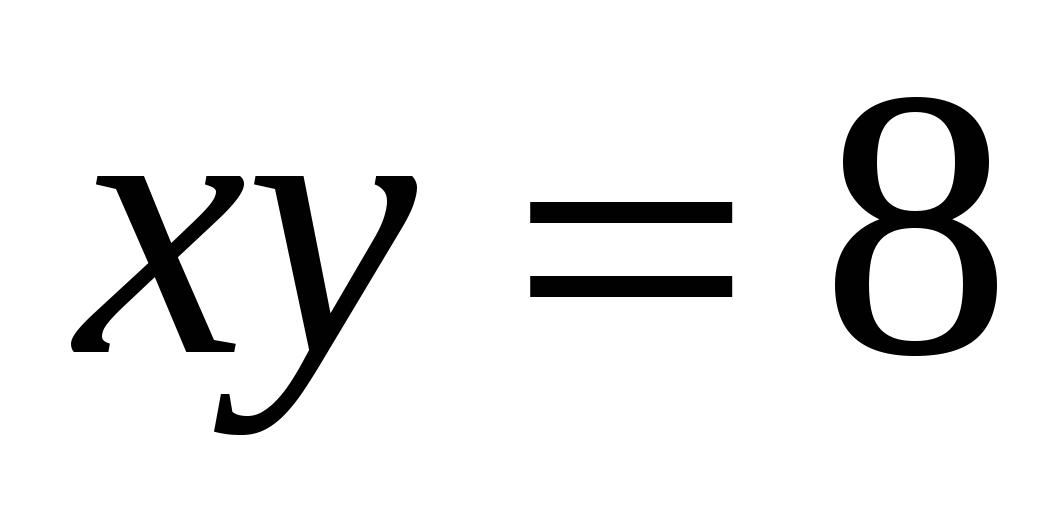 ,
, 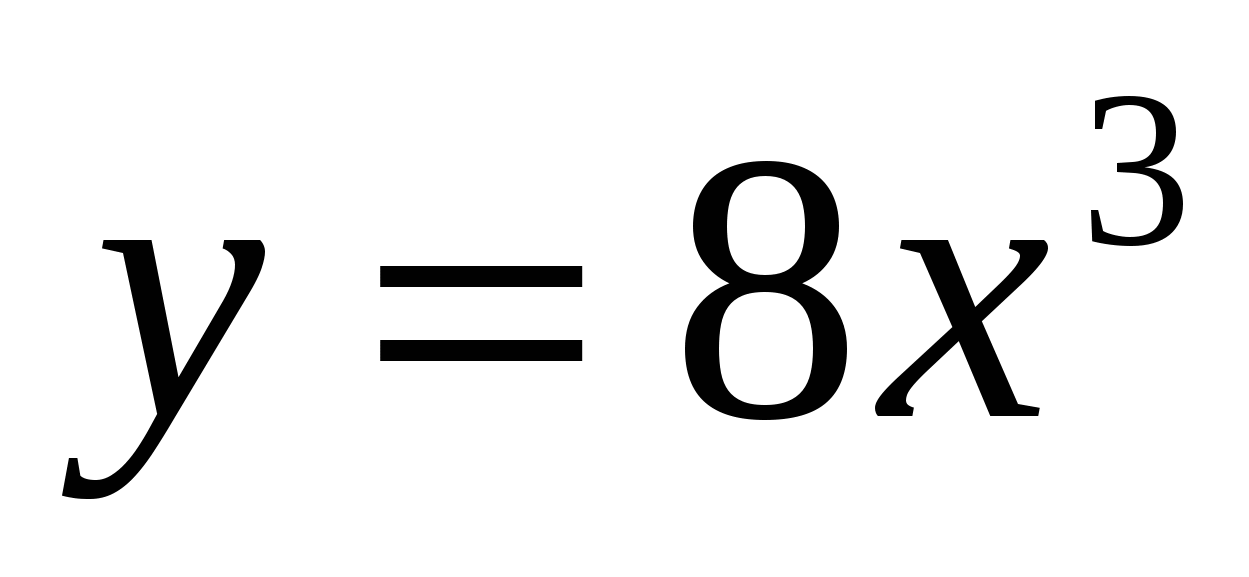 ,
, 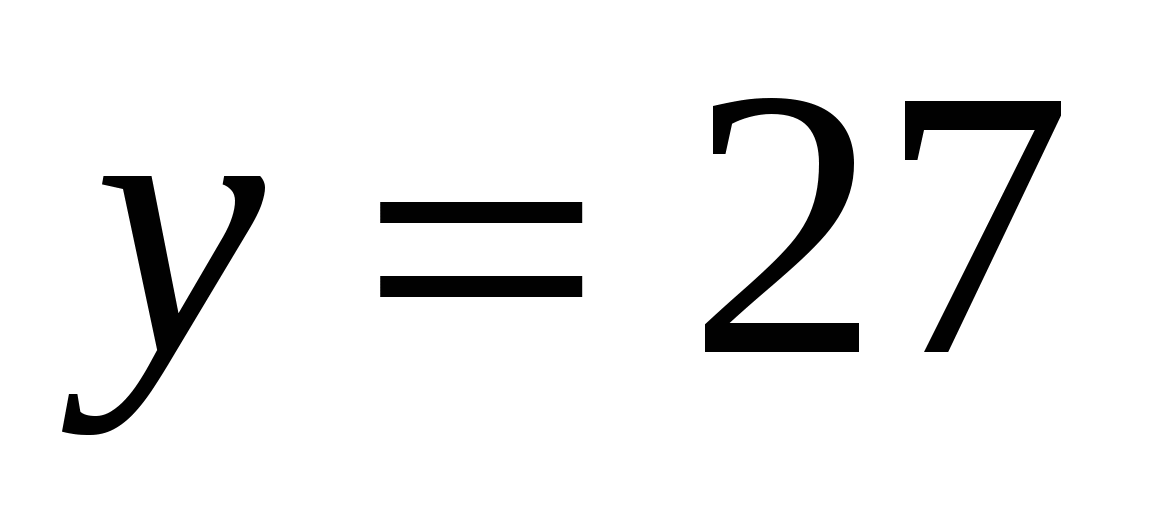
13
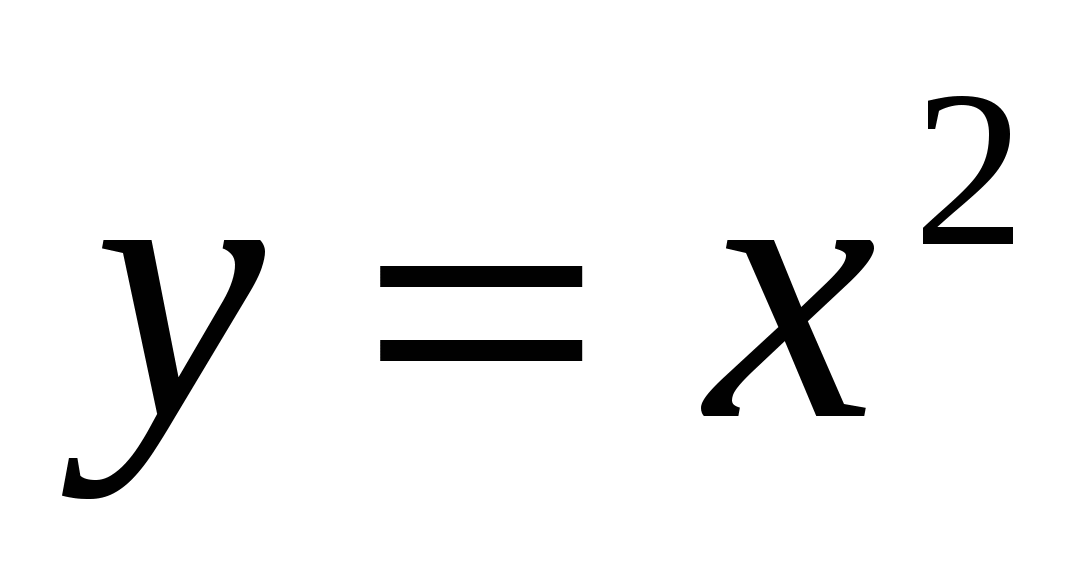 ,
, 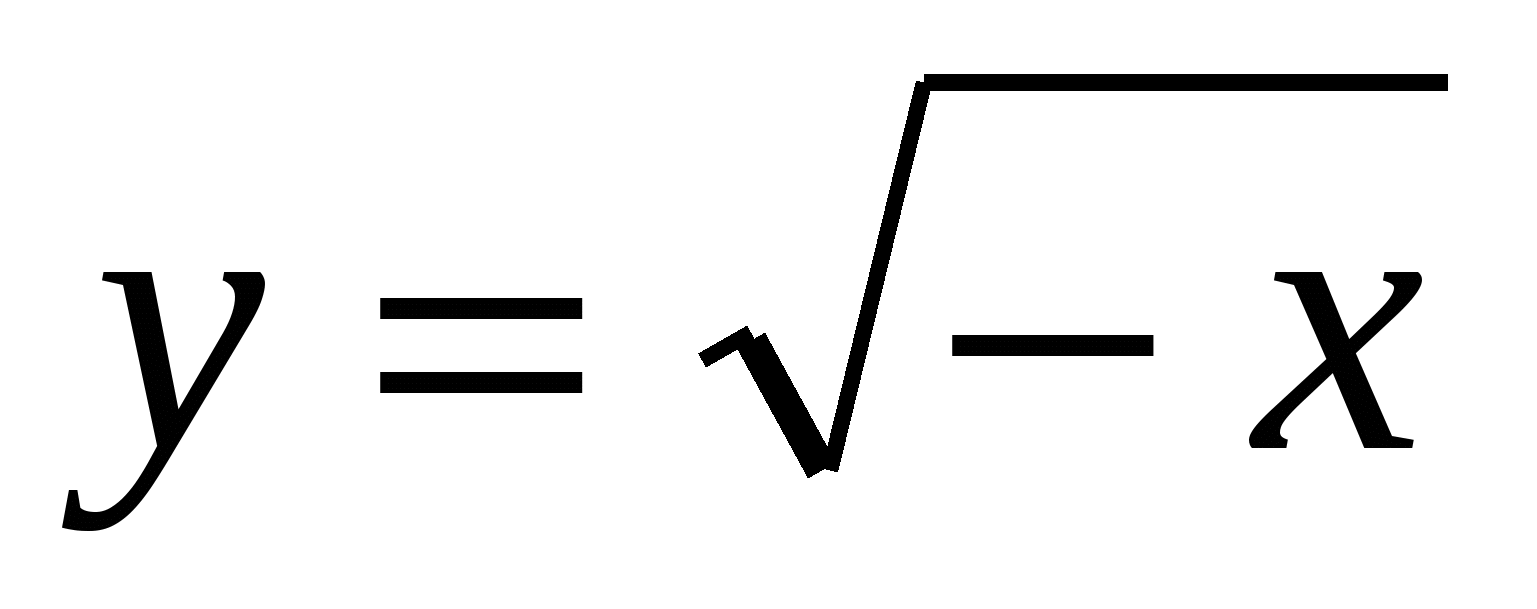
28
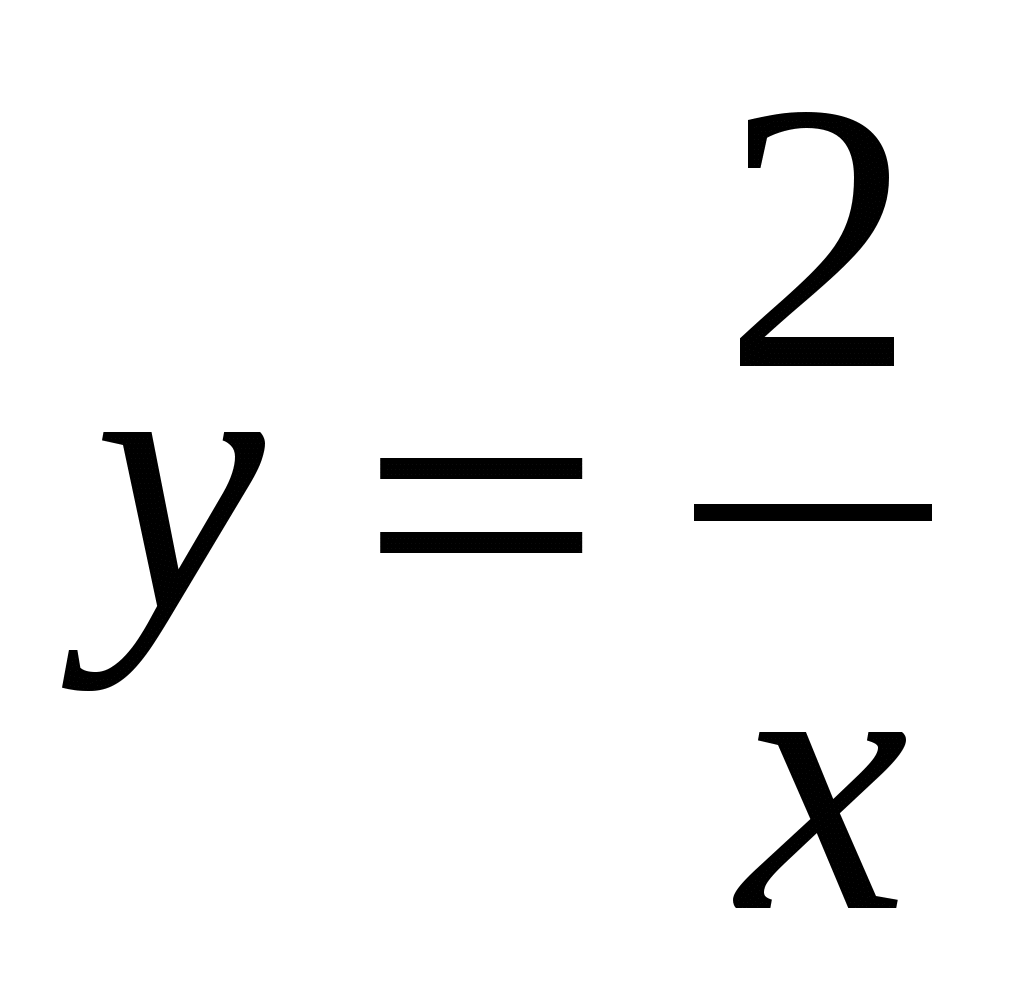 ,
, 
14
 ,
, 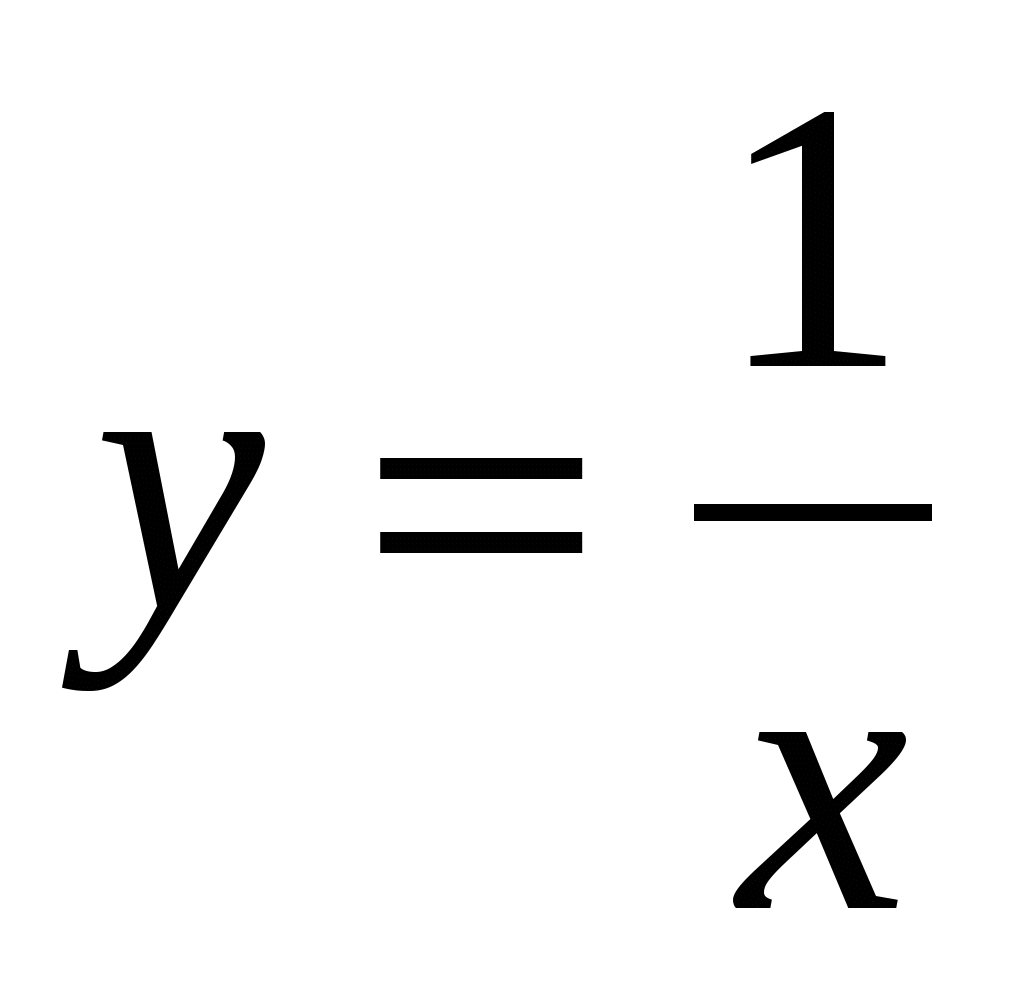 ,
, 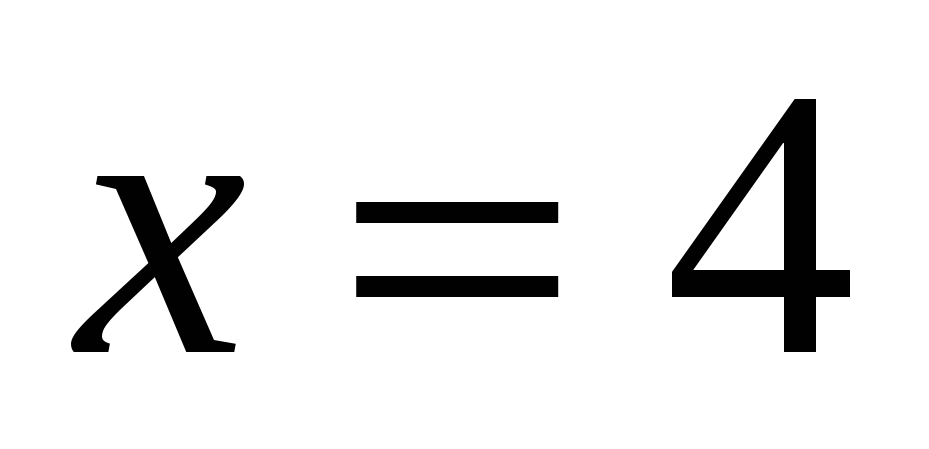
29
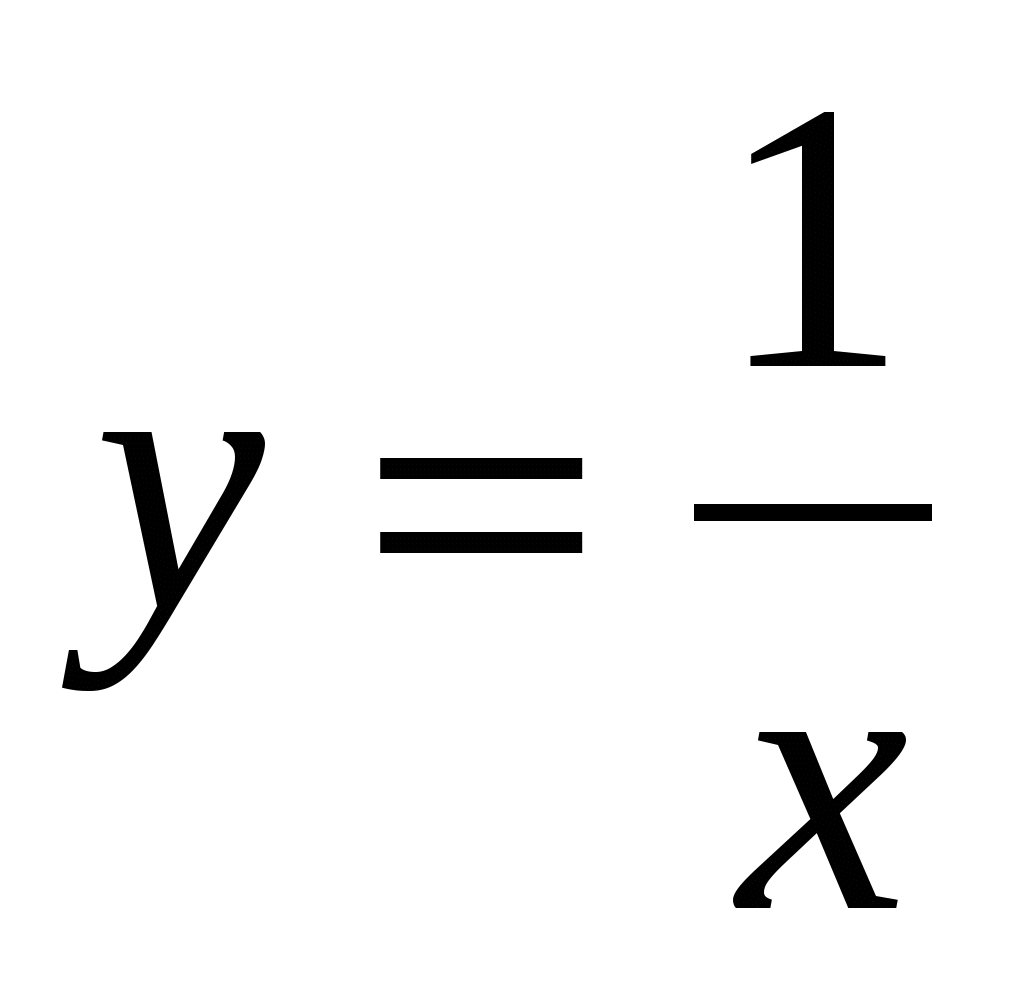 ,
, 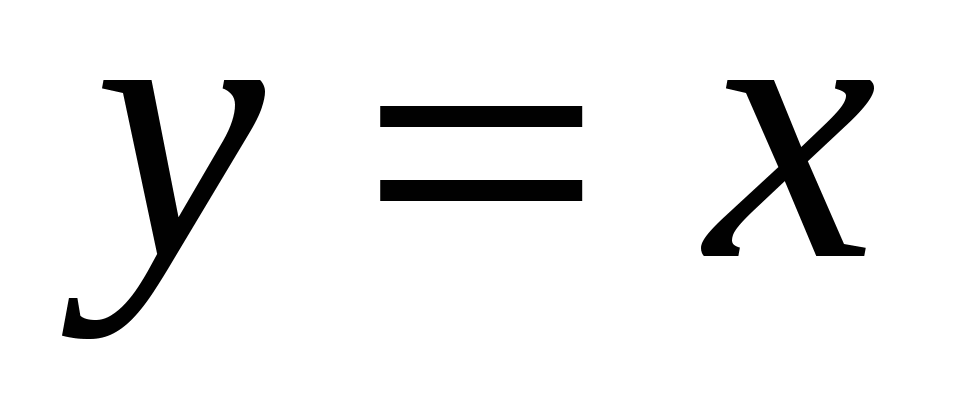 ,
, 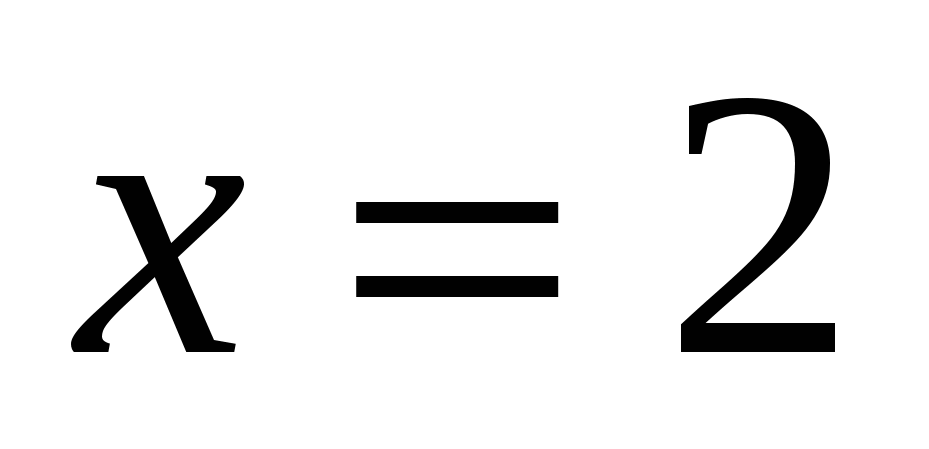
15
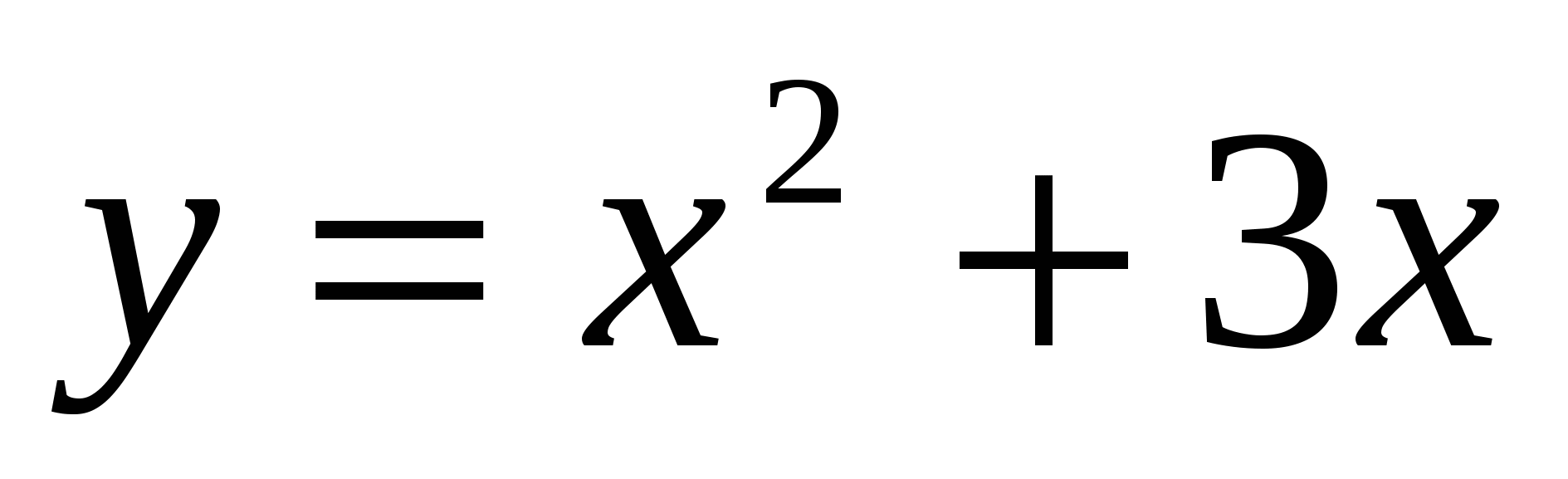 ,
, 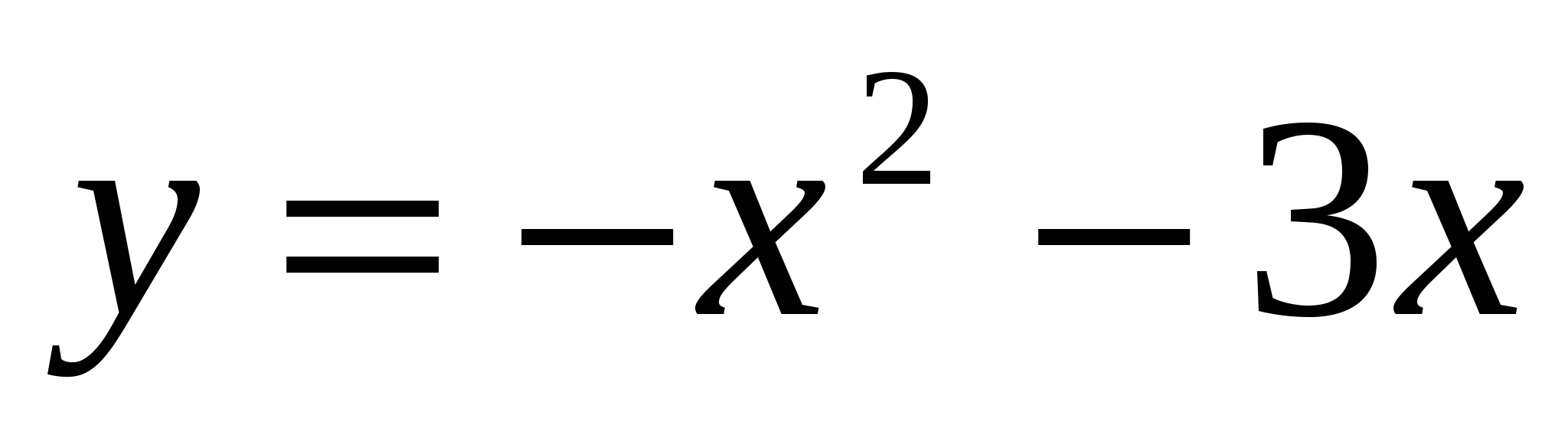
30
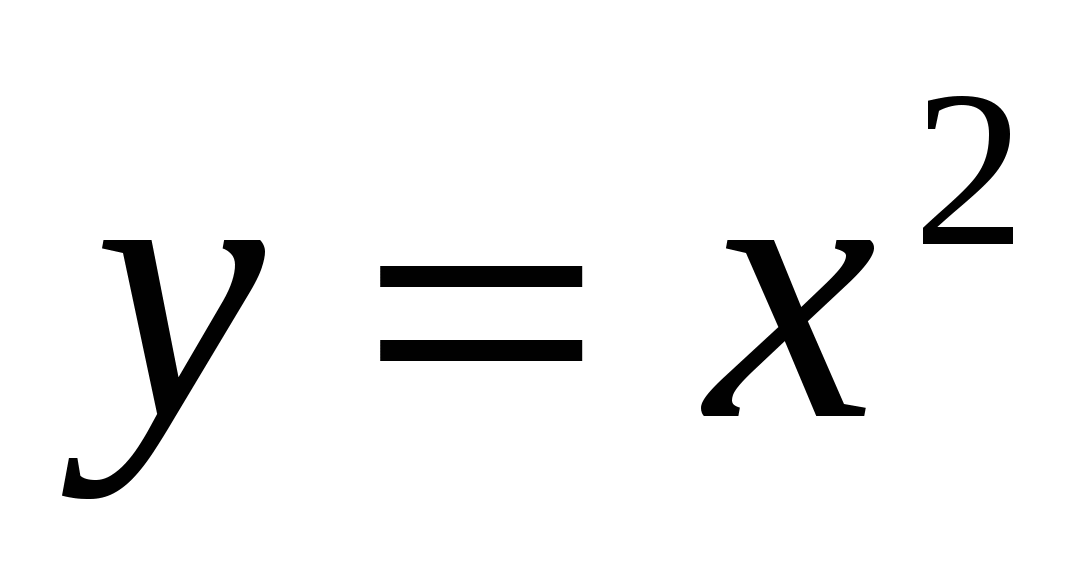 ,
, 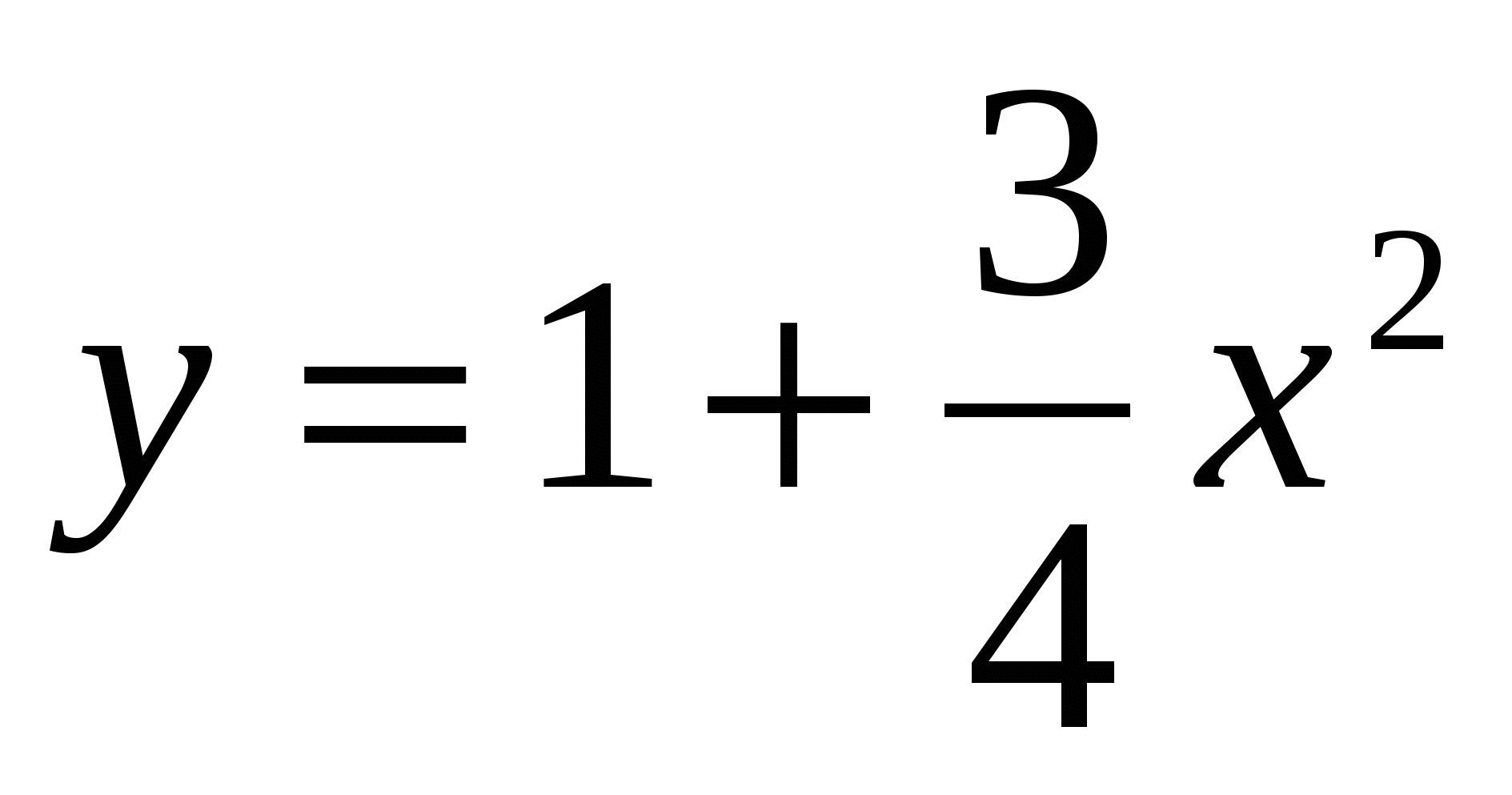
1.2. Вычисление объемов тел вращения
Пусть на отрезке  задана непрерывная функция
задана непрерывная функция 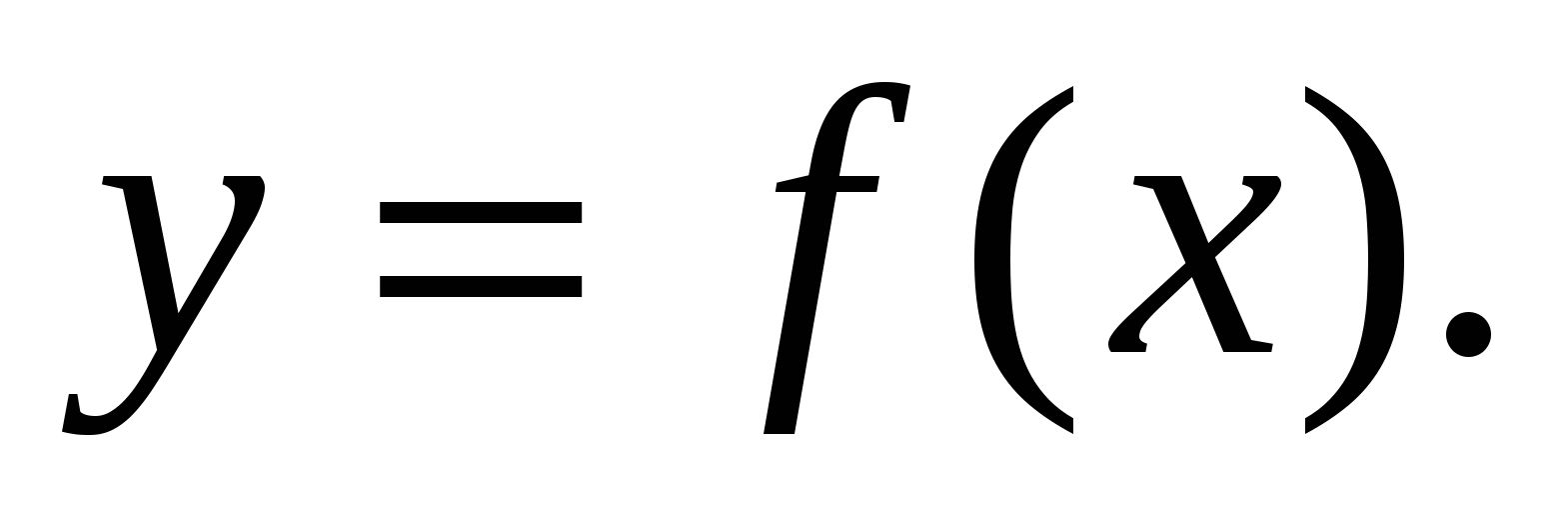 Необходимо найти объём
Необходимо найти объём 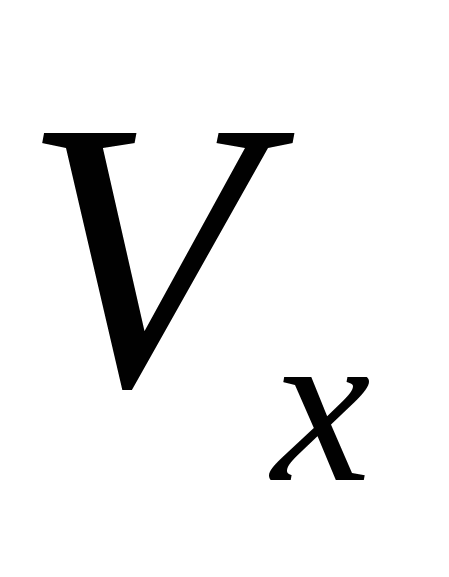 тела, образованного при вращении вокруг оси абсцисс криволинейной трапеции, ограниченной линиями
тела, образованного при вращении вокруг оси абсцисс криволинейной трапеции, ограниченной линиями 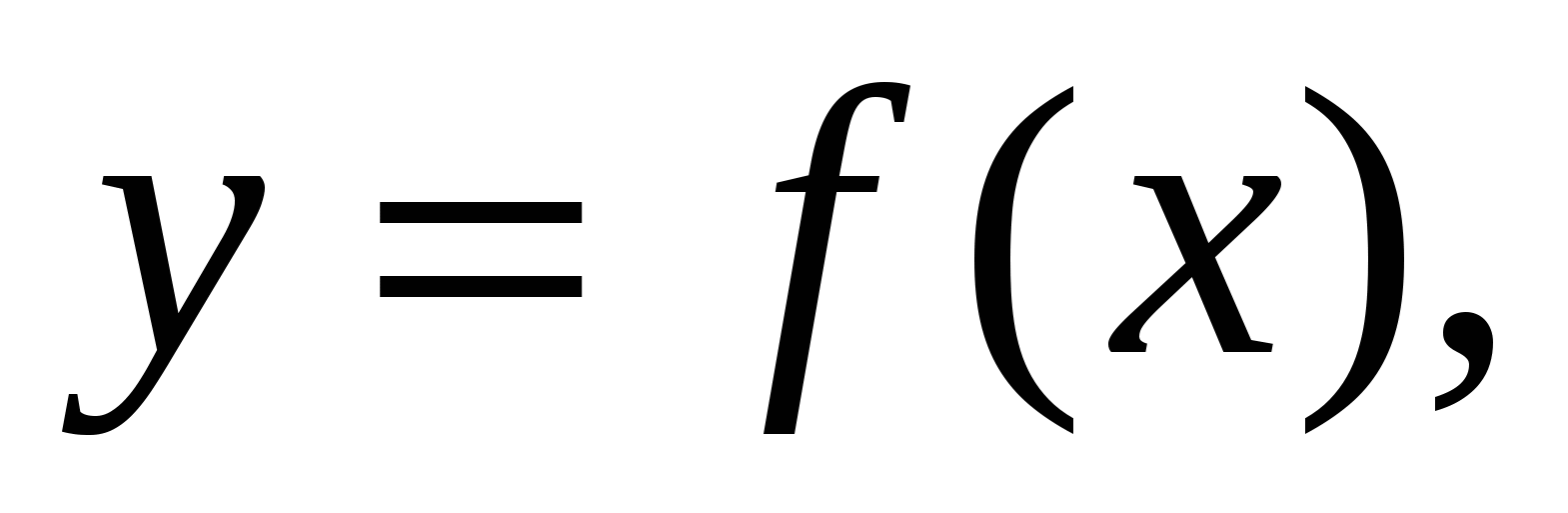
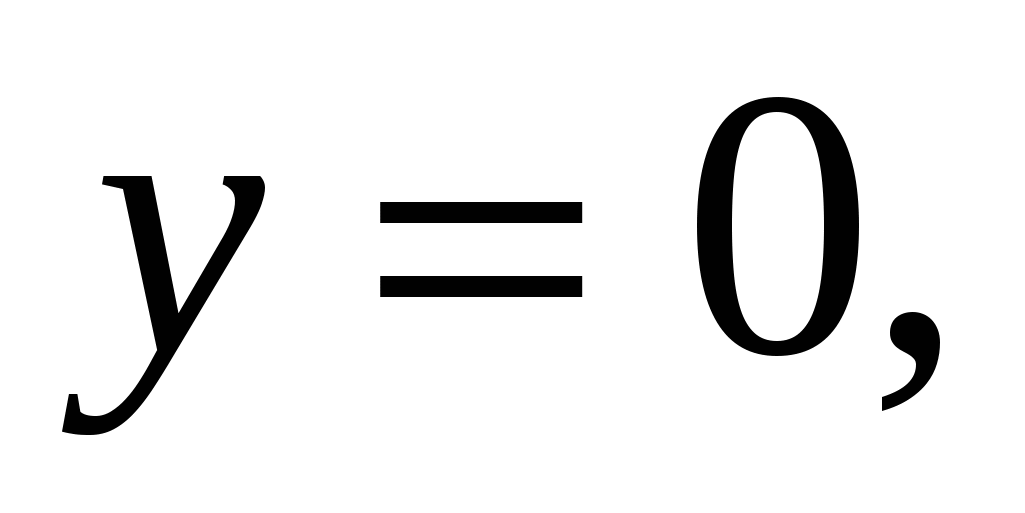
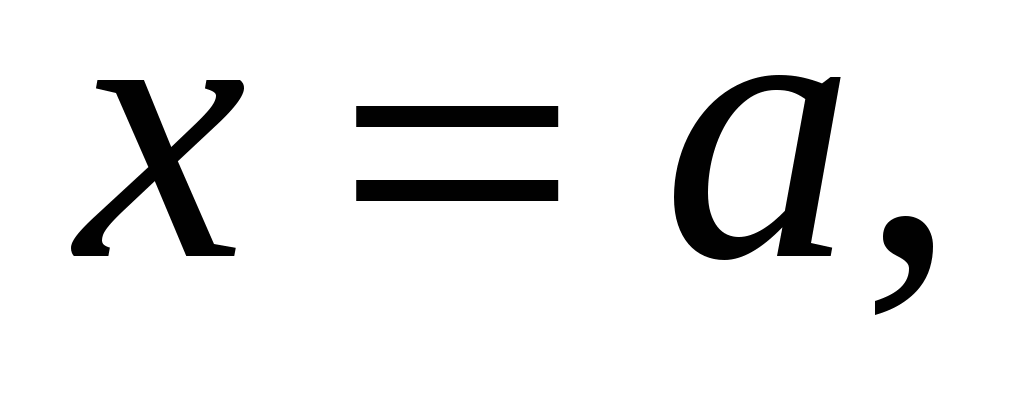
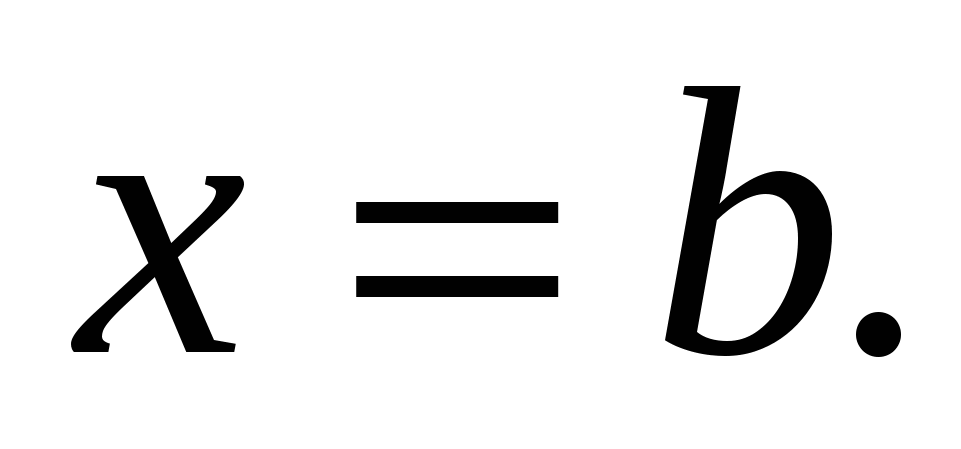
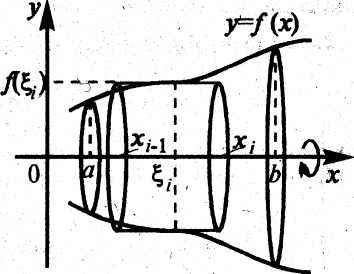
Рис. 1.9.
Для решения задачи разобьём отрезок  на элементарные отрезки точками:
на элементарные отрезки точками: 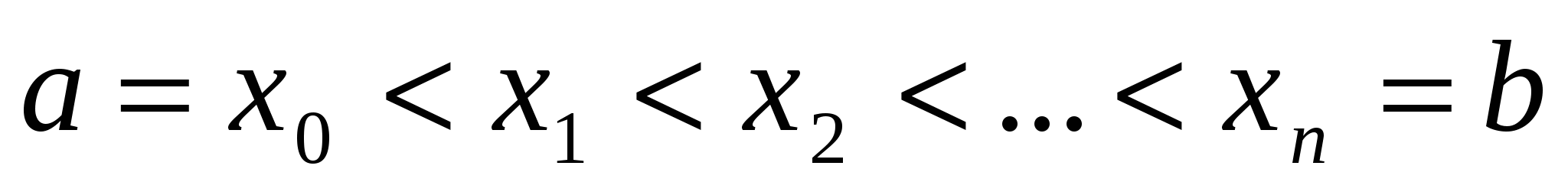 и на каждом из отрезков разбиения
и на каждом из отрезков разбиения 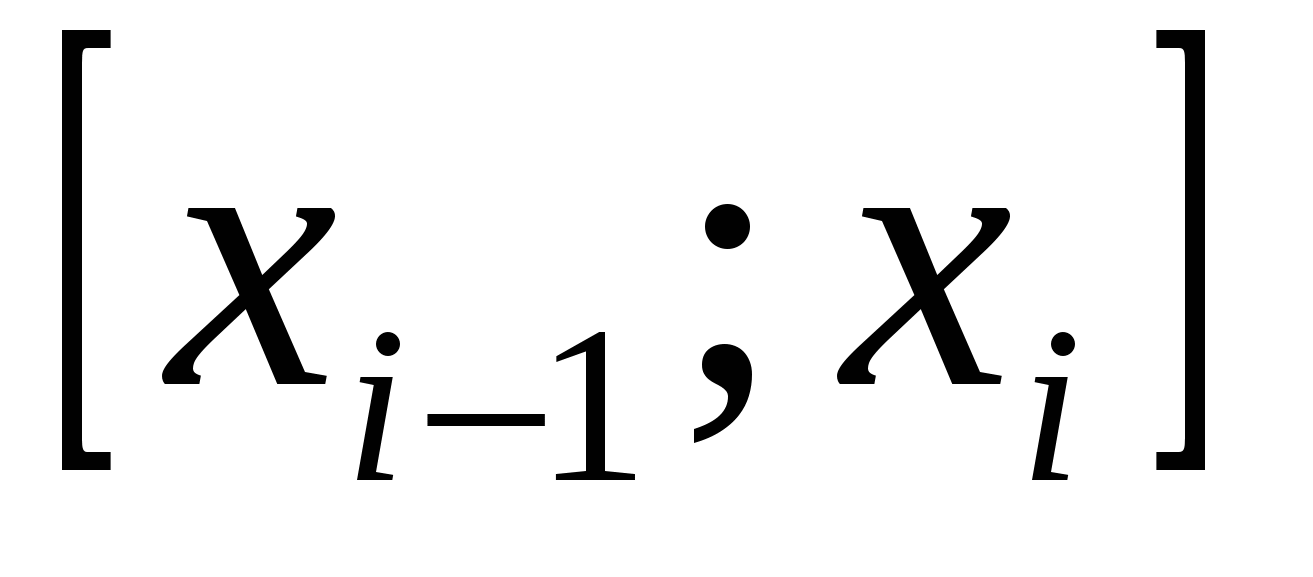 некоторым образом выберем точку
некоторым образом выберем точку 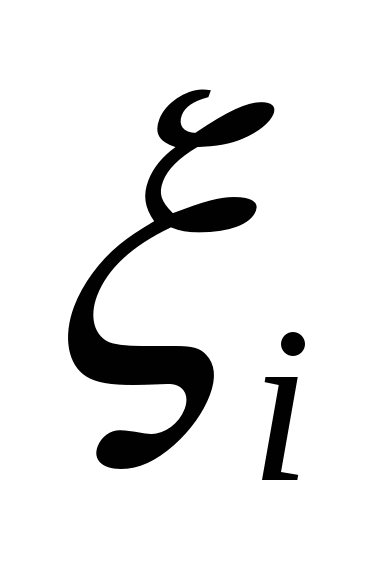 , где
, где 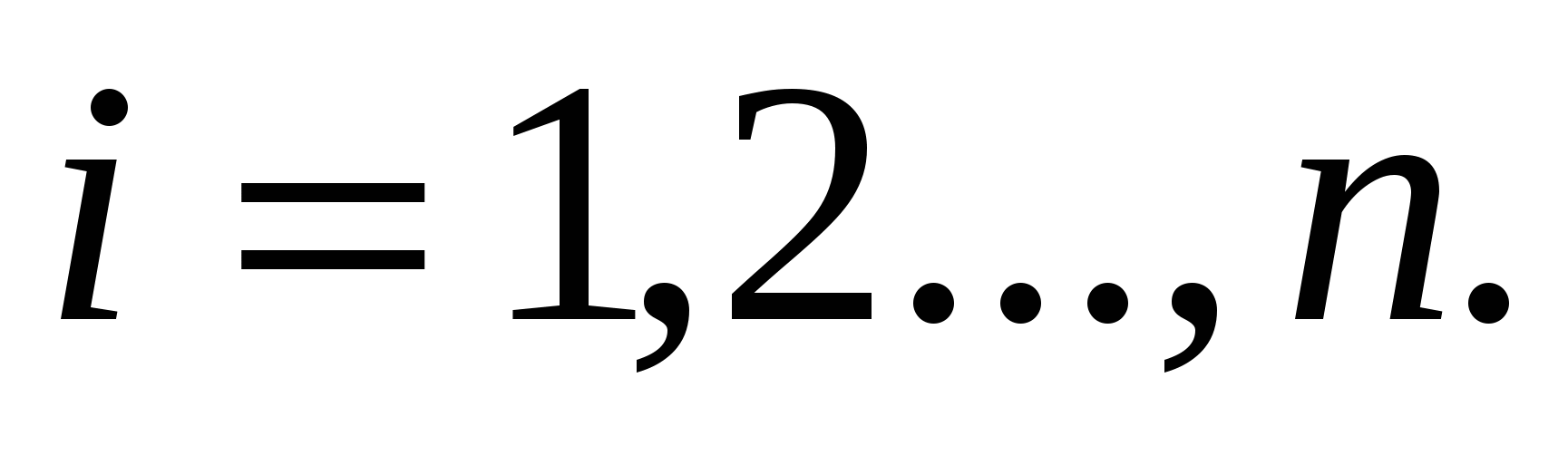 Тогда некоторое приближение для искомого объема даст следующая сумма
Тогда некоторое приближение для искомого объема даст следующая сумма 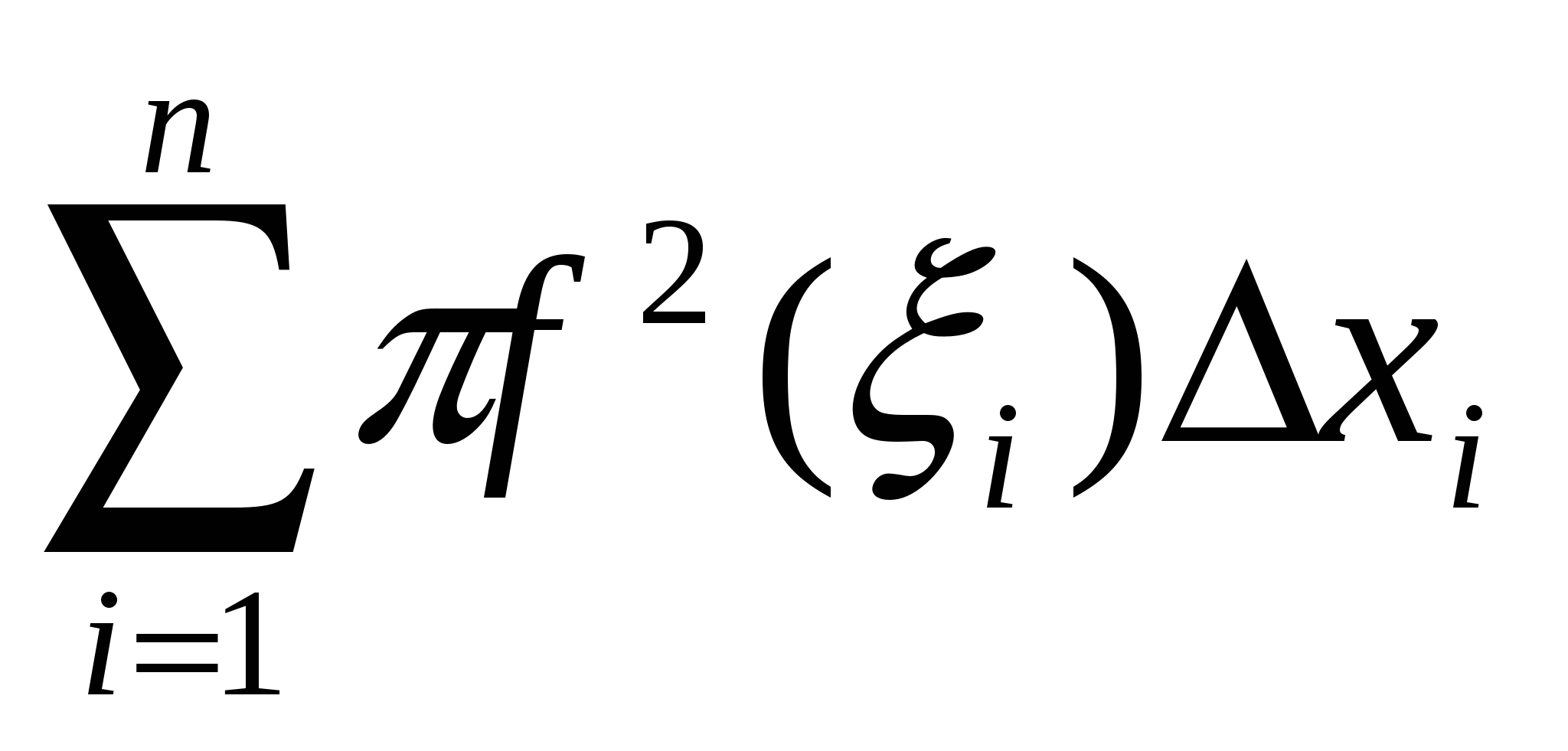
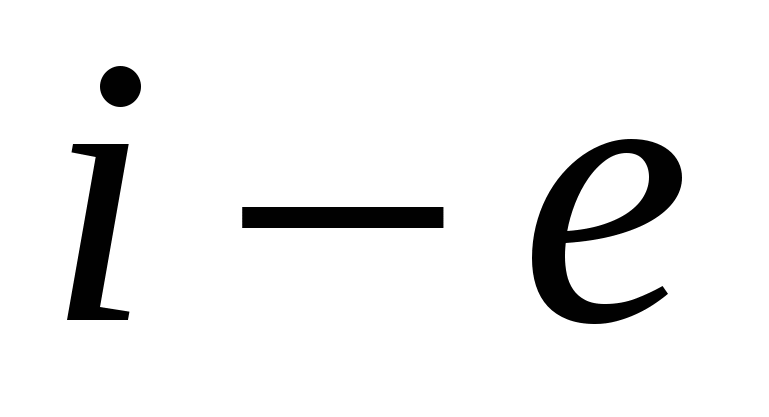 слагаемое которой
слагаемое которой ![]() - это объём цилиндра с высотой
- это объём цилиндра с высотой 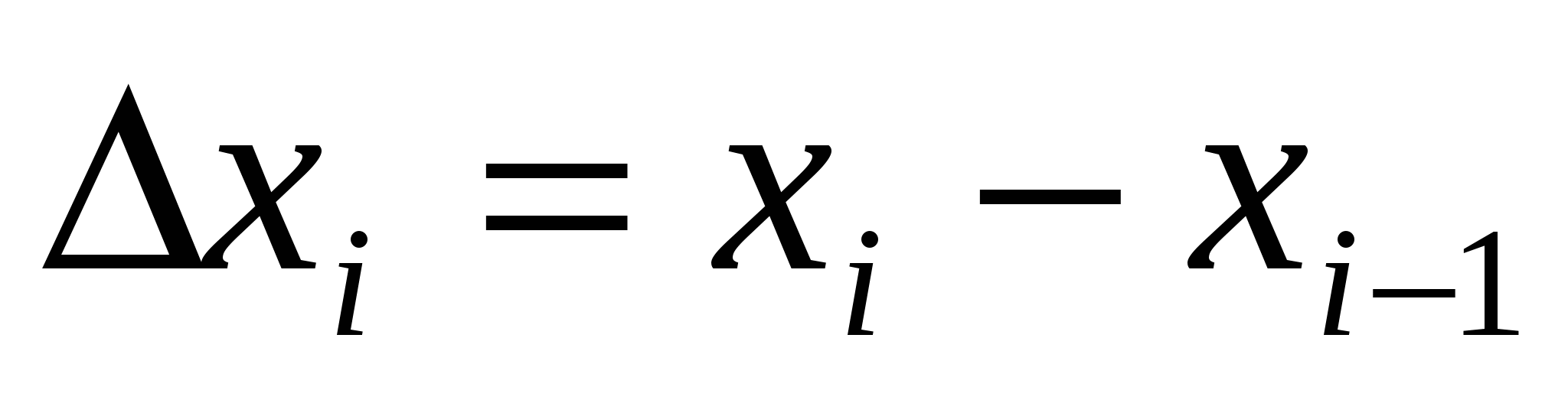 и радиусом основания
и радиусом основания 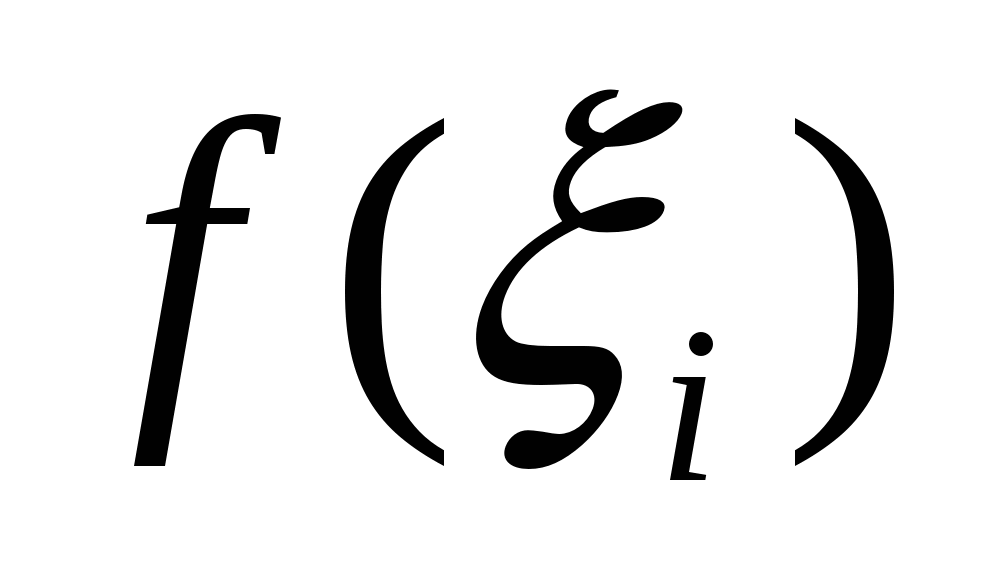 (см. рис. 1.9). Очевидно, что приближение для искомого объёма
(см. рис. 1.9). Очевидно, что приближение для искомого объёма 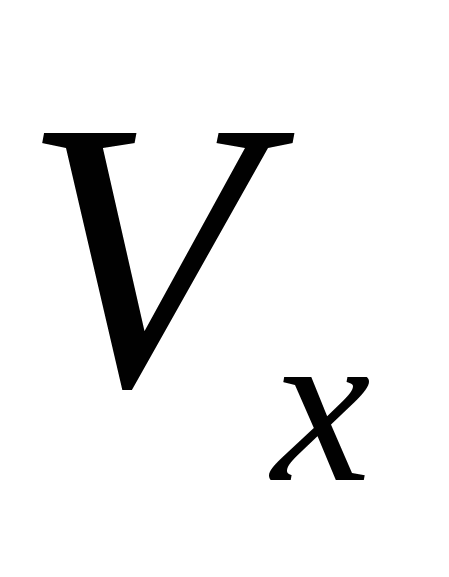 будет тем лучше, чем меньше длина отрезков разбиения
будет тем лучше, чем меньше длина отрезков разбиения 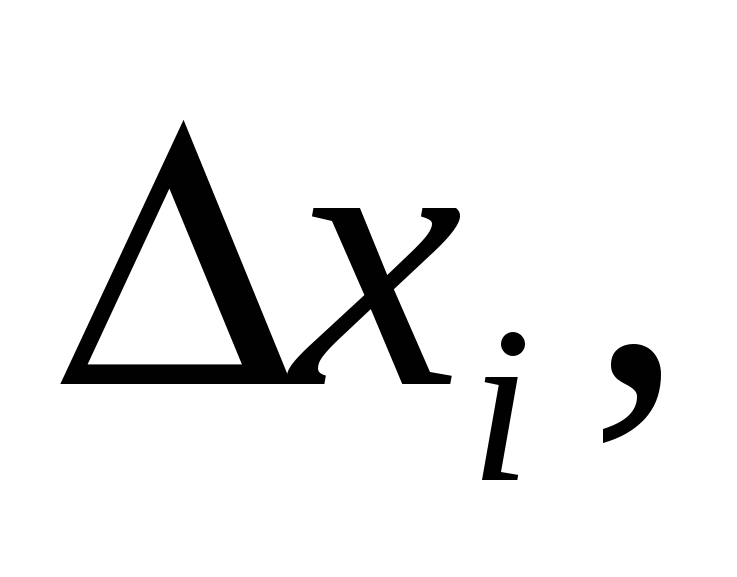 поэтому за искомый объём
поэтому за искомый объём ![]() естественно взять следующий предел
естественно взять следующий предел  ,
,
где 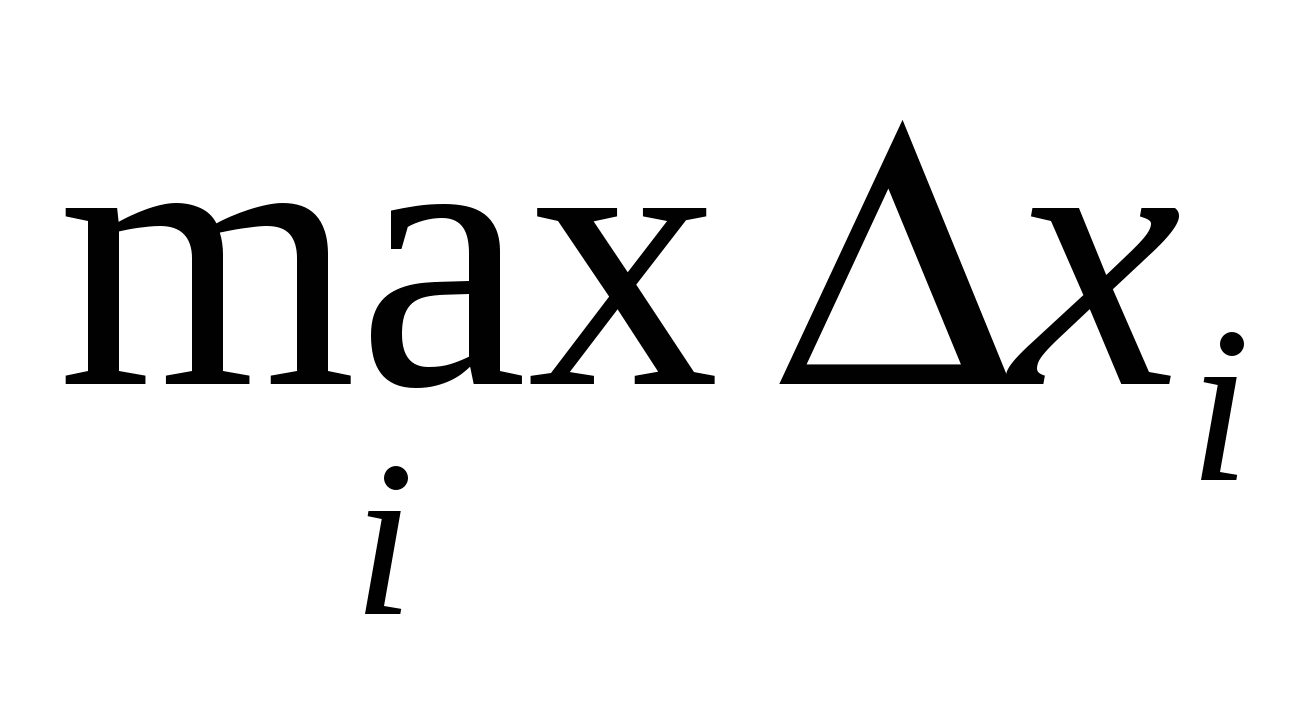 - максимальная из длин отрезков разбиения. Но выражение, стоящее в правой части последнего равенства, не что иное, как предел интегральной суммы для функции
- максимальная из длин отрезков разбиения. Но выражение, стоящее в правой части последнего равенства, не что иное, как предел интегральной суммы для функции 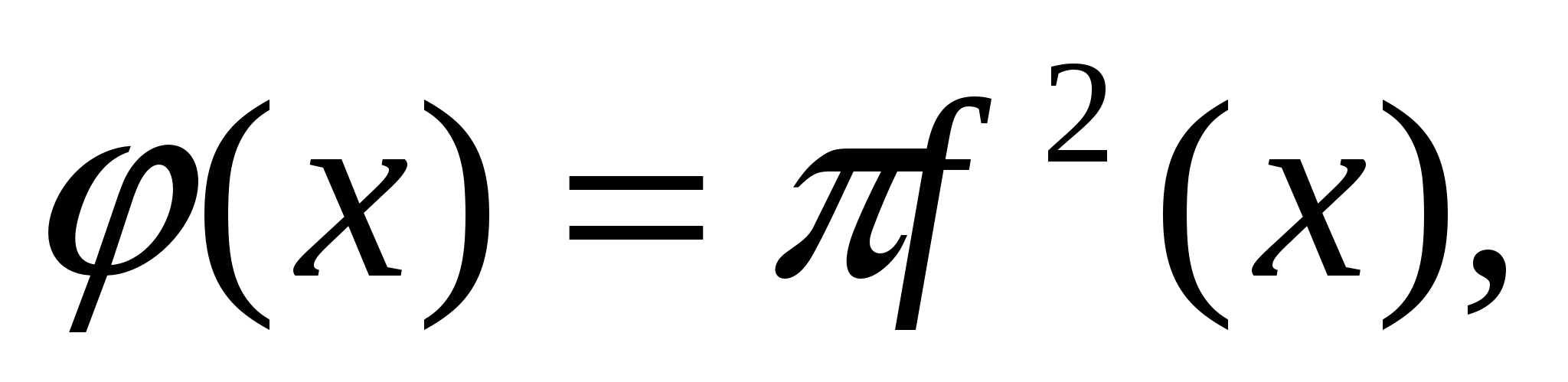 поэтому окончательно получаем
поэтому окончательно получаем
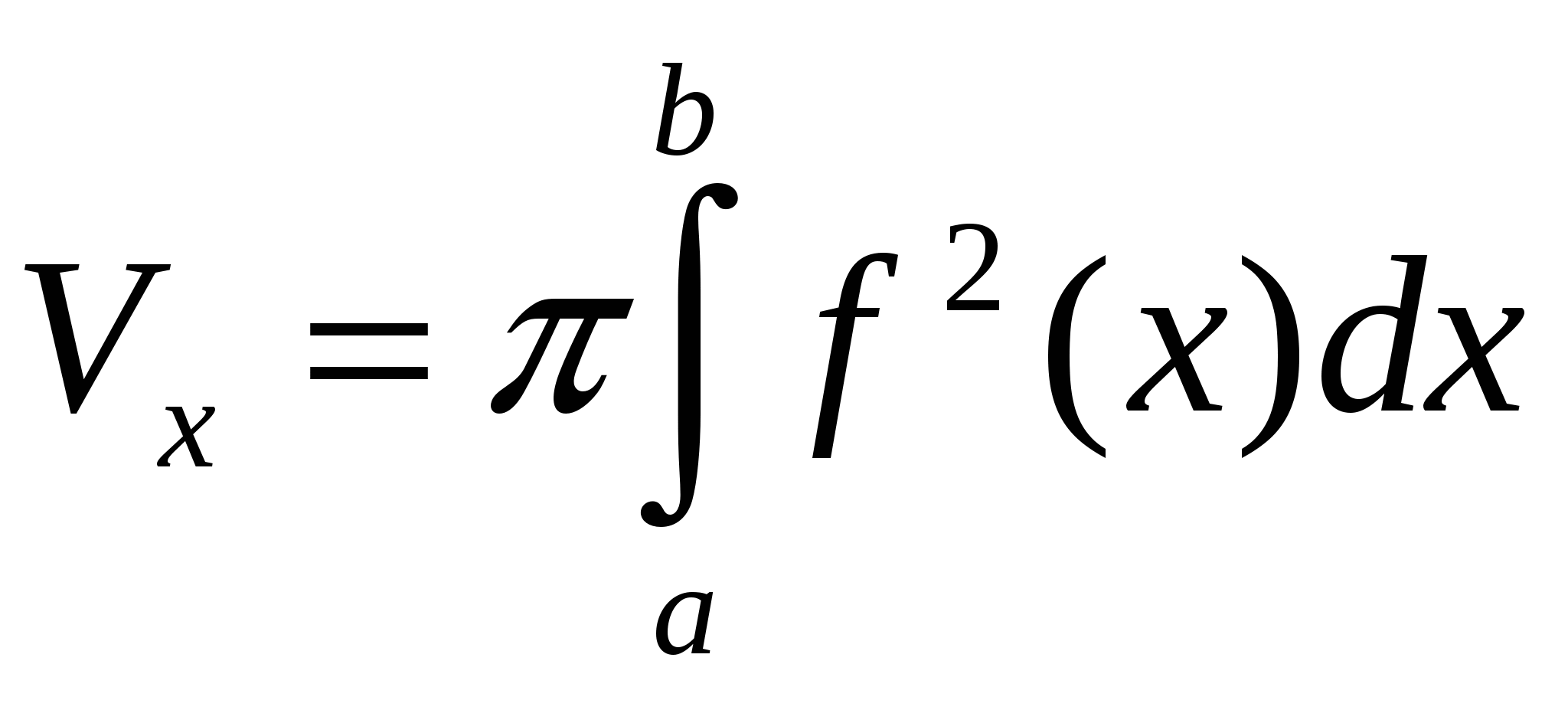 . (1.4)
. (1.4)
Пример 1.4. Вычислить объём тела, полученного от вращения фигуры, ограниченной линиями 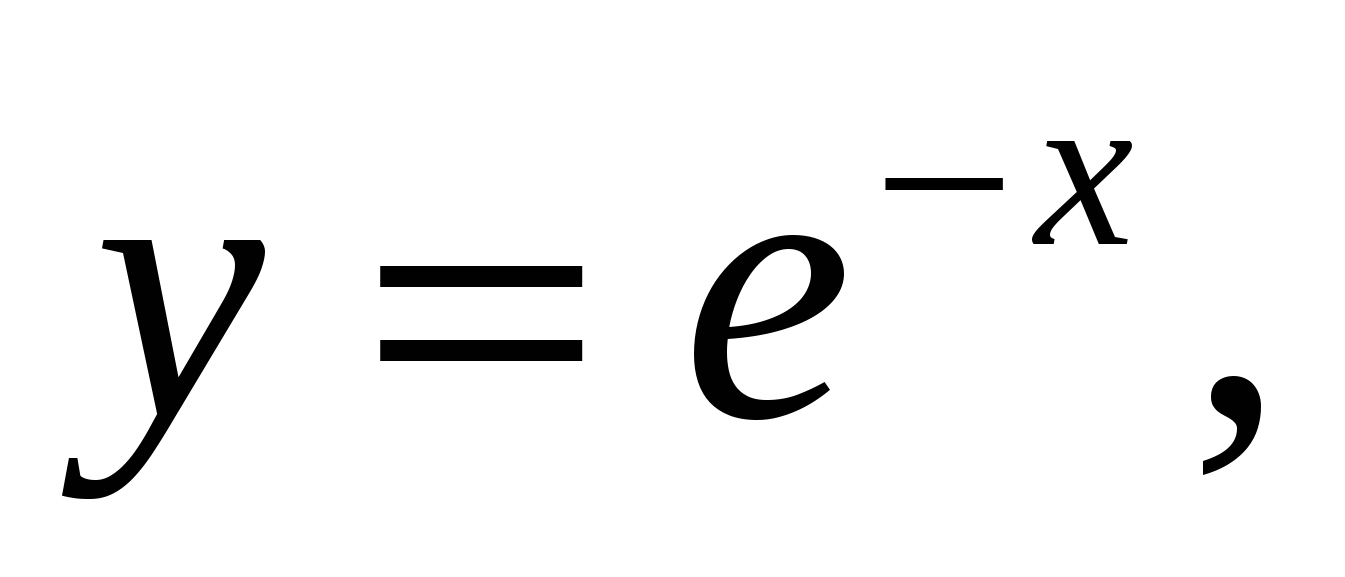
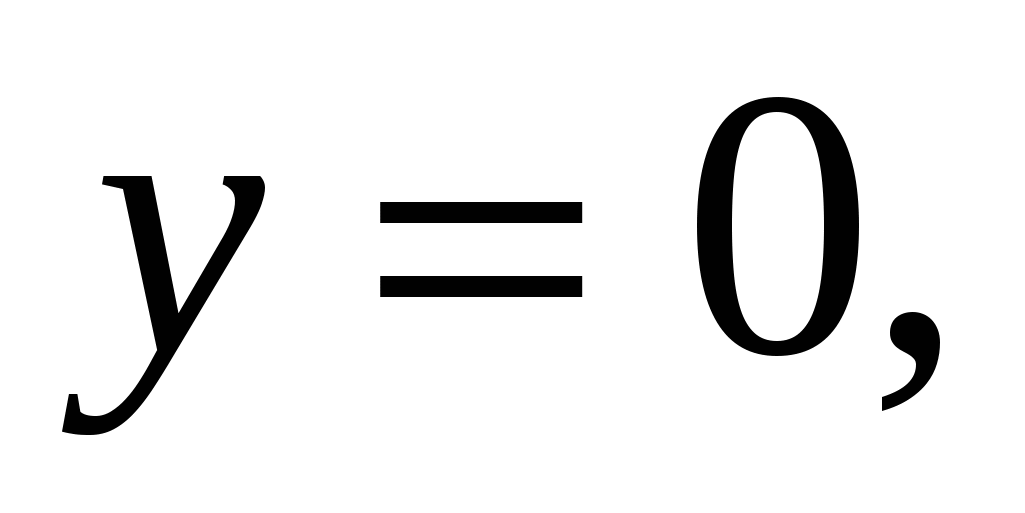

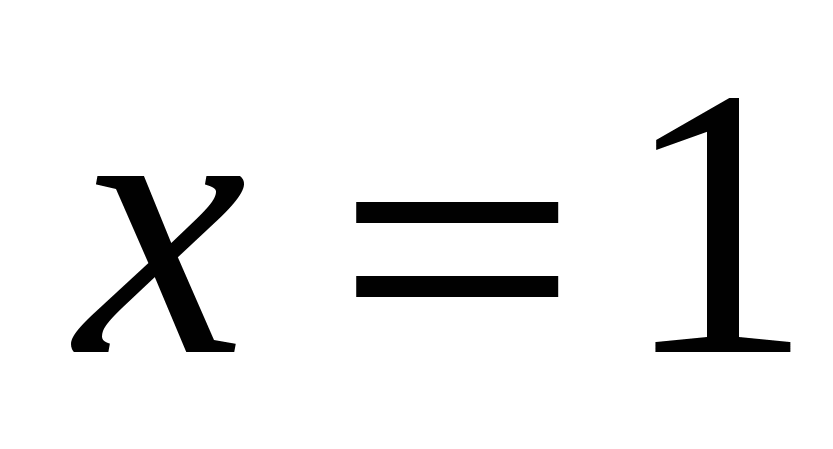 вокруг оси
вокруг оси 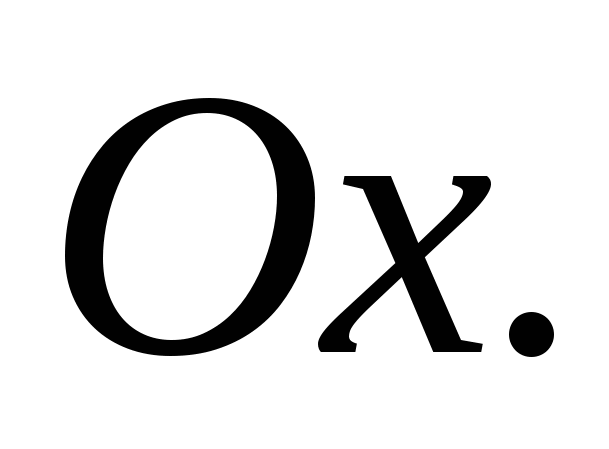
Решение:
По формуле (1.4) искомый объём 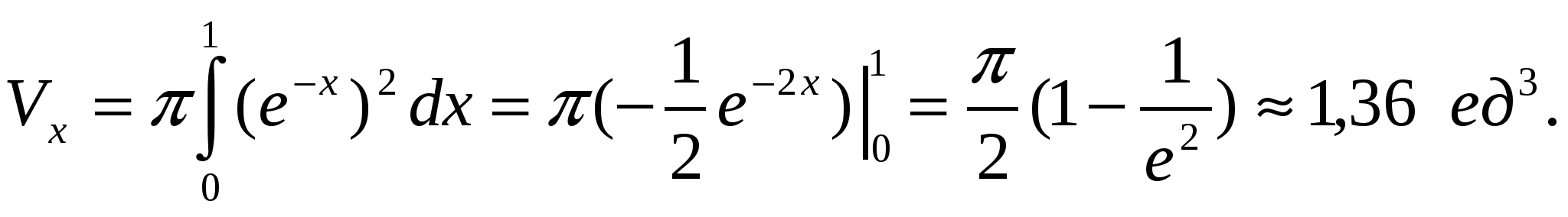
Пример 1.5. Найти объём тела, образованного вращением эллипса ![]() вокруг оси
вокруг оси 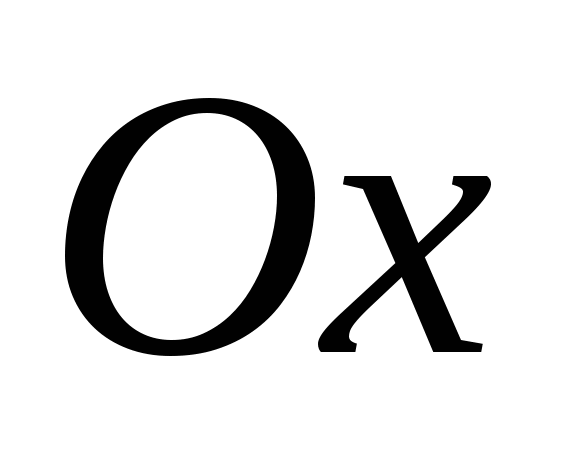 .
.
Решение:
Так эллипс симметричен относительно осей координат, то достаточно найти
половину искомого объёма. По формуле (1.4) имеем:
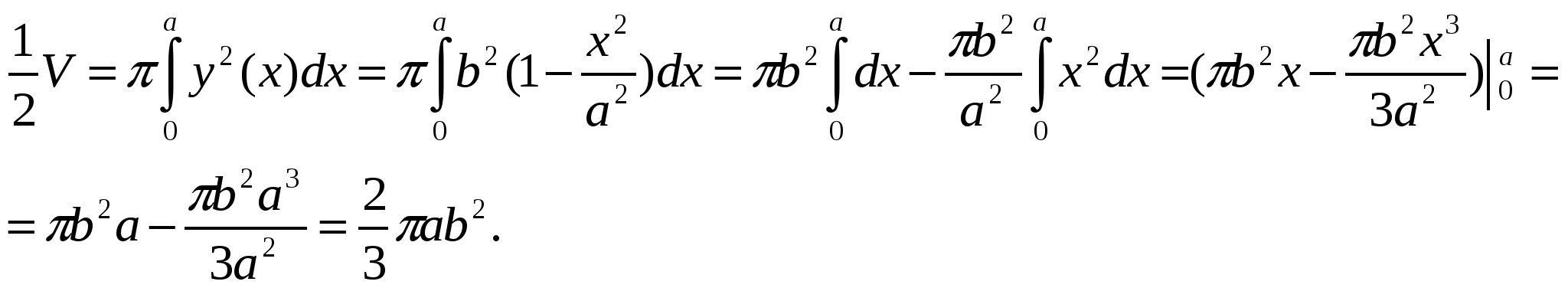
Следовательно, 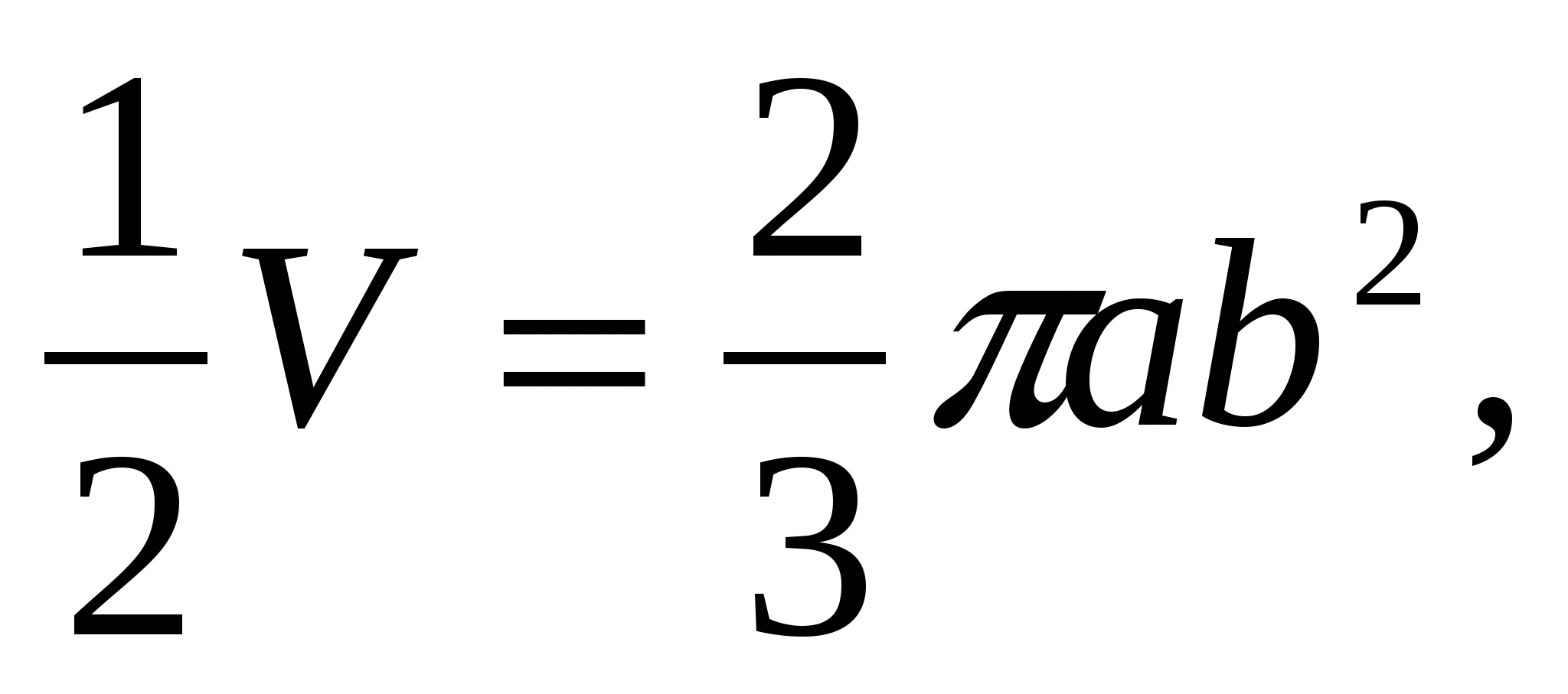 откуда
откуда 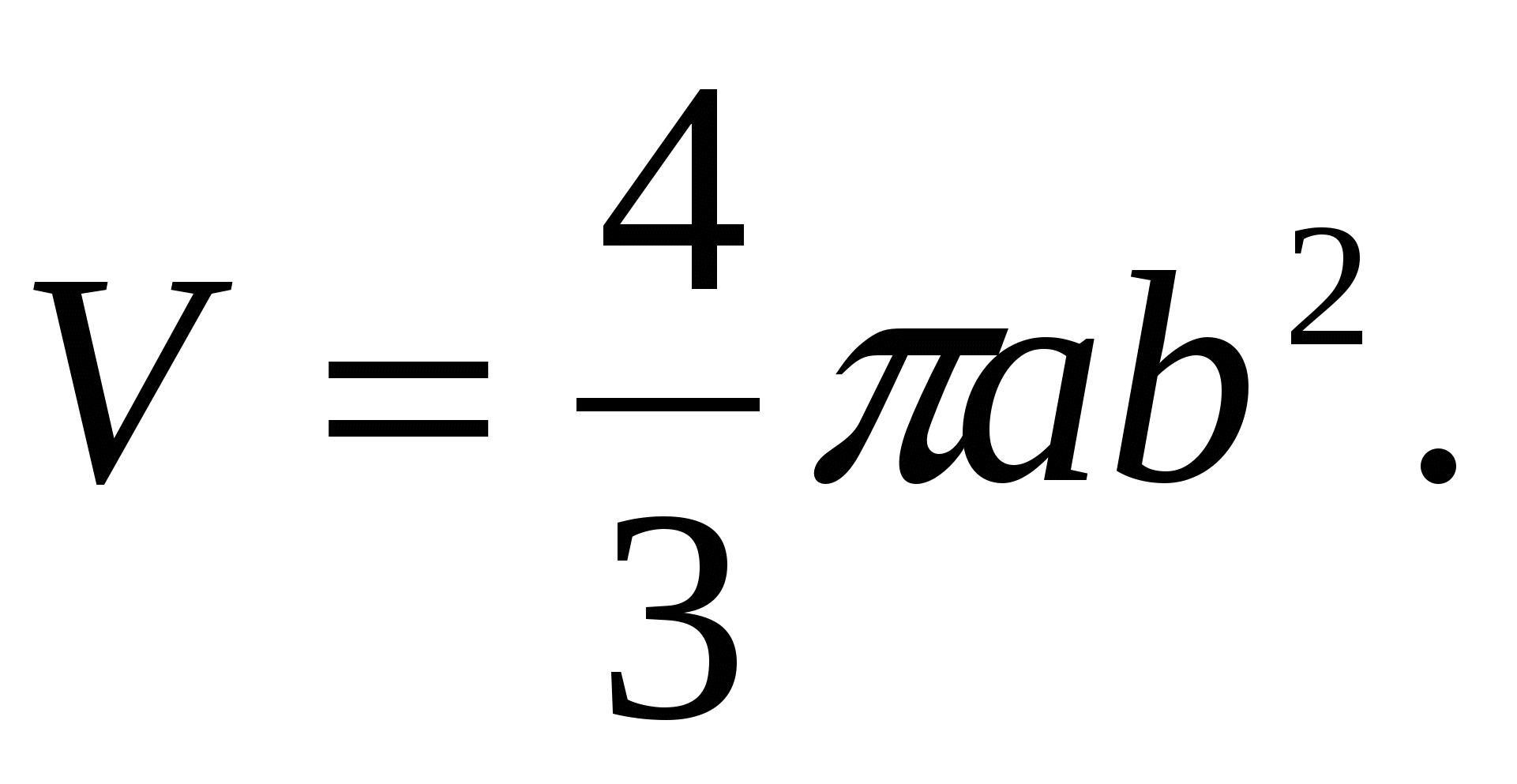
Если 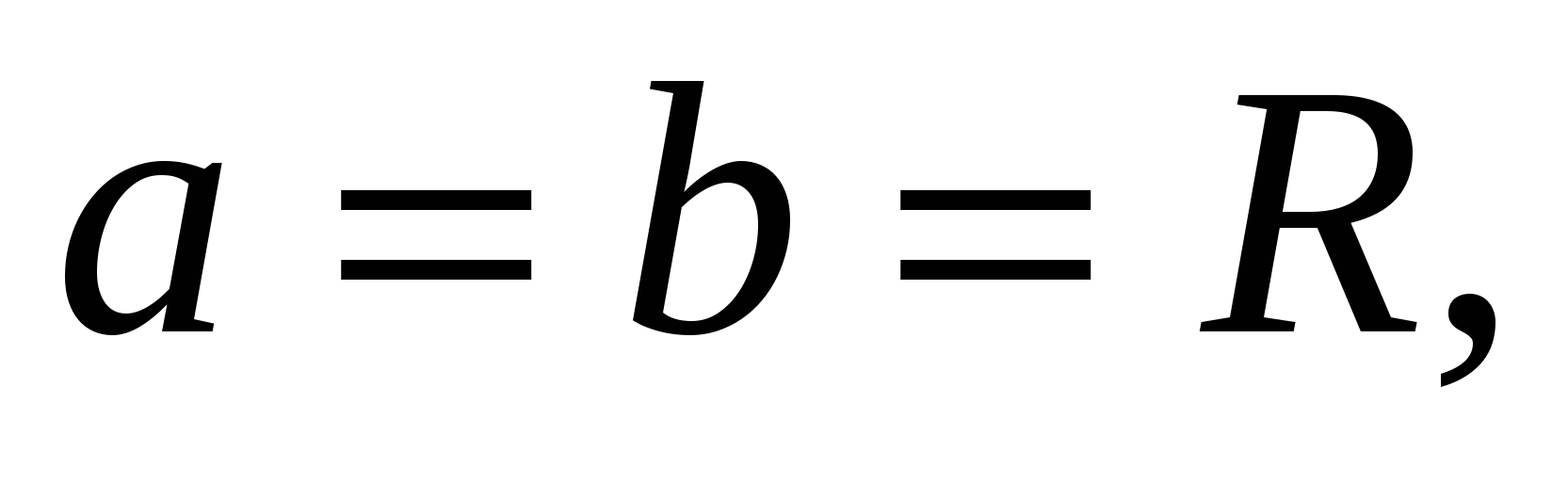 то эллипс является окружностью. Тогда объём тела вращения окружности вокруг оси
то эллипс является окружностью. Тогда объём тела вращения окружности вокруг оси 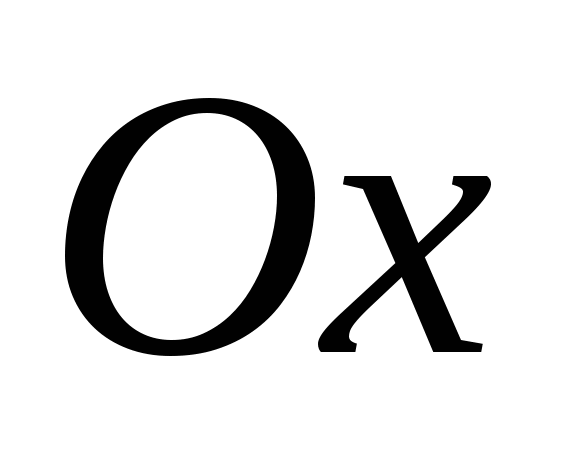 есть шар, объём которого
есть шар, объём которого
![]()
Формально заменяя в формуле (1.4) переменную  на
на 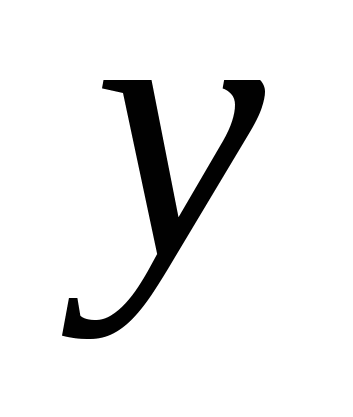 , получаем формулу для вычисления объёма
, получаем формулу для вычисления объёма 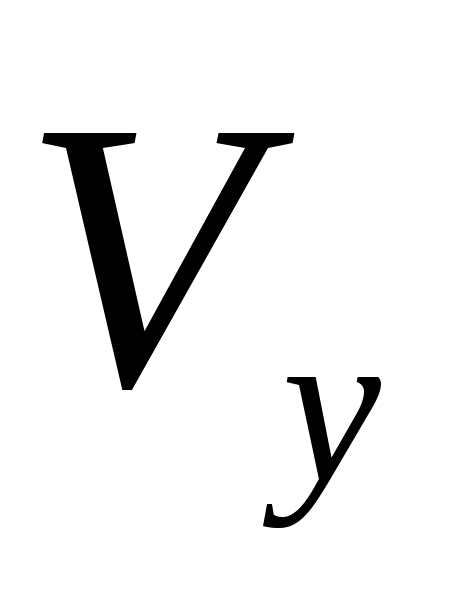 тела, полученного от вращения криволинейной трапеции вокруг оси ординат:
тела, полученного от вращения криволинейной трапеции вокруг оси ординат: 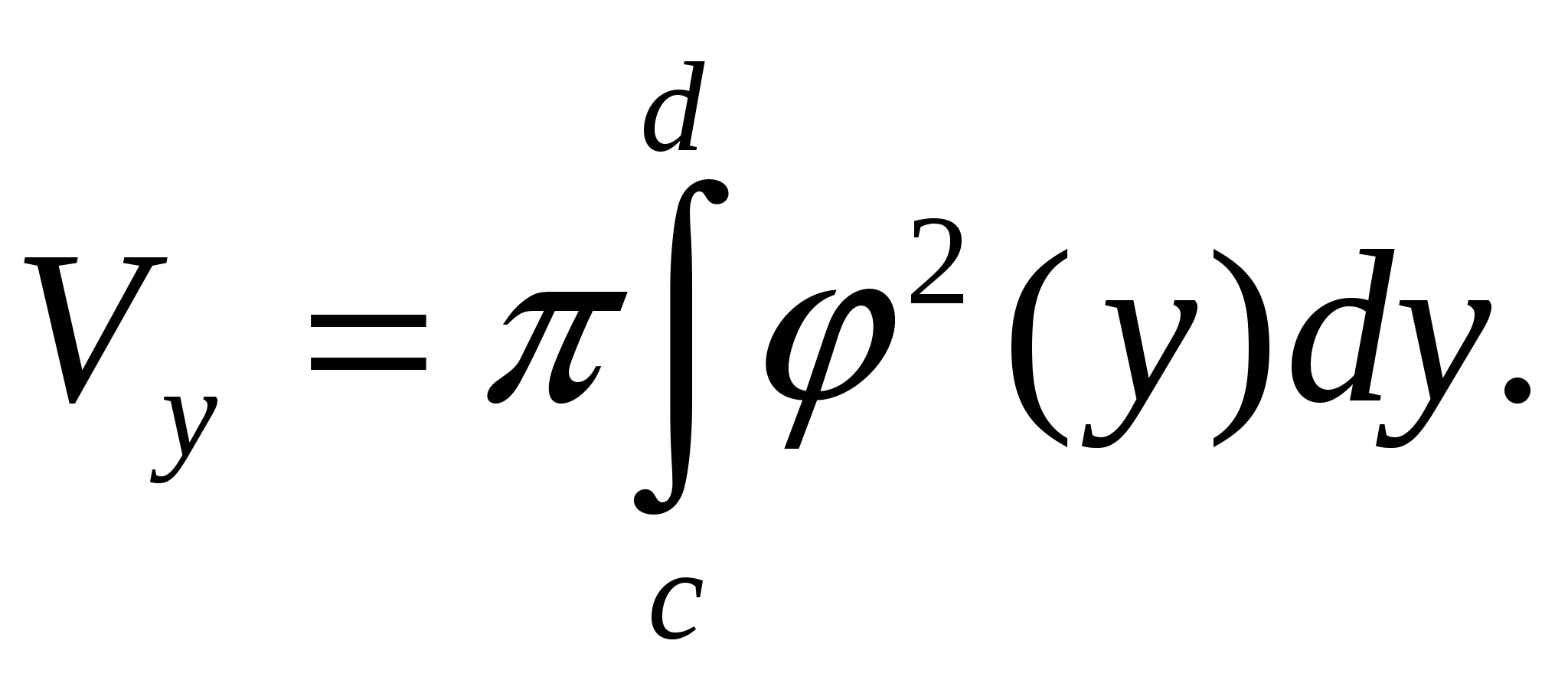 (1.5)
(1.5)
(на рис.1.10 вращаемая криволинейная трапеция заштрихована).
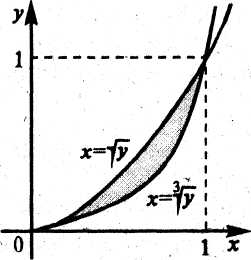
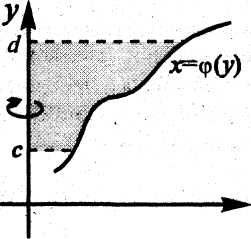
Рис 1.10. Рис. 1.11.
Пример 1.6. Найти объём тела, полученного от вращения вокруг оси ординат плоской фигуры, ограниченной линиями 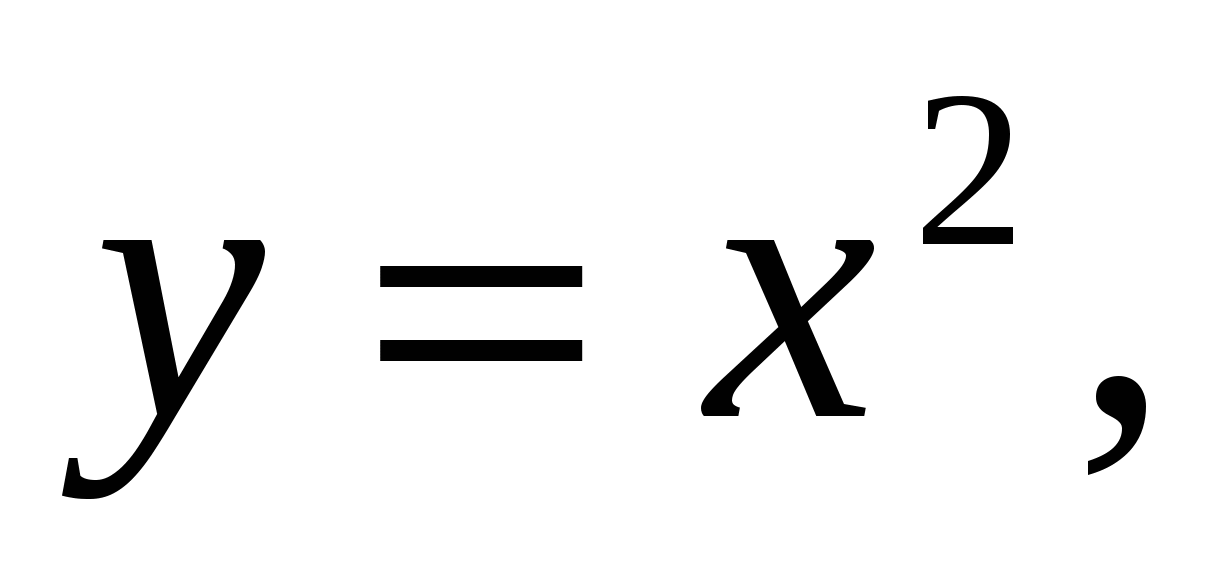
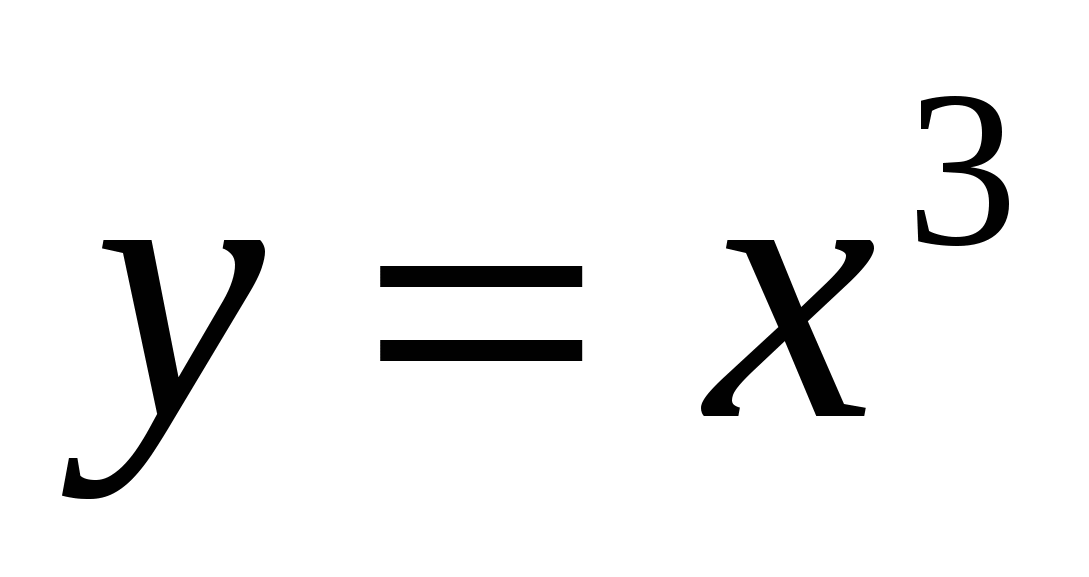 .
.
Решение:
Проецируя вращаемую фигуру на ось ординат (рис.1.11), убеждаемся, что искомый объём 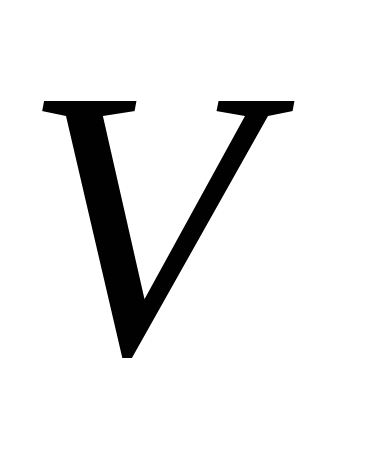 равен разности двух объёмов: объёма
равен разности двух объёмов: объёма ![]() , полученного от вращения вокруг оси ординат фигуры, ограниченной линиями
, полученного от вращения вокруг оси ординат фигуры, ограниченной линиями 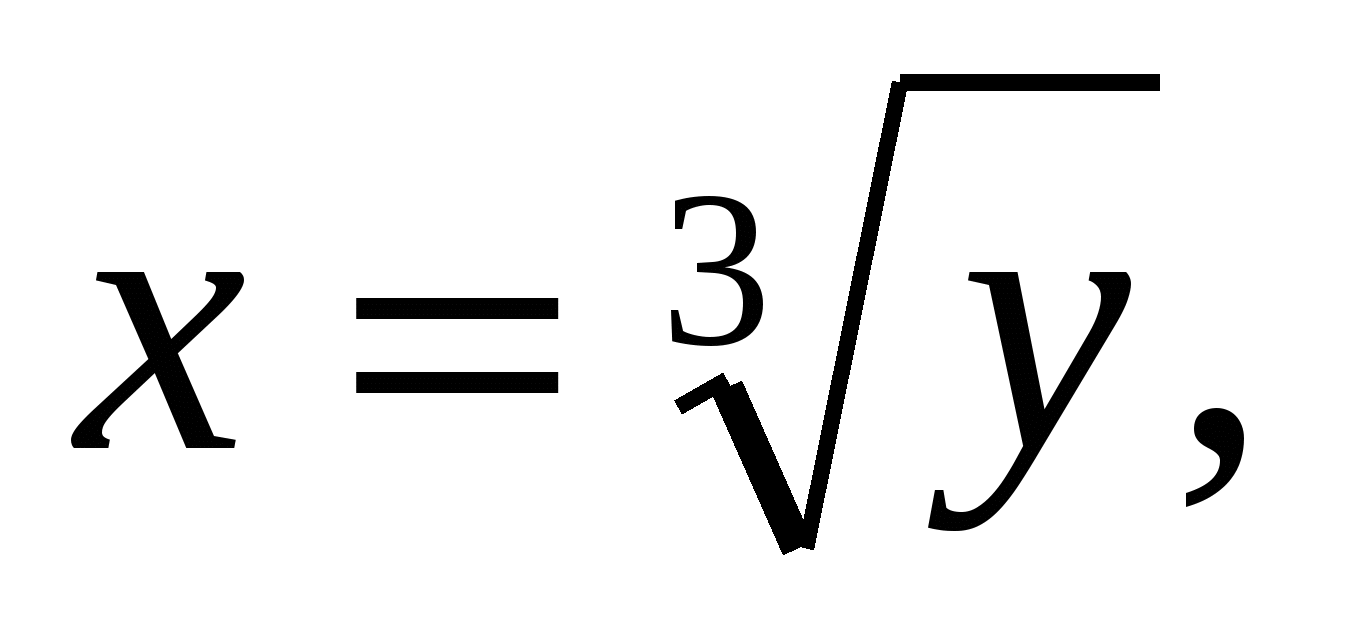

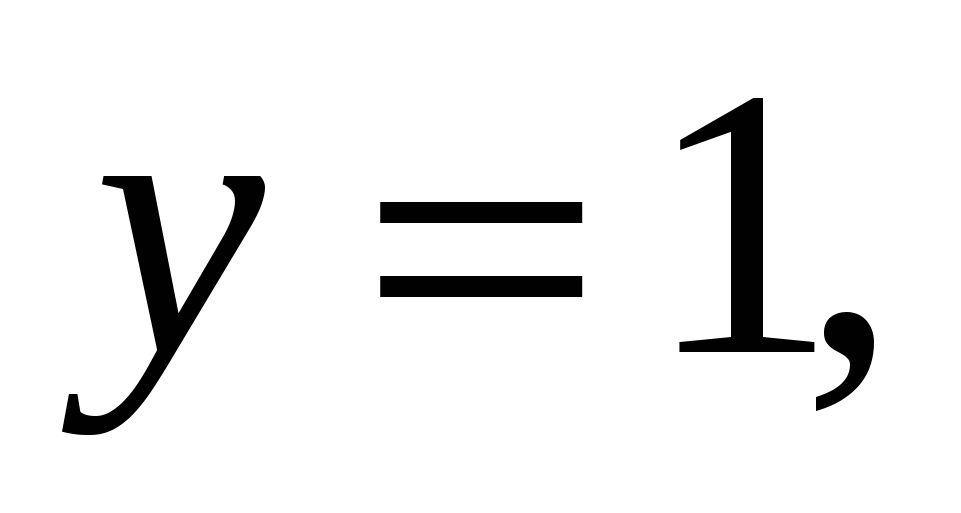 и объёма
и объёма  , для которого вращаемая фигура ограничена линиями
, для которого вращаемая фигура ограничена линиями 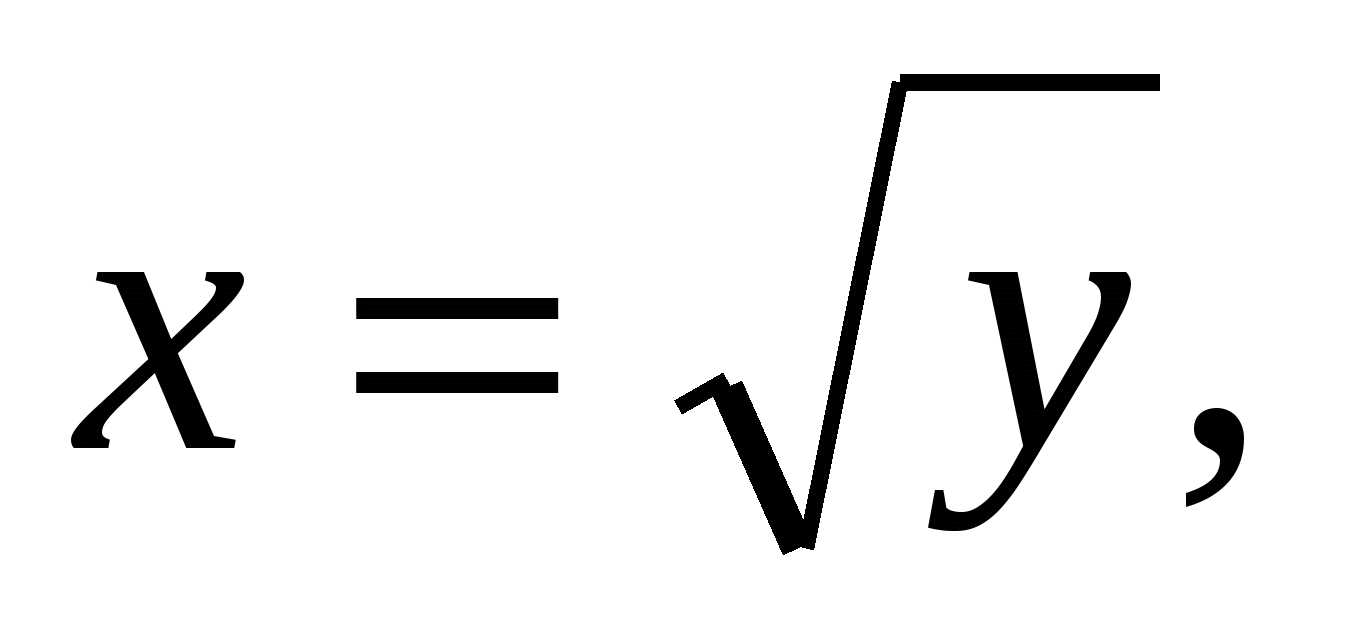

 . (С учётом предстоящего применения формулы (1.5) уравнения кривых записаны в виде
. (С учётом предстоящего применения формулы (1.5) уравнения кривых записаны в виде ![]() предполагающем переменную
предполагающем переменную 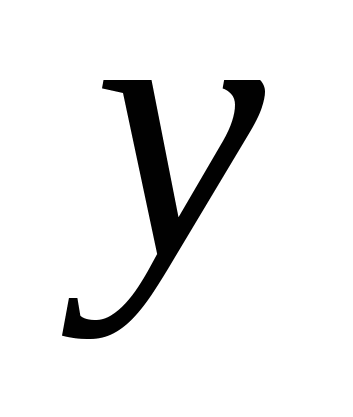 независимой). Применяя (1.5), получаем:
независимой). Применяя (1.5), получаем:
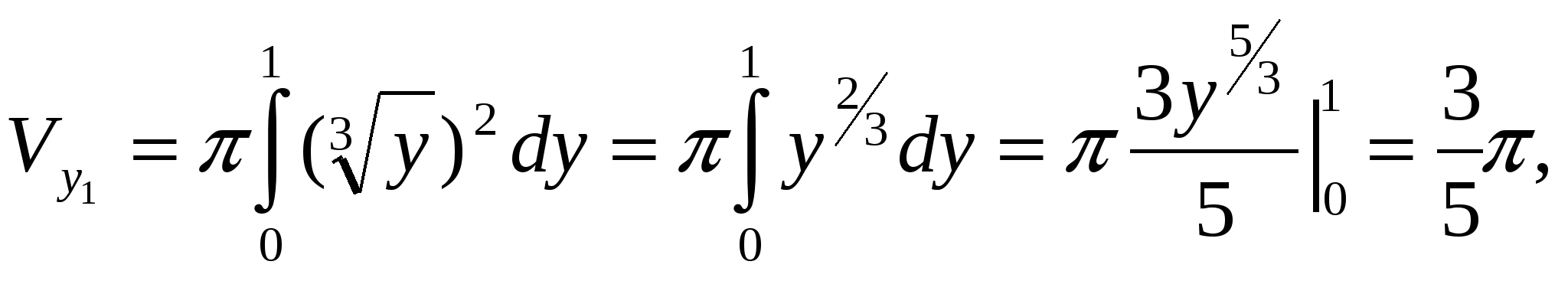
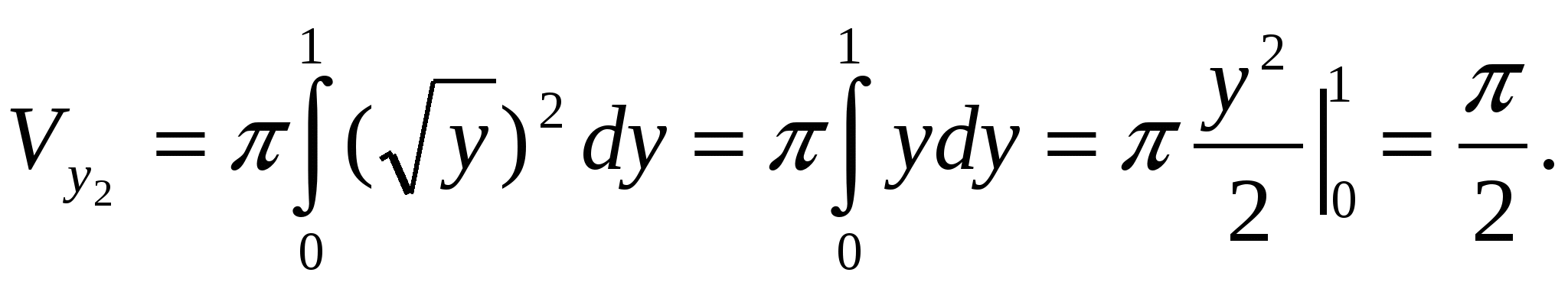
Окончательно 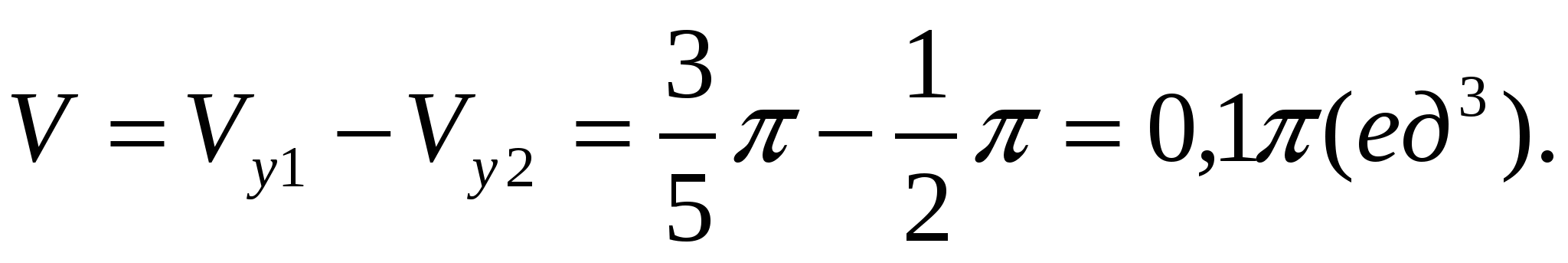
Упражнения для самостоятельной работы
Найти объём тела, образованного вращением фигуры, ограниченной линиями:
1.18. 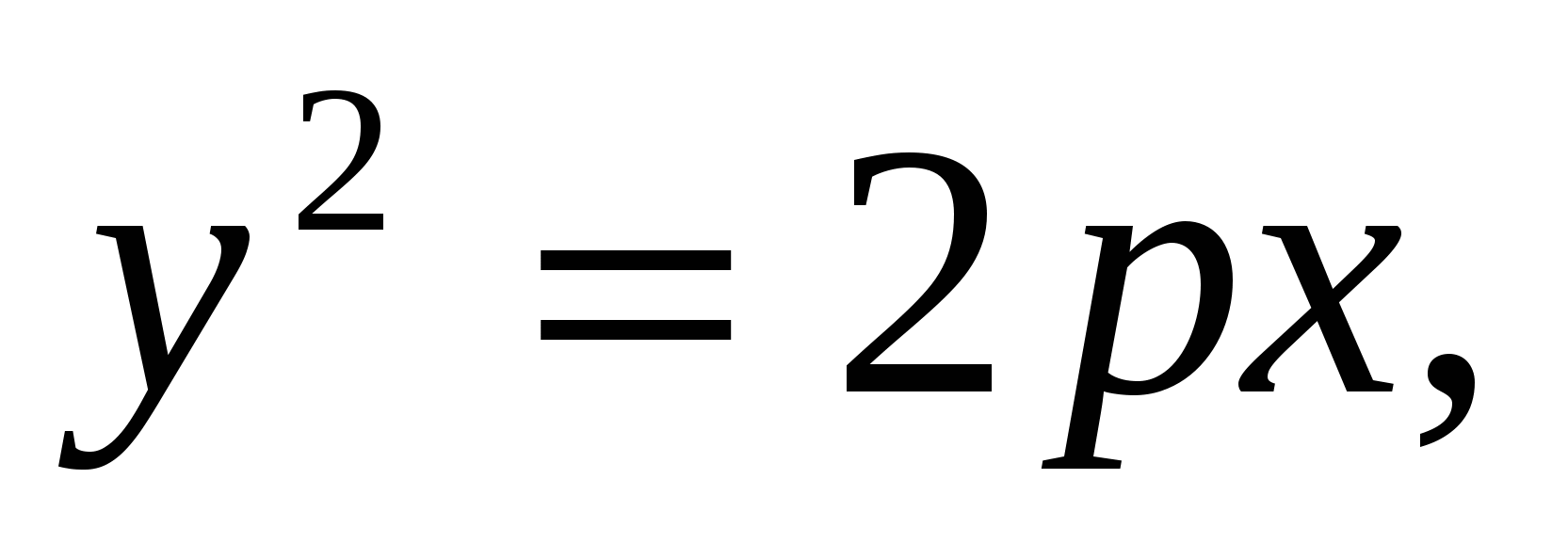
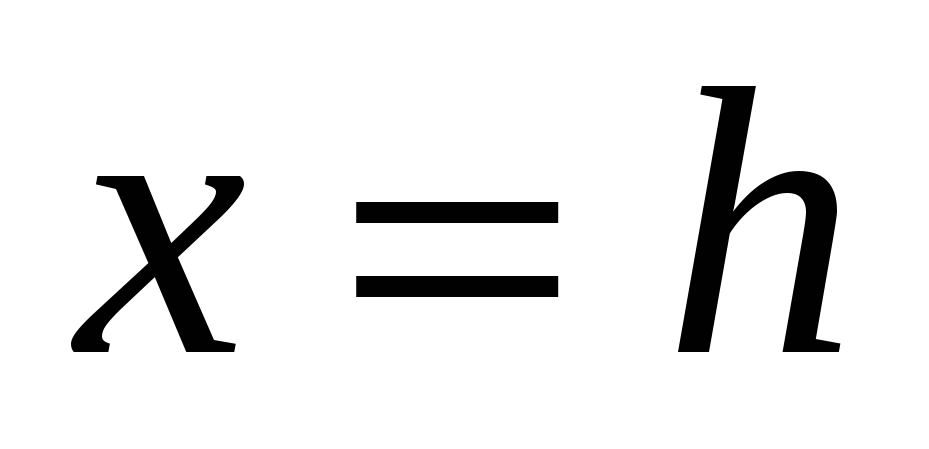 вокруг оси
вокруг оси 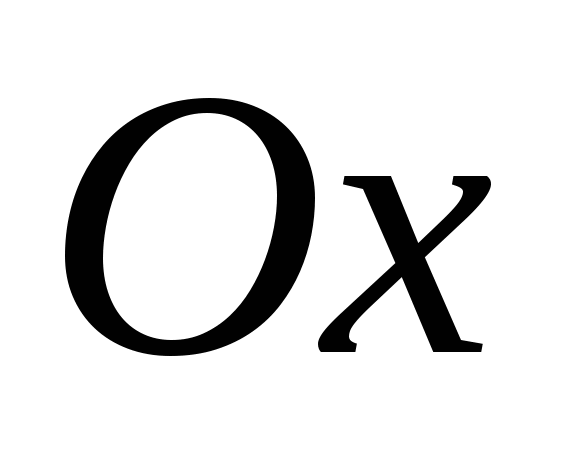
1.19. 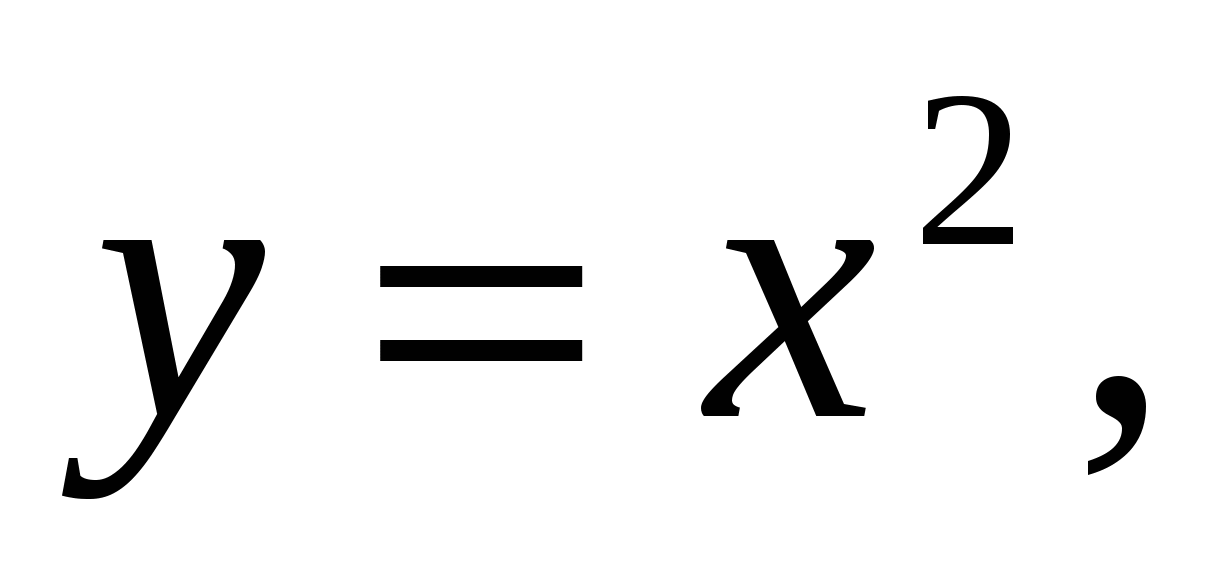
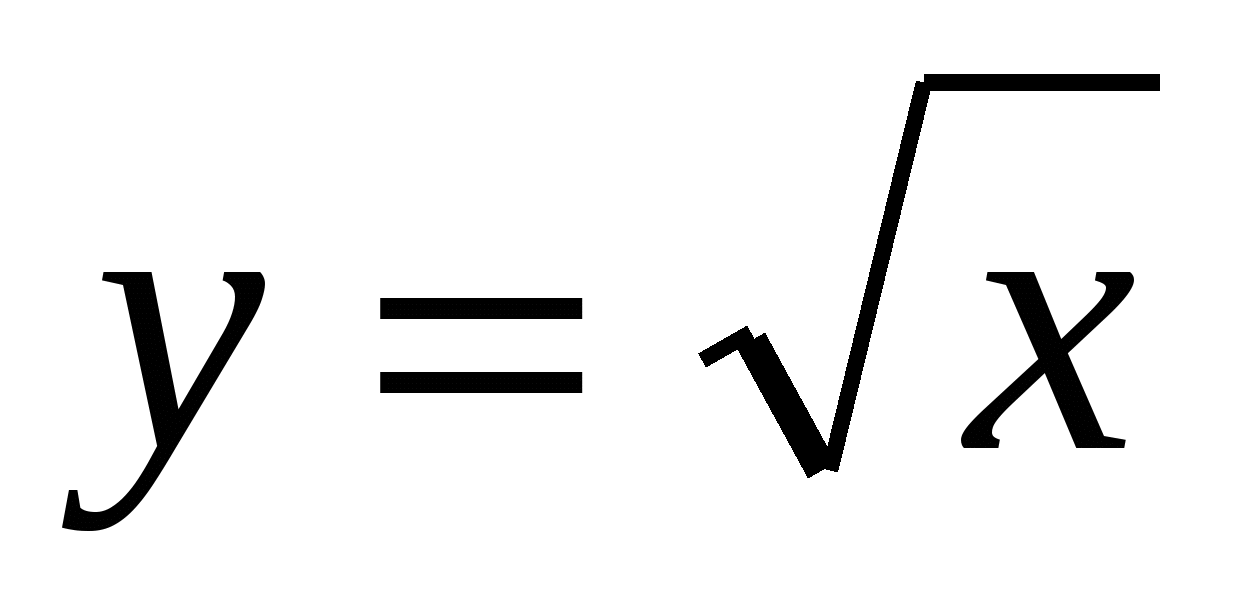 вокруг оси
вокруг оси 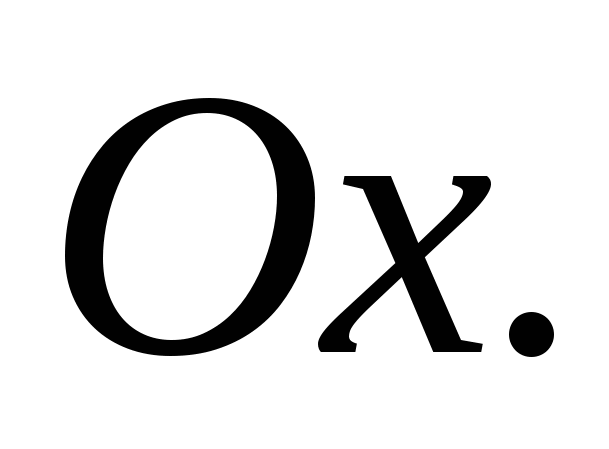
1.20. 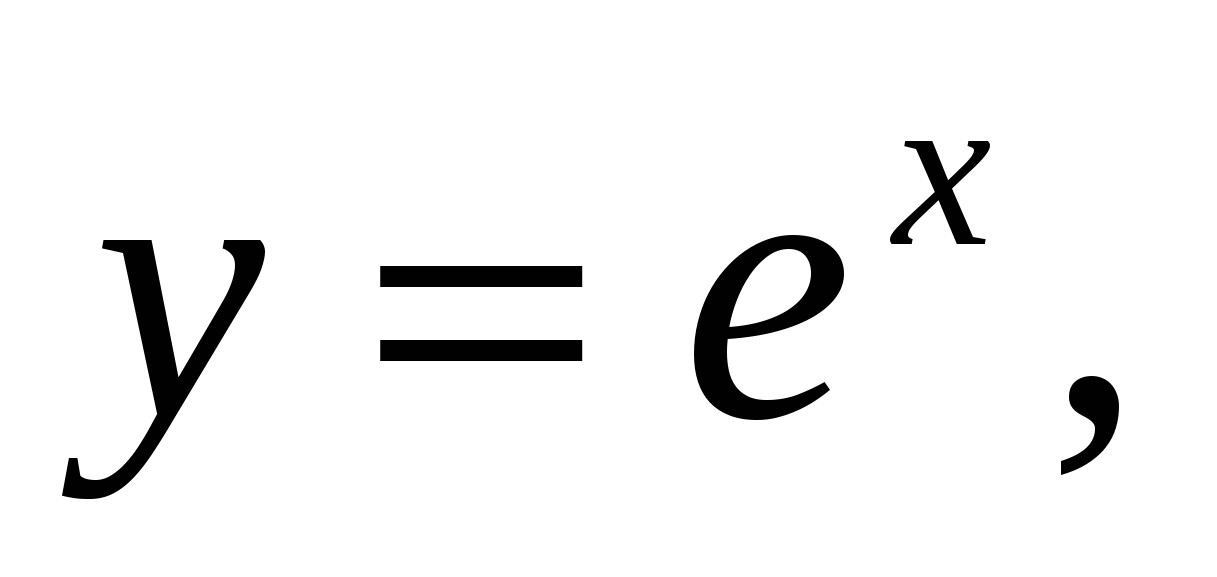

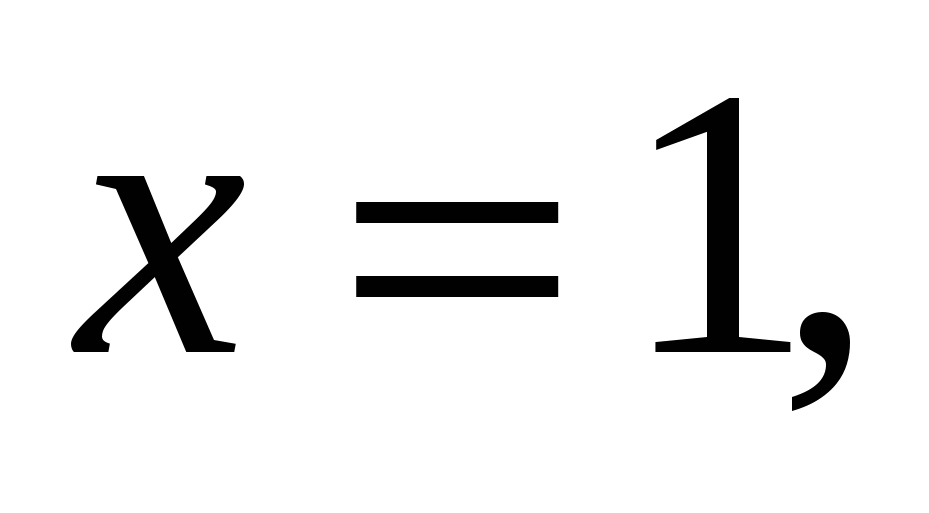
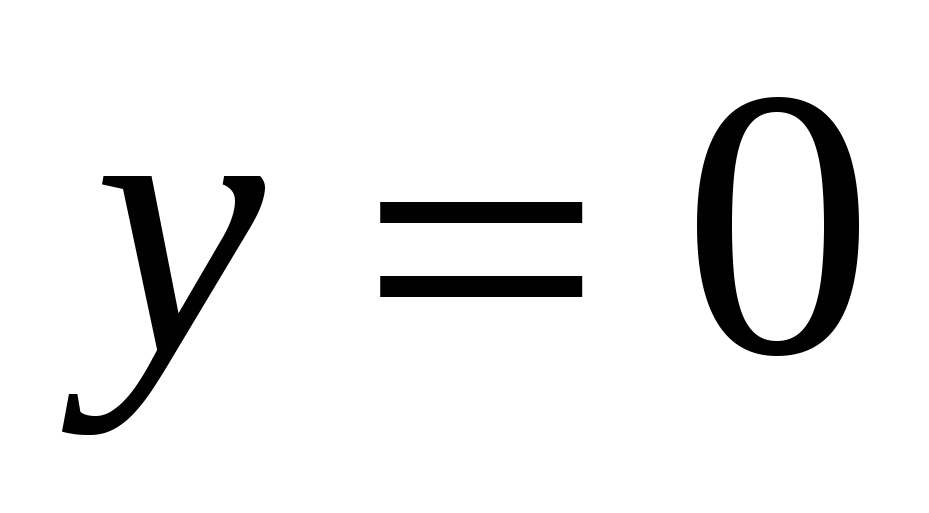 вокруг оси
вокруг оси 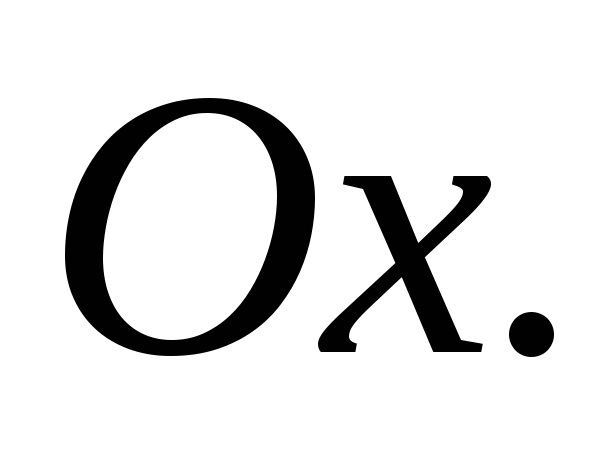
1.21. 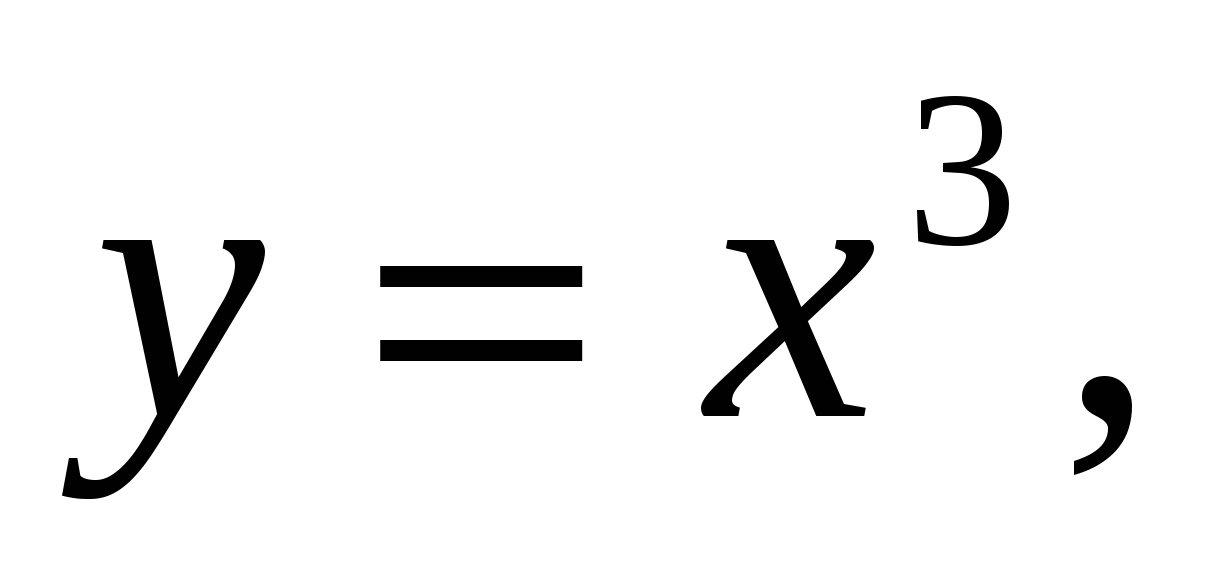
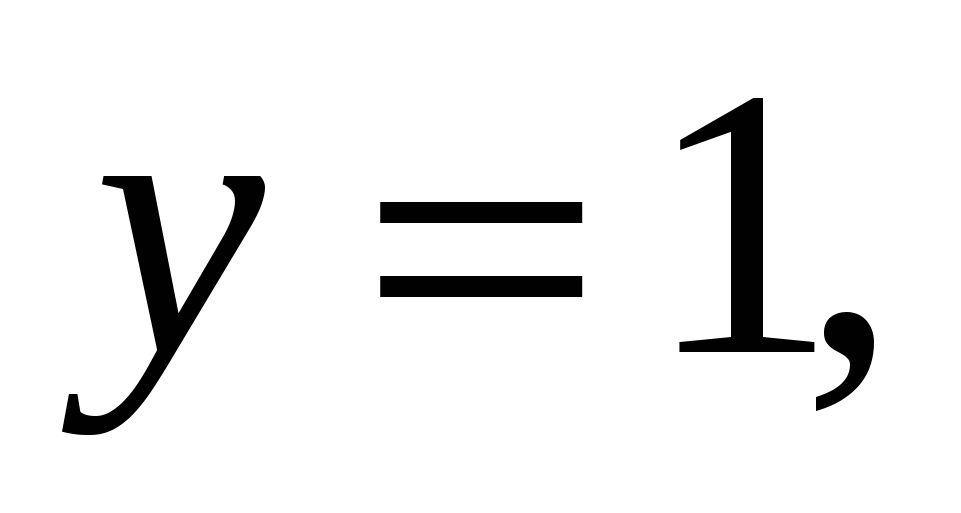
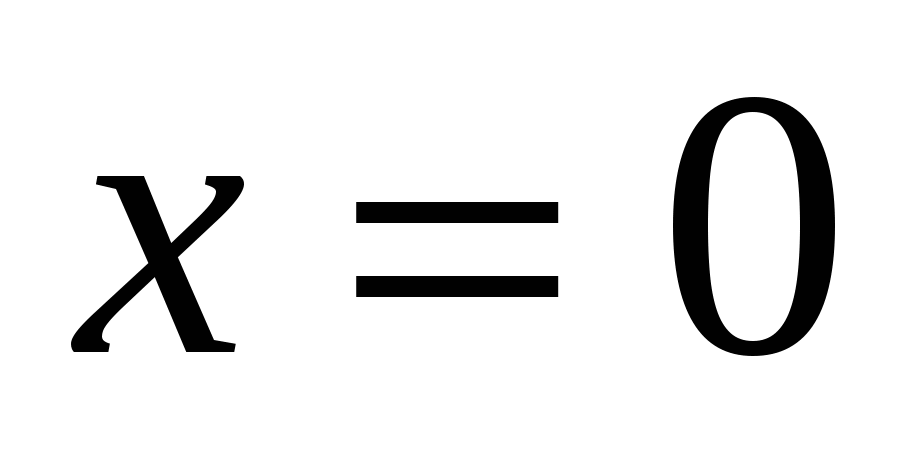 вокруг оси
вокруг оси 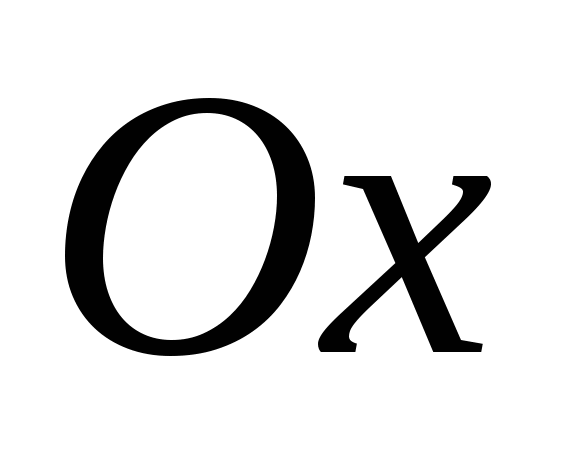
1.22. 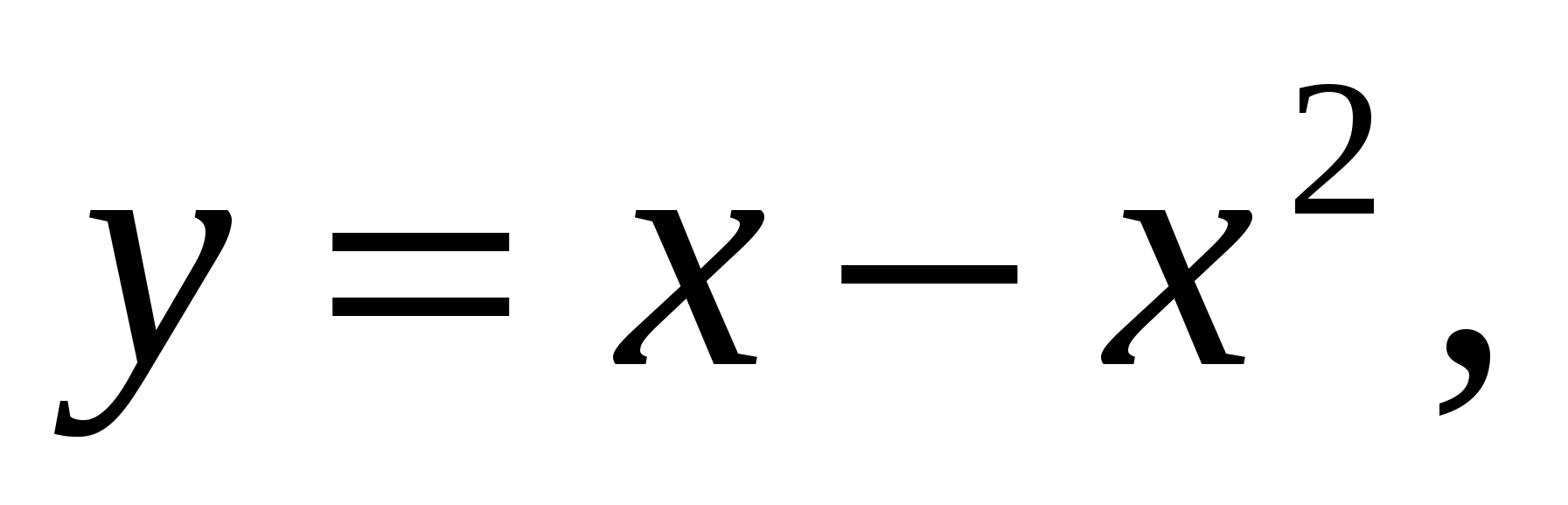
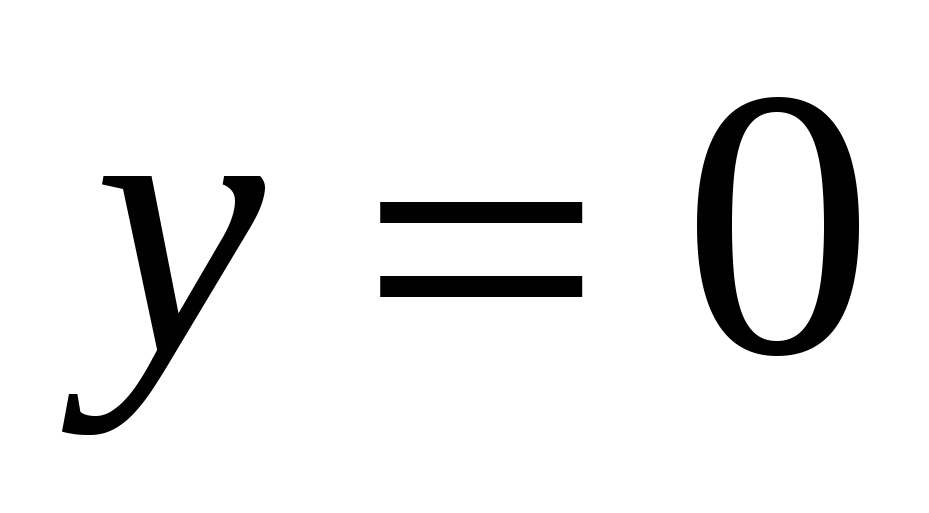 вокруг каждой из следующих прямых: 1)
вокруг каждой из следующих прямых: 1) 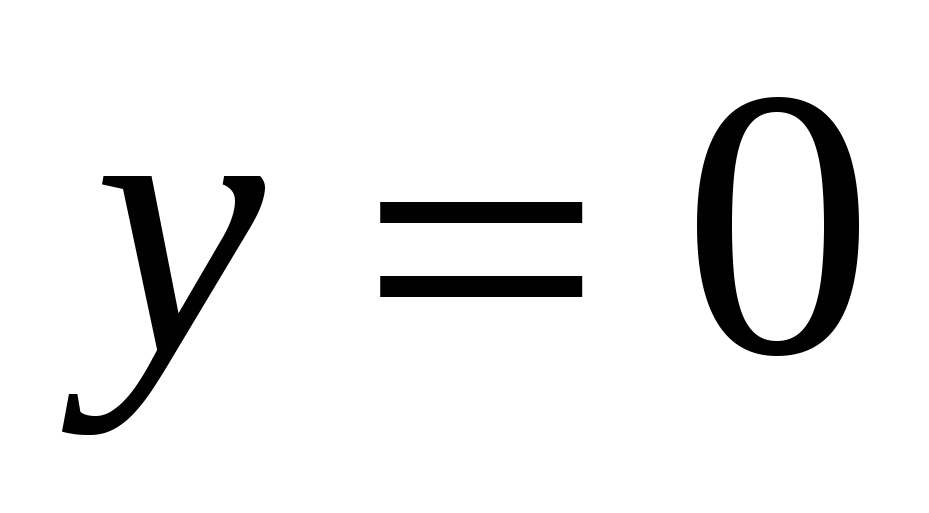 ,
,
2) 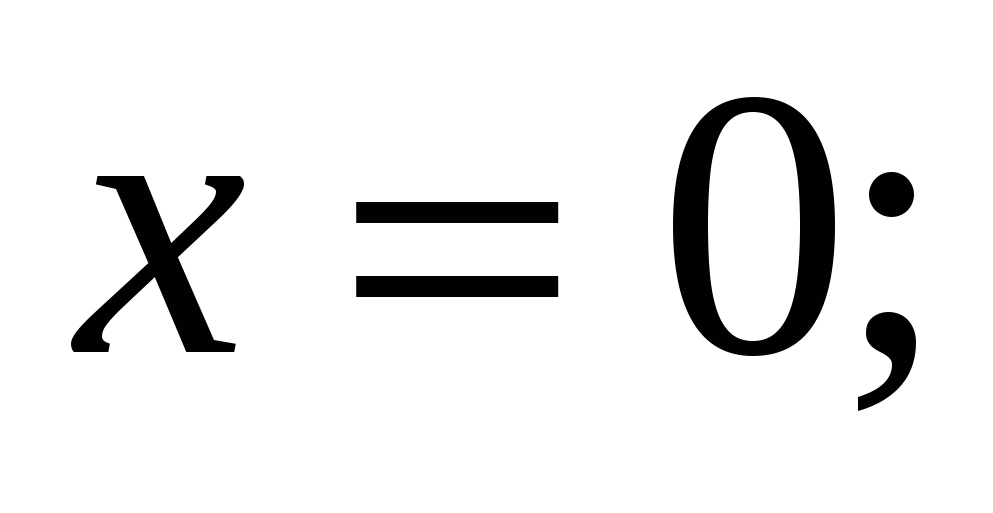 3)
3) 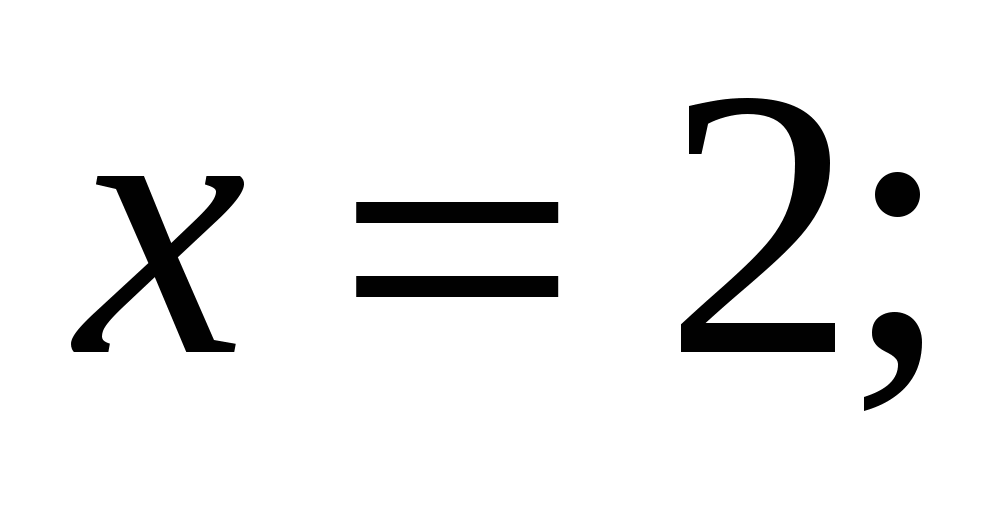 4)
4) 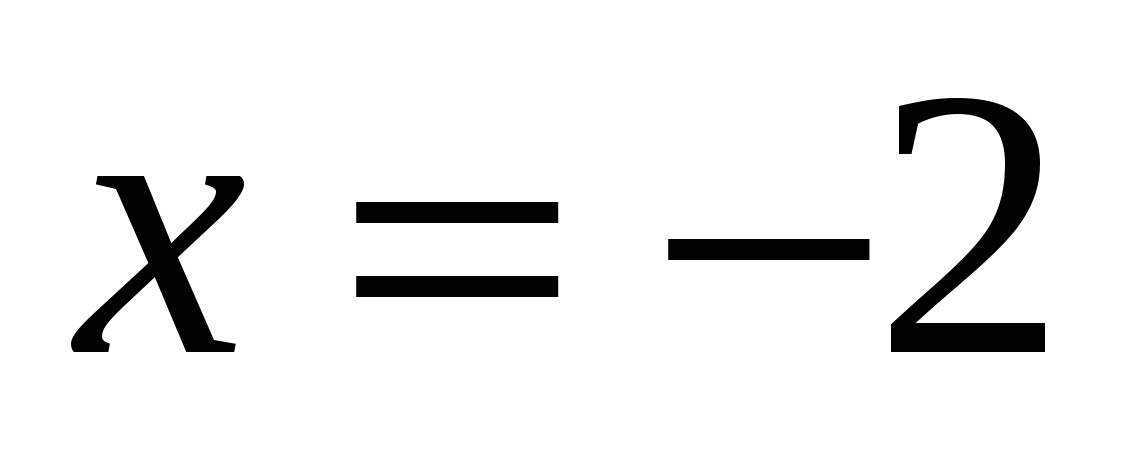 5)
5)  6)
6) 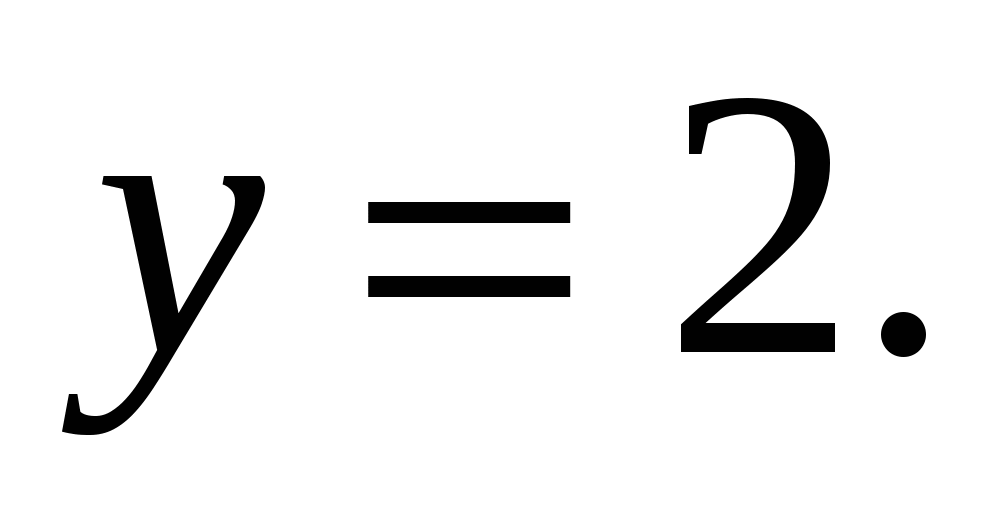
1.23. 
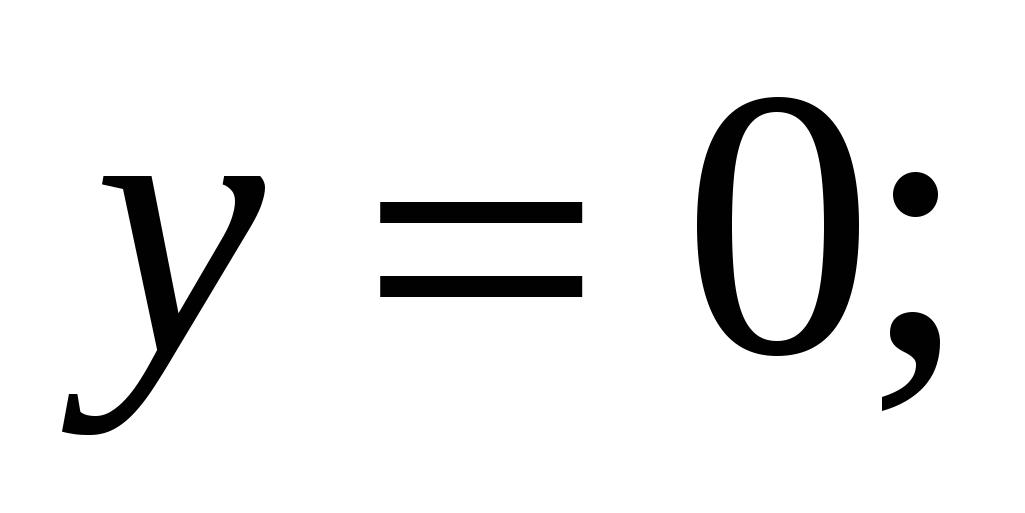
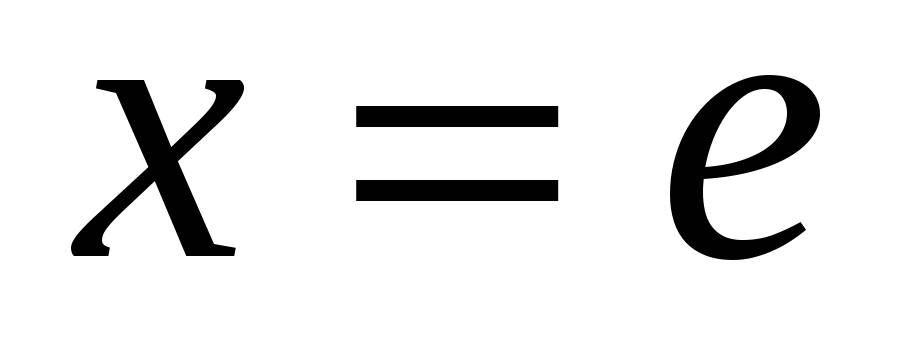 вокруг каждой из следующих прямых: 1)
вокруг каждой из следующих прямых: 1)![]() 2)
2) 3)
3)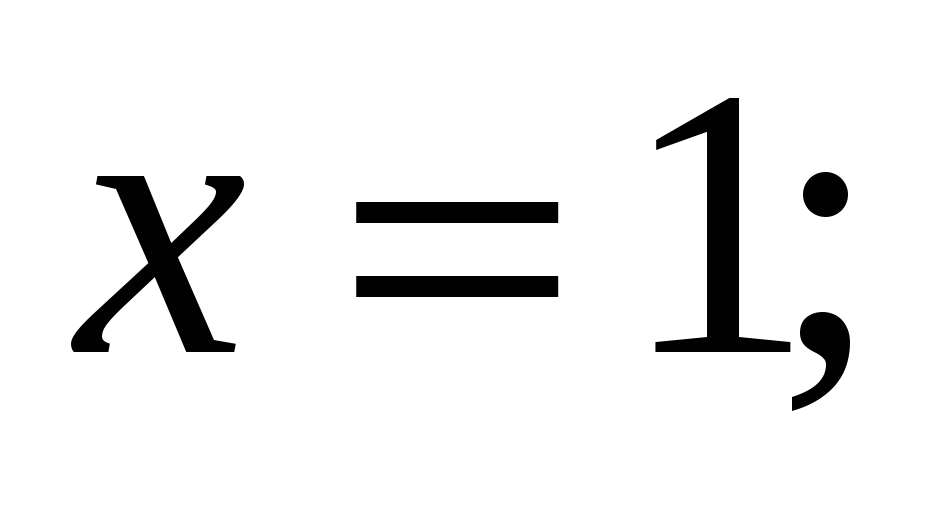 4)
4)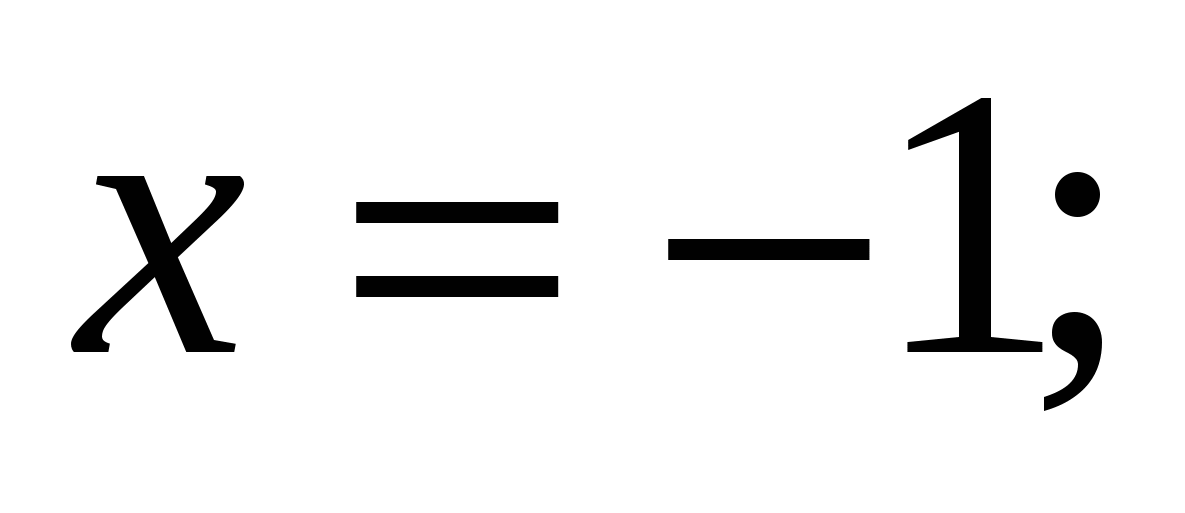 5)
5)
1.24. 
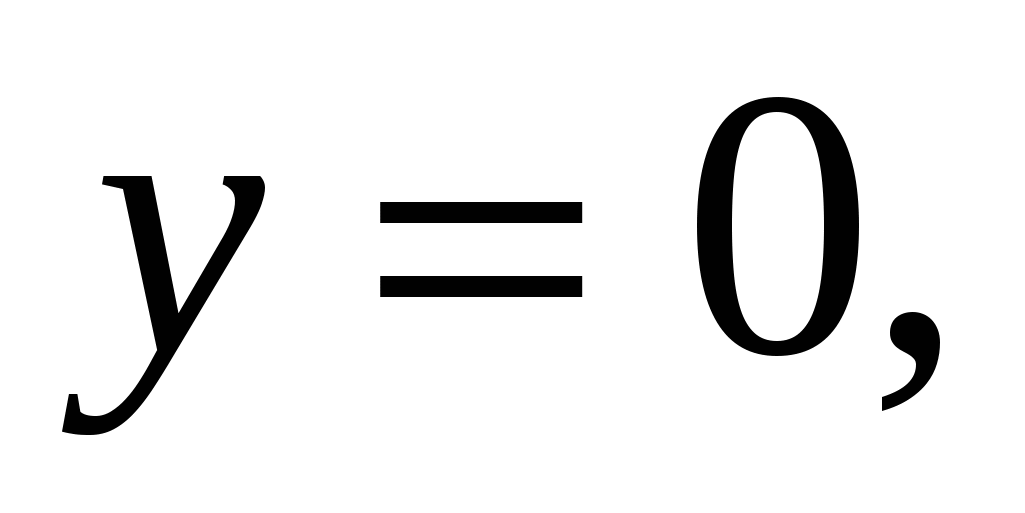
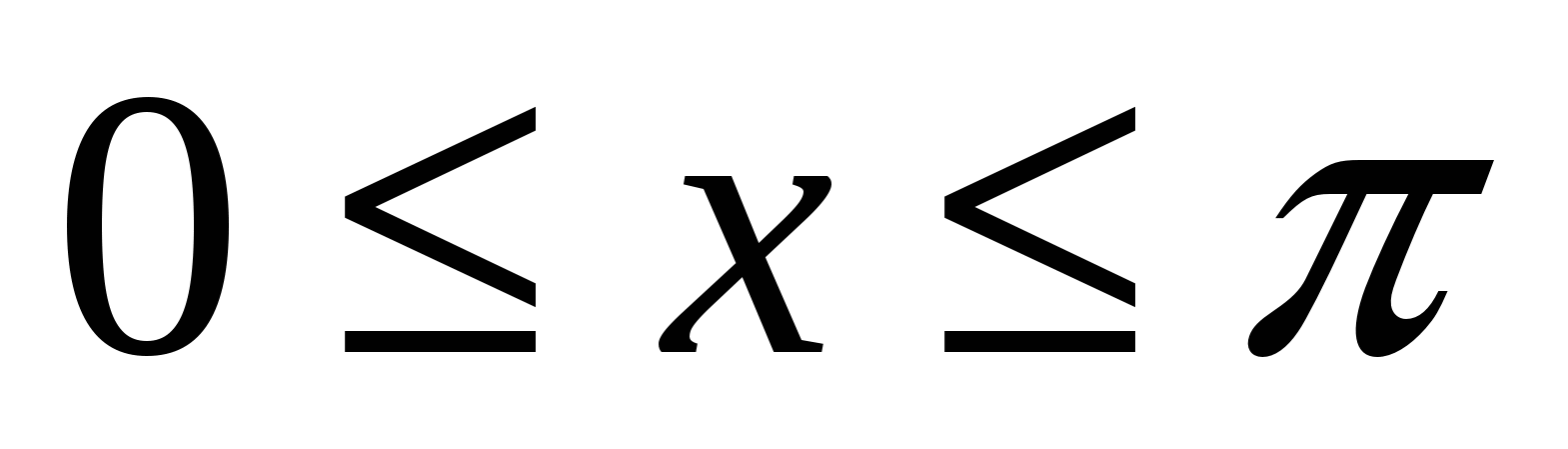 вокруг каждой из следующих прямых: 1)
вокруг каждой из следующих прямых: 1)![]() 2)
2)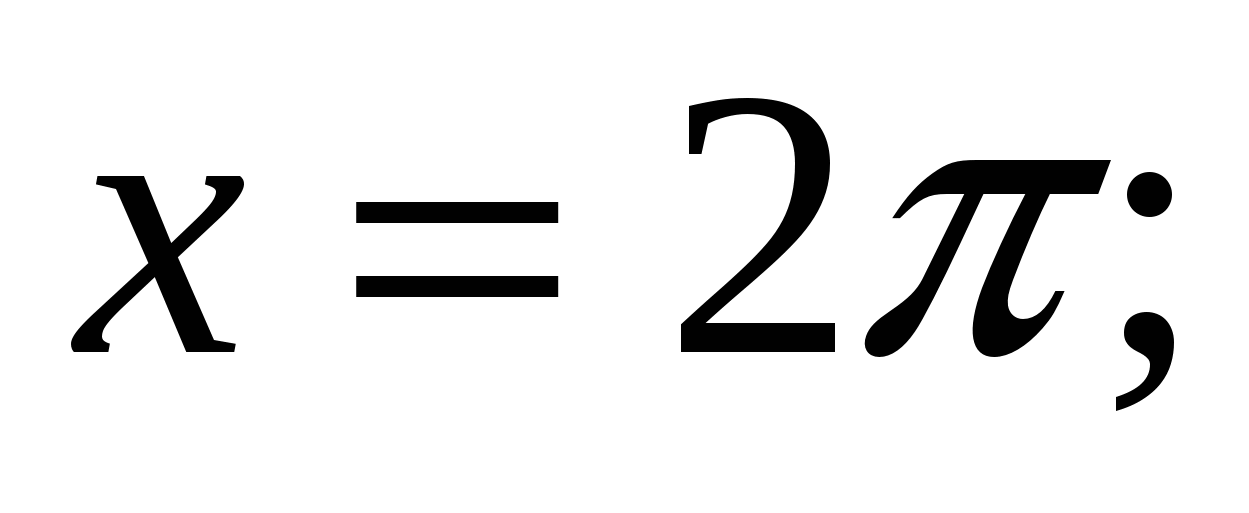 3)
3)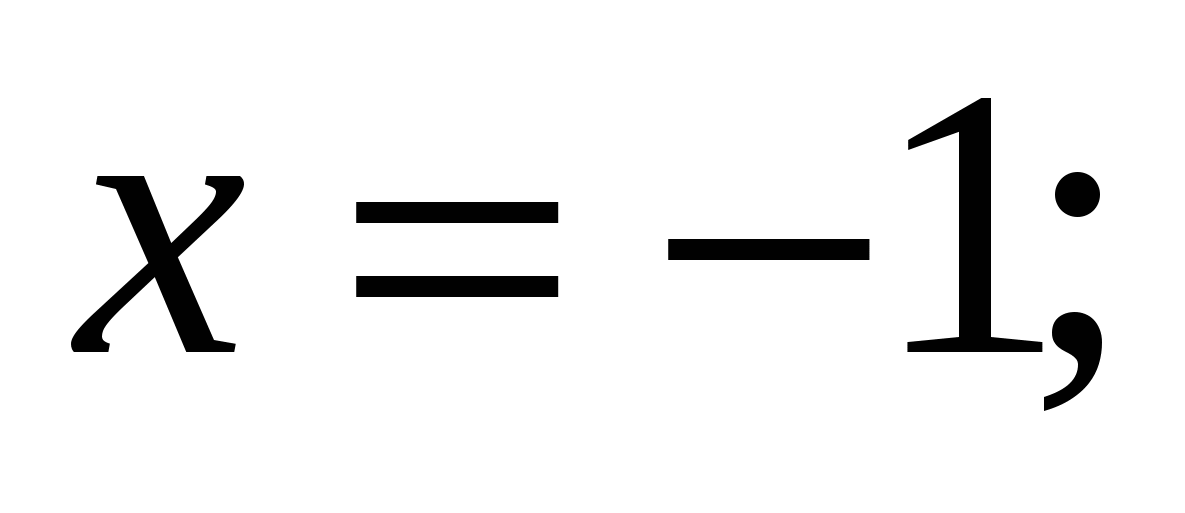 4)
4)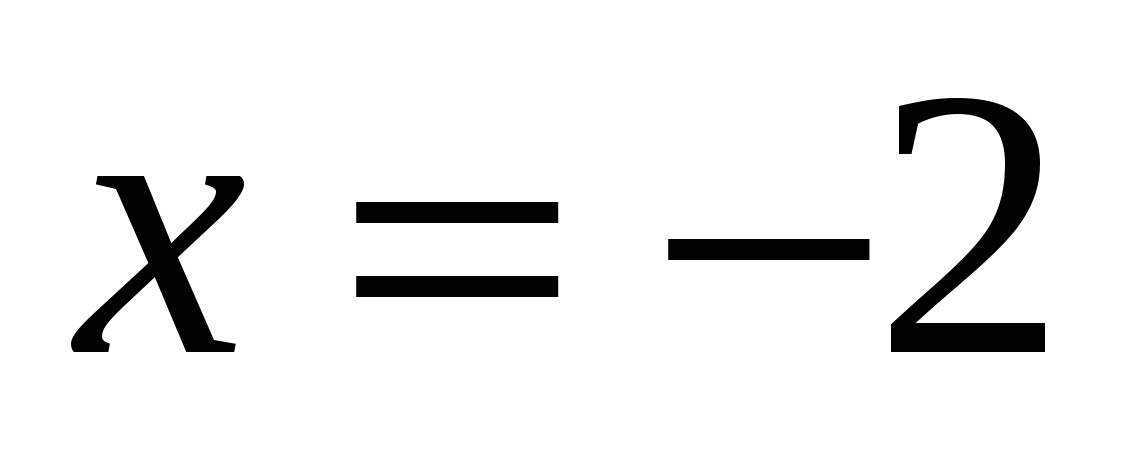 5)
5)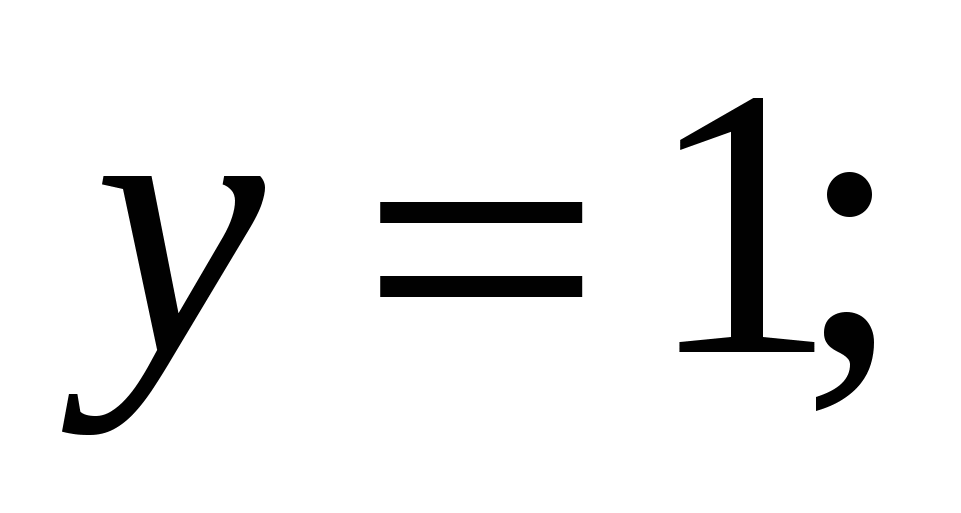 6)
6)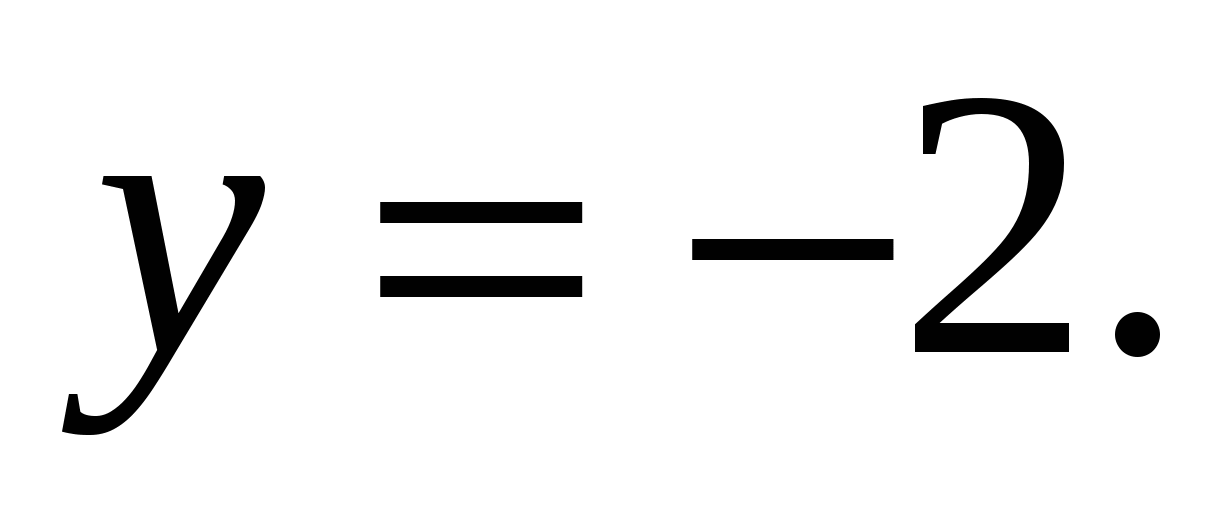
1.25. 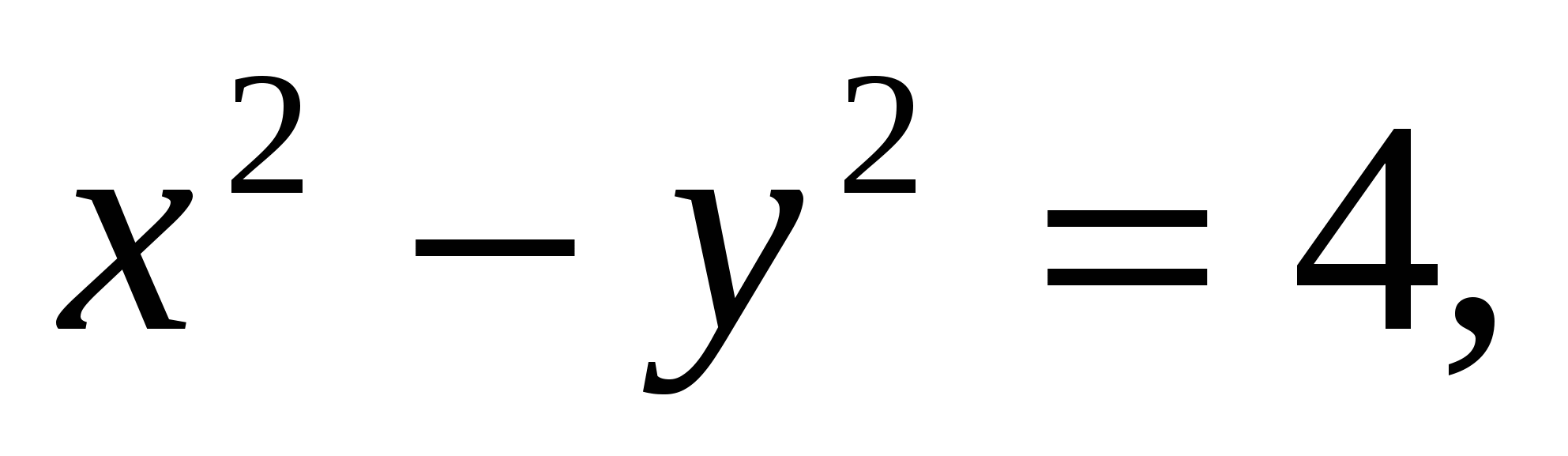
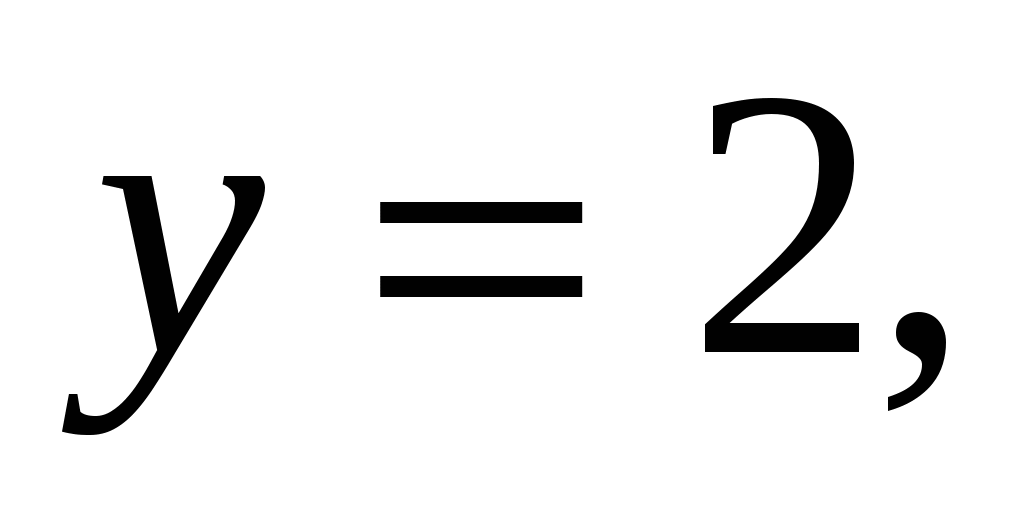
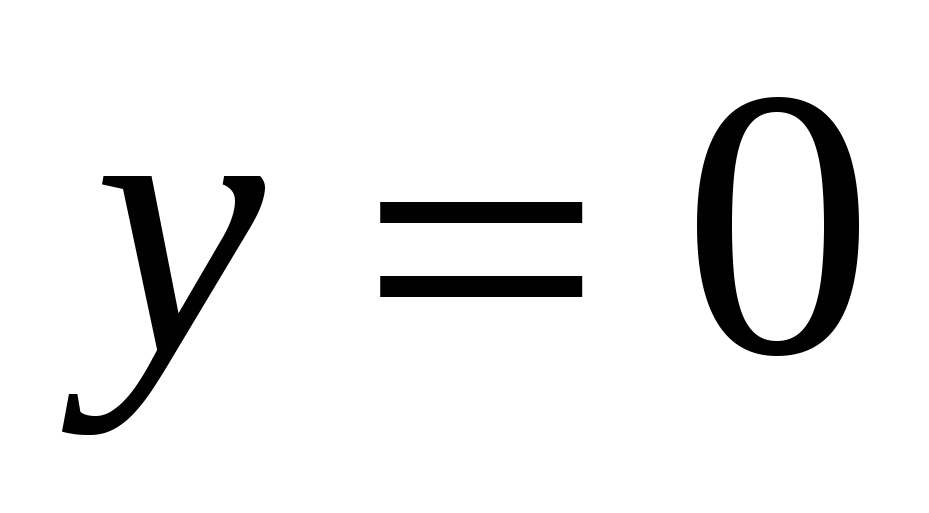 вокруг оси
вокруг оси 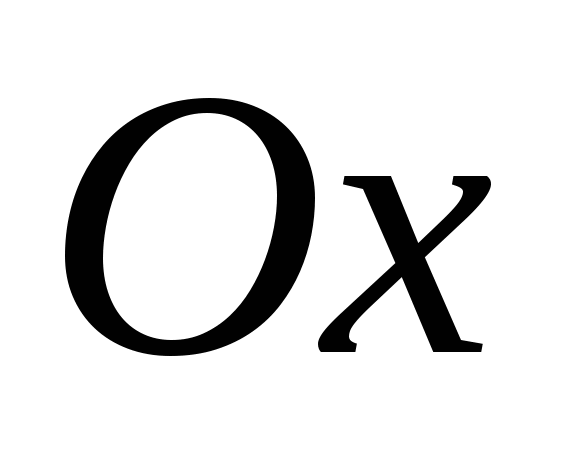
1.26. 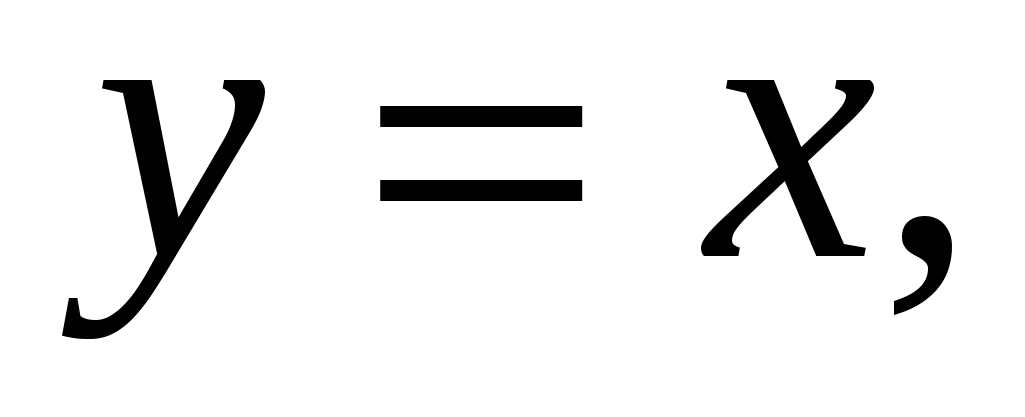
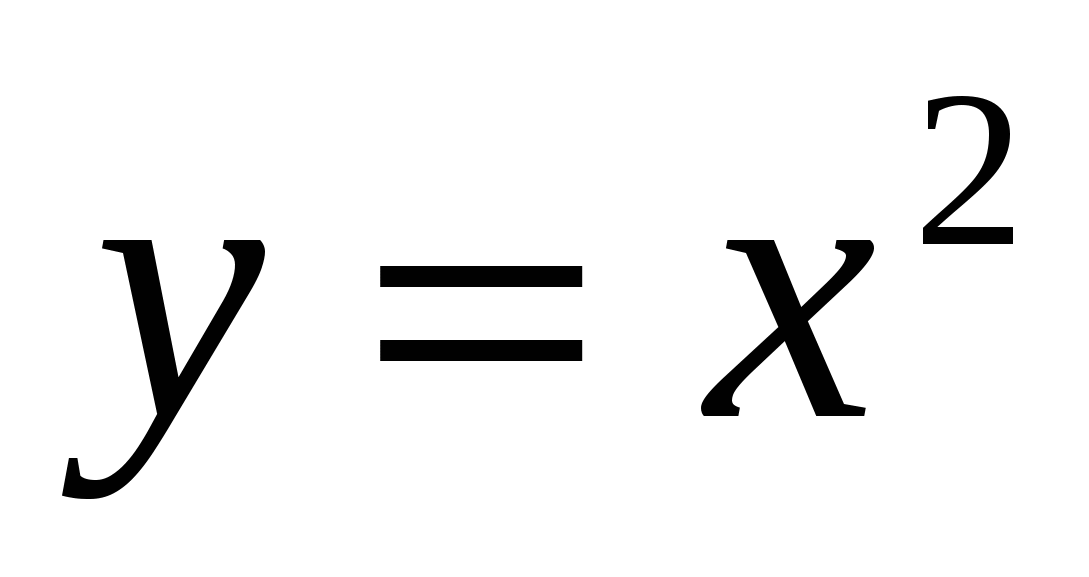 вокруг оси
вокруг оси 
1.27. 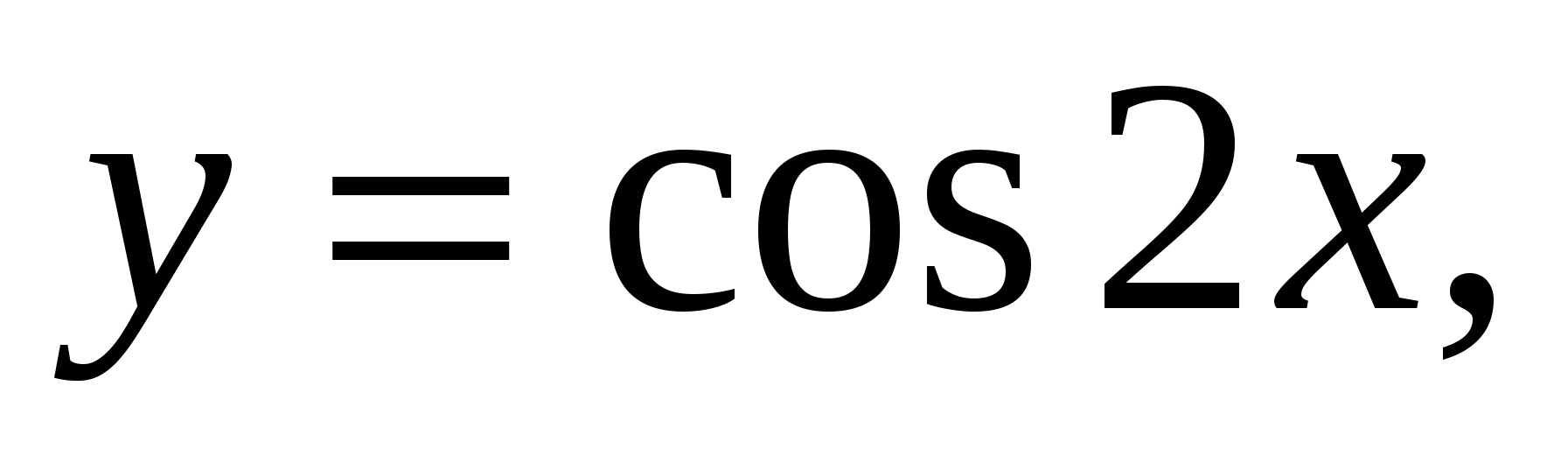

 где
где 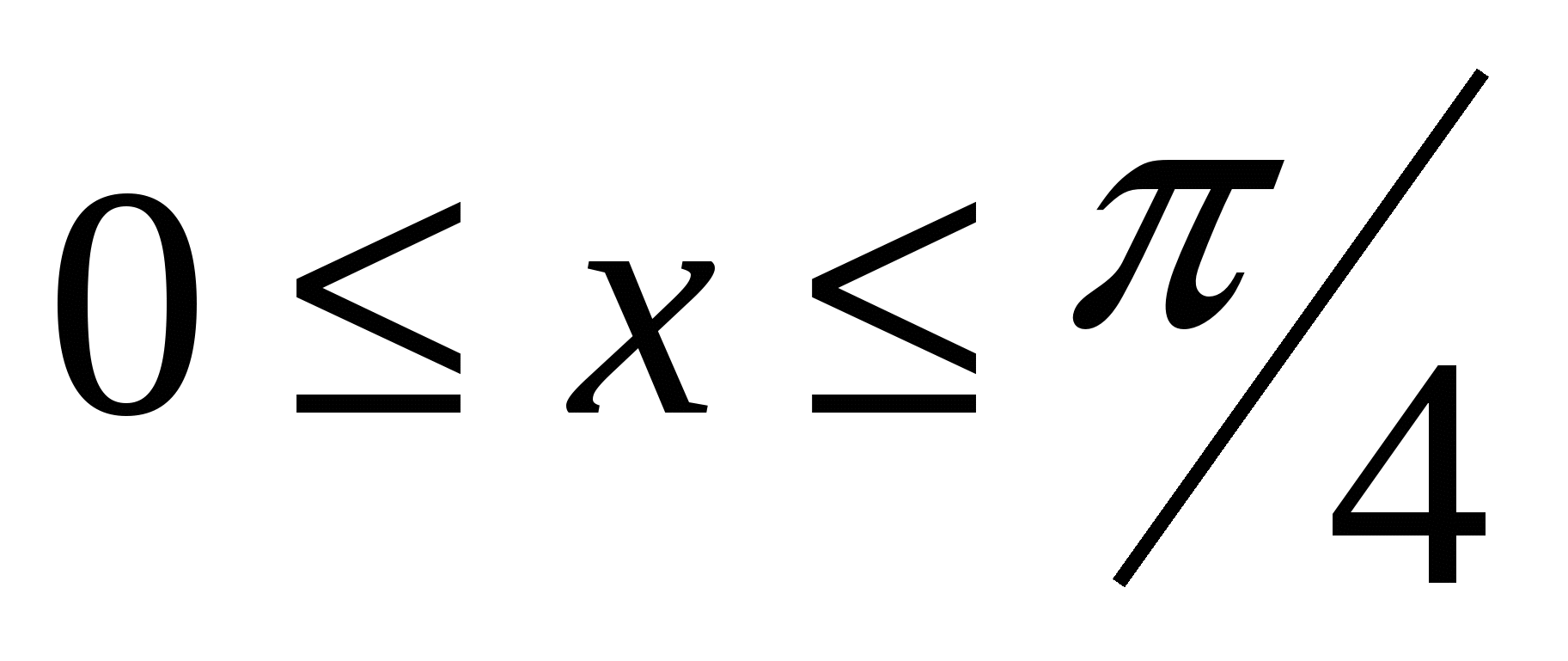 вокруг оси
вокруг оси 
1.28. 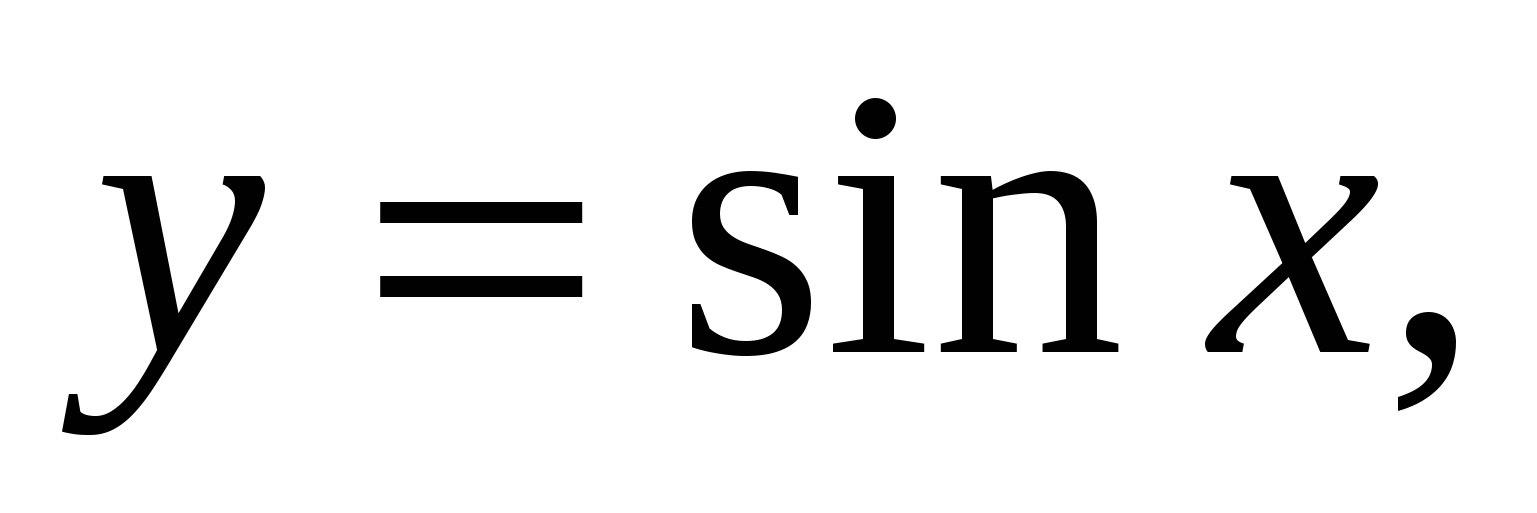
 где
где 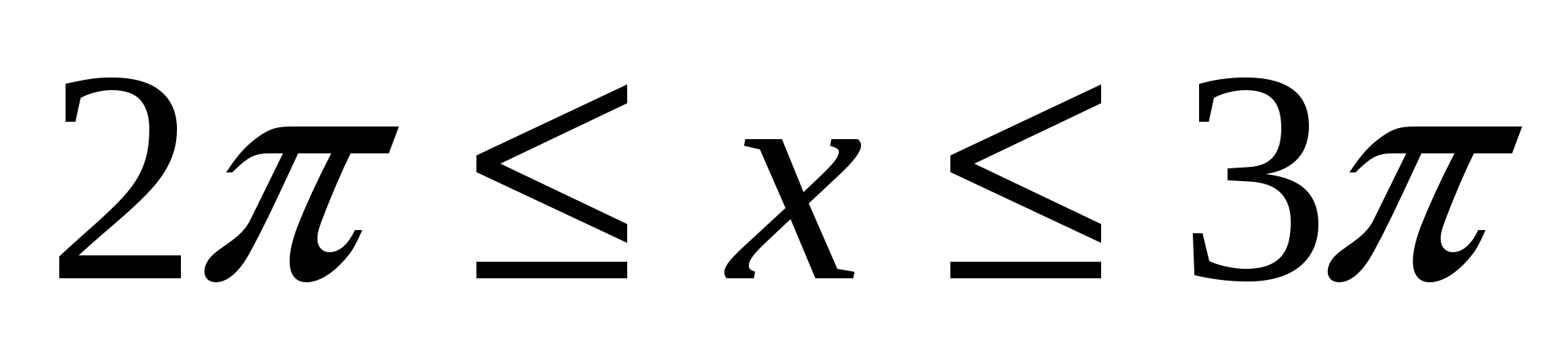 вокруг каждой из следующих прямых: 1)
вокруг каждой из следующих прямых: 1)![]() 2)
2)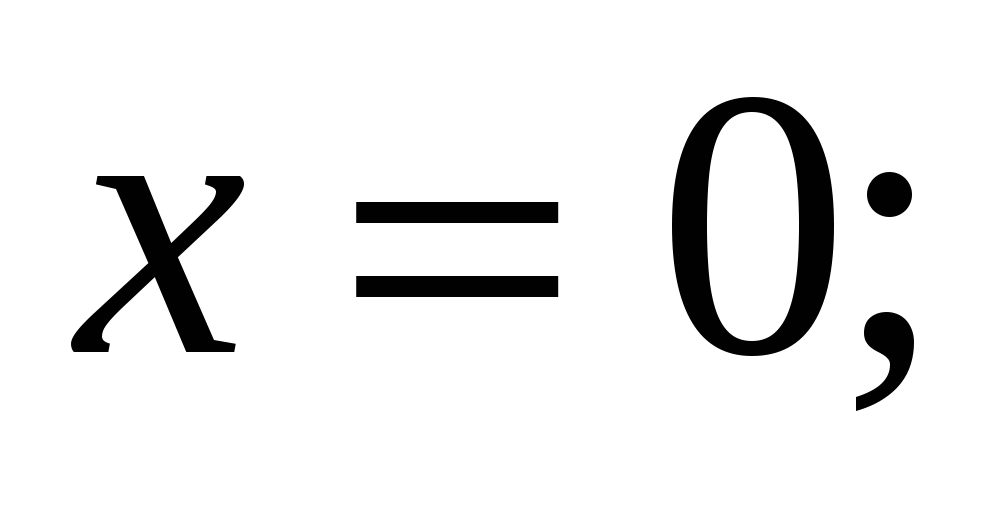 3)
3) 4)
4)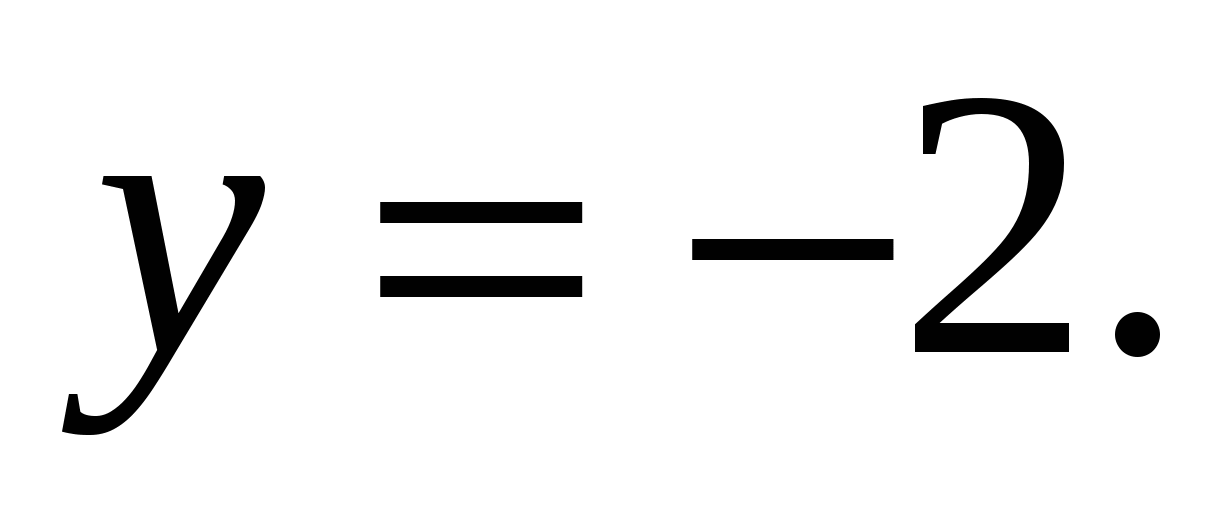

1.29. 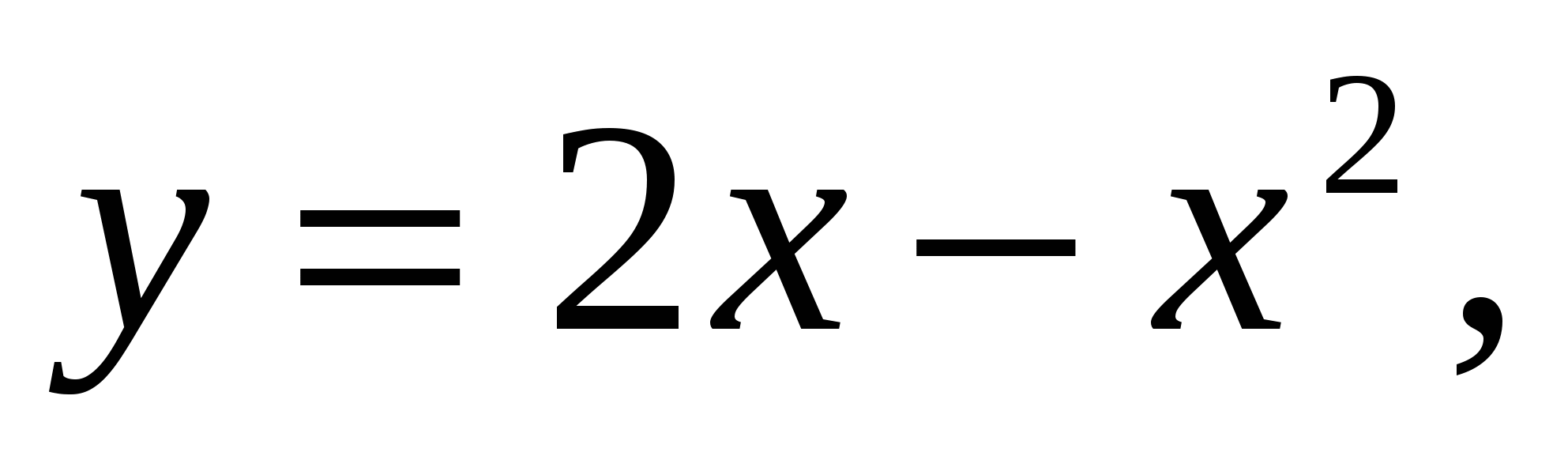
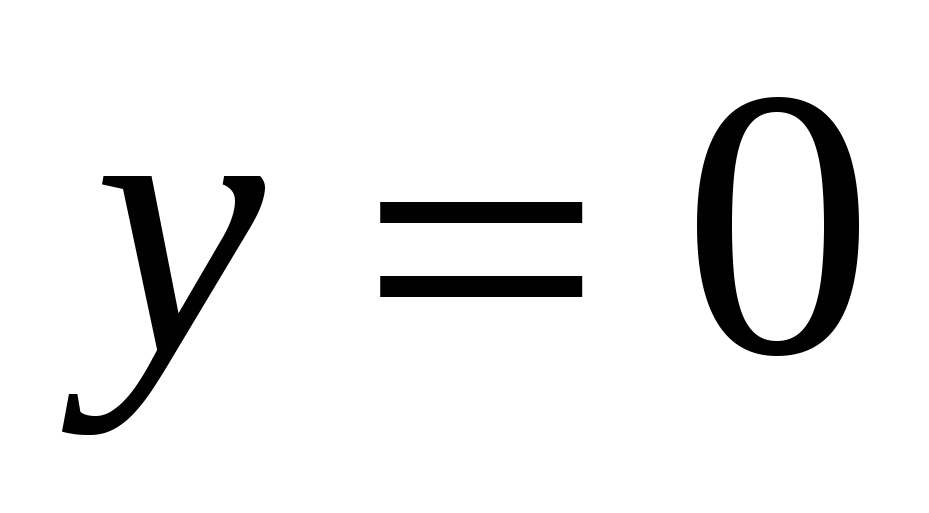 вокруг каждой из следующих прямых: 1)
вокруг каждой из следующих прямых: 1)![]() 2)
2)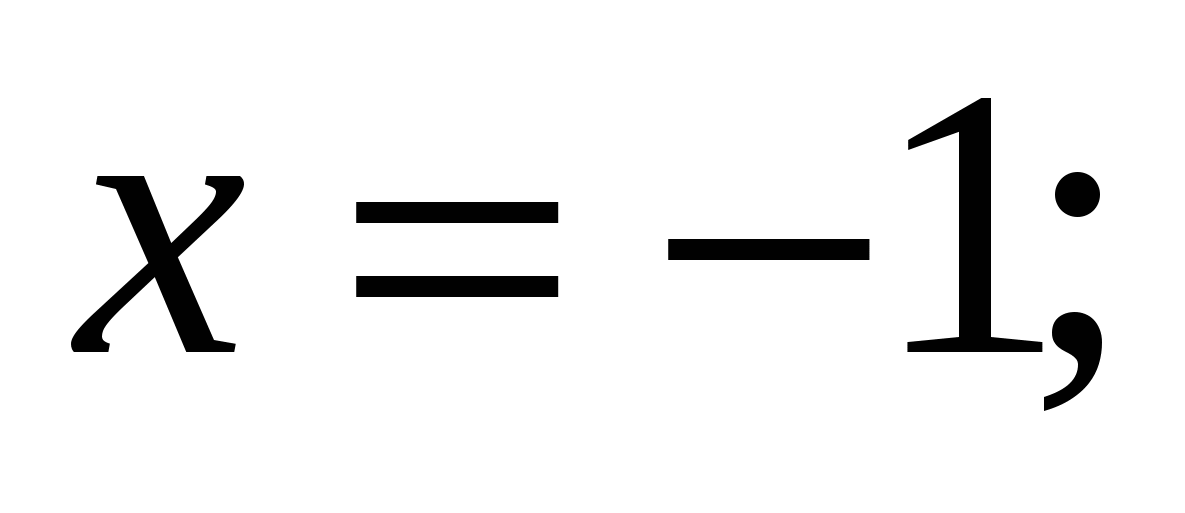 3)
3)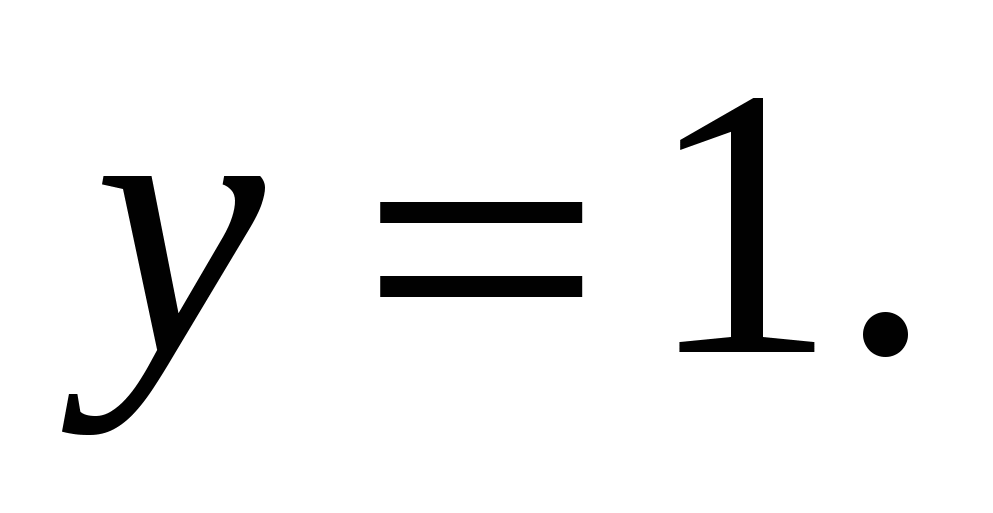
1.30. 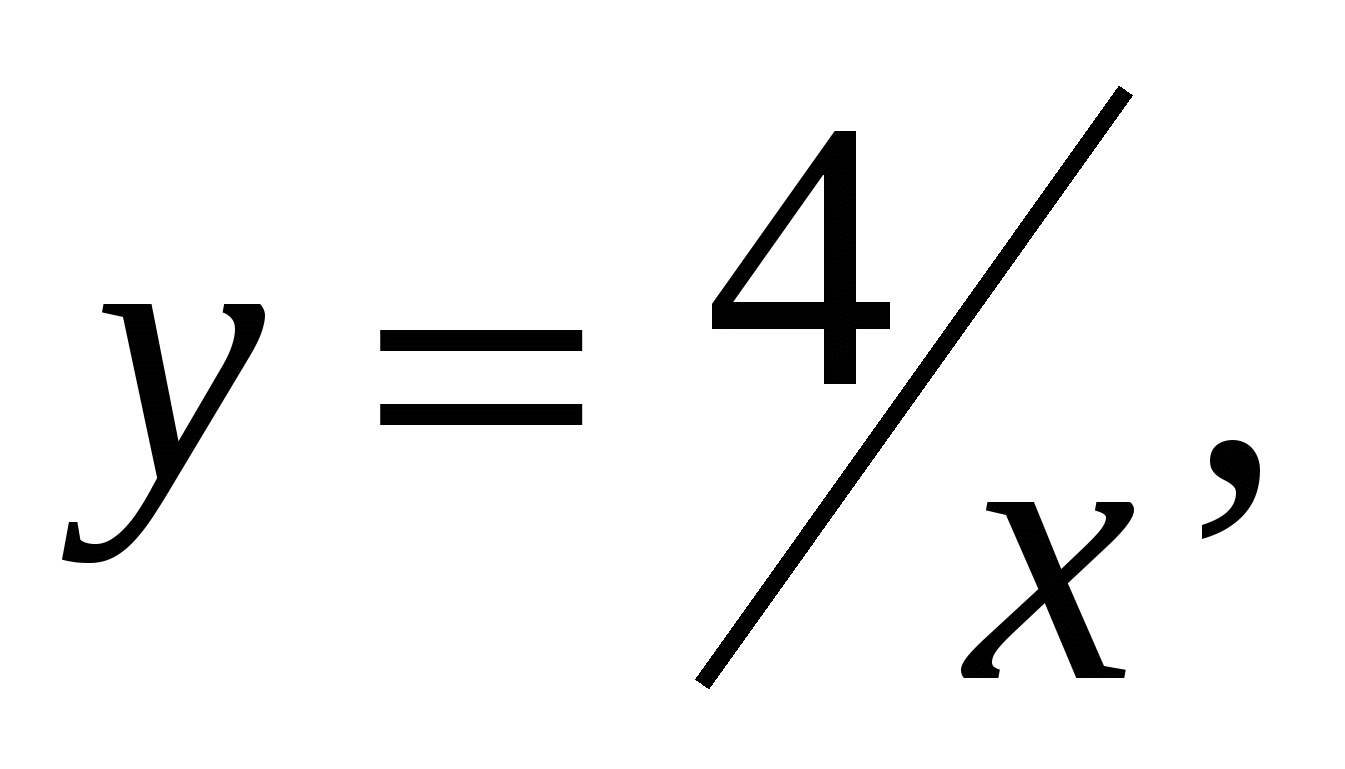
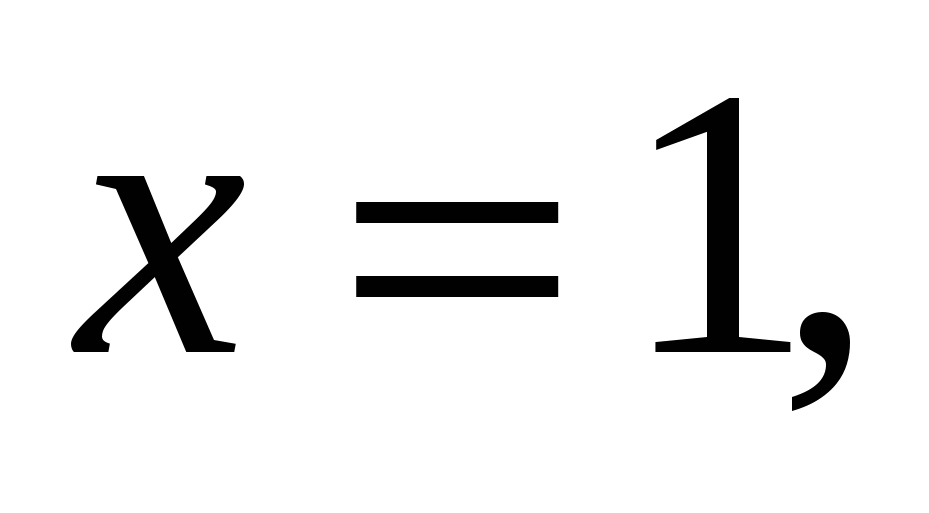
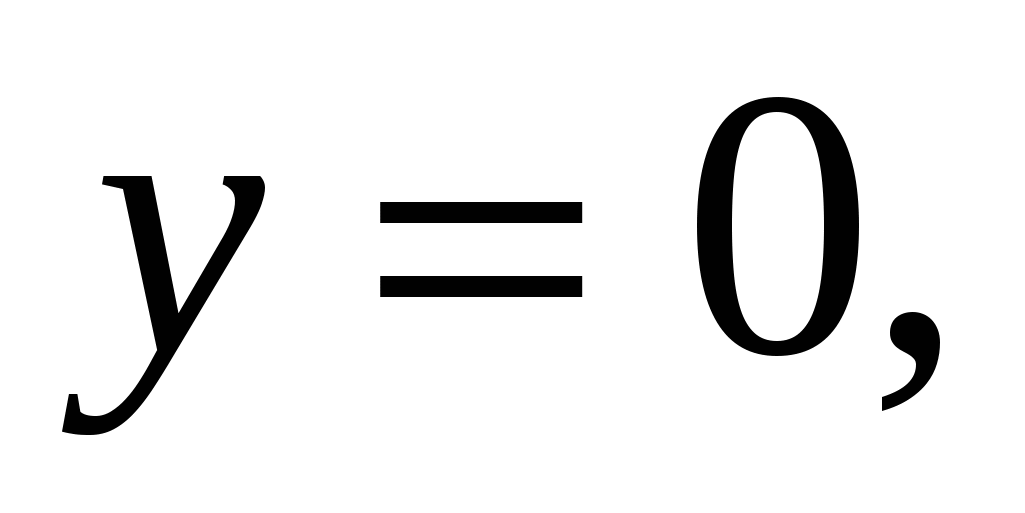
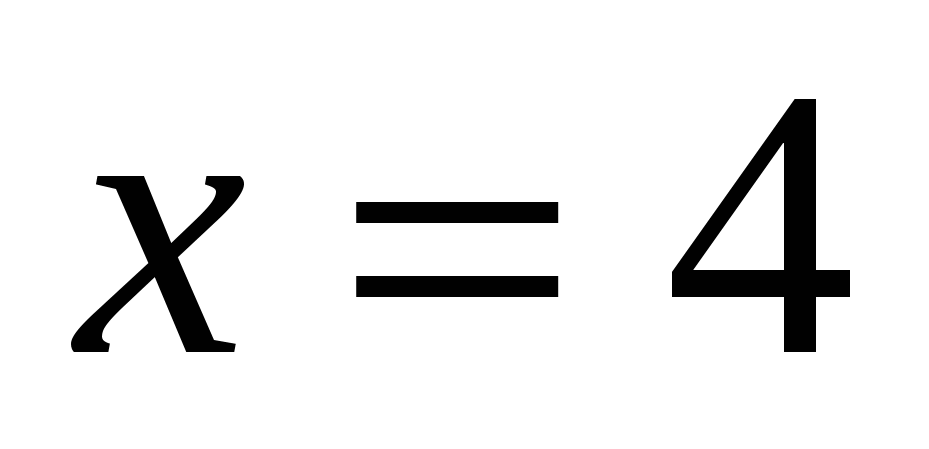 вокруг оси
вокруг оси 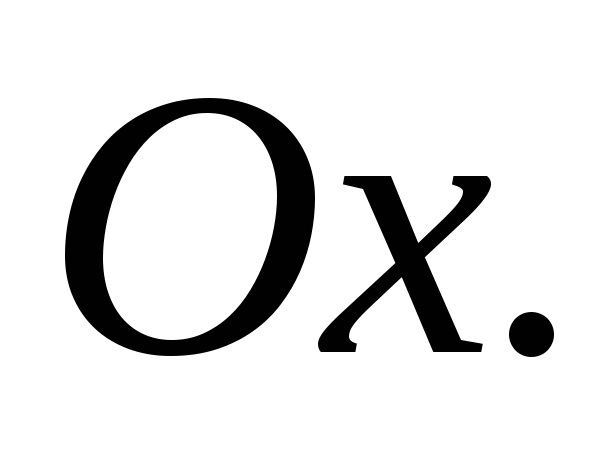

1.31. 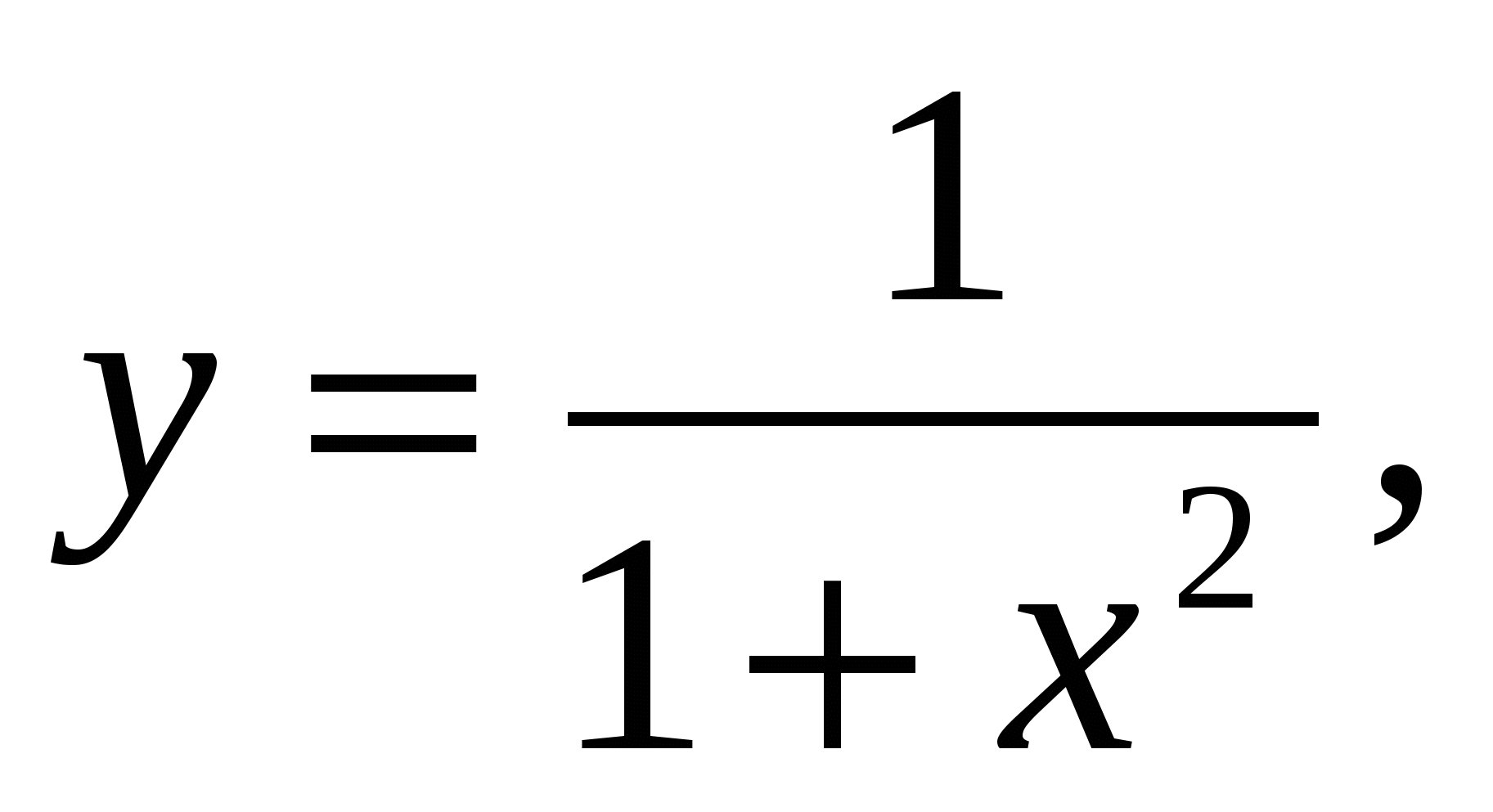
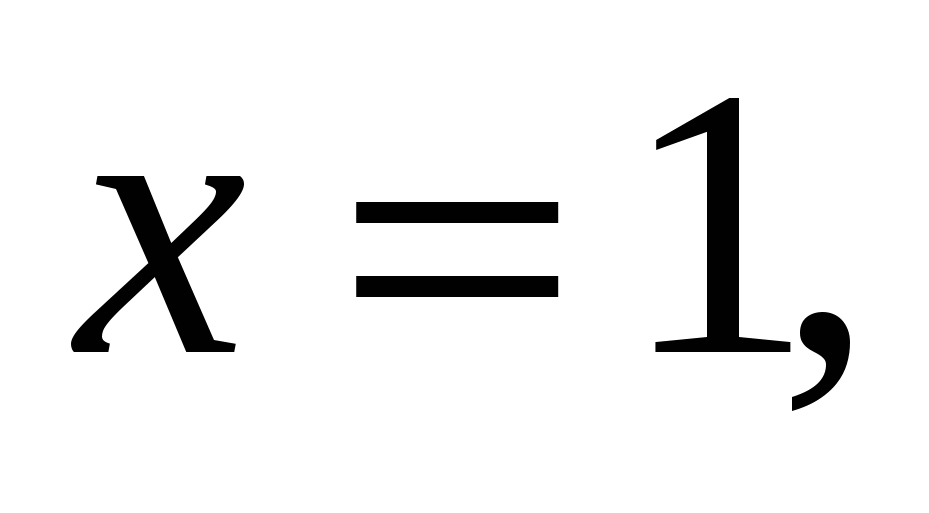
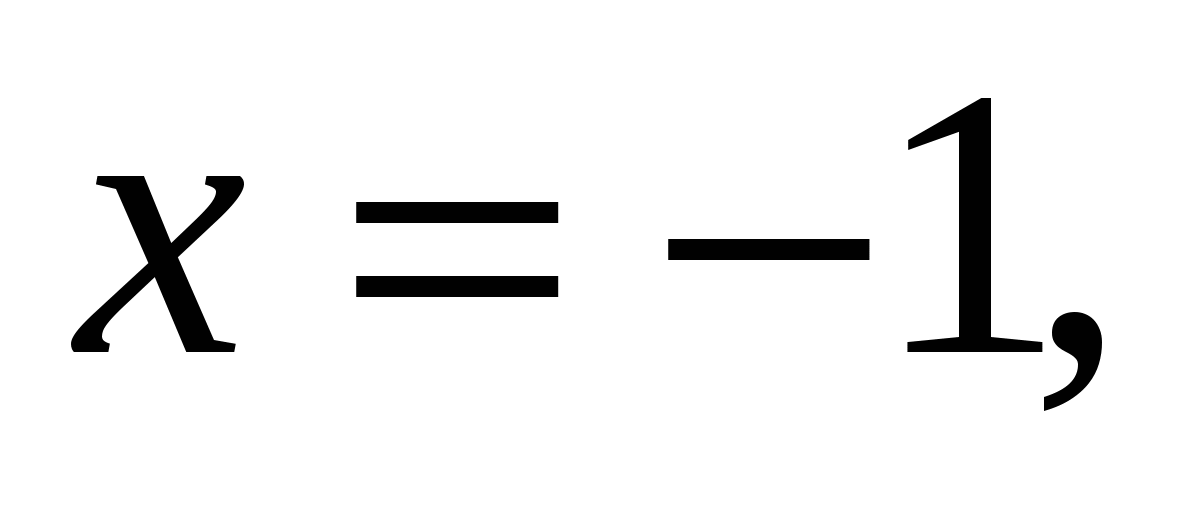
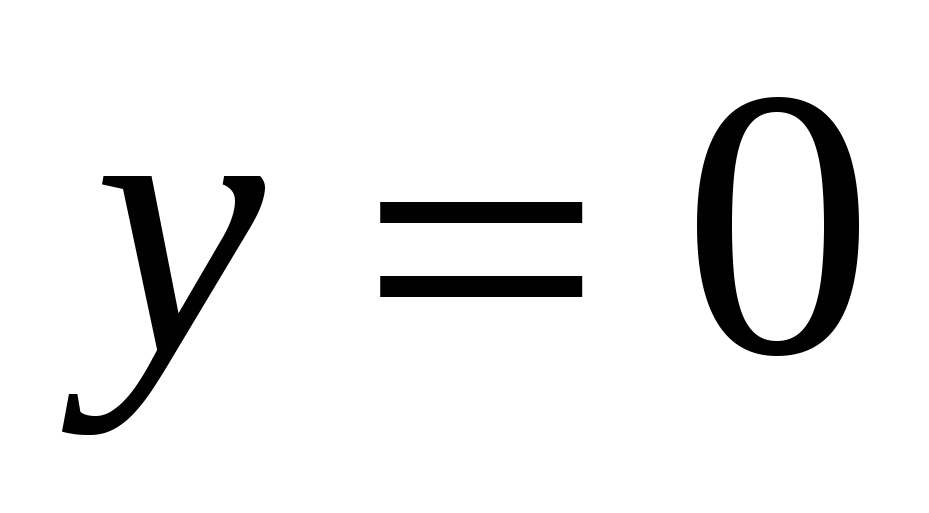 вокруг: 1) оси
вокруг: 1) оси  2)
2) 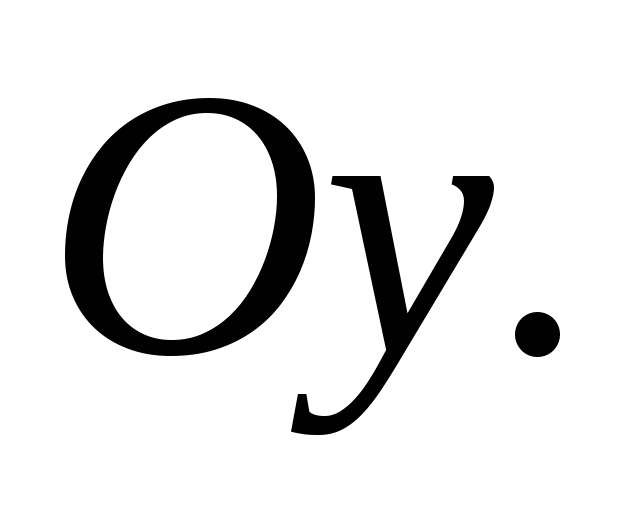
Индивидуальные задания
Раздел А
Задача.
Вычислить объем тела, образованного вращением вокруг заданной оси области, ограниченной графиками заданных функций (таблица 4).
Таблица4
№ вар
Заданные функции.
Задан
ось.
№ вар
Заданные функции.
Задан
ось.
1
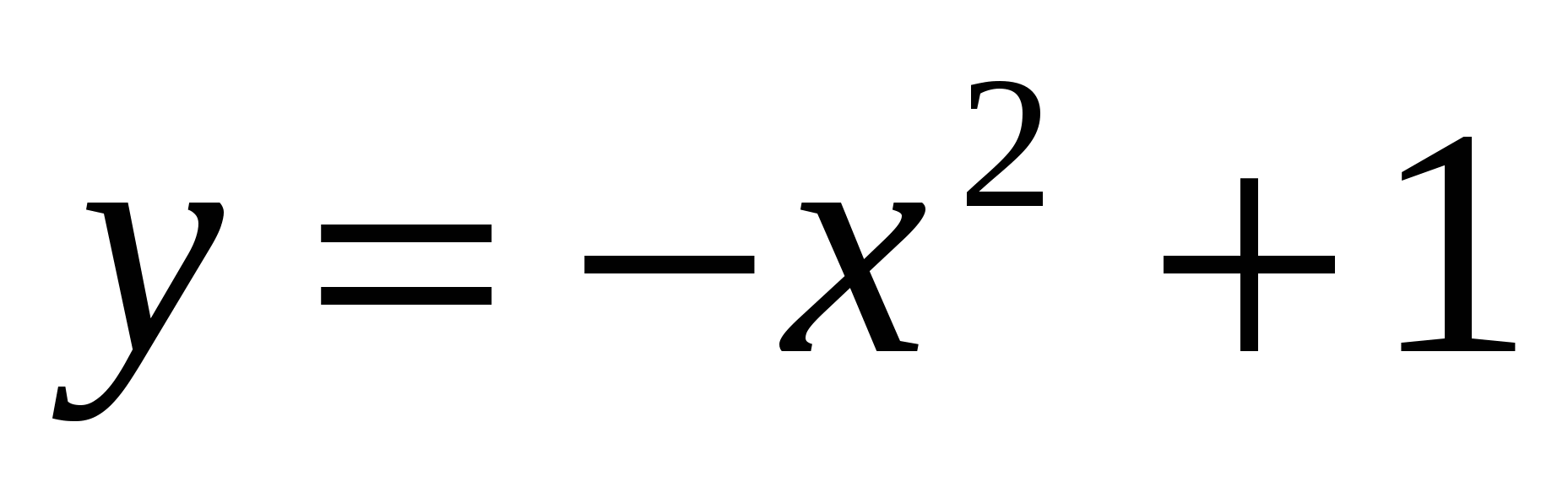 ,
, 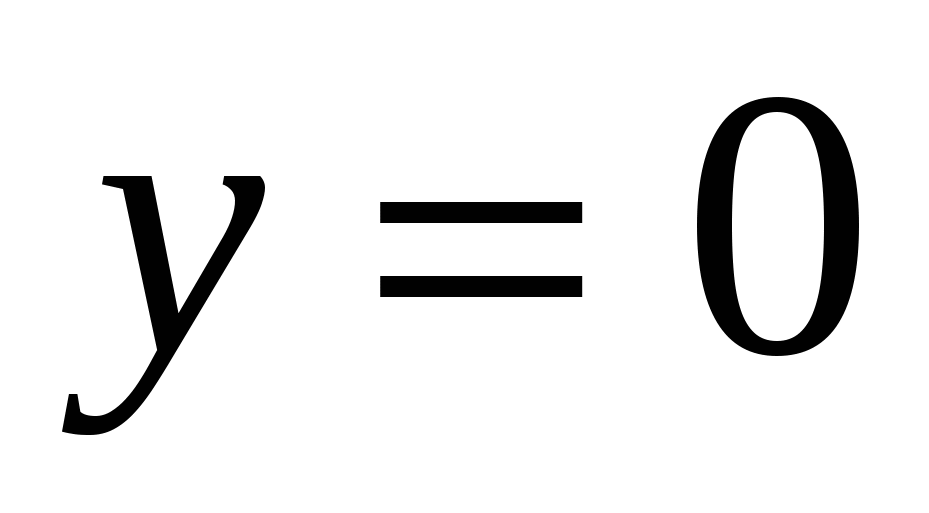
Ox
16
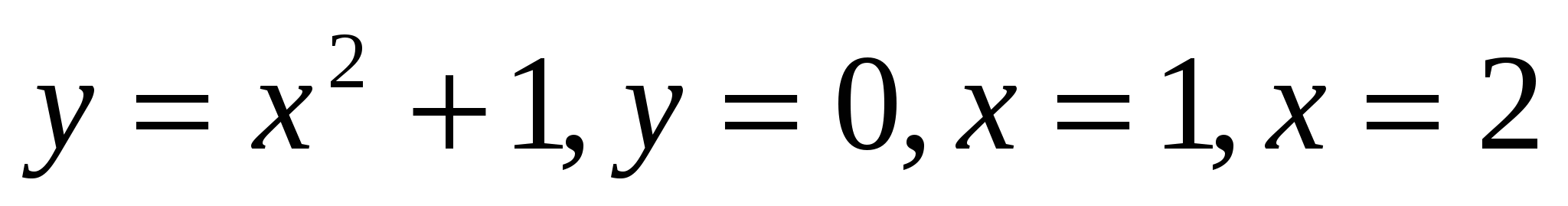
Oy
2
![]()

Oy
17
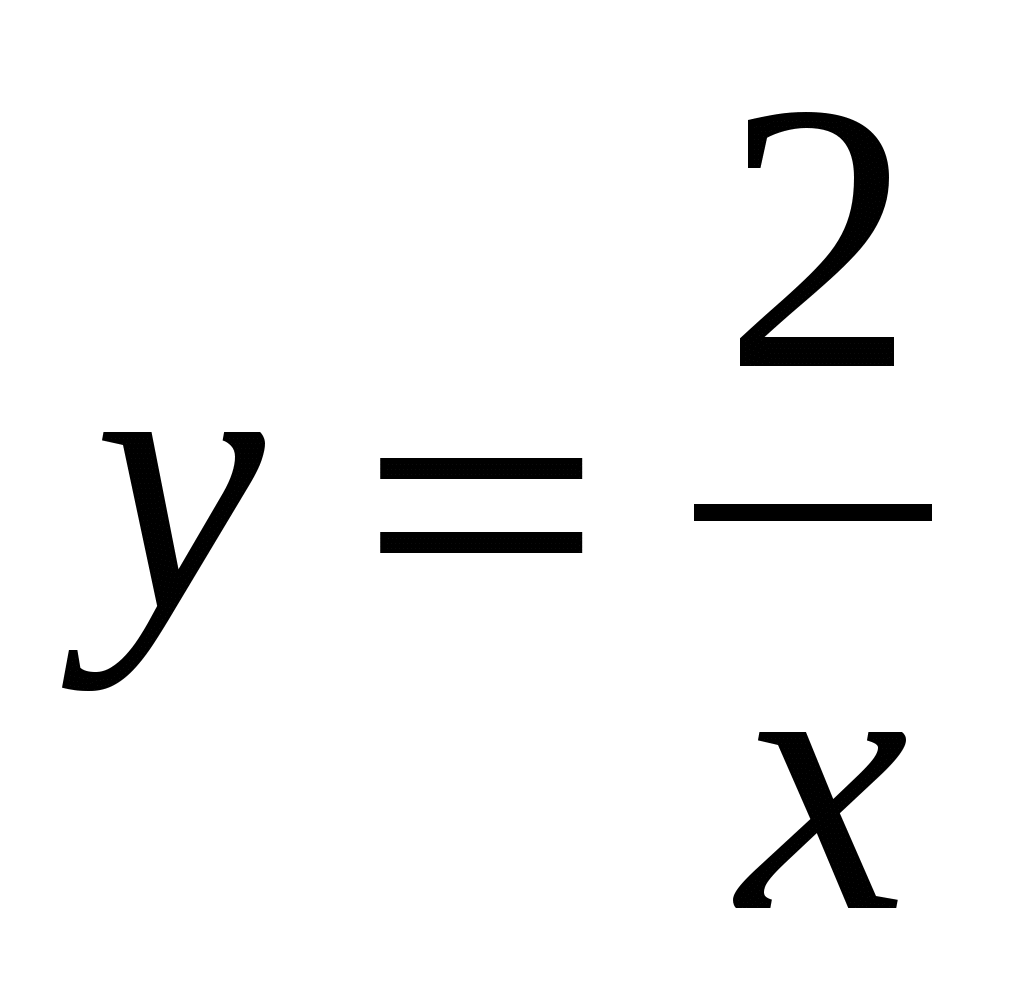 ,
, 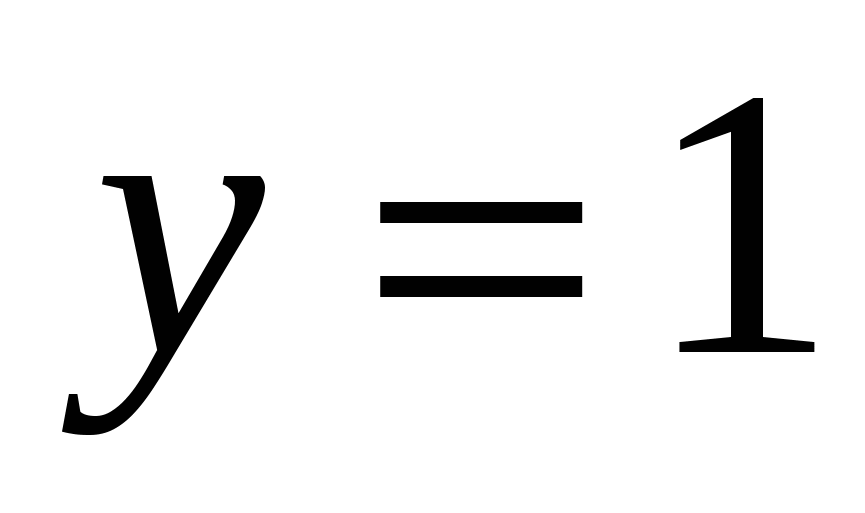 ,
, 
Ox
3
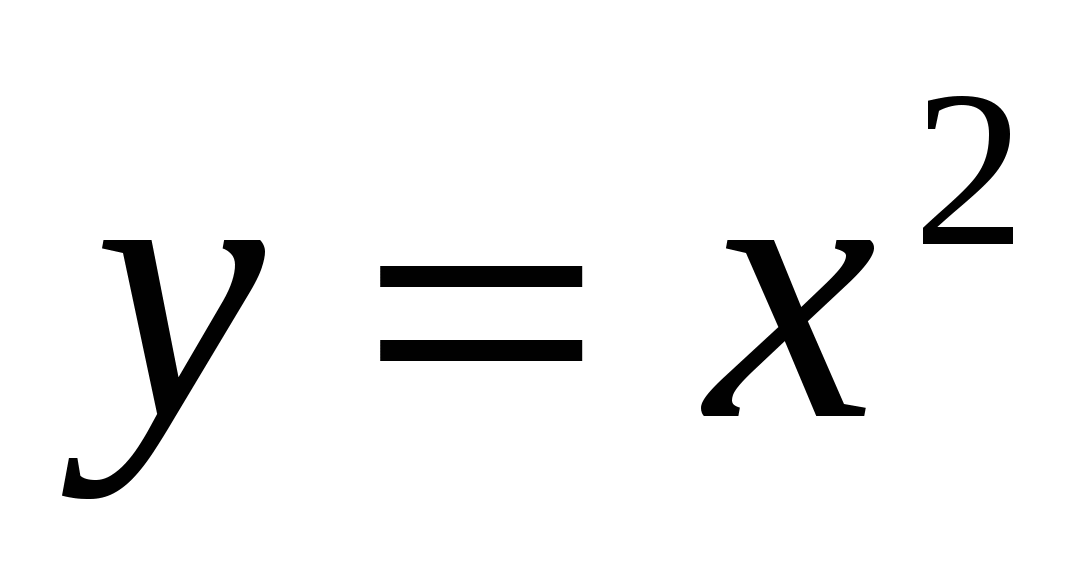 ,
, 
Oy
18
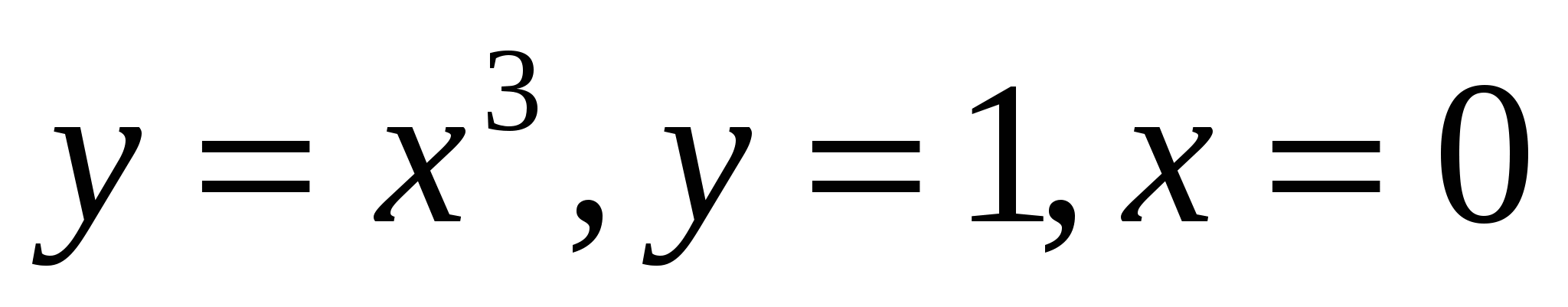
Oy
4
![]()
Oy
19
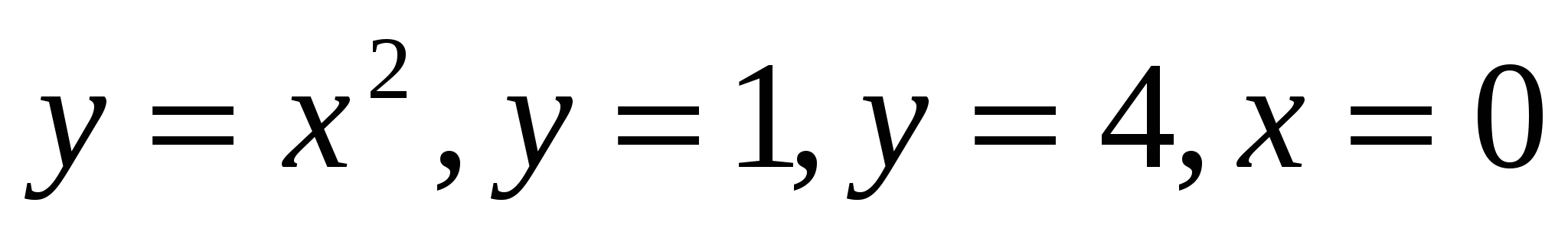
Oy
5

Ox
20
![]()
Oy
6
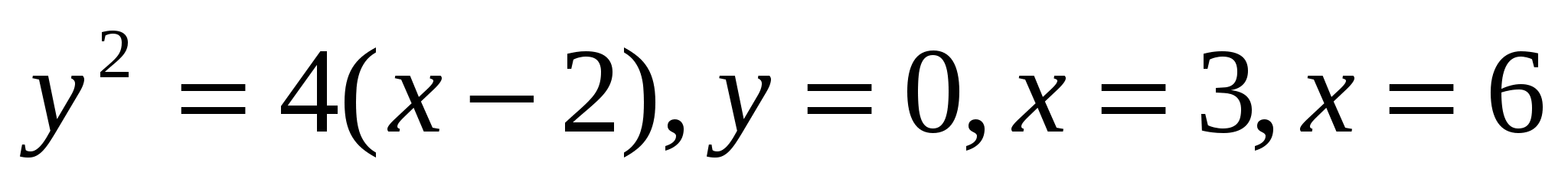
Ox
21
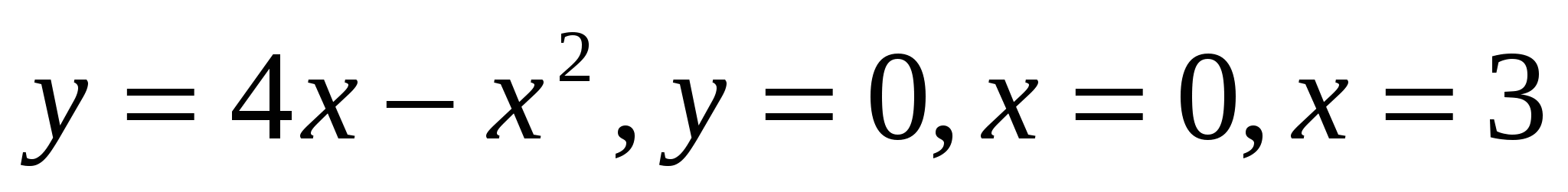
Ox
7
![]() ,
, 
Ox
22
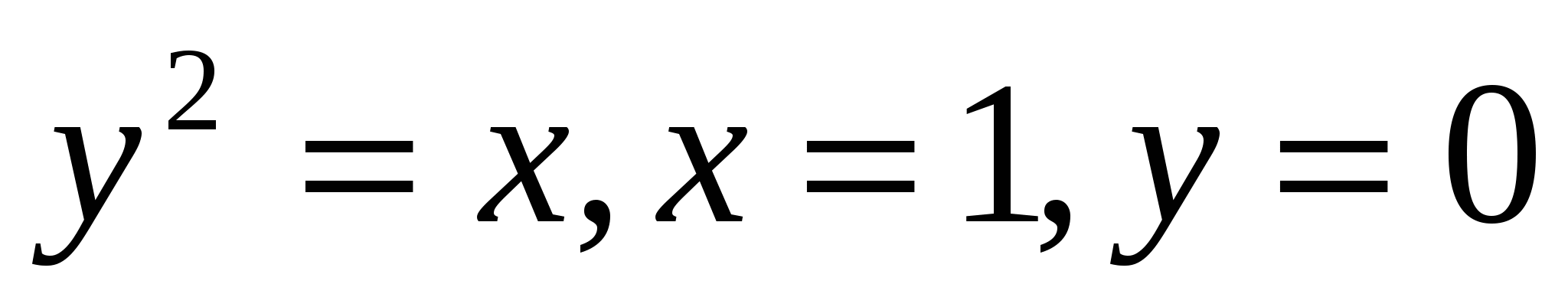
Ox
8
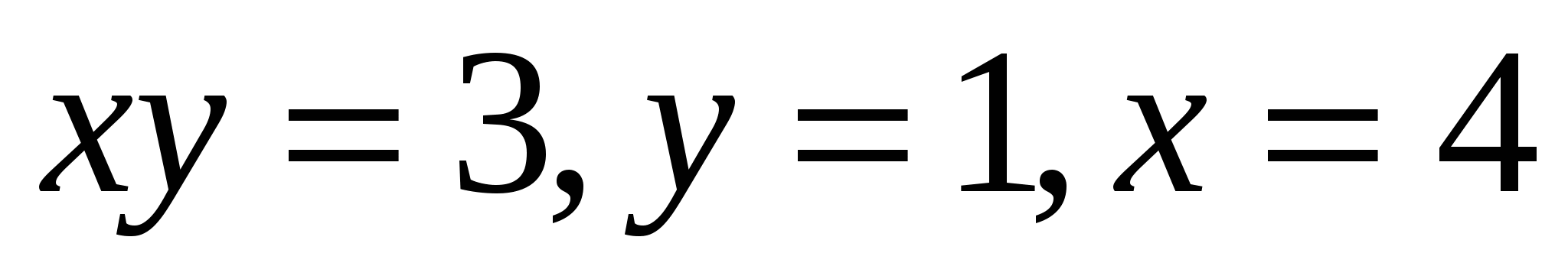
Oy
23
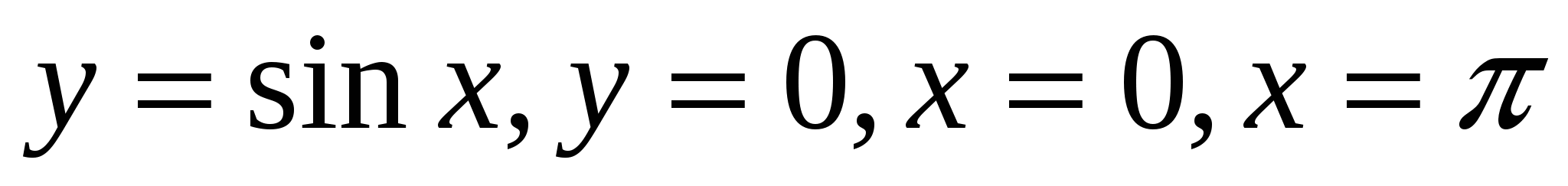
Ox
9
 ,
, 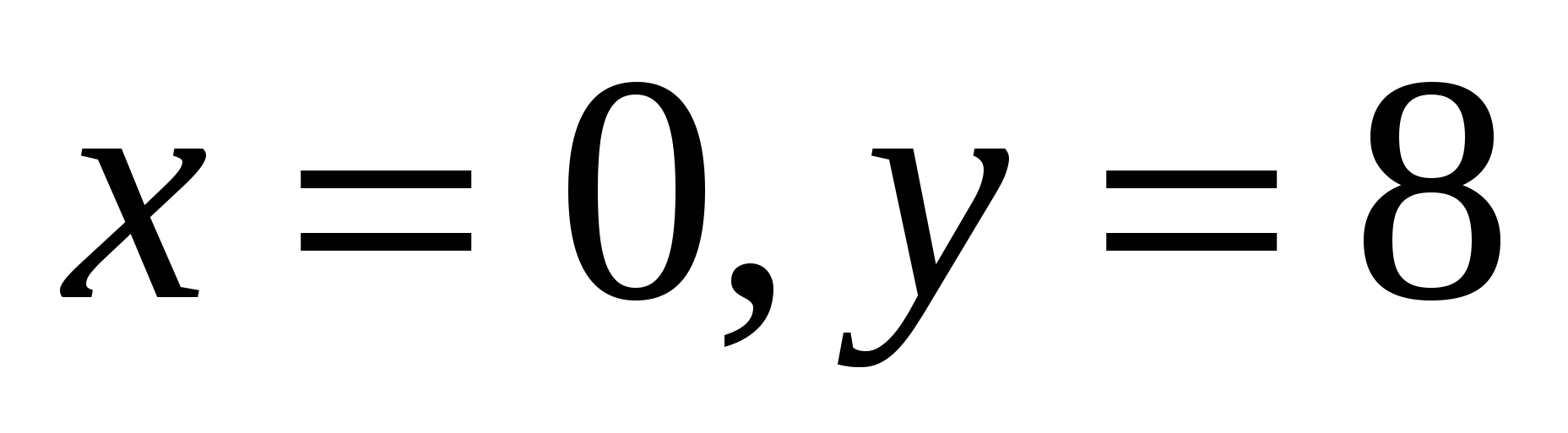
Ox
24
![]()
Ox
10
![]()
Oy
25
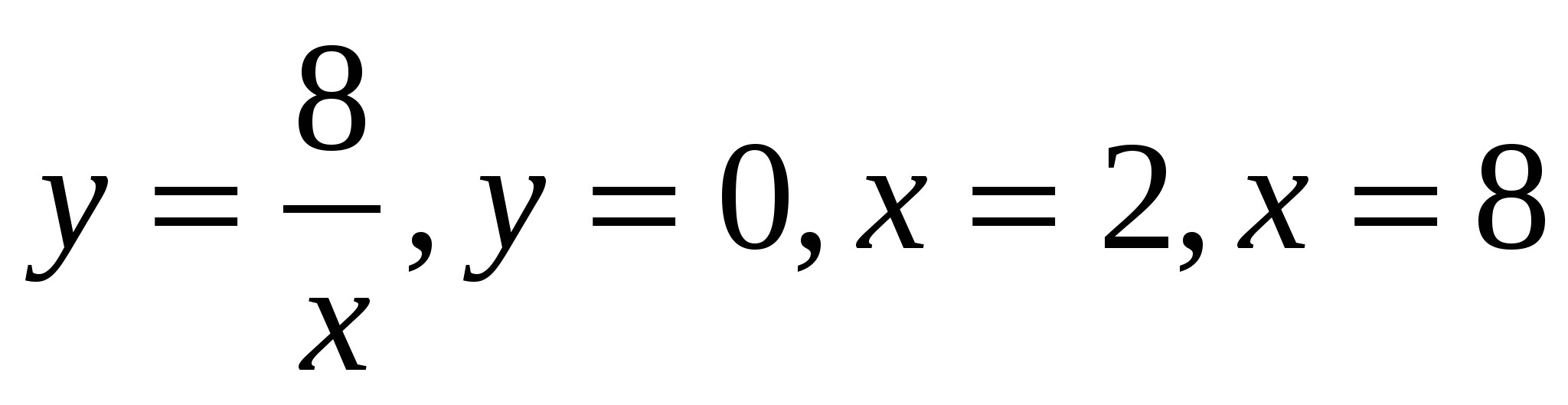
Ox
11

Ox
26
![]()
Ox
12
![]()
Oy
27

Ox
13
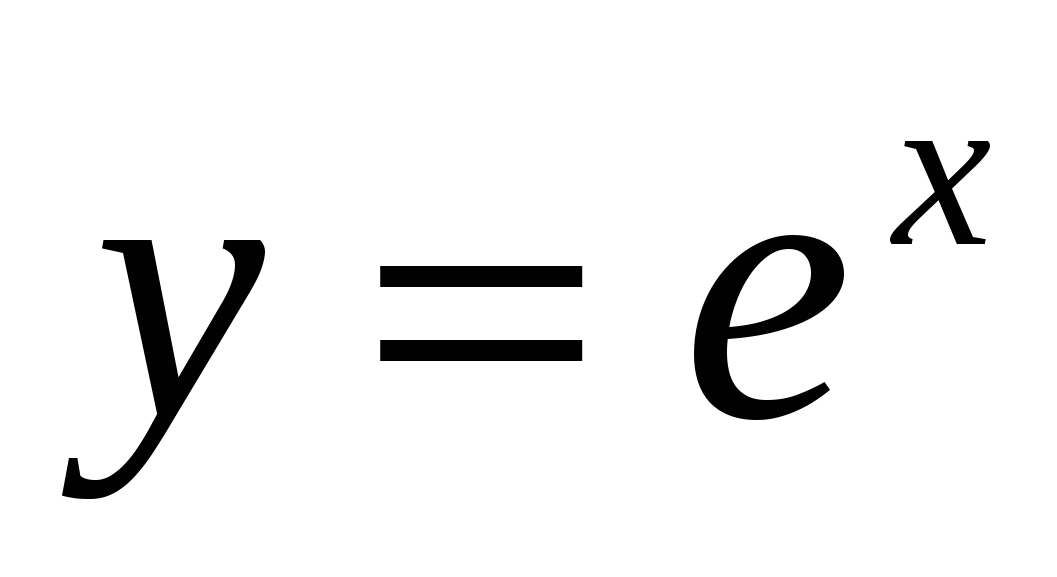 ,
, 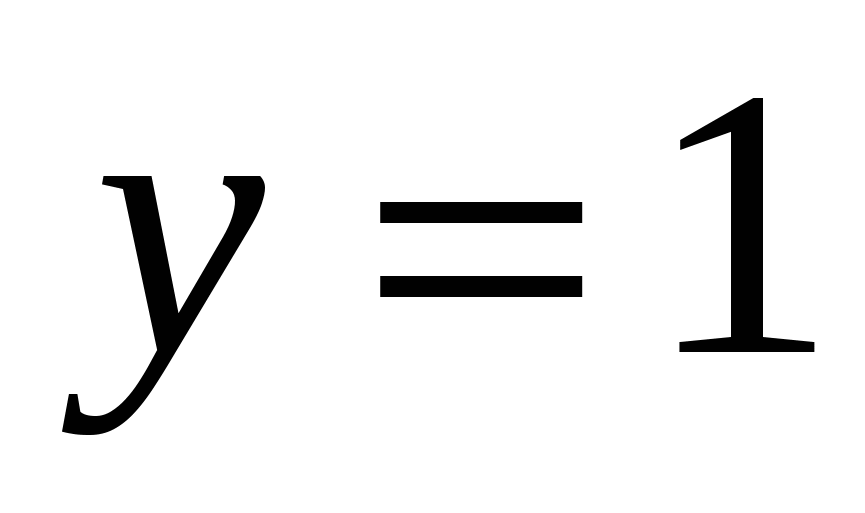 ,
, 
Ox
28
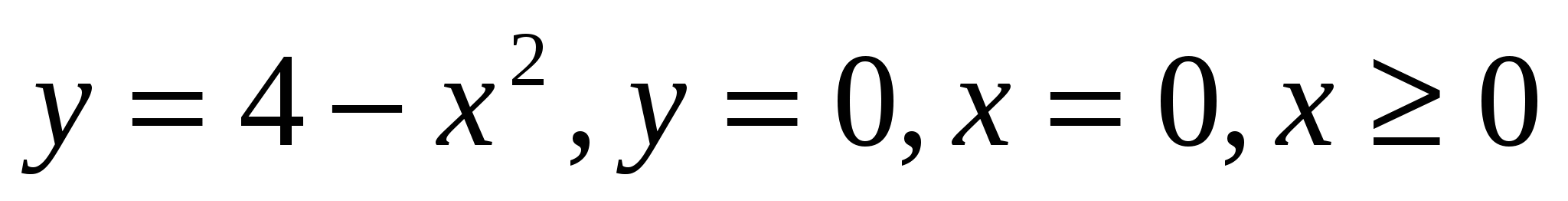
Ox
14
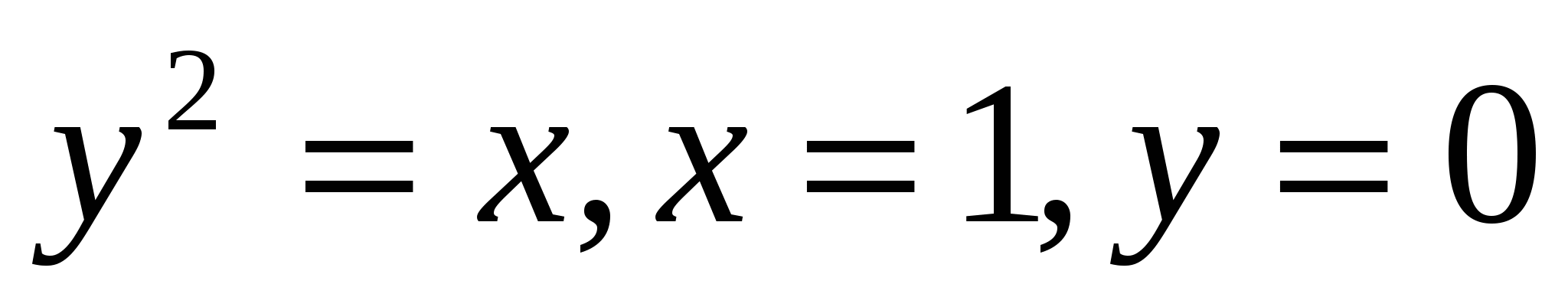
Oy
29
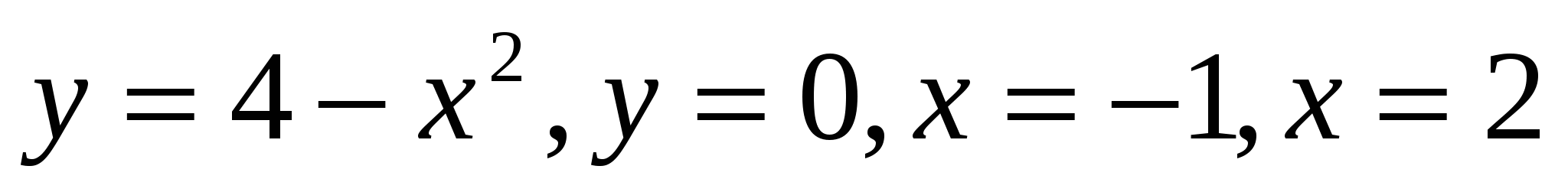
Ox
15
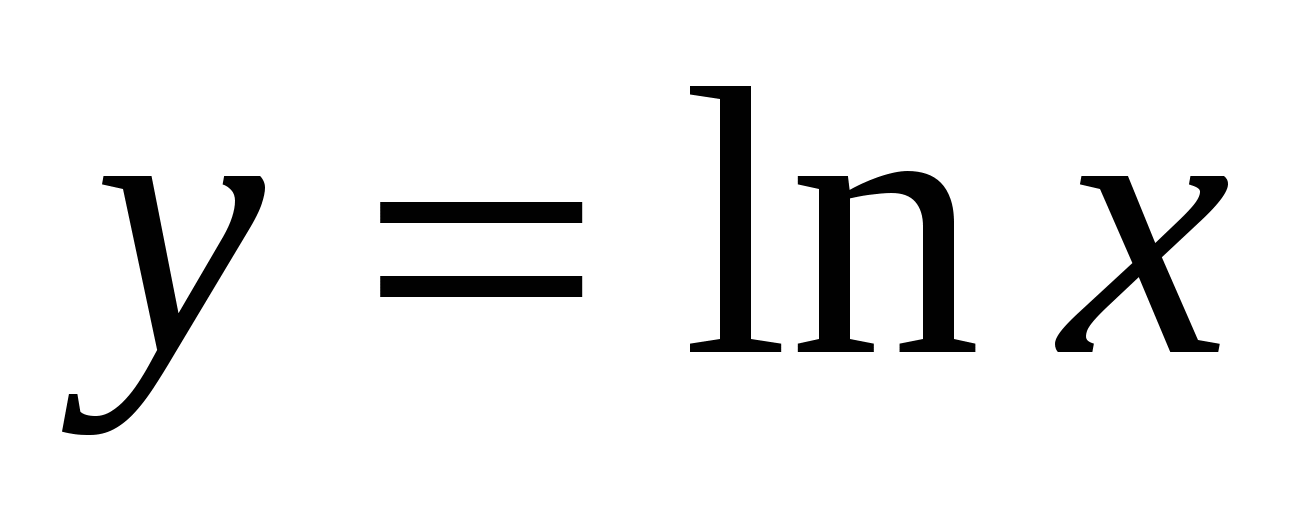 ,
, 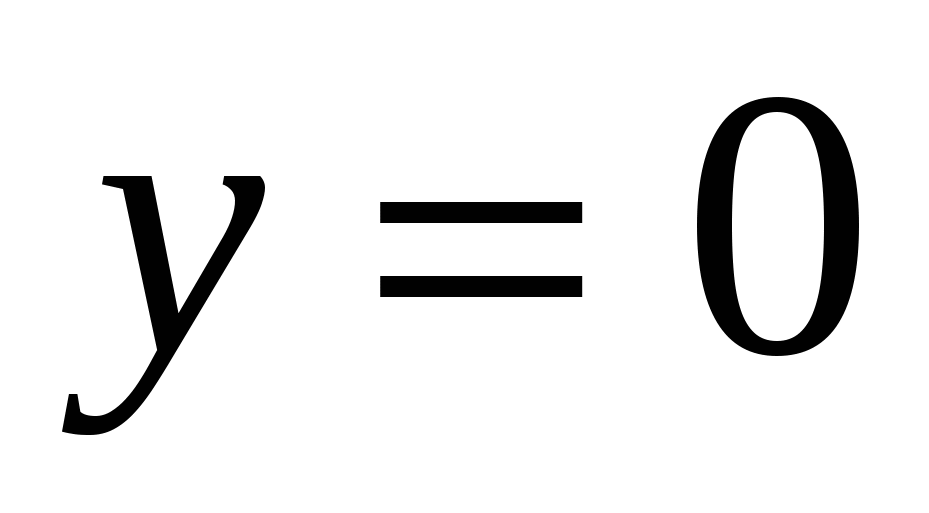 ,
, 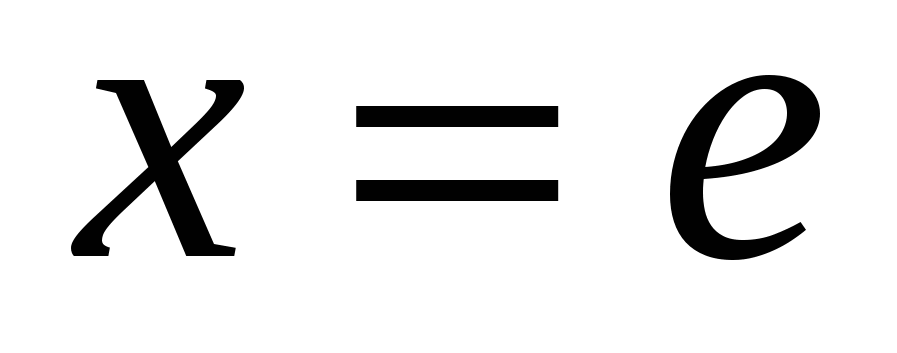
Ox
30
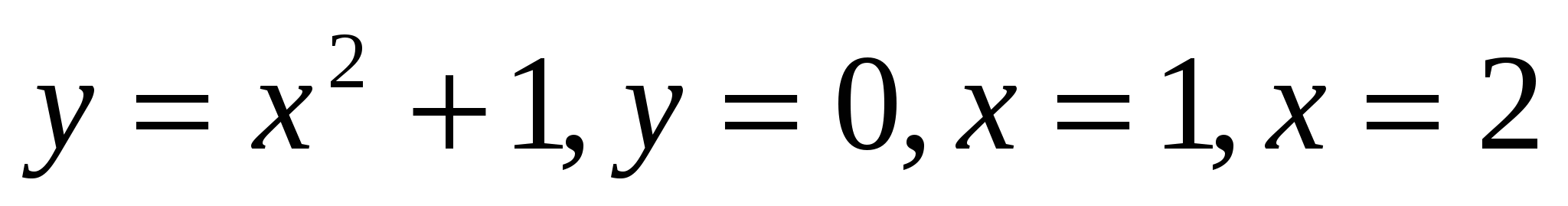
Ox
Раздел Б
Задача.
Вычислить объем тела, образованного вращением вокруг заданной оси области, ограниченной графиками заданных функций (таблица 5).
Таблица 5
№; вар
Заданные функции.
Задн
ная
ось.
№; вар
Заданные функции.
Задан-
ная
ось.
1
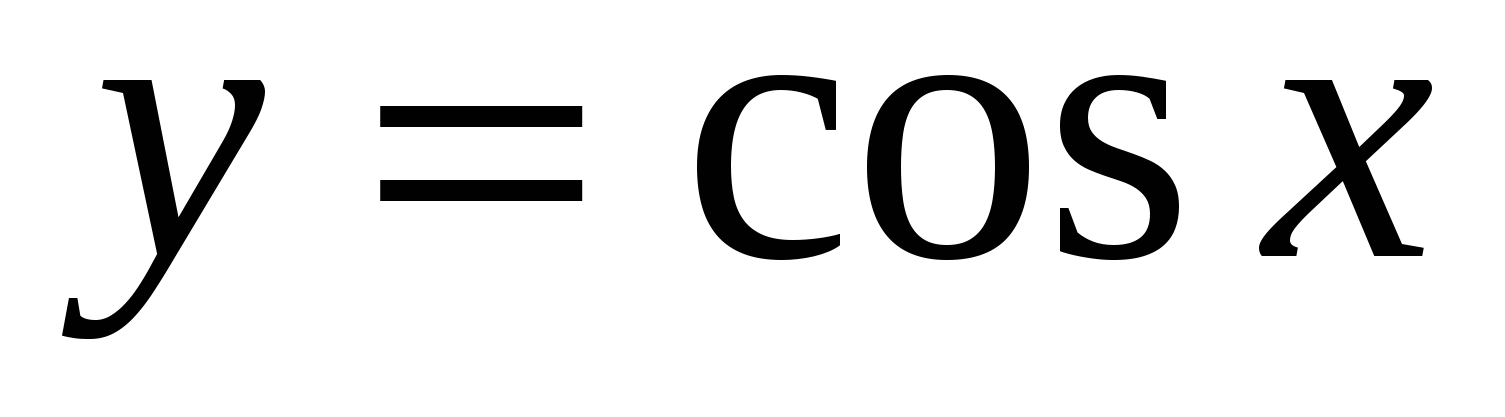 ,
,  ,
, 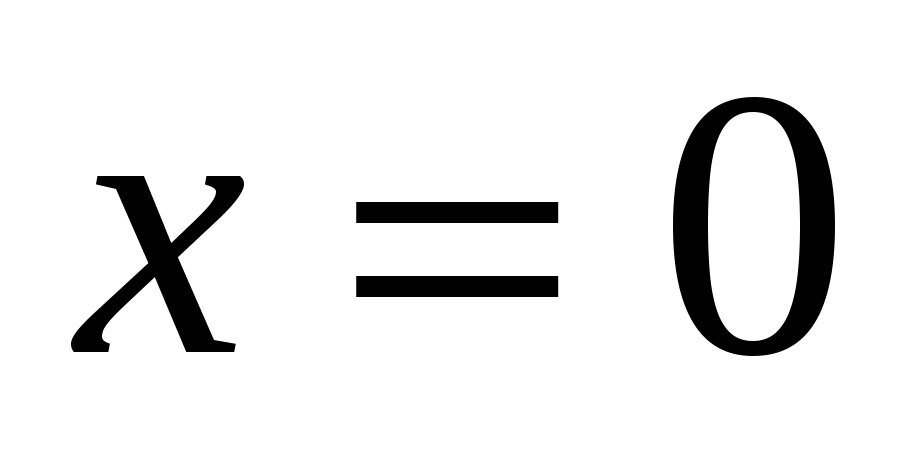
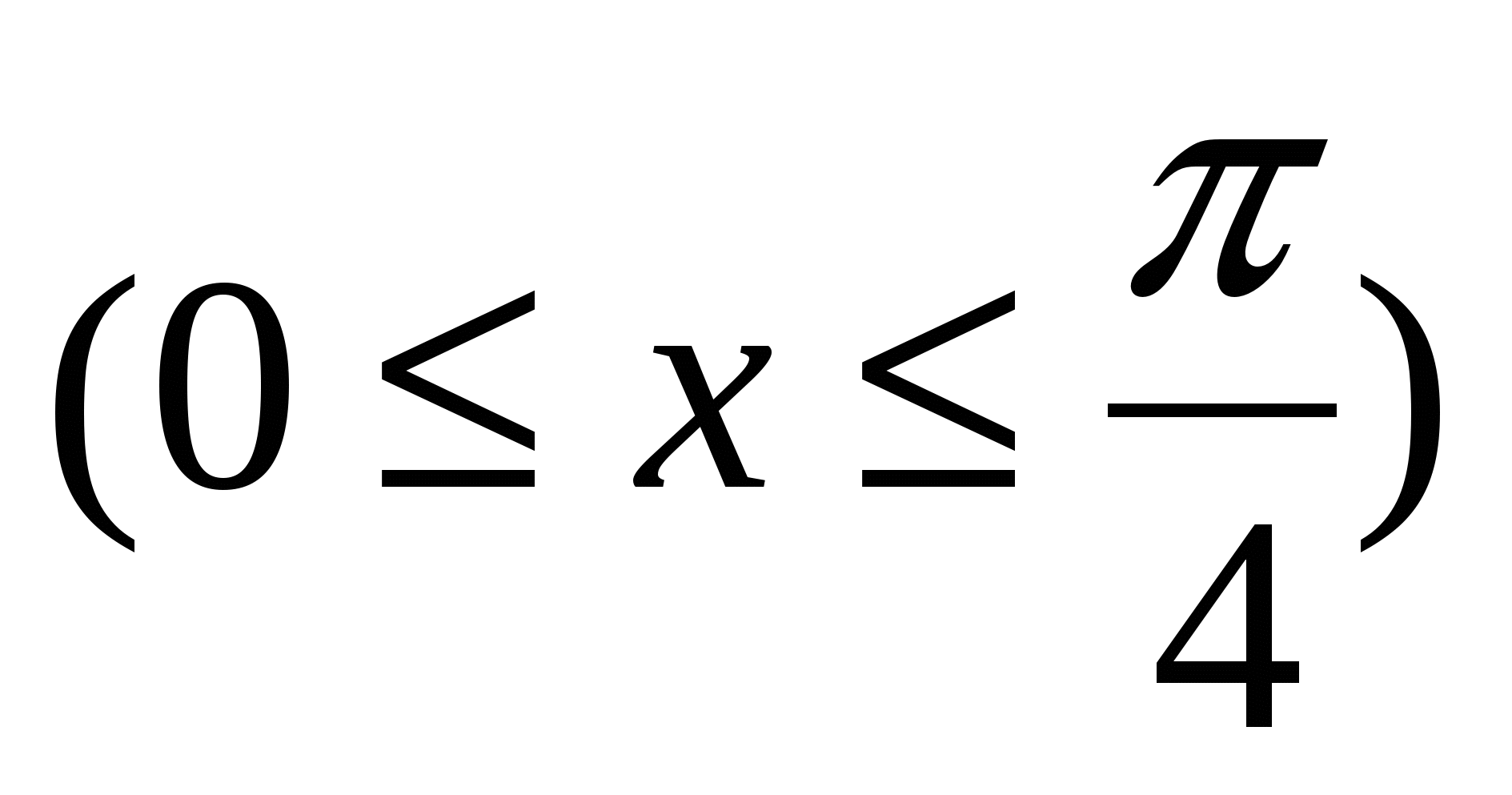
Ox
16
![]()
Ox
2

Оy
17
![]()
Ox
3
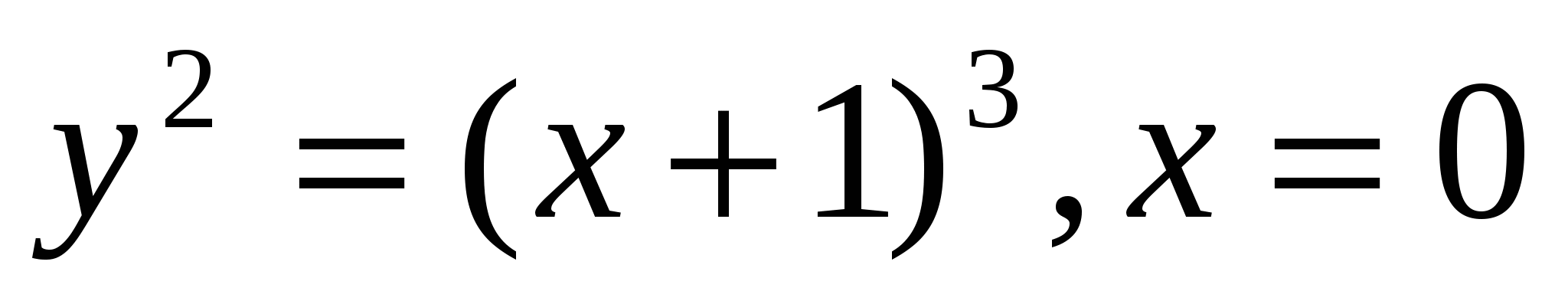
Oy
18
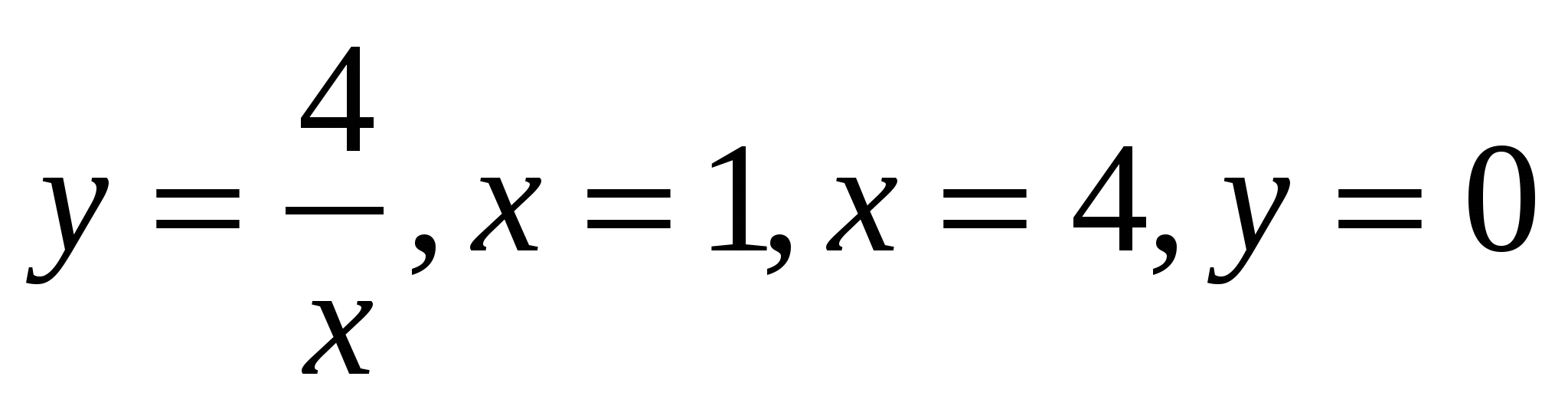
Oy
4
![]()
Oy
19
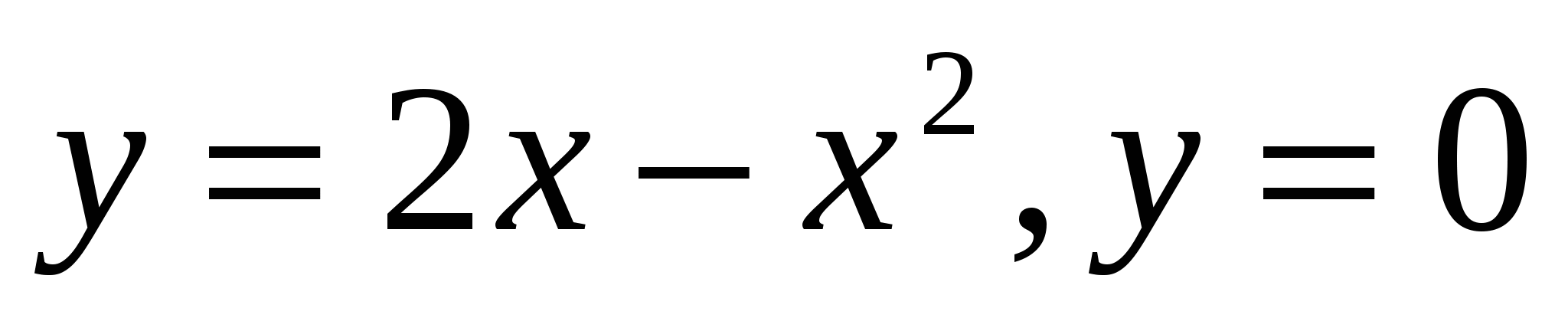
Oy
5
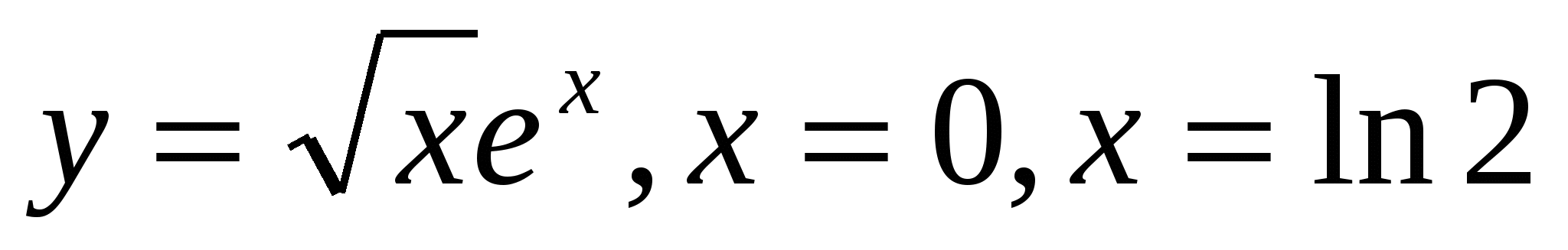
Ox
20
![]() ,
, 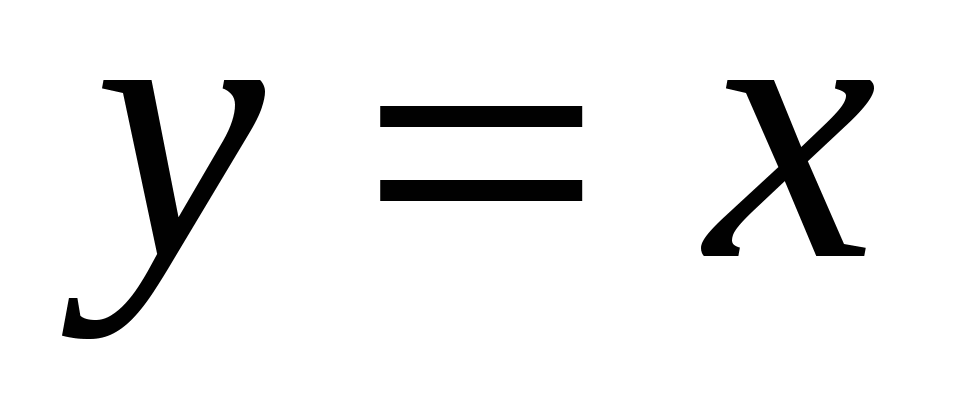
Ox
6

Ox
21
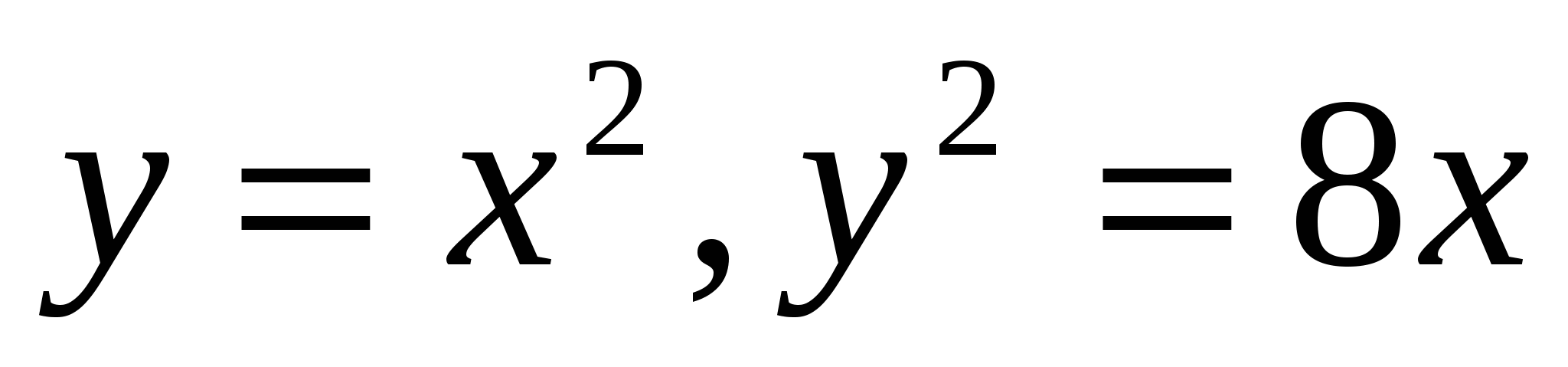
Ox
7

Ox
22

Ox
8
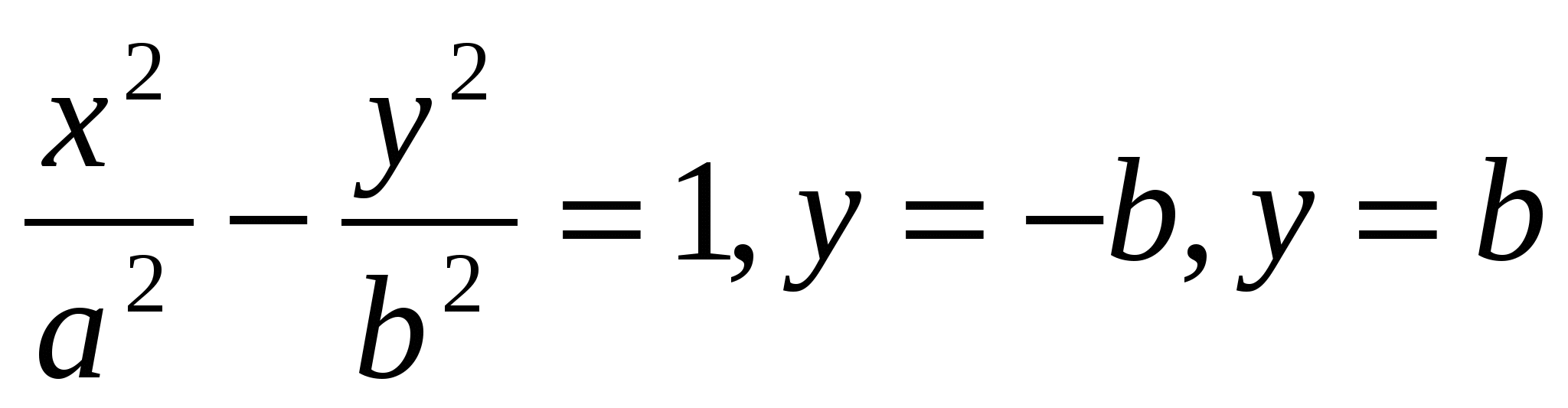
Oy
23
![]()
Oy
9
![]()
x=2
24
![]() ,
,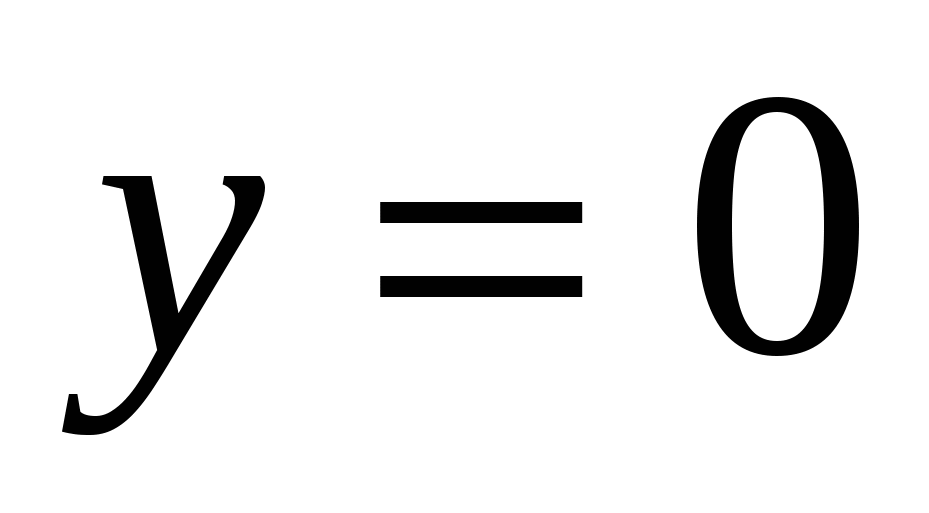 ,
,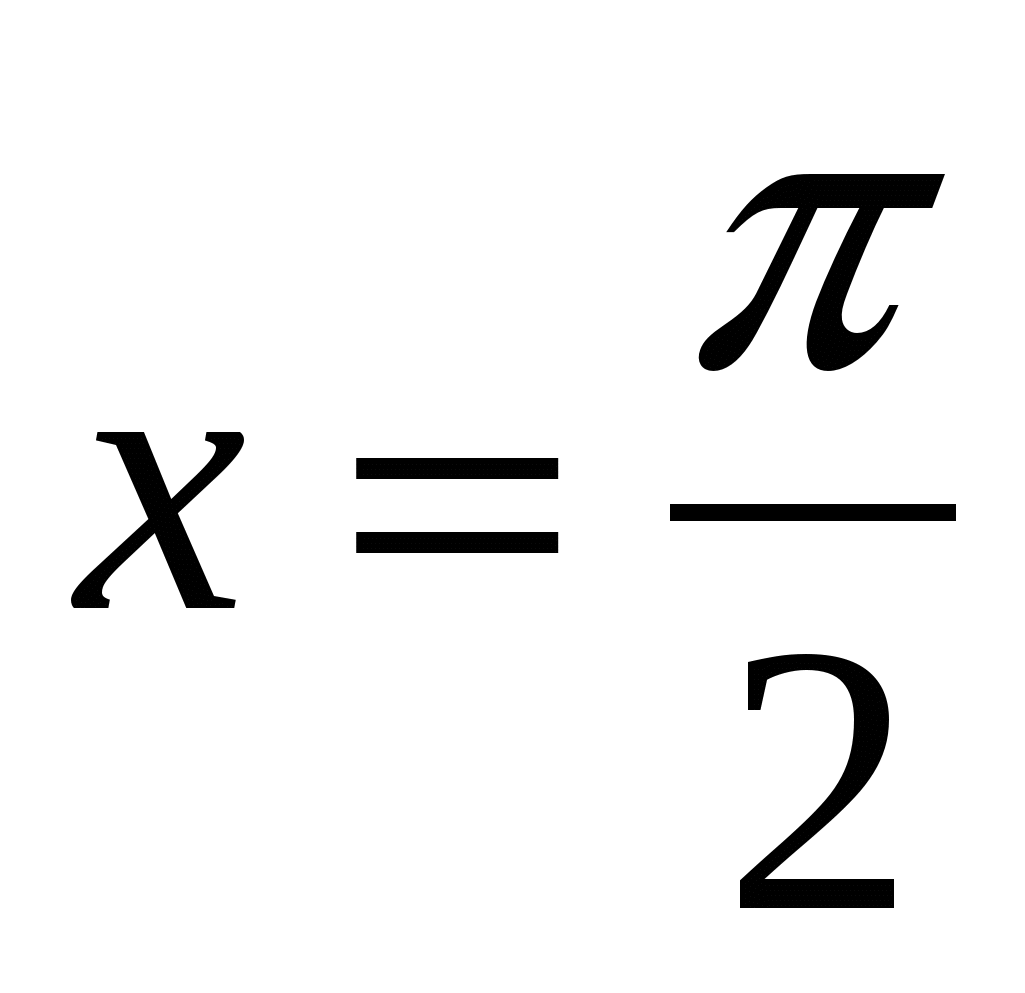

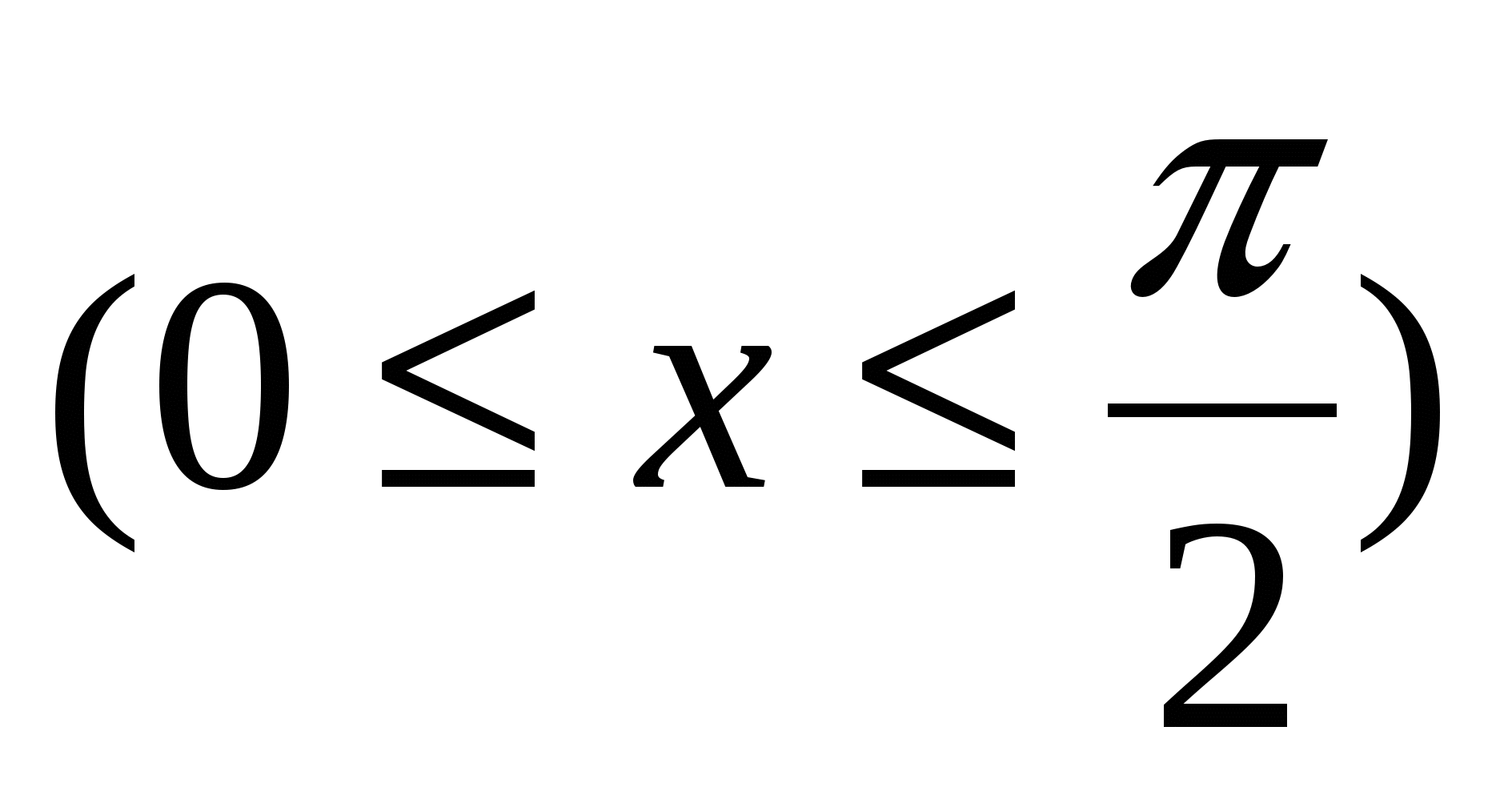
Ox
10
![]() при
при 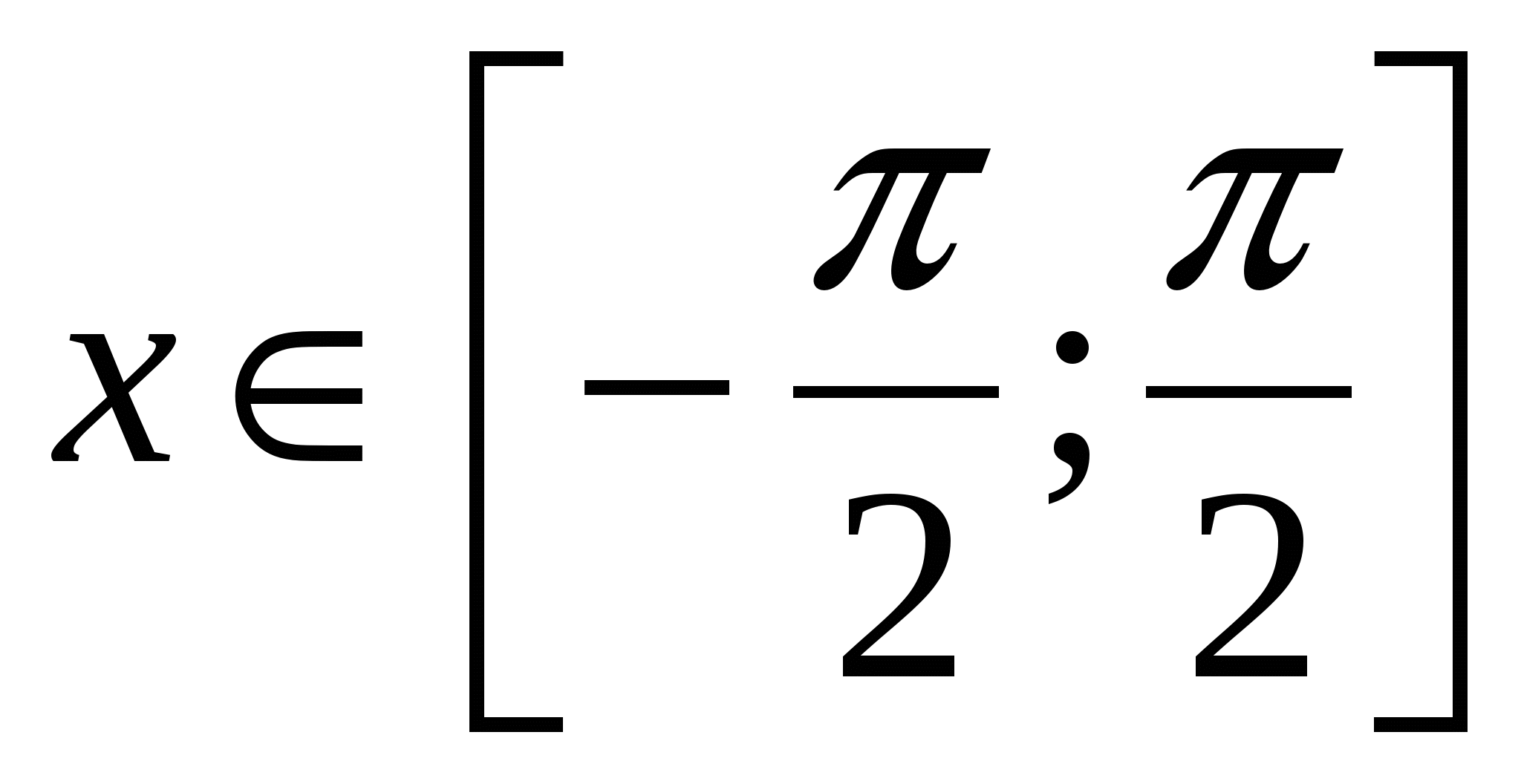
y=-1
25
![]() ,
, 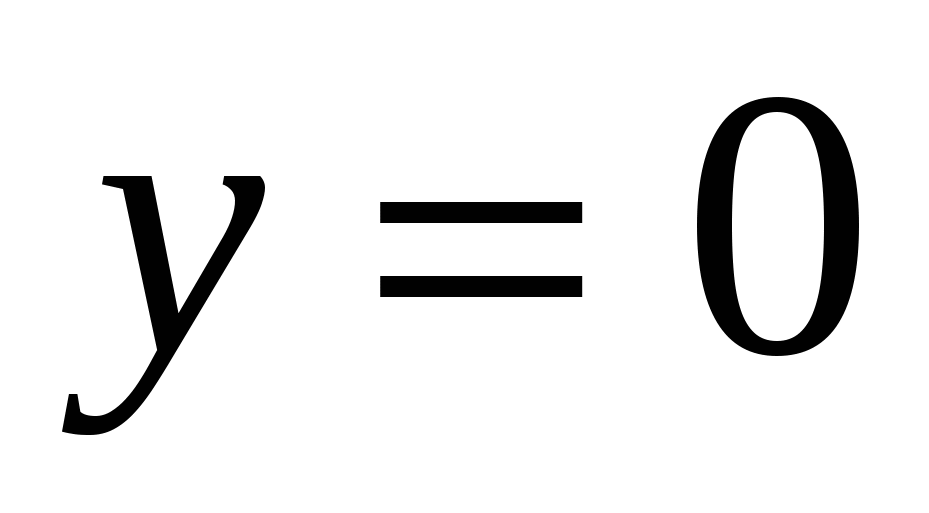
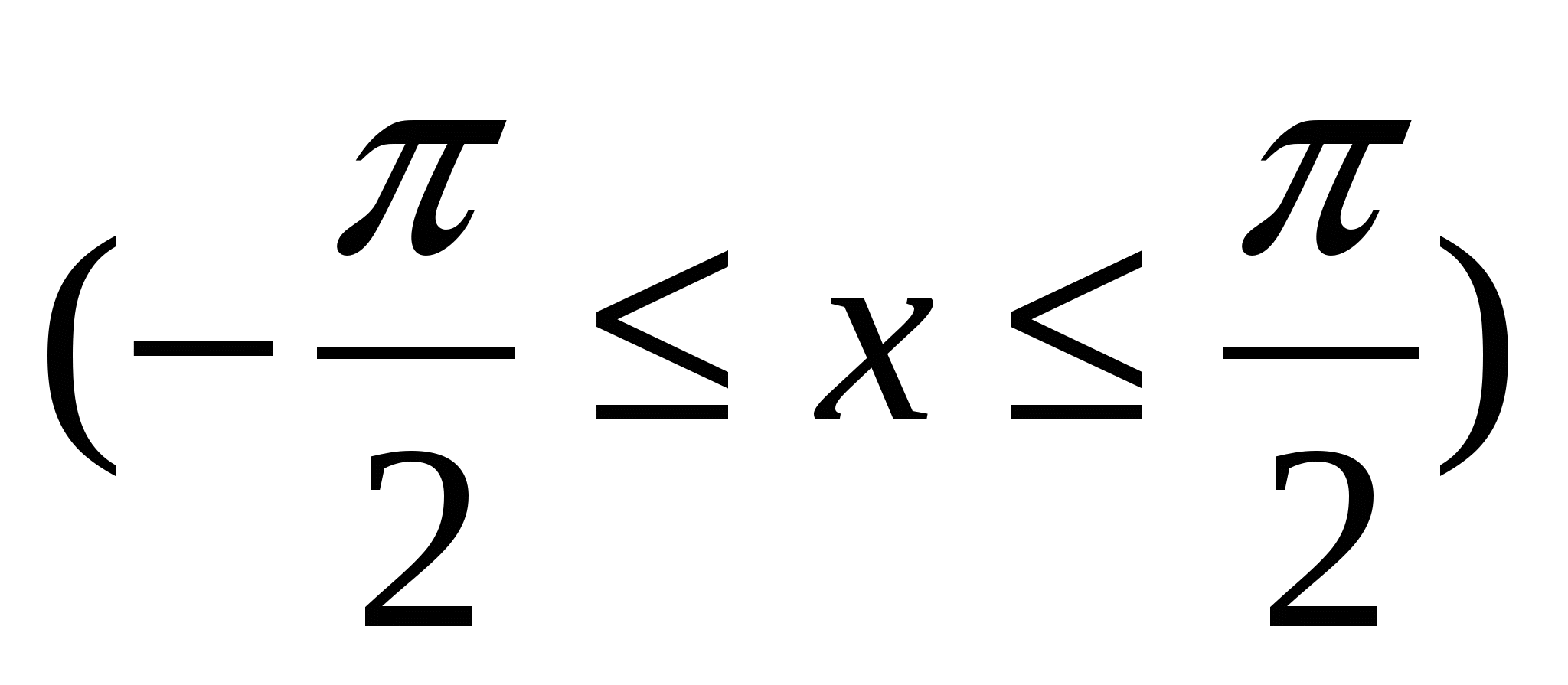
Ox
11
![]()
Oy
26
![]()
Oy
12
![]()
Ox
27
![]()
Oy
13
![]()
Oy
28
![]()
Oy
14
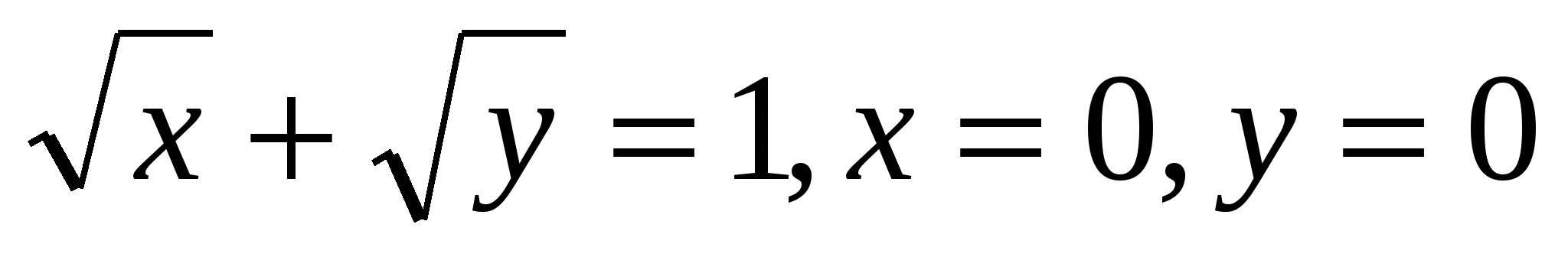
Oy
29
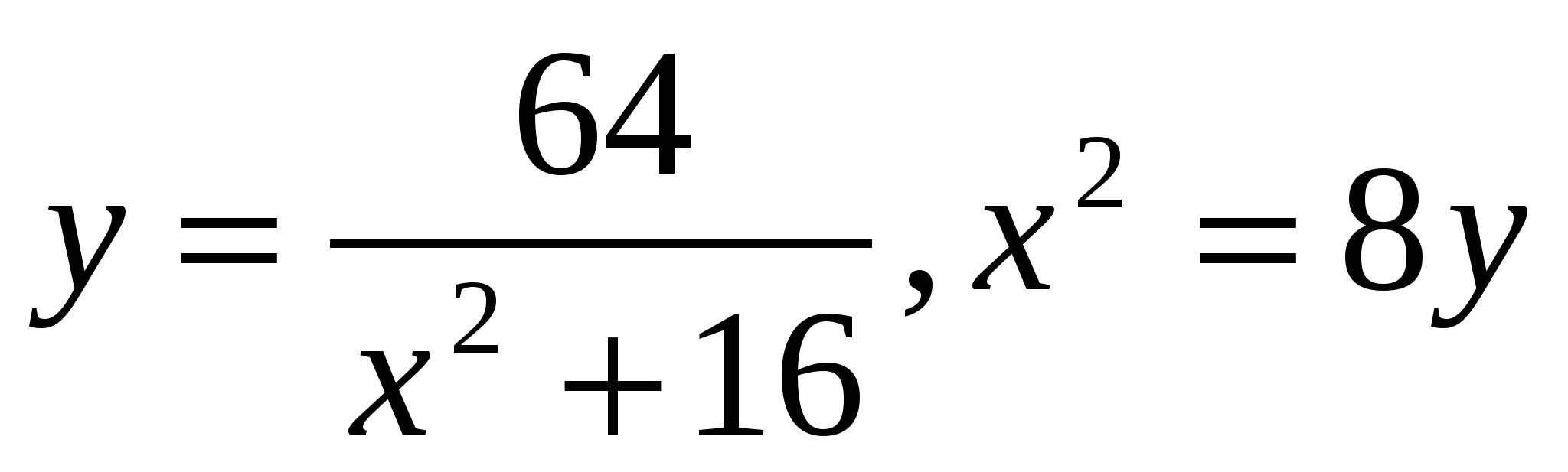
Ox
15
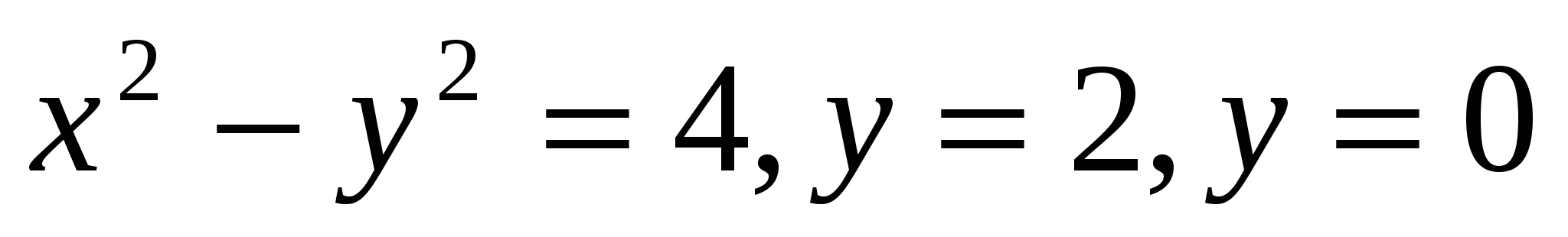
Ox
30
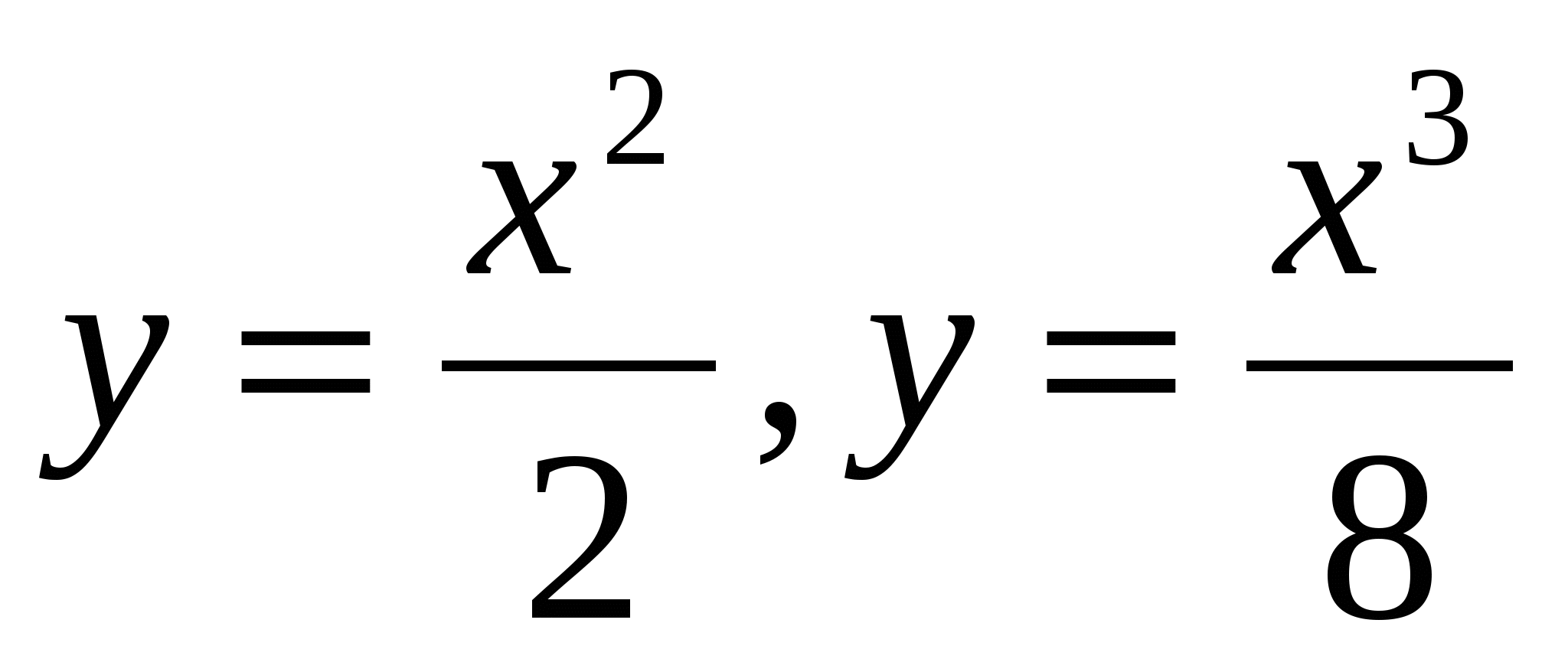
Ox
2. Применения определенного интеграла к решению физических и технических задач
2.1. Путь, пройденный телом
Из школьного курса известно, что путь, пройденный телом, перемещающимся со скоростью 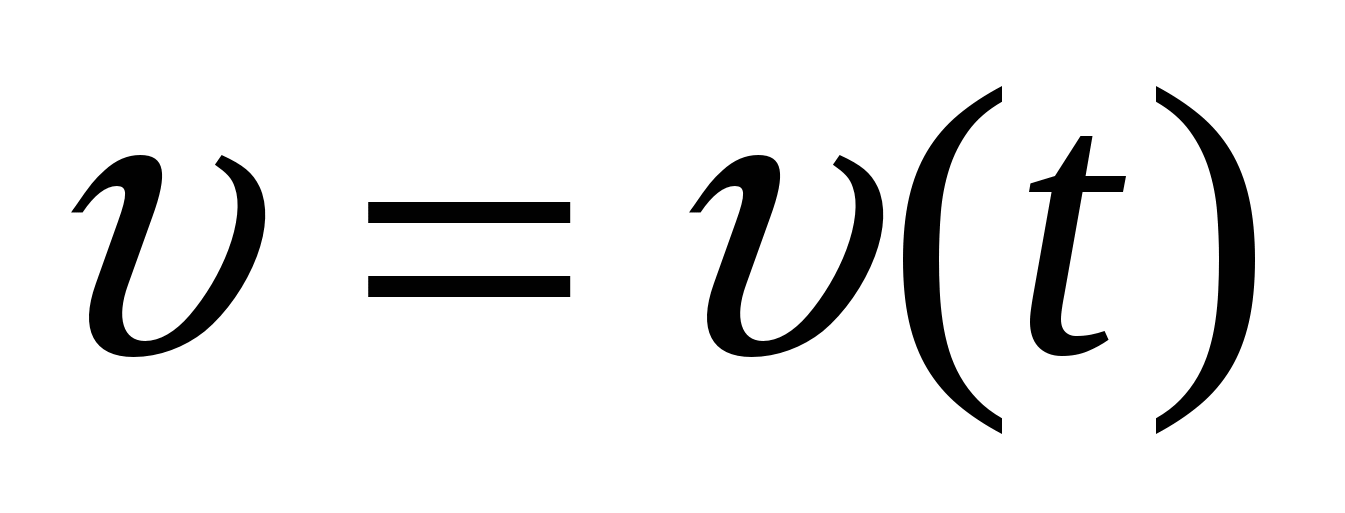 ,за промежуток времени
,за промежуток времени 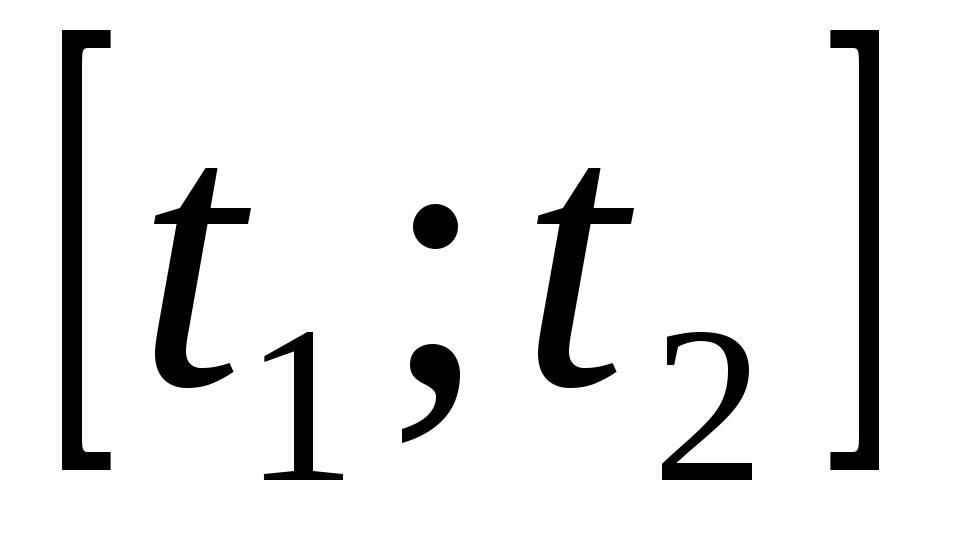 , выражается интегралом
, выражается интегралом
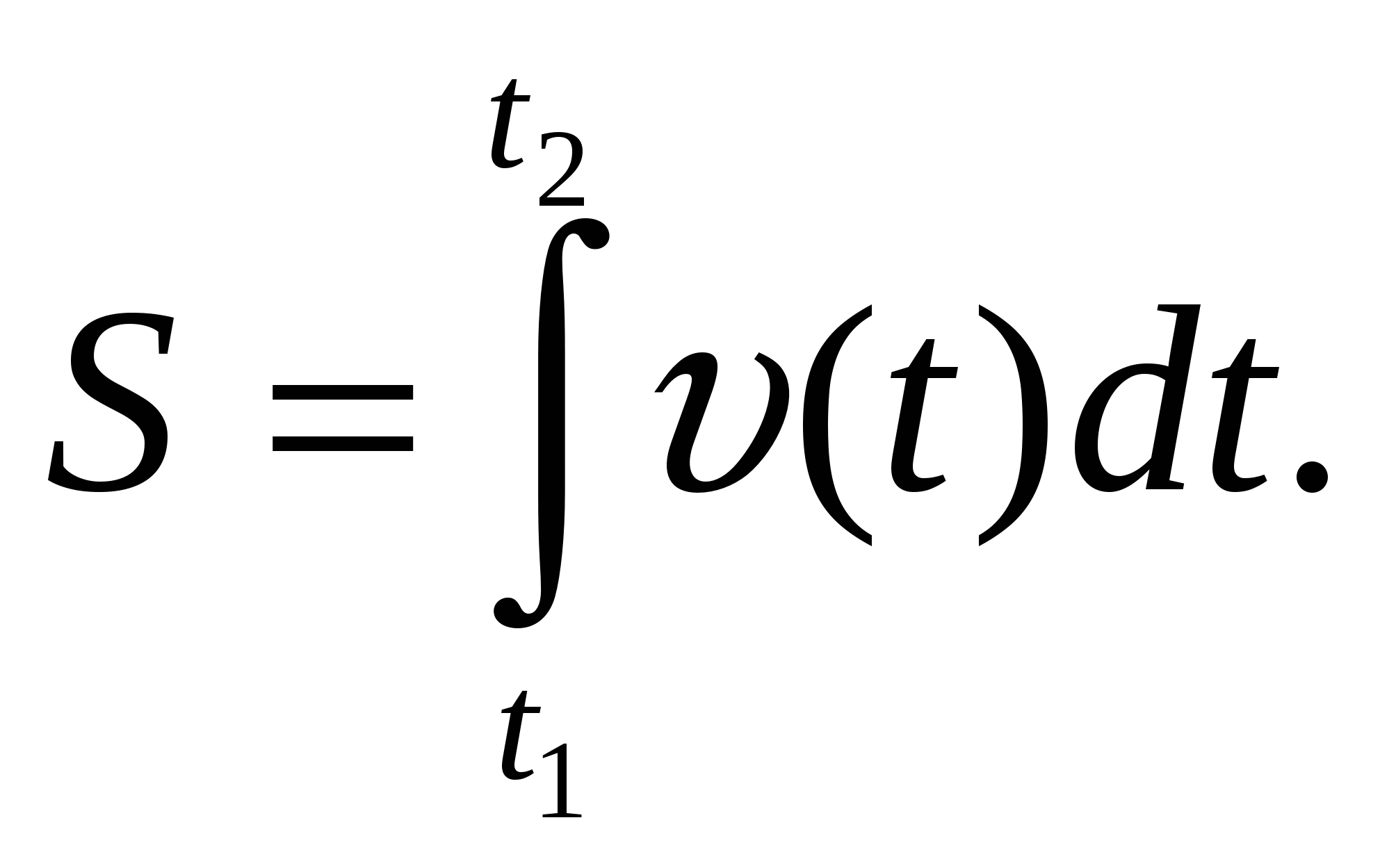 (2.1)
(2.1)
Пример 2.1. Автобус начинает двигаться с ускорением 1м/с2. Какой путь пройдет автобус за 12 секунд от начала движения?
Решение:
Скорость движения автобуса выражается формулой  м/с. Согласно формуле (2.1) находим путь, пройденный автобусом за время от
м/с. Согласно формуле (2.1) находим путь, пройденный автобусом за время от 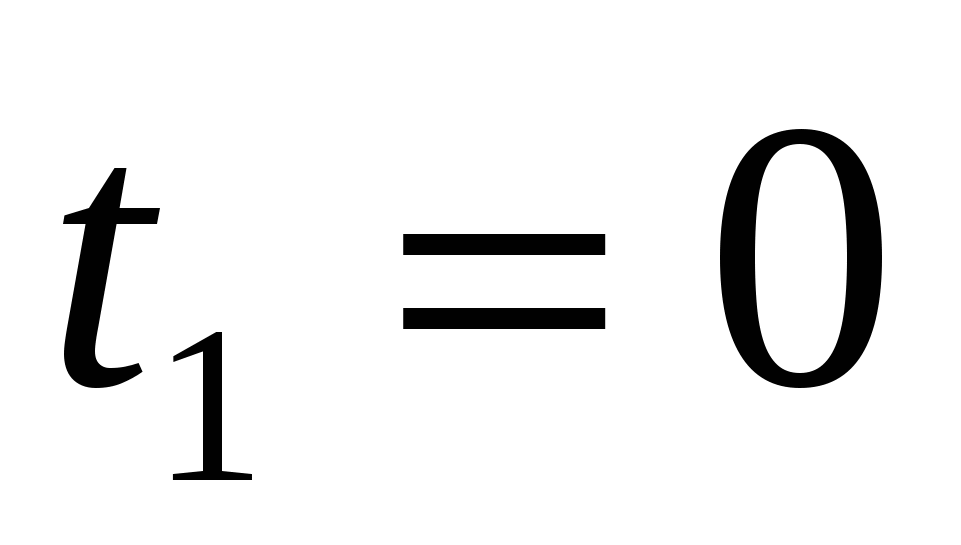 до
до  сек:
сек: 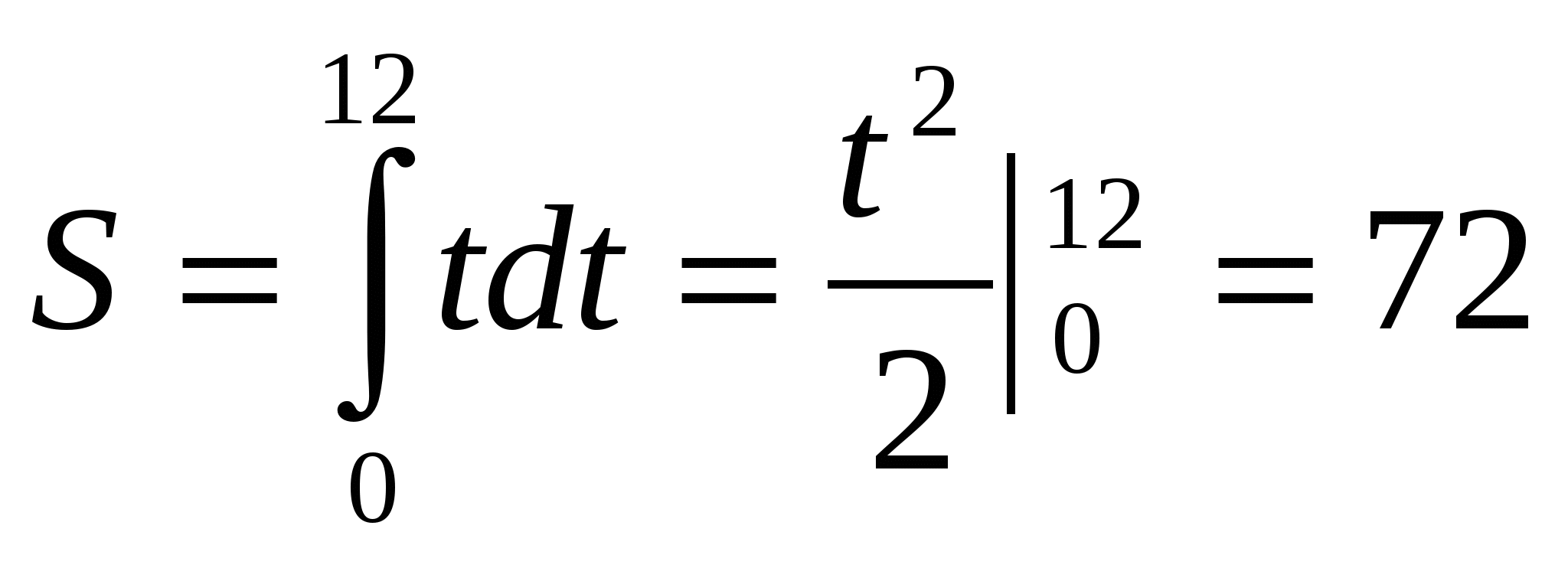 м.
м.
2.2. Работа переменной силы
Определенный интеграл широко применяется не только при вычислении различных геометрических величин, но и при решении ряда физических и технических задач. Так, например, известно, что работа  , совершаемая переменной силой
, совершаемая переменной силой ![]() на пути от точки
на пути от точки 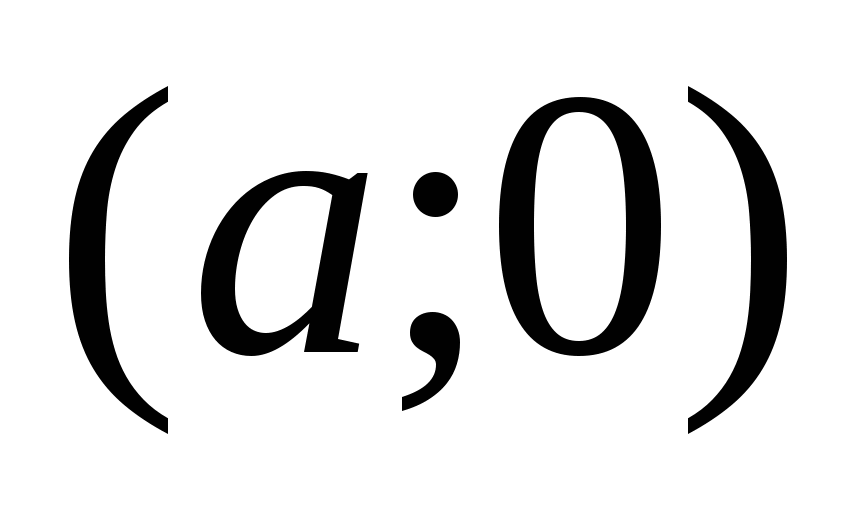 до точки
до точки  , вычисляется по
, вычисляется по
формуле
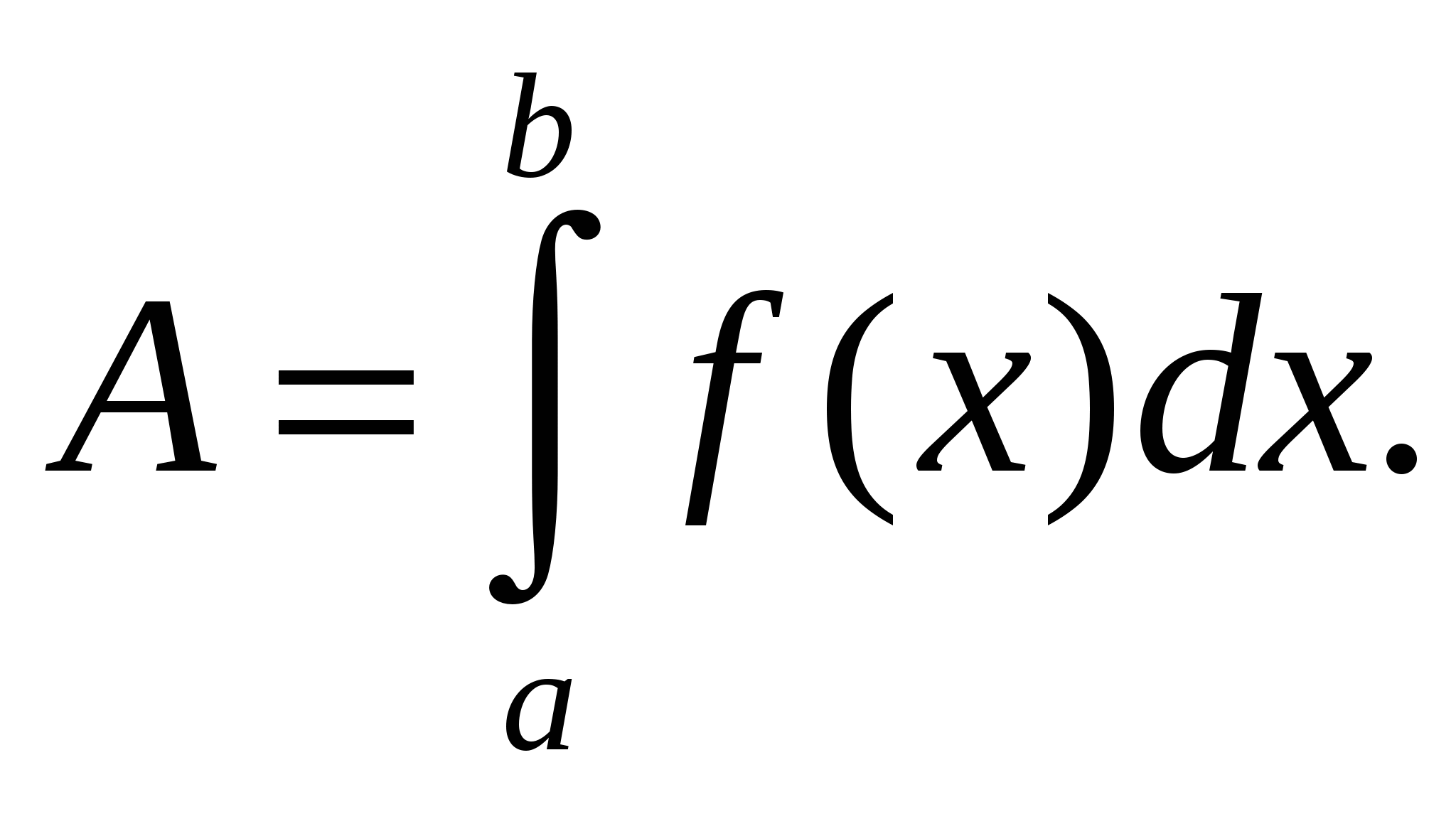 (2.2)
(2.2)
Пример 2.2. Какую работу надо совершить, чтобы растянуть пружину на 0,05 м, если известно, что для ее растягивания на 0,01 м нужна сила в 1  ?
?
Решение:
Согласно закону Гука сила 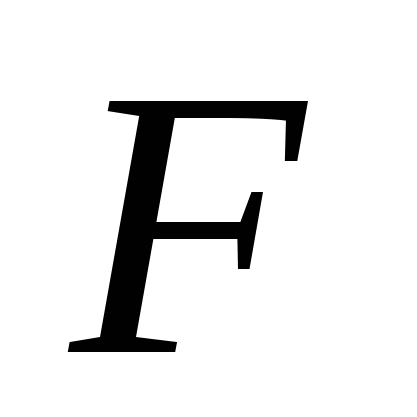 , растягивающая или сжимающая пружину на
, растягивающая или сжимающая пружину на  м, пропорциональна этому растяжению или сжатию, т. е.
м, пропорциональна этому растяжению или сжатию, т. е. 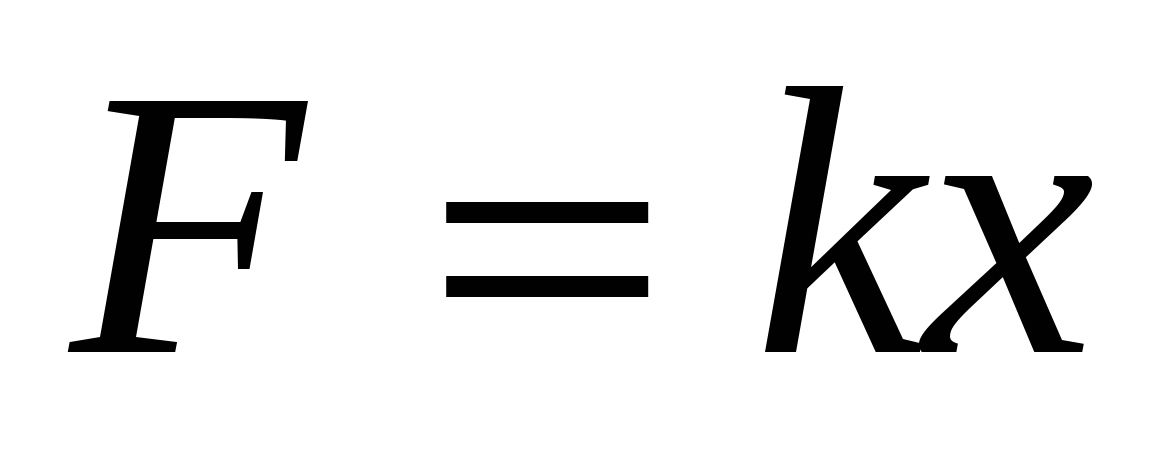 , где
, где 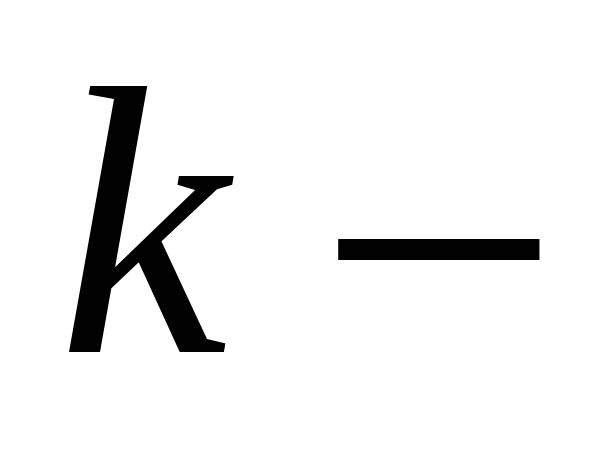 коэффициент пропорциональности. Из условия задачи известно, что для растяжения пружины на
коэффициент пропорциональности. Из условия задачи известно, что для растяжения пружины на 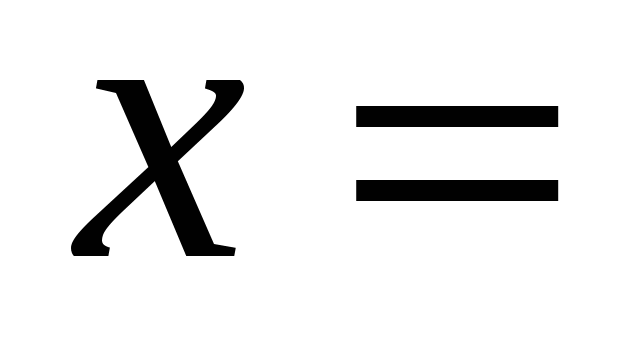 0,01м требуется сила
0,01м требуется сила ![]() Поэтому
Поэтому  , откуда
, откуда 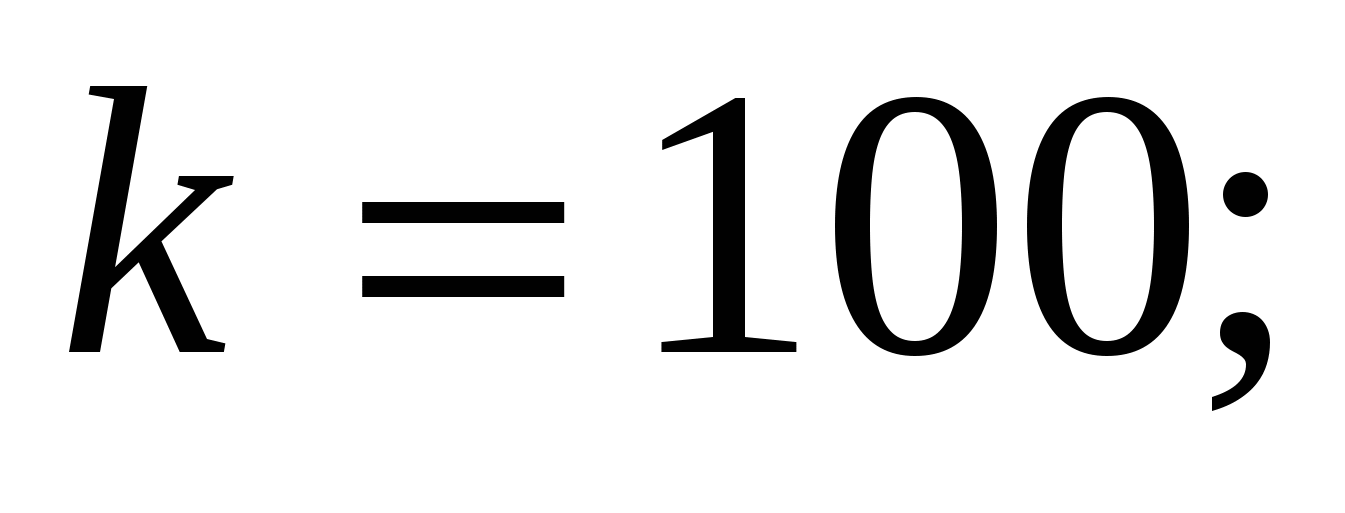 следовательно,
следовательно, 
В задаче требуется найти работу, совершаемую при растяжении пружины на 0,05м из состояния покоя, поэтому переменная  изменяется от
изменяется от 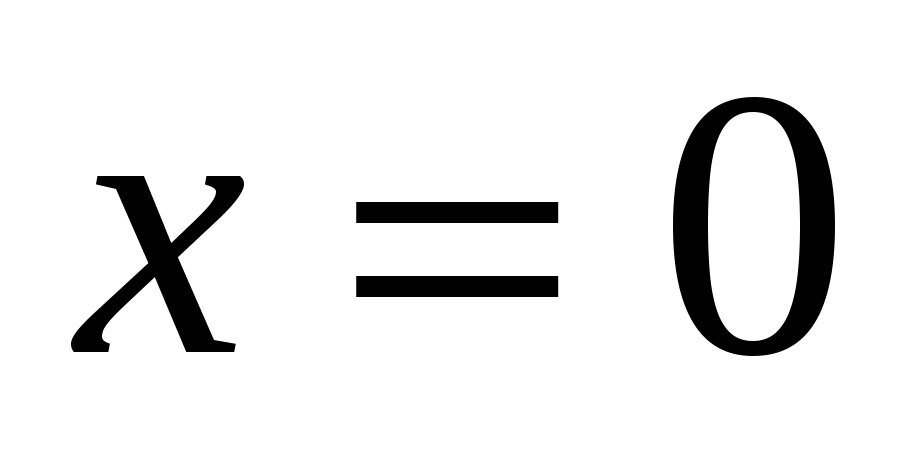 до
до 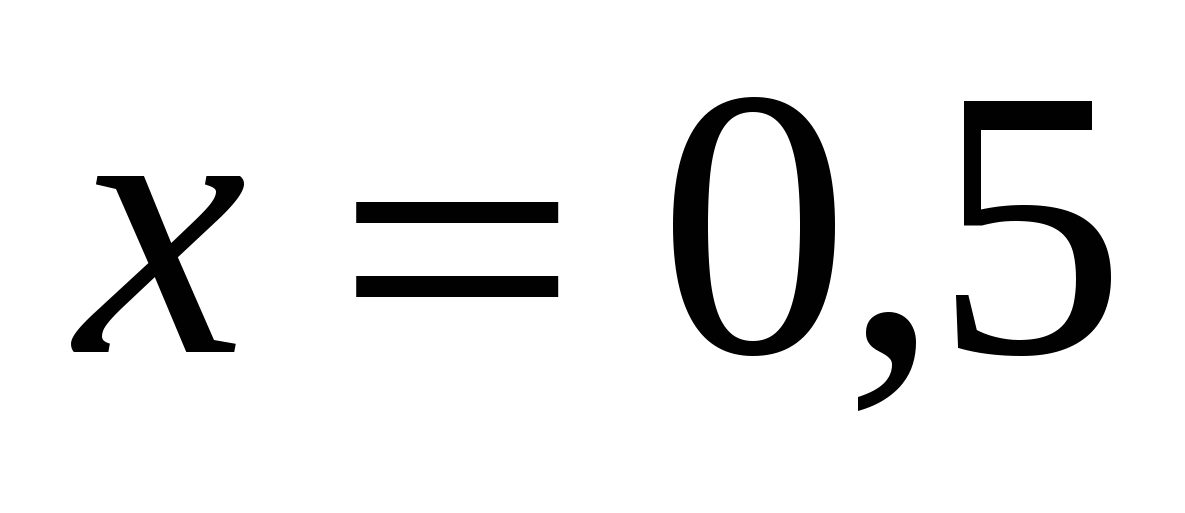 . Таким образом, подставив в формуле (2.2)
. Таким образом, подставив в формуле (2.2)  , найдем искомую работу
, найдем искомую работу ![]()
2.3. Вычисление силы давления жидкости
Согласно закону Паскаля величина силы 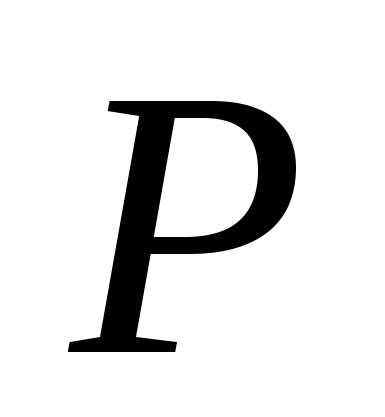 давления жидкости в ньютонах на горизонтальную площадку вычисляется по формуле
давления жидкости в ньютонах на горизонтальную площадку вычисляется по формуле
![]() , (2.3)
, (2.3)
где 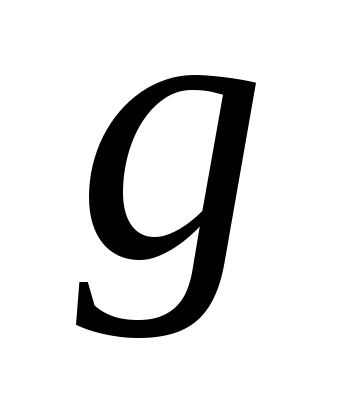 -ускорение свободного падения в м/с2,
-ускорение свободного падения в м/с2,  -плотность жидкости в кг/м2,
-плотность жидкости в кг/м2, ![]() -площадь площадки в м2,
-площадь площадки в м2, 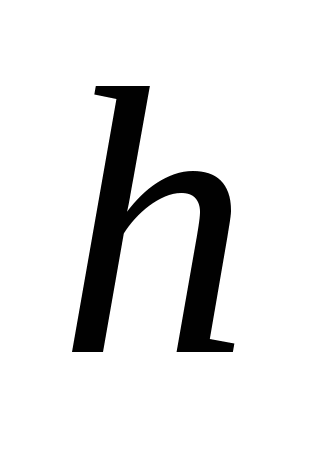 -глубина погружения площадки в м.
-глубина погружения площадки в м.
Если же площадка погружена в жидкость не горизонтально, то формула (2.3) неприменима, так как в этом случае сила 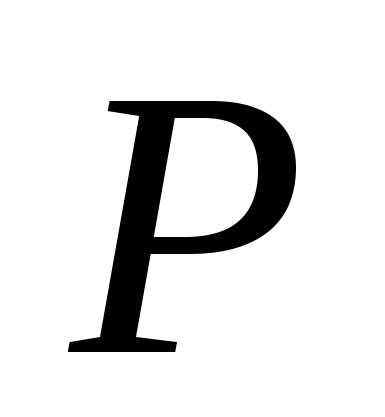 давления жидкости изменяется с глубиной. Рассмотрим задачу вычисления силы давления жидкости на вертикальную площадку.
давления жидкости изменяется с глубиной. Рассмотрим задачу вычисления силы давления жидкости на вертикальную площадку.
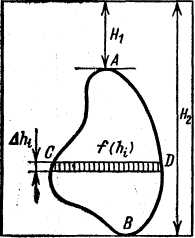
Задача. Пусть пластинка произвольной формы погружена вертикально в жидкость плотностью  так, что расстояние от поверхности жидкости до верхней точки
так, что расстояние от поверхности жидкости до верхней точки  пластинки равно
пластинки равно ![]() , а до ее нижней точки
, а до ее нижней точки ![]() равна
равна 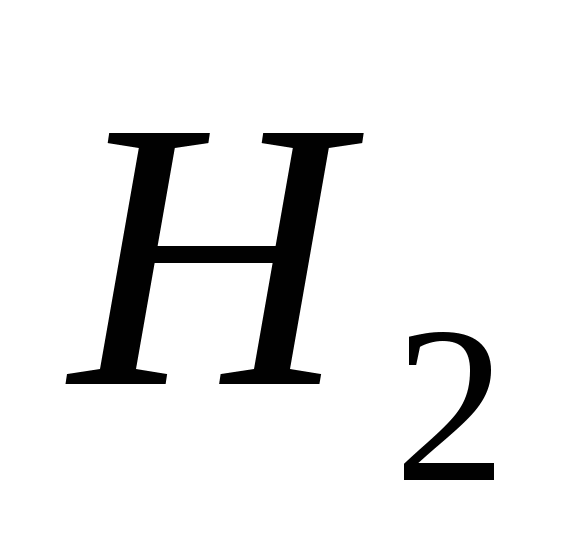 (рис.2.1).
(рис.2.1).
Требуется вычислить силу 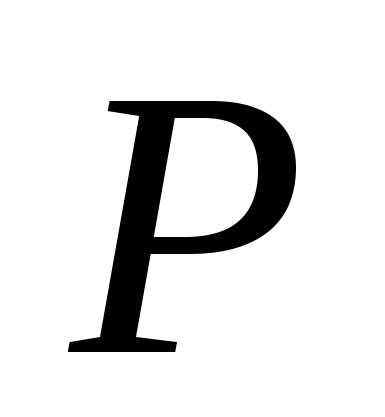 давления жидкости на пластинку.
давления жидкости на пластинку.
Решение:
 Р
Р 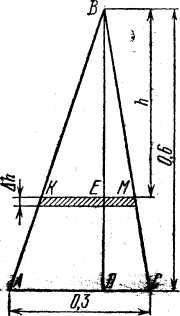 азобьем пластинку на
азобьем пластинку на 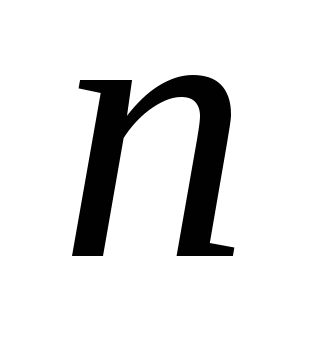 тонких полосок прямыми, параллельными поверхности жидкости:
тонких полосок прямыми, параллельными поверхности жидкости:
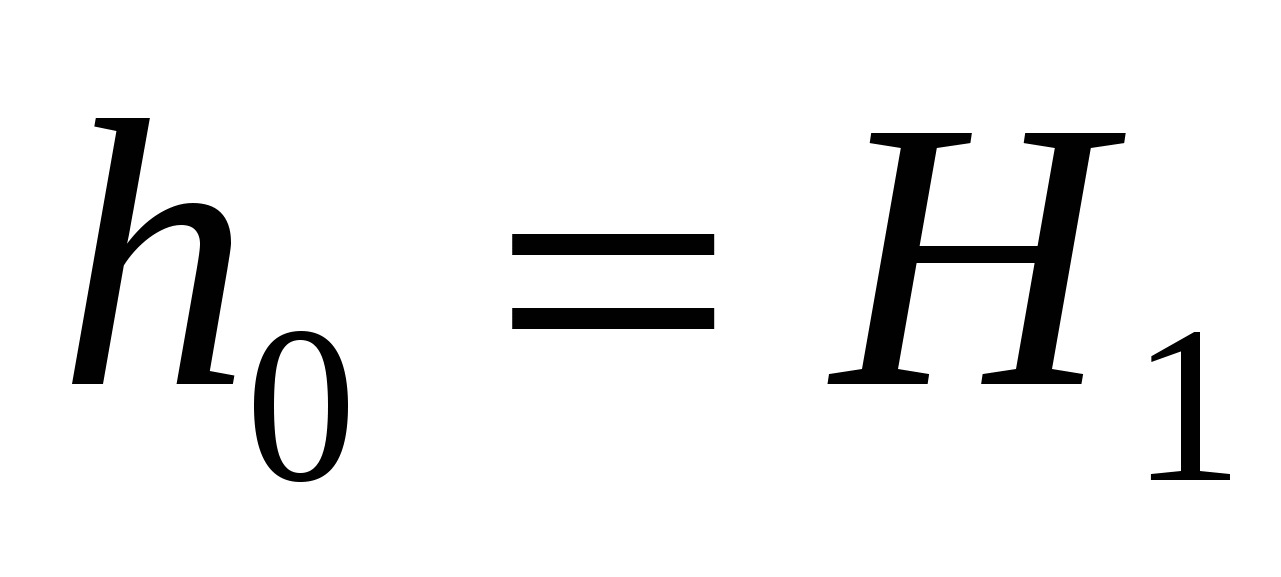 ,
,  .
.
Рис. 2.1. Рис. 2.2.
На глубине ![]() выделим одну из них (на рис. 2.1 она заштрихована) и обозначим через
выделим одну из них (на рис. 2.1 она заштрихована) и обозначим через 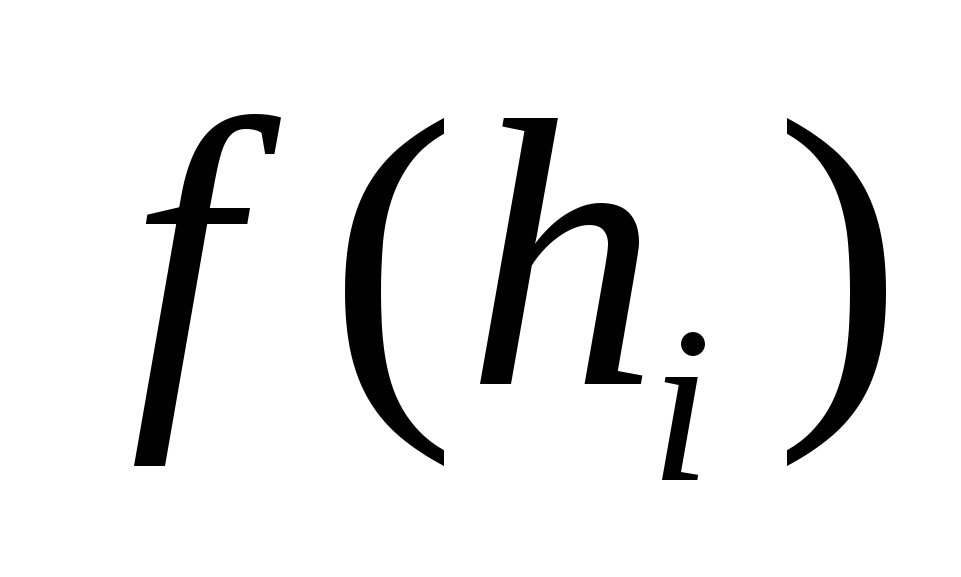 ее длину, а через
ее длину, а через ![]() - ее ширину. Приняв (с некоторой погрешностью) полоску за прямоугольник, находим ее площадь
- ее ширину. Приняв (с некоторой погрешностью) полоску за прямоугольник, находим ее площадь
![]()
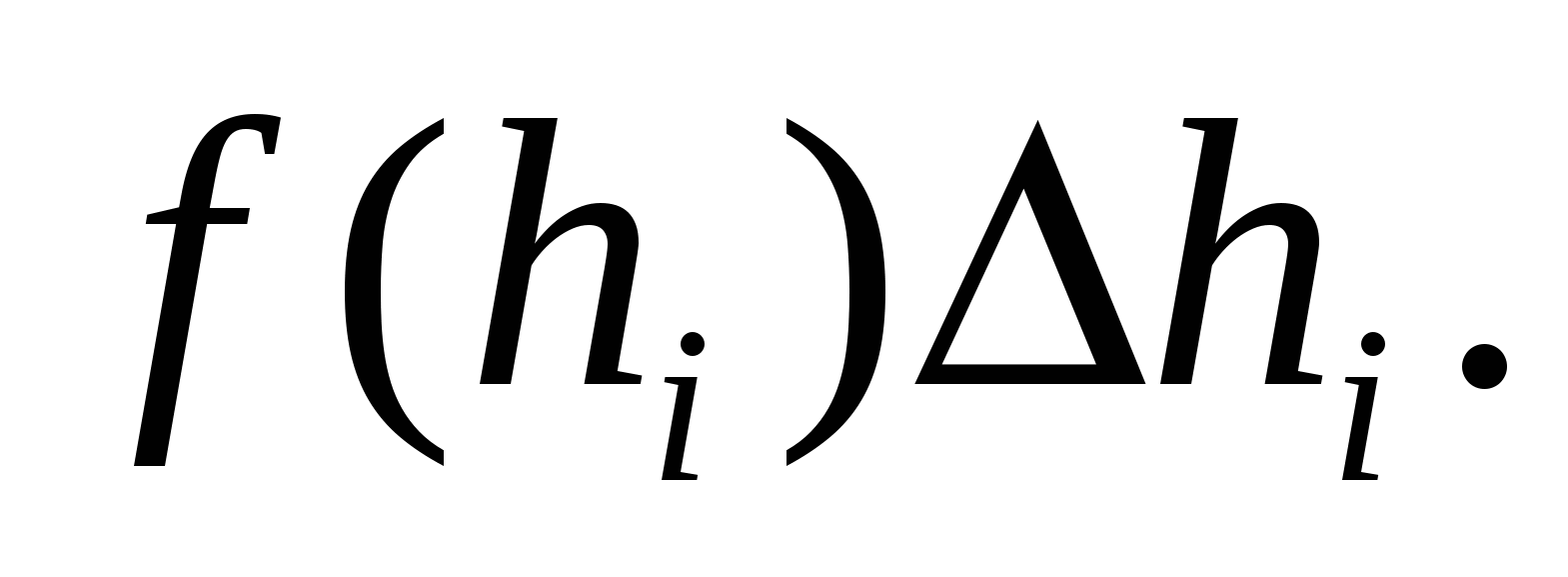
Предположим (также с некоторой погрешностью), что давление во всех точках рассматриваемой полоски одинаково и равно давлению на глубине 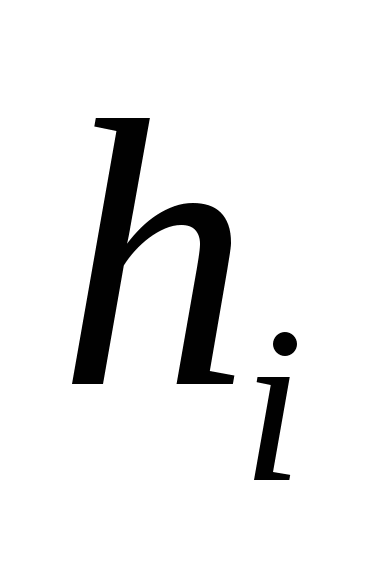 . Тогда силу
. Тогда силу  давления жидкости на полоску площади
давления жидкости на полоску площади  можно определить по формуле (2.3)
можно определить по формуле (2.3)  или
или  .
.
Суммируя элементарные давления  на каждую из
на каждую из 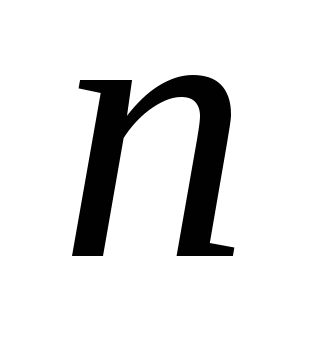 полосок, найдем приближенное значение силы
полосок, найдем приближенное значение силы 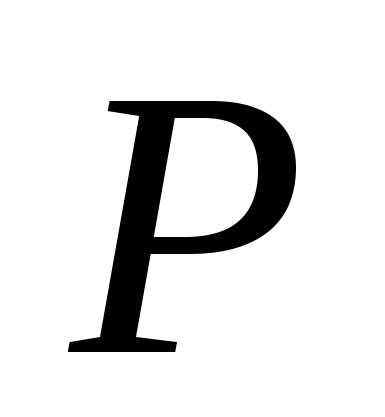 давления жидкости на всю пластинку
давления жидкости на всю пластинку
 . При неограниченном увеличении числа
. При неограниченном увеличении числа 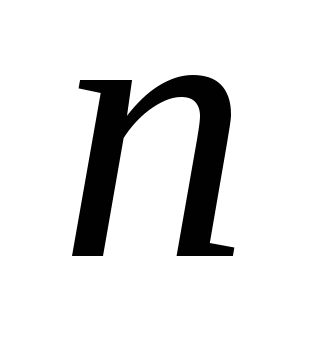 делений данной пластинки так, что
делений данной пластинки так, что 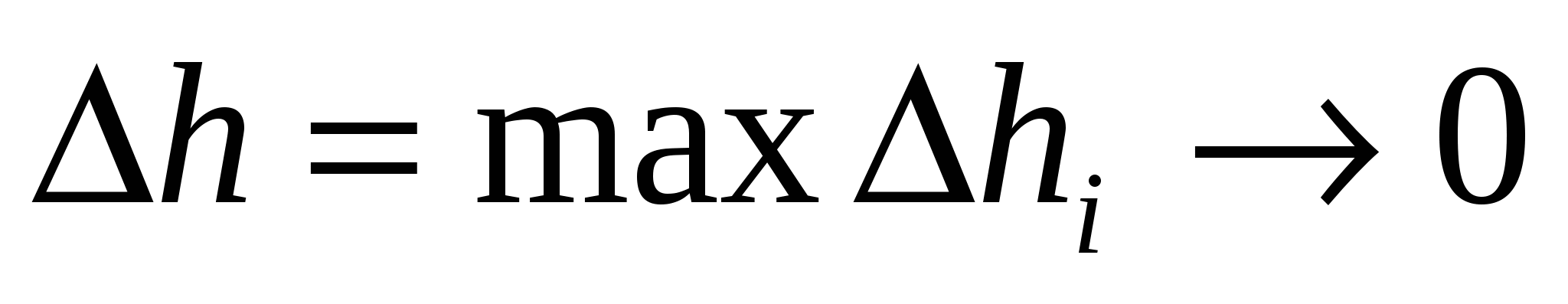 , по определению полагаем
, по определению полагаем
 .
.
Таким образом, сила давления жидкости на вертикальную пластинку вычисляется по формуле
 . (2.4)
. (2.4)
Пример 2.3. Треугольная пластинка с основанием 0,3м и высотой 0,6м погружена вертикально в воду так, что ее вершина лежит на поверхности воды, а основание параллельно ей. Вычислить силу давления воды на пластинку (рис.2.2).
Решение:
Выделим на глубине 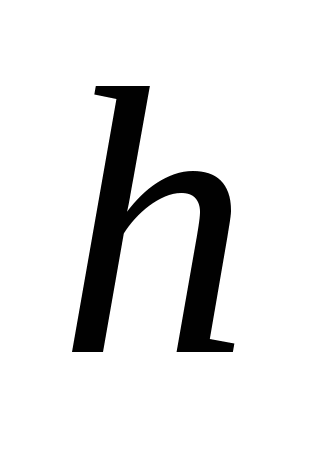 тонкую пластинку (на рис. 2.2 она заштрихована) и найдем ее длину
тонкую пластинку (на рис. 2.2 она заштрихована) и найдем ее длину 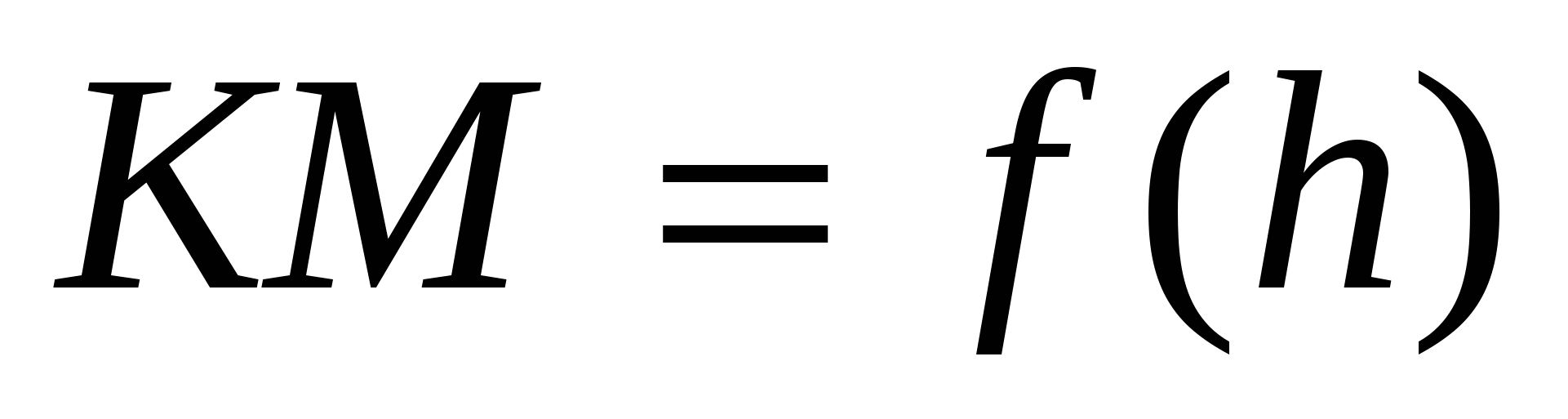 . Из подобия треугольников
. Из подобия треугольников 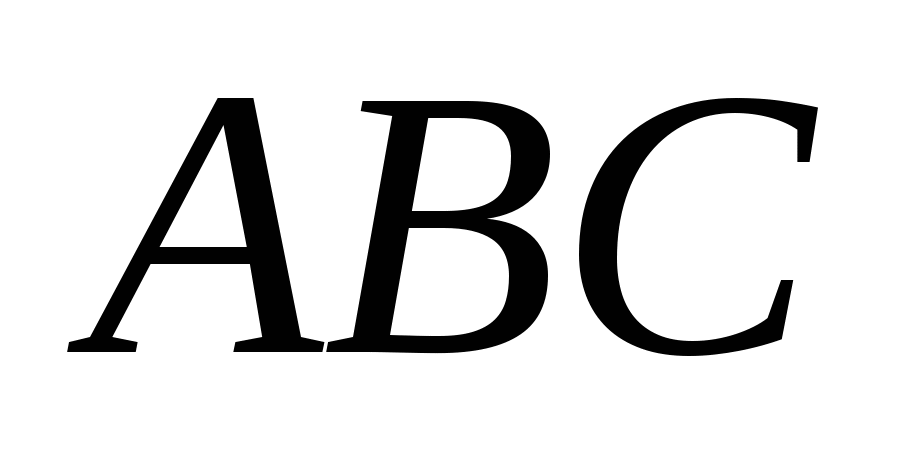 и
и 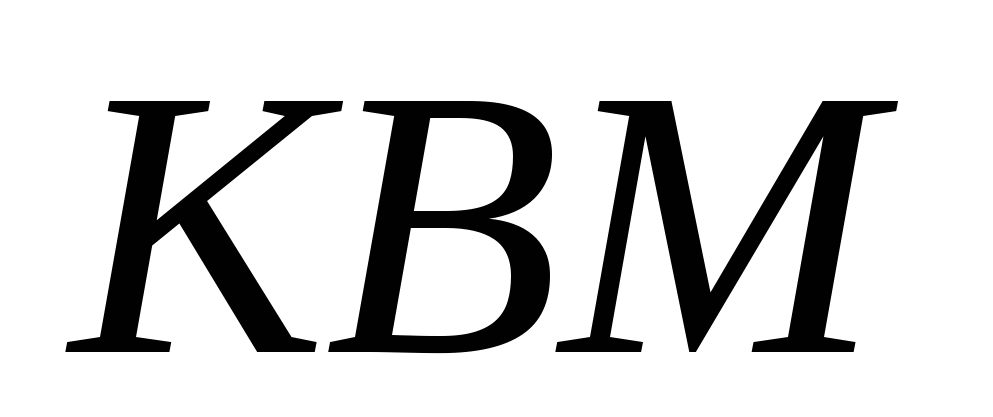 имеем
имеем
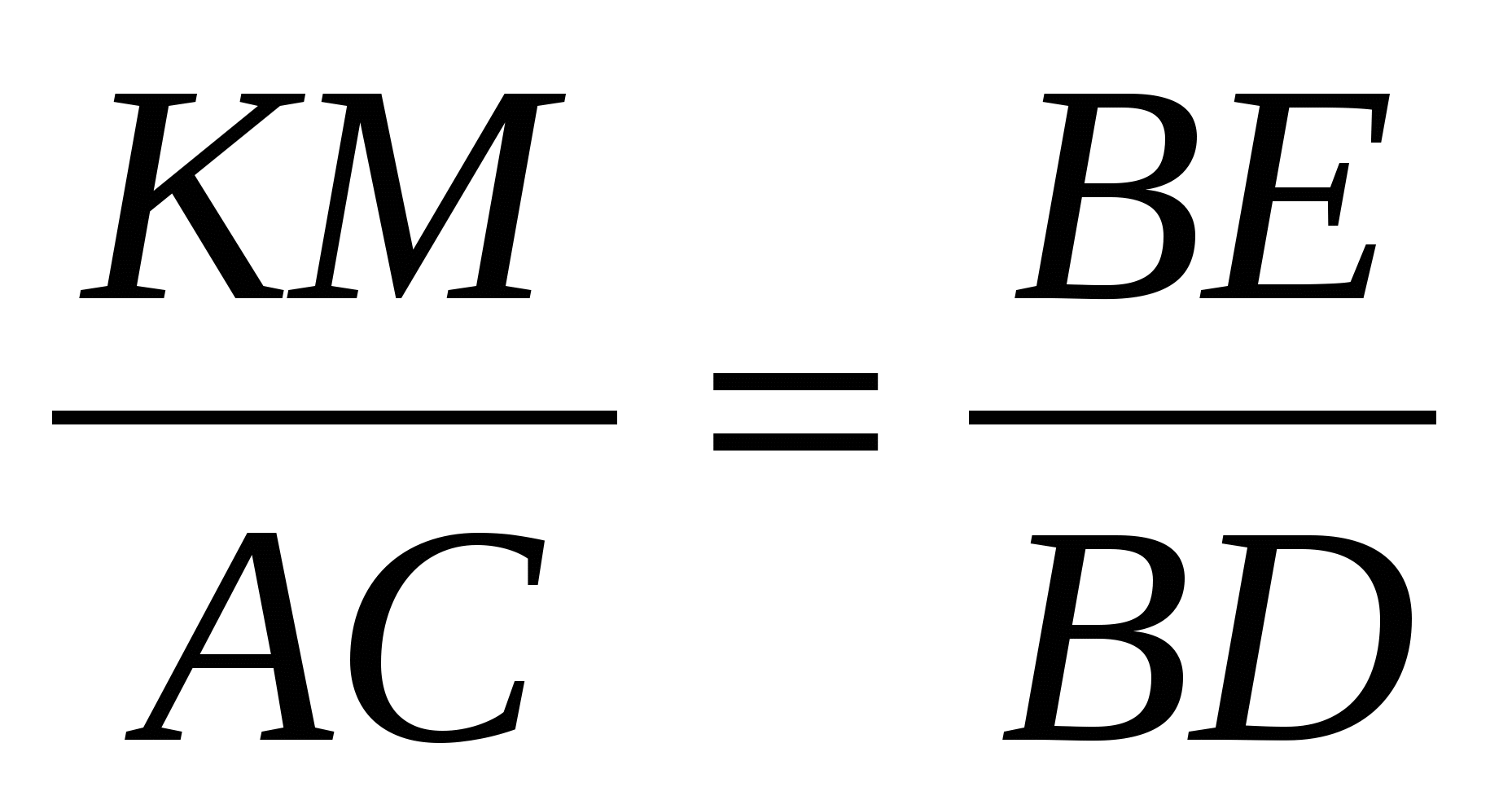 , или
, или 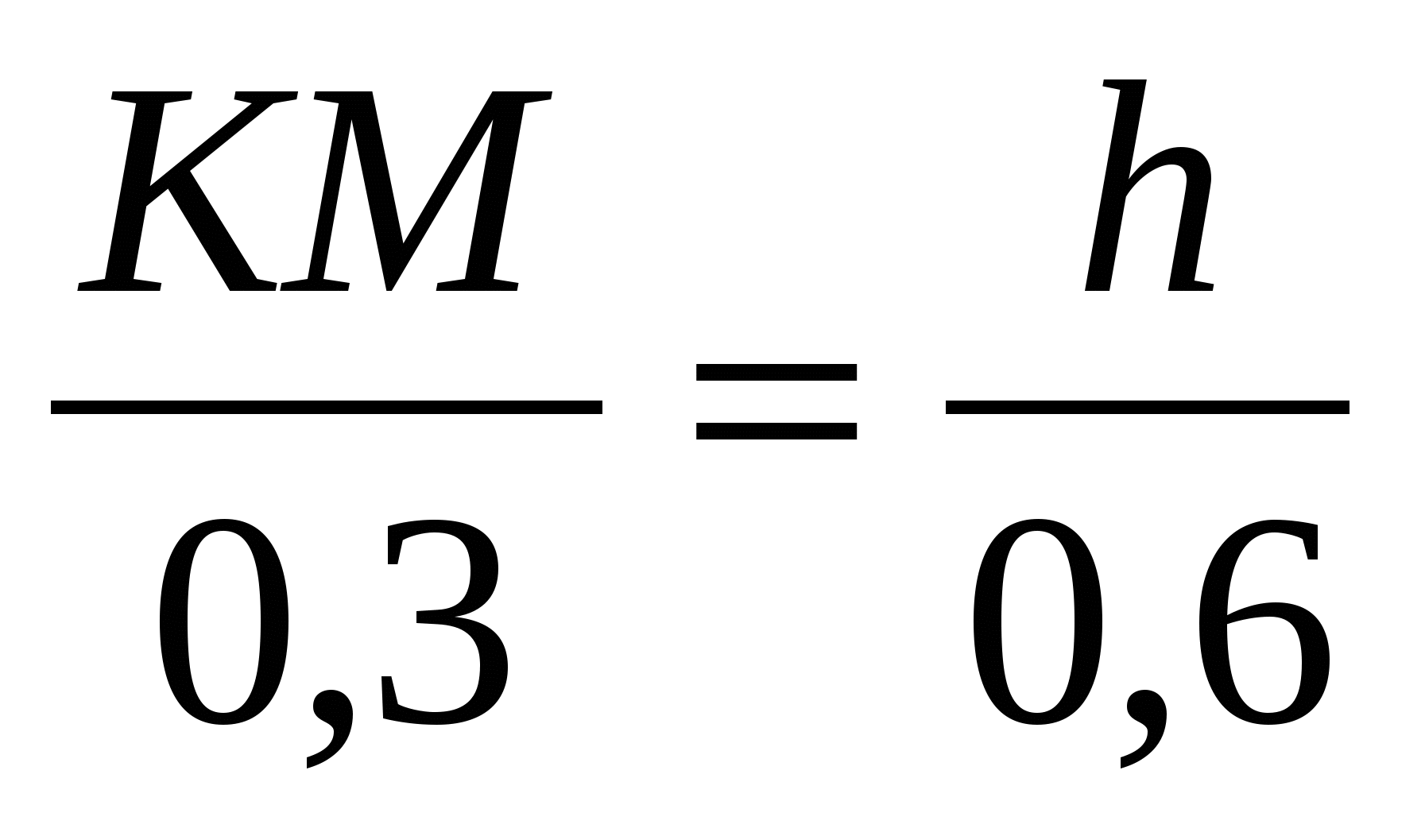 .
.
Отсюда 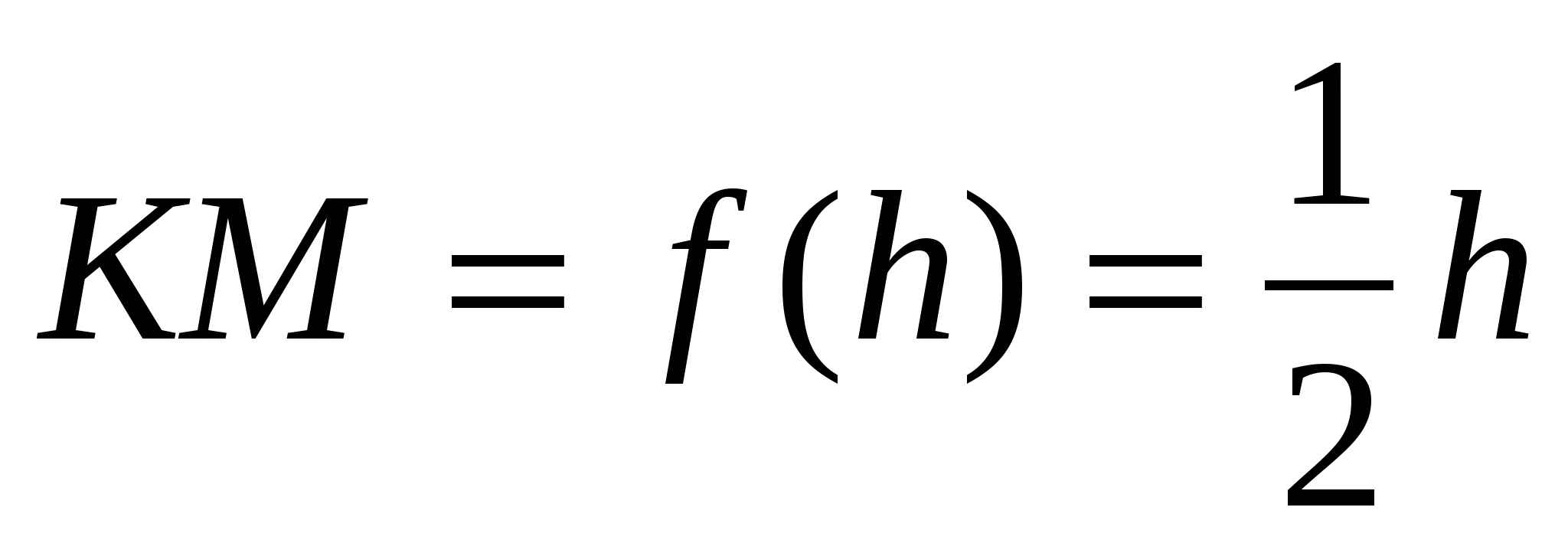 .
.
Так как вершина пластинки лежит на поверхности воды, а высота пластинки равна 0,6м, то в формуле (2.4) следует положить 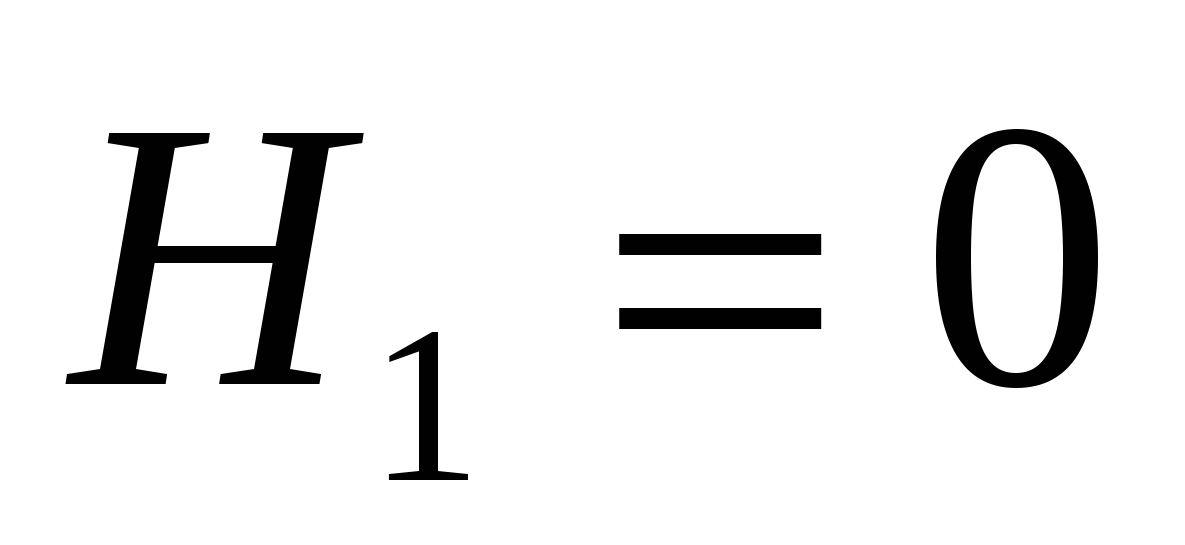 и
и 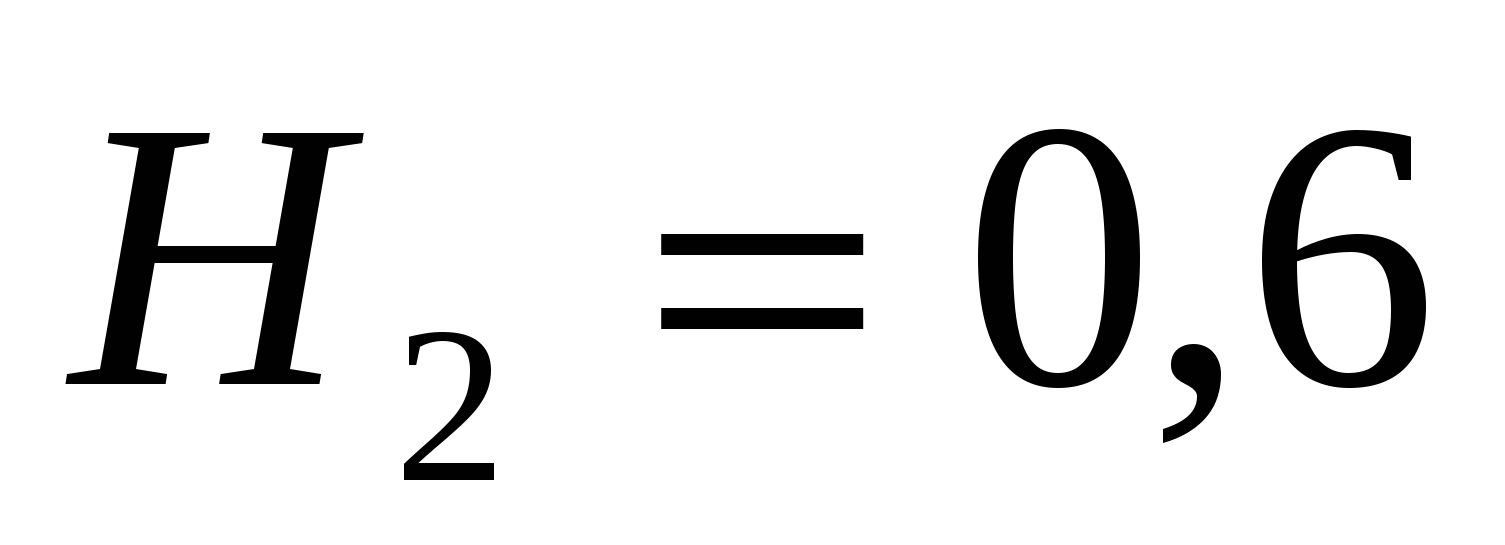 . Кроме этого,
. Кроме этого, 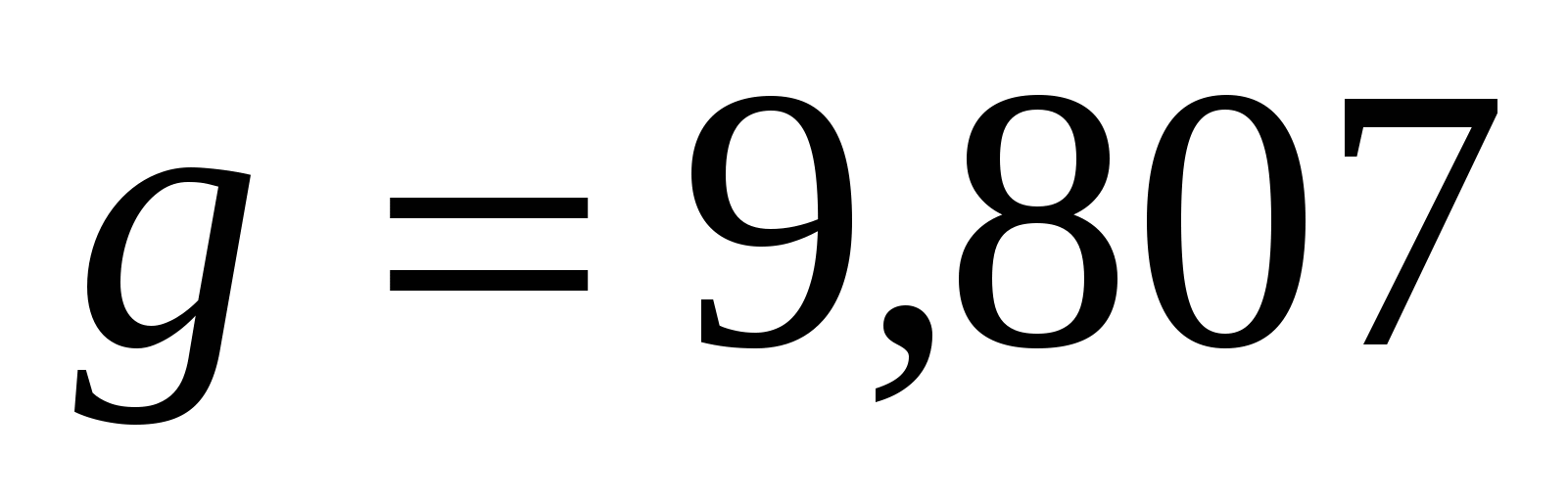 м/с2 и
м/с2 и 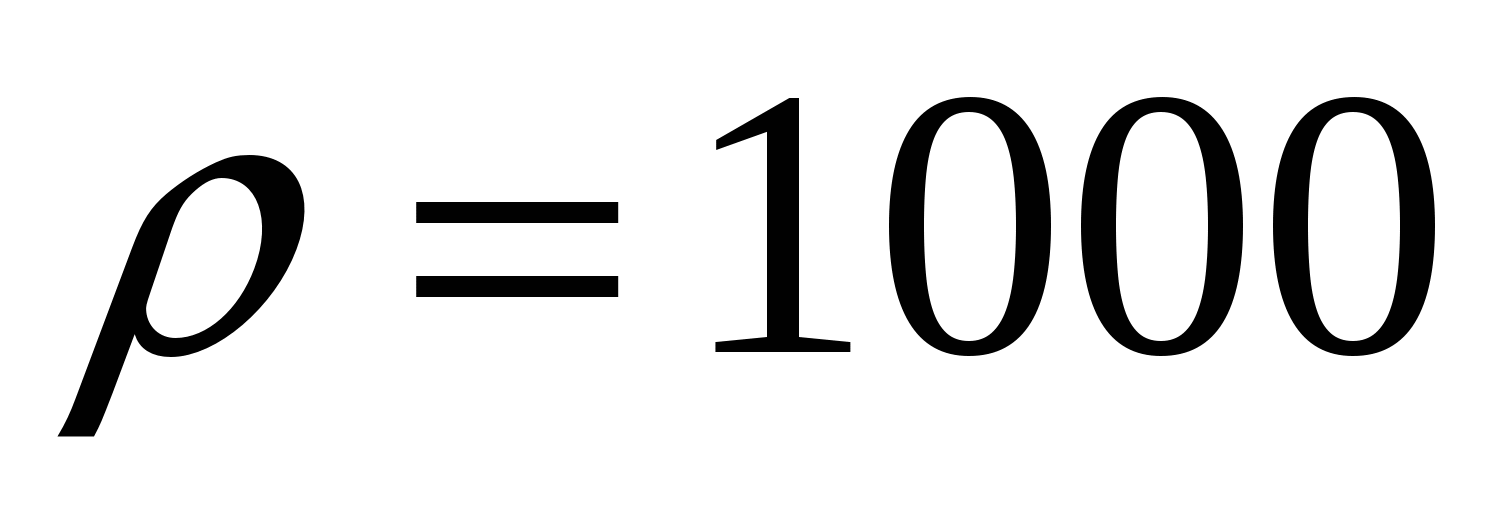 кг/м3, поэтому
кг/м3, поэтому
 .
.
Упражнения для самостоятельной работы
2.1.Определить давление воды на вертикальный прямоугольный шлюз с основанием 18 м и высотой 6 м.
2.2.При условиях предыдущей задачи найти, на какой глубине 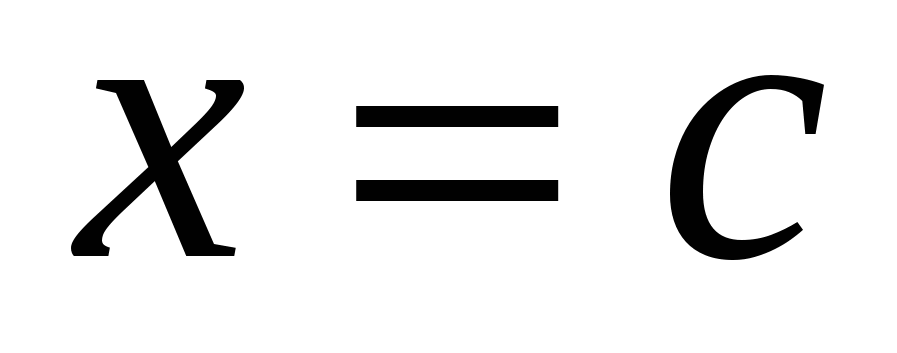 надо разделить шлюз горизонтальной прямой, чтобы давление воды на верхнюю и нижнюю части шлюза было одинаково.
надо разделить шлюз горизонтальной прямой, чтобы давление воды на верхнюю и нижнюю части шлюза было одинаково.
2.3.Найти давление воды на поверхность шара диаметром 4 м, если его центр находится на глубине 3 м от поверхности воды.
2.4.Вычислить работу, необходимую для выкачивания масла из вертикального цилиндрического резервуара высотой 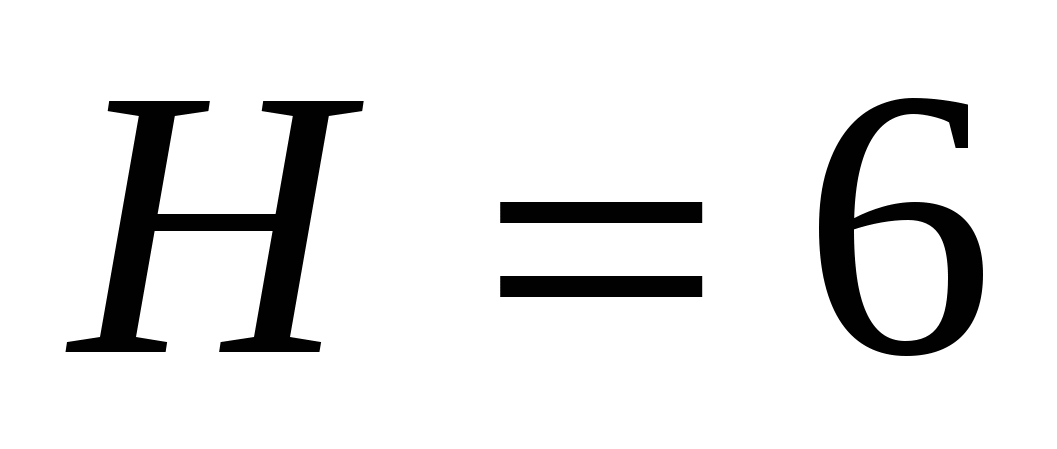 м и радиусом основания
м и радиусом основания 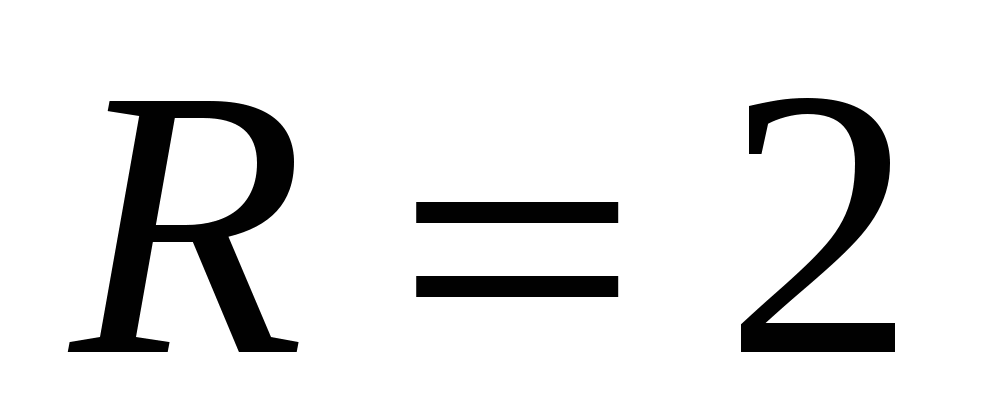 м. Плотность масла
м. Плотность масла ![]() .
.
2.5.При условиях предыдущей задачи вычислить работу, необходимую для выкачивания масла из цилиндрического резервуара, если его ось имеет горизонтальное направление.
2.6.Шар лежит на дне бассейна глубиной 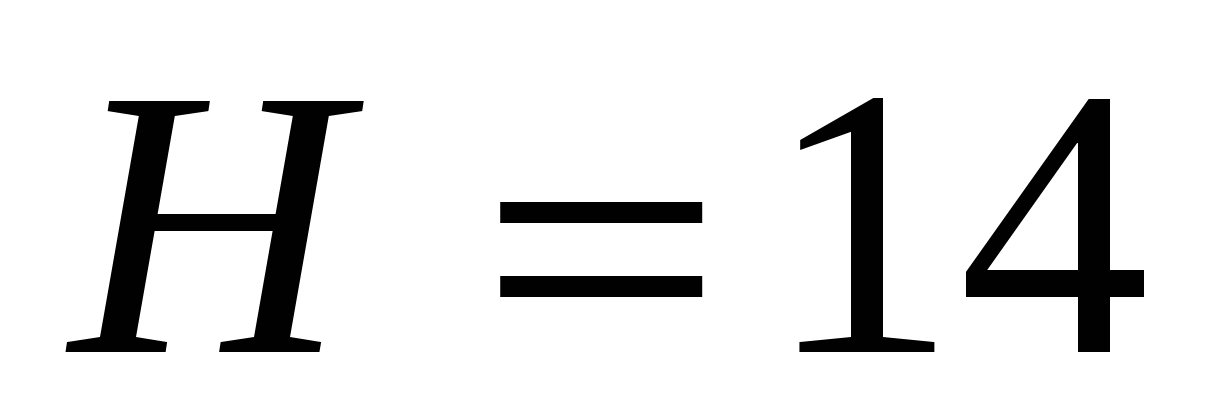 м. Определить работу, необходимую для извлечения шара из воды, если его радиус
м. Определить работу, необходимую для извлечения шара из воды, если его радиус 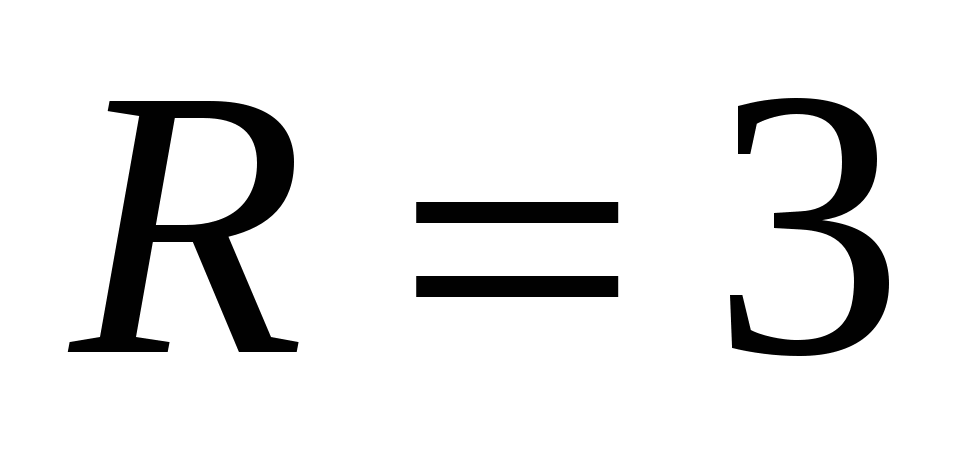 дм, а плотность
дм, а плотность 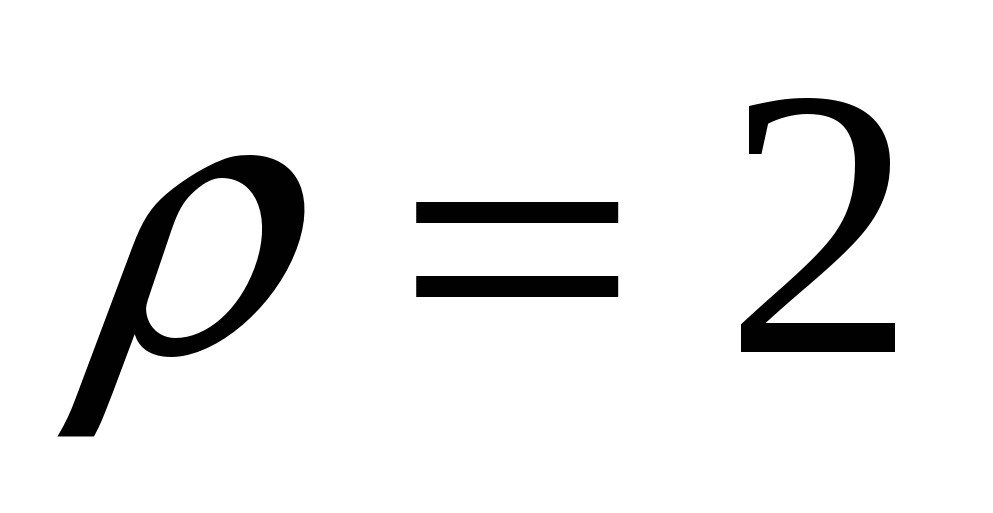 .
.
2.7.Определить работу, необходимую для запуска ракеты весом 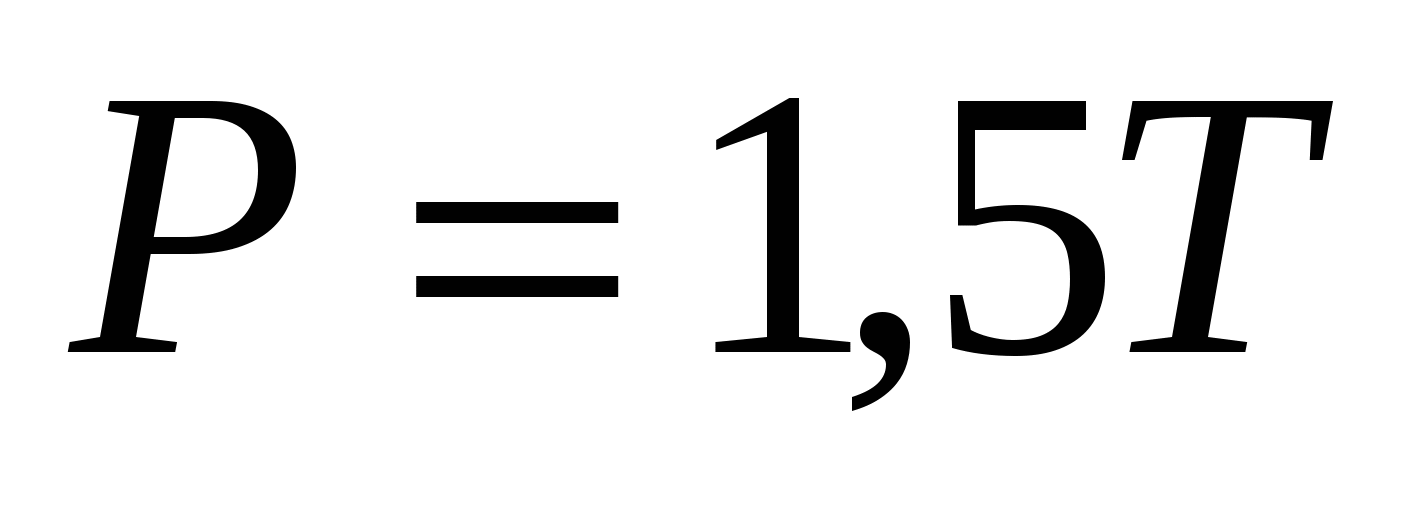 с поверхности земли на высоту
с поверхности земли на высоту  км.
км.
2.8.Какую работу надо совершить, чтобы растянуть пружину на 4 см, если известно, что от нагрузки в 1 она растягивается на 1 см?
она растягивается на 1 см?
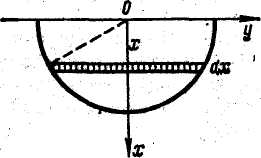
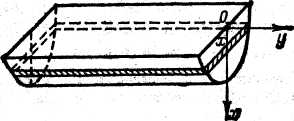
2.9.Найти работу, совершенную при выкачивании воды из корыта, имеющего форму полуцилиндра, длина которого  , радиус
, радиус 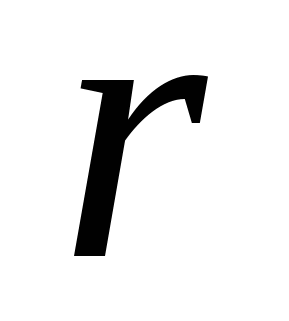 . (рис.2.3)
. (рис.2.3) 
Рис. 2.3. Рис.2.4.
2.10.Водопроводная труба имеет диаметр 6 см; один конец ее соединен с баком, в котором уровень воды выше верхнего края трубы, а другой закрыт заслонкой. Найти силу давления на заслонку.
2.11.Найти силу давления воды на вертикальную стенку в форме полукруга, диаметр которого 6 м и находится на поверхности воды (рис. 2.4) Плотность воды  .
.
2.12.Найти силу давления бензина, находящегося в цилиндрическом баке высотой 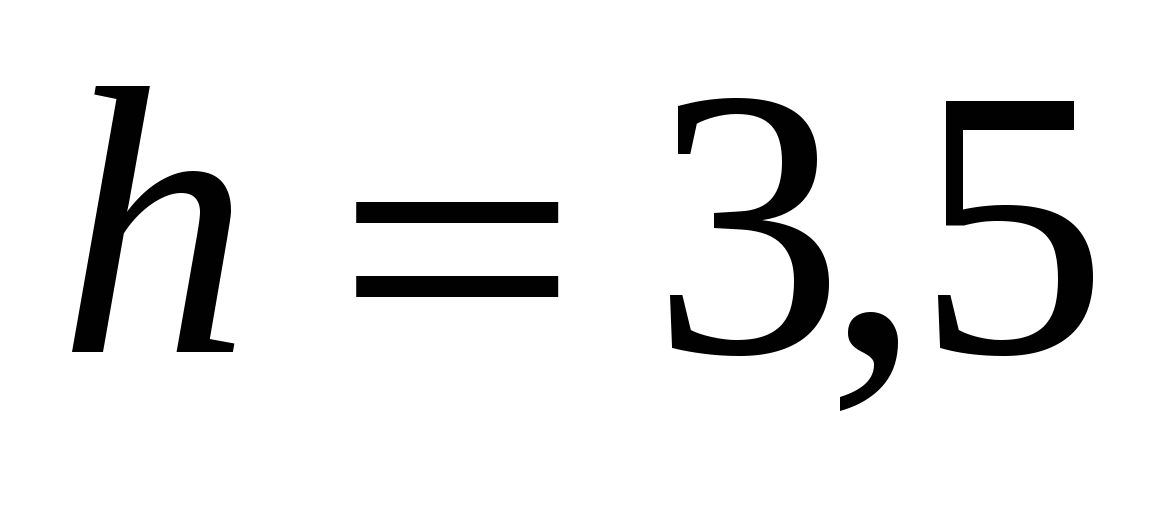 м и радиусом основания
м и радиусом основания 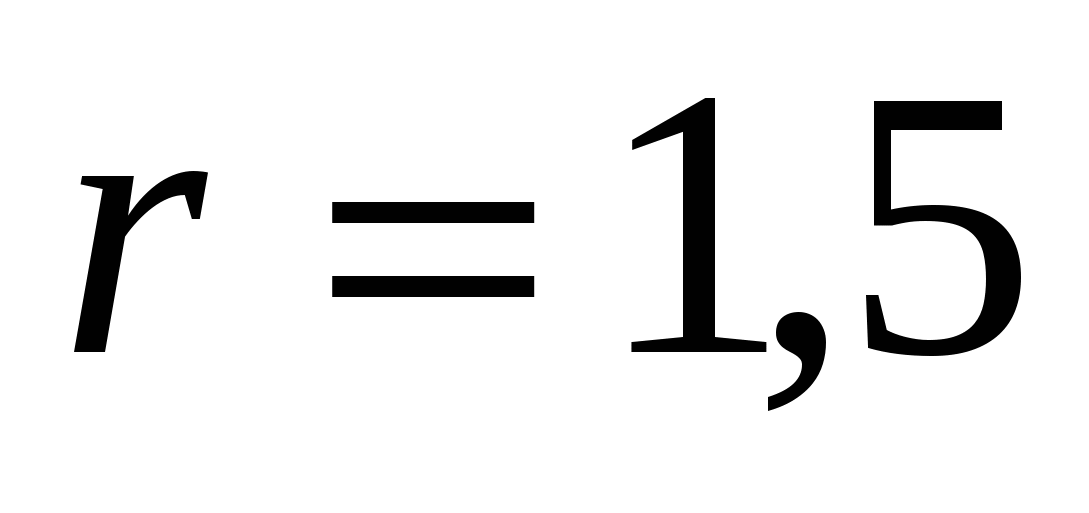 м, на его стенки, если
м, на его стенки, если ![]() .
.
Индивидуальные задания
Раздел А
Самостоятельно решите следующие задачи (номер варианта совпадает с номером задачи).
1.Скорость тела меняется по закону  м/с. Какой путь пройдет тело за 10 с? Чему равна средняя скорость движения?
м/с. Какой путь пройдет тело за 10 с? Чему равна средняя скорость движения?
2.Скорость автобуса при торможении изменяется по закону 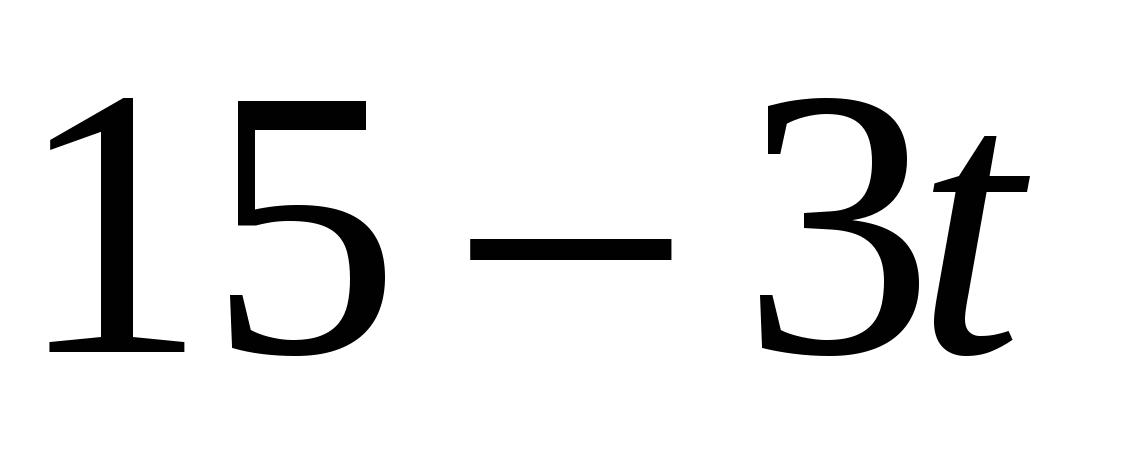 м/с. Какой путь пройдет автобус от начала торможения до полной остановки?
м/с. Какой путь пройдет автобус от начала торможения до полной остановки?
3.Какую работу нужно совершить, чтобы растянуть пружину на 10 см, если сила в 20 растягивает пружину на 5 см.
растягивает пружину на 5 см.
4.Вычислить работу, совершаемую при сжатии пружины на 0,04 м, если для сжатия ее на 0,01 м нужна сила в 10  ?
?
5.Для сжатия пружины на 0,03 м необходимо совершить работу 16 Дж. На какую длину можно сжать пружину, совершив работу в 144 Дж?
6.Вычислить работу, затраченную при сжатии пружины на 25 см, если известно, что при сжатии ее на 1 см необходима сила в 40  .
.
7.Силой в 80  пружина растягивается на 2 см. Первоначальная длина пружины равна 15 см. Какую работу надо совершить, чтобы растянуть ее до 20 см?
пружина растягивается на 2 см. Первоначальная длина пружины равна 15 см. Какую работу надо совершить, чтобы растянуть ее до 20 см?
8.Вычислить общую силу давления воды на дно и стенки аквариума, имеющего форму прямоугольного параллелепипеда, если стороны основания равны 0,9 м и 0,6 м, а высота равна 0,4 м. Аквариум доверху наполнен водой.
9.Вычислить силу давления воды на вертикальную плотину, имеющую форму равнобедренной трапеции, верхнее основание которой 38 м, нижнее 20 м и высота 12 м. Уровень воды доходит до верха плотины.
10.Цилиндрический резервуар наполнен маслом. Вычислить давление масла на боковую поверхность резервуара, если высота его 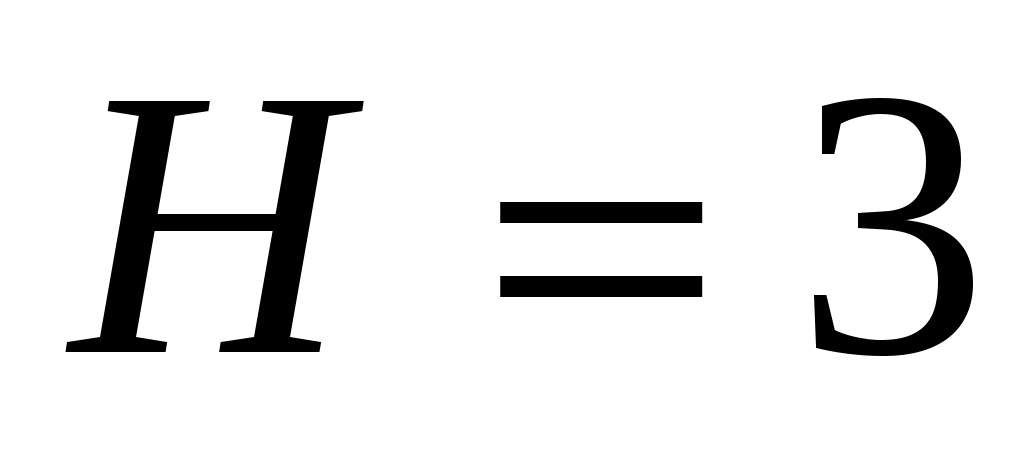 м и радиус основания
м и радиус основания ![]() м. Плотность масла
м. Плотность масла ![]() кг/м.
кг/м.
11.Треугольная пластина с основанием 0,9 м и высотой 0,12 м погружена в воду так, что ее вершина лежит на 0,03 м ниже поверхности воды, а основание параллельно ей. Вычислить силу давления воды на пластину.
12.Для растяжения пружины на 4 см необходимо совершить работу 24 Дж. На какую длину можно растянуть пружину, совершив работу в 150 Дж?
13.Рессора прогибается под нагрузкой 2 т на 105 см. Какую работу нужно затратить для деформации рессоры на 3 см? (Сила деформации пропорциональна величине деформации.)
14.Вода заполняет полностью резервуар кубической формы с ребром, равным 0,5 м. Найти силу давления воды на дно резервуара.
15. Вода заполняет полностью резервуар кубической формы с ребром, равным 0,5 м. Найти силу давления воды на боковую стенку.
16.Скорость движения точки 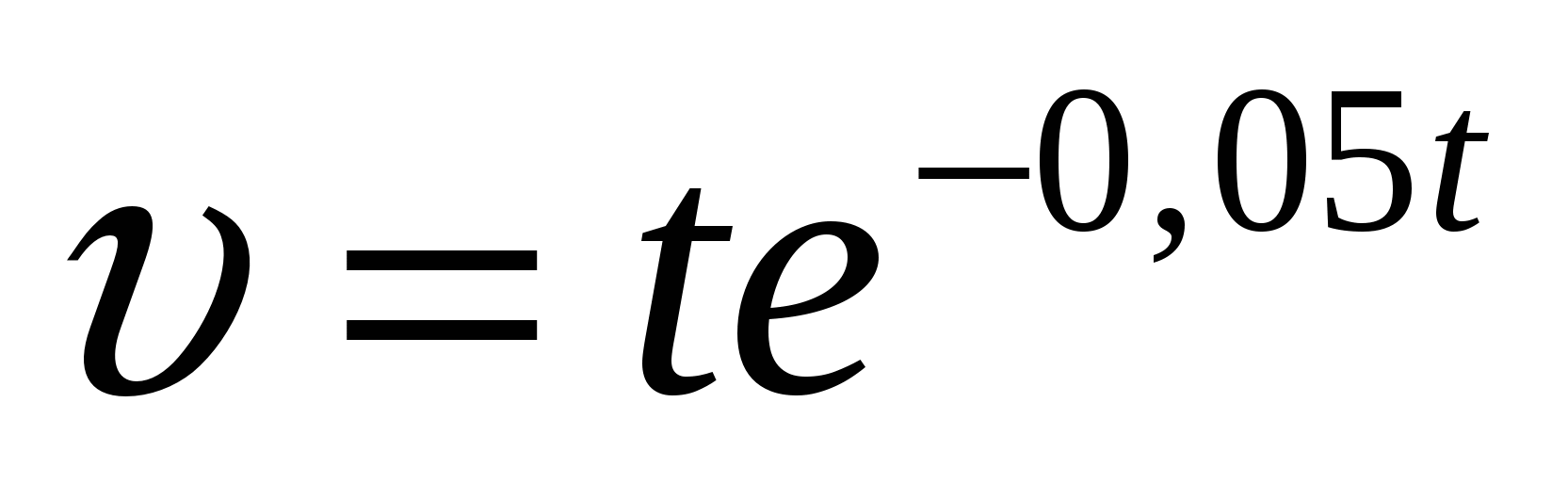 м/с. Найти путь пройденный точкой от начала движения до полной остановки.
м/с. Найти путь пройденный точкой от начала движения до полной остановки.
17.Найти давление спирта  , находящегося в цилиндрическом баке высотой 3 м и радиусом 4 м на боковую стенку бака.
, находящегося в цилиндрическом баке высотой 3 м и радиусом 4 м на боковую стенку бака.
18.Найти величину давления воды на прямоугольник, вертикально погруженный в воду, если известно, что основание его равно 8 м, высота 12 м, верхнее основание параллельно свободной поверхности воды и находится на глубине 5 м.
19.Вычислить силу, с которой вода давит на плотину, имеющую форму равнобочной трапеции, верхнее основание которой 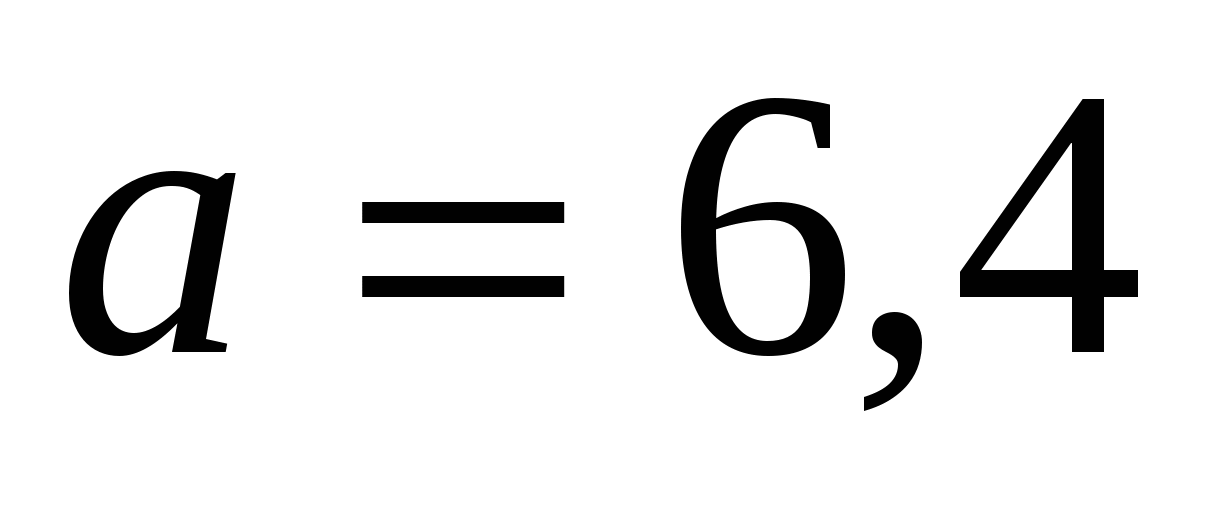 м, нижнее
м, нижнее  м, а высота
м, а высота 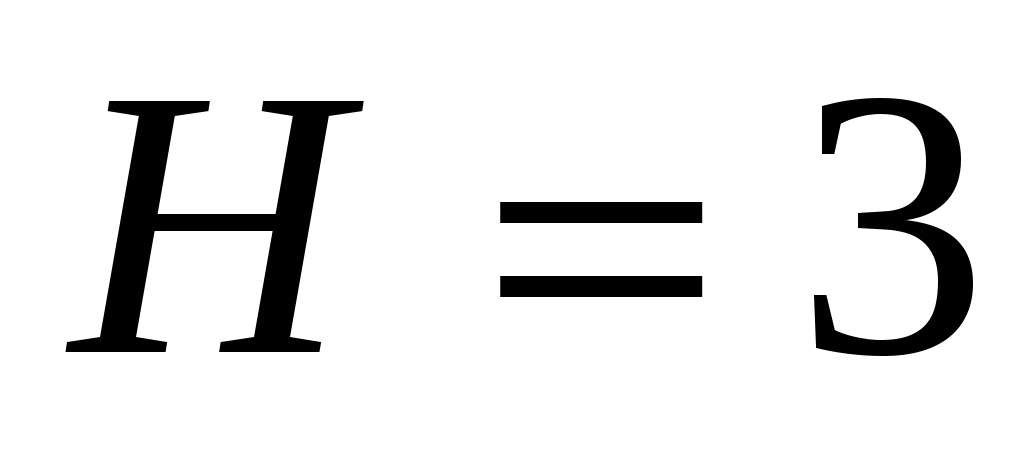 м.
м.
20.Найти центр тяжести площади фигуры, ограниченной параболой 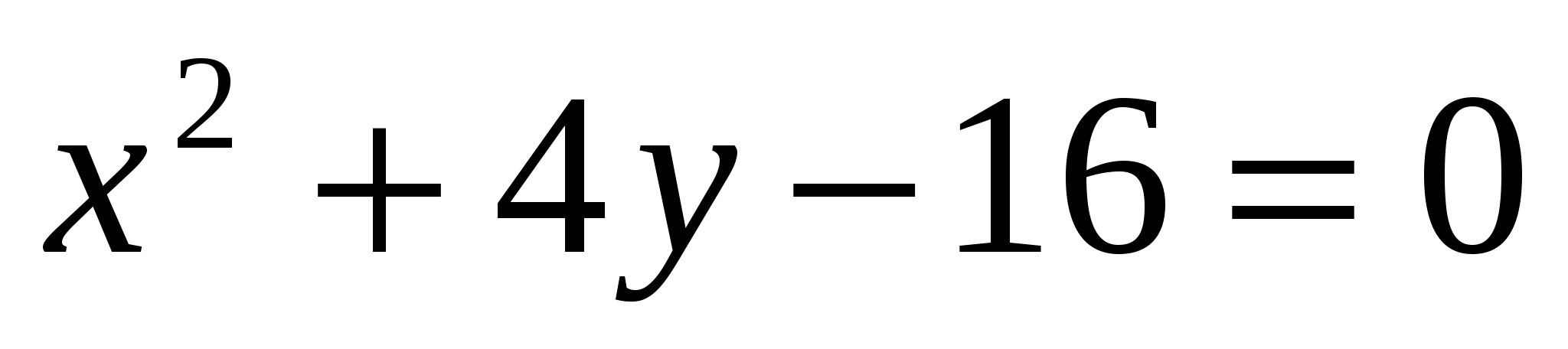 и осью
и осью 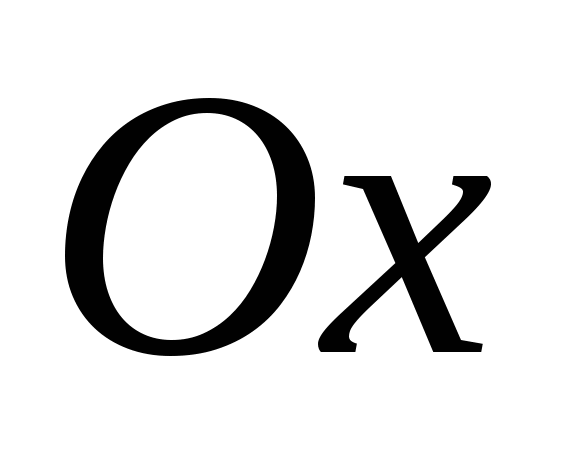 .
.
Раздел Б
1. Верхний край шлюза, имеющего форму квадрата со стороной, равной 8 м, лежит на поверхности воды. Определить величину давления на каждую из
частей шлюза, образуемую делением квадрата одной из его диагоналей.
2.Вычислить работу, необходимую для того, чтобы выкачать воду из полусферического сосуда, диаметр которого равен 20 м.
3.Вычислить работу, которую нужно затратить на выкачивание воды из цилиндрического бассейна с радиусом основания 0,5 м,если в начальный момент уровень воды в бассейне равен 2,8 м и на 0,2 м ниже выпускающего воду отверстия в цилиндре.
4.Котел имеет форму параболоида вращения глубиной 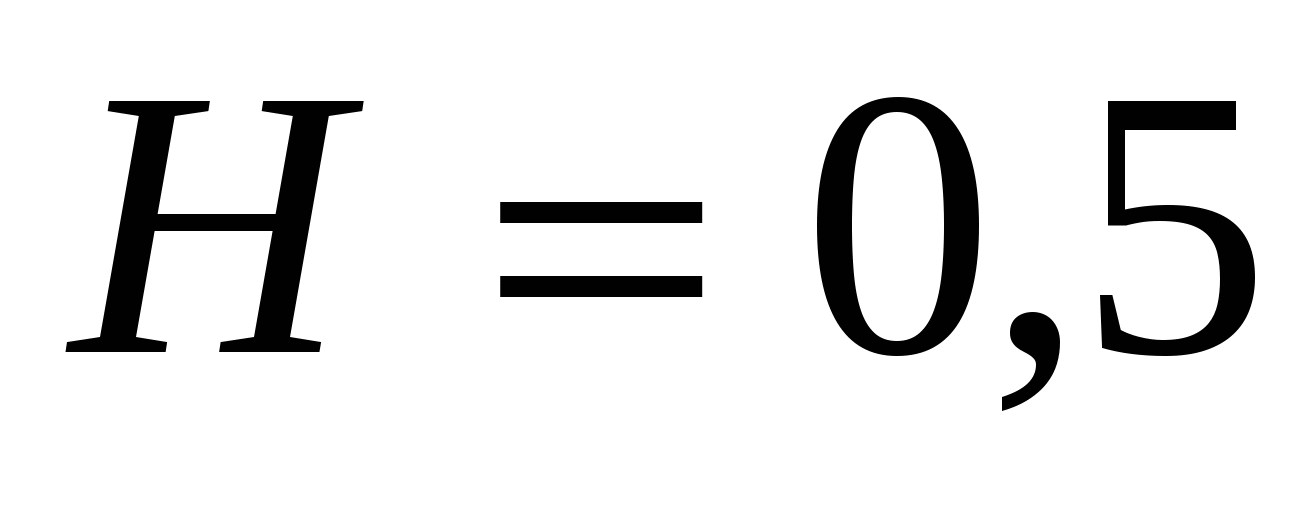 м и радиусом основания
м и радиусом основания 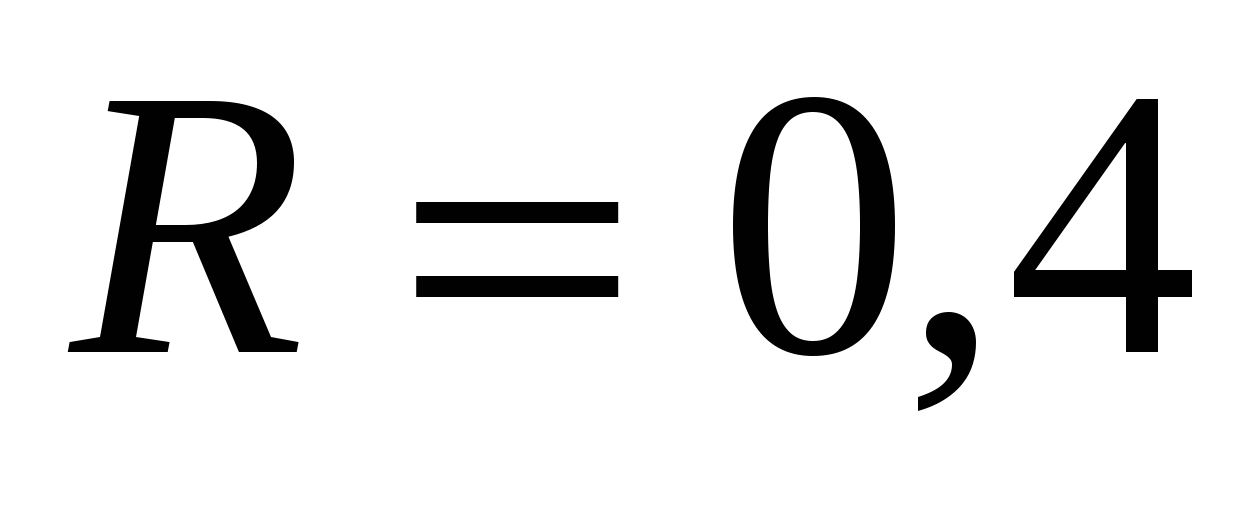 м. Определить работу, которую нужно затратить на выкачивание воды из такого наполненного котла.
м. Определить работу, которую нужно затратить на выкачивание воды из такого наполненного котла.
5.За какое время вода, наполняющая цилиндрический сосуд с площадью основания 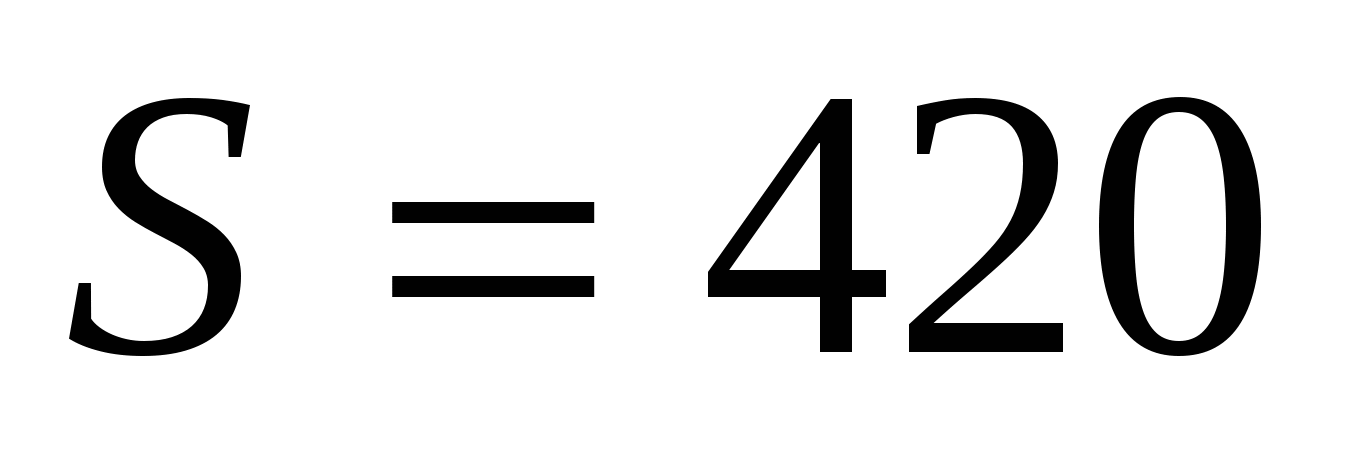 см2 и высотой
см2 и высотой  см, вытечет через отверстие на дне площадью
см, вытечет через отверстие на дне площадью  см2?
см2?
6.За какое время вода вытечет из конической воронки высотой ![]() см, радиусом нижнего основания
см, радиусом нижнего основания 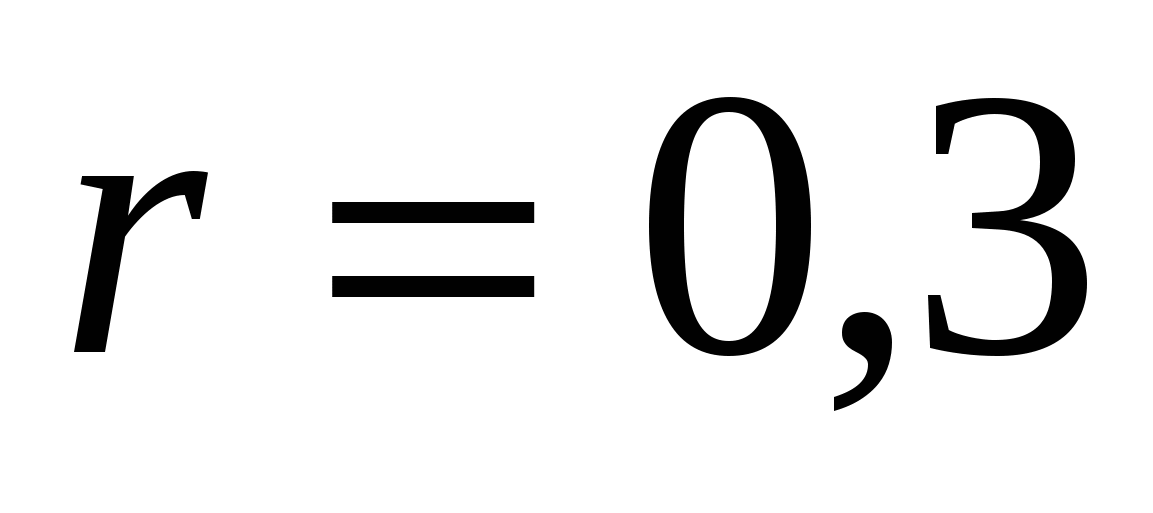 см и верхнего
см и верхнего 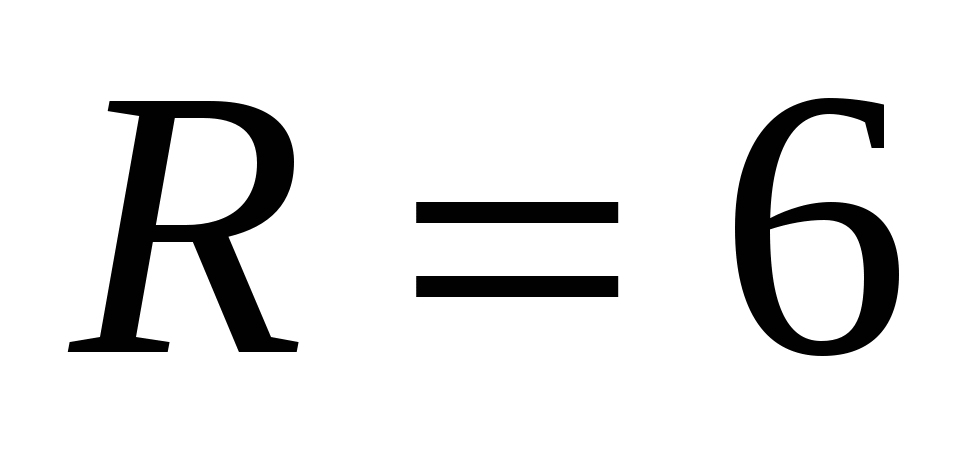 см?
см?
7.Цилиндрическая цистерна с горизонтальной осью наполовину наполнена маслом (удельный вес 0,9). Определить давление масла на каждую из плоских стенок цилиндра, если радиус ее равен 2 м.
Ответы
1.1. 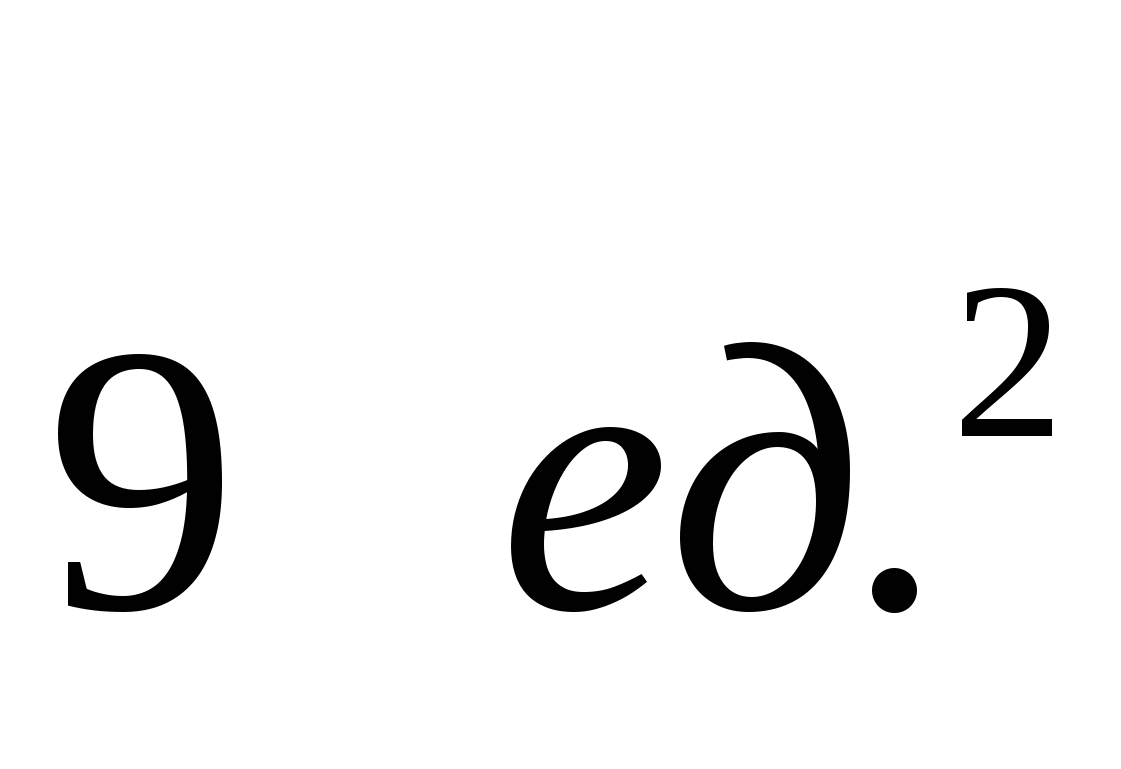 1.2.
1.2. 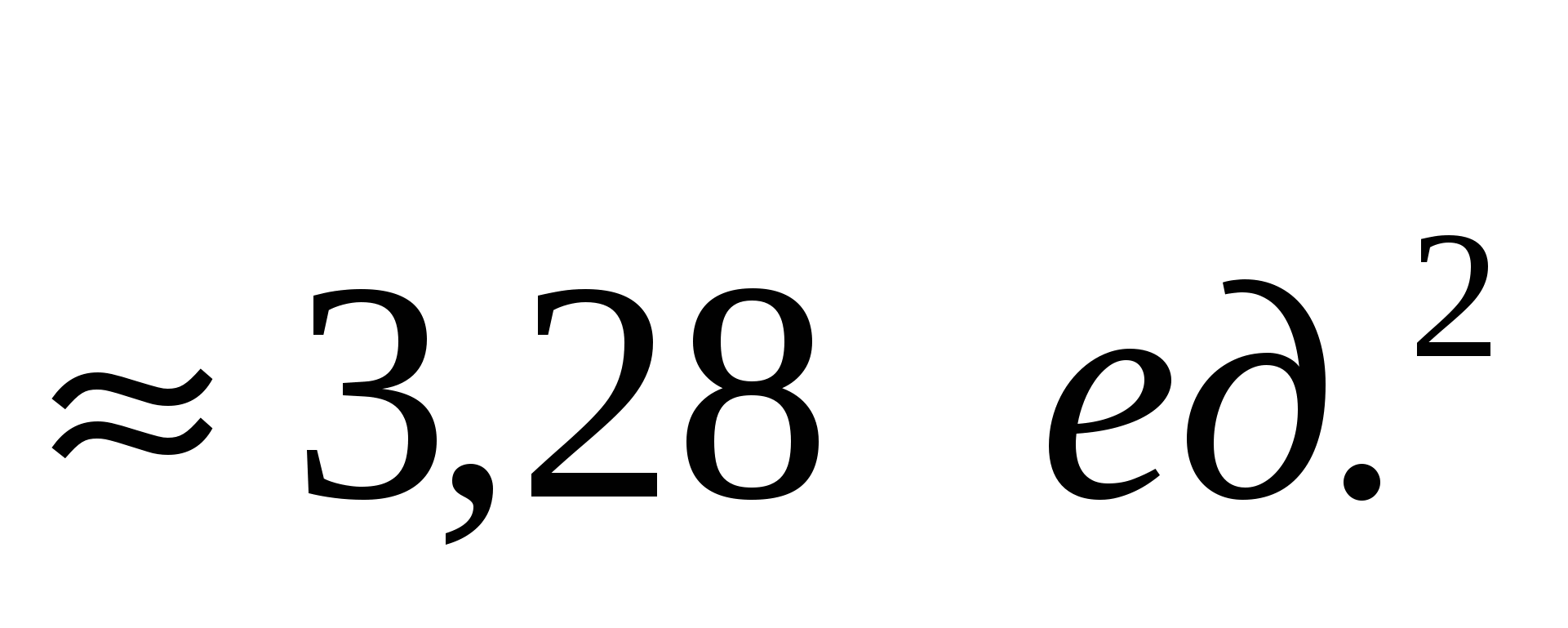 1.3.
1.3. 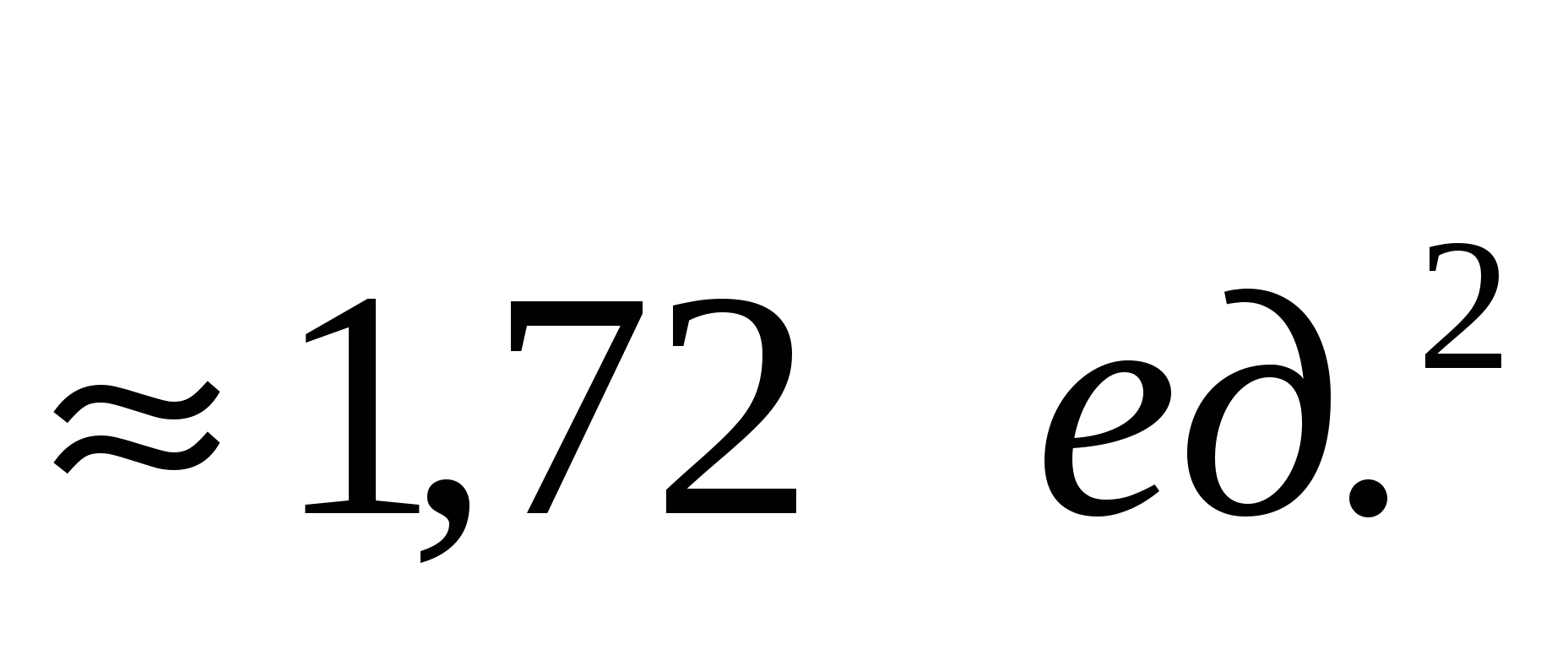 1.4.
1.4. 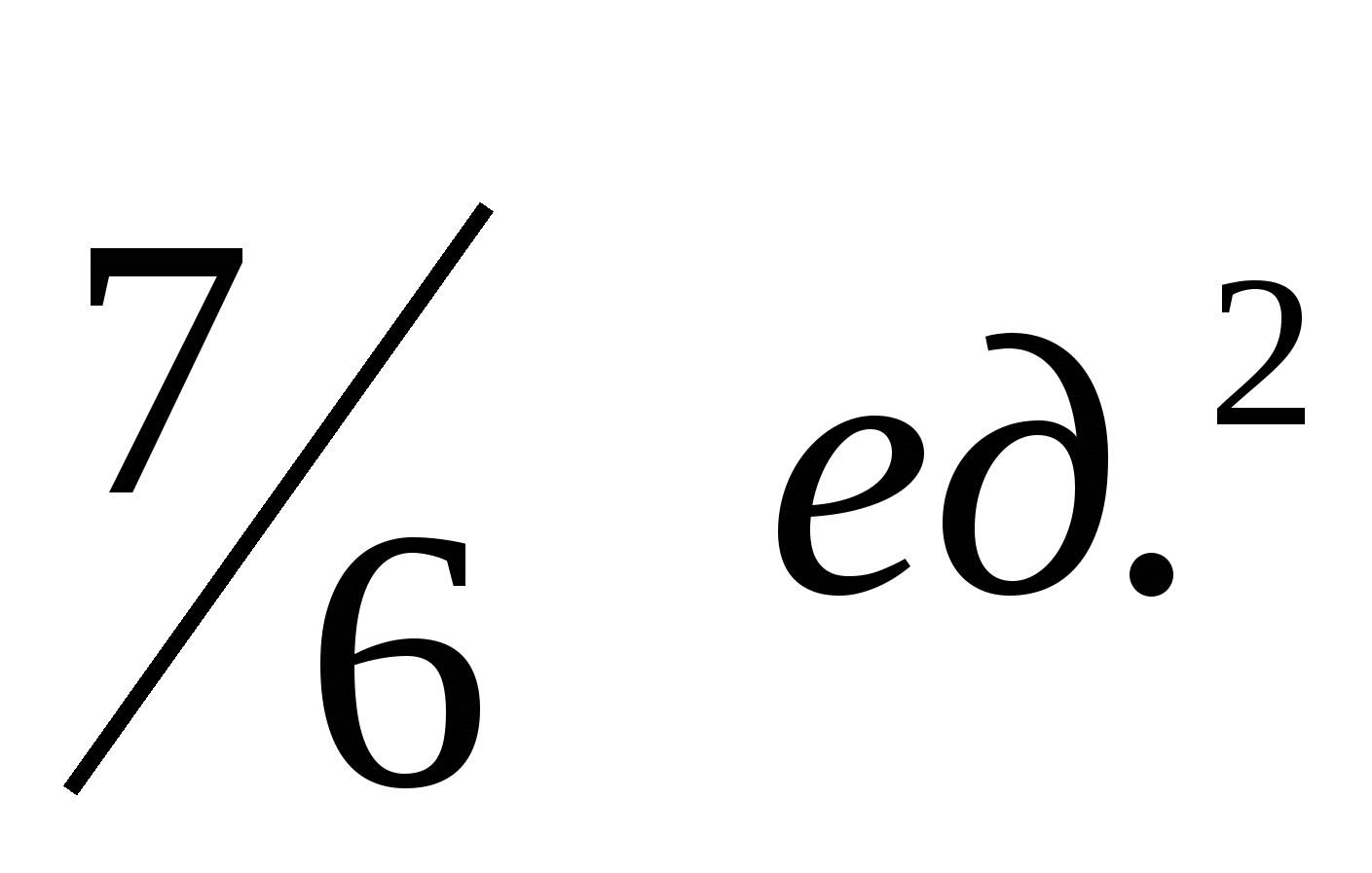 1.5.
1.5. 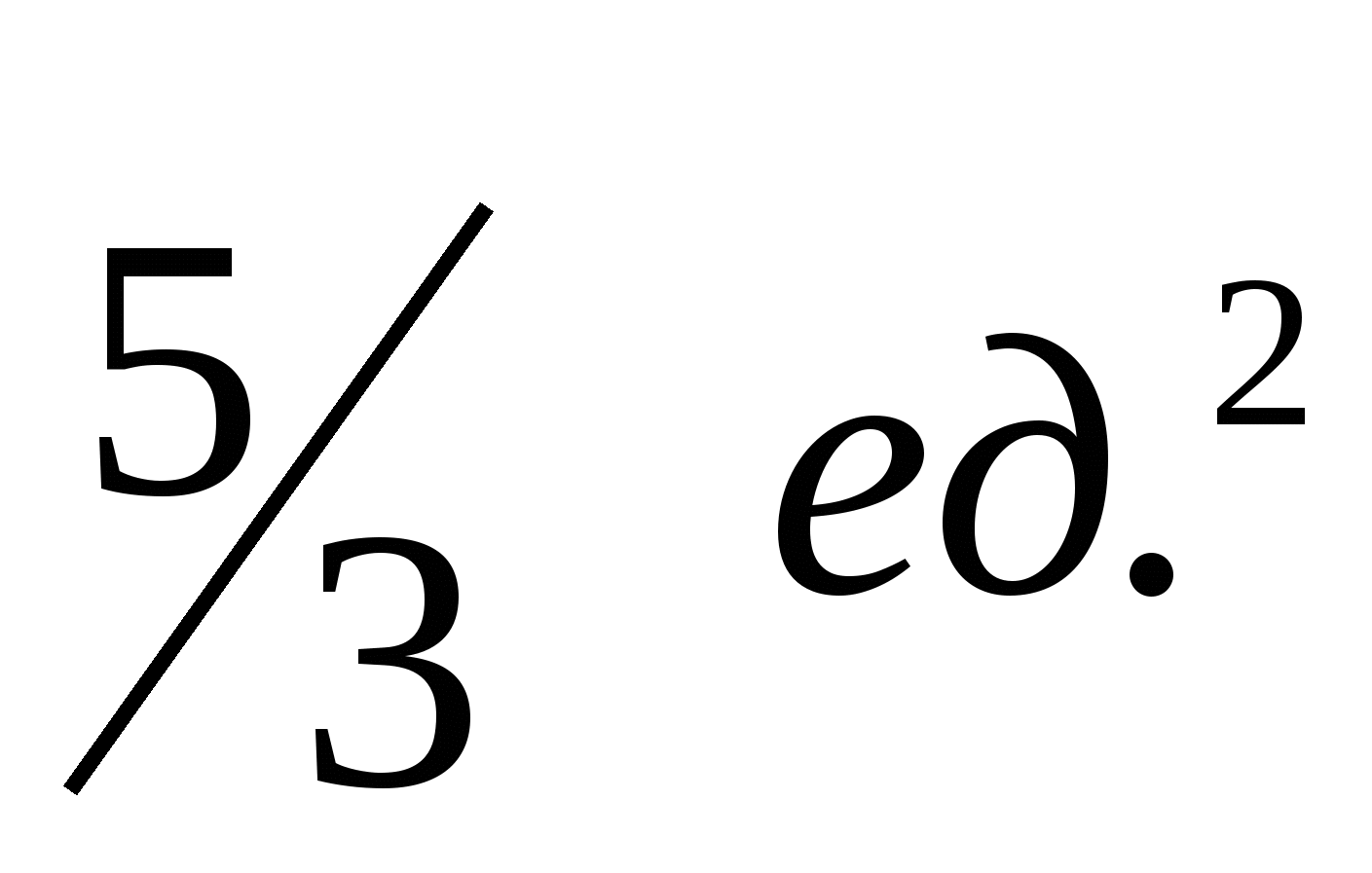

1.6.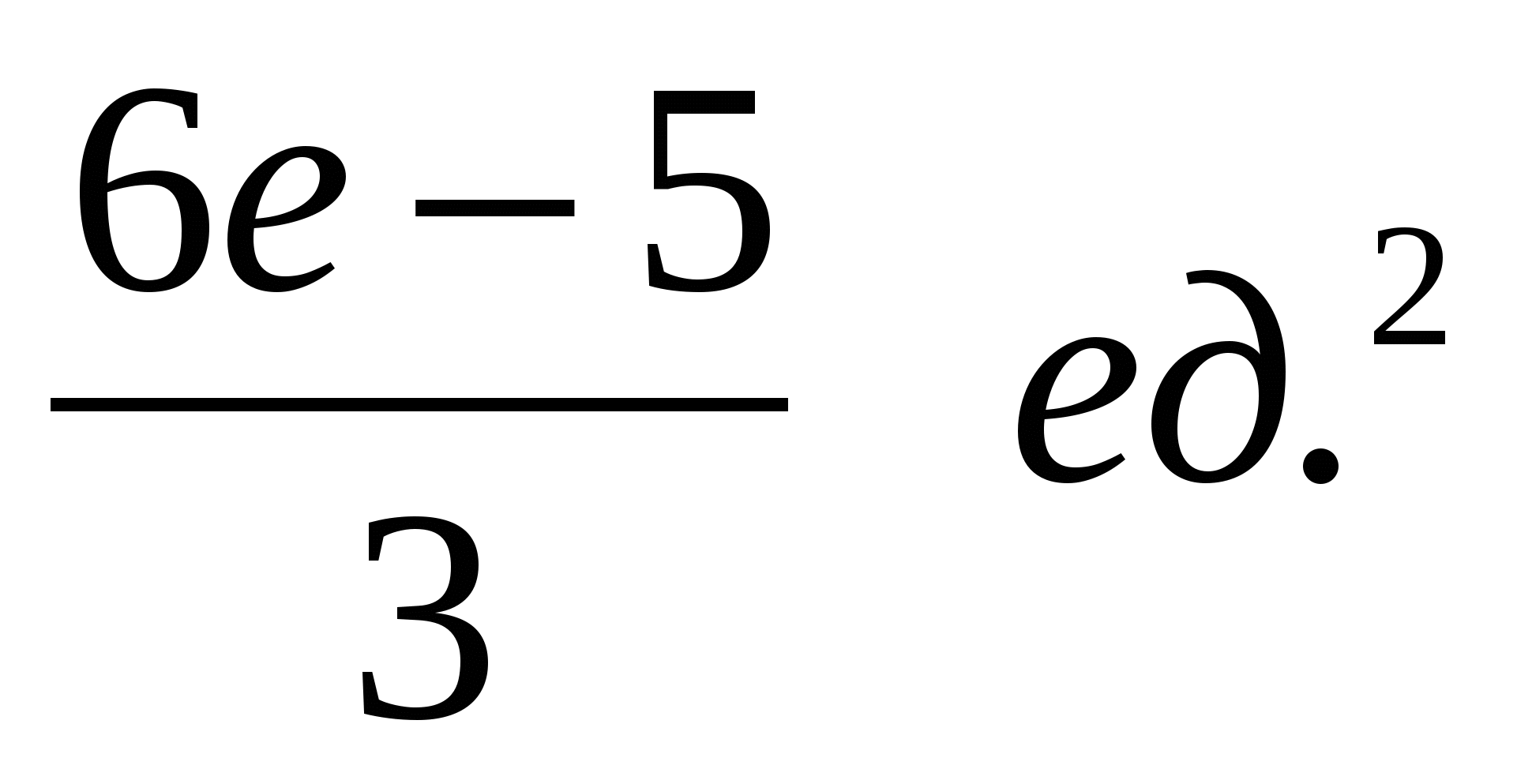 1.7.
1.7.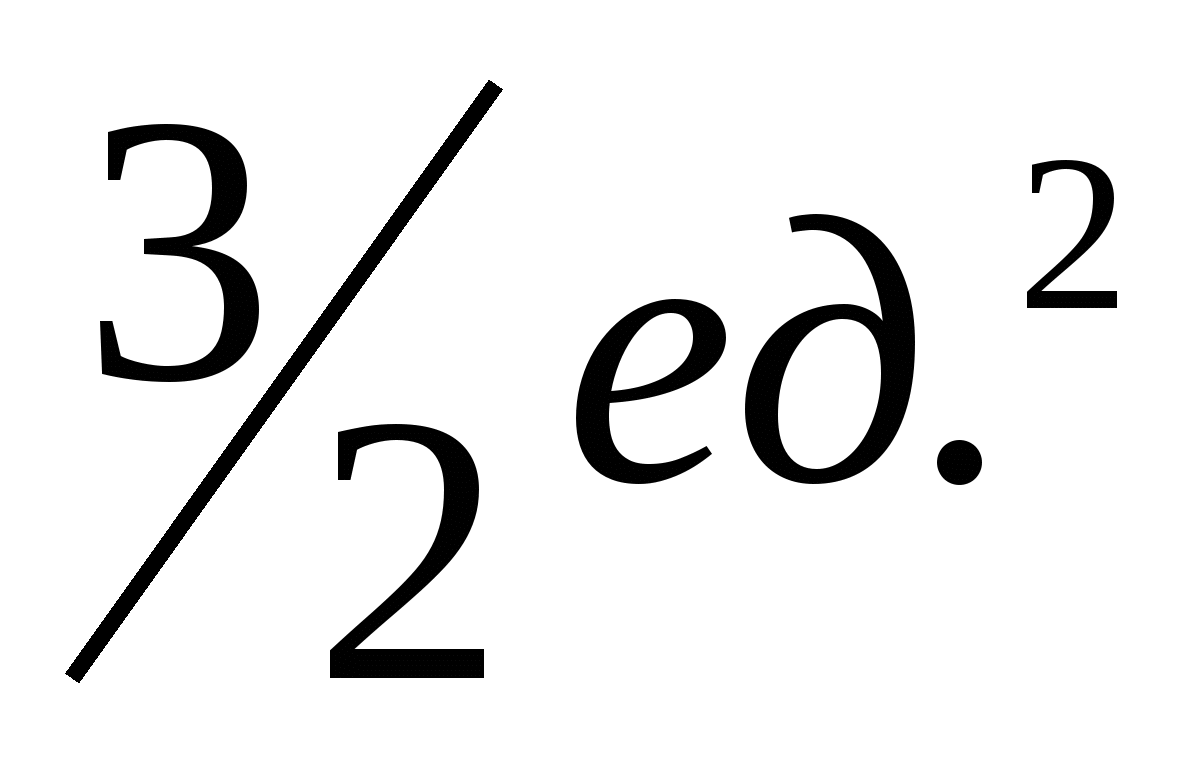 1.8.
1.8. 1.9.
1.9.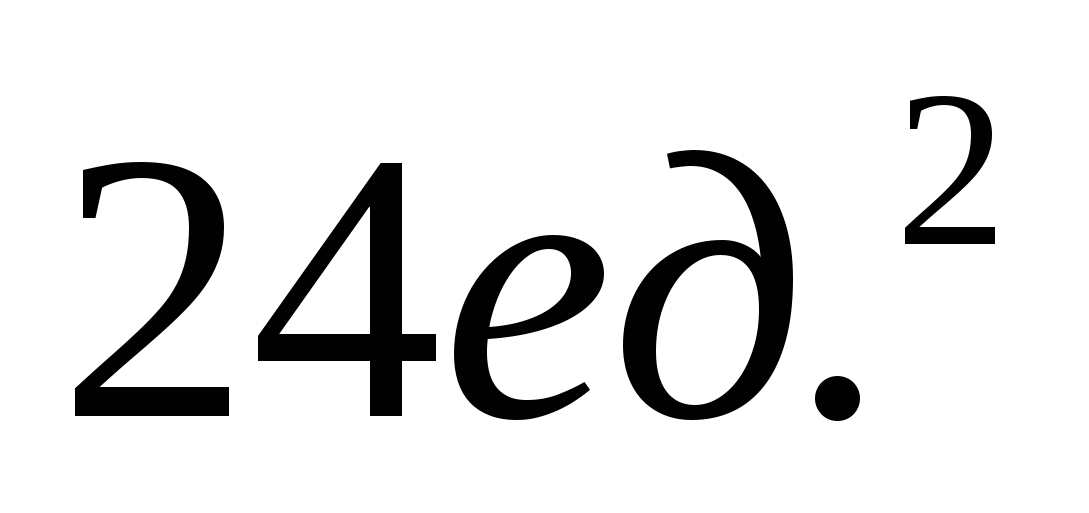 1.10.
1.10. 1.11.
1.11.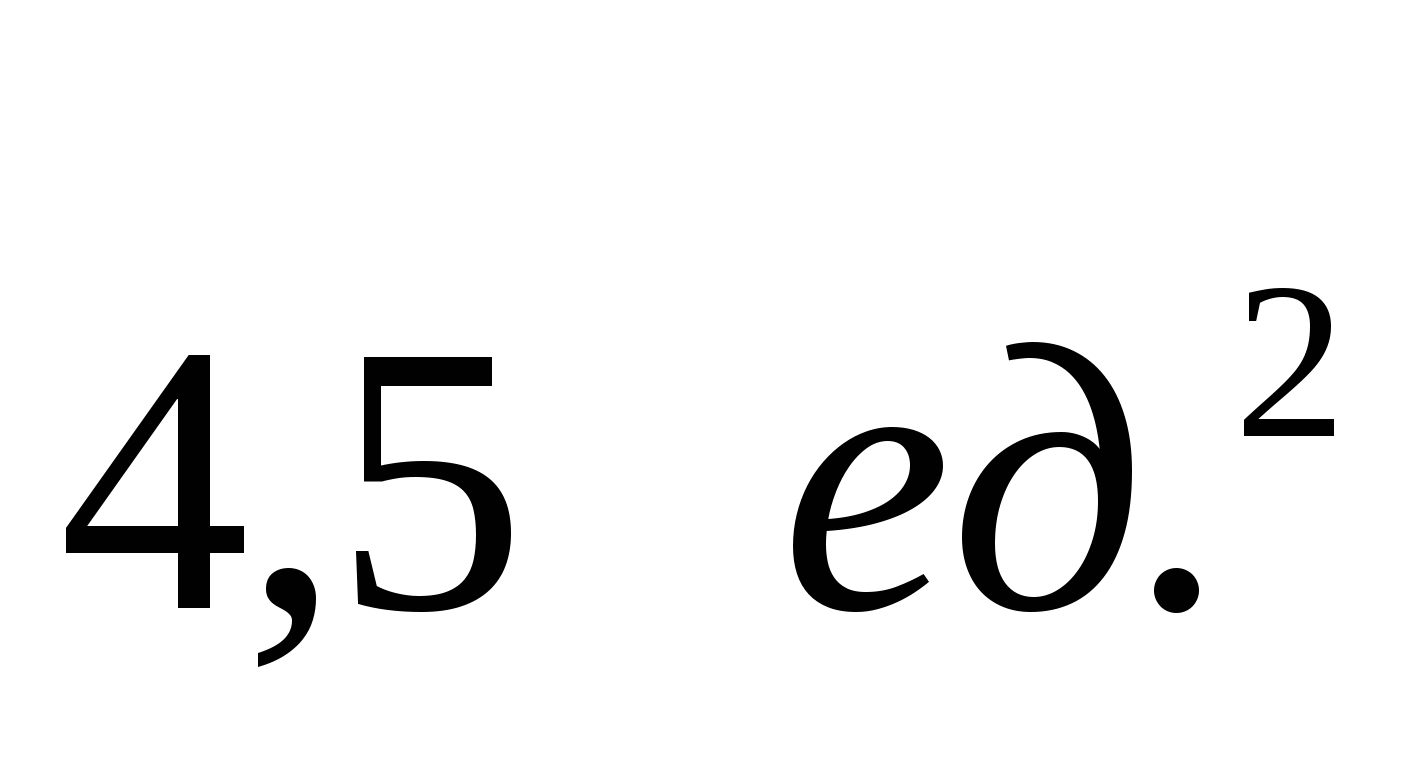 1.12.
1.12.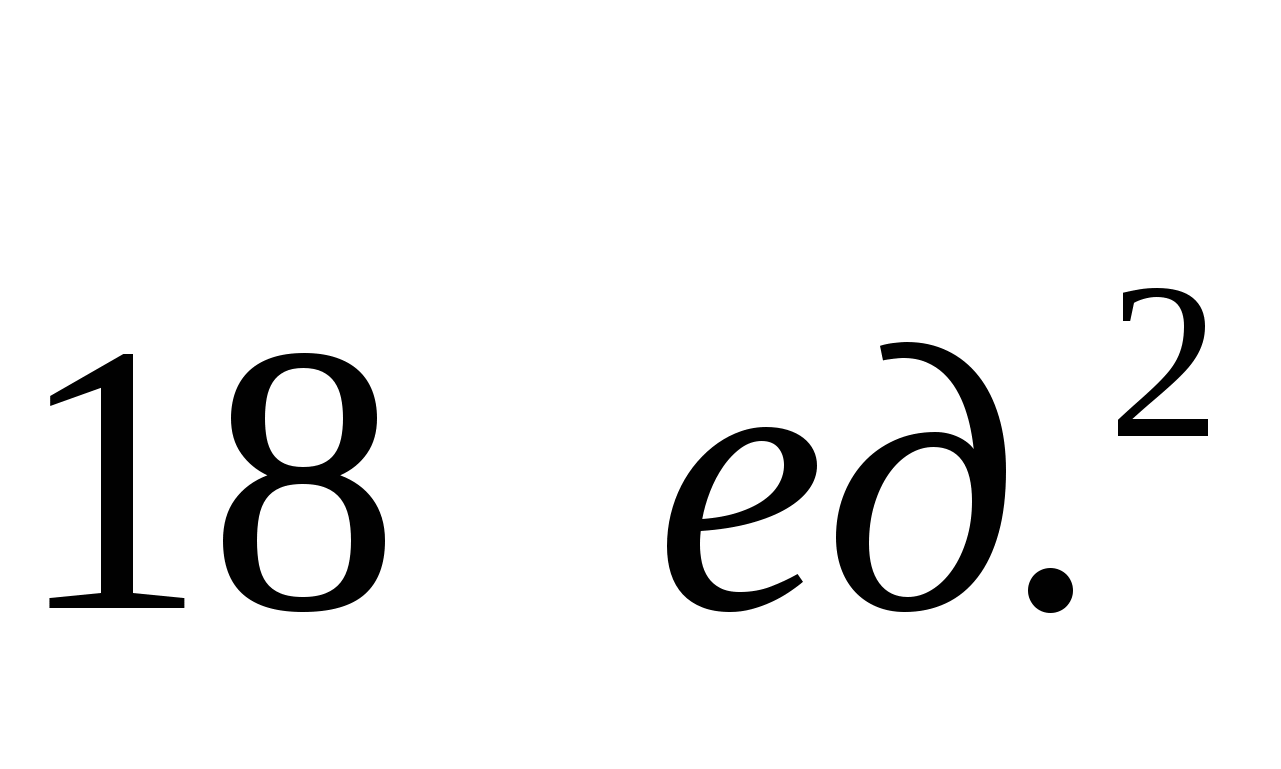 1.13.
1.13. 1.14.
1.14.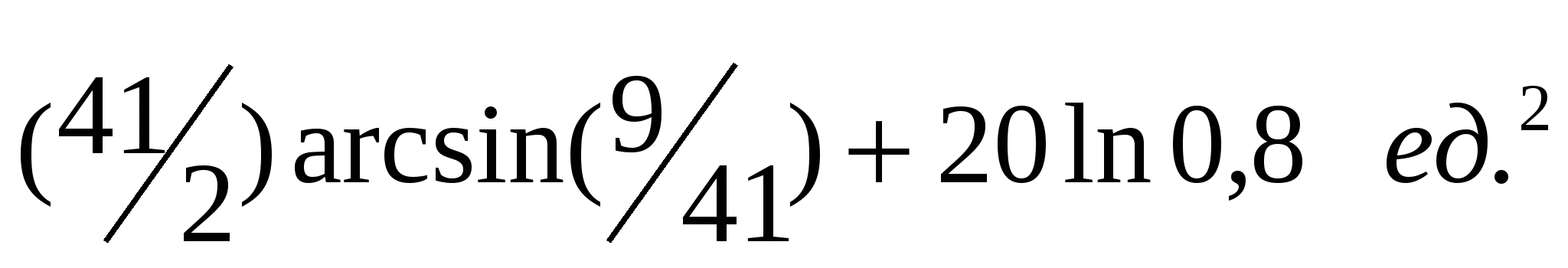 1.15.
1.15.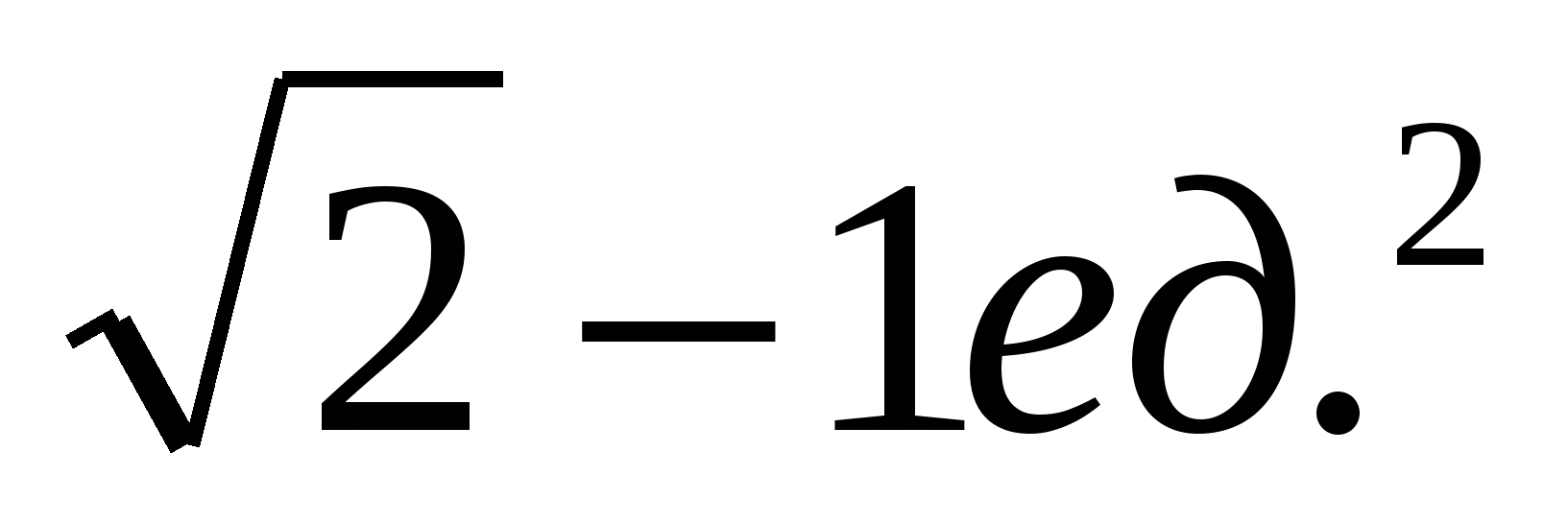 1.16.
1.16.  1.17.
1.17. 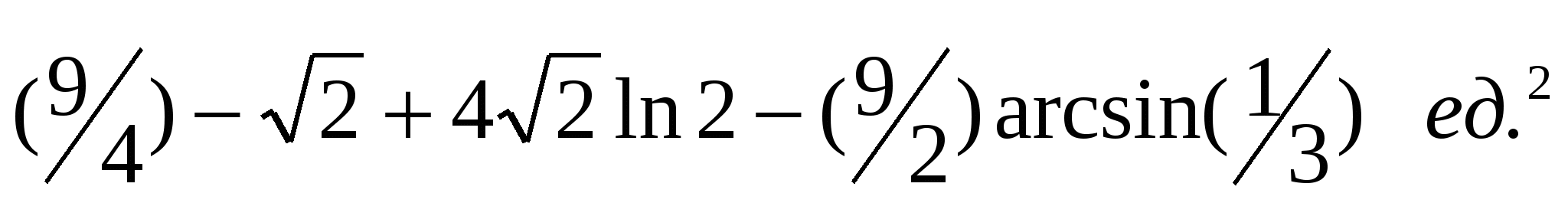
-------------------------------------------------------------------------------------------------------
1.18.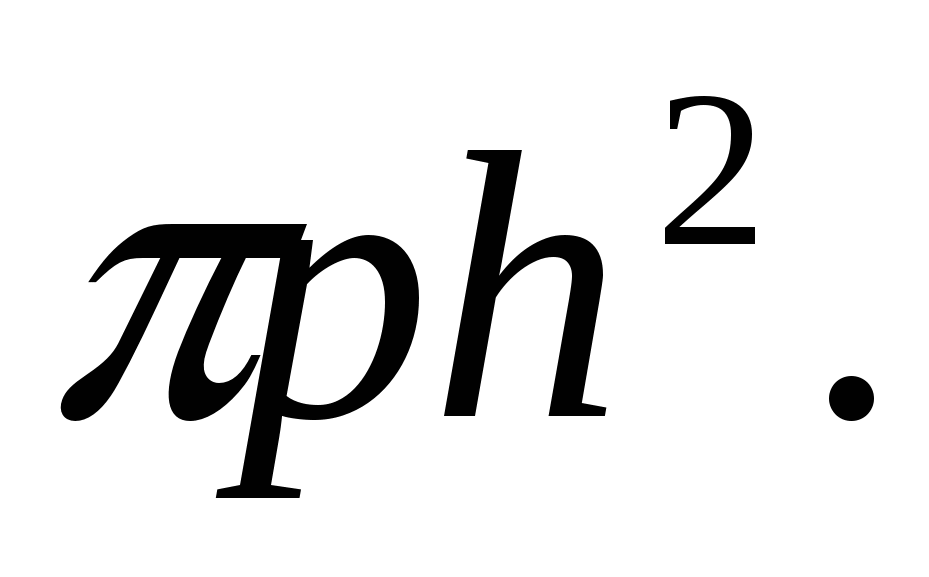 1.19.
1.19. .1.20.
.1.20.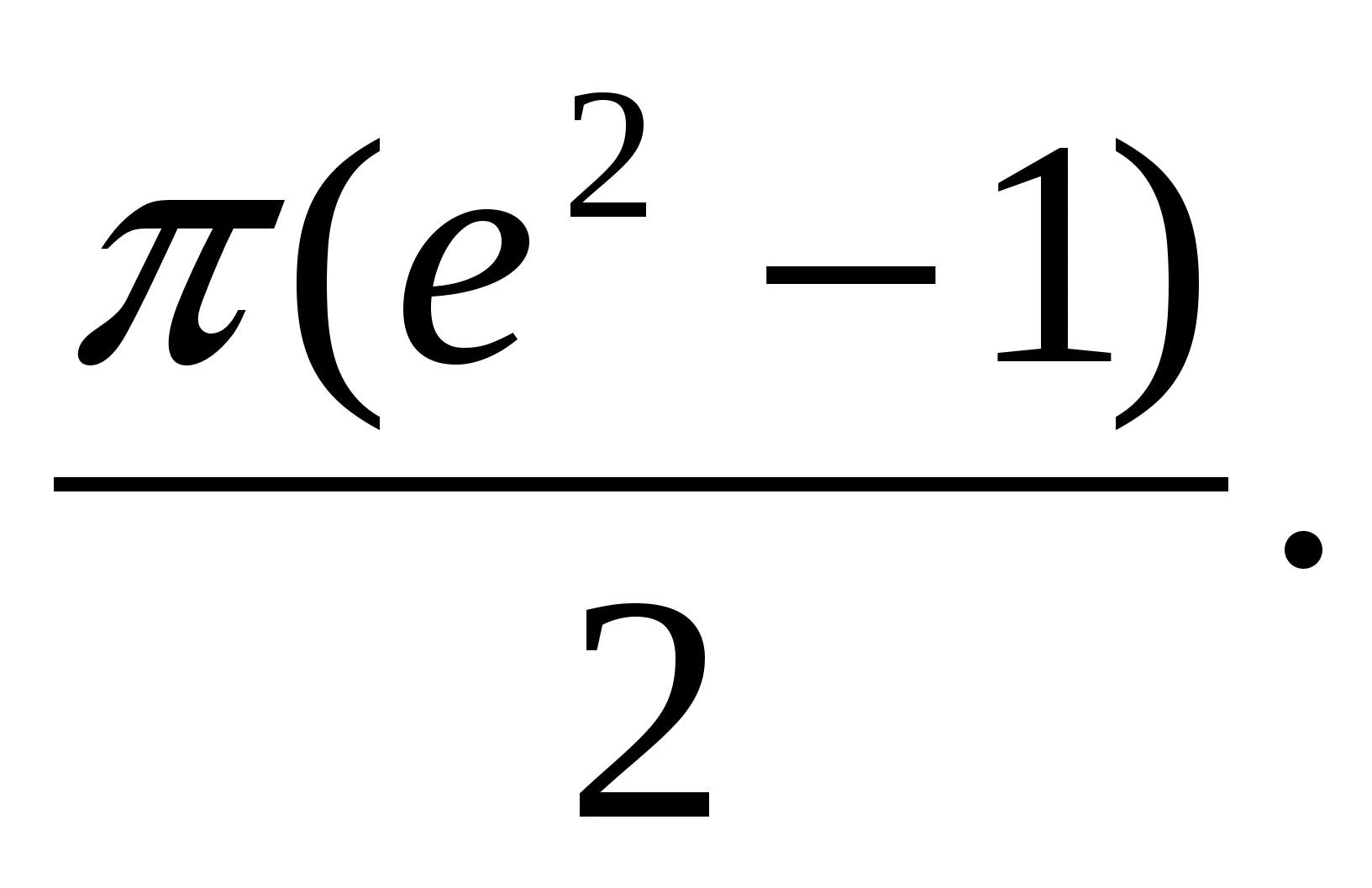 1.21.
1.21.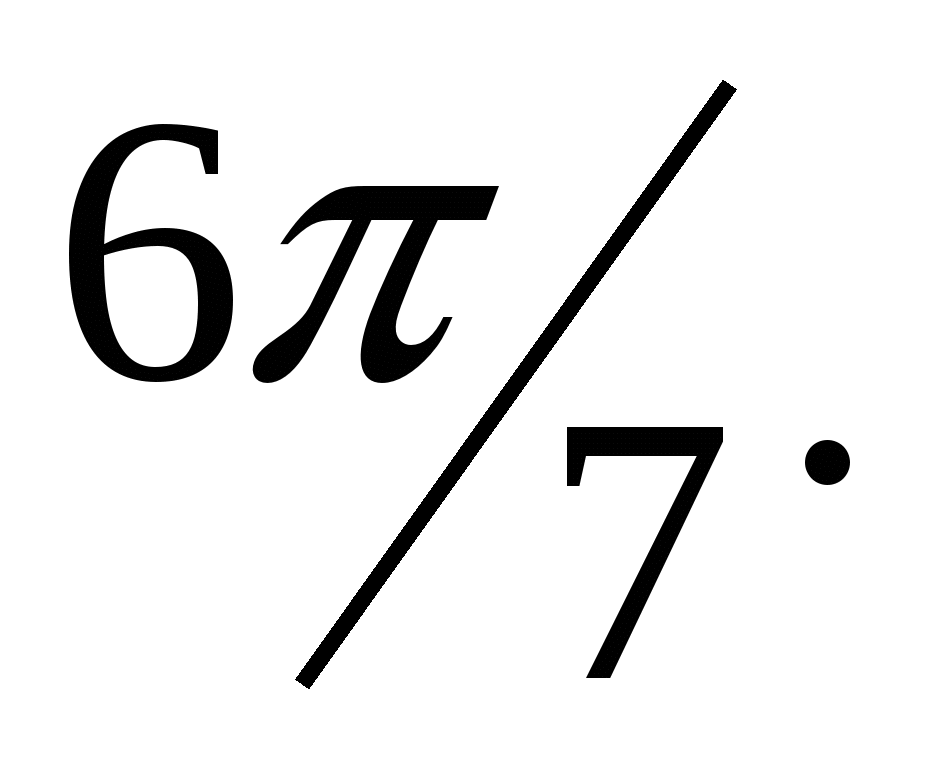
1.22.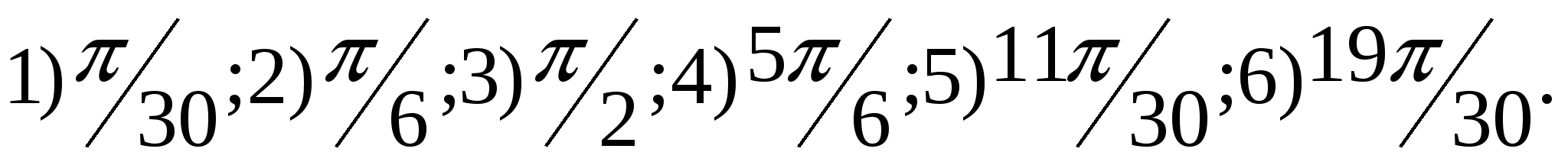
1.23.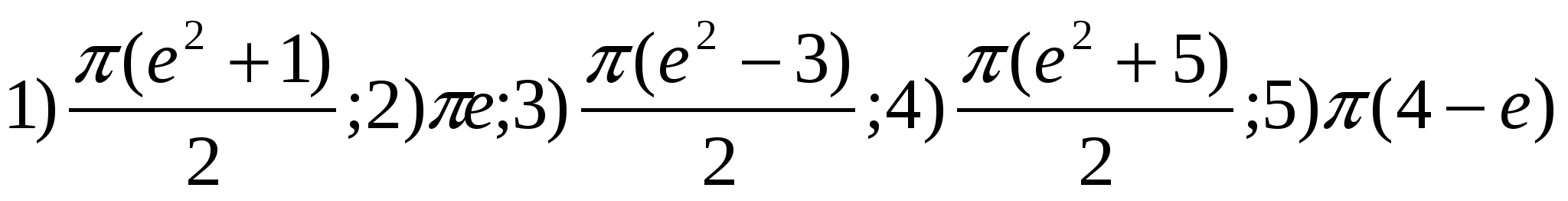 .
.
1.24.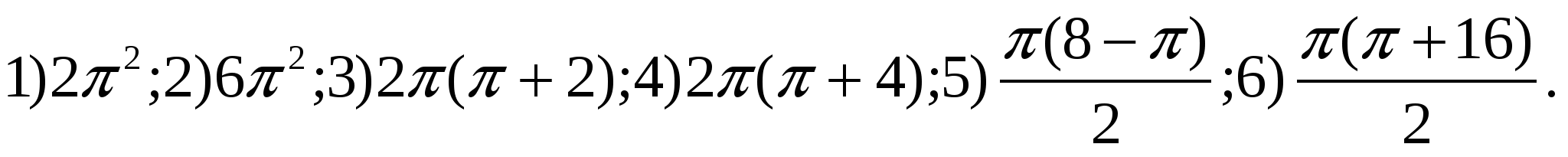 1.25.
1.25.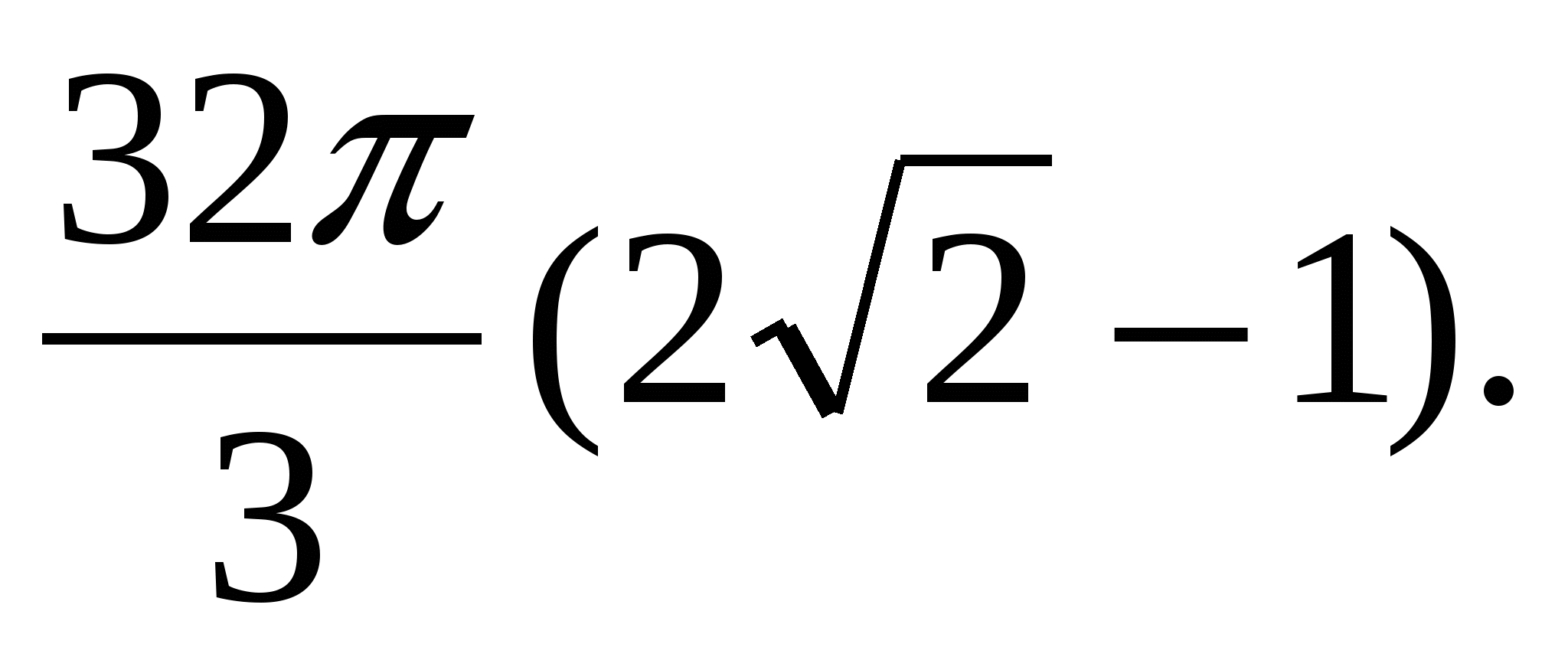 1.26.
1.26.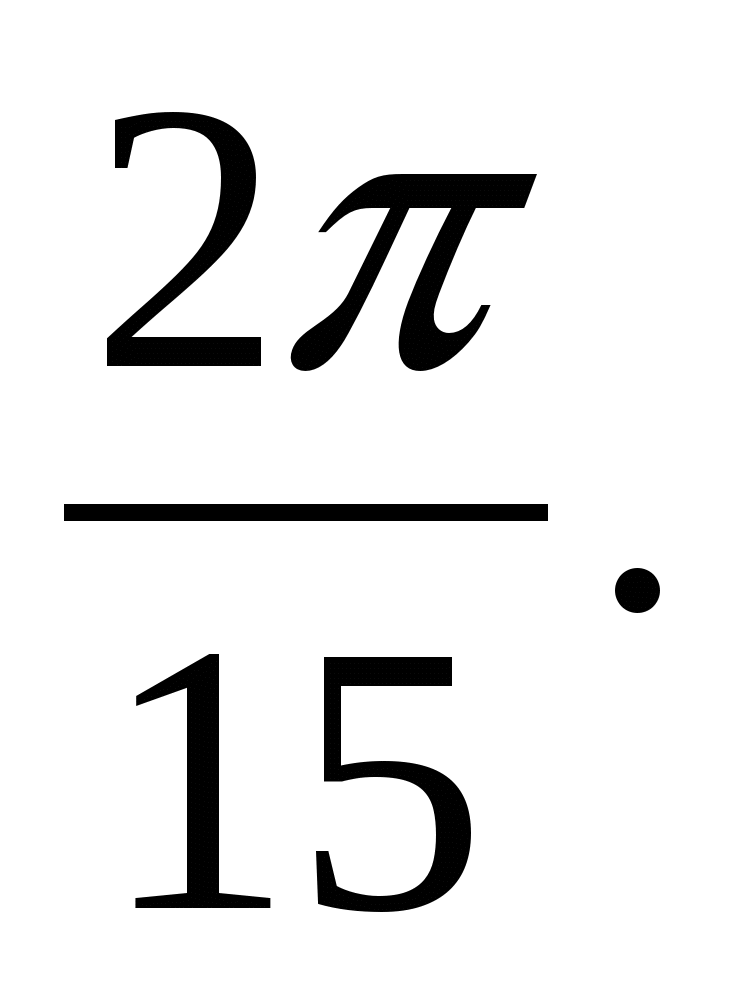 1.27.
1.27.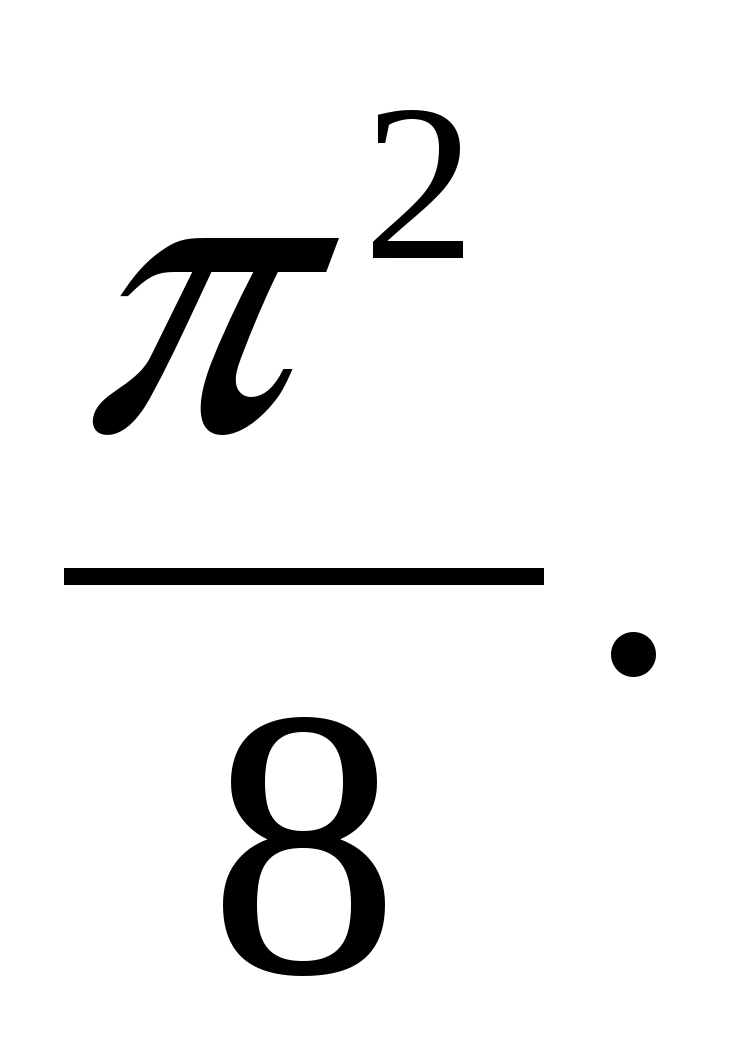 1.28.
1.28.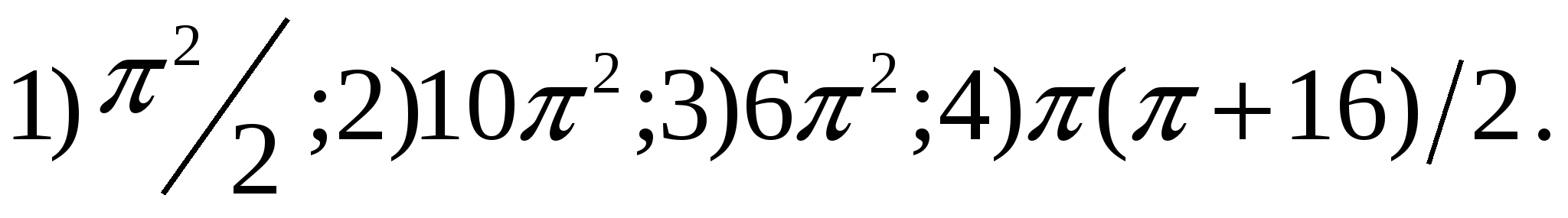 1.29.
1.29.
1.30. 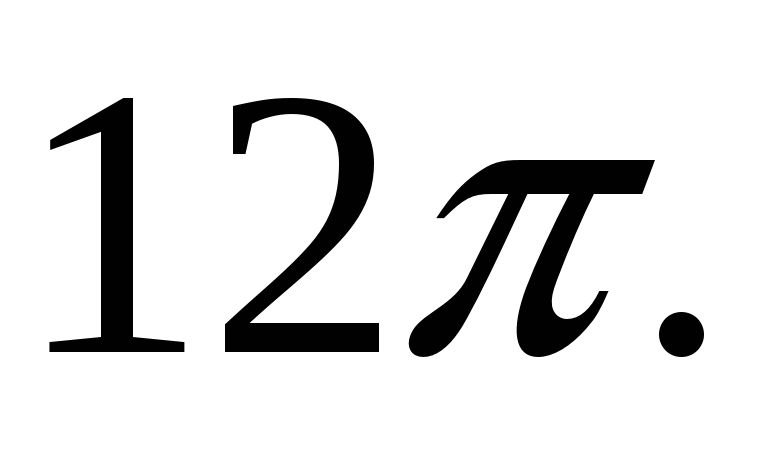 1.31.
1.31.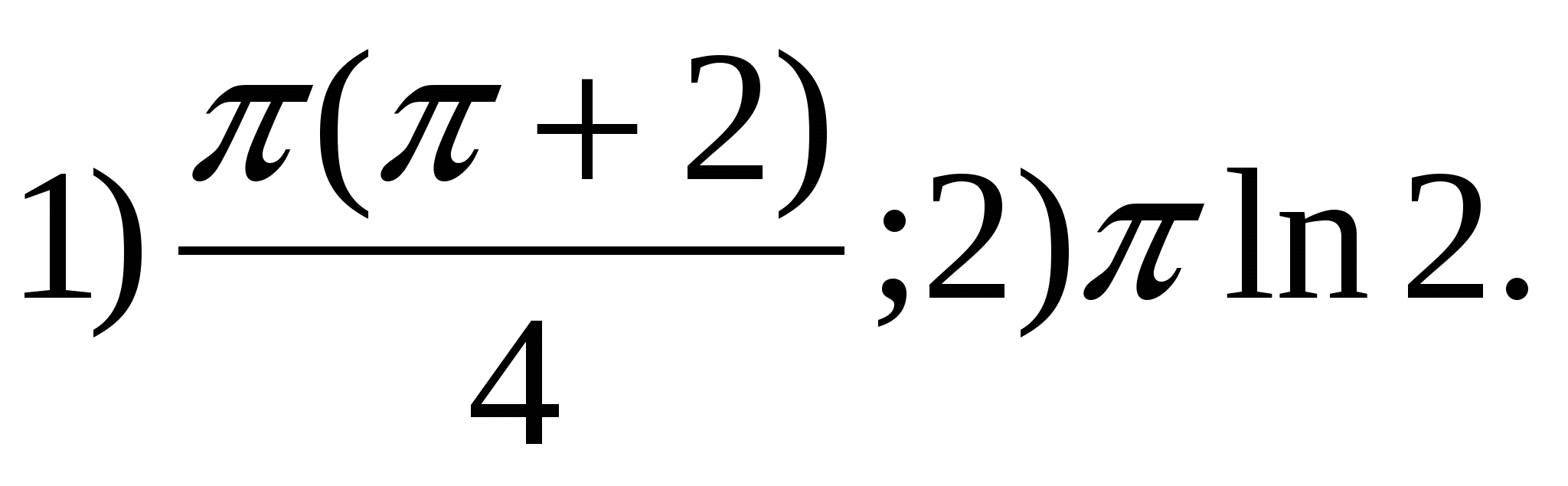
-------------------------------------------------------------------------------------------------------
2.1.  2.2.
2.2. 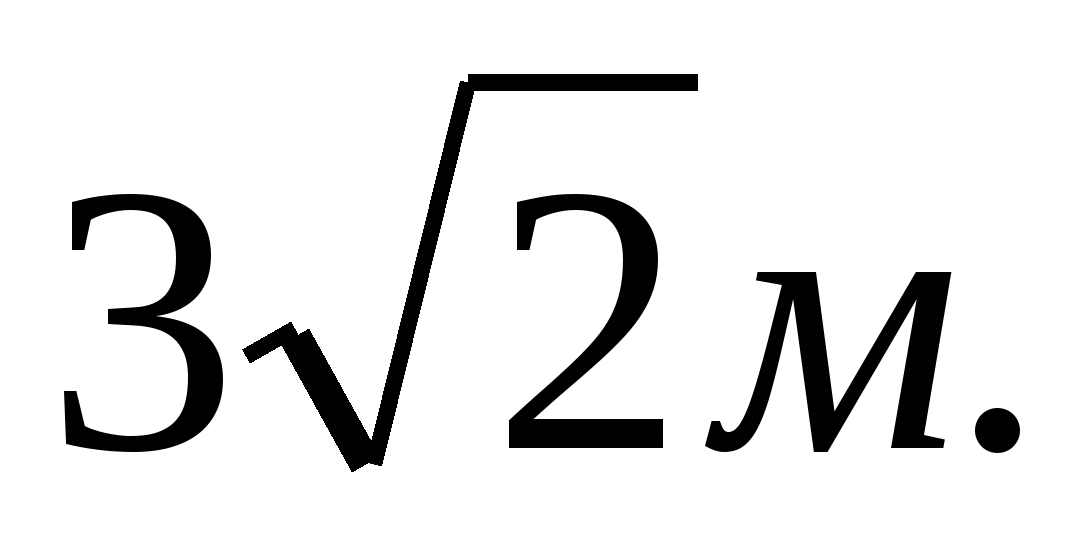 2.3.
2.3.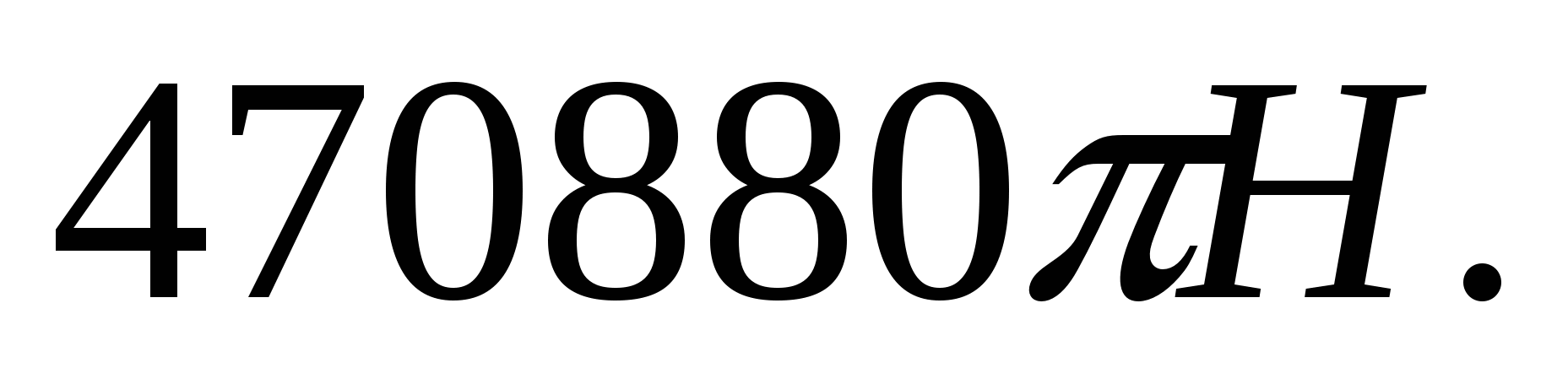 2.4.
2.4. 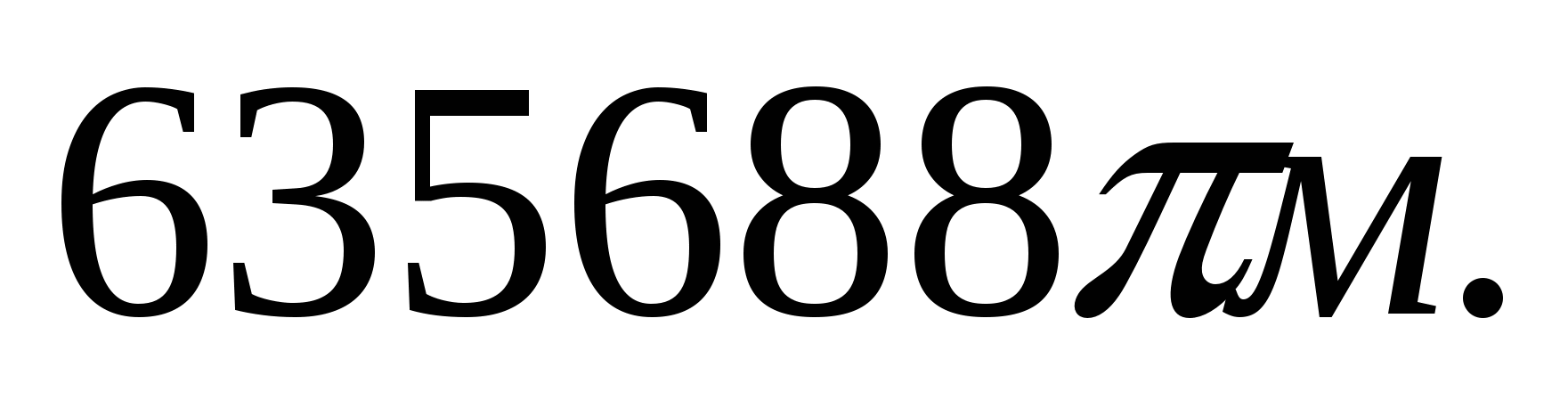 2.5.
2.5. 
2.6.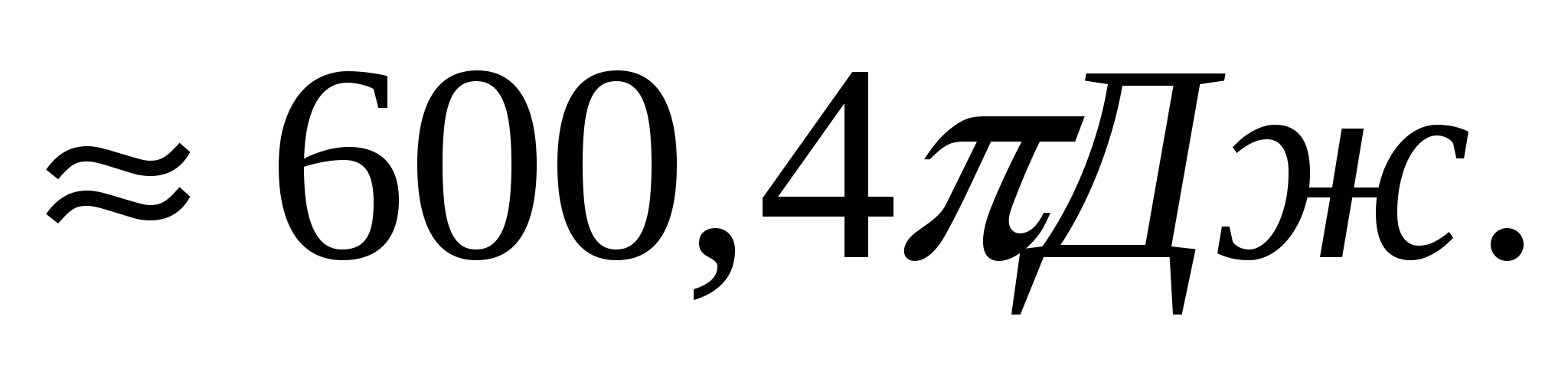 2.7.
2.7. 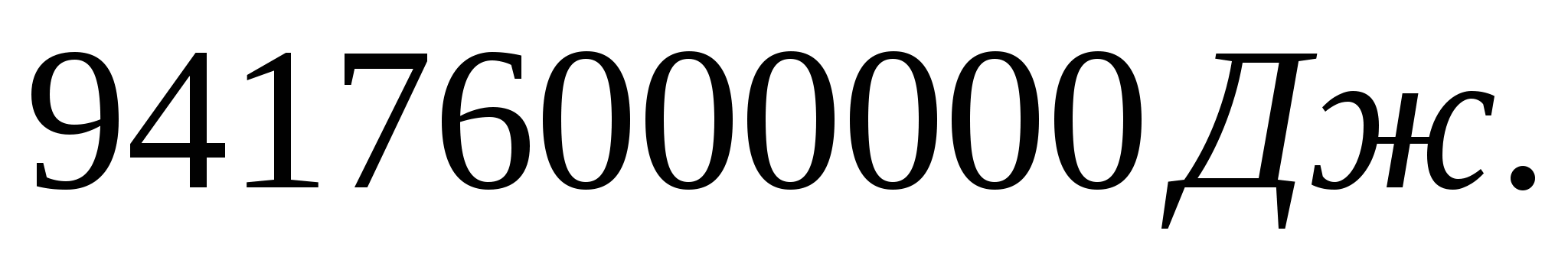 2.8.
2.8.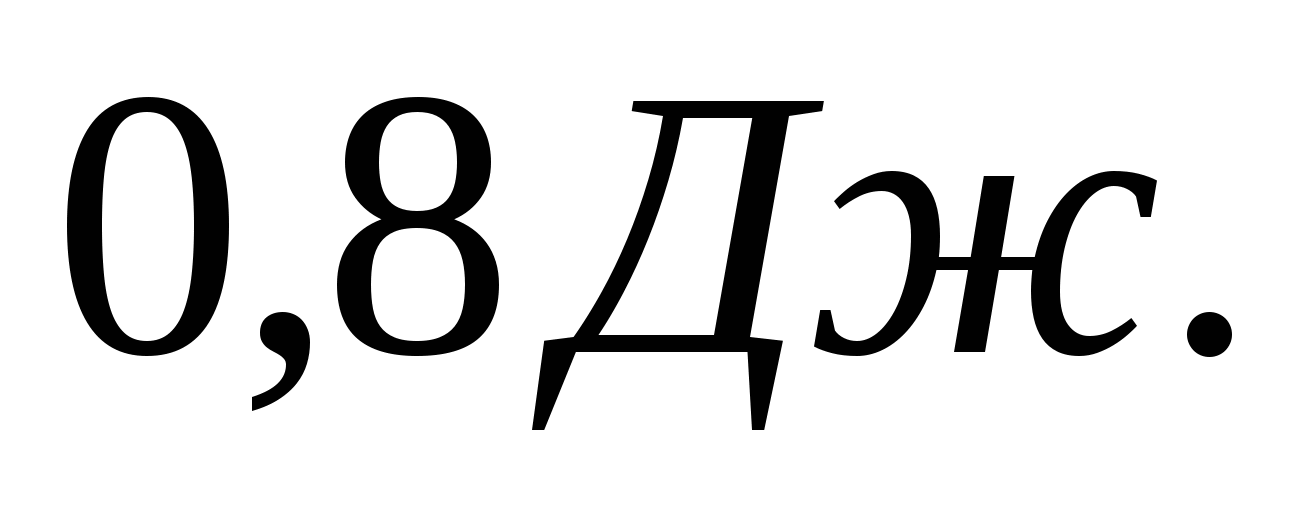 2.9.
2.9. 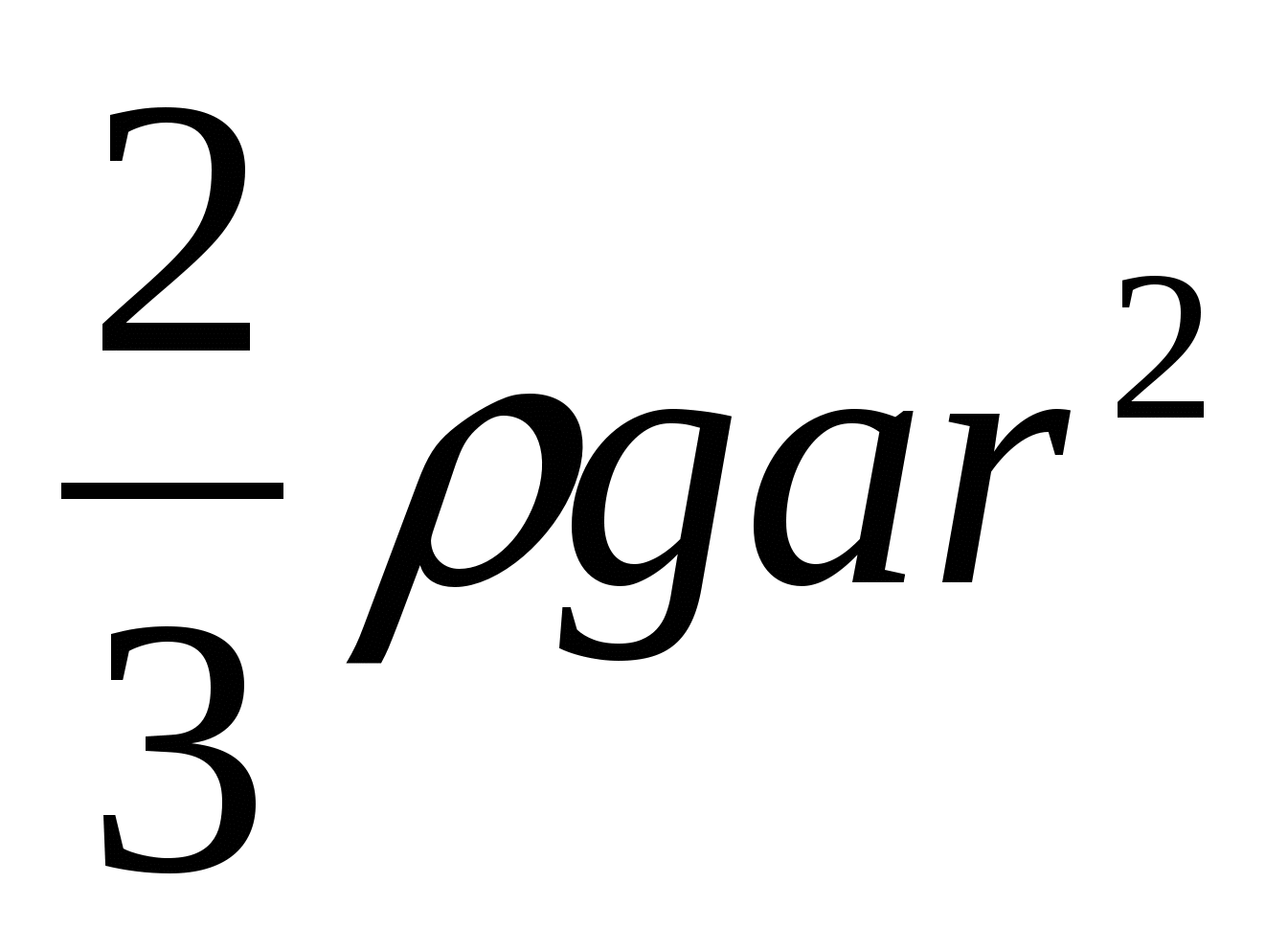 . 2.10.
. 2.10.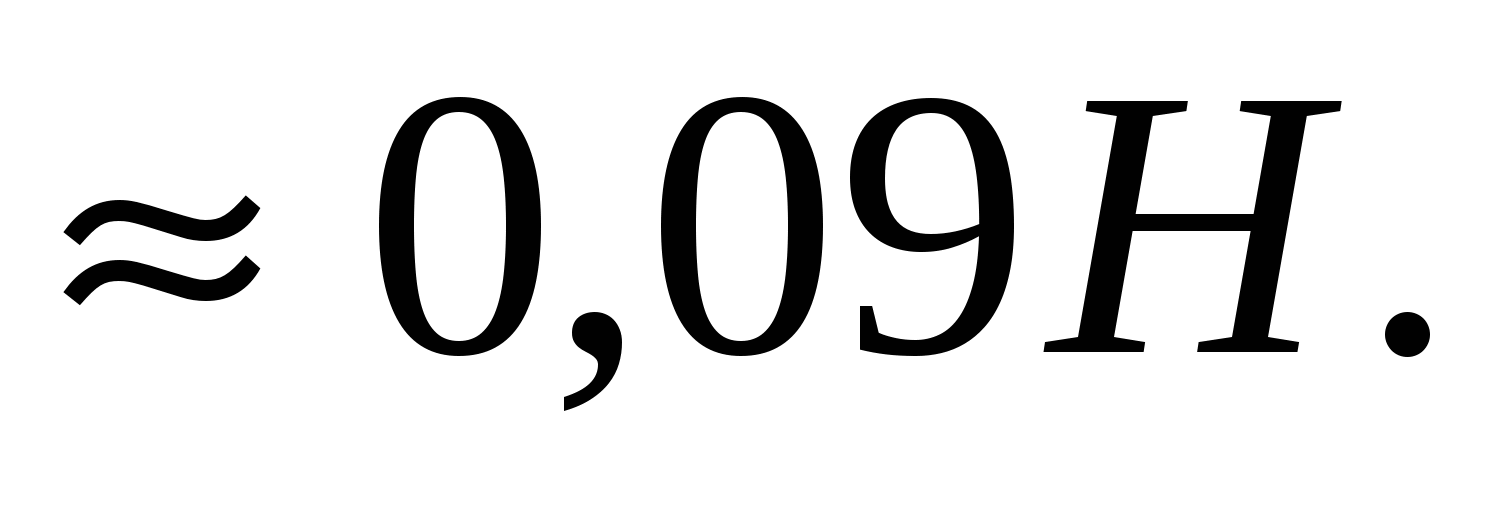
2.11. 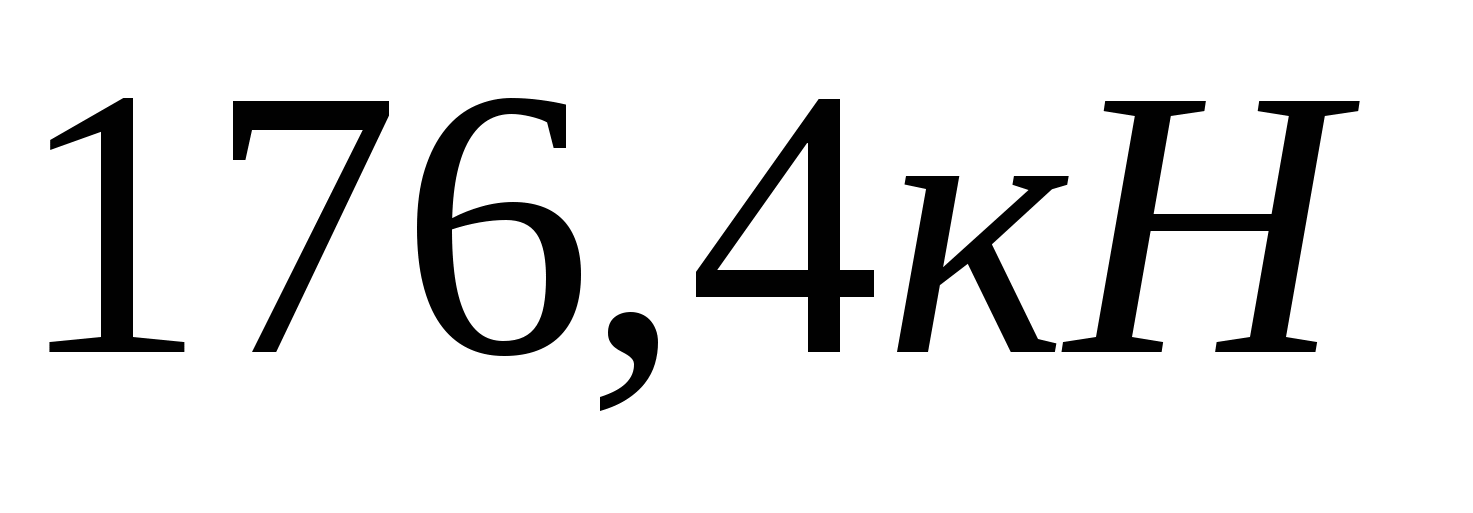 2.12.
2.12. 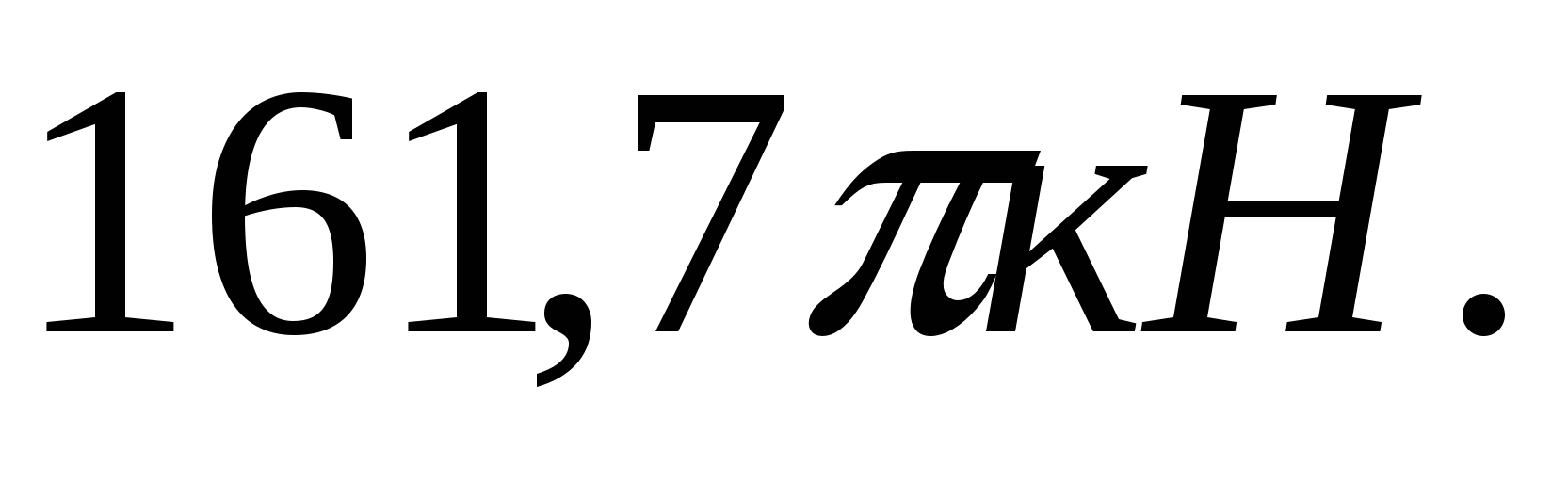 2.13.
2.13. 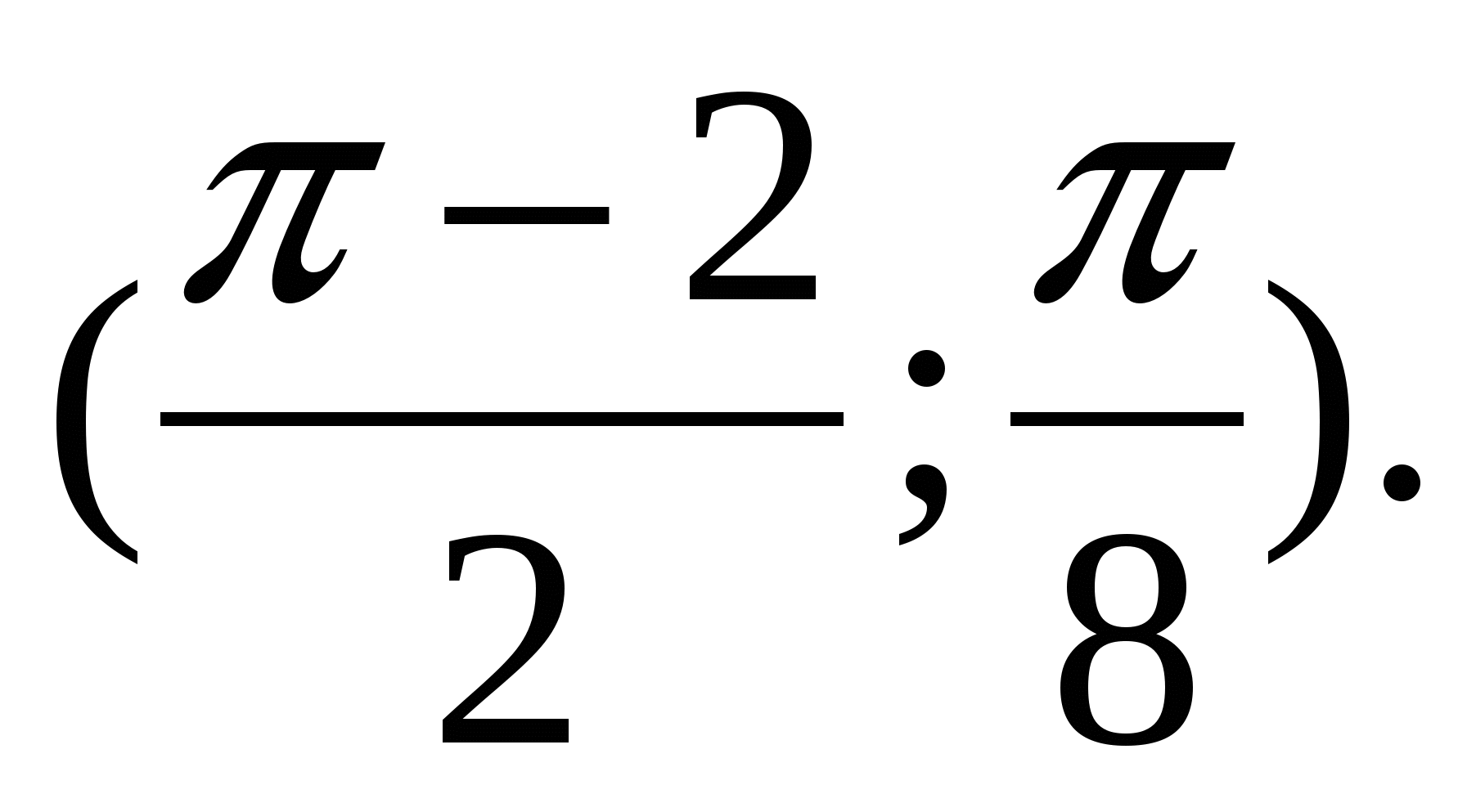 2.14.
2.14. 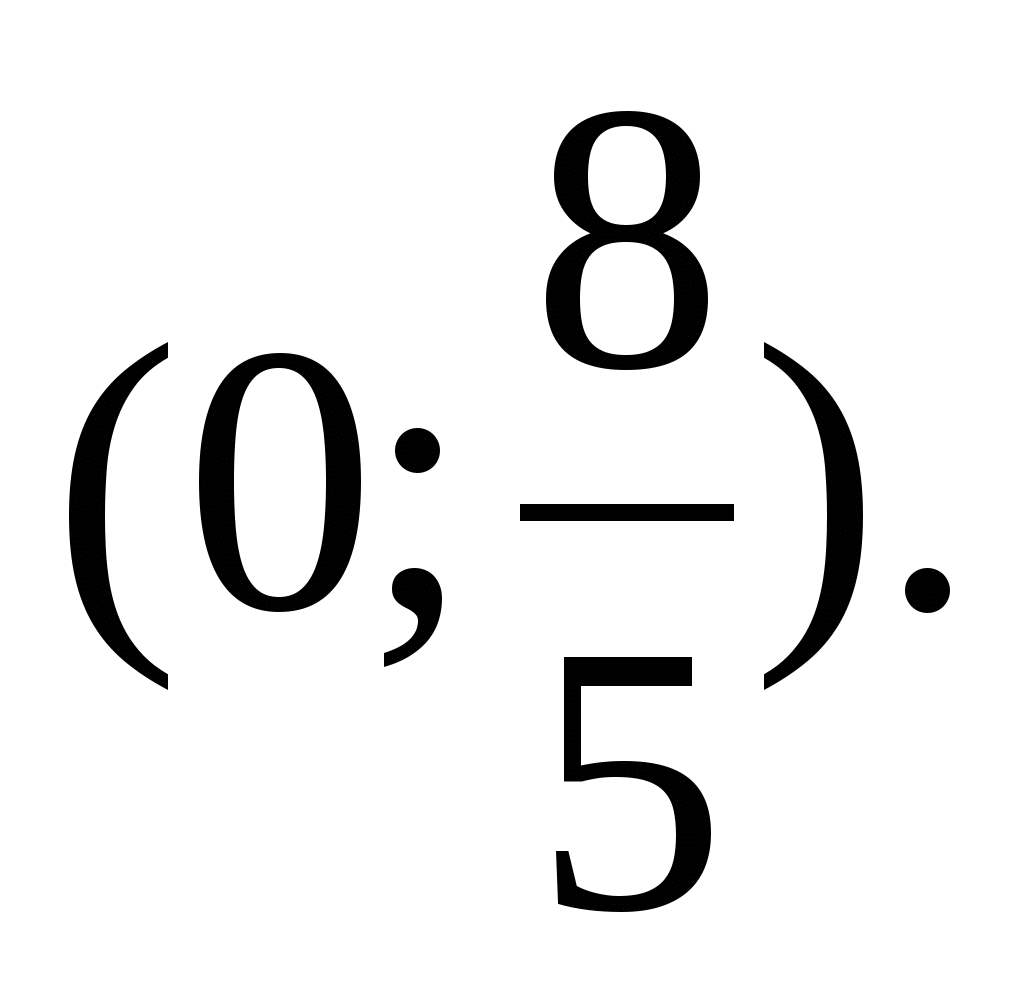
Литература
-
Баврин И.И. Высшая математика, М., Академия, 2002.
-
«Высшая математика для экономистов», под редакцией профессора Кремера Н. Ш., М., «ЮНИТИ», 2000г.
-
Пискунов Н. С. «Дифференциальное и интегральное исчисления», т. 1., М., «Наука», 1985г.
-
Марон И. А. «Дифференциальное и интегральное исчисление в примерах и задачах», М., «Наука», 1970г.
-
Данко П. Е., Попов А. Г., Кожевникова Т. Я., «Высшая математика в упражнениях и задачах», ч.I, М., «ОНИКС 21 век Мир и Образование», 2003г.
-
Шипачев В. С. «Задачник по высшей математике», М, «Высшая школа», 1998г.
-
Лунгу К.К., Письменный Д.Т., Федин С.Н., Шевченко Ю.А. «Сборник задач по высшей математике, М., «Рольф»,2001.
-
«Сборник задач по высшей математике для экономистов», под редакцией профессора Ермакова В.И., М., «Инфра- М», 2004.


