- Преподавателю
- Математика
- Методическая разработка «Производная и её применение»
Методическая разработка «Производная и её применение»
| Раздел | Математика |
| Класс | 10 класс |
| Тип | Другие методич. материалы |
| Автор | Хадеева З.М. |
| Дата | 01.10.2015 |
| Формат | doc |
| Изображения | Есть |
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РТ
ГАОУ ВО «Альметьевский государственный институт муниципальной службы»
Методическая разработка
По дисциплине: «Математика»
Для студентов ССУЗов по разделу
«Производная и её применение»
Составила: Хадеева Залфира Махмудовна
преподаватель математики
торгово-экономического факультета
среднего профессионального образования
Альметьевск, 2014
Содержание
Введение………………………………………………………………..………….3
Понятие производной…………………………………………………….………4
Геометрический и физический смысл производной ………………….……….5
Уравнение касательной к графику функции …………………………………..6
Вычисление производной………………………………………………….……7
Применение производной при исследовании функции…………………...…..9
Исследование функции……………………………………………….…..…….19
Задания для самостоятельных работ ……………………………….…..……22
Ответы………………………………………………………………….…..……24
Исторические сведения………………………………………………….….….25
Список использованных источников и литературы…………………..….….26
Введение
Преподавание математики не может стоять на должном уровне, а знания обучающихся не будут достаточно полными и прочными, если в работе преподавателя отсутствует система повторительно-обобщающих уроков. Правильно организованное заключительное повторение способствует объединению в целое материала, выделению общих идей, систематизирует знание учащихся путем раскрытия новых связей и углубления уже известного. При этом знания учащихся уточняются, становятся более прочными и осознанными, повышается их общая математическая культура.
В целях совершенствования преподавания математики целесообразно использовать обучение студентов решению задач, с помощью специально подобранных упражнений, учить их наблюдать, пользоваться аналогией, сравнениями и делать соответствующие выводы.
Работа имеет следующие задачи:
-
Обобщить и систематизировать теоретический материал по указанным темам;
-
Отработать навыки вычисления производной функции;
-
Овладеть умением применения геометрического и физического смысла производной;
-
Овладеть умением применения производной и ее графика при исследовании функции;
В этой работе рассмотрены разделы: понятие производной, физический геометрический смыслы производных, исследование функции с помощью производной.
По каждому разделу приведены теоретические материалы, набор различных заданий с решениями.
Данная работа может помочь учащимся овладеть конкретными математическими знаниями необходимыми для применения в практике, развить умственные способности, самостоятельно выполнять различные творческие работы.
-
Понятие производной
Определение. Производной функции y=f(x), заданной на некотором интервале (a;b), в точке х этого интервала, называют предел отношения приращения функции в этой точке к соответствующему приращению аргумента, когда приращение аргумента стремится к нулю.
Производную функции f(x) обозначают f '(x) и говорят: «эф штрих от икс». Следовательно,
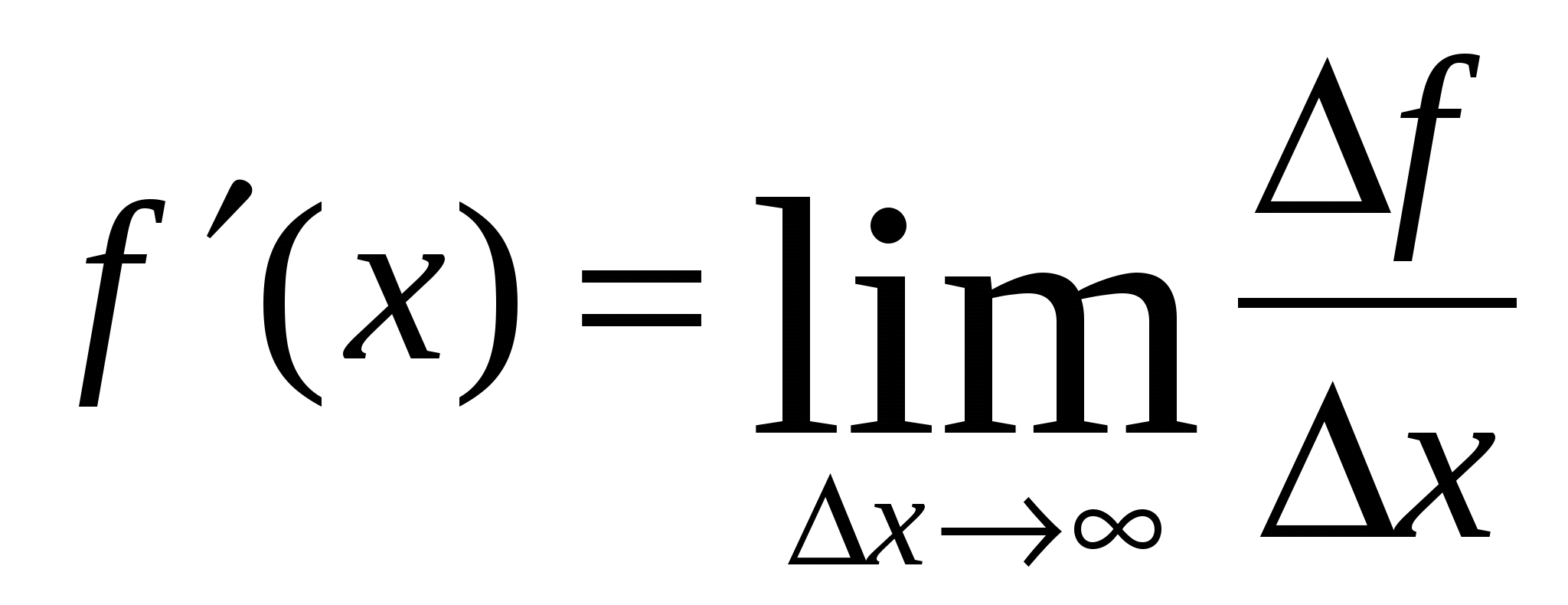 .
.
Алгоритм нахождения производной (для функции y=f(x)).
-
Зафиксировать значение х, найти f(x).
-
Дать аргументу х приращение ∆х, перейти в новую точку х+∆х, найти f(x+∆x).
-
Найти приращение функции: ∆у=f(x+∆x)-f(x).
-
Составим отношения
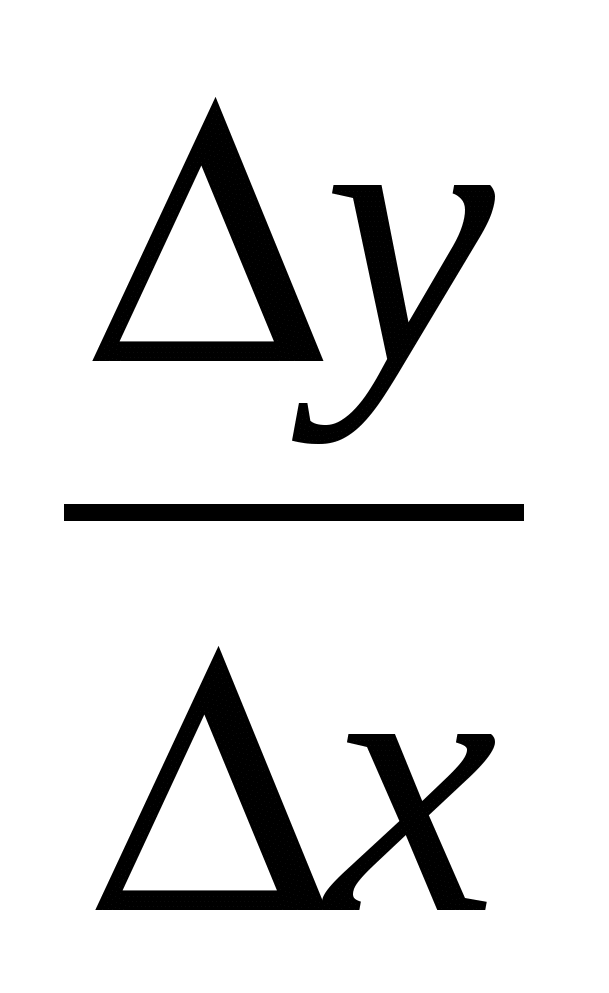 .
. -
Вычислить
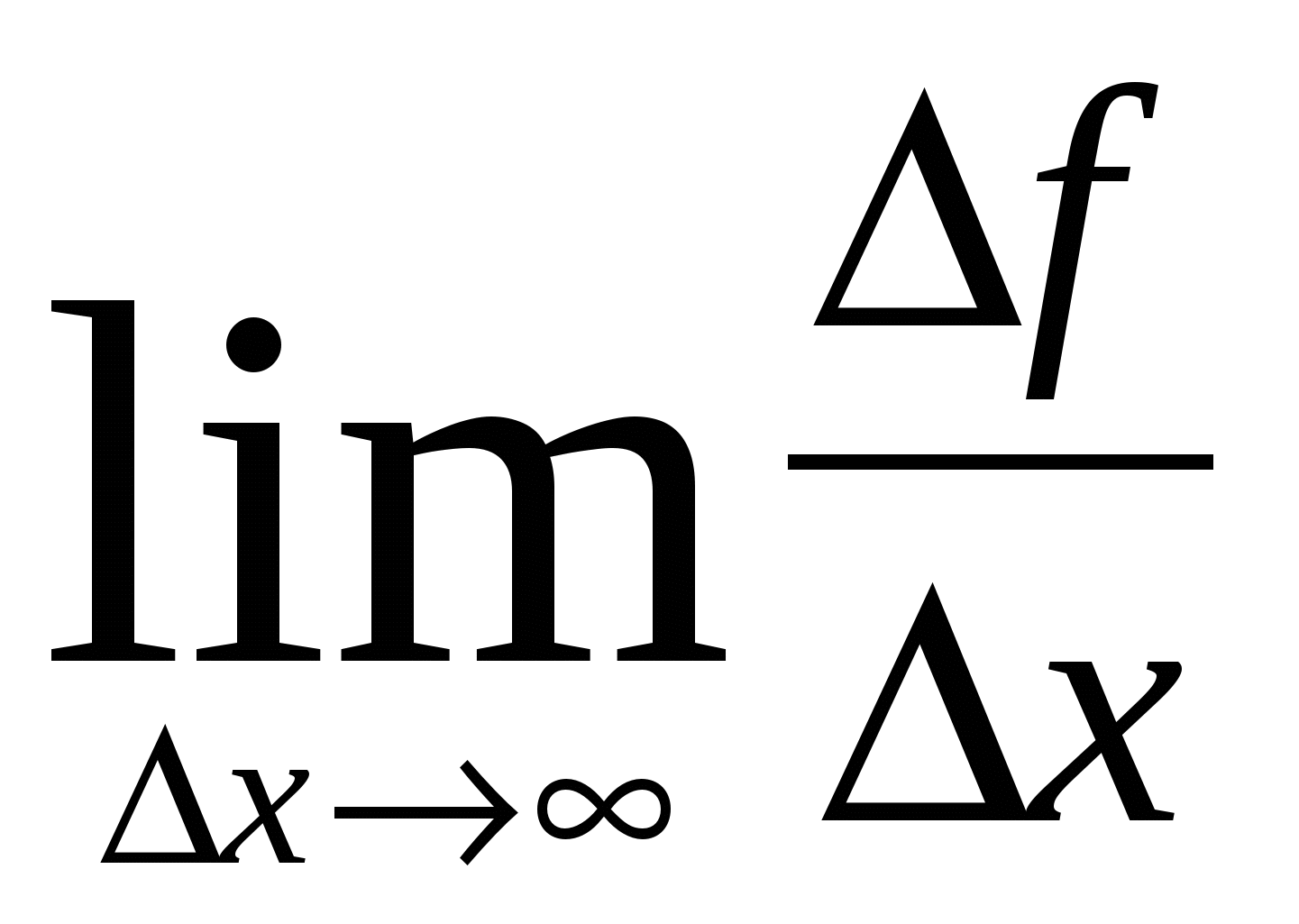 .
.
Этот предел и есть f '(x).
Пример. Найти производную функции у=2х+3 в точке х=3
1. 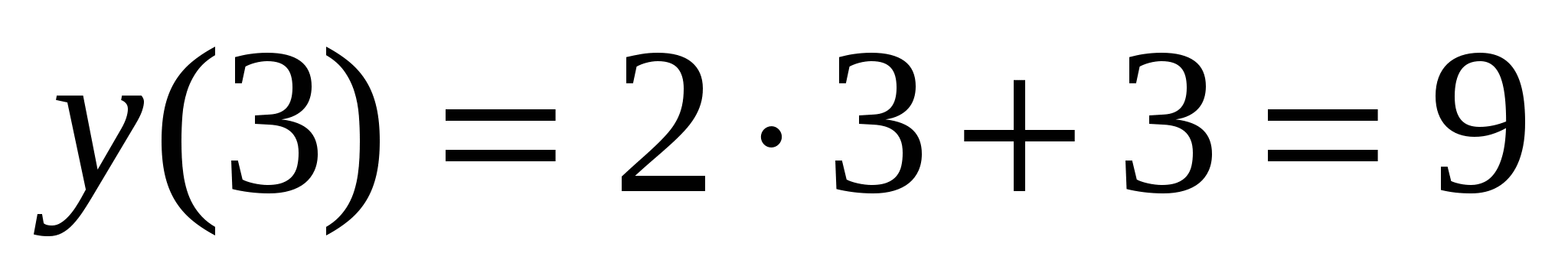 .
.
2. 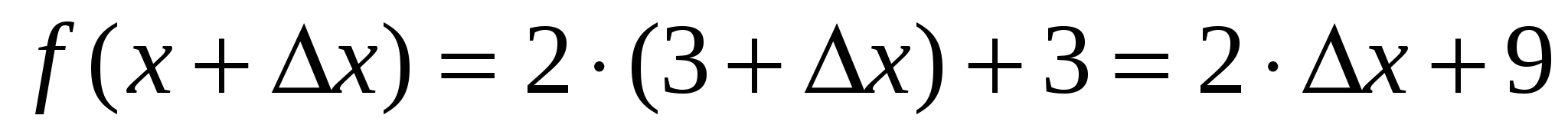 .
.
3. 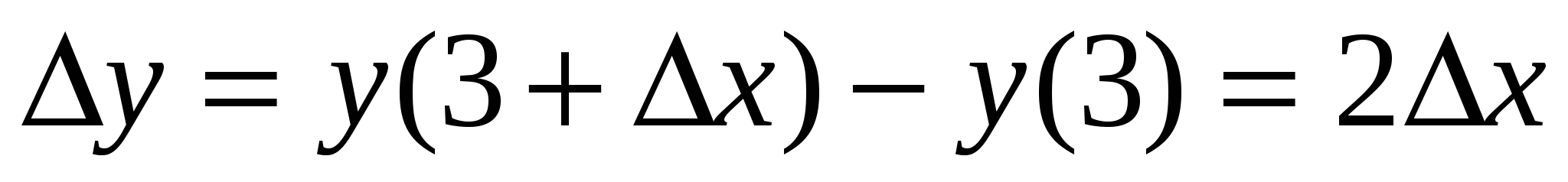 .
.
4. 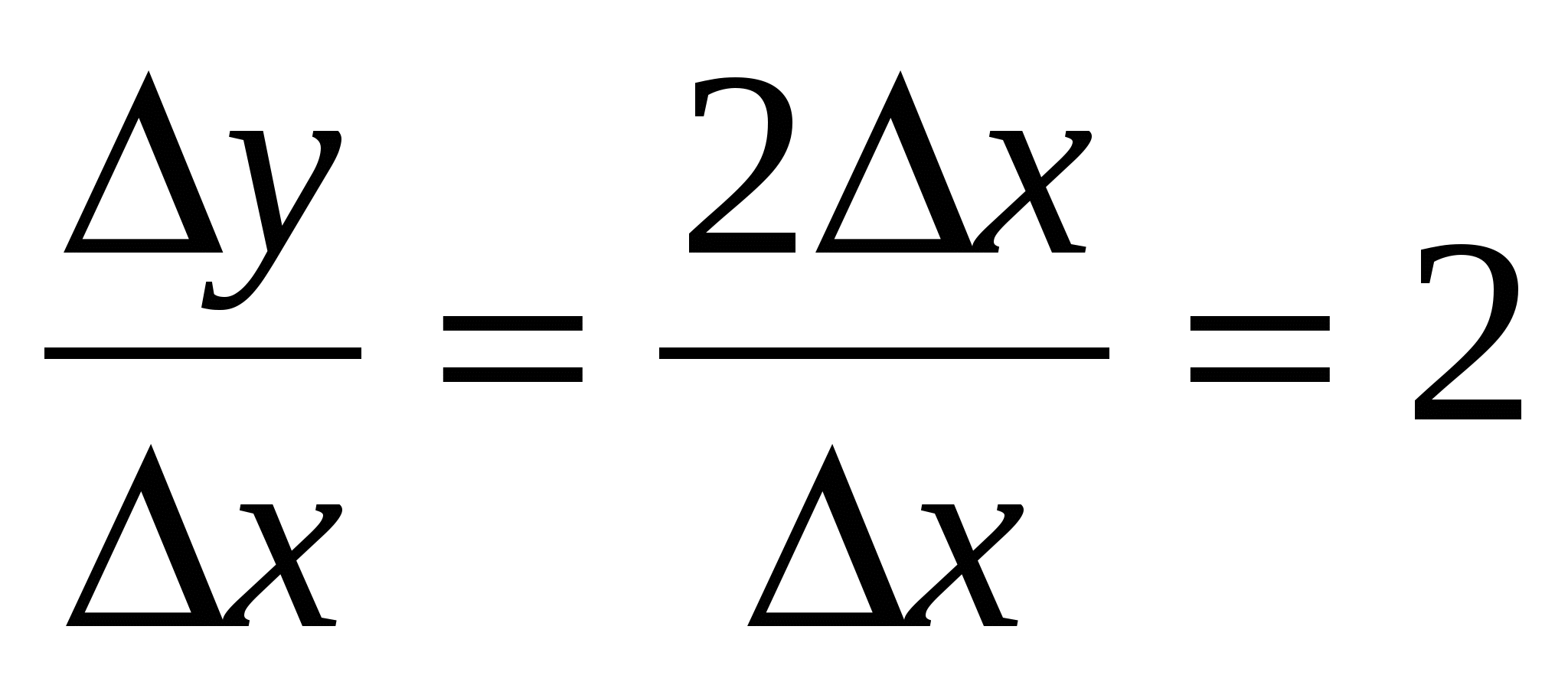 .
.
5. 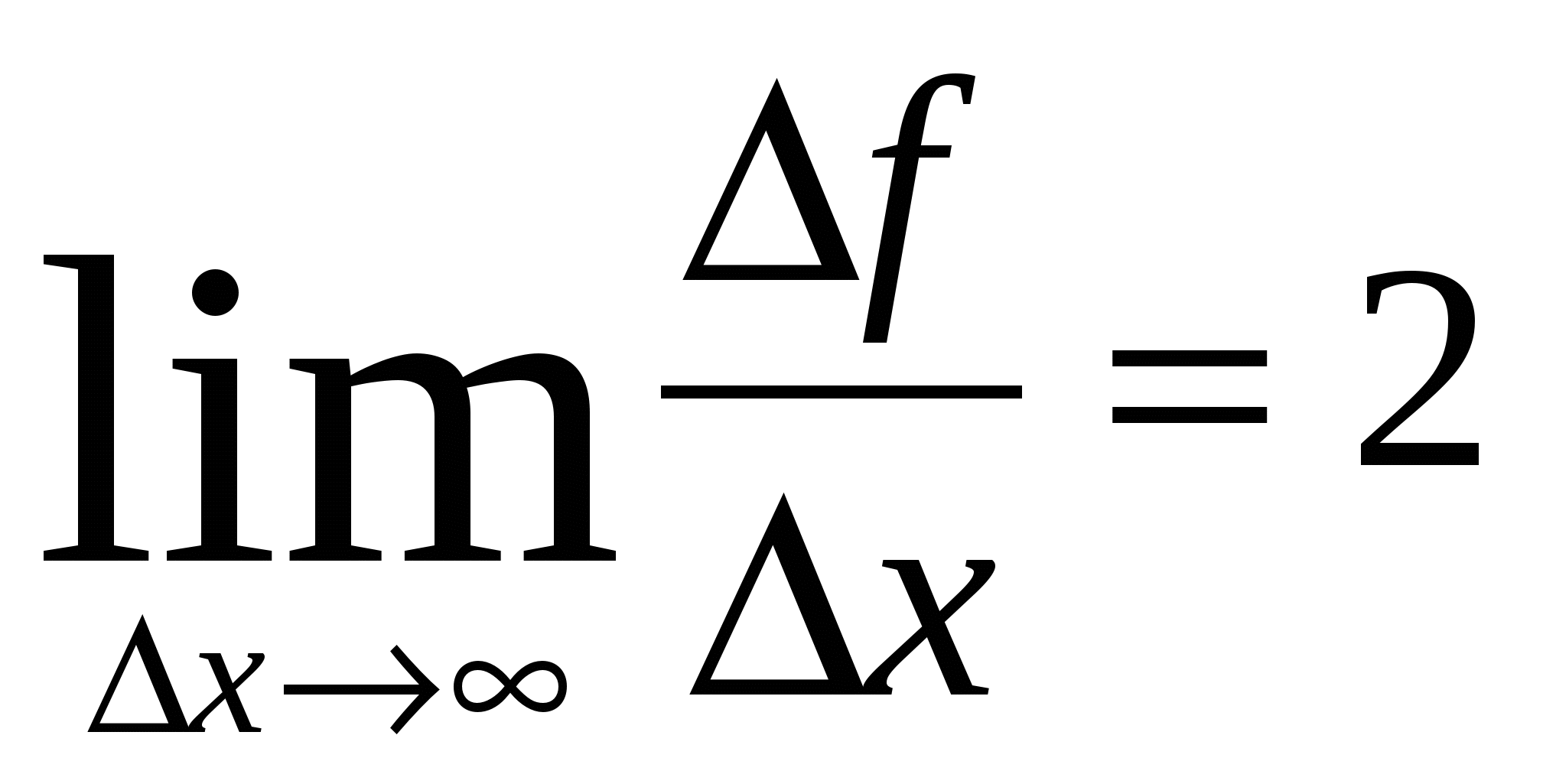 .
.
6. у '(3)=21
2 Геометрический и физический смысл производной
Если при прямолинейном движении путь s, пройденной точкой, есть функция от времени t, т.е. s=f(t), то скорость точки есть производная от пути по времени, т.е. v(t)=f '(t), этот факт выражает механический смысл производной.
Пример. Тело движется по прямой так, что расстояние S (в метрах) от него до точки В этой прямой изменяется по закону 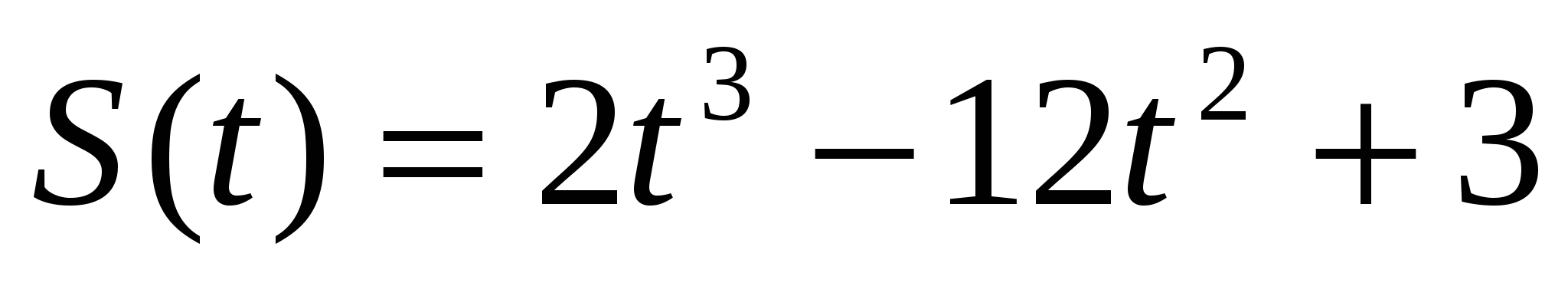 (t - время движения в секундах). Через сколько секунд после начала движения ускорение тела будет равно 36 м/
(t - время движения в секундах). Через сколько секунд после начала движения ускорение тела будет равно 36 м/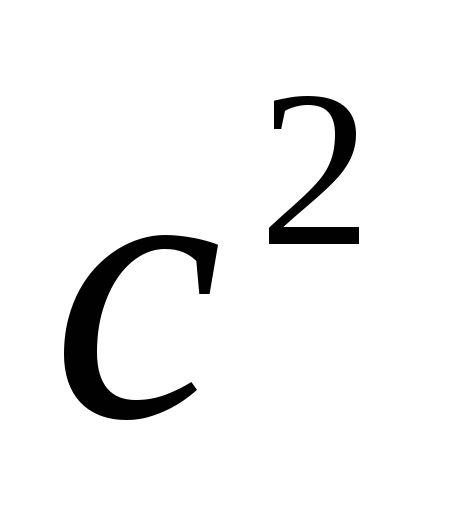 ?
?
Решение. Из механического смысла производной имеем скорость - это производная пути по времени. Скорость изменяется по закону 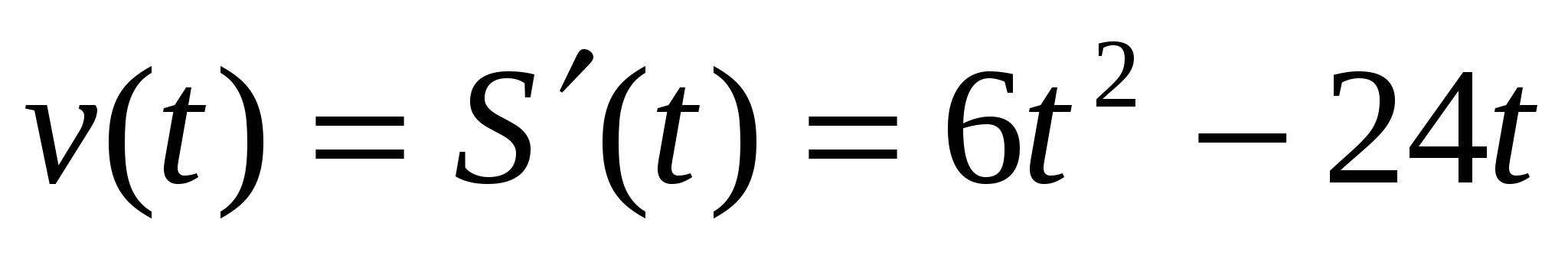 . Так как ускорение - это производная скорости по времени, то ускорение изменяется по закону
. Так как ускорение - это производная скорости по времени, то ускорение изменяется по закону 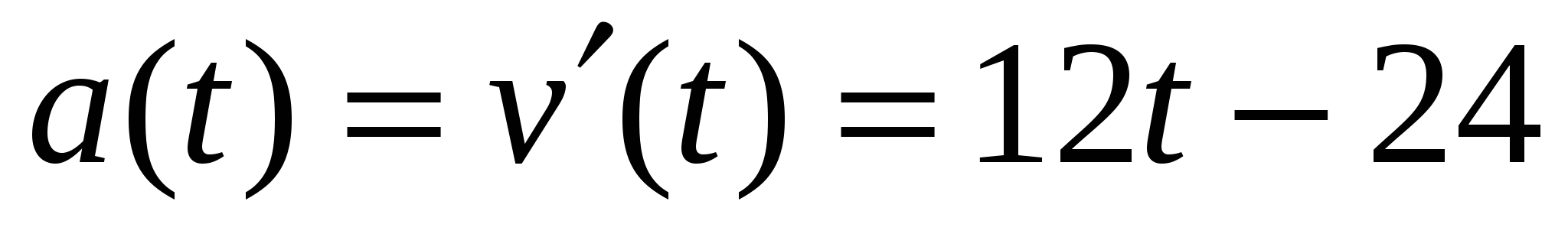 , с другой стороны ускорение равно 36 м/
, с другой стороны ускорение равно 36 м/![]() . Решим уравнение
. Решим уравнение  , t=5 c.
, t=5 c.
Ответ: через 5 секунд.
Если в точке 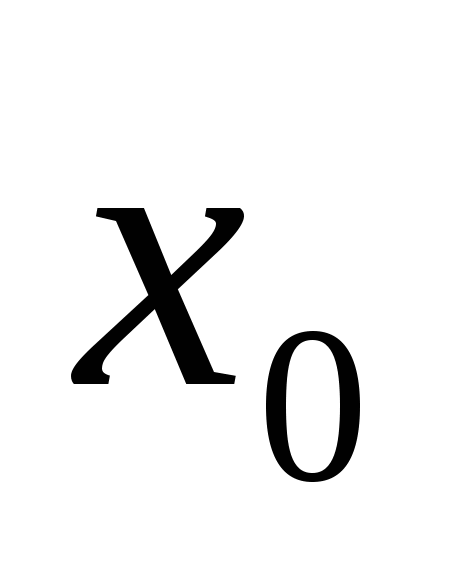 к графику функции y=f(x) проведена касательная, то число f '(
к графику функции y=f(x) проведена касательная, то число f '(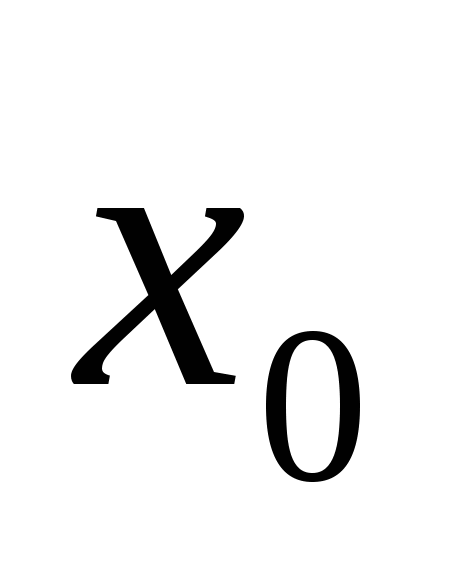 ) есть тангенс угла альфа между этой касательной и положительным направлением оси ОХ, т.е. f '(
) есть тангенс угла альфа между этой касательной и положительным направлением оси ОХ, т.е. f '(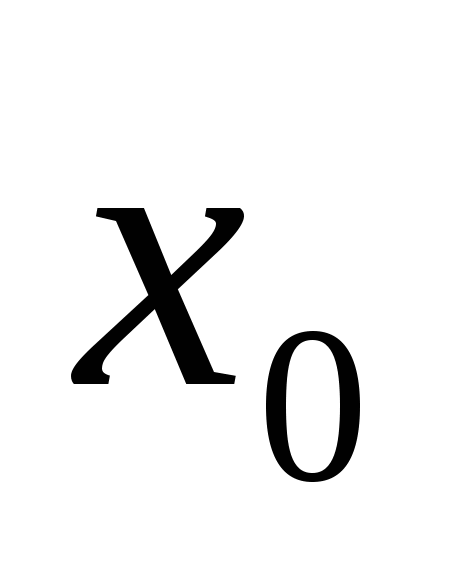 )=tgα. Этот угол называю углом наклона касательной. Этот факт выражает геометрический смысл производной.
)=tgα. Этот угол называю углом наклона касательной. Этот факт выражает геометрический смысл производной.
Пример.
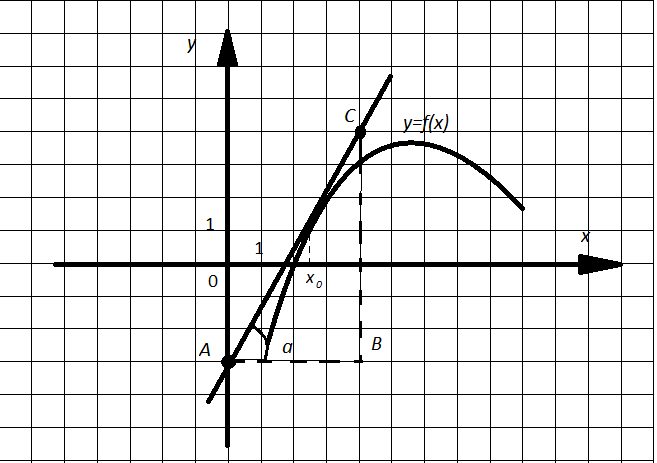
Рис. 1
На рисунке 1 изображен график функции y=f(x) и касательная к нему в точке с абсциссой 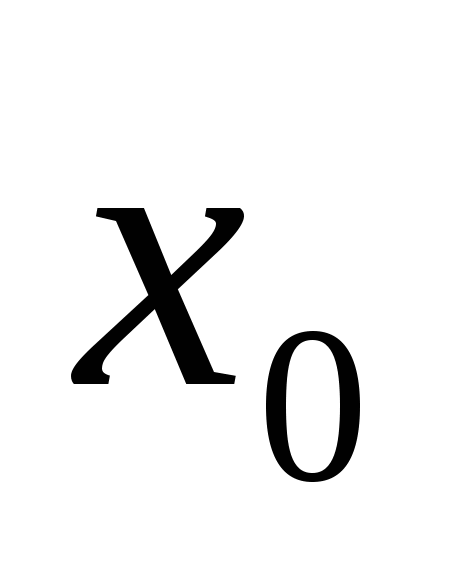 . Найдите значение производной функции f(x) в точке
. Найдите значение производной функции f(x) в точке 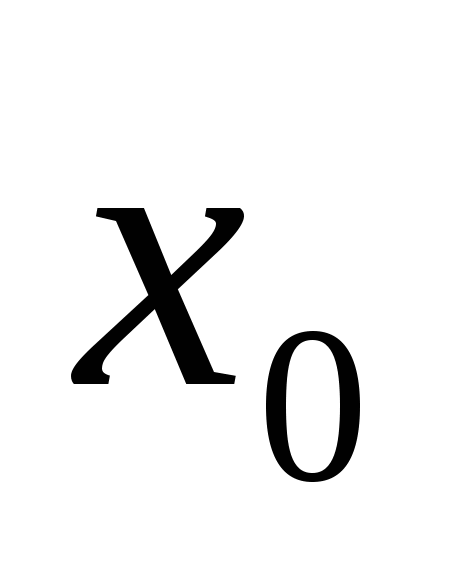 .
.
Решение. Значение производной f(x) в точке ![]() есть значение тангенса угла, образованного касательной к графику функции с положительным направлением оси ОХ. Из треугольника АВС (рис.1).
есть значение тангенса угла, образованного касательной к графику функции с положительным направлением оси ОХ. Из треугольника АВС (рис.1).
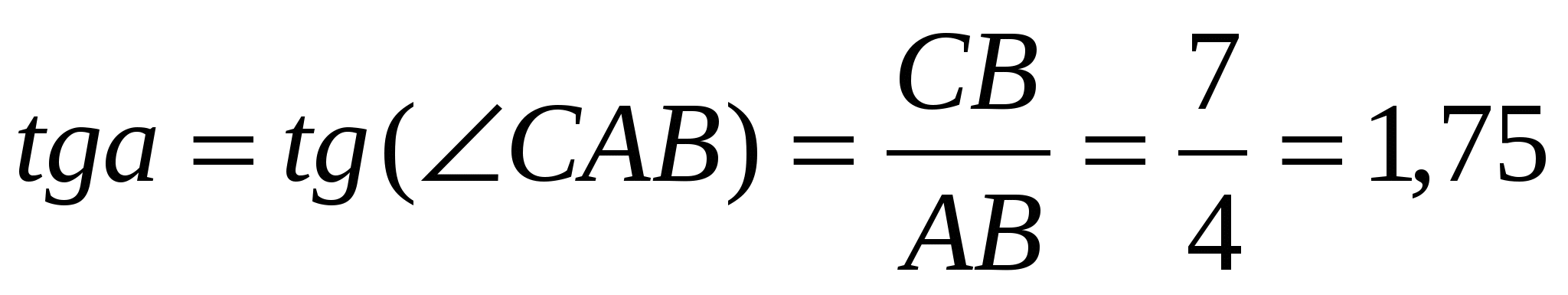 .
.
Ответ: 1,75.2
3 Уравнение касательной к графику функции
Уравнение касательной к графику функции y=f(x) в точке графика с абсциссой 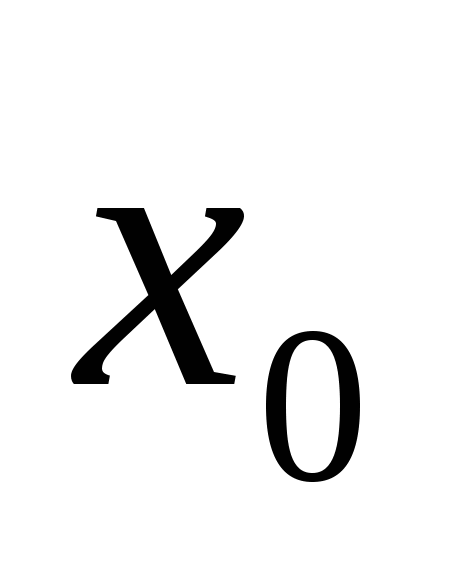 :
: 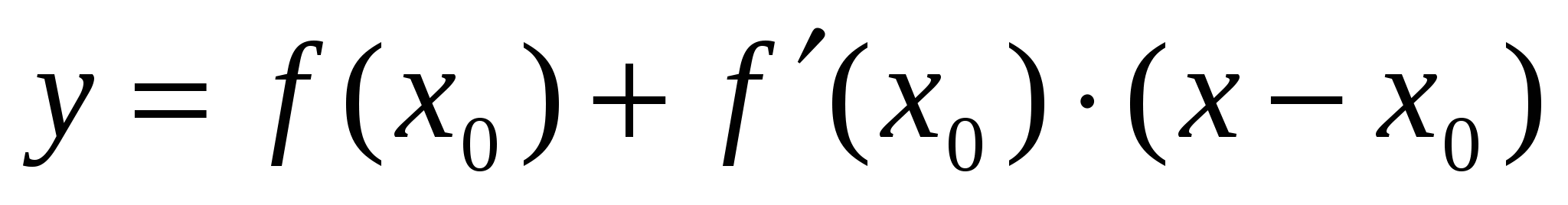 . Если функция f(x) не имеет производной в точке
. Если функция f(x) не имеет производной в точке 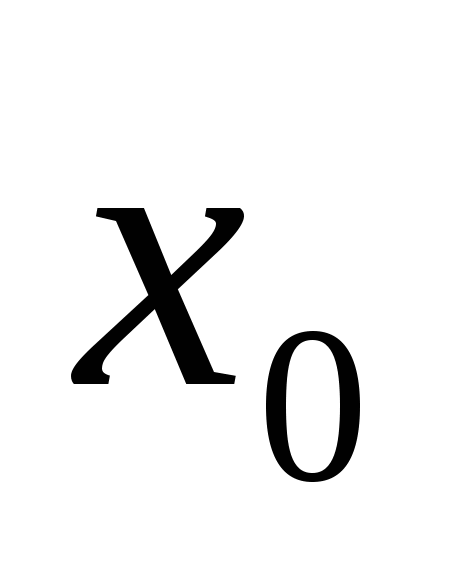 , но непрерывна в этой точке, то у графика функции в этой точке либо вообще нет касательной, либо есть вертикальная касательная.
, но непрерывна в этой точке, то у графика функции в этой точке либо вообще нет касательной, либо есть вертикальная касательная.
Алгоритм составления уравнения касательной к графику функции y = f(x)
1. Обозначить абсциссу точки касания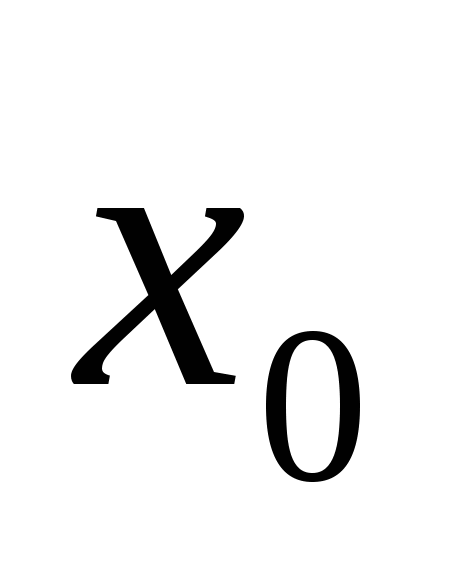 .
.
2.Вычислить f(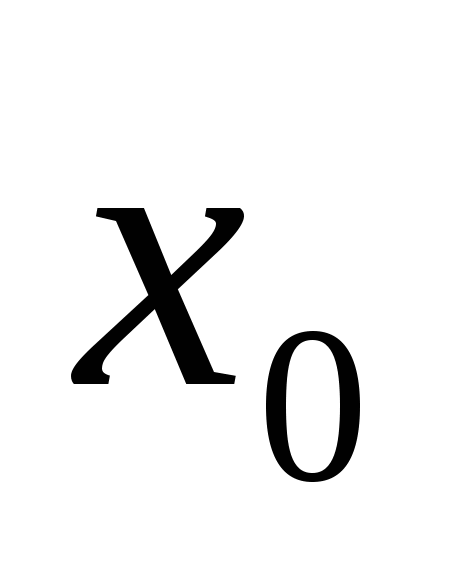 ).
).
3.Найти f '(x) и вычислить f '(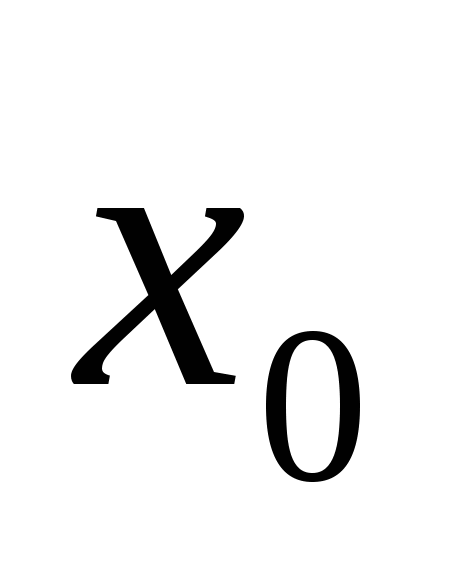 ).
).
4.Подставить найденные числа 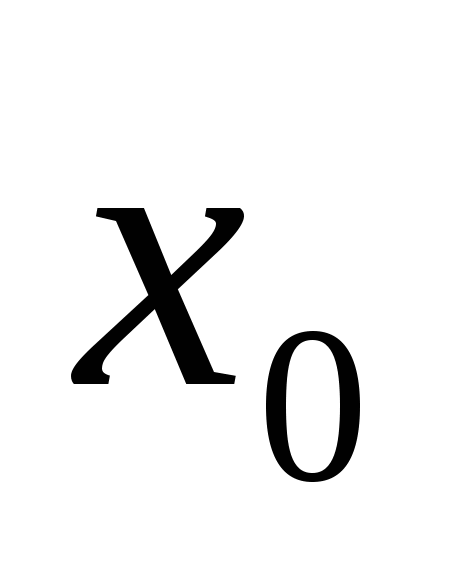 , f(
, f(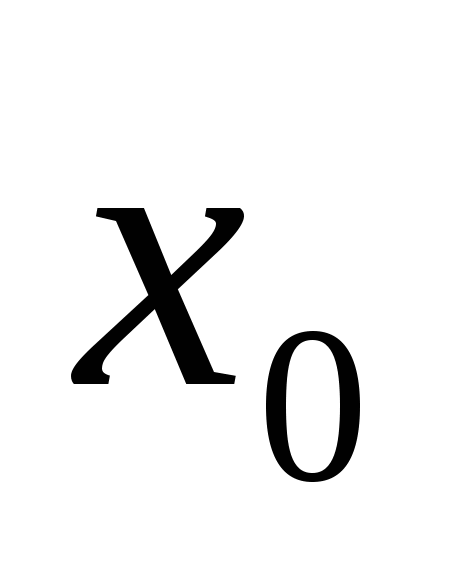 ), f '(
), f '(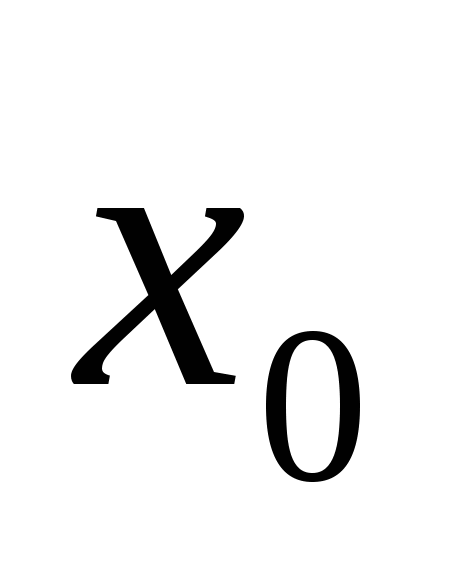 ) в общее уравнение касательной y = f(
) в общее уравнение касательной y = f(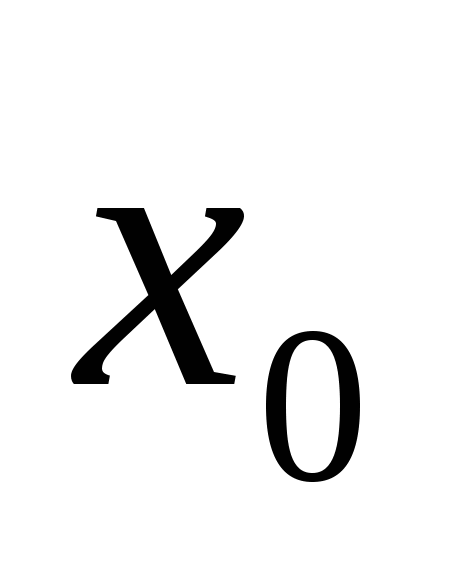 ) = f '(
) = f '(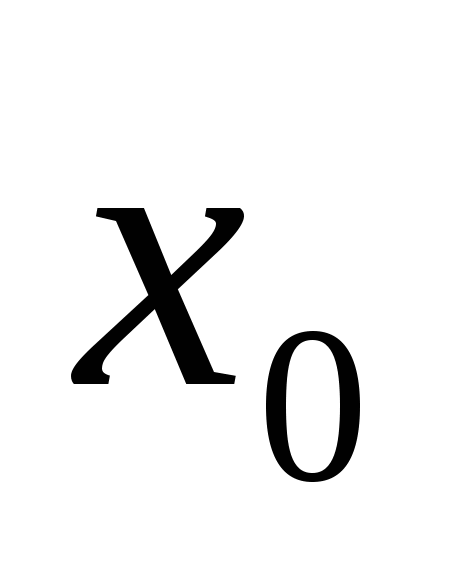 )(x -
)(x -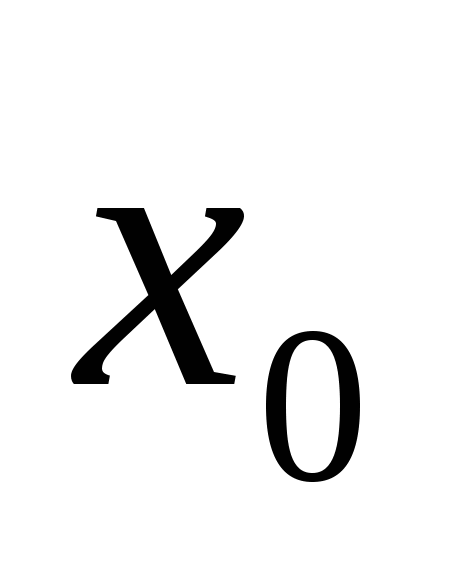 ).3
).3
4 Вычисление производных
Формулами дифференцирования обычно называют формулы для нахождения производных конкретных функций.
Формулы дифференцирования
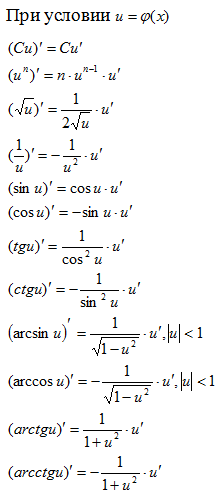
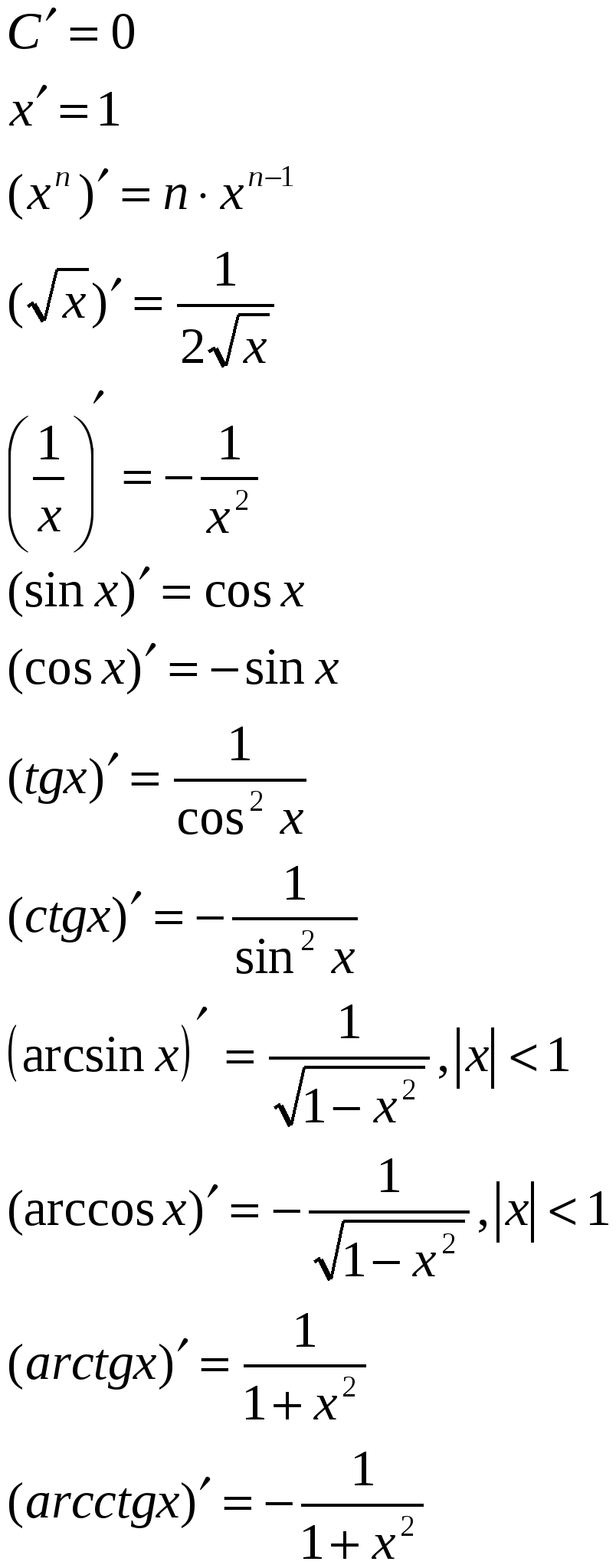
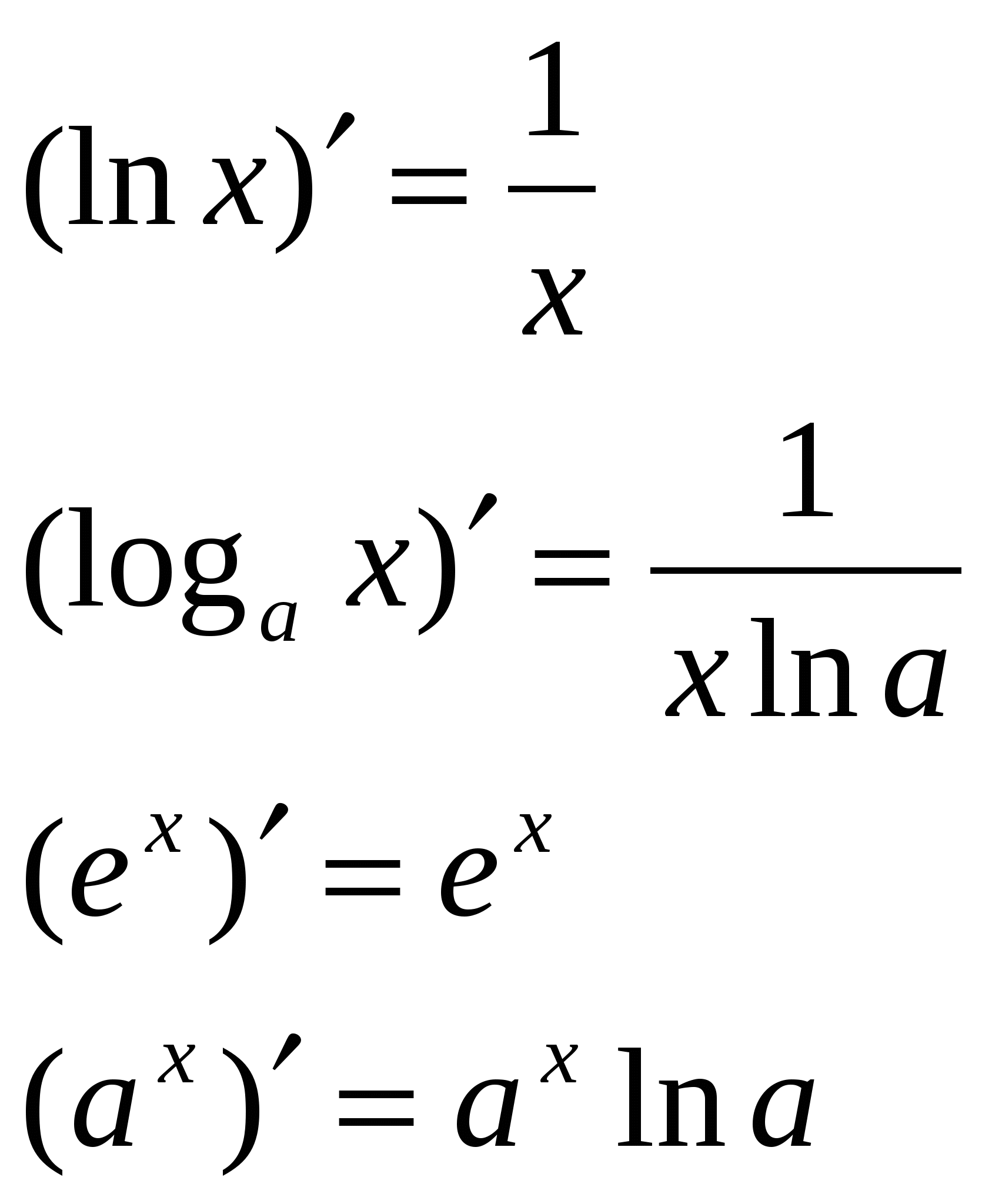
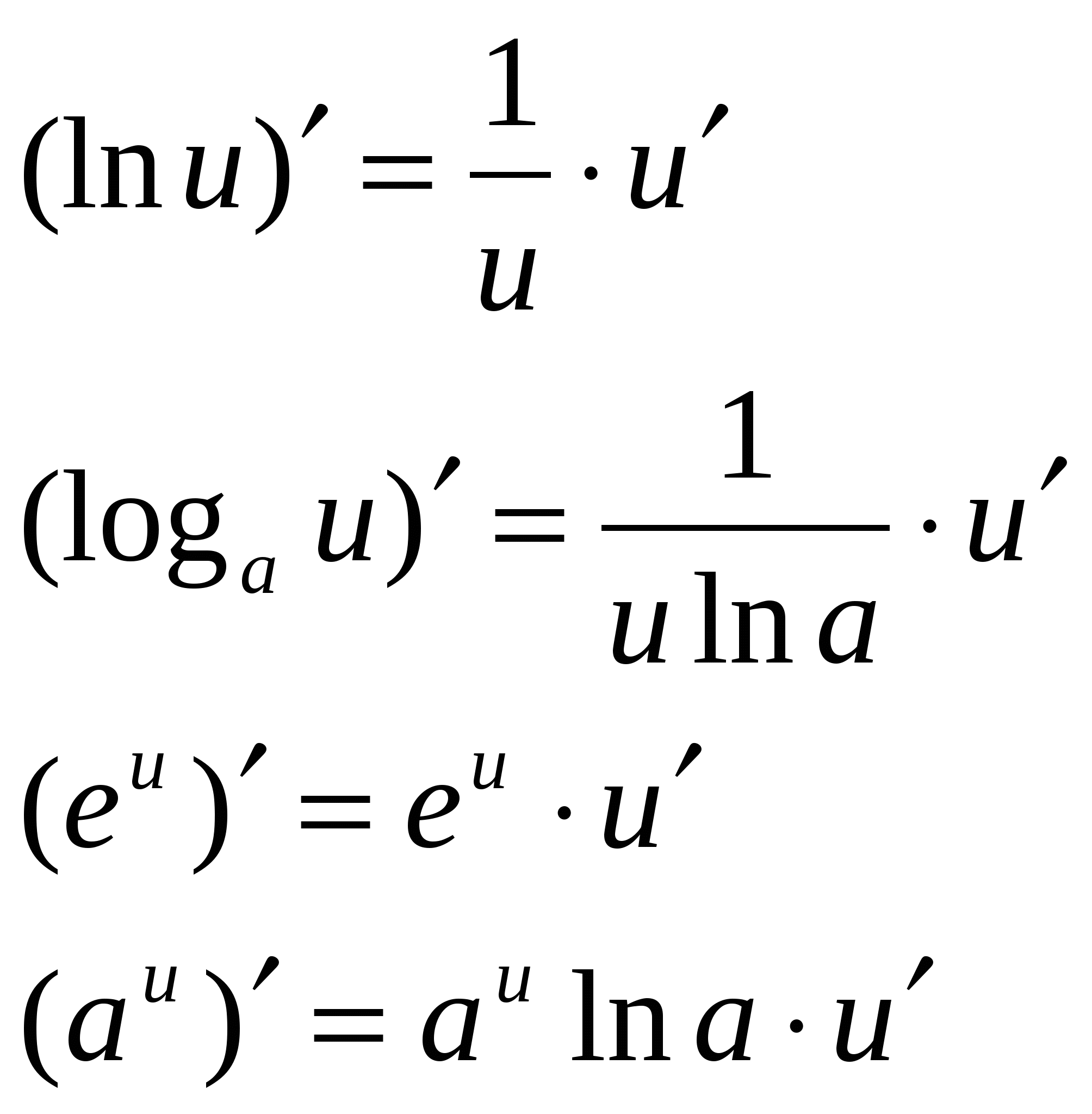
Правила дифференцирования
Теорема 1. Если функции y=f(x) и y=g(x) имеют производную в точке x, то и их сумма имеет производную в точке x, причем производная суммы равна сумме производных: 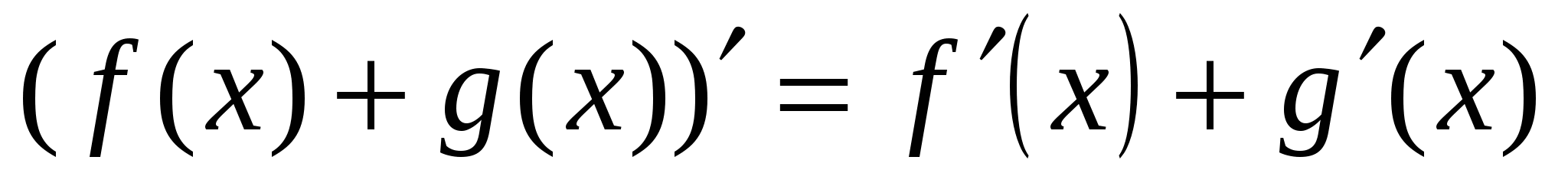 .
.
Теорема 2. Если функция y=f(x) имеет производную в точке х, то и функция y=kf(x) имеет производную в точке х, причем 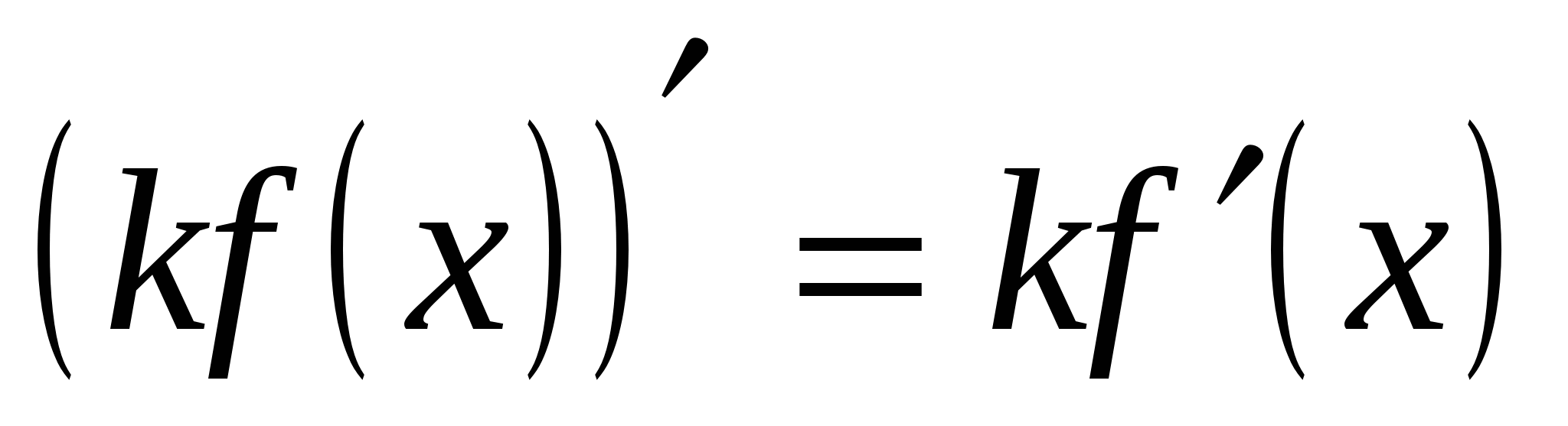 .
.
Теорема 3. Если функции y=f(x) и y=g(x) имеют производную в точке x, то и их произведение имеет производную в точке x, причем 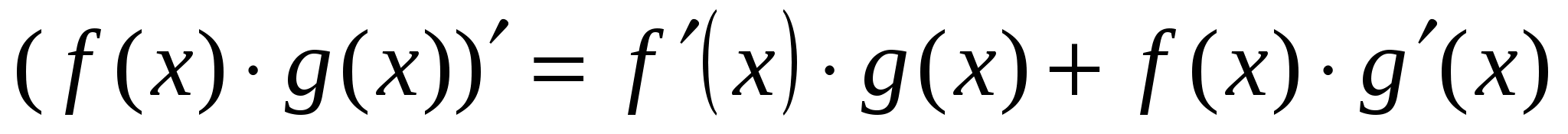 .
.
Теорема 4. Если функции y=f(x) и y=g(x) имеют производную в точке x и в этой точке g(x) ≠0, то функция 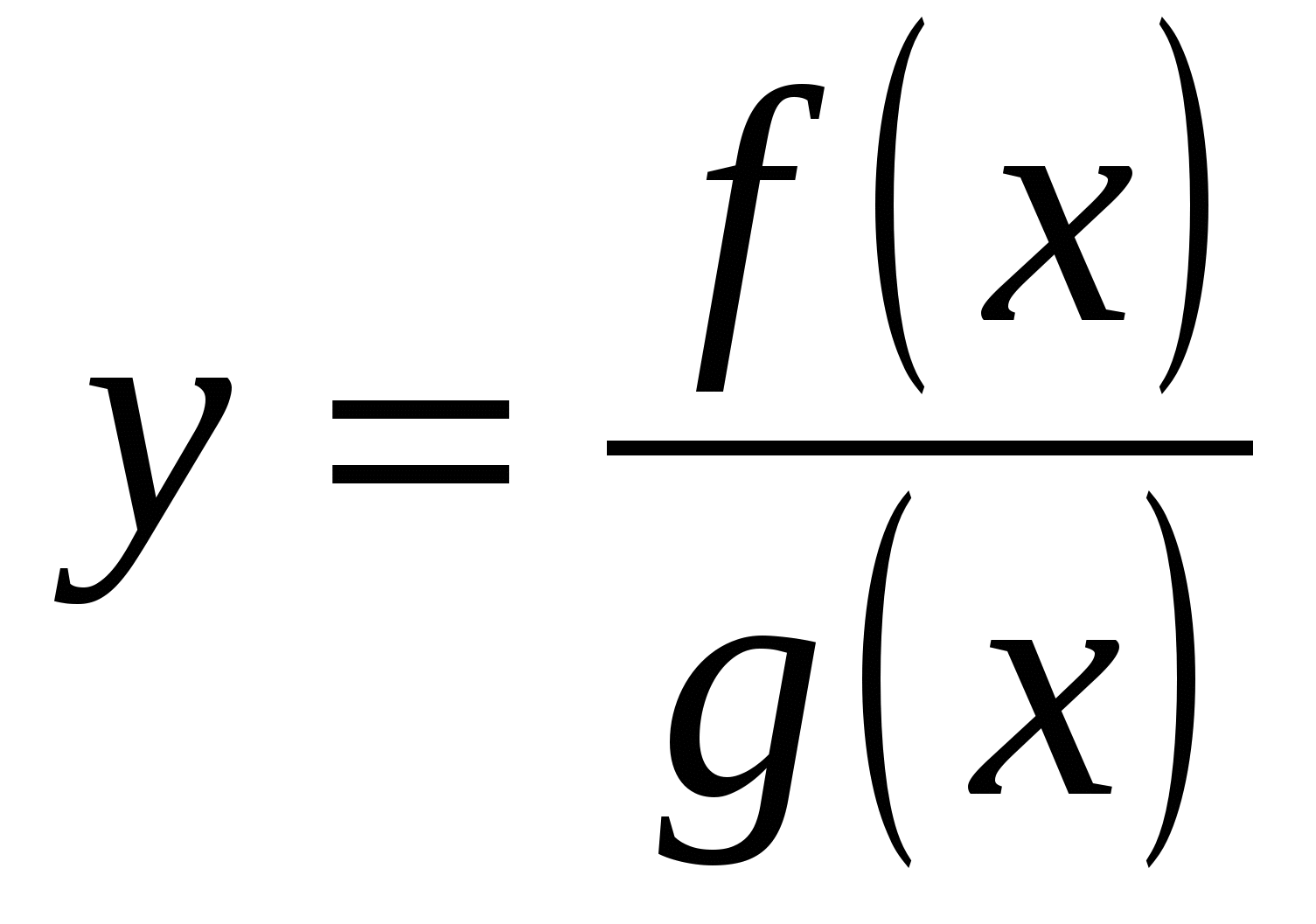 имеет производную в точке х, причем
имеет производную в точке х, причем 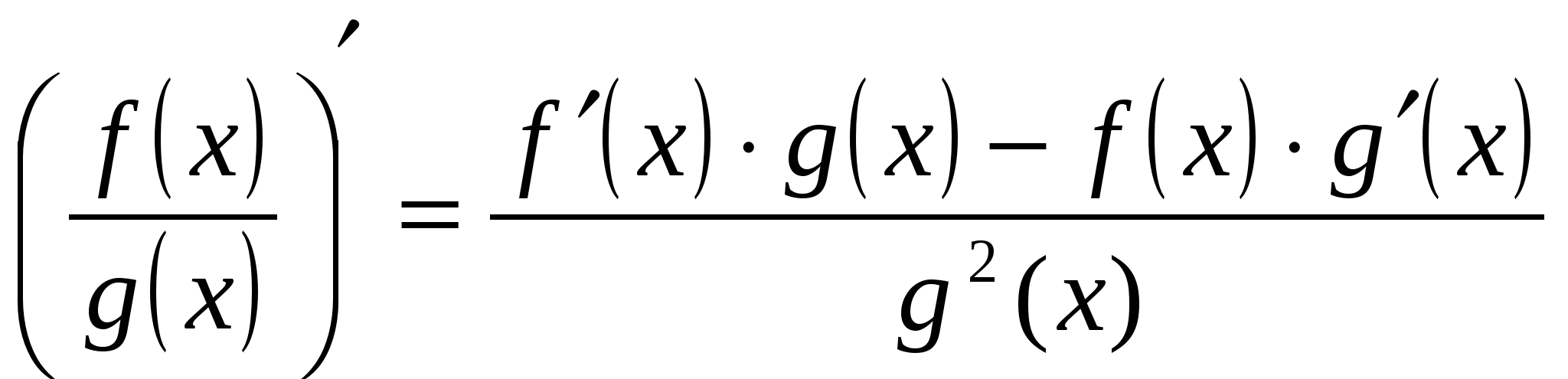 .
.
Теорема 5. Если функция f имеет производную в точке 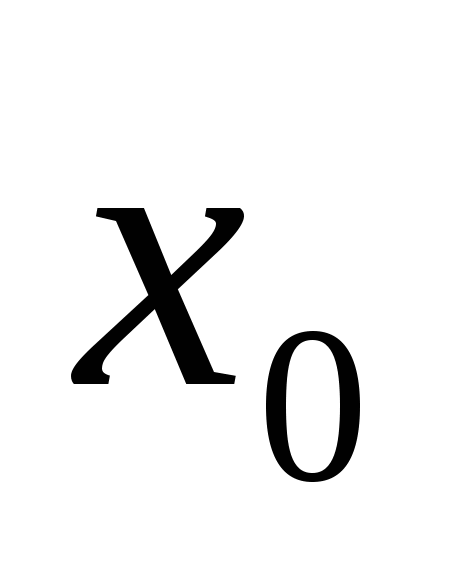 , а функция g имеет производную в точке
, а функция g имеет производную в точке 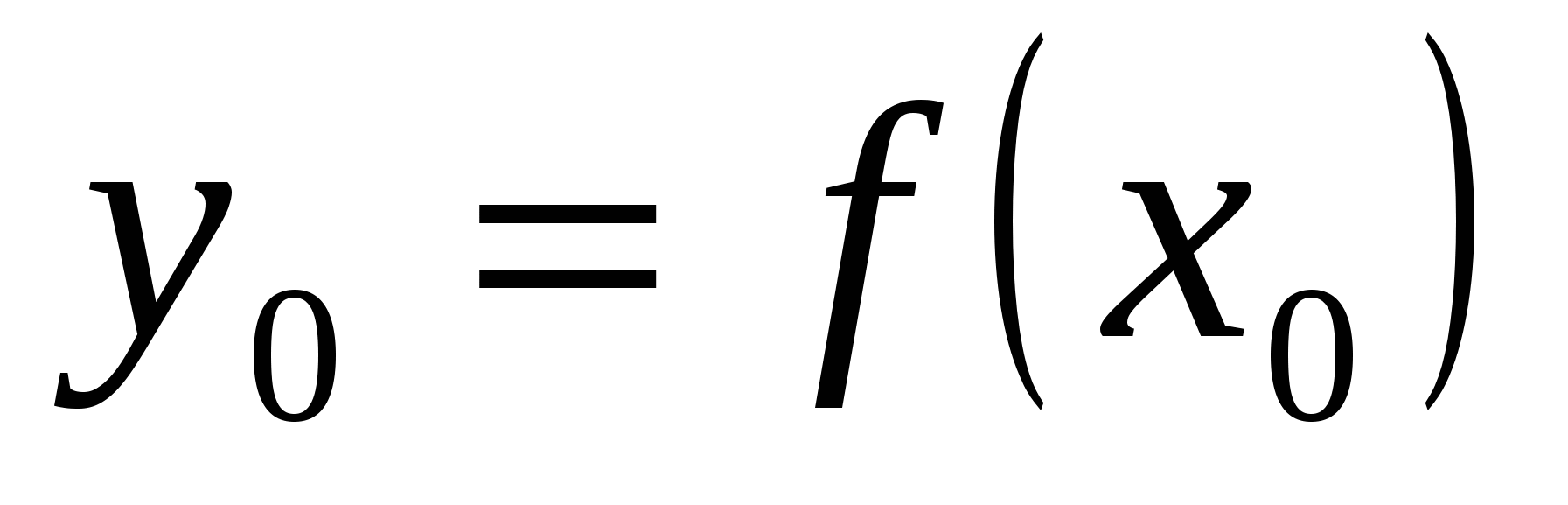 , то сложная функция
, то сложная функция ![]() также имеет производную в точке
также имеет производную в точке 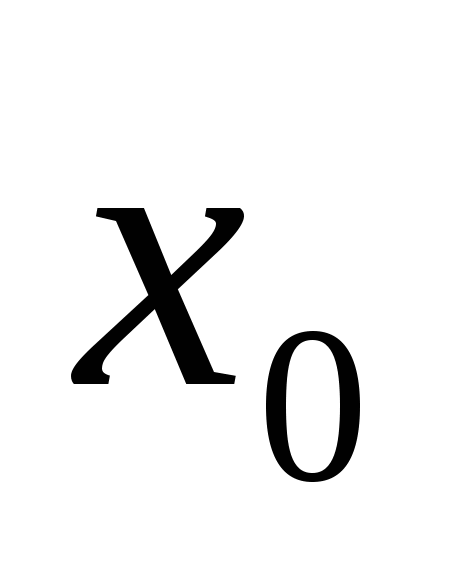 , причем
, причем 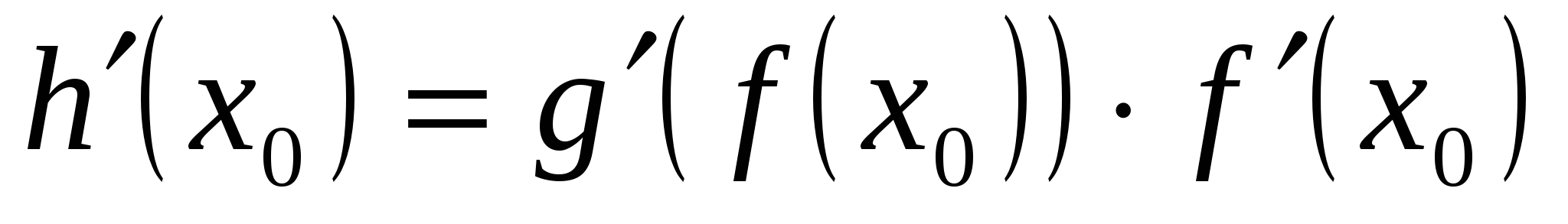 .4
.4
Пример. Найти производные функций
1. 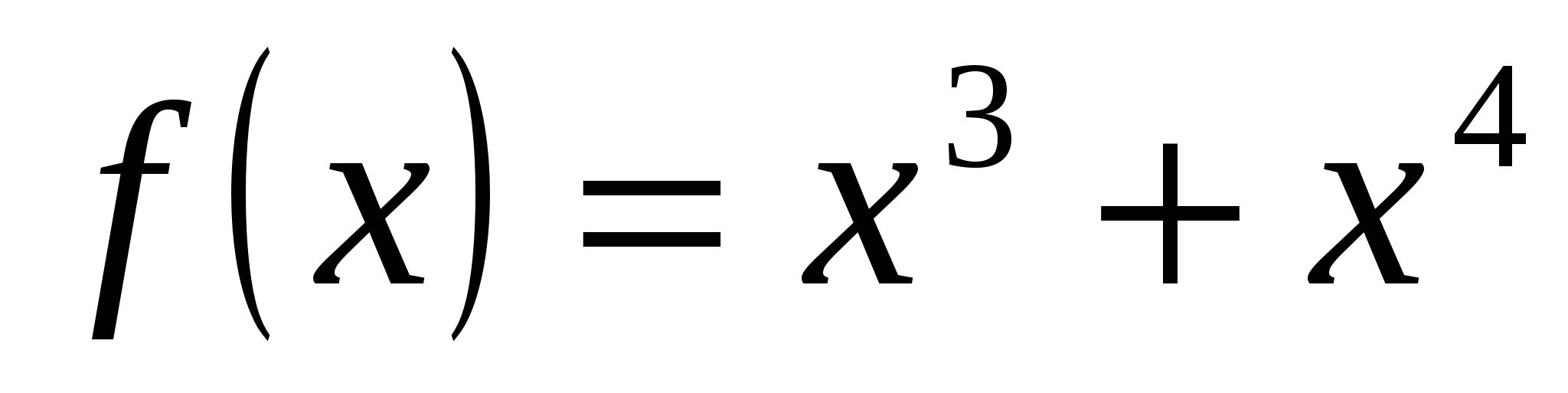 ;
;
2. 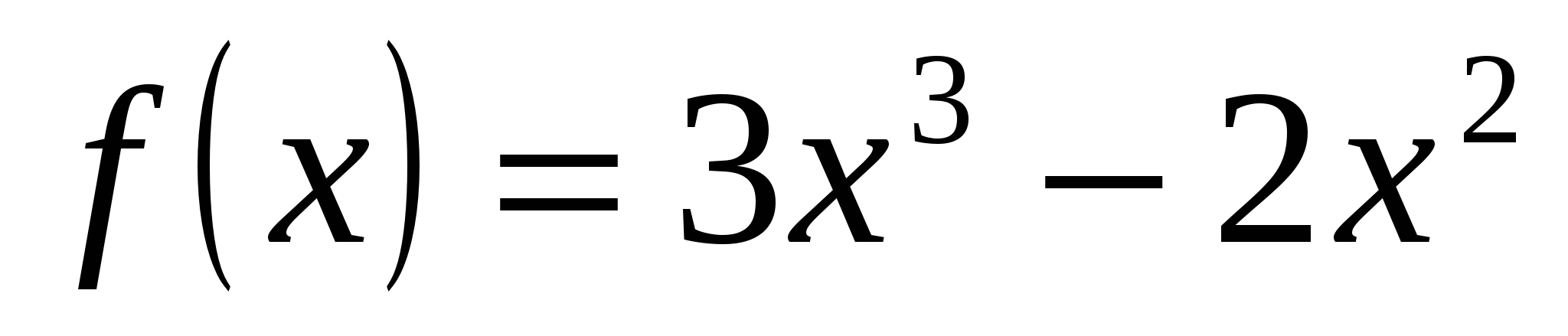 ;
;
3. 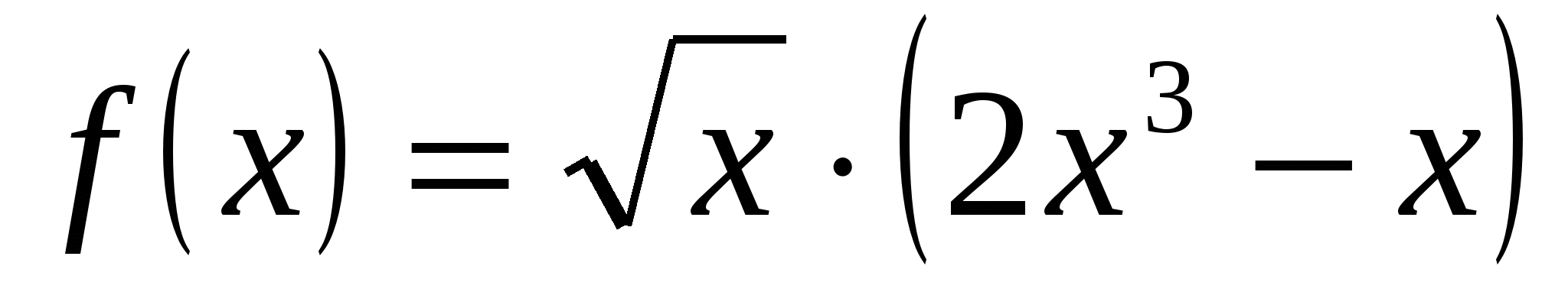 ;
;
4. 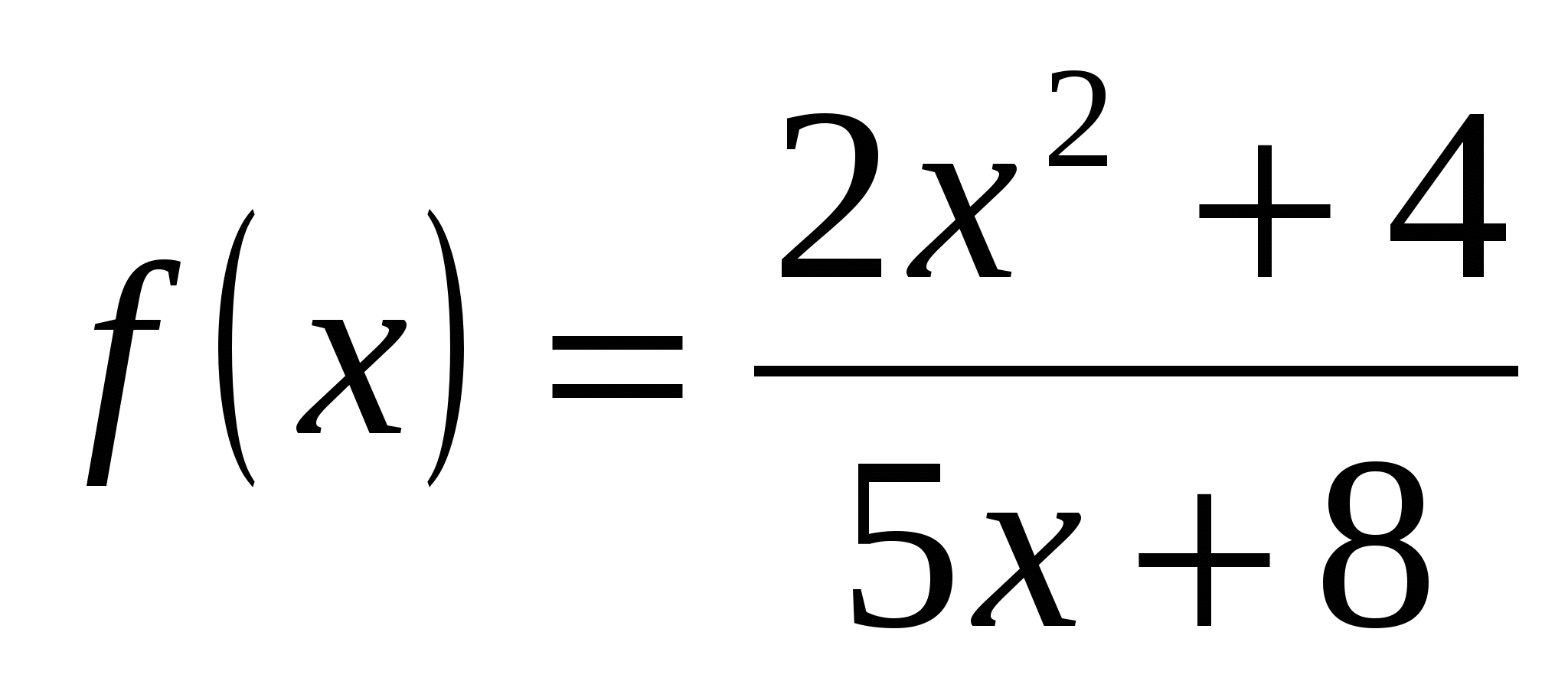 ;
;
5. 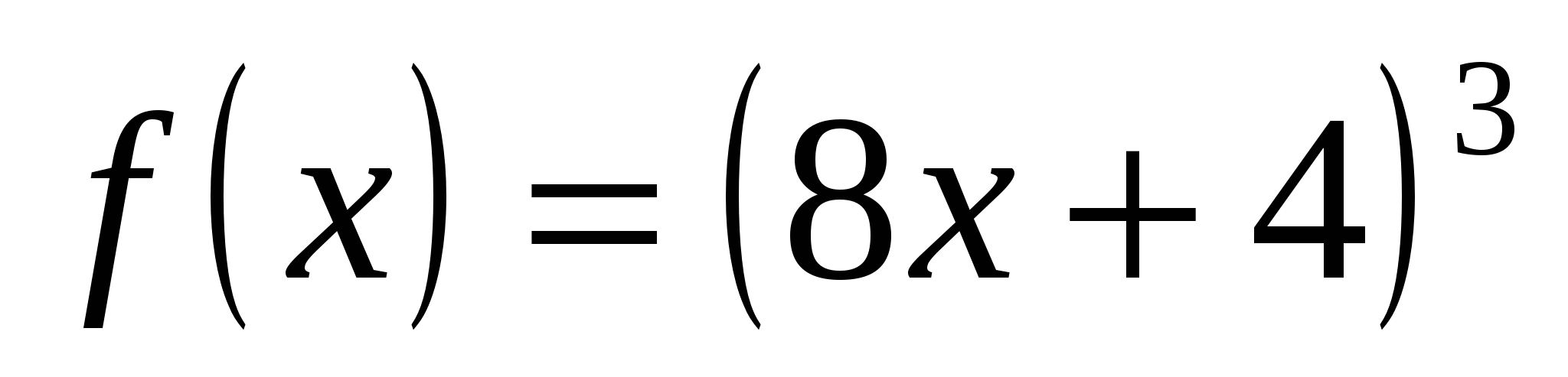 ;
;
Решение.
1. 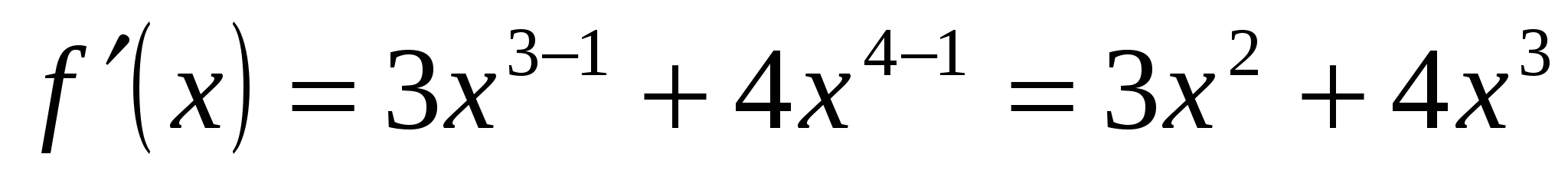 ;
;
2. 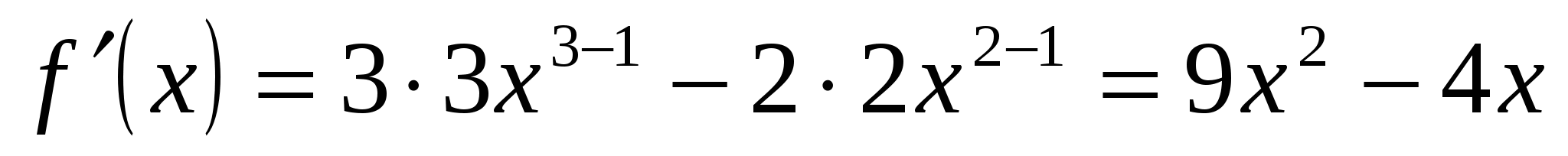 ;
;
3. 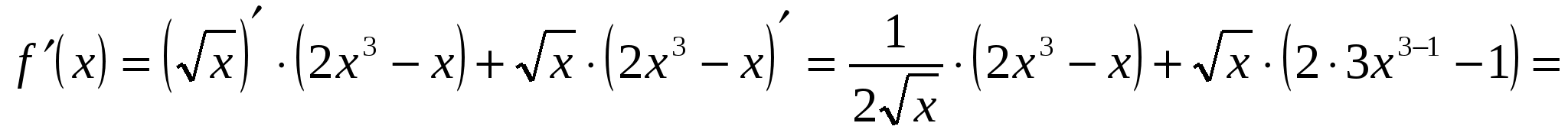
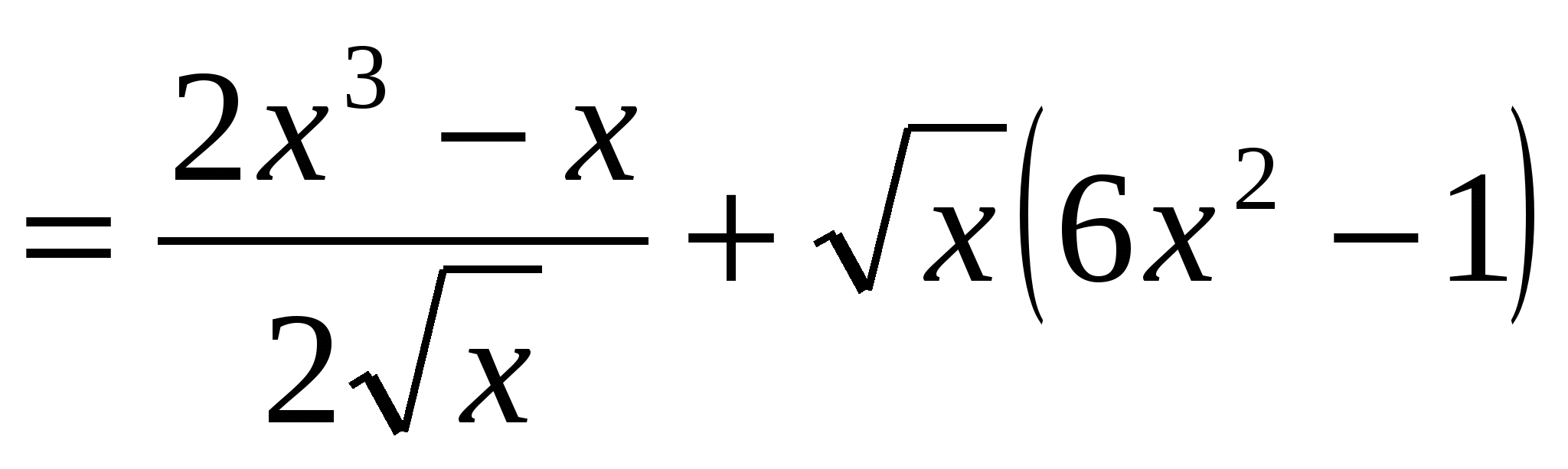 ;
;
4. 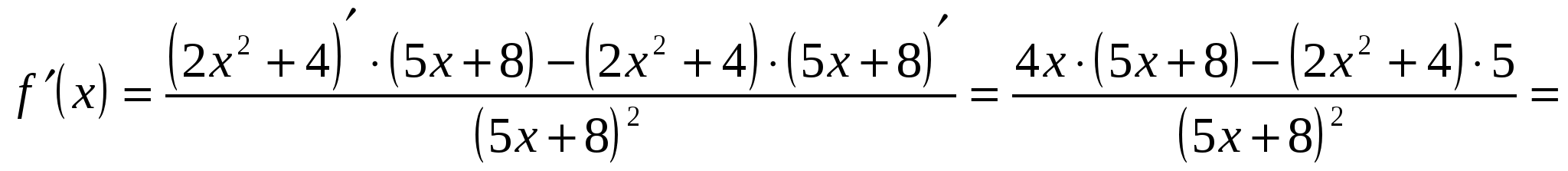
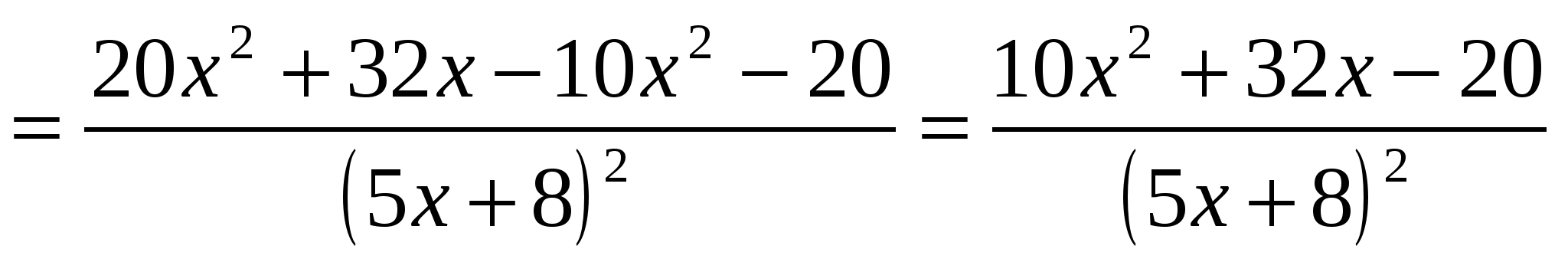 ;
;
5. 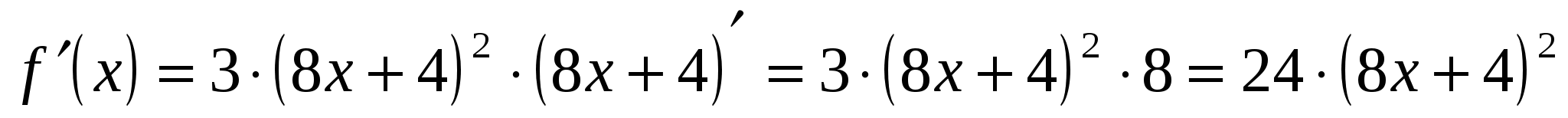 ;
;
5 Применение производной при исследовании функции
Пример 1.
Функция y=f(x) определена на промежутке (-5;9). На рисунке 2 изображен график производной этой функции. Определите число касательных к графику функции y=f(x), которые наклонены под углом 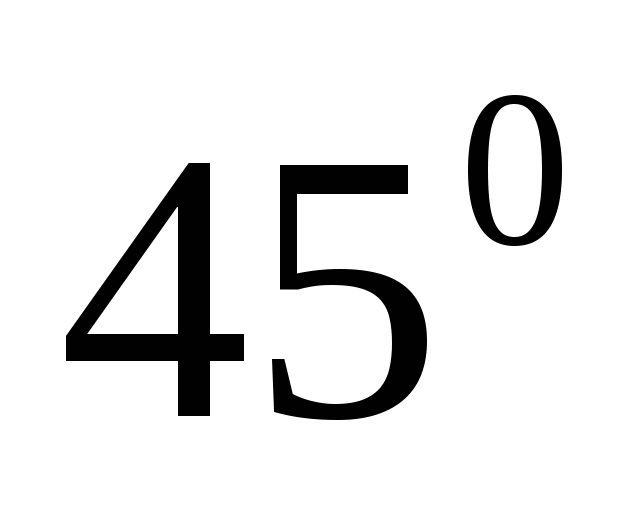 к положительному направлению оси абсцисс.
к положительному направлению оси абсцисс.
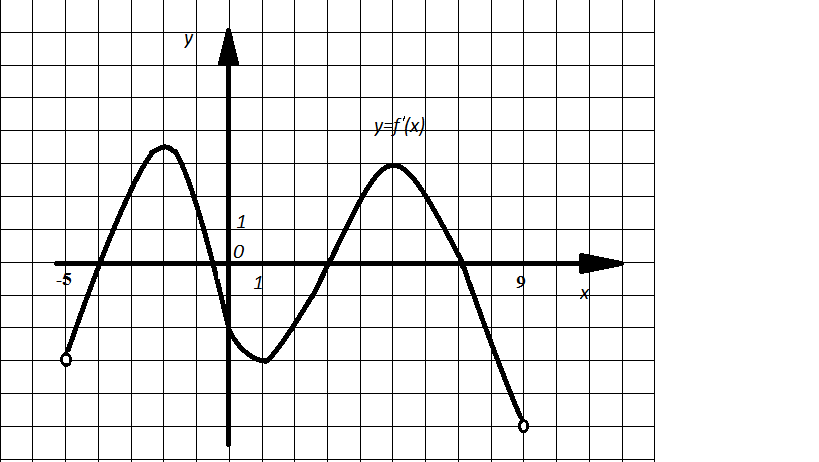
Рис.2
Решение. Пусть α -угол касательной, проведенной к графику функции y=f(x) в точке 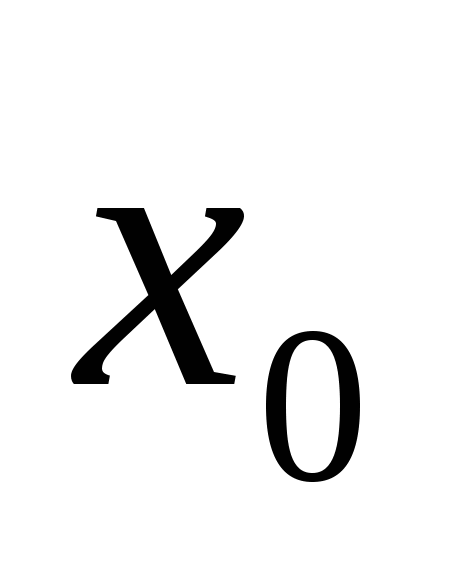 , и положительным направлением оси абсцисс, тогда
, и положительным направлением оси абсцисс, тогда 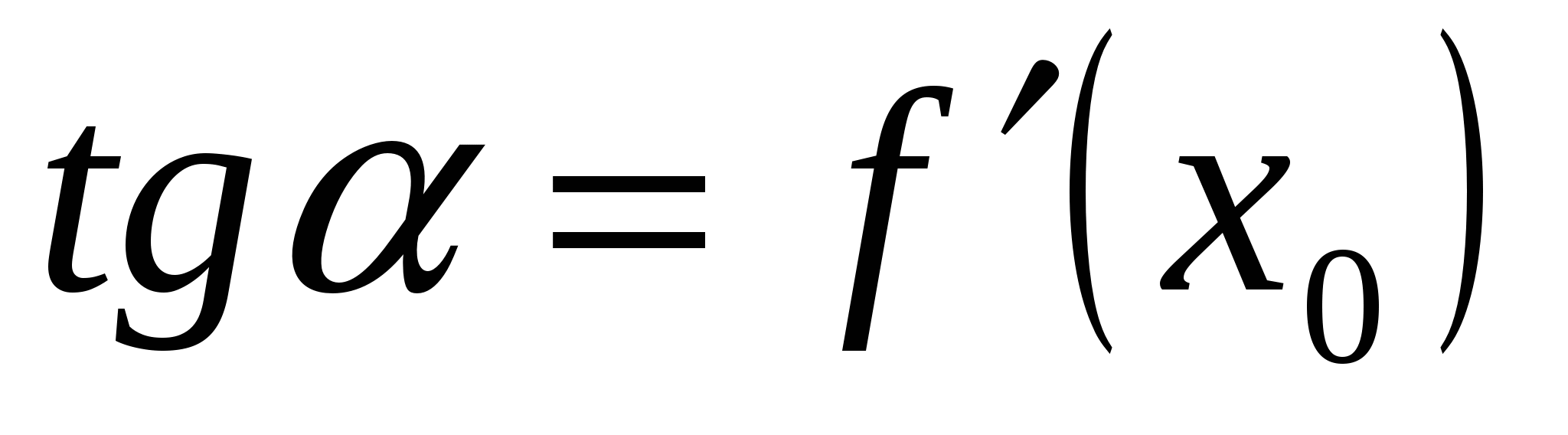 . Так как
. Так как 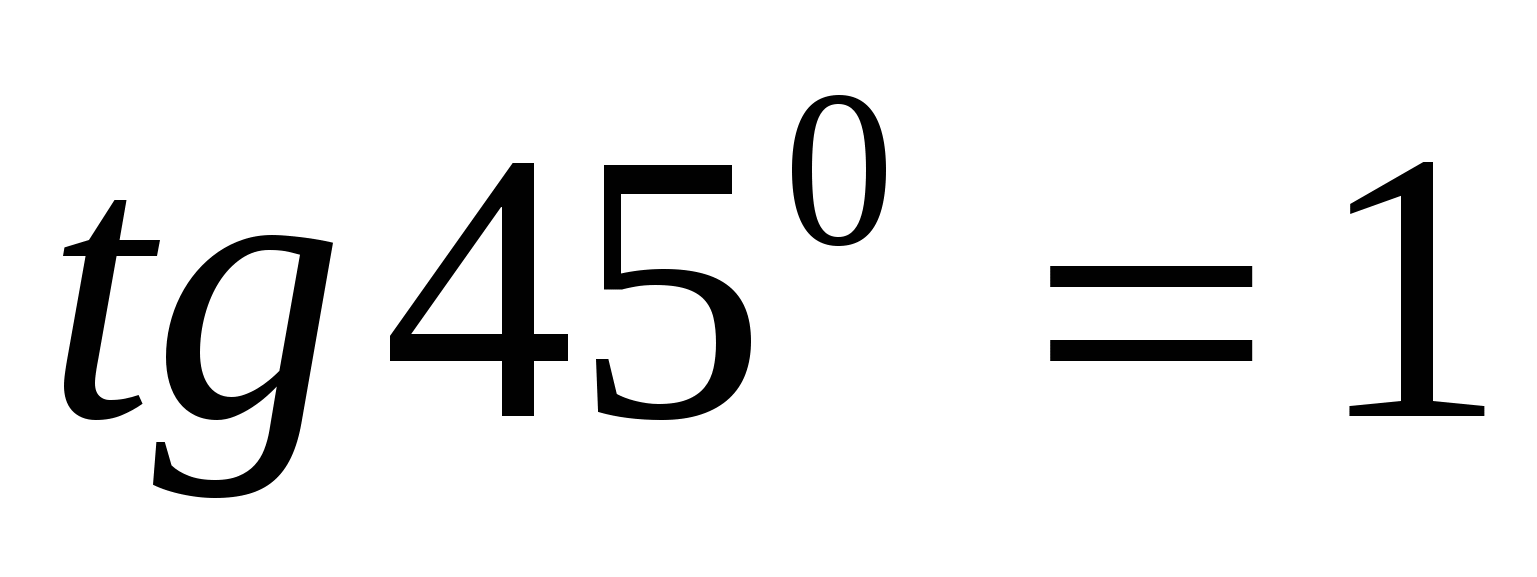 , то для решения задачи достаточно определить количество точек пересечения графика функции
, то для решения задачи достаточно определить количество точек пересечения графика функции ![]() и прямой у=1. Таких точек четыре.
и прямой у=1. Таких точек четыре.
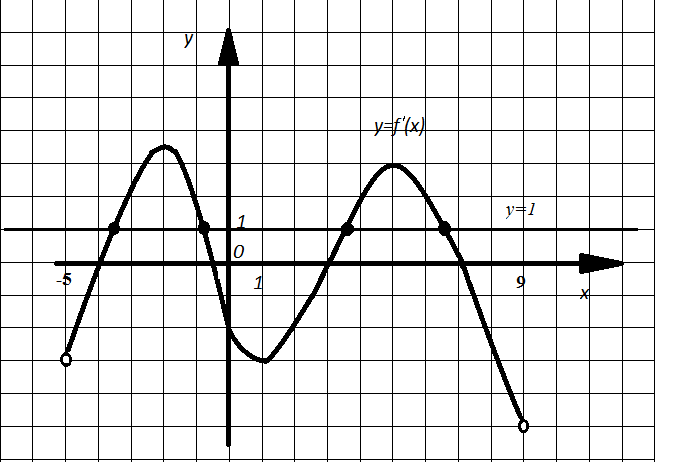
Рис. 3
Ответ: 4.
Пример 2. На рисунке 2 (см. пример 1) изображен график производной функции y=f(x) найдите абсциссу точки, в которой касательная к графику y=f(x) параллельна прямой у=1 или совпадает с ней.
Речение. Так как касательная параллельна прямой у=1, то ее угловой коэффициент равен 0 и тогда производная равна 0. По графику (рис.2) определяем, что производная обращается в ноль при х=-4; х=-0,5; х=3; х=7.
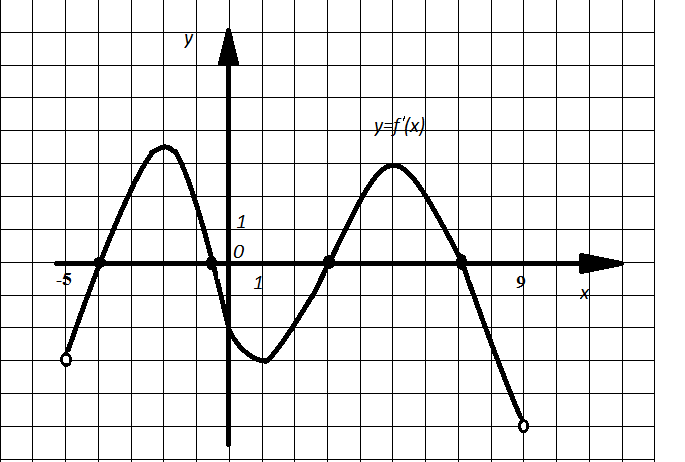
Рис. 4
Ответ: -4; -0,5; 3; 7.
Пример 3. На рисунке 5 изображен график функции y=f(x), определенной на промежутке 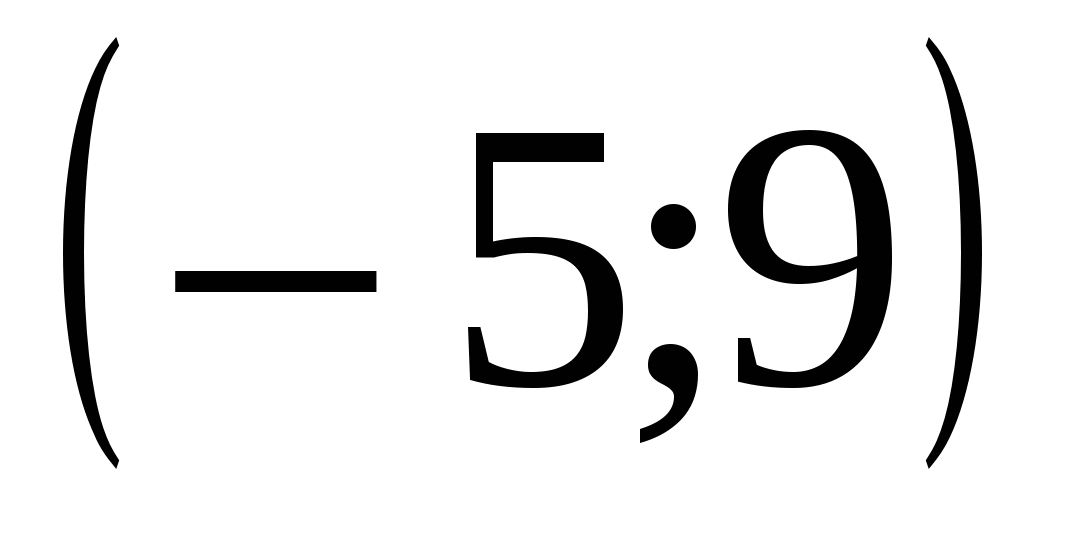 . Определите количество целых точек, в которых производная функции f(x) положительна.
. Определите количество целых точек, в которых производная функции f(x) положительна.
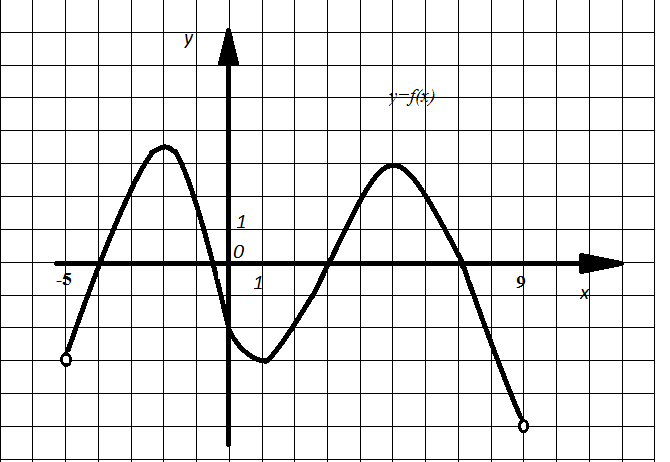
Рис. 5
Решение. Производная функции положительна в тех целых точках, которые принадлежат какому-нибудь промежутку возрастания, за исключением точек, в которых производная равна нулю (в этих точках касательная к графику функции параллельна оси ОХ) или не существует. По рисунку 2 определяем абсциссы таких точек: -4; -3; 2; 3; 4. Таких точек пять.
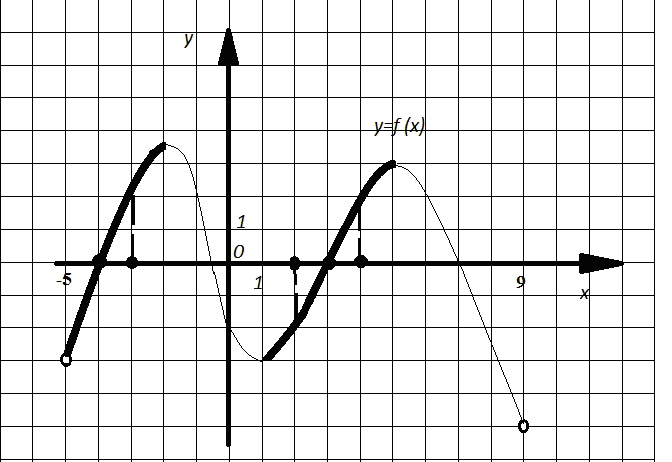
Рис. 6
Ответ: 5.
Пример 4. На рисунке 5 (см. пример 3) изображен график функции y=f(x), определенной на интервале (-5;9). Определите количество целых точек, в которых производная функции отрицательна.
Решение. Производная функции отрицательна в тех целых точках, которые принадлежат какому-нибудь промежутку убывания функции, за исключением точек, в которых производная равна нулю (в этих точках касательная к графику функции параллельна оси ОХ) или не существует. По рисунку определяем абсциссы таких точек: -1; 0; 6; 7; 8. Таких точек пять.
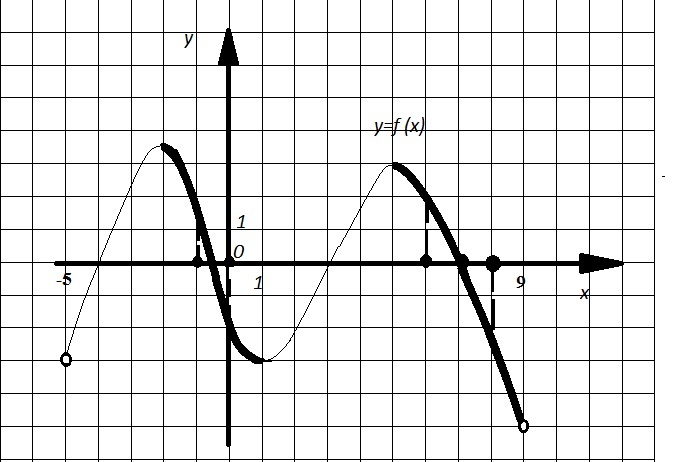
Рис. 7
Пример 5. На рисунке 2 (см. пример 1) изображен график производной функции y=f(x), определенной на интервале (-5;9). Найдите промежутки возрастания функции y=f(x). В ответе укажите длину наибольшего из них.
Решение. Промежуткам возрастания функции соответствуют промежутки, на которых производная данной функции положительна. По графику определяем, что наибольший из этих промежутков 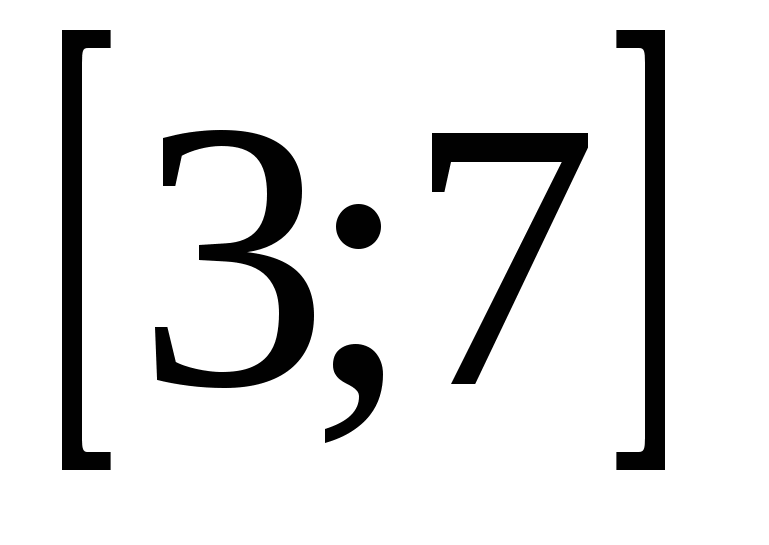 имеет длину 4.
имеет длину 4.
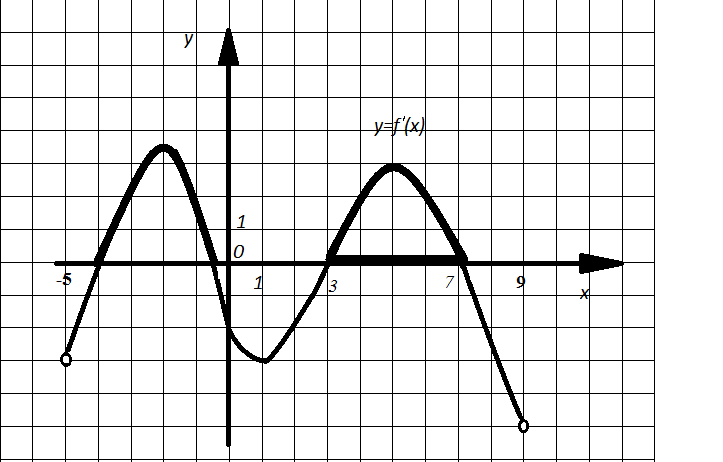
Рис. 8
Ответ: 4.
Пример 6. На рисунке 2 (см. пример 1) изображен график производной функции y=f(x), определенной на интервале (-5;9). Найдите промежутки убывания функции y=f(x). В ответе укажите длину наибольшего из них.
Решение. Промежуткам убывания функции соответствуют промежутки, на которых производная данной функции отрицательна. По графику определяем, что наибольший из этих промежутков 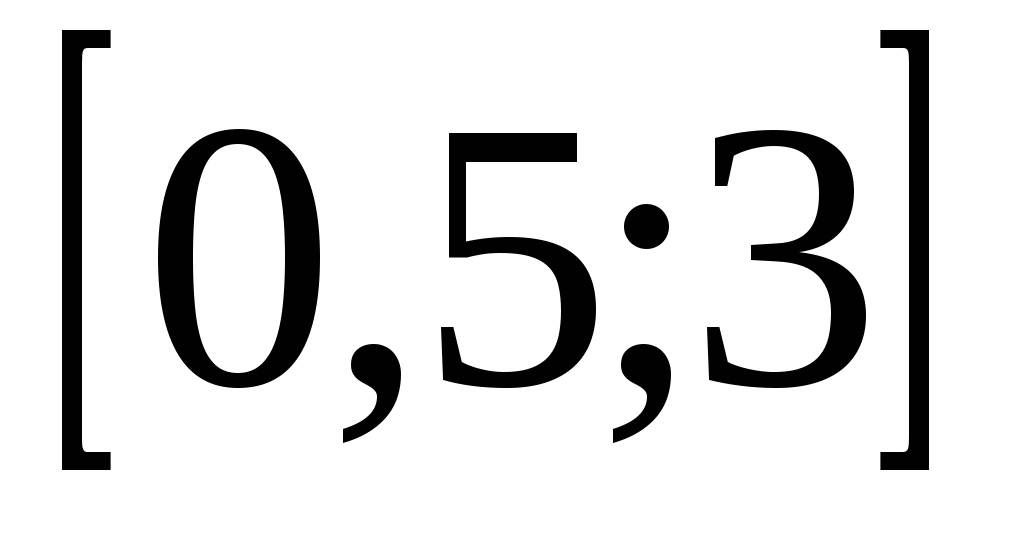 имеет длину 3,5.
имеет длину 3,5.
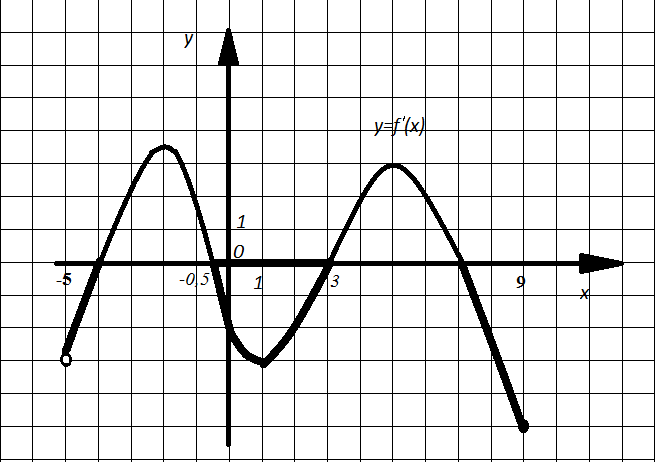
Рис. 9
Ответ: 3,5.
Пример 7. На рисунке 2 (см. пример 1) изображен график производной функции y=f(x), определенной на интервале (-5;9). Найдите количество точек максимума функции y=f(x).
Решение. Точек максимума здесь две, так как график производной 4 раза меняет знак на интервале (-5;9), из них два раза с плюса на минус. Это и есть точки максимума.
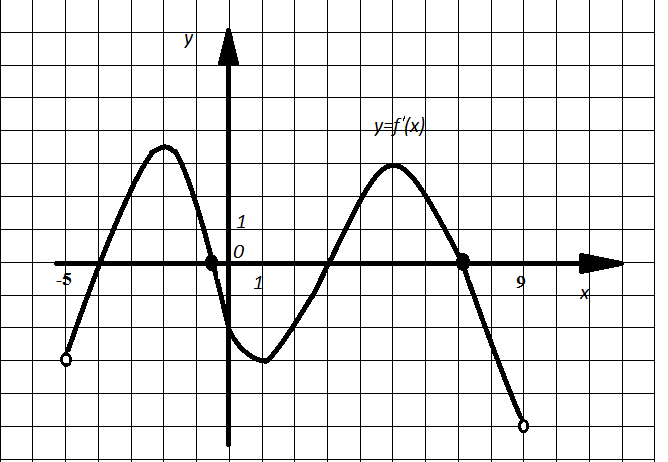
Рис. 10
Ответ: 2.
Пример 8. На рисунке 2 (см. пример 1) изображен график производной функции y=f(x), определенной на интервале (-5;9). Найдите точки минимума функции y=f(x).
Решение. На графике производной видно, что на интервале (-5;9)производная 4 раза меняет знак в точках х=-4; х=-0,5; х=3; х=7. Причем в точках х=-4; х=3 он меняется с минуса на плюс. Значит, эти точки являются точками минимума, так как в точках х=-4 и х=3 характер монотонности функции f(x) меняется с убывания на возрастание.
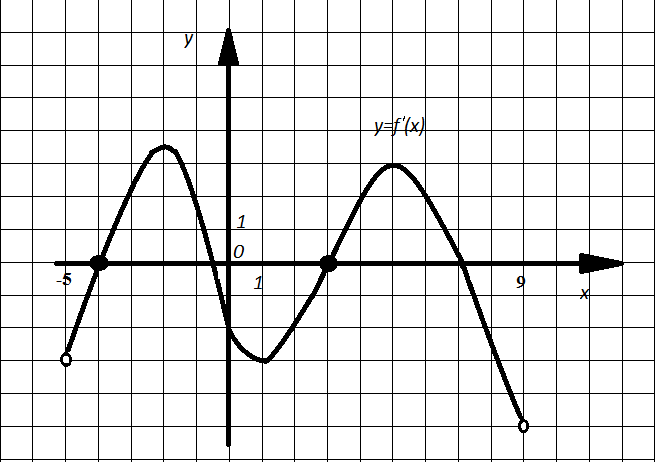
Рис. 11
Ответ: -4; 3.
Пример 9. На рисунке 2 (см. пример 1) изображен график производной функции y=f(x), определенной на интервале (-5;9). Найдите количество точек экстремума функции y=f(x).
Решение. На промежутке (-5;9) точек экстремума функции y=f(x) ровно четыре: -4; -0,5; 3; 7.

Рис. 12
Ответ: 4.
Пример 10. На рисунке 13 изображен график производной функции y=f(x), определенной на интервале (-5;4). Укажите абсциссы точек, в которой касательная к графику функции y=f(x) имеет наименьший и наибольший угловой коэффициент.
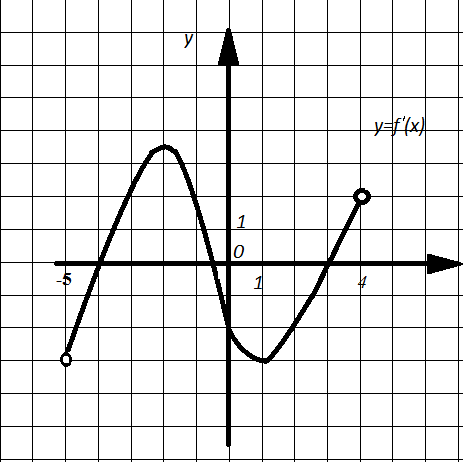
Рис. 13
Решение. Угловой коэффициент касательной 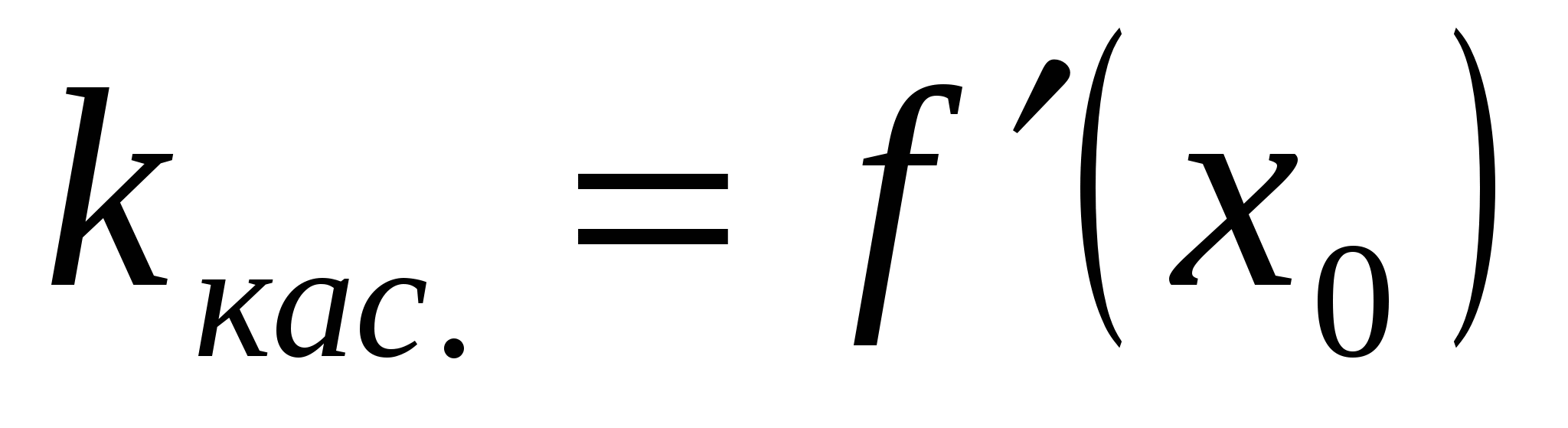 . По графику определяем, что наименьшее значение функция
. По графику определяем, что наименьшее значение функция 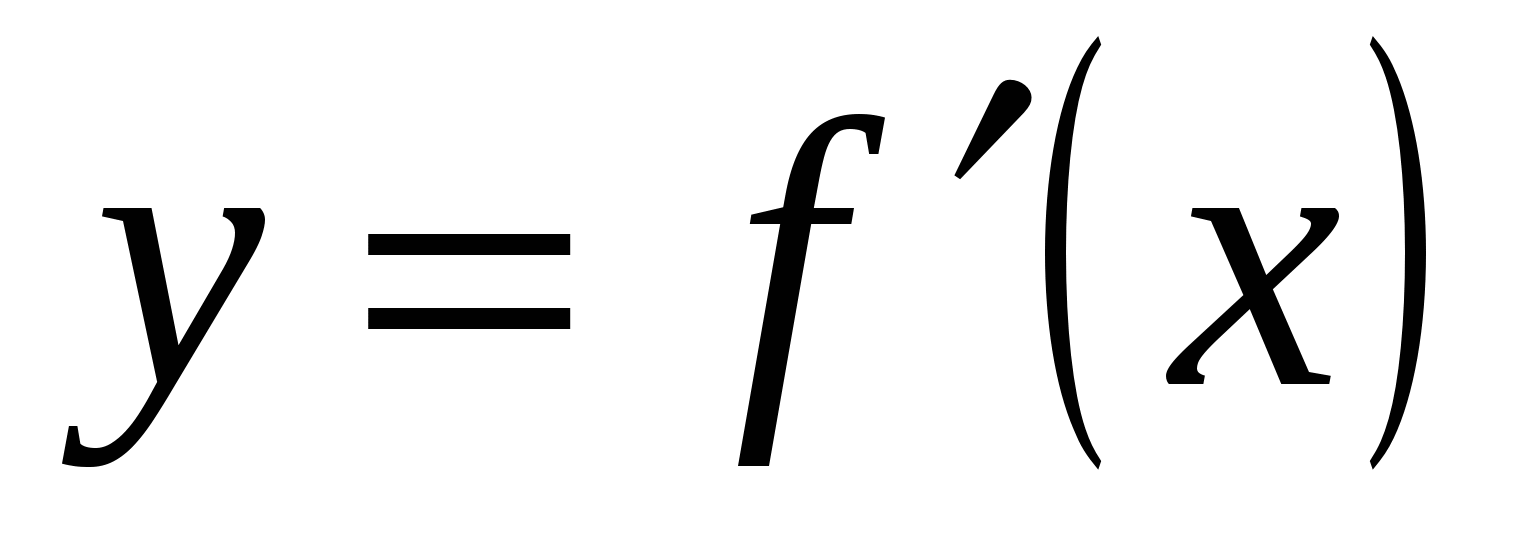 достигает при
достигает при 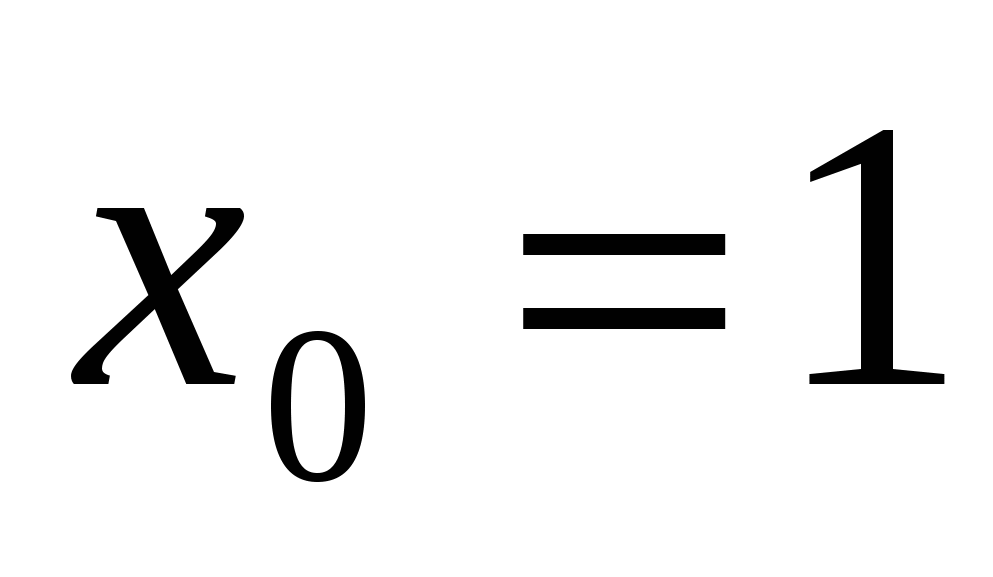 . А наибольшее значение функция
. А наибольшее значение функция 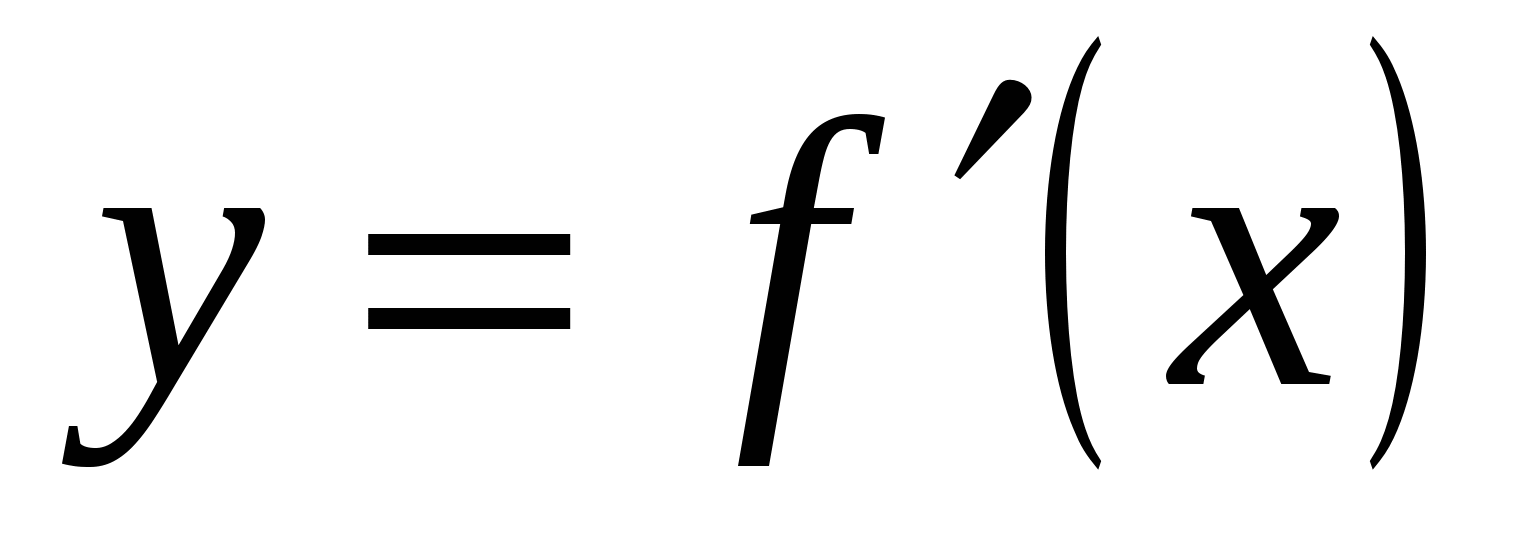 достигает при
достигает при 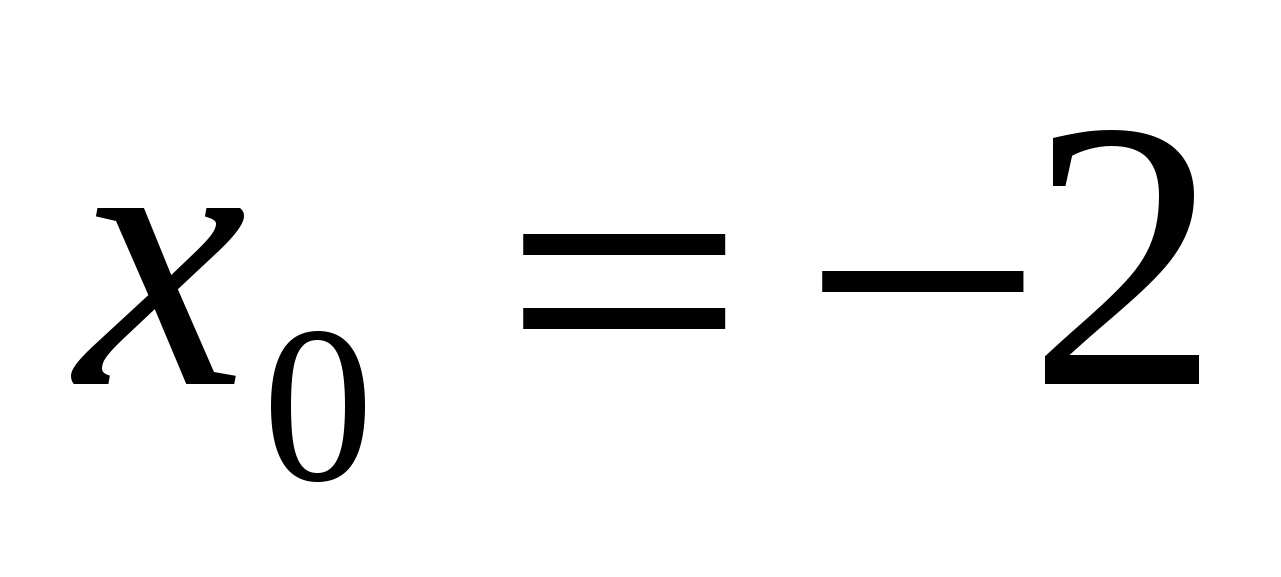 .
.
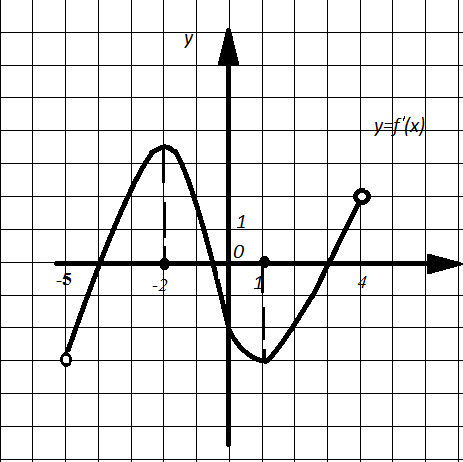
Рис. 14
Ответ: 1; -2.
Пример 11. На рисунке 2 (см. пример 1) изображен график производной функции y=f(x), определенной на интервале (-5;9). Найдите количество точек, в которых касательная к графику функции y=f(x) параллельна прямой у=-4х+3 или совпадает с ней.
Решение. Касательная к графику функции y=f(x) в некоторой точке параллельна прямой у=-4х+3, если значение производной функции в этой точке равно угловому коэффициенту прямой, то есть 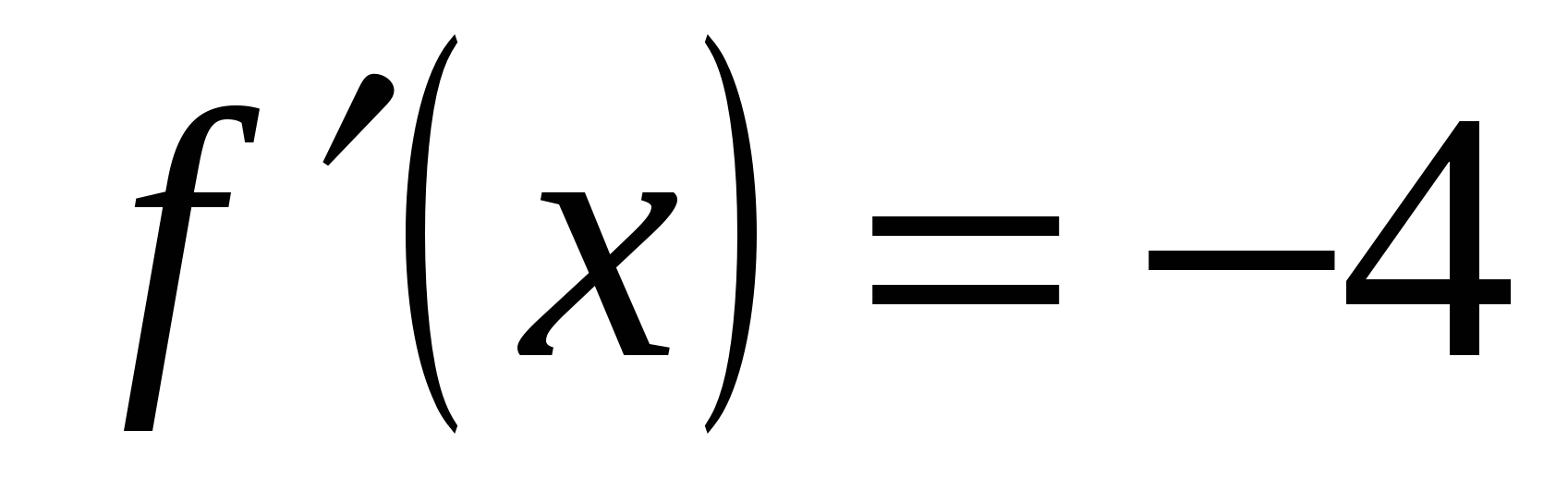 . По графику (рис. 15) видно, что
. По графику (рис. 15) видно, что ![]() принимает значение -4 в одной точке.
принимает значение -4 в одной точке.
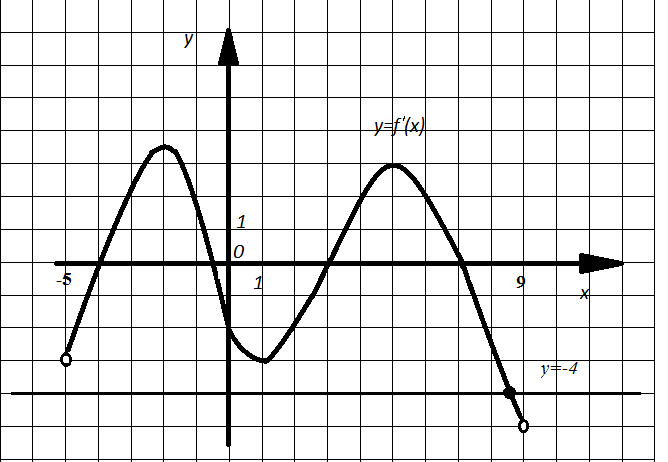
Рис. 15
Ответ: 1.
Пример 12. К графику функции y=f(x) проведена касательная в точке с абсциссой 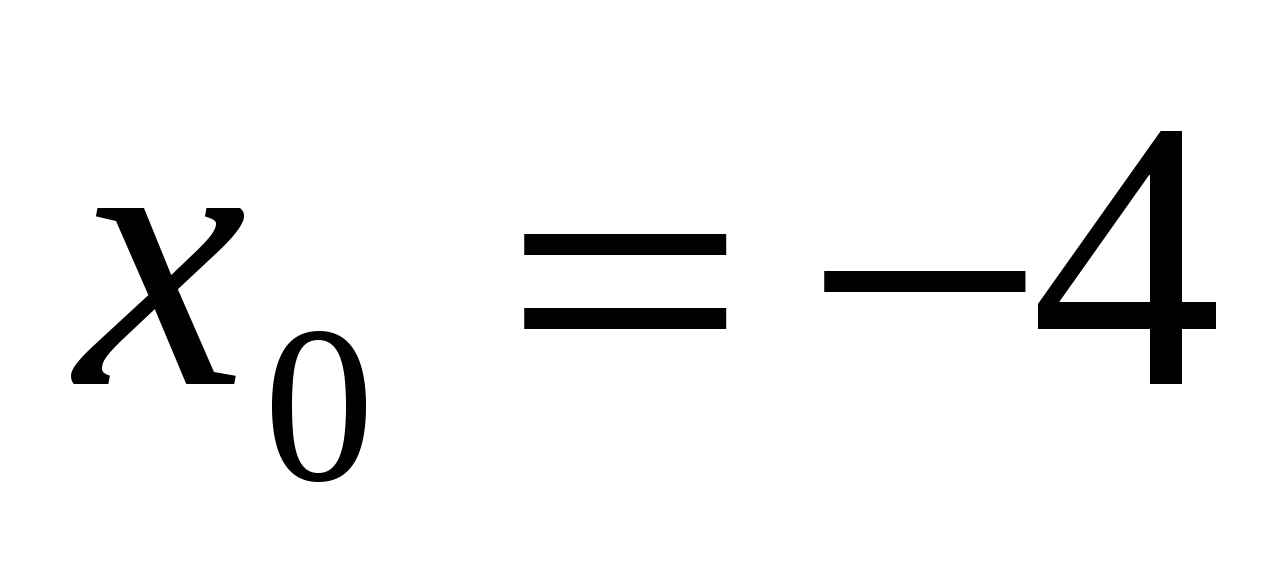 . На рисунке 16 изображен график производной этой функции. Определите градусную меру угла наклона касательной.
. На рисунке 16 изображен график производной этой функции. Определите градусную меру угла наклона касательной.
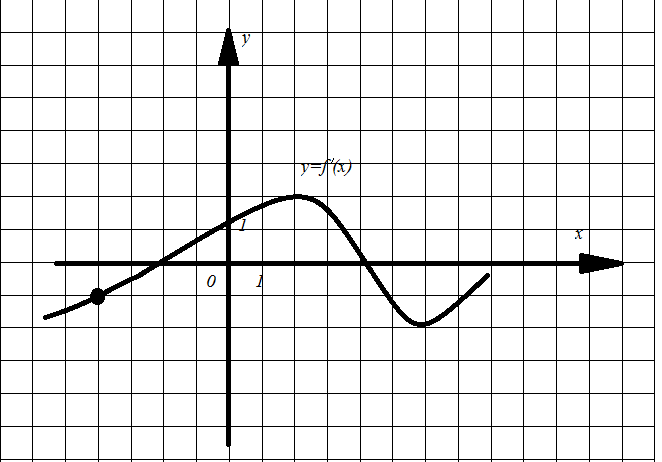
Рис. 16
Решение. Пусть  - угол наклона данной касательной к оси абсцисс. Так как
- угол наклона данной касательной к оси абсцисс. Так как 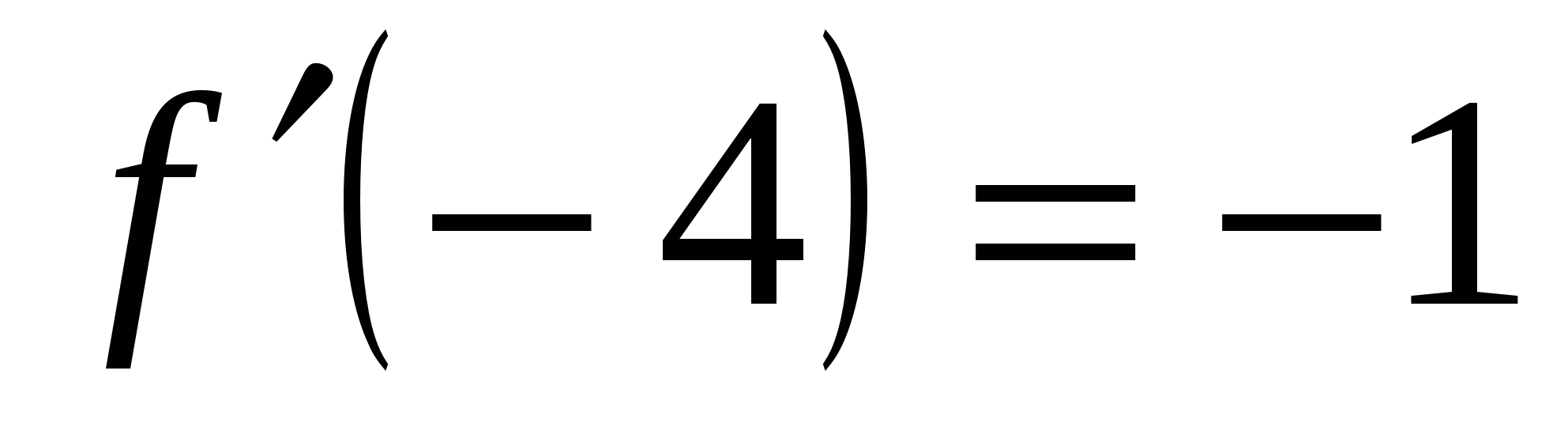 , то
, то 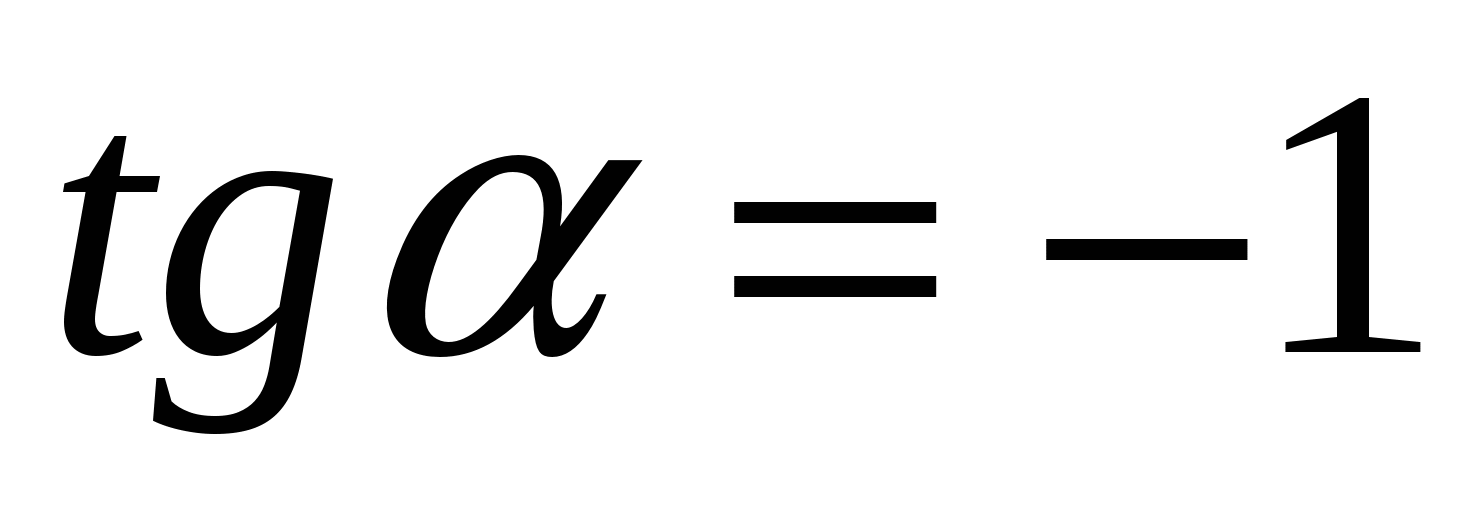 . Отсюда получаем
. Отсюда получаем 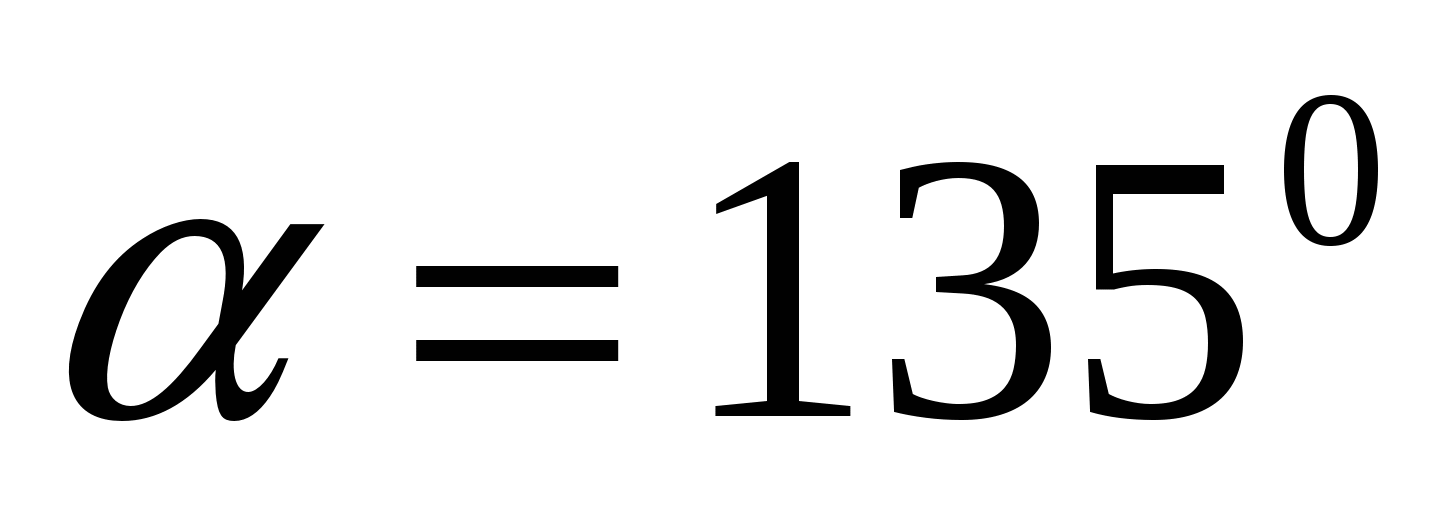 .
.
Ответ: 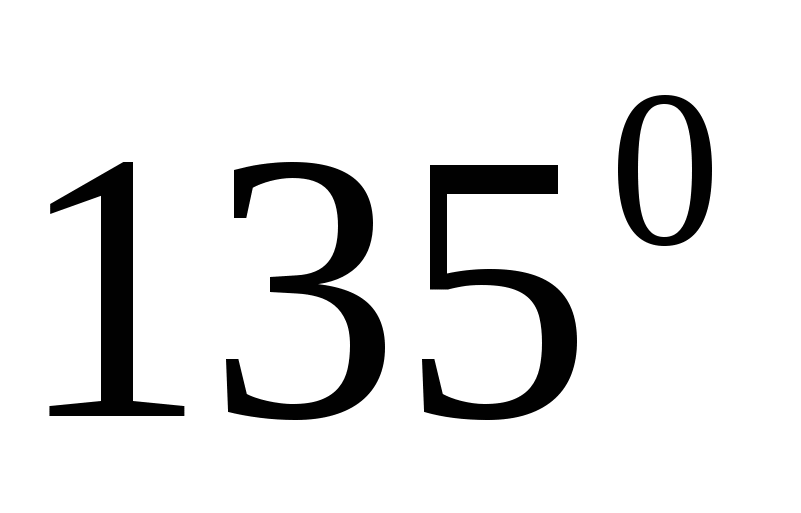 .
.
Пример 13. Найдите координаты точек, в которых касательные к графику функции 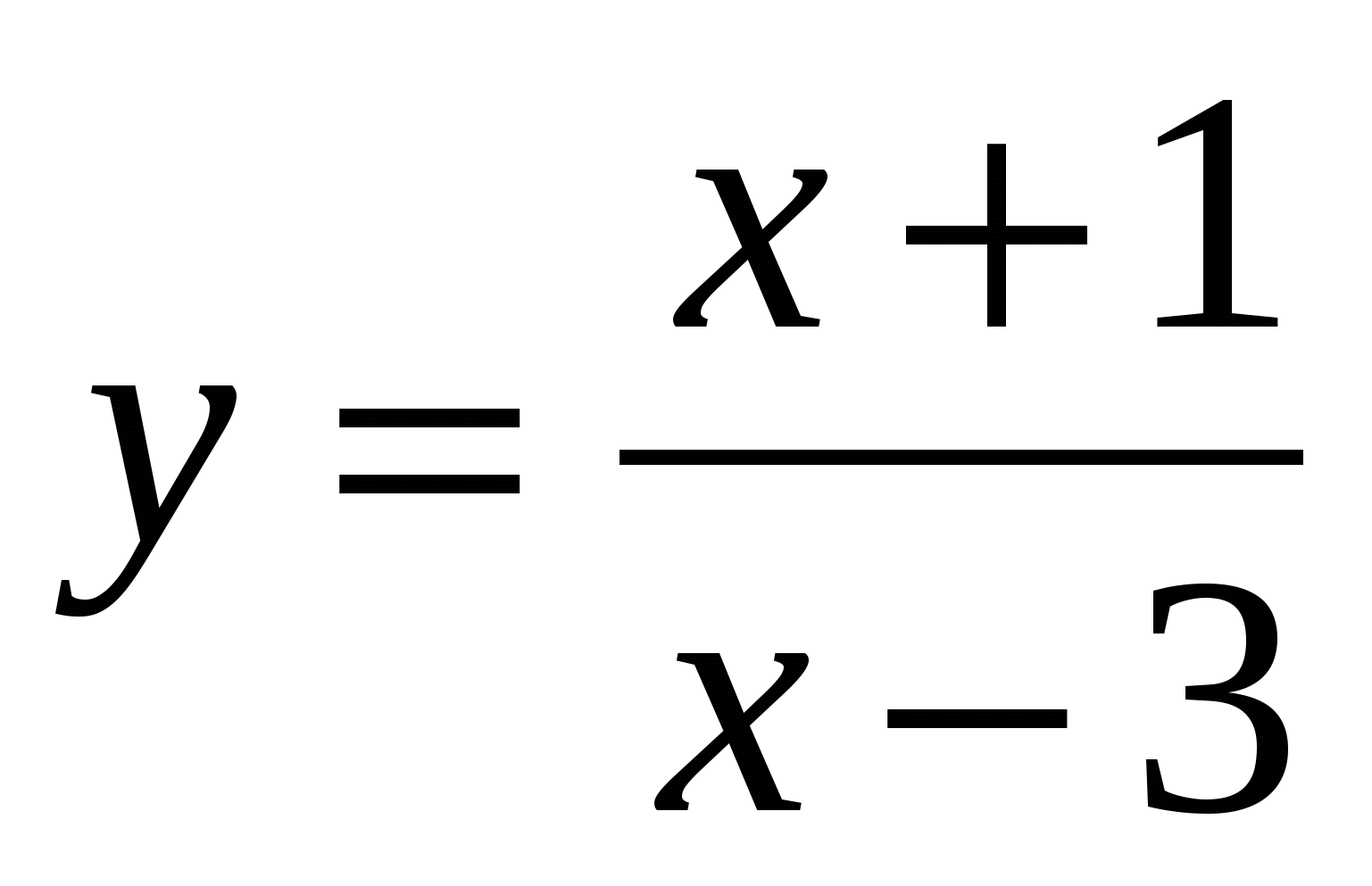 , имеющие угловой коэффициент -1, пересекают ось абсцисс.
, имеющие угловой коэффициент -1, пересекают ось абсцисс.
Решение. Найдем координаты точек, в которых касательные к графику имеют угловой коэффициент -1.
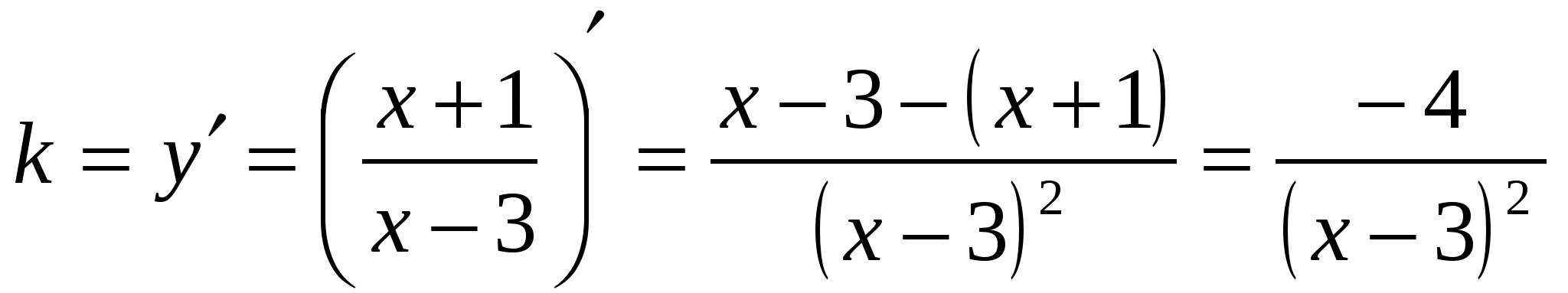 ;
;
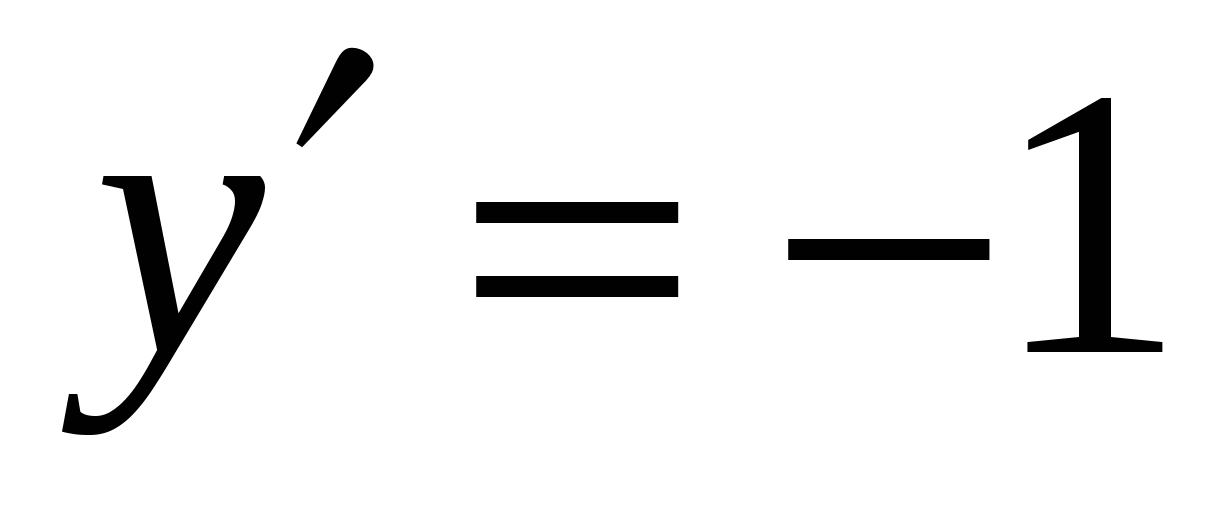
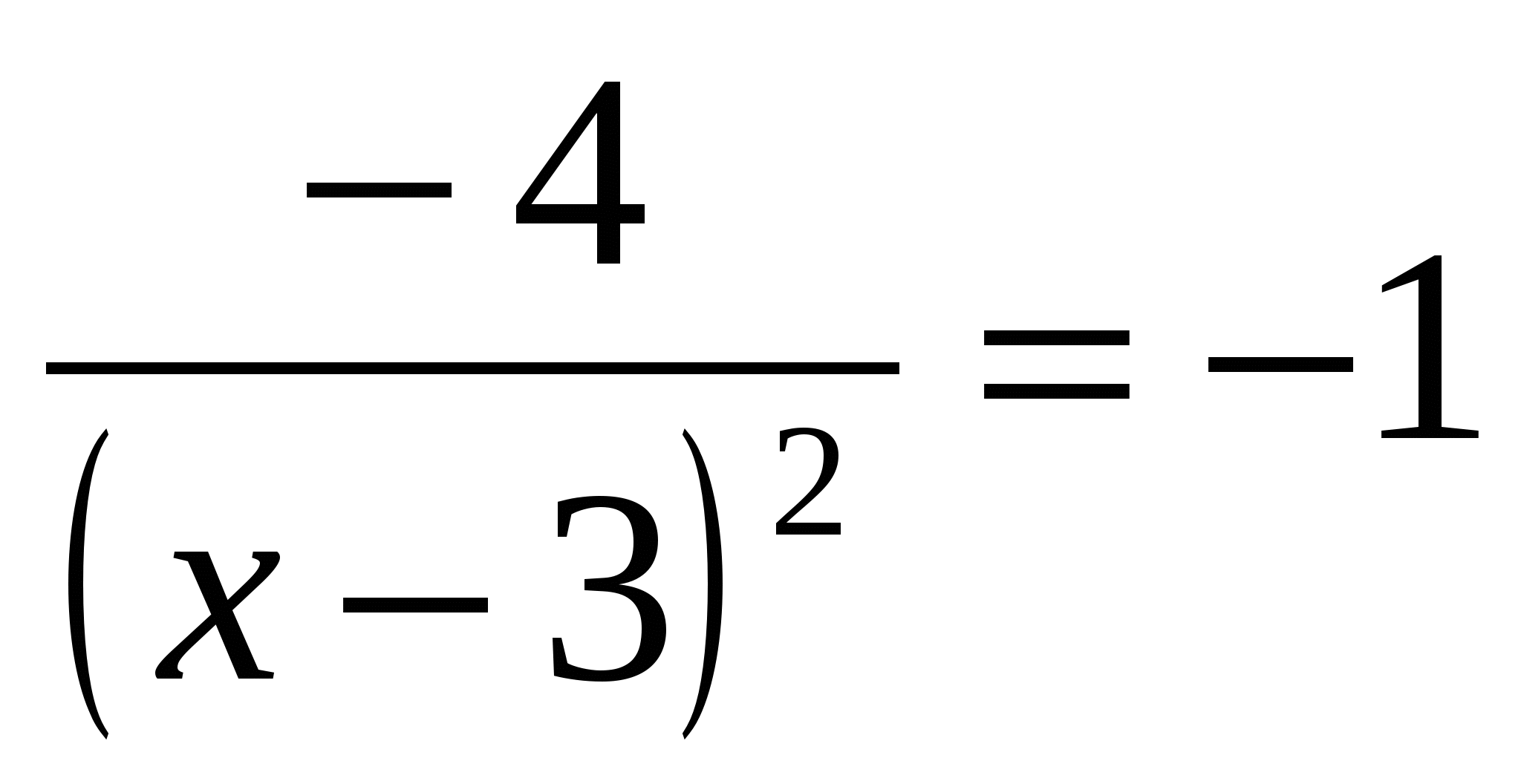
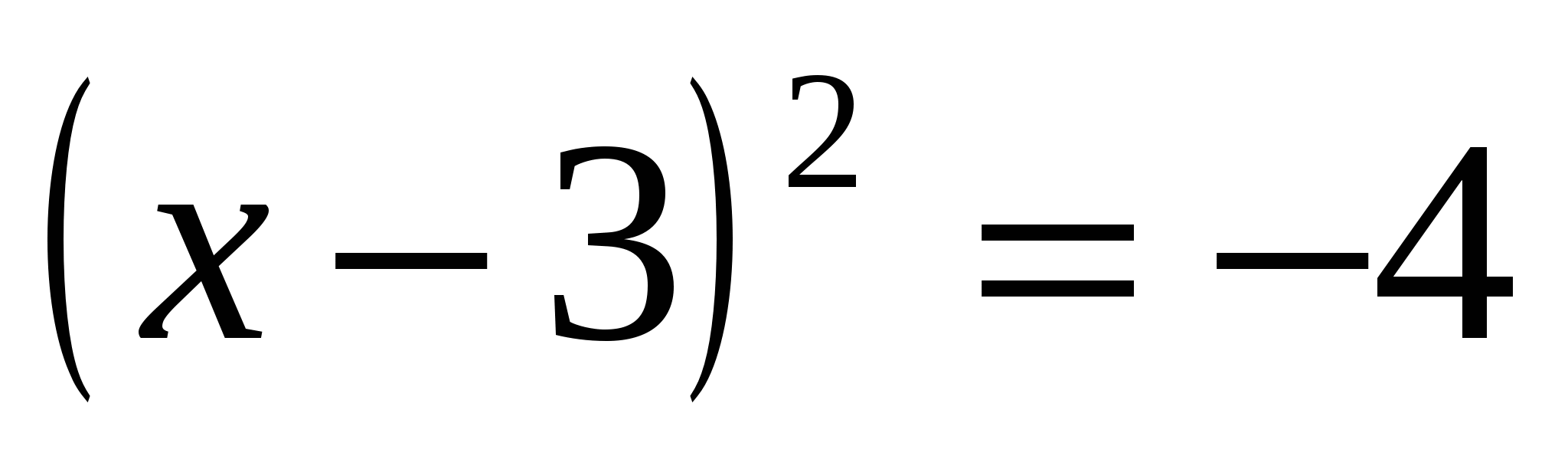 .
.
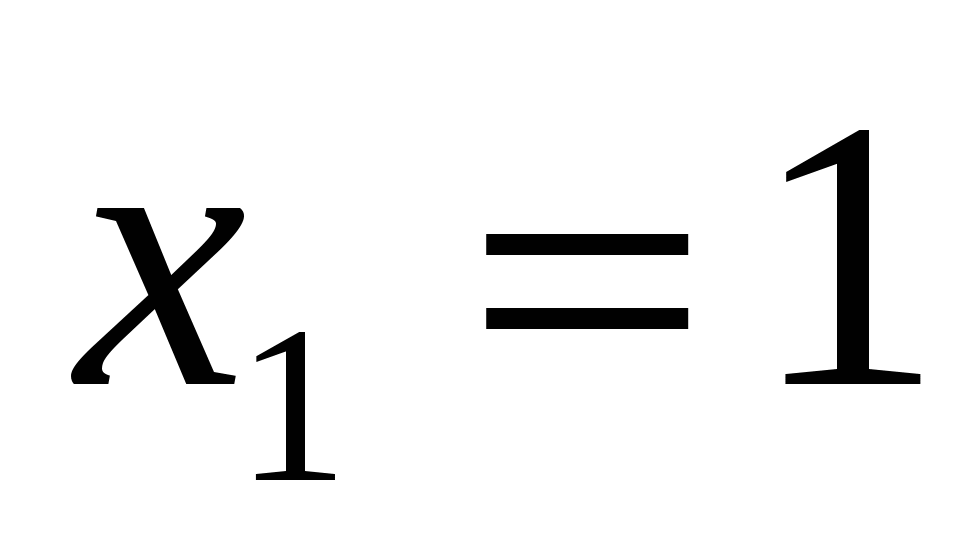
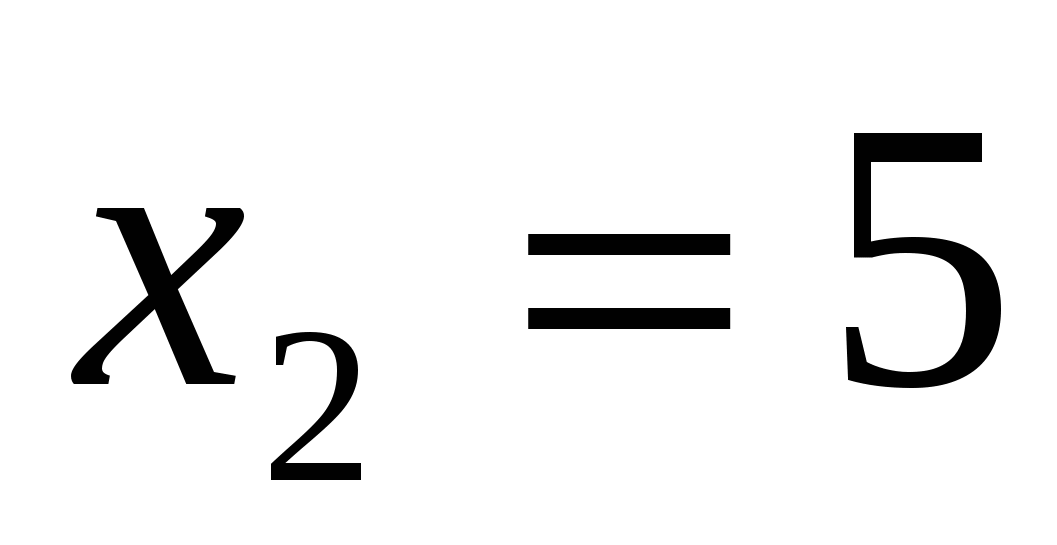
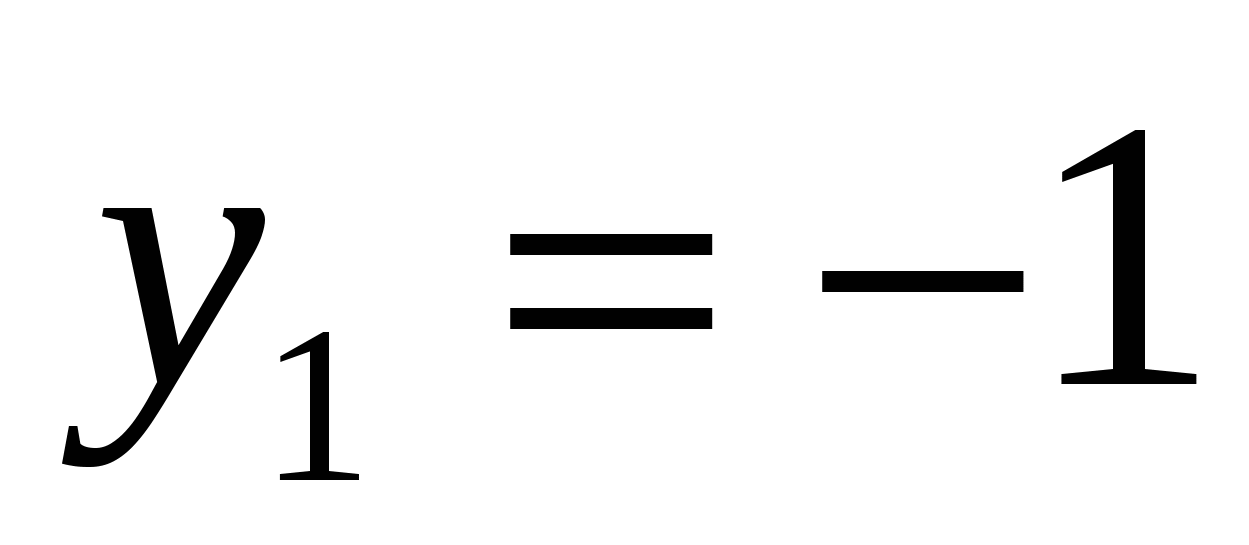
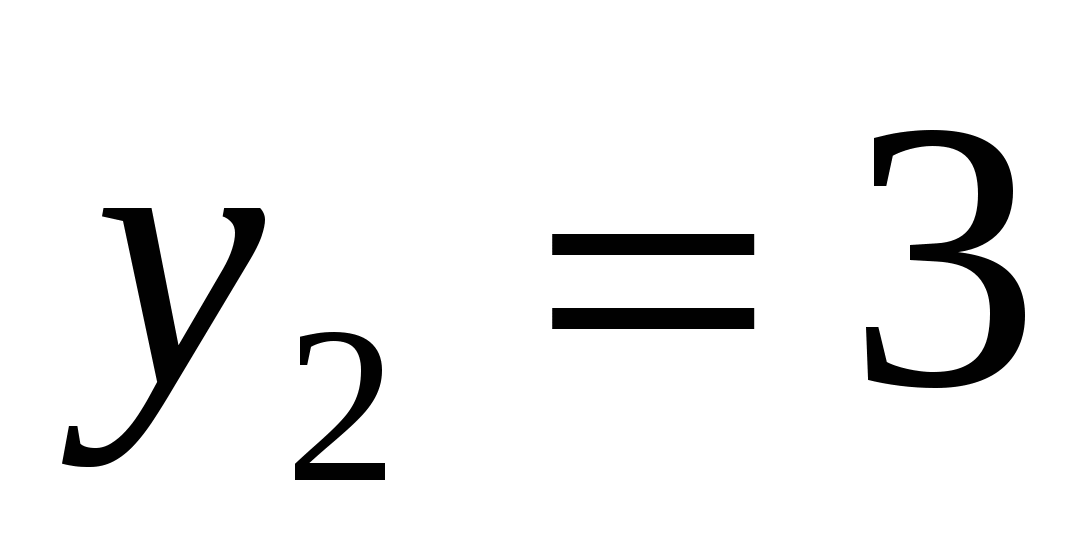 .
.
Запишем уравнения этих касательных:
1) 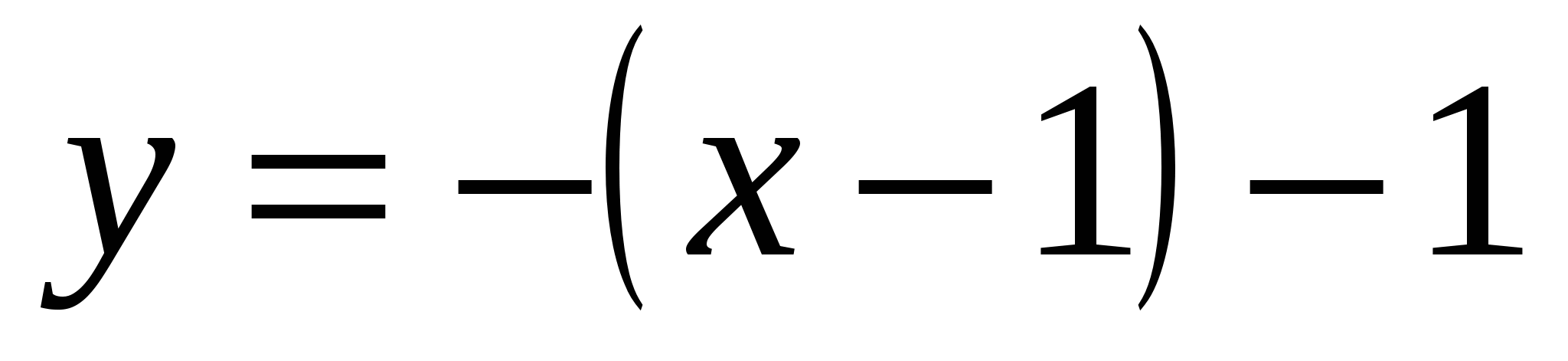
2) 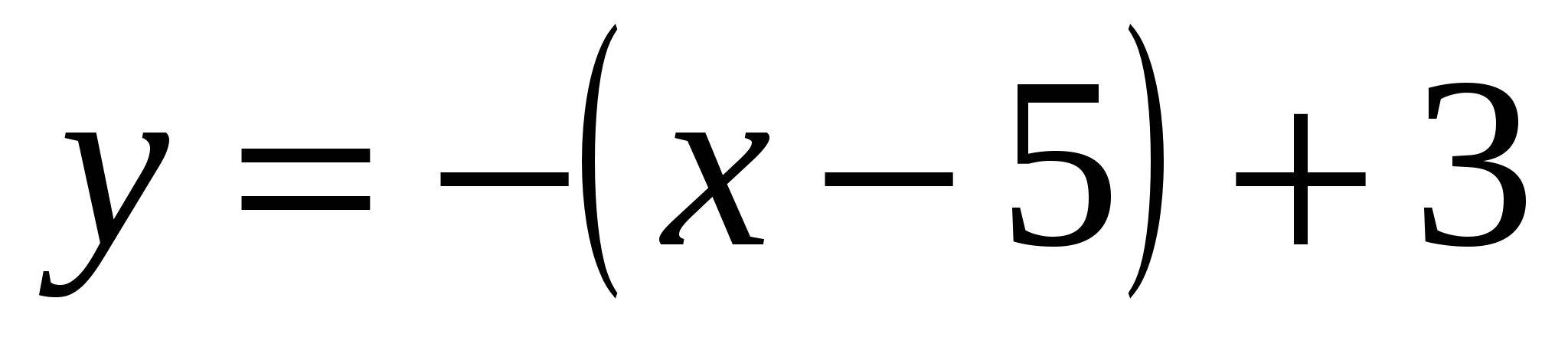 .
.
Касательные пересекают ось абсцисс, значит, у=0.
Таким образом,
-
х=0
-
х=8.
Ответ: (0;0), (8;0).
Пример 14. На рисунке 5 (см. пример 3) изображен график функции y=f(x), определенной на промежутке (-5;9). Найдите количество точек, в которых касательная к графику функции параллельна прямой y=-7.
Решение. Так как касательные параллельны прямой у=-7, то они параллельны оси ОХ, следовательно, производные функции f(x) в точках касания должны ровняться нулю. Это стационарные точки. На рисунке все они являются точками экстремума (максимумами или минимумами). Их три.
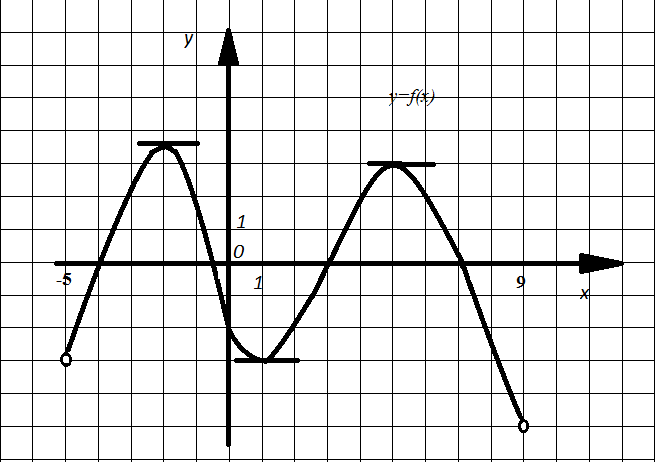
Рис. 17
Ответ: 3.
Пример 15. Дана кривая 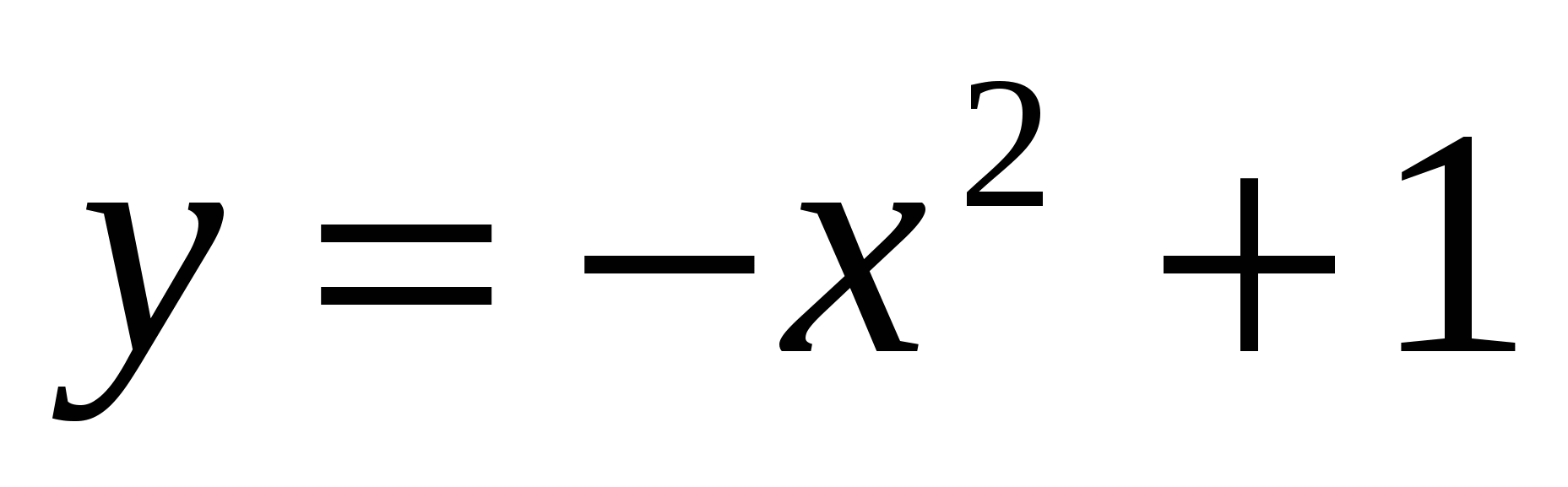 . Найти точку ее графика, в которой касательная параллельна прямой у=2х+3.
. Найти точку ее графика, в которой касательная параллельна прямой у=2х+3.
Решение. Так как касательная параллельна прямой у=2х+3, то угловой коэффициент касательной равен угловому коэффициенту прямой, то есть k=2, но согласно геометрическому смыслу производной 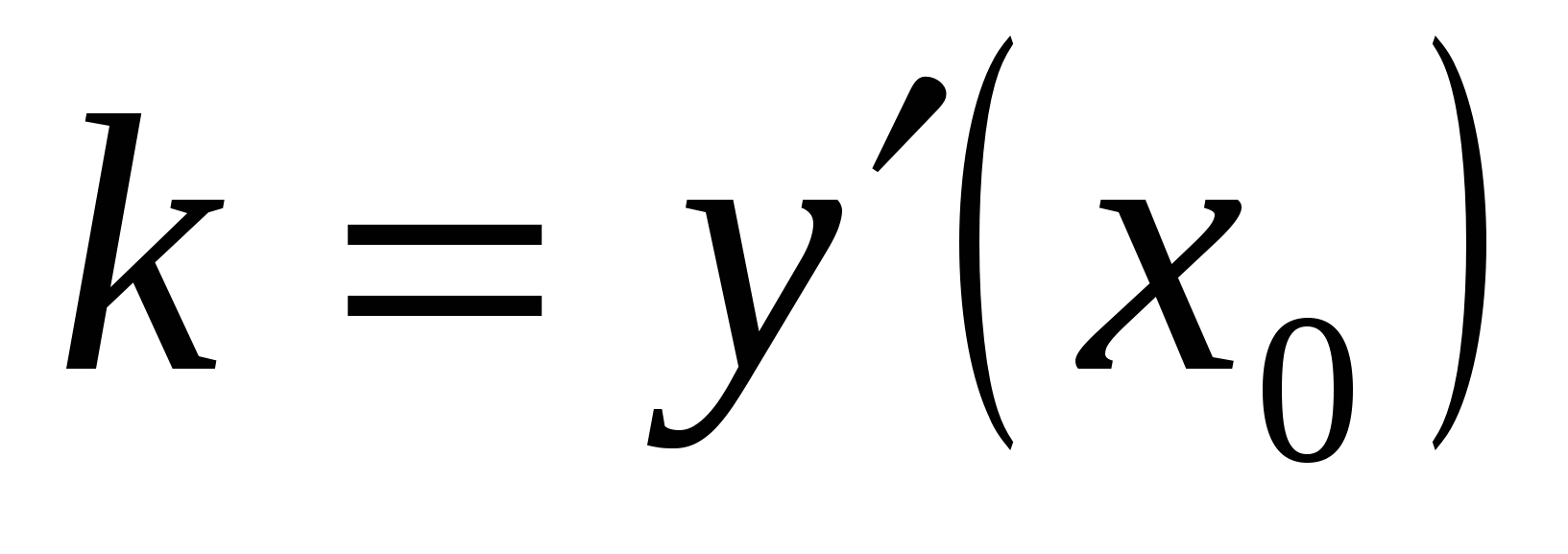 , значит, имеем
, значит, имеем 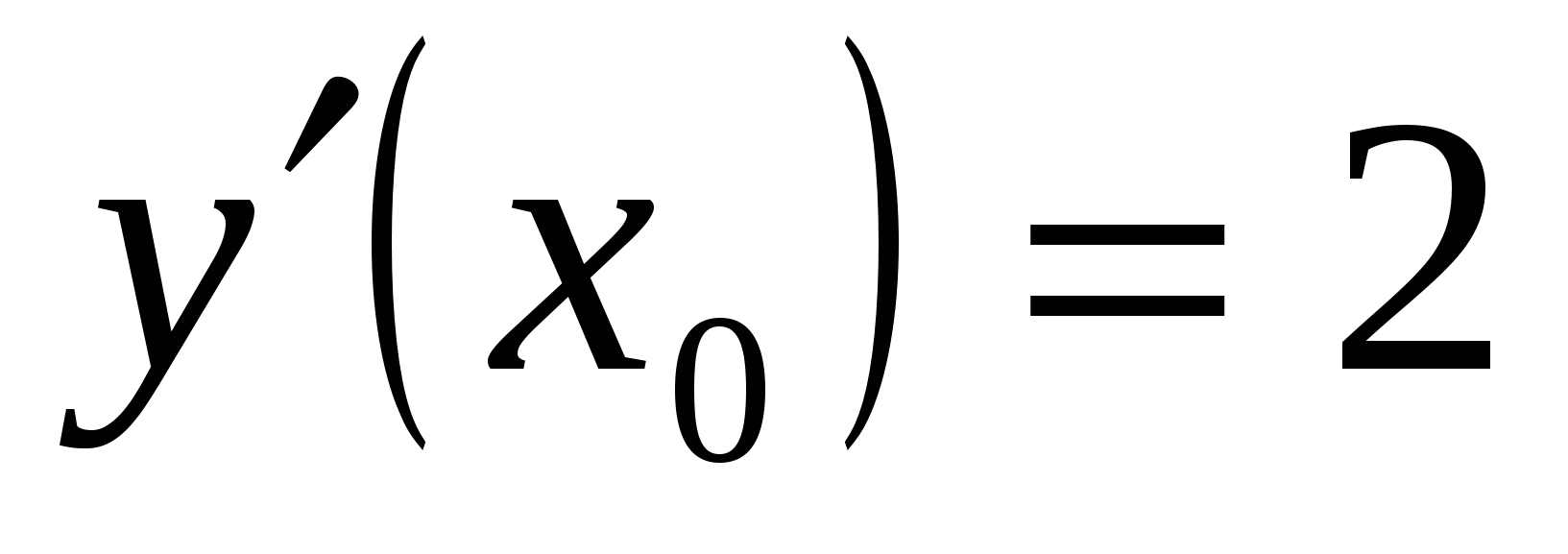 ,
, 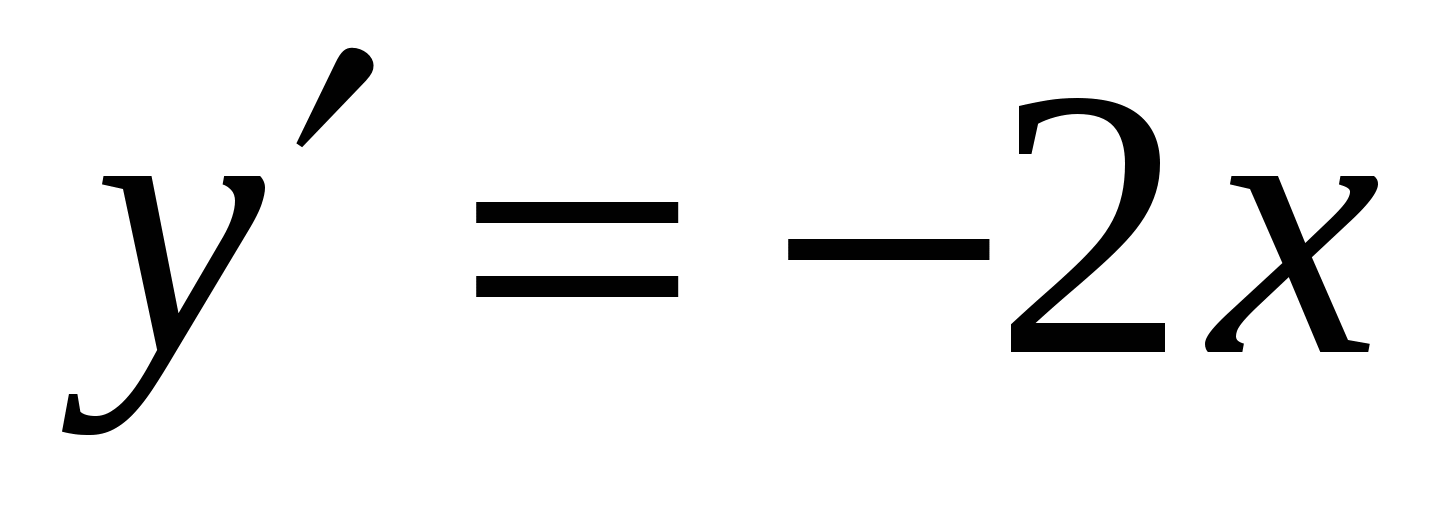 ,
, 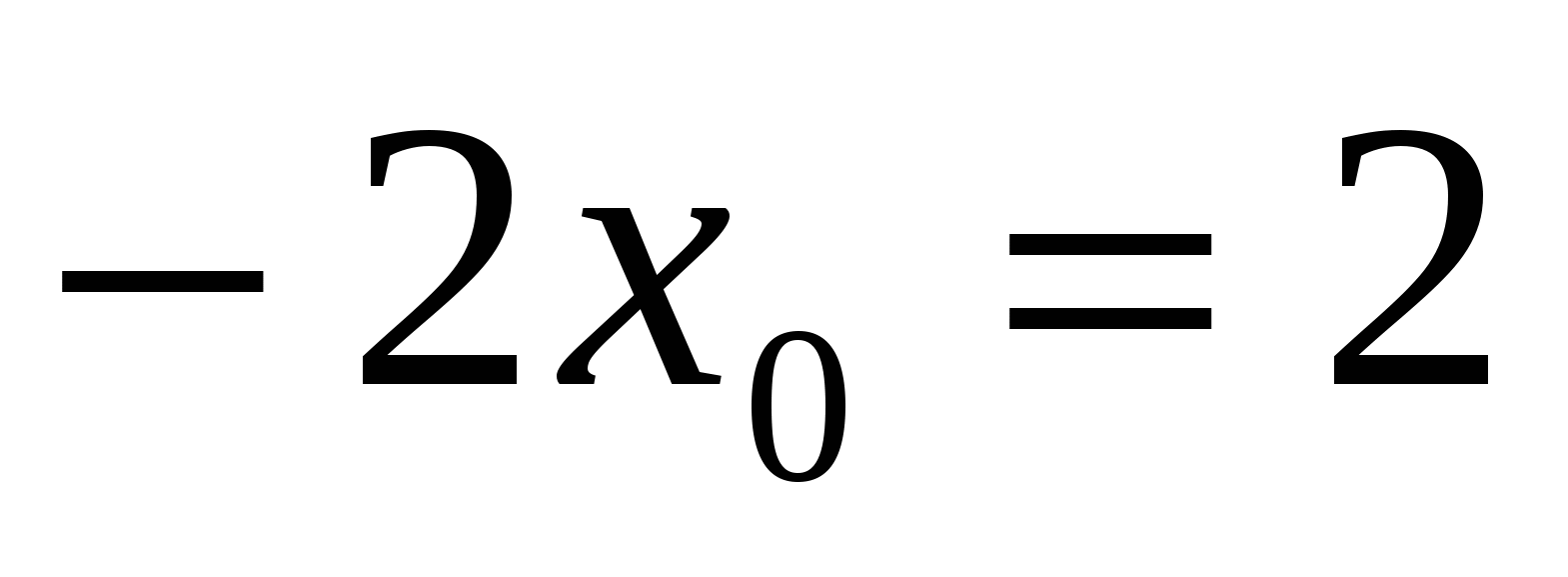 , отсюда
, отсюда 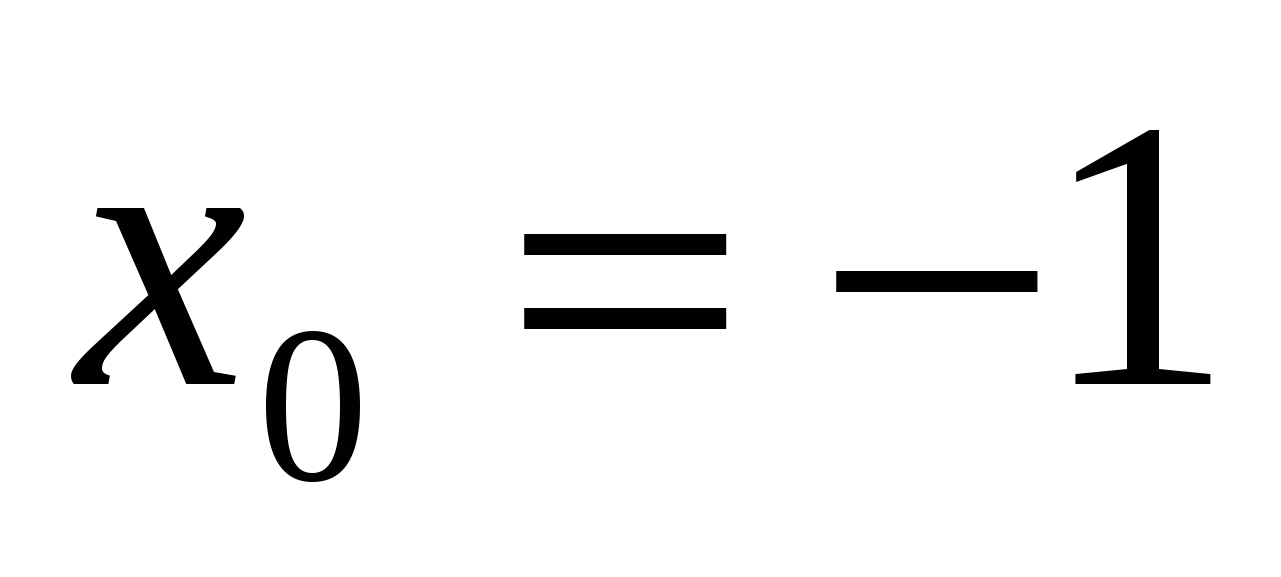 , а
, а 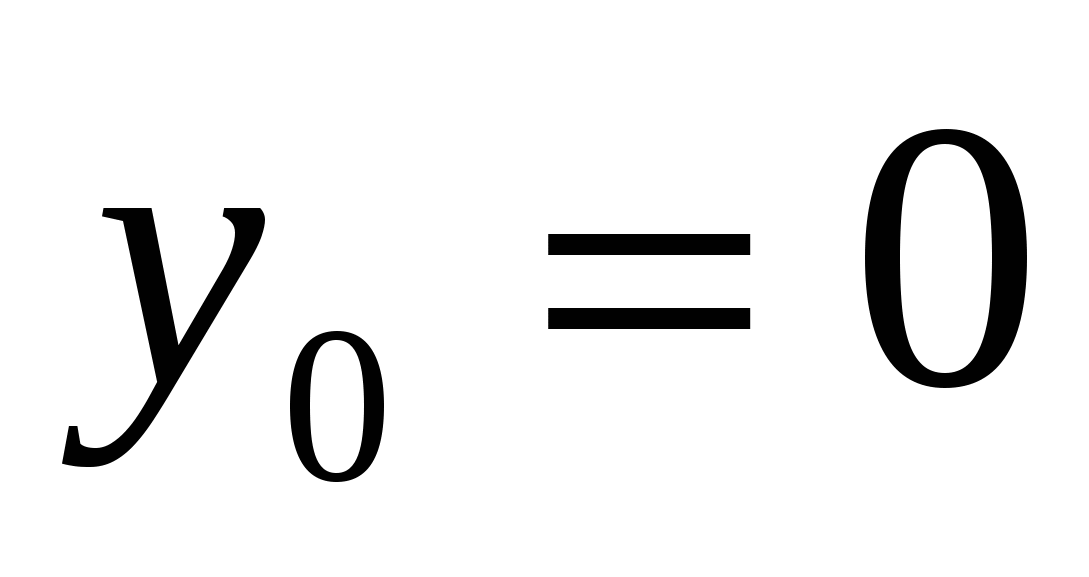 .
.
Итак, (-1;0) - искомая точка.
Ответ: (-1;0) .
6 Исследование функции
Пример 16. Исследовать функцию 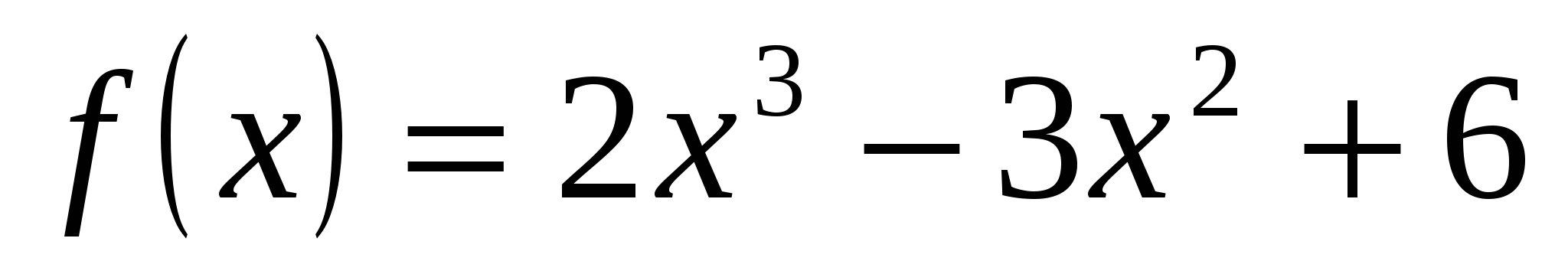 и построить ее график.
и построить ее график.
Решение.
-
Д(f)=R, Функция непрерывная на R, так как f(x) - многочлен.
-
Четность и нечетность функции, периодичность.
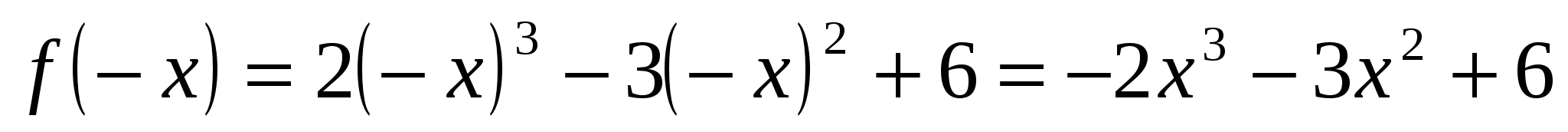
Функция не является ни четной, ни нечетной, так как не выполняются условия:
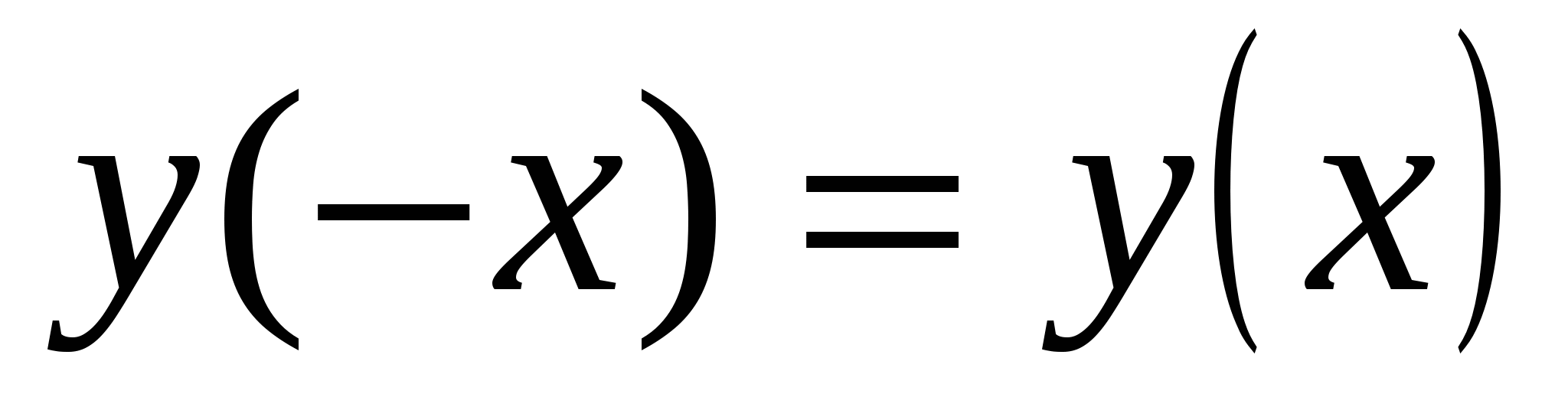 ,
, 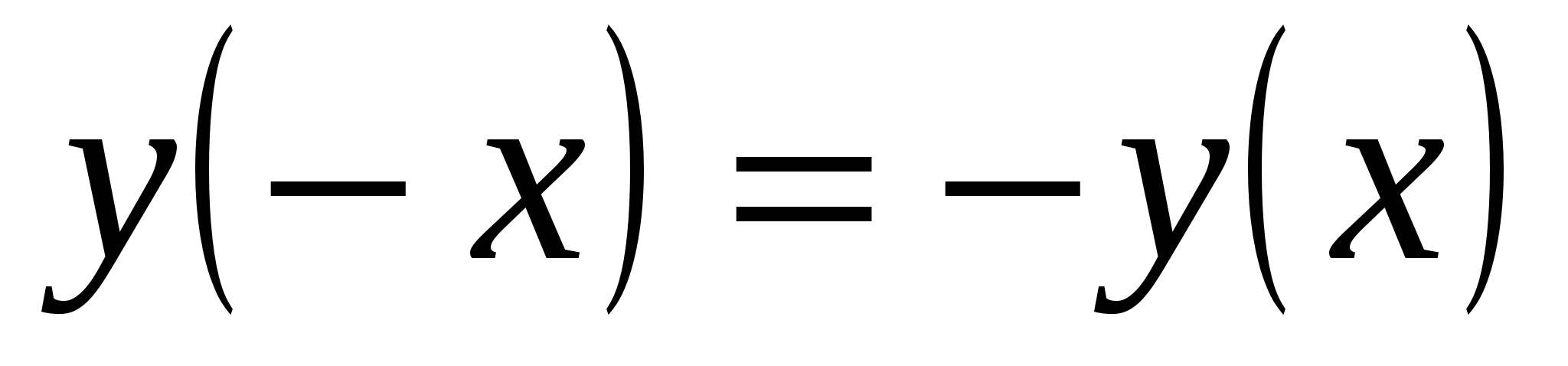 (функция общего вида). Функция не периодическая.
(функция общего вида). Функция не периодическая.
-
Найдем критические точки:
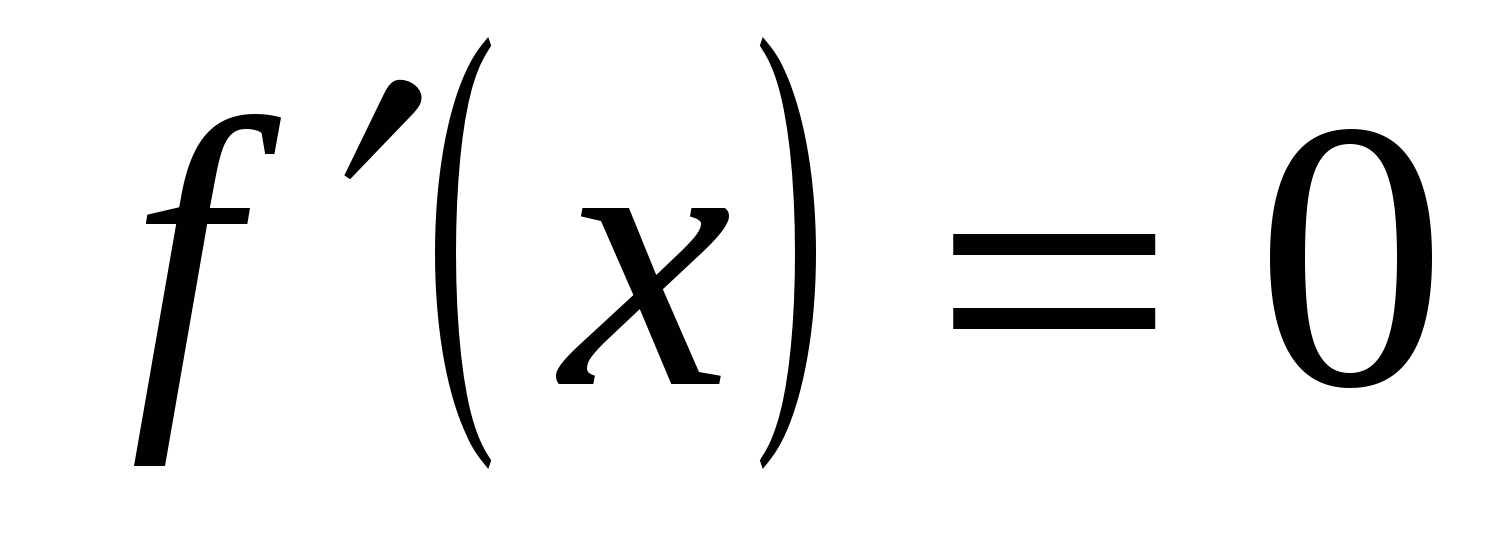 ,
,
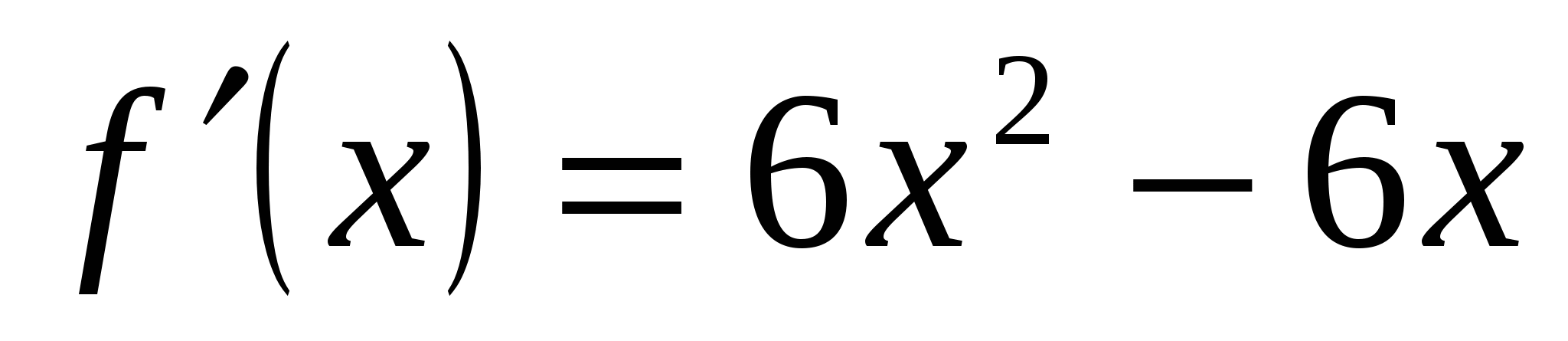
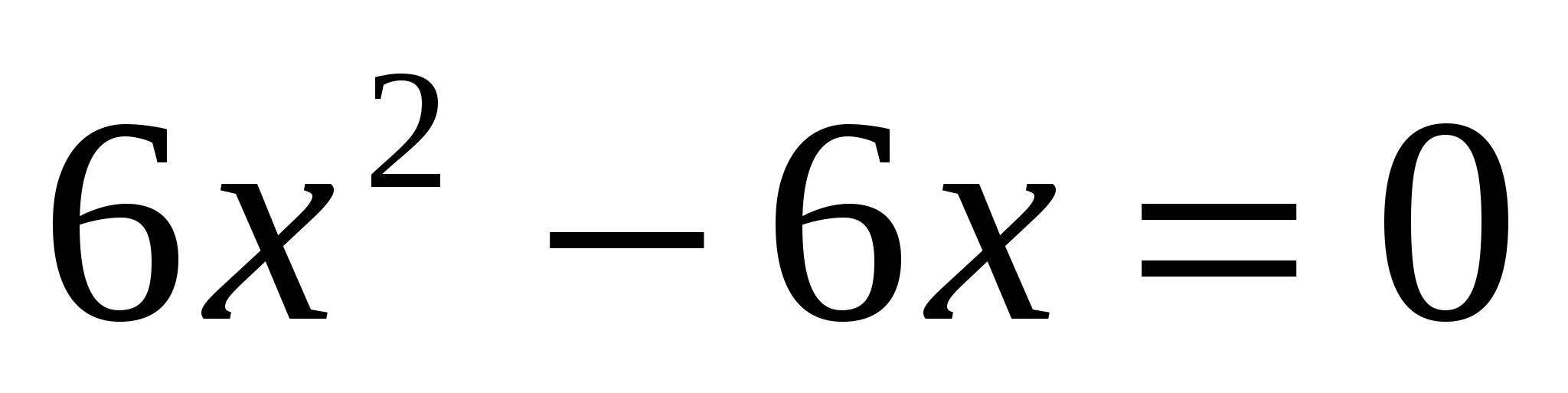
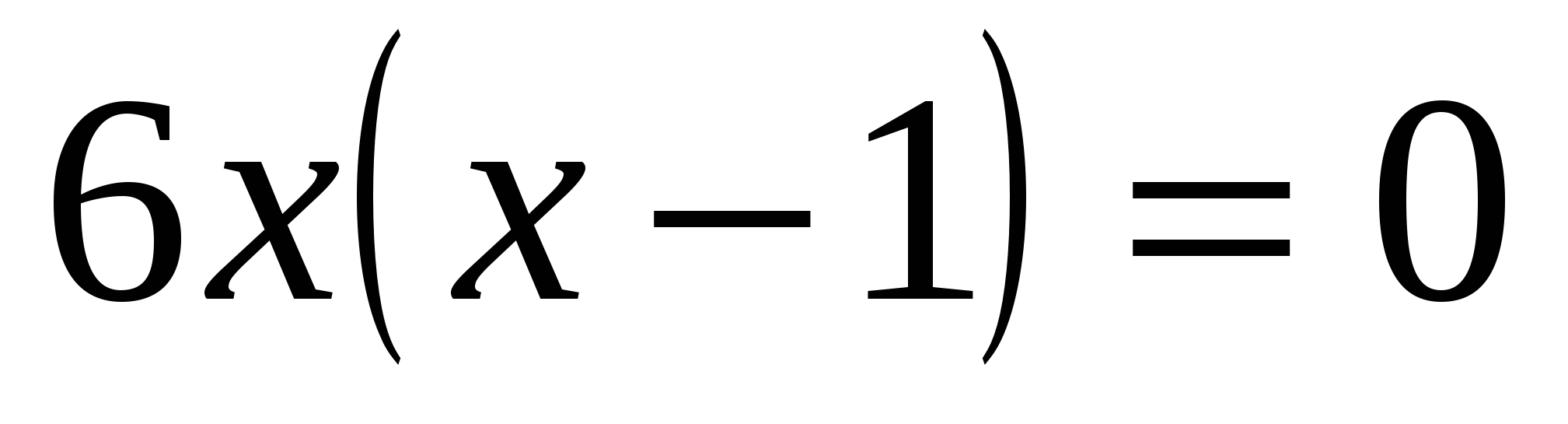
x=0 или x=1
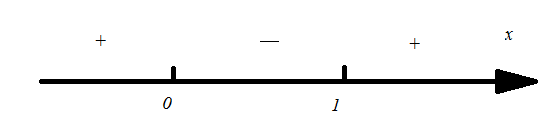
x
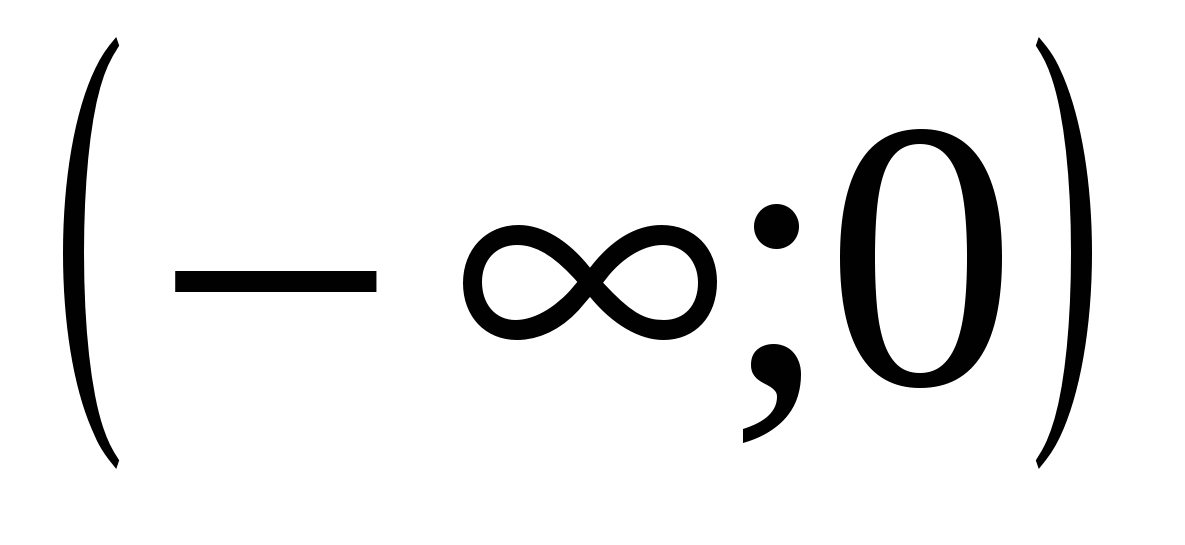
0
(0;1)
1
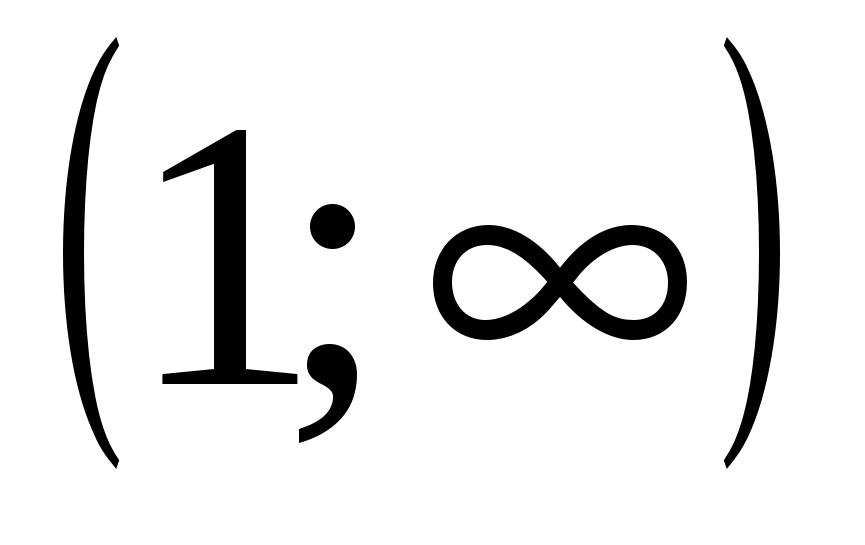
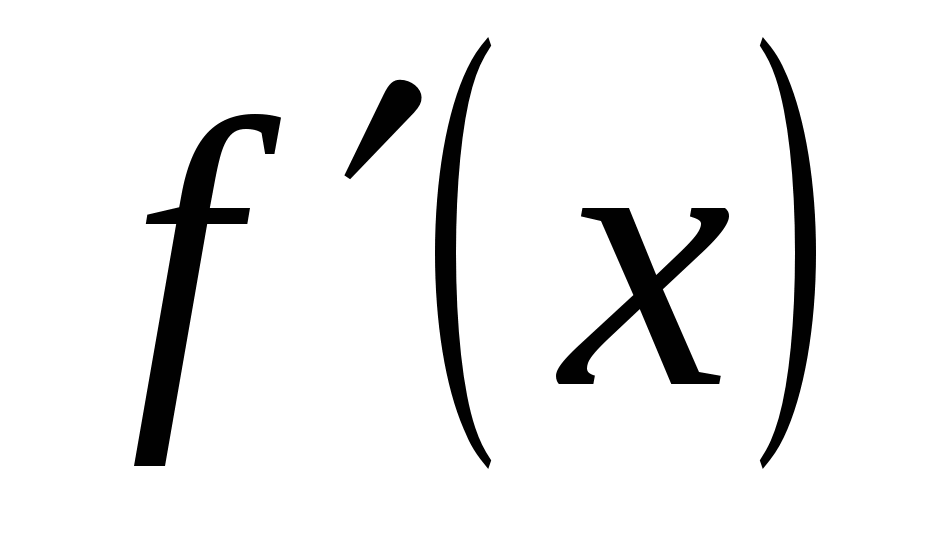
+
0
-
0
+
f(x)
6
5

max
min
4)
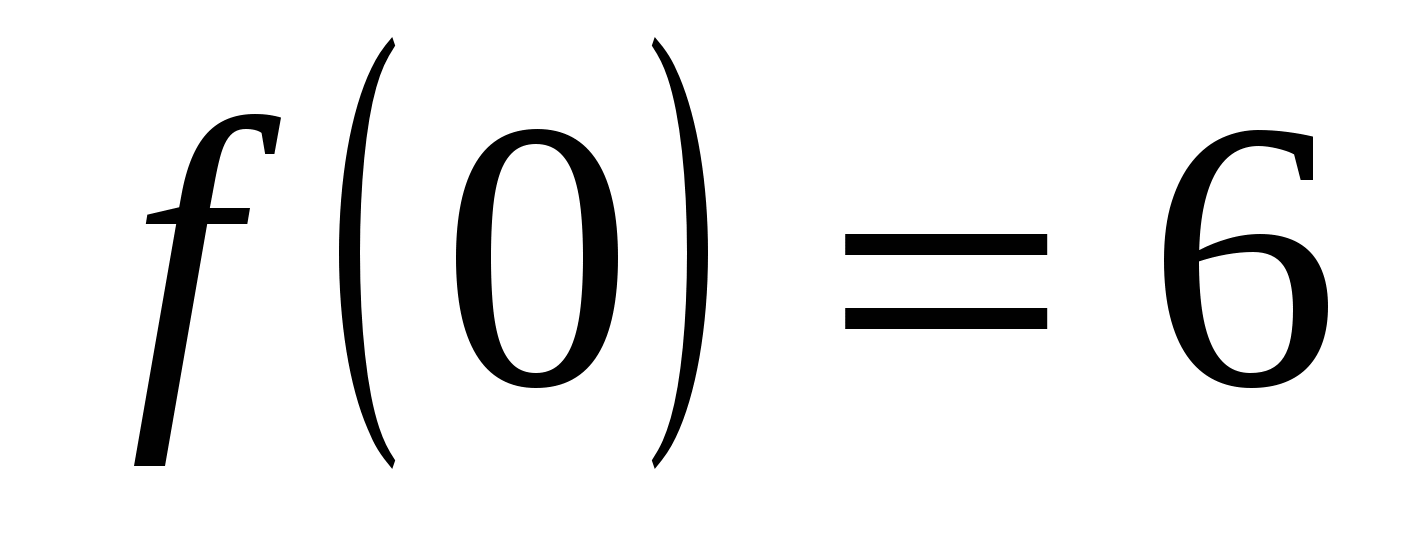 ; f(1)=2-3+6=5.
; f(1)=2-3+6=5.
Функция f(x) возрастает при 
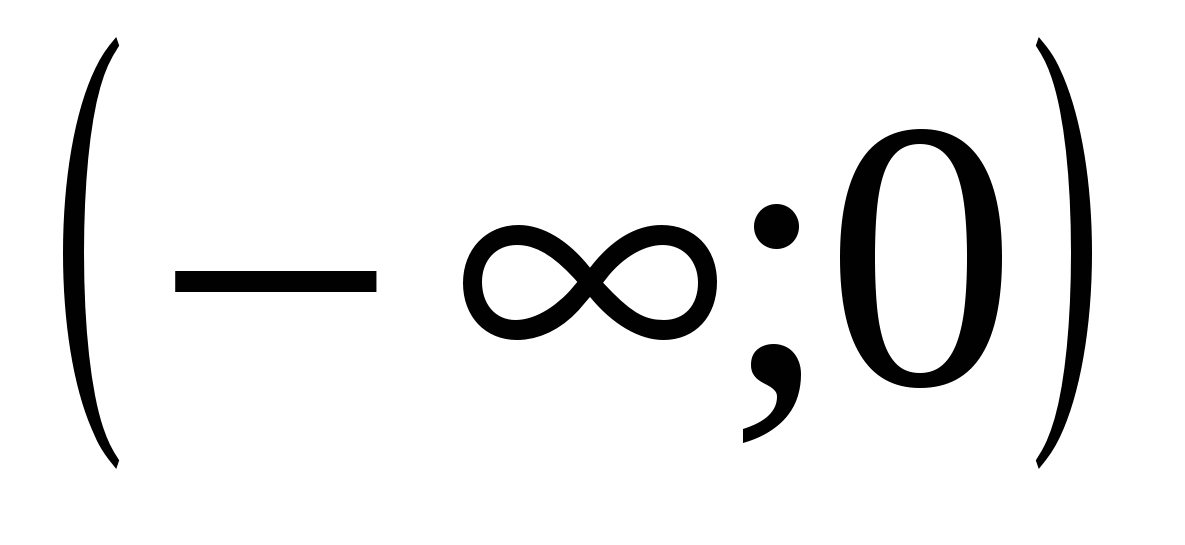

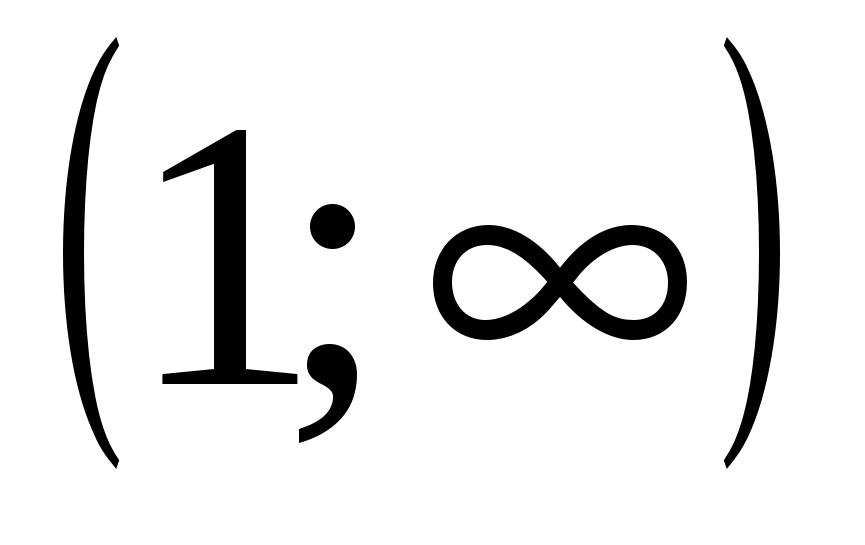 ;
;
Убывает при 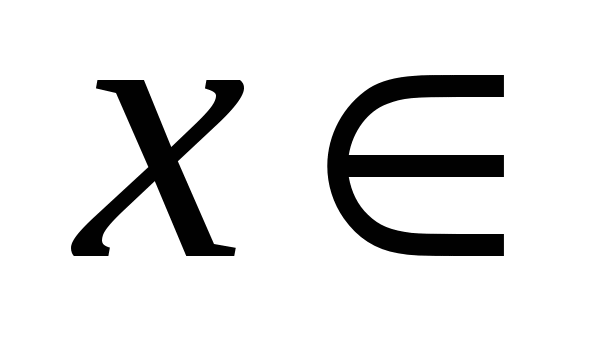 (0;1).
(0;1).
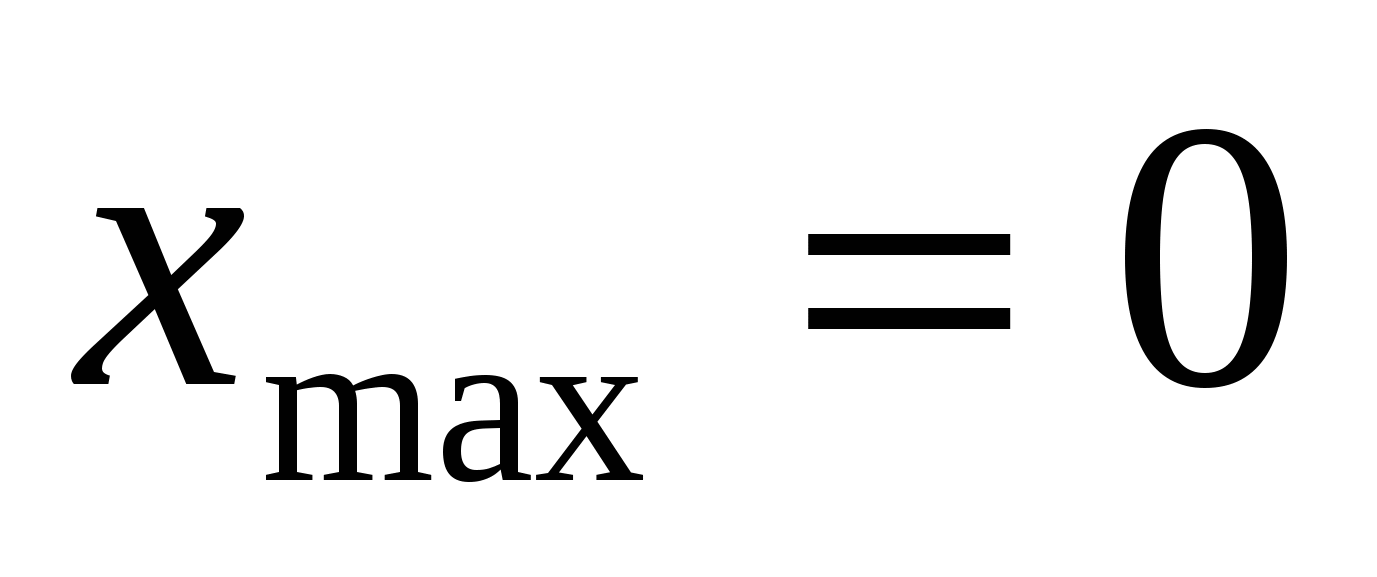 ,
, 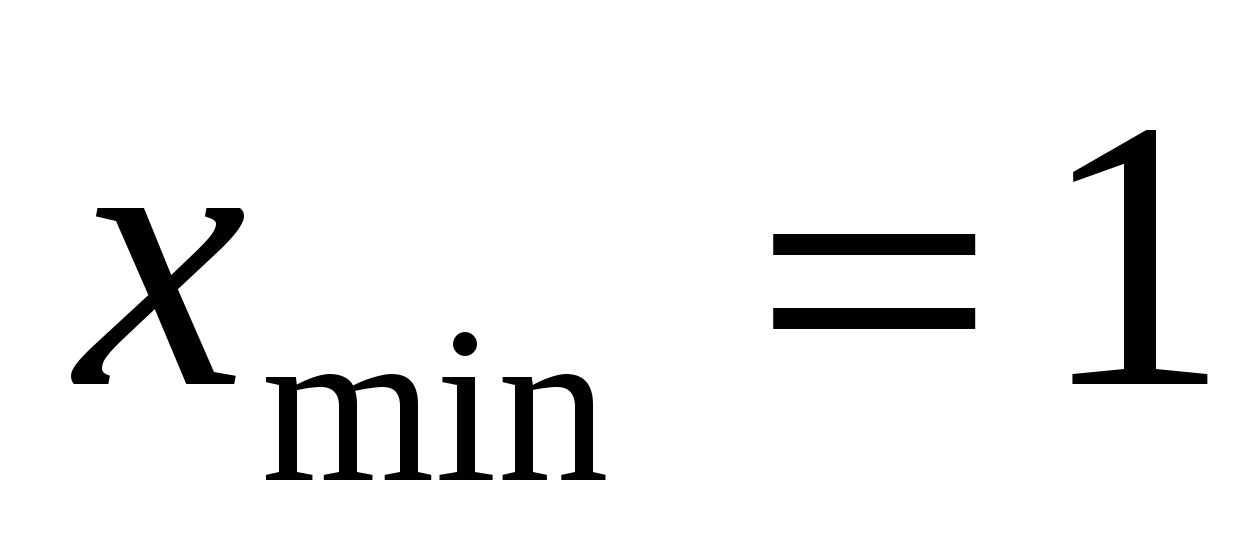 ,
, 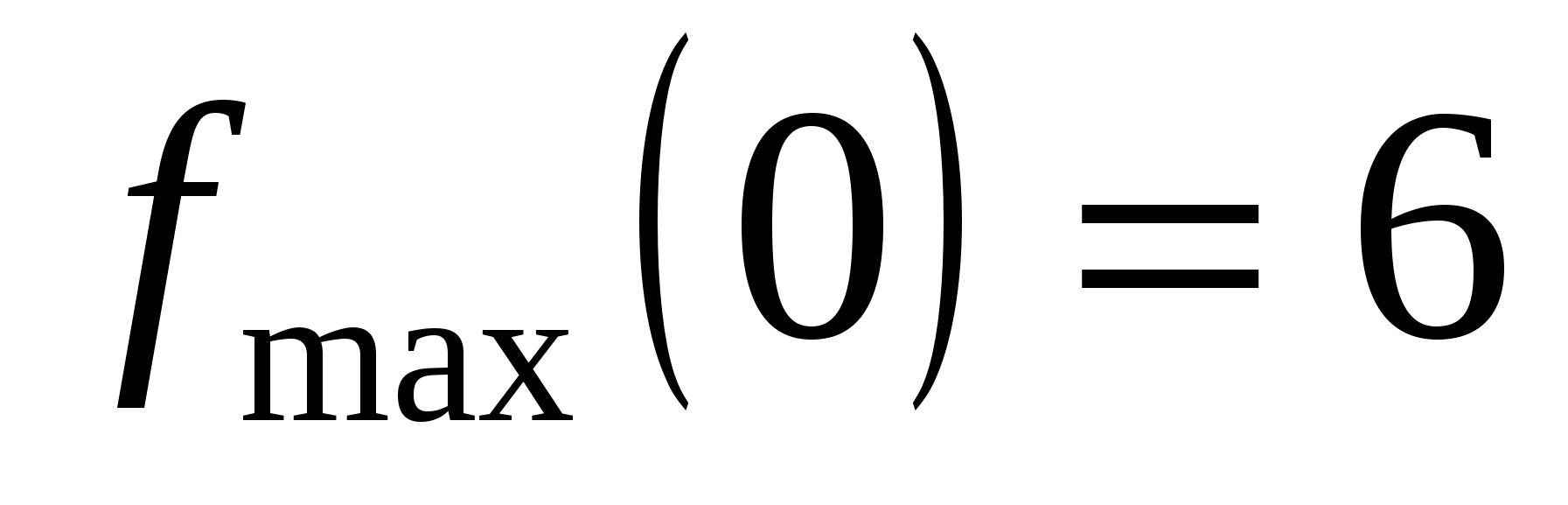 ,
, 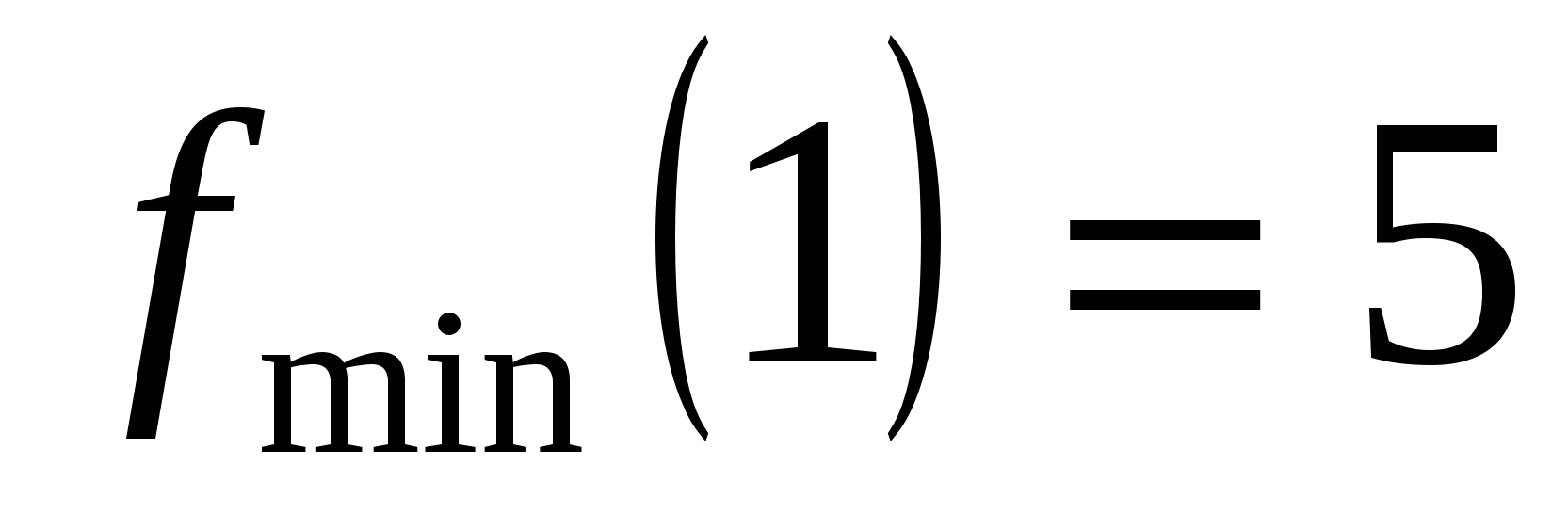 .
.
-
Найдем координаты некоторых точек графика:
если х= -1, то f(-1)=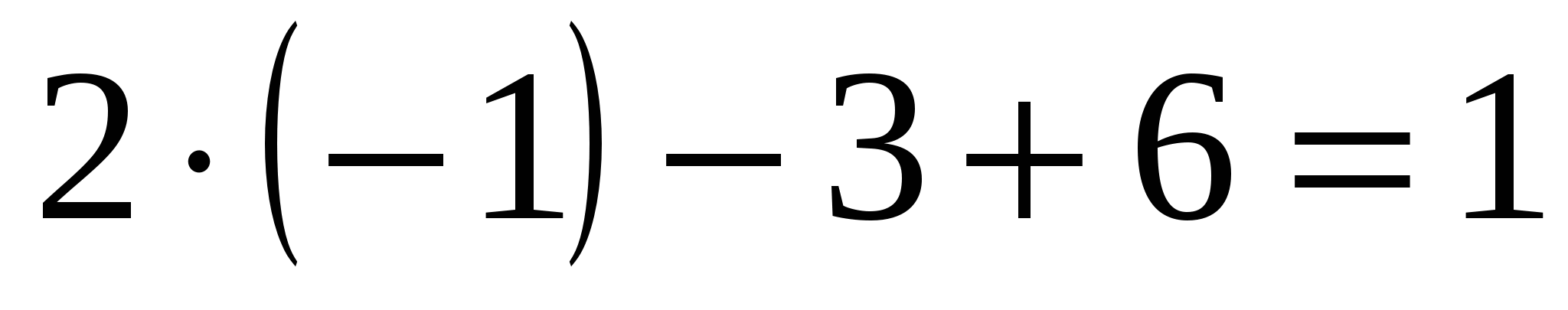 ;
;
если х=2, то 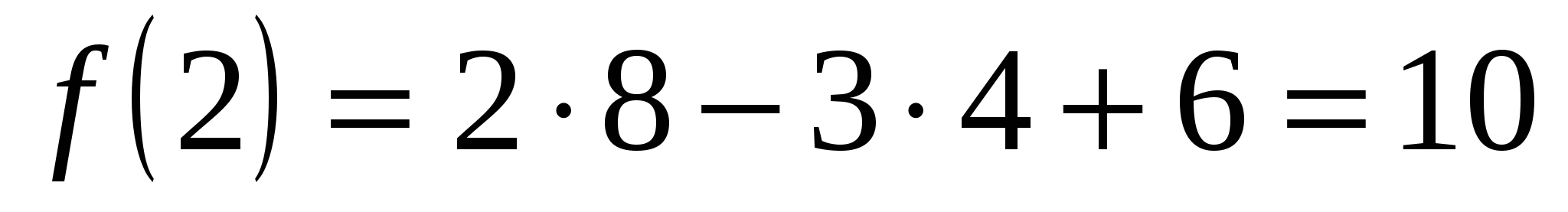 .
.
6)
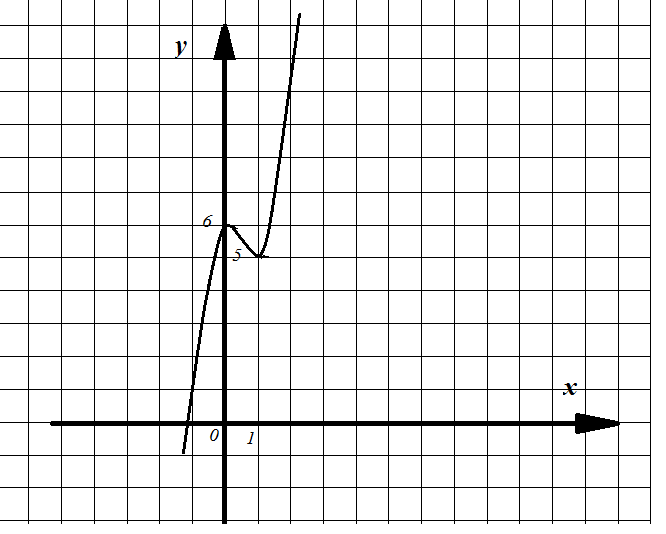
Рис. 18
Пример 17. написать уравнение касательной к графику функции 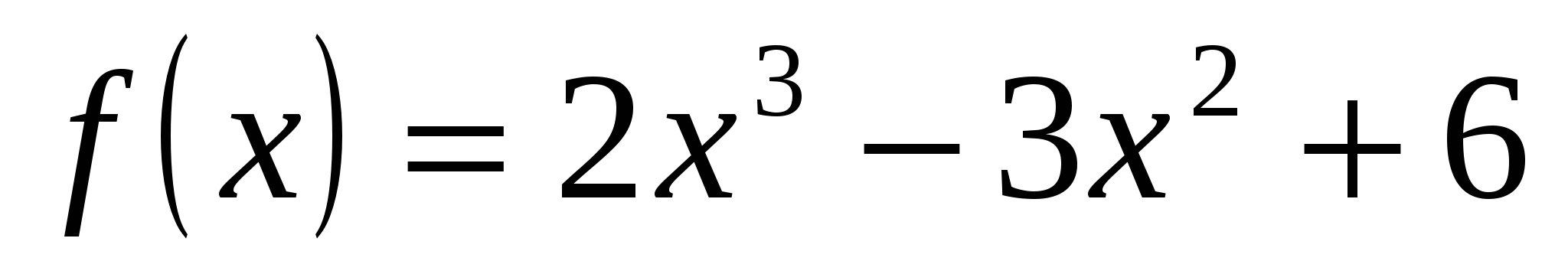 в точке с абсциссой
в точке с абсциссой 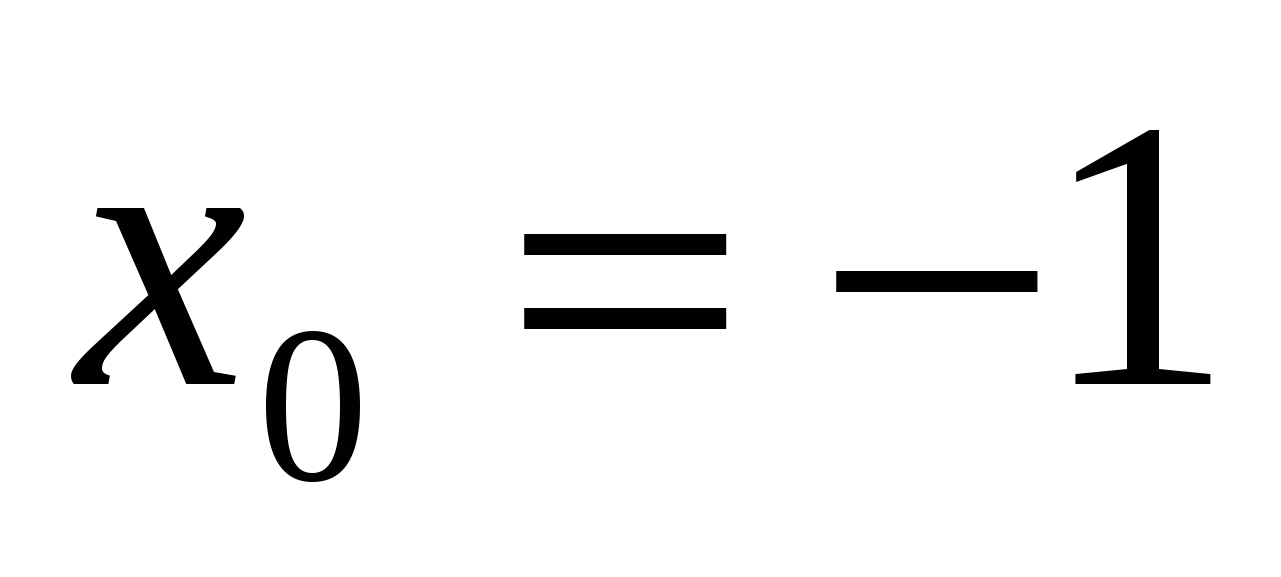 .
.
Решение. Напишем уравнение касательной к графику функции в точке 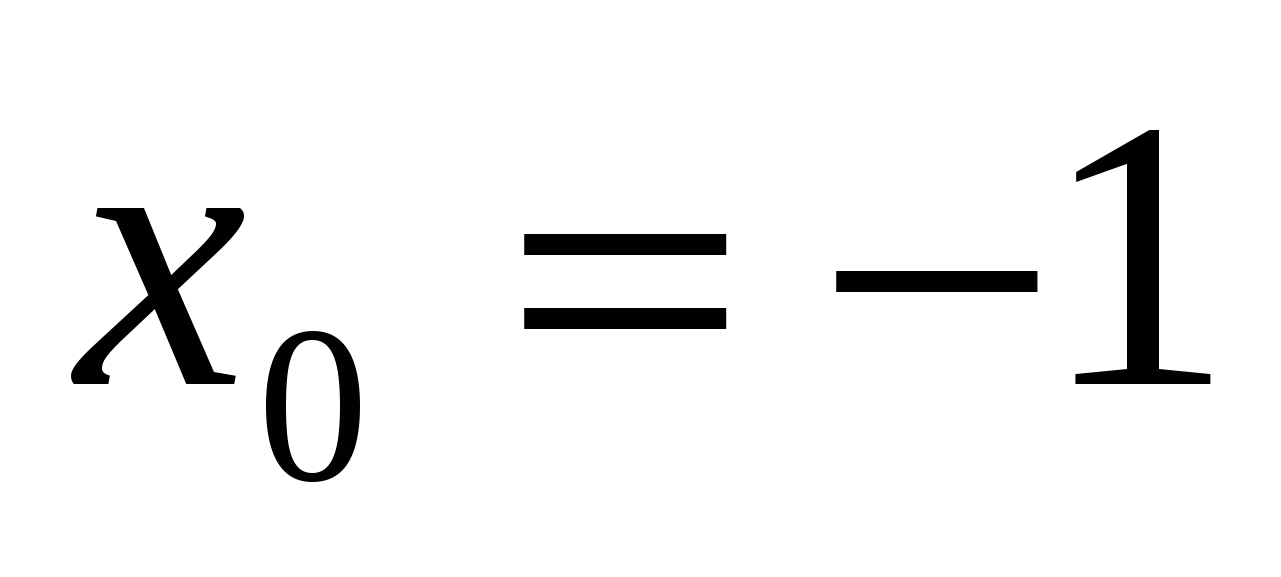 :
: 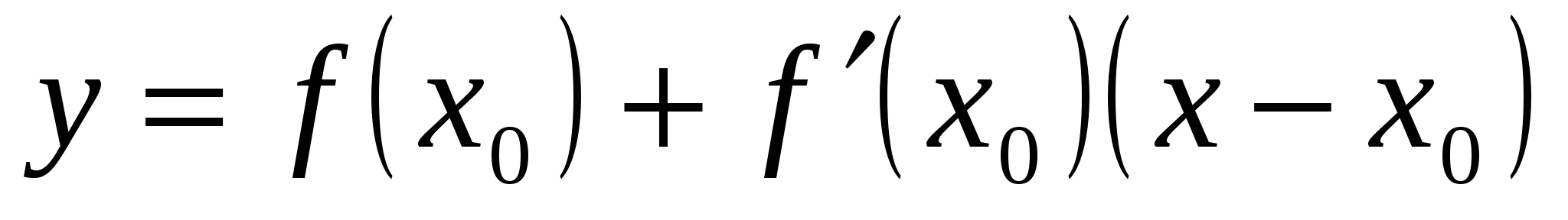 ;
;
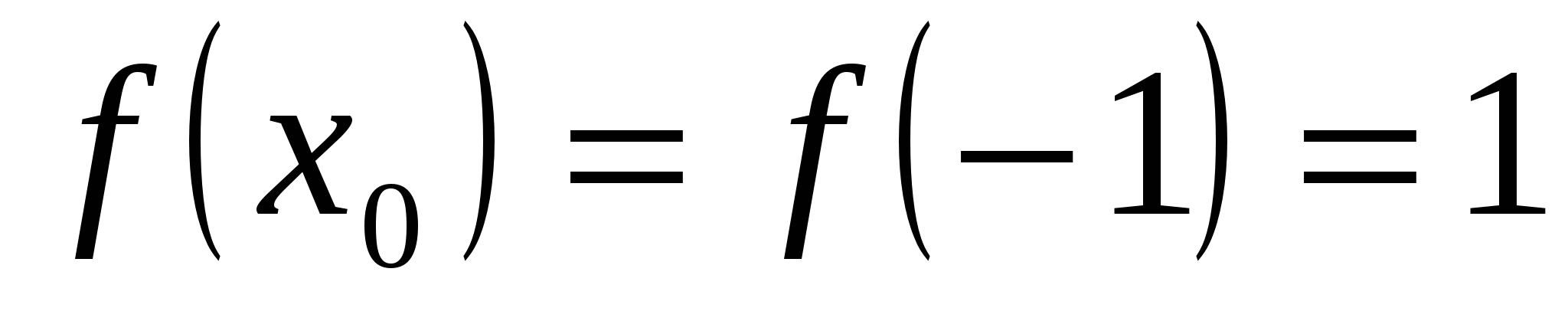 ;
;
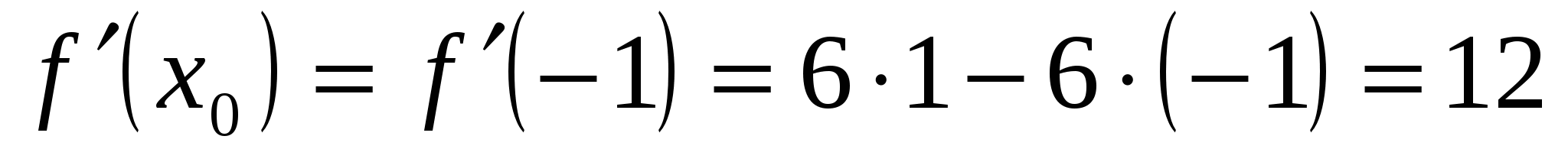 ;
;
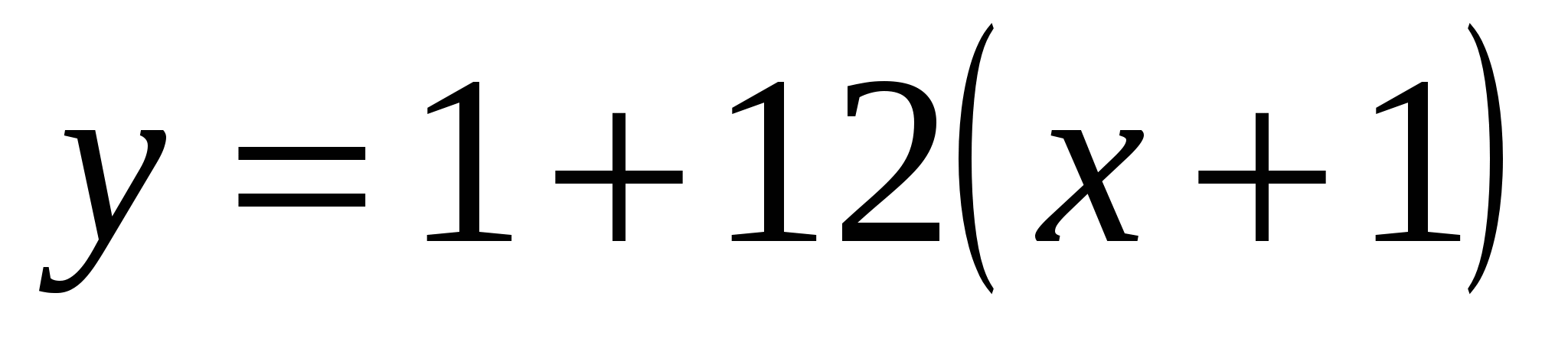 ;
;
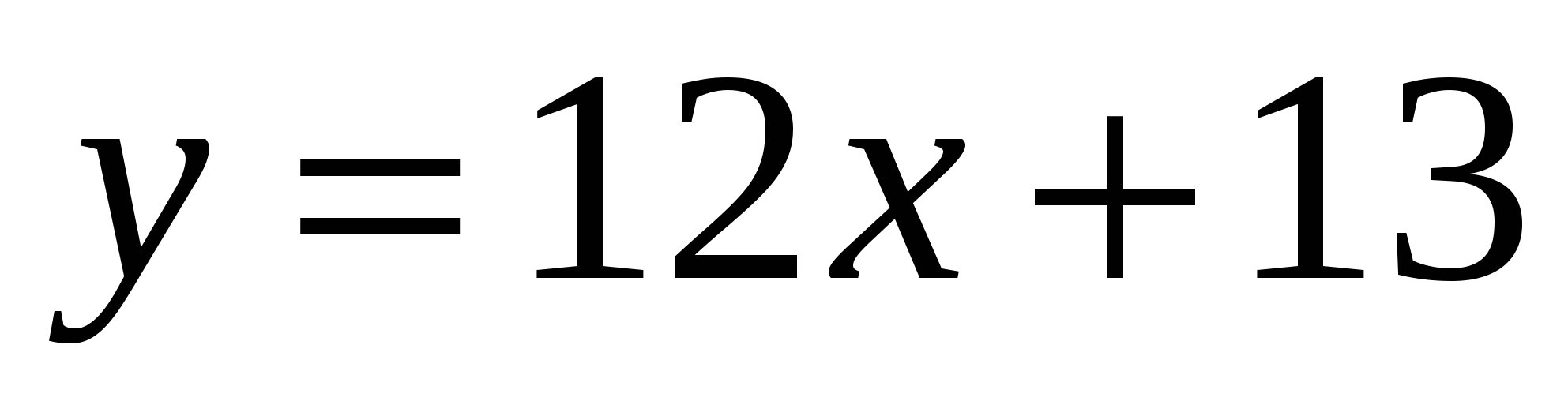 - уравнение касательной.
- уравнение касательной.
Пример 17. При каком значении а прямая у=3х+а является касательной к графику функции 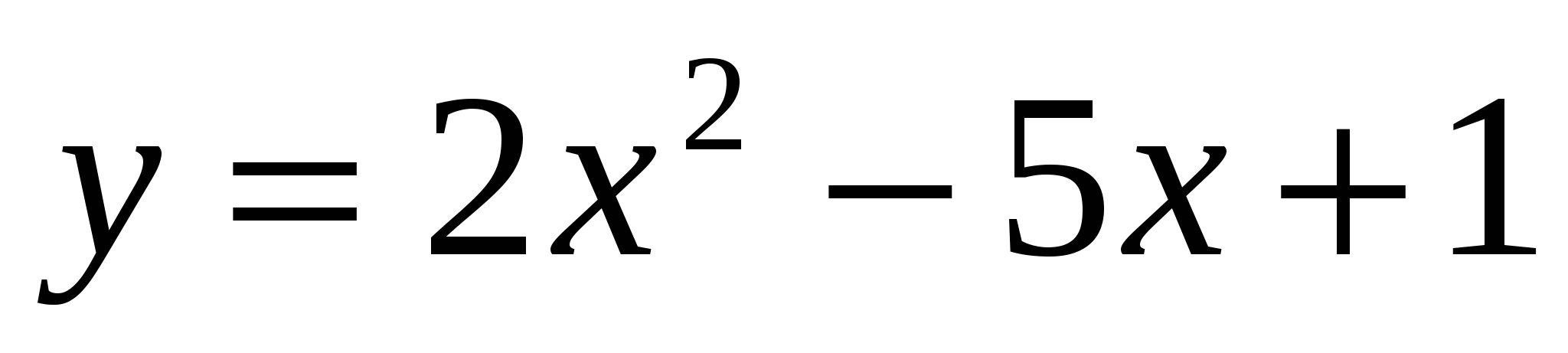 ?
?
Решение. Так как прямая у=3х+а является касательной к графику функции 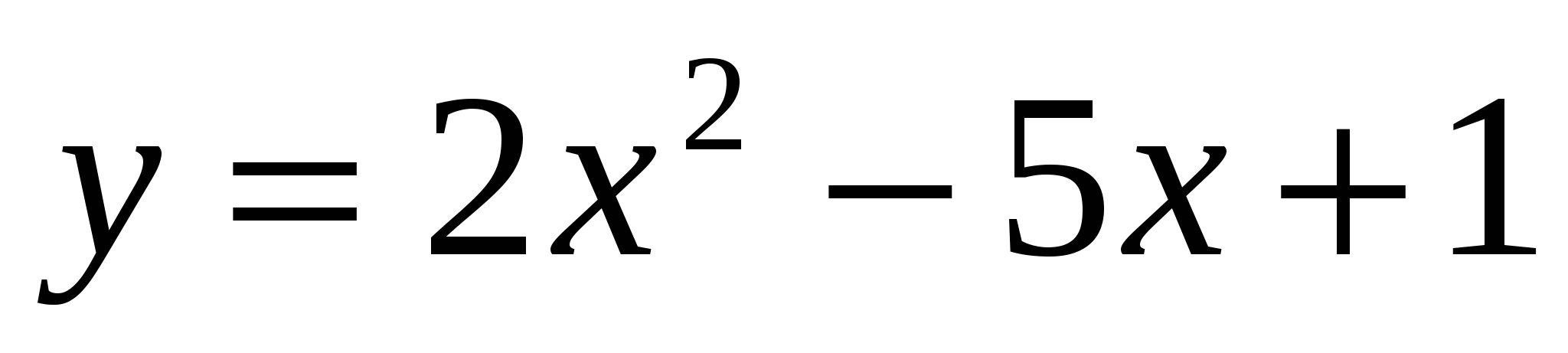 , то в точке касания угловой коэффициент касательной равен 3. Но угловой коэффициент касательной равен производной функции в этой точке, т.е.
, то в точке касания угловой коэффициент касательной равен 3. Но угловой коэффициент касательной равен производной функции в этой точке, т.е. 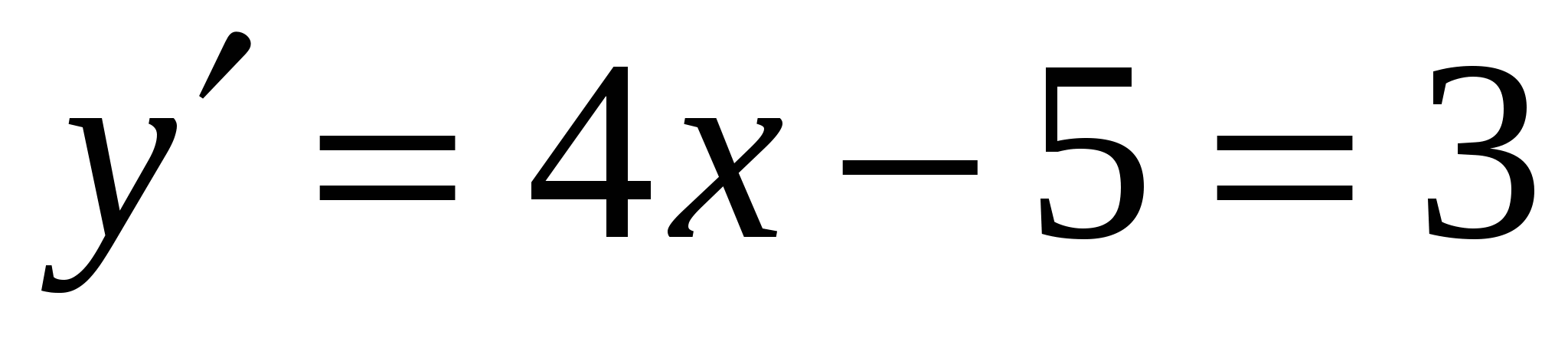 , откуда х=2. Следовательно, х=2 - абсцисса точки касания. Найдем а из условия равенства значений функций у=3х+а и
, откуда х=2. Следовательно, х=2 - абсцисса точки касания. Найдем а из условия равенства значений функций у=3х+а и 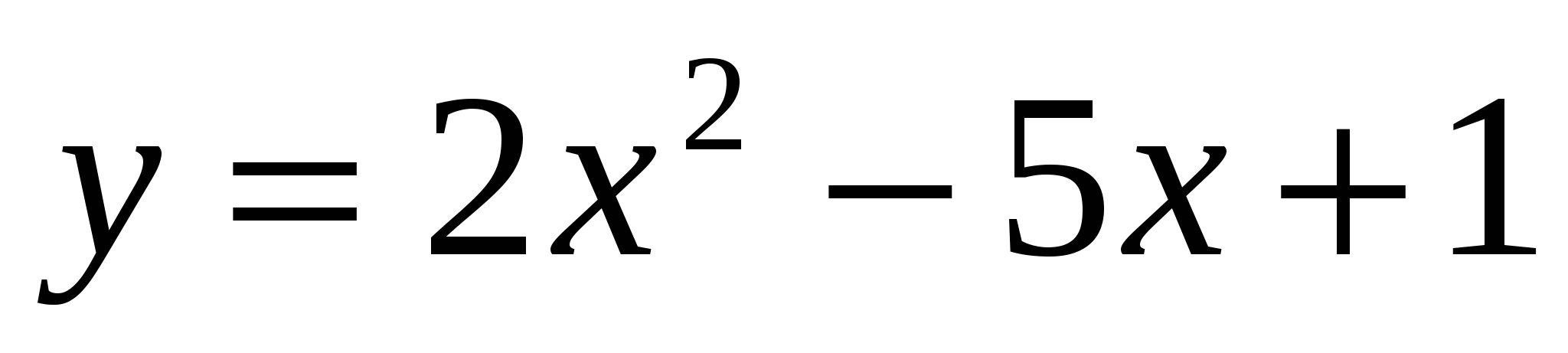 при х=2. Имеем
при х=2. Имеем 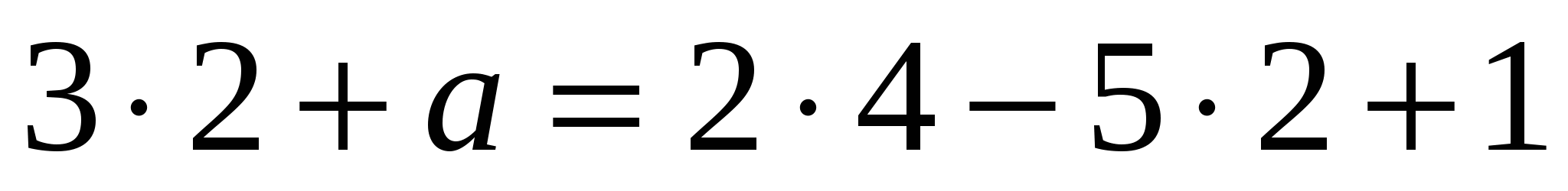 ; а= -7.
; а= -7.
Ответ: при а= -7.5
ЗАДАНИЯ ДЛЯ САМОСТОЯТЕЛЬНЫХ РАБОТ.
Задание 1. Найти производные функций.
А) 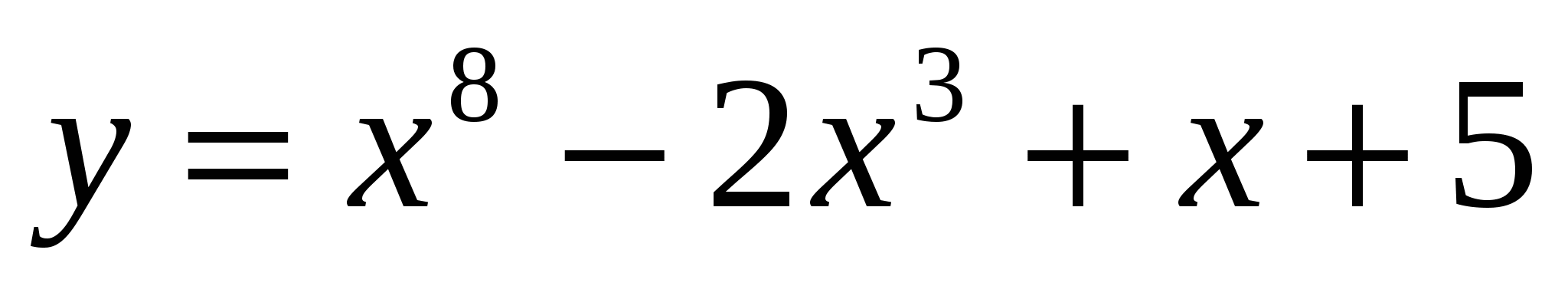 ;
;
Б) 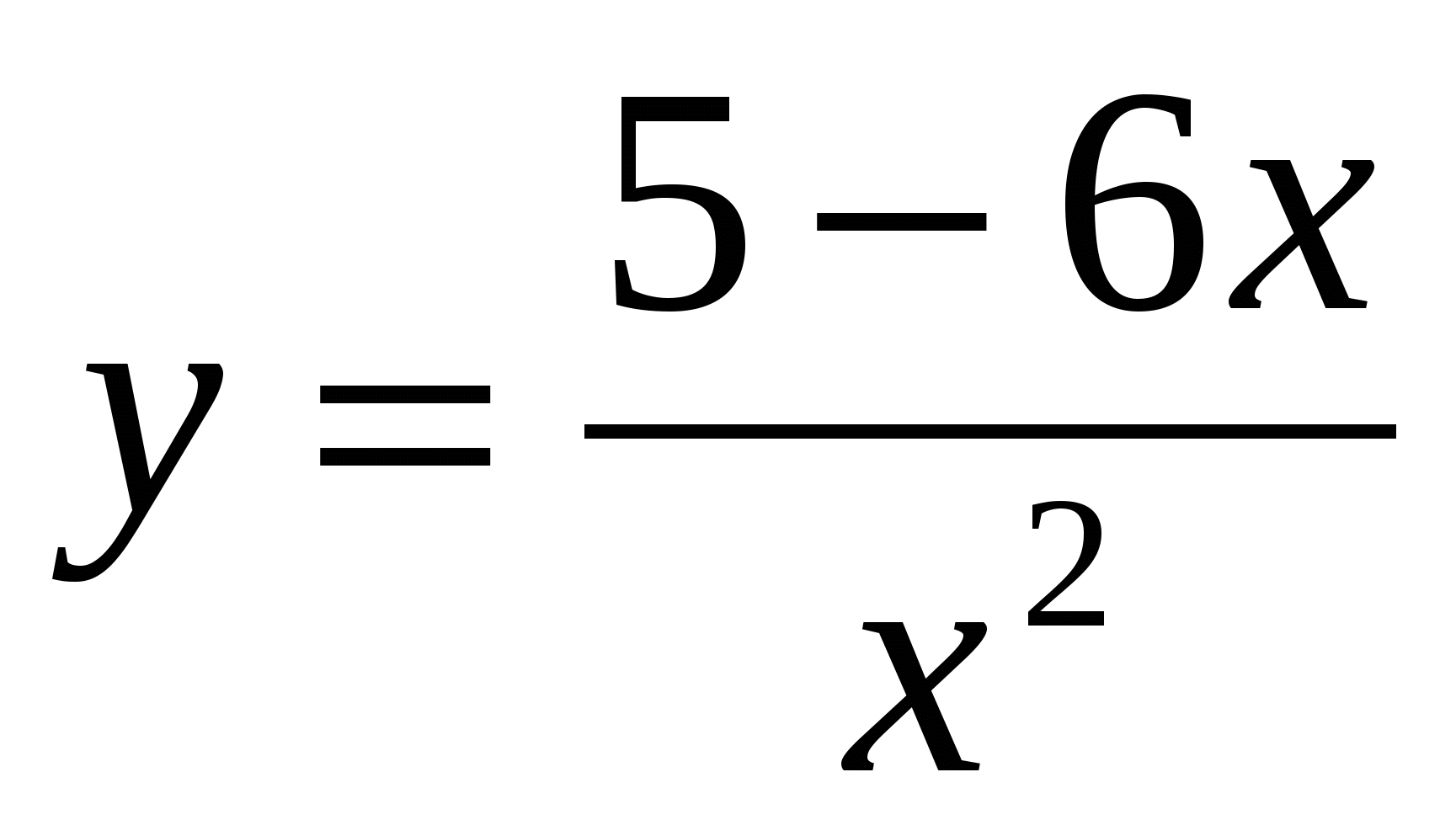 ;
;
В) 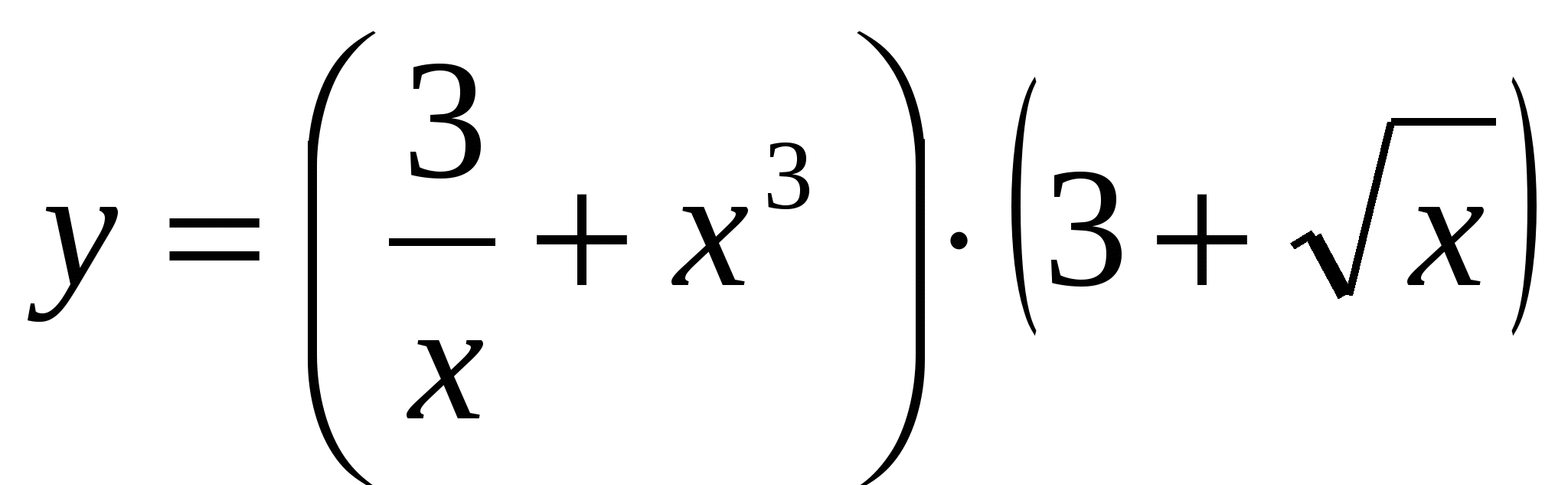 ;
;
Г) 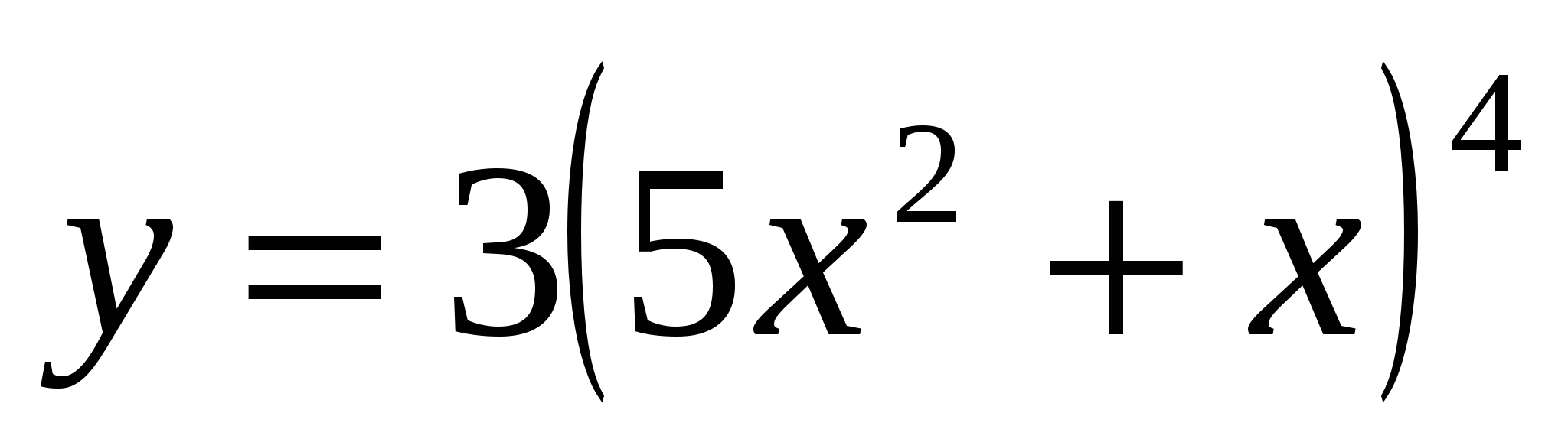 ;
;
Д) 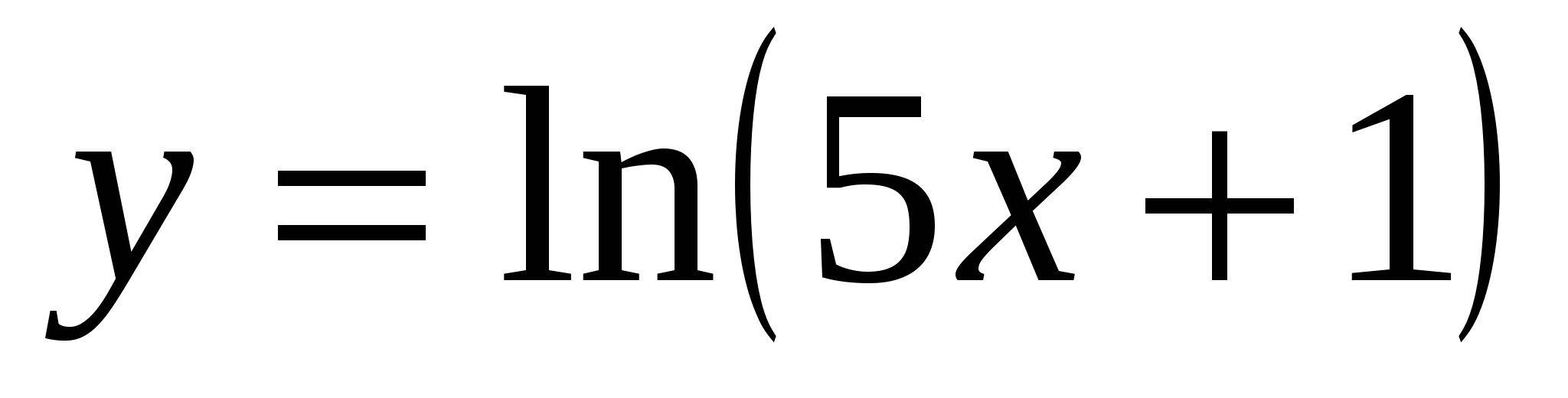 ;
;
Е) 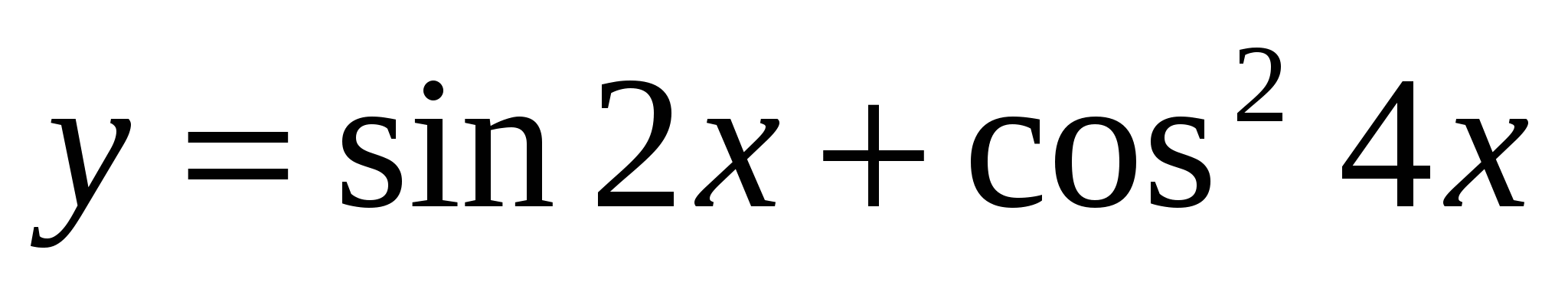 ;
;
Ж) 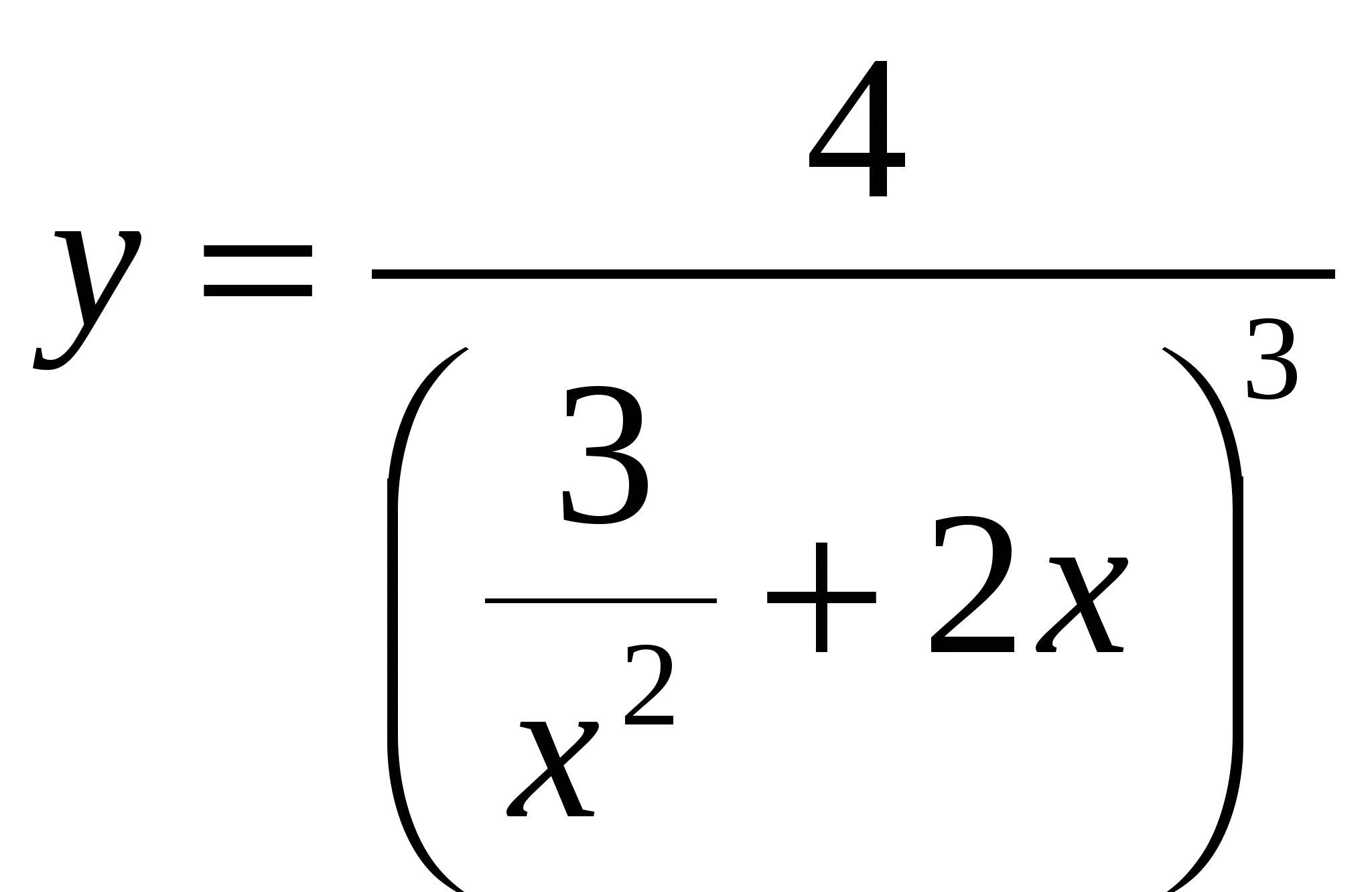 .
.
Задание 2. Напишите уравнение касательной к графику функции ![]() , параллельной прямой у= -32х+7.
, параллельной прямой у= -32х+7.
Задание 3. Функция y=f(x) определена на промежутке (-6;7). График ее производной изображен на рисунке 19. Укажите число промежутков убывания функции.
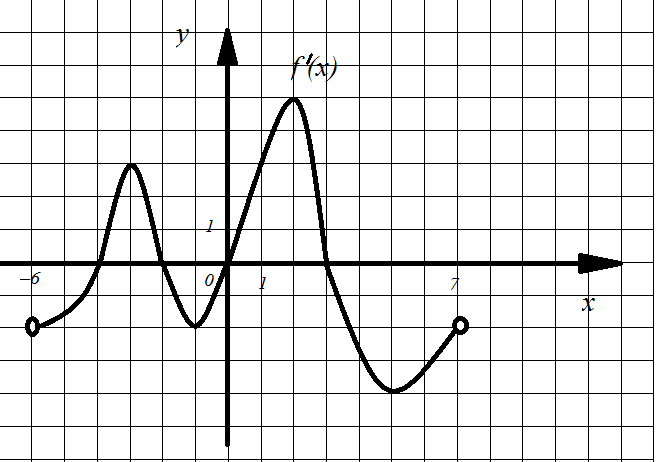
Рис. 19
Задание 4. На рисунке 19 изображен график производной функции y=f(x) найдите абсциссу точки, в которой касательная к графику y=f(x) параллельна прямой у=1 или совпадает с ней.
Задание 5. На рисунке 19 изображен график производной функции y=f(x), определенной на интервале (-6;7). Найдите промежутки возрастания функции y=f(x). В ответе укажите длину наименьшего из них.
Задание 6. На рисунке 19 изображен график производной функции y=f(x), определенной на интервале (-6;7). Найдите количество точек максимума функции y=f(x).
Задание 7. На рисунке 19 изображен график производной функции y=f(x), определенной на интервале (-6;7). Найдите точки минимума функции y=f(x).
Задание 8. На рисунке 19 изображен график производной функции y=f(x), определенной на интервале (-6;7). Найдите количество точек экстремума функции y=f(x).
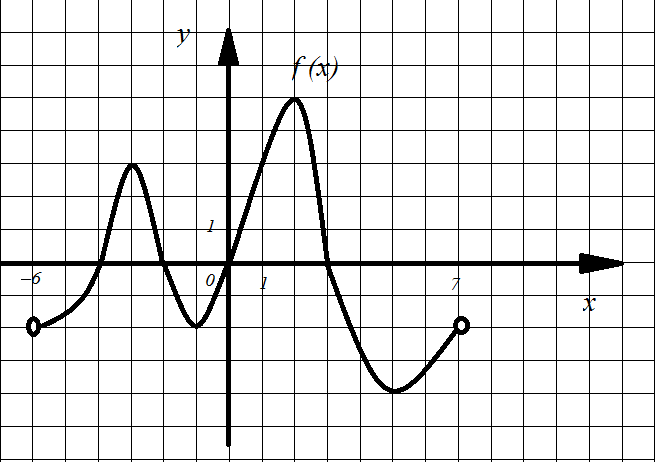
Рис. 20
Задание 9. На рисунке 20 изображен график функции y=f(x), определенной на интервале (-6;7). Определите количество целых точек, в которых производная функции отрицательна.
Задание 10. Исследовать функцию 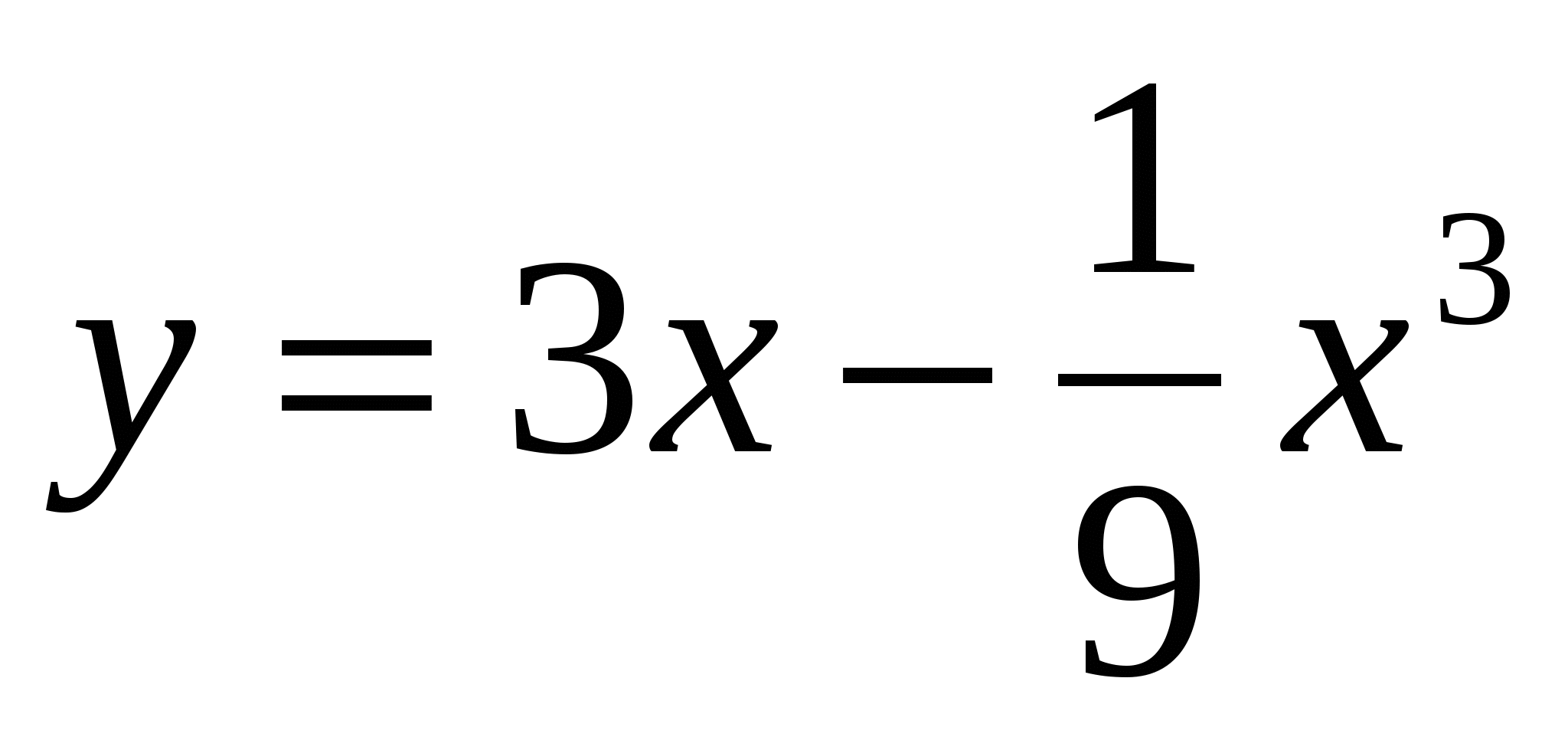 и построить ее график.
и построить ее график.
Ответы.
Задание 1. А) 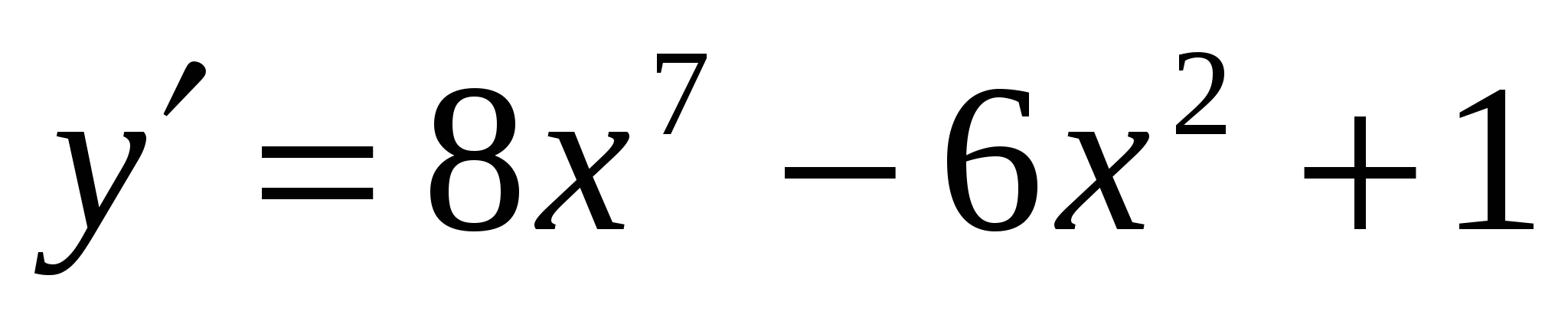 ; Б)
; Б) 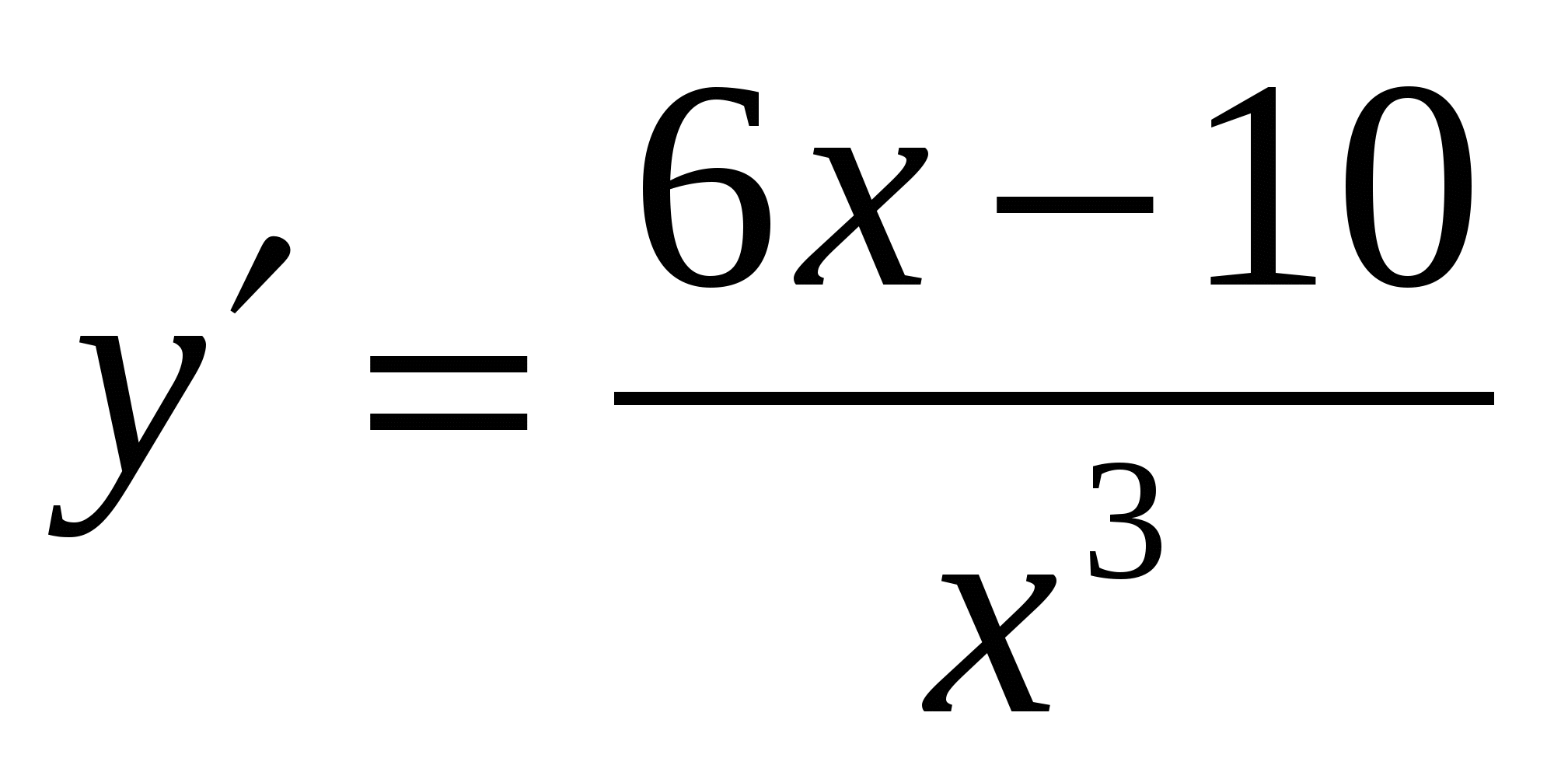 ;
;
В) 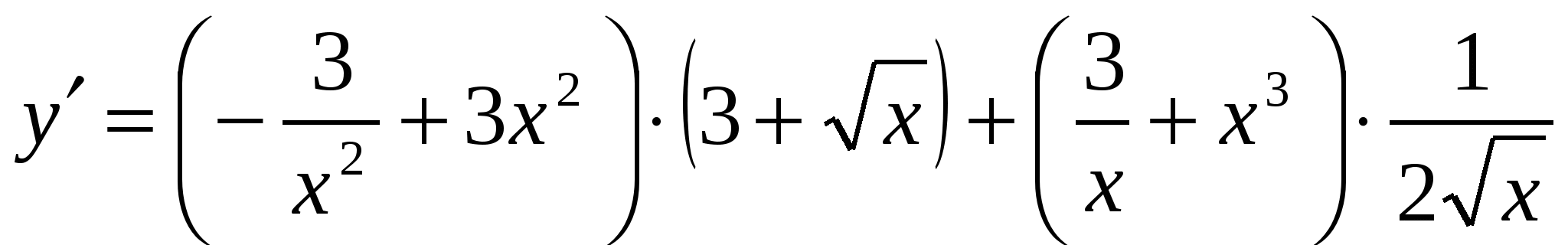 ; Г)
; Г) 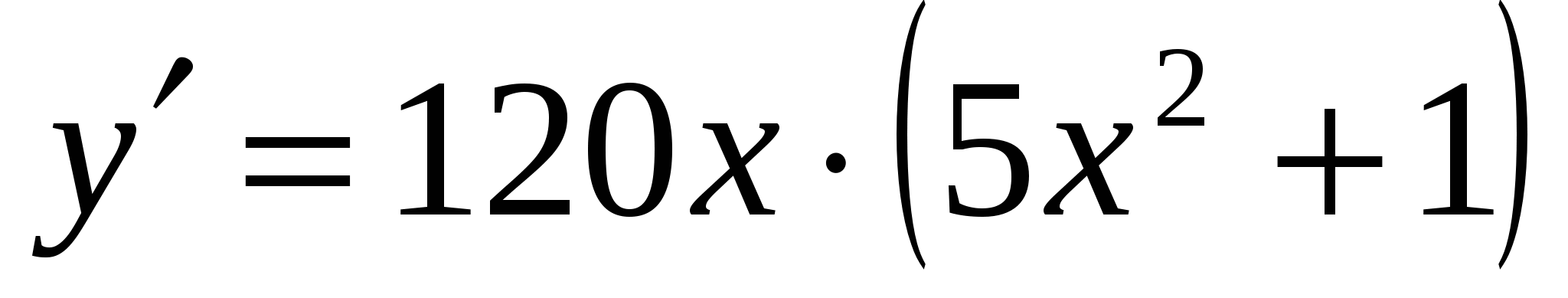 ;
;
Д) 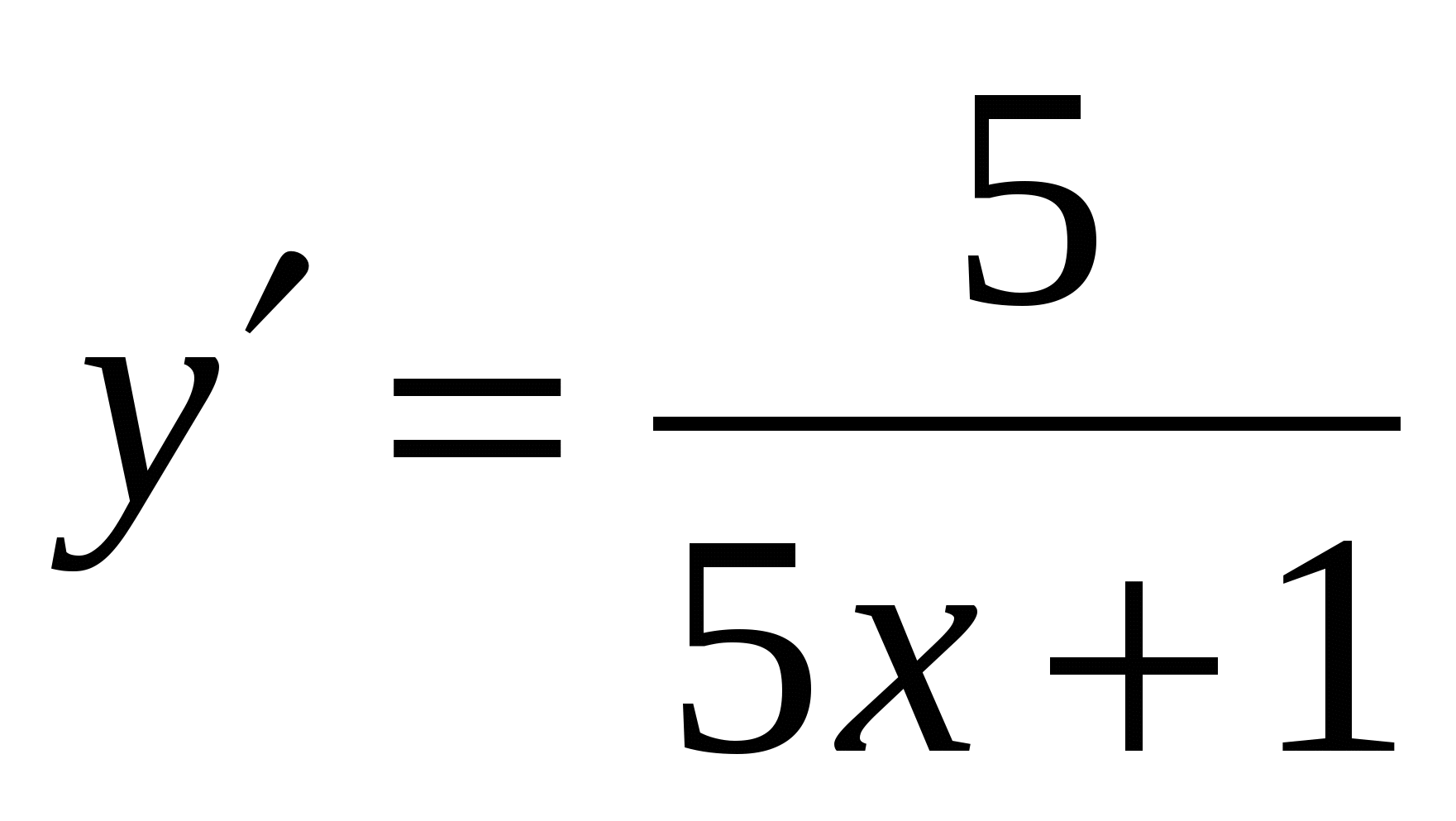 ; Е)
; Е) 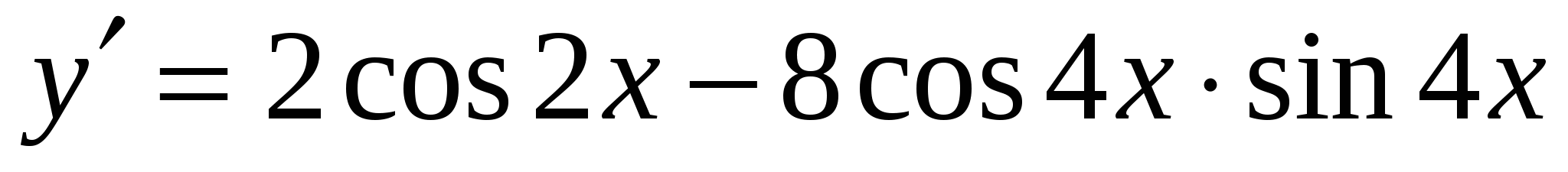 ; Ж)
; Ж) 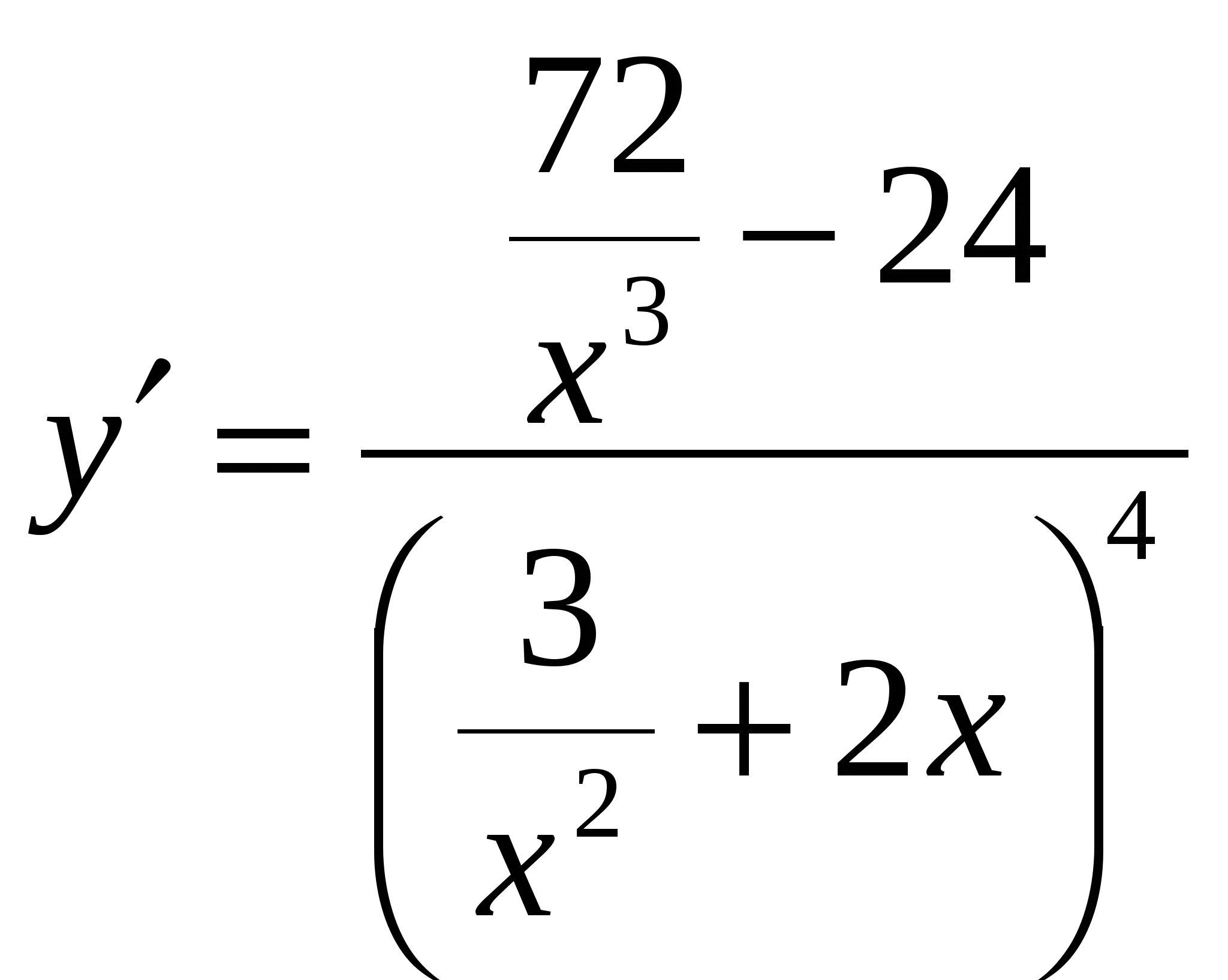 .
.
Задание 2. у=-32х-49.
Задание 3. Ответ: 3.
Задание 4. Ответ: 4 (-4; -2; 0; 3).
Задание 5. Ответ: 2.
Задание 6. Ответ: 2.
Задание 7. Ответ: 2.
Задание 8. Ответ: 4.
Задание 9. Ответ: 3.
Задание 10. 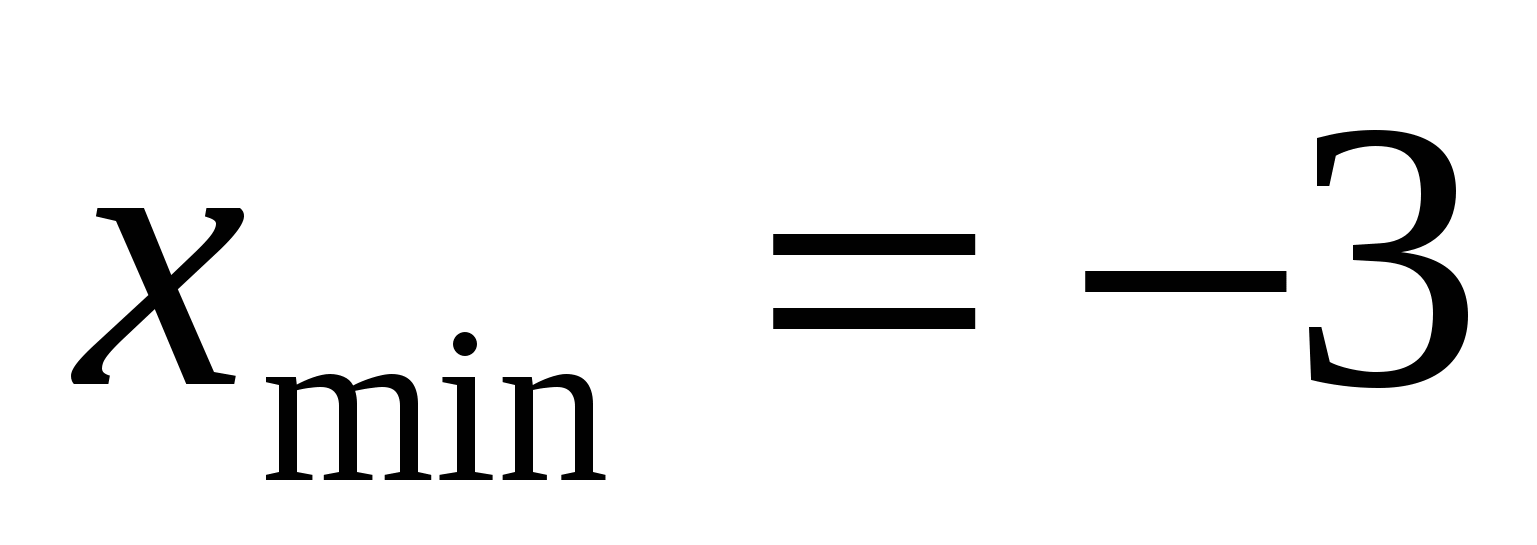 ,
, 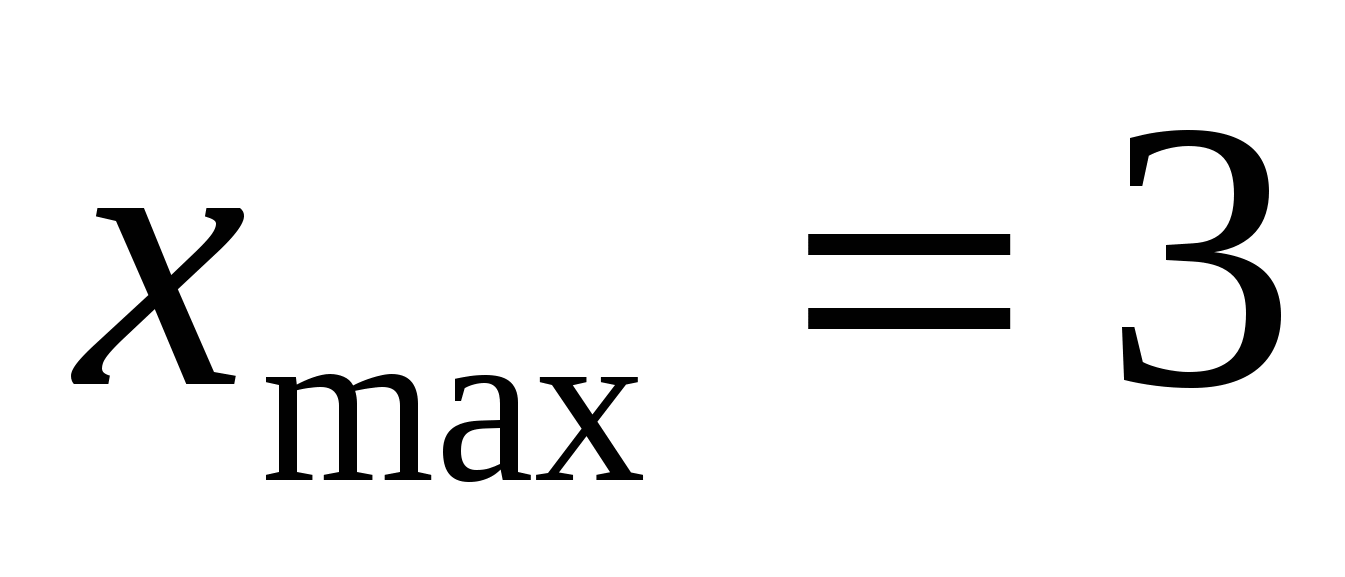 ,
, 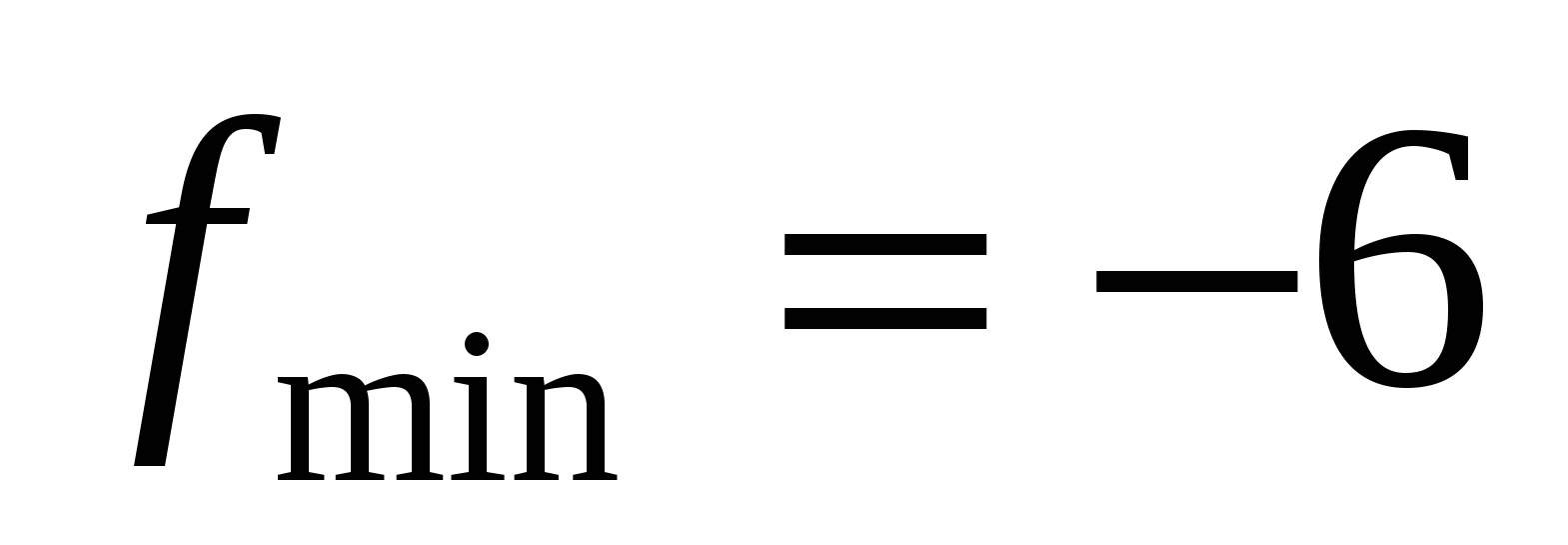 ,
, 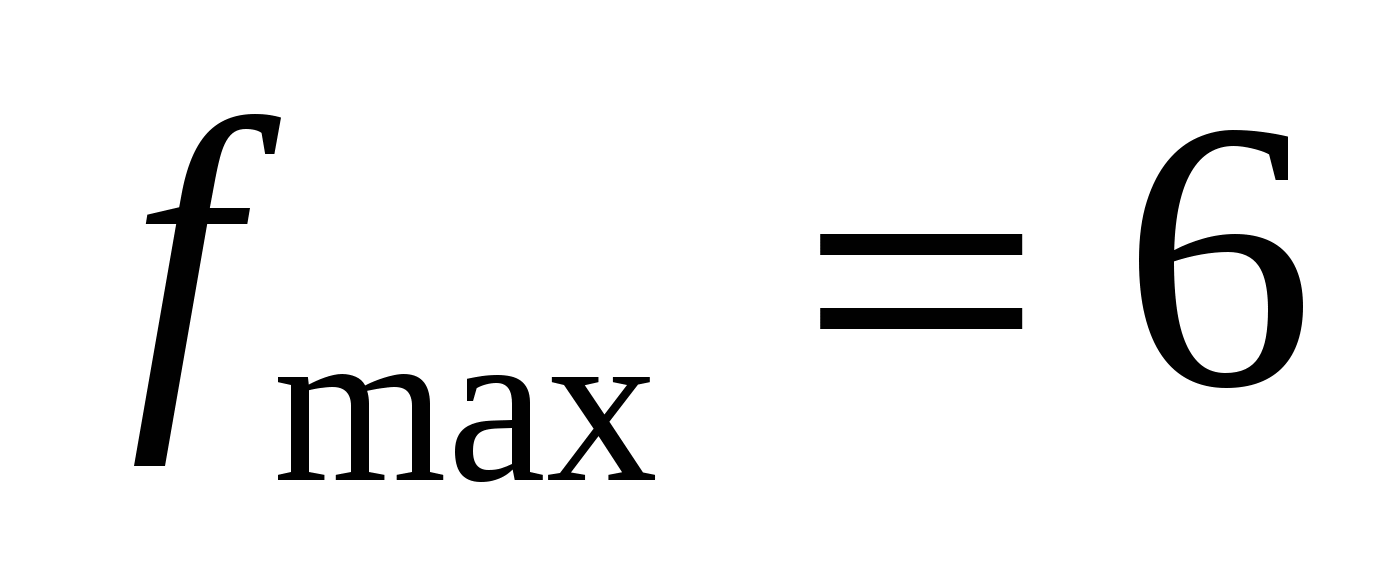 . Функция возрастает на промежутке
. Функция возрастает на промежутке 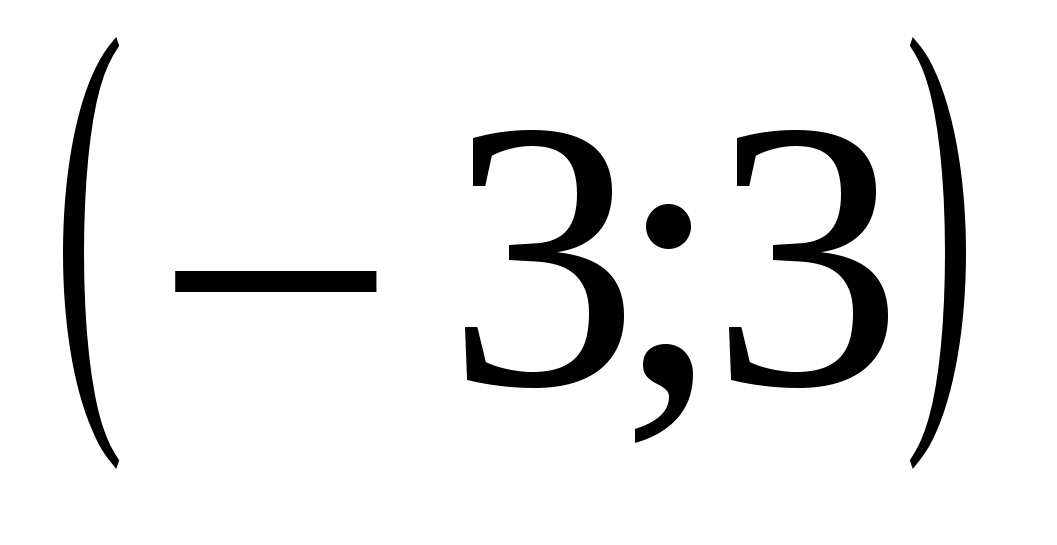 , убывает
, убывает 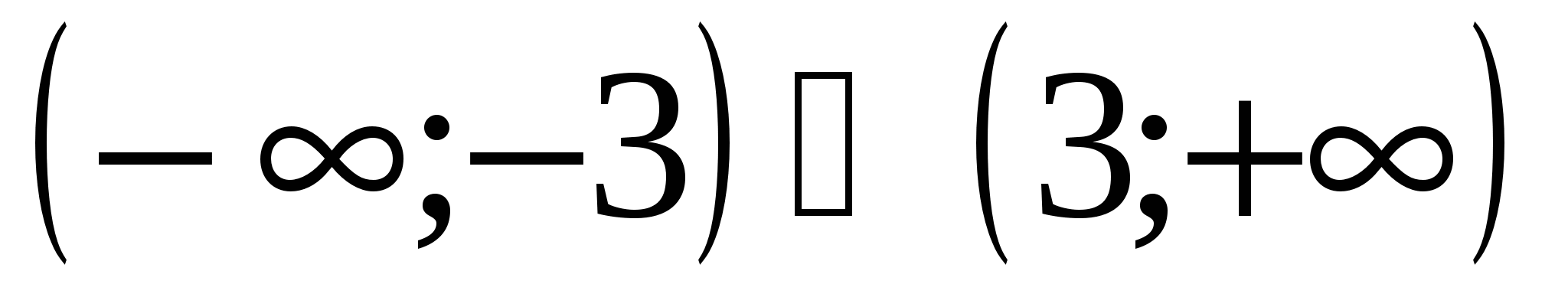 .
.
Историческая справка
В классическом дифференциальном исчислении производная чаще всего определяется через понятия теории пределов, однако исторически теория пределов появилась позже дифференциального исчисления. Русский термин «производная функции» впервые употребил В. Г. Болтянский, Что такое дифференцирование? В. И. Висковатов .
Общее понятие производной было сделано независимо друг от друга почти одновременно английским физиком и математиком И. Ньютоном и немецким философом и математиком Г. Лейбницом. Конец XVI - середина XVII веков ознаменовались огромным интересом ученых к объяснению движения и нахождению законов, которым оно подчиняется. Как никогда остро встали вопросы об определении и вычислении скорости движения и его ускорения. Решение этих вопросов привело к установлению связи между задачей о вычислении скорости движения тела и задачей проведения касательной к кривой, описывающей зависимость пройденного расстояния от времени. английским физиком и математиком И.Ньютоном. немецким философом и математиком Г.Лейбницем.6
Список использованных источников и литературы
-
Алгебра и начала математического анализа: учеб. для 10-11кл. общеобразоват. Учреждений/ А.Н.Комогоров, А.М.Абрамов, Ю.П.Дудницын и др.; под ред А.Н. Колмогорова.- 17-е изд.- М.: Просвещение, 2008.-384с.
-
Глейзер Г.И. /История математики в школе:9-10кл. пособие для учителей//Г.И.Глейзер.- М.:Просвещение, 1983,-351с.
-
Лаппо Л.Д./ ЕГЭ. Репетитор. Математика. Эффективная метолика//Л.Д.Лаппо, М.А. Попов.- 7-е изд., перераб. И доп. - М,: издательство «Экзамен», 2009.-383с.
-
Лысенко Ф.Ф/ Математика. Подготовка к ЕГЭ-2012:учебно-методическое пособие// Под редакцией Ф.Ф.Лысенко, С.Ю.Кулабухова. - Ростов-на-Дону:Легион-М,2011.-416с.
-
Мордкович А.Г./ Алгебра и начала анализа. 10-11 класс. В 2ч. Ч1. Учебник для общеобразовательных учреждений (профильный уровень). //А.Г.Мордкович, П.В.Семенов. - 5-е изд., стер. - М. : Мнемозина, 2008. - 424с.
-
Никольский С.М./ Алгебра и начала математического анализа, 11 класс: учеб. для общеобразоват. учреждений: базовый и профил. Уровни // С.М.Никольский, М.К.Потапов, Н.Н.Решетников, А.В.Шевкин. - 8-е изд. -М.: Просвещение, 2009. - 464 с.
1 Мордкович А.Г./ Алгебра и начала анализа. 10-11 класс. В 2ч. Ч1. Учебник для общеобразовательных учреждений (профильный уровень). //А.Г.Мордкович, П.В.Семенов. - 5-е изд., стер. - М. : Мнемозина, 2008. - С.325.
2 Мордкович А.Г./ Алгебра и начала анализа. 10-11 класс. В 2ч. Ч1. Учебник для общеобразовательных учреждений (профильный уровень). //А.Г.Мордкович, П.В.Семенов. - 5-е изд., стер. - М. : Мнемозина, 2008. - С.348.
3 Там же - С.346.
4 Алгебра и начала математического анализа: учеб. для 10-11кл. общеобразоват. Учреждений/ А.Н.Комогоров, А.М.Абрамов, Ю.П.Дудницын и др.; под ред А.Н. Колмогорова.- 17-е изд.- М.: Просвещение, 2008.-С.114.
5 Лаппо Л.Д./ ЕГЭ. Репетитор. Математика. Эффективная метолика//Л.Д.Лаппо, М.А. Попов.- 7-е изд., перераб. И доп. - М,: издательство «Экзамен», 2009.-С.245.
6 Глейзер Г.И. /История математики в школе:9-10кл. пособие для учителей//Г.И.Глейзер.- М.:Просвещение, 1983, - С48-49.


