- Преподавателю
- Математика
- Статья на тему: Функция
Статья на тему: Функция
| Раздел | Математика |
| Класс | - |
| Тип | Статьи |
| Автор | Максимова М.Н. |
| Дата | 16.02.2016 |
| Формат | doc |
| Изображения | Есть |
Функция, отображение, мощность
Часто говорят, что функция есть переменная величина, зависящая от другой переменной величины (аргумента). В применении к обычным функциям, изучаемым в школе, как y = sin x, это определение вполне подходит и может применяться в преподавании. Наша задача состоит в более точном уяснении сущности этого понятия и получении современного его определения. Прежде всего, если взять функцию
y = sin2x + cos2x,
то ее значение уже не зависит от значения x. Далее, под величинами принято понимать такие объекты, которые можно сравнивать между собой, т. е. такие, между которыми существуют отношения больше и меньше. Между тем в математике рассматриваются также и функции, для которых эти отношения не установлены, как, например, в случае комплексных чисел или вообще элементов некоторого множества. Внимательное рассмотрение показывает, что в понятии функции существенно не столько ее изменение с изменением аргумента, сколько сам закон соответствия, в силу которого по каждому значению аргумента однозначно определяется соответствующее ему значение функции. Так функцию
y = sin2x + cos2x
можно определить, просто сказав, что каждому действительному числу x она ставит в соответствие число 1. Соответствие есть закон, позволяющий для каждого элемента x некоторого множества X однозначно указать некоторый объект (соответствующий данному элементу). Эти слова лишь поясняют понятие соответствия, но не должны пониматься как его определение. Понятие соответствия, как и понятие множества, принимается за основное, не подлежащее определению. Тогда наиболее общее определение функции будет такое:
Определение. Функцией, заданной (или определенной) на некотором множестве X, называется соответствие, в силу которого любой элемент x множества X определяет некоторый (соответствующий ему) объект f(x).
Множество X называется областью определения функции, а множество Y - объектов, соответствующих всем элементам множества X, - областью значений функции.
Пример 1. Пусть y = sin x. За область определения функции можно принять множество действительных чисел. Тогда областью значений функции будет отрезок [-1, +1].
Пример 2. Пусть y = tg x. За область определения функции можно принять множество действительных чисел, отличных от чисел вида 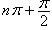 , где n пробегает все целые значения (т. к. для этих значений x функция не определена). Тогда областью значений функции будет множество всех действительных чисел.
, где n пробегает все целые значения (т. к. для этих значений x функция не определена). Тогда областью значений функции будет множество всех действительных чисел.
Пример 3. Функция Дирихле:

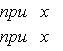
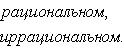
Область определения здесь - множество действительных чисел, область значений - множество {0, 1} из двух элементов.
Замечательно, что гениальный русский математик Н. И. Лобачевский более ста лет назад дал определение функции, весьма близкое к приведенному. В противовес господствовавшему тогда взгляду на функцию как на аналитическое выражение (т. е. как на формулу) он подчеркивал значение идеи соответствия в определении понятия функции.
"Это общее понятие, - писал Лобачевский о понятии функции, - требует, чтобы функцией от x называть число, которое дается для каждого x и вместе с x постепенно изменяется. Значение функции может быть дано или аналитическим выражением или условием, которое подает средство испытать все числа и выбирать одно из них, или, наконец, зависимость может существовать и оставаться неизвестной".
Весьма близким к понятию функции является понятие отображения.
Определение. Пусть даны два множества X и Y. Такое соответствие, при котором каждому элементу ![]() соответствует (единственный) элемент
соответствует (единственный) элемент 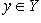 , называется отображением множества X в множество Y; в частности, если каждый элемент
, называется отображением множества X в множество Y; в частности, если каждый элемент ![]() соответствует по крайней мере одному элементу
соответствует по крайней мере одному элементу 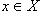 , то такое соответствие называется отображением X на Y.
, то такое соответствие называется отображением X на Y.
Если элементу x соответствует y, то y называется образом элемента x, а x - прообразом элемента y. Пишут: 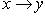 или y = f(x). Множество A всех элементов
или y = f(x). Множество A всех элементов 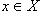 , имеющих один и тот же образ
, имеющих один и тот же образ ![]() , называется полным прообразом элемента y.
, называется полным прообразом элемента y.
Пример 4. Пусть D - множество действительных чисел. Соответствие 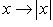 будет отображением множества D в себя же и отображением D на множество неотрицательных чисел. Прообразом числа 0 будет один 0, число y > 0 имеет два прообраза: +y и -y.
будет отображением множества D в себя же и отображением D на множество неотрицательных чисел. Прообразом числа 0 будет один 0, число y > 0 имеет два прообраза: +y и -y.
Пример 5. Поставим в соответствие каждой точке квадрата ее проекцию на основание. Получим отображение квадрата на отрезок. Полным прообразом каждой точки основания будет множество всех точек квадрата, лежащих на перпендикуляре к основанию, восстановленном в данной его точке.
Примеры 4 и 5 показывают, что при отображении множества X в Y, с одной стороны, некоторые элементы из Y могут вовсе не иметь прообразов, а, с другой стороны, могут быть элементы, имеющие несколько (даже бесконечно много) прообразов. Если нет ни того, ни другого, то отображение называется взаимно однозначным. Таким образом, приходим к следующему определению:
Определение. Взаимно однозначным соответствием между множествами X и Y (или отображением X на Y) называется соответствие (соответственно, отображение), обладающее следующими тремя свойствами: 1) каждому элементу множества X соответствует один и только один элемент множества Y; 2) двум различным элементам множества X всегда соответствуют два различных элемента множества Y; 3) всякий элемент множества Y соответствует хотя бы одному элементу множества X.
Заметим, что первые два свойства дают взаимно однозначные отображения X на некоторое подмножество Y. В этом случае говорят о взаимно однозначном отображении X в Y.
Если y = f(x) есть взаимно однозначное отображение X на Y, то каждому 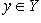 можно поставить в соответствие тот единственный элемент
можно поставить в соответствие тот единственный элемент 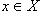 , образом которого при отображении f является y. Это соответствие называется обратным отображением для отображения f и обозначается через f -1. В качестве упражнения предлагается доказать, что f -1 есть также взаимно однозначное отображение Y на X и что обратным для отображения f -1 будет исходное отображение f.
, образом которого при отображении f является y. Это соответствие называется обратным отображением для отображения f и обозначается через f -1. В качестве упражнения предлагается доказать, что f -1 есть также взаимно однозначное отображение Y на X и что обратным для отображения f -1 будет исходное отображение f.
Определение. Два множества X и Y, между которыми можно установить взаимно однозначное соответствие, называются равномощными (или эквивалентными), что обозначается символом 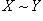 .
.
О равномощных множествах говорят также, что они имеют одинаковую мощность. Условимся считать, что пустое множество равномощно только самому себе.
Замечание. Выше мы дали определение понятия равномощности, но не понятие мощности. Можно сказать, что мощность есть то общее, что имеется у всех равномощных между собой множеств. Впрочем, всюду достаточно понятие равномощности.
Соотношение равномощности обладает следующими тремя основными свойствами:
1) рефлексивность: 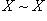 ;
;
2) симметрия: если 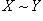 , то
, то 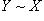 ;
;
3) транзитивность: если 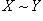 и
и 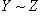 , то
, то 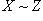 .
.
Для доказательства, например, первого из них достаточно каждому элементу 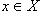 поставить в соответствие его же самого (тождественное отображение), что уже дает взаимно однозначное отображение множества X на себя. Остальные два свойства предлагается доказать самостоятельно.
поставить в соответствие его же самого (тождественное отображение), что уже дает взаимно однозначное отображение множества X на себя. Остальные два свойства предлагается доказать самостоятельно.
Мощность множества характеризует, так сказать, "количество" его элементов. Однако при этом может оказаться, что "часть равна целому", т. е. множество может иметь одинаковую мощность с его собственным подмножеством.
Пример 6. Функция y = 10x, где x - действительное число, устанавливает равномощность отрезка [0, 1] и в 10 раз более длинного отрезка [0, 10]. Таким образом, в смысле мощности "количество" точек обоих отрезков одинаково.
Пример 7. Два любых отрезка [a, b] и [c, d], а также два любых интервала (a, b) и (c, d) равномощны.
Для доказательства достаточно рассмотреть функцию
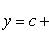
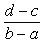
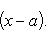
Во-первых, каждому действительному числу x однозначно соответствует y, причем легко видеть, что ![]() и
и 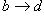 . Далее, пусть
. Далее, пусть
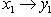
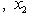
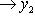 , и x1 < x2.
, и x1 < x2.
Примеры множеств. Примеров множеств можно привести сколько угодно. Так, можно говорить о множестве всех букв книги, причем одна и та же буква на разных страницах или разных строках одной страницы считается за два различных элемента множества, о множестве всех людей земного шара, причем надо сделать предположение, что в рассматриваемый момент времени никто не рождается и не умирает, о множестве молекул воды в данном стакане и т. д.
Все это - конечные множества. Приведем некоторые примеры бесконечных множеств, кроме упоминавшихся выше множеств натуральных чисел, четных натуральных чисел, рациональных чисел, действительных чисел и др.
Пусть a и b - два действительных числа, причем a < b. Множество всех действительных чисел x, для которых  , называется отрезком с концами a, b и обозначается через [a, b]. Множество (a, b) всех x, для которых a < x < b, называется интервалом с концами a, b. Далее полуинтервалами называются множества [a, b) тех x, для которых
, называется отрезком с концами a, b и обозначается через [a, b]. Множество (a, b) всех x, для которых a < x < b, называется интервалом с концами a, b. Далее полуинтервалами называются множества [a, b) тех x, для которых 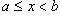 , и (a, b] тех x, для которых
, и (a, b] тех x, для которых 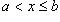 . Введем еще два символа:
. Введем еще два символа: 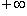 (плюс бесконечность),
(плюс бесконечность), 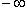 (минус бесконечность). Они не являются числами и вводятся лишь для удобства записи. Тем не менее для более легкого обращения с ними условимся говорить, что
(минус бесконечность). Они не являются числами и вводятся лишь для удобства записи. Тем не менее для более легкого обращения с ними условимся говорить, что ![]() больше, а
больше, а 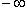 меньше любого действительного числа. Тогда можно ввести обозначения, аналогичные приведенным выше, для бесконечных полуинтервалов и интервалов. Именно:
меньше любого действительного числа. Тогда можно ввести обозначения, аналогичные приведенным выше, для бесконечных полуинтервалов и интервалов. Именно: ![]() - множество чисел x, для которых
- множество чисел x, для которых 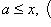
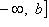 - множество чисел x, для которых
- множество чисел x, для которых ![]()
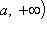 - множество чисел x, для которых
- множество чисел x, для которых ![]()
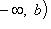 - множество чисел x, для которых
- множество чисел x, для которых ![]()
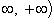 - множество всех действительных чисел.
- множество всех действительных чисел.
Согласно определению отрезка и интервала a < b и c < d. Следовательно, 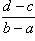
 . Поэтому y1 < y2. Итак, если
. Поэтому y1 < y2. Итак, если 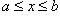 (или a < x < b), то и
(или a < x < b), то и 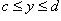 (соответственно, c < y < d). Значит, точкам отрезка [a, b] соответствуют точки отрезка [c, d], причем различные точки переходят в различные же (и то же верно в случае интервалов). Наконец, обратное отображение
(соответственно, c < y < d). Значит, точкам отрезка [a, b] соответствуют точки отрезка [c, d], причем различные точки переходят в различные же (и то же верно в случае интервалов). Наконец, обратное отображение
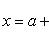
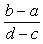
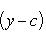
обладает теми же свойствами, откуда следует, что для каждого y из [c, d] найдется один (и даже только один) прообраз x из [a, b] (то же для интервалов). Этим доказано, что [a, b] ~ [c, d] (соответственно, (a, b) ~ (c, d)).
Пример 8. Функция y = tg x устанавливает эквивалентность интервала
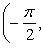

множеству всех действительных чисел.
Пример 9. Считая соответствующими друг другу числа, стоящие одно под другим в следующих строках:
1, 2, 3, ..., n , ...,
2, 4, 6, ..., 2n , ...,
1, 3, 5, ..., 2n-1, ...,
10, 100, 1000, ..., 10n , ...,
2, 3, 5, ..., pn , ... (pn - n-е - простое число),
заключаем, что множества всех натуральных чисел, четных чисел, нечетных чисел, степеней 10, простых чисел все имеют одну и ту же мощность, хотя первая из них является собственным надмножеством остальных.
Пример 10. Множество натуральных чисел равномощно множеству рациональных чисел. В самом деле, любое рациональное число, отличное от нуля, однозначно записывается в виде несократимой дроби ![]() , где принято q > 0 (т. е. знак отнесен к числителю).
, где принято q > 0 (т. е. знак отнесен к числителю).
Из возможных записей для нуля: 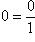
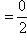
 выберем одну:
выберем одну: 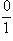 . Тогда запись вида
. Тогда запись вида 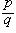 однозначно определена для всех рациональных чисел (в частности, при q = 1 получатся все целые числа).
однозначно определена для всех рациональных чисел (в частности, при q = 1 получатся все целые числа).
Высотой числа 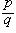 назовем натуральное число |p| + q, где |p| - абсолютная величина p. Тогда все рациональные числа можно расположить в одну последовательность, располагая их в порядке возрастания высоты, а числа с одинаковой высотой - в порядке возрастания числителя. Таким образом, получим последовательность
назовем натуральное число |p| + q, где |p| - абсолютная величина p. Тогда все рациональные числа можно расположить в одну последовательность, располагая их в порядке возрастания высоты, а числа с одинаковой высотой - в порядке возрастания числителя. Таким образом, получим последовательность
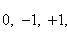
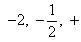
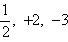
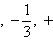
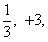
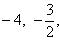
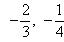
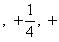
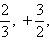
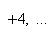
Так чисел данной высоты n - лишь конечное число [именно, не более 2(n - 1), т. к. числитель меняется от -(n - 1) до +(n - 1), исключая значение 0], то перед каждым данным числом в последовательности стоит лишь конечное число чисел. Поэтому, нумеруя числа последовательно по порядку натуральными числами, мы действительно занумеруем все рациональные числа, что и доказывает требуемую равномощность.


