- Преподавателю
- Математика
- ПРИЕМЫ И МЕТОДЫ РЕШЕНИЯ ГЕОМЕТРИЧЕСКИХ ЗАДАЧ НА ПОСТРОЕНИЕ
ПРИЕМЫ И МЕТОДЫ РЕШЕНИЯ ГЕОМЕТРИЧЕСКИХ ЗАДАЧ НА ПОСТРОЕНИЕ
| Раздел | Математика |
| Класс | - |
| Тип | Конспекты |
| Автор | Васильева И.А. |
| Дата | 10.09.2014 |
| Формат | doc |
| Изображения | Есть |
Муниципальное бюджетное общеобразовательное учреждение
«Гимназия №18»
«ПРИЕМЫ И МЕТОДЫ РЕШЕНИЯ
ГЕОМЕТРИЧЕСКИХ ЗАДАЧ НА ПОСТРОЕНИЕ»
М е т о д и ч е с к о е п о с о б и е
Васильева Ирина Александровна,
учитель математики
Старый Оскол
2014
«ПРИЕМЫ И МЕТОДЫ РЕШЕНИЯ
ГЕОМЕТРИЧЕСКИХ ЗАДАЧ НА ПОСТРОЕНИЕ»
Методическое пособие
Приемы указанные в методическом пособии служат конкретизацией тех общих методов решения задач на построение, которые освещаются в учебной литературе. Данное пособие следует рассматривать как дополнение к имеющимся учебникам геометрии.
-
ПРИЕМ ПРЕДВАРИТЕЛЬНОГО ИЗУЧЕНИЯ ЗАДАЧИ.
Всякая задача на построение имеет следующую структуру: «Даны некоторые фигуры /отрезки, прямые углы и т. п./. Построить фигуру, обладающую определенными свойствами.» Приступая к решению задачи, надо, прежде всего, хорошо понять ее содержание. Это означает, что необходимо: во-первых, уточнить условия задачи, т. е. выяснить, что в задаче дано; во-вторых, уточнить цель задачи, т.е. выяснить, какую фигуру требуется построить, какими свойствами должна обладать искомая фигура; в-третьих, сделать примерный чертеж, эскиз, набросок искомой фигуры. Последовательность этих действий образует прием предварительного анализа задачи, ее предварительного изучения. В качестве приема подвергнем предварительному изучению следующую задачу: «Построить равнобедренный треугольник по высоте и медиане, проведенных к боковой стороне».
В этой задаче даны два отрезка: обозначим их через а и h. Требуется построить равнобедренный треугольник АВС, в котором боковая сторона ВС равна данному отрезку а, а высота АD проведенная к стороне ВС равна данному отрезку h.
В качестве примера рассмотрим задачу: «построить треугольник по стороне, медиане и высоте, проведенным к этой стороне».
Предварительное изучение задачи. В задаче даны три отрезка. Обозначенными буквами a, ha, ma. требуется построить такой треугольник АВС, в котором сторона ВС равна данному отрезку а, высота AD = ha, а медиана АО равна данному отрезку ma(см. рис. 1).
Анализ. Пусть треугольник АВС - искомый. Рассмотрим треугольник ACD в этом треугольнике: угол ADO - прямой, катет AD равен отрезку ha, гипотенуза АО равна данному отрезку ma. По этим данным треугольник AOD можно легко построить. Располагая треугольником AOD, легко построить вершины В и С. таким образом, план построения ясен: вначале построить треугольник AOD, а затем - вершины В и С искомого треугольника.
Построение.
-
Построим прямоугольный треугольник АОD по гипотенузе АО, равной ma, и катету АD, равному ha.
-
На прямой ОD откладываем отрезки ОВ и ОС, равные
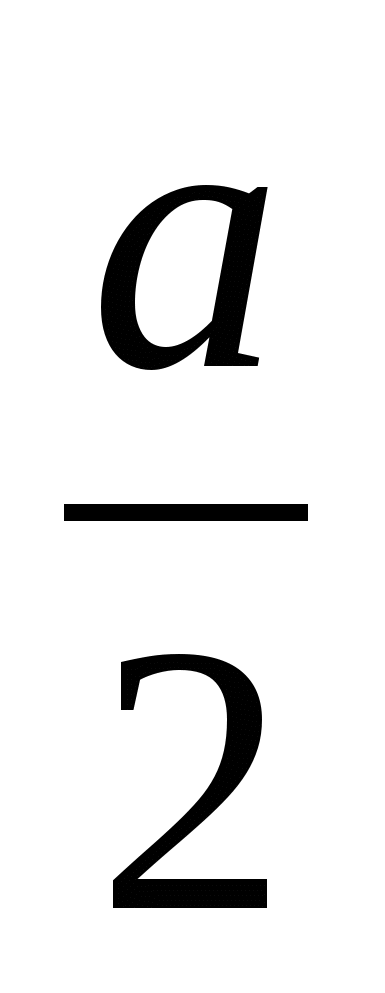 .
. -
Строим треугольник АВС.
Доказательство. В треугольнике АВС имеем: ВС = ВО + ОС = а; высота АD = ha по построению; медиана АО = ma по построению.
Исследование. Просматривая шаг за шагом выполненное построение, убеждаемся, что возможность построения треугольника АВС определяется возможностью построения треугольника AOD. Следовательно, если ha> ma, то треугольник нельзя - задача не имеет решений; если ha ≤ ma, то задача имеет единственное решение. Заметим, что при ha = ma треугольник АOD «вырождается» в отрезок.
A



 а
а
ha ha ma

m
 a
a
B C
D O
Рис 1.
2. Прием опорного треугольника.
Решение предыдущей задачи обладает интересной особенностью: в начале в составе искомого треугольника АВС был выделен вспомогательный треугольник АОD, затем выяснилось, что треугольник можно легко построить, и, наконец, было установлено, что располагая треугольником АОD можно легко построить треугольник АВС.
В этом и состоит сущность приема опорного треугольника: в составе искомой фигуры выделяют некоторый треугольник, который можно было бы легко построить /назовем такой треугольник опорным/, а затем выявляют возможность построения искомой фигуры, предполагая, что опорный треугольник уже построен.
Перечислим те простейшие построения, которые могут оказаться необходимыми при решении задач данным приемом.
-
Построение треугольника по трем сторонам.
-
Построение треугольника по двум сторонам и углу между ними.
-
Построение треугольника по стороне и двум прилежащим углам.
-
Построение треугольника по двум сторонам и углу, лежащему против одной из них.
-
Построение прямоугольного треугольника по гипотенузе и катету.
-
Построение прямоугольного треугольника по гипотенузе и острому углу.
-
Построение прямоугольного треугольника по катету и острому углу /противолежащему или прилежащему/.
Предлагаем читателю вспомнить перечисленные построения.
Приведем примерную форму анализа для задач, которые решаются с помощью приема опорного треугольника.
 Пусть... - искомая фигура /треугольник, параллелограмм, .../. рассмотрим треугольник. ... В нем известны ... . По этим данным такой треугольник можно построить. Располагая опорным треугольником, искомую фигуру можно построить следующим образом… .
Пусть... - искомая фигура /треугольник, параллелограмм, .../. рассмотрим треугольник. ... В нем известны ... . По этим данным такой треугольник можно построить. Располагая опорным треугольником, искомую фигуру можно построить следующим образом… .
3. Метод геометрических мест точек.
Общая характеристика метода. Задачу сводят к построению некоторой точки, которая должна удовлетворять двум условиям. Строят геометрическое место точек, удовлетворяющих первому условию. Затем строят геометрическое место точек, удовлетворяющих второму условию. Точка пересечения полученных линий и является искомой.
Что бы овладеть данным методом, необходимо знать и уметь строить известные геометрические места точек /множество точек/, обладающих некоторыми характеристическим свойством.
Примерная форма ответа для геометрических ситуаций на рис. 2-9:
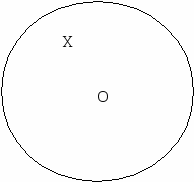
- точка Х удалена от … на расстояние, равное …; геометрическое место точек, удовлетворяющих этому условию, есть… .
-
точка X равноудалена от … ; геометрическое место точек, удовлетворяющих этому условию, есть … .
-
из точки X отрезок … виден под углом, равным … ; геометрическое место точек удовлетворяющих этому условию, есть … .
-
сумма квадратов расстояний /разность квадратов расстояний; отношения расстояний/ от искомой точки Х до данных точек … равна /равно/ … ; геометрическое место точек, удовлетворяющих этому условию, есть … .
Дано: АХ = р. Дано: отрезок ХУ
перпендикулярен
прямой а; ХУ = р.
Х
А Х
Х

Рис.2

 а
а
 У
У
Рис. 4.
Дано: Окружность ω1 и ω2 касаются Дано: ХА = ХВ
внешним образом; радиус окружностей
а и b. А

ω1 ω2



 Х
Х
Рис. 3 В рис. 5
Дано: прямые a и b параллельны; отрезки ХУ и ХZ перпендикулярны прямым а и в; ХУ = ХZ.
Дано: Окружность ω с центром Х, касается сторон данного угла.
 У
У






 Х А
Х А
Х




Z
Рис. 6 Рис. 7
Дано: 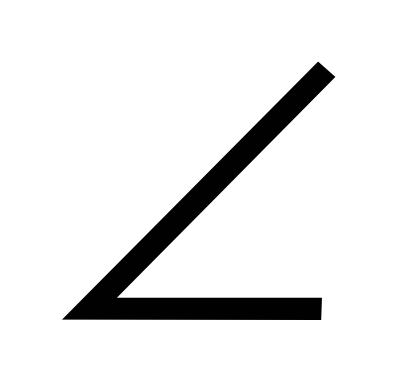 AХВ = 900
AХВ = 900

 Х .
Х .
А В
В
Рис. 8
 А
А
Дано: ХА = ХУ.

У
Рис. 10
Дано:
-
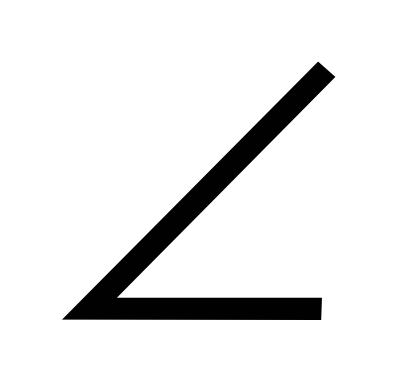 РХК = 900
РХК = 900 -
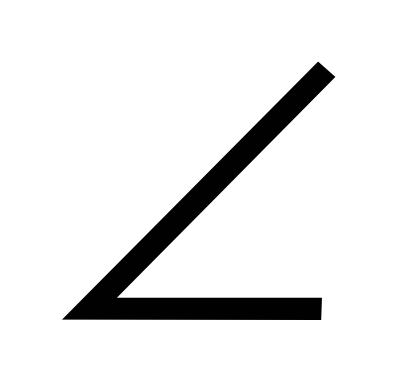 СХК = 900
СХК = 900 -
ХР : ХК = а : в, где а > в
-
ХС2 + ХК2 = с2
-
ХР2 - ХС2 = р2
-
ХК : ХС = а : в, где а > в
-
ХС2 + ХК2 = в2
-
ХР2 - ХС2 = с2.
Х



Р С К
Рис. 9
Что бы овладеть методом геометрических мест точек, необходимо уметь сводить построение некоторой фигуры к построению точки. Указанное сведение осуществляется обычно по следующему плану: а/ определяют, с каких элементов можно начать построение искомой фигуры. б/ выяснить, какие еще элементы искомой фигуры можно построить. в/ выяснить, какую точку или какие точки остается построить, что бы завершить построение искомой фигуры.
Первый вариант метода геометрических мест точек используется в задачах, состоящих в построении точки, которая должна принадлежать некоторой известной линии и удовлетворять некоторому условию. В таких задачах анализ удобно осуществлять по следующему плану.
-
Уточнить, какой известной линии должна принадлежать искомая точка.
-
Выяснить, какому условию должна удовлетворять эта точка.
-
Выяснить, что представляет собой геометрическое место точки, удовлетворяющих этому условию, и можно ли его построить.
-
Наметить план построения.
В качестве примера рассмотрим задачу: «На данной окружности ω найти точку, удаленную от данной прямой а на данное расстояние р» (рис. 11)
Анализ. 1. Искомая точка должна принадлежать данной окружности. 2. Искомая точка должна быть удалена от данной прямой а на данное расстояние р. 3. Геометрическое место точек, удовлетворяющих этому условию, есть пара прямых, параллельных прямой а. 4. Отсюда вытекает следующий план построения: построить в начале пару прямых, параллельных прямой а и отстоящих от нее на расстояние р, а затем построить точку пересечения построенных прямых с окружностью ω.




 р
р
ω

р Х У
а
р
рис. 11
Второй вариант метода геометрических мест точек используется в задачах, состоящих в построении точки, которая должна удовлетворять двум условиям. Для таких задач анализ удобно осуществлять по следующему плану.
-
Выяснить, какому условию должна удовлетворять искомая точка.
-
Выяснить, что представляет собой геометрическое место точек, удовлетворяющих этому условию, и можно ли построить это геометрическое место точек.
-
Выяснить, какому еще условию должна удовлетворять искомая точка.
-
Выяснить, что представляет собой геометрическое место точек, удовлетворяющих этому условию, и можно ли построить это геометрическое место точек.
-
Наметить план построения.
В качестве примера рассмотрим задачу: «построить точку, удаленную от данной точки на данное расстояние и равно удаленную от двух данных параллельных прямых» /рис. 12/.
Анализ. 1. Искомая точка Х должна быть удалена от данной точки А на данное расстояние р. 2. Геометрическое место точек удовлетворяющих этому условию, есть окружность радиуса р с центром в точке А. 3. Искомая точка Х должна быть равно удалена от данных параллельных прямых а и в. 4. Геометрическое место точек, удовлетворяющих этому условию, есть прямая, параллельная прямым а и в. 5. Отсюда вытекает построение: в начале постройте окружность радиуса р с центром А, затем построить прямую, параллельную прямым а и в и равноотстоящую от них, и, наконец, построить точки пересечения построенной прямой с и построенной окружности.
р

 а
а
 Х У
Х У
 с
с
 в
в
рис. 12
Третий вариант метода геометрических мест точек является наиболее распространенным и распространяется в задачах, состоящих в построении некоторых фигуры, отличной от точки. В таких задачах анализ начинается с выявления точки или точек, к построению которых может быть сведена данная задача. В свою очередь, для построения этих точек используется рассмотренные выше варианты данного метода. при отыскании плана построения в подобных задачах удобно придерживаться следующей схеме.
1. выяснить, к построению каких точек сводится данная задача /см. п. 4.4/.


Первый вариант метода г м. т.
-
выяснить, имеется ли некоторая известная линия, которой должна принадлежать искомая точка.
-
Выяснить, какому условию должна удовлетворять искомая точка.
-
Выяснить, что представляет собой г. м. т., удовлетворяющих этому условию и можно ли построить это г. м. т.
-
Наметить план построения искомой точки.
Второй вариант метода г. м. т.
-
Выяснить, какому условию должна удовлетворять искомая точка.
-
Выяснить, что представляет собой г. м. т., удовлетворяющих этому условию, и можно ли построить это г. м. т.
-
Выяснить, какому еще условию должна удовлетворять искомая точка.
-
Выяснить, что представляет собой г. м. т., удовлетворяющих этому условию, и можно ли построить это г. м. т.
-
Наметить план построения искомой точки.
или
Наметить построение искомой фигуры.
В качестве примера рассмотрим задачу: «Построим треугольник АВС, зная А, hв, mc». Обращаем внимание, что при письменном оформлении анализа целесообразно записать лишь его узловые моменты. В приводимом ниже анализе такие предположения подчеркнуты; остальные предположения раскрывают «внутреннюю» речь субъекта.
Анализ. Построение искомого треугольника можно начать с построения угла РАК, равного данному углу А. По этому задача сводится к построению точек В и С /рис. 13/. Искомая точка В принадлежит лучу АР на расстоянии, равное hв. Геометрическое место точек, удовлетворяющих последнему условию, есть пара прямых, параллельных прямой АВ и отстоящих от нее на расстояние равное hв. План построения точки В ясен. Переходим к точке С. Точка С принадлежит лучу АР. Точка С удалена от середины отрезка АВ - точки О - на расстояние mc. Геометрическое место точек, удовлетворяющих этому условию, есть окружность ω радиуса mc.Эту окружность можно построить. План построения точки С ясен. Ясен и план построения искомого треугольника.
Построение. Строим: 1. Угол РАК, равный данному углу А.
2. Прямые а и в параллельны прямой АР и отстоящая от нее на расстояние, равное hв.
-
АКВ = а
-
О - середина отрезка АВ
-
Окружность ω(О;mc)
-
С = ω АР
-
Треугольник АВС - искомый /рис. 13/
 hb
hb
mc
A
B a
O
hb A
 C P
C P
hb ω
рис. 13
Доказательство опускаем его в силу его очевидности.
Исследование. Просматривая шаг за шагом построение, видим, что задача может иметь ни одного, одного или два решения в зависимости от числа точек пересечения окружности с ω и луча АР.
Обращаем внимание, что в этой задаче построение точек В и С осуществлялось в соответствии с первым вариантом метода г м. т.
В качестве другого примера рассмотрим задачу: «построить треугольник АВС по следующим данным: а, А, р, где р2 = в2 - c2»
Анализ. Построение искомого треугольника можно начать с построения отрезка ВС, равного отрезку а, поэтому задача сводится к построению точки А. Из искомой точки А отрезок ВС виден под углом, равным данному углу А. Геометрическое место точек, удовлетворяющих этому условию, есть пара дуг вмещающих данный угол. Это г. м. т. можно построить. С другой стороны, разность квадратов расстояний точки А до точек С и В равна р2. Геометрическое место точек, удовлетворяющих этому условию, есть прямая, перпендикулярная лучу СВ и пересекающая этот луч в точке О, что СО = а/2 + р2/2а. Это г. м. т. можно построить. Отсюда вытекает следующий план построения: построить отрезок ВС, равный а, построить г. м. т., удовлетворяющих первому условию, построить г. м. т. удовлетворяющих второму условию, построить точку пересечения этих г. м. т., построить искомый треугольник АВС.
В этой задачи построение точки А осуществляется в соответствии со вторым вариантом метода г. м. т. Предлагаем читателю завершить решение данной задачи (построение, доказательство, исследование).
4. Метод спрямления
Опыт оказывает, что решение задач на построение полезно начинать как можно раньше, подбирая их по степени трудности. В школьных программах рассматриваются методом геометрических мест, методом подобия, методом преобразования фигур - перемещения (параллельный перенос, поворот, симметрия). Но нигде не упоминается метод спрямления. Я считаю, что решать достаточно сложные задачи на построение методом спрямления можно, а в математических классов нужно, с 7 класса. Ниже приведу решение таких задач.
Правильное, осмысленное решение задач на построение состоит из четырех частей:
1. Анализ.
2. Построение.
3. Доказательство (синтез).
4. Исследование.
1. Анализ. Составляется план решения. Для этого поступают так:
предполагают задачу решенной и делают от руки примерный чертеж искомой фигуры (не обязательно соответствующий размерам). Нужно найти такую зависимость между данными и искомыми величинами, которая позволила бы определить положение искомой точки, или отрезка, или угла, на нахождение которых нацелено решение задачи. При этом приходится проводить различные вспомогательные прямые, окружности, не редко даже на удачу, не зная заранее, приведет ли проведенная линия пользу или нет. Когда при помощи различных рассуждений и догадок зависимость между данными и искомыми величина определена, переходят ко второй части решения - построению.
2. Построение. Механическое выполнение тех приемов,
которые были выведены из плана решения
задачи, то есть анализа.
3. Доказательство. Когда искомая фигура построена, необходимо
доказать, что она удовлетворяет всем
требованиям задачи. При этом ход рассуждений будет обратный
тому, который применялся при анализе. Поэтому иногда доказательство
называют синтезом.
4. Исследование. Имеем целью выяснить, всегда ли задача
разрешима, сколько решений допускается
(одно или несколько). Необходимо рассмотреть всевозможные частные случаи, причем нужно выяснить, меняется ли ход решения в этих случаях и как именно.
Рассмотрим несколько задач, решаемых методом спрямления. Причем одну задачу дадим в подробном изложении, то есть опишем все четыре части решения. В остальных дадим только анализ.
Задача 1. Построить треугольник по данной стороне, углу, к ней
прилежащему, и сумме двух других сторон.
Дано:
a


 B
B
b+c c
 A
A


 a b
a b

 b
b




B C H D
1. Анализ. Пусть АВС - искомый.
Продолжим сторону ВА и на ее продолжении отложим АD = CA соединим C с D.
В CBD имеем BD = b + c, BC = a, CBD = B.
BCD можно построить по двум сторонам и углу между ними.
CAD равнобедренный, в котором АН высота и медиана.
Проведя серединный перпендикуляр (AH CD). Определим вершину А.
2. Построение. 1) CBD, где ВС = а, B и ВD = b + c;
2) HA СD и CH = HD.
3. Доказательство. АВС - искомый, так как он удовлетворяет всем
всем требованием задачи: BC = a; BA + AC = b + c;
В равен данному.
4. Исследование. Условие необходимое для решения задачи, b + c > a.
Докажем, что это условие и достаточно, то есть оно выполняется, то задача разрешима.
Если c + b > a, то в BDC C > D, а поэтому можно провести прямую линию AC по ACD к стороне CD, чтобы ACD = DC, что позволяет восстановить перпендикуляр к CD.
Задача разрешима при b + c > a и имеет одно решение.
Задача 2. Построить треугольник по разности сторон a и b, стороне c и B.
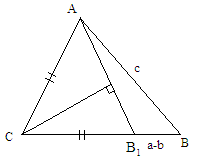
Анализ. Пусть АВС построен. Отложим на стороне ВС отрезок
СВ1 = АС, тогда В1В = a - b.
АВ1В возможно построить по двум сторонам и углу между ними: AB = c, B1B = a-b и В.
Для определения вершины С необходимо восстановить серединный перпендикуляр к стороне АВ1 (АСВ1 - равнобедренный) до пересечения с продолжением стороны ВВ1 (луч ВВ1).
Задача 3. Построить треугольник по двум углам и периметру.
C


 F
F




А В
Анализ. Пусть искомый . На продолжение стороны АВ в
обоих направлениях отложим отрезки DA = AC и BE = CB и соединим D с C и E c C, получим DEC, в котором DE = P (периметру).
Треугольник DAC и BEC - равнобедренные, и AK DC, где DK = KC и BF CE и CF = FE, что позволит определить вершины A и B. D = (1/2)* A, E = (1/2)* B (свойство внешнего угла треугольника).
Значит, задача сводится к построению DCE по стороне P и двум углам: D и E. Здесь произведено спрямление сторон AC и CB со стороной AB.
Задача 4. Постройте треугольник по данной стороне, углу, ей противолежащему, и разности двух других сторон.




 A
A
D
E b-c
B C
Анализ. Пусть ABC построен. На AC отложим AB и получим
точку D.
ABD - равнобедренный. В BDC известны две стороны: BC = a и
DC = b - c. определим BDC. Он внешний по отношению к AED, где
AEBD, причем BE = ED, до пересечения луча СD c EA дает положение точки А.
Задача 5. Построить по данной стороне, углу, ей противолежащему, и сумме двух других сторон.

 D
D



 А Е
А Е
В
С
Анализ. Пусть ABC построен. На луче ВА отложим отрезок АD = АС. Получим ADC - равнобедренный, в котором D = C = (1/2)* A (свойство внешнего угла треугольника).
Задача сводится к построению BDC по двум сторонам: BD = b + c, BC = a и углу D, противолежащему меньшей стороне а. Чтобы определить положение вершины А, достаточно ЕАпричем DE = EC.
Задача 6. Построить прямоугольный треугольник по сумме катета и гипотенузы и острому углу.


C1
 a
a


k

 a c
a c
A
C
Анализ. На продолжении гипотенузы отложим катет ВС, Получим С1А = а + с. С1ВС - равнобедренный. С1 = (1/2)*(1800-С1ВС) = (1/2)*(1800-(1800-СВА)) = (1/2)*СВА = (1/2)*(900-А).
АСС1 можно построить по стороне АС1 = а + с и двум углам: А С1 = (1/2)*(900-А).
Задача сведена к построению АСС1 и КВ АС1, причем С1К = КС. Так найдена вершина В.
Задача 7. Построить прямоугольный треугольник по катету и разности гипотенузы с другим катетом.
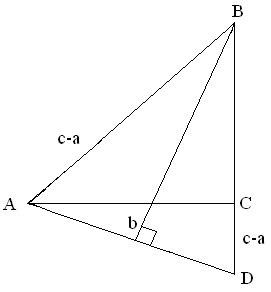
Анализ. Пусть АВС удовлетворяет условиям задачи. На
продолжении катета BC отложим CD = с - а, тогда
BD = а + с + а = с, отсюда ABD - равнобедренный: AB = DB = c. Первоначально можно построить ACD по двум катетам b и CD = c- a. Затем провести FBAD, причем AF = FD.
Задача 8. Построить АВС по углам A и В и разности сторон а - b.


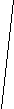 C
C

D


a-b
Q

A B
Анализ. Пусть АВС построен. В нем С = 1800 - (А +В).
(А + В).ACD - равнобедренный с углом при основании x. x = + C =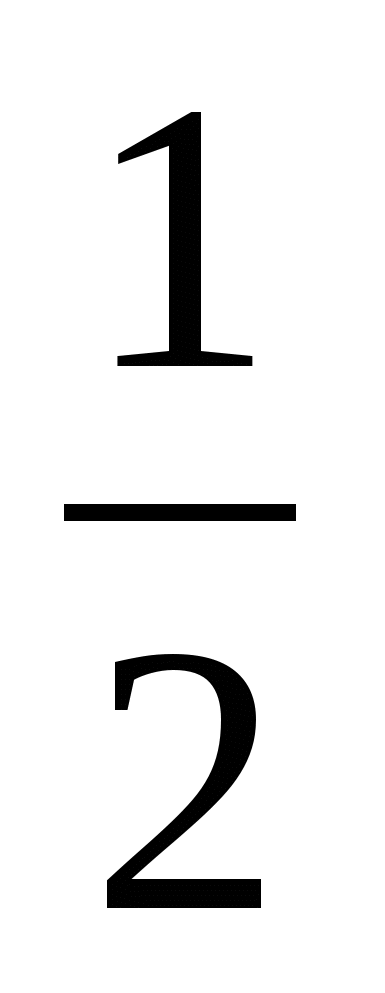 *(1800 - C) =
*(1800 - C) = 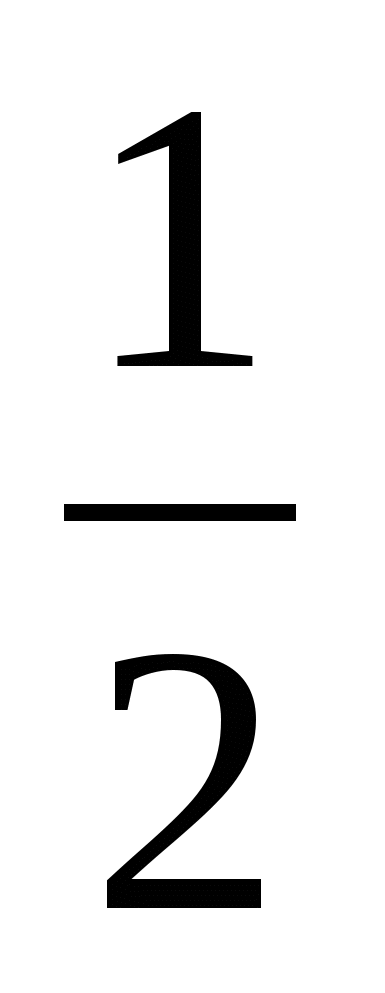 * (А + В).
* (А + В).
Необходимо вычислить АDB для построения ADB по стороне а - b и двум углам: В и ADB.
ADB = x +C = 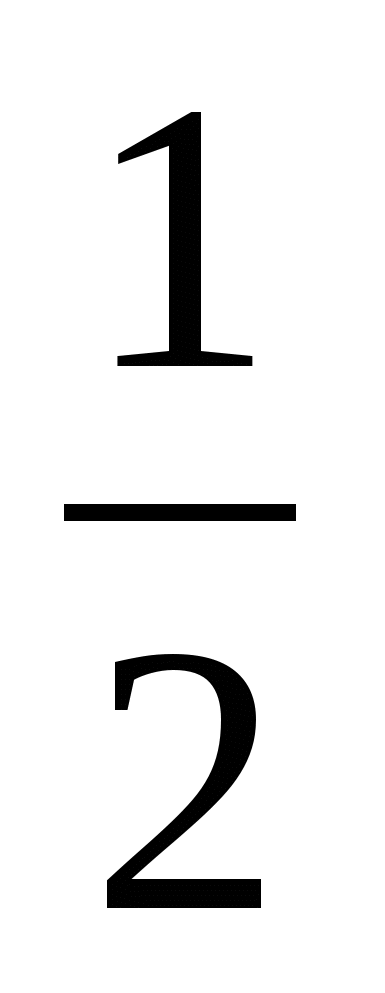 *(A+B)+1800 - (A+ C) = 1800 -
*(A+B)+1800 - (A+ C) = 1800 -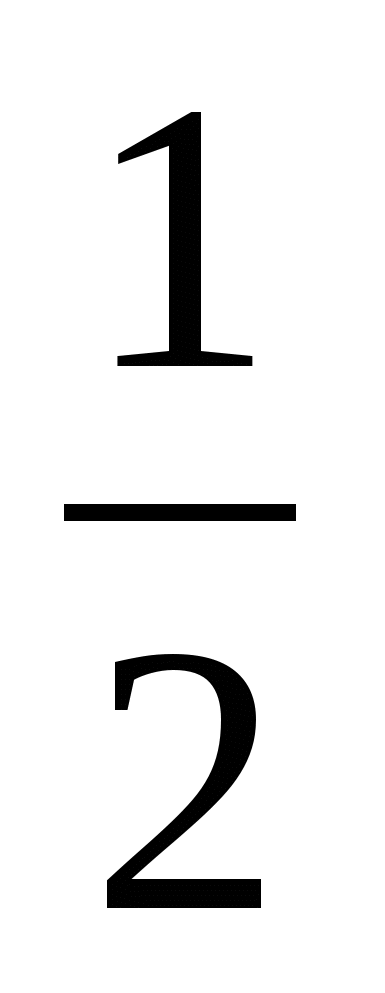 *(A+B).
*(A+B).
Таким образом, имеем возможность построить ADB.
Для получения вершины С есть несколько возможностей. Например от луча АВ отложить угол А до пересечения с продолжением стороны a - b; или восстановить серединный перпендикуляр QCAD до пересечения с продолжением стороны a - b.
Задача 9. Построить ABC , если даны: a; c - b;C- B.
Предварительно решим такую задачу:
В ABC проведена биссектриса угла при вершине А до пересечения с BC в точке D. На большей боковой стороне АС. Соединим D и E. Зная углы B и С, определить BDE.
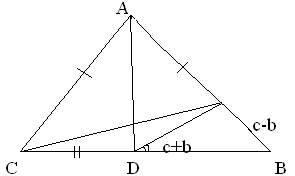
Решение. ADC = ADE по двум сторонам и углу между ними. Из этого следует, что AED = C и ED = CD. AED внешний по отношению к DEB, AED = EDB + B или C = EDB + B EDB = C- B.
Теперь решаем задачу на построение ABC, используя данные, полученные в предыдущей задаче.
Анализ. Задача сводится к построению DEB по стороне c-b, противолежащему углу C- B и в сумме сторон DE + DB = a, заключающих этот угол.
Спрямляем ED с BD (это уже имеется на чертеже)
ECD + CED = EDB ECD = 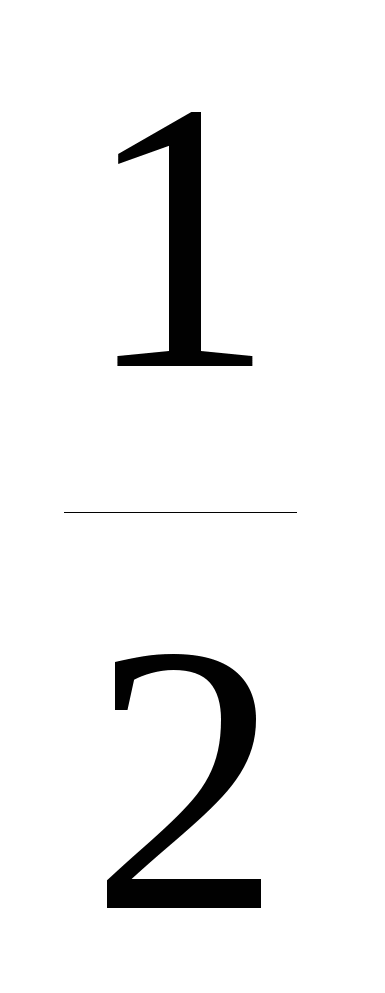 ( C - B)
( C - B)
CEB построим по сторонам EB = c - b; CB = a и углу ECD =  ( C- B).
( C- B).
D = MD CB (MD серединный перпендикуляр к CE).
DEB построен, и, чтобы построить ABC, нужно продолжить BE до пересечения с биссектрисой CED - получили точку А.
ВС = DE + DB = a.


