- Преподавателю
- Математика
- Методические приемы поиска решения задач по математике
Методические приемы поиска решения задач по математике
| Раздел | Математика |
| Класс | - |
| Тип | Другие методич. материалы |
| Автор | Богданова Ф.И. |
| Дата | 21.04.2014 |
| Формат | docx |
| Изображения | Есть |
Методические приемы поиска решения задач
Значительное количество задач предполагает при своем решении, как замечает И.Л. Никольская не творческую деятельность, а применение в основном определенного правила, формулы, определения, теоремы.
Например, для решения любого уравнения первой степени необходимо известные слагаемые перенести в правую часть, а слагаемые, содержащие неизвестные, перенести в левую часть, привести подобные члены и обе части уравнения разделить на коэффициент при неизвестном, если он отличен от нуля. Если он равен нулю, то поступают известным образом.
Приведенное правило - предписание алгоритмического типа, или алгоритм решения линейного уравнения. Правила сравнения чисел, действий над числами в различных числовых множествах, решения линейных, квадратных уравнений, неравенств - все это примеры алгоритмов. Под алгоритмом понимается точное общепонятное предписание о выполнении в определенной последовательности операций для решения любой из задач, принадлежащих некоторому классу [Никольская, Семенов, 1989].
Алгоритм может быть задан в виде таблицы, правила, формулы, определения, описания. Алгоритм может регламентировать действие с различной степенью подробности - свернутости, в зависимости от того, кому он предназначается. Если алгоритм предъявлен в форме последовательности команд, то это готовая программа действия. Приведем пример. Чтобы сложить десятичные дроби, нужно: 1) уравнять в этих дробях количество знаков после запятой; 2) записать их друг под другом так, чтобы запятая была записана под запятой; 3) выполнить сложение, не обращая внимания на запятую; 4) поставить в ответе запятую под запятой в данных дробях.
Если алгоритм задан в виде формулы, правила, таблицы, определения, то программы нет. Ее предстоит создать решающему задачу. Рассмотрим в качестве примера определение решения системы неравенств с переменной как значение переменной, при котором каждое из неравенств системы обращается в верное числовое неравенство. Определение подразумевает следующие шаги решения системы неравенств: 1) решить каждое неравенство; 2) найти пересечение полученных множеств.
Алгоритмы, как отмечает А.Б. Василевский, можно разделить на алгоритмы распознавания и преобразования. Признаки делимости, рассмотренные ранее алгоритмы подведения под определение и под понятие являются примерами алгоритмов распознавания. Алгоритмы по применению формул являются алгоритмом» преобразования. Однако при применении конкретной формулы, например, квадрата суммы двух чисел, вначале происходит узнавание формулы, доказательство того, что выбор формулы сделан правильно, а затем производится собственно преобразование: актуализация формулы и использование ее по шагам. Описанная деятельность состоит из следующих шагов: 1) найти первый член двучлена; 2) найти второй член двучлена; 3) возвысить первый член двучлена в квадрат; 4) составить произведение первого и второго членов двучлена; 5) удвоить результат предыдущего шага; 6) возвысить второй член двучлена в квадрат; 7) результаты третьего, пятого и шестого шагов сложить [Василевский, 1988].
Составлению, выделению алгоритмов, как отмечает Л.М. Фридман, необходимо специально обучать.
Это может происходить с помощью проведения обобщений при решении нескольких аналогичных задач. Необходимо обучать чтению формул словами, необходимо обучать переходу от речевой, формы в аналитическую и обратно, необходимо обучать строить программы действий в тех случаях, когда материал в книге или в рассказе предъявлен в описательной форме. Это и будет означать обучение применению теоретических знаний на практике и развитие алгоритмического мышления. Необходимо также обучать разворачивать, дополнять алгоритмы, предъявленные в готовой форме [Фридман, 2004].
Вторая рекомендация по использованию алгоритмов вытекает из положений теории деятельности. Она заключается в требовании проведения всех операций, содержащихся в алгоритме (правиле) во внешнем плане и в развернутой форме, т. е. в написании и проговаривании всех операций без пропусков [Никольская, Семенов, 1989].
Проиллюстрируем на примерах осуществление поиска решения стандартной задачи.
Задача 1. Выписать первые пять членов арифметической прогрессии, если а=10, d=4.
1) В задаче указан ее вид: имеем задачу на нахождение членов арифметической прогрессии.
2) Ищем способ решения задачи:
вспоминаем определение арифметической прогрессии: числовая последовательность, каждый член которой, начиная со второго, равен предшествующему члену, сложенному с одним и тем же числом (разностью прогрессии), называется арифметической прогрессией.
на основе этого определения составляем программу решения задачи: 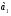 нам известно, поэтому находить будем
нам известно, поэтому находить будем 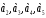 используя определение:
используя определение: 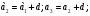 и т.д.
и т.д.
3) Проводим решение задачи по найденному способу.
Примеры задач, на которых показывается алгоритмические приемы поиска их решения, приведены в приложение 2. Урок с организацией поиска решения таких задач приводится в приложение 1.
Рассмотрим две задачи, которые можно решить с помощью одной и той же теоретической базы - с помощью векторов.
Задача 2. Доказать, что диагонали ромба перпендикулярны.
Доказательство. Пусть ABCD - ромб. Для доказательства введем два неколлинеарных вектора: ВА и ВС и выразим векторы АС и ВD, расположенные на диагоналях, через введенные (рис. 2.1).
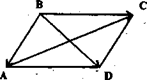
Рис. 2.1. Ромб ABCD
Чтобы доказать перпендикулярность векторов АС и BD, достаточно доказать равенство нулю их скалярного произведения.
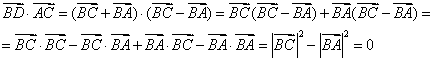
Равенство нулю скалярного произведения двух ненулевых векторов говорит о том, что косинус угла между ними равен 0°, а значит, угол между векторами - прямой, т. е. прямые, на которых располагаются рассматриваемые векторы, перпендикулярны.
Задача 3. Доказать с помощью векторов свойство средней линии трапеции.
Доказательство. Пусть АВСО - трапеция, точки Е и F-середины отрезка АВ и CD соответственно.
Введем векторы и выразим вектор EF из двух многоугольников:
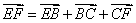 ;
; 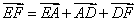 .
.
Сложим почленно полученные равенства:
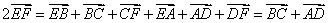 ,
,
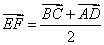 .
.
Последнее равенство можно интерпретировать следующим образом: т. к. векторы ВС и AD коллинеарны по определению трапеции, то и вектор EF также коллинеарен им, т. к. является линейной комбинацией этих векторов, а значит, отрезок EF параллелен основаниям трапеции. Т. к. векторы ВС и AD сонаправлены, то длина вектора 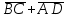 равна сумме длин векторов ВС и AD и, следовательно, длина вектора EF равна полусумме длин векторов ВС и AD. А значит, длина отрезка EF соответственно равна полусумме длин отрезков ВС и AD.
равна сумме длин векторов ВС и AD и, следовательно, длина вектора EF равна полусумме длин векторов ВС и AD. А значит, длина отрезка EF соответственно равна полусумме длин отрезков ВС и AD.
При решении рассмотренных выше задач, как отмечает А.Б. Василевский, можно выделить одинаковую схему - одинаковые шаги решения, а именно:
- введение удобным образом векторов;
- переформулирование условия и требования задачи на язык векторов;
- решение вновь сформулированной задачи с помощью векторного аппарата (определений, законов действий и т. д.);
- интерпретирование результатов, полученных на языке векторов, на обычный геометрический язык [Василевский, 1988, с. 126].
По выделенной схеме решается как вторая, так и третья задача. По этой же схеме с помощью векторного аппарата можно решить многие геометрические задачи. Перечисленные шаги образуют прием решения задач векторным методом.
Этот прием учитель может представить ученикам в готовом виде. Но, по мнению Г.И. Саранцева, большую познавательную ценность имеет работа по самостоятельному выделению учащимися под руководством учителя шагов приведенного приема. Некоторые методисты отрицательно относятся к решению типовых задач как к натаскиванию. Однако учащиеся, знакомые с приемом, умеют решить не одну конкретную задачу, а целый класс задач, к которым они подходят с более высоких позиций обобщения учебного материала. Материал лучше структурируется, повышаются его уровень системности, возможности учащихся при решении задач. Ученик, не владеющий наиболее распространенными типами задач, не сможет решить ни одной нестандартной задачи или будет делать это со значительно большим усилием, чем тот, у кого в запасе владение многими типами задач.
Четыре выделенных шага образуют прием по решению задач данного типа. Этот прием можно отнести к полуалгоритмическим приемам, т. к. знание его не обязательно приведет решающего к получению верного результата, но может существенно облегчить поиск. Алгоритмические предписания являются той базой, владение которой облегчает решение задач [Саранцев, 2005].
Подготовка к приему, как замечают М.Б. Балк и Г.Д. Балк, может быть организована задолго до явного введения самого приема. Учащиеся решают задачи, а учитель старается акцентировать их внимание на средствах решения, на последовательности одних и тех же шагов. Этот период можно назвать пропедевтическим, подготовительным в формировании приема. Следующий этап - этап явного введения приема (предписания) с помощью учащихся на основе сравнения процессов решения выделенных задач. Далее организуется работа по закреплению шагов предписания и применению всего приема.
Самостоятельно составленное учителем предписание требует предварительной проверки на решении нескольких задач и внесения в него при необходимости корректировки.
Далее остановимся на эвристических приемах поиска решения задач. Эвристики - это основная идея решения задачи. Знание эвристик не дает гарантии того, что будет решена любая задача. Эвристики лишь помогают квалифицированно делать попытки поиска решения. При решении некоторых задач может быть использовано несколько эвристик. Учителю необходимо знание эвристик для того, чтобы помочь учащимся обнаружить их в собственной (учащихся) деятельности, разобраться в сущности методов и научиться ими пользоваться. Приведем примеры наиболее часто используемых эвристик и соответственно задач, которые решаются с их помощью.
Метод восходящего анализа - решение задачи с конца, от требования - к условию. Эта эвристика осознанно или неосознанно, в большей или в меньшей степени используется при решении любой задачи.
Задача 4. Доказать, что в прямоугольном треугольнике биссектриса угла делит пополам угол между медианой и высотой, проведенные к гипотенузе (рис. 2.2).
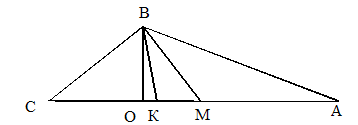
Рис. 2.2. Прямоугольный треугольник ABC
При использования метода анализа постоянно отыскивается ответ на вопрос, что достаточно найти, доказать, чтобы ответить на вопрос. Чтобы доказать равенство углов ОВК и КВМ, достаточно доказать равенство углов АВМ и СВО. А так как углы МВА и ВАМ равны, то для доказательства равенства углов СВО и МВА достаточно доказать равенство углов СВО и САВ. А доказать равенство этих углов уже не составит труда.
Достаточно универсальной является и другая эвристика - переформулирование. Суть этого эвристического приема заключается в том, что условия или требования, а возможно, то и другое одновременно, заменяются на новые, эквивалентные имеющимся, но позволяющие упростить поиск решения. В простейших случаях переформулировка - это замена термина его содержанием. Рассмотрим на примере эту эвристику.
Задача 5. Доказать, что середины оснований трапеции, точка пересечения диагоналей и продолжений боковых сторон лежат на одной прямой.
А.Б. Василевский отмечает, что поиск решения задачи облегчается, если задачу сформулировать иначе: доказать, что прямая, проходящая через точку пересечения диагоналей трапеции и точку пересечения продолжений боковых сторон, делит основания трапеции пополам. Задача при этом остается той же, но новая формулировка подсказывает определенный метод решения [Василевский, 1988, с. 162].
Доказательство 1. Используем утверждение: отрезок прямой, заключенный между боковыми сторонами трапеции и проходящий через точку пересечения диагоналей трапеции параллельно ее основаниям, делится этой точкой пополам.
1. Соединим отрезком точку пересечения продолжений боковых сторон трапеции Е и точку пересечения ее диагоналей О. ВС∩ЕО = М, АD∩ЕО = N. Докажем, что ВМ = МС и АN = ND (рис. 2.3). Из этого и будет следовать, что середины оснований трапеции тоже лежат на той же прямой ЕО. По-другому говоря, переформулируем данную задачу так: доказать, что прямая, проходящая через точку пересечения диагоналей трапеции и точку пересечения продолжений ее боковых сторон, делит основания трапеции пополам.
2. Предварительно через точку О параллельно основаниям данной трапеции проведем прямую, пересекающую ее боковые стороны АВ и CD в точках Р и Q соответственно, и докажем, что РО = ОQ. Действительно, ΔАОD ~ ΔВОС. Значит, 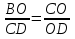 . Прибавив единицу к обеим частям этого равенства, получим
. Прибавив единицу к обеим частям этого равенства, получим
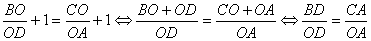 (1)
(1)
ΔВСD ~ ΔOQD, следовательно, 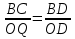 . Аналогично ΔВСА ~ ΔРOА и
. Аналогично ΔВСА ~ ΔРOА и 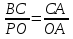 . Но
. Но 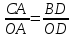 согласно формуле (1). Отсюда следует:
согласно формуле (1). Отсюда следует: 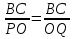 ↔ PO=OQ.
↔ PO=OQ.
3. ΔANE ~ ΔРОЕ и, значит, 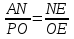 . Аналогично
. Аналогично 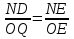 . Отсюда получаем, что
. Отсюда получаем, что 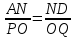 . Теперь уже видно, что из РО = ОQ следует, что АN = ND.
. Теперь уже видно, что из РО = ОQ следует, что АN = ND.
4. Точно также доказывается, что 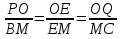
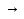 BM=MC.
BM=MC.
Замечание. Сделав два «шага», доказательство можно продолжить по-другому. После того, как доказано, что PO=OQ, имеем: середины оснований трапеции (М и N) и точка пересечения ее диагоналей (О) лежат на одной прямой. Действительно, все три указанные точки являются серединами отрезков прямых, проведенных параллельно основанию треугольника АDЕ, поэтому они принадлежат медиане этого треугольника, проведенной из вершины Е к основанию АD. Тем самым доказано, что Е, М, О и N лежат на одной прямой.
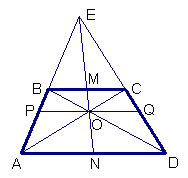
Рис. 2.3. Изображение отрезка PQ параллельного основаниям трапеции
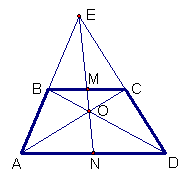
Рис. 2.4. Изображение трапеции ABCD
Доказательство 2. Используем признак подобия треугольников по двум углам (рис. 2.4).
1. Соединим точки Е и О. Докажем, что ВМ = МС и АN = ND (рис. 2.3).
2. Введем обозначения: ВМ = х, МС = у, АN = u, ND = v. Рассмотрим две пары подобных треугольников: ΔВМЕ ~ ΔANE и ΔМСЕ ~ ΔNDE. Из подобия ΔВМЕ и ΔANE следует 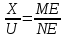 . Из подобия ΔМСЕ и ΔNDE следует
. Из подобия ΔМСЕ и ΔNDE следует 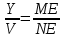 . Значит,
. Значит, 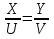 .
.
3. Рассмотрим еще две пары следующих подобных треугольников: ΔВМО ~ ΔNОD и ΔМОС ~ ΔАОN.
Из подобия ΔВМО и ΔNОD следует 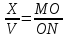 . Из подобия ΔМОС и ΔАОN следует
. Из подобия ΔМОС и ΔАОN следует  . Значит,
. Значит, 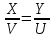 .
.
4. Осталось решить систему уравнений: 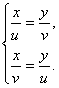
Перемножим левые и правые части соответствующих уравнений: 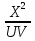 =
=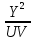
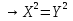
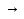 X=Y, т. е. ВМ = МС. Так как
X=Y, т. е. ВМ = МС. Так как 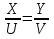 , то U=V, т. е. АN = ND.
, то U=V, т. е. АN = ND.
В качестве следующей эвристики рассмотрим метод суперпозиции - решение задач в частных случаях. Причем рассматриваемые частные случаи должны полностью исчерпывать все возможные случаи. Например, требуется доказать неравенство.
Задача 6. Доказать неравенство: а8 - а5 + а2 - а + 1 > 0.
Найти общее решение данной задачи можно, но довольно трудно, а решить ее в трех случаях, когда а < 0, 0 ≤ а ≤ 1, а >1, не представляет труда.
Например, если а < 0, то выражение слева можно представить как
а2(а6 + 1) - а(а4 + 1) + 1, которое принимает лишь положительные значения.
Если 0 ≤ а ≤ 1, то его можно представить как а8+ а2(1 - а3) + (1 - а), и тогда очевидно, что оно принимает положительные значения в рассматриваемом промежутке.
Если а >1, то выражение можно представить как а5(а3 - 1) + а2 - а + 1.
Рассмотренные три случая полностью исчерпывают все возможные значения параметра а.
Довольно часто при поиске решения задач может помочь еще одна эвристика - прием обобщения, когда вместо имеющейся задачи решается другая, более общая по отношению к данной.
Задача 7. Определить, какое число больше: 19971998 или 19981997.
Решение. Преобразование разности этих выражений к успеху не приводит. Но если выражения прологарифмировать: 1998 lg 1997 и 1997 lg1998, то вместо исходных можно сравнивать выражения 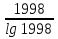 и
и 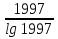 , тогда оказывается, что сравнивать надо два значения функции
, тогда оказывается, что сравнивать надо два значения функции 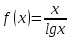 , т. е. требуется решить вопрос, какой характер монотонности имеет функция, а это стандартная задача.
, т. е. требуется решить вопрос, какой характер монотонности имеет функция, а это стандартная задача.
Очень важной эвристикой, используемой при решении большого числа задач, является выделение подзадач, решение которых не составляет труда, внутри основной задачи. Тем самым упрощается структура основной задачи.
Задача 8. Из двух пунктов, расстояние между которыми 100 км, выехали одновременно навстречу друг другу два велосипедиста. Скорость одного из них была 15 км/ч, а другого-10 км/ч. Вместе с первым велосипедистом выбежала собака со скоростью 20 км/ч. Встретив второго велосипедиста, собака повернула обратно и побежала навстречу первому велосипедисту. Встретив первого велосипедиста, она снова повернула. Собака бегала между велосипедистами до тех пор, пока велосипедисты встретились. Сколько километров пробежала собака?
Если решение задачи начинать с рассмотрения движения собаки и второго велосипедиста, то перед решающим встает необходимость рассматривать последовательность встречных движений, что может оказаться очень непростым делом. А если внутри основной задачи выделить в качестве элементарной подзадачи движение велосипедистов навстречу друг другу, в которой требуется определить время до их встречи, то сразу вырисовывается и вторая элементарная подзадача - движение собаки, скорость и время которой известны, а маршрут движения - безразличен.
Прием выделения подзадач внутри основной задачи, как отмечает Н.П. Кострикина, применяется при решении подавляющего большинства задач. Этот прием используется, в частности, когда решается любая задача на описанные и вписанные в сферу многогранники, когда требуется, например, доказать, что центр сферы, вписанной в правильную пирамиду, лежит на высоте пирамиды; что основание перпендикуляра, опущенного из любой точки высоты пирамиды на боковую грань, попадает на апофему боковой грани. Не зная, как решить задачу, решающий часто проводит рассуждения по схеме: «По данным задачи я могу найти то-то и то-то, а что это мне дает для решения основной задачи?» [Кострикина, 1991].
При решении ряда задач может оказаться полезным прием вспомогательных неизвестных - эвристика, используемая как при решении алгебраических задач, так и при решении геометрических задач. Рассматриваемый метод имеет три модификации: когда при замене число переменных или уменьшается, или увеличивается, или остается неизменным. Цепи введения вспомогательных неизвестных при этом различные. Рассмотрим две задачи.
Задача 9. Доказать, что при любых действительных, отличных от нуля х и у, справедливо неравенство:
3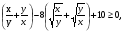 где
где 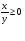 .
.
Пусть 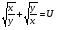 , тогда U2 =
, тогда U2 = 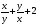 .
.
И вместо исходного неравенства получаем: 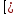
Неравенство (*) выполняется для всех U, кроме 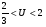
Однако 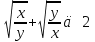 , т. е.
, т. е. 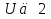 . Значит, исходное неравенство выполняется при всех допустимых значениях х и у.
. Значит, исходное неравенство выполняется при всех допустимых значениях х и у.
Задача 10. В качестве второго примера, когда при замене число переменных сохраняется, рассмотрим решение уравнения:
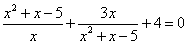 .
.
Замена 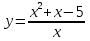 сводит исходное уравнение к достаточно хорошо известной форме
сводит исходное уравнение к достаточно хорошо известной форме 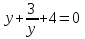 .
.
Малых изменений метод - эвристика, предполагающая замену одной модели другой, в результате незначительной, т.е. сохраняющей основные качественные характеристики первой модели, деформации.
Задача 11. Доказать неравенство 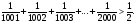
Решение. 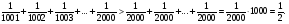
Задача 12. Что больше 1·2·3·…·20 или 1+2+3+…+1000000?
Решение. Имеем: 1+2+3+…+1000000 < 1000000+1000000+…+1000000 = 106 · 106 = 1012; 1·2·3·…·20 = 1·2·3·4·5·6·7·8·9·10·11·…·20 > 2·5·10·11·12·…·20 > 1012
Значит, 1·2·3·…·20 > 1+2+3+…+1000000.
Задача 13. Какое из чисел больше: а) 635 или 810?; б) 156 или 712?
Решение. а) 635 < 645 = (82)5 = 810; б) 156 < 166 = (42)6 = 412 < 712
Задача 14. Найти наибольшее значение выражения 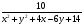
Решение. 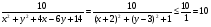
Равенство достигается, если 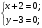
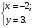
Ответ: Наибольшее значение выражения равно 10, при х = - 2, у = 3.
Задача 15. Найти наибольшее значение выражения
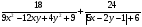
Решение. 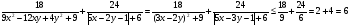
Равенство достигается, если 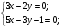
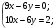
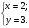
Ответ: Наибольшее значение выражения равно 6, при х = 2; у =3.
Задача 16. Найти наибольшее значение выражения
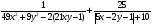
Решение. 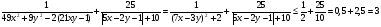 Равенство достигается, если
Равенство достигается, если 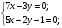
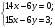
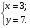
Ответ: Наибольшее значение выражения равно 3, при х = 3, у = 7.
Надо ли знакомить учащихся с эвристиками специально? Решающие находят, изобретают эвристики и сами. Но для этого нужны значительные усилия и время. Учителю полезно обратить внимание учащихся на метод, с помощью которого удалось осуществить поиск решения трудной задачи. Это можно сделать после решения задачи с помощью вопросов типа: «Как удалось переформулировать требование (условие) задачи?»; «Какие подзадачи удалось выделить, облегчив решение основной?»; «Как при решении задачи была использована аналогия?» Так постепенно вместе с учителем учащиеся осознают многие из используемых ими приемов, что позволит в дальнейшем сознательно привлекать их к решению других задач. При этом поиск решения становится более эффективным. Владение эвристиками расширяет творческие возможности учащихся.
Как правило, отмечает Л.М. Фридман, в чистом виде единичные эвристики при решении задач не применяются. Имеет место использование некоторой совокупности эвристик. Ни одна задача не обходится без методов анализа, переформулирования, выделения известных подзадач.
В методике Р.Г. Хазанкина, известного учителя из Белорецка, обучение эвристикам можно усмотреть в его методике решения «ключевых» задач. Ключевыми он называет задачи раздела, при решении которых раскрываются основные математические идеи, используемые для решения большого класса задач. Уроки решения «ключевых» задач проводятся в форме лекции, после чего учащиеся пытаются использовать рассмотренные идеи при решении других задач раздела.


