- Преподавателю
- Математика
- Ашық сабақ Қосарланған арифметикалық квадрат түбірлерді түрлендіру
Ашық сабақ Қосарланған арифметикалық квадрат түбірлерді түрлендіру
| Раздел | Математика |
| Класс | 11 класс |
| Тип | Конспекты |
| Автор | Артыкбаева Г.Д. |
| Дата | 05.11.2015 |
| Формат | docx |
| Изображения | Есть |
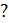 Сыныбы: 11 «Б»
Сыныбы: 11 «Б»
Сабақтың тақырыбы: Қайталау сабағы. (Қосарланған арифметикалық квадрат түбірлерді түрлендіру).
Сабақтың мақсаттары:
Білімділік мақсаты: Қосарланған арифметикалық квадрат түбірлерді түрлендіруде формулаларды қолдану алгоритмін қайталап үйрете отырып, терең де тиянақты саналы түрде білім негіздерін қалыптастыру;
Дамытушылық мақсаты: Оқушылардың логикалық ойлауын, ізденімпаздығын және жылдамдығын дамыту;
Тәрбиелік мақсат: Оқушыларды тиянақтылыққа тәрбиелеу.
Сабақтың түрі: білім мен білікті жетілдіру
Сабақтың әдіс-тәсілдері: түсіндірмелі иллюстрациялық, сұрақ-жауап, жекелей, жұппен жұмыс.
Пәнаралық байланыс: Әдебиет; тарих.
Көрнекілігі: Интерактивті тақта, плакаттар. Сабақтың барысы:
1. Ұйымдастыру кезеңі: Оқушыларды түгендеп, олардың сабаққа дайындығын тексеріп, сабақ мақсатын хабарлау.
Балалар, бүгінгі біздің сабағымызда, елбасының өскелең жас ұрпаққа айтылған өсиетіне назар аударайық: «Еліміздің ертеңі мен бүгіні - жас ұрпақтың қолында ...», - Н.Ә.Назарбаев айтқандай яғни, шарықтап шыңға ұмтылған Қазақстан, білімді де еңбекқор жастар, мына отырған сіздердің қолдарыңызда.
2. Үй тапсырмасын тексеру:
Өткенді қайталау:
1) Арифметикалық квадрат түбір деген не ?
2) Саннан квадрат түбір алу үшін бұл сан қандай болу керек ?
3) Теріс санның квадрат түбірі бар ма?
4) Оң санның неше квадрат түбірі бар?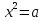 ,
, 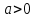 теңдеуінің неше түбірі бар
теңдеуінің неше түбірі бар
5) Арифметикалық квадрат түбір белгісінің басқаша атауы?
6) Квадрат түбірдің қасиеттерін ата?
7) Бөлшектің бөлімін иррационалдықтан босату дегеніміз?
8) Күрделі түбірлерді(радикалдарды)түрлендіру дегеніміз?
Жауаптары:
1)Теріс емес санның оң(теріс емес) квадрат түбірін оның арифметикалық квадрат түбірі деп атайды. Анықтама бойынша: 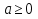 болғанда
болғанда 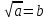 теңдігі орындалу үшін
теңдігі орындалу үшін 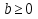 және
және 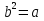 шарттары орындалу қажет.
шарттары орындалу қажет.
2)Берілген саннан квадрат түбір шығару үшін, ол сан теріс сан болмауы қажет, яғни бұл сан оң сан немесе нөлге тең болу қажет.
3) Түбірі жоқ. Себебі, егер  болса, онда
болса, онда 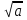 - өрнегінің мағынасы болмайды. Өйткені, кез келген санның квадраты теріс емес сан. Мысалы:
- өрнегінің мағынасы болмайды. Өйткені, кез келген санның квадраты теріс емес сан. Мысалы: 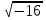 ;
; 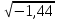 .
.
4)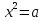 ,
, 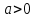 теңдеуінің екі түбірі бар:
теңдеуінің екі түбірі бар: 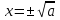 немесе
немесе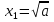 және
және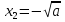 .
.
5)Арифметикалық квадрат түбір белгісінің басқаша атауы радикал деп аталады. Латын тілінен аударғанда «Radix» - түбір деген сөзінен шыққан.
6)Квадрат түбірдің қасиеттері:
1)Теорема1:Көбейтіндінің квадрат түбірі көбейткіштердің квадрат түбірлерінің көбейтіндісіне тең, яғни а≥0 және в≥0 болса, онда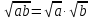 .
.
2) Теорема 2: Бөліндінің квадрат түбірі квадрат түбірлердің қатынасына тең, егер а≥0 және в>0 болса, онда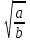 =
=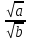 .
.
3) Теорема3: Кез келген х үшін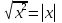 теңдігі орындалады.
теңдігі орындалады.
7) Бөлшектің бөлімін иррационалдықтан босату дегеніміз- берілген бөлшекті түрлендіру арқылы бөлімі рационал сан болатын бөлшекке келтіру.
8) Күрделі түбірлерді (радикалдарды) түрлендіру дегеніміз- сыртқы түбірден құтылу болып табылады.
3. Жаңа сабақ
Балалар, келесітұжырымдарға назар аударайық:«Математиканың өз тілі бар, ол-формулалар», - Софья Ковалевская.
«Формула -дегеніміз қандайда бір әріптер арқылы өрнектелген тепе-теңдік», - Н.Я. Виленкин. Яғни, математикада формулалардың маңызы зор. Онда, келесі күрделі радикал формулаларын берейік:
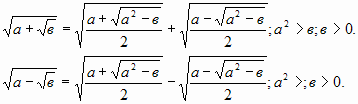
«Адамның денесі ғана емес, сонымен қатар миы да жаттығуды талап етеді. Математика ми гимнастикасы», - А.В. Суворов.
Онда, балалар келесі есептерді шығарайық:
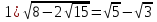 2)
2) 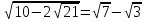
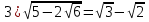 4)
4)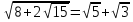
5) 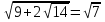 +
+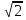 6)
6)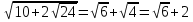
1. Өрнектің мәнін тап: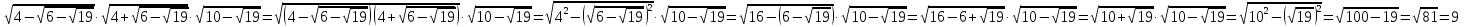
4.Сабақты бекіту: Қосарланған радикалдарды түрлендіруге болады:
1) Түбір астындағы өрнекті толық квадратқа келтіру арқылы;
2) 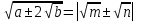
m+n m n
n
3) Күрделі радикал формулаларын қолдану арқылы есептеуге болады.
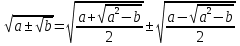 ,
,  ,
, 
4) «Дидактикалық материалдар» кітапшасынан есептер шығарту
5. Сабақты қорытындылау:
«Мейлі, сені бір түгелі, жүз ұстаз баулысын, - егер өзіңді өзің көндірмесең, өзің өзіңнен талап ете білмесең олар да дәрменсіз», - деген тұжырым арқылы сабақ түйінделеді.
6. Үй тапсырма:1) А.Әбілқасымова: № 95 (1,2,3);
2)Шыныбеков Ә.Н.: № 217; № 227,
3) З.Жумагулова (Дид. материал) №2, (бет: 38);
7. Бағалау
8. Рефлекция кезеңі (сабақ туралы нәтиже шығару): Балалар бүгінгі сабақ несімен ұнады?


