- Преподавателю
- Математика
- Решение рациональных уравнений методом введения новой переменной
Решение рациональных уравнений методом введения новой переменной
| Раздел | Математика |
| Класс | - |
| Тип | Другие методич. материалы |
| Автор | Куц Ф.И. |
| Дата | 25.02.2014 |
| Формат | docx |
| Изображения | Есть |
Муниципальное бюджетное образовательное учреждение
дополнительного образования детей дом детского творчества
г. Зверева Ростовской области
Решение рациональных уравнений
методом введения новой переменной.
Работа педагога дополнительного
образования
Куца Фёдора Ивановича
г. Зверево
2014г.
Рациональное уравнение - это уравнение вида f(x) = g(x), где f(x) и g(x) - рациональные выражения.
Содержание:
1) Биквадратные уравнения.
2) Замена переменных по явным признакам.
3)Уравнения вида (ax + b)(ax + c)(ax + d)(ax + e) = k, где b + e = c + d.
4) Возвратные уравнения четвертой степени.
5) Обобщенные возвратные уравнения четвертой степени.
6) Уравнения, содержащие переменную величину под знаком модуля.
7) Уравнения вида (ax2 + bx + c1)(ax2 + bx + c2) = k.
8) Уравнения вида (ax2 + b1x + c)(ax2 + b2x + c) = k x2.
9) Уравнения вида (ax2 + b1x + c1)(ax2 + b2x + c2) = k x2.
10) Уравнения вида А4(х) + В4(х) = С.
11) Уравнения с отрицательной степенью неизвестного.
12) Уравнения с взаимообратными выражениями.
13) Использование свойств пропорции.
14) Приведение к общему знаменателю.
1) Биквадратные уравнения.
Биквадратным называется уравнение вида ах4 + bх2 + с = 0.
Биквадратные уравнения решаются методом введения новой переменной: положив x2 = t (t > 0),
придём к квадратному уравнению at2 + bt + c = 0.
Пример 1. 2х4 + 3х2 - 5 = 0.
Решение. Введем новую переменную x2 = t, где t > 0, получим уравнение 2t2 + 3t -5 = 0.
Решив его, получим корни: t1 =1, t2 = - 5.
t2 = - 5 условию t > 0 не удовлетворяет.
Далее решаем уравнение х2 = 1, его корни х1,2 = ± 1.
Ответ: х1,2 = ± 1.
Пример 2. 4х4 - 17х2 -15 = 0.
Решение. Введем новую переменную x2 = t, где t > 0, получим уравнение 4t2 - 17t - 15 = 0.
D = b2 - 4ac = (- 17)2 - 4∙4∙ (- 15) = 529.
t1,2 = 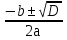 =
=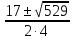 =
=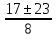 .
.
t1 = 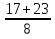 =
= 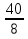 = 5;
= 5;
t2 =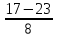 = -
= - 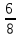 = -
= -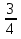 условию t > 0 не удовлетворяет.
условию t > 0 не удовлетворяет.
Далее решаем уравнение х2 = 5, его корни х1,2 = ± 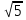 .
.
Ответ: х1,2 = ± 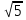 .
.
Пример 3. х4 - 37х2 + 36 = 0.
Решение. Введем новую переменную x2 = t, получим уравнение t2 - 37t + 36 = 0.
Решив его, получим корни: t1 =1, t2 = 36.
Далее решаем уравнения: 1) х2 = 1, х1,2 = ± 1.
2) х2 = 36, х1,2 = ± 6.
Ответ: х1,2 = ± 1; х3,4 = ± 6.
Пример 4. х4 + 37х2 +36 = 0.
Решение. Введем новую переменную x2 = t, где t > 0, получим уравнение t2 + 37t + 36 = 0.
Решив его, получим корни: t1 = -1, t2 = -36; которые не удовлетворяют условию t > 0,
следовательно, исходное уравнение корней не имеет.
Ответ. Корней нет.
2) Замена переменных по явным признакам.
Пример 5. (х2 - 2х)2 - 2(х2 - 2х) - 3 = 0.
Решение. Введя новую переменную х2 - 2х = t, получим уравнение t2 - 2t - 3 = 0, решив
которое, имеем: t1 = - 1, t2 = 3.
Далее решаем уравнения: 1) х2 - 2х = - 1; х2 - 2х + 1 = 0; (х - 1)2 = 0; х = 1. 2) х2 - 2х = 3; х2 - 2х - 3 = 0; по т., обр.т. Виета: х1 = - 1, х2 = 3.
Ответ: х1 = 1; х2 = - 1, х3= 3.
Пример 6. (2х2 + 3х -1)2 - 10х2 - 15х + 9 = 0.
Решение. (2х2 + 3х -1)2 -10х2 -15х + 5 + 4 = 0;
(2х2 + 3х -1)2 -5(2х2 + 3х - 1) + 4 = 0.
Введем новую переменную 2x2 +3х -1= t, получим уравнение t2 -5t + 4 = 0.
Решив его, получим корни: t1 =1, t2 = 4.
Далее решаем уравнения: 1) 2x2 + 3х -1 = 1; 2x2 + 3х - 2 = 0,его корни х1 = - 2; х2 = 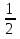 ,
,
2) 2x2 + 3х -1 = 4; 2x2 + 3х - 5 = 0,его корни х1 = 1; х2 = - 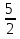 .
.
Корни исходного уравнения: х1 = 1; х2 = -2 х3 = 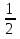 , х4 = -
, х4 = - 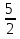 .
.
Ответ: х1 = 1; х2 = -2 х3 = 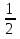 , х4 = -
, х4 = - 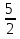 .
.
Пример 7. (х2 - 6х)2 - 2(х - 3)2 = 81.
Решение. Заметив, что х2 - 6х = (х - 3)2 - 9 и положив (х - 3)2 = у, где у ≥ 0, получим:
( у - 9)2 - 2у = 81, у2 - 18у + 81 - 2у - 81 = 0, у2 - 20у = 0, у (у - 20) = 0.
у1 = 0, у2 = 20.
Возвращаясь к переменной х, рассмотрим два случая:
1) (х - 3)2 = 0, х - 3 = 0, х = 3.
2) (х - 3)2 = 20, х - 3 = ±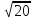 , х1,2 = 3 ±
, х1,2 = 3 ±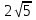 .
.
Корни исходного уравнения: х1 = 3, х2,3 = 3 ±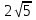 .
.
Ответ: х1 = 3, х2,3 = 3 ±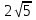 .
.
3)Уравнения вида (ax + b)(ax + c)(ax + d)(ax + e) = k, где b + e = c + d.
Пример 8. (х + 1)(х + 2)(х + 3)(х + 4) = 24.
Решение. Группируем скобки так, чтобы суммы свободных слагаемых были равными:
1 + 4 = 2 + 3.
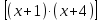 ∙
∙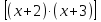 = 0.
= 0.
Перемножив вначале в первой квадратной скобке, а затем второй, имеем:
(х2 + 5х + 4)(х2 + 5х + 6) = 24.
Введя новую переменную x2 + 5х = t, получим уравнение (t + 4)(t + 6) = 24, откуда
t2 + 10t + 24 = 24; t2 + 10t = 0; (t + 10) t = 0.
t1 = - 10, t2 = 0.
Возвращаясь к переменной х, рассмотрим два случая:
1)х2 + 5х = - 10; х2 + 5х + 10 = 0. D = b2 - 4ac = 52 - 4∙1∙10 = - 15. Т.к. D < 0, то уравнение корней не имеет.
2)х2 + 5х = 0; х (х + 5) = 0,
х1 = 0, х2 = - 5.
Корни исходного уравнения: х1 = 0; х2 = - 5.
Ответ: х1 = 0; х2 = - 5.
Пример 9. х (х + 1)(х + 2)(х + 3) = 8.
Решение. Группируем множители так, чтобы суммы свободных слагаемых были равными:
0+3 = 1+2.
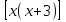 ∙
∙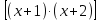 = 8.
= 8.
Перемножив в начале первый и второй множители, а затем третью и четвертую скобки имеем: (х2 + 3х) (х2 + 3х + 2) = 8.
Введя новую переменную x2 + 3х = t, получим уравнение t (t + 2) = 8, откуда
t2 + 2t = 8; t2 + 2t - 8 = 0. Решив квадратное уравнение, имеем корни: t1 = 2, t2 = - 4.
Возвращаясь к переменной х, рассмотрим два случая:
1) х2 + 3х = 2, х2 + 3х - 2 = 0. D = b2 - 4ac = 32 - 4∙1∙(- 2) = 17 .
х1,2 = 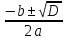 =
=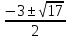 .
.
2) х2 + 3х = - 4, х2 + 3х + 4 = 0. D = b2 - 4ac = 32 - 4∙1∙4 = - 7. Т.к. D < 0, то уравнение корней не имеет.
Корни исходного уравнения: х1,2 = 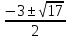 .
.
Ответ: х1,2 = 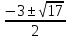 .
.
Пример 10. (2х + 3)(2х + 5)(2х + 7)(2х + 9) = 384. (1)
Решение. Если обозначить у = 2х +3, то исходное уравнение (1) примет вид:
у (у + 2) (у + 4) (у + 6) = 384.
Группируем множители так, чтобы суммы свободных слагаемых были равными: 0+6 = 2+4.
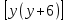 ∙
∙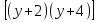 = 384.
= 384.
Перемножив в начале первый и второй множители, а затем третью и четвертую скобки имеем: (у2 + 6у) (у2 + 6у + 8) = 384. (2)
Если теперь обозначить z = у2 + 6у,
то последнее уравнение (2) запишется в виде:
z(z + 8) = 384,
z2 + 8z - 384 = 0. (3)
Решим уравнение (3):
z 1,2 = - 4 ±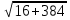 = - 4 ±
= - 4 ±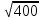 = - 4 ± 20.
= - 4 ± 20.
z1 = - 24, z2 = 16.
Возвращаясь к переменной у, рассмотрим два случая:
1) у2 + 6у = - 24.
у2 + 6у + 24 = 0, корней нет, т.к. D = b2 - 4ac = 36 - 96 = - 60 < 0.
2) у2 + 6у = 16.
у2 + 6у - 16 = 0, откуда у1 = - 8, у2 = 2.
Возвращаясь к переменной х, рассмотрим два случая:
1) 2х + 3 = - 8, откуда х = - 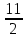 .
.
2) 2х + 3 = 2, откуда х = - 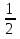 .
.
Корни исходного уравнения: х1 = - 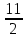 , х2 = -
, х2 = - 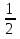 .
.
Ответ: х1 = - 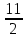 , х2 = -
, х2 = - 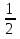 .
.
4) Возвратные уравнения четвертой степени.
Возвратным называется уравнение вида: ах4 + bх3 + сх2 ± bх + а = 0.
х = 0 не является корнем данного уравнения, поэтому можно разделить уравнение на х2 без потери корней, при этом получаем уравнение ах2 + bх + с ± 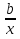 +
+ 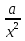 = 0, которое сводится к квадратному заменой х ±
= 0, которое сводится к квадратному заменой х ± 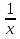 = t.
= t.
Пример 11. х4 - 2х3 - 22 х2 - 2х + 1 = 0.
Решение. Т.к. х = 0 не является корнем данного уравнения, то разделим обе части уравнение на х2: х2 - 2х - 22 - 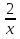 +
+ 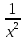 = 0; (х2 +
= 0; (х2 + 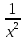 ) - 2∙(х +
) - 2∙(х + 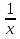 ) - 22 = 0.
) - 22 = 0.
Сделаем замену х + 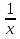 = t, тогда х2 + 2 +
= t, тогда х2 + 2 + 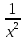 = t2, откуда х2+
= t2, откуда х2+ 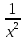 = t2 - 2 и уравнение сводится к виду: t2 - 2 - 2t - 22 = 0 , т.е. t2- 2t - 24 = 0, откуда t1 = 6, t2 = - 4.
= t2 - 2 и уравнение сводится к виду: t2 - 2 - 2t - 22 = 0 , т.е. t2- 2t - 24 = 0, откуда t1 = 6, t2 = - 4.
Возвращаясь к переменной х, рассмотрим два случая:
1) х + 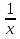 = 6, откуда х2 - 6х + 1 = 0, х1,2 = 3 ±
= 6, откуда х2 - 6х + 1 = 0, х1,2 = 3 ± 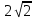 .
.
2) х + 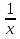 = - 4, откуда х2 + 4х + 1 = 0, х1,2 = - 2 ±
= - 4, откуда х2 + 4х + 1 = 0, х1,2 = - 2 ± 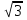 .
.
Корни исходного уравнения: х1,2 =3 ± 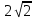 , х3,4 = - 2 ±
, х3,4 = - 2 ± 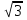 .
.
Ответ: х1,2 =3 ± 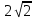 , х3,4 = - 2 ±
, х3,4 = - 2 ± 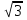 .
.
Пример 12. 2х4 - 15х3 +14 х2 + 15х + 2 = 0.
Решение. Т.к. х = 0 не является корнем данного уравнения, то разделим обе части уравнение на х2: 2х2 - 15х + 14 + 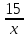 +
+ 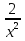 = 0; 2 (х2+
= 0; 2 (х2+ 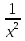 ) - 15(х -
) - 15(х - 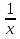 ) + 14 = 0.
) + 14 = 0.
Сделаем замену x - 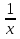 = t, тогда х2 - 2 +
= t, тогда х2 - 2 + 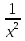 = t2, откуда х2 +
= t2, откуда х2 + 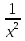 = t2 + 2 и данное уравнение сводится к виду 2(t2 + 2) - 15t + 14 = 0 , т.е. 2t2- 15t + 18 = 0.
= t2 + 2 и данное уравнение сводится к виду 2(t2 + 2) - 15t + 14 = 0 , т.е. 2t2- 15t + 18 = 0.
D = b2 - 4ac = (-15)2 - 4∙2∙18 = 225 - 144 = 81.
х1,2 = 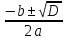 =
=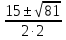 =
=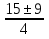 .
.
х1 =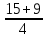 =
=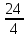 = 6, х2 =
= 6, х2 = 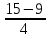 =
=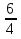 =
=  .
.
Возвращаясь к переменной х, рассмотрим два случая:
1) х - 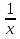 = 6, откуда х2 - 6х - 1 = 0, х1,2 = 3 ±
= 6, откуда х2 - 6х - 1 = 0, х1,2 = 3 ± 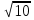 .
.
2) х - 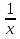 =
=  , откуда 2х2 - 3х - 2 = 0, х1 = 2, х2 = -
, откуда 2х2 - 3х - 2 = 0, х1 = 2, х2 = - 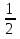 .
.
Корни исходного уравнения: х1,2 =3 ± 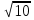 , х3 = 2, х4 = -
, х3 = 2, х4 = - 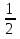 .
.
Ответ: х1,2 =3 ± 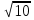 , х3 = 2, х4 = -
, х3 = 2, х4 = - 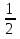 .
.
5) Обобщенные возвратные уравнения четвертой степени.
Обобщенным возвратным называется уравнение вида: ах4 + bх3 + сх2 ± dх + e = 0,
где 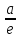 =
= 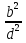 .
.
Пример 13. 3x4 - 2x3 - 31x2 + 10x +75 = 0.
Решение. Т.к. х = 0 не является корнем данного уравнения, то разделим обе части уравнения на
х2: 3x2 - 2x - 31 + 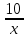 +
+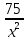 = 0; (3x2 +
= 0; (3x2 +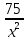 ) - (2x -
) - (2x - 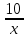 ) - 31 = 0; 3(x2 +
) - 31 = 0; 3(x2 +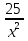 ) - 2(x -
) - 2(x - 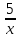 ) - 31 = 0.
) - 31 = 0.
Пусть t = x - 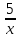 , тогда t2 = х2 - 10 +
, тогда t2 = х2 - 10 + 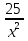 , откуда x2 +
, откуда x2 +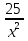 = t2 + 10 и данное уравнение сводится к
= t2 + 10 и данное уравнение сводится к
виду: 3(t2 +10) - 2t - 31 = 0, т. е. 3t2 - 2t - 1 = 0.
t1= 1, t2 = -  .
.
Возвращаясь к переменной х, рассмотрим два случая:
1) x - 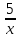 = 1, откуда x2 - x - 5 = 0.
= 1, откуда x2 - x - 5 = 0.
х1,2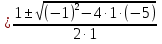 =
= 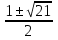 .
.
2) x - 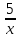 = -
= -  , откуда 3x2 + x - 15 = 0.
, откуда 3x2 + x - 15 = 0.
х1,2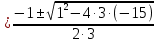 =
= 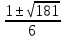 .
.
Корни исходного уравнения: х1,2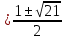 , х3,4 =
, х3,4 =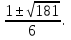
Ответ: х1,2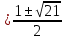 , х3,4 =
, х3,4 =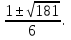
6) Уравнения, содержащие переменную величину под знаком модуля.
Пример 14. х2 +2|х| - 3 = 0.
Решение. Воспользовавшись тем, что х2 = |х|2, сделаем замену |х| = у, где у ≥ 0.
Получим у2 + 2у - 3 = 0, откуда у1 = 1, у2 = - 3.
у2 = - 3 не удовлетворяет условию у ≥ 0.
Возвращаясь к переменной х, рассмотрим уравнение
|х|= 1, откуда х1,2 = ±1.
Ответ: х1,2 = ±1.
Пример 15. х2 + 4х - 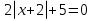
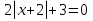 .
.
Решение. Чтобы можно было сделать замену, надо получить полный квадрат.
х2 + 4х + 4 - 2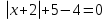
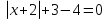 .
.
(х + 2)2 -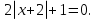
Замена: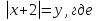 у ≥ 0.
у ≥ 0.
у2 - 2у + 1 = 0,
(у - 1)2 = 0,
у = 1.
Возвращаясь к переменной х, рассмотрим уравнение
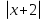 = 1, откуда х + 2 = 1 или х + 2 = - 1, т.е. х1 = -1, х2 = -3.
= 1, откуда х + 2 = 1 или х + 2 = - 1, т.е. х1 = -1, х2 = -3.
Ответ: х1 = -1, х2 = -3.
7) Уравнения вида (ax2 + bx + c1)(ax2 + bx + c2) = k.
Пример 16. (x2 - 3x + 1)(x2 - 3x + 3) = 3.
Введем новую переменную x2 - 3х + 1 = t, получим уравнение t (t +2) = 3, откуда t2 + 2t - 3 = 0.
Решив его, получим корни: t1 = 1, t2 = -3.
Далее решаем уравнения: 1) x2 - 3х + 1 = 1; x2 - 3х = 0, его корни х1 = 0; х2 = 3.
2) x2 - 3х +1 = - 3; x2 - 3х + 4= 0.
D = b2 - 4ac = (- 3)2 - 4∙1∙4 = - 7. Т.к. D < 0, то уравнение корней не имеет.
Корни исходного уравнения: х1 = 0; х2 = 3.
Ответ: х1 = 0; х2 = 3.
8) Уравнения вида (ax2 + b1x + c)(ax2 + b2x + c) = k x2.
Пример 17. (2x2 - 3x + 1)(2x2 + 5x + 1) = 9x2.
Решение. х = 0 не является корнем данного уравнения. Разделим обе части уравнения на х2 ≠ 0.
(2x - 3 + 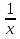 )(2x + 5 +
)(2x + 5 + 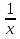 ) = 9. Введем замену 2x - 3 +
) = 9. Введем замену 2x - 3 + 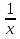 = у, тогда 2x + 5 +
= у, тогда 2x + 5 + 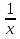 = у + 8.
= у + 8.
Данное уравнение примет вид: у (у + 8) = 9; у2 + 8у - 9 = 0. Откуда у1 =1, у2 = - 9.
Возвращаясь к переменной х, рассмотрим два случая:
1) 2x - 3 + 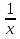 = 1; 2x2 - 3x + 1 = х; 2x2 - 4x + 1 = 0.
= 1; 2x2 - 3x + 1 = х; 2x2 - 4x + 1 = 0.
х1,2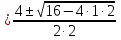 =
= 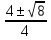 =
= 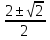 .
.
2) 2x - 3 + 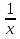 = - 9; 2x2 - 3x + 1 = - 9х; 2x2 + 6x + 1 = 0.
= - 9; 2x2 - 3x + 1 = - 9х; 2x2 + 6x + 1 = 0.
х1,2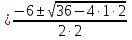 =
= 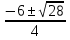 =
= 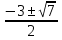 .
.
Корни исходного уравнения: х1,2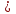
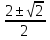 , х3,4
, х3,4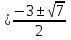 .
.
Ответ: х1,2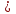
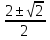 , х3,4
, х3,4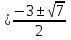 .
.
9) Уравнения вида (ax2 + b1x + c1)(ax2 + b2x + c2) = k x2.
Пример 18. (х2 + 5х + 6)(х2 + 20х + 96) = 4х2.
Решение. Разложим квадратные трехчлены на линейные множители:
х2 + 5х + 6 = (х + 2)(х + 3); х2 + 20х + 96 = (х + 8)(х + 12).
Исходное уравнение примет вид: (х + 2) (х + 3) (х + 8) (х + 12) = 4х2.
Группируем скобки так, чтобы произведения свободных слагаемых были равными:
2∙12 = 3∙8.Перемножим попарно первую и четвертую, вторую и третью скобки:
( х2 + 14х + 24) (х2 + 11х + 24) = 4х2.
х = 0 не является корнем исходного уравнения, следовательно, поделив на х2 ≠ 0
обе части уравнения, имеем: (х + 14 + 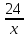 ) (х + 11 +
) (х + 11 + 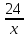 ) = 4.
) = 4.
Обозначив х + 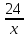 = у, получим уравнение: (у + 14) (у +11) = 4,
= у, получим уравнение: (у + 14) (у +11) = 4,
у2 + 25у +154 = 4; у2 + 25у +150 = 0.
у1 = -10, у2 = - 15.
Возвращаясь к переменной х, рассмотрим два случая:
1) х + 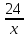 = -10; х2 + 10х + 24 = 0. х1 = - 4, х2 = - 6.
= -10; х2 + 10х + 24 = 0. х1 = - 4, х2 = - 6.
2) х + 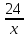 = -15; х2 + 15х + 24 = 0. х1,2
= -15; х2 + 15х + 24 = 0. х1,2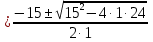 =
= 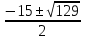 .
.
Корни исходного уравнения: х1 = - 4, х2 = - 6, х3,4= 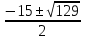 .
.
Ответ: х1 = - 4, х2 = - 6, х3,4= 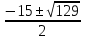 .
.
10) Уравнения вида А4(х) + В4(х) = С.
Уравнения вида А4(х) + В4(х) = С решаются заменой t = 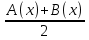 .
.
Пример 19. (х + 3)4 + (х + 1)4 = 20.
Решение. Введем замену t = 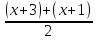 = х + 2, тогда х = t - 2.
= х + 2, тогда х = t - 2.
Сделаем замену (t +1)4 + (t -1)4 = 20.
Теперь возведем каждую скобку в четвертую степень, используя треугольник Паскаля:
t4 + 4t3 + 6t2 + 4t +1+ t4- 4t3 + 6t2 - 4t + 1 = 20.
Упростим уравнение, получим биквадратное уравнение относительно t:
2t4 + 12t2 - 18 = 0,
t4 + 6t2 - 9 = 0.
Пусть у = t2 , y > 0, тогда t1,2 = ±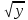 .
.
у2 + 6у - 9 = 0, у1,2 = -3 ± 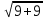 = -3 ± 3
= -3 ± 3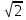 .
.
у1= -3 + 3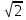 .
.
у2= -3 - 3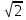 не удовлетворяет условию у > 0.
не удовлетворяет условию у > 0.
Следовательно, t1,2 = ±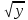 = ±
= ±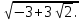
Откуда х1,2 = ±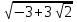 - 2.
- 2.
Ответ: х1,2 = - 2 ±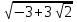 .
.
11) Уравнения с отрицательной степенью неизвестного.
Пример 20. 48 - 14х-1 + х-2 = 0.
Решение. Пусть t = x-1, тогда t2 = x-2, получим уравнение: t2 - 14t + 48 + 0.
Корни уравнения: t1= 8, t2 = 6.
Возвращаясь к переменной х, имеем:
1) x-1 = 8, откуда x1 = 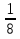 .
.
2) x-1 = 6, откуда x2 = 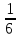 .
.
Корни исходного уравнения: x1 = 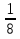 , x2 =
, x2 = 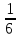 .
.
Ответ: x1 = 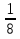 , x2 =
, x2 = 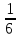 .
.
12) Уравнения с взаимообратными выражениями.
Пример 21. 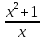 +
+ 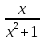 = 2,9.
= 2,9.
Решение. Пусть t = 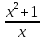 , (t ≠ 0), тогда
, (t ≠ 0), тогда 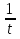 =
= 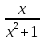 , получим уравнение: t +
, получим уравнение: t + 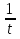 = 2,9.
= 2,9.
Откуда: t2 - 2,9t + 1 = 0.
D = b2 - 4ac = (-2,9)2 - 4∙1∙1= 8,41 - 4 = 4,41.
t1,2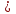
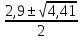 =
= 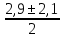 .
.
t1 = 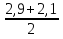 =
= 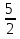 , t2 =
, t2 = 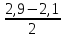 =
= 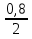 =
= 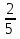 .
.
Возвращаясь к переменной х, имеем:
1) 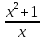 =
= 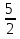 ; 2(х2 + 1) = 5х; 2х2 + 2 - 5х = 0; 2х2 - 5х + 2 = 0.
; 2(х2 + 1) = 5х; 2х2 + 2 - 5х = 0; 2х2 - 5х + 2 = 0.
Откуда: x1 = 2, x2 = 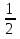 .
.
2) ) 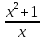 =
= 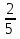 ; 5(х2 + 1) = 2х; 5х2 + 5 - 2х = 0; 5х2 - 2х + 5 = 0.
; 5(х2 + 1) = 2х; 5х2 + 5 - 2х = 0; 5х2 - 2х + 5 = 0.
D = b2 - 4ac = (-2)2 - 4∙5∙5= 4 - 100 = - 96 < 0. Корней нет.
Корни исходного уравнения: x1 = 2, x2 = 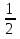 .
.
Ответ: x1 = 2, x2 = 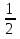
13) Использование свойств пропорции.
Пример 22. х2 + х + 1 = 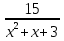 .
.
Решение. Пусть t = х2 + х + 1, тогда получаем уравнение: t = 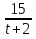 , откуда по свойствам пропорции имеем: t (t+ 2) = 15; t2 + 2t - 15 = 0.
, откуда по свойствам пропорции имеем: t (t+ 2) = 15; t2 + 2t - 15 = 0.
По теореме, обратной теореме Виета, t1 = - 5, t2 = 3.
Возвращаясь к переменной х, имеем:
1) х2 + х + 1 = - 5; х2 + х + 6 = 0.
D = b2 - 4ac =12 - 4∙1∙6 = - 23. Корней нет.
2) х2 + х + 1 = 3; х2 + х - 2 = 0. х1 = 1, х2 = -2.
При х1 = 1 и х2 = -2 знаменатель х2 + х + 3 ≠ 0, следовательно, х1 = 1 и х2 = -2 корни исходного уравнения.
Ответ: х1 = 1 , х2 = -2.
14) Приведение к общему знаменателю.
Пример 23.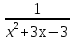 +
+ 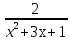 =
= 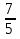 .
.
Решение. Пусть t = х2 + 3х, тогда 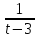 +
+ 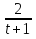 =
= 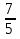 ;
; 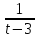 +
+ 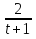 -
- 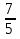 = 0;
= 0; 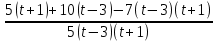 = 0;
= 0;
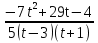 = 0; 5(t - 3)(t +1) ≠ 0.
= 0; 5(t - 3)(t +1) ≠ 0.
- 7t2 + 29t - 4 = 0; 7t2 - 29t + 4 = 0.
D = b2 - 4ac = (-29)2 - 4∙7∙4 = 841 - 112 = 729.
t1,2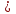
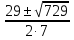 =
= 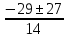 , t1 =
, t1 = 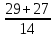 = 4, t2 =
= 4, t2 = 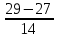 =
= 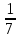 .
.
Оба корня удовлетворяют условию 5(t - 3)(t +1) ≠ 0.
Возвращаясь к переменной х, имеем:
1) х2 + 3х = 4; х2 + 3х - 4 = 0. х1 = 1, х2 = - 4.
2) х2 + 3х = 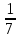 ; 7х2 + 21х = 1; 7х2 + 21х - 1= 0.
; 7х2 + 21х = 1; 7х2 + 21х - 1= 0.
D = b2 - 4ac = 212 - 4∙7∙(-1)= 441 +28 = 469.
х1,2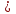
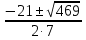 =
= 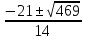 .
.
Корни исходного уравнения: х1 = 1, х2 = - 4, х3,4 =
= 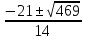 .
.
Ответ: х1 = 1, х2 = - 4, х3,4 =
= 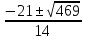 .
.
Литература:
Математика. Большой справочник для школьников и поступающих в вузы. М."Дрофа",1999г.
Математика. Учебное пособие для слушателей подготовительных курсов. Новочеркасск. НГМА,2003г.
Алгебра и начала анализа.10-11 классы: учеб. для общеобразовательных учреждений: базовый уровень / Ш.А. Алимов и др/-М. просвещение,2010г.
Алгебра. ЕГЭ: шаг за шагом /А.А. Черняк, Ж.А.Черняк,- Волгоград: Учитель,2012.
Математика. ЕГЭ- 2006,вступительные экзамены. Пособие для самостоятельной подготовки. Ростов-на-Дону, Легион, 2005.
Алгебра. В 2ч.Учебник для учащихся 8 класса общеобразовательных учреждений/ А.Г.Мордкович. - 10 -е изд. , стер. - М.: Мнемозина, 2008


