- Преподавателю
- Математика
- Дифференциальные уравнения для групп СПО
Дифференциальные уравнения для групп СПО
| Раздел | Математика |
| Класс | - |
| Тип | Конспекты |
| Автор | Алтухова В.А. |
| Дата | 24.10.2014 |
| Формат | docx |
| Изображения | Есть |

 Министерство просвещения ПМР
Министерство просвещения ПМР
ГОУ СПО « Рыбницкий политехнический техникум»
ПОСОБИЕ
ПО МАТЕМАТИКЕ
ТЕМА «Дифференциальные уравнения»
( для студентов и учащихся СПО)
Разработала - Томина Н.А. -преподаватель математики
высшей квалификационной
категории.
Рассмотрено и одобрено Рассмотрено и одобрено
на заседании методсовета на заседании ЦМК преподавателей
ГОУ СПО «РПТ» естественно-научных дисциплин
Протокол №_5 от 19.05.2014 г Протокол № 6 от 12.01. 2014 г.
Председатель методсовета Председатель ЦМК
___________Т.С.Штырбул ___________ А.Б.Женская
г.Рыбница
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ.
Введение
Многие физические законы, которым подчиняются те или иные явления, записываются в виде математического уравнения, выражающего определенную зависимость между какими-то величинами. Часто речь идет о соотношении между величинами, изменяющимися с течением времени, например экономичность двигателя, измеряемая расстоянием, которое автомашина может проехать на одном литре горючего, зависит от скорости движения автомашины. Соответствующее уравнение содержит одну или несколько функций и их производных и называется дифференциальным уравнением. (Темп изменения расстояния со временем определяется скоростью; следовательно, скорость - производная от расстояния; аналогично, ускорение - производная от скорости, так как ускорение задает темп изменения скорости со временем.) Большое значение, которое имеют дифференциальные уравнения для математики и особенно дляее приложений, объясняются тем, что к решению таких уравнений сводится исследование многих физических и технических задач. Дифференциальные уравнения играют существенную роль и в других науках, таких, как биология, экономика и электротехника; в действительности, они возникают везде, где есть необходимость количественного (числового) описания явлений (коль скоро окружающий мир изменяется во времени, а условия изменяются от одного места к другому).
В математике дифференциальные уравнения занимают особое место. Дело в том, что математическое исследование самых разнообразных явлений, происходящих в природе, часто приводит к решению таких уравнений, поскольку сами законы, которым подчиняется то или иное явление, записываются в виде дифференциальных уравнений.
Дифференциальные уравнения возникают во многих областях прикладной математики, физики, механики, техники и т.д. С их помощью описываются практически любые задачи динамики машин и механизмов. Существует множество методов решения дифференциальных уравнений через элементарные или специальные функции.
1. Цель дисциплины состоит в получении студентами прочных теоретических знаний и твердых практических навыков в области высшей математики. Такая подготовка необходима для успешного усвоения многих специальных дисциплин. Исследование многих процессов в промышленной технологии и экономике связано с разработкой соответствующих математических моделей, для успешного исследования которых будущий специалист должен получить достаточно серьёзную математическую подготовку.
2. Задачей дисциплины является изучение фундаментальных разделов высшей математики, которое составит основу математических знаний студента. Прочное усвоение современных математических методов позволит будущему специалисту решать в своей повседневной деятельности актуальные задачи практики, понимать написанные на современном научном уровне результаты других исследований и тем самым совершенствовать свои профессиональные навыки.
Примеры.
Следующие примеры позволяют лучше понять, как различные задачи формулируются на языке дифференциальных уравнений.
1) Закон распада некоторых радиоактивных веществ состоит в том, что скорость распада пропорциональна наличному количеству этого вещества. Если x - количество вещества в некоторый момент времени t, то этот закон можно записать так:
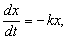
где 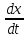 - скорость распада, а k - некоторая положительная постоянная, характеризующая данное вещество. (Знак «минус» в правой части указывает на то, что x убывает со временем; знак «плюс», подразумеваемый всегда, когда знак явно не указан, означал бы, что x возрастает со временем.)
- скорость распада, а k - некоторая положительная постоянная, характеризующая данное вещество. (Знак «минус» в правой части указывает на то, что x убывает со временем; знак «плюс», подразумеваемый всегда, когда знак явно не указан, означал бы, что x возрастает со временем.)
2) Емкость первоначально содержит 10 кг соли, растворенной в 100 м3воды. Если чистая вода вливается в емкость со скоростью 1 м3 в минуту и равномерно перемешивается с раствором, а образовавшийся раствор вытекает из емкости с такой же скоростью, то сколько соли окажется в емкости в любой последующий момент времени? Если x - количество соли (в кг) в емкости в момент времени t, то в любой момент времени t в 1м3раствора в емкости содержится 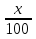 кг соли; поэтому количество соли убывает со скоростью
кг соли; поэтому количество соли убывает со скоростью 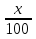 кг/мин, или
кг/мин, или
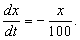
3) Пусть на тело массы m, подвешенное к концу пружины, действует возвращающая сила, пропорциональная величине растяжения пружины. Пусть x - величина отклонения тела от положения равновесия. Тогда по второму закону Ньютона, который утверждает, что ускорение (вторая производная от x по времени, обозначаемая d 2x/dt 2) пропорционально силе:
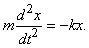
Правая часть стоит со знаком минус потому, что возвращающая сила уменьшает растяжение пружины.
4) Закон охлаждения тел утверждает, что количество тепла в теле убывает пропорционально разности температур тела и окружающей среды. Если чашка кофе, разогретого до температуры 90° С находится в помещении, температура в котором равна 20° С, то
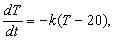
где T - температура кофе в момент времени t.
5) Министр иностранных дел государстваБлефуску утверждает, что принятаяЛиллипутией программа вооружений вынуждает его страну увеличить военные расходы на сколько это только возможно. С аналогичными заявлениями выступает и министр иностранных дел Лиллипутии. Возникающую в результате ситуацию (в простейшей интерпретации) можно точно описать двумя дифференциальными уравнениями. Пусть x и y - расходы на вооружение Лиллипутиии Блефуску. Предполагая, что Лиллипутия увеличивает свои расходы на вооружение со скоростью,пропорциональной скорости увеличения расходов на вооружение Блефуску, и наоборот, получаем:
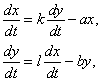
где члены -ax и -by описывают военные расходы каждой из стран,
k и l - положительные постоянные. (Эту задачу впервые таким образом сформулировал в 1939 Л.Ричардсон.)
После того, как задача записана на языке дифференциальных уравнений, следует попытаться их решить, т.е. найти величины,скоростиизменения которых входят в уравнения
Первоначальная математическая формулировка физической задачи обычно содержит упрощающие предположения; критерием их разумности может служить степень согласованности математического решения с имеющимися наблюдениями.
Основные понятия и определения.
Определение:
1.Уравнения, в которых неизвестными являются функции и в которые входят не только сами функции, но и их производные, называютсядифференциальными уравнениями.
2. Если в уравнение входят независимая переменная, неизвестная функция и ее первая производная, то это уравнение называется дифференциальным уравнением первого порядка.
3.Если в уравнение входит производная второго порядка от искомой функции, то уравнение называетсядифференциальным уравнением второго порядка.
Порядком дифференциального уравнения называется порядок старшей производной (искомой функции), входящей в это уравнение.
В общем случае дифференциальное уравнение первого порядка можно записать в следующем виде:
F(x;y;у`) = 0 , (1)
где у = у(х) - искомая неизвестная функция, у` = у`(х) - ее производная пох, аF-заданная функция переменных х, у, у`.
Функция 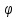 (х), х
(х), х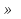 (а;b), называется решением дифференциального уравнения
(а;b), называется решением дифференциального уравнения
у`= f (х; у) (2) ,
если она имеет производную 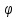 `(х)на(а; b) и если для любого х Є (а;b) справедливо равенство
`(х)на(а; b) и если для любого х Є (а;b) справедливо равенство
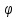 `(х) = f (х;
`(х) = f (х;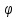 (х)).
(х)).
Другими словами, функция 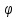 (х), х Є (а;b) , называется решением дифференциального уравнения (2), если уравнение (2) при подстановке ее вместоу обращается в тождество по х на интервале (а;b).
(х), х Є (а;b) , называется решением дифференциального уравнения (2), если уравнение (2) при подстановке ее вместоу обращается в тождество по х на интервале (а;b).
Аналогично определяется решение дифференциального уравнения (1) .
Задача нахождения уравнения решения уравнения (2), удовлетворяющего условию
у(х0) = у0 , (3)
где х0, у0- заданные числа, называется задачей Коши. Условие (3) называется начальным условием. Решение уравнения (2), удовлетворяющее начальному условию (3), называется решением задачи Коши.
Множество всех (или почти всех) решений дифференциального уравнения задается формулой
у = 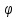 (х;С), (4) гдеС- произвольная постоянная.
(х;С), (4) гдеС- произвольная постоянная.
Функция (4), которая при каждом фиксированном значенииСкак функция от х является решением уравнения (2), называется общим решением уравнения (2).
Каждое решение уравнения (2), которое получается из общего решения (4) при конкретном значении постояннойС, называется частным решением. ПостояннаяСназывается постоянной интегрирования.
Умножив обе части уравнения (2) на дифференциал независимой переменной dx, получим уравнение, содержащее дифференциалы:
dy = f(x,y)dx. (5)
Уравнение (5) также называется дифференциальным уравнением первого порядка. Из определения дифференциала следует, что уравнение (5) равносильно уравнению (2).
Уравнения с разделяющимися переменными.
1.Определение.
Дифференциальное уравнение вида y =f(x)g(y), (1) где f(x) и g(y) - заданные функции, называютсяуравнениями с разделяющимися переменными.
=f(x)g(y), (1) где f(x) и g(y) - заданные функции, называютсяуравнениями с разделяющимися переменными.
Для тех у, для которых g(y)≠0, уравнение (1) равносильно уравнению р(у)у` = f(x) (2).
В этом уравнении переменная у присутствует лишь в левой части, а переменная х-лишь в правой части.
В дифференциалах уравнение (2) имеет вид:p(y)dy = f(x)dx (3)
Здесь слева стоит дифференциал некоторой функцииР(у), зависящей от у, а справа - дифференциал функции F(x), зависящей от х.
Проинтегрировав обе части уравнения (2) пох, получим
Р(у) = F(х) +С (4)
где С- произвольная постоянная. Формула (4) задает общее решение уравнения (2).
2.Правило нахождения общего решения.
Для нахождения общего решения дифференциального уравнения с разделяющимися переменными следует:
1) разделить переменные, т.е. преобразовать данное уравнение к виду
p(y)dy = f(x)dx ; (1)
2) проинтегрировать обе части полученного уравнения по у и по х соответственно, т.е. найти некоторую первообразную Р(у) функции р(у) и некоторую первообразную F (х) функции f(х);
3) написать уравнение Р(у) =F(х) + С (2),
гдеС- произвольная постоянная.
Решив уравнение (2) относительно у, получим общее решение дифференциального уравнения (1) :
у = 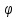 (х;С),
(х;С),
которое называется также общим решением данного уравнения.
Пример 1. Решить уравнение
у` = 1.
Решение:
Представим у`через 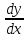 : у`=
: у`=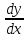 . Тогда
. Тогда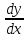 =1. Умножим обе части уравнения на dx, получим:dy= 1dx.
=1. Умножим обе части уравнения на dx, получим:dy= 1dx.
Интегрируем обе части уравнения: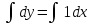 .
.
Отдельно найдем каждый интеграл:
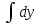 =у ;
=у ;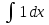 =х+С.
=х+С.
Приравниваем полученный результат:
у = х+С.
Итак, решением является функция у =х+С.
Ответ: у = х+С.
Пример 2. Решить уравнение
у` = х
Решение: Представим у` через 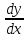 : у`=
: у`=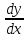 . Тогда
. Тогда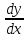 = х
= х
Умножим обе части уравнения на dx, получим :dy= хdx.
Интегрируем обе части уравнения: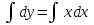 .
.
Отдельно найдем каждый интеграл:
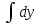 =у ;
=у ;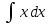 =
= 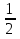 х2 + С.
х2 + С.
Приравниваем полученный результат: у = 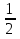 х2 + С.
х2 + С.
Итак, решением является у = 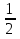 х2 + С.
х2 + С.
Ответ: у = 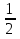 х2 + С.
х2 + С.
Пример 3. Решить уравнение
у` = ху.
Решение: Представим у` через 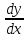 : у`=
: у`=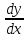 . Тогда
. Тогда 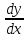 = ху
= ху
Умножим обе части уравнения на dx, получим :dy= хуdx.
Разделим обе части уравнения на у, получим :
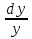 = хdx
= хdx
Интегрируем обе части уравнения: 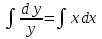
Отдельно найдем каждый интеграл:
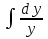 =
= 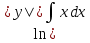 =
=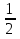 х2 + С.
х2 + С.
Приравнивая полученный результат, имеем: 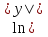 =
=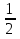 х2 + С1, где С1- произвольная постоянная. Отсюда следует, что
х2 + С1, где С1- произвольная постоянная. Отсюда следует, что
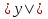 =
= 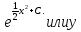 =C
=C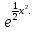 , где С=
, где С=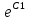
Таким образом, формула 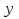 =C
=C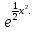 задает все решения уравнения.
задает все решения уравнения.
Ответ: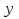 =C
=C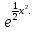
Пример 4. Решить уравнение
у`=ху2.
Решение: Представим у` через 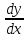 : у`=
: у`=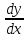 . Тогда
. Тогда 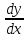 = ху2.
= ху2.
Умножим обе части уравнения на dx, получим :dy= ху2dx.
Разделив переменные, получим: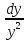 =
=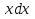
Проинтегрировав обе части уравнения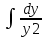 =
=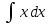 , получим:
, получим:
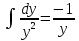 ;
;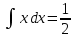 х2 + С и, следовательно,
х2 + С и, следовательно,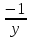 =
=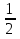 х2 + С .
х2 + С .
Таким образом, общее решение данного уравнения имеет вид:
у = - 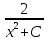 , где С - произвольная постоянная.
, где С - произвольная постоянная.
Ответ: у = - 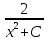
Пример 5.Решить уравнение
у`= - 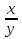 .
.
Решение. Представим у` через 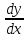 : у`=
: у`=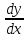 . Тогда
. Тогда 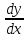 =-
=- 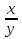 .
.
Разделив переменные: уdy = -xdx,
и проинтегрировав: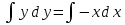 ,
,
получим: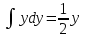 2,
2,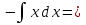 -
-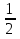 х2 + С
х2 + С
у2 +х2 =С.
Очевидно, что здесь С>0. ПоложимС=R2.
Полученное уравнение является уравнением окружности радиуса R с центром в точке (0;0). Оно при каждом фиксированном R>0 определяет две дифференцируемые функции
у= ±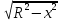 , х Є (а; b),
, х Є (а; b),
которые и являются решениями данного уравнения.
Ответ:у= ±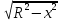 , х Є (а; b).
, х Є (а; b).
Пример 6. Решить уравнение у`= 1+у2.
Решение: Представим у`через 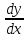 : у`=
: у`=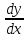 . Тогда
. Тогда 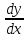 =1+у2
=1+у2
Разделив переменные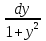 =dx и проинтегрировав обе части уравнения
=dx и проинтегрировав обе части уравнения
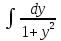 =
=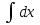 , получим:
, получим:
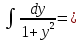 arctgy;
arctgy; 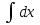 =х +С.
=х +С.
Итак:
arctgy = х +С, где С - произвольная постоянная. Отсюда следует, что
у= tg (х+ С).
Ответ: у= tg (х+ С).
Пример 7. Решить уравнение
(1+х)dу = 2уdх, если при х=0 у=4.
Решение.Разделив переменные, получим: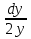 =
=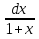 .
.
Проинтегрировав обе части уравнения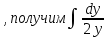 =
= 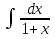
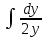 =
=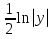 =
=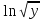 ;
; 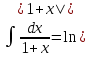 +С
+С
Итак,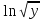 =
= 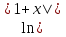 +С;
+С;
Находим значениеСиз условия х=0 иу=4; сделав подстановку, получим:
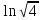 =
= 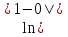 + С,
+ С, 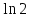 =
=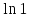 + С,
+ С, 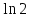 = 0 + С, С =
= 0 + С, С = 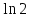 .
.
Итак,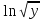 =
= 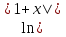 +
+ 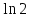 ;
; 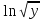 =
=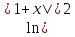 , у = 4(1 + 2)2
, у = 4(1 + 2)2
Ответ: у = 4(1 + 2)2.
Пример 8. Найти частные решения уравнения
dy +xdx = 2dx, если при х=1 у=1,5.
Решение. Разделив переменные и проинтегрировав обе части уравнения, получим
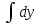 =
= 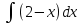 .
.
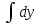 = y;
= y;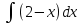 = 2х -
= 2х - 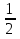 х2+ С.
х2+ С.
Итак, у = 2х - 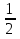 х2+ С.
х2+ С.
Ответ: у = 2х - 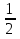 х2+ С.
х2+ С.
Находим значение С из условия х =1 при у = 1,5; сделав подстановку, получим:
1,5 = 2.1- 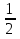 .12+ С, С = 1,5-1,5 = 0.
.12+ С, С = 1,5-1,5 = 0.
Итак, у = 2х -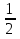 х2.
х2.
Ответ:у = 2х -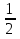 х2.
х2.
Упражнения для самостоятельного решения.
Решите уравнения:
1. у` = х +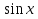 ;
;
2. у` = 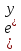 - 1;
- 1;
3. у` =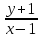 ;
;
4. у` = 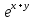 ;
;
5. (1+у2)dу - хdy = 0
6. у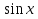 +
+ 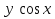 =0.
=0.
7.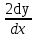 = 1+x2, если при х=0 у= 0.
= 1+x2, если при х=0 у= 0.
8. 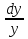 -dx =0, если при х = 0 у = 0.
-dx =0, если при х = 0 у = 0.
9. (1+у)dx - (1-x) dy = 0, если при х = 0 у = 1.
10.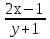 =
= 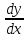 , если при х = 5 у = 0.
, если при х = 5 у = 0.
11. у`= 2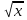
12. у`= 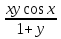
Линейные дифференциальные уравнения
первого порядка.
1.Общее решение линейного дифференциального уравнения первого порядка.
Дифференциальные уравнения вида
у` = f(x)y +g(x) (1)
называются линейными дифференциальными уравнениями первого порядка.
Если g(x) = 0, то линейное дифференциальное уравнение (1) называется однородным. Оно имеет вид
у`= f(x)y (2).
Уравнение (2) является уравнением с разделяющимися переменными. Все решения этого уравнения задаются формулой
у = С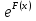 , (3)
, (3)
где F(x) -некоторая первообразная функции f(x), а С - произвольная постоянная. В частности, если функцияf(x) постоянная, например f(х)=k для любогох, то уравнение
у`= ky
имеет общее решение
у = С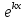 .
.
Если f(х) = 0, то уравнение (1) принимает вид
у` = g(х).
Как известно, общим решением этого уравнения будет
у = G(x)+ C,
где G(x) - некоторая первообразная функции g(x), а С- произвольная постоянная.
Теорема.Если у =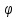 (х) - некоторое решение уравнения (1), то все решения этого уравнения задаются формулой
(х) - некоторое решение уравнения (1), то все решения этого уравнения задаются формулой
у = С 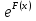 +
+ 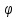 (х), (4)
(х), (4)
где С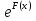 - общее решение однородного уравнения (2).
- общее решение однородного уравнения (2).
Для нахождения общего решения уравнения (1) достаточно найти хотя бы одно его частное решение.
Для линейного уравнения вида
у`= ky+b, (5)
где k и b - некоторые числа и k≠ 0, частное решение легко находится. Им будет постоянная функция у =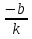 . Поэтому общее решение уравнения (5) имеет вид:
. Поэтому общее решение уравнения (5) имеет вид:
у = С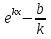 .
.
Пример 1. Решить уравнение
у`+2у+3 =0.
Решение: У этого уравнения k= -2, b=-3. Следовательно, общее решение определяется формулой
у = С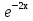 -
- 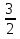 ,
,
где С-произвольная постоянная.
Ответ: у =С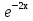 -
- 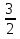 .
.
Пример 2. Найти общее решение дифференциального уравнения
у`+ ху =4х.
Решение. Подбором находим, что функция у=4 является решением данного линейного неоднородного уравнения. Найдем теперь общее решение соответствующего однородного уравнения:
у` + 4х =0.
По формуле 4 получаем, что общее решение этого уравнения имеет вид
у = С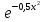 .
.
Общее решение данного уравнения задается формулой
у =С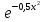 +4,
+4,
гдеС - произвольная постоянная.
Ответ: у = С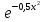 +4.
+4.
2.Применим теперь тот же способ решения к линейному уравнению общего вида
у`+ Р(х) у = Q(x). (6)
Полагаем у = uv, откуда у`=u`v+uv`, тогда уравнение (6) преобразуется в уравнение
u`v+uv`+ Р(х) uv = Q(x)
или v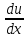 + u(
+ u(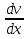 +P(x)v) = Q(x).
+P(x)v) = Q(x).
Пользуясь правом произвольного выбора одной из функций u или v, выбираем функцию v как одно из решений уравнения
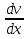 +P(x)v=0.
+P(x)v=0.
Разделив переменные в этом уравнении, находим
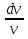 = -Р(х)dx,
= -Р(х)dx,
откуда
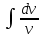 = -
= -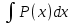 ,
, 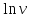 =-
=-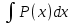
v= 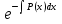 .
.
При таком выборе функции v уравнение (6) примет вид
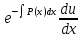 = Q(x),
= Q(x),
что дает 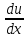 = Q(x)
= Q(x)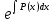 .
.
Интегрируя, находим
u =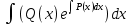 + C,
+ C,
и, наконец
у=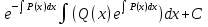 .
.
Таково общее решение линейного дифференциального уравнения (6).
Пример 3. Решить уравнение
у` + 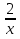 у = х2.
у = х2.
Решение: Будем искать решение данного уравнения в виде произведения двух функций u и v переменной х, т.е. положим
у= uv, отсюда
у`=u`v+uv`,
и данное уравнение преобразуется в уравнение
u`v+uv`+ 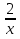 uv = х2 или u`v +(v`+
uv = х2 или u`v +(v`+ 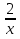 v) = х2.
v) = х2.
В целях упрощения уравнения выберем функцию v так, чтобы выражение v`+ 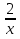 vобратилось в нуль (стоящее в скобках); иначе говоря, возьмем за функцию vодно из решений уравнения
vобратилось в нуль (стоящее в скобках); иначе говоря, возьмем за функцию vодно из решений уравнения
v`+ 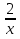 v=0.
v=0.
Представим это уравнение в виде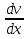 +
+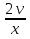 =0 и, разделяя переменные, получим
=0 и, разделяя переменные, получим
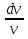 = -
= - 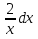
откуда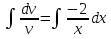 ,
,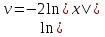 и
и
v= 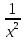 .
.
При таком выборе функции v уравнение приводится к виду
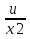 = х2 или
= х2 или 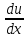 = х2.
= х2.
Отсюда du = x4dx, 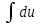 =
=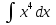 и
и
u =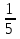 х5+С.
х5+С.
Мы положили у = uv. Следовательно, общее решение исходного уравнения получается в виде:
у = (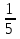 х5+С).
х5+С).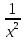 , или у=
, или у= 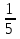 х3+Сх-2.
х3+Сх-2.
Ответ: у = 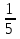 х3+Сх-2.
х3+Сх-2.
Пример 4 (задача). Электрическая цепь состоит из последовательно включенных источника тока, у которого напряжениеЕ, сопротивления R, самоиндукции L и выключателя, который включается при t=0. Найти зависимость I(t) силы тока от времени.
Решение: Для определения силы тока в электрической цепи из самоиндукцией пользуются формулой
L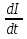 + RI = E.(1)
+ RI = E.(1)
Это линейное уравнение относительно неизвестной функции I(t). Необходимо найти частное решение этого уравнения при условии I(0)=0.
ПоложимI(t)=u(t)v(t) и вычислим I`=u`v +uv`.
Значения IиI` подставим в уравнение (1). Получим
L(u`v +uv`)+ Ruv = Eилиv`L+Rv=0иLu`v = E.
В первом уравнении разделим переменные 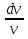 = -R
= -R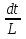 и отсюда получим v =
и отсюда получим v = 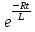 . Тогда второе уравнение имеет вид: L
. Тогда второе уравнение имеет вид: L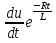 = E
= E
илиdu = 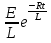 dt,
dt,
откуда, интегрируя, получим
u = 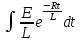 =
= 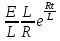 +C=
+C=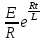 + C.
+ C.
Подставляя начальные условия I(0)=0, найдемС=- 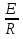 . Тогда
. Тогда
I= 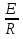 (1-
(1- 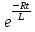 ). Так как функция
). Так как функция 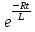 практически очень быстро убывает, то, отбрасывая ее, получим известное из физики соотношение I =
практически очень быстро убывает, то, отбрасывая ее, получим известное из физики соотношение I = 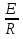 , которое называется законом Ома.
, которое называется законом Ома.
Пример 5. Найти кривую, которая проходит через точку (0;-2), чтобы угловой коэффициент касательной в произвольной ее точке был равен ординате этой точки, увеличенной на 3.
Решение: Составим дифференциальное уравнение по условию задачи. Поскольку угловой коэффициент касательной к кривой y= f(x)в точке (x,y) равен у`, то имеем уравнение у` = у + 3, решением которого есть 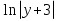 = х + С.Учитывая начальное условие, получим у =
= х + С.Учитывая начальное условие, получим у =  - 3.
- 3.
Ответ: у =  - 3.
- 3.
Упражнения для самостоятельного решения.
Решить уравнения:
1. у` + 4ху = х;
2. у` +4х2у = 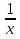 ;
;
3. у` - 3ху = 2;
4. у`- 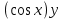 = х;
= х;
5. у` + у = 4;
6. у` + 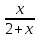 у = х;
у = х;
7. у`- (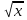 +3) = 1;
+3) = 1;
8. у` + 4х2у = 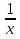 ;
;
9. у` +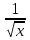 у = 4;
у = 4;
10. у`+ 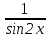 у = х.
у = х.
11.За 30 дней масса радиоактивного вещества уменьшилась на 50%.
Через какое время останется 1% от начального количества этого
вещества, если известно, что скорость распада радиоактивного
вещества пропорциональнанаявного его количества?
12.Скорость тела пропорциональна пройденному пути. За первые 10 с тело проходит 100 м, за 15 с -- 200 м. Какой путь пройдет тело за 20 с?
Линейные дифференциальные уравнения второго порядка с постоянными коэффициентами.
1.Дифференциальные уравнения второго порядка.
В общем случае дифференциальное уравнение второго порядка можно записать в виде
F(х; у; у`;у``) =0, (1)
где у = у(х) -искомая неизвестная функция, у`= у`(х) и у``= у``(х) -ее производные по х первого и второго порядков, а F - заданная функция переменных х, у, у`, у``.
Функция 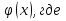 х
х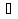 (а; b), называется решением дифференциального уравнения (1), если она имеет производные
(а; b), называется решением дифференциального уравнения (1), если она имеет производные 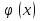 и
и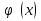 и если для любого х
и если для любого х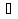 (а; b) справедливо равенство
(а; b) справедливо равенство
F(x,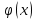 ,
,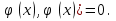
Другими словами, функция 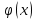 , х
, х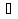 (а; b), называется решением уравнения (1), если при подстановке
(а; b), называется решением уравнения (1), если при подстановке 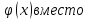 уэто уравнение обращается в тождество по х.
уэто уравнение обращается в тождество по х.
Дифференциальное уравнение вида
у``= f(х, у, у`), (2)
где f- заданная функция переменных х, у, у`, называется уравнением, разрешенным относительно второй производной.
2.Линейные однородные уравнения с постоянными коэффициентами.
Дифференциальные уравнения вида
у``+ ру`+qy = f(x), (1)
где p и q- некоторые числа, называются линейными дифференциальными уравнениями второго порядка. Функцияf(х)называется свободным членом или правой частью уравнения (1).
Если f (х)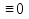 , то дифференциальное уравнение называется линейным дифференциальным уравнением. Оно имеет вид
, то дифференциальное уравнение называется линейным дифференциальным уравнением. Оно имеет вид
у``+ ру`+qy = 0 (2).
Решением данного уравнения является функция
у = С1у1+ С2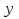 2,
2,
где у1иу2- два линейно независимых частных решения уравнения (2), С1 и С2- произвольные постоянные. Эти решения находят в виде у=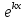 , где k- неопределенная постоянная. Для нахождения k составляют характеристическое уравнение
, где k- неопределенная постоянная. Для нахождения k составляют характеристическое уравнение
k2 + pk + q = 0, заменив у``= k2, y`= k, y = 1.
Решая уравнение (2), находим его корни k1 и k2. Возможны такие три случая.
1) Если k1 и k2- действительные и разные числа , то у1=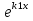 y2=
y2=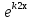 , а общее решение имеет вид у = С1
, а общее решение имеет вид у = С1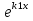 + С2
+ С2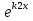 .
.
2) Если k1 = k2 = k, то у1=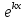 , у2= x
, у2= x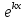 и
и
у = С1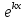 + С2x
+ С2x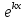 =
=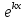 (С1+ С2х).
(С1+ С2х).
3) Корни k1 и k2 мнимые (k1=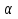 +
+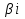 и k2 =
и k2 =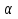 -
-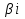 ,
, 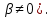
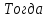 у1=
у1= 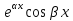 , у2=
, у2=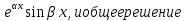 имеет вид
имеет вид
у= 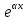 (С1
(С1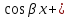 С2
С2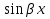 ).
).
Если, к примеру 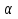 =0, то у = С1
=0, то у = С1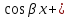 С2
С2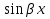 .
.
Пример 1. Найти все решения уравнения
у``- у = 0. (3)
Решение. Составим характеристическое уравнение, произведя замену:
у``= k,у=1; получим:
k2- 1 =0 и
k1=-1, k2= 1.
Тогда у1=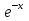 , у2=
, у2= и общее решение имеет вид
и общее решение имеет вид
у= С1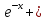 С2
С2 .
.
Ответ:у= С1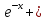 С2
С2 .
.
Пример 2. Найти все решения уравнения
у``+6у`+9 = 0.
Решение. Составим характеристическое уравнение, произведя замену у``=k2, y`=k, y=1
k2 + 6k + 9 = 0.
Корнем данного уравнения есть k1=k2= - 3. Поэтому у1=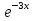 , у2=
, у2= 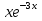 и общее решение у = С1
и общее решение у = С1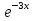 + С2
+ С2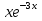 =
=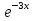 (С1 + С2х).
(С1 + С2х).
Ответ: у=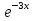 (С1 + С2х).
(С1 + С2х).
Пример 3. Найти все решения уравнения
у``- 7у`+ 6у = 0.
Решение. Запишем характеристическое уравнение для заданного дифференциального уравнения, заменив у``= k2, y`= k, y= 1.
Получим k2 -7k + 6 = 0. Корни этого уравнения k1= 1, k2 = 6. Поэтому
у1 = , у2 =
, у2 = 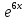 и общее решение у =С1
и общее решение у =С1 + С2
+ С2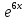 .
.
Ответ: у =С1 + С2
+ С2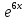 .
.
Пример 4. Найти общие решения уравнения
у`` - 2у` +17у= 0.
Решение. Запишем характеристическое уравнение для заданного дифференциального уравнения, произведя замену у``= k2, y`= k, y= 1.
Получим k2- 2k + 17 = 0.
Дискриминант этого уравнения D= (-2)2-4.1.17 = -64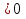 . Уравнение имеет два мнимых сопряженных корня k1 = 1+ 4i , k2= 1-4i
. Уравнение имеет два мнимых сопряженных корня k1 = 1+ 4i , k2= 1-4i
Итак, у1= 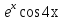 , у2=
, у2=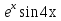 .
.
Общее решение у=С1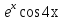 + С2
+ С2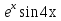 =
=  (С1
(С1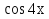 + С2
+ С2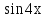 ).
).
Ответ: у =  (С1
(С1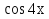 + С2
+ С2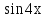 ).
).
Пример 5. Найти общие решения уравнения
у``+ 9у = 0.
Решение. Запишем характеристическое уравнение, заменив у``= k2, y= 1;
получим k2 + 9 = 0. Корни этого уравнения - мнимые k1=3i, k2=-3i.
Поэтому у1= С1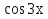 , у2 = С2
, у2 = С2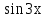 .
.
Общее решение у = С1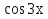 + С2
+ С2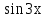 .
.
Ответ: у = С1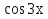 + С2
+ С2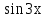 .
.
Пример 6. Решить задачу Коши:
у`` - 6у` +5у = 0, у(0)=2, у`(0) = -2.
Решение. Сначала найдем общее решение этого уравнения. Для этого составим характеристическое уравнение, произведя замену
у``= k2,y`= k,y= 1.
Получим k2 - 6k + 5 = 0 , где k1=1, k2=5. При этом у1=С1 , у2 = С2
, у2 = С2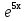 и общее решение имеет вид: у = С1
и общее решение имеет вид: у = С1 + С2
+ С2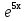 .
.
Теперь используем начальные условия для нахождения С1 и С2. Подставляя х=0 и у=2 в общее решение, получим
2=С1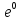 + С2
+ С2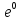 ; или С1+С2=2. Возьмем производную у` от общего решения: у`=С1
; или С1+С2=2. Возьмем производную у` от общего решения: у`=С1 + 5С2
+ 5С2 и подставим сюда значения х=0 и у
и подставим сюда значения х=0 и у =-2. Имеем
=-2. Имеем
-2= С1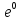 + 5С2
+ 5С2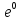 или С1+ 5С2 = -2. Для вычисления С1 и С2 необходимо решить систему уравнений:
или С1+ 5С2 = -2. Для вычисления С1 и С2 необходимо решить систему уравнений:
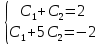
Решением этой системы уравнений есть С1=-1 и С2=3. Подставляя значения С1 и С2 в общее решение, получим искомое частное решение, т.е. решение задачи Коши:
у =- +3
+3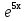
Ответ: у = - +3
+3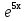 .
.
3.Линейные неоднородные дифференциальные уравнения
второго порядка с постоянными коэффициентами.
Эти уравнения имеют вид
у`` +py` + qy = Ф(x). (1)
Общее решение линейного неоднородного дифференциального уравнения (1) выражается суммой его частного решения и общего решения соответствующего линейного однородного уравнения:
у = у* + Y = у*+C1у1+ С2у2.
Для отыскания частного решения у*будем применять метод неопределенных коэффициентов, причем у следует искать в таком же виде, какой имеет Р(х) или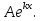
А) Подбор частного решенияу*, когда правая часть - многочлен. Если Р(х)- многочлен и q≠0, то у*следует искать в виде многочлена такой же степени. Это значит, что если, например, Р(х)=2х-3или х, то у* имеет вид Ах + В; если же Р(х)=х2 или х2+1, или х2 + х -1, то у* имеет вид Ах2+ Вх +С. При этом коэффициенты многочлена находятся из системы линейных алгебраических уравнений, которые получаются при подстановке в дифференциальное уравнение предполагаемого многочлена и его производных.
Б) Подбор частного решенияу*, когда правая часть - показательная функция. Если в правой части задана показательная функция а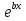 , то частное решениеу* следует искать в видеА
, то частное решениеу* следует искать в видеА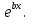 Для определения коэффициента Анужно подставить выражение А
Для определения коэффициента Анужно подставить выражение А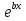 и его производные у*` и у*`` в данное уравнение и сопоставить полученное выражение левой части с правой. Если же характеристическое уравнение, соответствующее однородному уравнению, имеет корень х=b, то частное решение следует искать в виде у*= Ах
и его производные у*` и у*`` в данное уравнение и сопоставить полученное выражение левой части с правой. Если же характеристическое уравнение, соответствующее однородному уравнению, имеет корень х=b, то частное решение следует искать в виде у*= Ах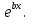
Если же правая часть - сумма функций различного вида, то частное решение составляется в виде суммы функций, соответствующих каждому слагаемому, т.е. при наличии, например, справа суммы х2+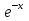 , у* подбирают в виде суммы Ах2+Вх+С+М
, у* подбирают в виде суммы Ах2+Вх+С+М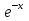 , причем каждое слагаемое проще определяется отдельно.
, причем каждое слагаемое проще определяется отдельно.
В)Подбор частного решения у*, когда правая часть - сумма тригонометрических функций. Если в правой части задана тригонометрическая функция а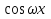 +b
+b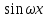 , то частное решение у* следует искать в видеА
, то частное решение у* следует искать в видеА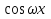 + В
+ В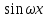 . КоэффициентыА и В будем искать методом неопределенных коэффициентов:
. КоэффициентыА и В будем искать методом неопределенных коэффициентов:
у*`= -А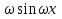 +В
+В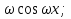 у*``= -А
у*``= -А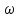 2
2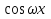 - В
- В 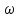 2
2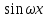 .
.
После несложных преобразований
(-А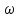 2 + В
2 + В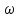 p + Aq)
p + Aq) 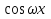 +( - В
+( - В 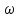 2+Ap
2+Ap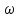 +Bq)
+Bq)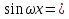 а
а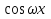 +b
+b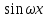 .
.
Для того чтобы функция у* являлась решением уравнения, нужно, чтобы это равенство былоа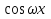 +b
+b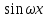 тождеством, а это возможно лишь при равенстве коэффициентов при
тождеством, а это возможно лишь при равенстве коэффициентов при 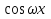 и
и 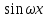 , соответственно в его левой и правой частяхОтсюда следует, что коэффициенты А и В должны удовлетворять системе уравнений
, соответственно в его левой и правой частяхОтсюда следует, что коэффициенты А и В должны удовлетворять системе уравнений 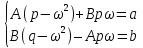
Система уравнений не будет иметь решения только в том случае, когда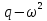 = 0 и р = 0.
= 0 и р = 0.
Если уравнение имеет вид у``+ 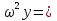 а
а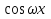 +b
+b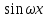 ,то его частное
,то его частное
у* = х(А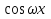 + В
+ В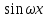 ) и А = -
) и А = - 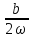 , B=
, B=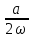 .
.
Пример 7. Найтиобщее решение уравнения
у``+ 2у` -3у = 1.
Решение. Подбором находим, что функция у* = - 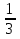 является частным решением данного уравнения. Найдем теперь общее решение линейного однородного уравнения
является частным решением данного уравнения. Найдем теперь общее решение линейного однородного уравнения
у``+ 2у` -3у=0.
Его характеристическое уравнение
k2 + 2k -3=0 имеет решения k1=-3, k2=1.
Следовательно, общее решение уравнения имеет вид:
Y=С1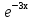 + С2
+ С2 .
.
Так как общее решение неоднородного уравнения является суммой некоторого его частного решения и общего решения соответствующего однородного уравнения, то общее решение уравнения задается формулой:
у = С1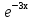 + С2
+ С2 -
-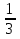 .
.
Ответ: у = С1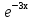 + С2
+ С2 -
-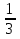 .
.
Пример 8. Найти общее решение уравнения
у``+ 2у`- 3у = х.
Решение. Частное решение уравнения будем искать в виде у* = Ах + В, где АиВ-неизвестные числа. Для этого вычислим первую и вторую производные функции у*:
у*` = (Ах +В)`= А, у*``= А`=0. Подставим у*, у*`,у*`` в данное уравнение, получим: 2А - 3Ах - 3В = х.
Из этого равенства следует, что 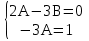 ,
,
и поэтомуА=-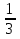 , В= -
, В= -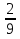 .
.
Следовательно, функция у*= -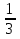 х -
х - 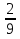 является частным решением уравнения.
является частным решением уравнения.
Для нахождения общего решения составим характеристическое уравнение
k2 + 2k -3=0 , корни которого k1=-3, k2=1.
Общее решение данного уравнения у=С1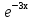 + С2
+ С2 -
-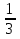 х -
х - 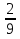 .
.
Ответ: у=С1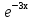 + С2
+ С2 --
--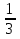 х -
х - 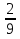 .
.
Пример 9. Найти решение дифференциального уравнения
у`` - 2у` = 24х.
Решение. Из характеристического уравнения k2 - 2k = 0 имеем k = 0 и k= 2. Поэтому общее решение однородного уравнения имеет вид
Y = С1+ С2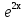 .
.
Частное же решение следует искать в виде у*= Ах2 + Вх. Тогда первая его производная будет у*` = 2Ах + В, а вторая производная у*``= 2А. Подставляя у* и его производные в данное дифференциальное уравнение, получим
2А - 4Ах + 2В = 24х, откуда, решая систему уравнений
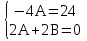 ,
,
находимА=- 6, В=- 6. Таким образому* = - 6х2 - 6х, а общее решение заданного уравнения у = Y+ у* =C1+C2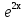 - 6x - 6x2.
- 6x - 6x2.
Ответ: у = C1+C2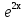 - 6x - 6x2.
- 6x - 6x2.
Пример 10. Найти решение дифференциального уравнения
у``- 3у` -4у = 9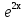 .
.
Решение. Составим характеристическое уравнение k2 - 3k - 4 = 0, его корни k1= -1, k2=4.
Частное решение у* будем искать в виде у* =А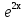 . Для определения коэффициента А подставим выражение А
. Для определения коэффициента А подставим выражение А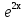 и его производные у*
и его производные у*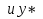 в данное уравнение:
в данное уравнение:
у*`=2А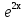 , у*``=4 А
, у*``=4 А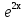 .
.
Подстановка этих выражений в уравнение дает
4 А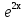 - 6 А
- 6 А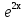 - 16 А
- 16 А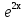 = 9
= 9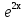 .
.
Отсюда -18А = 9 иА = - 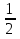 , т.е. у* = -
, т.е. у* = -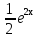 .
.
Общее решение имеем в виде у = С1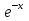 + С2
+ С2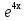 -
-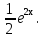
Ответ: у = С1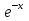 + С2
+ С2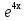 -
-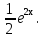
Пример 11. Найти решение дифференциального уравнения
у``+2у`-15у= -75х-2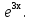
Решение. Корни характеристического уравнения k2+2k-15 = 0:
k=3 иk=-5.
Этим определяется вид частного решения у*= Ах + В + М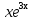 . Вычисления для
. Вычисления для 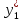 и
и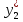 проведем раздельно:
проведем раздельно:
-
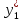 = Ах + В
= Ах + В 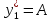
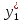 =0
=0 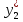 = М
= М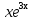
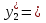 (М+3Мх)
(М+3Мх)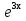
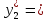 (6М+9Мх)
(6М+9Мх)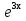
Подставив полученные выражения в данное дифференциальное уравнение, соответственно имеем:
-
-15Ах-15В+2А=-75х
откуда А = 5, В =
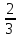
8М
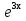 =-2
=-2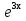
откуда М= -
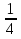
Таким образом, 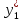 =5х+
=5х+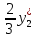 = -
= - 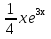 . Заметив, что
. Заметив, что
Y=С1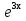 + С2
+ С2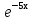 , получаем общее решение
, получаем общее решение
у=5х+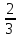 + (С1-
+ (С1- 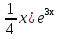 +С2
+С2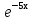 .
.
Ответ: у=5х+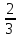 + (С1-
+ (С1- 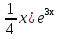 +С2
+С2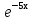 .
.
Пример 12. Найти общее решение уравнения
у``- 5у`+ 6у = 16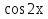 +28
+28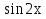 .
.
Решение. Составим характеристическое уравнение k2- 5k + 6 = 0,
его корни k1=2 и k2=3.
Общее решение Y= С1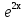 + С2
+ С2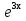 . В данном примере р =-5 , q = 6,
. В данном примере р =-5 , q = 6, 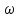 = 2,
= 2,
q -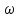 2= 6 - 22=2. Таким образом, вид частного решения
2= 6 - 22=2. Таким образом, вид частного решения
у*= А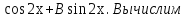 у*` и у*``.
у*` и у*``.
у*` = -2А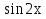 +2В
+2В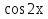 ;у*``=-4А
;у*``=-4А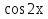 - 4В
- 4В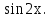
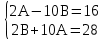
Решая эту систему, находим: А = 3, В = -1.
Следовательно, у* = 3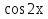 -
- 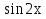 и общее решение данного уравнения будет такое у = С1
и общее решение данного уравнения будет такое у = С1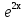 + С2
+ С2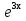 + 3
+ 3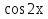 -
- 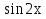 .
.
Ответ: у = С1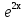 + С2
+ С2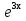 + 3
+ 3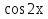 -
- 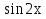 .
.
Пример 13. Найти общее решение уравнения
у``+4у = 6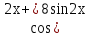 .
.
Решение. Составим характеристическое уравнениеk2+4 = 0 корни которого - мнимые числа k1= 2i , k2= -2i.
Общее решение Y= С1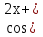 С2
С2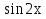 .
.
В данном уравнении 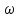 = 2, р = 0, q = 4, a = 6, b = 8. Согласно формулам
= 2, р = 0, q = 4, a = 6, b = 8. Согласно формулам
А = - 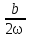 , B=
, B=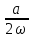
коэффициентыА и В частного решения у*= х (А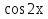 + В
+ В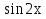 ) равны
) равны
А = 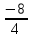 = - 2, В =
= - 2, В = 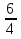 =
= 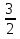 . и у*= х(-2
. и у*= х(-2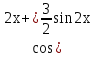 )
)
Следовательно, общее решение данного уравнения таково:у = Y + у*, и
у= С1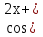 С2
С2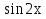 + х(-2
+ х(-2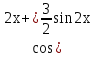 )
)
или у= (С1- 2х)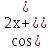 С2 +
С2 + 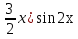 .
.
Ответ: у= (С1- 2х)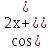 С2 +
С2 + 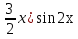 .
.
Пример 14. Найти частное решение уравнения
у``+9у = 12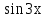 ,
,
удовлетворяющее следующим начальным условиям
у(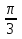 ) =
) = 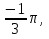 у`(
у`(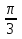 ) = 2.
) = 2.
Решение. Составляем характеристическое уравнение k2 + 9 =0корни которого k1=3i, k2= - 3i. Общее решение Y = С1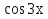 + С2
+ С2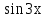 .
.
В данном уравненииа = 0, b = 12, 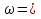 3. Следовательно, А = -
3. Следовательно, А = -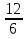 = - 2, В =
= - 2, В = 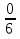 = 0; таким образом частное решение получим в виде
= 0; таким образом частное решение получим в виде
у*= - 2х 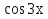
а общее решение примет вид
у =Y +у* = С1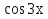 + С2
+ С2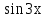 - 2х
- 2х 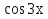 =(С1 - 2х)
=(С1 - 2х)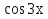 + С2
+ С2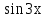 .
.
Отсюда у` = -3(С1 - 2х)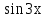 - 2
- 2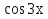 + 3С2
+ 3С2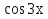 .
.
Используя начальные условия , получаем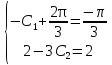
что дает С1=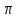 , С2= 0; искомое частное решение у = (
, С2= 0; искомое частное решение у = (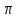 -2х)
-2х)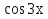
Ответ: у = (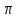 -2х)
-2х)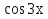 .
.
Пример 15. Ускорение прямолинейного движения тела равно 2м/с2. Выразить путьsтела как функцию времени t.
Решение. Согласно механическому смыслу второй производной функции имеем: s``=2.
Обозначим 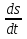 = p,
= p,
имеемs``=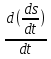 =
= 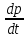 = 2,
= 2,
откуда dp = 2dtи p = 2t + C1.
Заменив р его выражением, получим:
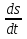 = 2t + C1, (2)
= 2t + C1, (2)
илиds =(2t + C1)dt,
отсюда s = 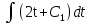 = t2 + C1t + C2. (3)
= t2 + C1t + C2. (3)
Для получения частного решения нужны начальные условия. Пусть при
t= 0, и 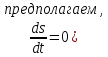 чтов начальный момент движения путь s и скорость
чтов начальный момент движения путь s и скорость 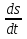 равны 0). Заменив t, sи
равны 0). Заменив t, sи 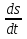 в уравнениях (2) и (3) нулями, получим С1= 0, С2= 0.
в уравнениях (2) и (3) нулями, получим С1= 0, С2= 0.
Таким образом, искомая зависимость будетs = t2.
Ответ:а)s =t2 + C1t + C2 ;б)s = t2.
Упражнения для самостоятельного решения.
1. у`` - 24у` + 3у =8х;
2. у`` - 4у` +3у = 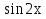 ;
;
3. у``- 3у`+ 2у = х2-1;
4. у``- 7у` - 8у = 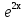 ;
;
5. у`` - 3у` - 4у = х2+ 1;
6. у``- 4у = 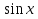 ;
;
7. у`` - 5у` + 4у =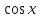
8. у`` - 3у` + 2у = х2+ 1;
9. у`` +9у = 15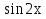 ;
;
10. у``+3у` - 4у = 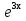 ;
;
11. у`` - 2у` = х;
12. у`` + 9у` = 9х.
13.Поезд, выйдя со станции, спустя t часов имеет ускорение
а=(3t2 -42t +80) км/час2.
Найти скорость в конце 2-го часа и расстояние, пройденное за
это время.
14.Ускорение прямолинейного движения пропорционально квадрату времени. Найти зависимость между s иt, если при t=0v=0, s =1 и при t=1 s = 2.
Заключение.
Данное пособие предназначено для студентов СПО и содержит понятия, определения, формулы и методы решения дифференциальных уравнений и имеет своей задачей помочь студентам СПО в овладениизнаний и методов решения дифференциальных уравнений. В пособии изложение материала проведено без использования теоретическо - множественной доказательной базы и тем отличается от учебников. По каждой теме даны способы решений некоторых видов уравнений с различными уровнями сложности, наиболее часто встречающихся в приложениях математики. Для более глубокого овладения приемамирешения дифференциальных уравнений студентам предлагаются упражнения для самостоятельного решения. Пособие отличается логическим единством и достаточной степенью подробности в изложении данного материала. Дифференциальные уравнения имеют большое применение в геометрии, механике, физике и других дисциплинах, а также в технике. Поэтому в пособии приведены примеры решения задач из различных областей, указанных ранее. Ввиду этого пособие может бытьиспользовано для приобретения и систематизации знаний студентов СПОпо решению обыкновенных дифференциальных уравнений и задач практического характера.
Литература.
-
Л.И.Дюженкова, Т.В. Носаль «Высшая математика» (практикум)
Киев «Высшая школа» 1991 г.
-
И.Л. Зайцев « Курс высшей математики» (для техникумов)
М. Высшая школа 1952 г.
-
Э.С. Маркович «Курс высшей математики»
М. «Высшая школа» 1972 г.
-
А.Г.Цыпкин «Справочник по математике для средних учебных заведений» М «Наука» 1988 г.
-
Под редакцией Г.Н.Яковлева «Алгебра и начала анализа» (математика для техникумов) Ч.2
М. «Наука» 1981 г.
Содержание.
-
Введение.
-
Основные понятия и определения.
-
Уравнения с разделяющимися переменными.
-
Линейные дифференциальные уравнения первого порядка.
-
Линейные дифференциальные уравнения второго порядка с постоянными коэффициентами.
5.1. Линейные дифференциальные уравнения второго порядка;
5.2. Линейные однородные дифференциальные уравнения с постоянными коэффициентами;
5.3. Линейные неоднородные дифференциальные уравнения второго порядка с постоянными коэффициентами.
6. Заключение.
7. Литература.
РЕЦЕНЗИЯ (внутренняя)
на работу «Пособие по математике»
«Дифференциальные уравнения».
Пособие по математике отражает структуру раздела «Дифференциальные уравнения», дается направление на изучение данного материала, на приобретение навыков решения задач и уравнений.
В математике дифференциальные уравнения занимают особое место. Дело в том, что математическое исследование самых разнообразных явлений, происходящих в природе, часто приводит к решению таких уравнений, поскольку сами законы, которым подчиняется то или иное явление, записываются в виде дифференциальных уравнений.
В пособии описаны способы решения дифференциальных уравнений первого и второго порядков, изложены приближенные методы решения дифференциальных уравнений. Даны основы теории обыкновенных дифференциальных уравнений, проанализированы дифференциальные уравнения второго порядка. Приводятся методы решения линейных дифференциальных уравнений с постоянными коэффициентами, линейных уравнений первого порядка; обсуждаются вопросы качественного исследования этих решений и условия решения задачи Коши.
Автор стремилась объединить строгость изложения теории дифференциальных уравнений с прикладной направленностью ее методов.
В связи с этим приведены многочисленные примеры из механики и физики. Отдельная глава посвящена линейным дифференциальным уравнениям второго порядка, к которым приводят многие прикладные задачи.Имеются также упражнения и задачи для самостоятельного решения. Материал пособия позволяет выработать практические навыки в решении и исследовании дифференциальных уравнений.
Преподаватель разработала своевременное пособие, в котором проведено логическое построение и изложение данного материала, что будет способствовать более успешному его усвоению.
Пособие предназначено для студентов техникумов и для преподавателей математики.
Рецензент: ______________Краснян Е.М. - преподаватель математики
высшей квалификационной
категории ГОУ СПО «РПТ»
РЕЦЕНЗИЯ (внешняя)
на пособие «Дифференциальные уравнения»
преподавателя Рыбницкого политехнического техникума
Томиной Надежды Алексеевны.
Пособие по математике отражает структуру раздела «Дифференциальные уравнения», дается направление на изучение данного материала, на приобретение навыков решения уравнений и задач.
В математике дифференциальные уравнения занимают особое место. Математическое исследование самых разнообразных явлений, происходящих в природе, часто приводит к решению таких уравнений, поскольку сами законы, которым подчиняются те или иные явления, записываются в виде дифференциальных уравнений. В работе изложены характерные особенности теории дифференциальных уравнений. Она оказывает большое влияние на развитие других областей математики. Теория дифференциальных уравнений является одним из самых больших разделов современной математики.
Пособие предназначено для студентов средних учебных заведений. В пособии приводятся краткие теоретические сведения и решения типовых задач по курсу обыкновенных дифференциальных уравнений.Отдельныйраздел посвящен линейным однородным дифференциальным уравнениям второго порядка, к которым приводят многие прикладные задачи. Имеются также задачи и упражнения для самостоятельного решения. Материал пособия позволяет выработать практические навыки в решении и исследовании дифференциальных уравнений, описывающих процессы в различных областях наук: механика, биология, электротехника и др. Пособие рассчитано на широкий круг читателей, интересующихся математикой: школьников старших классов, студентов, преподавателей.
Преподаватель разработала своевременное пособие, в котором проведено логическое построение и изложение данного материала, что будет способствовать более успешному его усвоению.
Рецензент: _________________Козак Л.Я. - кандидат технических наук,
доцент кафедры физики,
математики и информатики
46


