- Преподавателю
- Математика
- Методические указания к теме Многогранники
Методические указания к теме Многогранники
| Раздел | Математика |
| Класс | - |
| Тип | Конспекты |
| Автор | Кормачева Е.Е. |
| Дата | 06.01.2016 |
| Формат | docx |
| Изображения | Есть |
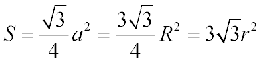
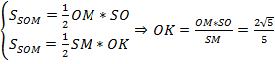
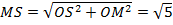
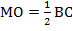
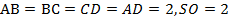
 ДЕПАРТАМЕНТ ОБРАЗОВАНИЯ ВОЛОГОДСКОЙ ОБЛАСТИ
ДЕПАРТАМЕНТ ОБРАЗОВАНИЯ ВОЛОГОДСКОЙ ОБЛАСТИ
БЮДЖЕТНОЕ ПРОФЕССИОНАЛЬНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
ВОЛОГОДСКОЙ ОБЛАСТИ
«КАДУЙСКИЙ ЭНЕРГЕТИЧЕСКИЙ КОЛЛЕДЖ»
ОДОБРЕНЫ:
методической цикловой комиссией
теоретических дисциплин
Протокол № 4 от 22.12.2014 г.
Председатель МЦК
__________________ Г.А. Веркина
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ СТУДЕНТОВ
ПО ТЕМЕ: «МНОГОГРАННИКИ»
дисциплины
«Математика»
для всех специальностей
Автор - составитель: Кормачева Е.Е, преподаватель
Кадуй
2014
Содержание
Пояснительная записка….………………………………….…………….5
1. Теоретическая часть …………………………………………………..6
2. Примеры решения задач………………………………………………
3. Задания для самостоятельной работы……………………………......9
Литература…….…………………………………………………………13
Пояснительная записка
Методические указания предназначены для студентов 1-2 курсов всех специальностей и профессий как руководство по выполнению различных видов внеаудиторной самостоятельной работы обучающихся по учебной дисциплине «Математика» раздела «Геометрия».
Целью изучения дисциплины является приобретение студентами систематических сведений об основных видах многогранников. На материале, связанном с изучением пространственных геометрических фигур, повторяются и систематизируются знания студентов о взаимном расположении точек, прямых и плоскостей в пространстве, об измерении расстояний и углов в пространстве.
Геометрия - один из важнейших компонентов математического образования, она необходима для приобретения конкретных знаний о пространстве и практически значимых умений, формирования языка описания объектов окружающего мира, развития пространственного воображения и интуиции. Изучение геометрии вносит вклад в развитие логического мышления и формирование понятия доказательства.
Данные указания содержат теоретическую часть изучаемого материала, знание которого необходимо по указанной теме. И ??
В результате изучения темы «Многогранники» студенты должны уметь: - изображать основные многогранники;
- выполнять чертежи по условиям задач;
- строить простейшие сечения куба, призмы, пирамиды;
- проводить доказательные рассуждения в ходе решения задач;
- использовать приобретенные знания и умения в практической деятельности и повседневной жизни.
Для более глубокого изучения темы «Многогранники» можно воспользоваться литературой, приведенной в методических указаниях, другими учебниками, а также конспектами лекций по курсу «Математика».
1. Теоретическая часть по теме «Многогранники»
1.1 Двугранный угол
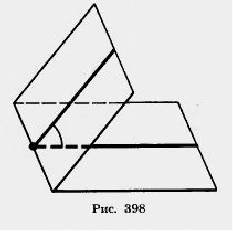
Двугранным углом называется фигура, образованная двумя полуплоскостями с общей ограничивающей их прямой (рис. 398). Полуплоскости называются гранями, а ограничивающая их прямая - ребром двугранного угла.
Плоскость, перпендикулярная ребру двугранного угла, пересекает его грани по двум полупрямым. Угол, образованный этими полупрямыми, называется линейным углом двугранного угла.
За меру двугранного угла принимается мера соответствующего ему линейного угла. Все линейные углы двугранного угла совмещаются параллельным переносом, а значит, равны. Поэтому мера двугранного угла не зависит от выбора линейного угла.
1.2 Трехгранный и многогранный угол
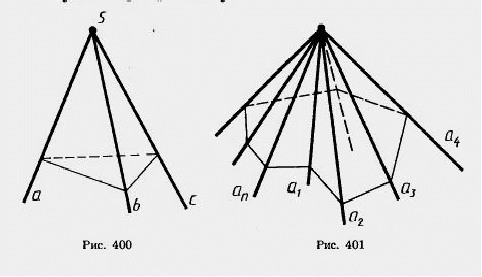
Рассмотрим три луча a, b, с, исходящие из одной точки и не лежащие в одной плоскости. Трехгранным углом (аbс) называется фигура, составленная из трех плоских углов (аb), (bс) и (aс) (рис. 400). Эти углы называются гранями трехгранного угла, а их стороны - ребрами.
Общая вершина плоских углов называется вершиной трехгранного угла.
Двугранные углы, образованные гранями трехгранного угла, называются двугранными углами трехгранного угла.
Аналогично определяется понятие многогранного угла (рис. 401).
1.3 Многогранник
В стереометрии изучаются фигуры в пространстве, называемые телами. Наглядно (геометрическое) тело надо представлять себе как часть пространства, занятую физическим телом и ограниченную поверхностью.
Многогранник называется выпуклым, если он расположен по одну сторону плоскости каждого плоского многоугольника на его поверхности. Общая часть такой плоскости и поверхности выпуклого многогранника называется гранью. Грани выпуклого многогранника являются плоскими выпуклыми многоугольниками. Стороны граней называются ребрами многогранника, а вершины - вершинами многогранника.
Куб есть выпуклый многогранник. Его поверхность состоит из шести квадратов: ABCD, BEFC, .... Они являются его гранями. Ребрами куба являются стороны этих квадратов: АВ, ВС, BE,.... Вершинами куба являются вершины квадратов: А, В, С, D, Е, ....У куба шесть граней, двенадцать ребер и восемь вершин.
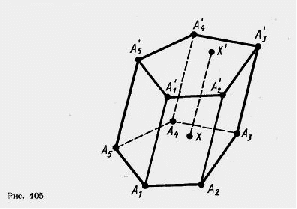
Призма
Призмой называется многогранник, который состоит из двух плоских многоугольников, лежащих в разных плоскостях и совмещаемых параллельным переносом, и всех отрезков, соединяющих соответствующие точки этих многоугольников (рис. 405). Многоугольники называются основаниями призмы, а отрезки, соединяющие соответствующие вершины,-
боковыми ребрами призмы.
Так как параллельный перенос есть движение, то основания призмы равны.
При параллельном переносе плоскость переходит в параллельную плоскость (или в себя), поэтому у призмы основания лежат в параллельных плоскостях.
Так как при параллельном переносе точки смещаются по параллельным (или совпадающим) прямым на одно и то же расстояние, то у призмы боковые ребра параллельны и равны.
Поверхность призмы состоит из оснований и боковой поверхности. Боковая поверхность состоит из параллелограммов. У каждого из этих параллелограммов две стороны являются соответствующими сторонами оснований, а две другие - соседними боковыми ребрами. Высотой призмы называется расстояние между плоскостями ее оснований. Отрезок, соединяющий две вершины призмы, не принадлежащие одной грани, называется диагональю призмы.
Призма называется n-угольной, если ее основания - n-угольники.
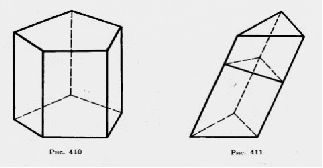
Прямая призма
Призма называется прямой, если ее боковые ребра перпендикулярны основаниям. В противном случае призма называется наклонной.
У прямой призмы боковые грани являются прямоугольниками. При изображении прямой призмы на рисунке боковые ребра обычно проводят вертикально.
Прямая призма называется правильной, если ее основания являются правильными многоугольниками.
Боковой поверхностью призмы (точнее, площадью боковой поверхности) называется сумма площадей боковых граней. Полная поверхность призмы равна сумме боковой поверхности и площадей оснований.
Теорема. Боковая поверхность прямой призмы равна произведению периметра основания на высоту призмы, т. е. на длину бокового ребра.
Параллелепипед
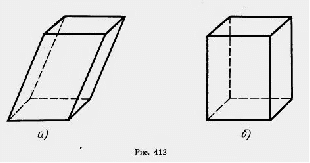
Если основание призмы есть параллелограмм, то она называется параллелепипедом. У параллелепипеда все грани - параллелограммы.
На рисунке 412, а изображен наклонный параллелепипед, а на рисунке 412, б - прямой параллелепипед.
Грани параллелепипеда, не имеющие общих вершин, называются противолежащими.
Теорема
У параллелепипеда противолежащие грани параллельны и равны.
Центральная симметрия параллелепипеда?
Теорема
Диагонали параллелепипеда пересекаются в одной точке и точкой пересечения делятся пополам.
Прямоугольный параллелепипед.
Прямой параллелепипед, у которого основанием является прямоугольник, называется прямоугольным параллелепипедом. У прямоугольного параллелепипеда все грани - прямоугольники.
Прямоугольный параллелепипед, у которого все ребра равны, называется кубом.
Длины непараллельных ребер прямоугольного параллелепипеда называются его линейными размерами (измерениями). У прямоугольного параллелепипеда три измерения.
Теорема
В прямоугольном параллелепипеде квадрат любой диагонали равен сумме квадратов трех его измерений.
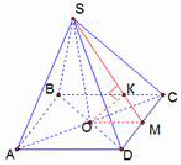
У прямоугольного параллелепипеда, как у всякого параллелепипеда, есть центр симметрии - точка пересечения его диагоналей. У него есть также три плоскости симметрии, проходящие через центр симметрии параллельно граням.
На рисунке 416 показана одна из таких плоскостей. Она проходит через середины четырех параллельных ребер параллелепипеда. Концы ребер являются симметричными точками.
Если у параллелепипеда все линейные размеры разные, то у него нет других плоскостей симметрии, кроме названных.
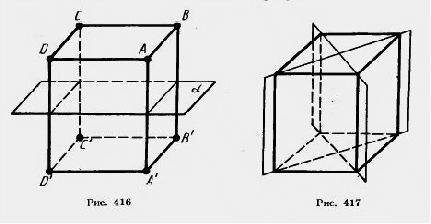
Если же у параллелепипеда два линейных размера равны, то у него есть еще две плоскости симметрии. Это плоскости диагональных сечений, показанные на рисунке 417.
Если у параллелепипеда все линейные размеры равны, т. е. он является кубом, то у него плоскость любого диагонального сечения является плоскостью симметрии. Таким образом, у куба девять плоскостей симметрии.
2. Задания для самостоятельной работы
2.1 Тест
1.Тело, поверхность которого состоит из конечного числа плоских многоугольников, называется:
а) четырехугольник
б) многоугольник
в) многогранник
г) шестиугольник
2. Вершины многогранника обозначаются:
а) а, в, с, д ...
б) А, В, С, Д ...
в) ав, сд, ас, ад ...
г) АВ, СВ, АД, СД ...
3. К многогранникам относятся:
а) параллелепипед
б) призма
в) пирамида
г) все ответы верны
4. Многогранник, который состоит из двух плоских многоугольников, совмещенных параллельным переносом, называется:
а) пирамидой
б) призмой
в) цилиндром
г) параллелепипедом
5. Отрезок, соединяющий две вершины призмы, не принадлежащие одной грани называется:
а) диагональю
б) ребром
в) гранью
г) осью
6. Если боковые ребра призмы перпендикулярны основанию, то призма является:
а) наклонной
б) правильной
в) прямой
г) выпуклой
7. У призмы боковые ребра:
а) равны
б) симметричны
в) параллельны и равны
г) параллельны
8. Если в основании призмы лежит параллелограмм, то она является:
а) правильной призмой
б) параллелепипедом
в) правильным многоугольником
г) пирамидой
9. Грани параллелепипеда не имеющие общих вершин, называются:
а) противолежащими
б) противоположными
в) симметричными
г) равными
10. Многогранник, который состоит из плоского многоугольника, точки и отрезков соединяющих их, называется:
а) конусом
б) пирамидой
в) призмой
г) шаром
11. Перпендикуляр, опущенный из вершины пирамиды на плоскость основания, называется:
а) медианой
б) осью
в) диагональю
г) высотой
12. Отрезки, соединяющие вершину пирамиды с вершинами основания, называются:
а) гранями
б) сторонами
в) боковыми ребрами
г) диагоналями
13. Точки не лежащие в плоскости основания пирамиды, называются:
а) вершинами пирамиды
б) боковыми ребрами
в) линейным размером
г) вершинами грани
14. Треугольная пирамида называется:
а) правильной пирамидой
б) тетраэдром
в) треугольной пирамидой
г) наклонной пирамидой
15. Высота боковой грани правильной пирамиды, проведенная из ее вершины, называется:
а) медианой
б) апофемой
в) перпендикуляром
г) биссектрисой
16. К правильным многогранникам не относится:
а)куб
б) тетраэдр
в) икосаэдр
г) пирамида
17. У куба все грани:
а) прямоугольники
б) квадраты
в) трапеции
г) ромбы
18. Высота пирамиды является:
а) осью
б) медианой
в) перпендикуляром
г) апофемой
19. Тело, состоящее из двух кругов и всех отрезков, соединяющих точки кругов называется:
а) конусом
б) шаром
в) цилиндром
г) сферой
20. Отрезки, соединяющие точки окружностей кругов, называются:
а) гранями цилиндра
б) образующими цилиндра
в) высотами цилиндра
г) перпендикулярами цилиндра
Критерии оценивания теста:
Оценка «5» - 18-20 баллов
Оценка «4» - 16-17 баллов
Оценка «3» - 14-15 баллов
2.2 Примеры решения задач
№1. В правильной четырехугольной пирамиде ребро основания и высота равны. Найти расстояние от центра основания до боковой грани.
Решение:
Пусть задана пирамида с основанием ABCD и вершиной S. Из условия ABCD - квадрат, пусть О - точка пересечения его диагоналей, тогда SO - высота пирамиды. . Требуется найти расстояния от точки О до плоскости CSD. Расстоянием от точки до плоскости называется длина перпендикуляра опущенного из заданной точки на
плоскость.
Пусть точка М - середина DС. Опустим перпендикуляр ОК на апофему SM. Докажем, что построенный таким образом отрезок ОК перпендикулярен всей плоскости CSD. Поскольку CD перпендикулярно всей плоскости MOS, то ОK перпендикулярно CD. Так, ОК есть перпендикуляр к плоскости CDS, его и требуется найти.
Рассмотрим прямоугольный треугольник MOS. В нем как средняя линия треугольника DBC. Имеем МО=1. SO по условию равно 2. Найдем гипотенузу MS по теореме Пифагора: .
Найдем площадь рассматриваемого треугольника двумя способами:
.
№2. Площадь боковой поверхности правильной треугольной призмы равна площади основания. Вычислите длину бокового ребра, если сторона основания 7см
Решение.
Площадь правильного треугольника в основании призмы находится по формуле:
Воспользуемся первой формулой.
По условию задачи a = 7 см
Так как площадь грани призмы в данном случае будет равна 7h, где h - высота бокового ребра, количество граней - три, то
49√3 / 4 = 3 * 7h
49√3 / 4 = 21h
откуда
h = 7√3 / 12
Ответ: длина бокового ребра правильной треугольной призмы равна 7√3 / 12
Задачи для самостоятельного решения
1. В прямой треугольной призме стороны основания равны 10см, 17см и 21 см, а высота призмы 18см. Найдите площадь сечения, проведенного через боковое ребро и меньшую высоту основания.
2. Боковое ребро наклонной призмы равно15 см и наклонено к плоскости основания под углом 30 градусов. Найдите высоту призмы.
3. В правильной четырехугольной призме площадь основания 144 см2 , а высота 14 см. Найдите диагональ призмы.
4. Расстояние между параллельными прямыми, содержащими боковые рёбра наклонной треугольной призмы, равны 2 см, 3 см и 4 см, а боковые ребра 5 см. Найдите боковую поверхность призмы.
5. У параллелепипеда три грани имеют площади 1 м2 , 2 м2 и 3 м2 . Чему равна полная поверхность параллелепипеда?
6. В прямом параллелепипеде стороны основания 3 см и 5 см, а одна из диагоналей основания 4 см. Найдите большую диагональ параллелепипеда, зная, что меньшая диагональ образует с плоскостью основания угол в 60 градусов.
7. В прямом параллелепипеде боковое ребро 1 м, стороны основания 23 дм и 11 дм, а диагонали основания относятся, как 2:3. Найдите площади диагональных сечений.
8. В прямоугольном параллелепипеде стороны основания 7 дм и 24 дм, а высота параллелепипеда 8 дм. Найдите площадь диагонального сечения.
Ответы к задачам:
1. 144 см2
2. 7,5 см
3. 22 см
4. 45 см2
5. 12 м2
6. 10 см
7. 2 м2 и 3 м2
8. 2 м2
Критерии оценивания решения задачи:
Оценка «5» - Задача решена верно, с полным теоретическим обоснованием по ходу решения.
Оценка «4» - Задача решена верно, с неполным теоретическим обоснованием.
Оценка «3» - Задача решена посредством оказания помощи преподавателя.
Оценка «2» - Решение неверное. Решение отсутствует.
Литература
1. Алимов Ш. А., Колягин Ю. М., Сидоров Ю. В., Фёдорова Н. Е., Шабунин М. И. под научным руководством академика Тихонова А. Н. Алгебра и начала математического анализа 10 - 11кл. - М. Просвещение, 2006.
2. Никольский С. М., Потапов М. К., Решетников Н. Н. и др. Алгебра и начала математического анализа (базовый и профильный уровни). 10 кл. - М., 2006.
3. Колягин Ю.М., Ткачева М.В, Федерова Н.Е. и др. под ред. Жижченко А.Б. Алгебра и начала математического анализа (базовый и профильный уровни). 10 кл. - М., 2005.
4. Ю.А. Глазков, И.К. Варшавский Тематические тесты алгебра 10 класс Издательство: М.: Центр тестирования МО РФ ISBN: 5-94635-048-Х, 2001.
Интернет ресурсы:
-
www/mathematics.ru
-
tutoronline.ru/
-
exponenta.ru


