- Преподавателю
- Математика
- Решетка нормальных подгрупп группы симметрии квадрата
Решетка нормальных подгрупп группы симметрии квадрата
| Раздел | Математика |
| Класс | - |
| Тип | Другие методич. материалы |
| Автор | Гмыза Д.Г. |
| Дата | 11.05.2015 |
| Формат | docx |
| Изображения | Есть |
РЕШЕТКА НОРМАЛЬНЫХ ПОДГРУПП ГРУППЫ СИММЕТРИИ КВАДРАТА
Д. Г. Гмыза, e-mail: [email protected].
АННОТАЦИЯ. Известно, что нормальные подгруппы любой группы образует модулярную решетку. В связи с этим в данной заметке построены решетки нормальных подгрупп группы симметрии треугольника и квадрата.
КЛЮЧЕВЫЕ СЛОВА: группа, нормальная подгруппа, модулярная решетка.
Группой называется множество G элементов произвольной природы, на котором задана бинарная операция 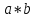 такая, что выполняются следующие условия:
такая, что выполняются следующие условия:
-
ассоциативность:
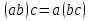 для любых элементов a, b, c из G;
для любых элементов a, b, c из G; -
в G существует такой элемент e, что
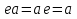 для любого элемента a из G, такой элемент e называется единицей группы G;
для любого элемента a из G, такой элемент e называется единицей группы G; -
для любого элемента a из G существует такой элемент
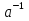 из G, что
из G, что 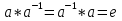 , такой элемент
, такой элемент 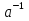 называется обратным к элементу a.
называется обратным к элементу a.
Алгебра (L; ⋀, ⋁) называется решеткой, если L непустое множество, а ⋀ и ⋁ - бинарные операции на L, которые идемпотентны, коммутативны, ассоциативны и удовлетворяют двум тождествам поглащения.
Связь между группой и решеткой непосредственно видна из следующей теоремы.
ТЕОРЕМА 1[1,2]. Нормальные подгруппы любой группы G образуют модулярную решетку.
Подгруппа некоторой группы называется нормальной подгруппой, если она переходит в себя при всех внутренних автоморфизмах группы. Другими словами, подгруппа N группы G называется нормальной подгруппой в G, если для любого элемента a из N и любого g из G элемент 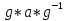 содержится в N.
содержится в N.
Пусть  обозначают соответственно вращения квадрата на 00, на 1800, на 900 и на 2700 в направлении указанном стрелкой, то есть
обозначают соответственно вращения квадрата на 00, на 1800, на 900 и на 2700 в направлении указанном стрелкой, то есть 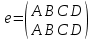 ,
, 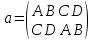 ,
, 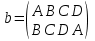 ,
, 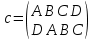 (рис а).
(рис а).
Можно составить таблицу умножения, где каждая строка, а также каждый столбец соответствует некоторому вращению, переводящему квадрат ABCD в себя. На пересечении строки, соответствующей преобразованию g2, мы будем ставить преобразование, равное 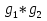 . Так, например, в клетку
. Так, например, в клетку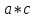 поставим:
поставим: 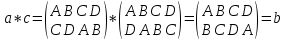 , то есть
, то есть 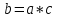 .
.
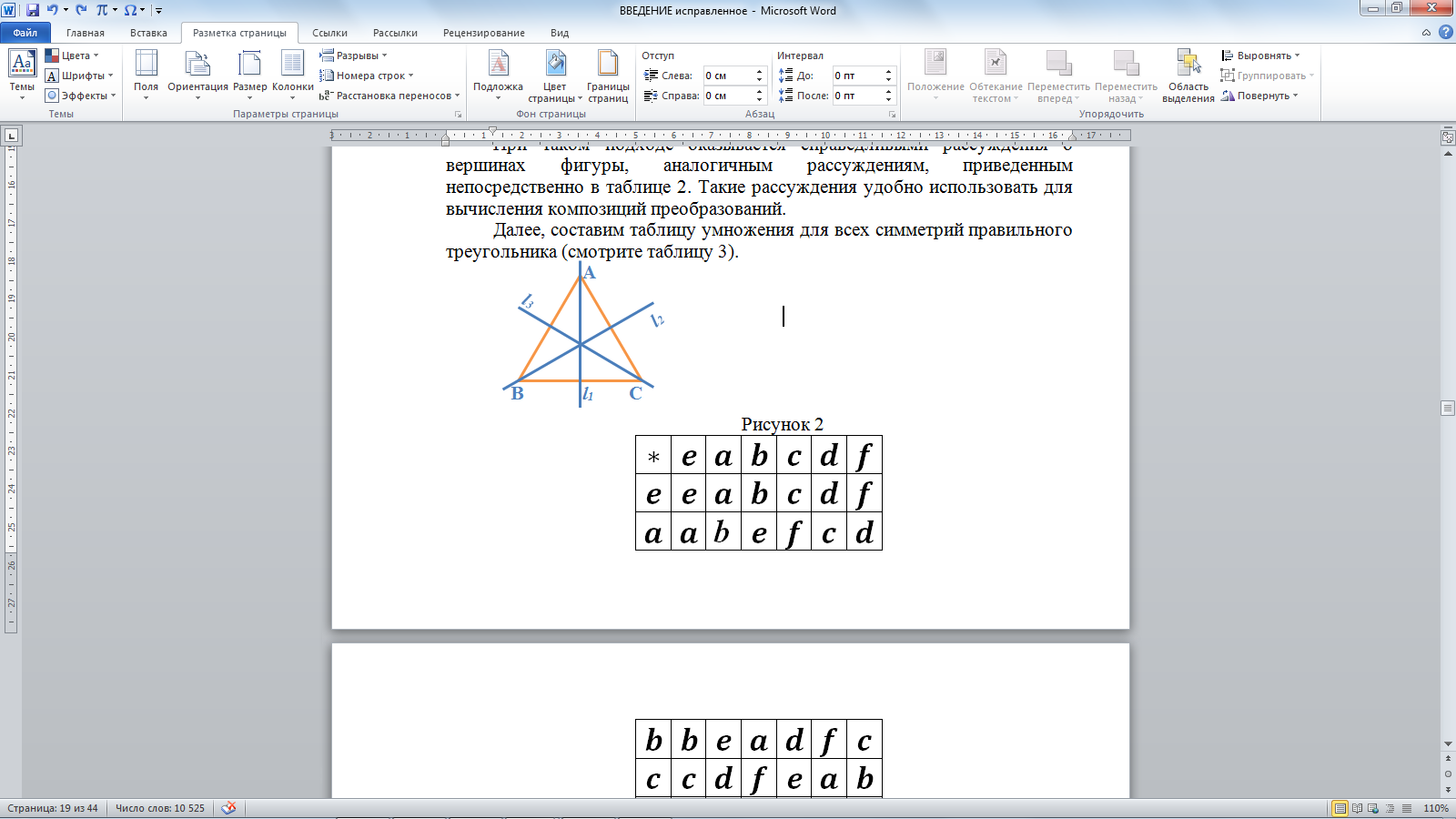
Кроме вращений, у квадрата имеется 4 симметрии, а именно, отражения относительно осей d, f, g и h. Эти преобразования мы обозначим соответственно: 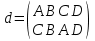 ,
, 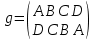 ,
, 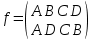 ,
, 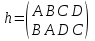 (рис б).
(рис б).
Элемент g стоящий на пересечении столбца а и строки h вычисляется так: 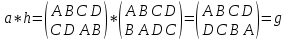 (таблица 1). Аналогично была заполнена другая часть таблицы 1.
(таблица 1). Аналогично была заполнена другая часть таблицы 1.
Непосредственно проверяется, что множество преобразований квадрата 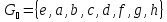 с таблицей 1 образует группу, которая называется группой симметрии квадрата.
с таблицей 1 образует группу, которая называется группой симметрии квадрата.
Далее, подгруппами в 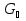 являются следующие: подгруппа вращений квадрата
являются следующие: подгруппа вращений квадрата 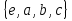 , подгруппа центральных симметрий
, подгруппа центральных симметрий 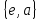 , 4 подгруппы отражений относительно осей симметрии:
, 4 подгруппы отражений относительно осей симметрии: 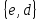 ,
, 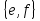 ,
, 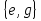 ,
, 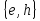 , и еще 2 подгруппы:
, и еще 2 подгруппы: 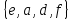 и
и 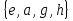 , 2 тривиальные подгруппы:
, 2 тривиальные подгруппы: 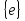 и вся группа
и вся группа 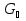 . Теперь среди этих 10 подгрупп выделим нормальных, для этого воспользуемся теоремой 2.
. Теперь среди этих 10 подгрупп выделим нормальных, для этого воспользуемся теоремой 2.
Если нормальная подгруппа в группе 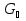 содержит элемент b или c, то она содержит всю подгруппу вращения квадрата, то есть получаем нормальную подгруппу
содержит элемент b или c, то она содержит всю подгруппу вращения квадрата, то есть получаем нормальную подгруппу 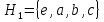 .
.
Имеем 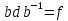 и
и 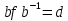 . Поэтому если один из элементов d, f входит в нормальную подгруппу, то и второй также входит в нормальную подгруппу. Так как
. Поэтому если один из элементов d, f входит в нормальную подгруппу, то и второй также входит в нормальную подгруппу. Так как 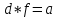 , то в этом случае элемент
, то в этом случае элемент 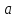 также входит в нормальную подгруппу. Получаем нормальную подгруппу
также входит в нормальную подгруппу. Получаем нормальную подгруппу  .
.
Так как 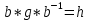 ,
,  и
и 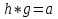 , то так же, как выше, получаем нормальную подгруппу
, то так же, как выше, получаем нормальную подгруппу  .
.
Если же нормальная подгруппа не содержит элементов 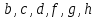 , то она совпадает с нормальной группой
, то она совпадает с нормальной группой 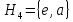 .
.
Следовательно, в силу теоремы 1 имеет следующую решетку (рис в).
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
-
Г. Гретцер, Общая теория решеток, М, Мир, 1982
-
Г. Биркгоф, Теория решеток, М, Наука, 1984
-
В. Н. Алексеев, Теория Абеля в задачах и решениях, М, Наука, 1976
и т.д.
-
.
e
a
b
c
d
f
e
e
a
b
c
d
f
a
a
b
e
f
c
d
b
b
e
a
d
f
c
c
c
d
f
e
a
b
d
d
f
c
b
e
a
f
f
c
d
a
b
e
Таблица 1
О
А
С
В
а)
б)
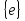
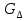
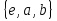
в)
Рис. 1
.
e
a
b
c
d
f
g
h
e
e
a
b
c
d
f
g
h
a
a
e
c
b
f
d
h
g
b
b
c
a
e
g
h
f
d
c
c
b
e
a
h
g
d
f
d
d
f
h
g
e
a
c
b
f
f
d
g
h
a
e
b
c
g
g
h
d
f
b
c
e
a
h
h
g
f
d
c
b
a
e
Таблица 2
О
D
A
BО
C
а)

б)
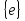
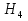
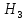
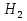
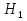
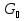
в)
Рис. 2


