- Преподавателю
- Математика
- Решение уравнений, содержащих переменную под знаком модуля
Решение уравнений, содержащих переменную под знаком модуля
| Раздел | Математика |
| Класс | - |
| Тип | Конспекты |
| Автор | Шиш Л.В. |
| Дата | 26.08.2014 |
| Формат | docx |
| Изображения | Есть |
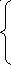
 Существенной характеристикой числа как в действительной, так и в комплексной области является понятие его абсолютной величины или модуля.
Существенной характеристикой числа как в действительной, так и в комплексной области является понятие его абсолютной величины или модуля.
Это понятие имеет широкое распространение в различных отделах физико-математических и технических наук.
В школьном курсе вводится понятие модуля числа и с помощью этого понятия формулируются правила действий над рациональными числами, понятие абсолютной погрешности приближенного числа, свойства арифметического квадратного корня, рассматриваются свойства корна n-степени, исследование функции.
В 6-ом классе можно решать уравнения вида |кх + в| = а,
в 7-ом классе вида |кх + в| = ах + с,
а также построение графиков функции вида:
у = к · |х| + в; у = |кх + в|; 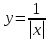 и др.,
и др.,
в 8-9-м классах графики функций вида у = |ах2 + вх + с|; у = 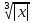 ; у =
; у = 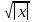 и др.
и др.
При построении графиков целесообразно использовать метод преобразований графиков (параллельный перенос, симметрия и др.).
Рассмотрим решения вопросов, связанных с понятием модуля, которые могут быть рассмотрены как на уроке, так и во внеклассной работе.
Основные определения и основные теоремы.
Определение 1.
Модулем действительного числа а называется неотрицательное число, взятое из двух чисел а или -а
а, если а >0
Из определения следует |а| = 0, если а = 0
- а, если а < 0
Теорема 1.
Противоположные числа имеют равные модули, т.е. |а| = |-а|
Теорема 2.
Модуль суммы конечного числа действительных чисел не превосходит сумму модулей слагаемых, т.е. |а1 + а2 + …+ аn| ≤ |а1| + |а2| + … + |аn|
Теорема 3. |а - в| ≤ |а| + |в|
Теорема 4. ||а| - |в|| ≤ |а ± в| ≤ |а| + |в|
Теорема 5. |а · в| = |а| · |в|
Теорема 6. 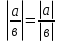 в ≠ 0
в ≠ 0
Пример. Решить уравнение: 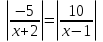
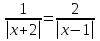
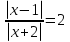 или
или 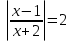
имеем 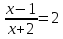 и
и 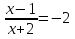 следовательно,
следовательно,
х1 = -5; х2 = -1
Решение уравнений
-
Решение уравнения вида |ƒ(х)| = а, где а ≥ 0
-
Решить уравнение: |х-3| = 2
|х - 3| =х - 3, х ≥ 3 х - 3 = 2 х1 = 5
-х + 3, х < 3 х - 3 = -2 х2 = 1
Пример № 2. Решить уравнение:
|sin x + cos x| = 1
Решение
|sin x + cos x| = 1 => sin х + cos х = 1
или sin x + cos x = -1
Решим эти два уравнения.
sin х + cos х = 1 sin х + cos х = -1
cos х - 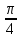 =
= 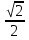 cos( х -
cos( х - 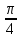 ) = -
) = - 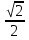
х = 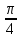 ±
± 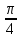 + 2πκ, κ
+ 2πκ, κ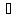 z х =
z х = 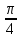 ±
± 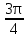 + 2πn, n
+ 2πn, n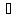 z
z
х1 = 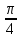 -
- 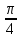 + 2πκ, κ
+ 2πκ, κ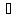 z х1 = -
z х1 = - 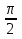 + 2πn, n
+ 2πn, n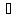 z
z
х1 = 2πκ, κ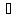 z х2 = π + 2πn, n
z х2 = π + 2πn, n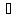 z
z
х2 = 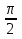 + 2πκ, κ
+ 2πκ, κ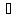 z
z
Общий вид решения будет х = 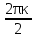
Ответ: 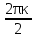 , κ
, κ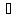 z
z
Уравнение вида ƒ|х| = а
Чтобы решить уравнение вида ƒ|х| = а рассмотрим решение двух систем:
ƒ(х) = а и ƒ(-х) = а
х ≥ 0 х ≤ 0
Функция g(х) = ƒ|х| - а четная.
Значения переменной, при которой функция обращается в нуль, будут противоположные числа. Поэтому достаточно найти решение одной из систем, второй корень будет противоположным ему числом.
Например: Решить уравнение х2 - |х| = 6
Решение
х, х ≥ 0
х2 - |х| = 6 по определению абсолютной величины |х| = - х, х < 0
данное уравнение распадается на совокупность двух смешанных систем
х2 - х = 6 и х2 + х = 6
х ≥ 0 х ≤ 0
Решим систему х2 - х - 6 = 0
х ≥ 0
Уравнению х2 - х - 6 = 0 удовлетворяют числа х1 = -2 и х2 = 3, из которых условию х ≥ 0 удовлетворяет х2 = 3.
Следовательно, корнями данного уравнения являются числа 3 и -3,
Ответ: 3, -3
Уравнение вида |ƒ(х)| = φ(х)
Данное уравнение |ƒ(х)| = φ(х) распадается на совокупность двух смешанных систем:
ƒ(х) = φ(х) ƒ(х) = -φ(х)
φ(х) ≥ 0 и φ(х) ≥ 0
Например:
-
Решить уравнение |3х - 7| = х - 2
Решение
|3х - 7| = х - 2
Решению подлежат две системы:
3х - 7 = х - 2 и 3х - 7 = 2 - х
х - 2 ≥ 0 х - 2 ≥ 0
2х = 5 и 4х = 9
х - 2 ≥ 0 х - 2 ≥ 0
х = 2,5 и х = 2,25
х - 2 ≥ 0 х - 2 ≥ 0
Числа 2,5 и 2,25 удовлетворяют данному уравнению
Ответ: 2,5; 2,25
-
Решить уравнение |х2 - 4| = х2 - 4
Решение
х2 - 4 = х2 - 4 и х2 - 4 = 4 - х2
х2 - 4 ≥ 0 х2 - 4 ≥ 0
х - любое число и х = ± 2
х ≥ 2 и х ≤ -2 х ≥ 2 х ≤ - 2
Ответ: уравнению удовлетворяют все значения х ≥2 и х ≤ - 2
-
Решить уравнение: |sin x| = sin x
Решение
sin x = sin x и sin x = -sin x
sin x ≥ 0 sin x ≥ 0
х - любое х = πκ, κ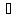 z
z
2πn ≤ х ≤ π + 2πn и 2πn ≤ х ≤ π + 2πn, n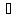 z
z
Ответ: 2πκ ≤ х ≤ π + 2πn, n 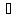 z
z
Уравнение вида |κ1х + в1| ± |κ2х + в2| ± …± |κnх + вn| = а
Для решения уравнения такого вида найдем абсциссы точек перелома графика функции - левой части этого уравнения, т.е. х1 = - 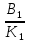 ; х2 = -
; х2 = - 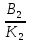 ; …. хn= -
; …. хn= - 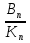 ;
;
пусть х1 < х2 < ……< хn
-
Данное уравнение последовательно рассмотрим на промежутках: (-∞; х1]; [х1; х2]; [х2; х3]; …. [хn; ∞).
На промежутке (-∞; х1] получим некоторое линейное уравнение ƒ1(х) = 0 и его корень х = а1.
Если а1 содержится в (-∞; х1], то а1 корень данного уравнения, а если не содержится, то а1 не является корнем данного уравнения. И так рассмотрим решение на каждом из промежутков.
Примеры.
-
Решить уравнение |х - 1| + |х - 2| = 1
Точки перелома х1 = 1, х2 = 2.
Решение уравнения рассмотрим на промежутках (-∞; 1]; [1; 2]; [2; ∞).
-
х < 1; - х + 1 - х + 2 = 1; -2х = 2; х = 1 Так как 1
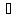 (-∞; 1], то х = 1
(-∞; 1], то х = 1
является корнем уравнения
-
1 ≤ х ≤ 2; х - 1 - х + 2 = 1; 0 · х = 0; х - любое число из множества [1; 2]
-
х ≥ 2 х - 1 + х - 2 = 1; 2х = 4; х = 2 2
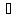 [2; ∞)
[2; ∞)
Ответ: [1; 2]
-
Решить уравнение:
|2х - 3| + |х - 3| - |4х - 1| = 0
Найдем точки перелома:
х1 = 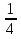 ; х2 = 1,5; х3 = 3
; х2 = 1,5; х3 = 3
Промежутки задания уравнения:
(-∞; 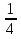 ]; [
]; [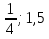 ]; [1,5; 3]; [3; ∞)
]; [1,5; 3]; [3; ∞)
1. х ≤ 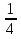 ; -2х + 3 - х + 3 + 4х - 1 = 0; х = -5
; -2х + 3 - х + 3 + 4х - 1 = 0; х = -5
-5 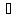 (-∞;
(-∞;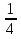 ] значит х = -5 корень уравнения
] значит х = -5 корень уравнения
2. 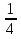 ≤ х ≤ 1,5; -2х + 3 - х + 3 - 4х + 1 = 0; х = 1
≤ х ≤ 1,5; -2х + 3 - х + 3 - 4х + 1 = 0; х = 1
1 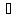 [
[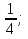 1,5] х = 1 корень уравнения
1,5] х = 1 корень уравнения
-
1,5 ≤ х ≤ 3; 2х - 3 - х + 3 - 4х + 1 = 0; -3х = -1; х =
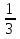
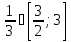 ; х =
; х = 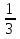 не является корнем уравнения
не является корнем уравнения
-
х ≥ 3; 2х - 3 + х - 3 - 4х + 1 = 0; х = -5 не является корнем уравнения
-5 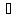 [3; ∞)
[3; ∞)
Ответ: -5; 1
3. Решить уравнение: | | | |х| - 2| -1| -2| = 2
Решение
По определению модуля имеем: | | |х| -2| -1| -2 = ± 2, т.е. два уравнения
Решим первое
Решим второе уравнение
| | | х| -2| -1| -2 = 2
| | | х| -2| -1| -2 = -2
| | | х| -2| -1| = 4
| | | х| -2| -1| = 0
| | х| -2| -1| = ±4
| | х| -2| = 1
| | х| -2| = 5 и | | х| -2| = -3
| х| -2 = ± 1
|х| - 2 = ± 5; ||х| -2| = -3 - не имеет решения; |х| = 3 или |х| = 1
х = ± 3 х = ± 1
|х| = 7 или |х| = -3 - нет решения
х = ±7
Ответ: ±1; ±3; ±7
Решите уравнения:
а) | | х - 1| - 1| = 2; б) |х - 3| = (х - 3)2
в) |х + 1| - |х - 1| = 2 г) |х| = х + 3
д) |х + 2| + |х| + |х - 2| = 4 е) log2 |х3 + 2х2 - 4х -2| = 2
ж) |sin 2х| =