- Преподавателю
- Математика
- Свойство биссектрисы угла треугольника
Свойство биссектрисы угла треугольника
| Раздел | Математика |
| Класс | - |
| Тип | Другие методич. материалы |
| Автор | Смирнова М.Н. |
| Дата | 24.10.2014 |
| Формат | doc |
| Изображения | Есть |
22
СОДЕРЖАНИЕ
Введение……………………………………………………………………. 2
-
Свойство биссектрисы треугольника и способы
доказательства …………………………………………………………4
-
Нахождение длины биссектрисы (формулы) ………………………7
-
Соотношения, связанные с биссектрисой………………………..…...13
4.Задачи…………………………………………………………………….16
5. Выводы…………………………………………………………………..20
6. Список литературы…………………………………………………….21
ВВЕДЕНИЕ
Цель работы:
Показать многообразие способов доказательства свойства биссектрисы треугольника.
Задачи:
-
Ознакомиться с литературой по данной теме, повторить ряд геометрических фактов, необходимых для проекта
-
Систематизировать теоретический материал, используемый для доказательства теоремы
-
Выяснить практическое применение формул для вычисления биссектрисы треугольника
-
Создание презентации к работе
Что мы знаем о биссектрисе угла треугольника? Наверное не так уж и много - определение биссектрисы; факт, что точка пересечения биссектрис является центром вписанной в треугольник окружности и свойство деления стороны биссектрисой на отрезки пропорциональные прилежащим сторонам.
В своей работе я постаралась систематизировать сведения и найти дополнительную информацию, которая углубляет знания об этом понятии в теории треугольников. С помощью научной литературы по теме и работы с научным руководителем, мы привели несколько способов доказательства свойства биссектрисы треугольника. При этом использовали следующие теоремы и понятия:
1.Теорему Фалеса о пропорциональных отрезках
2. Подобие треугольников
3. Применение формул площадей треугольника
4. Теорема синусов
Доказательство теоремы разными способами позволят повторить широкий спектр геометрических фактов, совершенствовать навыки применения разных методов и приемов решения задач, способствует более глубокому и прочному пониманию и запоминанию материала.
В работе значительно расширены сведения о биссектрисах треугольника:
-
приводятся 4 вида формул для вычисления биссектрисы треугольника, эти формулы имеют практическое применение;
-
выводятся формулы радиуса окружности, вписанной в треугольник;
-
формулируются свойства точки пересечения продолжения биссектрисы треугольника с описанной окружностью;
-
устанавливается взаимное расположение высоты, медианы и биссектрисы треугольника, проведенных из одной вершины ( 3 способа).
.
РАЗДЕЛ 1
Свойство биссектрисы треугольника и способы его доказательства.
Теорема.
Биссектриса делит сторону треугольника на отрезки пропорциональные двум другим сторонам 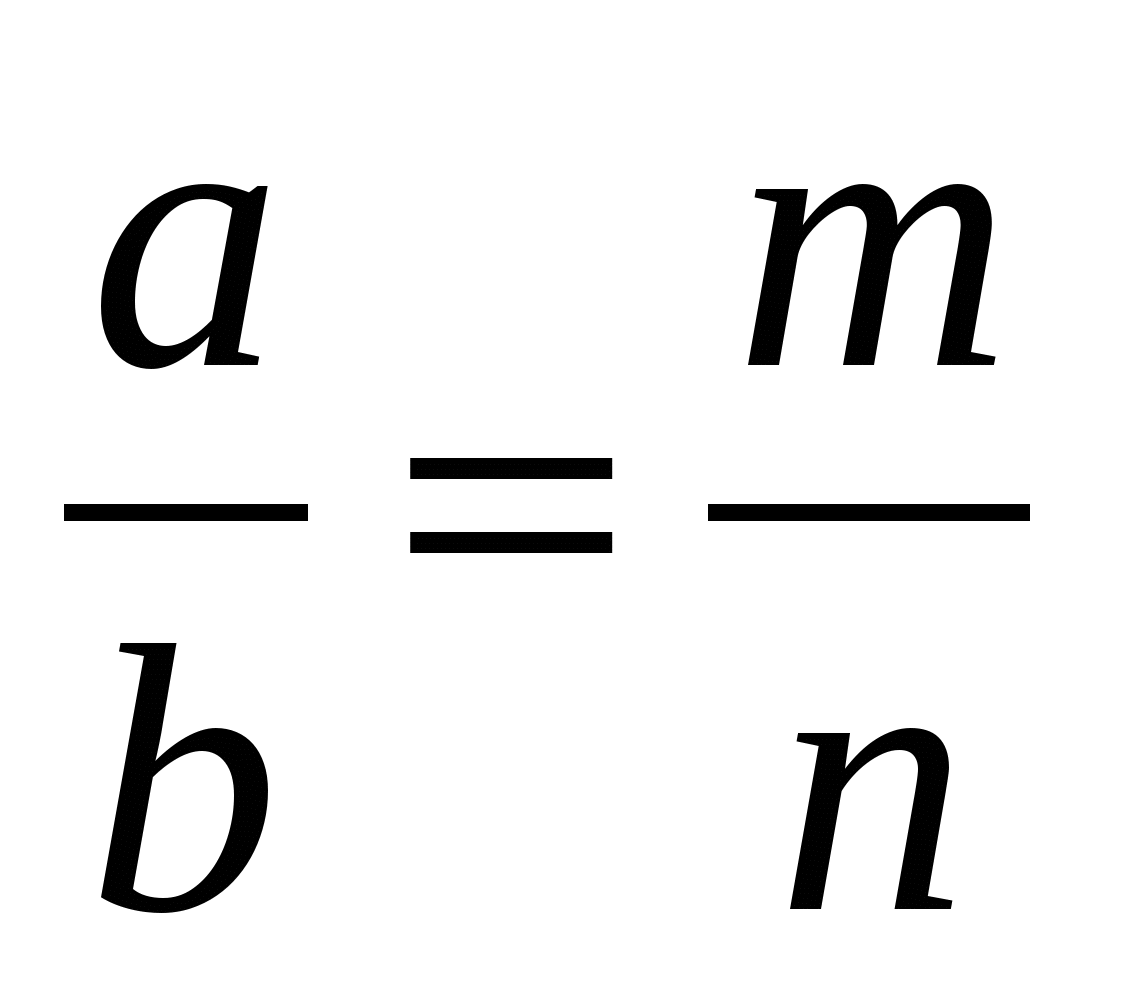 .
.
Дано: ∆ АВС, BD - его биссектриса.
Доказать: ![]()
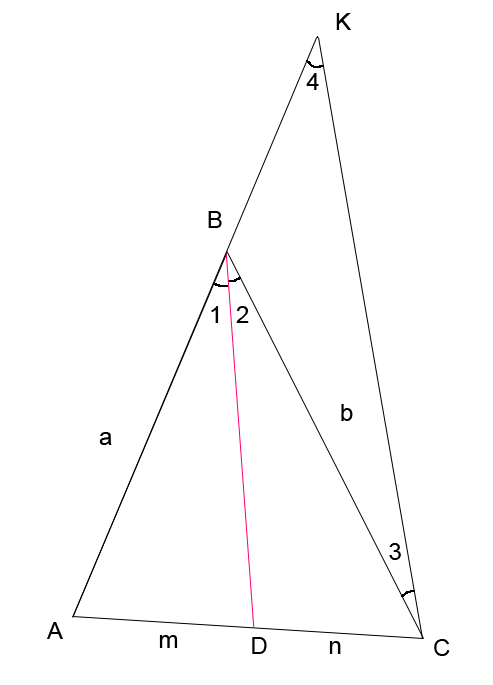 Рис. 1.1
Рис. 1.1
1. Применим к доказательству теорему Фалеса
Проведем прямую CK||BD и продолжим сторону AB до пересечения с этой прямой.  2 =
2 = 3 как внутренние накрест лежащие при параллельных прямых BD и KC и секущей BC.
3 как внутренние накрест лежащие при параллельных прямых BD и KC и секущей BC. ![]() 1 =
1 = ![]() 4 как соответственные углы при CK||BD и секущей BC.
4 как соответственные углы при CK||BD и секущей BC.
∆ BCK - равнобедренный. 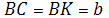
Тогда по теореме Фалеса: 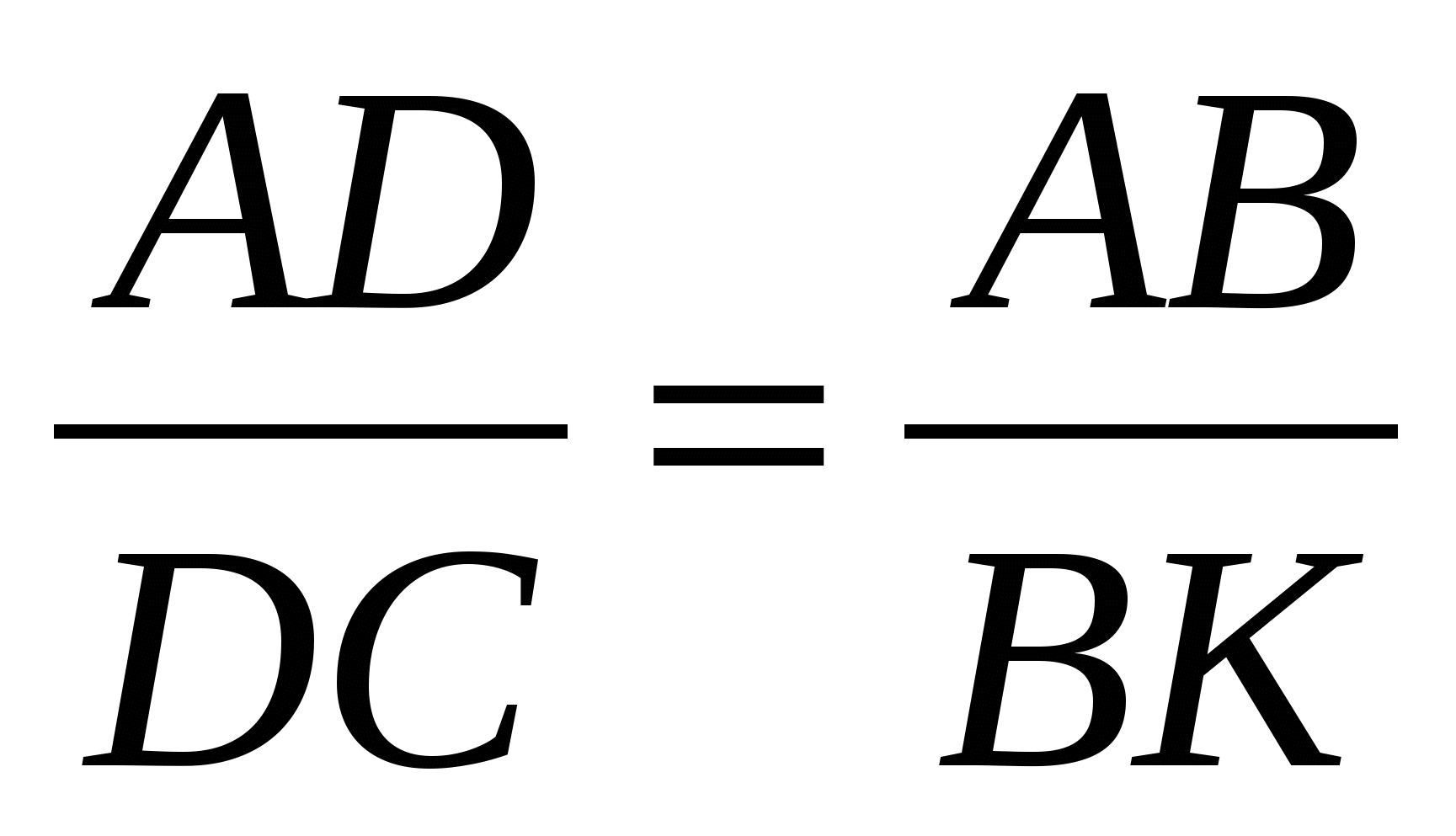
Т.е 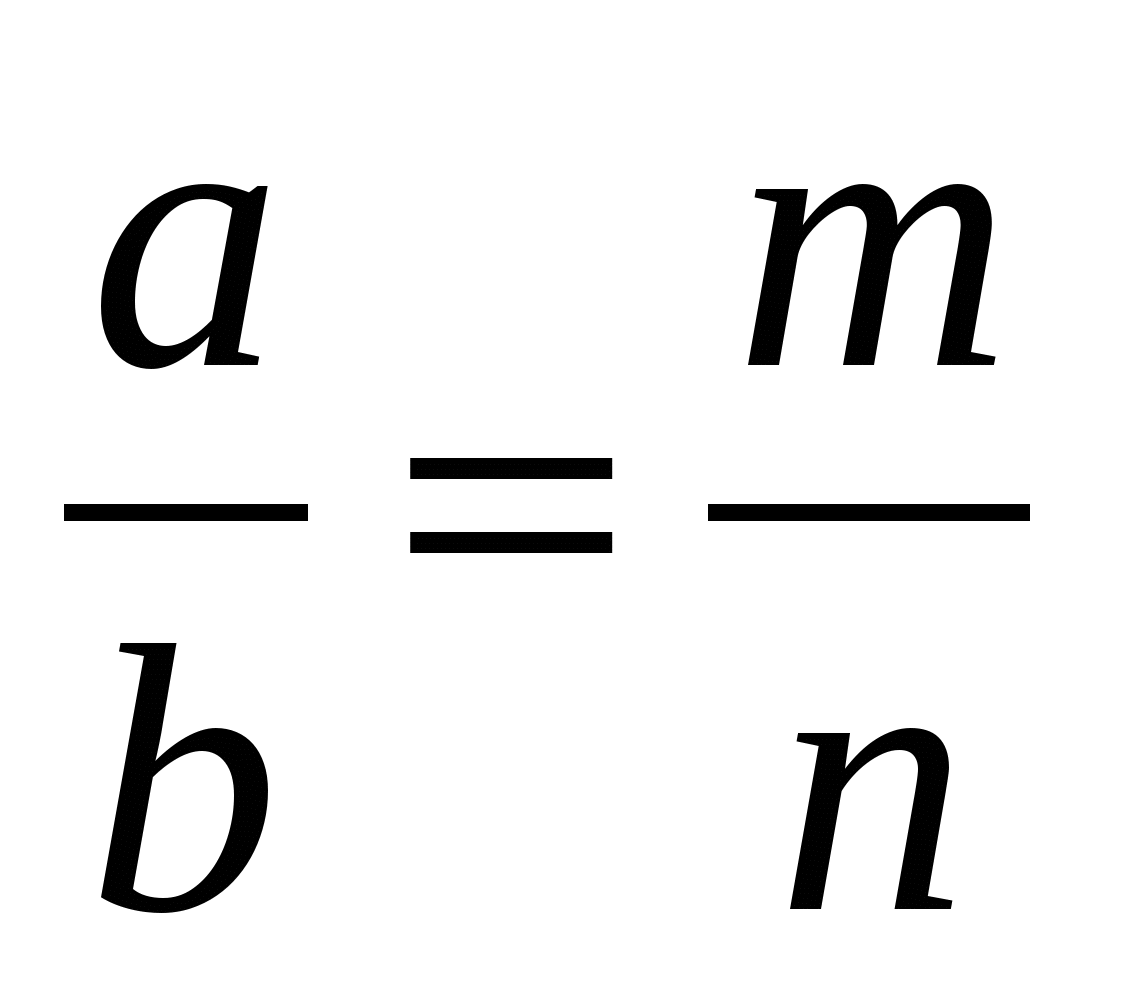 , что и требовалось доказать
, что и требовалось доказать
-
Применим подобие треугольников (рис. 1.2)
 Проведем перпендикуляры из вершин А и С на биссектрису и ее продолжение, тогда имеем:
Проведем перпендикуляры из вершин А и С на биссектрису и ее продолжение, тогда имеем:
Рис. 1.2
∆ AND ~ ∆ CMD (по двум углам). Из определения подобия треугольников следует пропорциональность соответствующих сторон:
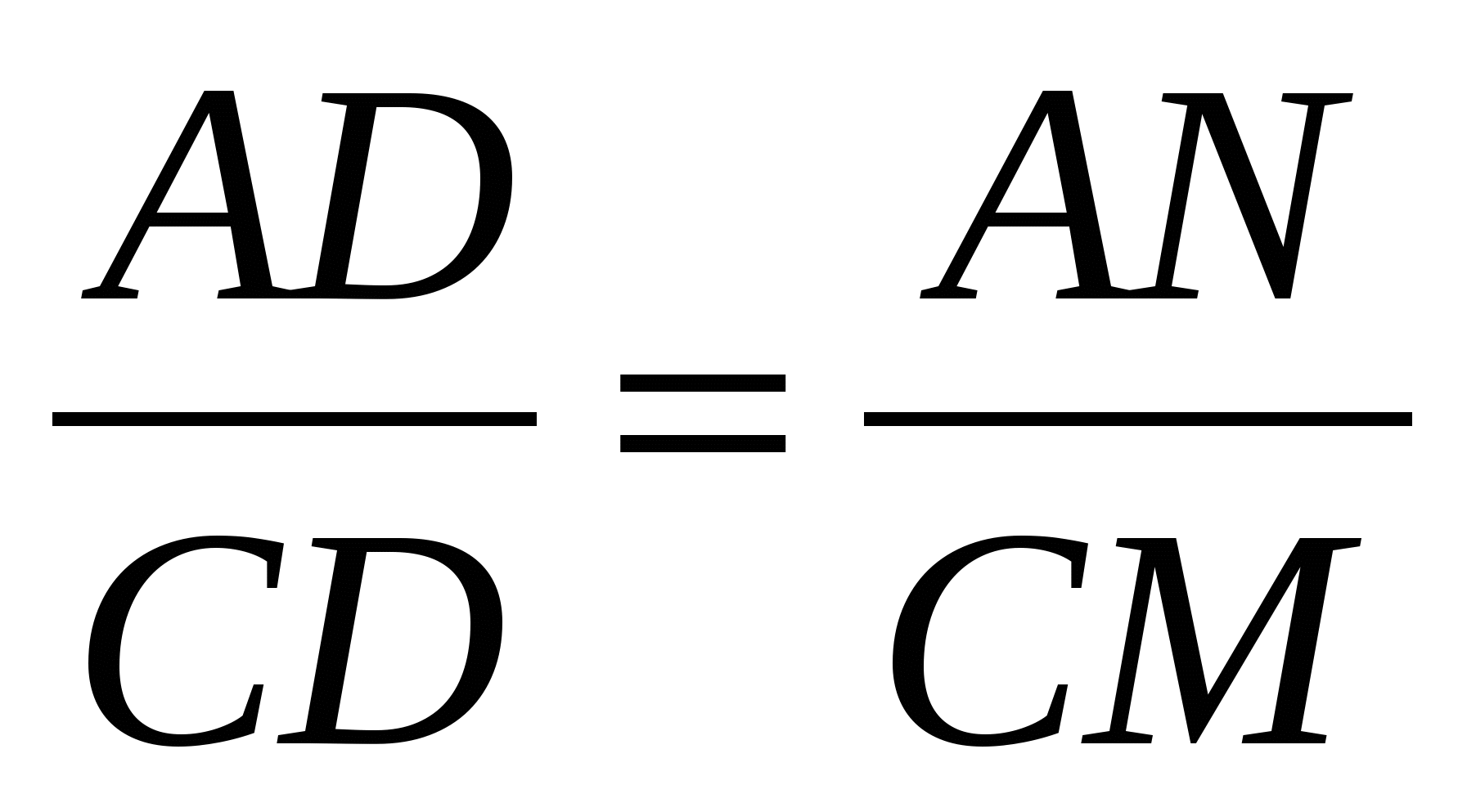 ,
, 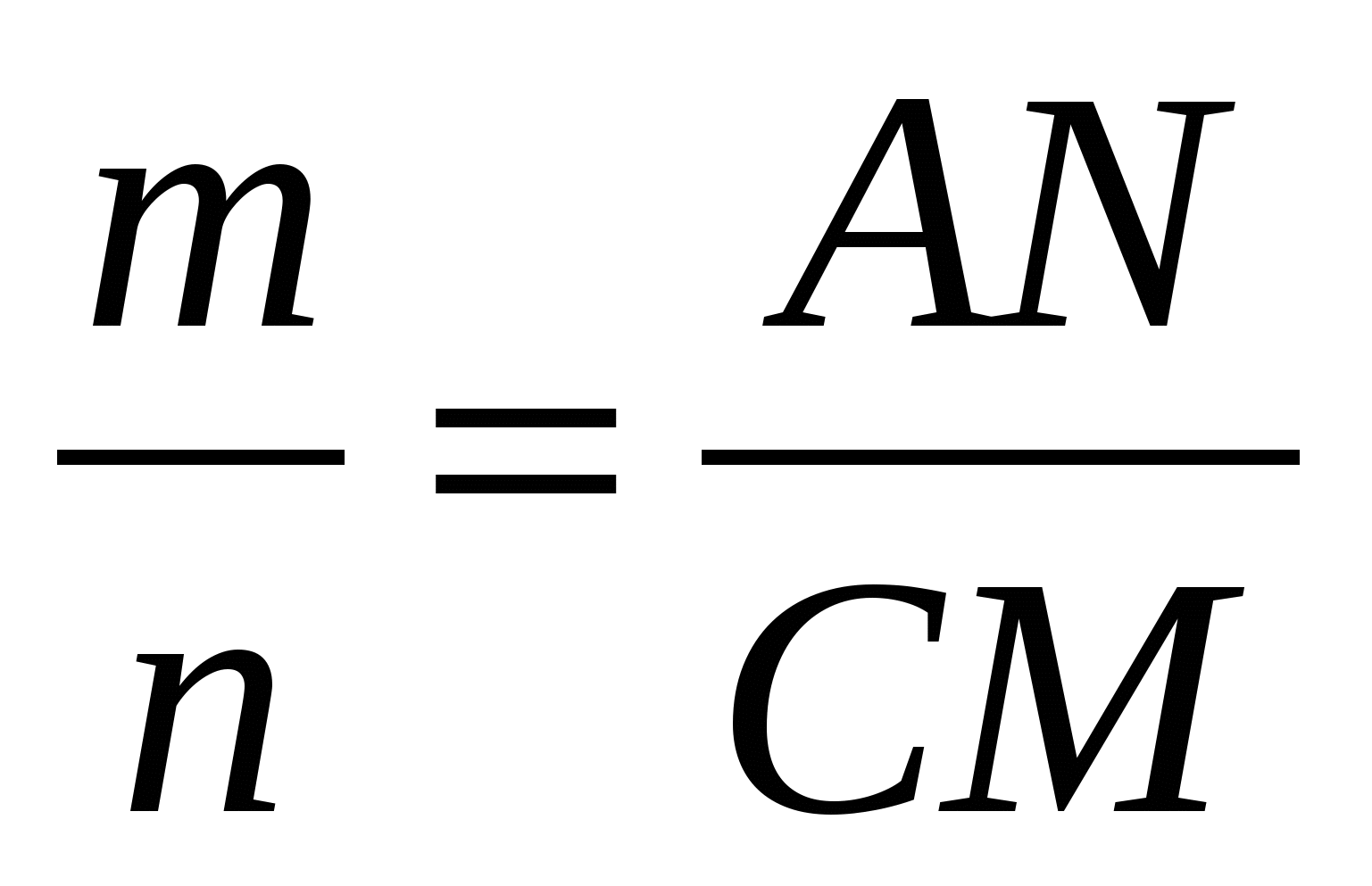 (*)
(*)
∆ ABN~ ∆ CBM, тогда 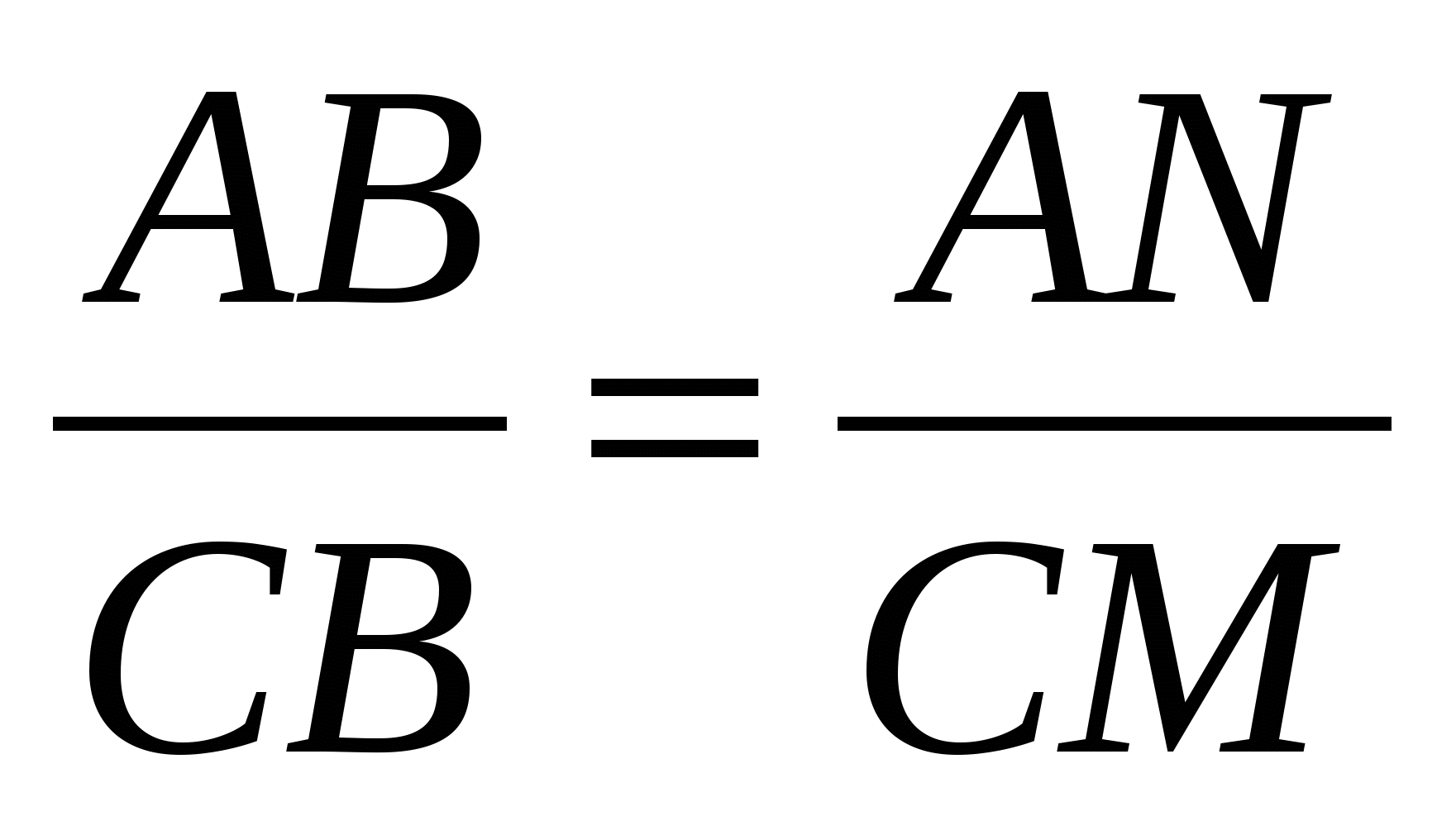 ;
; 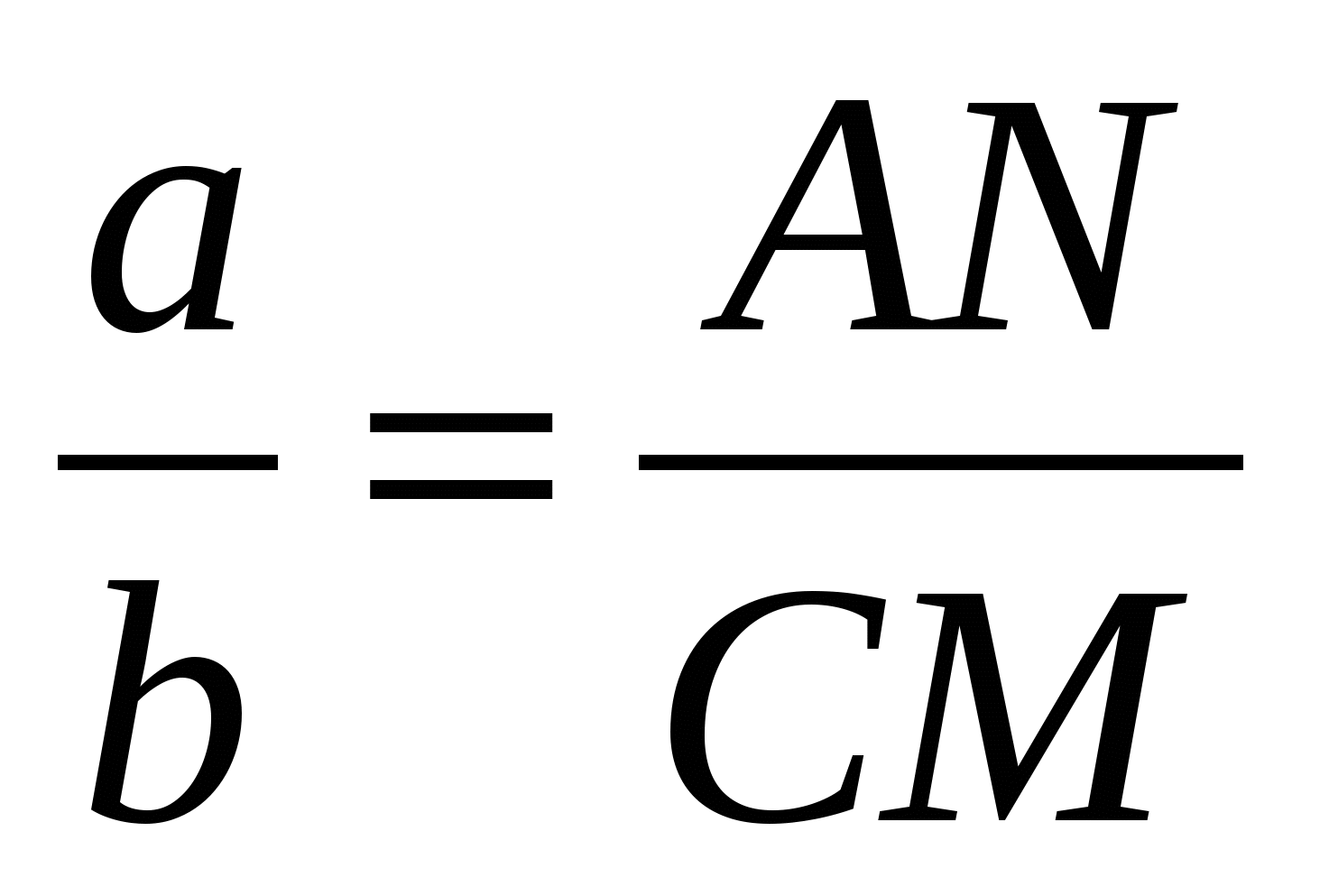 (**)
(**)
В равенствах (*) и (**) равны правые части, а значит: 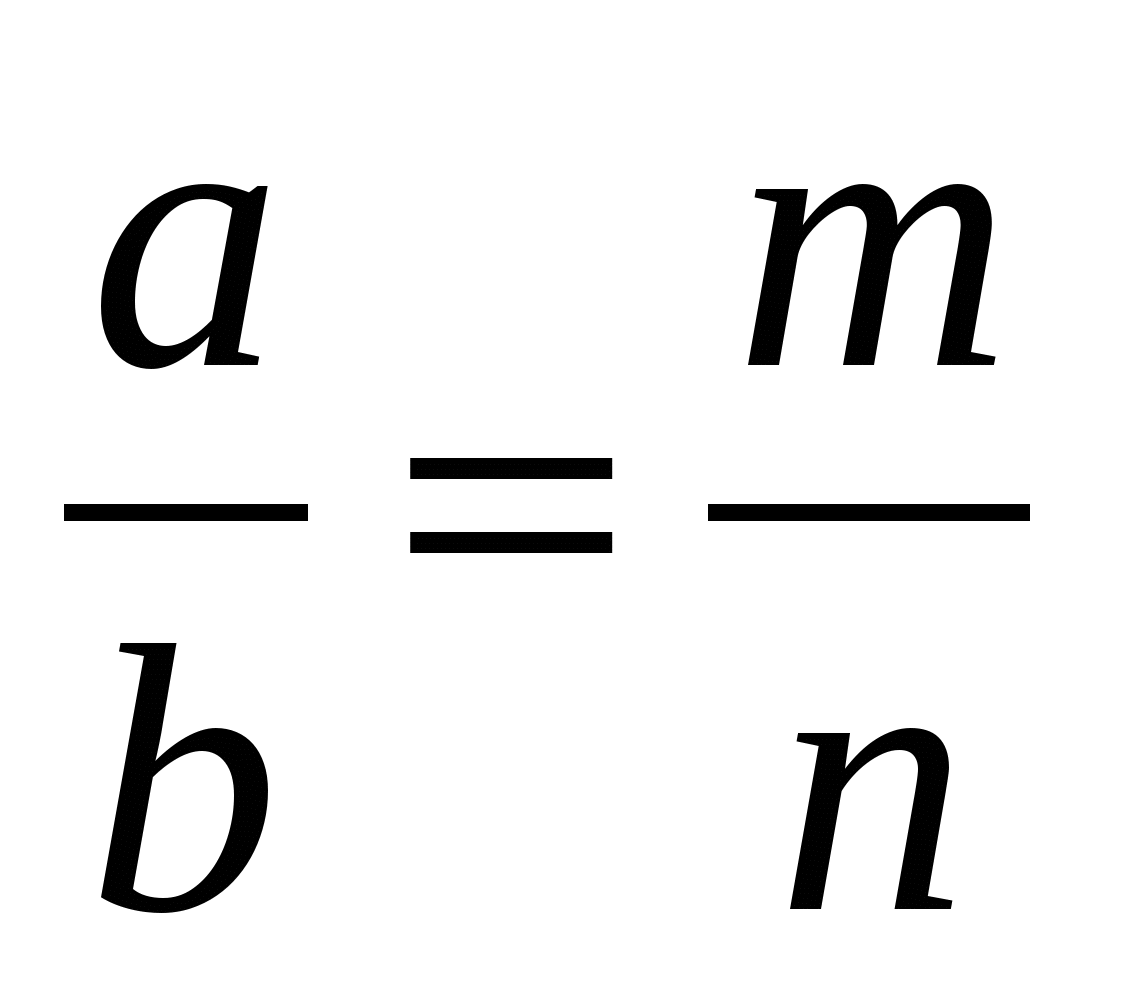
-
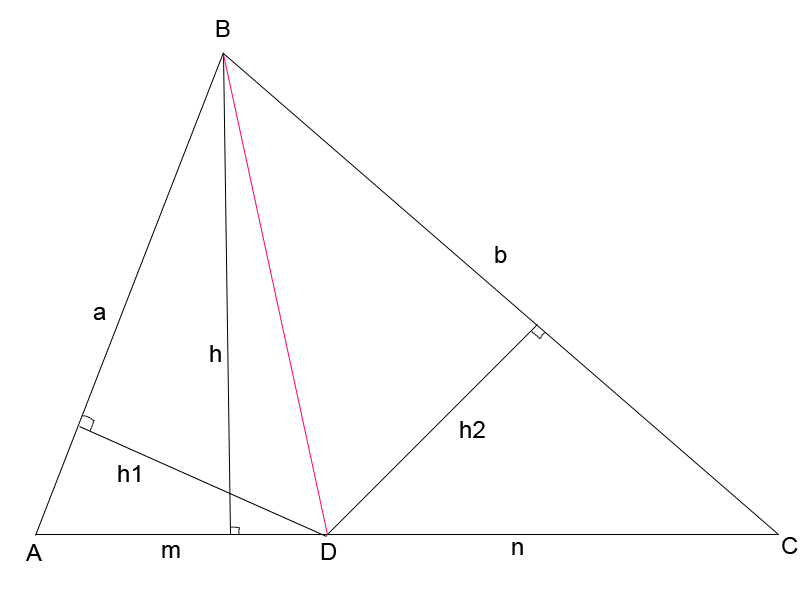 Применим формулы площади треугольника (рис. 1.3)
Применим формулы площади треугольника (рис. 1.3)
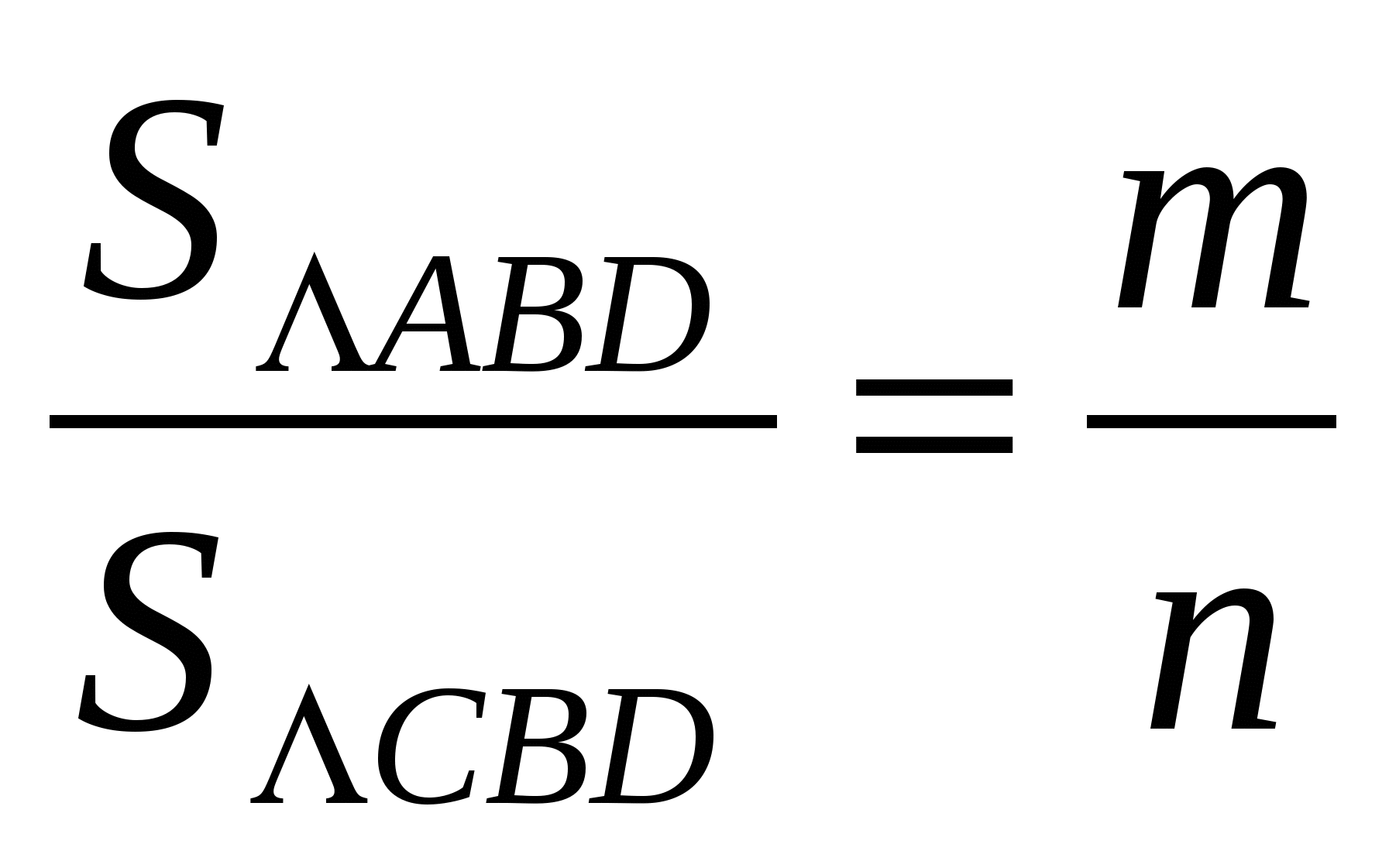
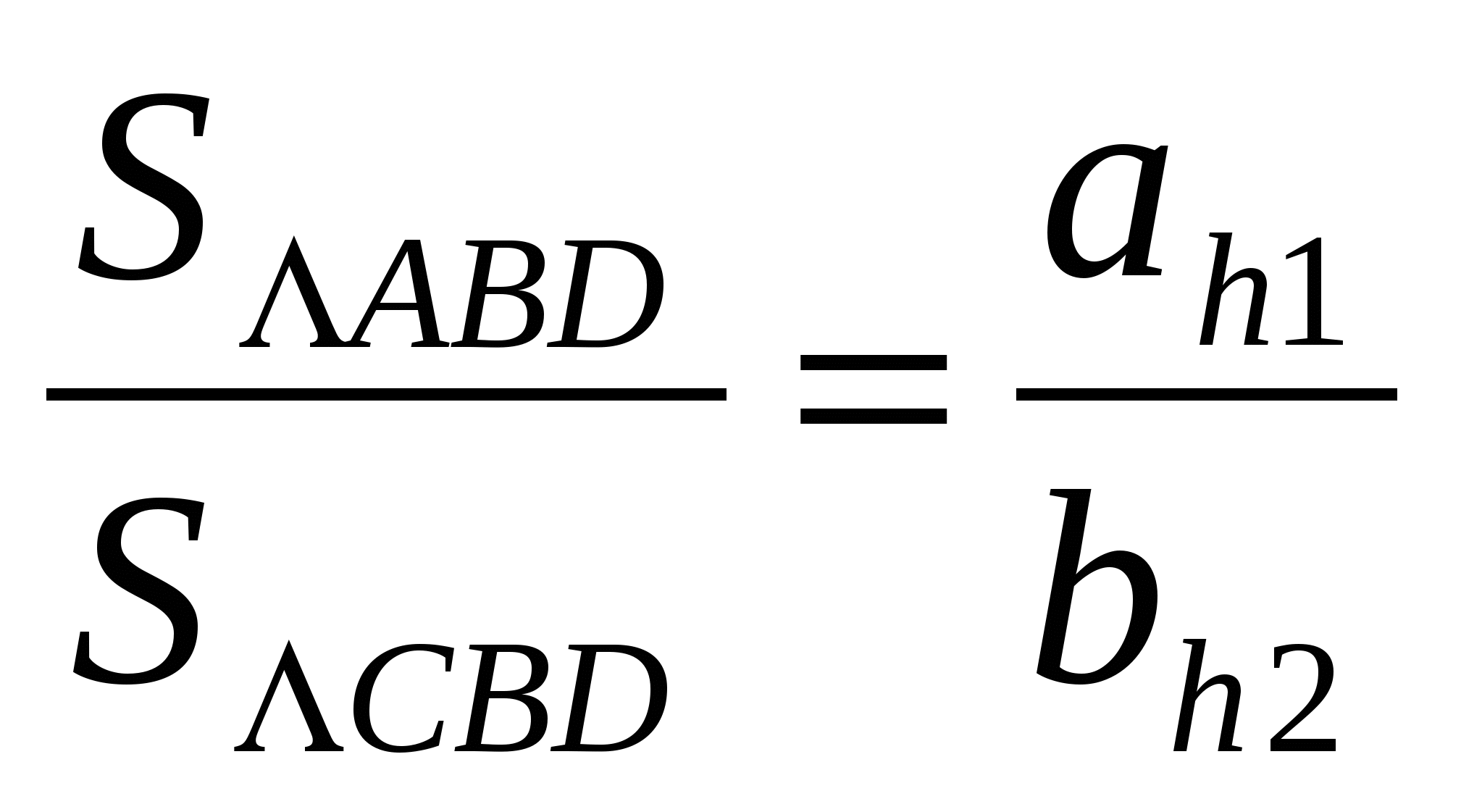
Точка D лежит на биссектрисе угла ABC, значит она равноудалена от его сторон, то есть 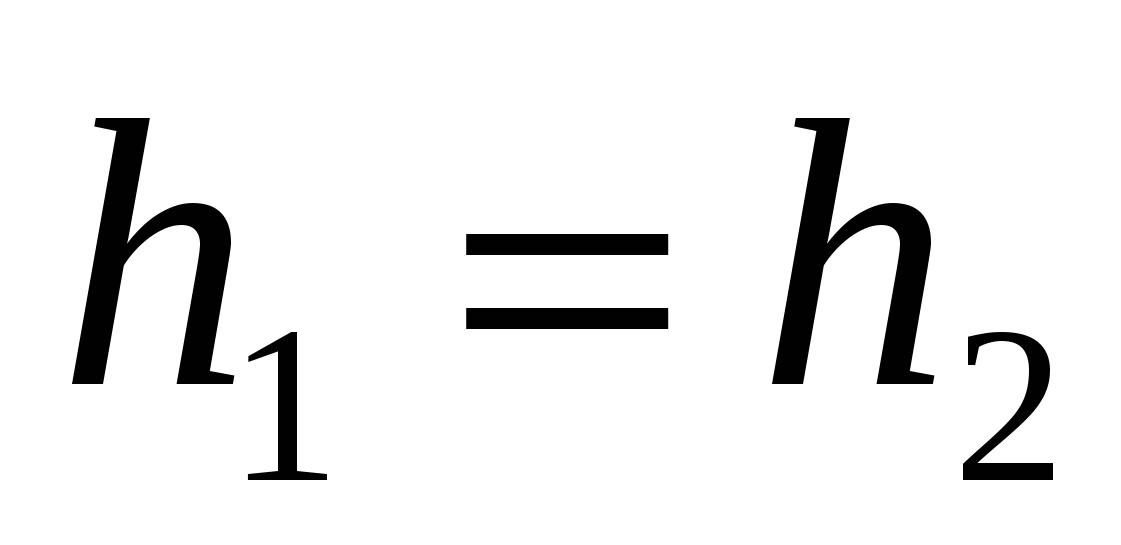
Тогда: 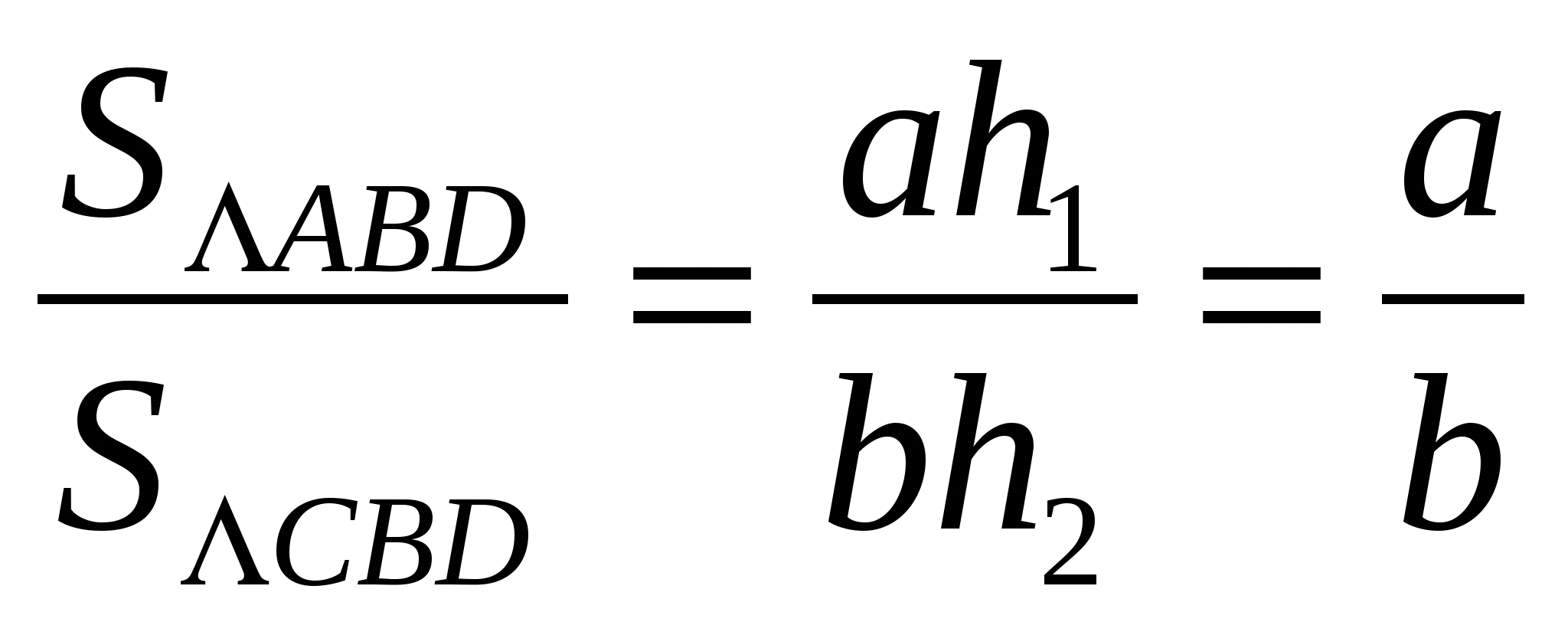
Получили, что 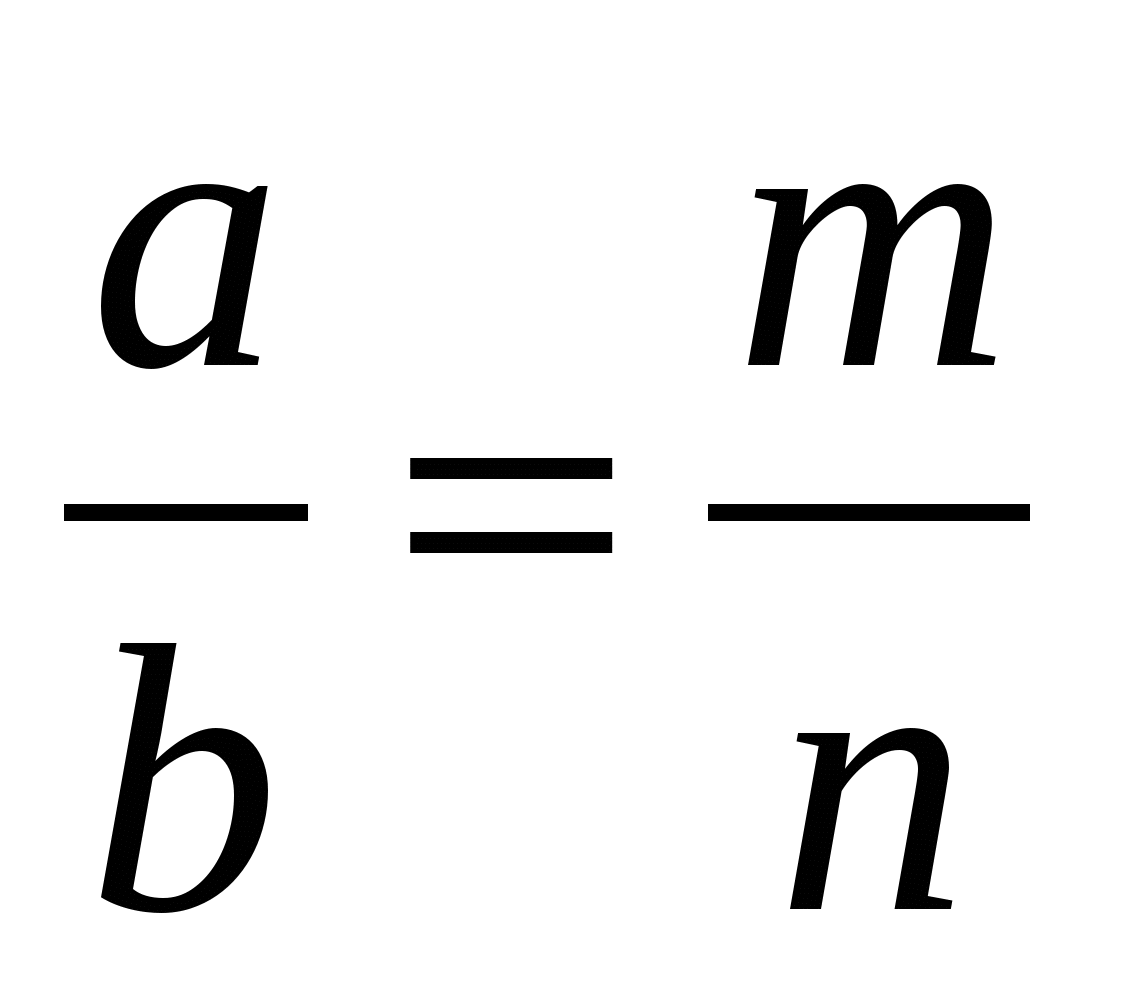
4. Применим теорему синусов
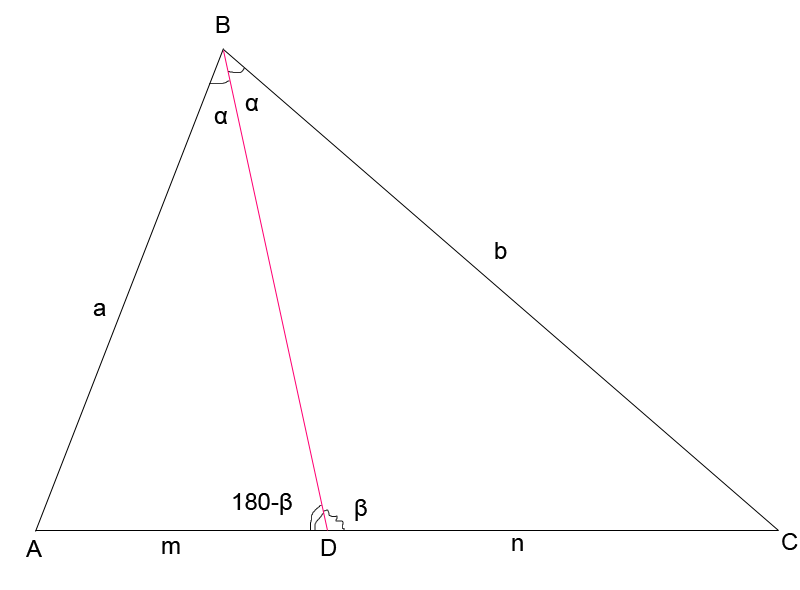 Рис. 1.4
Рис. 1.4
Из ∆ ABD по теореме синусов: 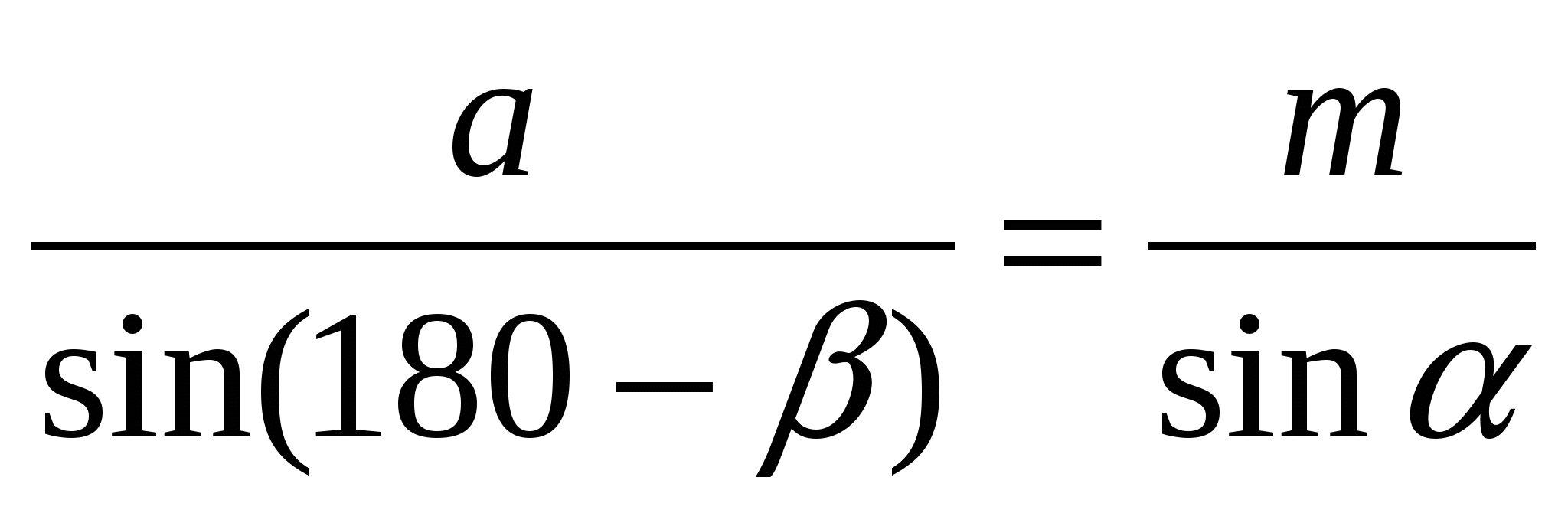 , или упростив, имеем:
, или упростив, имеем: 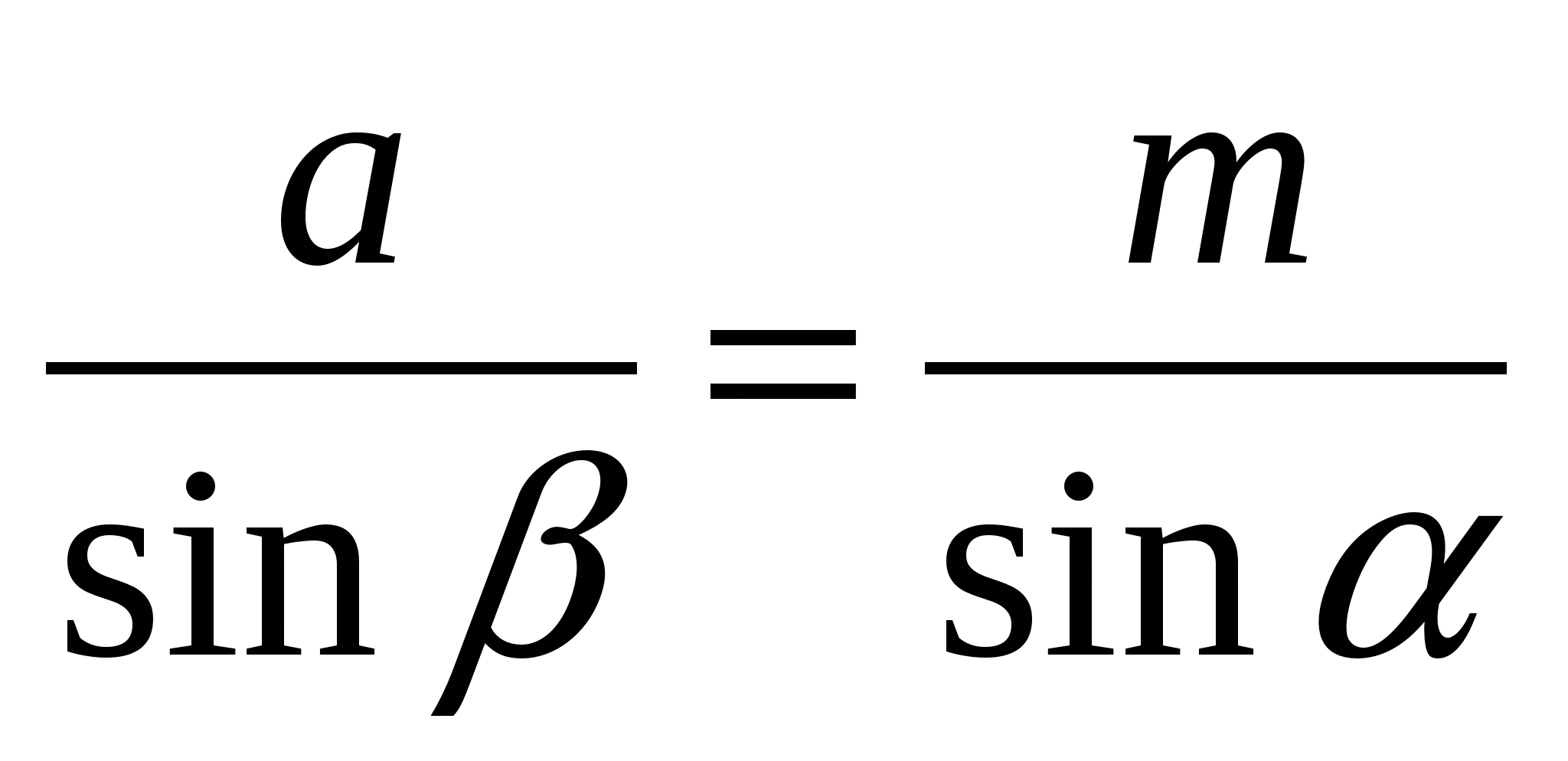 (*)
(*)
Из ∆ BDС по теореме синусов: 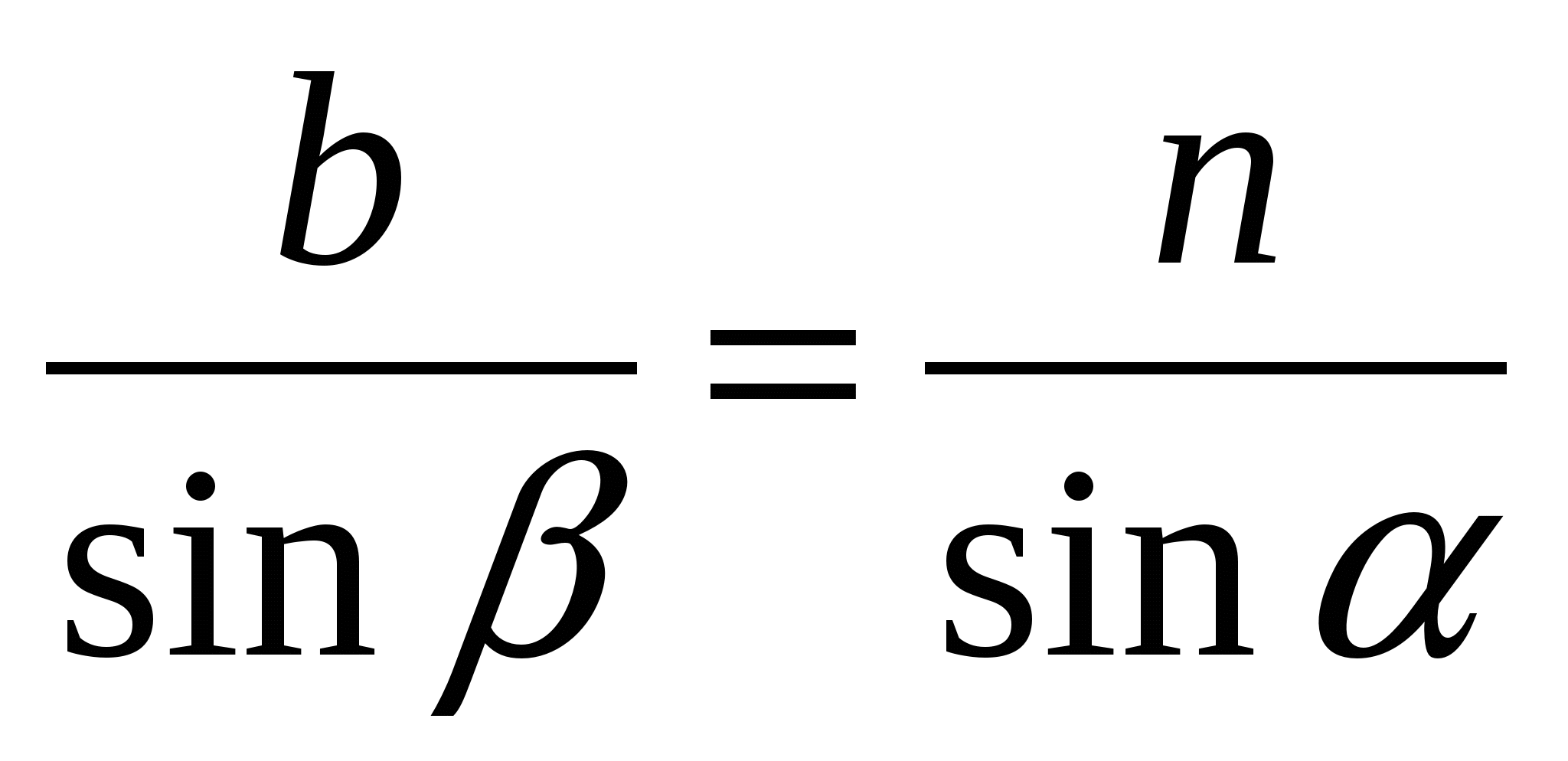 (**)
(**)
Разделим равенство (*) на (**), получим 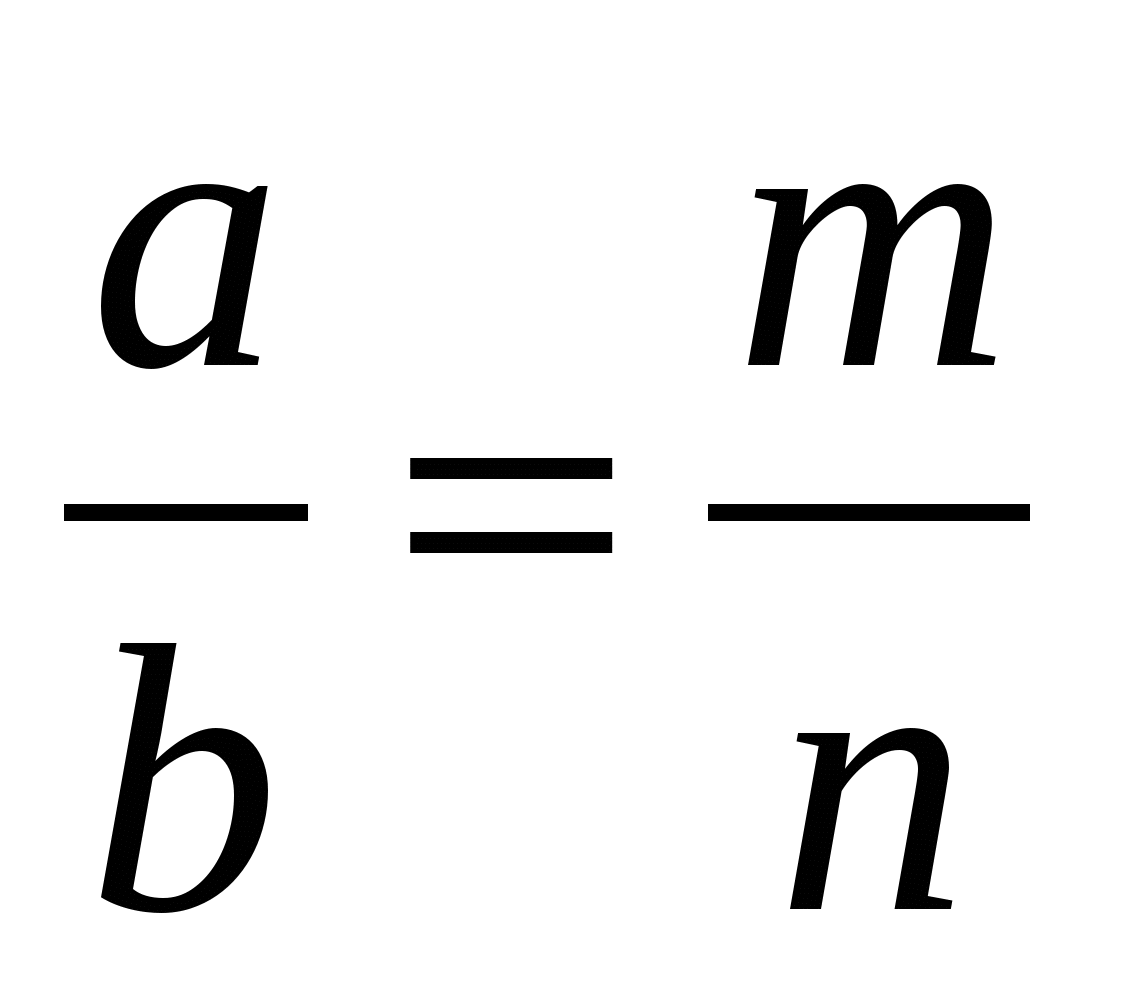
. 5. Докажем теорему, используя формулы площади треугольника (рис. 1.4) 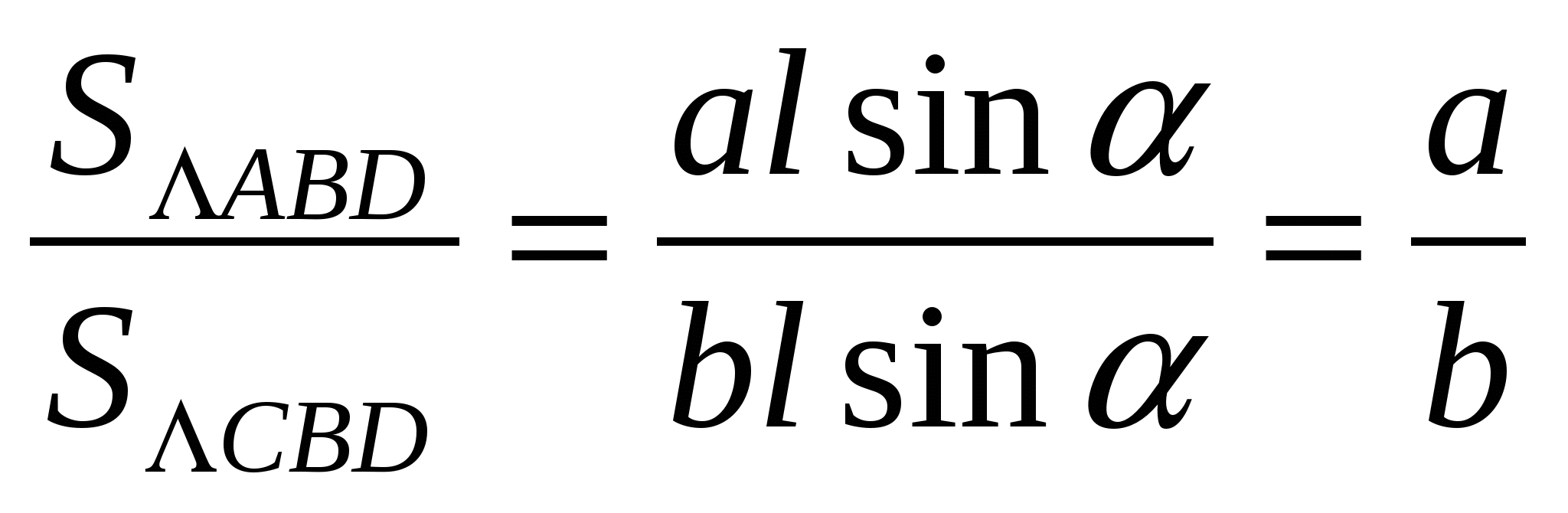
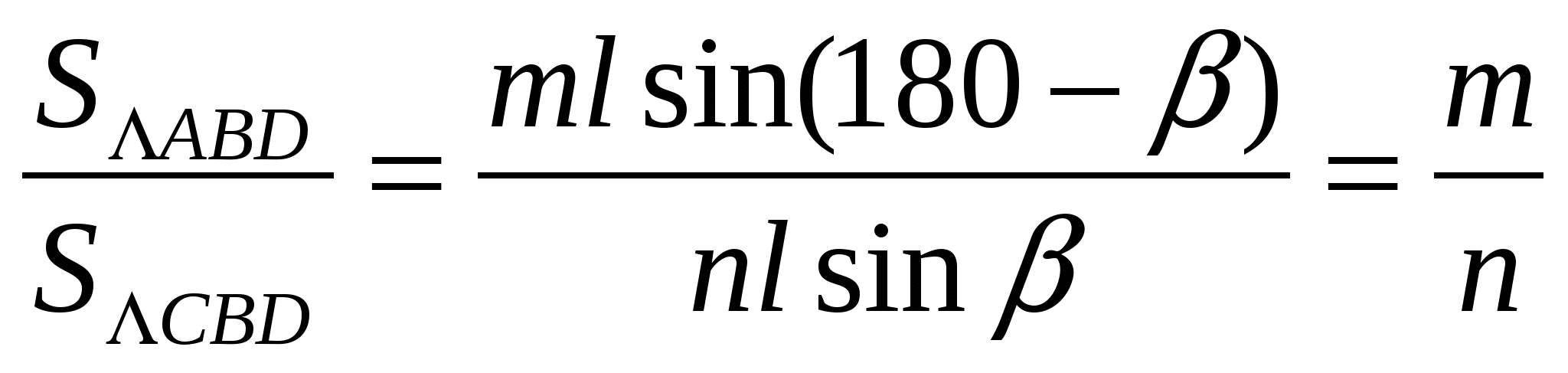
Получили 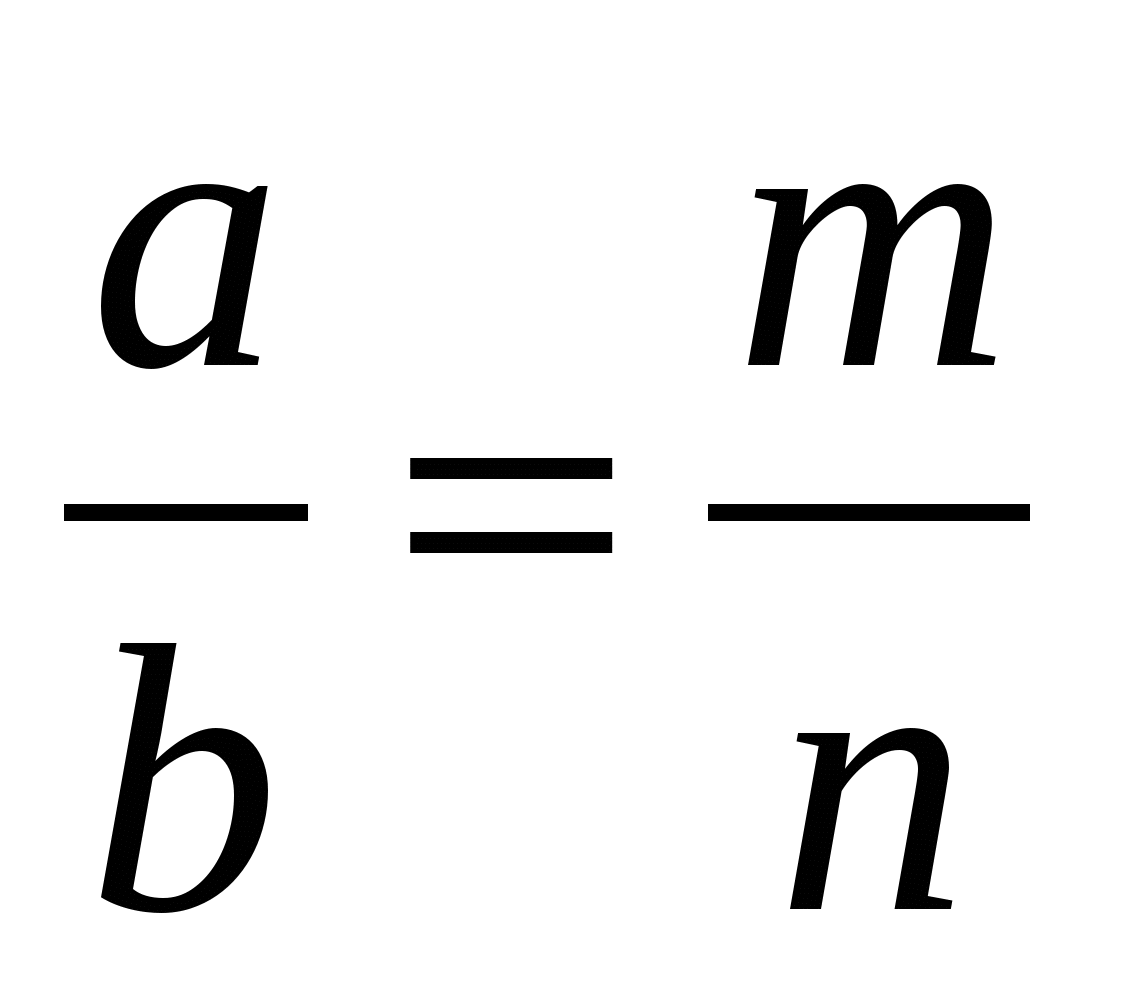
РАЗДЕЛ 2
Формулы для вычисления длины биссектрисы
В разделе выводятся четыре формулы для вычисления длины биссектрисы треугольника [3].
2.1. Длина биссектрисы через пропорциональные стороны и отрезки
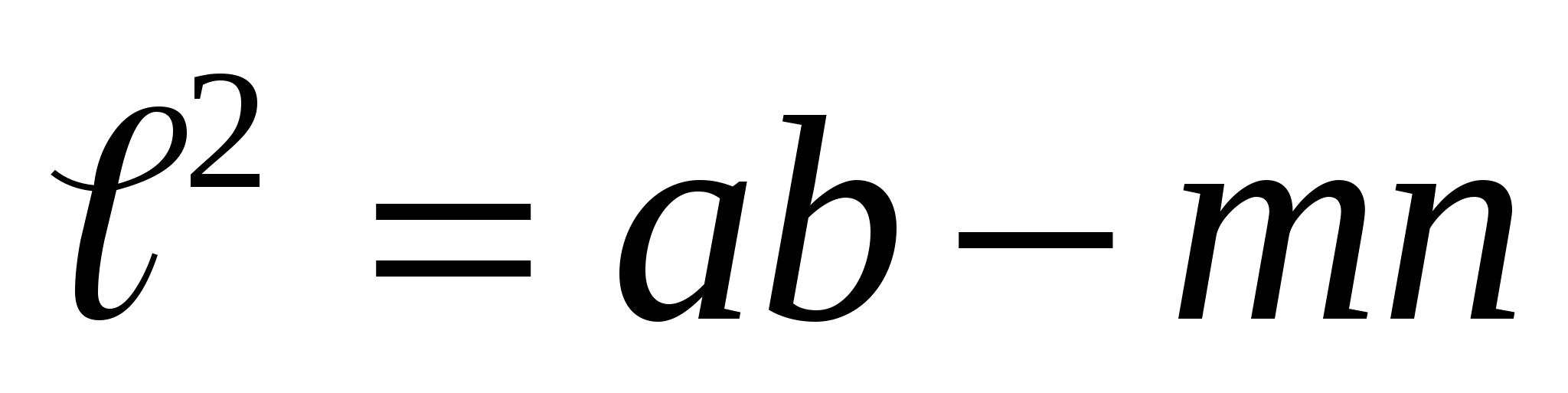

Рис. 2.1.1.
2.1.1.Доказательство. I способ - через вписанные углы (рис. 2.1.1).
Опишем вокруг ∆ABC окружность и продолжим биссектрису CD =l до
пересечения с окружностью, F - точка пересечения. Пусть DF= x.
Вписанные углы BFC и CAB равны, так как опираются на одну и ту же дугу BC. Тогда ∆FCB ~ ∆ACD по двум углам. У подобных треугольников соответствующие стороны пропорциональны:
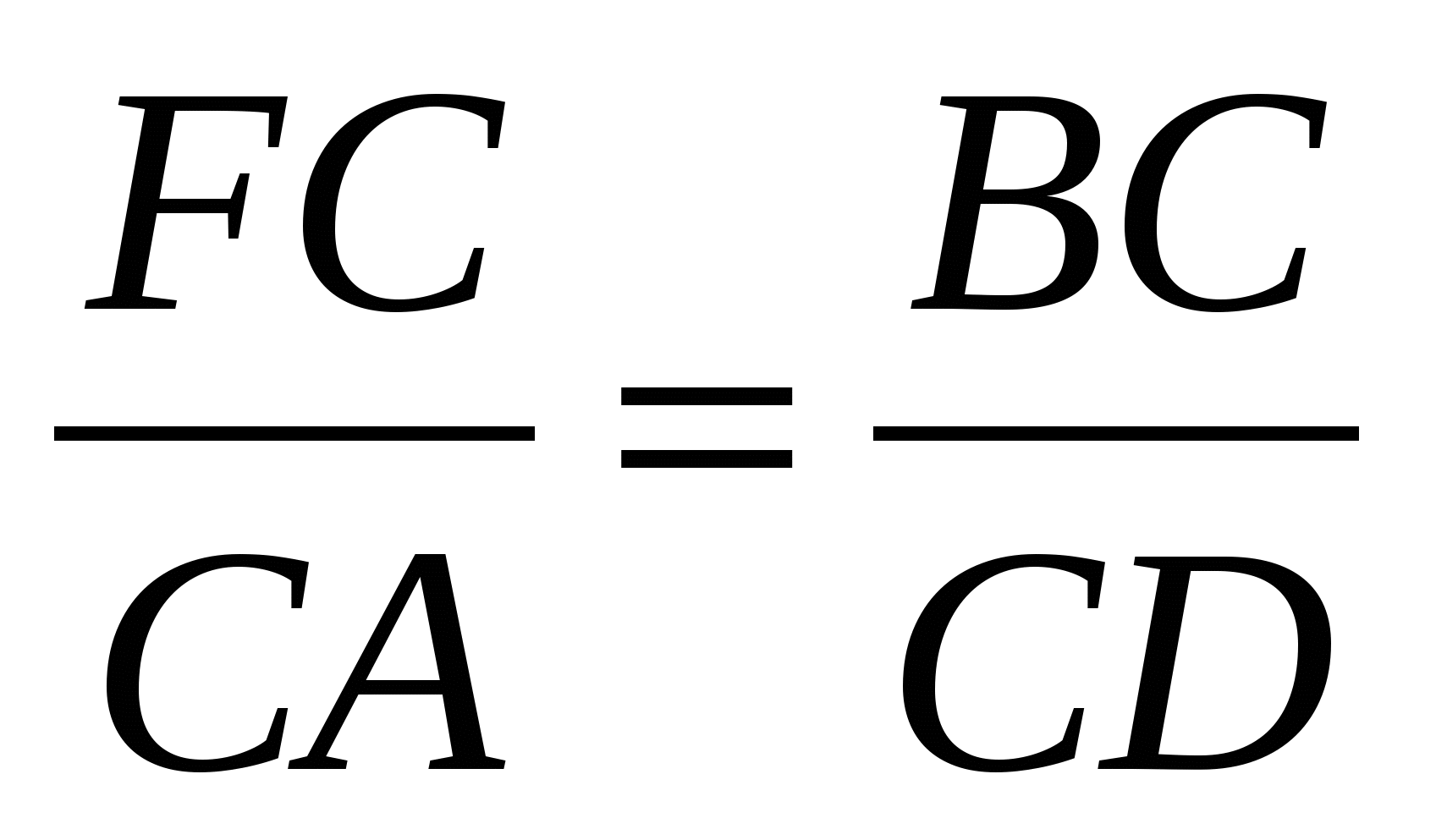 или
или 
Тогда 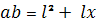 (1).
(1).
По свойству пересекающихся хорд 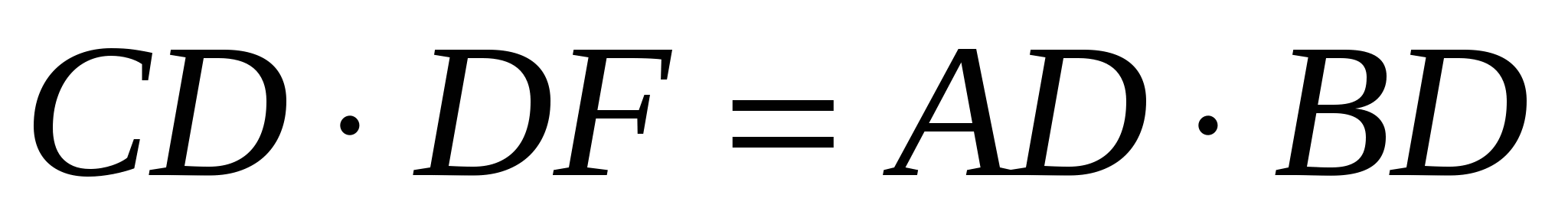
или 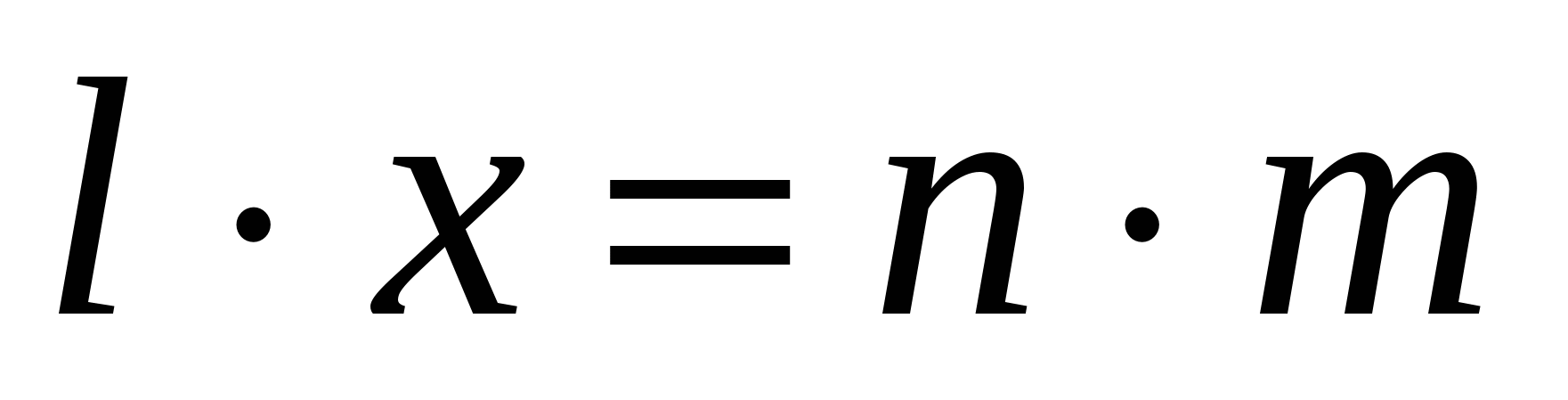 .
.
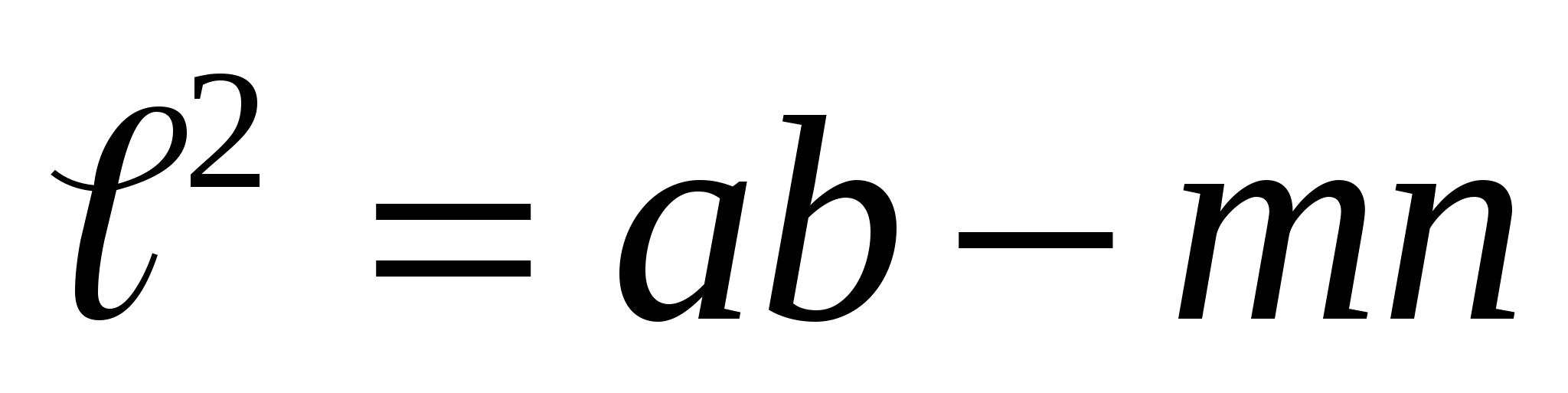 Подставим последнее равенств в формулу (1), получим
Подставим последнее равенств в формулу (1), получим
2.1.2.Доказательство. II способ - через теорему косинусов (рис.2.1.2)
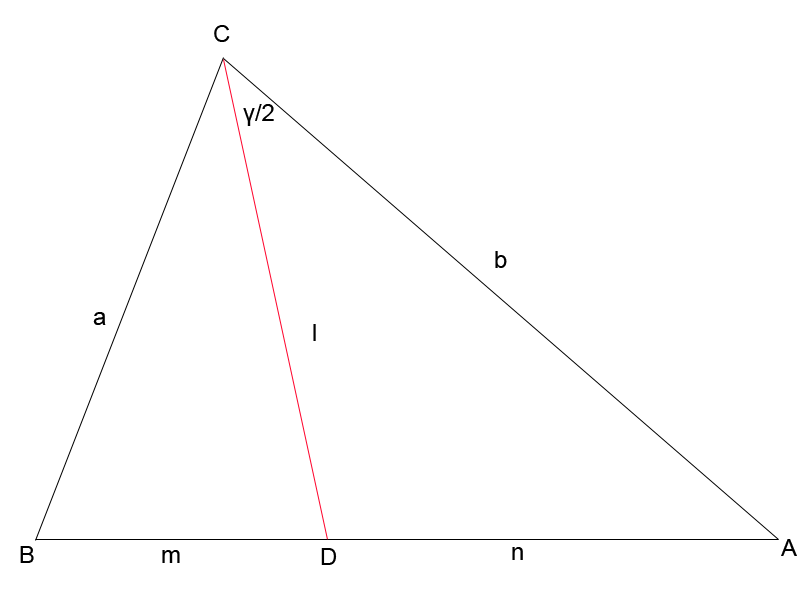 Рис 2.1.2
Рис 2.1.2
Из пропорции ![]() следует, что
следует, что 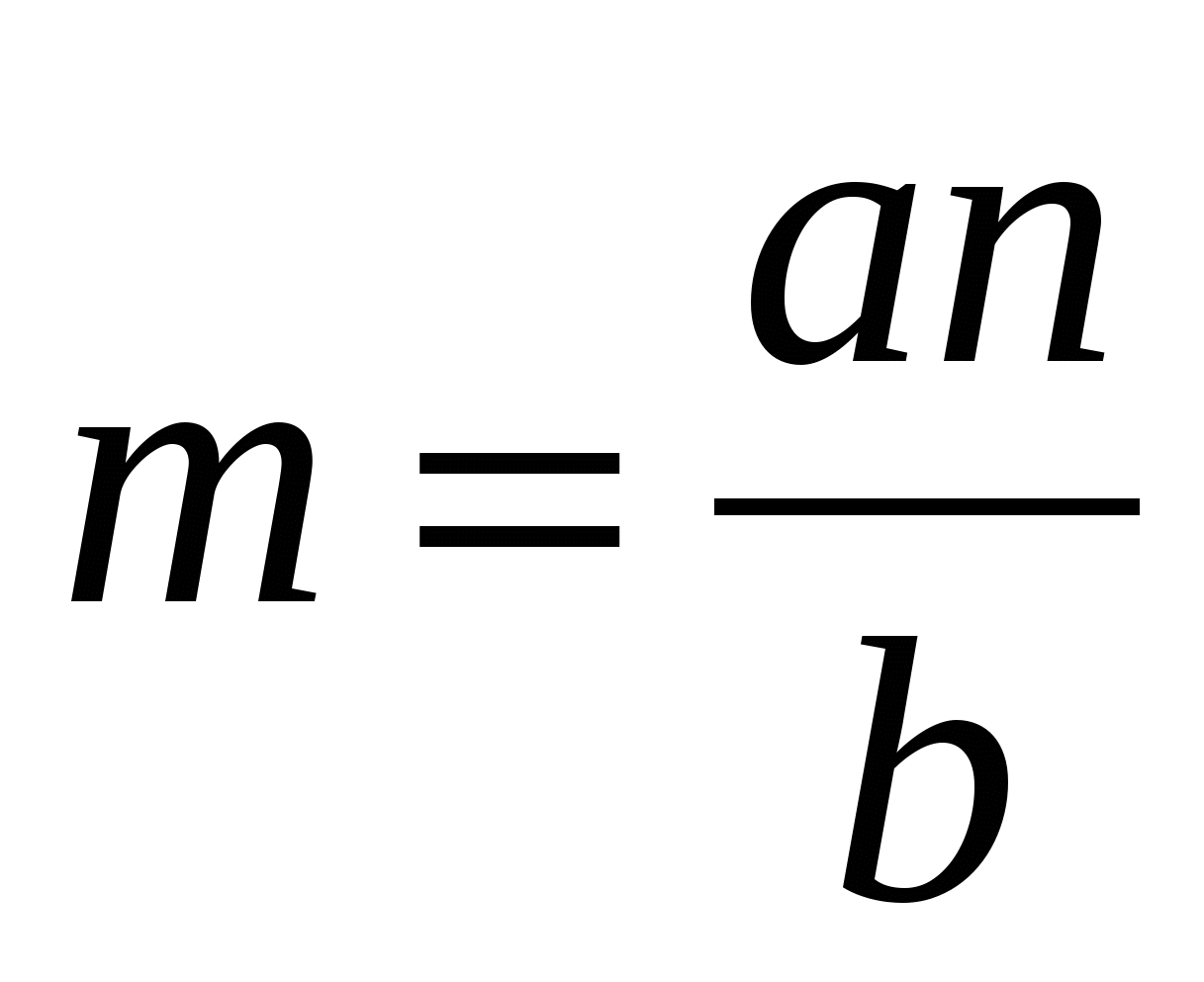 ,
, 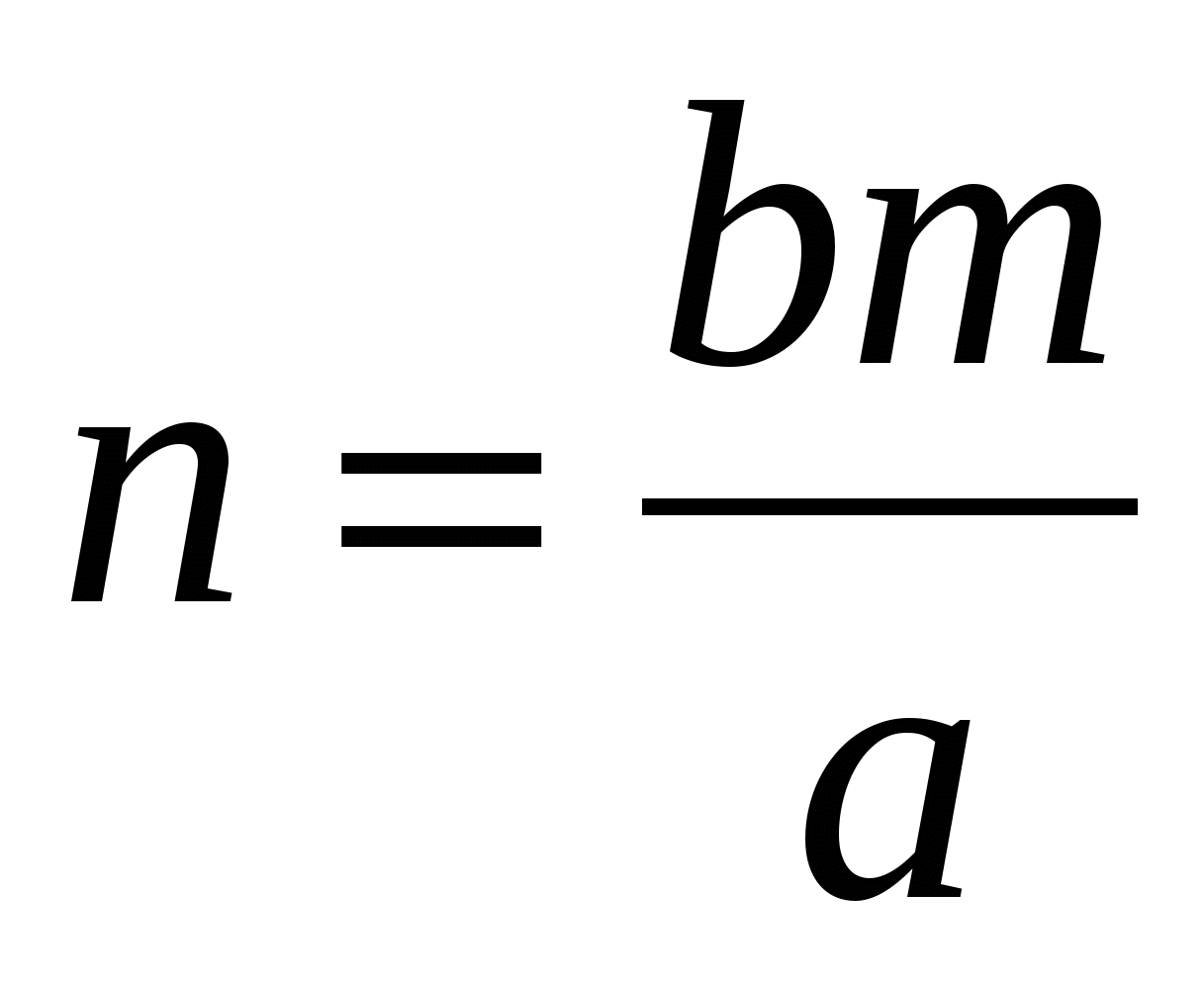 (2).
(2).
Из ∆ BCD 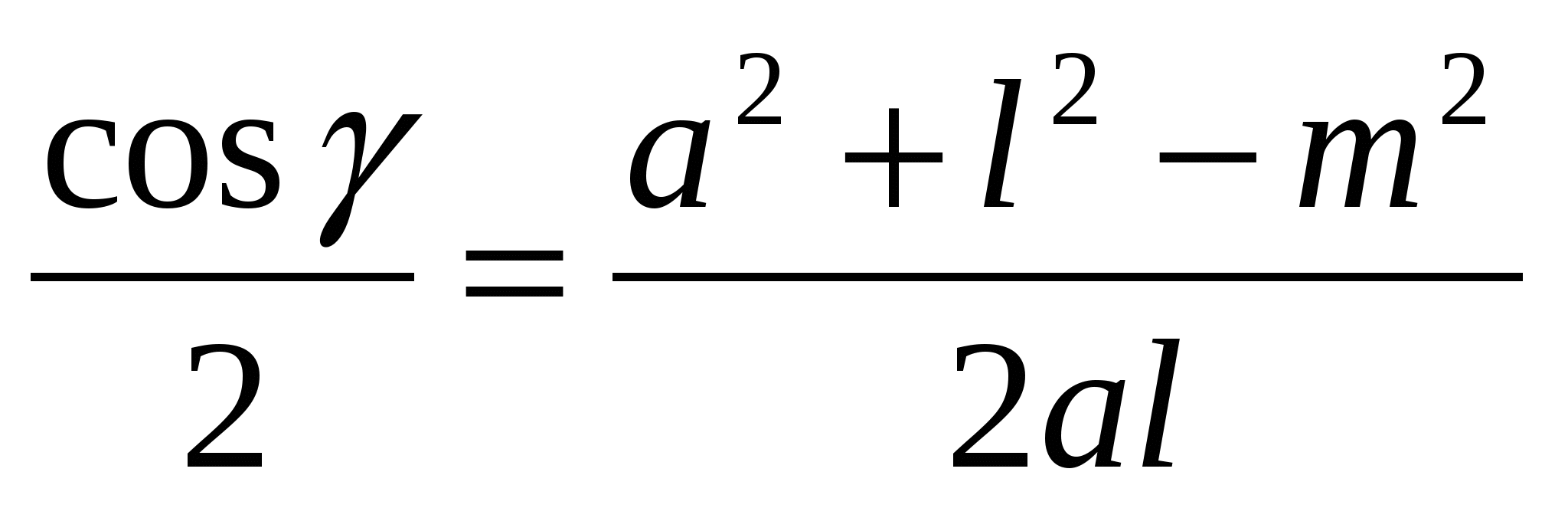 из теоремы косинусов.
из теоремы косинусов.
Из ∆ DCA 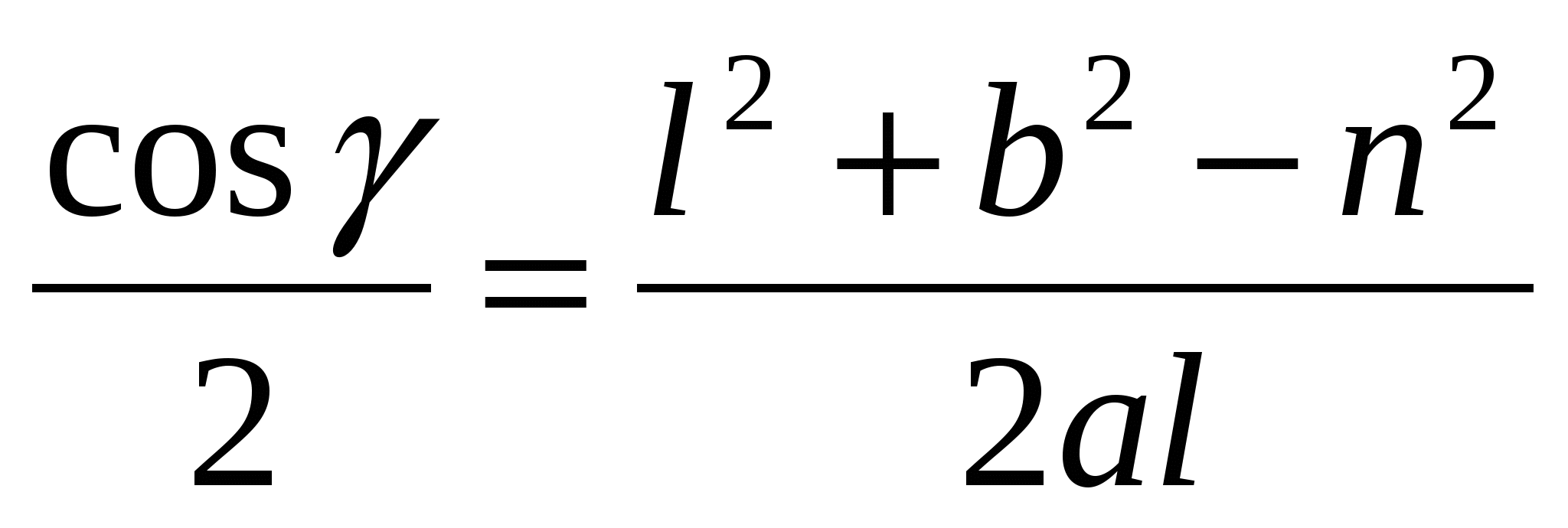 .
.
Получим равенство 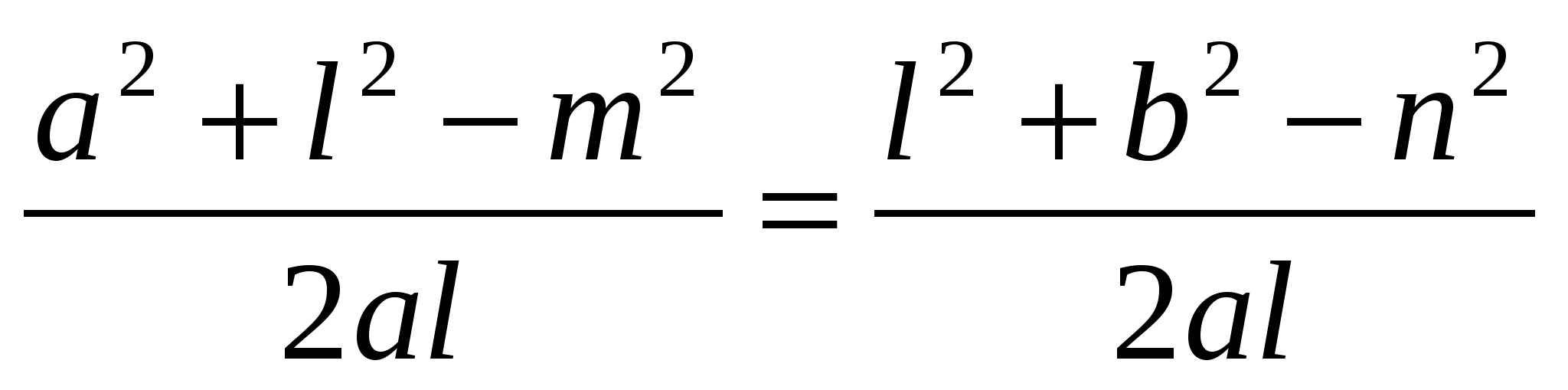 .
.
После умножения на 2abl получим:
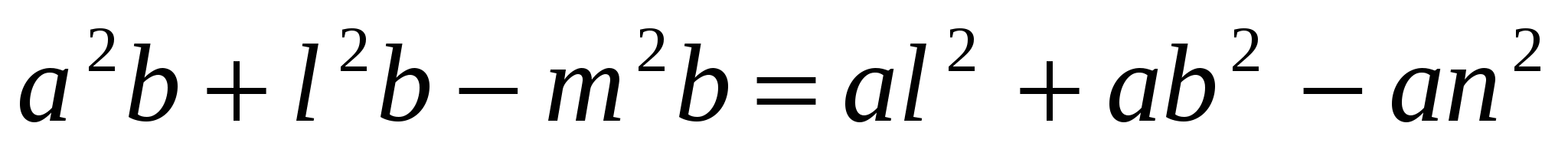 Перегруппировка слагаемых
Перегруппировка слагаемых
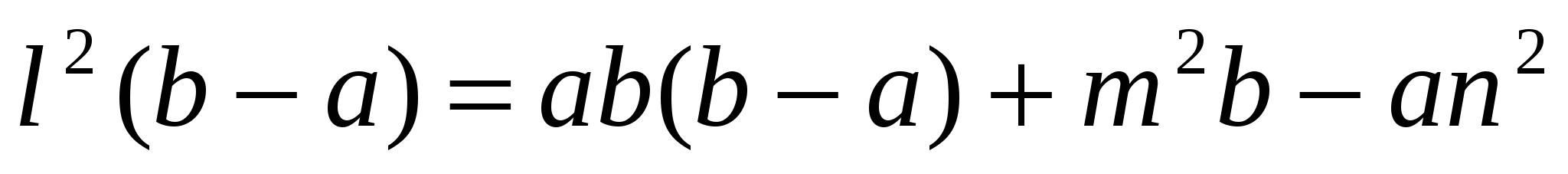 . Подставим формулы (2) в равенство вместо m и n
. Подставим формулы (2) в равенство вместо m и n 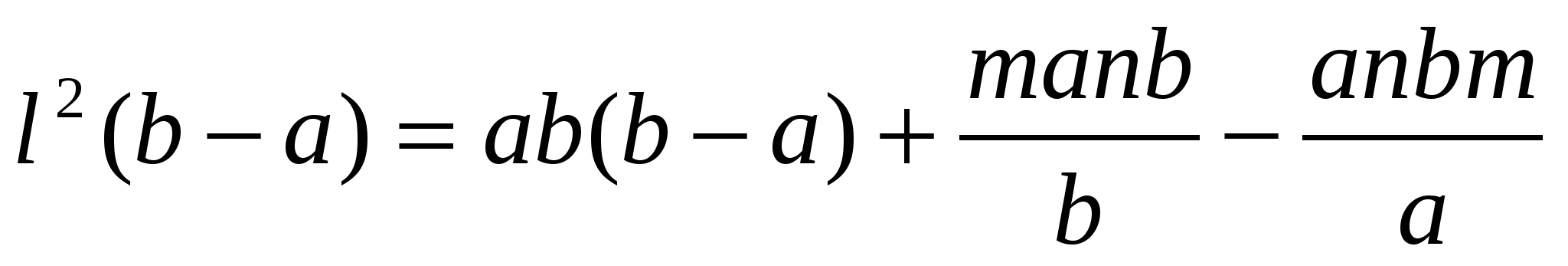
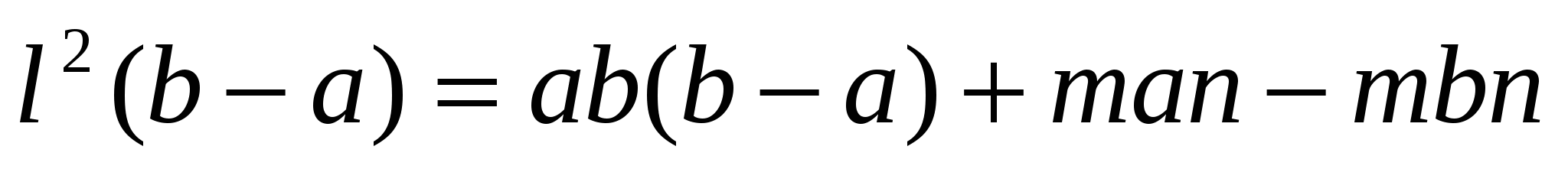
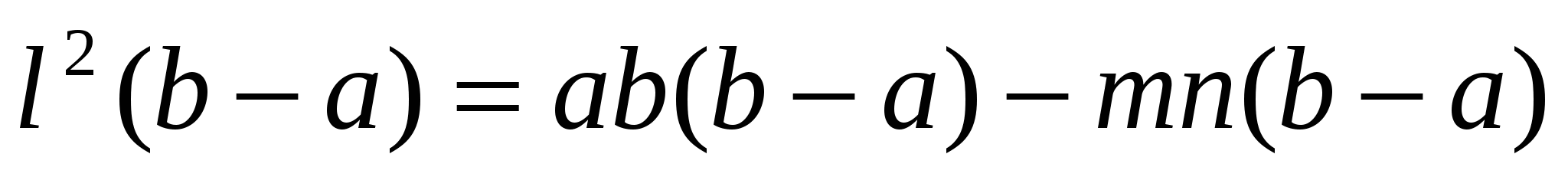
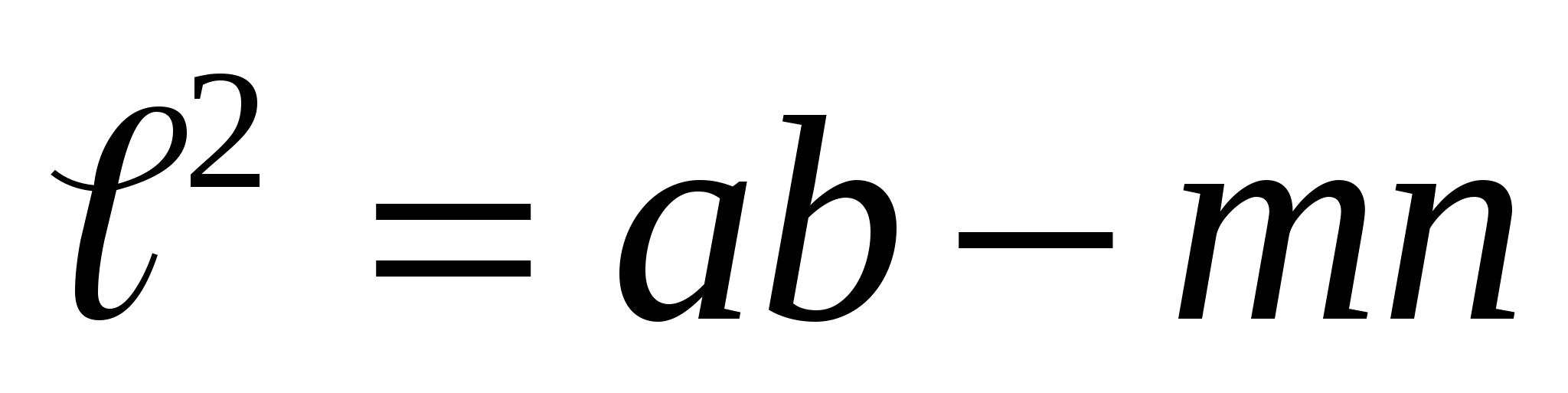
В случае, если ![]() делим на (b - a) и получаем
делим на (b - a) и получаем
2.2. Длина биссектрисы через две стороны и угол между ними (рис. 2.2)
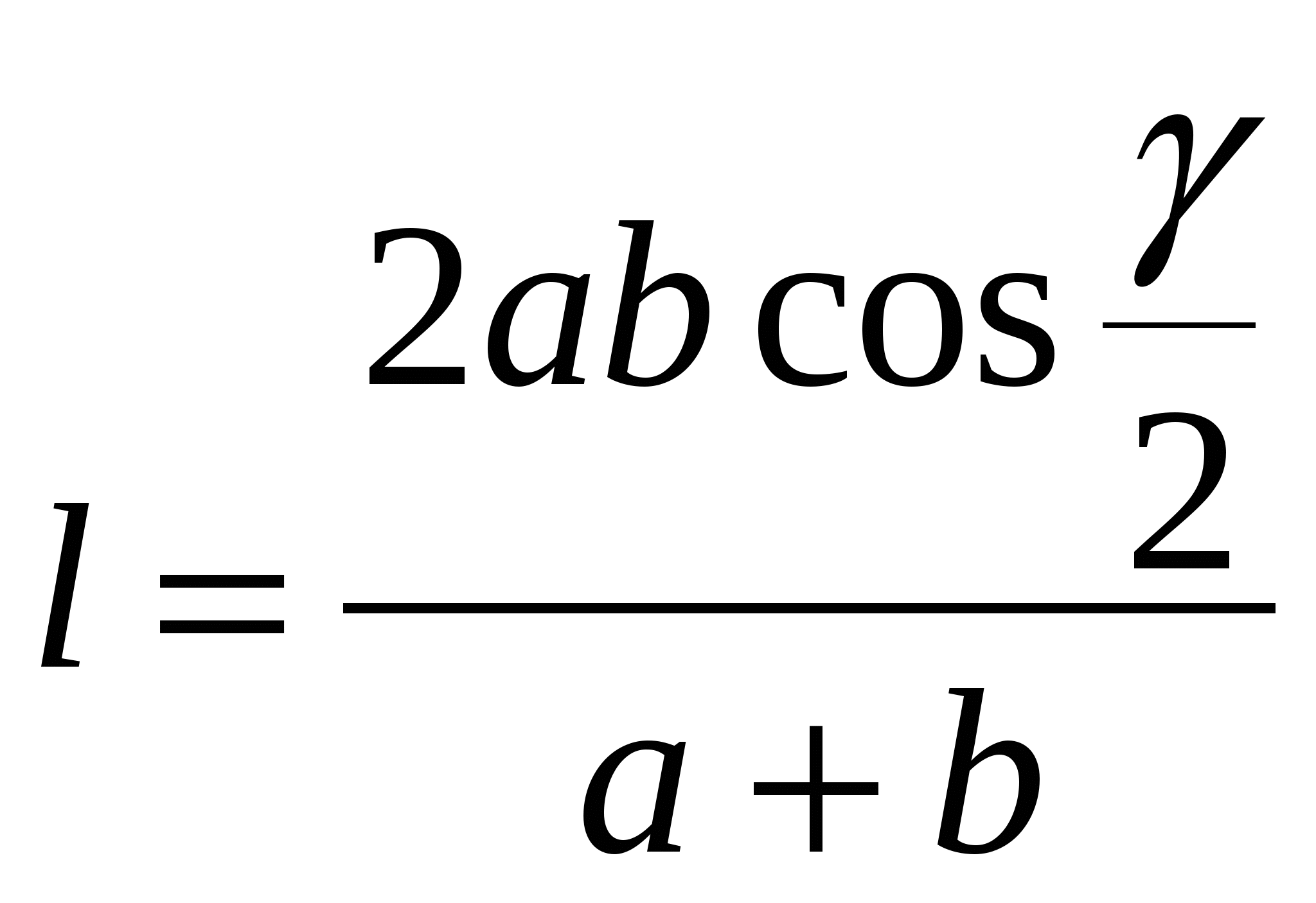
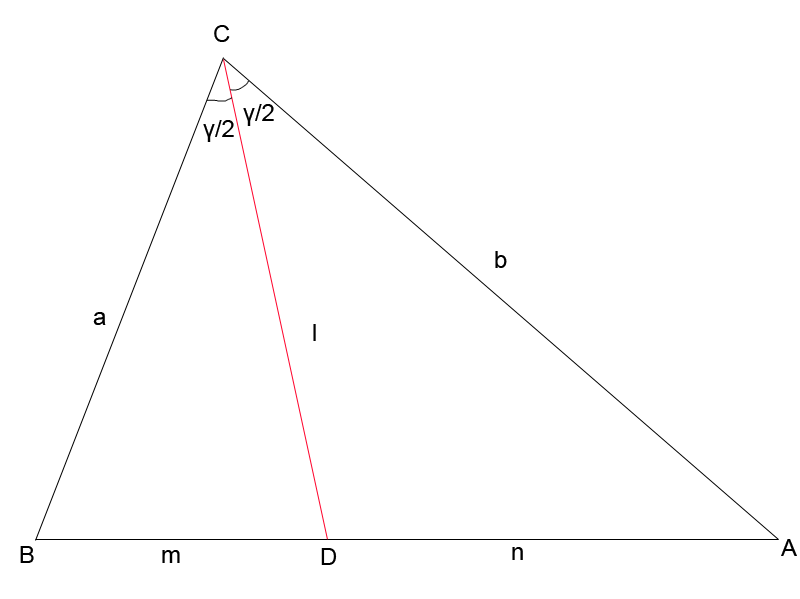
Рис. 2.2
Доказательство через площадь треугольника.
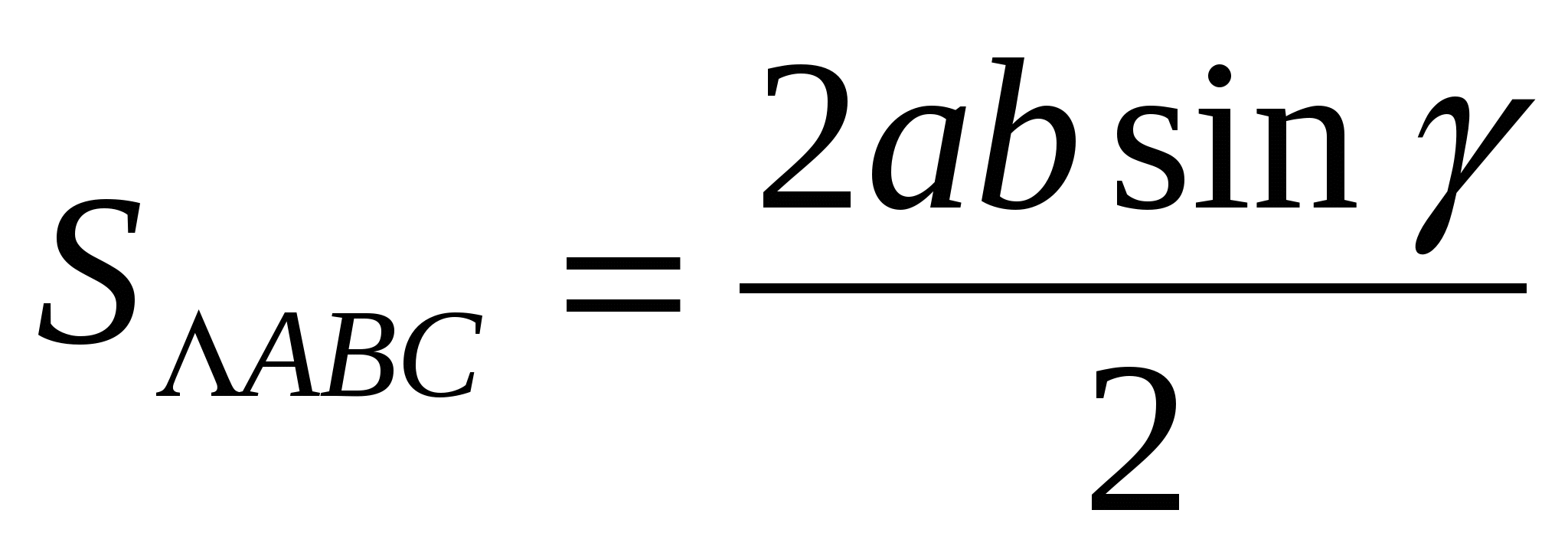
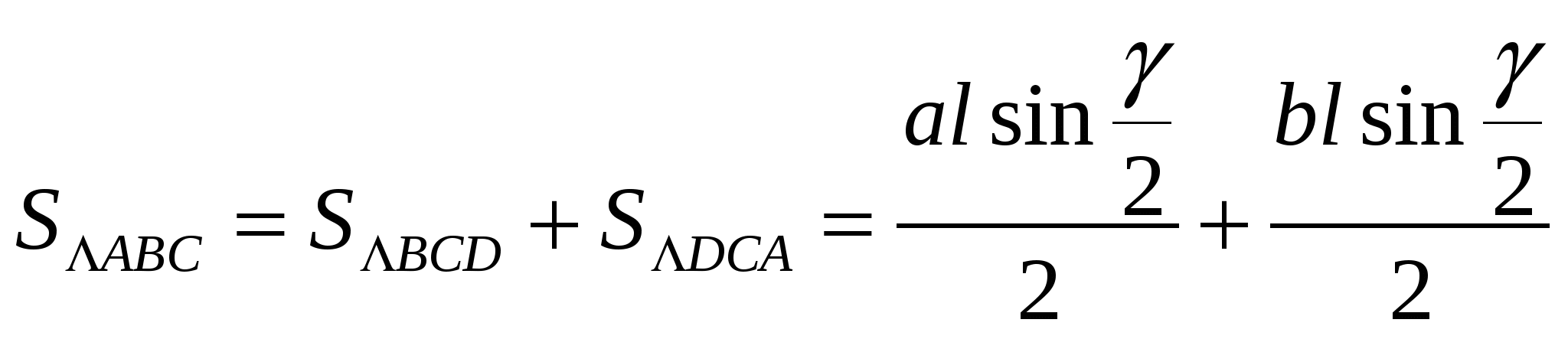
.
Равенство 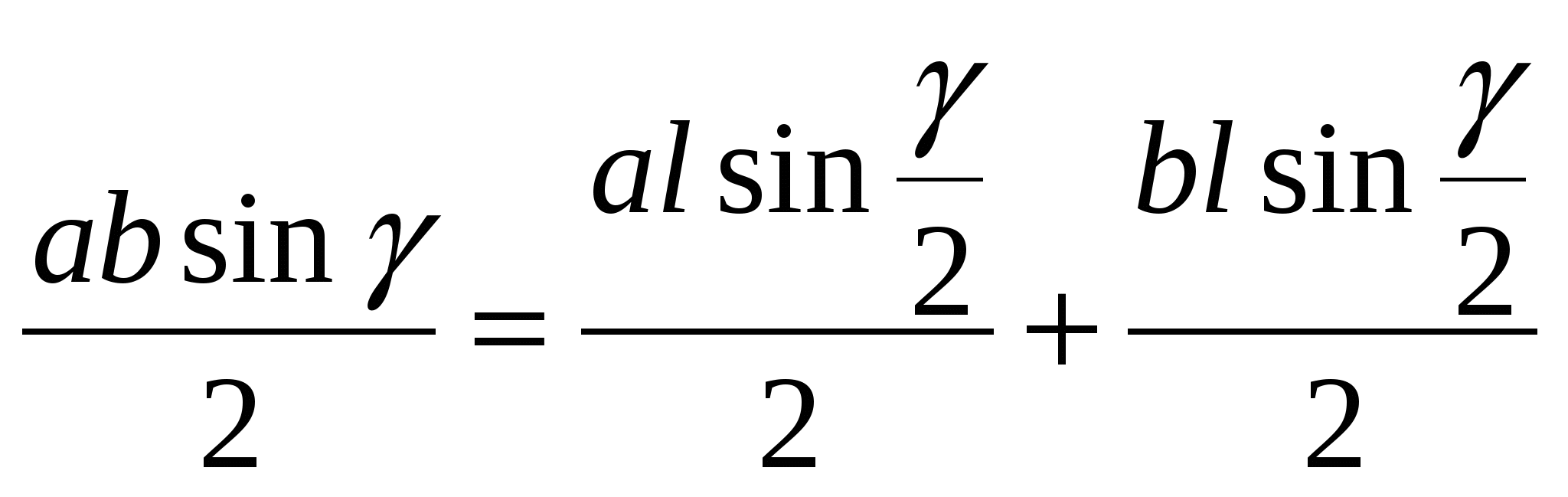 умножим на 2, а
умножим на 2, а 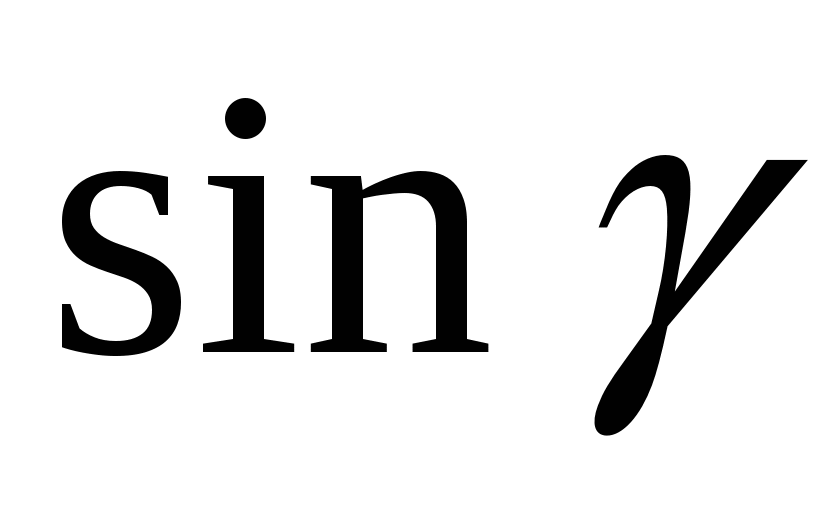 заменим по формулам двойного угла
заменим по формулам двойного угла ![]()
Так как 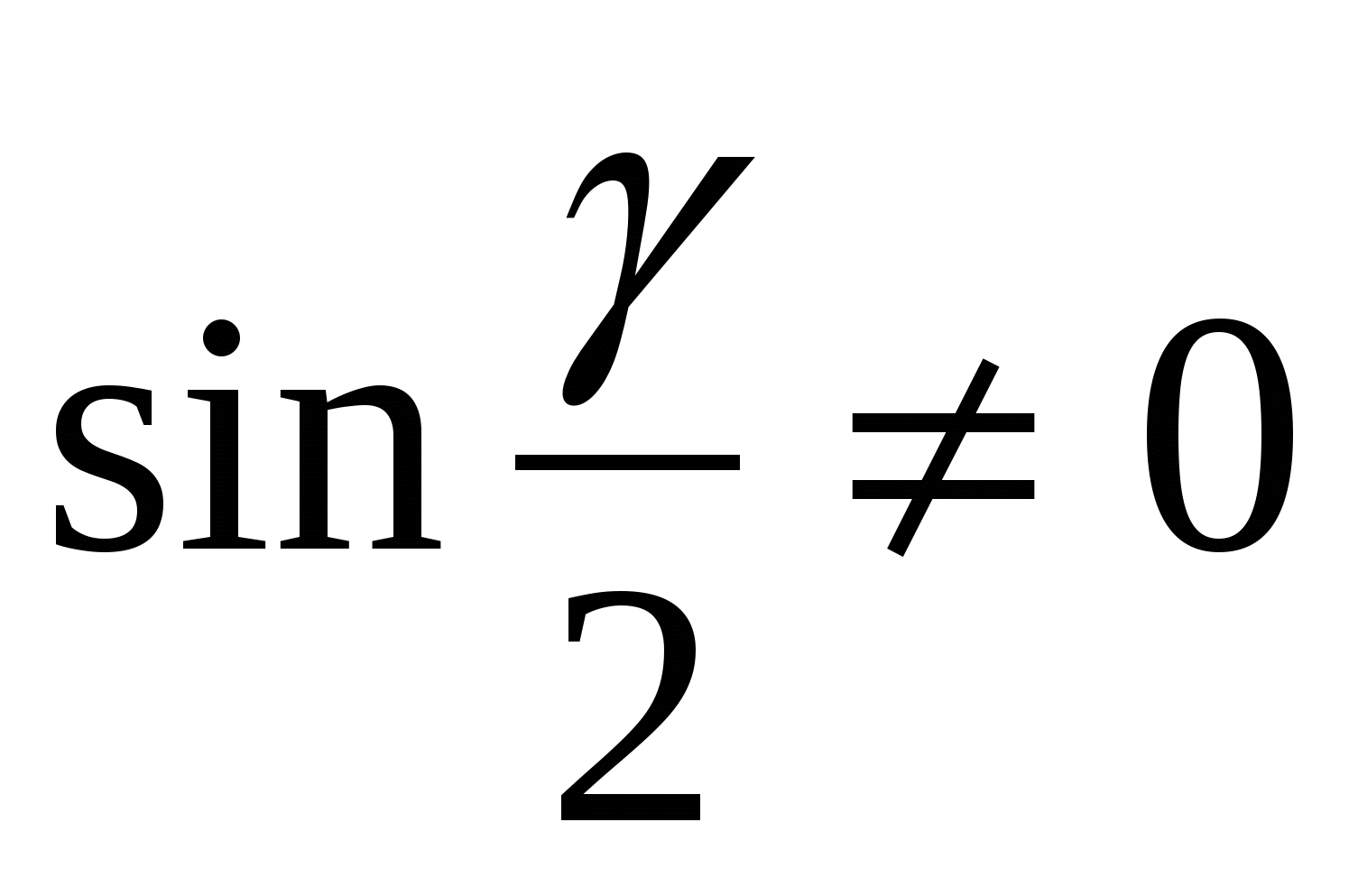 разделим на него и найдём l.
разделим на него и найдём l. 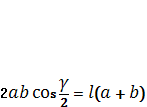 ;
;
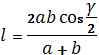
Следствие. В прямоугольном треугольнике угол 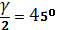 , поэтому биссектриса опущенная на гипотенузу равна
, поэтому биссектриса опущенная на гипотенузу равна 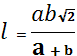 , где a и b - катеты.
, где a и b - катеты.
-
Длина биссектрисы через стороны треугольника (рис. 2.3)
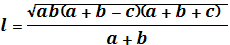
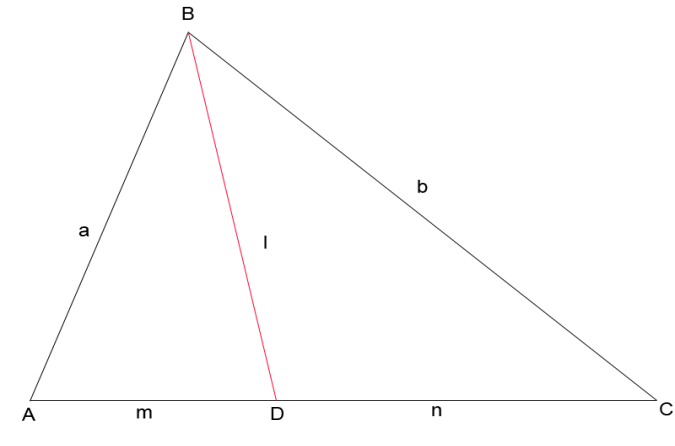 Рис. 2.3
Рис. 2.3
Выразим отрезки m и n через стороны треугольника, решив систему.
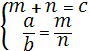 ;
; ![]() ;
; ![]()
![]() ;
; ![]() =c ;
=c ; 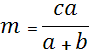 .
.
Аналогично 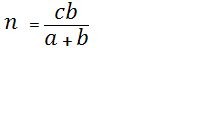 .
.
Подставим найденные выражения в формулу биссектрисы
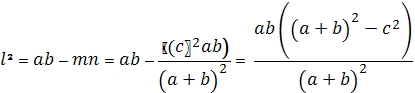
Тогда 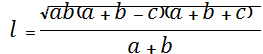 .
.
-
Угол между высотой и биссектрисой треугольника , проведенными
из одной вершины [1]
![]()
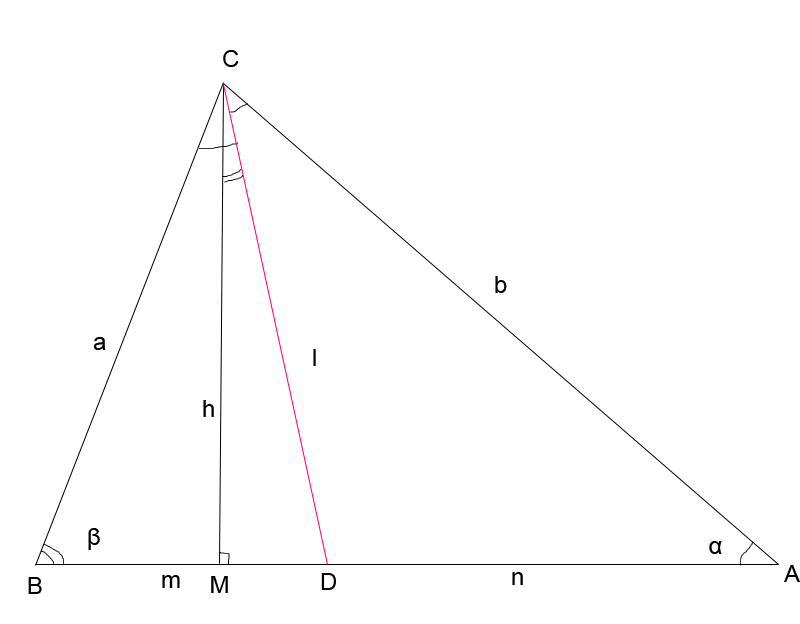 Рис. 2.4
Рис. 2.4
Пусть CM= h - высота, а CD= l биссектриса треугольника, проведенная из той же вершины. Найдем угол MCD между высотой и биссектрисой треугольника.
Из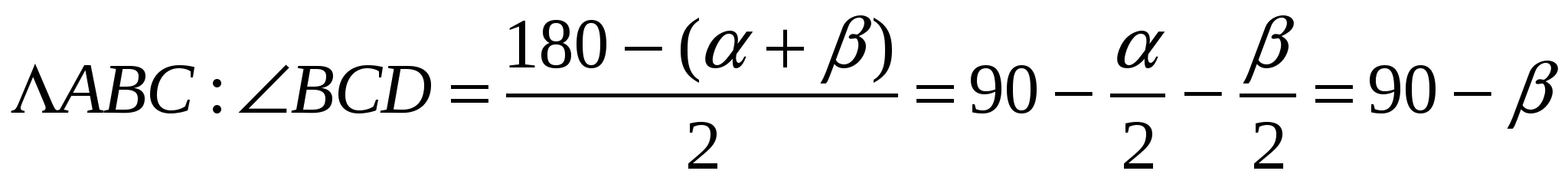
Из ∆BCM (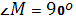 )
) BCM =
BCM =
 MCD=
MCD= BCD -
BCD -  BCM =
BCM = 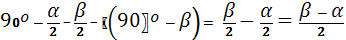 .
.
2.5.Длина биссектрисы через высоту 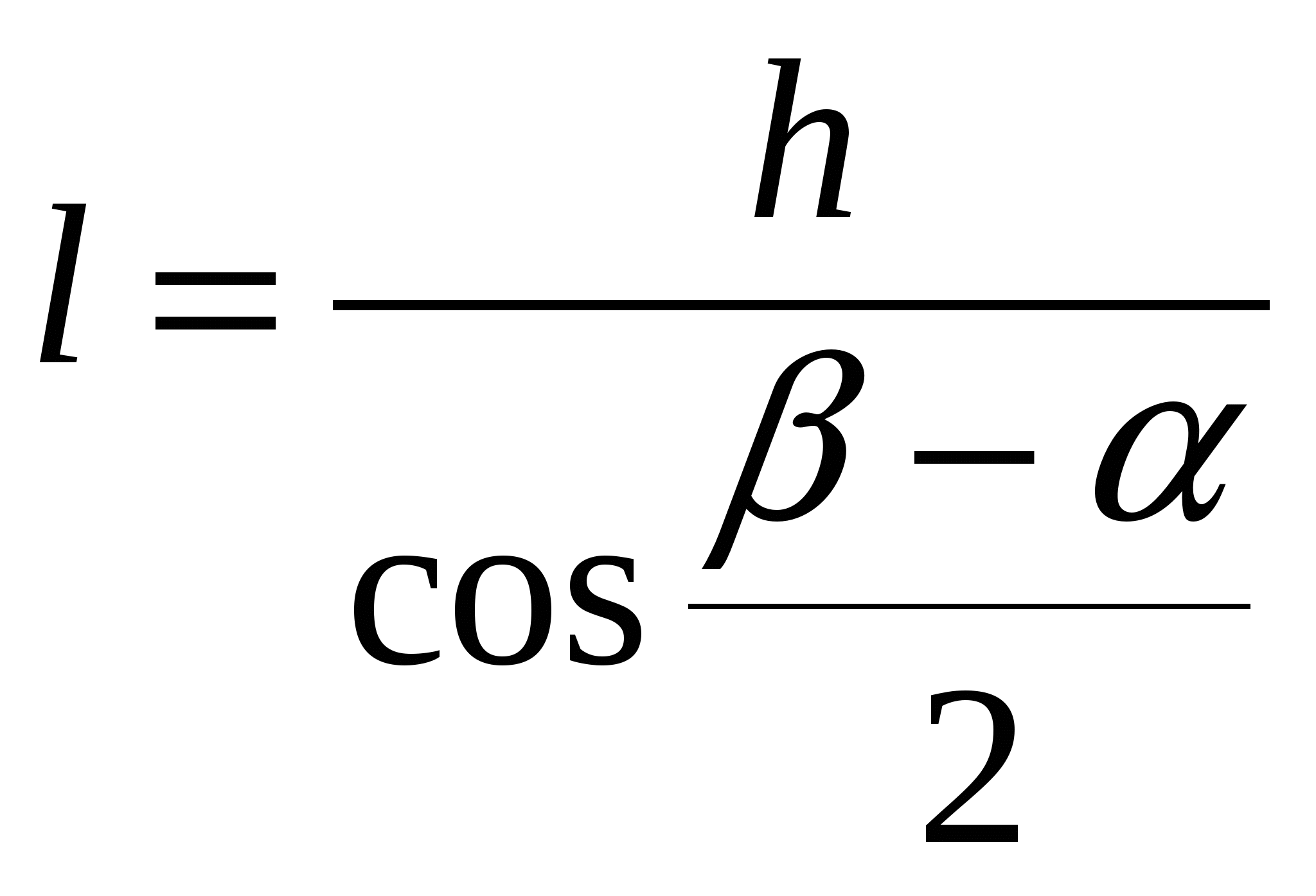 (рис. 2.4)
(рис. 2.4)
Из ∆CMD (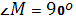 )
)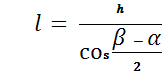 .
.
РАЗДЕЛ 3
Соотношения, связанные с биссектрисой
В разделе будет получено отношение, в котором биссектрисы треугольника делятся точкой пересечения; найден угол, образованный при пересечении биссектрис; установлена связь между сторонами треугольника и отрезками касательных ко вписанной в треугольник окружности.
3.1. Отношение , в котором биссектрисы треугольника делятся точкой пересечения (рис. 3.1)
Известно, что медианы треугольника точкой пересечения делятся в отношении 2:1, считая от вершины. Найдём, в каком отношении делятся биссектрисы точкой пересечении.
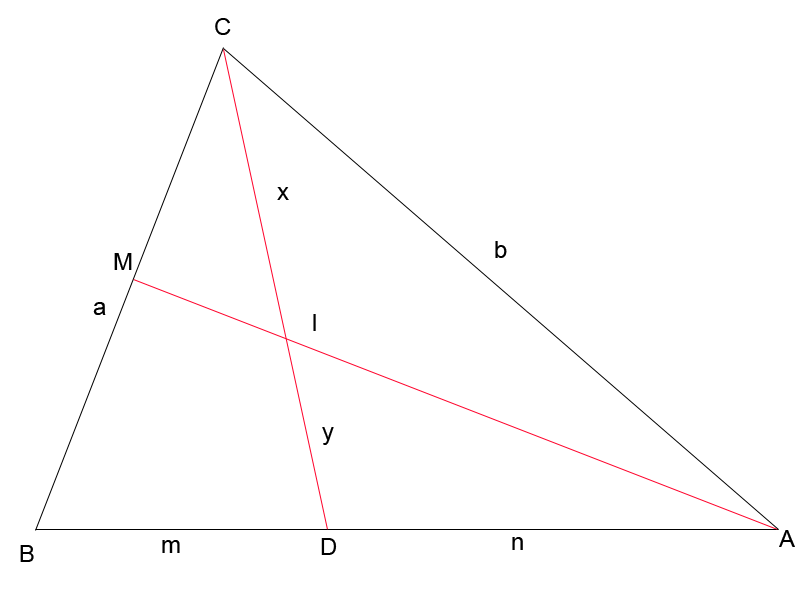
Рис. 3.1
Дано: биссектрисы CD и AM ∆АВС пересекаются в точке I (инцентр)
Пусть CI = x, а ID = y. Найдём отношение 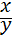 .
.
Из ∆ CDB по свойству биссектрис 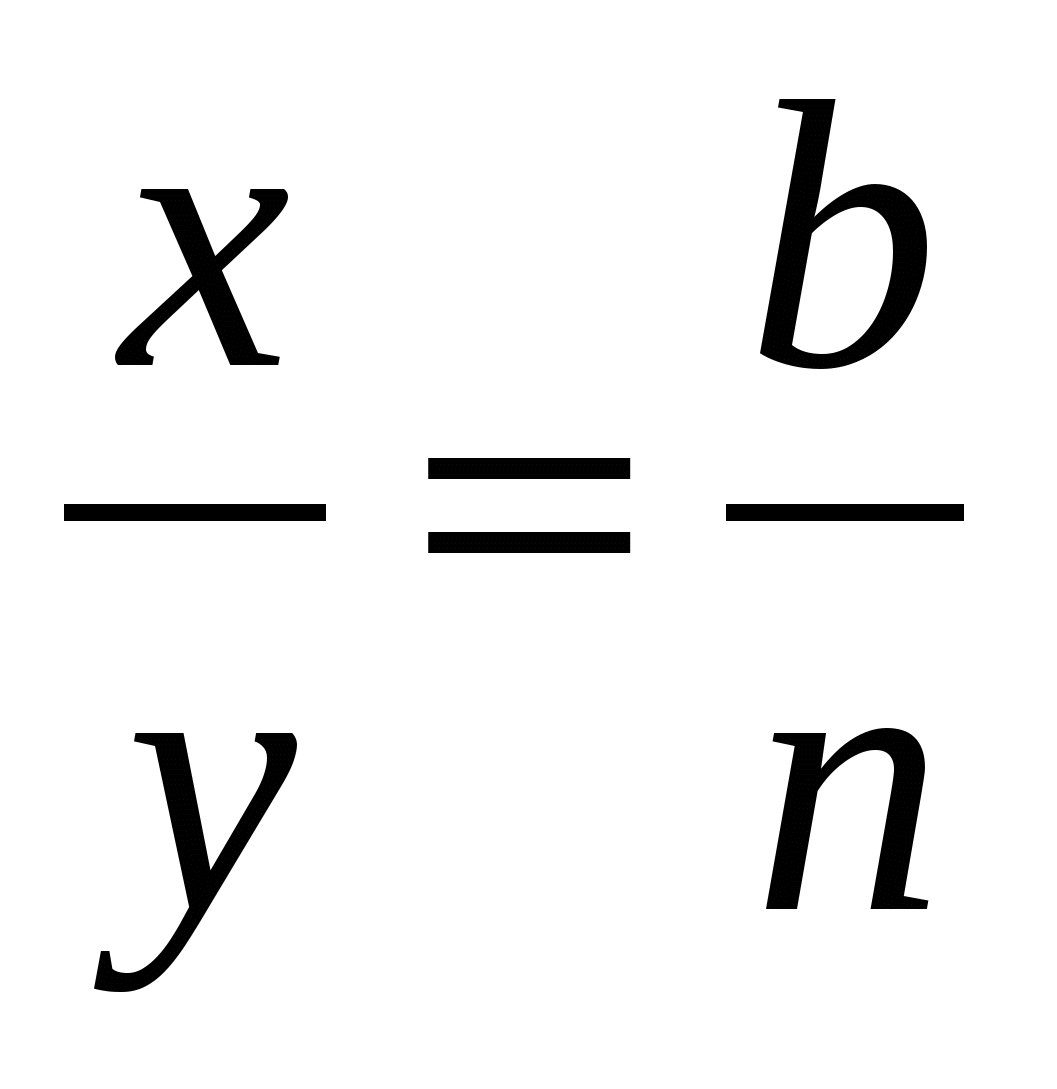 . Учитывая что
. Учитывая что 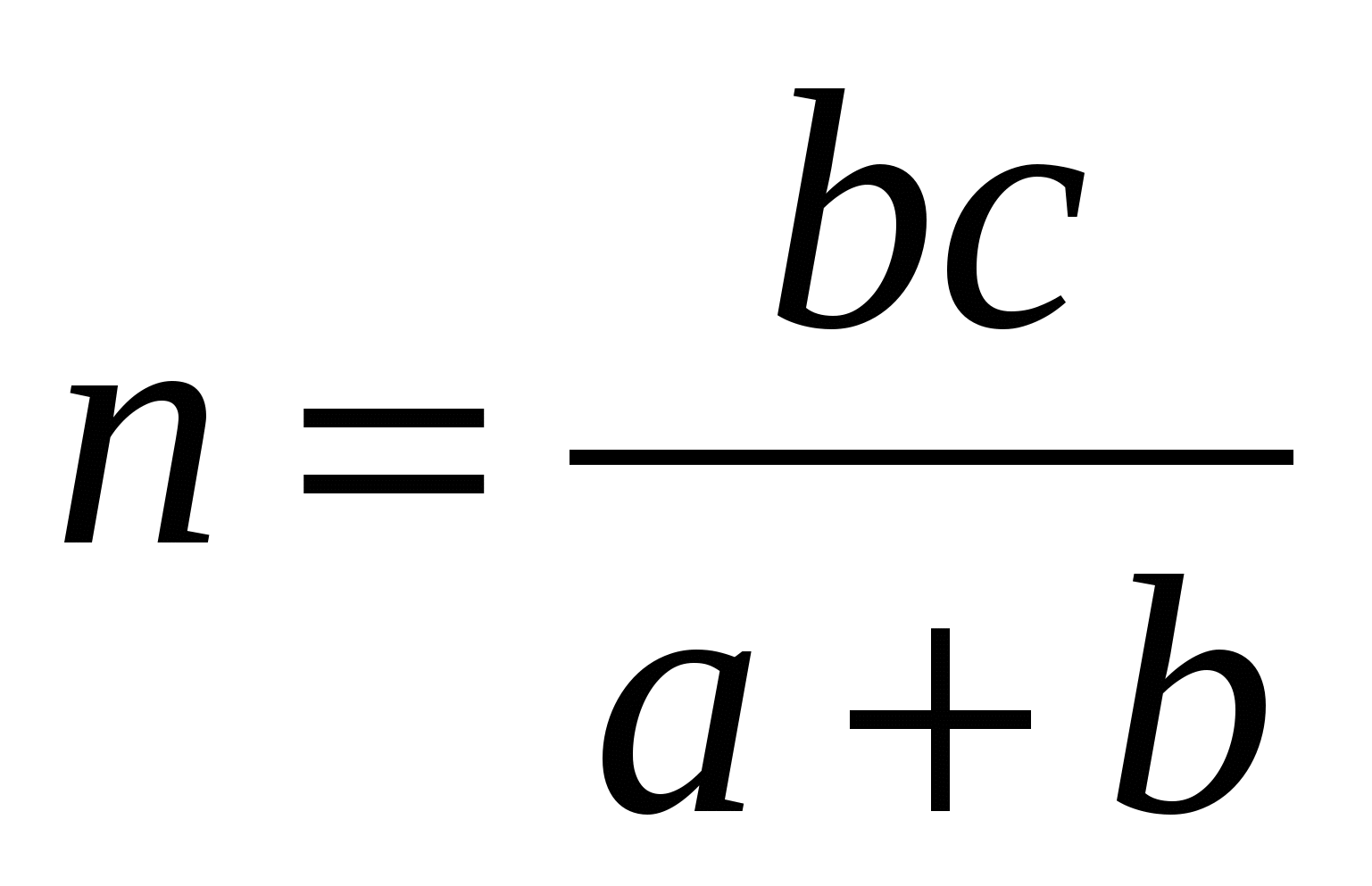 , находим
, находим 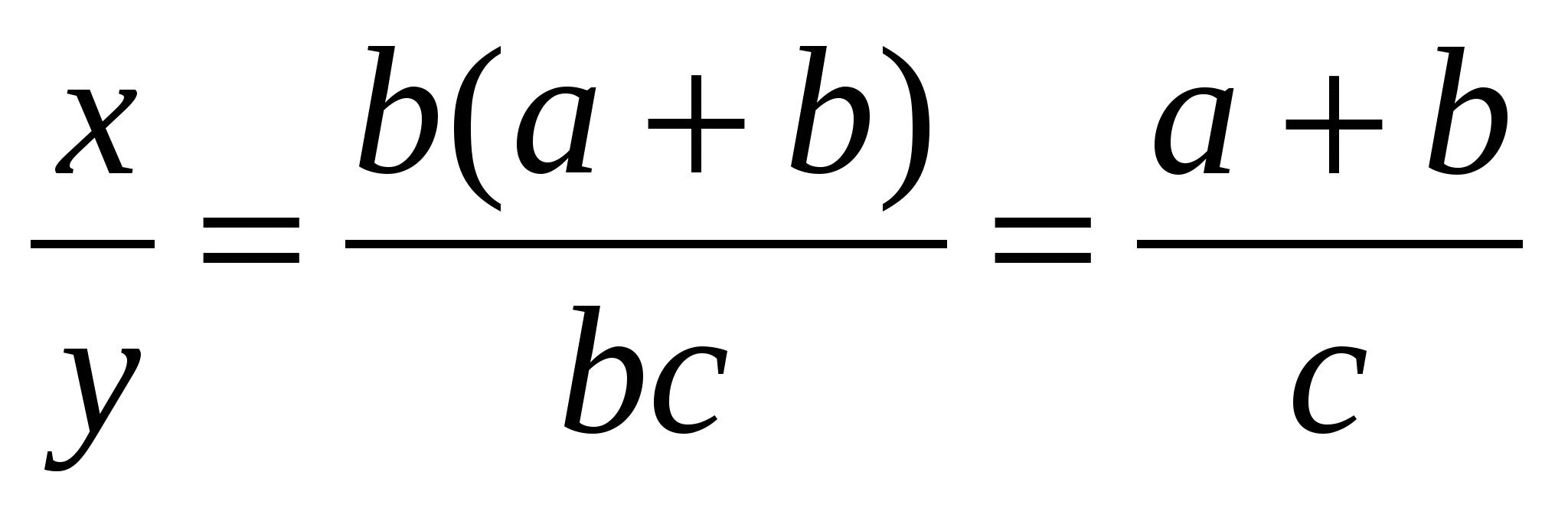 .
.
Получили соотношение 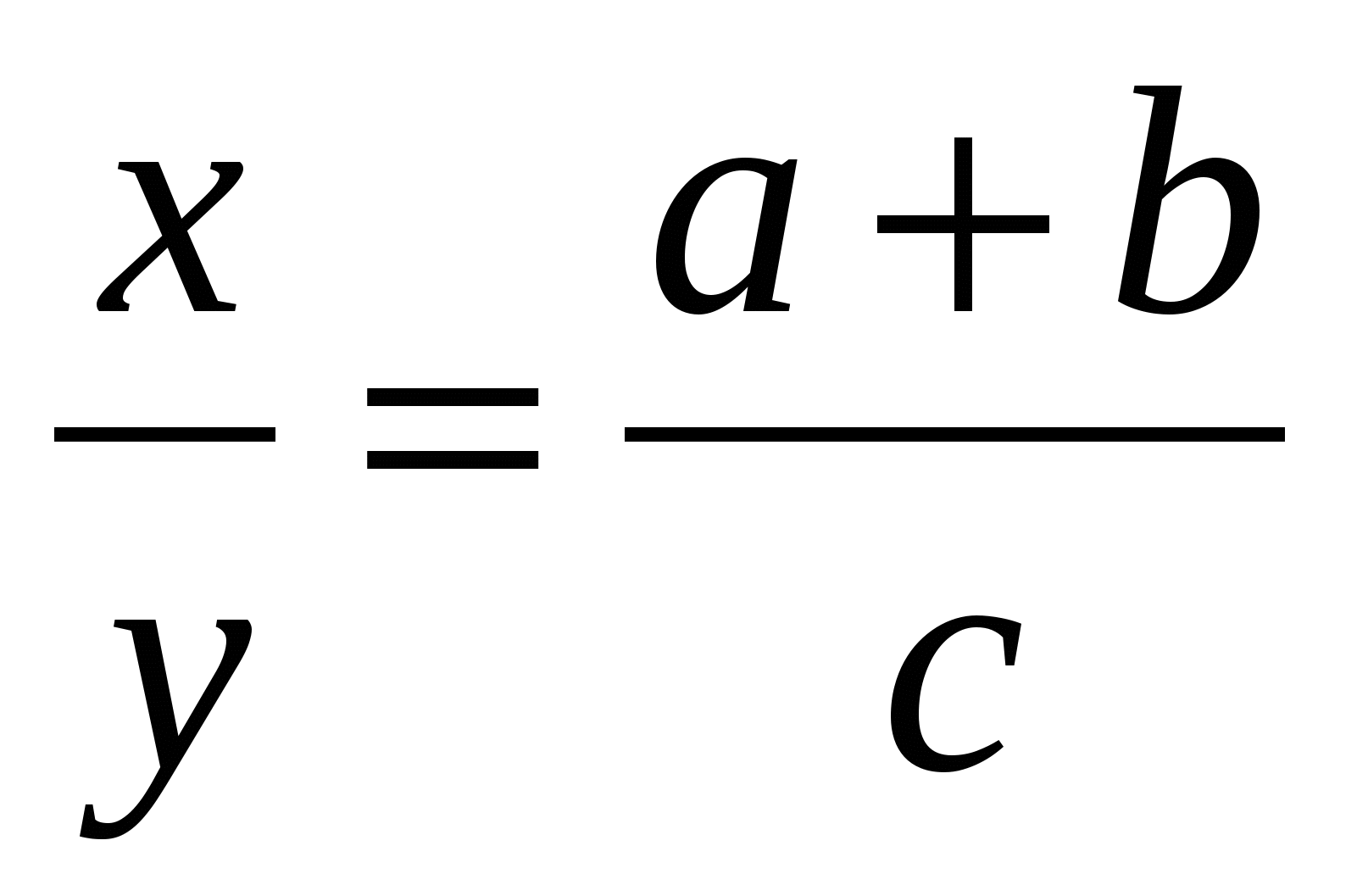
-
Угол , образованный при пересечении биссектрис,
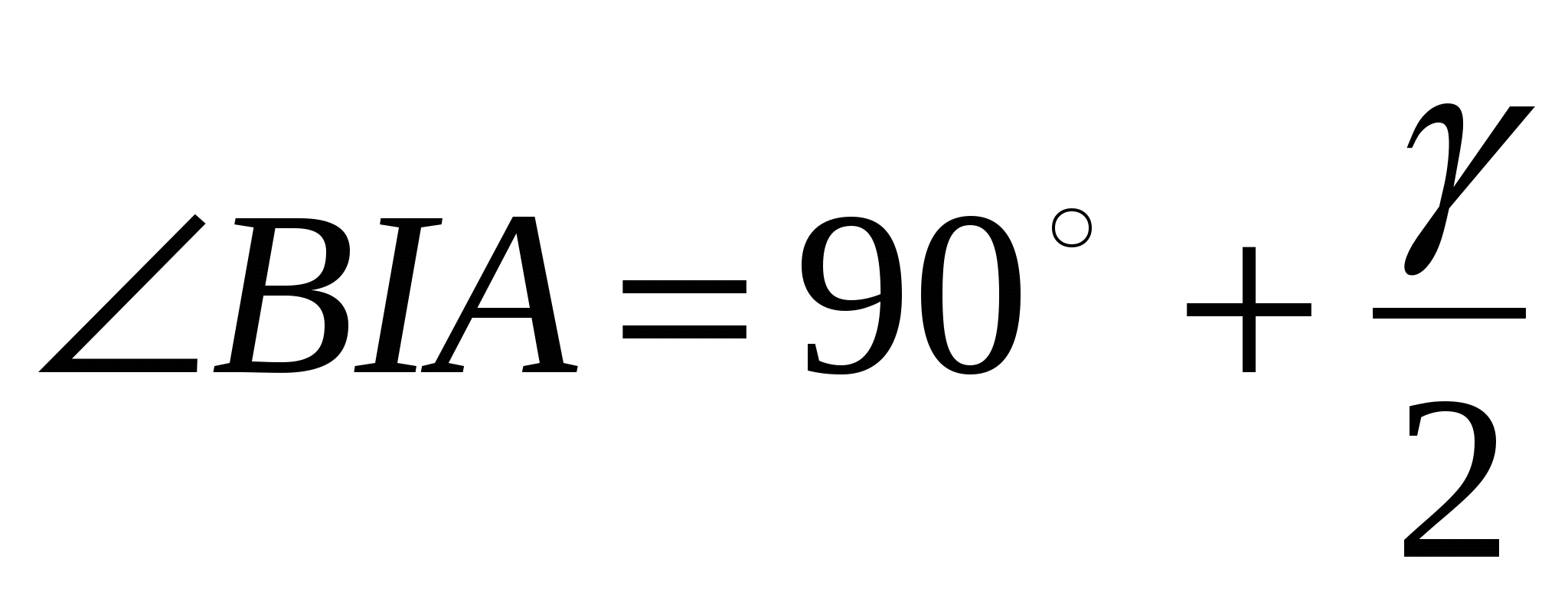
(рис. 3.2)
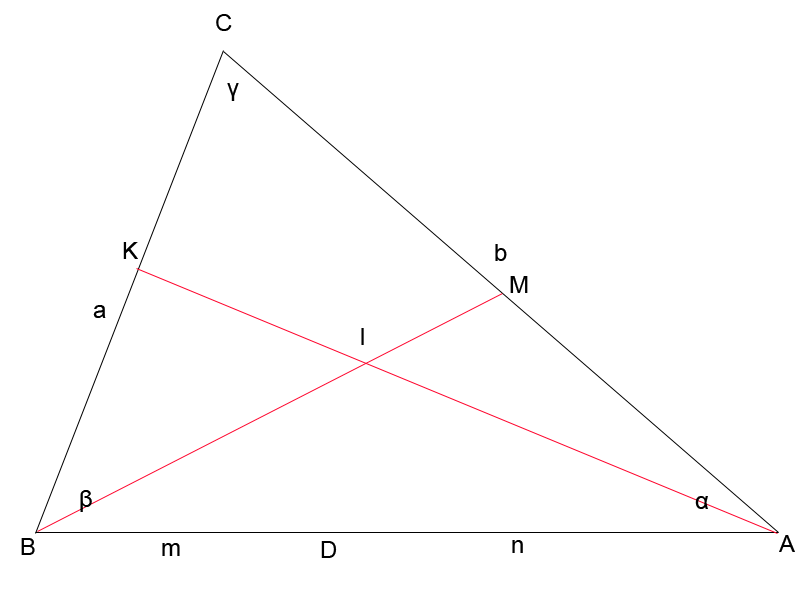
Рис. 3.2
Из 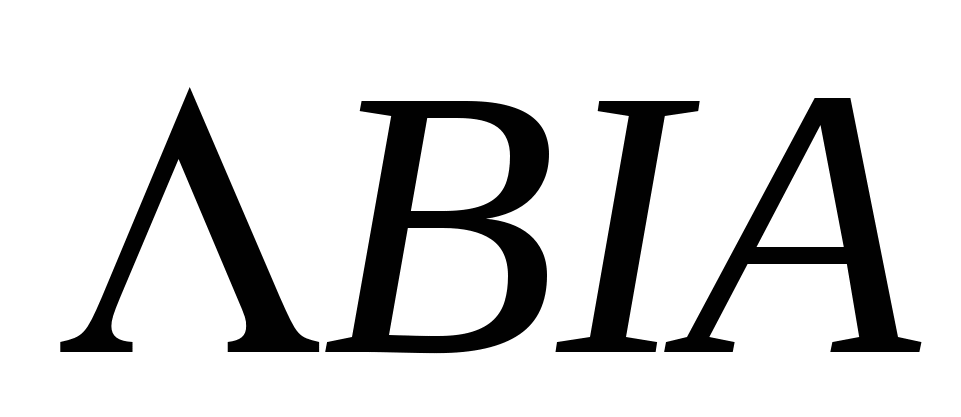 :
: 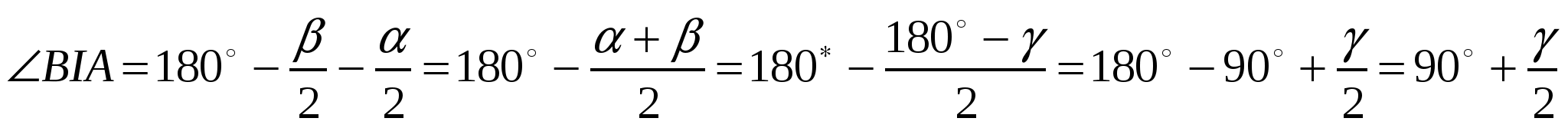
3.3 . Связь между сторонами треугольника и отрезками касательных к вписанной в треугольник окружности (рис. 3.3)
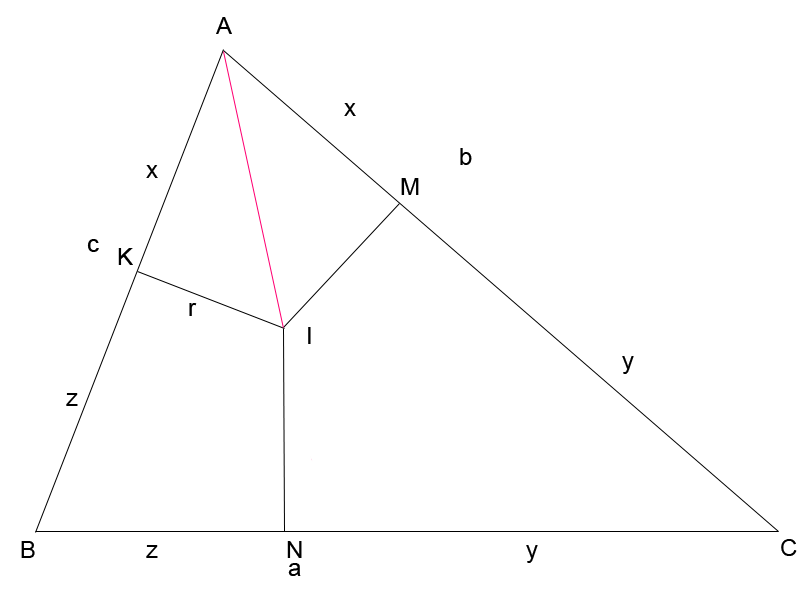
Рис. 3.3
В ∆АВС вписана окружность. Пусть М,К, N - точки касания окружности сторон треугольника. По свойству отрезков касательных, проведенных из одной точки, AM=AK=x, CM=CN=y, NB=KB=z . Тогда
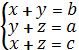 .
.
Сложив уравнения системы, получим
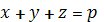 , где р - полупериметр.
, где р - полупериметр.
Вычитая из последнего равенства уравнения системы, получим
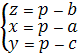
Формулы, выражающие отрезки касательных через стороны треугольника.
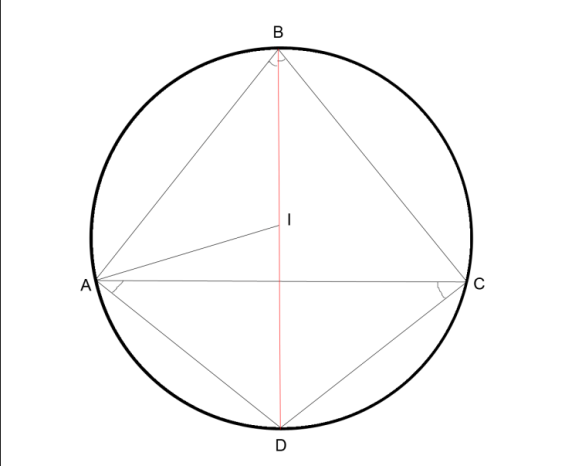
Привожу без доказательства утверждения о свойстве точки пересечения продолжения биссектрисы треугольника с описанной около него окружностью, о расположении биссектрисы треугольника. Эта часть работы будет продолжена.
1. Точка пересечения продолжения биссектрисы треугольника с описанной около него окружностью, равноудалена от двух других вершин и инцентра
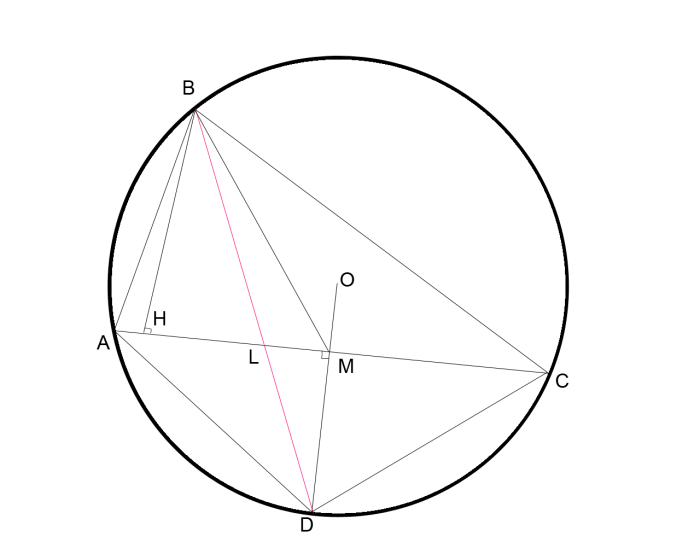
2. В неравнобедренном треугольнике биссектриса всегда расположена между высотой и медианой, проведенными из одной вершины.
Задачи
1. Дан треугольник ABC, в котором угол В = 30°, АВ = 4, ВС = 6. Биссектриса угла В пересекает сторону АС в точке D. Определите площадь треугольника ABD (рис. 1).
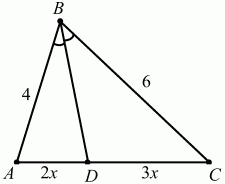
Рис. 1
Решение. По свойству биссектрисы AD/DC = AB/BC = 4/6 = 2/3.
Пусть AD = 2х; DC = Зх.
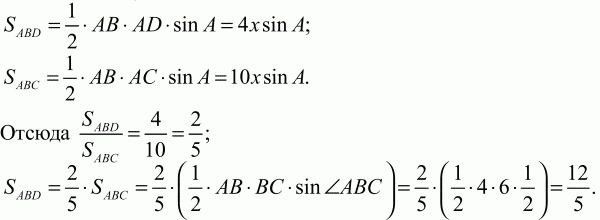
Ответ: 12/5.
Задача.
Стороны треугольника равны 10 см, 11 см и 12 см. Найти отрезки, на которые делит биссектриса треугольника среднюю сторону.
Дано: AC=10 см, BC=11 см, AB=12 см, AP = биссектриса.
Найти: CP и BP.
Решение:
По свойству биссектрисы треугольника:
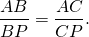
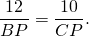
Пусть CP=x см, тогда BP=11-x см:
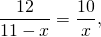
откуда по основному свойству пропорции
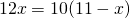
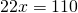
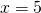
CP=5 см, BP=6 см.
Ответ: 5 см, 6 см.
Найти биссектрису угла B треугольника ABC и определить, в каком отношении центр вписанной в треугольник окружности делит эту биссектрису, если AB = 4, BC = 5 и AC = 6.
Решение
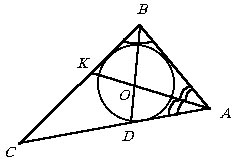
Пусть BD и AK - биссектрисы углов B и A треугольника ABC и O - центр вписанной окружности.
Так как AB = 4 и BC = 5, то по теореме о биссектрисе AD = 4t и CD = 5t, поэтому AC = 6 = 4t + 5t, т.е. 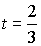 , и тогда
, и тогда ![]() .
.
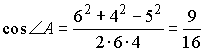 и
и
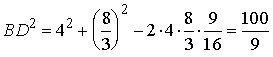 , т.е.
, т.е. 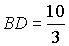 .
.
И, наконец, определим по теореме о биссектрисе из треугольника BAD, в каком отношении точка O делит отрезок BD:
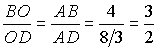 .
.
Ответ: 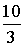 и
и 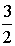 .
.
Найти биссектрисы острых углов в прямоугольном треугольнике, катеты которого равны 6 и 8 см.
Решение
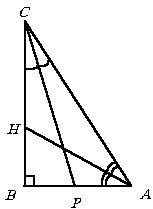
Пусть ABC - прямоугольный треугольник, у которого AB = 6, BC = 8, B = 90 °, P и H - основания биссектрис углов C и A соответственно. Тогда по теореме Пифагора 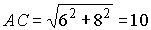 .
.
По теореме о биссектрисе BP = 8t и Pa = 10t , откуда AB = AB = 6 = 8t + 10t и 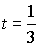 .
.
Поэтому 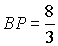 , и по теореме Пифагора
, и по теореме Пифагора 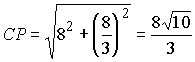 . Аналогично находим
. Аналогично находим 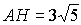 .
.
Ответ: 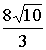 см,
см,  см.
см.
ВЫВОДЫ
В этой работе мы показали разнообразие способов доказательства свойства биссектрисы треугольника. Выведена формула для вычисления длины биссектрисы, рассмотрен ряд задач, которые были в заданиях на ЕГЭ разных лет. Доказано положение биссектрисы в неравнобедренном треугольнике. Показано отношение , в котором биссектрисы треугольника делятся точкой пересечения; определен угол , образованный при пересечении биссектрис. Для многих свойств приводится несколько способов доказательства.
Работая над проектом и находя различные способы доказательств, приобретаются логические навыки, умение анализировать и сопоставлять, сравнивать. С помощью доказанных свойств многие задачи решаются легче и доступней.
Данная работа может служить справочным материалом при подготовке к ЕГЭ, как в теоретическом, так и в практическом плане.
СПИСОК ЛИТЕРАТУРЫ
-
Шарыгин И.Ф. Учимся решать задачи по геометрии //Математика в школе.-1989.-№2. -С. 87-89.
-
Мерзляк А.Г., Полонский В.Б., Якир М.С. Геометрия .8 класс: Учебник. Харьков: Гимназия,2008.- С.83-84.
-
Биссектриса треугольника.- [Электронный ресурс] .-режим доступа: ru.wikipedia.org/
-
Апостолова Г.В. Геометрия .8 класс: Учебник. Киев: Генеза, 2008.-С.36-37.


