- Преподавателю
- Математика
- Проект «Теорема Птолемея для вписанного четырехугольника»
Проект «Теорема Птолемея для вписанного четырехугольника»
| Раздел | Математика |
| Класс | - |
| Тип | Конспекты |
| Автор | Кот В.И. |
| Дата | 09.01.2015 |
| Формат | doc |
| Изображения | Есть |
Мною проведено открытое факультативное занятие «Проект «Теорема Птолемея для вписанного четырехугольника» в 11 «А» классе гимназии № 1 г. Ивье. В результате получены положительные отзывы об этом занятии от коллег и администрации гимназии. Учащиеся подготовили и на занятии защитили семь разных доказательств теоремы Птолемея с помощью мультимедийных презентаций. Бегун Татьяна для доказательства теоремы Птолемея использовала подобие треугольников, Пешко Максим - теорему синусов, Гурина Юлия - теорему косинусов (попутно вывела формулу для выражения длины диагонали вписанного четырехугольника через его стороны), Садовский Дмитрий - метод площадей, Дмитриев Никита - педальный треугольник и прямую Симпсона, Ошейчик Мария - преобразование инверсии, Анацкий Денис - теорему Бретшнейдера, представляющую собой теорему косинусов для четырехугольника. Богданович Юлия и Богданович Иван представили свои решения вступительных задач по математике в вузы с использованием теоремы Птолемея. Таким образом, на проведенном факультативном занятии учащиеся углубили свои знания о вписанных четырехугольниках, убедились, что с помощью теоремы Птолемея можно доказать теорему Пифагора, теорему косинусов для треугольника, вывести формулы синуса суммы и синуса разности, что теорема Птолемея до сих пор является источником для множества обобщений и плодотворных идей.
Теорема Птолемея
Если четырехугольник ABCD (рис. 1) вписан в окружность, то произведение его диагоналей равно сумме произведений его противоположных сторон:
AC . BD = AB . CD + AD . BC
Данная теорема установлена Клавдием Птолемеем во втором веке нашей эры.
► Первое доказательство будет в основном следовать доказательству самого Птолемея, приведенному им в книге «Альмагест». Используется подобие треугольников.
На чертеже (рис. 1) изображен данный четырехугольник ABCD, его диагонали АС и ВD и описанная около него окружность. 
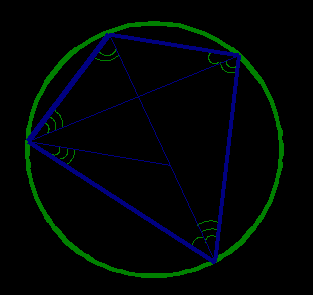
Рис. 1
Проведем из точки B отрезок BE до пересечения с диагональю AC таким образом, чтобы CBE = ABD.  Углы BCЕ и BDA равны как вписанные, опирающиеся на одну и ту же дугу AB. Тогда
Углы BCЕ и BDA равны как вписанные, опирающиеся на одну и ту же дугу AB. Тогда треугольники ABD и СBЕ подобны (по двум углам). Отсюда следует, что
треугольники ABD и СBЕ подобны (по двум углам). Отсюда следует, что 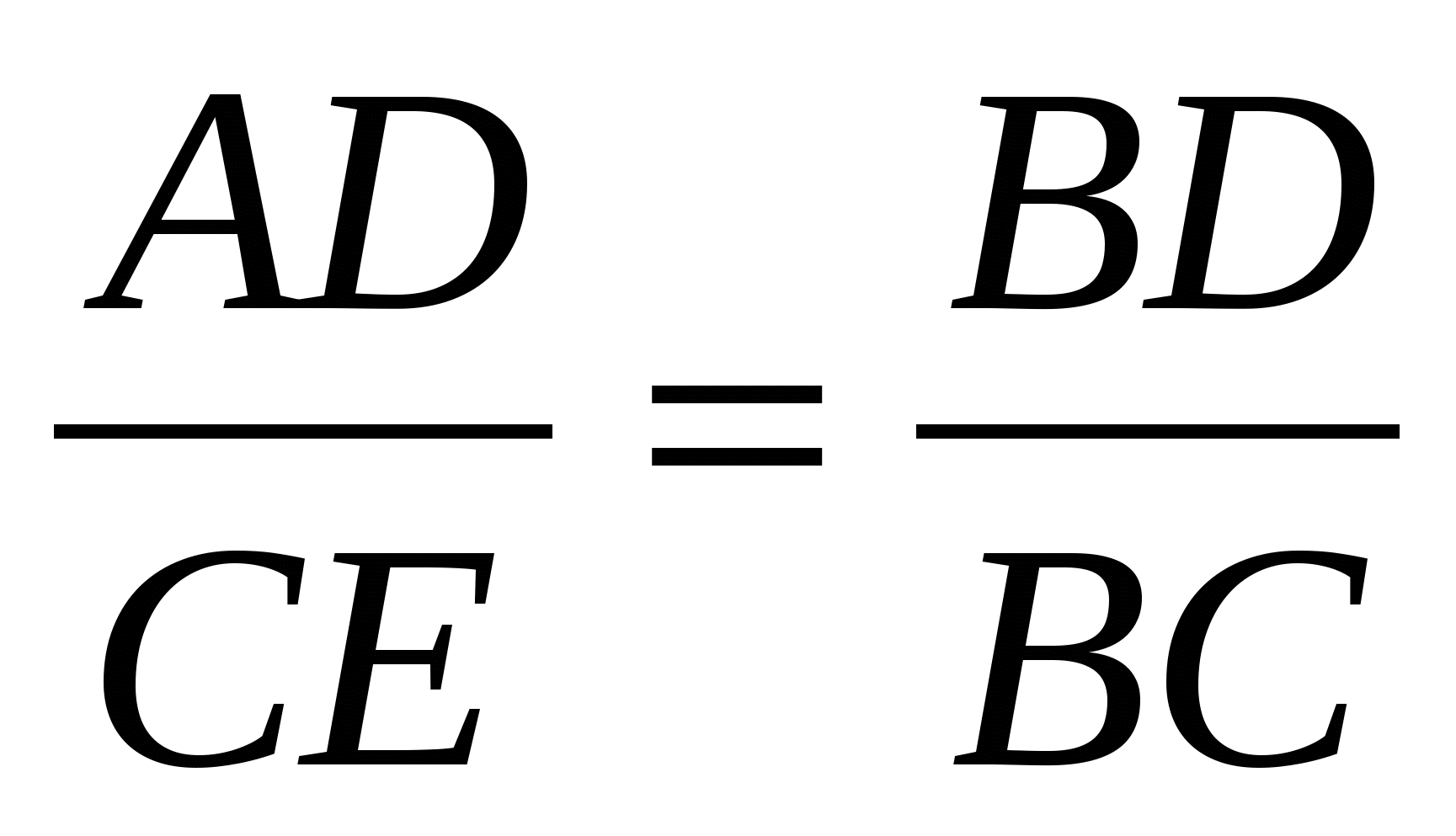 и, следовательно, далее имеем:
и, следовательно, далее имеем:
AD . BC = BD . CE. (2)
 Подобны также треугольники ABE и DBC, так как ABE = DBC и BAE = BDC.
Подобны также треугольники ABE и DBC, так как ABE = DBC и BAE = BDC.
Отсюда следует, что 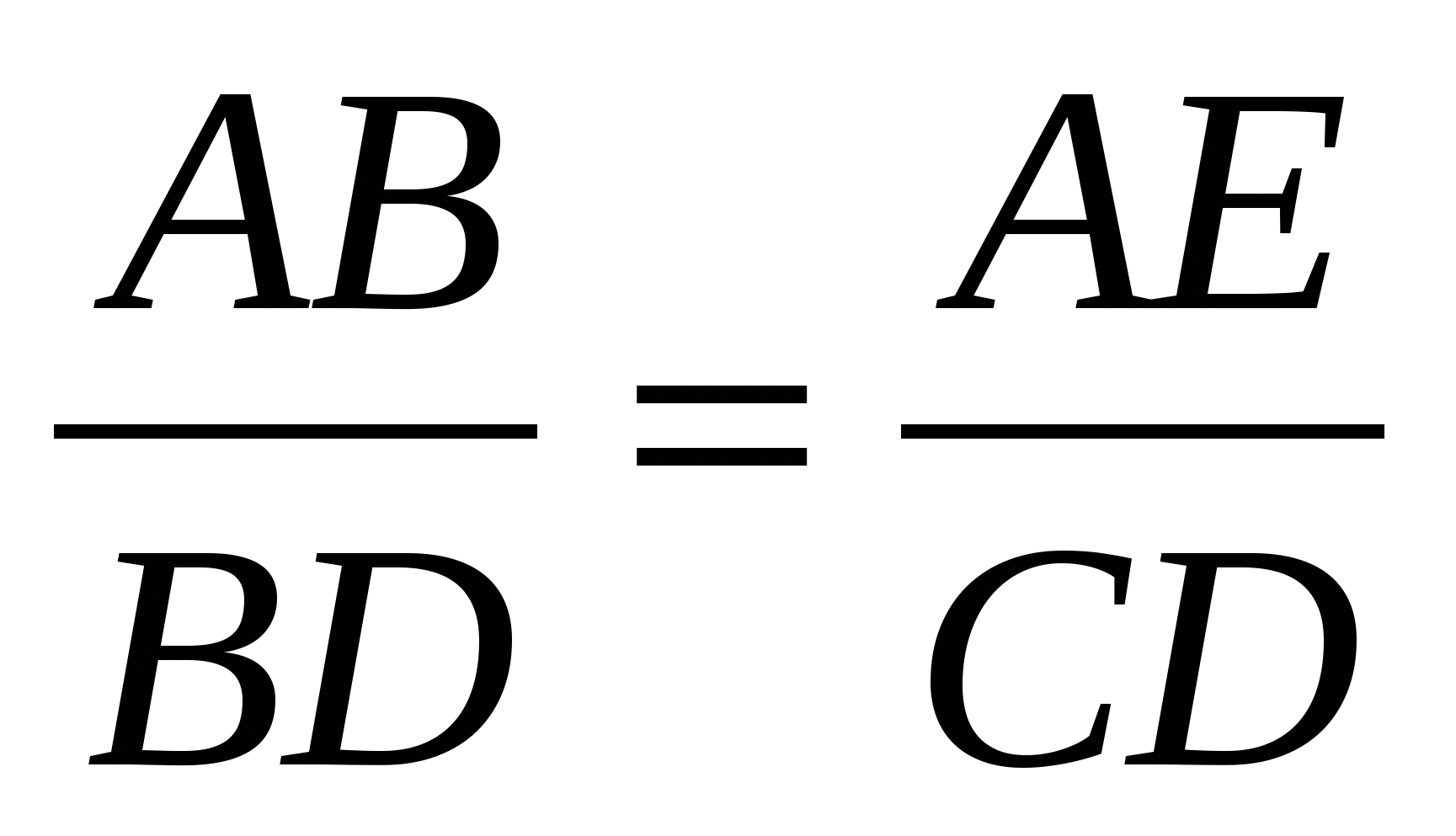 и затем имеем:
и затем имеем:
AB . CD = BD .AE. (3)
Сложим соответственно левые и правые части равенств (2) и (3). Получим
AD . BC + AB . CD = BD . CE + BD . AE или
AD . BC + AB . CD = BD . (CE + AE) , то есть
AD . BC + AB . CD = BD . AC, что и требовалось.
Замечание. К этому же можно прийти, введя другие обозначения.
Если АВ = ![]() ВС =
ВС =  СD =
СD = 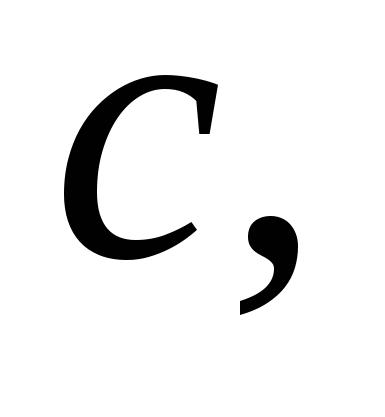 DА =
DА = 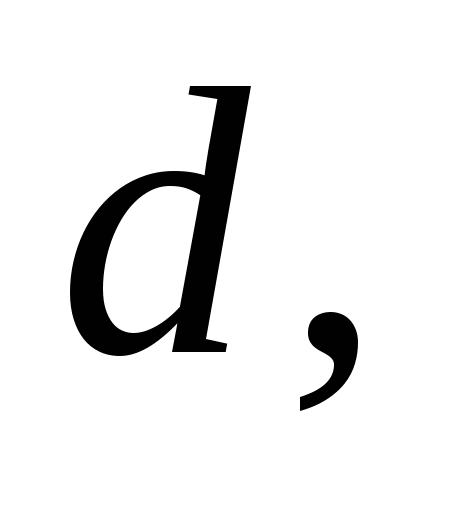 АС =
АС = 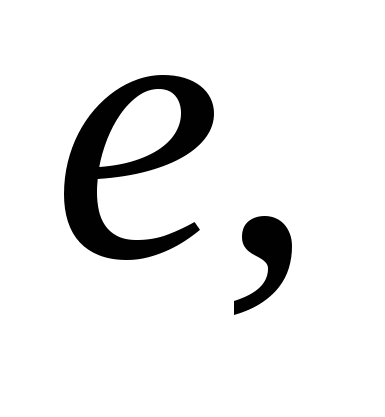 ВD =
ВD = 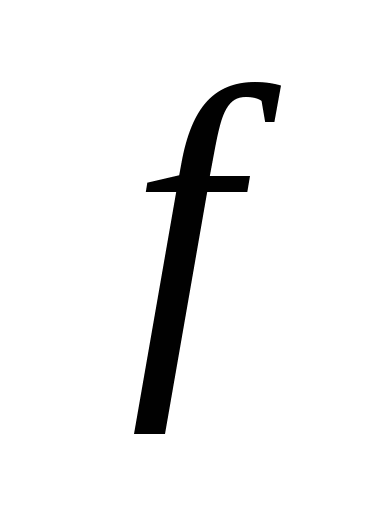 , то выберем на диагонали АС точку Е так, чтобы угол СВЕ был равен
, то выберем на диагонали АС точку Е так, чтобы угол СВЕ был равен 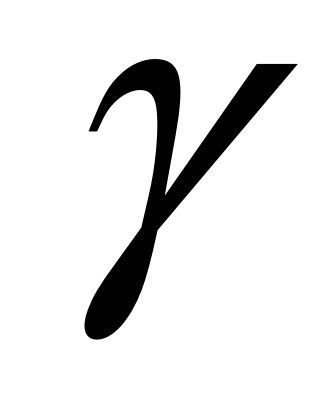 .
.
Тогда треугольники СВЕ и DВА подобны.
Поэтому ЕС : 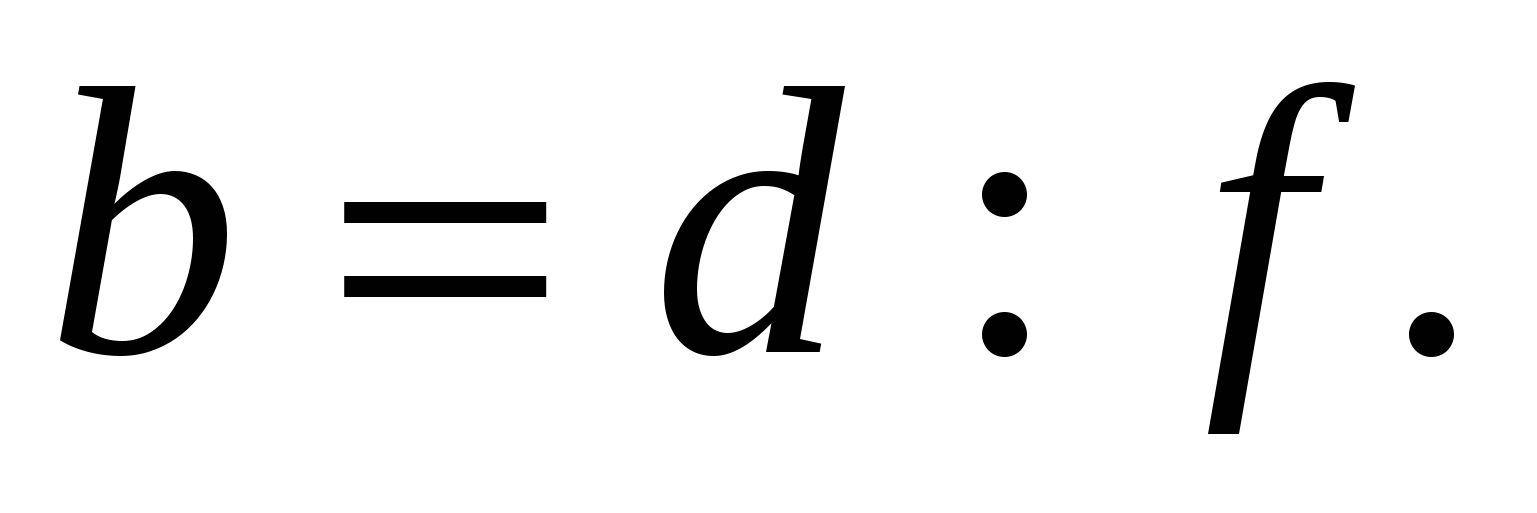
Из подобия треугольников АВЕ и DВС (углы АВЕ и DВС равны как равносоставленные) получаем АЕ : 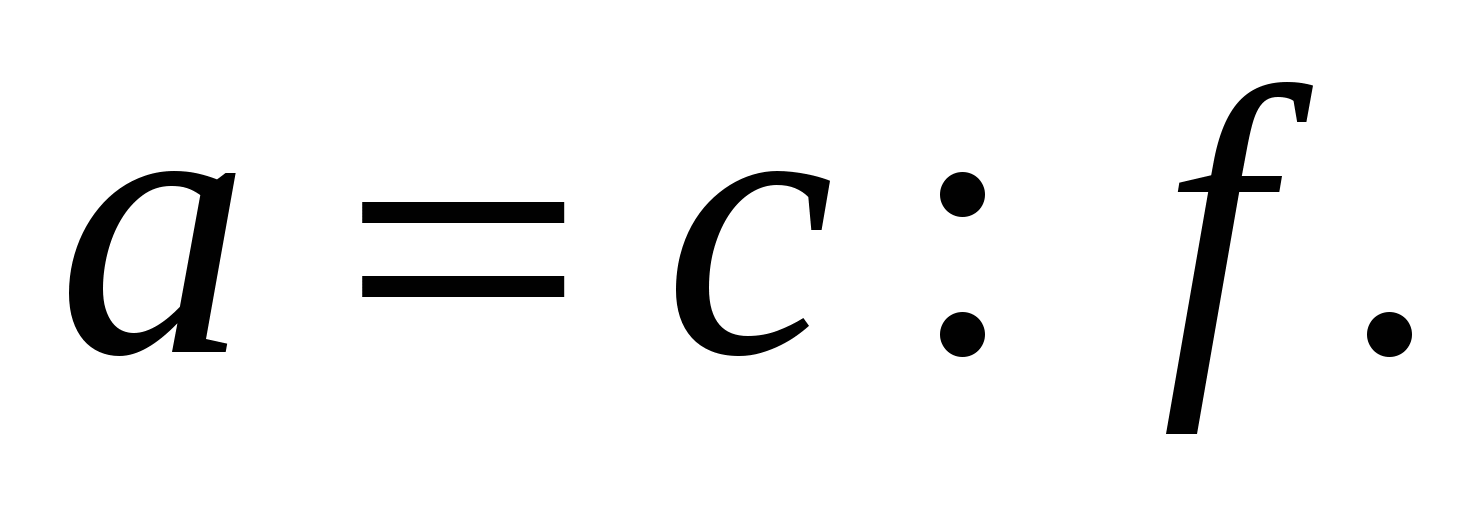
Значит, ЕС = 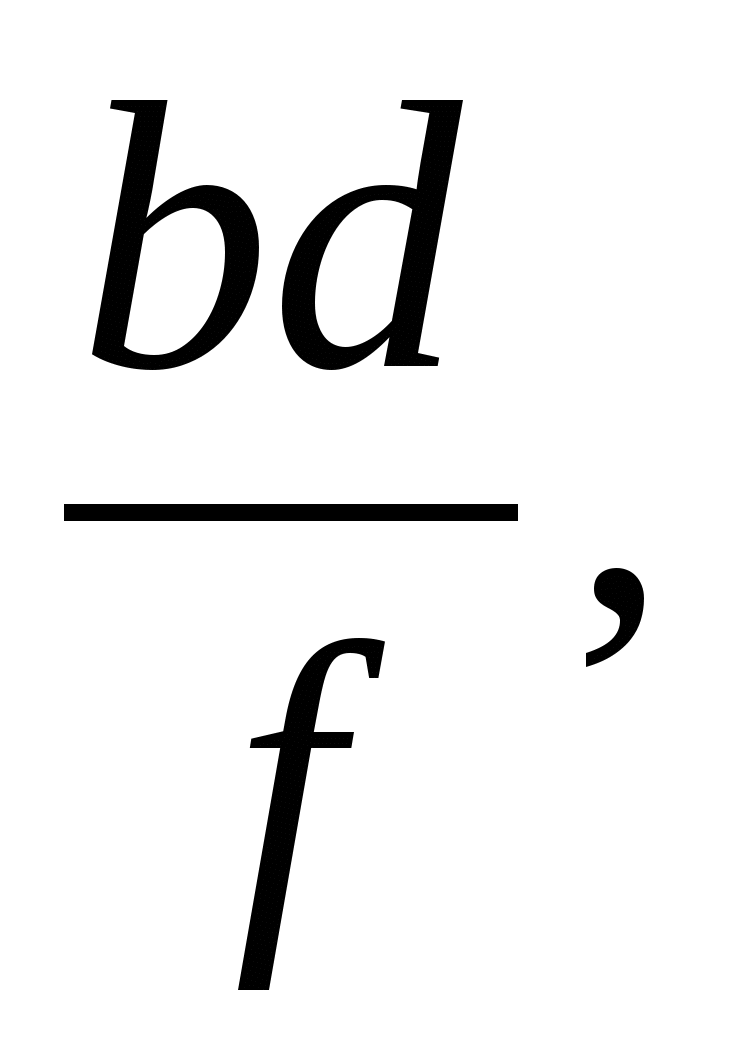 АЕ =
АЕ = 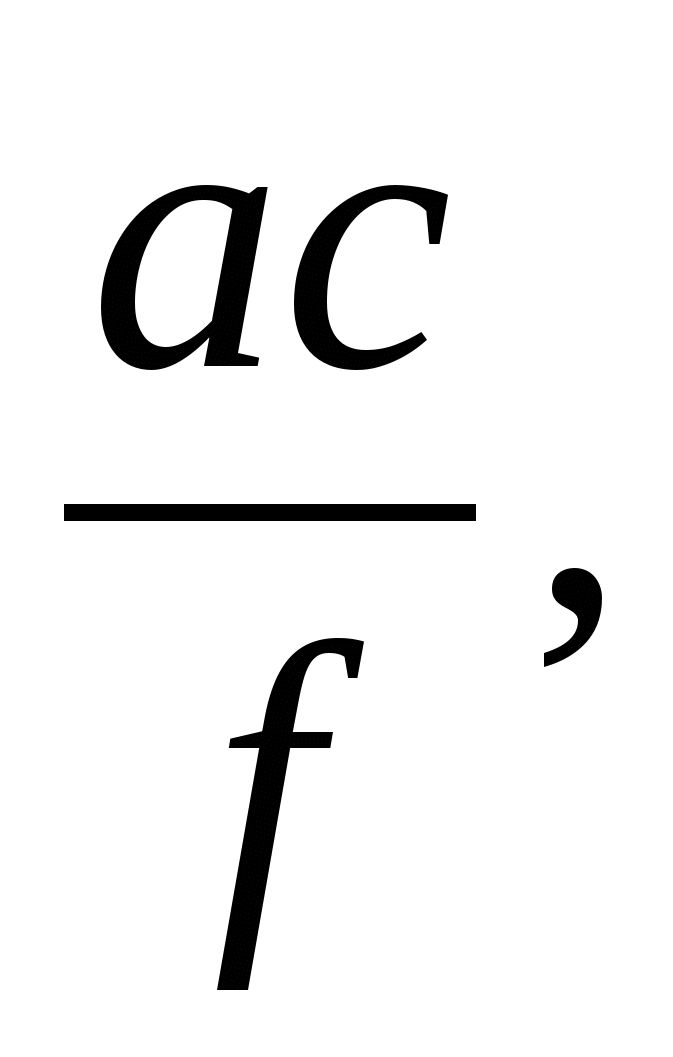 АЕ + ЕС =АС,
АЕ + ЕС =АС, 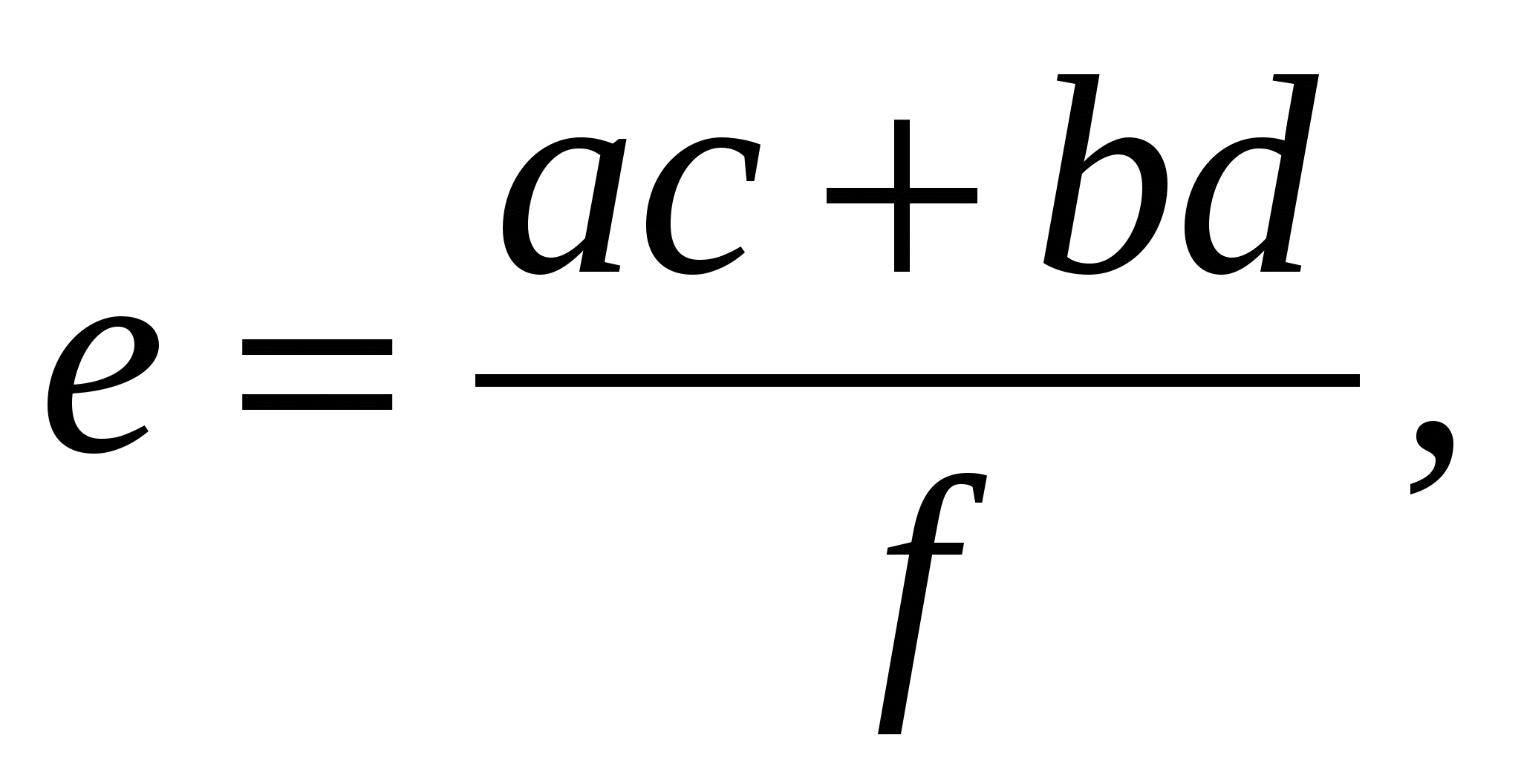
отсюда 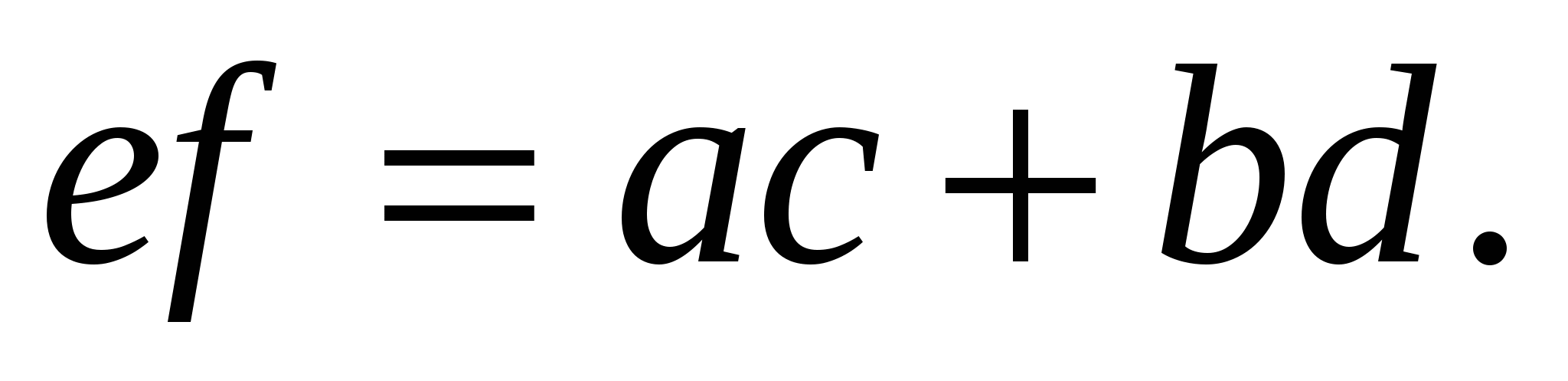
Теорема Птолемея доказана. ◄
(Справедлива и теорема, обратная теореме Птолемея).
►► Второе доказательство. Используется теорема синусов.
Так как четырехугольник вписанный, то кроме входящих в условие теоремы величин целесообразно рассмотреть радиус круга R и углы четырехугольника. Введя углы, мы сможем использовать свойство вписанного четырехугольника.

Рис. 1
Итак, пусть 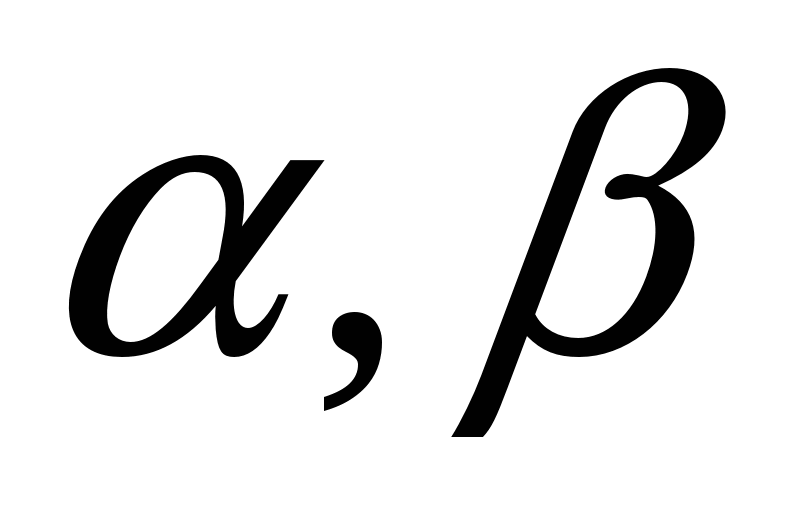 и
и 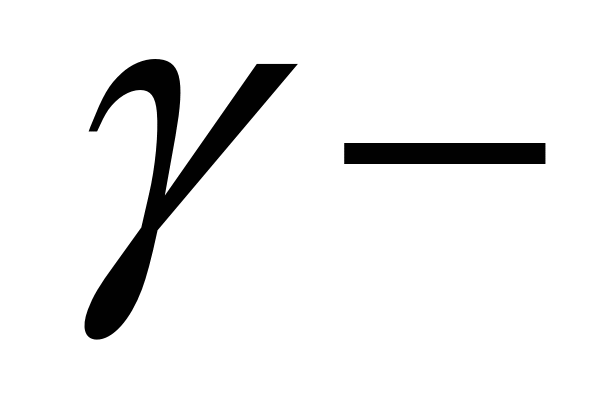 вписанные углы, опирающиеся соответственно на стороны АВ, ВС и АD (рис. 1).
вписанные углы, опирающиеся соответственно на стороны АВ, ВС и АD (рис. 1).
Тогда  DВС =
DВС =  DАС =
DАС = 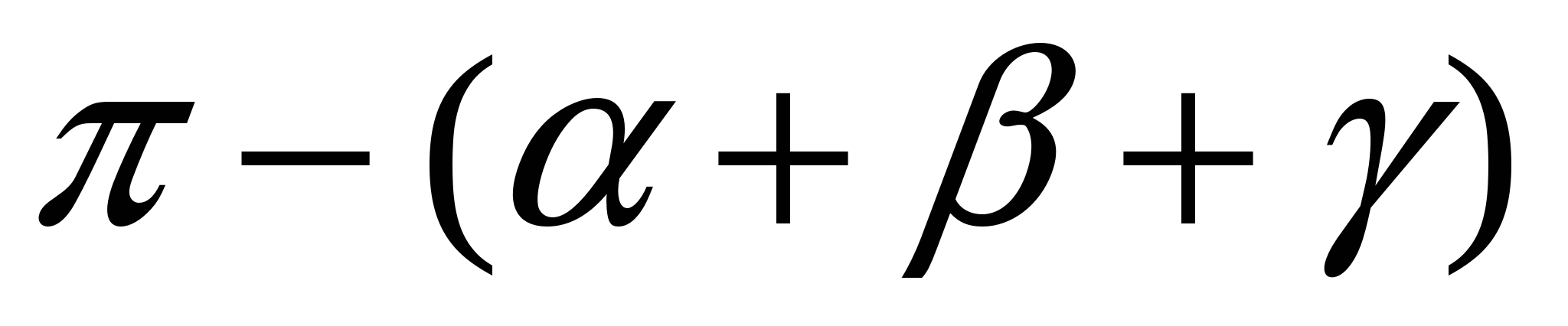 .
.
По теореме синусов
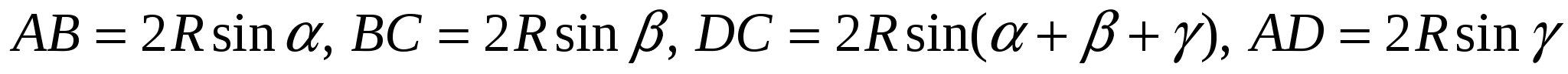 .
.
Следовательно, 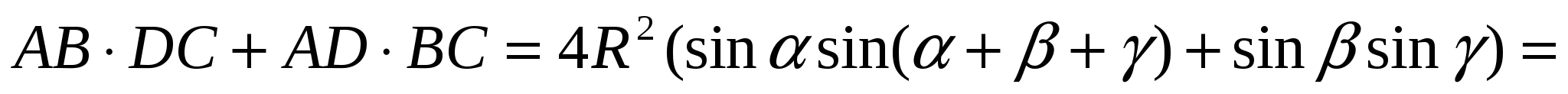
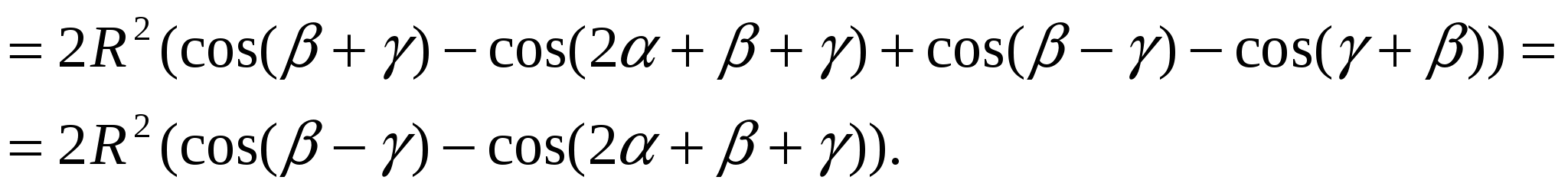
Так как 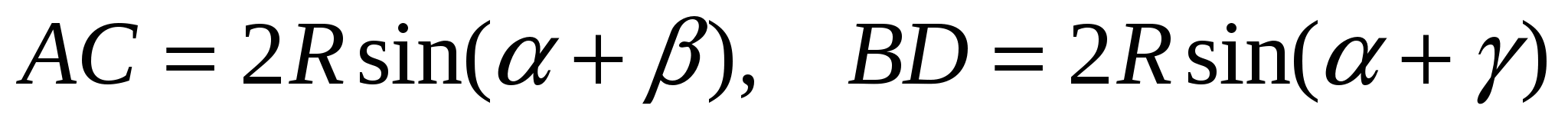 ,
,
то 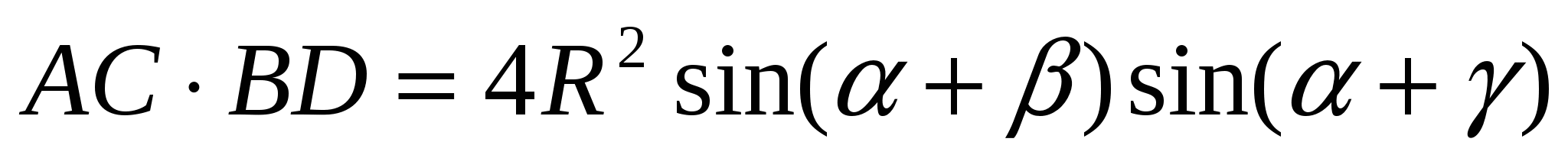 =
=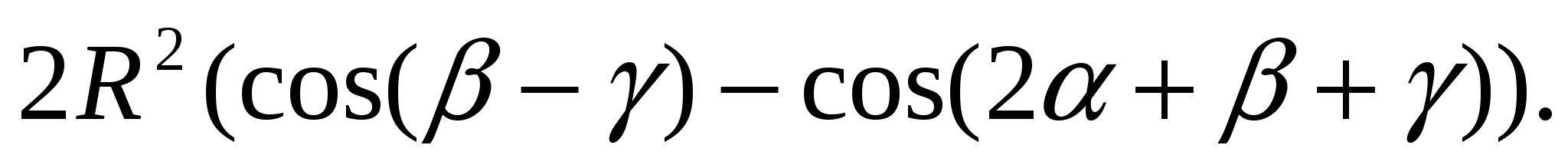
Значит, 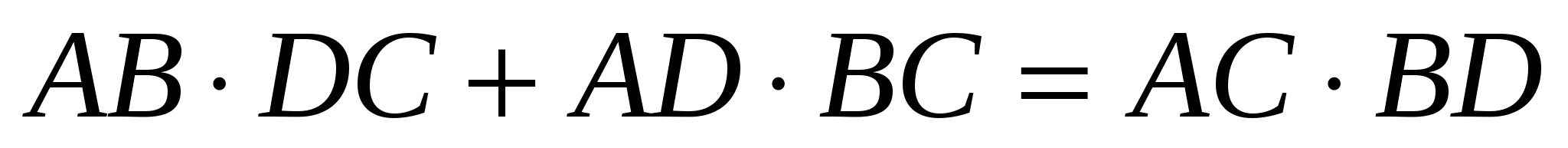 .◄
.◄
►►► Третье доказательство. Используется теорема косинусов.

Рис. 1
Пусть АВ = ![]() ВС =
ВС =  СD =
СD = 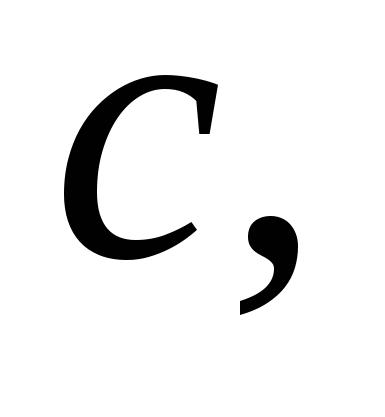 DА =
DА = 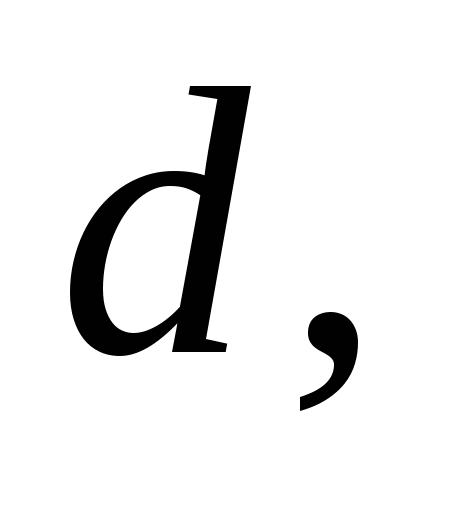 АС =
АС = 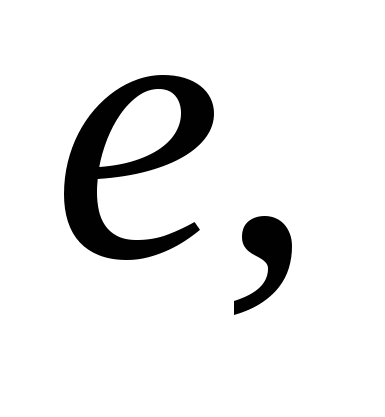 ВD =
ВD = 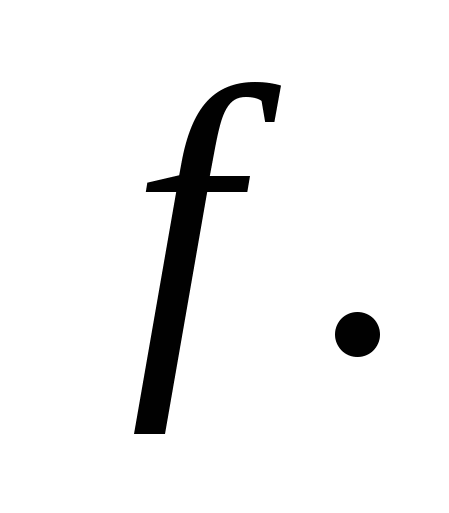
Нужно доказать, что 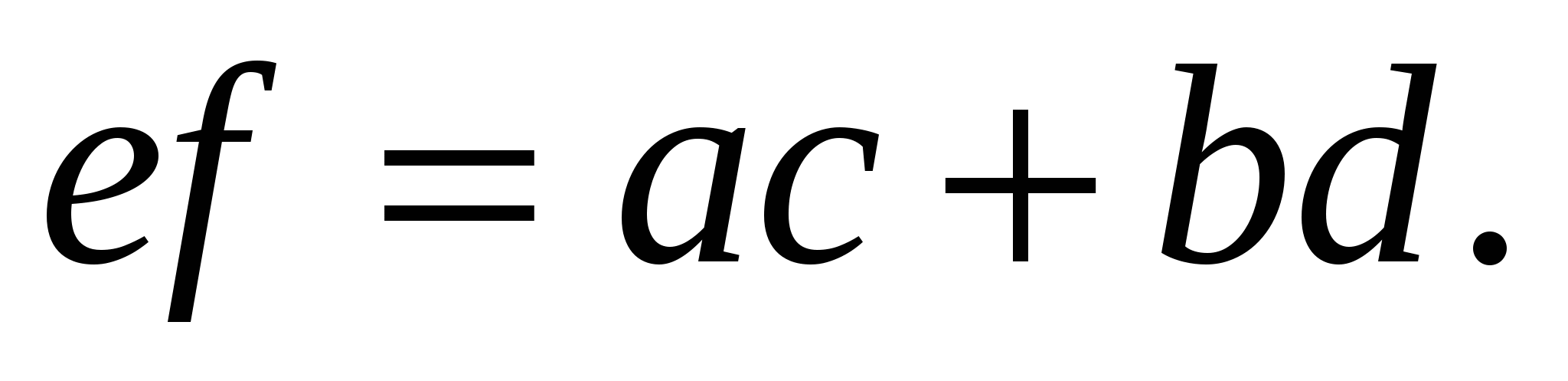
По теореме косинусов имеем:
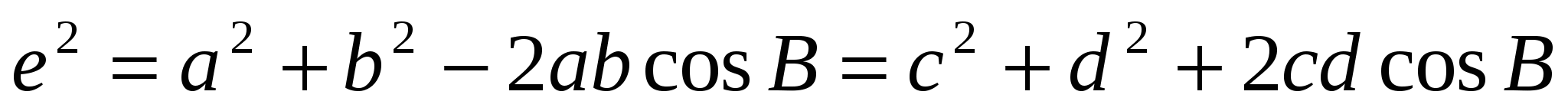 .
.
Избавляясь от косинусов и раскладывая на множители, получаем:
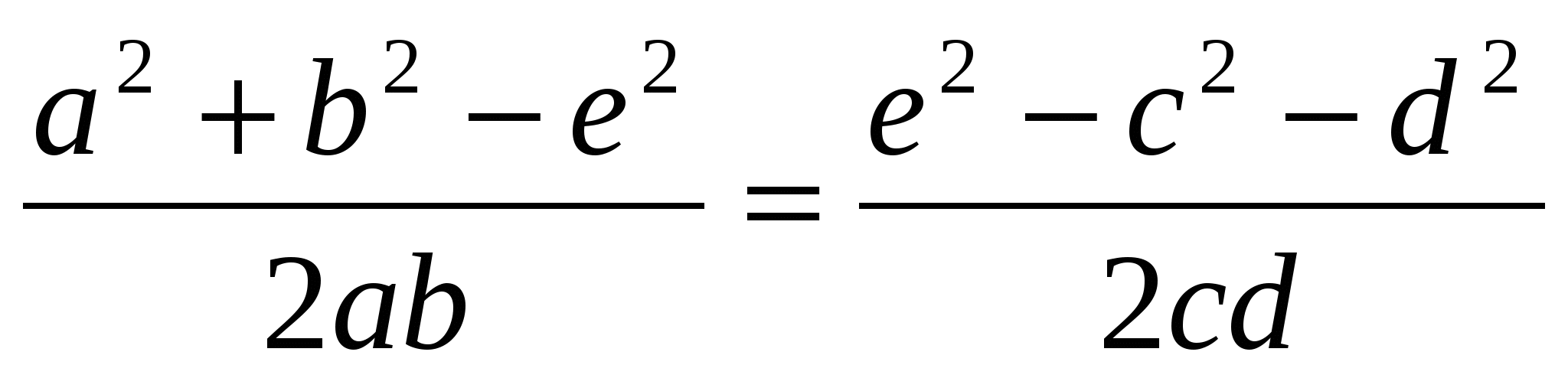 ,
,
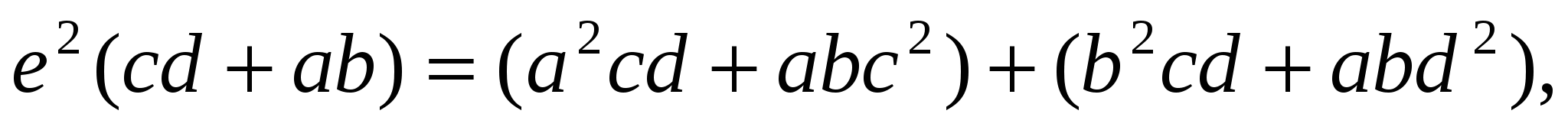
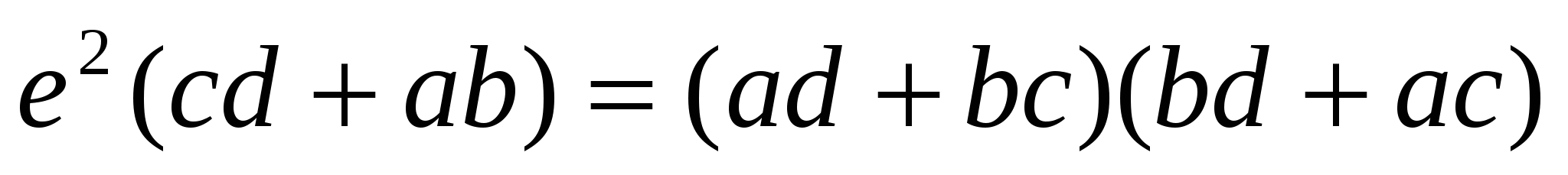

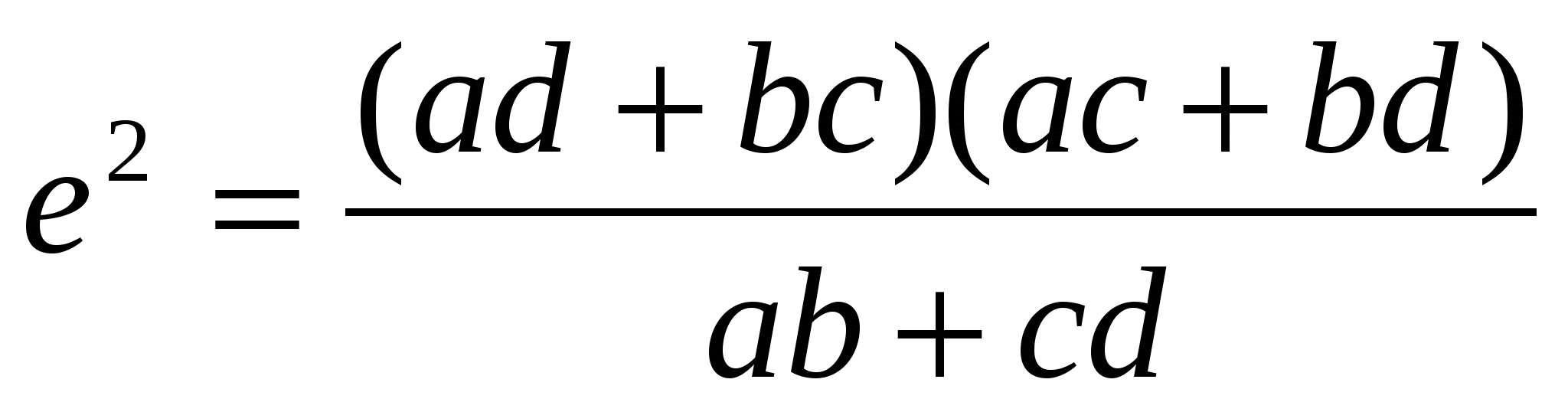 .
.
Аналогично, 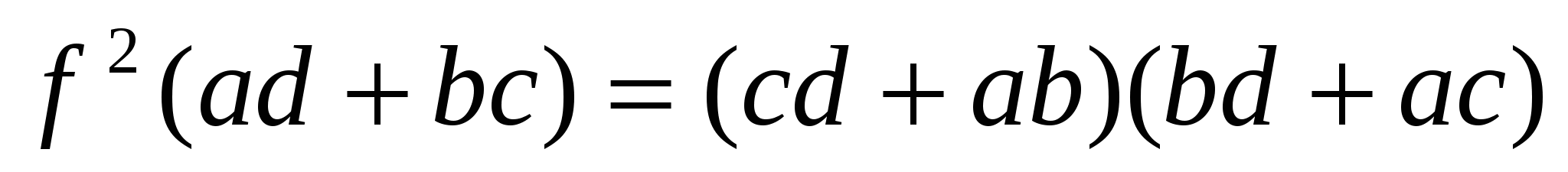

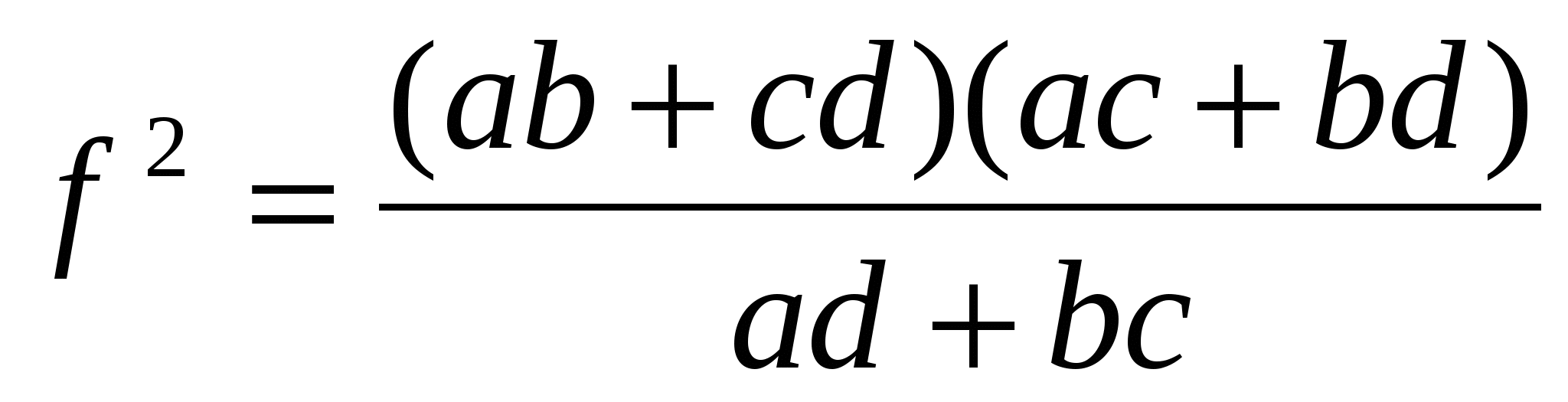 .
.
Перемножив последние два равенства и произведя соответствующие сокращения, найдем:
 ,
,
откуда и следует утверждение теоремы Птолемея. ◄
►►►► Четвертое доказательство. Используется метод площадей.
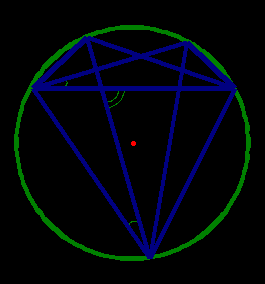
Рис. 2
Будем применять те же обозначения, что и в предыдущем доказательстве.
Найдем площадь S четырехугольника АВСD двумя способами.
-
Площадь выпуклого четырехугольника равна половине произведения диагоналей на синус угла между ними:
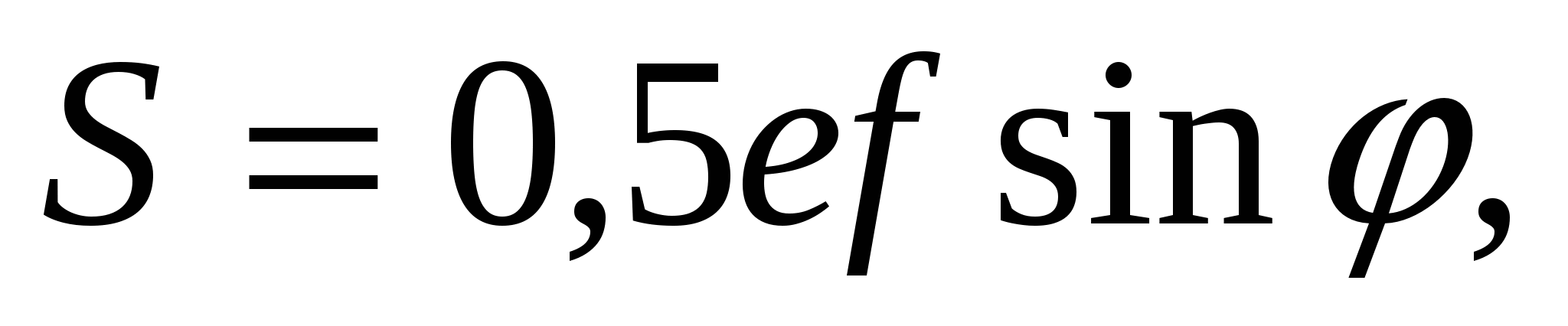 где
где 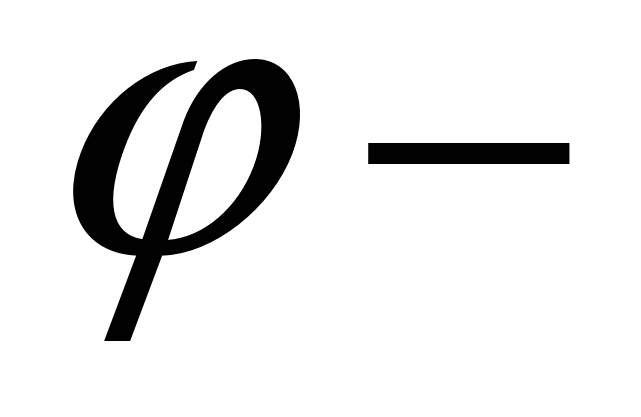 угол между диагоналями.
угол между диагоналями.
-
Рассмотрим на дуге АВС (рис. 2) точку В´ такую, что АВ = СВ´. Поскольку треугольники АВС и СВ´А равны, то равны и их площади. Тогда равны площади четырехугольников АВСD и АВ´СD.
Разобьем вновь полученный четырехугольник АВ´СD на два треугольника диагональю DВ´.
Площадь треугольника АВ´D равна 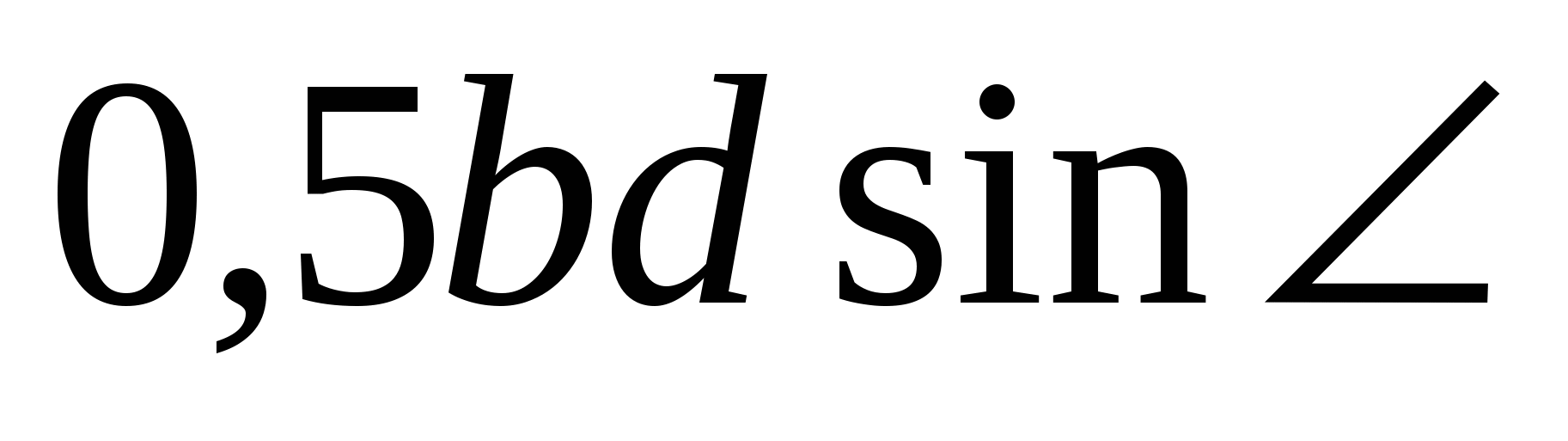 DAВ´,
DAВ´,
площадь треугольника СВ´D равна 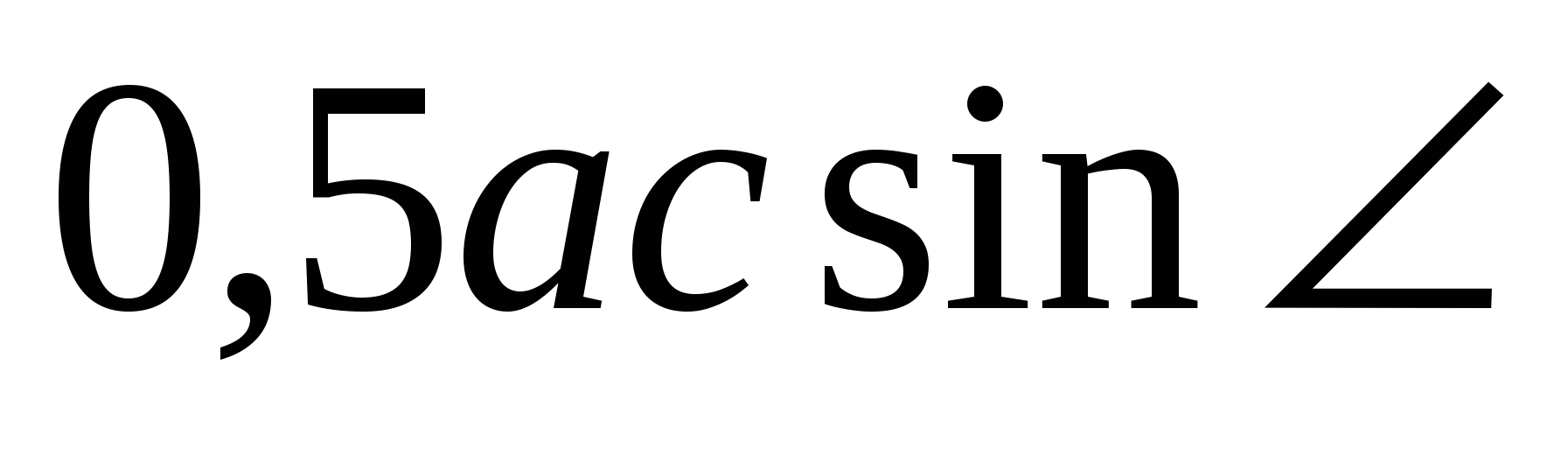 DCВ´.
DCВ´.
Так как четырехугольник АВ´СD вписанный, то углы DАВ´ и DСВ´ в сумме дают 180º и поэтому синусы этих углов совпадают.
Остается заметить, что
 DAВ´=
DAВ´=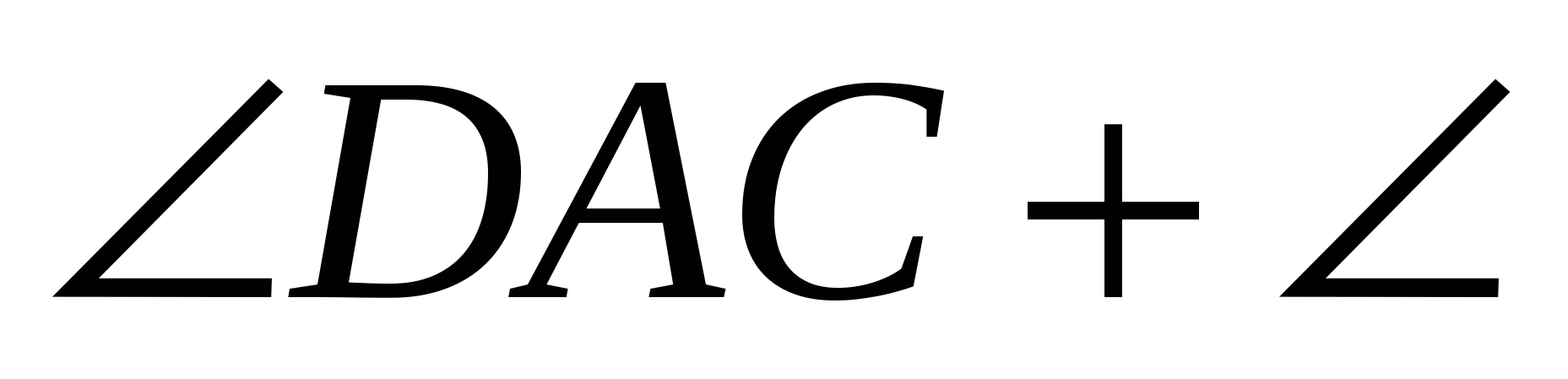 CAВ´ =
CAВ´ = 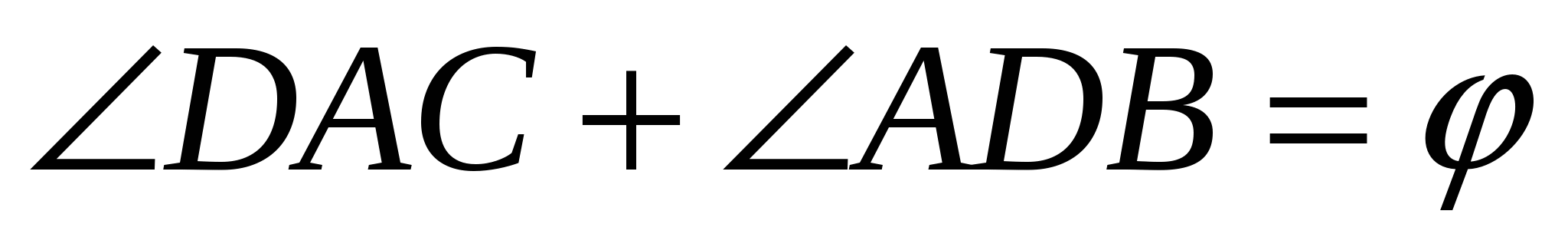
по теореме об угле между пересекающимися хордами.
Складывая площади треугольников и приравнивая результат к площади четырехугольника, получаем
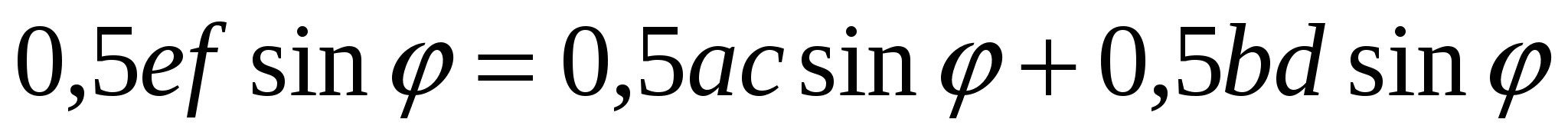 , откуда
, откуда 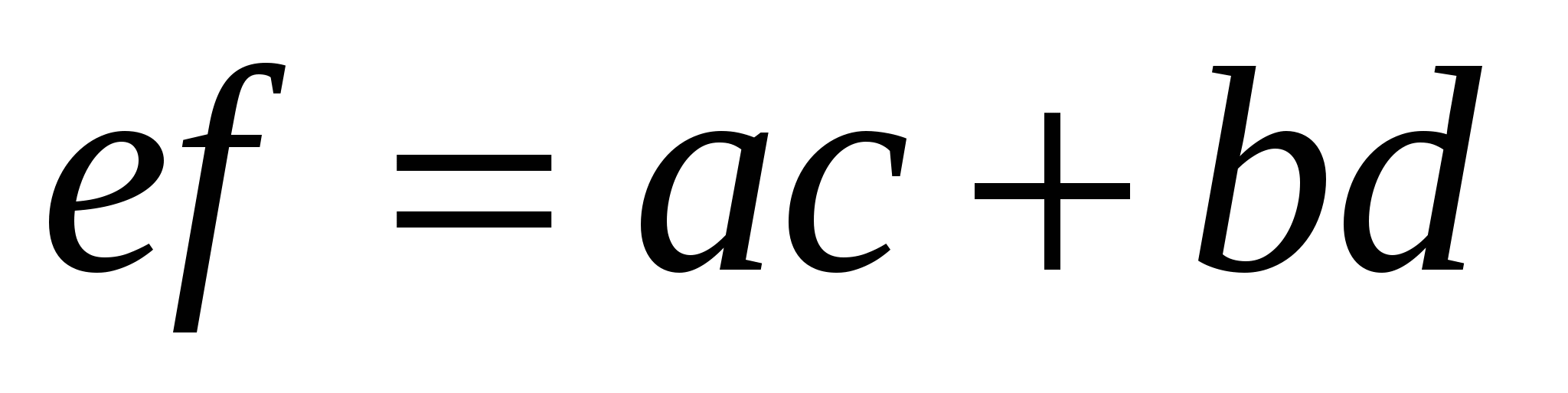 ,
,
что и требовалось доказать. ◄
Замечание. Та же идея может быть реализована по-другому. Покажем возникающие при этом нюансы.
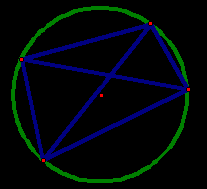
Рис. 3
Произведение диагоналей четырехугольника АВСD (рис. 3) равно площади этого четырехугольника S, деленной на 0,5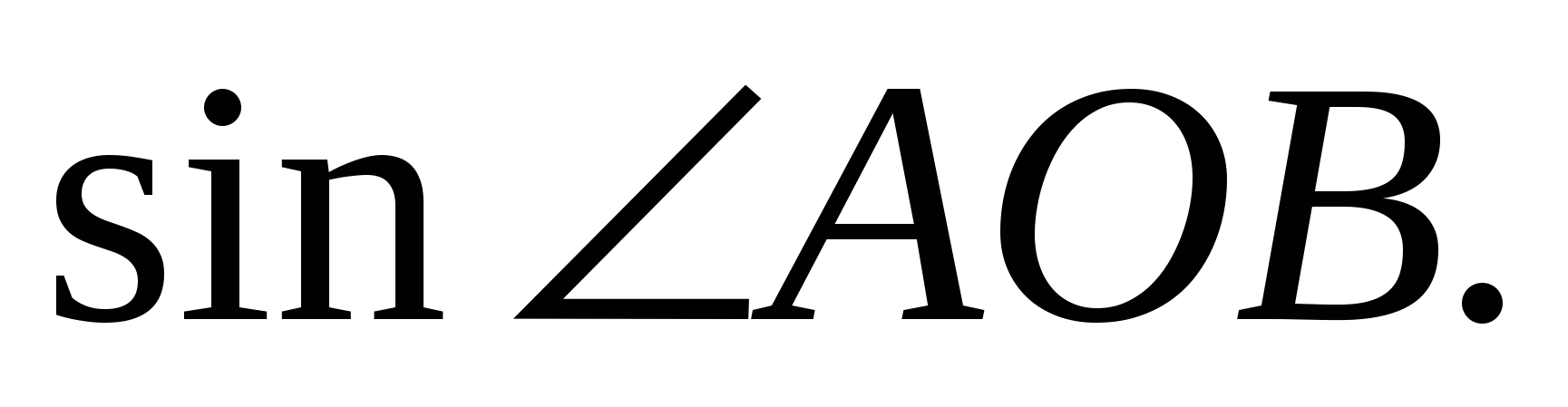
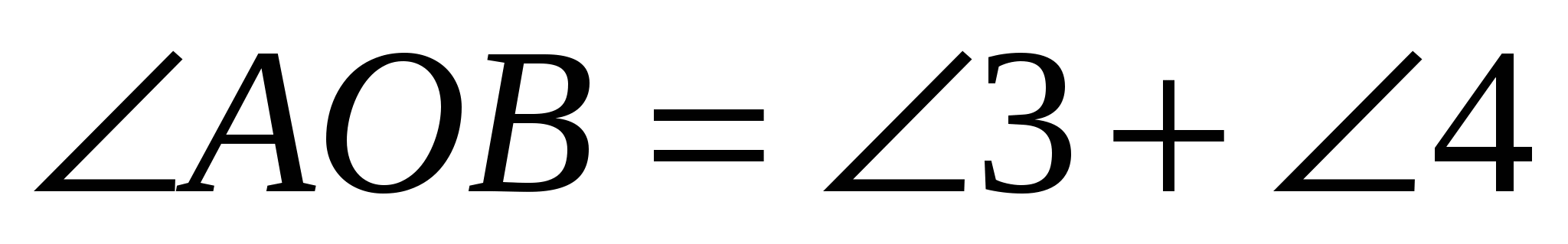 (как внешний угол треугольника ВОС).
(как внешний угол треугольника ВОС).
Остается показать, что и
АВ · DС + ВС · DА = S : 0,5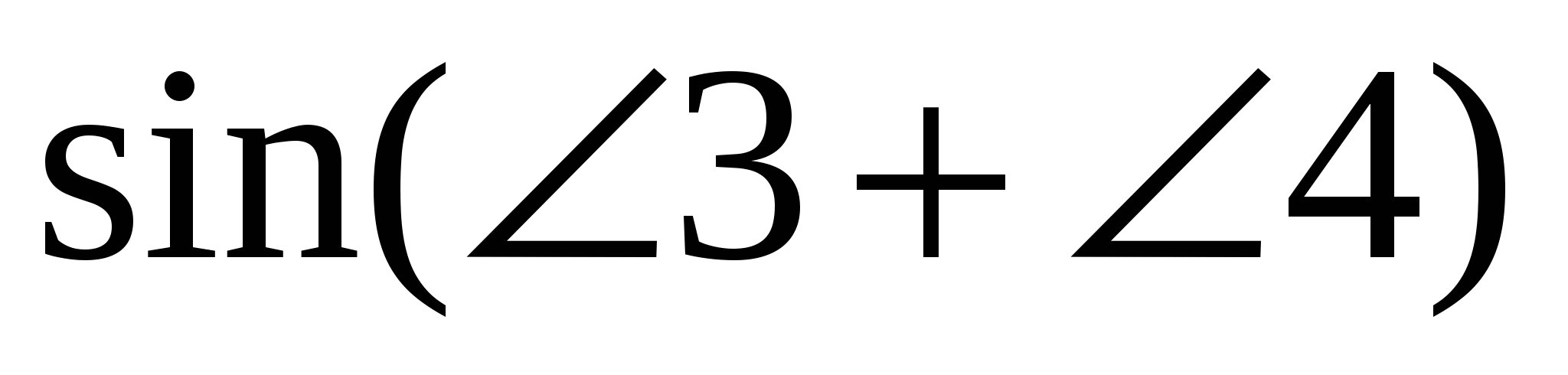 .
.
Для этого заметим, что площадь четырехугольника АВСD не изменится, если треугольник ВСD «перевернуть», поменяв местами вершины В и D (рис. 4).
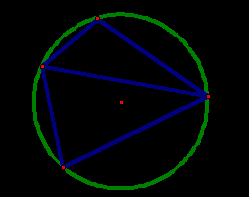
Рис. 4
Тогда 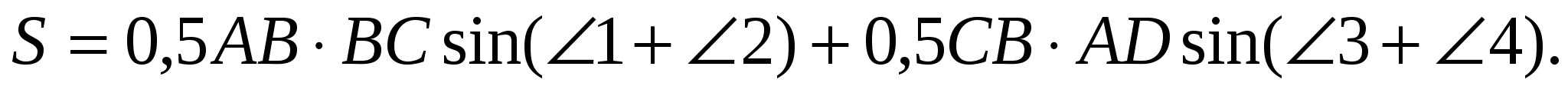
После этого учтем, что в полученном четырехугольнике сумма противоположных углов равна 180º, т. е.
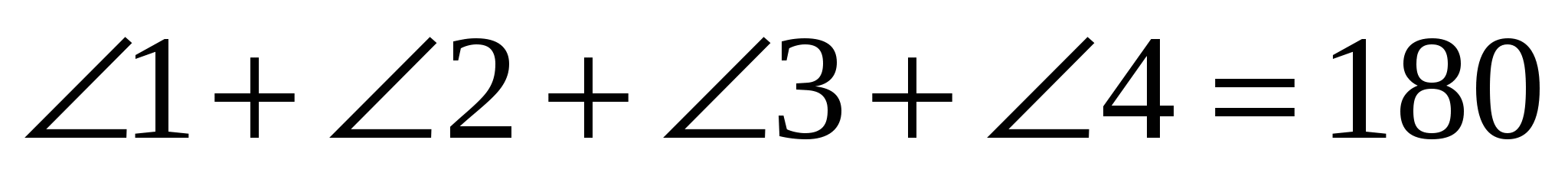 º, откуда следует,
º, откуда следует,
что 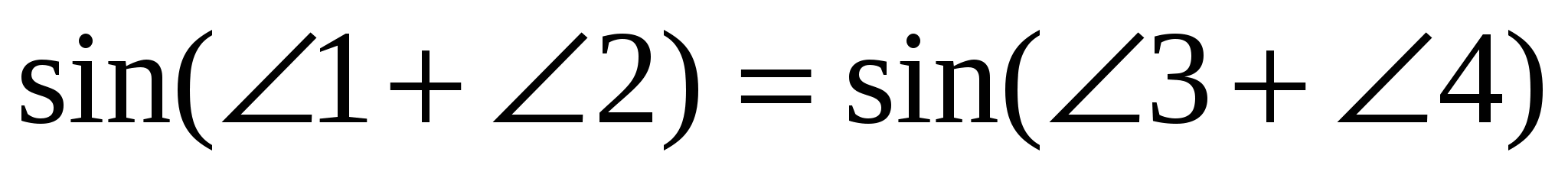 и
и
АС · DВ =АВ · DС + ВС · DА.
►►►►►Пятое доказательство. Используется прямая Симпсона.
Здесь потребуются некоторые дополнительные сведения из геометрии треугольника.
Определим такое понятие как педальный треугольник. Пусть Р - любая точка внутри треугольника АВС, и пусть перпендикуляры, опущенные из точки Р на его стороны ВС =  , СА =
, СА = 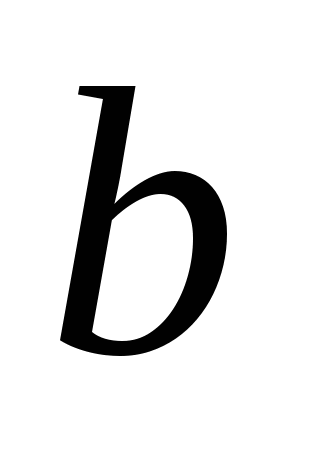 , АВ =
, АВ = 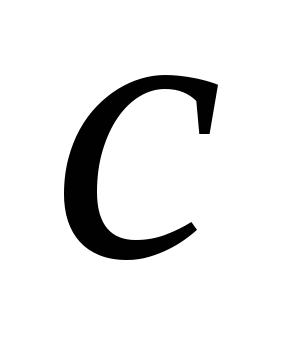 будут
будут 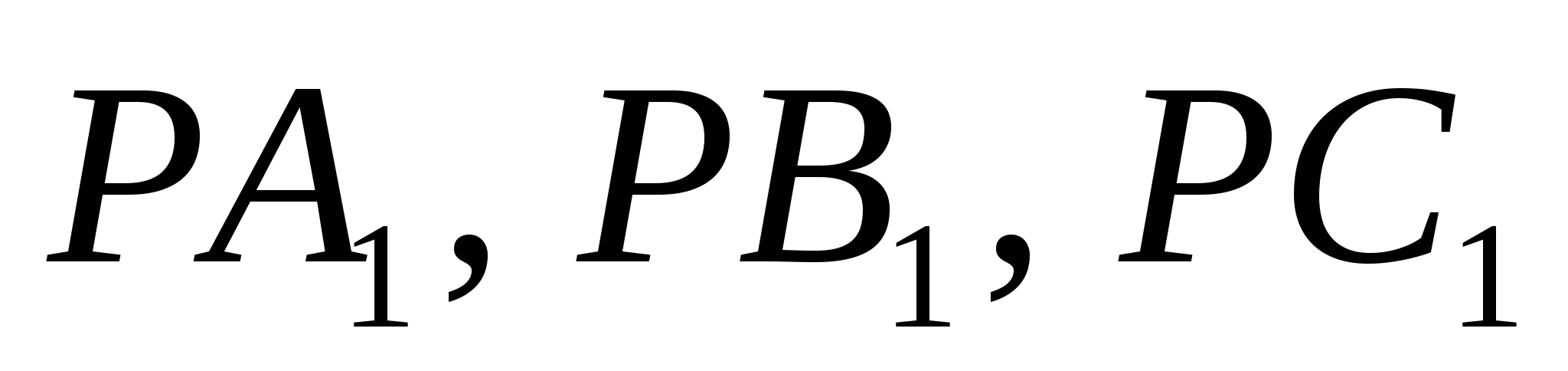 .
.
Тогда треугольник 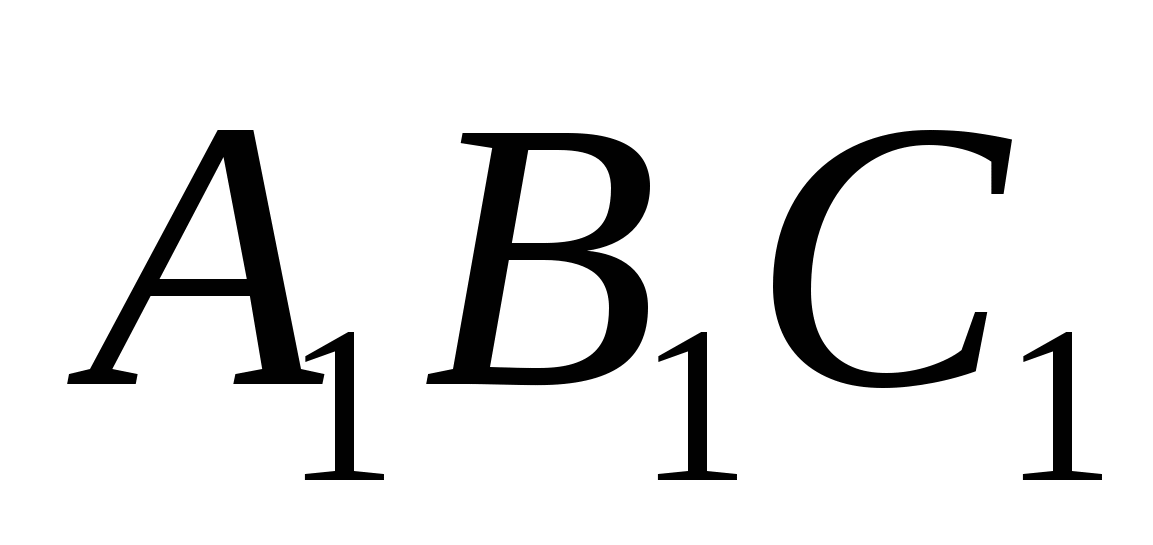 , вершинами которого являются основания этих перпендикуляров, называется педальным треугольником точки Р относительно треугольника АВС
, вершинами которого являются основания этих перпендикуляров, называется педальным треугольником точки Р относительно треугольника АВС
(например, треугольник с вершинами в точках касания вписанной окружности со сторонами данного треугольника - педальный треугольник центра вписанной окружности).
Прямые углы в точках 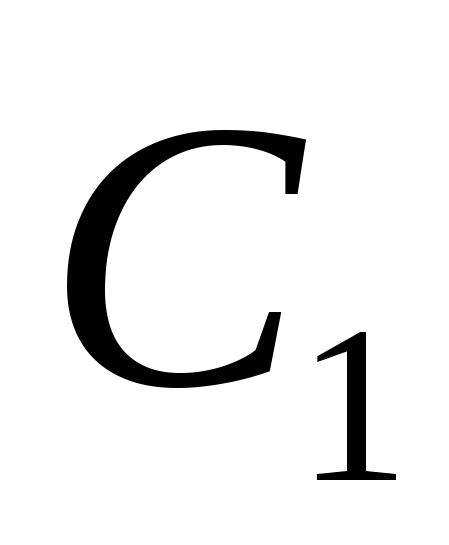 и
и 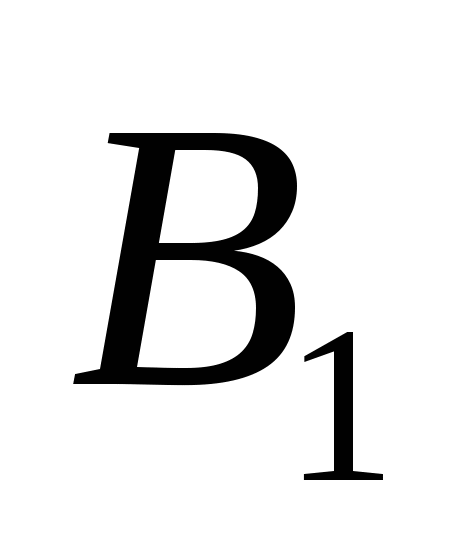 (рис. 5) указывают на то, что эти точки лежат на окружности с диаметром АР;
(рис. 5) указывают на то, что эти точки лежат на окружности с диаметром АР;
другими словами, точка Р лежит на окружности, описанной вокруг треугольника 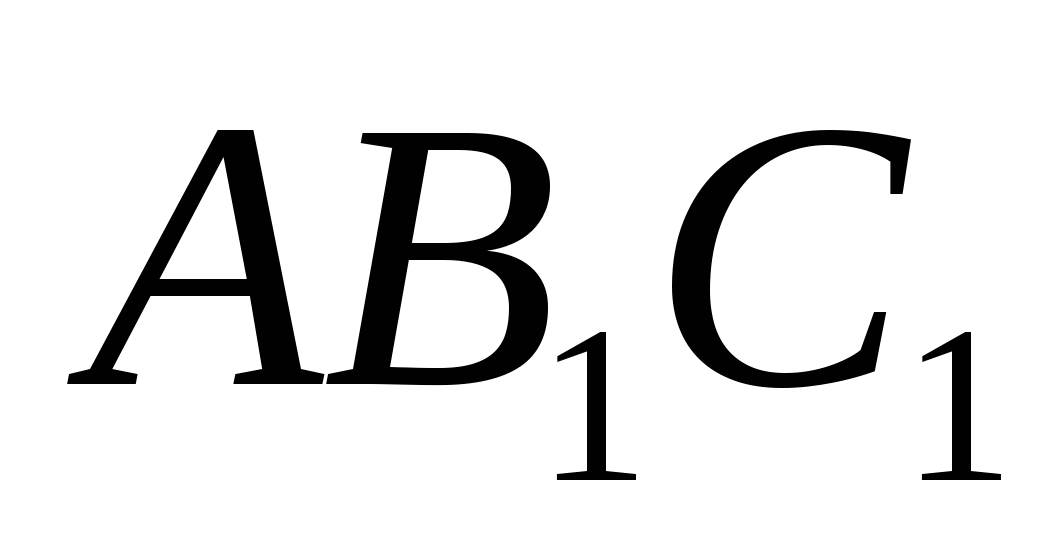 .
.
Применяя теорему синусов к этому треугольнику, а также к самому треугольнику АВС, получим
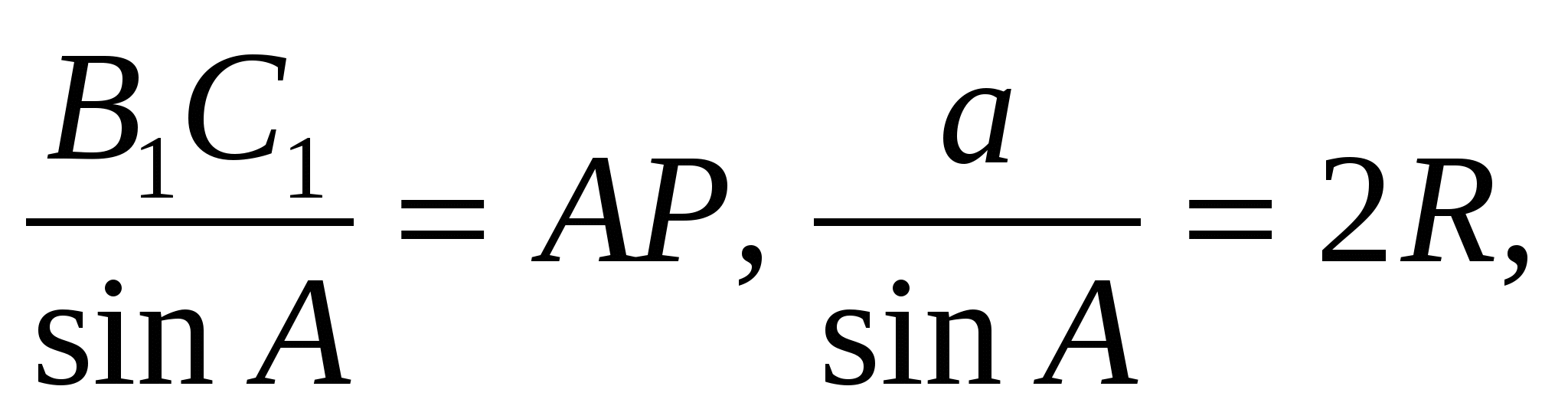
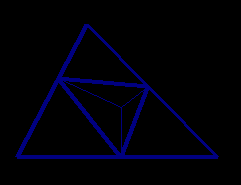
Рис. 5
откуда 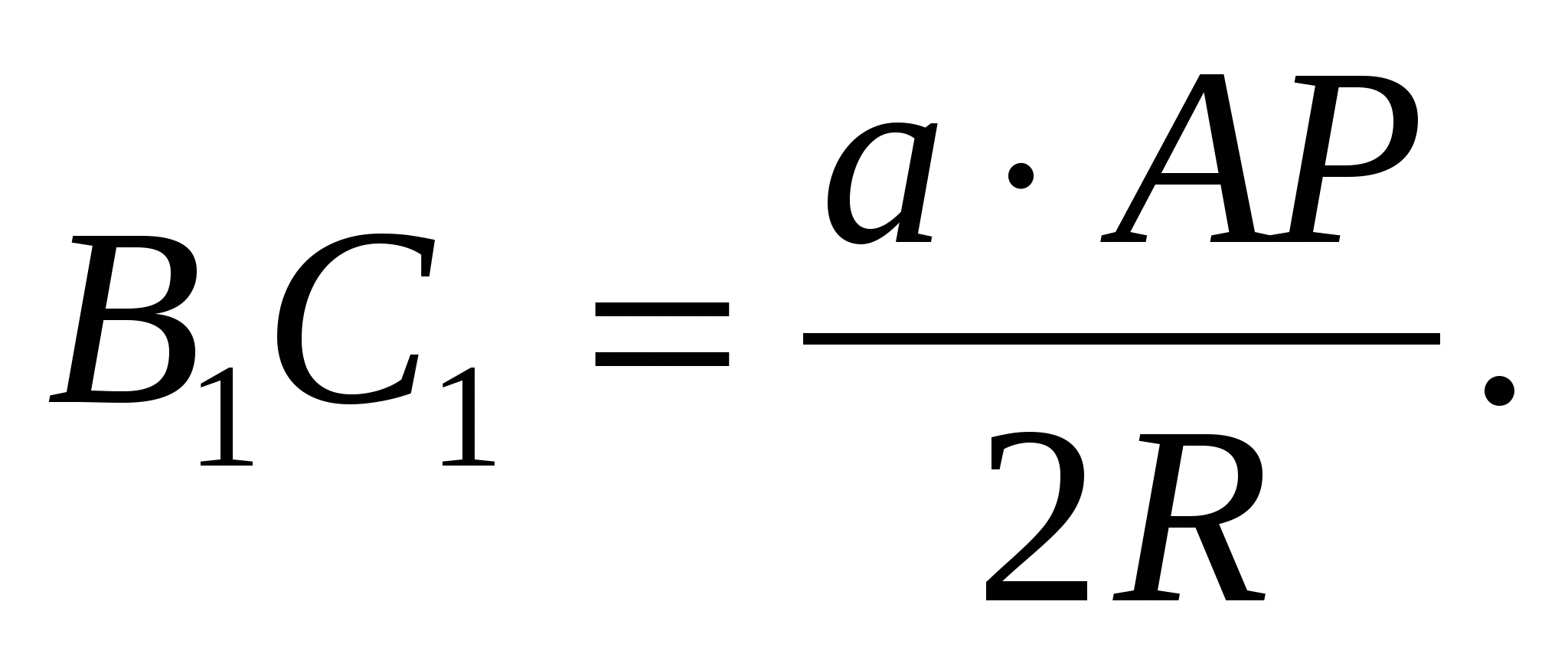 Аналогично,
Аналогично, 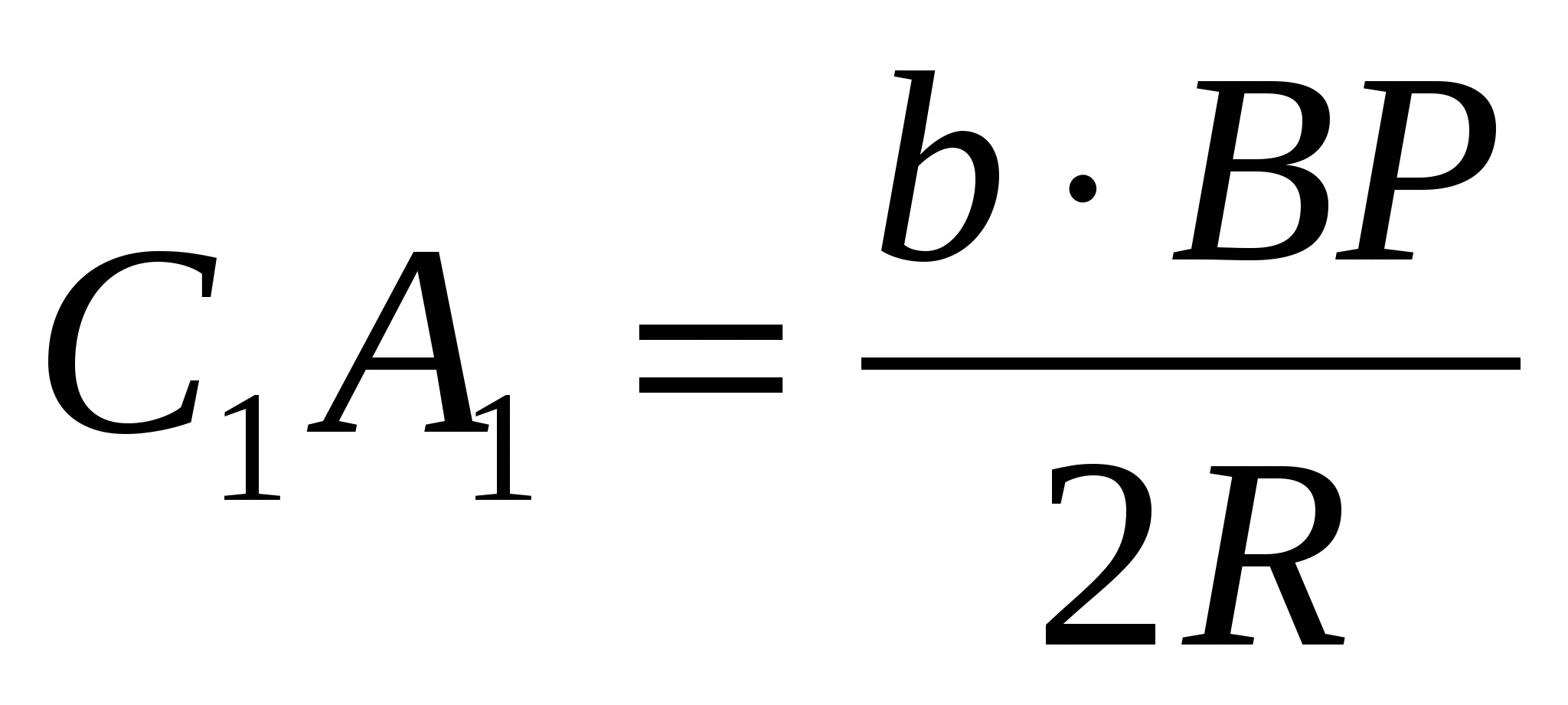 и
и 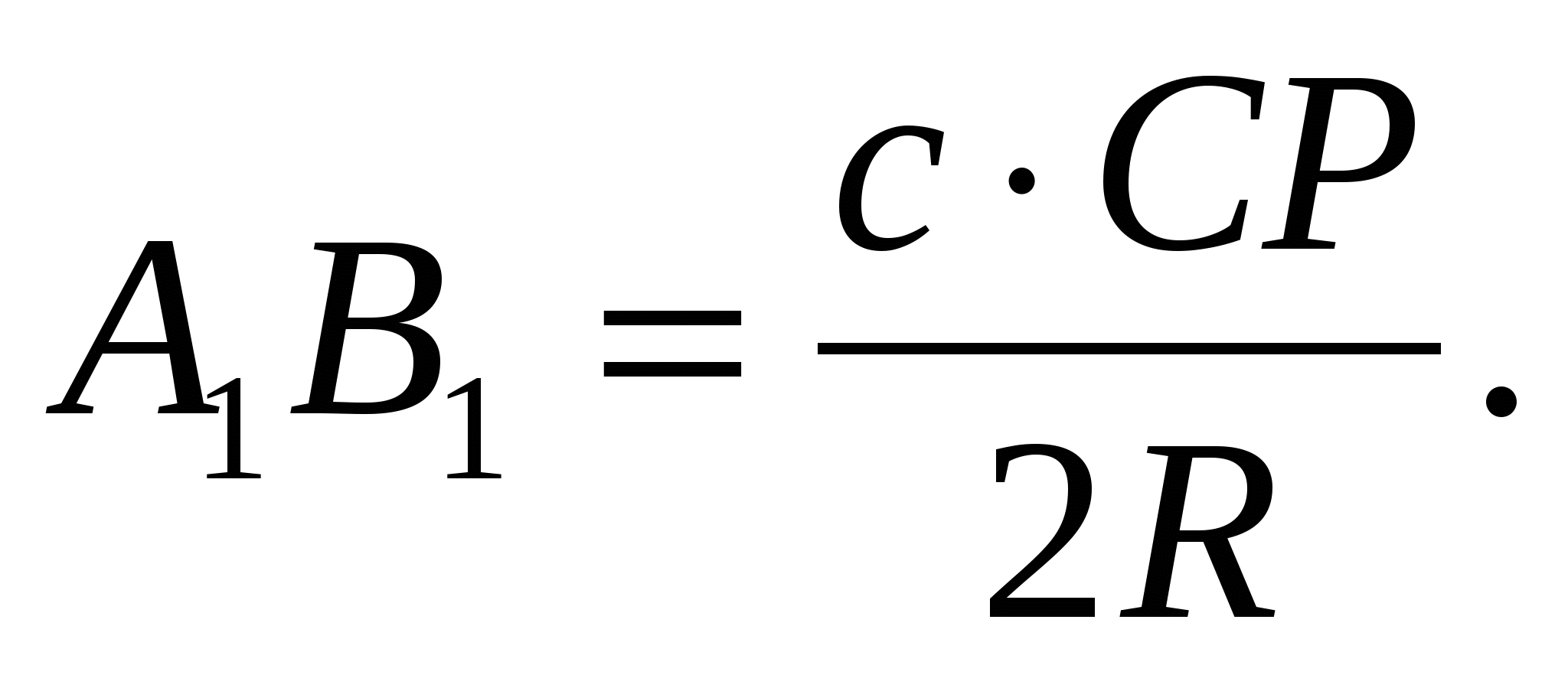
Таким образом, если расстояния от педальной точки до вершин треугольника АВС равны 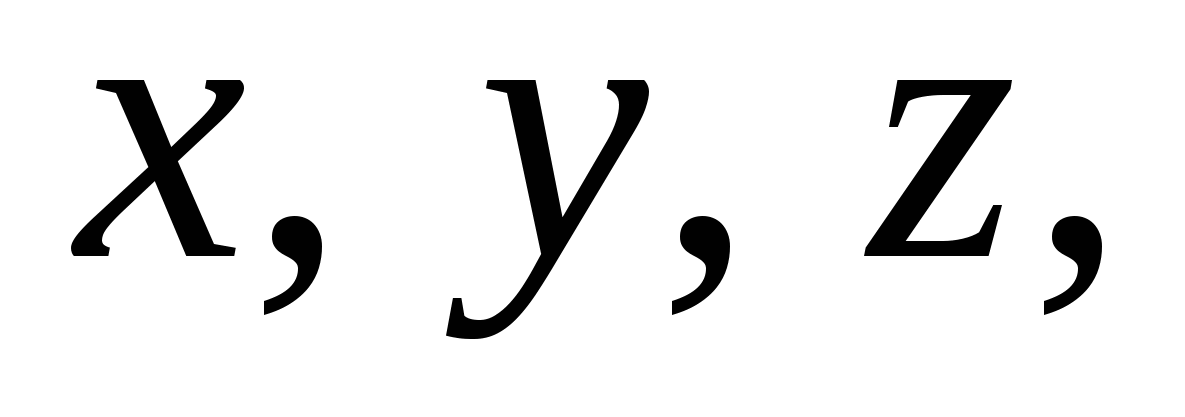 то длины сторон педального треугольника равны соответственно
то длины сторон педального треугольника равны соответственно
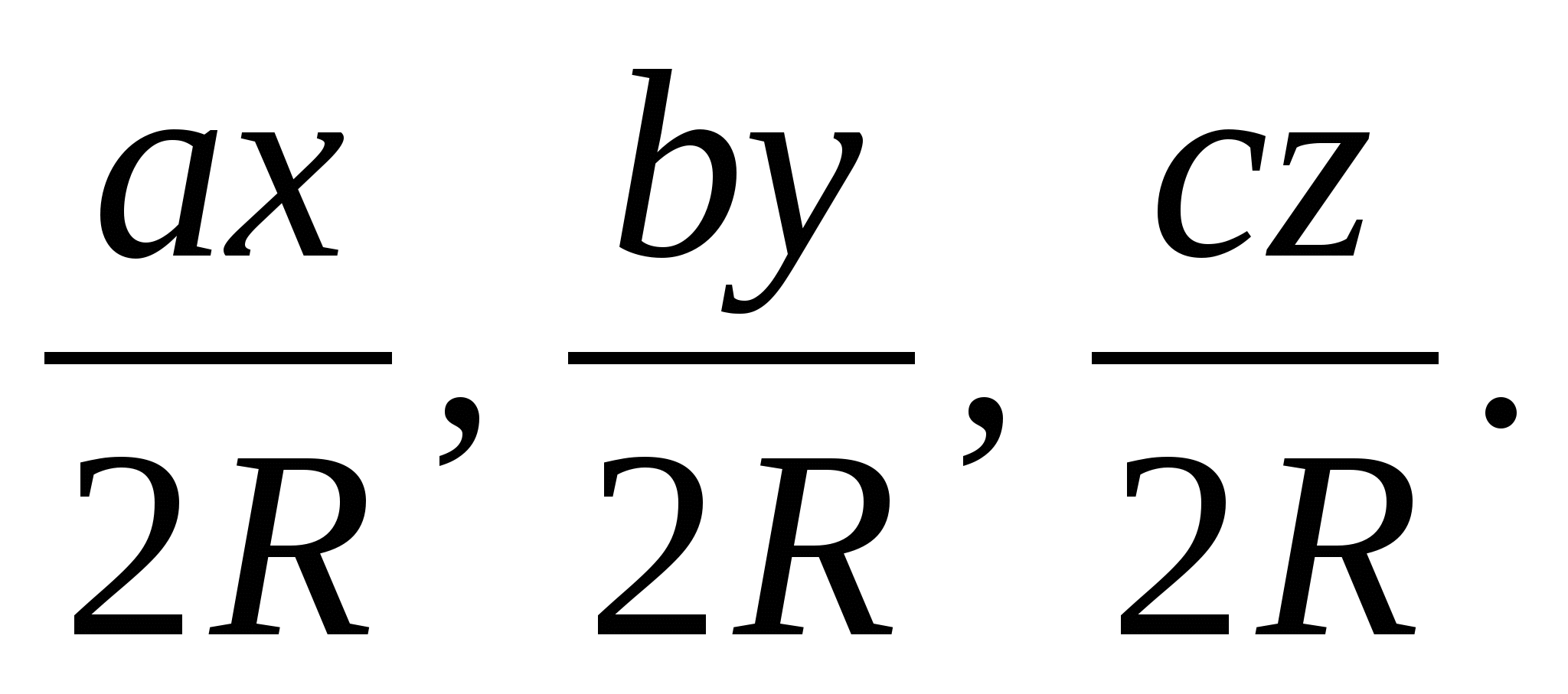
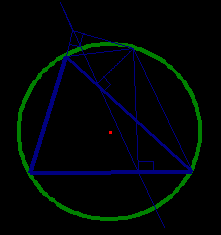
Рис. 6
Теперь рассмотрим тот особый случай, когда точка Р лежит на описанной окружности вокруг треугольника АВС (рис. 6).
Тогда педальный треугольник 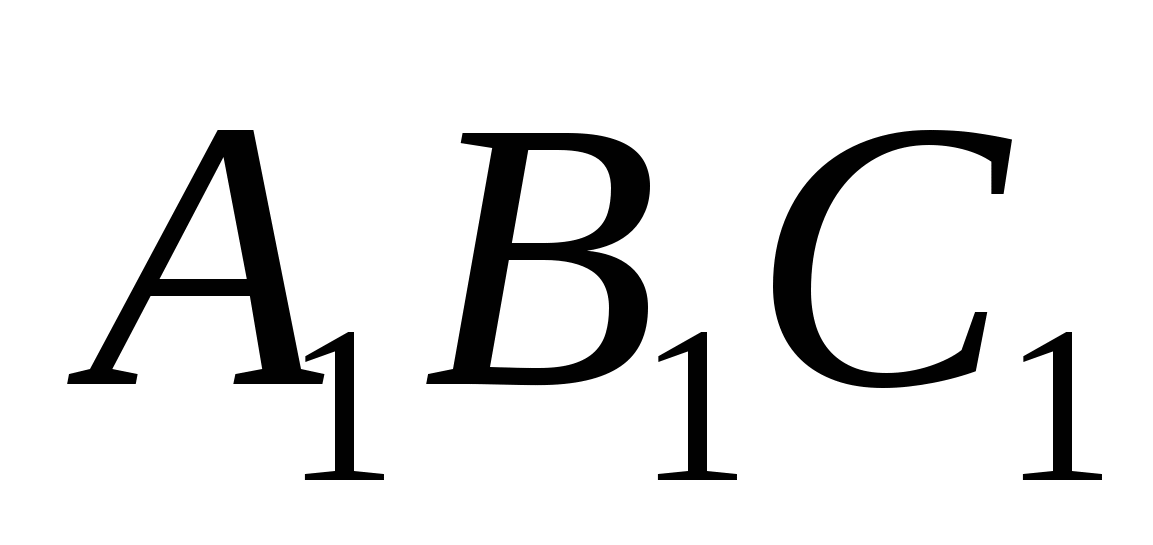 «вырождается» в прямую, называемую прямой Симпсона.
«вырождается» в прямую, называемую прямой Симпсона.
Хотя «педальный треугольник» 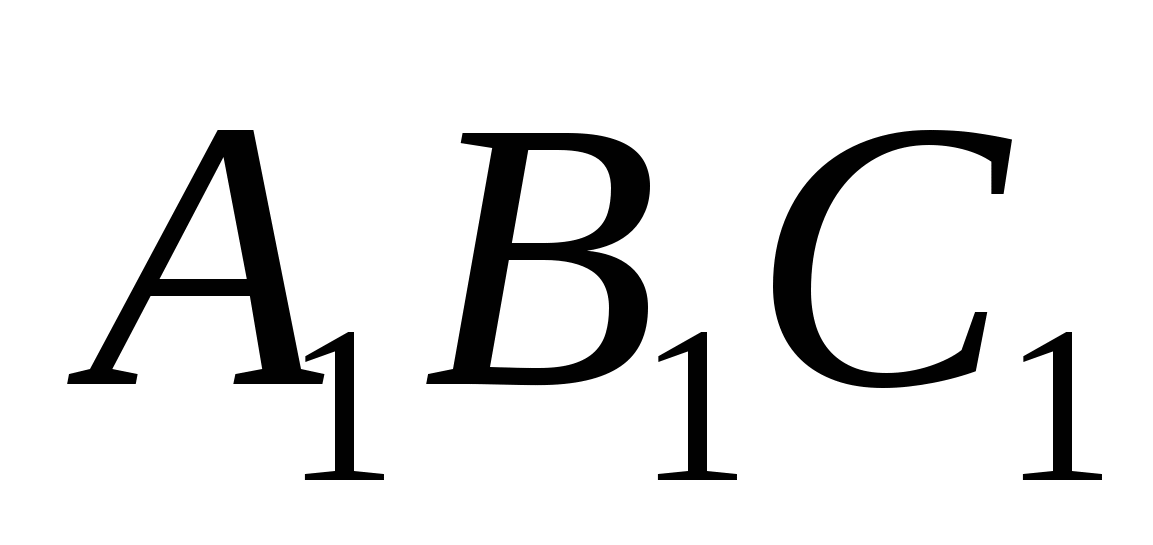 вырожден, длины его «сторон» все еще могут быть вычислены с помощью формул:
вырожден, длины его «сторон» все еще могут быть вычислены с помощью формул:
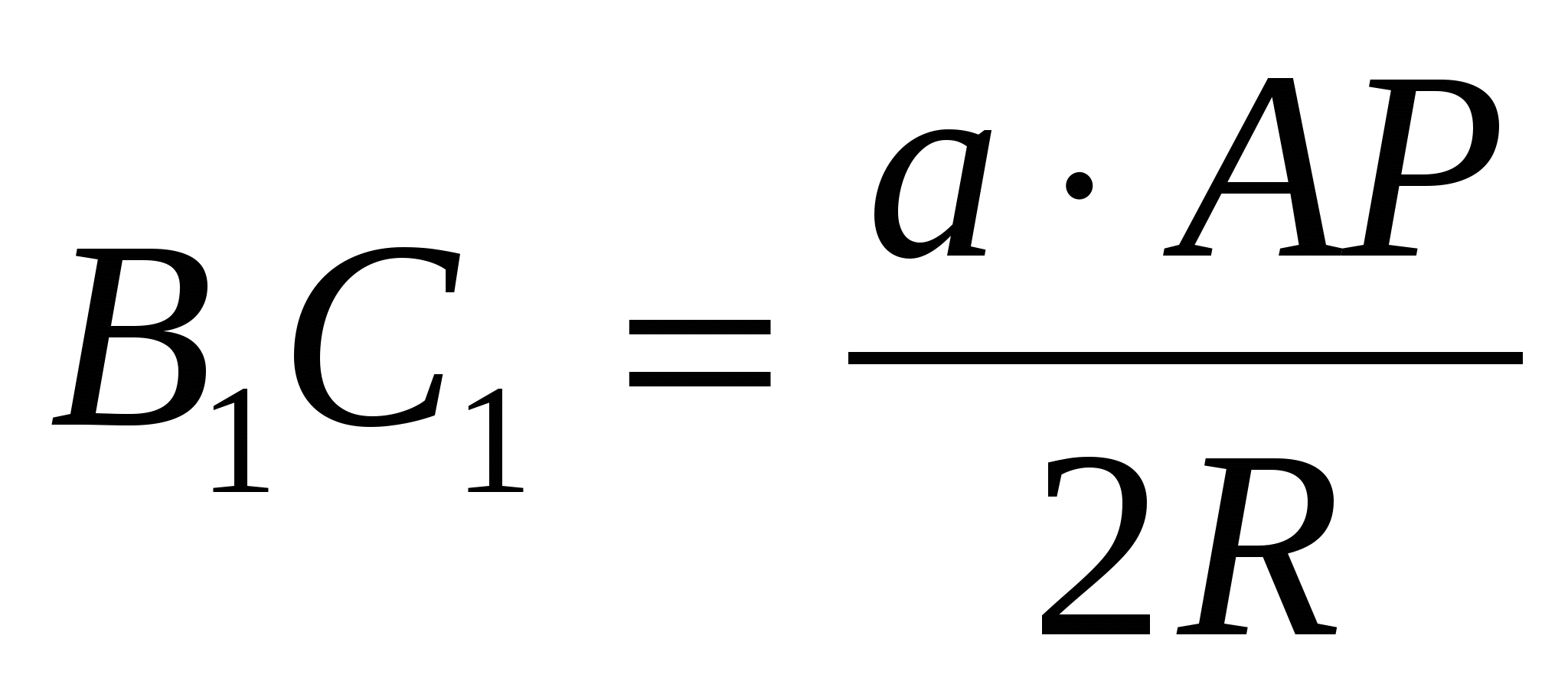 ,
, 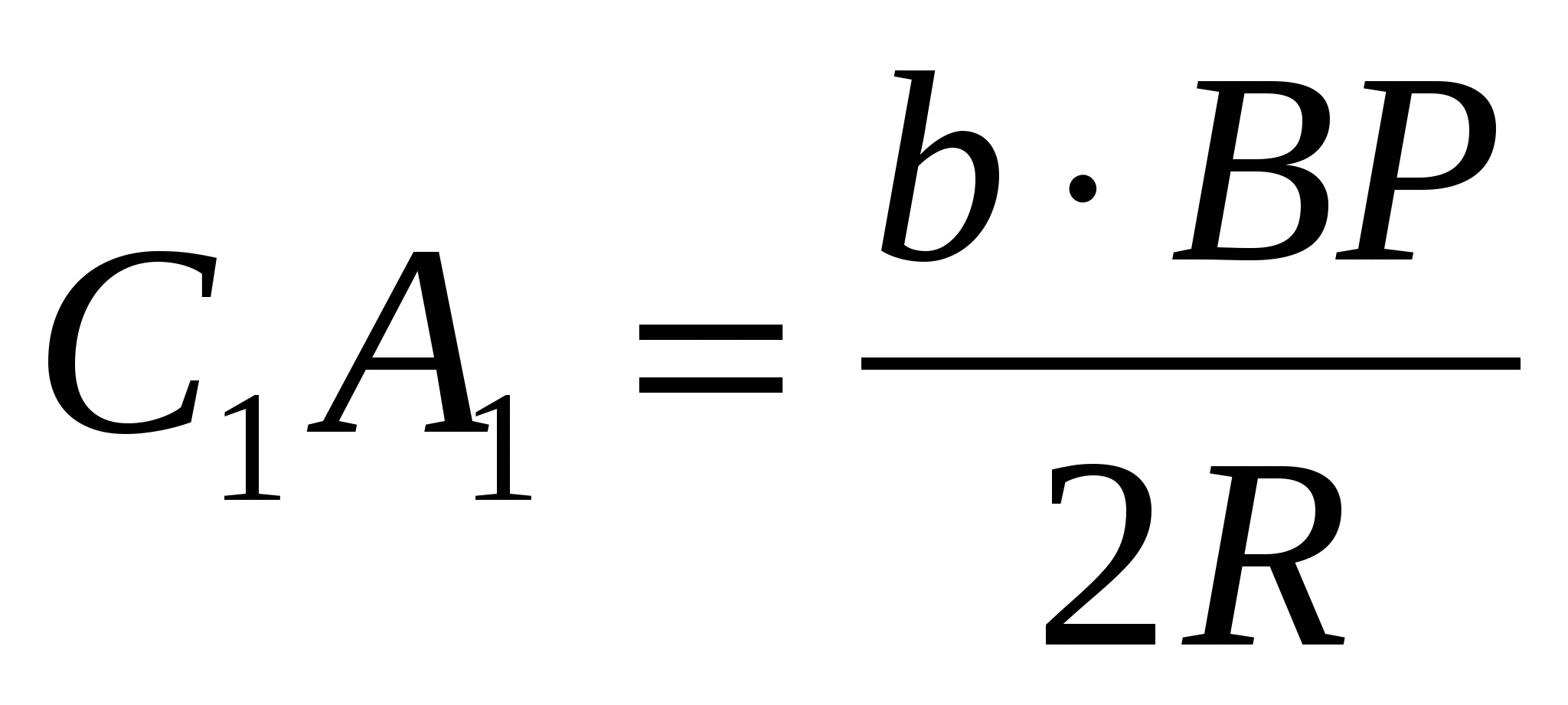 ,
, 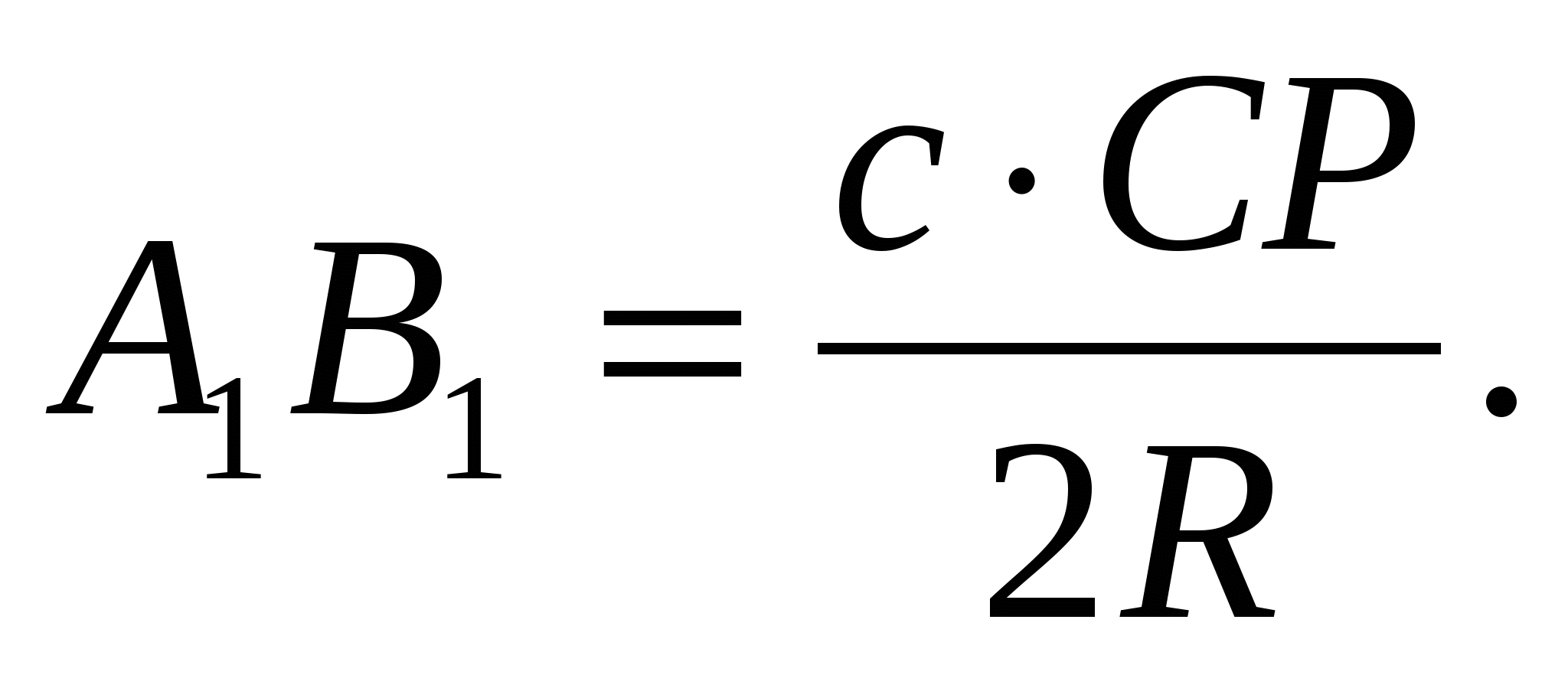
Так как 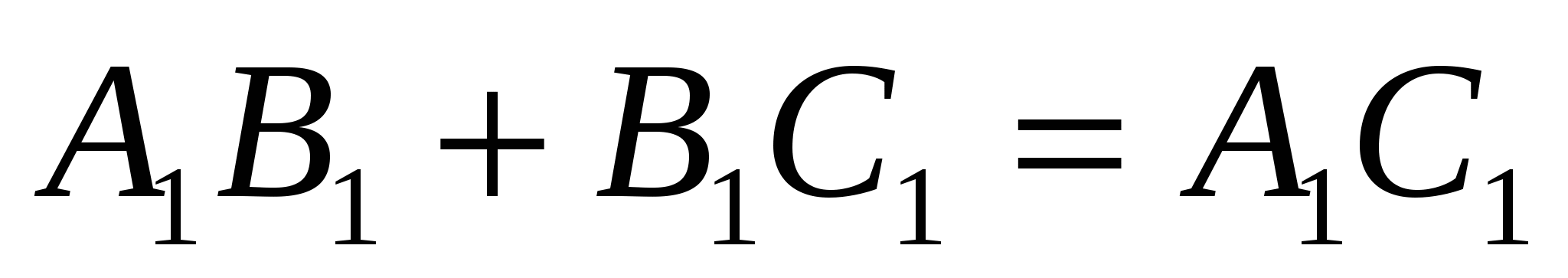 , то
, то 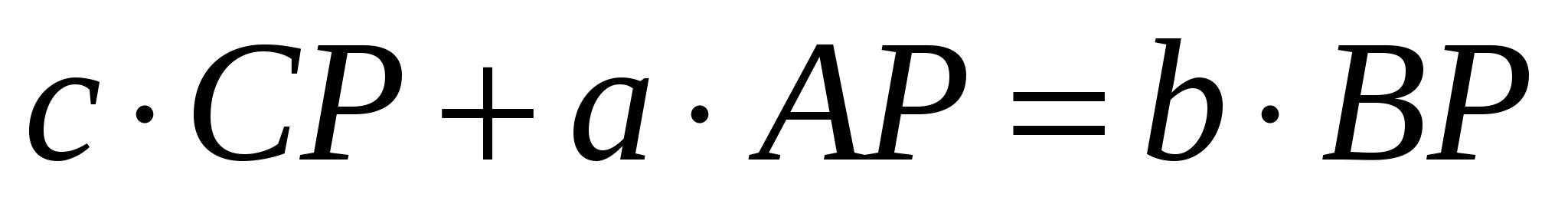 , т. е.
, т. е.
АВ · СР + ВС · АР = АС · ВР.
Так как АВСР - вписанный четырехугольник, то таким образом мы доказали теорему Птолемея. ◄
►►►►►►Шестое доказательство. Используется преобразование, которое называется инверсией.
Рис. 7
Пусть задана некоторая окружность S с центром О и радиусом r (рис. 7).
Каждой точке Х, отличной от точки О, поставим в соответствие точку Х´ на луче ОХ, такую, что ОХ´·ОХ = 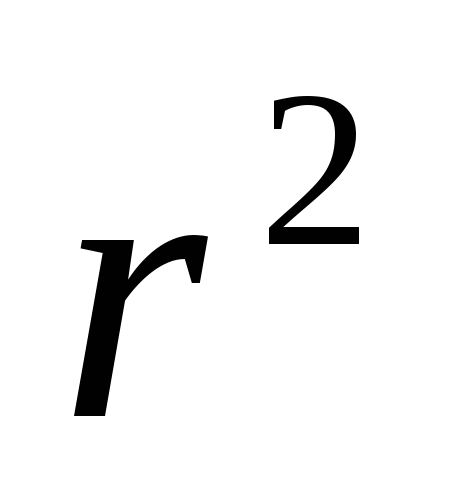 .
.
Это преобразование и называется инверсией относительно окружности S.
Лемма (об инверсии). Пусть А´ и В´ − образы точек А и В при инверсии с центром О и радиусом r.
Тогда треугольники ОАВ и ОВ´А´ подобны и 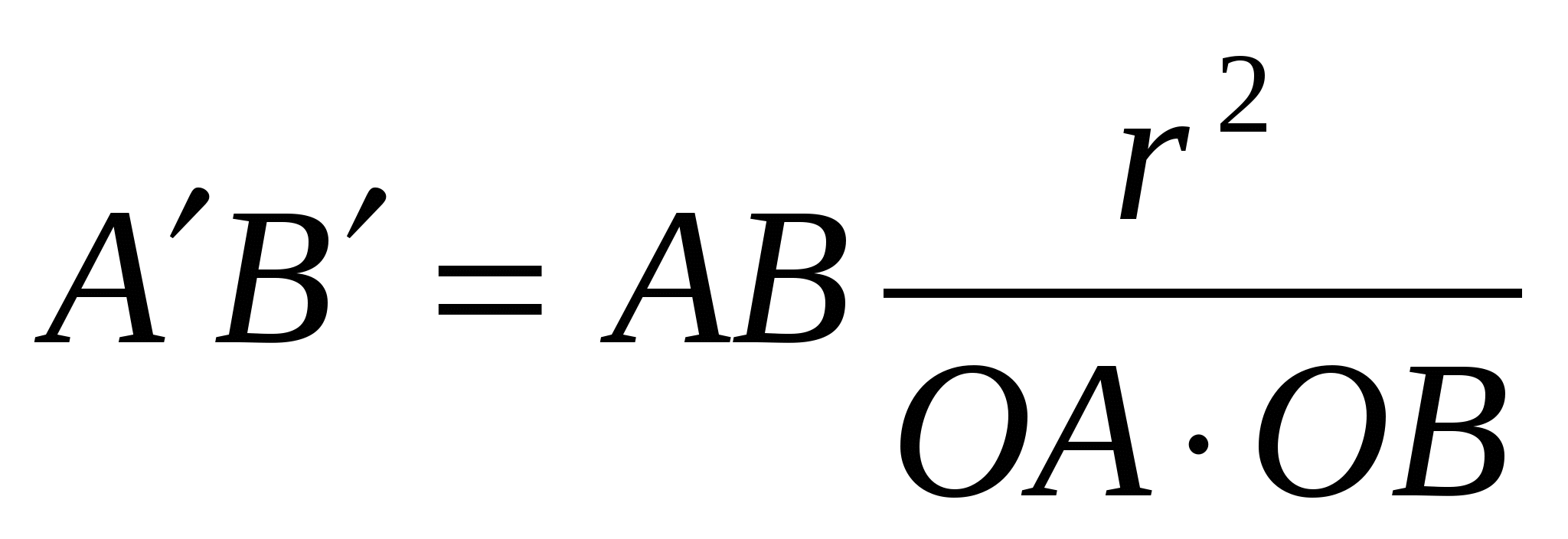 (рис.8).
(рис.8).
Приведем рассуждения, доказывающие утверждение леммы.
По определению инверсии выполняются равенства 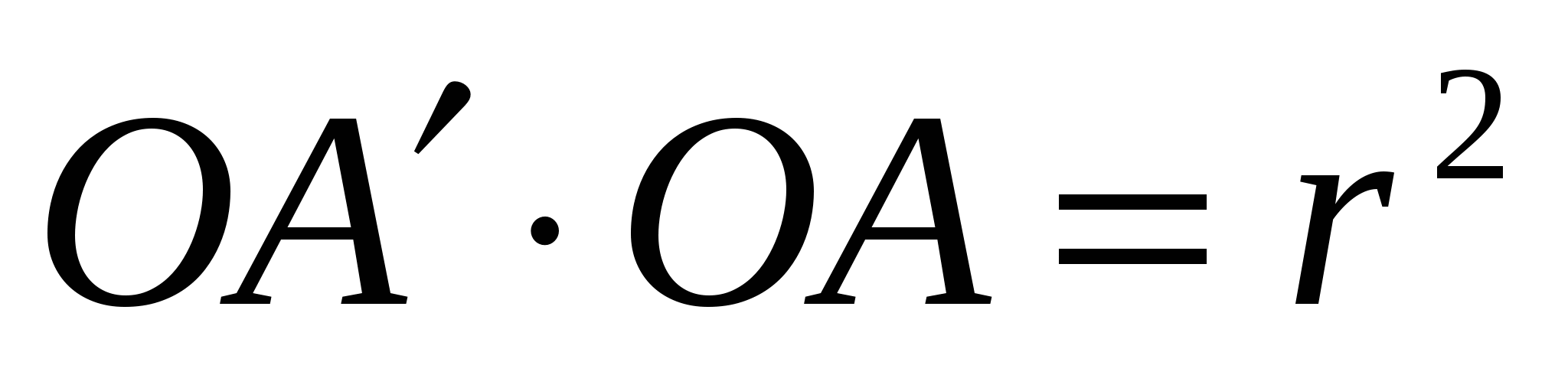 ,
, 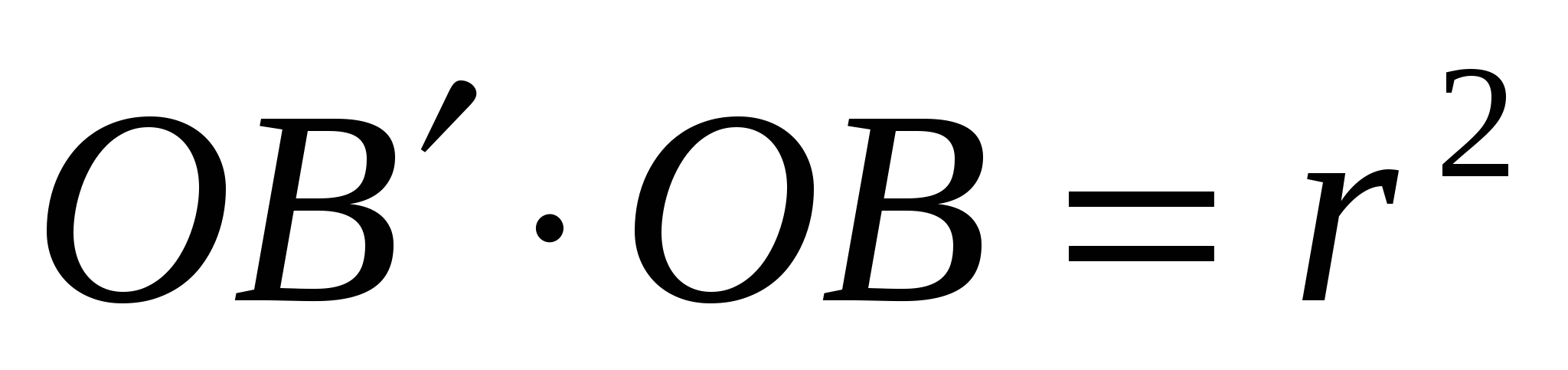 .
.
Следовательно, 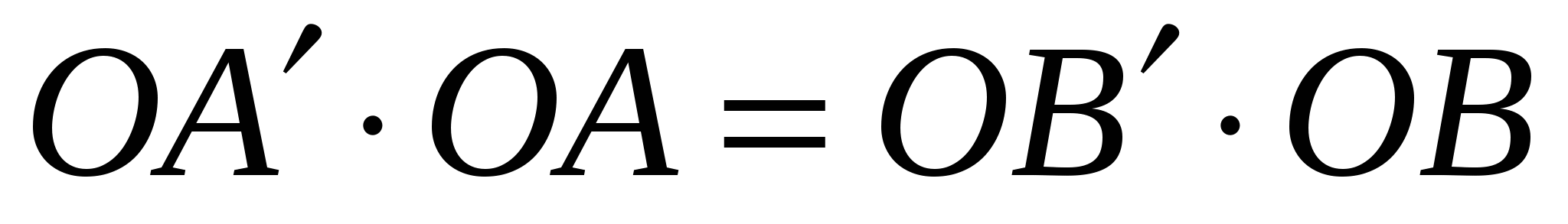 , и поэтому
, и поэтому 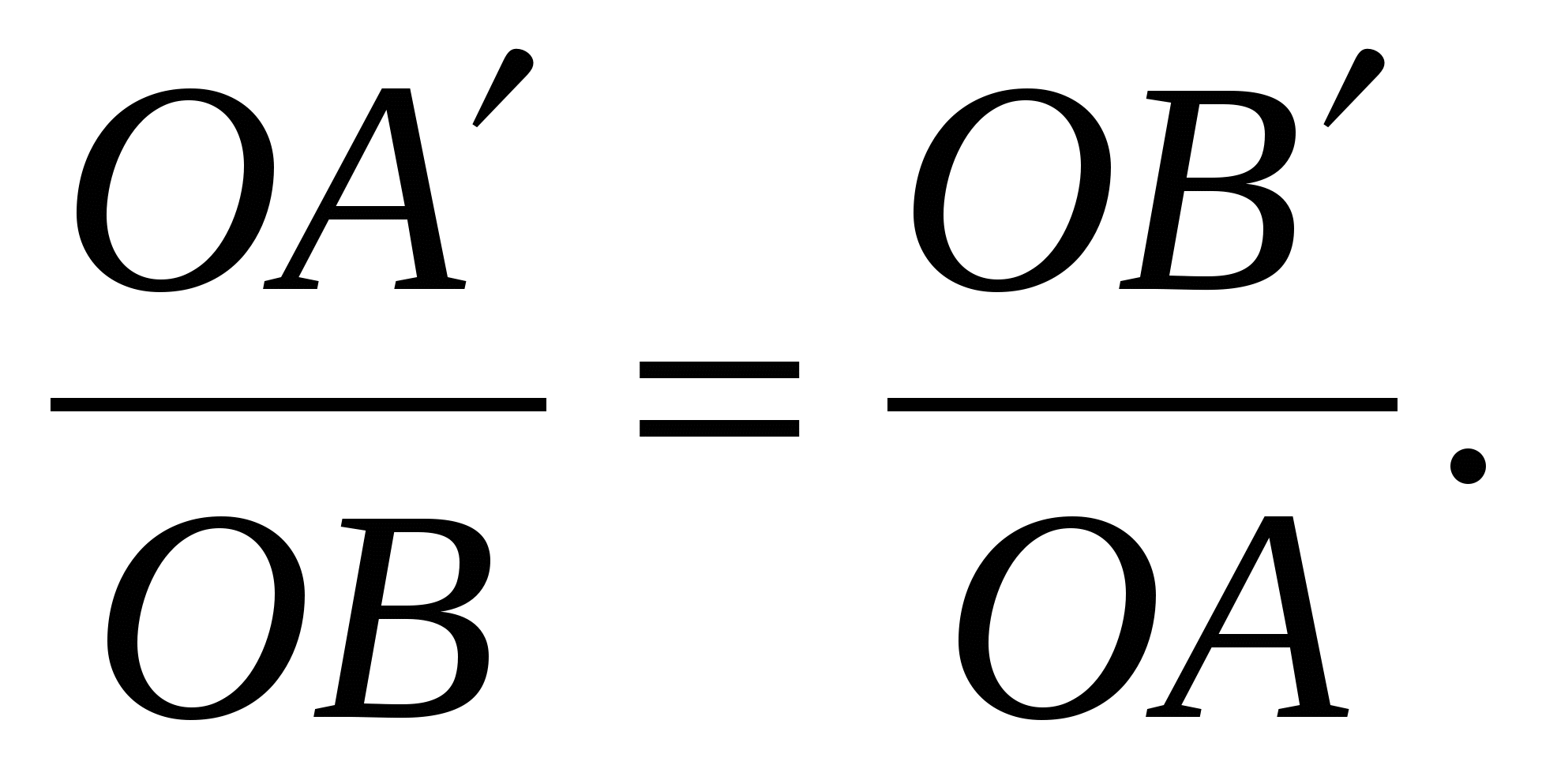

Рис. 8
Значит, треугольники ОАВ и ОВ´А´ подобны (имеют общий угол при вершине О и их стороны, идущие от этой вершины, пропорциональны).
При этом вершине А соответствует вершина В´, а вершине В - вершина А´.
Но тогда и 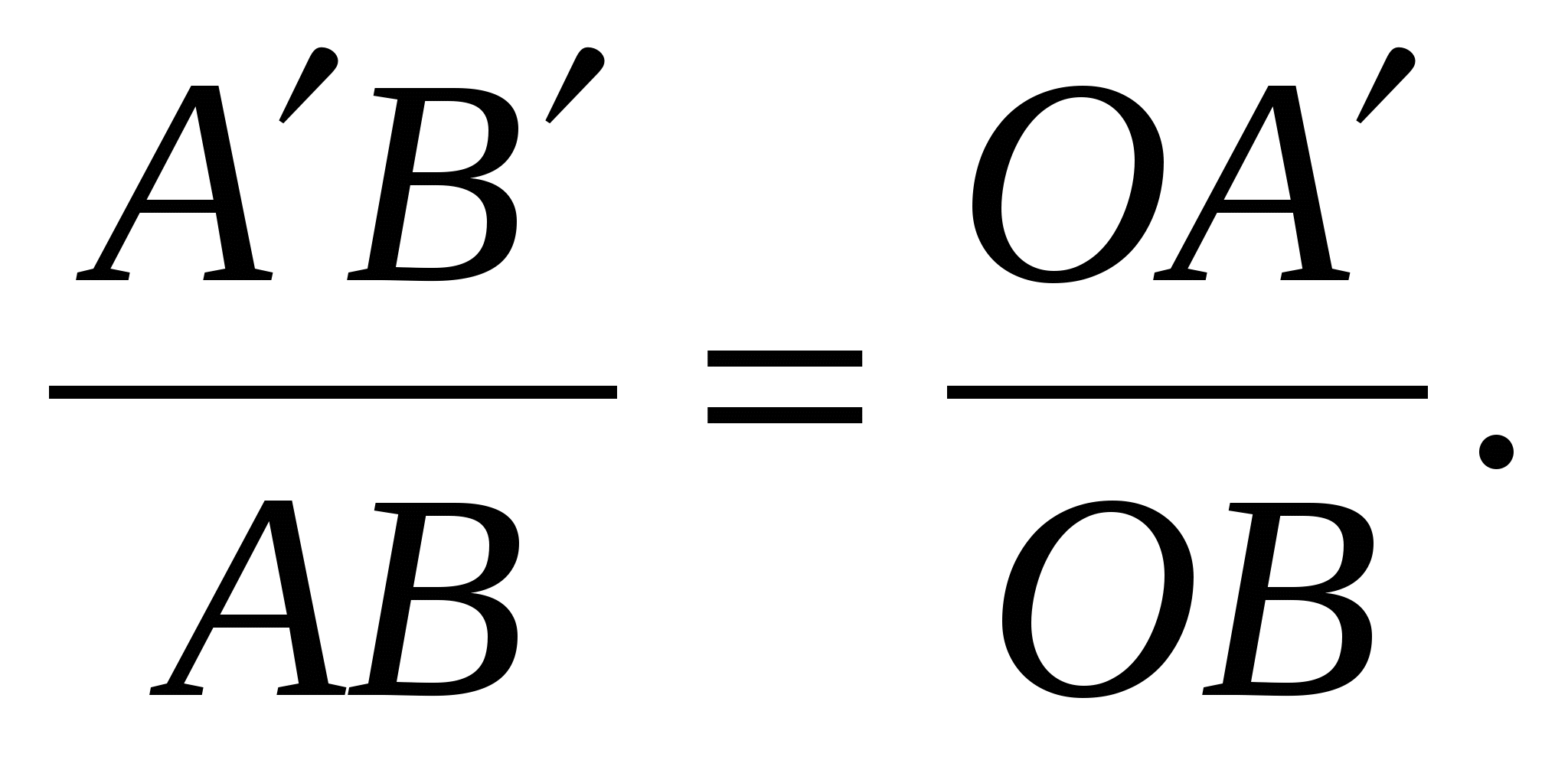
Из этого равенства имеем: 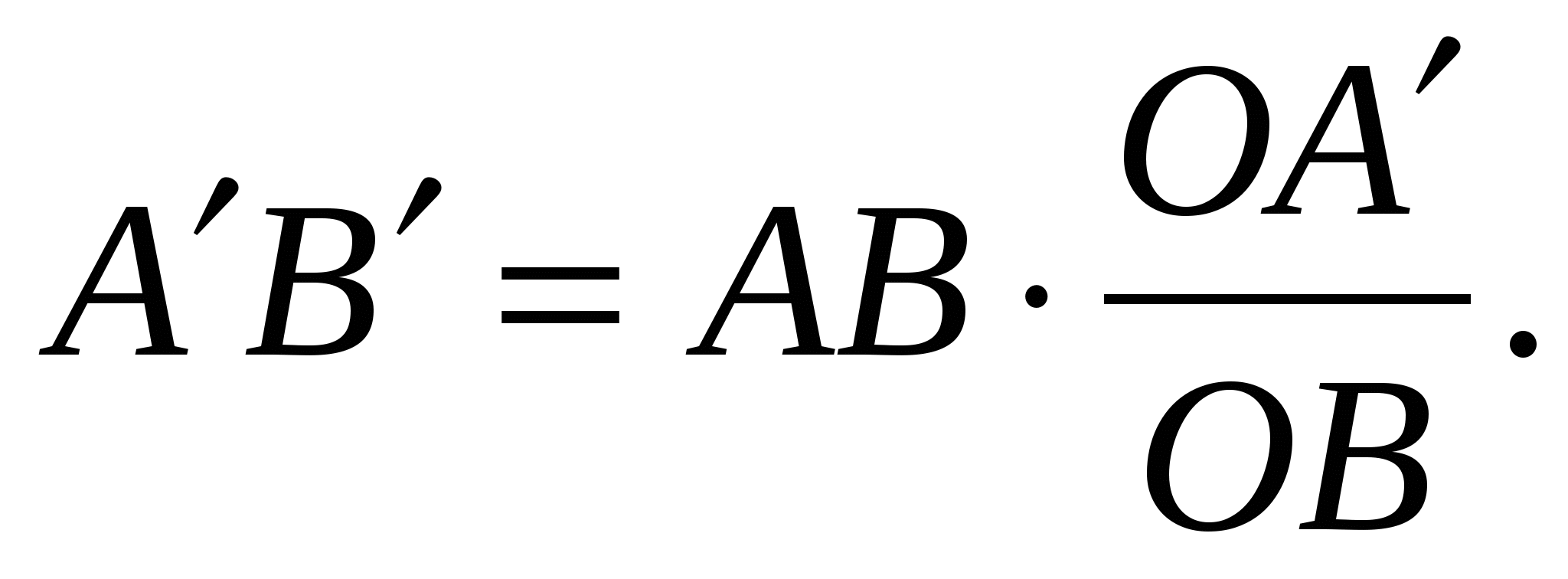
Подставляя сюда выражение из определения 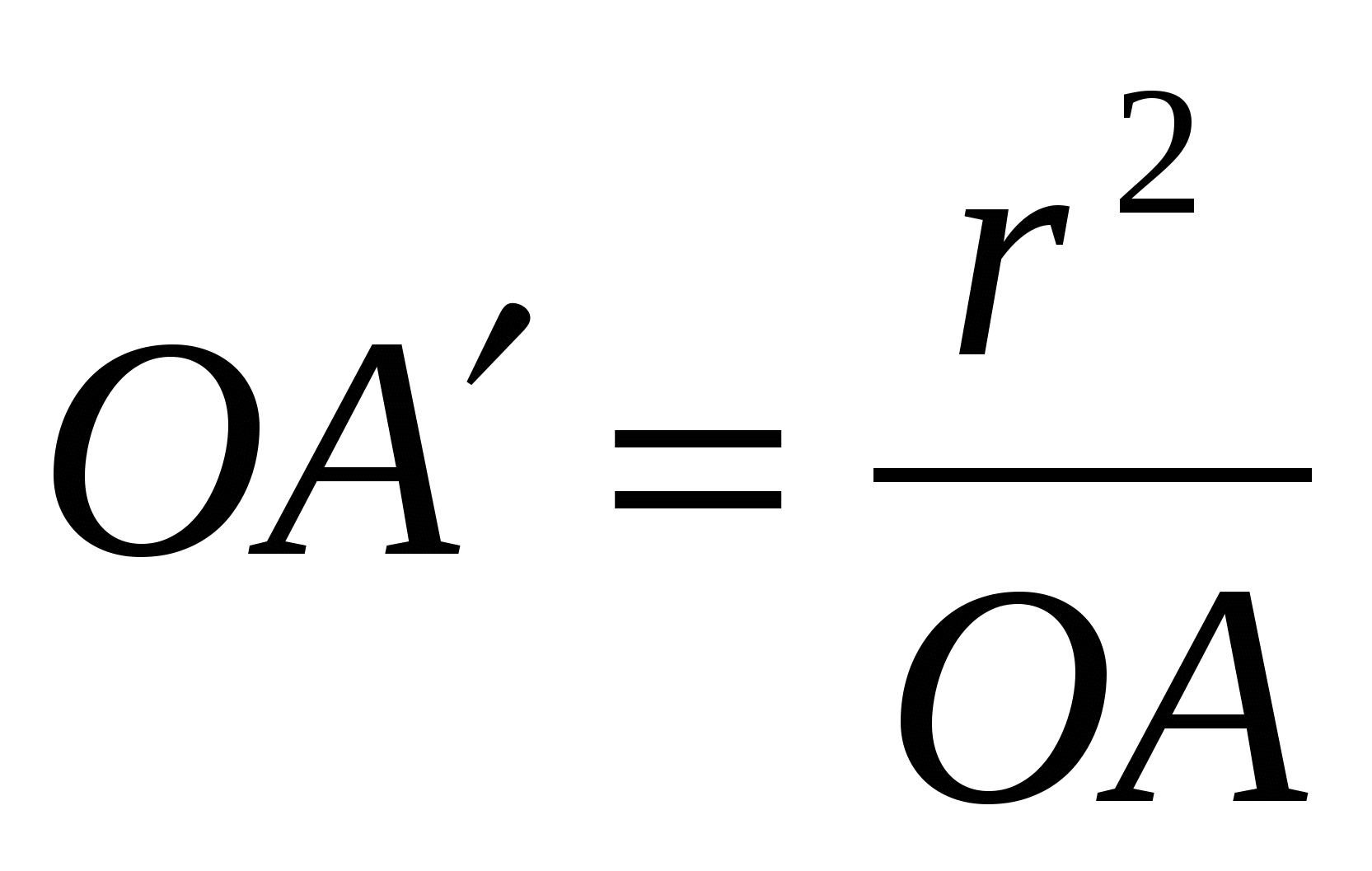 , получаем
, получаем 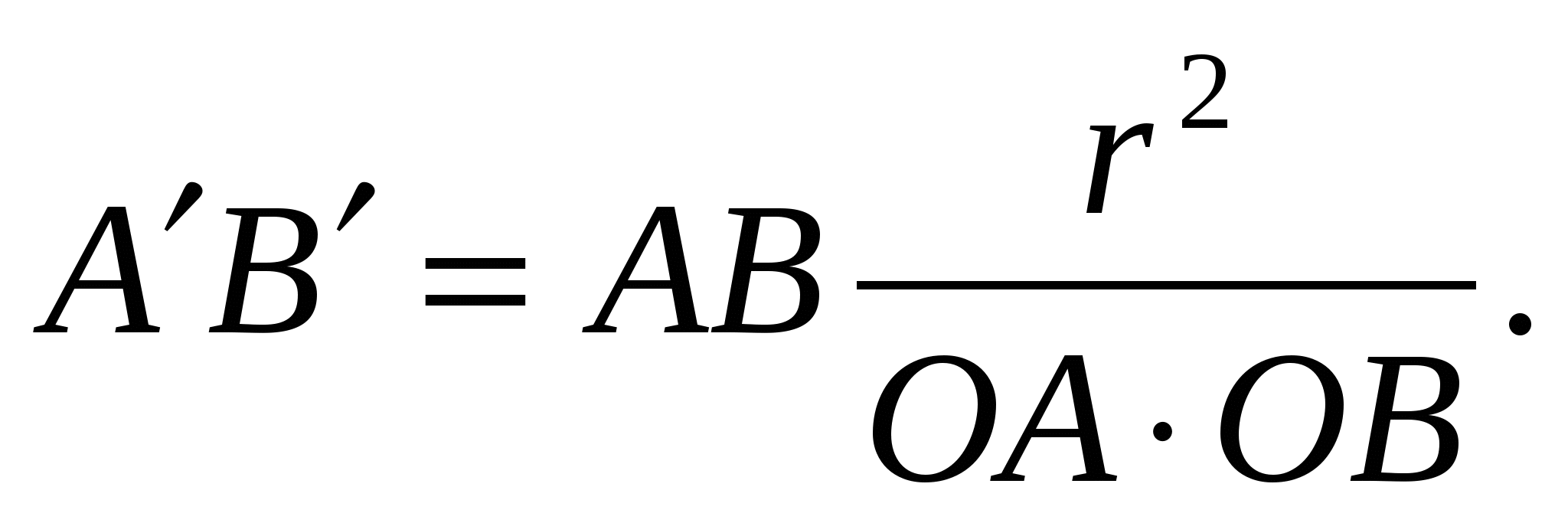 Лемма доказана.
Лемма доказана.
Итак, пусть четырехугольник АВСD вписан в окружность S (рис. 9).
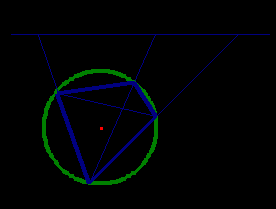
Рис. 9
По теореме об инверсии эту окружность инверсия I с центром в точке D (и любым радиусом) переведет в прямую p, не проходящую через точку D.
Точки 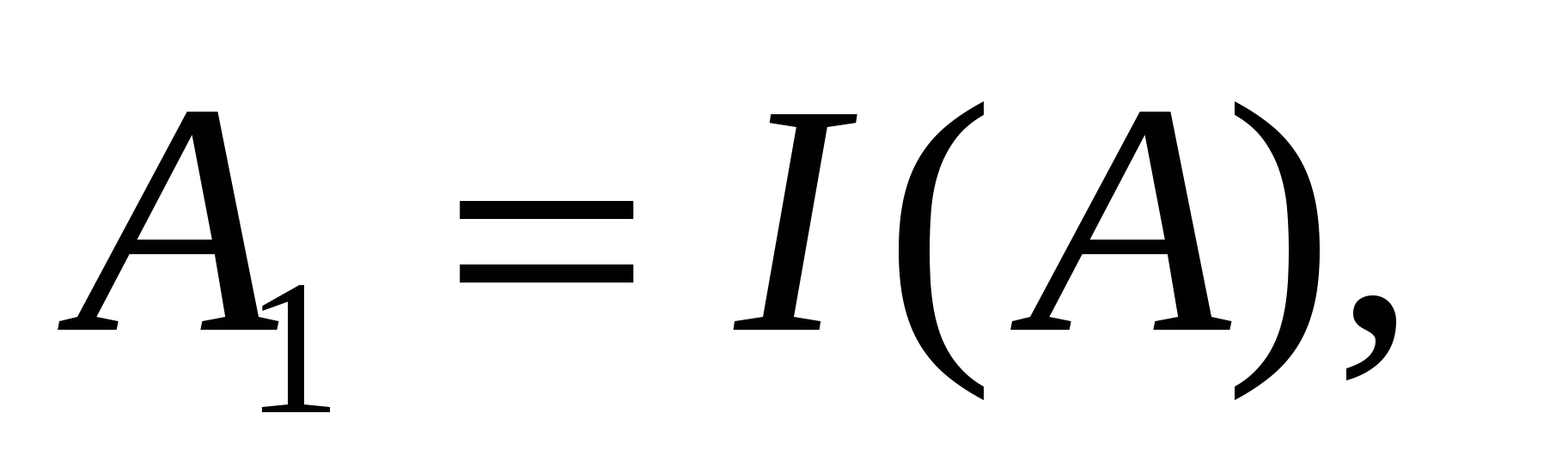
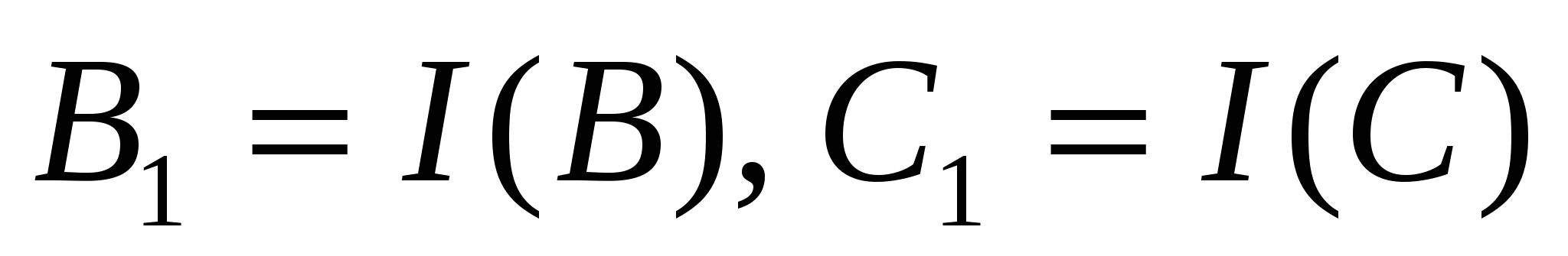 лежат на прямой p,
лежат на прямой p,
причем точка 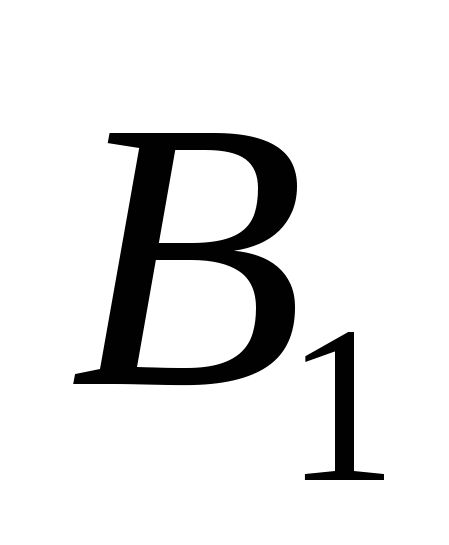 лежит на отрезке
лежит на отрезке 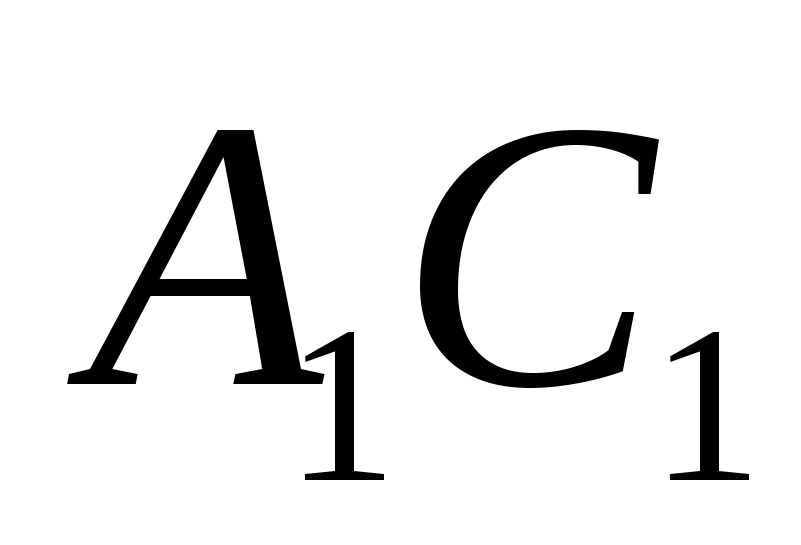 .
.
Поэтому 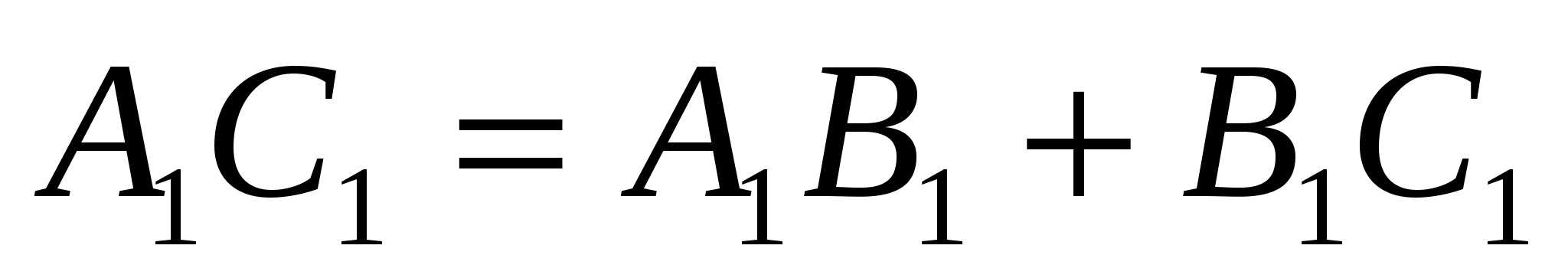 .
.
По лемме об инверсии
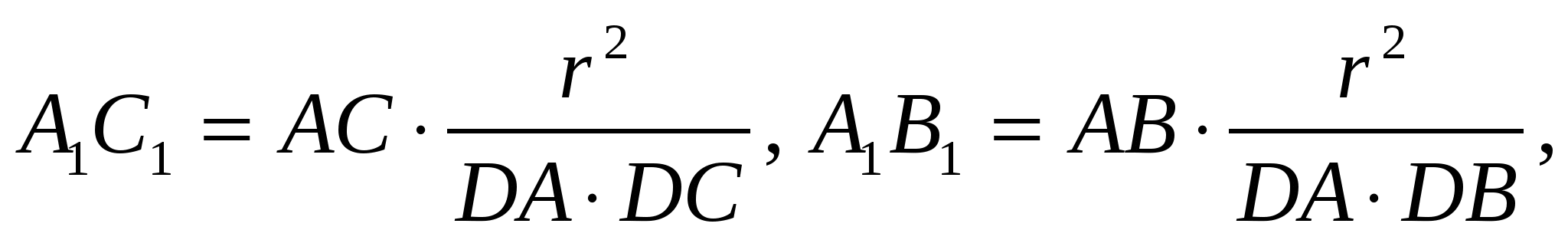
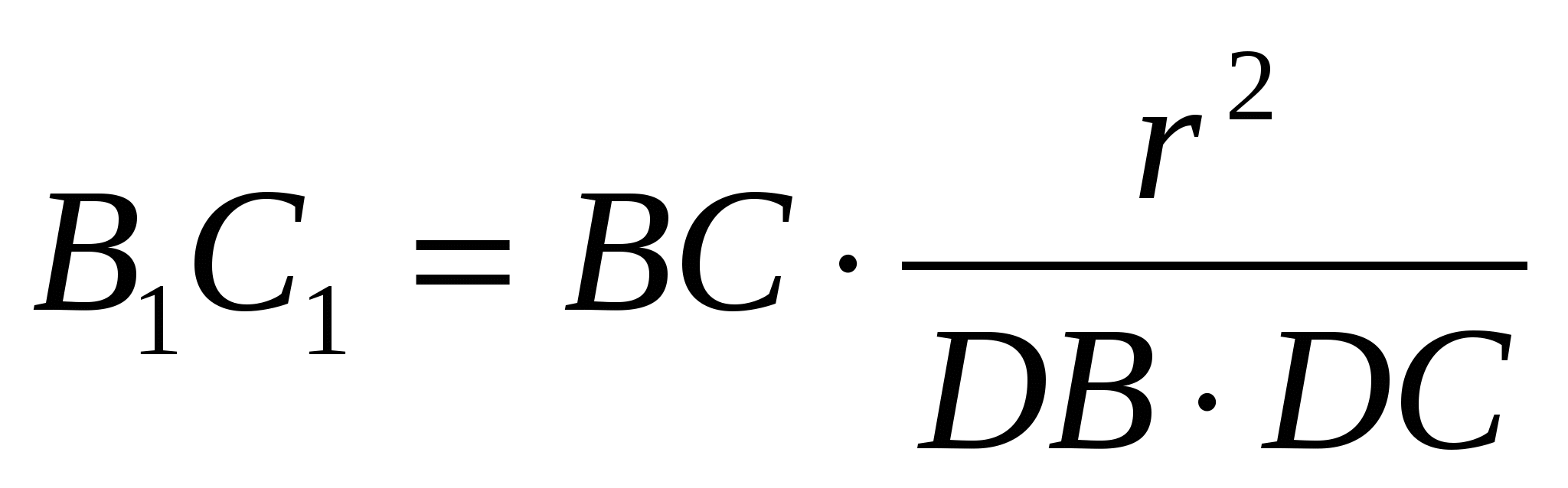 .
.
Подставив эти выражения в равенство 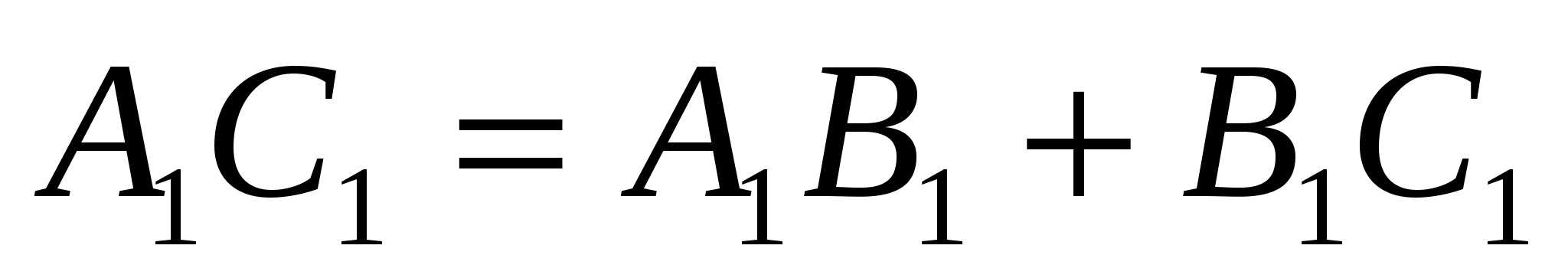 , получаем:
, получаем:
АС · DВ = АВ · DС + ВС · DА,
что и требовалось доказать. ◄
Приведенные доказательства на самом деле не исчерпывают всех возможных доказательств теоремы Птолемея.
Седьмое доказательство Теорема Птолемея может быть, например, получена и как следствие теоремы Бретшнейдера (теоремы косинусов для четырехугольника), которая утверждает следующее.
Квадрат произведения диагоналей выпуклого четырехугольника равен сумме квадратов произведений его противоположных сторон без удвоенного произведения всех четырех сторон четырехугольника и косинуса суммы двух его противолежащих углов,
т. е. 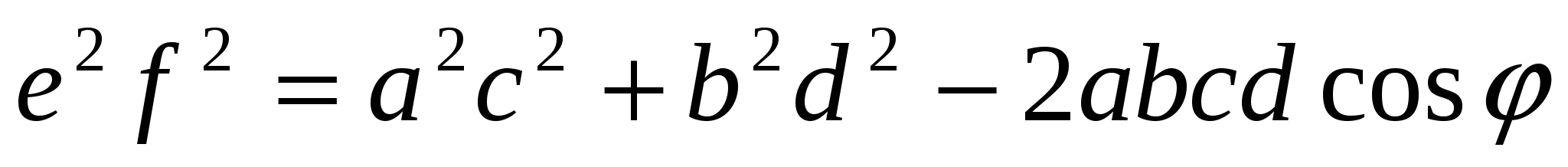 ,
,
где 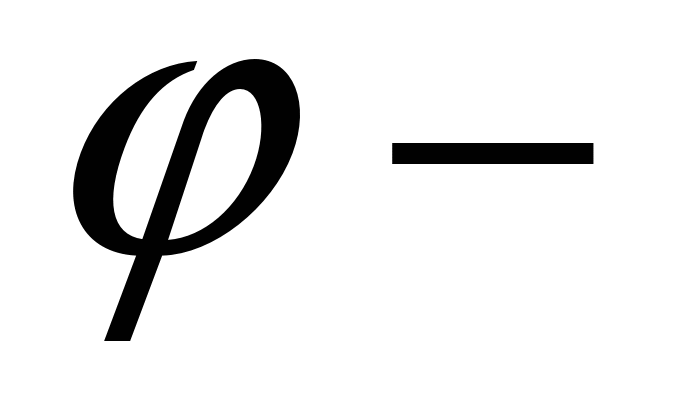 угол, равный сумме углов А и С или В и D,
угол, равный сумме углов А и С или В и D,
так как 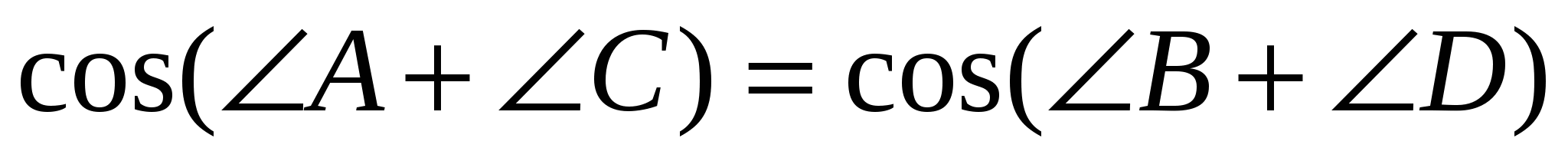 .
.
Поскольку во вписанном четырехугольнике сумма двух противоположных углов равна 180º, то по теореме Бретшнейдера в этом случае
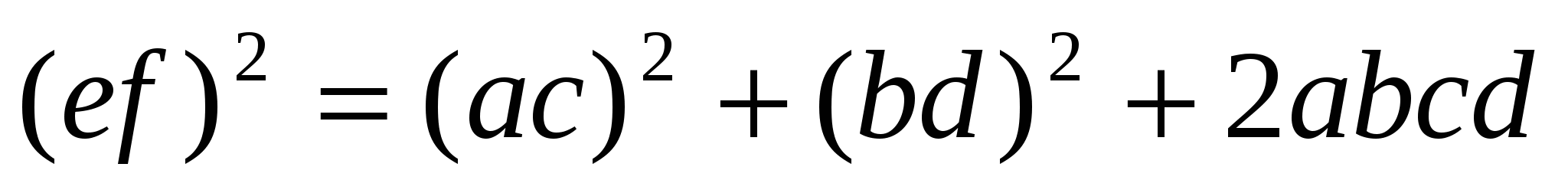
или 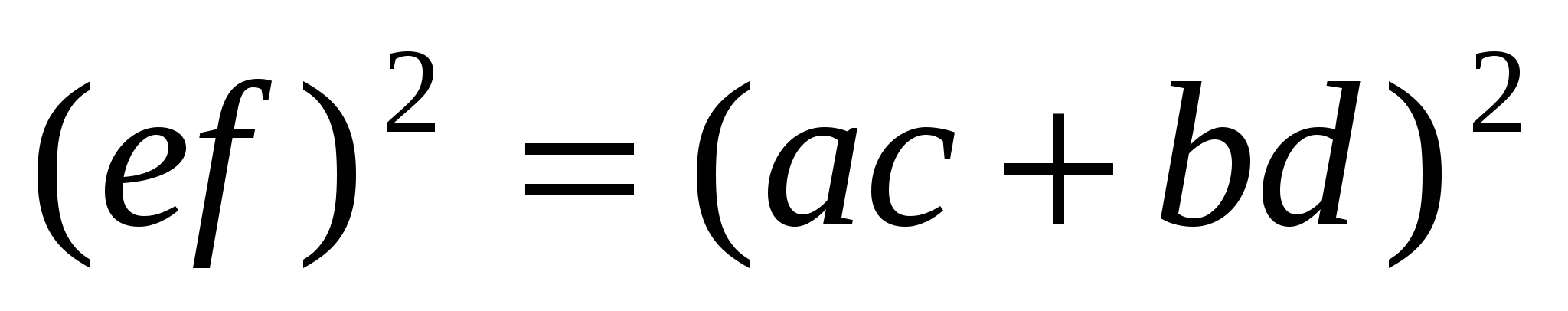 , т. е.
, т. е. 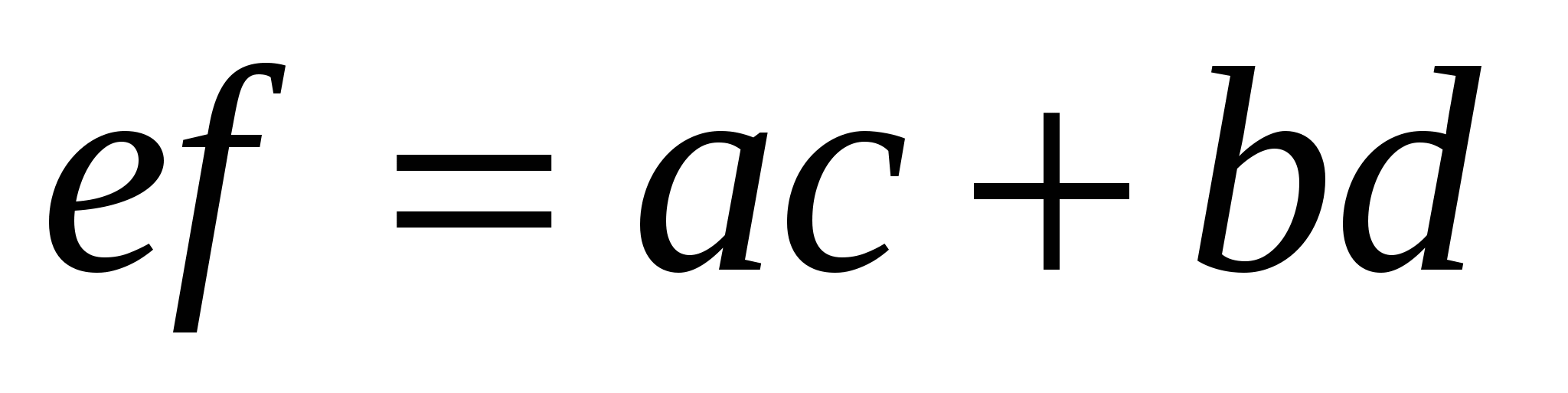 .
.
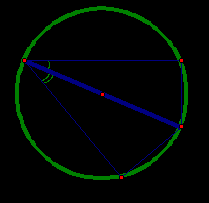
Рис. 10
Эта теорема понадобилась Клавдию Птолемею (ок.100 - ок.178) - знаменитому древнегреческому астроному и математику, жившему в Александрии, для составления таблицы синусов, точнее, таблицы длин хорд.
Если АС - диаметр окружности, то теорема Птолемея перепишется в виде
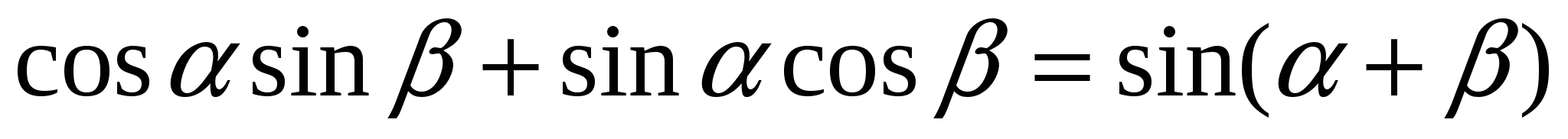 ;
;
если же в качестве диаметра взять сторону АВ, то получим формулу для синуса разности этих углов (рис. 10).
Именно эти частные случаи использовал Птолемей для составления своих таблиц, очень нужных для астрономических расчетов.
В эпоху средневековья книга Птолемея, в которой содержались обширные сведения по астрономии, получила распространение в странах арабского Востока; астрономы называли ее там «Аль Маджисти» − «Величайшее», отсюда и происходит ее название «Альмагест».
Заметим, что если около выпуклого четырехугольника нельзя описать окружность, то произведение его диагоналей меньше суммы произведений противоположных сторон. Докажем это.
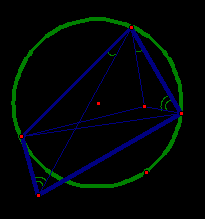
Рис. 11
Пусть для определенности в данном четырехугольнике АВСD  АВС +
АВС +  АDС < 180º. Тогда вершина D лежит вне окружности, проведенной через вершины А, В и С.
АDС < 180º. Тогда вершина D лежит вне окружности, проведенной через вершины А, В и С.
Пусть  DВС
DВС 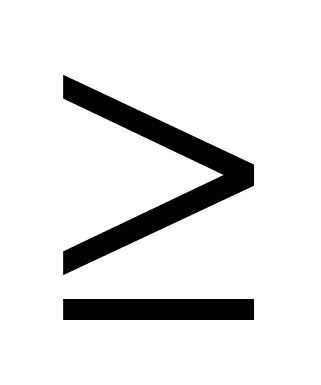
 АВD.
АВD.
Построим (как на рис. 11)  СВК =
СВК =  АВD,
АВD,  ВСК =
ВСК =  АDВ и проведем отрезок АК.
АDВ и проведем отрезок АК.
Тогда 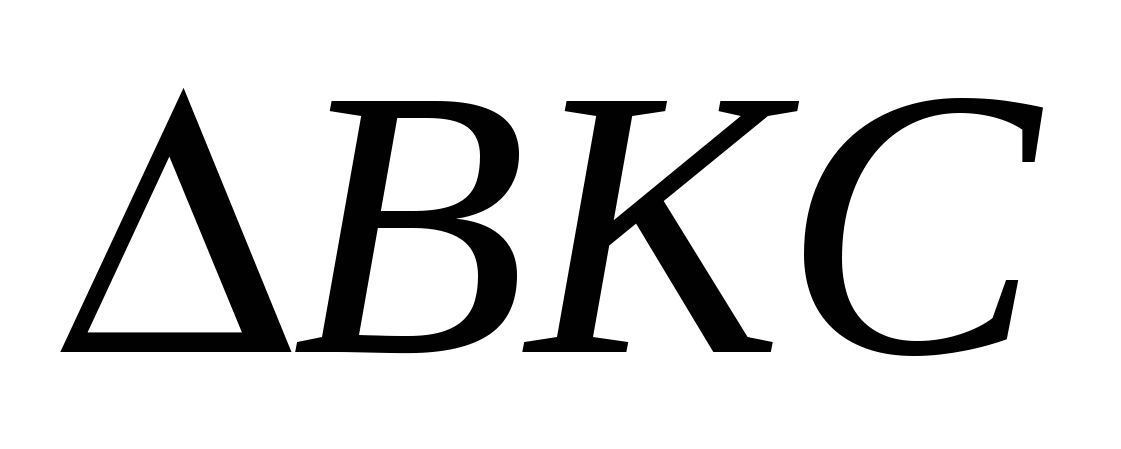 ~
~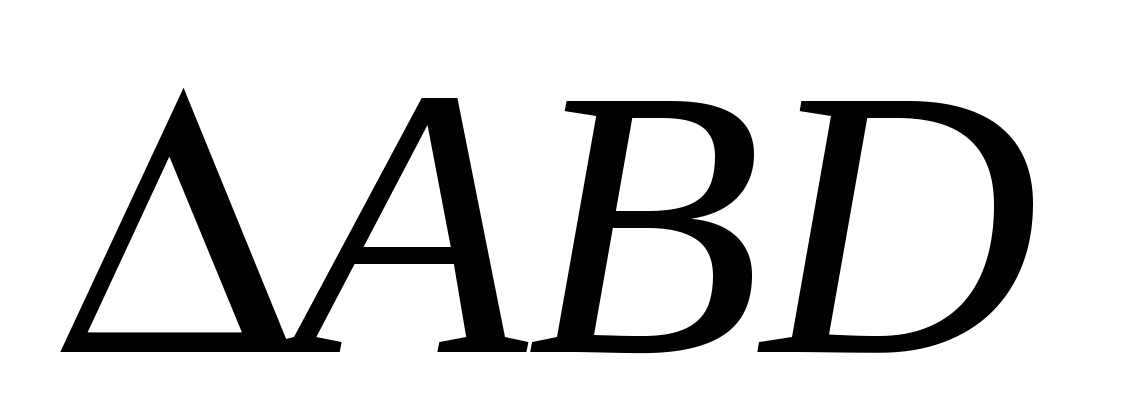 , а поэтому
, а поэтому
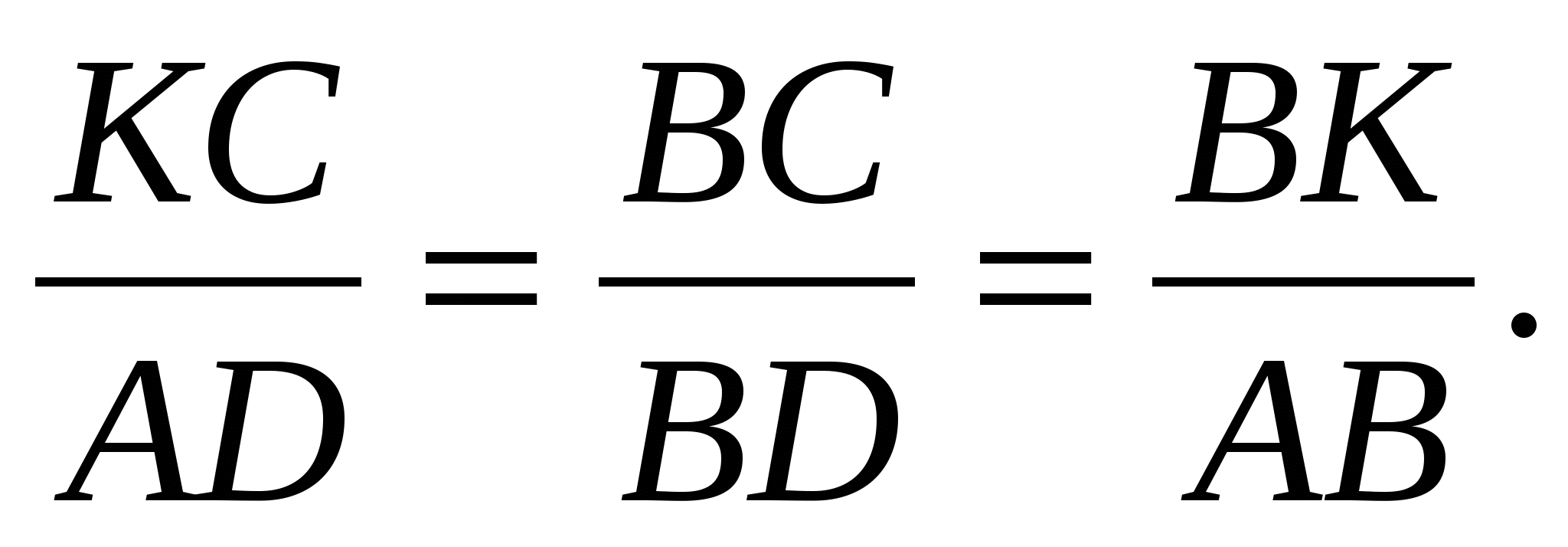 (4)
(4)
Следовательно, АD · ВС = ВD · КС. (5)
Так как ![]() DВС =
DВС =  АВК,
АВК,
а из (4) следует, что 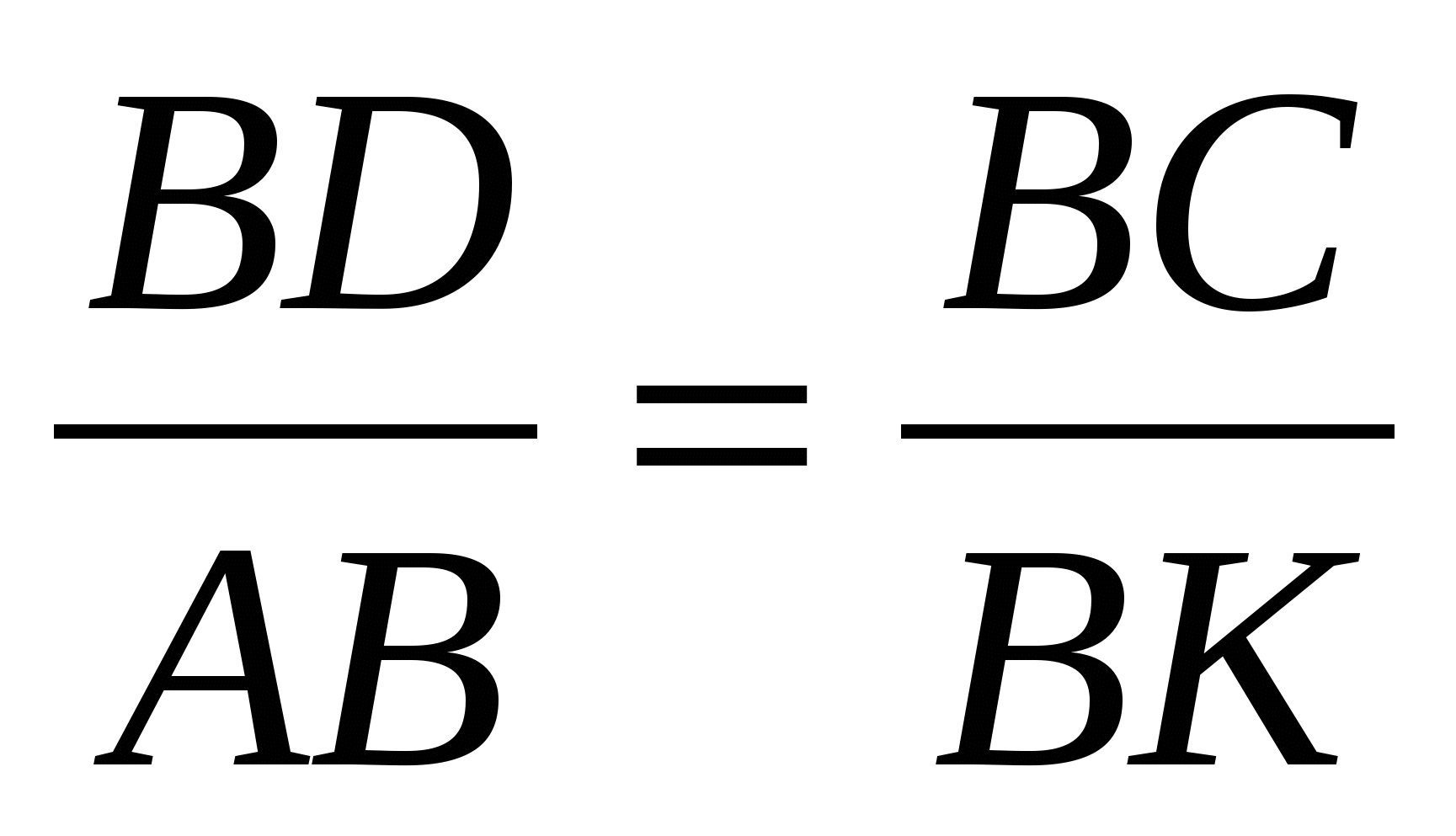 , то
, то 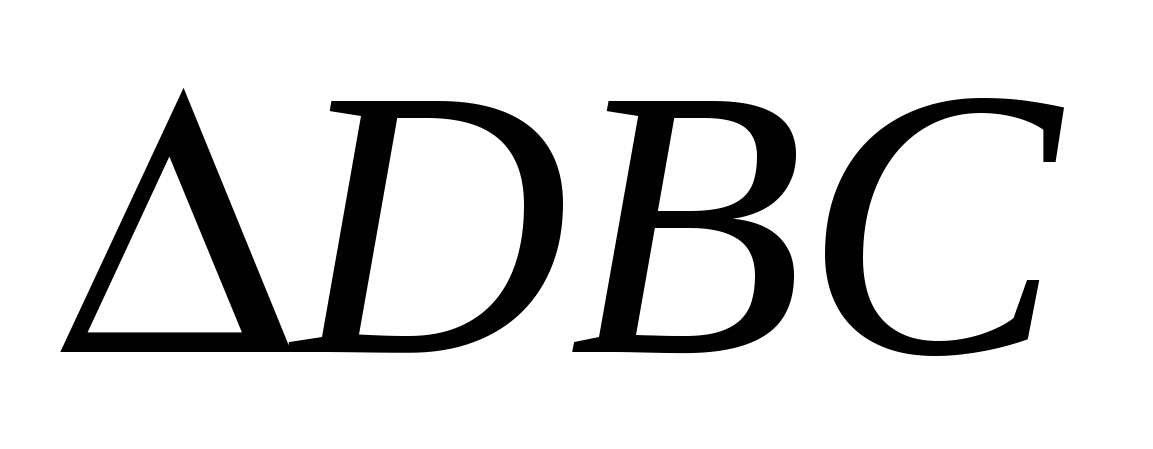 ~
~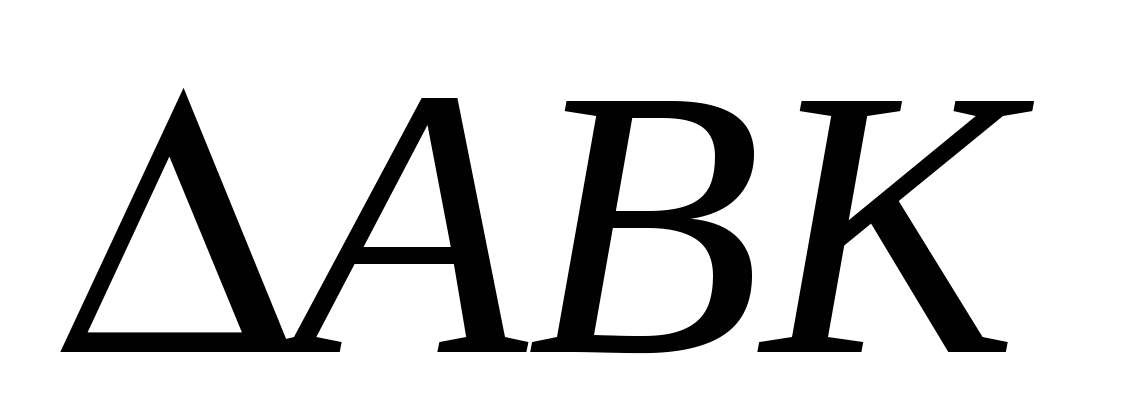 .
.
Из подобия этих треугольников вытекает, что 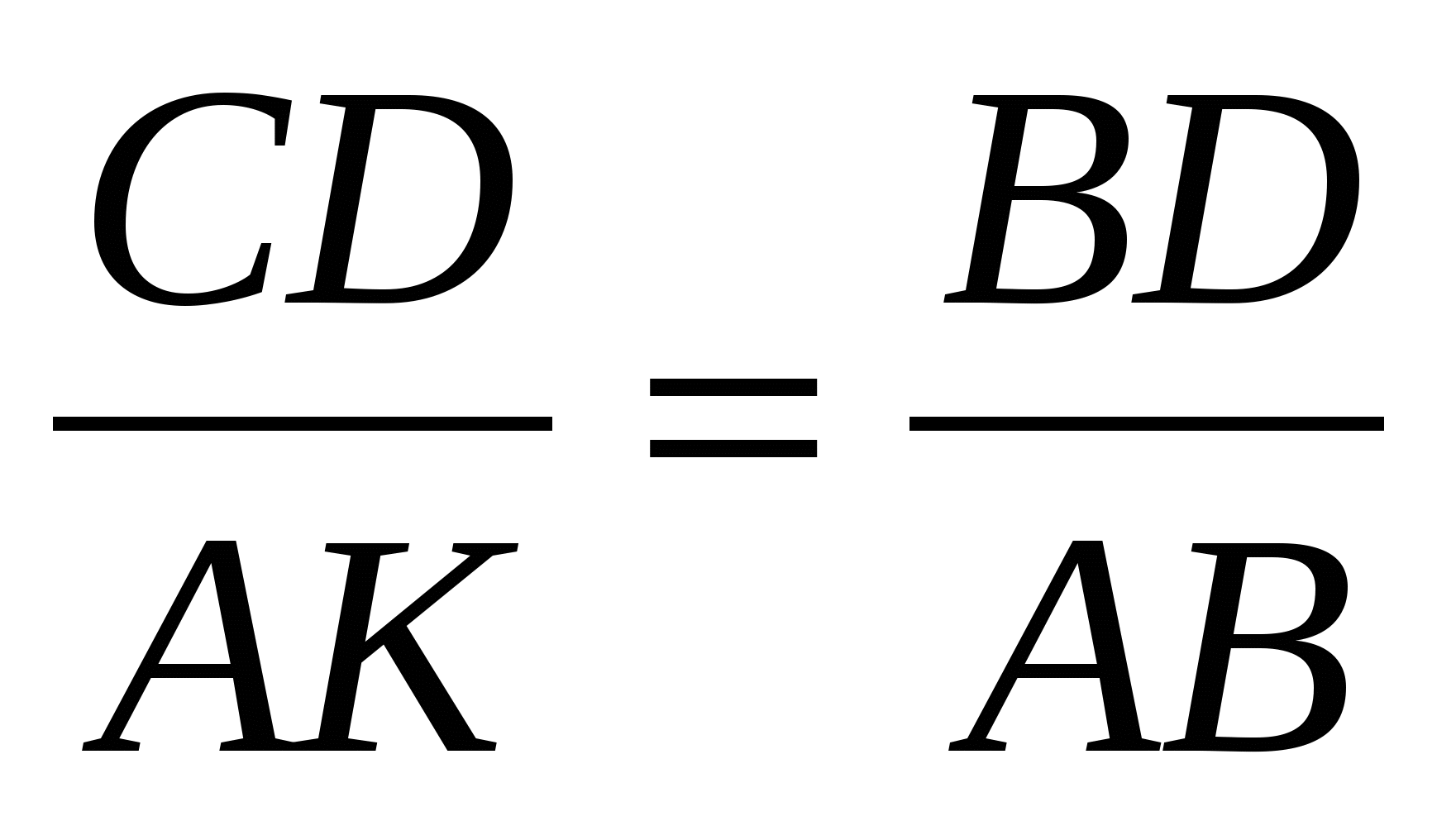 ,
,
т. е.
АВ · СD = ВD · АК. (6)
Сложив (5) и (6) получаем:
АD · ВС + АВ · СD = ВD(АК + КС). (7)
Но точка К не лежит на прямой АС, поскольку  ВСК, равный
ВСК, равный  АDВ, имеющему вершину вне круга, меньше вписанного угла АСВ.
АDВ, имеющему вершину вне круга, меньше вписанного угла АСВ.
Следовательно,
АК + КС > АС. (8)
Поэтому из (7) и (8) имеем:
АС · ВD < AD · BC + AB · CD.
Значит, для любого выпуклого четырехугольника АВСD имеет место неравенство
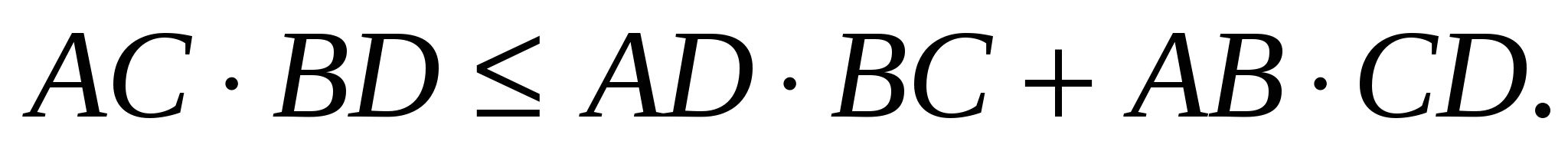
Рассмотрим теперь теорему, представляющую обобщение теоремы Птолемея.
В ней речь пойдет о четырех окружностях, касающихся внутренним (внешним) образом некоторой окружности в вершинах вписанного в нее четырехугольника.
Вместо расстояния между двумя вершинами А и В принимается касательное расстояние 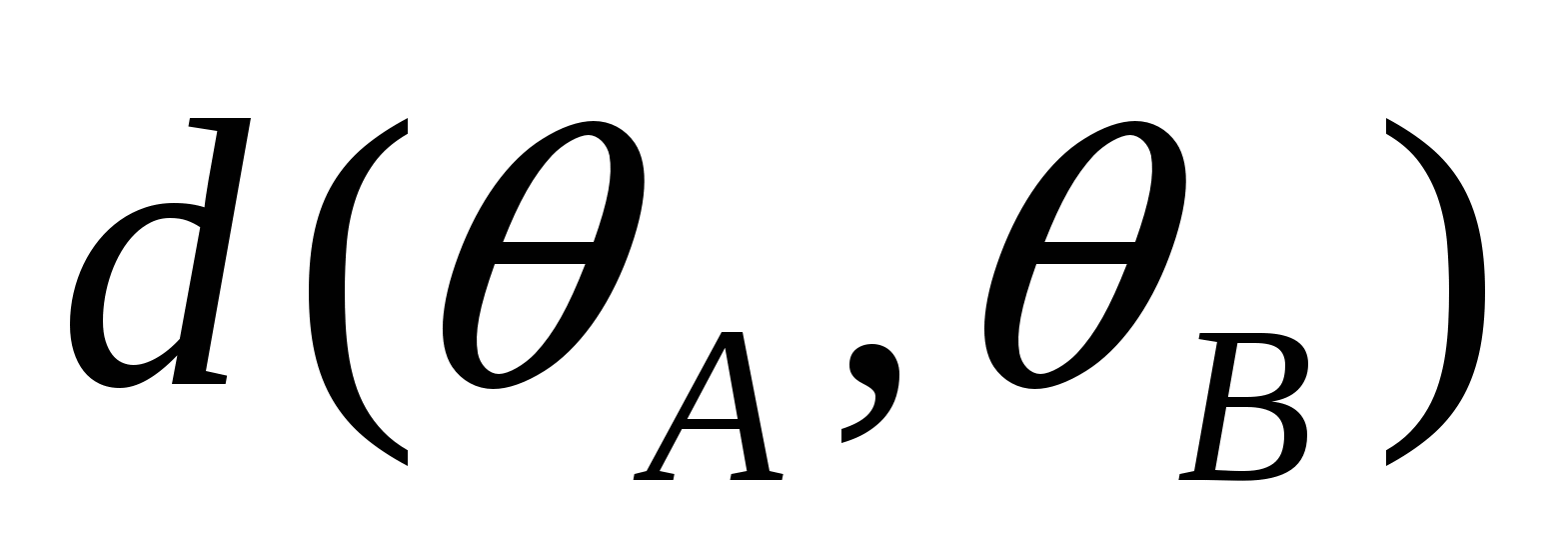 между соответствующими двумя окружностями
между соответствующими двумя окружностями  ,
, 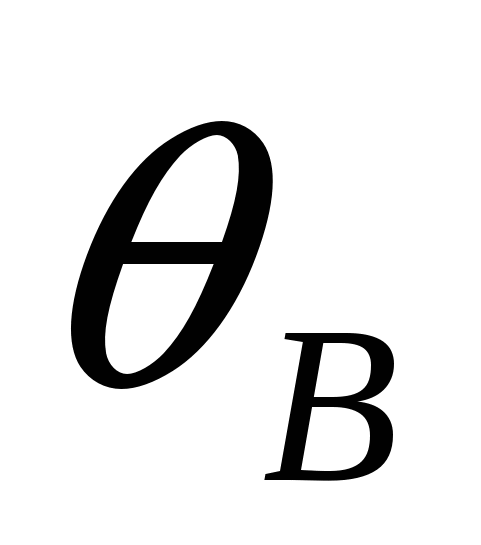 .
.
Под касательным расстоянием 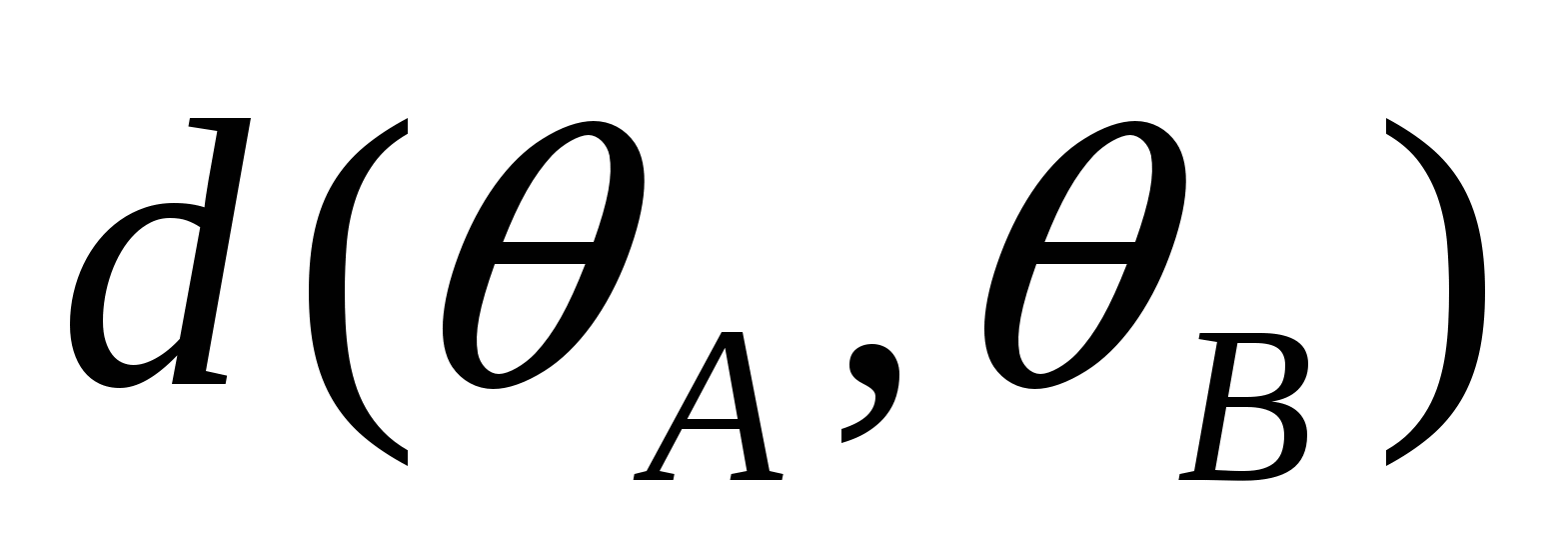 подразумевается расстояние между двумя точками касания общей внешней касательной этих двух окружностей (рис. 12).
подразумевается расстояние между двумя точками касания общей внешней касательной этих двух окружностей (рис. 12).
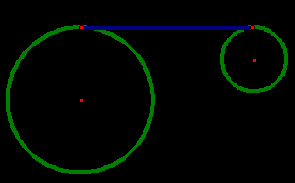
Рис.12
Обобщенная теорема Птолемея.
Если окружности  ,
, 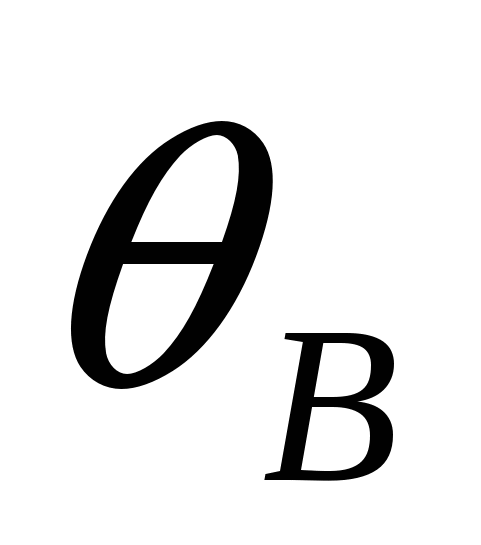 ,
, 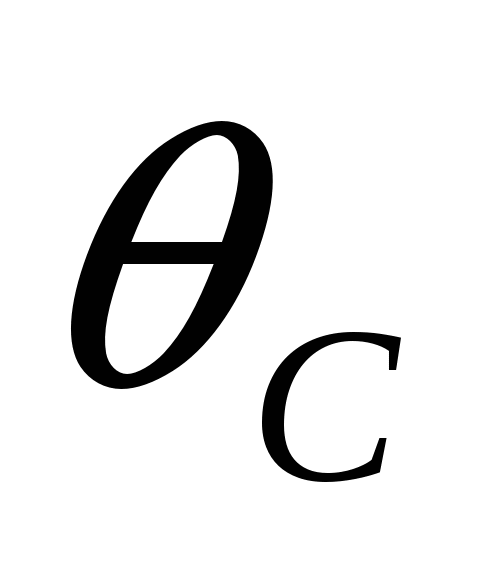 ,
, 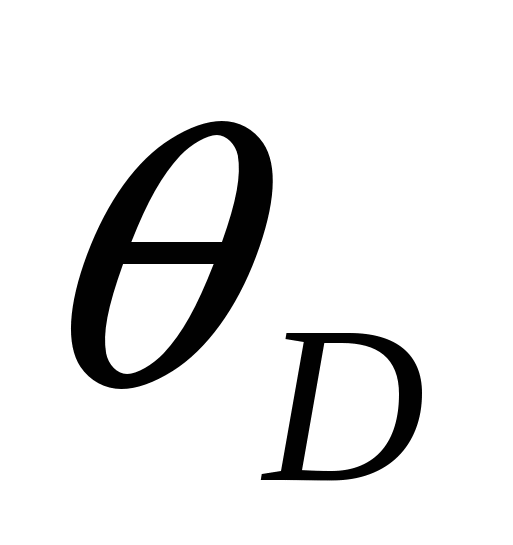 касаются окружности
касаются окружности  внутренним (внешним) образом в вершинах А, В, С, D выпуклого четырехугольника АВСD, вписанного в
внутренним (внешним) образом в вершинах А, В, С, D выпуклого четырехугольника АВСD, вписанного в  , то касательные расстояния между парами окружностей связаны соотношением:
, то касательные расстояния между парами окружностей связаны соотношением:
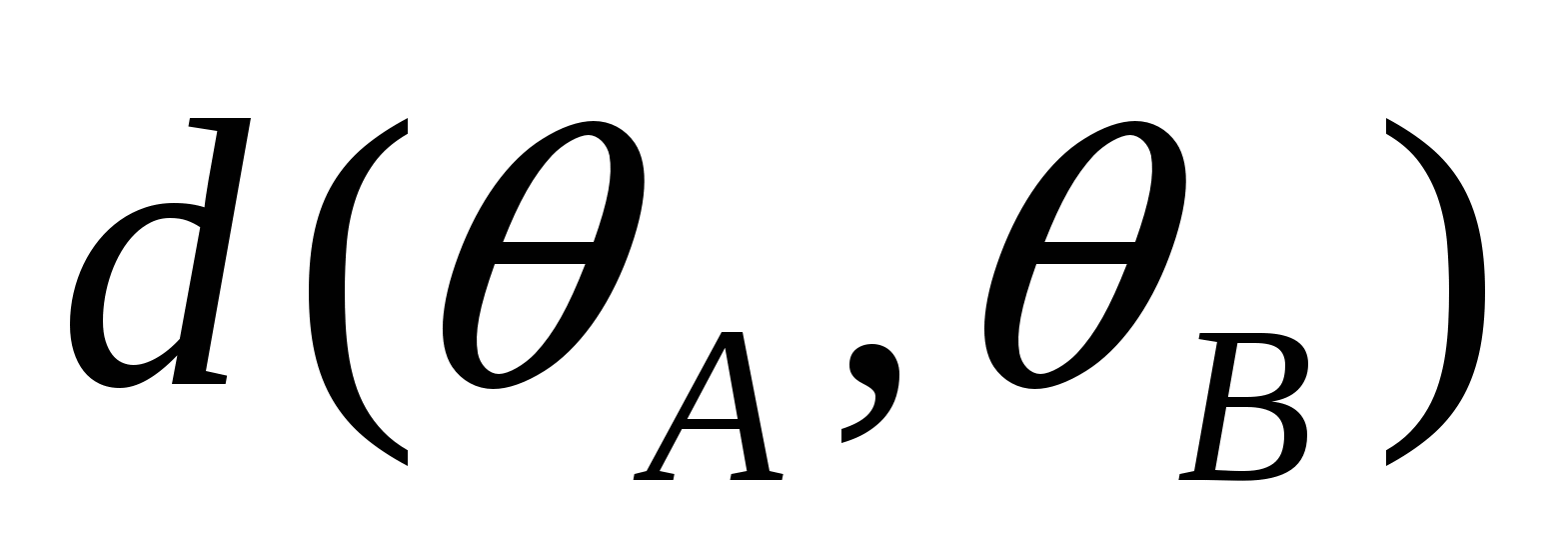 ·
·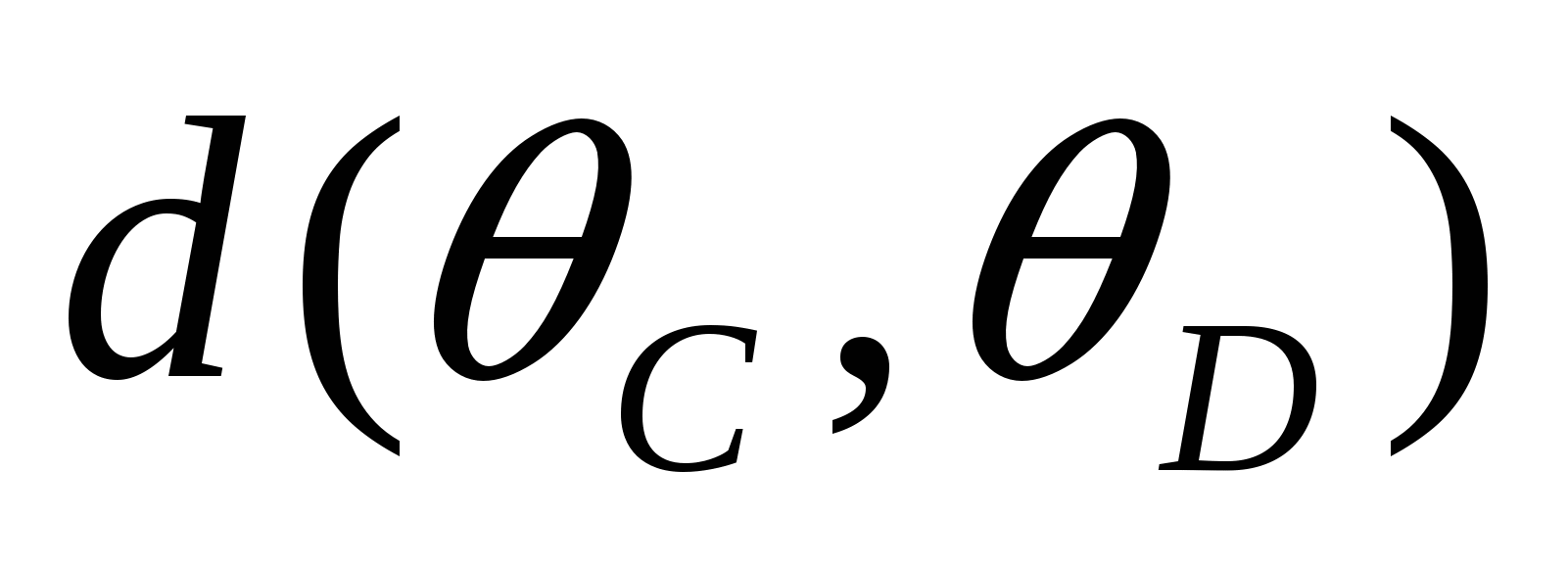 +
+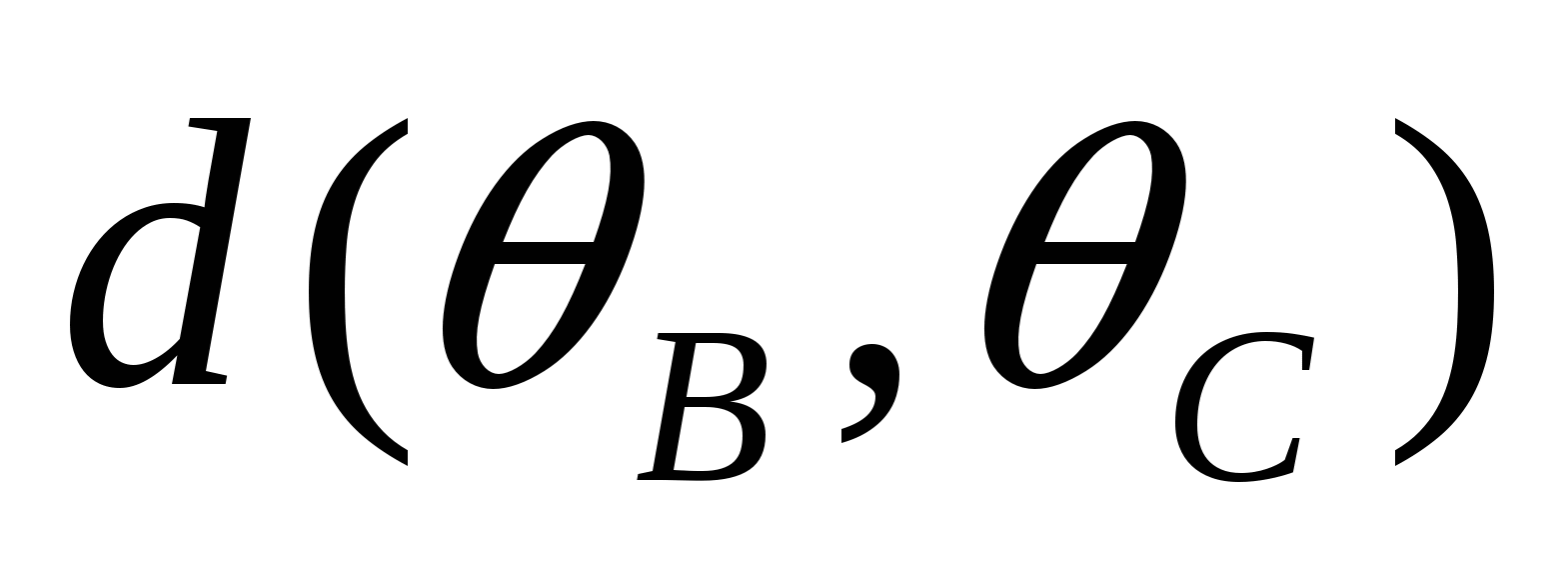 ·
·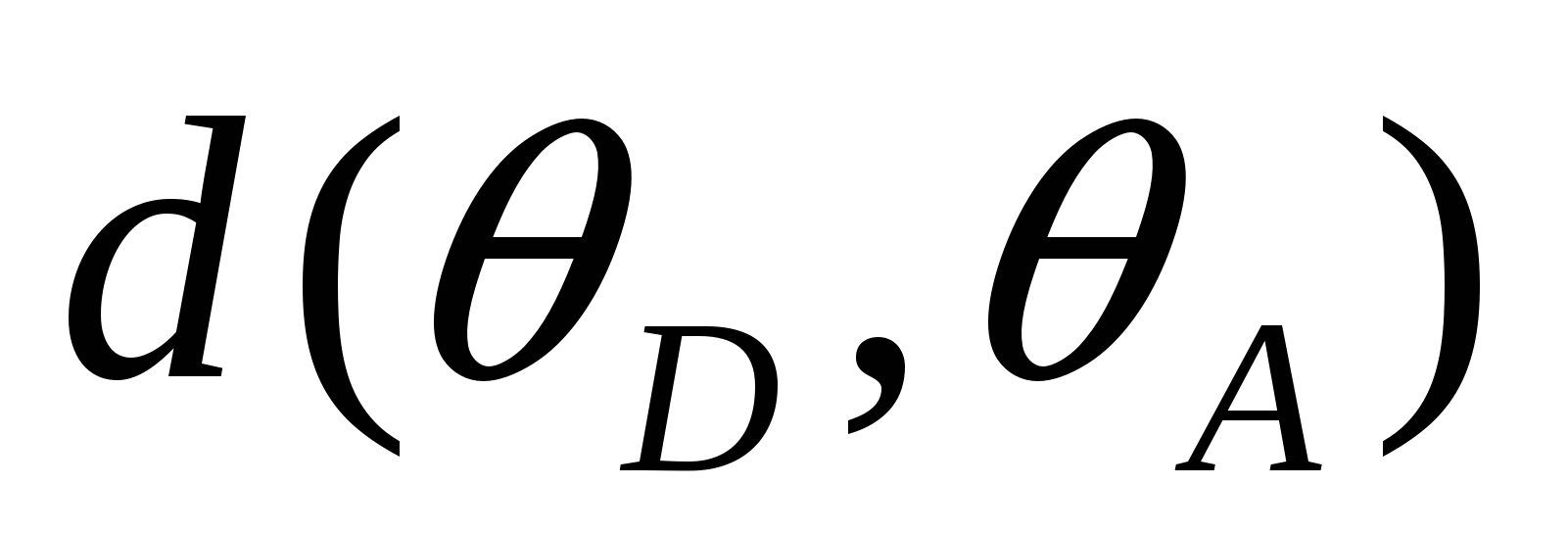 =
=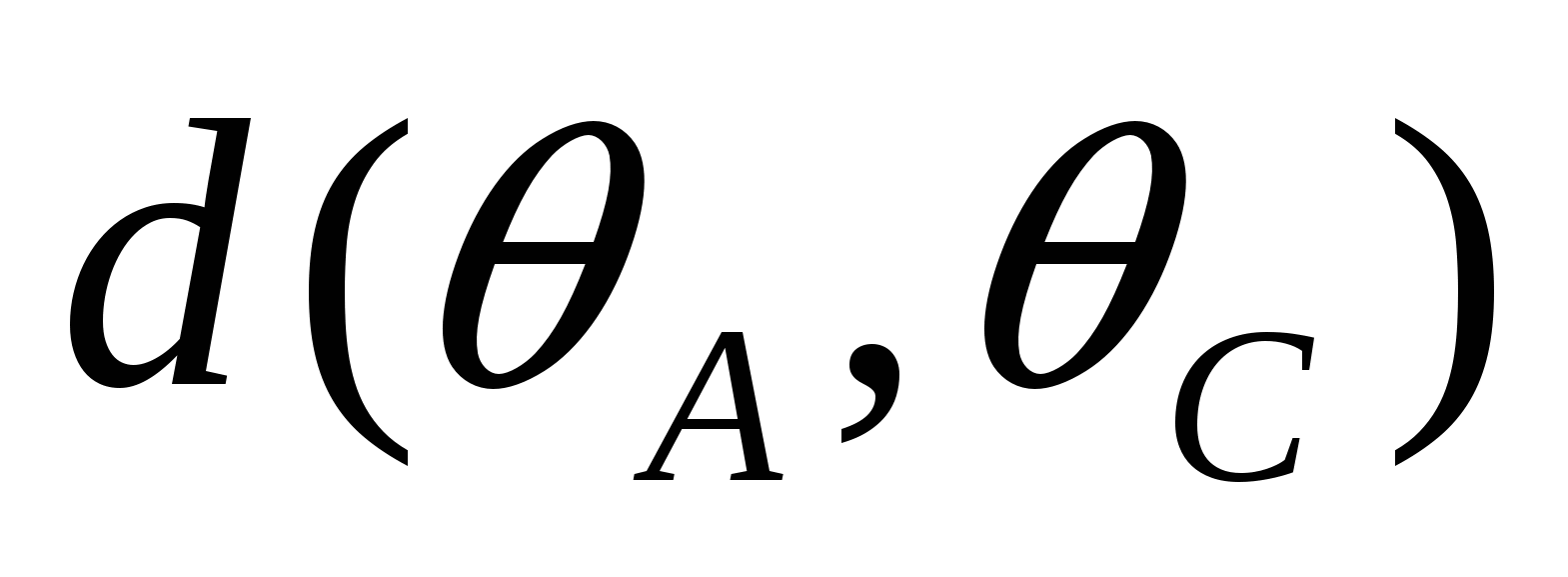 ·
·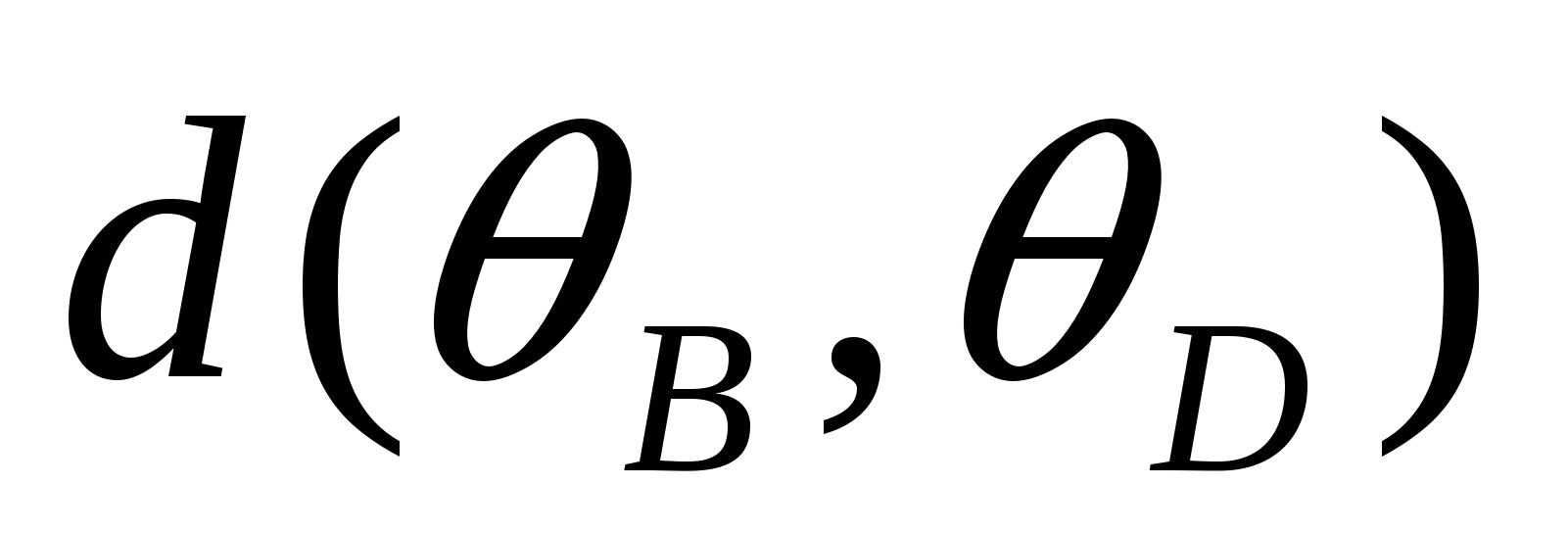 .
.
Замечание. Если  ,
, 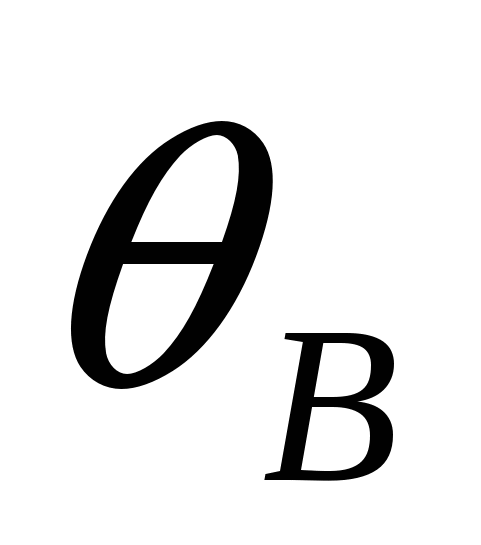 ,
, 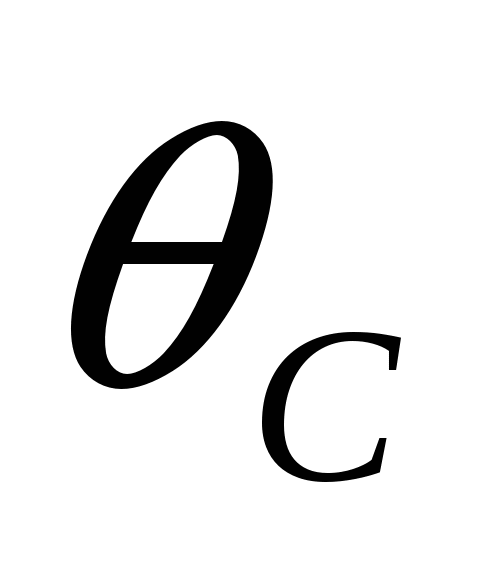 ,
, 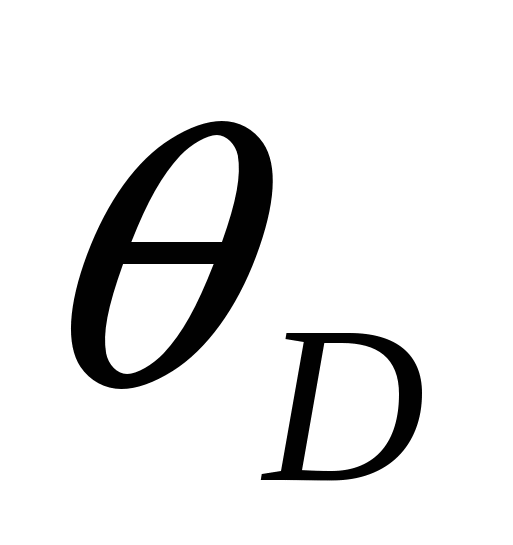 − окружности нулевого радиуса, то получаем обычную теорему Птолемея.
− окружности нулевого радиуса, то получаем обычную теорему Птолемея.
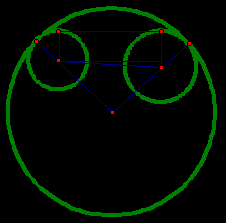
Рис. 13
Прежде чем непосредственно перейти к доказательству обобщенной теоремы Птолемея, вычислим касательное расстояние 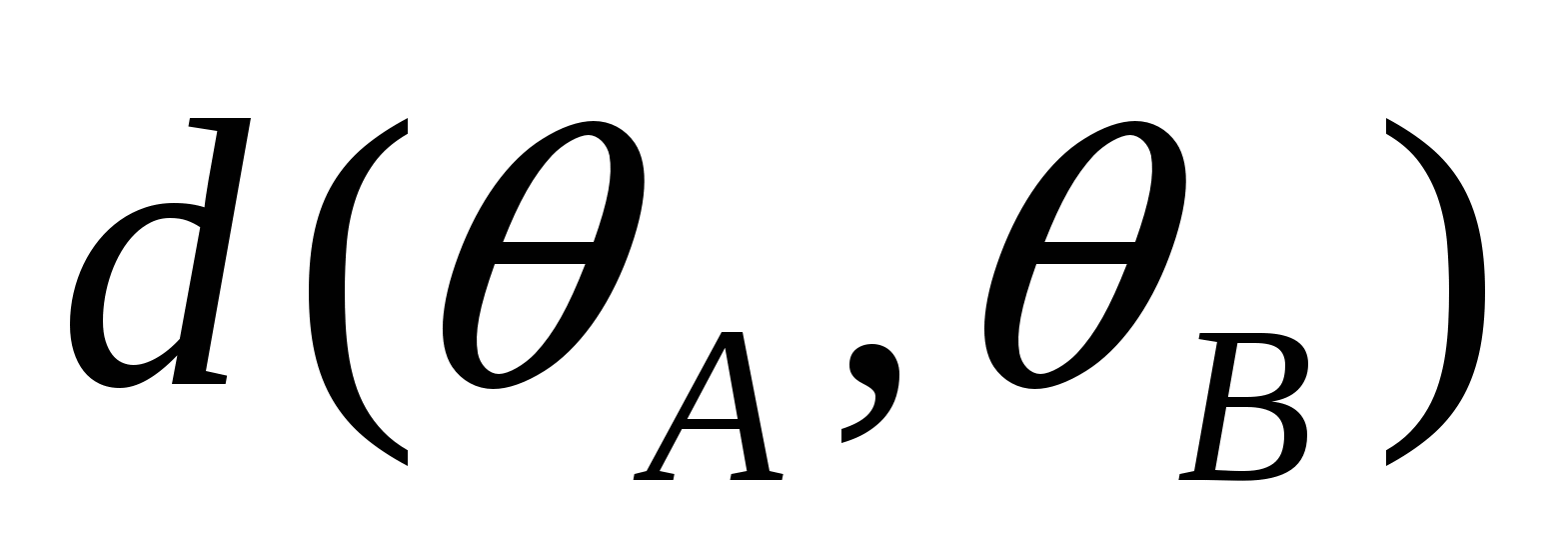 между окружностями
между окружностями  и
и 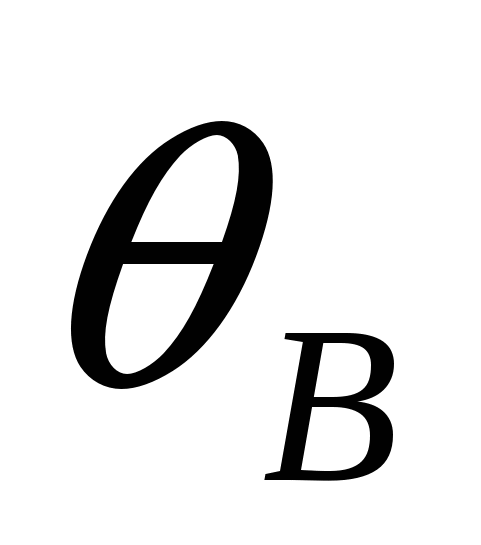 , если дана окружность
, если дана окружность ![]() (О,R) и две касающиеся ее внутренним образом в точках А и В окружности
(О,R) и две касающиеся ее внутренним образом в точках А и В окружности 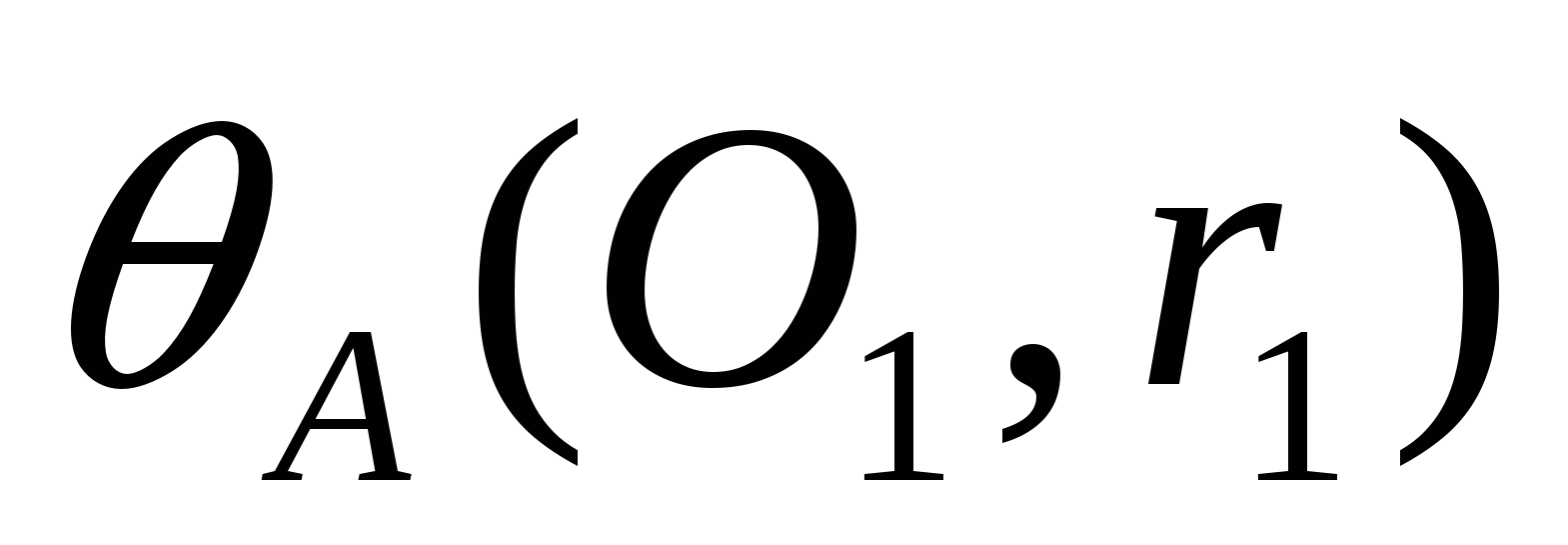 и
и 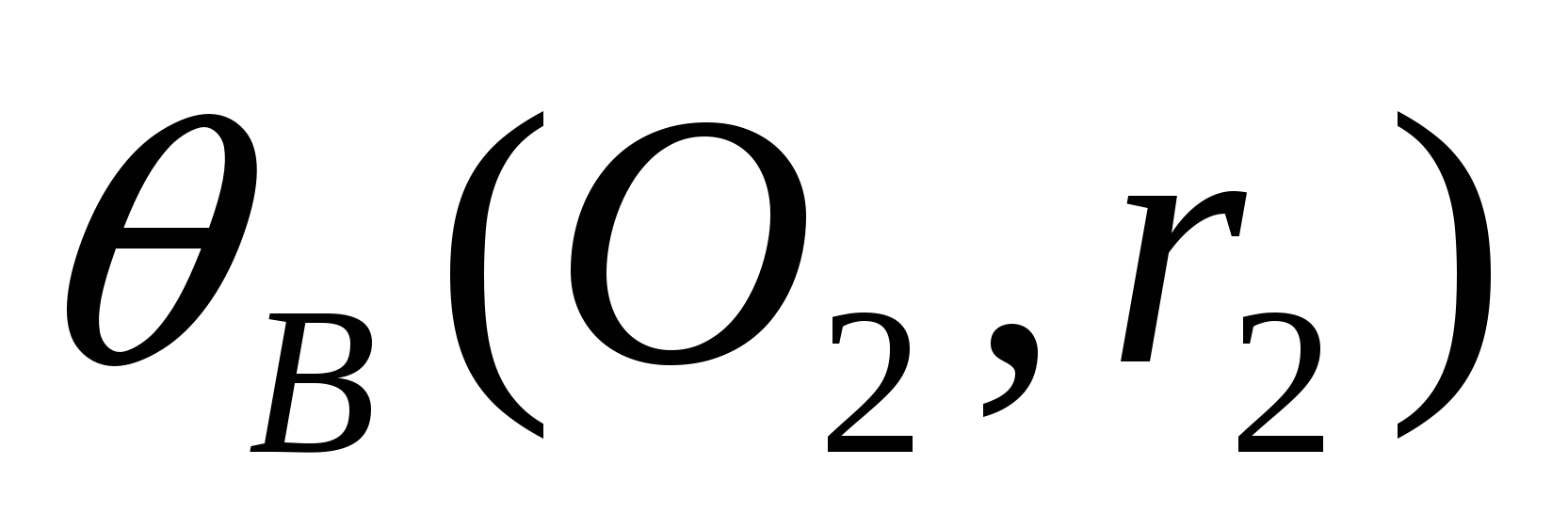 .
.
Пусть общая внешняя касательная касается  в точке
в точке  , а
, а 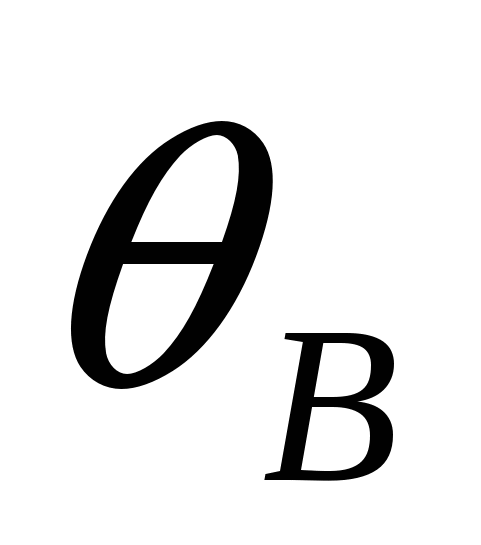 − в точке
− в точке 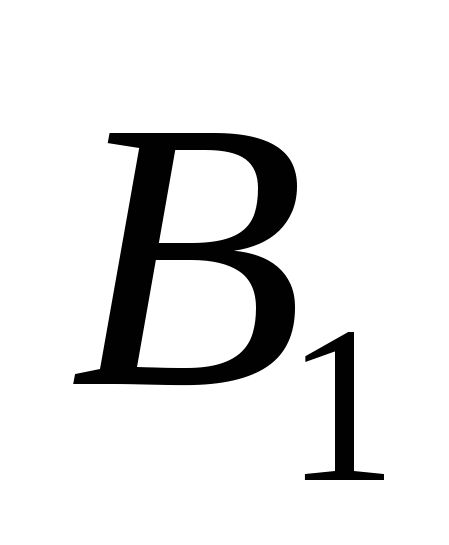 (рис. 13).
(рис. 13).
Тогда 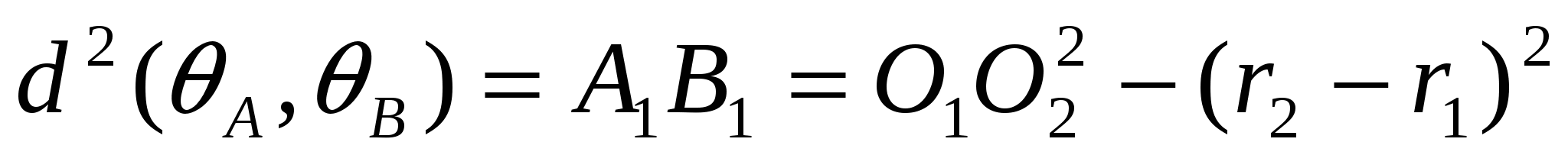 ,
,
где 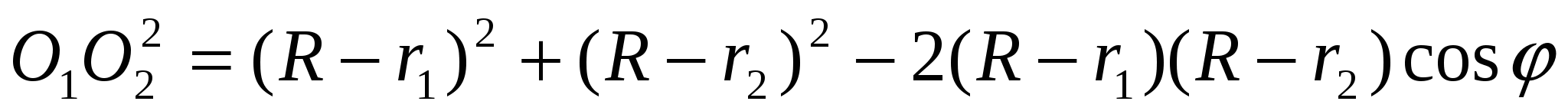 .
.
Далее, 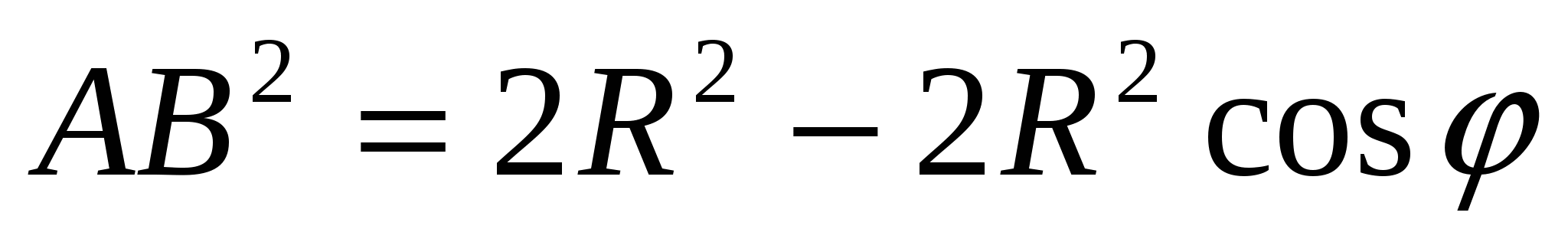 , где
, где  .
.
Из записанных уравнений следует после исключения 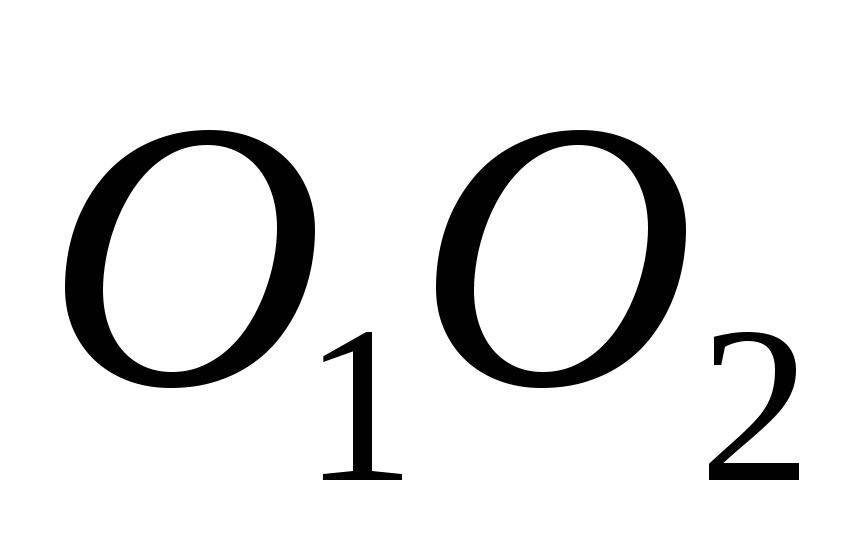 и
и 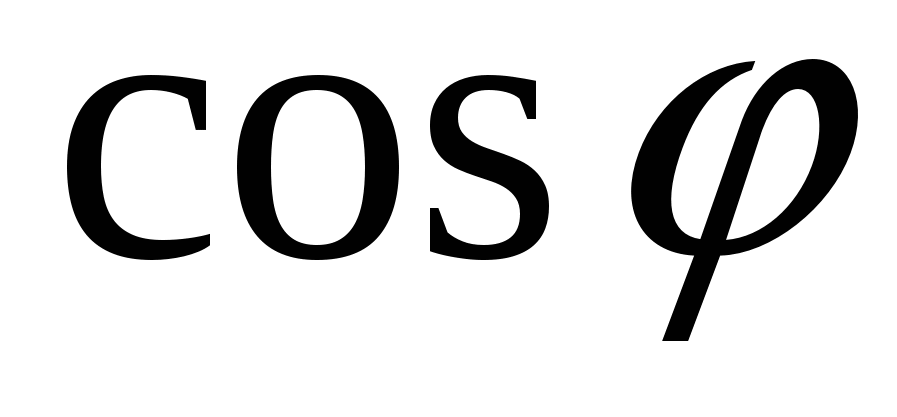 равенство
равенство
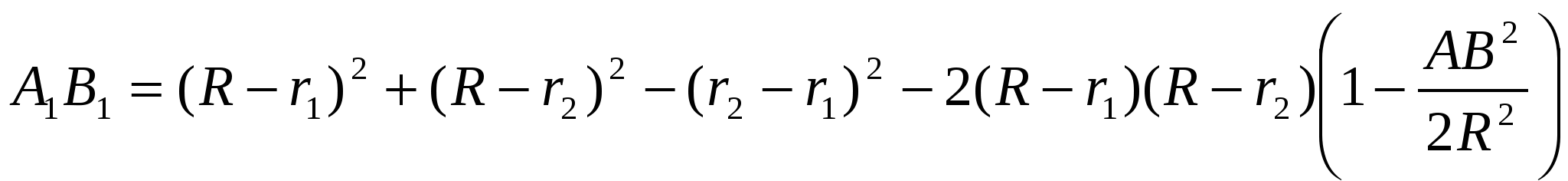
или, после преобразований,
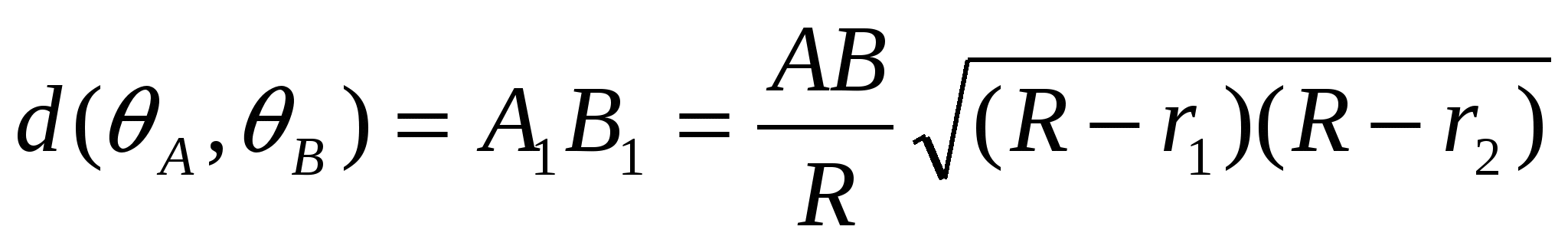 .
.
Теперь докажем обобщенную теорему Птолемея.
Впишем в окружность  четырехугольник АВСD и построим четыре окружности
четырехугольник АВСD и построим четыре окружности  ,
, 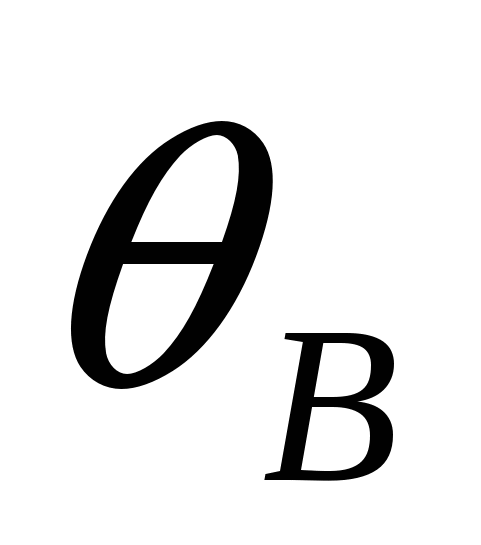 ,
, 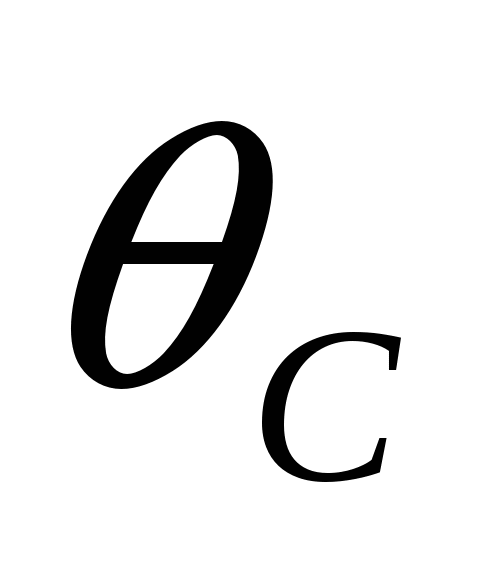 ,
, 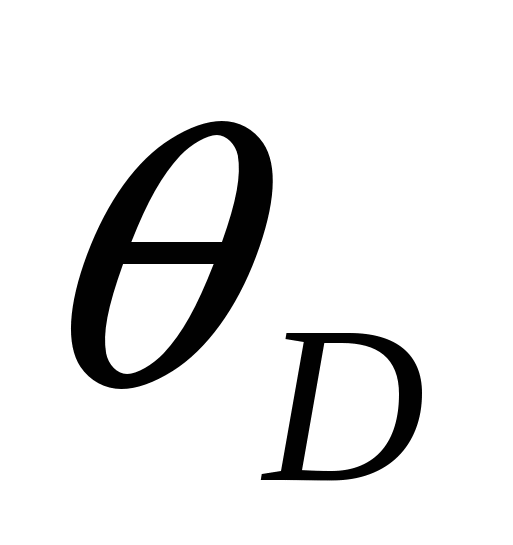 , касающиеся
, касающиеся  внутренним образом в точках А, В, С, D (рис. 14).
внутренним образом в точках А, В, С, D (рис. 14).
Тогда согласно полученной формуле имеем:
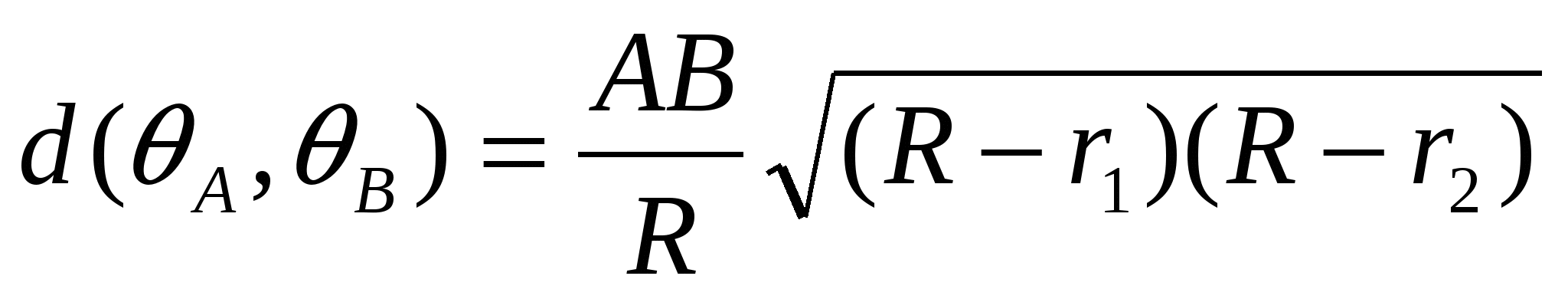 ,
, 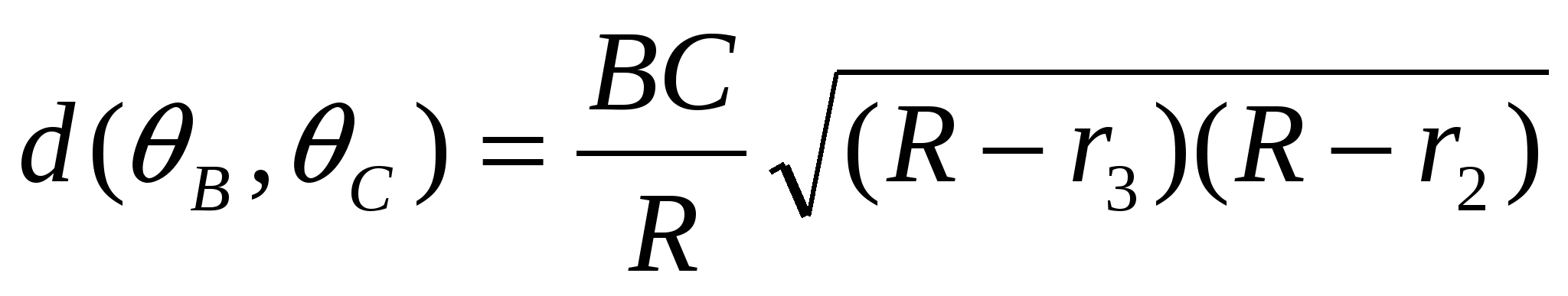 ,
,
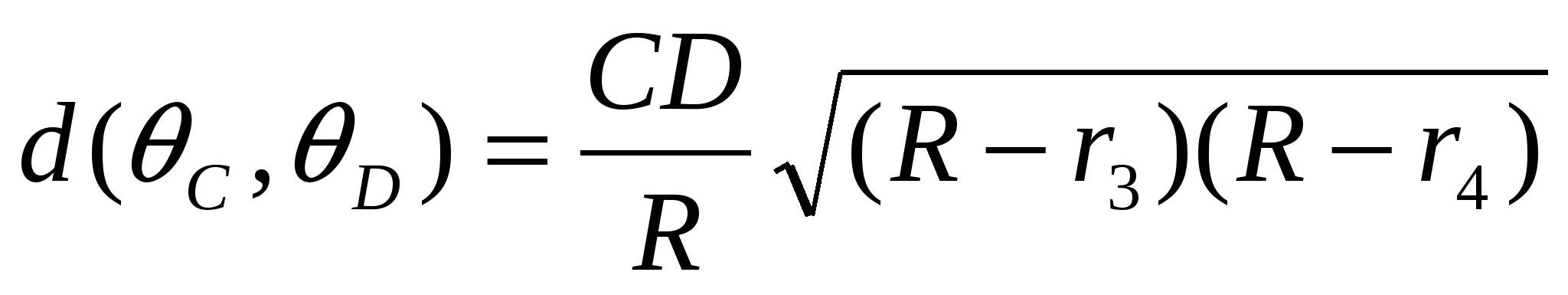 ,
, 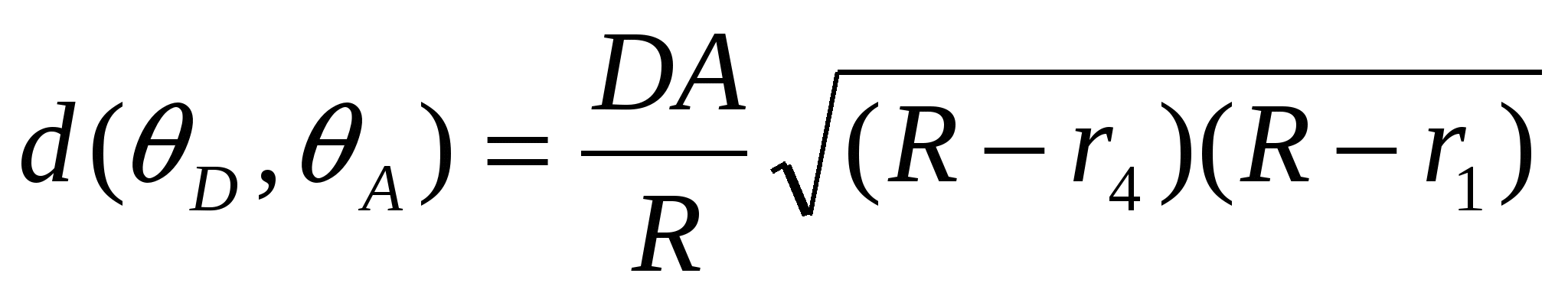 ,
,
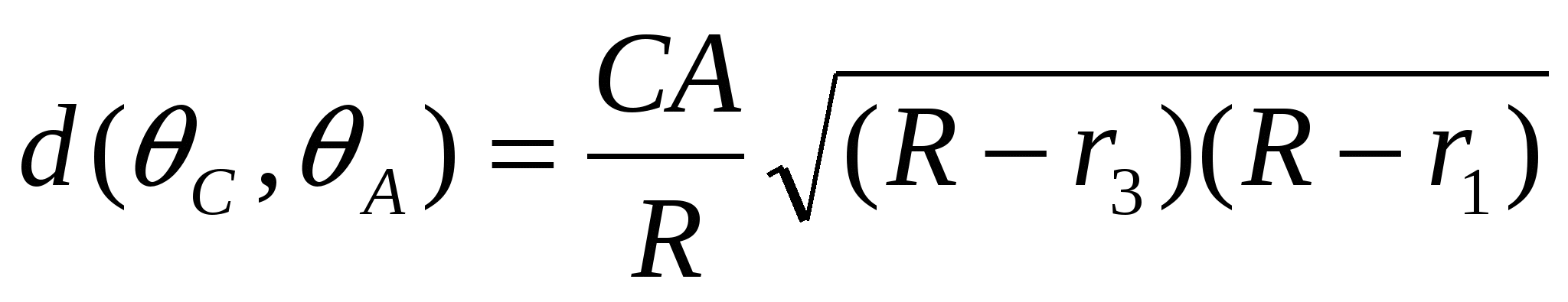 ,
, 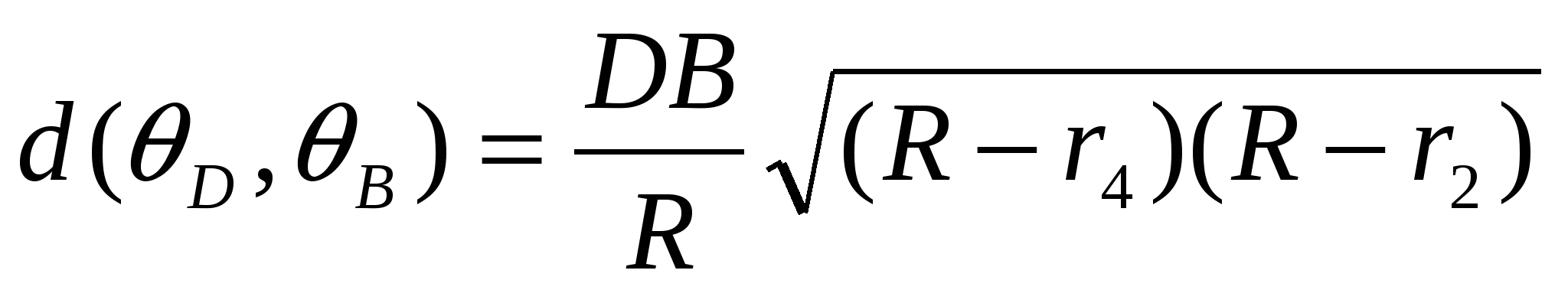 .
.
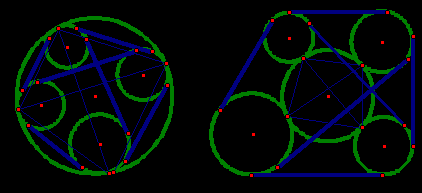
Рис. 14 Рис. 15
Подставим эти выражения для
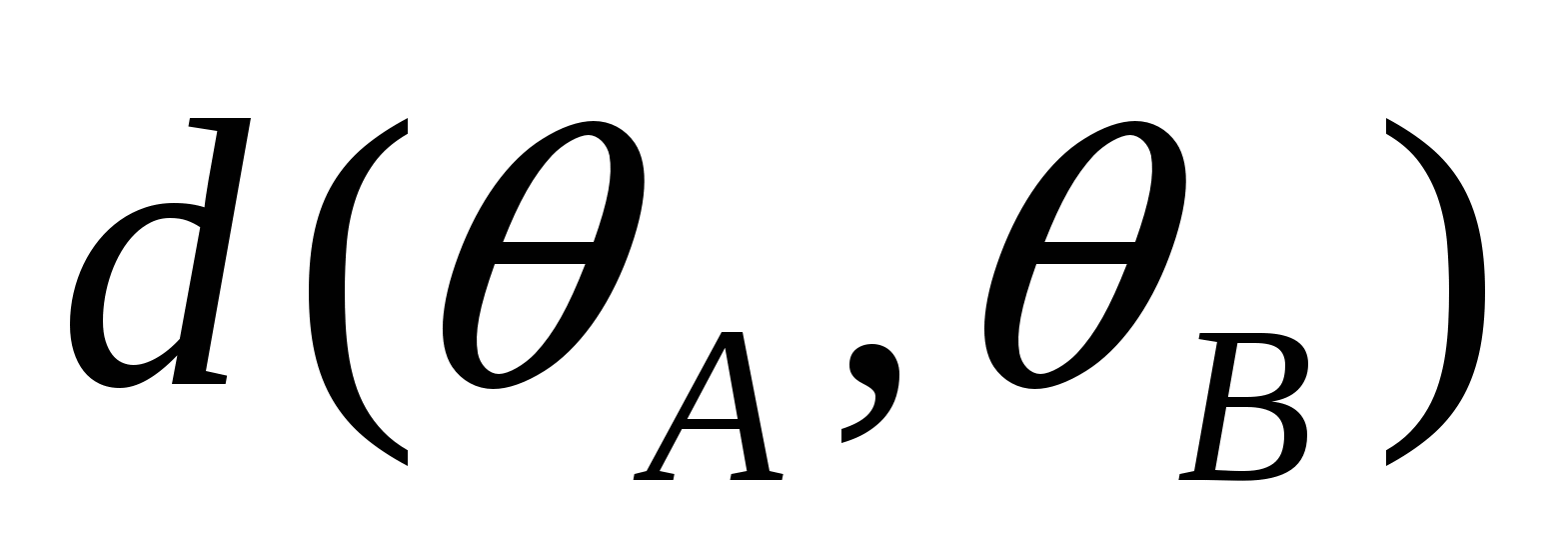 ,
, 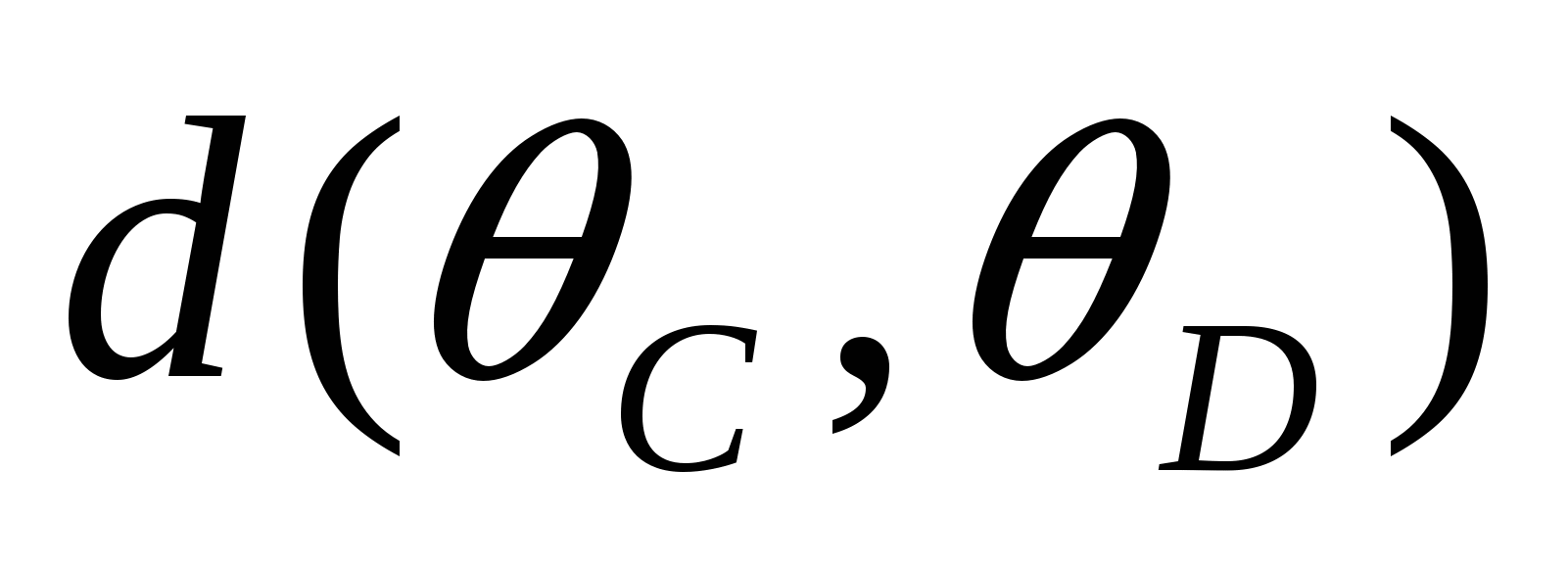 ,
, 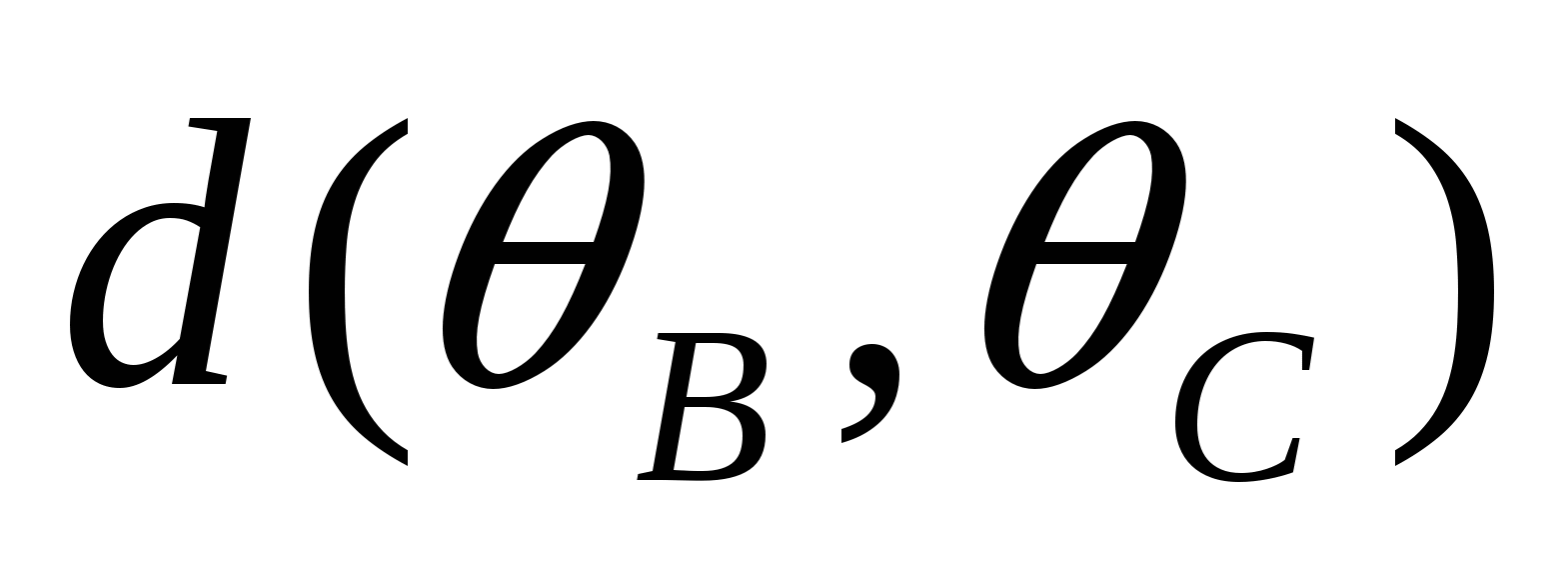 ,
, 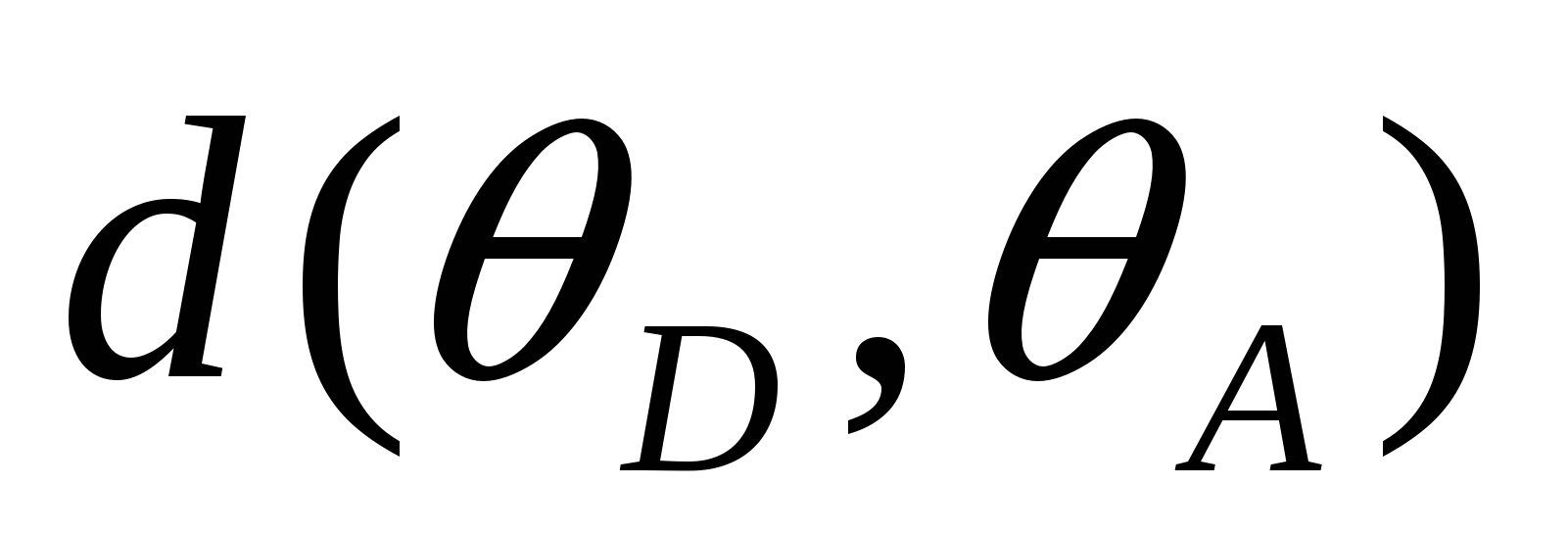 ,
,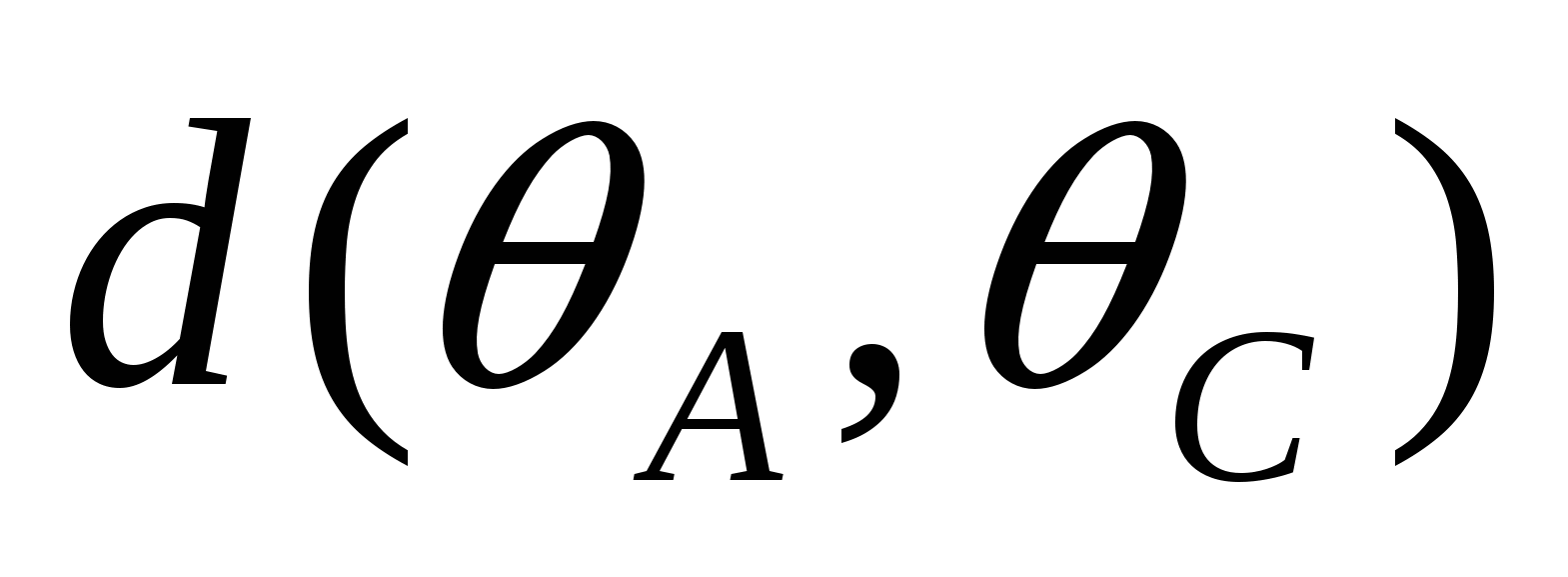 ,
, 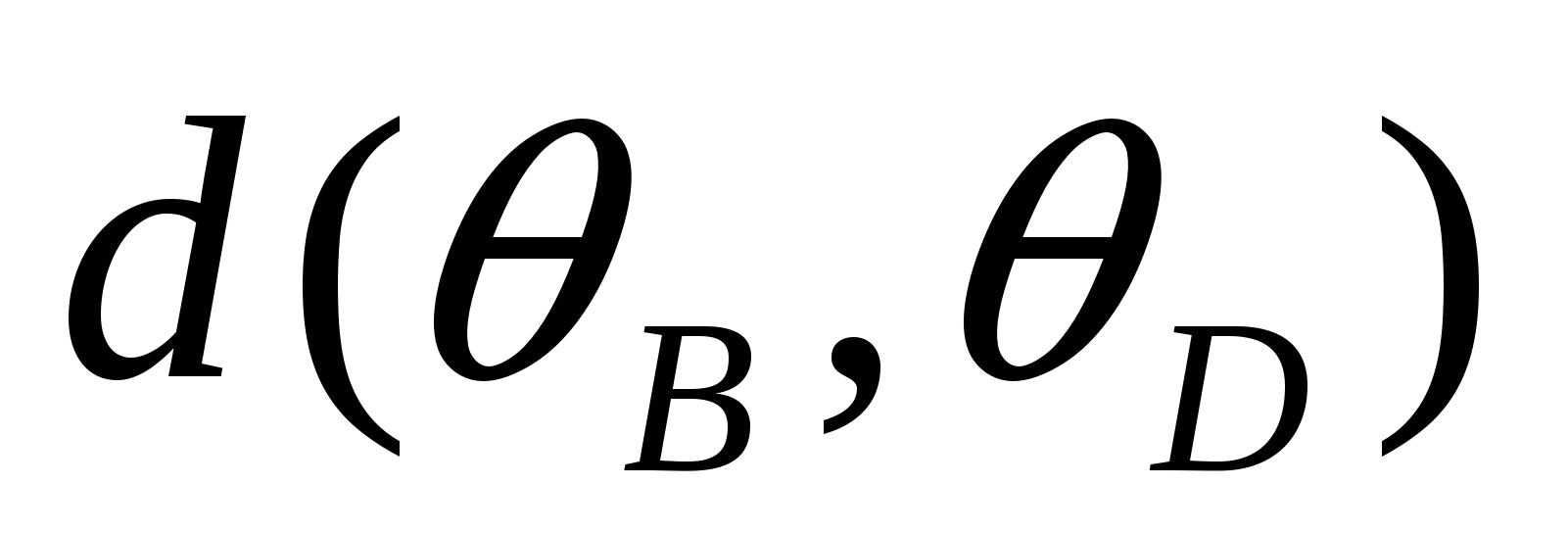
в равенство
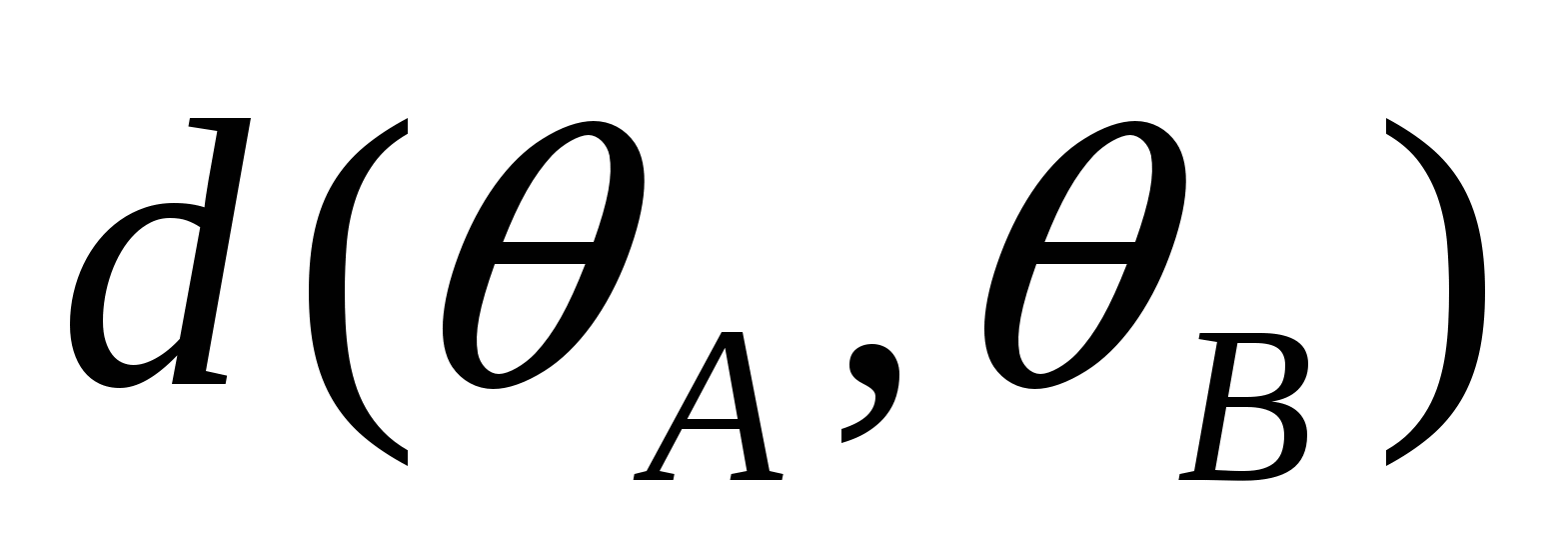 ·
·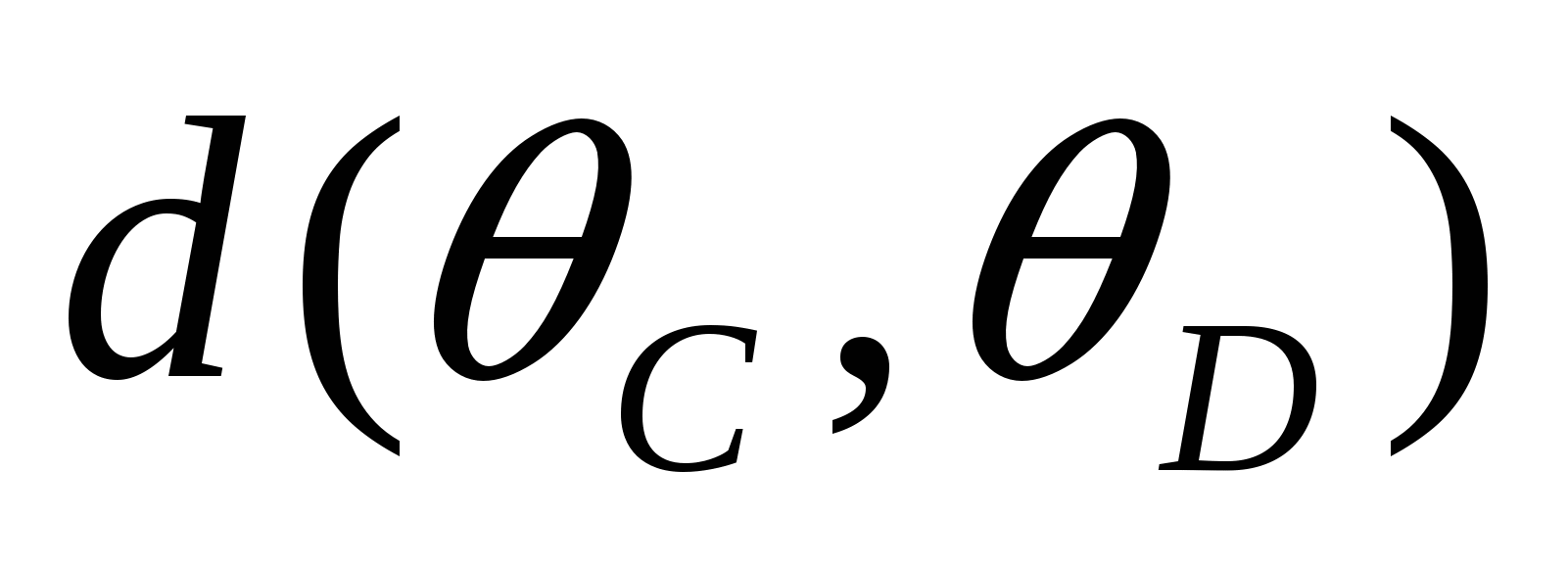 +
+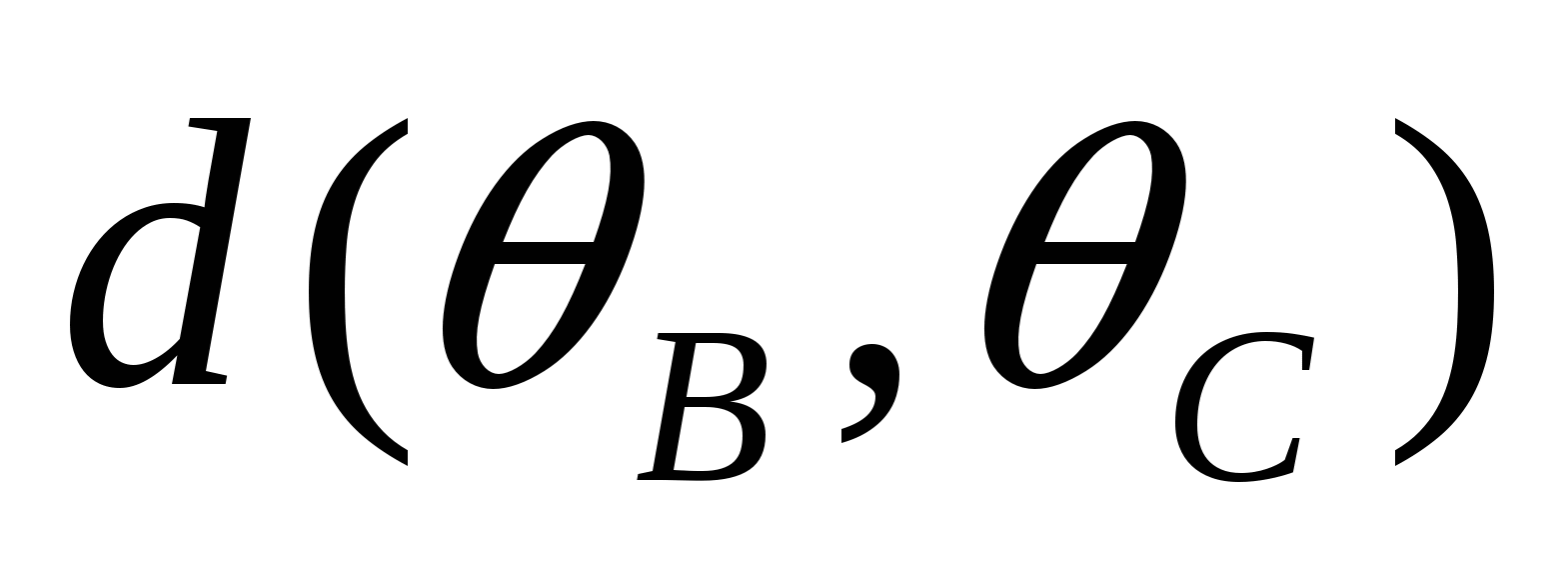
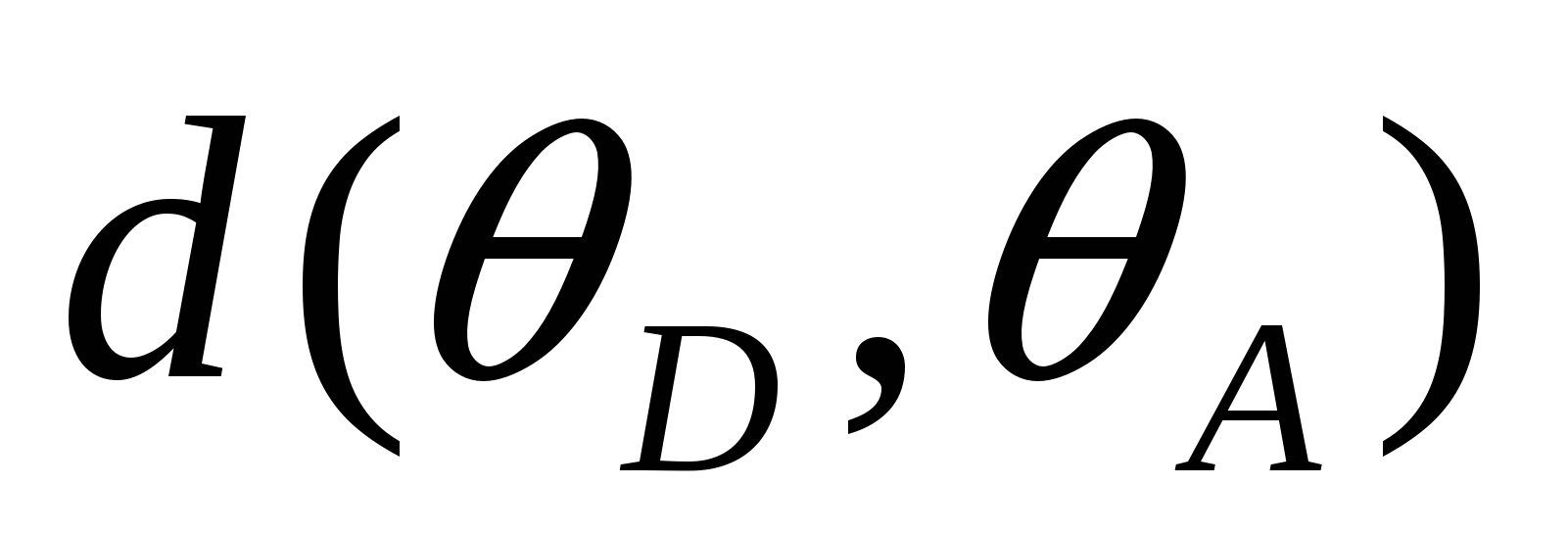 =
=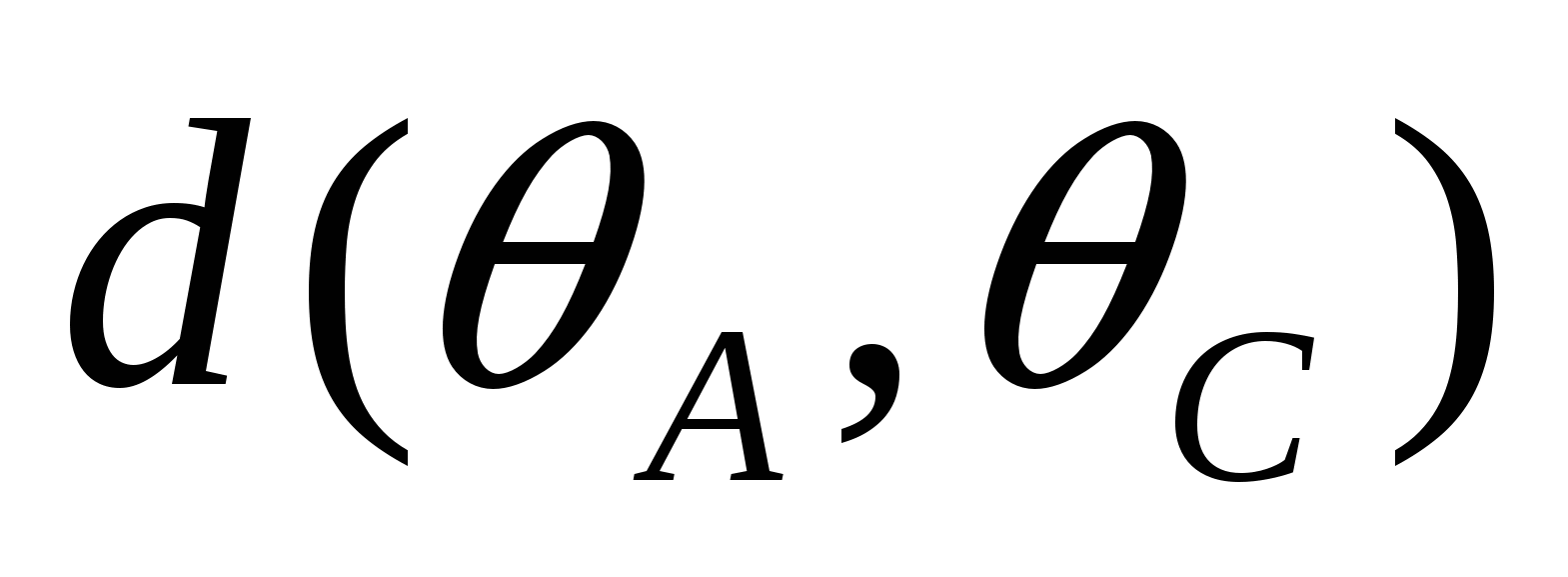
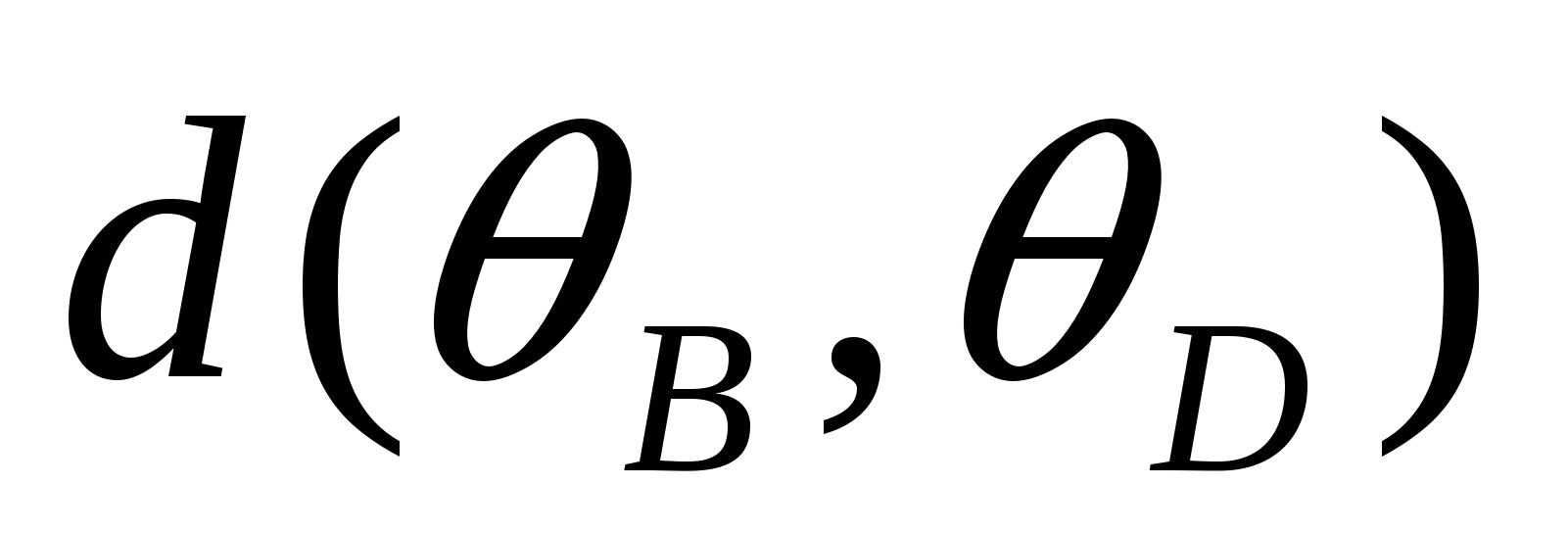 .
.
В результате получим равенство, равносильное следующему:
АС · DВ = АВ · DС + ВС · DА,
что верно для четырехугольника АВСD по обычной теореме Птолемея.
Тем самым, ввиду равносильности соответствующих равенств, обобщенная теорема Птолемея доказана для четырех окружностей, касающихся  внутренним образом.
внутренним образом.
Она же остается в силе и для четырех окружностей, касающихся  внешним образом (рис. 15).
внешним образом (рис. 15).
Отличие здесь только в том, что если две окружности  и
и 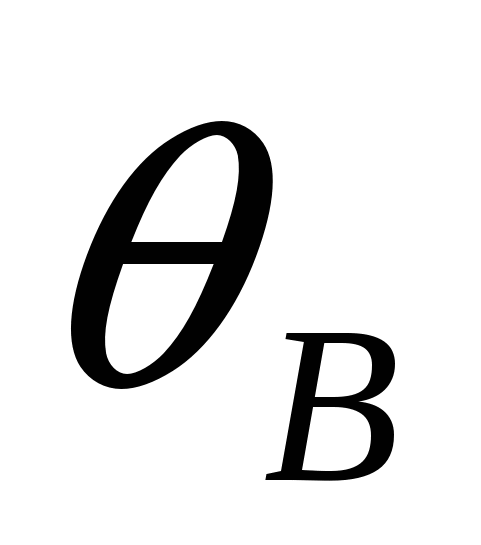 касаются
касаются  внешним образом, то
внешним образом, то
![]() .
.
В качестве геометрического практикума по применению теоремы Птолемея решим с ее помощью задачи.
1. Из концов диаметра, равного 25 см, проведены по одну сторону от него две хорды длиной 24 см и 20 см. Определите расстояние между концами хорд, не лежащими на диаметре.
► Имеем: АВ = 25 см, АС = 24 см, ВD = 20 см,  АСВ =
АСВ =  АDВ = 90º (рис. 16). Из треугольника АDВ по тереме Пифагора АD =
АDВ = 90º (рис. 16). Из треугольника АDВ по тереме Пифагора АD = 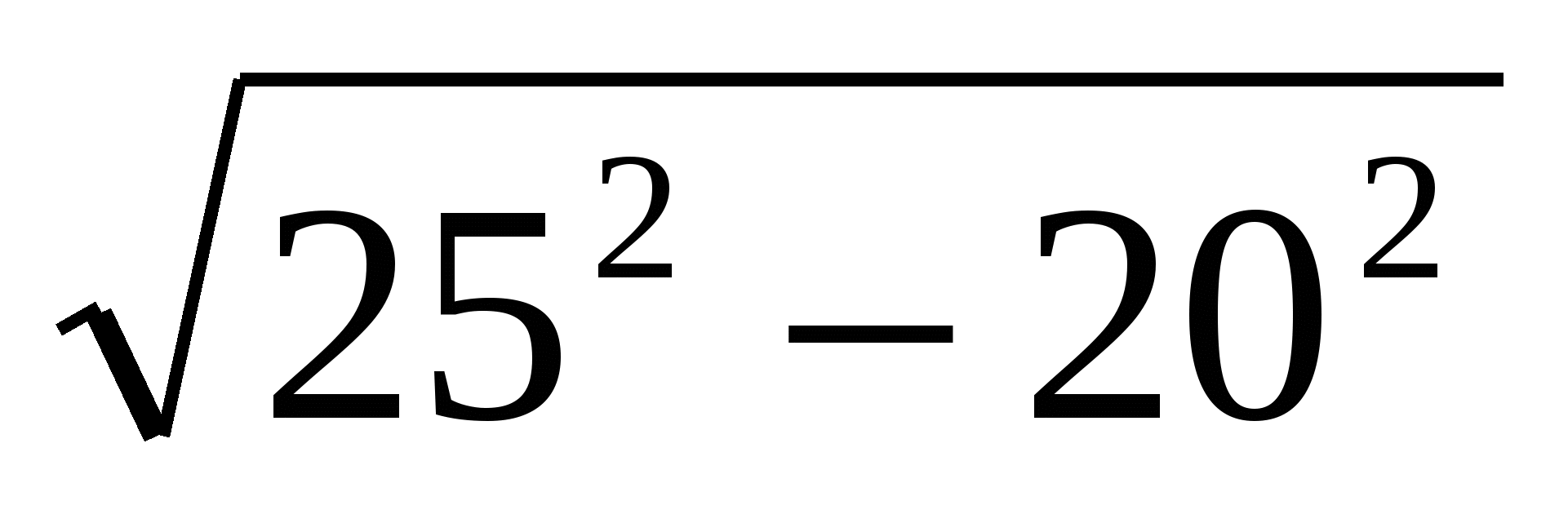 =15(см). Аналогично из треугольника АВС получаем: ВС =
=15(см). Аналогично из треугольника АВС получаем: ВС = 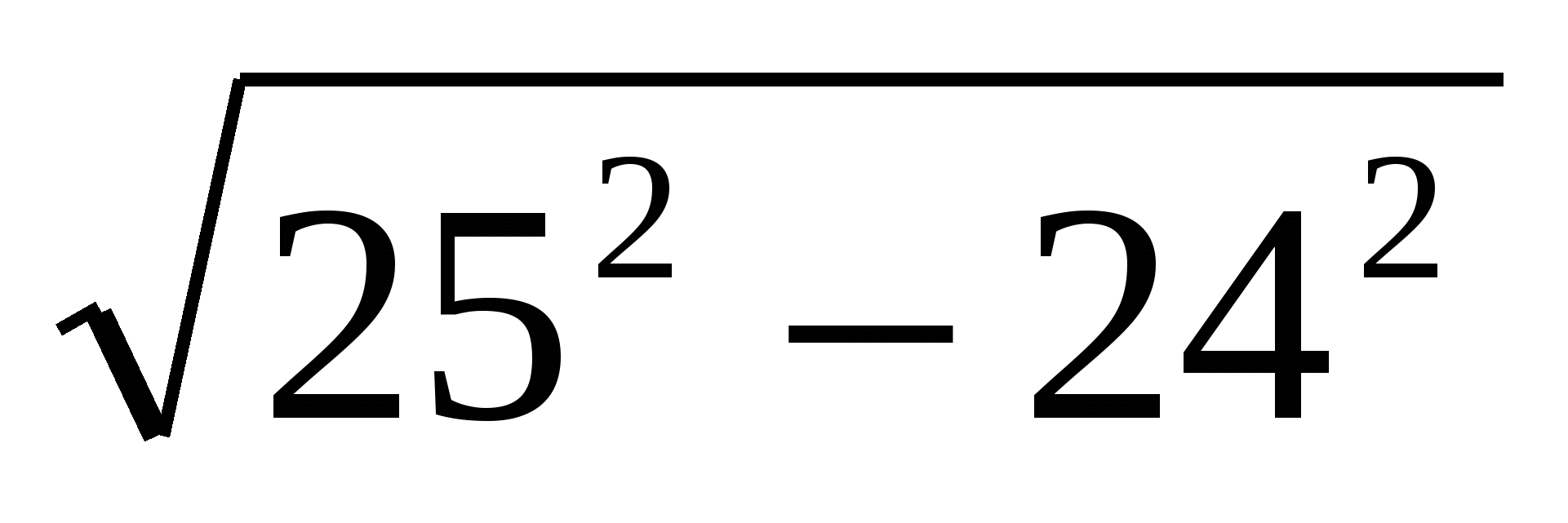 = 7 (см).
= 7 (см).
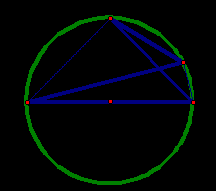
Рис. 16
Введем обозначения: ВО = х, DО = 20 - х, СО = у,
АО = 24 - у. По свойству пересекающихся хорд (АС и ВD):
(20 - х) · х = (24 - у) · у.
Из прямоугольного треугольника ОСВ: 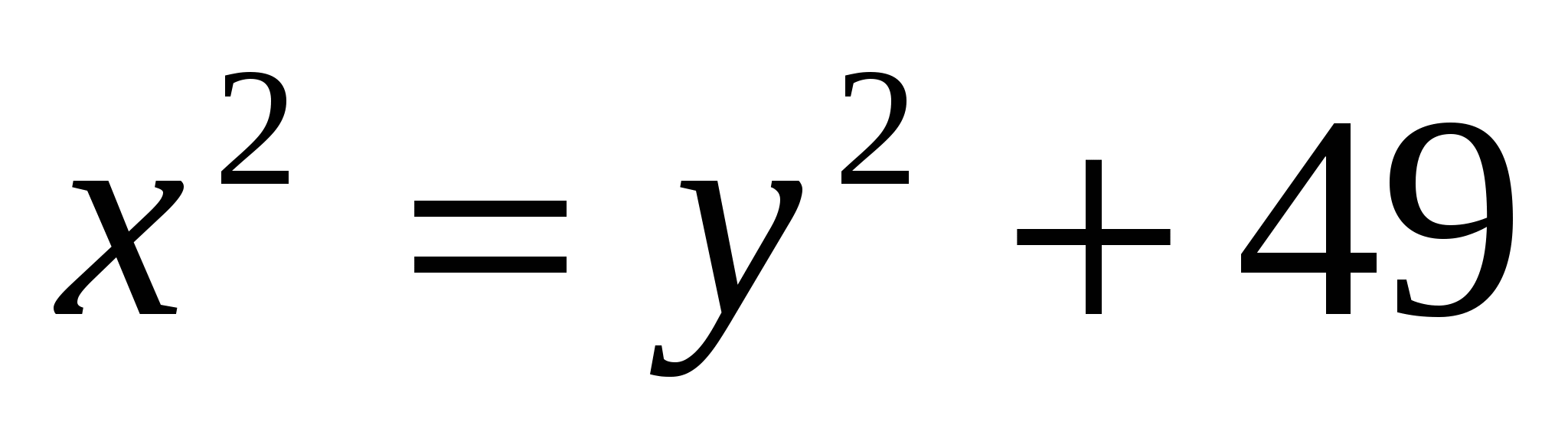 . Решаем систему уравнений:
. Решаем систему уравнений:
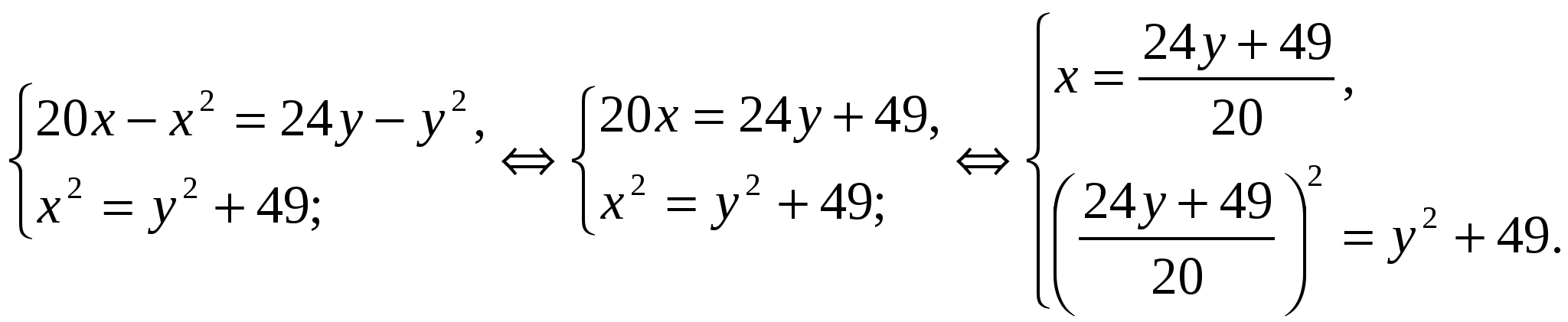
Из второго уравнения последней системы находим: у = 5, 25, т. е. СО = 5, 25 см, тогда х = 8, 75, т. е. ВО = 8, 75 см.
Треугольники DОС и АОВ подобны ( DОС =
DОС =  АОВ как вертикальные,
АОВ как вертикальные,  ВDС =
ВDС =  ВАС как вписанные и опирающиеся на одну и ту же дугу). Значит,
ВАС как вписанные и опирающиеся на одну и ту же дугу). Значит, 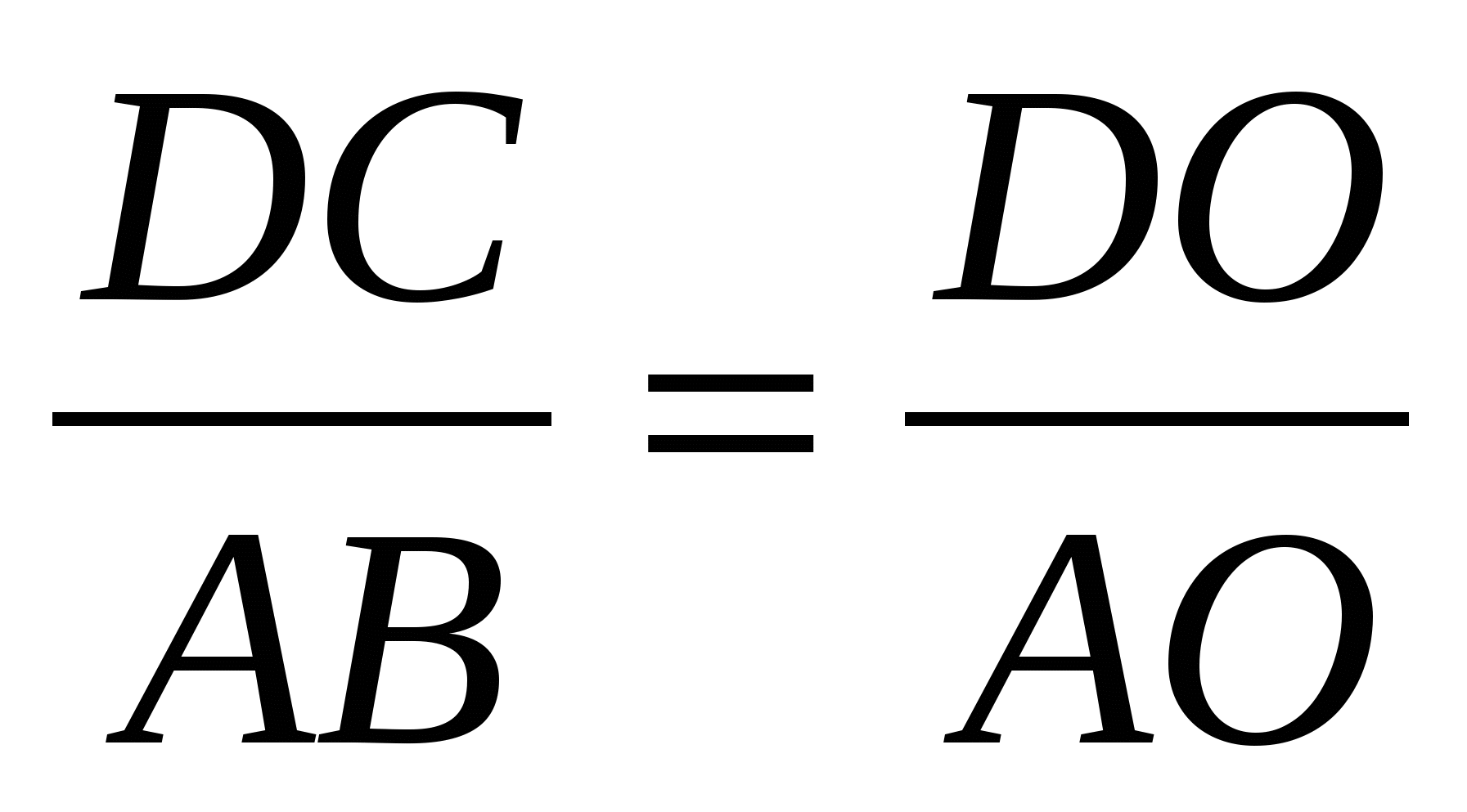 . Отсюда DС = 15 см. ◄
. Отсюда DС = 15 см. ◄
►► Используется теорема Птолемея.
Имеем: АВ = 25 см, АС = 24 см, ВD = 20 см,  АСВ =
АСВ =  АDВ = 90º (рис. 16).
АDВ = 90º (рис. 16).
Из треугольника АDВ по тереме Пифагора АD = 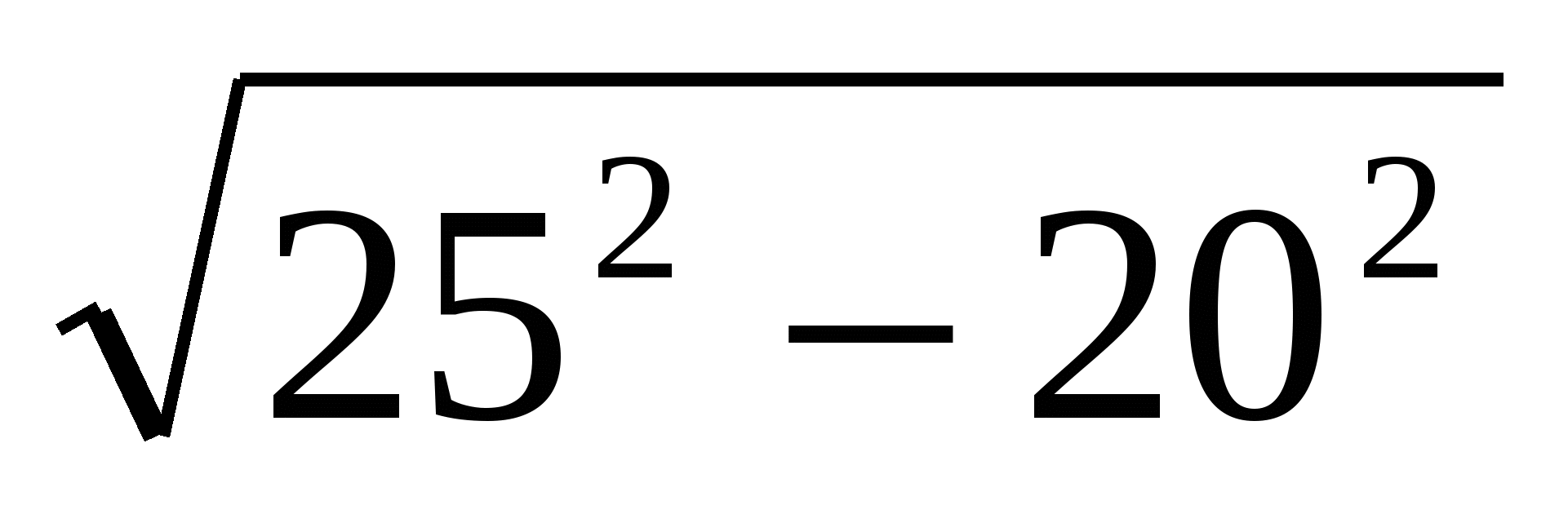 =15(см). Аналогично из треугольника АВС получаем: ВС =
=15(см). Аналогично из треугольника АВС получаем: ВС = 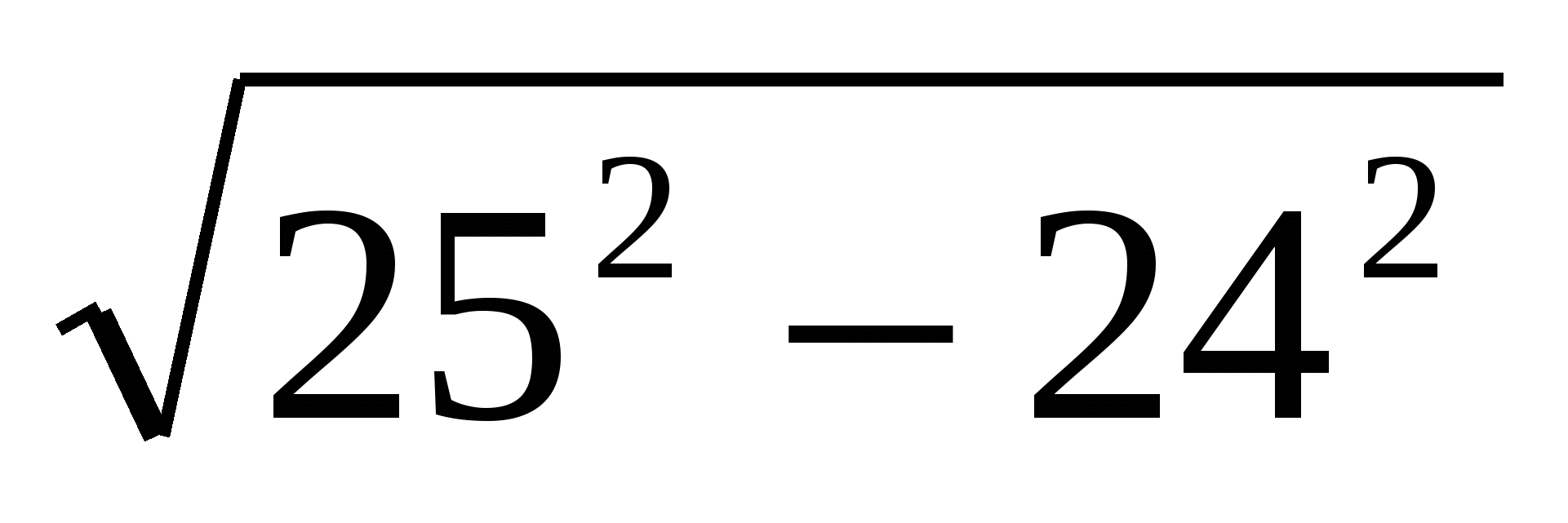 = 7 (см).
= 7 (см).
Четырехугольник АВСD - вписанный.
По теореме Птолемея
АС · DВ = АВ · DС + ВС · DА, т. е.
24 · 20 = 15 · 7 + 25 · DС. Отсюда DС = 15 см.
Ответ: 15 см. ◄
2. Четырехугольник АВСD вписан в окружность, причем  АСD = 90º,
АСD = 90º,  АСВ =
АСВ =  ВАD, АD = 2, СD =
ВАD, АD = 2, СD = 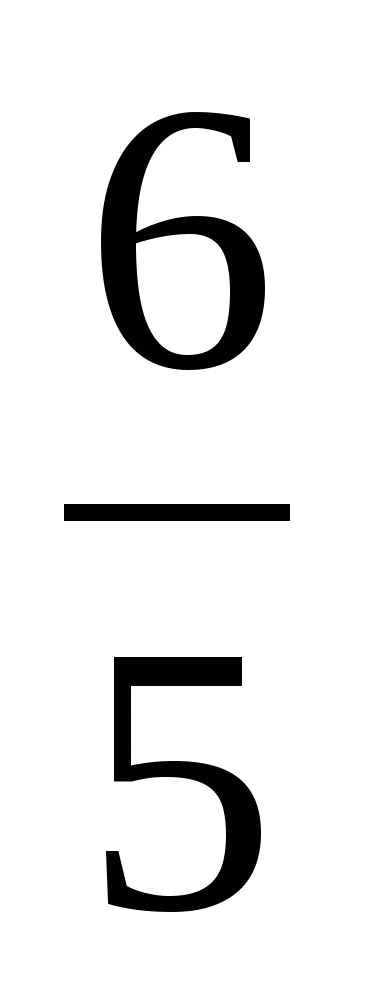 . Найдите ВС.
. Найдите ВС.
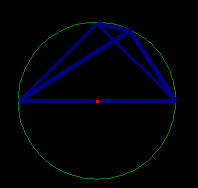
Рис. 17
► Используется теорема Птолемея.
Из условия следует, что АD - диаметр,  АВD = 90º, АВ = ВD (рис. 17). Следовательно, треугольник АВD - равнобедренный прямоугольный, откуда АВ = ВD =
АВD = 90º, АВ = ВD (рис. 17). Следовательно, треугольник АВD - равнобедренный прямоугольный, откуда АВ = ВD = 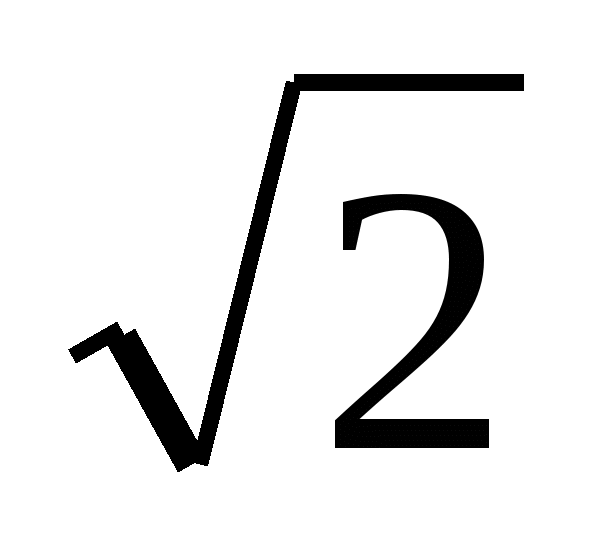 . Далее, из прямоугольного треугольника АСD находим катет АС. Он равен 8/5. Осталось применить теорему Птолемея:
. Далее, из прямоугольного треугольника АСD находим катет АС. Он равен 8/5. Осталось применить теорему Птолемея: 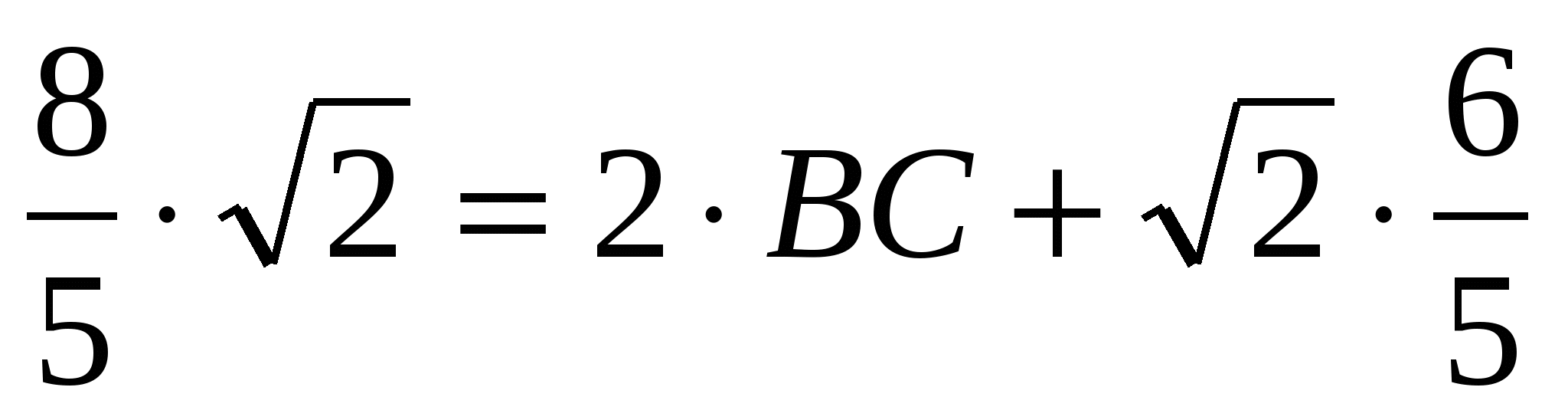 .
.
Ответ: 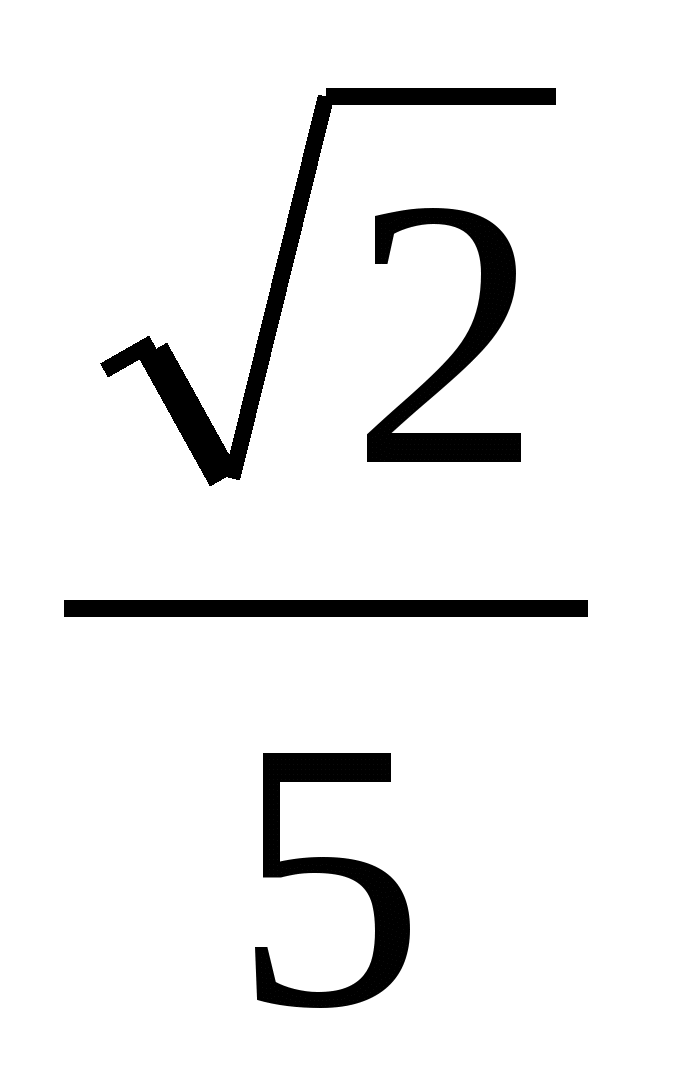 .◄
.◄
►►Установив, что АВ = 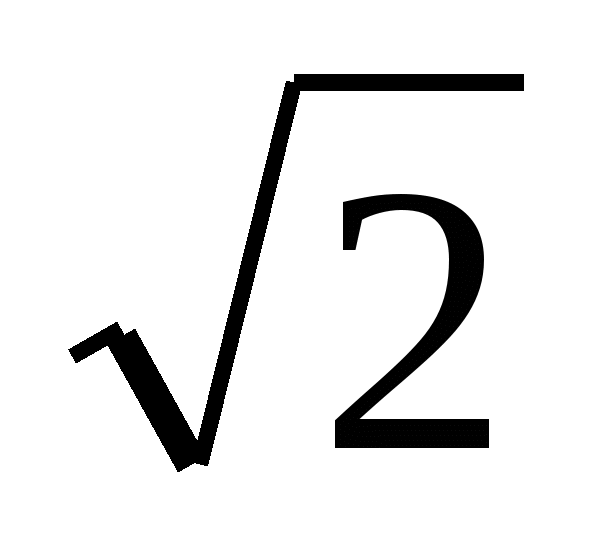 , АС = 8/5,
, АС = 8/5,  АСВ = 45º (см. первое решение), дальше применим теорему косинусов (
АСВ = 45º (см. первое решение), дальше применим теорему косинусов (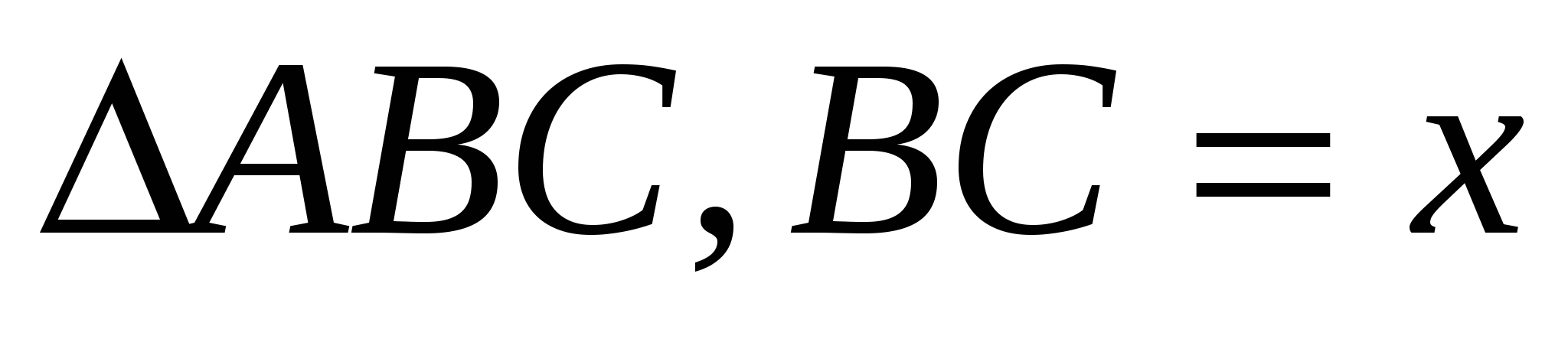 , (рис. 17)):
, (рис. 17)): 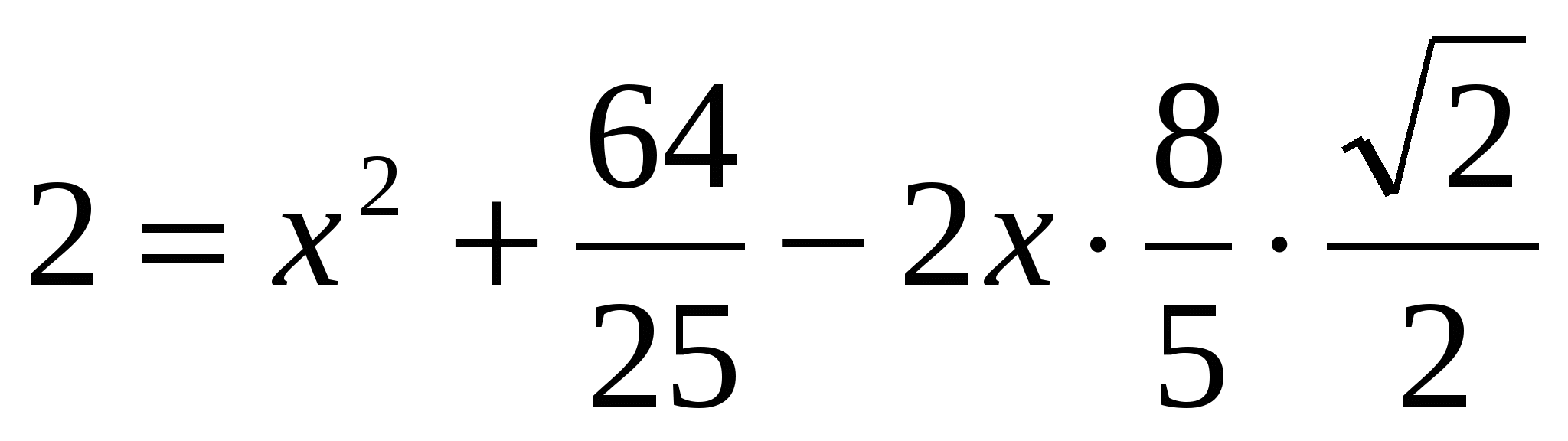 . Решая полученное квадратное уравнение, найдем два его корня:
. Решая полученное квадратное уравнение, найдем два его корня: 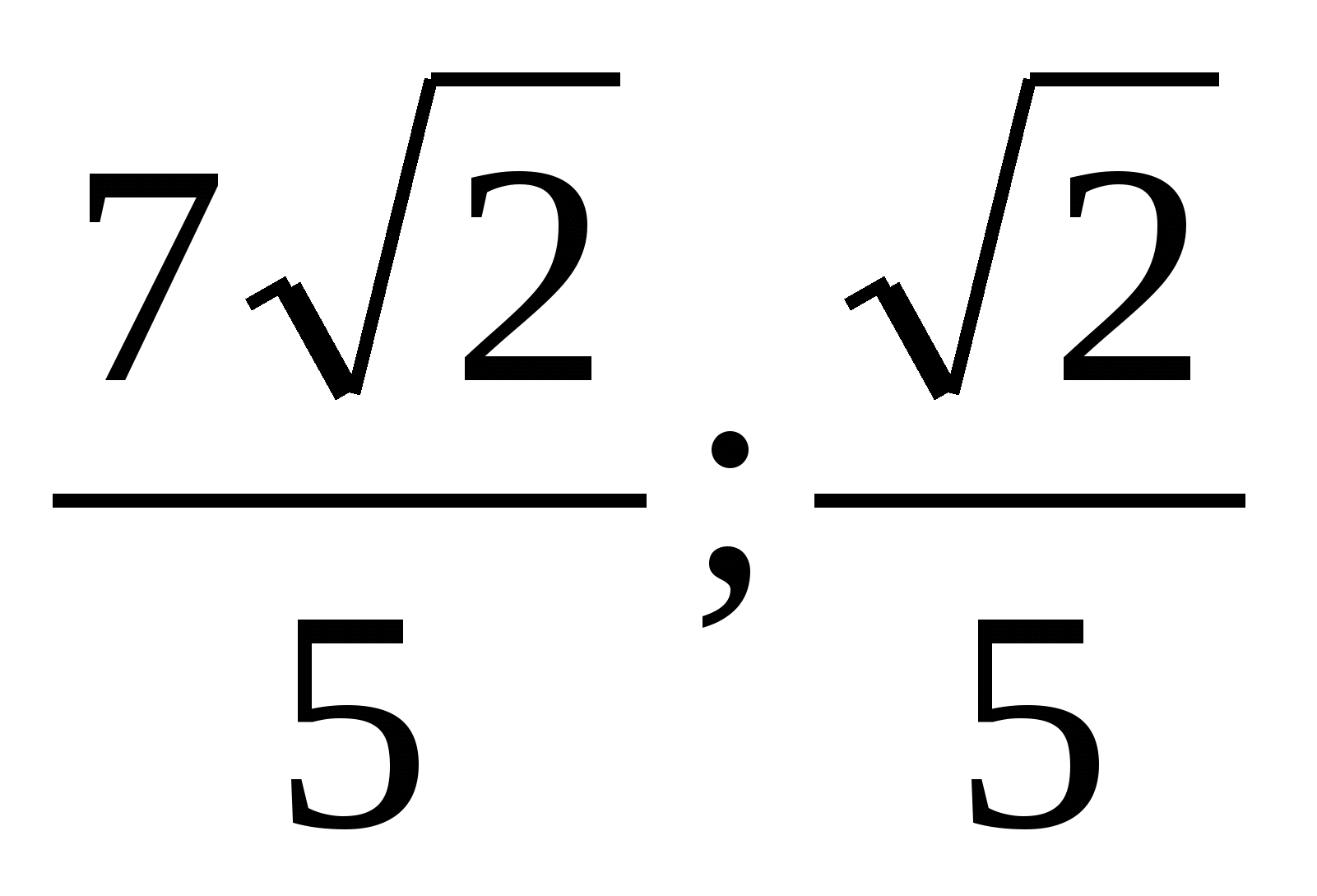 . Один из них
. Один из них 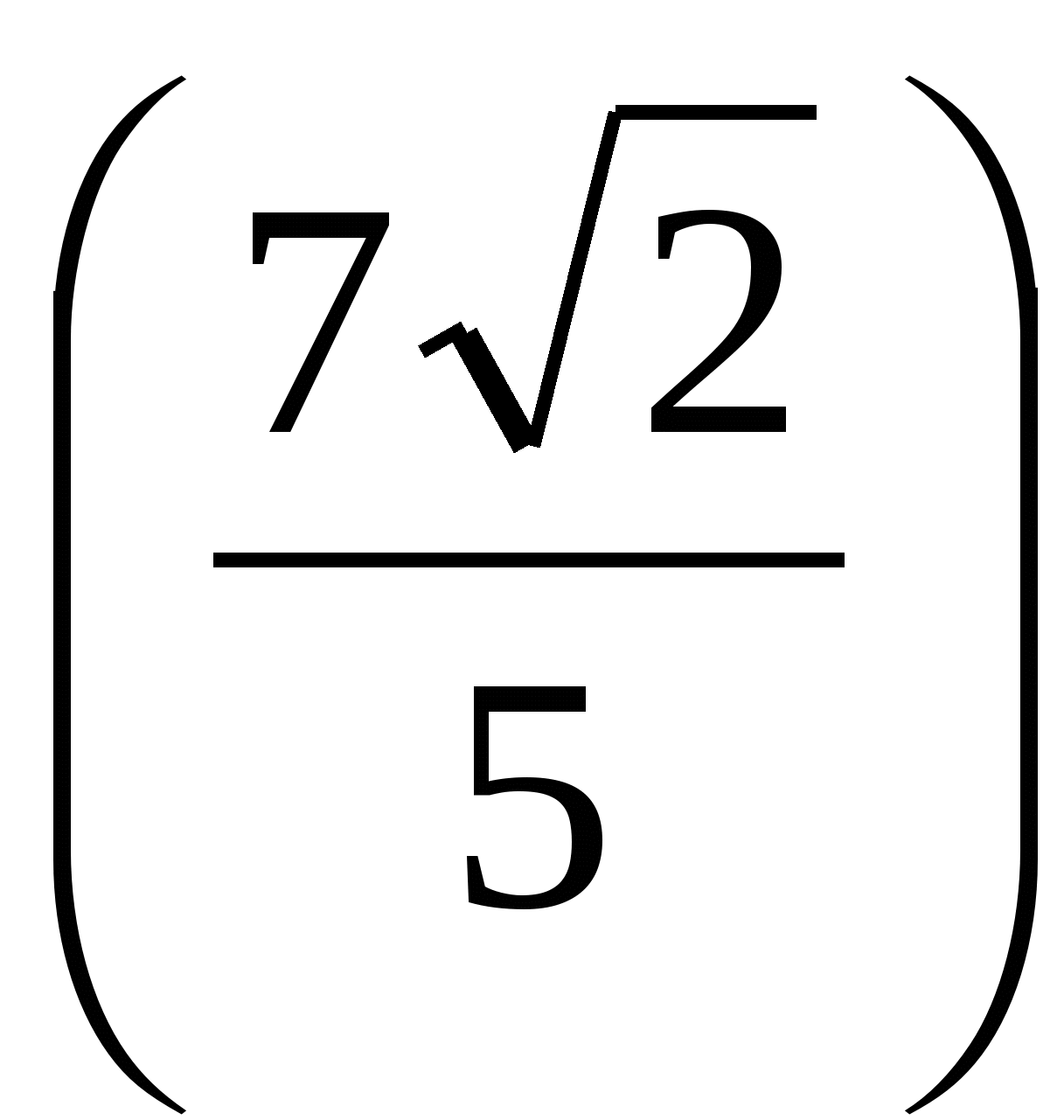 посторонний, так как по условию ВС < АВ. Ответ:
посторонний, так как по условию ВС < АВ. Ответ: 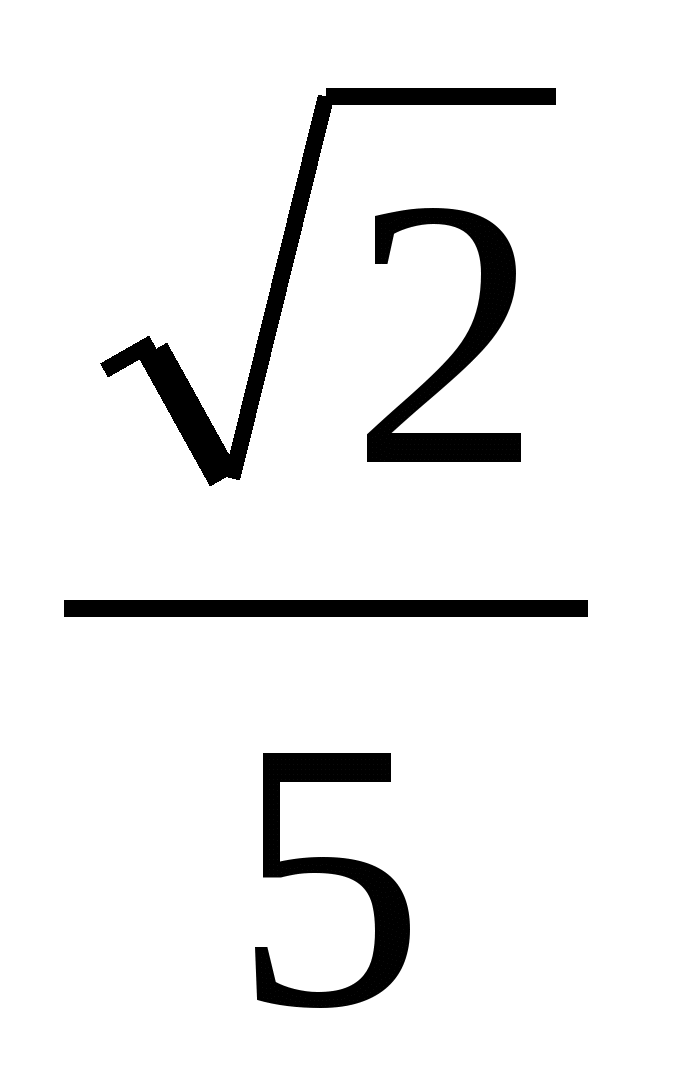 .◄
.◄


