- Преподавателю
- Математика
- Методическая разработка Метод математической индукции
Методическая разработка Метод математической индукции
| Раздел | Математика |
| Класс | - |
| Тип | Другие методич. материалы |
| Автор | Бершак Л.М. |
| Дата | 20.01.2015 |
| Формат | rar |
| Изображения | Есть |
МБОУ лицей «Технико-экономический»
МЕТОД МАТЕМАТИЧЕСКОЙ ИНДУКЦИИ
Автор: Бершак Л.М
МЕТОД МАТЕМАТИЧЕСКОЙ ИНДУКЦИИ.
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
Методическая разработка «Метод математической индукции» составлена для обучающихся 10 класса математического профиля.
Первоочередные цели : познакомить обучающихся с методом математической индукции и научить применять его при решении различных задач.
В методической разработке рассматриваются вопросы элементарной математики: задачи на делимость, доказательство тождеств, доказательство неравенств, предлагаются задачи различной степени сложности, в том числе и задачи, предлагаемые на олимпиадах.
Роль индуктивных выводов в экспериментальных науках очень велика. Они дают те положения, из которых потом путем дедукции делаются дальнейшие умозаключения. Название метод математической индукции обманчиво - на самом деле этот метод является дедуктивным и дает строгое доказательство утверждениям, угаданным с помощью индукции. Метод математической индукции содействует выявлению связей между различными разделами математики, помогает развитию математической культуры обучающегося.
СОДЕРЖАНИЕ
Определение метода математической индукции. Полная и неполная индукции. Доказательство неравенств. Доказательство тождеств. Решение задач на делимость. Решение различных задач по теме «Метод математической индукции».
ЛИТЕРАТУРА ДЛЯ УЧИТЕЛЯ
1. М.Л.Галицкий. Углубленное изучение курса алгебры и математического анализа. - М.Просвещение.1986.
2. Л.И.Звавич. Алгебра и начала анализа. Дидактические материалы. М.Дрофа.2001.
3. Н.Я.Виленкин. Алгебра и математический анализ. М Просвещение.1995.
4. Ю.В.Михеев. Метод математической индукции. НГУ.1995.
ЛИТЕРАТУРА ДЛЯ ОБУЧАЮЩИХСЯ
1. Н.Я.Виленкин. Алгебра и математический анализ. М Просвещение.1995.
2. Ю.В.Михеев. Метод математической индукции. НГУ.1995.
КЛЮЧЕВЫЕ СЛОВА
Индукция, аксиома, принцип математической индукции, полная индукция, неполная индукция, утверждение, тождество, неравенство, делимость.
ДИДАКТИЧЕСКОЕ ПРИЛОЖЕНИЕ К ТЕМЕ
«МЕТОД МАТЕМАТИЧЕСКОЙ ИНДУКЦИИ».
Урок № 1.
Определение метода математической индукции.
Метод математической индукции является одним из высокоэффективных методом поиска новых результатов и доказательства истинности выдвинутых предположений. Хотя этот метод в математике и не нов, но интерес к нему не ослабевает. Впервые в четком изложении метод математической индукции был применен в 17 веке выдающимся французским ученым Блезом Паскалем при доказательстве свойств числового треугольника, носящего с того времени его имя. Однако идея математической индукции была известна еще древним грекам. В основе метода математической индукции лежит принцип математической индукции, который принимается как аксиома. Идею математической индукции рассмотрим на примерах.
Пример № 1.
Квадрат делится отрезком на две части, затем одна из полученных частей делится на две части и так далее. Определить, на какое число частей разделится квадрат через п шагов?
Решение.
После первого шага мы, по условию, получим 2 части. На втором шаге мы одну часть оставляем без изменений, а вторую - делим на 2 части и получаем 3 части. На третьем шаге мы 2 части оставляем без изменений, а третью делим на две части и получаем 4 части. На четвертом шаге мы 3 части оставляем без изменений, а последнюю часть делим на две части и получаем 5 частей. На пятом шаге мы получим 6 частей. Напрашивается предложение, что через п шагов мы получим (п+1) часть. Но это предложение нужно доказать. Предположим, что через к шагов квадрат разобьется на (к+1) часть. Тогда на (к+1) шаге мы к частей оставим без изменения, а (к+1) часть делим на две части и получим (к+2)части. Замечаете, что так можно рассуждать как угодно долго, до бесконечности. То есть, наше предположение, что через п шагов квадрат будет разбит на (п+1) часть, становится доказанным.
Пример № 2.
У бабушки был внучек, который очень любил варенье, и особенно то, что в литровой банке. Но бабушка не разрешала его трогать. И задумал внучек обмануть бабушку. Он решил съедать каждый день по 1/10 л из этой банки и доливать её водой, тщательно перемешав. Через сколько дней бабушка обнаружит обман, если варенье остается прежним на вид при разбавлении его водой на половину?
Решение.
Найдем, сколько чистого варенья останется в банке через п дней. После первого дня в банке останется смесь, состоящая на 9/10 из варенья и на 1/10 из воды. Через два дня из банки исчезнет 1/10 смеси воды и варенья и останется ( в 1л смеси находится 9/10л варенья, в 1/10л смеси находится 9/100лваренья)
9/10 - 9/100=81/100=(9/10)2л варенья. На третий день из банки исчезнет 1/10л смеси, состоящей на 81/100 из варенья и на19/100 из воды. В 1л смеси находится 81/100л варенья, в 1/10л смеси 81/1000л варенья. 81/100 - 81/1000=
=729/1000=(9/10)3л варенья останется через 3 дня, а остальное будет занимать вода. Выявляется закономерность. Через п дней в банке останется (9/10)пл варенья. Но это, опять, только наше предположение.
Пусть к - произвольное натуральное число. Предположим, что через к дней в банке останется (9/10)кл варенья. Посмотрим, что же тогда будет в банке еще через день, то есть, через (к+1) день. Из банки исчезнет 1/10л смеси, состоящей из (9/10)кл варенья и воды. В 1л смеси находится (9/10)кл варенья, в 1/10л смеси (9/10)к+1л варенья. Теперь мы смело можем заявлять, что через п дней в банке останется (9/10)пл варенья. Через 6 дней в банке будет 531444/1000000л варенья, через 7 дней - 4782969/10000000л варенья, то есть меньше половины.
Ответ: через 7 дней бабушка обнаружит обман.
Попытаемся выделить самое основное в решениях рассмотренных задач. Каждую из них мы начинали решать с рассмотрения отдельных или, как говорят, частных случаев. Затем на основе наших наблюдений, мы высказывали некоторое предположение Р(п), зависящее от натурального п.
-
утверждение проверили, то есть доказали Р(1), Р(2), Р(3);
-
предположили, что Р(п) справедливо при п=к и вывели, что тогда оно будет справедливо и при следующем п, п=к+1.
А затем рассуждали примерно так: Р(1) верно, Р(2) верно, Р(3) верно, Р(4) верно,…, значит верно Р(п).
Принцип математической индукции.
Утверждение Р(п), зависящее от натурального п, справедливо при всех натуральных п, если
1) доказана справедливость утверждения при п=1;
2) из предположения справедливости утверждения Р(п) при п=к следует
справедливость Р(п) при п=к+1.
В математике принцип математической индукции выбирается, как правило, в качестве одной из аксиом, определяющих натуральный ряд чисел, и, следовательно, принимается без доказательства. Метод доказательства по принципу математической индукции обычно называется методом математической индукции. Заметим, что этот метод широко применяется при доказательстве теорем, тождеств, неравенств при решении задач на делимость и многих других задач.
Урок № 2
Полная и неполная индукция.
В случае, когда математическое утверждение касается конечного числа объектов, его можно доказать, проверяя для каждого объекта, например, утверждение «Каждое двузначное четное число является суммой двух простых чисел». Метод доказательства, при котором мы проверяем утверждение для конечного числа случаев, называется полной математической индукцией. Этот метод применим сравнительно редко, так как утверждения чаще всего рассматриваются на бесконечных множествах. Например, теорема «Любое четное число равно сумме двух простых чисел» до сих пор ни доказана, ни опровергнута. Если бы мы даже проверили эту теорему для первого миллиарда, это бы ни на шаг не приблизило бы нас к её доказательству.
В естественных науках применяют неполную индукцию, проверяя эксперимент несколько раз, переносят результат на все случаи.
Пример № 3.
Угадаем с помощью неполной индукции формулу для суммы кубов натуральных чисел.
Решение.
13=1; 13+23=(1+2)2; 13+23+33=(1+2+3)2; 13+23+33+43=(1+2+3+4)2;
13+23+33+43+53=(1+2+3+4+5)2; …; 13+23+…+n3=(1+2+…+n)2.
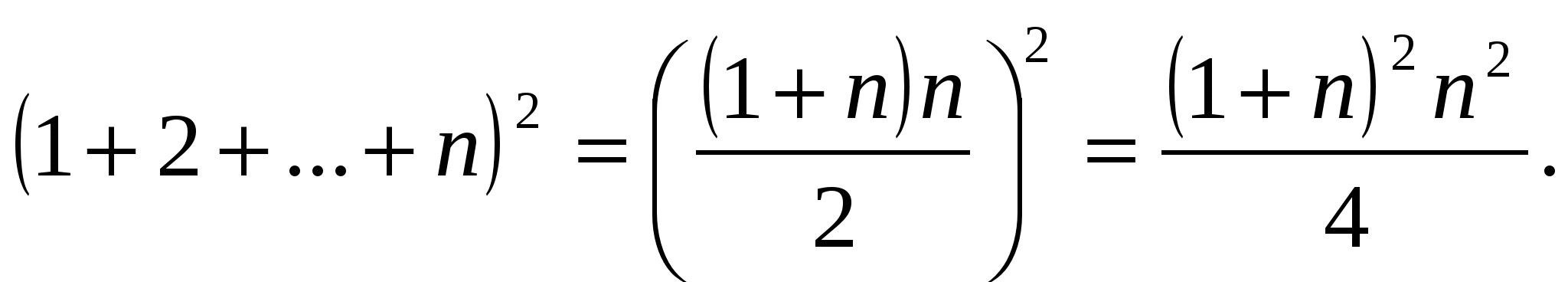
Доказательство.
Пусть верно для п=к. 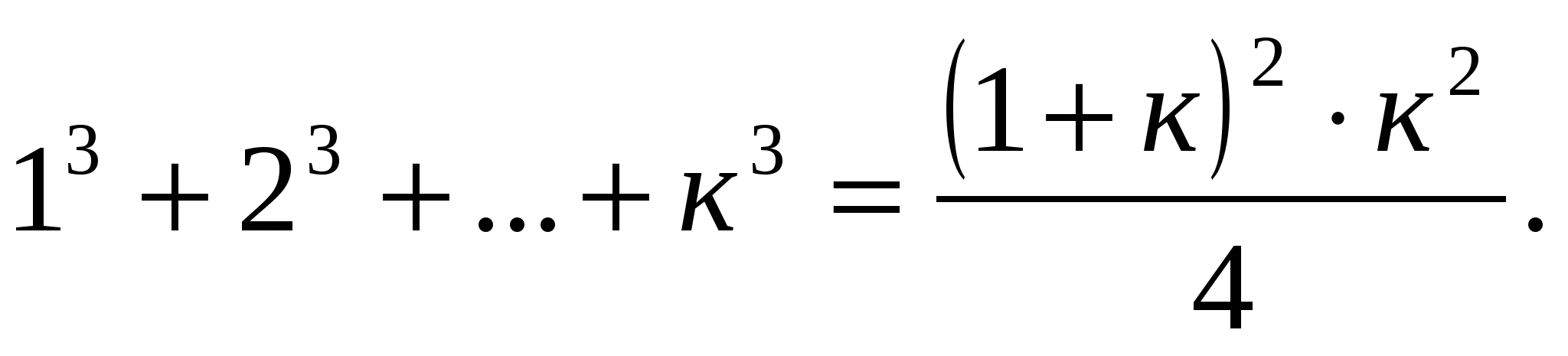
Докажем, что верно для п=к+1.
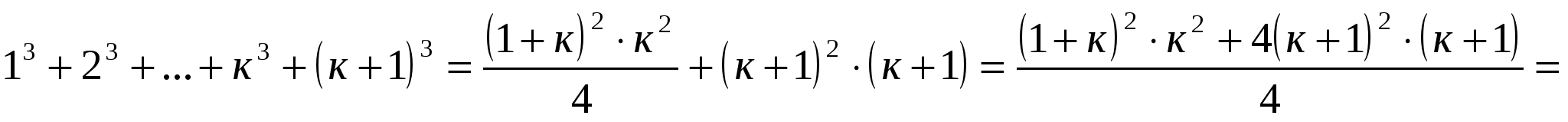
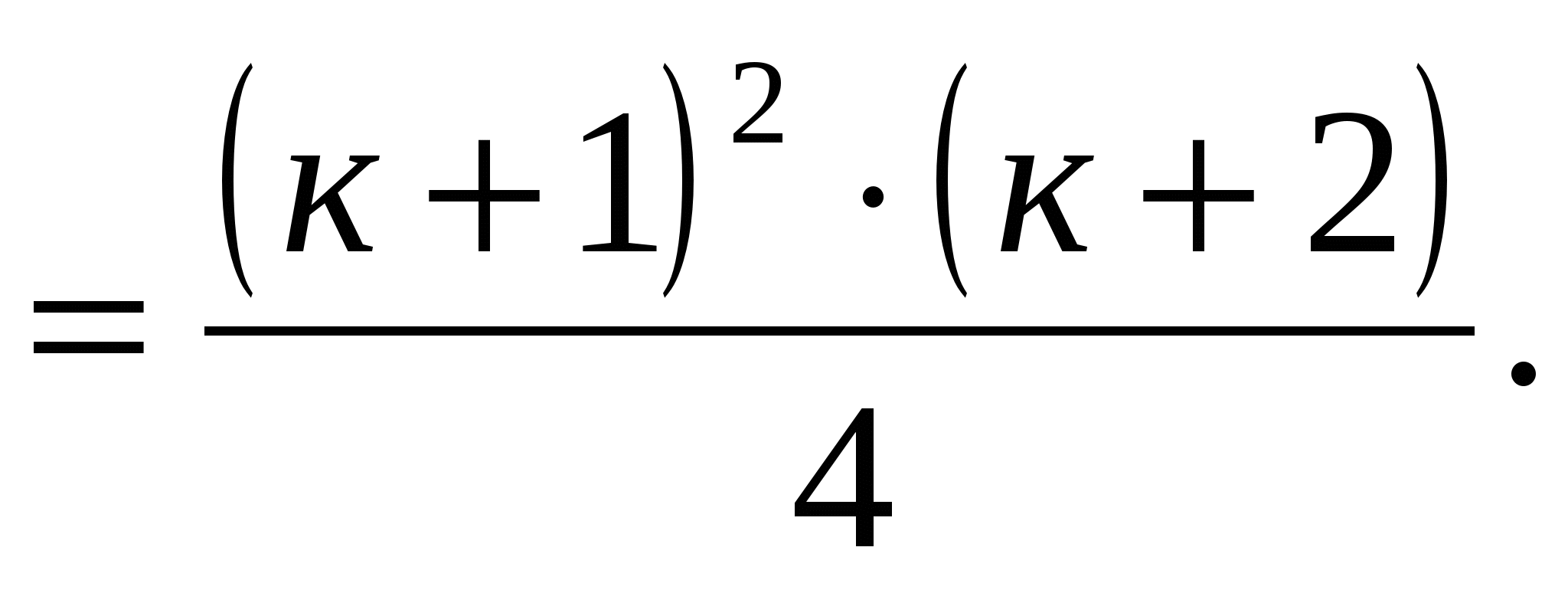
Вывод: формула для суммы кубов натуральных чисел верна для любого натурального п.
Пример № 4.
Рассмотрите равенства и догадайтесь, к какому общему закону подводят эти примеры.
Решение.
1=0+1
2+3+4=1+8
5+6+7+8+9=8+27
10+11+12+13+14+15+16=27+64
17+18+19+20+21+22+23+24+25=64+125
……………………………………………………………..
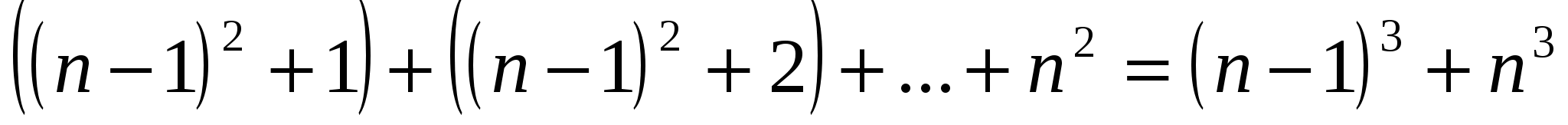
Пример № 5.
Запишите в виде суммы следующие выражения:
1) 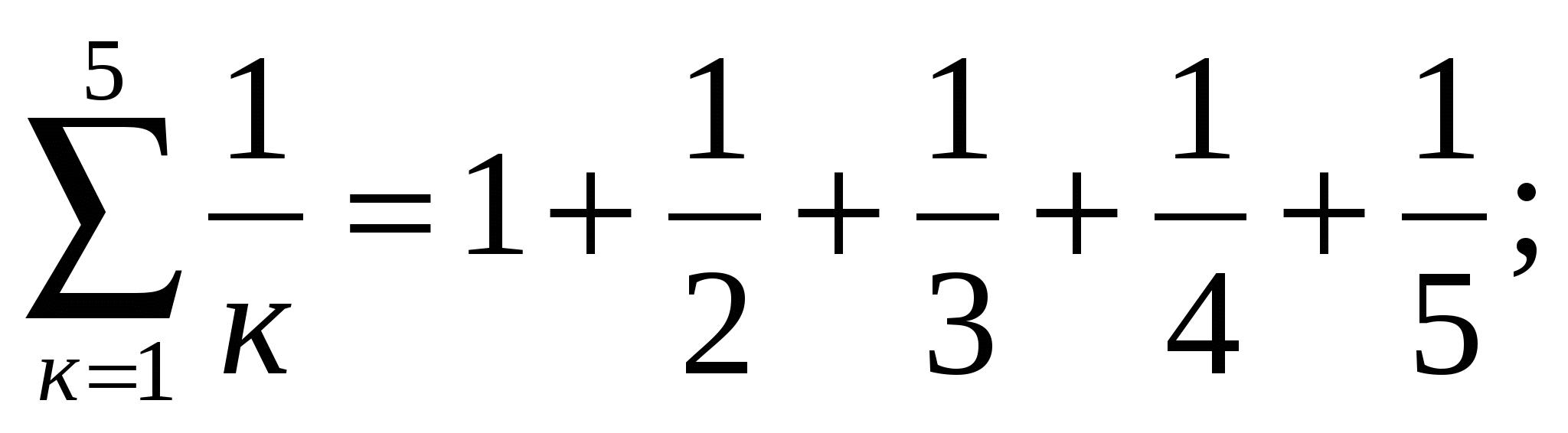 2)
2) 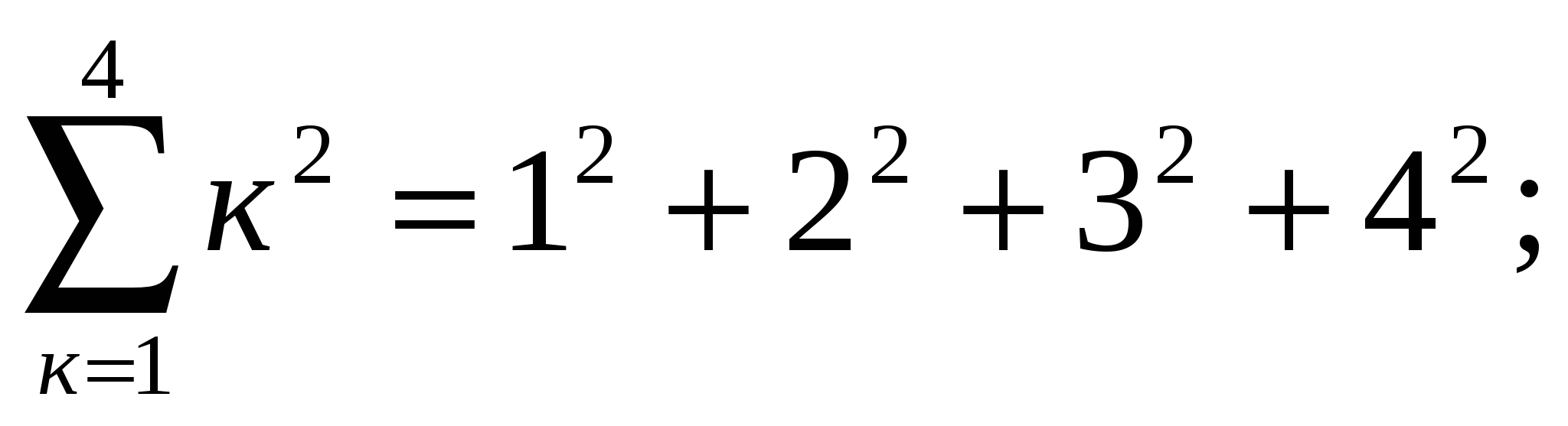 3)
3)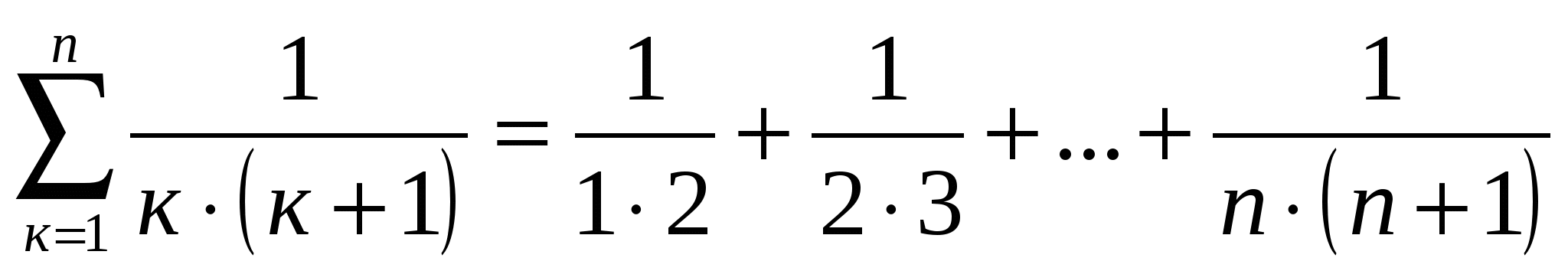 ; 4)
; 4) 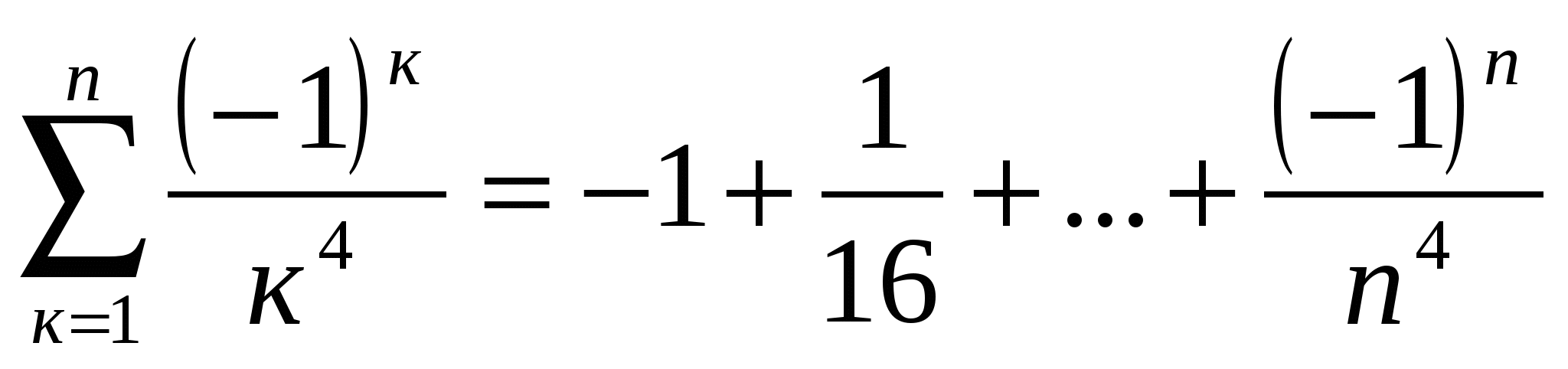 .
.
![]() греческая буква «сигма».
греческая буква «сигма».
Пример № 6.
Запишите следующие суммы с помощью знака 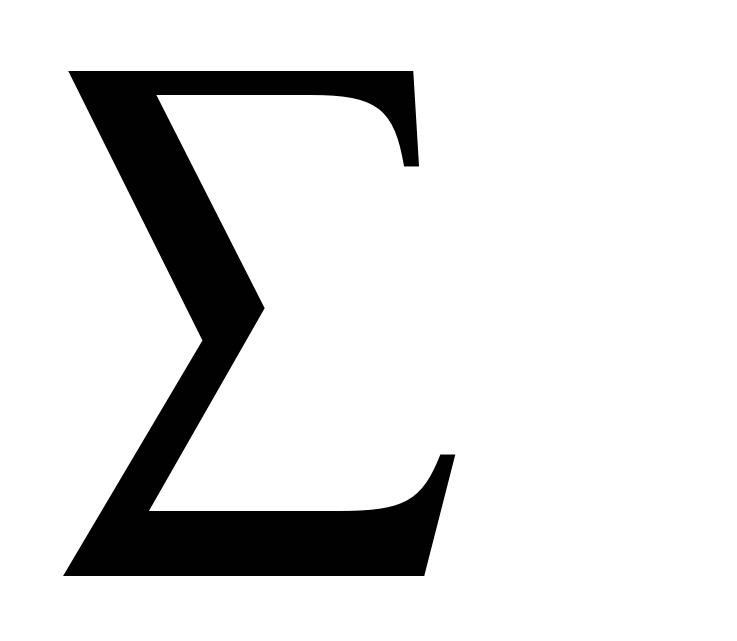 :
:
1)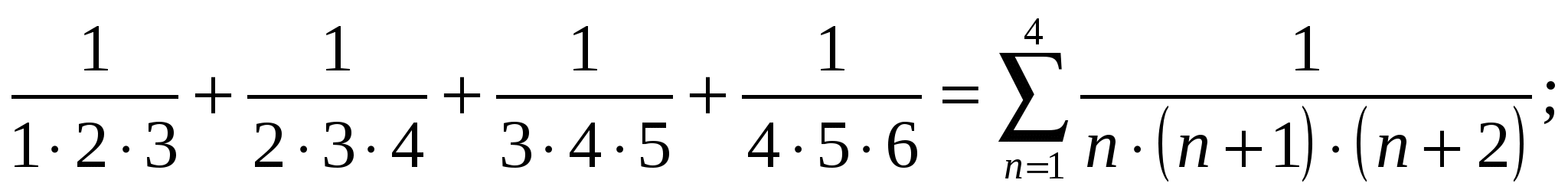
2) 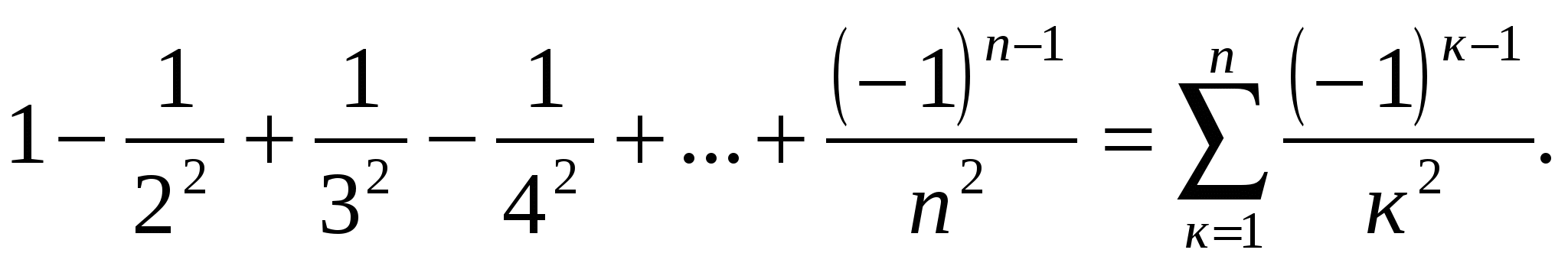
Пример № 7.
Запишите следующие выражения в виде произведений:
1) 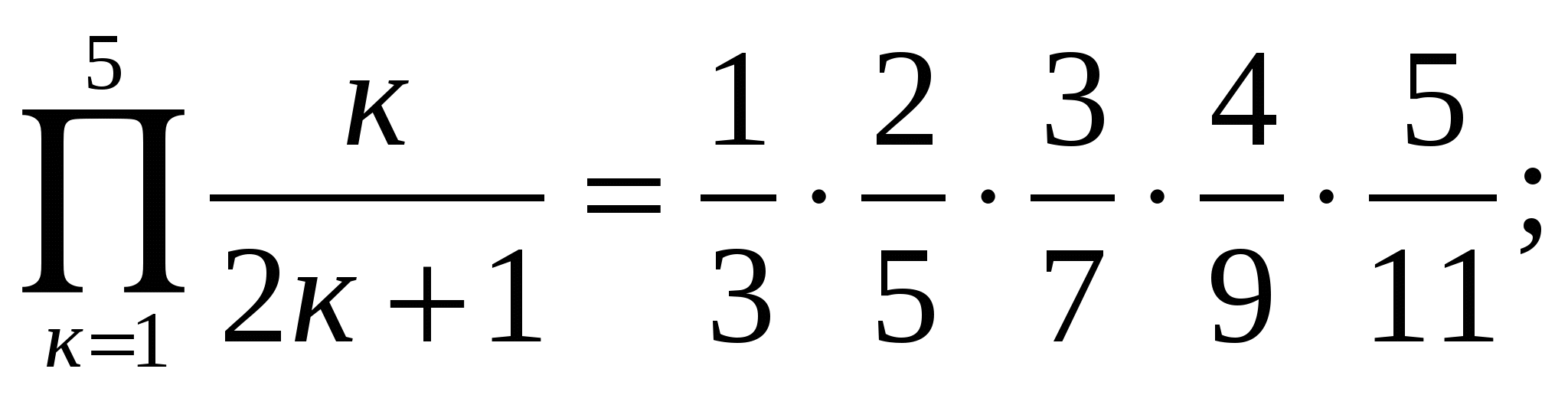
2) 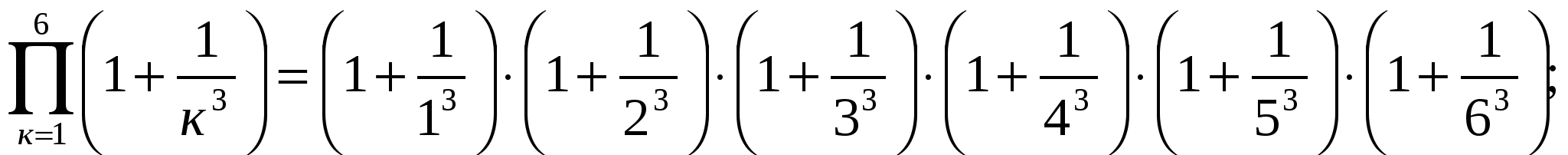
3) 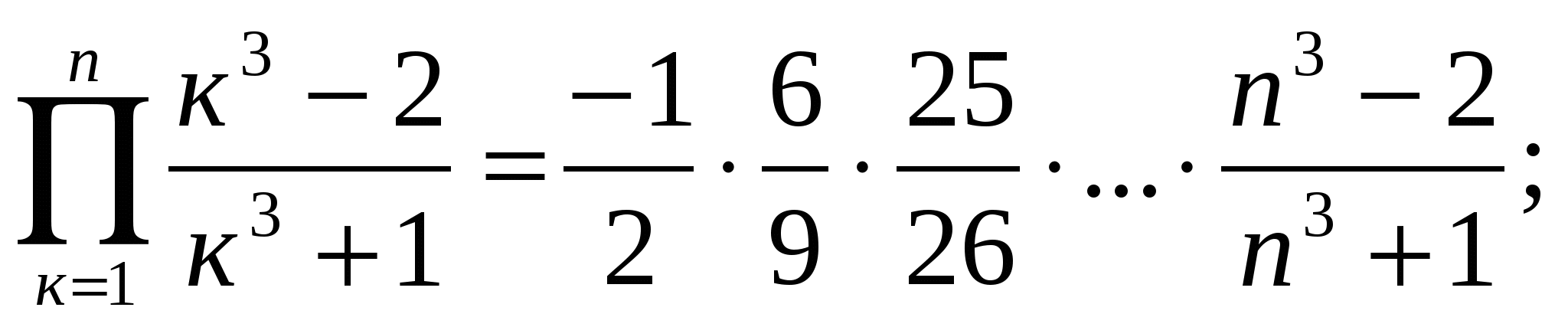 4)
4) 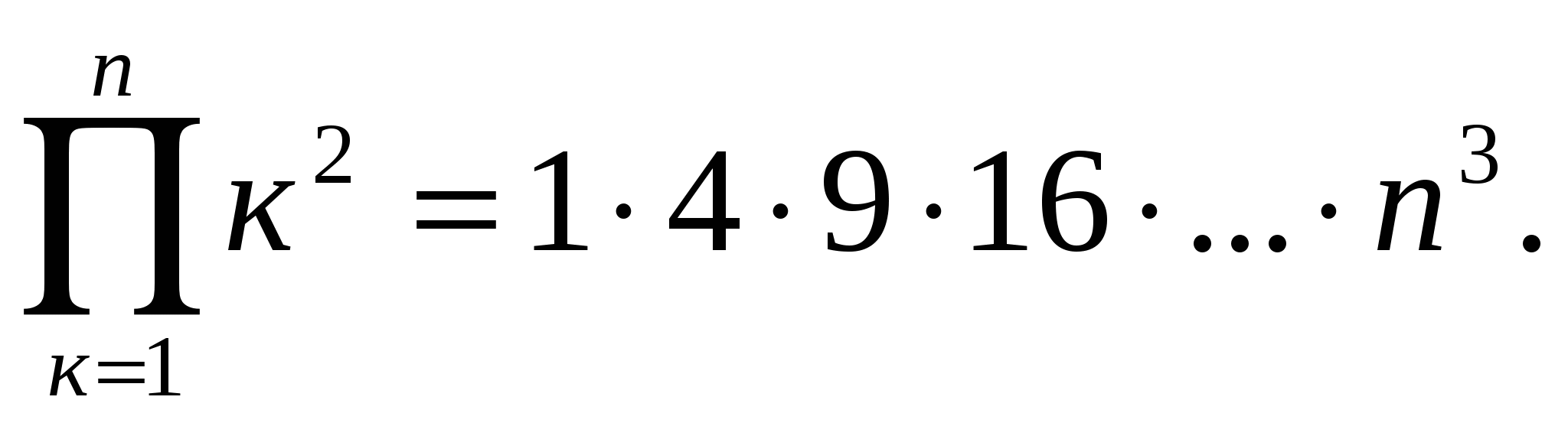
Пример № 8.
Запишите следующие произведения с помощью знака 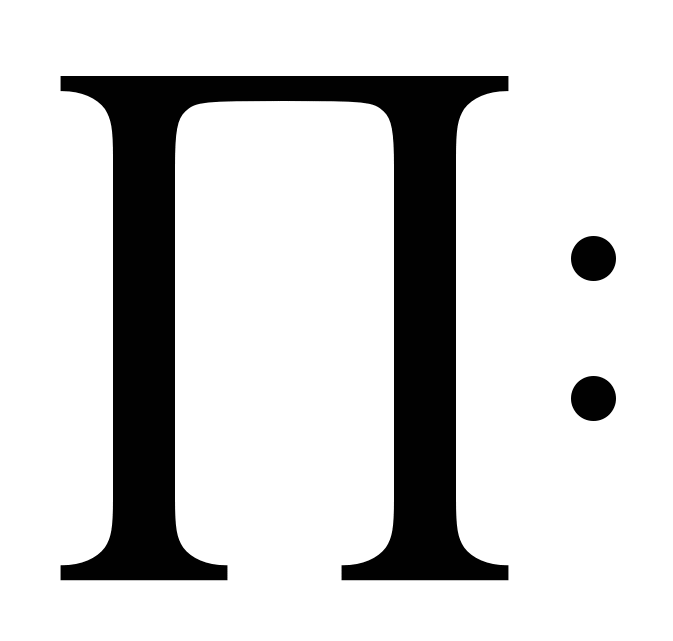
( прописная греческая буква «пи» )
1) 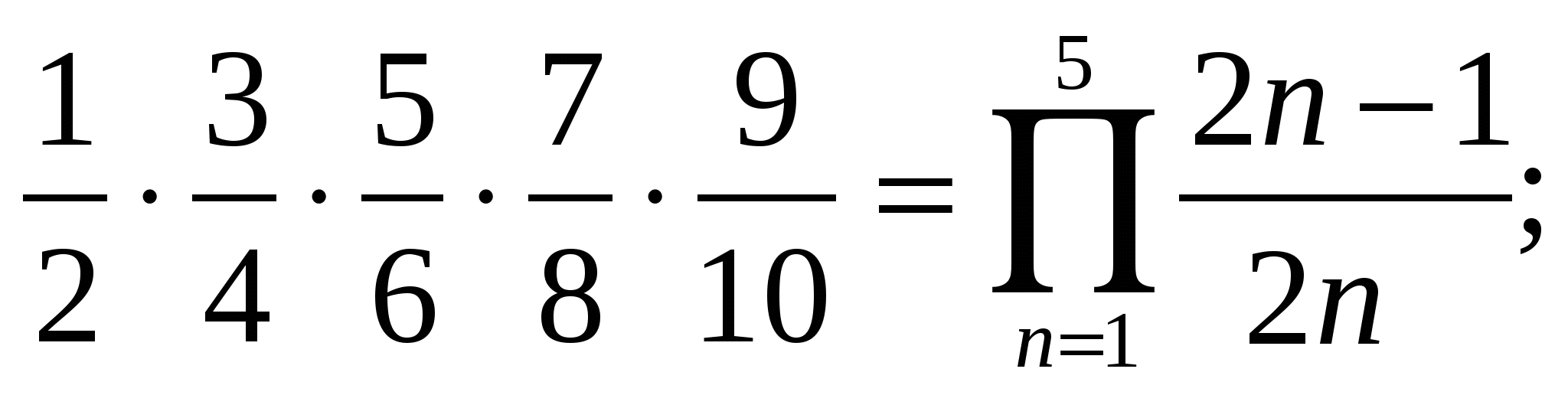 2)
2) 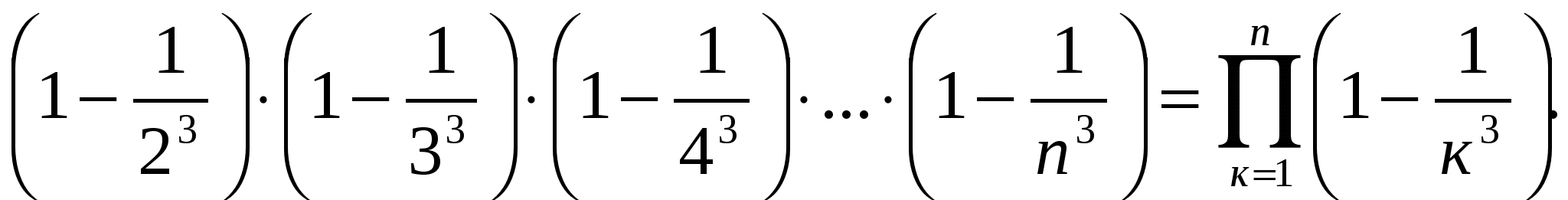
Пример № 9.
Вычисляя значение многочлена  f(n)=n2+n+11, при п=1,2,3,4.5,6,7 можно сделать предположение, что при любом натуральном п число f(n) простое.
f(n)=n2+n+11, при п=1,2,3,4.5,6,7 можно сделать предположение, что при любом натуральном п число f(n) простое.
Верно ли это предположение?
Решение.
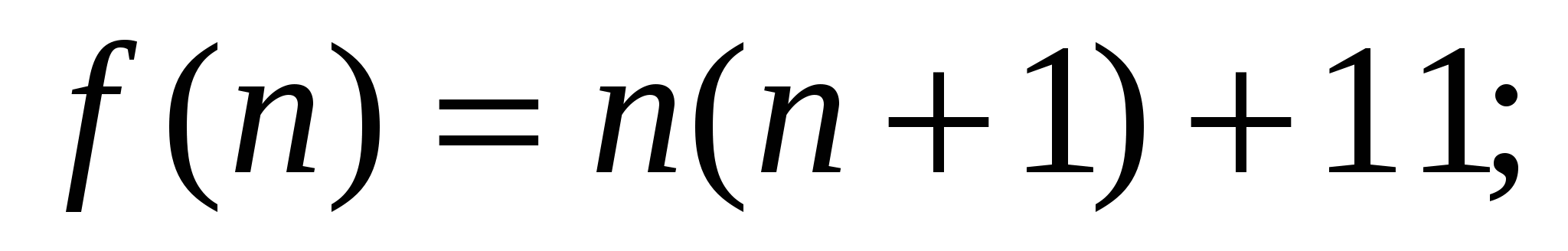
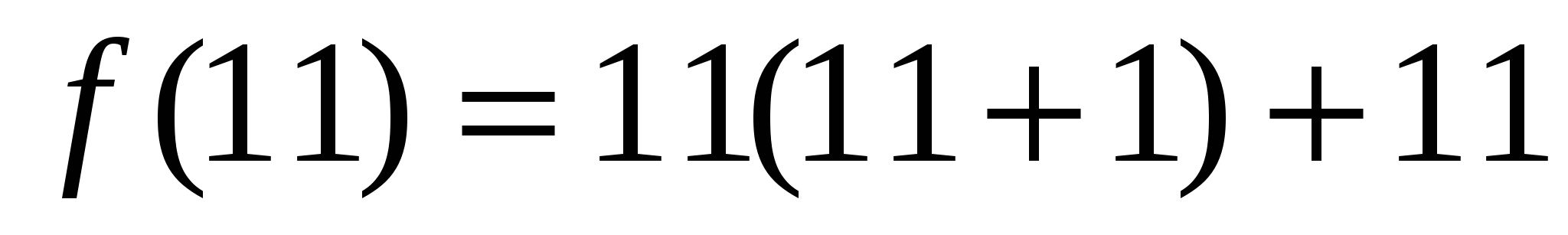 ;
; 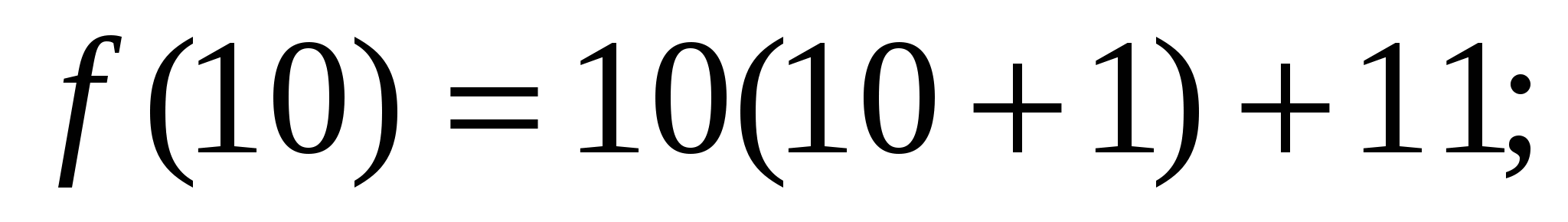
Если каждое слагаемое суммы делится на число, то сумма делится на это число, 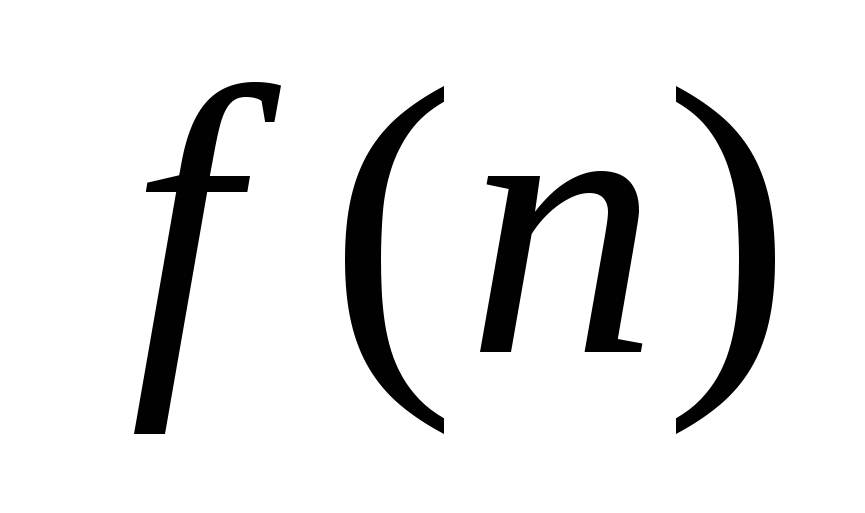 не является простым числом при любом натуральном п.
не является простым числом при любом натуральном п.
Разбор конечного числа случаев играет важную роль в математике: не давая доказательства того или иного утверждения, он помогает угадать правильную формулировку этого утверждения, если она ещё неизвестна. Именно так член Петербургской академии наук Гольдбах пришел к гипотезе, что любое натуральное число, начиная с двух, является суммой не более чем трёх простых чисел.
Урок № 3.
Доказательство тождеств методом математической индукции.
Метод математической индукции позволяет доказывать различные тождества.
Пример № 10. Докажем, что для всех п выполняется тождество
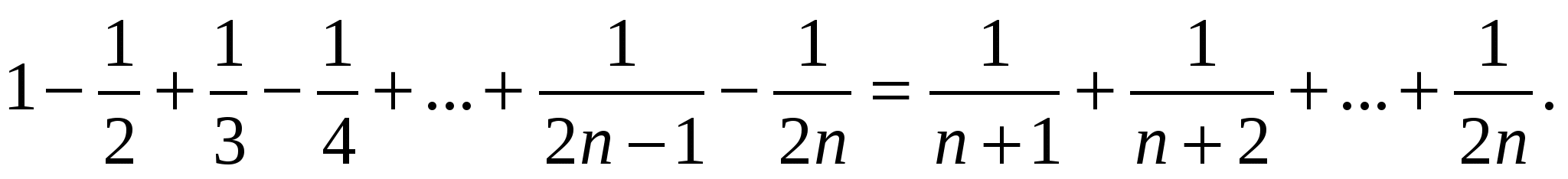
Решение.
Положим 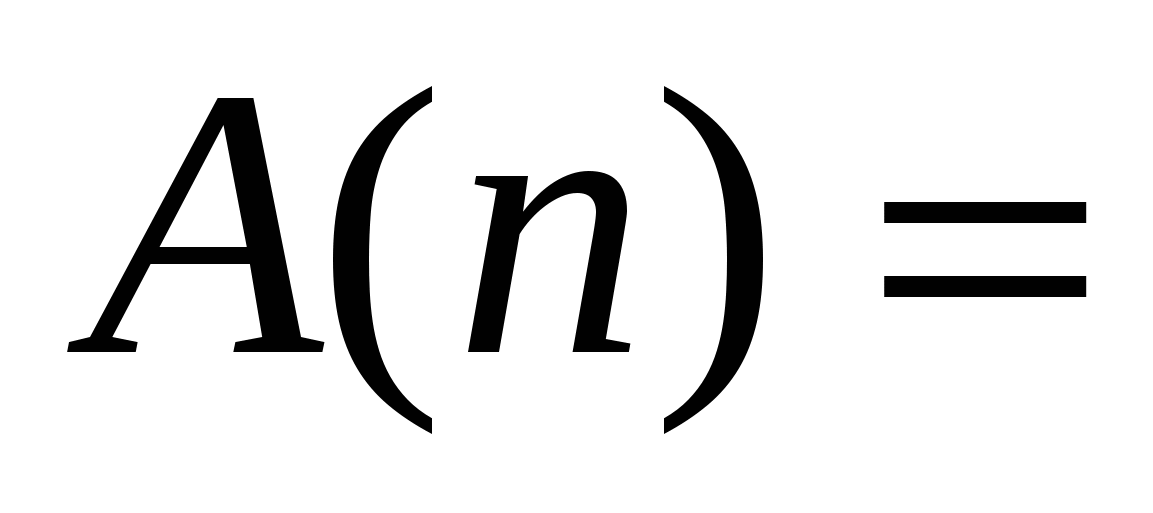
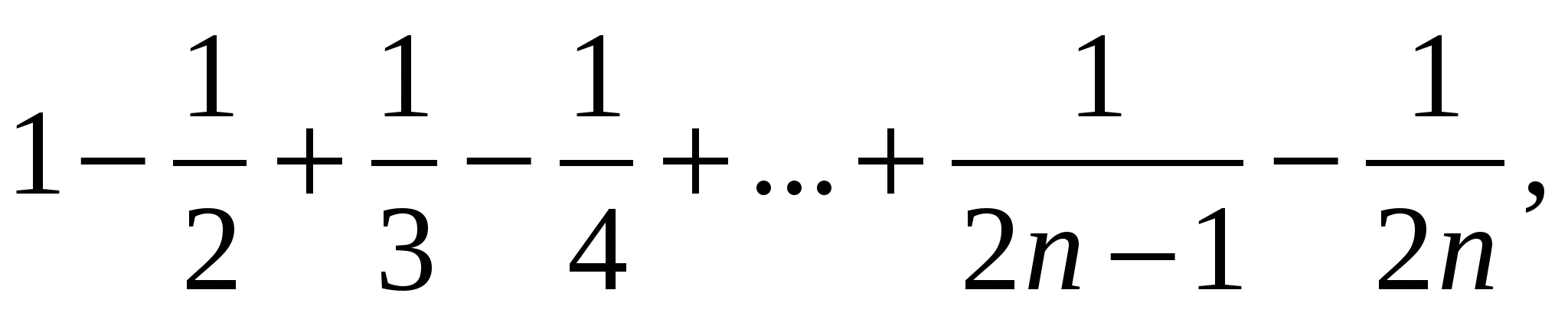
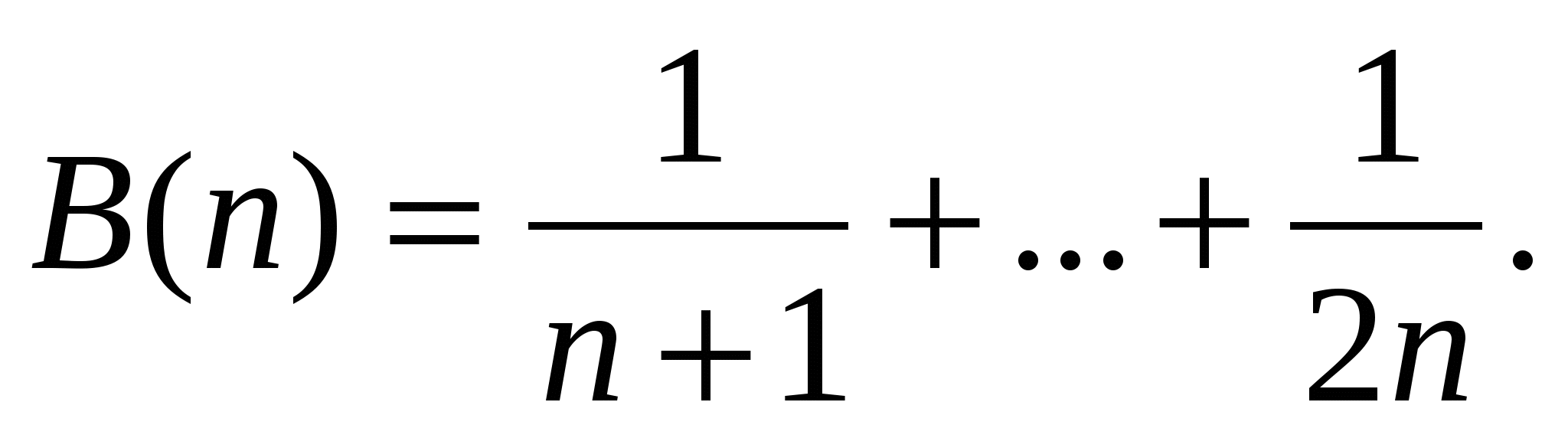
Нам надо доказать, что 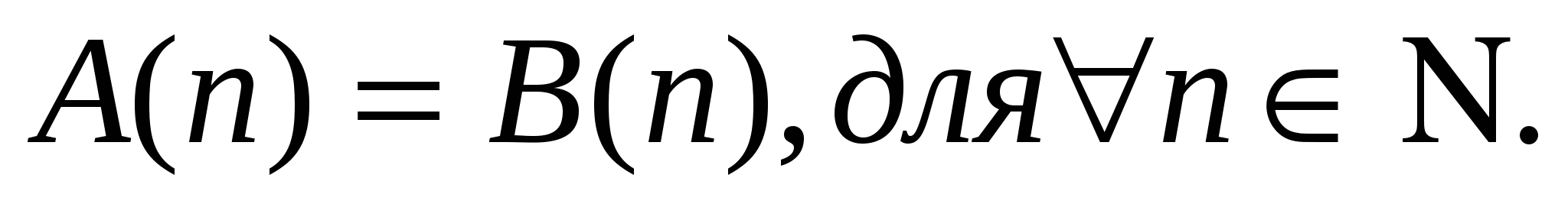
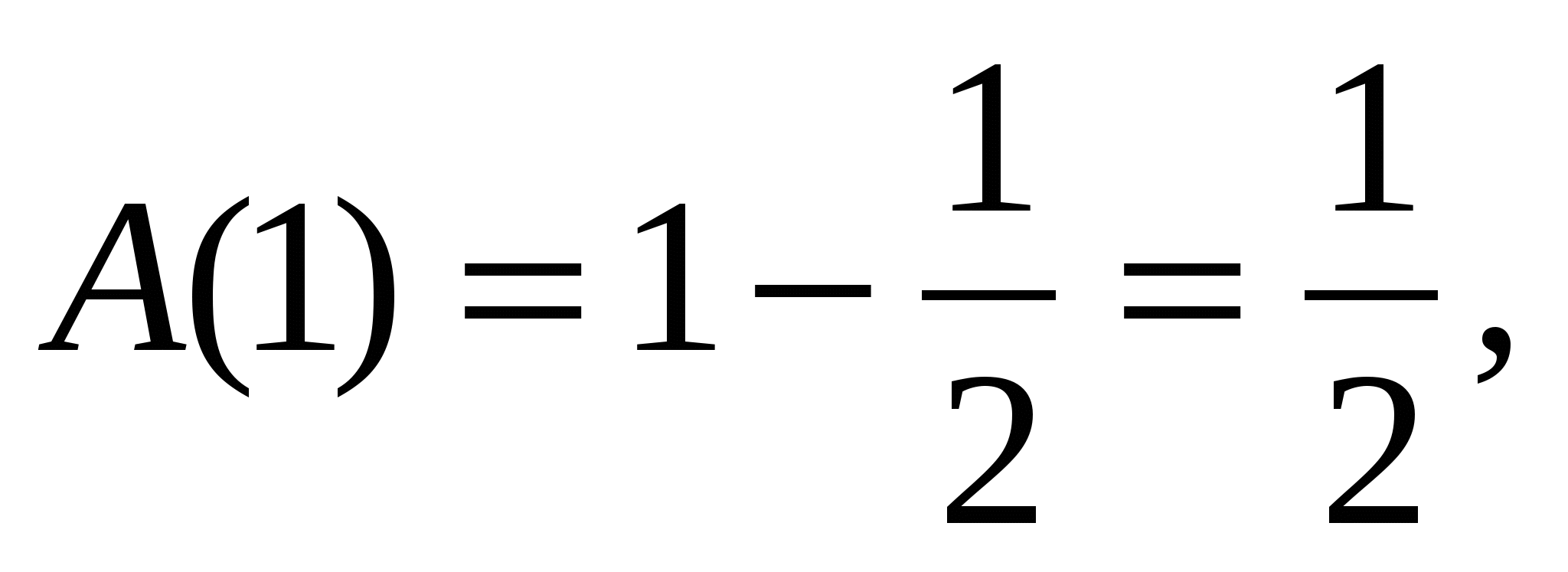
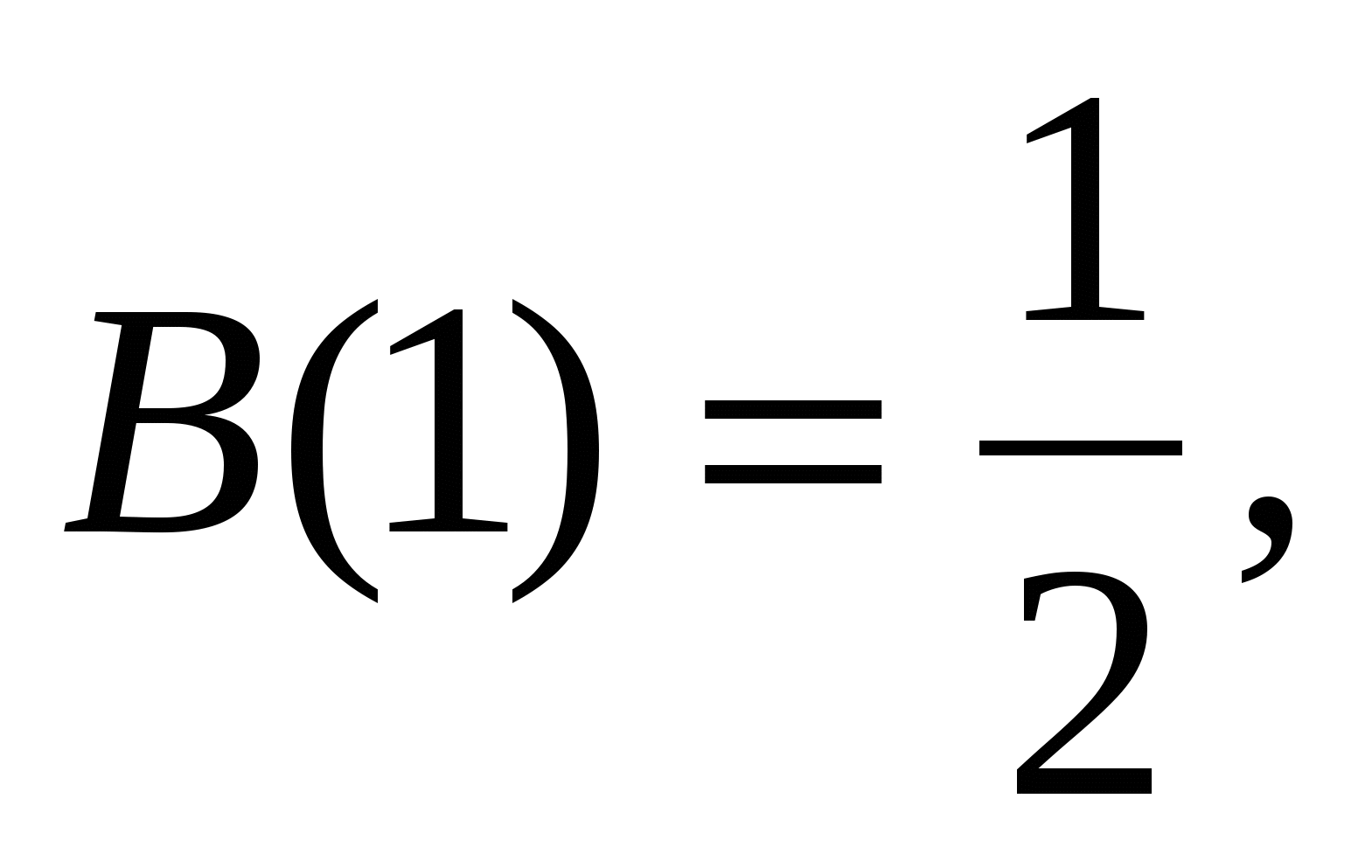
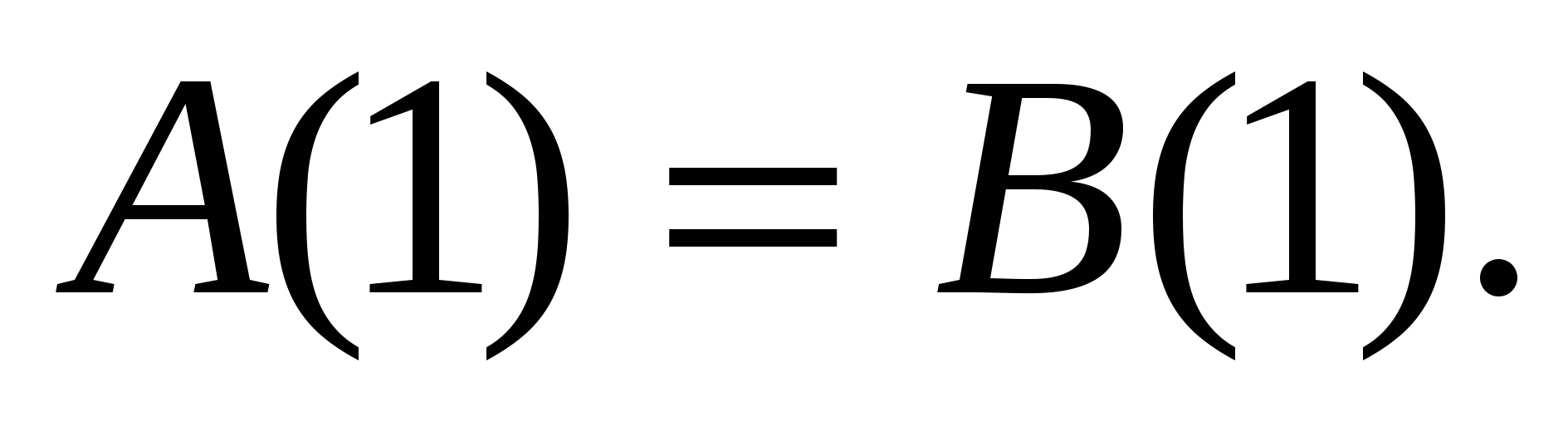
Докажем, что ![]() Тогда из истинности тождества
Тогда из истинности тождества
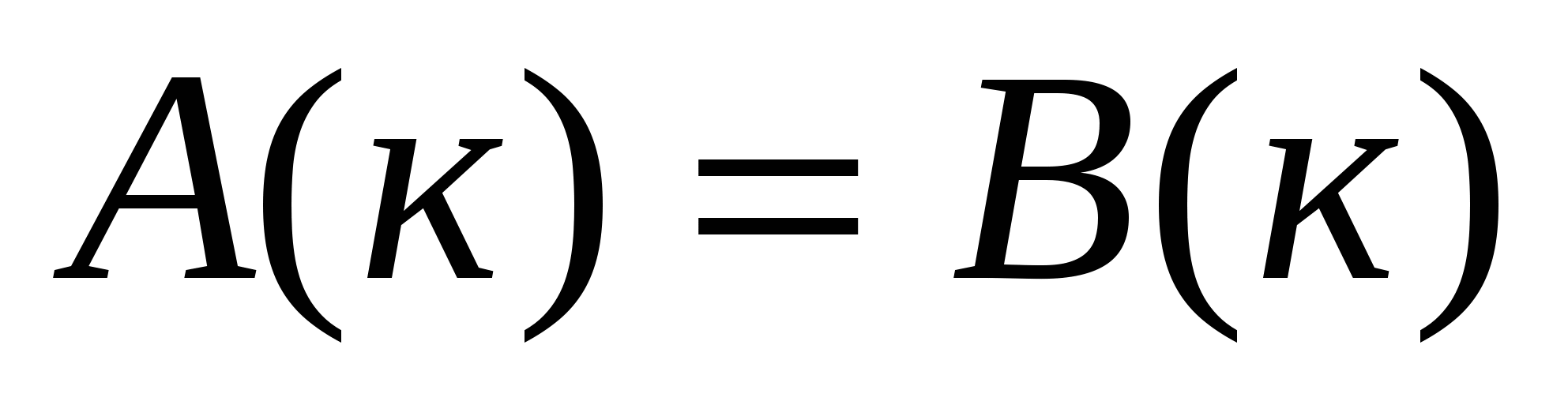 следует истинность тождества
следует истинность тождества 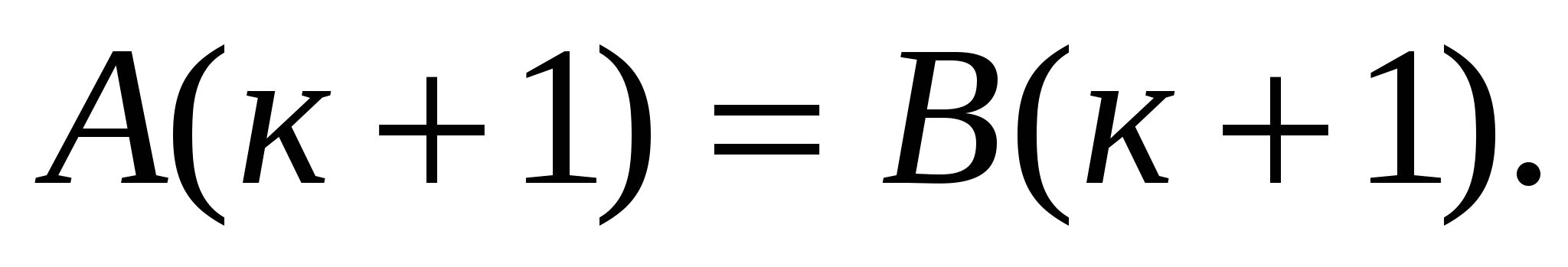
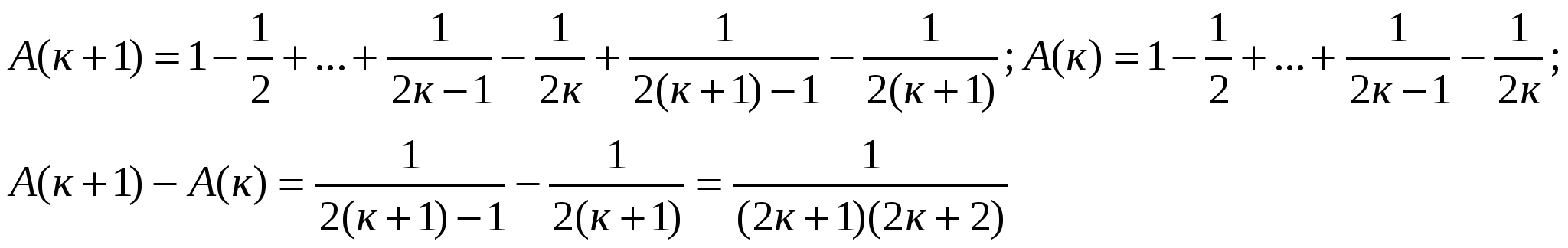
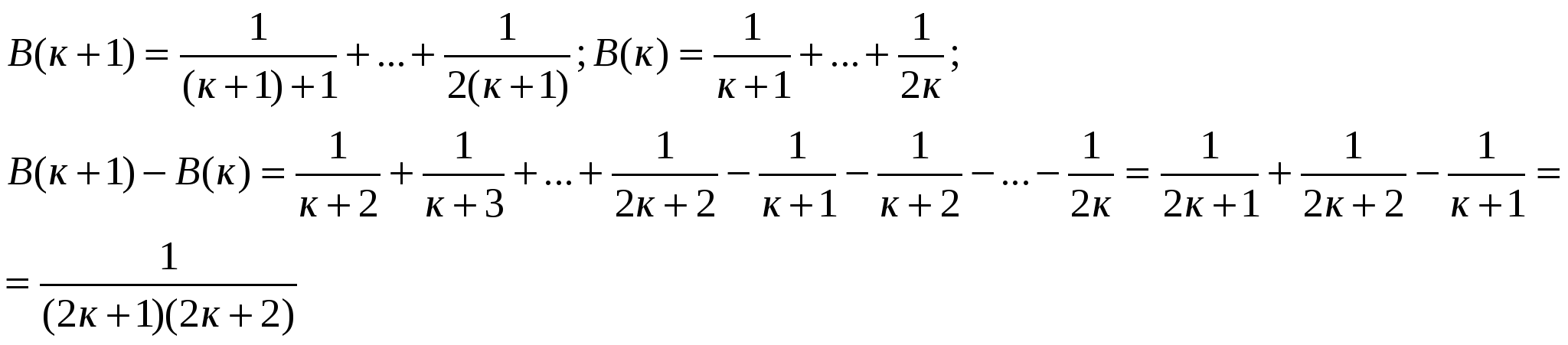
По принципу математической индукции доказана истинность тождества при всех п.
Пример № 11.
Докажем тождество 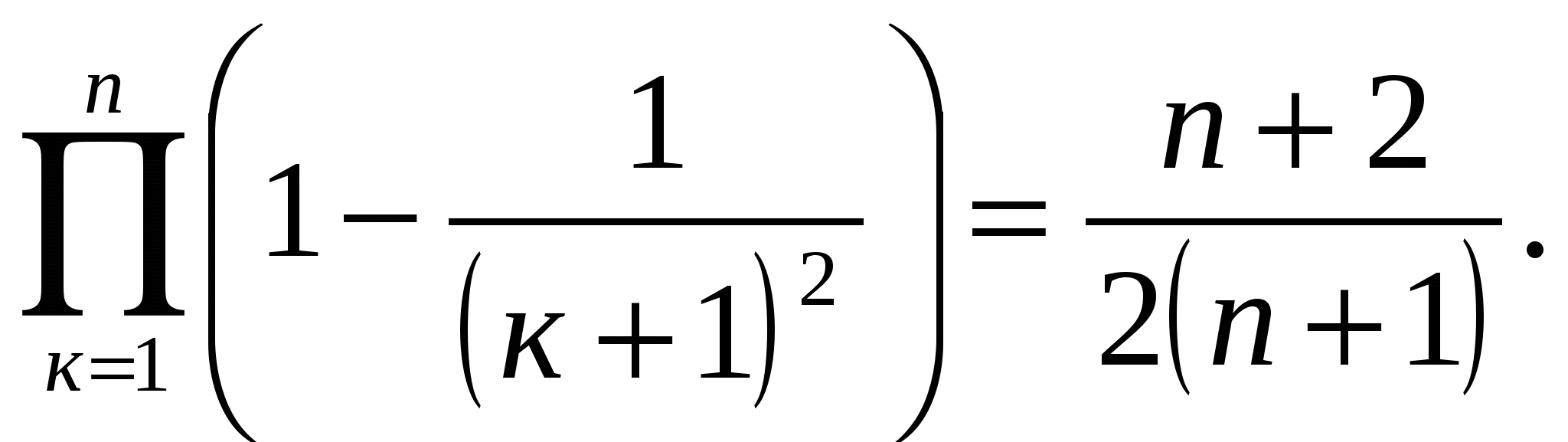
Доказательство.
-
пусть п=1.
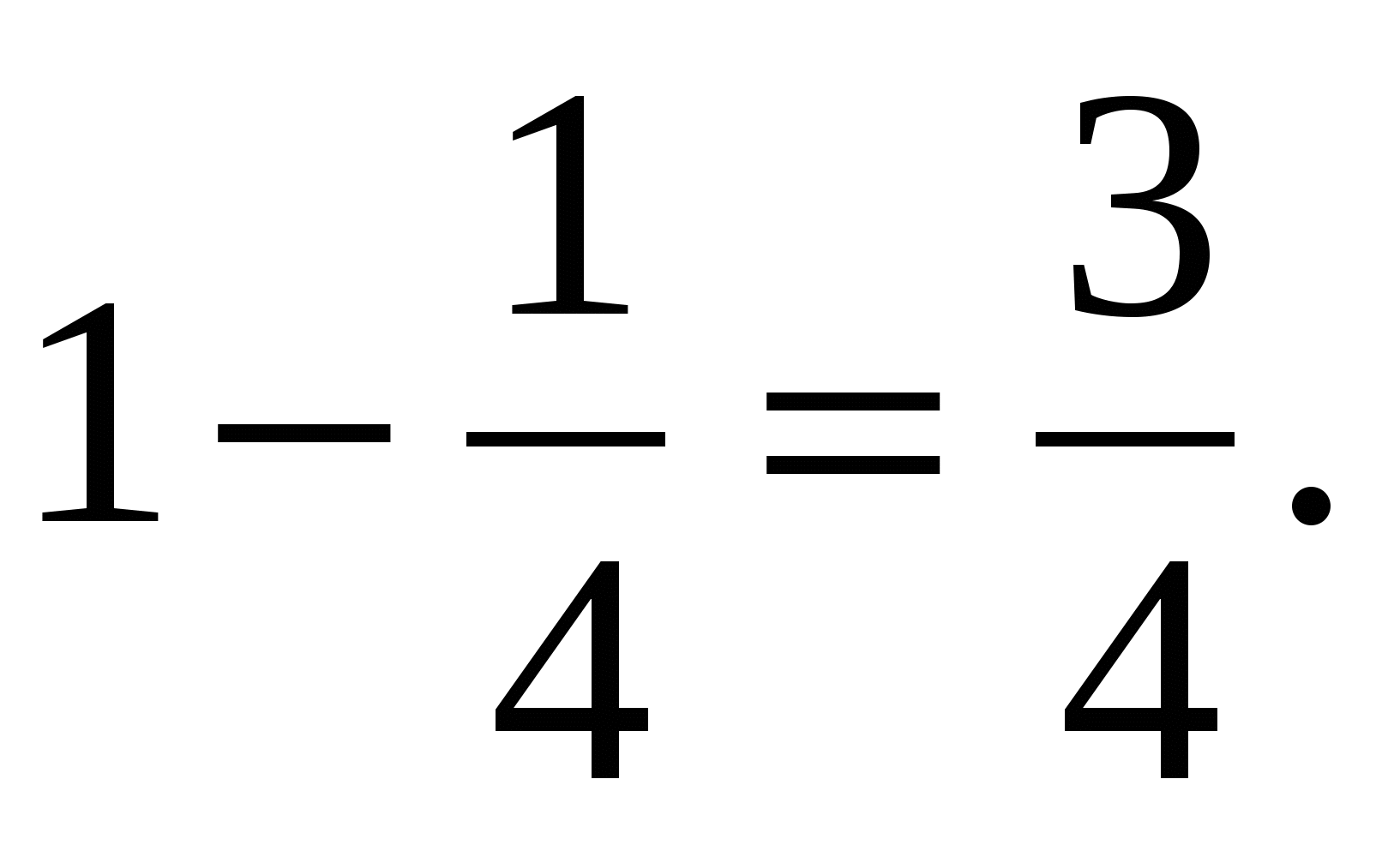
-
пусть п=к.
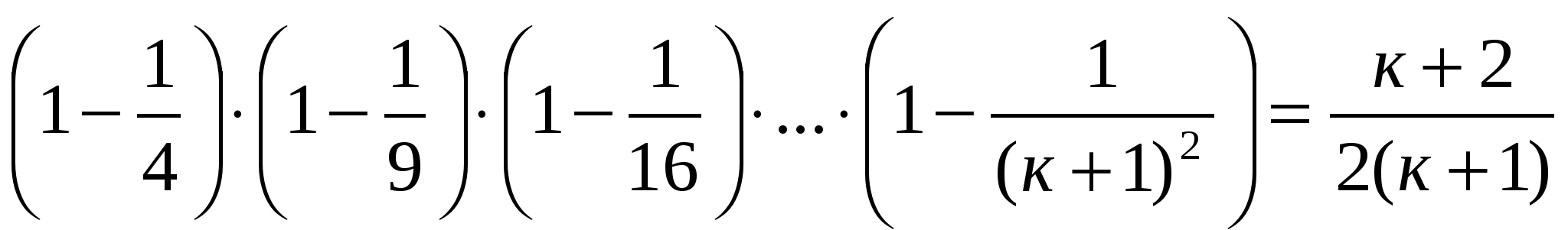
-
пусть п=к+1.
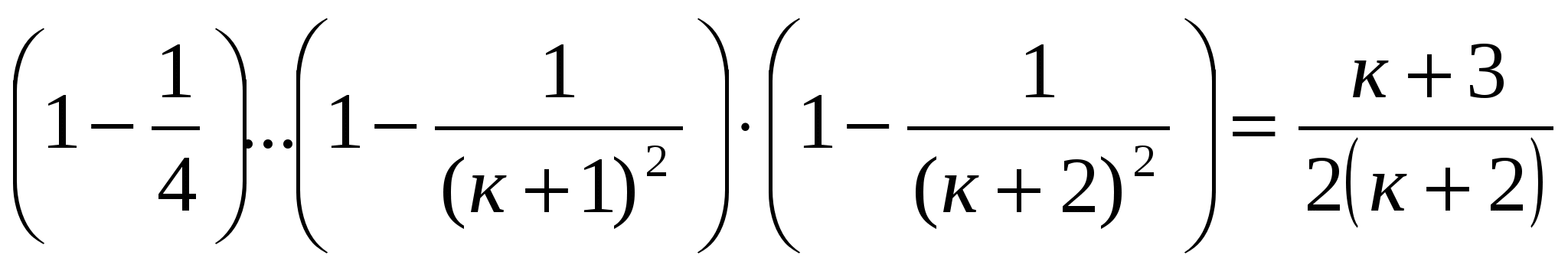 . Разделим
. Разделим
почленно получившиеся равенства.
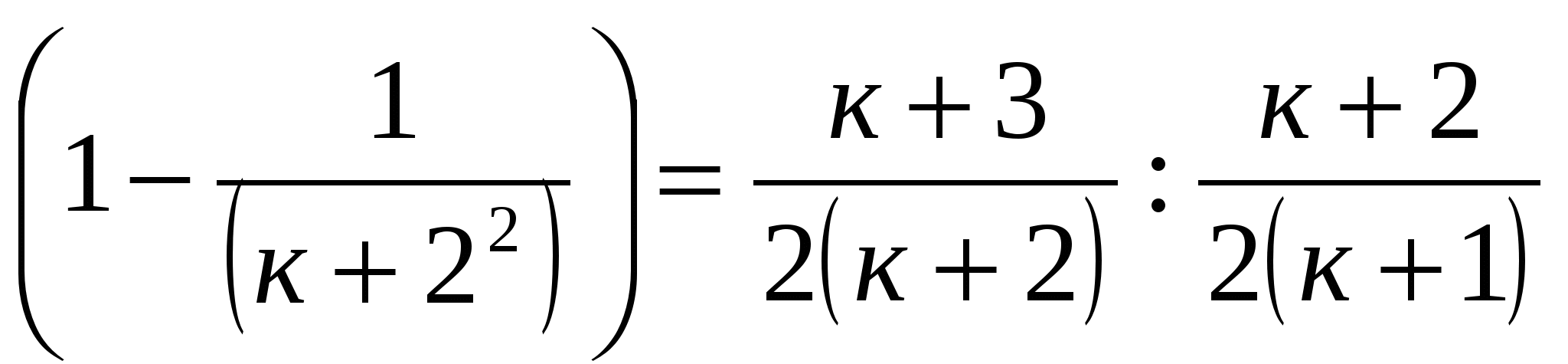 ;
; 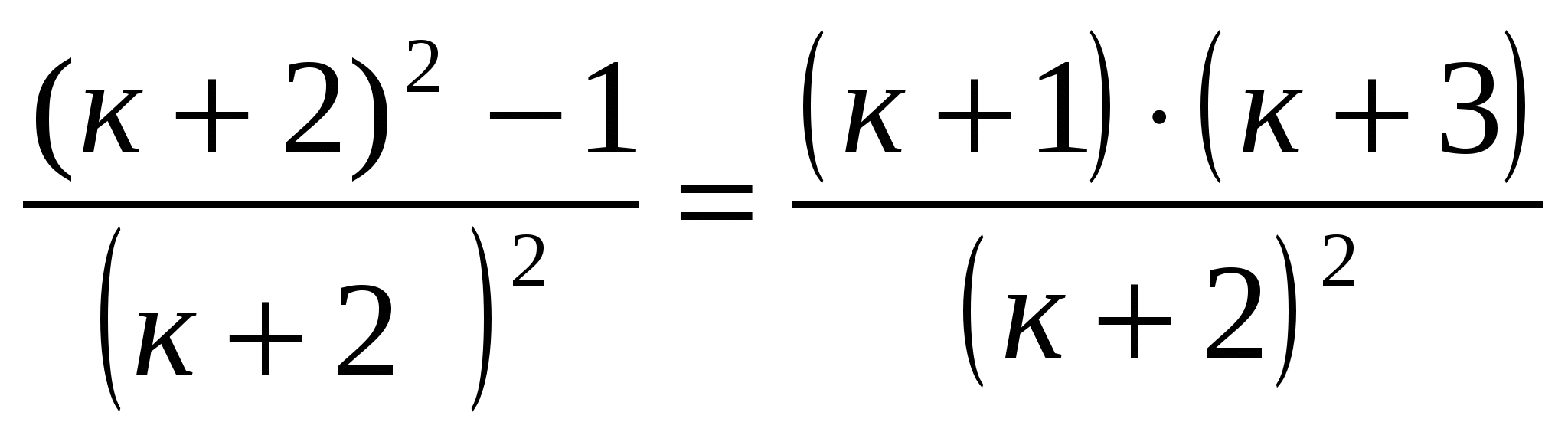 . Значит, данное тождество истинно для всех п.
. Значит, данное тождество истинно для всех п.
Урок № 4.
Доказательство тождеств методом математической индукции.
Пример № 12. Докажем тождество 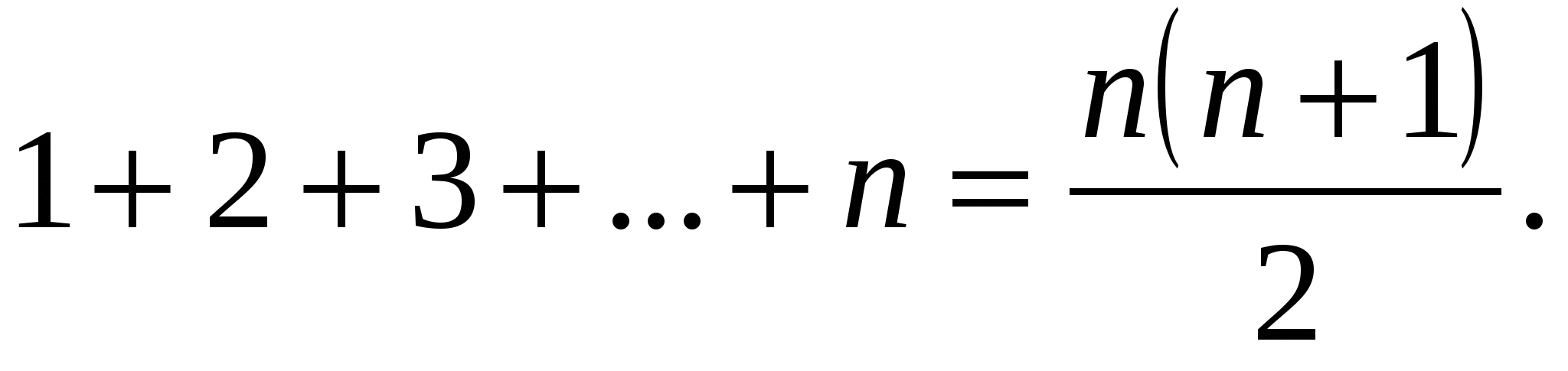
Доказательство.
-
п=1.
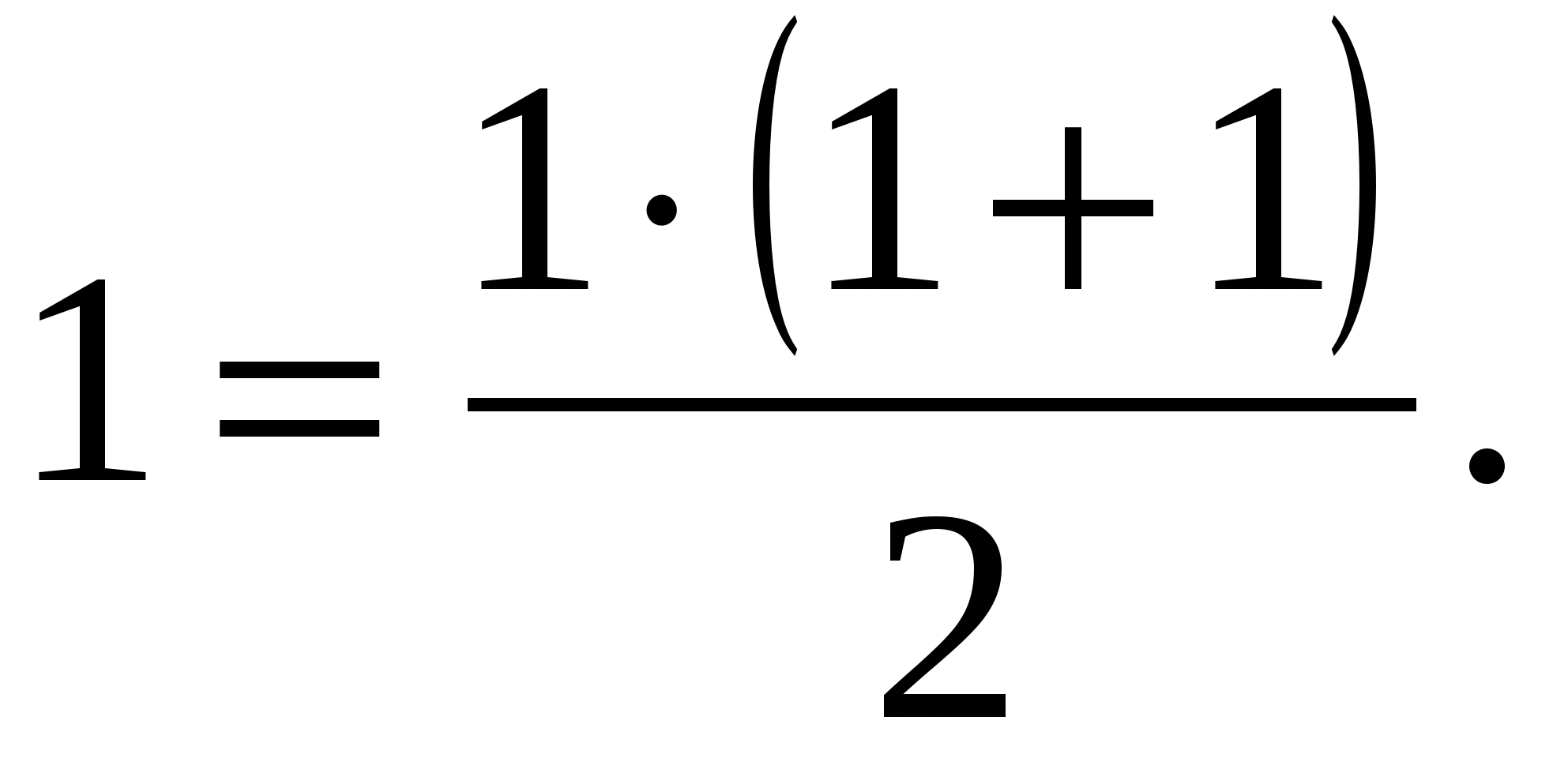
-
п=к.
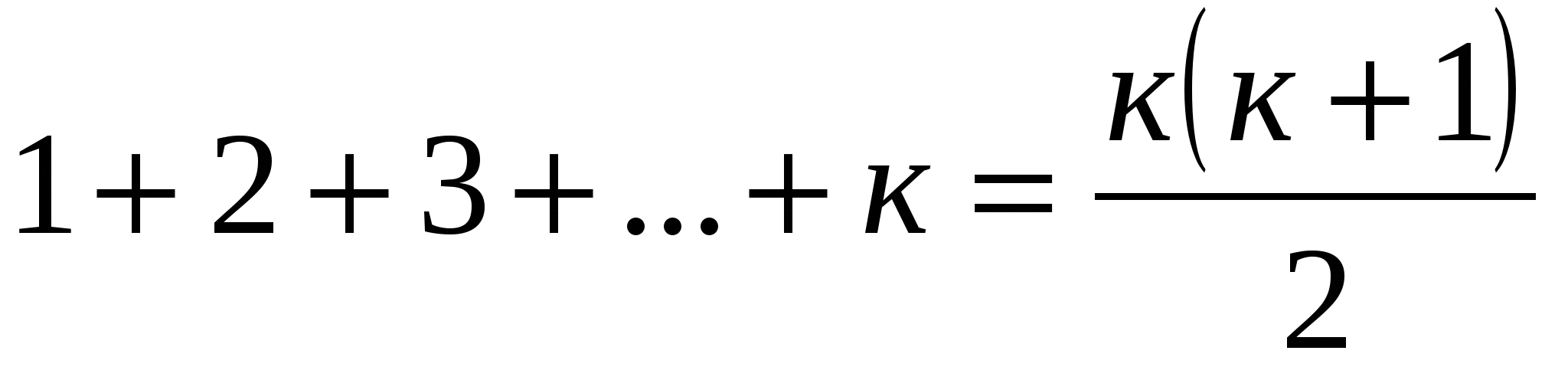 , допустим, что равенство выполняется.
, допустим, что равенство выполняется. -
п=к+1.
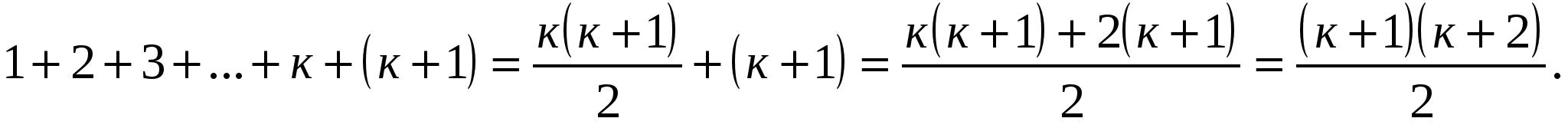
Применяя принцип математической индукции, доказали, что равенство верно при всех п.
Пример № 13. Докажем тождество 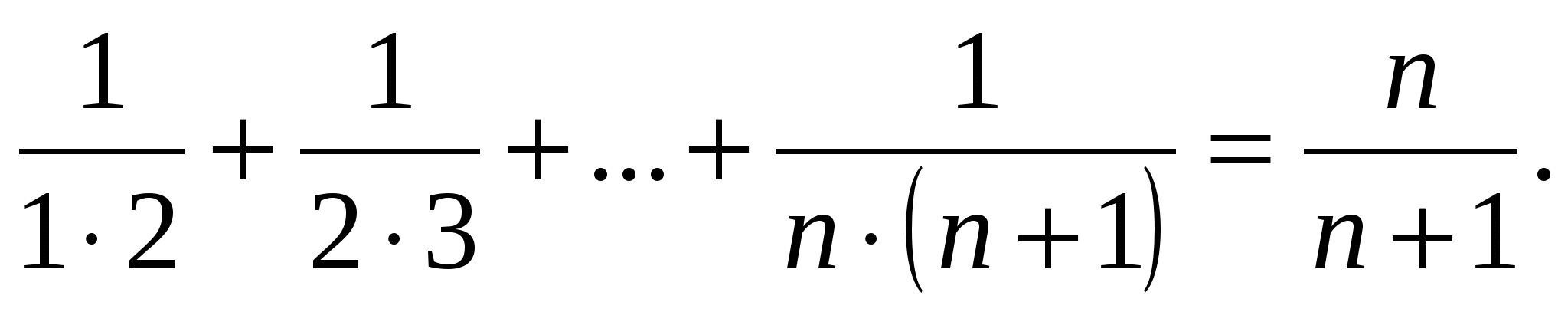
Доказательство.
-
п=1;
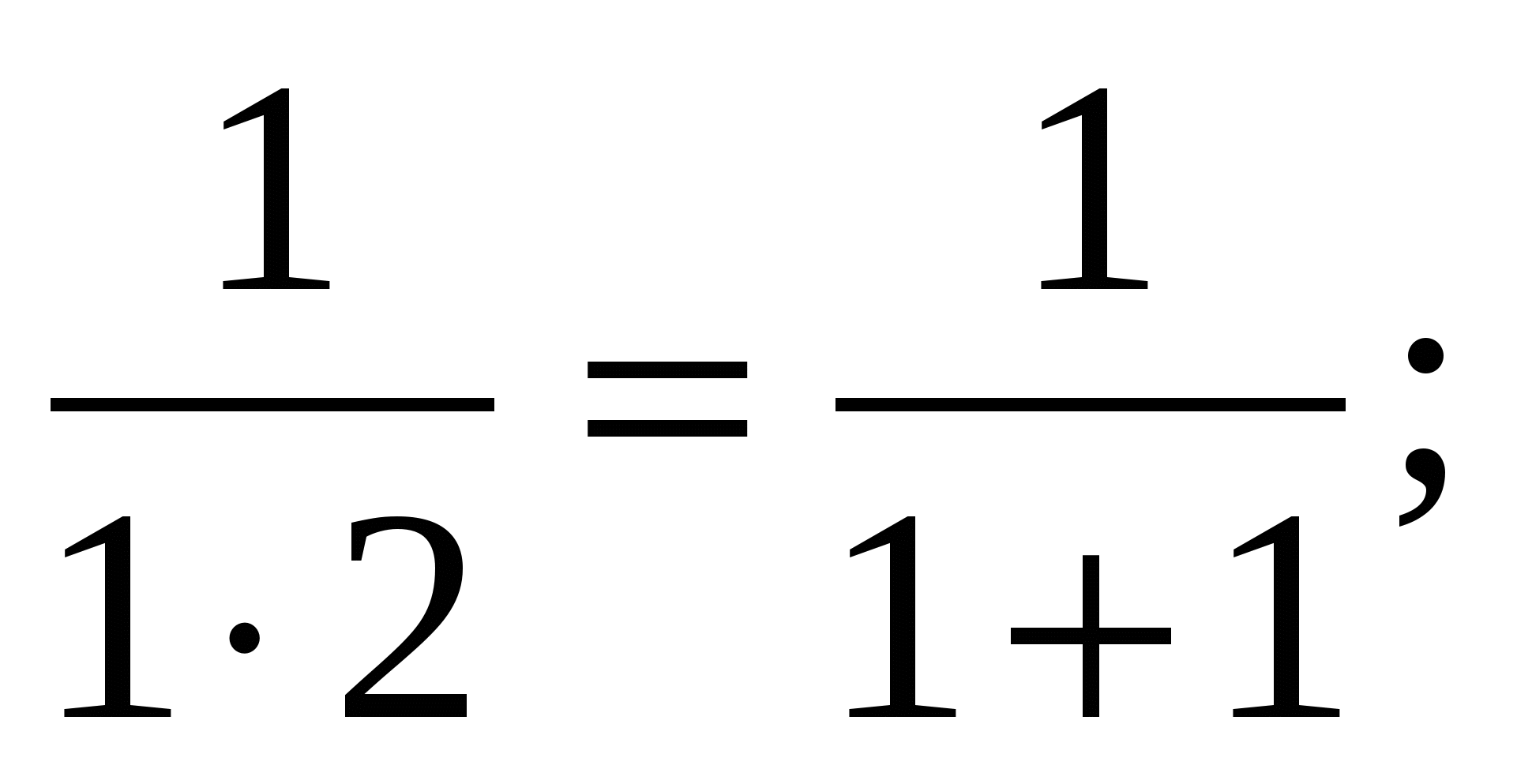 п=2;
п=2; 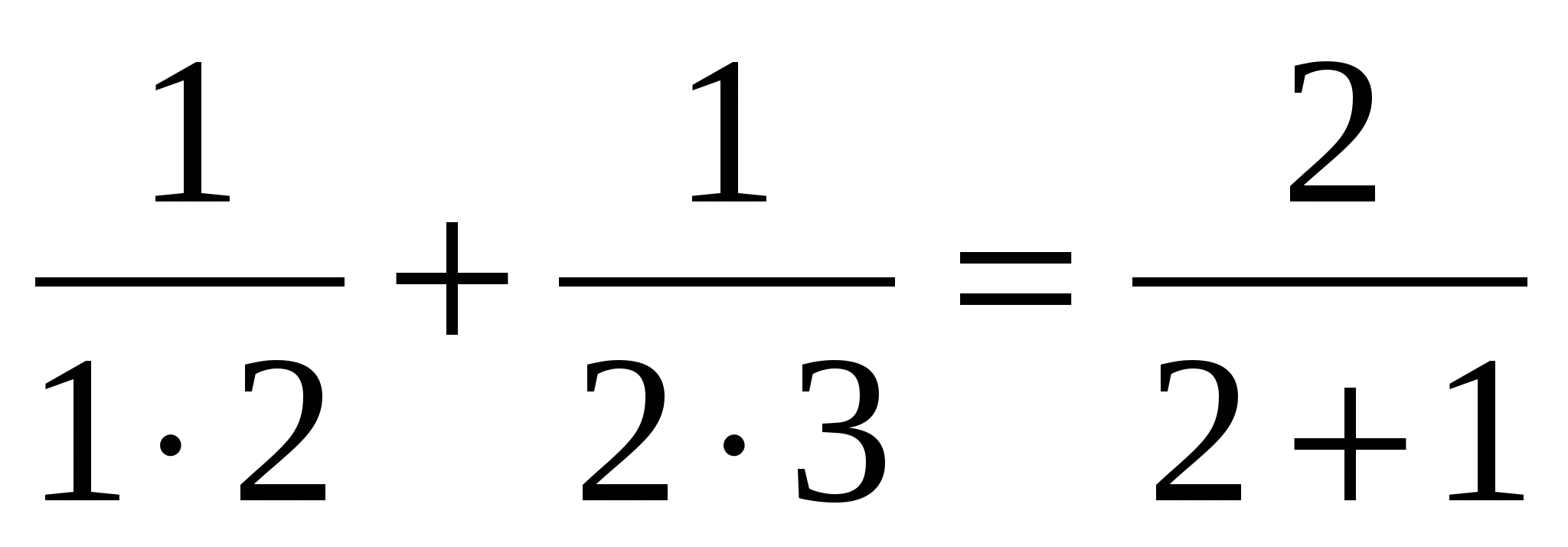 ;
; -
п=к;
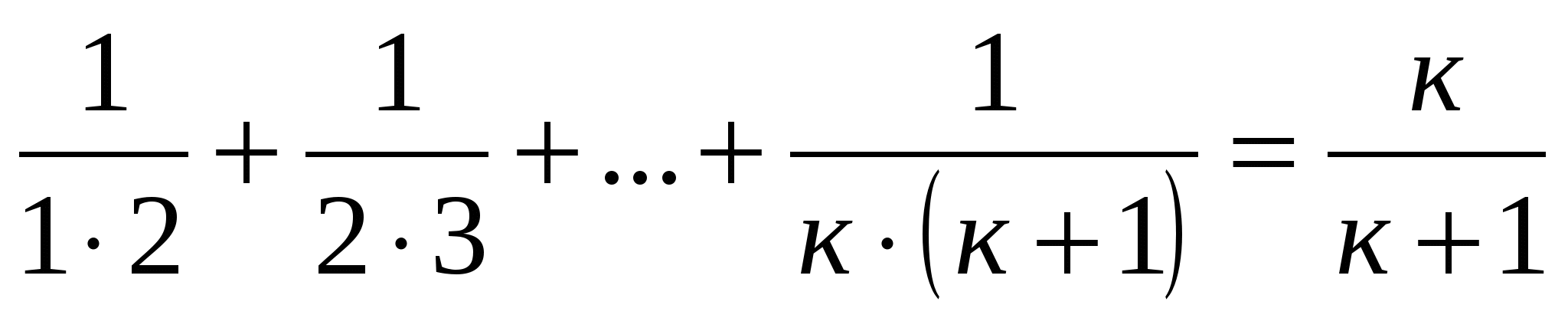 - это равенство выполняется при любом натуральном к;
- это равенство выполняется при любом натуральном к; -
докажем, что равенство выполняется при п=к+1.
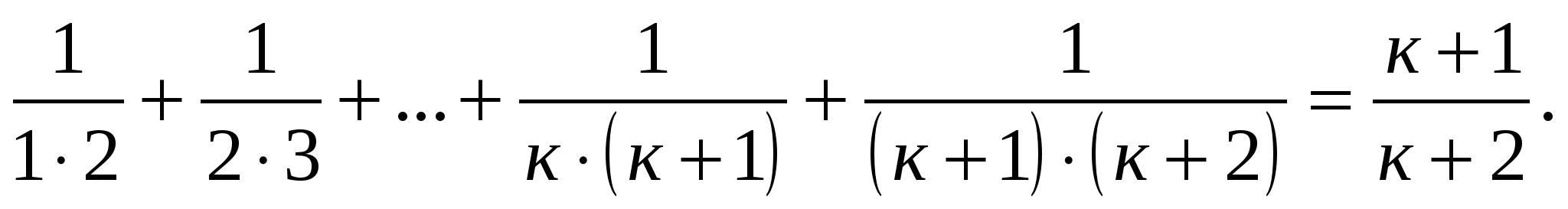
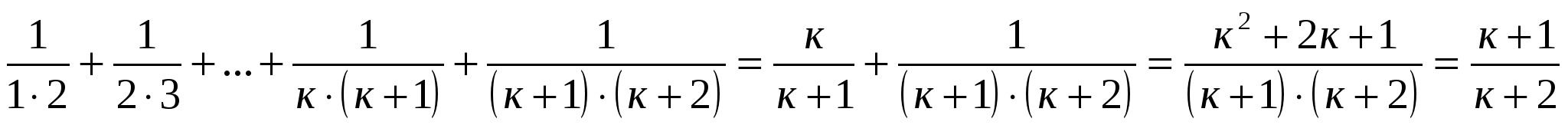 Применяя принцип математической индукции, доказали, что утверждение верно при любом натуральном п.
Применяя принцип математической индукции, доказали, что утверждение верно при любом натуральном п.
Пример № 14. Докажем тождество 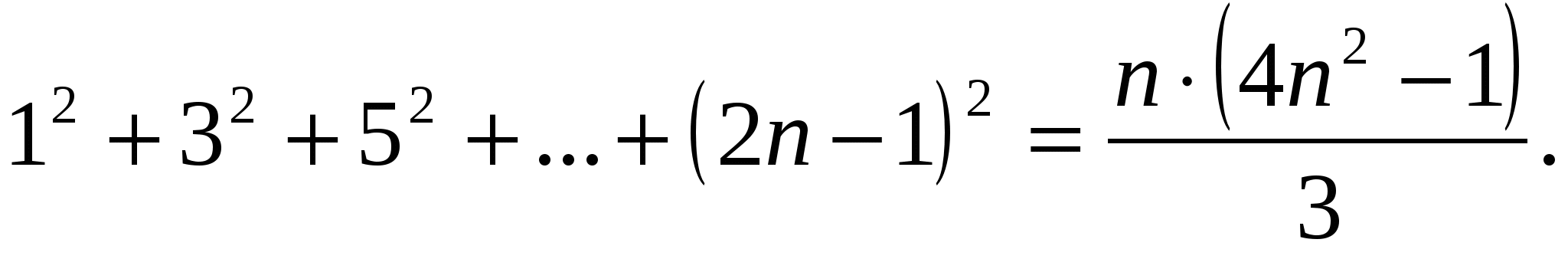
Доказательство.
-
п=1;
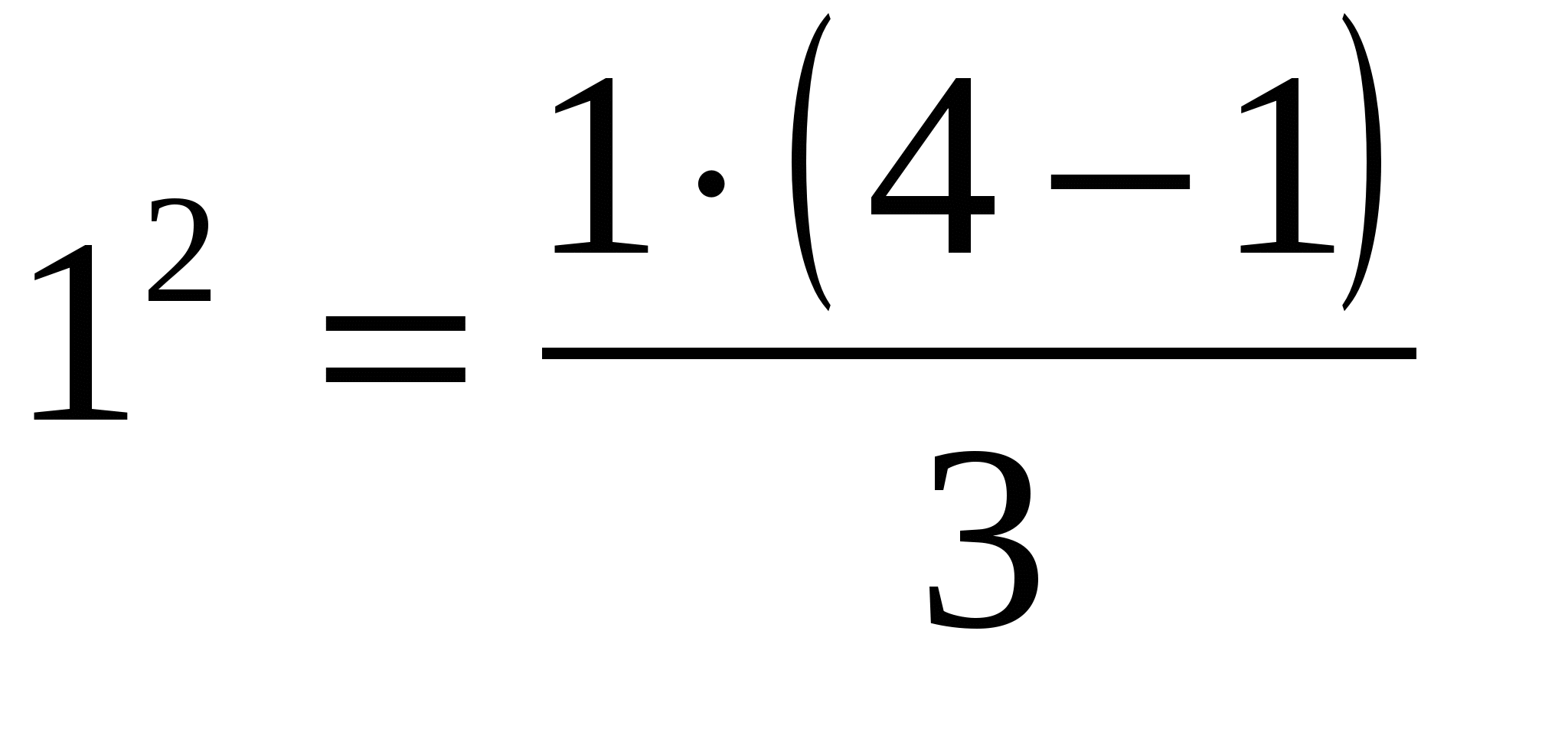 ;
; -
п=к; предположим, что верно равенство
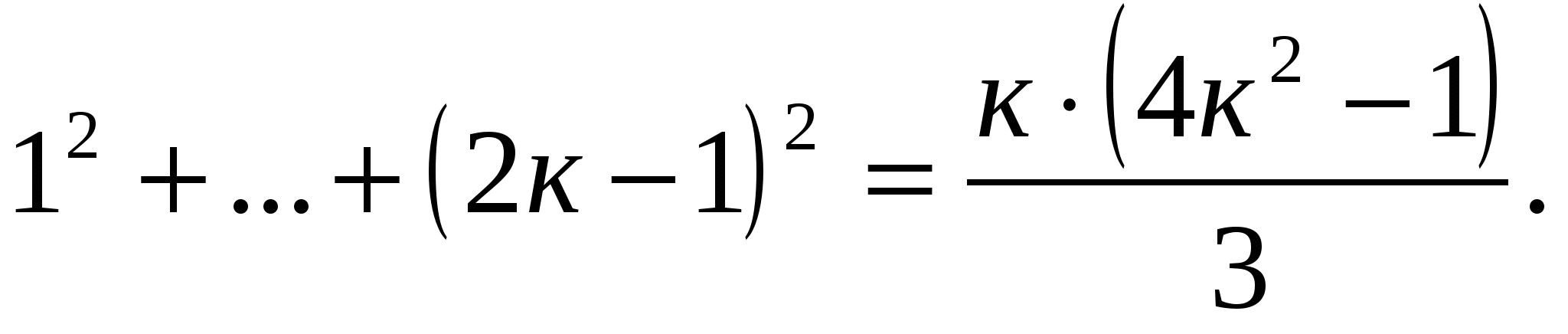
-
п=к+1; докажем, что верно равенство
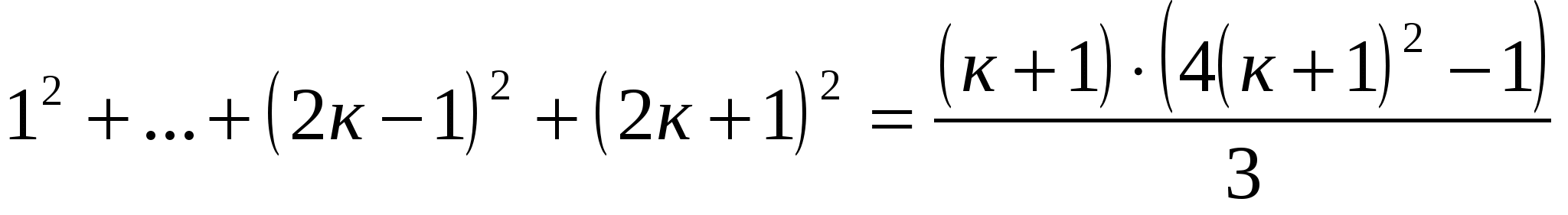 .
.
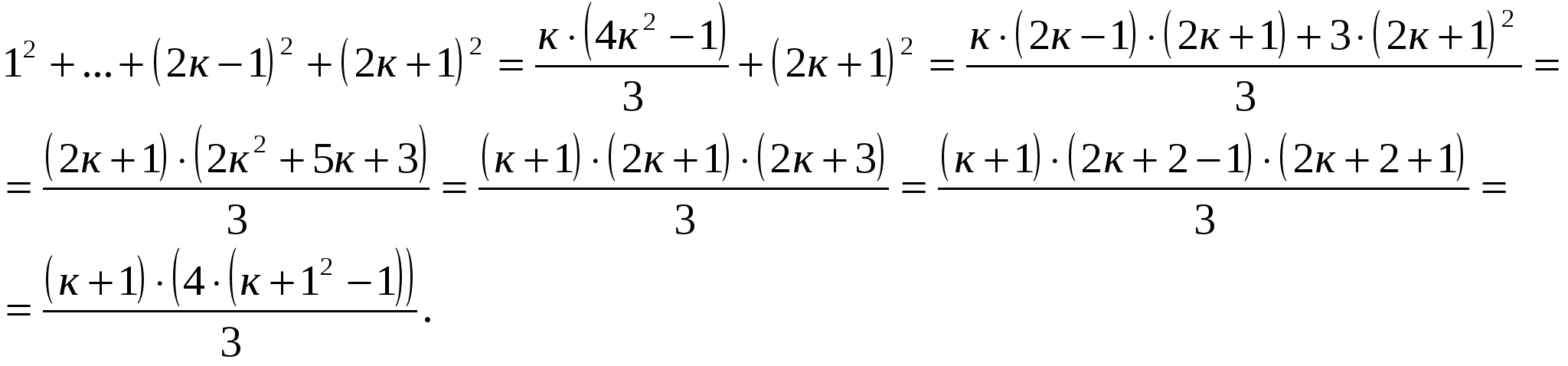
Пример № 15. Докажем тождество 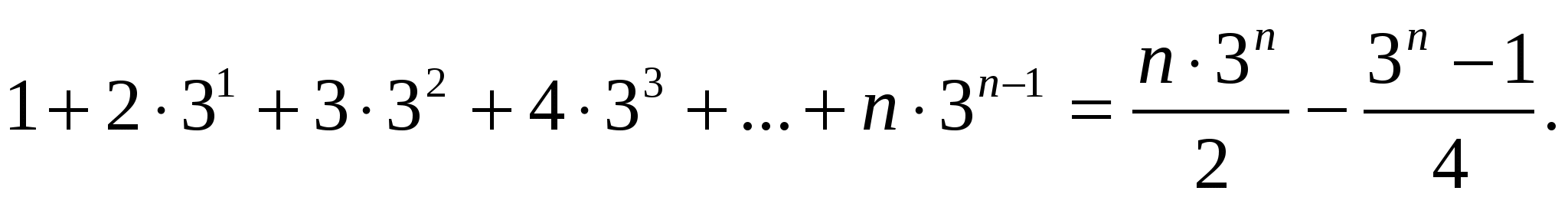
1) п=1; 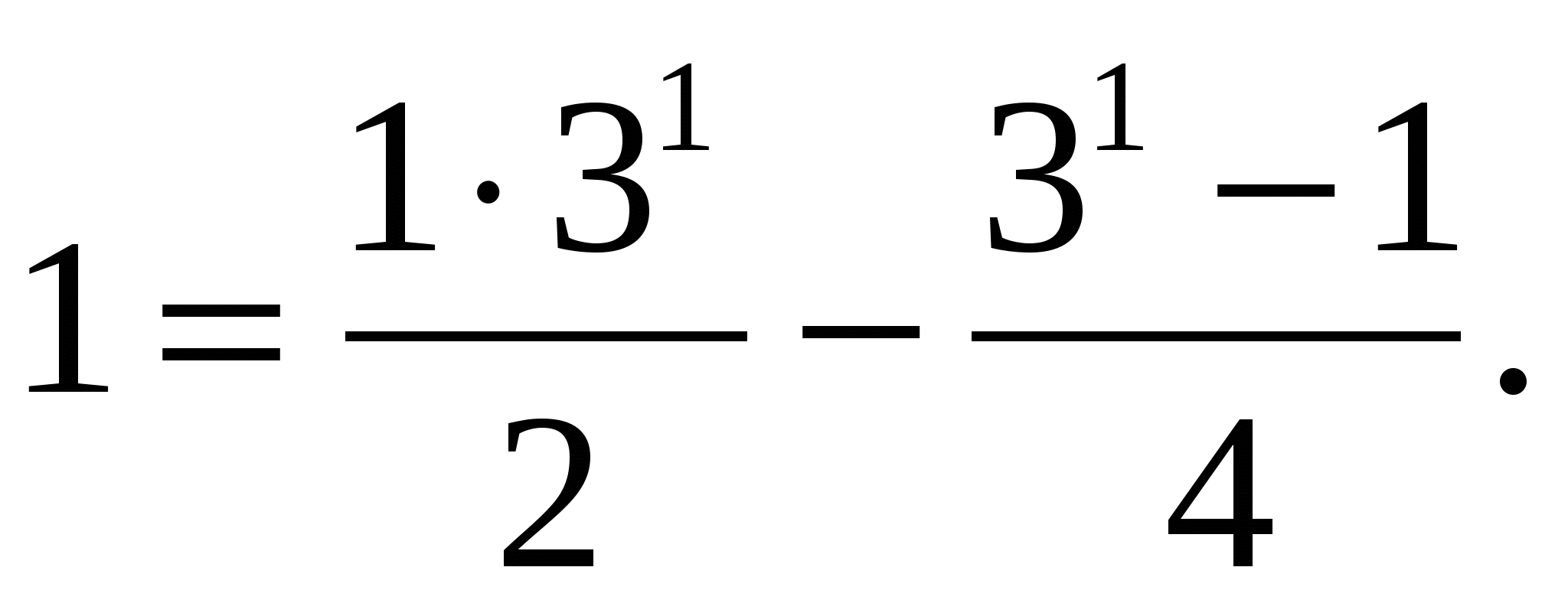
2) для п=к выполняется равенство 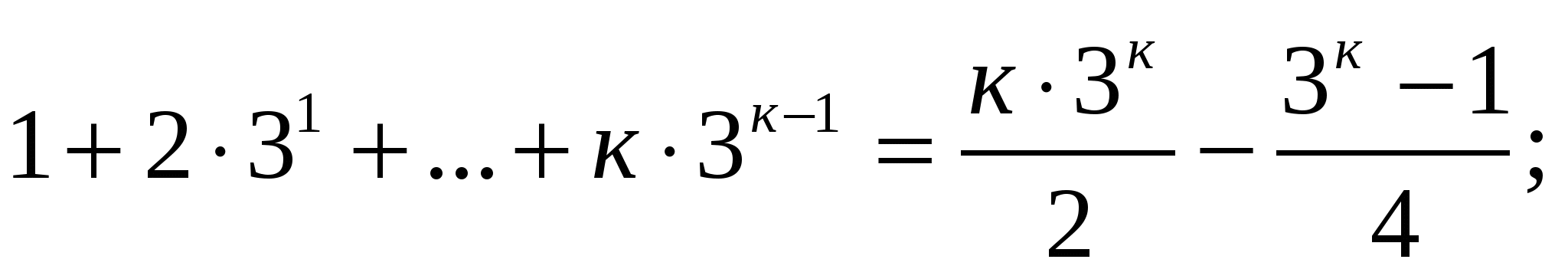
3) докажем, что равенство выполняется для п=к+1:
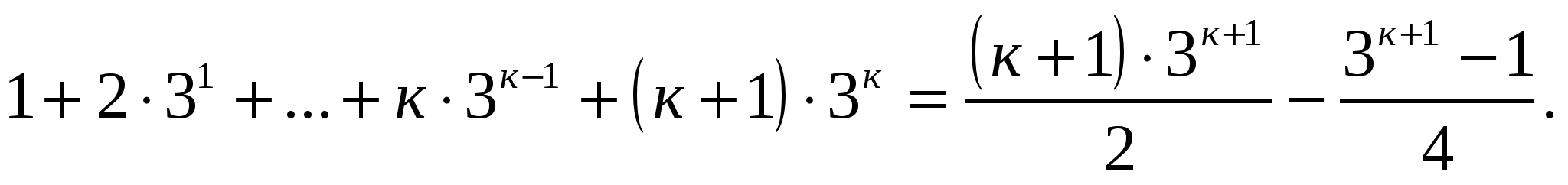
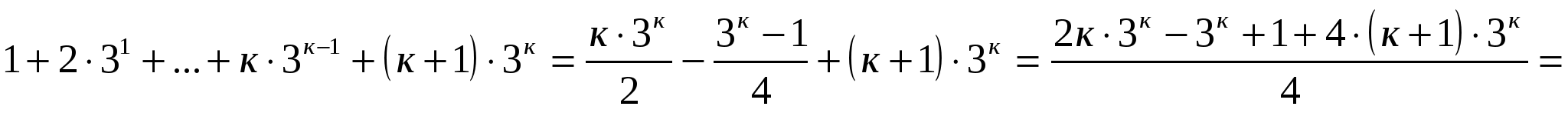
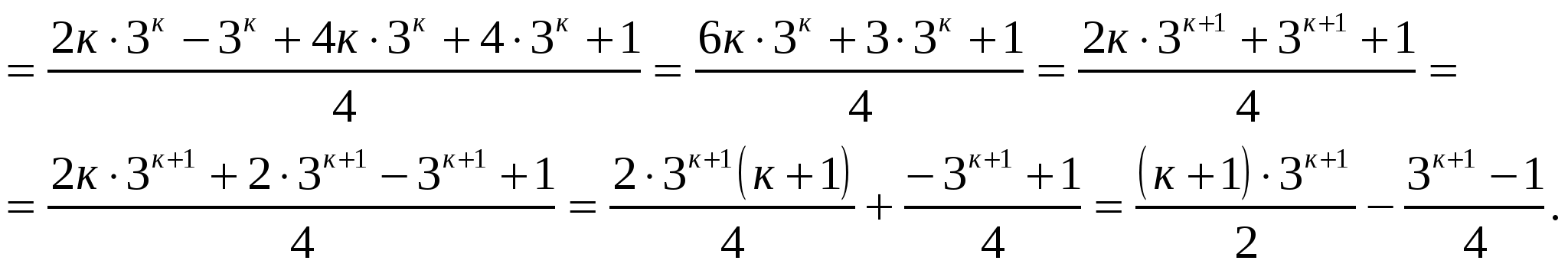
Вывод: тождество справедливо для любого натурального п.
Пример № 16. Докажем тождество
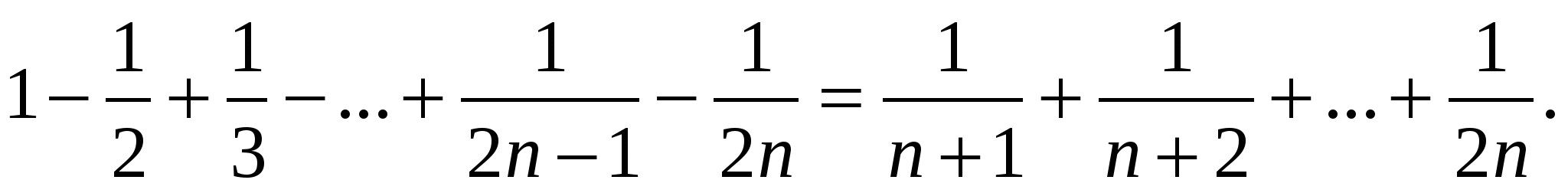
Доказательство.
Если п=1, то ![]()
Пусть тождество выполняется при п=к.
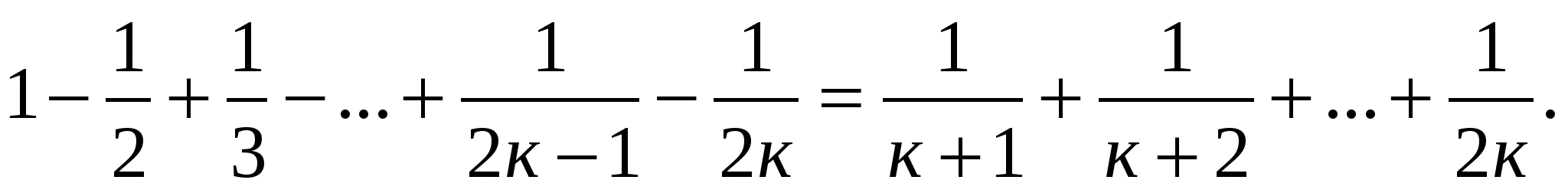
Докажем, что тождество выполняется при п=к+1.
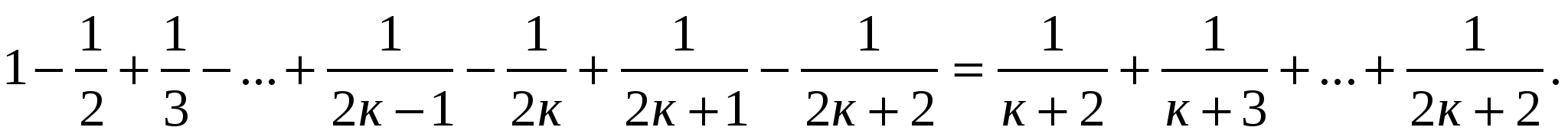
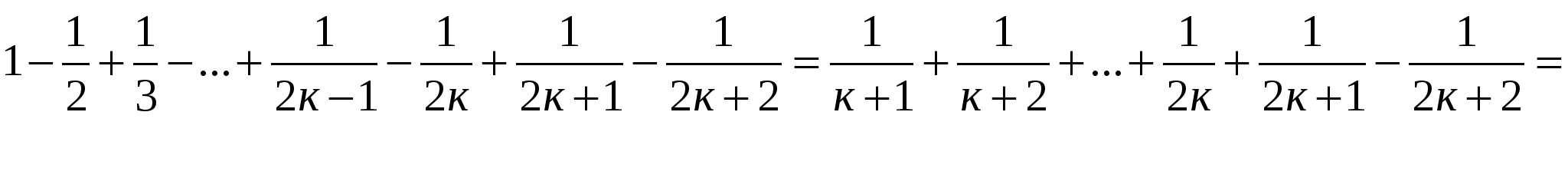
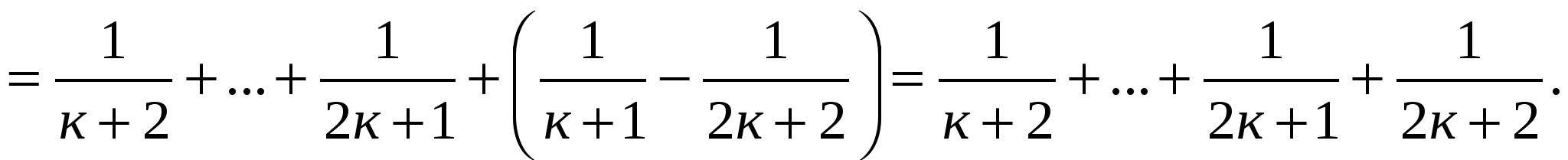
Тогда тождество справедливо для любого натурального п.
Урок № 5.
Доказательство тождеств методом математической индукции.
Пример № 17. Докажем тождество
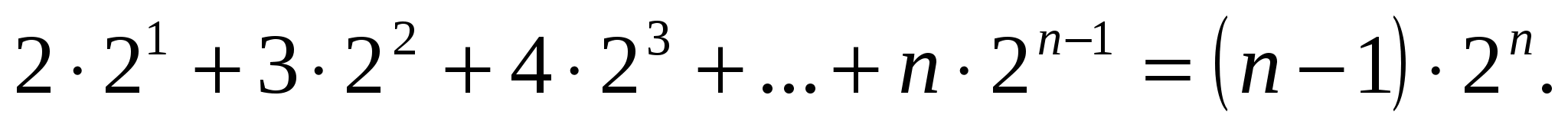
Доказательство.
Если п=2, то получаем верное равенство: 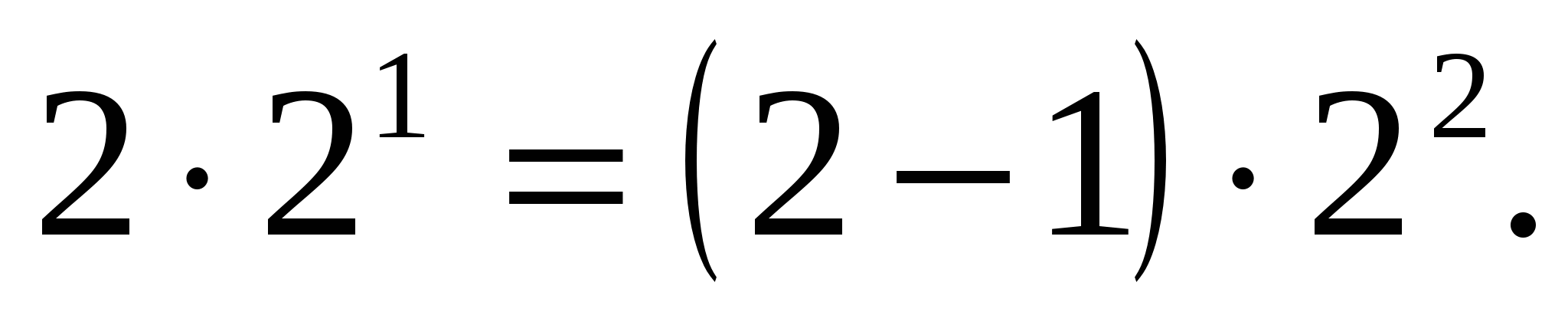
Пусть равенство верно при п=к: 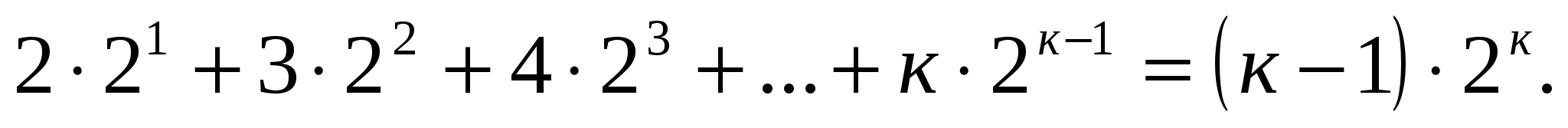
Докажем справедливость утверждения при п=к+1.
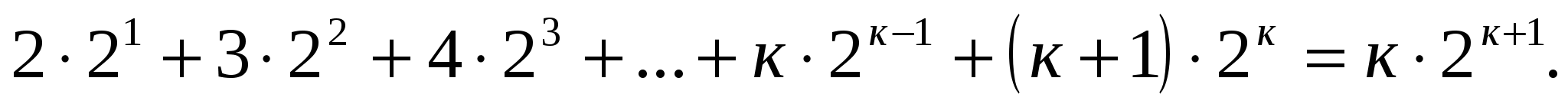
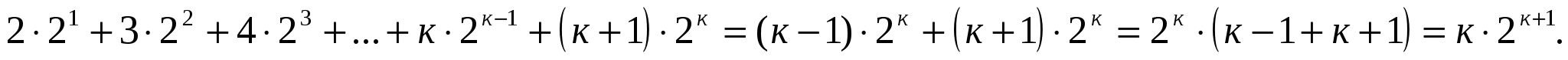 Согласно принципу математической индукции, тождество доказано.
Согласно принципу математической индукции, тождество доказано.
Пример № 18. Докажем тождество 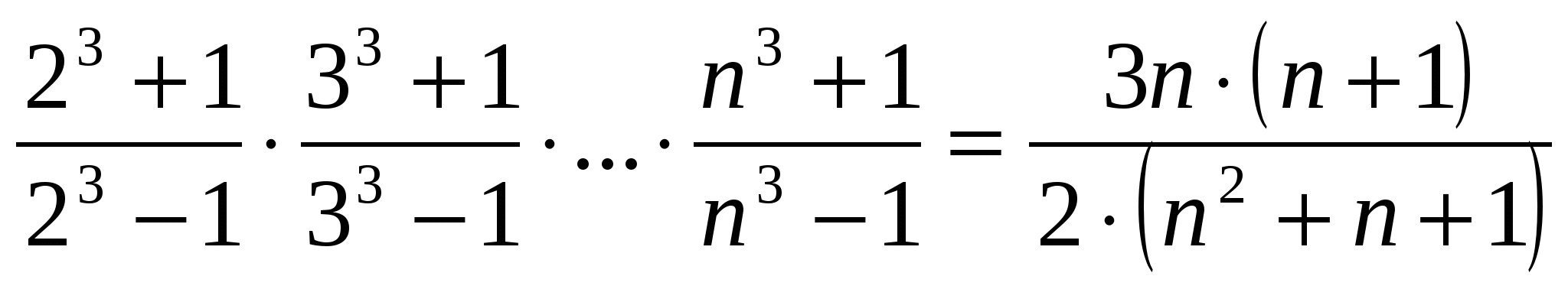 при п≥2.
при п≥2.
При п=2 это тождество перепишется в очень простом виде 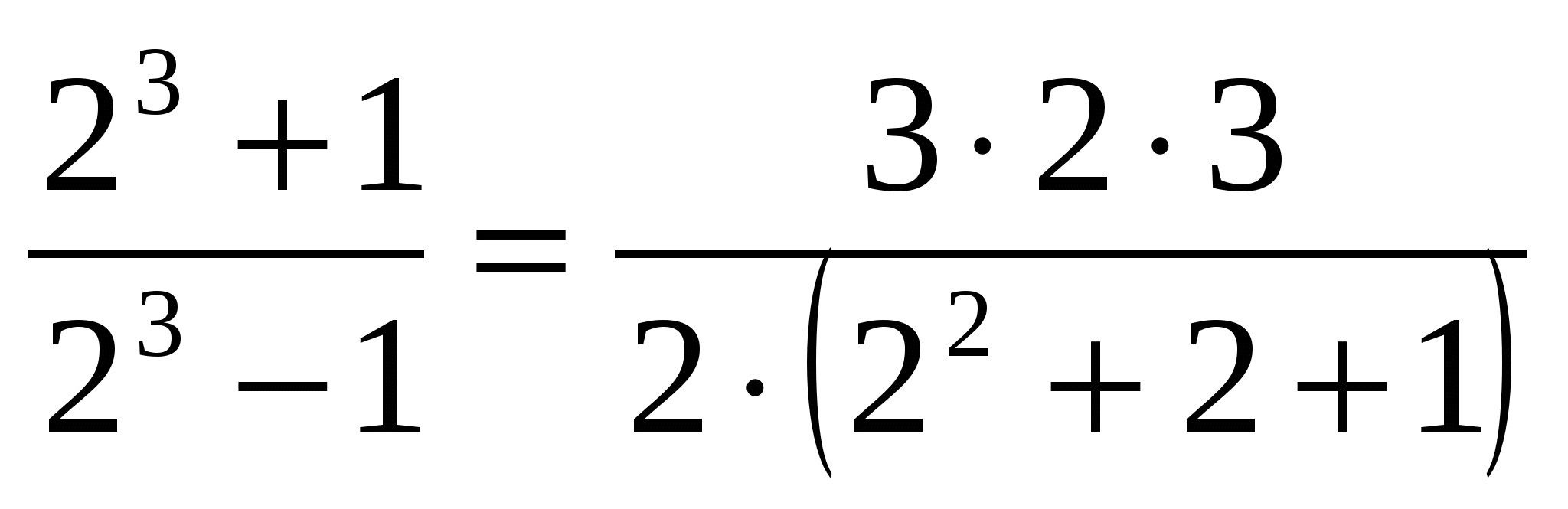
и, очевидно, верно.
Пусть при п=к действительно
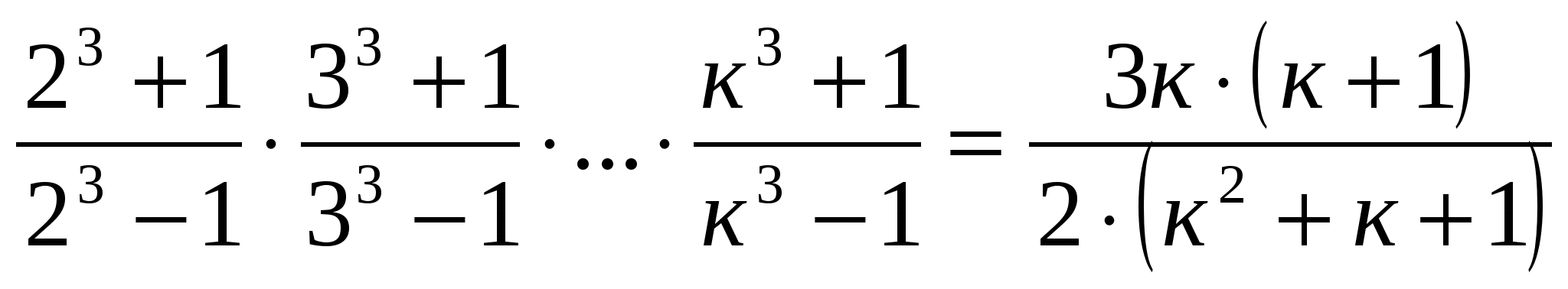 .
.
Докажем справедливость утверждения при п=к+1, то есть выполняется равенство: 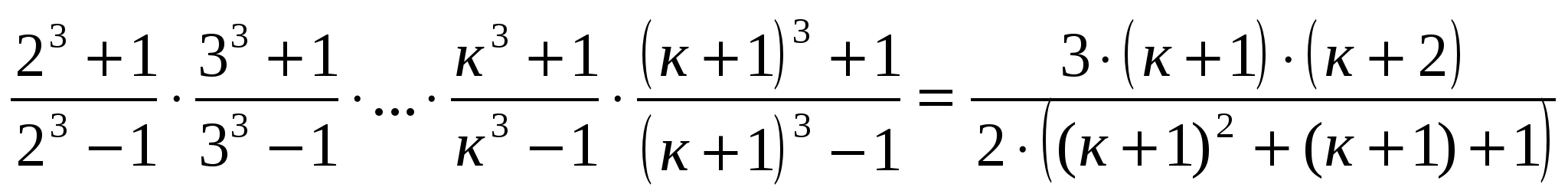 .
.
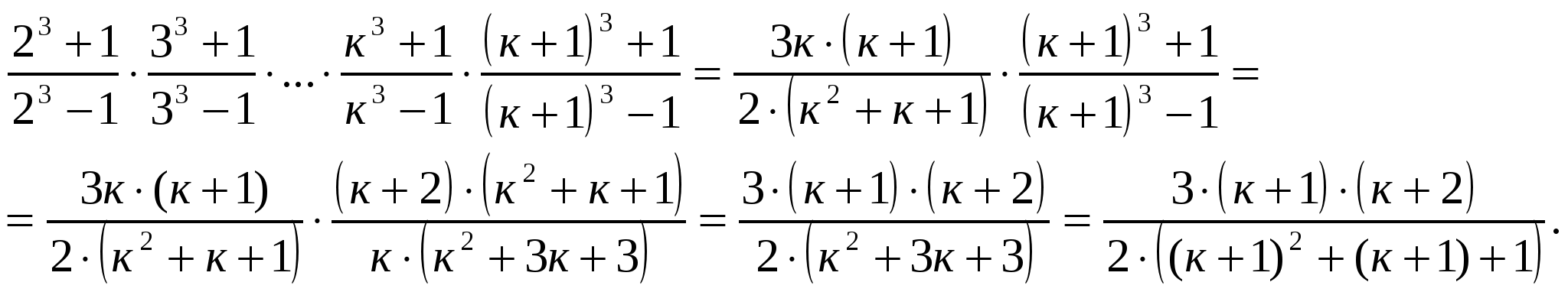
Итак, мы доказали, что тождество верно при любом натуральном п≥2.
Пример № 19. Докажем тождество 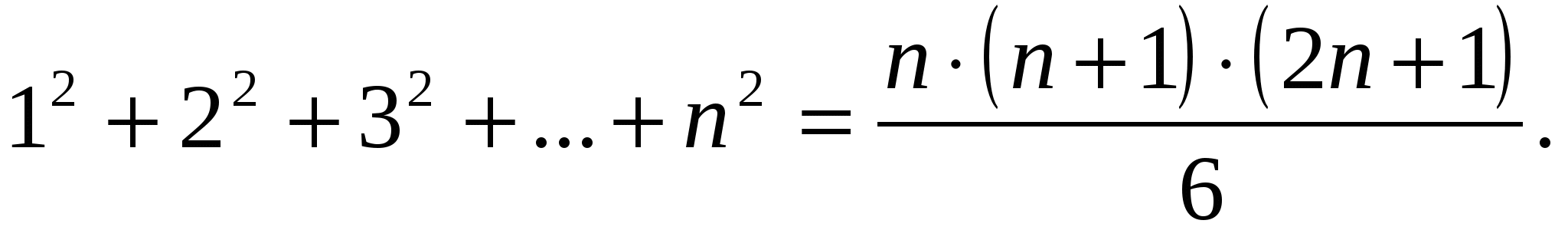
При п=1 получим верное равенство: 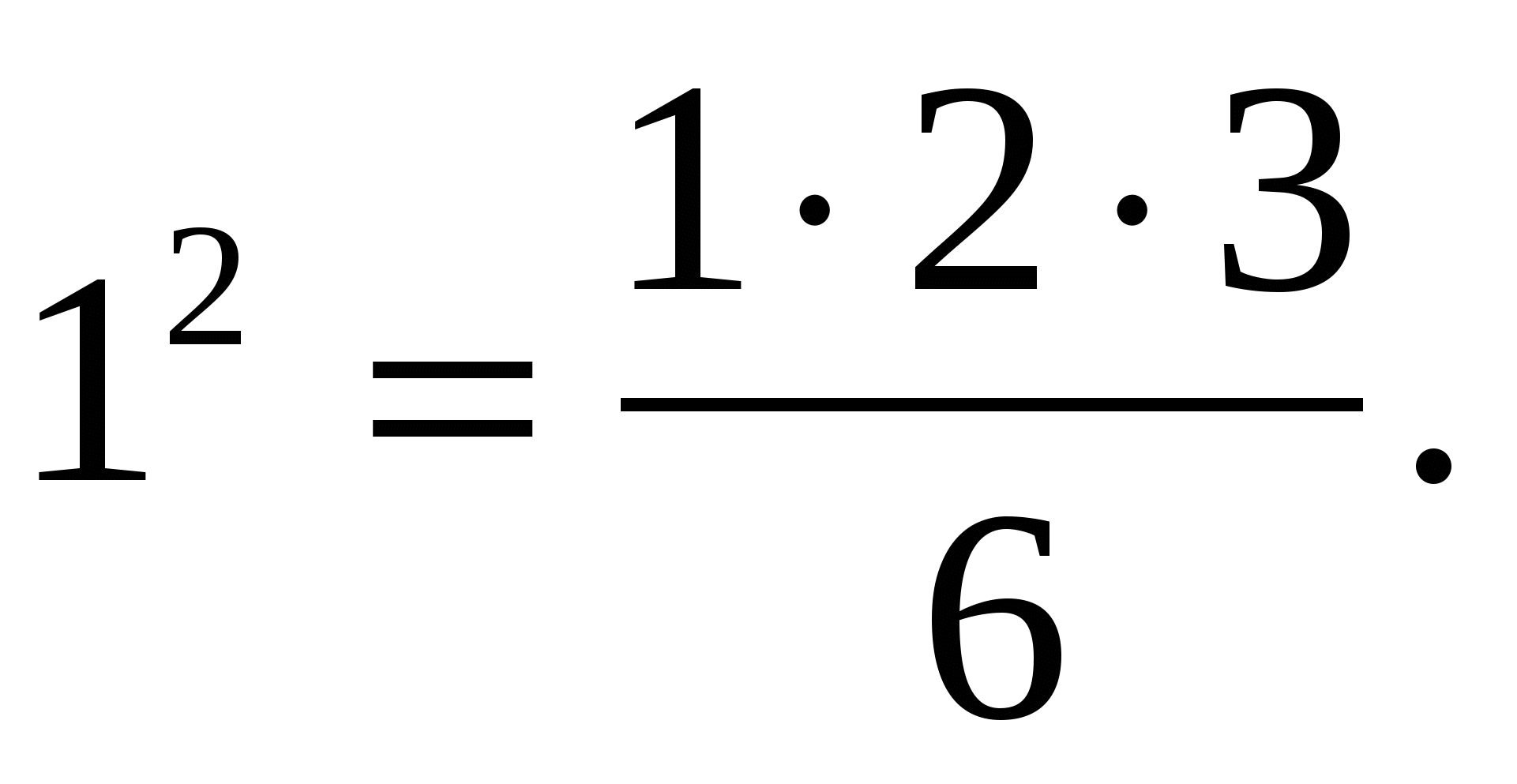
Предположим, что при п=к получаем также верное равенство:
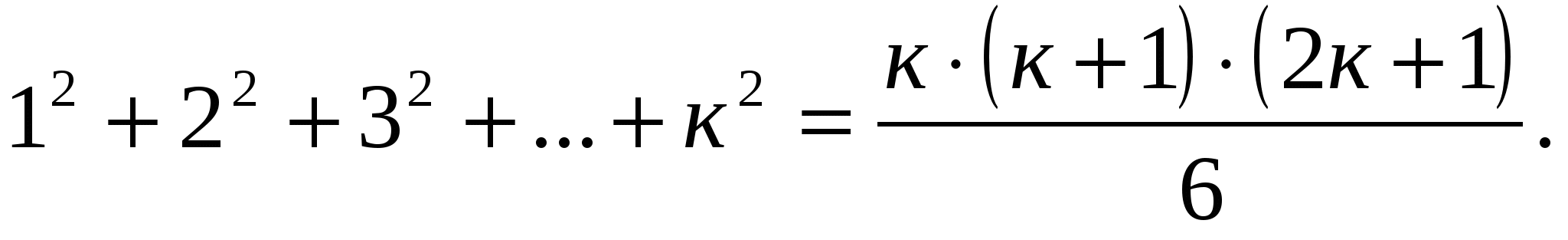
Докажем, что наблюдается справедливость равенства при п=к+1:
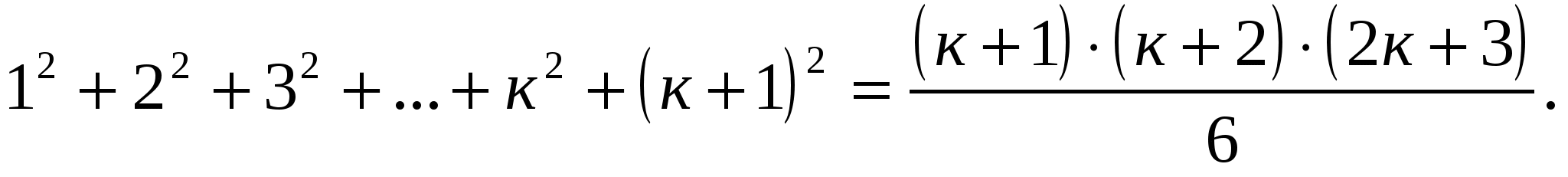
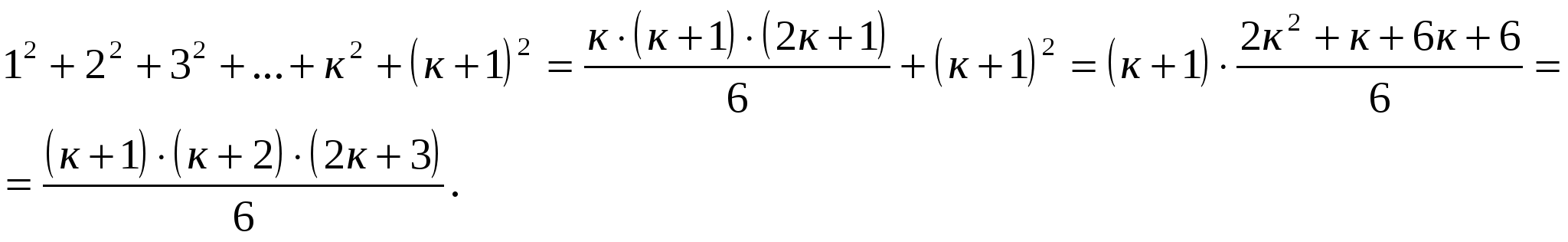
Тогда тождество справедливо при любом натуральном п.
Урок № 6.
Решение задач на делимость.
Пример № 20. Доказать методом математической индукции, что
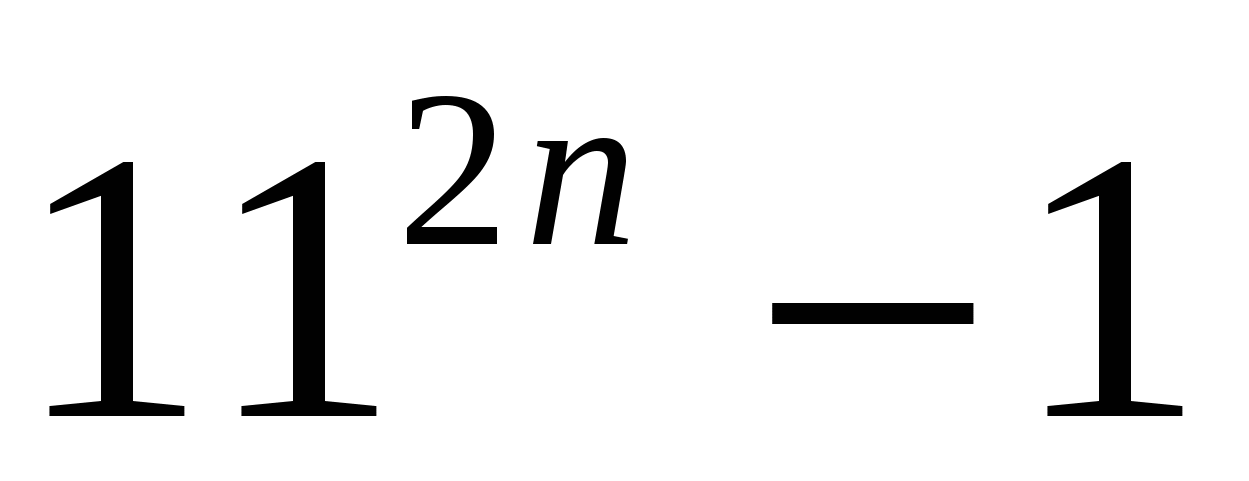 делится на 6 без остатка.
делится на 6 без остатка.
Доказательство.
При п=1 наблюдается деление на 6 без остатка, 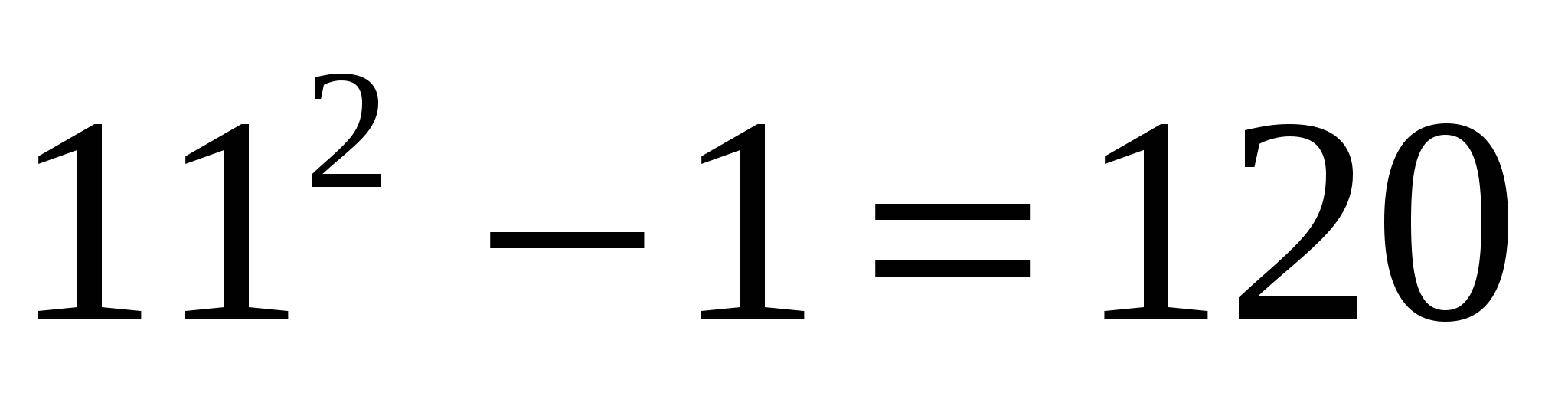 .
.
Пусть при п=к выражение 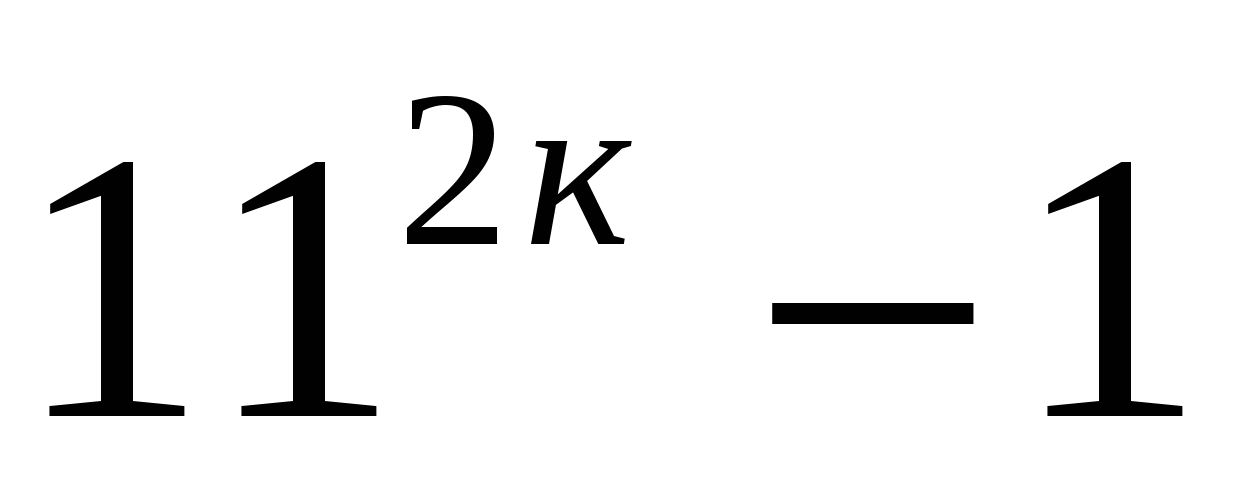 кратно 6.
кратно 6.
Докажем, что при п=к+1 выражение 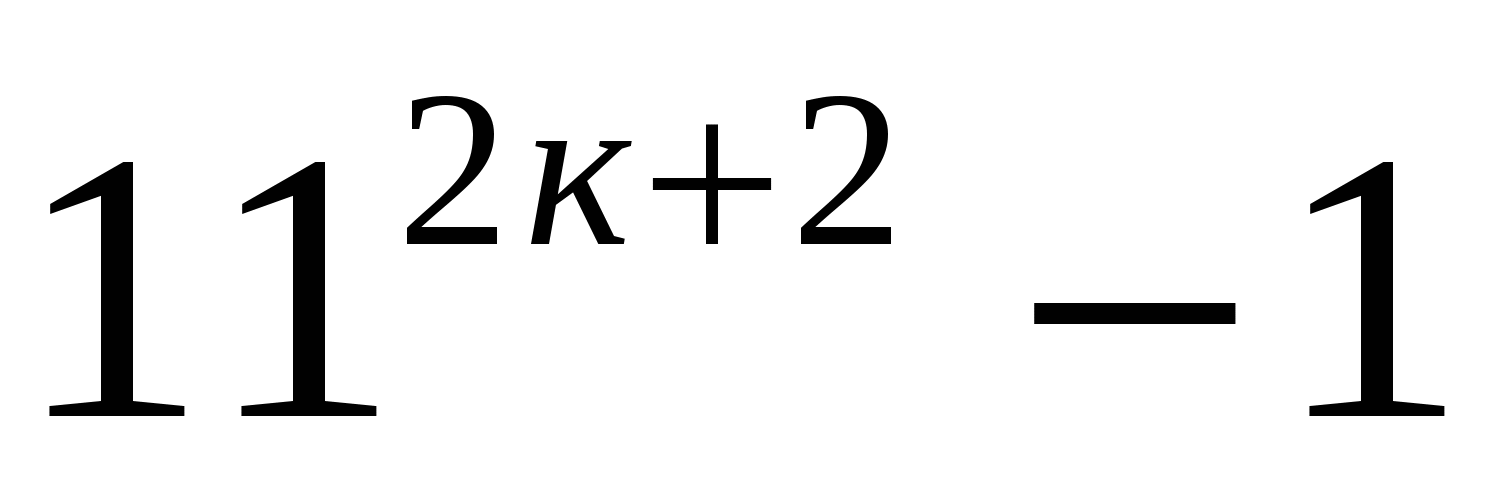 кратно 6.
кратно 6.
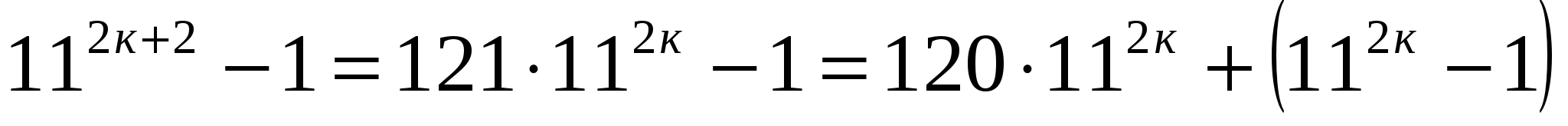 . Каждое слагаемое кратно 6, следовательно сумма кратна 6.
. Каждое слагаемое кратно 6, следовательно сумма кратна 6.
Пример № 21. Доказать делимость выражения 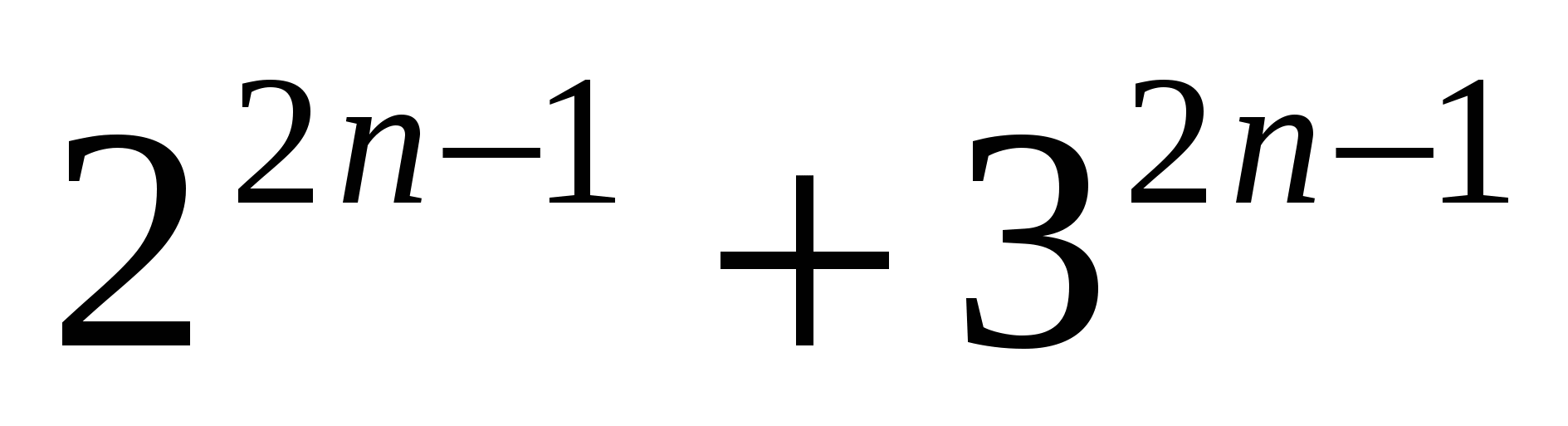 на 5 без остатка.
на 5 без остатка.
Доказательство.
При п=1 выражение делится без остатка 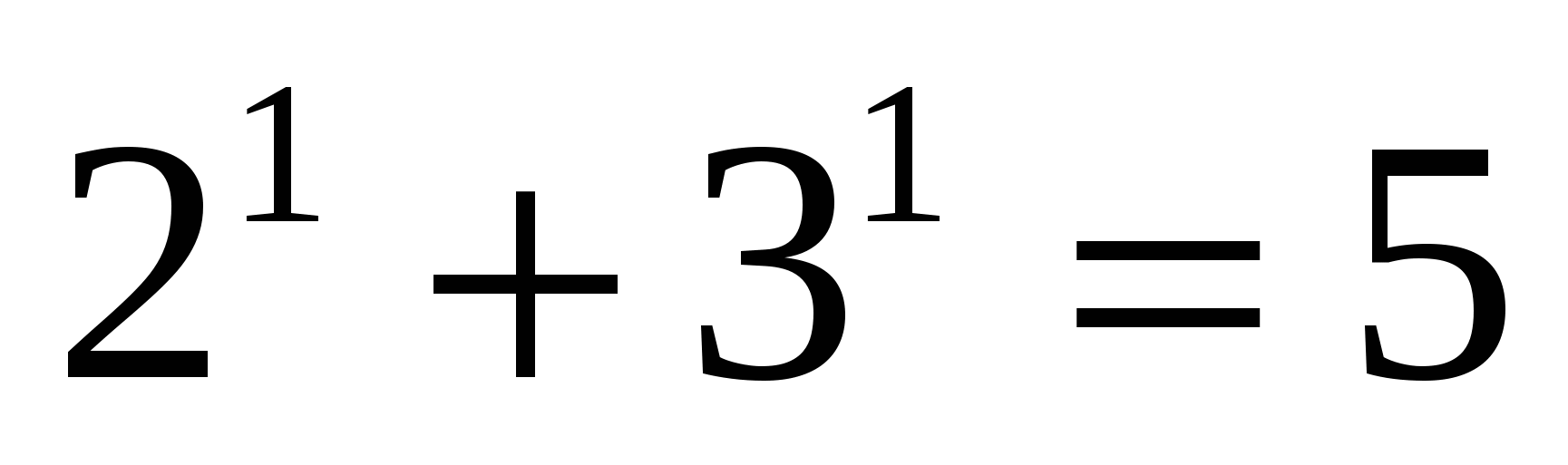 .
.
Пусть при п=к выражение 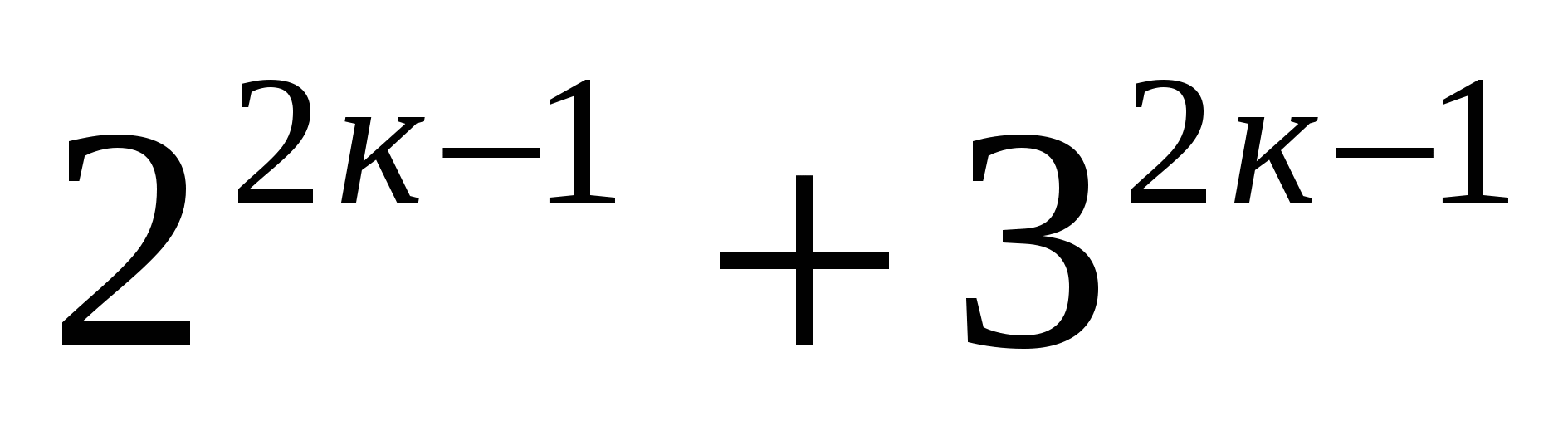 также делится на 5 без остатка.
также делится на 5 без остатка.
При п=к+1 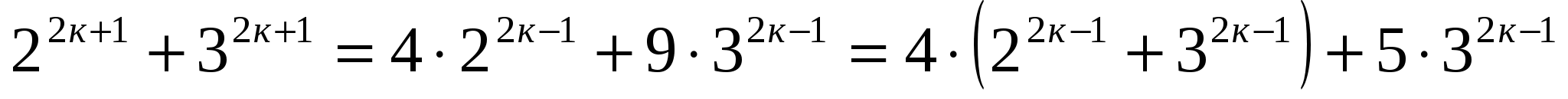 делится на 5.
делится на 5.
Пример № 22. Доказать делимость выражения 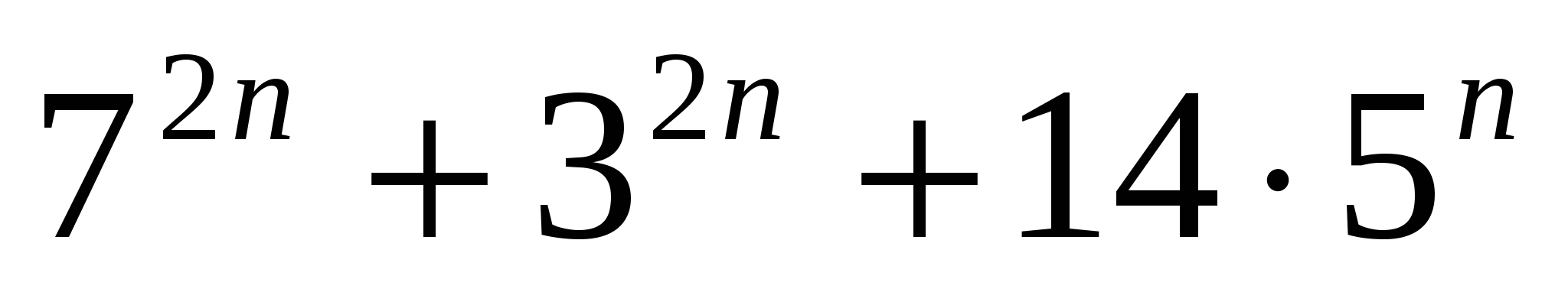 на 16.
на 16.
Доказательство.
При п=1 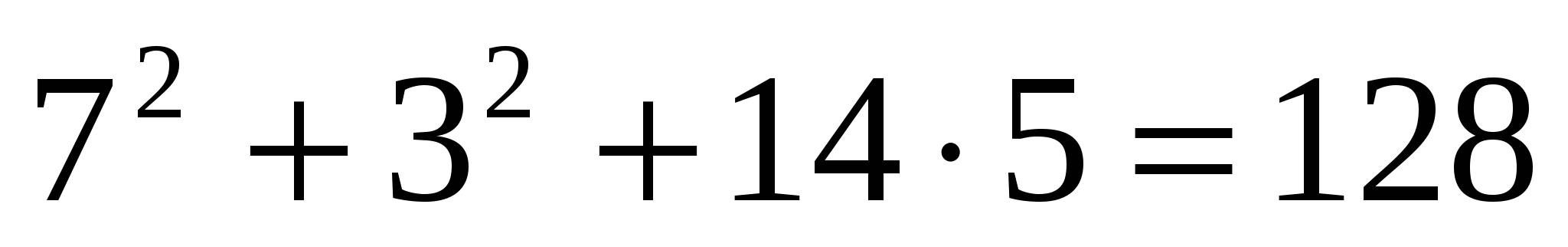 кратно 16.
кратно 16.
Пусть при п=к ![]() кратно 16.
кратно 16.
При п=к+1 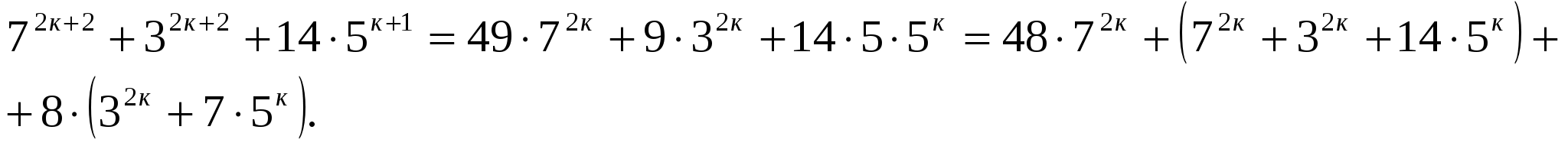
Все слагаемые делятся на 16: первое - очевидно, второе по предположению, а в третьем - в скобках стоит четное число.
Пример № 23. Доказать делимость 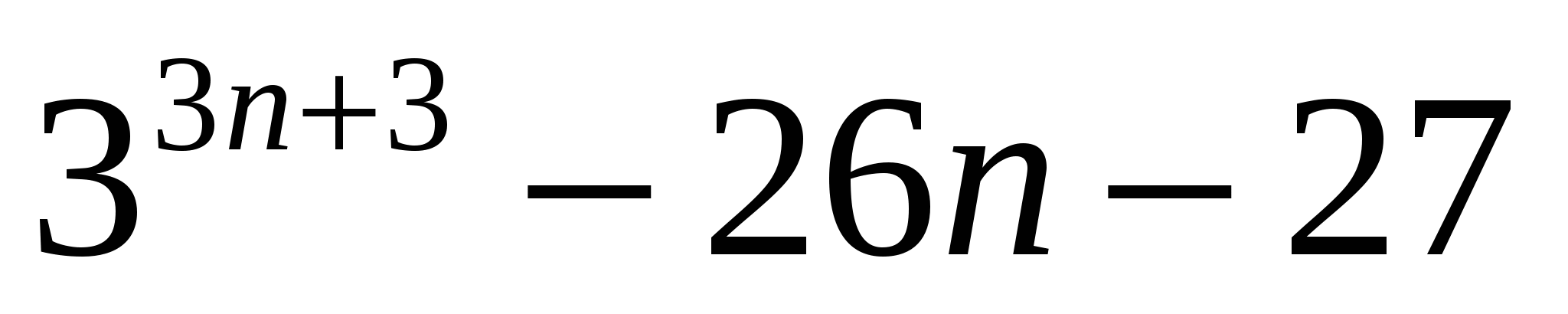 на 676.
на 676.
Доказательство.
Предварительно докажем, что 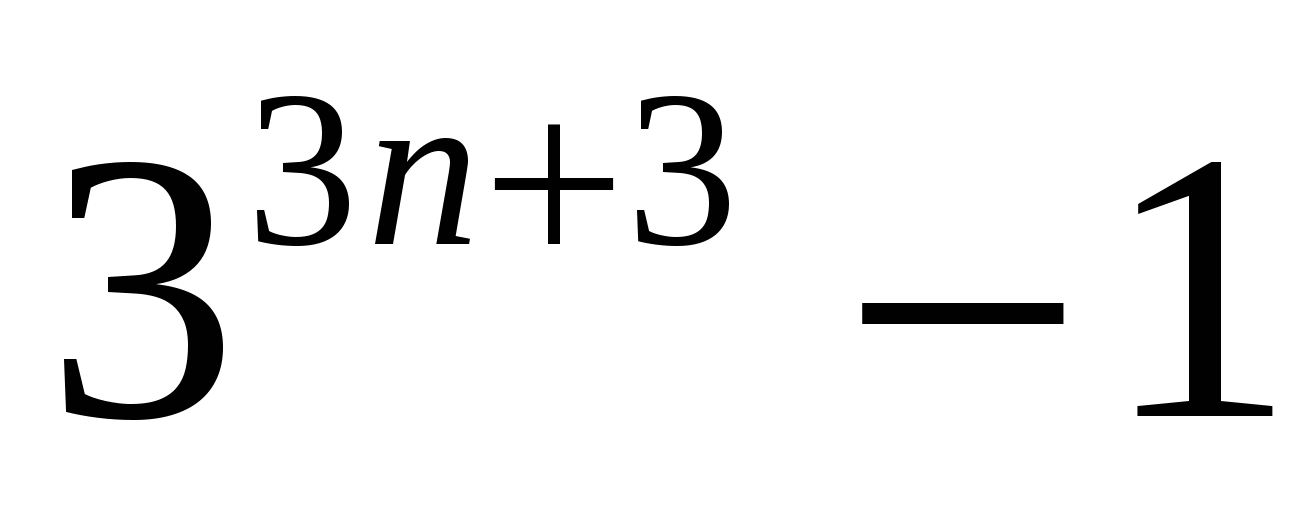 делится на
делится на 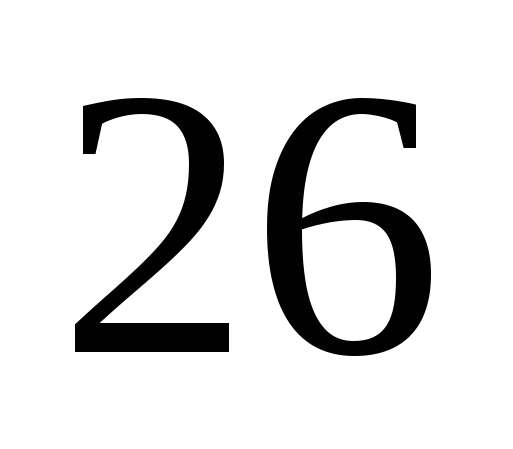 .
.
При п=0 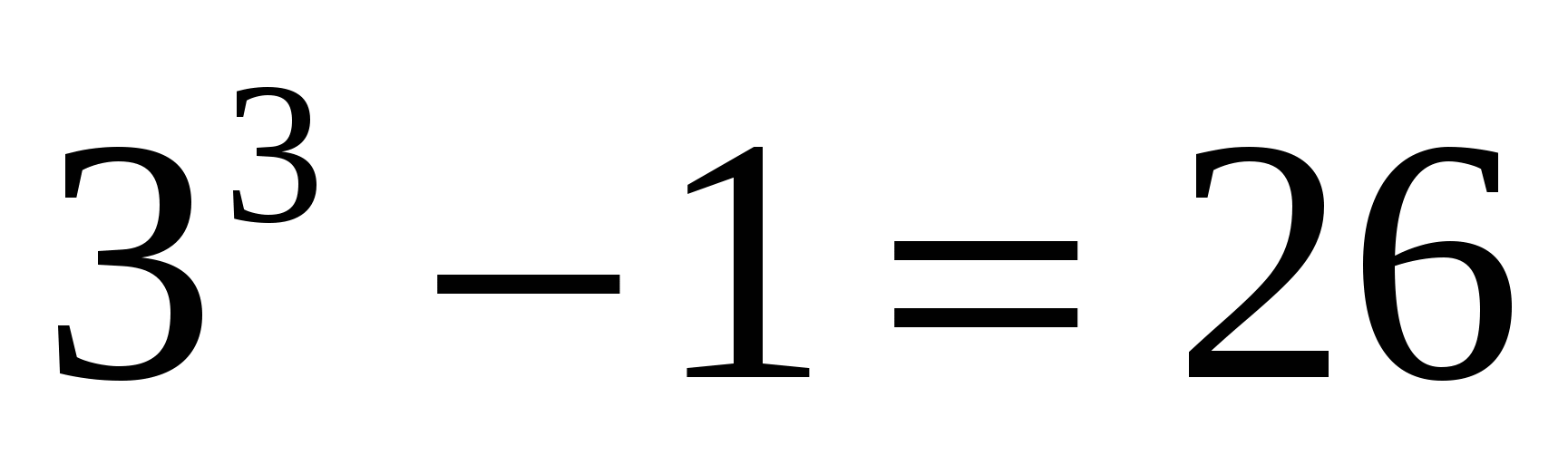 .
.
Пусть при п=к ![]() делится на 26.
делится на 26.
Тогда при п=к+1 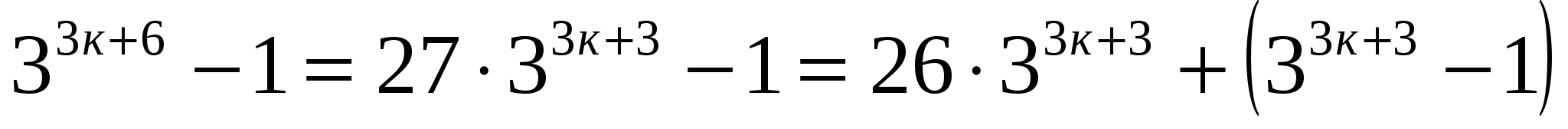 делится на 26.
делится на 26.
Теперь проведем доказательство утверждения, сформулированного в условии задачи.
При п=1 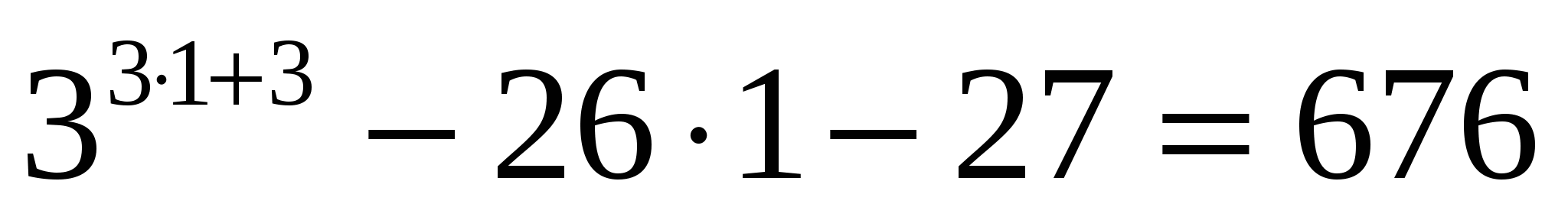 делится на 676.
делится на 676.
При п=к верно, что 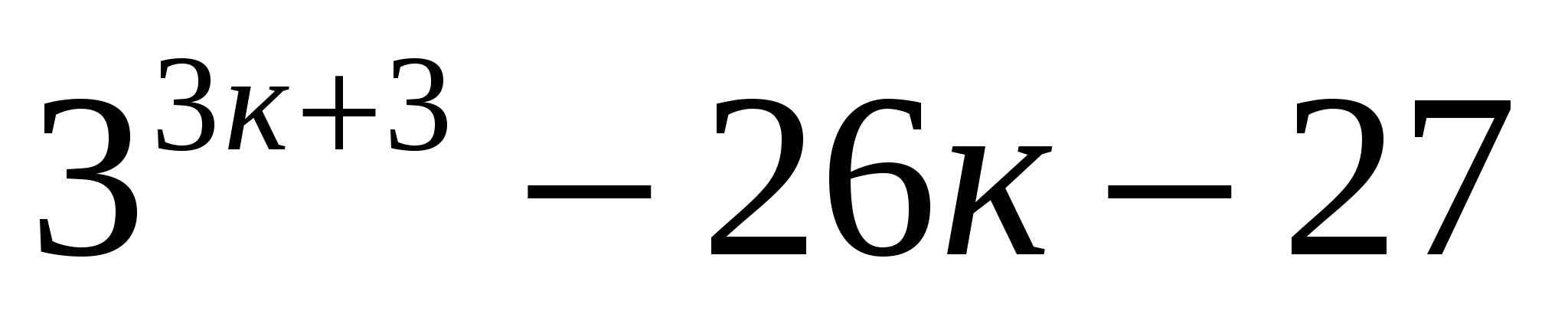 делится на 262.
делится на 262.
При п=к+1 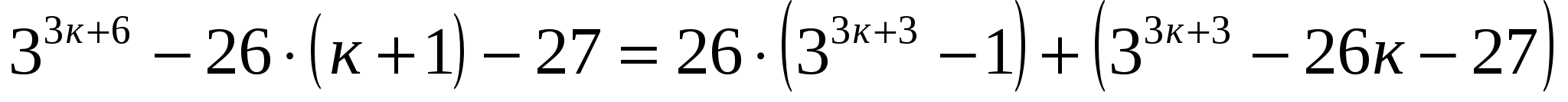 .
.
Оба слагаемых делятся на 676; первое - потому, что мы доказали делимость на 26 выражения, стоящего в скобках, а второе делится по предположению индукции.
Урок № 7.
Решение задач на делимость.
Пример № 24.
Доказать, что ![]() делится на 5 без остатка.
делится на 5 без остатка.
Доказательство.
При п=1 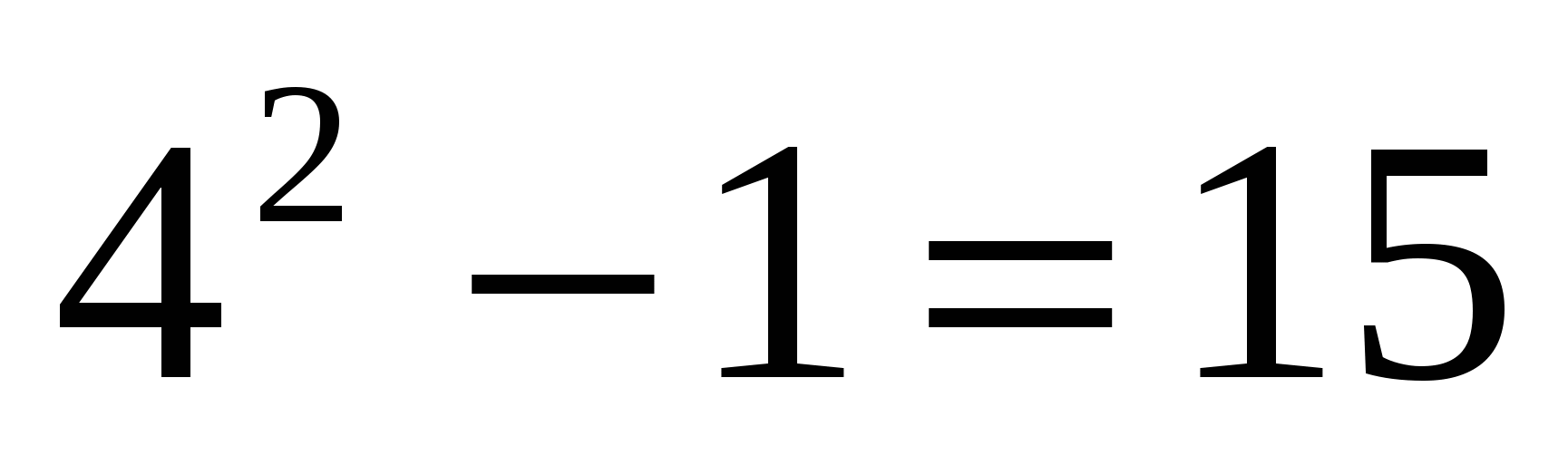 делится на 5.
делится на 5.
При п=к 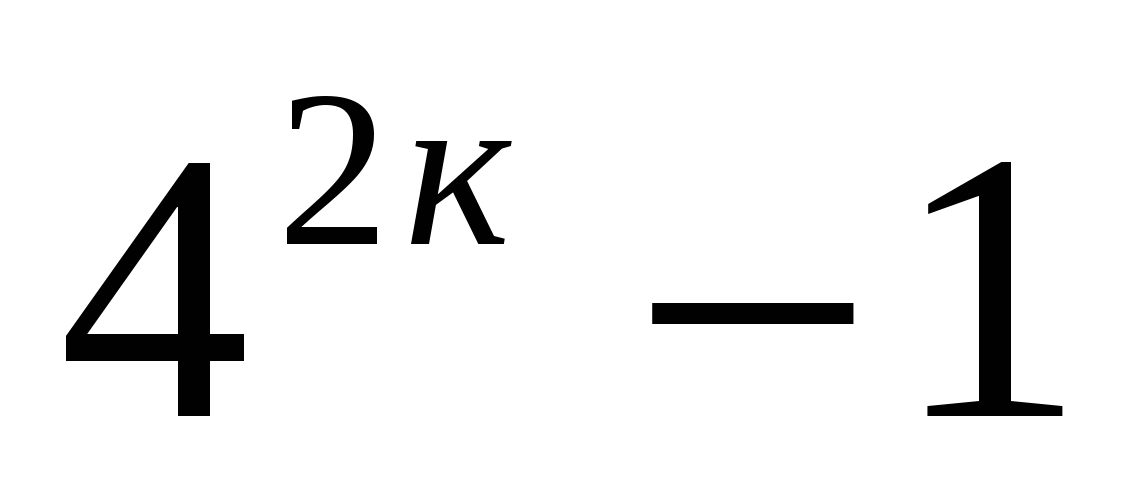 делится на 5 без остатка.
делится на 5 без остатка.
При п=к+1 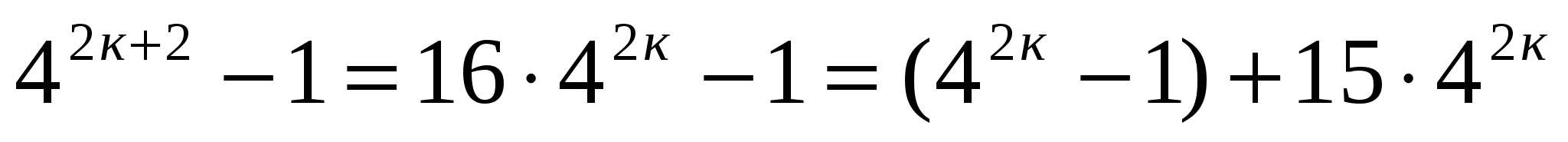 каждое слагаемое делится на 5 без остатка.
каждое слагаемое делится на 5 без остатка.
Пример № 25.
Доказать, что ![]() делится на 6 без остатка.
делится на 6 без остатка.
Доказательство.
При п=1 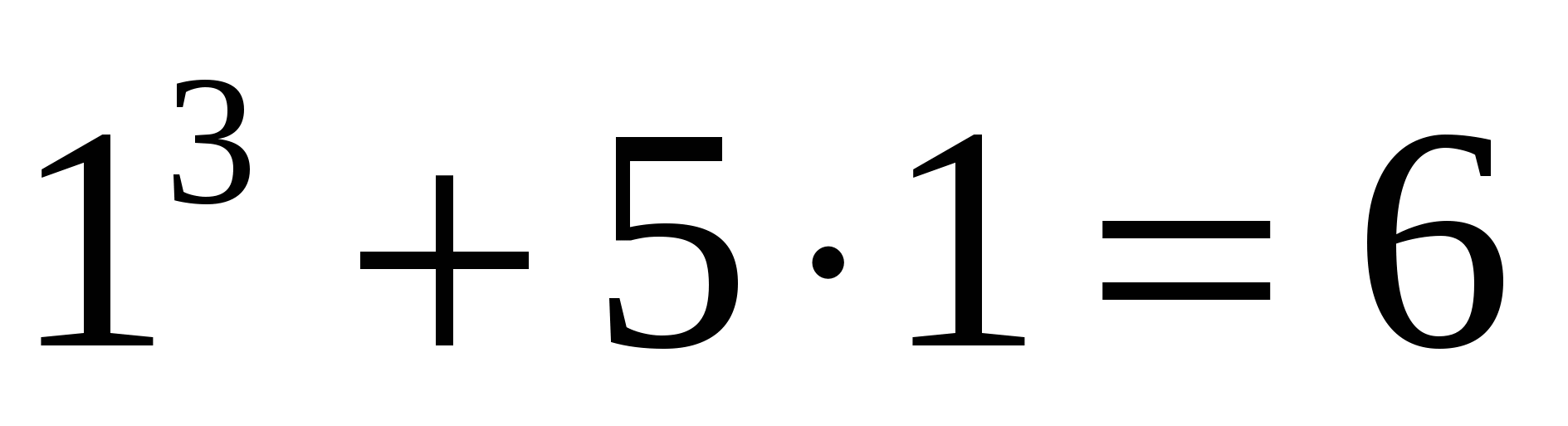 делится на 6 без остатка.
делится на 6 без остатка.
Пусть при п=к ![]() делится на 6 без остатка.
делится на 6 без остатка.
При п=к+1 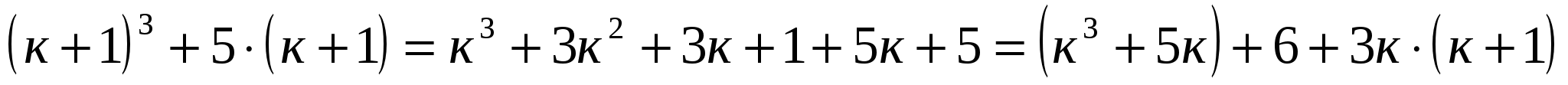 делится на 6 без остатка, так как каждое слагаемое делится на 6 без остатка: первое слагаемое - по предположению индукции, второе - очевидно, третье - потому, что
делится на 6 без остатка, так как каждое слагаемое делится на 6 без остатка: первое слагаемое - по предположению индукции, второе - очевидно, третье - потому, что 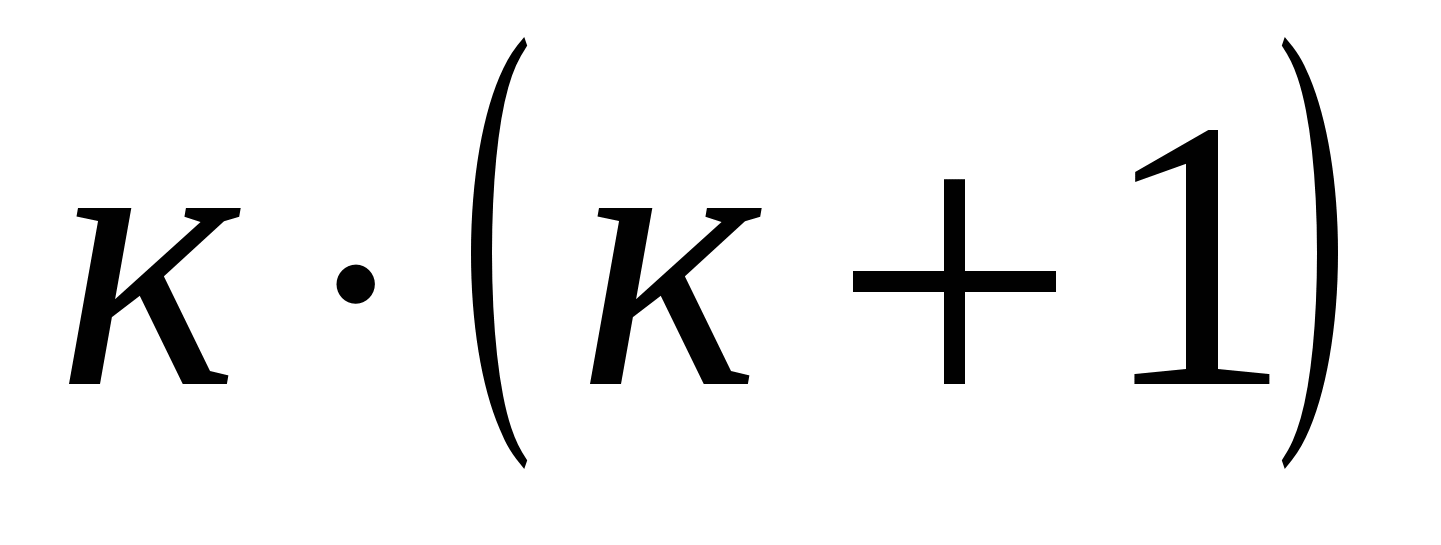 четное число.
четное число.
Пример № 26.
Доказать, что ![]() при делении на 9 дает остаток 1.
при делении на 9 дает остаток 1.
Доказательство.
Докажем, что ![]() делится на 9.
делится на 9.
При п=1 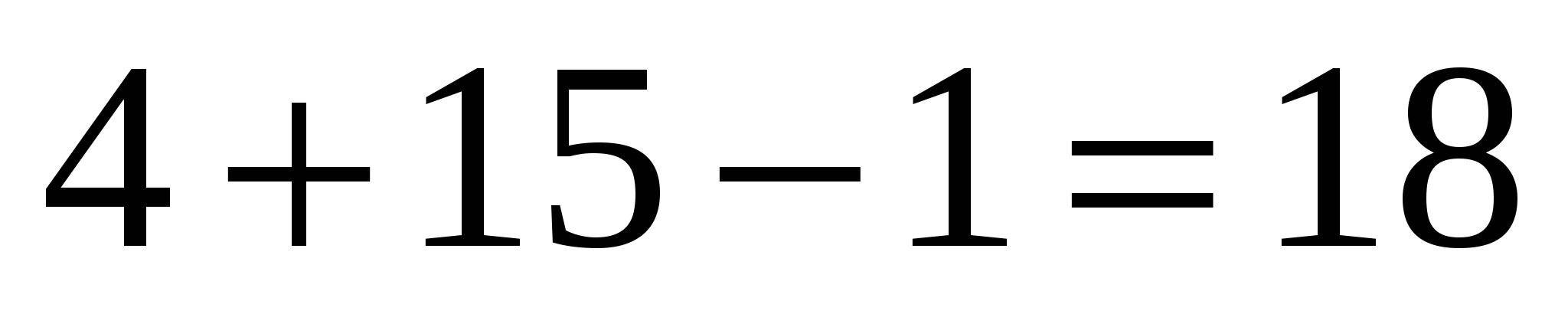 делится на 9. Пусть при п=к
делится на 9. Пусть при п=к 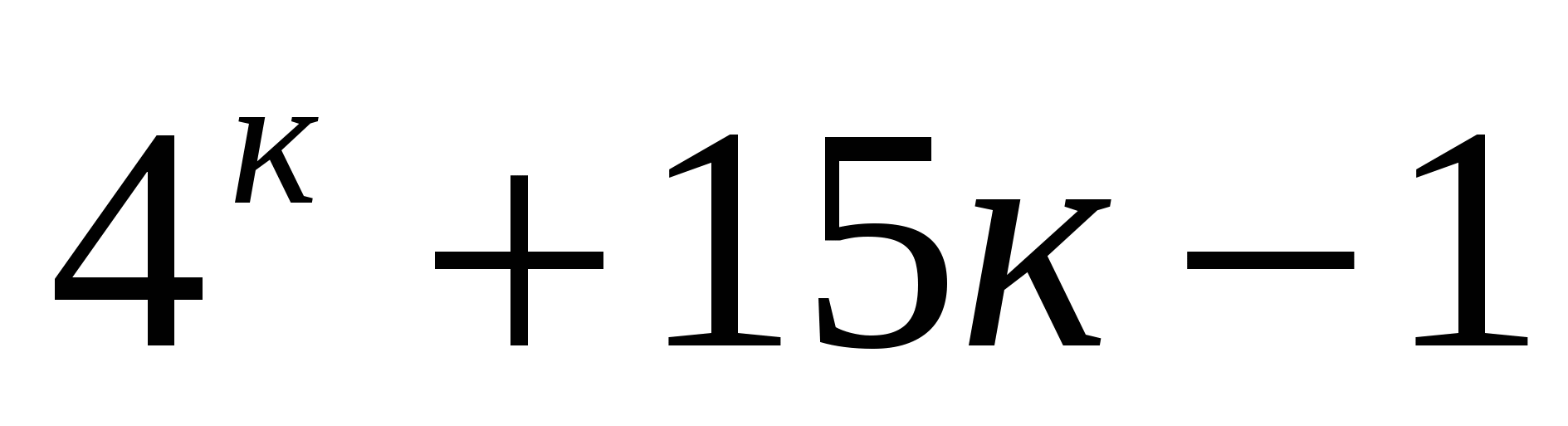 делится на 9.
делится на 9.
При п=к+1 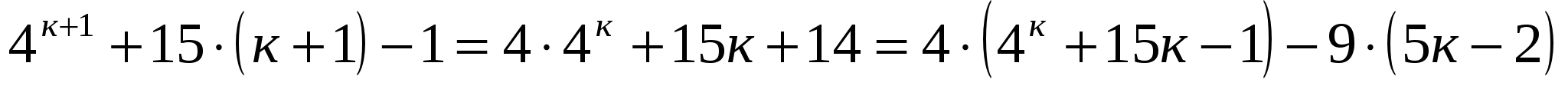 делится на 9.
делится на 9.
Пример № 27.
Доказать, что ![]() делится на 15 без остатка.
делится на 15 без остатка.
Доказательство.
При п=1 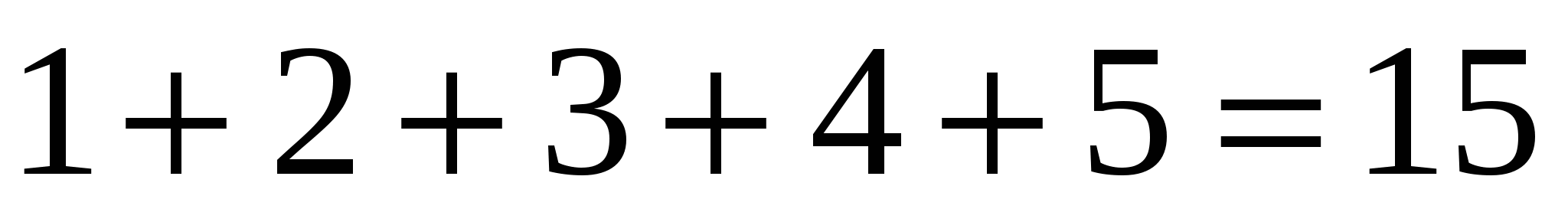 делится на 15.
делится на 15.
Пусть при п=к ![]() делится на 15 без остатка.
делится на 15 без остатка.
При п=к+1 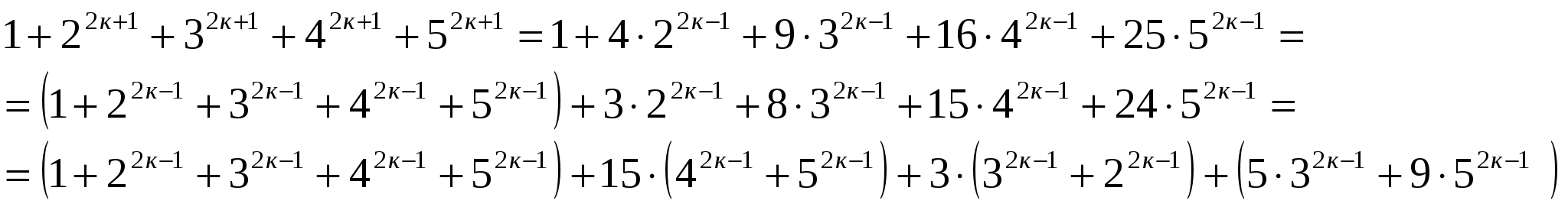
Первое слагаемое кратно 15 по предположению индукции, второе слагаемое кратно 15 - очевидно, третье слагаемое кратно 15, так как 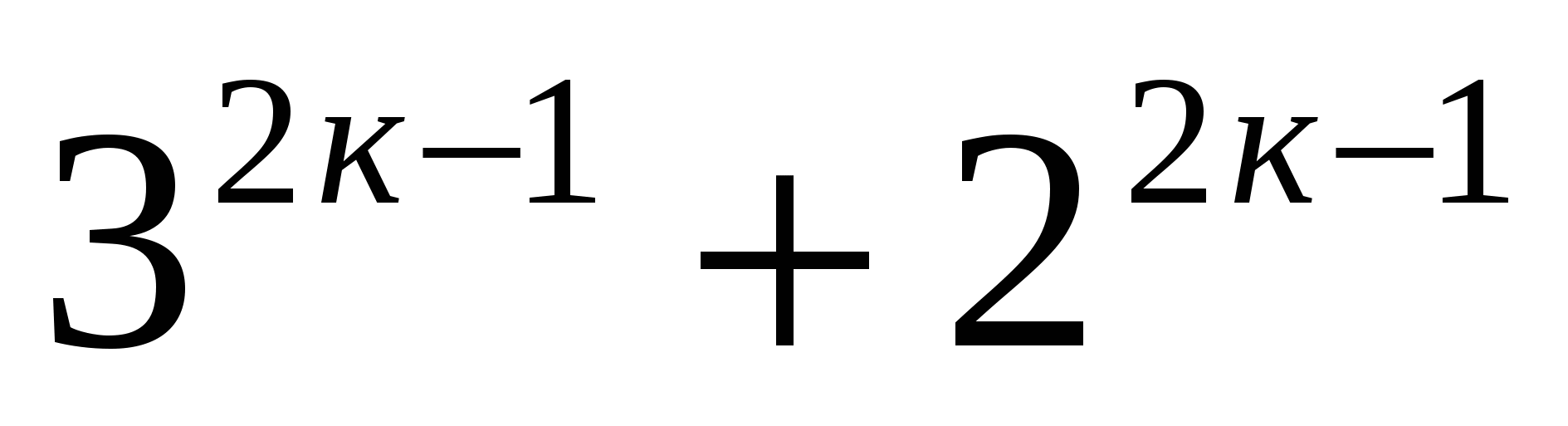 кратно 5 ( доказано в примере № 21), четвертое и пятое слагаемые также кратны 5, что очевидно, тогда сумма кратна 15.
кратно 5 ( доказано в примере № 21), четвертое и пятое слагаемые также кратны 5, что очевидно, тогда сумма кратна 15.
Урок № 8-9.
Доказательство неравенств методом математической индукции
Пример № 28. Доказать, что справедливо неравенство 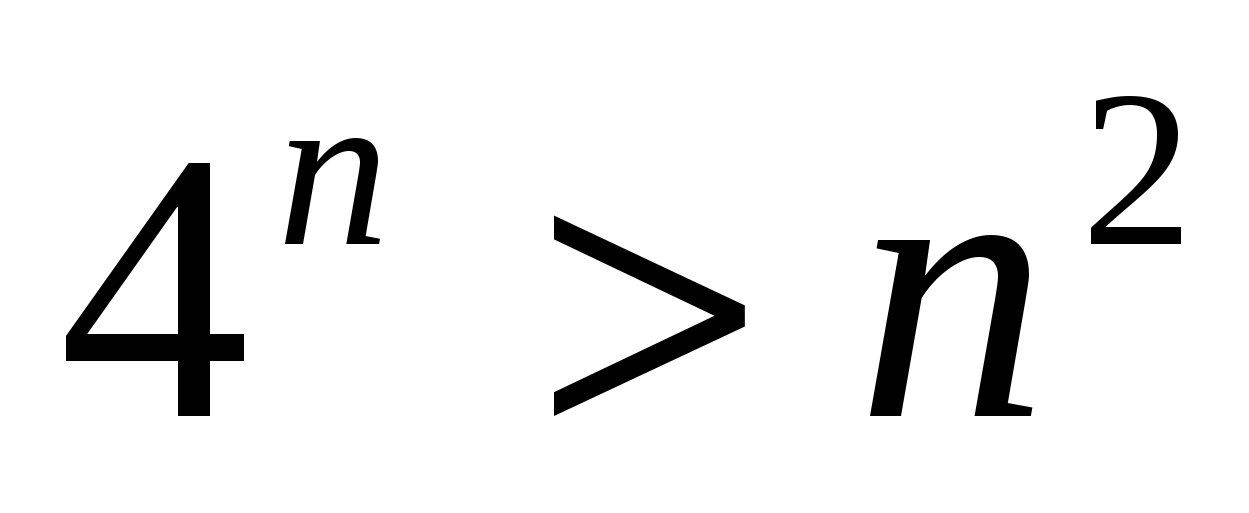 .
.
При п=1 имеем 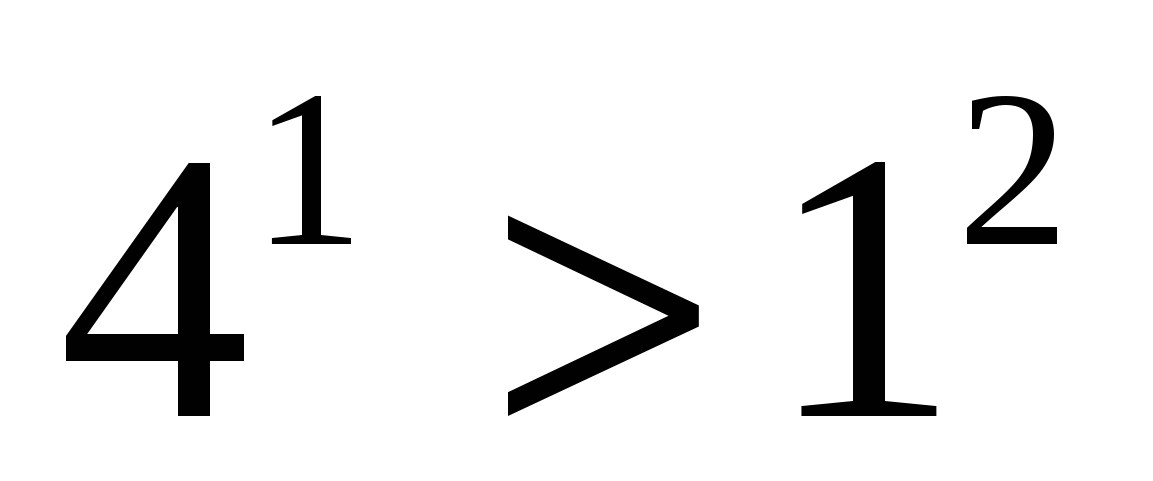 - верно.
- верно.
Пусть при п=к 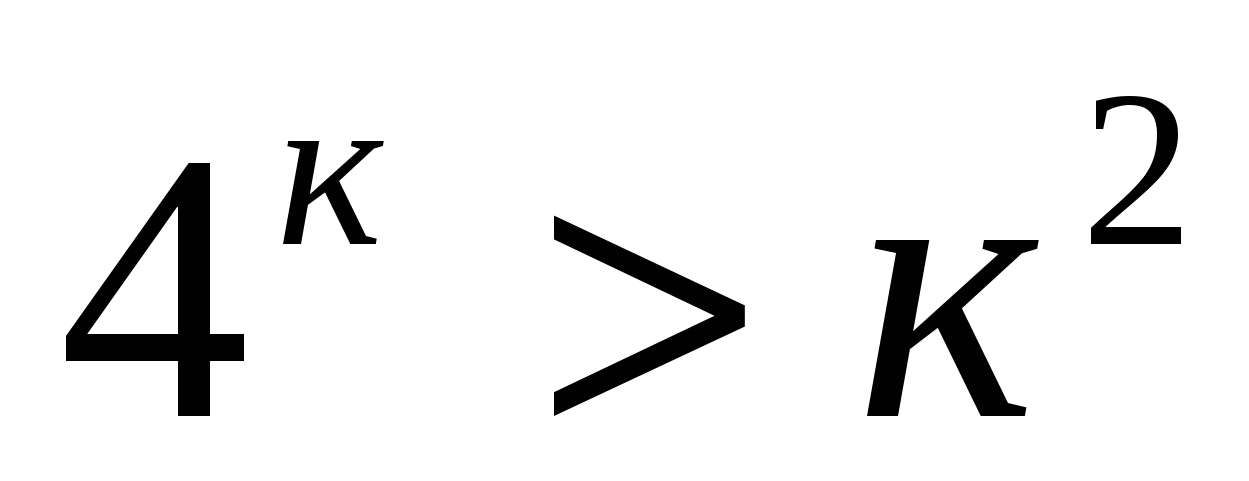 - верное неравенство.
- верное неравенство.
При п=к+1
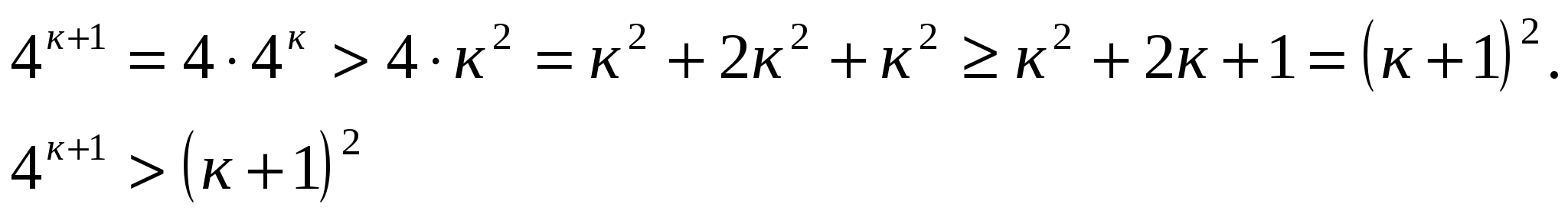
Тогда неравенство справедливо для любого натурального п.
Пример № 29. Доказать, что справедливо неравенство 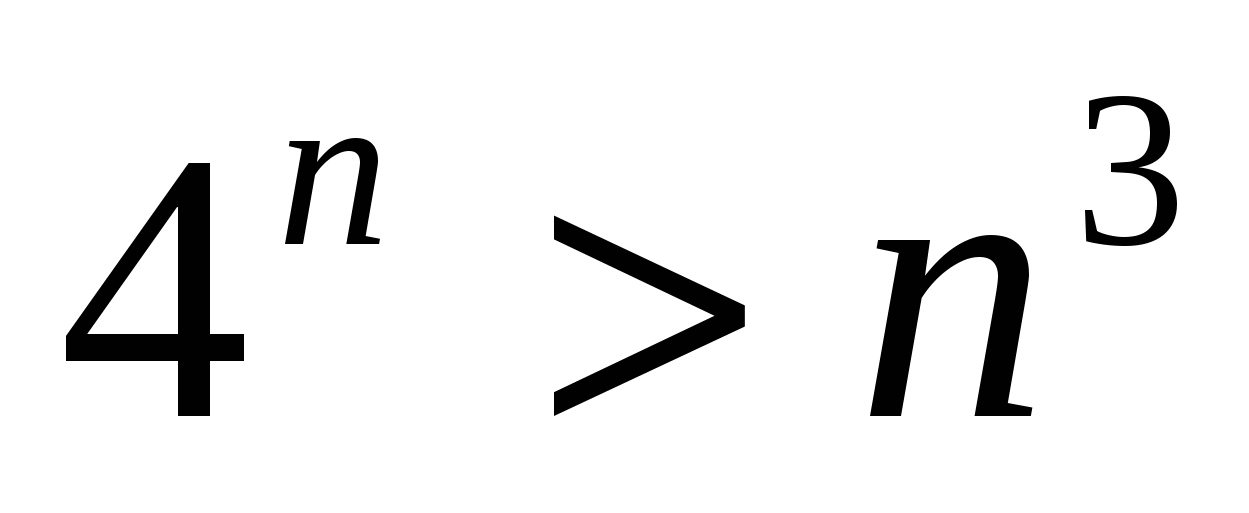 при любом п.
при любом п.
При п=1 получим верное неравенство 4 >1.
Пусть при п=к справедливо неравенство 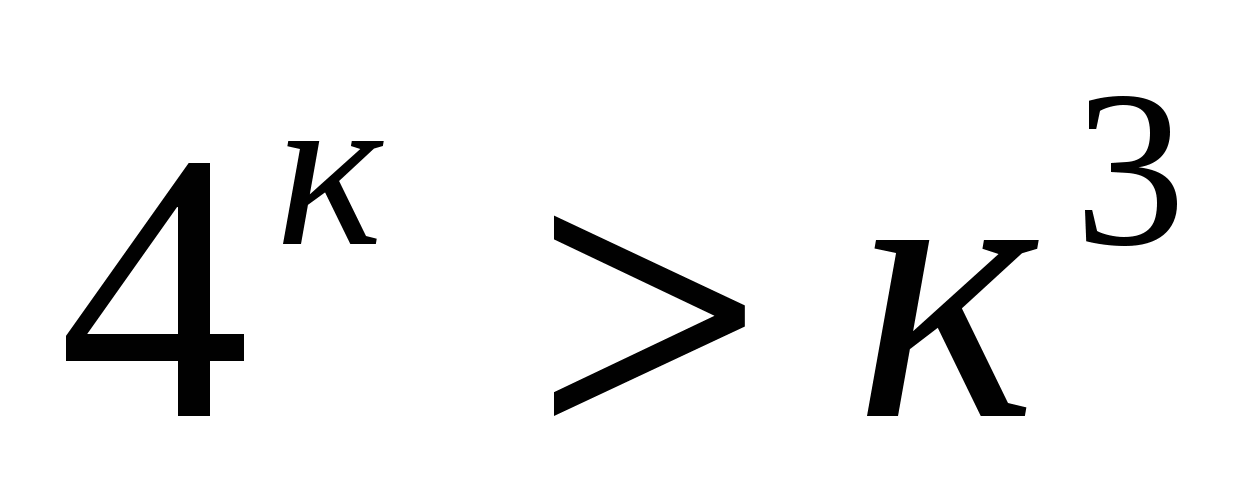 .
.
Докажем, что при п=к+1 справедливо неравенство 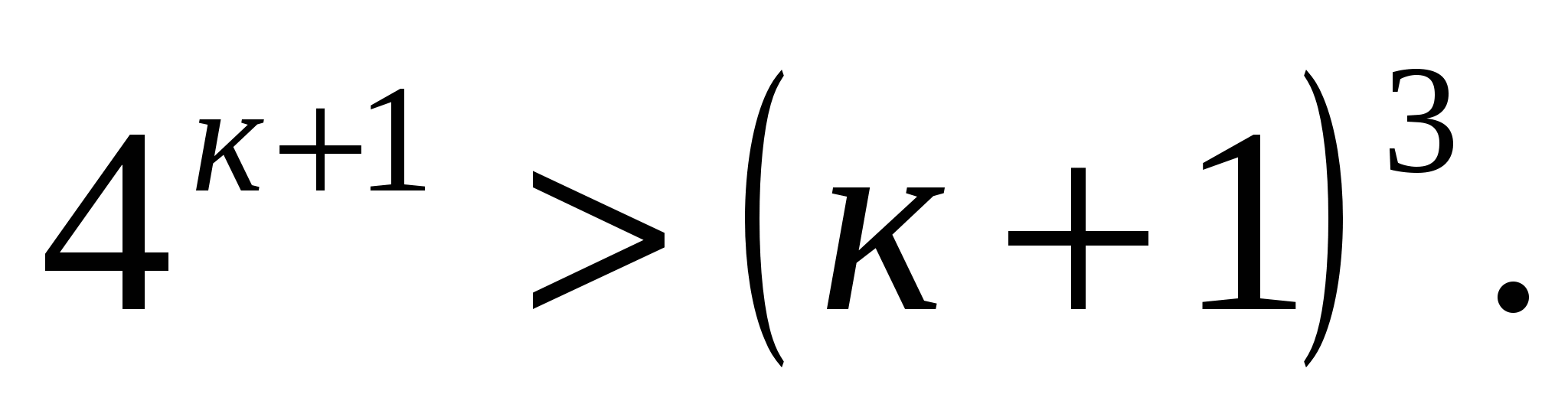
Для любого натурального к наблюдается неравенство 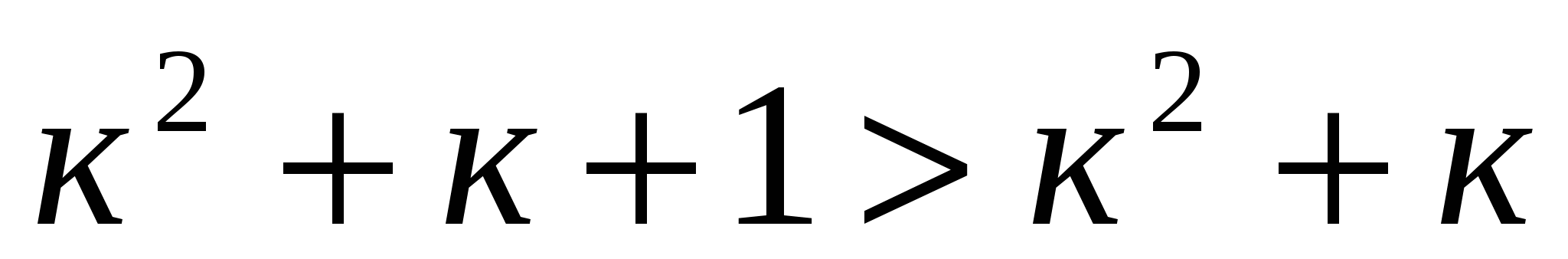 .
.
Если 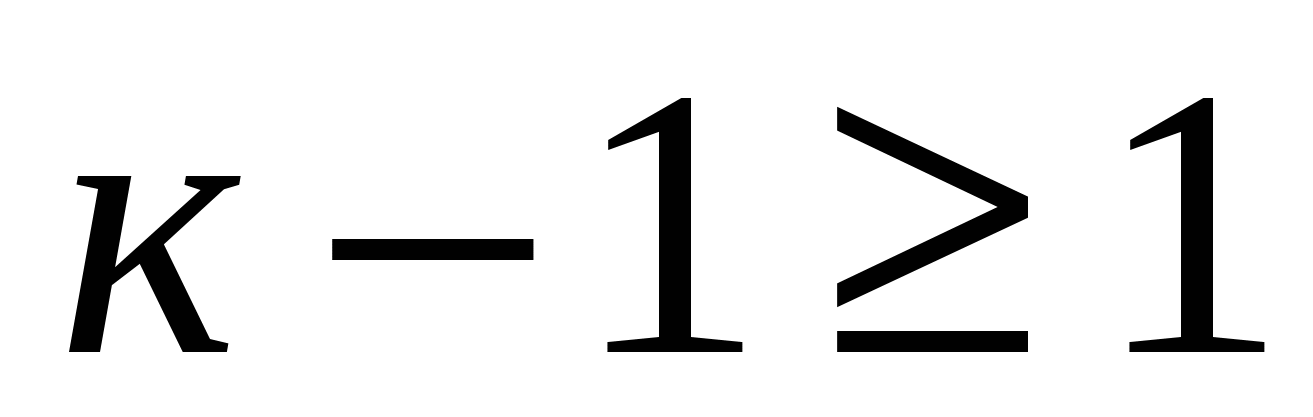 при
при 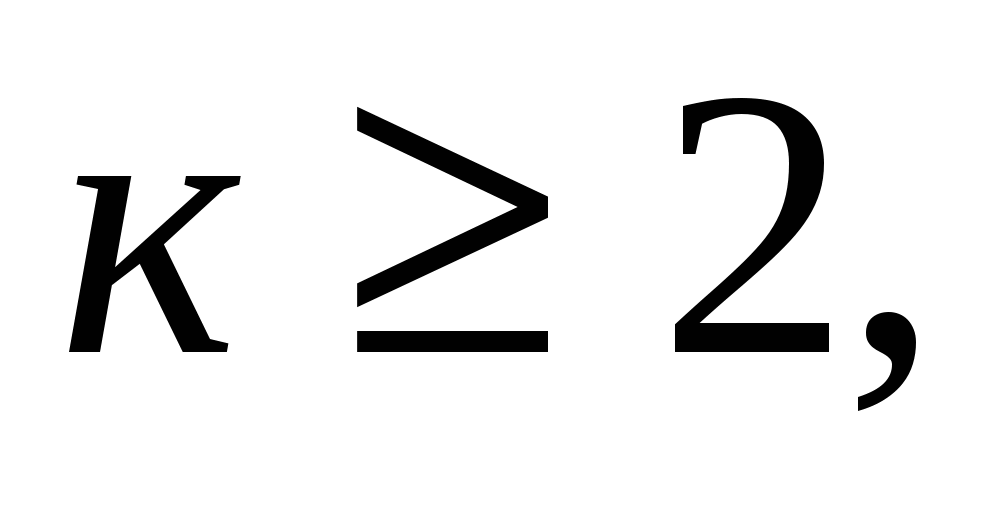 то
то 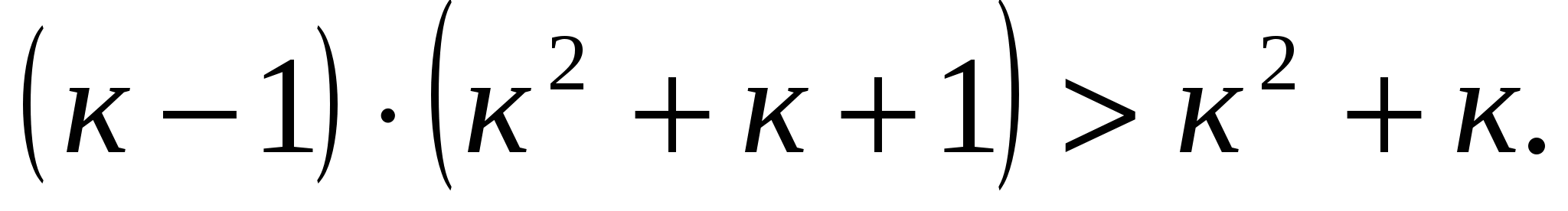
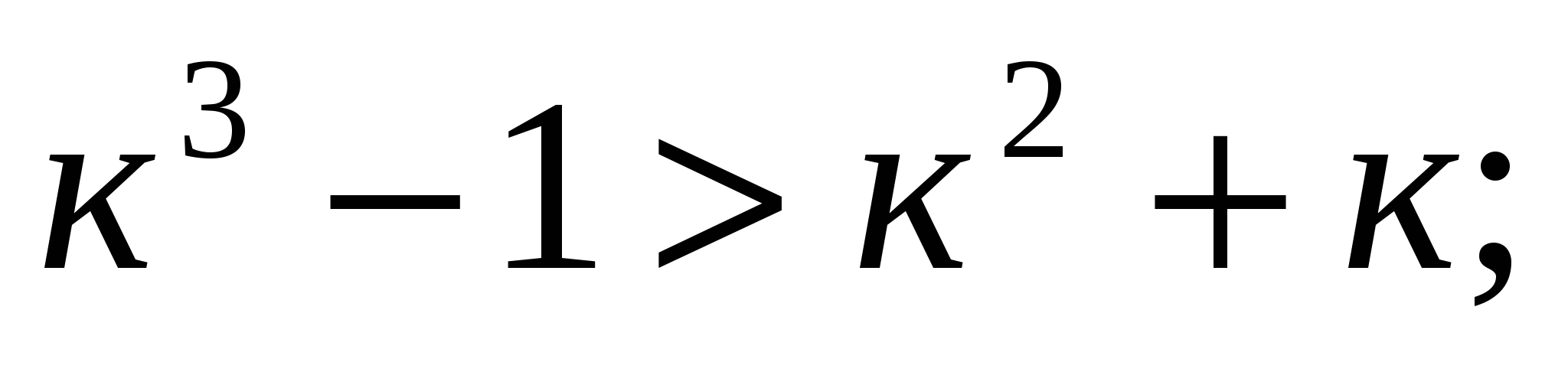
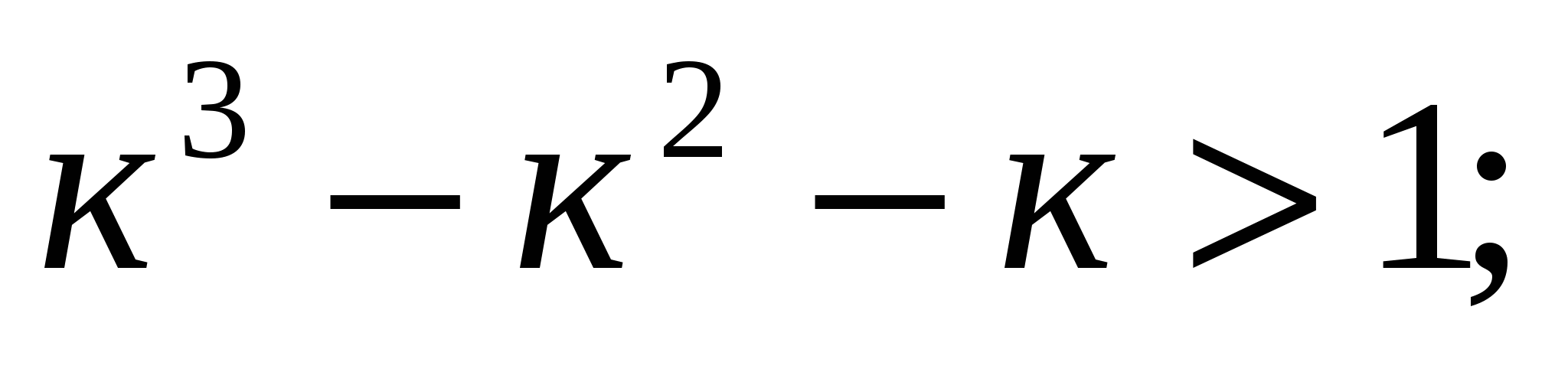
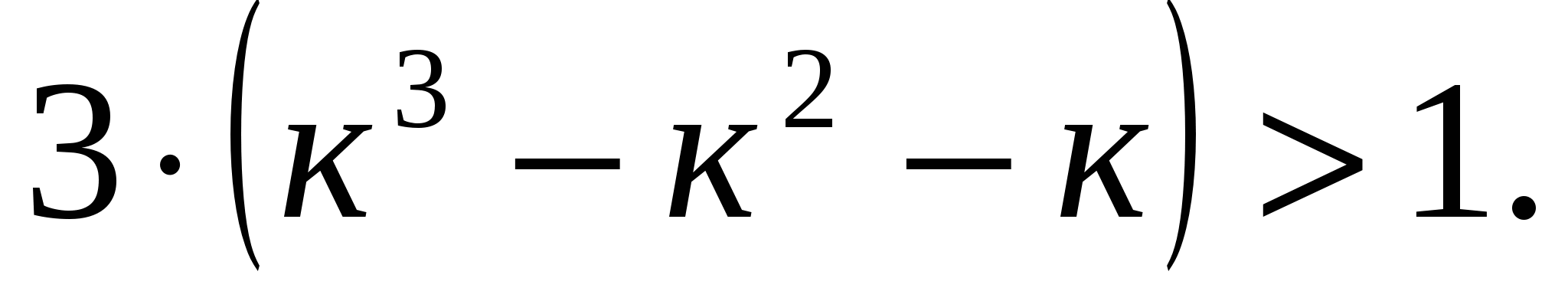
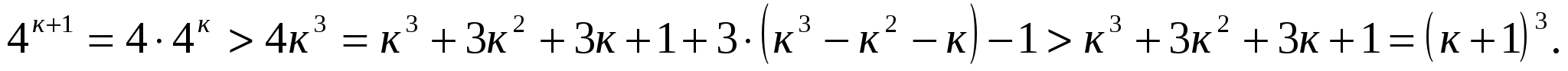
Пример № 30. Доказать справедливость неравенства
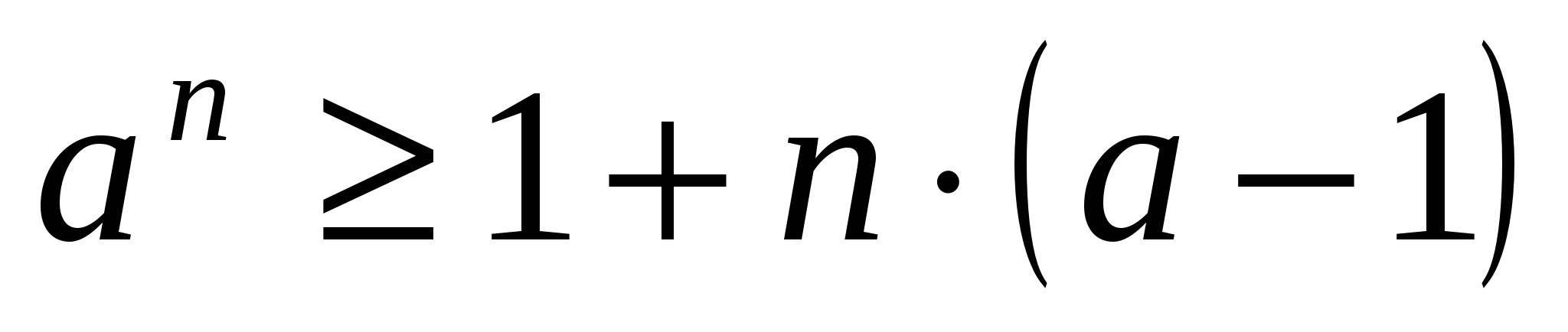 при любом натуральном п и любом
при любом натуральном п и любом ![]()
Пусть п=1 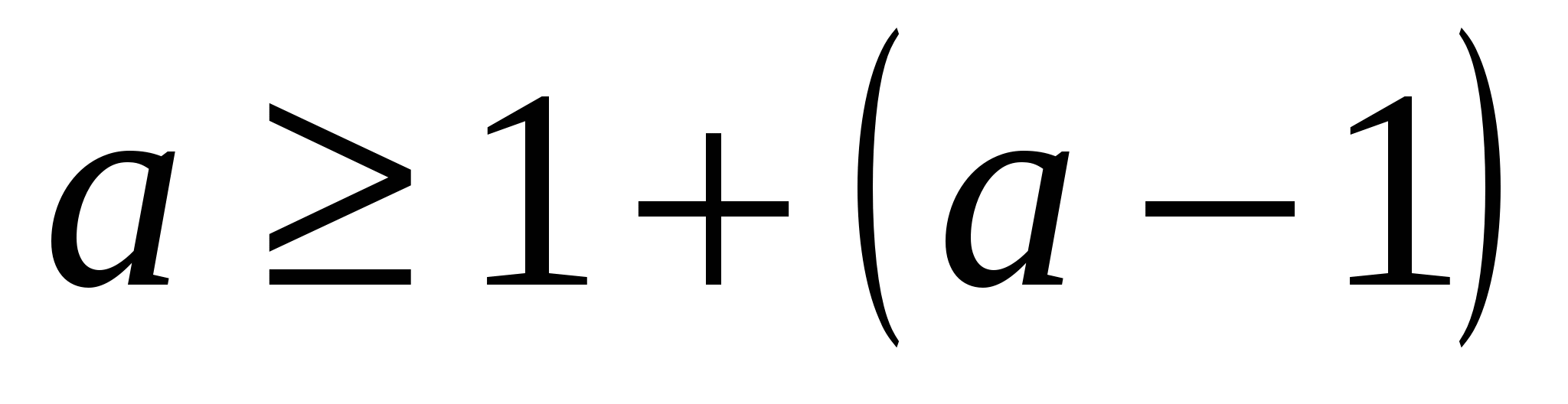 , верно.
, верно.
Предположим, что неравенство выполняется при п=к: 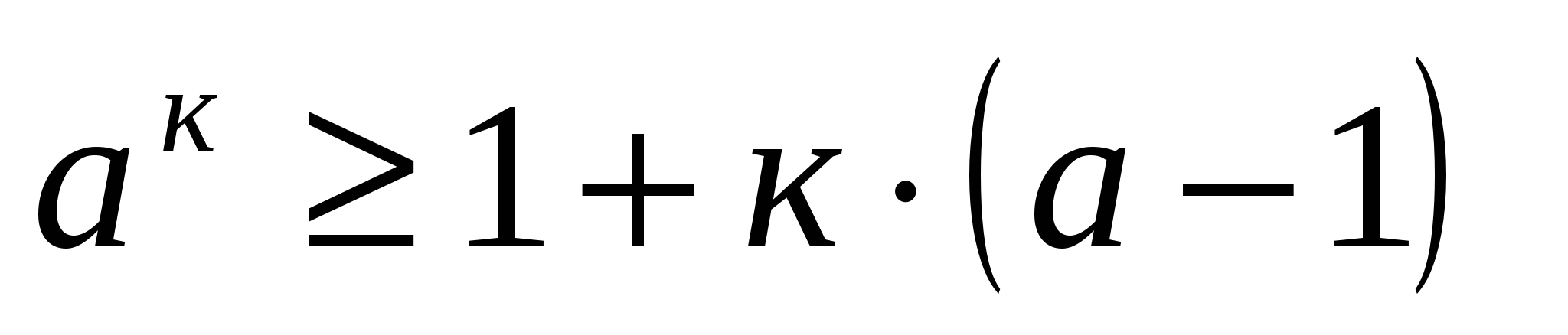 .
.
При п=к+1 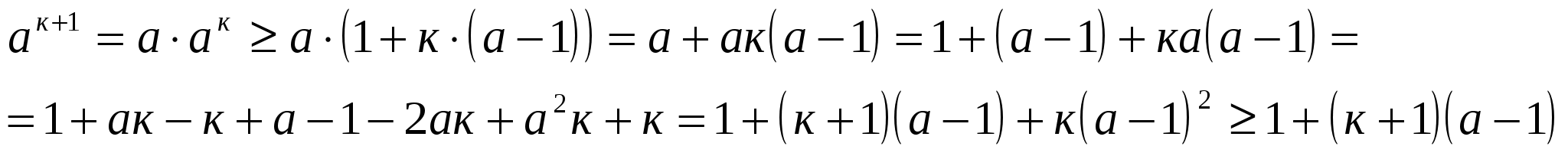
Пример № 31. Доказать справедливость неравенства
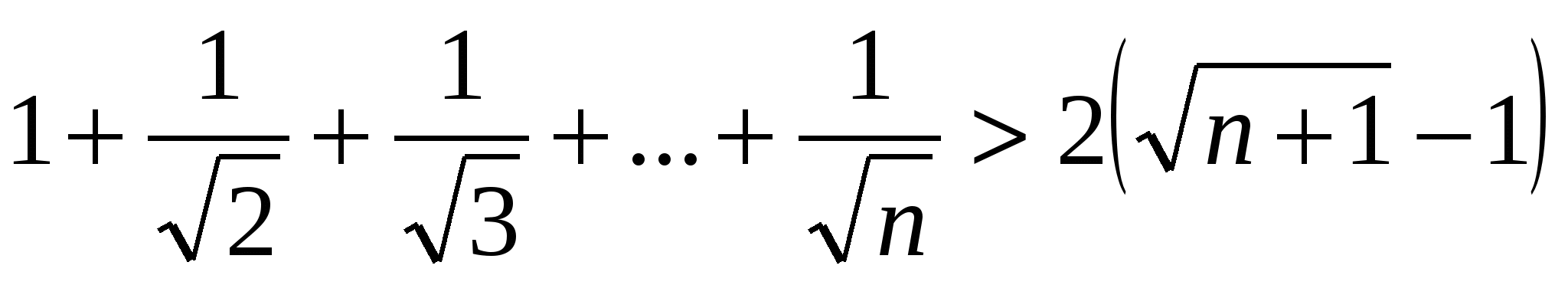 при любом натуральном п.
при любом натуральном п.
Докажем сначала, что при любом натуральном т справедливо неравенство
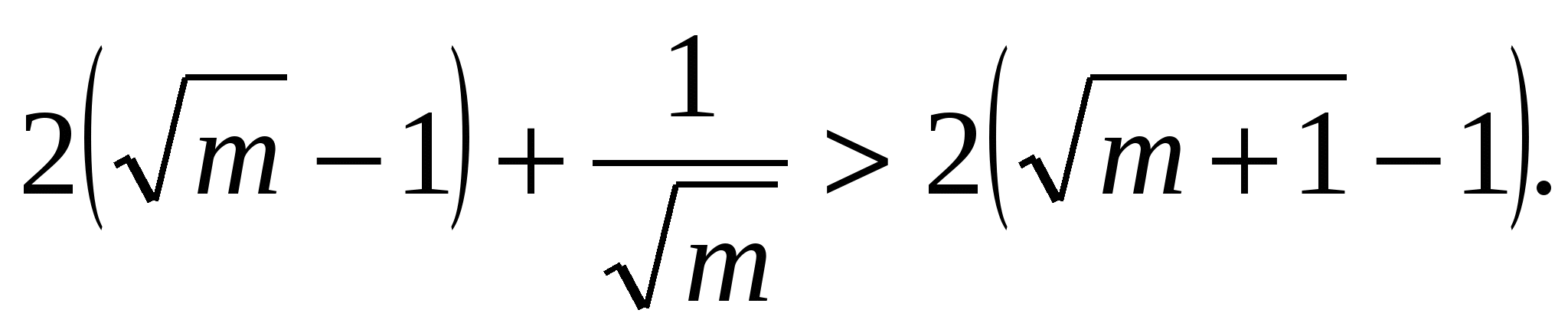 Умножим обе части неравенства на
Умножим обе части неравенства на 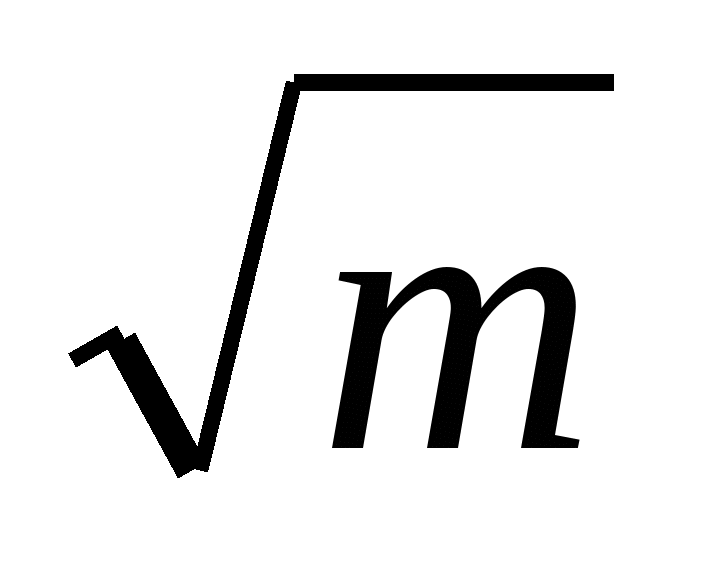 . Получим равносильное неравенство
. Получим равносильное неравенство 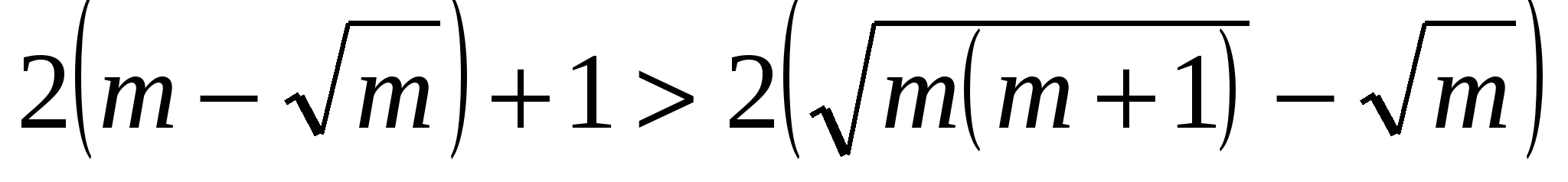 или
или 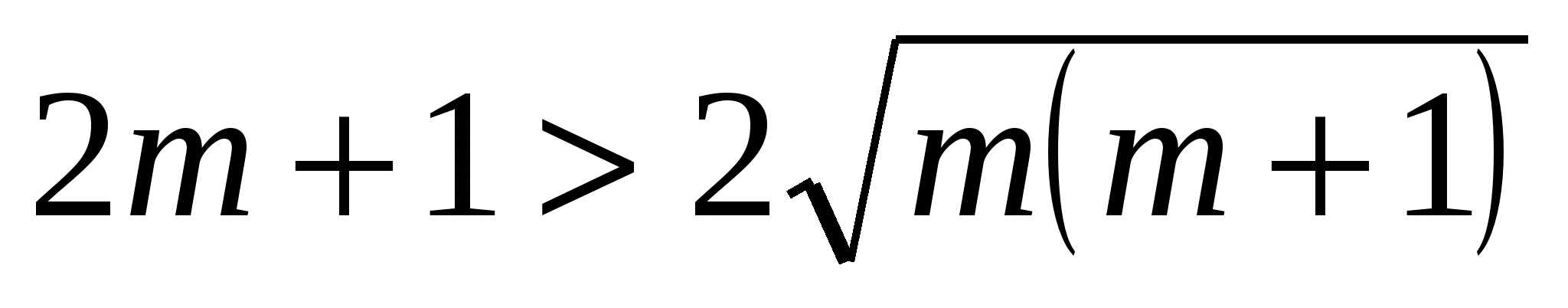 ;
; 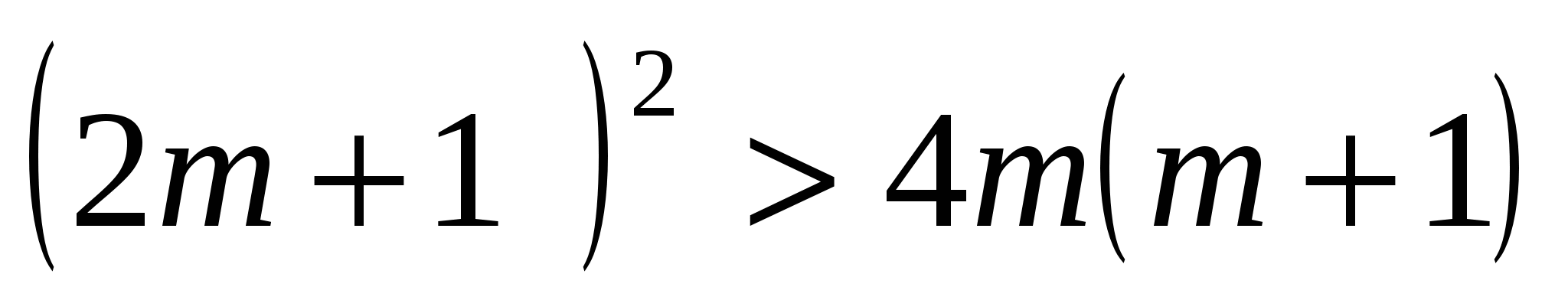 ;
; 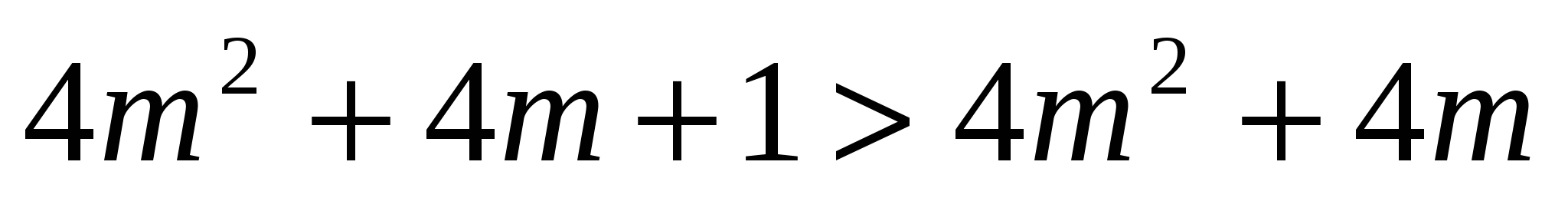 - это неравенство выполняется при любом натуральном т.
- это неравенство выполняется при любом натуральном т.
При п=1 исходное неравенство верно 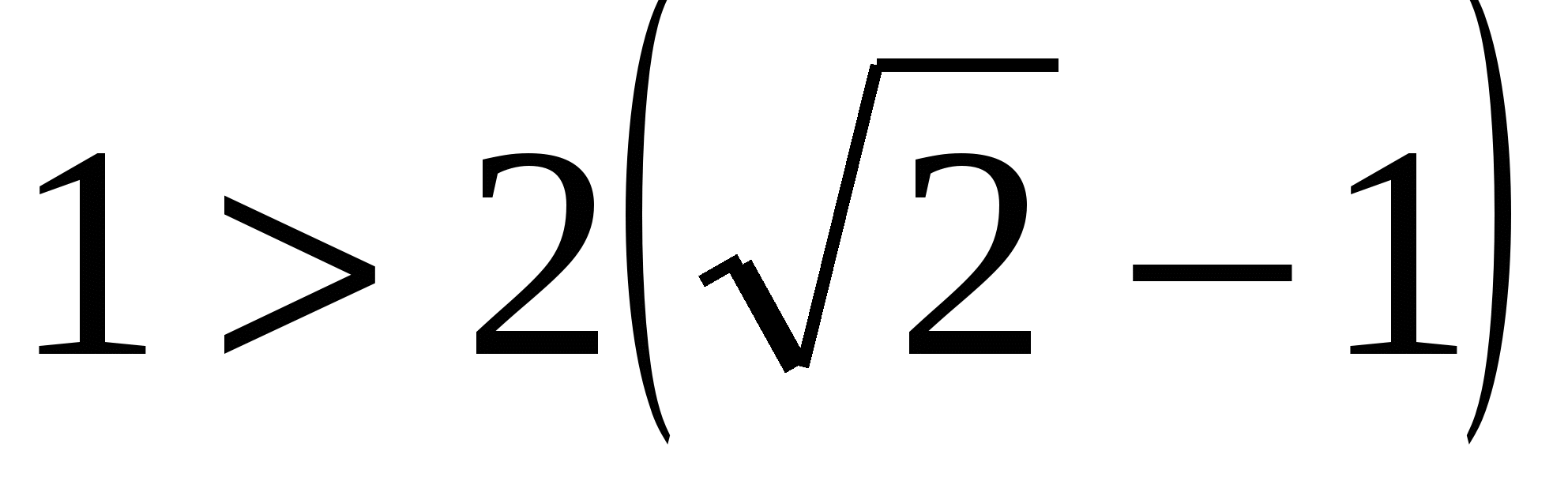 ;
; 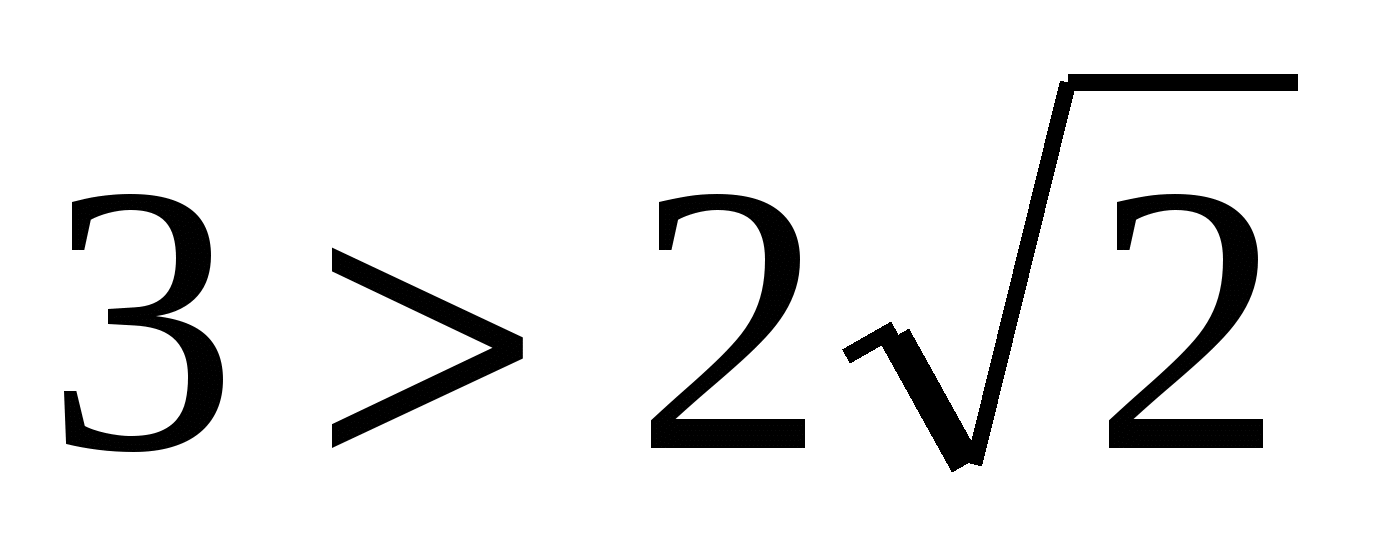 ;
; 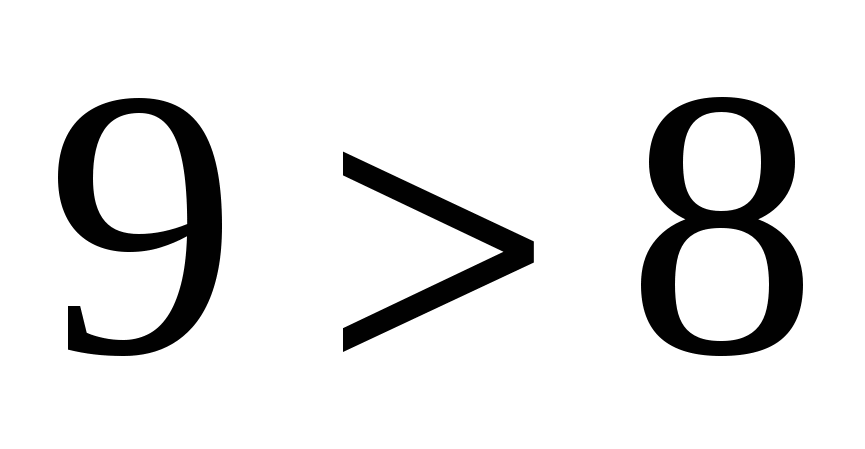 .
.
Пусть неравенство выполняется при п=к: 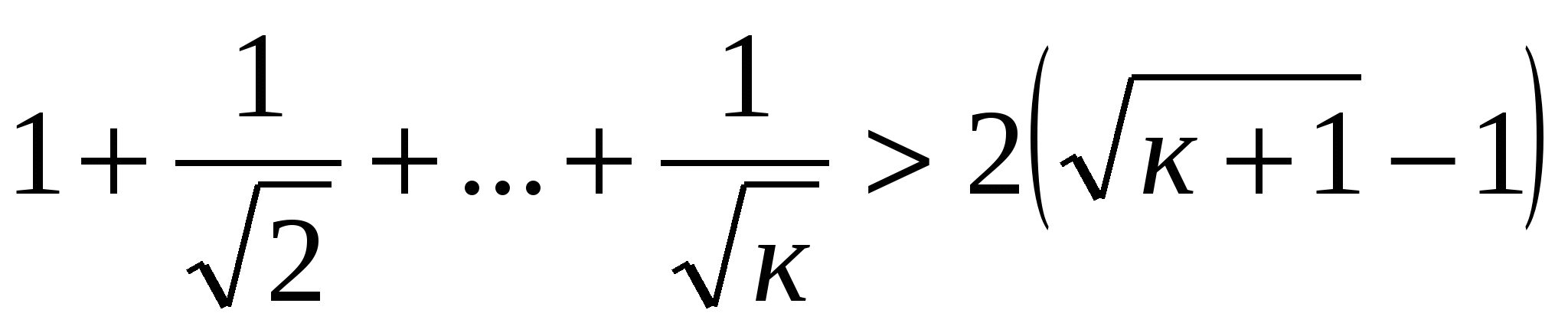 .
.
При п=к+1 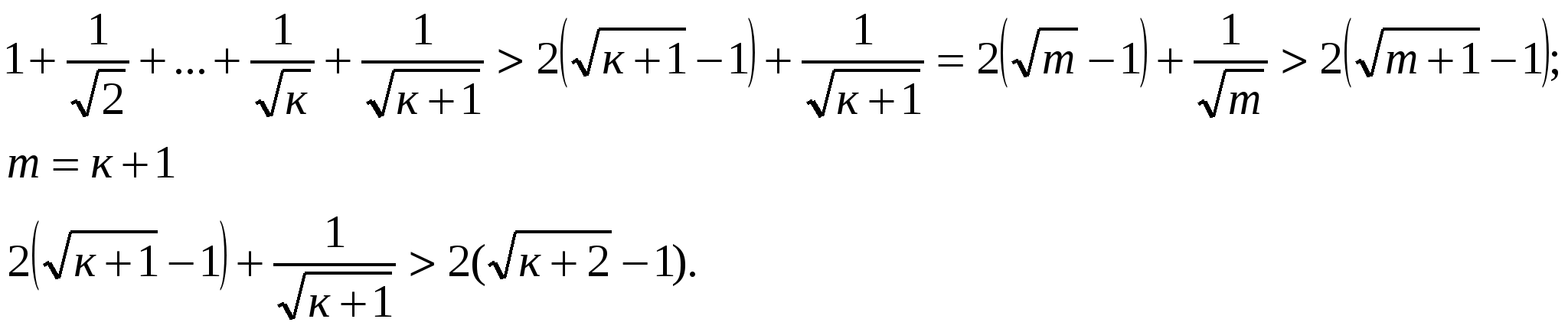
Урок № 10.
Решение задач по теме
Метод математической индукции.
Пример № 32. Доказать неравенство Бернулли.
Если 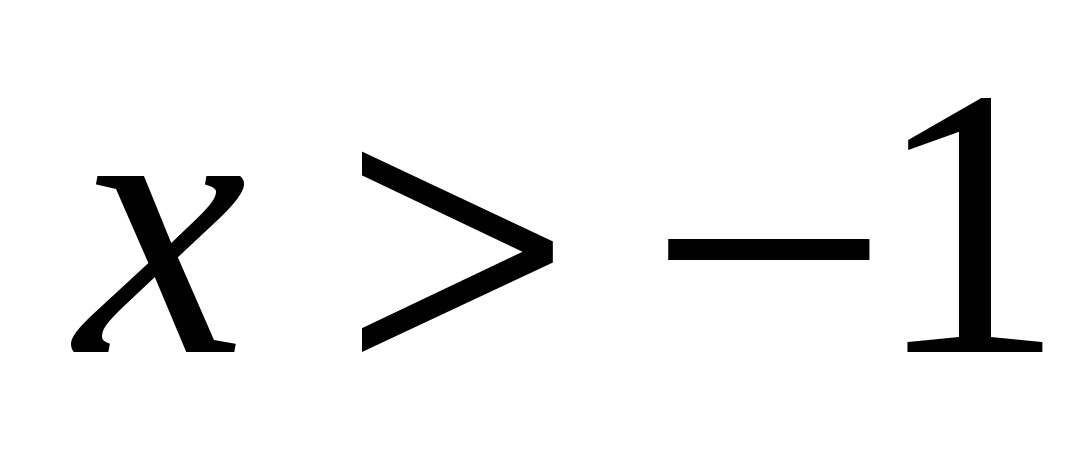 , то для всех натуральных значений п выполняется неравенство
, то для всех натуральных значений п выполняется неравенство
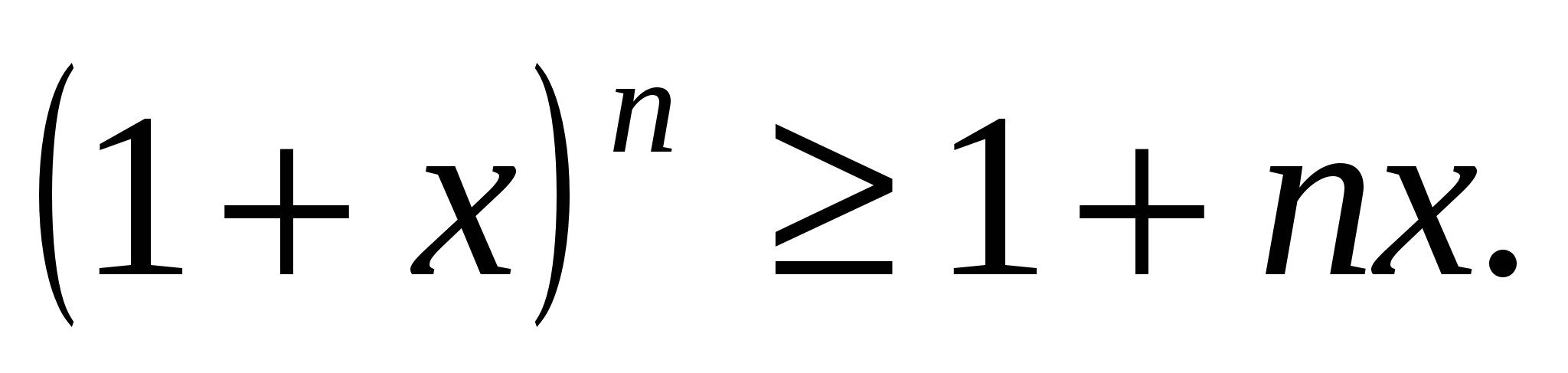
Доказательство.
При п=1 доказываемое неравенство принимает вид 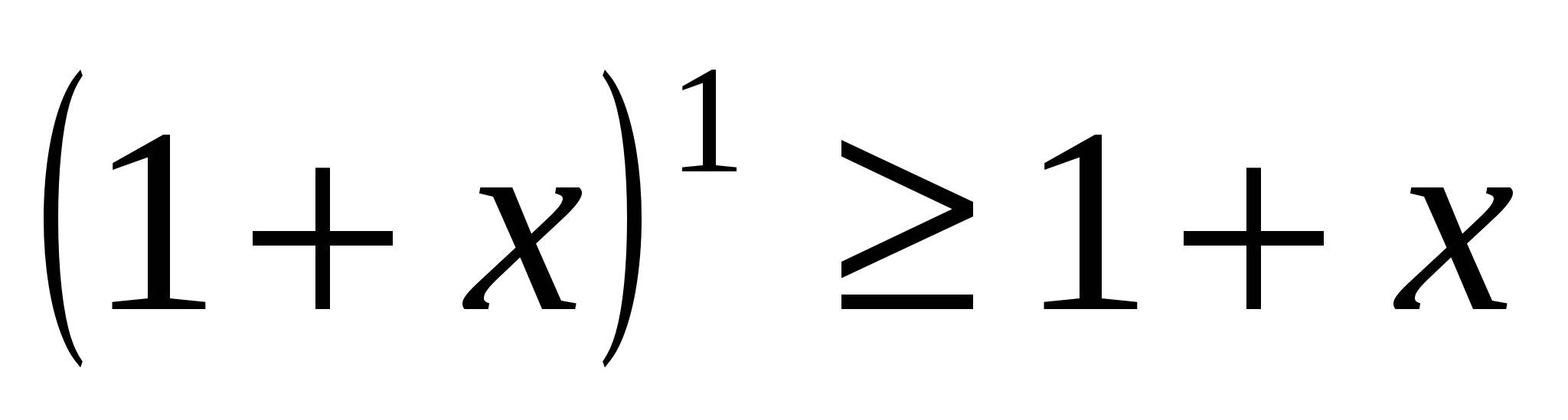 и, очевидно, справедливо. Предположим, что оно верно при п=к, то есть что
и, очевидно, справедливо. Предположим, что оно верно при п=к, то есть что 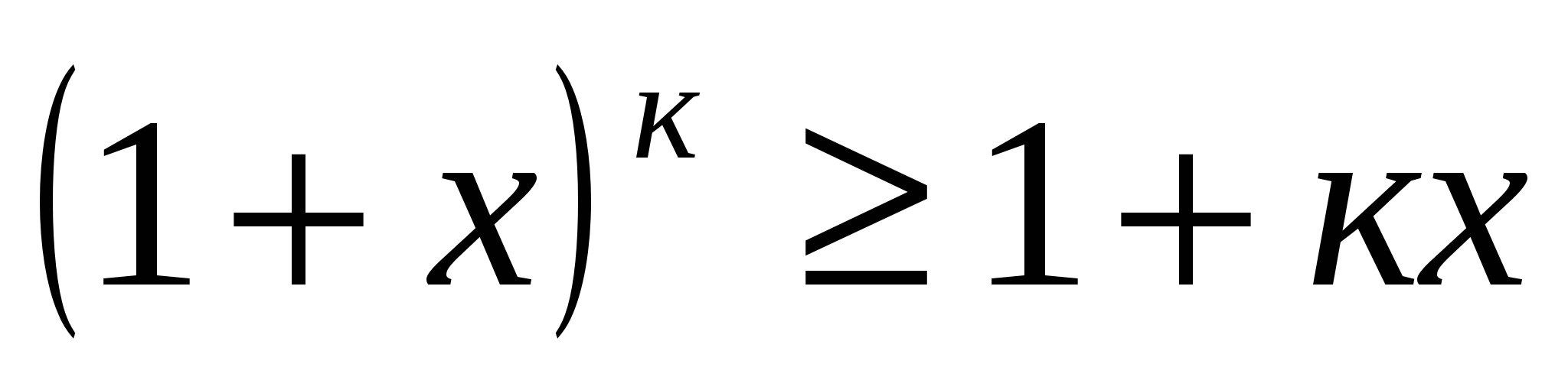 .
.
Так как по условию 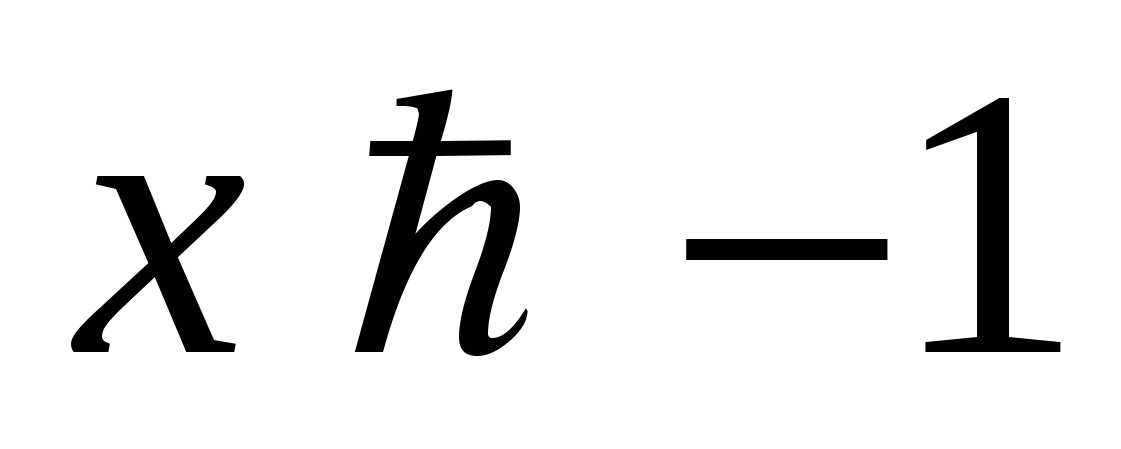 , то
, то 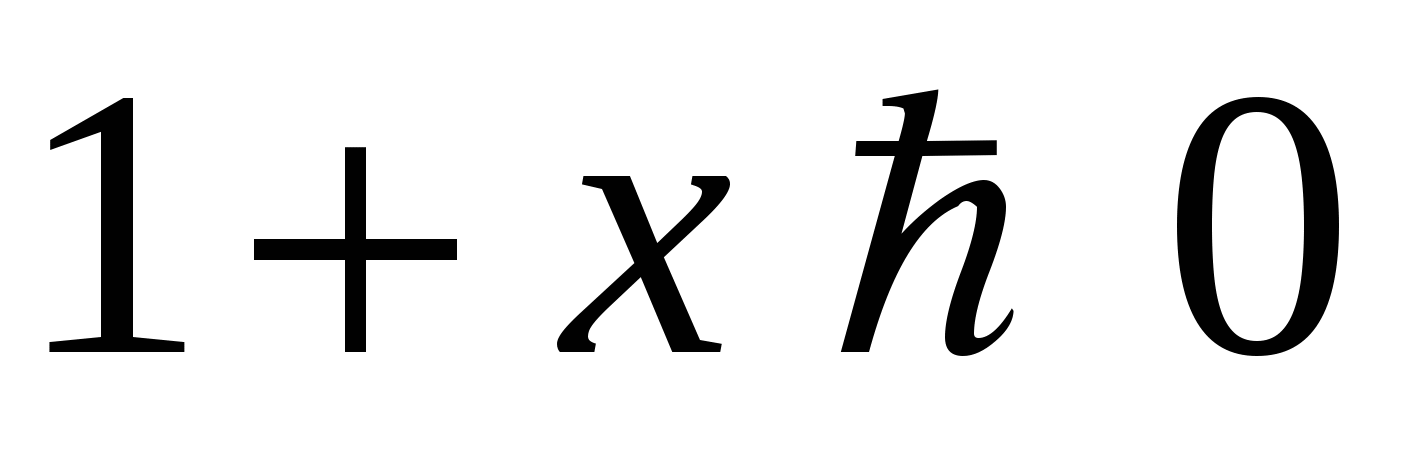 , и потому неравенство не изменит смысла при умножении обеих его частей на
, и потому неравенство не изменит смысла при умножении обеих его частей на 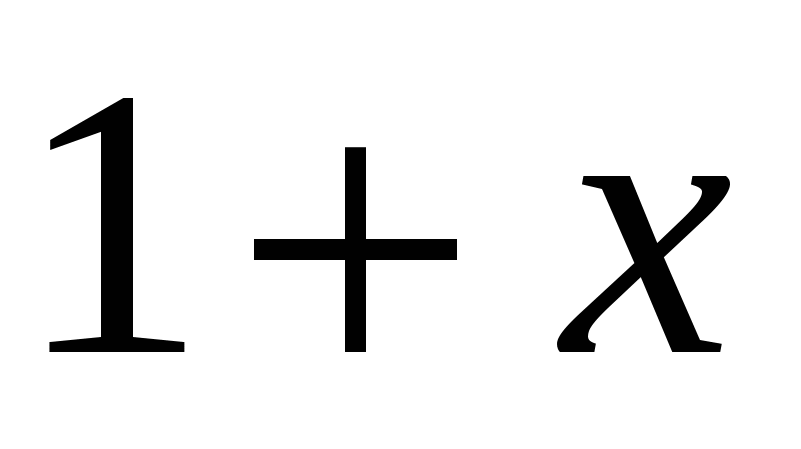 :
:
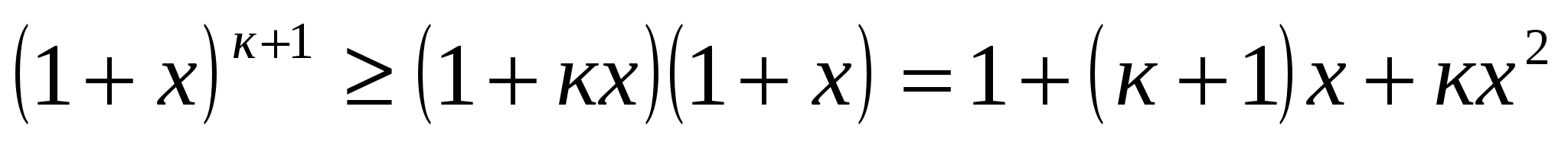 . Так как
. Так как 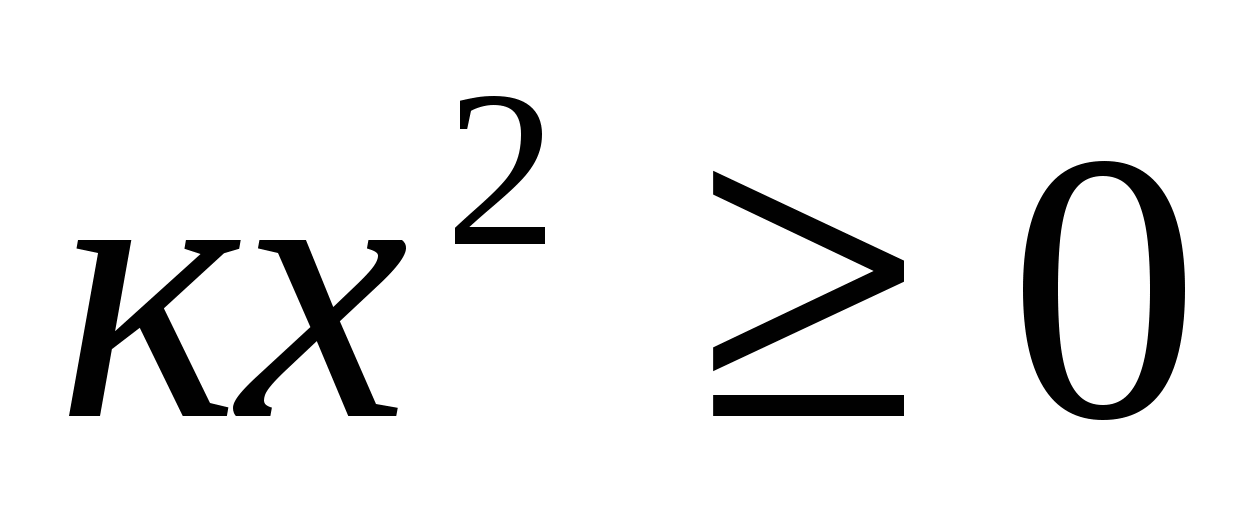 , то получаем, что
, то получаем, что
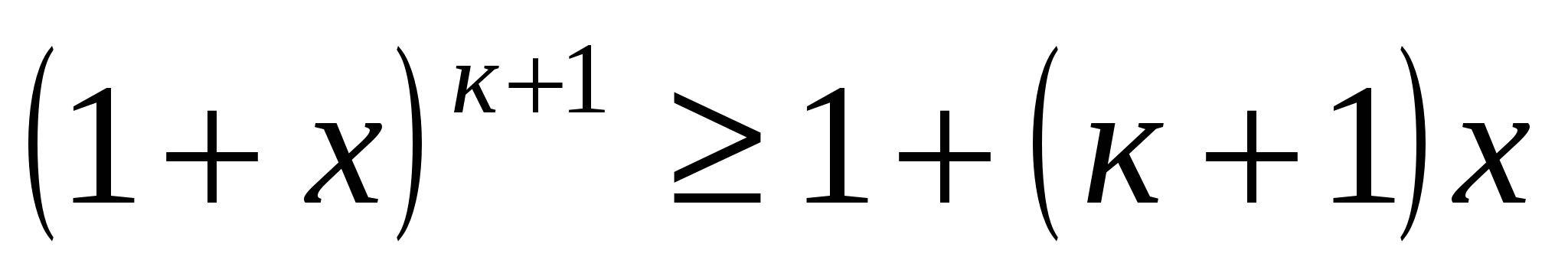 .
.
Итак, неравенство верно при п=1, а из его истинности при п=к следует, что оно истинно и при п=к+1. Значит, в силу математической индукции оно имеет место для всех натуральных п.
Например, 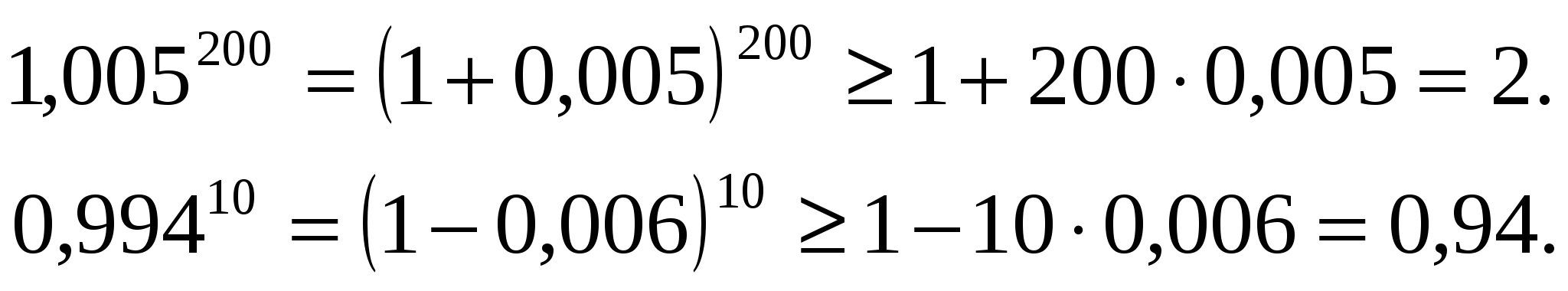
Пример № 33. Найти все натуральные значения п, для которых справедливо неравенство 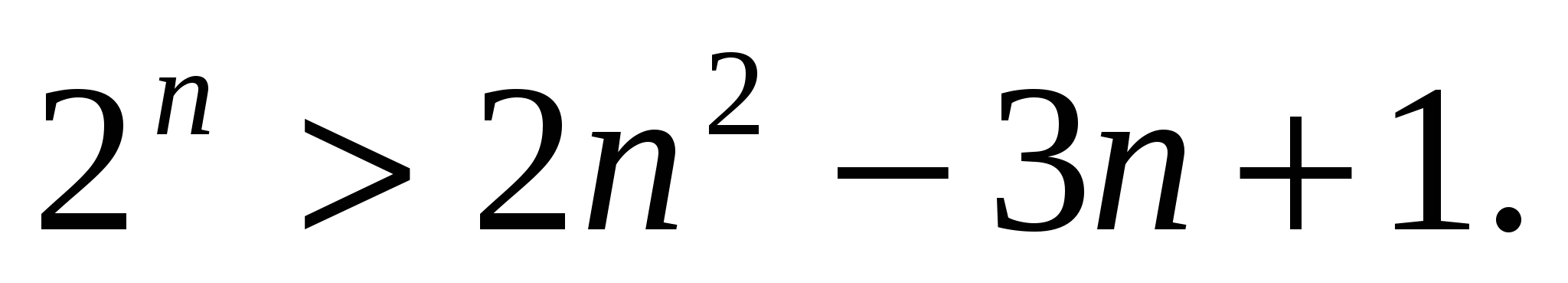
Решение.
При п=1 неравенство справедливо. При п=2 неравенство также справедливо.
При п=3 неравенство уже не выполняется. Лишь при п=6 неравенство выполняется, так что за базис индукции можно взять п=6.
Предположим, что неравенство справедливо для некоторого натурального к:
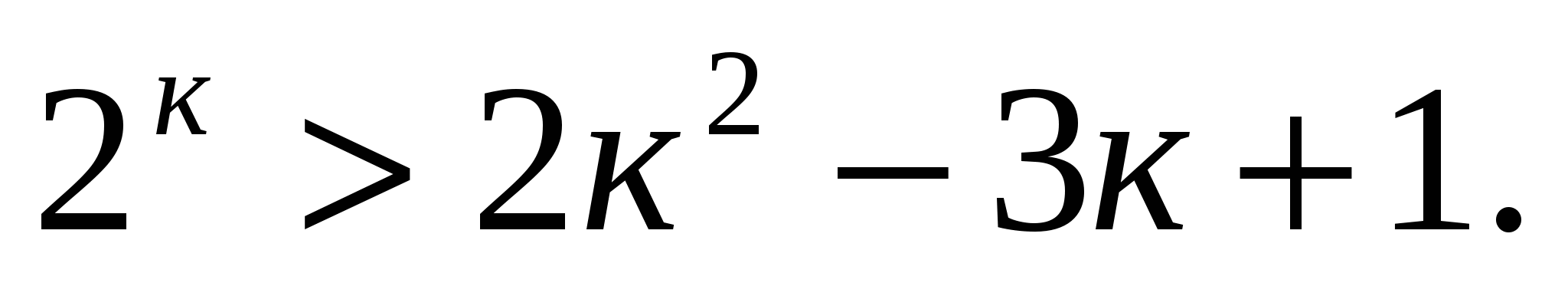 Рассмотрим неравенство
Рассмотрим неравенство 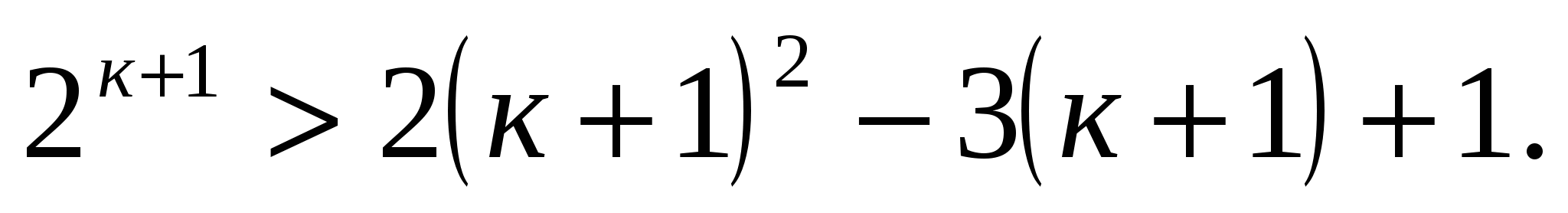
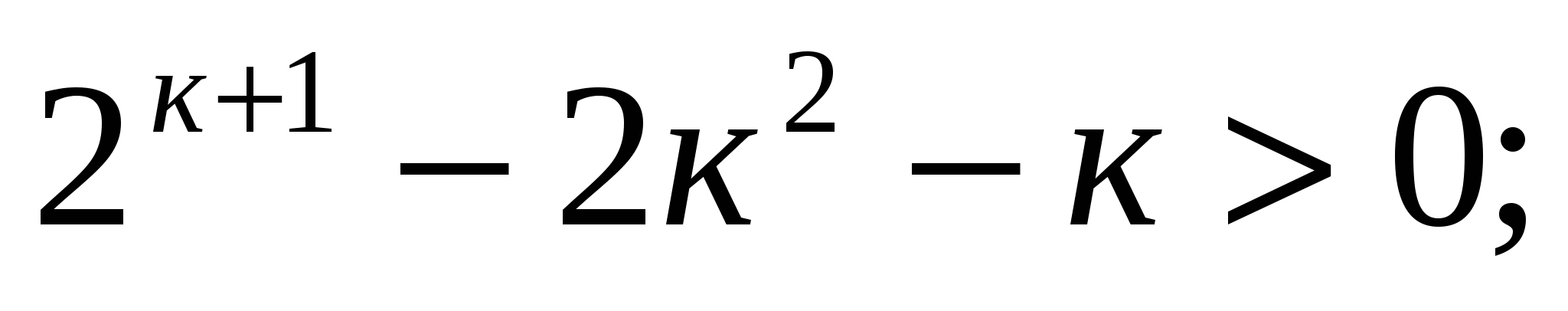
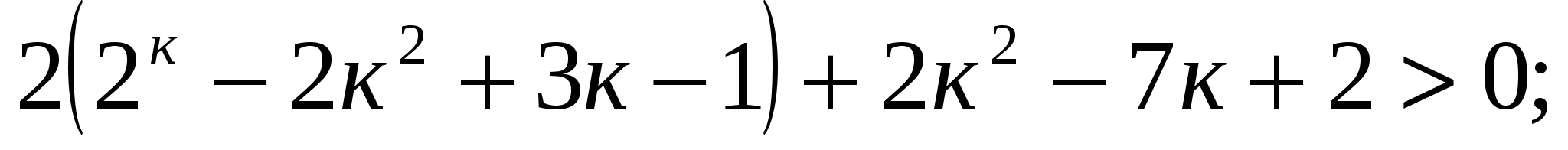
Последнее неравенство выполняется, если 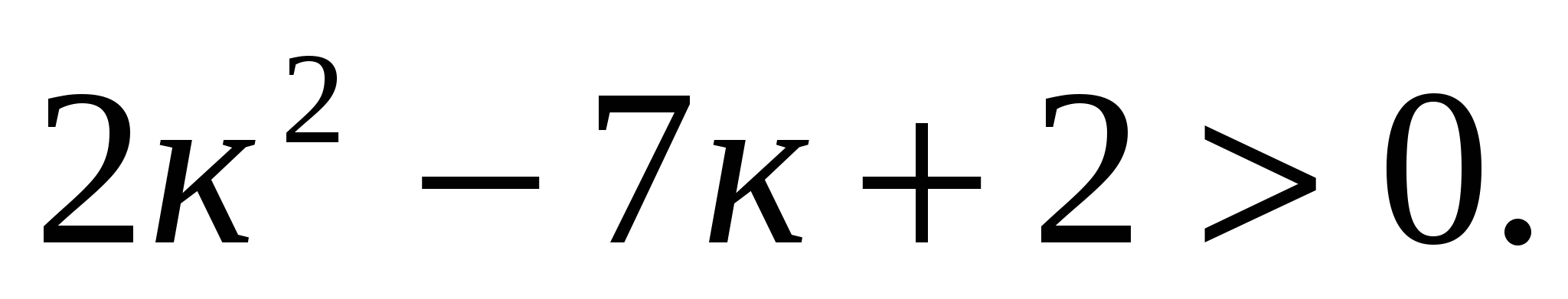
При к=6 неравенство справедливо. Пусть имеет место неравенство при к=т
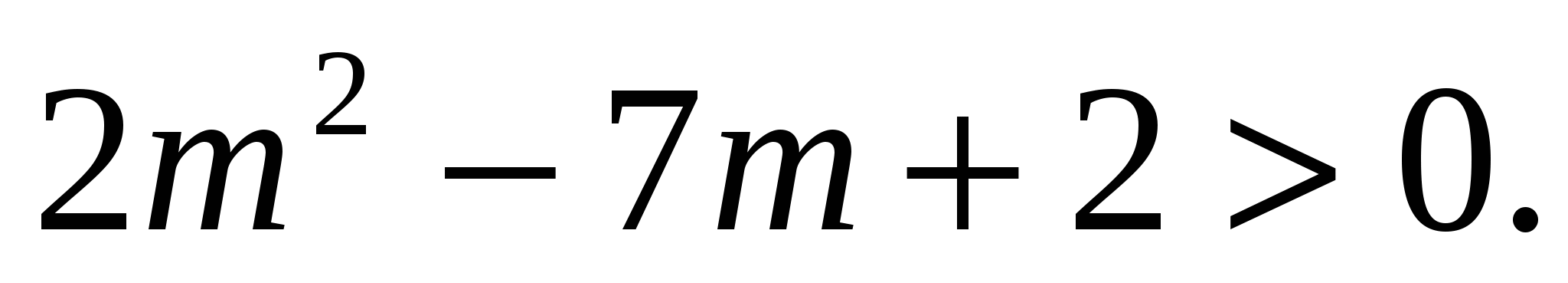 Докажем справедливость неравенства
Докажем справедливость неравенства 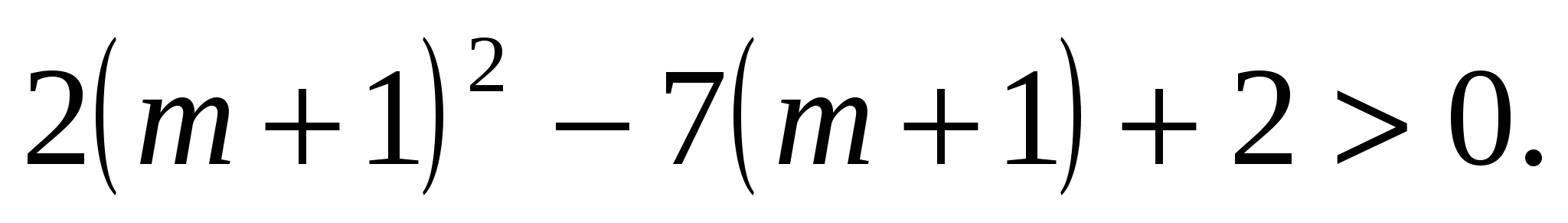
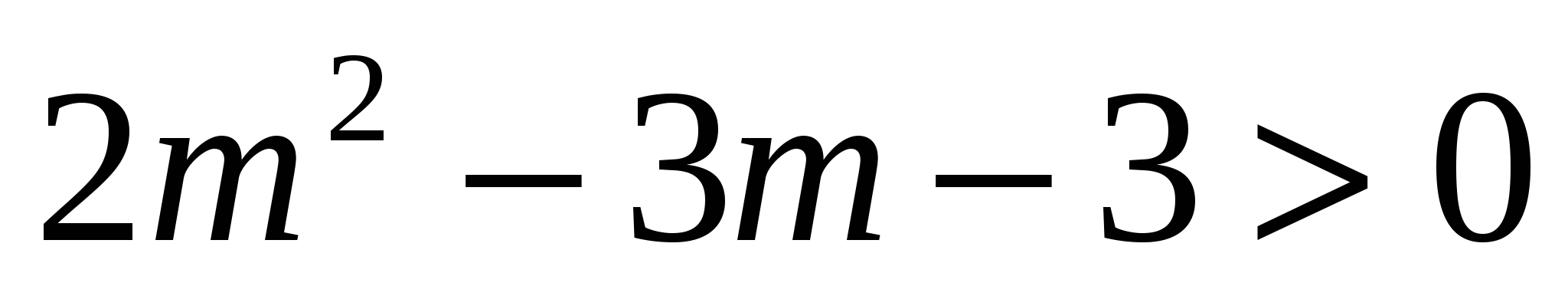 при любом натуральном т, так как дискриминант квадратного трехчлена отрицательный.
при любом натуральном т, так как дискриминант квадратного трехчлена отрицательный.
Таким образом, неравенство 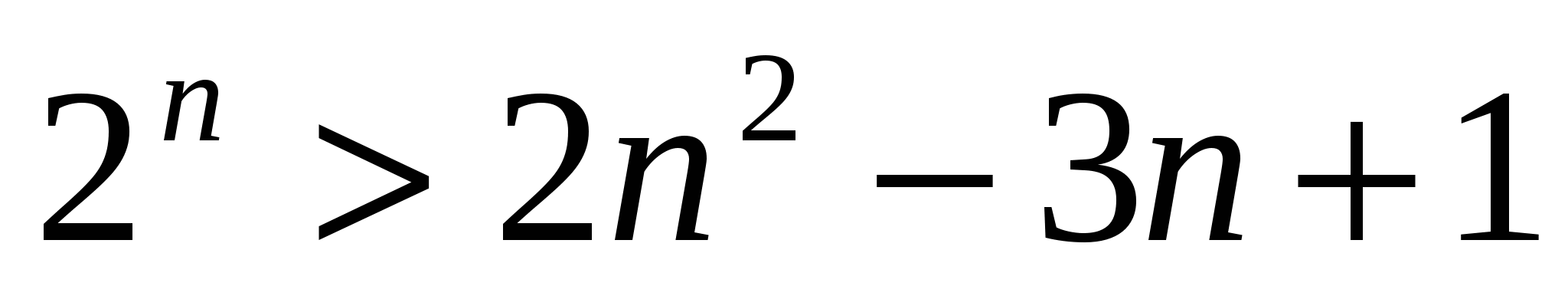 справедливо при п=1, п=2, п≥6, где п - натуральное число.
справедливо при п=1, п=2, п≥6, где п - натуральное число.
Пример № 34. Доказать неравенство для натуральных п≥10: 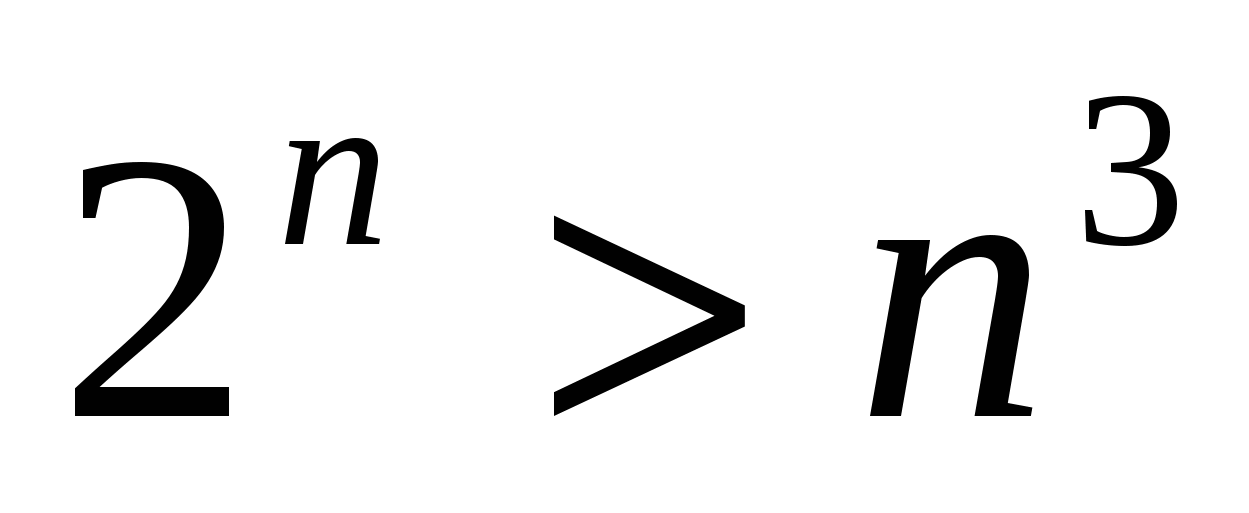 .
.
Доказательство.
При п=10 неравенство справедливо. Пусть неравенство справедливо при п=к: 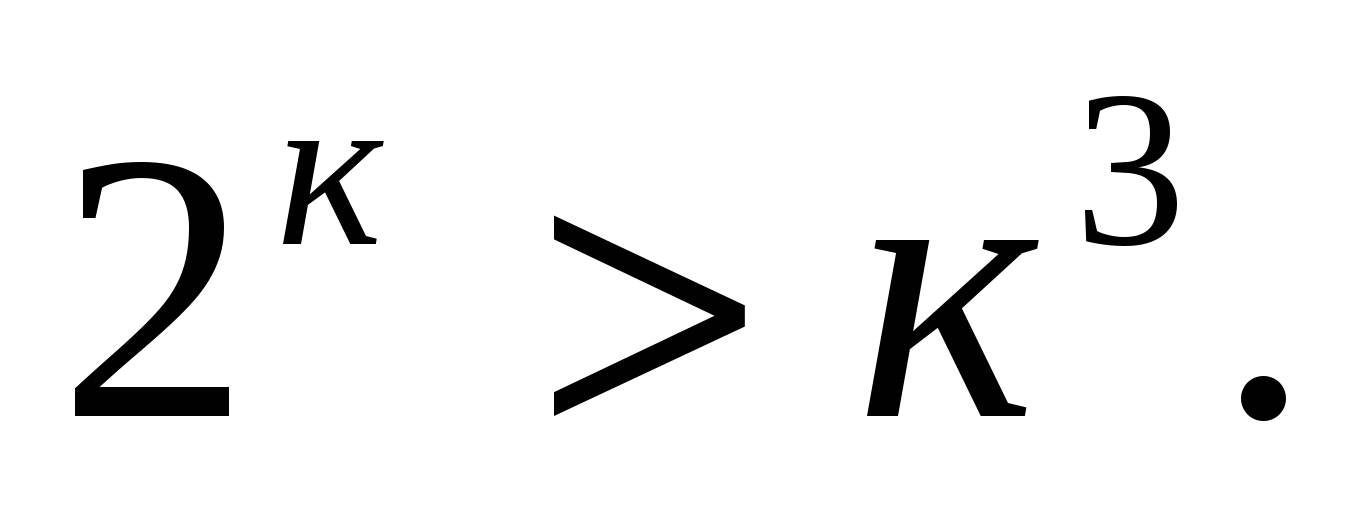 Докажем справедливость неравенства
Докажем справедливость неравенства 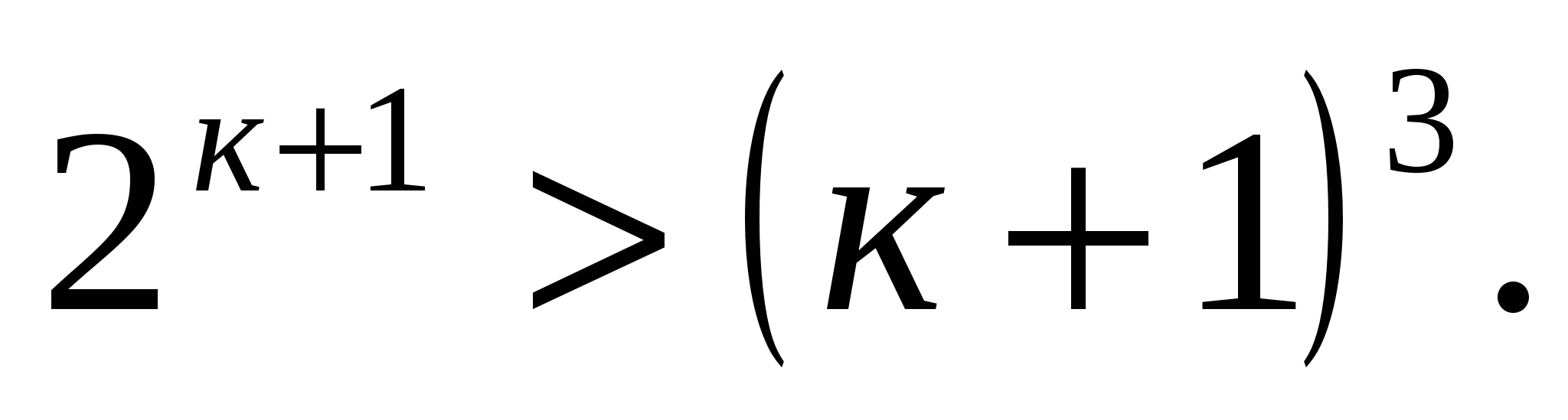
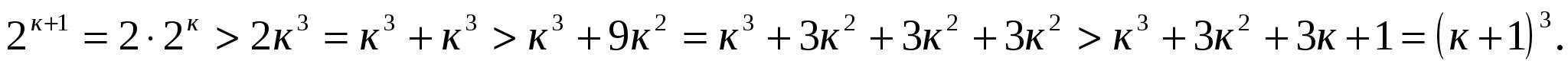
При доказательстве учитывалось то, что п≥10.
Урок № 11.
Решение задач по теме
Метод математической индукции
Пример №35.
Докажите методом математической индукции, что
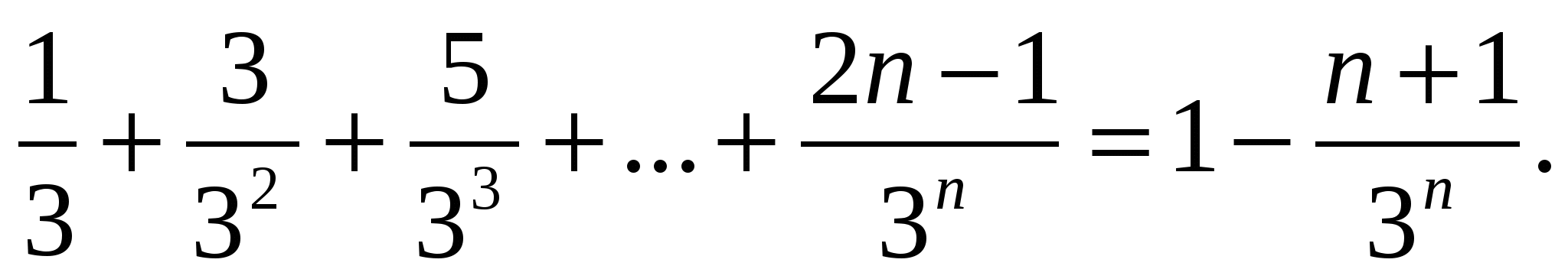
Доказательство.
Обозначим данное утверждение через Р(п), где п - натуральное число. Убедимся, что Р(1) справедливо: 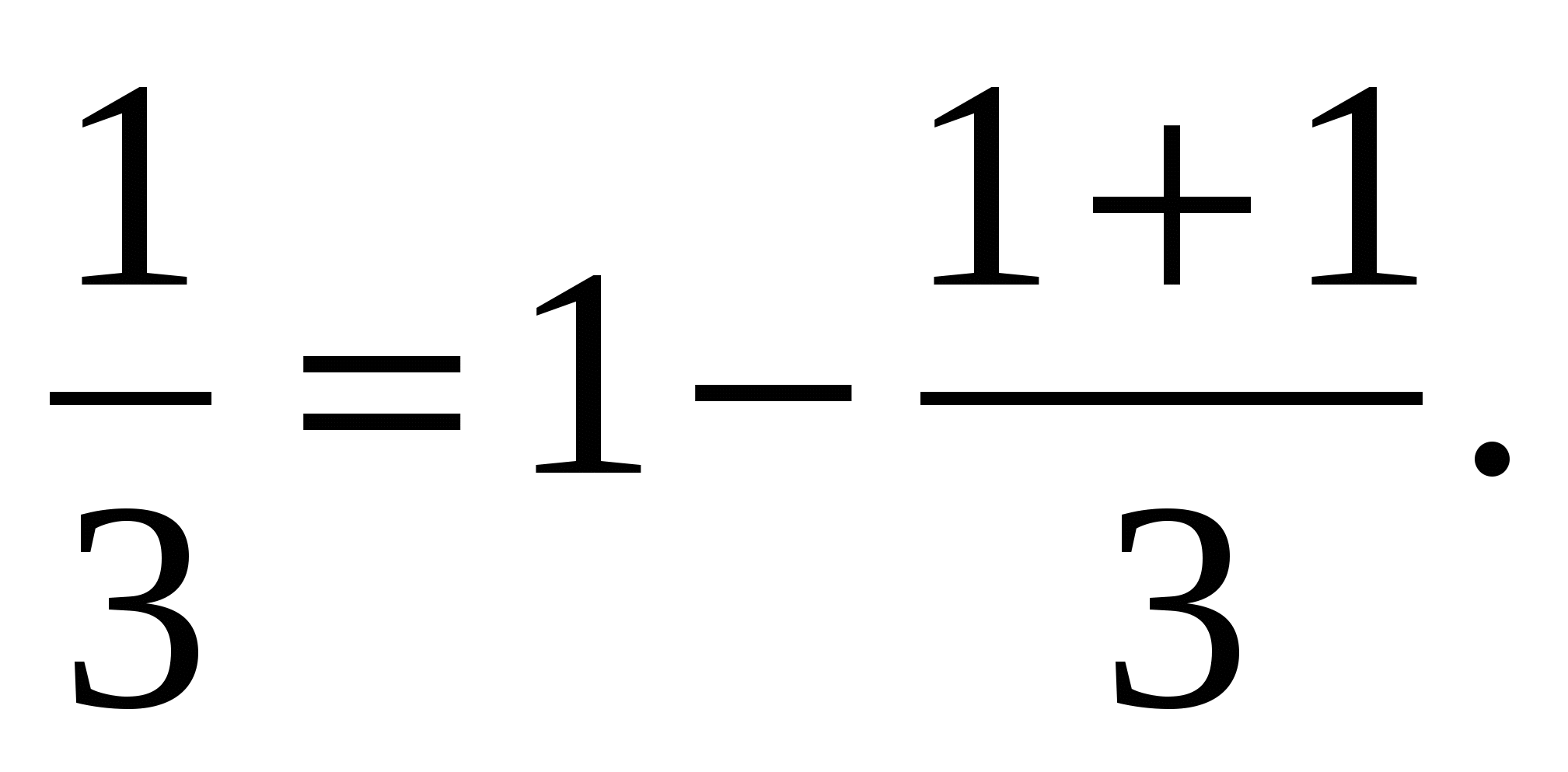
Предположим, что утверждение Р(к): 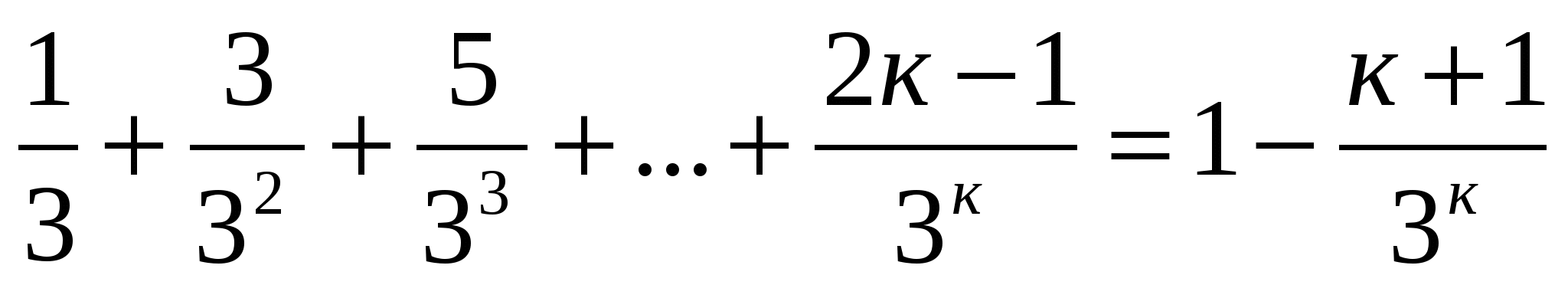 - справедливо. Убедимся в справедливости утверждения Р(к+1).
- справедливо. Убедимся в справедливости утверждения Р(к+1).
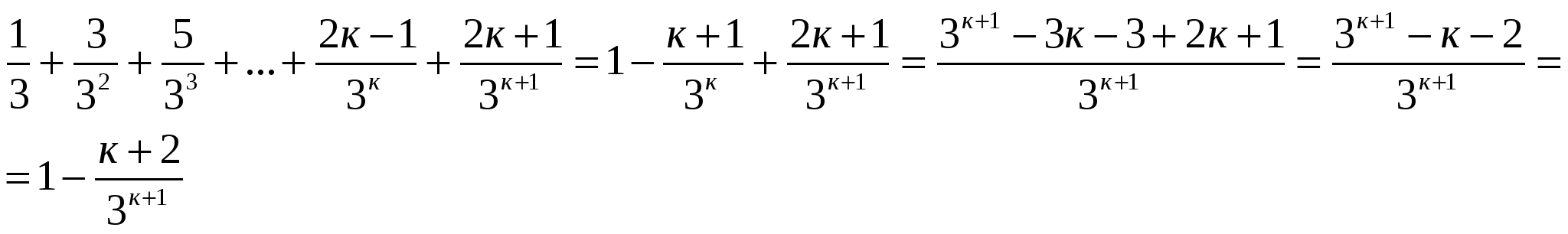
По принципу математической индукции утверждение справедливо для любого натурального п.
Пример № 36.
Докажите, что ![]() делится на 81 при натуральных п.
делится на 81 при натуральных п.
Доказательство.
Если п=1, то ![]() - кратно 81. Если п=2, то
- кратно 81. Если п=2, то 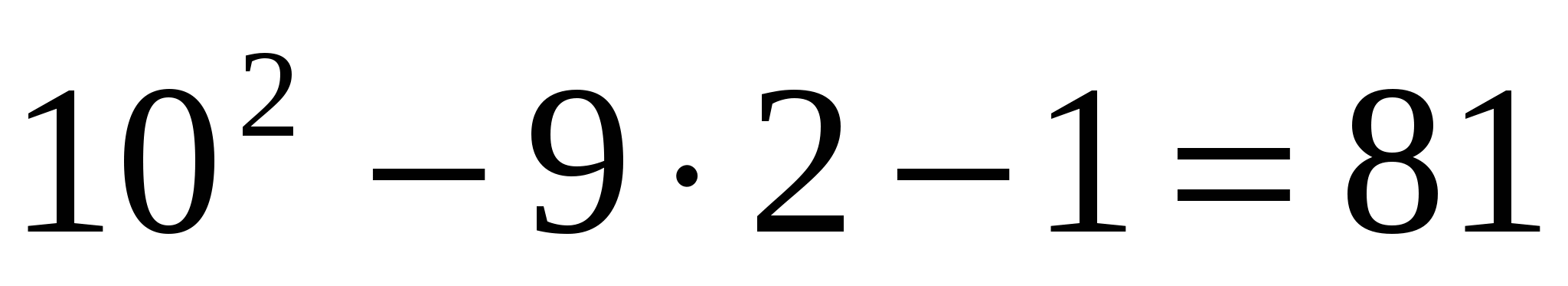 - кратно 81. Пусть
- кратно 81. Пусть 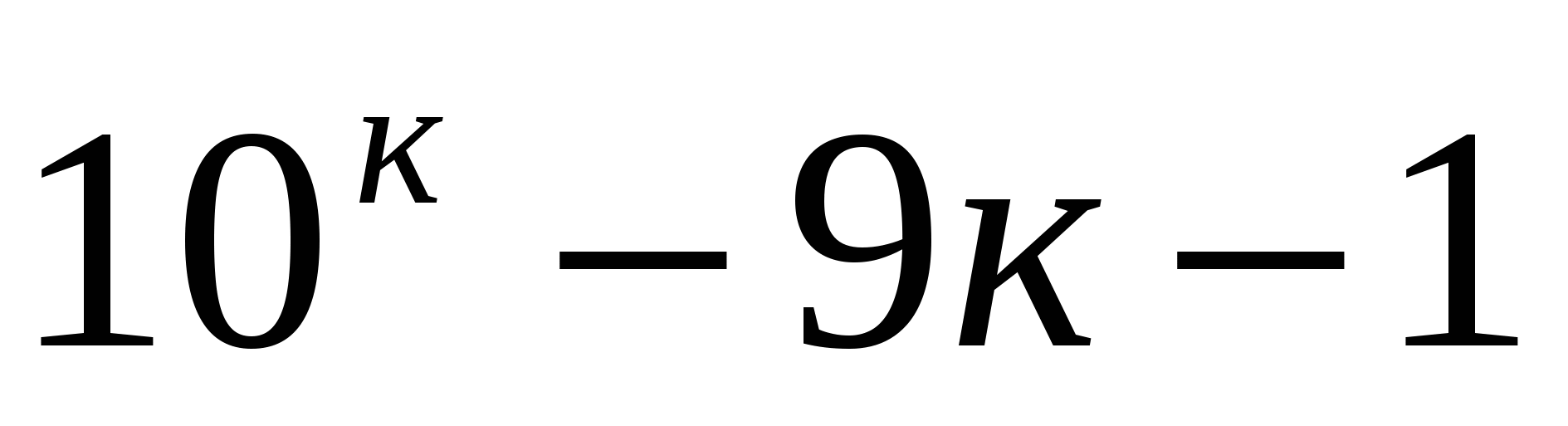 кратно 81. Докажем, что
кратно 81. Докажем, что ![]() кратно 81.
кратно 81.
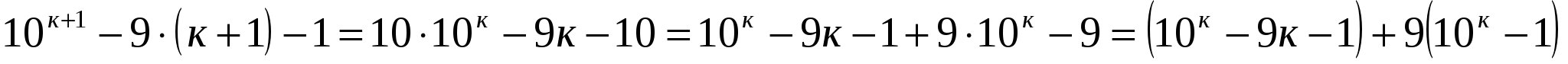 - кратно 81, так как каждое слагаемое кратно 81.
- кратно 81, так как каждое слагаемое кратно 81.
Тогда по принципу математической индукции неравенство делится на 81 при любом натуральном значении п.
Пример № 37.
Докажем, что ![]()
Доказательство.
Если п=1, 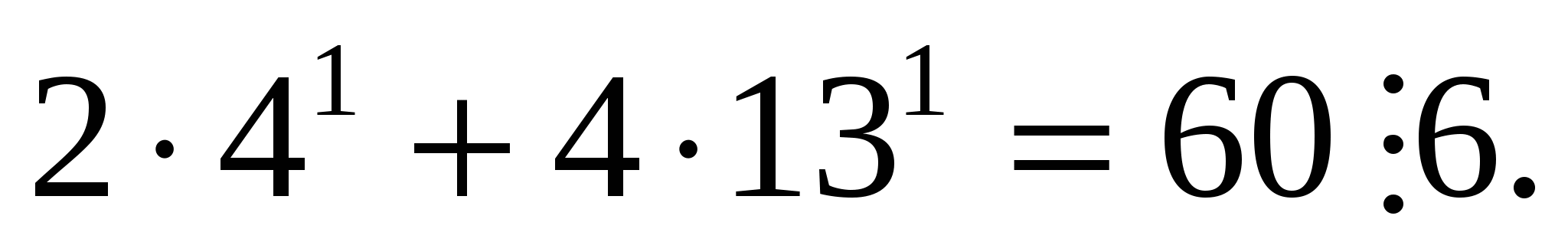 Предположим, что при п=к
Предположим, что при п=к 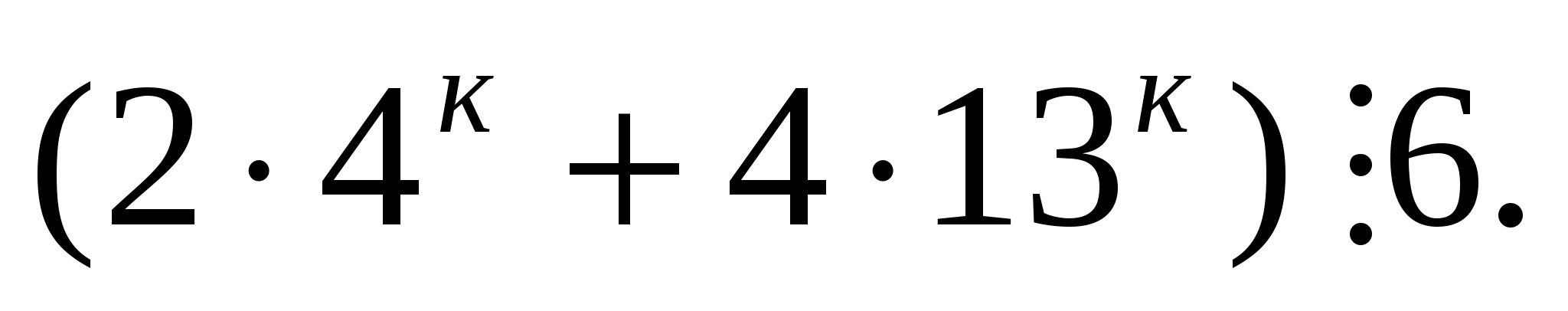
Докажем, что при п=к+1 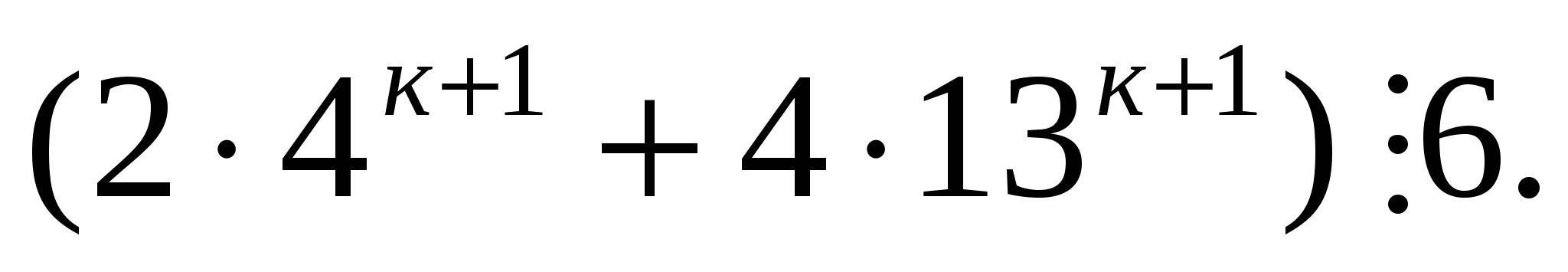
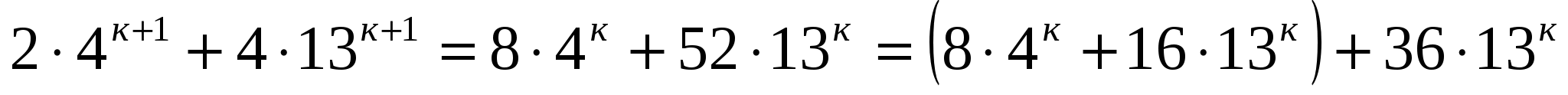 - оба слагаемых кратны 6.
- оба слагаемых кратны 6.
Тогда 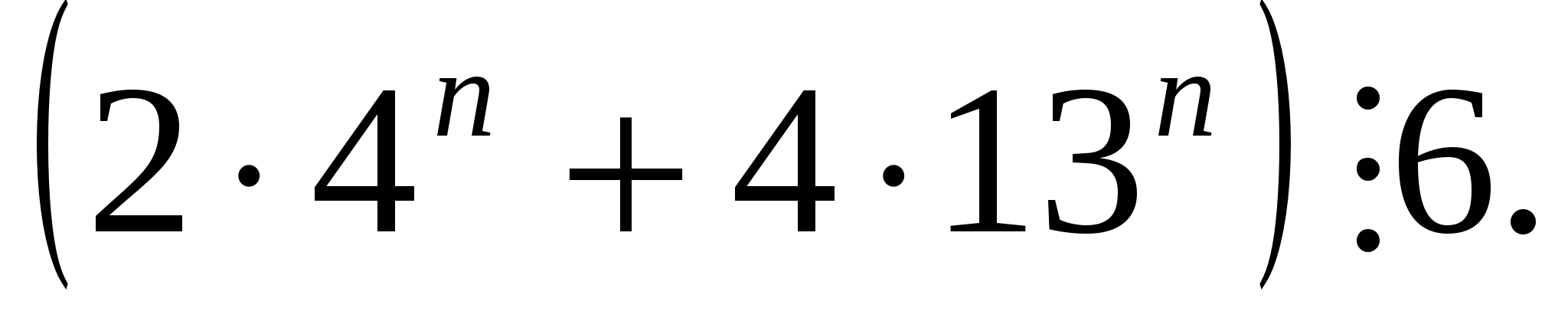
Урок № 12.
Контрольная работа по теме
Метод математической индукции
Вариант № 1.
-
Докажите методом математической индукции, что
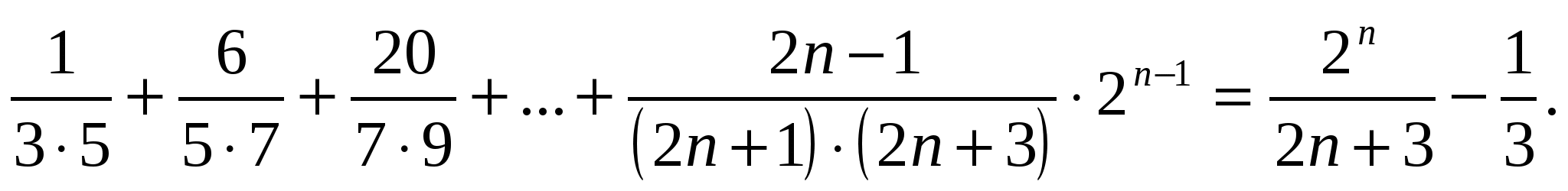
Доказательство.
Обозначим данное утверждение через Р(п), где п натуральное число. Р(1)- справедливо, так как при п=1 левая и правая части равенства принимают равные значения. Докажем, что 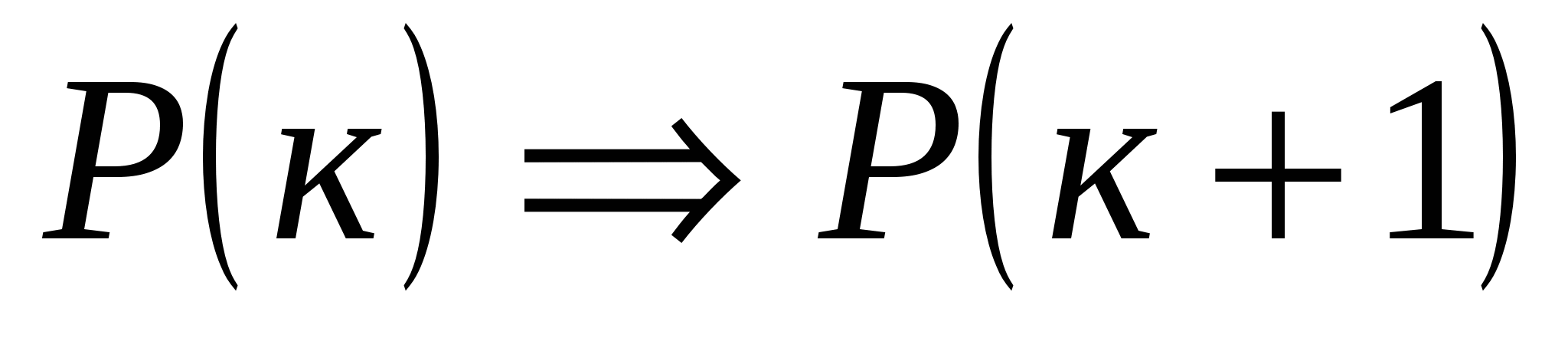 ,
, 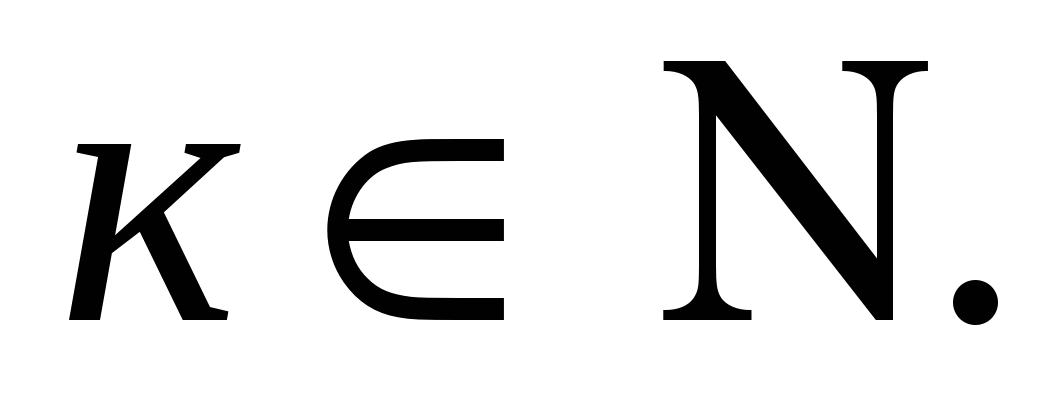
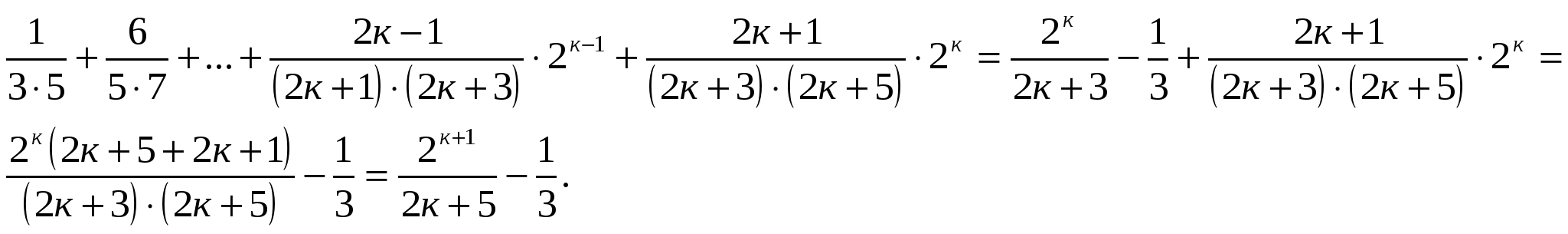 Итак, утверждение справедливо при п=1, и из его справедливости при п=к следует, что оно верно и при п=к+1. Значит, утверждение справедливо для любого натурального значения п.
Итак, утверждение справедливо при п=1, и из его справедливости при п=к следует, что оно верно и при п=к+1. Значит, утверждение справедливо для любого натурального значения п.
-
Докажите, что
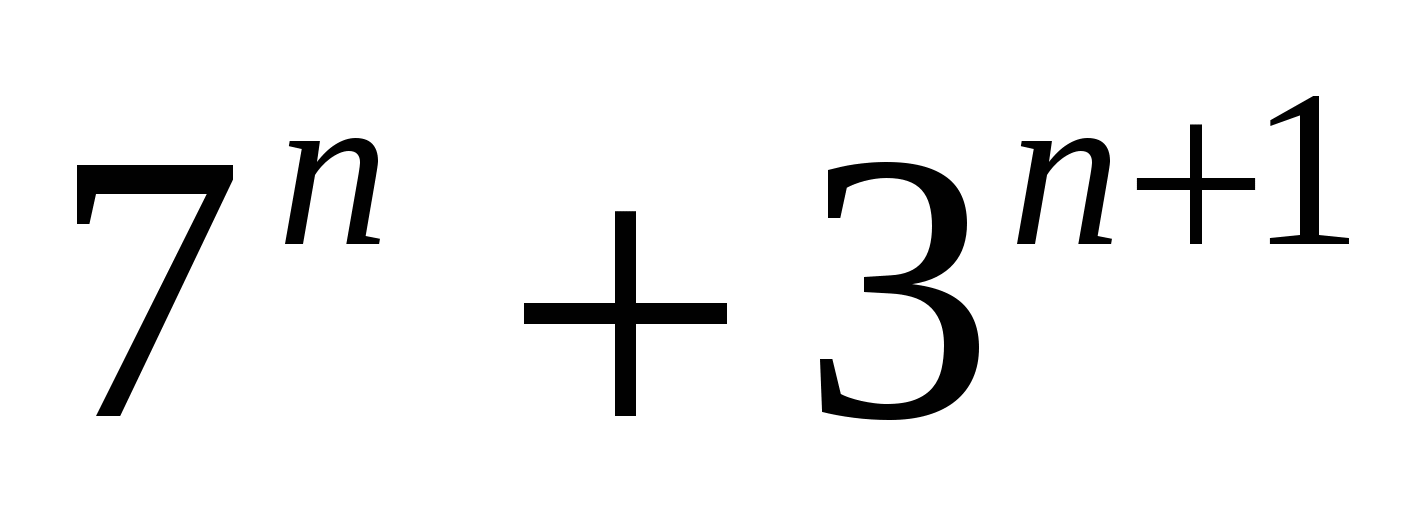 делится на 4 при всех натуральных значениях п.
делится на 4 при всех натуральных значениях п.
Доказательство.
Обозначим данное утверждение через Р(п), где п - натуральное число.
Утверждение Р(1) справедливо. Действительно, 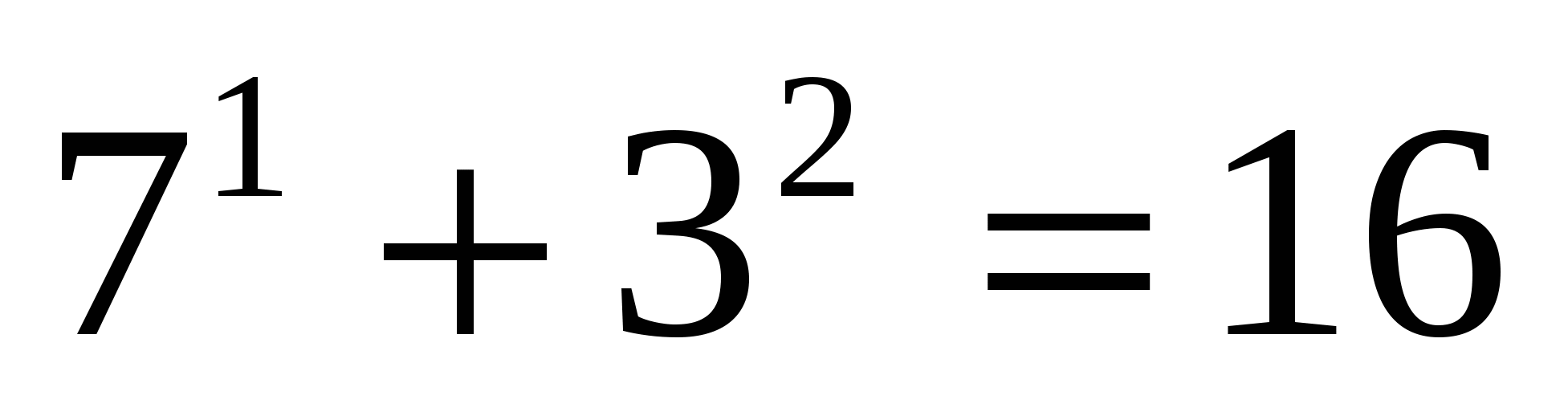 - -кратно 4.
- -кратно 4.
Докажем, что ![]()
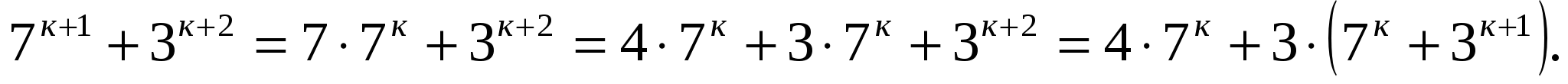 Сумма кратна 4, так как каждое слагаемое кратно 4. Утверждение доказано.
Сумма кратна 4, так как каждое слагаемое кратно 4. Утверждение доказано.
3. Последовательность 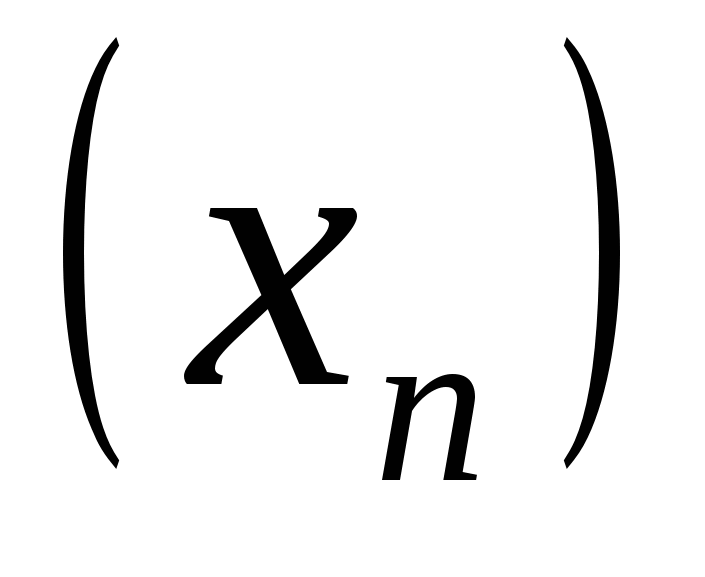 задана рекуррентно:
задана рекуррентно: 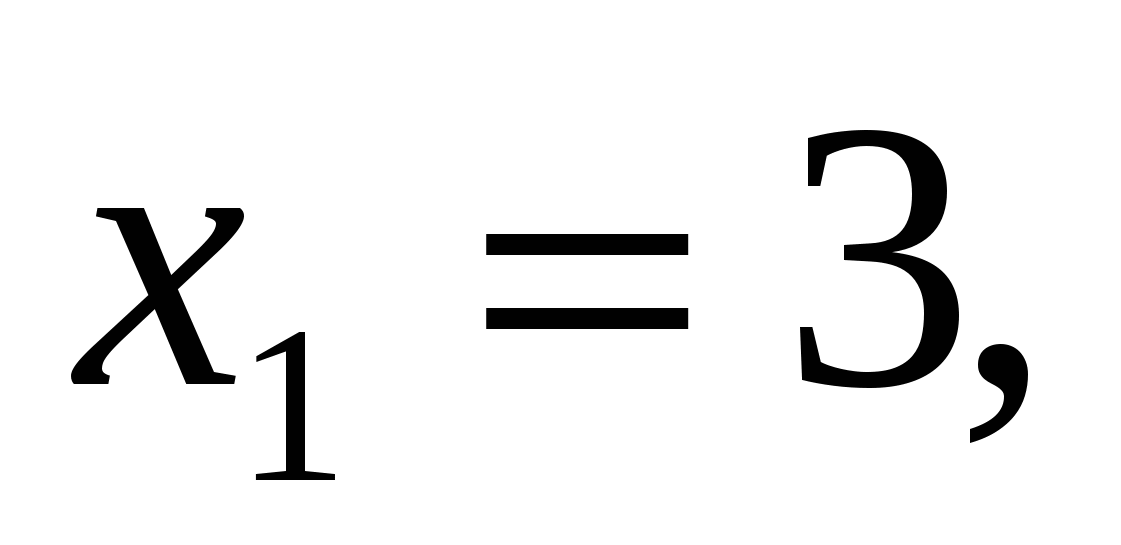
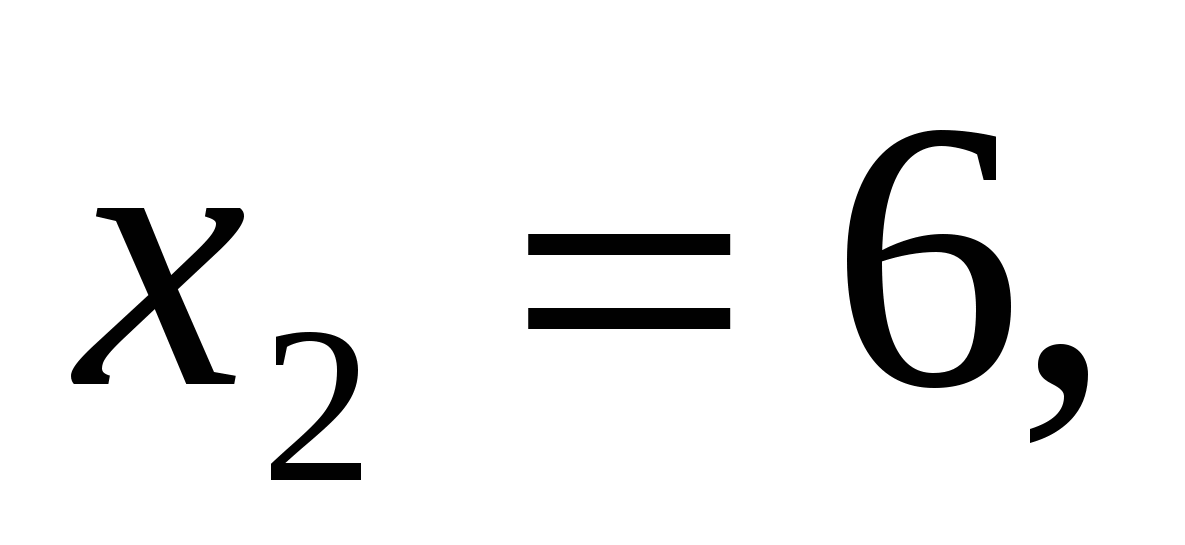
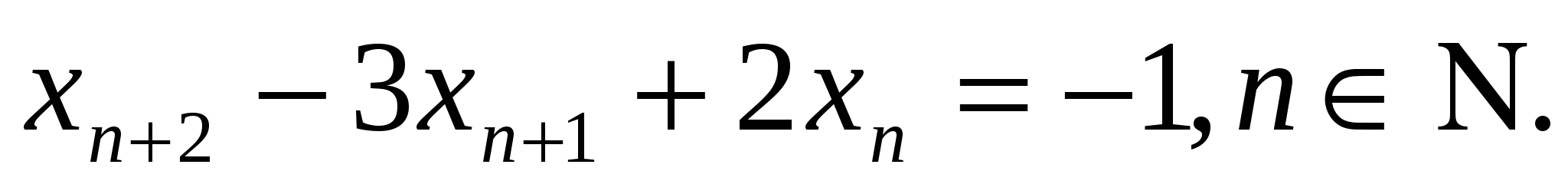 Докажите, что
Докажите, что 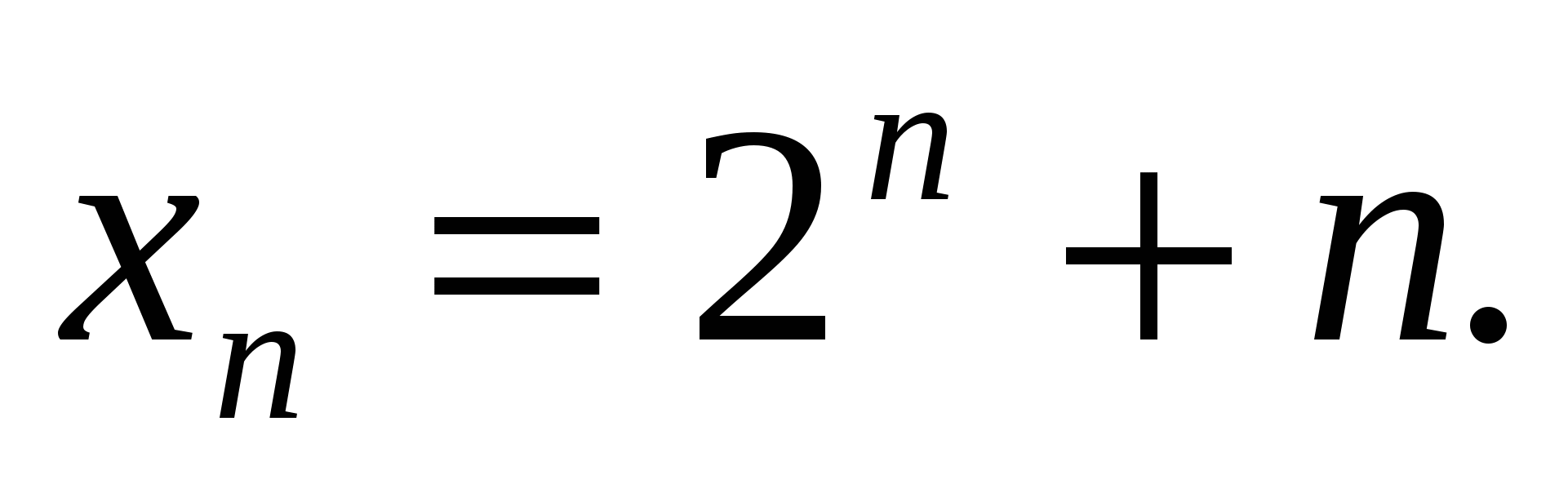
Доказательство.
При п=1 и п=2 утверждение справедливо. 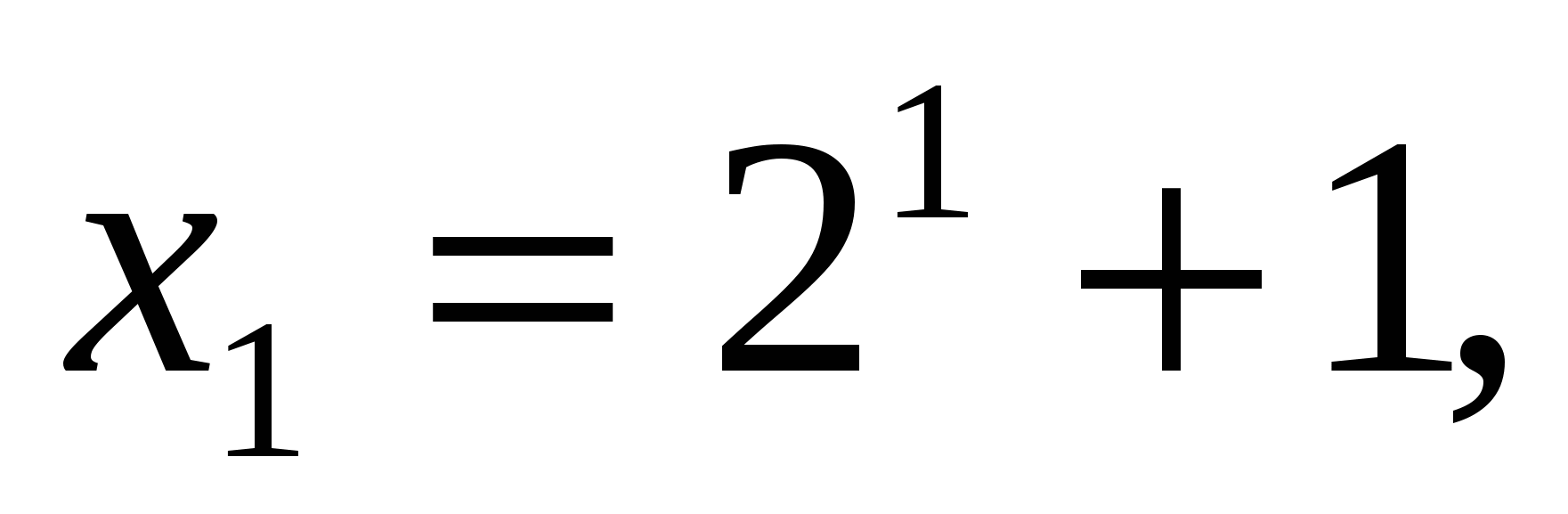
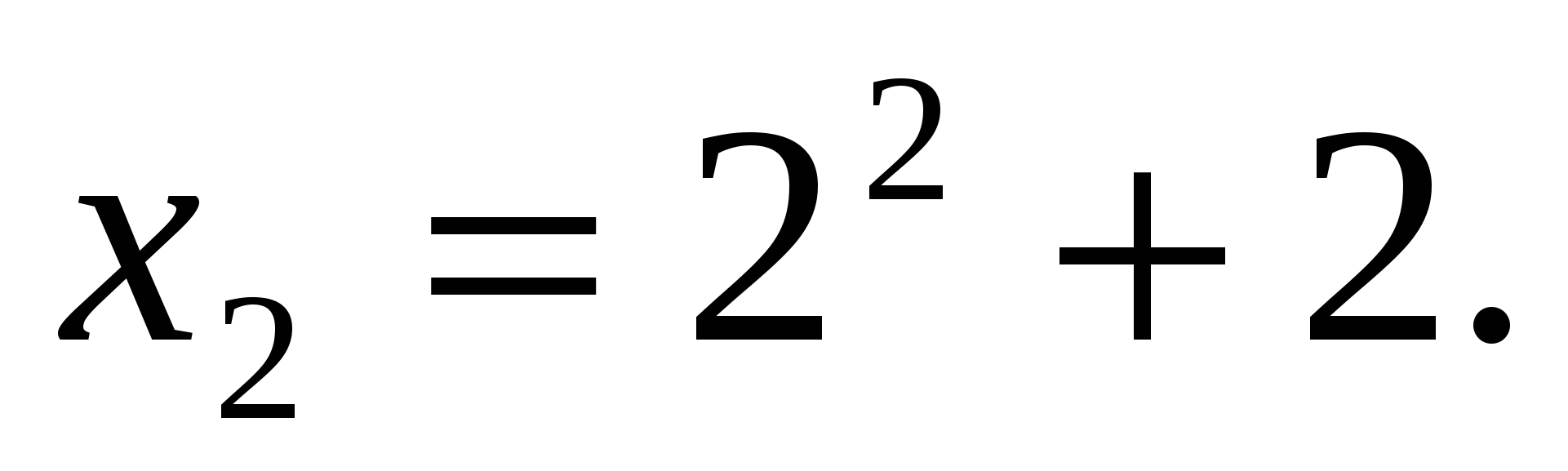
Пусть 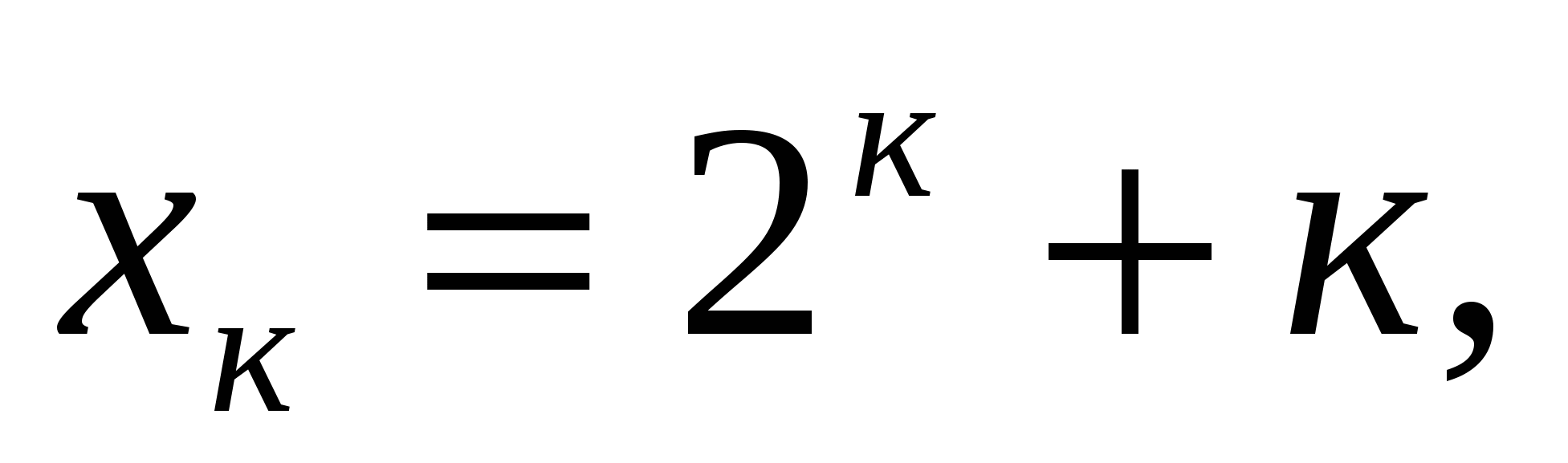
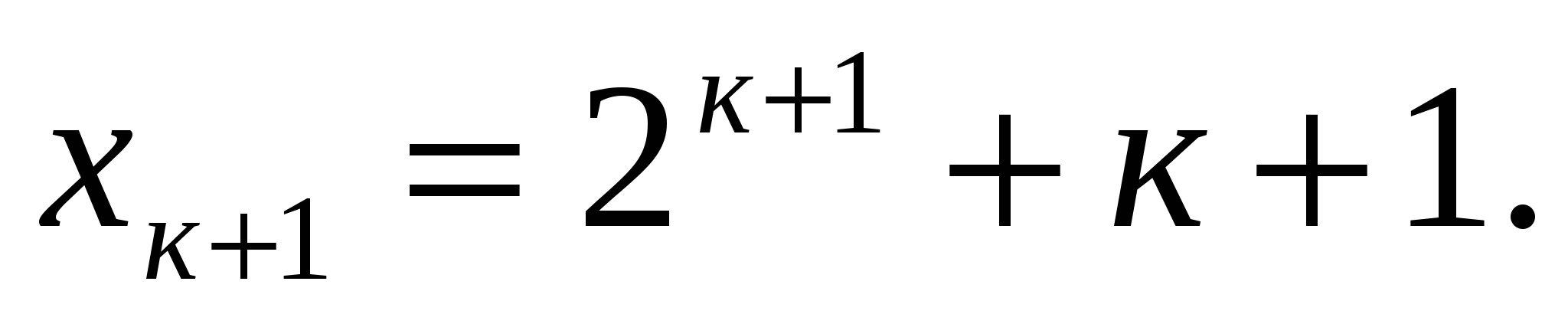 Докажем, что тогда
Докажем, что тогда 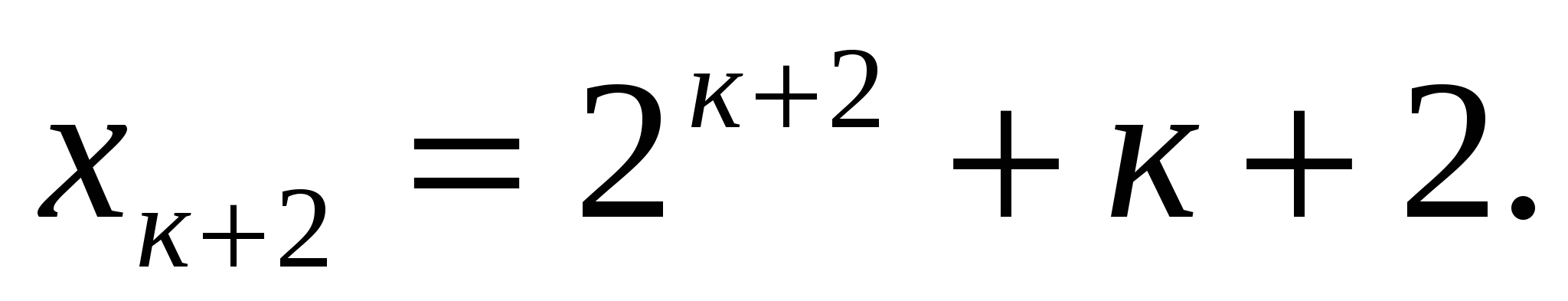
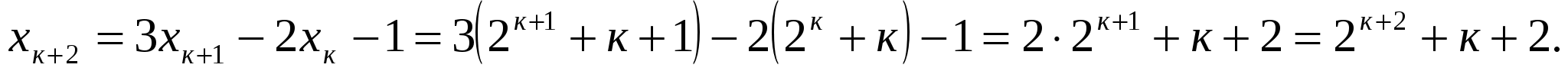
Итак, утверждение справедливо при п=1 и при п=2, а из его справедливости при п=к и п=к+1 следует, что оно справедливо и при п=к+2. Значит, оно имеет место для всех натуральных значений п.
Вариант № 2.
-
Докажите методом математической индукции, что
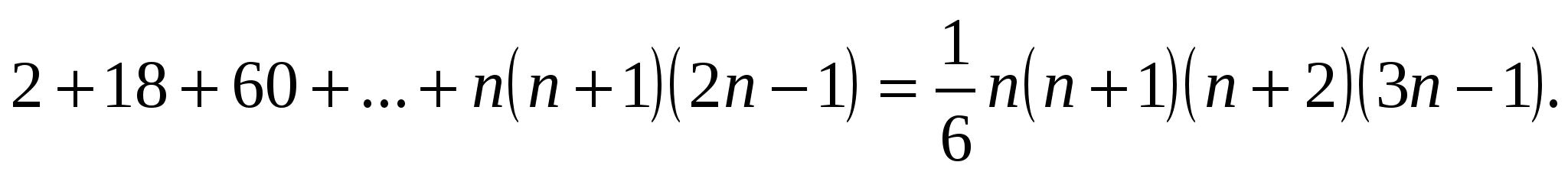
Доказательство.
Обозначим данное утверждение через Р(п), где п - натуральное число.
Р(1) справедливо: 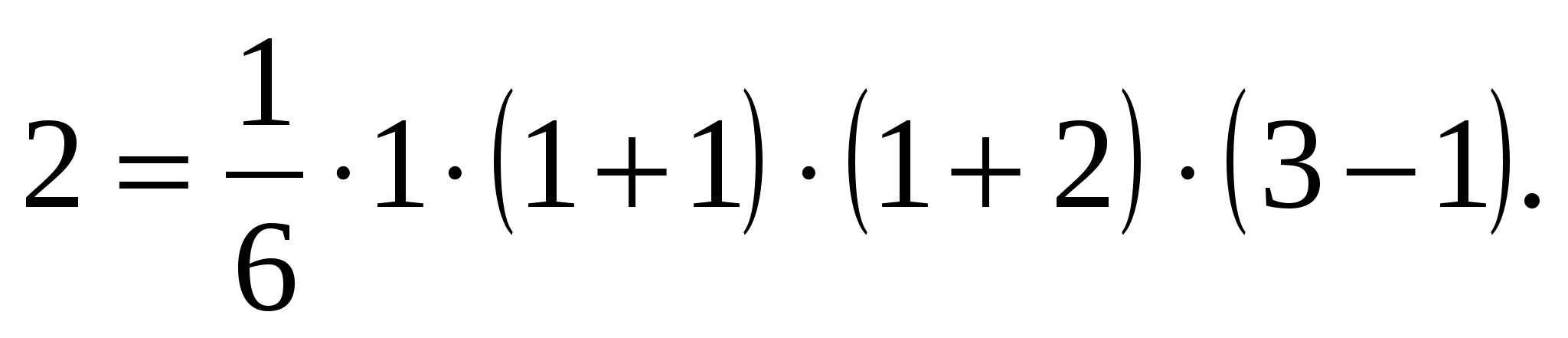
Предположим, что утверждение Р(к) справедливо, где к - натуральное число:
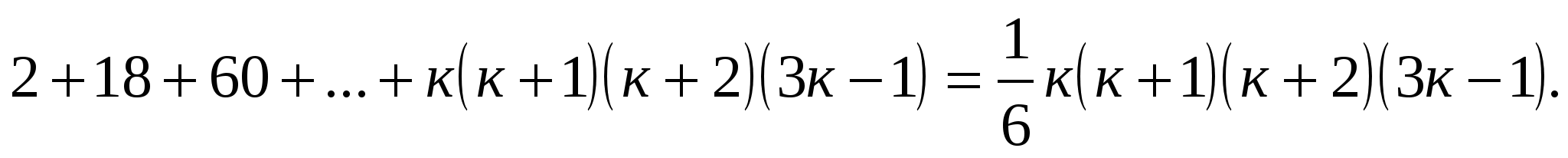
Докажем, что ![]()
Мы должны доказать, что справедливо неравенство:
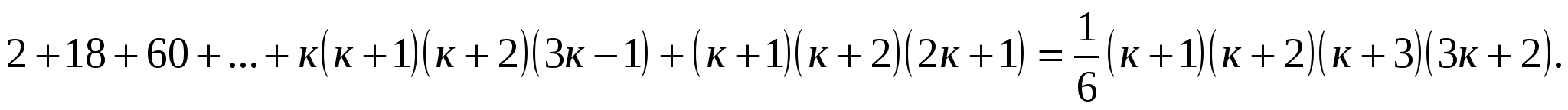
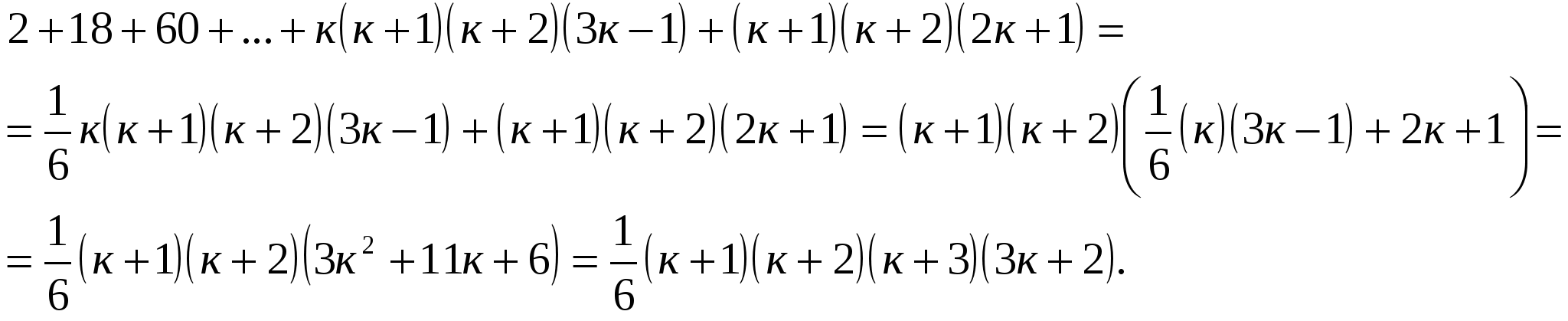
По принципу математической индукции утверждение справедливо для любого натурального п.
-
Докажите, что
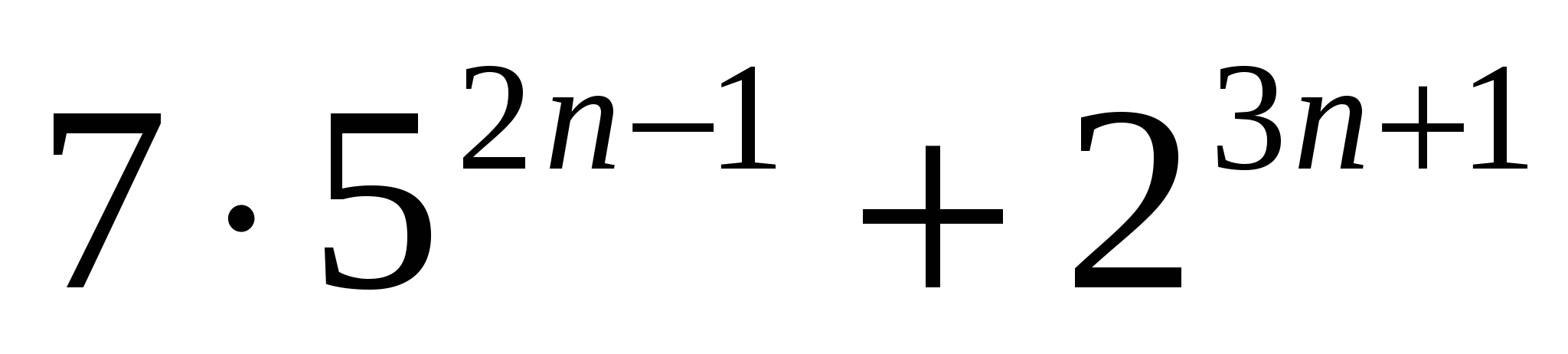 делится на 17 при любом натуральном п.
делится на 17 при любом натуральном п.
Доказательство.
Пусть 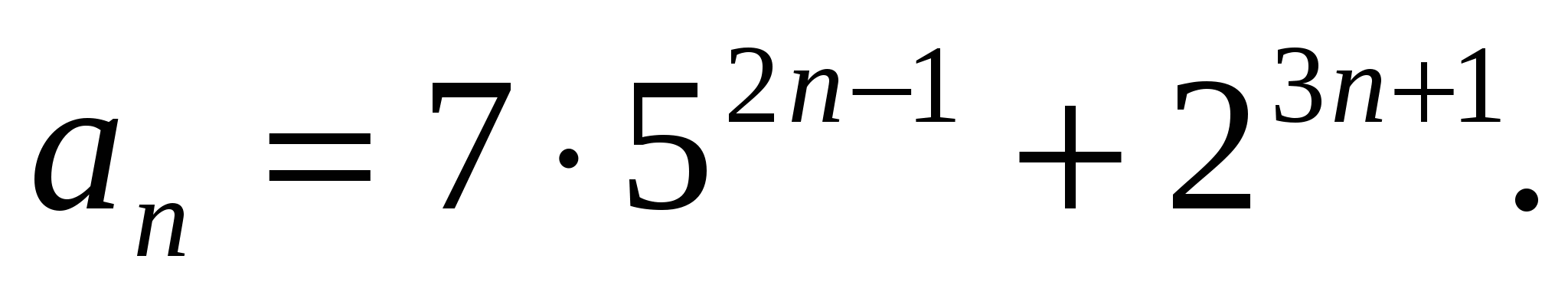
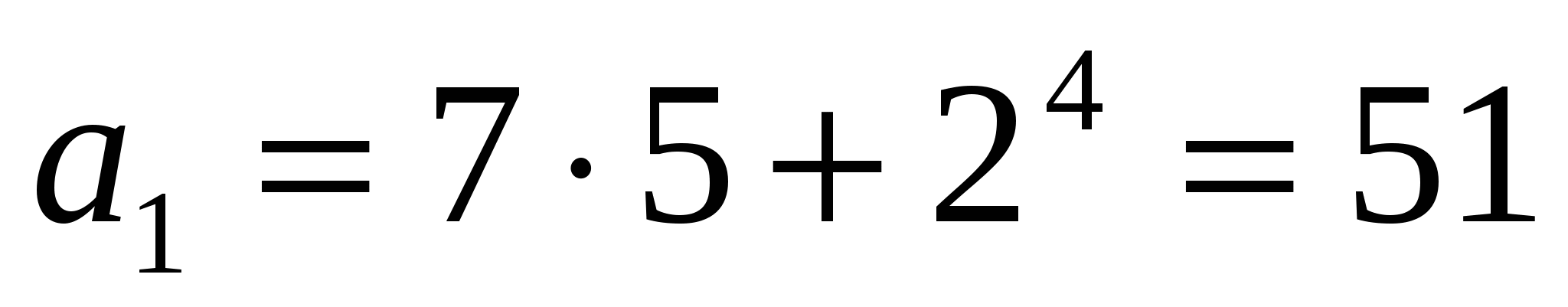 - кратно 17. Пусть
- кратно 17. Пусть 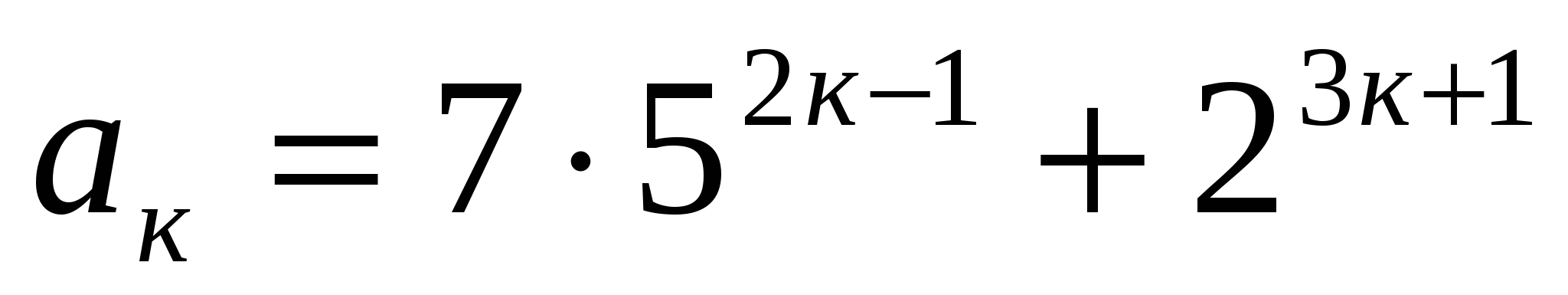
кратно 17. Докажем, что ![]() кратно 17.
кратно 17.
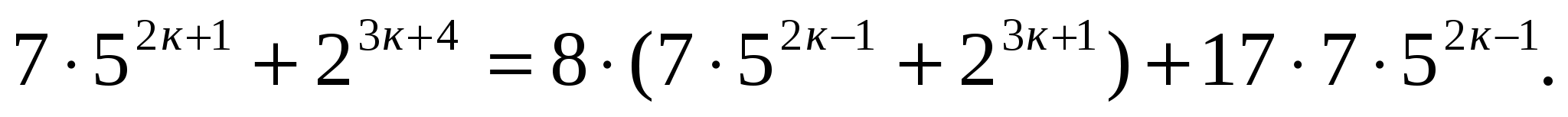 Каждое слагаемое суммы кратно 17.
Каждое слагаемое суммы кратно 17.
-
Докажите, что при
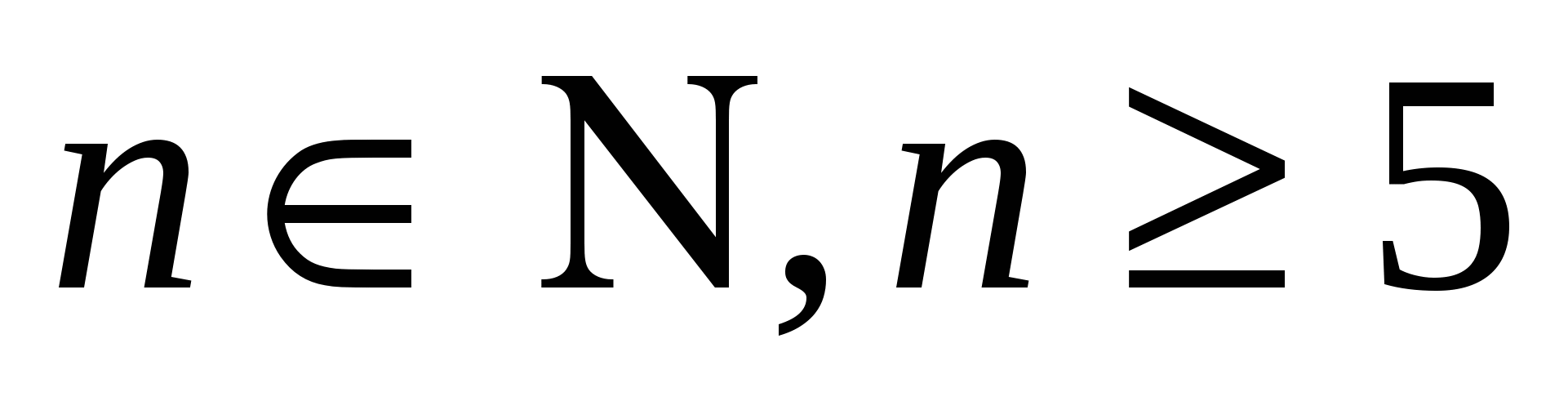 справедливо неравенство
справедливо неравенство
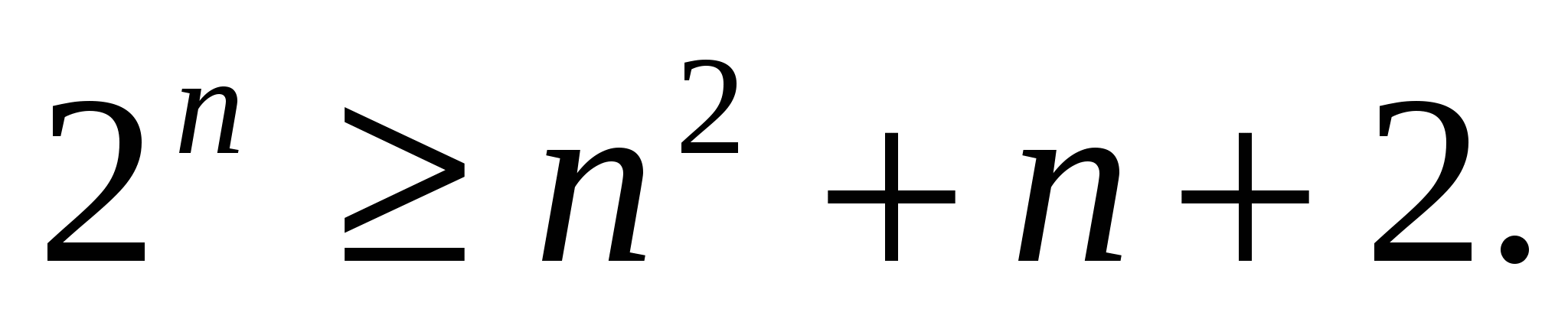
Доказательство.
При п=5 неравенство справедливо: 32≥32.
Пусть неравенство справедливо при п=к: 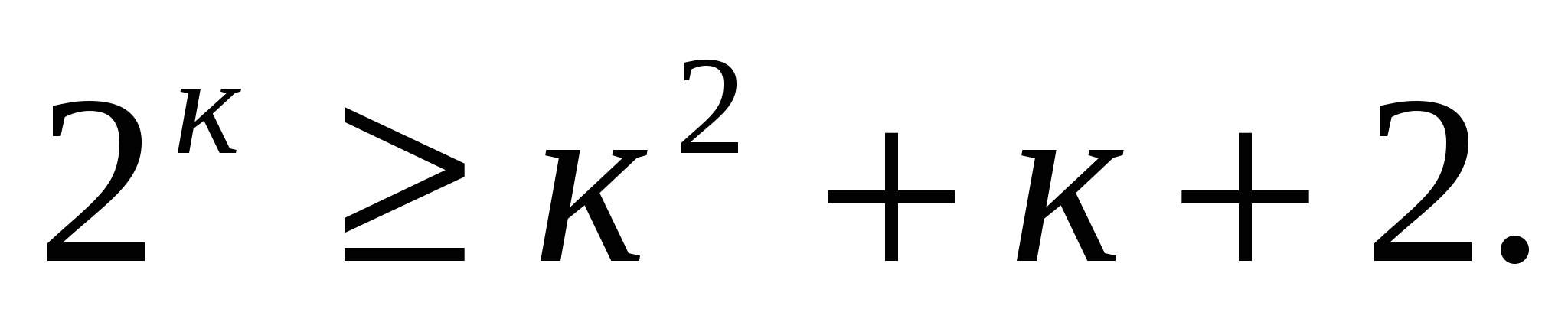
Докажем, что неравенство справедливо при п=к+1.
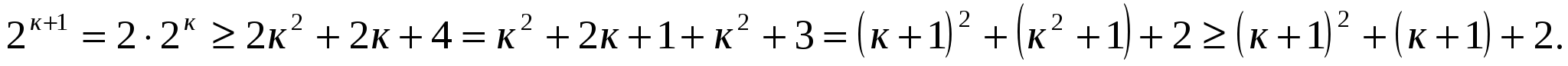
Итак, неравенство справедливо при п=5, из его справедливости при п=к следует справедливость при п=к+1. Значит, неравенство справедливо при п≥5, где п - -натуральное число.
17


