- Преподавателю
- Математика
- Самостоятельная внеаудиторная работа по теме Цилиндр
Самостоятельная внеаудиторная работа по теме Цилиндр
| Раздел | Математика |
| Класс | - |
| Тип | Конспекты |
| Автор | Кудравец Н.М. |
| Дата | 12.09.2015 |
| Формат | doc |
| Изображения | Есть |
Самостоятельное изучение материала, предваряющее изучение темы в аудитории (домашнее задание)
Занятие 3.
Тема: «Тела вращения. Цилиндр. Площадь полной и боковой поверхности цилиндра»
(разработал преподаватель математики Кудравец Н.М.)
Цель самостоятельной работы:
-
ввести понятие цилиндрической поверхности, цилиндра и его элементов, ввести формулы для вычисления боковой и полной поверхности цилиндра, научиться решать задачи по данной теме
Результаты деятельности студентов по данной теме (что у вас должно быть в тетрадях):
-
определения основных понятий темы, свойств пирамид;
-
построение кругового и прямого кругового цилиндра и его сечений;
-
ответы на вопросы;
-
самостоятельное решение задач.
Основные понятия по теме «Правильная пирамида»: цилиндрическая поверхность,круговой цилиндр, образующие, основания цилиндра, радиус цилиндра, высота цилиндра, осевое сечение цилиндра.
I. Подготовка к изучению темы.
Отгадайте загадку и найдите общее во всех перечисленных предметах загадки
Один мы есть предпочитаем,
Другим - мы талию спасаем,
Третьим же мышцы подкачаем.
Четвёртым - транспорт подкуём,
И пятый - на воду бросаем.
А их геометрическую форму
Одним лишь, словом называем
Что это за слово?
На рисунке 1 вы можете «тот самый» тор среди прочих фигур
 Рисунок 1
Рисунок 1
-
Изучение понятия «Тела вращения»
Определение 1.
Тела вращения - объёмные тела, возникающие при вращении плоской геометрической фигуры, ограниченной кривой, вокруг оси, лежащей в той же плоскости.
Примеры образования тел вращения (см. рис. 1):
-
Шар - образован полукругом, вращающимся вокруг диаметра разреза
-
Цилиндр - образован прямоугольником, вращающимся вокруг одной из сторон
-
Конус - образован прямоугольным треугольником, вращающимся вокруг одного из катетов
-
Тор - образован кругом, вращающимся вокруг прямой, не пересекающей его.
III. Изучение понятия «Цилиндр»
Предварительно посмотрите ролик x-uni.com/video/s457.
Задание 1.
Выполните конспект следующего материала и рисунки 2 и 3 в тетрадь.
Цилиндр
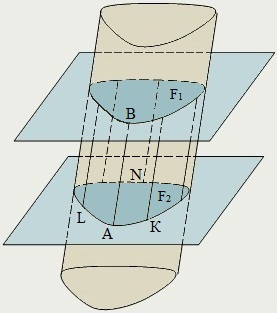
Рисунок 2
Определение 2.
Цилиндрическая поверхность-поверхность, образуемая движением прямой (в каждом своём положении называемой образующей) вдоль кривой (называемой направляющей) так, что прямая постоянно остаётся параллельной своему начальному положению.
Прямая АВ - образующая;
кривая AKNLA - направляющая.
Бесконечный цилиндр - тело, ограниченное цилиндрической поверхностью.
Определение 3.
Цилиндр-геометрическое тело, ограниченное цилиндрической поверхностью и двумя параллельными плоскостями, пересекающими её.
Часть поверхности цилиндра, ограниченная цилиндрической поверхностью, называется боковой поверхностью цилиндра.
Высотой цилиндра называется расстояние между плоскостями его оснований.
Другая часть, ограниченная параллельными плоскостями - это основания цилиндра.
Отрезок АВ - образующая;
фигуры F1 и F2 - основания.
У цилиндра:
-
основания равны;
-
образующие параллельны и равны.
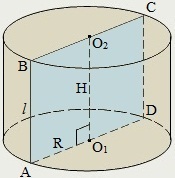
Рисунок 3
Определение 4.
Цилиндр, у которого основания перпендикулярны образующим и являются кругами, называется прямым круговым цилиндром (часто, и далее, - просто цилиндром).
Прямой круговой цилиндр можно получить вращением прямоугольника вокруг одной из его сторон.
Радиусом цилиндра называется радиус его основания.
Осью цилиндра называется прямая, проходящая через центры его оснований. Ось цилиндра параллельна образующим.
Осевым сечением цилиндра называется сечение цилиндра плоскостью, проходящей через его ось. Осевым сечением цилиндра (прямого кругового цилиндра) является прямоугольник.
AO1- радиус цилиндра;
AB, CD - образующие цилиндра;
O1O2- ось цилиндра;
AB, CD,O1O2- высоты цилиндра;
ABCD- осевое сечение цилиндра.
Боковая поверхность прямого кругового цилиндра равна произведению длины окружности основания на высоту:
Sбок = 2πRH.
Полная поверхность цилиндра вычисляется по формуле:
Sп= Sбок + 2Sосн= 2πR(H + R).
-
Закрепление пройденного материала
Задание 2.
Запишите в тетрадь примеры домашних предметов, имеющих форму цилиндра (не менее семи)
Задание 3.
Решите задачи в тетради.
1) Чему равен радиус основания, если осевым сечением цилиндра является квадрат 25 м2?
2) Сколько квадратных метров листовой жести пойдет на изготовление трубы длиной 4 м и диаметром 20 см, если на швы необходимо добавить 2,5% площади её боковой поверхности?
-
Вопросы к теме:
-
Чем отличается цилиндрическая поверхность от цилиндра?
-
Что такое образующая?
-
Какой цилиндр называется прямым круговым?
-
Вращением какой фигуры получается прямой цилиндр?
-
Что такое осевое сечение цилиндра?


