- Преподавателю
- Математика
- Конспеут урока Математика и экономика
Конспеут урока Математика и экономика
| Раздел | Математика |
| Класс | - |
| Тип | Конспекты |
| Автор | Луконина С.А. |
| Дата | 03.03.2015 |
| Формат | doc |
| Изображения | Есть |
Тема 8. Простейшие экономико-математические модели.
Время: 2 часа
Цель лекции: Познакомить слушателей с возможностями использования математического аппарата дифференциального исчисления и систем линейных алгебраических уравнений в экономических расчётах.
План лекции:
-
Простые и сложные проценты.
-
Задачи на экстремум в экономике.
-
Понятие эластичности в микроэкономике.
-
Модель Леонтьева межотраслевого баланса.
-
Простые и сложные проценты.
Предоставляя свои денежные средства в долг, их владелец получает определенный доход в виде процентов, начисляемых по некоторому алгоритму в течение некоторого промежутка времени. Известны две основные схемы дискретного начисления:
-
схема простых процентов;
-
схема сложных процентов.
В финансовых расчётах процентом P называют сумму, уплачиваемую за использование предоставленных средств S. Величина 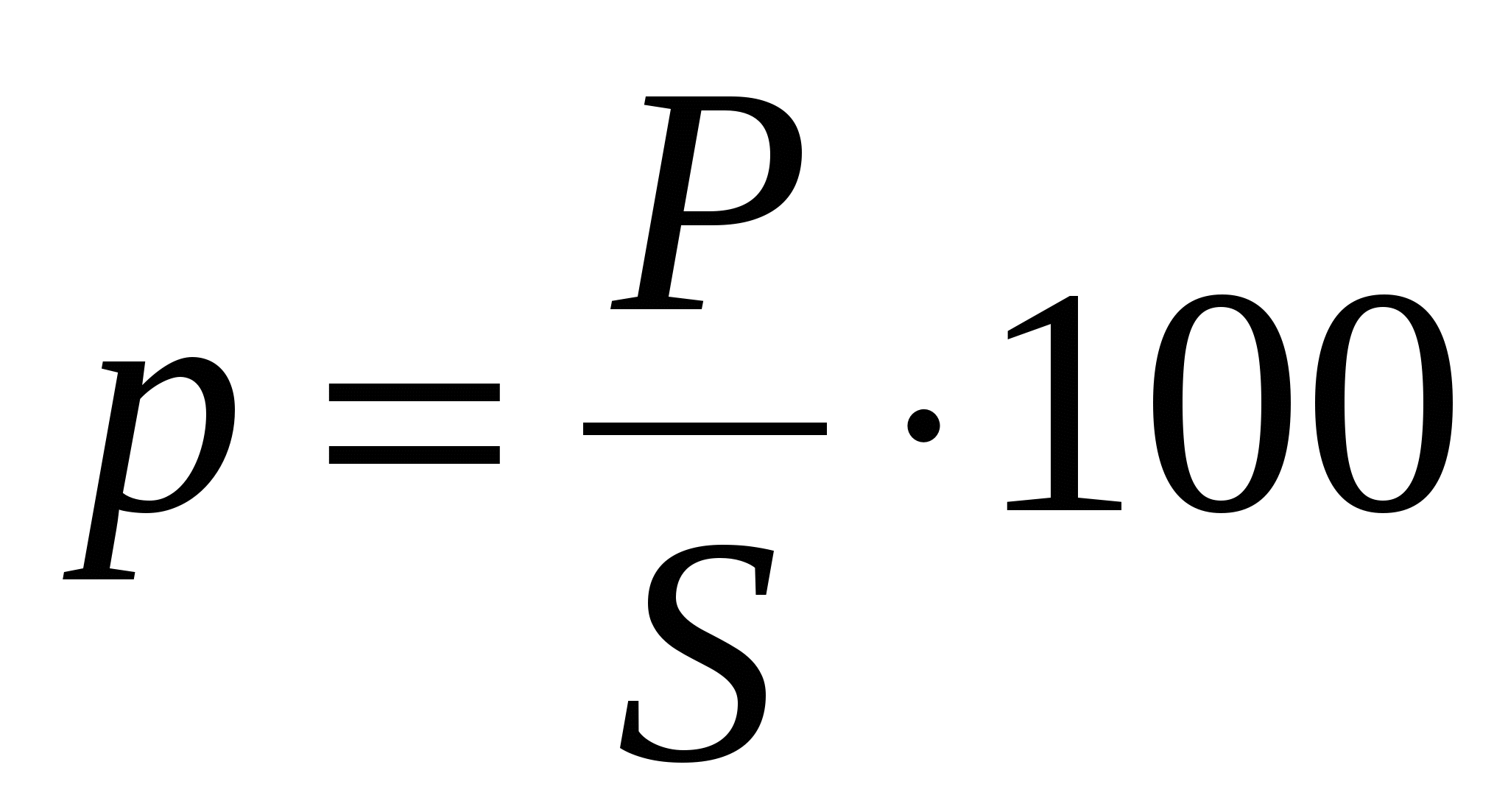 называется процентной ставкой. По истечению договорного срока (например, 1 год), инвестор получает сумму
называется процентной ставкой. По истечению договорного срока (например, 1 год), инвестор получает сумму 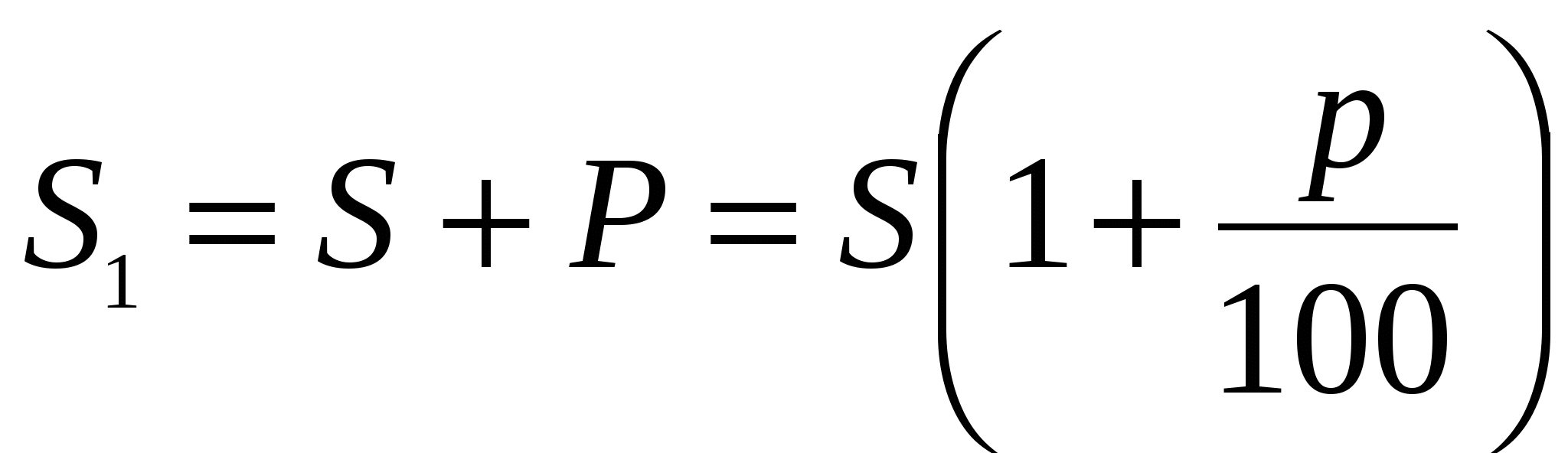 . Число
. Число 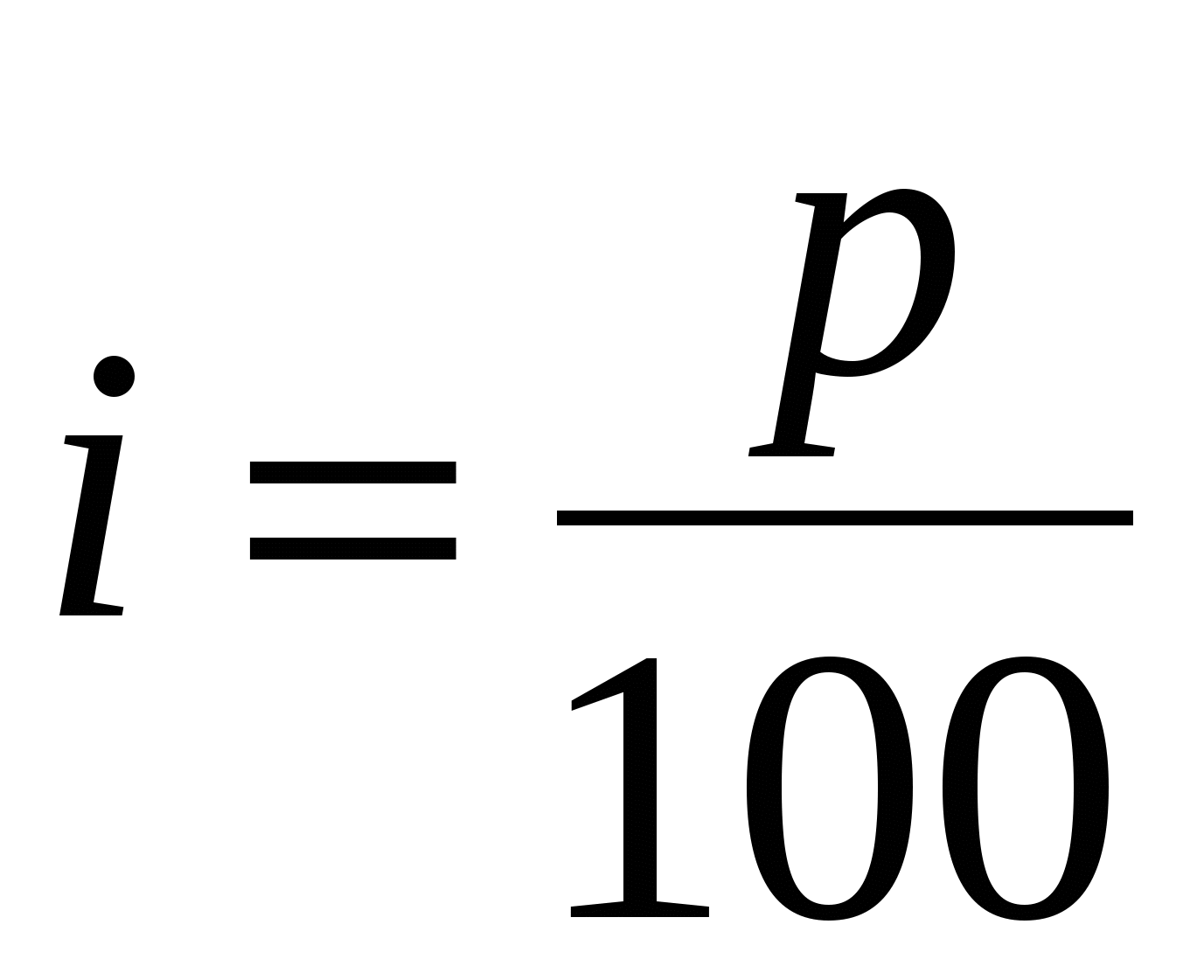 называют удельной процентной ставкой.
называют удельной процентной ставкой.
Схема простых процентов предполагает неизменность базы, с которой происходит начисление, т.е. на процент Р, добавленный к сумме S, процент не начисляется и тогда сумма Sп, накопленная за п лет, вычисляется по формуле:
![]() .
.
Считается, что инвестиция сделана на условиях сложного процента, если очередной годовой доход исчисляется не с исходной величины инвестированного капитала, а с общей суммы, включающей также и ранее начисленные и невостребованные инвестором проценты.
Сумма, накопленная за п лет при сложном проценте, определяется формулой:
![]() .
.
Величину 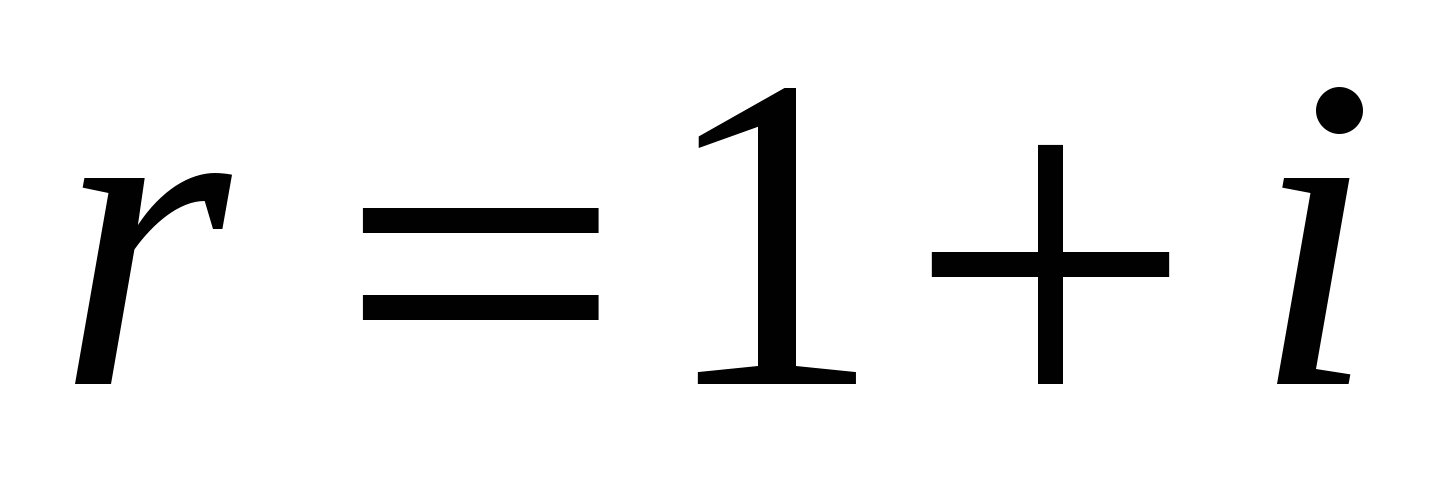 называют коэффициентом сложного процента.
называют коэффициентом сложного процента.
Величина вклада при сложных процентах, начисляемых т раз в год:
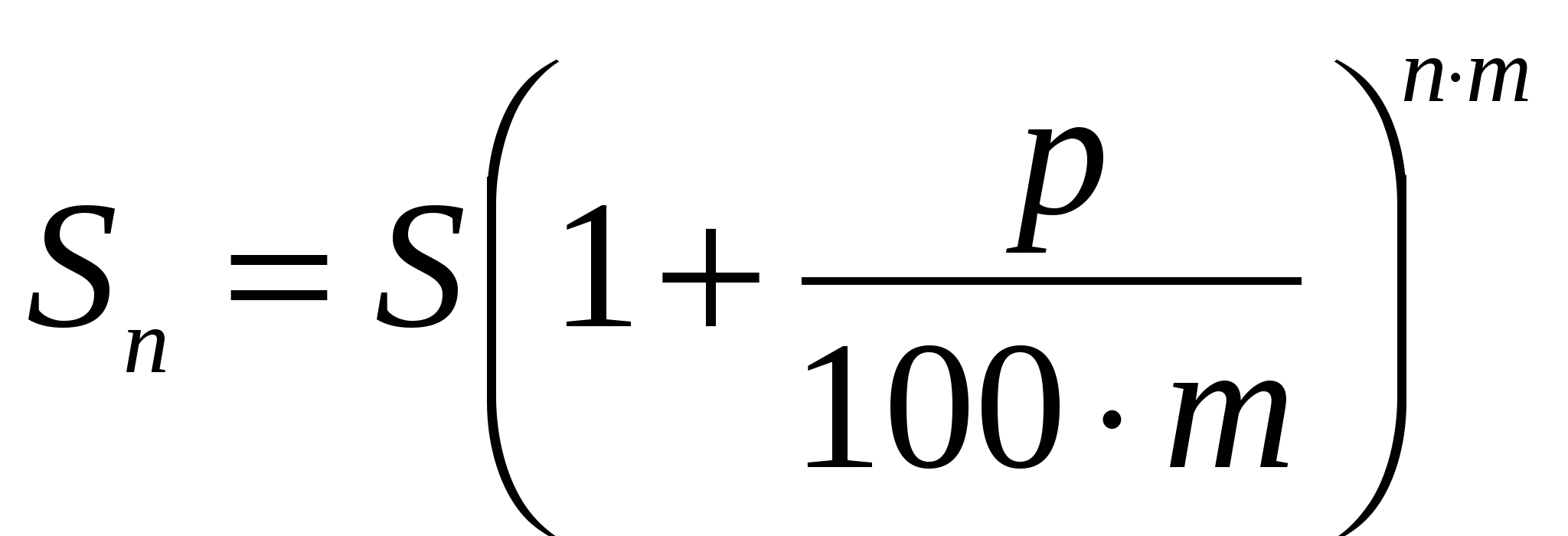
Использование в расчетах сложного процента в случае многократного его начисления более логично, поскольку в этом случае капитал, генерирующий доходы, постоянно возрастает. При применении простого процента доходы по мере их начисления целесообразно снимать для потребления или использования в других инвестиционных проектах или текущей деятельности.
Формула сложных процентов является одной из базовых формул в финансовых вычислениях вообще и при оценке инвестиционных проектов в частности, поэтому, для удобства пользования значения множителя 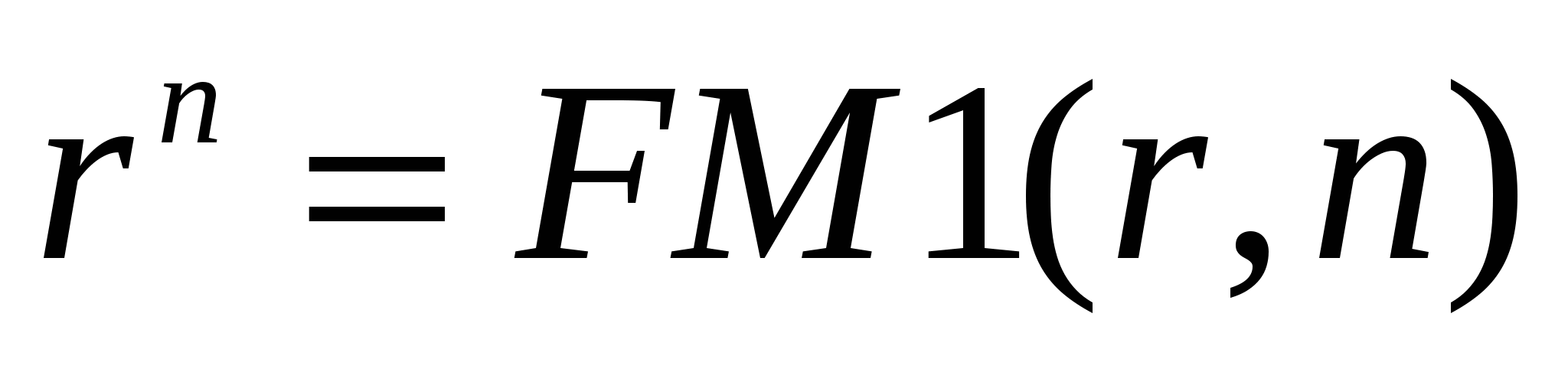 табулируют для различных значений r и n. Тогда формула алгоритма наращения по схеме сложных процентов переписывается следующим образом:
табулируют для различных значений r и n. Тогда формула алгоритма наращения по схеме сложных процентов переписывается следующим образом:
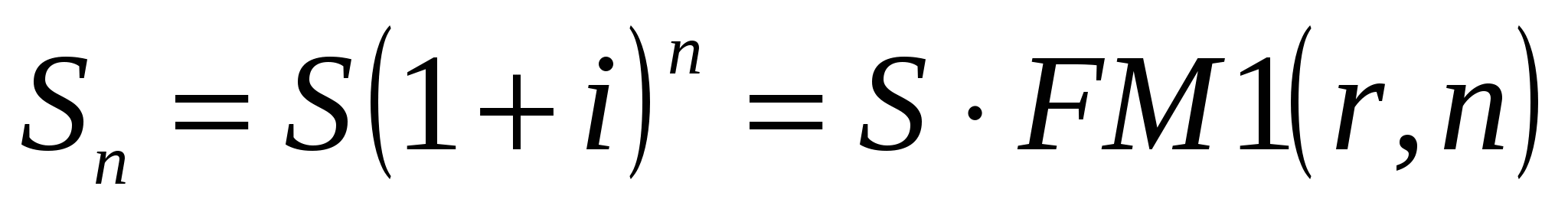 ,
,
где 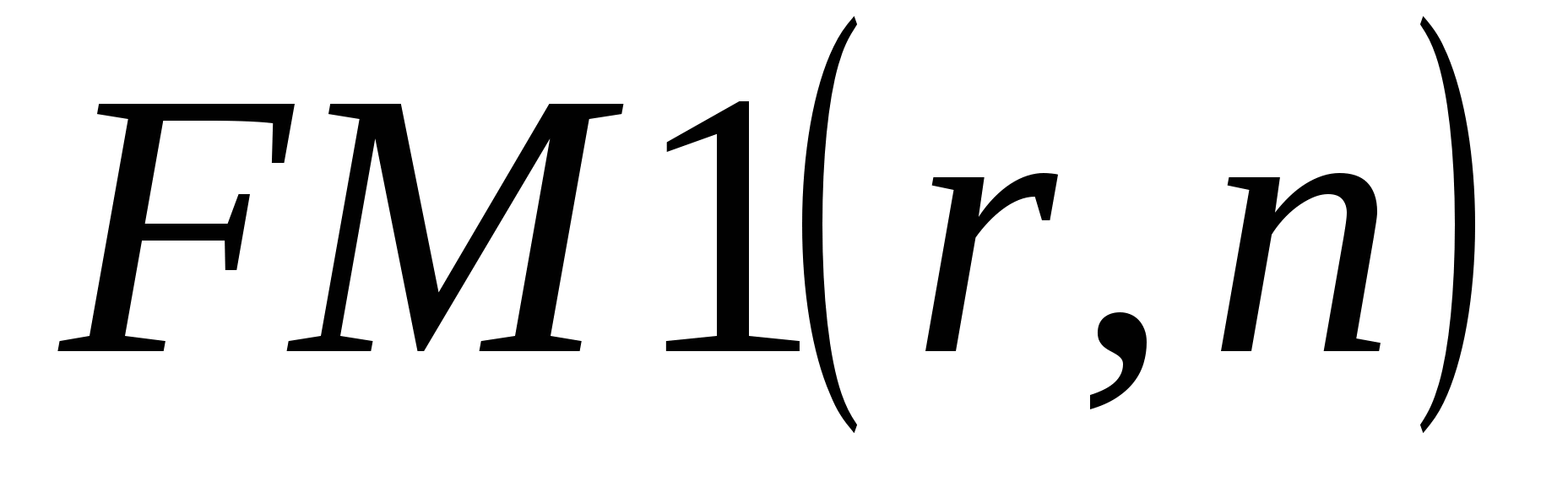 ‒ мультиплицирующий множитель.
‒ мультиплицирующий множитель.
Экономический смысл множителя 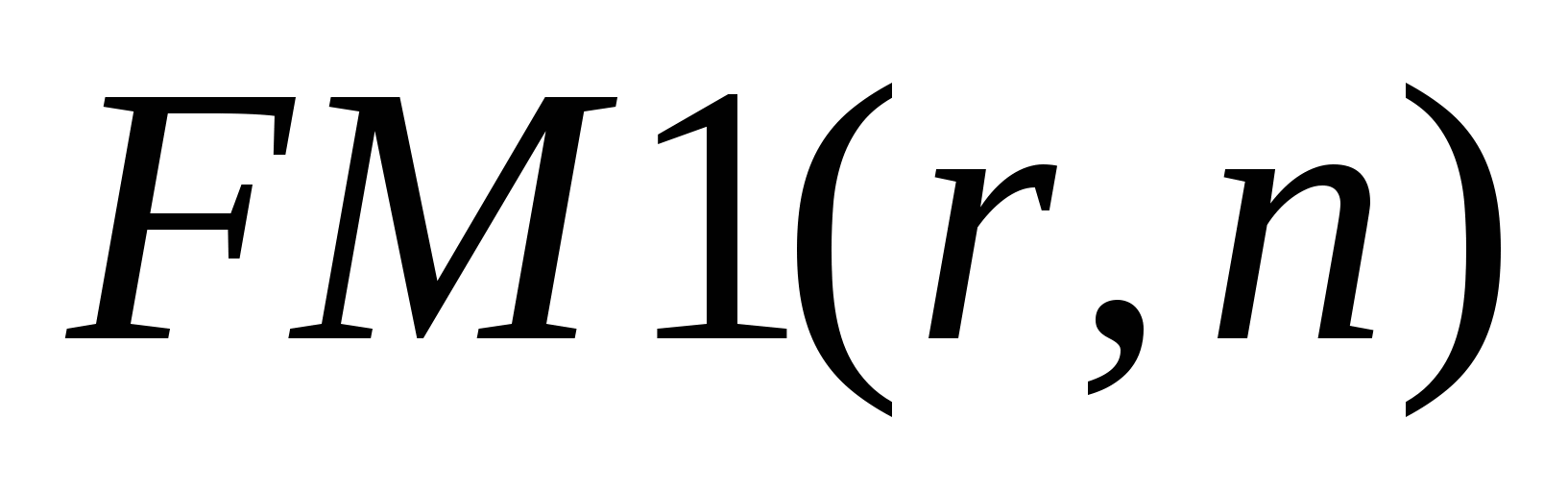 состоит в следующем: он показывает, чему будет равна одна денежная единица (один рубль, один доллар, одна иена и т.п.) через n периодов при заданной процентной ставке.
состоит в следующем: он показывает, чему будет равна одна денежная единица (один рубль, один доллар, одна иена и т.п.) через n периодов при заданной процентной ставке.
Методы оценки инвестиционных проектов.
Оценивая целесообразность финансовых вложений в тот или иной вид бизнеса, исходят из того, является это вложение более прибыльным (при допустимом уровне риска), чем вложения в государственные ценные бумаги, или нет.
Основная идея этих методов заключается в оценке будущих поступлений 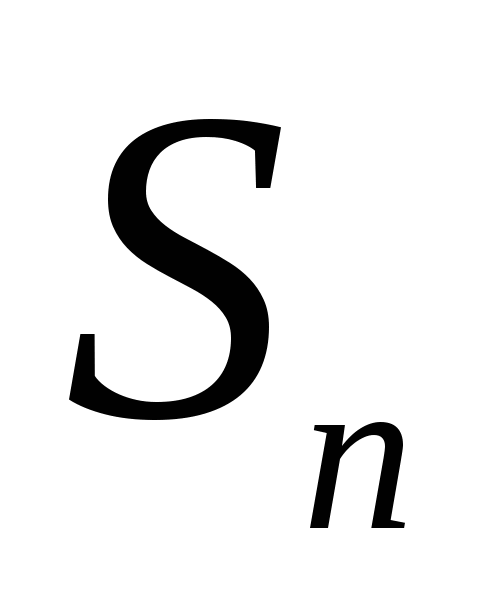 (например, в виде прибыли, процентов, дивидендов) с позиции текущего момента. При этом, сделав финансовые вложения, инвестор обычно руководствуется тремя посылами:
(например, в виде прибыли, процентов, дивидендов) с позиции текущего момента. При этом, сделав финансовые вложения, инвестор обычно руководствуется тремя посылами:
а) происходит перманентное обесценение денег (инфляция);
б) темп изменения цен на сырье, материалы и основные средства, используемые предприятием, может существенно отличаться от темпа инфляции;
в) желательно периодическое начисление (или поступление) дохода, причем в размере не ниже определенного минимума.
Базируясь на этих посылах, инвестор должен оценить, какими будут его доходы в будущем, какую максимально возможную сумму допустимо вложить в данное дело исходя из прогнозируемой его рентабельности.
Базовая расчетная формула для такого анализа является следствием формулы
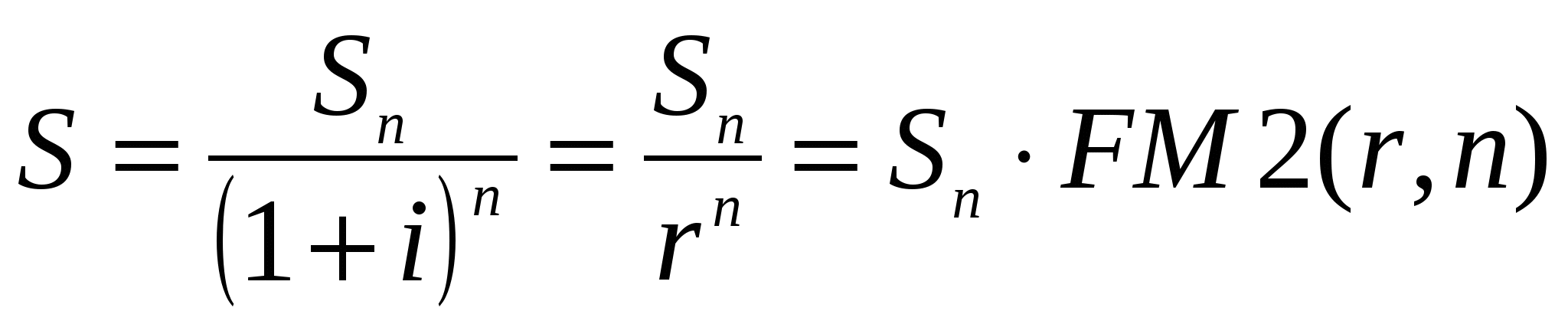 ,
,
где: 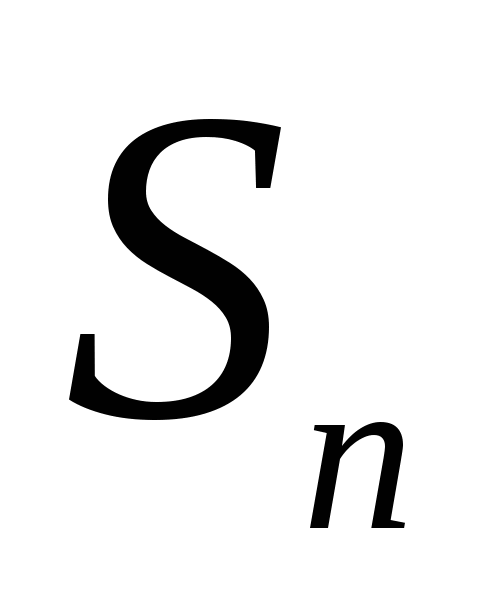 - доход, планируемый к получению в п-ом году;
- доход, планируемый к получению в п-ом году;
S - текущая (или приведенная) стоимость, т.е. оценка величины 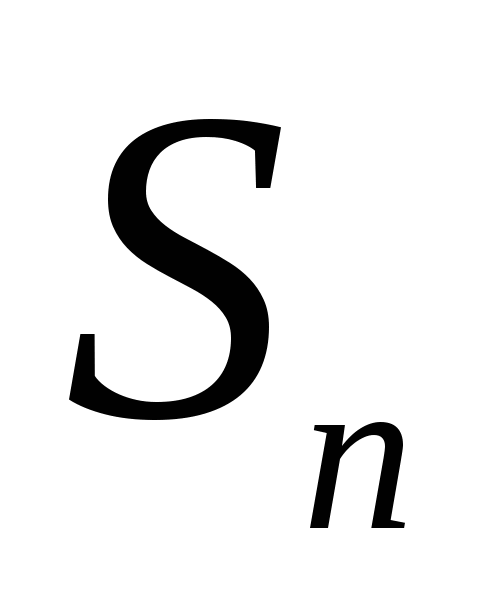 с позиции текущего момента;
с позиции текущего момента;
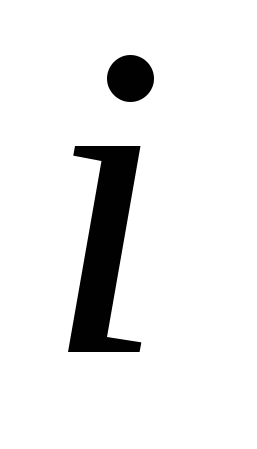 ‒ коэффициент дисконтирования.
‒ коэффициент дисконтирования.
Экономический смысл такого представления заключается в следующем: прогнозируемая величина денежных поступлений через n - лет (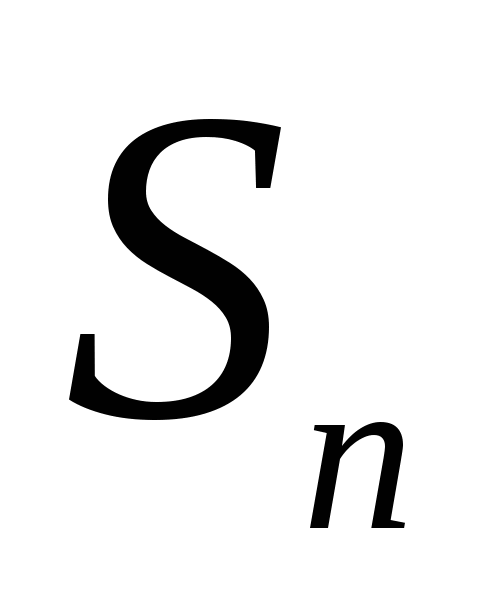 ) с позиции текущего момента будет меньше и равна S (поскольку знаменатель дроби больше единицы. Это означает также, что для инвестора сумма S в данный момент времени и сумма
) с позиции текущего момента будет меньше и равна S (поскольку знаменатель дроби больше единицы. Это означает также, что для инвестора сумма S в данный момент времени и сумма 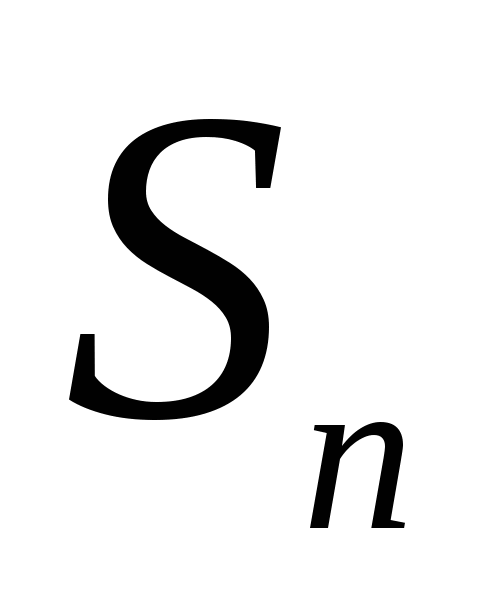 через n - лет одинаковы по своей ценности. Используя эту формулу, можно приводить в сопоставимый вид оценку доходов от инвестиций, ожидаемых к поступлению в течение ряда лет.
через n - лет одинаковы по своей ценности. Используя эту формулу, можно приводить в сопоставимый вид оценку доходов от инвестиций, ожидаемых к поступлению в течение ряда лет.
-
Задачи на экстремум в экономике.
Алгоритм решения задачи на определение наибольшего или наименьшего значений:
-
Этап построения математической модели (этап формализации).
-
выявляем оптимизируемую величину (прибыль, расходы на производство и т.п.). и обозначаем её у;
-
одну из неизвестных величин (цену товара, величину спроса, объём производства и т.п.) считаем независимой переменной и обозначаем х. Устанавливаем реальные границы изменения х в соответствии с условием задачи;
-
исходя из конкретных условий задачи, выражаем у через х и известные величины.
-
Этап исследования математической модели.
-
для полученной функции находим максимум или минимум (в зависимости от требований задачи) на промежутке реального изменения х.
-
Этап интерпретации результатов.
-
Интерпретируем полученные результаты для данных задачи.
Данный алгоритм подходит и для функции с двумя переменными.
-
Понятие эластичности в микроэкономике.
Для исследования экономических процессов и решения прикладных задач используется понятие эластичности функции.
Эластичностью функции (с точки зрения математики) 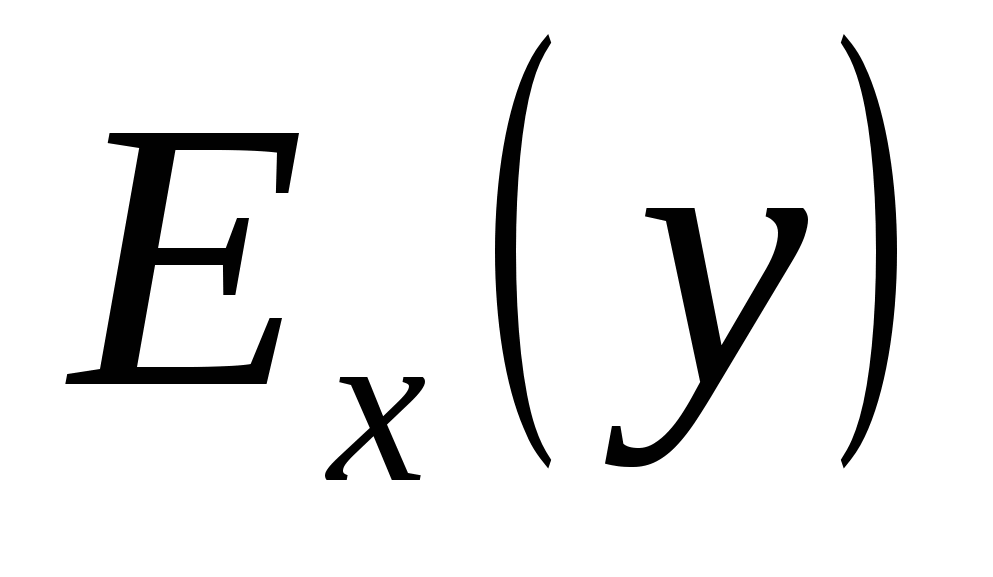 называется предел отношения относительного приращения функции к относительному приращению аргумента при
называется предел отношения относительного приращения функции к относительному приращению аргумента при 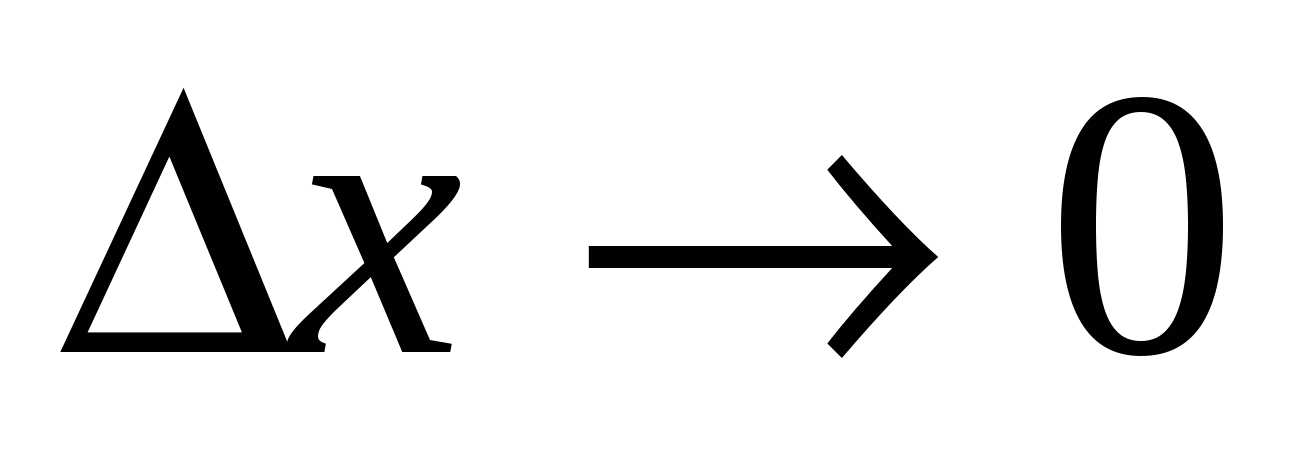 .
.
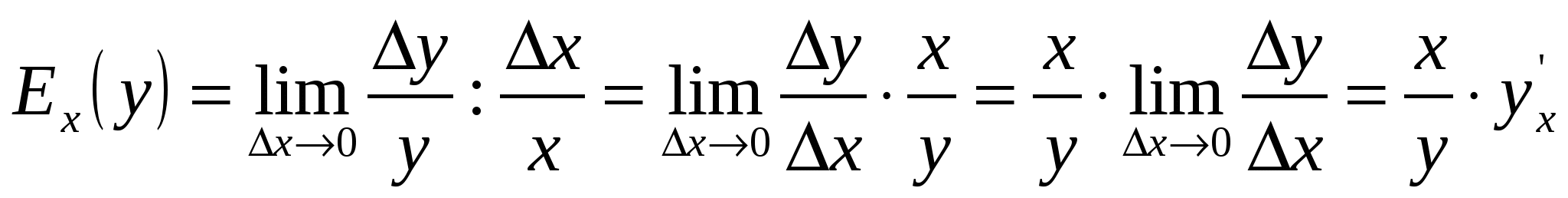

![]()
Экономический смысл эластичности функции в том, что она выражает приближённый процентный прирост значения функции при приращении аргумента на 1%.
Свойства эластичности:
-
Эластичность ‒ безразмерная величина, т.е. её значение не зависит от единиц измерения величин х и у.
-
Эластичность произведения двух функций равна сумме эластичностей этих функций.
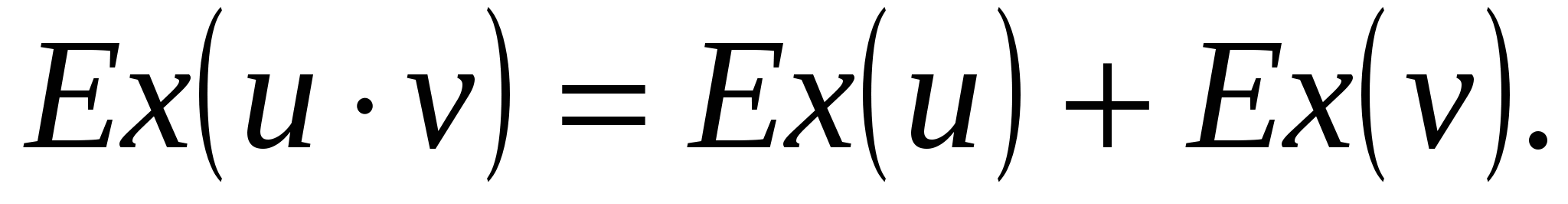
-
Эластичность частного двух функций равна разности эластичностей этих функций.
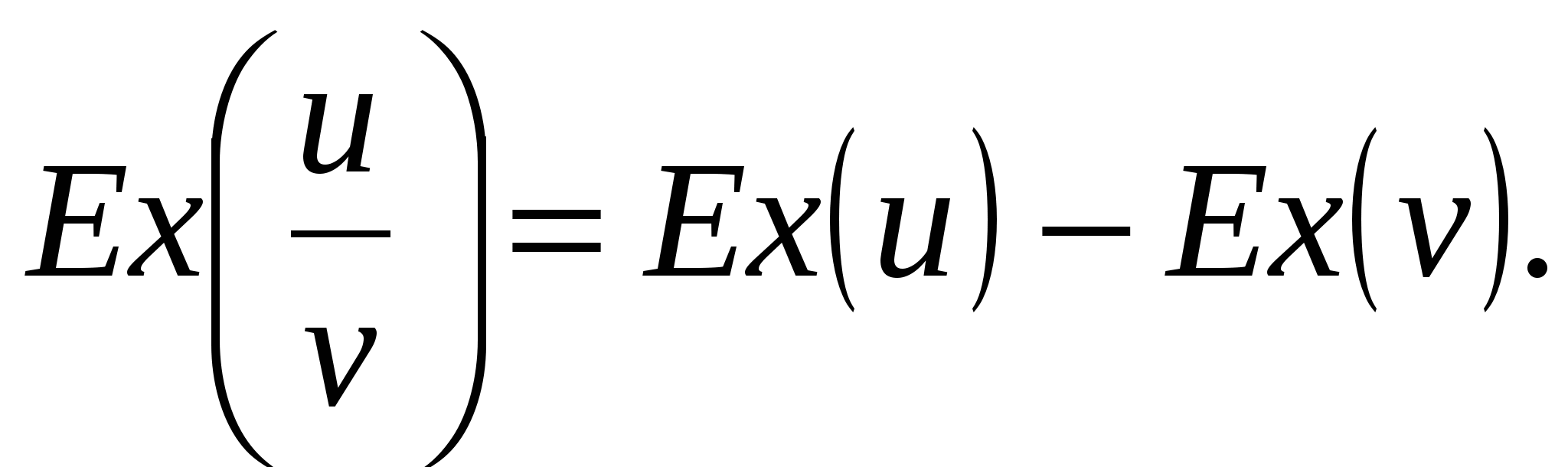
Эластичность спроса q относительно цены p.
Пусть спрос зависит от цены по закону 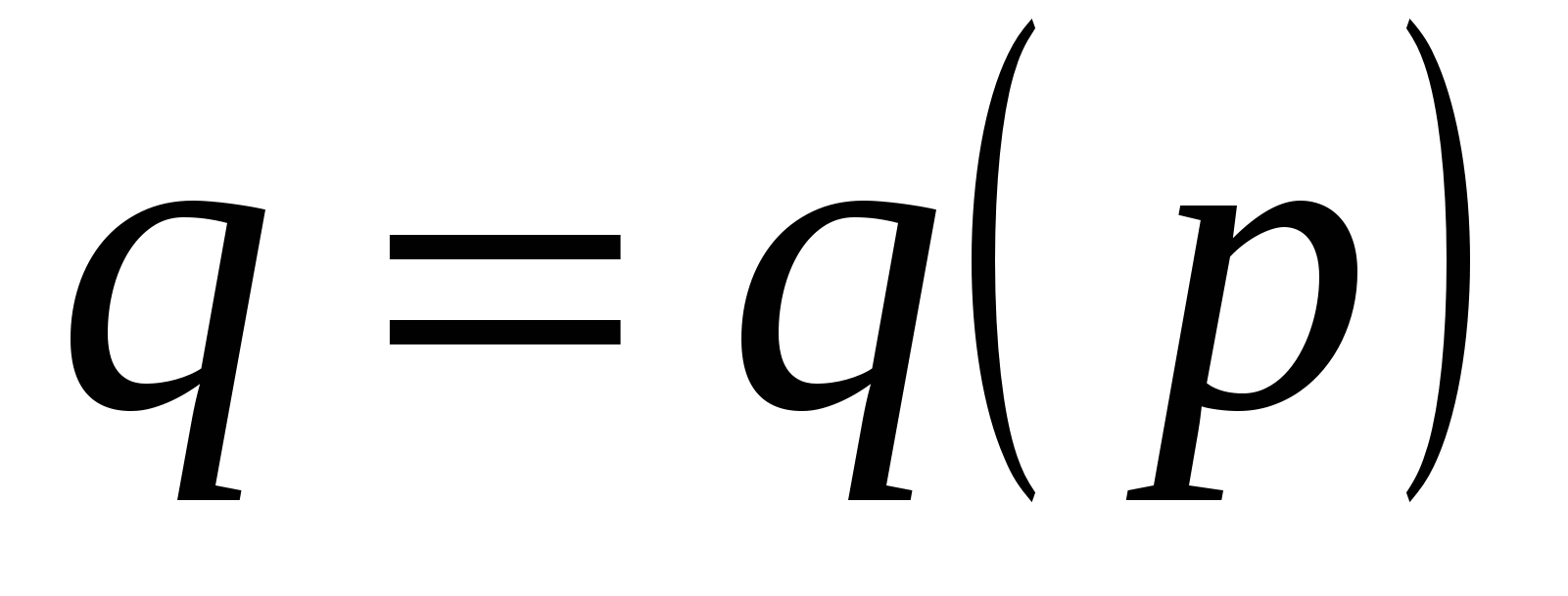 . Функция
. Функция 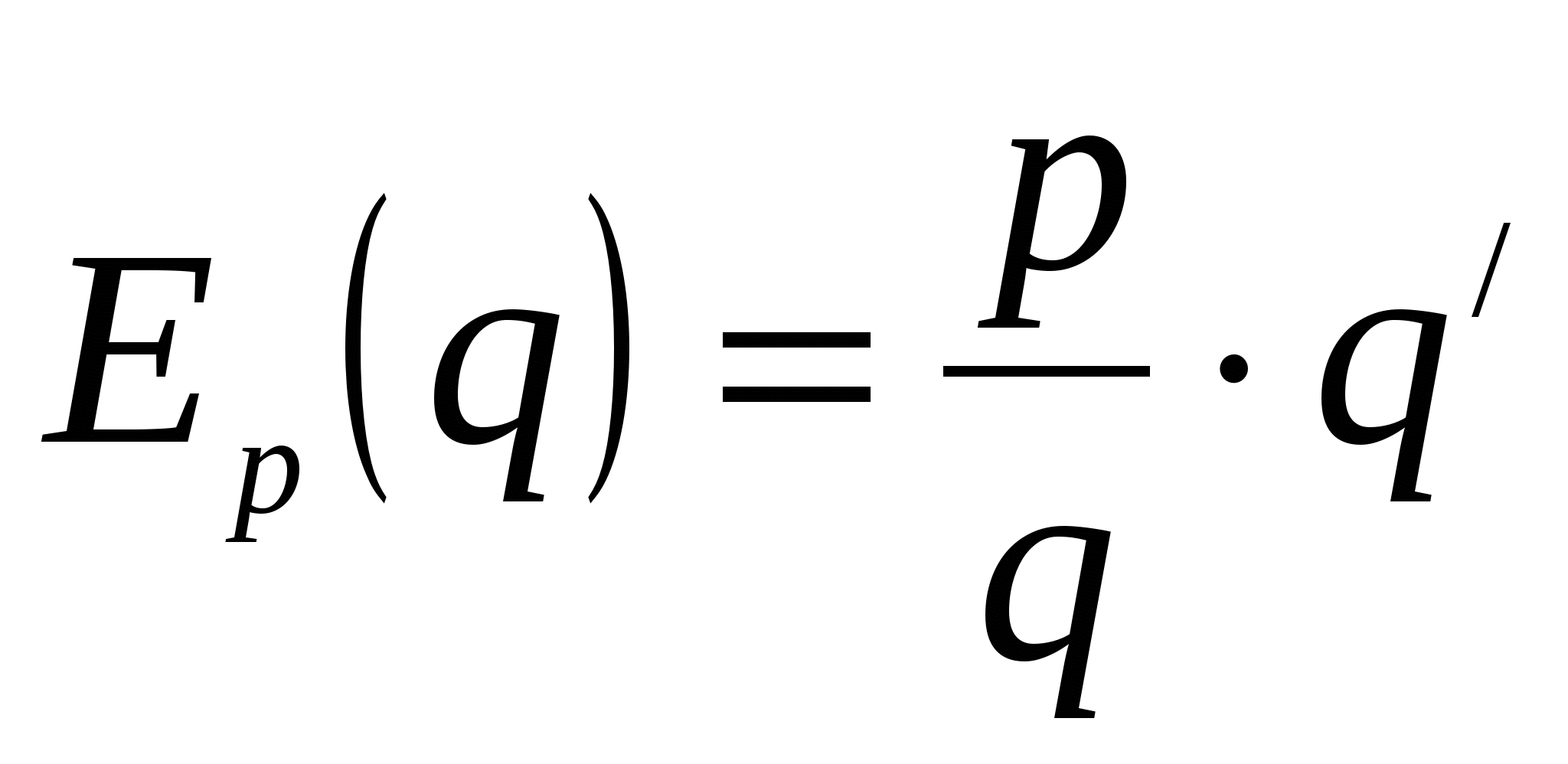 показывает, как изменится спрос на данный товар, если цена изменится на 1%. Так как обычно
показывает, как изменится спрос на данный товар, если цена изменится на 1%. Так как обычно 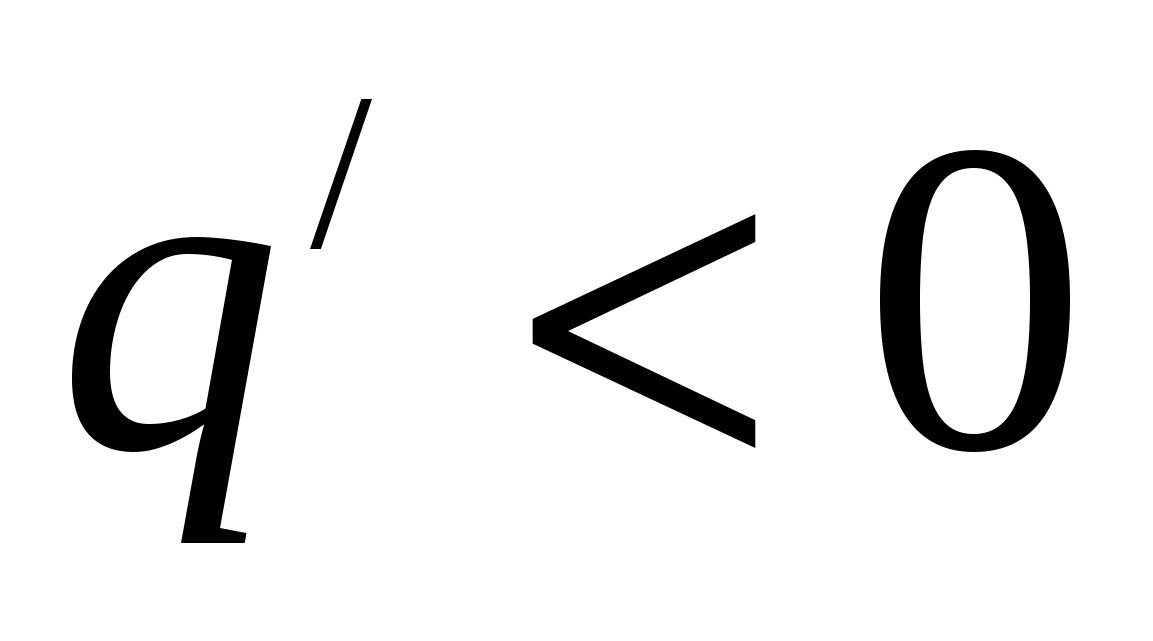 , т.е. с увеличением цены спрос падает, то
, т.е. с увеличением цены спрос падает, то ![]() берут со знаком «‒», т.е.
берут со знаком «‒», т.е. 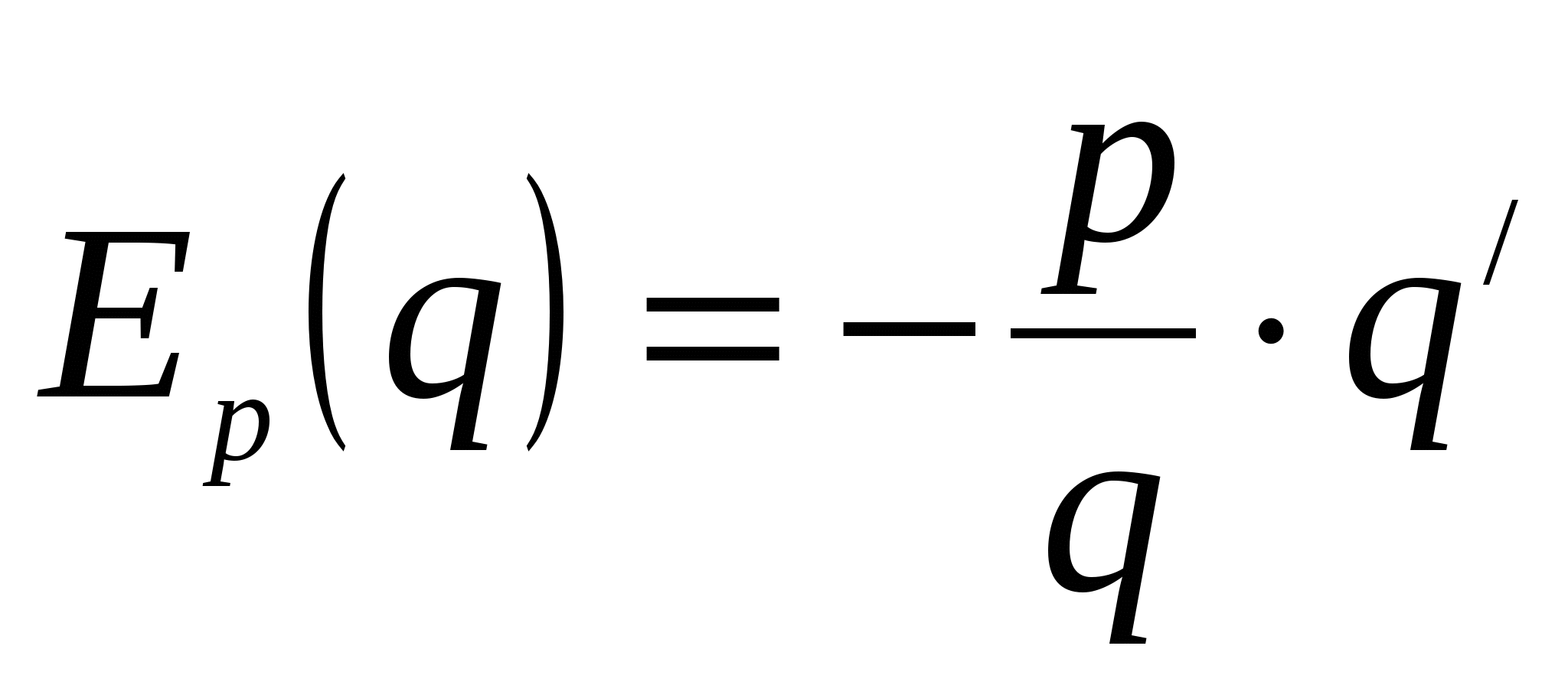 .
.
Если 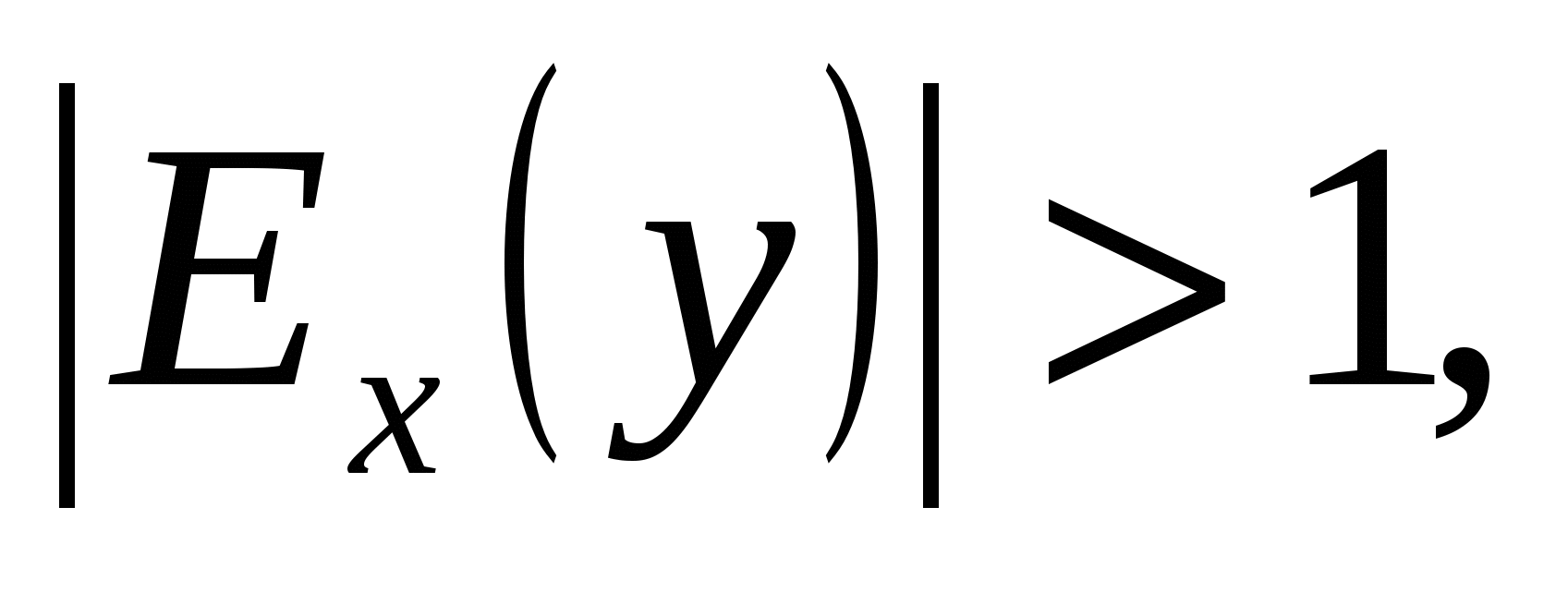 то говорят, что спрос эластичен; если
то говорят, что спрос эластичен; если ![]() то не эластичен; если же
то не эластичен; если же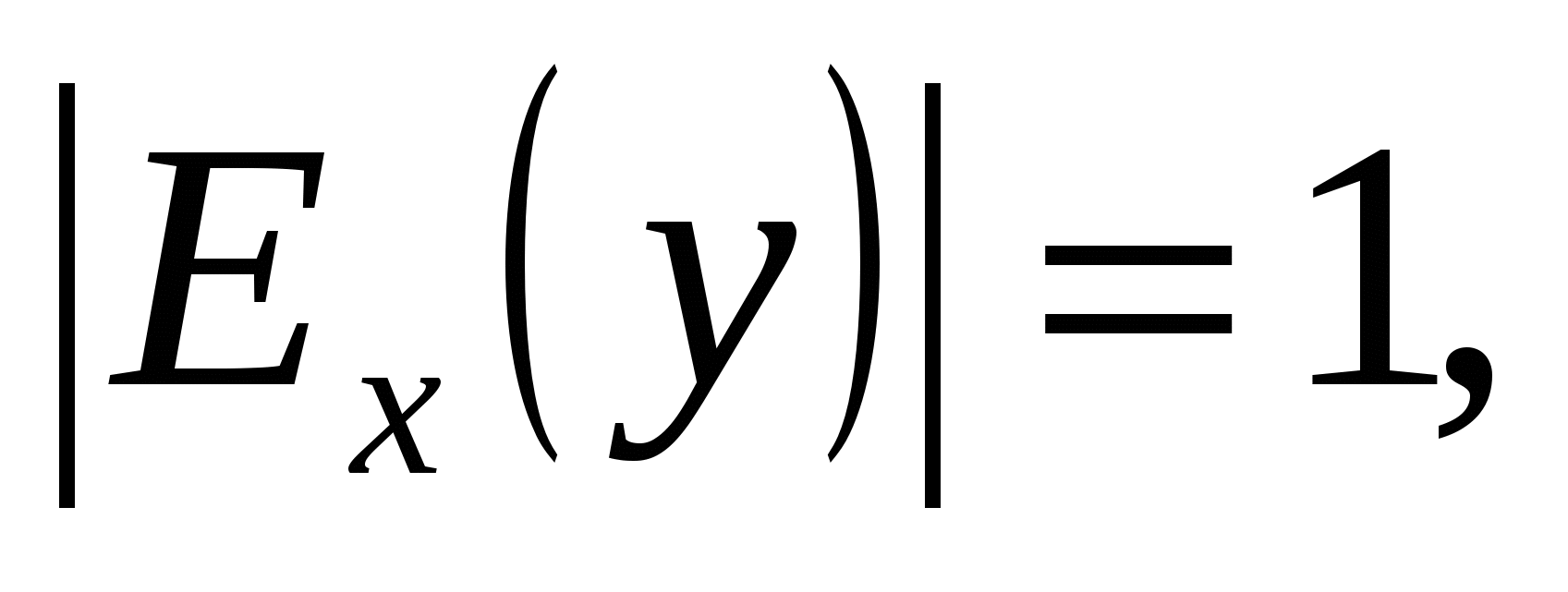 то спрос нейтрален.
то спрос нейтрален.
Перекрестная эластичность спроса по цене характеризует относительное изменение величины спроса на один товар или услуги при изменении цены на другие (замещающие или дополняющие) на один процент.
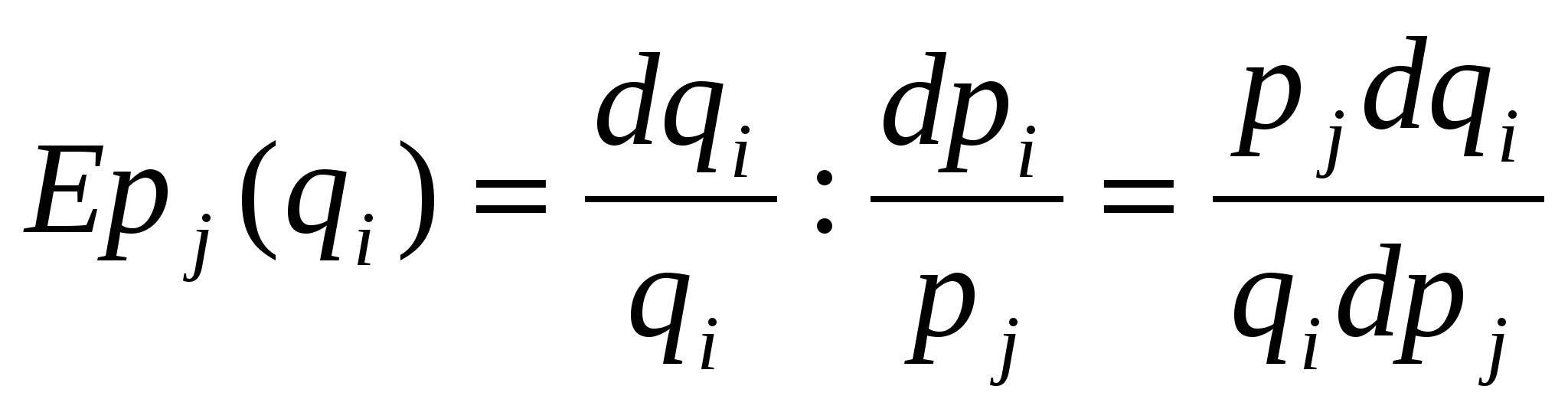
Положительный знак в (10) свидетельствует о замещаемости, а отрицательный - о дополняемости.
Эластичность спроса q относительно дохода r.
Пусть 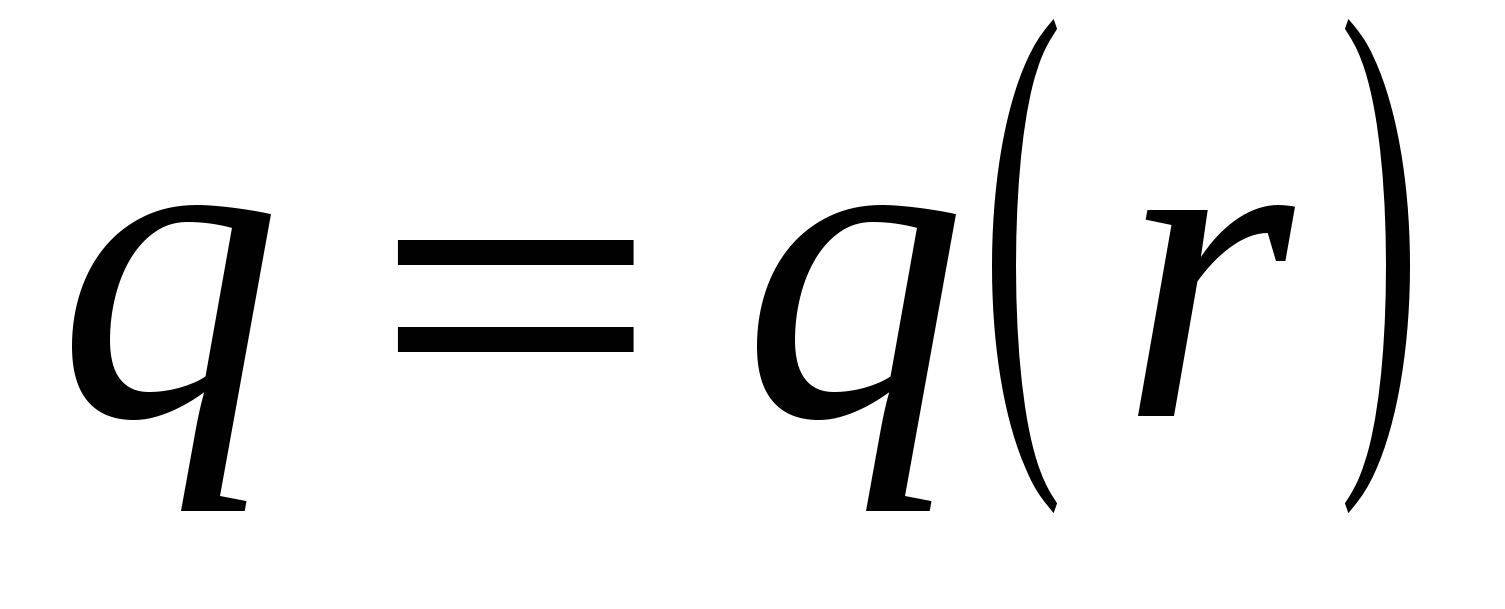 ‒ закон зависимости спроса от дохода. Тогда
‒ закон зависимости спроса от дохода. Тогда 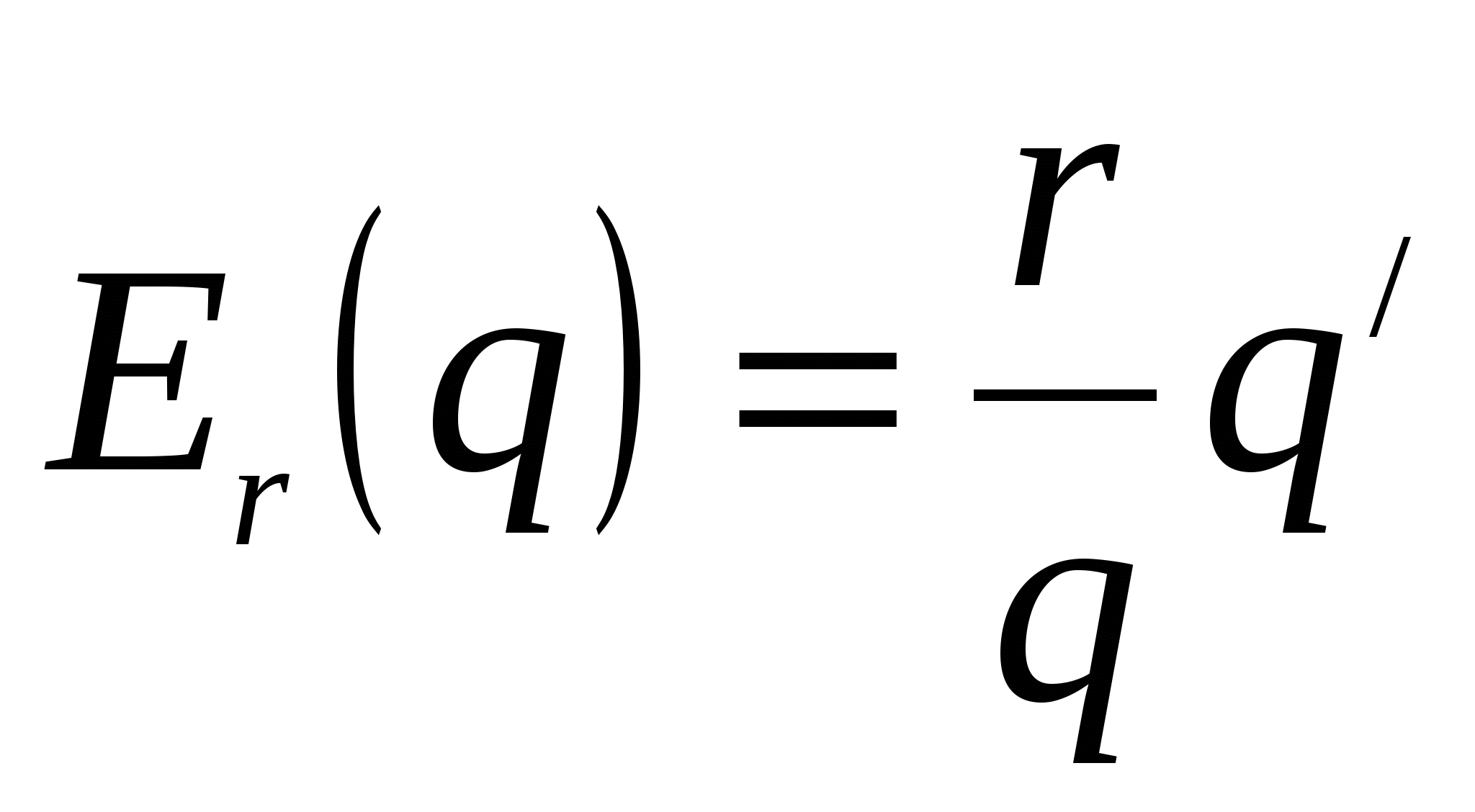 есть эластичность спроса относительно дохода, она показывает как изменится спрос на данный товар, если доход изменится на 1%.
есть эластичность спроса относительно дохода, она показывает как изменится спрос на данный товар, если доход изменится на 1%.
Аналогично можно определить эластичность предложения s относительно цены р или дохода r:
![]() и
и 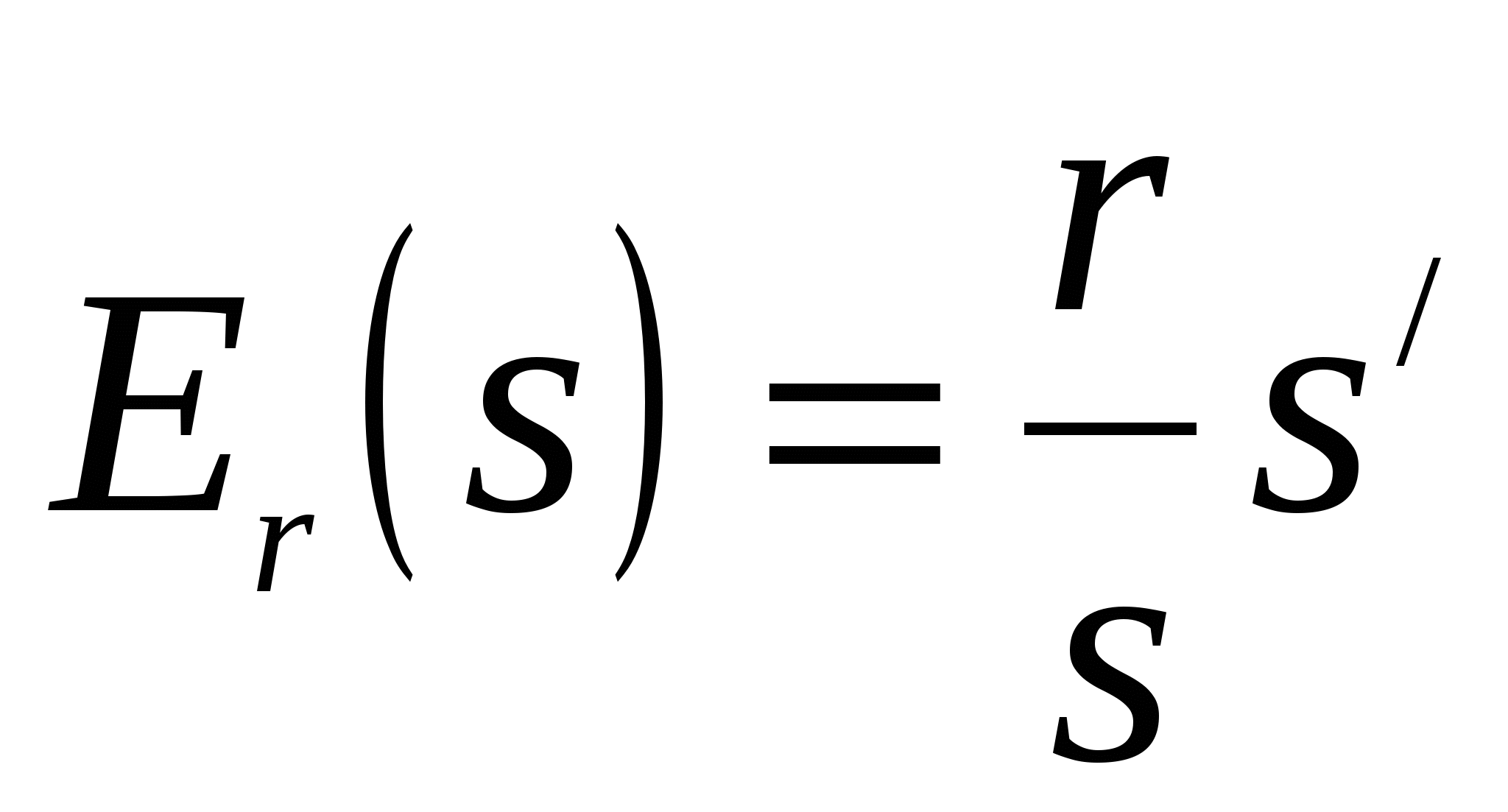
Ценовая эластичность ресурсов.
![]()
Характеризует относительное изменение величины спроса на какой-либо ресурс (например, труд) при изменении цены этого ресурса (зарплаты) на один процент.
Эластичность замещения одного ресурса другим
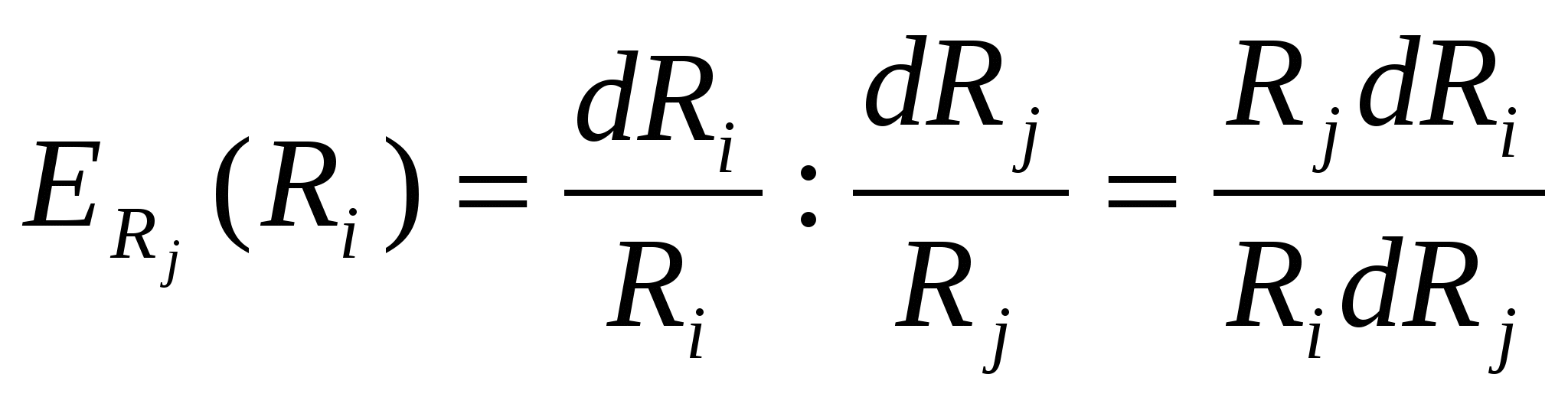
Характеризует необходимое изменение величины одного ресурса (капитала) при изменении количества другого ресурса (труда) на один процент с тем, чтобы выпуск при этом не сократился.
Пример 1: Функция спроса: 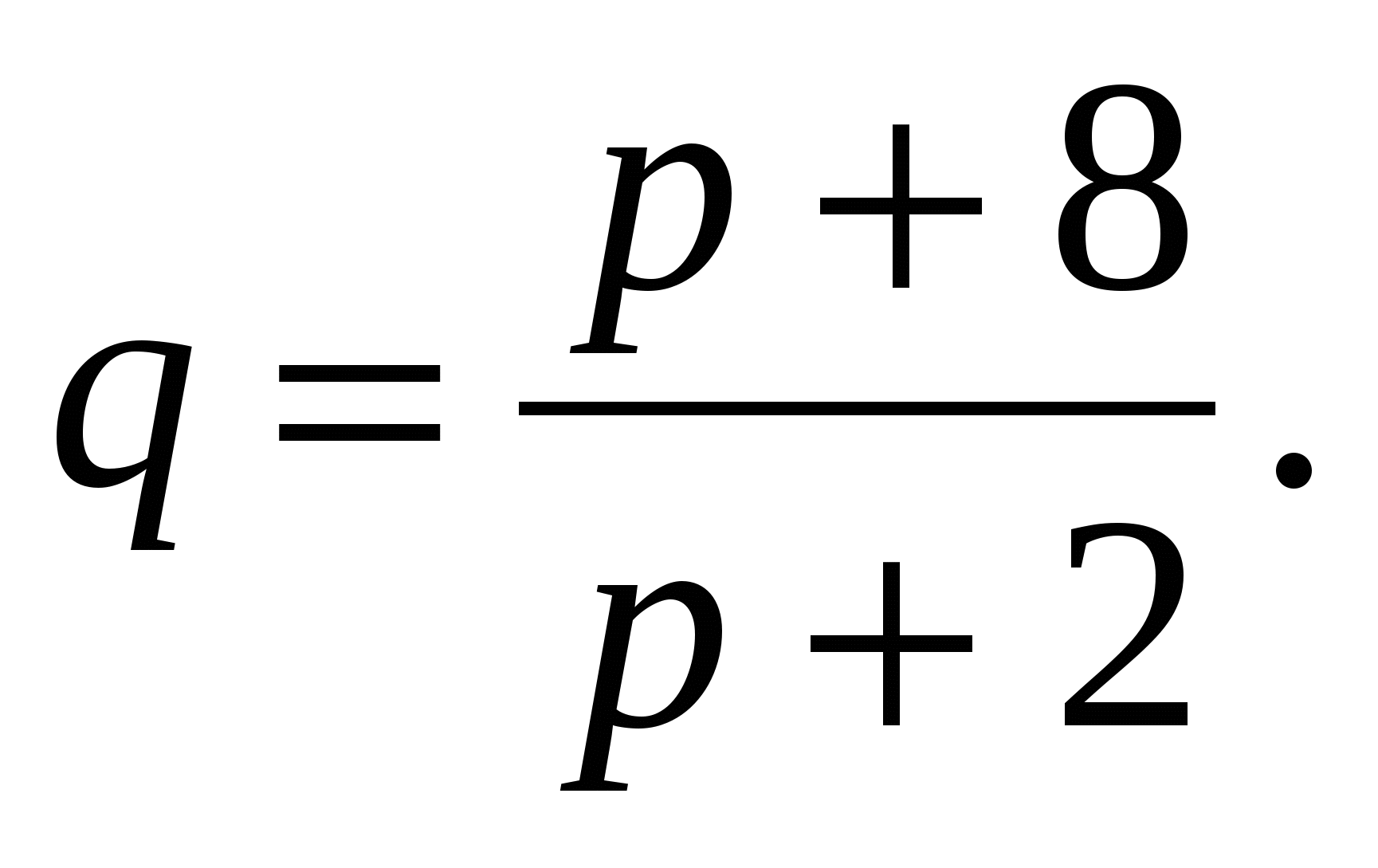 Функция предложения: S = p + 0,5. Здесь р(руб) - цена товара, q(шт.) - количество покупаемого товара; S(шт.) - количество предлагаемого на продажу товара в единицах времени.
Функция предложения: S = p + 0,5. Здесь р(руб) - цена товара, q(шт.) - количество покупаемого товара; S(шт.) - количество предлагаемого на продажу товара в единицах времени.
Найти: а) равновесную цену: q= S; б) эластичность спроса и предложения для этой цены.
Решение: а) ![]() p = 2 руб.
p = 2 руб.
б) 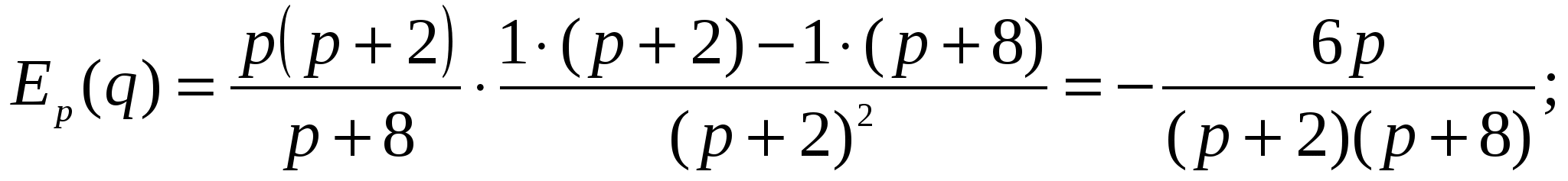
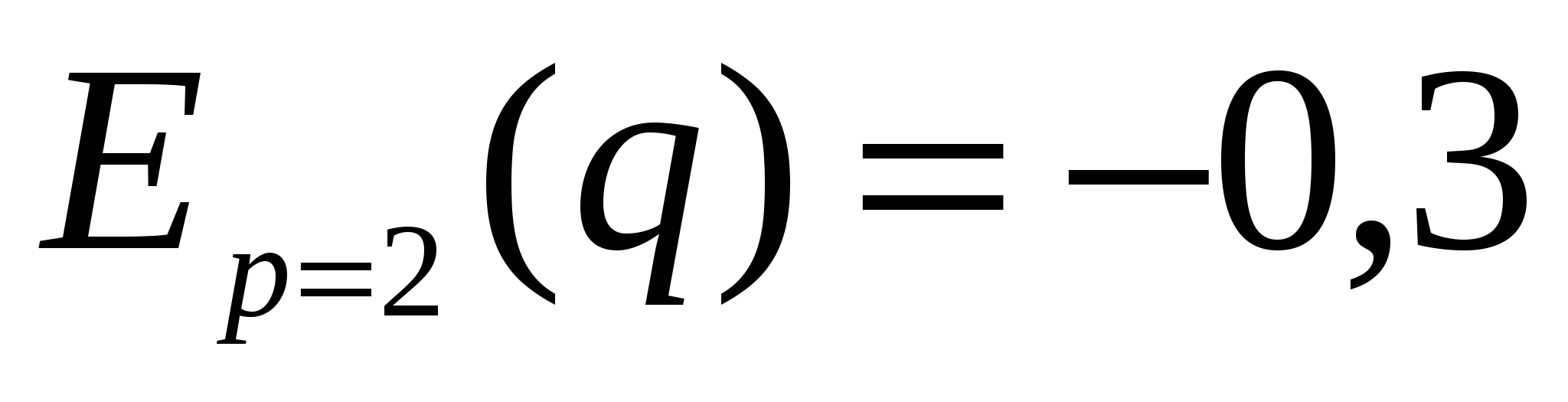 ;
; 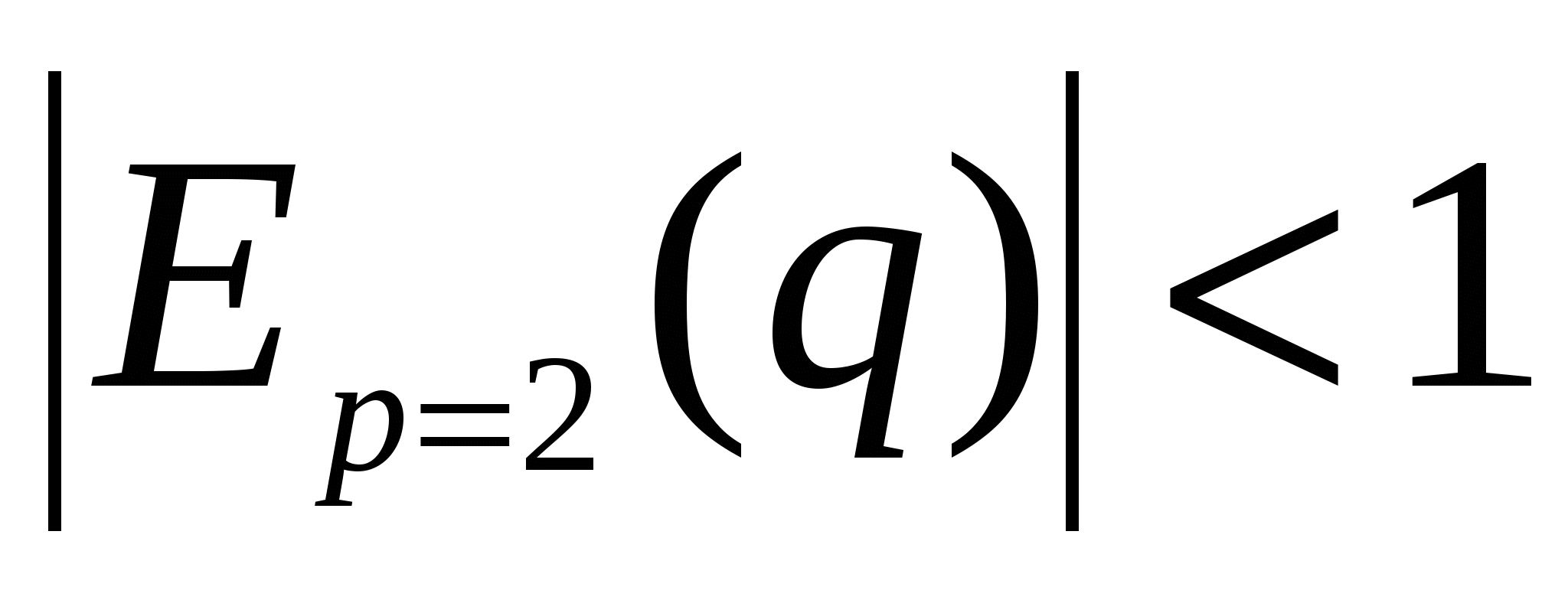 неэластична
неэластична
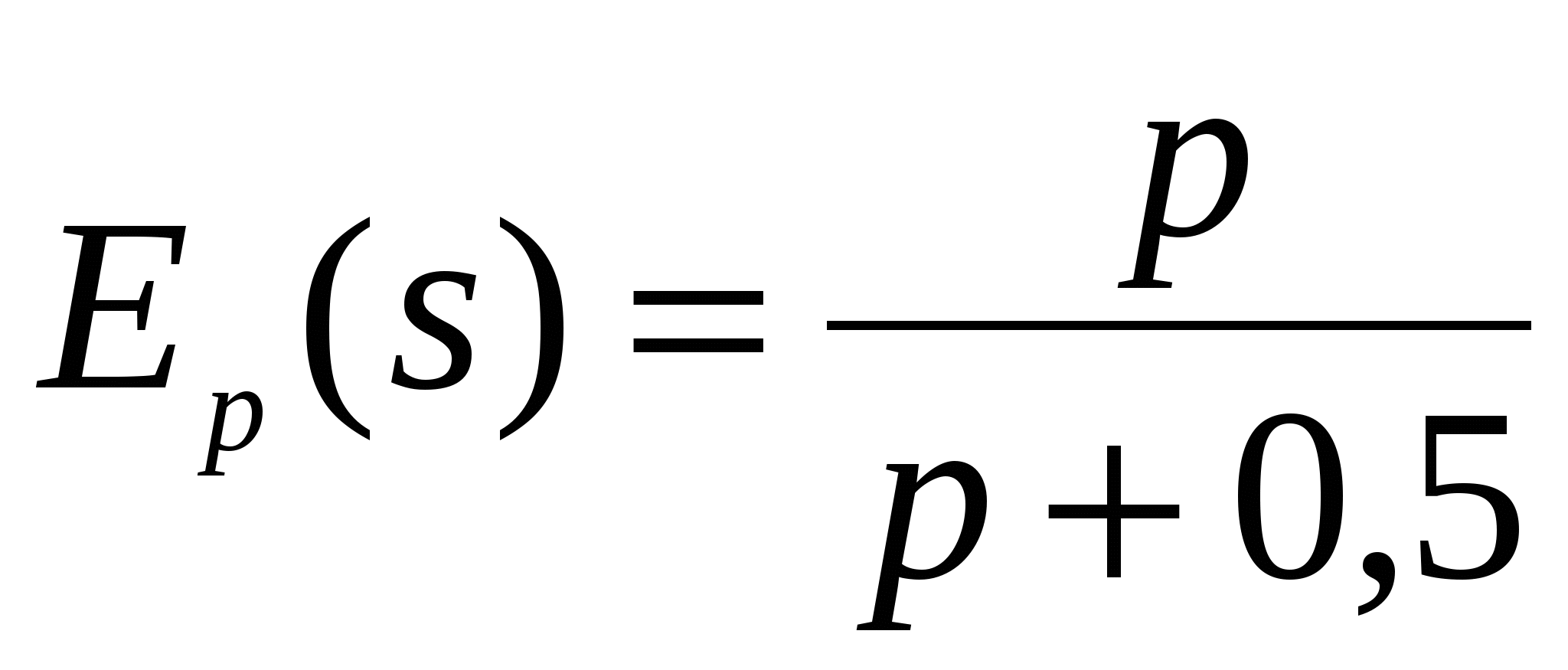
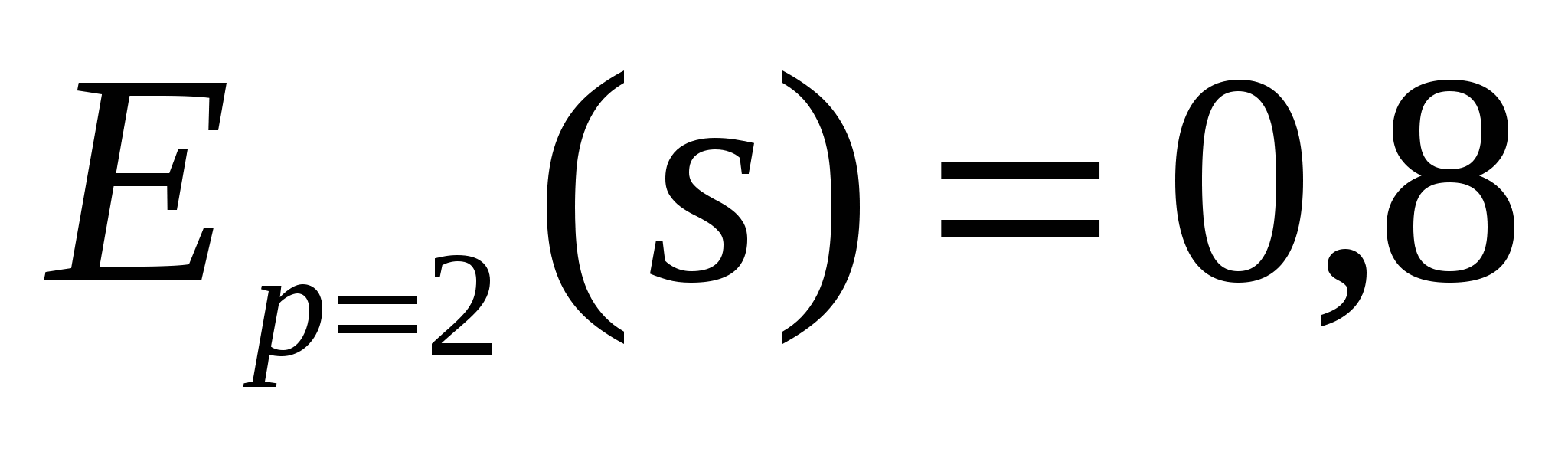 ;
; 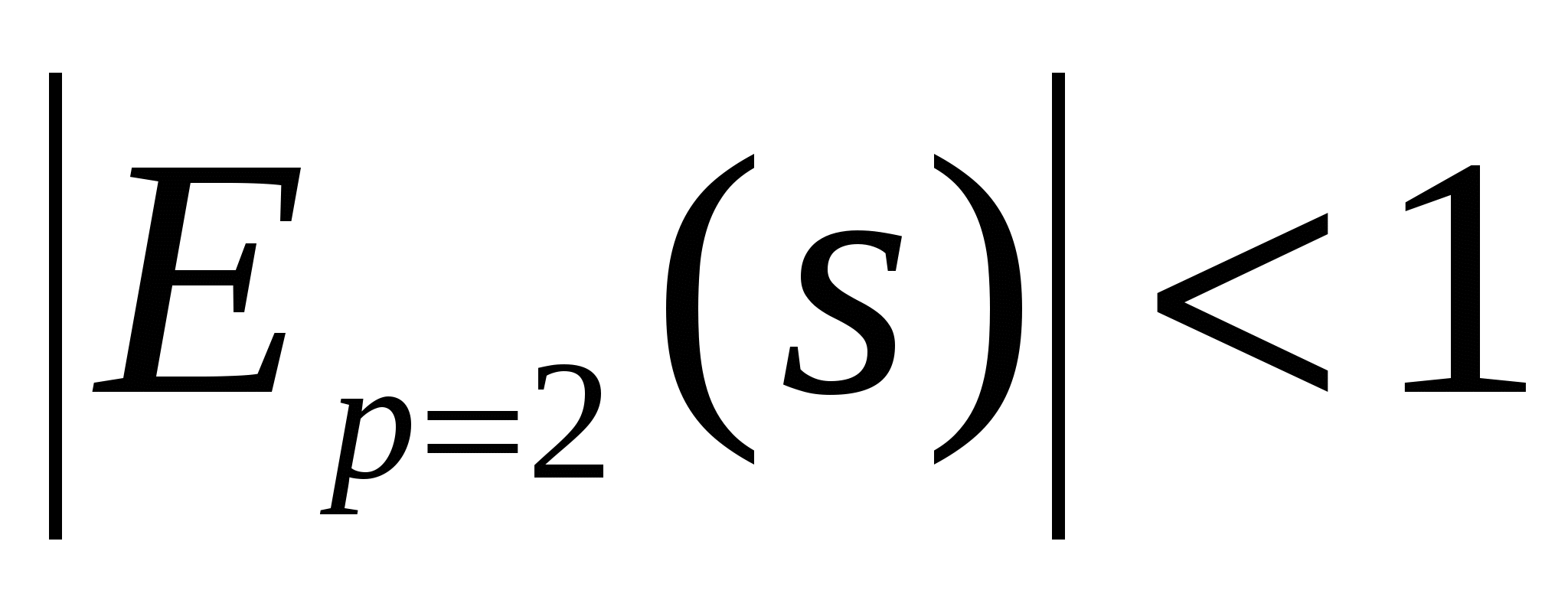 неэластична.
неэластична.
Следовательно изменение цены не приведет к резкому изменению спроса и предложения. При увеличении цены р на 1% спрос уменьшится на 0,3%, а предложение увеличится на 0,8%.
Пример 2: Функция спроса y от цены х продукта имеет вид 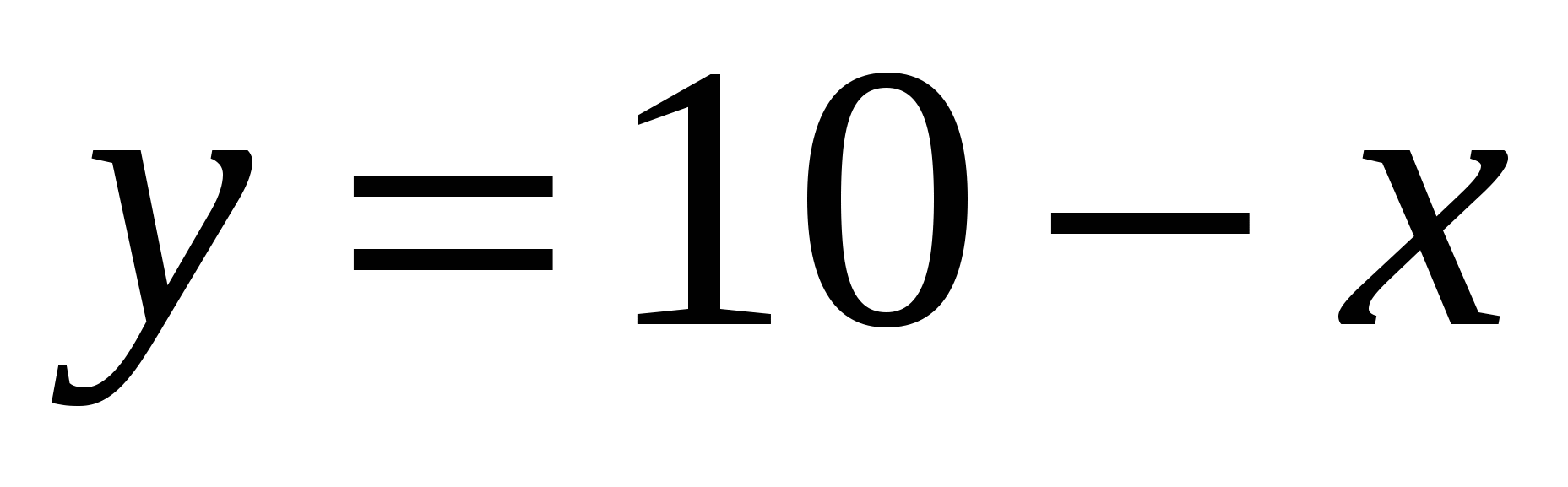 . Найти коэффициент эластичности спроса при цене товара
. Найти коэффициент эластичности спроса при цене товара 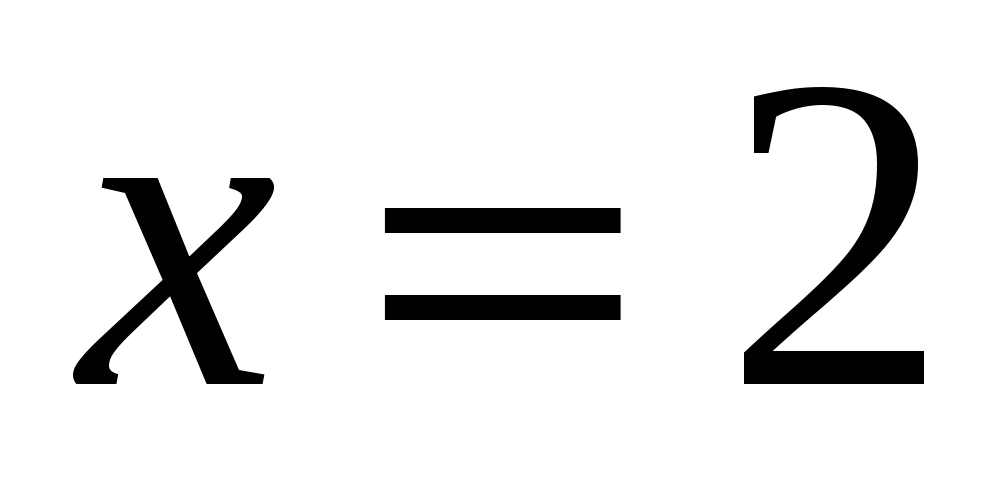 единицы.
единицы.
Решение. Коэффициент эластичности спроса равен
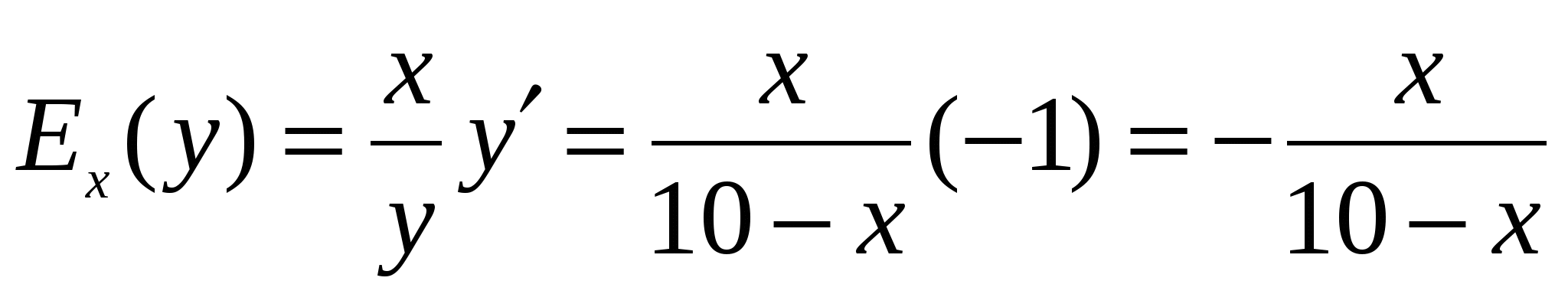 .
.
При 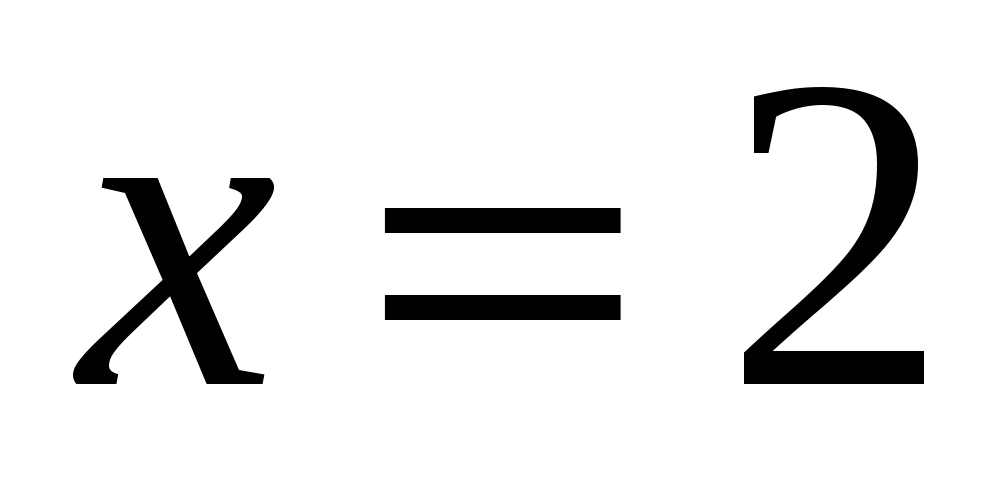 получаем
получаем 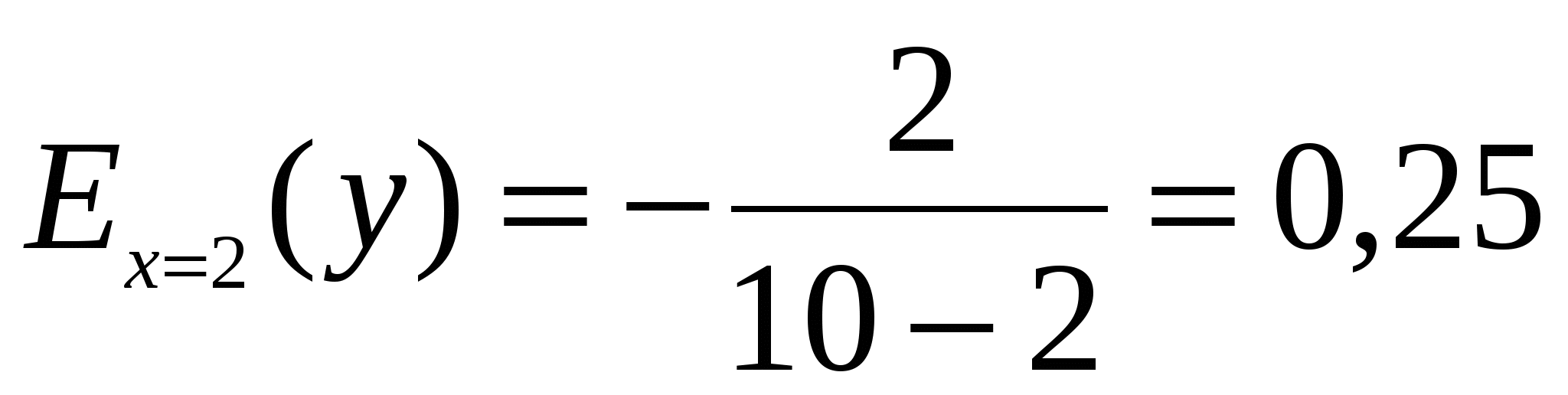 , т.е. при повышении цены на 1% спрос на товар уменьшится на 0,25%. Так как
, т.е. при повышении цены на 1% спрос на товар уменьшится на 0,25%. Так как 
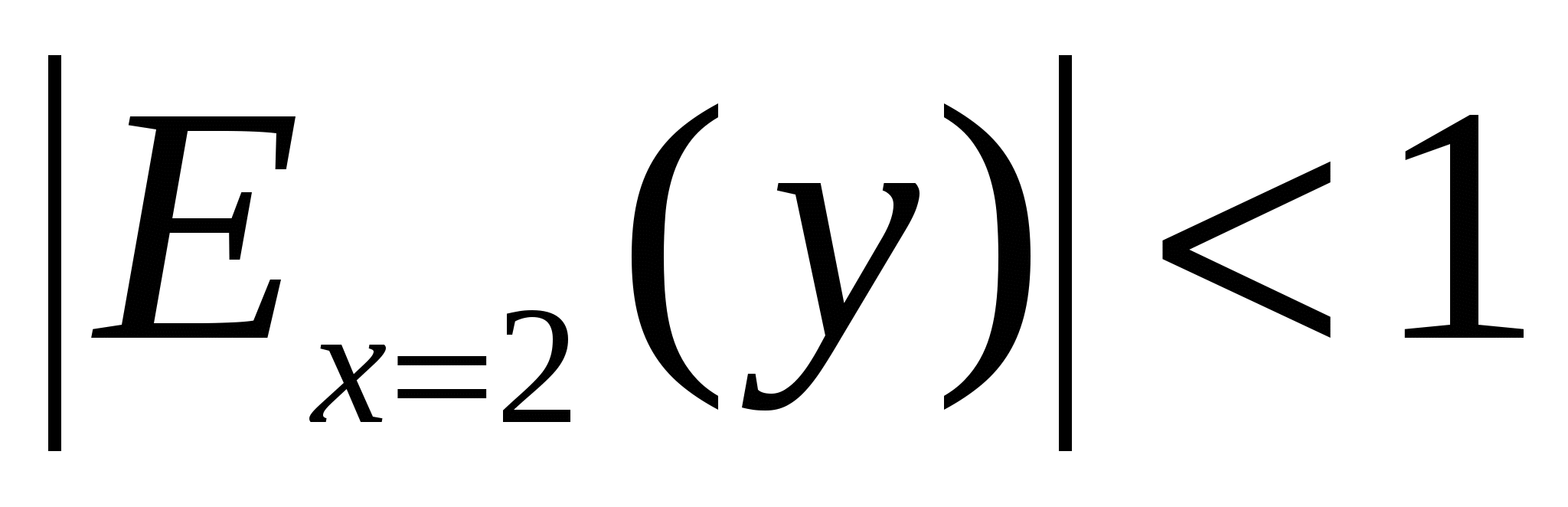 , то спрос при цене
, то спрос при цене 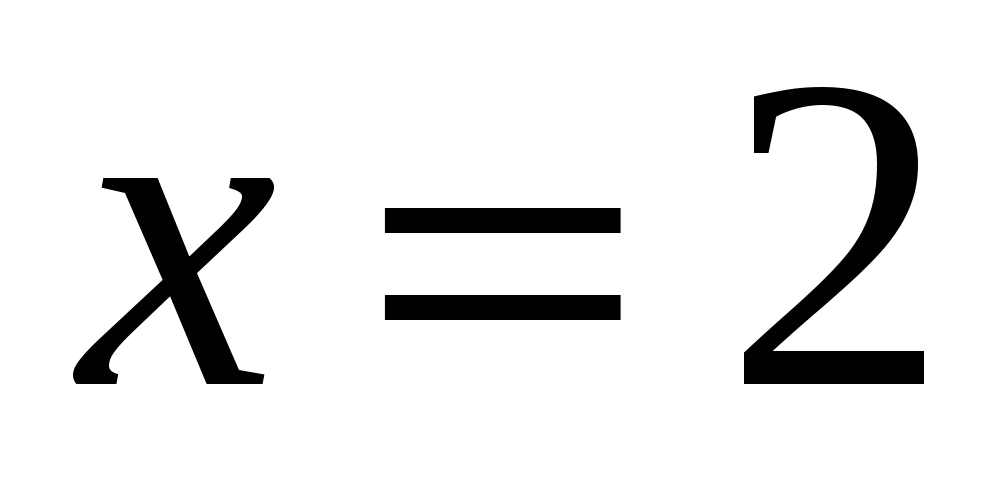 единицы не эластичен.
единицы не эластичен.
-
Модель Леонтьева межотраслевого баланса.
Макроэкономика функционирования многоотраслевого хозяйства требует баланса между отдельными отраслями. Впервые математическая модель межотраслевого баланса была сформулирована в 1936 году американским экономистом Василием Васильевичем Леонтьевым, который попытался проанализировать причины экономической депрессии США 1929-1932 гг. Эта модель основана на алгебре матриц и использует аппарат матричного анализа.
Рассмотрим взаимодействие п отраслей экономики. Каждая отрасль выпускает определённый продукт, для производства которого требуется продукция каждой из этих п отраслей.
Введем следующие обозначения:
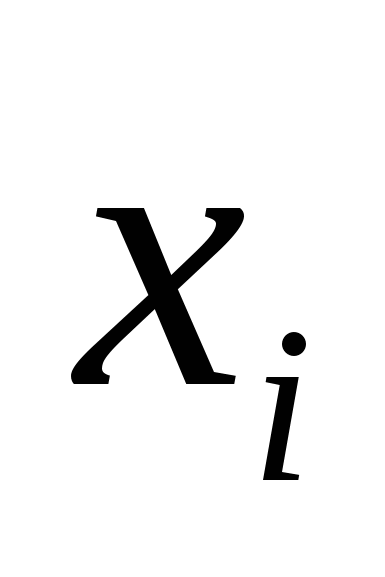 ‒ общий объем продукции i-ой отрасли (её валовой выпуск);
‒ общий объем продукции i-ой отрасли (её валовой выпуск);
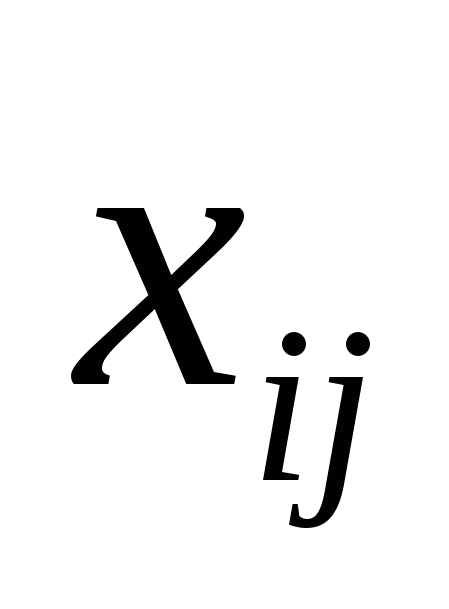 ‒ объем продукции i-ой отрасли, потребляемый j-ой отраслью при производстве продукции объёма
‒ объем продукции i-ой отрасли, потребляемый j-ой отраслью при производстве продукции объёма ![]() ;
;
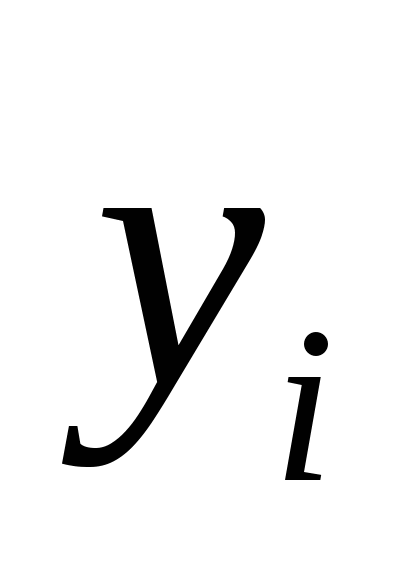 ‒ объем продукции i - ой отрасли, предназначенный для реализации (потребления) в непроизводственной сфере (продукт конечного потребления). К нему относятся личное потребление граждан, удовлетворение общественных потребностей, содержание государственных институтов и т.д.
‒ объем продукции i - ой отрасли, предназначенный для реализации (потребления) в непроизводственной сфере (продукт конечного потребления). К нему относятся личное потребление граждан, удовлетворение общественных потребностей, содержание государственных институтов и т.д.
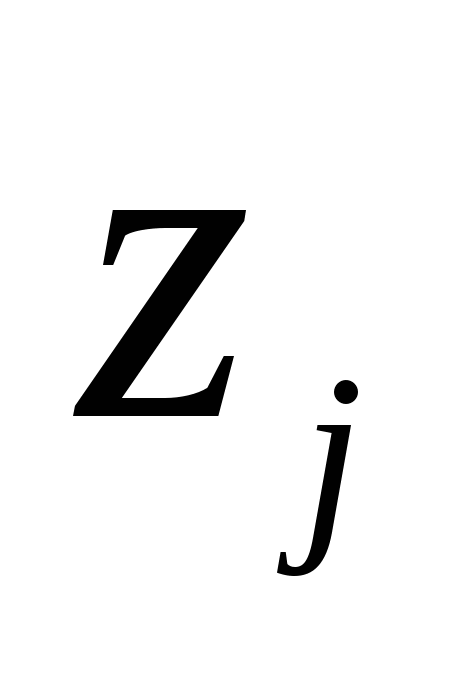 - условно чистая продукция, которая включает оплату труда, чистый доход и амортизацию.
- условно чистая продукция, которая включает оплату труда, чистый доход и амортизацию.
Единицы измерения всех указанных величин могут быть или натуральными (кубометры, тонны, штуки и т.п.), или стоимостными. В зависимости от этого различают натуральный и стоимостный межотраслевые балансы. Мы будем рассматривать стоимостный баланс.
Для наглядного выражения взаимной связи между отраслями используют таблицы определённого вида, которые называют таблицами межотраслевого баланса.
Потребляющие
отрасли
Производящие
отрасли
1
2
…
п
Конечный
продукт
Валовой
продукт
1
x11
x12
…
x1n
у1
х1
2
x21
x22
…
x1n
у2
х2
…
…
…
…
…
…
…
п
xn1
xn2
…
xnm
уn
хп
Условно чистая
продукция
![]()
![]()
…
![]()
![]()
Валовой продукт
х1
х2
…
хп
![]()
Рассматривая схему баланса по столбцам, можно заметить, что итог материальных затрат любой потребляющей отрасли и её условно чистой продукции равен валовой продукции этой отрасли.
Данный вывод можно записать в виде соотношения:
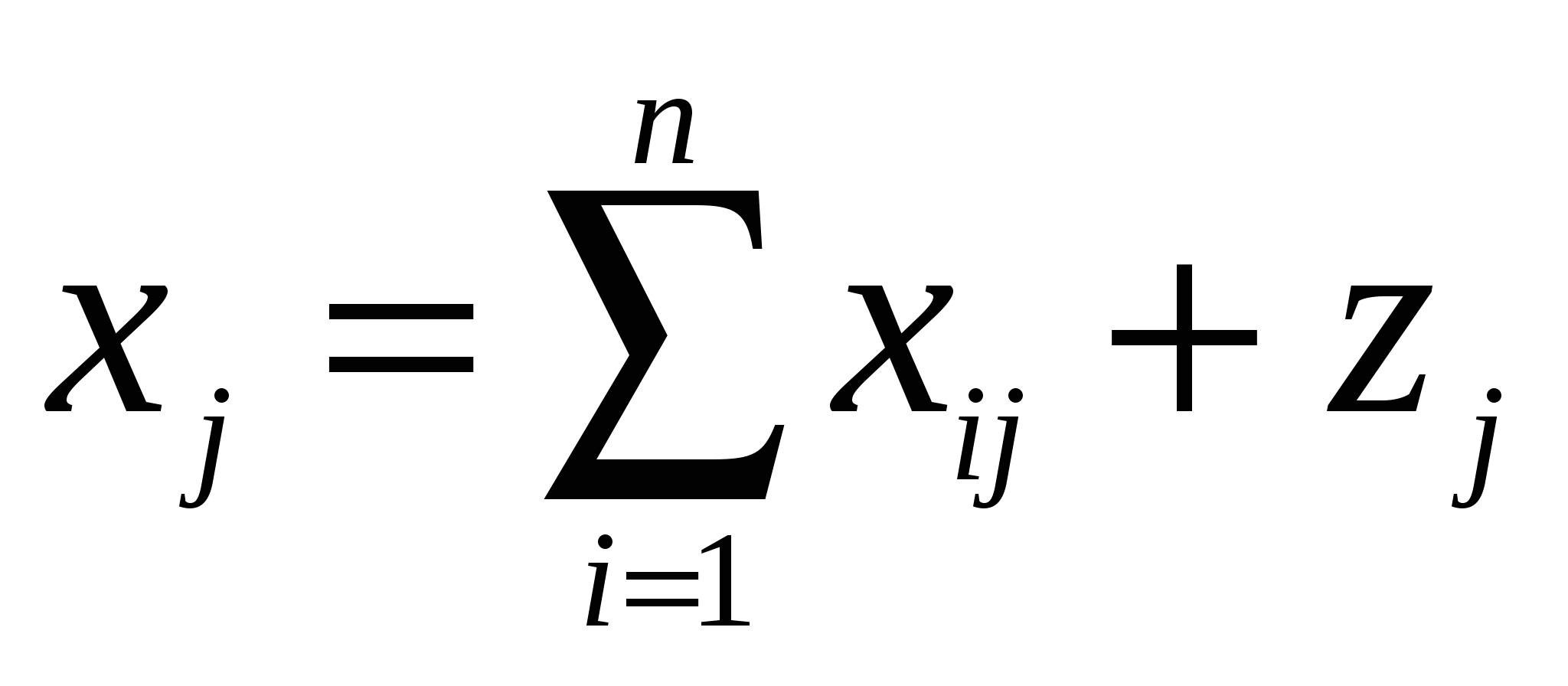 , j =1,…,п. (1)
, j =1,…,п. (1)
Рассматривая схему МОБ по строкам для каждой производящей отрасли, замечаем, что валовая продукция той или иной отрасли равна сумме материальных затрат потребляющих её продукцию отраслей и конечной продукции данной отрасли:
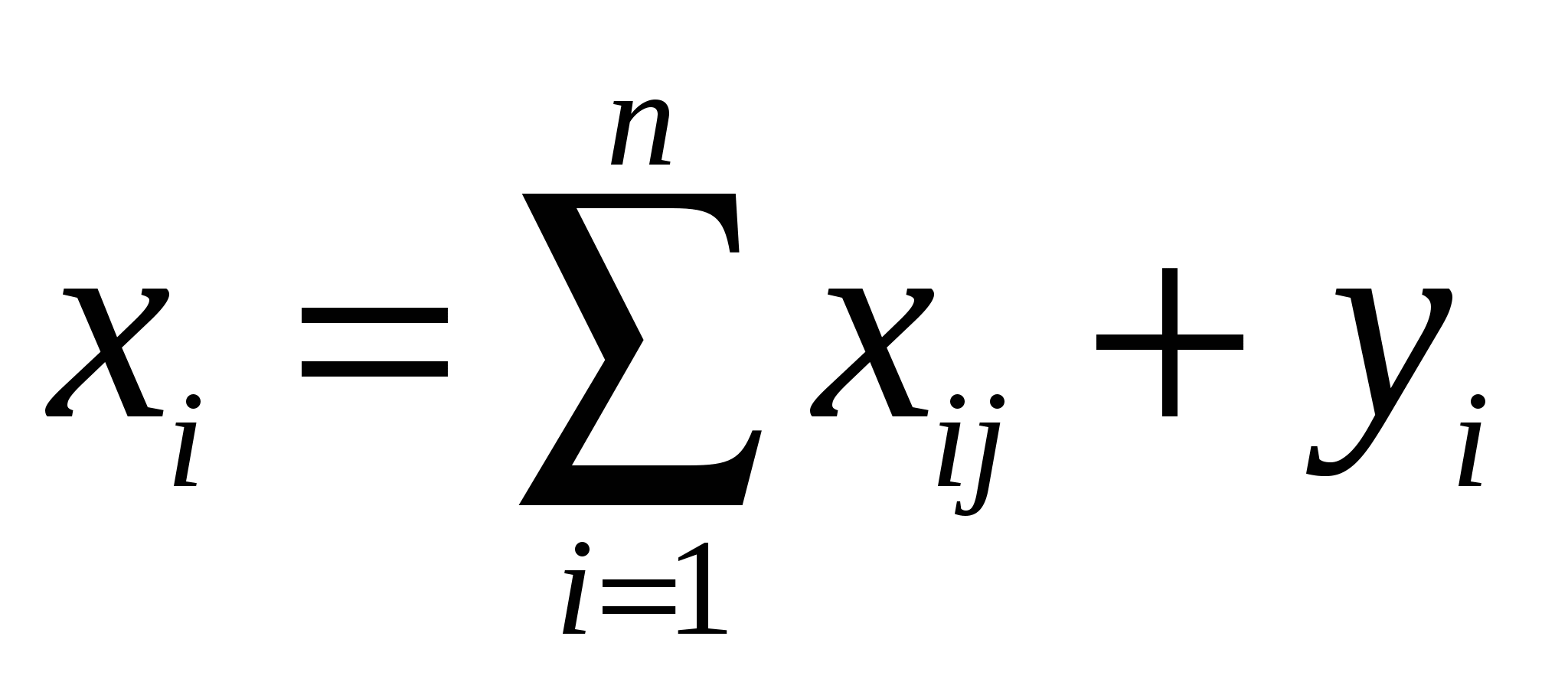 , i = 1,…,п. (2)
, i = 1,…,п. (2)
Балансовый характер таблицы выражается в том, что
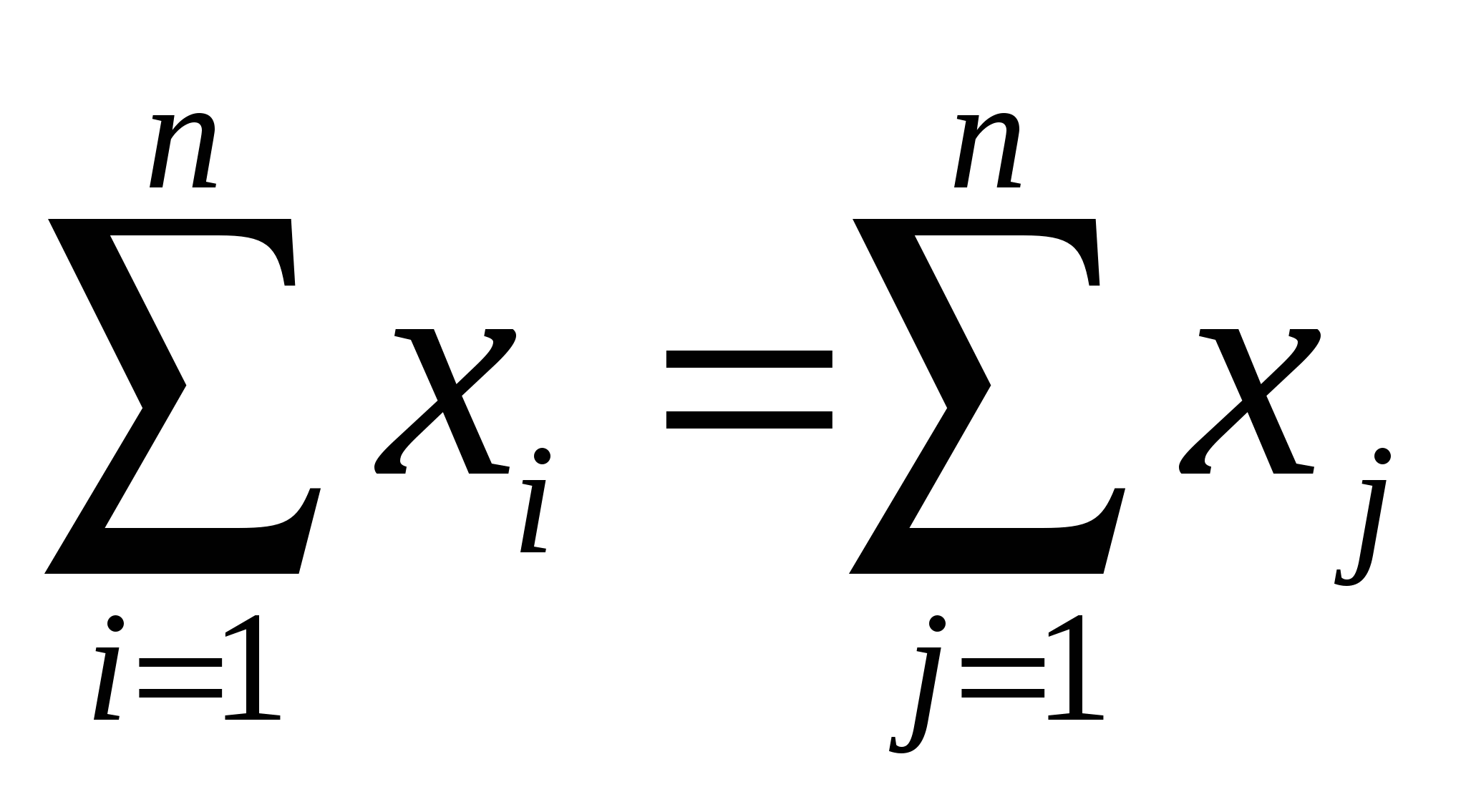
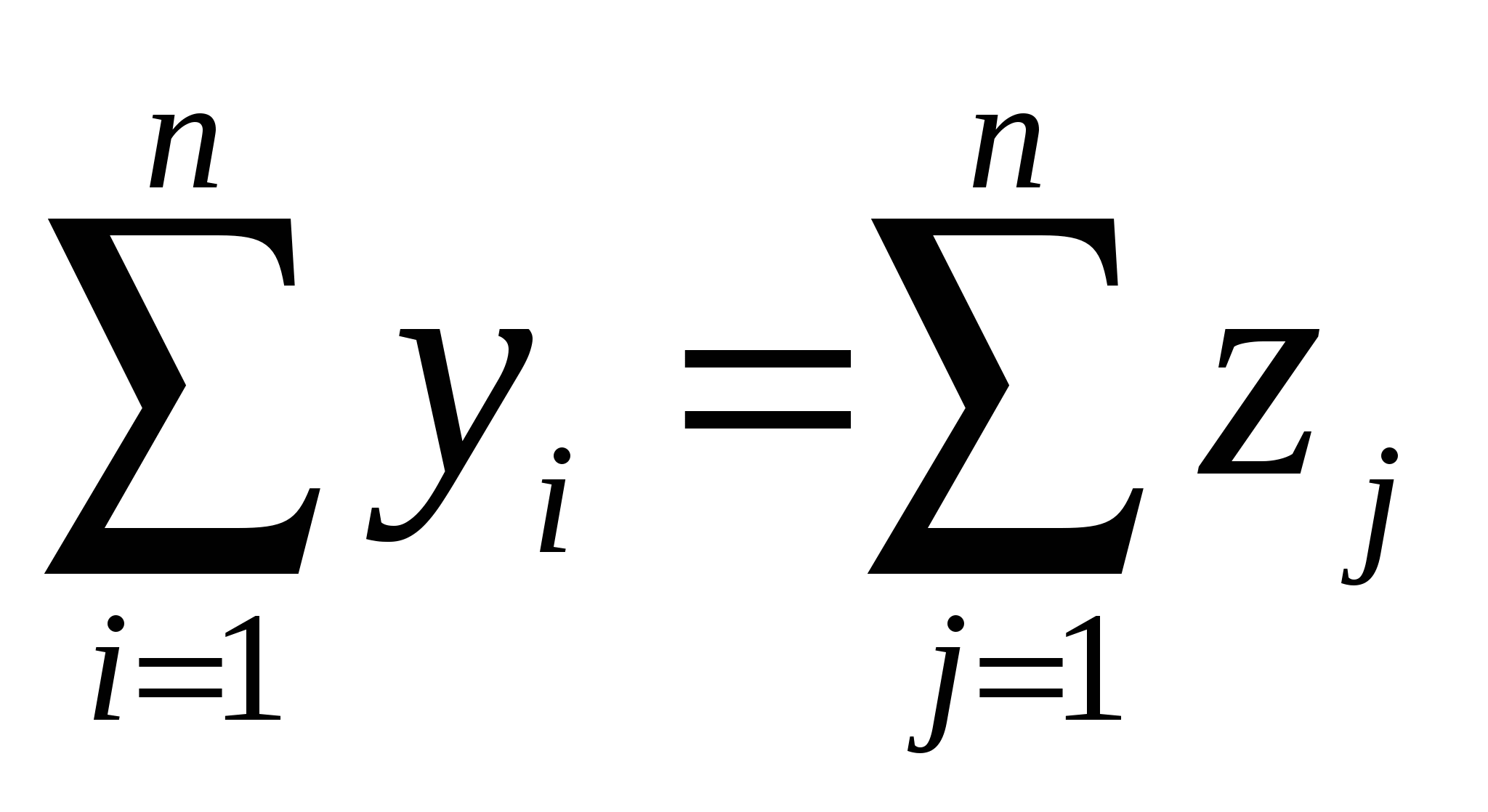
Основу экономической модели МОБ составляет технологическая матрица коэффициентов прямых затрат А(аij).
Коэффициент прямых материальных затрат аij показывает, сколько необходимо единиц продукции i-ой отрасли для производства единицы продукции отрасли j: 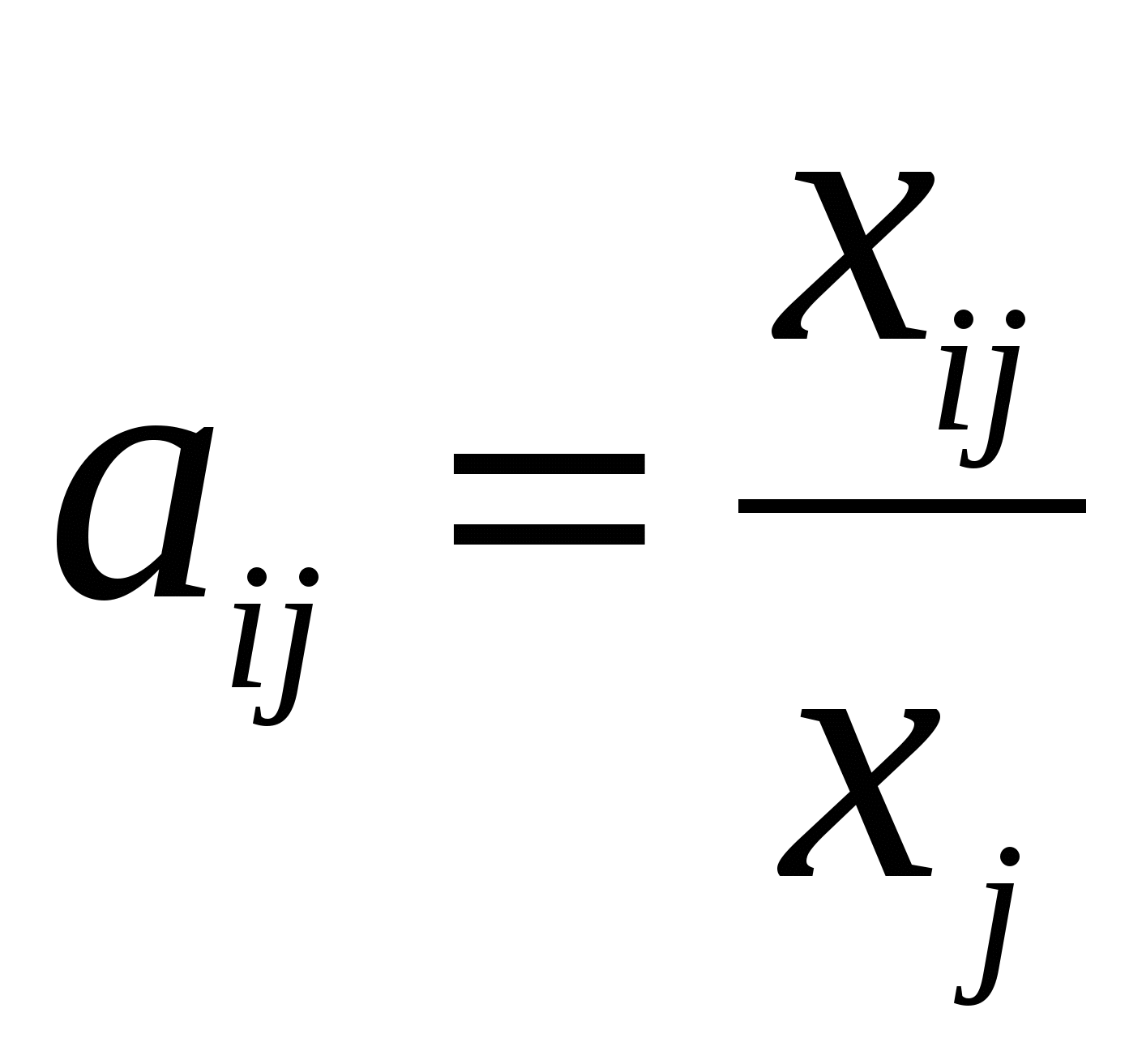 ,
, 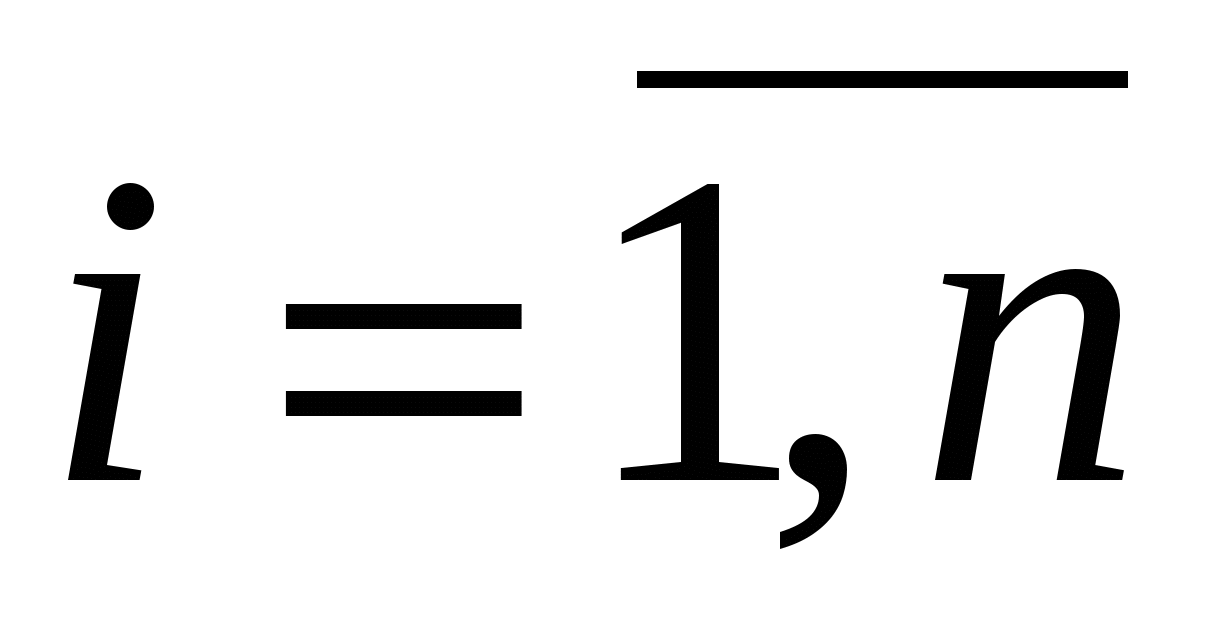 ,
, 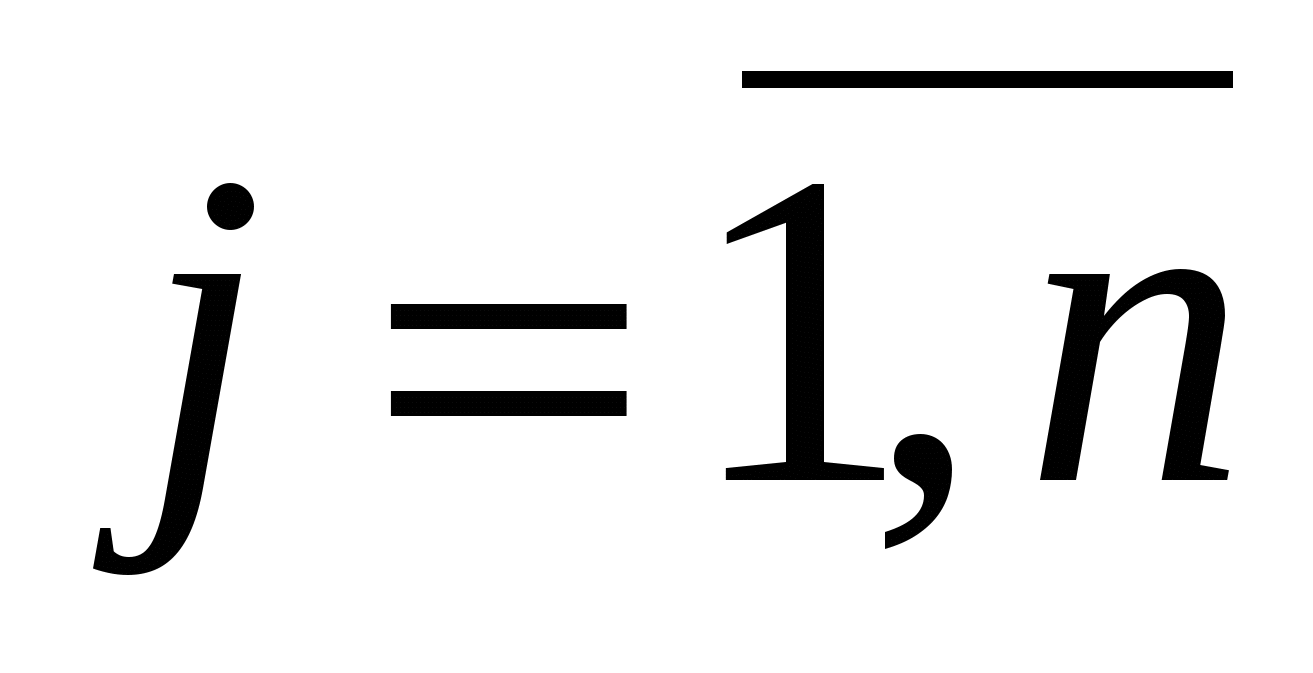 . (3)
. (3)
Выдвигаются два важных предположения:
-
Сложившуюся технологию производства считаем неизменной. Таким образом, матрица А(аij) постоянна.
-
Постулируем свойство линейности существующих технологий: для выпуска отраслью j любого объёма продукции хj необходимо затратить продукцию отрасли i в количестве
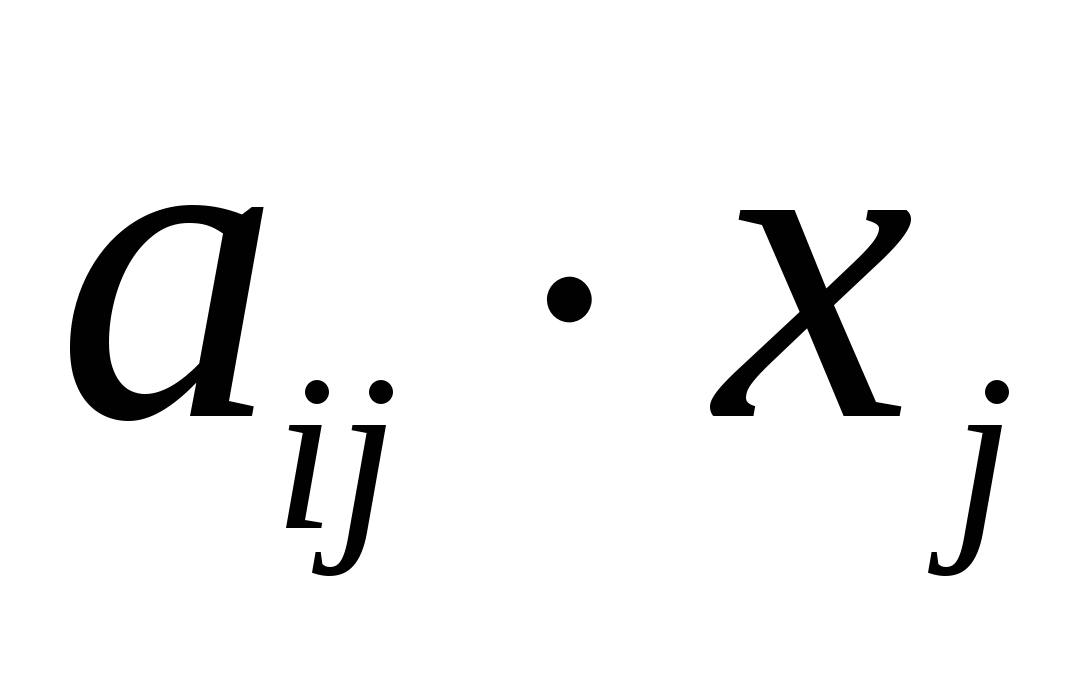 , т.е. материальные издержки пропорциональны объёму производимой продукции:
, т.е. материальные издержки пропорциональны объёму производимой продукции: 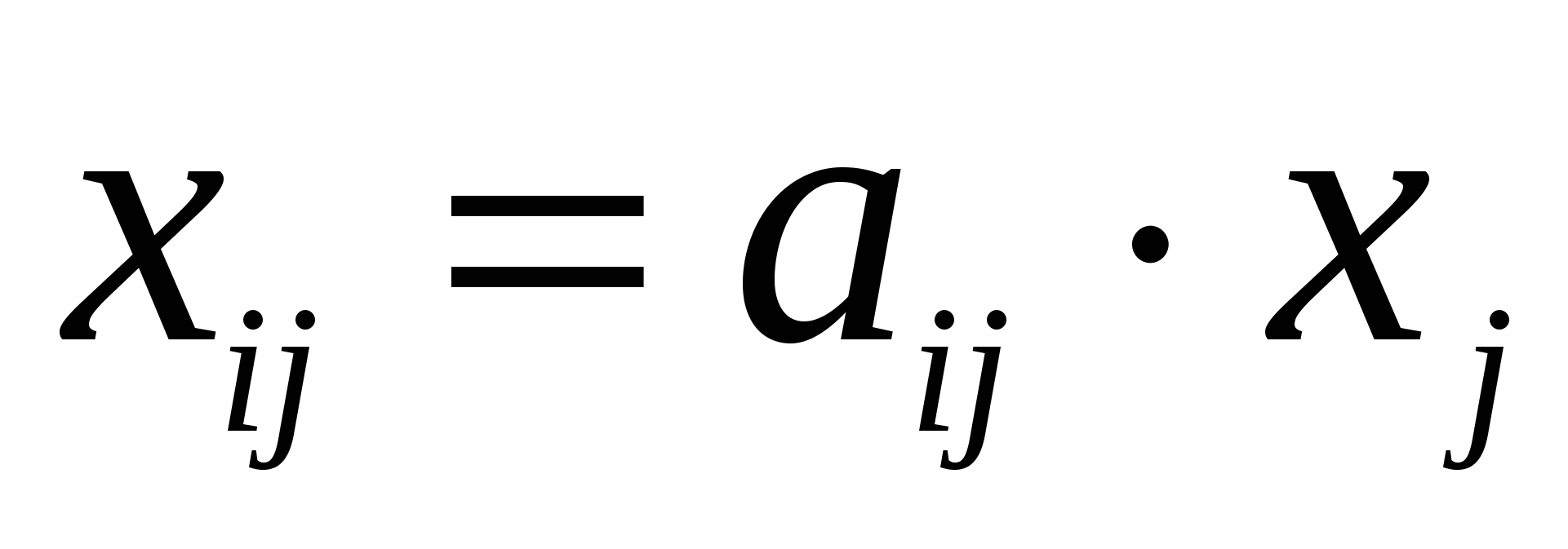 (4)
(4)
Подставляя (4) в (2), получаем 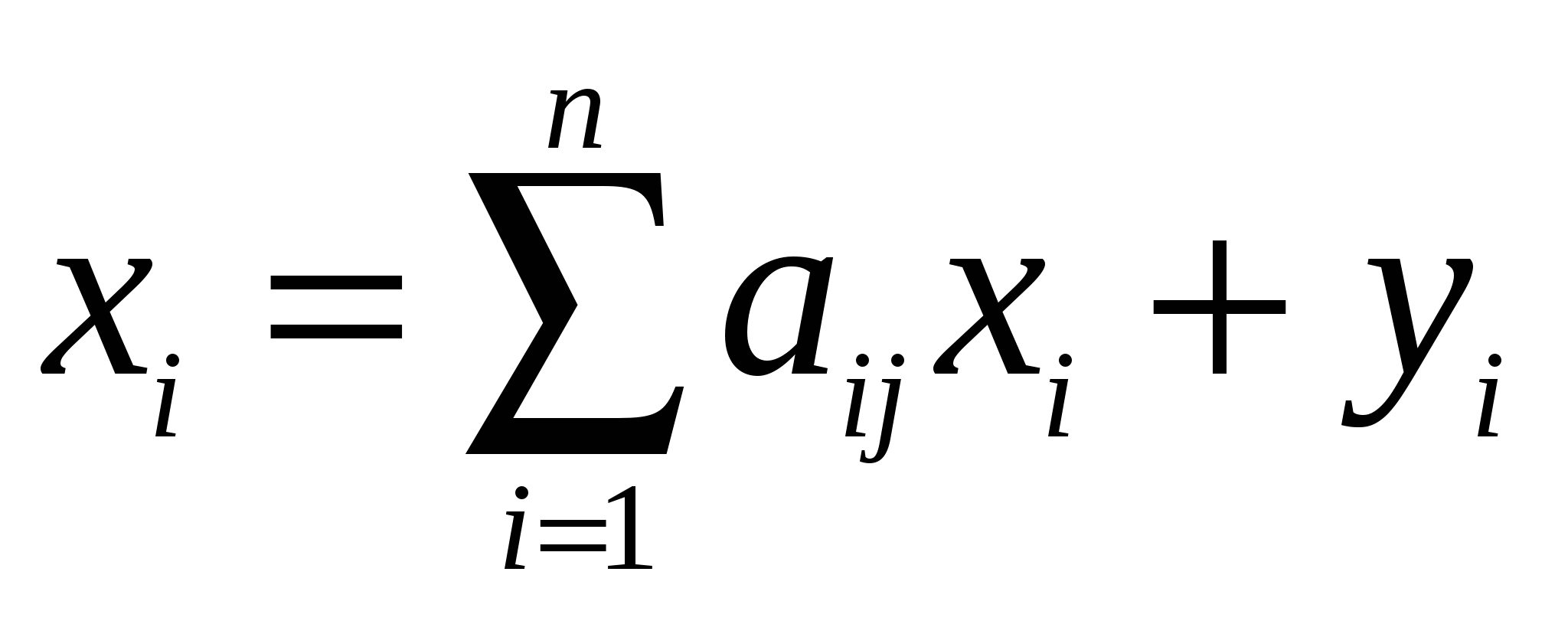 (5)
(5)
или в матричной форме Х=АХ+Y (6)
С помощью этой модели можно выполнять три вида плановых расчётов:
-
задавая для каждой отрасли величины валовой продукции (хi), можно определить объёмы конечной продукции каждой отрасли (уj):
Y=(E-A)X; (7)
-
задавая величины конечной продукции всех отраслей (уj), можно определить величины валовой продукции каждой отрасли (хi), т.е. определить объём производства, необходимый для удовлетворения данного конечного спроса:
X=(E-A)-1Y (8)
Если решение системы (7) существует для любой неотрицательной матрицы Y, то модель Леонтьева (и матрица А) называется продуктивной. Плановые расчёты по модели Леонтьева можно выполнять, если соблюдаются условия продуктивности.
Матрица  называется матрицей полных затрат.
называется матрицей полных затрат.
Для того чтобы матрица коэффициентов прямых материальных затрат А была продуктивной, необходимо и достаточно, чтобы выполнялось одно из перечисленных ниже условий:
-
матрица (Е-А) неотрицательно обратима, т.е. существует обратная матрица (Е-А)-10;
-
матричный ряд Е+А+А2+А3+…=
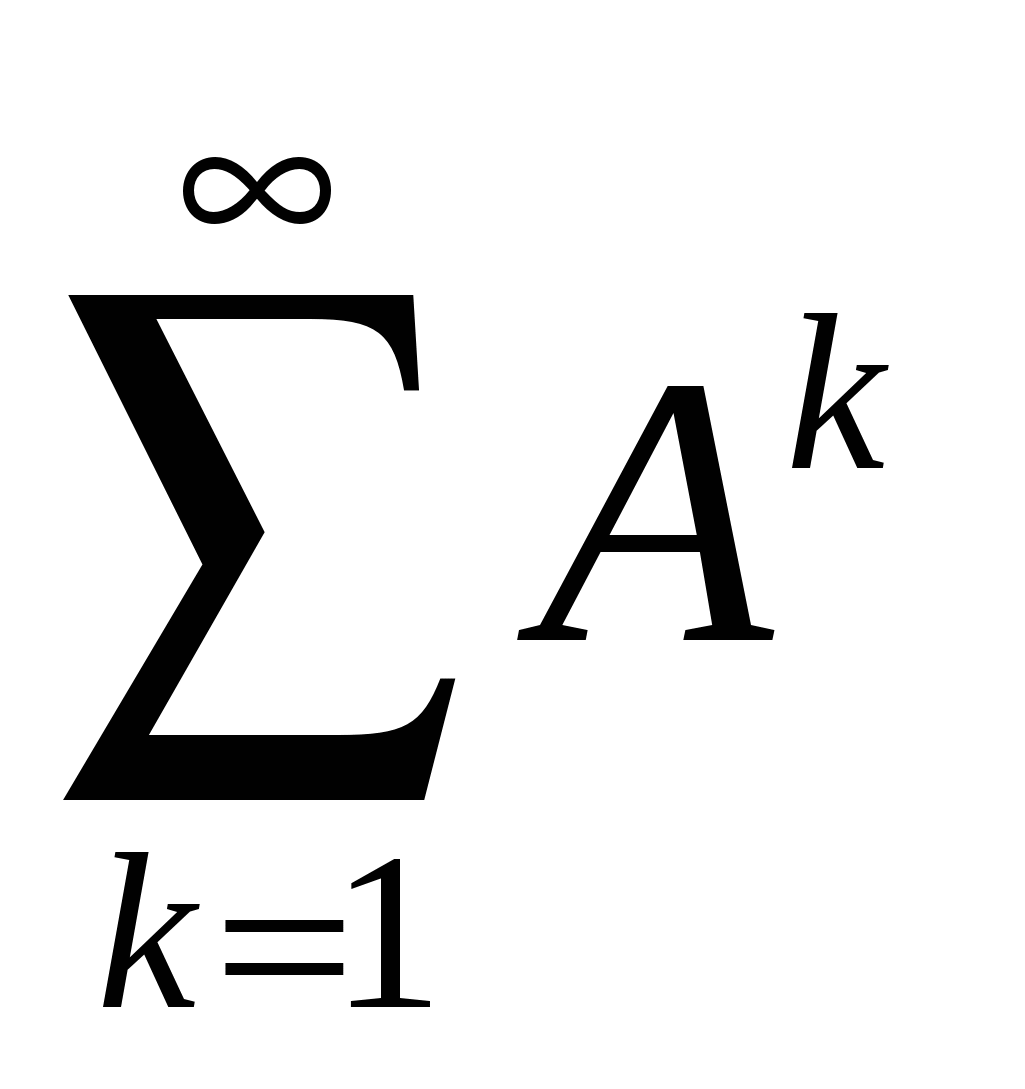 сходится, причём его сумма равна обратной матрице (Е-А)-1
сходится, причём его сумма равна обратной матрице (Е-А)-1
В=(Е-А)-1= Е+А+А2+А3+… ;
-
наибольшее по модулю собственное значение
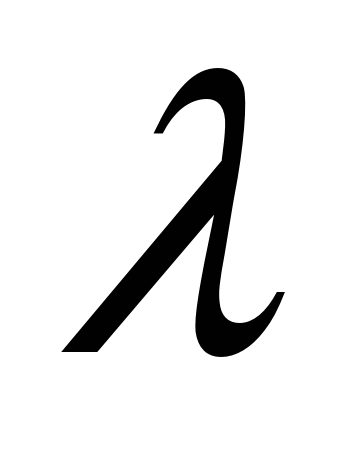 матрицы А, т.е. решение характеристического уравнения Е-А=0, строго меньше единицы;
матрицы А, т.е. решение характеристического уравнения Е-А=0, строго меньше единицы; -
все главные миноры матрицы (Е-А), т.е. определители матриц, образованные элементами первых строк и первых столбцов этой матрицы, порядка от 1 до п, положительны.
Более простым способом проверки продуктивности матрицы А является ограничение на величину её нормы, в данном случае на величину наибольшей из сумм элементов матрицы А в каждом столбце. Если норма матрицы А строго меньше единицы, то эта матрица продуктивна. Данное условие является достаточным, но не необходимым условием продуктивности, поэтому матрица А может оказаться продуктивной и в случае, когда её норма больше единицы.
10


