- Преподавателю
- Математика
- Задачи, решаемые векторным способом
Задачи, решаемые векторным способом
| Раздел | Математика |
| Класс | - |
| Тип | Другие методич. материалы |
| Автор | Ильина Е.Е. |
| Дата | 26.10.2014 |
| Формат | docx |
| Изображения | Есть |

















































 Задачи, решаемые векторным способом.
Задачи, решаемые векторным способом.
 1.Основные задачи о прямых и плоскостях.
1.Основные задачи о прямых и плоскостях.
1.Уравнение прямой, проходящей через две точки.
Пусть в пространстве задана общая декартова система координат и две точки М1 и М2 с координатами (x1,y1,z1) и (x2,y2,z2). Чтобы написать уравнение прямой М1М2, примем М1 за начальную точку, а 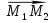 за направляющий вектор. Этот вектор не нулевой, если точки не совпадают.
за направляющий вектор. Этот вектор не нулевой, если точки не совпадают.
Получаем 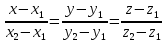 . Если в этих равенствах какой-либо из знаменателей равен нулю, то следует приравнять нулю соответствующий числитель.
. Если в этих равенствах какой-либо из знаменателей равен нулю, то следует приравнять нулю соответствующий числитель.
В планиметрии задача решается также. Отличие только в том, что координаты точек теперь (x1,y1) и (x2,y2), и мы получаем 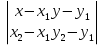 =0.
=0.
2.Уравнение плоскости, проходящей через три точки.
Пусть М1, М2,М3 - не лежащие на одной прямой точки с координатами (x1,y1,z1), (x2,y2,z2) и (x3,y3,z3) в общей декартовой системе координат. Выберем М1 в качестве начальной точки, а 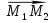 и
и 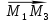 в качестве направляющих векторов. Тогда получим уравнение плоскости
в качестве направляющих векторов. Тогда получим уравнение плоскости 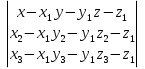 =0.
=0.
3. Параллельность прямой и плоскости.
Пусть известен направляющий вектор прямой a(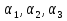 ), а плоскость задана одним из уравнений (
), а плоскость задана одним из уравнений (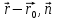 )=0 или (
)=0 или (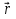 -
-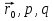 )=0. Прямая параллельна плоскости (а возможно, и лежит в ней) тогда и только тогда, когда соответственно (
)=0. Прямая параллельна плоскости (а возможно, и лежит в ней) тогда и только тогда, когда соответственно (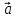 ,
,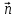 )=0 или (
)=0 или (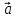 ,
,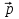 ,
,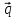 )=0. Если плоскость задана линейным уравнением Ax+By+Cz+D=0, то условию параллельности - A
)=0. Если плоскость задана линейным уравнением Ax+By+Cz+D=0, то условию параллельности - A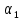 +B
+B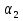 +C
+C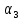 =0. Пусть прямая задана системой уравнений
=0. Пусть прямая задана системой уравнений 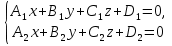 .
.
Тогда получаем A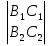 + B
+ B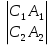 + C
+ C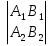 =0, или
=0, или 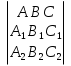 =0.
=0.
Все приведенные здесь условия являются не только необходимыми, но и достаточными.
4. Расстояние от точки до плоскости.
Пусть дана плоскость с уравнением (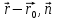 )=0 и точка М с радиус вектором
)=0 и точка М с радиус вектором 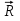 . Рассмотрим вектор
. Рассмотрим вектор 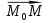 =
=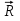 -
-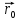 , соединяющий начальную точку плоскости с М(рис 1).Расстояние от точки до плоскости равно модулю его скалярной проекции на вектор
, соединяющий начальную точку плоскости с М(рис 1).Расстояние от точки до плоскости равно модулю его скалярной проекции на вектор 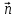 , то есть h=
, то есть h= . Если в декартовой прямоугольной системе координат точка М имеет координаты (X,Y,Z), то равенство запишется следующим образом h=
. Если в декартовой прямоугольной системе координат точка М имеет координаты (X,Y,Z), то равенство запишется следующим образом h= 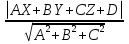
М
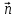
h
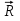
М0
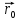
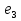
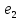
O 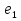
рис.1
5. Расстояние от точки до прямой.
Если прямая задана уравнением 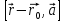 =0, то можем найти расстояние h от точки М с радиус - вектором
=0, то можем найти расстояние h от точки М с радиус - вектором 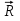 до этой прямой, разделив площадь параллелограмма, построенного на векторах
до этой прямой, разделив площадь параллелограмма, построенного на векторах 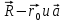 , на длину его основания (рис 2). Результат можно записать формулой h=
, на длину его основания (рис 2). Результат можно записать формулой h= 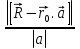 .
.
Для прямой в пространстве мы не будем получать координатной записи этого выражения.
Рассмотрим прямую на плоскости, заданную уравнением Ax+By+C=0 в декартовой прямоугольной системе координат. Пусть M0(x0,y0) - начальная точка прямой, а M(X,Y)- некоторая точка плоскости. В качестве направляющего вектора возьмём вектор 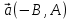 . Площадь параллелограмма равна S=
. Площадь параллелограмма равна S=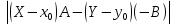 . Тогда S=
. Тогда S=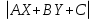 и h =
и h = 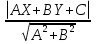 .
.
М
h
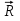
М0
e3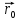 e2
e2
О e1
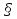 2.Доказательства и решения задач.
2.Доказательства и решения задач.
Задача 1: Доказать, что диагонали ромба взаимно перпендикулярны.
Доказательство: Пусть ABCD - данный ромб (рис.3). Введем обозначения 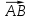 =
=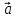 ,
, 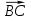 =
=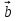 . Из определения ромба следует
. Из определения ромба следует 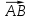 =
=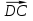 =
=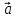 ,
, 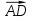 =
=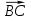 =
=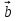 .
.
По определению суммы и разности векторов 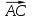 =
=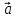 +
+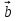 ;
;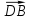 =
=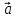 -
-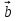 .
.
Рассмотрим 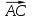 *
*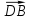 =
=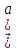 +
+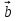 )(
)(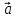 -
-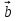 )=
)=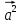 -
-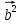 . Так как стороны ромба равны, то
. Так как стороны ромба равны, то 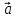 =
=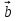 . Следовательно,
. Следовательно, 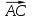 *
*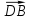 =0. Из последнего условия следует что,
=0. Из последнего условия следует что, 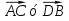 , что и требовалось доказать.
, что и требовалось доказать.
A
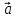
D B
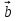
C
рис.3
Задача 2: Даны два вектора 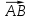 и
и 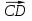 , причем А(-1;2;4), В (-4;5;4), С(-1;-2;2) и D(2;1;5). Определить, перпендикулярны они друг другу или нет.
, причем А(-1;2;4), В (-4;5;4), С(-1;-2;2) и D(2;1;5). Определить, перпендикулярны они друг другу или нет.
Решение: Найдем сначала координаты векторов.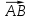 =(-3;3;0) и
=(-3;3;0) и 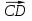 =(3;3;3).
=(3;3;3).
Вычислим теперь скалярное произведение этих векторов:
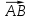 *
*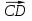 =(-3)*3 +3*3+0*3 = 0.
=(-3)*3 +3*3+0*3 = 0.
Последнее и означает, что 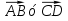
Задача 3: Дан произвольный треугольник АВС. Доказать, что можно построить треугольник, стороны которого равны и параллельны медианам треугольника АВС.
B B1
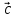
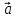
F D A1
A E 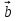 C C1
C C1
рис.4 рис.5
Решение: Обозначим медианы треугольника АВС через ВЕ, СF и обозначим векторы, идущие вдоль сторон треугольника АВС, через 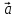 ,
,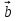 ,
, 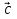 :
:
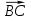 =
=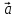 ,
, 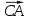 =
=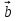 ,
,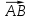 =
=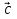 . Тогда
. Тогда 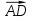 =
=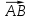 +
+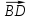 =
=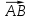 +
+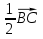 =
=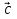 +
+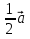 . Аналогично определяются и другие медианы:
. Аналогично определяются и другие медианы: 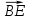 =
=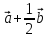 ,
, 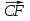 =
=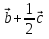 .
.
Так как, в силу замкнутости 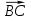 +
+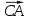 +
+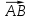 =
=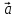 +
+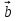 +
+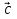 =0б то мы имеем
=0б то мы имеем 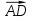 +
+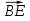 +
+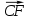 =(
=(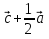 )+(
)+(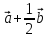 )+(
)+(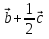 )=
)=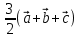 =
=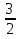 *0=0. Следовательно, отложив от точки В, вектор
*0=0. Следовательно, отложив от точки В, вектор 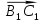 =
=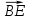 и от точки С1 - вектор
и от точки С1 - вектор 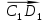 =
= 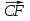 , мы получим.
, мы получим.
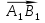 +
+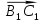 +
+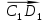 =
=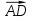 +
+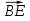 +
+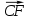 =0.
=0.
А это значит (в силу условия замкнутости), что ломаная А1В1С1D1 является замкнутой, т.е. точка D1 совпадает с А1.
Таким образом, мы получаем треугольник А1В1С1 (рис.5), стороны которого равны и параллельны медианам АD, ВЕ, СF исходного треугольника.
Задача 4: Доказать, что для любого треугольника имеет место формула
c2 = a2+b2-2ab*соsС (теорема косинусов)
Решение. Положим: 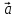 =
= 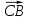 ,
, 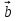 =
= 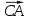 ,
, 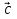 =
=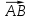 (рис.6).
(рис.6).
Тогда 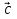 =
= 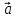 -
-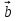 , и мы имеем (учитывая, что угол между векторами
, и мы имеем (учитывая, что угол между векторами 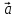 и
и 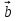 равен С): с2 =(а-b)2 = а2 -2аb + b2 = а2-2аb*соsС+ b2.
равен С): с2 =(а-b)2 = а2 -2аb + b2 = а2-2аb*соsС+ b2.
A
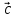
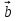
B 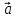 C
C
рис.6
Задача 5: Докажите, что сумма квадратов диагоналей параллелограмма равна сумме квадратов его сторон.
Решение: Пусть четырехугольник АВСD - параллелограмм (рис.7). Имеем векторные равенства 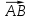 +
+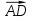 =
=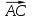 ,
, 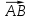 -
-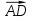 =
=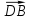 . Возведем эти равенства в квадрат. Получим:
. Возведем эти равенства в квадрат. Получим: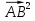 +2
+2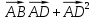 =
=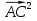 ,
, 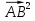 -2
-2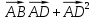 =
=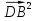
Сложим эти равенства почленно. Получим: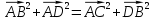 так как у параллелограмма противолежащие стороны равны, то это равенство и означает, что сумма квадратов диагоналей параллелограмма равна сумме квадратов его сторон, что и требовалось доказать.
так как у параллелограмма противолежащие стороны равны, то это равенство и означает, что сумма квадратов диагоналей параллелограмма равна сумме квадратов его сторон, что и требовалось доказать.
B C
A D
рис.7
Задача 6: Даны три точки: А(1;1), В(-1;0), С(0;1). Найдите такую точку D(х;y), чтобы векторы 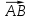 и
и 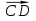 были равны.
были равны.
Решение: Вектор 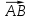 имеет координаты (-2, -1). Вектор
имеет координаты (-2, -1). Вектор 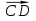 имеет координаты (х-0, y-1). Так как
имеет координаты (х-0, y-1). Так как 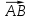 =
= 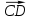 , то х-0 = -2, y-1 = -1. Отсюда находим координаты точки D: х =-2, y = 0.
, то х-0 = -2, y-1 = -1. Отсюда находим координаты точки D: х =-2, y = 0.
Задача 7: Даны два вектора 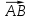 и
и 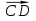 , причем А(-1;2;4), В(-4;5;4), С(-1;-2;2), D (2;1;5).Определить, перпендикулярны они друг другу или нет.
, причем А(-1;2;4), В(-4;5;4), С(-1;-2;2), D (2;1;5).Определить, перпендикулярны они друг другу или нет.
Решение: Найдем сначала координаты векторов. 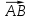 (-3;3;0) и
(-3;3;0) и 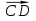 (3;3;3).
(3;3;3).
Вычислим теперь скалярное произведение этих векторов:
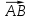 *
*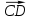 = (-3)*3 + 3*3 + 0*3 = 0.
= (-3)*3 + 3*3 + 0*3 = 0.
Последнее означает, что 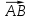
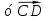
Задача 8: Доказать, что прямая проведенная через середины оснований трапеции, проходит через точку пересечения продолжений боковых сторон.
Доказательство: Пусть ABCD - данная трапеция, М и N - середины оснований BC и AD, а O-точка пересечения прямых AB и CD (рис.8). Докажем, что точка О лежит на прямой MN.
Треугольник OAD и OBC подобны по первому признаку подобия треугольников, поэтому 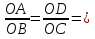 k. Так как
k. Так как 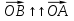 и
и 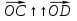 , то
, то 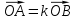 ,
, 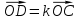 . Точка М - середина отрезка ВС, поэтому
. Точка М - середина отрезка ВС, поэтому 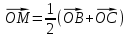 . Аналогично
. Аналогично 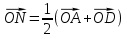 .
.
Подставив в это выражение равенство для 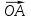 и
и 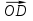 , получим:
, получим:
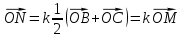 .
.
Отсюда следует, что векторы 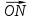 и
и 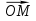 коллинеарны, и , значит, точка О лежит на прямой MN.
коллинеарны, и , значит, точка О лежит на прямой MN.
О
B M C
A N D
рис.8
Задача 9: Доказать что средняя линия трапеции параллельна основаниям и равна их полусумме.
Доказательство: Пусть MN - средняя линия трапеции ABCD (рис.9). Докажем, что MN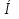 AD и MN=
AD и MN=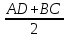 .
.
По правилу многоугольника 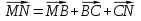 и
и 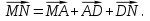 Сложив эти равенства получим:
Сложив эти равенства получим:
2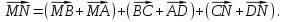
Но M и N- середины сторон AB и CD, поэтому 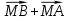 =
=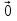 и
и 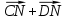 =
=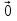 . Следовательно, 2
. Следовательно, 2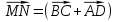 , откуда
, откуда 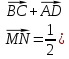 ).
).
Так как векторы 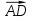 и
и 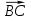 сонаправлены, то векторы
сонаправлены, то векторы 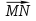 и
и 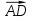 также сонаправлены, а длина вектора
также сонаправлены, а длина вектора 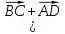 ) равна AD+BC. Отсюда следует MN
) равна AD+BC. Отсюда следует MN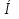 AD и MN=
AD и MN=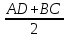 , что и требовалось доказать.
, что и требовалось доказать.
B C
M N
A D
рис.9


