- Преподавателю
- Математика
- Задача Архимеда. Урок одной задачи
Задача Архимеда. Урок одной задачи
| Раздел | Математика |
| Класс | 9 класс |
| Тип | Конспекты |
| Автор | Садикова Э.Ф. |
| Дата | 31.10.2015 |
| Формат | doc |
| Изображения | Есть |
Урок одной задачи
в 9 классе физико-математического профиля.
Тема: Задача Архимеда.
Цели:
- познакомить учащихся с авторской задачей Архимеда, позволяющей понять его гениальность;
- повторить теоретические положения планиметрии;
- рассмотреть несколько способов решения задачи;
- воспитывать у учащихся умение видеть красоту и изящество решения геометрических задач, культуру геометрического построения;
- развивать способность анализировать, умение по-разному взглянуть на один и тот же вопрос.
I. Ребята, сегодня мы с вами решим следующую задачу Архимеда.
З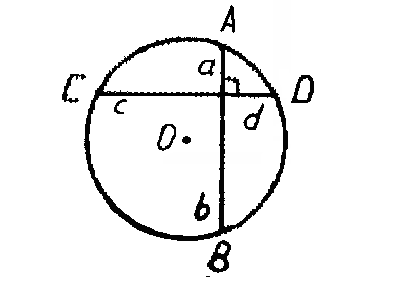 адача:
адача:
Хорды АВ CD окружности радиуса R перпендикулярны и делятся точкой пересечения на отрезки а, b, с и d (рис. 1). Докажите, что сумма квадратов этих (отрезков есть величина постоянная для данной окружности, равная квадрату ее диаметра, то есть
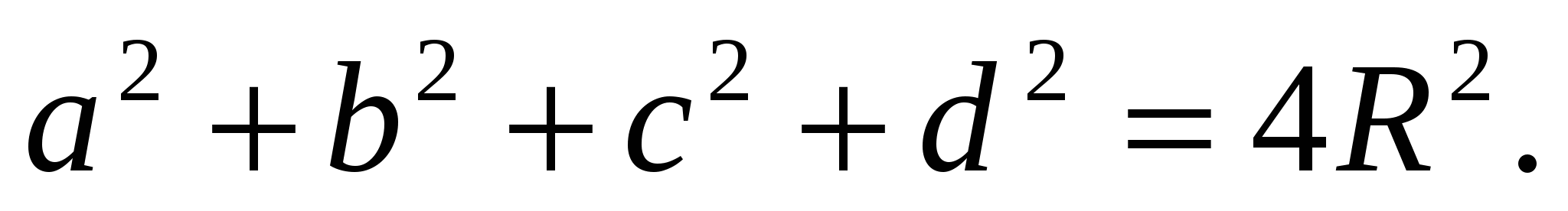
Рис. 1
Мы посвятим урок данной задаче, потому что эта задача:
1) задача Архимеда (287-212 гг. до н.э.), позволяющая понять его гениальность;
2) она - конкурсная - во многих вузах ее предлагают на вступительных экзаменах;
3) она позволяет повторить ряд важнейших фактов и задач планиметрии;
4) она трудная!;
5) она решается удивительно красиво и изящно и различными способами.
II. Решение задачи различными способами.
1) Авторское решение задачи.
Пусть а, b, с, d - данные отрезки хорд АВ и СD (рис. 2). Пусть АD = х, ВС = у. Тогда по теореме Пифагора для треугольника АED:
![]() (1)
(1)
А по теореме Пифагора для треугольника ВЕС:
![]() (2)
(2)
Проведем АК // СD. Тогда ВК = 2R - диаметр (так как  КАВ = 90°).
КАВ = 90°).
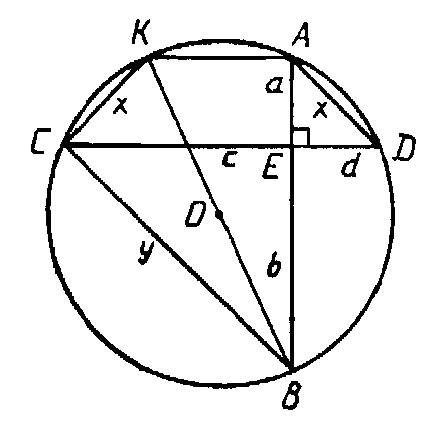
Рис.2
CKAD - равнобочная трапеция, поскольку в окружность можно вписать только равнобокую трапецию, СК =АD = х. 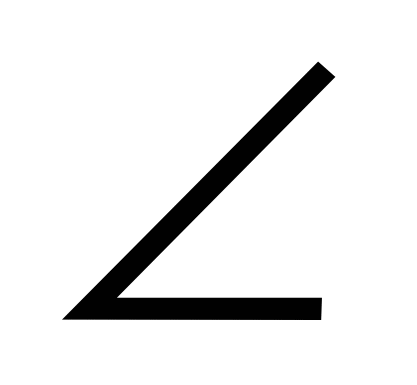 КСВ = 90° (опирается на диаметр). Тогда по теореме Пифагора для треугольника КСВ имеем:
КСВ = 90° (опирается на диаметр). Тогда по теореме Пифагора для треугольника КСВ имеем:
![]()
Воспользовавшись равенствами (1) и (2), получаем требуемое:
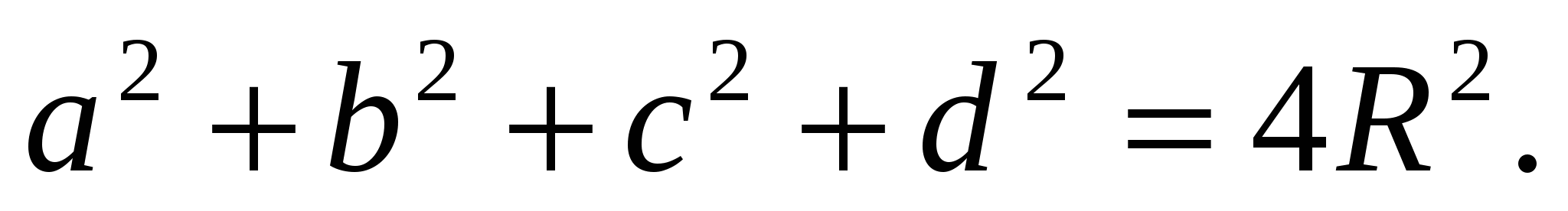
Задача решена!
2) Решение задачи с использованием тригонометрических формул.
К тем же обозначениям (рис. 1 и 2) добавим следующие (рис. 3):
![]() САЕ =
САЕ =  ,
, 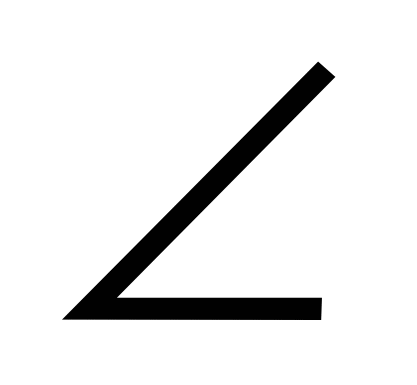 АСЕ =
АСЕ = 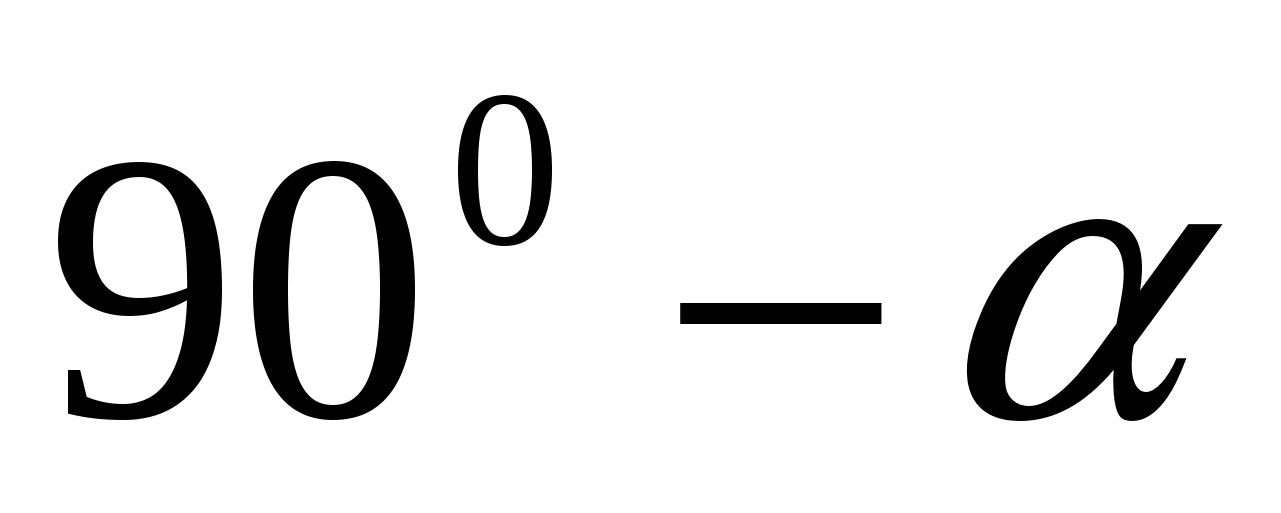
(из прямоугольного треугольника АЕС). Тогда по расширенной теореме синусов для треугольника САВ:
![]() или
или 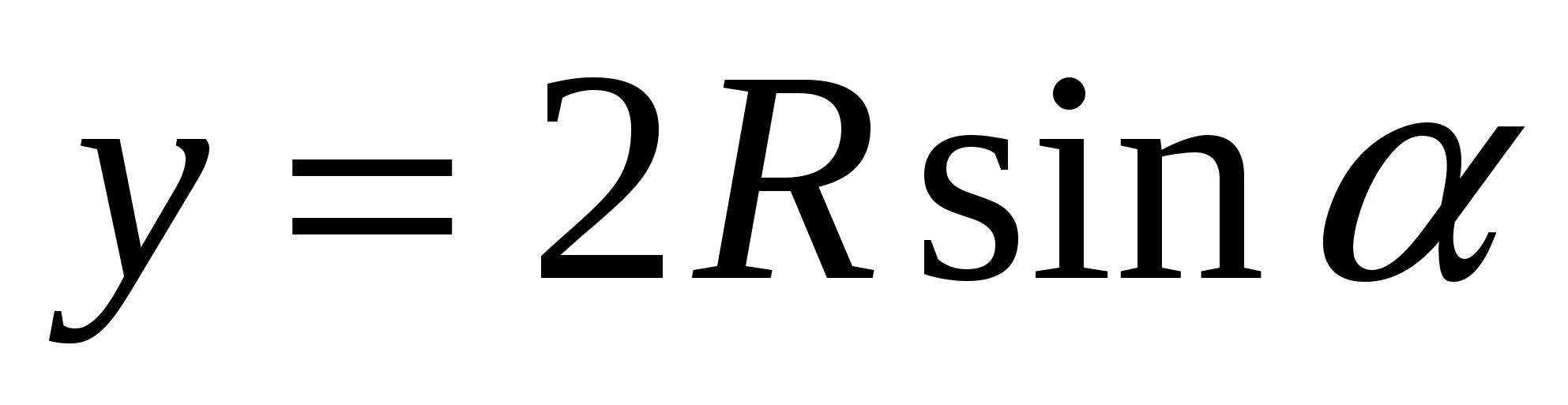 .
.
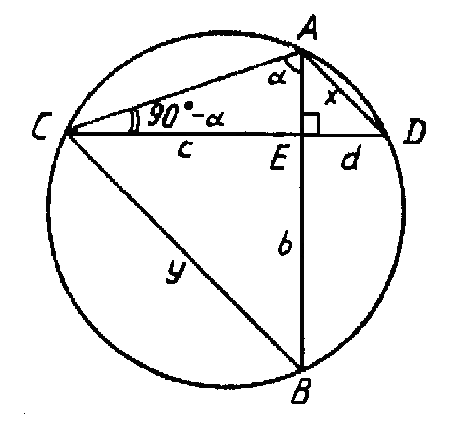
Рис. 3
Для треугольника АСD по расширенной теореме синусов имеем
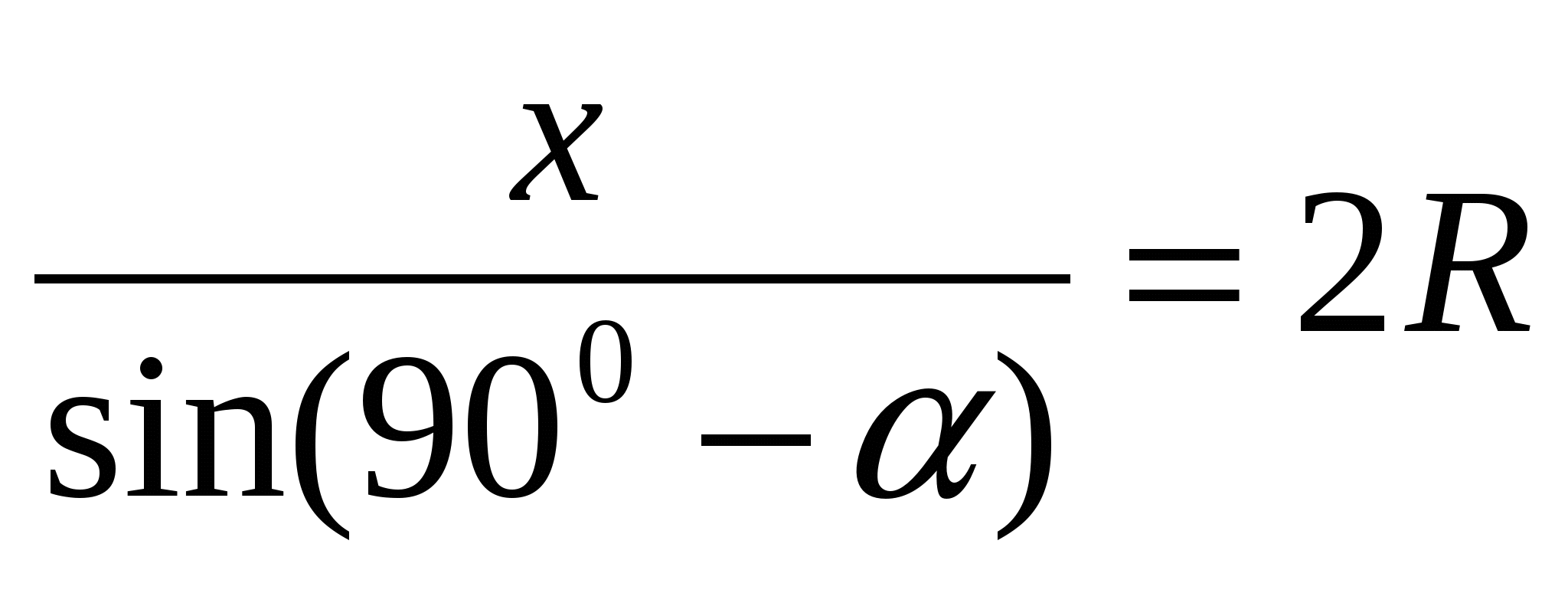 или
или 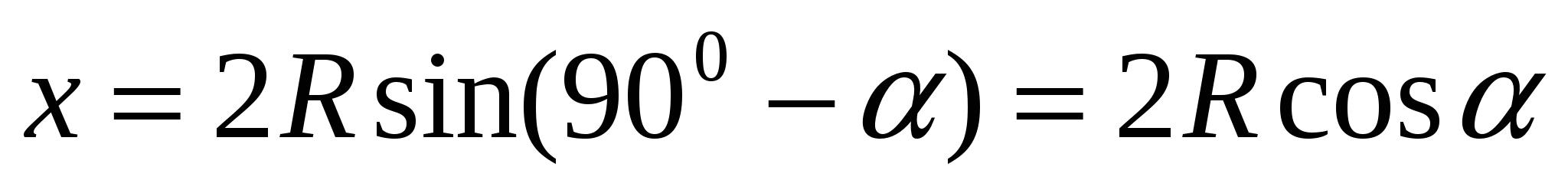 .
.
Итак,
![]() , (3)
, (3)
![]() . (4)
. (4)
Возведем обе части равенств (3) и (4) в квадрат и сложим:
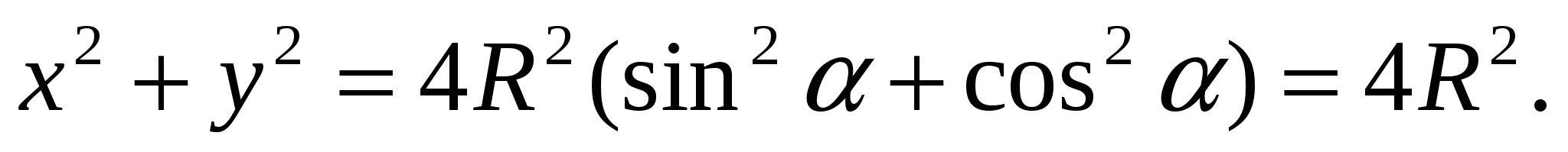
С учетом равенств (1) и (2) задача решена:
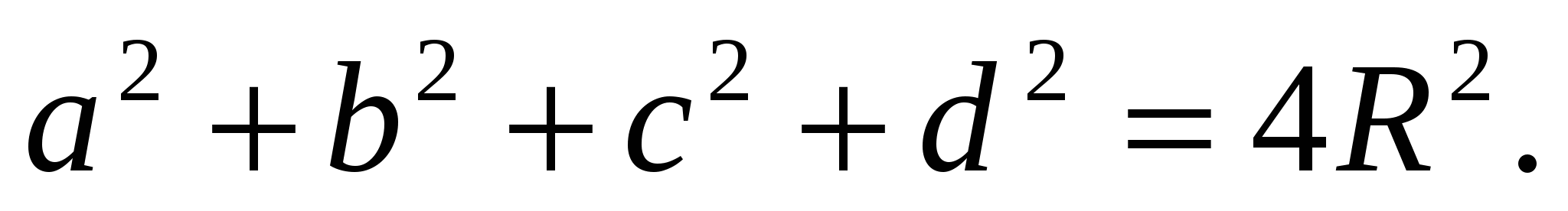
3) Использование симметрии.
1-ый способ.
Воспользуемся свойством угла с вершиной внутри круга.
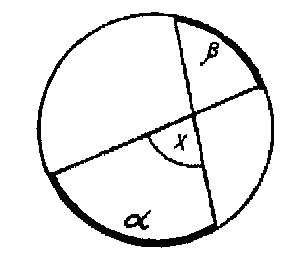
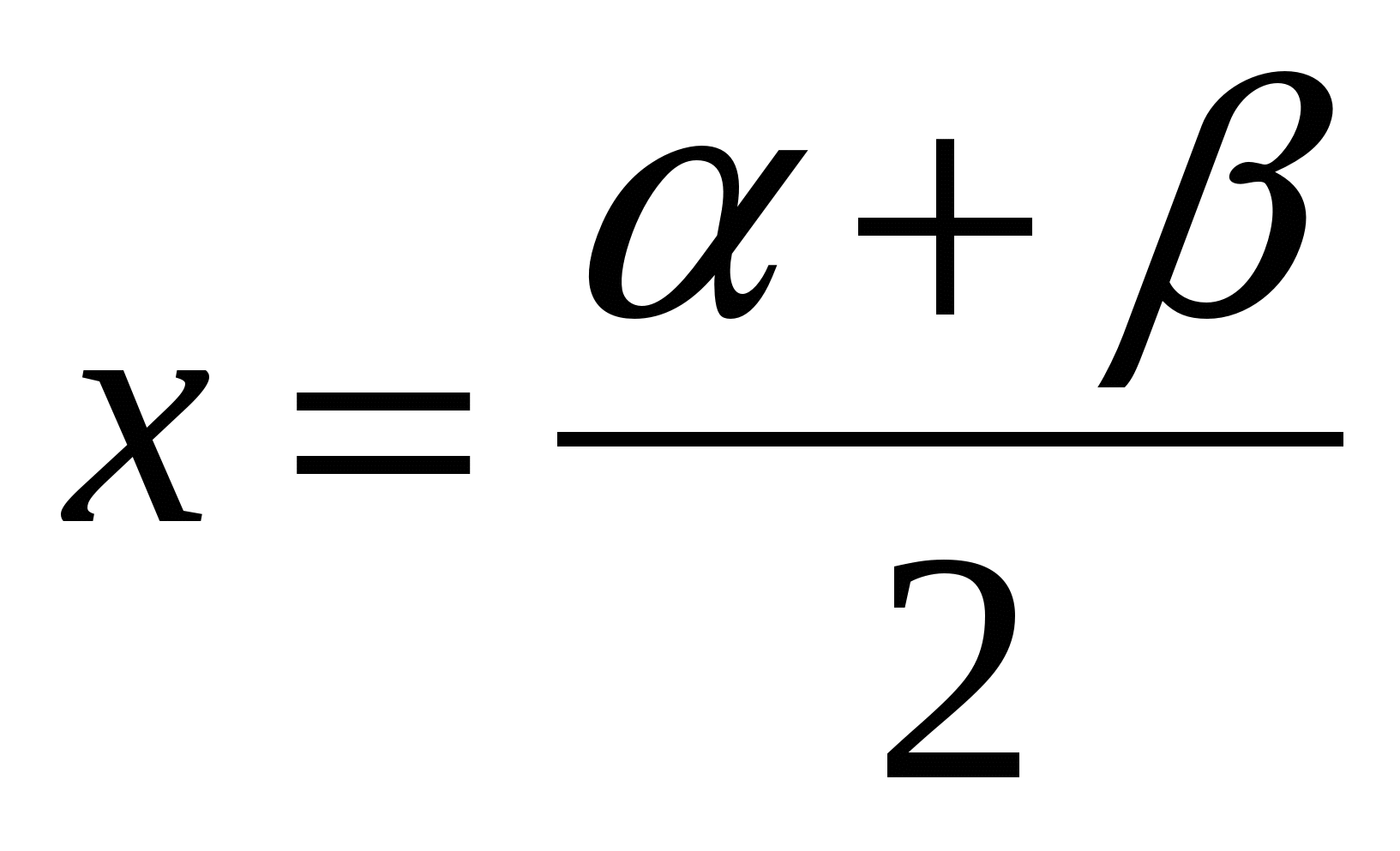
Рис. 4
Согласно свойству угла с вершиной внутри круга полусумма дуг АD и ВС равна 90° (рис. 5).
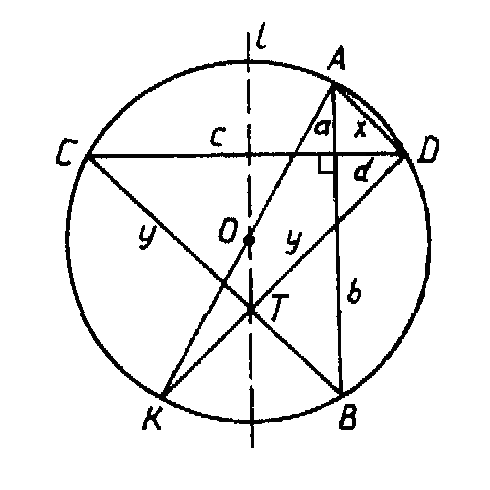
Рис.5
Тогда
![]() AD+
AD+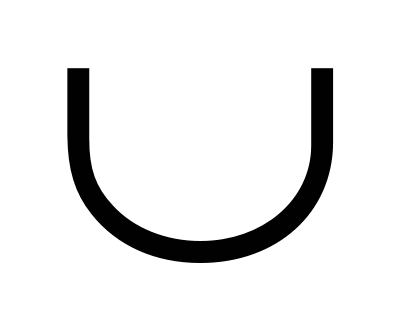 BC=180°. (*)
BC=180°. (*)
Проведем прямую 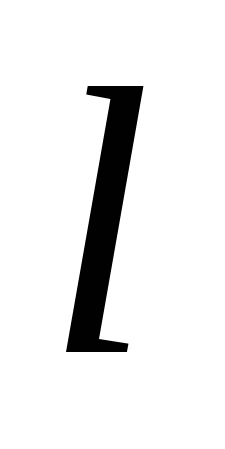 , содержащую диаметр, так что
, содержащую диаметр, так что ![]() // АВ. Из соображений симметрии
// АВ. Из соображений симметрии
DK=BC=y.
Тогда и дуга DК равна дуге ВС (равные хорды стягиваются равными дугами). Значит,
![]() AD+
AD+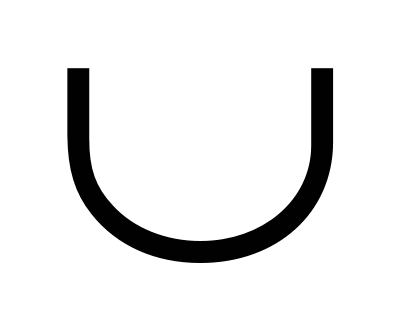 DK=180°.
DK=180°.
Если это так, то АК - диаметр, и 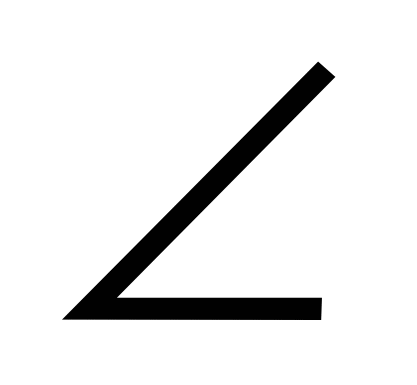 ADK= 90°. По теореме Пифагора для треугольника АDK
ADK= 90°. По теореме Пифагора для треугольника АDK
![]() ,
,
что равносильно решению задачи.
2-ой способ.
Построим отрезок ТК, симметричный АВ относительно центра окружности O (рис.6).
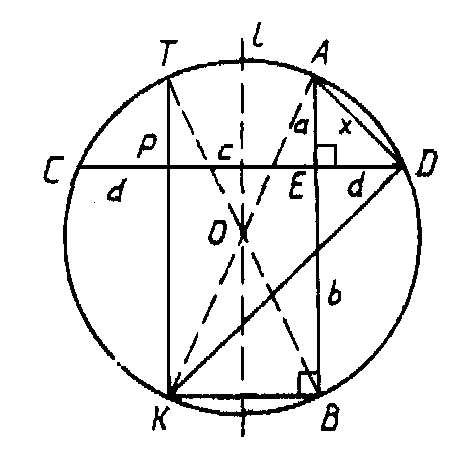
Рис. 6
В силу симметрии ТК=АВ, СР=ЕD=d, РК=ВЕ=b. Очевидно, что РD=c. Из прямоугольного треугольника DРК имеем
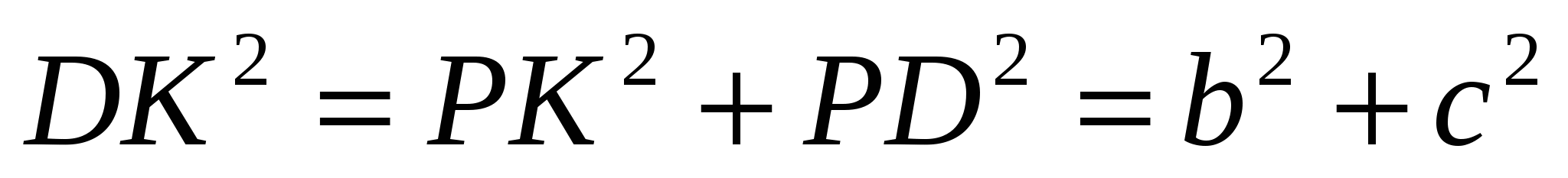
Очевидно, что АК - диаметр (так как АВКТ - прямоугольник), и тогда 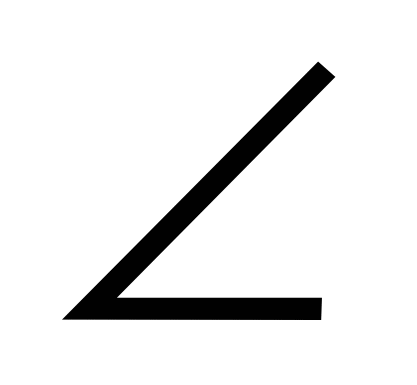 ADK = 90°. По теореме Пифагора для треугольника АDК
ADK = 90°. По теореме Пифагора для треугольника АDК
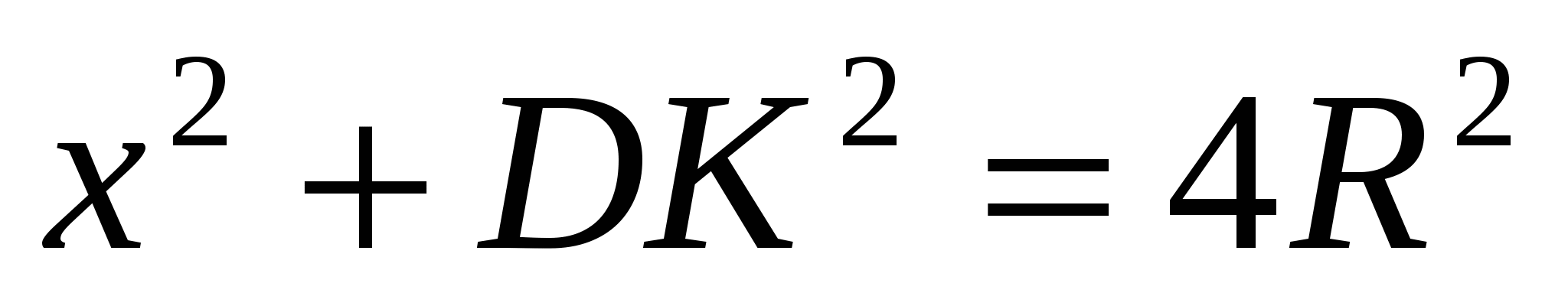 , или
, или 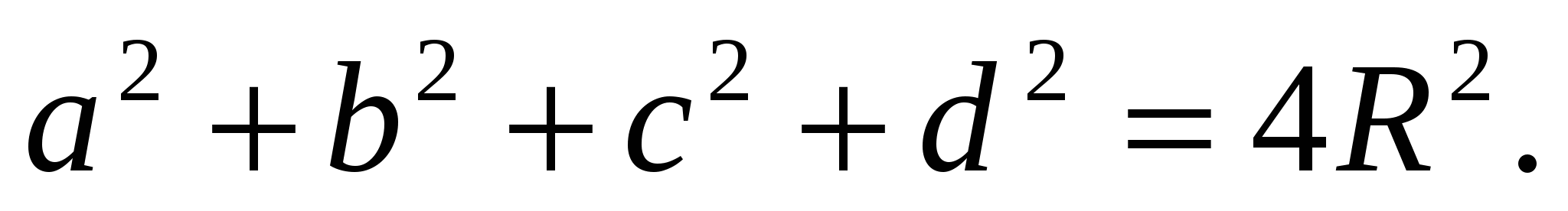
Задача решена!
3-ий способ
Воспользуемся тем же рисунком. ВК = с - d; АВ = a + b, и 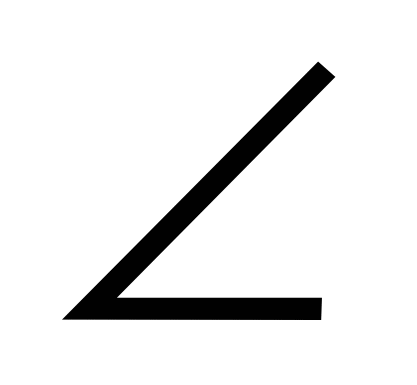 ABK = 90°АВК - 90° (опирается на диаметр). Тогда
ABK = 90°АВК - 90° (опирается на диаметр). Тогда
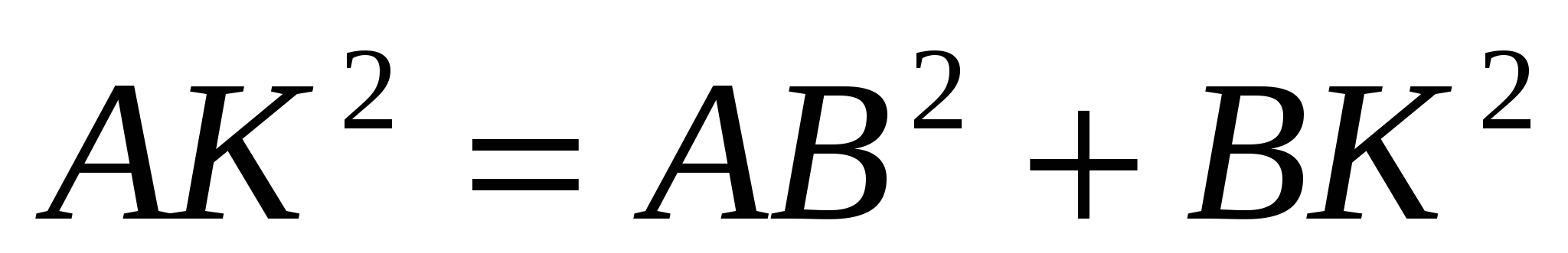 ,
,
или
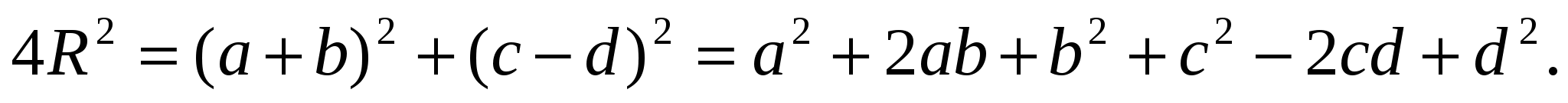
Но по известной задаче о равенстве произведений отрезков хорд ab=cd. Тогда 2аb и -2cd сократятся! Решение задачи получено.
4) Использование формулы 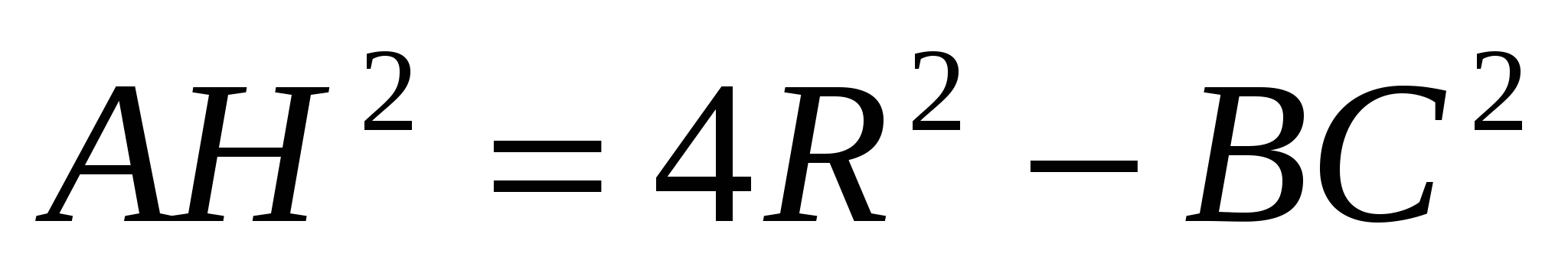 .
.
Проведем в треугольнике АВС высоту АК (рис. 7).
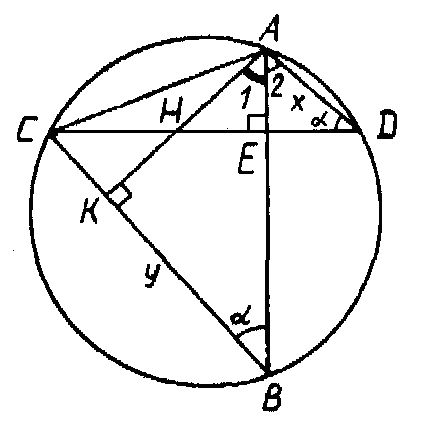
Рис. 7
Тогда H - ортоцентр (точка пересечения высот) в треугольнике АВС. Покажем, что АН =AD = х.
Действительно, ![]() АDС =
АDС =  АВС =
АВС =  (вписанные, опирающиеся на одну дугу). Тогда
(вписанные, опирающиеся на одну дугу). Тогда ![]() 1 = 90° -
1 = 90° -  (из
(из  АВК) и
АВК) и 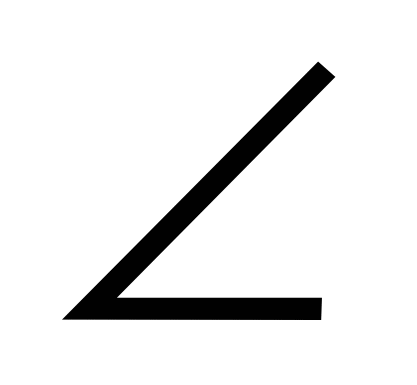 2 = 90° -
2 = 90° -  (из
(из  АDE). Поскольку АЕ - высота и биссектриса в
АDE). Поскольку АЕ - высота и биссектриса в  АDH, то он - равнобедренный, и
АDH, то он - равнобедренный, и
АН = AD = x.
Далее применим хорошо известную нам формулу
![]() . (5)
. (5)
Следовательно,
![]() , т.е.
, т.е. 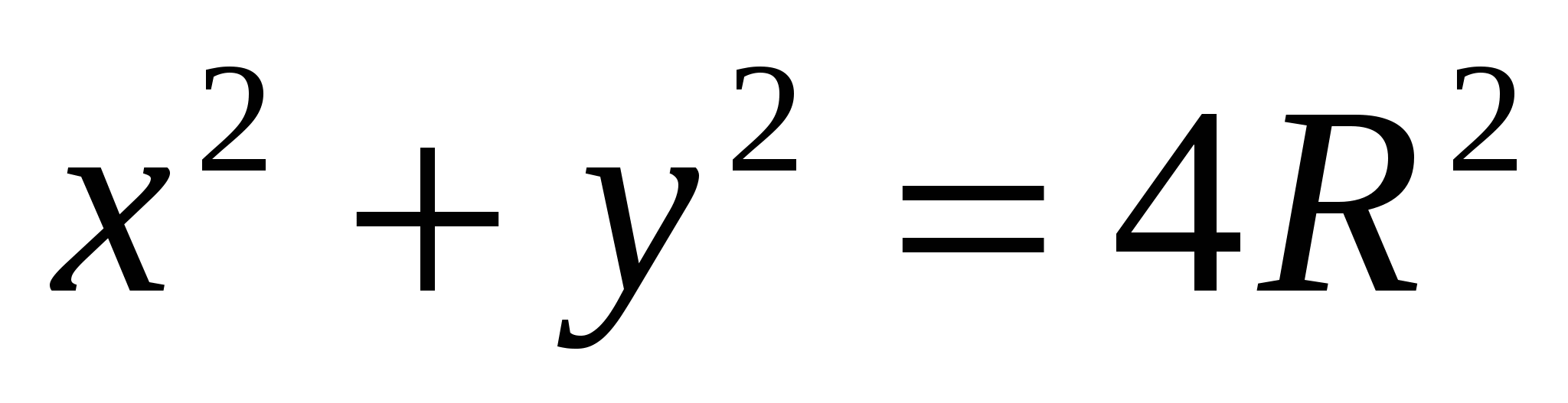 .
.
5) Использование свойства ортоцентра.
Свойство ортоцентра: «Точки, симметричные ортоцентру относительно сторон треугольника, принадлежат описанной окружности».
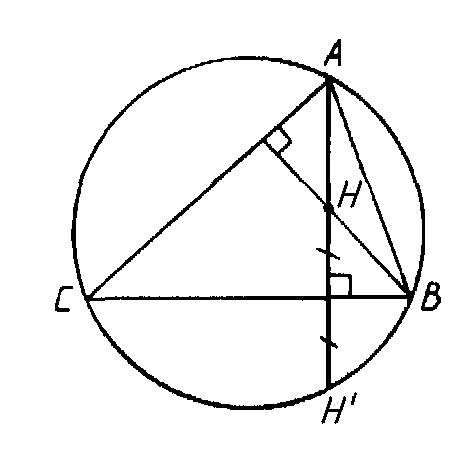
Рис.8
Точки Н и Н' симметричны друг другу относительно стороны ВС (рис. 8).
С учетом вышесказанного способ выглядит так (хорда СО опущена вниз для удобства работы с рис. 9):
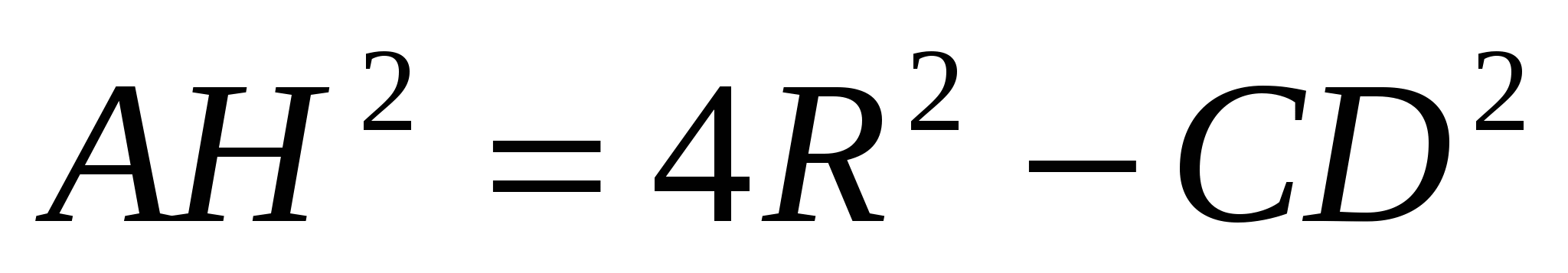 ,
,
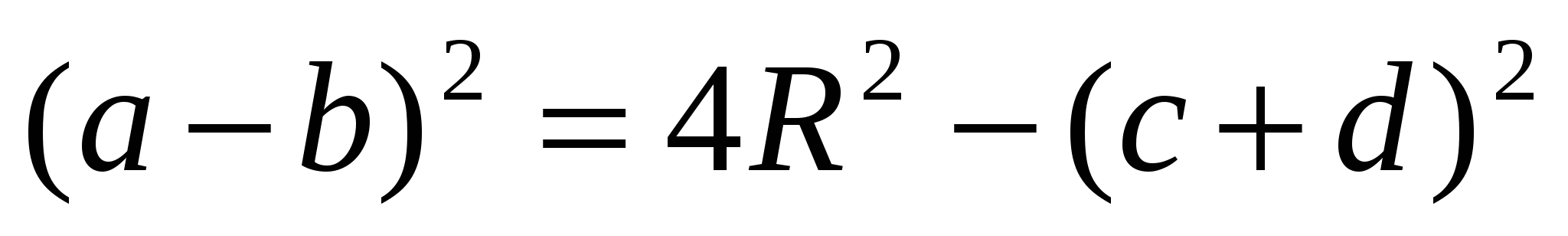 ,
,
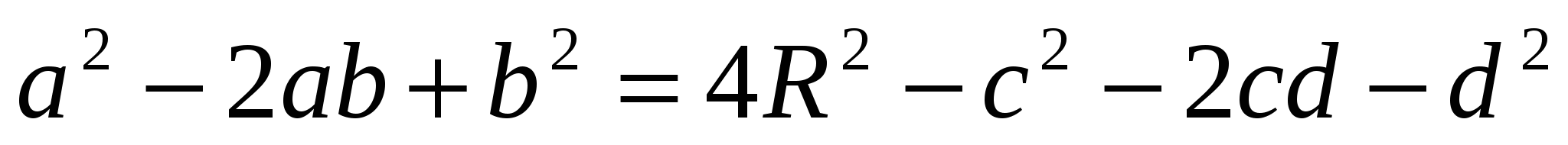 .
.
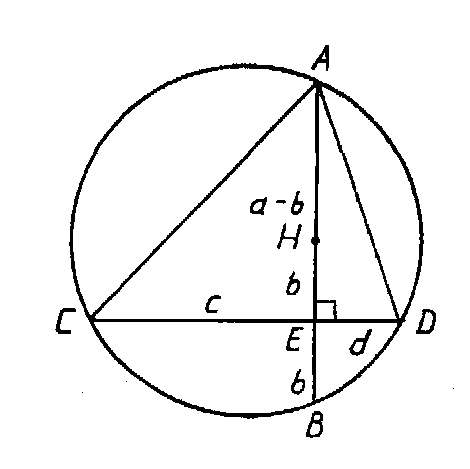
Рис.9
Но аb = cd - из равенства произведения отрезков хорд. Тогда
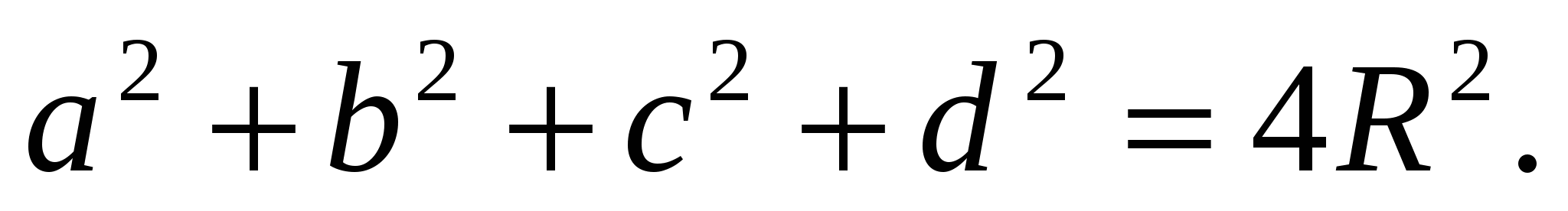
Задача решена!
6) Векторное решение.
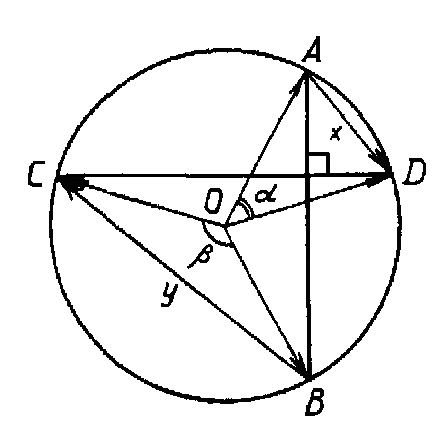
Рис. 10
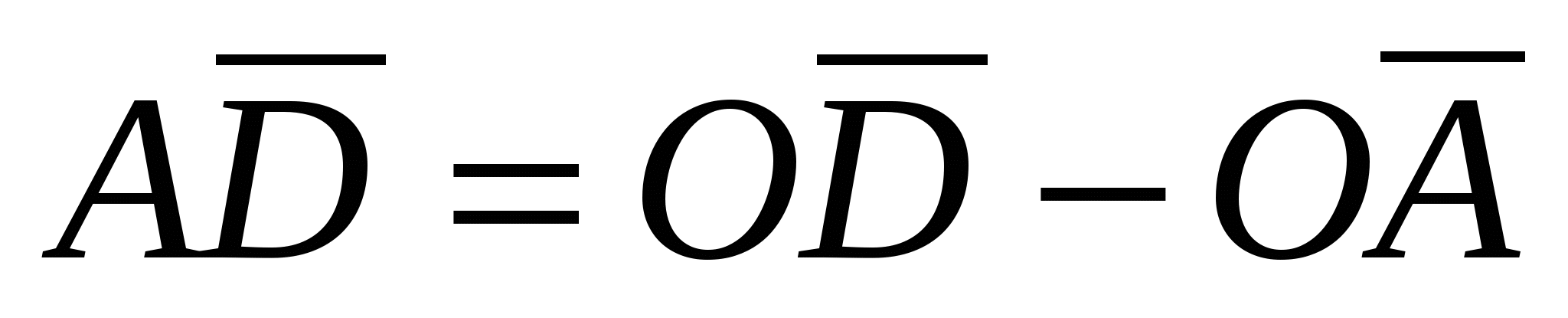 ;
; 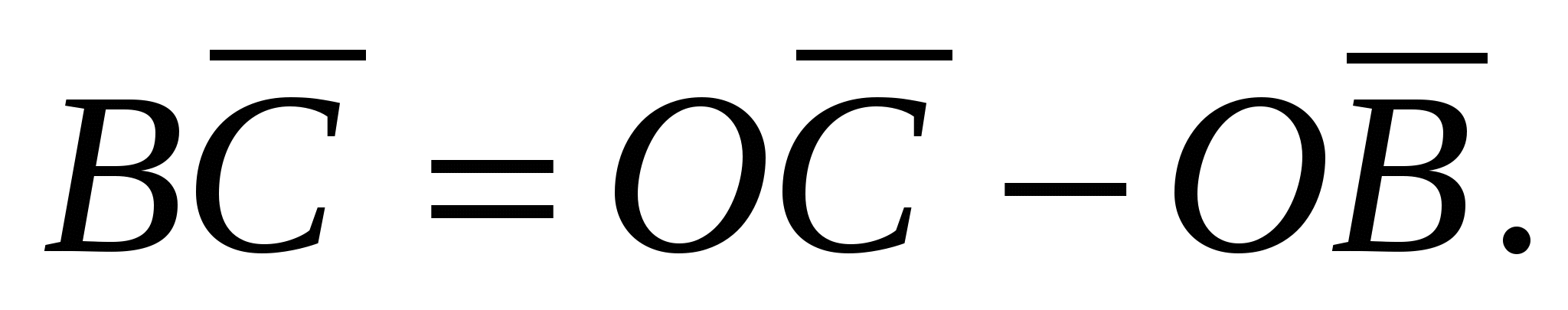
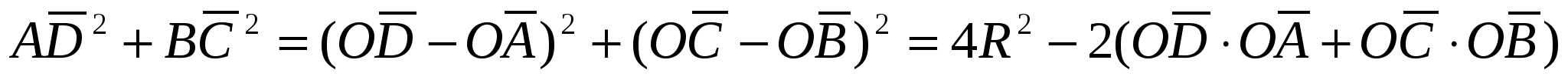 ,
,
![]() , (6)
, (6)
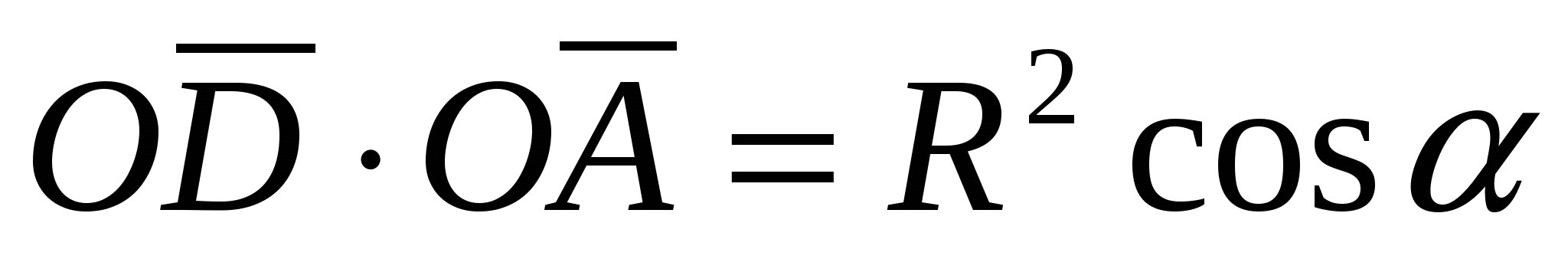 ,
, 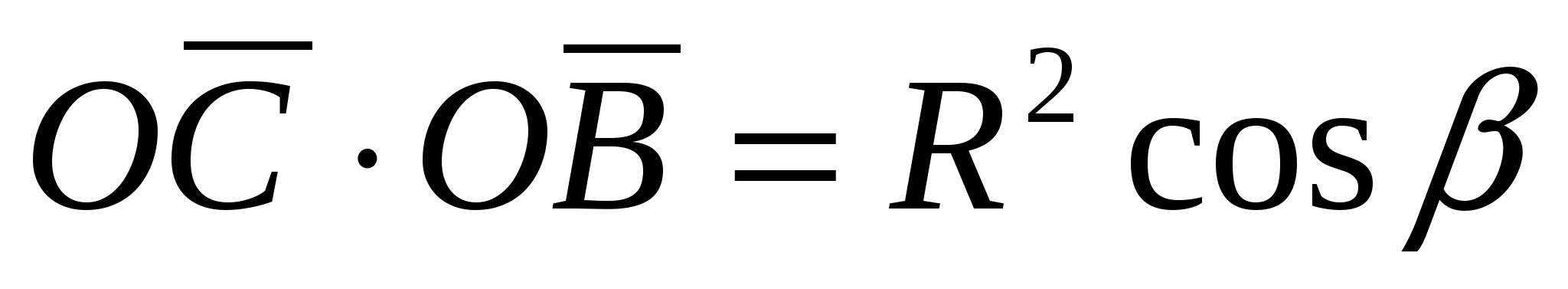 .
.
Докажем, что ![]() ;
;
![]() AD+
AD+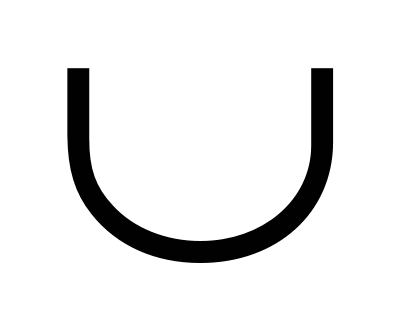 BC=180° - см. формулу (*),
BC=180° - см. формулу (*),
А углы  и
и 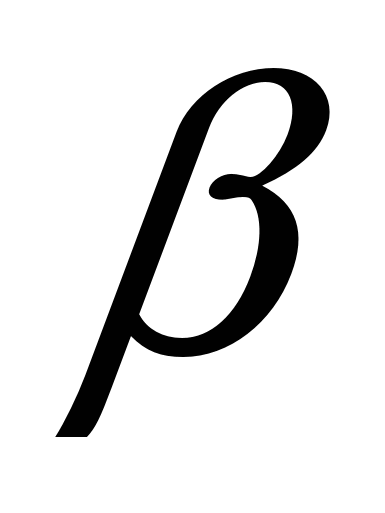 - центральные, равные соответственно дугам AD и ВС.
- центральные, равные соответственно дугам AD и ВС.
Тогда 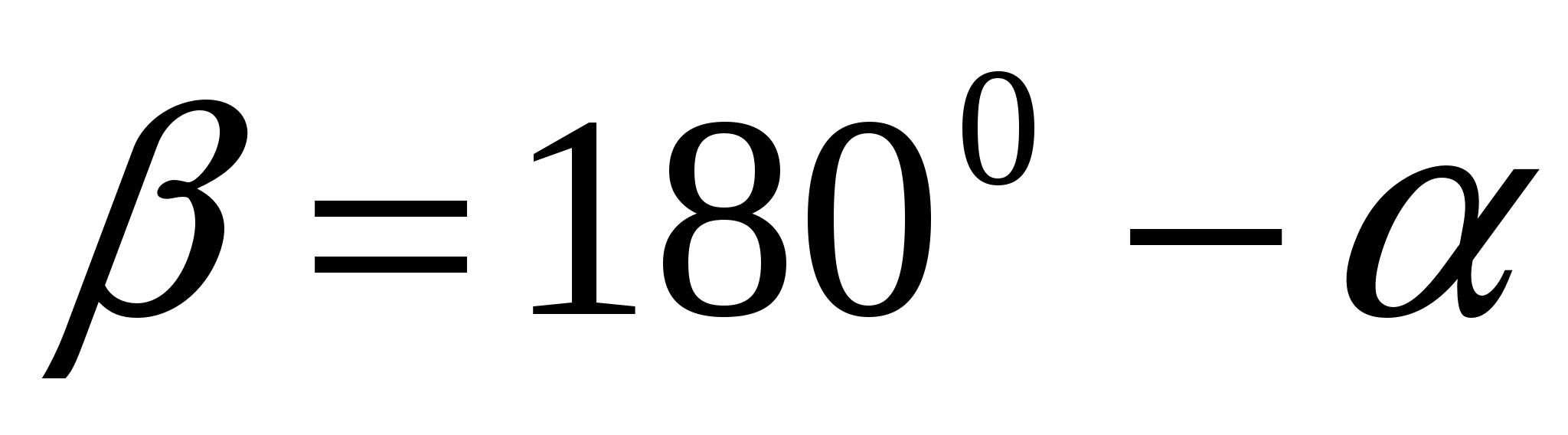 , и
, и 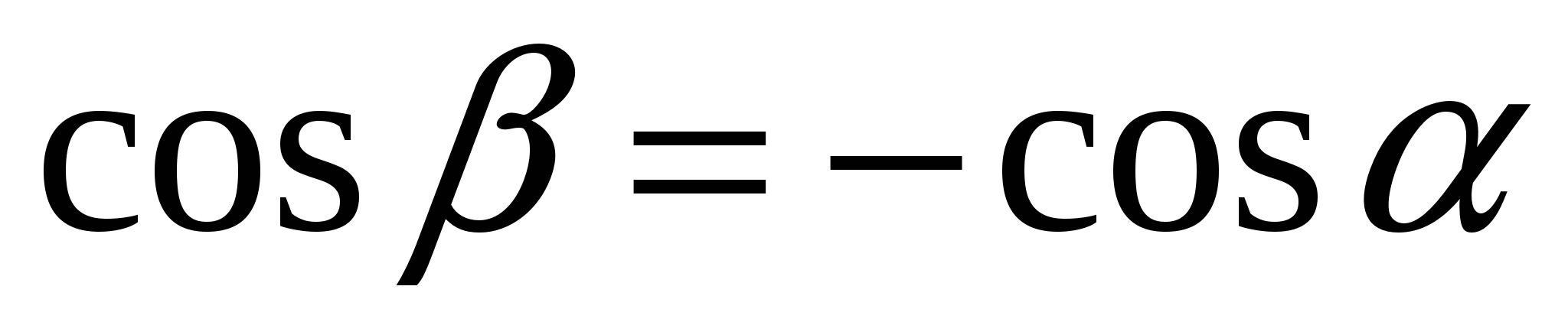 , откуда следует, что
, откуда следует, что
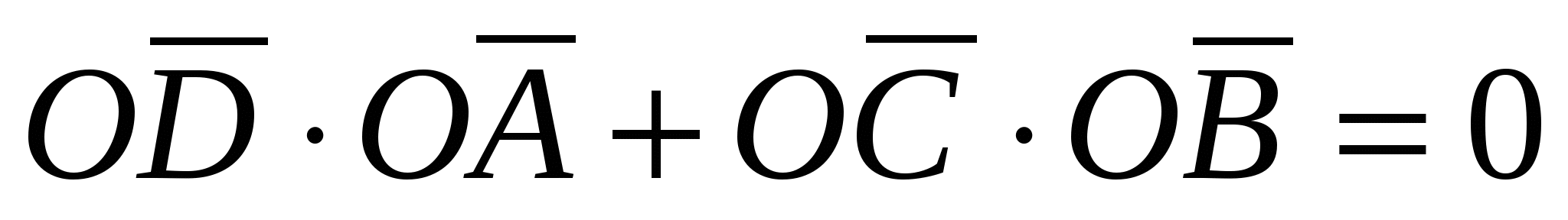 .
.
По формуле (6):
![]() .
.
Задача решена!
III. Итоги урока
IV. Домашнее задание. Решить задачу Архимеда методом координат.


