- Преподавателю
- Математика
- Олимпиадные задания. 10 класс. Оценивание с критериями
Олимпиадные задания. 10 класс. Оценивание с критериями
| Раздел | Математика |
| Класс | 10 класс |
| Тип | Тесты |
| Автор | Дунаева О.А. |
| Дата | 21.02.2016 |
| Формат | doc |
| Изображения | Есть |
Муниципальный этап Российской олимпиады по математике 2011-12 учебного года
10 класс (c решениями)
Время решения - 4 часа
-
Два натуральных числа в сумме составляют 2011, причем второе число получается из первого вычеркиванием последней цифры. Найдите все такие числа.
Ответ: 1829 и 182.
Решение. Обозначим второе число за 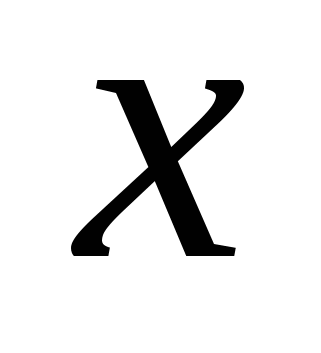 . Тогда первое число имеет вид
. Тогда первое число имеет вид 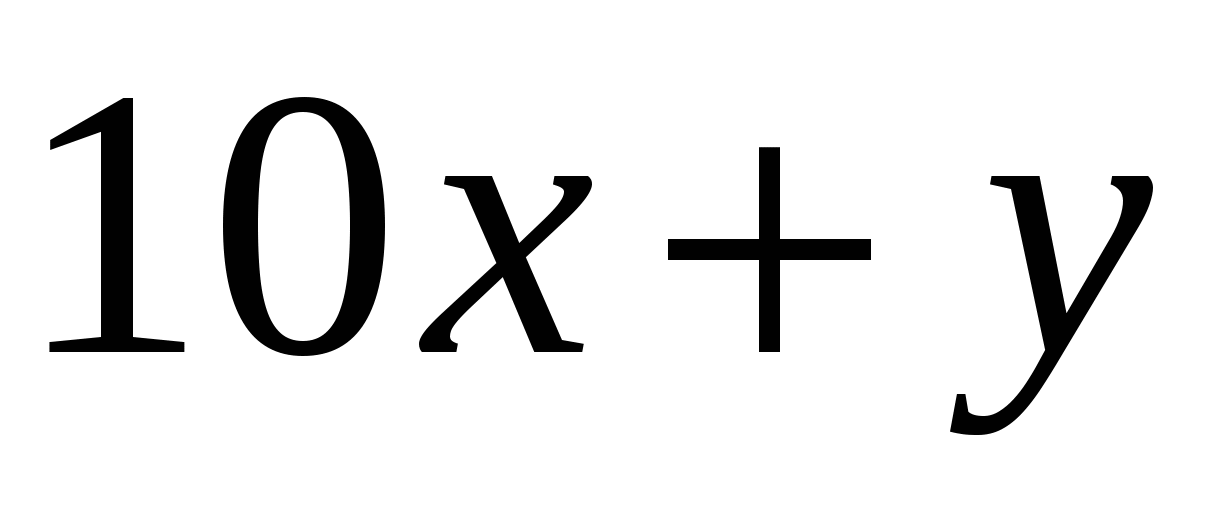 , где
, где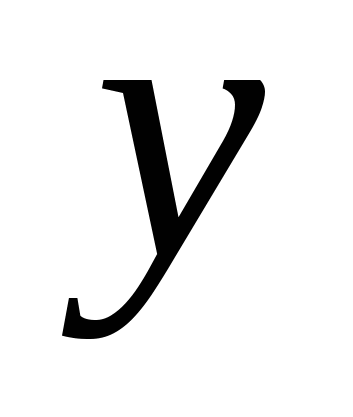 цифра. Из условия задачи получаем, что
цифра. Из условия задачи получаем, что 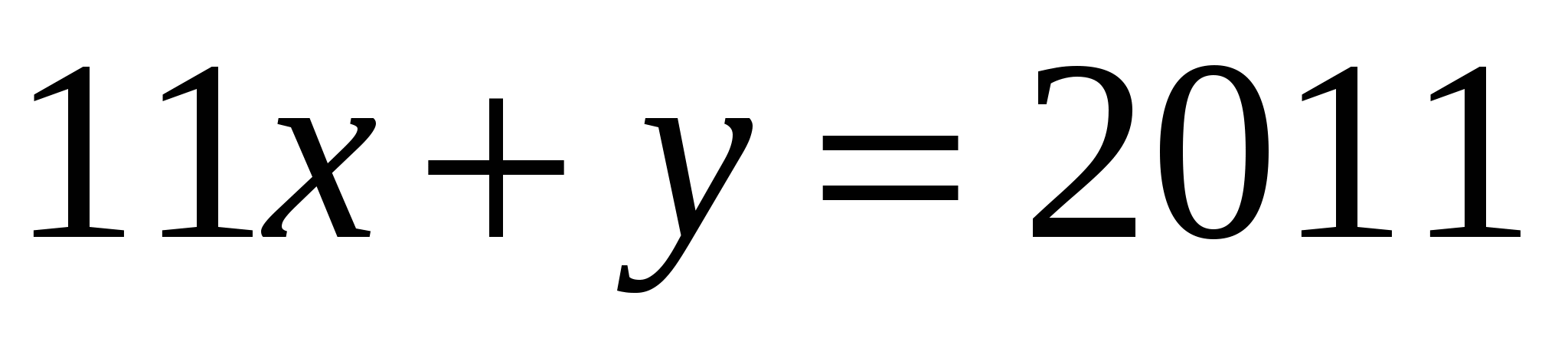 , а тогда
, а тогда 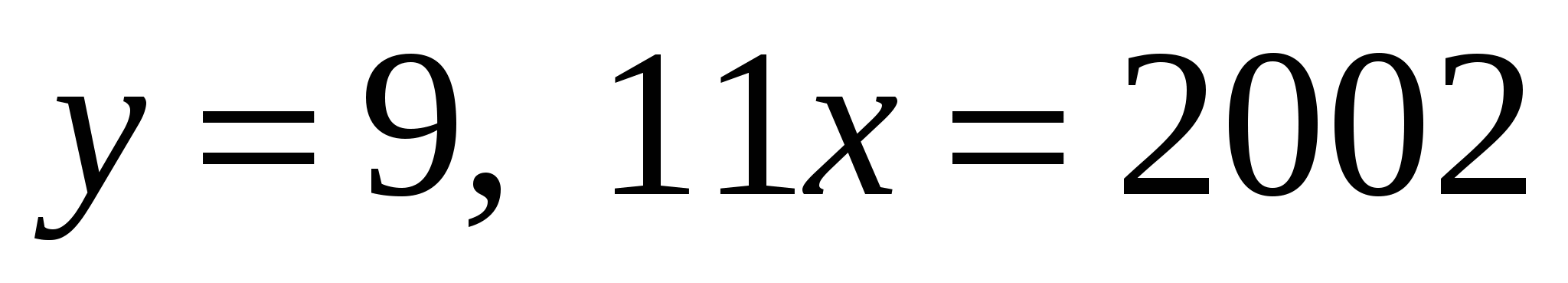 , откуда
, откуда 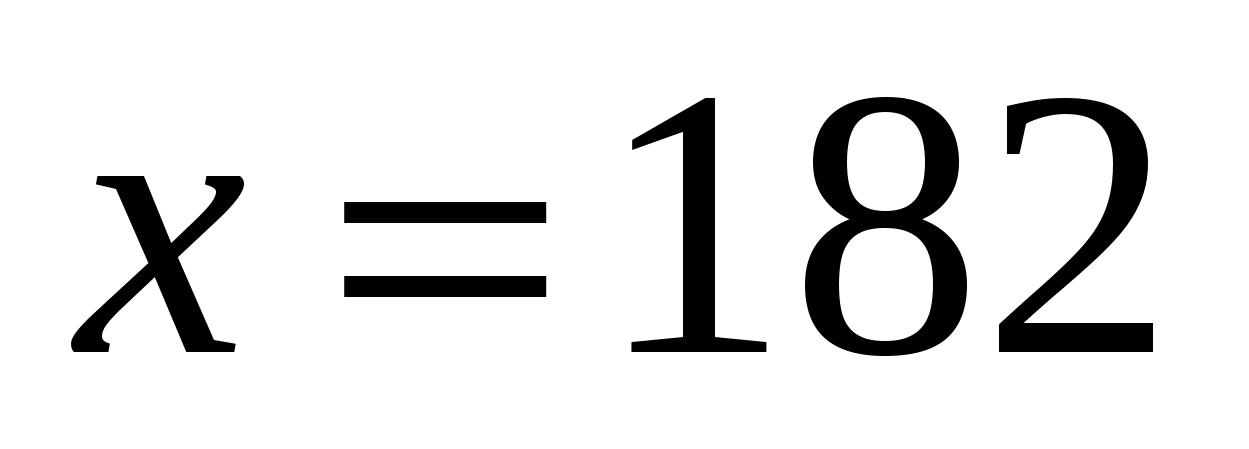 .
.
Критерии. Ответ без доказательства единственности - 3 балла.
-
На плоскости отмечены четыре точки А, В, С и D. Известно, что АВ СD, BC AD. Доказать, что AC BD.
Решение. Легко видеть, что точки А, В и С не могут лежать на одной прямой. Следовательно, они образуют треугольник, в котором точка D есть пересечение двух высот: CD и AD. Но тогда ВD - третья высота треугольника АВС, и она перпендикулярна стороне АС.
Критерии. Не доказано, что точки А, В и С не могут лежать на одной прямой - не более 5 баллов.
-
Два графика
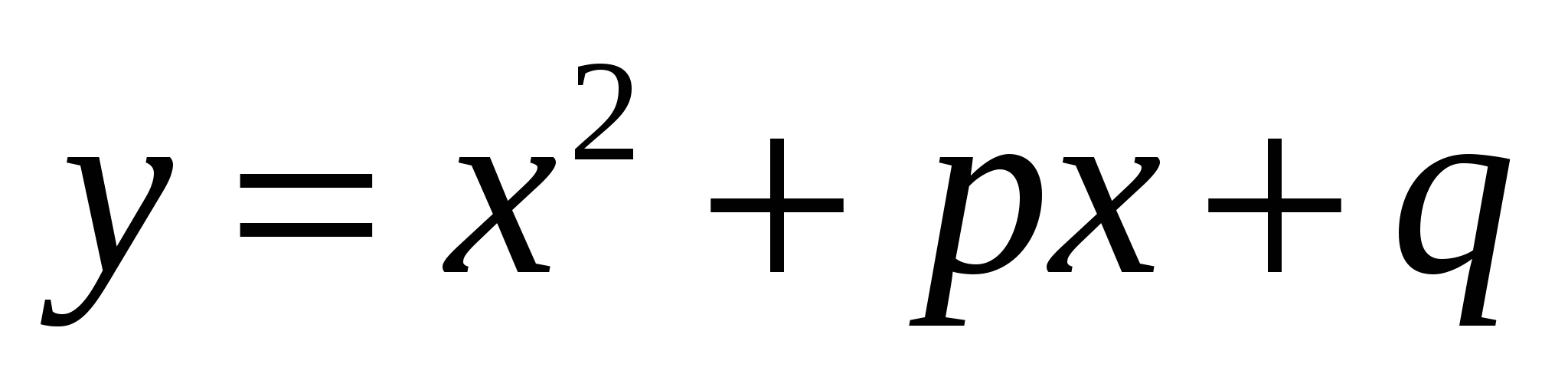 и
и 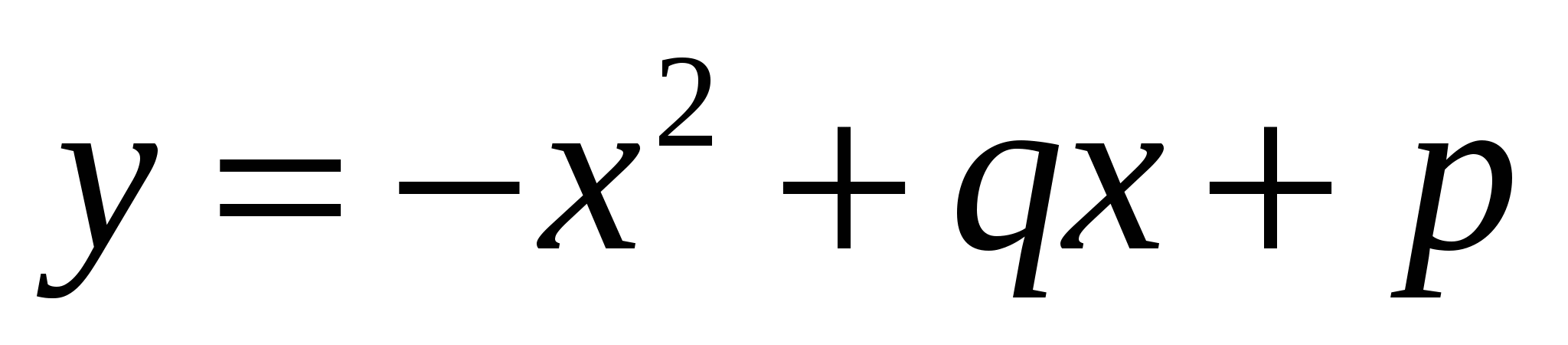 имеют единственную общую точку. Чему равна абсцисса этой точки?
имеют единственную общую точку. Чему равна абсцисса этой точки?
Ответ: 0 или 2. Решение. Из условия следует, что уравнение 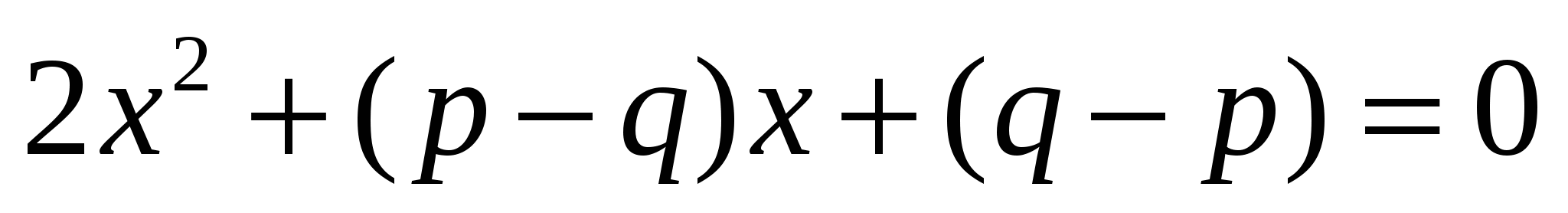 имеет единственное решение, которое нужно найти. Дискриминант этого уравнения равен
имеет единственное решение, которое нужно найти. Дискриминант этого уравнения равен ![]() , а корни
, а корни 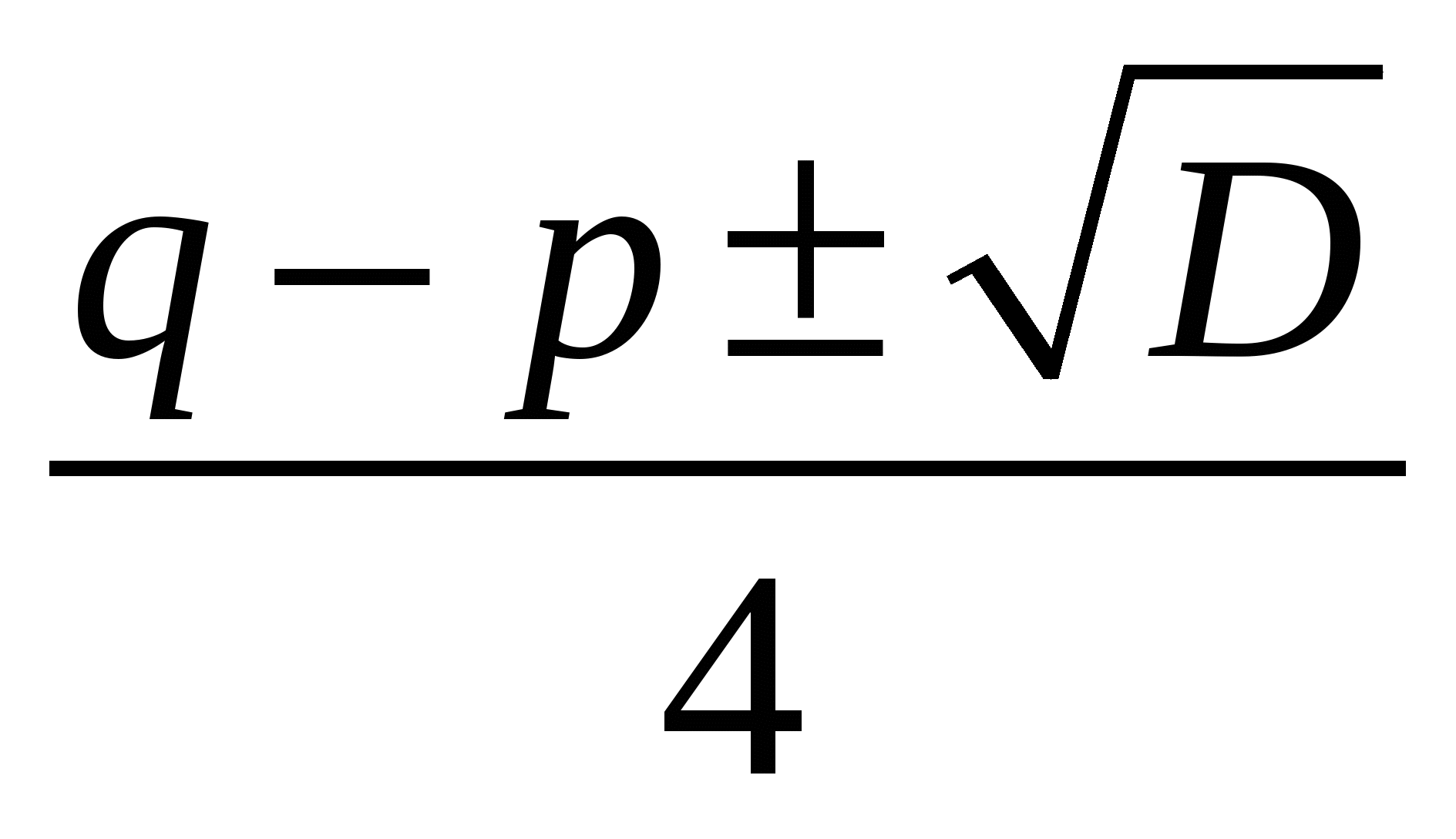 . Поскольку согласно условию
. Поскольку согласно условию ![]() , имеем
, имеем 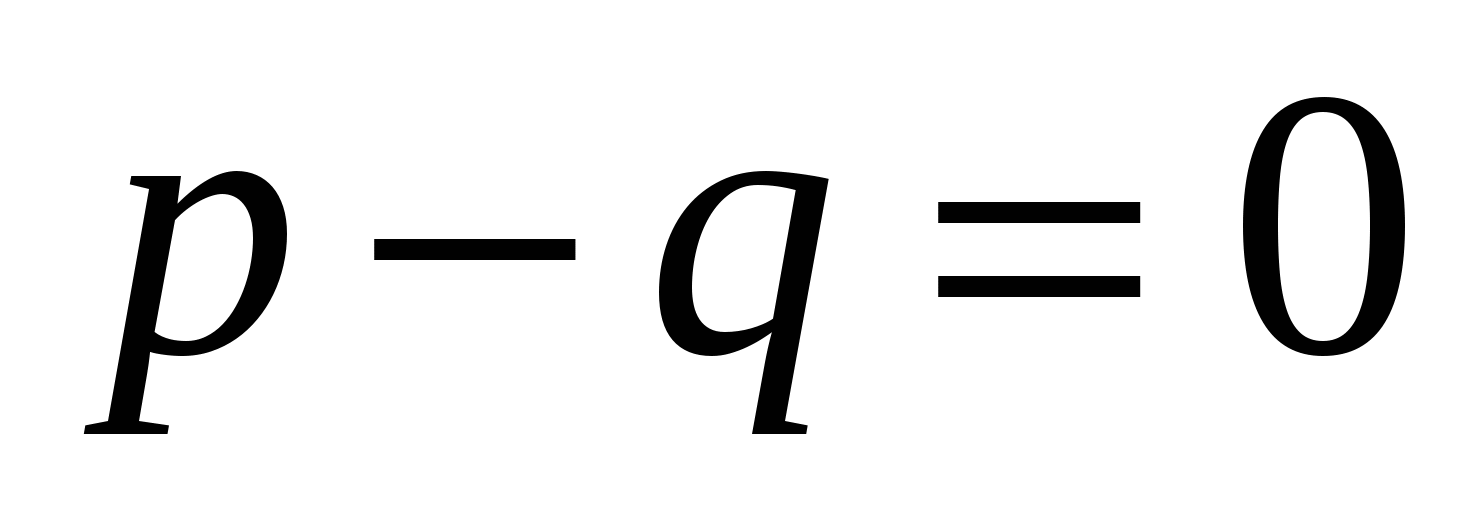 или
или 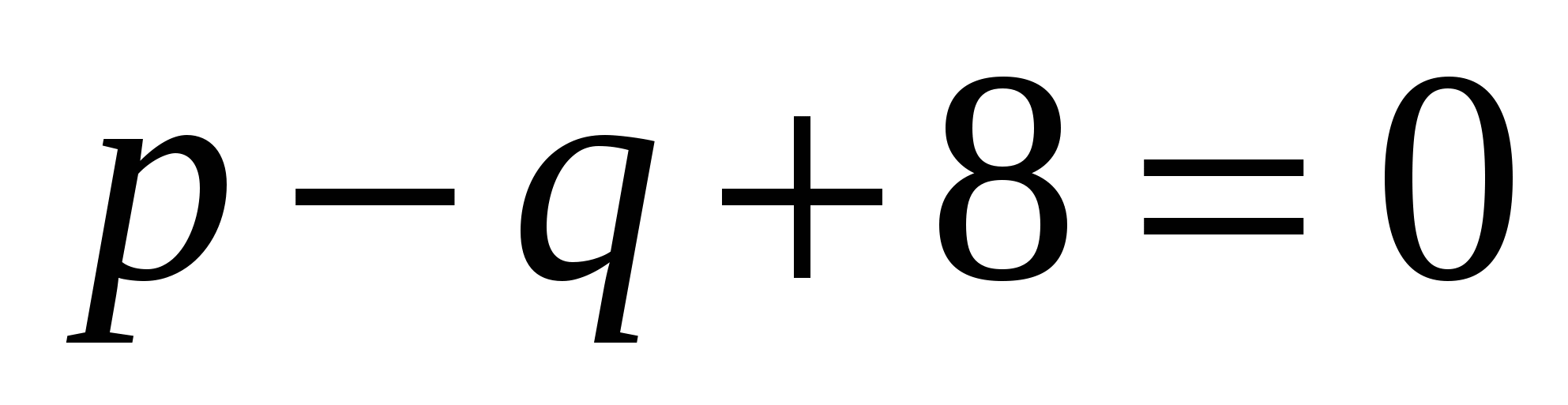 , то есть
, то есть 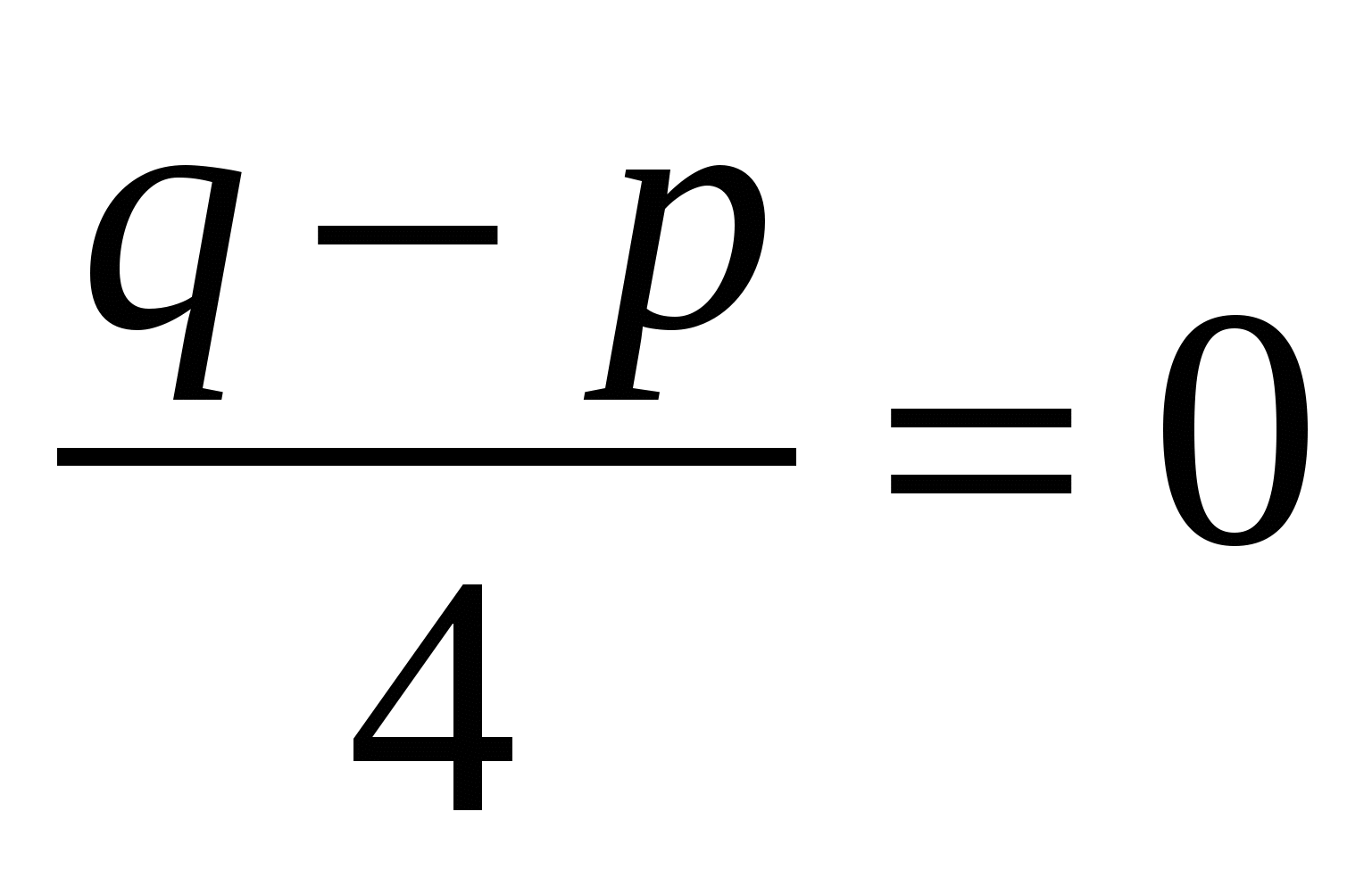 или
или 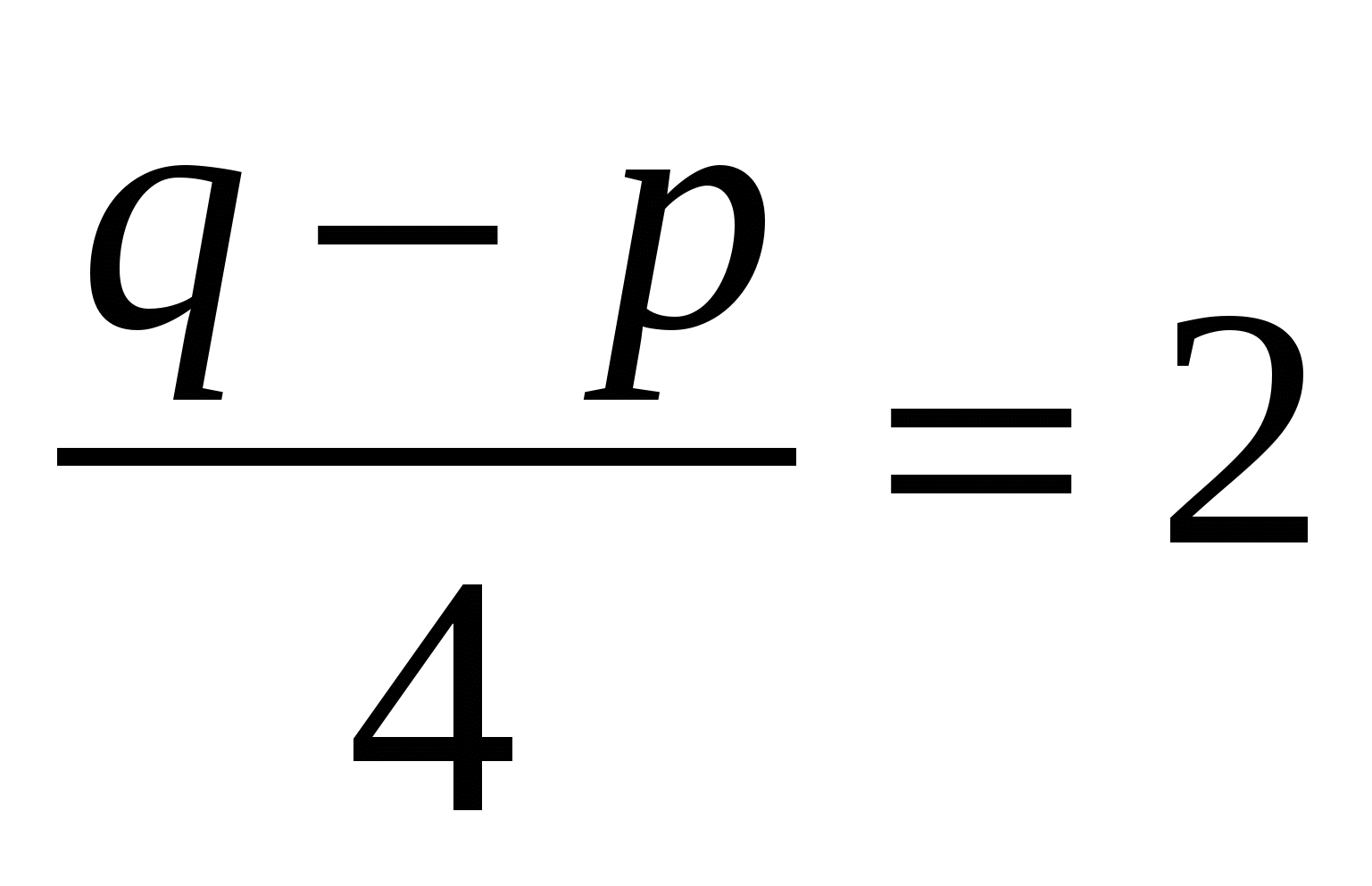 .
.
Критерии. Найден один ответ - 1 балл, оба ответа без обоснования, что других нет, - 3 балла.
-
В клетках прямоугольной таблицы записаны натуральные числа. За один ход разрешается либо умножить на 2 все числа строки, либо вычесть 1 из всех чисел столбца. Докажите, что за несколько ходов можно добиться того, чтобы во всех клетках таблицы стояли нули.
Решение. Выберем произвольный столбец и будем вычитать из всех элементов столбца 1 до тех пор, пока наименьшее из чисел столбца не станет равным 1. Если не все числа столбца стали равными 1, то поступим так: умножим на 2 все строки, в которых стоят 1 выбранного столбца, и снова вычтем из всех элементов столбца 1. В результате все 1 останутся 1, а остальные числа уменьшатся на 1. Очевидно, что после нескольких таких операций все числа выбранного столбца станут равными 1. Теперь можно вычесть из всех элементов столбца 1, и он станет нулевым. Выберем другой столбец и теми же действиями добьемся, чтобы он стал нулевым. Заметим, что, работая со вторым столбцом, мы не изменим уже полученные нули в первом столбце. Последовательно делая нулевыми один столбец за другим, получим таблицу из одних нулей.
Критерии. Если показано, как получить нулевой столбец, то не менее 4 баллов.
-
На пост мэра баллотировались три кандидата. Кандидат А заявил: «Я умнее Б». Кандидат Б заявил: «Я честнее В». Кандидат В заявил: «Я богаче А». Известно, что самый богатый солгал, самый умный сказал правду, а самый честный был третий. Кто из кандидатов был самый богатый?
Ответ: самый богатый Б. Решение. Кандидат В не может быть самым богатым, так как в противном случае он сказал правду, что противоречит условию. Допустим, самый богатый - А. Но тогда В солгал, значит согласно условию он не может быть самым умным, значит, самый умный - Б, самый честный - В. Но тогда Б сказал правду и он честнее В. Мы получили противоречие. Значит, самым богатым может быть только Б. Нетрудно убедиться, что такая ситуация возможна.
Критерии. Если найден ответ без обоснования или с неверным обоснованием - 1 балл. Если задача решается перебором, то следить за тем, чтобы были рассмотрены все варианты, в противном случае перебор решением не считать.


