- Преподавателю
- Математика
- Метод координат в задачах типа С2
Метод координат в задачах типа С2
| Раздел | Математика |
| Класс | - |
| Тип | Конспекты |
| Автор | Дряева М.Г. |
| Дата | 30.11.2014 |
| Формат | docx |
| Изображения | Есть |
13
1. Система координат в пространстве.
Выберем начало координат. Проведем три взаимно перпендикулярные оси х, y и z . Выберем масштаб.
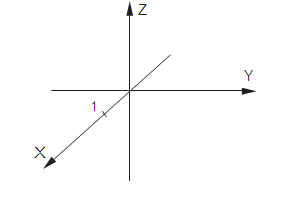
Получилась система координат в трехмерном пространстве.
Каждая точка характеризуется тремя числами - координатами по x, y и z. Запись M(−1; 3; 2) означает, что координата точки M по x (абсцисса) равна −1, координата по y (ордината) равна 3, а координата по z (аппликата) равна 2.
Векторы в пространстве определяются так же, как и на плоскости.
Это направленные отрезки, имеющие начало и конец. Только в пространстве вектор задается тремя координатами x, y и z:
ﺂ؟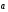 (xa; ya; za)
(xa; ya; za)
Чтобы найти координаты вектора, так же, как и на плоскости, из координаты конца надо вычесть координату начала.
1.
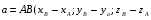
2.
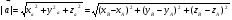
Если точка M - середина отрезка AB, то ее координаты находятся по формуле:
3. 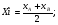
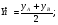
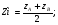
4. 
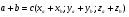 - сумма векторов.
- сумма векторов.
5. 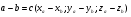 - разность векторов.
- разность векторов.
6. 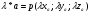 - произведение вектора на число.
- произведение вектора на число.
7. 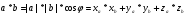 - скалярное произведение векторов
- скалярное произведение векторов
8. 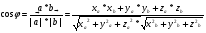 - косинус угла между векторами.
- косинус угла между векторами.
2. Введение системы координат.
Метод координат - это, конечно, очень хорошо, но в настоящих задачах C2 никаких координат и векторов нет, поэтому их надо вводить.
Самое замечательное свойство заключается в том, что не имеет никакого значения как именно вводить систему координат. Если все вычисления будут правильными, то и ответ будет правильным.
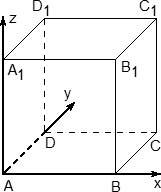
2.1 Координаты куба.
Система координат вводится очень просто:
-
Начало координат - в точке A
-
Если ребро куба не указано, то принимаем его за единичный отрезок;
-
Ось x направляем по ребру АВ, у - по ребру АD, а ось z - по ребру AA1 .
Теперь у каждой вершины куба есть координаты:
A (0; 0; 0), B (1; 0; 0), C (1; 1; 0), D (0; 1; 0),
A1 (0; 0;1) B (1; 0; 1) C1 (1; 1; 1), D1 (0; 1; 1).
2.2 Координаты правильной треугольной призмы
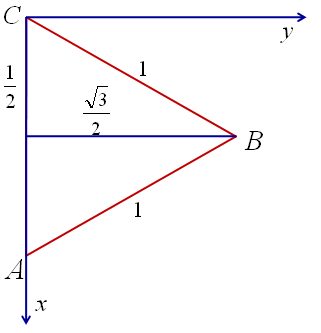
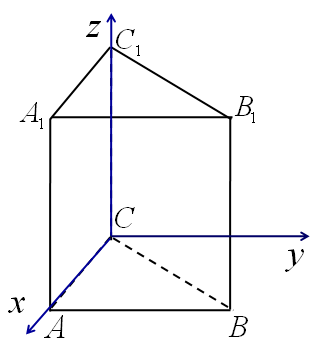
A (1; 0; 0), B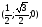 , C (0; 0; 0), A1 (1; 0; 1), B1
, C (0; 0; 0), A1 (1; 0; 1), B1 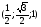 , C1 (0; 0; 1).
, C1 (0; 0; 1).
2.3 Координаты правильной шестиугольной призмы
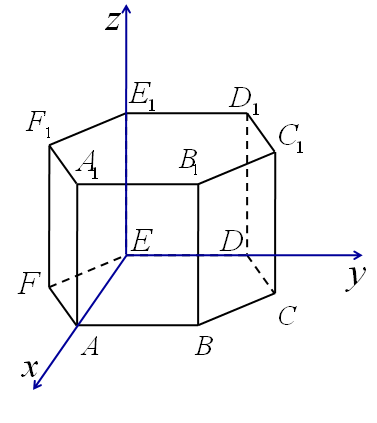
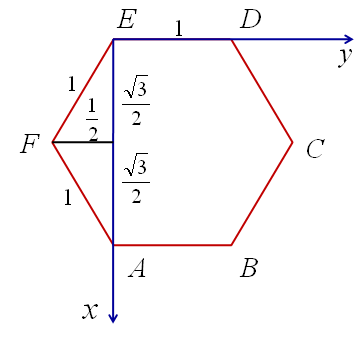
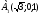
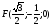
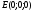
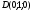
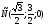
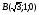
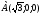
, , , , , , ,
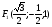
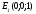
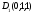
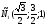
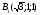
, , , , .
2.4 Координаты правильной четырехугольной пирамиды
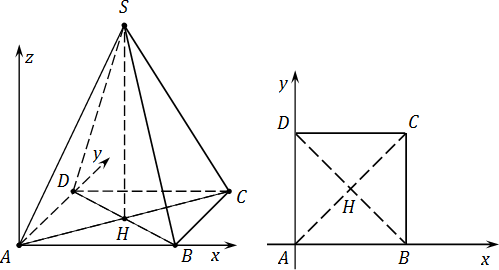
Введем систему координат с началом в точке А
A (0; 0; 0), B (1; 0; 0), C (1; 1; 0), D (0; 1; 0), H (0,5; 0,5; 0).
Найдем координаты точки S. Рассмотрим треугольники ASH и ABH
-
AS = AB = 1 по условию;
-
Угол AHS = AHB = 90°, поскольку SH - высота, а AH ⊥ HB как диагонали квадрата;
-
Сторона AH - общая.
Следовательно, прямоугольные треугольники ASH и ABH равны по одному катету и гипотенузе. Значит, SH = BH = 0,5 · BD. Но BD - диагональ квадрата со стороной 1. Поэтому имеем:
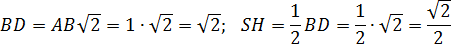
Итак, координаты точки S:
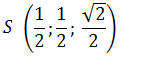
Рассмотрим случай, если боковые ребра пирамиды не равны ребрам основания. В этом случае рассмотрим треугольник AHS: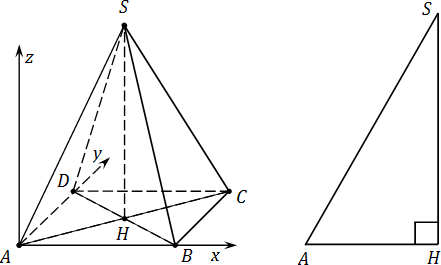
Треугольник AHS - прямоугольный, причем гипотенуза AS - это одновременно и боковое ребро исходной пирамиды SABCD. Катет: AH = 0,5 · AC. Оставшийся катет SH найдем по теореме Пифагора. Это и будет координата z для точки S.
3. Матрицы и определители второго и третьего порядка.
Определение: Таблица, составленная из четырёх чисел 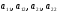 называется квадратной матрицей второго порядка. Числа
называется квадратной матрицей второго порядка. Числа 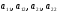 называют элементами матрицы.
называют элементами матрицы.
Определение: Число ∆ называется определителем или детерминантом матрицы.
∆=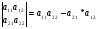
Определитель третьего порядка можно вычислить так:
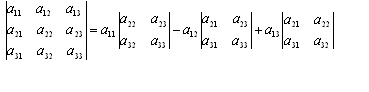
4. Метод координат в пространстве
4.1 Угол между прямыми.
Вычисление направляющих векторов для прямых.
В задаче С2 прямые всегда задаются парой точек. Если ввести систему координат и рассмотреть вектор с началом и концом в этих точках, получим направляющий вектор для прямой.
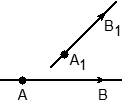
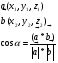
α-угол между прямыми
3.1 Угол между двумя прямыми - это угол между их направляющими векторами.
Задача 1.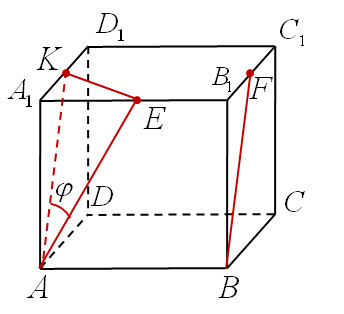
В единичном кубе ABCDA1B1C1D1 найдите угол между прямыми AE и BF, где E - середина ребра A1B1, где Е - середина ребра А1В1 а F - середина ребра B1C1.
Решение (1 способ)
K- середина A1D1 AK║BF угол KAE = φ
По теореме Пифагора
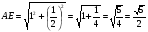
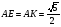
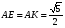
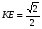
По теореме косинусов для ∆ AKE
KE² = AE² + AK² - 2 * AE *AK * cos φ
cos φ=0,8 φ=arccos0.8
Решение (2 способ)
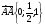
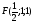
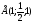
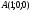
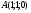
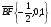
С помощью векторов и координат легко найти угол между прямыми.
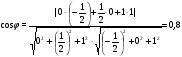
А если требуется найти угол между плоскостями или между прямой и плоскостью, то для этого нам понадобится уравнение плоскости в пространстве.
4.2 Плоскость в пространстве задается уравнением.
Ax+By+Cz+D=0,
где A, B и С - координаты вектора, перпендикулярного этой плоскости. Его называют нормалью к плоскости.
Чтобы написать уравнение плоскости, берем координаты трех принадлежащих ей точек. Подставляем их по очереди в уравнение плоскости. Решаем полученную систему.
Напишем уравнение плоскости, проходящей через точки M (1; 0; 1), N(2; -2; 0) и К (4; 1; 2)
Уравнение плоскости выглядит так:
Ax+By+Cz+D=0
Получим систему из трех уравнений:
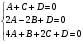
В ней четыре неизвестных: A, B, С и D. Поэтому одну из них мы выберем сами, а другие выразим через нее. Правило - простое вместо одной из переменных можно взять любое число, не равное нулю.
Решив систему, получим:
A=-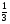 B=-
B=-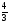 C=
C=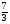
Уравнение плоскости MNK имеет вид:
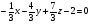
Умножим обе части уравнения на -3. Тогда коэффициенты станут целыми:
x+4y+7z+6-0
Вектор 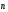 (1; 4; -7) - это нормаль к плоскости MNK.
(1; 4; -7) - это нормаль к плоскости MNK.
Если плоскость проходит через начало координат, то D=0 (так как D≠0 не позволит получить верное числовое равенство).
Уравнение плоскости, проходящей, через заданную точку 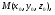 имеет вид:
имеет вид:
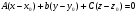
Уравнение плоскости можно составить и с помощью определителя третьего порядка :
Пусть имеем точки
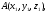
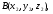
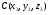 ,
,
Тогда уравнение плоскости, проходящей через эти три точки ,будет иметь вид:
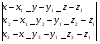 =0
=0
4.3 Угол между плоскостями равен углу между нормалями к этим плоскостям:
cos φ= 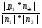
При пересечении двух плоскостей образуется четыре угла . Мы берем меньший из них. Поэтому в формуле стоит модуль скалярного произведения - чтобы косинус угла был неотрицателен.
Задача 2
В кубе ABCDA1B1C1D1 точки E и F с середины ребер соответственно A1B1 и
A1D1. Найдите косинус угла между плоскостями AEF и BDD1.
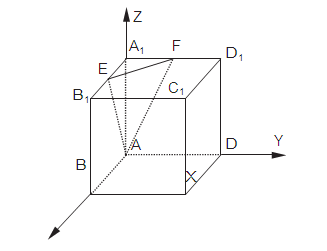
Видно, что плоскости AEF и BDD1 пересекаются где-то вне куба. В классическом решении пришлось бы строить пересечения. Но координатный метод значительно всё упрощает. Достаточно отметить координаты нужных точек и найти угол между нормалями к плоскостям AEF и BDD1.
A(0; 0; 0), C(1; 1; 0)
Сначала - нормаль к плоскости BDD1. Мы можем подставить координаты точек B, D и D1 в уравнение плоскости и найти координаты вектора нормали. А можно увидеть нужную нормаль на чертеже. Ведь плоскость BDD1 - это диагональное сечение куба. Вектор 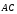 перпендикулярен этой плоскости.
перпендикулярен этой плоскости.
Итак, первый вектор нормали у нас уже есть: 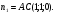
Напишем уравнение плоскости AEF.
A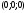 E
E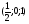 F
F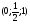
Составим уравнение плоскости:
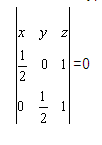
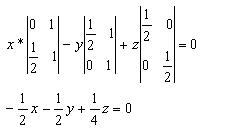

Уравнение плоскости AEF: 2x+2y-z=0
Нормаль к плоскости AEF: 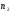 (2; 2; -1)
(2; 2; -1)
Найдем угол между плоскостями: 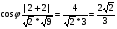
4.4 Угол между прямой и плоскостью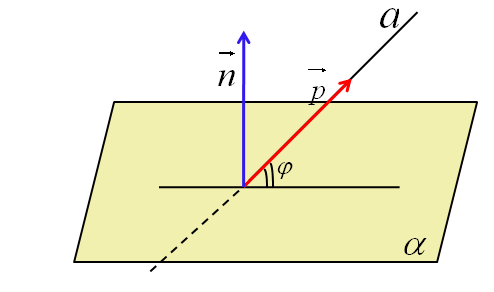
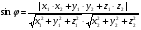

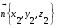
Задача 3.
В правильной четырехугольной пирамиде SABCD, все ребра которой равны 1, найдите угол между прямой DE, где E-середина апофемы SF грани ASB грани и плоскостью ASC
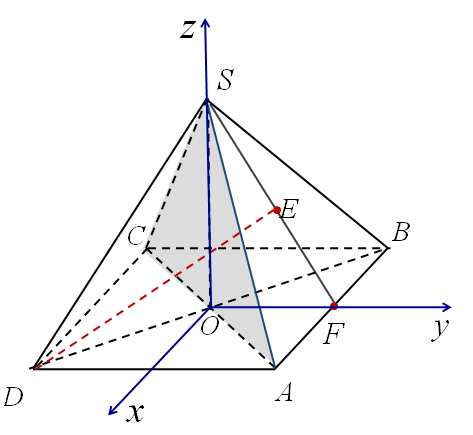
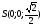
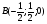
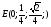
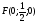

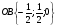
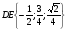
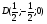
OB - вектор нормали плоскости ASC
DE - направляющий вектор прямой
OB - 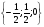 - вектор нормали плоскости ASC
- вектор нормали плоскости ASC
DE - 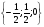 - вектор направляющей вектор прямой DE
- вектор направляющей вектор прямой DE
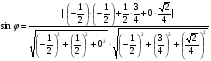
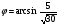
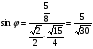 Ответ:
Ответ:
4.5 Расстояние от точки до плоскости
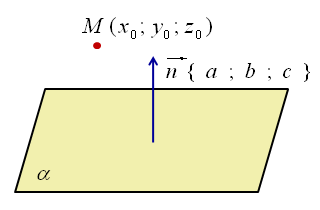
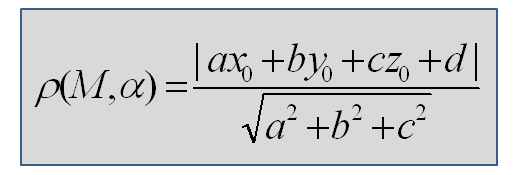
Задача 4
В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 , все рёбра которой равны 1, найдите расстояние от точки E до прямой B1C1.
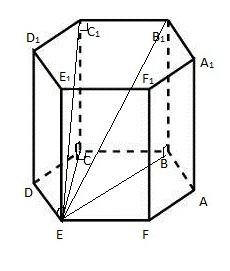
Решение (1 способ)
1) Рассмотрим ΔCDE:
по теореме косинусов:
СЕ2 = 2СD2 - 2CD2 cos120° = 2 + 2*1/2 = 3 =>
CE = 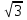
2) Рассмотрим ΔС1СЕ: он прямоугольный, т.к. С1С перпендикулярна плоскости нижнего основания => CC1 перпендикулярна СЕ.
По теореме Пифагора:
С1Е2 = (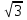 )2 + 12 = 4, С1Е = 2
)2 + 12 = 4, С1Е = 2
3) Рассмотрим ΔBCE: он прямоугольный , т.к. 120° - 60°:2 = 90° (из ΔCDE)
ВЕ2 = (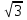 )2 + 12 = 4, ВЕ = 2
)2 + 12 = 4, ВЕ = 2
4) Рассмотрим ΔВВ1Е: он прямоугольный, т.к. ВВ1 перпендикулярна ВЕ,
по теореме Пифагора:
В1Е2 = В1В2 + ВЕ2 = 4 + 1 = 5, ВЕ = 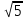
5) Рассмотрим ΔВ1С1Е:
С1Е = 2, С1В1 = 1, В1Е = 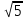 , т.е. 22 + 12 = (
, т.е. 22 + 12 = (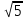 )2. Таким образом, по теореме обратной теореме Пифагора, ΔВ1С1Е - прямоугольный, угол В1С1Е = 90°
)2. Таким образом, по теореме обратной теореме Пифагора, ΔВ1С1Е - прямоугольный, угол В1С1Е = 90°
6) Искомое расстояние от точки Е до прямой В1С1 - это длина С1Е = 2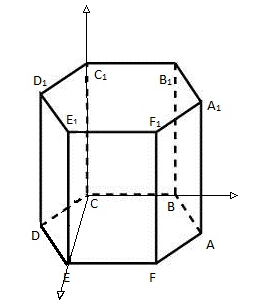
2 способ
1) Поместим призму в прямоугольную систему координат, расположив координатные оси, как показано на рисунке. СС1, СВ и СЕ попарно перпендикулярны, поэтому можно направить вдоль них координатные оси. Получаем координаты:
С1 (0;0;1), Е (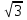 ;0;0), В1 (0;1;1)
;0;0), В1 (0;1;1)
2) Найдем координаты векторов С1В1 и С1Е:
С1В1 (0;1;0), С1Е (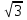 ;0;-1).
;0;-1).
3) Найдем косинус угла между С1В1 и С1Е, используя скалярное произведение векторов С1В1 и С1Е:
cosβ = 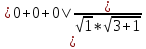 = 0 => β = 90° => C1E - искомое расстояние.
= 0 => β = 90° => C1E - искомое расстояние.
4) С1Е = 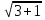 =2
=2
4.6 Расстояние между скрещивающимися прямыми
в пространстве - это длина их общего перпендикуляра. Общий перпендикуляр скрещивающихся прямых - отрезок с концами на этих прямых, перпендикулярный обеим этим прямым.
Если прямые в пространстве пересекаются, расстояние между ними считается равным 0.
Пусть есть не пересекающиеся в пространстве прямые a и b.
Построим плоскости α и β так, чтобы эти плоскости были параллельны, плоскость α содержала в себе прямую a, плоскость β содержала в себе прямую b.
Расстоянием между прямыми a и b будет расстояние между плоскостями α и β.
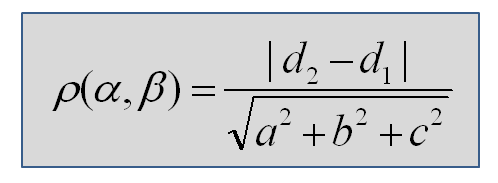
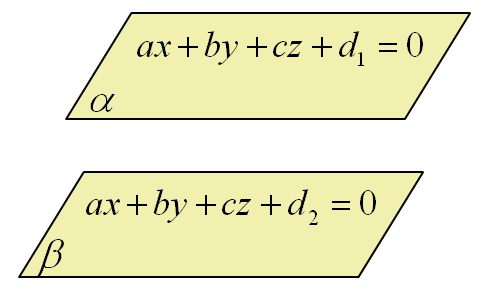
Литература:
-
Александров А.Д. и др
. Геометрия для 10-11 классов: Учеб. пособие для учащихся школ и классов с углубленным изучением математики . Просвещение, 1992.
2. Ю.М.Нейман, Т.М. Королева, Е.Г. Маркарян .
Математика: ЕГЭ: Учебно-справочные материалы «Просвещение», 2011.
3 . Погорелов А.В.
Геометрия: Учеб. для 7-11 кл. сред. шк., 4-е изд. - М.: Просвещение, 1993.
4. Смирнов В. А.
ЕГЭ 2011. Математика. Задача С2. Геометрия. Стереометрия
. Под ред. А. Л. Семенова и И.В.Ященко. МЦНМО, 2011.
5. Холева, О. В.
Нахождение углов между прямыми и плоскостями (координатно-векторный метод) . Математика в школе. - 2011. - №4.


