- Преподавателю
- Математика
- Статья по истории образования
Статья по истории образования
| Раздел | Математика |
| Класс | - |
| Тип | Другие методич. материалы |
| Автор | ЮЛИНА Н.А. |
| Дата | 25.09.2014 |
| Формат | doc |
| Изображения | Есть |
УДК 51(091)
Изложение основ арифметики и алгебры в учебниках
Л. Эйлера и Т.Ф. Осиповского. Сходство и различие
О.О. Барабанов, Н.А. Юлина
Аннотация. Исследуется эволюция научно-педагогической математической мысли в российском образовании второй половины XVIII - начала XIX века путём сопоставления учебников Л. Эйлера «Руководство к арифметике» (1740), «Универсальная арифметика» (1768) и первого тома «Курса математики» (1802) Т.Ф. Осиповского. Первый аспект сравнения - состав математического практикума, второй - проблема имени и значения.
Введение. В 2007 году весь научный мир отмечал трёхсотлетие со дня рождения великого математика Леонарда Эйлера, который прославился не только своими теоремами, но и фундаментальными трудами в области математического образования. Известно, какое важное значение имели для России учебники Л. Эйлера [1] (далее просто «Руководство к арифметике I») и [2] (далее просто «Универсальная арифметика I»). Эти учебники (далее просто Учебники Эйлера) были обращены к широким слоям общества и содержали изложение основ математики, начиная с самых элементарных азов и заканчиваясь алгеброй рациональных, иррациональных, логарифмических выражений, прогрессий и простейших рядов. Гений Л. Эйлера обеспечил этим учебникам высокий уровень математической строгости и четкую последовательность изложения материала. Учебники Эйлера на протяжении многих десятилетий надёжно служили математическому образованию в России. Однако в силу ещё недостаточной развитости российского образования круг читателей Учебников Эйлера был первоначально весьма узким и имел к тому же сословный характер.
Наиболее внимательными читателями Учебников Эйлера были, разумеется, ещё немногочисленные отечественные математики-педагоги, такие как Н.Г. Курганов, Д.С. Аничков, С.Е. Гурьев, Е.Д. Войтяховский, Т.Ф. Осиповский и др. Не собираясь соперничать с великим Л. Эйлером в научном плане, каждый из них приходил к необходимости собственного изложения тех разделов математики, которые составили содержание Учебников Эйлера. Модификации, предпринятые отечественными авторами по материалу Учебников Эйлера, в основном сводились к стилистическим изменениям. Однако с точки зрения педагогической целесообразности эти изменения приобретали содержательный смысл. Кроме того, российские интерпретаторы Л. Эйлера снабжали свои курсы оригинальными задачами и не боялись высказывать собственные мысли методологического характера. Для сопоставления с Учебниками Эйлера мы избрали первый том «Курса математики» Т.Ф. Осиповского [3], как лучший (см. [4]) из российских учебников по арифметике и алгебре на начало XIX века.
Основной целью настоящей работы является исследование эволюции научно-педагогической математической мысли в российском образовании второй половины XVIII - начала XIX века путём сопоставления Учебников Эйлера и соответствующего материала из первого тома «Курса математики» Т.Ф. Осиповского. Более точно, сопоставляться будут: «Руководство к арифметике I» Эйлера и «Частная арифметика» - первая часть первого тома «Курса математики» Т.Ф. Осиповского, и, отдельно, «Универсальная арифметика I» Эйлера и «Общая арифметика или алгебра I» - первое отделение второй части первого тома «Курса математики» Т.Ф. Осиповского. Первый аспект сравнения - состав математического практикума. Второй аспект кратко можно сформулировать как «проблема имени и значения». Начнём, однако, с кратких исторических справок.
Учебники Леонарда Эйлера: «Руководство к арифметике I», «Универсальная арифметика I». «Руководство по арифметике I» написано Л. Эйлером в 1735 году на немецком языке. На русский язык первую часть этого руководства перевёл адъюнкт Академии наук В.Е. Ададуров. Она была издана в 1740 году. Перевод на русский язык второй части «Руководства по арифметике», выполненный студентом В. Кузнецовым, был издан в 1760 году.
В «Руководстве к арифметике I» излагаются законы арифметики и алгоритмы решения простейших арифметических задач. Обстоятельный анализ «Руководства к арифметике I» содержится в работе [5]. В этой работе отмечается, что первостепенную роль Л. Эйлер в своём учебнике отводил теории.
Продолжением «Руководства к арифметике I» стала «Универсальная арифметика I», которую Л. Эйлер, уже будучи слепым, продиктовал своему слуге. Перевод на русский язык первого тома «Универсальной арифметики», выполненный студентами П. Иноходцевым и И. Юдиным, был издан в 1768 году при Императорской Академии Наук и предшествовал изданию немецкого подлинника «Vollständige Anleitung zur Algebra, St-Peterburg, 1770» (в буквальном переводе на русский - «Полное руководство по алгебре») в двух томах. Разницу в названиях следует понимать как дань, отданную переводчиками традиции, восходящей к И. Ньютону, лекции по алгебре которого были опубликованы в 1707 году Вистоном под заглавием «Arithmetica Universalis». Согласно [6] «Универсальная арифметика I» Л. Эйлера определила основное содержание и характер учебного предмета алгебры вплоть до начала XX века и стала прототипом учебника элементарной алгебры. Этот учебник неоднократно перерабатывался и был переведён на многие европейские языки. Так, к французскому переводу Алгебры Эйлера Ж. Лагранж написал свои знаменитые прибавления, относящиеся к неопределённому анализу.
«Курс математики» Тимофея Фёдоровича Осиповского. Известно, что Леонард Эйлер написал много книг и статей, причём значительная часть из них была издана при его жизни. В этом к нему судьба благоволила. Нельзя сказать того же самого про другого фигуранта нашего сопоставления - Тимофея Фёдоровича Осиповского (02.02.1766-12.06.1832). Судьба последнего была более чем драматична, см. [7, 8], а имя оказалось полузабыто. Эти обстоятельства заставляют нас уделить личности Т.Ф. Осиповского здесь чуть больше места, чем предписано темой статьи. Т.Ф. Осиповский родился в селе Осипово Ковровского уезда Владимирской губернии в семье попа. Для получения образования юный Тимофей был отдан во Владимирскую семинарию. В числе лучших 150 учеников духовных семинарий России в 1783 (в год смерти Л. Эйлера) Т.Ф. Осиповский был переведен в только что открытую Петербургскую учительскую семинарию. После окончания семинарии (1786) Т.Ф. Осиповский был назначен преподавателем математических наук и русской словесности в главном народном училище в Москве. Там Т.Ф. Осиповский приступил к разработке собственного крупного сочинения, названного им «Курсом математики». В марте 1800 Т.Ф. Осиповский возвращается в Петербургскую учительскую гимназию уже как профессор физики и математики. В это время Московский университет приглашает его возглавить кафедру математики, а Академия наук предлагает ему вступить в число её членов со званием адъюнкта математики. По правилам тех лет для перехода на новую государственную должность нужно было подать прошение на отставку с занимаемой должности. Это условие было противно независимому характеру Т.Ф. Осиповского. Прошение он не подал.
В конце 1802 Т.Ф. Осиповскому было предложено место профессора математики в открываемом Харьковском университете. «По чрезвычайному обременению делами, - пишет Т.Ф. Осиповский, - от коего я даже сделался болен, подумав несколько недель, решился я принять сие предложение, но с тем, чтобы мне не проситься у начальства, а чтобы попечитель сам просил меня у начальства». Так в 1803 Т.Ф. Осиповский оказался в Харькове и как член комитета правления университета с головой погрузился в организационные хлопоты. С момента открытия университета в 1805 и по 1820 Т.Ф. Осиповский читал различные курсы: так называемую чистую математику, прикладную математику, механику, оптику и астрономию. В 1813 Т.Ф. Осиповский избирается ректором, затем переизбирается на следующие трехлетия в 1816 и в 1819. Однако в 1817 году Министерство народного просвещения было преобразовано в Министерство духовных дел и народного просвещения. Одновременно уходит от дел граф С.О. Потоцкий, идеальный попечитель первого устава Российских университетов. Его сменил вице-председатель Библейского общества, мистик З.Я. Карнеев, который считал своим долгом бороться против приверженцев рационального знания. Под покровительством влиятельного попечителя в университете немедленно формируется партия «мистиков», а попросту - невежественных карьеристов, любимым занятием которых было исследование потустороннего смысла чисел и прочее мракобесие. Судьба Т.Ф. Осиповского, одним из девизов которого был «я не знаю никаких таинств в числах», была тем самым предрешена. Осенью 1819 на математическом факультете вводится курс богопознания. Студенты, в большинстве своём ученики Т.Ф. Осиповского, этот курс игнорируют. Это служит основанием для доноса попечителю на ректора. В результате, в ноябре 1820 года Т.Ф. Осиповского (ректора!) увольняют без объяснения причин. Попутно лишают диплома лучшего ученика Тимофея Фёдоровича - Михаила Васильевича Остроградского. Это был глубоко несправедливый поступок властей, нанесший чувствительную рану Харьковскому университету.
После увольнения из Харьковского университета и переезда в Москву Тимофей Федорович живёт на пенсию, недостаточную для его семьи (жена и пять несовершеннолетних детей). Однако материальные трудности не сломили дух Т.Ф. Осиповского как ученого. К нему, также как к М.В. Ломоносову, можно отнести слова Г.В. Белинского «гений умеет торжествовать над всеми препятствиями, какие ни противопоставляет ему враждебная судьба». Он завершает перевод четвёртого тома «Небесной механики» П. Лапласа, в своём отверженном положении умудряется опубликовать две работы по астрономии и продолжает перерабатывать свой объемистый четырехтомный «Курс математики». В 1826, 1831 годах Т.Ф. Осиповский предлагает Министерству издать полностью четыре тома своего «Курса математики», а также сделанный им перевод «Небесной механики», но каждый раз получает отказ.
Научные интересы Т.Ф. Осиповского не ограничивались областью математики. Выдающийся русский учёный оставил после себя оригинальные работы по философии, астрономии, оптике, электричеству и механике. Однако наиболее крупным его произведением, одновременно научным и учебным, стал «Курс математики». Высокие научные и методические достоинства этого курса позволили использовать его не только в университетах, но и в гимназиях, где в сокращенном виде он был официально основным руководством с 1805 по 1812. Первый том «Курса математики», выдержавший три издания, был посвящён, в основном, алгебре, второй том (1801) - геометрии, третий том (1820) - дифференциальным уравнениям и вариационному исчислению, четвёртый (неизданный) том - дифференциальной геометрии. О высоких качествах «Курса математики» Т.Ф. Осиповского писали многие авторы, см., например, [9-12]. Ограничимся здесь только одним отзывом: «Курс математики» Осиповского может быть поставлен наряду с лучшими руководствами того времени; … избравши образцом преимущественно Эйлера, Осиповский по ясности и строгости изложения был достойным последователем великого математика» [9, с. 85-86].
Сравнение математических практикумов по арифметике у Л. Эйлера и Т.Ф. Осиповского. Состав математического практикума в «Руководстве к арифметике I» Л. Эйлера ранее анализировался в работе [5], где предложена классификация задач по их содержательной направленности. Указывается, что «всего в конце глав I-й части Л. Эйлер приводит 38 задач. Из них: на библейские сюжеты - 2, на исторические темы - 3, о размерах Земли - 3, о числе песчинок (по Архимеду) - 1, вычисление дат - 3, вычисление времени - 1, численность войска - 1, денежные расчёты - 8, без конкретного содержания - 16».
Следует отметить, что квалификация фрагмента текста как задачи не всегда имеет однозначное разрешение. Так, иногда трудно провести границу между понятиями пример и задача. Автор [5] пошёл по простому пути. В качестве задач он считал только те вопросы из «Руководства к арифметике I», которые снабжались авторскими номерами. Однако кроме этих вопросов Л. Эйлер, непосредственно в тексте, приводит ещё два невыделенных специальными номерами вопроса, которые по смыслу равнозначны вопросам пронумерованным. На стр. 267 «Руководства к арифметике I» [1] формулируется следующий вопрос:
«Ежели из четырёх человек первый имеет 560 рублей, второй в 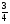 против того числа, которое имеет первый, третий в
против того числа, которое имеет первый, третий в  против второго, а четвёртый в
против второго, а четвёртый в 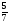 против третьего: то спрашивается, по сколько три последние человека денег имеют?». Разрешение этого вопроса приводится тут же.
против третьего: то спрашивается, по сколько три последние человека денег имеют?». Разрешение этого вопроса приводится тут же.
А на стр. 279 читаем: «Ежели 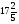 надобно умножить чрез
надобно умножить чрез 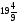 , то произведение найдётся следующим образом…»
, то произведение найдётся следующим образом…»
Очевидно, что оба приведённых фрагмента следует квалифицировать как задачи. Первая из них, по классификации [5], относится, очевидно, к денежным расчётам, вторая - «без конкретного содержания».
На наш взгляд выбранная в работе [5] классификация не удачна для сравнения математических практикумов различных авторов. В самом деле, несерьёзно, например, выглядит класс задач «О числе песчинок». В Таблице 1 предлагается более крупная тематическая классификация задач по прикладному принципу, которая позволяет объективно сравнивать два математических практикума - у Л. Эйлера и Т.Ф. Осиповского. Поясним, что задачи, попавшие в класс «Русский изоморфизм» относятся исключительно к произнесению чисел по-русски. Как видим, задачи такого рода имеют значительное место в «Руководстве по арифметике I» Л. Эйлера и полностью отсутствуют в руководстве Т.Ф. Осиповского. Другое важное различие двух руководств заключается в преобладании задач с абстрактным содержанием у Л. Эйлера по сравнению с Т.Ф. Осиповским.
В задачах из руководства Т.Ф. Осиповского участвуют либо метрологические, либо финансовые, либо торговые, либо домоводческие, либо военные, либо маркитанские операции. В своё время в работе [10] был поднят вопрос о доминировании библейских сюжетов в «Руководстве к арифметике I» Л. Эйлера. В работе [5] отмечено, что по библейским сюжетам у Л. Эйлера имеется всего лишь две задачи. У Т.Ф. Осиповского задач с библейским содержанием нет.
Для полноты картины приводим две аналогичные арифметические задачи из того и другого курса.
Задача из «Руководства к арифметике I» Л. Эйлера. «Ежели бы некоторое войско расположено было продолговатым квадратом, так чтоб в длину онаго квадрата стояло 156, и в ширину 97 человек: спрашивается, из коликаго числа людей состояло бы в таком случае всё оное войско?» [1, глава IV].
Задача из первого тома «Курса математики» Т.Ф. Осиповского. «В некотором полку находится 1372 человека рядовых солдат, и на каждого в год дается жалованья по 7 руб. 45 коп. или по 745 копеек. Спрашивается, сколько на всех их в год выходит?» [3, §6].
Все арифметические задачи у Л. Эйлера снабжены подробными решениями, а у Т.Ф. Осиповского имеется 8 задач (31%) только с одними ответами.
Из приведённых примеров задач у Л.Эйлера и Т.Ф. Осиповского может сложиться ложное впечатление о тривиальности и скучности предмета арифметики в их изложении. Что это далеко не так, видно, например, из следующего фрагмента в «Курсе математики» Т.Ф. Осиповского.
«Положим, что должно раздробить в одинаковые части дроби 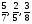 . Для сего помножим числитель и знаменатель каждой дроби на произведение прочих знаменателей, то есть числитель и знаменатель первой дроби помножим на произведение 5 и 8 или на 40; второй дроби числитель и знаменатель на произведение 7 и 8, то есть на 56; третьей дроби числитель и знаменатель на произведение 7 и 5, то есть на 35; тогда вместо первой дроби получится
. Для сего помножим числитель и знаменатель каждой дроби на произведение прочих знаменателей, то есть числитель и знаменатель первой дроби помножим на произведение 5 и 8 или на 40; второй дроби числитель и знаменатель на произведение 7 и 8, то есть на 56; третьей дроби числитель и знаменатель на произведение 7 и 5, то есть на 35; тогда вместо первой дроби получится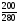 , вместо второй
, вместо второй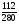 , вместо третьей
, вместо третьей 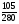 , кои (по §14.3) будут равны прежним дробям. Сие известно в Арифметике под именем приведения дробей к одному знаменателю.
, кои (по §14.3) будут равны прежним дробям. Сие известно в Арифметике под именем приведения дробей к одному знаменателю.
Можно также привесть разные части в одинаковые мелкие доли и следующим образом. Пусть будут предложены те же самые дроби 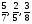 . Перемножим все знаменатели между собою, от чего получится 280. Сие число показывать будет, в какие части единицы или меры все дроби приводить будем, то есть сколько частей равных в одной единице предполагать будем. Итак, найдем сколько сих частей в
. Перемножим все знаменатели между собою, от чего получится 280. Сие число показывать будет, в какие части единицы или меры все дроби приводить будем, то есть сколько частей равных в одной единице предполагать будем. Итак, найдем сколько сих частей в 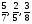 частях единицы содержится. Каждая седьмая часть единицы будет содержать сих частей
частях единицы содержится. Каждая седьмая часть единицы будет содержать сих частей 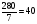 , а в пяти частях таких будет
, а в пяти частях таких будет 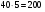 ; пятая часть единицы будет содержать
; пятая часть единицы будет содержать 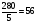 , а две таких части 112;
, а две таких части 112; 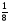 часть единицы содержать будет
часть единицы содержать будет 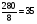 , а
, а 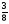 будет содержать 105; по сему показанные дроби превратятся в дроби
будет содержать 105; по сему показанные дроби превратятся в дроби 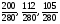 как и выше найдено: и когда много дробей в одинаковые части приводить должно, то сей второй прием бывает гораздо легче первого» [3, §16].
как и выше найдено: и когда много дробей в одинаковые части приводить должно, то сей второй прием бывает гораздо легче первого» [3, §16].
Последняя фраза Т.Ф. Осиповского звучит интригующе. Понять её можно только в предположении, что операции деления и умножения примерно равносложны. Такой, кстати, взгляд характерен для современной нам компьютерной арифметики. Предположим, что складываются  дробей
дробей 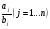 , где для простоты положим числа
, где для простоты положим числа 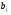 , не имеющими общих делителей. Тогда первый приём приведения к общему знаменателю
, не имеющими общих делителей. Тогда первый приём приведения к общему знаменателю 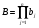 включает суммирование
включает суммирование  произведений
произведений 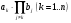 и, тем самым, требует
и, тем самым, требует 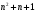 операций умножения и деления. Второй же приём включает суммирование
операций умножения и деления. Второй же приём включает суммирование 
 членов
членов 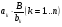 и, тем самым, требует всего
и, тем самым, требует всего 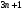 операций умножения и деления. Таким образом, второй приём имеет временную сложность (как сейчас принято говорить) на порядок меньше! Вот, оказывается, что имел в виду Т.Ф. Осиповский, говоря «второй прием бывает гораздо легче первого». Любопытно, что Л. Эйлер, заглядывая, вероятно, на столетия вперёд, даже не упоминает о первом приёме, который, кстати, наиболее привычен для современной средней школы.
операций умножения и деления. Таким образом, второй приём имеет временную сложность (как сейчас принято говорить) на порядок меньше! Вот, оказывается, что имел в виду Т.Ф. Осиповский, говоря «второй прием бывает гораздо легче первого». Любопытно, что Л. Эйлер, заглядывая, вероятно, на столетия вперёд, даже не упоминает о первом приёме, который, кстати, наиболее привычен для современной средней школы.
Сравнение математических практикумов по алгебре у Л. Эйлера и Т.Ф. Осиповского. Для классификации алгебраических задач у Л. Эйлера и Т.Ф. Осиповского приходится применять другой принцип, нежели для задач арифметических. Более того, по-видимому, невозможно ограничится одной единственной шкалой. Мы в данном исследовании опираемся на две различные шкалы сравнения: «алгебраическую» и «прикладную». В первой шкале осуществляется разделение на классы, отвечающие различным алгебраическим инструментам (Таблица 2). Во второй шкале осуществляется разделение на классы, отвечающие различным родам предметной деятельности (Таблица 3).
И у Л. Эйлера и у Т.Ф. Осиповского все алгебраические задачи снабжены полными решениями. По количеству имеется практическое совпадение. Тематические различия незначительны, если не считать превосходства Т.Ф. Осиповского по темам «Биномиальный ряд» и «Логарифмы» и превосходства Л. Эйлера по темам «Рациональные выражения» и «Арифметическая прогрессия». Отметим, что к арифметической прогрессии Л. Эйлер относился с особенной любовью, вводя в рассмотрение далёкие от приложений фигурные (или многоугольные) числа для вычисления сумм арифметических прогрессий.
Общим для Л. Эйлера и Т.Ф. Осиповского является старательное рассмотрение только таких алгебраических задач, которые не приводят к случаю имени (буквы) с отрицательным значением. Впрочем, об этом следует сказать подробнее.
Проблема имени и значения. В истории развития человеческой мысли эта проблема занимает одно из главных мест. Вероятно, первая по времени постановка проблемы имени содержится в диалоге Платона «Кратил». По мнению А.Ф. Лосева «Кратил» принадлежит к числу довольно трудных и замысловатых диалогов Платона» [13, с.594]. В диалоге «Кратил» Сократ говорит, что «об именах немалая есть наука» [13, с.416.]. Однако древнегреческая философия не ушла дальше этимологического толкования имени, понимая под ним зависящую от неё сущность. У Платона имя было не просто идентификатором сущности, которая скрывалась за знаком (именем), но его второй природой. Это отношение к имени довлело над человеческой мыслью около двух тысячелетий. Такое стародавнее отношение к имени удивительным образом сохранилось и до наших дней (об этом говорят современные и газетные и телевизионные материалы). Однако для научного языка естествознания понятие имени имеет очень конкретный и отчётливый смысл. Здесь нет и не может быть мистификаций. За именем в науке, будь то математика, физика, химия, биология, психология и т.п., скрывается объект из заранее определённого класса. Как правило, это объект абстрактного характера, но он является математическим образом реального объекта.
Происхождение имени для неопределённого объекта имеет богатую историю. Возможны самые различные взгляды на этот вопрос. Нас, однако, в рамках данного исследования интересует чисто математический аспект. Если исходить из этой предпосылки, то зародышем «имени» было само понятие числа.
Известно, что в древнегреческой науке каждое число было персональным и наделённым собственным смыслом [14]. Об этом язвительно писал Николай Гумилёв в стихотворении «Слово»:
А для низкой жизни были числа,
Как домашний, подъяремный скот,
Потому что все оттенки смысла
Умное число передаёт.
Заметим, что числа из первого десятка снабжались ещё и теологическим толкованием [15]. В неопределённые времена Древней Греции не существовало ещё понятий величины и значения, а понятие «число» вмещало в себе весь тот комплекс атрибутов, которые составили современное содержание науки. С развитием человеческой мысли эти атрибуты породили, и, наверняка, породят ещё новые смыслы. Об этом хорошо написано в том же стихотворении «Слово» Николая Гумилёва:
Патриарх седой, себе под руку
Покоривший и добро и зло,
Не решаясь обратиться к звуку,
Тростью на песке чертил число.
Великий поэт понимает здесь под словом и звуком, разумеется, имя!
Ф. Виет (XVI век) одним из первых предложил обозначать неизвестные числа буквами. Фактически, это означало настоящую научную революцию. Предложение Ф. Виета автоматически потребовало введение новых понятий - величины и значения. Лучше даже сказать, что произошло первое расщепление понятия величины на имя и значение. Однако под величиной и древние греки, и Ф. Виет, и его великие восприемники (И. Ньютон, Г. Лейбниц и др.) понимали исключительно материальный объект, что требовало в качестве значения величины использовать только положительные числа. Эта концепция величины была стандартом в течение нескольких веков. Даже нуль входил в математический обиход, как значение величины, с большим трудом.
Во избежание недоразумения заметим, что отрицательные числа во всю использовались. Однако отрицательные и комплексные числа в начале XIX в. по-прежнему доставляли немало беспокойства, так как интуитивно казались неприемлемыми. В XIX в., как и в предыдущие столетия, многие их все ещё просто отвергали или довольно злобно критиковали их использование [16, с.179].
Всё-таки избежать использования отрицательных чисел было невозможно. Это хорошо видно и по учебникам Л. Эйлера и по учебнику Т.Ф. Осиповского. Но отрицательные числа не допускались в качестве значений величины! То есть, буква, например, а в любом математическом тексте первой половины XIX века обозначала исключительно положительное число или, в крайнем случае, нуль. В качестве подтверждения этого факта приведём отношение к отрицательным числам знаменитого французского геометра Лазара Николы Карно (1753-1823). Л. Карно прямо утверждал: нелепо думать, будто что-то может быть меньше, чем ничто. Отрицательные числа, по мнению Л. Карно, можно вводить в алгебру как некие фиктивные величины, облегчающие вычисления, но, разумеется, это не настоящие величины, и они могут приводить к неверным заключениям [16, с.180].
Как считает известный историк математики Морис Клайн, «в первой половине XIX в. логические основания алгебры характеризовались попросту их полным отсутствием» [16, с.184].
Научная практика именовать неопределённые объекты произвольной природы и оперировать этими именами начала формироваться с середины XIX века и даже сейчас она не проникла в некоторые очень важные области человеческой практики - к примеру, в бухгалтерию. Что касается математики, то в качестве полноправных значений величины отрицательные числа были допущены только к середине XIX века одновременно с комплексными числами, чем мы обязаны геометрической интерпретации тех и других.
Наиболее значительным продвижением в разработке теории имени следует, вероятно, считать исследования Г. Фреге (1848-1925) - немецкого логика, математика и философа. Основной идеей Г. Фреге было расщепление понятия имени, которое он назвал семантическим треугольником, в одной из вершин которого располагается имя, в другой - обозначаемая этим именем вещь, в третьем - выражаемый этим именем смысл.
Вполне возможно, что история с расщеплением понятия величины (или понятия имени по Г. Фреге) ещё не завершена. Так, уже в наше время в связи с развитием компьютерной техники возник и широко употребляется новый атрибут понятия «величина» - адрес.
Нельзя забывать и об очень важном педагогическом аспекте обучения понятию величины современных школьников и студентов. Дело в том, что в своём интеллектуальном развитии молодой человек с помощью образовательных общественных институтов (семья, детский сад, начальная, средняя, высшая школа) проходит путь, пройденный уже до него мировой наукой. Если учесть какими драматическими, а порой и трагическими, обстоятельствами сопровождался путь науки, то становится понятна сложность задачи современной педагогики, состоящей в том, чтобы за исключительно короткое время сообщить неподготовленному уму ученика знания, накопленные многими поколениями учёных. Современное обучение понятию величины начинается ещё в начальной школе через введение буквенных обозначений. Затем основной задачей становится создание устойчивой привычки к буквенным алгебраическим операциям. Существует тонкая грань между необходимым объёмом времени для создания такой привычки и требованиями других образовательных задач (история, грамматика и т.д.).
Говоря о современной школе, уместно процитировать знаменитого французского историка Марка Блока: «Вовсе не так уж редко, как обычно думают, случается, что для достижения полной ясности надо в исследовании доходить вплоть до нынешних дней» [17, с. 29]. Дело в том, что в связи с сокращением часов, отводимых на изучение математики, большинство современных школьников не по своей вине вынуждены остановиться на условном историческом рубеже мышления времён Л. Эйлера и Т.Ф. Осиповского. Например, уже не удивительно встретить студента первого или второго курса высшего учебного заведения России, которому затруднительно выполнить операцию  .
.
Имя и значение у Эйлера. В статье I главы I первой части «Универсальной арифметики I» Эйлер даёт следующее понятие величины: «всё, что увеличиться или уменьшиться может, или к чему прибавить или убавить можно, называется величина или количество».
В этом определении великий математик создаёт лукавую предпосылку для того, чтобы оперировать с именами величин с отрицательными или комплексными значениями. Фактически, в этом определении Л. Эйлер избегает материализации понятия величины. Однако фраза Л. Эйлера написана так, что все его читатели, включая Т.Ф. Осиповского, понимали под величиной Л. Эйлера именно положительное количество. В последующем тексте «Универсальной арифметики I» Л. Эйлер неоднократно отождествляет величину с числом (§12, §16).
В главе II «Универсальной арифметики I» Л. Эйлер переходит к буквенным обозначениям величин, нигде не поясняя, что за его буквами скрываются положительные числа.
Отрицательные числа Л. Эйлер вводит в главе II первой части «Универсальной арифметики I». То, что именами отрицательных чисел у Л. Эйлера становятся исключительно 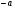 или
или 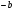 , видно из §31, §32 «Универсальной арифметики I».
, видно из §31, §32 «Универсальной арифметики I».
Наиболее отчётливо взгляд Эйлера на буквенные обозначения проявляется в главе XIII §139 и §140.
«Видели уже мы, что квадраты как из положительных так и отрицательных, (прибыточных или убыточных) чисел, суть всегда положительные или с знаком 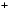 ; ибо
; ибо 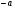 умноженное на
умноженное на 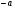 даёт также
даёт также 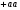 , как и
, как и 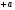 умноженное на
умноженное на 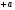 . Для сей причины в прежней главе брали мы числа, из коих квадратной корень извлечь должно, за числа положительныя.
. Для сей причины в прежней главе брали мы числа, из коих квадратной корень извлечь должно, за числа положительныя.
И так ежели случится из отрицательнаго числа извлечь корень квадратной, то конечно должно быть тут великому сомнению, потому что нет никакого такого числа, котораго бы квадрат был отрицательное число; как напр. когда похочешь иметь квадратной корень числа 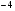 , то сему числу должно быть такому, которое бы само собою помножено, произвело
, то сему числу должно быть такому, которое бы само собою помножено, произвело 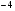 ; следовательно искомое число ни
; следовательно искомое число ни 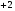 , ни
, ни 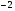 быть не может, ибо как
быть не может, ибо как 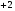 , так и
, так и 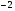 помножены будучи сами собою в произведении дают
помножены будучи сами собою в произведении дают 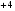 , а не
, а не 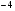 ».
».
Этот отрывок ещё раз подтверждает замалчиваемую самим автором (Л. Эйлером) мысль о том, что буква (имя) скрывает за собой нечто материальное, а, следовательно, положительное число. К тому же самому выводу приходим при чтении §147, §157 «Универсальной арифметики I».
В итоге этого краткого анализа отношения Л. Эйлера к понятиям величины, знака и числа можно утверждать, что Л. Эйлер, избегая строгих определений, предчувствовал какие-то новые связи между ними и возможные новые смыслы, которыми будут наделены эти понятия впоследствии. По крайней мере, в силу своей богатой алгебраической практики Л. Эйлер наверняка понимал эффективность мысленного игнорирования материализации математической величины. Это обеспечивало серьёзные упрощения математических выкладок, что также наверняка Л. Эйлер испытал в своих исследованиях. Уместно в связи с этим упомянуть одну фразу А. Уайтхеда: «Великие успехи мышления часто оказываются результатом счастливых заблуждений. Эти заблуждения возникают в результате упрощений» [18, с.349].
К таким успехам мышления вполне можно отнести современное понимание взаимоотношения имени и значения в математике: за именем может скрываться не только число, но и функция, матрица, векторное поле, граф и т.д. Это позволяет разворачивать различные алгебраические структуры над множествами объектов очень сложной природы и решать с помощью этих структур важнейшие задачи теоретического и прикладного характера.
Имя и значение у Т.Ф. Осиповского. Определение величины у Т.Ф. Осиповского лишено абстрактного смысла, который можно усмотреть у Л. Эйлера (см. выше). Т.Ф. Осиповский придаёт понятию величины совершенно конкретный физический смысл:
«Все то, что может быть подвергнуто измерению, называется величиною; и наука о величинах называется Математикою.
Различие величин произвело различные части Математики; и поелику число различных величин неопределенно, по сему и число частей Математики пределов не имеет.
Когда измерять хотим какую-нибудь величину, то берем для сего какую-нибудь известную величину того же рода, и рассматриваем сколько раз сия величина в исследуемой нами содержится: от сего происходят числа, кои по сему не что иное суть, как содержания величины взятой за меру в величинах исследуемых. И как за меру может быть взята величина и менее и более той, которую исследуем, по сему и числа могут произойти или целые, когда величина, за меру взятая, в исследуемой величине несколько раз нацело содержится, или дроби, когда исследуемая величина часть своей меры составляет.
Величина, за меру принимаемая, как легко видеть можно, не что иное есть, как единица в сравнении с исследуемой величиной; и ежели исследуемая величина изображена будет чрез свою меру, то она называется количеством; ибо количество единиц или количество частей, в ней содержащихся, будет изображать, сколь она велика.
Следовательно, величина и количество суть вещи однозначимые; с той только разностью, что величину можно вообразить без всякого сравнения с другою подобною ей величиною; количество же не иначе понять можно, как посредством сравнения сея величины с подобною ей взятою за меру величиною.
Поелику каждая часть Математики исследует величины свои чрез сравнение их с другими подобными им величинами, и как от сего происходят числа, следовательно, каждая часть Математики иметь должна дело с числами; по сему необходимо всем прочим частям Математики предшествовать должна наука о числах. Наука сия называется Арифметикою».
Из этого отрывка мы видим, что с одной стороны Т.Ф. Осиповский придерживается понятия величины по Л. Эйлеру, с другой стороны сужает это понятие до требований непосредственной измеряемости.
Строго говоря, Л. Эйлер избегает формулировки понятия величины. Затем он это понятие использует под различными названиями: величина, число, количество.
Т.Ф. Осиповскому этого показалось недостаточно. Поэтому он и ввёл своё довольно неожиданное по своей строгости для начала XIX века определение величины (см. выше).
Безусловно, внедрять математические знания в умы неподготовленных учеников можно только на материалистической основе. Затем, после привычки к алгебраическим упражнениям можно надеяться на безупречное оперирование именами переменных. По-видимому, Т.Ф. Осиповский и преследовал эту цель.
Отличие структуры первого тома «Курса математики» Т.Ф. Осиповского от учебников Л. Эйлера. Известна педагогическая проблема выбора между подробнейшим изложением материала и лаконичным его представлением. Эту проблему Т.Ф. Осиповский решил в пользу компактификации изложения Л. Эйлера в одном учебнике с существенными добавлениями своих оригинальных задач. Кроме того, первый том «Курса математики» Т.Ф. Осиповского значительно превосходил по содержанию Учебники Эйлера.
Заключение. В результате проведённого анализа можно констатировать следующее:
- Т.Ф. Осиповский, как и Л. Эйлер решал одну и ту же задачу первоначального обучения русского юношества математике;
- дидактика Т.Ф. Осиповского вполне соответствовала тем шестидесяти годам, которые прошли со времени издания «Руководства к арифметике I» Л. Эйлера. Именно, упростился язык, исключились из рассмотрения те лингвистические аспекты, которым придавал значение Л. Эйлер (они стали неактуальны в связи с определённым расширением сферы народного образования, точнее класса педагогов), значительно сократилось изложение различных разделов начального курса математики, весь материал приобрёл откровенную прикладную направленность;
- значительным отличием учебника Т.Ф. Осиповского от курса Л. Эйлера явилось компактификация материала (50 стр. против 300 стр.) без ущерба содержанию.
Список использованной литературы
-
Эйлер Л. Руководство к арифметике для употребления гимназии Императорской Академии наук. Часть I. - СПб, 1740.
-
Эйлер Л. Универсальная арифметика. Т.I. - СПб, 1768.
-
Осиповский Т.Ф. Курс математики. Т.I. - СПб, Импер. Академия Наук, 1802.
-
Сушкевич А.К. Материалы к истории алгебры в России / Историко-математические исследования. Выпуск IV. Под ред. Г.Ф. Рыбкина и А.П. Юшкевича. - М.: Гос. изд-во технико-теоретической литературы, 1951, С.237-451.
-
Хармац А.Г. Создание Л. Эйлером учебника арифметики нового типа с повышенной в нём ролью теории / Учёные записки МОПИ. Т.202. Вып.6. - М.: 1968, С.373-378.
-
Беляев В.И. «Универсальная арифметика» Л. Эйлера - прототип учебников элементарной алгебры / Из опыта преподавания математики в VIII-X классах средней школы. Под ред. П.В. Стратилатова. - М.: Учпедгиз, 1955, С.130-142.
-
Чириков Г.С. Тимофей Федорович Осиповский // Русская старина, 1876, ноябрь, С. 463-490.
-
Барабанов О.О., Юлина Н.А. Тимофей Фёдорович Осиповский в оценках потомков // Рождественский сборник. Выпуск XIII. Сост. И.Н. Зудина, О.А. Монякова. - Ковров, «Маштекс», 2006, С. 21-26.
-
Сухомлинов М. Материалы по истории образования в России // Журнал министерства народного просвещения, 1865 г., октябрь, С. 9-172.
-
Прудников В.Е. Русские педагоги-математики. Пособие для учителей. - М.: Государственное учебно-педагогическое издание министерства просвещения РСФСР, 1956.
-
Ланков А.В. К истории развития передовых идей в русской методике математики. Пособие для учителей. - М.: Государственное учебно-педагогическое издание министерства просвещения РСФСР, 1951.
-
Бахмутская Э.Я. Тимофей Федорович Осиповский и его "Курс математики" / Историко-математические исследования. Выпуск V. Под ред. Г.Ф.Рыбкина и А.П.Юшкевича. - М.: Гос. изд-во технико-теоретической литературы, 1952, С. 28-74.
-
Платон. Сочинения в трёх томах. Под общ. ред. А.Ф. Лосева и В.Ф. Асмуса. Т. 1. - М.: Мысль, 1968.
-
Щетников А.И. Пифагорейское учение о числе и величине. 6-е изд. - Новосибирск, Артель «Напрасный труд», 2006.
-
Теологумены арифметики. Перевод В.В. Бибихина и А.И. Щетникова. Общая редакция перевода, вступит. статья и комм. А.И. Щетникова. - Новосибирск, Артель «Напрасный труд», 2007.
-
Клайн М. Математика. Утрата определенности. - М: Мир, 1984.
-
Блок М. Апология истории или ремесло историка. - М.: Наука, 1986.
-
Уайтхед А. Избранные работы по философии - М.: Прогресс, 1990.


