- Преподавателю
- Математика
- Реферат по математике на тему Аттрактор Лоренца
Реферат по математике на тему Аттрактор Лоренца
| Раздел | Математика |
| Класс | - |
| Тип | Другие методич. материалы |
| Автор | Уильямс М.(. |
| Дата | 16.05.2015 |
| Формат | docx |
| Изображения | Есть |
Реферат
По дисциплине: Математика
" Аттрактор Лоренца "
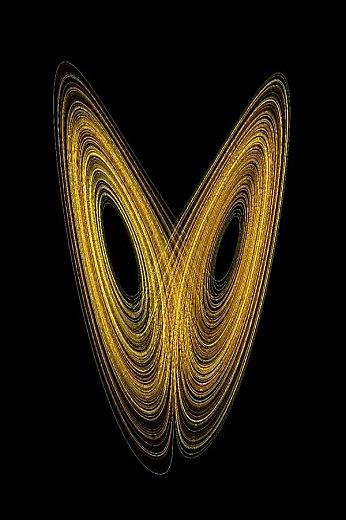
Аттрактор Лоренца
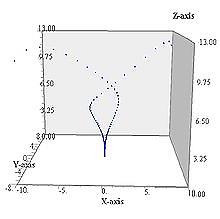
решение системы при r=0,3
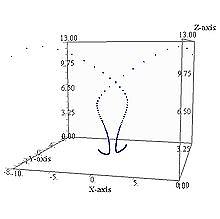
решение системы при r=1,8
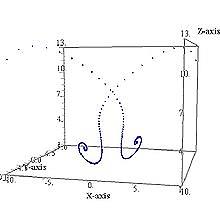
решение системы при r=3,7
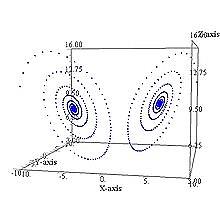
решение системы при r=10
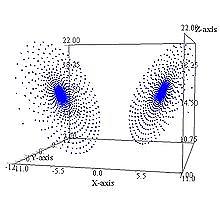
решение системы при r=16
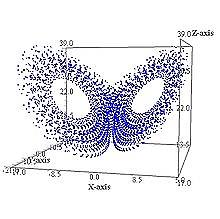
решение системы при r=24,06
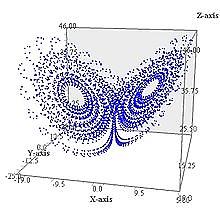
решение системы при r=28 ― собственно, это и есть аттрактор Лоренца
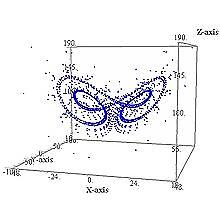
решение системы при r=100 ― виден режим автоколебаний в системе
Аттрактор Лоренца (от англ. to attract - притягивать) ― компактное инвариантное множество 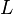 в трехмерном фазовом пространстве гладкого потока, которое имеет определённую сложную топологическую структуру и является асимптотически устойчивым, оно устойчиво по Ляпунову и все траектории из некоторой окрестности
в трехмерном фазовом пространстве гладкого потока, которое имеет определённую сложную топологическую структуру и является асимптотически устойчивым, оно устойчиво по Ляпунову и все траектории из некоторой окрестности 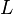 стремятся к
стремятся к 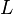 при
при 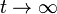 (отсюда название).
(отсюда название).
Аттрактор Лоренца был найден в численных экспериментах Лоренца, исследовавшего поведение траекторий нелинейной системы:
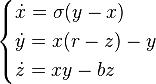
при следующих значениях параметров: σ=10, r=28, b=8/3. Эта система вначале была введена как первое нетривиальное галёркинское приближение для задачи о конвекции морской воды в плоском слое, чем и мотивировался выбор значений σ, r и b, но она возникает также и в других физических вопросах и моделях:
-
конвекция в замкнутой петле;
-
вращение водяного колеса;
-
модель одномодового лазера;
-
диссипативный гармонический осциллятор с инерционной нелинейностью.
Исходная гидродинамическая система уравнений:
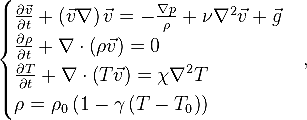
где 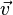 - скорость течения,
- скорость течения, 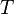 - температура жидкости,
- температура жидкости, 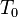 - температура верхней границы (на нижней поддерживается
- температура верхней границы (на нижней поддерживается 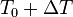 ),
), 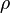 - плотность,
- плотность, 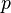 - давление,
- давление, 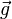 - сила тяжести,
- сила тяжести, 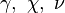 - соответственно коэффициент теплового расширения, коэффициент температуропроводности и кинематической вязкости.
- соответственно коэффициент теплового расширения, коэффициент температуропроводности и кинематической вязкости.
В задаче о конвекции модель возникает при разложении скорости течения и температуры в двумерные ряды Фурье и последующей их «обрезки» с точностью до первых-вторых гармоник. Кроме того, приведённая полная система уравнений гидродинамики записывается в приближении Буссинеска. Обрезка рядов в определённой мере оправдана, так как Сольцмен в своих работах продемонстрировал отсутствие каких-либо интересных особенностей в поведении большинства гармоник.
Применимость и соответствие реальности
Обозначим физический смысл переменных и параметров в системе уравнений применительно к упомянутым задачам.
-
Конвекция в плоском слое. Здесь x отвечает за скорость вращения водяных валов, y и z - за распределение температуры по горизонтали и вертикали, r - нормированное число Рэлея, σ - число Прандтля (отношение коэффициента кинематической вязкости к коэффициенту температуропроводности), b содержит информацию о геометрии конвективной ячейки.
-
Конвекция в замкнутой петле. Здесь x - скорость течения, y - отклонение температуры от средней в точке, отстоящей от нижней точки петли на 90°, z - то же, но в нижней точке. Подведение тепла производится в нижней точке.
-
Вращение водяного колеса. Рассматривается задача о колесе, на ободе которого укреплены корзины с отверстиями в дне. Сверху на колесо симметрично относительно оси вращения льётся сплошной поток воды. Задача равнозначна предыдущей, перевернутой «вверх ногами», с заменой температуры на плотность распределения массы воды в корзинах по ободу.
-
Одномодовый лазер. Здесь x - амплитуда волн в резонаторе лазера, y - поляризация, z - инверсия населённостей энергетических уровней, b и σ - отношения коэффициентов релаксации инверсии и поля к коэффициенту релаксации поляризации, r - интенсивность накачки.
Стоит указать, что применительно к задаче о конвекции модель Лоренца является очень грубым приближением, весьма далёким от реальности. Более-менее адекватное соответствие существует в области регулярных режимов, где устойчивые решения качественно отображают экспериментально наблюдаемую картину равномерно вращающихся конвективных валов (Ячейки Бенара). Хаотический режим, присущий модели, не описывает турбулентной конвекции в силу существенной обрезки исходных тригонометрических рядов.
Интересным является существенно большая точность модели при некоторой её модификации, применяемая в частности для описания конвекции в слое, подвергаемом вибрации в вертикальном направлении либо переменному тепловому воздействию. Такие изменения внешних условий приводят к модулированию коэффициентов в уравнениях. При этом высокочастотные Фурье-компоненты температуры и скорости существенно подавляются, улучшая соответствие модели Лоренца и реальной системы.
Примечательно везение Лоренца при выборе значения параметра  , так как система приходит к странному аттрактору только при значениях, больших 24,74, при меньших поведение оказывается совершенно иным.
, так как система приходит к странному аттрактору только при значениях, больших 24,74, при меньших поведение оказывается совершенно иным.
Поведение решения системы
Рассмотрим изменения в поведении решения системы Лоренца при различных значениях параметра r. На иллюстрациях к статье приведены результаты численного моделирования для точек с начальными координатами (10,10,10) и (-10,-10,10). Моделирование производилось с помощью приведённой ниже программы, написанной на языке Фортран, построение графиков по полученным таблицам - из-за слабых графических возможностей Фортрана с помощью Compaq Array Viewer.
-
r<1 - аттрактором является начало координат, других устойчивых точек нет.
-
1<r<13,927 - траектории спирально приближаются (это соответствует наличию затухающих колебаний) к двум точкам, положение которых определяется формулами:
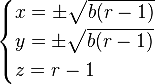
Эти точки определяют состояния стационарного режима конвекции, когда в слое формируется структура из вращающихся валов жидкости.
-
r≈13,927 - если траектория выходит из начала координат, то, совершив полный оборот вокруг одной из устойчивых точек, она вернется обратно в начальную точку - возникают две гомоклинические петли. Понятие гомоклинической траектории означает, что она выходит и приходит в одно и то же положение равновесия.
-
r>13,927 - в зависимости от направления траектория приходит в одну из двух устойчивых точек. Гомоклинические петли перерождаются в неустойчивые предельные циклы, также возникает семейство сложно устроенных траекторий, не являющееся аттрактором, а скорее наоборот, отталкивающее от себя траектории. Иногда по аналогии эта структура называется «странным репеллером» (англ. to repel - отталкивать).
-
r≈24,06 - траектории теперь ведут не к устойчивым точкам, а асимптотически приближаются к неустойчивым предельным циклам - возникает собственно аттрактор Лоренца. Однако обе устойчивые точки сохраняются вплоть до значений r≈24,74.
При больших значениях параметра траектория претерпевает серьезные изменения. Шильников и Каплан показали, что при очень больших r система переходит в режим автоколебаний, при этом, если уменьшать параметр, будет наблюдаться переход к хаосу через последовательность удвоений периода колебаний.
Значимость модели
Модель Лоренца является реальным физическим примером динамических систем с хаотическим поведением, в отличие от различных искусственно сконструированных отображений («зуб пилы», «тент», преобразование пекаря, отображение Фейгенбаума и др.).
Программы, моделирующие поведение системы Лоренца
Borland C
#include
#include
void main()
{
double x = 3.051522, y = 1.582542, z = 15.62388, x1, y1, z1;
double dt = 0.0001;
int a = 5, b = 15, c = 1;
int gd=DETECT, gm;
initgraph(&gd, &gm, "C:\\BORLANDC\\BGI");
do {
x1 = x + a*(-x+y)*dt;
y1 = y + (b*x-y-z*x)*dt;
z1 = z + (-c*z+x*y)*dt;
x = x1; y = y1; z = z1;
putpixel((int)(19.3*(y - x*0.292893) + 320),
(int)(-11*(z + x*0.292893) + 392), 9);
} while (!kbhit());
closegraph();
}
Mathematica
data = Table[
With[{N = 1000, dt = 0.01, a = 5, b = 1 + j, c = 1},
NestList[Module[{x, y, z, x1, y1, z1},
{x, y, z} = #;
x1 = x + a (-x + y) dt;
y1 = y + (b x - y - z x) dt;
z1 = z + (-c z + x y) dt;
{x1, y1, z1}] &,
{3.051522, 1.582542, 15.62388}, N
]
],
{j, 0, 5}];
Graphics3D@MapIndexed[{Hue[0.1 First[#2]], Point[#1]} &, data]
Borland Pascal
Program Lorenz;
Uses CRT, Graph;
Const
dt = 0.0001;
a = 5;
b = 15;
c = 1;
Var
gd, gm: Integer;
x1, y1, z1, x, y, z: Real;
Begin
gd:=Detect;
InitGraph(gd, gm, 'c:\bp\bgi');
x := 3.051522;
y := 1.582542;
z := 15.62388;
While not KeyPressed Do Begin
x1 := x + a*(-x+y)*dt;
y1 := y + (b*x-y-z*x)*dt;
z1 := z + (-c*z+x*y)*dt;
x := x1;
y := y1;
z := z1;
PutPixel(Round(19.3*(y - x*0.292893) + 320),
Round(-11*(z + x*0.292893) + 392), 9);
End;
CloseGraph;
ReadKey;
End.
FORTRAN
program LorenzSystem
real,parameter::sigma=10
real,parameter::r=28
real,parameter::b=2.666666
real,parameter::dt=.01
integer,parameter::n=1000
real x,y,z
open(1,file='result.txt',form='formatted',status='replace',action='write')
x=10.;y=10.;z=10.
do i=1,n,1
x1=x+sigma*(y-x)*dt
y1=y+(r*x-x*z-y)*dt
z1=z+(x*y-b*z)*dt
x=x1
y=y1
z=z1
write(1,*)x,y,z
enddo
print *,'Done'
close(1)
end program LorenzSystem
QBASIC/FreeBASIC(«fbc -lang qb»)
DIM x, y, z, dt, x1, y1, z1 AS SINGLE
DIM a, b, c AS INTEGER
x = 3.051522: y = 1.582542: z = 15.62388: dt = 0.0001
a = 5: b = 15: c = 1
SCREEN 12
PRINT "Press Esc to quit"
WHILE INKEY$ <> CHR$(27)
x1 = x + a * (-x + y) * dt
y1 = y + (b * x - y - z * x) * dt
z1 = z + (-c * z + x * y) * dt
x = x1
y = y1
z = z1
PSET ((19.3 * (y - x * .292893) + 300), (-11 * (z + x * .292893) + 360)), 9
WEND
END
JavaScript и HTML5
var cnv = document.getElementById("cnv");
var cx = cnv.getContext('2d');
var x = 3.051522, y = 1.582542, z = 15.62388, x1, y1, z1;
var dt = 0.0001;
var a = 5, b = 15, c = 1;
var h = parseInt(cnv.getAttribute("height"));
var w = parseInt(cnv.getAttribute("width"));
var id = cx.createImageData(w, h);
var rd = Math.round;
var idx = 0;
i=1000000; while (i--) {
x1 = x + a*(-x+y)*dt;
y1 = y + (b*x-y-z*x)*dt;
z1 = z + (-c*z+x*y)*dt;
x = x1; y = y1; z = z1;
idx=4*(rd(19.3*(y - x*0.292893) + 320) + rd(-11*(z + x*0.292893) + 392)*w);
id.data[idx+3] = 255;
}
cx.putImageData(id, 0, 0);
IDL
PRO Lorenz
n=1000000 & r=dblarr(n,3) & r[0,*]=[3.051522,1.582542,15.62388] & a=5. & b=15. & c=1.
FOR i=0.,n-2. DO r[i+1,*]=r[i,*] + [ a*(r[i,1]-r[i,0]), b*r[i,0]-r[i,1]-r[i,2]*r[i,0], r[i,0]*r[i,1]-c*r[i,2] ]*0.0001
plot,19.3*(r[*,1]-r[*,0]*0.292893)+320.,-11*(r[*,2]+r[*,0]*0.292893)+392.
END
Литература
-
Кузнецов С. П., Лекция 3. Система Лоренца; Лекция 4. Динамика системы Лоренца. // Динамический хаос (курс лекций). - М.: Физматлит, 2001.
-
Saltzman B. Finite amplitude free convection as an initial value problem. // Journal of the atmospheric science, № 7, 1962 - p. 329-341.
-
Лоренц Э. Детерминированное непериодическое движение // Странные аттракторы. - М., 1981. - С. 88-116.


