- Преподавателю
- Математика
- Урок Начала теории графов (9 класс)
Урок Начала теории графов (9 класс)
| Раздел | Математика |
| Класс | 9 класс |
| Тип | Конспекты |
| Автор | Моторина Е.А. |
| Дата | 05.01.2016 |
| Формат | docx |
| Изображения | Есть |
Урок «Начала теории графов»
факультативного курса «теория графов и их приложения» (9 класс)
Начнем изучать теорию графов с задачи, вводя новые понятия по ходу рассмотрения: «Шахматный турнир проводится по круговой системе. Это означает, что каждая пара игроков встречается между собой ровно один раз. В турнире участвуют семь школьников. Известно, что Ваня сыграл шесть партий, Толя - пять, Леша и Дима - по три, Семен и Илья - по две, Женя - одну. С кем сыграл Леша?»
Для решения этой задачи школьнику не требуется как-либо специальных знаний из теории графов, достаточно лишь начальных сведений - понятий вершины и ребра, графа и подграфа, смежности вершин, степени вершины. Чтобы показать это изложим решение данной задачи сначала на интуитивном уровне, а затем формализуем его.
Представим школьный турнир в виде графа: пусть каждому из школьников соответствует одна вершина графа, и в случае, если два школьника сыграли партию, соединим соответствующие вершины ребром. Для краткости обозначим вершины: вершина 1 соответствует Ване, вершина 2 - Толе, вершина 3 - Леше, вершина 4 - Диме, вершина 5 - Семену, вершина 6 - Илье и вершина 7 - Жене.
На первом этапе решения зададим пустой граф (рис. 1)
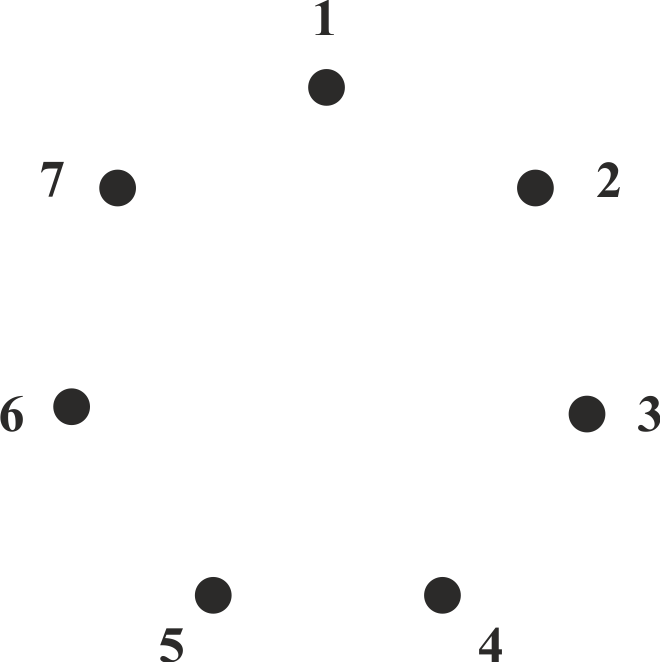
Рис. 1
Выберем школьника, сыгравшего партии со всеми остальными - он должен сыграть на одну партию меньше числа участников, то есть 6 партий. В нашем случае - это Ваня, которому соответствует вершина 1. Соединим ее ребрами со всеми остальными вершинами - ведь Ваня сыграл со всеми школьниками, им сопоставленными. Отметим кружком вершину 1 как вершину для которой установлены все связи и которые не изменятся (рис. 2)
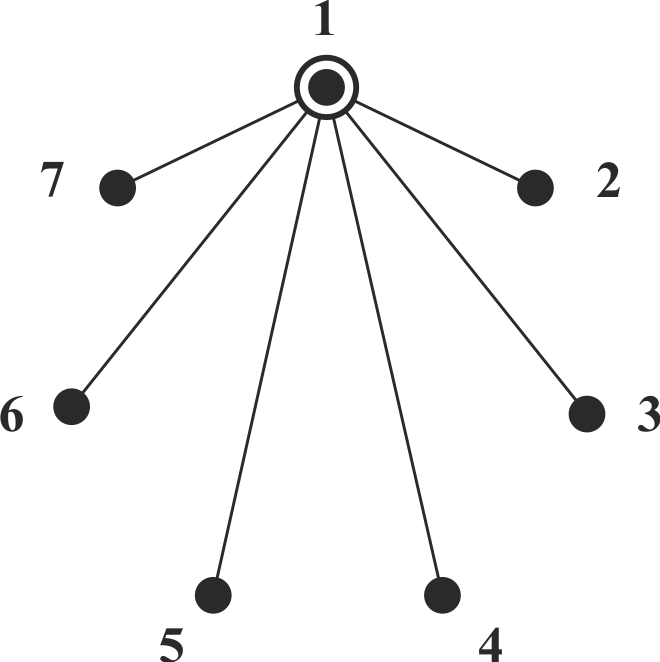
Рис. 2
Далее замечаем, что Женя сыграл всего одну партию, и ее он мог сыграть только с Ваней. Поэтому вершину 7, которая соответствует Жене тоже можно отметить кружком (рис. 3)
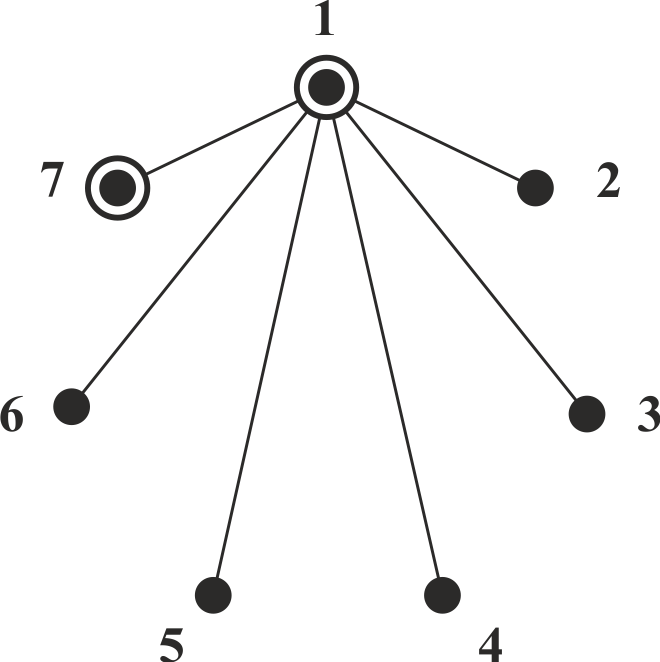
Рис. 3
Выберем школьника, сыгравшего партии со всем, кроме Жени, так как известно, что Женя сыграл только с Ваней. Он должен был сыграть 5 партий, причем одну из них с Ваней, и она уже отмечена на графе. В нашем случае, это Толя. Тогда наш граф примет вид как на рис. 4.
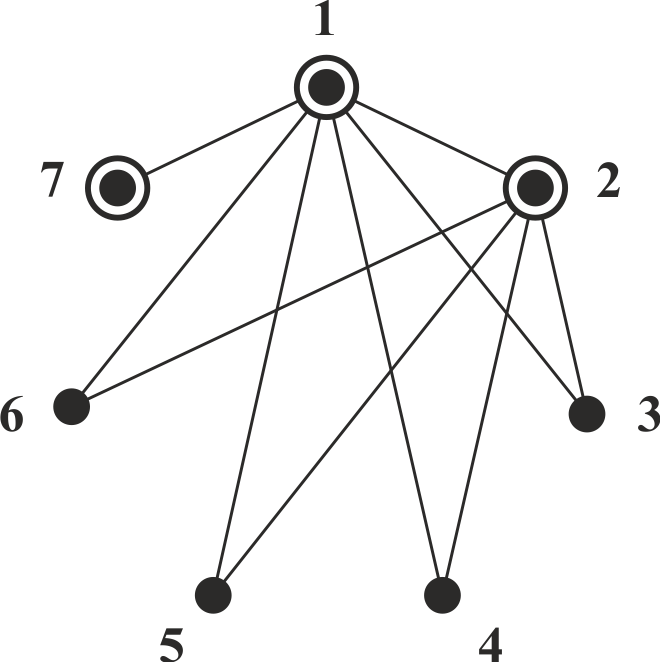
Рис. 4
Замечаем, что для Семена (вершина 5) и Ильи (вершина 6), которые сыграли по 2 партии также установлены все школьники, с которыми они сыграли, и эти вершины тоже можно отметить (рис. 5).
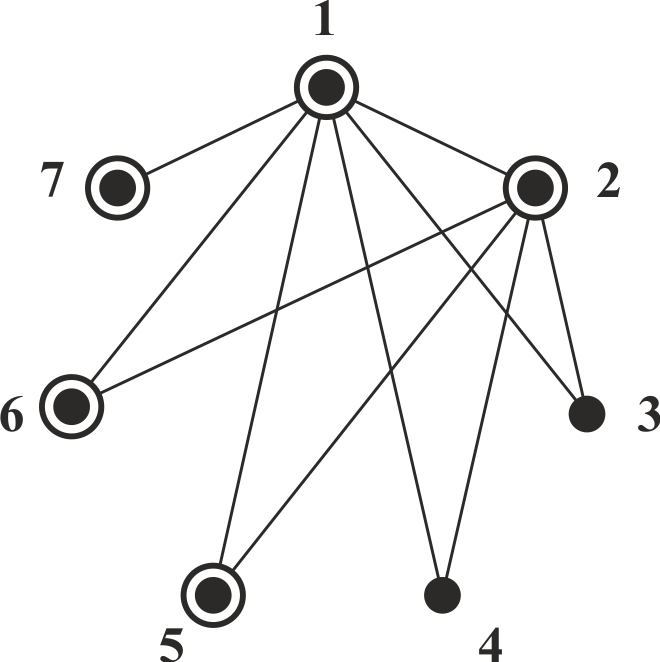
Рис. 5
В графе остались лишь две неотмеченные вершины, которые соответствуют Леше и Диме, сыгравшим по 3 партии. Поскольку в графе уже присутствуют ребра, соответствующие двум партиям, сыгранным Лешей и двум партиям, сыгранным Димой, а все остальные вершины - отмечены, то Леша с Димой эту третью партию могли сыграть только друг с другом (рис. 6).
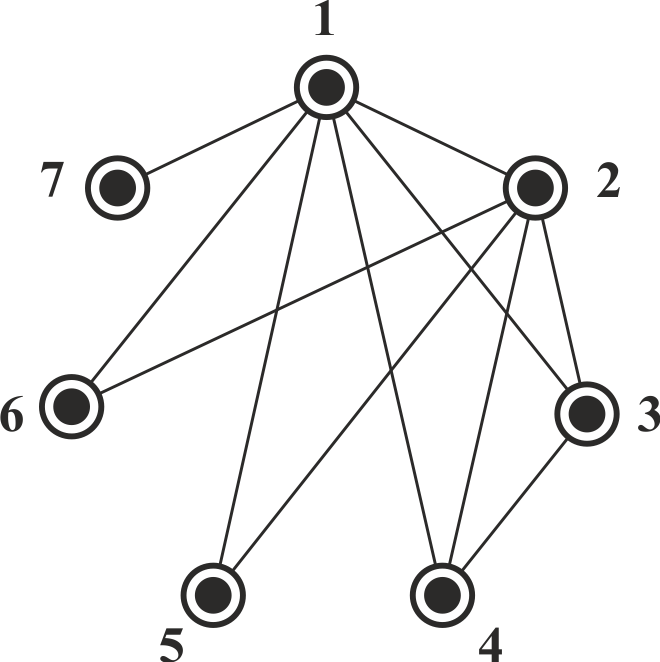
Рис. 6
Итак, мы получили граф полностью отражающий все партии, сыгранные участниками турнира. Установим, с кем сыграл Леша. Ему соответствует вершина 3, которая соединена ребрами с вершинами 1, 2 и 4. Таким образом, Леша сыграл с Ваней, Толей и Димой.
При решении этой задачи на интуитивном уровне, нам потребовались лишь понятия графа, вершины и ребра. Однако после того, как эта задача решена, целесообразно ввести понятия смежности вершин, степени или валентности (обозначим ее deg (v)) вершины и подграфа, а затем разобрать более формализованное решение этой задачи. Представим этот вариант решения (изображения подграфов G1 и G2 для краткости изложения приводить не будем).
Пусть G - граф встреч игроков. Поскольку deg (1) = 6, то эта вершина соединена со всеми вершинами графа G, а так как deg (7) = 1, то она смежна только с вершиной 1. Рассмотрим подграф G1, порожденный множеством вершин {2, 3, 4, 5, 6}. Этот подграф получается из графа G удалением вершин 1 и 7 и всех ребер, выходящих из этих вершин. Поэтому в графе G1, который имеет 5 вершин (рис. 7 а), степени вершин будут deg (2) = 4, deg (3) = deg (4) = 2, deg (5) = deg(6) = 1.
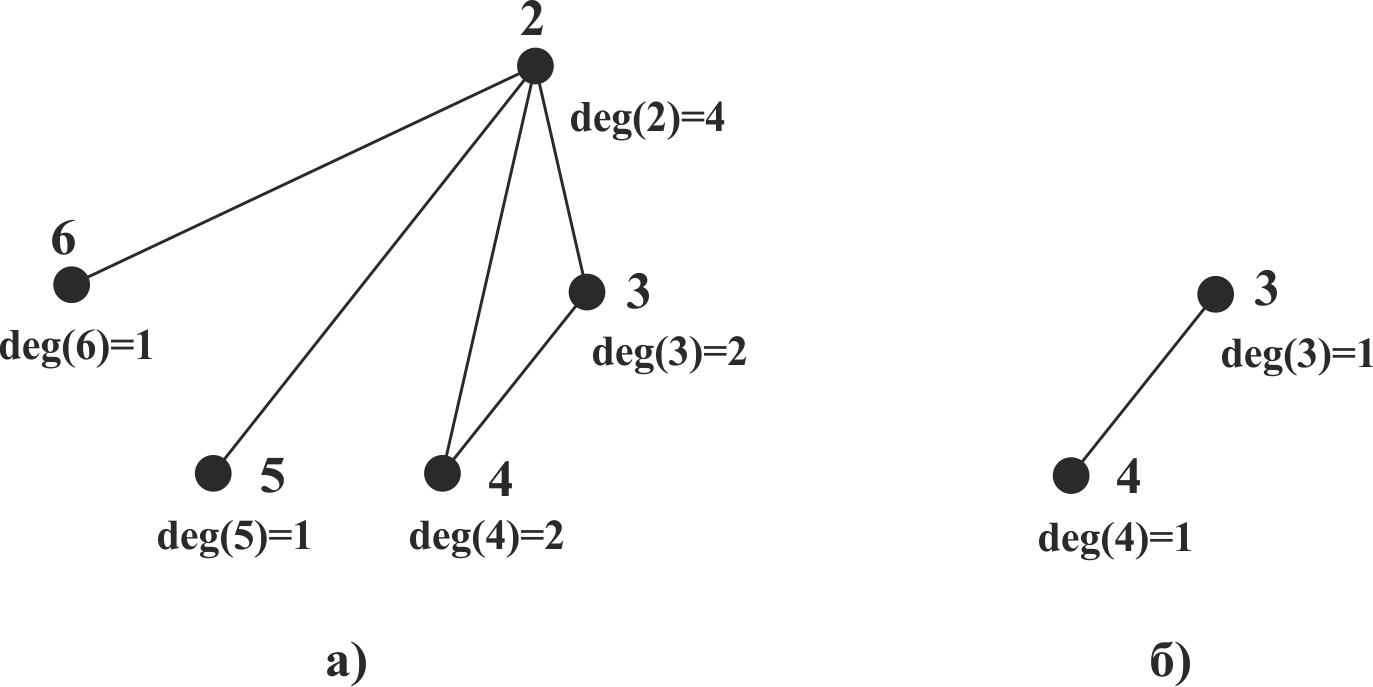
Рис. 7
В графе G1 вершина 2 будет смежной со всеми вершинами, а вершины 5 и 6 - только с вершиной 2. Рассмотрим граф G2, порожденный множеством вершин {3,4}. Этот граф получается из графа G1 после удаления вершин 2, 5, 6 и всех ребер, выходящих из этих вершин. В графе G2 степени вершин 3 и 4 равны единице (см. рис. 7 б).
Возвратив удаленные вершины 2, 5, 6, получим граф G1. Возвратив теперь удаленные вершины 1 и 7, получим требуемый граф G (см. рис. 6). По этому графу можно также определить, с кем встречались остальные школьники.
Как видно из представленного примера задачи, она не требуют большого объема знаний теории графов от школьников, но нацелена на умение рассуждать, использовать различные стратегии решения. Как правило, учащиеся начинают решения подобных задач с попыток «угадать» решение. Однако поняв, что «угадывание» не может учесть все критерии условия, учащиеся вынуждены переходить к планированию стратегии решения задачи, попытке наглядного ее представления с помощью графа, и наконец, к рассуждениям. Все это подчеркивает важность и эффективность теории графов в формировании компетенции и умения применять индуктивные и дедуктивные способы рассуждений, видеть различные стратегии решения задач.
Для занятий по теории графов со старшими школьниками, способными к построению и формализации алгоритмов решений, целесообразно также использовать средства специализированных математических пакетов. В качестве такового, можно предложить бесплатный математический пакет Scilab, имеющий в своем составе библиотеку Metanet, позволяющую оперировать с графами [3].
Литература
-
Мельников О.И. Теория графов в занимательных задачах. Изд. 3-е, испр. и доп. - М.: Книжный дом «ЛИБРОКОМ», 2009
-
Моторина Е.А. Роль и место теории графов в курсе математики общеобразовательной школы / Е.А. Моторина // Педагогические технологии в современном образовании. Часть II: материалы II Международной научно - практической конференции (г. Чебоксары, 16 июня 2014г.). - Образовательный центр «INCEPTUM», 2014. - 526с.
-
Моторина Е.А. Графы в Scilab [Текст] / Е. А. Моторина // Педагогическое мастерство: материалы V междунар. науч. конф. (г. Москва, ноябрь 2014 г.). - М.: Буки-Веди, 2014.
Study of the Elements of Graph Theory in Optional Classes in Secondary School
E.A. Motorina
Gymnasium No 3, Russia, 414000 Astrakhan, pl. Shaumyan, 1a
e-mail: [email protected]
The article discusses the role of graph theory as a model to help solve problems in various areas of human activity are considered competence, which contributes to the formation of the study of graph theory in school, is an illustration for an example of the problem.


