- Преподавателю
- Математика
- Исследовательская работа Софизмы и парадоксы
Исследовательская работа Софизмы и парадоксы
| Раздел | Математика |
| Класс | - |
| Тип | Другие методич. материалы |
| Автор | Рыскина М.В. |
| Дата | 07.03.2015 |
| Формат | docx |
| Изображения | Есть |
VII районная научно-практическая конференция исследовательских, проектных и творческих работ учащихся «Первые шаги в науку»
Софизмы и парадоксы
Исследовательская работа
Автор работы:
Агеева Ирина Юрьевна,
ученица 10 класса
МБОУ «Инсарская СОШ №2»
Руководитель работы:
Рыскина Маргарита Валерьевна,
учитель математики
МБОУ «Инсарская СОШ №2»
Инсар 2015
Содержание.
Введение………………………………………………………...3
-
Определение софизма……………………………………4
-
Софизмы в математике…………………………………..4
-
Алгебраические софизмы………………………..5
-
Геометрические софизмы………………………..6
-
-
Определение парадокса………………………………….7
-
Парадоксы в математике………………………………...7
-
Оптические парадоксы………………………………......9
Заключение…………………………………………………10
Литература………………………………………………….11
Приложения………………………………………………...12
Введение
«Предмет математики настолько серьёзен,
что полезно не упускать случаев
сделать его немного занимательным»
Б. Паскаль
Актуальность: и парадоксы, и софизмы очень поучительны и интересны. Необходимо различать между собой софизмы и парадоксы. Практика обучения математике показывает, что поиск заключенных в софизме ошибок, ясное понимание их причин ведут к осмысленному постижению математики. Такой подход при обучении математике способствует более глубокому ее пониманию и осмыслению и, кроме того, показывает, что математика - это живая наука, а не собрание закостенелых догм, выдуманных по чьей-то злой воле.
Софизм - это ложное высказывание, кажущееся правильным, но содержащее скрытую логическую ошибку.
Знаменитый русский физиолог И.П.Павлов говорил, что "правильно понятая ошибка - это путь к открытию". Софизмы способствовали повышению строгости математических рассуждений и содействовали более глубокому уяснению понятий и методов математики. Для изучающих математику софизмы полезны тем, что развивают логическое мышление, наблюдательность и вдумчивость, приучают тщательно следить за точностью формулировок, правильностью записей и чертежей. Разбор софизмов увлекателен - это изящная гимнастика для ума.
Парадокс - это утверждение, резко расходящееся с общепринятыми мнениями, отрицание того, что представляется "безусловно правильным". Само греческое слово, от которого произведено слово "парадокс", буквально означало "необычное, странное, невероятное".Парадокс в современном значении - это два противоположных утверждения, для каждого из которых имеются убедительные аргументы.
Предмет исследования: софизмы и парадоксы
Цель: изучить данную тему, а именно, узнать что такое софизмы и парадоксы.
Гипотеза исследования: математика без софизмов и парадоксов существовать не может.
Задачи:
1. Познакомиться с парадоксами и софизмами; узнать, в чем их отличие.
2. Понять, как найти ошибку во внешне безошибочных рассуждениях?
3. Узнать, как проклассифицировать «парадоксы» и «софизмы», по каким критериям?
4. Обобщить найденный материал.
-
Определение софизма
Софизм (от греч. - мастерство, умение, хитрая выдумка, уловка, мудрость) - ложное умозаключение, которое, тем не менее, при поверхностном рассмотрении кажется правильным. Софизм основан на преднамеренном, сознательном нарушении правил логики.
Что же такое математический софизм? Математический софизм - удивительное утверждение, в доказательстве которого кроются незаметные, а подчас и довольно тонкие ошибки. История математики полна неожиданных и интересных софизмов, разрешение которых порой служило толчком к новым открытиям. Очень часто понимание ошибок в софизме ведет к пониманию математики в целом, помогает развивать логику и навыки правильного мышления. Если нашел ошибку в софизме, значит, ты ее осознал, а осознание ошибки предупреждает от ее повторения в дальнейших математических рассуждениях. Софизмы не приносят пользы, если их не понимать. Что касается типичных ошибок в софизмах, то они таковы: запрещенные действия, пренебрежение условиями теорем, формул и правил, ошибочный чертеж, опора на ошибочные умозаключения. Нередко, ошибки, допущенные в софизме, настолько умело скрыты, что даже опытный математик не сразу их выявит. Именно в этом и проявляется связь математики и философии в софизмах. На самом деле, софизм- гибрид не только математики и философии, но и логики с риторикой. Основные создатели софизмов - древнегреческие ученые-философы, но тем не менее, они создавали математические софизмы, основываясь на элементарных аксиомах, что еще раз подтверждает связь математики и философии в софизмах. Кроме того, очень важно правильно преподнести софизм, так, чтобы докладчику поверили, а значит, необходимо владеть даром красноречия и убеждения. Группа древнегреческих ученых, начавшая заниматься софизмами как отдельным математическим явлением, назвала себя софистами
-
Софизмы в математике
Как было сказано ранее, в математических софизмах чаще всего используются «запрещенные действия» либо не учитываются условия применимости теорем, формул или правил. Часто понимание людьми ошибок в софизме ведет к пониманию математики в целом, развивает логику и навыки правильного мышления. Поиск ошибки в софизме ведет к ее пониманию и осознанию, а осознавая ошибку, человек имеет больше шансов ее не допустить. Также, в истории развития математики софизмы способствовали повышению точности формулировок и более глубокому пониманию понятий математики. Математические софизмы делятся на алгебраические и геометрические.
-
Алгебраические софизмы
Алгебра - один из больших разделов математики, принадлежащий наряду с арифметикой и геометрией к числу старейших ветвей этой науки. Задачи, а также методы алгебры, отличающие её от других отраслей математики, создавались постепенно, начиная с древности. Алгебра возникла под влиянием нужд общественной практики, в результате поисков общих приёмов для решения однотипных арифметических задач. Приёмы эти заключаются обычно в составлении и решении уравнений. Т.е. алгебраические софизмы - намеренно скрытые ошибки в уравнениях и числовых выражениях.
Всякое число равно своему удвоенному значению.
Запишем очевидное для любого числа a тождество a2 - a2 = a2 - a2, вынесем a в левой части за скобку, а правую часть разложим на множители по формуле разности квадратов, получим a(a - a) = (a + a)(a - a). Разделив обе части на (a - a), получим a = a + a, или a=2a.
Итак, всякое число равно своему удвоенному значению.
Разбор софизма. Здесь ошибочен переход к равенству a=2a. В самом деле, число a-a, на которое делится равенство a(a - a) = (a + a)(a - a) равно нулю. А мы прекрасно знаем, что на ноль делить нельзя.
Чётное число равно нечётному.
Возьмём произвольное чётное число 2n, где n-любое целое число, и запишем тождество 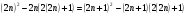 , в справедливости которого нетрудно убедиться, раскрыв скобки.
, в справедливости которого нетрудно убедиться, раскрыв скобки.
Прибавив к обеим частям этого тождества 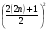 , перепишем его в следующем виде:
, перепишем его в следующем виде: 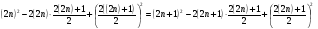 ,
,
или в таком: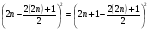 ,
,
Откуда следует, что 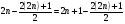 , или 2n=2n+1,
, или 2n=2n+1,
что означает равенство чётного числа нечётному.
Разбор софизма. Из равенства квадратов не следует равенство величин.
Сумма любых двух одинаковых чисел равна нулю.
Возьмём произвольное не равное нулю число a и напишем уравнение x=a. Умножая обе его части на (-4а), получим -4ах=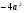 . Прибавляя к обеим частям последнего равенства
. Прибавляя к обеим частям последнего равенства 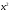 и перенеся член
и перенеся член 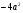 влево с противоположным знаком, получим
влево с противоположным знаком, получим 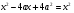 , откуда, замечая, что слева стоит полный квадрат, имеем
, откуда, замечая, что слева стоит полный квадрат, имеем
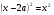 , или х-2а=х. Заменяя в последнем равенстве х на равное ему число а, получим а-2а=а, или -а=а, откуда 0=а+а, т. е. сумма двух произвольных одинаковых чисел а равна 0.
, или х-2а=х. Заменяя в последнем равенстве х на равное ему число а, получим а-2а=а, или -а=а, откуда 0=а+а, т. е. сумма двух произвольных одинаковых чисел а равна 0.
Разбор софизма. Когда мы имеем полный квадрат 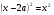 , то /х-2а/=/х/, а так x=a, то 2а-x=x.
, то /х-2а/=/х/, а так x=a, то 2а-x=x.
2.2.Геометрические софизмы
Геометрические софизмы - это умозаключения или рассуждения, обосновывающие какую-нибудь заведомую нелепость, абсурд или парадоксальное утверждение, связанное с геометрическими фигурами и действиями над ними.
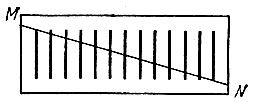
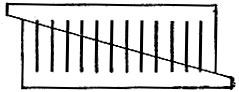
Загадочное исчезновение.
У нас есть произвольный прямоугольник (приложение 1), на котором начерчено 13 одинаковых линий на равном расстоянии друг от друга. Теперь «разрежем» прямоугольник прямой MN, проходящей через верхний конец первой и нижний конец последней линии. Сдвигаем обе половины вдоль по этой линии и замечаем, что линий вместо 13 стало 12. Одна линия исчезла бесследно. Куда исчезла 13-я линия?
Разбор софизма. 13-я линия удлинила каждую из оставшихся на 1/12 своей длины.
Земля и апельсин.
Вообразим, что земной шар обтянут по экватору обручем и что подобным же образом обтянут и апельсин по его большому кругу. Далее вообразим, что окружность каждого обруча удлинилась на 1м. Тогда обручи отстанут от поверхности тел и образуют некоторый зазор. Где зазор будет больше: у апельсина или у Земли?
Разбор софизма. Пусть длина окружности земного шара = C, а апельсина с метрам. Тогда радиус Земли R = C/2p и радиус апельсина r = c/2 p. После прибавки к радиусам 1 метра окружность обруча у Земли будет C + 1, а у апельсина c + 1. Радиусы их соответственно будут: (C + 1)/2p и (c + 1)/2 p. Если из новых радиусов вычтем прежние, то получим в обоих случаях одно и то же. (C + 1)/2p - C/2p = 1/2p - для Земли, (c + 1)/2p - c/2p = 1/2p - для апельсина. Итак, у Земли и у апельсина получается один и тот же зазор в 1/2p метра (примерно 16 см)
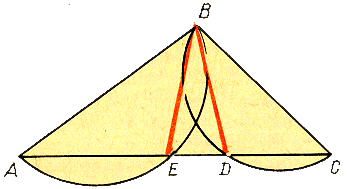
Два перпендикуляра.
Попытаемся «доказать», что через точку, лежащую вне прямой, можно провести два перпендикуляра к этой прямой (приложение2) . С этой целью возьмём треугольник ABC. На сторонах AB и BC этого треугольника, как на диаметрах, построим полуокружности. Пусть эти полуокружности пересекаются со стороной AC в точках E и D. Соединим точки E и D прямыми с точкой B. Угол AEB прямой, как вписанный, опирающийся на диаметр; угол BDC также прямой. Следовательно, BE ^ AC и BD ^ AC. Через точку B проходят два перпендикуляра к прямой AC. В чём ошибка?
Разбор софизма. Рассуждения опирались на ошибочный чертёж. В действительности полуокружности пересекаются со стороной AC в одной точке, т.е. BE совпадает с BD.
-
Определение парадокса.
Парадокс (греч. "пара" - "против", "докса" - "мнение") - это нечто необычное и удивительное, то, что расходится с привычными ожиданиями, здравым смыслом и жизненным опытом.
Парадокс близок софизму. С софизмом их различает то, что парадокс - не преднамеренно полученный противоречивый результат. Таким образом, парадокс не ошибка, однако его появление нельзя объяснить и желанием сознательно исказить положение дел или незнанием какой-то детальной информации. Парадокс коренится глубже и свидетельствует об объективно сложившемся противоречивом состоянии дел, в котором никто не виноват. Парадокс принято также называть антиномией (греческого αντινομια, буквально - противоречие в законе, парадокс,- ситуация, когда в теории доказаны два взаимно исключающие друг друга суждения, причём каждое из этих суждений выведено убедительными с точки зрения данной теории средствами). Парадокс - высказывание, истинность которого не очевидна, справедливое, но неожиданное утверждение. Математический парадокс - высказывание, которое в данной теории равным образом может быть доказано и как истинна, и как ложь. Парадокс - это рассуждение, доказывающее как истинность, так и ложность некоторого суждения, иными словами, доказывающее как это суждение, так и его отрицание.
-
Парадоксы в математике.
Парадоксы были типичными способами постановки проблем в античном мышлении. Сначала парадоксы рассматривались только как продукт философских измышлений, теперь наука признала их полноправными членами сообщества научных проблем.
Парадоксы возникают в современных прикладных науках также часто, как и в древних. В VII в. до н. э. вавилонские жрецы-астрологи заметили, что некоторые планеты временами замедляют движение, пятятся назад, а затем снова продолжают движение в обычном направлении. Гераклид Пантийский смог объяснить "явление блуждающих светил" с помощью математической теории эпицикла. Но при этом оставались другие проблемы - не все светила вели себя по этой схеме. Долгое время ученые с помощью своих теорий (геометрическая, механическая) не могли объяснить "дуализм света" (XVIII-XIX вв.), только предположение Д.К. Максвелла о электромагнитной природе света разрешило эту проблему. Таким образом, можно считать, что парадоксы возникают в науке там, где теория не описывает процессы должным образом. Разрешение таких парадоксальных явлений ведет в свою очередь к возникновению новых теорий.
Парадокс Банаха - Тарского.
Парадокс Банаха - Тарского, или парадокс удвоения шара, говорит, что трёхмерный шар равносоставлен двум своим копиям (приложение 3). Разделяя шар на конечное число частей, мы интуитивно ожидаем, что, складывая эти части вместе, можно получить только сплошные фигуры, объём которых равен объёму исходного шара. Однако это справедливо только в случае, когда шар делится на части, имеющие объём. Суть парадокса заключается в том, что в трёхмерном пространстве существуют неизмеримые множества, которые не имеют объёма. Очевидно, что «куски» в таком разбиении не могут быть измеримыми (и невозможно осуществить такое разбиение какими-либо средствами на практике).
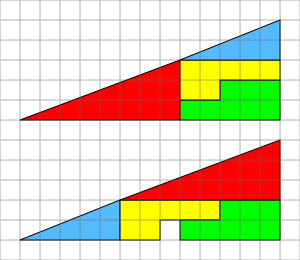
Задача о треугольнике.
Дан прямоугольный треугольник 13×5 клеток, составленный из 4 частей (приложение 4). После перестановки частей при визуальном сохранении изначальных пропорций появляется дополнительная, не занятая ни одной частью, клетка. 1) Перестановка частей. 2) Разрезанный треугольник. 3) «Гипотенуза» на самом деле является ломаной линией. Площади закрашенных фигур, разумеется, равны между собой (32 клетки), однако, то, что визуально наблюдается как треугольники 13×5, на самом деле таковым не является, и имеет разные площади (S13×5 = 32,5 клетки). То есть ошибка, замаскированная в условии задачи, состоит в том, что начальная фигура поименована треугольником (на самом деле это - вогнутый 4-угольник). Это отчётливо заметно на рисунках 1 и 2 - «гипотенузы» верхней и нижней фигур проходят через разные точки: (8,3) вверху и (5,2) - внизу. Секрет в свойствах синего и красного треугольников. Это легко проверить вычислениями. Отношения длин соответствующих сторон синего и красного треугольников не равны друг другу (2/3 и 5/8), поэтому эти треугольники не являются подобными, а значит, имеют разные углы при соответствующих вершинах. Если нижние стороны этих треугольников параллельны, то гипотенузы в обоих треугольниках 13×5 на самом деле являются ломаными линиями (на верхнем рисунке создаётся излом внутрь, а на нижнем - наружу). Если наложить верхнюю и нижнюю фигуры 13×5 друг на друга, то между их «гипотенузами» образуется параллелограмм, в котором и содержится «лишняя» площадь. На рисунке 3 этот параллелограмм приведён в верных пропорциях. По словам Мартина Гарднера, эту задачу изобрёл иллюзионист-любитель из Нью - Йорка Пол Карри в 1953.
Исчезающий квадрат.
Маленький квадрат «исчезает» и «появляется» при повороте частей (приложение 5). Этот парадокс объясняется тем, что сторона (и площадь) нового большого квадрата немного отличается от стороны́(и площади) того, который был в начале. Если в качестве первой фигуры принять тот квадрат, в середине которого нет маленького ромба, дальнейший анализ заметно упростится. Таким образом, можно заключить, что ошибка, замаскированная в условии, состоит в том, что центры вращения составляющих 4-угольников находятся не там, где это представляется при визуальном осмотре картинки (не в точках пересечения их диагоналей). Они находятся в вершинах квадрата, повёрнутого относительно первого квадрата, хотя его стороны параллельны сторонам второго.
5. Оптические парадоксы
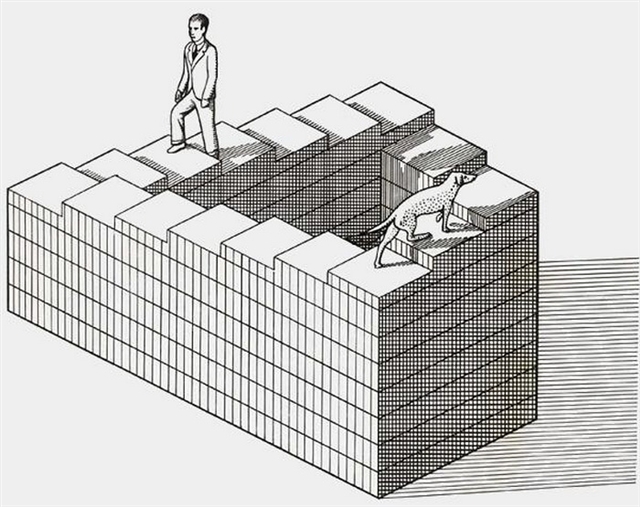
Невозможная фигура - один из видов оптических парадоксов, фигура, кажущаяся на первый взгляд проекцией обычного трёхмерного объекта, при внимательном рассмотрении которой становятся видны противоречивые соединения элементов. Создаётся иллюзия невозможности существования такой фигуры в трёхмерном пространстве. Две известные невозможные фигуры - невозможный треугольник (приложение 6) и невозможный х-зубец (приложение 7). Направление в изобразительном искусстве, нацеленное на изображение невозможных фигур, называется имп-арт. Имп-арт образовано от английского impossible art - невозможное искусство. Целью имп-арта является изображение невозможных фигур и объектов, т.е. оптической иллюзии изображения трехмерного объекта элементы которого расположены в противоречивой, препятствующей однозначному восприятию взаимосвязи. Основателем направления невозможного искусства - имп-арта (imp-art, impossible art) по праву называют шведского художника Оскара Рутесварда. Первую невозможную фигуру он изобразил еще в 30-ые годы XX века - это был невозможный треугольник состоящий из 9 кубиков (приложение 8). Все кубики реальны, но их расположение в трехмерном пространстве невозможно. Этот же художник создал и прототип "невозможной лестницы". Самую известную классическую фигуру "Невозможный треугольник" (приложение 9)создал английский математик Роджер Пенроуз. Он использовал линейную перспективу, а не параллельную, что придало картине глубину и выразительность и, следовательно, большую степень невозможности. Наиболее известным художником имп-арта стал М. К. Эшер. Среди наиболее известных его произведений - картины "Водопад" ( приложение10) и "Восхождение и спуск" (приложение11). Художник использовал эффект "бесконечной лестницы", открытый Рутесвардом. На полотне изображены два ряда человечков: при движении по часовой стрелке человечки постоянно поднимаются, а при движении против часовой стрелки спускаются. Именно ему принадлежит знаменитая фраза «Рисовать - значит обманывать».
Заключение
О математических софизмах и парадоксах можно говорить бесконечно много, как и о математике в целом. Изо дня в день рождаются новые софизмы и парадоксы, некоторые из них останутся в истории, а некоторые просуществуют один день.
Математические софизмы - это лишь часть одного большого течения. Поиск заключенных в софизме ошибок, ясное понимание их причин ведет к осмысленному изучению математики. Обнаружение и анализ ошибки, заключенной в софизме, очень часто оказывается более поучительным, чем просто разбор решений «безошибочных» задач. Эффектная демонстрация «доказательства» явно неверного результата, демонстрация того, к какой нелепице приводит пренебрежение каким-либо математическим правилом, и последующий поиск и разбор ошибки, позволяют понять и «закрепить» математическое правило или утверждение.
Некоторые софизмы приходилось разбирать по нескольку раз, чтобы действительно в них разобраться, некоторые же наоборот, казались очень простыми. Исторические сведения о софистике и софистах помогли нам разобраться, откуда же все-таки началась история софизмов.
Парадоксы - это неожиданные утверждения, противоречащие здравому смыслу или общепризнанным научным теориям. Очень часто их рассматривают как ошибки, хотя в большинстве случаев они таковыми не являются. Обычно парадоксы построены на логически верных заключениях, но их противоречивый результат не является преднамеренным (этим они отличаются от софизмов). Парадоксы известны науке уже более двух тысяч лет. В античные времена были описаны многие парадоксы и для некоторых из них ученые до сих пор не могут найти объяснения и решения. Открываются парадоксы и в наши дни. Обычно подобные открытия сопровождаются кризисами в науке, разрушением старых, проверенных временем теорий и попытками создать новые, которые способны объяснить появившиеся противоречия. Парадоксы присутствуют везде - и в повседневной жизни, и в науке. Практически в каждой научной области исследования существуют свои парадоксы.
Прослеживая историю математики, можно сказать, что во все времена математику спасала какая-нибудь новая идея. Она придавала математике строгость, восстанавливая ее авторитет. Поэтому не стоит бояться парадоксов, ибо они являются двигателями науки.
Благодаря софизмам и парадоксам можно научиться искать ошибки в рассуждениях других, научится грамотно строить свои рассуждения и логические объяснения.
«Все, что без этого было темно, сомнительно и неверно,
математика сделала ясным, верным и очевидным»
М. Ломоносов
Литература
-
«Математические софизмы». Книга для учащихся 7-11 классов. Авторы: А.Г. Мадера, Д.А. Мадера. Издательство Москва «Просвещение» 2003.
-
«Математическая шкатулка». Автор: Ф.Ф. Нагибин. Государственное учебно-педагогическое издательство министерства просвещения РСФСР 1961.
-
«Математика после уроков». Пособие для учителей. Авторы: М.Б.Балк, Г.Д.Балк. Издательство Москва «Просвещение», 1971.
-
«Парадоксы науки». Автор: А.К.Сухотин. Издательство "Молодая гвардия", 1978 г.
Приложения
Приложение 1
Геометрические софизмы
«Загадочное исчезновение»
Приложение 2
Геометрические софизмы
«Два перпендикуляра»
Приложение 3
Парадоксы в математике
«Парадокс Банаха - Тарского»

Приложение 4
Парадоксы в математике
«Задача о треугольнике»
Приложение 5
Парадоксы в математике
«Исчезающий квадрат»

Приложение 6
Оптические парадоксы
«Невозможный треугольник»

Приложение 7
Оптические парадоксы
«Невозможный х-зубец»

Приложение 8
Оптические парадоксы
«Невозможный треугольник, состоящий из девяти кубиков»

Приложение 9
Оптические парадоксы
«Невозможная лестница»
Приложение 10
Оптические парадоксы
«Восхождение и спуск»

Приложение 11
Оптические парадоксы
«Водопад»



