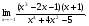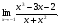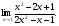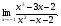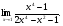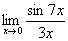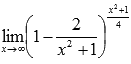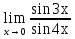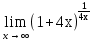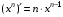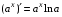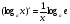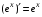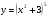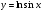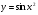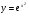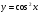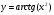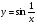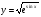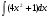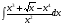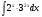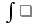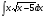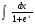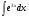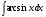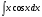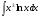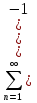- Преподавателю
- Математика
- Методические указания по самостоятельной внеаудиторной работе по высшей математике
Методические указания по самостоятельной внеаудиторной работе по высшей математике
| Раздел | Математика |
| Класс | - |
| Тип | Другие методич. материалы |
| Автор | Цыбикова М.Г. |
| Дата | 22.09.2015 |
| Формат | docx |
| Изображения | Есть |
Содержание
-
Пояснительная записка
4
-
Краткий тематический план видов самостоятельной работы
6
-
Карта самостоятельной работы студентов
7
-
Порядок выполнения самостоятельной работы студентами
10
-
Приложение 1
32
Пояснительная записка
Тенденция современного образования - самостоятельное приобретение знаний под руководством преподавателя.
Самостоятельность - это свобода, независимость, своеобразие, что обозначает не только самостоятельное добывание знаний, но и самостоятельное принятие решений, а, значит, умение брать на себя ответственность.
Самостоятельность - это то качество, которое наряду с активностью, компетентностью, профессиональной мобильностью необходимо современному специалисту.
Для развития этих качеств студенту необходимо заниматься самостоятельной работой.
Самостоятельная работа студентов предполагает многообразные виды индивидуальной и коллективной деятельности студентов, осуществляемые под руководством, но без непосредственного участия преподавателя в специально отведенное для этого аудиторное и внеаудиторное время. Самостоятельная работа - это особая форма обучения по заданию преподавателя, выполнение которой требует творческого подхода и умения получать знания самостоятельно.
Методические указания по выполнению самостоятельной работы внеаудиторной работы для студентов по специальности СПО 230111 Компьютерные сети разработаны в соответствии с рабочей программой учебной дисциплины «Элементы высшей математики».
По учебному плану на изучение учебной дисциплины студентами дневной формы обучения предусмотрено всего 120 часов, из них лекций - 32 часа, практических и лабораторных занятий - 48 часов, самостоятельных занятий - 40 часов.
В результате освоения дисциплины обучающийся должен уметь:
- выполнять операции над матрицами и решать системы линейных уравнений;
- применять методы дифференциального и интегрального исчисления;
- решать дифференциальные уравнения.
В результате освоения дисциплины обучающийся должен знать:
- основы математического анализа, линейной алгебры и аналитической геометрии;
- основы дифференциального и интегрального исчисления.
Методические указания для самостоятельной работы студентов содержат информацию о том, сколько и какие темы выносятся на самостоятельное изучение, основную и дополнительную литературу, вопросы для самопроверки.
Выполненная работа позволит приобрести не только знания, но и умения, навыки, а также поможет выработать свою методику подготовки, что очень важно в дальнейшем процессе обучения. Если потребуется консультация, то ее можно получить у преподавателя в соответствии с графиком консультаций.
Сроки выполнения и виды отчётности самостоятельной работы определяются преподавателем и доводятся до сведения студентов в начале изучения междисциплинарного курса.
Оценка выполненных заданий в баллах проставляется преподавателем в карте-маршруте внеаудиторной самостоятельной работы (приложение 1).
Итоговая сумма набранных студентом баллов, суммируясь с результатами оценки аудиторной работы, составит рейтинговый показатель студента, который может учитываться при проведении итогового контроля.
Перед тем, как приступить к решению примеров, студенту рекомендуется изучить теоретическую часть по теме.
При необходимости можно обратиться за консультацией к преподавателю.
Необходимо сдать выполненные самостоятельные работы преподавателю в срок, определенный педагогом.
Краткий тематический план видов самостоятельной работы
Наименование и краткая характеристика
Кол-во
часов
Вид работы
1
2
3
Тема 1. Элементы линейной алгебры
6
Матрицы и определители
2
Решение примеров
Системы линейных уравнений
4
Решение примеров
Тема 2. Элементы аналитической геометрии
6
Векторы. Операции над векторами.
4
Решение примеров
Прямая на плоскости. Кривые второго порядка.
2
Решение примеров
Тема 3. Основы математического анализа
26
Теория пределов. Предел функции.
2
Решение примеров
Два замечательных предела
2
Решение примеров
Непрерывность функции.
2
Решение примеров
Сложная функция
2
Решение примеров
Производная функции
4
Решение примеров
Дифференциал функции
2
Решение примеров
Функции нескольких переменных
2
Решение примеров
Применение производных в исследовании функций
2
Решение примеров
Неопределенный интеграл
2
Решение примеров
Определенный интеграл
2
Решение примеров
Числовые ряды. Основные свойства рядов.
2
Решение примеров
Признаки сходимости рядов. Знакопеременные ряды. Функциональные ряды.
2
Решение примеров
Тема 4. Обыкновенные дифференциальные уравнения
2
Дифференциальные уравнения первого порядка
2
Решение примеров
Дифференциальные уравнения второго порядка
Итого
40
Карта самостоятельной работы студента
Методические указания по выполнению самостоятельной работы студентами по учебной дисциплине «Элементы высшей математики», состоят из карты самостоятельной работы студента и порядка выполнения самостоятельной работы студентом.
Из данной карты студенты узнают наименования тем, которые вынесены на самостоятельное изучение, обязательные и предоставленные по выбору формы самостоятельной работы, основную и дополнительную литературу.
В карте самостоятельной работы студента предложены названия тем (разделов), наименования вопросов, количество часов для выполнения, форма осуществления работы (обязательная и по выбору студента), а также основная и дополнительная литература, необходимая для выполнения предложенных заданий. Для выполнения самостоятельной работы студентам разрешается пользоваться учебной литературой, которая предложена в списке рекомендуемой литературы или другими источниками по усмотрению студентов. Данная информация представлена в таблице 1.
Задания должны выполняться в тетради (клетчатой) для самостоятельной работы студентов. Работа, выполненная небрежно, будет возвращена студенту без проверки. В тетради оставляют поля шириной 4-5 см.
Если требуется чертеж, то его выполняют карандашом, с помощью чертежных инструментов. При построении чертежа соблюдается масштаб.
Решение задачи или примера должно сопровождаться необходимыми вычислениями, формулами и пояснениями.
Если работа выполнена неудовлетворительно, то студент исправляет её и представляет вторично, или по указанию преподавателя выполняет другой вариант.
Таблица 1
Карта самостоятельной работы студента
№ п/п
Наименование темы
Кол-во часов
Вопросы, рассматриваемые в теме
Обязательная форма осуществления самостоятельной работы
Методы проверки самостоятельной работы, разработанные преподавателем
Основная и дополнительная
литература
1
2
3
4
5
6
8
Тема 1. Элементы линейной алгебры
6
1
Матрицы и определители
2
Матрица, операции над матрицами, определитель
Решение примеров
Проверка выполненных заданий
Омельченко В.П., Курбатова Э.В. Математика. 5-е издание. Ростов-на-Дону: Феникс, 2011
2
Системы линейных уравнений
4
Решение линейных уравнений методом Крамера и методом Гаусса
Решение примеров
Проверка выполненных заданий
«--«--
Тема 2. Элементы аналитической геометрии
6
1
Векторы. Операции над векторами.
4
Векторы, коллинеарные, компланарные векторы, скалярное произведение векторов, модуль вектора, угол между векторами, операции над векторами
Решение примеров
Проверка выполненных заданий
«--«--
2
Прямая на плоскости. Кривые второго порядка.
2
Прямая на плоскости, уравнения прямых
Кривые второго порядка
Решение примеров
Проверка выполненных заданий
«--«--
Тема 3. Основы математического анализа
26
1
Теория пределов. Предел функции.
2
Предел функции
Свойства пределов
Решение примеров
Проверка выполненных заданий
«--«--
2
Два замечательных предела
2
Первый замечательный предел
Второй замечательный предел
Решение примеров
Проверка выполненных заданий
«--«--
3
Непрерывность функции.
2
Непрерывность функции
Точки разрыва
Решение примеров
Проверка выполненных заданий
«--«--
4
Сложная функция
2
Сложная функция
Решение примеров
Проверка выполненных заданий
«--«--
5
Производная функции
4
Производная функции
Таблица производных
Решение примеров
Проверка выполненных заданий
«--«--
6
Дифференциал функции
2
Дифференциал функции
Свойства дифференциалов
Решение примеров
Проверка выполненных заданий
«--«--
7
Функции нескольких переменных
2
Функция нескольких переменных
Решение примеров
Проверка выполненных заданий
«--«--
8
Применение производных в исследовании функций
2
Частная производная
Полный дифференциал
Решение примеров
Проверка выполненных заданий
«--«--
9
Неопределенный интеграл
2
Неопределенный интеграл
Решение примеров
Проверка выполненных заданий
«--«--
10
Определенный интеграл
2
Определенный интеграл
Решение примеров
Проверка выполненных заданий
«--«--
11
Числовые ряды. Основные свойства рядов.
2
Числовые ряды
Основные свойства рядов
Решение примеров
Проверка выполненных заданий
12
Признаки сходимости рядов. Знакопеременные ряды. Функциональные ряды.
2
Признаки сходимости рядов
Знакопеременные ряды
Функциональные ряды
Решение примеров
Проверка выполненных заданий
Тема 4. Обыкновенные дифференциальные уравнения
2
1-2
Дифференциальные уравнения первого порядка
Дифференциальные уравнения второго порядка
2
Дифференциальные уравнения
Общее и частное решения
Дифференциальные уравнения первого порядка
Дифференциальные уравнения второго порядка
Решение примеров
Проверка выполненных заданий
«--«--
Порядок выполнения самостоятельной работы студентом
Тема 1.1. Матрицы и определители
Цель: закрепление навыков вычисления определителей, выполнения операций над матрицами.
Теоретическая часть
Определение 1. Матрицей размером m×n называется прямоугольная таблица чисел, состоящая из m строк и n столбцов. Эту таблицу обычно заключают в круглые скобки.
Определение 2. Две матрицы A и B называются равными, если они имеют одинаковое число строк и столбцов и их соответствующие элементы равны, aij = bij.
Так если 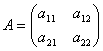 и
и 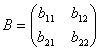 , то A=B, если a11 = b11, a12 = b12, a21 = b21 и a22 = b22.
, то A=B, если a11 = b11, a12 = b12, a21 = b21 и a22 = b22.
Определение 3. Суммой двух матриц A и B называется матрица C, которая определяется по правилу:
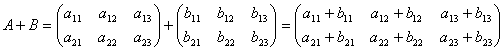 .
.
Определение 4. Произведение матрицы A на число k есть новая матрица, которая определяется по правилу 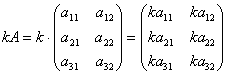 или
или 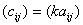 .
.
Формула 1. Формула нахождения определителя второго порядка:
det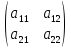 =
= 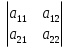 =
= 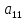 *
*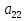 -
- 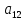 *
*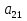 .
.
Формула 2. Формула нахождения определителя третьего порядка:
det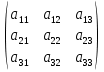 =
=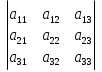 =
=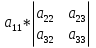 -
- 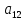 *
*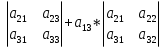 .
.
Задания:
-
Даны матрицы:
-
А =
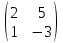 ;
;
В = 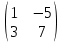
-
А =
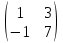 ;
;
В = 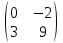
-
А =
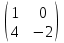 ;
;
В = 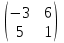
-
А =
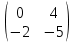 ;
;
В = 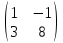
Выполнить операции над матрицами:
-
Сложение матриц;
-
Умножение матрицы на число 5;
-
Умножение матриц
-
Найти определитель матрицы:
-
А =
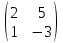 ;
;
В = 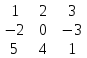
-
А =
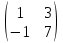 ; В =
; В = 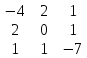
-
А =
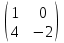 ;
;
В = 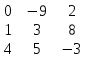
-
А =
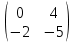 ;
;
В = 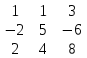
Тема 1.2. Системы линейных уравнений
Цель: закрепление навыков решения систем уравнений методом Крамера и Гаусса.
Теоретическая часть
Системой m линейных уравнений с n неизвестными называется система вида
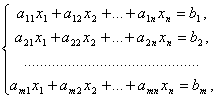
где aij и bi (i=1,…,m; b=1,…,n) - некоторые известные числа, а x1,…,xn - неизвестные. В обозначении коэффициентов aij первый индекс i обозначает номер уравнения, а второй j - номер неизвестного, при котором стоит этот коэффициент.
Коэффициенты при неизвестных будем записывать в виде матрицы, которую назовём матрицей системы.
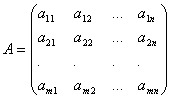
Числа, стоящие в правых частях уравнений, b1,…,bm, называются свободными членами.
Правило Крамера
Рассмотрим систему 3-х линейных уравнений с тремя неизвестными:
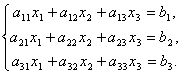
Определитель третьего порядка, соответствующий матрице системы, т.е. составленный из коэффициентов при неизвестных,

называется определителем системы.
Составим ещё три определителя следующим образом: заменим в определителе D последовательно 1, 2 и 3 столбцы столбцом свободных членов
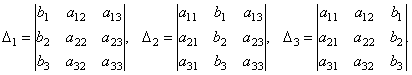
Тогда можно доказать следующий результат.
Теорема (правило Крамера). Если определитель системы Δ ≠ 0, то рассматриваемая система имеет одно и только одно решение, причём
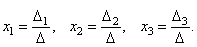
Пример. Решить систему уравнений:
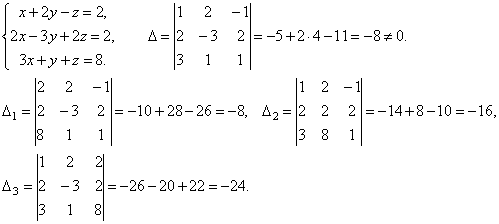
Итак, х=1, у=2, z=3.
Задание:
Решить системы уравнений методом Крамера.
-
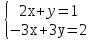 ;
;
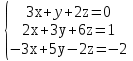
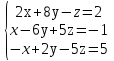
Тема 2.1. Векторы. Операции над векторами.
Цель: закрепление навыков нахождения координат, модулей, произведения векторов, угла между векторами.
Теоретическая часть
Вектором называется направленный отрезок прямой. Точка А называется началом вектора, точка В - концом. Вектор обозначается особым символом над буквенным обозначением - стрелкой: 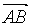 . При этом первым указывается начало вектора, или же
. При этом первым указывается начало вектора, или же 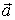 . Прямая, на которой лежит вектор, называется линией действия вектора.
. Прямая, на которой лежит вектор, называется линией действия вектора.
Координаты вектора
Пусть вектор 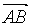 имеет началом точку А(ха, уа) и концом точку В(хb, yb). Координатами вектора
имеет началом точку А(ха, уа) и концом точку В(хb, yb). Координатами вектора 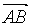 будем называть числа АВх = хb - ха, АВу = уb - уа, АВz = zb - zа.
будем называть числа АВх = хb - ха, АВу = уb - уа, АВz = zb - zа.
Равные векторы
Два вектора называются равными, если один из них может быть получен параллельным переносом другого
Два вектора называются одинаково направленными, если они параллельны и у равных им векторов, имеющих общее начало, концы располагаются по одну сторону от начала
Два вектора называются противоположно направленными, если они параллельны и у равных им векторов, имеющих общее начало, концы располагаются по разные стороны от начала
Нулевым вектором называется вектор, у которого начало совпадает с его концом. Нулевой вектор имеет нулевые координаты.
Длина отрезка, изображающего вектор, называется длиной вектора или модулем вектора. Из формулы расстояния между двумя точками следует формула для нахождения длины вектора
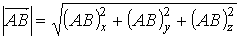 .
.
Два вектора называется коллинеарными, если они лежат на одной прямой или на параллельных прямых.
Если векторы коллинеарны, то их соответствующие координаты пропорциональны. И обратно, если у двух векторов соответствующие координаты пропорциональны, то векторы коллинеарны.
Формула скалярного произведения векторов:
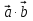 =
= 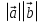 cos
cos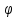 , где
, где 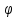 - угол между векторами
- угол между векторами 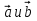 .
.
Формула скалярного произведения векторов, заданных координатами:
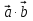 = x1 x2 +y1 y2 +z1 z2.
= x1 x2 +y1 y2 +z1 z2.
Формула угла между векторами:
cos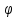 =
= 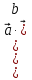 , или в координатах:
, или в координатах:
cos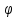 =
= 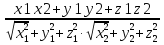 .
.
Задания:
-
Даны точки:
-
А(4; 2), В(6; 1), С(2; 5).
-
А(2; 2), В(5; 0), С(6; 8).
-
А(-2; 0), В(9; 1), С(3; 4).
-
А(5; -2), В(12; 3), С(-7; 9).
Найти координаты векторов АВ, АС, ВС.
-
Найти косинус угла между векторами:
-
a (4; 3; 0) и b(0; 12; 5);
-
a (2; 1; 3) и b(-2; 10; 4);
-
a (3; 2; 1) и b(7; -2; 5);
-
a (0; 5; 4) и b(-3; 10; -4).
-
Найти модуль вектора:
-
a (4; 3; 0) и b(0; 12; 5);
-
a (2; 1; 3) и b(-2; 10; 4);
-
a (3; 2; 1) и b(7; -2; 5);
-
a (0; 5; 4) и b(-3; 10; -4).
-
Найти скалярное произведение векторов
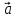 и
и 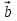 , если:
, если:
-
 =2,
=2, 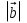 =5,
=5, 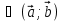 =
= 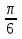 .
. -
 =4,
=4, 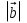 =3,
=3, 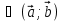 =
= 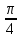 .
. -
 =6,
=6, 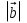 =6,
=6, 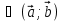 =
=  .
. -
 =8,
=8, 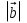 =10,
=10, 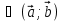 =
= 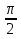 .
.
Тема 2.2. Прямая на плоскости. Кривые второго порядка.
Цель: закрепление навыков составления уравнений прямых, нахождения угла между прямыми, расстояния от точки до прямой.
Теоретическая часть
Уравнения прямой:
-
А(x-x0) + B(y-y0) = 0 - уравнение прямой, проходящей через точку М0(x0, y0) перпендикулярно нормальному вектору
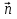 = {A, B}.
= {A, B}. -
Ах + Ву + С = 0 - общее уравнение прямой.
-
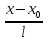 =
=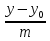 - уравнение прямой, проходящей через точку М0(x0, y0) параллельно направляющему вектору
- уравнение прямой, проходящей через точку М0(x0, y0) параллельно направляющему вектору 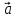 = {l,m} (каноническое уравнение прямой).
= {l,m} (каноническое уравнение прямой). -
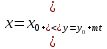 , t
, t - параметрические уравнения прямой.
- параметрические уравнения прямой. -
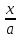 +
+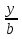 =1 - уравнение прямой в отрезках, где a и b - величины направленных отрезков, отсекаемых на координатных осях Оx и Oy соответственно.
=1 - уравнение прямой в отрезках, где a и b - величины направленных отрезков, отсекаемых на координатных осях Оx и Oy соответственно. -
Уравнение прямой, проходящей через две точки
Пусть в пространстве заданы две точки M 1 (x 1, y 1, z 1) и M2 (x 2, y 2, z 2), тогда уравнение прямой, проходящей через эти точки:
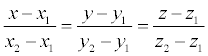
-
y - y0 =k(x - x0) - уравнение прямой, проходящей через точку М0(x0, y0), k - угловой коэффициент прямой, равный тангенсу угла наклона прямой к положительному направлению оси Ох.
-
y = kx + b - уравнение прямой с угловым коэффициентом k; b -величина отрезка, отсекаемого прямой к положительному направлению оси Ох.
-
tg
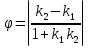 - тангенс острого угла между двумя прямыми y = k1x+b1 и y = k2x+b2.
- тангенс острого угла между двумя прямыми y = k1x+b1 и y = k2x+b2. -
k1 = k2 и k2 = -
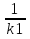 - условия параллельности и перпендикулярности двух прямых y = k1x+b1 и y = k2x+b2.
- условия параллельности и перпендикулярности двух прямых y = k1x+b1 и y = k2x+b2. -
d =
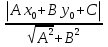 - расстояние от точки М0(x0, y0) до прямой Ах + Ву + С = 0.
- расстояние от точки М0(x0, y0) до прямой Ах + Ву + С = 0. -
x =
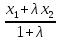 , y =
, y = 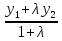 ,
, 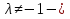 координаты точки М(х, у), делящей отрезок М1М2 в отношении
координаты точки М(х, у), делящей отрезок М1М2 в отношении 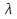 , М1(x1, y1), М2(x2, y2).
, М1(x1, y1), М2(x2, y2). -
x =
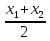 , y =
, y = 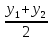 - координаты середины отрезка М1М2, М1(x1, y1), М2(x2, y2).
- координаты середины отрезка М1М2, М1(x1, y1), М2(x2, y2).
Задания:
1. Составить уравнение прямой, проходящей:
-
через точку А(-2, -3) и начало координат.
-
через точку А(3, 5) и начало координат.
2. Определить угол между прямыми:
-
y = -3 x + 7; y = 2 x + 1.
-
y = 2 x + 2; y = 5 x + 3.
-
Даны вершины треугольника АВС: А(-2,3), В(1,12), С(11,6).
Найти:
1) уравнение стороны АВ;
2) уравнение высоты СD, опущенной из вершины С на сторону АВ;
3) уравнение медианы АЕ;
4) уравнение окружности, для которой медиана АЕ служит диаметром.
4. В треугольнике с вершинами А(2,3), В(-1,0), С(4,1) найти длину высоты, опущенной из вершины А на сторону ВС.
Тема 3.1. Теория пределов. Предел функции.
Цель: закрепление навыков нахождения пределов, раскрытия неопределенностей.
Теоретическая часть
Постоянное число b называется пределом функции f(x) при 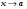 , если для любого малого, наперёд заданного, положительного числа
, если для любого малого, наперёд заданного, положительного числа  найдётся положительное число
найдётся положительное число 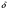 такое, что для всех х
такое, что для всех х а и удовлетворяющих неравенству
а и удовлетворяющих неравенству 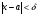 будет выполняться неравенство
будет выполняться неравенство 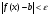
Обозначение: 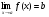 .
.
Вычисление пределов:
1 тип. Предел делителя не равен нулю. В этом случае подставляем вместо переменной её предельное значение и вычисляем полученное выражение.
2 тип. 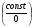 Предел делителя равен нулю. В этом случае предел дроби равен бесконечности.
Предел делителя равен нулю. В этом случае предел дроби равен бесконечности.
3 тип. 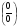 Пределы делителя и делимого равны нулю.
Пределы делителя и делимого равны нулю.
В этом случае получим неопределённость 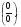 для раскрытия которой нужно выполнить некоторые преобразования данного выражения:
для раскрытия которой нужно выполнить некоторые преобразования данного выражения:
- разложить на множители числитель и знаменатель дроби, затем сократить дробь, подставить вместо переменной её предельное значение и вычислить или
- умножить числитель и знаменатель дроби на сопряжённое выражение, сократить и подставить предельное значение переменной.
Замечание: 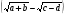 и
и 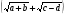 - сопряжённые выражения.
- сопряжённые выражения.
4 тип. 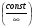 Предел делителя равен ∞, а предел делимого - конечное число. В этом случае предел частного равен 0.
Предел делителя равен ∞, а предел делимого - конечное число. В этом случае предел частного равен 0.
5 тип. 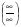 Пределы делителя и делимого равны
Пределы делителя и делимого равны 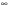 .
.
Если предел делителя и делимого равны 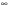 , то получится выражение, не имеющее смысла (неопределённость
, то получится выражение, не имеющее смысла (неопределённость 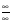 ). Для раскрытия этой неопределённости нужно числитель и знаменатель дроби разделить на переменную в наивысшей степени.
). Для раскрытия этой неопределённости нужно числитель и знаменатель дроби разделить на переменную в наивысшей степени.
Задание: Найти предел функции:
Тема 3.2. Два замечательных предела.
Цель: закрепление навыков нахождения пределов с использованием двух замечательных пределов.
Теоретическая часть
1) 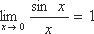 - первый замечательный предел.
- первый замечательный предел.
2) 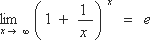 - второй замечательный предел.
- второй замечательный предел.
3) 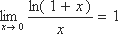 - замечательный логарифмический предел.
- замечательный логарифмический предел.
4) 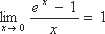 - замечательный показательный предел.
- замечательный показательный предел.
5) 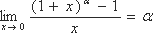 - замечательный степенной предел.
- замечательный степенной предел.
Задание: Найти предел функции с помощью двух замечательных пределов:
Тема 3.3. Непрерывность функции.
Цель: закрепление навыков нахождения пределов с использованием двух замечательных пределов.
Теоретическая часть
Функцию y = f(x) называют непрерывной на отрезке [a, b], если она непрерывна во всех внутренних точках этого отрезка, а на его концах, т.е. в точках a и b, непрерывна соответственно справа и слева.
Определение. Функция f(x) называется непрерывной в точке x0, если 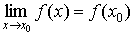 .
.
Определение. Функция f(x) называется непрерывной на множестве Х, если она непрерывна в каждой точке этого множества.
Разрывы функции
Определение. Точки, где функция f(x) не является непрерывной, называются точками разрыва функции f(x).
Для классификации точек разрыва рассмотрим предел слева 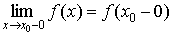 и предел справа
и предел справа  функции f(x). Тогда имеет место следующая классификация точек разрыва.
функции f(x). Тогда имеет место следующая классификация точек разрыва.
1. Устранимый разрыв.
Он имеет место, когда выполнено условие 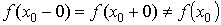 .
.
В данном случае достаточно изменить значение функции в точке x0, чтобы разрыва не стало.
2. Разрыв первого рода (скачок).
Разрыв первого рода (скачок) получается тогда, когда односторонние пределы 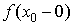 и
и 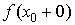 существуют, конечны, но не равны между собой, то есть
существуют, конечны, но не равны между собой, то есть 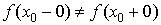 .
.
3. Разрыв второго рода.
Если хотя бы один из 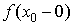 и
и 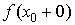 равен ±¥ или не существует, то говорят, что функция f(x) имеет в точке x0 разрыв второго рода.
равен ±¥ или не существует, то говорят, что функция f(x) имеет в точке x0 разрыв второго рода.
Задание: Исследовать функцию и построить график.
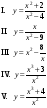
Тема 3.4. Производная функции
Цель: закрепление навыков нахождения производных функций.
Теоретическая часть
Таблица производных основных элементарных функций
-
-
(C)' = 0
11.
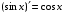
-
(u
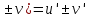
12.
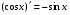
-
(uv)' = u'v + uv'
13.
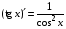
-
(
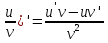
14.
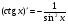
-
(Cu)' = Cu'
15.
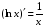
16.
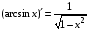
7.
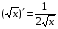 ; 11)
; 11) 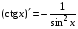 ;
; 17.
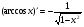 ;
; 18.
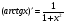
19.
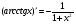
-
Задания:
-
Выучить таблицу производных.
-
Найти производные.
y = x2 + 2x - 1
y= x*2x3
y = ln x + ax
y = sin x + cos x
y = 2x + x2
y = sin ex
y = x2*3x
y = x*(1-lnx)
y = sinx *ex
y = 5arccosx + 5arcsinx
Тема 3.5. Сложная функция
Цель: закрепление навыков нахождения пределов с использованием двух замечательных пределов.
Теоретическая часть
Если функция y зависит от переменной u, т. е. у = f (u), u 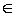 U, а u, в свою очередь, является какой-либо функцией от независимой переменной х, т. е u = g (x), х
U, а u, в свою очередь, является какой-либо функцией от независимой переменной х, т. е u = g (x), х 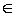 Х, то переменная у называется функцией от функции (или сложной функцией) от x и записывается в виде Y = f(u), u = g(x), или y = f[g(x)].
Х, то переменная у называется функцией от функции (или сложной функцией) от x и записывается в виде Y = f(u), u = g(x), или y = f[g(x)].
Если f и g - дифференцируемые функции, то сложная функция 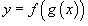 также дифференцируема по x и ее производная равна
также дифференцируема по x и ее производная равна
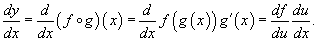
Данная формула показывает, что производная сложной функции равна произведению производной внешней функции на производную от внутренней функции. Важно, однако, что производная внутренней функции вычисляется в точке x, а производная внешней функции - в точке u = g(x)!
Задание: Найти производные сложных функций:
Тема 3.6. Дифференциал функции
Цель: закрепление навыков нахождения дифференциалов функций.
Теоретическая часть
Дифференциалом функции f(x) в точке х называется главная линейная часть приращения функции.
Обозначается dy или df(x).
Из определения следует, что dy = f(x)x или dy = f(x)dx.
Можно также записать: 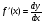
Свойства дифференциала:
Если u = f(x) и v = g(x) - функции, дифференцируемые в точке х, то непосредственно из определения дифференциала следуют следующие свойства:
-
d(u v) = (u v)dx = udx vdx = du dv;
-
d(uv) = (uv)dx = (uv + vu)dx = vdu + udv;
-
d(Cu) = Cdu;
-
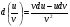 .
.
Дифференциал сложной функции
Пусть y = f(x), x = g(t), т.е. у - сложная функция.
Тогда dy = f(x)g(t)dt = f(x)dx.
Задания:
-
Выучить свойства дифференциала функции.
-
Найти дифференциалы функций:
y = ln2x
y = (arcsin x)2
y = x4 - e2x
y = arcos(1+x2)
Тема 3.7. Функции нескольких переменных
Цель: закрепление навыков нахождения частных производных функции нескольких переменных и полного дифференциала функции.
Теоретическая часть
Переменная u=f(x, y, z, ..,t) называется функцией нескольких переменных, если для любой совокупности значений (x, y, z, ..,t) ставится в соответствие вполне определенное значение переменной u.
Частная производная
Частной производной функции u = f(x, y) по переменной х называется предел отношения частного приращения этой функции по переменной х к приращению рассматриваемой независимой переменной, когда последнее стремится к нулю:
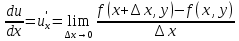 . Аналогично определяем частную производную по переменной у.
. Аналогично определяем частную производную по переменной у.
Нахождение частных производных
При определении частных производных каждый раз изменяется только одна переменная, остальные переменные рассматриваются как постоянные. В результате каждый раз мы рассматриваем функцию только одной переменной и частная производная совпадает с обычной производной этой функции одной переменной. Отсюда правило нахождения частных производных: частная производная по рассматриваемой переменной ищется как обычная производная функции одной этой переменной, остальные переменные рассматриваются как постоянные величины. При этом оказываются справедливыми все формулы дифференцирования функции одной переменной (производная суммы, произведения, частного).
Частные дифференциалы и полный дифференциал функции
Частный дифференциал функции - это произведение частной производной по одной из независимых переменных на дифференциал этой переменной.
dxu = 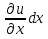 ; dyu =
; dyu = 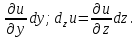
Полный дифференциал du функции u - это сумма частных дифференциалов функции u=f(x, y, z).
du = 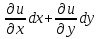 +
+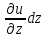 .
.
Задание:
-
Найти частные производные и полный дифференциал функции.
u = x3 + y2
u = 3cos(x-y)
u = 4ex-y
u = ln(x*y)
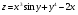
Тема 3.8. Применение производных в исследовании функций
Цель: закрепление навыков раскрытия неопределенностей с помощью правила Лопиталя.
Задания:
-
Выучить правило Лопиталя.
-
Найти пределы, используя правило Лопиталя:
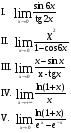
Тема 3.9. Неопределенный интеграл
Цель: закрепление навыков нахождения неопределенного интеграла.
Теоретическая часть
Если функция  является первообразной для функции
является первообразной для функции 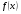 , выражение
, выражение 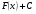 называется неопределенным интегралом и обозначается символом
называется неопределенным интегралом и обозначается символом 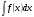 . Таким образом можно записать:
. Таким образом можно записать:
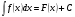 (8.3)
(8.3)
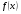 - подынтегральная функция;
- подынтегральная функция;
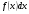 - подынтегральное выражение;
- подынтегральное выражение;
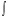 - знак неопределенного интеграла;
- знак неопределенного интеграла;
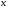 - переменная интегрирования.
- переменная интегрирования.
Свойства неопределенного интеграла
1. Дифференциал от неопределенного интеграла равен подынтегральному выражению:
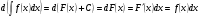
2. Производная от неопределенного интеграла равна подынтегральной функции.
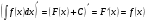
3. Неопределенный интеграл от дифференциала некоторой функции равен этой функции плюс произвольная постоянная.
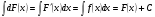
4. Неопределенный интеграл от алгебраической суммы конечного числа функций равен алгебраической сумме неопределенных интегралов от каждого слагаемого в отдельности, т.е.:
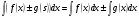
5. Постоянный множитель можно вынести за знак неопределенного интеграла, т.е.:
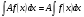
Таблица интегралов
1. 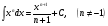
2. 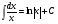
3. 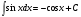
4. 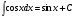
5. 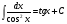
6. 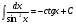
7. 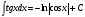
8. 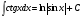
9. 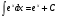
10. 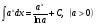
11. 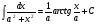
12. 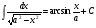
13. 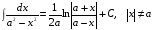
14. 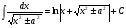
Основные методы вычисления неопределенного интеграла
Пусть требуется найти неопределенный интеграл 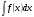 , причем непосредственно подобрать первообразную не представляется возможным, но известно, что она существует. В этом случае применяются различные методы интегрирования, благодаря которым исходный интеграл можно привести к интегралу табличного вида. Рассмотрим некоторые из этих методов.
, причем непосредственно подобрать первообразную не представляется возможным, но известно, что она существует. В этом случае применяются различные методы интегрирования, благодаря которым исходный интеграл можно привести к интегралу табличного вида. Рассмотрим некоторые из этих методов.
1. Метод непосредственного интегрирования. Используя свойства неопределенного интеграл, а также выполняя элементарные математические преобразования подынтегральной функции, исходный интеграл можно привести к неопределенному интегралу табличного вида.
2. Замена переменной. Пусть требуется найти неопределенный интеграл 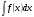 . Сделаем замену в подынтегральном выражении, положив
. Сделаем замену в подынтегральном выражении, положив 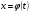 , где
, где 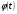 - монотонная непрерывная функция, которая имеет непрерывную производную. Тогда
- монотонная непрерывная функция, которая имеет непрерывную производную. Тогда 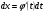 . В этом случае имеет следующее равенство:
. В этом случае имеет следующее равенство:
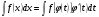
3. Интегрирование по частям. Пусть 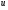 и
и 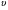 - две дифференцируемые функции от переменной
- две дифференцируемые функции от переменной 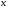 . Тогда дифференциал произведения вычисляется по формуле:
. Тогда дифференциал произведения вычисляется по формуле:
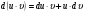
Интегрируя, получим:
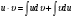
Отсюда:
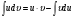
Последняя формула называется формулой интегрирования по частям.
Задание: Найти неопределенный интеграл:
-
Методом непосредственного интегрирования
-
Методом подстановки
-
Методом интегрирования по частям
Тема 3.10. Определенный интеграл
Цель: закрепление навыков нахождения пределов с использованием двух замечательных пределов.
Теоретическая часть
-
Постоянный множитель можно выносить за знак определенного интеграла:
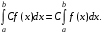
-
Определенный интеграл от суммы функций равен сумме интегралов от слагаемых:
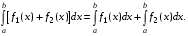
-
Если на отрезке
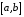 функции
функции 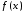 и
и 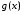 удовлетворяют условию
удовлетворяют условию 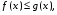 то
то
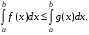

-
Теорема о среднем. Если функция
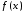 непрерывна на
непрерывна на 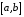 , то существует точка
, то существует точка 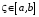 такая, что
такая, что
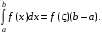

-
Для любых трех чисел a, b, c имеет место равенство
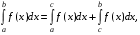
если только все эти интегралы существуют.
Теорема:
-
Если
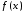 - непрерывная функция, то определенный интеграл
- непрерывная функция, то определенный интеграл 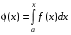 с переменным верхним пределом является первообразной для функции
с переменным верхним пределом является первообразной для функции 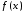 , т.е.
, т.е.
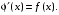
2. Формула Ньютона-Лейбница. Если F(x) - произвольная первообразная для непрерывной на 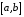 функции
функции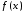 , то имеет место равенство
, то имеет место равенство
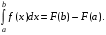
В дальнейшем вместо 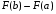 будет удобнее писать
будет удобнее писать 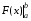 .
.
Методы вычисления определенных интегралов:
1. Метод непосредственного интегрирования. Используя свойства неопределенного интеграл, а также выполняя элементарные математические преобразования подынтегральной функции, исходный интеграл можно привести к неопределенному интегралу табличного вида.
2. Замена переменной. Пусть требуется найти неопределенный интеграл 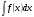 . Сделаем замену в подынтегральном выражении, положив
. Сделаем замену в подынтегральном выражении, положив 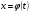 , где
, где 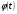 - монотонная непрерывная функция, которая имеет непрерывную производную. Тогда
- монотонная непрерывная функция, которая имеет непрерывную производную. Тогда 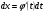 . В этом случае имеет следующее равенство:
. В этом случае имеет следующее равенство:
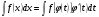
3. Интегрирование по частям. Пусть 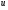 и
и 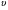 - две дифференцируемые функции от переменной
- две дифференцируемые функции от переменной 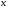 . Тогда дифференциал произведения вычисляется по формуле:
. Тогда дифференциал произведения вычисляется по формуле:
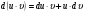
Интегрируя, получим:
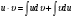
Отсюда:
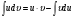
Последняя формула называется формулой интегрирования по частям.
Задания: Вычислить определенные интегралы:
-
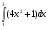
-
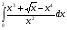
-
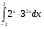
-
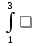
-
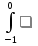
-
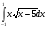
-
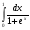
-
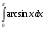
-
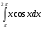
-
Вычислить площади фигур, ограниченных графиками функций:
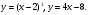
Тема 3.11. Числовые ряды. Основные свойства рядов. Признаки сходимости рядов.
Цель: закрепление навыков нахождения пределов с использованием двух замечательных пределов.
Теоретическая часть
Сумма членов бесконечной числовой последовательности 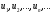 называется числовым рядом.
называется числовым рядом.
Суммы 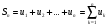 , n = 1, 2, … называются частными (частичными) суммами ряда.
, n = 1, 2, … называются частными (частичными) суммами ряда.
Ряд 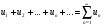 называется сходящимся, если сходится последовательность его частных сумм. Сумма сходящегося ряда - предел последовательности его частных сумм.
называется сходящимся, если сходится последовательность его частных сумм. Сумма сходящегося ряда - предел последовательности его частных сумм.
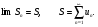
Если последовательность частных сумм ряда расходится, т.е. не имеет предела, или имеет бесконечный предел, то ряд называется расходящимся и ему не ставят в соответствие никакой суммы.
Свойства рядов:
1) Сходимость или расходимость ряда не нарушится, если изменить, отбросить или добавить конечное число членов ряда.
2) Рассмотрим два ряда 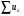 и
и 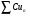 , где С - постоянное число.
, где С - постоянное число.
Теорема. Если ряд 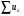 сходится и его сумма равна S, то ряд
сходится и его сумма равна S, то ряд 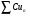 тоже сходится, и его сумма равна СS. (C 0)
тоже сходится, и его сумма равна СS. (C 0)
3) Рассмотрим два ряда 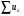 и
и 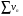 . Суммой или разностью этих рядов будет называться ряд
. Суммой или разностью этих рядов будет называться ряд 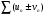 , где элементы получены в результате сложения (вычитания) исходных элементов с одинаковыми номерами.
, где элементы получены в результате сложения (вычитания) исходных элементов с одинаковыми номерами.
Теорема. Если ряды 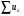 и
и 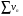 сходятся и их суммы равны соответственно S и , то ряд
сходятся и их суммы равны соответственно S и , то ряд 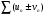 тоже сходится и его сумма равна S + .
тоже сходится и его сумма равна S + .
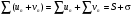
Разность двух сходящихся рядов также будет сходящимся рядом.
Сумма сходящегося и расходящегося рядов будет расходящимся рядом.
Признак сходимости Даламбера:
-
Если
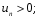
-
2) существует
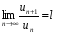 , тогда
, тогда 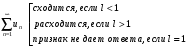
1 признак сравнения: Пусть даны два положительных ряда: 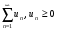 и
и 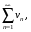
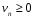 . Если выполняется неравенство:
. Если выполняется неравенство: 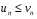 , начиная с некоторого n, то из сходимости ряда второго (большего) ряда - следует сходимость первого (меньшего) ряда. А из расходимости ряда меньшего ряда следует расходимость ряда большего.
, начиная с некоторого n, то из сходимости ряда второго (большего) ряда - следует сходимость первого (меньшего) ряда. А из расходимости ряда меньшего ряда следует расходимость ряда большего.
Признак Коши
Теорема. Если 1) 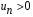 и 2) существует
и 2) существует 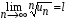 ,
,
Тогда 
Задания:
-
Исследовать на сходимость ряд, применяя признак Даламбера:
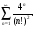
-
Исследовать ряд на сходимость, применяя первый признак сравнения:
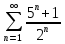
-
Исследовать ряд на сходимость, применяя признак Коши:
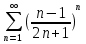
Тема 3.12. Знакопеременные ряды. Функциональные ряды
Цель: закрепление навыков нахождения пределов с использованием двух замечательных пределов.
Теоретическая часть
Знакочередующимися называются ряды, члены которых поочерёдно то неотрицательны, то отрицательны.
Достаточный признак сходимости знакочередующегося ряда (признак Лейбница). Если:
1. Последовательность, составленная из модулей членов знакочередующегося ряда, монотонно убывает, т.е. 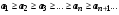 ;
;
2. Выполняется необходимый признак сходимости ряда, т.е. ![]() ,
,
то ряд сходится. Его сумма по абсолютной величине не превосходит абсолютную величину первого члена.
Пусть функция 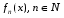 определена в области
определена в области 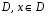 .
.
Выражение 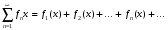 называется функциональным рядом.
называется функциональным рядом.
Пример.
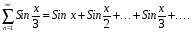
Функциональный ряд называется сходящимся в области 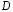 , если существует предел частичных сумм этого ряда, то есть
, если существует предел частичных сумм этого ряда, то есть 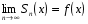 .
.
Задания:
-
Исследовать ряды на сходимость:
-
Разложить в ряд Маклорена:
f(x) = 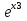
Тема 4.1-4.4 Обыкновенные дифференциальные уравнения
Цель: закрепление навыков решения дифференциальных уравнений.
Теоретическая часть
Дифференциальное уравнение - это равенство, содержащее производные или дифференциалы неизвестной функции.
Общий вид дифференциального уравнения:
F(x, y, y', …, y(n)) = 0 - неявная форма,
где х - независимая переменная; y - неизвестная функция; y' - ее производная первого порядка и т.д.
Если из уравнения можно выразить y', то оно примет вид: y' = f(x, y) - явная форма. Это уравнение первого порядка, разрешенное относительно производной.
Порядок n старшей производной, входящей в уравнение, называется порядком уравнения.
Всякая функция, подстановка которой вместе с ее производной в дифференциальное уравнение обращает его в тождество, называется решением уравнения.
Общее решение - это решение, зависящее от произвольных постоянных. Оно содержит столько независимых переменных, каков порядок уравнения. Общее решение дифференциального уравнения - семейство функций y = (x, C), удовлетворяющее этому уравнению при произвольном значении постоянных С.
Например, для дифференциального уравнения xy' - 2x2 = 0 функция y = x2 будет решением, так как при ее подстановке левая часть уравнения тождественно обращается в нуль: x*2x - 2x2 =0.
Частное решение - это решение, получающееся из общего решения при конкретных определенных значениях произвольных постоянных y = (x, C0).
Уравнение первого порядка P(x, y)dx + Q(x, y)dy = 0 называется уравнением с разделяющимися переменными, если функции P и Q разлагаются на множители, зависящие каждый только от одной переменной:
f1(x) f2(y)dx + φ1(x) φ2(y)dy = 0.
В таком уравнении после деления его членов на f2(y)*φ1(x) переменные разделяются:
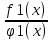 dx +
dx + 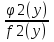 dy = 0, и каждый член уравнения зависит от одной переменной.
dy = 0, и каждый член уравнения зависит от одной переменной.
Общий интеграл уравнения находится почленным интегрированием:
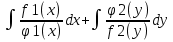 = 0.
= 0.
Линейное дифференциальное уравнение первого порядка - это уравнение вида:
y' + P(x)y = q(x), где P(x) и q(x) - непрерывные функции.
Название уравнения «линейное» связано с тем, что неизвестная функция и ее производная входят в первой степени, т.е. линейно.
-
Линейное однородное уравнение будет, если q(x)
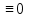 , т.е. это уравнение вида:
, т.е. это уравнение вида:
y' + P(x)y = 0. Это уравнение с разделяющимися переменными и его решение будет иметь вид: y = C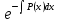 .
.
-
Линейное неоднородное уравнение будет, если функция q(x) не равна тождественно нулю:
q(x)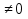 : y' +P(x)y = q(x). Общее решение линейного уравнения первого порядка находится методом вариации постоянной и имеет вид:
: y' +P(x)y = q(x). Общее решение линейного уравнения первого порядка находится методом вариации постоянной и имеет вид:
y(x) = 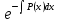 [C +
[C + 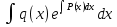 ].
].
Уравнения вида a0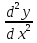 +a1
+a1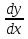 +a2y = 0 называются линейными однородными уравнениями второго порядка с постоянными коэффициентами.
+a2y = 0 называются линейными однородными уравнениями второго порядка с постоянными коэффициентами.
Общий интеграл находится с помощью характеристического уравнения a0k2 + a1k +a2 = 0, которое получается из этого уравнения, если, сохраняя в нем все коэффициенты ai, заменить функцию y единицей (y=1), а все ее производные - соответствующими степенями k. При этом:
-
Если все корни характеристического уравнения действительные и различные, то общий интеграл имеет вид: y = C1
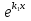 + C2
+ C2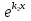 .
. -
Если характеристическое уравнение имеет корни действительные и равные (k1 = k2 = k), то y = C1
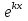 + C2
+ C2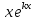 .
. -
Если корни мнимые (k=
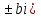 , то y = C1cosbx + C2 sinbx.
, то y = C1cosbx + C2 sinbx. -
Если корни комплексные (k=a
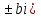 , то y = eax(C1cosbx + C2 sinbx).
, то y = eax(C1cosbx + C2 sinbx).
Задания:
-
Выучить определения.
-
Найти решения дифференциальных уравнений:
-
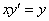 ;
; -
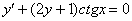 ;
; -
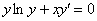 ;
; -
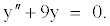 .
.
Приложение 1
Карта-маршрут внеаудиторной самостоятельной работы
по дисциплине_______________________________________________студента ___________________________,
ФИО
курс____, группа_______, специальность Компьютерные сети
Тема
Задания внеаудиторной самостоятельной работы студента
Кол-во баллов
1.1
1.2
2.1
2.2
3.1
3.2
3.3
3.4
3.5
3.6
3.7
3.8
3.9
3.10
3.11
3.12
4.1-4.2
2 ч.
4 ч.
4 ч.
2 ч.
2 ч.
2 ч.
2 ч.
2 ч.
4 ч.
2 ч.
2 ч.
2 ч.
2 ч.
2 ч.
2 ч.
2 ч.
2 ч.
3 б.
2 б.
4 б.
4 б.
5 б.
4 б.
5 б.
8 б.
11 б.
4 б.
5 б.
5 б.
13 б.
10 б.
4 б.
3 б.
8 б.
1.1
1.2
2.1
2.2
3.1
3.2
3.3
3.4
3.5
3.6
3.7
3.8
3.9
3.10
3.11
3.12
4.1-4.2