- Преподавателю
- Математика
- Параметр в квадратном уравнении
Параметр в квадратном уравнении
| Раздел | Математика |
| Класс | - |
| Тип | Конспекты |
| Автор | Дряева М.Г. |
| Дата | 20.12.2014 |
| Формат | doc |
| Изображения | Есть |
Решение квадратных уравнений с параметрами
Если в уравнении некоторые коэффициенты заданы не конкретными числовыми значениями, а обозначены буквами, то они называются параметрами, а уравнение - параметрическим.
Научиться решать любые задачи с параметрами, используя какой-то алгоритм или формулы, нельзя. Надо использовать соображения, рассматривать их как задачи исследовательские.
Уравнение вида ах2 + bх + с = 0, а ≠ 0, где коэффициенты а, b, с - любые действительные числа, называется квадратным.
Выражение b2 - 4ас называют дискриминантом квадратного уравнения.
Если D < 0, то квадратное уравнение не имеет действительных корней.
Если D= 0, то квадратное уравнение имеет единственный действительный корень 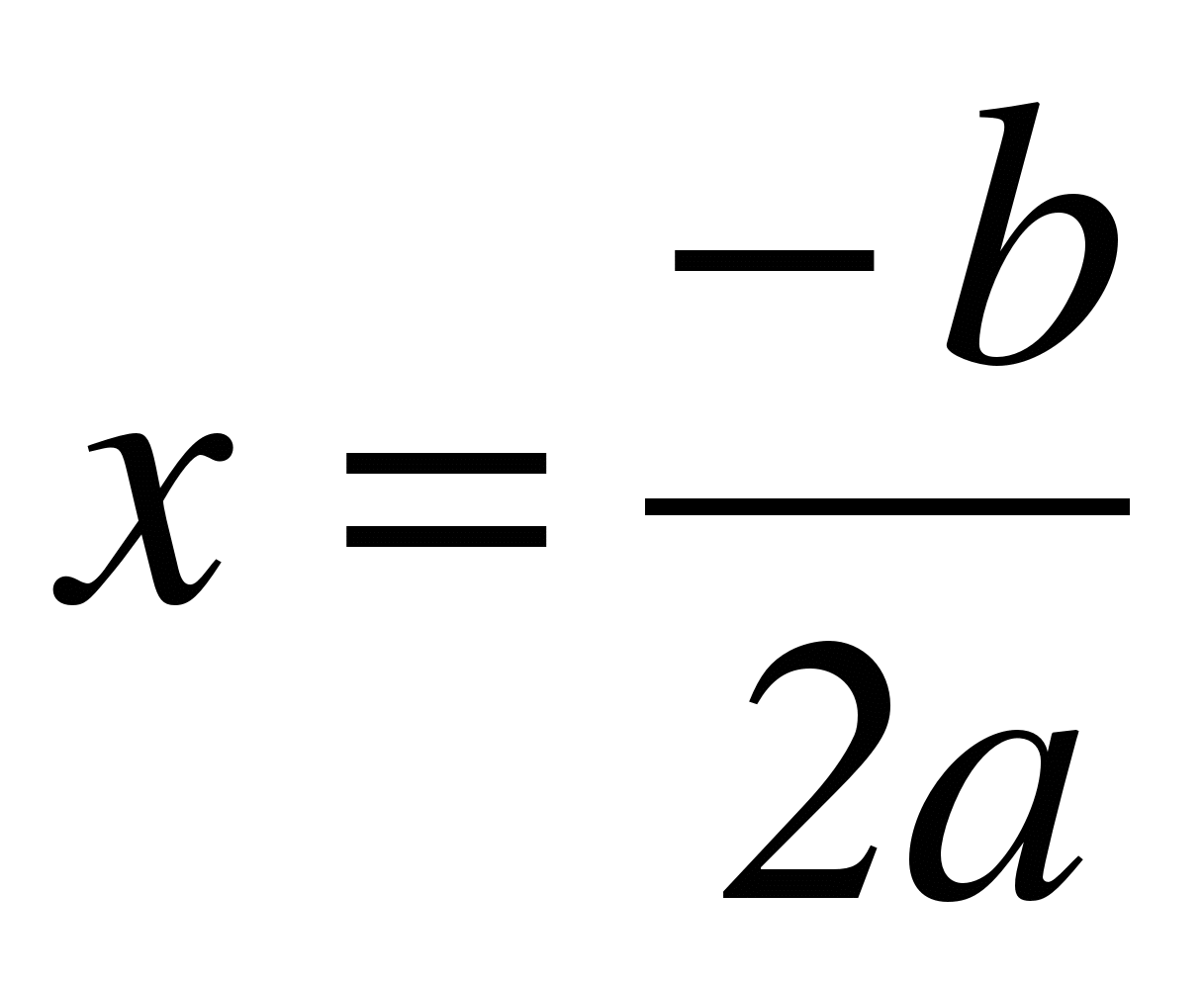 (или говорят, что это уравнение имеет два кратных корня
(или говорят, что это уравнение имеет два кратных корня 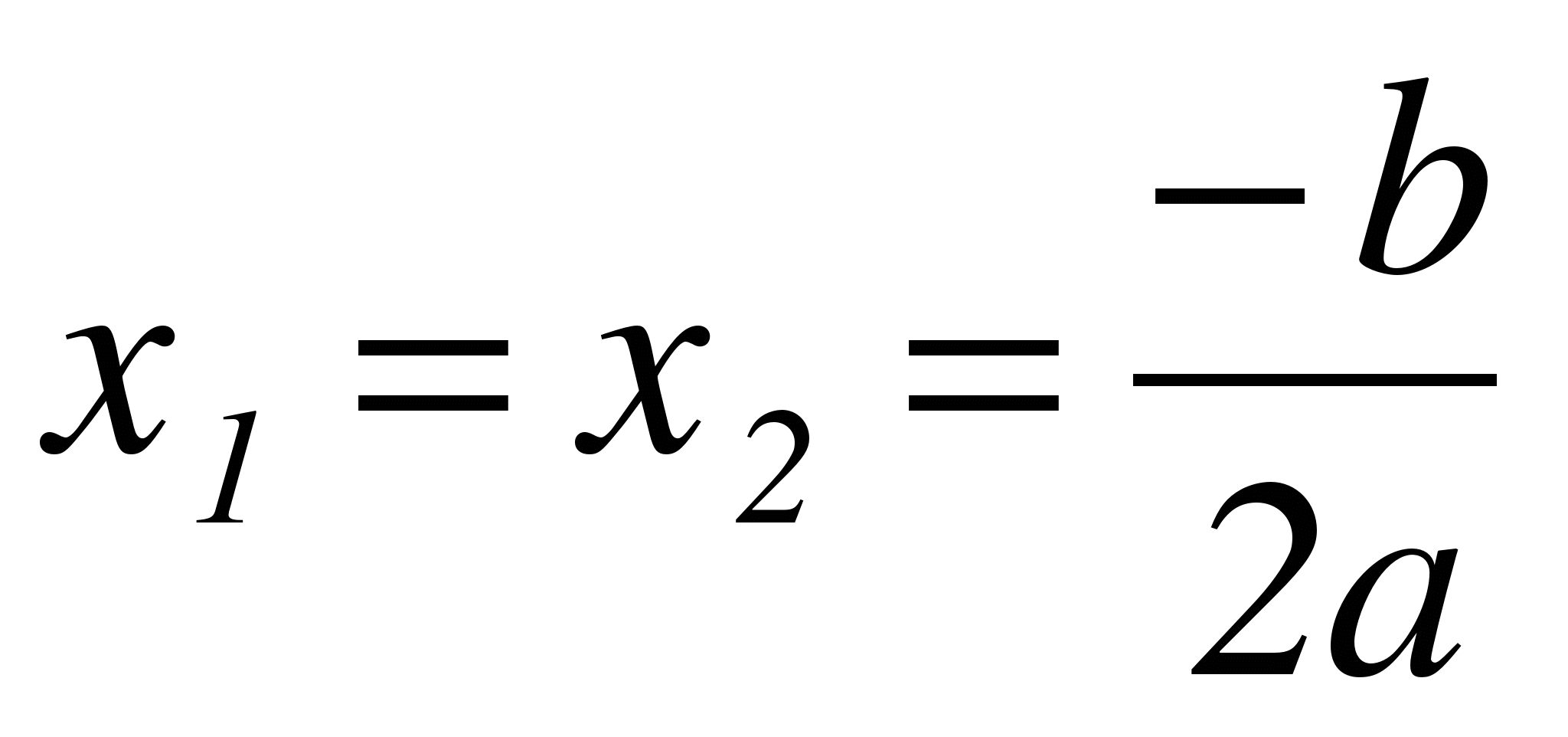 ).
).
Если D > 0, то квадратное уравнение имеет два различных действительных корня 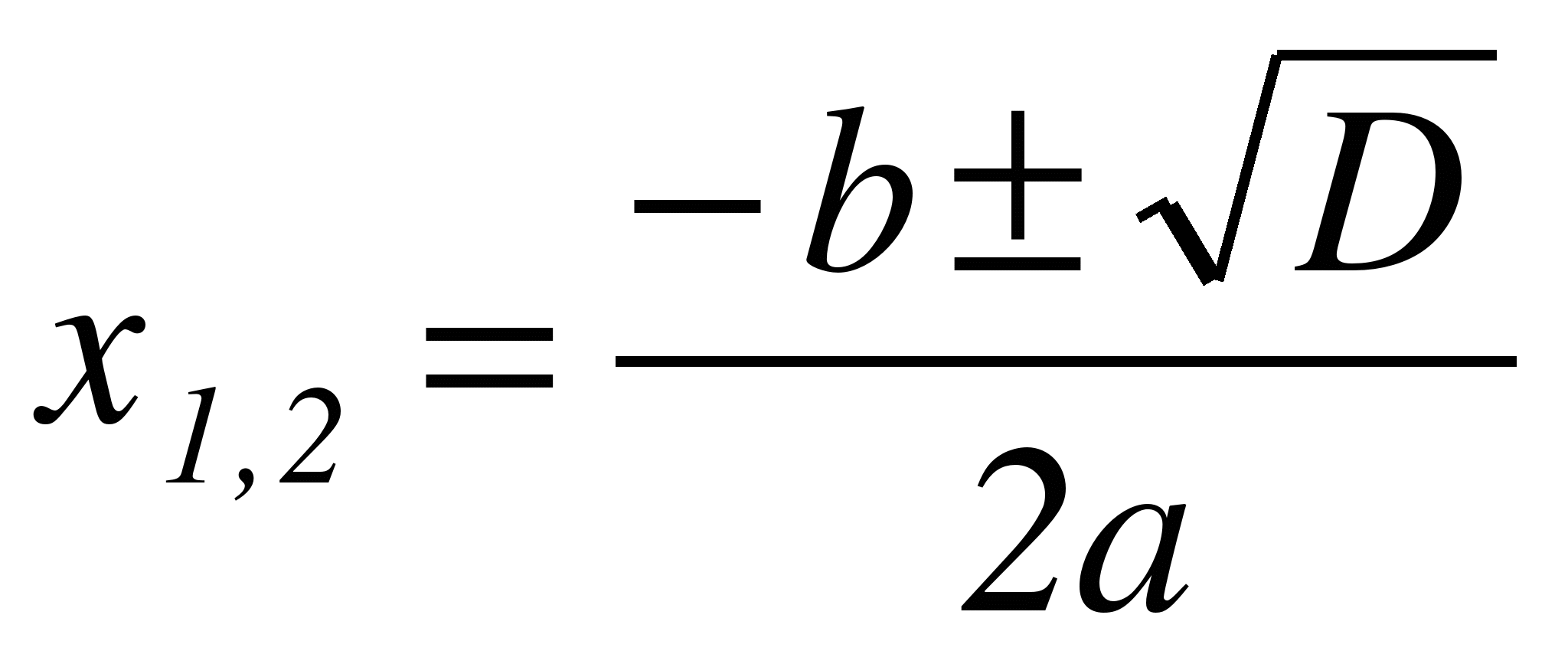 .
.
Теорема Виета. Если х1, х2 - корни квадратного уравнения ах + bх + с = 0,
а ≠ 0, то сумма корней равна 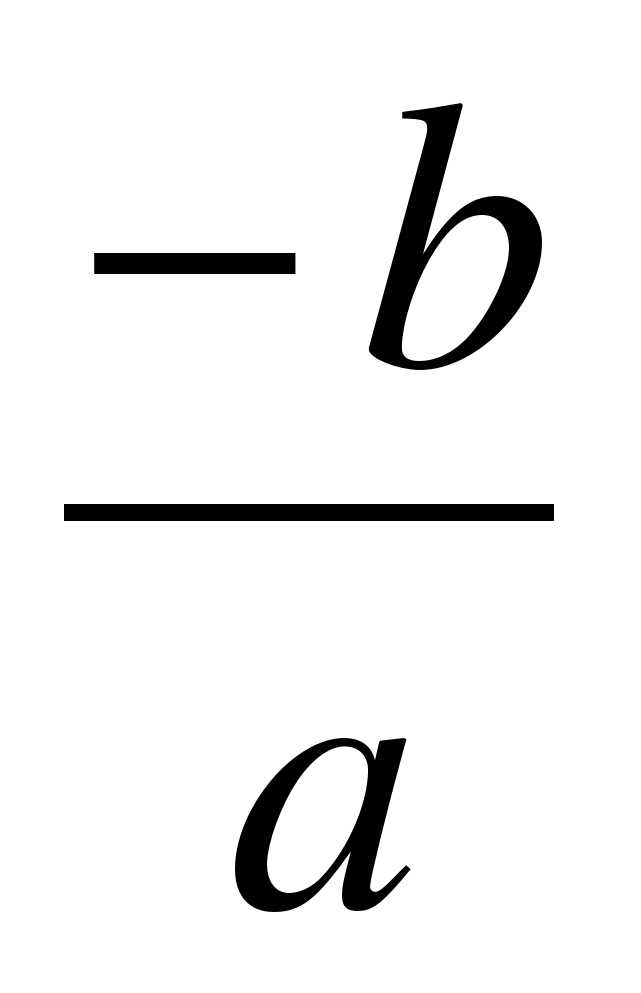 , а их произведение равно
, а их произведение равно 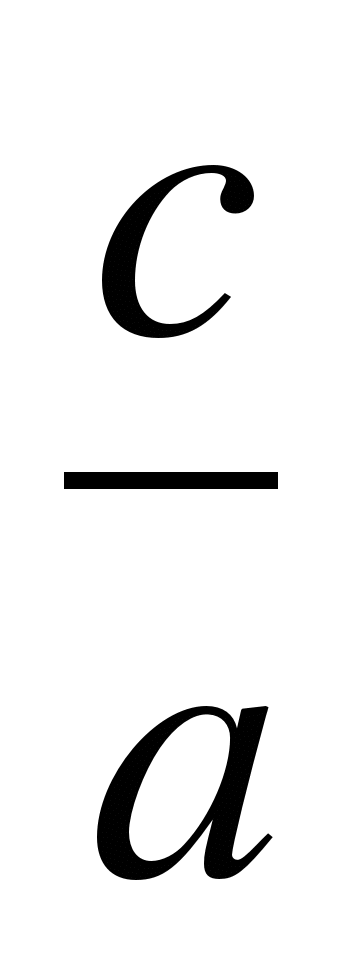 .
.
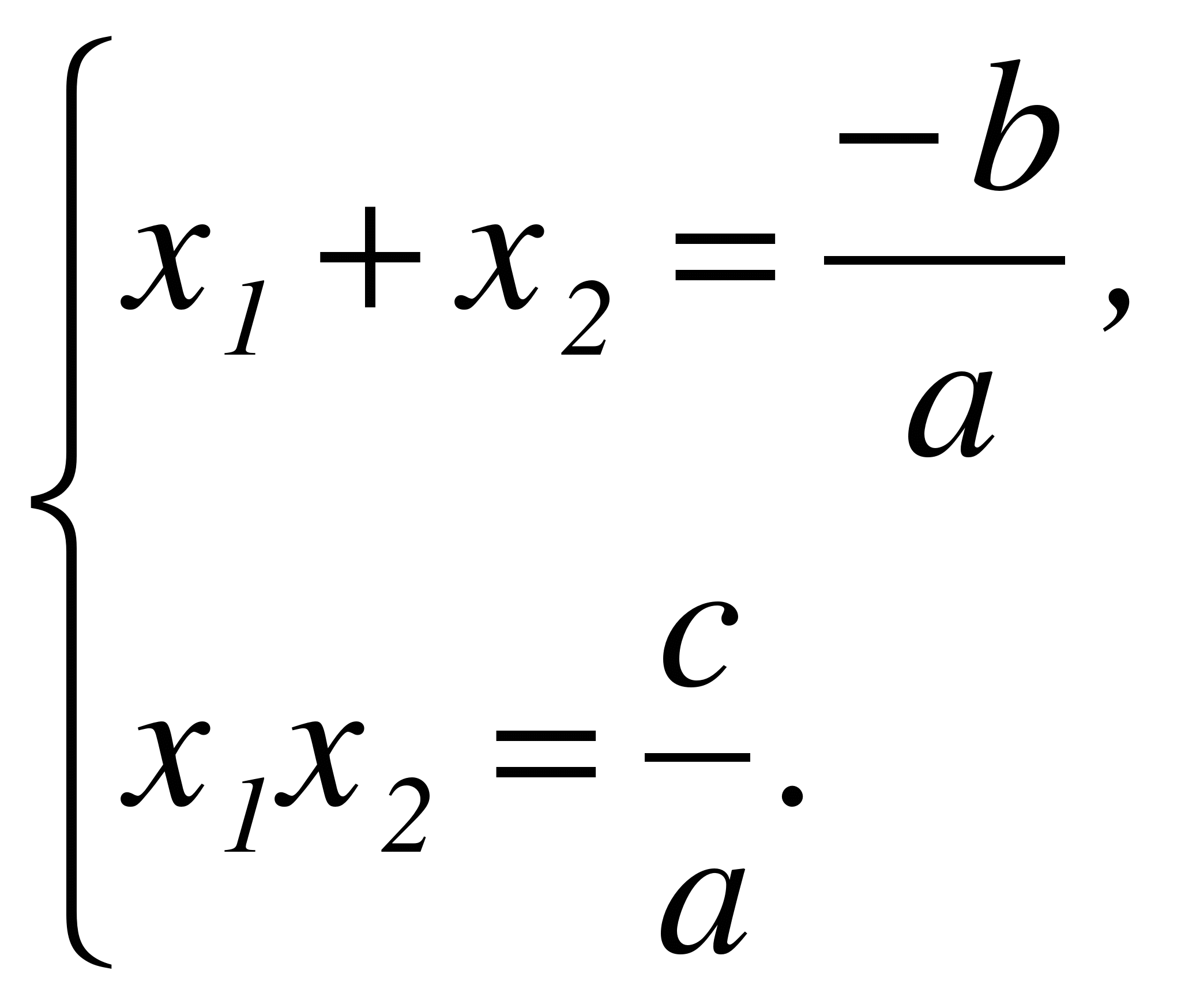
Обратное утверждение: Если числа х1, х2 таковы, что
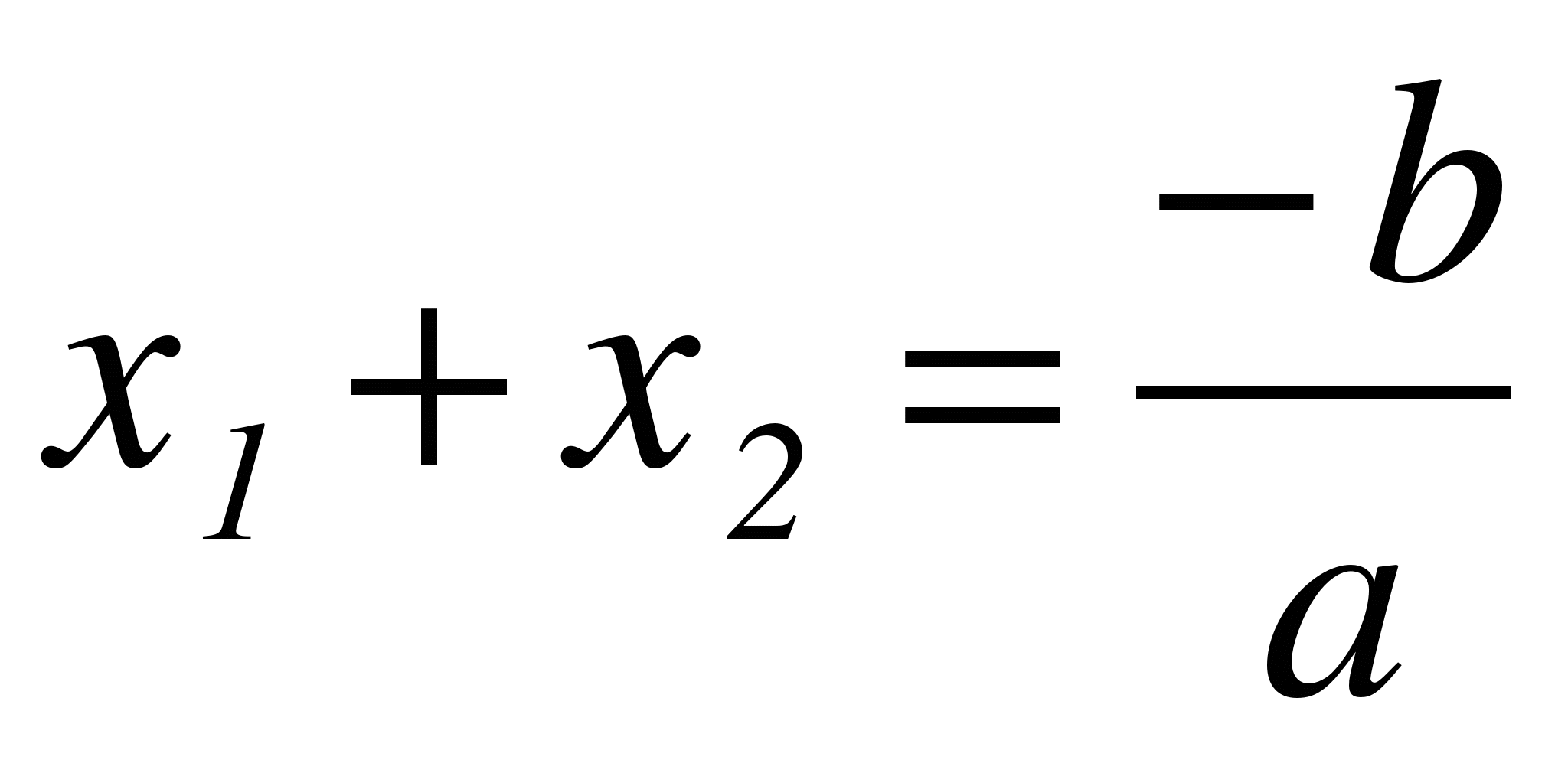 ,
, 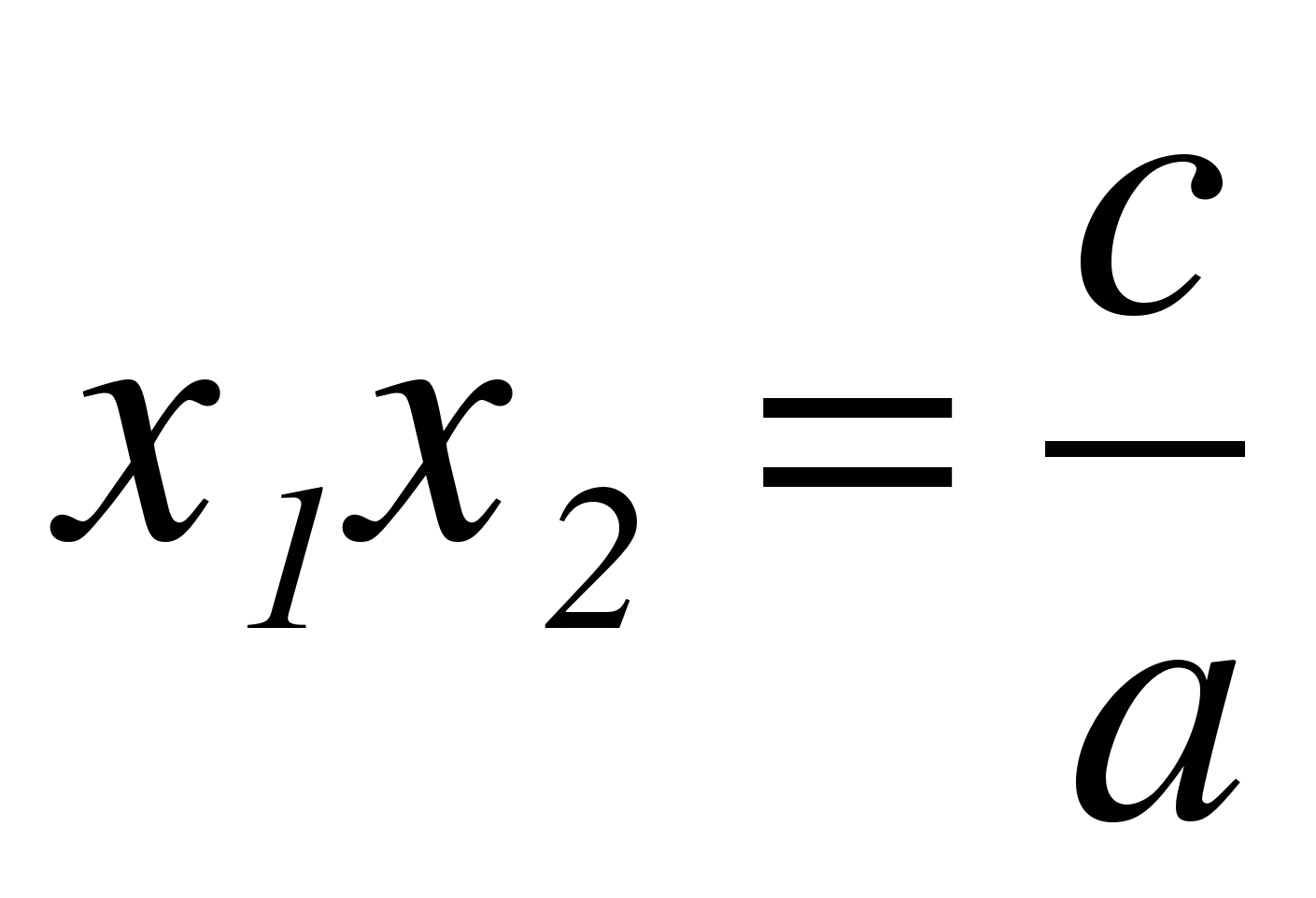 , то эти числа - корни уравнения ах2 + bх + с = 0, а ≠ 0.
, то эти числа - корни уравнения ах2 + bх + с = 0, а ≠ 0.
Значения параметра, при которых или при переходе через которые происходит качественное изменение уравнения, можно назвать контрольными или особыми. Очень важно уметь находить их.
При решении квадратного уравнения с параметрами контрольными будут те значения параметра, при которых коэффициент при х2 обращается в нуль.
Если этот коэффициент равен нулю, то уравнение превращается в линейное;
если же этот коэффициент отличен от нуля, то имеем квадратное уравнение (в этом и состоит качественное изменение уравнения).
Понятие квадратного трехчлена и его свойства.
Квадратным трехчленом называется выражение вида ax²+bx+c, где a≠0. Графиком соответствующей квадратичной функции является парабола.
При a<0 ветви параболы направлены вниз; при a>0 ветви направлены вверх.
Выражение x²+px+q называется приведенным квадратным трехчленом.
В зависимости от величины дискриминанта D=b²- 4ac возможны следующие случаи расположения графика квадратного трехчлена:
при D>0 существуют две различные точки пересечения параболы с осью Ох (два различных корня трехчлена);
при D=0 эти две точки сливаются в одну, то есть парабола касается оси Ох (один корень трехчлена);
при D<0 точек пересечения с осью Ох нет (и корней трехчлена нет).
В последнем случае при а>0 парабола лежит целиком выше оси Ох,
при а<0- целиком ниже оси Ох
«Белое пятнышко» в теме «Квадратный трёхчлен и квадратичная функция» может привести к появлению «мёртвых зон» и провалов в наших знаниях элементарной математики. Кстати, преподаватели мехмата МГУ О. Черкасова и А. Якушева утверждают: « Во многих так называемых задачах повышенной сложности «торчат уши квадратного трехчлена».
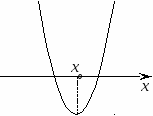
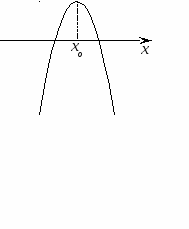
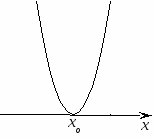
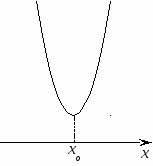
. Расположение параболы по отношению к оси абсцисс
в зависимости от коэффициента а и дискриминанта.
a > 0
a < 0
D > 0
D = 0

D < 0

Теоремы о знаках корней квадратного трехчлена.
Теорема 1. Для того, чтобы корни квадратного трехчлена имели одинаковые знаки, необходимо и достаточно выполнения соотношений:
D=b²-4ac>0; x1•x2=c/a>0. При этом оба корня будут положительны, если выполняется условие : x1+x2= -b/a>0 ,
а оба корня будут отрицательны, если x1+x2= -b/a<0.
Теорема 2. Для того, чтобы корни квадратного трехчлена имели разные знаки, необходимо и достаточно выполнения соотношения x1•x2=c/a<0.
В данном случае нет необходимости проверять знак дискриминанта, поскольку при выполнении условия c/a<0 будет выполняться и условие c•a<0, а это значит, что дискриминант D=b²-4ac>0.
Расположение корней квадратного трехчлена
Рассмотрим теперь особенности расположения корней квадратного трехчлена с заданными свойствами на координатной плоскости.
Решение задач, для которых характерны следующие формулировки : при каких значениях параметра корни ( только один корень) больше (меньше, не больше, не меньше) заданного числа р; корни расположены между числами p и q и т.д.; опирается на утверждения о расположении корней квадратичной функции.
При решении многих задач требуется знание следующих теорем и следствий.
Пусть f(х) = ах2 + bx + с имеет действительные корни х1, х2 (которые могут быть кратными), а М, N - какие-нибудь действительные числа, причем М < N. Тогда:
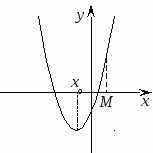
Теорема 1. Для того чтобы оба корня квадратного трехчлена были меньше, чем число М (то есть лежали на числовой оси левее, чем точка М), необходимо и достаточно выполнение следующих условий:
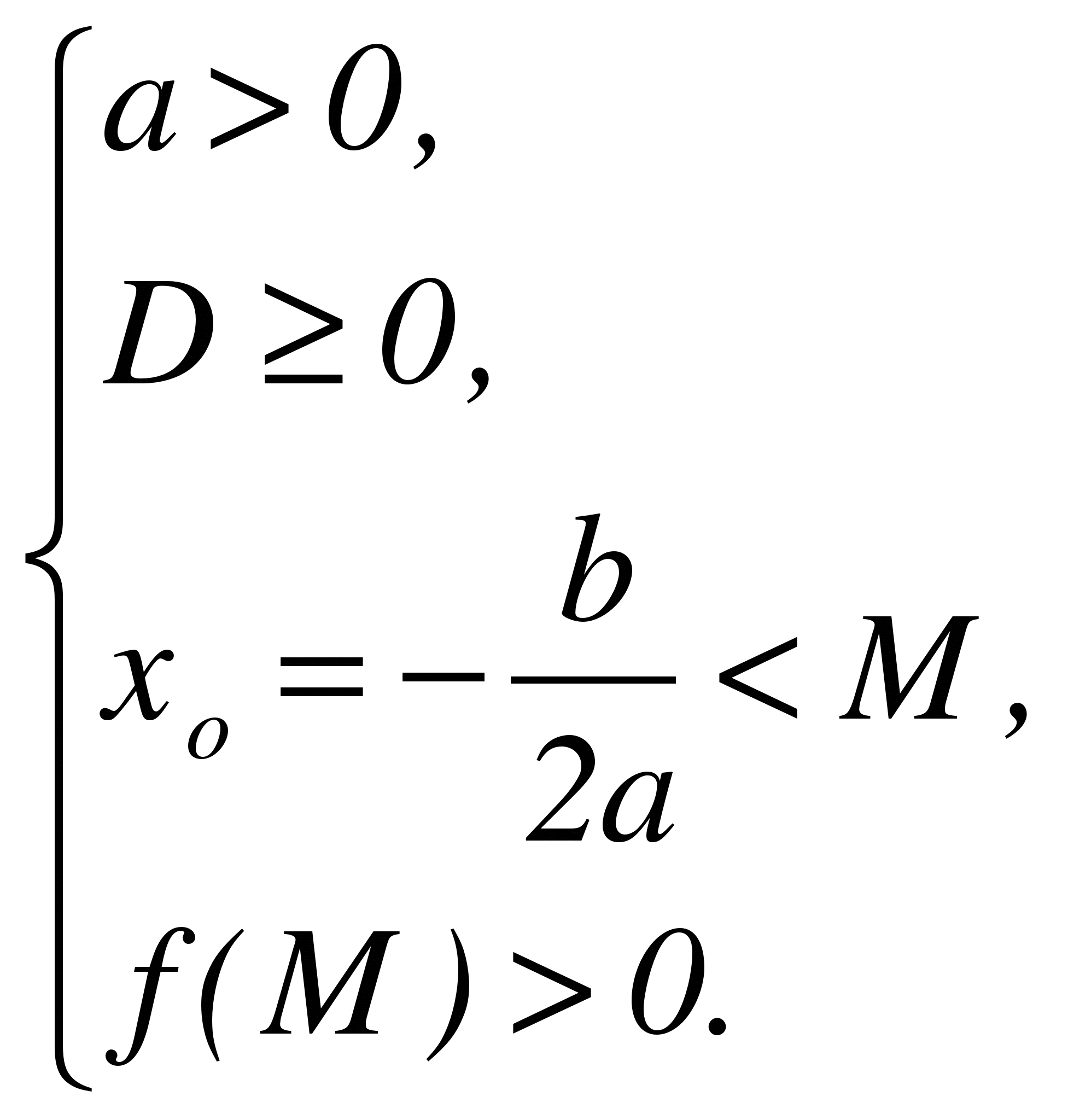 или
или 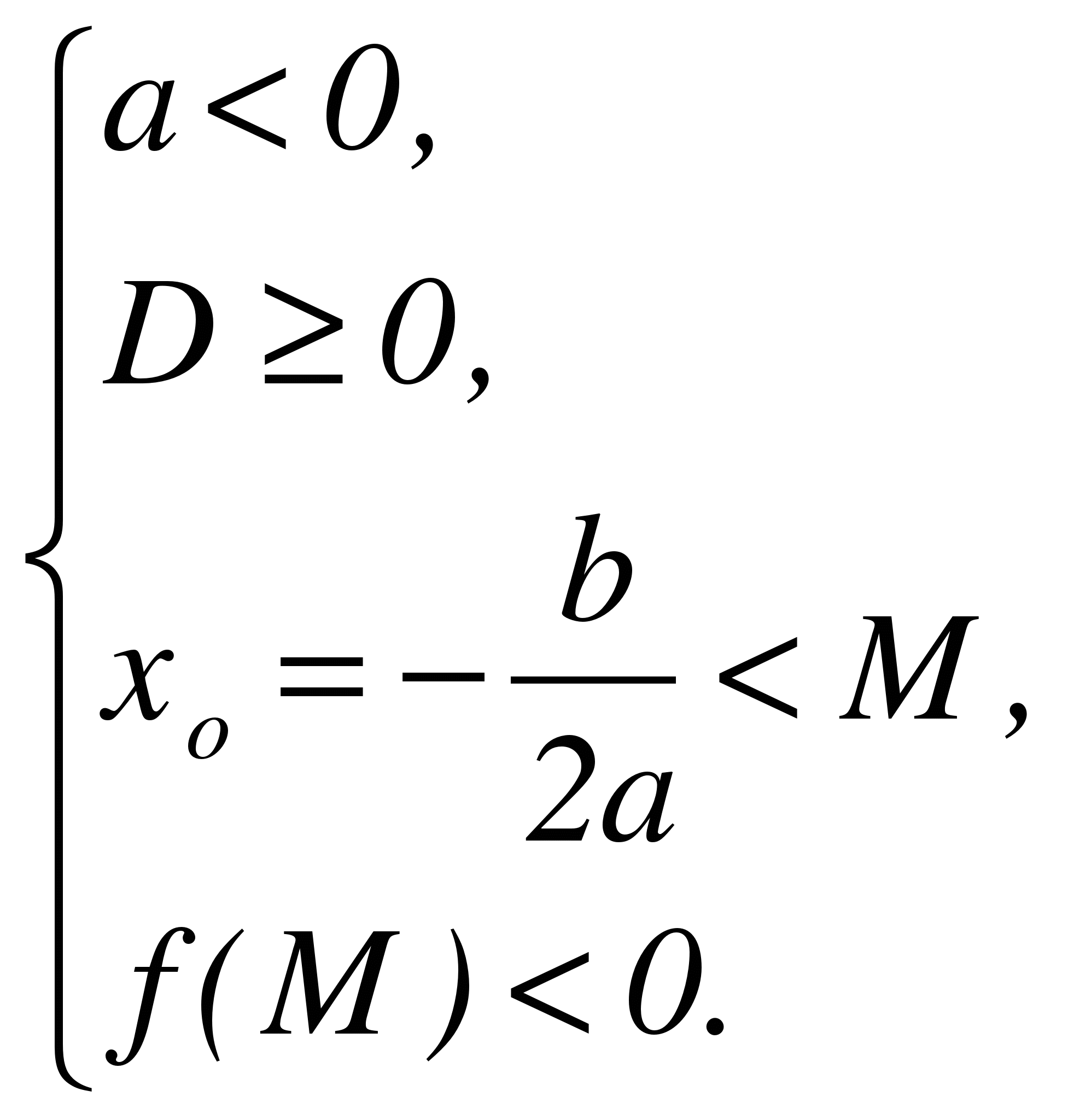
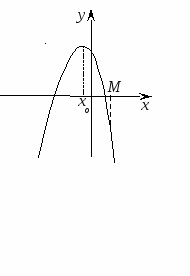
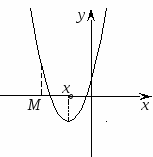
Теорема 2. Для того чтобы один из корней квадратного трехчлена был меньше, чем число М, а другой больше, чем М (то есть точка М лежала бы между корнями), необходимо и достаточно выполнение следующих условий:
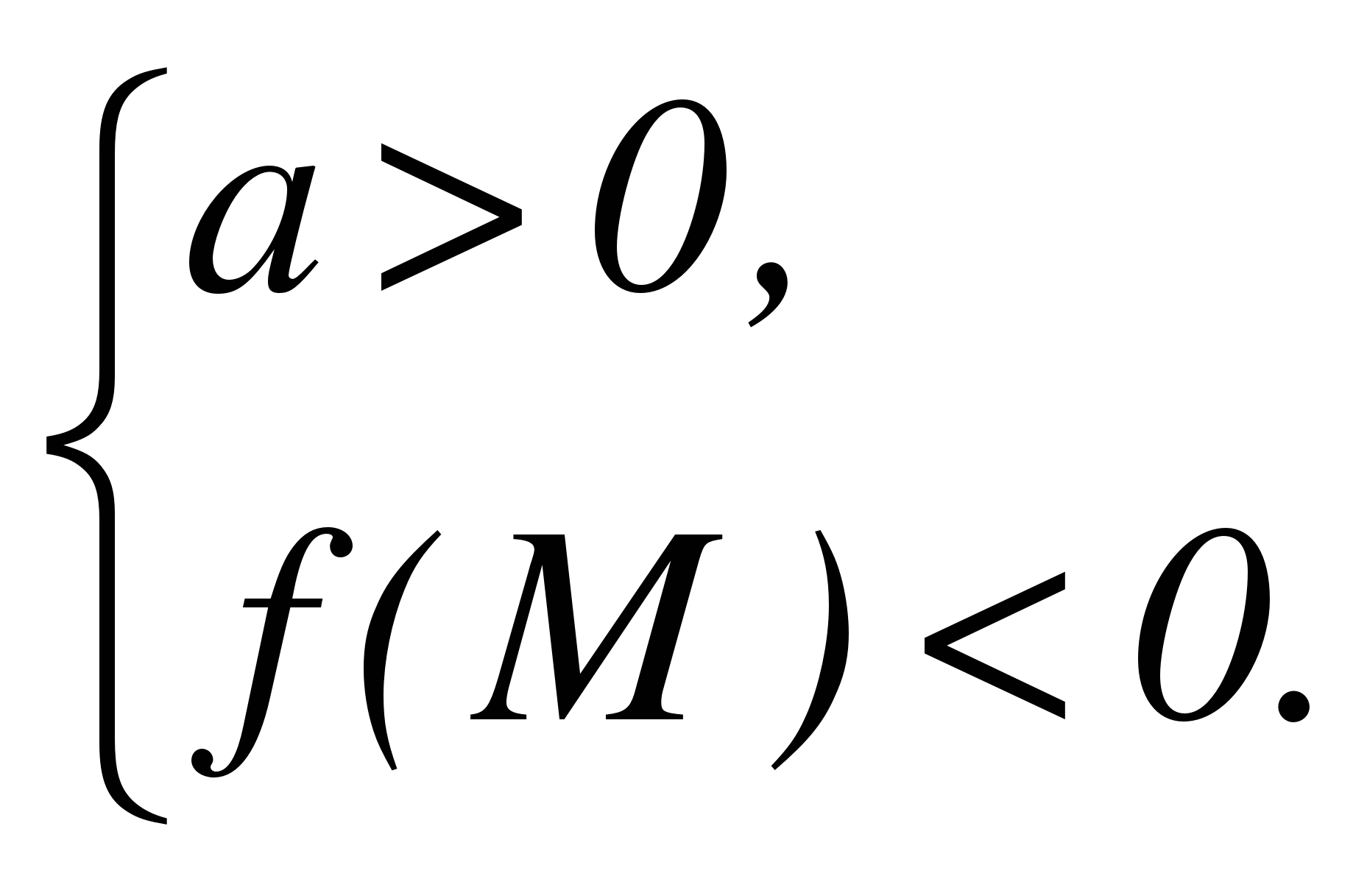 или
или 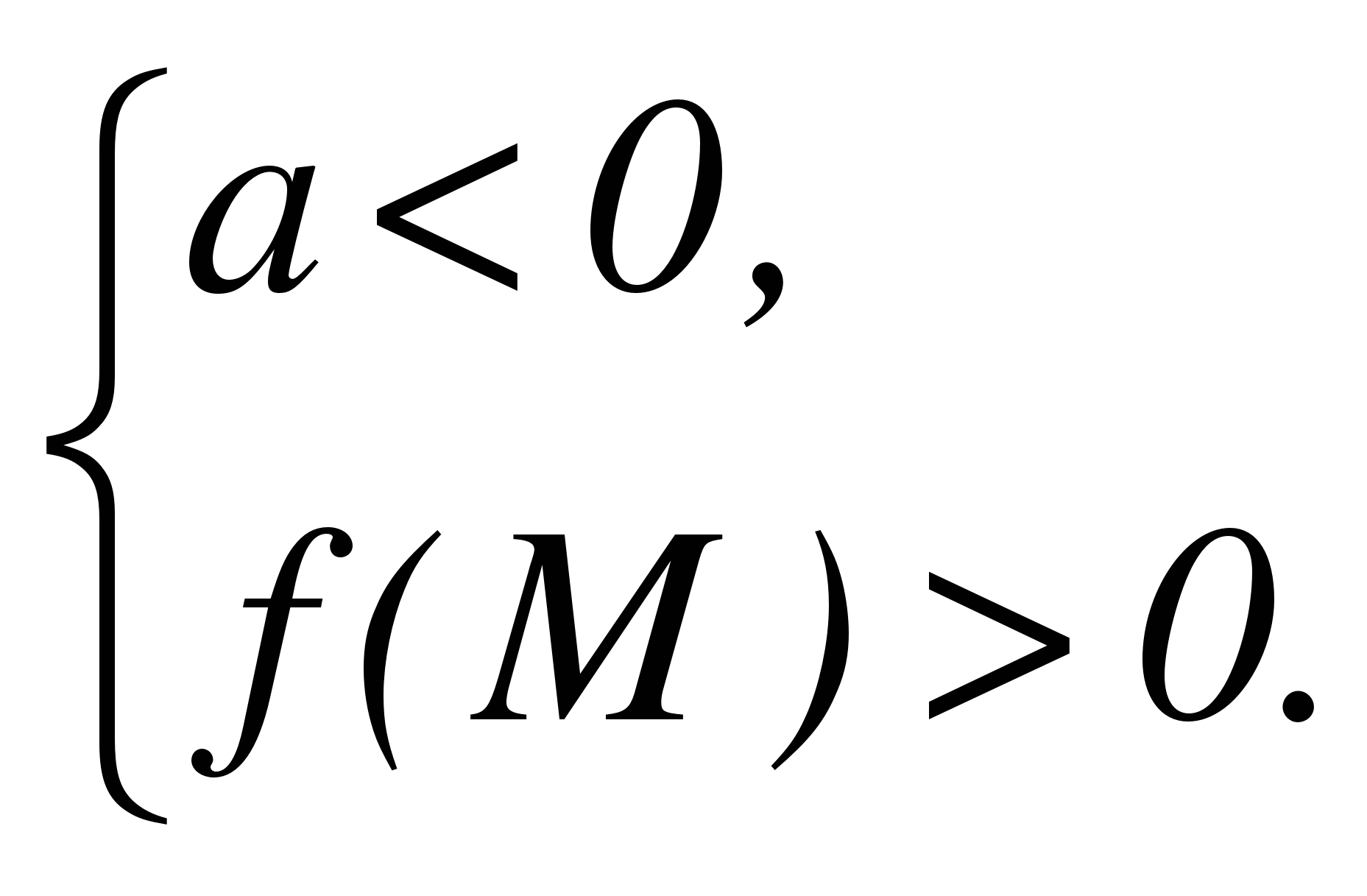
Эти две системы можно заменить формулой 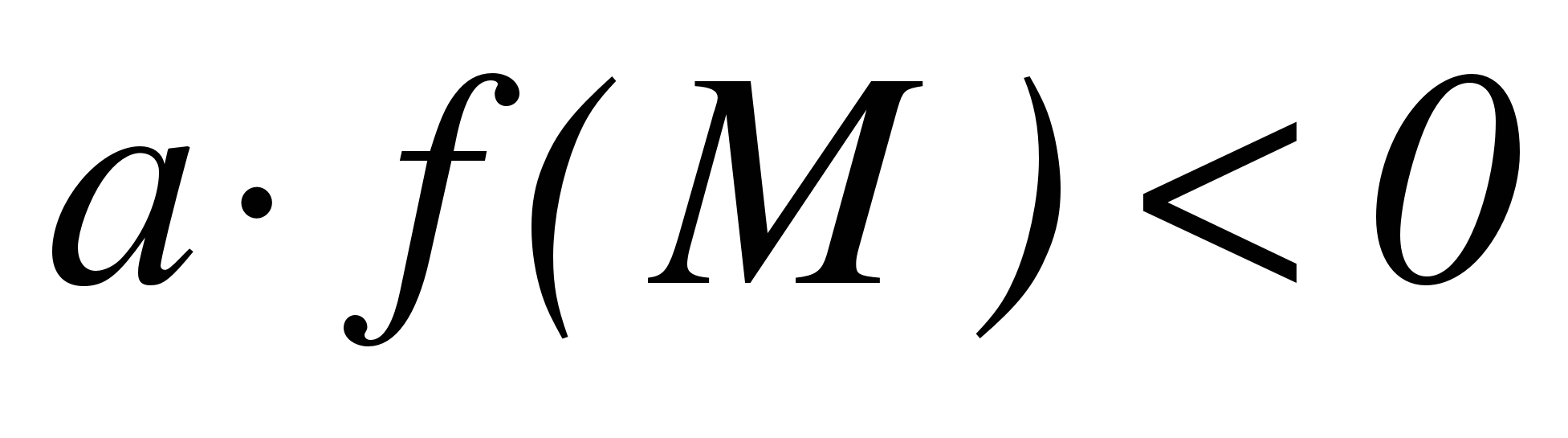 .
.
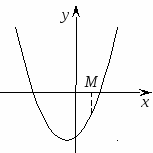
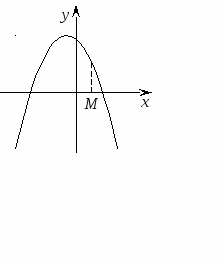
Теорема 3. Для того чтобы оба корня квадратного трехчлена были больше, чем число М (то есть лежали на числовой оси правее, чем точка М), необходимо и достаточно выполнение следующих условий:
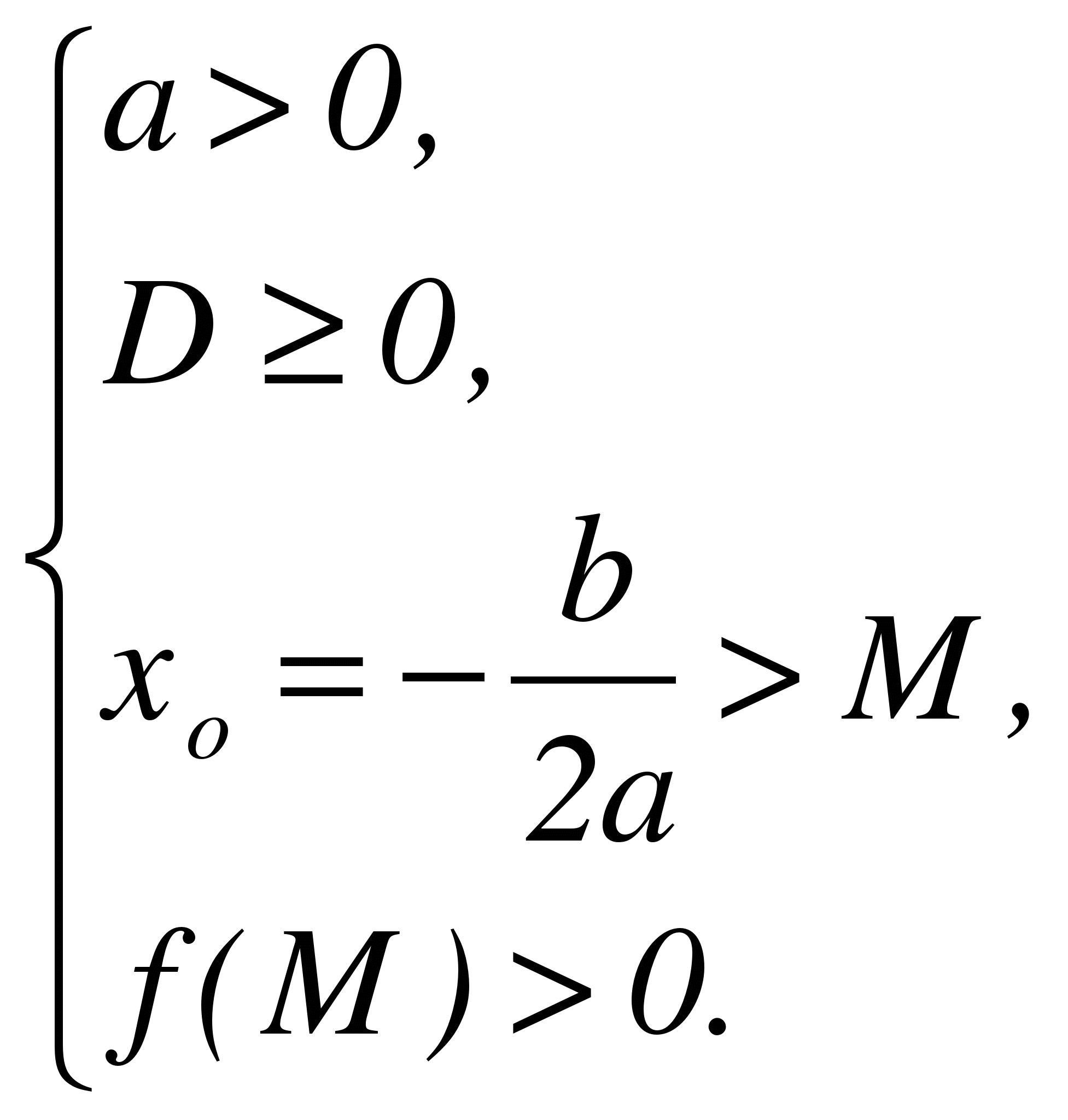 или
или 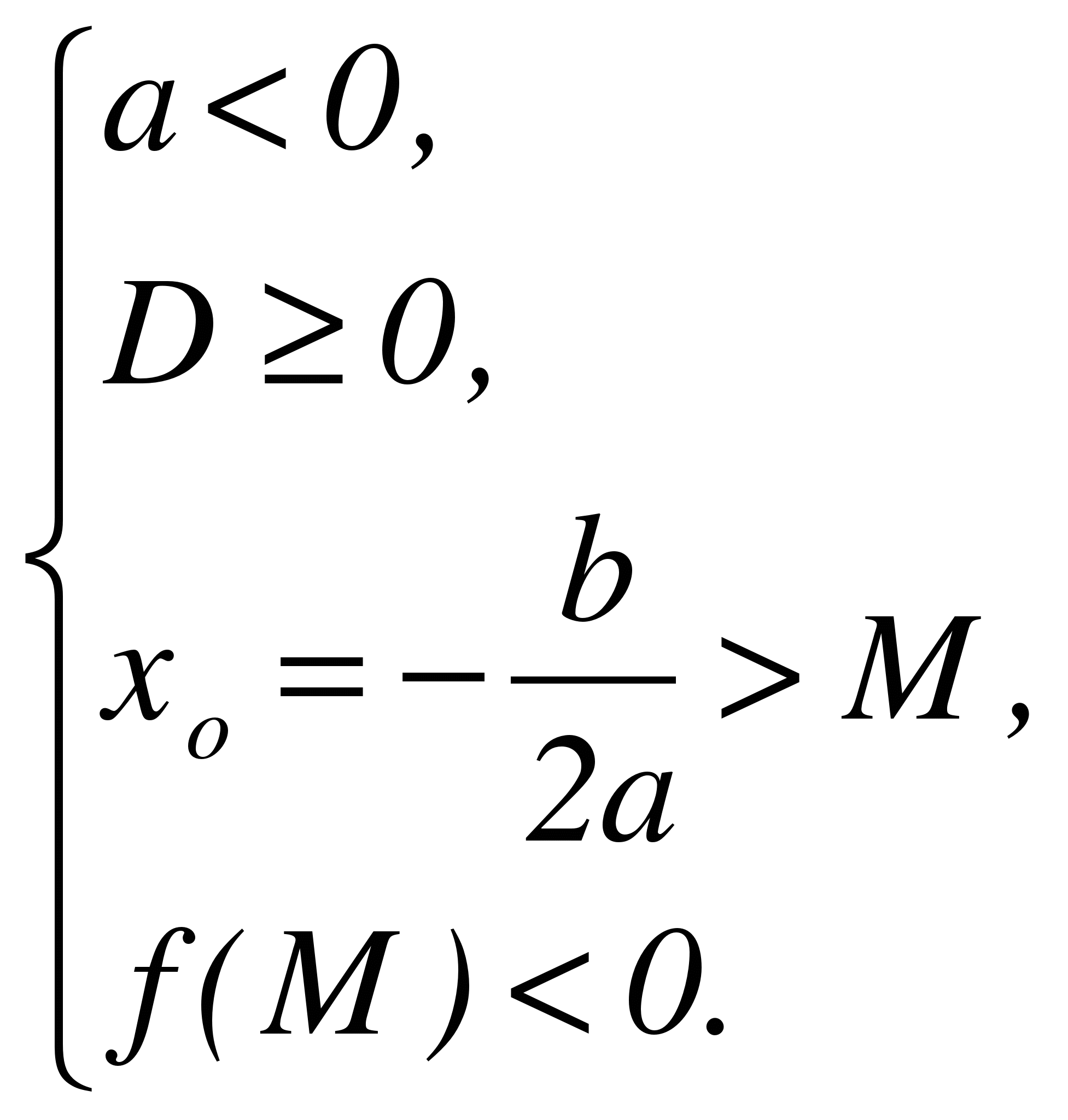
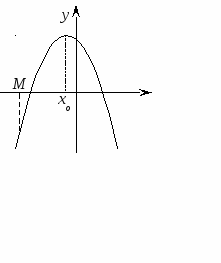
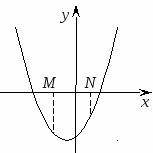
Следствие 1. Для того , чтобы оба корня квадратного трехчлена были меньше, чем число М, но меньше, чем число N (то есть лежали в интервале между М и N, необходимо и достаточно выполнение следующих условий:
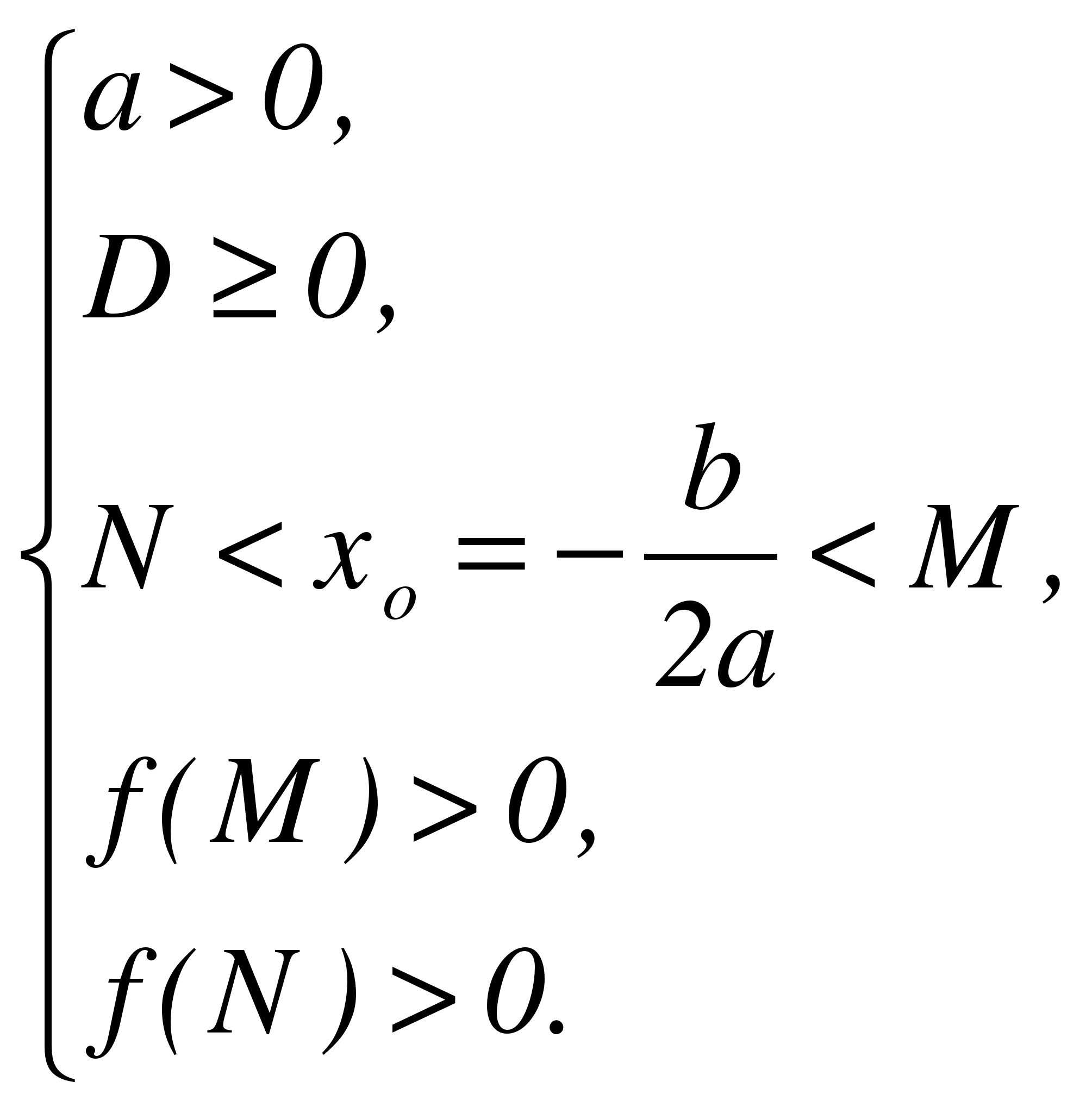 или
или 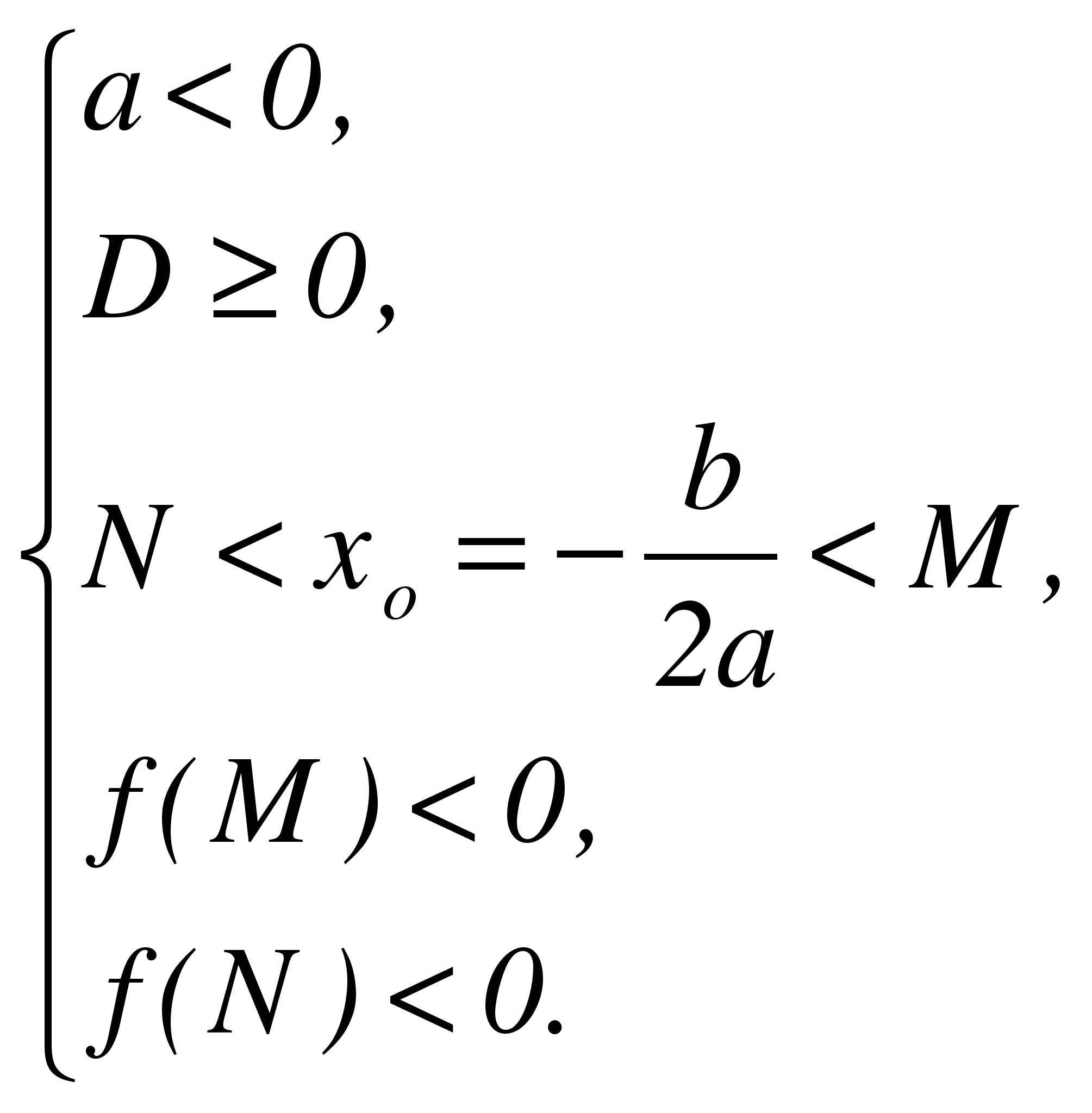
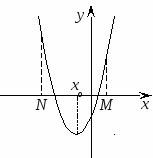
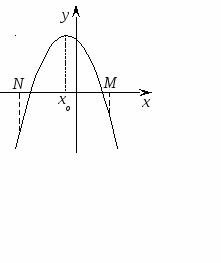
Следствие 2. Для того чтобы больший корень квадратного трехчлена лежал в интервале между М и N, необходимо и достаточно выполнение следующих условий:
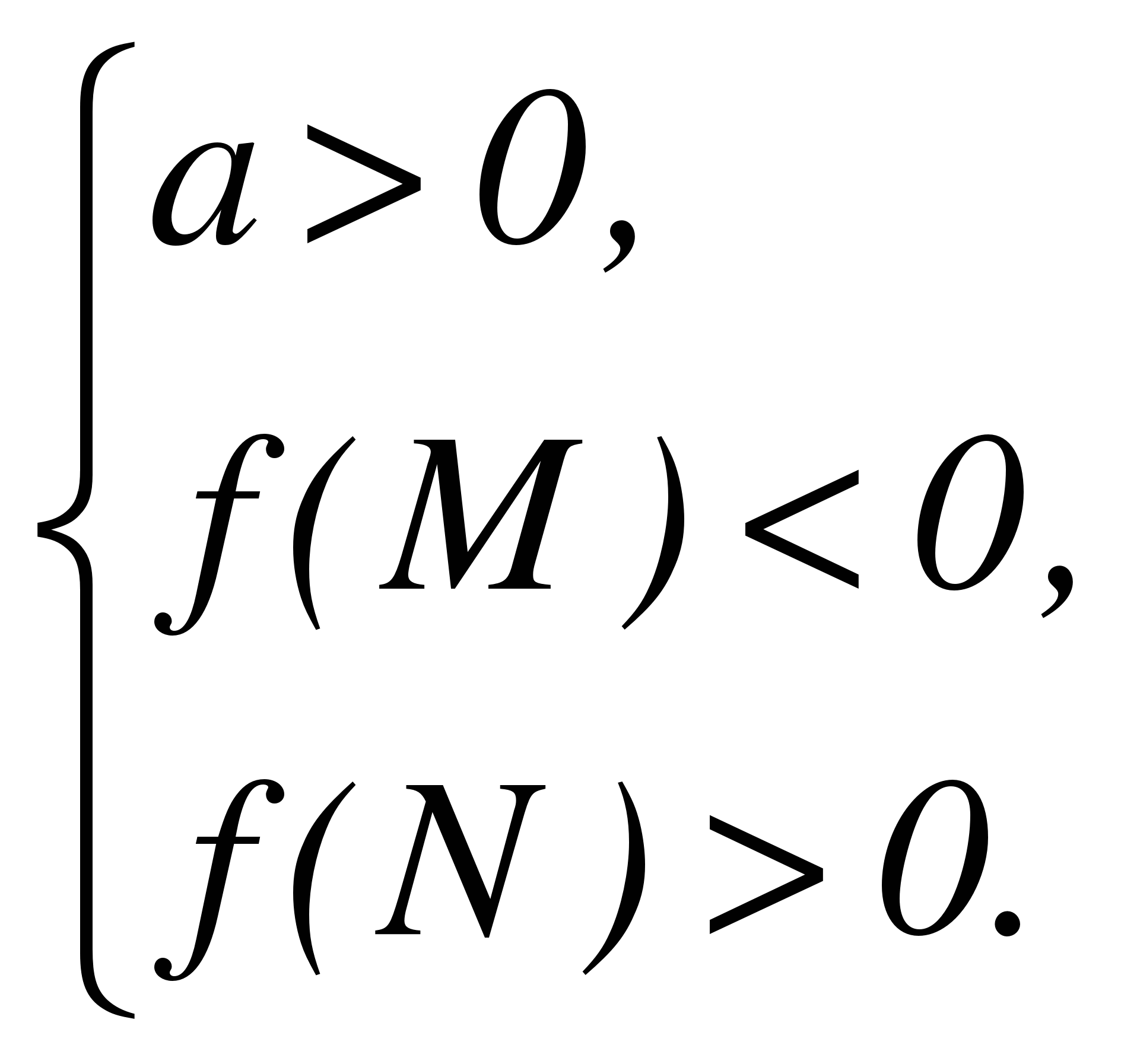 или
или 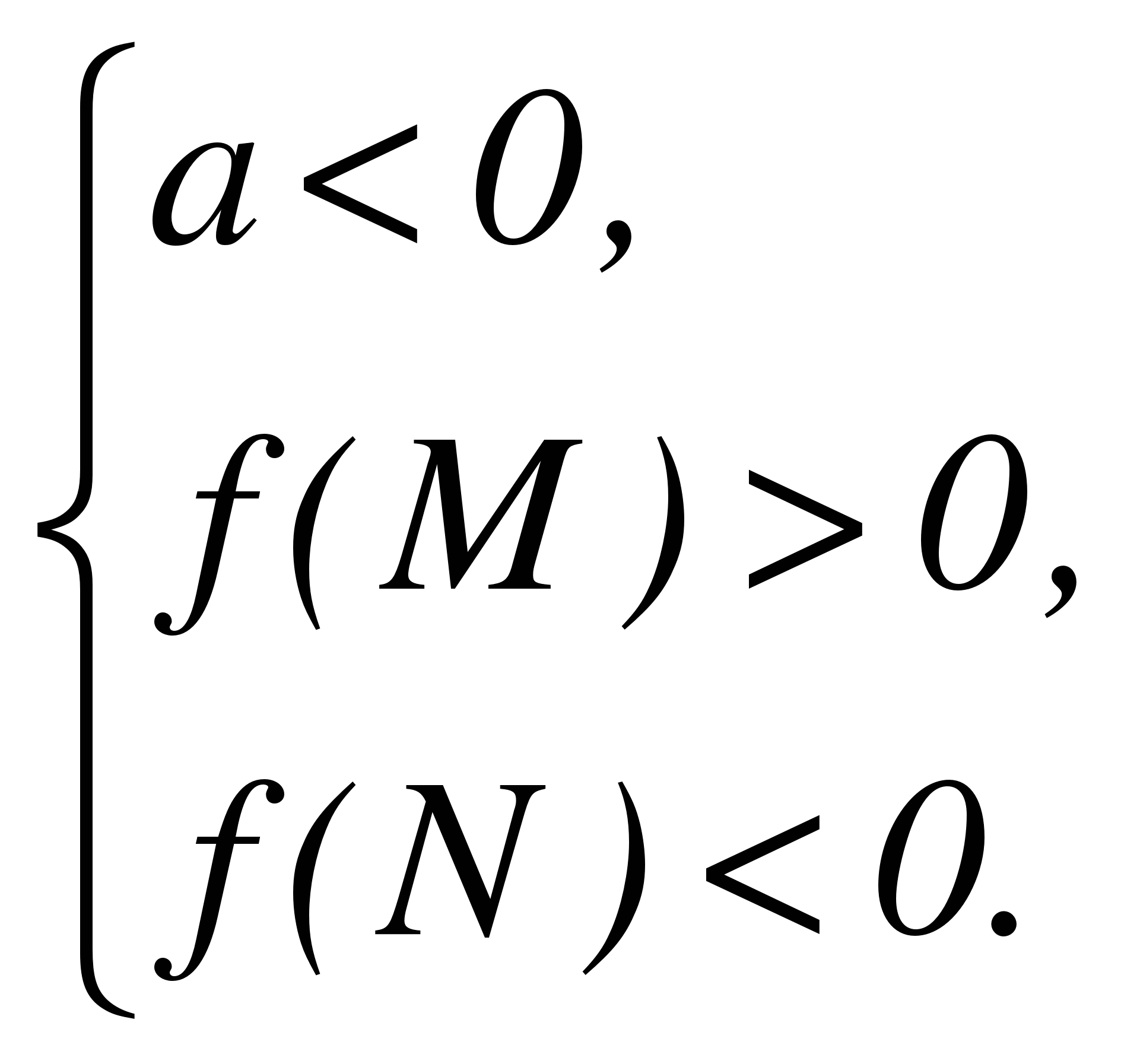
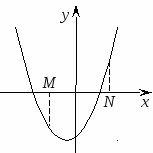
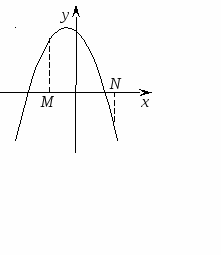
Следствие 3. Для того чтобы только меньший корень квадратного трехчлена лежал в интервале между М и N, необходимо и достаточно выполнение следующих условий:
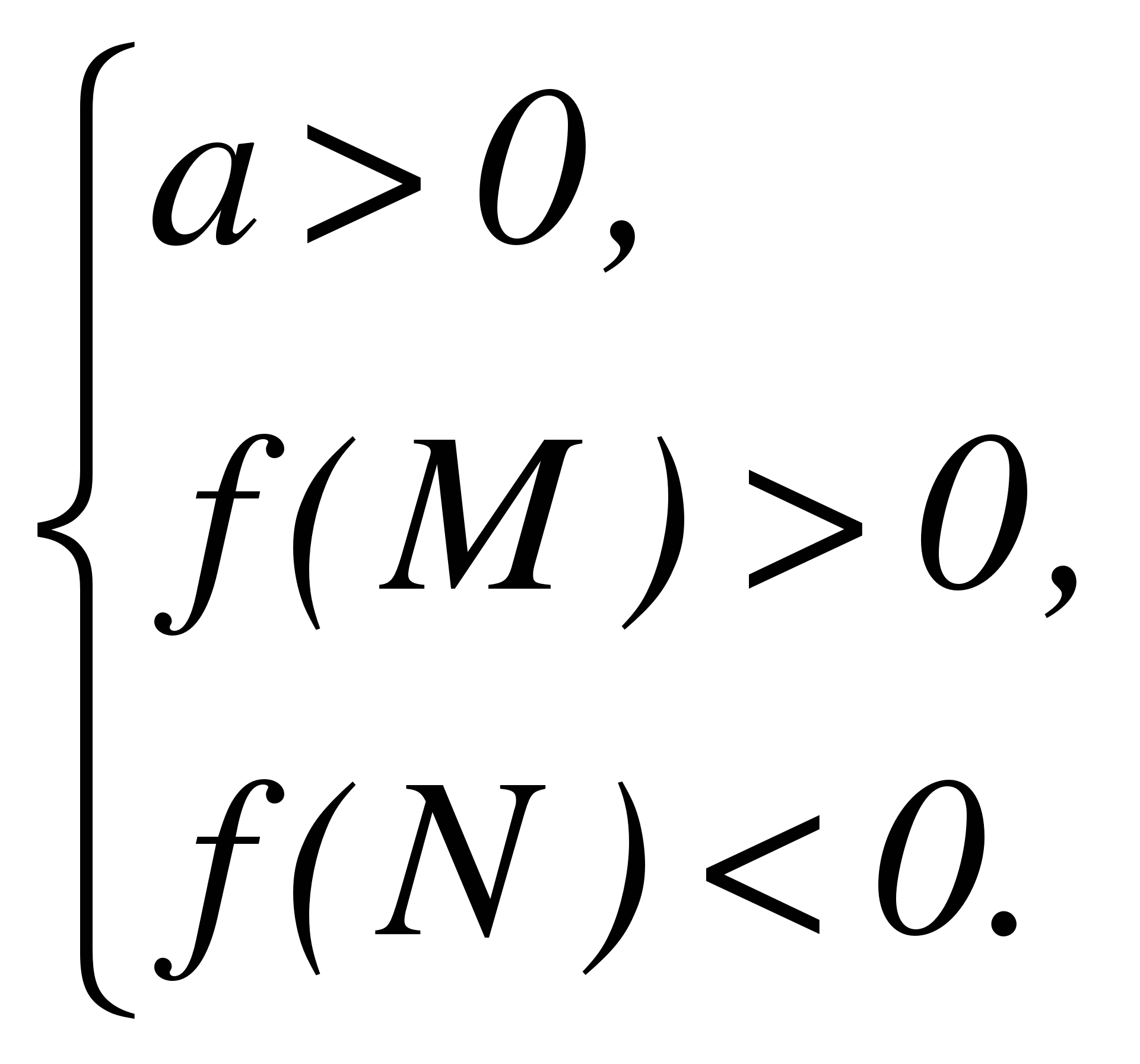 или
или 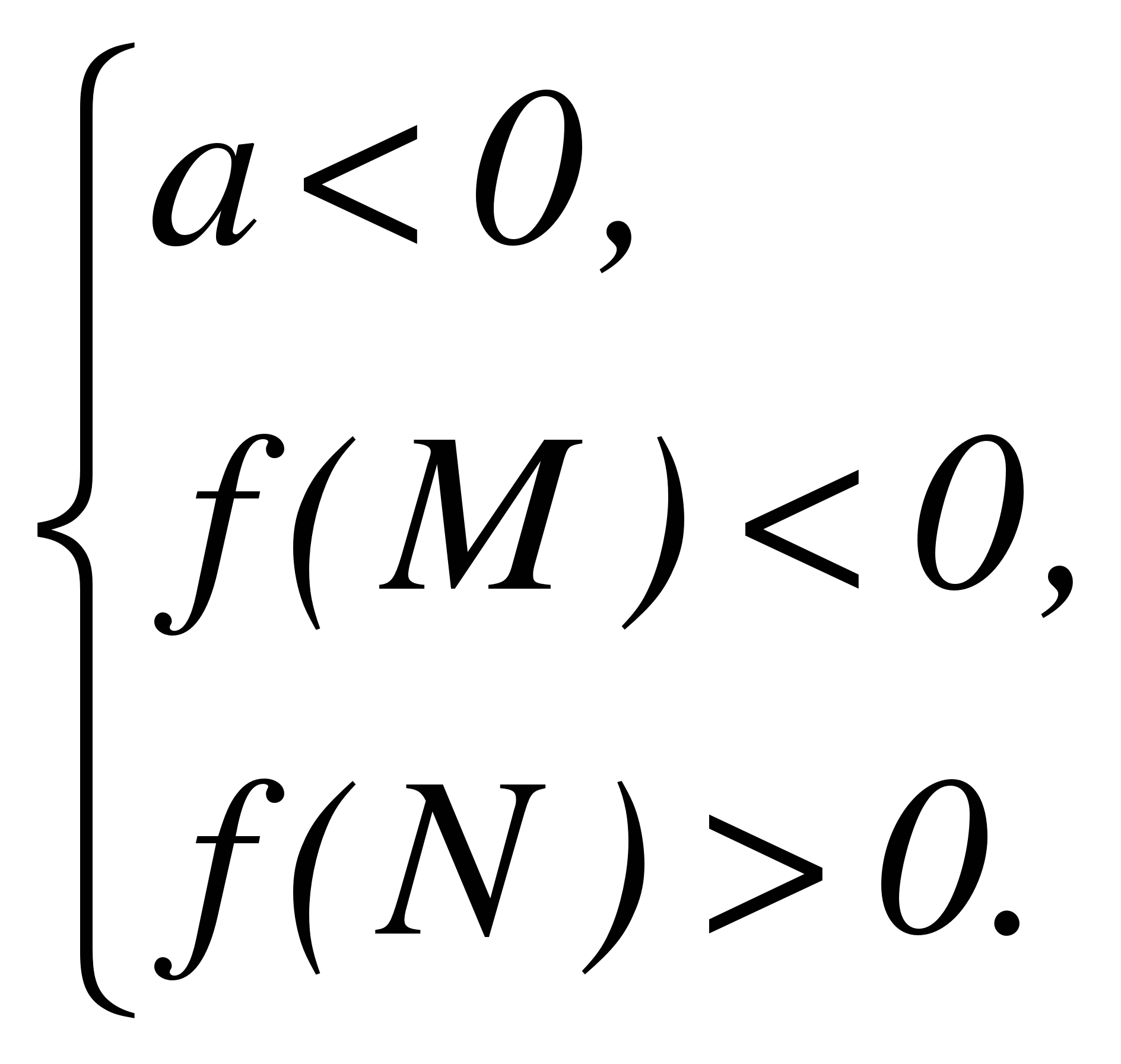
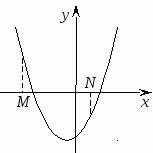
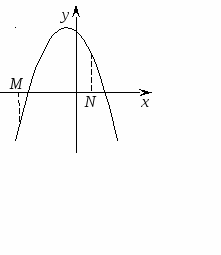
Следствие 4. Для того чтобы один из корней квадратного трехчлена был меньше, чем число М, но меньше, а другой больше, чем число N (то есть отрезок МN лежал внутри интервала между корнями), необходимо и достаточно выполнение следующих условий:
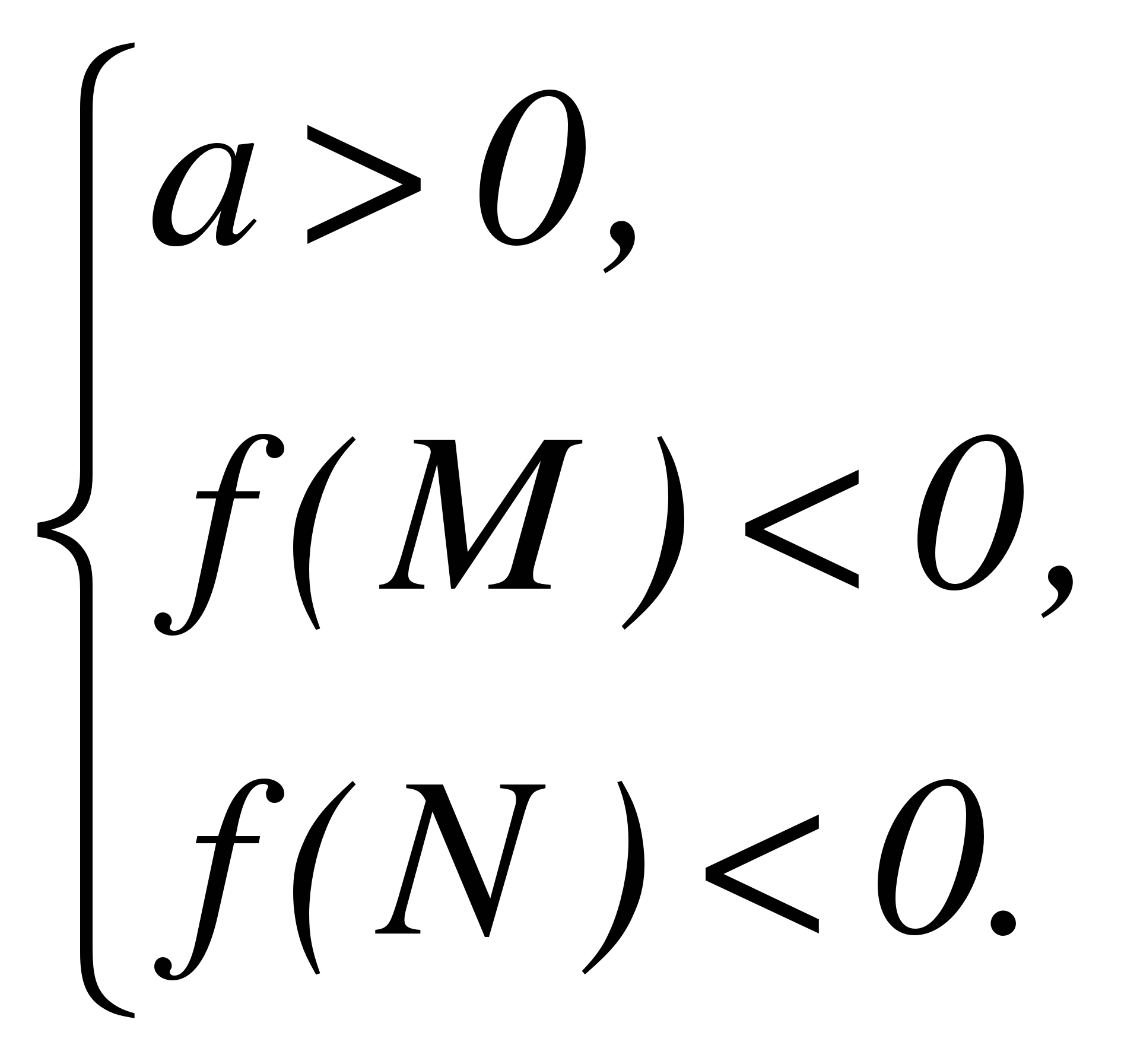 или
или 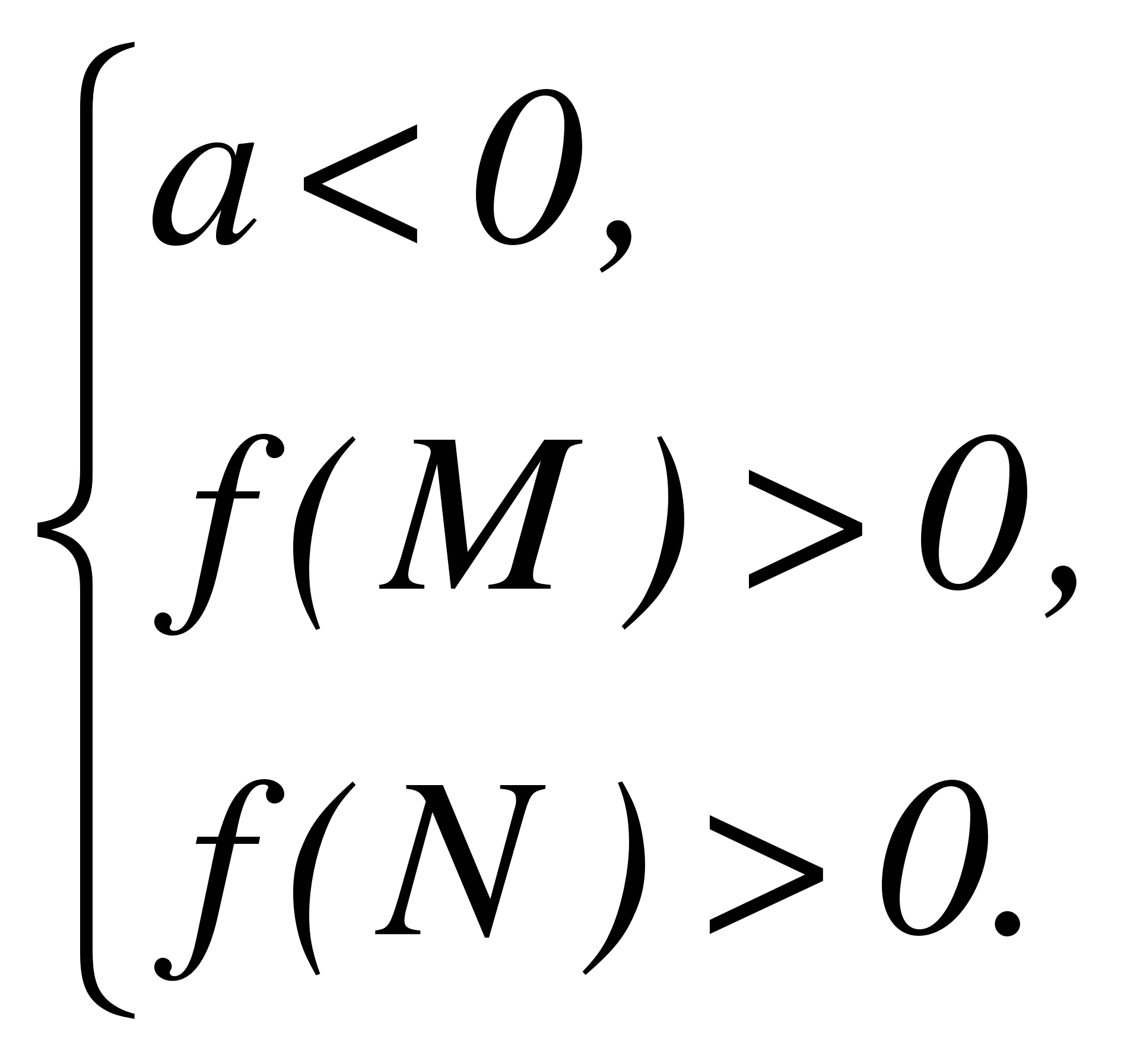
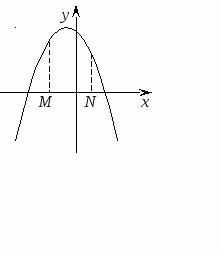
Акцентировать внимание надо на то, что здесь контрольными являются: направление ветвей параболы, знаки значений f(M), f(N), расположение вершины параболы..
Задача 1. При каких значениях параметра а уравнение х2+2∙(а+1)х+9=0 имеет два различных положительных корня?
Решение. Так как по условию корни различны, то D>0. Воспользуемся теоремой 1(о знаках корней квадратного трехчлена). Составим систему :
 D= (a+1)2- 9 >0, (a-2)∙(a+4)>0,
D= (a+1)2- 9 >0, (a-2)∙(a+4)>0,
x1∙x2=9>0, <=> a< -1.
-2∙(a+1)>0.
Решив последнюю систему, получим , что -∞<a< -4 . Ответ:- ∞<a< -4 .
Задача 2. При каких значениях параметра а уравнение х2-4х + (4-а2)=0
имеет два корня разных знаков?
Решение. Воспользуемся теоремой 2 ( о знаках корней квадратного трехчлена). Запишем условие:
4-а2 <0 а2 > 4 │а│> 2 => а< -2 и а> 2. Ответ: а<-2 и а>2 .
Задача 3. При каких значениях параметра а уравнение х2 - 2ах + а2 - а- 6 =0 имеет два разных отрицательных корня?
Решение. Воспользуемся теоремой 1 (о расположении корней квадратного трехчлена) и запишем систему :
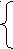 D>0 , а+6>0,
D>0 , а+6>0,
x0<0 , a<0,
f(0)>0 ; a2-a-6>0.
Решив последнюю систему, получим -6<a<-2 . Ответ : -6<a<-2.
Задача 4. При каких значениях параметра а число 2 находится между корнями квадратного уравнения х2 + (4а+5)∙х + 3-2а =0.
Решение. Пусть х1 и х2 корни квадратного трехчлена, причем х1<2<х2. Воспользуемся теоремой 2 (о расположении корней квадратного трехчлена) и запишем систему :
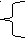 D= 16a2 +48a +13 >0,
D= 16a2 +48a +13 >0,
F(2)= 22 + (4a+5)∙2 +3- 2a<0. Решив систему, получим
17+6а<0 или а < -17/6 . Ответ: а< -17/ 6.
Задача 5. При каких значениях параметра а корни уравнения
4х2 - 2х + а =0 находятся между числами -1 и 1?
Решение. Так как корни находятся между числами -1 и 1,
То -1<х1<1 и -1<х2<1. Воспользуемся
Следствием 1 и составим систему :
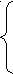
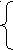 -1< х0= 2/4< 1, 6 + а >0 ,
-1< х0= 2/4< 1, 6 + а >0 ,
4∙(4+2+а)>0, => 2 + а >0 ,
4∙(4 -2+а)>0, 4 - 16а>0;
D=(-2)2 - 4∙4а >0;
Решив систему, получим -2< а < ¼. Ответ: -2< а < ¼.
Теорема Виета и задачи с параметрами.
Задача 6 . При каких значениях параметра a сумма квадратов корней уравнения 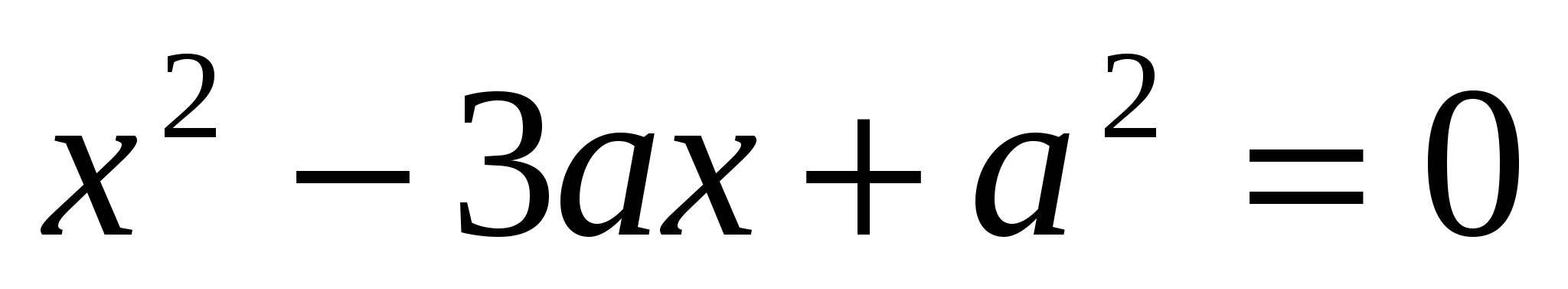 равна
равна 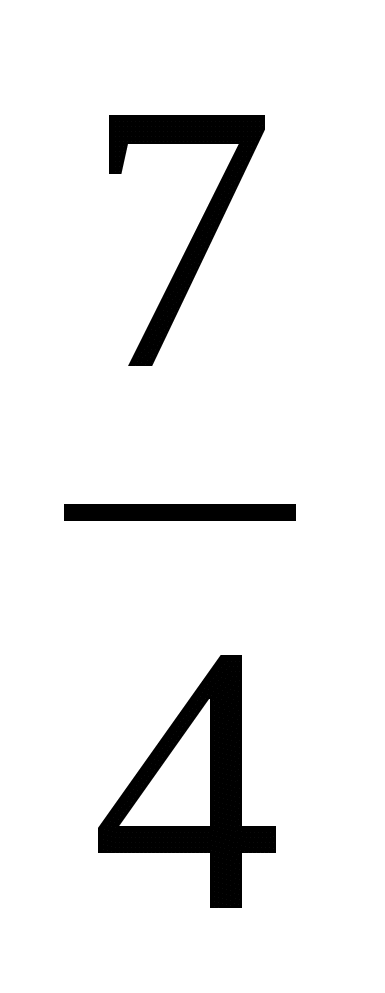 ?
?
Решение. Найдем дискриминант 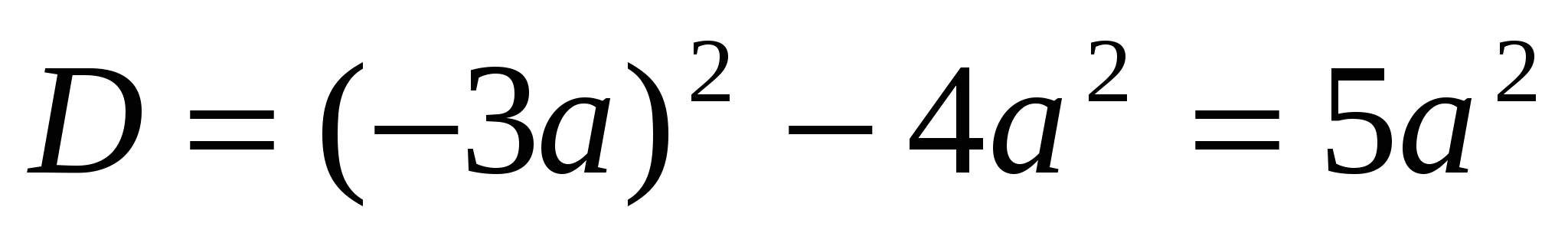 . Уравнение имеет два корня при любом a. Используя теорему Виета, найдем
. Уравнение имеет два корня при любом a. Используя теорему Виета, найдем
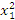 +
+ 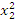 =(
=(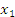 +
+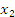 )²-2
)²-2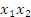 =(3a)²-2a²
=(3a)²-2a²
Поскольку 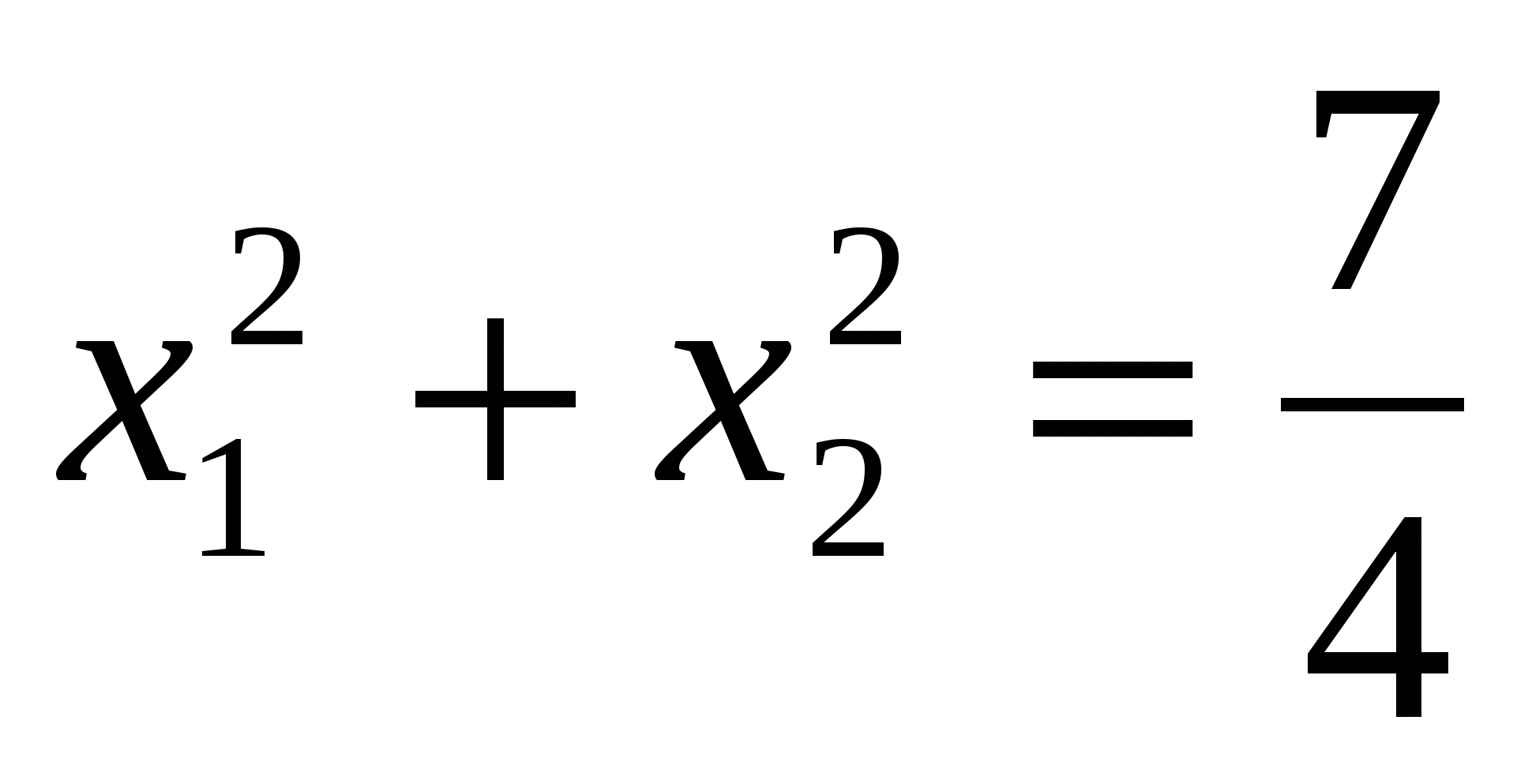 , то
, то 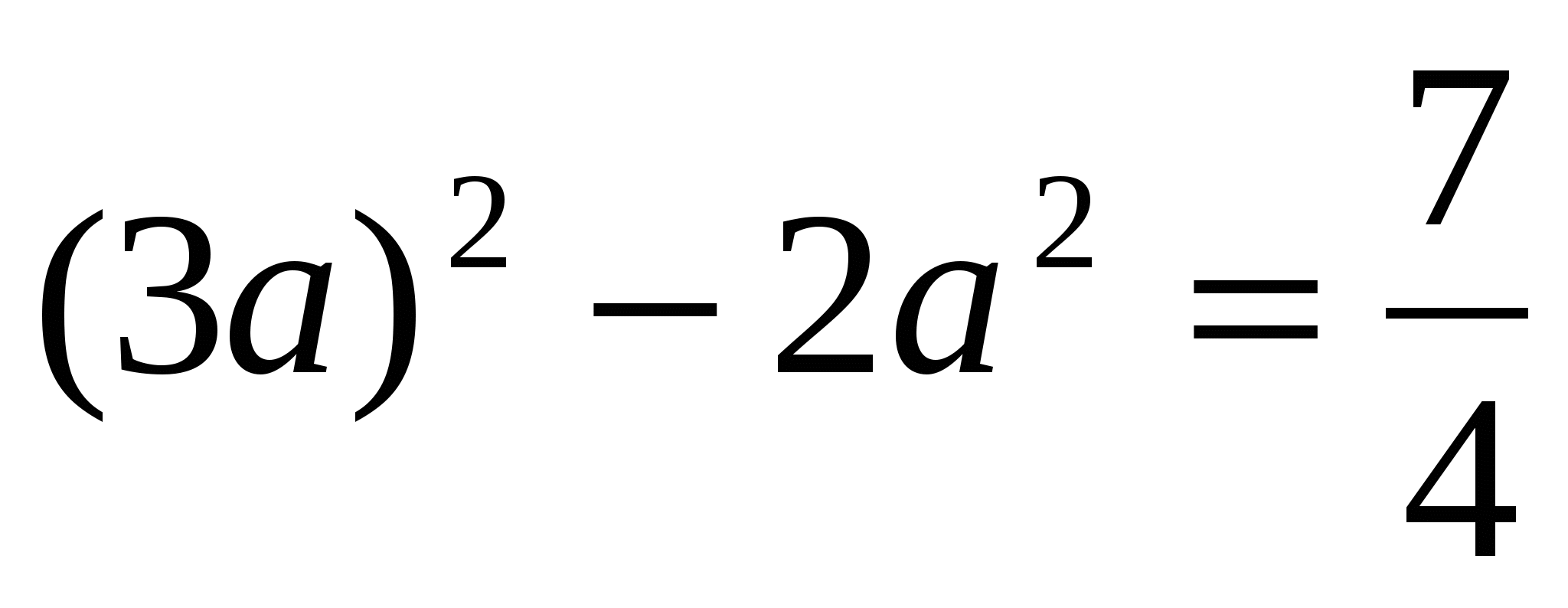 , a=0,5; -0,5. Ответ: a=0,5; -0,5.
, a=0,5; -0,5. Ответ: a=0,5; -0,5.
Задача7 . При каком значении m сумма квадратов корней уравнения
х2 + (2 - m)x - m - 3 = 0 минимальна?
Решение: Найдём х12 + х22 = (х1 + х2)2 - 2х1х2 = (m - 2)2 - 2(-m - 3) = m2 - 4m + 4 + 2m + 6 = m2 - 2m +10 = m2 - 2m + 1 + 9. Наименьшее значение трёхчлена m2 - 2m +10 достигается при m =1. Ответ: 1

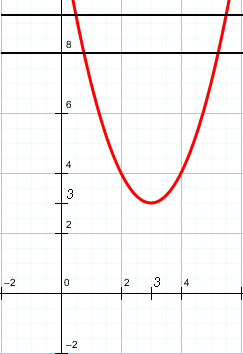
 Задача 8. Найти все значения параметра а, при которых модуль разности корней уравнения x2 -6x+12+a2 -4a =0принимает наибольшее значение.
Задача 8. Найти все значения параметра а, при которых модуль разности корней уравнения x2 -6x+12+a2 -4a =0принимает наибольшее значение.
Решение: Пусть
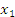 ,
,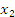 -корни уравнения, тогда |
-корни уравнения, тогда |![]() -
-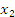 |
|
-расстояние между корнями, и оно, по условию, должно быть наибольшим.
Уравнение запишем в виде: 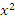 -6x+12=-a²+4a
-6x+12=-a²+4a
и решим его графически.
у=x²-6x+12
,
D=36-48=-12<0
![]() =3, yв =3
=3, yв =3
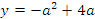 -прямая, параллельная оси ОХ.
-прямая, параллельная оси ОХ.
Чем выше она пройдет, тем больше расстояние между корнями ,т.е. надо узнать, при каком значении а функция у=y(a)=a²+4a
принимает наибольшее значение .
Графиком является парабола, ветви которой направлены вниз.
Функция достигает наибольшего значения при 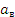 =2.
=2.
 .
.
.
Ответ: 2.
Графический способ определения числа корней уравнения с параметром.
Рациональность любого верного решения опирается на условия задачи и напрямую зависит от них. Иногда графический метод помогает быстрее и удобнее решить задачу.
Остановимся на нахождении числа решений уравнений с параметрами, в которых под знаком модуля находится квадратный трёхчлен.
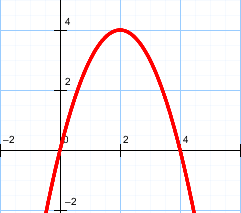
Задача 9. Найдите число решений уравнения
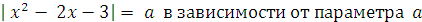 .
.
Решение: Построим график функции 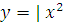 - 2x - 3 | .
- 2x - 3 | .
Выделим полный квадрат: 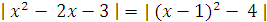
(1; -4) -координаты вершины параболы
Уравнение 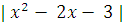 = a имеет столько решений, сколько
= a имеет столько решений, сколько
раз прямая у = а пересекает график функции 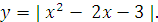
если ![]() , то графики не имеют общих точек, т.е. нет решения;
, то графики не имеют общих точек, т.е. нет решения;
если ![]() , то графики имеют две общие точки , т.е. два решения;
, то графики имеют две общие точки , т.е. два решения;
если 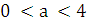 , то графики имеют четыре общие точки - четыре решения;
, то графики имеют четыре общие точки - четыре решения;
если ![]() , то графики имеют три общие точки , т.е. три решения;
, то графики имеют три общие точки , т.е. три решения;
если ![]() , то графики имеют две общие точки , т.е. два решения.
, то графики имеют две общие точки , т.е. два решения.
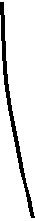
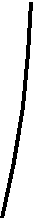 у
у
 y = a (
y = a (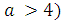

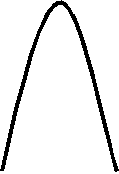 4 y = a (
4 y = a ( 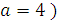
 y = a (
y = a ( 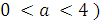
 х
х
 y = a (
y = a ( 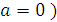
y = a ( 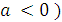
Задача 10. Для каждого значения параметра а определите число решений
уравнения 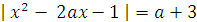 .
.
Решение: Здесь в отличие от предыдущего уравнения параметр а входит в выражение, как стоящее под знаком модуля, так и находящееся вне его. Преобразуем левую часть данного уравнения:
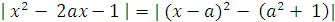 .
.
Строим схематически график левой части данного уравнения с учётом того, что дискриминант квадратного трёхчлена 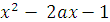 всегда положителен:
всегда положителен: 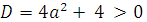 .
.
Проводим горизонтальные прямые - графики функции у = а + 3
При различных значениях параметра а.
Если 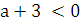 , т.е.
, т.е. 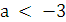 , то графики
, то графики 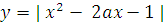 и
и
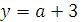 не пересекаются, и значит, нет решений.
не пересекаются, и значит, нет решений.
Если а + 3 = 0, т.е. а = -3, то графики пересекаются в двух точках
-уравнение имеет два решения.
Если 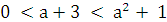 , то графики имеют четыре общие точки ,
, то графики имеют четыре общие точки ,
а уравнение - четыре решения.
Найдём, при каких значениях а уравнение будет иметь четыре решения. Для этого решим двойное неравенство
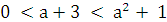 , или
, или
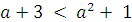
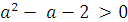
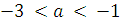
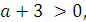
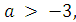
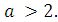
Значит, при 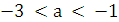 и
и 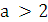 уравнение имеет четыре решения. Если
уравнение имеет четыре решения. Если 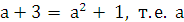 = -1 и а = 2, то графики имеют три
= -1 и а = 2, то графики имеют три
Общие точки . Значит, уравнение имеет три решения.
Если же 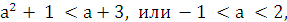 то графики пересекаются в двух точках , т.е. уравнение имеет два решения.
то графики пересекаются в двух точках , т.е. уравнение имеет два решения.
у

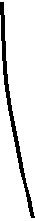
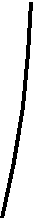 y = a+3
y = a+3 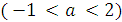



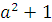 y = a+3 (
y = a+3 (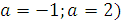
y = a + 3 (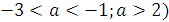


 х
х
Графический метод не дает в большинстве случаев точного решения уравнения, однако, часто оказывается более эффективным, чем аналитический, т.к. он может быть полезен для наглядной иллюстрации
рассуждений. Но не стоит забывать о его «подводных рифах», так как иногда не все решения можно увидеть . В силу ограниченности наших графических возможностей абсолютно точный график в принципе построить нельзя, поэтому слепо доверять рисунку может быть просто опасно. Более того, часто случается, что при решении задач подобным способом не обойтись без аналитических формул и вычислений.
Список литературы
1. Амелькин В.В.
Задачи с параметрами - М.: Асар, 1996.
2. Горнштейн П.И., Полонский В.Б., Якир М.С.
Задачи с параметрами. - М.: Илекса, 2005.
3. Дорофеев Г.В.
Решение задач, содержащих параметр
4 .Локоть В.В.
«Задачи с параметрами. Линейные и квадратные уравнения, неравенства и системы» Учебное пособие М. АРКТИ, 2005(Абитуриент);
5. Цыганов Ш.
Десять правил расположения корней квадратного трехчлена
Математика. - 2002. №18.-с. 19-23.
6. Цыганов Ш.
Квадратные трехчлены и параметры
Математика. - 1999. №5. -с. 4-9.
7. С.В. Кравцев, Ю.Н. Макаров
Методы решения задач по алгебре от простых до самых сложных.


