- Преподавателю
- Математика
- Элективный курс Функция: просто, сложно, интересно
Элективный курс Функция: просто, сложно, интересно
| Раздел | Математика |
| Класс | 9 класс |
| Тип | Другие методич. материалы |
| Автор | Черных А.Н. |
| Дата | 22.11.2015 |
| Формат | doc |
| Изображения | Есть |
Элективный курс по математике.
Функция: просто, сложно, интересно.
Составил Черных А.Н.
Пояснительная записка
Начиная с 7 класса в центре внимания школьной математики находится понятие функции. Однако размеры школьного учебника, количество часов, выделяемых на изучение темы "Функция" в разных классах, не позволяют показать в сколько-нибудь полном объеме все многообразие задач, требующих для своего решения функционального подхода, научить учащихся глубоко понимать и использовать свойства функции; нет времени изложить историю возникновения этого интереснейшего раздела в школьном курсе математики.
С другой стороны, авторы контрольно-измерительных материалов ЕГЭ уделяют много внимания проверке умений читать по графику свойства функции, использовать их в решении уравнений и неравенств. Тесты итоговой аттестации по математике за курс основной школы предполагают наличие у школьников подобных знаний, поэтому формировать основы этих знаний необходимо начинать как можно раньше.
Курс "Функция: просто, сложно, интересно" позволит углубить знания учащихся по истории возникновения понятия, по способам задания функций, их свойствам, а также раскроет перед школьниками новые знания об обратных функциях и свойствах взаимно обратных функций, выходящие за рамки школьной программы.
Ц е л ь: создание условий для обоснованного выбора учащимися профиля обучения в старшей школе через оценку собственных возможностей в освоении математического материала на основе расширения представлений о свойствах функций.
З а д а ч и:
- закрепление основ знаний о функциях и их свойствах;
- расширение представлений о свойствах функций;
- формирование умений "читать" графики и называть свойства по формулам;
- вовлечение учащихся в игровую, коммуникативную, практическую деятельность как фактор личностного развития.
Курс предназначен для учащихся 9 классов средних общеобразовательных учреждений, реализующих предпрофильную подготовку. Рассчитан на 17 часов аудиторного времени.
Включенный в программу материал имеет познавательный интерес для учащихся и может применяться для разных групп школьников вследствие своей обобщенности и практической направленности. Развертывание учебного материала четко структурировано и соответствует задачам курса.
Формами итоговой аттестации являются представление "Портфеля достижений", а также дидактическая игра "Восхождение на вершину знаний".
"Портфель достижений", на наш взгляд, должен включать:
- конспекты занятий;
- схему исследования функции;
- самостоятельные исследования свойств функций (не менее четырех);
- "Применение функций в природе и технике" (информация в любой форме);
- тесты (не менее двух);
- анализ собственных успехов (в любой форме);
- описание своего участия в игре, баллы, набранные в ней.
Требования к усвоению курса.
Учащиеся должны знать:
- понятие функции как математической модели, описывающей разнообразие реальных зависимостей;
- определение основных свойств функции (область определения, область значений, четность, возрастание, экстремумы, обратимость и т. д.);
Учащиеся должны уметь:
- правильно употреблять функциональную терминологию;
- исследовать функцию и строить ее график;
- находить по графику функции ее свойства.
Тематическое планирование учебного материала
Тема
Кол-во часов
Технология
реализации
Подготовительный этап: постановка цели, проверка владения базовыми навыками
1
Беседа, тестирование
Историко-генетический подход к понятию "функция"
1
Лекция, демонстрация диафильма
Способы задания функций
1
Беседа, практикум
Четные и нечетные функции
2
Беседа, практикум
Монотонность функции
2
Лекция, практикум, тестирование
Ограниченные и неограниченные функции
2
Семинар, практикум
Исследование функции элементарными способами
2
Практикум, тестирование
Построение графиков функций
2
Практикум тестирования
Функционально-графический метод решения уравнений
2
Беседа, практикум
Функция: сложно, просто, интересно
1
Дидактическая игра "Восхождение на вершину знаний"
Функция: просто, сложно, интересно
1
Презентация "Портфеля достижений"
Занятие 1
Постановка цели.
Проверка владения базовыми умениями
Цели: проверка и актуализация базовых знаний.
Х о д з а н я т и я
На данном занятии надо рассказать о целях и задачах изучения курса, о важности получаемых знаний для итоговой аттестации как в основной так и в средней школе. Объяснить, как получить зачет, что такое "Портфель достижений". Проверка базовых знаний осуществляется за счет вводного тестирования.
I. Тест.
В а р и а н т I
1. Какая из функций, приведенных ниже, является линейной:
а)  ; б)
; б)  ; в)
; в) ![]() .
.
2. Область определения функции  :
:
а)  ; б)
; б)  ; в)
; в) ![]() ?
?
3. Найдите значение функции  при
при ![]() :
:
а) 0; б) - 2; в) - 0,8.
4. На рис. 82 (а, б, в) найдите точку  , симметричную точке
, симметричную точке  относительно оси ординат.
относительно оси ординат.
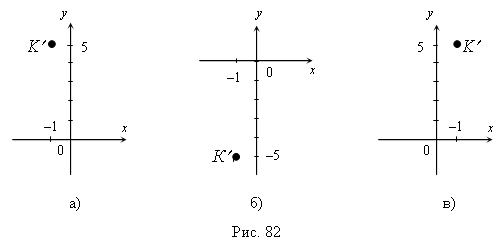
5. На рис. 83 (а, б, в) найдите точку А', симметричную точке  относительно начала координат.
относительно начала координат.
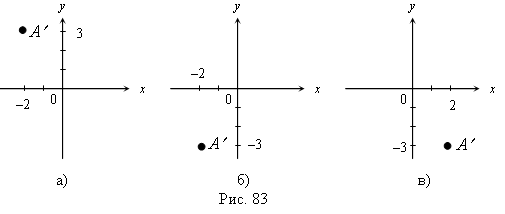
6. Функция  при
при  :
:
а) возрастает; б) убывает; в) постоянна.
7. График функции  называется:
называется:
а) прямой; б) гиперболой; в) параболой.
8. Какой из графиков параллелен прямой  :
:
а)  ; б)
; б)  в)
в) ![]() .
.
9. Графику какой функции принадлежит точка ![]() :
:
а)  ; б)
; б)  ; в)
; в) ![]() ?
?
10. Найдите координаты точки пересечения графиков функций  и
и  :
:
а)  ; б)
; б)  ; в)
; в) ![]() .
.
Ключ к тесту:
1
2
3
4
5
6
7
8
9
10
б
а
а
б
в
а
б
б
б
в
В а р и а н т II
1. Какая из функций, приведенных ниже, линейная:
а)  ; б)
; б)  ; в)
; в) ![]() ?
?
2. Область определения функции  :
:
а)  ; б)
; б)  ; в)
; в) ![]() .
.
3. Найдите значение функции  при
при ![]() :
:
а) 3; б) 12; в)  .
.
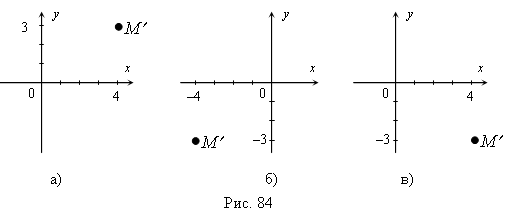
4. На рис. 84 (а, б, в) найдите точку М', симметричную точке  относительно начала координат.
относительно начала координат.
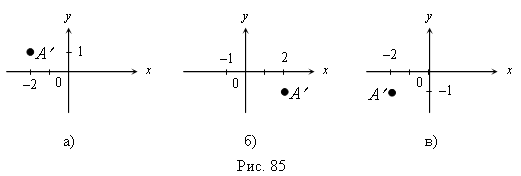
5. На рис. 85 (а, б, в) найдите точку А', симметричную А (2, 1) относительно оси ординат.
6. Функция  при
при  :
:
а) возрастает; б) убывает; в) постоянна.
7. График функции  называется:
называется:
а) прямой; б) гиперболой; в) параболой.
8. Какой из графиков параллелен прямой  :
:
а)  ; б)
; б)  ; в)
; в) ![]() .
.
9. Какому из графиков принадлежит точка ![]() ?
?
а)  ; б)
; б)  ; в)
; в) ![]() .
.
10. Найдите координаты точки пересечения графиков функций  и
и  :
:
а)  ; б)
; б)  ; в)
; в) ![]() .
.
Ключ к тесту:
1
2
3
4
5
6
7
8
9
10
а
б
а
в
а
б
в
а
б
в
II. Актуализация базовых знаний.
О п р е д е л е н и е: Зависимость переменной у от переменной х называется функцией, если каждому значению х соответствует единственное значение у. При этом используют запись y = f(x).
Переменную х называют независимой переменной, или аргументом, а переменную у - зависимой переменной. Говорят, что у является функцией от х.
Значение у, соответствующее заданному значению х, называют значением функции.
Все значения, которые принимает независимая переменная, образуют область определения функции; все значения, которые принимает зависимая переменная, образуют множество значений функции. Они обозначаются ![]() и
и  соответственно.
соответственно.
Если функция задана формулой, то считают, что область определения состоит из всех значений независимой переменной, при которых эта формула имеет смысл.
Для закрепления учащимся предлагается ответить на вопросы.
1. Найдите область определения функции, заданной формулой:
а)  ; б)
; б)  ; в)
; в) ![]() ; г)
; г)  ;
;
д)  ; е)
; е)  ; ж)
; ж) ![]() .
.
О т в е т: а) все числа, кроме 1; б)  ; в) все числа; г) все числа, кроме 0 и 1; д)
; в) все числа; г) все числа, кроме 0 и 1; д)  ; е)
; е) ![]() ; ж) все отрицательные числа и 0.
; ж) все отрицательные числа и 0.
Далее повторяются функции, уже известные из школьной программы.
1.  - линейная функция, графиком которой является прямая.
- линейная функция, графиком которой является прямая.
2.  - функция обратно пропорциональной зависимости, графиком которой является гипербола.
- функция обратно пропорциональной зависимости, графиком которой является гипербола.
3.  - квадратичная функция, графиком которой является парабола.
- квадратичная функция, графиком которой является парабола.
4.  - степенная функция, графиком которой является кубическая парабола.
- степенная функция, графиком которой является кубическая парабола.
Для закрепления можно задать вопросы:
1. Формула y = -5x + 6 задает некоторую функцию. Найдите значение функции, соответствующее значениям аргумента: -1,2; 2,8. При каком значении аргумента значение функции равно 6; 8; 100?
О т в е т: 12; -8; 0; -0,4; -18,8.
2. Заполните таблицу:
х
2
1,6



О т в е т: 4; -1; 5; -16.
3. Найдите значение функции, соответствующее значению аргумента, если это возможно,  ; 16; 1,21; -25;
; 16; 1,21; -25;  .
.
О т в е т: 4; 1,1; не существует;  .
.
Занятие 2
Историко-генетический подход
к понятию "функция"
Цели: раскрыть сложный исторический путь понятия "функция"; вызвать чувство сопричастности к поиску гениальных ученых.
Х о д з а н я т и я
У ч и т е л ь. Понятие функции уходит своими корнями в ту далекую эпоху, когда люди впервые поняли, что окружающие их явления взаимосвязаны. Они еще не умели считать, но уже знали, что чем больше оленей удастся убить на охоте, тем дольше племя будет избавлено от голода; чем сильнее натянута тетива лука, тем дальше полетит стрела.
С развитием скотоводства и земледелия, ремесла и обмена увеличилось количество известных людям зависимостей между величинами. Многие из них выражались с помощью чисел. Это позволило формулировать их словами: "больше на", "меньше на", "больше во столько-то раз". Если за одного быка давали 6 овец, то двух обменивали уже на 12; если из одного ведра глины можно было сделать 4 горшка, то из 3 - 12. Такие расчеты привели к представлениям о пропорциональности величин.
Высокого уровня достигла математика в Древнем Вавилоне. Чтобы облегчить вычисления, вавилоняне составили таблицы обратных чисел, таблицы квадратов и кубов чисел и даже таблицы для суммы квадратов чисел и их кубов. Говоря современным языком, это было табличное задание функций  ;
;  ;
; ![]() ,
,  . Разумеется, путь от составления таблиц до создания общего понятия функциональной зависимости был еще очень долог, но первые шаги по этому пути уже были сделаны.
. Разумеется, путь от составления таблиц до создания общего понятия функциональной зависимости был еще очень долог, но первые шаги по этому пути уже были сделаны.
Многое из того, что сделали древнегреческие математики, тоже могло привести к возникновению понятия о функции. Они нашли много различных кривых, неизвестных в Египте и Вавилоне, изучили зависимости между отрезками диаметров и хорд в круге, эллипсе и других линиях.
Арабские ученые ввели новые тригонометрические таблицы и усовершенствовали таблицы хорд, составленные Птолемеем. В исследованиях аль-Бируни впервые встречаются мысли о "всех таблицах", то есть о всевозможных зависимостях между величинами.
Исследования общих зависимостей началось в XIV веке. Среди схоластов возникла школа, утверждавшая, что качества могут быть более или менее интенсивными (платье человека, свалившегося в воду, мокрее, чем у того, кто лишь попал под дождь). Французский ученый Николай Оресм стал изображать интенсивности длинами отрезков. Важным достижением Оресма была попытка классифицировать получившиеся графики. Он выделил три типа качеств: равномерные (то есть с постоянной интенсивностью), равномерно-неравномерные (для которых скорость изменения интенсивности постоянна) и неравномерно-неравномерные (все остальные), а также указал характерные свойства этих графиков.
Идеи Оресма намного обогнали тогдашний уровень науки. Чтобы развивать их дальше, нужно было уметь выражать зависимости между величинами не только графически, но и с помощью формул, а буквенной алгебры в то время еще не существовало.
На протяжении XVI и XVII вв. в естествознании произошла революция, приведшая к глубочайшим изменениям не только в технике (астрономы узнали о спутниках Юпитера и пятнах на Солнце, инженеры придумали новые машины и усовершенствовали часы, мореплаватели открыли новые континенты и таинственные страны), но и в мировоззрении людей. Они стали смотреть на мир не как на поле приложения божесвенной воли, а как на механизм, управляемый своими законами. И основной задачей науки стало открытие этих законов, описание их в терминах математики.
Чтобы создать математический аппарат для изучения движений, понадобилось понятие переменной величины. Это понятие было введено в науку французским философом и математиком Рене Декартом (1596-1650 гг.). Декарту удалось уничтожить пропасть, существовавшую со времен древнегреческой математики, между геометрией и арифметикой. При записи зависимостей между величинами Декарт стал применять буквы. Отношения между известными и неизвестными величинами Декарт выражал в виде уравнений. Чтобы наглядно изображать уравнение, он заменял все величины длинами отрезков. По сути дела, здесь была заложена идея метода координат. Одновременно с Декартом к мысли о соответствии между линиями и уравнениями пришел другой французский математик - Пьер Ферма (1601-1665 гг.).
После того как в науку вошли переменные величины, были изучены траектории движущихся точек, достигла расцвета вычислительная математика и была создана буквенная алгебра, внимание ученых обратилось к изучению соответствий между величинами. В своей "Геометрии" Декарт писал: "Придавая линии у последовательно бесконечное количество различных значений, мы найдем также бесконечное количество значений х и, таким образом, получим бесконечное количество различных точек…; они опишут требуемую кривую линию". Здесь ясно выражена идея функциональной зависимости величин у и х, идея геометрического выражения этой зависимости.
Функция - основное понятие математического анализа. Но вначале оно было очень расплывчатым, не имело сколько-нибудь точного описания.
Термин "функция" ввел в математику Готфрид Лейбниц (1646-1716 гг.). Он употреблял его в очень узком смысле, связывая только с геометрическими образами.
Лишь И. Бернулли дал определение функции, свободное от геометрического языка: "Функцией переменной величины называется количество, образованное каким угодно способом преобразования этой переменной величины и постоянных".
Определение Бернулли опиралось не только на работы Лейбница и его школы, но и на исследования великого математика и физика Исаака Ньютона (1643-1727 гг.), который изучил колоссальное число самых различных функциональных зависимостей и их свойств. Вместо слова функция Ньютон применял термин "ордината". Он сводил изучение геометрических и физических зависимостей к изучению этих ординат, а сами ординаты описывал различными аналитическими выражениями.
Один из самых замечательных математиков XVIII в. - Леонард Эйлер (1707-1783 гг.), - вводя в своем учебнике понятие функции, говорил лишь, что "когда некоторые количества зависят от других таким образом, что при изменении последних и сами они подвергаются изменению, то первые называются функциями вторых".
В развитие понятия функции внесли свой вклад французский математик Ж. -Б.Фурье (1768-1830 гг.), русский ученый Н. И. Лобачевский (1792-1856 гг.), немецкий математик Дирихле (1805-1859 гг.) и другие ученые, и общепризнанным стало следующее определение: "Переменная величина у называется функцией переменной величины х, если каждому значению величины х соответствует единственное определенное значение величины у".
Однако некоторых математиков подобное определение не совсем удовлетворяло. Ведь в нем термин "функция" определяется через понятия, которые достаточно неопределенны и расплывчаты ("зависимость", "соотвествтие"). Некоторое успокоение пришло с созданием теории множеств, начала которой были заложены в конце XIX в. Георгом Кантором. Все вроде встало на свои места. Пусть Х и Y - два множества. Множество F пар ![]() , где
, где ![]() ,
,  называется функцией, если для любого
называется функцией, если для любого  существует единственное
существует единственное ![]() , такое, что
, такое, что ![]() . Концепции теории множеств произвели огромное впечатление на многих математиков, бывших свидетелями зарождения новой теории. Давид Гильберт, известный немецкий математик, сказал о теории множеств: "Я считаю, что она представляет собой высочайшее проявление человеческого гения и одно из самых высоких достижений чисто духовной деятельности человека".
. Концепции теории множеств произвели огромное впечатление на многих математиков, бывших свидетелями зарождения новой теории. Давид Гильберт, известный немецкий математик, сказал о теории множеств: "Я считаю, что она представляет собой высочайшее проявление человеческого гения и одно из самых высоких достижений чисто духовной деятельности человека".
Подводя итоги, следует сказать, что в зависимости от природы множеств Х и Y термин "функция" в различных разделах математики имеет ряд полезных синонимов: отображение, соответствие, преобразование, оператор, функционал и т. д.
Рассмотрим их на простых примерах.
1. Отображение. Когда функцию  называют отображением, значение
называют отображением, значение  , которое она принимает на элементе
, которое она принимает на элементе  , обычно называют образом элемента х. Например, можно задать отображение множества
, обычно называют образом элемента х. Например, можно задать отображение множества  на множество
на множество ![]() так, что образом элементов 2, 3, 5 будет 2, а 4 3. То есть каждому числу соответствует количество его делителей.
так, что образом элементов 2, 3, 5 будет 2, а 4 3. То есть каждому числу соответствует количество его делителей.
2. Соответствие. Пусть А - множество квадратов. Каждый квадрат  имеет сторону вполне определенной длины
имеет сторону вполне определенной длины  . Соответствие
. Соответствие ![]() порождает функцию.
порождает функцию.
3. Преобразование. Если на прямой ввести две системы координат  и
и  , имеющие одинаковый масштаб (единицу длины), то координаты х и х' одной и той же точки прямой в этих системах будут связаны соотношением
, имеющие одинаковый масштаб (единицу длины), то координаты х и х' одной и той же точки прямой в этих системах будут связаны соотношением  , где с - координата начала отсчета в системе
, где с - координата начала отсчета в системе  . Функция
. Функция  - называется преобразованием. Такой термин чаще встречается в геометрии и физике.
- называется преобразованием. Такой термин чаще встречается в геометрии и физике.
4. Оператор - это функция, преобразующая одни функции в другие. Например: любой радиоприемник - оператор, преобразующий электромагнитный сигнал, поступающий на вход приемника, в звуковой на его выходе. Среди числовых функций оператором можно назвать функции, задающие геометрические преобразования графиков. Например,  - оператор сдвига функции на величину с.
- оператор сдвига функции на величину с.
5. Функции, определенные на функциях и принимающие числовые значения, называют функционалом. Например, любой числовой функции, определенной на отрезке  , поставим в соответствие длину кривой графика этой функции на этом отрезке.
, поставим в соответствие длину кривой графика этой функции на этом отрезке.
Таким образом, функция - одно из основных математических и общенаучных понятий, выражающее зависимость между переменными величинами. Каждая область знаний: физика, химия, биология, социология, лингвистика и т. д. - имеет свои объекты изучения, устанавливает свойства и взаимосвязи этих объектов. Математика рассматривает абстрактные переменные величины и в отвлеченном виде изучает различные законы их взаимосвязи, которые на математическом языке называются функциями.
Мы будем изучать числовые функции и их свойства.
М е т о д и ч е с к о е з а м е ч а н и е. Ясно, что лекционный материал такого объема трудно воспринимать. Но, во-первых, слушатели - учащиеся 9 класса, выбравшие этот курс; во-вторых, в процессе рассказа о функциях демонстрируются фрагменты диафильма: "Функция" (математика, 6 кл.) (Ю. Н. Макарычев. Студия "Диафильм". - Москва, 1982 г.), где на конкретных ярких примерах показаны соответствия, отображения; в-третьих, в качестве разрядки ребятам можно предложить следующие вопросы:
1) Прочитайте фамилии известных математиков, внесших свой вклад в формирование понятия "функция", зашифрованные анаграммами:
а) НОТЮНЬ; г) НАКТОР;
б) ЛИДЕРИХ; д) РЕЙЛЭ.
в) ЛОЙБАСИКЧЕВ;
2) Впишите в оставшиеся клетки фамилии известных ученых, внесших свой вклад в развитие понятия "функция".
3) Можно также предложить придумать различные степени интенсивности качеств по Оресму, например, у костра жарче, чем у свечи.
И наконец в-четвертых, никто не запрещает учителю сократить данный здесь материал, предложить учащимся часть его найти самостоятельно и т. д.
Занятие 3
Способы задания функций
Цели: повторить и углубить знания о способах задания функций; осуществить эвристические пробы по переходу от одного способа к другому.
Х о д з а н я т и й
У ч и т е л ь. Задать функцию f - значит, указать ее область определения  , множество значений
, множество значений  и множество пар
и множество пар  . Поскольку во многих случаях
. Поскольку во многих случаях ![]() и
и  находятся из множества пар
находятся из множества пар  , то достаточно каким-то способом задать эти пары.
, то достаточно каким-то способом задать эти пары.
Табличное задание функции - частный случай задания функции с помощью пар; таблица - это особая форма записи пар, первые компоненты которых записаны в одном столбце (одной строке), а вторые - в другом.
Например:
х
1
2
3
4
f(x)
12
6
4
3


Ясно, что табличный способ находит свое применение в практике, те же таблицы Брадиса.
З а д а н и я д л я с а м о с т о я т е л ь н о г о р е ш е н и я.
Назовите  и
и  . Является ли заданная в таблице функция - числовой?
. Является ли заданная в таблице функция - числовой?
З а д а н и е 1. Результаты измерений сопротивления r (Ом) медного стержня при различных значениях температуры t (С) представлены в табл.
t
19,1
25,0
30,1
36,0
50,0
r
76,3
77,8
79,75
80,80
85,10
З а д а н и е 2. Дальность полета вертолетов S (км) задана таблицей:
Марка вертолета
Ми-4П
Ми-6
Ми-8
Ка-18
Ка-26
S
740
810
650
400
304
Задает ли таблица функцию? Числовую функцию? Что в таблице принято за значения аргумента?
Графическое задание функции. Графиком функции  называется изображение на координатной плоскости множества пар
называется изображение на координатной плоскости множества пар  .
.
Для того чтобы множество точек координатной плоскости являлось графиком некоторой функции, необходимо и достаточно, чтобы любая прямая, параллельная оси Оу, пересекалась с указанным графиком не более чем в одной точке.
З а д а н и я д л я с а м о с т о я т е л ь н о г о р е ш е н и я.
З а д а н и е 3. На рис. 86 изображены графики тормозного пути автомобиля на сухом (I), мокром (II) асфальте и в гололед (III).
1) При каких условиях удлиняется тормозной путь?
2) Каков примерно тормозной путь при каждом состоянии асфальта при скорости 50 км/ч?
3) Какую скорость следует выбрать для безопасного движения:
а) на мокром асфальте;
б) в гололед?
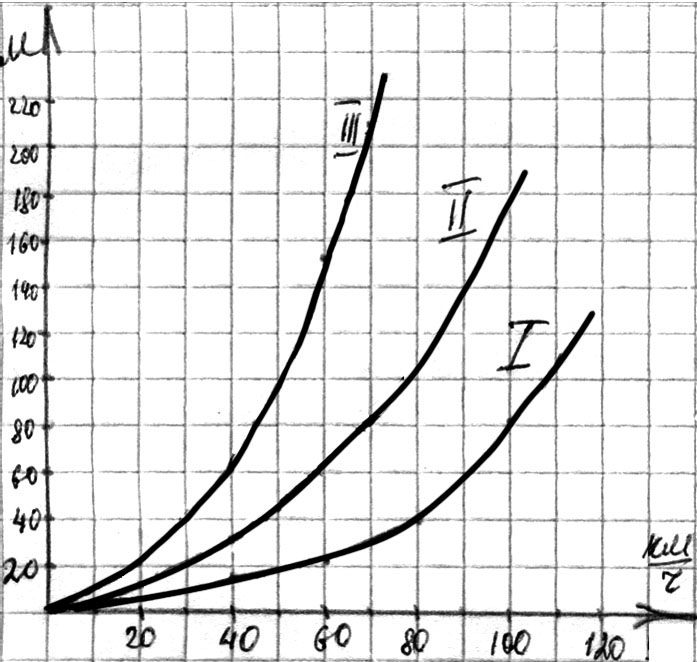
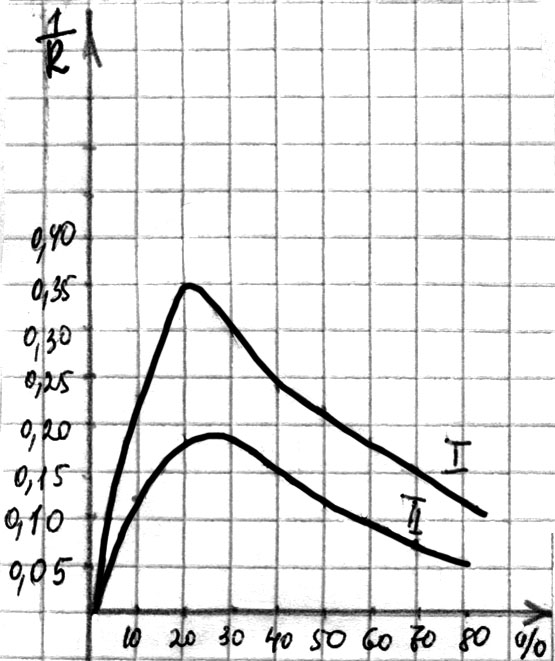
Рис. 86 Рис. 87
З а д а н и е 4. На рис. 87 показано графически влияние доли фосфорной кислоты в растворе при заданной температуре на электрическую проводимость раствора (кривая I при температуре 75 С, кривая II при 25 С). Укажите наибольшую электрическую проводимость в каждом из двух случаев. При какой концентрации раствора она наступает?
Аналитический способ задания функции.
Функция может быть задана в виде формулы ![]() , где переменная х - элемент множества значений аргумента, а переменная у - соответствующее значение функции.
, где переменная х - элемент множества значений аргумента, а переменная у - соответствующее значение функции.
Можно привести примеры элементарных функций, изученных ранее.
Большинство функций, заданных формулами, пришло из решения конкретных задач.
Например, в листе жести прямоугольной формы (длина сторон а = 600 мм, b = 400 мм) нужно вырезать прямоугольное отверстие, площадь которого S = 800 см2, а края должны быть на одинаковом расстоянии от краев листа. Вычислите это расстояние.
Р е ш е н и е:
Пусть искомое расстояние х мм, тогда ![]() ,
,  , при данных а и b.
, при данных а и b.
 . Функция
. Функция ![]() задает формулу для решения всех задач такого типа.
задает формулу для решения всех задач такого типа.
Если подставить S, то найдем искомое х, решив уравнение:

х1 = 100
х2 = 400.
Очевидно, что 400 мм не удовлетворяет условию.
О т в е т: 100 мм.
З а д а н и я д л я с а м о с т о я т е л ь н о г о р е ш е н и я.
З а д а н и е 5. Всякое оборудование в процессе эксплуатации изнашивается, его ценность при этом уменьшается. Пусть первоначальная стоимость оборудования А0 руб. уменьшается на k % в год. Составьте формулу стоимости оборудования в процессе его эксплуатации.
О т в е т:  , где t - количество лет.
, где t - количество лет.
З а д а н и е 6. Задайте формулой функции, заданные табличным способом:
а)
x
-2
-1
0
1
2
y
-4
-3
-2
-1
0
О т в е т:  .
.
б)
х





0

у
6,25
4
2,25
1
0,25
0

О т в е т:  .
.
З а д а н и е 7. Задайте формулами функции, изображенные на рис. 88.
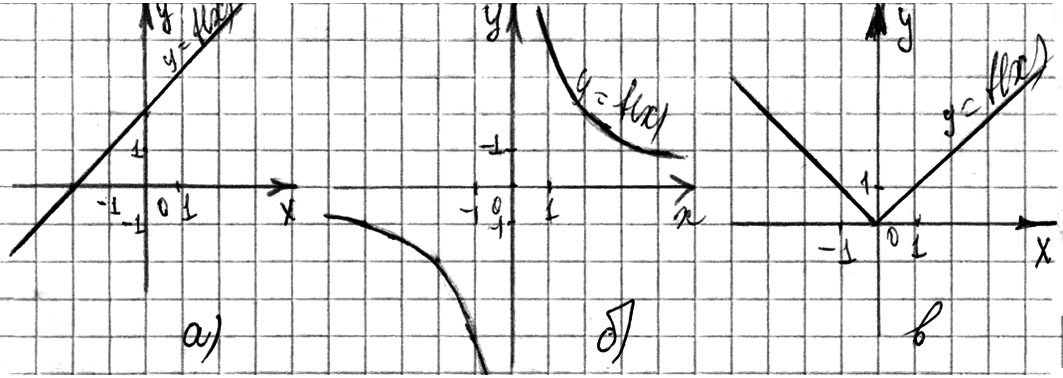
Рис. 88
О т в е т: а)  ; б)
; б)  ; в)
; в) ![]() .
.
З а д а н и е 8. По таблице значений переменных х и у определите вид зависимости между ними:

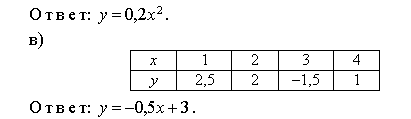
Далее можно предложить ребятам самим загадать соседу функцию.
Занятие 4
Четные и нечетные функции
Цели: сформировать понятие четности и нечетности функций; научить определять и использовать эти свойства.
Х о д з а н я т и я
У ч и т е л ь. Рассмотрим функцию  . Эта функция определена на множестве R действительных чисел и обладает свойством
. Эта функция определена на множестве R действительных чисел и обладает свойством 
 ,
, ![]() , то есть вообще
, то есть вообще  для любого
для любого ![]() . Такие функции называются четными.
. Такие функции называются четными.
О п р е д е л е н и е: Функция f, заданная на множестве Х, называется четной, если для любого xX верно равенство f(-x) = f(x).
Выполнение равенства  означает, что для любого
означает, что для любого  и
и  , то есть область определения четной функции есть множество, симметричное относительно нуля. Значит, если функция задана на несимметричном относительно О множестве, она не является четной. Например,
, то есть область определения четной функции есть множество, симметричное относительно нуля. Значит, если функция задана на несимметричном относительно О множестве, она не является четной. Например,  ,
,  - несимметрична относительно О, значит, функция
- несимметрична относительно О, значит, функция  не является четной. Отсюда следует такое правило.
не является четной. Отсюда следует такое правило.
А л г о р и т м в ы я с н е н и я ч е т н о с т и ф у н к ц и и.
1. Найти  .
.
2. Выяснить, симметрична ли  относительно О.
относительно О.
3. Выяснить, выполняется ли равенство  .
.
Например. Исследуйте на четность функцию

1.  .
.
2.  симметрична относительно О.
симметрична относительно О.
3. 
 - функция h четная.
- функция h четная.
Докажем, что график четной функции симметричен относительно оси ординат.
Д о к а з а т е л ь с т в о.
Пусть  - произвольная точка графика G четной функции f с областью определения Х. Тогда
- произвольная точка графика G четной функции f с областью определения Х. Тогда  , но и
, но и ![]() , то есть точка
, то есть точка  . Но точки
. Но точки ![]() и
и  симметричны относительно оси Оу. Значит, вместе с каждой своей точкой
симметричны относительно оси Оу. Значит, вместе с каждой своей точкой ![]() график G четной функции содержит и симметричную относительно оси Оу ей точку, то есть график четной функции симметричен относительно оси ординат.
график G четной функции содержит и симметричную относительно оси Оу ей точку, то есть график четной функции симметричен относительно оси ординат.
Это свойство графика четной функции находит свое отражение в задачах.
Например.
1. Построить график функции  , если известно, что f - четная функции и задана часть графика для
, если известно, что f - четная функции и задана часть графика для ![]() (см. рис. 89).
(см. рис. 89).
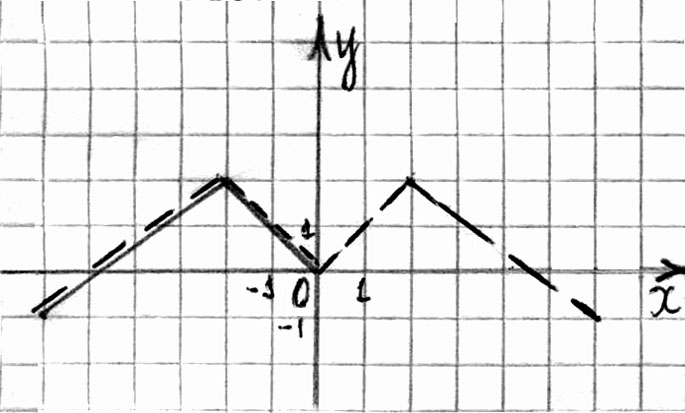
Рис. 89
2. Среди функций на рис. 90 найдите четную (ЕГЭ - 2002).
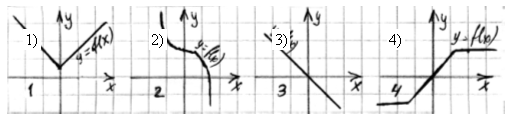
Рис. 90
Ответ: 1)
О п р е д е л е н и е. Функция g, заданная на множестве X, называется нечетной, если для любого xX верно равенство g(-x) = -g(x).
Алгоритм выяснения нечетности.
1. Найти  .
.
2. Выяснить, симметрична ли  относительно О.
относительно О.
3. Выяснить, выполняется ли равенство  .
.
Ясно, что график нечетной функции симметричен относительно начала координат. Учащимся вполне по силам доказать это самостоятельно.
П р и м е р. Доказать, что  - нечетная.
- нечетная.
1.  .
.
2.  - симметрична относительно О.
- симметрична относительно О.
3.  .
.
Рассмотрим свойства четных и нечетных функций.
1. Пусть f - функция, заданная на множестве  , где а - некоторое положительное число или знак , принимает положительные значения при
, где а - некоторое положительное число или знак , принимает положительные значения при  .
.
Тогда:
а) если f - четная функция, то при ![]() значения ее положительны;
значения ее положительны;
б) если f - нечетная, то при  значения функции отрицательны.
значения функции отрицательны.
Это следует, например, из симметрии графиков.
З а д а н и я д л я с а м о с т о я т е л ь н о г о р е ш е н и я.
З а д а н и е 1. Докажите, что функция f - четная, а функция g - нечетная, если:
а)  ; г)
; г)  ;
;
б)  ; д)
; д)  ;
;
в)  ; е)
; е)  .
.
З а д а н и е 2. Исследуйте на четность функцию:
а)  ; г)
; г)  ;
;
б)  ; д)
; д)  ;
;
в)  ; е)
; е)  .
.
О т в е т: а) ни четная, ни нечетная; б) нечетная; в) четная; г) четная; д) нечетная, е) четная.
З а д а н и е 3. Докажите, что если график функции f.
а) симметричен относительно оси У, то f - четная функция;
б) симметричен относительно начала координат, то f - нечетная функция.
Р е ш е н и е.
Докажем п. б).
Вместе с точкой  графику функции принадлежит точка
графику функции принадлежит точка  , то есть
, то есть ![]() и
и  . Что и требовалось доказать.
. Что и требовалось доказать.
З а д а н и е 4. Даны функции  и
и ![]() .
.
Найдите:
а) область определения функции f;
б)  ;
;
в) пересечение  и
и  ;
;
г) исследуйте  на четность.
на четность.
Р е ш е н и е.
а)  , то есть
, то есть ![]() ;
;
б)  , то есть
, то есть ![]() или
или  ;
;
в)  и
и  - симметрична относительно нуля;
- симметрична относительно нуля;
г)  , - четная функция
, - четная функция
З а д а н и е 5. Известно, что f - четная функция и  ,
,  ,
, ![]() . Найдите
. Найдите ![]() .
.
О т в е т: 8; 12; 3.
З а д а н и е 6. Известно, что g - нечетная функция и  ,
,  ,
, ![]() . Найти
. Найти ![]() .
.
О т в е т: 5; -3; -7.
З а д а н и е 7. Значение выражения  при
при  равно 13,57728. Найдите значение этого выражения при х = 0,8.
равно 13,57728. Найдите значение этого выражения при х = 0,8.
У к а з а н и е: убедиться, что  - четная.
- четная.
З а д а н и е 8. Постройте график четной функции, если при  ее значения могут быть найдены по формуле:
ее значения могут быть найдены по формуле:
а)  ; б)
; б)  ; в)
; в)  .
.
З а д а н и е 9. Постройте график нечетной функции g, если известно, что ее значения при  могут быть найдены по формуле:
могут быть найдены по формуле:
а)  ; б)
; б)  ; в)
; в) ![]() .
.
З а д а н и е 10. Почему график нечетной функции не может пересекать ось Оу в точке, отличной от начала координат?
О т в е т: одному значению х = 0 будет соответствовать 3 значения у.
З а д а н и е 11. При каком условии линейная функция  является:
является:
а) нечетной; б) четной функцией?
О т в е т: а)  ; б)
; б)  .
.
З а д а н и е 12. Может ли функция быть одновременно четной и нечетной?
О т в е т: нет.
З а д а н и е 13. Известно, что f и g - четные функции. Является ли четной функция:
а)  ; в)
; в)  ;
;
б)  ; г)
; г)  .
.
О т в е т: а), б), в), г) - четная.
З а д а н и е 14. Известно, что f и g - нечетные функции. Исследуйте на четность функцию:
а)  ; в)
; в)  ;
;
б)  ; г)
; г)  .
.
О т в е т: а), б) - нечетные; в), г) - четные.
З а д а н и е 15*. Исследуйте на четность функции:
а)  ;
;
б)  ;
;
в)  .
.
О т в е т: а), в) - четные; б) - нечетная.
З а д а н и е 16*. Исследуйте на четность функцию:
а)  ;
;
б)  .
.
О т в е т: а) - нечетная; б) - четная.
Занятие 5
Монотонность функции
Цели: осознать понятие "возрастание", "убывание" функции; научить находить промежутки монотонности по графику и формулам.
Х о д з а н я т и я
Рассмотрим график функции (рис. 91).
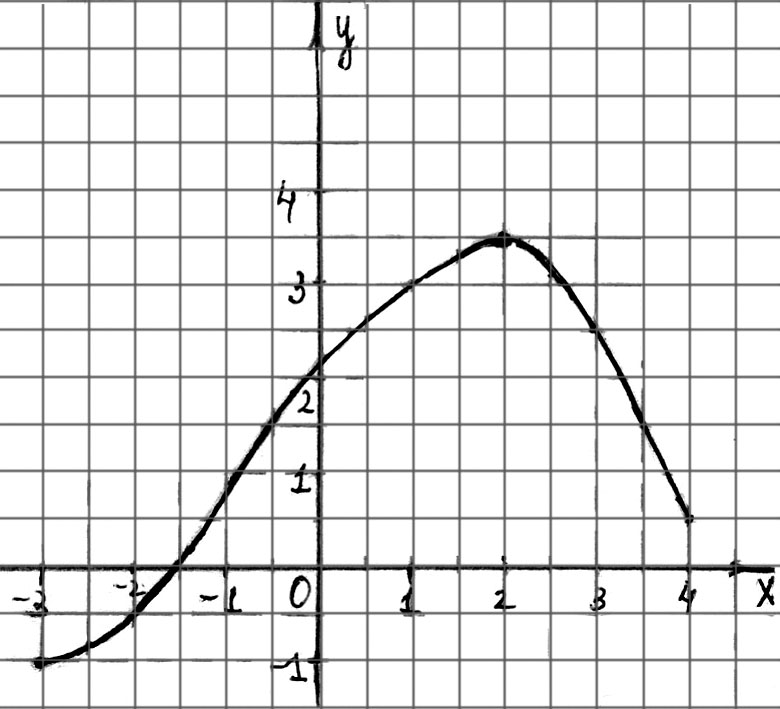
Рис. 91
По графику функции видно, что  ,
, ![]() .
.
На множестве  с возрастанием аргумента, возрастают и значения функции.
с возрастанием аргумента, возрастают и значения функции.
На множестве  с возрастанием аргумента значения функции убывают.
с возрастанием аргумента значения функции убывают.
О п р е д е л е н и е. Функция f называется возрастающей на множестве Х, если большему значению аргумента из этого множества соответствует большее значение функции.
Функция f называется убывающей на множестве Х, если большему значению аргумента из этого множества соответствует меньшее значение функции.
Иначе эти определения формулируются так: функция f называется возрастающей на множестве Х, если для любых двух значений аргумента х1 и х2 множества Х, таких, что  , выполняется неравенство
, выполняется неравенство  .
.
Очевидно, что для убывающей на Х функции из условия  следует
следует ![]() .
.
Функция возрастающая на множестве Х или убывающая на этом множестве называется монотонной на множестве Х.
Свойства монотонности функций
С в о й с т в о 1. Монотонная функция каждое свое значение принимает лишь при одном значении аргумента.
Д о к а з а т е л ь с т в о:
Допустим, что это утверждение неверно, то есть существует  , где f - монотонная (строго возрастающая или строго убывающая функция). Пусть для определенности
, где f - монотонная (строго возрастающая или строго убывающая функция). Пусть для определенности  . Тогда из возрастания функции f следует, что
. Тогда из возрастания функции f следует, что  . А если функция f убывает, то
. А если функция f убывает, то  . Таким образом, равенство невозможно.
. Таким образом, равенство невозможно.
С в о й с т в о 2. Если функция  монотонная на множестве Х и сохраняет на этом множестве знак (то есть все ее значения являются положительными или отрицательными), то функция
монотонная на множестве Х и сохраняет на этом множестве знак (то есть все ее значения являются положительными или отрицательными), то функция  имеет на множестве Х противоположный характер монотонности.
имеет на множестве Х противоположный характер монотонности.
Д о к а з а т е л ь с т в о:
Пусть функция  возрастающая на множестве Х. Возьмем на множестве Х значения
возрастающая на множестве Х. Возьмем на множестве Х значения ![]() и
и  , такие, что
, такие, что  и рассмотрим разность
и рассмотрим разность  ; рассмотрим
; рассмотрим ![]()
 , значит
, значит ![]() , то есть функция g убывает на Х.
, то есть функция g убывает на Х.
Случай убывания f учащиеся рассматривают самостоятельно.
С в о й с т в о 3. Пусть f - монотонная функция на множестве Х и  при всех
при всех ![]() . Тогда:
. Тогда:
1) Если функция f возрастает на множестве Х, то функция  также возрастает на множестве Х;
также возрастает на множестве Х;
2) если функция f убывает на множестве Х, то функция  также убывает на множестве Х.
также убывает на множестве Х.
Д о к а з а т е л ь с т в о:
Пусть  , где
, где ![]() ,
,  . Из курса алгебры известно, что из условия
. Из курса алгебры известно, что из условия  следует
следует  . Тогда для возрастающей функции из условия
. Тогда для возрастающей функции из условия  следует
следует ![]() , то есть функция
, то есть функция  возрастает.
возрастает.
Убывание рассматривается аналогично.
С в о й с т в о 4. Монотонная функция обратима.
О п р е д е л е н и е. Функции f и g называются взаимно обратными, если:
1) область определения функции f совпадает с множеством значений функции g;
2) множество значений функции f совпадает с областью определения функции g;
3) y0 = f(x0) тогда и только тогда, когда x0 = g(y0) (для любого х0 из области определения функции f и любого y0 из области определения функции g).
Свойство 4 следует из свойства 1, так как каждому значению функции f будет соответствовать единственное значение аргумента Х. То есть можно задать функцию g, отвечающую выше приведенным условиям.
З а м е ч а н и е. Графики взаимно обратных функций симметричны относительно прямой у = х.
П р и м е р 1. Докажите, что функция y = 7x + 2 возрастает на R.
Р е ш е н и е:
Пусть  . Тогда
. Тогда ![]() и
и  .
.
Найдем разность  .
.
Значит  , то есть функция у возрастает.
, то есть функция у возрастает.
П р и м е р 2. Докажите, что функция  убывает на промежутке
убывает на промежутке  и возрастает на промежутке
и возрастает на промежутке ![]() .
.
Р е ш е н и е:
Пусть  из области определения функции.
из области определения функции.
Тогда 

 .
.
Оценим знак разности исходя из условий задачи.
а) Если  , то
, то  ,
, ![]() и
и  , а так как знаменатель дроби тоже больше 0, то дробь больше нуля, то есть из условия
, а так как знаменатель дроби тоже больше 0, то дробь больше нуля, то есть из условия  следует, что
следует, что ![]() и функция возрастает при
и функция возрастает при ![]() ;
;
б) Если  , то
, то  ,
, ![]() , то есть
, то есть ![]() , значит, числитель дроби - отрицательное число, знаменатель дроби - положительное число и дробь отрицательна. Значит, на промежутке
, значит, числитель дроби - отрицательное число, знаменатель дроби - положительное число и дробь отрицательна. Значит, на промежутке ![]() функция убывает.
функция убывает.
П р и м е р 3. Вычислить характер монотонности функции
 .
.
I способ.
Раскроем модуль по определению:

Ясно, что у = 4 - постоянная функция.
Остается выяснить поведение функций  и
и ![]() . Это можно сделать по определению возрастания и убывания (см. пример 1) или можно вспомнить, что линейная функция при
. Это можно сделать по определению возрастания и убывания (см. пример 1) или можно вспомнить, что линейная функция при  возрастает, а при
возрастает, а при  убывает.
убывает.
О т в е т:  убывает на промежутке
убывает на промежутке  и возрастает на
и возрастает на ![]() .
.
II способ.
Построим график линейного сплайна (см. рис. 92).
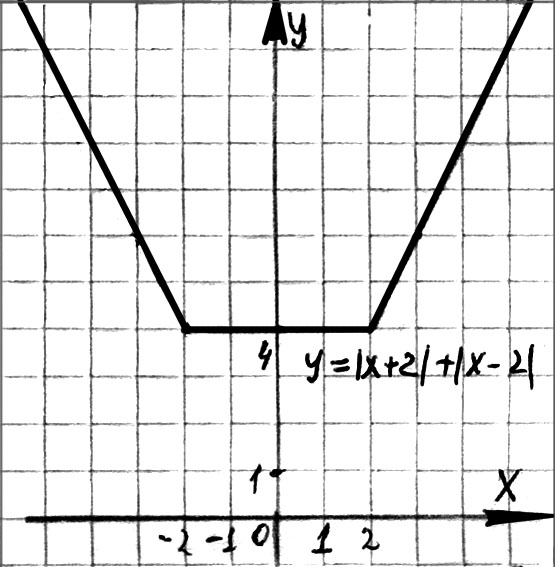
Рис. 92
x
-3
-2
2
3
y
6
4
4
6
О т в е т: у возрастает при  ; у убывает при
; у убывает при  .
.
П р и м е р 4. Найдите функцию, обратную функции ![]() , где
, где ![]() .
.
Р е ш е н и е:
На промежутке  данная функция убывает.
данная функция убывает.
Ребята легко проверяют это самостоятельно. Для получения формулы функции, обратной данной, заменим переменную х на у, у на х в аналогическом задании функции и из полученной формулы выразим у:
 ,
,  .
.
Решим квадратное уравнение относительно у.

 .
.
Для того чтобы выбрать знак перед радикалом, обратим внимание на область определения данной в задании функции ![]() ; по определению обратной функции, этот промежуток - множество значений искомой функции, значит
; по определению обратной функции, этот промежуток - множество значений искомой функции, значит  .
.
Заметим, что нам легко найти множество значений первоначальной функции. Для этого найдем область определения ![]() ,
,  . Значит, таково множество значений данной функции.
. Значит, таково множество значений данной функции.
З а д а н и я д л я с а м о с т о я т е л ь н о г о р е ш е н и я.
З а д а н и е 1. Существуют ли функции, имеющие симметричную относительно нуля область определения и являющиеся:
а) четными убывающими;
б) нечетными убывающими;
в) четными возрастающими;
г) нечетными возрастающими.
Приведите примеры.
З а д а н и е 2. На рис. 93 изображен график функции  . Укажите промежутки возрастания и убывания функции.
. Укажите промежутки возрастания и убывания функции.
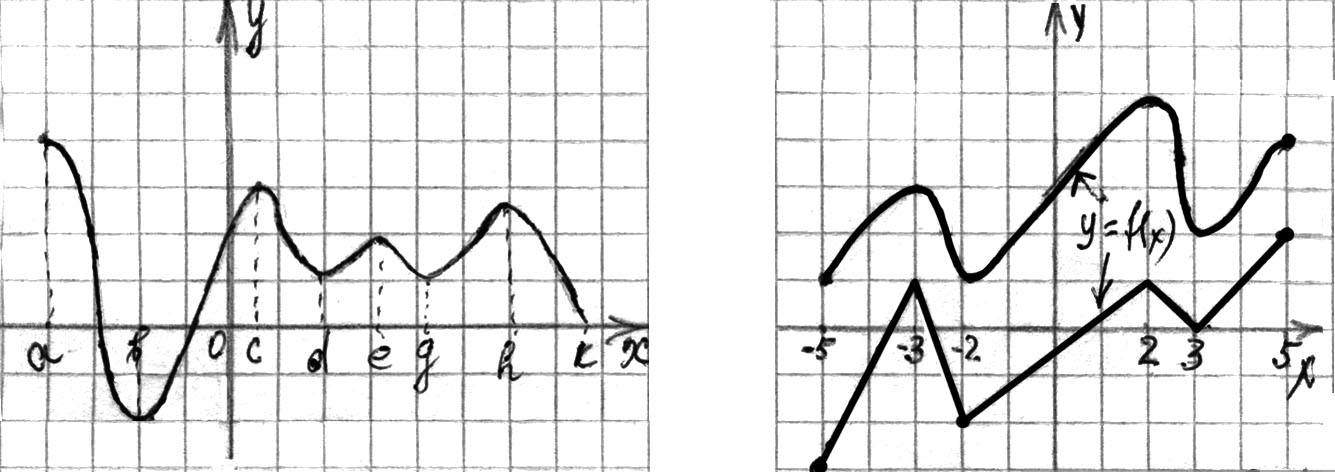
Рис. 93 Рис. 94
З а д а н и е 3. Функция f является возрастающей и  . Может ли она быть:
. Может ли она быть:
а) всюду положительной;
б) всюду отрицательной.
Приведите графические примеры.
З а д а н и е 4. Постройте график функции, которая бы возрастала на  ;
;  и
и ![]() и убывала на
и убывала на ![]() и
и  .
.
О т в е т: два из возможных графиков изображены на рис. 94.
Необходимо обязательно разъяснить ребятам, что ответ не будет однозначным.
З а д а н и е 5. Приведите примеры физических и химических процессов, которые можно описать с помощью монотонных и немонотонных функций.
З а д а н и е 6. Функции f и g возрастают на промежутке Х. Верно ли, что функции:
а)  ,
,  и
и ![]() возрастают на Х?
возрастают на Х?
б)  ,
,  убывают на Х?
убывают на Х?
З а д а н и е 7. Используя определения возрастания и убывания функции на промежутке докажите, что функция:
а)  убывает на
убывает на ![]() ;
;
б)  возрастает на
возрастает на ![]() .
.
З а д а н и е 8. Используя определения возрастания и убывания функции на промежктке, докажите, что функция:
а)  убывает на
убывает на ![]() ;
;
б)  возрастает на
возрастает на ![]() .
.
З а д а н и е 9. Построив график функции, определите промежутки возрастания и убывания функции:

З а д а н и е 10. Укажите, какие из функций, заданных графически на рис. 95, обратимы, какие - необратимы.
Постройте графики функций, обратных обратимым.
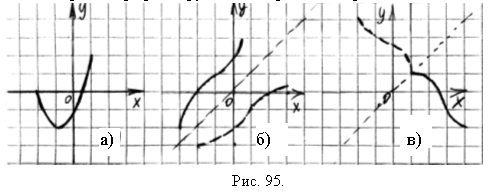
З а д а н и е 11. Найдите функцию, обратную данной. Укажите область определения и область значений обратной функции. Постройте графики данной и обратной функции в одной системе координат.
а)  ; б)
; б)  ; в)
; в) ![]() при
при  ;
;
г)  ; д)
; д)  при
при ![]() .
.
О т в е т: а)  ; б)
; б)  ; в)
; в) ![]() ; г)
; г)  ; д)
; д) ![]() .
.
З а д а н и е 12. Функция задана с помощью пар:
а)  ;
;
б)  .
.
Является ли соответствие, обратное данному, функцией?
З а д а н и е 13. Покажите, что функции являются обратимыми и обратны каждая себе:
а)  ; б)
; б)  .
.
Каковы особенности графика функции, обратной самой себе?
Р е ш е н и е:
1. Докажем обратимость:
Пусть  из
из  .
.
Тогда рассмотрим
 ,
,
так как знаменатель будет положительным для любых  и
и  из
из ![]() и любых
и любых ![]() и
и  из промежутка
из промежутка  .
.
2. Переобозначим:



 .
.
З а д а н и е 14. Верно ли, что графики взаимно обратных функций могут пересекаться на прямой у = х?
Занятие 6
Ограниченные и неограниченные функции
Цели: ввести понятие "ограниченность функций", "наибольшее и наименьшее значения функций"; учить осуществлять эвристические пробы по нахождению множества значений функции.
Х о д з а н я т и я
У ч и т е л ь. Рассмотрим рис. 96.
На нем изображен график функции  .
.
График этой функции полностью заключен между прямыми y = -3 и  . Для всех значений аргумента
. Для всех значений аргумента  выполняеся условие
выполняеся условие  .(*)
.(*)
Очевидно что неравенство (*) легко можно заменить -3 f(x) 3 или - 4 f(x) 4. Все они будут верными. Тогда легко понять определение.
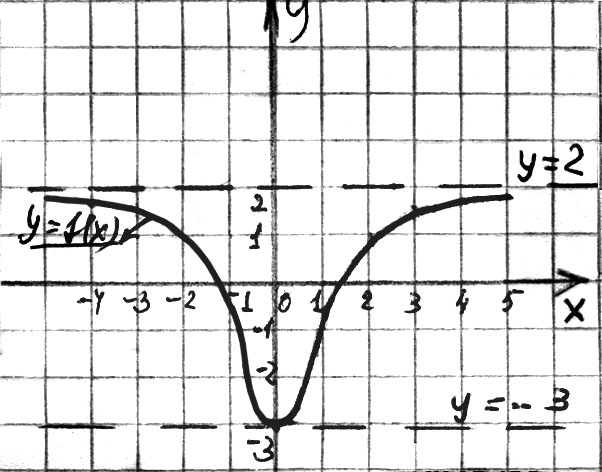
Рис. 96
О п р е д е л е н и е. Функция f, называется ограниченной на множестве X, если существует таое число c > 0, что для любого значения аргумента xX выполняется равенство |f(x)| c.
Например, функция  ограниченная, для всех
ограниченная, для всех  , так как
, так как ![]() .
.
Функция  тоже ограниченная.
тоже ограниченная.

 , то есть
, то есть  и
и  , значит,
, значит,  , в силу возрастания функции у.
, в силу возрастания функции у.
Если функция не ограничена на множестве Х, то она называется неограниченной на этом множестве.
Например,  - неограниченная функция, это легко видно графически.
- неограниченная функция, это легко видно графически.
Можно рассматривать функции, ограниченные снизу или сверху. Например, функция  ограничена снизу. Очевидно, что для всех х, отличных от 0, значения этой функции положительны. А функция
ограничена снизу. Очевидно, что для всех х, отличных от 0, значения этой функции положительны. А функция  ограничена только сверху и неограничена снизу.
ограничена только сверху и неограничена снизу.
С понятием ограниченности находится рядом понятие "наибольшее или наименьшее значение функции".
О п р е д е л е н и е. Если функция f на множестве X имеет наименьшее значении, то это означает, что на множестве X найдется такое х = а, что при всех xX выполняется неравенство f(а) f(x).
О п р е д е л е н и е. Если функция f на множестве X имеет наибольшее значении, то это означает, что найдется такое х = а, что при всех xX выполняется неравенство f(а) f(x).
Очевидно, что если функция имеет наибольшее или наименьшее значение, то она ограничена. Обратное утверждение неверно. Например, функция  при
при  ограничена снизу. Но наименьшего значения она не имеет.
ограничена снизу. Но наименьшего значения она не имеет.
Докажем это. Допустим противное, то есть что найдется такое  , что
, что ![]() для всех
для всех ![]() ,
,  . Рассмотрим
. Рассмотрим  . Тогда
. Тогда ![]() , то есть нашлось х такое, что
, то есть нашлось х такое, что  . Что противоречит условию, так как
. Что противоречит условию, так как  - наименьшее значение функции. Значит, наименьшего значения эта функция не имеет.
- наименьшее значение функции. Значит, наименьшего значения эта функция не имеет.
П р и м е р 1. Доказать, что  ограниченная. Найдем множество значений этой функции.
ограниченная. Найдем множество значений этой функции.
I способ. Очевидно, что эта функция возрастающая, значит обратима. Найдем обратную функцию и область ее определения - множество значений данной функции  .
.
Область ее определения  , значит, значения функции
, значит, значения функции  не превосходят по модулю 1, то есть функция f ограничена .
не превосходят по модулю 1, то есть функция f ограничена .
З а м е ч а н и е. Ясно, что f(0) = 0, то есть 0 тоже входит во множество значений функции f. Обратная функция на самом деле имеет вид:

Очевидно, что это решение довольно трудное. Возможно, легче будет другой способ.
II способ.
Пусть  - произвольное значение f. Это число является значением функции f, если уравнение
- произвольное значение f. Это число является значением функции f, если уравнение  имеет корни. Решим его.
имеет корни. Решим его.  ,
,  . При
. При ![]()
 , то есть уравнение имеет корень, равный 0. При
, то есть уравнение имеет корень, равный 0. При  уравнение квадратное, D = 1 -
уравнение квадратное, D = 1 -
![]() ,
,  ,
, ![]() ,
,  .
.
Значит, при  уравнение имеет корни, то есть область значений функции
уравнение имеет корни, то есть область значений функции  - функция ограничена.
- функция ограничена.
П р и м е р 2. Исследуйте на ограниченность ![]() .
.
Раскроем модуль по определению:

Ясно, что функция ограничена снизу.
Можно было построить график линейного сплайна и увидеть это.
З а д а н и я д л я с а м о с т о я т е л ь н о г о р е ш е н и я.
З а д а н и е 1. Исходя из графических представлений, выясните, ограничены ли функции:
а)  ; г)
; г)  ;
;
б)  ; д)
; д)  .
.
в)  ;
;
О т в е т: а), б) - неограничены; в), г), д) - ограничены снизу.
З а д а н и е 2. Найдите область значений функции, сделайте вывод о ее ограниченности.
а)  ; в)
; в)  ;
;
б)  ; г)
; г)  .
.
О т в е т: а)  , ограничена снизу; б)
, ограничена снизу; б)  , ограничена снизу; в)
, ограничена снизу; в)  , ограничена; г)
, ограничена; г)  , не ограничена.
, не ограничена.
З а д а н и е 3. Найдите множество значений функции:
а)  ; О т в е т:
; О т в е т: ![]() ;
;
б)  ; О т в е т:
; О т в е т:![]() ;
;
в)  ;
;
Р е ш е н и е.  .
.
О т в ет: ![]() .
.
г)  .
.
Р е ш е н и е.  ;
;  ; так как
; так как ![]() принимает значения
принимает значения  , то
, то  .
.
О т в е т:  .
.
З а д а н и е 4. Найдите множество значений функции:
а) 
Р е ш е н и е:
Найдем функцию, обратную  на
на ![]() .
.
 .
.
Чтобы ее множество значений было  , надо, чтобы был
, надо, чтобы был  , то есть множество значений первоначальной функции
, то есть множество значений первоначальной функции  .
.
Найдем функцию, обратную  , это
, это ![]() . Из первоначального условия
. Из первоначального условия  следует, что в обратной функции область определения
следует, что в обратной функции область определения  , что является множеством значений данной.
, что является множеством значений данной.
Объединив полученные промежутки, имеем: ![]() .
.
О т в е т:  .
.
б) 
Р е ш е н и е:
Рассмотрим  ; выясним, является ли она монотонной на
; выясним, является ли она монотонной на  . Пусть
. Пусть ![]() , тогда
, тогда ![]()

 . Первая скобка меньше нуля из условия
. Первая скобка меньше нуля из условия  , а вторая меньше нуля из условия, что
, а вторая меньше нуля из условия, что  , значит
, значит ![]() . Поэтому произведение положительно, и значит, что на промежутке
. Поэтому произведение положительно, и значит, что на промежутке  функция
функция  возрастает; значит, ее значения принадлежат
возрастает; значит, ее значения принадлежат  .
.
Аналогично, на промежутке  функция
функция  убывает; значит, ее значения принадлежат
убывает; значит, ее значения принадлежат  .
.
Объединив полученные промежутки, имеем: ![]() .
.
Ответ:  .
.
в) 
Р е ш е н и е:
Построим график заданной функции (см. рис. 97).
О т в ет:  .
.
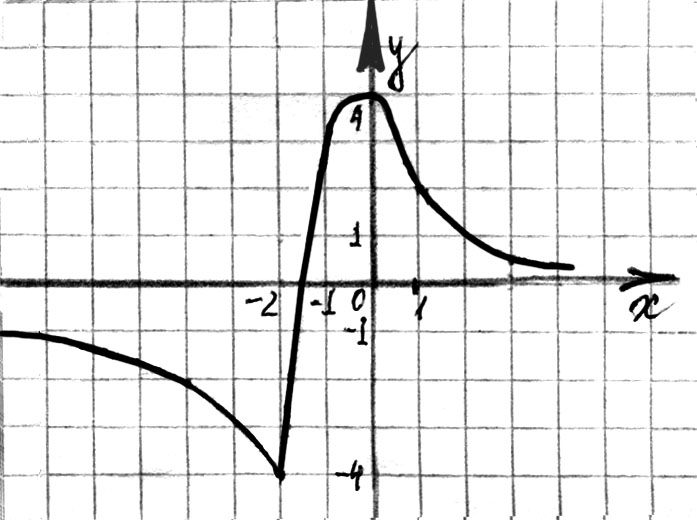
Рис. 97
З а м е ч а н и е. Очевидно, каждое из заданий этого номера можно решить всеми указанными способами. Надо побуждать ребят к применению различных способов решения одного и того же задания.
З а д а н и е 5. Найдите наибольшее значение функции и значение аргумента при котором оно достигается:
а)  ; б)
; б)  , если
, если ![]() .
.
О т в е т: а)  ; б)
; б)  .
.
З а д а н и е 6. Найдите наименьшее значение функции и значение аргумента, при котором оно достигается:
а)  ; б)
; б)  .
.
О т в е т: а) унаим. =  ; б) унаим. =
; б) унаим. =  .
.
З а д а н и е 7. Приведите пример непрерывной монотонной функции f с областью определения  , у которой
, у которой  - наименьшее значение функции;
- наименьшее значение функции;  - наибольшее значение функции.
- наибольшее значение функции.
З а д а н и е 8. Известно, что непрерывная функция f на промежутке  возрастает. Найдите наименьшее и наибольшее значения функции f и область ее значений.
возрастает. Найдите наименьшее и наибольшее значения функции f и область ее значений.
Занятие 7
Исследование функций
элементарными способами
Цели: составить схему исследования функции, исследовать по схеме элементарные функции.
Х о д з а н я т и я
У ч и т е л ь. В младших классах мы легко читали информацию по графику функции. Сейчас добавился ряд свойств, которые также хорошо видны на графике, то есть он дает наиболее наглядное представление о функции. Но если функция задана таблицей или аналитически, то построить график труднее. Надо провести ее исследование.
В процессе эвристической беседы составляется схема исследования функции.
Схема исследования функции
1) Найти область определения функции. Если она явно не указана, то речь идет о допустимых значениях независимой переменной в данной формуле.
2) Выяснить четность (нечетность) функции. Достаточно исследовать ее при  в случае положительного ответа.
в случае положительного ответа.
3) Найти множество значений функции.
4) Найти нули функции и промежутки, в которых функция принимает положительные и отрицательные значения.
5) Найти промежутки возрастания и убывания функции.
6) Можно выяснить поведение функции при стремлении х к  .
.
Для этого надо знать, является ли функция непрерывной. По этому поводу есть несколько утверждений:
Функция  , где
, где ![]() - многочлен, является непрерывной функцией на всей области ее определения, то есть на множестве R.
- многочлен, является непрерывной функцией на всей области ее определения, то есть на множестве R.
График функции  , где
, где ![]() и
и  - многочлены имеет разрывы в точках, в которых многочлен
- многочлены имеет разрывы в точках, в которых многочлен  обращается в нуль. Если многочлен
обращается в нуль. Если многочлен  не имеет корней, то функция непрерывна на множестве R.
не имеет корней, то функция непрерывна на множестве R.
П р и м е р. Исследовать функцию  .
.
1)  , так как
, так как ![]() не обращается в нуль ни при каком х.
не обращается в нуль ни при каком х.
2) Так как область определения симметрична относительно нуля, проверим функцию на четность и нечетность.
 - четная.
- четная.
3) Найдем множество значений.
Так как  , то
, то  , но
, но ![]() , значит
, значит ![]() .
.
Значит, 1 - наибольшее значение функции.
Наименьшего значения у функции нет.
Функция ограничена.
4) Так как  , то нулей нет и функция положительна при любом значении х.
, то нулей нет и функция положительна при любом значении х.
5) Ясно, что при 
 возрастает, тогда функция
возрастает, тогда функция  убывает при
убывает при ![]() .
.
Значит, при  наша функция убывает, а в силу четности при
наша функция убывает, а в силу четности при  функция возрастает.
функция возрастает.
6) Если  , то знаменатель функции тоже стремится к
, то знаменатель функции тоже стремится к  , а значит, функция будет принимать очень маленькие значения, то есть стремиться к 0.
, а значит, функция будет принимать очень маленькие значения, то есть стремиться к 0.
Проведенное исследование поможет легко построить и график функции. Но такая задача на этом занятии не стоит.
З а д а н и я д л я с а м о с т о я т е л ь н о г о р е ш е н и я.
З а д а н и е 1. Найдите область определения функции:
а)  ; в)
; в)  ;
;
б)  ; г)
; г)  .
.
О т в е т: а)  ; б)
; б)  ;
;
в)  ; г)
; г)  .
.
З а д а н и е 2. Является ли четной или нечетной функция:
а)  ; в)
; в)  ;
;
б)  ; г)
; г)  .
.
О т в е т: а) нечетная; б) четная; в) нечетная; г) ни четная, ни нечетная.
З а д а н и е 3. Найдите множество значений функции:
а)  ; б)
; б)  ; в)
; в) ![]() .
.
О т в е т: а)  или
или  ; б)
; б) ![]() ; в)
; в) 
 .
.
З а д а н и е 4. Найдите нули функции и промежутки знакопостоянства:
 .
.
О т в е т: нули х = 2; х = 7; функция положительна при  ,
, ; функция отрицательна, если x
; функция отрицательна, если x ,
, ![]() .
.
З а д а н и е 5. Найдите промежутки возрастания и убывания функции:
а)  ; б)
; б)  ; в)
; в) ![]() .
.
О т в е т: а) убывает на  , возрастает на
, возрастает на  ; б) убывает на
; б) убывает на ![]() , возрастает на
, возрастает на ![]() ; в) убывает на
; в) убывает на ![]() , возрастает на
, возрастает на ![]() .
.
З а д а н и е 6. Проведите исследование функции.
а)  ; б)
; б)  ; в)
; в) ![]() .
.
О т в е т: а)  , функция нечетная,
, функция нечетная,  ,
,  при
при ![]() ,
,  при
при ![]() ; возрастает на
; возрастает на ![]() , убывает на
, убывает на ![]() и на
и на ![]() ;
;
б)  , функция четная,
, функция четная,  , возрастает на
, возрастает на ![]() , убывает на
, убывает на ![]() ;
;
в)  , функция четная,
, функция четная,  , убывает на
, убывает на ![]() , возрастает на
, возрастает на ![]() ;
;  при
при ![]() ,
,  при
при ![]() .
.
Занятие 8
Построение графиков функций
Цели: показать практическое применение предварительного исследования функций, заданных формулами для наглядного представления их с помощью графиков и более подробного исследования с его помощью.
Х о д з а н я т и я
Ясно, что исследование функции по схеме дает о ней некоторое представление, но часто кажется ребятам просто гимнастикой ума. Поэтому на этом занятии надо научить их применять исследование для построения графика.
П р и м е р 1. Пусть дана функция  .
.
Исследуем ее.
1)  .
.
2) Функция нечетная, так как  .
.
3)  .
.
4) Нулей нет. При 
 .
.
5) Пусть  , тогда
, тогда ![]()

 .
.
При  это произведение отрицательно.
это произведение отрицательно.
При  это произведение положительно.
это произведение положительно.
Значит, функция убывает на  и возрастает на
и возрастает на ![]() .
.
6) Если  и
и  , то
, то ![]() .
.
Если  и
и  , то
, то ![]() .
.
Исходя из этих данных, можно построить график функции  (см. рис. 98).
(см. рис. 98).
Возьмем дополнительные точки:
х


1
2
4
у


2


Вторая ветвь графика получается с помощью симметрией относительно начала координат, в силу нечетности функции.
Очевидно, что график дает возможность добавить некоторые свойства функции.
Определение. Точка  из области определения функции f называется точкой максимума этой функции, если существует такая окрестность точки
из области определения функции f называется точкой максимума этой функции, если существует такая окрестность точки ![]() , что для всех
, что для всех ![]() из этой окрестности
из этой окрестности  .
.
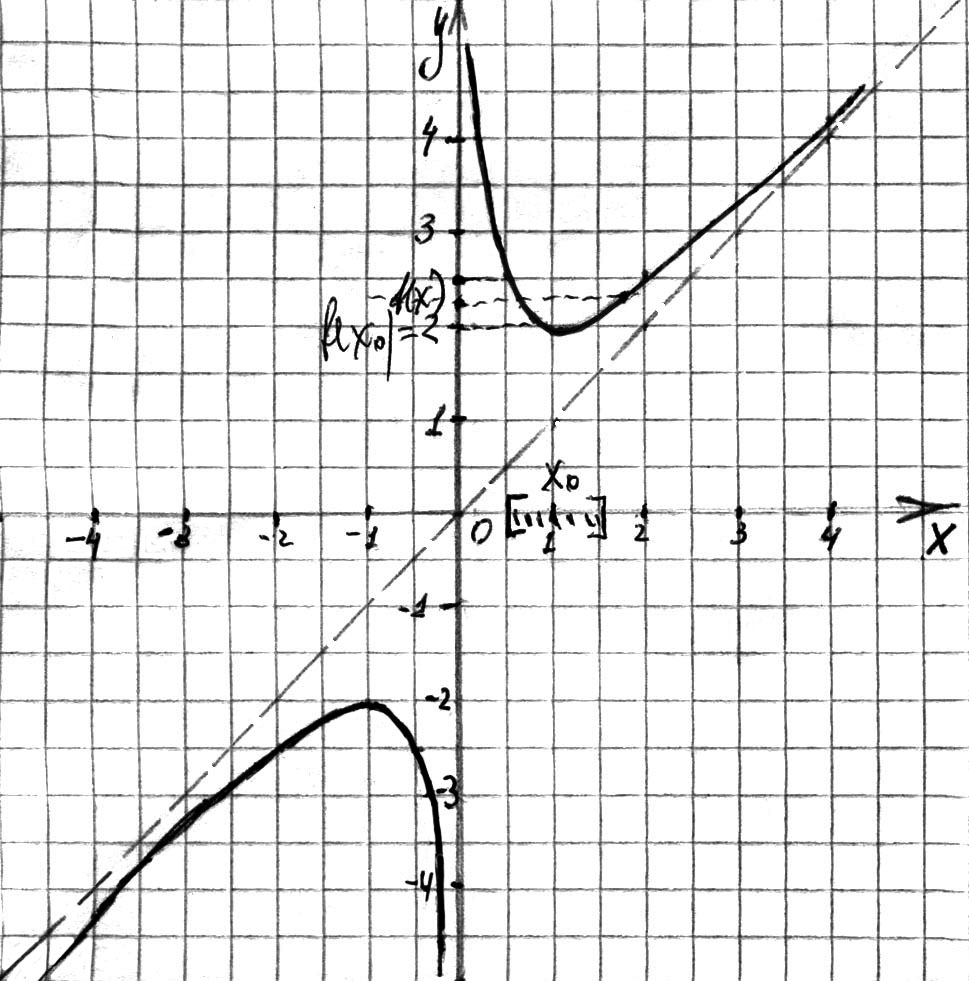
Рис. 98
Окрестностью точки  называется отрезок
называется отрезок  , где а - некоторое маленькое пложительное число.
, где а - некоторое маленькое пложительное число.
О п р е д е л е н и е. Точка x0 из области определения функции f называется точкой минимума этой функции, если существует такая окрестность точки x0, что для всех х x0 из этой окрестности f(x) > f(x0).
Заметим, что точки  и
и ![]() полностью удовлетворяют этим определениям. Пусть
полностью удовлетворяют этим определениям. Пусть  , тогда окрестность точки 1 - отрезок
, тогда окрестность точки 1 - отрезок  ; для всех точек этого отрезка
; для всех точек этого отрезка  , значит
, значит ![]() - точка минимума. Аналогично,
- точка минимума. Аналогично,  - точка максимума функции.
- точка максимума функции.
Точки максимума и минимума называются точками экстремума, а значения функции в этих точках - экстремумами функции.
Заметим, что при  график приближается к оси ординат, а при
график приближается к оси ординат, а при  и
и  график приближается к прямой у = х.
график приближается к прямой у = х.
Эти прямые называются асимптотами графика функции.
О п р е д е л е н и е. Асимптотой называется прямая линия, к которой неограниченно приближается график функции по мере удаления его от начала координат в бесконечность.
П р и м е р 2. Построить график функции ![]() .
.
Исследуем функцию по схеме.
1)  .
.
Точки  и
и  - точки разрыва.
- точки разрыва.
2) Ввиду несимметричности области определения функция не может быть ни четной, ни нечетной.
3)  найти довольно трудно. Пусть b - некоторое значение функции. Найдем, для каких b функция существует.
найти довольно трудно. Пусть b - некоторое значение функции. Найдем, для каких b функция существует.



 для любого b.
для любого b.
Значит,  .
.
4)  при
при  .
.
Для определения промежутков знакопостоянства решим неравенство  ; получим, что
; получим, что ![]() при
при  и
и ![]() и соответственно
и соответственно ![]() при
при  и
и ![]() .
.
5) Рассмотрим 
 на каждом из интервалов
на каждом из интервалов  ;
;  ;
; ![]() . Эта разность положительна при
. Эта разность положительна при  . Значит, функция возрастает на каждом интервале.
. Значит, функция возрастает на каждом интервале.
6) При 
 , при
, при ![]() слева
слева ![]() ,
,  справа
справа  , при
, при ![]() аналогично. Исходя из полученного исследования, построим график (см. рис. 99).
аналогично. Исходя из полученного исследования, построим график (см. рис. 99).
Добавим, глядя на график, что прямые  и
и ![]() являются вертикальными асимптотами графика функции.
являются вертикальными асимптотами графика функции.
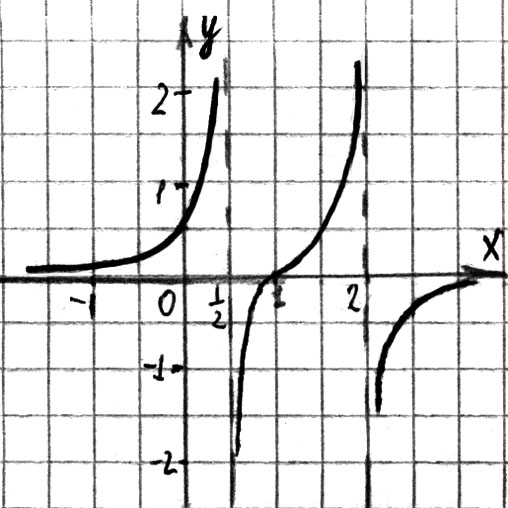
Рис. 99
Эта функция не имеет экстремумов.
З а д а н и я д л я с а м о с т о я т е л ь н о г о р е ш е н и я.
З а д а н и е 1. В результате исследования некоторой функции выяснилось, что:
1) D(f):(-; +);
2) f - четная, непрерывная функция;
3)  ;
;
4)  ,
,  при
при ![]() ;
;
5) функция f возрастает на  ;
;
6) при x > + ∞  .
.
Изобразите схематически график функции (см. рис. 100).
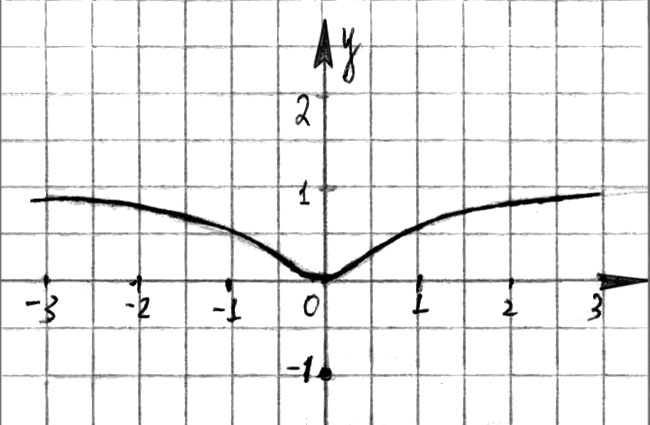
Рис. 100
З а д а н и е 2. Проведите исследование и постройте график функции:
а)  ; в)
; в)  ;
;
б)  ; г)
; г)  .
.
О т в е т:
а) 1)  ;
;
2) четная;
3)  ;
;
4)  для любых х;
для любых х;
5) убывает на промежутке [0; +), возрастает на промежутке
(-; 0];
6) при 
 (рис. 101)
(рис. 101)
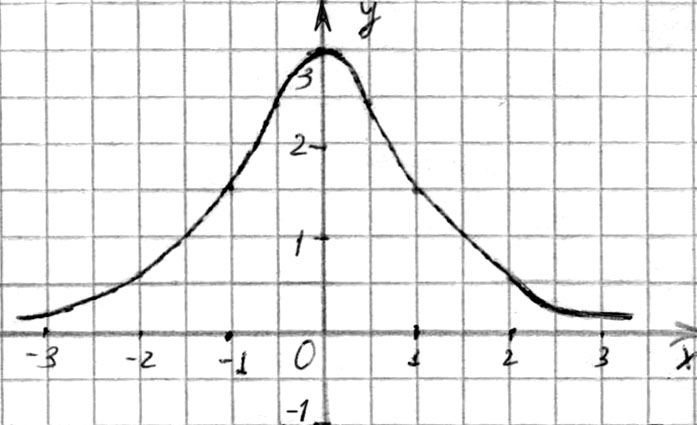
Рис. 101
б) 1)  ;
;
2) четная;
3)  ;
;
4) нулей нет,  всегда;
всегда;
5) убывает на промежутке (-; 0], возрастает на промежутке
[0; +);
6) при 
 (см. рис. 102).
(см. рис. 102).
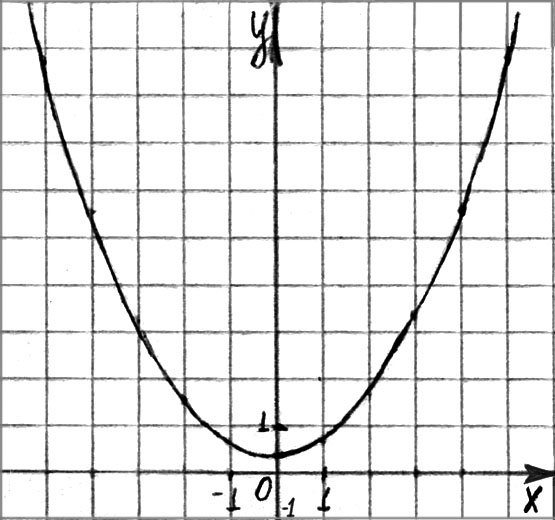
Рис. 102
в) 1) D(f) = [-4; 4];
2) четная;
3) E(f) = [0; 4];
4) у = 0 при х = ± 4;
5) убывает при х[0; 4], возрастает при х[-4; 0];
6) при х = 0 у = 4 - наибольшее значение (рис. 103).
г) 1)  ;
;
2) четная;
3)  ;
;
4)  при
при  ;
;
5) на промежутке [4; +) f возрастает, на промежутке (-; -4]
f убывает.
6) при  f(x) + (см. рис. 104).
f(x) + (см. рис. 104).
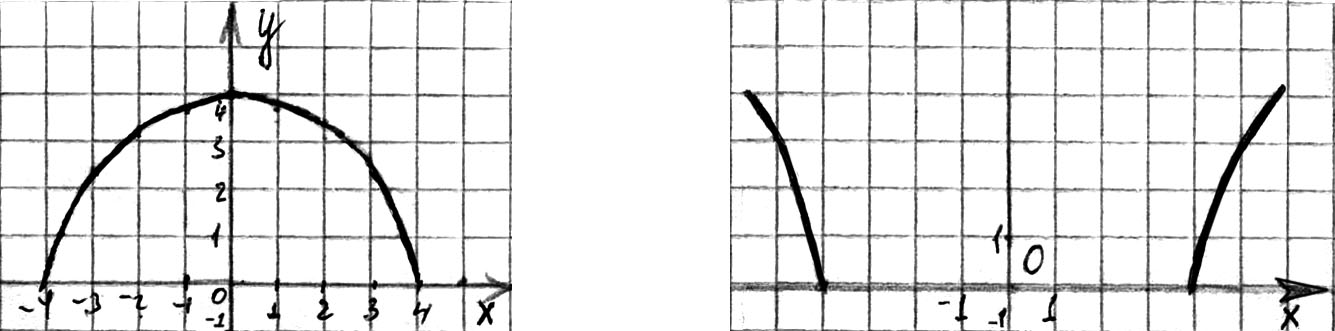
Рис. 103 Рис. 104
З а д а н и е 1. Постройте график функции и по графику исследуйте функцию:
а) 
б) 
О т в е т:
а) См рис. 105.
1)  ;
;
2) у - ни четная, ни нечетная;
3)  , у ограничена сверху; наибольшее значение 3;
, у ограничена сверху; наибольшее значение 3;
4) у = 0 при  , х = -1,
, х = -1, ![]() ,
,  ,
, ![]() ;
;
 при
при  ;
;
 при
при  ;
;
5) у возрастает при  ;
;
у убывает при  ;
;
6) точки минимума:  ,
, ![]() ,
,  ,
, ![]() ;
;
минимумы:  ;
;
точки максимума:  , х = 0, х = 2, х = 4;
, х = 0, х = 2, х = 4;
максимумы:  ,
,  ,
, ![]() ,
,  .
.
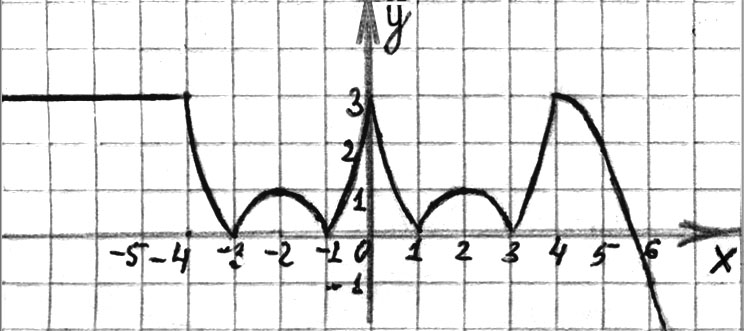
Рис. 105
б) См. рис. 106;
1)  ;
;
2) у - четная.
3)  , ограничена снизу, наименьшее значение у = 0;
, ограничена снизу, наименьшее значение у = 0;
4)  , при
, при ![]() ,
,  ,
, ![]() ;
;
5) у возрастает при  ;
;
у убывает при  ;
;
6) точки минимума:  ,
, ![]() ,
,  ; минимум: у = 0;
; минимум: у = 0;
точки максимума:  ,
,  ; максимум: у = 1.
; максимум: у = 1.
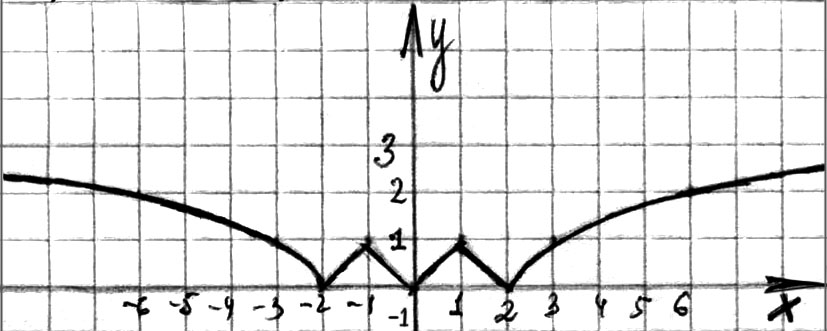
Рис. 106
Занятие 9
Функционально-графический метод
решения уравнений
Цели: закрепить знания и умения по исследованию функций и построению графиков в практической ситуации при решении уравнений.
Х о д з а н я т и я
Ребята должны понять, что исследование функций и построение графиков порой существенно облегчает решение уравнений, позволяет определить число корней, угадать значения корня.
У ч и т е л ь. Для того чтобы решить уравнение с одним неизвестным графическим способом, нужно, перенося все его члены в левую часть, представить это уравнение в виде  . После этого необходимо построить график функции
. После этого необходимо построить график функции  . Абсциссы точек пересечения или касания этого графика с осью х равны корням исходного уравнения. Если таких точек нет, то уравнение не имеет решений.
. Абсциссы точек пересечения или касания этого графика с осью х равны корням исходного уравнения. Если таких точек нет, то уравнение не имеет решений.
В ряде случаев при решении уравнений с одним неизвестным целесообразней воспользоваться другим способом. Для этого уравнения записывается в виде  и заменяется системой
и заменяется системой  решаемой графически. Абсциссы точек пересечения или касания графиков f1(x) и f2(x) равны корням исходного уравнения.
решаемой графически. Абсциссы точек пересечения или касания графиков f1(x) и f2(x) равны корням исходного уравнения.
В некоторых случаях построение графиков функций можно заменить опорой на какие-либо свойства функций.
Если, например, одна из функций  ,
, ![]() возрастает, а другая убывает, то уравнение
возрастает, а другая убывает, то уравнение  либо не имеет корней, либо имеет один корень, который иногда можно угадать. Или другая разновидность функционально-графического метода: если на промежутке Х наибольшее значение одной из функций
либо не имеет корней, либо имеет один корень, который иногда можно угадать. Или другая разновидность функционально-графического метода: если на промежутке Х наибольшее значение одной из функций  ,
, ![]() равно А и наименьшее значение другой функции тоже равно А, то уравнение
равно А и наименьшее значение другой функции тоже равно А, то уравнение  равносильно системе
равносильно системе  .
.
П р и м е р 1. Решить уравнение  .
.
Изобразим в одной системе координат (см. рис. 107) графики функций  и
и  .
.
Графики пересеклись в точке (-1; 2). Следовательно, корень данного уравнения  .
.
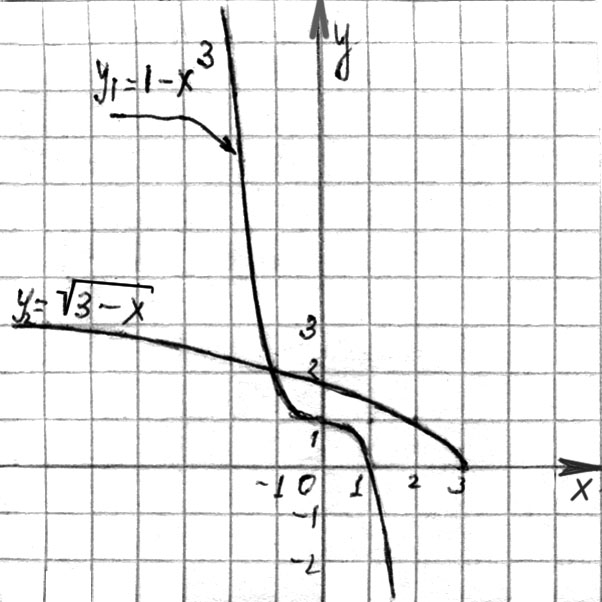
Рис. 107
П р и м е р 2. Решить уравнение  .
.
Перепишем уравнение в виде  . Очевидно, что
. Очевидно, что ![]() является корнем данного уравнения. А в силу того, что
является корнем данного уравнения. А в силу того, что  возрастает на R, а
возрастает на R, а  убывает на R, других корней нет.
убывает на R, других корней нет.
П р и м е р 3. Решить уравнение  .
.
Наименьшее значение функции  равно 0, наибольшее значение функции
равно 0, наибольшее значение функции  также равно 0.
также равно 0.
Значит, уравнение равносильно системе 
Отсюда  - корень уравнения.
- корень уравнения.
П р и м е р 4. (ЕГЭ).
Нечетная функция  определена на всей числовой прямой. Для всякого неположительного значения переменной х значение этой функции совпадает со значением функции
определена на всей числовой прямой. Для всякого неположительного значения переменной х значение этой функции совпадает со значением функции  . Сколько корней имеет уравнение
. Сколько корней имеет уравнение  ?
?
Р е ш е н и е.
Ясно, что  при
при  ,
, ![]() ,
,  ,
, ![]() .
.
В силу нечетности  будет равна 0 в точках
будет равна 0 в точках  ,
,  и
и ![]() , так как ее график симметричен относительно начала координат. То есть уравнение
, так как ее график симметричен относительно начала координат. То есть уравнение ![]() имеет 3 корня.
имеет 3 корня.
З а д а н и я д л я с а м о с т о я т е л ь н о г о р е ш е н и я.
З а д а н и е 1. Решите уравнение:
а)  ; б)
; б)  .
.
О т в е т: а) х = 1 - подбором, слева возрастающая функция, справа - убывающая, значит, других корней нет; б)  , слева - функция возрастающая на
, слева - функция возрастающая на  , справа - постоянная, других корней нет.
, справа - постоянная, других корней нет.
З а д а н и е 2. Решите уравнение:
а)  ; б)
; б)  .
.
О т в е т: а)  ,
,  ,
, ![]() (см. рис. 108); б)
(см. рис. 108); б) ![]() ,
,  (см. рис. 109).
(см. рис. 109).
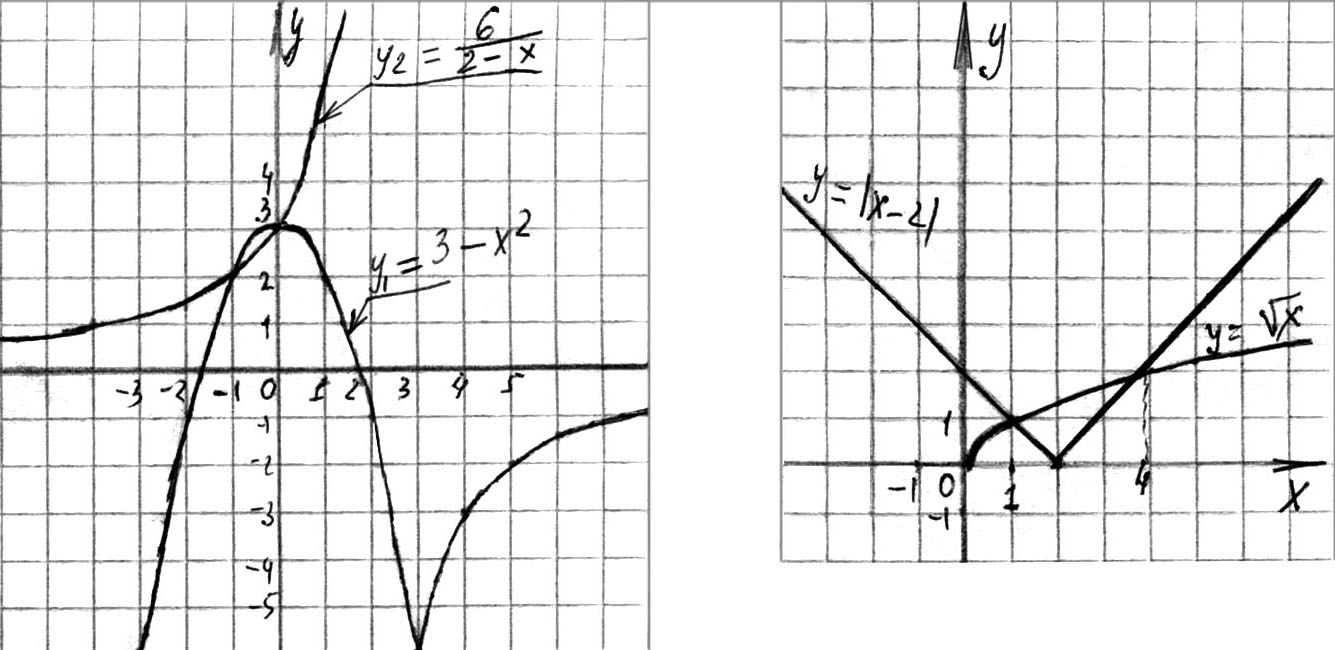
Рис. 108 Рис. 109
З а д а н и е 3. Известно, что уравнение ![]() , где
, где ![]() - четная функция, область определения которой - множество действительных чисел, имеет пять корней. Докажите, что среди корней есть число 0.
- четная функция, область определения которой - множество действительных чисел, имеет пять корней. Докажите, что среди корней есть число 0.
З а д а н и е 4. Решите уравнение:
а)  ; б)
; б)  .
.
О т в е т: а) , слева ограниченная функция, множество значений
, слева ограниченная функция, множество значений  , справа наименьшее значение 1; б)
, справа наименьшее значение 1; б)  , наибольшее значение слева 3, справа наименьшее значение тоже 3.
, наибольшее значение слева 3, справа наименьшее значение тоже 3.
После изучения нескольких тем можно и нужно проводить контроль знаний учащихся с помощью тестов, возможные варианты которых предлагаются ниже.
Поскольку в двух из них содержится по 5 заданий, то критерий их оценки соответствует 5-балльной системе. При 10 заданиях "отлично" ставится за 10 заданий; "хорошо" - 8-9 заданий; "удовлетворительно" - 5-7 заданий.
Тест 1
Понятие функции, способы задания
В а р и а н т I
1. Вычислите значение функции  в точке
в точке  :
:
а)  ; б)
; б)  ; в) 2; г)
; в) 2; г)  .
.
2. Найдите недостающую координату точки ![]() , если она принадлежит графику функции
, если она принадлежит графику функции  :
:
а)  ; б)
; б)  ; в)
; в) ![]() ; г)
; г)  .
.
3. Найдите область определения функции  :
:
а)  ; б)
; б)  ; в) (-; 1]; г) (-; -1].
; в) (-; 1]; г) (-; -1].
4. Зависимость  имеет вид либо
имеет вид либо  , либо
, либо ![]() , либо
, либо ![]() . Задайте формулой функцию, заданную парами
. Задайте формулой функцию, заданную парами  ,
,  :
:
а)  ; б)
; б)  ; в)
; в) ![]() ; г)
; г)  .
.
5. Постройте график функции, заданной формулой

Ключ к тесту:
1
2
3
4
5
б
а
в
в
см. рис. 110
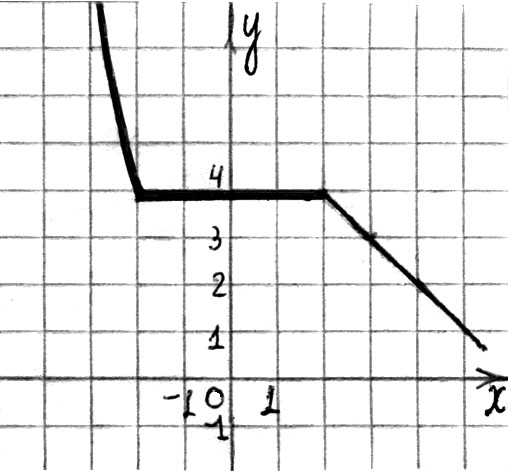
Рис. 110
В а р и а н т II
1. Вычислите значение функции  при
при ![]() :
:
а)1; б)  ; в)
; в)  ; г) 2.
; г) 2.
2. Найдите недостающую координату точки ![]() , если она принадлежит графику функции
, если она принадлежит графику функции  :
:
а) 1; б)  ; в) 2; г) 4.
; в) 2; г) 4.
3. Найдите область определения функции  :
:
а)  ; б)
; б)  ; в)
; в) ![]() ; г)
; г)  .
.
4. Зависимость  имеет вид либо
имеет вид либо  , либо
, либо ![]() , либо
, либо ![]() . Задайте формулой функцию, заданную парами
. Задайте формулой функцию, заданную парами  ,
,  :
:
а)  ; б)
; б)  ; в)
; в) ![]() ; г)
; г)  .
.
5. Постройте график функции, заданной формулой:

Ключ к тесту:
1
2
3
4
5
б
а
г
а
см рис. 111
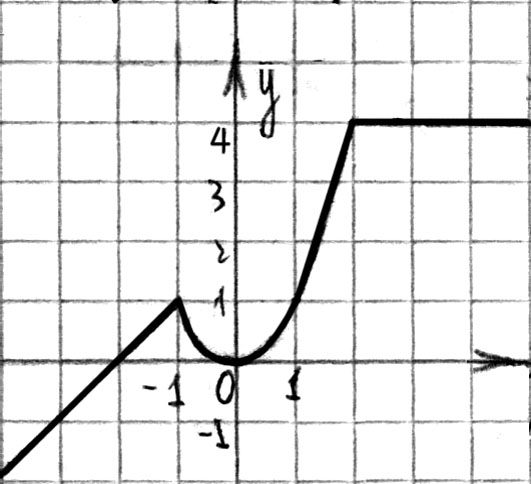
Рис. 111
Тест 2
Свойства функции
В а р и а н т I
1. Функция  задана графиком на отрезке
задана графиком на отрезке  . Укажите множество ее значений (см. рис. 112):
. Укажите множество ее значений (см. рис. 112):
а)  ; б)
; б)  ;
;
в)  ; г)
; г)  .
.
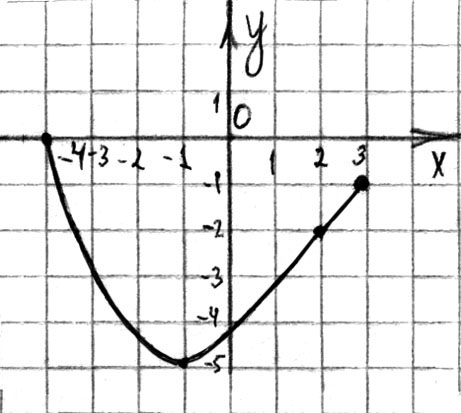
Рис. 112
2. Укажите график нечетной функции (см. рис. 113):
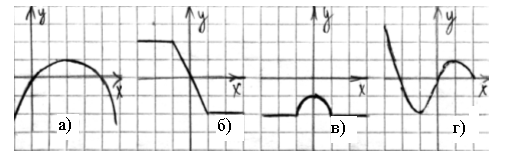
Рис. 113
3. Функция задана графиком на промежутке ![]() . Укажите расстояние между точками экстремумов:
. Укажите расстояние между точками экстремумов:
а) 0; б) 5; в) 3; г) 4.
4. Укажите рисунок, на котором изображен график функции, принимающей на промежутке  только положительные значения.
только положительные значения.
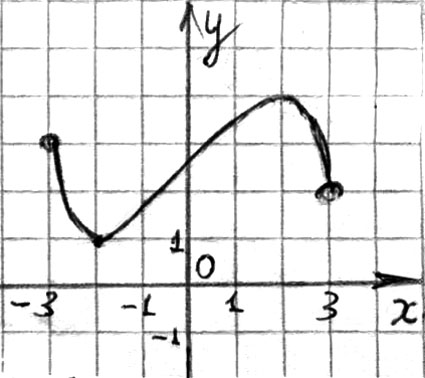
Рис. 114
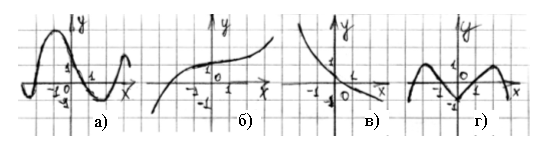
Рис. 115
5. Функция  задана графиком на промежутке
задана графиком на промежутке  . Укажите наибольший промежуток, на котором функция убывает:
. Укажите наибольший промежуток, на котором функция убывает:
а)  ; б)
; б)  ; в)
; в) ![]() ; г)
; г)  .
.
Ключ к тесту:
1
2
3
4
5
б
б
г
б
в
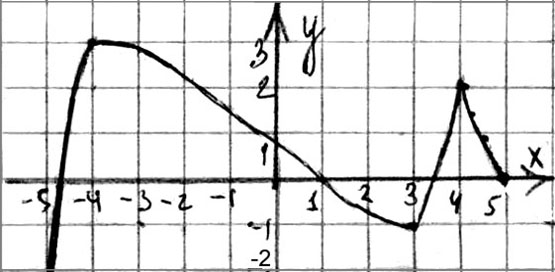
Рис. 116
В а р и а н т II
1. Функция  задана графиком на отрезке
задана графиком на отрезке  . Укажите множество ее значений (см. рис. 117):
. Укажите множество ее значений (см. рис. 117):
а)  ; б)
; б)  ;
;
в)  ; г)
; г)  .
.
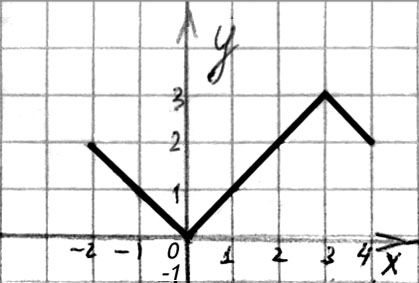
Рис. 117
2. Укажите график четной функции (см. рис. 118):
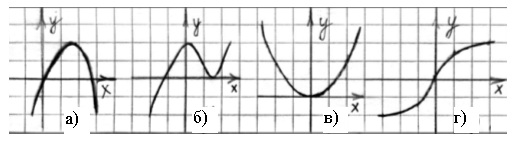
Рис. 118
3. Функция задана графиком (рис. 119). Укажите количество точек минимума:
а) 5; б) 4; в) 3; г) 0.
4. Функция задана графиком (рис. 120). Укажите промежуток, на котором она принимает только отрицательные значения:
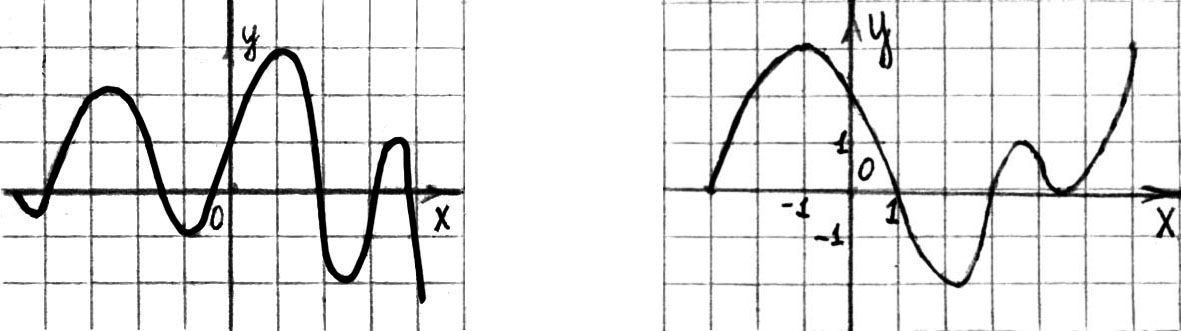
Рис. 119 Рис. 120
а)  ; б)
; б)  ; в)
; в) ![]() ; 4)
; 4)  .
.
5. Укажите промежуток возрастания функции ![]() , заданной графиком на отрезке
, заданной графиком на отрезке  (рис. 121).
(рис. 121).
а)  ; б)
; б)  ; в)
; в) ![]() ; г)
; г)  .
.
Ключ к тесту:
1
2
3
4
5
а
в
в
а
б
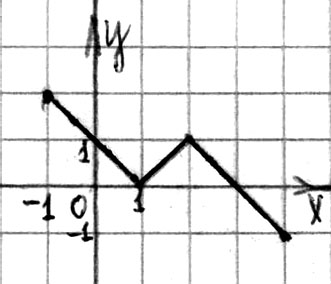
Рис. 121
Тест 3
В а р и а н т I
Установите, истинные или ложные следующие утверждения:
1. Область определения функции  - это промежуток
- это промежуток  .
.
2. Функция  - четная.
- четная.
3. Функция  - ограниченная.
- ограниченная.
4. Функция  возрастает при
возрастает при  .
.
5. Функция  убывает на промежутке
убывает на промежутке  и на промежутке
и на промежутке
 .
.
6. Функция  имеет нули
имеет нули ![]() ,
,  .
.
7. Функции  и
и  являются взаимно обратными.
являются взаимно обратными.
8. Множество значений функции  - промежуток
- промежуток  .
.
9. Уравнение  имеет 2 корня:
имеет 2 корня:  и
и  .
.
10. Решением уравнения  являются числа
являются числа  ,
,  ,
, ![]() .
.
О т в е т ы:
1
2
3
4
5
6
7
8
9
10
ист.
ист.
ложн.
ист.
ист.
ист.
ложн.
ист.
ложн.
ложн.
Установите, истинные или ложные следующие утверждения:
В а р и а н т II
1. Область определения функции  -
- ![]() .
.
2. Функция  - нечетная.
- нечетная.
3. Функция  ограничена снизу.
ограничена снизу.
4. Функция  убывает при
убывает при ![]() .
.
5. Функция  возрастает при
возрастает при 
6. Функция  имеет нули
имеет нули ![]() ,
,  .
.
7. Функции  и
и  взаимно обратные.
взаимно обратные.
8. Множество значений функции у = 8 - х2 - промежуток (-; 8].
9. Корнями уравнения  являются числа
являются числа ![]() и
и  .
.
10. Решением уравнения  являются числа
являются числа  ,
,  ,
, ![]() .
.
О т в е т ы:
1
2
3
4
5
6
7
8
9
10
ист.
ист.
ист.
ист.
ложн.
ист.
ложн.
ист.
ложн.
ложн.
Занятие 10
Игра "восхождение на вершину знаний"
Цели: создать ситуацию успеха в процессе проверки, коррекции и демонстрации знаний, умений и навыков.
Правила игры.
Все учащиеся, посещающие курсы, делятся на группы по 2-4 человека. Для выстраивания маршрута вдоль горы к вершине знаний ребятам предлагается подкинуть кубик, на гранях которого написаны задания.
Найдите значения функции в точке  :
:
1)  ;
;  ; 4)
; 4) ![]() ;
;  ;
;
2)  ;
;  ; 5)
; 5) ![]() ;
;  ;
;
3)  ;
;  ; 6)
; 6) ![]() ;
;  .
.
О т в е т: 1) 1; 2) 2; 3) 3; 4) 4; 5) 5; 6) 6.
Рис. 122 Рис. 123
Ясно, что ответ, полученный ребятами, показывает, в каком порядке им предстоит выполнять задания, то есть определяет маршрут движения по горе (рис. 122). Задания ребята выбирают сами, отрывая один из лепестков цветка, на обороте которого записано задание (рис. 123).
Ответы, полученные группой, проверяет учитель, он же отмечает флажками на рисунке горы скорость продвижения группы.
На одном из этапов каждая группа должна оформить решения у доски, изложив при этом теоретический материал. Так как на каждом этапе каждая группа выполняет задание из разных тем, то очевидно, что на доске окажется панорама тем, изученных на курсе. Во время выступления групп у доски ребята набирают баллы индивидуально за заданный уточняющий вопрос, с целью помочь ответить товарищам (1 балл) или за дополнение ответа (1 балл). Кроме того, за проход каждого этапа вместе с группой ребята получают баллы - 5 баллов за I этап и далее на 1 балл больше за каждый следующий.
В о з м о ж н ы е э т а п ы.
I. "Задай функцию формулой".
II. "Четно или нечетно".
III. "Возрастает? Убывает!"
IV. "Прочитай свойства".
V. "Исследуй функцию".
VI. "Построй график".
I. "Задай функцию формулой".
На обороте лепестков цветка с сердцевиной I записаны следующие задания:
Функция задана таблицей и может быть записана в виде одной из формул:  ,
,  ,
, ![]() ,
,  , где
, где ![]() . Запишите соответствующую формулу.
. Запишите соответствующую формулу.

О т в е т: а)  ; б)
; б)  ; в)
; в) ![]() ; г)
; г)  ; д)
; д) ![]() .
.
II. "Четно или нечетно".
На обороте лепестков цветка с цифрой II на сердцевине записаны следующие задания:
Выясните, четной или нечетной является функция:
а)  ; г)
; г)  ;
;
б)  ; д)
; д)  .
.
в)  ;
;
О т в е т: а, в - четные; б, г, д - нечетные.
III. "Возрастает? Убывает?"
Цветок с цифрой III.
Докажите, что функция:
а)  возрастает на промежутке
возрастает на промежутке  ;
;
б)  убывает на промежутке
убывает на промежутке  ;
;
в)  возрастает на промежутке
возрастает на промежутке  ;
;
г)  убывает на промежутке
убывает на промежутке  ;
;
д)  возрастает на R.
возрастает на R.
IV. "Прочитай свойства".
Цветок с цифрой IV.
Ребятам предлагаются графики (рис. 124-128), по которым они должны прочитать свойства функции, записанные в схеме исследования, а также добавить все, что они могут прочитать, и ответить на вопрос: "Сколько корней имеет уравнение  ?".
?".
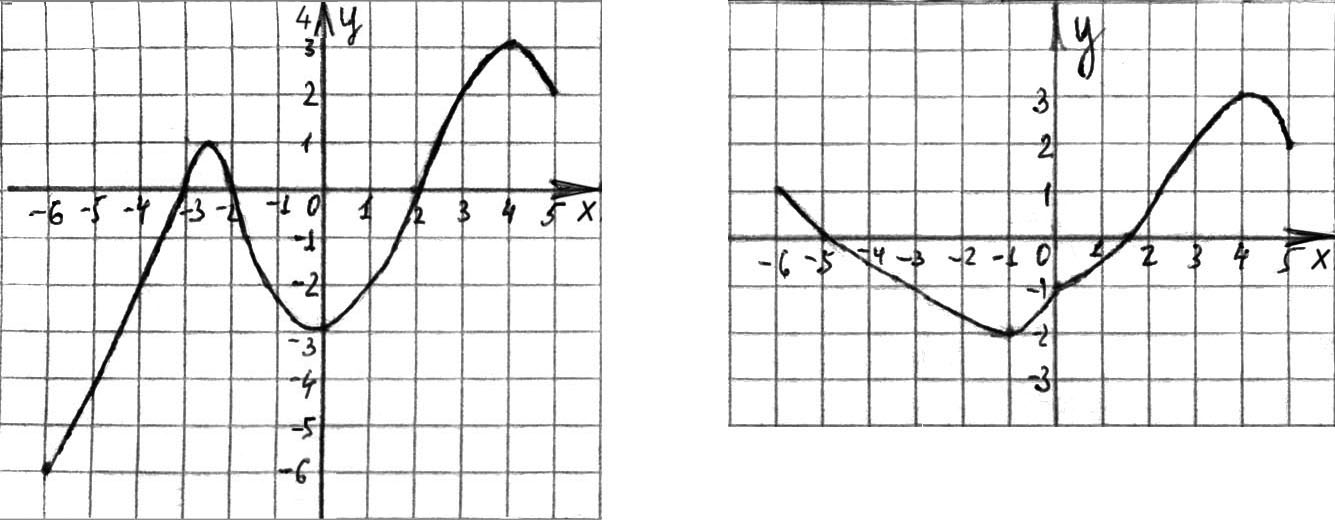
а = -2 а = 3
Рис. 124 Рис. 125
О т в е т:
 ;
;
 ;
;
ни четная, ни нечетная; возрастает на  ,
,  ; убывает на
; убывает на ![]() ,
,  ; точки максимума:
; точки максимума: ![]() и 4; точка минимума: 0.
и 4; точка минимума: 0.
Уравнение  имеет
имеет
3 корня.
 при
при ![]() ,
,  ,
,  ;
;  при
при ![]() ,
,  ;
;  при
при ![]() ,
,  .
.
О т в е т:
 ;
;
 ;
;
ни четная, ни нечетная возрастает на  ; убывает на
; убывает на ![]() ,
,  ;
;
точка максимума: 4; точка минимума: 1.
Уравнение  имеет 1 корень.
имеет 1 корень.
 при
при ![]() ,
,  ,
,
 при
при ![]() ;
;
 ;
;  при
при ![]() .
.
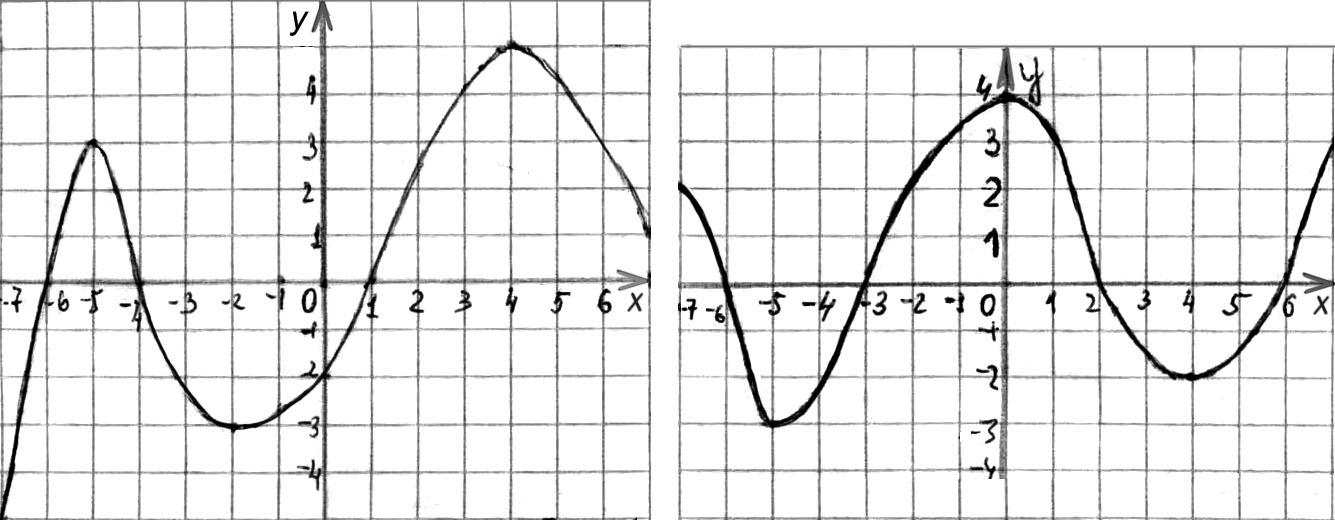
а = -2 а = 3
Рис. 126 Рис. 127
О т в е т:
 ;
;
 ;
;
ни четная, ни нечетная;
возрастает при  ,
,  , убывает при
, убывает при  ,
,  ;
;
О т в е т:
 ;
;
 ;
;
ни четная, ни нечетная;
возрастает на  ,
, 
убывает на  ,
, 
 при
при ![]() ,
,  ,
,  ;
;
 при
при ![]() ,
,  ;
;
 при
при ![]() ,
,  .
.
Уравнение  имеет
имеет
4 корня.
 при
при ![]() ,
,  ,
,  ,
,  ;
;
 при
при ![]() ,
,  ,
,  ;
;
 при
при ![]() ,
,  .
.
Уравнение  имеет
имеет
4 корня.
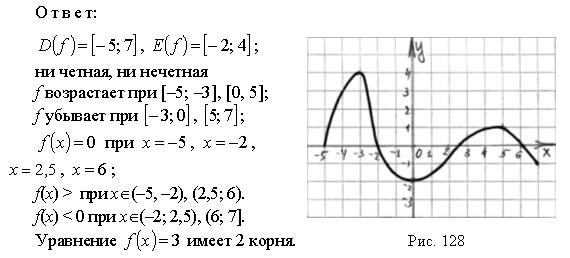
V. "Исследуй функцию".
Цветок с цифрой V.
а)  ; г)
; г)  ;
;
б)  ; д)
; д)  .
.
в)  ;
;
О т в е т: д)  ,
,  ; ни четная ни нечетная; f возрастает на промежутке
; ни четная ни нечетная; f возрастает на промежутке  , убывает на
, убывает на  ;
;  при
при ![]() ,
,  ;
; ![]() при
при  ;
;  при
при ![]() .
.
V. "Исследуй функцию".
Цветок с цифрой V.
а)  ; г)
; г)  ;
;
б)  ; д)
; д)  .
.
в)  ;
;
О т в е т: д)  ,
,  ; ни четная ни нечетная; f возрастает на промежутке
; ни четная ни нечетная; f возрастает на промежутке  , убывает на
, убывает на  ;
;  при
при ![]() ,
,  ;
; ![]() при
при  ;
;  при
при ![]() .
.
VI. "Построй график".
Цветок с цифрой VI.
Используя приведенные ниже свойства функции, постройте график непрерывной функции:
а)  ;
;
 .
.
В левом конце функция принимает наибольшее значение, 2 - единственная точка экстремума (см. рис. 129).
б)  ;
;
 ;
;
f убывает на  и
и ![]() ,
,
f возрастает на  .
.
Принимает отрицательные значения в точках x (1; 2]
(1; 2]
(см. рис. 130 (а, б).
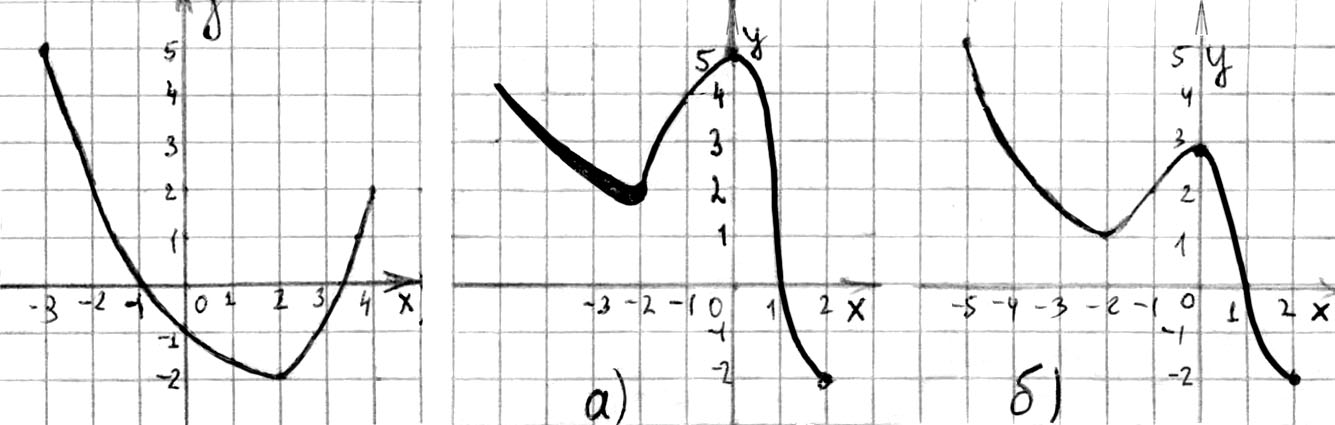
Рис. 129 Рис. 130
в)  ;
;
 ;
;
возрастает на  ,
,
убывает на  .
.
Нули функции при х = 0 и х = 3
(см. рис. 131).
г)  ;
;
 ;
;
возрастает на  ,
,
убывает на  ,
,  .
.
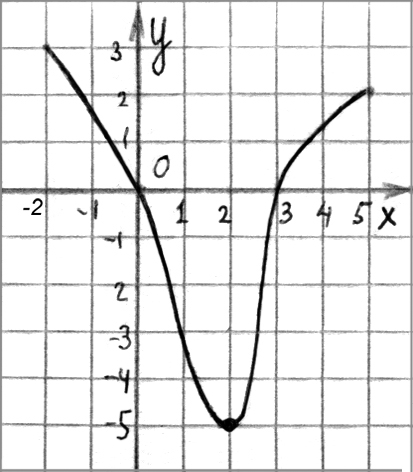
Рис. 131
Нули функции при х = -1 и х = 3 (см. рис. 132).
д)  ;
;
 ;
;
возрастает на  и
и  ,
,
убывает на  .
.
Нули функции при х = 0 и х = 4 (см. рис. 133).
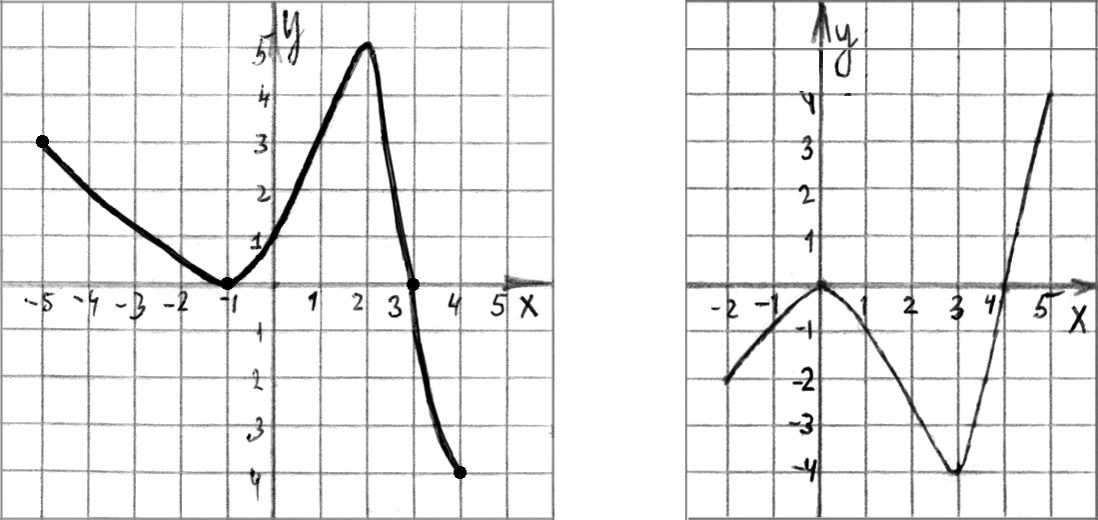
Рис. 132 Рис. 133
Ясно, что группы не смогут закончить выполнение своих заданий одновременно, поэтому заранее готовятся карточки с занимательными вопросами по изученным темам.
Например:
а) Дана функция  . Напишите в порядке взрастания числа f(-30), f(50), f(0), f(1), f(-5), f(10), f(-51).
. Напишите в порядке взрастания числа f(-30), f(50), f(0), f(1), f(-5), f(10), f(-51).
б) Задумана степенная функция с натуральными показателями. Придумайте один вопрос, который достаточно задать для установления ее четности или нечетности.
Занятие 11
Представление
"Портфеля достижений"
Цели: создание ситуации успеха в процессе оценки и самооценки знаний по темам курса.
Начиная с 5-6 занятия слушатели курса могут готовить к представлению "портфеля достижений". Если учащийся его подготовил, то на любом занятии он может его представить. Поэтому на последнем занятии часть доски, стенды уже украшены достигнутыми ребятами результатами работы; некоторые выступают повторно (с самыми интересными сообщениями), некоторые только представляют то, чего они достигли.
На этом же занятии можно провести тест, проверяющий уровень интереса к данному курсу, и выставить зачеты.
Литература
1. Баранова, Т., Кочетков, К., Семенов А. Школьный интеллектуальный марафон. Математика // Прил. К газете "Первое сентября", № 5, 33, 1995., № 35, 1999., № 34, 2004.
2. Виленкин, Н. Я. Функции в природе и технике. Книга для внеклассного чтения IX-X кл. - М.: Просвещение, 1978. - 192 с.: ил.
3. Галицкий, М. Л. и др. Сборник задач по алгебре для 8-9 классов. Учеб. пособие для учащихся шк. и классов с углубл. изуч. курса математики / М. Л. Галицкий, А. М. Гольдман, М. И. Звавич. - М.: Просвещение, 1992. - 271 с.: ил. ISBN 5-09-003875-9.
4. Депман, И. Я., Виленкин, Н. Я. За страницами учебника математики: Пособие для учащихся 5-6 кл. сред. шк. - М.: Просвещение, 1989. - 287 с.: ил. ISBN 5-09-000412-9.
5. Доброва, О. Н. Задания по алгебре и математическому анализу: Пособие для учащихся 9-11 кл. общеобразоват. учреждений. - М.: Просвещение, 1996. - 352 с.: ил. ISBN 5-09-007091-1.
6. Дорофеев, Г. В., Бунимович, Е. А., Кузнецова, Л. В., Мишаева, С. С., Суворова, С. Б., Мищенко, Т. М., Рослова, Л. О. Курс по выбору для IX класса. "Избранные вопросы математики" // Журнал "Математика в школе", № 10, 2003. - С. 12-33.
7. Дорофеев, Г. В., Муравин, Г. К., Седова, Е. А. Математика. 11 кл. Подготовка к письменному экзамену за курс средней школы. Решение задач с методическими комментариями. - М.: Дрофа, 2000. - 352 с.: ил. - Библиотека учителя, ISBN 5-7107-3407-1.
8. Единый государственный экзамен 2002: контрольные измерительные материалы: Математика / Л. О. Денищева, Е. М. Бойченко, Ю. А. Глазков и др. - М.: Просвещение, 2002, - 217 с. - ISBN 5-09-011853-1.
9. Зельманзон, М., Хлобыстова, Л. Самосовмещения квадрата и тайнопись // "Квант", № 12, 1980. - С. 32-34.
10. Канин, Е. С. и др. Упражнения по началам математического анализа в 9-10 классах: кн. для учителя / Е. С. Канин, Е. М. Канина, М. Д. Чернявский. - М.: Просвещение, 1986. - 160 с.
11. Коробова, Л. Математические загадки детективного сюжета: интегрированный урок математики и литературы. "Математика" //Прил. к газете "Первое сентября", № 19, 1998.
12. Крамор, В. С. Повторяем и систематизируем школьный курс алгебры и начала анализа. - М.: Просвещение, 1990. - 416 с.: ил. ISBN 5-09-001292-4.
13. Крамор, В. С. Повторяем и систематизируем школьный курс геометрии. - М.: Просвещение, 1992. - 320 с.: ил. - ISBN 5-09-003862-7.
14. Кудрявцев, С. В. и др. Дидактические материалы по алгебре для 7 класса: Пособие для учителя / С. В. Кудрявцев, Ю. Н. Макарычев, Е. М. Сорокина. 3-е изд., перераб. - М.: Просвещение, 1986. - 176 с.
15. Макарычев, Ю. Н., Миндюк, Н. Г. Алгебра: Доп. главы к шк. учеб. 9 кл.: Учеб. пособие для учащихся шк. и кл. с углубл. изуч. математики / Под ред. Г. В. Дорофеева. - М.: Просвещение, 1997. - 224 с.: ил. ISBN 5-09-00700-х.
16. Факультативный курс по математике: Учеб. пособие для 7-9 кл. сред. шк. / Сост. И. Л. Никольская. - М.: Просвещение, 1991. - 383 с.: ил. - ISBN 5-09-001287-3.
17. Фелкон Тэвис, Джуди Хиндлей, Рут Томисон, Хизер Эмери. Краткий курс юного шпиона / Авт. лит. обработки Анна Данковцева. - М.: АСТ-ПРЕСС, 1997.
18. Энциклопедический словарь юного математика / Сост. А. П. Савин. - М.: Педагогика, 1985. - 352 с.: ил.


