- Преподавателю
- Математика
- Методические указания по выполнению самостоятельных работ на тему: Эмпирическая формула
Методические указания по выполнению самостоятельных работ на тему: Эмпирическая формула
| Раздел | Математика |
| Класс | - |
| Тип | Другие методич. материалы |
| Автор | Николаева Л.Н. |
| Дата | 11.09.2015 |
| Формат | doc |
| Изображения | Есть |
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
ПО ВЫПОЛНЕНИЮ САМОСТОЯТЕЛЬНЫХ РАБОТ
для студентов технологического отделения специальностей
260807 и 100114
по дисциплине «Математика»
Чебоксары 2013
ГАПОУ СПО «Чебоксарский техникум технологии питания и коммерции»
Минобразования Чувашии
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
ПО ВЫПОЛНЕНИЮ САМОСТОЯТЕЛЬНЫХ РАБОТ
для студентов технологического отделения специальностей
260807 и 100114
по дисциплине «Математика»
Составитель: Николаева Л.Н.
Рекомендованы к печати методическим
советом ЧТТПиК
Протокол № от «___» _______ 20__ года
Электронная копия находится
у руководителя ИМЦ
Чебоксары, 2015
Содержание
Введение ………………………………………………………………….4
Эмпирическая формула. ..……………………………………………………….5
Задания для самостоятельного выполнения……………………………………10
Использованная литература……………………………………………………..13
Введение.
Методическое указание предназначено для студентов, изучающих предмет «Математика». Данное самостоятельная работа по математике предполагает выполнение задания, позволяющего освоить один из методов нахождения эмпирической формулы, на основе опытных данных полученных при выполнении работ из сферы профессиональной деятельности.
Самостоятельная работа - это одна из форм учебной работы, которая ориентирована на изучение и закрепление учебного материала, его более глубокое усвоение и формирование умения применять теоретические знания в практических, прикладных целях.
Предложенная задача, требующая от студентов навыков самостоятельного изучения понятия эмпирическая формула и метода наименьших квадратов и закрепления полученных знаний на примере составления эмпирической формулы при решении прикладной задачи из сферы профессиональной деятельности.
Практическая работа предполагает самостоятельное, внеаудиторное выполнение.
Для выполнения самостоятельной работы рекомендуется изучение нового материала и двух примеров решения задач с помощью метода наименьших квадратов.
Эмпирическая формула.
Формула, полученная на основании экспериментальных данных, называется эмпирической. Построение эмпирической формулы по экспериментальным данными состоит из двух этапов: 1) подбор вида эмпирической формулы, зависящей от параметров; 2) нахождение этих параметров по некоторому критерию.
Во многих случаях характер зависимости между переменными не сразу определяется. Практически вид эмпирической формулы (приближающей функции)можно определить визуально: по таблице наблюдений (опыта) строится точечный график функциональной зависимости, а затем проводится кривая, по возможности наилучшим образом отражающая характер расположения точек. По расположению точек выбирается функция.
Обычно в экономических исследованиях рассматриваются следующие функциональные зависимости:
y= ax+b;
y= ax2+bx+c;
y= a*Lgx+b;
y= a/x+b;
y= axb;
y= abx
Метод наименьших квадратов.
Метод наименьших квадратов (МНК) - один из методов теории ошибок для оценки неизвестных величин по результатам измерений, содержащим случайные ошибки.
Метод наименьших квадратов применяют также для приближенного представления заданной функции другими (более простыми) функциями и часто МНК оказывается полезным при обработке наблюдений.
Очень часто, особенно при анализе эмпирических данных возникает необходимость найти в явном виде функциональную зависимость между величинами x и y , которые получены в результате измерений.
При аналитическом исследовании взаимосвязи между двумя величинами x и y производят ряд наблюдений, и в результате получается таблица значений (Рис.1):
X
x1
x2
…
xi
…
xn
Y
y1
y2
…
yi
…
yn
Рис.1. Таблица значений x и y
Эта таблица обычно получается как итог каких-либо экспериментов (наблюдений), в которых xi (независимая величина) задается экспериментатором, а yi получается в результате опыта (наблюдений). Поэтому значения yi называются опытными или эмпирическими значениями. Между величинами x и y существует функциональная зависимость, но её аналитический вид обычно неизвестен, поэтому возникает практически важная задача - найти эмпирическую формулу:
 (1)
(1)
(где  - параметры), значения которой при
- параметры), значения которой при  возможно мало отличались бы от опытных значений
возможно мало отличались бы от опытных значений 
Обычно указывается класс функций (например, множество линейных, степенных, показательных и т. п.), из которого выбирается функция  , и далее определяются наилучшие значения параметров.
, и далее определяются наилучшие значения параметров.
Если в эмпирическую формулу (1) подставить исходные  , то получим теоретические значения
, то получим теоретические значения  , где
, где 
Согласно методу наименьших квадратов, наилучшими коэффициентами ![]() считаются те, для которых сумма квадратов отклонений найденной эмпирической функции от заданных значений функции
считаются те, для которых сумма квадратов отклонений найденной эмпирической функции от заданных значений функции 

 (2)
(2)
будет минимальной.
Геометрический смысл метода наименьших квадратов.
Каждая пара чисел  из исходной таблицы определяет точку
из исходной таблицы определяет точку  на плоскости XOY. Используя формулу (1) при различных значениях коэффициентов
на плоскости XOY. Используя формулу (1) при различных значениях коэффициентов  можно построить ряд кривых, которые являются графиками функции (1). Задача состоит в определении коэффициентов
можно построить ряд кривых, которые являются графиками функции (1). Задача состоит в определении коэффициентов  таким образом, чтобы сумма квадратов расстояний по вертикали от точек
таким образом, чтобы сумма квадратов расстояний по вертикали от точек  до графика функции (1) была наименьшей (рис. 2).
до графика функции (1) была наименьшей (рис. 2).




 y
y 















 yn
yn  Мn
Мn
yi Мi
di
y1 М1 M3
М4 Мi+1
y2 М2
x1 x2 xi xn x
Рис.2. Геометрический смысл метода наименьших квадратов.
Построение эмпирической формулы состоит из двух этапов: выяснение общего вида формулы и определение её наилучших параметров.
Если неизвестен характер зависимости между данными величинами x и y, то вид эмпирической зависимости является произвольным. Предпочтение отдается простым формулам, обладающим хорошей точностью. Удачный выбор эмпирической формулы в значительной мере зависит от знаний исследователя в предметной области, используя которые, он может указать класс функций из теоретических соображений. Большое значение имеет изображение полученных данных в декартовых иди специальных системах координат (полулогарифмической, логарифмической и т. д.). По положению точек можно примерно угадать общий вид зависимости путем установления сходства между построенным графиком и образцами известных кривых.
Определение наилучших коэффициентов  , входящих в эмпирическую формулу производят хорошо известными аналитическими методами.
, входящих в эмпирическую формулу производят хорошо известными аналитическими методами.
Для того, чтобы найти набор коэффициентов  , которые доставляют минимум функции S, определяемой формулой (2), используем необходимое условие экстремума функции нескольких переменных - равенство нулю частных производных. В результате получим нормальную систему для определения коэффициентов
, которые доставляют минимум функции S, определяемой формулой (2), используем необходимое условие экстремума функции нескольких переменных - равенство нулю частных производных. В результате получим нормальную систему для определения коэффициентов 
 (3)
(3)
Значит, нахождение коэффициентов  сводится к решению системы (3).
сводится к решению системы (3).
Эта система упрощается, если эмпирическая формула (1) линейна относительно параметров  , тогда система (3) будет линейной. Конкретный вид системы (3) зависит от того, из какого класса эмпирических формул находится зависимость (1).
, тогда система (3) будет линейной. Конкретный вид системы (3) зависит от того, из какого класса эмпирических формул находится зависимость (1).
В случае линейной зависимости у=ах+bсистема примет вид:
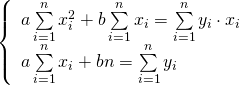 (4)
(4)
Эта линейная система может быть решена любым известным способом (методом подстановки, методом уравнивания коэффициентов, методом Крамера)
Пример 1.
Нахождение параметров линейной зависимости у=ax+b. Пусть на основании опыта получена следующие пары чисел (хi;yi), которые изображены на координатной плоскости. 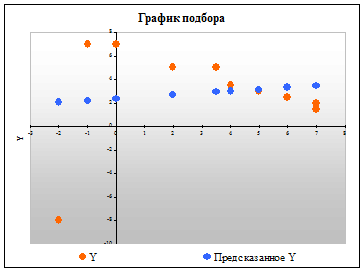
Решение:Для расчёта коэффициентов а и b составим следующую таблицу:
i
yi
xi
x2i
yixi
1
-8
-2
4
16
2
7
-1
1
-7
3
7
0
0
0
4
5
2
4
10
5
5
3,5
12,25
17,5
6
3,5
4
16
14
7
3
5
25
15
8
2,5
6
36
15
9
2
7
49
14
10
1,5
7
49
10,5
Σ
28,5
31,5
196,25
105
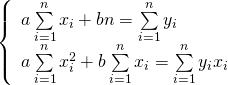 (4)
(4)
Подставляя из таблицы в систему уравнений (4), полученные данные, имеем:
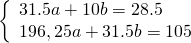
Для решения системы линейных уравнений и определения параметров, воспользуемся методом Крамера.
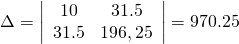
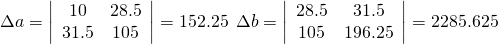
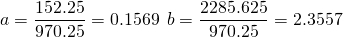
Уравнение прямой принимает следующий вид: y=0.1569X+2.3557
Всего один выброс (экстремальная точка с координатами -2; -8 на диаграмме рассеяния) может полностью изменить наклон регрессионной линии и, следовательно, вид зависимости между переменными. Такие выбросы могут исказить оценки модели, сдвигая линию регрессии в определенном направлении и, тем самым, вызывая смещение коэффициентов регрессии. На случай появления выбросов, должны быть предусмотрены корректировки, основанные на использовании "принципов статистического контроля", т. е. значения, выходящие за определенный диапазон, который определяется в терминах, кратных сигма, т.е. стандартных отклонений, могут быть преобразованы или вовсе пропущены, и только после этого должны вычисляться окончательные оценки параметров модели (уравнения) регрессии.
Пример 2. Нахождение параметров линейной зависимости у=ax+b.
Приводятся данные о росте производительности труда и снижении себестоимости работ за 5 лет некоторого предприятия по отношению к базисным данным , принимаемым за единицу:
Год
2007
2008
2009
2010
2011
Производительность труда, хi
1.05
1.09
1.13
1.18
1.24
Себестоимость продукции, yi
0.98
0.95
0.93
0.90
0.88
Предполагая, что зависимость себестоимости продукции от производительности труда является линейной: y=f(x)=ax + b, найдите параметры a и b , применяя метод наименьших квадратов.
Решение: Для расчёта коэффициентов a и b составим следующую таблицу:
i
xi
yi
xi2
xi yi
1
1.05
0.98
1.1025
1.0290
2
1.09
0.95
1.1881
1.0355
3
1.13
0.93
1.2769
1.0509
4
1.18
0.90
1.3624
1.0620
5
1.24
0.88
1.5376
1.0912
∑
5.69
4.64
6.4975
5.2686
С учётом данных таблицы составим систему уравнений:
6,4975a+5.69b=5,2686
5,69а+5b=4,64
Решим систему методом подстановки, выразим переменную а из первого уравнения системы и подставим во второе уравнение:
a=(5.2686 - 5.69b) / 6,4975
5,69[(5.2686 - 5.69b) / 6,4975] +5b=4.64
Решением второго уравнения будет b≈1,53. После подстановки находим а≈ -0,52.Получаем, решение этой системы: а≈ -0,52, b≈1,53.Таким образом, функция, приближённо выражающая зависимость себестоимости продукции у от производительности труда х в течение рассматриваемого пятилетия, имеет вид: у=-0,52х +1,53.
Вывод: Так как -0,52 ﮮ 0, то функция у=-0,52х +1,53 является убывающей, и поэтому чем выше производительность труда, тем ниже себестоимость продукции на предприятии. Ответ: -0,52; 1,53
Задания для самостоятельного выполнения.
Производительность труда на предприятии по годам приведена в таблице. Найдите:
-
линейную зависимость производительности труда по годам у= aх+b;
-
предполагаемую производительность на 10 -ый год работы.
1.
х i, лет
1
2
3
4
5
6
7
8
yi, тыс.шт. в год
63
95
139
161
202
241
268
288
2.
х i, лет
1
2
3
4
5
6
7
8
yi, тыс.шт. в год
14,7
16,5
16,5
18,1
21,5
22,3
23,5
24,1
3.
х i, лет
1
2
3
4
5
6
7
8
yi, тыс.шт. в год
100
156
170
184
194
205
220
229
4.
х i, лет
1
2
3
4
5
6
7
8
yi, тыс.шт. в год
120
140
230
370
445
570
655
770
5.
х i, лет
1
2
3
4
5
6
7
8
yi, тыс.шт. в год
69,1
167,4
265,2
362
460,6
556,2
675,5
755
6.
х i, лет
1
2
3
4
5
6
7
8
yi, тыс.шт. в год
66,5
168,4
270,1
372
474,8
576,6
678,6
735,5
7.
х i, лет
1
2
3
4
5
6
7
8
yi, тыс.шт. в год
6,2
9,6
13,9
16,2
20,3
24,1
26,6
27,9
8.
х i, лет
1
2
3
4
5
6
7
8
yi, тыс.шт. в год
100,2
155,5
170,2
183,7
194,5
204,6
220,1
229,5
9.
х i, лет
1
2
3
4
5
6
7
8
yi, тыс.шт. в год
623,5
675,4
746,2
828,8
890,5
959,3
1028,2
1105,8
10.
х i, лет
1
2
3
4
5
6
7
8
yi, тыс.шт. в год
2
4,9
7,9
11,1
14,1
17
21,1
23,9
11.
х i, лет
1
2
3
4
5
6
7
8
yi, тыс.шт. в год
2,9
6,1
9,2
11,8
16
18,8
21,9
23,5
12.
х i, лет
1
2
3
4
5
6
7
8
yi, тыс.шт. в год
20
50
70
100
130
150
180
210
13.
х i, лет
1
2
3
4
5
6
7
8
yi, тыс.шт. в год
39
55
67
82
94
110
123
138
14.
х i, лет
1
2
3
4
5
6
7
8
yi, тыс.шт. в год
40
250
470
650
990
1080
1300
1450
15.
х i, лет
1
2
3
4
5
6
7
8
yi, тыс.шт. в год
64
96
140
162
203
242
269
290
16.
х i, лет
1
2
3
4
5
6
7
8
yi, тыс.шт. в год
66
99
139
162
205
243
271
289
17.
х i, лет
1
2
3
4
5
6
7
8
yi, тыс.шт. в год
147
165
165
181
215
223
235
241
18.
х i, лет
1
2
3
4
5
6
7
8
yi, тыс.шт. в год
10
15,6
17
18,4
19,4
20,5
22
22,9
19.
х i, лет
1
2
3
4
5
6
7
8
yi, тыс.шт. в год
12
14
23
37
44,5
57
65,5
77
20.
х i, лет
1
2
3
4
5
6
7
8
yi, тыс.шт. в год
69
167
265
362
460
556
675
755
21.
х i, лет
1
2
3
4
5
6
7
8
yi, тыс.шт. в год
66
168
270
372
474
576
678
735
22.
х i, лет
1
2
3
4
5
6
7
8
yi, тыс.шт. в год
62
96
139
162
203
241
266
279
23.
х i, лет
1
2
3
4
5
6
7
8
yi, тыс.шт. в год
100
155
170
183
194
204
220
229
24.
х i, лет
1
2
3
4
5
6
7
8
yi, тыс.шт. в год
623
675
746
828
890
959
1028
1105
25.
х i, лет
1
2
3
4
5
6
7
8
yi, тыс.шт. в год
20
49
79
111
141
170
211
239
26.
х i, лет
1
2
3
4
5
6
7
8
yi, тыс.шт. в год
29
61
92
118
160
188
219
235
27.
х i, лет
1
2
3
4
5
6
7
8
yi, тыс.шт. в год
21
51
71
101
131
151
181
211
28.
х i, лет
1
2
3
4
5
6
7
8
yi, тыс.шт. в год
3,9
5,5
6,7
8,2
9,4
11
12,3
13,8
29.
х i, лет
1
2
3
4
5
6
7
8
yi, тыс.шт. в год
4
25
47
65
99
108
130
145
30.
х i, лет
1
2
3
4
5
6
7
8
yi, тыс.шт. в год
6,4
9,6
14
16,2
20,3
24,2
26,9
29
Использованная литература:
-
Сборник задач по высшей математике для экономистов.: под редакцией проф. В.И. Ермакова , Москва, Инфра - М: 2003, 315с
-
Справочник по высшей математике.: М.Я. Выгодский.: Москва. 2011, 523с
-
Математика. Задачи с экономическим содержанием.: пособие/ С.Л. Гуринович. _ Минск: Новое знание, 2008. - 264с
-
Интернет.


