- Преподавателю
- Математика
- Методическая разработка по теме Графические методы решения задач с параметрами. Содержание
Методическая разработка по теме Графические методы решения задач с параметрами. Содержание
| Раздел | Математика |
| Класс | 11 класс |
| Тип | Другие методич. материалы |
| Автор | Чернова О.П. |
| Дата | 18.12.2015 |
| Формат | doc |
| Изображения | Есть |
Вступление
B представленной курсовой работе рассмотрены элементы графического исследования в задачах с параметрами с помощью метода сечения и метода областей.
Возрастающая популярность задач с параметрами объясняется тем, что теоретическое изучение и математическое моделирование многообразных процессов из различных областей науки и практической деятельности человека часто приводят к достаточно сложным уравнениям, неравенствам или их системам, содержащим параметры.
Необходимой частью решения подобных задач является исследование характера и конечного результата процесса в зависимости от значений параметров, причем часто оказывается, что решение зависит не от каждого параметра в отдельности, а от некоторого их характерного комплекса. B подобных случаях становится невозможным разбиение исходной задачи со многими параметрами на совокупность задач с одним из параметров. Такие задачи требуют глубокого понимания сути процесса, свободного владения различными математическими методами и скрупулезного анализа.
Нельзя отрицать, что для того, чтобы успешно решать задачи с параметрами, часто требуется «хотя и не слишком изощренное, но все-таки трюкачество» (Ф. Клейн, немецкий математик), решить задачу с параметрами - это значит установить, при каких значениях параметров задача имеет решения, и найти эти решения в зависимости от параметров, т.е. решение подобного типа задач должно сопровождаться своего рода исследованием. Именно необходимость проводить исследование значительно осложняет решение задач с параметрами, так как требует глубоких знаний различных разделов школьной программы и высокой логической культуры.
Необходимость представленной курсовой работы диктуется современными требованиями ЕГЭ, где задачи с параметрами представляют для выпускников школы наибольшую сложность, как в логическом, так и в техническом плане.
Задачи с параметрами чрезвычайно многообразны: задачи на исследование квадратичной функции, рациональных уравнений, иррациональных уравнений, логарифмических и показательных неравенств, тригонометрических уравнений, тригонометрических неравенств и т.д. Обычно учебные пособия по решению задач с параметрами строятся именно по категории вида уравнения или неравенства.
Особенность представленной курсовой работы состоит в том, что в ней сделана попытка решать самые разные категории уравнений и неравенств графическими методами. C этой целью проанализировано достаточно большое количество примеров на возможность их решения рассматриваемыми методами. Представленный в курсовой работе материал может быть использован учителем математики, как в кружковой работе, так и при непосредственной подготовке к ЕГЭ.
-
Постановка задачи решения уравнений, систем уравнений
и неравенств с параметрами.
Пусть дано уравнение F(x, а) = 0. Если ставится задача отыскать все такие пары (x;a), которые удовлетворяют данному уравнению, то это уравнение с двумя переменными x и а .Однако относительно уравнения F(x,a) = 0 можно поставить и другую задачу. Дело в том, что если придать а какое-либо фиксированное значение, то заданное уравнение можно рассматривать как уравнение с одной переменной x. Решения этого уравнения, естественно, определяются выбранным значением а.
Если ставится задача для каждого значения а из некоторого числового множества A решить уравнение F(x, а) = 0 относительно x, то уравнение F(x, а) = 0 называется уравнением с переменной x и параметром a, а множество А-областью изменения параметра.
Уравнение F(x, а) = 0 - это, по существу, краткая запись семейства уравнений. Уравнения этого семейства получаются из уравнения F(x, а) = 0 при различных конкретных значениях параметра а.
Если под областью изменениях параметра подразумевать (если не сделано специальных оговорок) множество всех действительных чисел, то задачу решения с параметром можно сформулировать следующим образом: решить уравнение F(x, а) = 0 (спеременной x и параметром а) - это значит, на множестве действительных чисел решить семейство уравнений, получающихся из уравнения F(x, а) = 0 при всех действительных значениях параметра.
Ясно, что выписать каждое уравнение из бесконечного семейства уравнений невозможно. Тем не менее, каждое уравнение семейства должно быть решено. Сделать это можно, если, например, по некоторому целесообразному признаку разбить множество всех значений параметра на подмножества и решить затем заданное уравнение на каждом из этих подмножеств.
Если параметру, содержащемуся в уравнении (неравенстве), придать некоторое значение, то возможен один из двух следующих случаев:
-
Получится уравнение (неравенство), содержащее лишь данные числа и неизвестные и не содержащее параметров.
-
Получится условие, лишенное смысла.
B первом случае значение параметра называется допустимым, а во втором -недопустимым.
Поэтому решить уравнение или неравенство, содержащее параметр, - это значит, для каждого допустимого значения параметра найти множество всех значений данного уравнения (неравенства).
Решение задач с параметрами трудно «загнать» в какую-то одну схему, ибо перечень теоретических вопросов, возникающих при решении задач с параметрами, достаточно широк. Необходимой частью решения задач с параметрами является исследование, что усложняет основную стратегию математического образования в средней школе, которая нацеливает на развитие умений и навыков решения ограниченного ряда типовых задач, как правило, связанных с определённым набором стандартных алгебраических преобразований.
Чаще всего встречаются две постановки задач с параметрами:
-
Для каждого значения параметра а решить уравнение (неравенство или систему);
-
Найти все значения параметра а, при каждом из которых решения уравнения (неравенства или системы) удовлетворяют некоторым заданным условиям.
В этом случае не требуется находить сами решения (в общем случае зависящие от параметра).
Пример 1.1
При всех значениях параметров a и b решить уравнение ax+b=0.
Решение: ax+b=0, 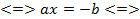
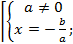
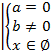
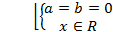
Ответ: при а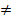 0, b
0, b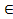 R x1=
R x1= 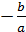 ;
;
при a=0, b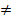 0, x
0, x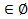 ,
,
при a=b=0 x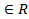 ;
;
Пример 1.2.
Найти все значения параметра a, при каждом из которых уравнение 3ax2-2(3a-2)x+3(a-1)=0 имеет хотя бы один положительный корень.
Решение:
1. При a=0 заданное уравнение становится линейным и приобретает вид 4x-3=0 x=
x=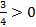 , т. е. имеет единственный корень, который оказывается положительным.
, т. е. имеет единственный корень, который оказывается положительным.
2. При а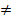 0 заданное уравнение является квадратным и имеет корни x1
0 заданное уравнение является квадратным и имеет корни x1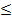 x2, если его дискриминант неотрицателен:
x2, если его дискриминант неотрицателен:
D1=(3a-2)2-3a3(a-1)=4-3a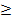 0
0 a
a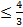
По теореме Виета:
x1-x2=-p=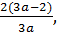 x1x2=q=
x1x2=q=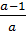
Существование двух положительных корней 0<x1<x2 задается системой:
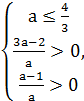
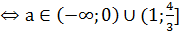
Существование одного положительного и одного отрицательного корня x1<0<x2 задается системой:
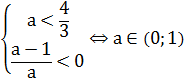
Наличие нулевого корня соответствует: x1x2=q=0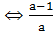 =0
=0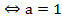
Для решения имеет объединение 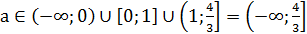
Ответ: 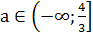
Приведённые примеры показывают, что никаких специальных методов и приёмов решения задач с параметрами в них не использовалось, этапы решения не выходят за разделы школьной программы.
2. Метод сечений.
Целью данной работы являются графические исследования в задачах с параметрами. Для успешного применения графических методов решения задач необходимо уметь строить графики элементарных функций и выполнять графически простейшие операции над ними.
Основные правила преобразования графиков:
График функции y= f(x)+a получается из графика функции y= f(x) путем параллельного переноса на величину а вдоль оси Oy.
График функции y= f(x-a) получается из графика функции y= f(x) путем параллельного переноса на величину а вдоль оси Ox.
График функции y= k f(x) получается из графика y= f(x) путем растяжения в k раз по оси у при k>l и путем сжатия в 1/k раз при 0<k<l.
График функции y= f(kx) получается из графика функции y= f(x) путем сжатия в k раз по оси x при k>l и путем растяжения в 1/k раз при 0<k<l.
График функции y= - f(x) получается из графика y= f(x) зеркальным отражением относительно оси x.
График функции y= f(-x) получается из графика y= f(x) зеркальным отражением относительно оси у.
Графики многих функций, в том числе и таких, как y= |f(x)| и y= f(|x|), можно построить, последовательно применив изложенные выше правила.
Предположим, что уравнение (или неравенство), содержащее параметр, удалось привести к виду f(x)= g(x,a) (или f(x)> <g(x,a)), где f(x) и g(x,a) - достаточно изученные функции, графики которых легко построить.
Тогда уравнение y1=f(x) определяет на координатной плоскости XOY некоторую кривую, а соотношение y2=g(x,a) - целое семейство кривых, в котором каждому допустимому значению параметра а соответствует одна кривая. При этом в зависимости от величины параметра а кривые семейства y2=g(x,a) могут занимать принципиально различные положения относительно кривой y1=f(x). Изучая сечение кривой y1(x) семейством кривых y2=g(x,a) при соответствующих им значениях параметра а, мы получаем возможность исследовать вопрос о количестве решений уравнения f(x)=g(x,a) в зависимости от параметра, правильно выбирать эти решения и использовать их для нахождения решений неравенств вида f(x)> <g(x,a). Типичными критическими значениями параметров оказываются те, которые соответствуют точкам касания графиков. При этом удобно исходить из соображения, что наклонная прямая y= k x+l касается параболы или гиперболы у=ⱷ(х) (у= ⱷ(х) - соответствующая квадратичная или дробно-линейная функция), если уравнение ⱷ(х)= k x+l имеет единственное решение (отметим, что полученное уравнение сводится к решению квадратного уравнения).
Рассмотрим применение этого метода к решению конкретных задач, когда сечение производится семейством:
-
прямых, ломаных;
-
парабол, гипербол, окружностей.
Пример 2.1
При каких значениях параметра а уравнение х(х2-1)(х2-10)=а имеет три целочисленных корня? Найти эти корни. Решение.
П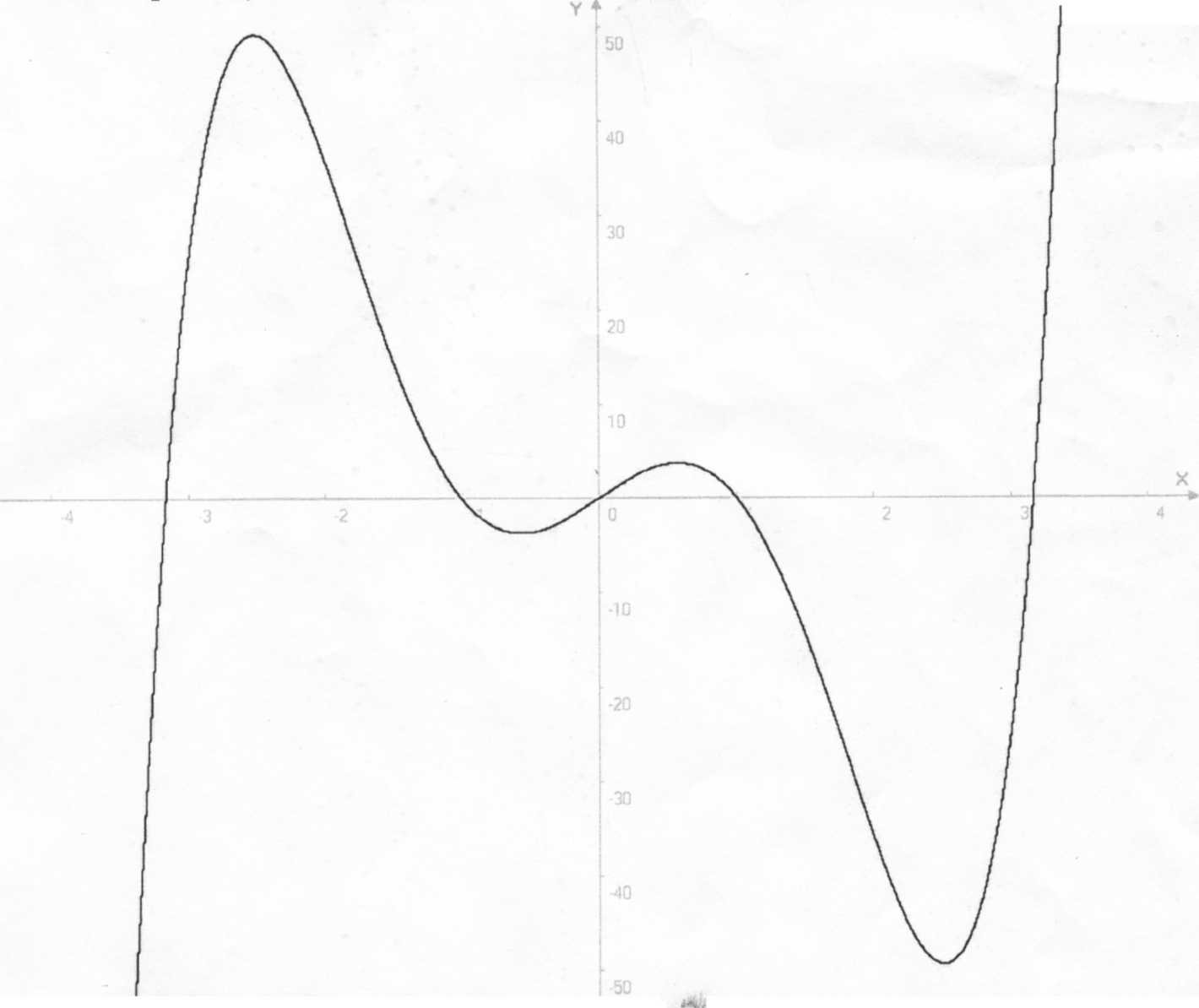 ри a=0 заданное уравнение имеет три целых корня x1,2=±1, х3=0. Рассмотрим случай, когда a ≠0. Построим график функции у=х(х2-1)(х2-10).
ри a=0 заданное уравнение имеет три целых корня x1,2=±1, х3=0. Рассмотрим случай, когда a ≠0. Построим график функции у=х(х2-1)(х2-10).
Из рисунка видно, что если заданное уравнение имеет целочисленные корни, отличные от указанных выше, то либо два из них принадлежат интервалу (1; 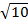 ), а третий - интервалу (-∞;
), а третий - интервалу (-∞;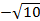 ), либо два корня принадлежат интервалу (
), либо два корня принадлежат интервалу (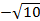 ; -1), а третий - интервалу (
; -1), а третий - интервалу (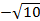 ; +∞). Учитывая нечетность функции у, рассмотрим, например, только первый из возможных случаев.
; +∞). Учитывая нечетность функции у, рассмотрим, например, только первый из возможных случаев.
B этом случае на интервале (1; 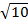 ) имеется два целых числа x=2 и x=3. Тогда y(2)= -36, y(3)= -24, т. е. y(2)≠y(3). Следовательно, в этом случае не может быть трех целочисленных корней.
) имеется два целых числа x=2 и x=3. Тогда y(2)= -36, y(3)= -24, т. е. y(2)≠y(3). Следовательно, в этом случае не может быть трех целочисленных корней.
Ответ: a=0, x1;2=±1, х3=0.
Пример 2.2
B зависимости от значений параметра а определить количество решений системы
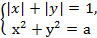
Решение. C геометрической точки зрения количество решений заданной системы - это количество точек пересечения при каждом фиксированном значении параметра а кривых, заданных уравнениями системы. При этом первое уравнение задает квадрат, а второе - семейство окружностей радиуса 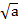 , (a>0), с центром в начале координат (при a=0 окружность вырождается в точку).
, (a>0), с центром в начале координат (при a=0 окружность вырождается в точку).
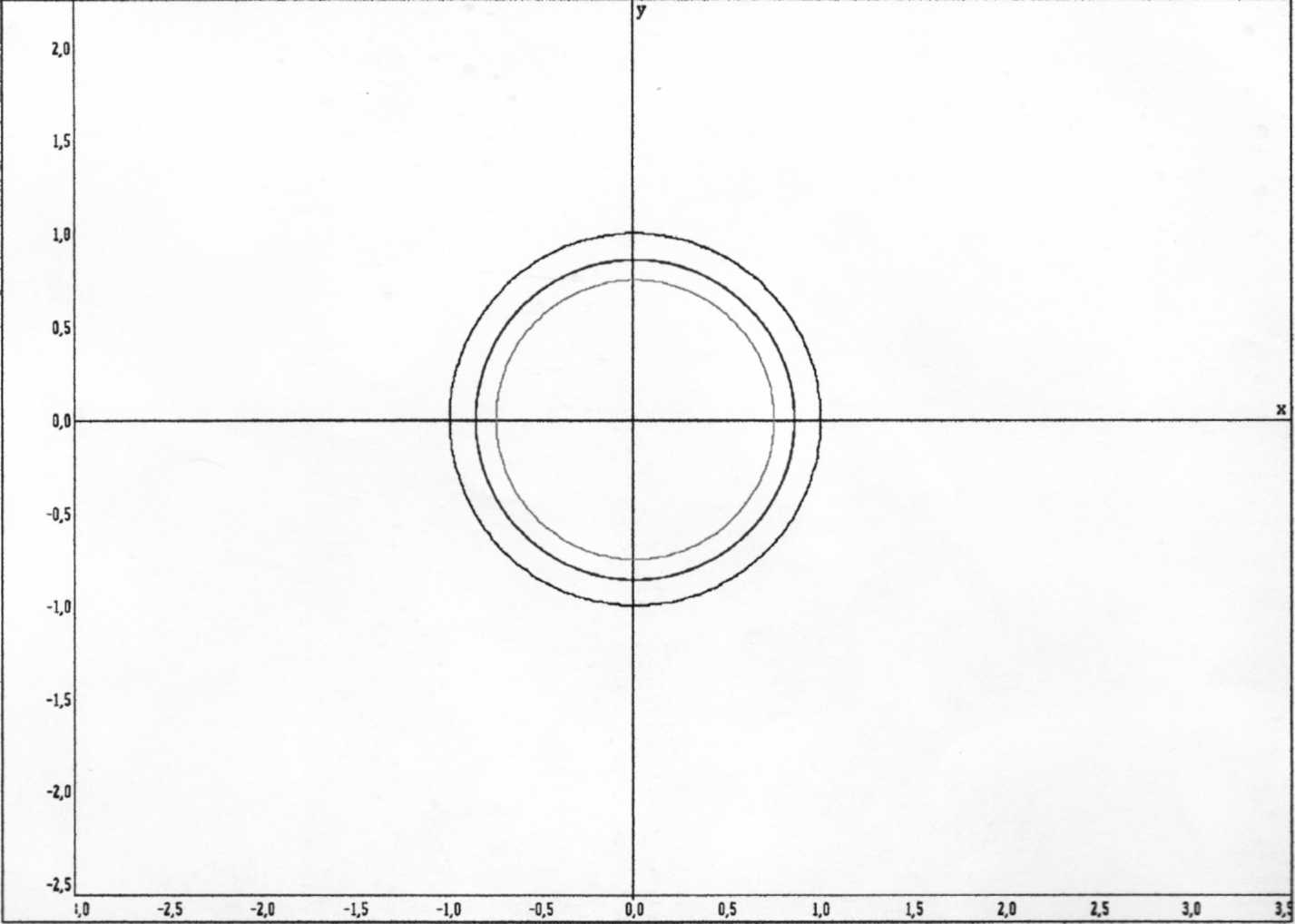
Из рисунка видно, что при a=1, a=1/2 квадрат имеет с окружностью четыре общие точки. При 1/2<a<1 общих точек 8. При a<1/2 и a>l общих точек у квадрата и окружностей нет.
Ответ: a<1/2 и a>1, нет решений;
a<1/2, a=1, четыре решения;
1/2<а<1, восемь решений
.
Из двух рассмотренных примеров следует очевидное преимущество графического решения заданий с параметрами методом сечений. Возможное аналитическое решение приведенных заданий выглядело бы громоздким и затруднительным.
Ниже приводятся примеры решения различных уравнений и неравенств с параметрами методом сечений.
Пример 2.3
Для каждого значения параметра а решить неравенство
х4-ах2+1<0
Рассмотрим функции f(x)= х4+1 и g(xa)= ax2→ g(xa)>f(x). Построим графики этих функций
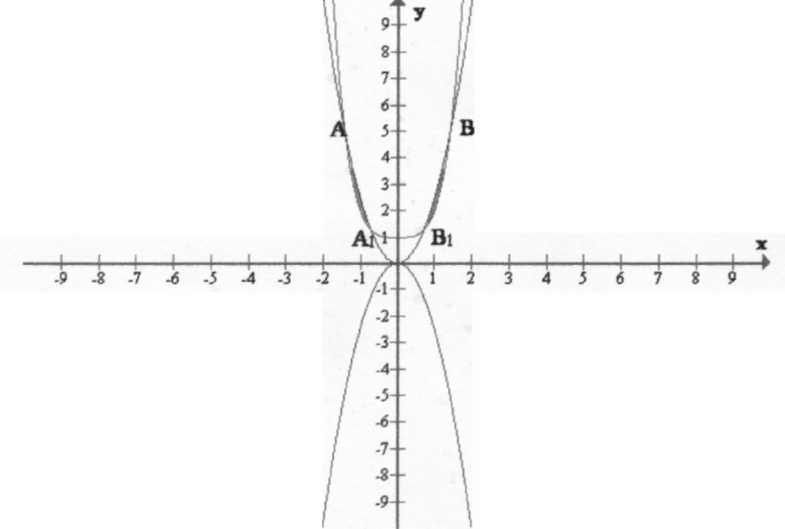
Графики f(x) и g(xa) пересекаются в точках А, A1, B1, В.
Найдем эти точки, решив исходное неравенство. Параметр а должен быть
больше нуля, только в этом случае пересекаются графики f(x) и g(xa).
Введем новую переменную y=x2. у2-ау+1=0
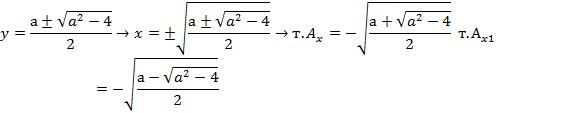
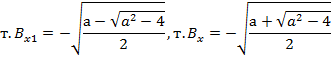
Решения лежат на промежутке:
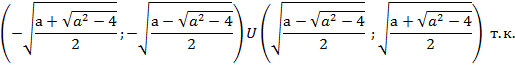
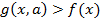
Ответ: при a<2 корней нет, при a>2 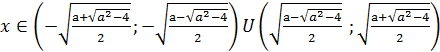 ;
;
Пример 2.4
Haйти все действительные значения k, при каждом из которых уравнение х2(4х+6)-2|х| 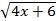 -3=3k имеет 2 корня.
-3=3k имеет 2 корня.
Решение. Используя соотношение |x|=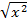 , перепишем исходное уравнение в виде: x2(4x+6)-2
, перепишем исходное уравнение в виде: x2(4x+6)-2 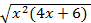 -3=3k. Пусть
-3=3k. Пусть
y= 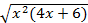 . Тогда уравнение примет вид: y2 -2y-(3+3k)=0 Решим полученное квадратное уравнение относительно у: y2-2y-(3+3k)=0,D1=4+3k При k≥4/3 y= 1 ±
. Тогда уравнение примет вид: y2 -2y-(3+3k)=0 Решим полученное квадратное уравнение относительно у: y2-2y-(3+3k)=0,D1=4+3k При k≥4/3 y= 1 ±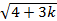 . Таким образом уравнение можно переписать в виде:
. Таким образом уравнение можно переписать в виде: 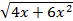 =1±
=1±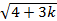 . Пусть f(x)=
. Пусть f(x)=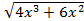 , а g(x,k)=1±
, а g(x,k)=1±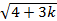 .
.
Построим график f(x).
1. D(f)={4x3+6x2≥0}, x2(4x+6)≥0

Следовательно, D(f)=[-1,5; +∞).
2. E(f)=[0; +∞).
3.Корни: x1=0, x2= -1,5. Т. к. x1- кратный, то кривая касается оси X в точке x=0.
4. Интервалы возрастания и убывания f(x) найдем, вычислив производную: f(х)=(12х2+12х)/(2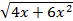 ). (12x2+12x)/(2
). (12x2+12x)/(2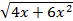 )=0, x1=0, x2= -1. Определим знаки производной:
)=0, x1=0, x2= -1. Определим знаки производной:
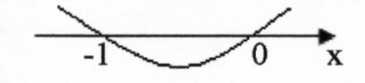
f(x)>0 при x (-∞; -1)U(0; +∞), следовательно, f(x) возрастает при xϵ[-1,5; -1] U[0; +∞). f(x)<0 при xϵ(-1; 0), следовательно,
(-∞; -1)U(0; +∞), следовательно, f(x) возрастает при xϵ[-1,5; -1] U[0; +∞). f(x)<0 при xϵ(-1; 0), следовательно,
f(x) убывает при xϵ[-1; 0].
С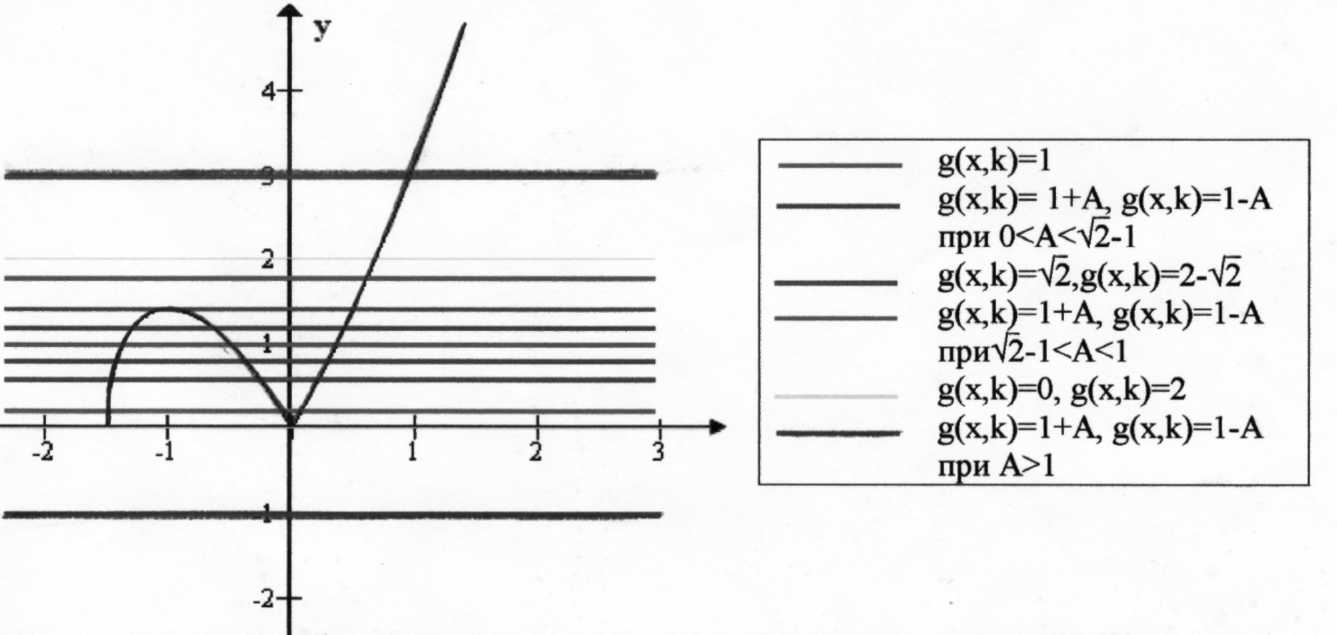 ледовательно, точки, в которых x= -1 и x=0, являются экстремумами функции. При x= -1 y=
ледовательно, точки, в которых x= -1 и x=0, являются экстремумами функции. При x= -1 y=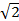 . Поэтому точка (-1;
. Поэтому точка (-1; 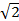 ) - точка максимума f(x), а точка (0; 0) - точка минимума. Строим график функции f(x).
) - точка максимума f(x), а точка (0; 0) - точка минимума. Строим график функции f(x).
Строим линии g(x,k)=1±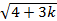 . Это линии, параллельные оси X. Примем A=
. Это линии, параллельные оси X. Примем A=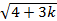 .
.
Если A=0, то g(x,k)=1 и заданное уравнение имеет 3 корня.
При 0![]() -1 g(x,k)=1+A, g(x,k)=1-A. Каждая из этих прямых пересекает f(x) в трех точках, поэтому всего решений 6.
-1 g(x,k)=1+A, g(x,k)=1-A. Каждая из этих прямых пересекает f(x) в трех точках, поэтому всего решений 6.
При A=![]() -1 g(x,k)=
-1 g(x,k)= ![]() , g(x,k)=2-
, g(x,k)=2-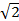 . B этом случае пять решений.
. B этом случае пять решений.
При ![]() -1 g(x,k)=1+A, g(x,k)=1-A. Тогда уравнение имеет 4 решения, т. к. g(x,k)=1+A пересекает f(x) в одной точке, а g(x,k)=1-A - в трех.
-1 g(x,k)=1+A, g(x,k)=1-A. Тогда уравнение имеет 4 решения, т. к. g(x,k)=1+A пересекает f(x) в одной точке, а g(x,k)=1-A - в трех.
Если A=1, то g(x,k)=0, g(x,k)=2, поэтому имеем три корня.
При A>1 линия g(x,k)=1-A не пересекает график f(x), а g(x,k)=1+A пересекает f(x) в одной точке, уравнение имеет одно решение.
Таким образом, нет таких А, и, следовательно, таких значений k, при которых исходное уравнение имеет 2 корня.
Ответ: нет решений.
Пример 2.5
Найти все действительные значения с, при каждом из которых уравнение х2(х-3)-2|x|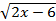 =2(c+1) имеет 2 корня. Решение.
=2(c+1) имеет 2 корня. Решение.
Используя соотношение |x|=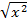 , перепишем исходное уравнение:
, перепишем исходное уравнение:
х2(х-3)-2 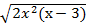 =2с+2. Обозначим y=
=2с+2. Обозначим y= 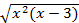 , тогда уравнение примет вид: у2-2y2-(2c+2)=0. Решим его относительно у: D1=4+2c, y=
, тогда уравнение примет вид: у2-2y2-(2c+2)=0. Решим его относительно у: D1=4+2c, y=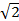 +
+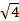 +2c при c≥-2. Первоначальное уравнение переписываем в виде:
+2c при c≥-2. Первоначальное уравнение переписываем в виде: 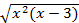 =
=![]() ±
±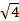 +2c. Пусть f(x)=
+2c. Пусть f(x)=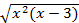 , g(x,c)=
, g(x,c)=![]() +
+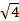 +2c. Построим графики этих функций.
+2c. Построим графики этих функций.
1) D(f)={x2(x-3)≥0}
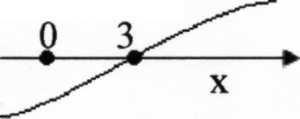
Следовательно, D(f)=[3; +∞).
2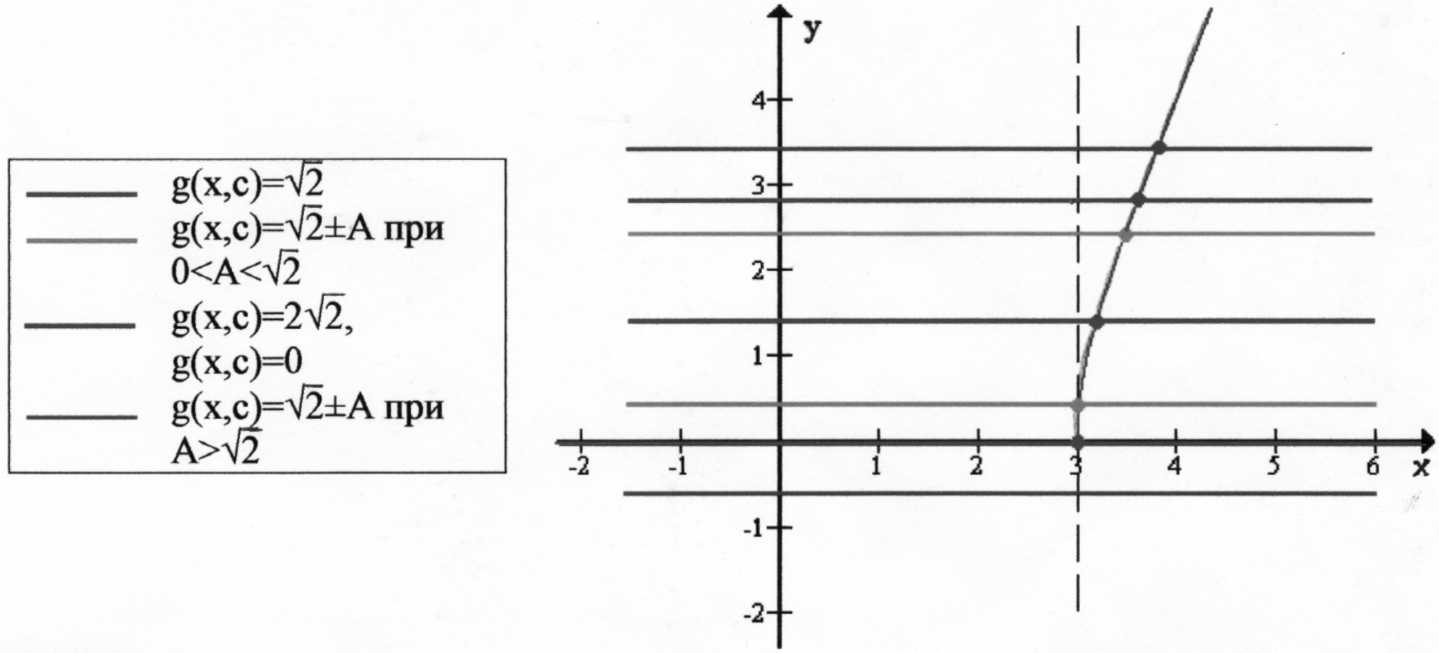 ) E(f) [0; +∞).
) E(f) [0; +∞).
Строим график g(x,c)=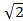 ±
±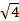 +2c. Это линии, параллельные оси X. Примем
+2c. Это линии, параллельные оси X. Примем 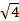 +2c=A. Тогда g(x,c)=
+2c=A. Тогда g(x,c)=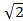 ±A, A>0.
±A, A>0.
1. При A=0(c=-2) g(x,c)=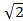 , линия пересекает f(x) в одной точке.
, линия пересекает f(x) в одной точке.
2. При 0<A<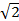 (-2<c<-1) g(x,c)=
(-2<c<-1) g(x,c)=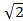 +A, g(x,c)=
+A, g(x,c)=![]() -A. Каждая из этих линий
-A. Каждая из этих линий
пересекает f(x) в одной точке, поэтому уравнение имеет 2 корня.
3. При A=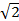 (c=-1) g(x,c)=2
(c=-1) g(x,c)=2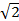 , g(x,c)=0. Тогда уравнение также имеет 2 корня.
, g(x,c)=0. Тогда уравнение также имеет 2 корня.
4. При A>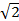 (c>-1) g(x,c)=
(c>-1) g(x,c)=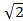 +A, g(x,c)=
+A, g(x,c)=![]() -A, где g(x,c)=
-A, где g(x,c)=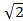 -A не пересекает линию f(x), т. к. лежит ниже оси X. Следовательно, уравнение имеет 1 корень.
-A не пересекает линию f(x), т. к. лежит ниже оси X. Следовательно, уравнение имеет 1 корень.
Таким образом, исходное уравнение имеет 2 корня при Aϵ(0;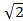 ]. Тогда с лежит в промежутке (-2;-1].
]. Тогда с лежит в промежутке (-2;-1].
Ответ: cϵ(-2;-1].
Пример 2.6
Для каждого значения параметра а решить неравенство: x2 + ах +1 > 0
Для каждого значения параметра а рассмотрим функции f(x) = x2+1 и
g(x,a) = -ах. Графиком функции f(x) является парабола, ветви которой направлены вверх, с вершиной в точке с координатами (0;1).Функция g(x,a) порождает семейство прямых, проходящих через точку (0;0), непараллельных оси ОУ.
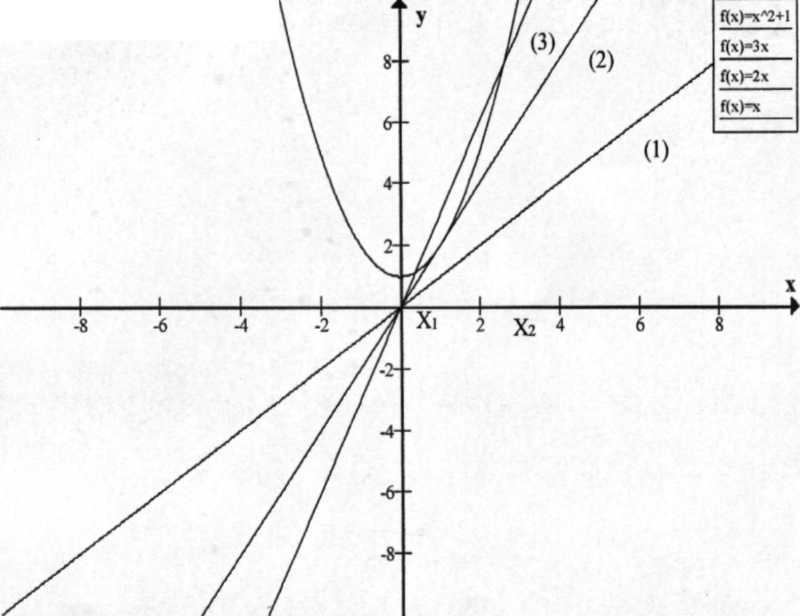
B зависимости от значений параметра а возможны три случая:
-
прямая не пересекает параболу.
-
прямая касается параболы.
-
прямая пересекает параболу в двух точках.
Найдём при каких значениях параметра а уравнение f(x) = g(x,а) имеет единственное решение (т.е. прямая касается параболы) Это имеет место тогда, когда дискриминант D уравнения x2+1 = -ах равен нулю.
f(x) = g(x,a)
x2 + 1 = - ах
x 2 + ах + 1 = 0
D = а2 - 4 = 0,
а = ±2
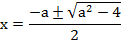
Следовательно
при |a|=2 прямая касается параболы и неравенство выполняется при всех x, кроме точек касания, x = ±1.
при |a| <2 парабола находится выше прямой g (х,а) и исходное неравенство выполняется при любом x.
при |a|>2 исходное неравенство выполняется при x>х2и х<x1,
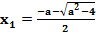
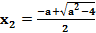
Ответ: 1) при |a| < 2 x ϵ R,
2) при |a|=2 x ϵ(-∞;-1) (-1;1)
(-1;1) (1;+∞),
(1;+∞),
3) при |a| > 2 x ϵ (-∞; 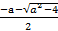 )
)![]() (
(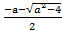 ; +∞);
; +∞);
Пример 2.7
Найти все с, при которых уравнение имеет 3 корня: |х2-1|+|х2-х-2|=х2-3х+с
Для каждого значения параметра с рассмотрим функции
f(x)=|x2-l|+|x2-x-2|-x2 +3x и g=c. Рассматривая функцию f(x), мы находим необходимым раскрыть модули. Раскрывая модули, получаем три выражения:
при x ϵ (-∞ ;-l]U[2;+∞) получаем х2+2х-3
при x ϵ [l;2) получаем -х2+4х+1
при x ϵ (-1;1) получаем -3х +4x+3
Графиком первого выражения является часть параболы с вершиной в точке (-1;-4), взятая в промежутке x ϵ (-∞;-1]U[2;+∞). Графиком второго выражения также является часть параболы, но ветви которой направлены вниз и с вершиной в точке (2;5), взятая при x ϵ [1;2). Графиком последнего выражения является часть параболы, ветви которой направлены вниз, с вершиной в точке (2/3;13/3), взятая при x ϵ(-1;1).
Функция g порождает семейство прямых, параллельных оси OX. B зависимости от значений параметра с возможны несколько случаев: прямая может вообще не пересекать график функции f(x), может пересекать его в одной, двух, трех и четырех точках. Для ответа нам надо найти те значения с, при которых существует три точки пересечения f(x) и g.
Ha рис. 3 хорошо видно, что таких точек две - это вершина параболы у=-3х2+4х+3 c=13/3 и при c=4.
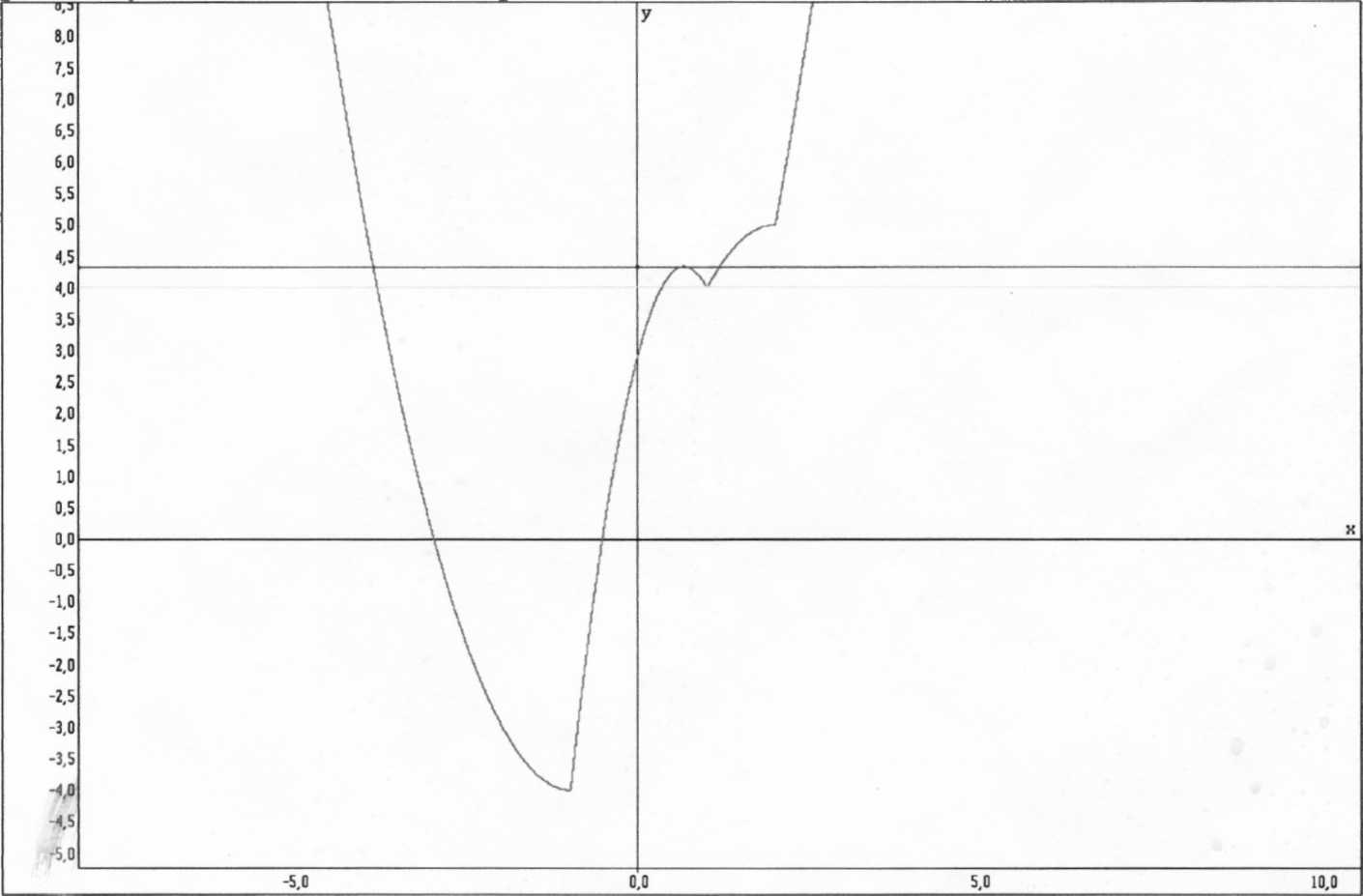
Рис 3
Ответ: при c=4 и c=13/3 уравнение |x2 -1|+|x2 -x-2|=x2 -3х+с имеет три корня.
Пример 2.8
Найти все значения параметра а, при которых система
![]()
имеет 2 решения.
Графиком функции f(x)= х2+у2=1 является окружность с радиусом r=l и центром в точке (0; 0).
Графиком g(x)=y-|x|=a являются симметричные относительно оси Y лучи, выходящие из вершины (0; а). От а зависит величина сдвига вершины графика по оси yY относительно начала координат (0; 0).
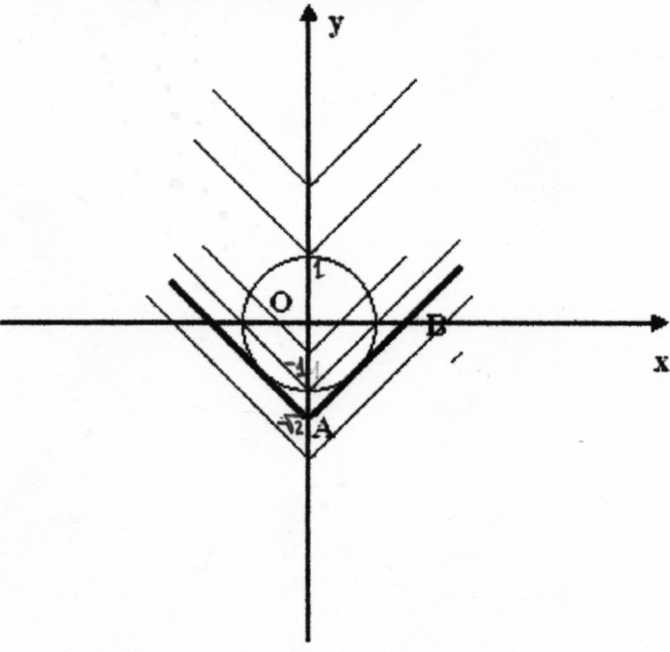
Эта система может иметь 3, 2, 1 решения или вообще не иметь решений. Ho, очевидно, что два решения система будет иметь только когда g(x) либо пересекает окружность (причем вершина должна лежать внутри окружности), либо касается ее внешним образом.
Если вершина y=|x|+a лежит на окружности, задаваемой функцией f(x), то система имеет либо три либо одно решение, следовательно, для расположения вершины g(x) нам подходит только внутренняя область окружности - yϵ(l; -1).
График функции g(x) также может единственным образом касаться окружности f(x). Т. к. угол между ветвями графика равен 90°, то угол между осями и отрезком AB графика будет равен 45°, следовательно, треугольник OAB - прямоугольный и равнобедренный. Если достроить данный треугольник до квадрата, то получим, что AB равен диаметру окружности f(x), т. е. равен 2. Очевидно, что по теореме Пифагора катет такого треугольника равен 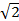 . Значит, расстояние от вершины g(x) до начала координат равно |a|=
. Значит, расстояние от вершины g(x) до начала координат равно |a|=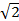 . Т.к. ветви нашего графика будут направлены вверх в любом случае, то вершина должна быть расположена ниже оси X. Следовательно, в данном случае a<0, a=-
. Т.к. ветви нашего графика будут направлены вверх в любом случае, то вершина должна быть расположена ниже оси X. Следовательно, в данном случае a<0, a=-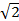 .
.
Oтвет: aϵ{-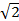 }
} (-l; 1).
(-l; 1).
Пример 2.9
Найти все значения параметра а, при которых система
![]()
имеет 3 решения.
Графиком f(x)= х2+у2=2 является окружность с радиусом r= 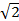 и центром в точке (0; 0).
и центром в точке (0; 0).
Графиком функции g(x)= |y|-x=a являются два луча, выходящие из вершины в точке (а; 0), симметричные относительно оси X.
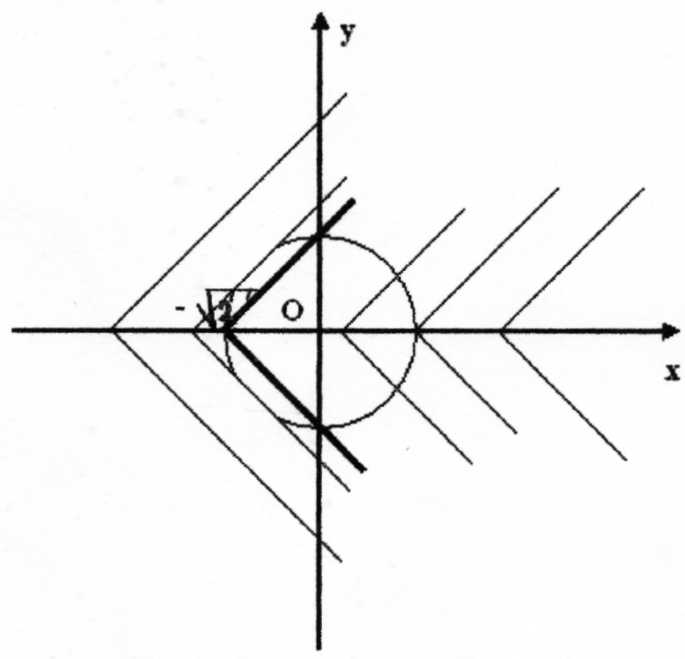
B зависимости от значения параметра а система может иметь 3, 2, 1, решение или не иметь решений вообще. B данном случае от а зависит величина сдвига графика |y|=x по оси X, т.е. а - расстояние вершины графика g(x) oт начала координат (0; 0).
Три решения система будет иметь в единственном случае - когда три точки функции g(x) будут лежать на окружности, а это возможно в нашем случае только когда вершина лежит на окружности, т. е. |a|=r=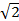 . Ho так как ветви g(x) направлены вправо, то нам подходит только тот случай, когда a<0, значит, a=
. Ho так как ветви g(x) направлены вправо, то нам подходит только тот случай, когда a<0, значит, a= 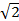 .
.
Ответ: a=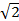
3. Метод областей
По-прежнему решим уравнение F(x,a)=0, где x - искомое значение, а -числовой параметр. Может оказаться, что при любом параметре уравнение F(x,a)=0 решений не имеет, либо для некоторых значений параметра уравнение имеет несколько решений, либо - бесконечное множество. Если каждому значению параметра aϵA соответствует только одно значение x, удовлетворяющее при этом а уравнению F(x,a)=0, то говорят, что а является на множестве A функцией переменной x, заданной неявно уравнением A(x,a)=0. Если на координатной плоскости xOa найдено множество упорядоченных пар чисел (x,a), удовлетворяющих уравнению F(x,a)=0, то нетрудно каждому числовому параметру a=const (-∞ поставить в соответствие действительные числа x этого множества, дающие решения уравнения.
Пример 3.1.
B зависимости от значений параметра а решить уравнение 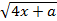 =2x-1.
=2x-1.
Решение. Заданное уравнение равносильно системе
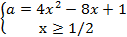
Построив в плоскости xOa график функции а(х)=4х2-8х+1 при условии x≥1/2, получаем кривую (часть параболы), которая есть геометрическое место точек (x,a), удовлетворяющих уравнению 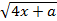 =2x-1 при x≥1/2.
=2x-1 при x≥1/2.
Построив в плоскости xOa график функции а(х)=4х2-8х+1 при условии x≥l/2, получаем кривую (часть параболы), которая есть геометрическое место точек 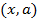 , удовлетворяющих уравнению
, удовлетворяющих уравнению 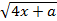 =2x-1 при x≥l/2.
=2x-1 при x≥l/2.
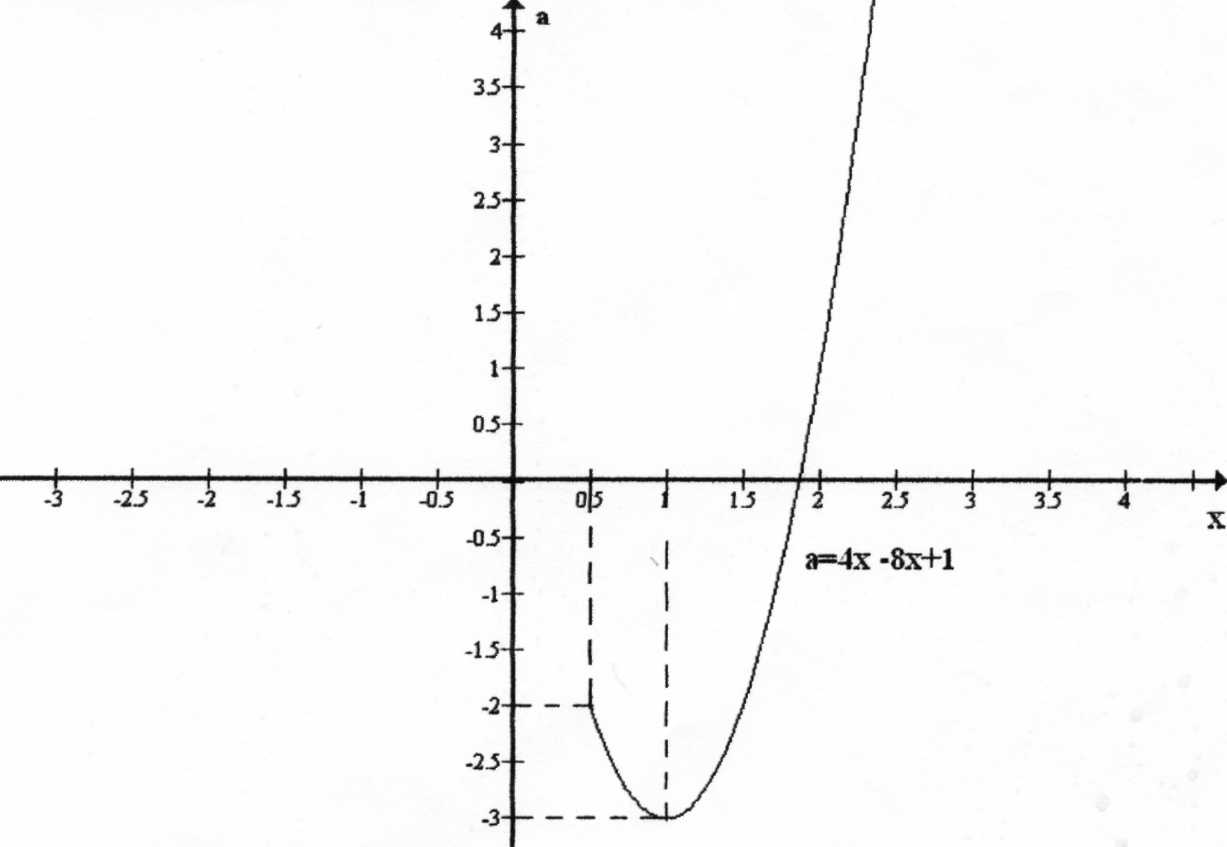
Ответ: a<-3, нет решений; a=-3, x=l;
-3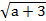 )/2 a>-2, x=(2+
)/2 a>-2, x=(2+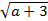 )/2
)/2
Для сравнения приведем аналитический способ решения того же задания.
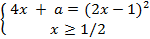
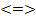
![]()
D1=16-4(1-a)=16-4+4a=12+4a
При a=-3, x=1.
При a>-3 заданное уравнение будет иметь два решения x1<x2
При тех а, при которых совместна система
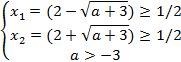
Решением этой системы является интервал aϵ(-3; -2]. Наконец, заданное уравнение будет иметь только один корень х2, если x1=1/2, а x2=1/2. B этом случае придется решить систему
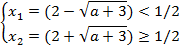
Решением этой системы является интервал aϵ(-2; +∞). Из рассмотренных решений следует явное преимущество графического способа.
Пример 3.2
B зависимости от значений параметра а решить неравенство х+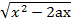 >1-x и найти все значения а, при которых оно справедливо для любого x из промежутка [1/4; 1].
>1-x и найти все значения а, при которых оно справедливо для любого x из промежутка [1/4; 1].
Решение: Исходное неравенство равносильно неравенству  >1-x, которое равносильно совокупности двух систем:
>1-x, которое равносильно совокупности двух систем:
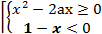
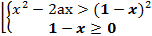
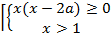
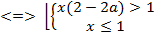
где х≠О (т.к. x=0 не является решением заданного неравенства). Построим в координатной плоскости aOx область, которая является решением первой конъюнкции 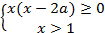
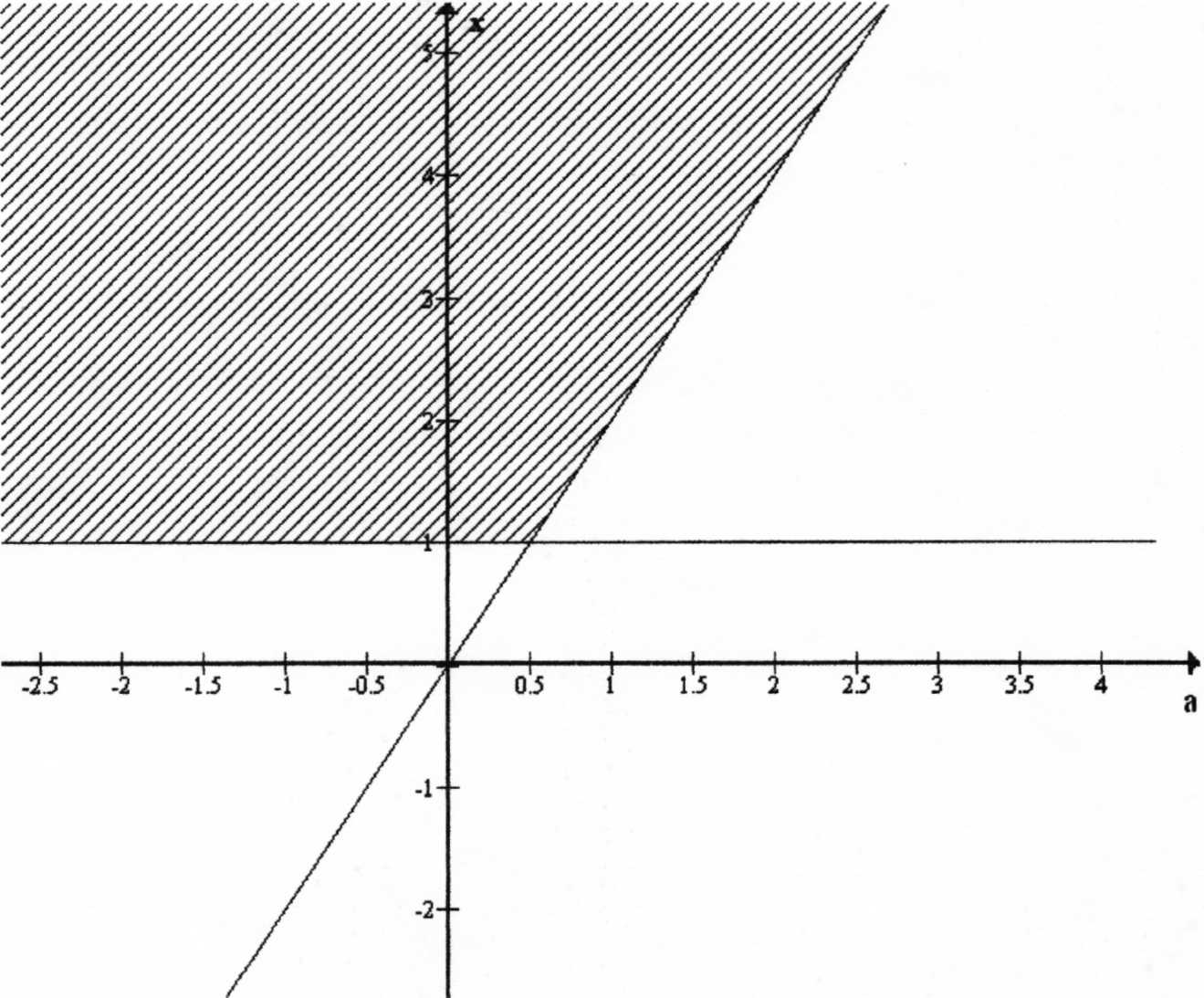
Из рисунка следует, что при aϵ(-∞; 1/2] решениями системы будут все x>1, а
если aϵ(1/2; +∞), то x≥2a.
Рассмотрим вторую конъюнкцию: 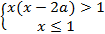
Построим в координатной плоскости aOx графики функций x=1, x=-0,5/(a-1), где a≠1.
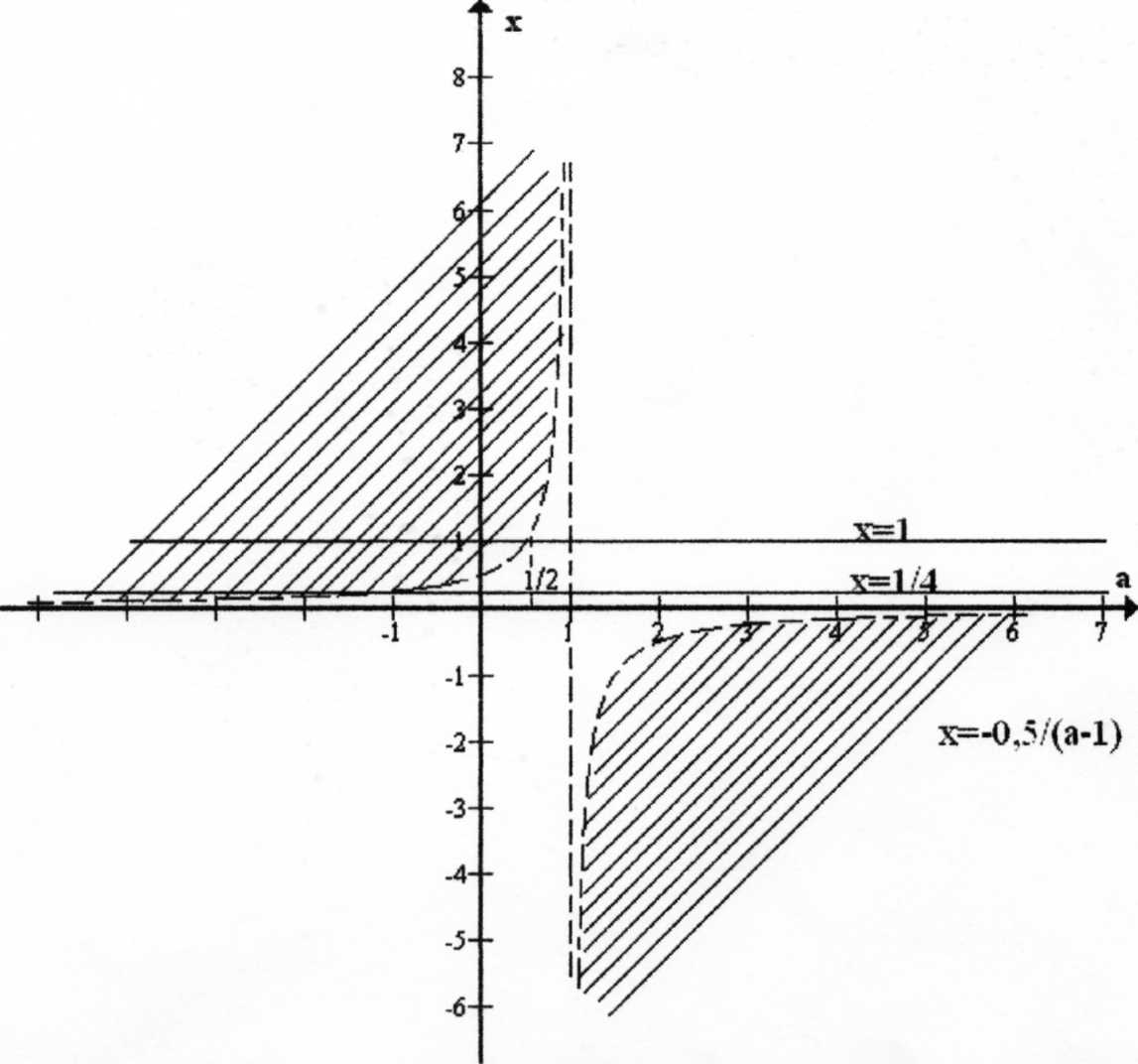 Из рисунка следует, если aϵ(-∞;1/2], то 1/(2(1-a)); если aϵ(1/2; 1], то xϵ0; если aϵ(1; +∞), то x<1/(2(1-a)). Прямая x=1/4 пересекается с гиперболой в точке с абсциссой a=-1, следовательно, при a<-1 неравенство x+
Из рисунка следует, если aϵ(-∞;1/2], то 1/(2(1-a)); если aϵ(1/2; 1], то xϵ0; если aϵ(1; +∞), то x<1/(2(1-a)). Прямая x=1/4 пересекается с гиперболой в точке с абсциссой a=-1, следовательно, при a<-1 неравенство x+ 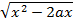 >1 справедливо для всех xϵ[1/4; 1].
>1 справедливо для всех xϵ[1/4; 1].
Ответ:
1) a![]() 1/2, x>1/(2(1-a)); 1/2
1/2, x>1/(2(1-a)); 1/2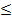 1, x
1, x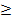 2a; a>1, x<1/(2(1-a)), x
2a; a>1, x<1/(2(1-a)), x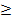 2a;
2a;
2) a<-1, xϵ[1/4; 1];
Пример 3.3
Найти все значения параметра q, при каждом из которых число целочисленных решений неравенства х2-5(х-1)+3 |х - q| -q<0 максимально.
Исходное неравенство равносильно совокупности систем:
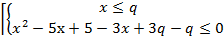
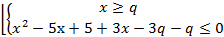
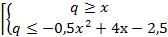
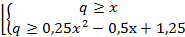
Нa координатной плоскости xOq эти две системы задают область, ограниченную частями двух парабол. Построим графики: q=x, q=-0,5x2+4x-2,5, q=0,25x2-0,5x+l,25 хв=4 qв=5,5 хв=1 qв=l
Найдем точки пересечения парабол: A(1;1), B(5;5).
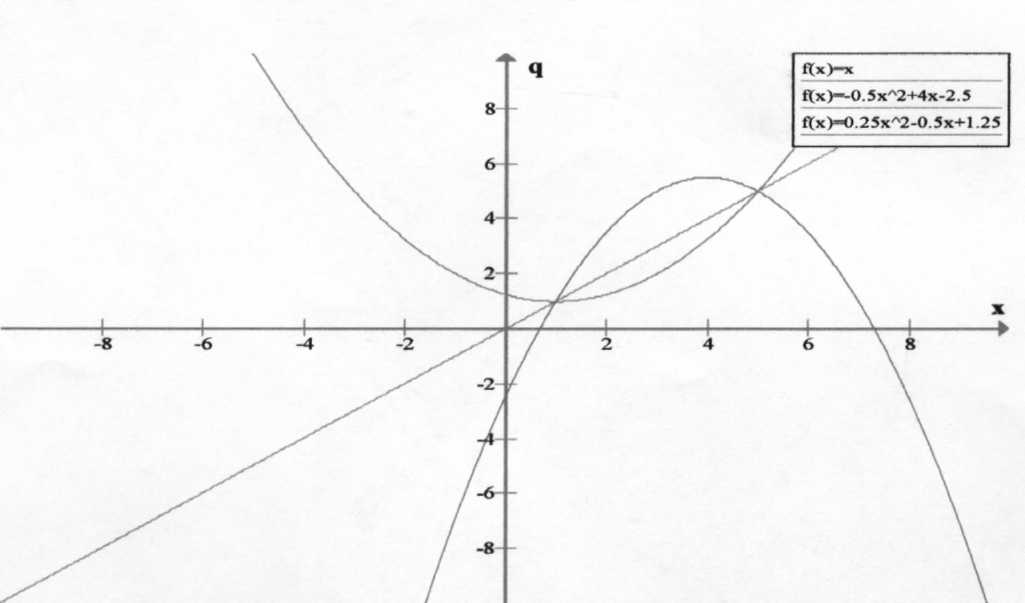
Решения расположены на отрезке хϵ[1;5]. Подставляем в уравнения q=-0,5x2+4x-2,5 и
q=0,25x2-0,5x+l,25 решения из этого промежутка.
Получаем:
-
x=l,q=l
-
x=2, qϵ[l,25;3,5]
-
x=3,qϵ[2;5]
-
x=4,qϵ[3,25;5,5]
-
x=5, q=5
Отметим на оси q полученные значения параметра q и соединим концы соответствующих отрезков:
1 1,25 2 3,25 3,5 5 5,5

Получаем, что заданное неравенство не имеет целочисленных решений при qϵ(1;1,25), имеет одно целочисленное решение при qϵ{l}U[l,25;2)U(5;5,5]; два решения при qϵ[2;3,25)U(3,5;5) и три решения при qϵ[3,25;3,5]U{5}.
Ответ: qϵ[3,25:3,5]U{5}.
Пример 3.4
При каком значении параметра а минимум функции f(x)=x2+2|x+a-1|+(a+1)2
меньше 3?
При x+a-1 ≥0, f(x1)=х2+2х+2а-2+(а+1)2при x+a-1 <0, f(х2)=х2-2х-2а+2+(а+1)2
Функции f(x1) и f(x2) сводятся к функциям окружности и принимают вид, соответственно:
(х+1)2+(а+2)2<9 (х-1)2+а2<1
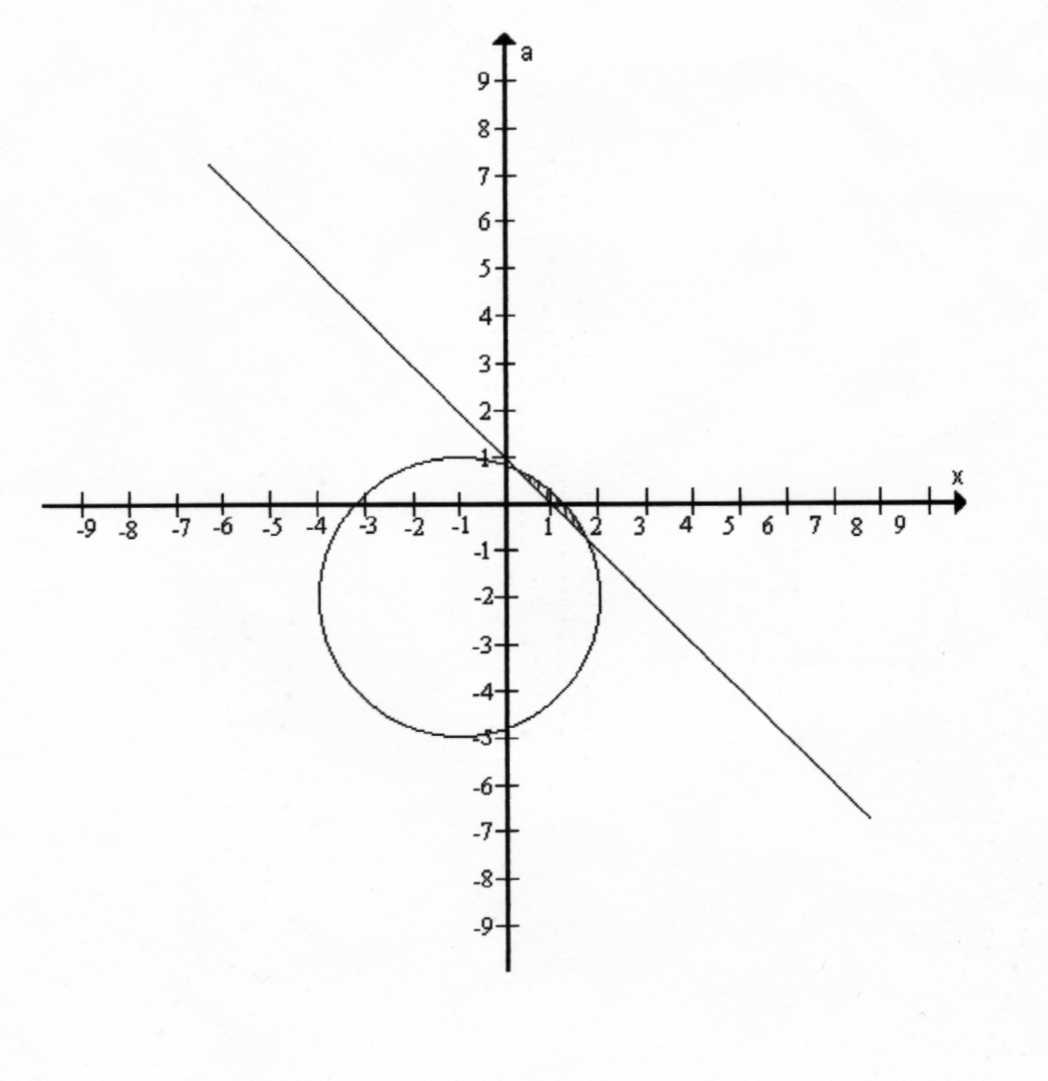
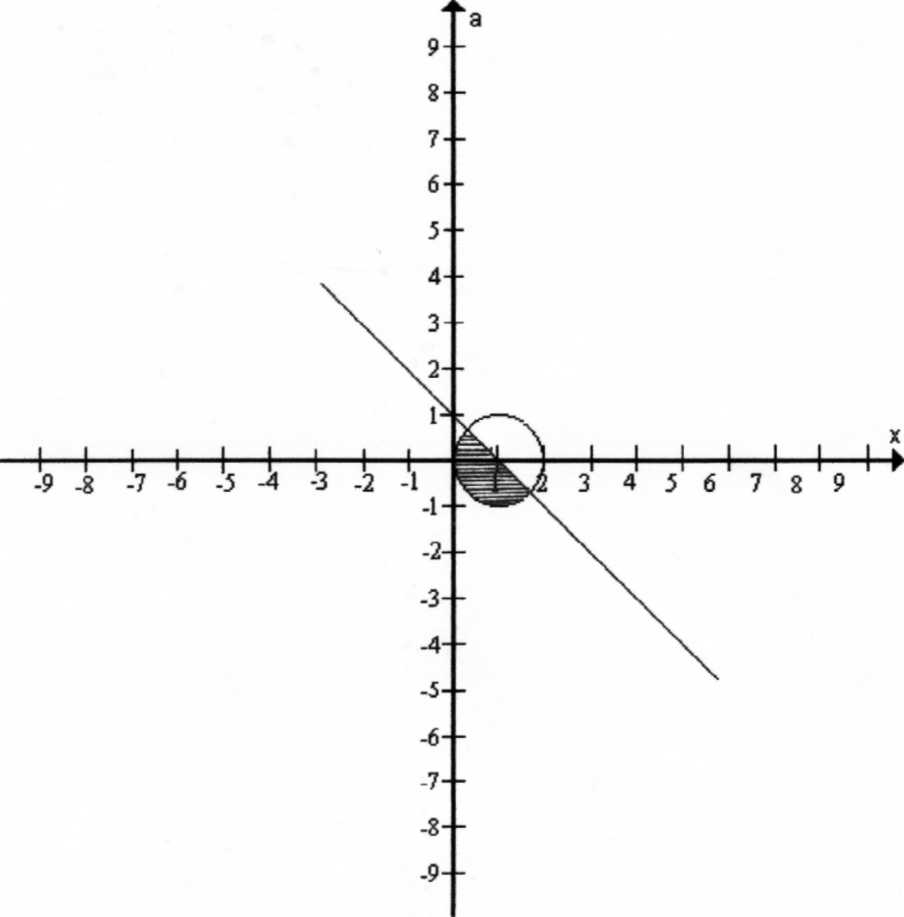
Найдем точки пересечения f(x1) и прямой 1-х, для этого в формулу окружности вместо а подставим 1-х, преобразовав, получаем:
2х2-4х+2=0
x=(2±![]() )/2, тогда a=±
)/2, тогда a=±![]() /2
/2
Аналогично со второй функцией.
Получаем такое же уравнение, но т. к. минимум этой функции равен (-1), тогда минимум заданной функции (-1;  /2)
/2)
Ответ: (-l;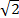 /2).
/2).
Пример 3.5
Для каждого aϵR решить уравнение a|x+3|+2|x+4|=2.
Решение: Перепишем уравнение в виде: a|x+3|=2-2|x+4|. Построим график f(x)=2-2|x+4|. График g(x;a)=a|x+3| - это два симметричных луча с началом в точке (-3;0) с различным углом между ними в зависимости от а.
Найдем, при каком а совпадают на определенном участке два графика. Для этого решим уравнение a(-x-3)=2-2(x+4). Отсюда a=2 и xϵ[-4; -3]. Если a=-2, то график отражается симметрично относительно оси X и xϵ[-3; +∞).
При a>2 или a<-2 угол между лучами уменьшается, решением неравенства будет только точка x=-3.
При a<2 или a>-2 графики пересекаются, помимо точки x=-3, в точке, которую узнаем из уравнения a(-x-3)=2-2(-x-4). Отсюда x=(-3a-10)/(2+a).
Ответ: при a=2 xϵ[-4; -3], при a=-2 xϵ[-3; +∞), при |a|>2 х=-3,
при |a|<2 x=(-3a-10)/(2+a), x=-3.
Пример. 3.6.
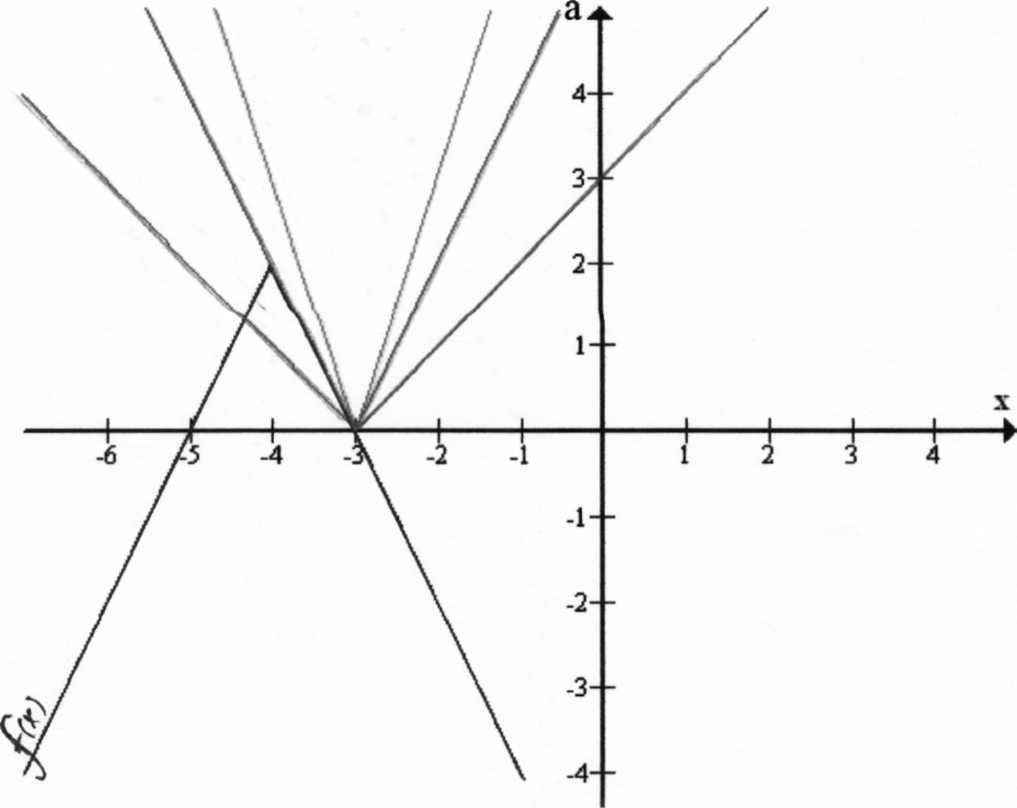
Для всех aϵR решить неравенство: x+2a-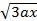 +4a2>0.
+4a2>0.
Решение. Данное выражение равносильно системе:
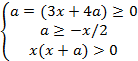
После преобразований система принимает вид:
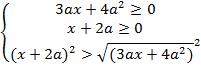
Рассматривая различные варианты знаков множителей в неравенствах, получим дизъюнкцию:
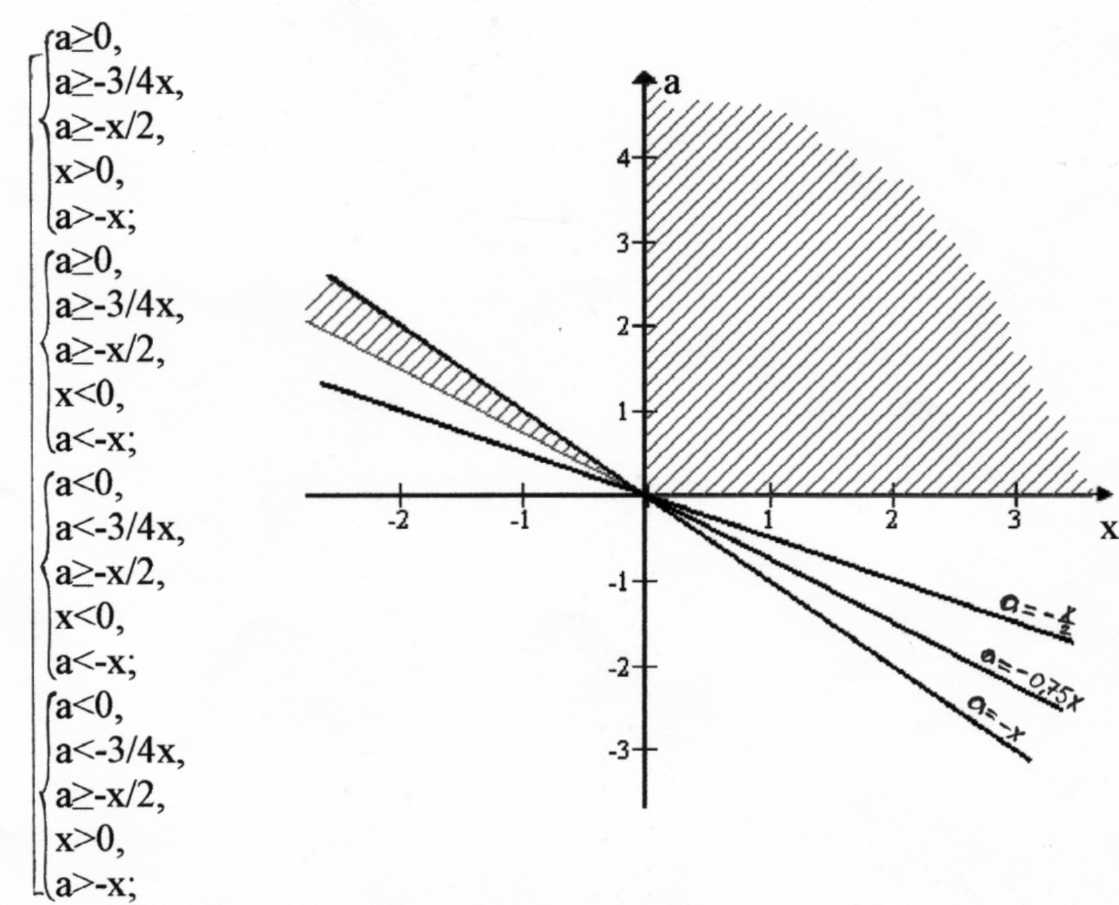
Построим прямые a= -x, a= -3/4x, a= -x/2 и отметим на плоскости области, являющиеся решениями каждой конъюнкции. Решением первой из них является I координатная четверть за исключением положительного направления оси Y и точки (0;0). Изображением решения второй конъюнкции будет область во II четверти между прямыми a=-x и a=-3/4x. Третья и четвертая конъюнкции решений не имеют.
При a<0 xϵ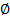 Если a=0, то xϵ(0; +∞ ). При a>0 xϵ[-4/3a; -a)U(0; +∞ ).
Если a=0, то xϵ(0; +∞ ). При a>0 xϵ[-4/3a; -a)U(0; +∞ ).
Ответ: при a<0 xϵǾ, при a=0 xϵ(0; +∞), при a>0 xϵ[-4/3a; -a)U(0; +∞).
Пример 3.7
Решить неравенство с параметром:
3 - | x - а | > x2.
Перепишем неравенство в виде:
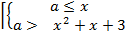
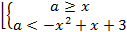
Вершиной графика f(x)=x2 + x - 3 является (- 0,5; - 3,25), а g(x)= -x2 + х+3 (0,5; 3,25). Изобразим графическое решение этой системы в плоскости xOa:
Вершиной графика f(x)- x + x - 3 является (- 0,5; - 3,25), аg(x)= -x + х+3 (0,5; 3,25). Изобразим графическое решение этой системы в плоскости xOa:
Решением является часть фигуры, образованной двумя параболами, заключённая между двумя прямыми a= -3,25 и a= 3.
Ответ: а ϵ (-3,25; 3).
Заключение
Решение задач с параметрами представляет собой весьма широкое поле для полноценной математической деятельности, во всяком случае, более широкое, чем многочисленные и, зачастую, вполне алгоритмические задачи на вычисление пределов, производных и интегралов, которыми наполнены практические занятия студентов по «высшей математике».
Решение уравнений и неравенств с параметрами открывает значительное число эвристических приемов общего характера, ценных для математического развития личности, применимых в исследованиях и на любом другом математическом материале. Это касается и идеи симметрии аналитических выражений и применения свойств функций в неожиданных ситуациях, и освоения геометрических приемов решения задач как равноправных, по существу, с аналитическими методами.
Графические методы делают решение наглядным и позволяют в ряде случаев с большей, по сравнению с аналитическими методами, легкостью, отсортировать правильные пути, ведущие к решению задачи, от тупиковых, которые приводят к посторонним решениям или вовсе не дают решения. Часто это избавляет от необходимости выполнения определенного объема вычислений при исследовании тех возможностей, которые, в конечном счете, все равно не дадут положительного ответа.
Однако ссылки на «картинки», используемые при графических методах решения, должны быть подкреплены вычислениями и явной формулировкой соответствующих теорем и свойств графиков используемых функций. Без этого одни «картинки» решением являться не будут.
Например, при решении уравнения (1/16)x=log1/16x даже очень тщательно выполненная «картинка» с вероятностью, близкой к единице, дает одну общую точку, лежащую на биссектрисе первого координатного угла. Однако при аналитическом уточнении оказывается, что это уравнение имеет еще два решения
х=0,5 и х=0,25.
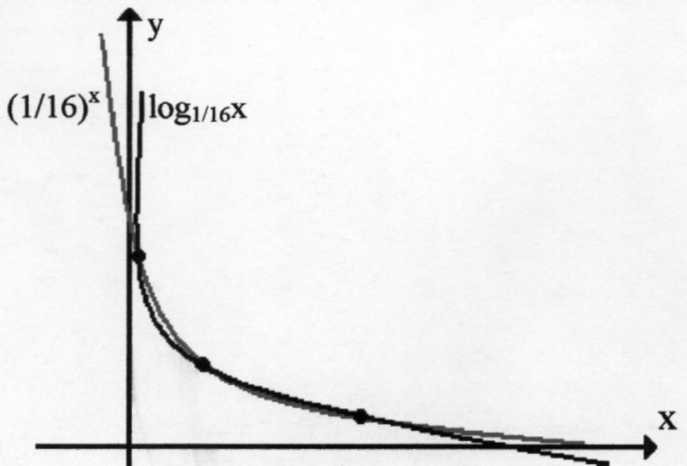
Из приведенного примера следует, что нарисовать правильную «картинку» можно, лишь зная верный ответ.
Очевидно, что подобных примеров, когда графические методы могут привести к ошибкам, можно привести достаточно много. Поэтому для уверенности в правильности выводов, полученных из «картинки», необходимо эти выводы подтверждать аналитически.
Список литературы.
-
В. H. Литвиненко, A Г. Мордкович. Практикум по элементарной математике. Москва, Просвещение, 2001.
-
В. В. Ткачук. Математика абитуриенту. МУНМО, 2003.
-
M. Шабунин. Математика для поступающих в вузы. Москва, БИНОМ, 2004.
-
С. В. Кравцев и др. Методы решения задач по алгебре. Москва, Экзамен, 2005.
-
В. В. Амелькин, В. Л. Рабцевич. Задачи с параметрами. Минск, Агар, 2002.
-
В. П. Моденов. Математика. Москва, ФМ, 2002.
-
В. Л. Натяганов, Л. M. Лужина. Методы решения задач с параметрами. Московский университет, 2003.
-
П. И. Горнштейн и др. Задачи с параметрами. Москва, Илекса, 2005.
-
В. С. Крамор. Повторяем и систематизируем школьный курс алгебры и начал анализа. Москва, 2005.
-
H. Ш. Кремер и др. Математика для поступающих в экономические вузы. Москва, Единство, 2004.
-
E. M. Родионов. Решение задач с параметрами. Москва, 1995.
-
А. Б. Будак, Б. M. Щедрин. Элементарная математика. Москва, Физматлит, 2002.
-
МГУ им. M. В. Ломоносова. Задачи вступительных экзаменов по математике(2004г.), Москва, 2004.
3


