- Преподавателю
- Математика
- Методическая разработка урока по математике: Десятичные и натуральные логарифмы
Методическая разработка урока по математике: Десятичные и натуральные логарифмы
| Раздел | Математика |
| Класс | - |
| Тип | Конспекты |
| Автор | Арцыбашева Н.В. |
| Дата | 13.10.2015 |
| Формат | docx |
| Изображения | Есть |
Тема занятия: «Десятичные и натуральные логарифмы».
Цели занятия:
1)обучающие
- ввести понятие десятичного и натурального логарифма, познакомить обучающихся с историей возникновения логарифмов. Отработать навыки решения упражнений с натуральными и десятичными логарифмами.
2)развивающие
- развитие познавательного интереса;
- усвоение принципов мыслительной деятельности (анализ, сравнение, синтез, выделение главного, систематизация , классификация);
- развитие интеллектуальной сферы (внимание, память);
- развитие речи;
- развитие эмоциональной сферы;
- развитие способностей (индивидуально).
3)воспитательные
- воспитание сознательного отношения к учебе;
- воспитание сознательной дисциплины;
- воспитание культуры умственного труда;
- воспитание культуры поведения;
- воспитание эстетической культуры.
Тип занятия: изучение нового материала.
Ход занятия
I.Организационный этап.
II.Новый материал.
1.Десятичные логарифмы
Среди различных оснований для вычисления логарифмов чаще всего используется число 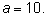 Логарифмы по такому основанию называются десятичными и имеют специальное обозначение:
Логарифмы по такому основанию называются десятичными и имеют специальное обозначение: 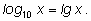
Особое положение десятичных логарифмов связано с использованием десятичной системы счисления. Если мы запишем положительное число x в стандартной форме, т. е. в виде 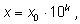 где
где 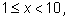 то получим, что
то получим, что 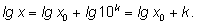 Но
Но 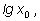 если
если 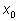 лежит в указанном интервале, является положительным числом, меньшим 1. Это означает, что мы представили
лежит в указанном интервале, является положительным числом, меньшим 1. Это означает, что мы представили 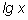 как сумму целого числа и положительной дроби, меньшей единицы, т. е. k - это целая часть десятичного логарифма числа x. По десятичной записи числа x мы сразу можем приблизительно определить его десятичный логарифм.
как сумму целого числа и положительной дроби, меньшей единицы, т. е. k - это целая часть десятичного логарифма числа x. По десятичной записи числа x мы сразу можем приблизительно определить его десятичный логарифм.
В частности, десятичный логарифм целого числа, записанного k десятичными знаками, лежит в пределах от 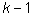 до k.
до k.
Натуральные логарифмы, число e
Есть одно основание, которое в расчетах используется не реже, чем число 10. Это знаменитое число e, введенное Эйлером. Это число не является рациональным, лежит между 2 и 3, и его первые десятичные знаки таковы: e=2,718281828… .
Логарифмы по этому основанию называются натуральными и обозначаются с помощью знака 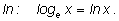
Чем же замечательно число e ? С помощью степени с произвольным действительным показателем мы определим показательную функцию 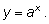 Показательная функция при
Показательная функция при 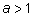 растет очень быстро, быстрее любой степени. Можно определить скорость роста этой функции аналогично тому, как в физике, исходя из функции, задающей положение y точки в момент времени x, определяют ее мгновенную скорость. Оказывается, что показательная функция растет так быстро, что скорость ее роста пропорциональна значению самой этой функции. Этот коэффициент зависит от а и участвует во многих расчетах. Число e - это такое число, что скорость роста показательной функции с основанием e просто равна значению этой функции, т. е. коэффициент пропорциональности, о котором шла речь выше, равен единице, что, конечно, сильно облегчает расчеты.
растет очень быстро, быстрее любой степени. Можно определить скорость роста этой функции аналогично тому, как в физике, исходя из функции, задающей положение y точки в момент времени x, определяют ее мгновенную скорость. Оказывается, что показательная функция растет так быстро, что скорость ее роста пропорциональна значению самой этой функции. Этот коэффициент зависит от а и участвует во многих расчетах. Число e - это такое число, что скорость роста показательной функции с основанием e просто равна значению этой функции, т. е. коэффициент пропорциональности, о котором шла речь выше, равен единице, что, конечно, сильно облегчает расчеты.
Связь между десятичными и натуральными логарифмами осуществляется с помощью модуля перехода k:
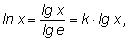 где
где 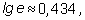 а
а 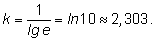
Примеры
Вычисление десятичных логарифмов
1) 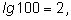 так как
так как 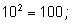
2) 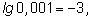 так как
так как 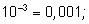
3) 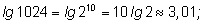
4) 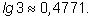
Нахождение порядка числа x, т. е. числа 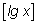
1) 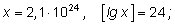
2) 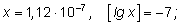
3) 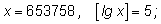
4) 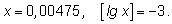
Порядки k знаменитых констант
Масса покоя электрона (в кг)
9,11 × 10-31
k = -31
Электрический заряд (в А × с)
1,60 × 10-19
k = -19
Скорость света (в м/с)
2,99 × 108
k = 8
Диаметр Солнца (в м)
1,39 × 109
k = 9
Диаметр нашей Галактики (в м):
7,7 × 1019
k = 19
Масса Земли (в кг)
5,98 × 1024
k = 24
Приближенные формулы для числа e
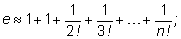
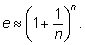
2.Исторический экскурс.
На всем протяжении XVI века быстро возрастало количество приближенных вычислений, прежде всего в астрономии. Исследование планетных движений требовало колоссальных расчетов.
Астрономы просто могли утонуть в невыполнимых расчетах. Очевидные трудности возникали и в других областях, таких как финансовое и страховое дело. Основную трудность представляли умножение и деление многозначных чисел, особенно же тригонометрических величин.
Иногда для приведения умножения к более легкому сложению и вычитанию пользовались таблицами синусов и косинусов. Была также составлена таблица квадратов до 100 000, с помощью которой умножение можно было производить по определенному правилу.
Однако эти приемы не давали удовлетворительного решения вопроса. Его принесли с собой таблицы логарифмов.
«Открытие логарифмов опиралось на хорошо известные к концу XVI века свойства прогрессий, - пишут М.В. Чириков и А.П. Юшкевич. - Связь между членами геометрической профессии и арифметической прогрессией не раз отмечалась математиками, о ней говорилось еще в «Псаммите» Архимеда. Другой предпосылкой было распространение понятия степени на отрицательные и дробные показатели, позволившее перенести только что упомянутую связь на более общий случай...
Многие... авторы указывали, что умножению, делению, возведению в степень и извлечению корня в геометрической прогрессии соответствуют в арифметической - в том же порядке - сложение, вычитание, умножение и деление. Здесь уже скрывалась идея логарифма числа как показателя степени, в которую нужно возвести данное основание, чтобы получить это число. Оставалось перенести знакомые свойства прогрессии с общим членом на любые действительные показатели. Это дало бы непрерывную показательную функцию, принимающую любые положительные значения, а также обратную ей логарифмическую. Но эту идею глубокого принципиального значения удалось развить через несколько десятков лет».
Логарифмы изобрели независимо друг от друга Непером и Бюрги лет на десять позднее. Их цель была одна - желание дать новое удобное средство арифметических вычислений. Подход же оказался разный. Непер кинематически выразил логарифмическую функцию, что позволило ему по существу вступить в почти неизведанную область теории функций. Бюрги остался на почве рассмотрения дискретных прогрессий. Надо заметить, что у обоих определение логарифма не походило на современное.
Первый изобретатель логарифмов - шотландский барон Джон Непер (1550-1617) получил образование на родине в Эдинбурге. Затем после путешествия по Германии, Франции и Испании, в возрасте двадцати одного года, он навсегда поселился в семейном поместье близ Эдинбурга. Непер занялся главным образом богословием и математикой, которую изучал по сочинениям Евклида, Архимеда, Региомонтана, Коперника.
«К открытию логарифмов, - отмечают Чириков и Юшкевич, - Непер пришел не позднее 1594 года, но лишь двадцать лет спустя опубликовал свое «Описание удивительной таблицы логарифмов» (1614), содержавшее определение Неперовых логарифмов, их свойства и таблицы логарифмов синусов и косинусов от 0 до 90 градусов с интервалом в 1 минуту, а также разности этих логарифмов, дающие логарифмы тангенсов. Теоретические выводы и объяснения способа вычисления таблицы он изложил в другом труде, подготовленном, вероятно, до «Описания», но изданном посмертно, в «Построении удивительной таблицы логарифмов» (1619). Упомянем, что в обоих сочинениях Непер рассматривает и некоторые вопросы тригонометрии. Особенно известны удобные для логарифмирования «аналогии», т. е. пропорции Непера, применяемые при решении сферических треугольников по двум сторонам и углу между ними, а также по двум углам и прилежащей к ним стороне.
Непер с самого начала вводил понятие логарифма для всех значений непрерывно меняющихся тригонометрических величин - синуса и косинуса. При тогдашнем состоянии математики, когда еще не было аналитического аппарата исчисления бесконечно малых, естественным и единственным средством для этого являлось кинематическое определение логарифма. Быть может, здесь не остались без влияния и традиции, восходившие к оксфордской школе XIV века».
В основе определения логарифма у Непера лежит кинематическая идея, обобщающая на непрерывные величины связь между геометрической профессией и арифметической прогрессией показателей ее членов.
Теорию логарифмов Непер изложил в сочинении «Построение удивительных таблиц логарифмов», посмертно опубликованном в 1619 году и переизданном в 1620 году его сыном Робертом Непером.
Вот выдержки из нее - «Таблица логарифмов - небольшая таблица, с помощью которой можно узнать посредством весьма легких вычислений все геометрические размеры и движения. Она по справедливости названа небольшой, ибо по объему превосходит таблицы синусов, весьма легкой, потому что с ее помощью избегают всех сложных умножений, делений и извлечений корня, и все вообще фигуры и движения измеряются посредством выполнения более легких сложения, вычитания и деления на два. Она составлена из чисел, следующих в непрерывной пропорции.
Если из полного синуса с добавленными семью нулями ты вычтешь его 10000000-ую часть, а из полученного таким образом числа - его 10000000-ую часть и так далее, то этот ряд можно легко продолжить до ста чисел в геометрическом отношении, существующем между полным синусом и синусом, меньшим его на единицу, а именно между 10000000 и 9999999, и этот ряд пропорциональных мы назовем Первой таблицей.
Вторая таблица следует от полного синуса с шестью добавленными нулями через пятьдесят других чисел, пропорционально убывающих в отношении, которое является простейшим и возможно более близким к отношению между первым и последним числами Первой таблицы.
Поскольку первое и последнее числа Первой таблицы суть 10000000.0000000 и 9999900.004950, то в этом отношении трудно образовать пятьдесят пропорциональных чисел. Близким и в то же время простым отношением является 100000 к 99999, которое можно с достаточной точностью продолжить, добавив к полному синусу шесть нулей и последовательно вычитая из предшествующего его 100000-ую часть. Эта таблица содержит, кроме полного синуса, являющегося первым числом, еще пятьдесят пропорциональных чисел, последнее из которых (если ты не ошибешься) будет 9995001.222927.
Третья таблица состоит из шестидесяти девяти столбцов и в каждом столбце расположено двадцать одно число, следующее в отношении, которое является простейшим и возможно более близким к отношению, существующему между первым и последним членами Второй таблицы.
Поэтому ее первый столбец может быть очень легко получен из полного синуса с пятью добавленными нулями и из последующих чисел вычитанием из них 2000-ой части.
Первые числа всех столбцов следуют от полного синуса с добавленными четырьмя нулями в отношении, которое является простейшим и близким к отношению, существующему между первым и последним числами первого столбца...
В том же отношении должна быть образована прогрессия со второго числа первого столбца для вторых чисел всех столбцов, и с третьего для третьих, и с четвертого для четвертых, и соответственно с остальных для остальных.
Таким образом, из любого числа предыдущего столбца вычитанием его сотой части получается число того же порядка следующего столбца...
.... этих трех таблиц (после их составления) достаточно для вычисления таблицы логарифмов».
В 1620 году швейцарец Иост Бюрги (1552-1632) - высококвалифицированный механик и часовых дел - мастер опубликовал книгу «Таблицы арифметической и геометрической прогрессий, вместе с основательным наставлением, как их нужно понимать и с пользой применять во всяческих вычислениях» (1620)
Как писал сам Бюрги, он исходил из соображений о соответствии между умножением в геометрической прогрессии и сложением в арифметической. Задача состояла в выборе прогрессии со знаменателем, достаточно близким к единице, с тем, чтобы ее члены следовали друг за другом с интервалами, достаточно малыми для практических вычислений.
Однако таблицы Бюрги не получили значительного распространения. Они не могли конкурировать с таблицами Непера, более удобными и к тому времени уже широко известными.
Ни у Непера, ни у Бюрги не было, строго говоря, основания логарифмов, поскольку логарифм единицы отличается от нуля. И значительно позднее, когда уже перешли к десятичным и натуральным логарифмам, еще не было сформулировано определение логарифма, как показателя степени данного основания.
В руководствах оно появляется впервые, вероятно, у В Гардинера (1742). Впрочем, сам Гардинер использовал при этом бумаги преподавателя математики В Джонса Широкому распространению современного определения логарифма более других содействовал Эйлер, который применил в этой связи и термин «основание».
Термин «логарифм» принадлежит Неперу, он возник из сочетания греческих слов «отношение» и «число», и означает «число отношения». Хотя первоначально Непер пользовался другим термином - «искусственные числа»
Таблицы Непера, приспособленные к тригонометрическим вычислениям, были неудобны для действий с данными числами. Чтобы устранить эти недостатки, Непер предложил составить таблицы логарифмов, приняв за логарифм единицы нуль, а за логарифм десяти просто единицу. Это предложение он сделал в ходе обсуждения с посетившим его в 1615 году профессором математики Грешем колледжа в Лондоне Генри Бригсом (1561 - 1631), который и сам задумывался, как усовершенствовать таблицы логарифмов. Заняться осуществлением своего плана Непер не мог из-за пошатнувшегося здоровья, но указал идею двух вычислительных приемов, развитых далее Бригсом.
Бриге опубликовал первые результаты своих кропотливых вычислений - «Первую тысячу логарифмов» (1617) в год смерти Непера. Здесь даны были десятичные логарифмы чисел от 1 до 1000 с четырнадцатью знаками Большинство десятичных логарифмов простых чисел Бриге нашел с помощью извлечения квадратных корней Позднее, уже став профессором в Оксфорде, он выпустил «Логарифмическую арифметику» (1624). В книге содержались четырнадцатизначные логарифмы чисел от 1 до 20 000 и от 90 000 до 100 000.
Оставшийся пробел был восполнен голландским книготорговцем и любителем математики Андрианом Флакком (1600-1667). Несколько ранее семизначные десятичные таблицы логарифмов синусов и тангенсов вычислил коллега Бригса по Грешем колледжу, воспитанник Оксфордского университета Эдмунд Гунтер (1581-1626), опубликовавший их в «Своде треугольников» (1620).
Открытие Непера в первые же годы приобрело исключительно широкую известность. Составлением логарифмических таблиц и совершенствованием их занялись очень многие математики. Так, Кеплер в Марбурге в 1624-1625 годах применил логарифмы к построению новых таблиц движений планет. В приложении ко второму изданию «Описания» Непера (1618) было вычислено и несколько натуральных логарифмов. Здесь можно усмотреть подход к введению предела. Вероятнее всего, это дополнение принадлежит В. Отреду. Вскоре лондонский учитель математики Джон Спейделл издал таблицы натуральных логарифмов чисел от 1 до 1000. Термин «натуральные логарифмы» ввели П. Менголи (1659), а несколько позднее - Н Меркатор (1668).
Практическое значение вычисленных таблиц было очень велико. Но открытие логарифмов имело также глубочайшее теоретическое значение. Оно вызвало к жизни исследования, о которых не могли и мечтать первые изобретатели, преследовавшие цель только облегчить и ускорить арифметические и тригонометрические выкладки с большими числами. Открытие Непера, в частности, открыло путь в область новых трансцендентных функций и сообщило мощные стимулы в развитии анализа.
III.Итог занятия.
Домашнее задание: конспект, доклады.


