- Преподавателю
- Математика
- Курсовая работа: Метод координат и его применение
Курсовая работа: Метод координат и его применение
| Раздел | Математика |
| Класс | - |
| Тип | Другие методич. материалы |
| Автор | Перевалова О.А. |
| Дата | 23.01.2015 |
| Формат | doc |
| Изображения | Есть |
Метод координат и его применение
Курсовая работа
Содержание
Введение 3
- Исследовать использование «метода координат» при решении геометрических задач; 5
- установить какой из методов решения лучше; 5
- освоить координатный метод решения задач. 5
2.Метод координат на плоскости 6
2.3. Полярная система координат на плоскости 13
3.Метод координат в пространстве 14
3.1. Декартова прямоугольная система координат в пространстве 14
3.2. Цилиндрическая система координат в пространстве 16
3.3. Сферическая система координат 18
Сферическая система координат определяется так: 19
Заключение 32
Список литературы 33
Приложение 1. Задачи, решаемые методом координат с решениями. 35
Введение
Метод координат имеет применение во многих областях современной человеческой деятельности, он лежит в основе таких наук, как механика, геодезия, астрономия.
Первоначально идея координат зародилась в древности в связи с потребностями астрономии, географии, живописи. Так, на стене одной из древнеегипетских погребальных камер была обнаружена квадратная сетка (палетка), которой пользовались для увеличения изображений. Древнегреческий астроном Клавдий Птолемей применил географические координаты для определения местонахождения мореплавателя. Идеей координат пользовались в середине века для определения положения светил на небе, для определения места на поверхности Земли. Прямоугольной сеткой пользовались художники эпохи Возрождения. Применять координаты в математике впервые стали Ферма и Декарт. В 1637 году вышла книга Декарта «Рассуждения о методе», в которой наряду с общими философскими рассуждениями о материи значительное место уделяется универсальной математике. В разделе этой книги «Геометрия» Декарт предложил новый метод - метод координат, который позволил переходить от точки к паре чисел, от линии к уравнению, от геометрии к алгебре. Главное достижение Декарта - построение аналитической геометрии, в которой геометрические задачи переводились на язык алгебры при помощи метода координат. Но у Декарта в точном виде еще не было того, что сегодня называется декартовой системой координат. Декарт начал с того, что перевел на алгебраический язык задачи на построение циркулем и линейкой, и при этом многие трудные геометрические задачи становятся почти тривиальными.
Немалой заслугой Декарта было введение удобных обозначений, сохранившихся до наших дней: латинских букв x, y, z - для неизвестных; a, b, c - для коэффициентов, x2, y5, a7- для степеней.
Основное новшество Декарта - введение переменных величин как координатных отрезков переменной длины, характеризующих положение точек на плоскости и своими концами описывающих при движении различные кривые.
Идея геометрии Декарта состоит в том, что геометрический объект задается уравнением, связывающим переменные величины. По свойствам уравнения судят о свойствах геометрического объекта.
Декарт считается одним из основателей новой математики. Его имя сохранили термины: «декартовы координаты», «декартов лист», «правило знаков Декарта», «метод неопределенных коэффициентов Декарта».
Развитие идей Декарта впоследствии привело к появлению новой ветви математики - аналитической геометрии. В ней точка определяется системой чисел (ее координат), и, следовательно, геометрические факты записываются в виде соотношений между координатами.
Основные понятия в аналитической геометрии взяты из обычной, но записываются языком алгебры, становящейся вследствие этого средством исследования геометрических форм.
Характерной особенностью метода координат является определение геометрических фигур уравнениями, что позволяет производить геометрические исследования и решать геометрические задачи средствами алгебры.
Придавая геометрическим исследованиям алгебраический характер, метод координат переносит в геометрию наиболее важную особенность алгебры - единообразие способов решения задач. Если в арифметике и элементарной геометрии приходится, как правило, искать для каждой задачи особый путь решения, то в алгебре и аналитической геометрии решения проводятся по общему для всех задач плану, легко приспособляемому к любой задаче. Можно сказать, что аналитическая геометрия занимает такое же положение по отношению к элементарной геометрии, какое алгебра занимает относительно арифметики. Перенесение в геометрию свойственных алгебре и поэтому обладающих большой общностью способов решения задач составляет главную ценность метода координат. Следует, однако, предостеречь читателя от пренебрежительного отношения к приёмам элементарной геометрии, так как в отдельных случаях они позволяют находить изящные решения, более простые, чем получаемые методом координат.
Другое достоинство метода координат состоит в том, что его применение избавляет от необходимости прибегать к наглядному представлению сложных пространственных конфигураций.
Таким образом, метод координат имеет важное практическое значение и следовательно цель данной работы заключается в следующем: изучить основы «метода координат» и его применение.
Задачи данной работы:
- Исследовать использование «метода координат» при решении геометрических задач;
- установить какой из методов решения лучше;
- освоить координатный метод решения задач.
-
Сущность метода координат
Сущность метода координат как метода решения задач состоит в том, что, задавая фигуры уравнениями и выражая в координатах различные геометрические соотношения, мы можем решать геометрическую задачу средствами алгебры. Обратно, пользуясь координатами, можно истолковывать алгебраические и аналитические соотношения и факты геометрически и таким образом применять геометрию к решению алгебраических задач.
Метод координат - это универсальный метод. Он обеспечивает тесную связь между алгеброй и геометрией, которые, соединяясь, дают «богатые плоды», какие они не могли бы дать, оставаясь разделенными.
В некоторых случаях метод координат дает возможность строить доказательства и решать многие задачи более рационально, красиво, чем чисто геометрическими способами. Метод координат связан, правда, с одной геометрической сложностью. Одна и та же задача получает различное аналитическое представление в зависимости от того или иного выбора системы координат. И только достаточный опыт позволяет выбирать систему координат наиболее целесообразно.
-
Метод координат на плоскости
2.1. Аффинная система координат на плоскости.
Определение. Аффинная система координат (или аффинным репером) на плоскости называется упорядоченная тройка точек этой плоскости не лежащих на одной прямой: R={О, Е1, Е2}.
Рассмотрим тогда векторы: е1= ОЕ1 и е2 = ОЕ2 (рис. 1). Поскольку точки О, Е1, Е2, не лежат на одной прямой, поэтому векторы е1и е2 не коллинеарны, следовательно, они образуют базис совокупности V2 всех векторов плоскости. Таким образом, мы приходим к упорядоченной тройке R={О, е1, е2}, состоящей из точки О и двух неколлинеарных векторов е1и е2.
О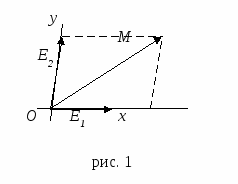 братно если дана упорядоченная тройка R={О, е1, е2}, состоящая из точки О и двух неколлинеарных векторов е1и е2, то от неё легко перейти к тройке R={О, Е1, Е2}, отложив векторы е1и е2 от точки О и взяв соответственно концы этих векторов Е1 и Е2: е1= ОЕ1 и е2 = ОЕ2. Ясно, что точки О, Е1, Е2, не будут лежать на одной прямой, так как векторы е1и е2 не коллинеарны.
братно если дана упорядоченная тройка R={О, е1, е2}, состоящая из точки О и двух неколлинеарных векторов е1и е2, то от неё легко перейти к тройке R={О, Е1, Е2}, отложив векторы е1и е2 от точки О и взяв соответственно концы этих векторов Е1 и Е2: е1= ОЕ1 и е2 = ОЕ2. Ясно, что точки О, Е1, Е2, не будут лежать на одной прямой, так как векторы е1и е2 не коллинеарны.
Таким образом, мы приходим к выводу, что задание на плоскости системы координат как упорядоченной тройки точек R={О, Е1, Е2}, не лежащих на одной прямой, равносильно заданию её как упорядоченной тройки R={О, е1, е2}, состоящей из точки О и двух неколлинеарных векторов е1и е2. В результате в геометрическую картину, составленную из точек, вводятся векторы.
Первая точка О в системе координат R называется началом системы координат, а векторы е1 и е2 - её базисными или координатными векторами. Прямая ОЕ1 с направляющим вектором е1 называется координатной осью Ох, или осью абсцисс, а прямая ОЕ2 с направляющим вектором е2 называется координатной осью Оу, или осью ординат.
Пусть на плоскости задана система координат R={О, е1, е2} и произвольная точка М. Вектор ОМ = rм называется радиус-вектором точки М относительно точки О (или системы координат R).
Определение. Координатами точки М в системе координат R={О, е1, е2} называются координаты её радиус-вектора ОМ в базисе е1, е2, то есть коэффициенты х, у в его разложении в линейную комбинацию векторов базиса: М(х, у)R ОМ = хе1+ уе2.
Итак, понятие координат точки тесно связывается с понятием координат вектора, а понятие системы координат для точек - с понятием базиса векторов. «Привязывая» векторный базис к фиксированной точке плоскости (началу координат), мы приходим к системе координат для точек. Если тот же векторный базис «привязать» к другому началу, мы получим другую систему координат для точек.
Векторы а и в коллинеарны тогда и только тогда, когда их координаты пропорциональны.
Каждой точке М плоскости поставим в соответствие вектор ОМ. Координаты вектора ОМ называются координатами точки М в данной аффинной системе координат. При этом если ОМ = (х, у), то пишут: М (х, у).
Пусть прямые, проведенные через точку М параллельно осям координат, пересекают оси координат соответственно в точках М1 и М2 (рис. 2).
Тогда имеем ОМ = ОМ1 + ОМ2.
С другой стороны, ОМ = хе1+ уе2.
Следовательно, х =ОМ1 / е, у = ОМ2 / е2.
Точки Е1 и Е2имеют координаты: Е1 (1; 0), Е2 (0;1).
Если на плоскости даны две точки А (х1, у1) и В (х2, у2), то координаты вектора АВ вычисляются так:
АВ = ОВ - ОА = (х2 - х1, у2 - у1).
Пусть точка С делит отрезок АВ в данном отношении: ![]()
Т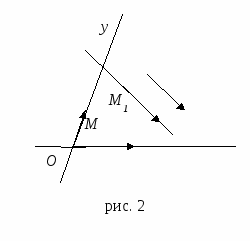 огда
огда 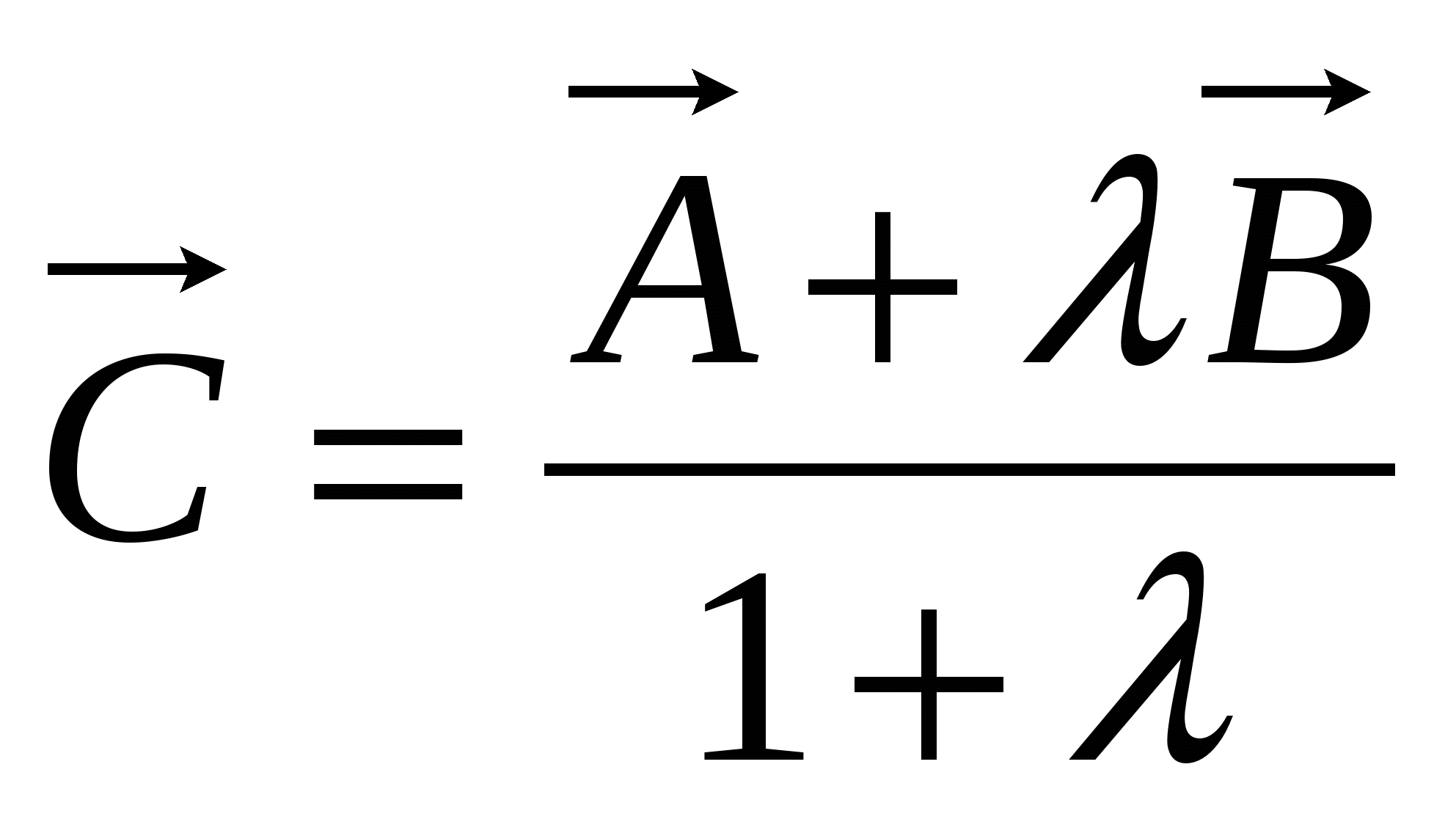 . Из правил действии над векторами в координатах следует, что координаты точки С определяются формулами:
. Из правил действии над векторами в координатах следует, что координаты точки С определяются формулами:
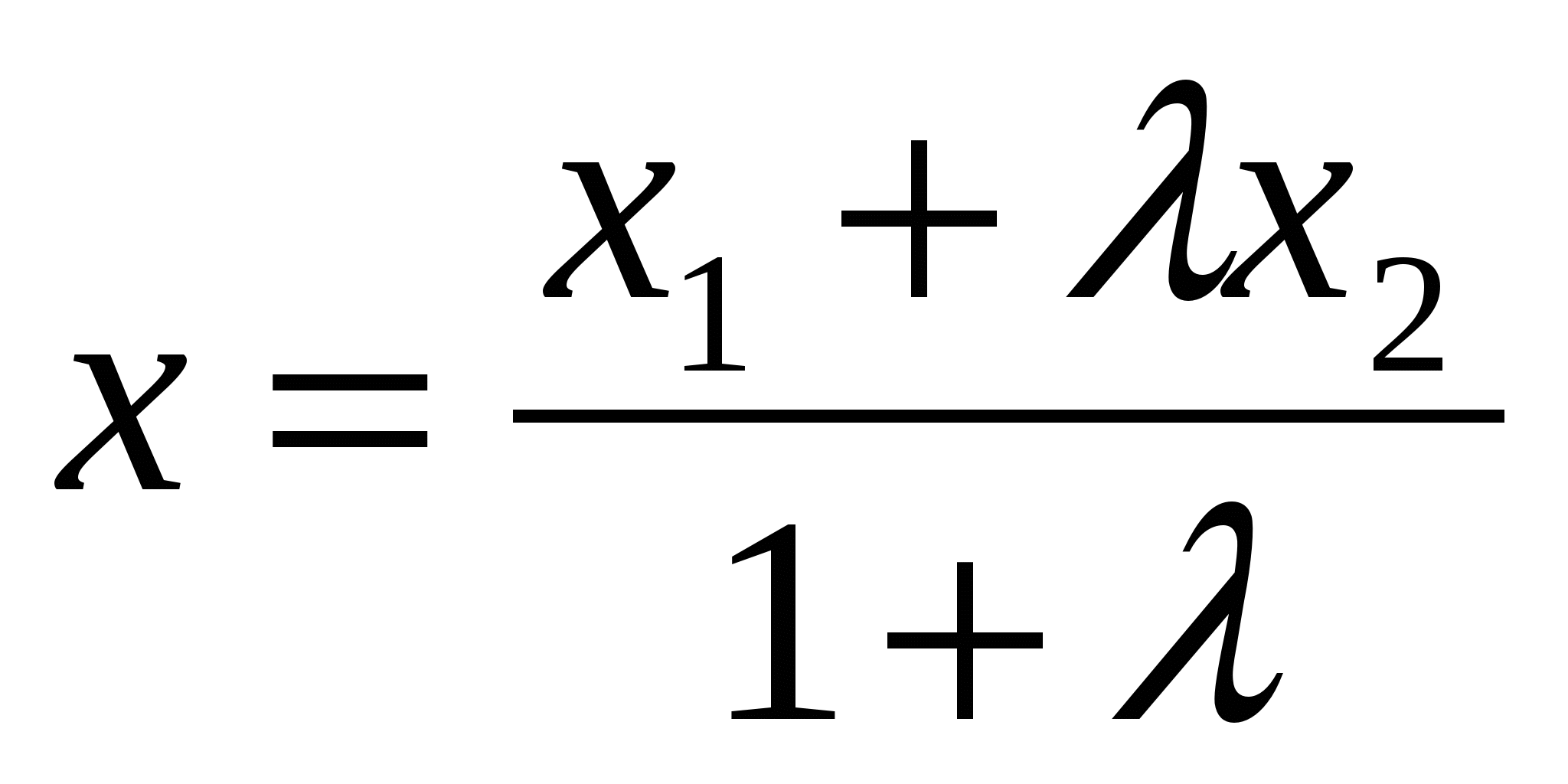 ,
, 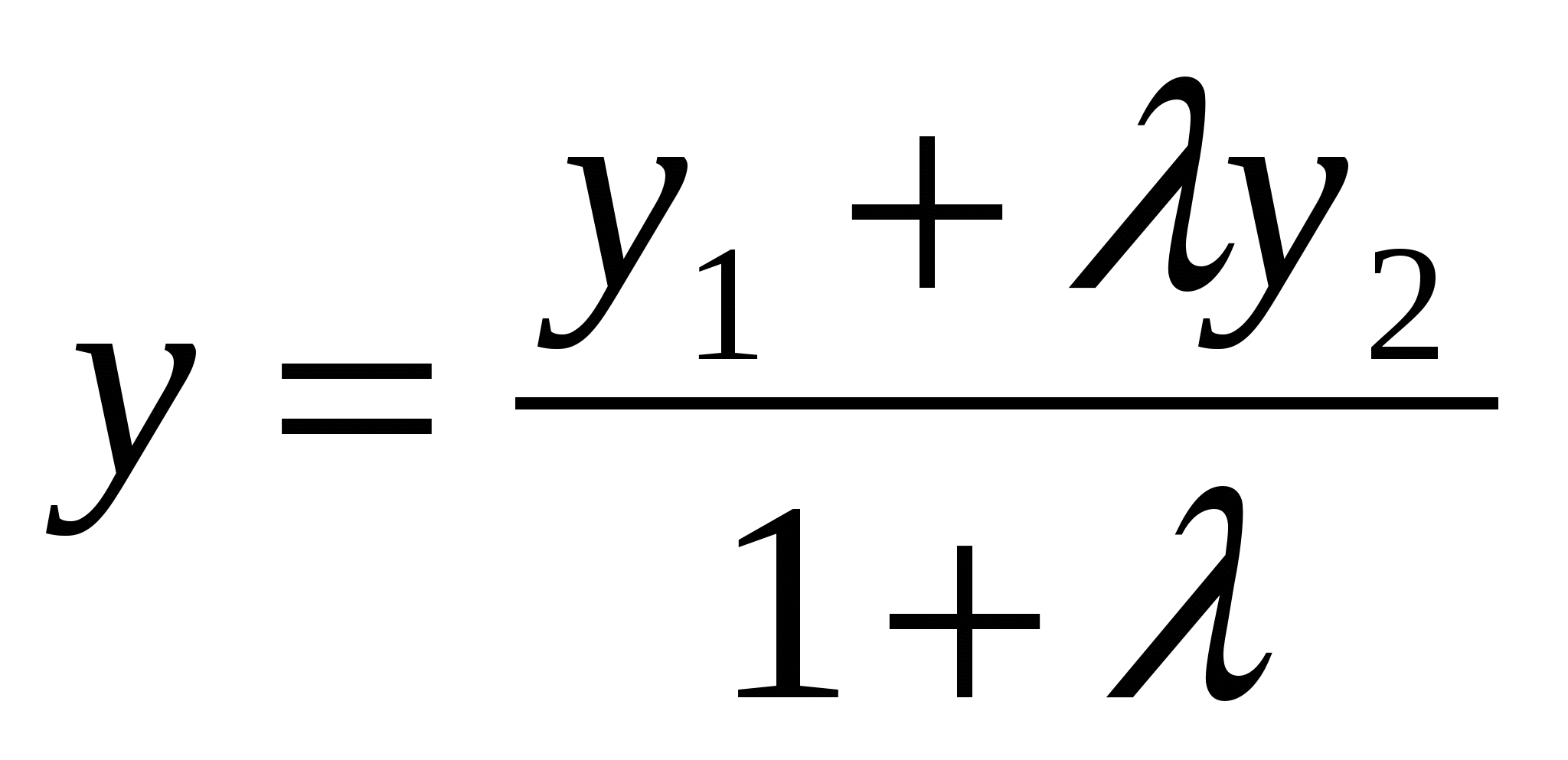
В частности, если С - середина отрезка АВ, то
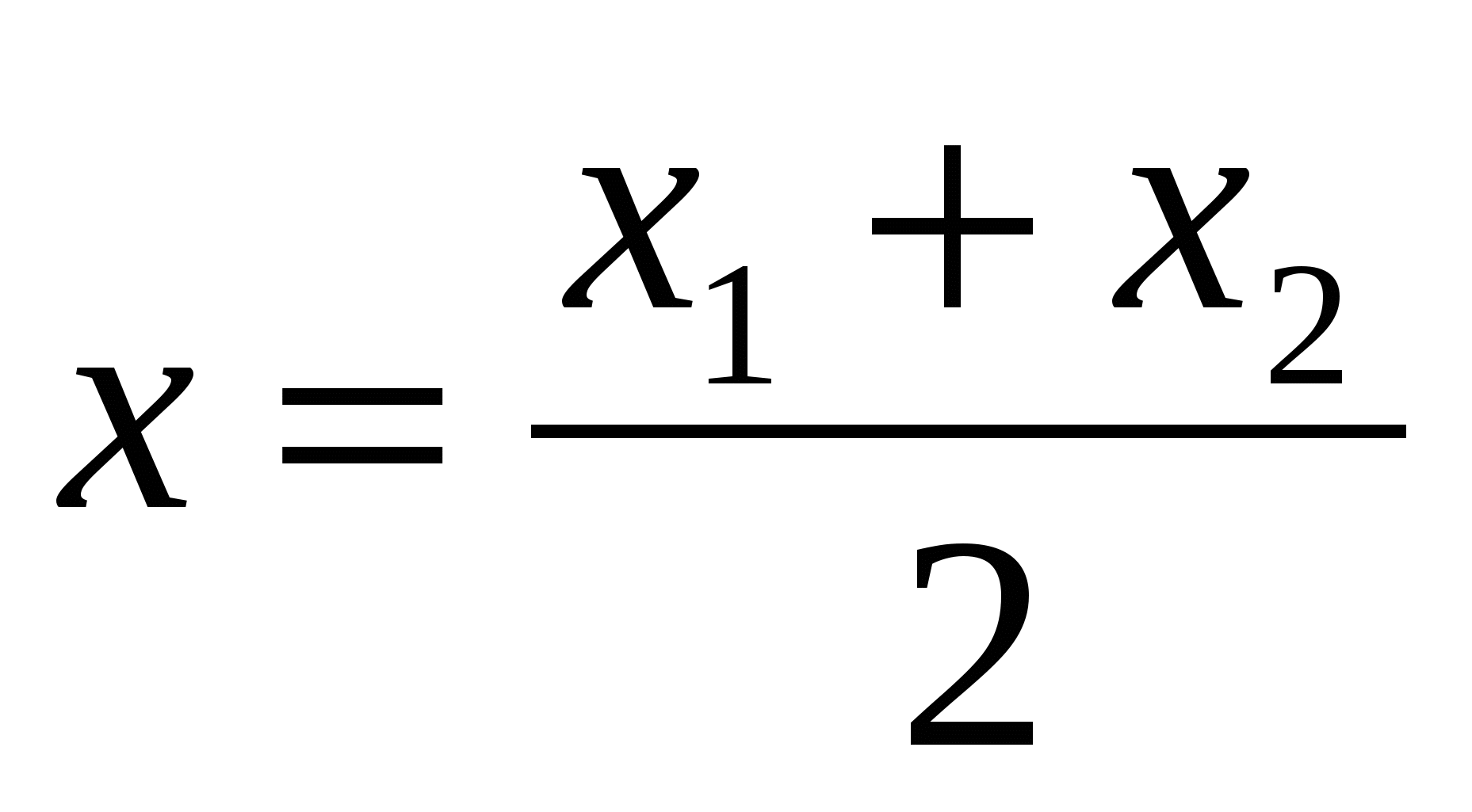 ,
, 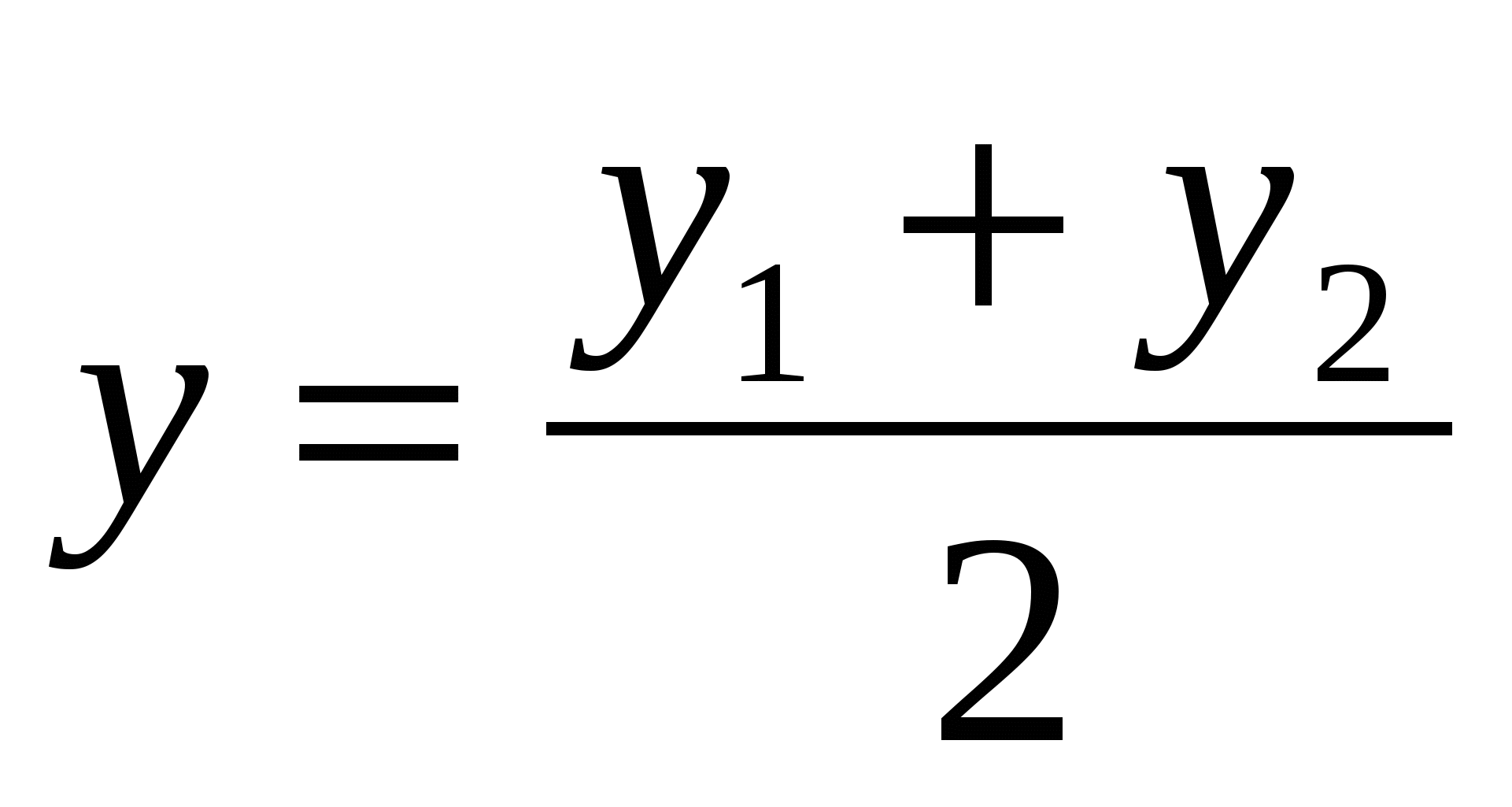
Рассмотрим различные способы задания прямой на плоскости.
Пусть требуется написать уравнение прямой l, заданной в некоторой аффинной системе координат точкой М1 (х1, у1) и ненулевым вектором 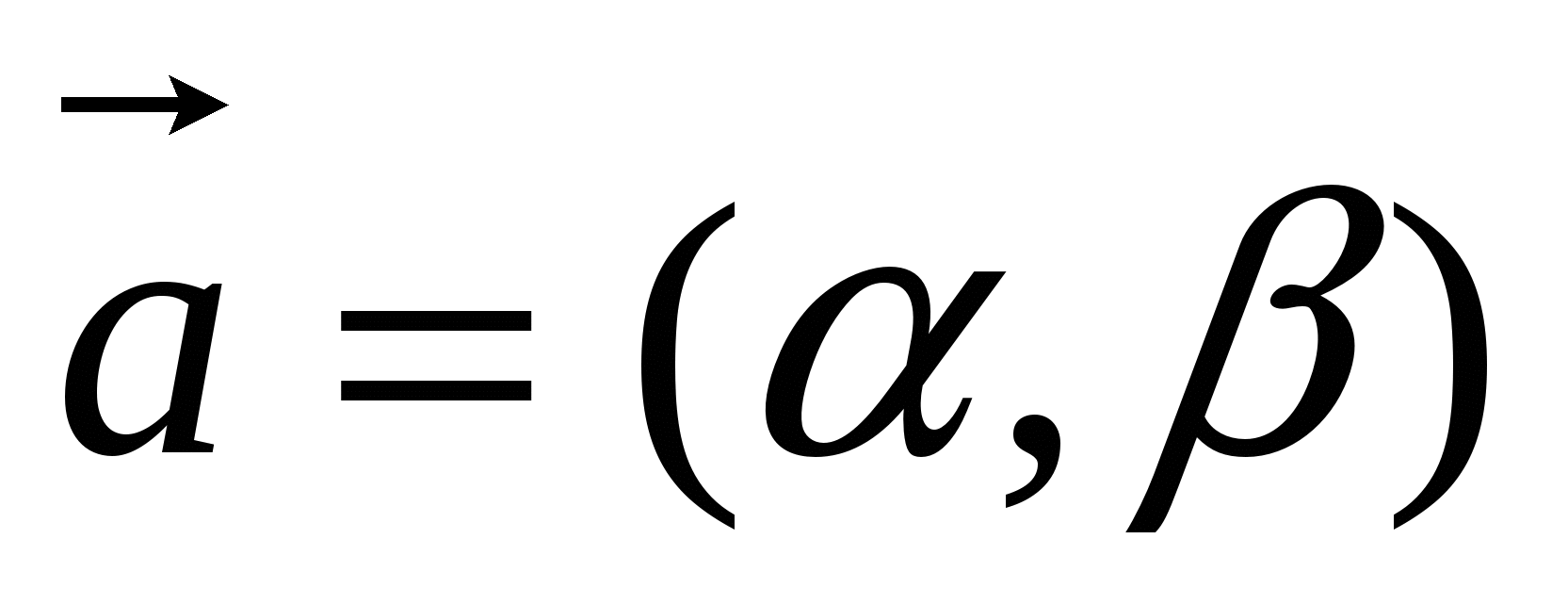 , параллельным прямой l (рис. 2).
, параллельным прямой l (рис. 2).
Вектор а будет называться направляющим вектором прямой l .
Пусть М (х, у) - произвольная точка прямой l . Тогда, согласно условию, векторы 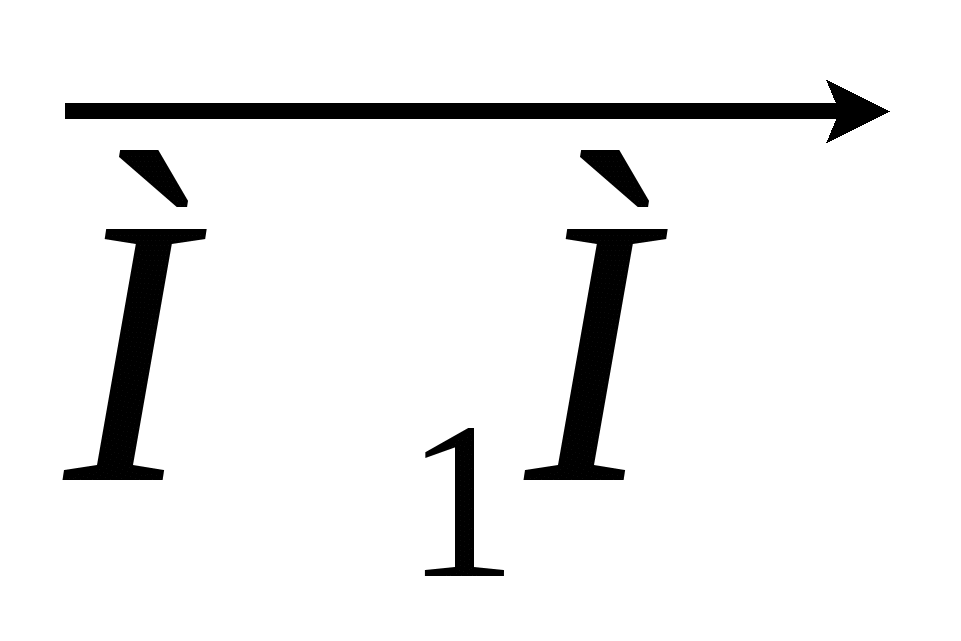 и а коллинеарны тогда и только тогда, когда выполняется равенство
и а коллинеарны тогда и только тогда, когда выполняется равенство 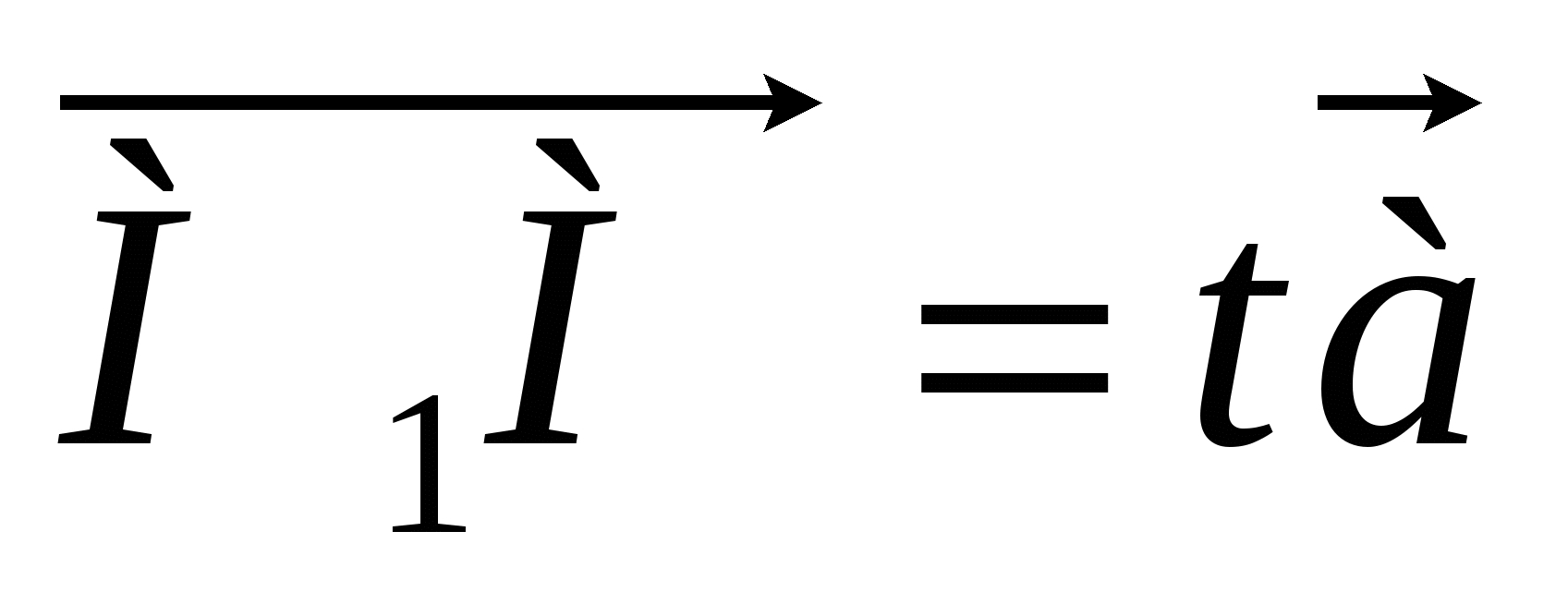 , или
, или
ОМ = ОМ1 + tа,
где t - некоторое число (параметр). Это соотношение в координатах запишется так:
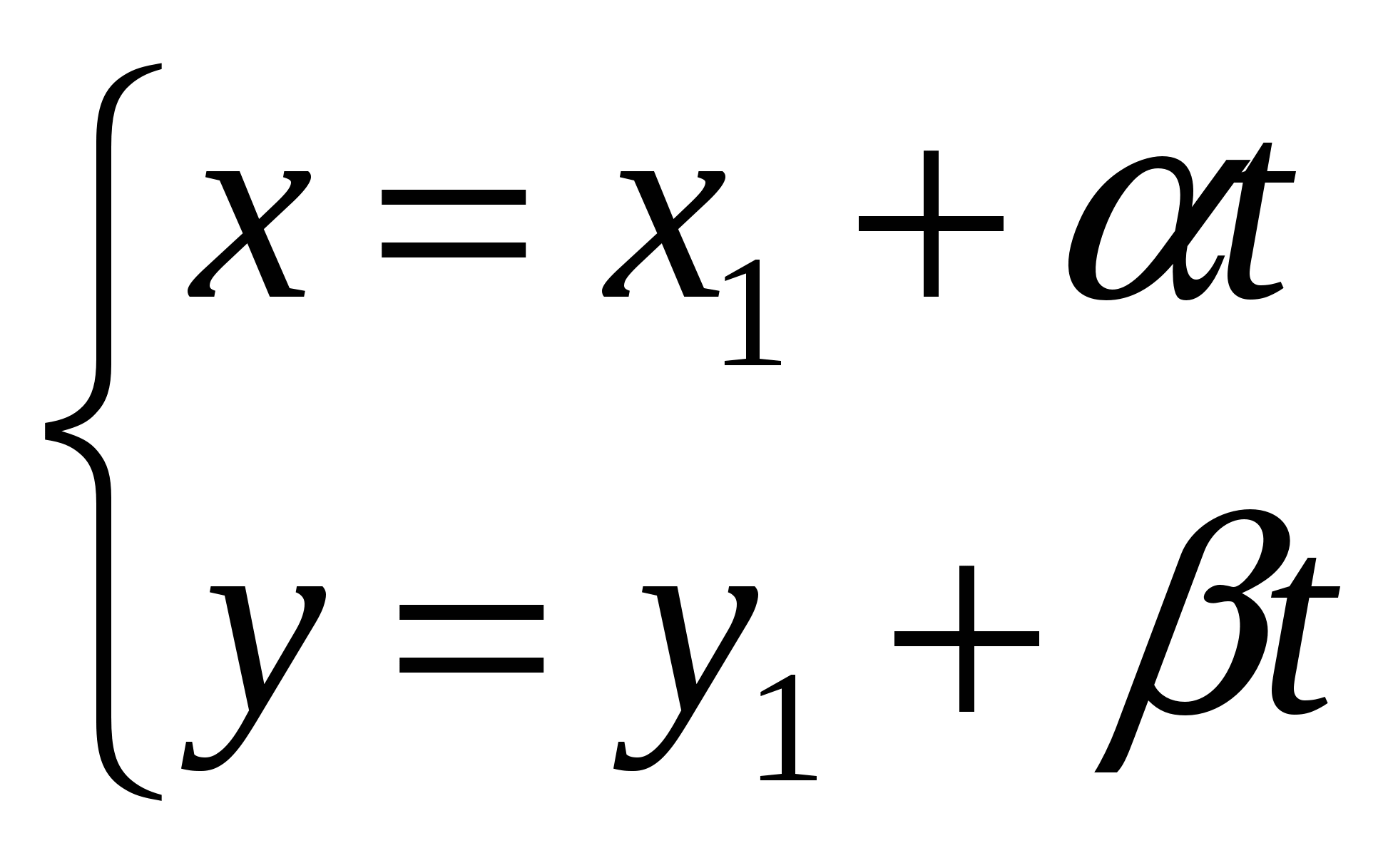
Полученные уравнения называют параметрическими уравнениями прямой.
При 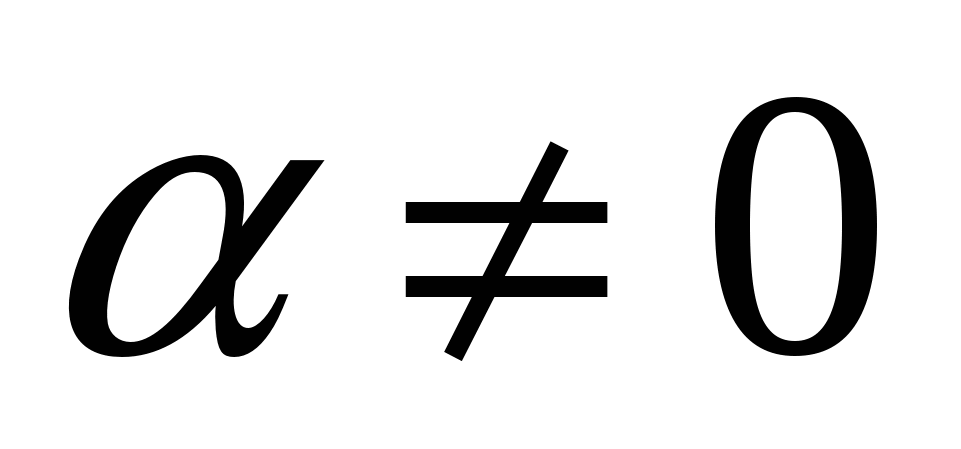 и
и 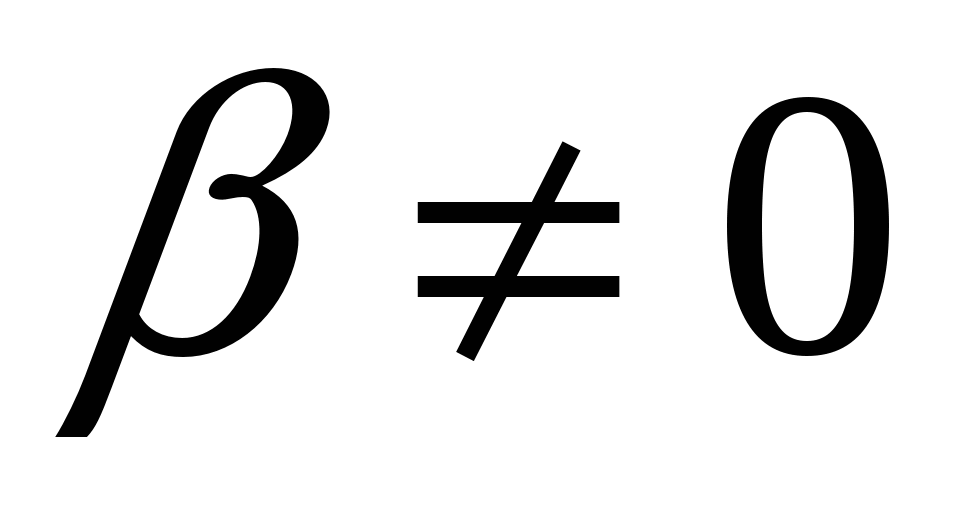 эти уравнения равносильны следующему уравнению первой степени:
эти уравнения равносильны следующему уравнению первой степени:
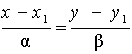
Если прямая задана двумя различными точками: А (х1, у1) и В (х2, у2), то вектор АВ = (х2 - х1, у2 - у1) является направляющим вектором прямой l. Следовательно, при х1 х2 и у1
х2 и у1 у2 получаем уравнение
у2 получаем уравнение
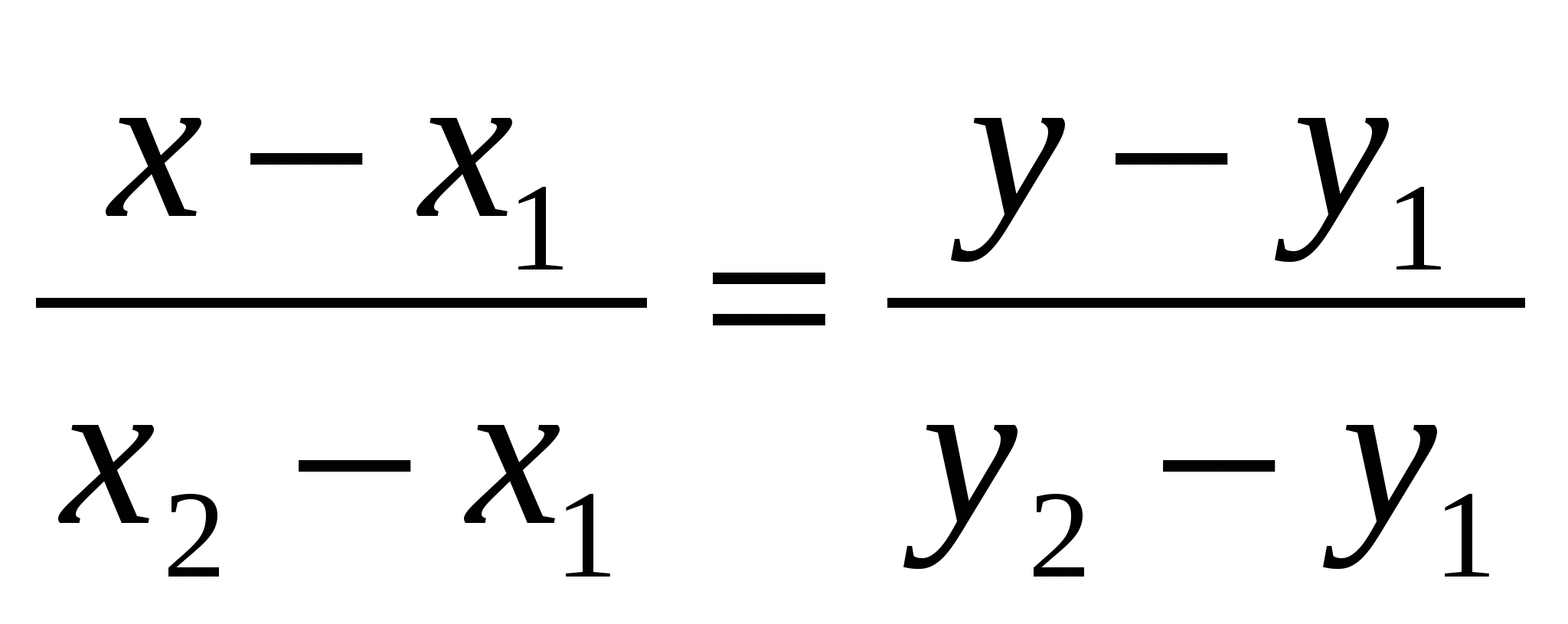 ,
,
которое называется уравнением прямой, проходящей через две точки.
В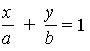 частности, если прямая l проходит через точки А (а, 0) и В (0, b), отличные от начала координат, то уравнение прямой принимает вид
частности, если прямая l проходит через точки А (а, 0) и В (0, b), отличные от начала координат, то уравнение прямой принимает вид
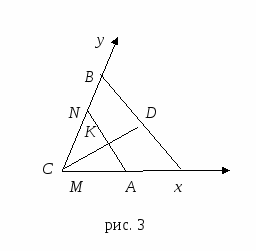
Это уравнение называется уравнением прямой в отрезках.
Исключая из параметрических уравнений прямой параметр t. При ![]() получим уравнение:
получим уравнение:
у- у1 = k (х- х1),
где 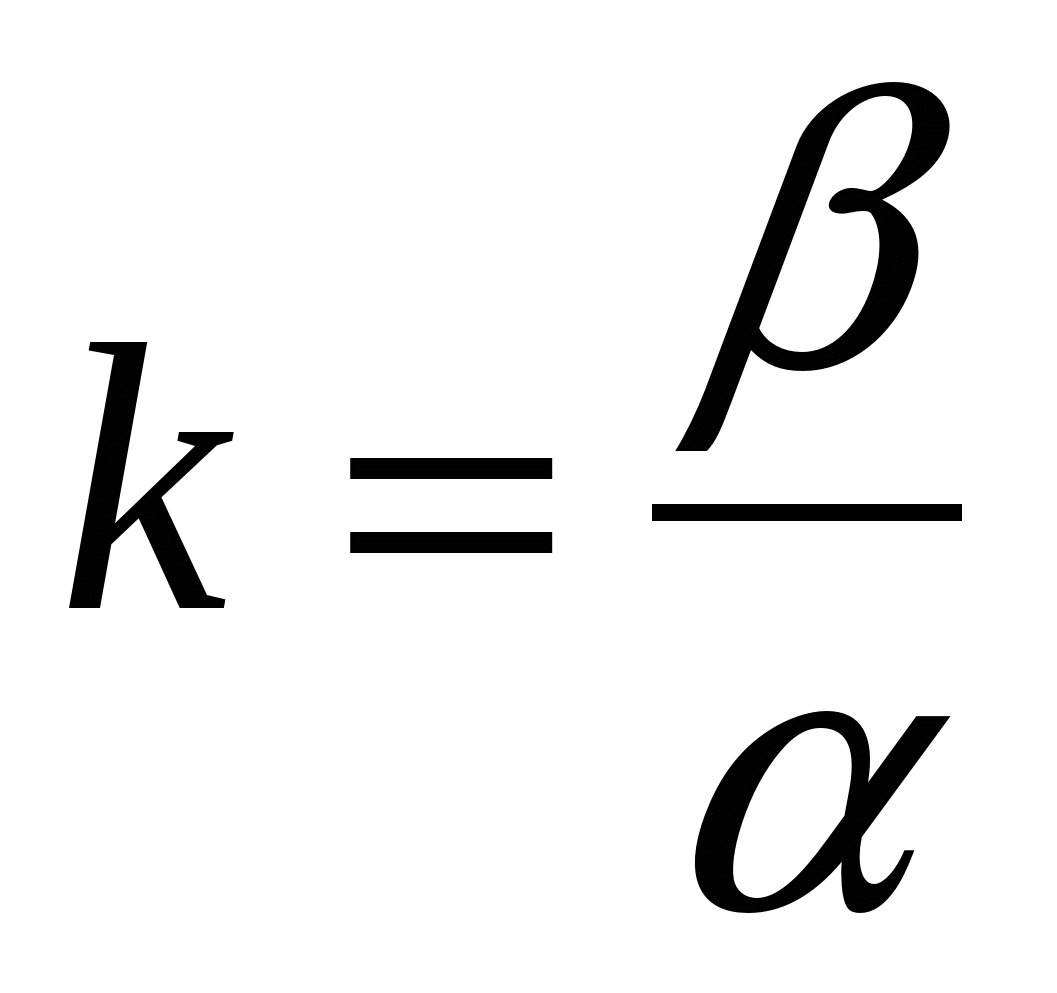 . Число k называют угловым коэффициентом прямой. В частном случае, при х1 = 0 и у1 = b, уравнение принимает вид
. Число k называют угловым коэффициентом прямой. В частном случае, при х1 = 0 и у1 = b, уравнение принимает вид
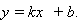
Если же ![]() , то прямая l параллельна оси Оy, а её уравнение запишется так:
, то прямая l параллельна оси Оy, а её уравнение запишется так:
х = х1.
Таким образом, всякую прямую на плоскости можно задать уравнение первой степени Ах + Ву + С = 0, где хотя бы одно из чисел А и В отлично от нуля. Верно и обратное предложение: всякое уравнение первой степени Ах + Ву + С = 0 есть уравнение некоторой прямой в аффинной системе координат на плоскости.
При 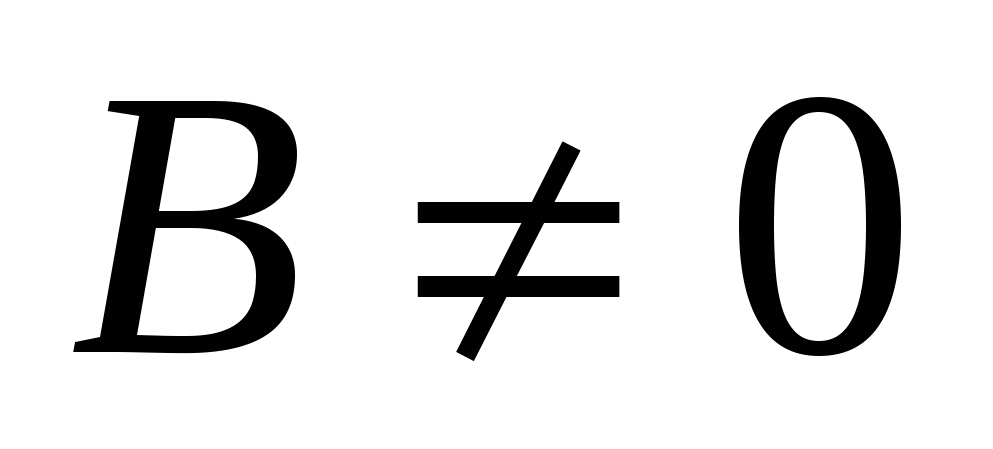 уравнение Ах + Ву + С = 0 приводится к виду у = kх + b, где
уравнение Ах + Ву + С = 0 приводится к виду у = kх + b, где
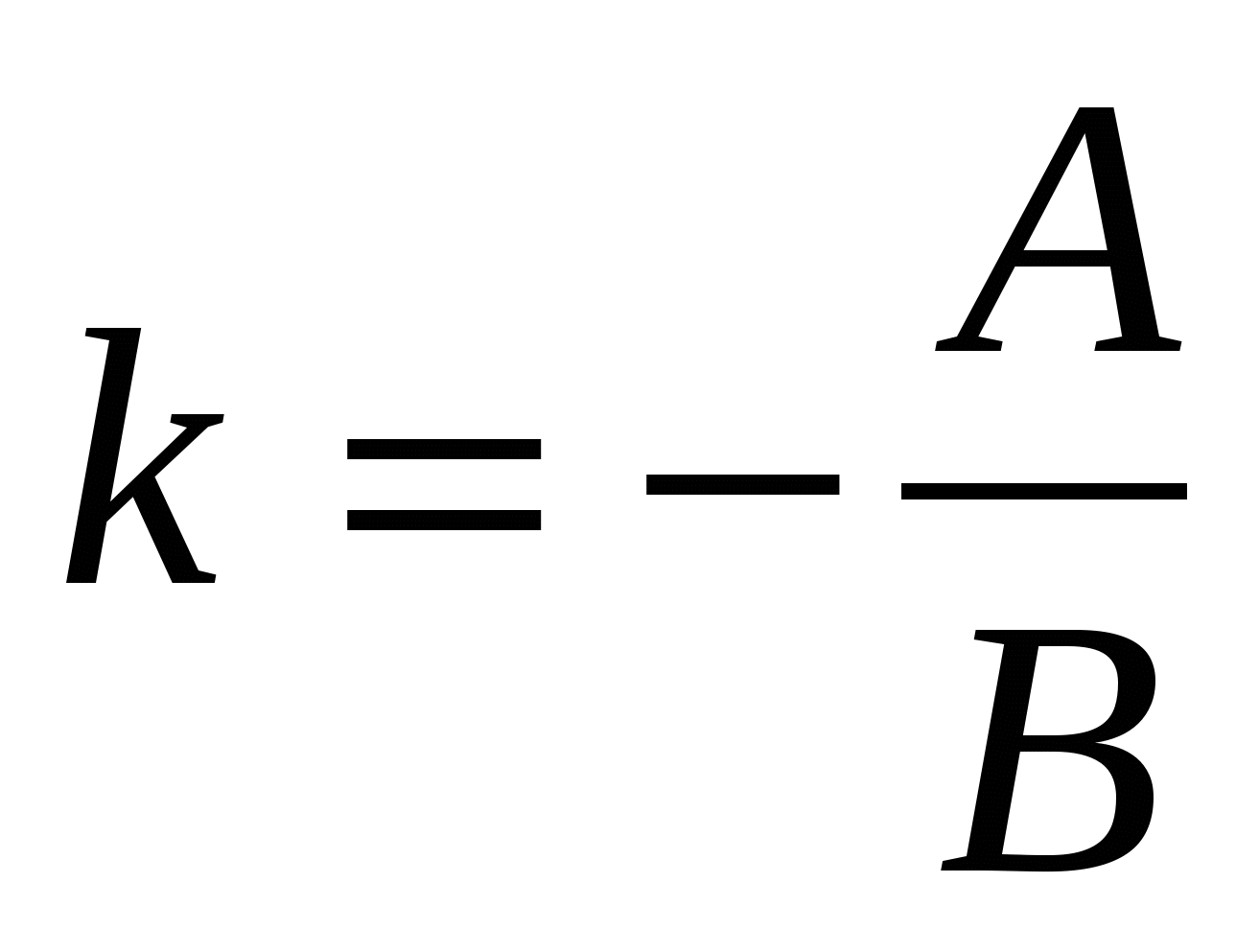 ,
, 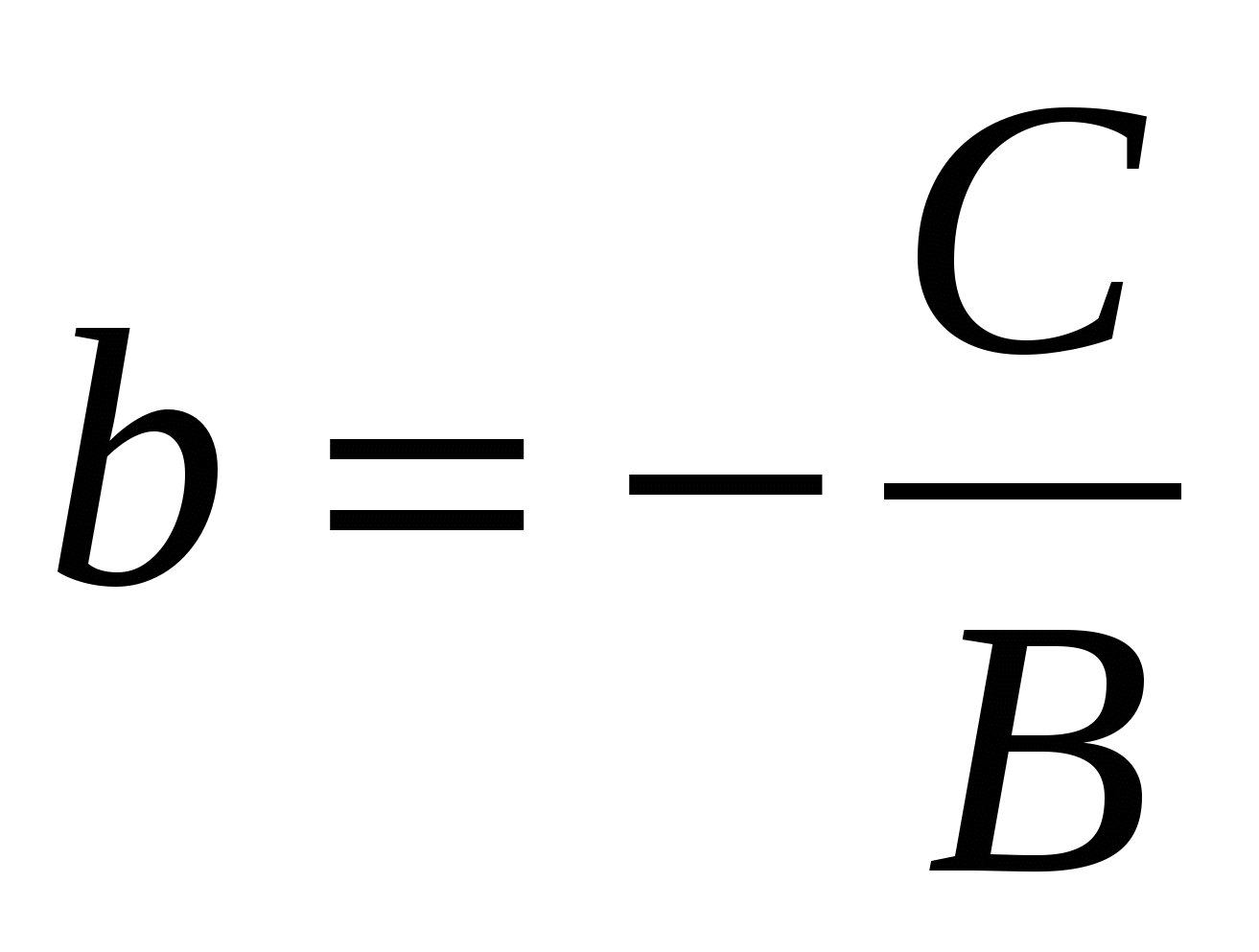
Если же В = 0 и 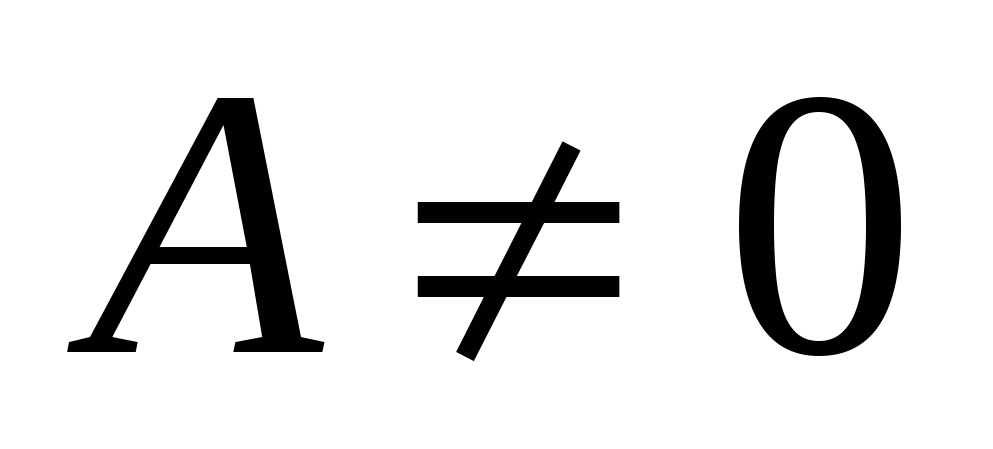 , то оно принимает вид х = а, где
, то оно принимает вид х = а, где 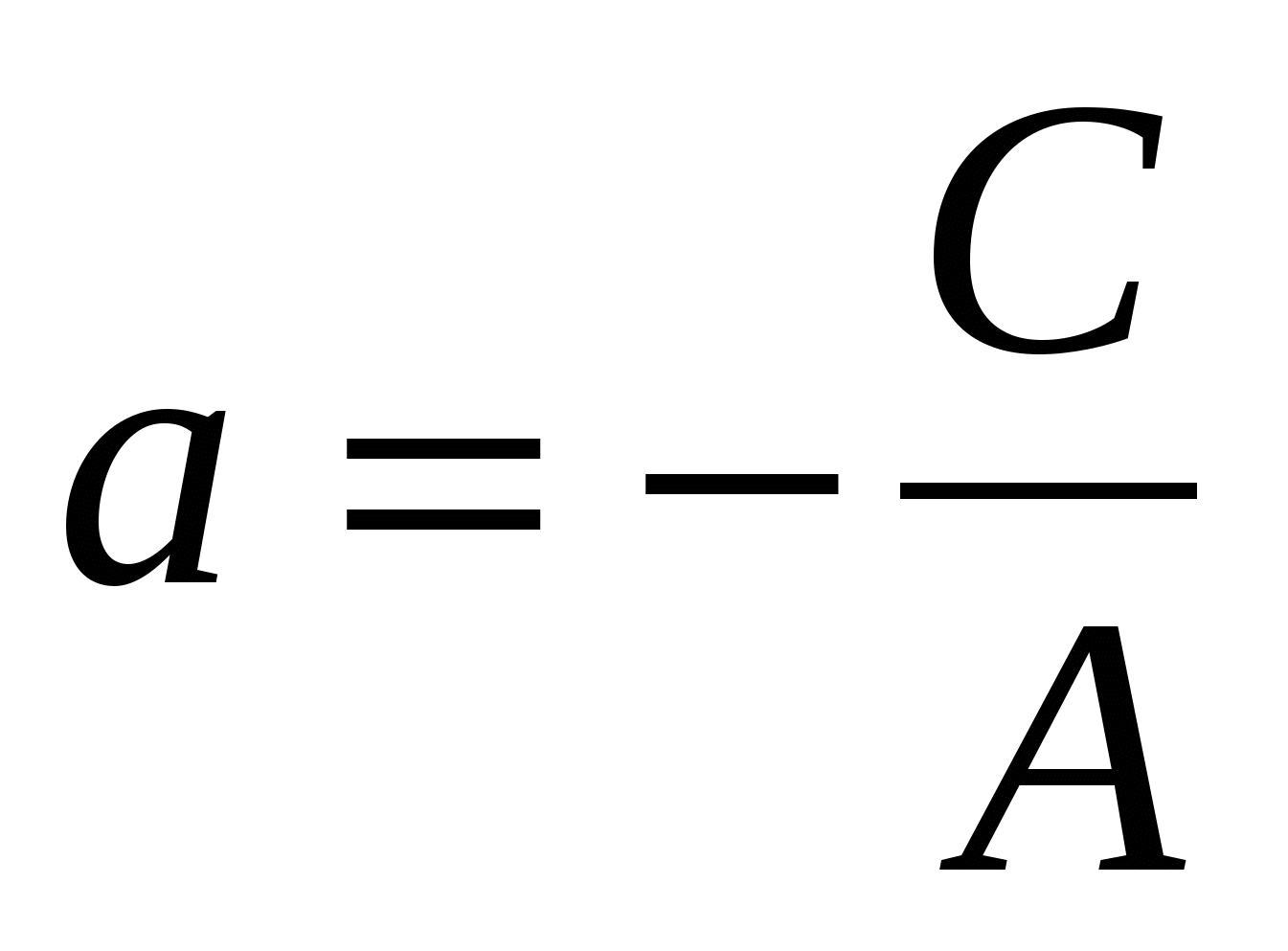 .
.
2.2. Декартова система координат на плоскости. Прямая и окружность.
Определение. Декартовой (или ортонормированной, или прямоугольной) системой координат на плоскости называется такая аффинная система координат, базисные векторы которой ортонормированны, то есть имеют единичные длины и ортогональны (перпендикулярны). Обозначение R = {O, i, j}; так что |i| = |j| = 1, i перпендикулярен j.
П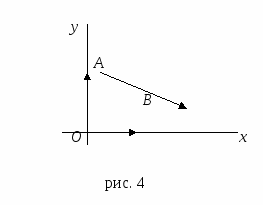 ри решении задач, в которых существенную роль играет понятие расстояния между двумя точками, применяется, декартова или прямоугольная система координат.
ри решении задач, в которых существенную роль играет понятие расстояния между двумя точками, применяется, декартова или прямоугольная система координат.
Пусть даны две точки: А (х1, у1) и В (х2, у2). Тогда, как известно,
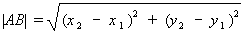 .
.
Пользуясь формулой, запишем уравнение окружности с центром в точке С (a, b) и радиусом r:
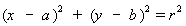 .
.
Вышеизложенная теория прямой справедлива и для прямоугольной системы координат. В частности, при решении задач пользуются уравнением прямой с угловым коэффициентом k, проходящей через точку А (х1, у1):
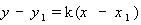 .
.
Отсюда следует, что угловой коэффициент прямой, заданной двумя точками А (х1, у1) и В (х2, у2), вычисляется по формуле
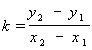
У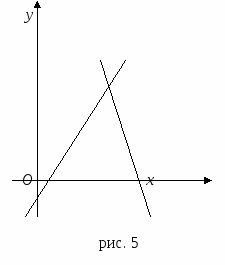 гловой коэффициент в прямоугольной системе координат имеет следующий геометрический смысл:
гловой коэффициент в прямоугольной системе координат имеет следующий геометрический смысл: 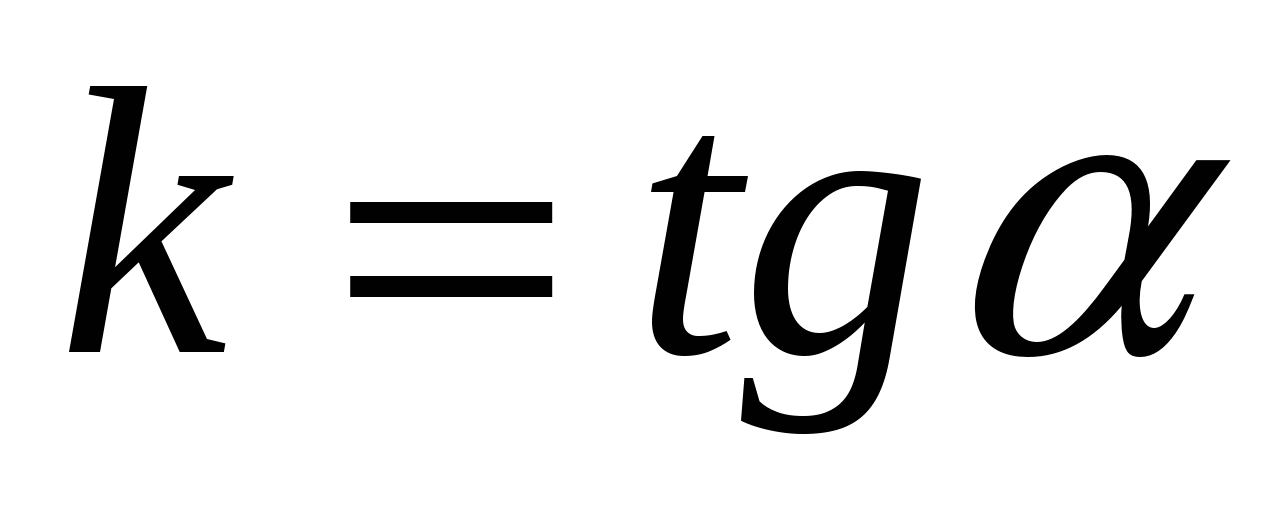 , где
, где  - величина угла от оси абсцисс до прямой l.
- величина угла от оси абсцисс до прямой l.
Пусть прямые l1 и l2 заданы своими уравнениями с угловыми коэффициентами: у = k1х + b1 и у = k2х + b2.
Если l1 || l2, то 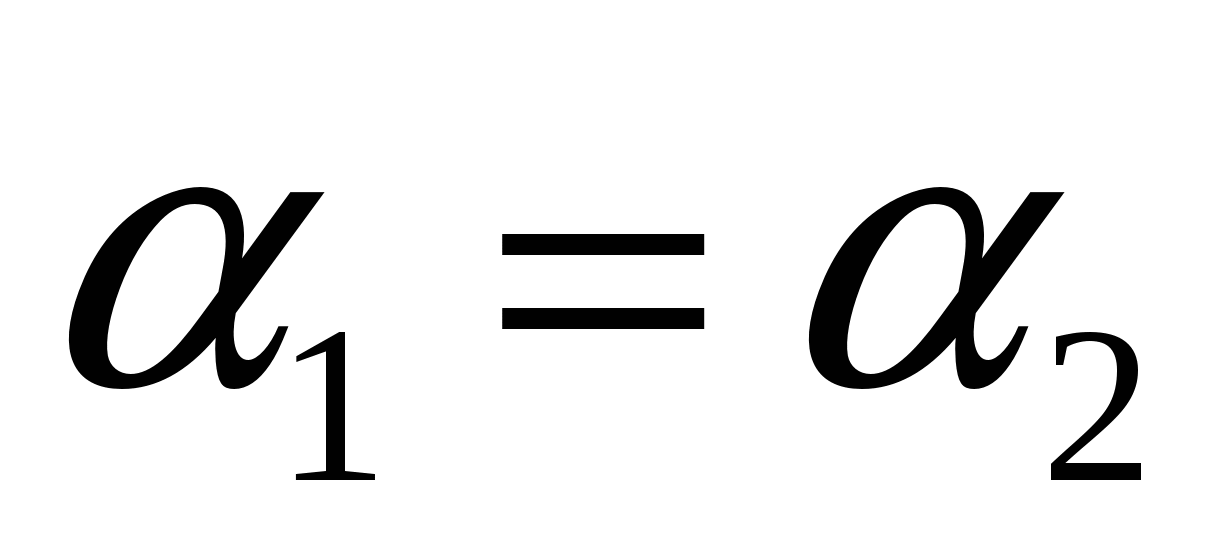 , поэтому k1 = k2, и обратно, т.е. условие k1 = k2 выражает признак параллельности прямых l1 и l2.
, поэтому k1 = k2, и обратно, т.е. условие k1 = k2 выражает признак параллельности прямых l1 и l2.
Введем формулу для вычисления угла  между пересекающимися прямыми l1 и l2 (рис. 5).
между пересекающимися прямыми l1 и l2 (рис. 5).
Так как 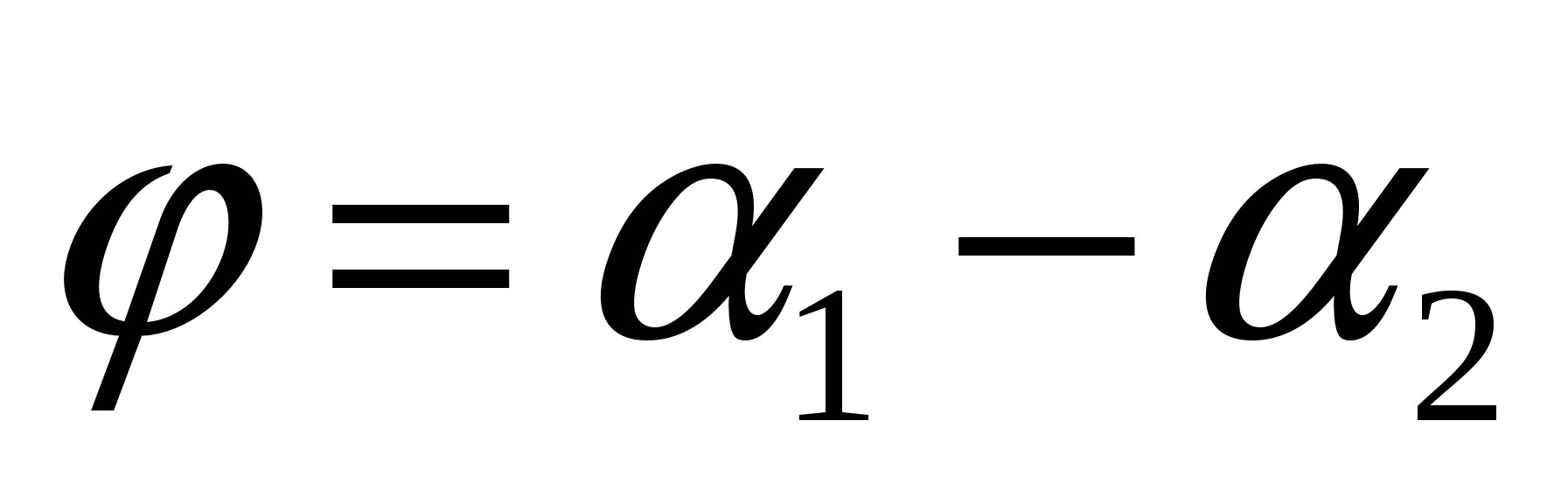 и
и 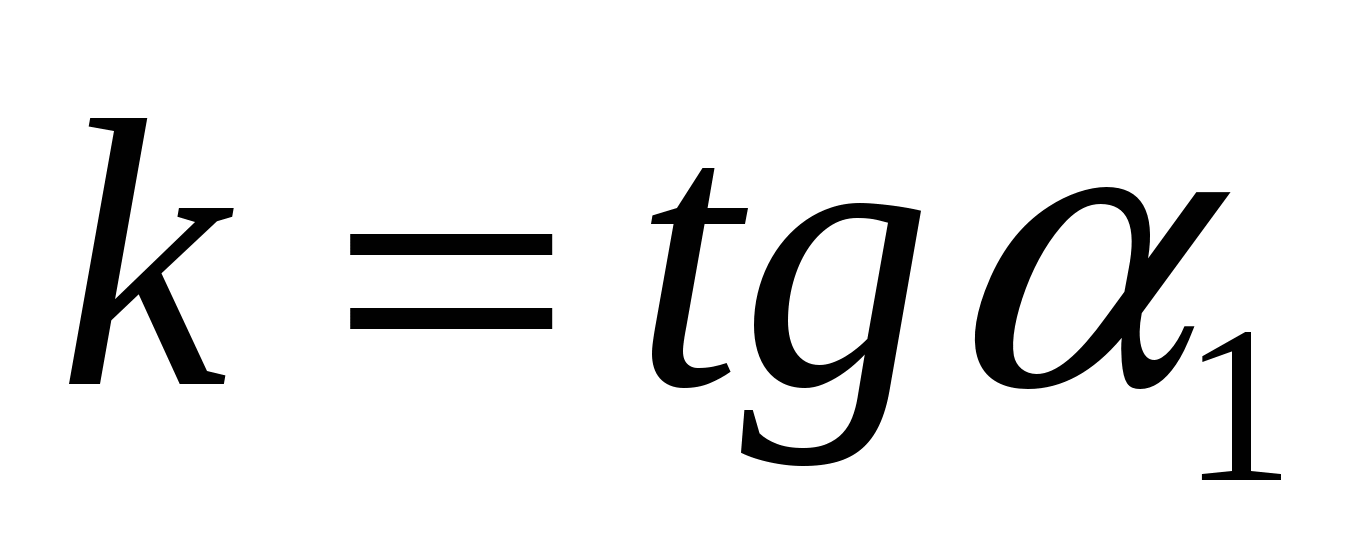 ,
, 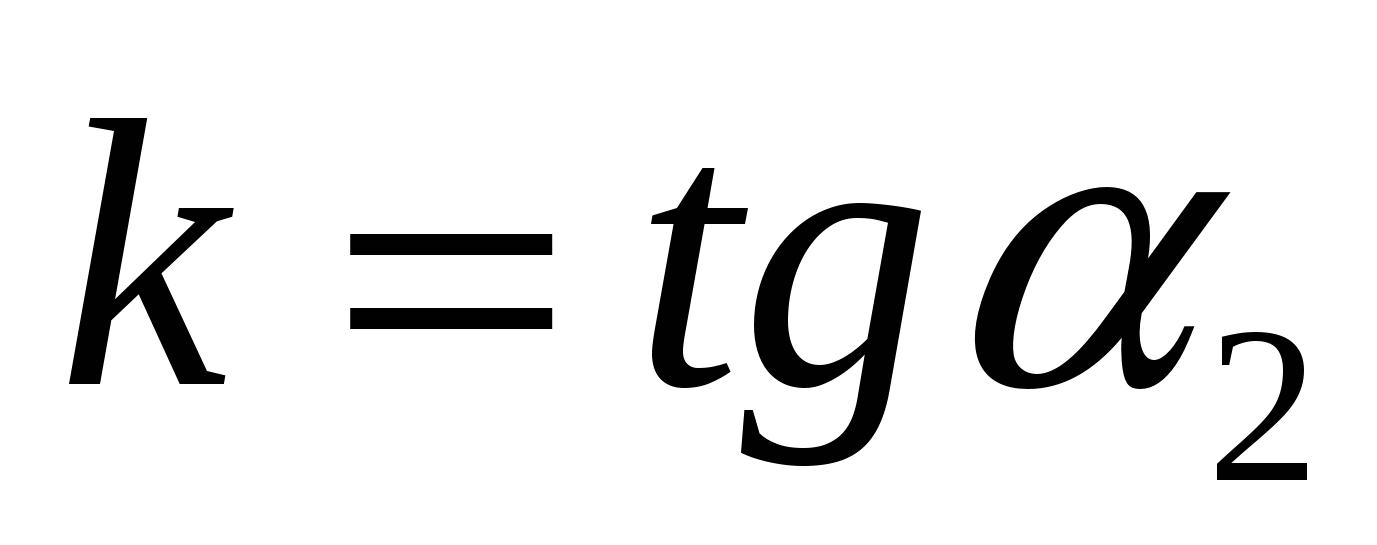 , то
, то
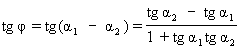
или
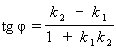
Полученную формулу для вычисления угла от прямой l1 до прямой l2 можно записать и так:
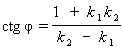
Отсюда следует, что 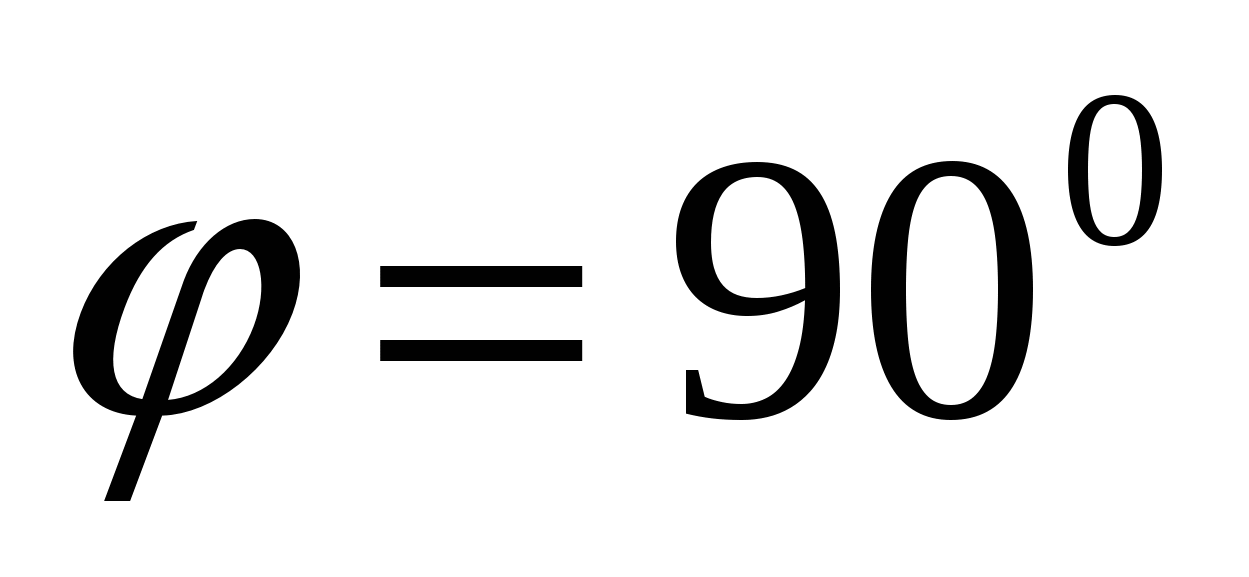 тогда и только тогда, когда k1k2 = - 1, т.е. условие k1k2 = - 1 выражает признак перпендикулярности прямых l1 и l2.
тогда и только тогда, когда k1k2 = - 1, т.е. условие k1k2 = - 1 выражает признак перпендикулярности прямых l1 и l2.
Приступая к решению геометрической задачи, следует рационально выбрать систему координат, присоединить её к данной фигуре наиболее естественным образом. Желательно, чтобы данные точки располагались на осях координат, тогда среди координат будут нули. Это позволит упростить вычисления.
2.3. Полярная система координат на плоскости
У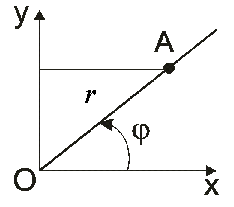 равнения многих кривых удобно задавать не в декартовой системе, а в других системах координат. Координатами называются числа, при помощи которых можно определить положение точки. Например, положение точки на поверхности земного шара определяются ее географическими координатами - шириной и долготой. Одной из важных систем координат на плоскости является полярная система координат.
равнения многих кривых удобно задавать не в декартовой системе, а в других системах координат. Координатами называются числа, при помощи которых можно определить положение точки. Например, положение точки на поверхности земного шара определяются ее географическими координатами - шириной и долготой. Одной из важных систем координат на плоскости является полярная система координат.
Полярная система координат задается точкой О и лучом ОА с началом в этой точке. Точка О называется полюсом, ось ОА - полярной осью. Полярными координатами точки М называются ее расстояние r от полюса и угол ![]() , который направленный отрезок ОМ образует с полярной осью.
, который направленный отрезок ОМ образует с полярной осью.
Координата r называется полярным радиусом, а координата 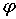 - полярным углом точки М. При этом употребляют запись М(r,
- полярным углом точки М. При этом употребляют запись М(r, 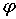 ) . Из определения полярных координат следует, что r
) . Из определения полярных координат следует, что r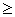 0. Координата
0. Координата 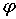 определяется неоднозначно, так как координатам (r,
определяется неоднозначно, так как координатам (r, 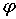 ) и (r,
) и (r, 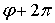 ), соответствует одна и та же точка. Если наложить на
), соответствует одна и та же точка. Если наложить на 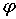 условие 0
условие 0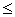
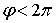 или
или ![]() , то координата
, то координата ![]() становится однозначной. При
становится однозначной. При 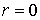 точка
точка ![]() совпадает с полюсом, а координата
совпадает с полюсом, а координата 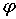 не определена. Кривые могут задаваться уравнениями в полярных координатах так же, как они задаются уравнениями в декартовых координатах.1
не определена. Кривые могут задаваться уравнениями в полярных координатах так же, как они задаются уравнениями в декартовых координатах.1
3.Метод координат в пространстве
3.1. Декартова прямоугольная система координат в пространстве
Координаты точек и векторов.
Декартова прямоугольная система координат в пространстве задается тремя попарно перпендикулярными осями координат с общим началом:
Ох - ось абсцисс, Оу - ось ординат, Оz - ось аппликат.
Плоскости Оху, Оуz, Ozx называются плоскостями координат. Система координат Охуz называется правой, если для наблюдателя, стоящего на плоскости Оху и расположенного так, что ось Оz направлена от ног к голове, кратчайший поворот, совмещающий положительное направление оси Ох с положительным направлением оси Оу, происходит против часовой стрелки. Если же такой поворот происходит по часовой стрелке, то система называется левой. Названия "правая система" и "левая система" объясняются тем, что оси координат правой системы направлены как большой, указательный, средний палец правой руки, расположенные попарно перпендикулярно друг другу, а оси левой системы - как пальцы левой руки.2
Радиус-вектором точки М относительно декартовой прямоугольной системы координат Охуz называется вектор 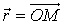 . Координатами точки М относительно декартовой прямоугольной системы координат называются проекции ее радиус-вектора на оси координат:
. Координатами точки М относительно декартовой прямоугольной системы координат называются проекции ее радиус-вектора на оси координат:
х=Прх 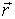 , у=Пру
, у=Пру 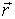 , z=Прz
, z=Прz 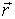 , т.е. скалярные величины направленных отрезков
, т.е. скалярные величины направленных отрезков 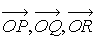 на осях Ох, Оу, Оz:
на осях Ох, Оу, Оz:
х=(ОР)х, у=(ОQ)y, z=(OR)z,
где P, Q, R - проекции точки М на оси Ох, Оу, Оz соответственно. При этом пишут 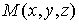
Существует определения координат вектора.
Определение. Координатами вектора 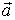 относительно декартовой прямоугольной системы координат Охуz называются его проекции на оси координат: ах=Прх
относительно декартовой прямоугольной системы координат Охуz называются его проекции на оси координат: ах=Прх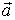 , ау=Пру
, ау=Пру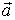 , аz=Прz
, аz=Прz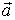 . При этом употребляется запись
. При этом употребляется запись 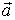 =( ах ,ау, аz).
=( ах ,ау, аz).
Координаты вектора равны разностям между координатами его конца и начала: если 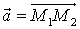 , то
, то
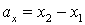 ,
, 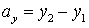 ,
, ![]() выражение координат вектора через координаты его начала и конца. Действительно,
выражение координат вектора через координаты его начала и конца. Действительно, 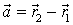 . Следовательно,
. Следовательно,
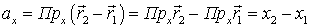 .
.
Аналогичным образом можно найти выражения для ![]() ,
, 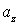 .
.
3.2. Цилиндрическая система координат в пространстве3
Цилиндрические координаты - трехмерный аналог полярных, в котором точка P представляется трехкомпонентным кортежем (r,θ,h). В терминах декартовой системы координат,
-
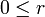 (радиус) - расстояние от оси z к точке P,
(радиус) - расстояние от оси z к точке P, -
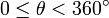 (азимут или долгота) - угол между положительной («плюсовой») частью оси x и прямой линии, мысленно проведённой от полюса до точки P, спроектирован на xy-плоскость
(азимут или долгота) - угол между положительной («плюсовой») частью оси x и прямой линии, мысленно проведённой от полюса до точки P, спроектирован на xy-плоскость -
h (высота) - расстояние (с учетом знака) от xy-плоскости до точки P.
Цилиндрические координаты полезны для изучения систем, симметричных вокруг некой оси. Например, длинный цилиндр в декартовых координатах имеет уравнение 2x + 2y = 2c, тогда как в цилиндрических оно выглядит как r = с
Пример: Найти центр тяжести однородного тела, ограниченного сферой 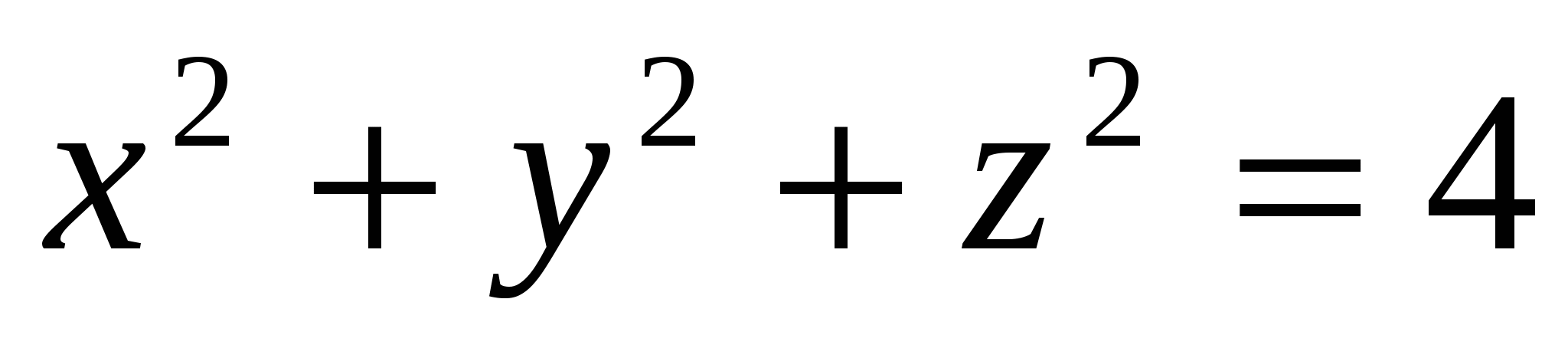 и параболой
и параболой 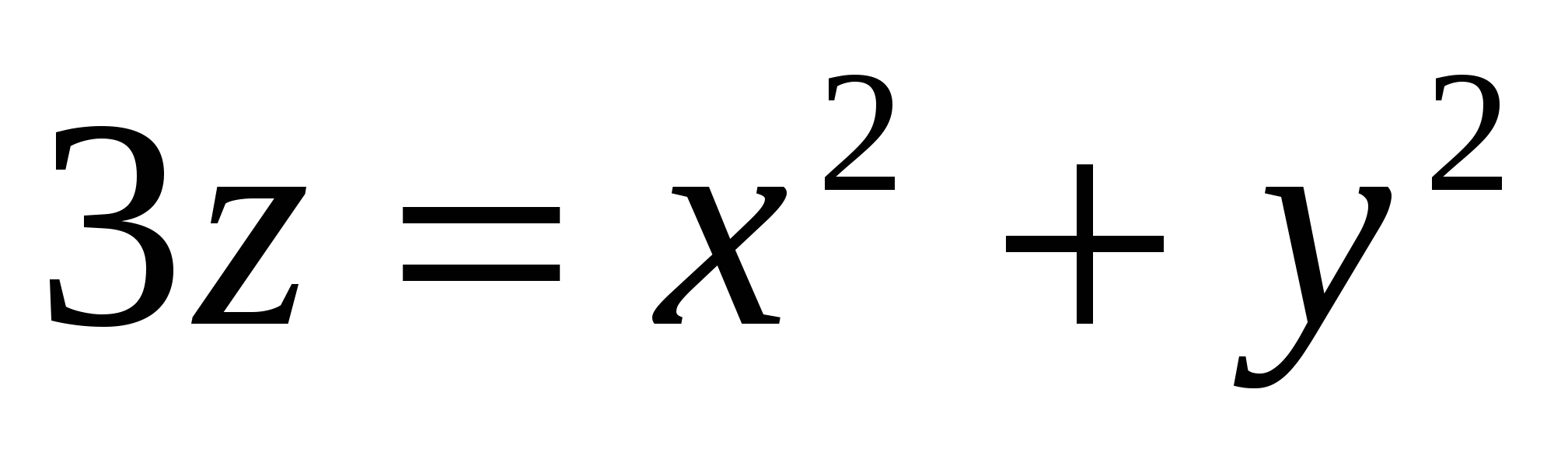 .
.
В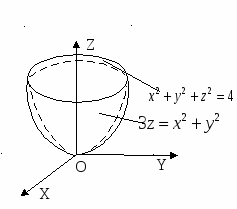 оспользуемся формулами
оспользуемся формулами 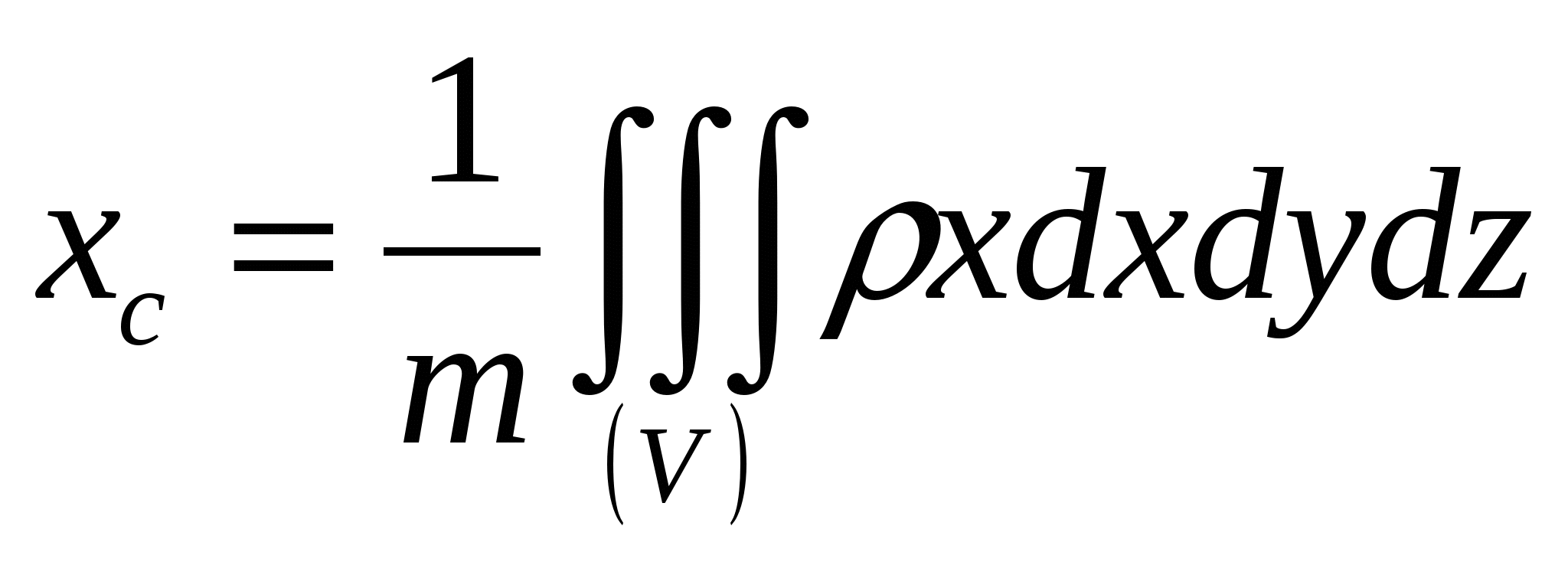 ,
, 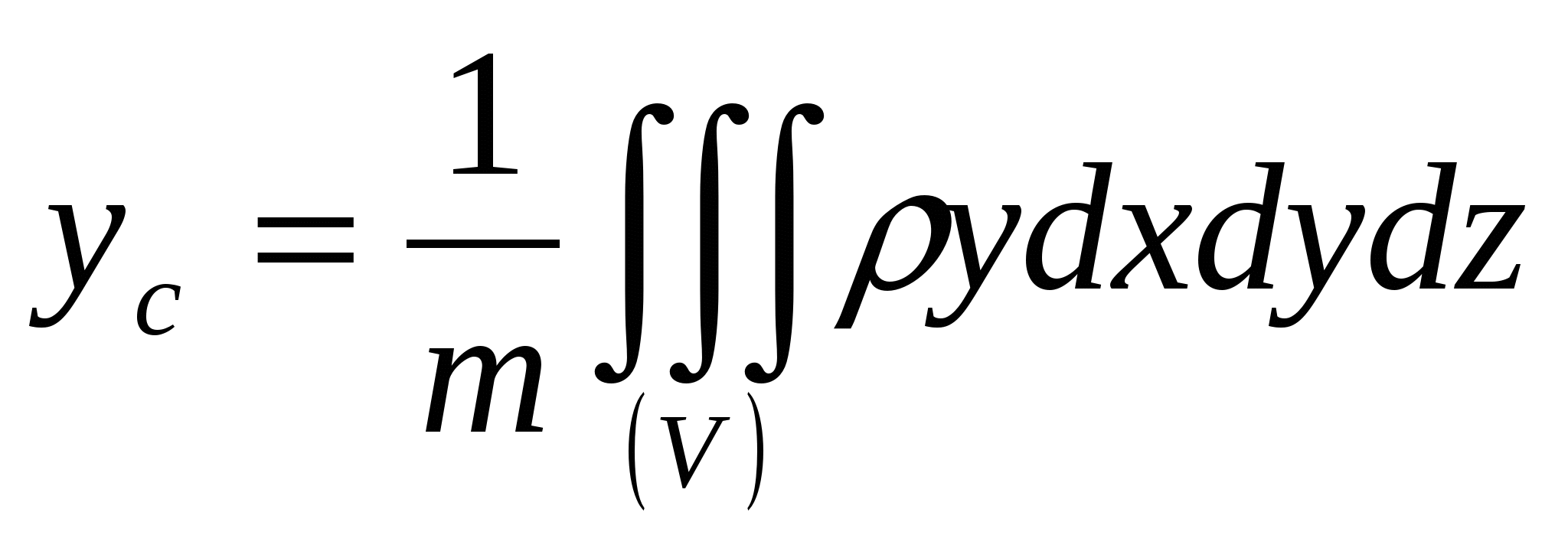 ,
, 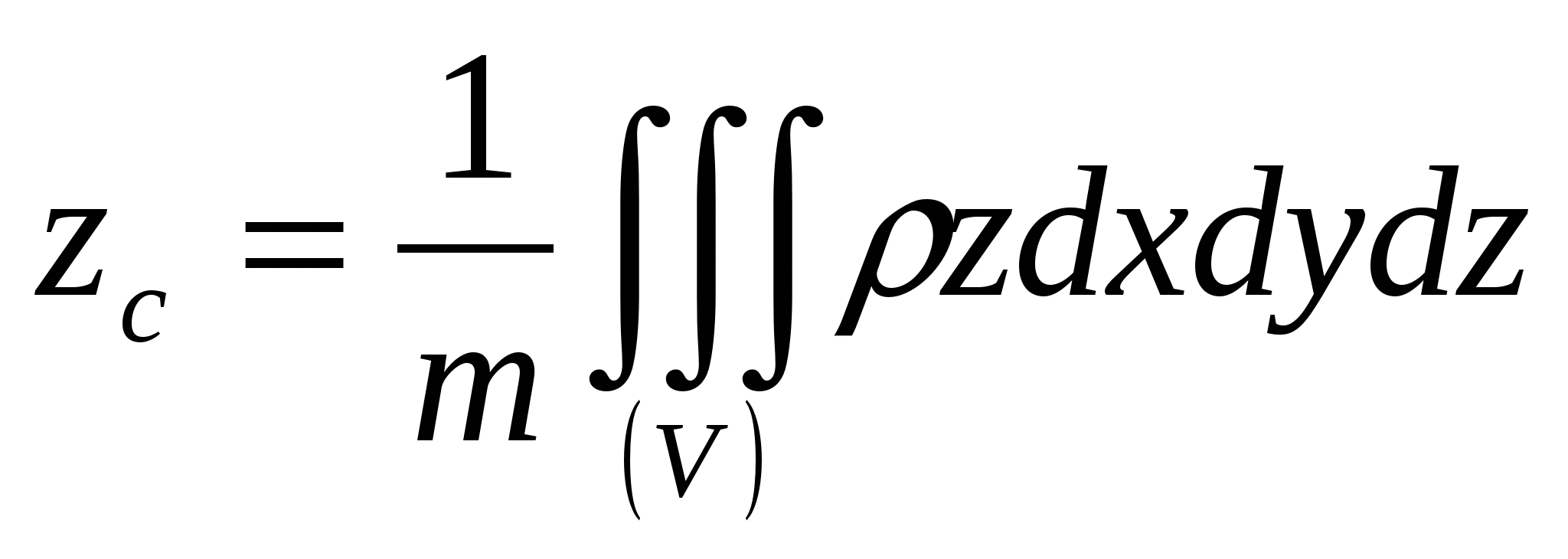 ,
,
где ρ - плотность тела в точке (x,y,z), а m - масса тела: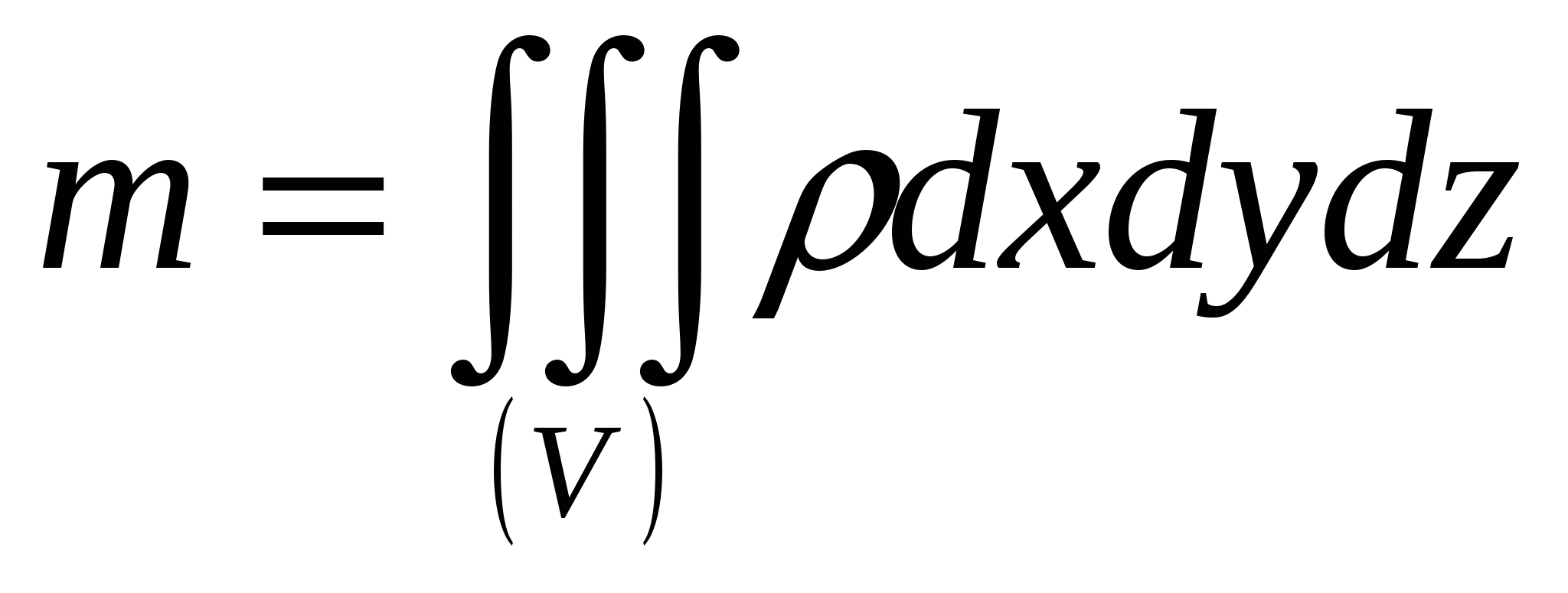 . в которых положим ρ=1. Тело симметрично, центр тяжести лежит на оси Oz, поэтому
. в которых положим ρ=1. Тело симметрично, центр тяжести лежит на оси Oz, поэтому 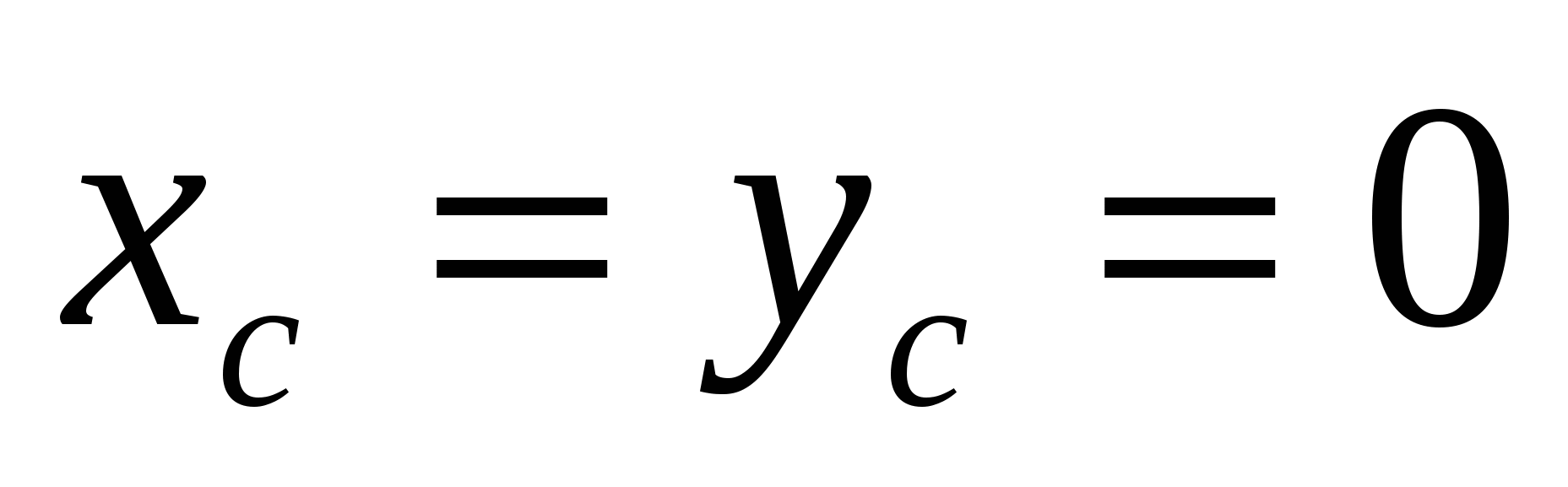 и необходимо найти аппликату центра тяжести тела, т.е.
и необходимо найти аппликату центра тяжести тела, т.е. 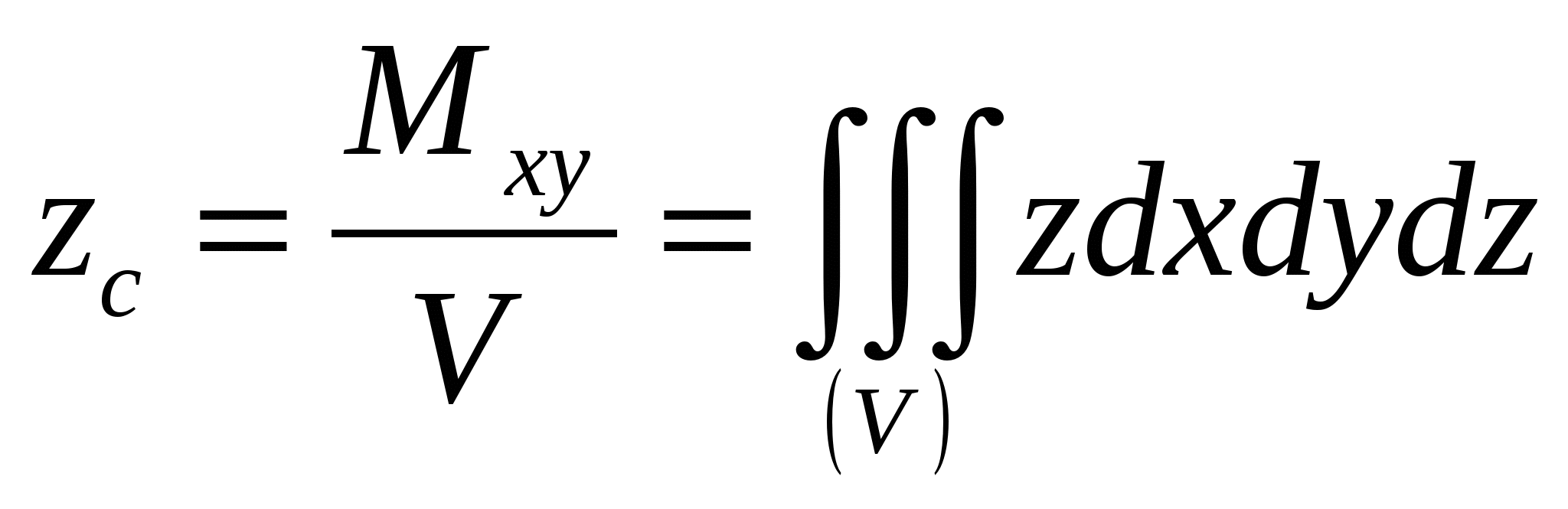 . Т.к. тело симметричное, то в цилиндрической системе координат определяющие неравенства запишем в виде (рассмотрим первую четверть координатной системы.):
. Т.к. тело симметричное, то в цилиндрической системе координат определяющие неравенства запишем в виде (рассмотрим первую четверть координатной системы.):
(V1): 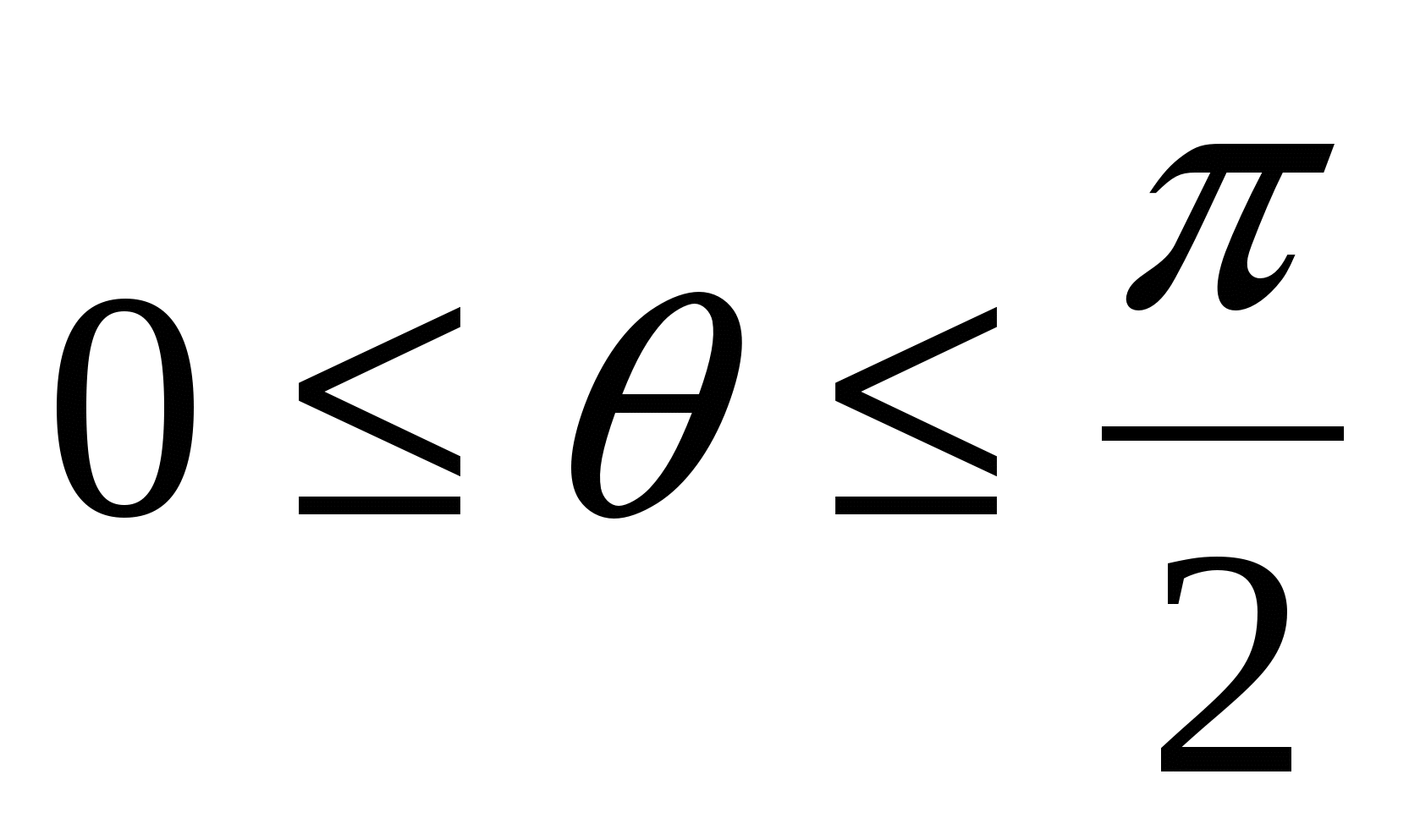 ,
,  ,
, 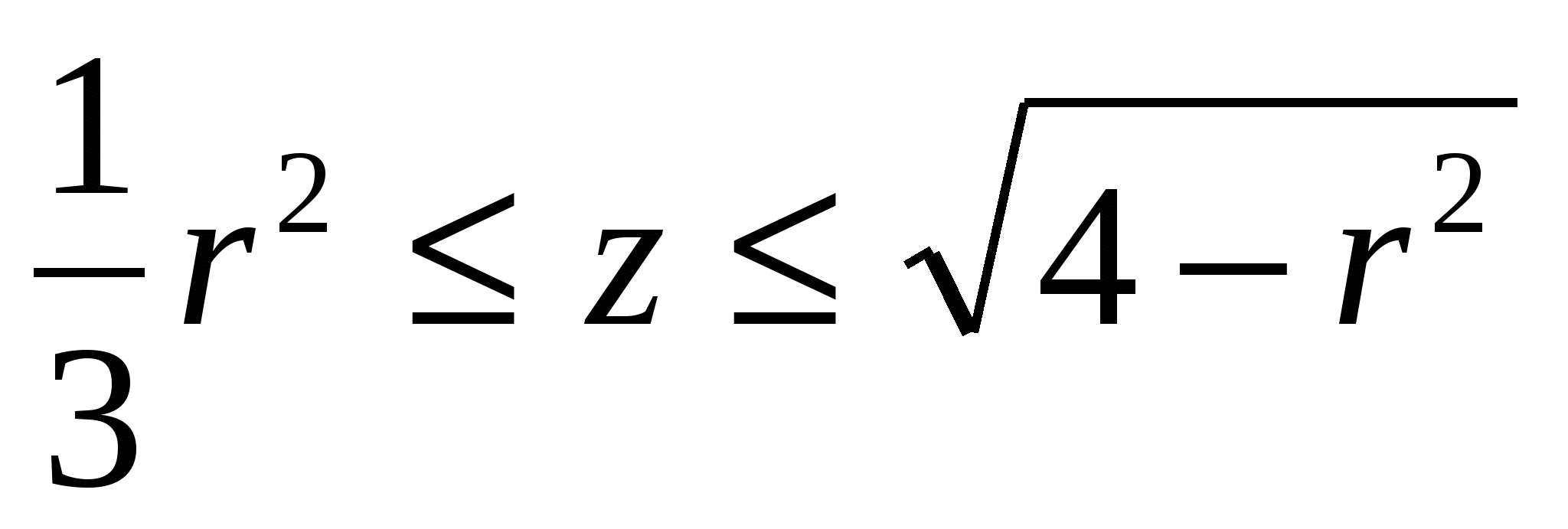 , а интеграл в виде
, а интеграл в виде 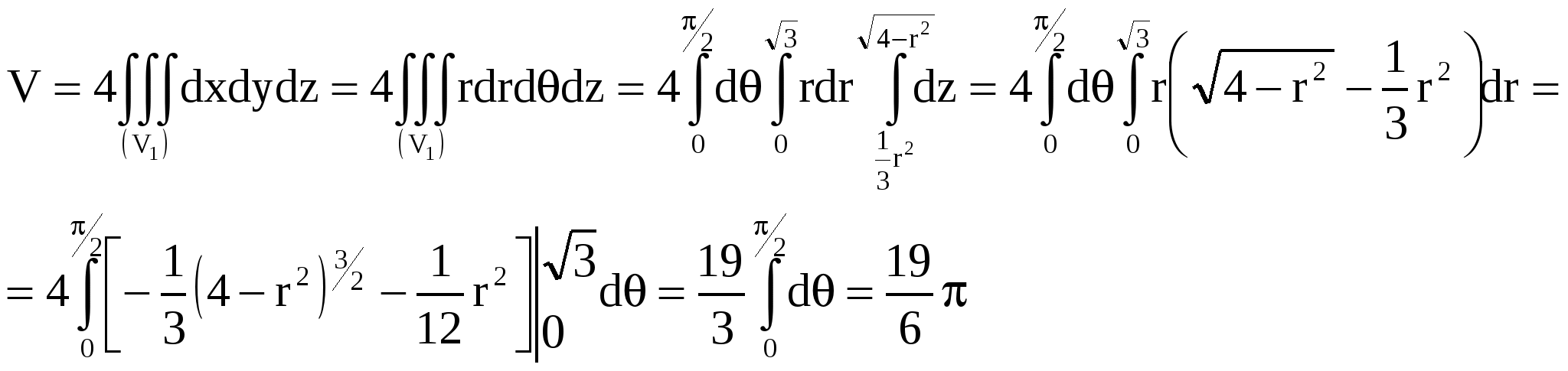
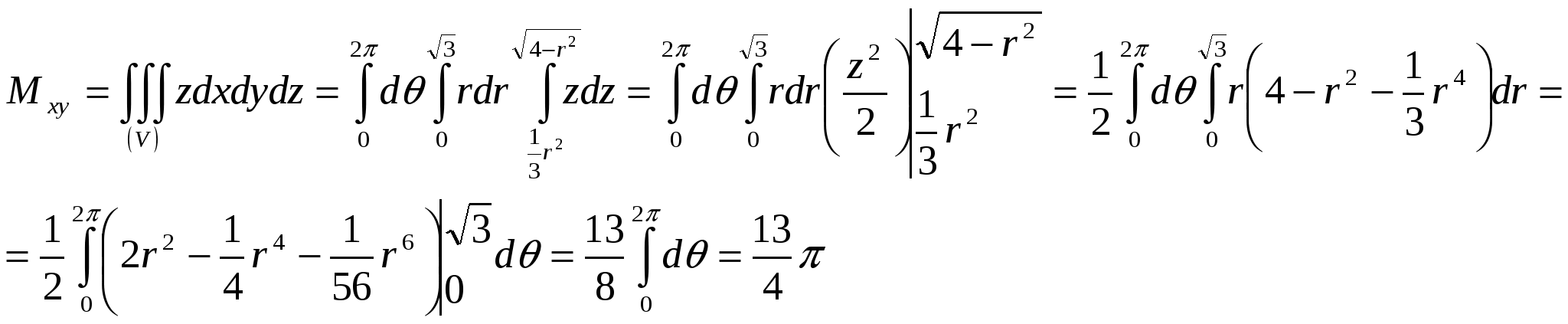 Следовательно,
Следовательно, 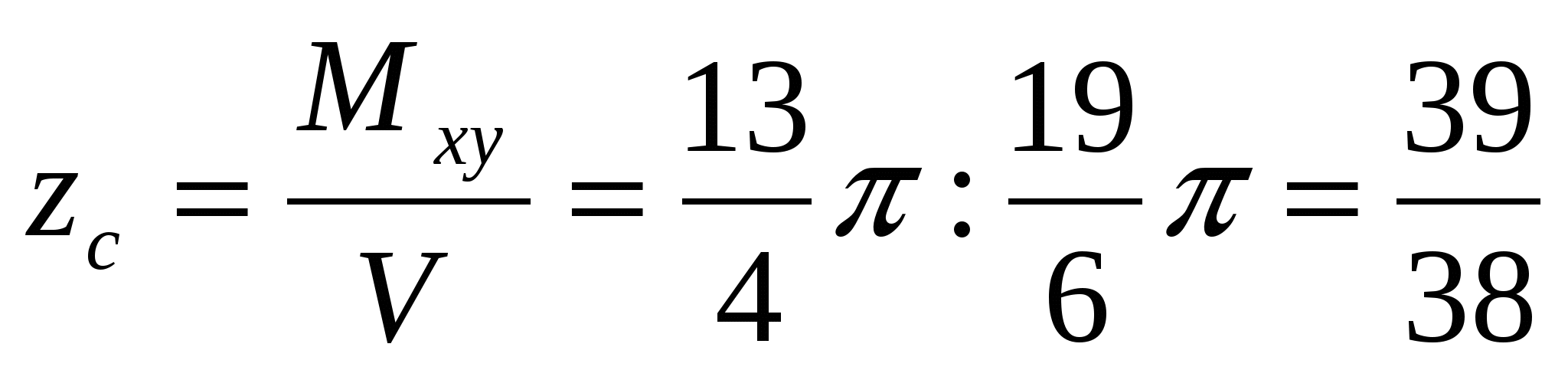 . Таким образом, центр тяжести данного тела находится в точке
. Таким образом, центр тяжести данного тела находится в точке 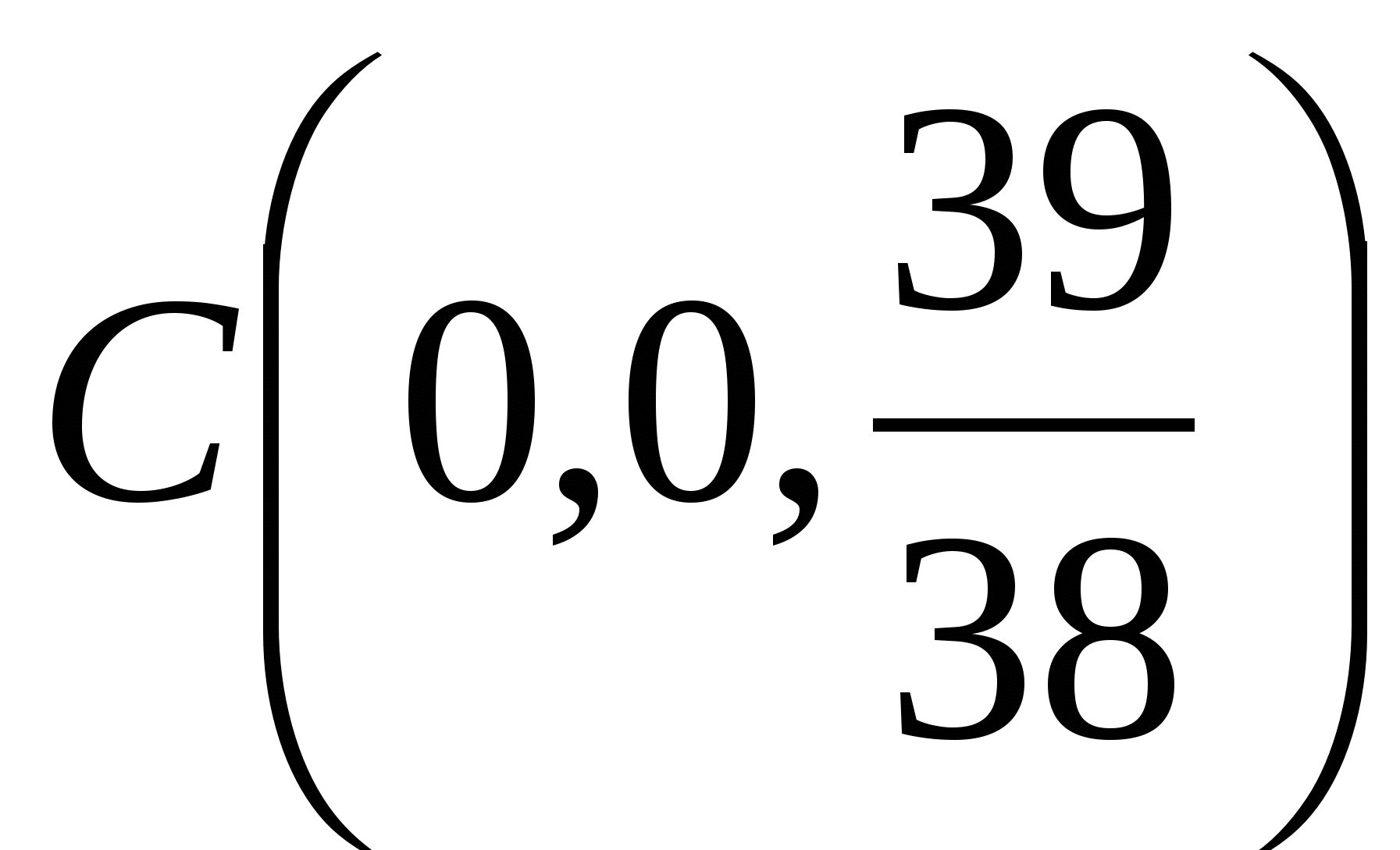 .
.
Замечание. Неравенства, определяющие область V1 получены следующим образом. Уравнение 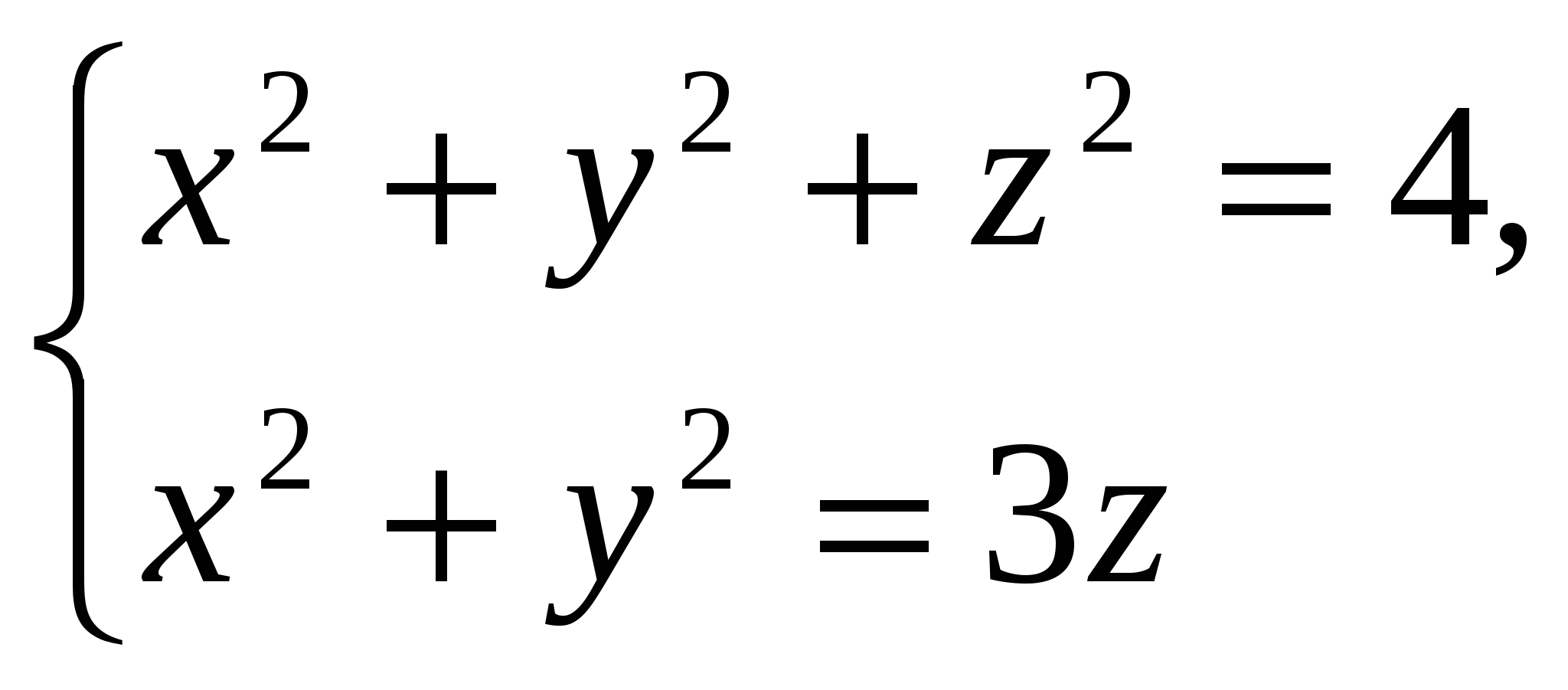 определяется пересечением параболоида
определяется пересечением параболоида 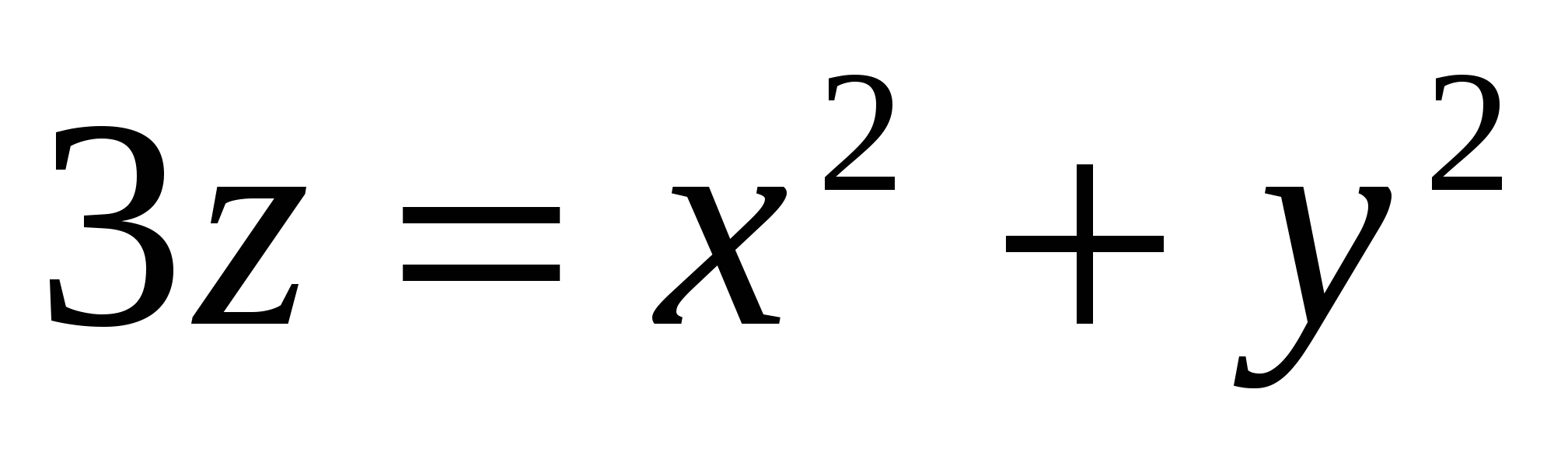 и сферы
и сферы 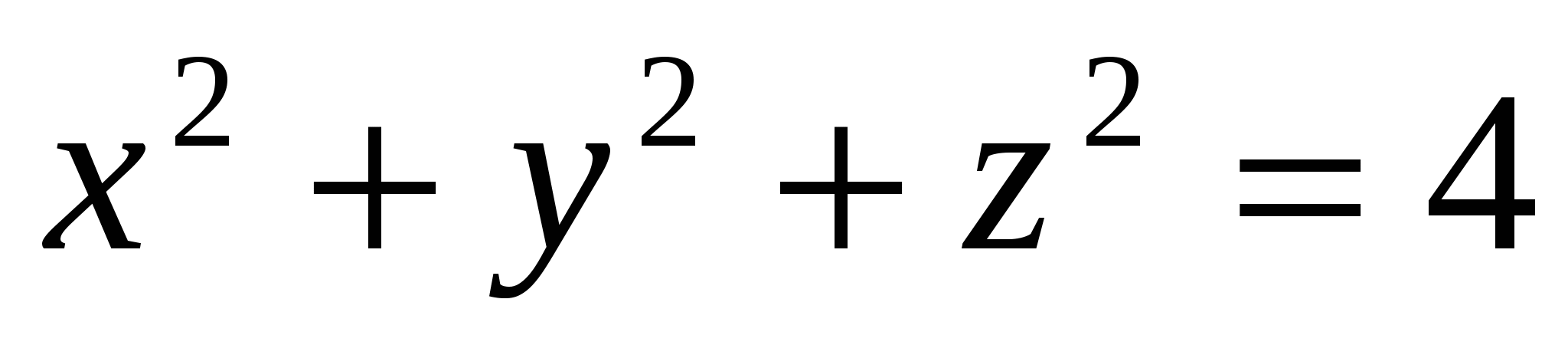 . Откуда,
. Откуда, 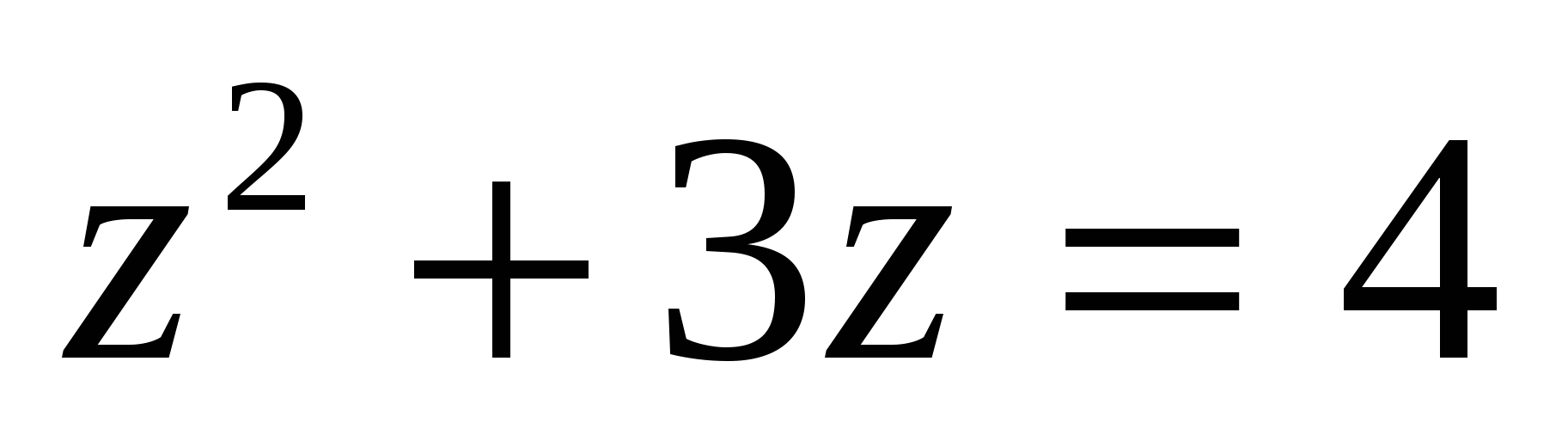 , z=1 и в цилиндрической системе координат
, z=1 и в цилиндрической системе координат 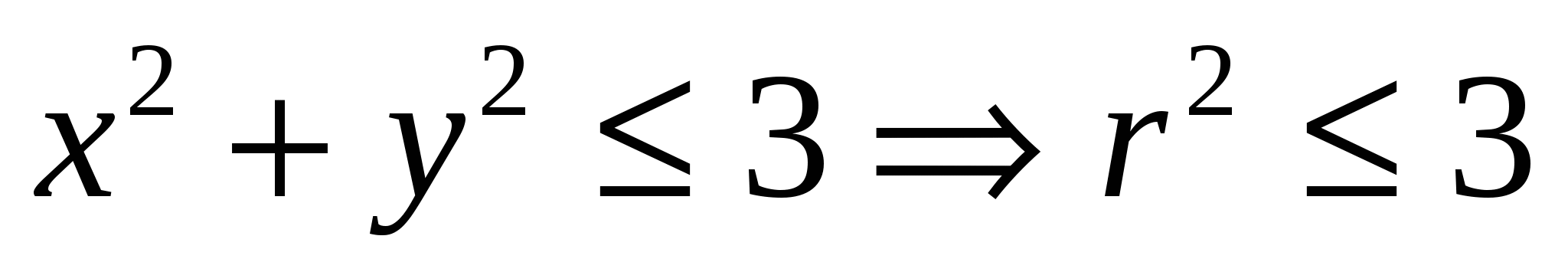 . Следовательно,
. Следовательно, ![]() ; функции
; функции 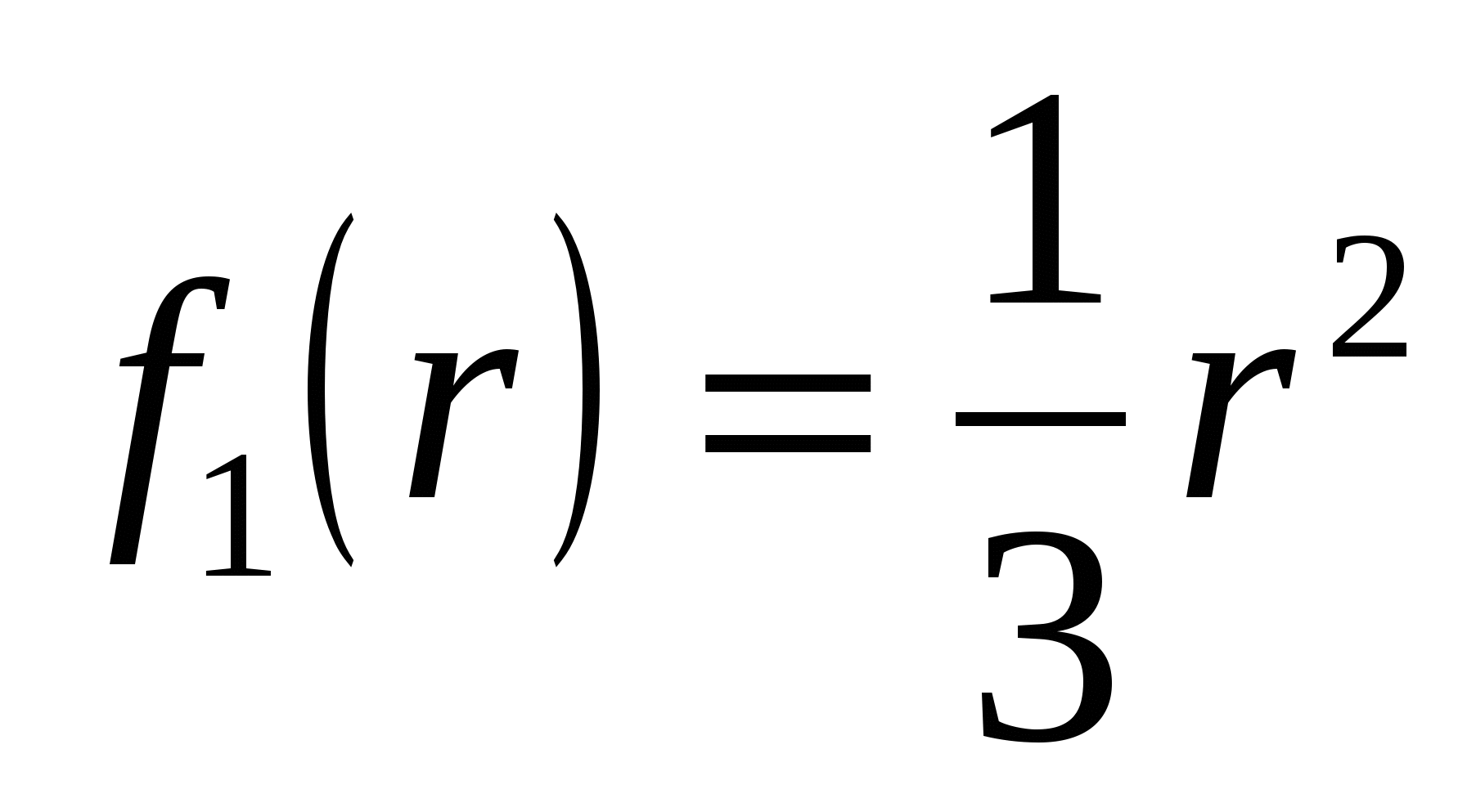 ,
, 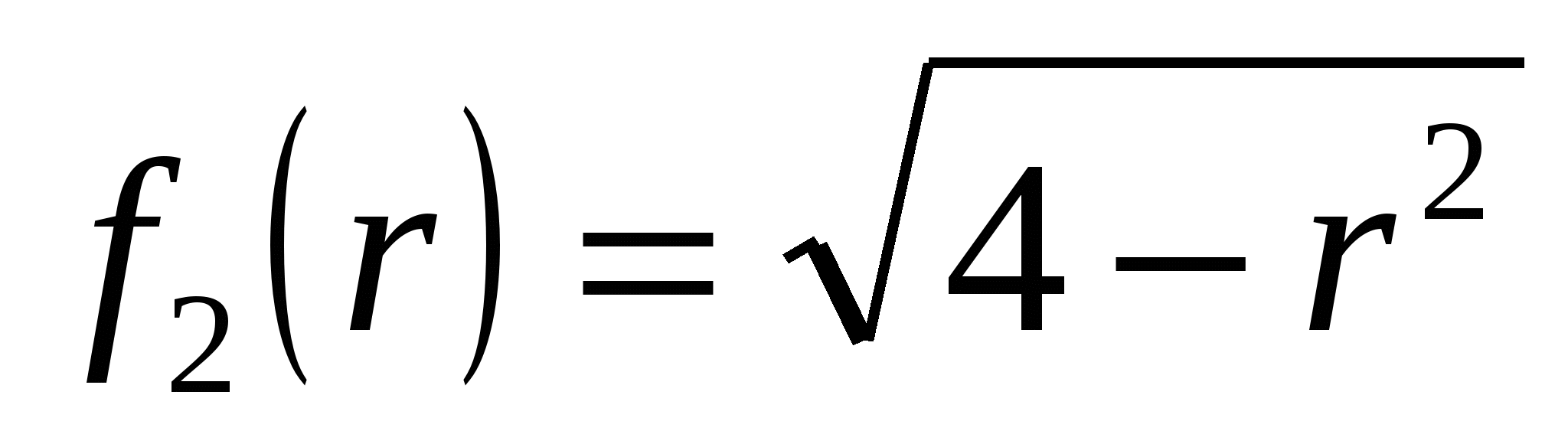 ; а
; а 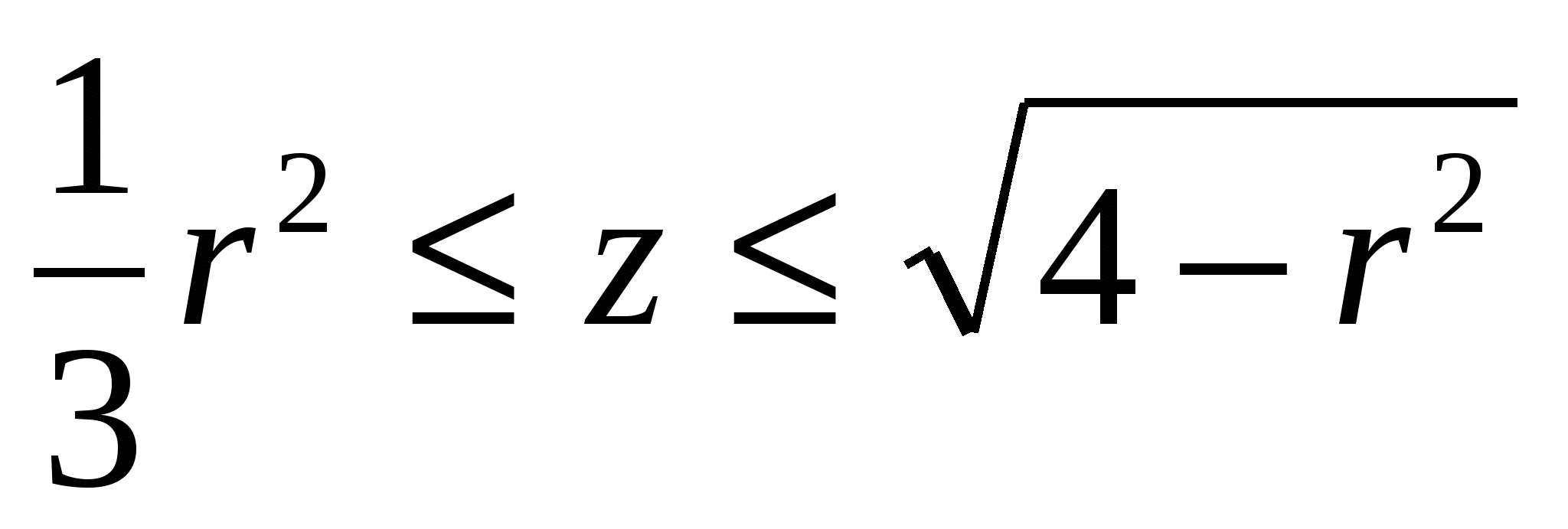 .
.
Необходимо отметить, что при решении данной задачи не было необходимости выполнять чертеж. Достаточно записать неравенства, определяющие область V.
 3.3. Сферическая система координат
3.3. Сферическая система координат
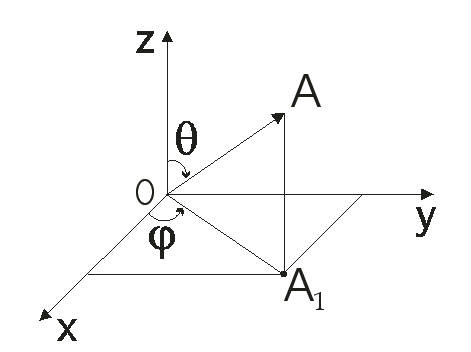
Сферическая система координат определяется так4:
Для любой точки А, с прямоугольными координатами (x ; у, z) не совпадающий с началом координат, проводится радиус- вектор ОА, затем проецируется на плоскость xOy, тогда ОА1 =пр(хоу)ОА = угол отсчитывается от оси Ох, а угол в плоскости ZOA от оси Оz. Тогда три параметра ( , , ) образуют сферическую систему координат.
Величину называют сферическим радиусом, - широтой, - долготой. Для 0 широта и долгота неопределенна.
При =90 сферическая система координат вырождается в полярную.
Если полюс и полярная ось совпадают соответственно с началом O и осью Ox прямоугольной системы координат, то при условии, что для измерения , x, y, z использованы равные единицы масштаба, декартовы и сферические координаты связаны соотношениями.
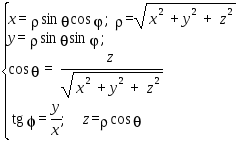 .
.
Стереографической проекцией называется проекция сферы из одного полюса (скажем южного) на касательную плоскость к другому полюсу (северному). Стереографическая проекция является взаимно однозначным отображением сферы с выколотой точкой на плоскость. С ее помощью можно получать плоское изображение сферы (например, земной поверхности или « небесной сферы»), и поэтому ею с давних времен пользуются астрономы и картографы.
И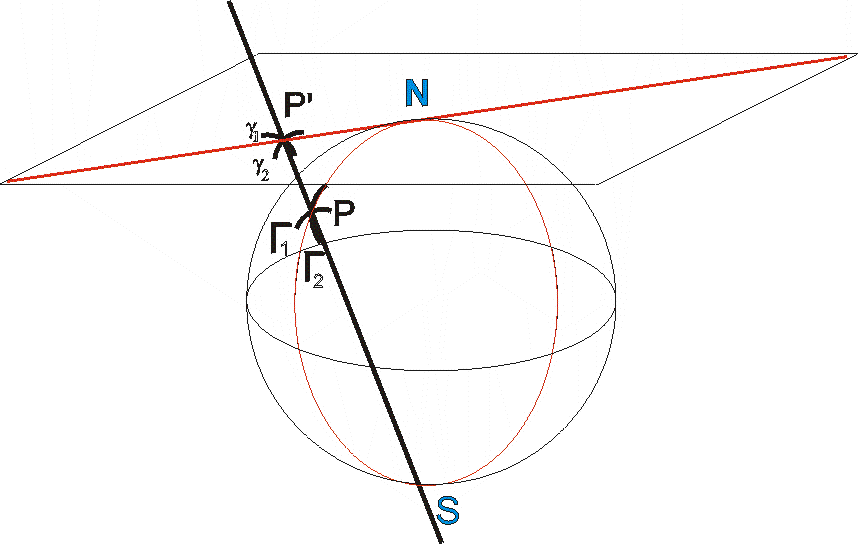 зобретение стереографической проекции обычно приписывают греческому астроному Гиппарху, жившему 160-125 гг. до н. э.; впоследствии, ее использовали навигаторы, кристаллографы, геологи и всесторонне изучали математики. Стереографическая проекция лежит в основе работы астролябии.
зобретение стереографической проекции обычно приписывают греческому астроному Гиппарху, жившему 160-125 гг. до н. э.; впоследствии, ее использовали навигаторы, кристаллографы, геологи и всесторонне изучали математики. Стереографическая проекция лежит в основе работы астролябии.
Первое свойство сферической проекции - оно сохраняет углы между линиями. Рассмотрим, например, пересечение линий Г1 и Г2 на сфере. Угол ( Г1, Г2) измеряется углом между большими окружностями сферы, касающимися кривых Г1, Г2 в точке их пересечения или углом между касательными к этим окружностям прямыми. Пусть Г1 и Г2 перешли при проекции в 12 . Нужно доказать равенство. (Г1 ;Г2) = ( g1 ; g2).
Не нарушая общности, можно предположить, что Г1 проходит через полюсы сферы. Тогда нужно доказать равенство углов UPW и UP'W.
Для этого рассмотрим плоскость = (МSV), параллельную и проходящую через полюс S, и плоскость (MPV), касающуюся сферы в точке Р. Эти плоскости пересекаются по прямой МV и значит, они симметричны относительно плоскости МОV. Отсюда следует равенство углов UPW и TSR. Но из параллельности плоскостей и сразу следует UP'W =TSR, откуда UPW=UP'W.
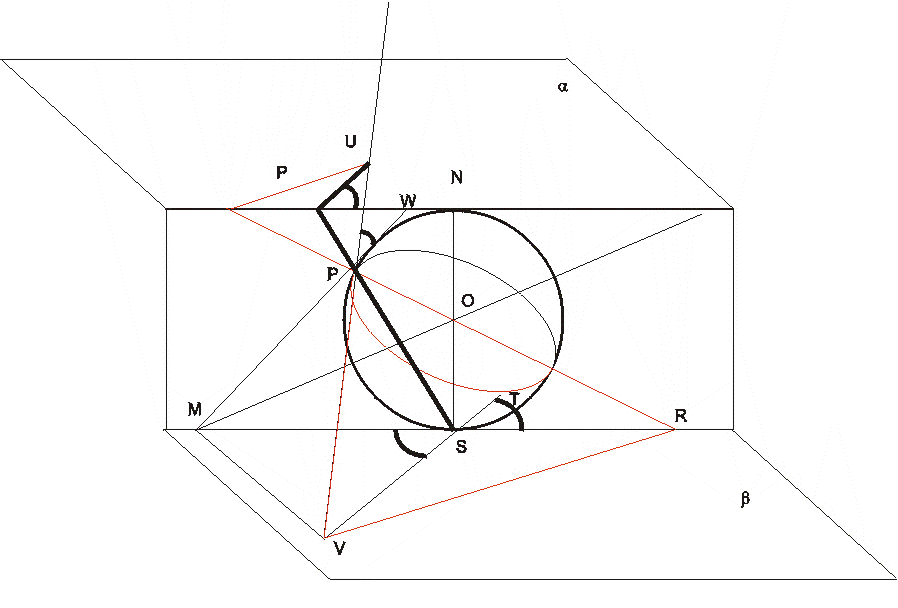 Второе свойство стереографической проекции: окружности на сфере переходят в прямые или окружности на плоскости .
Второе свойство стереографической проекции: окружности на сфере переходят в прямые или окружности на плоскости .
Сразу видно, что окружность на сфере, проходящая через полюс S, отображается на прямую. Покажем, что все другие окружности на сфере стереографическая проекция переводит в окружности на . Для этого вспомним, что плоская кривая, составляющая прямые углы со всевозможными лучами, исходящими из одной точки, является окружностью.
Пусть окружность l проектируется на кривую l', Pl и P' - образ Р. Пусть Q - точка пересечения перпендикуляра к плоскости окружности l , проходящего через ее центр I, и касательной QP к сфере в точке P. Пусть Q' - точка пересечения SQ с . Ясно, что QP l; значит, по первому свойству, QP l' и в силу замечания из предыдущего абзаца это значит, что l' - окружность.
Третье свойство стереографической проекции: при вращении сферы относительно оси, проходящей через точки S и N, стереографическая проекция произвольной точки P на сфере будет вращаться около (SN). Другими словами, параллели сферы проектируются в концентрические окружности плоскости , и проекция вращающейся по параллели точки станет вращаться по такой окружности.
Четвертое свойство стереографической проекции; если Р' - проекция точки Р, то |SP| |SP'| = d2 , где d/2 - радиус сферы. Доказательство легко получить из подобия прямоугольных треугольников SP'N и SPN.
С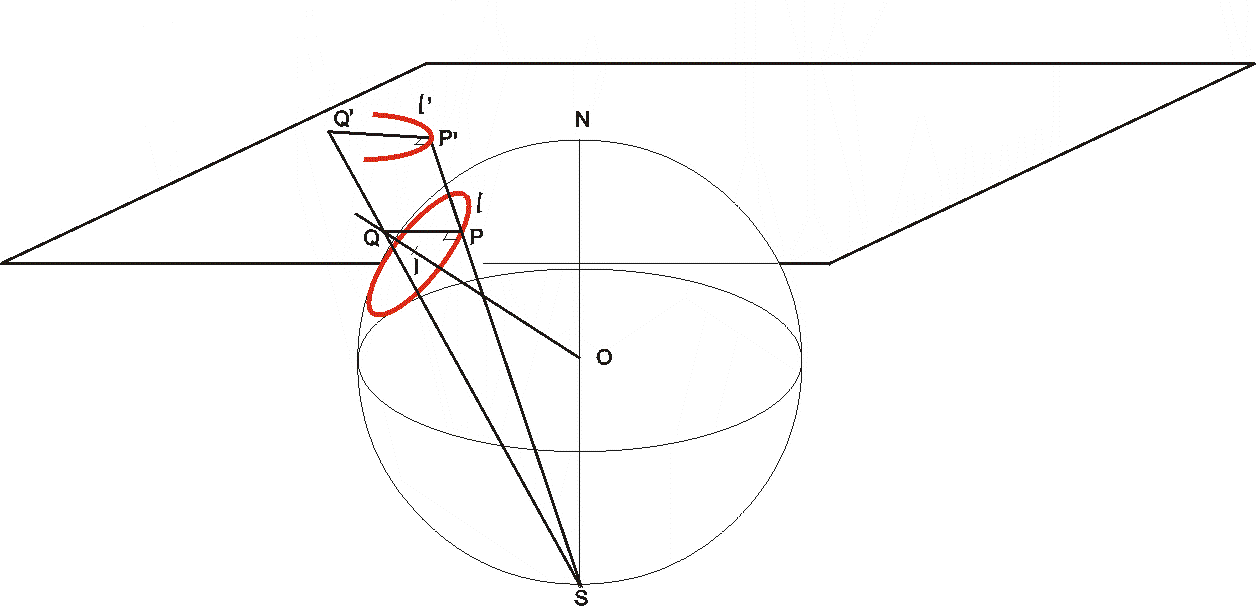 тереографическая проекция и её свойства лежат в основе конструкции и принципа действия астролябии. Название этого прибора означает «схватывают звезды». Схватывание это состоит в измерении координат интересующего нас светила. Сам прибор - сложная металлическая конструкция; он состоит из «паука», вращающегося по криволинейной координатной сетке - «паутине».
тереографическая проекция и её свойства лежат в основе конструкции и принципа действия астролябии. Название этого прибора означает «схватывают звезды». Схватывание это состоит в измерении координат интересующего нас светила. Сам прибор - сложная металлическая конструкция; он состоит из «паука», вращающегося по криволинейной координатной сетке - «паутине».
Пример. Найти объем, ограниченный поверхностями 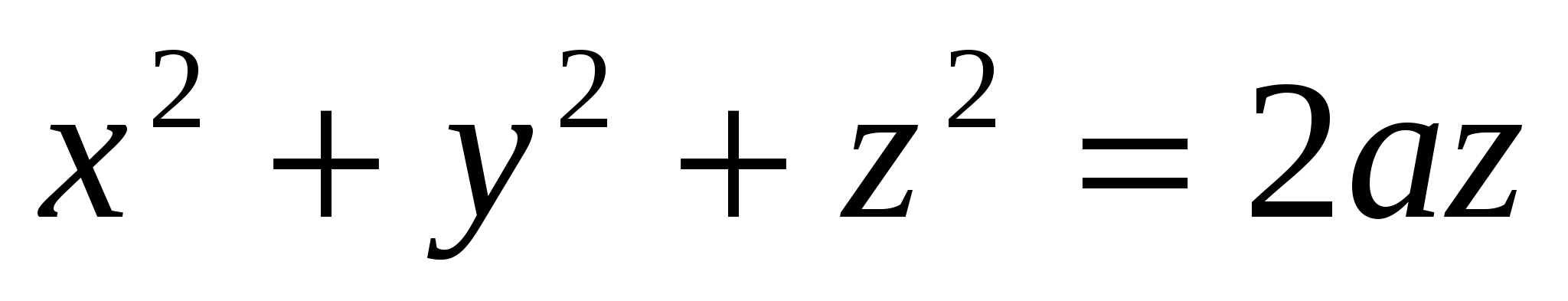 ,
, 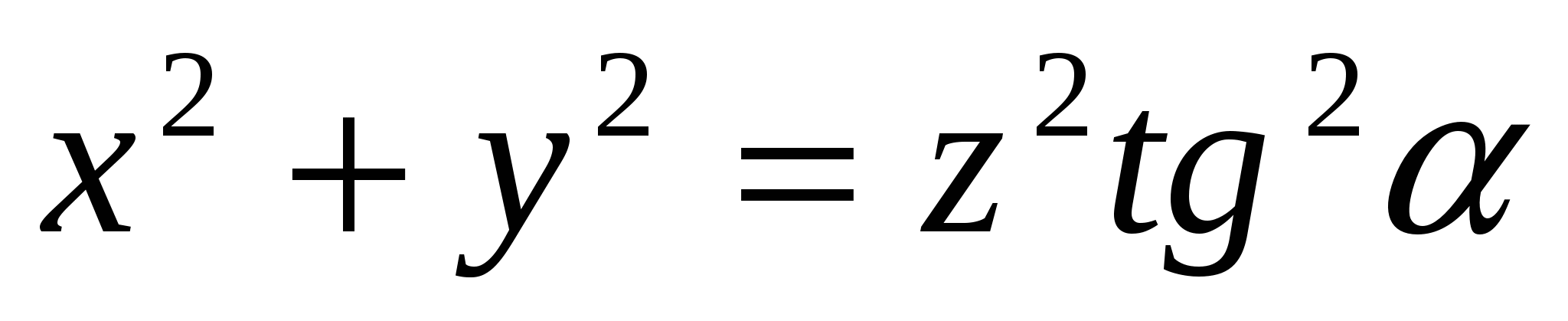 ,
, 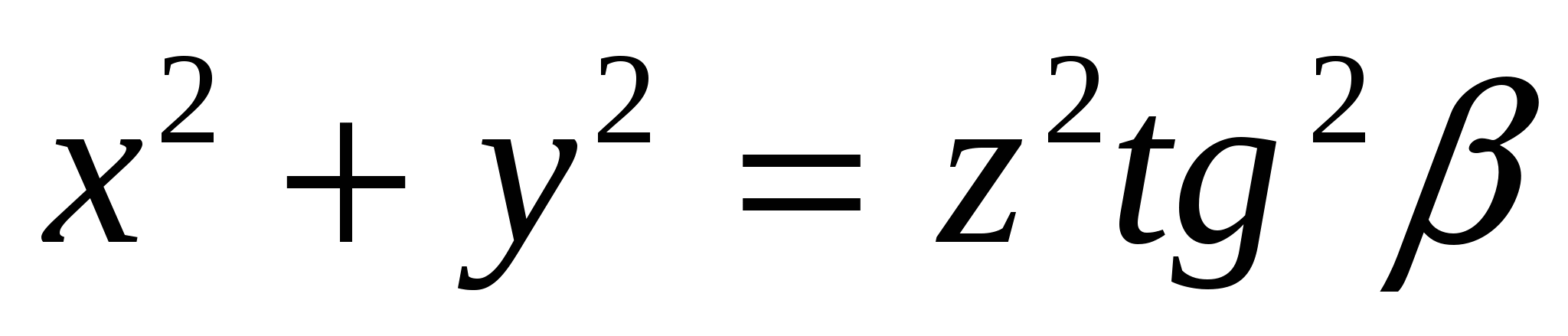 , где α<β.
, где α<β.
Область изменения переменных характеризуется неравенствами: ![]() ,
, 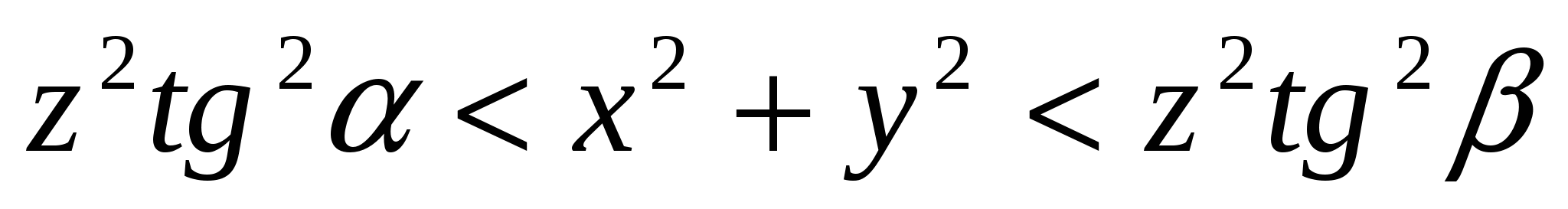 .
.
Решение: Введем сферические координаты по формулам: 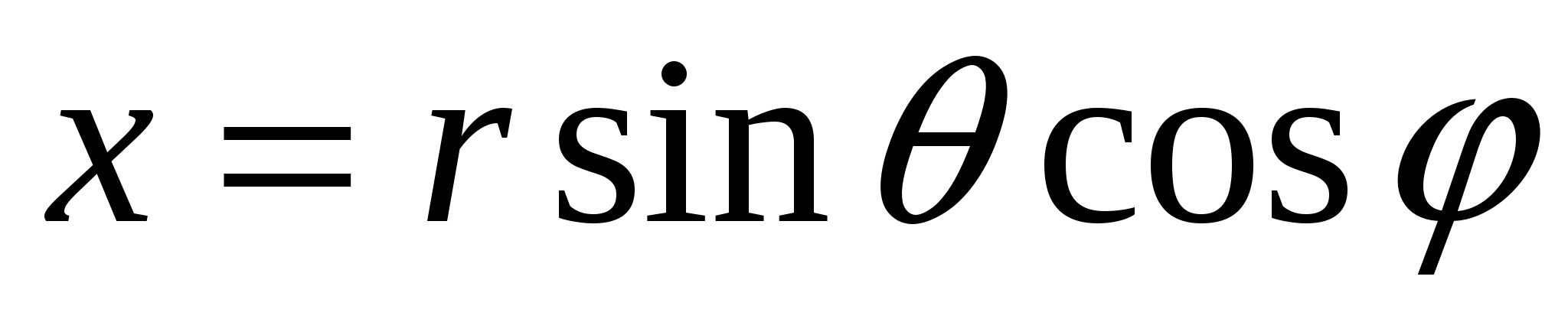 ,
, 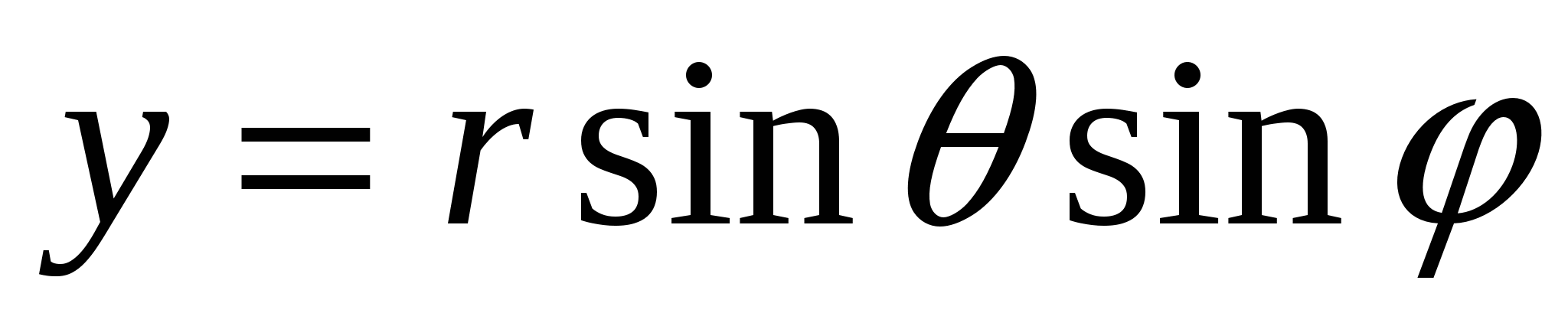 ,
, 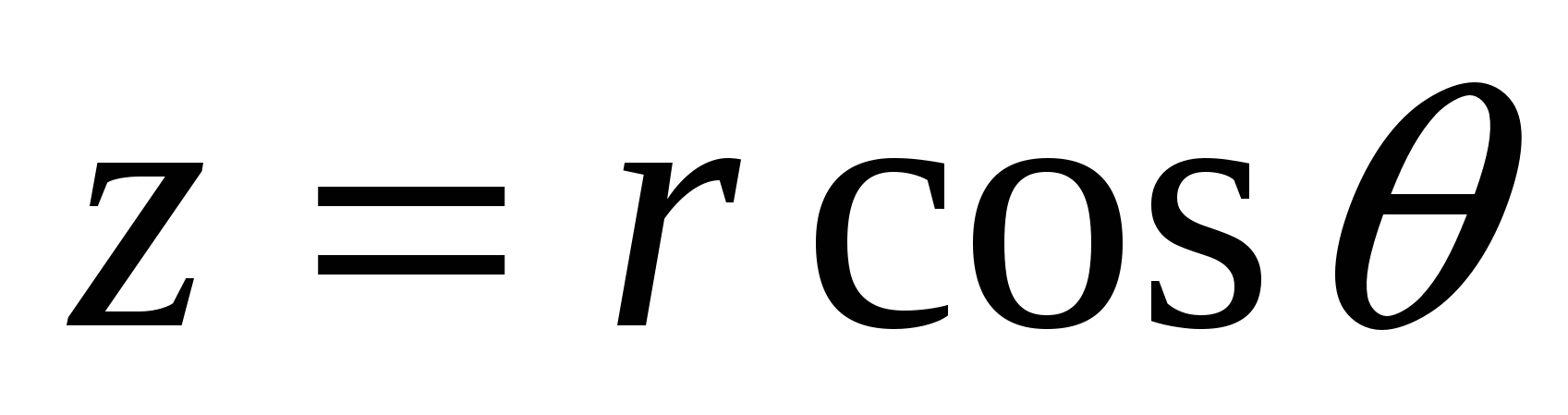 .
.
При этом якобиан удобно вычислить по формуле J=J1J2, где J1 -якобиан преобразования ![]() ,
, 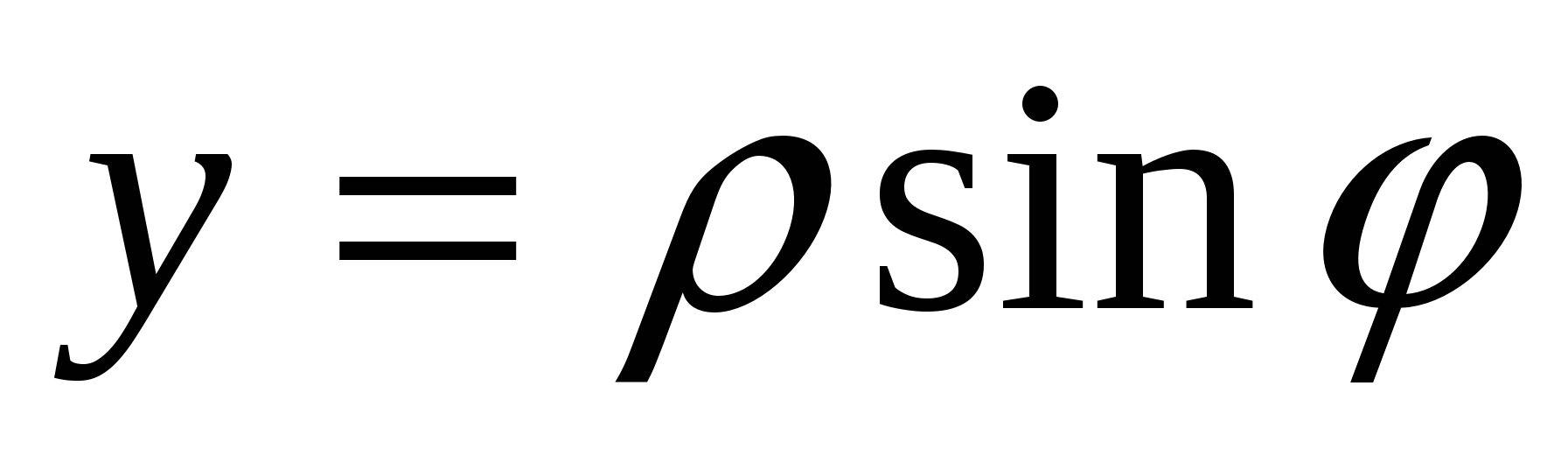 , z=z, равный ρ (J1= ρ), а J2 - якобиан преобразования
, z=z, равный ρ (J1= ρ), а J2 - якобиан преобразования 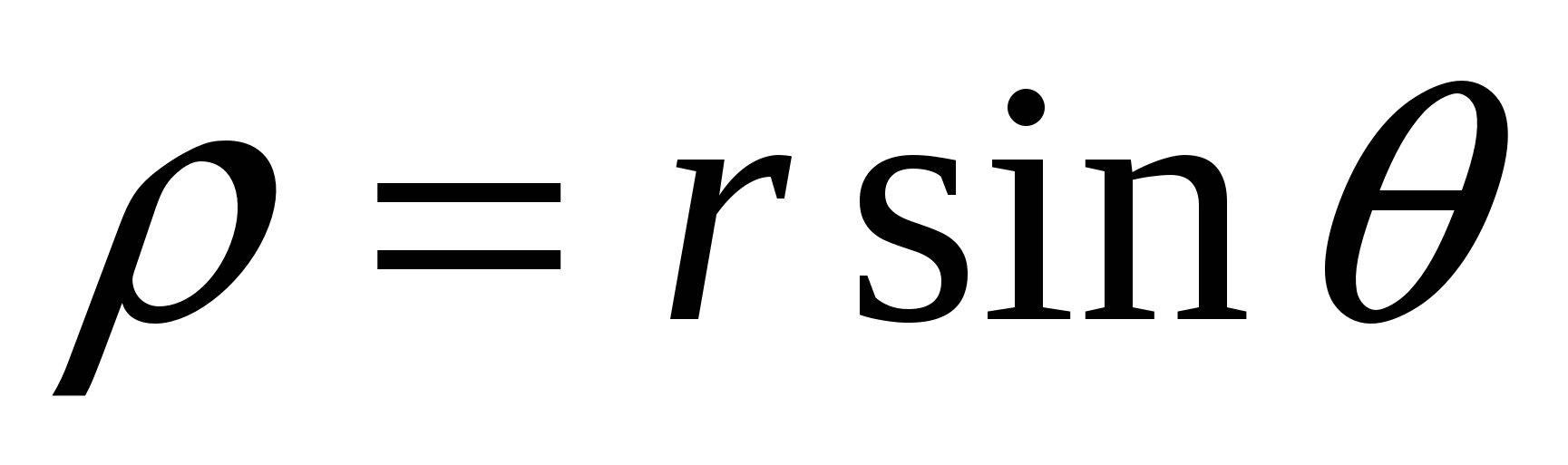 ,
, 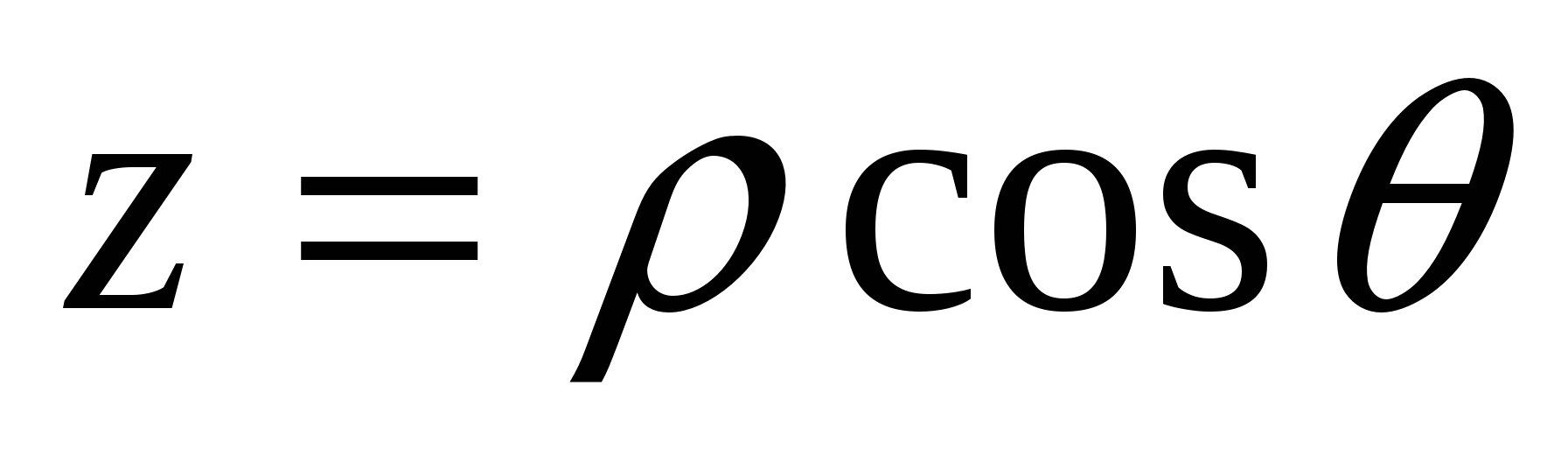 , φ=φ, равный r. Таким образом,
, φ=φ, равный r. Таким образом, 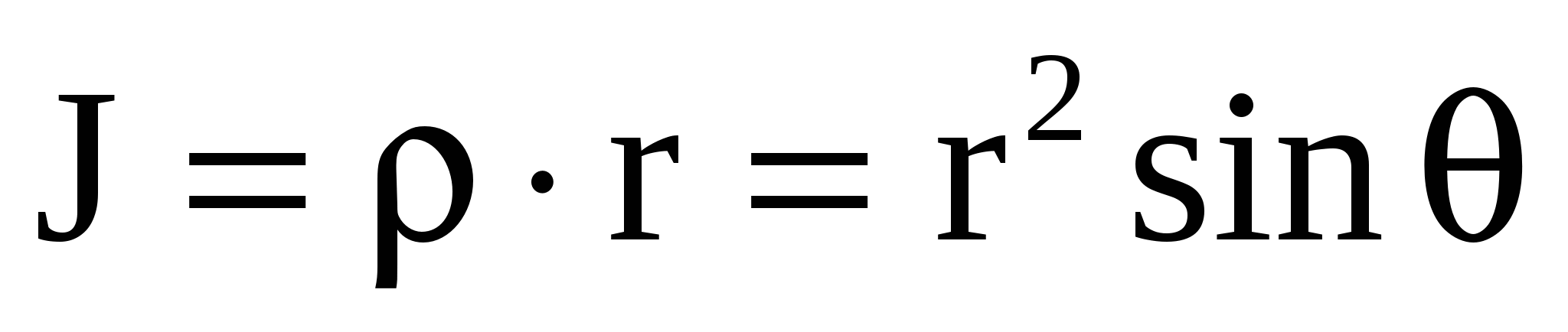 .
.
Область новых переменных характеризуется следующими неравенствами: 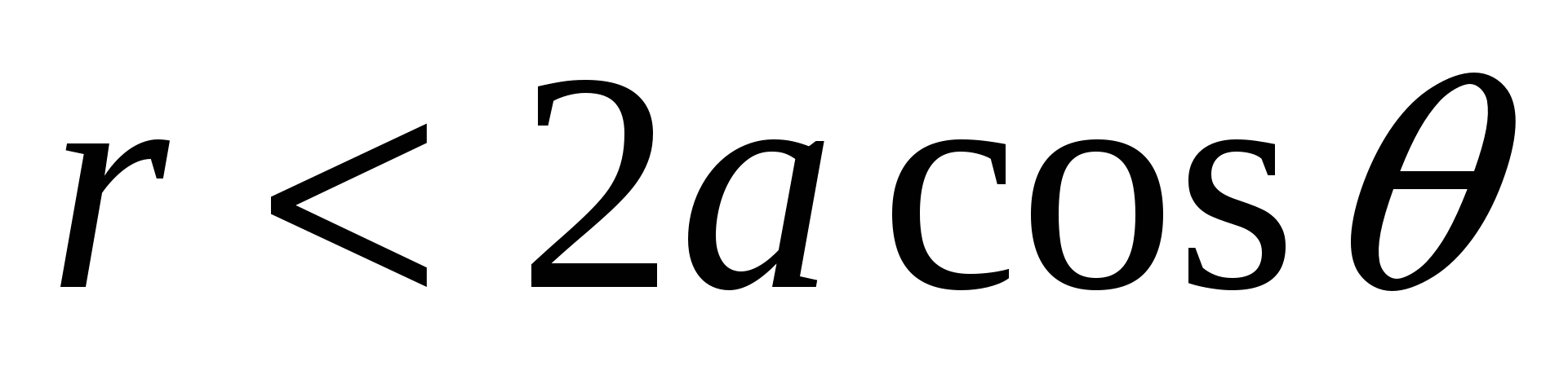 ,
, 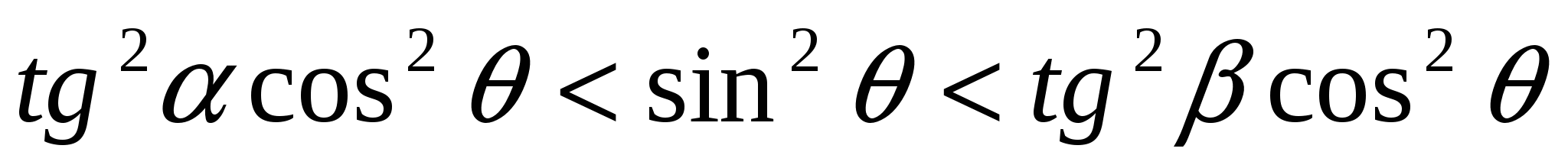 .
.
Так как z>0, то и cos θ>0, поэтому окончательно имеем неравенства: 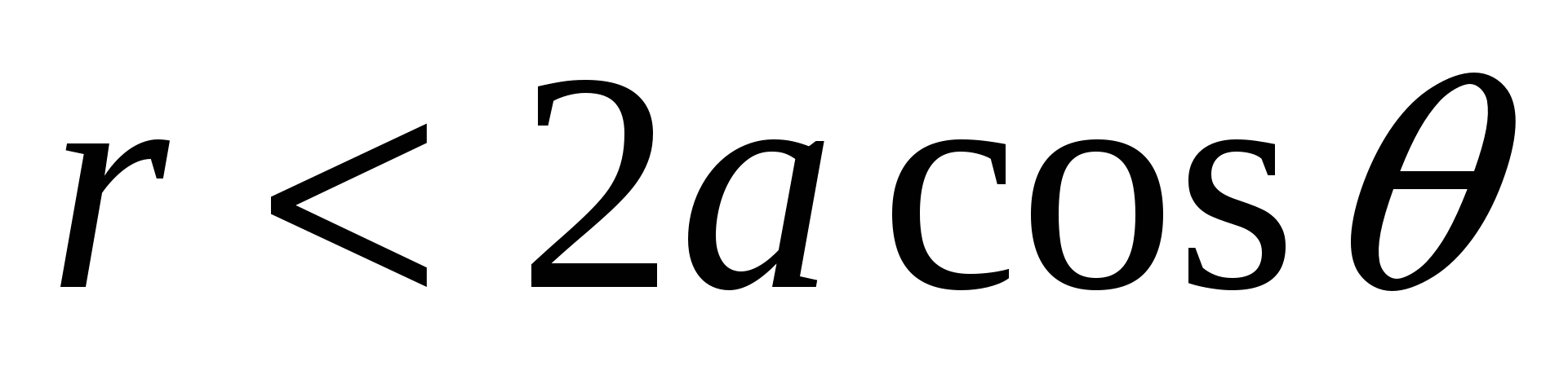 ,
, 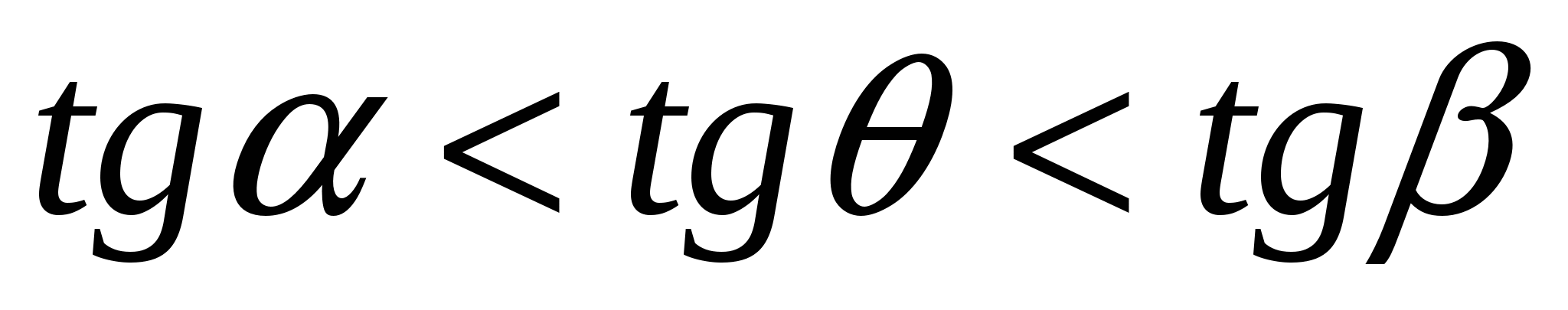 .
.
Таким образом, при любых данных r и θ переменное φ может иметь любые значения от 0 до 2π, переменное r может при данном θ изменяться от 0 до 2acosφ, а угол θ может изменятся от α до β. Итак, объем вычисляем по формуле:
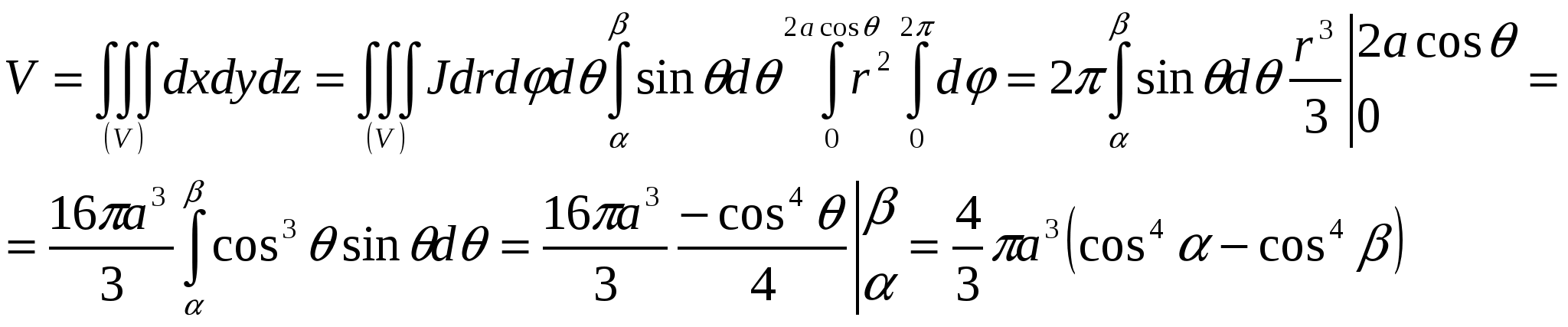
4. Уравнения геометрических мест точек
4.1. Определение геометрического места точек
Геометрическое место точек - это множество всех точек, удовлетворяющих определённым заданным условиям.
Пример 1. Срединный перпендикуляр любого отрезка есть геометрическое место точек (т.е. множество всех точек), равноудалённых от концов этого отрезка. Пусть PO AB и AO = OB:
Тогда, расстояния от любой точки P, лежащей на срединном перпендикуляре PO, до концов A и B отрезка AB одинаковы и равны d. Таким образом, каждая точка срединного перпендикуляра отрезка обладает следующим свойством: она равноудалена от концов отрезка.
Пример2. Окружность - это геометрическое место точек (т.е. множество всех точек), равноудалённых от её центра (одна из этих точек - А).
Тогда отрезок, соединяющий центр окружности с какой-либо её точкой, называется радиусом и обозначается r или R. Часть плоскости, ограниченная окружностью, называется кругом. Часть окружности AmB, называется дугой. Прямая PQ, проходящая через точки M и N окружности, называется секущей, а её отрезок MN, лежащий внутри окружности - хордой. Хорда, проходящая через центр круга например, BC называется диаметром и обозначается d или D. Диаметр - это наибольшая хорда, равная двум радиусам (d = 2r). Предположим, дана точка А (7; 3; 5); эта запись означает, что точка А определяется координатами х = 7, у = 3, z = 5. Если масштаб для построения чертежа задан или выбран, то откладывают на оси х от некоторой точки О отрезок ОАХ, равный 7 единицам, и на перпендикуляре к этой оси, проведенном из точки Ах, отрезки АХА' = 3 ед. и АХА" = 5 ед. Получаем проекции А' и А". Для построения достаточно взять только ось х. Принимая оси проекций за оси координат, можно найти координаты точки по данным ее проекциям. Например, отрезок ОАХ - выражает абсциссу точки А, отрезок АХА' - ее ординату, отрезок АХА" - аппликату. Если задается лишь абсцисса, то этому соответствует плоскость, параллельная плоскости, определяемой осями у и z. Действительно, такая плоскость является геометрическим местом точек, у которых абсциссы равны заданной величине. Если задаются две координаты, то этим определяется прямая, параллельная соответствующей координатной оси.
Например, имея заданными абсциссу и ординату, получаем прямую, параллельную оси z (это прямая АВ). Она является линией пересечения двух плоскостей _ и _, где _ - геометрическое место точек с равными ординатами. Прямая АВ служит геометрическим местом точек, у которых равны между собой абсциссы и равны между собой ординаты. Если задаются все три координаты, то этим определяется точка. Точка К, полученная в пересечении трех плоскостей, из которых _ есть геометрическое место точек по заданной абсциссе, _ - по заданной ординате и _ - по заданной аппликате. Точка может находиться в любом из восьми октантов. Следовательно, нужно знать не только расстояние данной точки от той или иной плоскости координат, но и направление, по которому надо это расстояние отложить; для этого координаты точек выражают относительными числами.
4.2. Определение уравнения геометрического места точек
Уравнением линии называется уравнение с переменными x и y, которому удовлетворяют координаты любой точки этой линии и только они.
Входящие в уравнение линии переменные x и y называются текущими координатами, а буквенные постоянные - параметрами.
Чтобы составить уравнение линии как геометрического места точек, обладающих одинаковым свойством, нужно:
1) взять произвольную (текущую) точку M(x, y) линии;
2) записать равенством общее свойство всех точек M линии;
3) входящие в это равенство отрезки (и углы) выразить через текущие координаты точки M(x, y) и через данные в задаче.
В прямоугольных координатах уравнение прямой на плоскости задается в одном из следующих видов:
1. Уравнение прямой с угловым коэффициентом
y = kx + b, (1)
где k - угловой коэффициент прямой, т. е. тангенс того угла, который прямая образует с положительным направлением оси Ox, причем этот угол отсчитывается от оси Ox к прямой против часовой стрелки, b - величина отрезка, отсекаемого прямой на оси ординат. При b = 0 уравнение (1) имеет вид y = kx и соответствующая ему прямая проходит через начало координат.
Уравнением (1) может быть определена любая прямая на плоскости, не перпендикулярная оси Ox.
Уравнение прямой с угловым коэффициентом разрешено относительно текущей координаты y.
2. Общее уравнение прямой
Ax + By + C = 0. (2)
Частные случаи общего уравнения прямой:
а) Если C = 0, уравнение (2) будет иметь вид
Ax + By = 0,
и прямая, определяемая этим уравнением, проходит через начало координат, так как координаты начала координат x = 0, y = 0 удовлетворяют этому уравнению.
б) Если в общем уравнении прямой (2) B = 0, то уравнение примет вид
Ax + С = 0, или 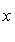
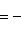
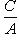 .
.
Уравнение не содержит переменной y, а определяемая этим уравнением прямая параллельна оси Oy.
в) Если в общем уравнении прямой (2) A = 0, то это уравнение примет вид
By + С = 0, или 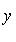
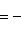
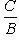 ;
;
уравнение не содержит переменной x, а определяемая им прямая параллельна оси Ox.
Следует запомнить: если прямая параллельна какой-нибудь координатной оси, то в ее уравнении отсутствует член, содержащий координату, одноименную с этой осью.
г) При C = 0 и A = 0 уравнение (2) принимает вид By = 0, или y = 0.
Это уравнение оси Ox.
д) При C = 0 и B = 0 уравнение (2) запишется в виде Ax = 0 или x = 0.
Это уравнение оси Oy.
3. Уравнение прямой в отрезках на осях
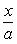
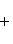
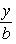
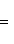
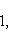 (3)
(3)
где a - величина отрезка, отсекаемого прямой на оси Ox; b - величина отрезка, отсекаемого прямой на оси Oy.
Каждый из этих отрезков отложен от начала координат.
Особенности этого уравнения такие: в левой части уравнения между дробями сосит знак плюс, величины a и b могут быть как положительными, так и отрицательными, правая часть уравнения равна единице.
4. Нормальное уравнение прямой
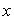
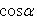
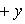
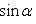
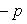
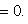 (4)
(4)
Здесь p - длина перпендикуляра, опущенного из начала координат на прямую, измеренная в единицах масштаба, а ![]() - угол, который этот перпендикуляр образует с положительным направлением оси Ox. Отсчитывается этот угол от оси Ox против часовой стрелки. Для приведения общего уравнения прямой (2) к нормальному виду обе его части надо умножить на нормирующий множитель:
- угол, который этот перпендикуляр образует с положительным направлением оси Ox. Отсчитывается этот угол от оси Ox против часовой стрелки. Для приведения общего уравнения прямой (2) к нормальному виду обе его части надо умножить на нормирующий множитель:
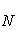
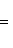
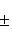
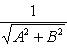
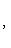 (5)
(5)
причем перед дробью следует выбрать знак, противоположный знаку свободного члена C в общем уравнении прямой (2).
Особенности нормального уравнения прямой: сумма квадратов коэффициентов при текущих координатах равна единице, свободный член отрицателен, а правая его часть равна нулю.
5. Построение прямой по ее уравнению
Прямая вполне определена, если известны две принадлежащие ей точки. Для того чтобы построить прямую по ее уравнению, надо, пользуясь этим уравнением, найти координаты двух ее точек. Твердо следует помнить, что если точка принадлежит прямой, то координаты этой точки удовлетворяют уравнению прямой.
При практическом построении прямой по ее уравнению наиболее точный график получится тогда, когда координаты взятых для ее построения двух точек - целые числа.
Если прямая определена общим уравнением Ax + By + C = 0 и 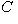
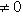 , то для ее построения проще всего определить точки пересечения прямой с координатными осями.
, то для ее построения проще всего определить точки пересечения прямой с координатными осями.
Укажем, как определить координаты точек пересечения прямой с координатными осями. Координаты точки пересечения прямой с осью Ox находят из следующих соображений: ординаты всех точек, расположенных на оси Ox, равны нулю. В уравнении прямой полагают, что y равно нулю, и из полученного уравнения находят x. Найденное значение x и есть абсцисса точки пересечения прямой с осью Ox. Если окажется, что x = a, то координаты точки пересечения прямой с осью Ox будут (a, 0).
Чтобы определить координаты точки пересечения прямой с осью Oy, рассуждают так: абсциссы всех точек, расположенных на оси Oy, равны нулю. Взяв в уравнении прямой x равным нулю, из полученного уравнения определяют y. Найденное значение y и будет ординатой пересечения прямой с осью Oy. Если окажется, например, что y = b, то точка пересечения прямой с осью Oy имеет координаты (0, b).
Пример 1. Прямая 2x + y - 6 = 0 пересекает ось Ox в точке (3, 0). Действительно, взяв в этом уравнении y = 0, получим для определения x уравнение 2x - 6 = 0, откуда x = 3.
Чтобы определить точку пересечения этой прямой с осью Oy, положим в уравнении прямой x = 0. Получим уравнение y - 6 = 0, из которого следует, что y = 6. Таким образом, прямая пересекает координатные оси в точках (3, 0) и (0, 6).
Если же в общем уравнении прямой C = 0, то прямая, определяемая этим уравнением, проходит через начало координат. Таким образом, уже известна одна ее точка, и для построения прямой остается только найти еще одну ее точку. Абсциссу x этой точки задают произвольно, а ординату y находят из уравнения прямой.
Пример 2. Прямая 2x - 4y = 0 проходит через начало координат. Вторую точку прямой определим, взяв, например, x = 2. Тогда для определения y получаем уравнение 2*2 - 4y = 0; 4y = 4; y = 1. Итак, прямая 2x - 4y = 0 проходит через точки (0, 0) и (2, 1).
Если прямая задана уравнением y = kx + b с угловым коэффициентом, то из этого уравнения уже известна величина отрезка b, отсекаемого прямой на оси ординат, и для построения прямой остается определить координаты еще только одной точки, принадлежащей этой прямой. Если в уравнении y = kx + b 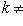
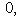
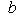
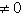 , то легче всего определить координаты точки пересечения прямой с осью Ox. Выше было указано, как это сделать.
, то легче всего определить координаты точки пересечения прямой с осью Ox. Выше было указано, как это сделать.
Если же в уравнении y = kx + b b = 0, то прямая проходит через начало координат, и тем самым уже известна одна принадлежащая ей точка. Чтобы найти еще одну точку, следует дать x любое значение и определить из уравнения прямой значение y, соответствующее этому значению x.
5. Применение и значение метода координат
Мысль о возможности систематического применения метода координат в научных исследованиях зародилась несколько тысяч лет тому назад. Известно, например, что астрономы древнего мира, используя специальные системы координат на воображаемой небесной сфере, определяли положение наиболее ярких звёзд, составляли карты звёздного неба, вели отличавшиеся большой точностью наблюдения за перемещением Солнца, Луны и планет относительно неподвижных звёзд. В более позднюю эпоху широко развилось использование системы географических координат для составления карт земной поверхности и определения местонахождения корабля в открытом море. Однако до XVII века применение метода координат имело односторонний характер: им пользовались, по сути, только для указания положения определённого объекта - неподвижного (гора, мыс) или движущегося (корабль, планета).
Метод координат представляет собой глубокий и мощный аппарат, позволяющий привлекать для исследования геометрических объектов. Благодаря универсальности подхода к решению различных задач, метод аналитической геометрии стал основным методом геометрических исследований и широко применяется в других областях точного естествознания - механике, физике.
Сферическая система координат широко применяется в астрономии, в частности при расчетах траектории движения спутников и других объектов. Пример ее использования астролябия.
Стереографическая проекция является взаимно однозначным отображением сферы с выколотой точкой на плоскость. С ее помощью можно получать плоское изображение сферы (например, земной поверхности или « небесной сферы»), и поэтому ею с давних времен пользуются астрономы и картографы.
Изобретение стереографической проекции обычно приписывают греческому астроному Гиппарху, жившему 160-125 гг. до н. э.; впоследствии, ее использовали навигаторы, кристаллографы, геологи и всесторонне изучали математики. Стереографическая проекция лежит в основе работы астролябии.
Полярная система координат двумерная и поэтому может применяться только в тех случаях, когда местонахождение точки определяется на плоскости, или для случая однородности свойств системы в третьем измерении, например, при рассмотрении течения в круглой трубе. Лучшим контекстом применения полярных координат являются случаи, тесно связанные с направлением и расстоянием от некоторого центра. Например, в приведённых выше примерах видно, что простых уравнений в полярных координатах достаточно для определения таких кривых как спираль Архимеда, уравнения которых в прямоугольной системе координат гораздо сложнее. Кроме того, многие физических системы - такие, которые содержат тела, движущиеся вокруг центра, либо явления, распространяющиеся из некоторого центра - гораздо проще моделировать в полярных координатах. Причиной создания полярной системы координат было исследование орбитального и движения по кругу.
Полярную систему координат часто применяют в навигации, поскольку пункт назначения можно задать как расстояние и направление движения от отправной точки. Например, в авиации, для навигации применяют несколько изменённую версию полярных координат. 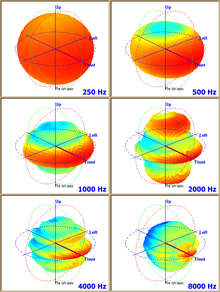
Системы с радиальной симметрией очень хорошо подходят для описания в радиальных координатах, где полюс системы координат совпадает с центром симметрии. В качестве примера можно привести уравнение тока грунтовых вод в случае радиально симметричных колодцев. Системы с центральными силами также подходят для моделирования в полярных координатах. К таким системам относятся гравитационные поля, подчиняющиеся закону обратно-квадратичной зависимости, так и системы с точечными источниками энергии, такие как радиоантенны.
Фронт мощности звуковой волны промышленного громкоговорителя показан в сферических полярных координатах при шести частотах. Трёхмерное моделирование звука динамиков может использоваться для прогнозирования их эффективности. Необходимо сделать несколько диаграмм в 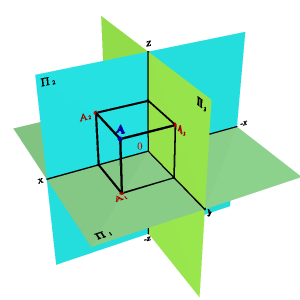 полярных координатах для широкого диапазона частот, поскольку фронт существенно меняется в зависимости от частоты звука. Полярные диаграммы помогают увидеть, что многие громкоговорители с понижением частоты звука теряют направленность.
полярных координатах для широкого диапазона частот, поскольку фронт существенно меняется в зависимости от частоты звука. Полярные диаграммы помогают увидеть, что многие громкоговорители с понижением частоты звука теряют направленность.
В инженерной деятельности при изучении свойств геометрических объектов используют прямоугольную систему координат, отличающуюся от декартовой системы координат, применяемой в математике, направлением осей.
Заключение
Трудно переоценить значение декартовой системе координат в развитии математики и её приложений. Огромное количество задач, требовавших для решения геометрической интуиции, специфических методов получило решение, состоящее в аккуратном проведении алгебраических выкладок. Метод координат лежит в основе расчетов сложных физических процессов, траектории движения космических и наземных объектов и т.д.
Сферическая и полярная системы координат иногда бывают удобней прямоугольной декартовой, особенно в задачах, связанных с окружностями или дугами кривых. Метод координат позволяет быстро и красиво решать сложные геометрические задачи, он имеет ряд преимуществ по сравнению с векторным методом, даёт наглядное представление на координатной плоскости и в пространстве сложных зависимостей, выраженных формулами, уравнениями. Графики функций позволяют описать свойства этих функций. Многие линии, фигуры можно описать в координатах. Векторный и координатный методы тесно связаны друг с другом. Выбор зависит от условия задачи, поставленного вопроса. Нельзя сказать, что какой-то из методов решения лучше или проще для целой серии задач. Выбор системы координат для конкретных задач более конкретен.
При практическом применении понятия координат координаты предмета, рассматриваемого условно как точка, могут быть определены лишь приближённо. Задание координат предмета означает, что точка, определяемая этими координатами, либо является одной из точек этого предмета либо достаточно близка к нему.
В результате исследования можно сделать вывод, что метод координат (и математика в целом) развивается исходя из практических нужд. В том числе метод координат играет огромную роль не только в геометрии, алгебре, математическом анализе, но и в таких направлениях как физика, динамика, география, астрономия, механика и многие др.
Список литературы
-
Моденов П.С., Аналитическая геометрия, М., 1969.
-
Атанасян Л.С., Геометрия, часть 1, М., Просвещение, 1967.
-
Атанасян Л.С., Геометрия, часть 1, Учебное пособие для студентов математических факультетов педагогических институтов, М., Просвещение, 1973.
-
Выгодский М.Я., Справочник по высшей математике, М., 1972.
-
Понтрягин Л.С., Метод координат. М., Наука, 1977.
-
Ефимов Н.В., Краткий курс аналитической геометрии, 9 изд., М., Наука, 2003.
-
Ильин В.А., Позняк Э.Г. Аналитическая геометрия, М., ФИЗМАТЛИТ, 2003.
-
Атанасян Л.С., Базылев В.Т. и др., Геометрия, М., Просвещение, 1986.
-
Погорелов А.В., Аналитическая геометрия, 4 изд., М., Наука, 2004.
-
Постников М.М., Аналитическая геометрия, М., Техника, 2004.
-
Энциклопедия элементарной математики. Геометрия, том 4
-
Атанасян Л.С., Сборник задач по геометрии, часть 1, М., 1973.
-
Базылев В.Т. и др., Сборник задач по геометрии, М., 1980.
-
Прасолов В.В., Задачи по стереометрии, М., 1989.
-
Прасолов В.В., Задачи по планиметрии, часть 2, М., 1986.
-
Интернет ресурс: matschool2005.narod.ru/Lessons/Lesson8.htm
Приложение 1. Задачи, решаемые методом координат с решениями.
Задача 1. Даны уравнения одной из сторон ромба х-3у + 10 = 0 и одной из его
диагоналей х + 4у - 4 = 0; диагонали ромба пересекаются в точке (0; 1). Найти уравнение остальных сторон ромба.
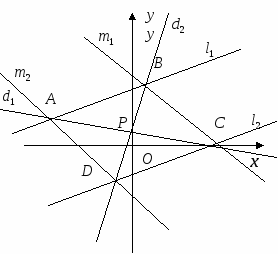
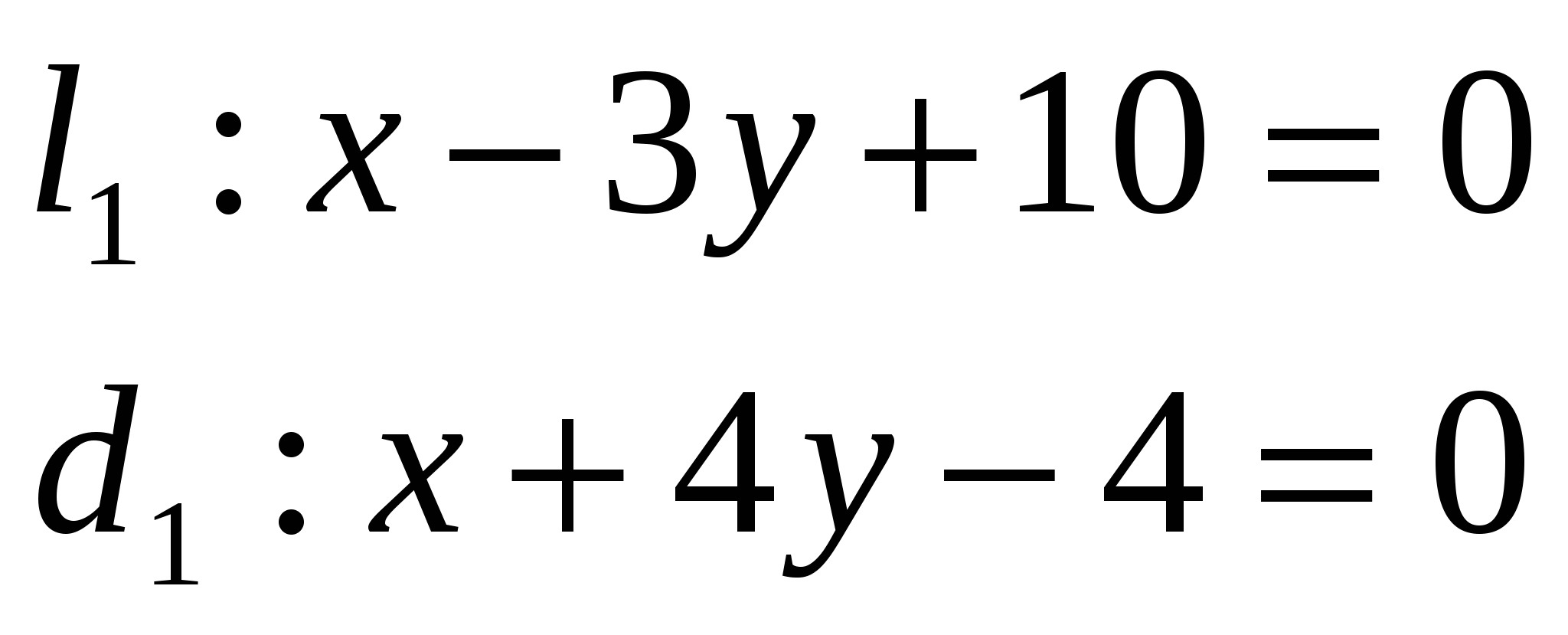
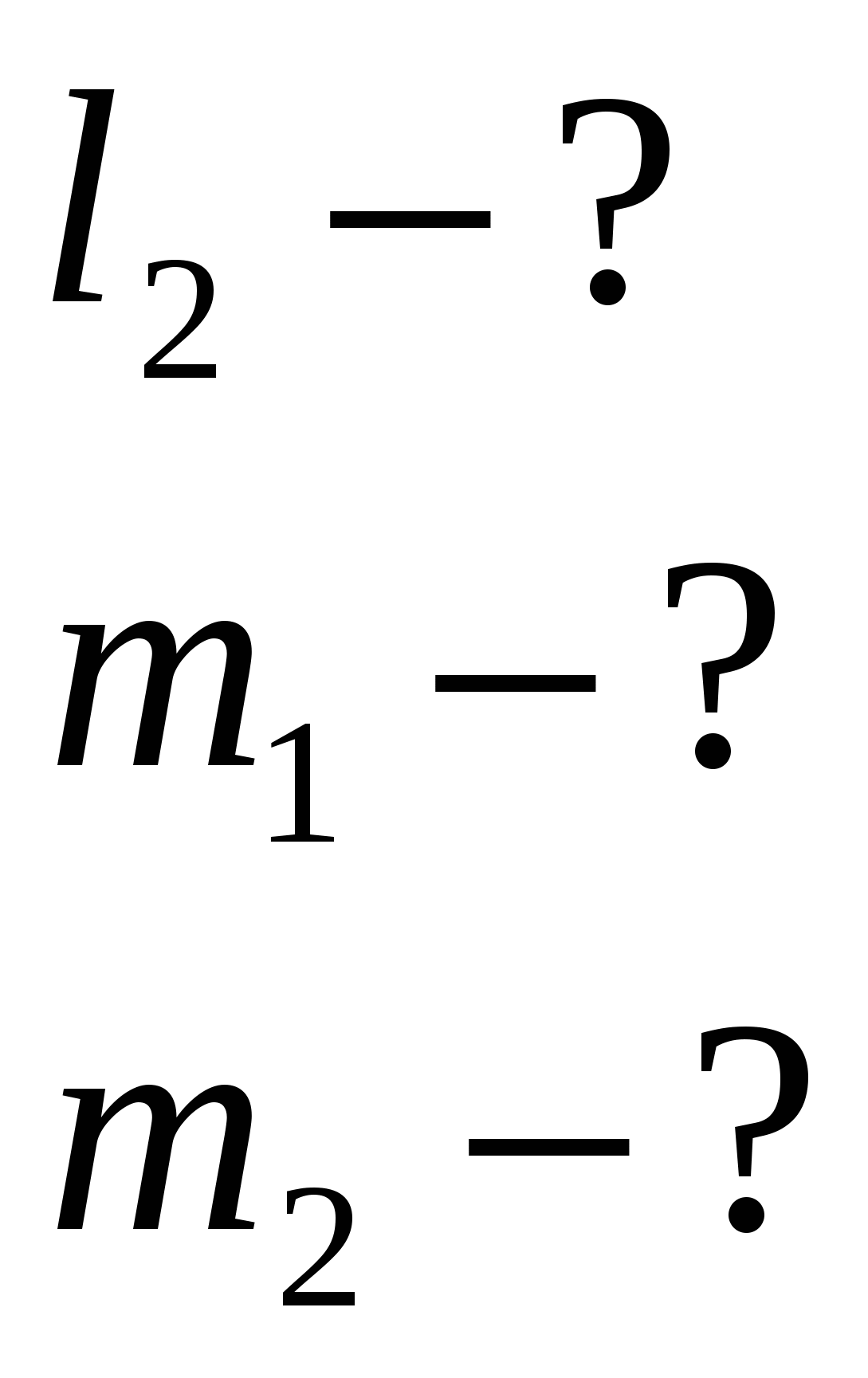
Решение:
Найдем т. пересечения 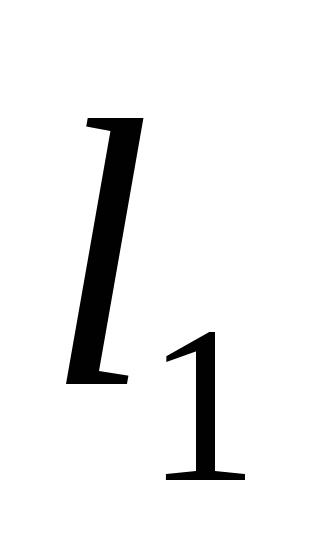 и
и 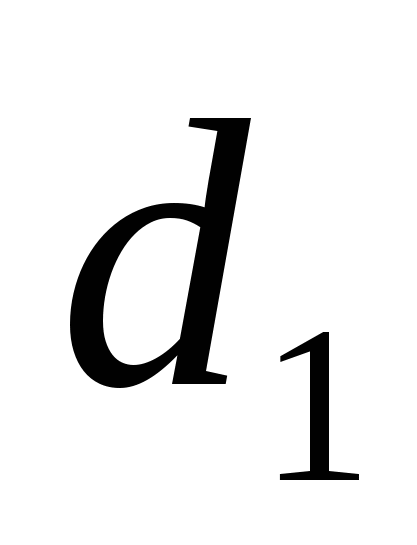 :
: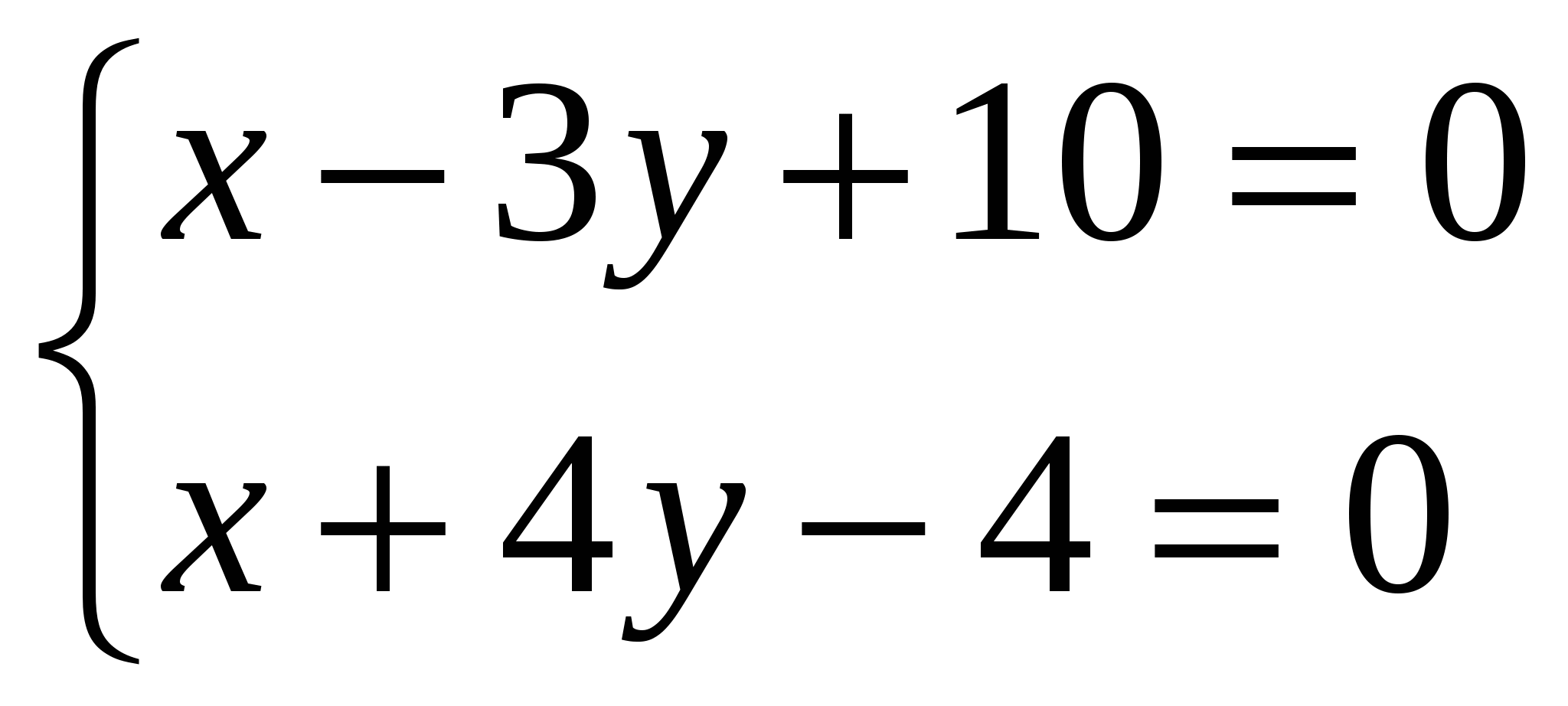
![]()

 =>
=> 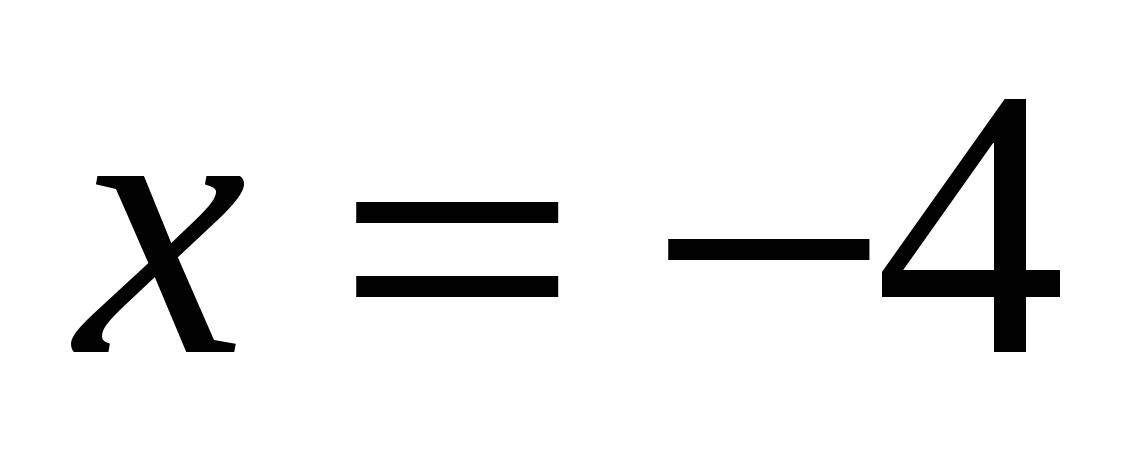 A(-4;2)
A(-4;2)
Т.к P - середина отрезка AC, то
![]()
![]() => C(4;0). Через точку C направим прямую, параллельную
=> C(4;0). Через точку C направим прямую, параллельную 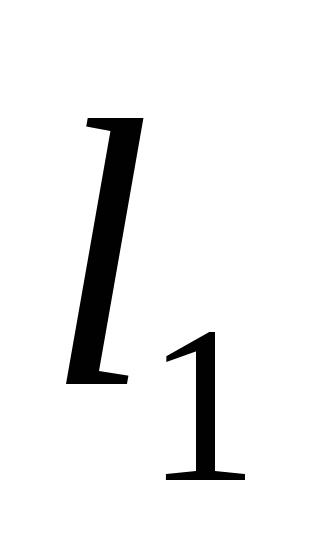 (т.е. найдем
(т.е. найдем 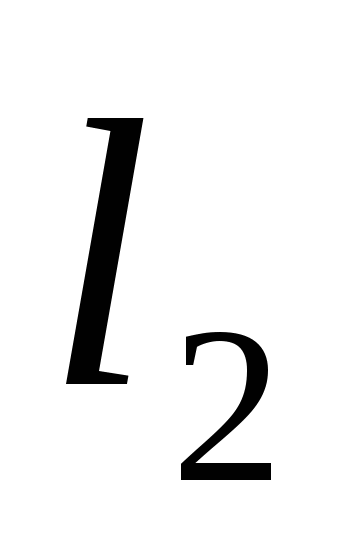 ).
). 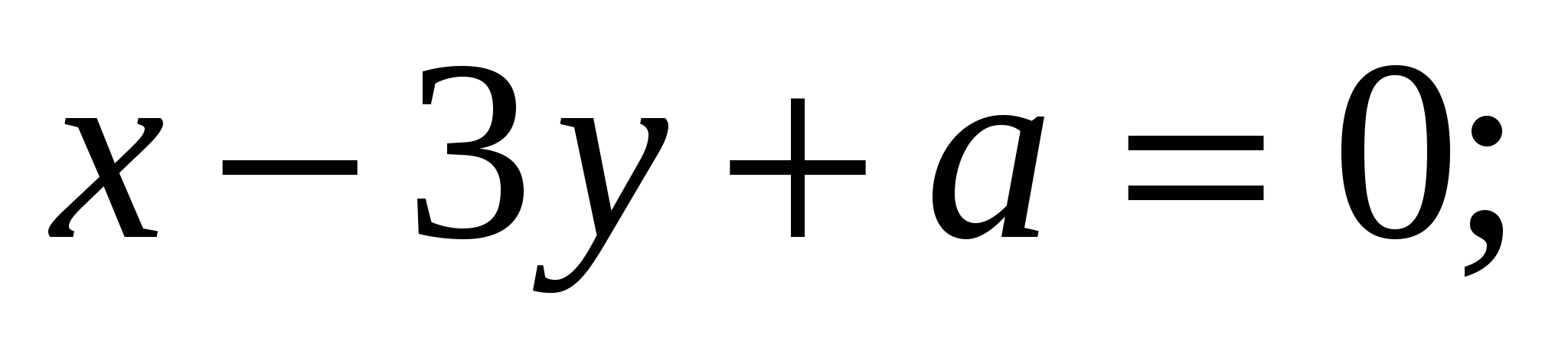
 =>
=> 
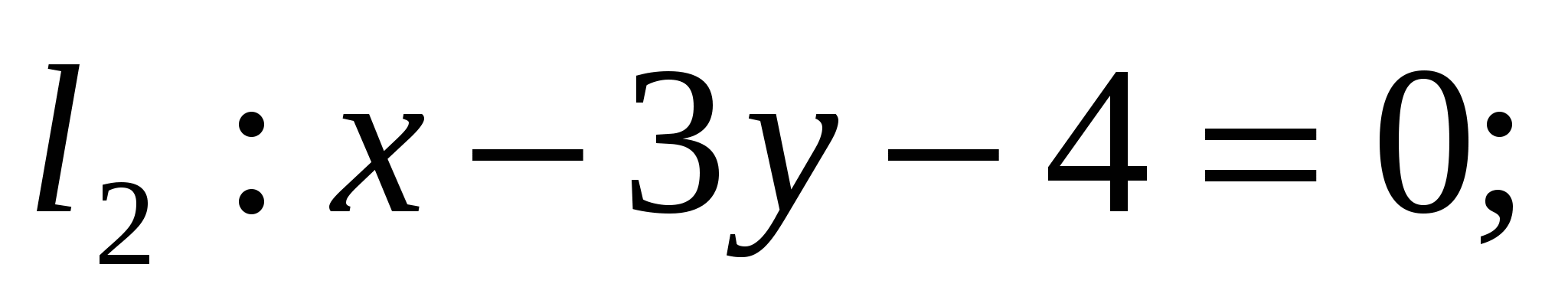 По свойству ромба:
По свойству ромба: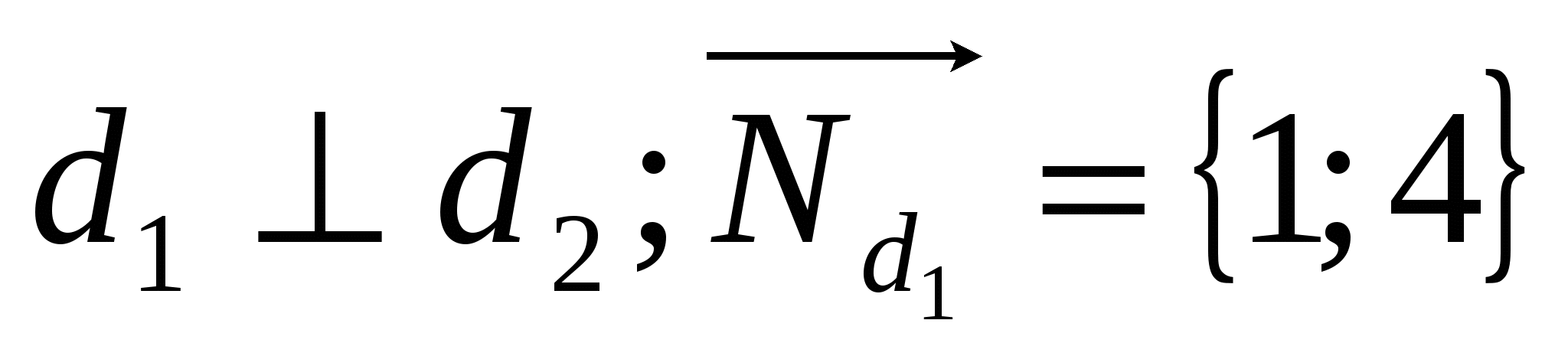 =>
=> 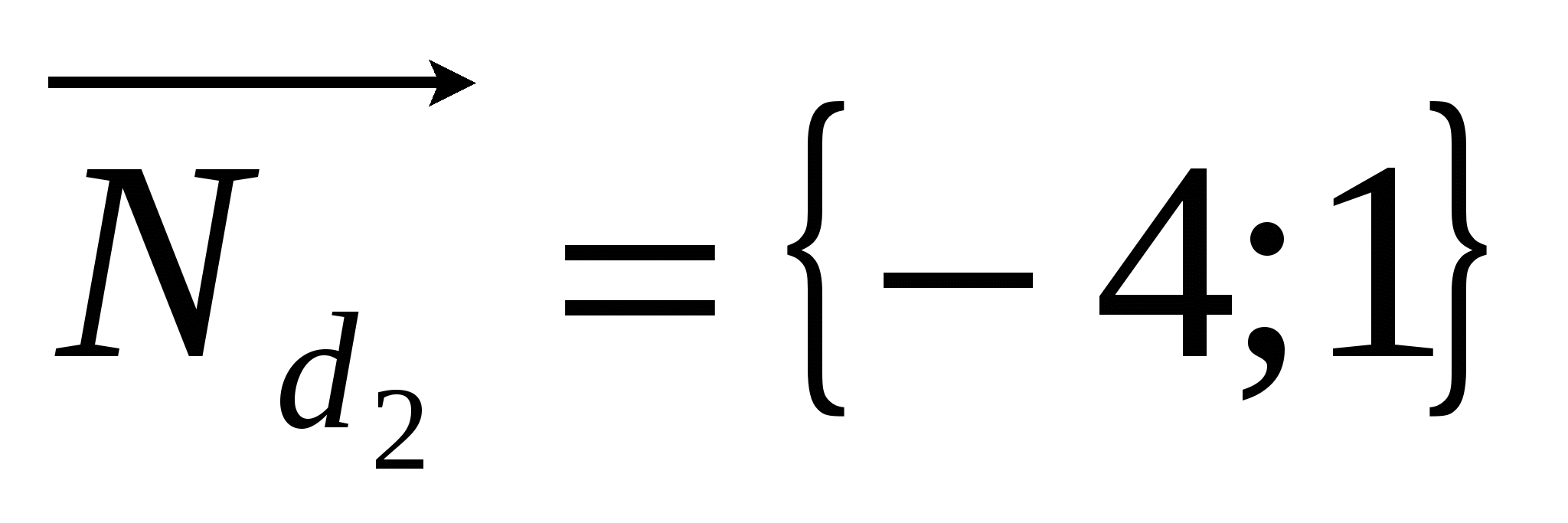 ;
; 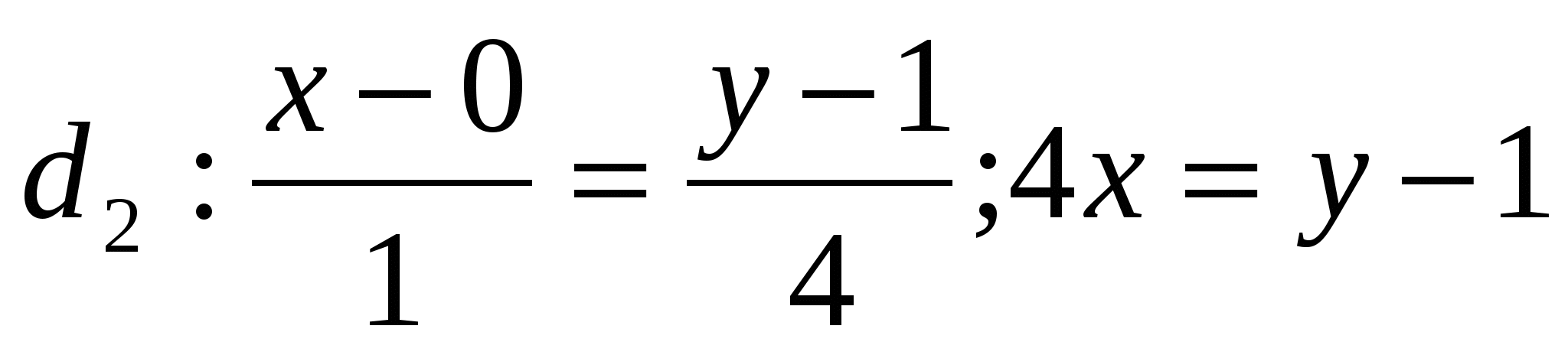 =>
=> 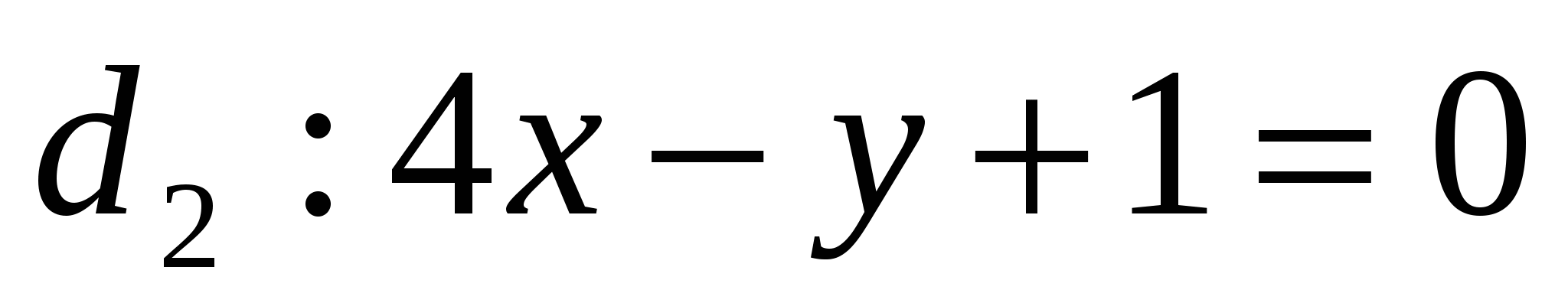
![]()
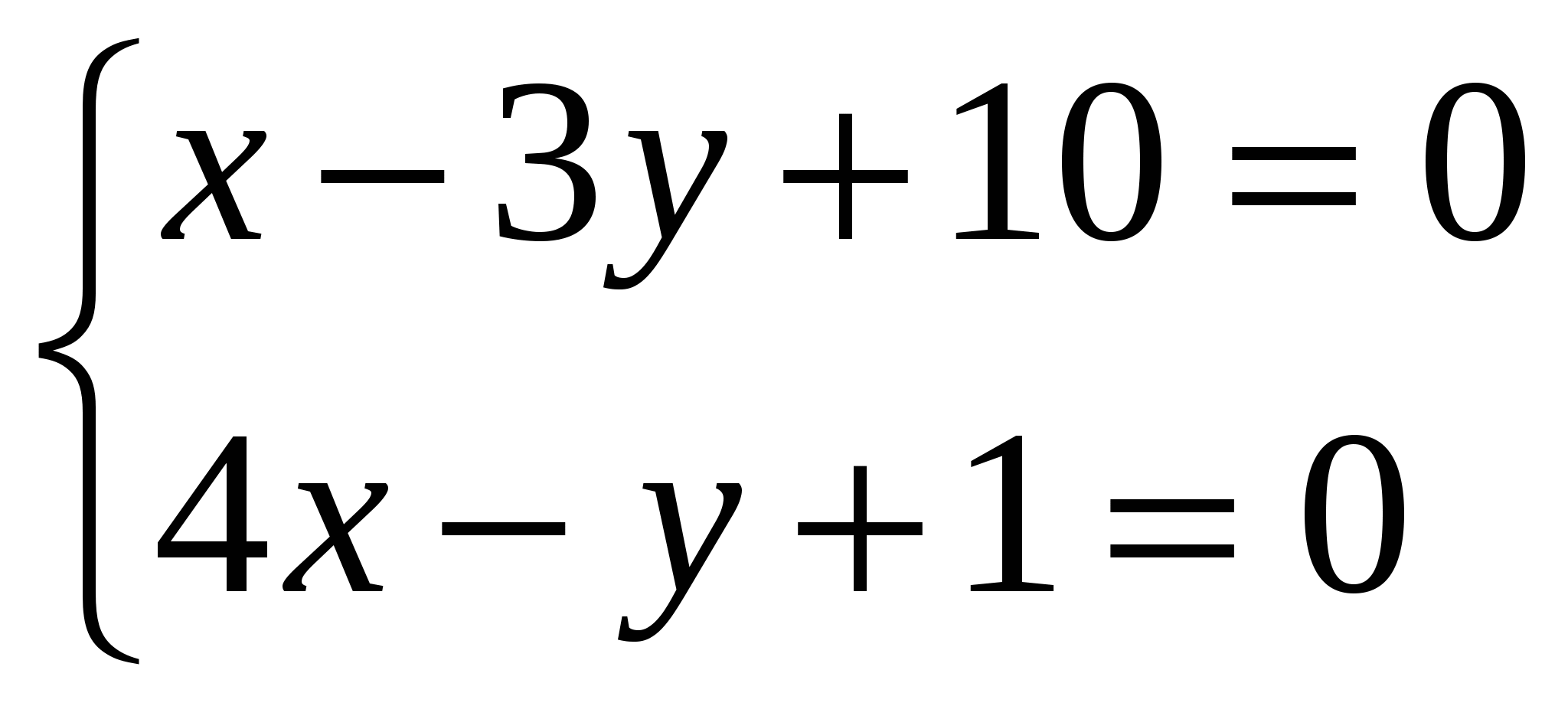 ;
; 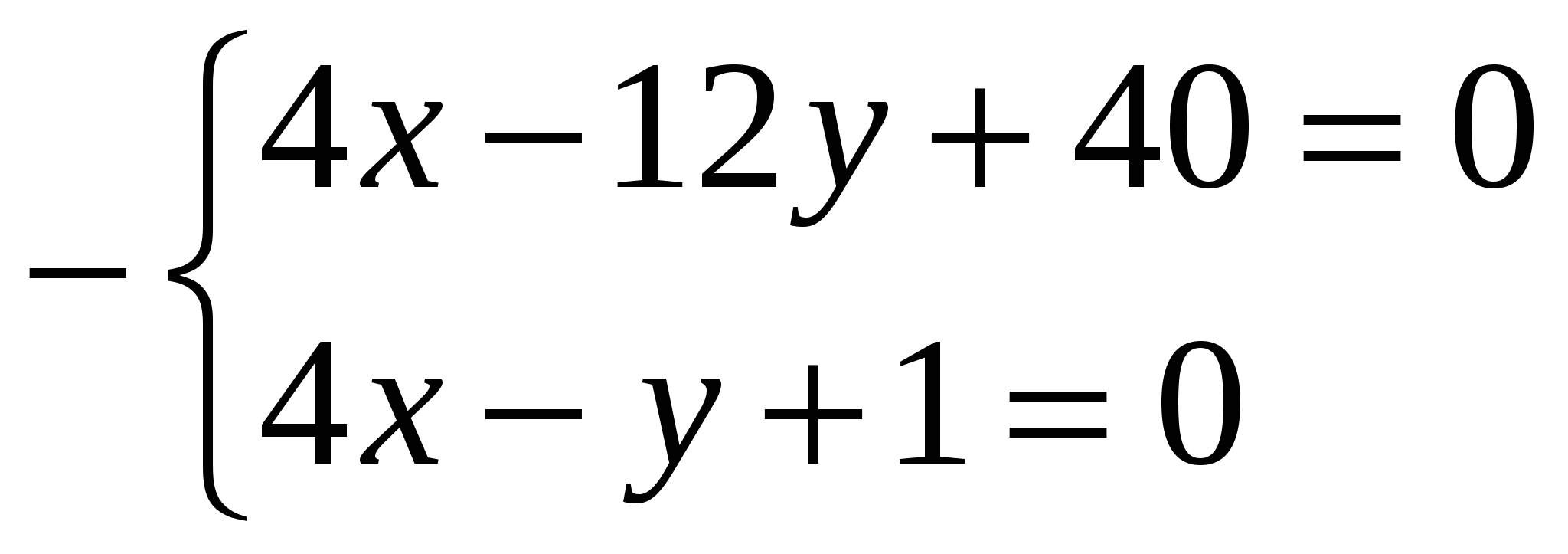 ;
; 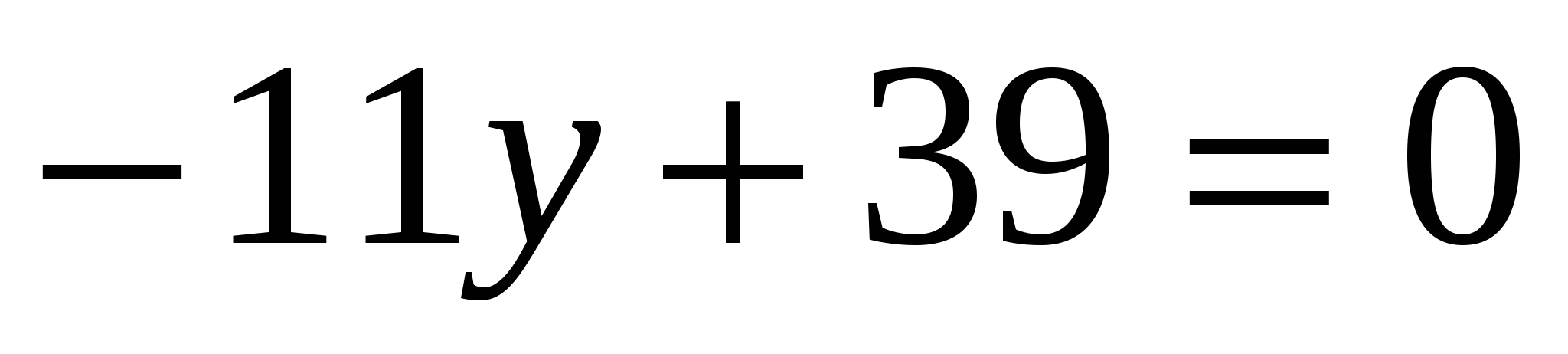 ;
; 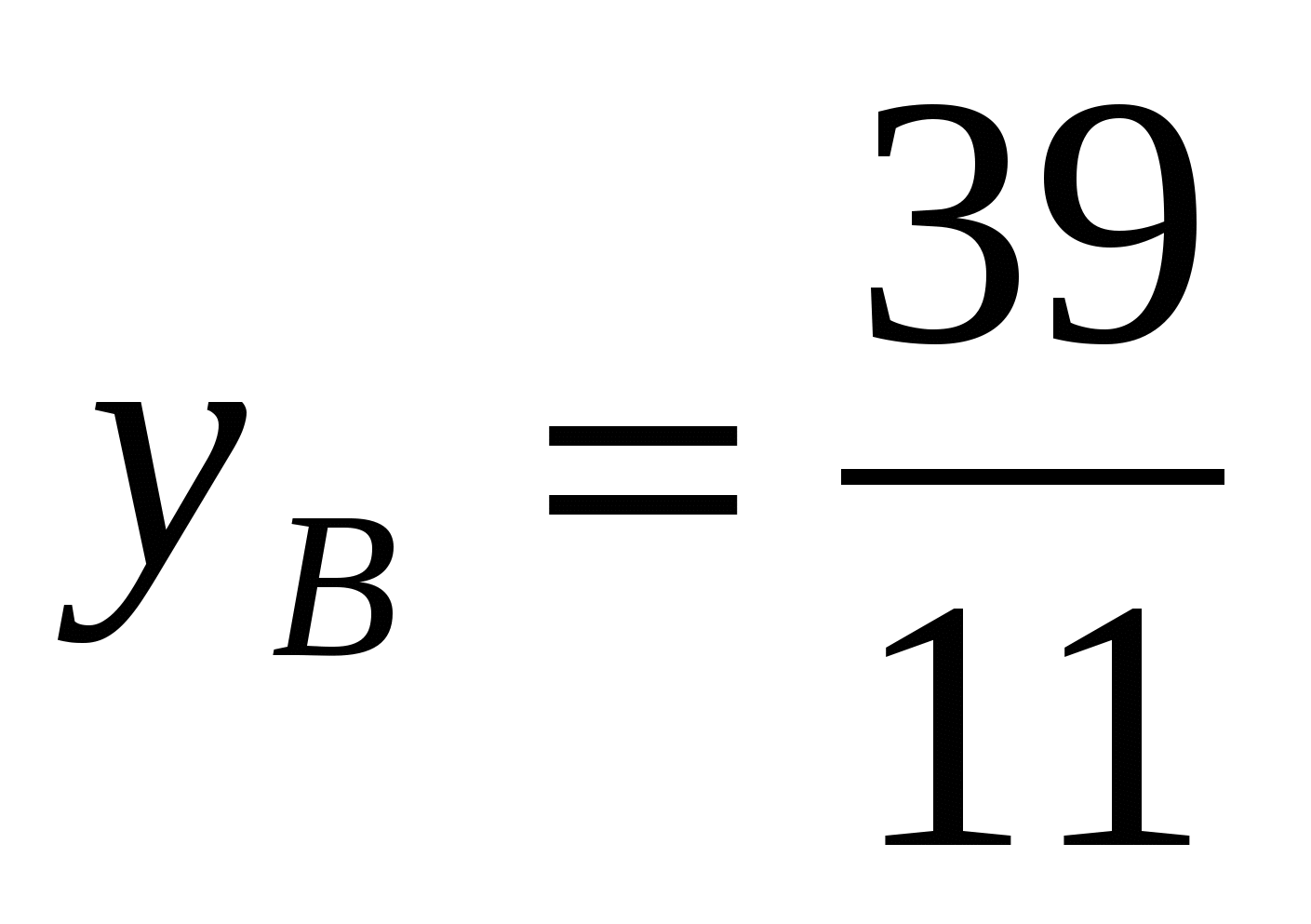 =>
=> 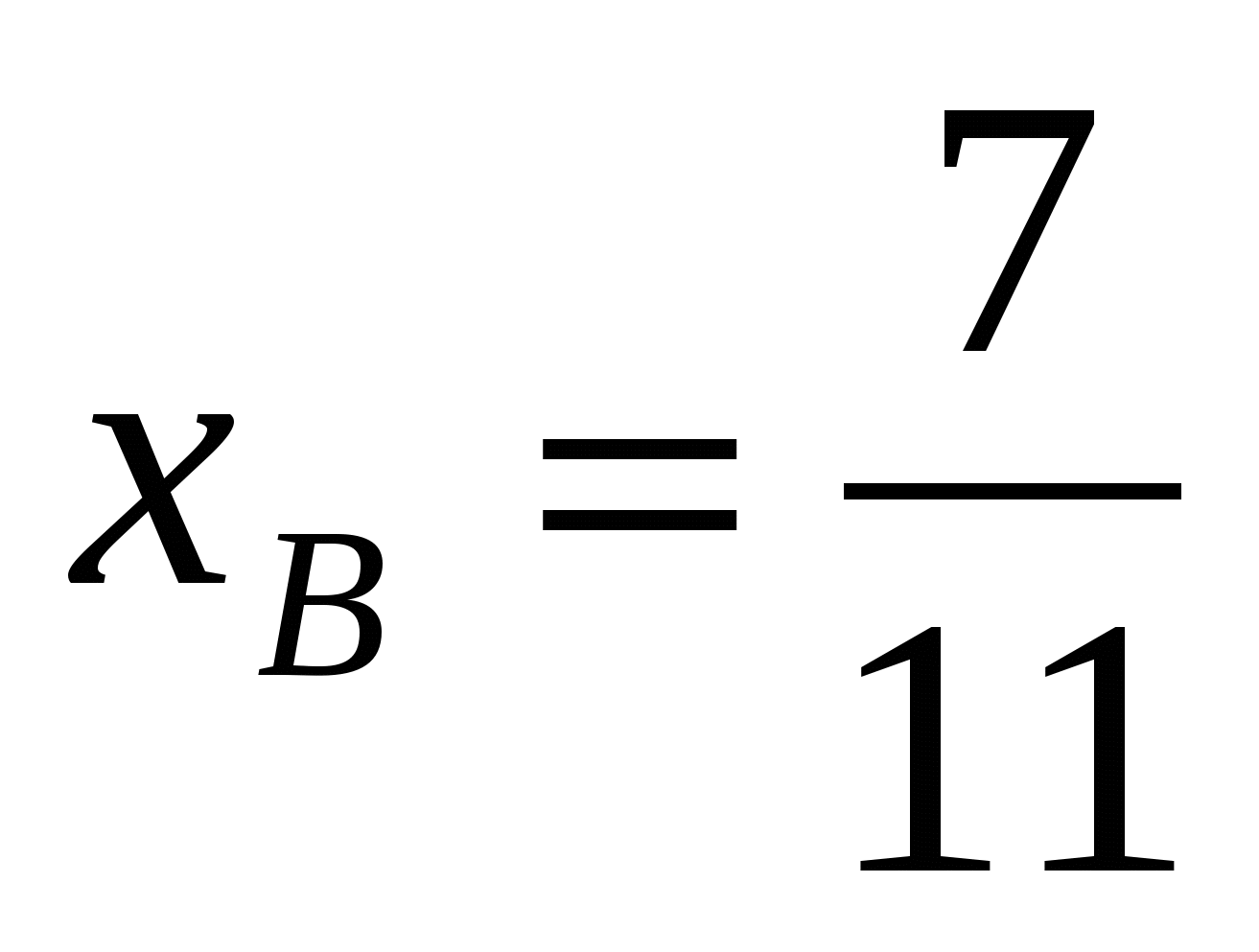
![]()
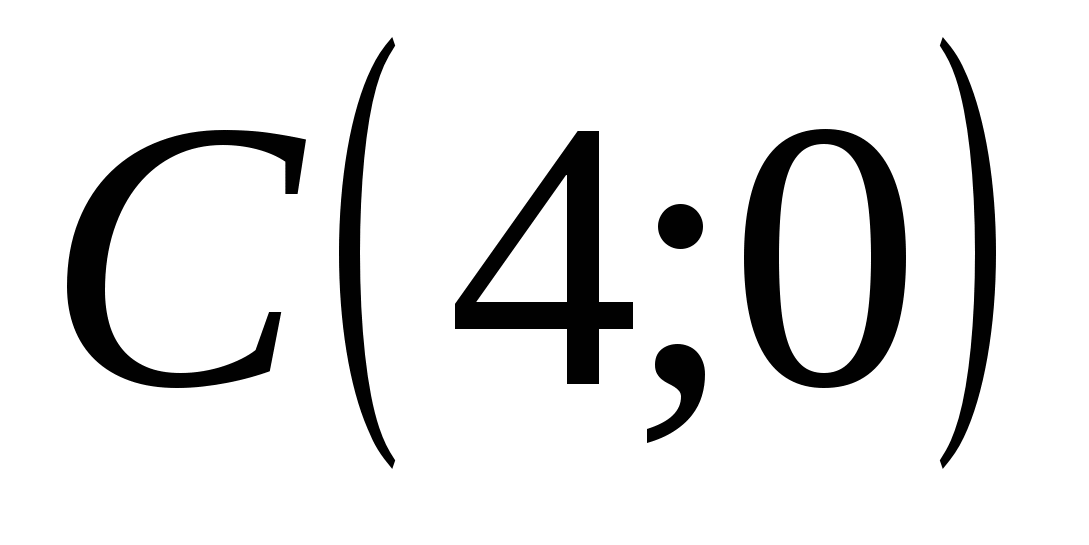 ; По формуле прямой, проходящей через две точки, найдем
; По формуле прямой, проходящей через две точки, найдем 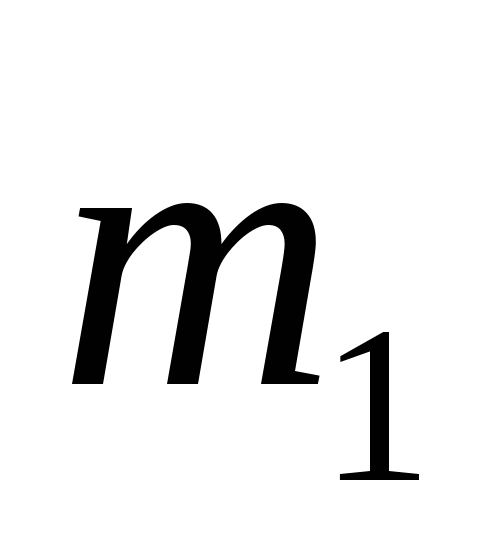
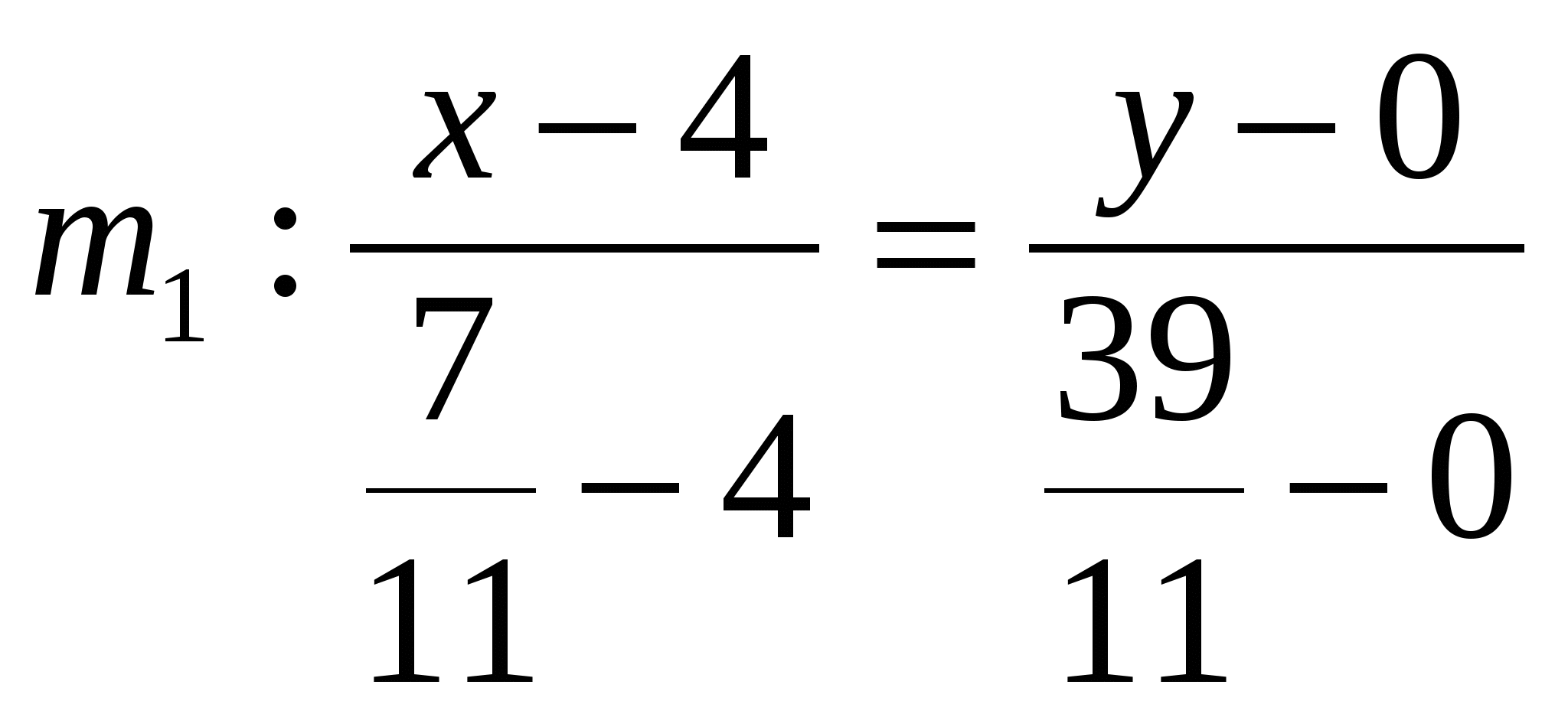 ;
; 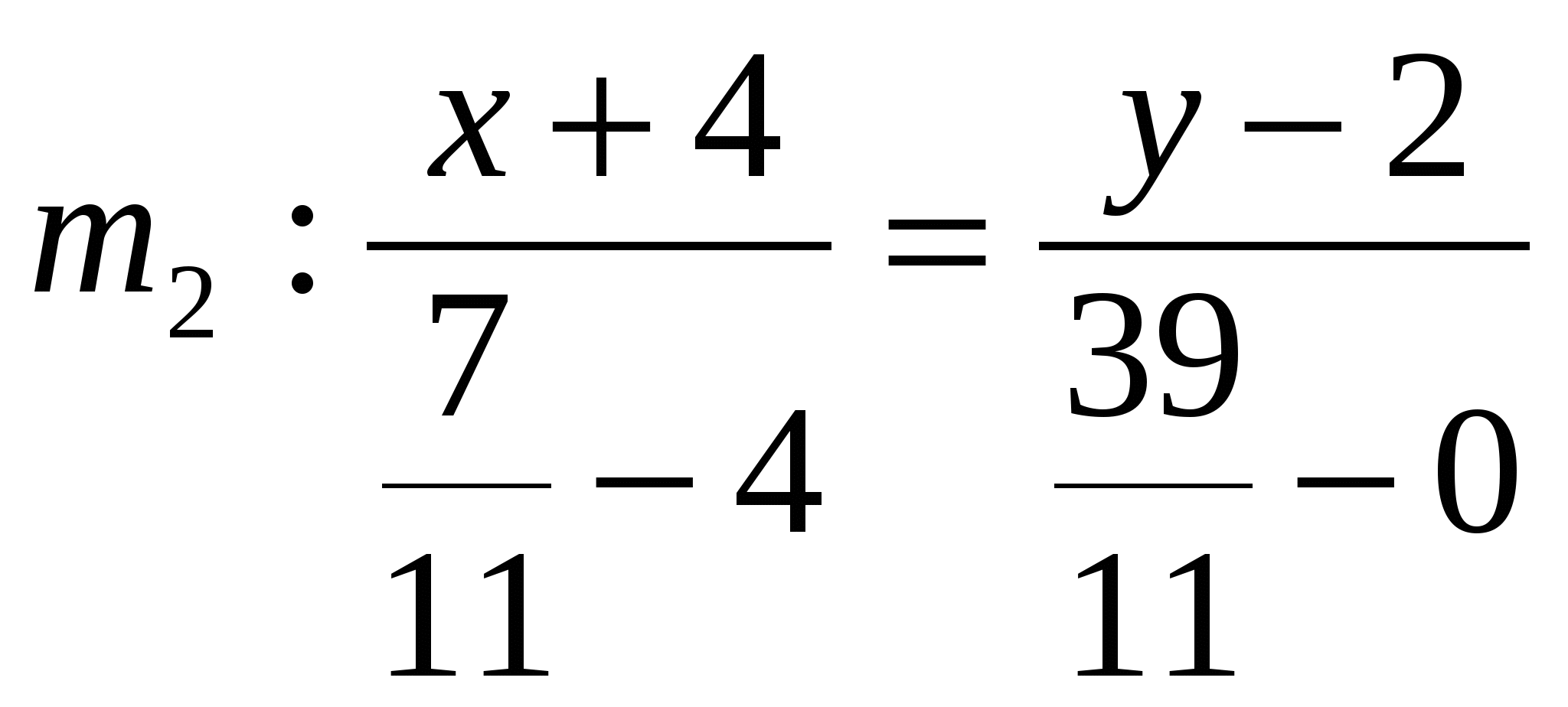
Задача 2. Даны координаты вершин треугольника АВС. Найти длины медианы, высоты, биссектрисы, проведенных из вершины А. Вычислить внутренний угол при вершине В.
А (8;0), В(-4; -5); С(-8;-2).
Решение:
1) 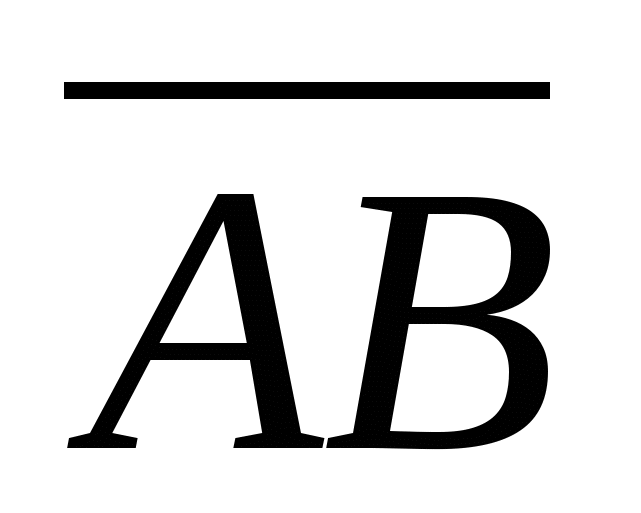 ={-12; -5}, |
={-12; -5}, |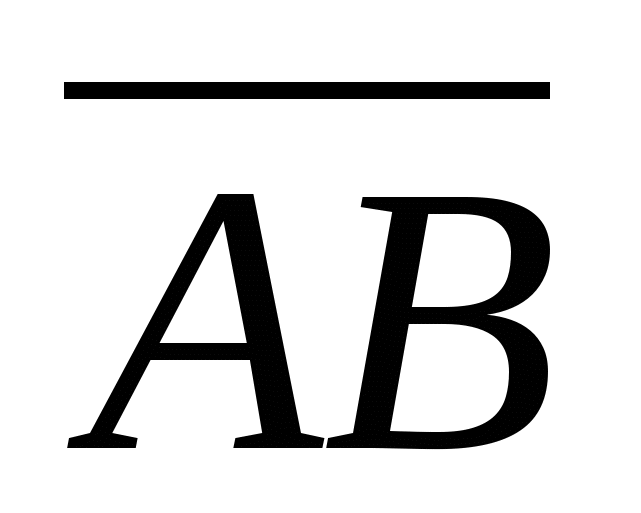 |=13
|=13
![]() = {-4; 3}, |
= {-4; 3}, |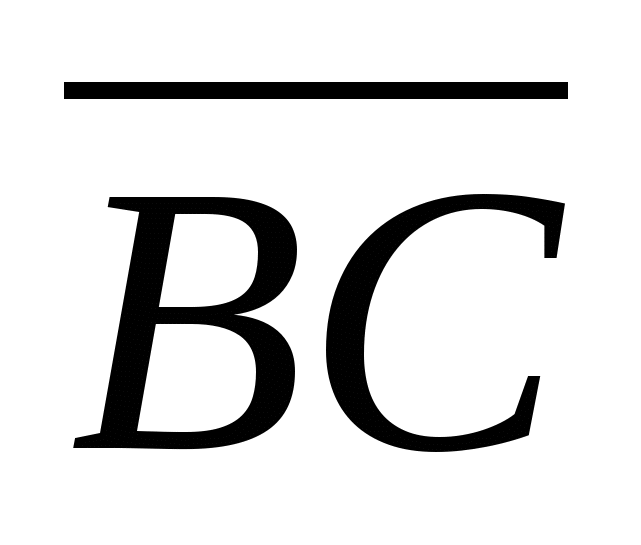 |=5
|=5
![]() = {-16; -2}, |
= {-16; -2}, |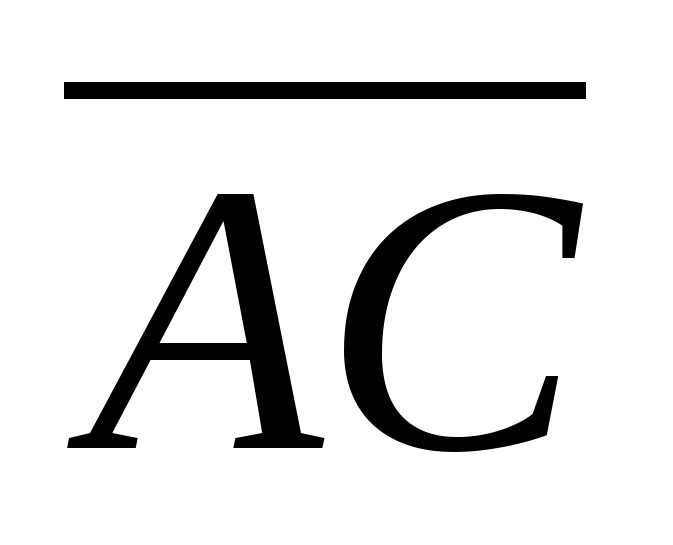 |=
|=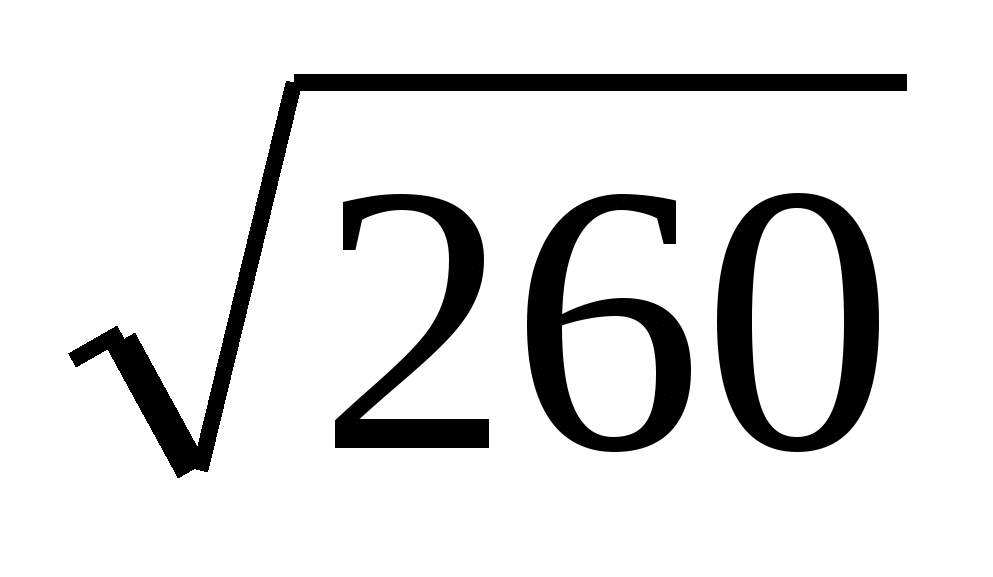 =
=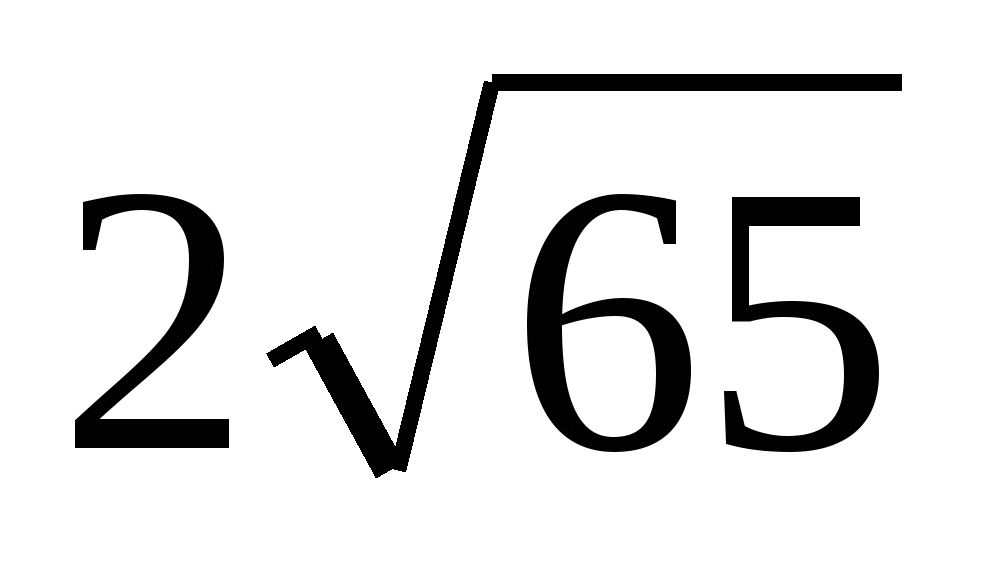
A


y
x

C
L
M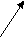
H
B
2) 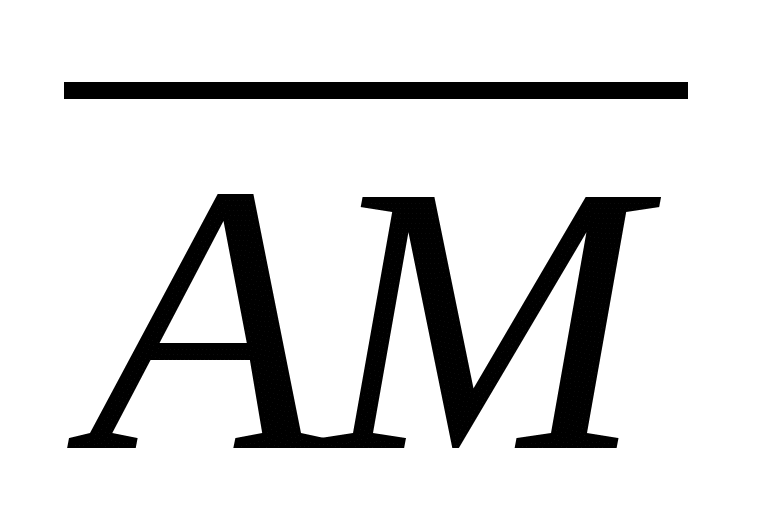 =0.5(
=0.5(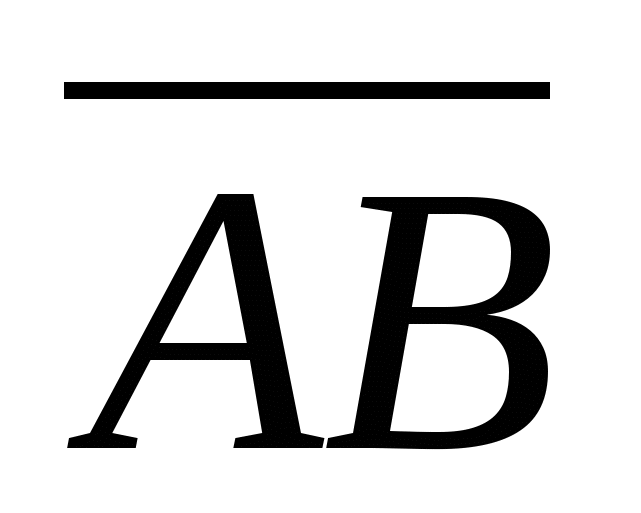 +
+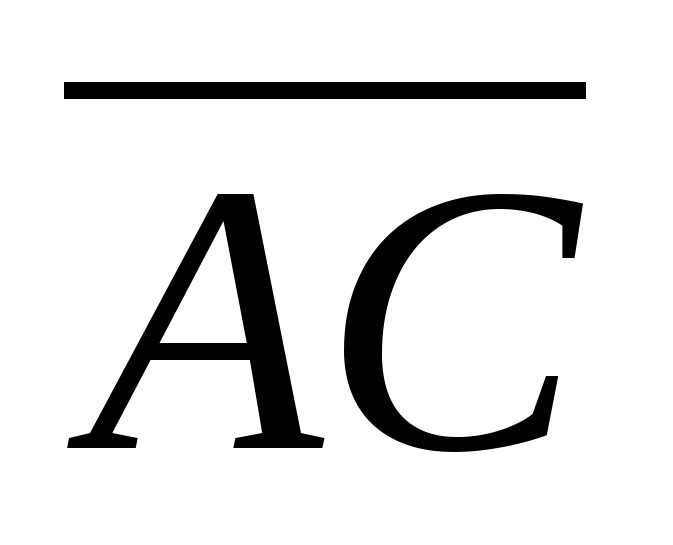 )=0.5{-12-16;-5-2}={-28;-7}
)=0.5{-12-16;-5-2}={-28;-7}
|![]() | =
| = 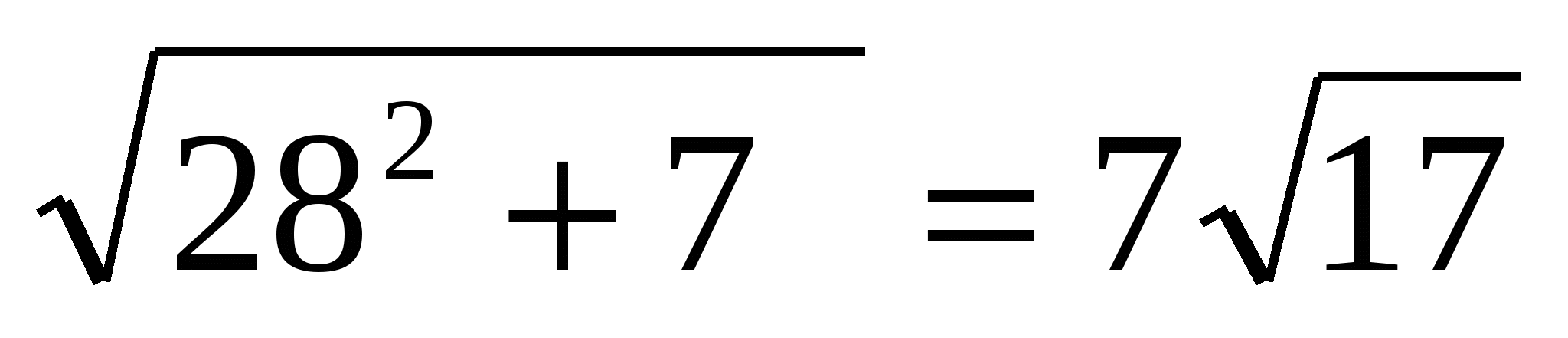
x +4
=
y + 5
-4
33) Имеем уравнение прямой ВС:
3x + 4y + 32 = 0.
|![]() | = ρ(A, BC) =
| = ρ(A, BC) =
|3∙8+4∙0+32|
=![]()
![]()
4) Найдем уравнение прямой AL:
![]() ;
; 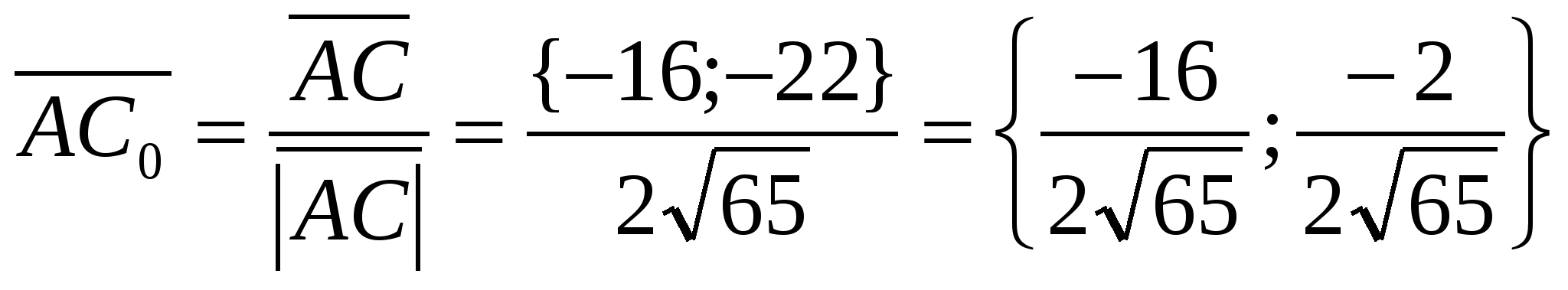 ;
;
![]()
Значит,
![]() .
.
Тогда, 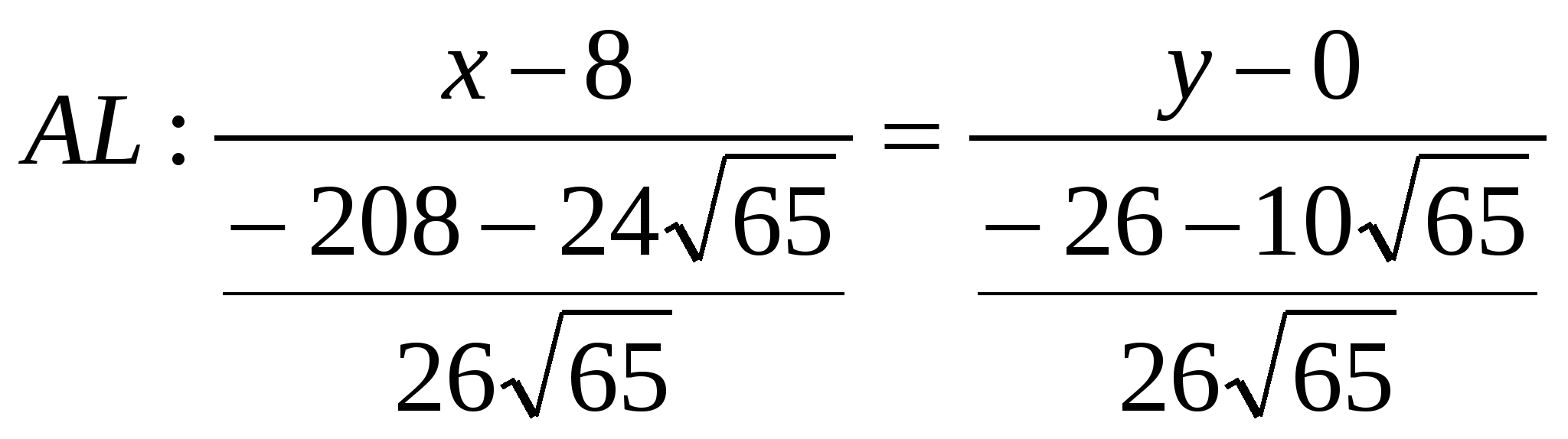 или
или 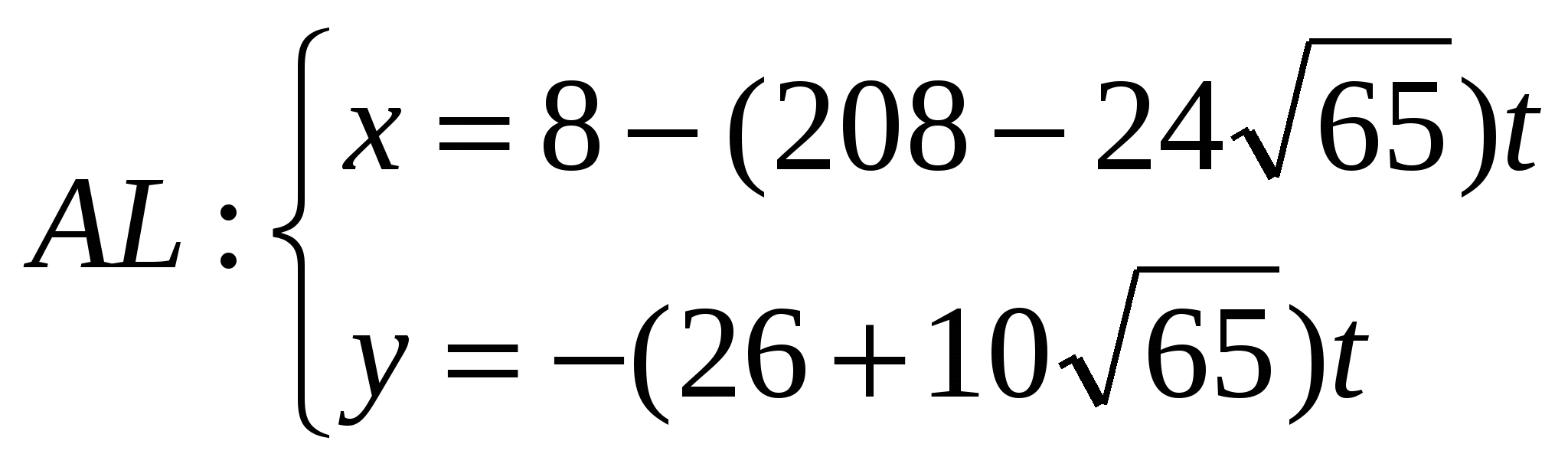
Найдем точку L - точку пересечения прямых AL и BC:
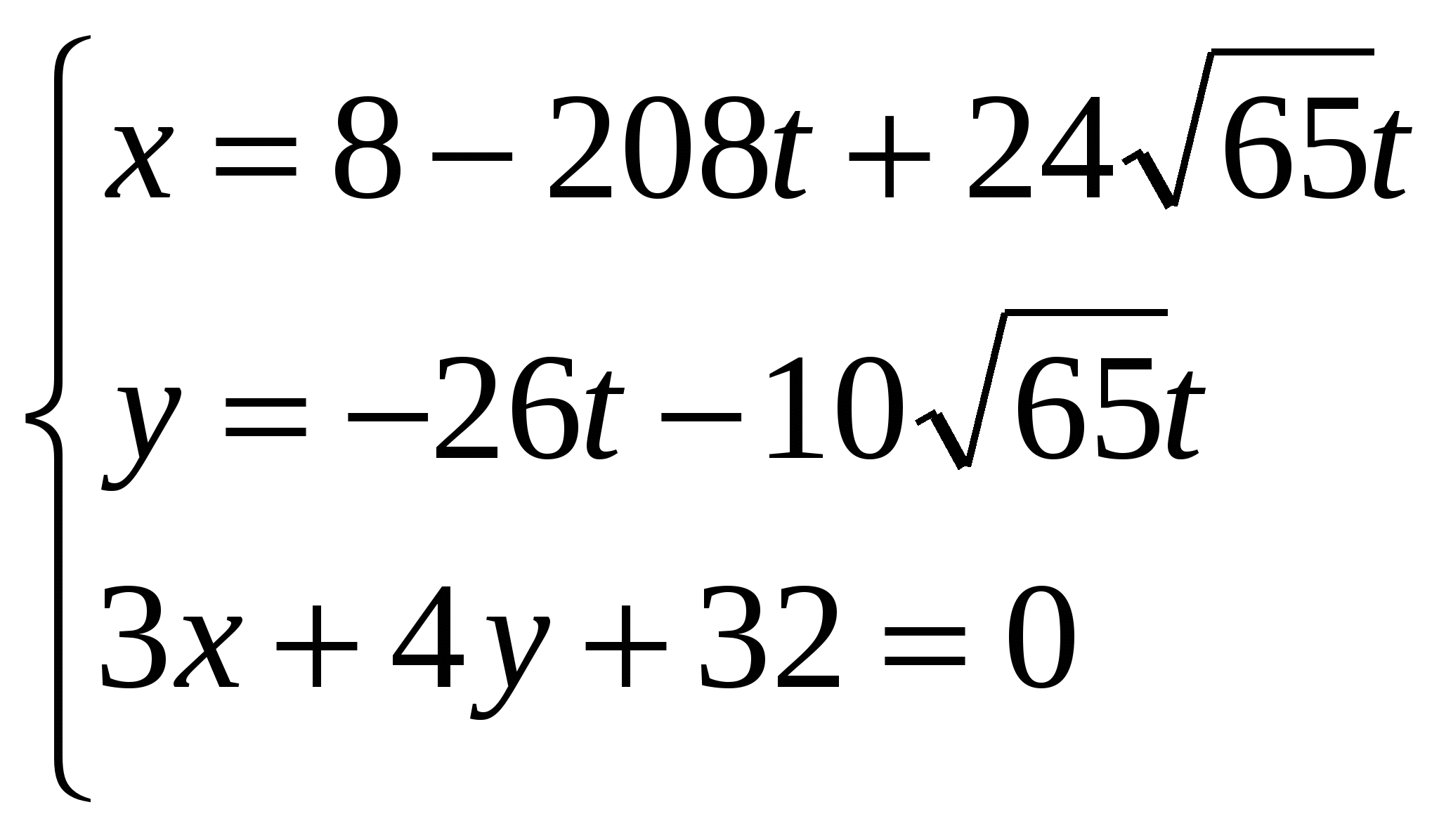 ;
; 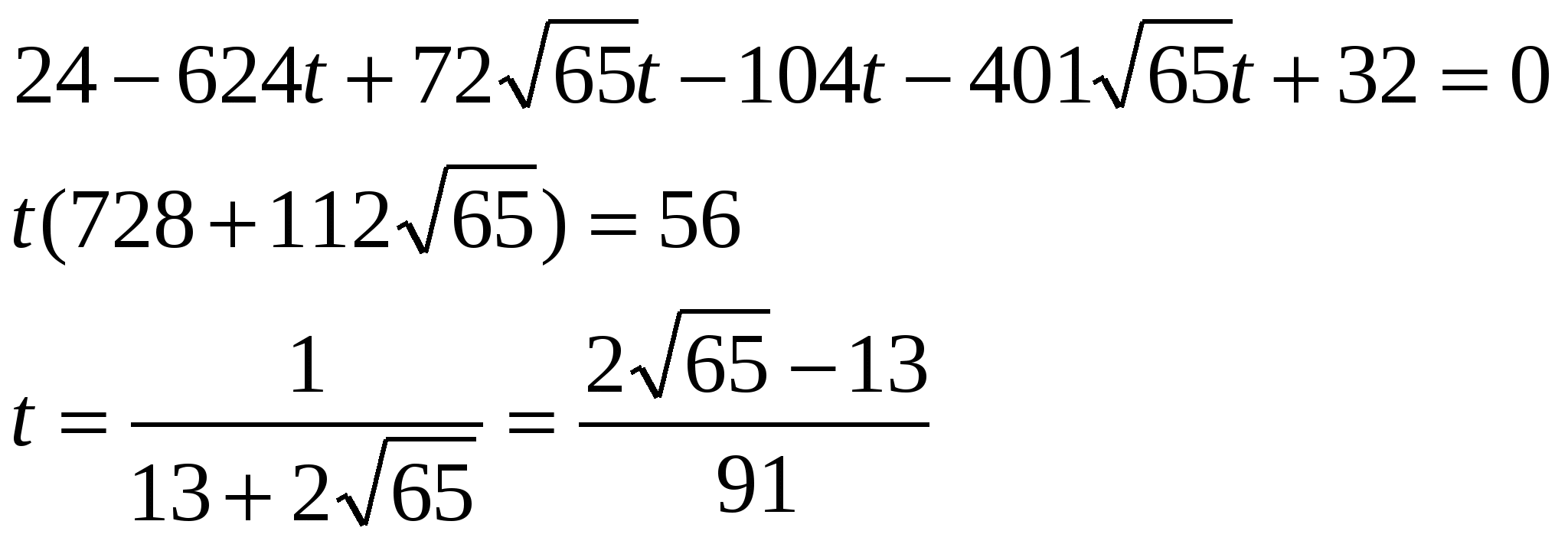
Тогда 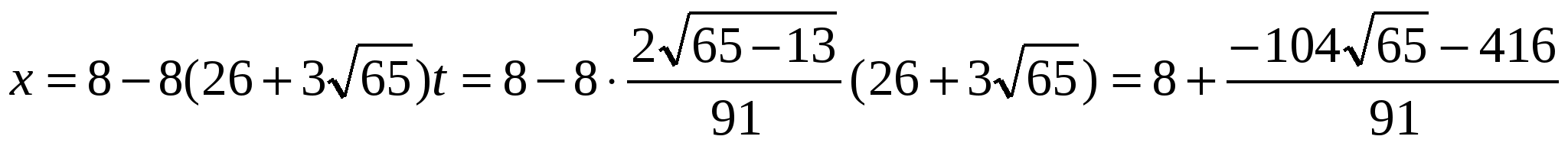
и 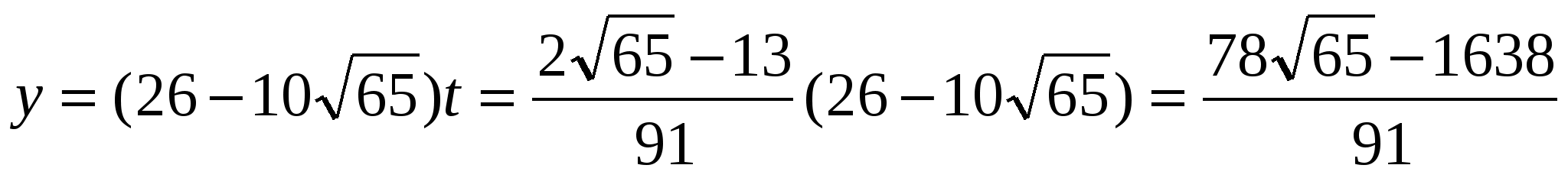 .
.
Итак, 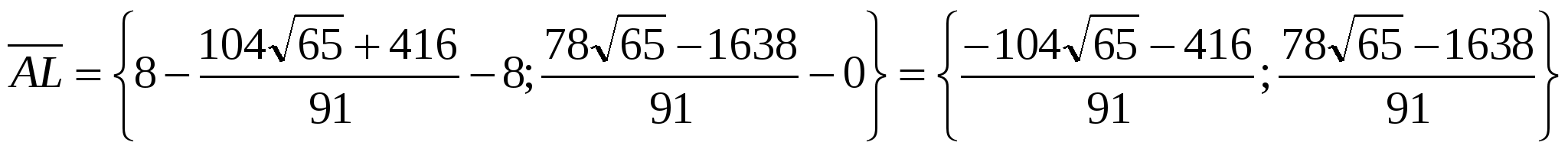
и
![]()
5) 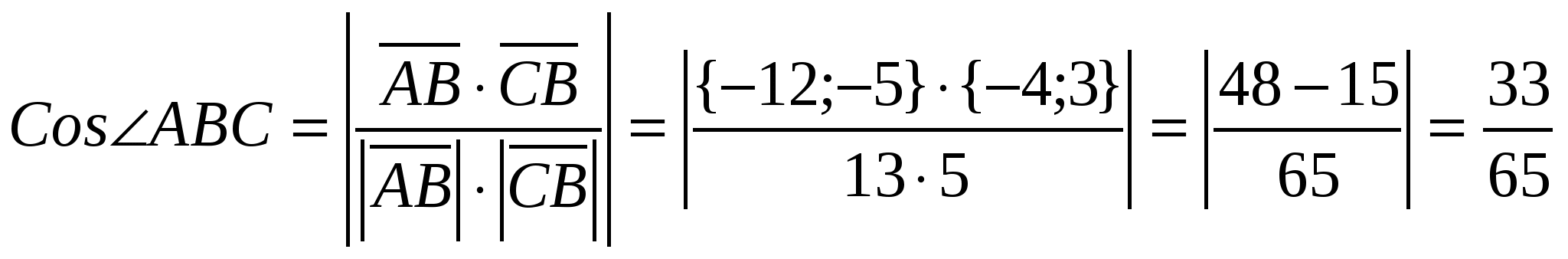
![]()
Ответ: 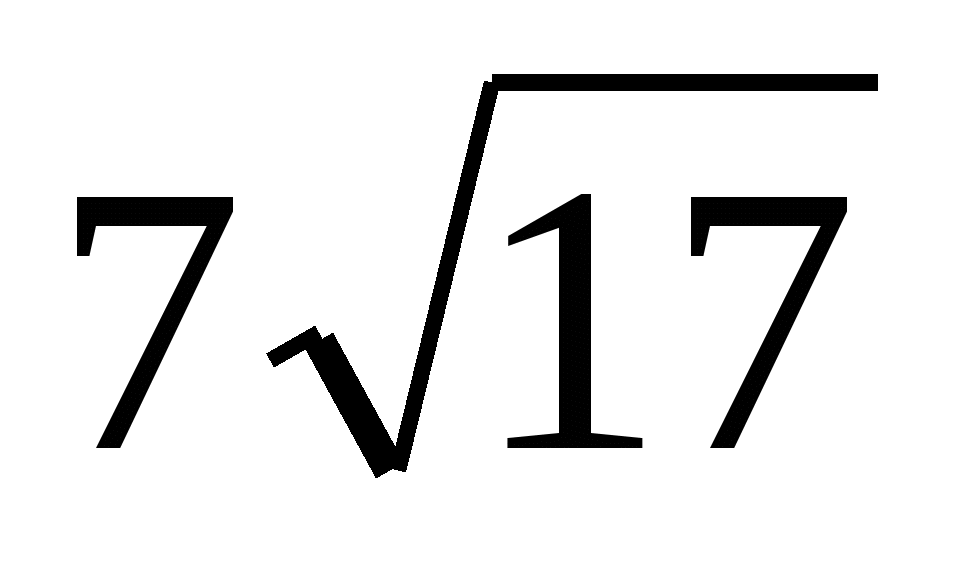 ;
; 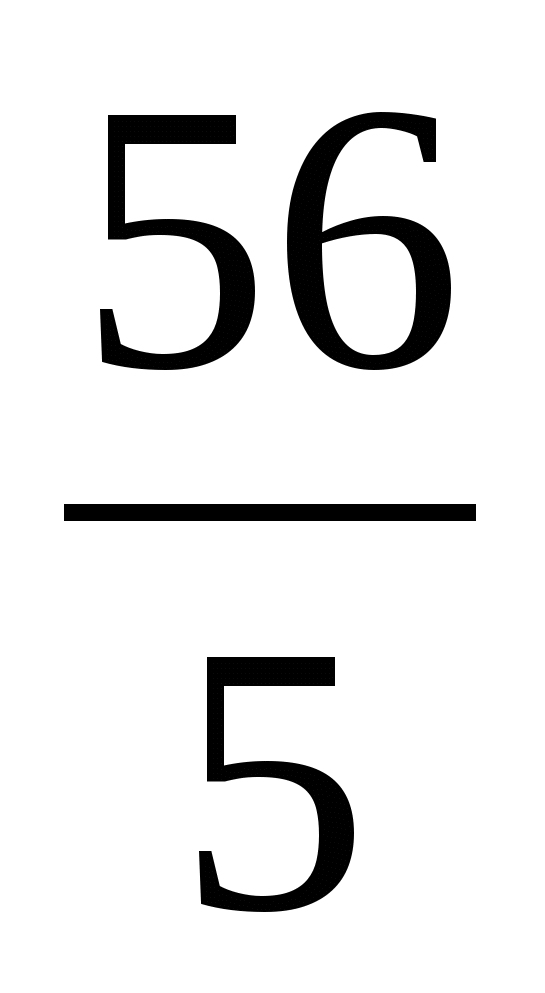 ;
; ;
; 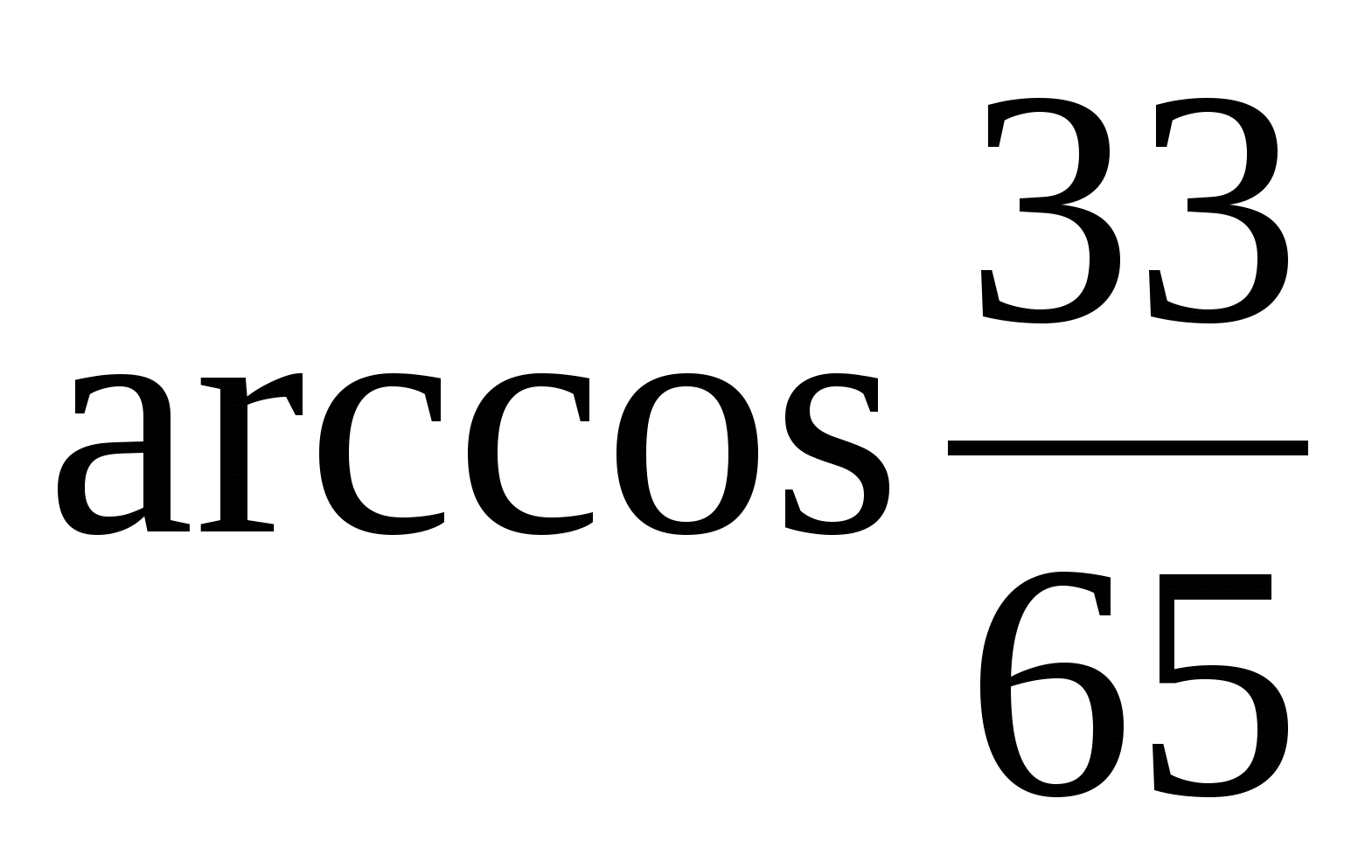
Задача 3. Найти точки пересечения кривой второго порядка 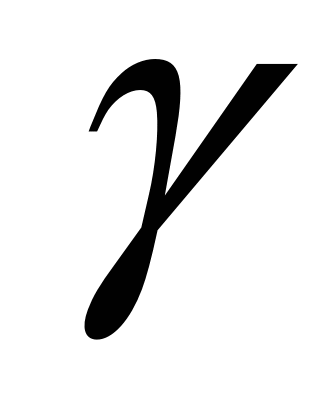 с прямой (а):
с прямой (а):
![]()
Решаем систему: 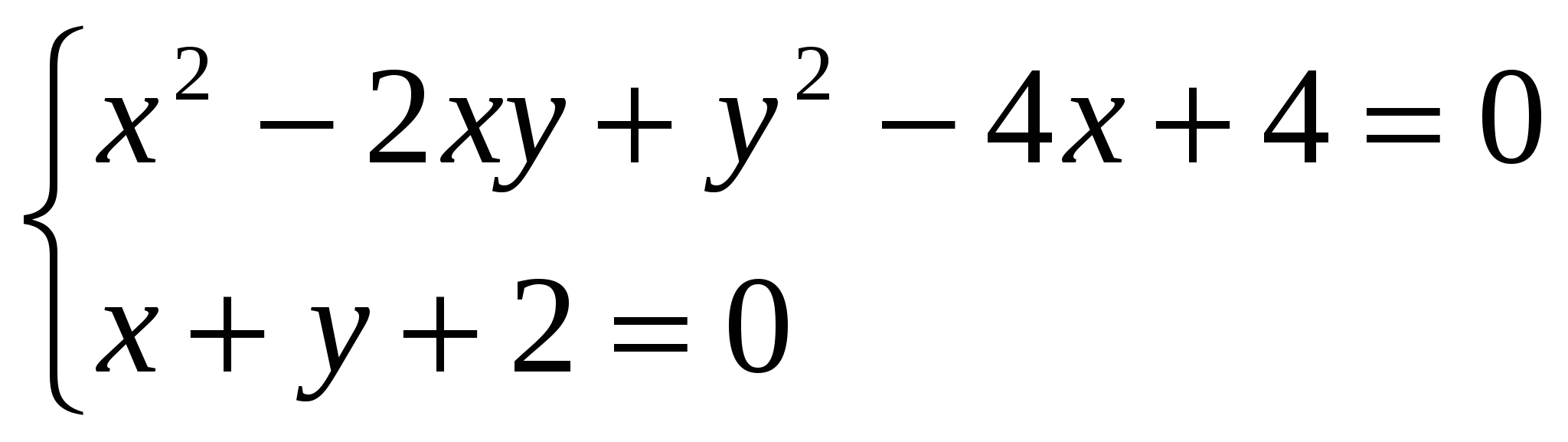 ;
; 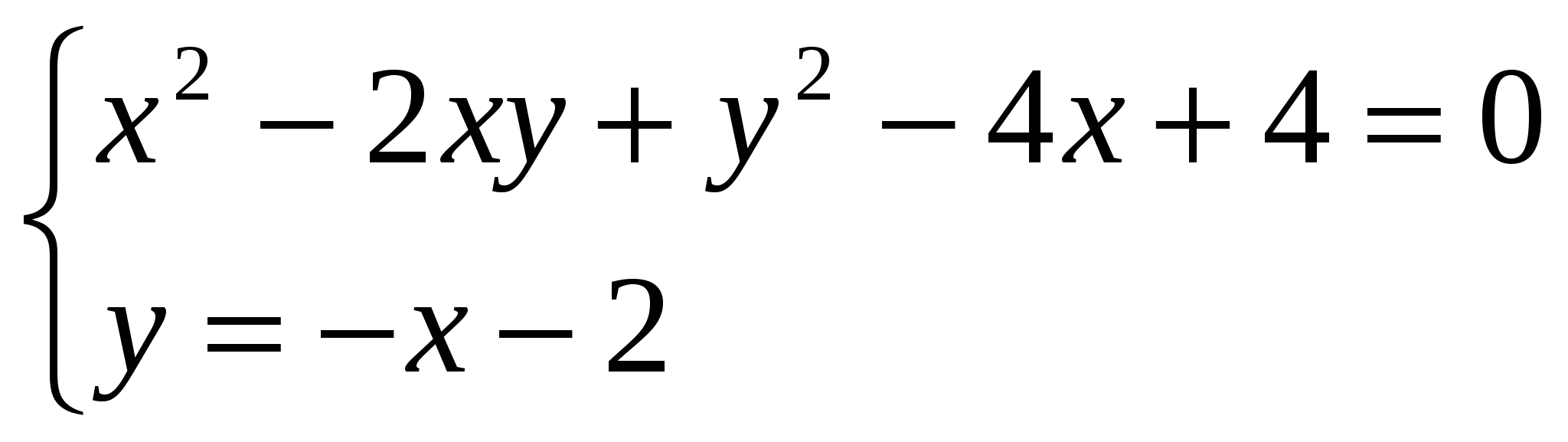 ;
;
Подставляем в первое уравнение и получаем: 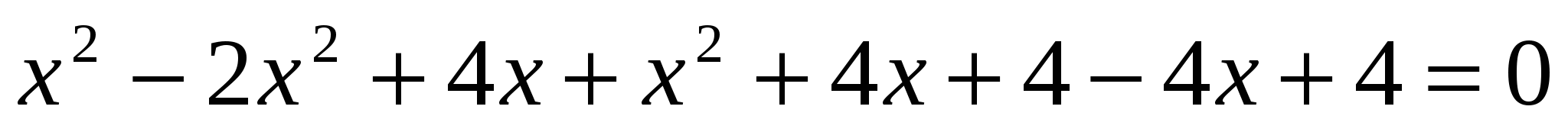
![]() D<0 => нет точек пересечения
D<0 => нет точек пересечения
Ответ: нет точек пересечений
Задача 4. Полюс полярной системы координат совпадает с началом декартовых прямоугольных координат, а полярная ось направлена по биссектрисе первого координатного угла. Даны полярные координаты точек 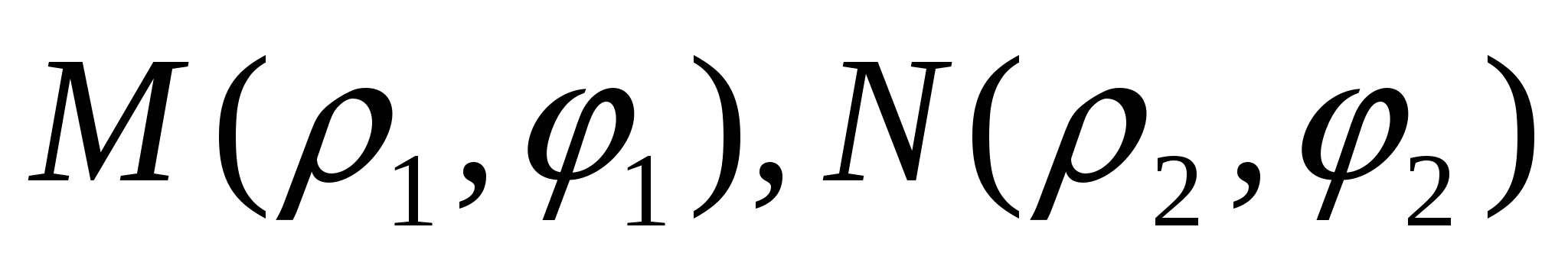 . Определить декартовы прямоугольные координаты этих точек.
. Определить декартовы прямоугольные координаты этих точек.
![]()
M(xM; yM), где
xM=ρ1Cos (φ1+π/4) = Cos(25π/12) = Cos(π/12),
yM=ρ1Sin (φ1+π/4) = Sin(25π/12) = Sin(π/12).
N(xN; yN), где
xN=ρ2Cos (φ2+π/4) = 2Cos(π +π/4) =-2Cos(π/4)=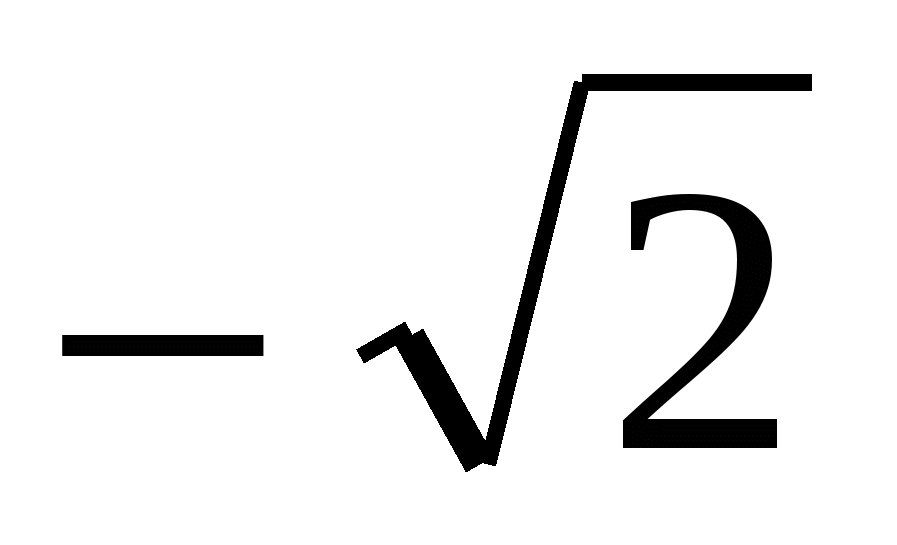 ,
,
yN=ρ2Sin (φ2+π/4) = 2Sin(π +π/2) = -2Sin(π/4)= 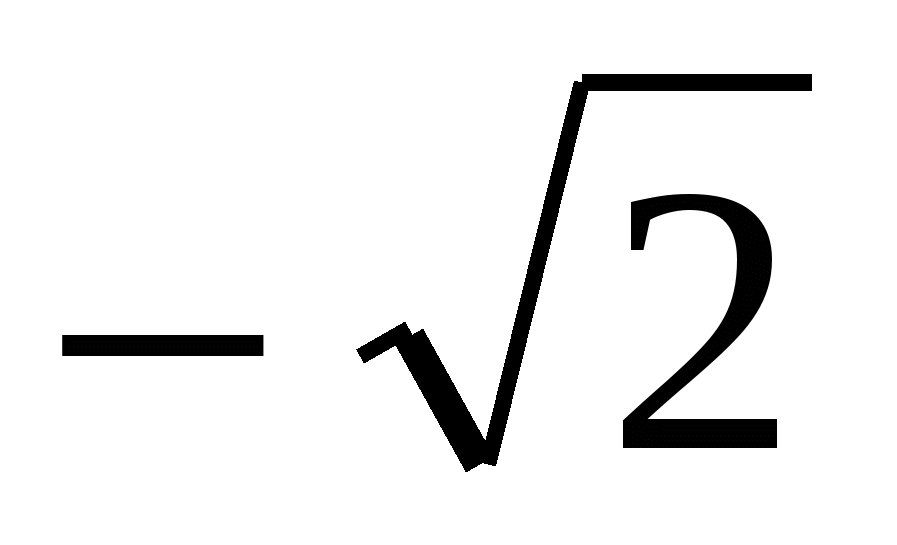 .
.
Ответ: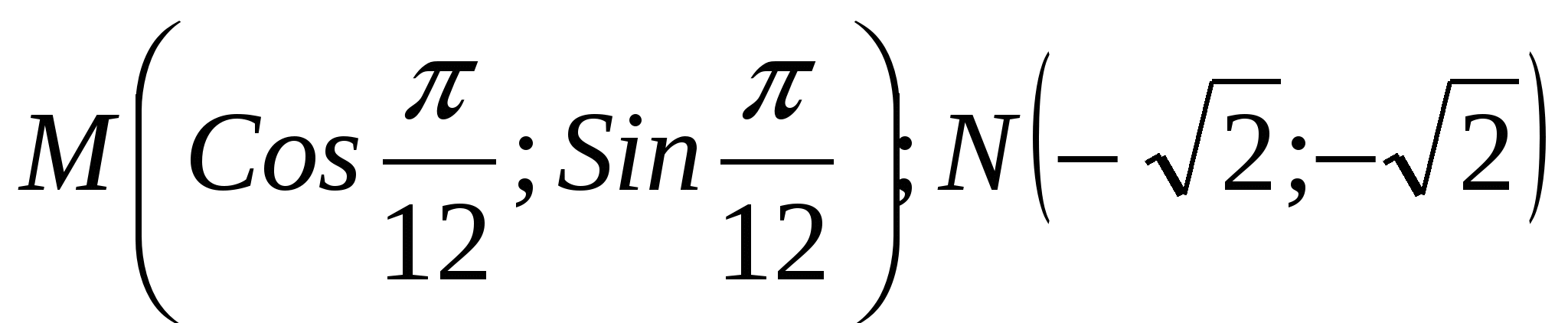
Задача 5. Для векторов 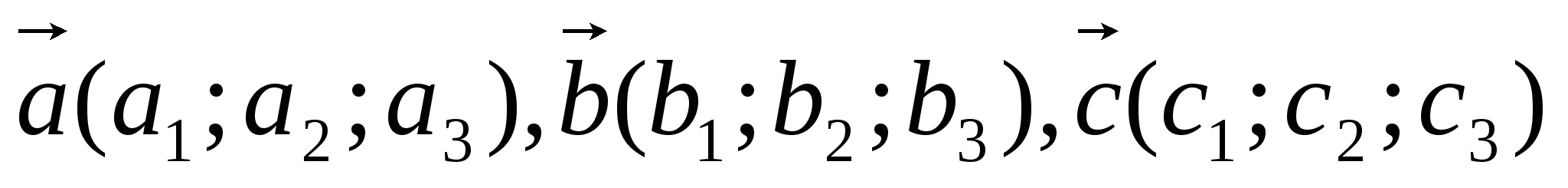 , заданных в ортонормированном базисе
, заданных в ортонормированном базисе 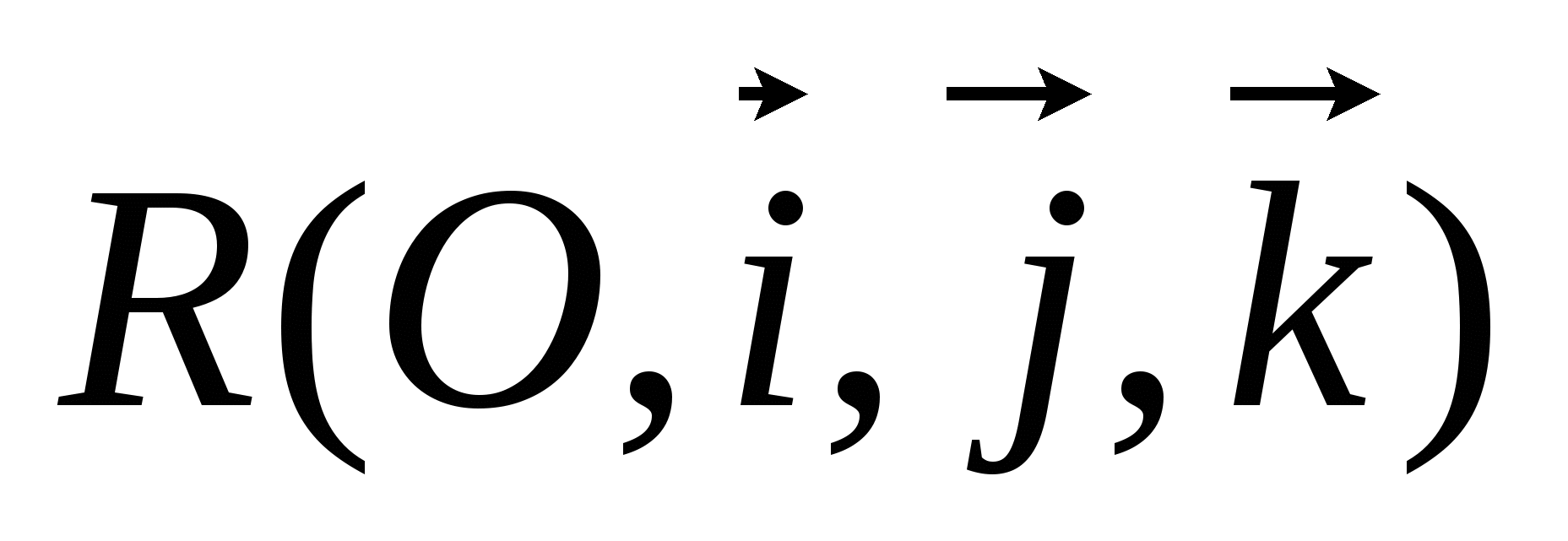 найдите:
найдите:
-
направляющие косинусы вектора
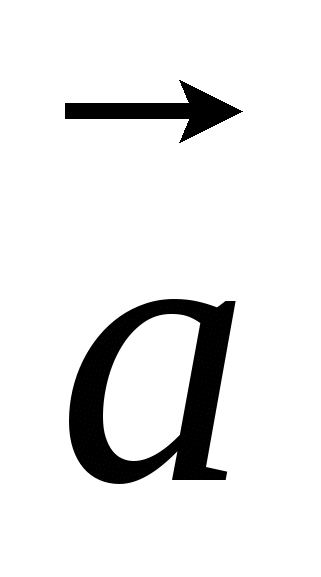 ;
; -
площадь параллелограмма, построенного на векторах
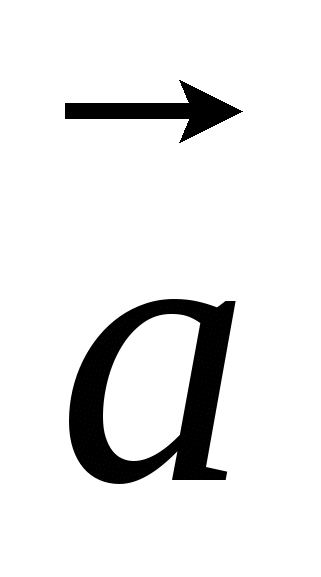 и
и 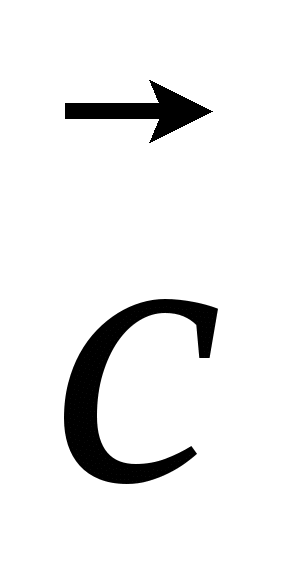 , имеющих общее начало;
, имеющих общее начало; -
объем пирамиды, построенной на векторах
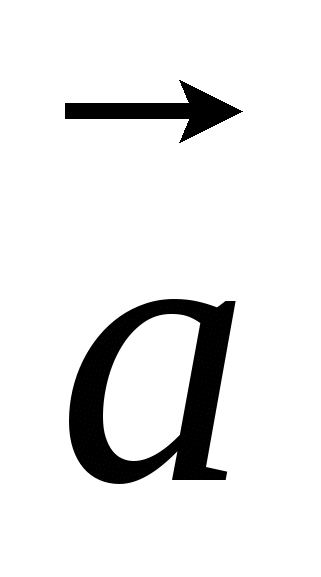 ,
,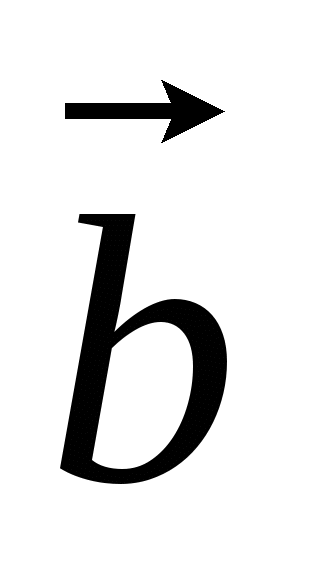 и
и  , имеющих общее начало.
, имеющих общее начало.
![]()
1) 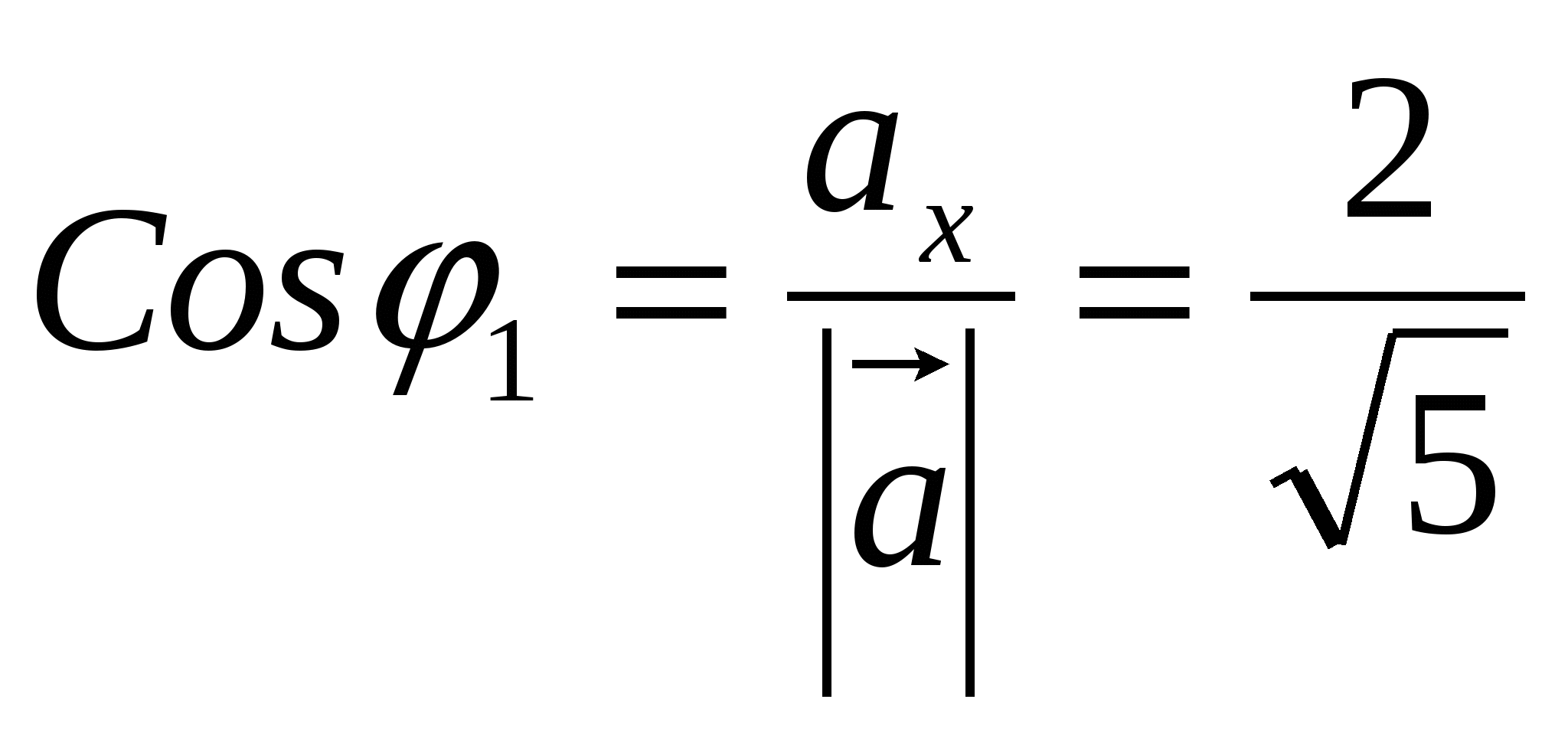 ;
; 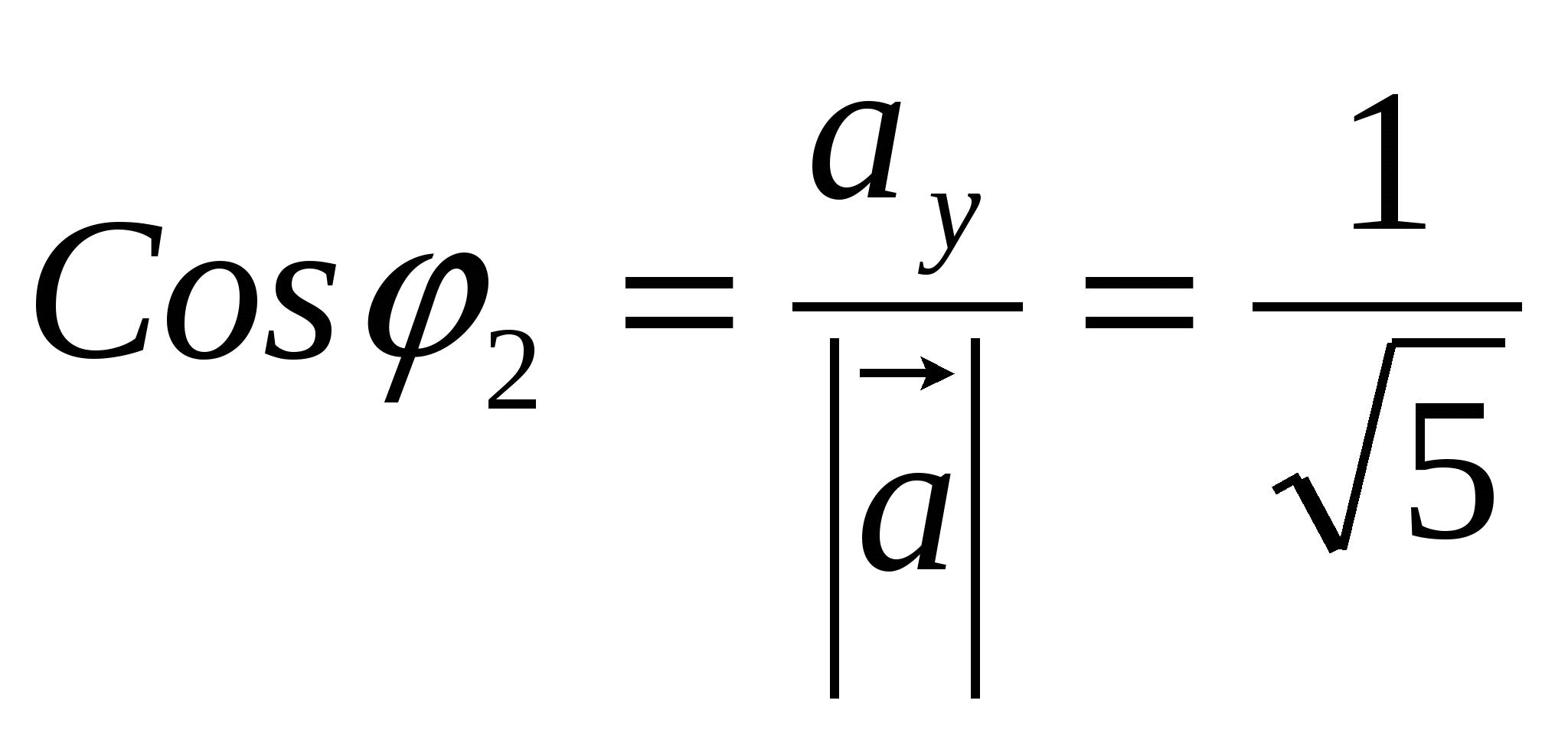 ;
; 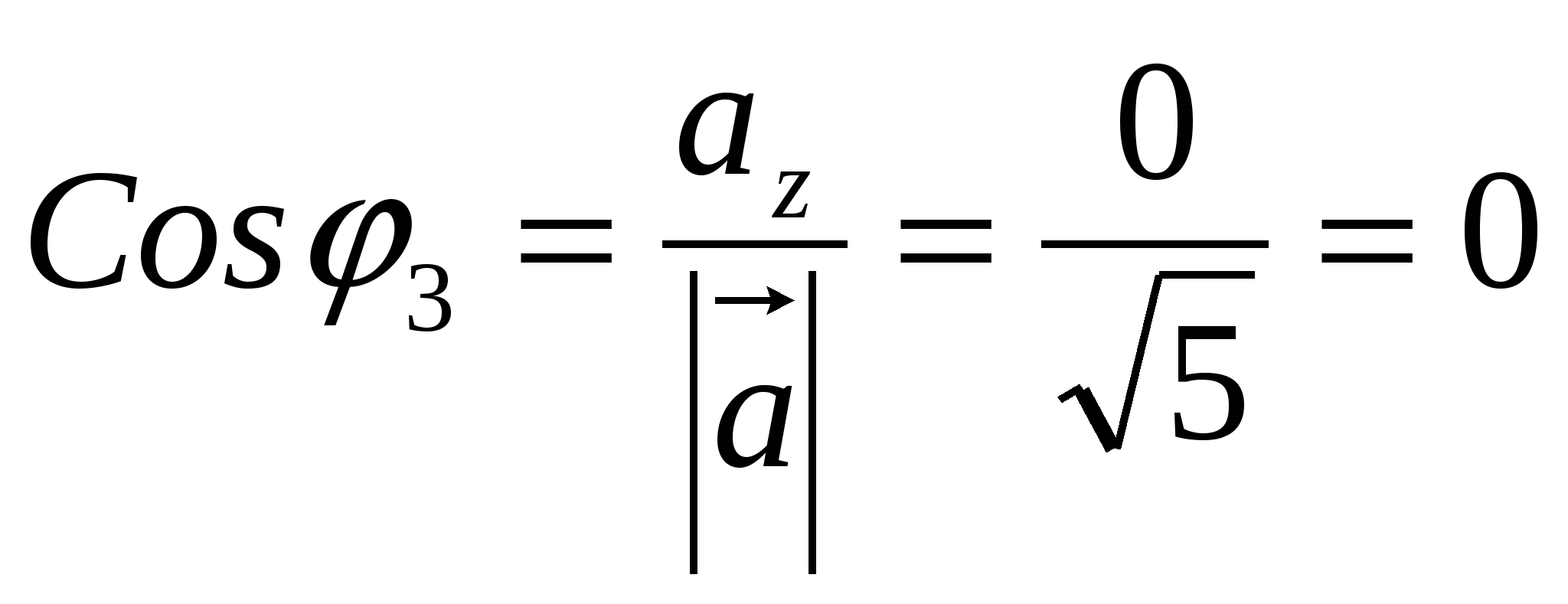
2) 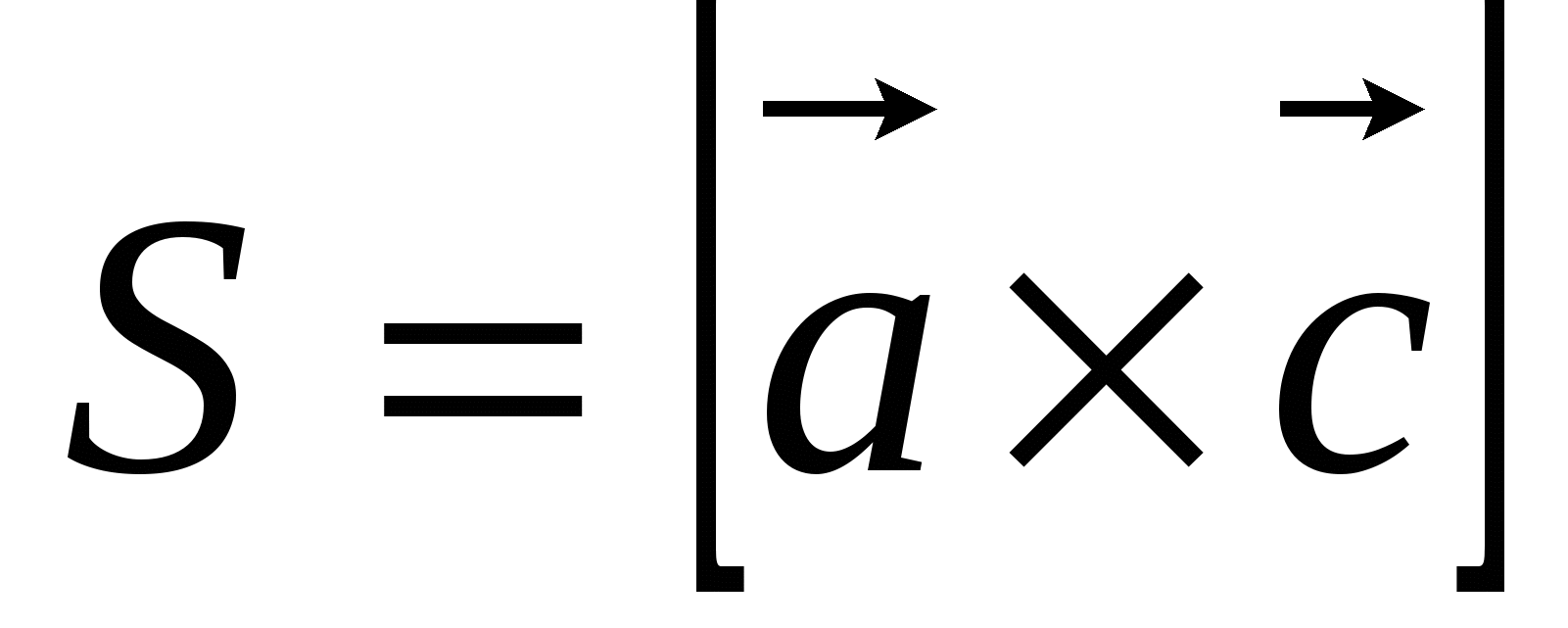 ;
; 
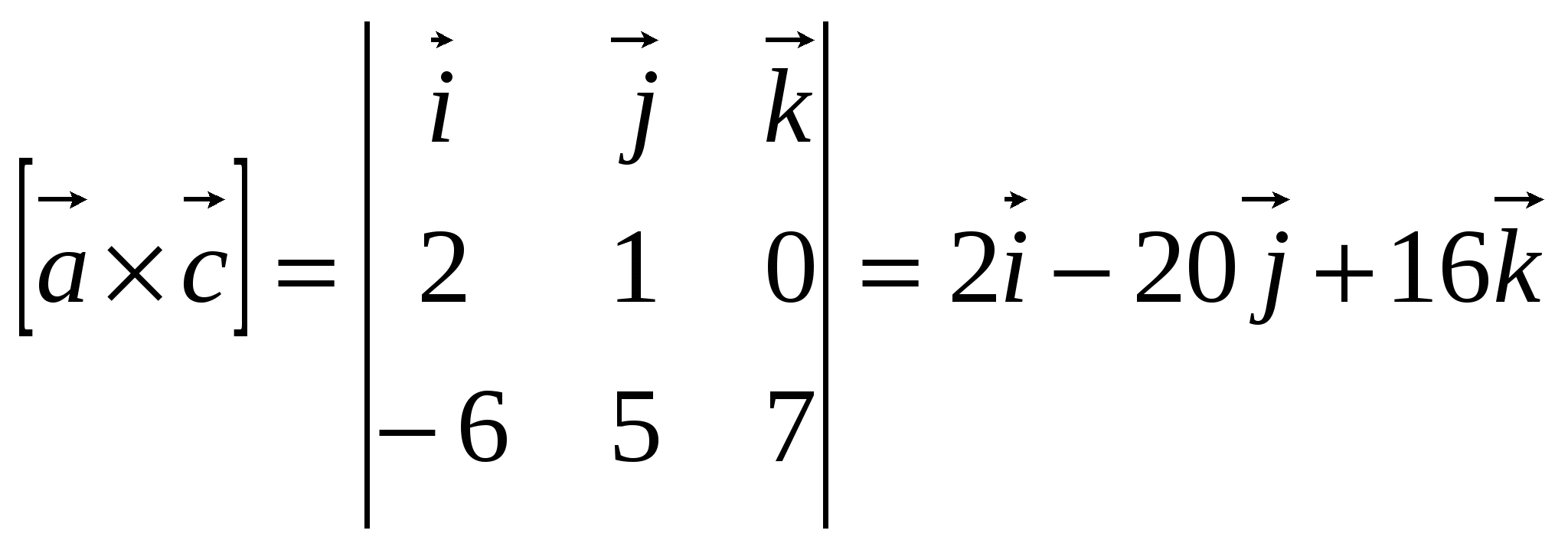 ;
; 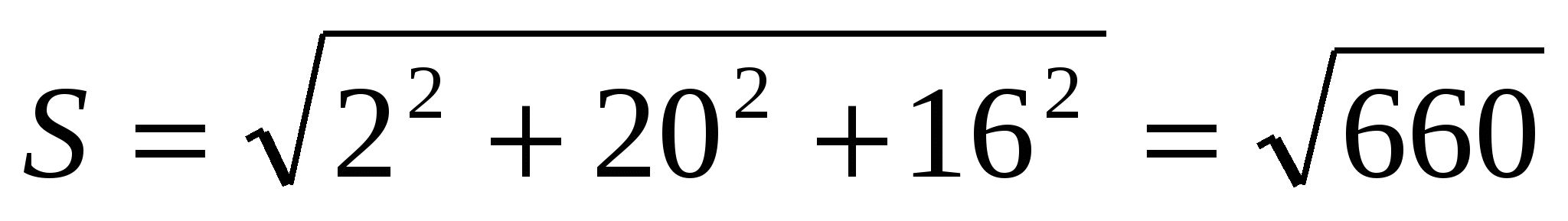
3) 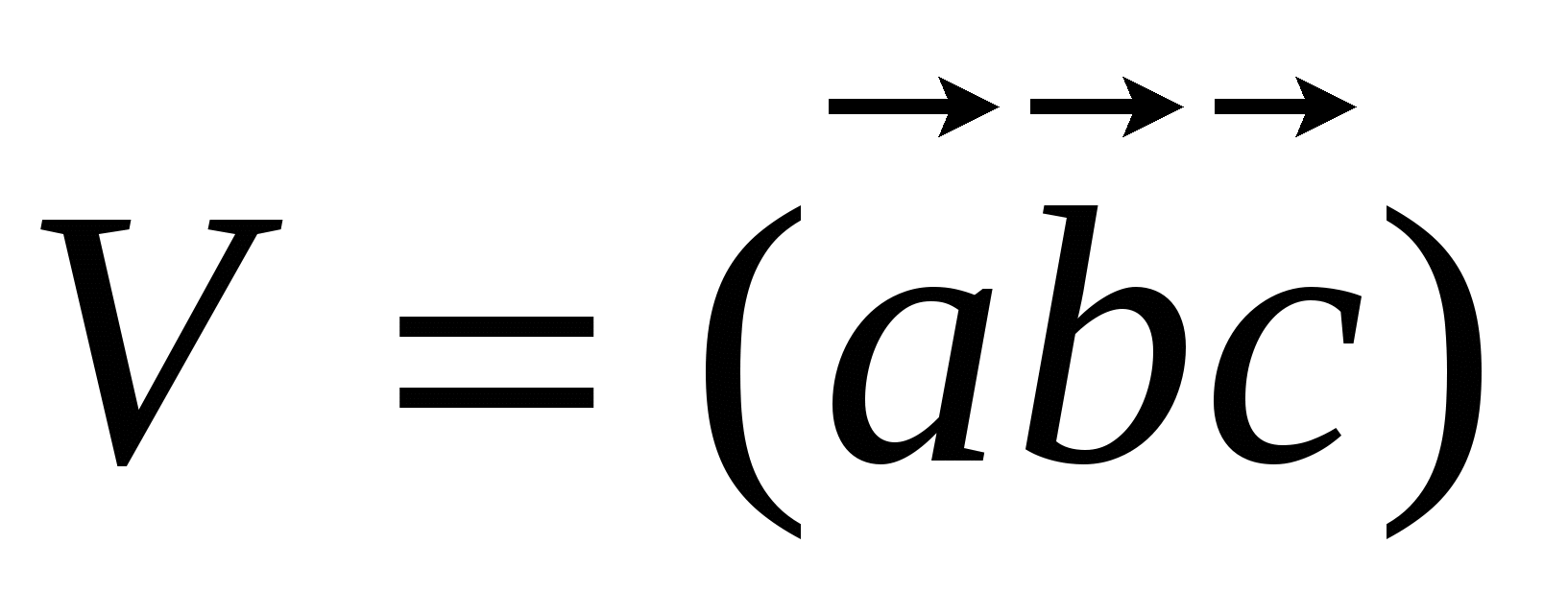
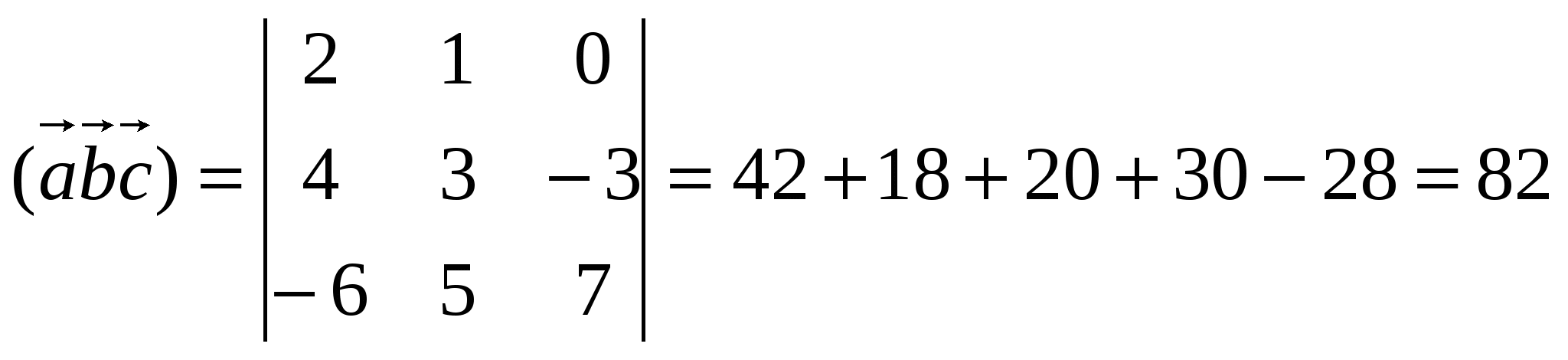
Ответ: 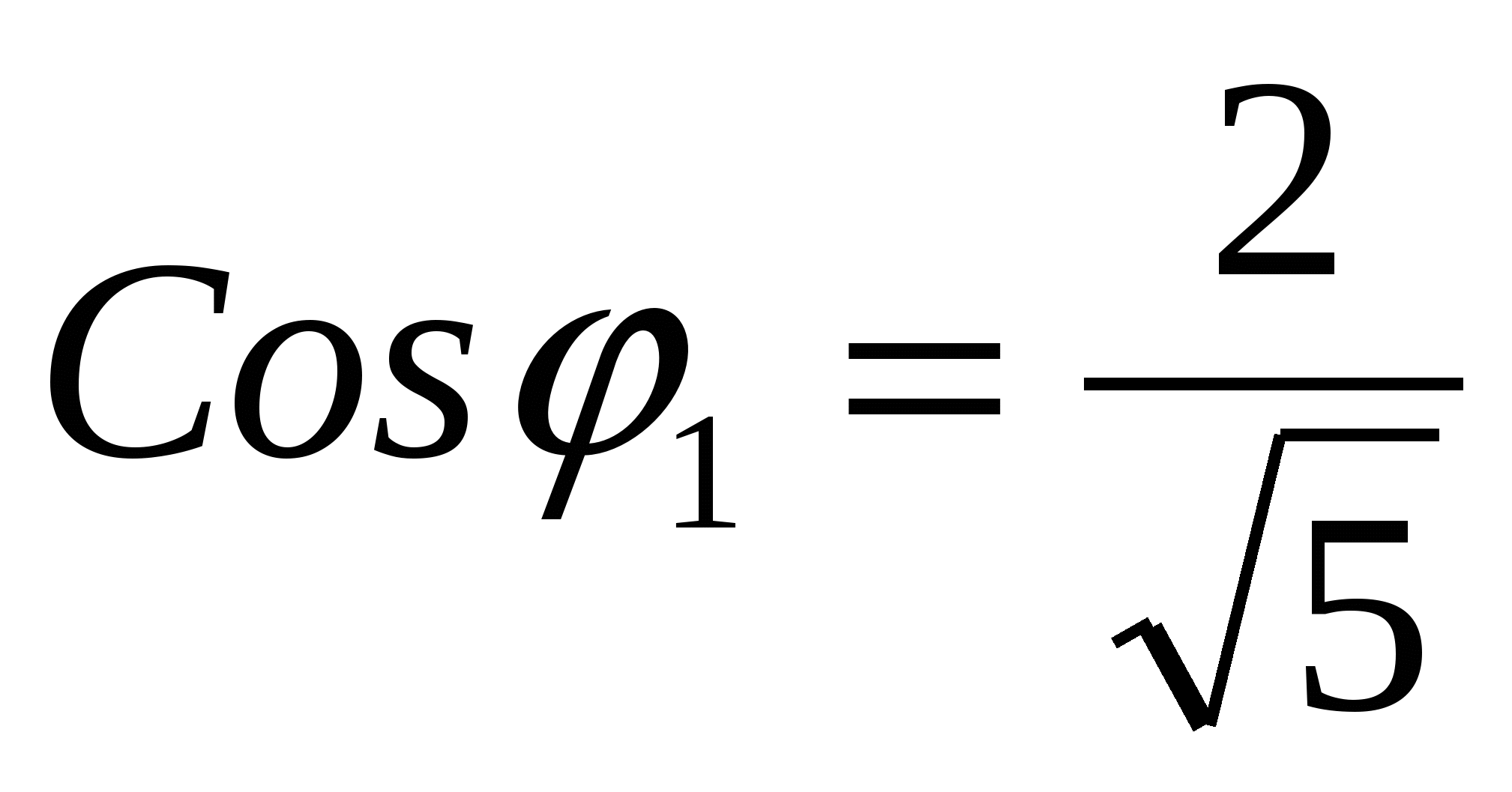 ;
; 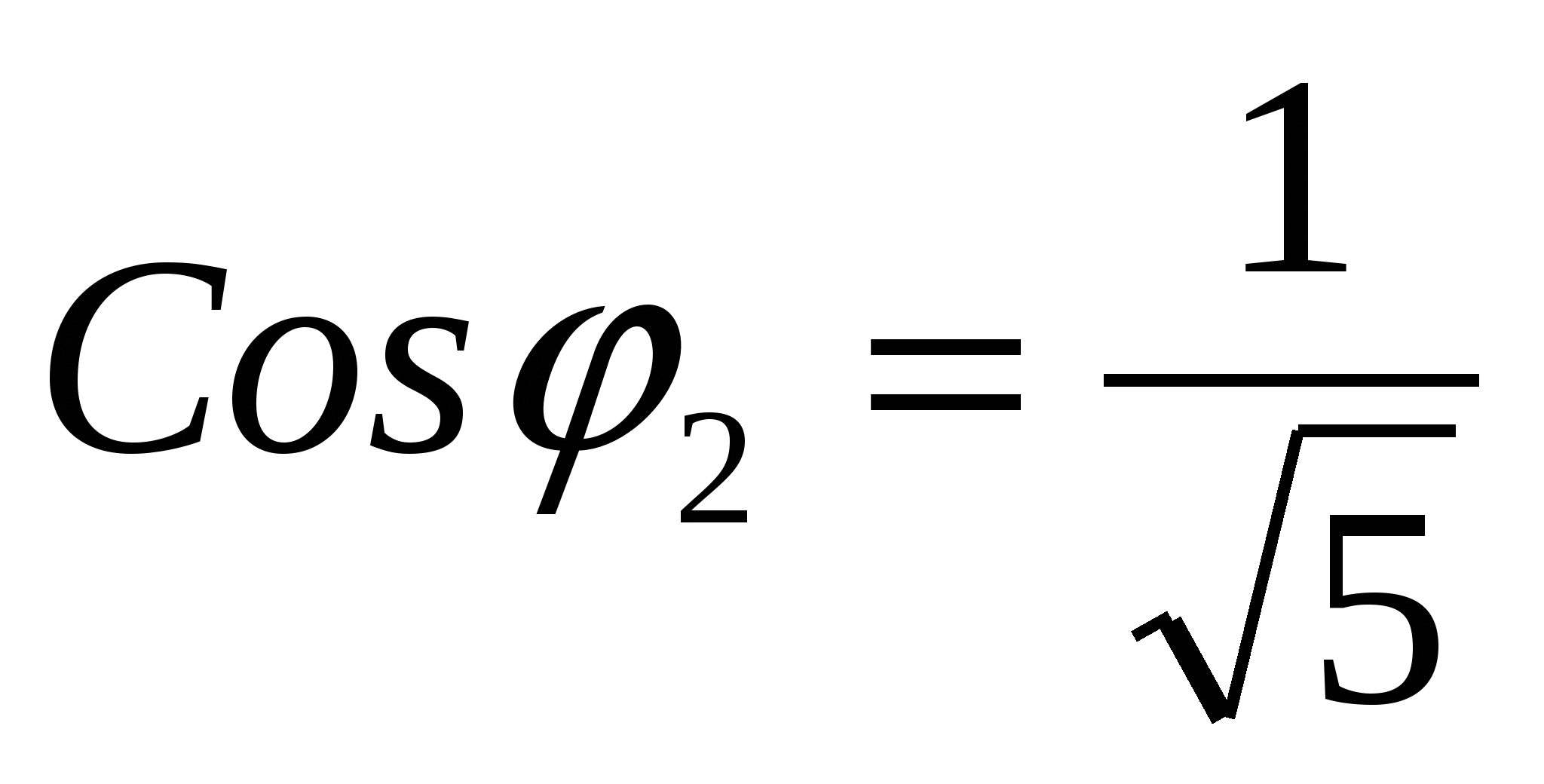 ;
; 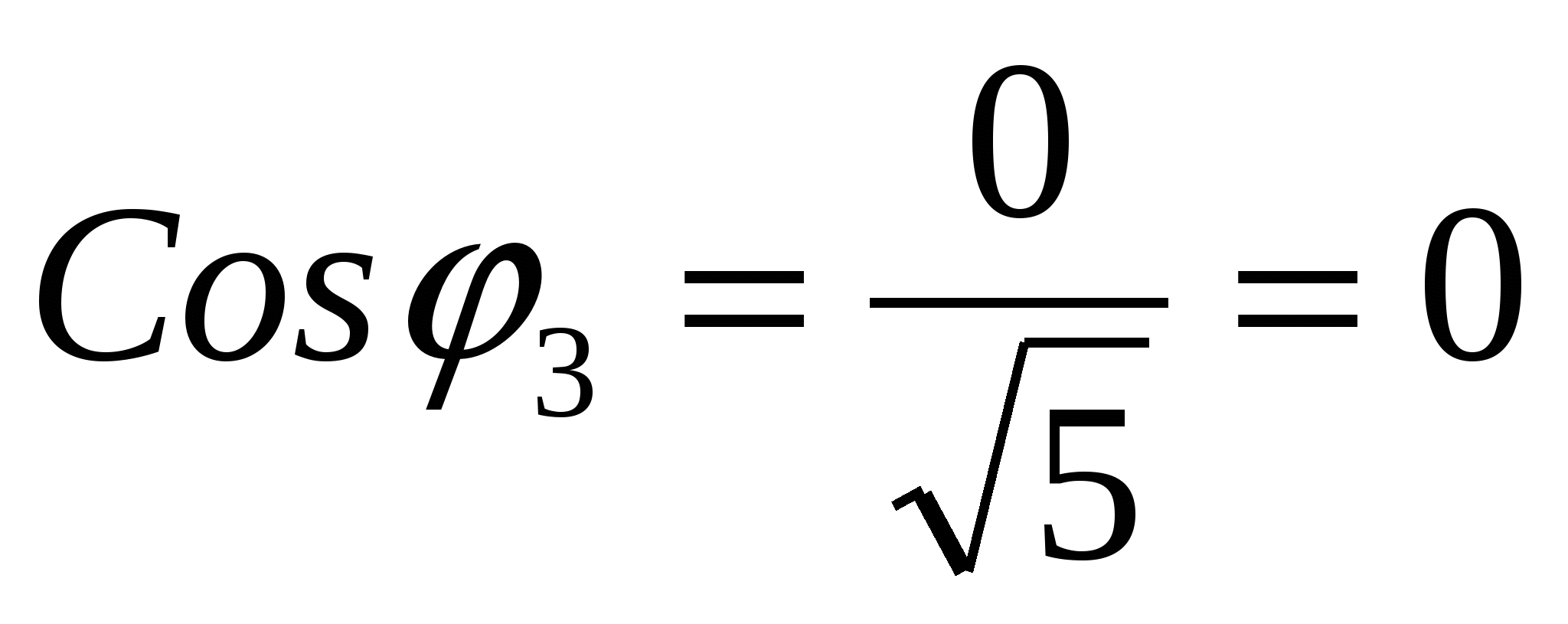 ;
;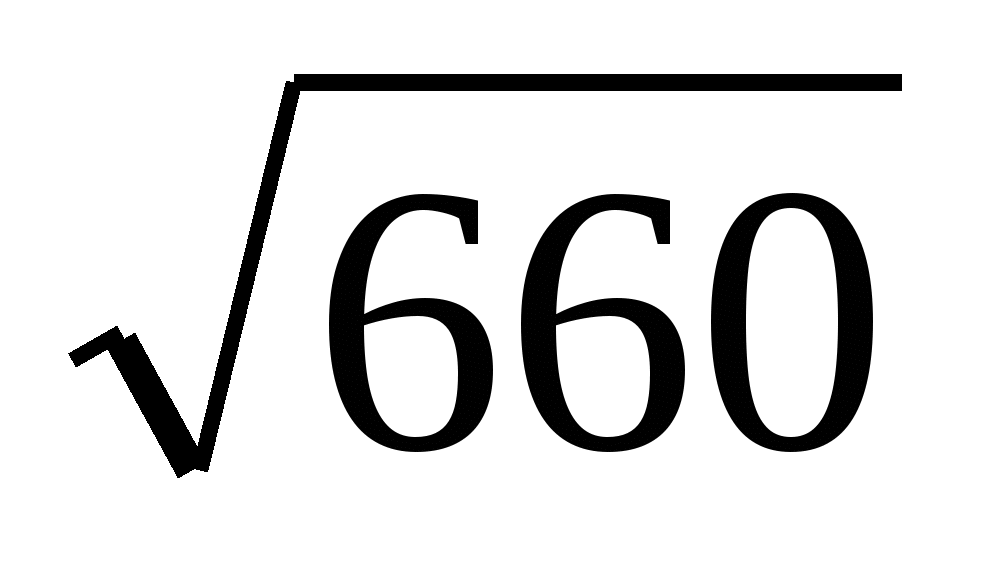 ; 82.
; 82.
Задача 6. С помощью преобразования поворота прямоугольной декартовой системы привести к каноническому виду уравнение кривой второго порядка
29x2 + 144xy + 71y2 - 40x + 30y - 50 = 0.
Написать формулы преобразования и изобразить данную кривую на чертеже.
Решение:
При повороте системы координат на угол φ наблюдается следующая зависимость между старыми и новыми координатами:
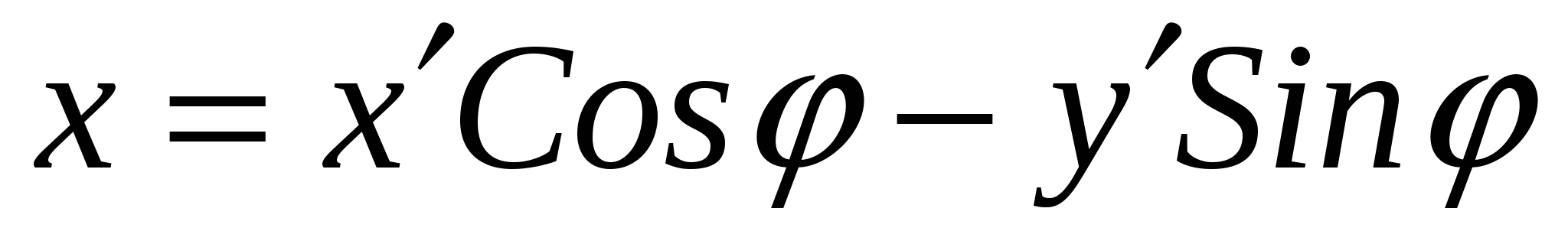
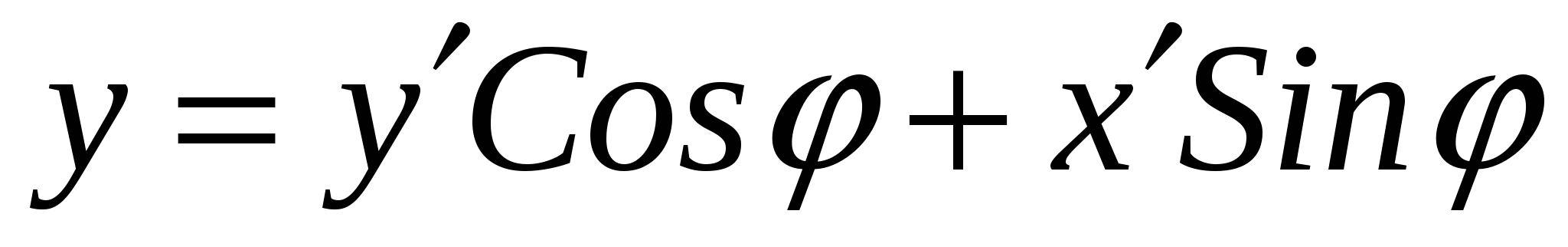 .
.
Тогда общее уравнение кривой второго порядка
Ax2 + 2Bxy + Cy2 + Dx + Ey + F = 0
преобразуется следующим образом:
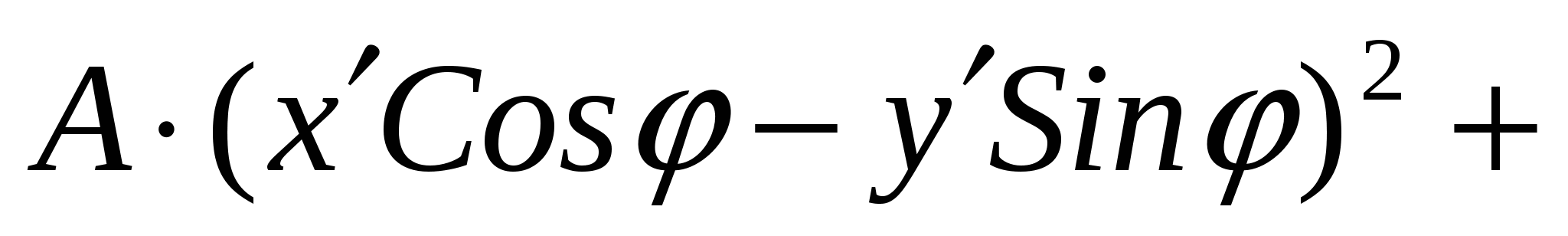
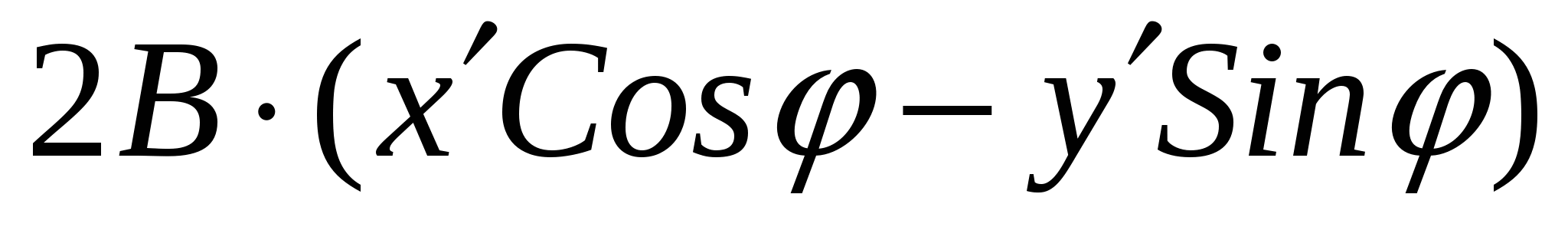
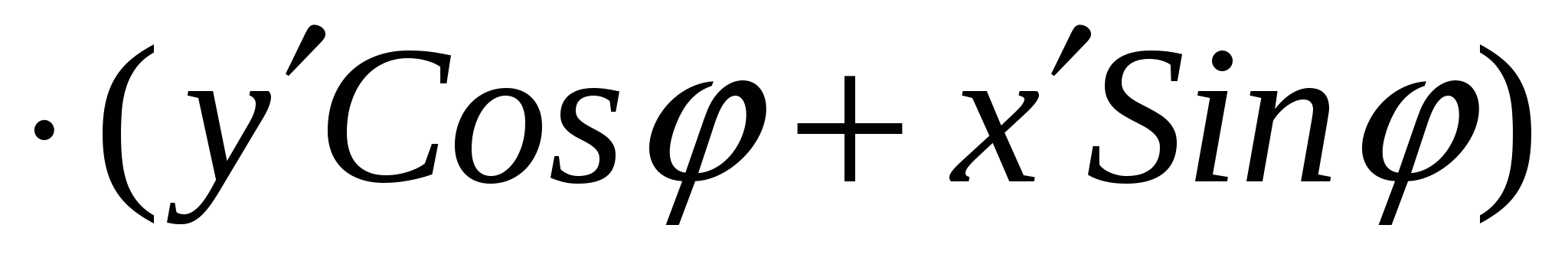 +
+
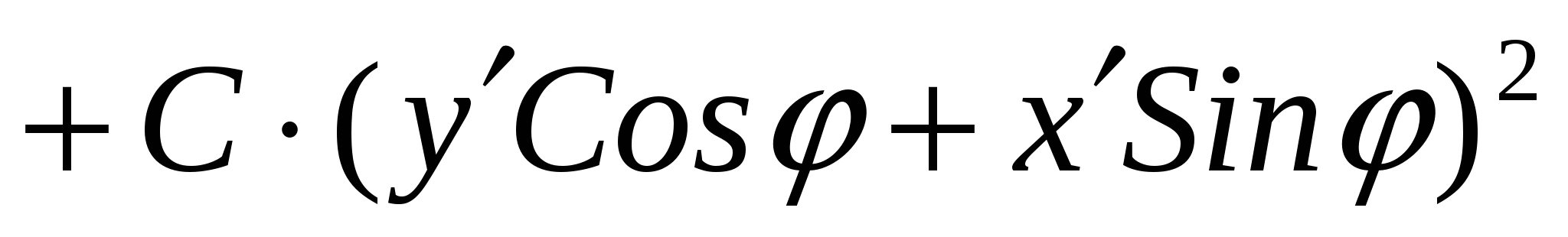 +
+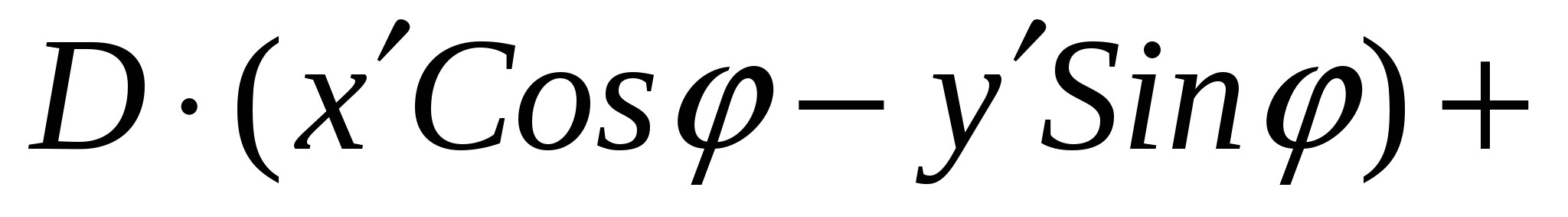
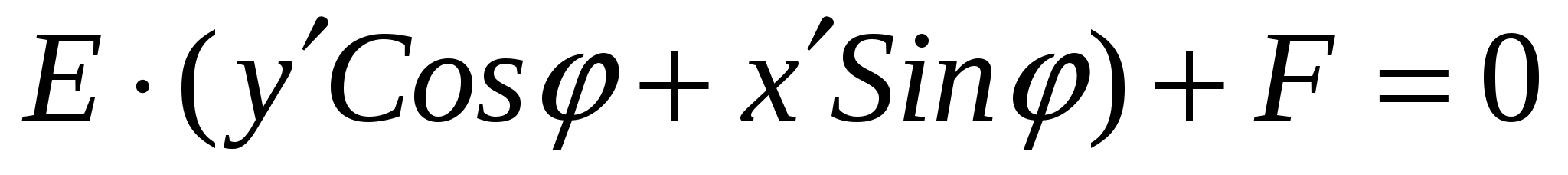
Раскроем скобки. Получим
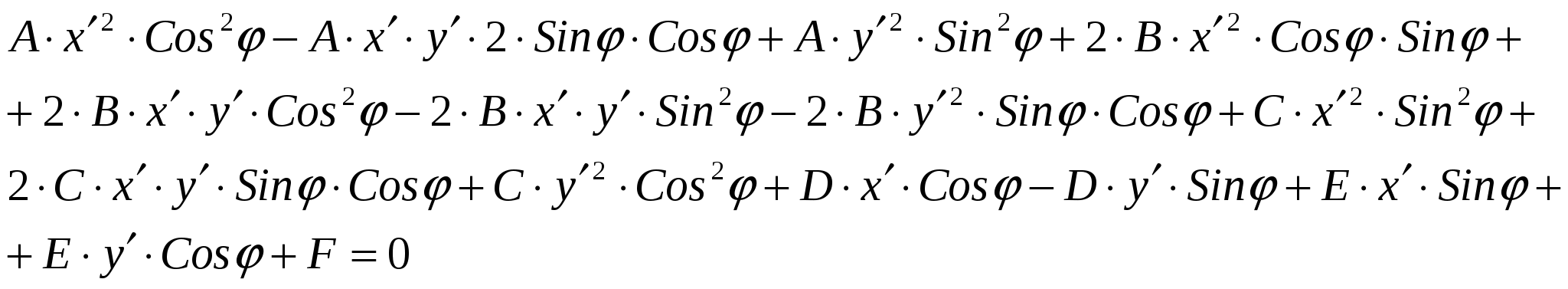
или
![]() , где
, где
![]()
![]()
![]()
![]()
![]() .
.
Для того, чтобы избавиться от перекрестного члена необходимо повернуть систему координат на такой угол φ, чтобы 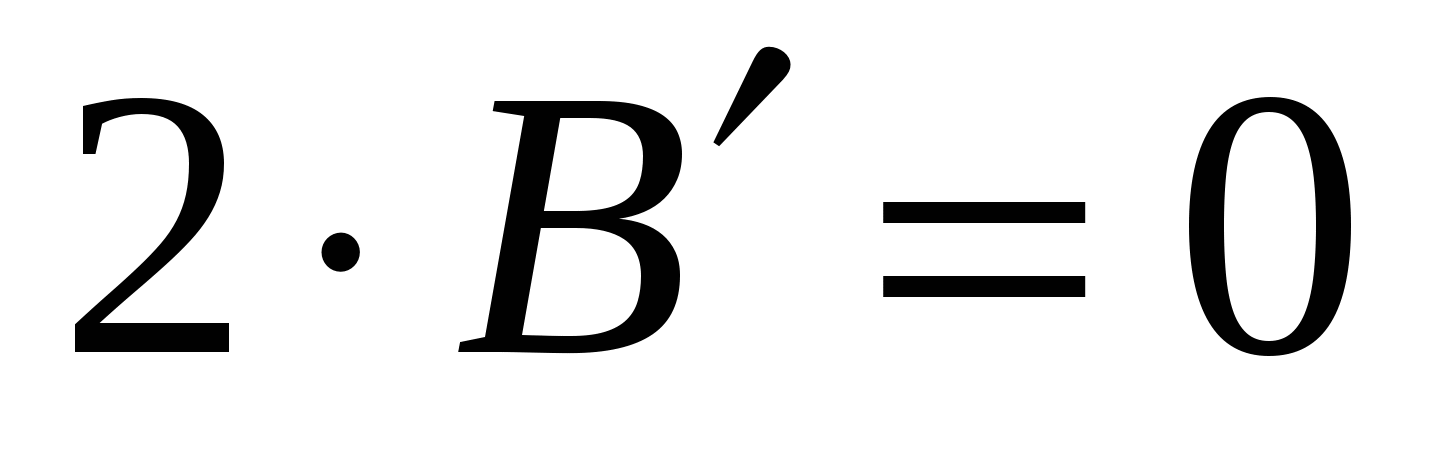 , т.е.
, т.е.
![]()
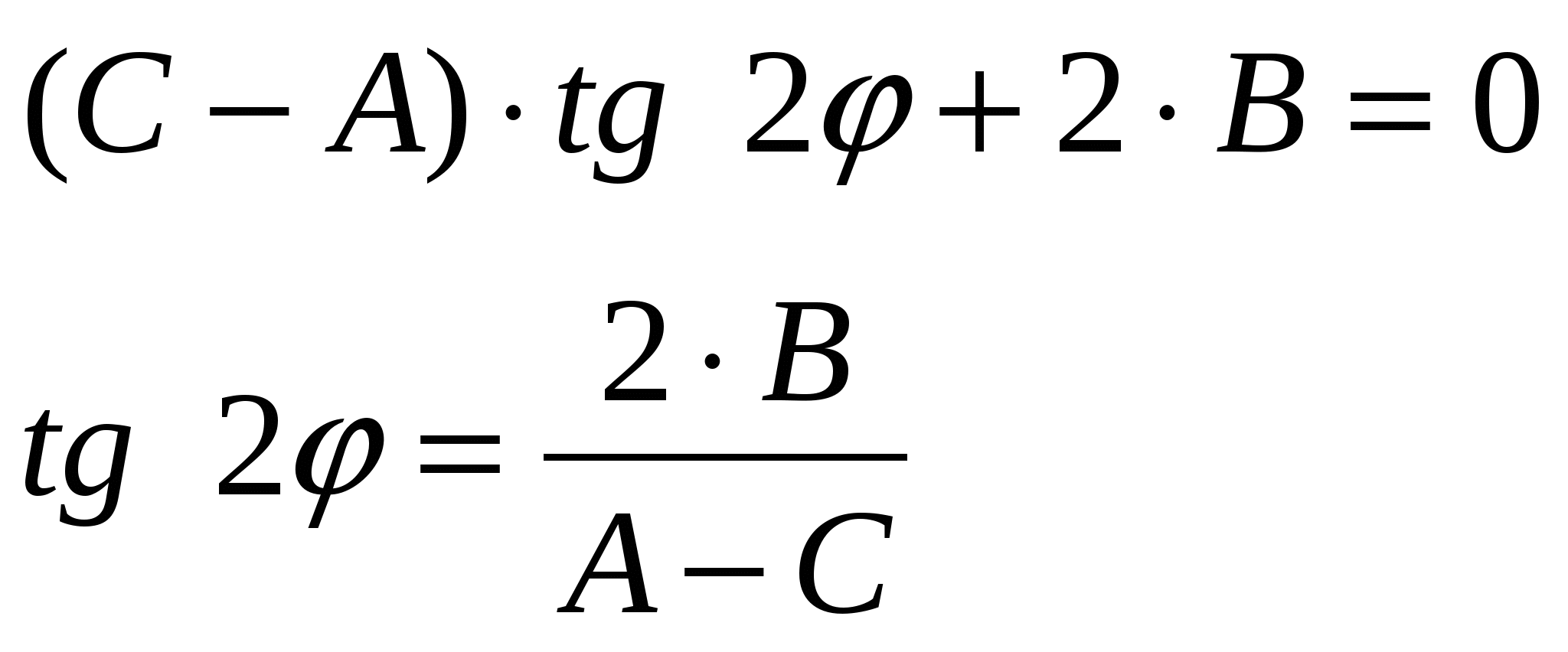
![]()
Найдем 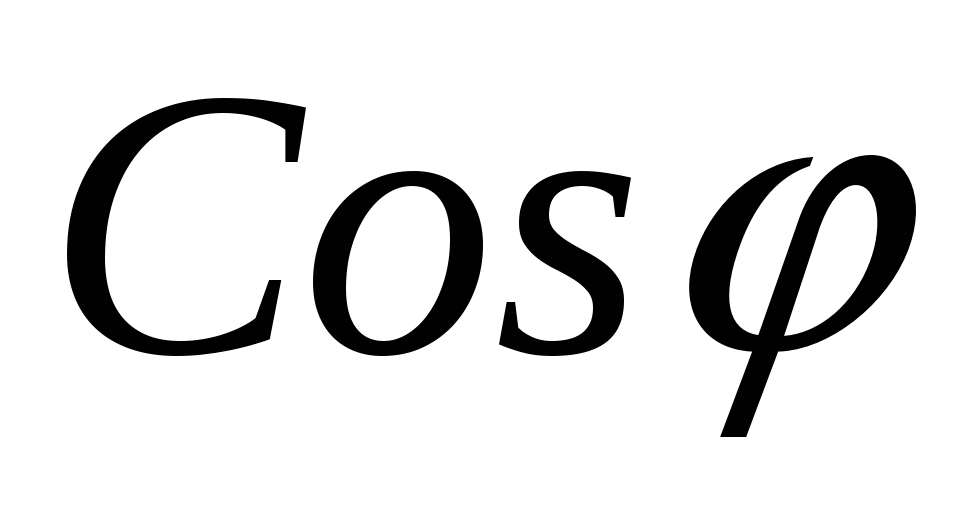 :
:
![]() где
где 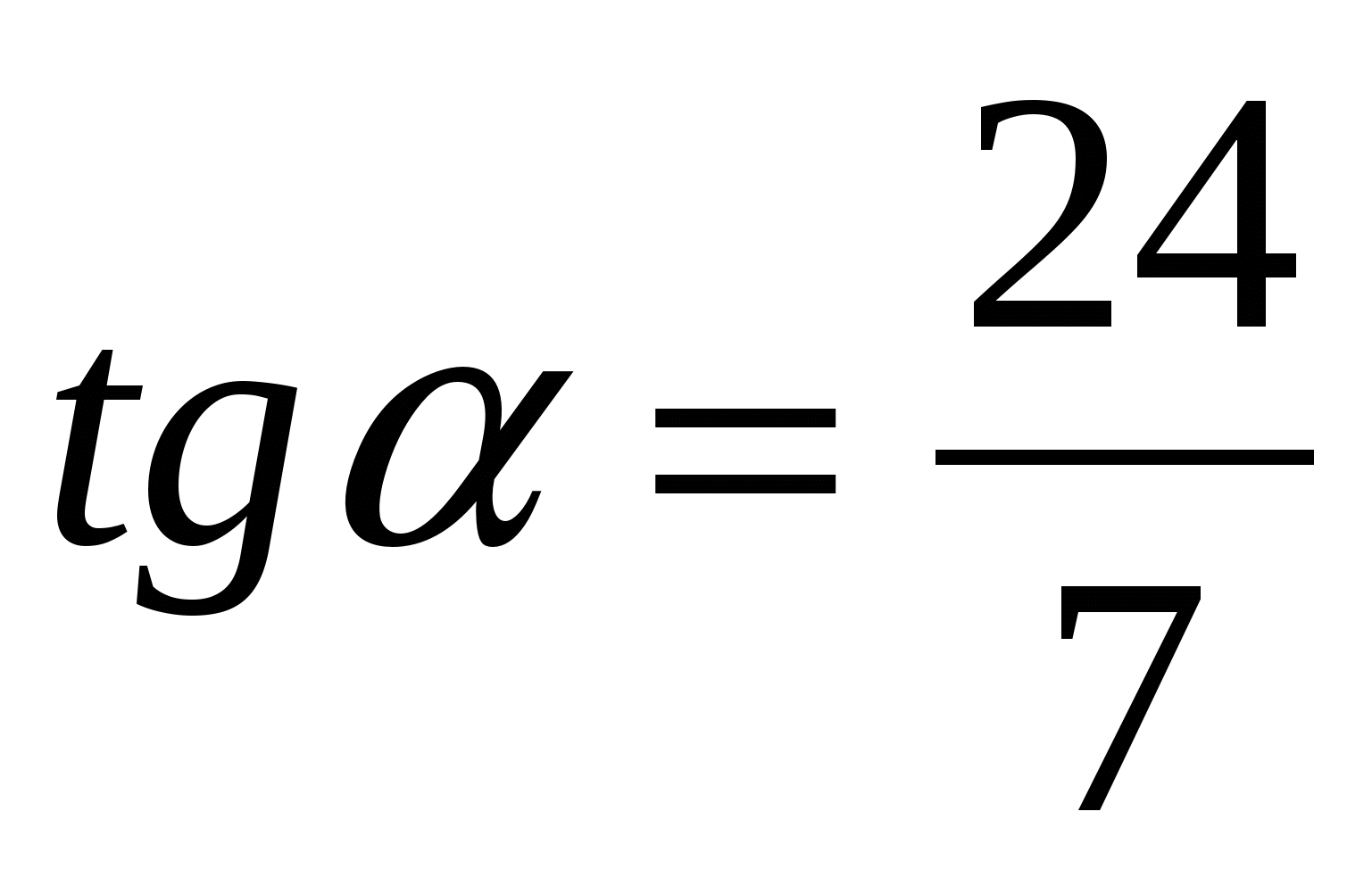 .
.
Тогда
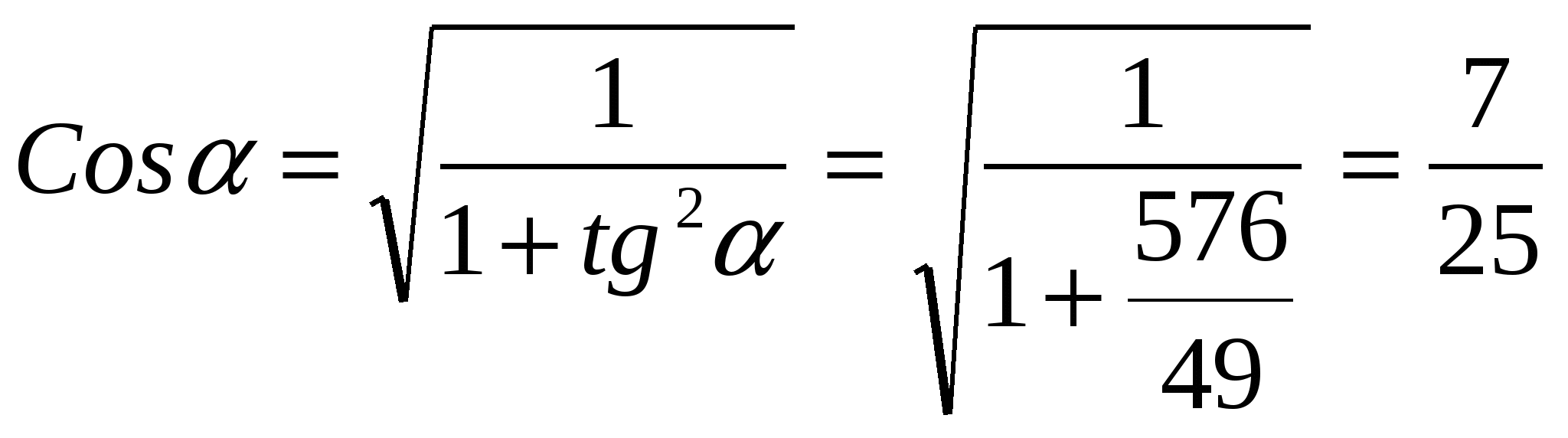
и
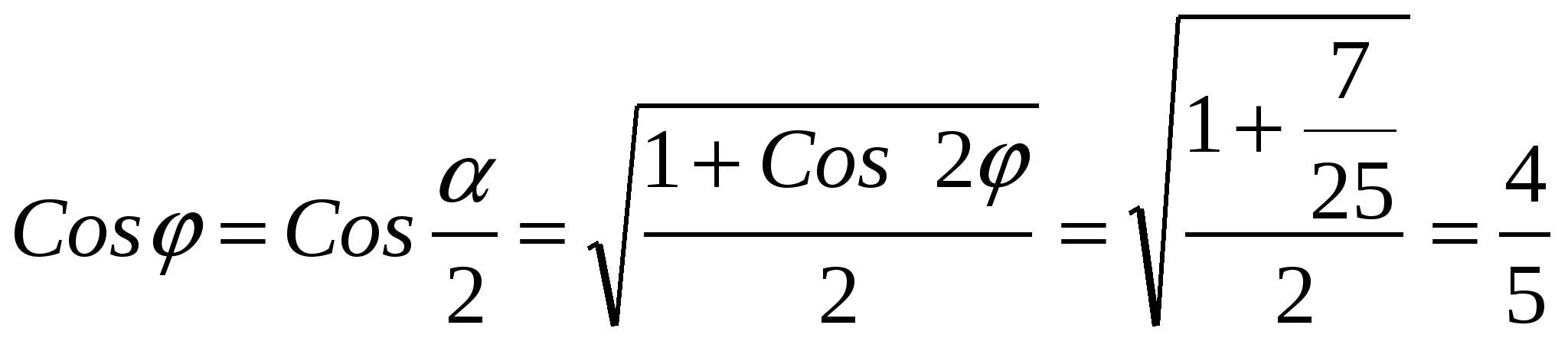 ;
; 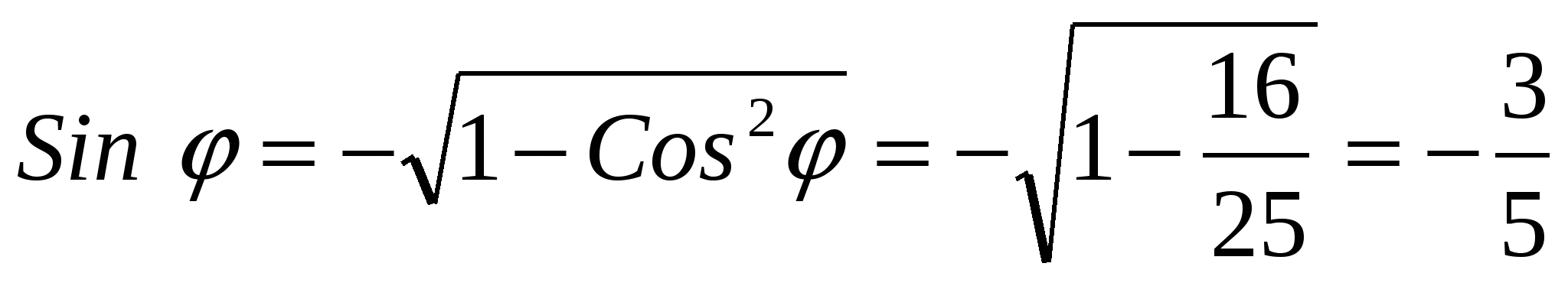 .
.
Имеем: 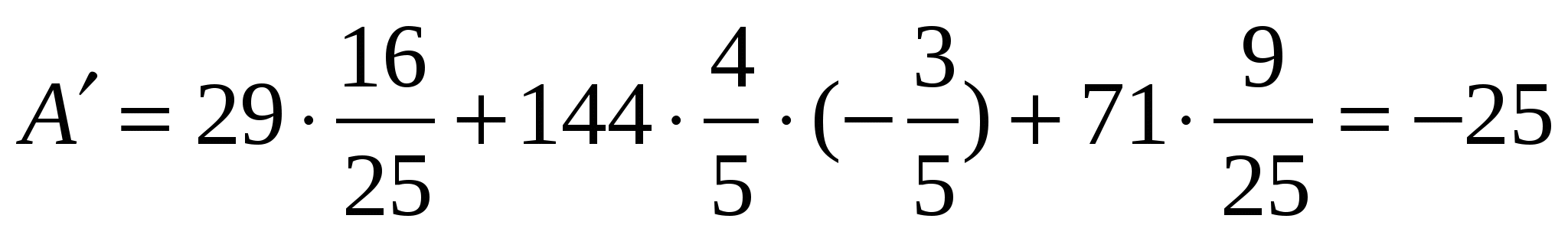
![]()
![]()
![]()
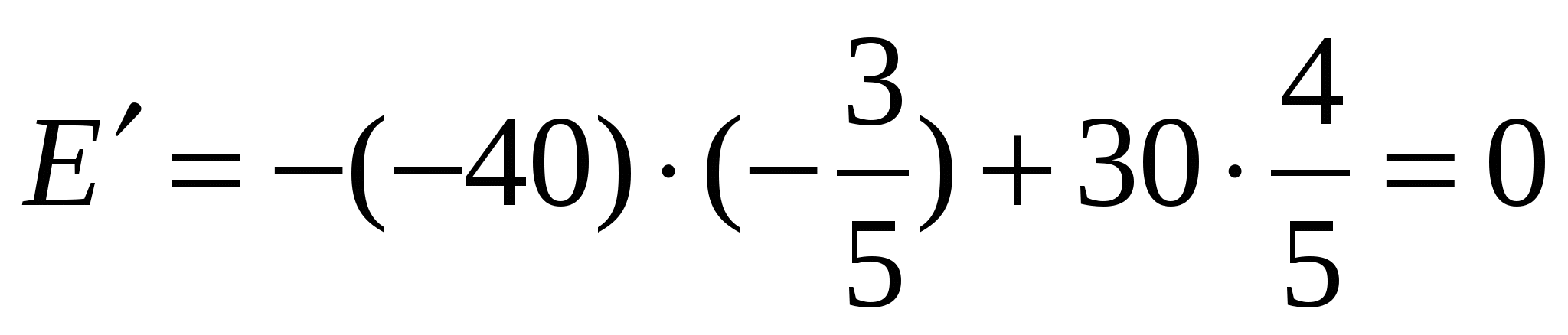 .
.
Получили: 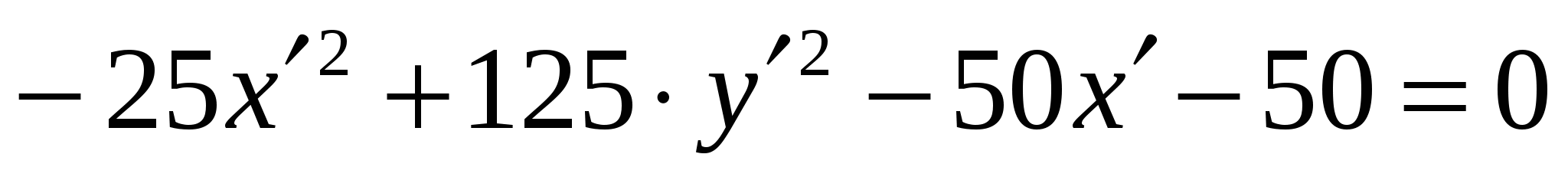
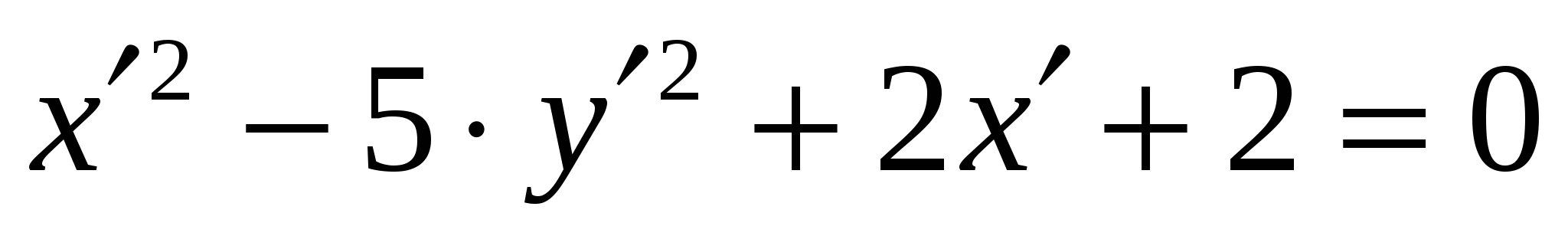
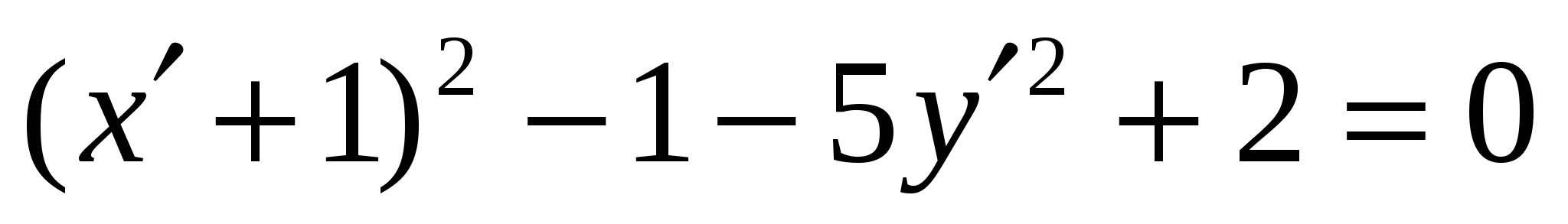
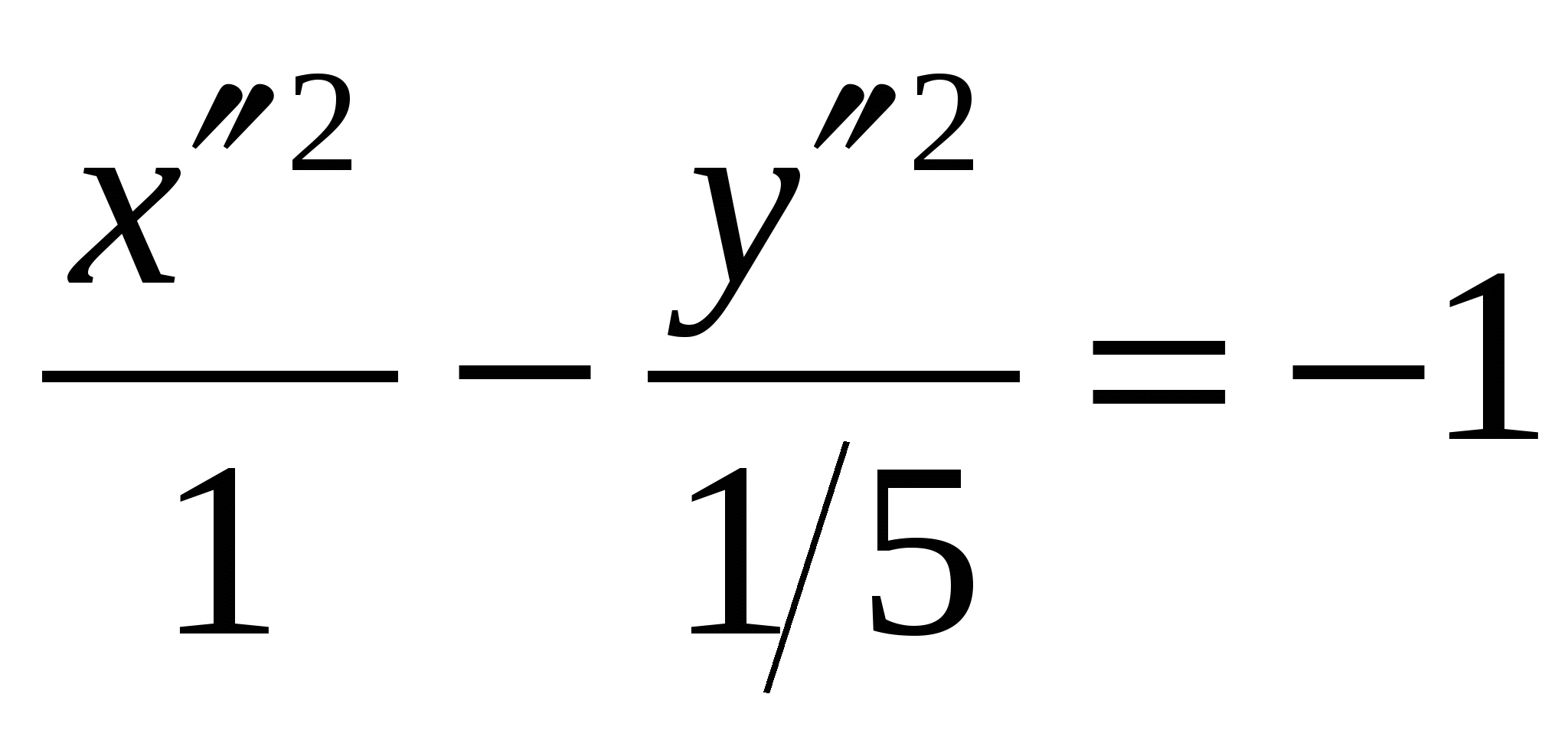 , где
, где 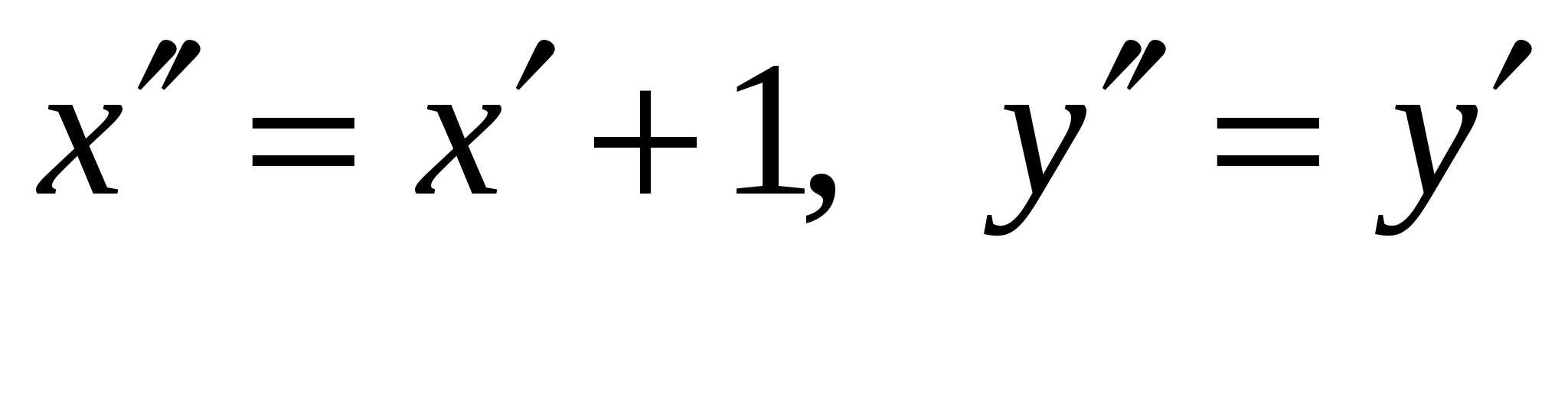 .
.
Канонический вид уравнения заданной кривой: 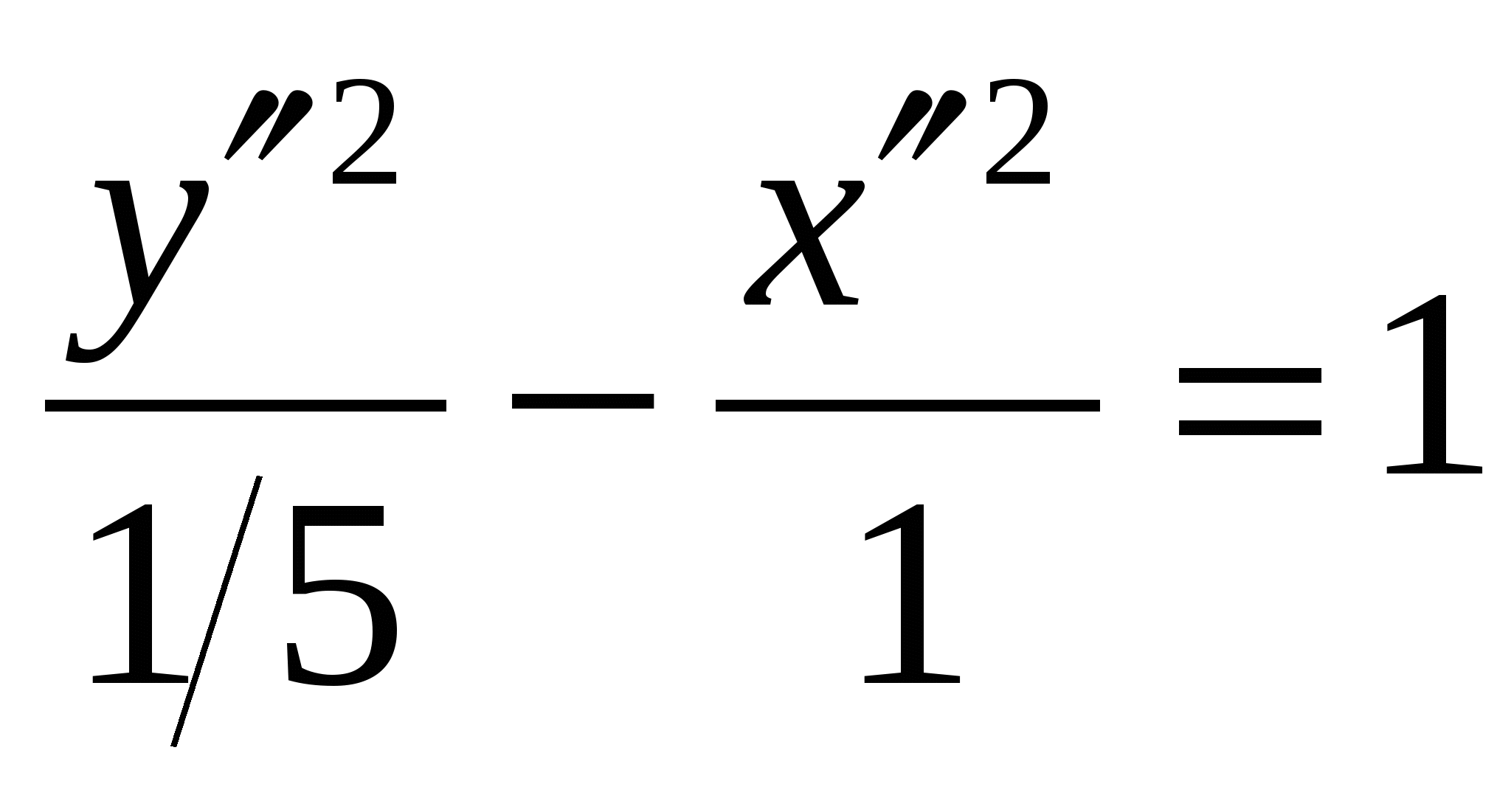
Это гипербола с вершинами в точках 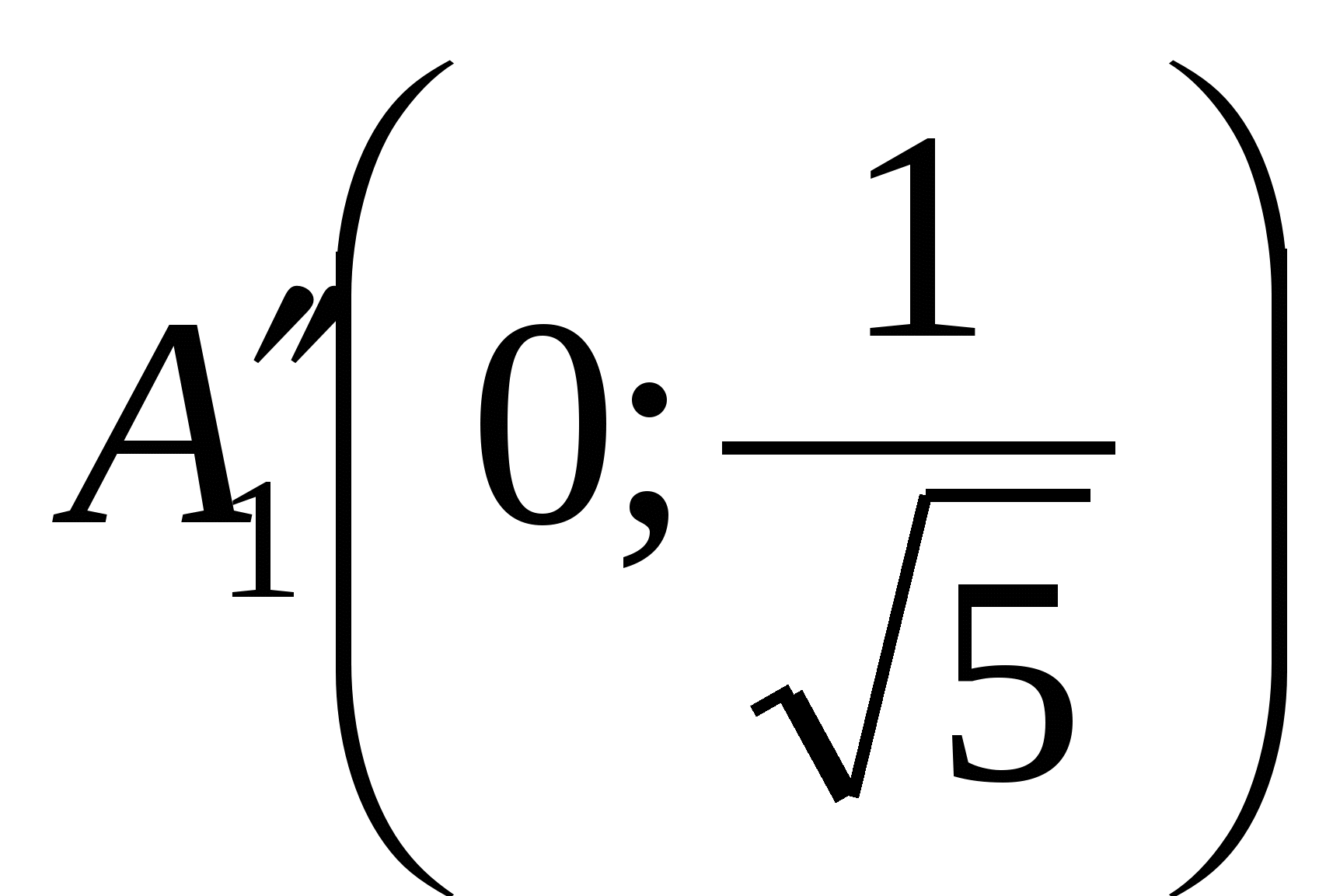 и
и 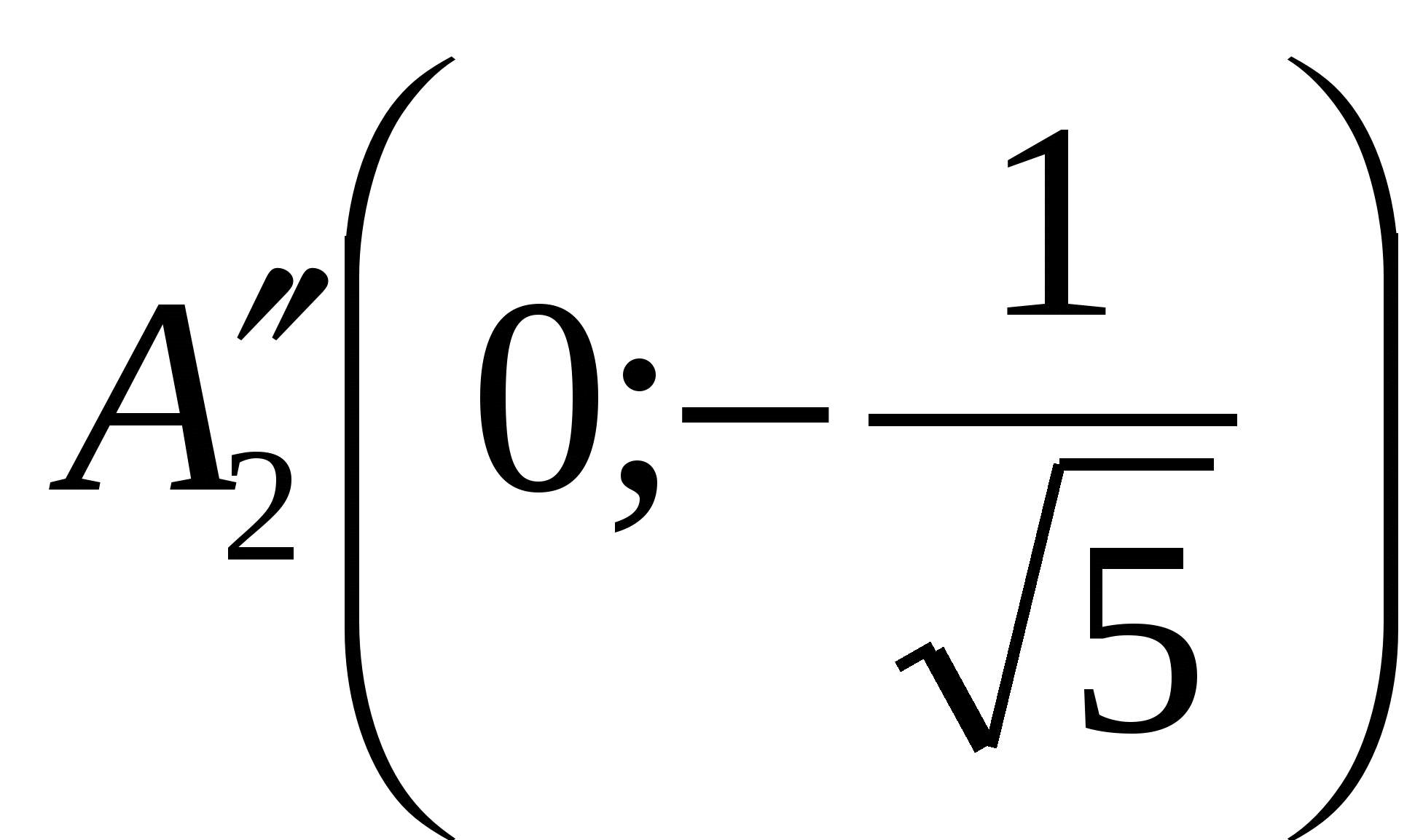 ; асимптотами
; асимптотами 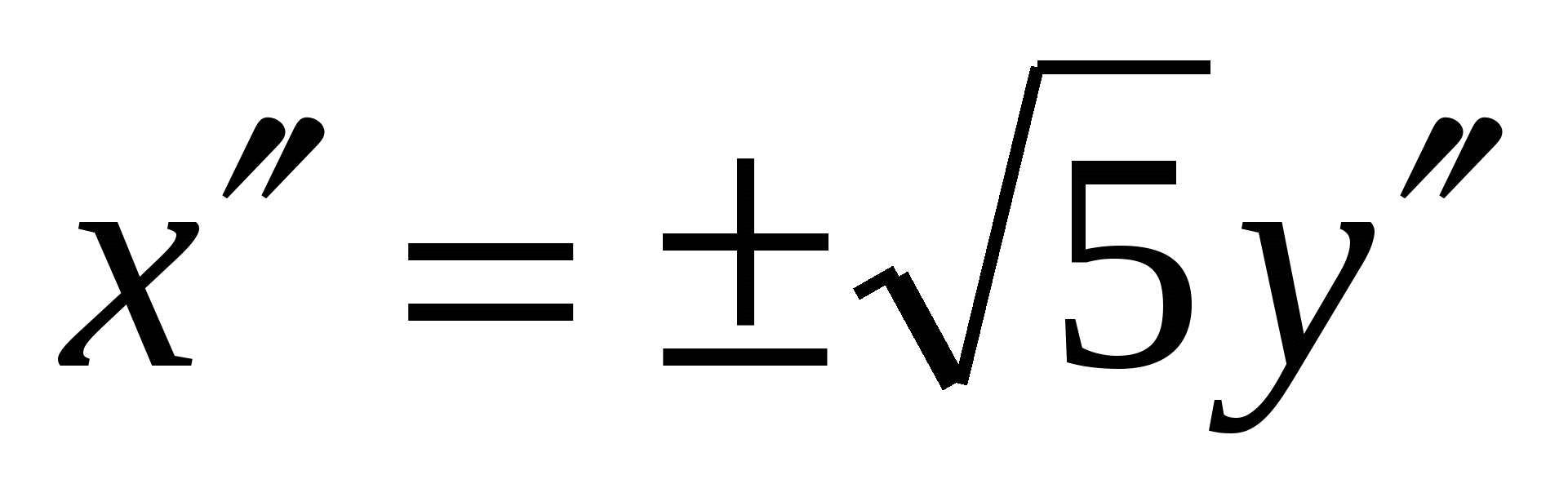 и фокусами
и фокусами 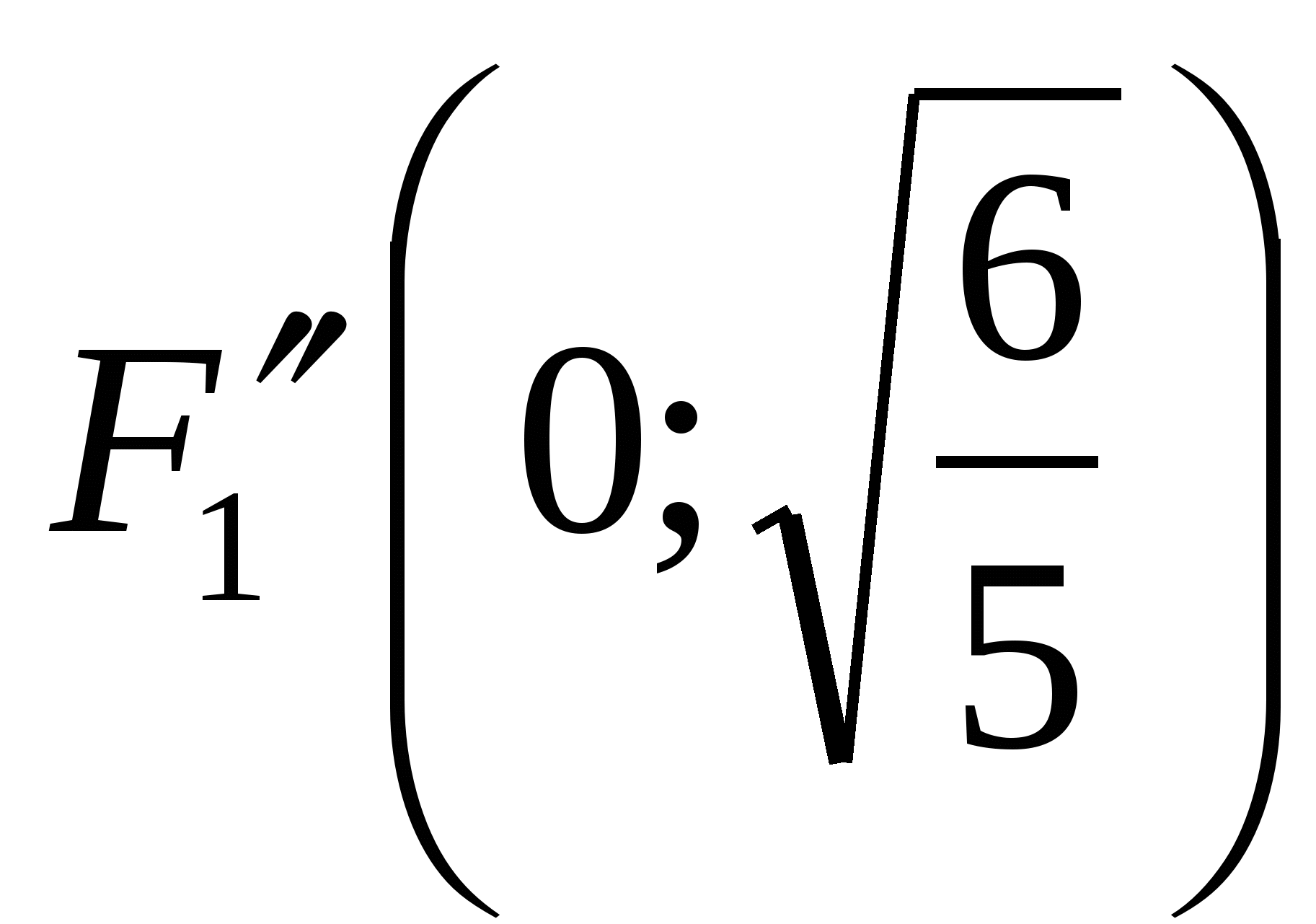 и
и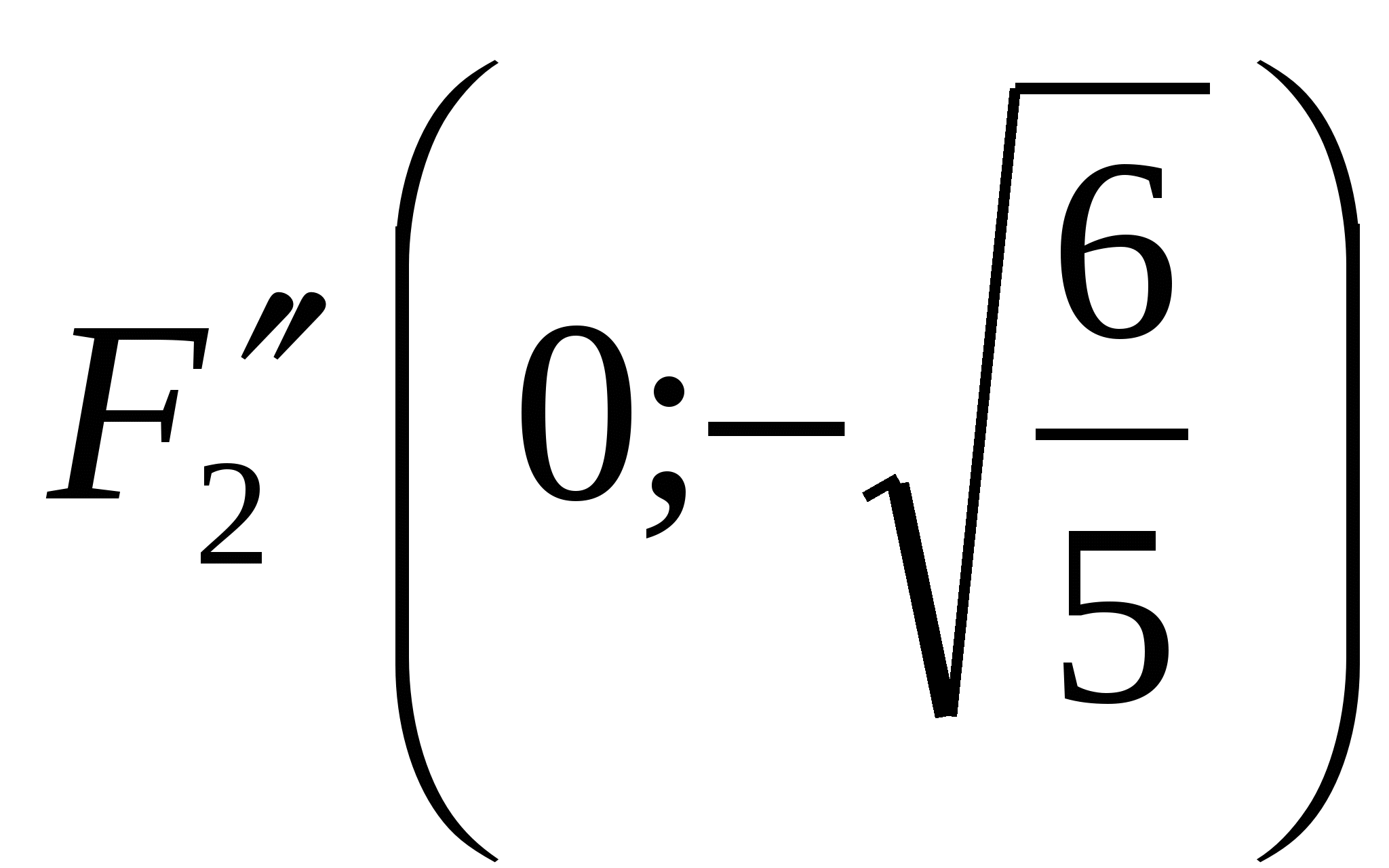
Ответ: 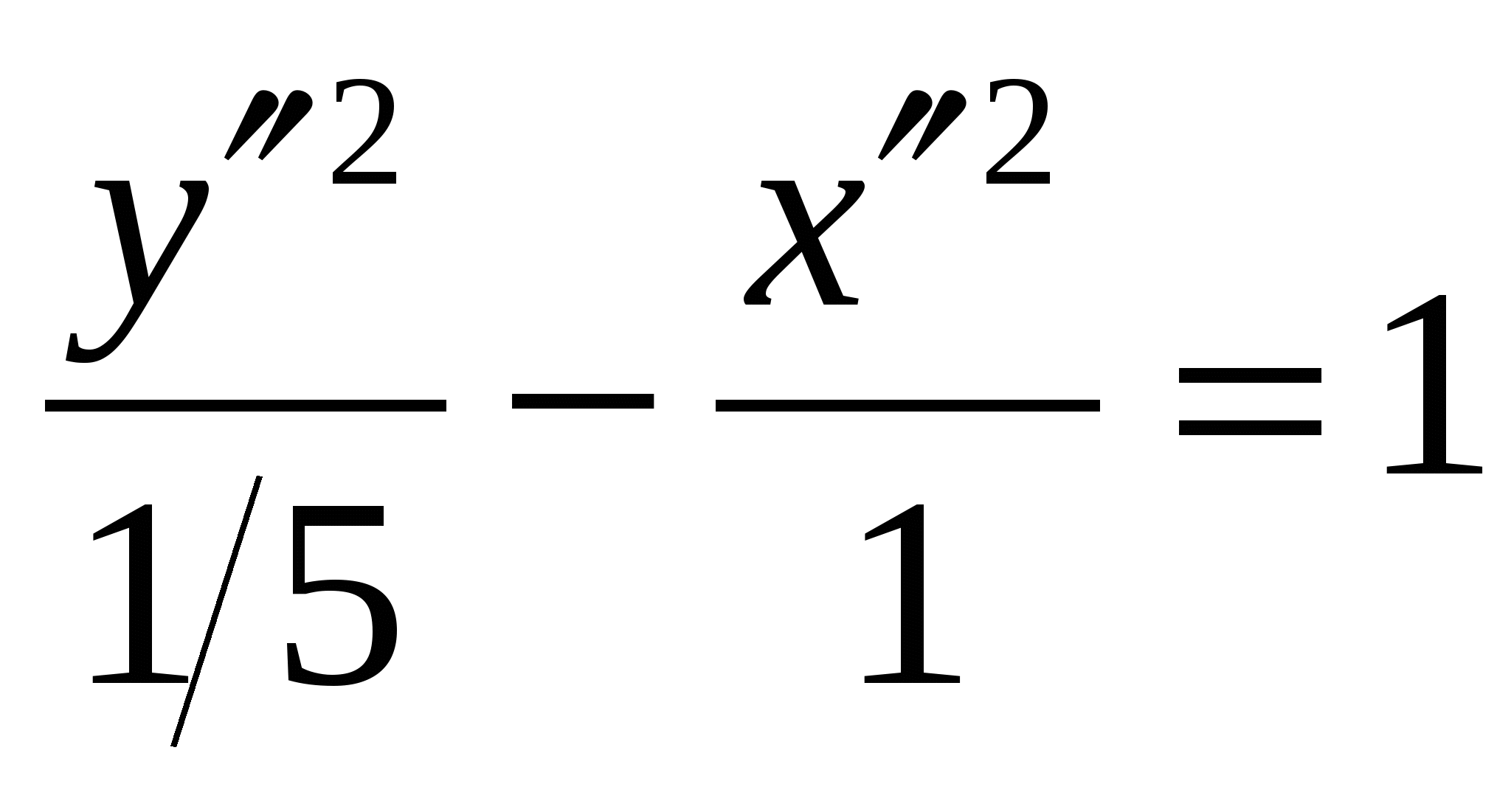
Задача 7. Привести уравнение кривой к каноническому виду и построить кривую на плоскости:
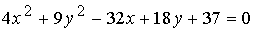 .
.
Решение:
Имеем: a11 = 4, a22 = 9, a12 = 0, a1 = −16, a2 = 9, a0 = 37. Тогда
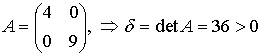 , то есть уравнение задает кривую эллиптического типа. Так как
, то есть уравнение задает кривую эллиптического типа. Так как 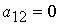 , то выделяем "полный квадрат":
, то выделяем "полный квадрат":
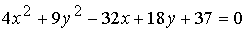
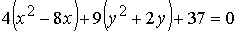 ;
;
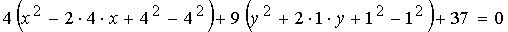 ;
;

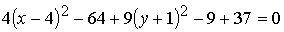 ;
;
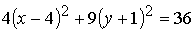
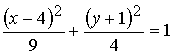 .
.
Сделаем замену:
 .
.
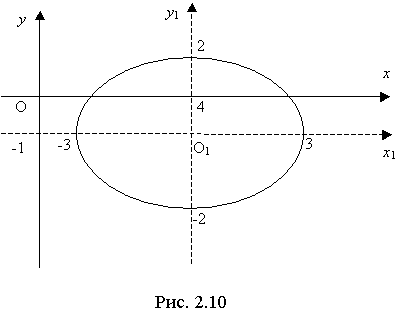
В системе координат 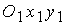 уравнение имеет вид:
уравнение имеет вид:
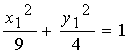 .
.
Таким образом, данное уравнение определяет эллипс с полуосями 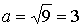 и
и 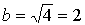 , с центром в точке
, с центром в точке 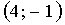 . Строим чертеж .
. Строим чертеж .

Задача 8.
Решение:

Ответ: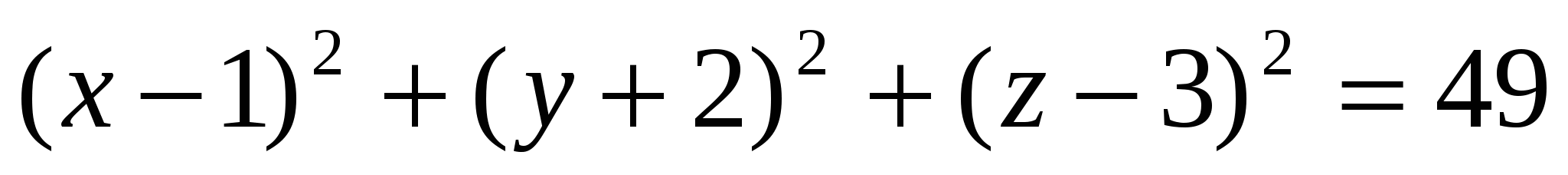

Задача 9.


Ответ: 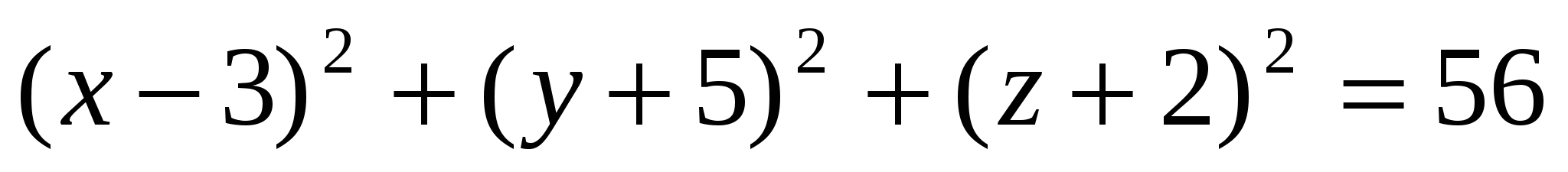
Задача 10. Привести уравнение кривой к каноническому виду и построить кривую на плоскости:
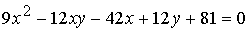 .
.
(1)
Решение:
Имеем: a11 = 9, a12 = −6, a22 = 0, a1 = −21, a2 = 6, a0 = 81. Тогда
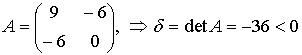
то есть уравнение (1) задает кривую гиперболического типа. Далее находим:
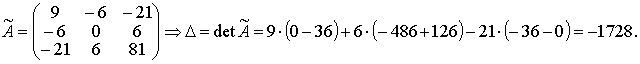
Найдем собственные значения:
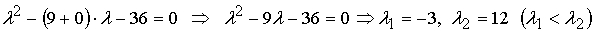 .
.
Тогда угол поворота равен 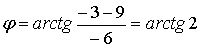
Далее найдем координаты α, β нового центра О1 системы координат 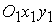 .
.
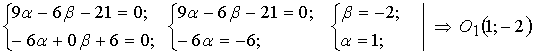 .
.
Уравнение (1) в системе 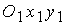 примет вид:
примет вид:
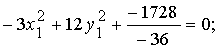
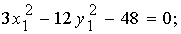
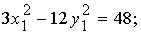
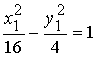 .
.
(2)
Уравнение (2) задает гиперболу, у которой 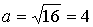 и
и 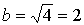 , фокусы гиперболы лежат на оси О1х1.
, фокусы гиперболы лежат на оси О1х1.
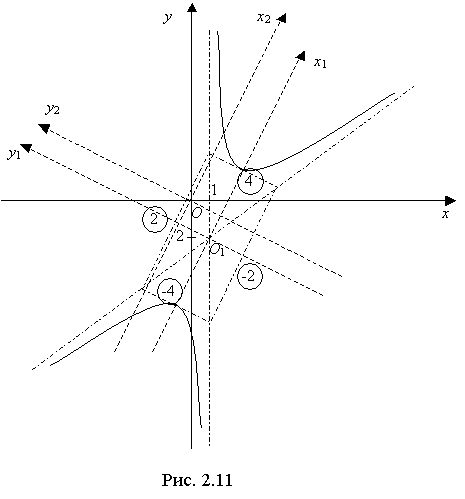
Строим гиперболу на плоскости 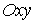 по плану :
по плану :
╥ поворачиваем ось 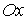 на угол
на угол 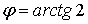 против часовой стрелки, для этого строим прямую
против часовой стрелки, для этого строим прямую 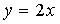 (так как
(так как 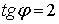 ); в результате получаем систему координат
); в результате получаем систему координат 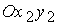 ;
;
╥ на плоскости 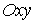 отмечаем точку
отмечаем точку 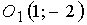 , через эту точку проводим две прямые, параллельные осям
, через эту точку проводим две прямые, параллельные осям 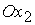 и
и 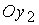 ; получаем систему координат
; получаем систему координат 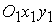 ;
;
╥ в системе 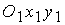 строим гиперболу, согласно уравнению (2).
строим гиперболу, согласно уравнению (2).
Задача 11. Уравнение прямой x + 3y - 4 = 0 привести к нормальному виду.
Решение.
Нормирующий множитель определяется по формуле
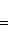
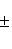
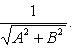
Здесь A = 1; B = 3. Перед корнем надо выбрать знак, противоположный знаку свободного члена в заданном уравнении, т. е. знак плюс. Тогда нормирующий множитель
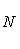
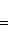
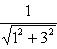
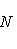
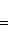
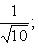
после умножения обеих частей уравнения на N уравнение примет вид
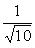
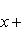
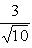
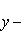
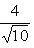
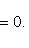
Задача 12. Общее уравнение прямой 4x - 3y + 12 = 0 представить в виде: 1) с угловым коэффициентом; 2) в отрезках на осях и 3) в нормальном виде. Построить эту прямую.
Решение.
1) Уравнение прямой с угловым коэффициентом имеет вид y = kx + b. Чтобы заданное уравнение преобразовать к этому виду, разрешим его относительно y: 3y = 4x + 12, 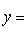
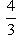
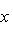
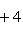 .
.
Сравнивая с уравнением y = kx + b, видим, что здесь угловой коэффициент прямой 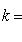
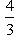 , а величина отрезка, отсекаемого прямой на оси ординат, b = 4 (если уравнение прямой дано в общем виде Ax + By + C = 0, то ее угловой коэффициент легко получить, если разделить коэффициент при x на коэффициент при y и взять полученное частное с обратным знаком
, а величина отрезка, отсекаемого прямой на оси ординат, b = 4 (если уравнение прямой дано в общем виде Ax + By + C = 0, то ее угловой коэффициент легко получить, если разделить коэффициент при x на коэффициент при y и взять полученное частное с обратным знаком 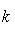
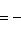
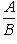 ).
).
2) В отрезках на осях уравнение прямой имеет вид
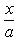
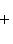
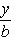
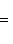
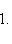 (1)
(1)
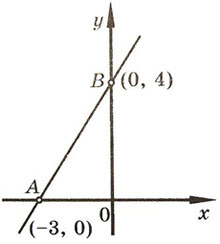
Чтобы определить величины отрезков, отсекаемых заданной прямой 4x - 3y + 12 = 0, поступим так: в уравнении прямой положим y = 0. Получаем 4x + 12 = 0, а x = -3. Значит, наша прямая пересекает ось Ox в точке с координатами (-3, 0) и в уравнении (1) величина отрезка a = -3.
Полагая в нашем уравнении x = 0, определим ординату точки пересечения прямой с осью ординат. Будем иметь
-3y + 12 = 0; y = 4.
Точка пересечения прямой с осью ординат имеет координаты (0, 4), и в уравнении (1) величина отрезка b = 4.
Таким образом, наше уравнение в отрезках на осях будет иметь вид
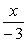
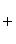
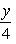
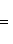
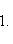
3) Чтобы привести уравнение к нормальному виду, обе его части следует умножить на нормирующий множитель 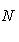
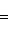
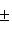
 , выбрав перед корнем знак, противоположный знаку свободного члена в общем уравнении прямой. В нашем случае свободный член в общем уравнении прямой равен +12, а поэтому перед корнем в нормирующем множителе должен быть выбран противоположный знак, т. е. знак минус, и так как A = 4, B = -3, то
, выбрав перед корнем знак, противоположный знаку свободного члена в общем уравнении прямой. В нашем случае свободный член в общем уравнении прямой равен +12, а поэтому перед корнем в нормирующем множителе должен быть выбран противоположный знак, т. е. знак минус, и так как A = 4, B = -3, то 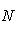
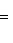
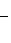
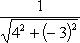
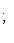
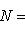
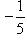 .
.
Умножая на 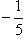 обе части уравнения 4x - 3y + 12 = 0, приведем его к нормальному виду
обе части уравнения 4x - 3y + 12 = 0, приведем его к нормальному виду
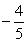
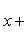
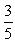
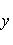
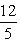
Запомнить: В нормальном уравнении прямой сумма квадратов коэффициентов при текущих координатах должна быть равна единице, а свободный член должен быть отрицательным. Эти два требования в полученном нами последнем уравнении, как легко проверить, выполнены. В пункте 2 решения мы получили уравнение прямой в отрезках на осях: a = -3, b = 4. Зная эти отрезки, мы легко построим нашу прямую (см. рисунок).
Задача 13. Найти длину перпендикуляра, опущенного из начала координат на прямую 3x - 6y + 5 = 0, а также координаты основания этого перпендикуляра.
Решение.
Приведем данное уравнение к нормальному виду:
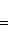
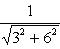
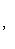
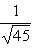
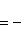
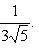
После умножения на нормирующий множитель уравнение примет вид
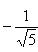
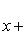
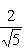
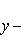
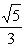
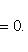
Из сравнения с 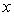
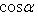
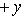
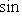
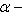
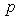
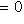 заключаем, что
заключаем, что 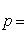
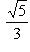 .
.
Для определения координат основания этого перпендикуляра из рисунка
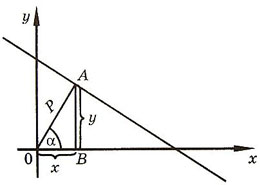
получим формулы
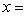
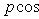
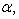
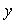
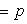
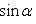
(эти формулы верны при любом расположении прямой относительно координатных осей).
как видно из уравнения 
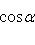

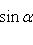
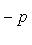
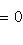
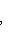
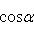
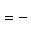
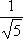
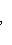
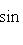
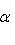
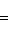
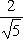 и искомые координаты основания перпендикуляра равны
и искомые координаты основания перпендикуляра равны
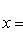
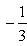
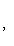
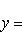
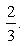
Задача14.Найти геометрическое место точек, равноудаленных от двух данных точек.
Решение.
Возьмем прямоугольную систему координат, и пусть две данные точки B и C лежат на оси абсцисс и имеют координаты (x1, 0) и (x2, 0) (см. рисунок). Пусть точка A принадлежит искомому геометрическому месту. Обозначим ее координаты через x и y: A(x, y).
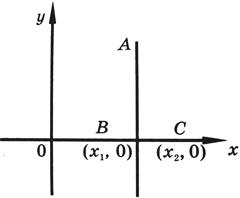
На основании формулы для определения расстояния между двумя точками 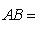
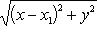
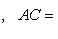
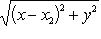 , значит, так как по условию AB = AC, можем написать, что
, значит, так как по условию AB = AC, можем написать, что 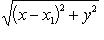
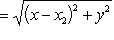 . Это и есть уравнение искомого геометрического места.
. Это и есть уравнение искомого геометрического места.
Возводя в квадрат обе части искомого равенства, будем иметь
(x - x1)2 + y2 = (x - x2)2 + y2.
После очевидных упрощений получим 2x(x2 - x1) = (x2 - x1)(x2 + x1); сокращая на 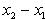
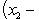
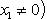 , имеем 2x = x1 + x2, или
, имеем 2x = x1 + x2, или ![]()
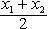 .
.
Это уравнение прямой, перпендикулярной оси Ox и проходящей через середину отрезка BC.
Итак, искомым геометрическим местом является прямая, перпендикулярная к отрезку BC, соединяющему данные точки, и проходящая через его середину.
Замечание. При решении задачи нам пришлось уничтожить радикалы в уравнении искомого геометрического места
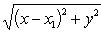
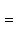
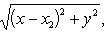 (1)
(1)
в результате чего было получено уравнение
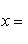
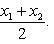 (2)
(2)
Из алгебры известно, что возведение обеих частей уравнения в квадрат может привести к уравнению, которое не равносильно (не эквивалентно) исходному. Это значит, что уравнение, полученное от возведения в квадрат обеих частей исходного уравнения, может иметь решения, не удовлетворяющие исходному уравнению, т. е. иметь так называемые "посторонние" корни. Поэтому всегда в тех случаях, когда обе части уравнения приходится возводить в квадрат, следует ставить вопрос об эквивалентности полученного и исходного уравнений.
В интересующем нас случае вопрос ставится так: не содержит ли линия (2) точек, которых нет на линии (1), т. е. таких, координаты которых не удовлетворяют уравнению (1) и таким образом не удовлетворяют исходному условию AB = AC.
Чтобы убедиться в том, что линия (2) не содержит точек, которых нет в линии (1), надо показать, что уравнение (2) может быть преобразовано в уравнение (1).
Произведя в обратном порядке операции, с помощью которых было получено уравнение (2), мы придем к уравнению (x - x1)2 + y2 = (x - x2)2 + y2, откуда следует, что
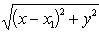
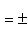
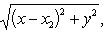 (3)
(3)
т. е. что 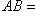
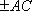 ; отсюда видно, что или AB - AC = 0, или AB + AC = 0.
; отсюда видно, что или AB - AC = 0, или AB + AC = 0.
Но AB > 0 и AC > 0, а следовательно, ![]()
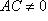 , так как сумма двух положительных величин не может быть равна нулю, а потому остается только одно равенство AB - AC = 0, т. е. AB = AC, и знак минус перед правой частью уравнения (3) должен быть отброшен. Поскольку из уравнения (1) получается уравнение (2) и обратно - из уравнения (2) следует уравнение (1), то эти уравнения равносильны (эквивалентны). Таким образом, поставленный вопрос решен: линия (2) не содержит таких точек, которых нет на линии (1).
, так как сумма двух положительных величин не может быть равна нулю, а потому остается только одно равенство AB - AC = 0, т. е. AB = AC, и знак минус перед правой частью уравнения (3) должен быть отброшен. Поскольку из уравнения (1) получается уравнение (2) и обратно - из уравнения (2) следует уравнение (1), то эти уравнения равносильны (эквивалентны). Таким образом, поставленный вопрос решен: линия (2) не содержит таких точек, которых нет на линии (1).
Задача 15. Найти уравнение геометрического места точек, произведение расстояний которых до двух данных точек A и B есть величина постоянная, равная a2. Длину AB считать равной 2a.
Решение.
Проведем вывод уравнения в прямоугольных координатах. Направим ось Ox по прямой, соединяющей A и B, как обычно, вправо, начало координат поместим в середине отрезка AB, ось Oy направим вверх по перпендикуляру к оси Ox. Длина отрезка AB по условию равна 2a (AB = 2a); тогда точки A и B будут иметь координаты: A(-a, 0); B(a, 0). Пусть точка M принадлежит кривой. Ее координаты обозначим через x и y (см. рисунок).
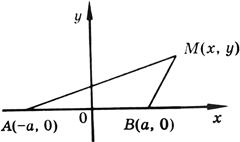
Из условия задачи AM * BM = a2. По формуле расстояния между двумя точками
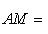
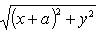
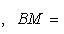
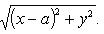
Значит, 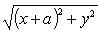
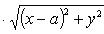
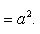
Возведем обе части этого уравнения в квадрат:
[(x + a)2 + y2][(x - a)2 + y2] = a4,
Или [(x2 + y2 + a2) + 2ax][(x2 + y2 + a2) - 2ax] = a4;
(x2 + y2 + a2)2 - 4a2x2 = a4.
Упрощая, получаем (x2 + y2)2 = 2a2(x2 - y2).
Это и есть искомое уравнение.
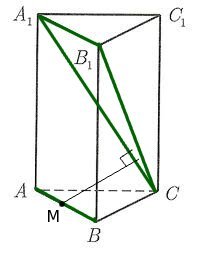
Задача 16. В правильной треугольной призме ![]() , все ребра которой равны 1, найдите расстояние между прямыми
, все ребра которой равны 1, найдите расстояние между прямыми 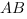 и
и ![]() :
:
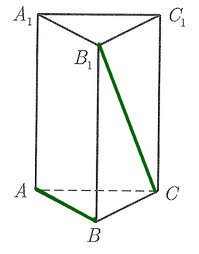 Как мы помним из геометрического метода решения этой задачи, расстояние между прямыми
Как мы помним из геометрического метода решения этой задачи, расстояние между прямыми 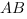 и
и 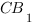 есть расстояние от точки
есть расстояние от точки 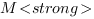 до плоскости
до плоскости ![]() :
:
Решение:
Рассстояние 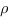 от точки
от точки ![]() до плоскости
до плоскости ![]() вычисляется по такой формуле:
вычисляется по такой формуле:
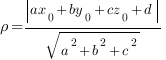
Поместим нашу призму в систему координат. Если мы решаем задачу с кубом или прямоугольным параллелепипедом, то выбор системы координат очевиден: мы помещаем начало координат в одну из вершин куба, а оси направляем вдоль ребер. В случае призмы это не столь очевидно.
Нам надо выбрать систему координат таким образом, чтобы координаты точки 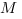 и точек
и точек ![]() ,
, 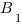 и
и ![]() , задающих плоскость
, задающих плоскость 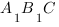 вычислялись наиболее простым способом и содержали как можно больше нулей. Поэтому удобно выбрать систему координат вот таким образом:
вычислялись наиболее простым способом и содержали как можно больше нулей. Поэтому удобно выбрать систему координат вот таким образом:
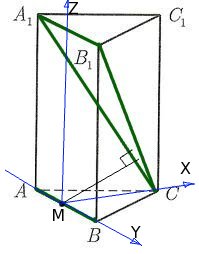 Запишем координаты нужных нам точек:
Запишем координаты нужных нам точек:
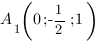
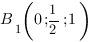
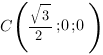
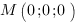
Чтобы найти коэффициенты 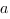 ,
, 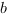 ,
, 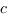 и
и ![]() в уравнении
в уравнении ![]() плоскости
плоскости ![]() , примем коэффициент
, примем коэффициент ![]() , и подставим координаты точек
, и подставим координаты точек 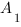 ,
, 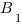 и
и ![]() в уравнение плоскости. Получим систему уравнений:
в уравнение плоскости. Получим систему уравнений:
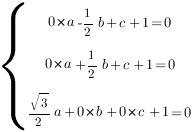
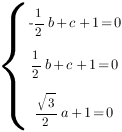
Отсюда:
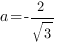 ,
,
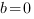 ,
,
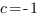
Подставим значения коэффициентов и координаты точки ![]() в формулу для расстояния. Получим:
в формулу для расстояния. Получим:
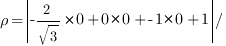
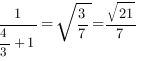
Ответ: 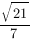
Задача 17. В единичном кубе 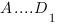 найдите расстояние от точки
найдите расстояние от точки 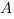 до плоскости
до плоскости ![]() .
.
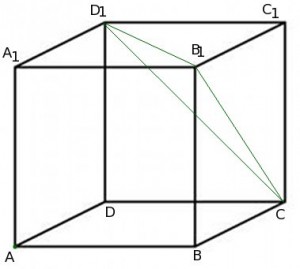 Решение:
Решение:
Рассстояние 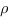 от точки
от точки ![]() до плоскости
до плоскости ![]() вычисляется по такой формуле:
вычисляется по такой формуле:
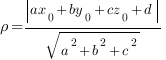
Чтобы воспользоваться этой формулой, поместим куб в систему координат:
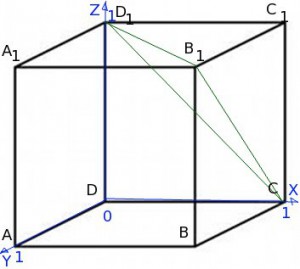 В задаче роль точки
В задаче роль точки 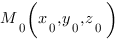 играет точка
играет точка ![]() . То есть
. То есть ![]() ,
, 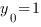 ,
, ![]()
Теперь задача найти коэффициенты 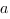 ,
, 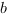 ,
, 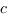 и
и ![]() в уравнении
в уравнении ![]() плоскости
плоскости ![]() .
.
Плоскость 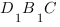 определяется тремя точками
определяется тремя точками 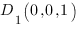 ,
, 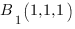 и
и ![]() . Если координаты точек подставим в уравнение плоскости
. Если координаты точек подставим в уравнение плоскости 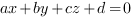 , то получим верное равенство.
, то получим верное равенство.
Коэффициент 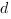 в уравнении плоскости можно принять равным 1.
в уравнении плоскости можно принять равным 1.
Чтобы найти коэффициенты 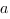 ,
, 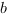 и
и 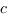 , подставим координаты точек
, подставим координаты точек 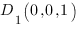 ,
, 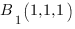 и
и ![]() в уравнение плоскости
в уравнение плоскости 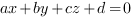 . Получим систему уравнений:
. Получим систему уравнений:
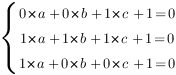
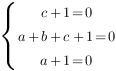
Отсюда: 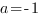 ,
, 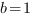 ,
, ![]()
Подставим координаты точки 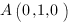 и значения коэффициентов в формулу для расстояния:
и значения коэффициентов в формулу для расстояния:
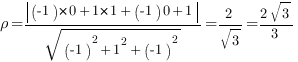
Ответ: 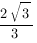
1 Постников М.М., Аналитическая геометрия, М., Техника, 2004.
2 Энциклопедия элементарной математики. Геометрия, том 4.
3 Выгодский М.Я., Справочник по высшей математике, М., 1972.
4 Понтрягин Л.С., Метод координат. М., Наука, 1977.


