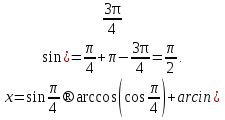- Преподавателю
- Математика
- КЕРІ ТРИГОНОМЕТРИЯЛЫҚ ФУНКЦИЯЛАРМЕН БАЙЛАНЫСТЫ ЕСЕПТЕР. ШЕШУ ӘДІСТЕРІ
КЕРІ ТРИГОНОМЕТРИЯЛЫҚ ФУНКЦИЯЛАРМЕН БАЙЛАНЫСТЫ ЕСЕПТЕР. ШЕШУ ӘДІСТЕРІ
| Раздел | Математика |
| Класс | - |
| Тип | Другие методич. материалы |
| Автор | Серикболкызы Н.С. |
| Дата | 13.11.2015 |
| Формат | docx |
| Изображения | Есть |
КЕРІ ТРИГОНОМЕТРИЯЛЫҚ ФУНКЦИЯЛАРМЕН БАЙЛАНЫСТЫ ЕСЕПТЕР. ШЕШУ ӘДІСТЕРІ.
Кері тригонометриялық функциялармен байланысты есептер әдетте оқушыларға жеткілікті дәрежеде қиындықтар туғызады. Себебі, қолданыстағы оқу құралдары мен бағдарламаларда ондай есептерге жеткілікті түрде көңіл бөлінбейді, анықтамаларынан кейін белгілі тепе-теңдіктерді келтіріп, функциялардың мәндерін табуға мысалдар келтірумен шектеледі, ал теңдеулер мен теңсіздіктерді шешу тәсілдері туралы мағлұматтар жоқтың қасында. Сол себепті, ондай есептерді қалай шешілетініне байланысты «табиғаттары» әртүрлі бірнеше мысалдардың шығару жолдарын келтіріп отырмыз. Негізінен, осы функциялардан пайда болған есептер көбінесе стандартты емес есептер класына жататыны анық. [1]
Кейінгі жылдары оқушыларды ҰБТ-ға даярлауға көбірек назар бөлетіндіктен, оларды стандарттық, трафареттік есептерді шығарумен шектейді. Көп жағдайда есептің шартына терең үңіліп, жеткілікті талқылау жасамай, алдыңғы есептерге ұқсас шешуге тырысады.
Біздің айтайық дегеніміз оқушылардың ой-өрісінің дұрыс дамып жетілуі үшін стандартты емес есептерді шешуге баулып, олардың қабілетін жандандыру болып табылады. Осындай есептерді шығару кезінде оқушылардың математикалық мәдениеті артып, логикалық даму жолына өз ықпалын тигізетініне ешбір күмәніміз жоқ, сол кезде ғана еңбегіміздің нәтижесі оң болатынына кәміл сенеміз. Осы мақалада әртүрлі типті есептердің шешу жолдарын келтіреміз, ал анықтамалар мен негізгі қатынастар белгілі деп санаймыз.
-
Алгебралық теңдеуге айналдырып шешу (айнымалыны ауыстыру).
Кейбір кері тригонометриялық функциялардан (КТФ) жасалған теңдеулер мен теңсіздіктерді қолайлы ауыстырма енгізіп, алгебралық түрге айналдыруға болады. Тек қана КТФ шектелгендігіне байланысты жаңа айнымалыға қойылатын табиғи шарттарды естен шығармасақ болғаны.
1- мысал. 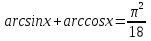 теңдеуін шешейік.
теңдеуін шешейік.
Шешуі: Берілген теңдеу 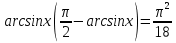 теңдеуіне эквивалентті, онда
теңдеуіне эквивалентті, онда 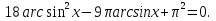
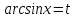 деп белгілесек,
деп белгілесек, 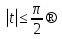
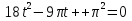 ⇒
⇒ 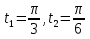 .
. 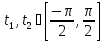
Сондықтан a) 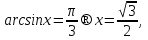 b)
b) 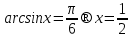 .
.
Жауабы: 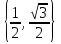 .
.
2-мысал.  теңсіздігін шешейік.
теңсіздігін шешейік.
Шешуі: 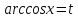 десек,
десек, 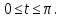 Онда
Онда 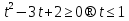 немесе
немесе 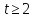 . Ал
. Ал 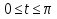 ескеріп,
ескеріп, 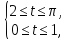 қос теңсіздіктерін аламыз.
қос теңсіздіктерін аламыз. 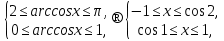
Жауабы: 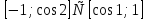 .
.
3-мысал. 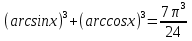 теңдеуін шешейік.
теңдеуін шешейік.
Шешуі: Теңдеу 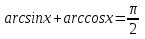 тепе-теңдігіне арналған стандартты мысал болып табылады.
тепе-теңдігіне арналған стандартты мысал болып табылады. 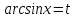 ,
, 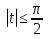 деп белгілесек, онда жоғарыдағы қатынасты ескеріп
деп белгілесек, онда жоғарыдағы қатынасты ескеріп 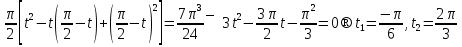 .
. 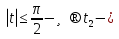 бөгде түбір. Сонымен , t
бөгде түбір. Сонымен , t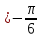 , онда
, онда 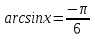 ,
, 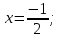
Жауабы: 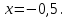
Осындай әдіспен шығарылған теңдеулерге тексеру жүргізбеуге де болады, себебі есептің шығару жолынан қосымша шешім пайда болуы мүмкін емес.
-
Аттас КТФ арқылы жасалған теңдеулер мен теңсіздіктер.
Аттас КТФ-дан тұратын теңдеулер мен теңсіздіктерді шешкен кезде көбінесе КТФ-ның монотондық қасиетін басшылыққа алады. Өздерінің анықталу облыстарында 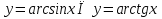 өседі де, ал
өседі де, ал 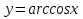 пен
пен  кемиді. Сол себепті төмендегі мәндес көшу қатынастарына келеміз:
кемиді. Сол себепті төмендегі мәндес көшу қатынастарына келеміз:
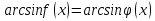

 немесе
немесе 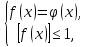


 f
f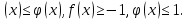
Дәл осылайша басқа да КТФ-тар үшін эквивалентті қатынастар орын алады.
а) теңдеуінде қай жүйені шешу қолайлы екендігі тек қана 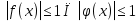 теңсіздігінің қарапайым шешілуіне тікелей байланысты.
теңсіздігінің қарапайым шешілуіне тікелей байланысты.
1-мысал. 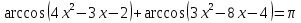 .
.
Шешуі: 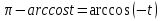 теңдігінен төмендегі эквивалентті түрлендірулер орын алады:
теңдігінен төмендегі эквивалентті түрлендірулер орын алады: 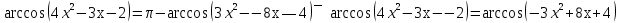
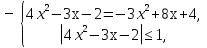 ⇔
⇔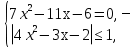
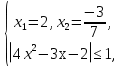 ⇒
⇒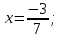
Жауабы:  .
.
2-мысал. 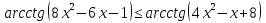 теңсіздігін шешейік.
теңсіздігін шешейік.
Шешуі: Берілген теңсіздік 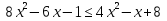 қатынасына мәндес,
қатынасына мәндес,
 немесе
немесе 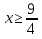 .
.
Жауабы: (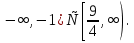
3-мысал. 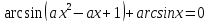 параметрлі теңдеуді шешейік.
параметрлі теңдеуді шешейік.
Шешуі: Берілген теңдеуден 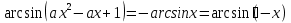 қатынасы шығады. Олай болса
қатынасы шығады. Олай болса
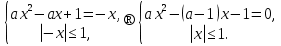
Екі жағдайға тоқталайық.
-
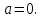 Онда жүйеден ⇒
Онда жүйеден ⇒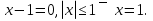
-
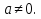 Жүйенің квадрат теңдеуінен
Жүйенің квадрат теңдеуінен 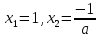 аламыз.
аламыз.
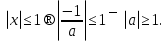 Егер
Егер 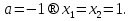 Ал егер
Ал егер 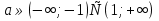 ⇒ теңдеу әртүрлі екі түбірге ие болады.
⇒ теңдеу әртүрлі екі түбірге ие болады.
Жауабы: егер 
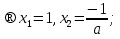 егер
егер
параметр  ның басқа мәндерінде шешімі жоқ.
ның басқа мәндерінде шешімі жоқ.
-
Әр аттас КТФ арқылы жасалған теңдеулер мен теңсіздіктер.
Теңдеулер мен теңсіздіктердің екі жағында әртүрлі КТФ лар болса, белгілі тригонометриялық тепе
лар болса, белгілі тригонометриялық тепе теңдікті қолдануға болады. Осындай типтес теңдеулер мен теңсіздіктерді шешкенде түрлендірудің мәндестігіне ешқандай көңіл бөлмей, теңдеудің салдарына көшіп, содан кейін түбірлерге тексеру жасасақ жеткілікті.
теңдікті қолдануға болады. Осындай типтес теңдеулер мен теңсіздіктерді шешкенде түрлендірудің мәндестігіне ешқандай көңіл бөлмей, теңдеудің салдарына көшіп, содан кейін түбірлерге тексеру жасасақ жеткілікті.
Мысал үшін, 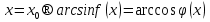 теңдеуінің шешімі болсын.
теңдеуінің шешімі болсын.  деп белгілеу енгізейік. Онда
деп белгілеу енгізейік. Онда 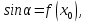
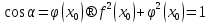 .
.
Сондықтан 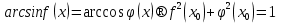 . (1)
. (1)
Осыған ұқсас тұжырымнан келесі қатынастарға келеміз:
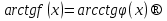
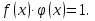 (2)
(2)
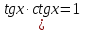 формуласы қолданылған) ;
формуласы қолданылған) ;
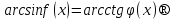
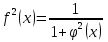 , (3)
, (3)
(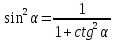 қатынасынан);
қатынасынан);
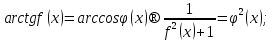 (4)
(4)
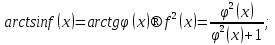 (5)
(5)
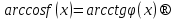
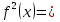
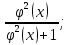 (6)
(6)
Ескерту. Әрбір (1)-(4) теңдеулерінің түбірі болып бір уақытта 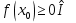
 орын алатын
орын алатын 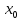 саны табылады. Себебі, қарсы жағдайда қатынастың екі бөлігінің мәндерінің жиыны қиылыспайды.
саны табылады. Себебі, қарсы жағдайда қатынастың екі бөлігінің мәндерінің жиыны қиылыспайды.
1-мысал. 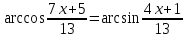 теңдеуін шешейік.
теңдеуін шешейік.
Шешуі: (1) теңдіктен 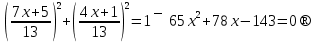

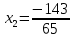 .
. 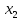 түбірі бөгде.
түбірі бөгде.
Жауабы: 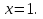
2-мысал. 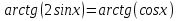 теңдеуін шешейік.
теңдеуін шешейік.
Шешуі: (2) теңдіктен 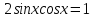 ⇔
⇔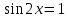 ⇔
⇔ аламыз. Бұдан
аламыз. Бұдан 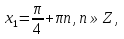
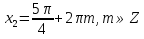 шығады.
шығады. 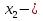 бөгде түбір болып табылады.
бөгде түбір болып табылады.
Жауабы: 
3-мысал.  теңсіздігін шешейік.
теңсіздігін шешейік.
Шешуі: функциясын енгізіп
функциясын енгізіп  теңсіздігін шешу үшін интервалдар әдісін қолданайық.
теңсіздігін шешу үшін интервалдар әдісін қолданайық.
Алдымен  функциясының анықталу облысы
функциясының анықталу облысы  тауып алайық, кері функциялардың анықтамаларынан
тауып алайық, кері функциялардың анықтамаларынан 
 =
= Енді
Енді  тің нөлдерін анықтайық.
тің нөлдерін анықтайық.
Ол үшін  теңдеуін шығарамыз.
теңдеуін шығарамыз. 
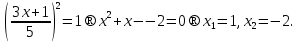
 бөгде түбір, себебі
бөгде түбір, себебі 
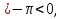
 болғандықтан интервал әдісінен
болғандықтан интервал әдісінен  орынды болатынын көреміз.
орынды болатынын көреміз.
Жауабы: .
.
Ескерту: Интервал әдісіне жүгінбей  анықталу облысында
анықталу облысында 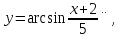 ал
ал 
 болатынын ескеріп берілген теңсіздіктің шешімі
болатынын ескеріп берілген теңсіздіктің шешімі  кесіндісі екеніне көз жеткізуге болады. Дегенмен, интервал әдісі әмбебап, функцияның монотондық қасиеті болмаған жағдайына да қолдануға болады.
кесіндісі екеніне көз жеткізуге болады. Дегенмен, интервал әдісі әмбебап, функцияның монотондық қасиеті болмаған жағдайына да қолдануға болады.
-
Теңдеудің екі жағынан тригонометриялық функцияны алу тәсілі.
Теңдеудің екі жағынан тригонометриялық функцияны алғанда берілген теңдеудің салдары шығады. Бірақ бұл амал қауіпті, себебі ол кезде теңдеудің шешімін алуымызда, жоғалтуымызда мүмкін. Біріншіден, әртүрлі монотондық облыста жатқан әртүрлі аргументтердің тригонометриялық функциясының мәні бірдей болуы мүмкін. Ал екінші жағынан, жаңадан пайда болған теңдеудің мүмкін мәндер жиыны (ММЖ) бастапқы теңдеудің ММЖ-на қарағанда тар немесе кең болуы мүмкін.
1-мысал. 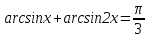 теңдеуін шешейік.
теңдеуін шешейік.
Шешуі: 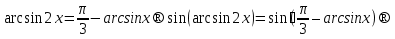

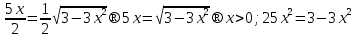
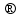
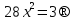
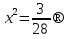
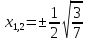 ; Тексеруден
; Тексеруден 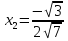 бөгде түбір болатынын көреміз.
бөгде түбір болатынын көреміз.
Жауабы: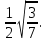
2-мысал. 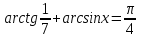 теңдеуін шешейік.
теңдеуін шешейік.
Шешуі:
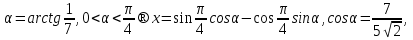
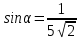 болғандықтан
болғандықтан 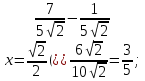
Енді бөгде түбір болмайтынына көз жеткізейік. Расында да солай, себебі анықтама бойынша 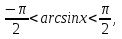 ал
ал 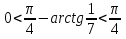 теңсіздігінен берілген теңдеудің екі жағыда синус функциясының монотондық (өспелі) облысында жататынын көреміз.
теңсіздігінен берілген теңдеудің екі жағыда синус функциясының монотондық (өспелі) облысында жататынын көреміз.
Жауабы: 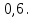
-
Кері тригонометриялық функциялардың монотондық және шектелгендік қасиеттерін қолдану тәсілі.
Қайсыбір теңдеулер мен теңсіздіктерді шешкенде (әрине КТФ арқылы жасалған) тек қана шектелгендігі мен монотондылығына сүйеніп шығарылатын есептер бар. Ондай кезде келесі теоремаларды басшылыққа алады.
Теорема 1. Егер  монотонды
монотонды 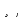 онда
онда 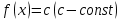
теңдеуінің бірден артық шешімі жоқ.
Теорема 2. Егер  - өспелі, ал
- өспелі, ал 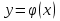 кемімелі функциялар болса, онда
кемімелі функциялар болса, онда 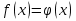 теңдеуінің бірден артық шешімі болмайды.
теңдеуінің бірден артық шешімі болмайды.
Теорема 3. Егер 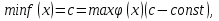 онда
онда 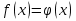 теңдеуі
теңдеуі
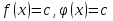 жүйесіне эквивалентті. ( 3 теореманы қолданып шығаратын әдісті кейде мажорант немесе min-max әдісі деп те айтады ).
жүйесіне эквивалентті. ( 3 теореманы қолданып шығаратын әдісті кейде мажорант немесе min-max әдісі деп те айтады ).
1-мысал. 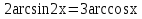 теңдеуін шешейік.
теңдеуін шешейік.
Шешуі: берілген теңдеудің шешімі. 2 теорема бойынша - ол жалғыз шешім.
берілген теңдеудің шешімі. 2 теорема бойынша - ол жалғыз шешім.
Жауабы: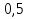 .
.
2-мысал. 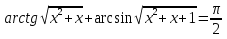 теңдеуін шешейік.
теңдеуін шешейік.
Шешуі: 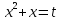 деп белгілейік. Онда теңдеу
деп белгілейік. Онда теңдеу 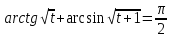
түріне енеді. 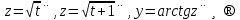
 1-теорема бойынша
1-теорема бойынша 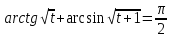 теңдеудің бірден артық түбірі болмайды.
теңдеудің бірден артық түбірі болмайды. 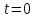 осы теңдеудің түбірі екені анық. Сол себепті
осы теңдеудің түбірі екені анық. Сол себепті 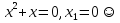
 .
.
Жауабы: 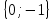 .
.
3-мысал. 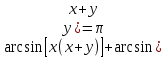 теңдеуін шешейік.
теңдеуін шешейік.
Шешуі: 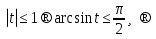 теңдеудің сол жағы
теңдеудің сол жағы 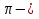 ден артпайды. Теңдік таңбасы
ден артпайды. Теңдік таңбасы 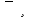 , егер әрбір қосылғыш
, егер әрбір қосылғыш 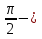 ге тең болса. Сонымен, теңдеу
ге тең болса. Сонымен, теңдеу 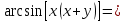
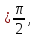
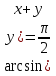 жүйесіне мәндес.
жүйесіне мәндес.
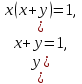 ⇒
⇒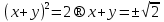 ⇒
⇒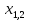 =
=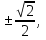
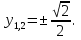
Жауабы: ( ), (-
), (-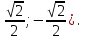
4-мысал. 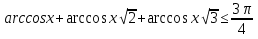 теңсіздігін шешейік.
теңсіздігін шешейік.
Шешуі: Сол жағы 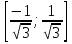 кесіндісінде кемімелі
кесіндісінде кемімелі  функциясының анықтамасынан бір уақытта
функциясының анықтамасынан бір уақытта 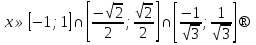
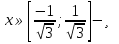 .
. 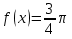 теңдеуі 1-теорема бойынша жалғыз түбірге ие болады, ол мән
теңдеуі 1-теорема бойынша жалғыз түбірге ие болады, ол мән 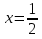 ;
; 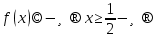
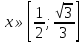 .
.
Жауабы: 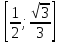 .
.
-
Тригонометриялық ауыстырма.
КТФ арқылы жасалған трансценттік теңдеуді тригонометриялық ауыстырма арқылы тригонометриялық теңдеуге айналдырып, стандартты емес әдіске жататын теңдеуге келтіріп шешуге болады. Әдетте алгебралық өрнектер белгілі тригонометриялық формулаларға ұқсас болып келсе, ондай ауыстырмалар нәтижелі болып табылады. Кең тараған түріне төмендегі өрнектер жатады:
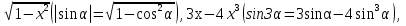
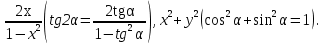 Осы әдісті келесі жалғыз мысал арқылы түсіндірейік.
Осы әдісті келесі жалғыз мысал арқылы түсіндірейік.
Мысал: 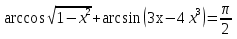 теңдеуін шешейік.
теңдеуін шешейік.
Шешуі: 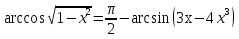 түрінде жазсақ, екі жағыда
түрінде жазсақ, екі жағыда 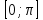 кесіндісінде жатқан бұрыш, онда екі жағынан косинусты алсақ (монотонды облысы) қосымша түбір пайда болмайды, сол себепті
кесіндісінде жатқан бұрыш, онда екі жағынан косинусты алсақ (монотонды облысы) қосымша түбір пайда болмайды, сол себепті 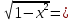

Теңдеуді шешу үшін 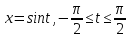 ауыстырмасын қолданамыз, онда
ауыстырмасын қолданамыз, онда 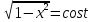 ,ал
,ал 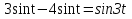 болғандықтан
болғандықтан 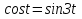 тригонометриялық теңдеуіне келеміз.
тригонометриялық теңдеуіне келеміз. 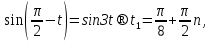
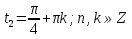 шешімдерін аламыз. Осылардың ішінде
шешімдерін аламыз. Осылардың ішінде 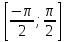 сегментінде тек
сегментінде тек
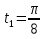 ;
; 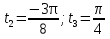 немесе
немесе 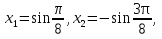
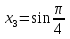 түбірлері жатады. Енді қажетті тексерулерді жүргізейік (ол үшін бастапқы теңдеуге апарып қоямыз).
түбірлері жатады. Енді қажетті тексерулерді жүргізейік (ол үшін бастапқы теңдеуге апарып қоямыз).
-
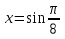 ⇒
⇒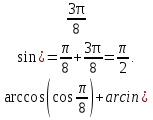
-

=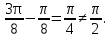
Жауабы: 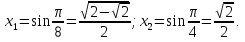
Ең соңында функциялардың бар болу облыстарын қолданып үш айнымалыдан тәуелді функциялармен иррационал функциялардың комбинациясынан жасалған күрделі теңдеудің шешімін келтірейік.
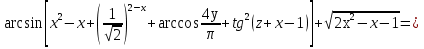
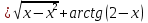 .
.
Алдымен берілген теңдеуге енетін 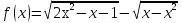 функциясының анықталу облысын анықтайық. Ол
функциясының анықталу облысын анықтайық. Ол  жүйесі арқылы табылады, оның жалғыз шешімі
жүйесі арқылы табылады, оның жалғыз шешімі 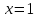 интервал әдісін қолданып, қарапайым теңсіздіктерден аламыз.
интервал әдісін қолданып, қарапайым теңсіздіктерден аламыз.
Сонымен, 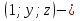 үштігі берілген теңдеудің шешімі екен, соған апарып қойсақ
үштігі берілген теңдеудің шешімі екен, соған апарып қойсақ 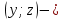 тер үшін
тер үшін 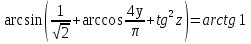 теңдеуіне келеміз. Ал
теңдеуіне келеміз. Ал
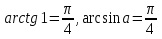 ⇔ егер
⇔ егер 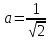 болатынын ескерсек, соңғы теңдеу
болатынын ескерсек, соңғы теңдеу 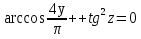 түріндегі теңдеуге айналады. Анықтама бойынша
түріндегі теңдеуге айналады. Анықтама бойынша  ⇒
⇒ 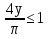 ⇒
⇒ 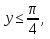 және
және 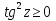 ⇒
⇒ 
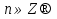 олай болса
олай болса 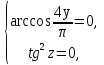 жүйесін аламыз,одан
жүйесін аламыз,одан 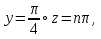
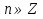
шығады. Сонымен, берілген теңдеудің шешімі 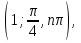
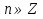 шексіз жиыны табылатынын көреміз.
шексіз жиыны табылатынын көреміз.
Ескерту. Стандартты әдіспен шешілмейтін теңдеулерде жауаптары ақырлы немесе шексіз жиын бола беретінін көреміз. Бұл қасиет теңсіздіктер үшін де орын ала беретін құбылыс, белгісіздердің саны артық болса да. Мысал үшін,
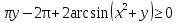 теңсіздігінің
теңсіздігінің 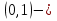 жалғыз шешімі де, ал
жалғыз шешімі де, ал 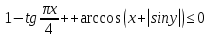 шешімі
шешімі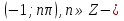 саналатын жиын.
саналатын жиын.
Сонымен, біз бірнеше есептердің шығару жолдарын келтірдік, әрине, кері тригонометриялық функциялар арқылы жасалған әртүрлі типті есептер жиынын қамту ешқашан да мүмкін емес. Айтайық дегеніміз, тек қана күрделілігі жоғары, стандартты емес есептерді шығару кезінде оқушылардың зерттеушілік қасиеті дамып, әр деңгейдегі математика пәні бойынша олимпиадаға қатысуға қызығушылығын тудыратыны сөзсіз.параметрден тәуелді немесе жүйелерден тұратын жаттығулар мүлде қарастырылған жоқ. Оларды келешектің еншісіне қалдырдық. КТФ - ға арналған талай оқу құралдары бар, негізгілері әдебиеттер тізімінде келітірілген.
ӘДЕБИЕТТЕР ТІЗІМІ:
-
Олехник С.Н. и др. Нестандартные методы решения. Уравнения и неравенства. Справочник. Москва, МГУ, 1997,-219 стр.
-
Фалин Г.И., Фалин А.И. Обратные тригонометрические функции. 10-11 классы. Изд. «Экзамен», Москва,2012,-221 с.
-
Гельфанд И.М. и др. Тригонометрия. МЦНМО, АО «Московские учебники», М., 2003-200с,
-
Супрун В.П. Математика для старшеклассников. Нестандартные методы решения задач. М., Книж.дом «ЛИБРОКОМ», 2009,-272 стр.
-
Егерев В.К. и др. 4х100 задач., Москва, Linka-Press, 1993,-262 с.
-
Арлазаров В.В. и др. Лекции по математике для физико-математических школ, часть II, Уч. пособие.- М., Изд. ЛКИ, 2008.-264с.