- Преподавателю
- Математика
- Урок Олимпиада 10 - класс
Урок Олимпиада 10 - класс
| Раздел | Математика |
| Класс | 10 класс |
| Тип | Другие методич. материалы |
| Автор | Бомуратов Т.Б. |
| Дата | 06.01.2016 |
| Формат | doc |
| Изображения | Есть |
Математика
10 класс.
1. Решить уравнение в целых числах:
(x - y)3 + (y - z)3 + (z - x)3 = 30. ( 6 баллов)
Решение. Преобразовав данное уравнение, получим:
3(x - y)(y - z)(z - x) = 30 или (x - y)(y - z)(z - x) = 10.
Значит, целые числа (x - y), (y - z), (z - x) - делители числа 10, сумма этих делителей равна нулю. Не трудно убедиться, что таких делителей у числа 10 нет.
2. Из трехзначного числа вычли сумму его цифр. С полученным числом сделали то же самое и так далее, 100 раз. Доказать, что в результате получится нуль. ( 6 баллов)
Решение. Так как 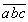 - (a + b + c) = 9 (11a + b), то первая разность делится на 9. Сумма ее цифр делится на 9, значит, вторая, и, аналогично, все остальные разности будут делиться на 9.
- (a + b + c) = 9 (11a + b), то первая разность делится на 9. Сумма ее цифр делится на 9, значит, вторая, и, аналогично, все остальные разности будут делиться на 9.
Сумма цифр трехзначного числа, делящегося на 9, может быть равна 9, 18 или 27. Значит, за 100 операций число либо станет равным 0, либо уменьшится не менее чем на 900. Поэтому, любое число, меньшее 900, станет равным нулю.
Пусть число не менее 900. Тогда после первого хода получится число, кратное 9, от 900 - 9 = 891 до 999 - 27 = 972. Таких чисел 9. Перебором можно убедиться, что они также обратятся в 0 через 99 операций.
3. Существуют ли всюду определенные функции f(x) и g(у), что для любых х и у выполняется f(x) g(y) = x + y - 1? ( 6 баллов)
Решение. Пусть такие функции существуют. Тогда при любом y
при x = 0: f (0) g (y) = y - 1,
при x = 1: f (1) g (y) = y.
Очевидно, что f (0) ≠ 0, f (1) ≠ 0, отсюда
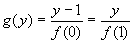 .
.
Это равенство выполняется не при всех y (при y = 0 оно неверно), значит, таких функций не существует.
4. Решить уравнение
![]() . (6 баллов)
. (6 баллов)
Р е ш е н и е. Подстановка y = x + 7 делает рассматриваемое уравнение симметричным:
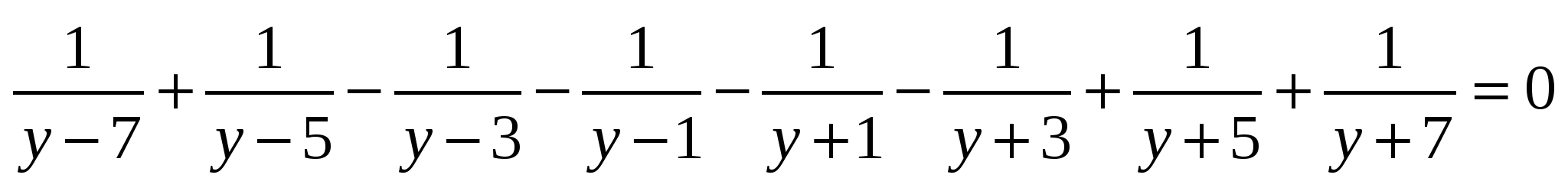 .
.
Сгруппируем следующим образом
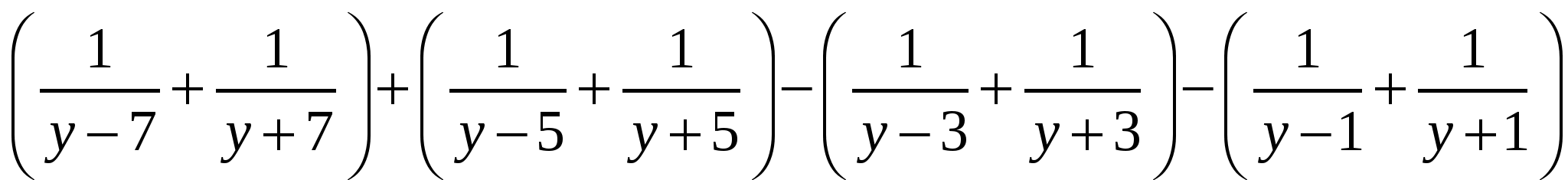 = 0.
= 0.
Это даёт
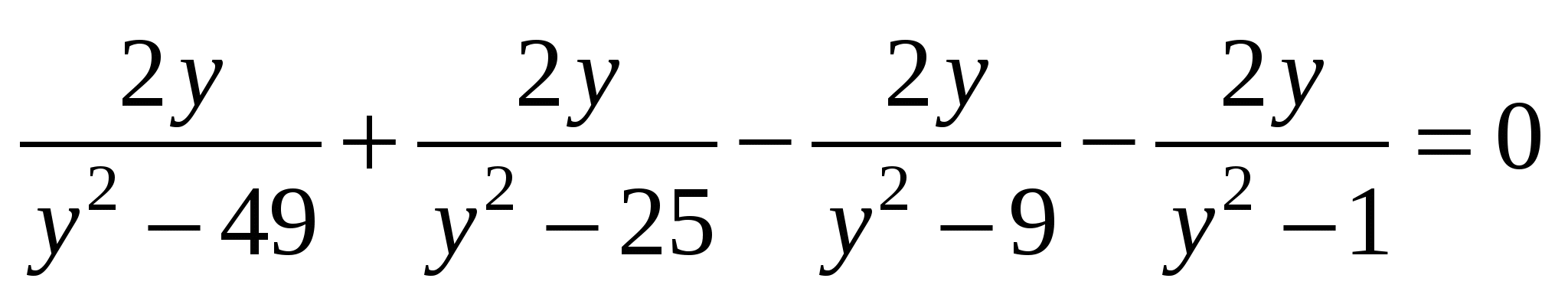 ,
,
т.е.
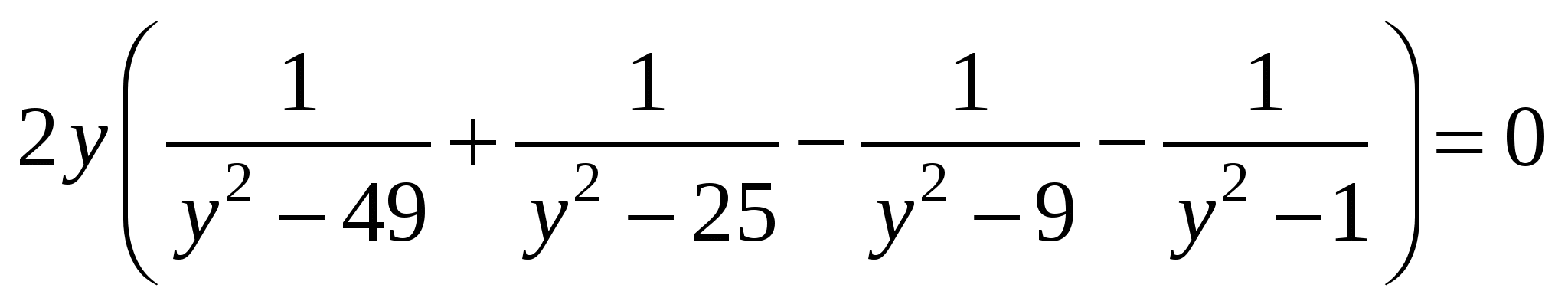 ,
,
откуда y = 0, т.е. x = 7, или (после подстановки z = y2)
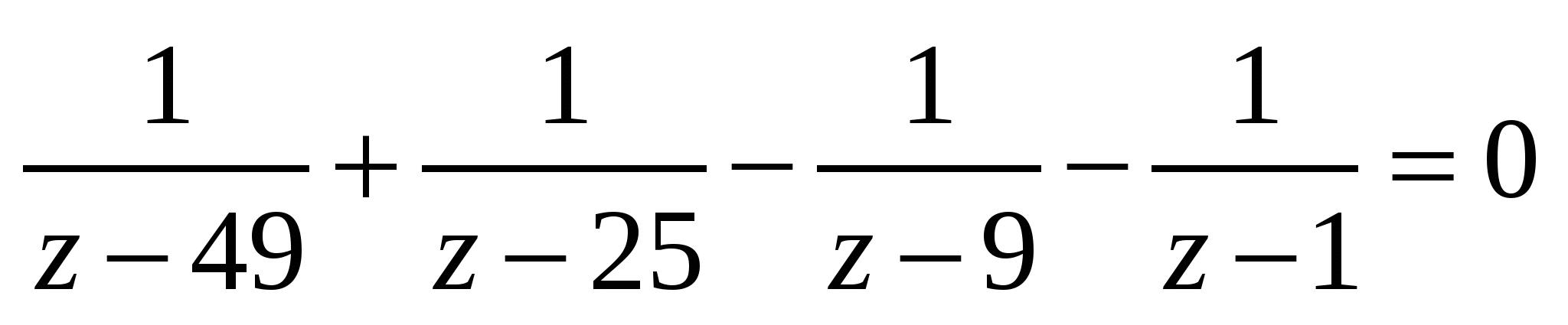 .
.
Группируем
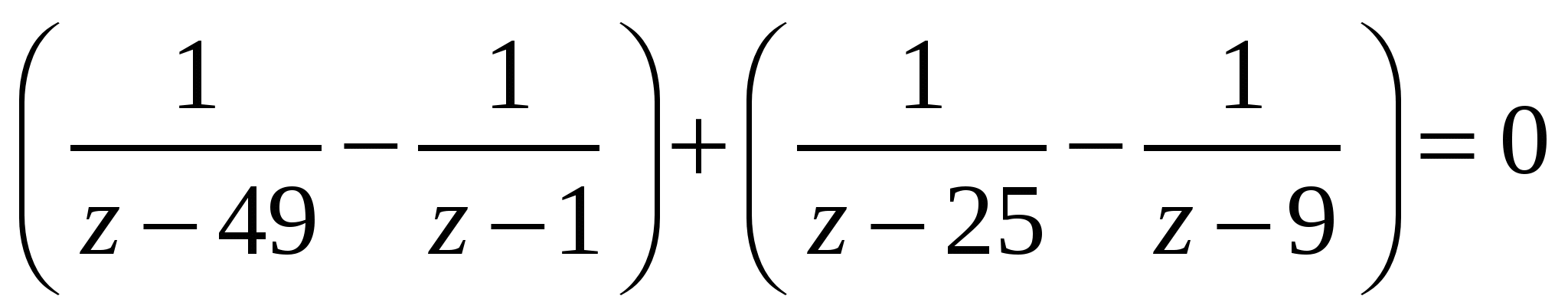 .
.
Это даёт
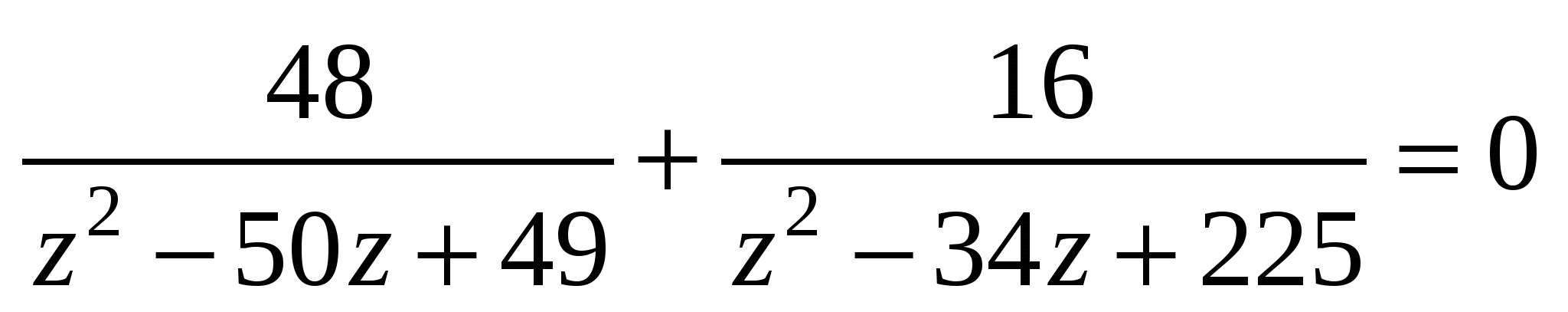 .
.
Сокращая на 16 и приводя к общему знаменателю, получаем
3(z2 - 34z + 225) + (z2 - 50z + 49) = 0
и, разумеется, z 1, z 9, z 25, z 49. Приводя подобные, имеем 4z2 - 152z + 724 = 0, откуда, сокращая на 4, получаем z2 - 38z + 181 = 0. Корнями этого уравнения являются
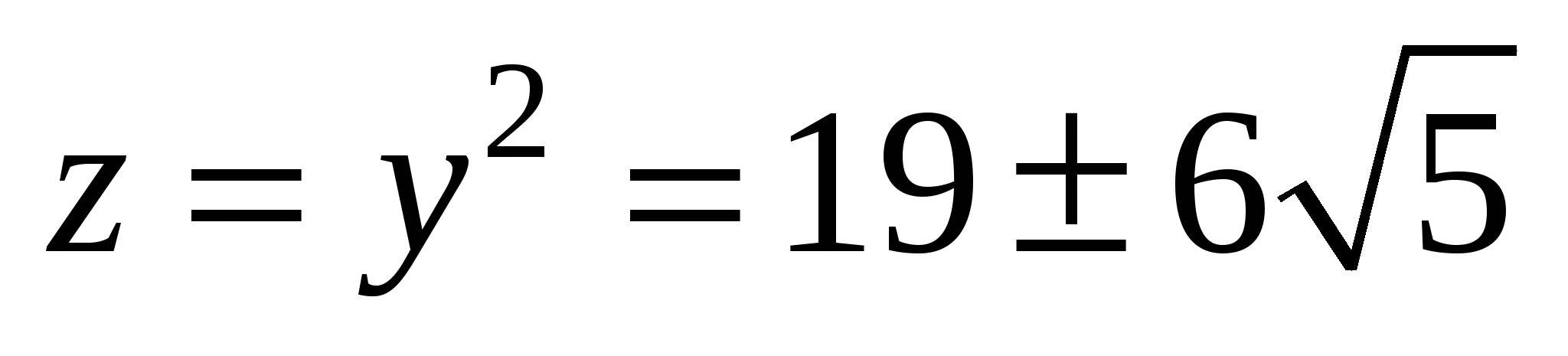 ,
,
откуда 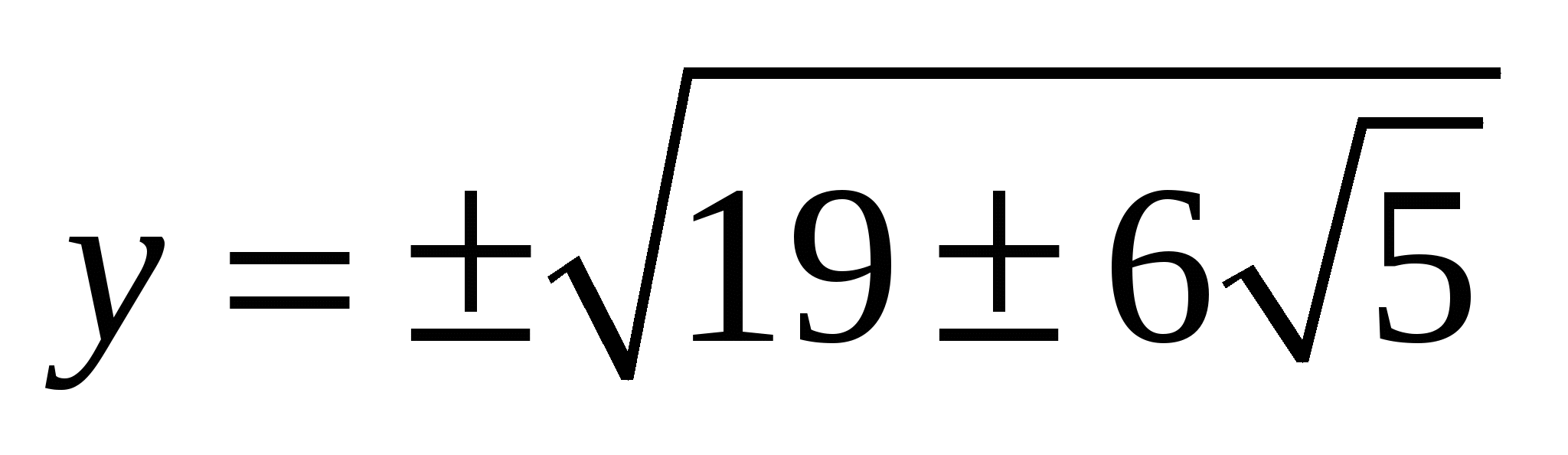 и, наконец,
и, наконец, 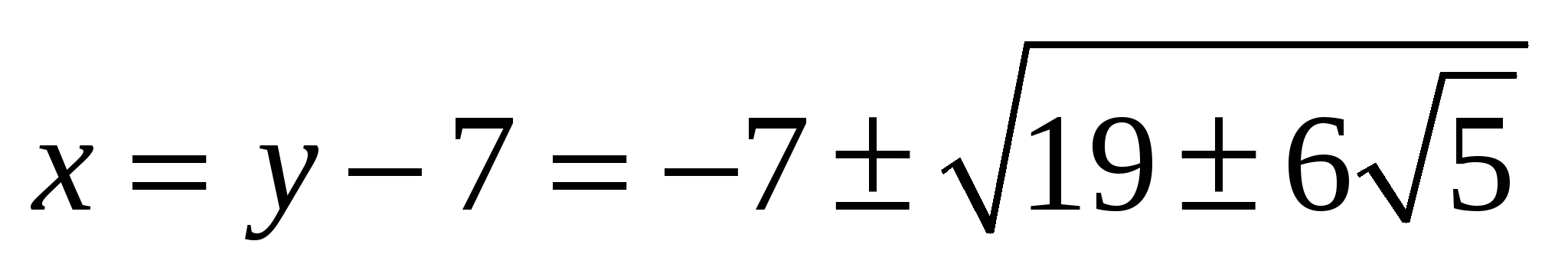 , причём возможны различные комбинации знаков.
, причём возможны различные комбинации знаков.
О т в е т: x = 7, 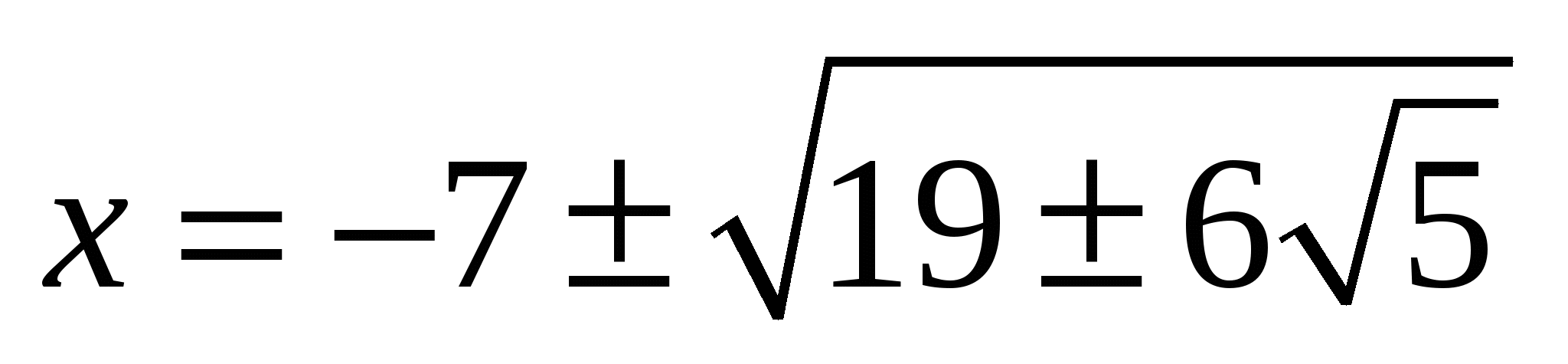 .
.
5. В выпуклом четырёхугольнике ABCD с внутренними углами < 180о точка E - точка пересечения диагоналей, F1, F2 - площади треугольников ABE, CDE, F - площадь четырёхугольника ABCD. Доказать, что 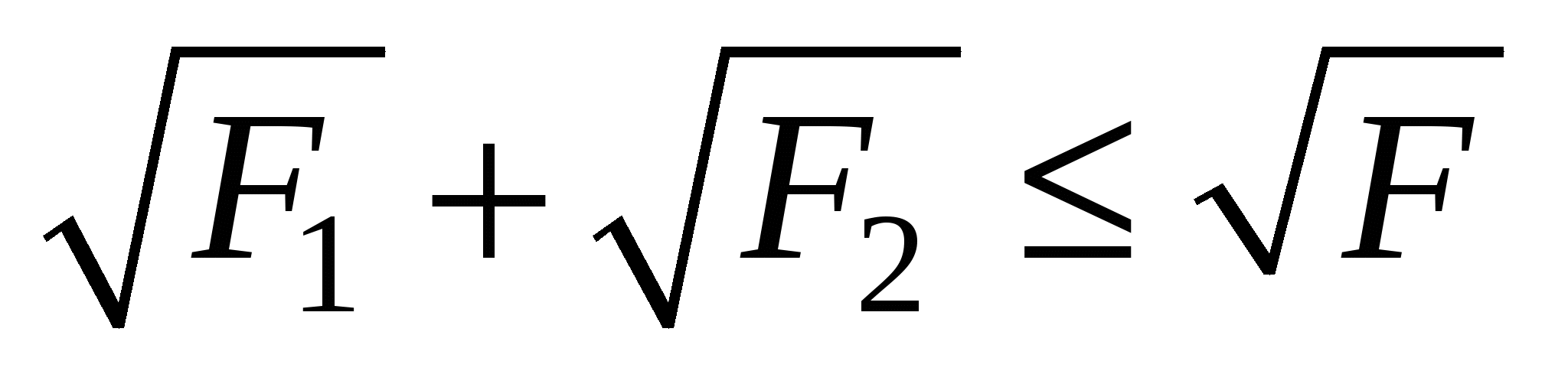 . В каком случае возможно равенство? (6 баллов)
. В каком случае возможно равенство? (6 баллов)
Р е ш е н и е.
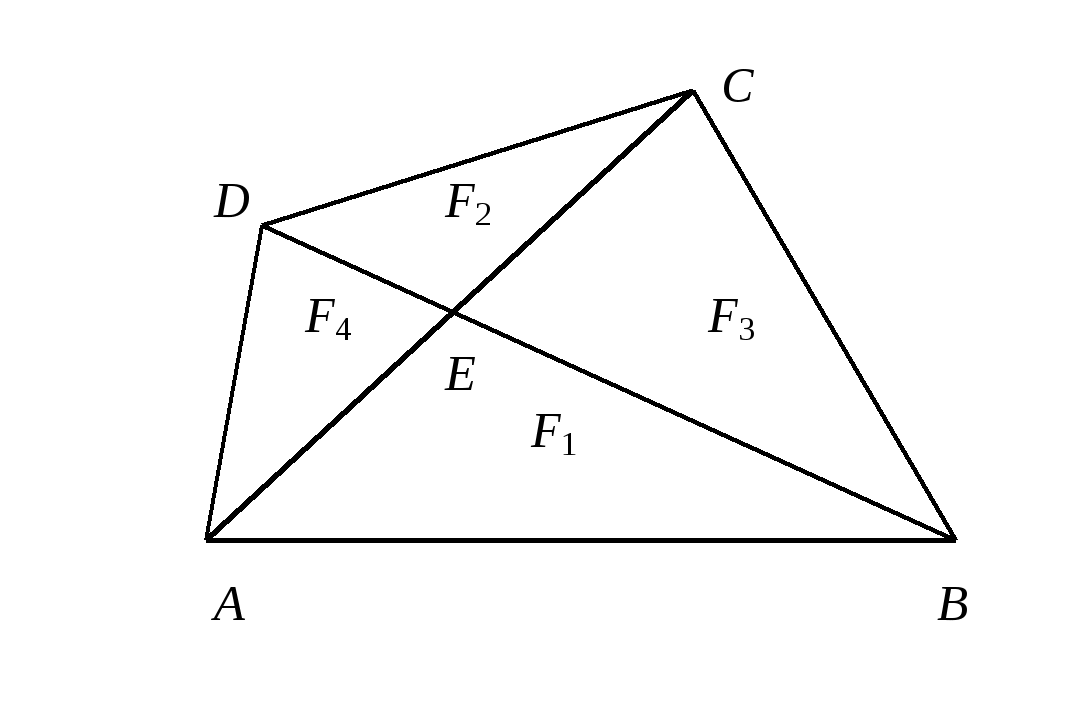
Имеем F = F1 + F2 + F3 + F4. Доказываемое неравенство равносильно тогда неравенству
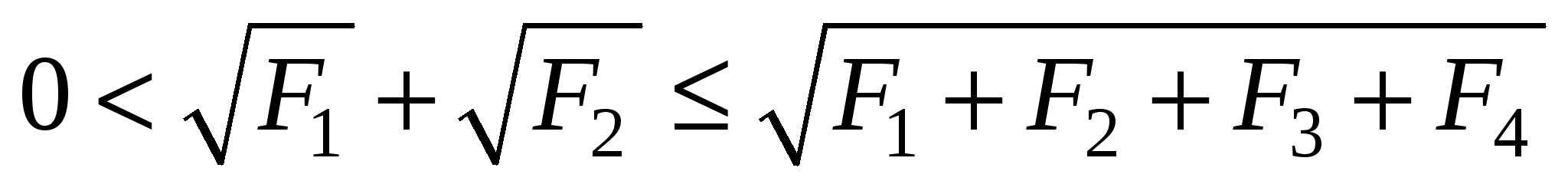 .
.
После возведения в квадрат получаем, что последнее равносильно неравенству
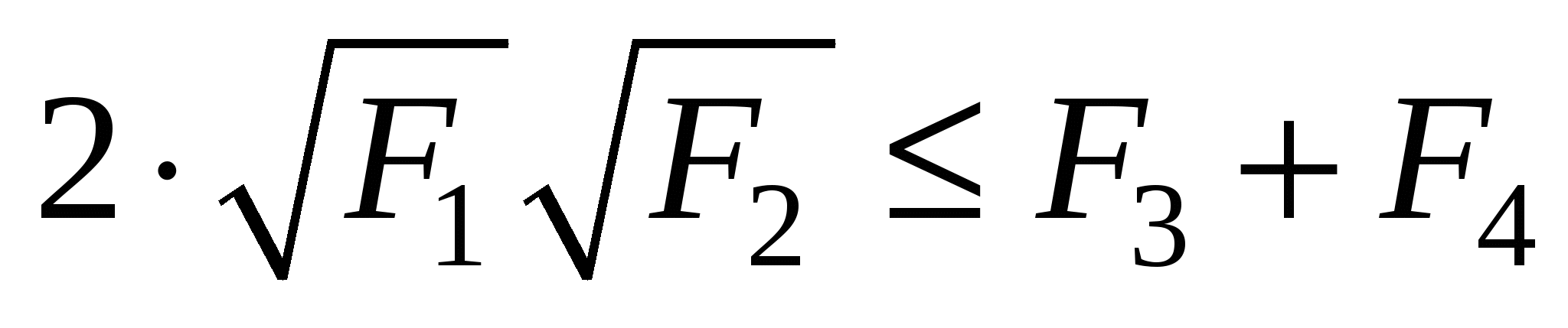 .
.
Треугольники ABE и ADE имеют одинаковую высоту, следовательно, 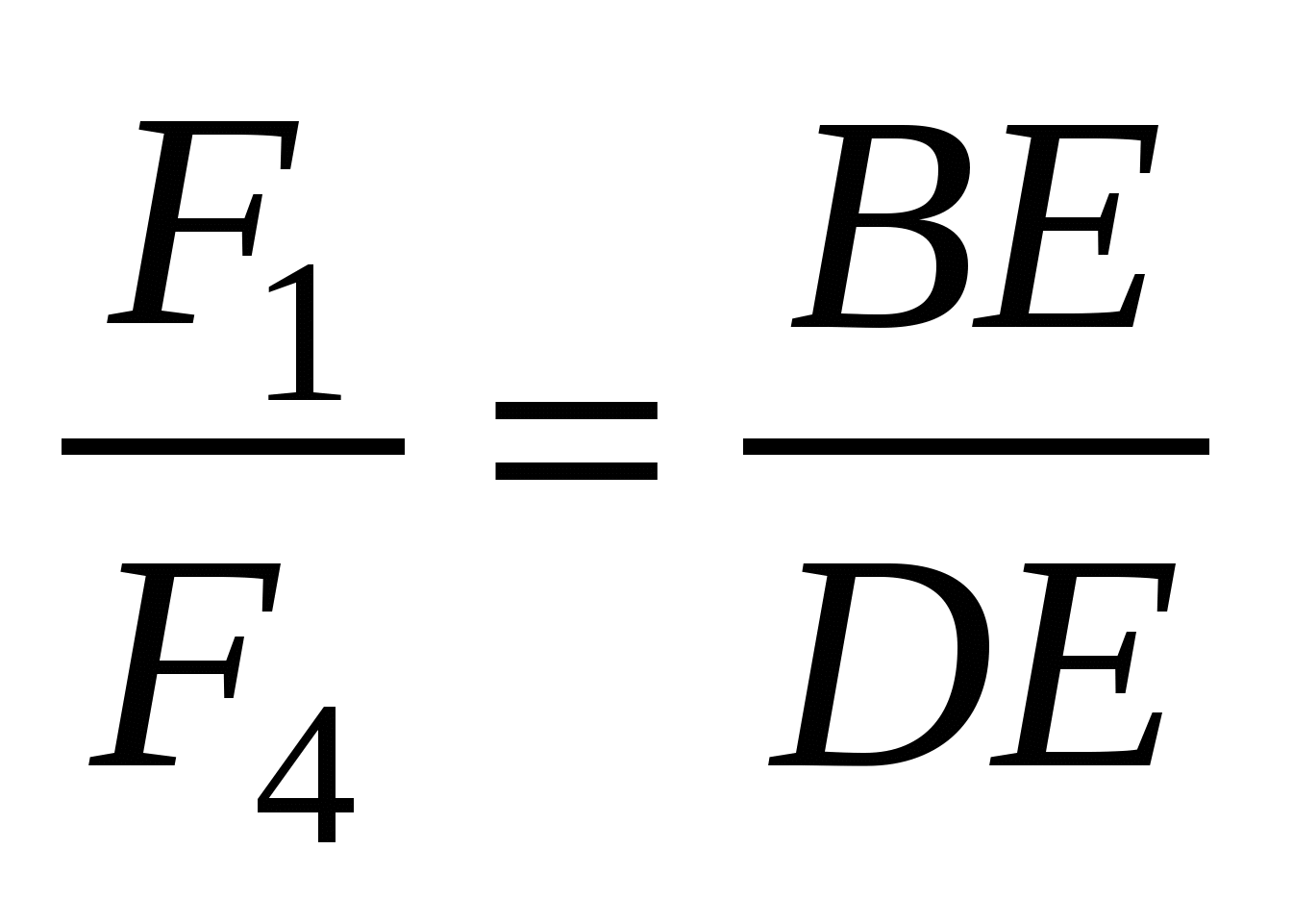 . Аналогично,
. Аналогично, 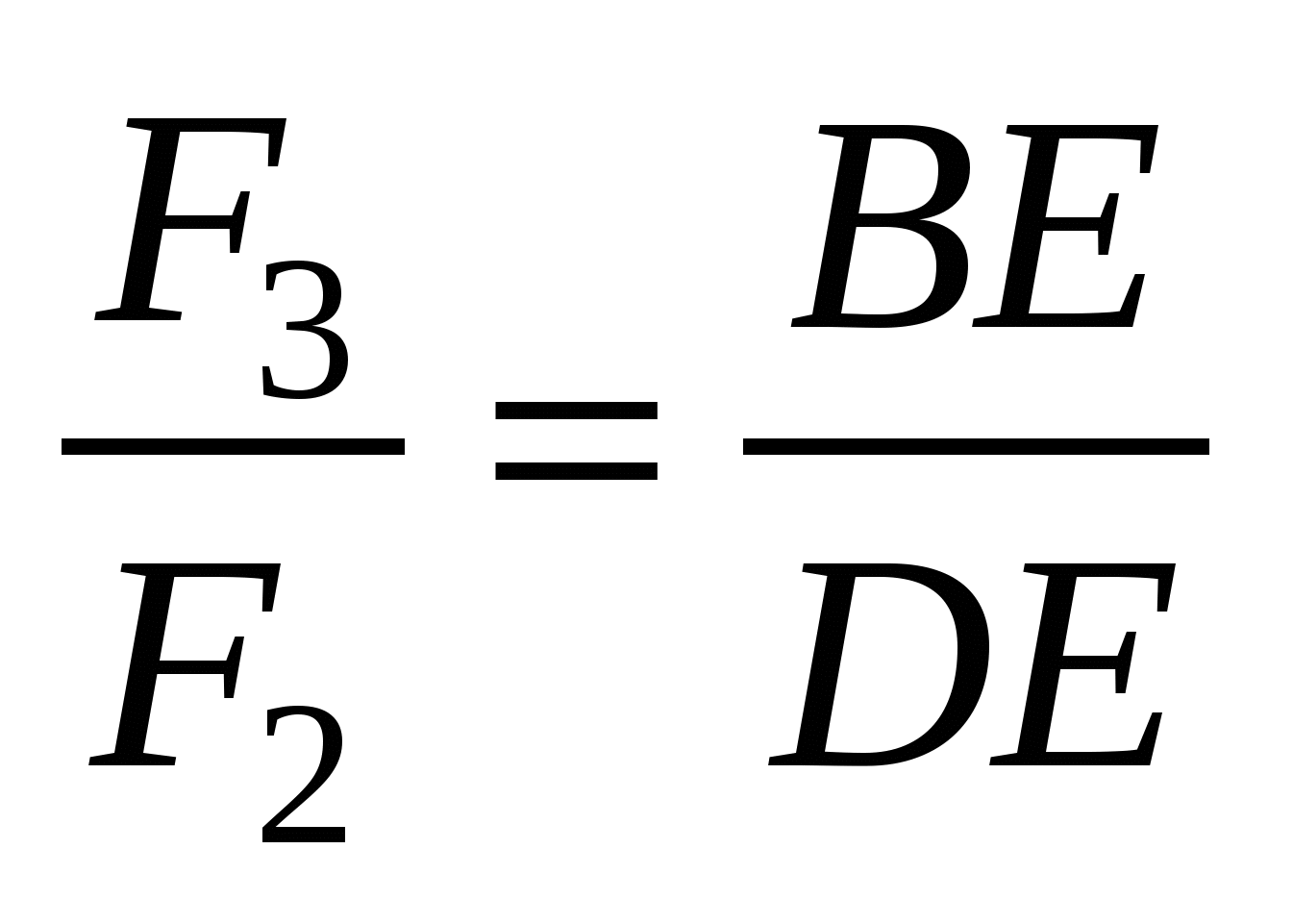 . Отсюда получаем
. Отсюда получаем 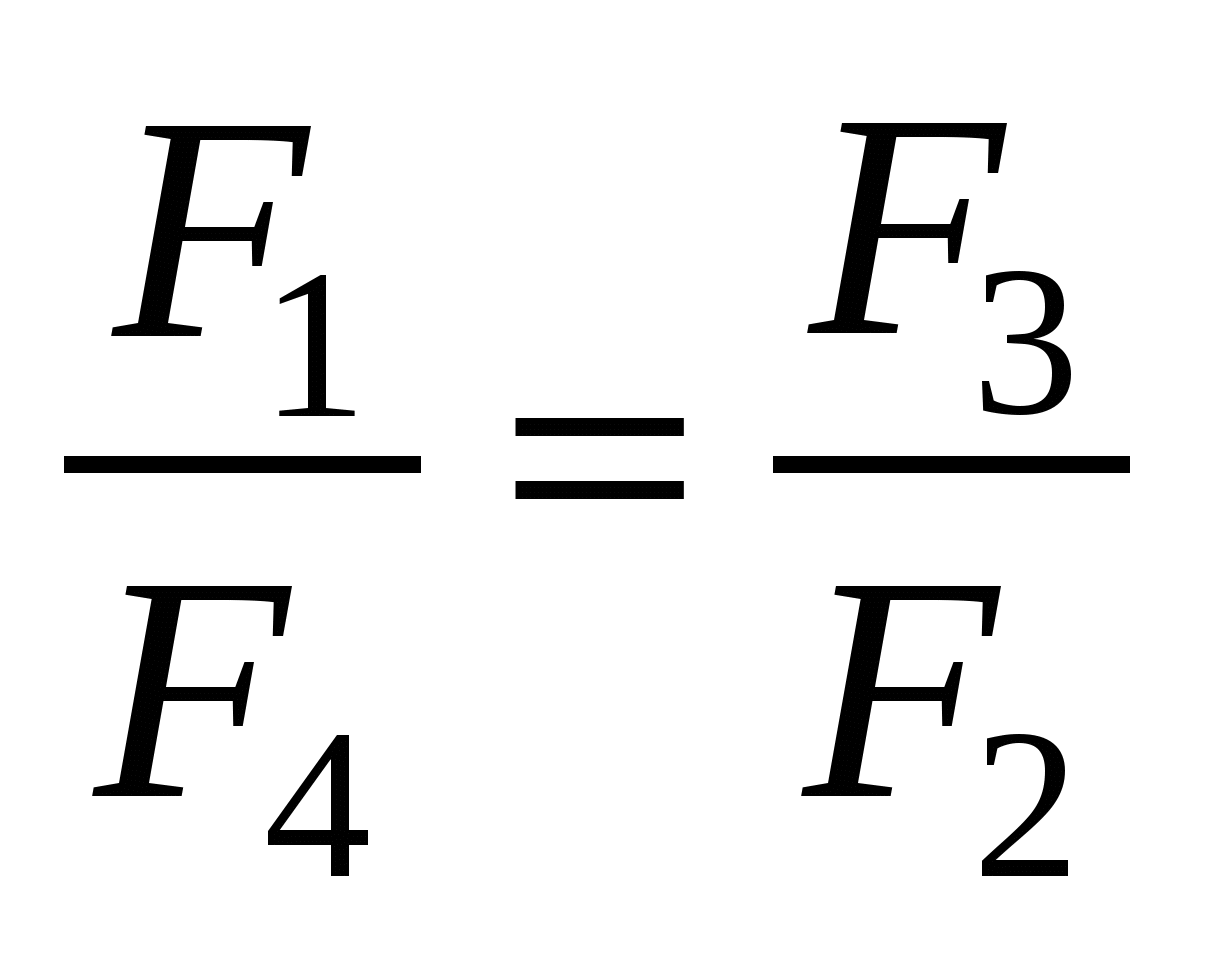 , так что F1F2 = F3F4. Доказываемое неравенство сводится тогда к такому:
, так что F1F2 = F3F4. Доказываемое неравенство сводится тогда к такому: 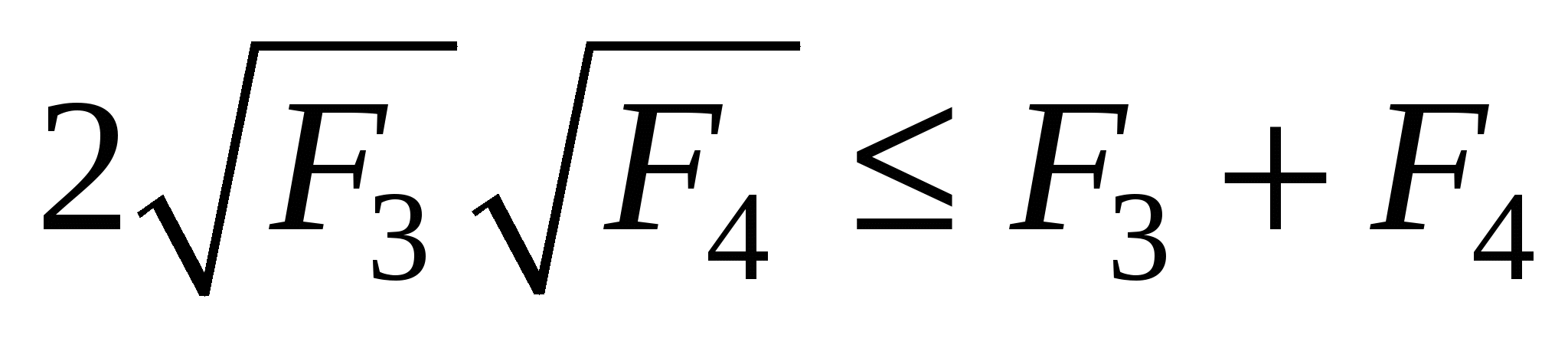 . Это последнее неравенство очевидно, поскольку F3 -
. Это последнее неравенство очевидно, поскольку F3 - 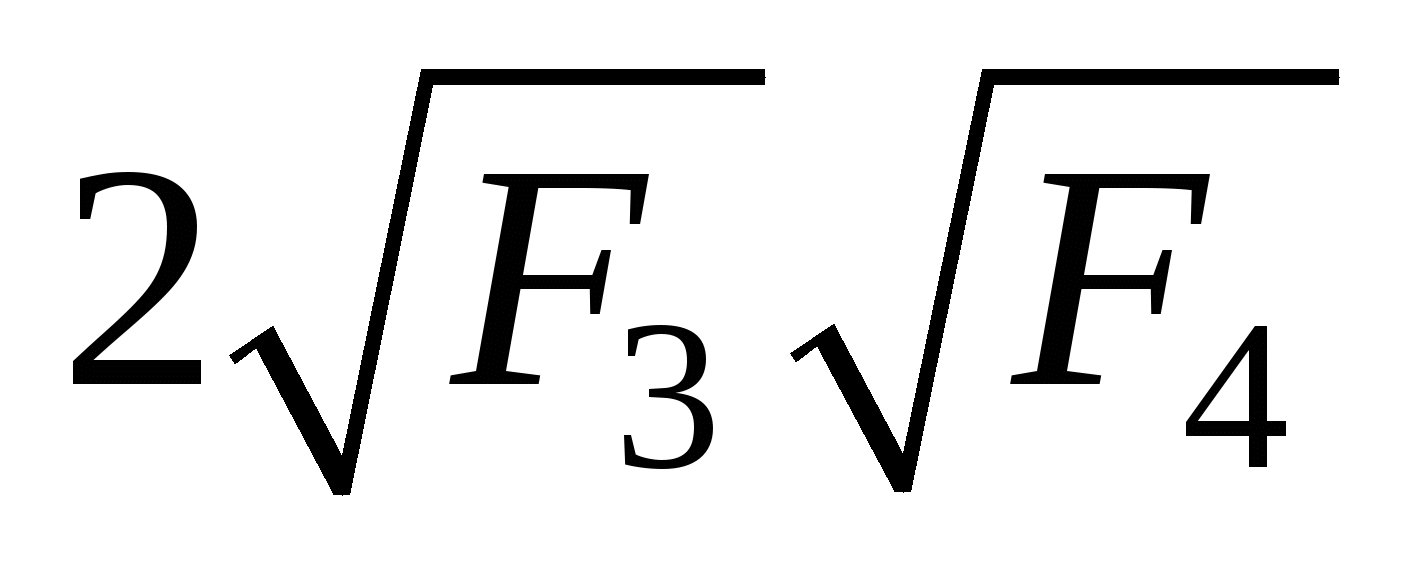 + F4 =
+ F4 = ![]() 0.
0.
Равенство достигается в случае F3 = F4. В свою очередь это равносильно условию SABD = F1 + F4 = F1 +
+ F3 = SABC. Но треугольники ABC и ABD имеют общее основание AB, следовательно, должны иметь одинаковые высоты. А это выполняется в случае, когда AD параллельно CD, т.е. когда ABCD - трапеция.


