- Преподавателю
- Математика
- Исследовательская работа ученика по математике и литературе
Исследовательская работа ученика по математике и литературе
| Раздел | Математика |
| Класс | 9 класс |
| Тип | Другие методич. материалы |
| Автор | Викулова О.А. |
| Дата | 27.07.2015 |
| Формат | docx |
| Изображения | Есть |




























Научно-исследовательская работа
по математике
Математика в искусстве
Автор:
Викулов Виталий Игоревич,
ученик 9 Б класса МБОУ СШ №30
г. Дзержинска Нижегородской обл.
Руководители:
Бойко Галина Ивановна,
учитель математики
МБОУ СШ №30
Викулова Ольга Анатольевна,
учитель русского языка и литературы,
педагог-психолог
МБОУ СШ №30
Оглавление
Введение
3
1.
«Золотые» понятия геометрии
4
1.1.
Золотое сечение
4
1.2.
Ряд Фибоначчи
4
1.3.
Золотой треугольник
5
1.4.
Золотой прямоугольник
6
1.5.
Звездчатый пятиугольник
6
2.
Математика в скульптуре
7
3.
Математика в архитектуре
9
4.
Математика в живописи
10
5.
Математика и декоративно - прикладное искусство
14
6.
Математика в литературе
15
7.
Математика в поэзии
18
8.
Математика в музыке
19
Заключение
21
Список использованной литературы
22
Введение
Математика владеет не только истиной, но и высшей красотой отточенной и строгой, возвышенно чистой и стремящейся к подлинному совершенству, которое свойственно лишь величайшим образцам искусства.
Б. Рассел.
С детства я люблю рассматривать альбомы по искусству, где много удивительных по своей красоте картин, портретов, икон. Мне нравятся пейзажные произведения И. Шишкина и И.Айвазовского, портреты кисти В. Перова и И.Крамского, сюжетная живопись Тициана и В.Васнецова, картины на библейские сюжеты Рафаэля и А.И. Иванова. Некоторые произведения живописи просто завораживают. Я давно хотел найти объяснение, в чём же их притягательность.
Когда-то давно мама рассказывала мне про золотое сечение в иконописи, но я ещё не очень понимал, что такое пропорции, да и математику считал сухой и нудной наукой. Другое дело, - литература! Звучные стихи, интересные образы, которые можно не только представить, но и сыграть на сцене.
И тут появилась мысль, почему бы не сопоставить математику и искусство. Тема исследования: «Математика в искусстве» прозвучала для меня как-то неестественно гротескно, но я сразу почувствовал: эта тема - моя!
Цель моей работы очевидна:
- раскрыть связь математики и искусства,
доказав при этом возникшую у меня гипотезу о том, что математика как наука имеет свои каноны красоты, которые используются в разных видах искусства.
Для этого мне необходимо решить следующие задачи:
-
познакомиться с новыми математическими понятиями (золотой треугольник, золотое сечение, золотой прямоугольник, золотая спираль, параллельный перенос, проекция);
-
произвести анализ разных видов искусства: живописи, архитектуры, скульптуры, литературы, музыки, прикладного искусства;
-
показать присутствие в них понятий арифметики, алгебры, геометрии;
-
произвести практическое исследование, как красота определённого произведения искусства (картины, архитектурного строения, литературного произведения) связана с математикой;
-
на основании всего изложенного сформулировать вывод о том, какую роль играет математика в искусстве.
-
«Золотые» понятия геометрии
Геометрия владеет двумя сокровищами. Это теорема Пифагора и деление отрезка в крайнем и среднем отношениях. Первое сравнимо с мерой золота, второе же больше напоминает драгоценный камень.
Иоганн КеплерНауку и искусство можно назвать «двумя крыльями культуры, они - дополняющие друг друга противоположности, две грани одного и того же процесса - творчества» (11, 4).
Искусство дарит нам красоту образов, соразмерность линий, гармонию красок и звуков. Но именно математика подарила нам такие понятия, как гармония, симметрия, пропорция, которые и определяют красоту и соразмерность образа, создаваемого искусством.
С головой окунувшись в эту тему, я пытался понять, что же роднит «царицу наук» (математику) и «божественное наслаждение» (искусство). За ответом я обратился к древним философам, которые относили математику к числу искусств, и узнал о золотых понятиях геометрии.
-
Золотое сечение
Золотым сечением (делением) и даже "божественной пропорцией" (10, 34) называли математики древности и средневековья деление отрезка, при котором длина всего отрезка так относится к длине его большей части, как длина большей части к меньшей
с:b = b:a
Это отношение приближенно равно 1,618.
a
c
Поскольку я ещё в школе не проходил такие уравнения, поэтому я взял готовые ответы древних учёных, которые высчитали это соотношение.
Они исходят из следующего: если принять длину всего отрезка за единицу с = 1,
то b = х, а = 1-х.
Длина отрезка b, которая вычисляется по формуле: 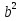 = с
= с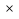 a, то есть
a, то есть
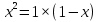 , будет выражена числом φ (фи), равным примерно 0,618…
, будет выражена числом φ (фи), равным примерно 0,618…
Тогда длина отрезка а будет равна 1- 0,618 = 0,382
Такое деление отрезка со времён древних греков называется делением отрезка в крайнем и среднем отношении. Оно часто используется в искусстве.
-
Ряд Фибоначчи
С историей золотого сечения косвенным образом связано имя итальянского математика монаха Леонардо из Пизы, более известного под именем Фибоначчи (сын Боначчи). Он много путешествовал по Востоку, познакомил Европу с индийскими (арабскими) цифрами. В 1202 г вышел в свет его математический труд «Книга об абаке» (счетной доске), в котором были собраны все известные на то время задачи. Одна из задач гласила «Сколько пар кроликов в один год от одной пары родится». Размышляя на эту тему, Фибоначчи выстроил такой ряд цифр:
Месяцы 0 1 2 3 4 5 6 7 8 9 10 11 12 и т.д.
Пары кроликов 0 1 1 2 3 5 8 13 21 34 55 89 144 и т.д
Ряд чисел 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55 и т.д. получил название ряда Фибоначчи. Особенность последовательности чисел состоит в том, что каждый ее член, начиная с третьего, равен сумме двух предыдущих 2 + 3 = 5; 3 + 5 = 8; 5 + 8 = 13, 8 + 13 = 21; 13 + 21 = 34 и т.д., а отношение смежных чисел ряда приближается к отношению золотого сечения. Числа 0.618 и 0.382 являются коэффициентами последовательности Фибоначчи.
У этой последовательности очень интересное соотношение с числом фи: если разделить каждый член этого ряда на предыдущий, полученные результаты будут стремиться к числу 1,618.
1/1=1, 2/1=2, 3/2=1.5, 5/3=1.66, 13/8=1.625, 21/13=1.615, 34/21=1.619, 55/34=1.617, 89/55=1.6181, Чем дальше продолжать считать, тем ближе можно подойти к числу фи, но дойти до него невозможно, потому что у него нет арифметического решения.
Эту последовательность можно изобразить графически, в виде так называемой спирали Фибоначчи.
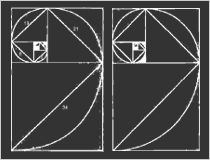
Рис. 1. Спираль Фибоначчи
«Эта спираль почти идентична логарифмической спирали фи, известной как спираль золотого сечения. Разница заключается в том, что спираль Фибоначчи - это интерпретация (при помощи целых чисел) арифметически невозможной спирали золотого сечения, у которой нет ни конца, ни начала. У спирали Фибоначчи есть определенное начало» (10,3).
На пропорции b:a = с:b базируются основные геометрические фигуры.
С числом φ связаны понятия о золотом треугольнике, золотом прямоугольнике и золотой спирали.
-
Золотой треугольник
Золотым треугольником называют равнобедренный треугольник, у которого отношение длины боковой стороны к длине основания равняется 1,618. Одним из таких треугольников является треугольник с боковой стороной Ф и основанием 1. Одно из замечательных свойств такого треугольника состоит в том, что длины биссектрис углов при его основании равны длине самого основания.
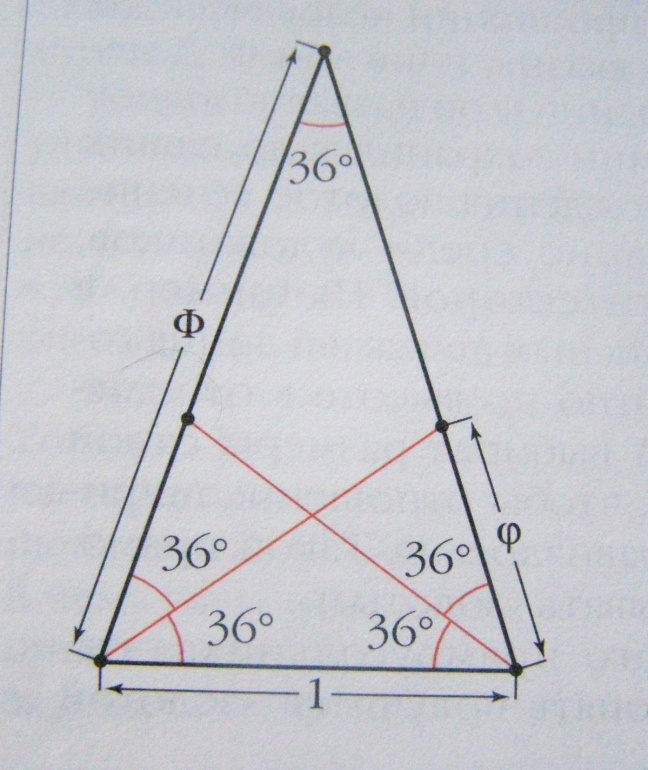
Рис.2. Золотой треугольник
-
Золотой прямоугольник
Золотой прямоугольник - прямоугольник, у которого отношение смежных сторон дает пропорцию Фидия 1,618. «Золотой прямоугольник» обладает интересным свойством: если от него отрезать квадрат, то останется вновь «золотой прямоугольник». Так можно продолжать до бесконечности. Если провести диагонали первого и второго прямоугольников, то точка О их пересечения принадлежит всем получаемым «золотым прямоугольникам».
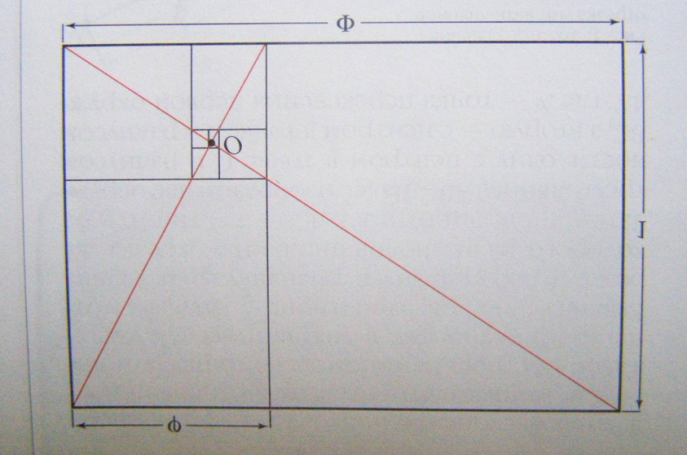
Рис. 3. Золотой прямоугольник
-
Звёздчатый пятиугольник
Каждая из пяти линий, составляющая эту фигуру, делит другую в отношении золотого сечения, а концы звезды являются золотыми треугольниками.
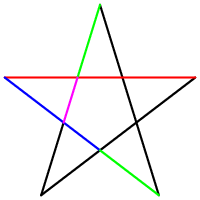
Рис. 4. Звездчатый треугольник
Золотая пропорция - это такое соотношение сторон, которое наиболее приятно глазу. Она и создаёт гармонию, без которой невозможно ни одно совершенное творение природы и человека-творца. Поэтому любое великое творение подчинено законам математики. Я и попробую рассмотреть, как проявляются эти законы в различных видах искусства.
-
Математика в скульптуре
Мы… никогда бы не стали разумными, если бы исключили число из человеческой природы.
Платон.
Скульптура как вид искусства, воспроизводящий тело человека, связано с пропорциями "золотого сечения", которые и создают впечатление гармонии и красоты, поэтому скульпторы используют их в своих произведениях. Ещё древнегреческие скульпторы утверждали, что талия делит совершенное человеческое тело в отношении «золотого сечения».
Великий древнегреческий скульптор Фидий, в честь которого и названо число фи, часто использовал "золотое сечение" в своих произведениях. Самыми знаменитыми из них были статуя Зевса Олимпийского (она считалась одним из чудес света) и Афины Парфенос .
Венера Милосская - статуя богини Афродиты, признана эталоном женской красоты именно потому, что её тело содержит золотое сечение. Как видно из рисунка, расстояние статуи Венеры Милосской от талии до стопы кратно 0,618 ; от макушки до талии кратно 0,382, т.е. составляет золотую пропорцию.
Эталон мужской красоты - знаменитая статуя Аполлона Бельведерского, также соответствовала золотой пропорции: a кратно 0,618, b кратно 0,382.
Одним из высших достижений классического греческого искусства может также служить статуя Дорифора (что означает копьеносец), изваянная Поликтетом в V веке до н.э. Эта статуя считается наилучшим примером для анализа пропорций идеального человеческого тела, установленных античными греческими скульпторами, и напрямую связана с золотым сечением и числом фи = 0,618.
Оно представлено в статуе несколько раз. Это отношение расстояния
-
От талии до стопы к расстоянию от макушки до талии,
-
От талии до шеи к длине головы,
-
От подбородка до линии бровей к расстоянию от линии бровей до макушки,
-
От талии до колена к расстоянию колена до стопы.
Все эти отношения приближены к 1,618.
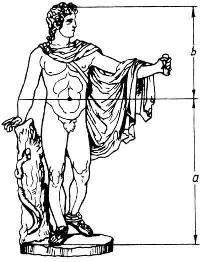
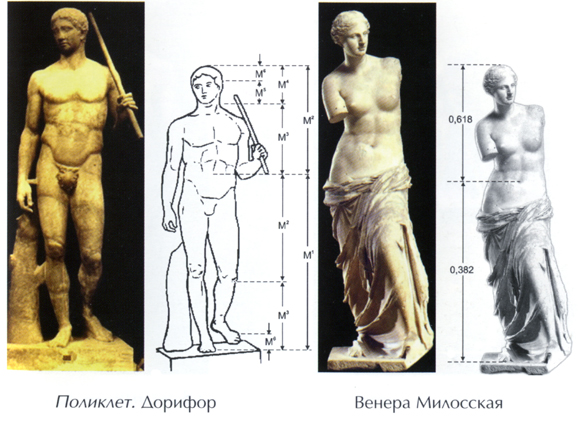
Рис. 5 Золотое сечение в скульптурах
Практическое исследование
Я решил проверить, есть ли золотое сечение в скульптурах нашего города Дзержинска Нижегородской области. Наглядный пример, - памятник В. В. Маяковскому. Конечно, оригинал мне измерить не удалось, поэтому я измерил на фотографии расстояние от талии до стопы и от макушки до талии. В.Маяковский, конечно, не Аполлон Бельведерский (хотя стихи у него замечательные), но золотое сечение в нём тоже присутствует:
c=5,02
a=1,92 a : 5 = 0,384
b=3,1 b : 5 = 0,62 - число, близкое к фи 0,618
b : а = с : b
3,1 : 1,92 =1,614
5,02 : 3,1 =1,619
Оба эти значения близки к отношению золотого сечения 1,618
Я много раз проходил мимо этого памятника, но мне и в голову не приходило, что в скульптурах нашего современного города есть что-то общее с античной скульптурой.

c
a
Рис.6. Золотая пропорция в скульптуре В.В. Маяковского
-
Математика в архитектуре
Математика - такое же подлинное искусство, как пластические искусства и музыка… Она особенно связана с великими архитектурами…
О. Шпенглер
"Золотое сечение" дает наиболее спокойное соотношение размеров тех или иных длин и в архитектуре. В книгах о "золотом сечении" можно найти мнения о том, что «в архитектуре, как и в живописи, все зависит от положения наблюдателя» (9,67), и что, если некоторые пропорции в здании «с одной стороны кажутся образующими "золотое сечение", то с других точек зрения они будут выглядеть иначе».(9, 68) .
Одним из красивейших произведений древнегреческой архитектуры является Парфенон (V в. до н. э.). Отношение высоты здания к его длине равно фи. Золотое сечение представляет собой и верх здания.

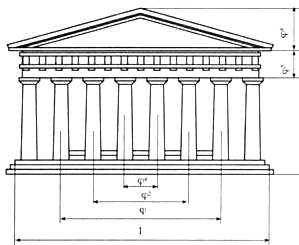
Рис. 7. Парфенон
Даже внутри Парфенона можно увидеть золотые прямоугольники. 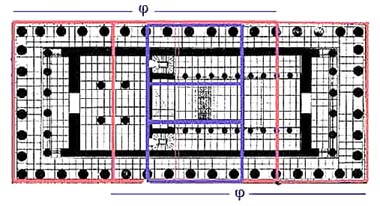
Рис. 8. Внутреннее строение Парфенона
Отношение сторон прямоугольника приближено к 1.618 и создаёт идеальную пропорцию.
Практическое исследование
Я обнаружил в нашем городе здание, похожее на древнегреческой Парфенон. Это здание Кукольного театра. Даже на глаз видно, что колонны и крыша здания создают золотое сечение. А последовательность колонн очень напоминает последовательность Фибоначчи, как и колонны Парфенона.
с = 1,7
b = 1,05
а = 0,65
b:а = 1,05:0,65 = 1,615
с:b = 1,7:1, 05 = 1, 619

c
φ
φ²
a
1
Рис. 9. Золотая пропорция и ряд Фибоначчи в Дзержинском Театре Кукол
-
Математика в живописи
Человек по натуре своей - художник.
Он всюду так или иначе стремится
вносить в свою жизнь красоту.
М. Горький.
В эпоху Возрождения художники открыли, что «любая картина имеет определенные точки, невольно приковывающие наше внимание, так называемые зрительные центры. При этом абсолютно неважно, какой формат имеет картина - горизонтальный или вертикальный. Таких точек всего четыре, и расположены они на расстоянии 3/8 и 5/8 от соответствующих краев плоскости». ( 2, 67).
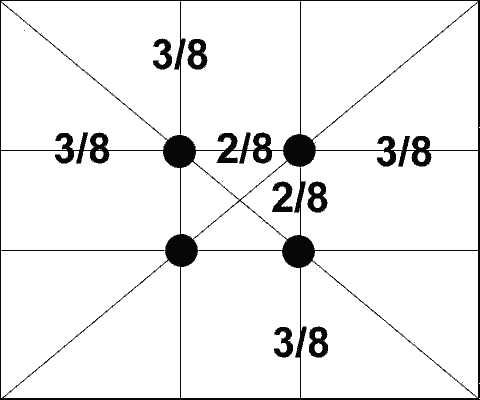
Рис. 10. Зрительные центры на плоскости
Данное открытие у художников того времени получило название "золотое сечение" картины. Поэтому, для того чтобы привлечь внимание к главному элементу картины, необходимо совместить этот элемент с одним из зрительных центров. Было так же определено, что больше всего внимания при рассматривании прямоугольного рисунка придается центральной части, образованной точками, которые делят этот рисунок в золотой пропорции.
Картина«Тайная вечеря» Леонардо да Винчи примечательна тем, что построена на прямоугольниках. Соответствующие прямоугольники в картине - "золотые".
В центре художник помещает фигуру Христа, выделяя ее просветом двери. Апостолов он сознательно отодвигает от Христа, чтобы еще более акцентировать его место в композиции. Наконец, в этих же целях он заставляет сходиться все перспективные линии в точке, непосредственно расположенной над головой Христа. Учеников Леонардо да Винчи разбивает на четыре симметрические группы, полные жизни и движения. Стол он делает небольшим, а трапезную - строгой и простой. Это дает ему возможность сосредоточить внимание зрителя на фигурах, обладающих огромной пластической силой. Во всех этих приемах сказывается глубокая целеустремленность творческого замысла, в котором все взвешено и учтено.

Рис. 11. «Тайная вечеря» Леонардо да Винчи
«Джоконда» - пожалуй, одно из самых загадочных и таинственных произведений Леонардо да Винчи. Портрет Моны Лизы привлекает тем, что композиция рисунка построена на "золотых треугольниках", точнее на треугольниках, являющихся кусками правильного звездчатого пятиугольника. «Зрачок левого глаза, через который проходит вертикальная ось полотна, находится на пересечении двух биссектрис верхнего золотого треугольника, которые с одной стороны, делят пополам углы при основании золотого треугольника, а с другой стороны - в точках пересечения с боковыми сторонами золотого треугольника делят их в пропорции золотого сечения». (2, 88). Благодаря ему, в изображении главной героине картины соблюдается строгая пропорциональность, которая придает ей красоту и правильные очертания. Мона Лиза - пример идеального изображения человека.


Рис. 12. «Мона Лиза (Джоконда)» Леонардо Да Винчи.
На картине И.И. Шишкина "Сосновая роща" просматриваются мотивы золотого сечения. Ярко освещенная солнцем сосна, стоящая на первом плане, делит длину картины приблизительно в золотом сечении. Справа от сосны - небольшой пригорок, освещенный солнцем. Он делит в золотом сечении правую часть картины по горизонтали. Слева от большой сосны находится множество сосен. При желании можно с успехом продолжить деление картины в пропорциях золотого сечения.
Наличие в картине ярких вертикалей и горизонталей, делящих ее в отношении золотого сечения, придает ей характер уравновешенности и спокойствия, в соответствии с замыслом художника.


Рис. 13. «Сосновая роща» И.И. Шишкин.
Когда же замысел художника иной, если, скажем, он создает картину с бурно развивающимся действием, подобная геометрическая схема композиции (с преобладанием вертикалей и горизонталей) становится неприемлемой.
В отличие от золотого сечения ощущение динамики, волнения проявляется сильней всего в другой простой геометрической фигуре - спирали. Многофигурная композиция, выполненная в 1509 - 1510 годах Рафаэлем как раз отличается динамизмом и драматизмом сюжета.
На подготовительном эскизе Рафаэля проведены красные линии, идущие от смыслового центра композиции - точки, где пальцы воина сомкнулись вокруг лодыжки ребенка, - вдоль фигур ребенка, женщины, прижимающей его к себе, воина с занесенным мечом и затем вдоль фигур такой же группы в правой части эскиза. Если соединить эти куски кривой пунктиром, то с большой точностью получается золотая спираль. Это можно проверить, измеряя отношение длин отрезков, высекаемых спиралью на прямых, проходящих через начало кривой.
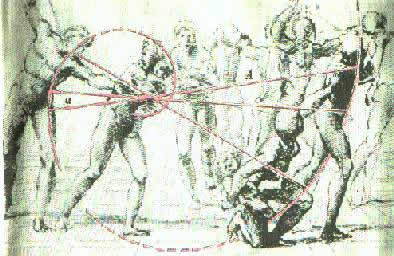
Рис. 14. «Избиение младенцев» Рафаэль.
Картина «Святое семейство» Микеланджело признана одним из шедевров западноевропейского искусства эпохи Возрождения. Гармонический анализ показал, что композиция картины тоже, как и остальные, основана на золотом сечении. «Элементы этой картины образуют звездчатый пятиугольник. Каждая из пяти линий, составляющих эту фигуру, делит другую в отношении золотого сечения, а концы звезды являются золотыми треугольниками». (4, 90).

Рис. 15. «Святое семейство» Микеланджело.
Практическое исследование
Нерукотворный образ Иисуса Христа. Ясный взор, светлый лик, от которого веет божественным светом. В чём секрет такого сильного воздействия на все лучшие струны человеческой души? До того, как я взялся за эту тему, я считал, что ответ кроется в изяществе тонких черт лица сына Божьего: длинный нос, строго очерченная линия бровей, высокий чистый лоб... Я думал, что это и создаёт то неповторимое выражение, которое называют божественным. Теперь я наглядно убедился, что божественный свет - это и есть идеальные пропорции золотого сечения, т. е. «божественная пропорция».
19,4 : 12 = 1,616
12 : 7,4 = 1,62
Даже репродукция «Нерукотворного Спаса», на которой я измерил черты лица Иисуса Христа, отражает его божественные пропорции, близкие к числу 1,618.
7,4 см
19,4см
12 см

Рис. 15. Спас Нерукотворный
-
Математика и декоративно - прикладное искусство
Симметрия… есть идея, с помощью которой человек веками пытался объяснить и создать порядок, красоту и совершенство.
Г. Вейль
Практическое исследование
Декоративно-прикладное искусство как вид творческой деятельности по созданию предметов быта, также отражает художественно - эстетические потребности людей, поэтому не обходится без математической точности рисунка. И главную роль здесь играет соблюдение закона симметрии.
У нас дома много предметов городецкой росписи, они и стали предметом моего исследования.
Наиболее распространенными мотивами этого вида прикладного искусства являются цветы: розы, ромашки, купавки с симметричными листьями. Их расположение на предмете быта (блюде, доске) тоже симметрично относительно центральной точки плоскости изделия или центральной и смежных линий. Таким образом, рисунок может иметь несколько симметричных относительно друг друга фигур. Даже непохожие друг на друга цветы (роза и купавка) развёрнуты и расположены по принципу осевой или центральной симметрии. На изделии они становятся симметричными друг другу.
листья


Рис. 16. Городецкая роспись
На основе симметрии создаются целые композиции. Например, «Венок». Он напоминает «цветочную полосу», но только замкнутую по краю блюда или крышки шкатулки. На рисунке он изображён на каёмке тарелки.
Цветочные композиции обычно симметричны не только по расположению мотивов, но и по распределению цвета.
При изображении фигур (коня или птицы) мотивы могут быть как симметричными, так и асимметричными. Они располагаются по сторонам цветущего дерева или внутри цветочной гирлянды. Иногда, среди симметрично написанного цветочного орнамента располагаются две птицы, асимметричные по рисунку, иногда различные по цвету. Иногда, при выполнении мастером композиции из нескольких предметов (например, разделочных досок), симметрия проявляется в композиции двух крайних досках. На них могут изображаться различные мотивы цветов либо при написании птиц будут использоваться два мотива: «петух» и «курочка».


Рис. 17. Осевая симметрия в изделиях городецкой росписи
-
Математика в литературе
Гуманитарные науки... только тогда будут удовлетворять человеческую мысль, когда в движении своём они встретятся с точными науками и пойдут с ними рядом...
А. П. Чехов.
Литература содержит достаточно много математики, особенно геометрии. Этот факт был отмечен, как математиками, так и литературными критиками.
«Многие произведения художественной литературы построены на передвижении в пространстве. Сюда можно отнести жанры путевых заметок, путешествия. Повествование разворачивается от некоей точки отсчета, приобретает скорость, «перемещается» и оканчивает свое движение». (11, 12).
Практическое исследование
Я бы выделил 3 вида художественных произведений, основанных на перемещении:
-
Линейные перемещения. Сюжет произведения здесь построен на перемещении главного героя по некоей прямой линии. В математике оно представляет собой отрезок, начало которого соответствует завязке, а конец - развязке сюжета. Таким образом построены, например, «Железная дорога» Н. А. Некрасова и «Путешествие из Петербурга в Москву» А.Н. Радищева, где герой совершает путешествие по железной дороге. То же самое движение происходит в русских народных сказках, где Иван-царевич идёт прямо, никуда не сворачивая.
-
Перемещение по плоскости. Такие произведения имеют несколько сюжетных линий, объединённых одним действующим лицом, путешествия которого рассосредоточены по времени («Сентиментальное путешествие» Д. Стерна, «Письма русского путешественника» Н.М. Карамзина), или несколько главных действующих лиц, которые развивают одну сюжетную линию («Дети капитана Гранта» Ж. Верна). Математически это может выглядеть, как ломаная линия, несколько отрезков, не связанных между собой, или несколько разнонаправленных отрезков, которые впоследствии сходятся в одной точке.
-
Перемещение в трёхмерном пространстве. Образцом этого вида произведений является « Из пушки на луну» Ж. Верна, где и с точки зрения литературы, и с точки зрения математики передвижение происходит в трёхмерном пространстве, где отрезки движения группы персонажей создают стереометрическую фигуру. Сюда же можно отнести и такие произведения многие произведения жанра приключений и фантастики («Вокруг света за 80 дней» Ж. Верна, «Гарри Поттер» Дж. Роллинг).
-
Перемещение с использованием параллельного переноса. Он осуществляется рассказчиком произведения и проецируется в другое место пространства на литературного героя. Литература в этом случае пользуется указательными местоимениями: «здесь», «тут» означают местонахождение рассказчика, а «там» - нахождение персонажа за пределами расположения авторского пространства. Геометрически же получается две равные фигуры, одна из которых создаётся из отрезков движения героя произведения и рассматривается, как результат параллельного переноса фигуры автора произведения. (Такую конструкцию можно обнаружить в «Путешествии Гулливера»).
Вообще, литература часто использует математический приём параллельного переноса и проецирования: параллельные образы (автор и его герой, герой и его психологический двойник - у А.С. Пушкина, Х.К. Андерсена, Е. Шварца), приём психологического параллелизма, когда прослеживается параллель между состоянием природы и состоянием литературного героя (у И.С. Тургенева, Н. А. Некрасова).
Особое внимание мне хотелось бы уделить произведениям, целиком построенным по математическим принципам:
-
Сказки Льюиса Кэрролла
«Алиса в стране чудес» и «Алиса в зазеркалье».
Льюис Кэрролл как математик (Чарльз Л.Доджсон) экспериментирует с героями и пространством: меняет и перемещает точки отсчета, нарушает линейность, «разрушает все логические основания трехмерного восприятия».
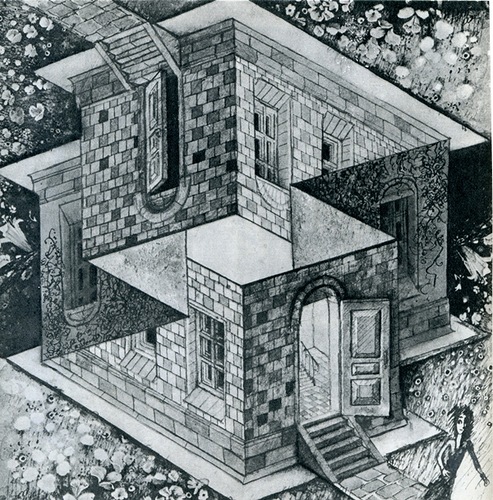
Рис. 18. Иллюстрация к книге Л. Кэрролл «Алиса в стране чудес».
На рисунке видно искажение трёхмерного пространства, благодаря которому создаётся зазеркальность восприятия мира главной героиней произведения и его читателями.
Здесь можно увидеть разные виды движения по плоскости: от разных точек, в разных направлениях, ведь персонажи сказки разыгрывают шахматную партию, где Льюис Кэрролл определил каждому герою - шахматной фигуре своё движение по плоскости. Если нарисовать траектории движения фигур, то получится интересная закономерность: все линии сведутся к отрезкам, связующей нитью которых станет ломаная линия главной героини Алисы, пересекающая каждый из этих отрезков, параллельно которой будет построена линия движения Чёрной королевы, сопровождающей Алису по зазеркалью.
В основе «Алисы в зазеркалье» лежит принцип осевой симметрии. Оно и понятно, ведь Алиса попадает в мир зазеркалья, где всё должно быть обратной копией реального мира.
Все действующее лица сказки симметричны.
БЕЛЫЕ ФИГУРЫ:
Труляля, Единорог, Овца, Белая Королева, Белый Король, Старичок, Белый Рыцарь, Траляля
БЕЛЫЕ ПЕШКИ:
Маргаритка, Зай Атс, Устрица, Крошка Лили, Лань, Устрица, Болванс Чик, Маргаритка
--------------------------------------------------------------------------------------------------------------------------- Маргаритка, Чужестранец, Устрица, Тигровая Лилия, Роза, Устрица, Лягушонок, Маргаритка
:ЧЕРНЫЕ ПЕШКИ
Шалтай-Болтай, Плотник, Морж, Черная Королева, Черный Король, Ворон, Черный Рыцарь, Лев
:ЧЕРНЫЕ ФИГУРЫ
(Пунктиром показана ось симметрии).
Образцом симметрии здесь являются Труляля и Траляля - "зеркальные" близнецы. Симметричны не только их движения, но и поступки и даже мысли.
- То же самое, - сказал Труляля.
- Самое, самое, - подтвердил Траляля.
Белый Рыцарь сам является симметричной фигурой. Он поет о попытке втиснуть правую ногу в левый башмак и постоянно меняет правую и левую стороны так же, как и направления.
В книге много примеров «симметричных отношений». Чтобы приблизиться к Черной Королеве, Алиса идет в противоположном направлении; в вагоне поезда кондуктор ей говорит, что она едет не в ту сторону; у короля - два Гонца, "один, чтобы бежал туда, другой - чтобы бежал оттуда". Белая Королева объясняет преимущества "жизни назад"; пироги в Зазеркалье сначала раздают гостям, а потом уж режут. Принцип симметрии помогает автору выразить главную тему сказки - тему вывернутого наизнанку зеркального мира.
Льюис Кэрролл использует и принцип параллельности, которая прослеживается в параллельных действиях персонажей (движения по шахматной доске Алисы и белого Рыцаря, параллельные вопросы двух королев) и параллельности их мыслей.
Но параллельны ещё и сами персонажи. Действующие лица, играющие роль белых фигур, параллельны чёрным фигурам.
Б
Е
Л
Ы
Е
Труляля
Маргаритка
Маргаритка
Шалтай-Болтай
Ч
Ё
Р
Н
Ы
Е
Единорог
Зай Атс
Чужестранец
Плотник
Овца
Устрица
Устрица
Морж
Белая Королева
Крошка Лили
Тигровая Лилия
Черная Королева
Белый Король
Лань
Роза
Черный Король
Старичок
Устрица
Устрица
Ворон
Белый Рыцарь
Болванс Чик
Лягушонок
Черный Рыцарь
Траляля
Маргаритка
Маргаритка
Лев
Рис. 19. Схема параллельной расстановки персонажей в сказке «Алиса в Зазеркалье»
И это ещё не всё. В параллельных снах Алисы и Черного Короля наблюдается своеобразный пример бесконечно убывающей последовательности: Алиса видит во сне Короля, который видит во сне Алису, которая видит Короля, который видит Алису, и так далее.
В книге не раз говорится о шпоре-штопоре, которую Чёрный рыцарь заносит то на левое, то на правое стремя, в результате чего как бы вкручивается в шлем. Эта шпора представляет собой не что иное, как спираль.
В сказке «Алиса в стране чудес» мы наблюдаем ещё один вид перемещения. Это перемещение Алисы по числовой прямой, где она изначально находится в нулевой точке отсчёта. Откусив от гриба с левой стороны, она уменьшается, откусив же с правой - напротив, вырастает. Движение направо - это увеличение, т.к. это движение связано с натуральным рядом чисел, а движение налево - уменьшение, т.к. это движение по отрицательному ряду числовой прямой.
Вообще в книге много подобных инверсий (изменений в росте). Например, вместо большой девочки и маленького щенка - маленькая девочка и большой щенок; маленькие слоны и огромные насекомые. Это можно считать проецированием.
-
Сказка В. Губарева «Королевство кривых зеркал».
Принцип симметричного построения образа мы видим также в сказке В. Губарева «Королевство кривых зеркал». В Зазеркалье главная героиня Оля встречается с Яло, которая оказывается ее симметричным двойником. "Видишь, у меня всё наоборот: у тебя родинка на правой щеке, а у меня на левой".
Имена Оли и Яло также симметричны. Симметрия в этом произведении помогает читателям понять сущность каждого персонажа. Все имена в сказке перевернуты и читаются "наоборот".
Вот положительные герои: А вот отрицательные:
Гурд - Друг Нушрок - Коршун
Аксал - Ласка Анидаг - Гадина
Бар - Раб Абаж - Жаба
Кстати, великое произведение древности «Слово о полку Игореве» построено математически. В основе памятника древней русской литературы, состоящего из девяти песен, лежит круговая композиция. А если есть круг, значит, есть и его диаметр. Петербургский поэт А. Чернов разделил число стихов во всех трех частях (их 804) на число стихов в первой и последней части (256), получается 3,14, то есть число пи.
-
Математика в поэзии
Истинная поэзия - это математика слова.
А. Блок.
Я бы добавил ещё, что поэзия - это математика ритма и поэтического сюжета. Ритм любого стихотворения строится на математической закономерности соотношения безударных и ударных звуков. Так выстраивается математическая последовательность поэтических размеров, где | - ударный звук, а _- безударный:
Ямб: _ | _ | _ | _ | _ | _ | _ | _ | _ | _ | _ | _ | _ | _ | _ | _ |
Хорей: | _ | _ | _ | _ | _ | _ | _ | _ | _ | _ | _ | _ | _ | _ | _ | _
Дактиль: | _ _ | _ _| _ _ | _ _| _ _ | _ _| _ _ | _ _| _ _| _ _ | _ _| _ _
Анапест: _ | _ _| _ _ | _ _| _ _ | _ _| _ _ | _ _| _ _| _ _ | _ _| _ _| _
Амфибрахий: _ _ | _ _| _ _ | _ _| _ _ | _ _| _ _ | _ _| _ _| _ _ | _ _| _ _|
В поэзии существует и принцип симметрии. Есть необычный тип стихотворной формы - палиндром, когда слово или фраза читается одинаково как слева направо, так и справа налево. Классический пример палиндрома Афанасия Фета: А роза упала на лапу Азора. В обратном направлении читается так же, как и в прямом. А у Велемира Хлебникова есть целые палиндромические стихотворения:
Мороз в узел, лезу взором.
Солов зов, воз волос.
Колесо. Жалко поклаж. Оселок.
Сани, плот и воз, зов и толп и нас.
Горд дох, ход дрог.
И лежу. Ужели?
Зол, гол лог лоз.
Многими исследователями было замечено, что в стихотворениях существуют кульминационные пункты, которые делят стихотворение в пропорции золотого сечения. Например, в стихотворении А.С. Пушкина "Сапожник"(13 строк) выделяется две смысловые части: первая в 8 строк и вторая (мораль притчи) в 5 строк (13, 8, 5 - числа ряда Фибоначчи).
Практическое исследование
Композиция стиха нередко выстраивается по математическому принципу параллельности - параллельности образов и состояний.
Например, в известном всем стихотворении А.С. Пушкина «Зимнее утро» состояние природы (чудесный день) и состояние автора (радость, чудесное настроение) параллельны.
Кроме того, здесь можно наблюдать математическое явление параллельного переноса состояния природы на состояние человека через лирического героя стихотворения. Такой приём в литературе называется психологическим параллелизмом:
-
природа
Грустное состояние
человек
Вечор, ты помнишь, вьюга злилась,
На мутном небе мгла носилась;
Луна, как бледное пятно,
Сквозь тучи мрачные желтела…
И ты печальная сидела…
Радостное состояние
Мороз и солнце; день чудесный!
Под голубыми небесами
Великолепными коврами,
Блестя на солнце, снег лежит;
Прозрачный лес один чернеет,
И ель сквозь иней зеленеет,
И речка подо льдом блестит…Пора, красавица, проснись!..
Навстречу северной Авроры,
Звездою севера явись!..
Приятно думать у лежанки…
Скользя по утреннему снегу,
Друг милый, предадимся бегу Нетерпеливого коня …
-
Математика в музыке
Каждая математическая пропорция остается одинаковой как в малом, так и в большом масштабе, подобно тому, как в пении одна октава относится к другой: одна из них выше, другая ниже, тон же единый.
А. Дюрер
Теорию музыки нельзя представить без математики: длительность нот и пауз, музыкальный размер, ритм, темп - всё это имеет прямое отношение к математике. Без знания математики невозможно сыграть ни одну мелодию.
Размер представляет собой математические дроби:

Рис. 20. Музыкальный размер
Длительность нот - это не что иное, как деление целого на дроби:
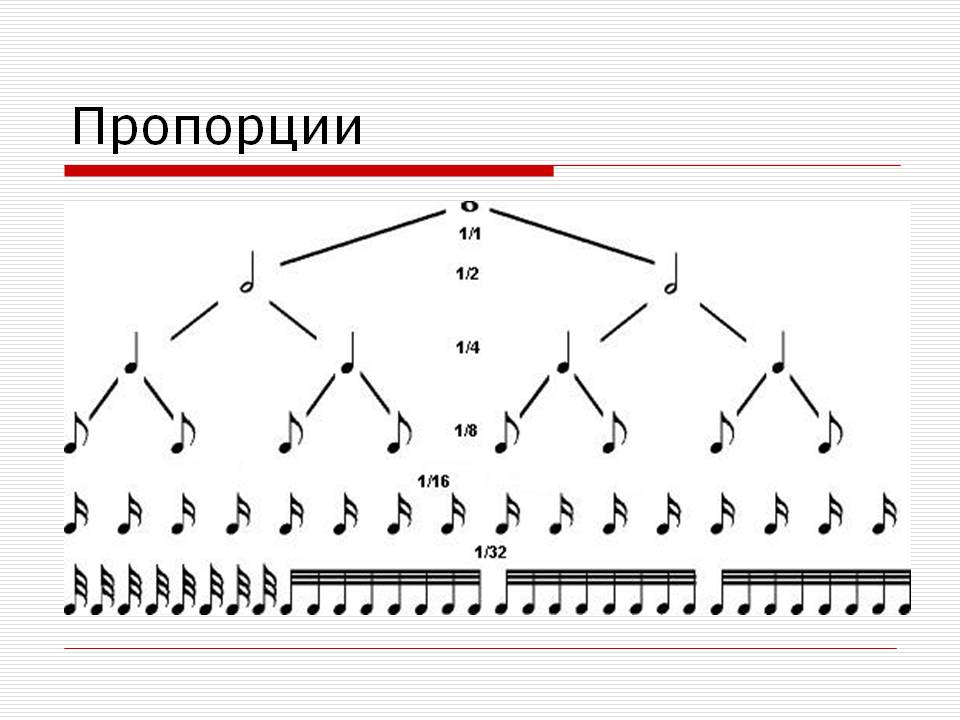
Рис. 21. Длительность нот
Транспонирование мелодии (перенос на одинаковое количество нотных ступеней) можно сравнить с математической проекцией или параллельным переносом.
Даже музыкальные инструменты (гитара, скрипка, виолончель) имеют форму близкую к параметрам золотого сечения. «Знаменитые итальянские мастера музыкальных инструментов Маджини, Амати, Гварнери, Страдивари сознательно применяли геометрию пентаграммы и тему золотого сечения в очертаниях своих несравненных скрипок». Журнал «Европа», 1925г. (4, 56)
Ещё один интересный пример. В 1925 году искусствовед Л.Л.Сабанеев, проанализировав 1770 музыкальных произведений 42 авторов, показал, что «подавляющее большинство выдающихся сочинений можно легко разделить на части или по теме, или по интонационному строю, или по ладовому строю, которые находятся между собой в отношении золотого сечения.
Причем, чем талантливее композитор, тем в большем количестве его произведений найдено золотых сечений. У Аренского, Бетховена, Бородина, Гайдна, Моцарта, Скрябина, Шопена и Шуберта золотые сечения найдены в 90% всех произведений». (4, 89). По мнению Сабанеева, золотое сечение приводит к впечатлению особой стройности музыкального сочинения.
Музыке свойственна математическая точность. Но математическому анализу подлежат не только длительность звуков (нот) и размер, а также и звук, и тембр, и лад, и гармония. Английский математик Сильвестр называл музыку математикой чувств, а математику - музыкой разума.
Заключение
Если вы хотите участвовать в большой жизни, то наполняйте свою голову математикой, пока есть к тому возможность. Она окажет вам потом огромную помощь во всей вашей работе. М.И. Калинин
Благодаря этой работе я больше углубился в математику и понял, как интересна эта наука, как много общего у неё с искусством. Я увидел в ней то, чего не замечал раньше: все виды искусства построены на математике. Я узнал, что величественные скульптуры античности, красивейшие архитектурные сооружения эпохи Возрождения, поражающие воображения картины известных мастеров кисти строятся по математическим расчётам. И чем точнее эти расчёты, чем более они приближены к математическим канонам, тем величественнее и притягательнее выглядит произведение искусства.
Работая над этой темой, я стал внимательнее вглядываться и вслушиваться в то, что находится вокруг меня: городские постройки, лица людей, природа, музыка. И всюду мне попадаются свидетельства того, что здесь поработал великий творец - математика.
Теперь я точно знаю, что ответ на вечный вопрос:
в чем бессмертие искусства, - кроется в математике!
Список использованной литературы
-
Бобров С. П. «Новое о стихосложении А. С. Пушкина» М.: Просвещение, 2005.
-
Волошинов А. В. «Математика и искусство» М.: Просвещение, 2000.
-
Востоков А. Х. « Опыт о русском стихосложении» СПб. 1987.
-
Давыдов М. «Красота математики». Н. Новгород, 2007.
-
Депман И. Я. Виленкин Н. Я. «За страницами учебника математики» М.: Просвещение, 1989 С.
-
Каменева Т. А. Козлов А.М. « Золотой треугольник в задачах» М.: Чистые пруды, 2008.
-
Кондратов А. М. « Математика и поэзия» М.: Знание, 1962.
-
Кордемский. Б. А. «Увлечь школьников математикой» М.: Просвещение, 1981.
-
А. В. Фарков. «Внеклассная работа по математике 5 - 11 классы» М.: Айрис-пресс, 2006.
-
И. Ф. Шарыгин Л.Н. Ерганжиева. «Наглядная геометрия» М.: Чистые пруды, 1995.
-
Нафиков Н.Н. « Гипотеза об истоках золотого сечения», Ж. "Математика в школе"
№ 3, 1994.
Список использованных источников информации
-
bymath.net
-
exponenta.ru
-
proza.ru
25


