- Преподавателю
- Математика
- Нестандартные методы решения задач
Нестандартные методы решения задач
| Раздел | Математика |
| Класс | - |
| Тип | Другие методич. материалы |
| Автор | Рыбенкова М.П. |
| Дата | 26.08.2015 |
| Формат | doc |
| Изображения | Есть |
Нестандартные методы решения уравнений.
Рыбенкова М.П.
МБОУ «Школа 140»
Н.Новгород.
Оглавление.
Глава I. Методические рекомендации к изучению нестандартных
методов решения уравнений.
-
Особенности обучения во втором концентре.
1.2. Нестандартные методы.
1.3. Развитие творческого мышления при решении уравнений нестандартными методами.
1.4.Методические рекомендации при организации занятий по решению уравнений нестандартными методами.
Глава I I. Нестандартные методы решения уравнений.
2.1. Решение уравнений с помощью исследования ОДЗ
2.2.Решение уравнений с использованием множества значений
2.3.Использование монотонности функций при решении уравнений
2.4.Использование эквивалентности при решении уравнений
2.5.Использование четности функций при решении уравнений
2.6.Использование векторов при решении уравнений
2.7.Использование неравенства между средним арифметическим
и средним геометрическим при решении уравнений
Заключение.
Список литературы.
ГЛАВА I. Методические рекомендации к изучению нестандартных методов решения.
1.1.Особенности обучения во втором концентре.
« Деятельности нельзя научить, но ею можно овладеть».1
В условиях современной школы перед учителем стоит задача так организовать учебный процесс, чтобы школа стала не местом приобретения суммы знаний, а средой для развития личности, для овладения интеллектуальными приёмами, необходимыми в будущем. Особенно это важно в старших класса, для выпускников, которым совсем скоро предстоит адаптироваться во взрослой жизни, самостоятельно принимать решения, брать на себя ответственность.
При организации уроков в 10 -11 классах, в том числе практических занятий, учителю, прежде всего, необходимо учитывать особенности концентрической структуры образования.
Обучение в рамках первого концентра предполагает изучение фактов. В 5 -9 классах ученик знакомится с фактами, накапливает их, систематизирует и усваивает, приобретая минимум математических знаний.
Второй концентр предполагает принципиально новый уровень усвоения учебного материала. Учитель ориентирует учащихся не на информационный, а на проблемный принцип усвоения. Таким образом, в центре внимания проблемное обучение математики. Сущность проблемного обучения заключается в постановке проблемы, задачи, требующей разрешения. Это обучение, основанное на активном привлечении учащихся к учебному процессу. В связи с этим существенно меняются функции учителя и ученика, цели обучения.
Если в рамках первого концентра преобладает сообщение учителем новой информации, то есть информационно - репродуктивный уровень, то во втором концентре упор делается на познание сути математического процесса, на установление причинно - следственных связей, на определение места и роли события, на анализ фактов самими учащимися под руководством учителя.
Таким образом, ученик превращается в субъекта учебной деятельности, а задача учителя - организаторская, управляющая (учитель - менеджер урока). Учебные проблемы легко обнаруживаются при установлении связей между теориями и фактами, между теориями и понятиями, между отдельными понятиями и т.д. Так, например, проблема, почему одни и те же, скажем, иррациональные уравнения нельзя решить путем возведения в одну и ту же степень левой и правой частей уравнений.
1.2«Нестандартные» методы.
Какие же методы называются нестандартными? « Нестандартные методы решения уравнений - это такие нетипичные методы, содержащие в себе оригинальную, творческую идею, это не традиционные методы, далекие от шаблона. Оценка метода решения уравнения с позиции традиционности (нестандартности) во многом субъективна: на сколько непривычен для учащегося предложенный прием, настолько он и нестандартен. И, наверное, самая высокая степень нестандартности идеи - это ее неожиданность.
Понятие «нестандартный» метод является относительным. Как только учитель познакомит учащихся с такими методами решения уравнений, они перестают быть «нестандартными».
Нестандартные задачи, опять - таки условно, можно разделить на два типа: нестандартные и стандартные по внешнему виду. Довольно часто задача первого типа представляет нечто вроде «функционального винегрета», т.е. ее конструируют функции из различных разделов математики. Например: 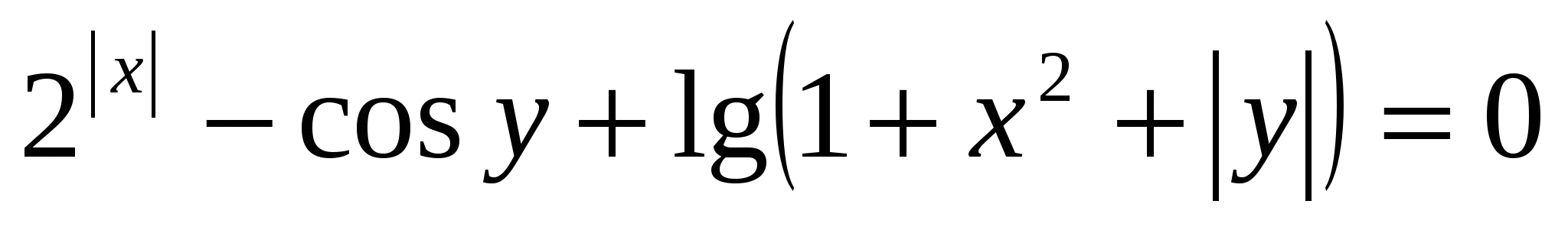 .
.
С задачами второго типа иная ситуация. Их внешняя «успокоительная стандартность» - своего рода коварство. Зачастую по закону зловредности длинное решение менее замаскировано, чем короткое. В таких случаях бывает полезно еще раз проанализировать условие задачи, а самое главное, попытаться найти ее конкретные особенности, позволяющие обнаружить ее традиционную идею. Поэтому для решения такого рода задач особенно важны такие качества, как сообразительность, интуиция, высокая логическая культура. При этом вовсе не хотим сказать, что второй тип задач более сложный, чем первый: ощущение необходимости поиска нетрадиционной идеи еще не означает, что такова будет найдена2.
Универсального метода, позволяющего решить любое уравнение, любую нестандартную задачу, к сожалению, нет. Но, чтобы добиться хороших результатов, надо соблюдать следующие методические приемы:
1)Вызвать интерес к решению той или иной задачи. (Можно научить решать такие уравнения только в том случае, если у ученика будет желание.) Умение учителя отбирать интересные задачи.
2)Задачи не должны быть слишком легкими или слишком трудными, чтобы ученик не потерял веру в себя не предлагать ученикам те задачи, которые они заведомо не решат.
3)Если не решат заданную задачу, то не предлагать ее решение, а подсказать идею решения, или план, или вспомогательные задания.
4)Отмечать успехи учащихся в решении такого типа задач.
5)Нет ничего плохого в том, что при решении таких задач ученик обратился к кому-то за помощью, ему интересна задача, а изучение способа решения, предложенного кем-то другим, будет способствовать накоплению определенного запаса математических фактов.
1.3.Развитие творческого мышления при решении уравнений нестандартными методами.
Самостоятельный поиск нетрадиционного способа решения уравнения, ведущего к быстрому и рациональному способу решения, способствует развитию творческого мышления.
Психологами было затрачено много усилий и времени на выяснение того, как человек решает новые, необычные, нестандартные, творческие задачи. Однако до сих пор ясного ответа на вопрос о психологической природе творчества нет. Наука располагаем только некоторыми данными, позволяющими частично описать процесс решения человеком такого рода задач, охарактеризовать условия, способствующие и препятствующие нахождению правильного решения.
Мышление отличается от других психологических процессов тем, что оно почти всегда связано с присутствием проблемной ситуации, задачи которую нужно решить. В мышлении на основе информации делаются определенные теоретические и практические выводы.
Мышление - это движение идей, раскрывающее суть вещей. Eго итогом является не образ, а некоторая мысль, идея.
Что же такое творческое мышление? Одним из первых попытался сформулировать ответ на данный вопрос Дж.Гилфорд. Он считал, что «творческость» мышления связана с доминированием в нем четырех особенностей
A. Оригинальность, нетривиальность, необычность высказываемых идей, ярко выраженное стремление к интеллектуальной новизне. Творческий человек почти всегда и везде стремится найти свое собственное, отличное от других решение.
Б Семантическая гибкость, т.е. способность видеть объект под новым углом зрения, обнаруживать его новое использование, расширять функциональное применение на практике.
B. Образная адаптивная гибкость, т.е. способность изменить восприятие объекта таким образом, чтобы видеть его новые, скрытые от наблюдения стороны.
Г. Семантическая спонтанная гибкость, т.е. способность продуцировать разнообразные идеи в неопределенной ситуации, в частности в такой, которая не содержит ориентиров для этих идей.3
В ходе исследований творческого мышления были выявлены условия, которые способствуют быстрому нахождению решения творческой задачи:
1.Если в прошлом определенный способ решения человеком некоторых задач оказался достаточно успешным, то это обстоятельство побуждает его и в дальнейшем придерживаться данного способа решения. При встрече с новой задачей человек стремится применить его в первую очередь.
2.Чем больше усилий было потрачено на то, чтобы найти и применить на практике новый способ решения задачи, тем вероятнее обращение к нему в будущем. Психологические затраты на обнаружение некоторого нового способа решения пропорциональны стремлению использовать его как можно чаще на практике.
3.Максимум эффективности в решении интеллектуальных задач достигается при оптимальной мотивации и соответствующем уровне эмоционального возбуждения. Этот уровень для каждого человека сугубо индивидуален
Условия, которые препятствуют быстрому нахождению решения творческой задачи:
1.Возникновение стереотипа мышления, который в силу указанных выше условий мешает человеку отказаться от прежнего и искать новый, более подходящий путь решения задачи.
Один из способов преодоления такого сложившегося стереотипа состоит в том, чтобы на некоторое время вообще прекратить попытки решения задачи, а затем вернуться к ней, с твердой установкой пробовать для поиска решения только новые пути.
2.Интеллектуальные способности человека, как правило, страдают от частых неудач, и боязнь очередной неудачи начинает автоматически возникать при встрече с новой задачей. Она порождает защитные реакции, которые мешают творческому мышлению, обычно связанному с риском для собственного «Я». В итоге человек теряет веру в себя, у него накапливаются отрицательные эмоции, которые мешают ему думать. Чувство успеха для усиления интеллектуальных потенций людей столь же необходимо, как и ощущение правильности какого-либо движения для его усвоения.
Чем больше знаний имеет человек, тем разнообразнее будут его подходы к решению творческих задач. Однако соответствующие знания должны быть разнонаправленными, так как они обладают способностью ориентировать мышление на различные подходы к решению.
1.4.Методические рекомендации при организации занятий по решению уравнений нестандартными методами.
Почему уравнения? В течение всех лет обучения в школе решают различные виды уравнений: линейных, квадратных, дробно - рациональных, тригонометрических, показательных, логарифмических и т. д., но проблема остается: решение уравнений один из наиболее трудных заданий по математике. Даже если ученик правильно проводит тождественные преобразования, входящих в него выражений, безошибочно вычисляет. Нужно знать какие способы, в каких ситуациях применять, а это умение вырабатывается при знании различных методов решения и большой практике.
Если ученик научится решать уравнения. Он эти знания перенесет на решение неравенств, систем уравнений и неравенств. В нестандартных методах используются свойства всех функций входящих в состав уравнений, знания скалярного произведения векторов, неравенство между средним арифметическим и средним геометрическим положительных чисел, и многое другое. Это вырабатывает умения переносить знания с одного предмета на другой, и на другие учебные ситуации. Вооружив ученика различными методами решения уравнений, его мышление претерпевает изменения, учащайся сам начинает предлагать различные подходы к решению уравнений, предлагая порой интересные нестандартные решения. Его уже не пугает сложный вид порой и нестандартного уравнения, применяя различные способы решения которого нестандартность улетучивается.
Для углубления знаний по методам решения уравнений используются индивидуально-групповые занятия, начиная с третьей четверти.
Основная задача наших занятий: как можно полнее развить потенциальные творческие способности каждого ученика, не ограничивая заранее уровень сложности решения задач. Как видим, личная цель - подготовки к конкурсному экзамену - совпадает с общественной- повышением уровня математической подготовки выпускников средней школы. Не зависимо от цели у учащихся повышается интерес к математике, к творческим заданиям. Ориентируя школьников на поиски красивых изящных решений математических задач, учитель тем самым способствует эстетическому воспитанию учащихся и повышению их математической культуры. Главная цель задач - развить творческое и математическое мышление учащихся, заинтересовать их математикой, привести к «открытию» математических фактов.
Следует отметить тот факт, что любая математическая задача, решаемая на уроках, на внеклассных занятиях или дома должна обязательно чему-нибудь научить учащихся. Решение каждой задачи должно быть шагом вперед в развитии математических знаний, умений и навыков учащихся, должно обогащать их знания и опыт, учить их ориентироваться в различных ситуациях.
Систематическая работа по изучению способов решения уравнений поможет учащимися не только научиться решать задачи, но и самим их предлагать. Умение находить нестандартные, более рациональные пути решения уравнений, свидетельствует о культуре их мышления, хорошо развитых математических способностях.
Учитель должен помнить, что решение задач является не самоцелью, а средством обучения. Обсуждение найденного решения, поиск других способов решения, закрепление в памяти тех приемов, которые были использованы, выявление условий возможности применения этих приемов, обобщение данной задачи - все это дает возможность школьникам учиться на задаче. Именно через задачи учащиеся могут узнать и глубоко усвоить новые математические факты, овладеть новыми математическими методами, накопить определенный опыт, сформировать умения самостоятельно и творчески применять полученные знания.
Чтобы добиться эффективности этих занятий необходимо выполнение следующих правил.
1)Новые идеи, не опирающиеся на дополнительные теоретические сведения, следует вводить через уравнения по схеме; уравнение - самостоятельный поиск решения - разбор ее решения - выделение идеи.
2) При решении таких заданий должен работать принцип регулярности, основная работа происходит не в классе, а дома.
3)Не стоит загружать ученика большой по объему, но не сложной работой, также как нельзя ставить перед ним непосильную задачу.
4) Ученик имеет право отложить трудную задачу( уравнение), если он над ее решением потрудился определенное время, и она у него не получилась. В этом случае процесс усвоения новых идей будет более эффективным.
5) Приветствуется правильная идея, в период накопления идей или же при решении трудных задач.
6) Полезно приводить различные приемы и методы решения одного и того же уравнения, а затем обсудить решения на предмет рациональности, красоты, нестандартности решения. При отыскании различных способов решения задач у школьника формируется познавательный интерес, развиваются творческие способности, вырабатываются исследовательские навыки.
7)Постоянный повтор при решении ранее изученных методов решения
применять полученные знания.
ГЛАВА 2. НЕСТАНДАРТНЫЕ МЕТОДЫ РЕШЕНИЯ УРАВНЕНИЙ.
Собранные здесь уравнения не являются очень сложными ,но по мере занятий усложняются. Некоторые методы решения уравнений условно можно назвать нестандартными.
Решение уравнений с помощью исследования ОДЗ.
Областью допустимых значений (сокращенно ОДЗ) уравнения называется множество тех значений неизвестного, при которых имеют смысл его левая и правая части.
В этом пункте мы рассматриваем решение иррациональных уравнений, которые можно решать стандартным путем, избавляясь от иррациональности, а затем выполнить проверку. Но такой способ ведет к громоздким вычислениям, к решению рациональных уравнений четвертой, шестой степени, которые решить очень сложно. При решении некоторых уравнений знание ОДЗ уравнения и применение некоторых оценок позволяет найти все его корни или доказать, что их нет.
Предлагаю ученикам решить 2 таких уравнения дома, перед занятием. Чаще всего они пытаются решить эти уравнения, избавляясь от иррациональности, но находятся 1-2 человека в классе, которые выбирают рациональный путь решения, что радует. Затем совместно рассматриваем оба способа решения уравнений.
Примеры.
1)Решить уравнение 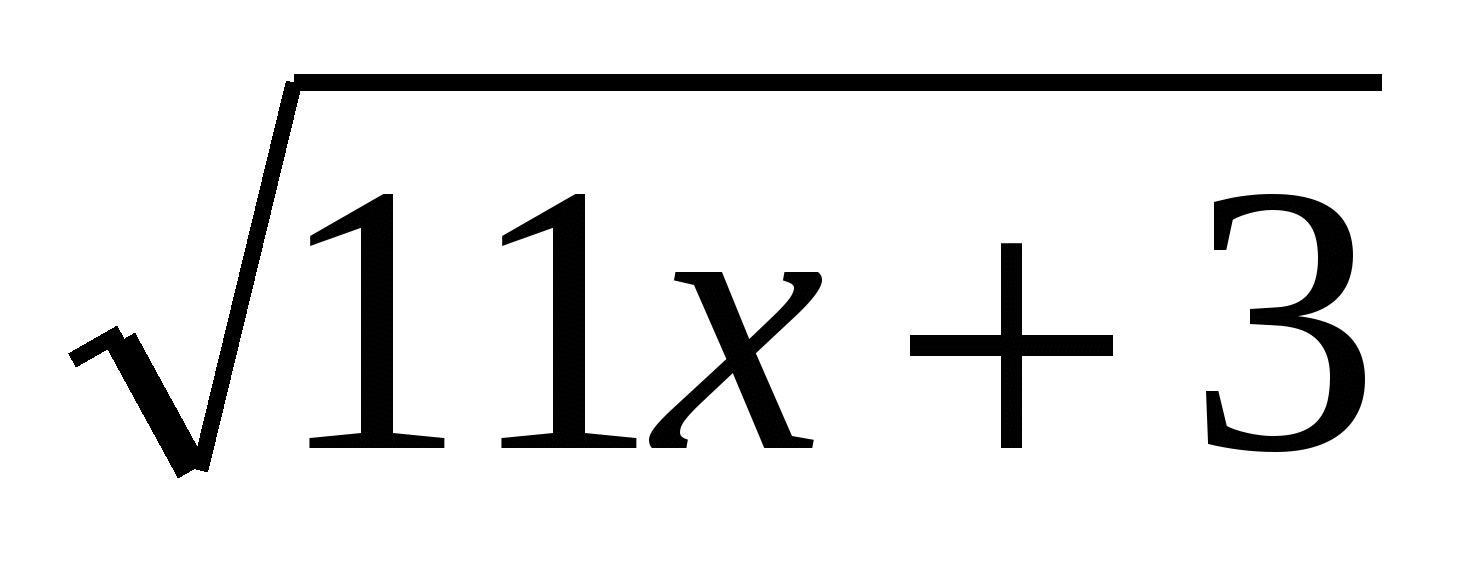 -
-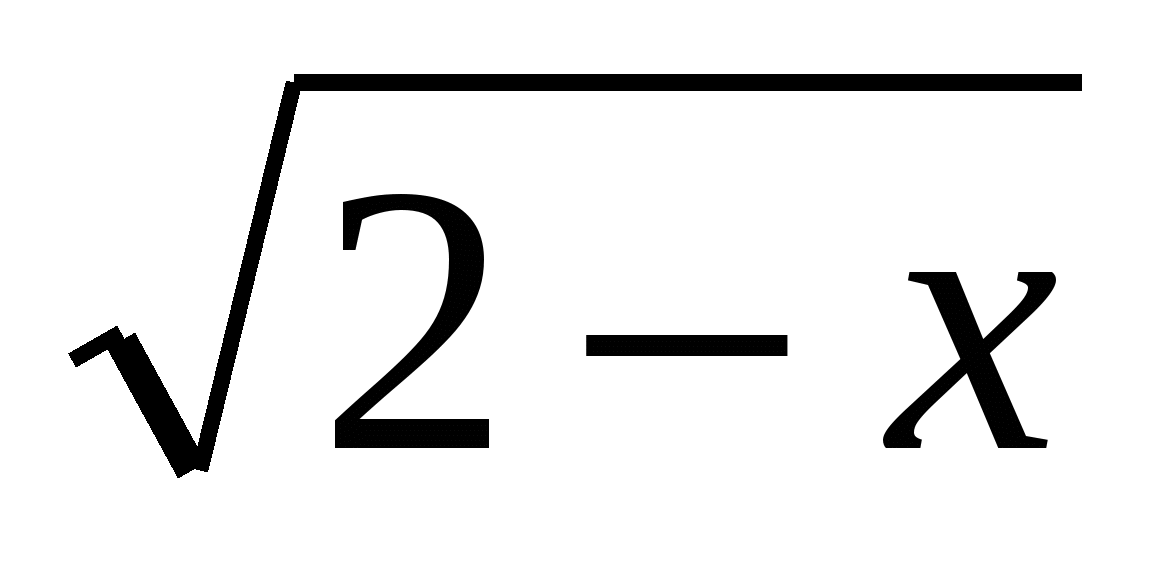 =
=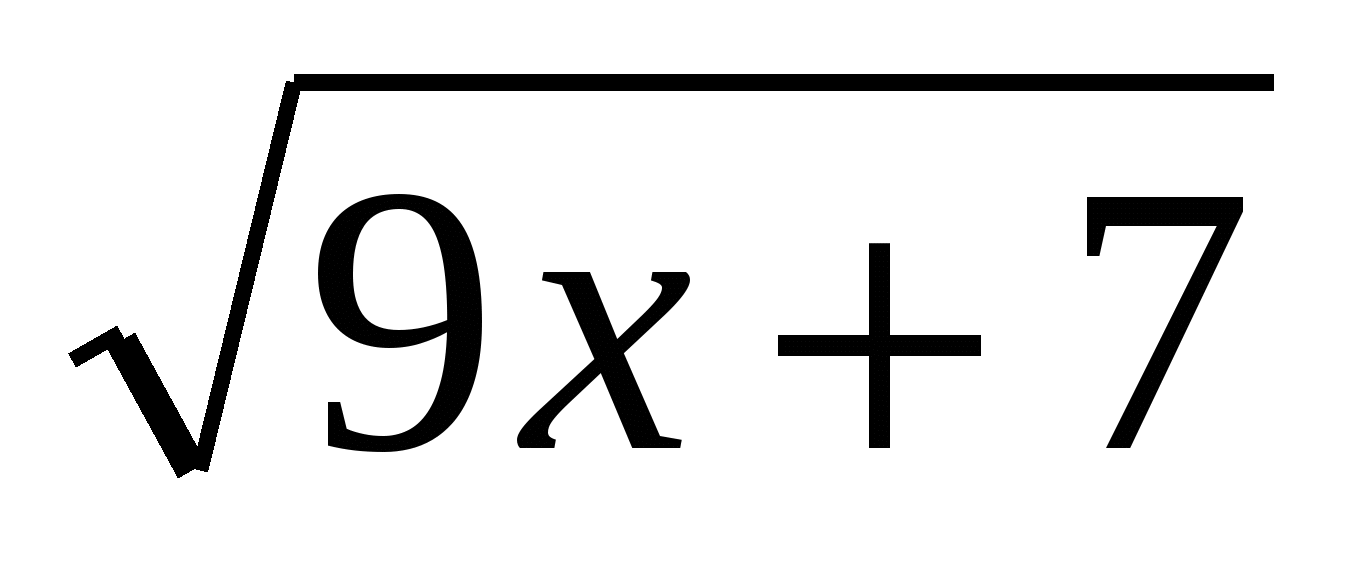 -
-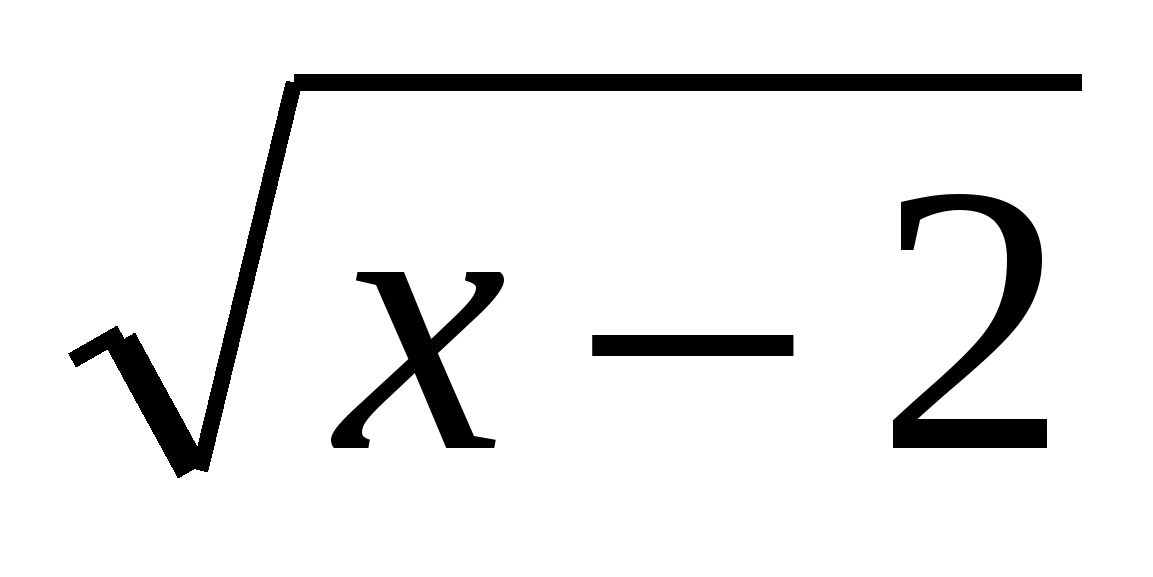
Решение: видно, что для решения этого уравнения можно возвести в квадрат обе части уравнения, что возможно позволит избавиться от иррациональности
11х+3-2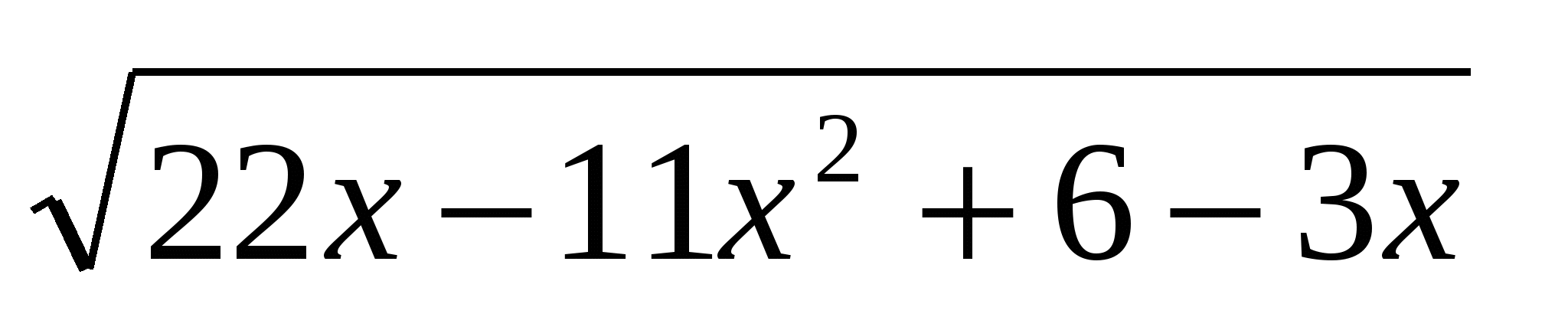 +2-х=9х+7-2
+2-х=9х+7-2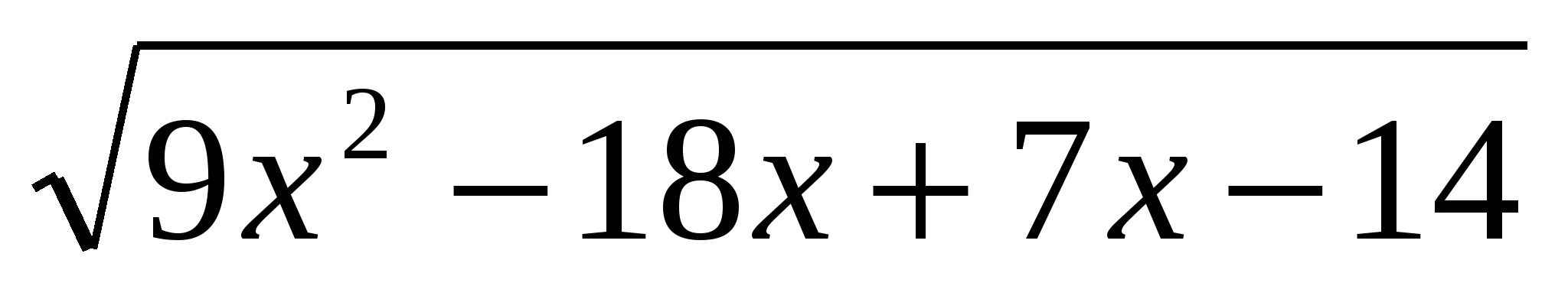 +х-2
+х-2
Приведем подобные 10х+5-2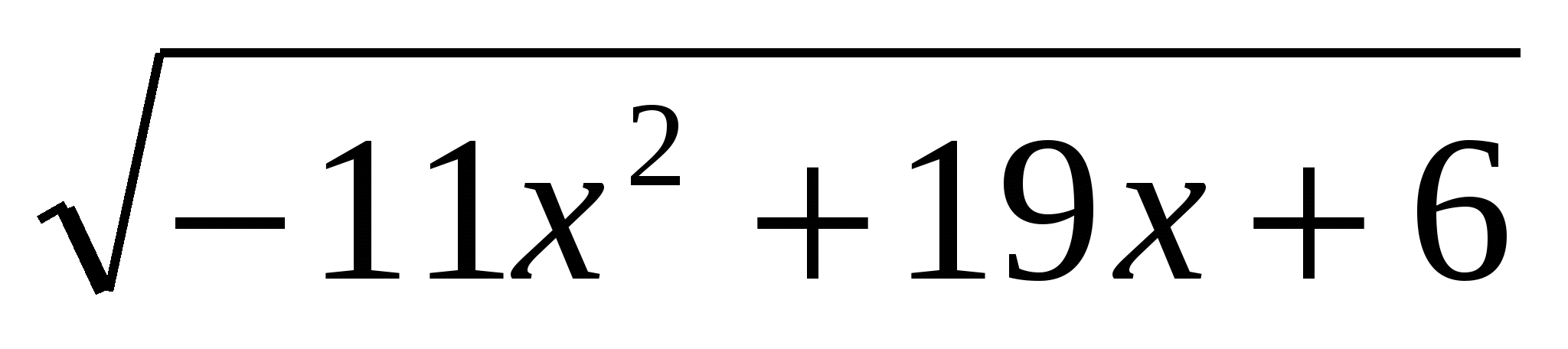 =10х+5-2
=10х+5-2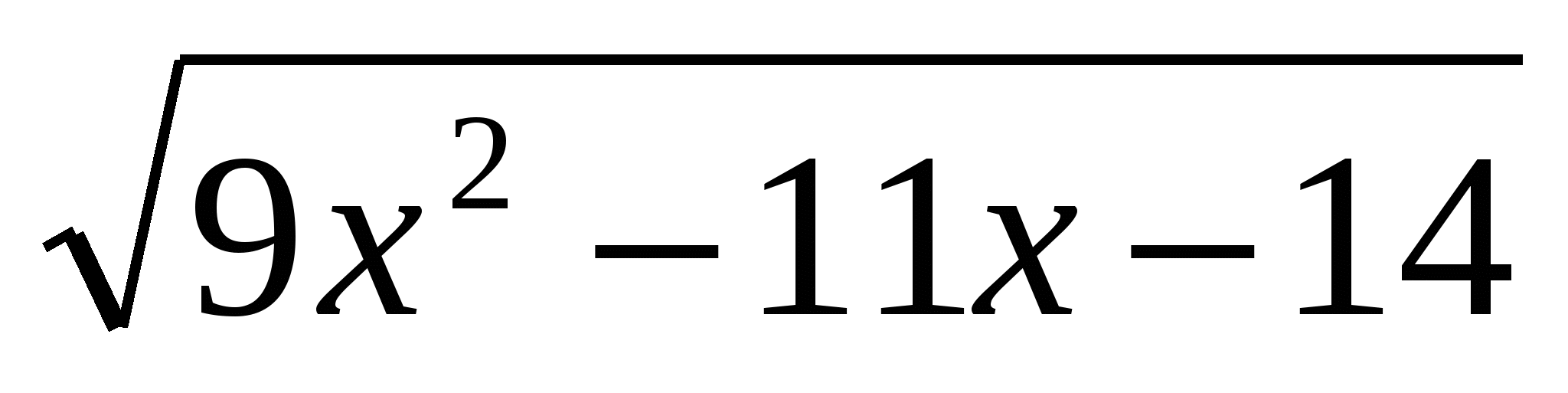
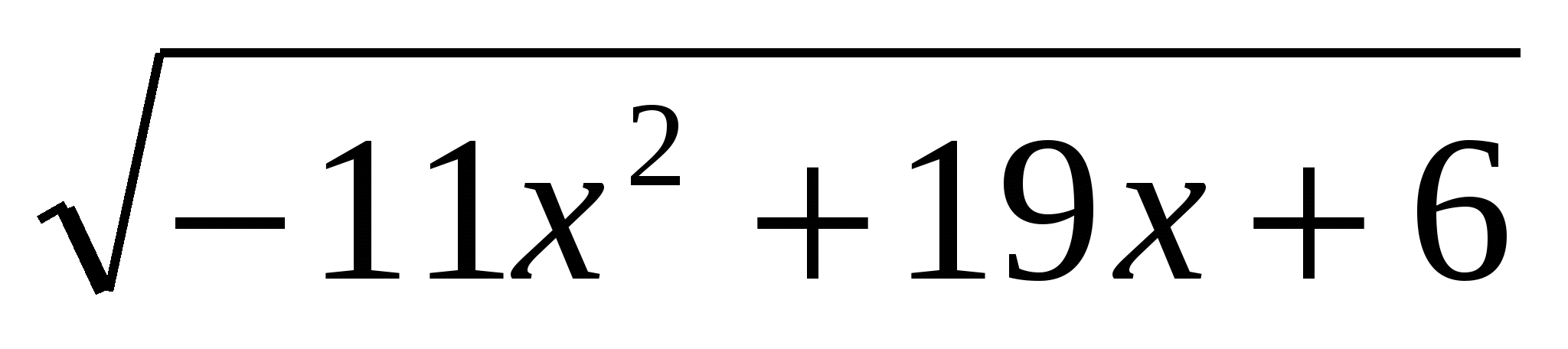 =
=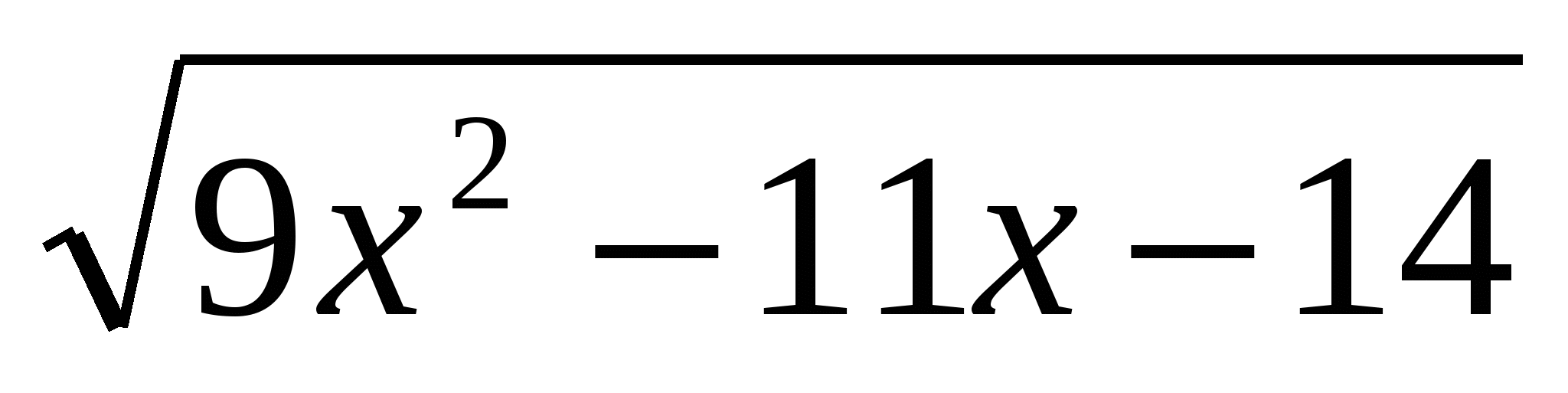 .
.
После возведения в квадрат обеих частей уравнения, приведем подобные и получим стандартное квадратное уравнение
20х2-30х-20=0,
2х2-3х-2=0,
х1=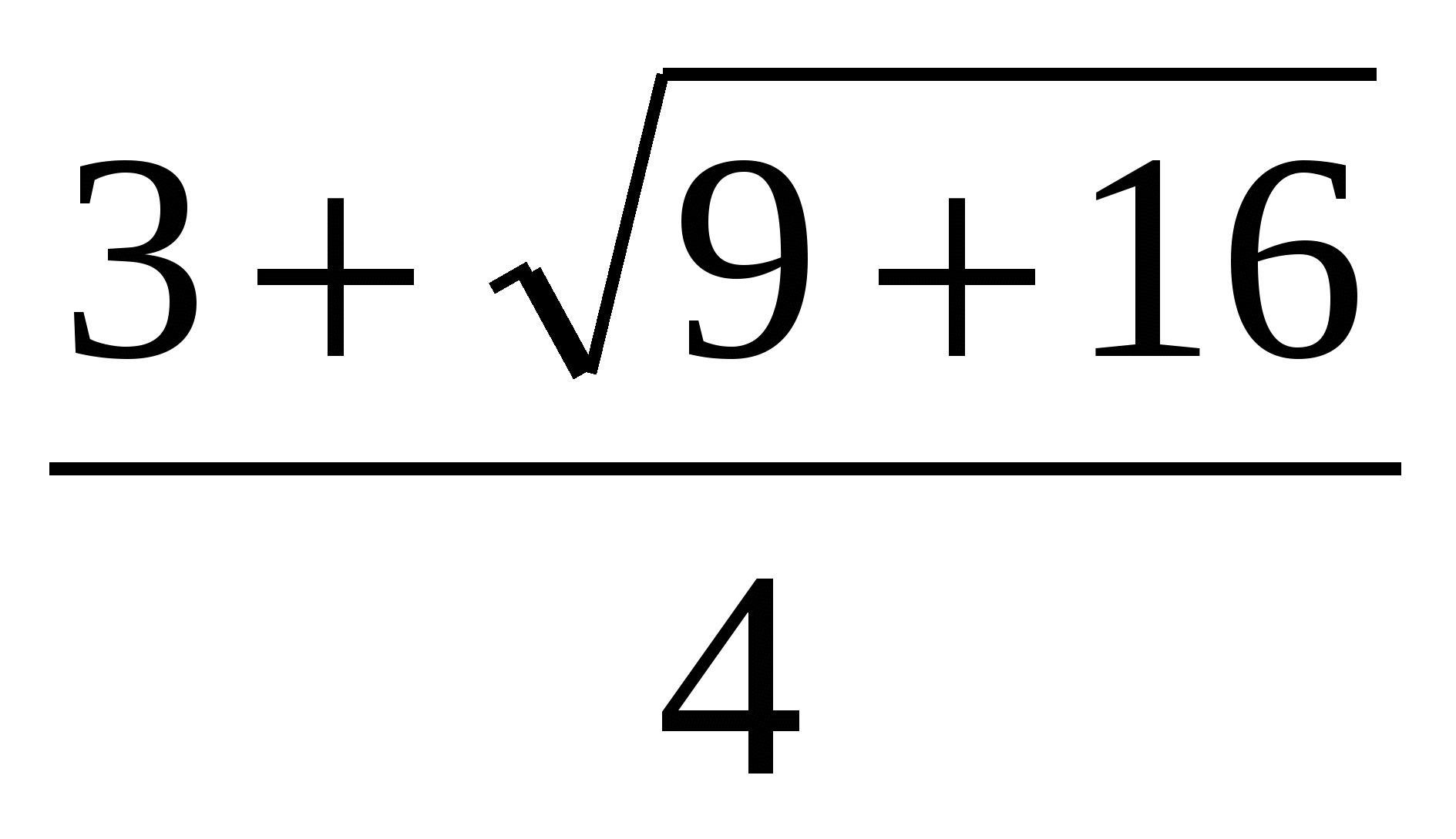 , х1=2 х2=
, х1=2 х2=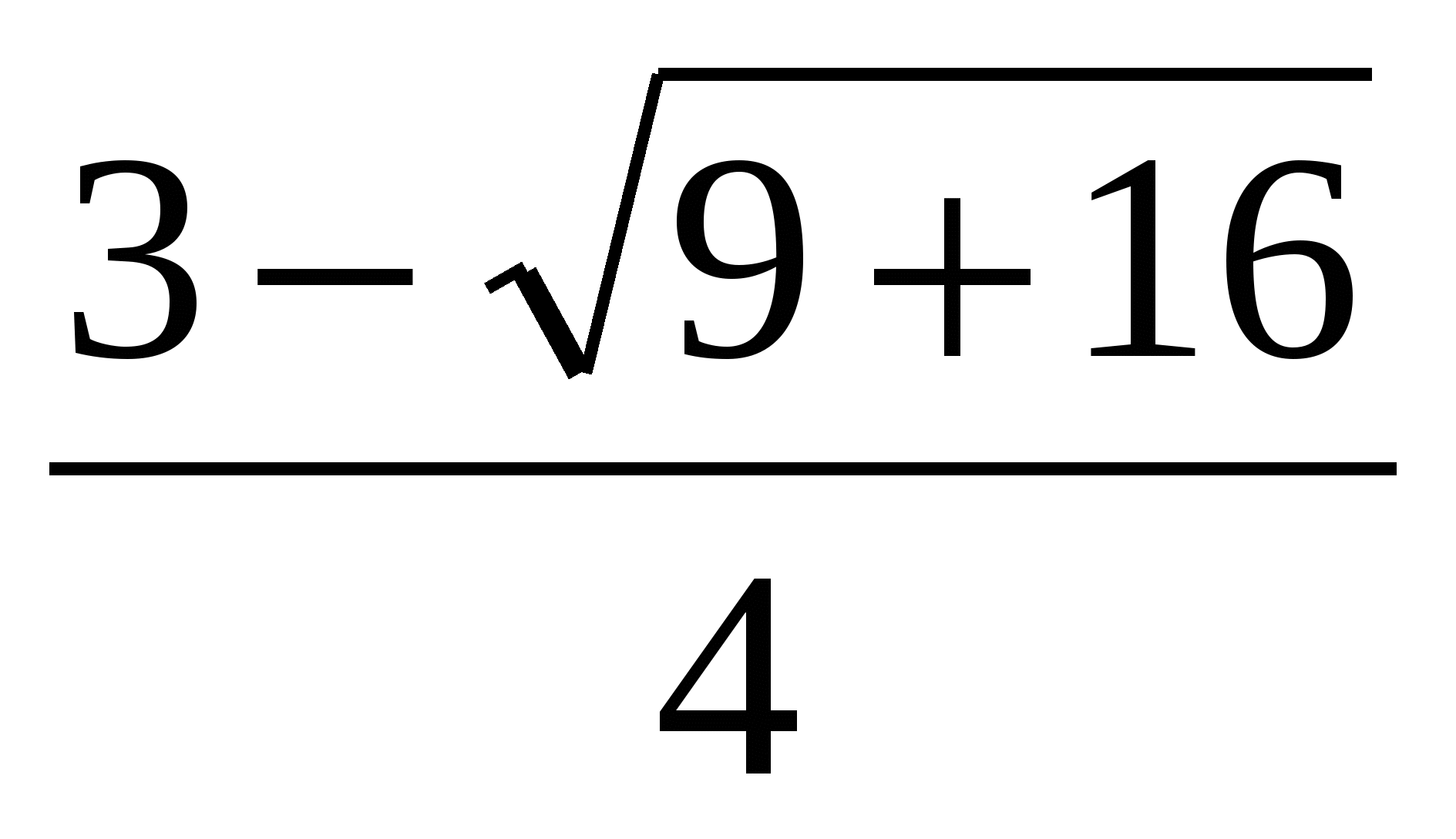 , х2=-0,5
, х2=-0,5
Полученные корни необходимо проверить, т.к. при возведении в квадрат, возможно приобретение посторонних корней.
Проверка:
х=2, 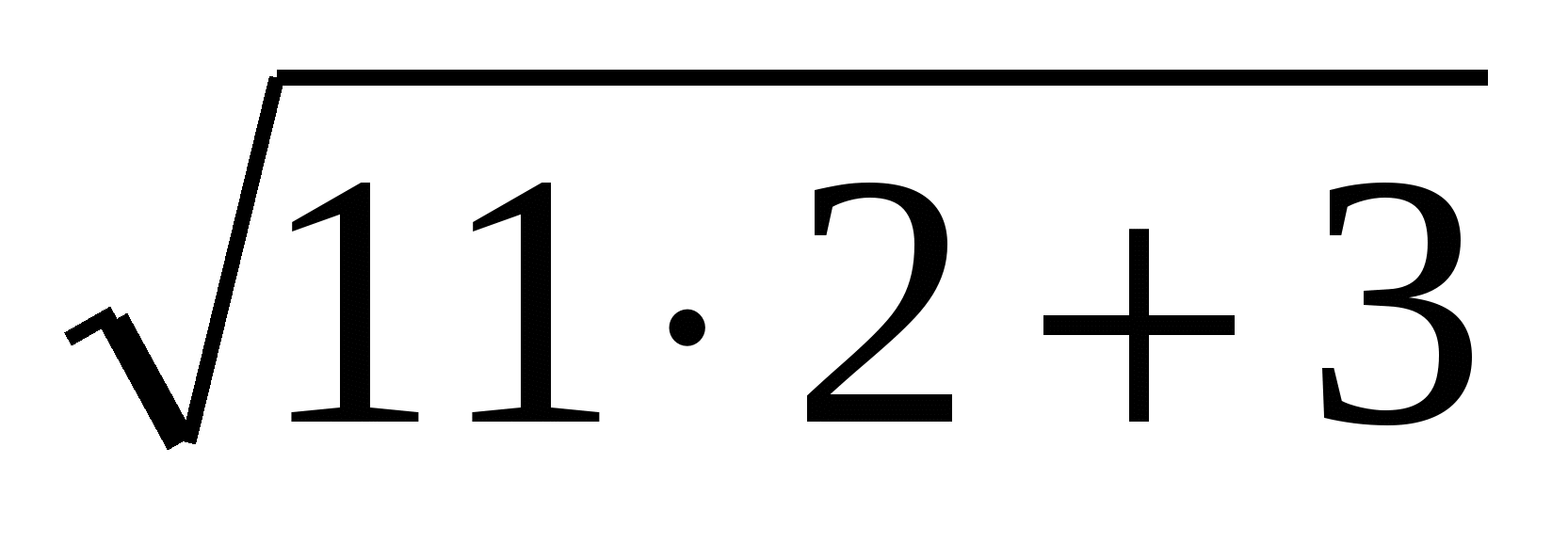 -
-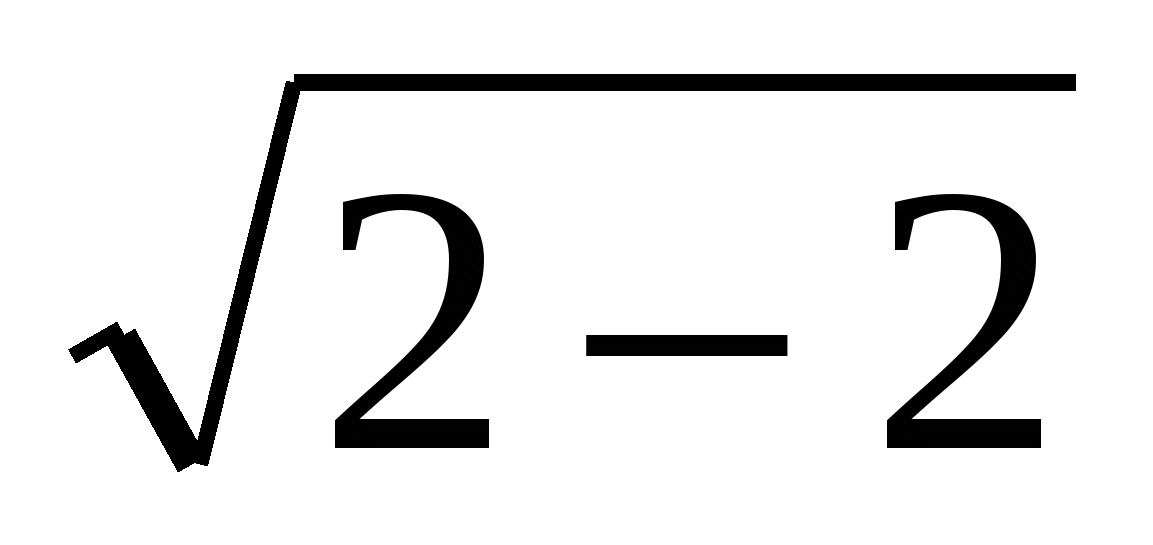 =5,
=5,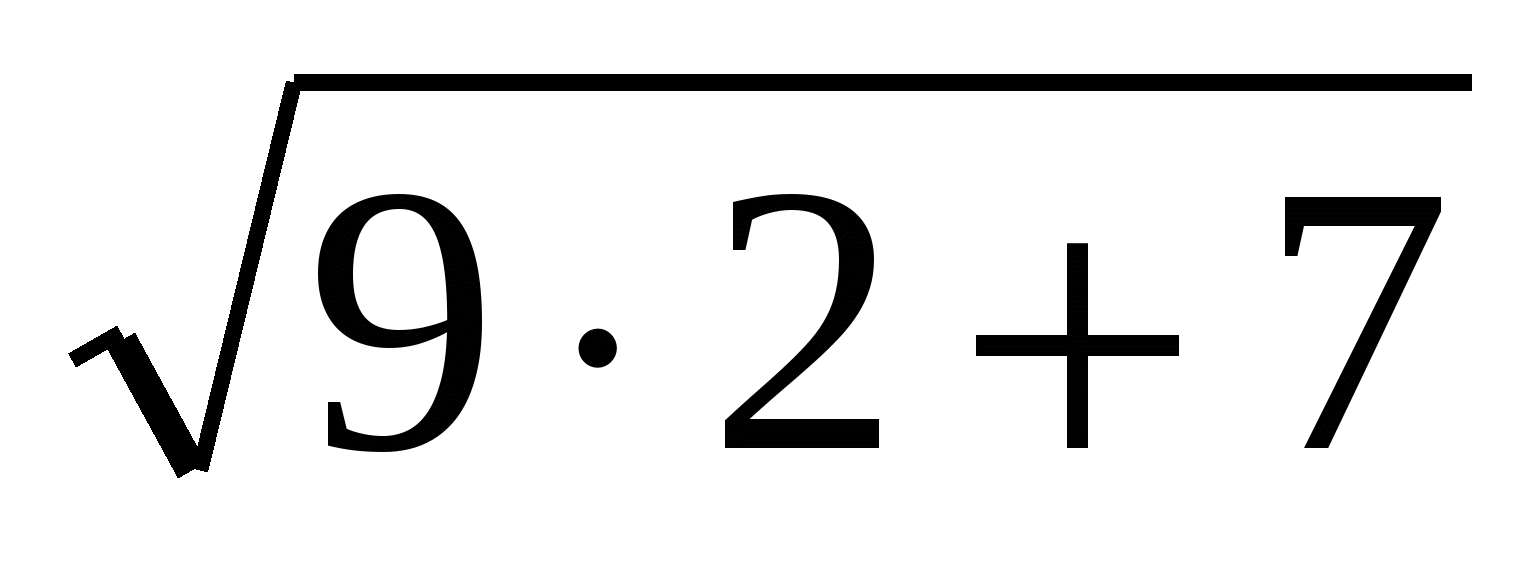 -
-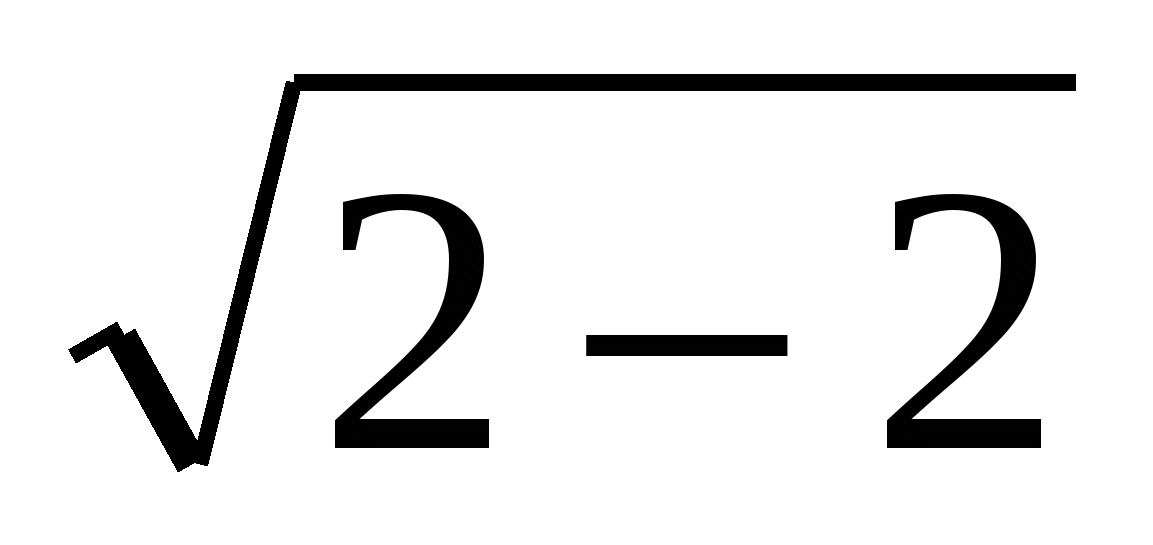 =5, 5=5
=5, 5=5 х=2 корень данного уравнения
х=2 корень данного уравнения
х=-0,5 ,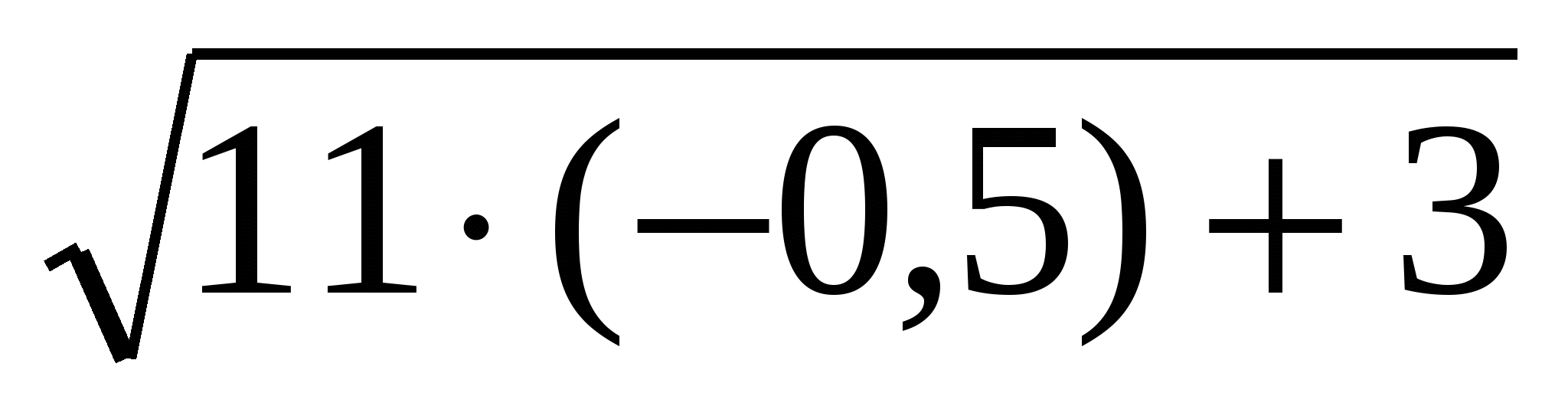 -
-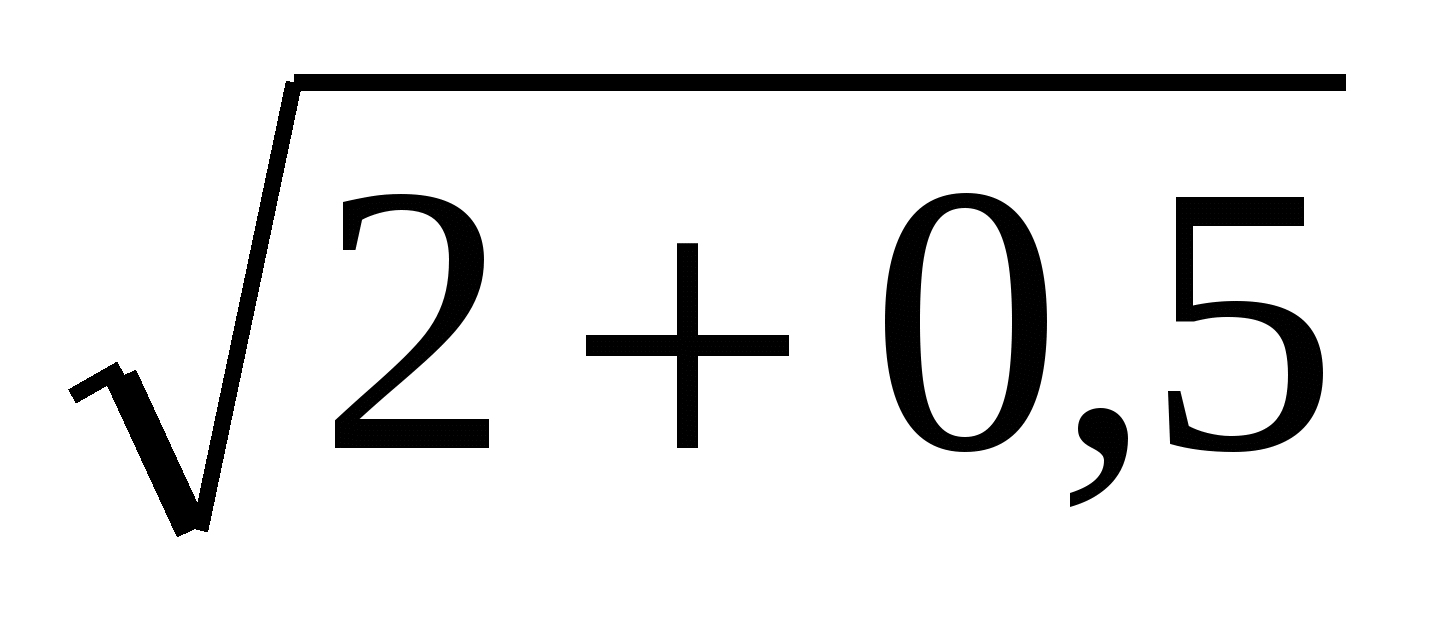 =
=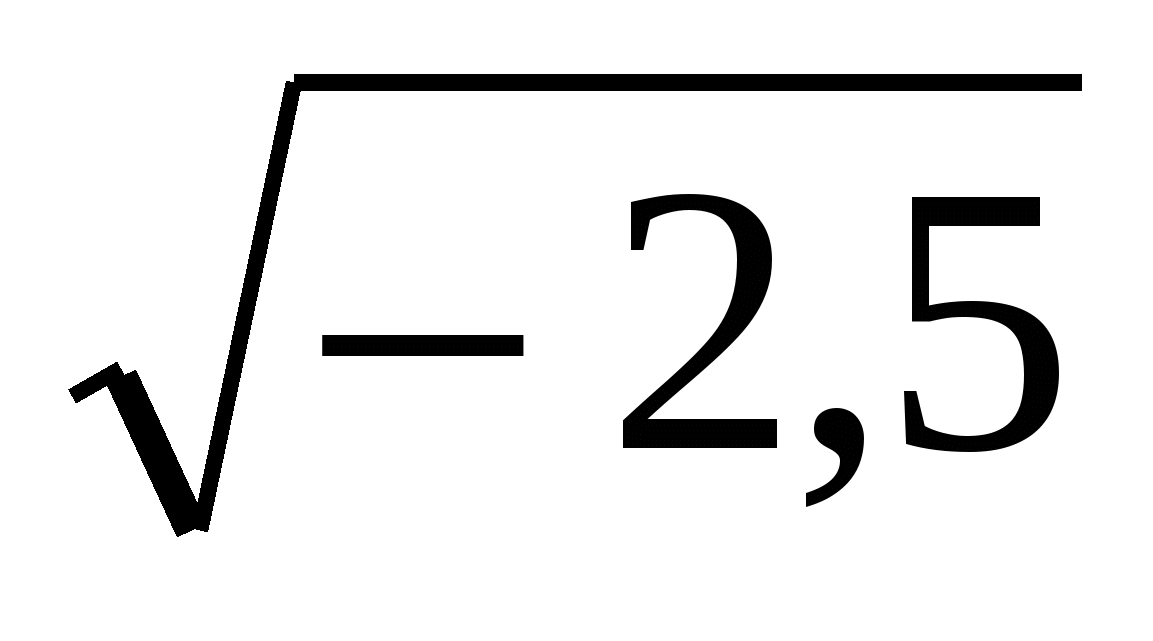 -
-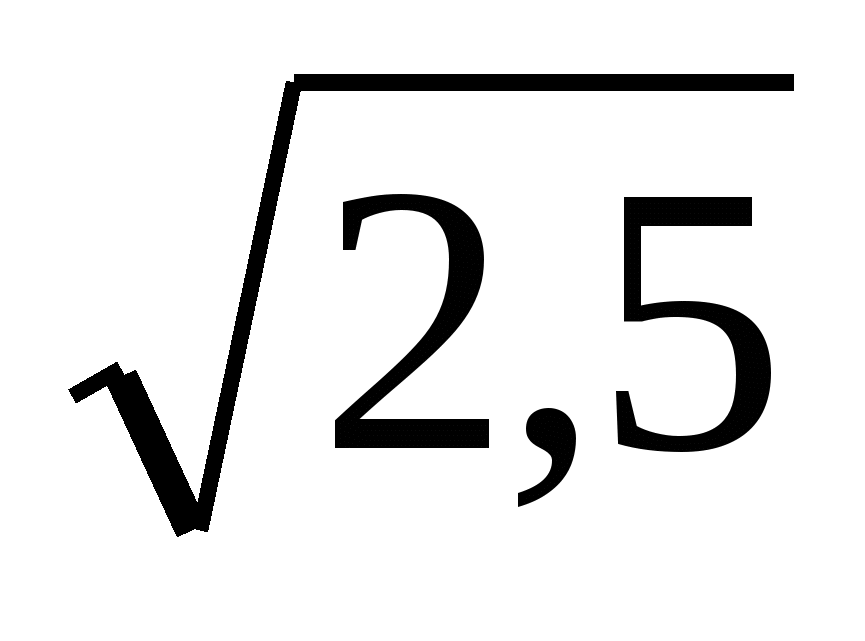
 х=-0,5-посторонний корень.
х=-0,5-посторонний корень.
Ответ: х=2
Однако, сравнив области определения функций у=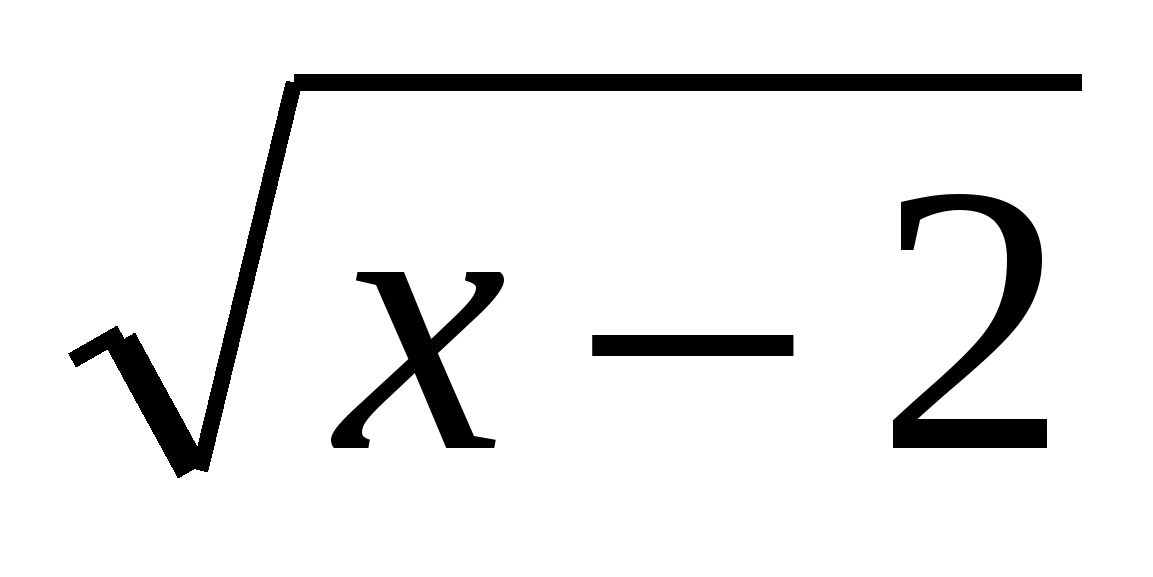 , (х-2
, (х-2 0, х
0, х 2) и у=
2) и у=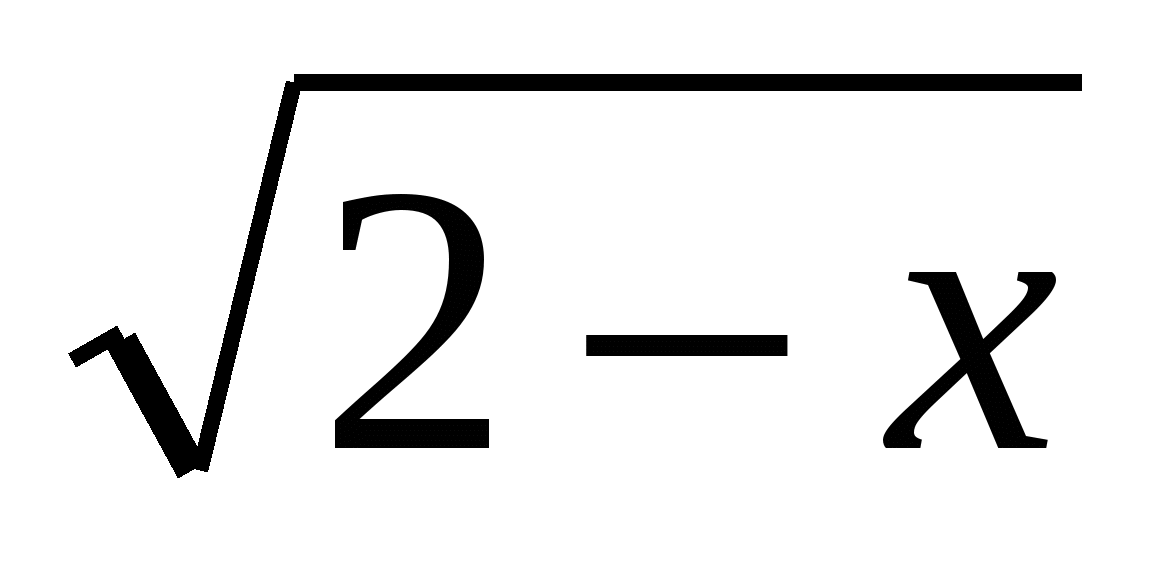 , (2-х
, (2-х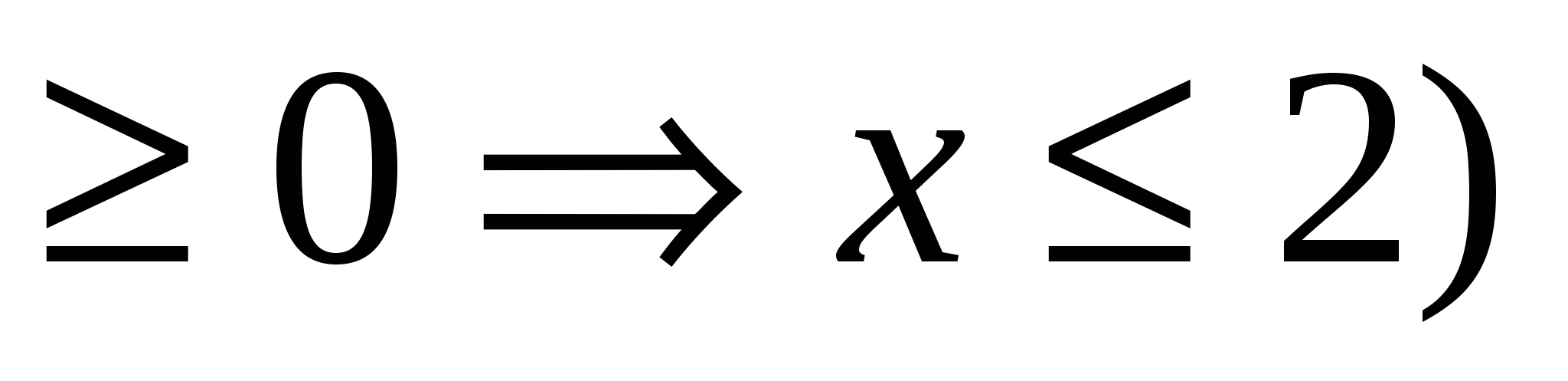 , приходим к выводу, что область определения исходного уравнения х=2. Подставив х=2 в данное уравнение, приходим к выводу, что х=2 единственный корень этого уравнения.
, приходим к выводу, что область определения исходного уравнения х=2. Подставив х=2 в данное уравнение, приходим к выводу, что х=2 единственный корень этого уравнения.
Ответ: х=2.
Очевидно, что решать данное уравнение вторым способом удобнее и быстрее чем первым. Рассмотрим еще несколько таких уравнений.
2)Решить уравнение 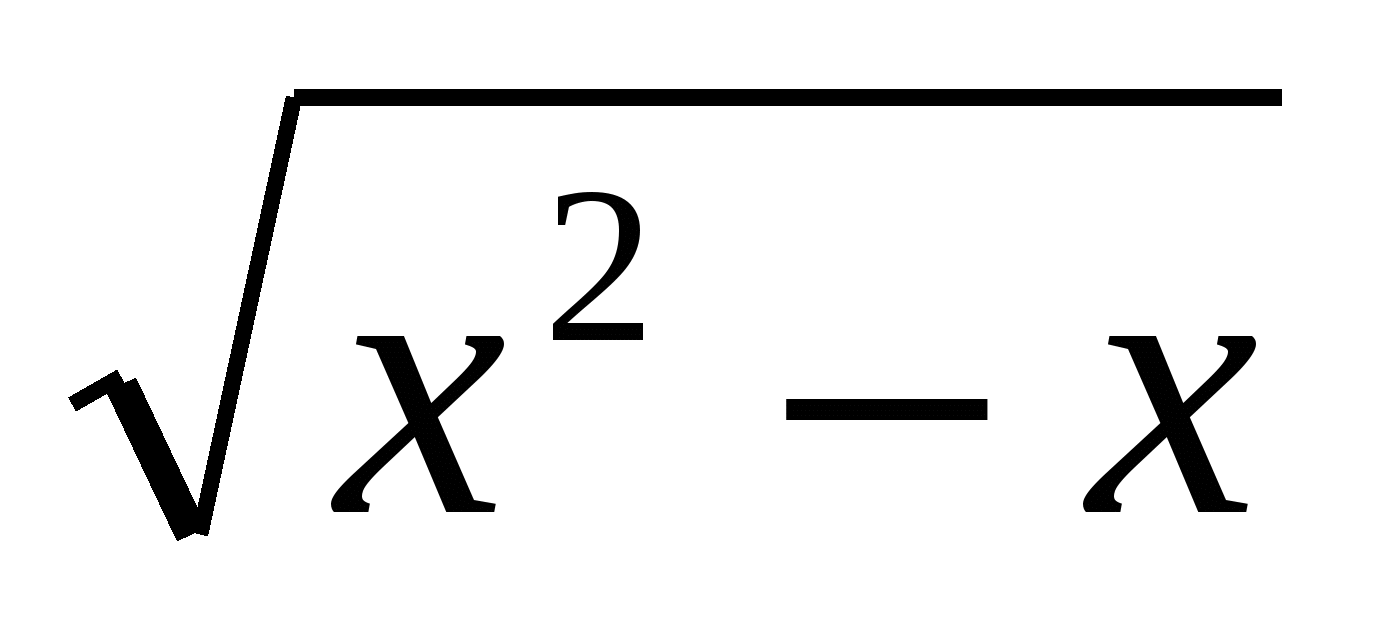 +
+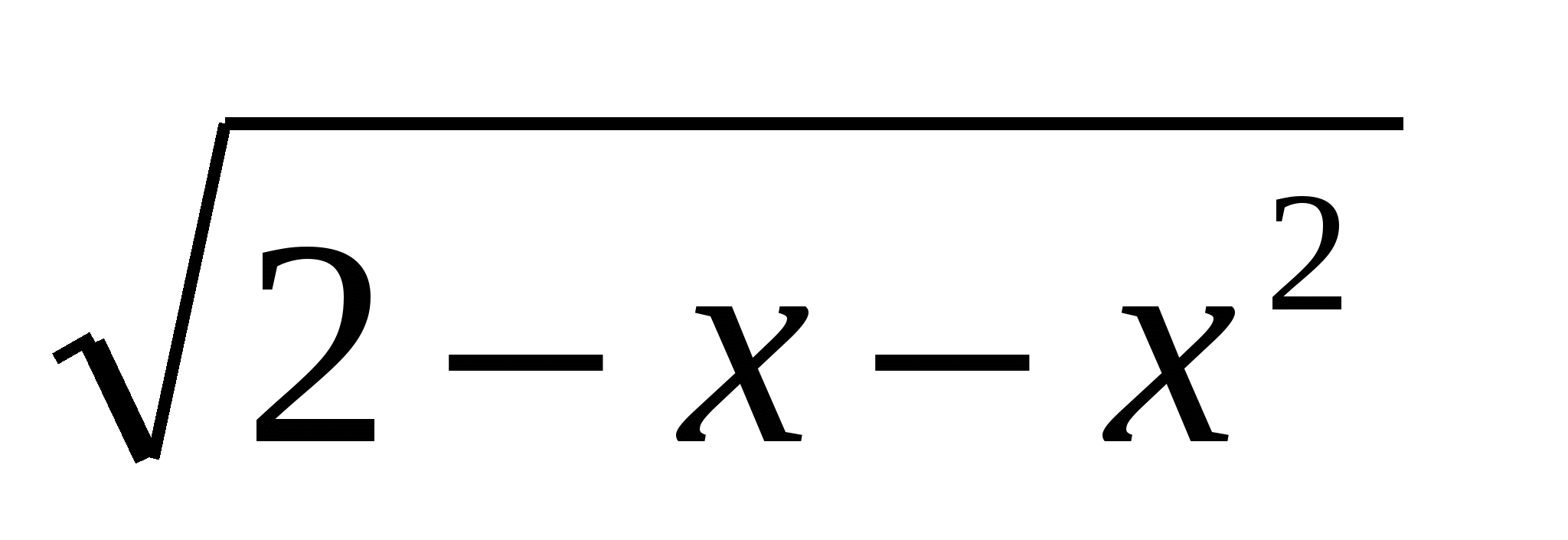 =
=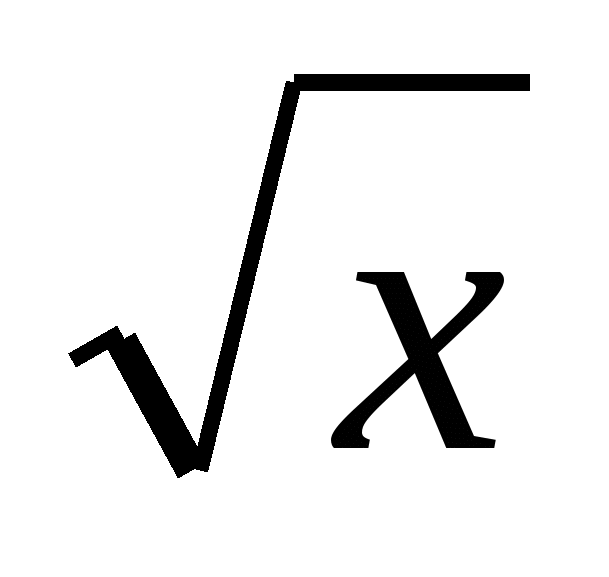 -1.
-1.
 Решение: найдем ОДЗ этого уравнения. Для этого нужно решить систему неравенств:
Решение: найдем ОДЗ этого уравнения. Для этого нужно решить систему неравенств:  х2-х
х2-х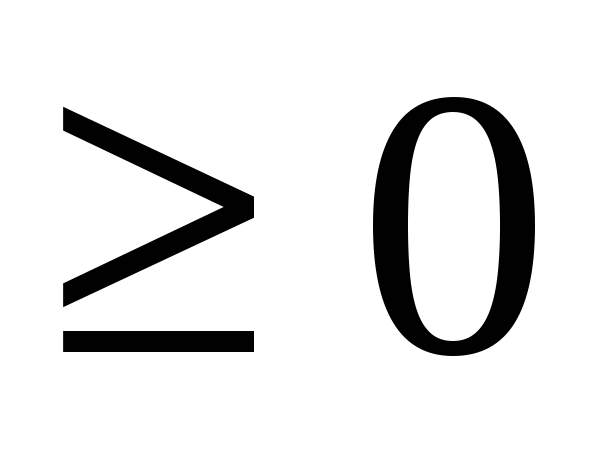 ,
,
2-х-х2>0,
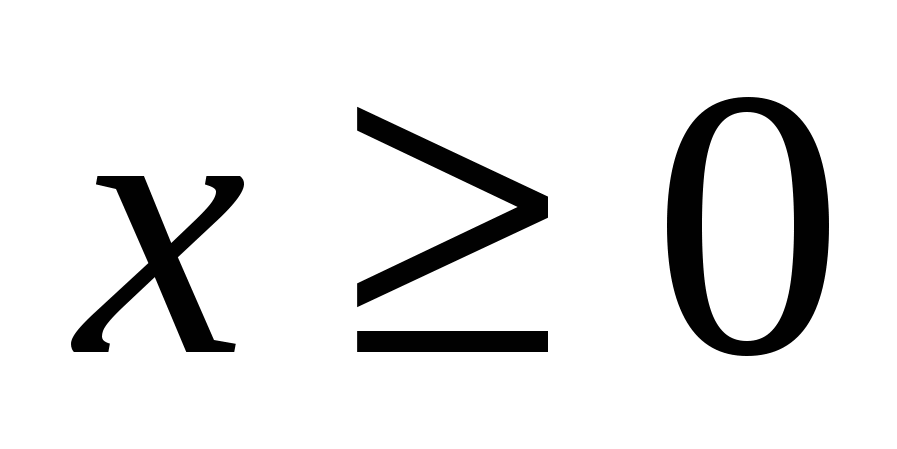 , х=0, х=1
, х=0, х=1
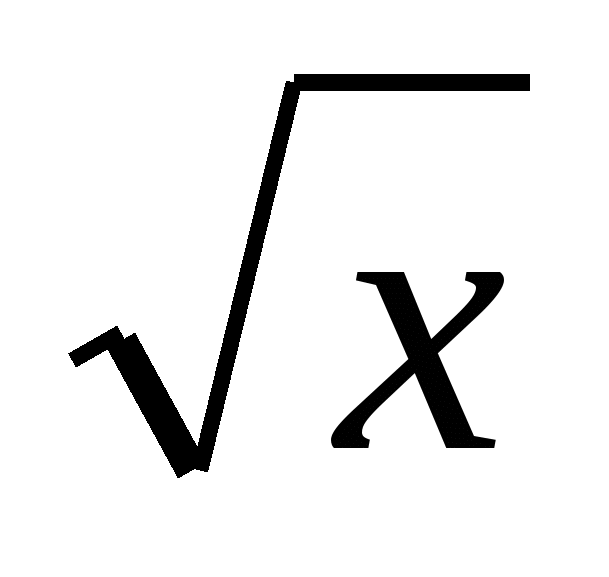 -1
-1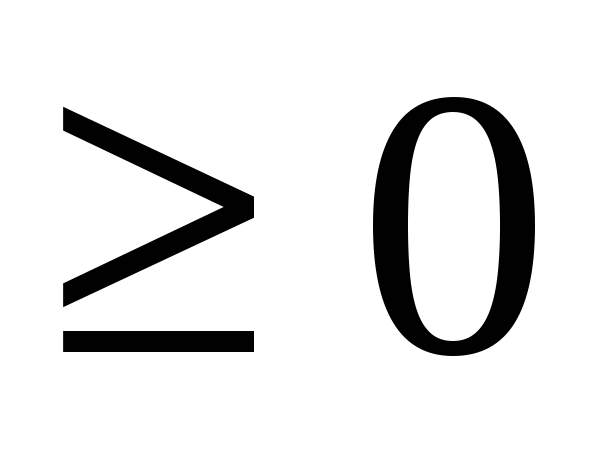
![]()
Итак, ОДЗ этого уравнения является двух элементное множество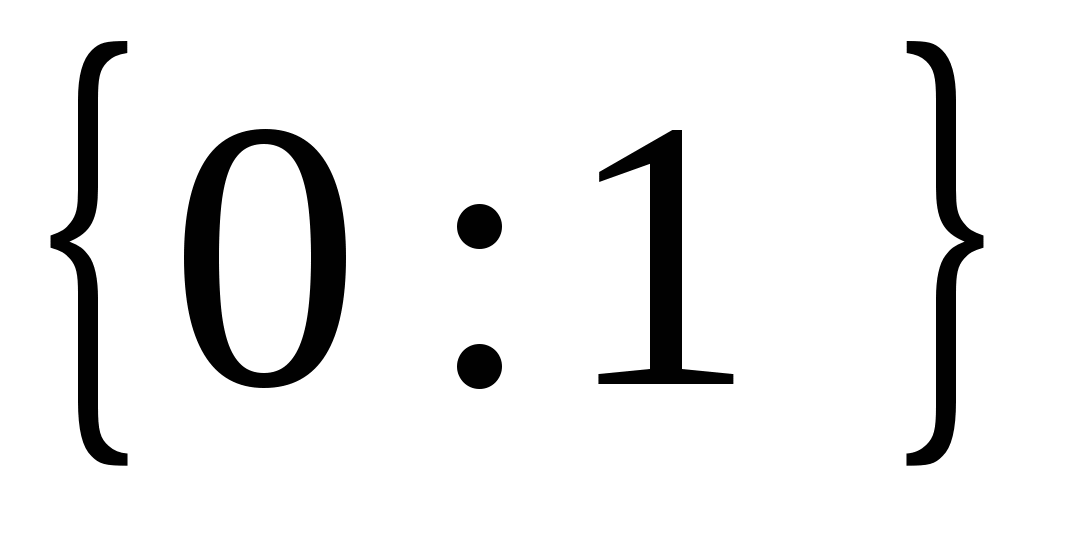 . Проверим, являются ли эти значения корнями уравнения:
. Проверим, являются ли эти значения корнями уравнения:
х=0 , 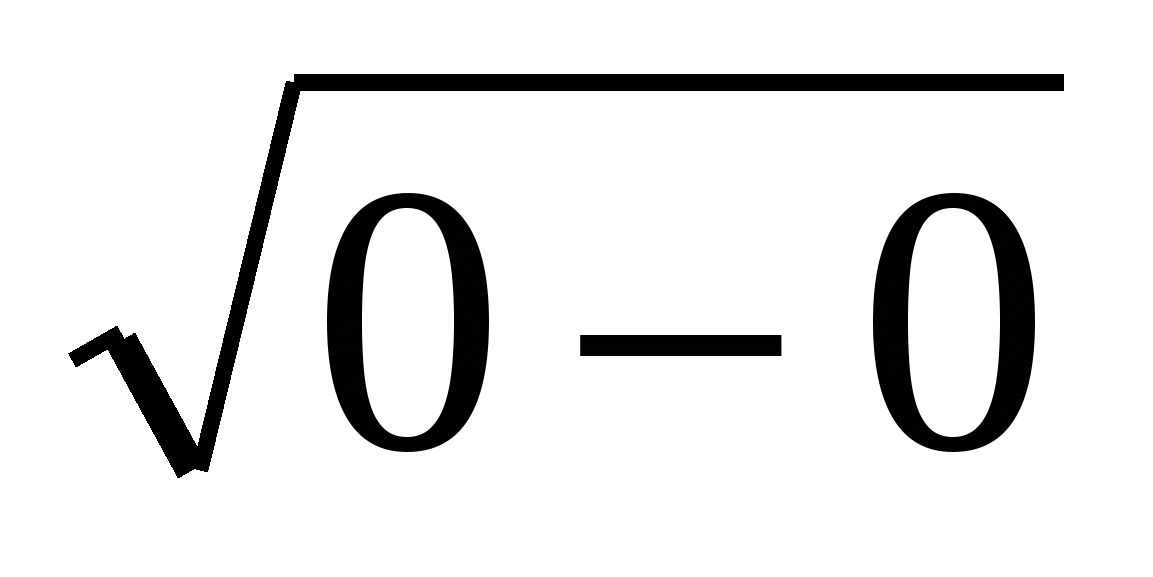 +
+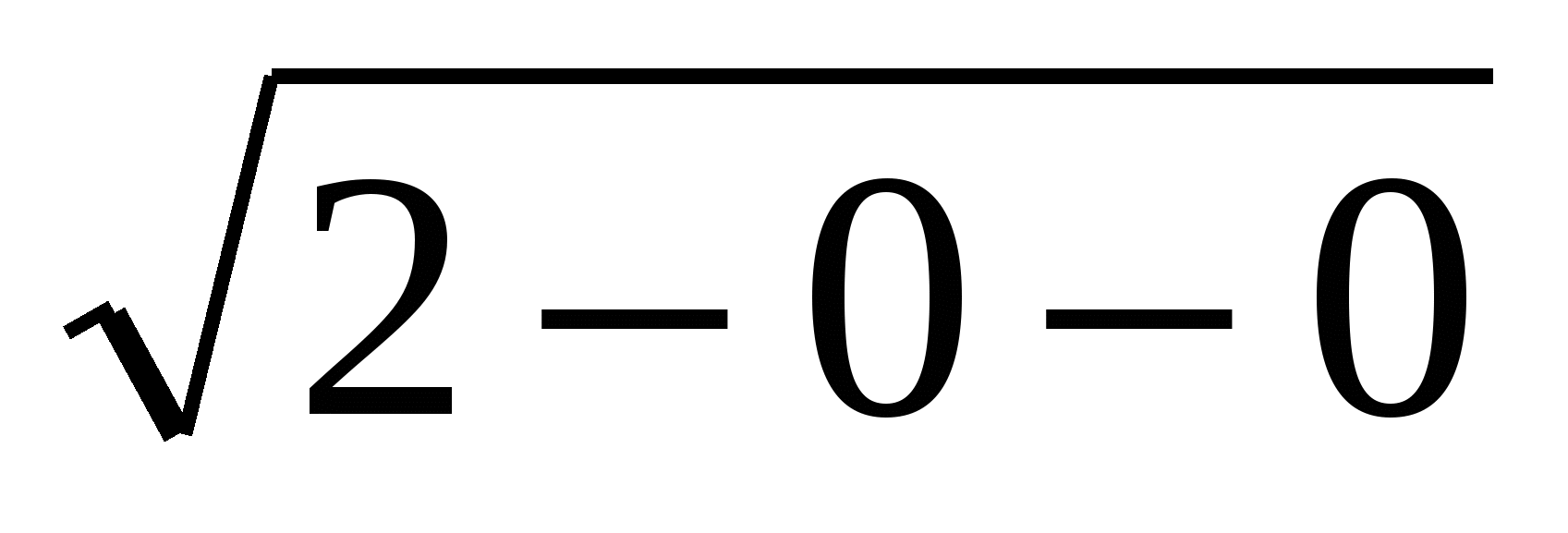 =
=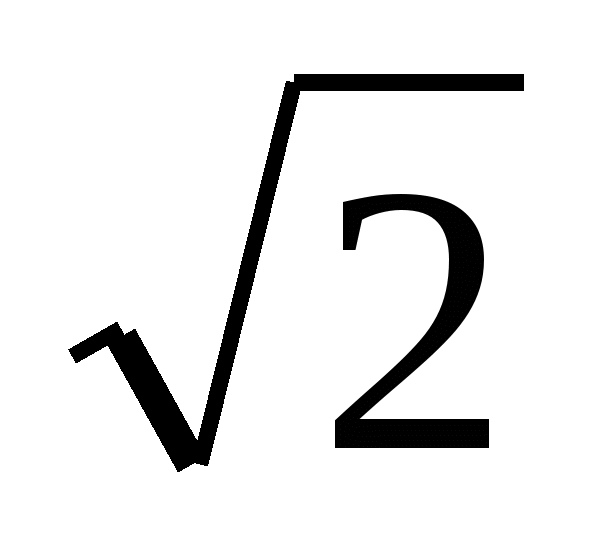
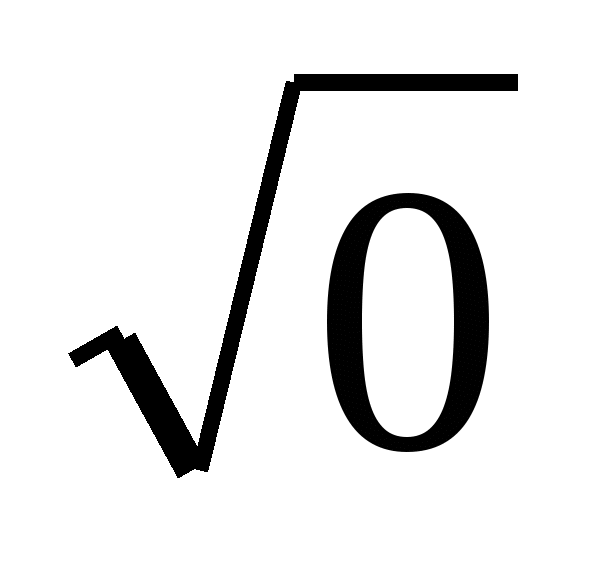 -1 =-1,
-1 =-1, 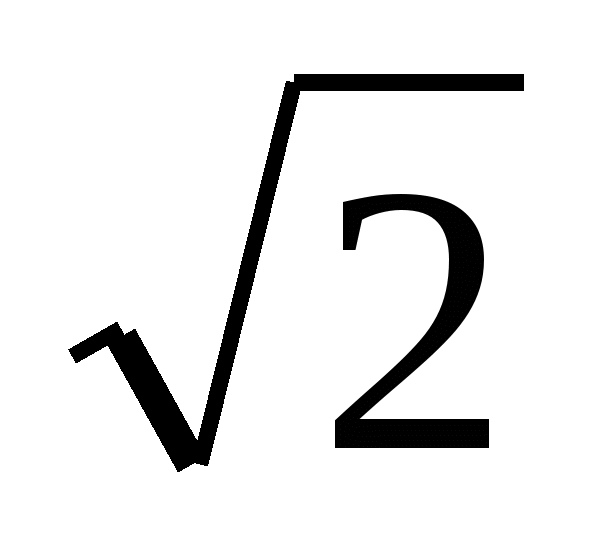
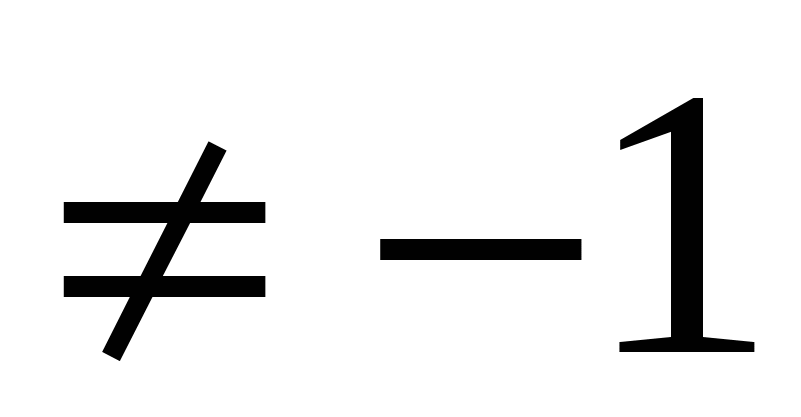 , х=0 - не является корнем уравнения.
, х=0 - не является корнем уравнения.
х =1 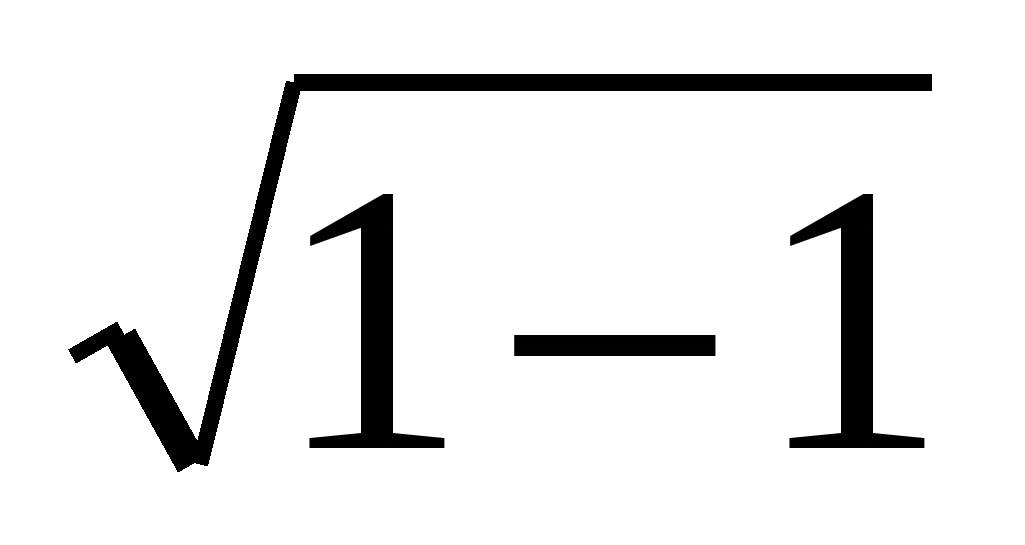 +
+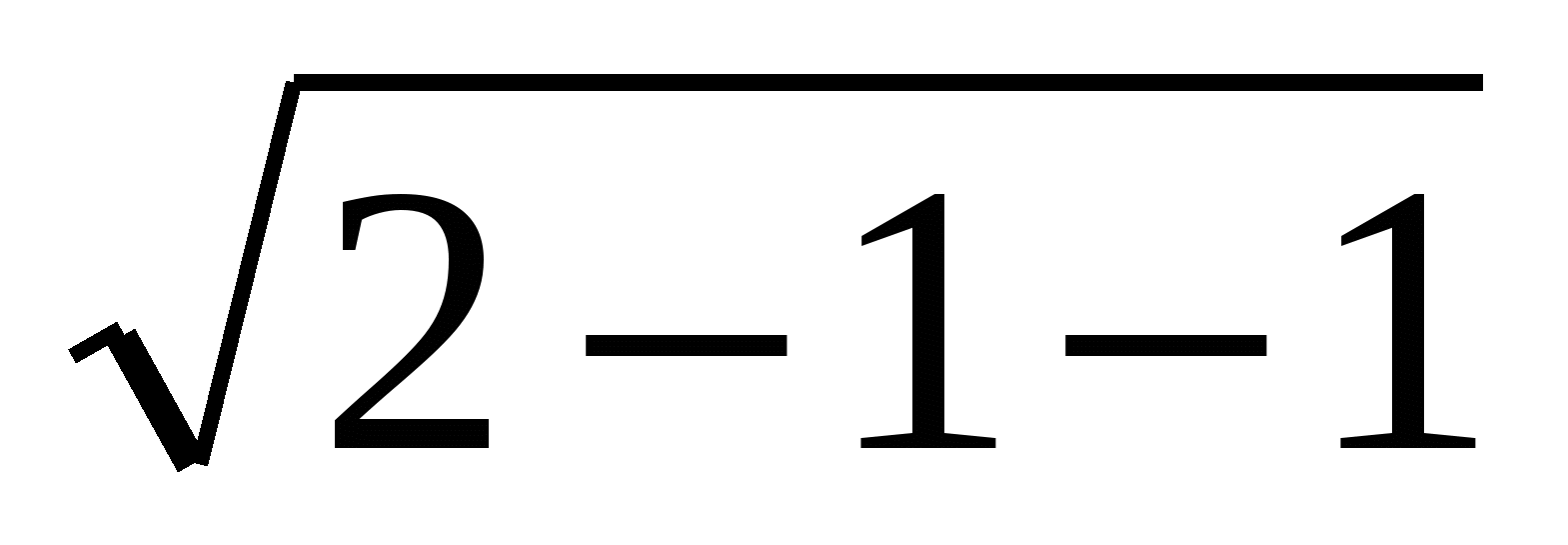 =0
=0
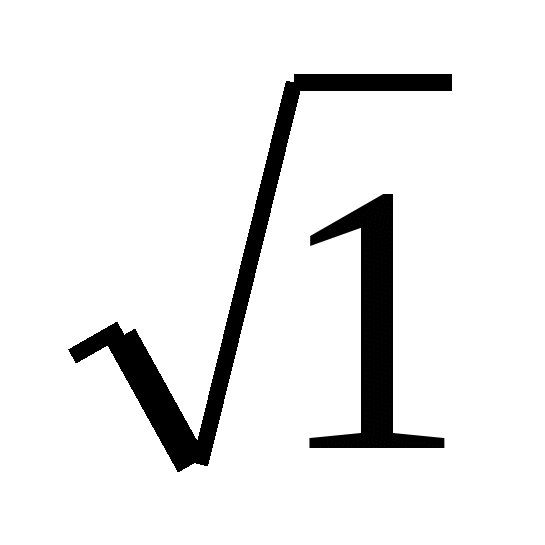 -1=0, 0=0
-1=0, 0=0 х=1- корень уравнения.
х=1- корень уравнения.
Ответ: х=1.
3) Сколько корней имеет уравнение.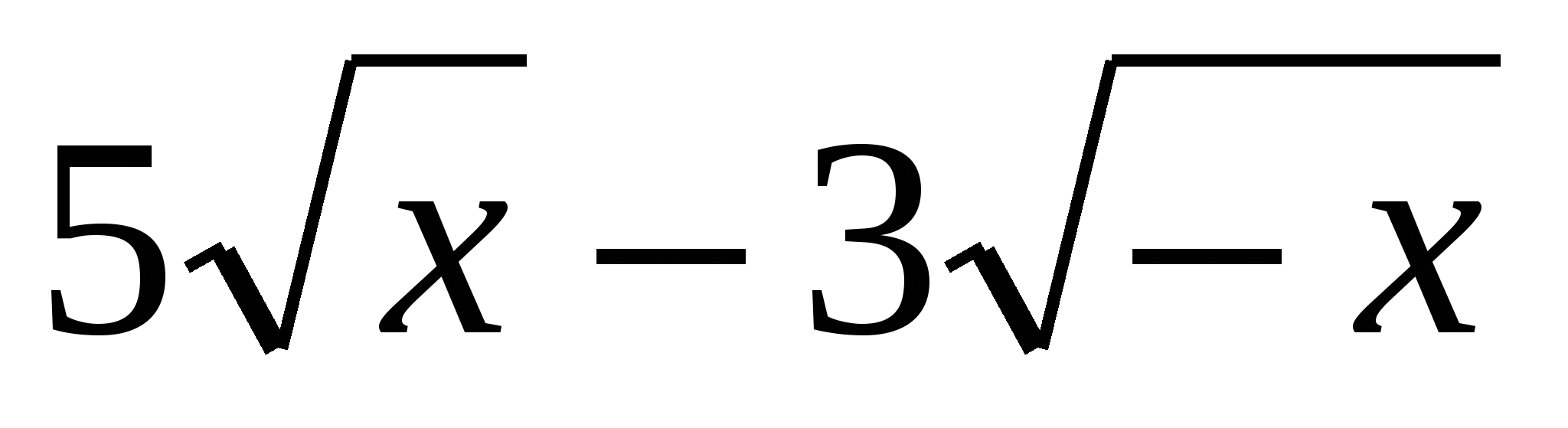
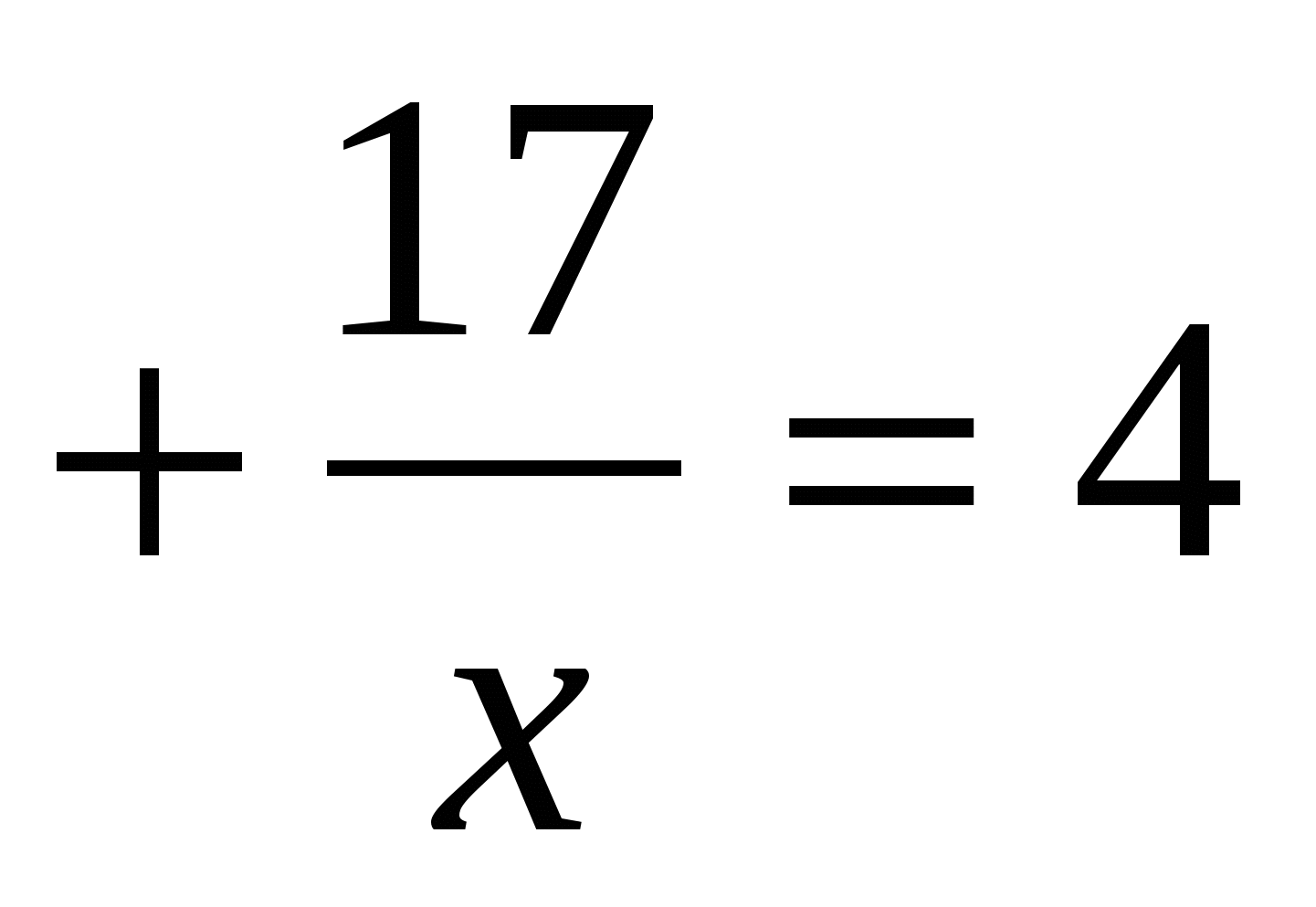
Р ешение:
ешение: 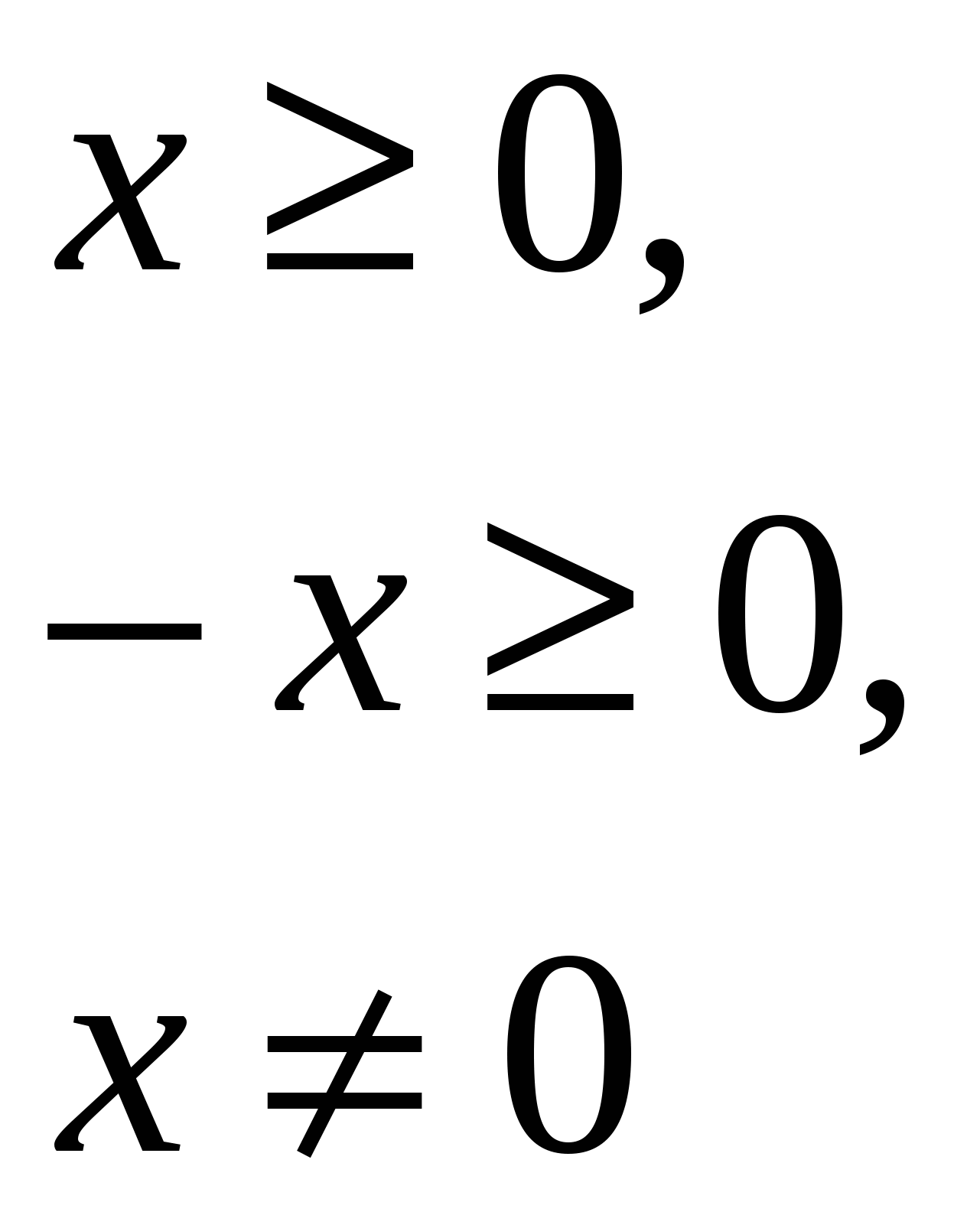
Данное уравнение не определено не при каких действительных х.
Ответ: уравнение не имеет корней.
4) Решить уравнение: 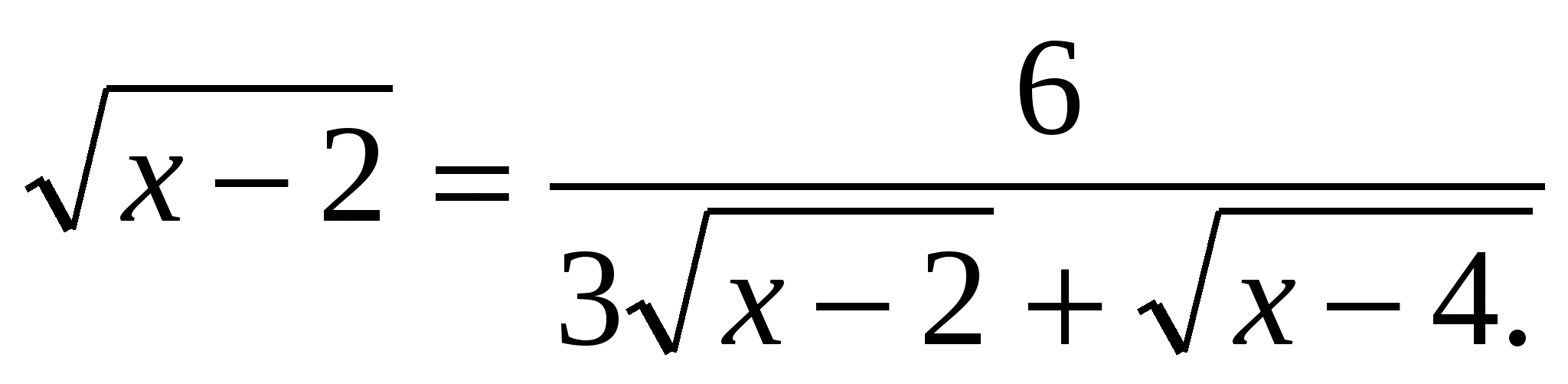
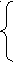 Решение: область определения уравнения:
Решение: область определения уравнения: 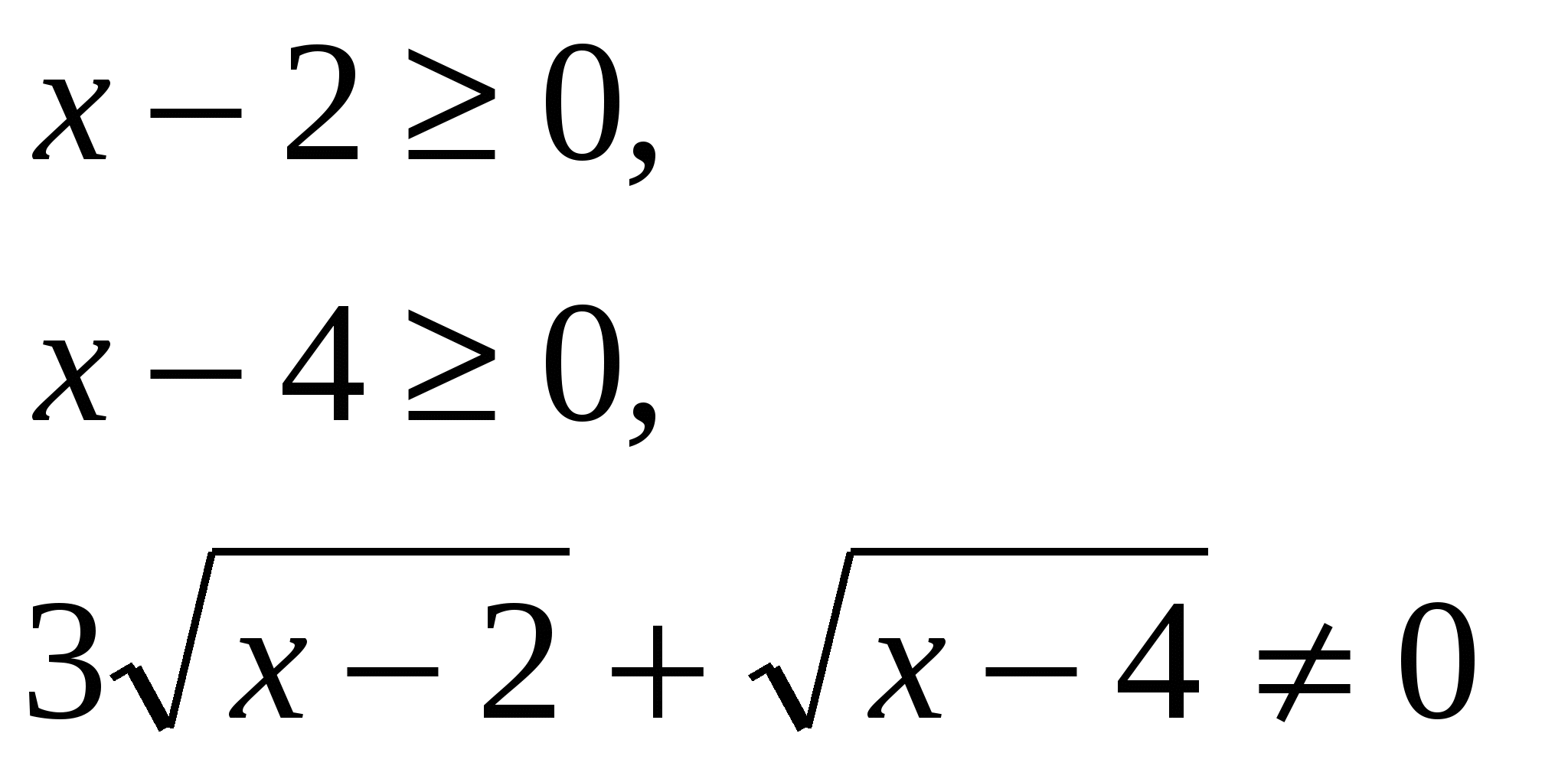
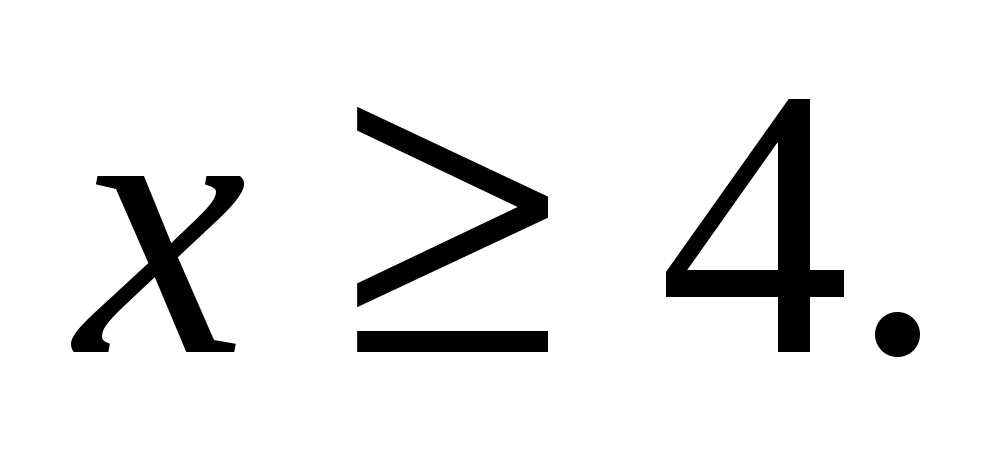
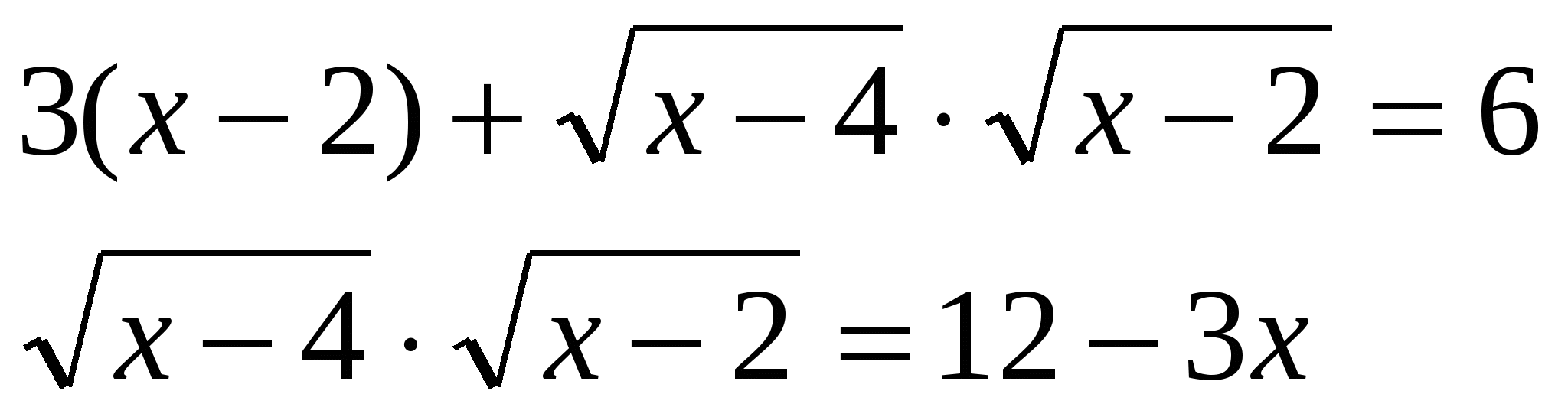
Это уравнение равносильно следующей системе:
(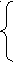 х-4)(х-2)=(12-3х)2,
х-4)(х-2)=(12-3х)2,
12-3х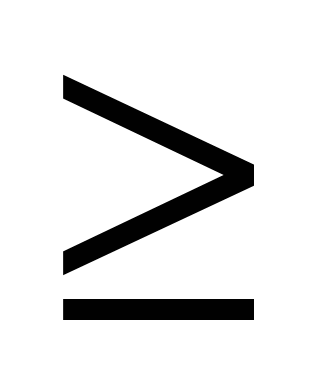 0.
0.
12-3х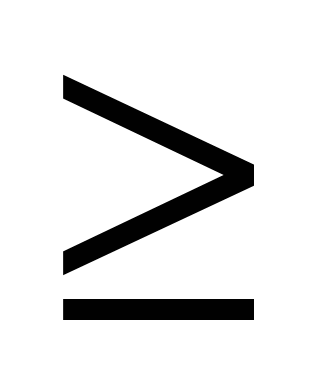 0, х
0, х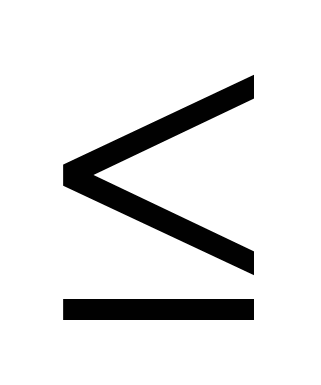 4.
4.
Учитывая область определения уравнения, единственно возможным корнем может быть только х=4, проверим: 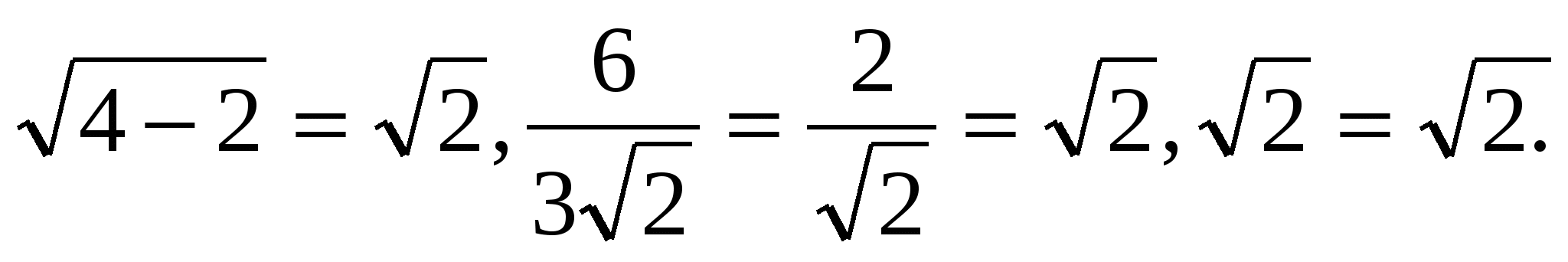
х=4- корень уравнения.
Ответ: х=4.
5)Решить уравнение: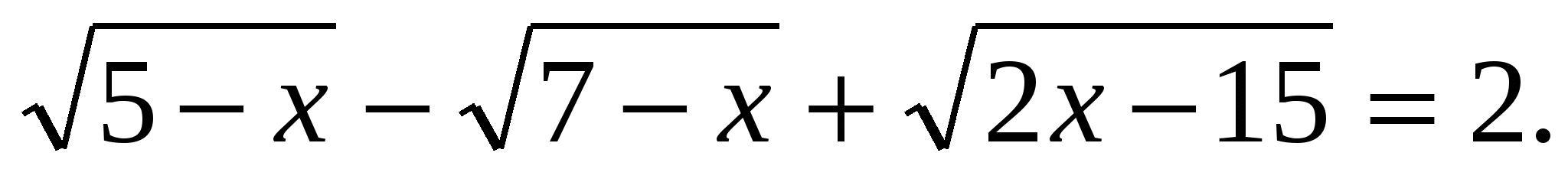
Решение: Попытки решить уравнение, производя последовательное возведение в квадрат и единение радикала, ведут здесь к уравнению четвертой степени и заводят в тупик. Выпишем условия, при которых выражения, входящие в левую часть данного уравнения, имеют смысл.
5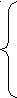
 -х
-х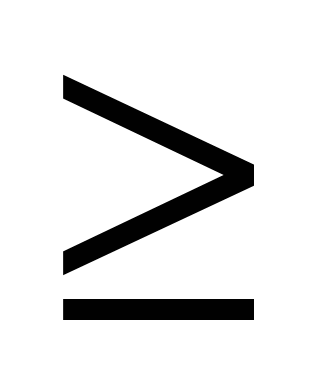 0, х
0, х 5,
5,
7-х 0, х
0, х 7, нет решения.
7, нет решения.
2х-15. х![]() 7,5.
7,5.
Видим, что нет таких действительных х при которых было бы определено данное уравнение.
Ответ: нет корней.
Решение уравнений с использованием множества значений.
При решении некоторых уравнений нахождение множества значений существенно облегчает задачу решения уравнений. Этот метод довольно часто встречается у ребят с развитой культурой мышления. Легко усваивается, они пытаются часто применять его при решении других уравнений.
1)Решить уравнение: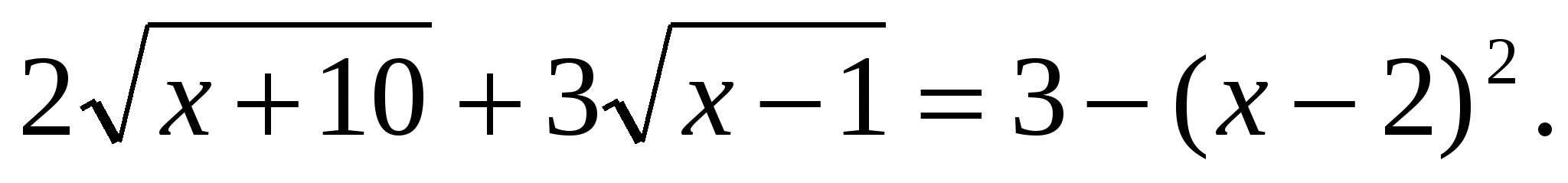
 Решение: найдем область определения данного уравнения:
Решение: найдем область определения данного уравнения: 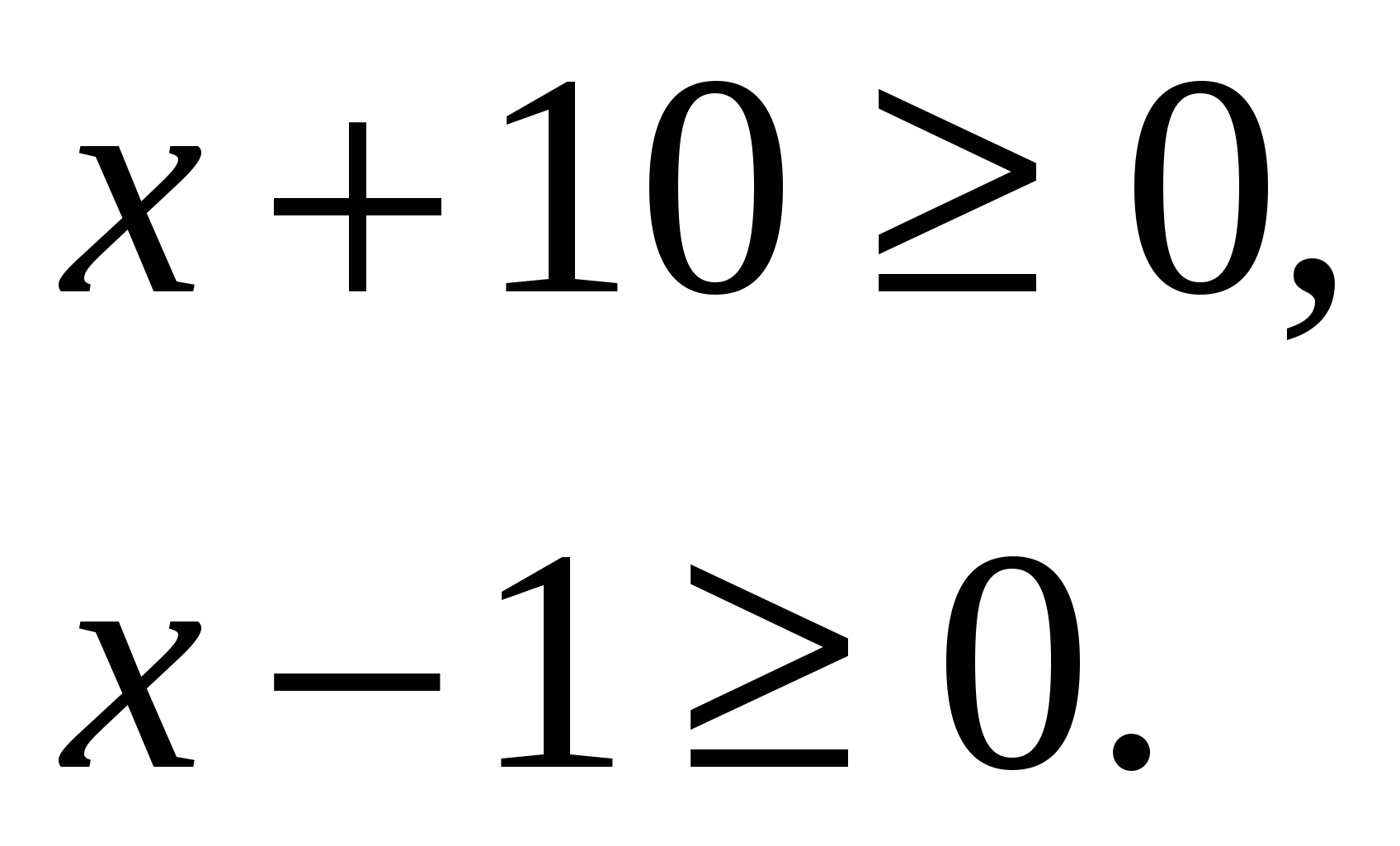
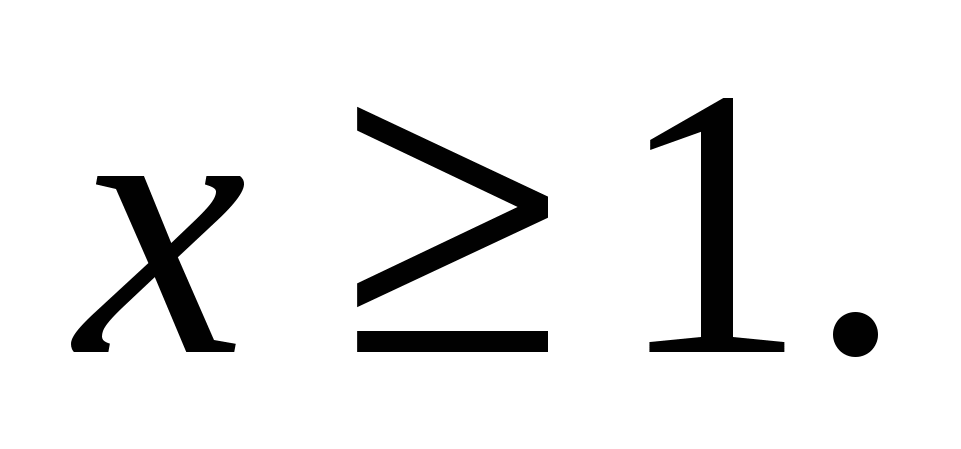
Оценим правую и левую части уравнений: 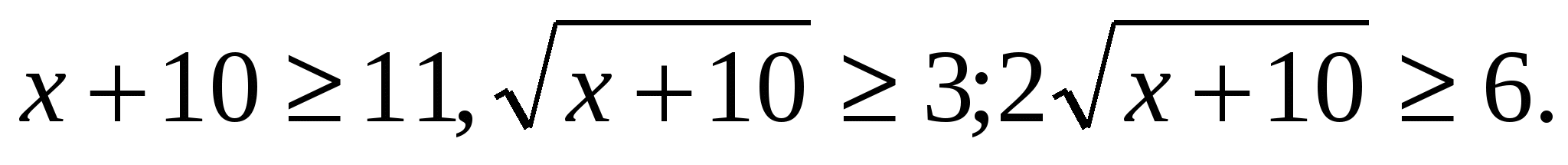 т.е.
т.е.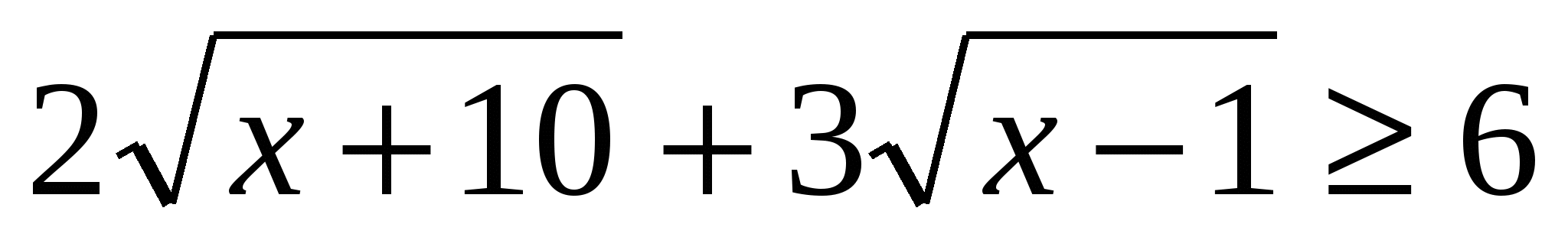 , а
, а 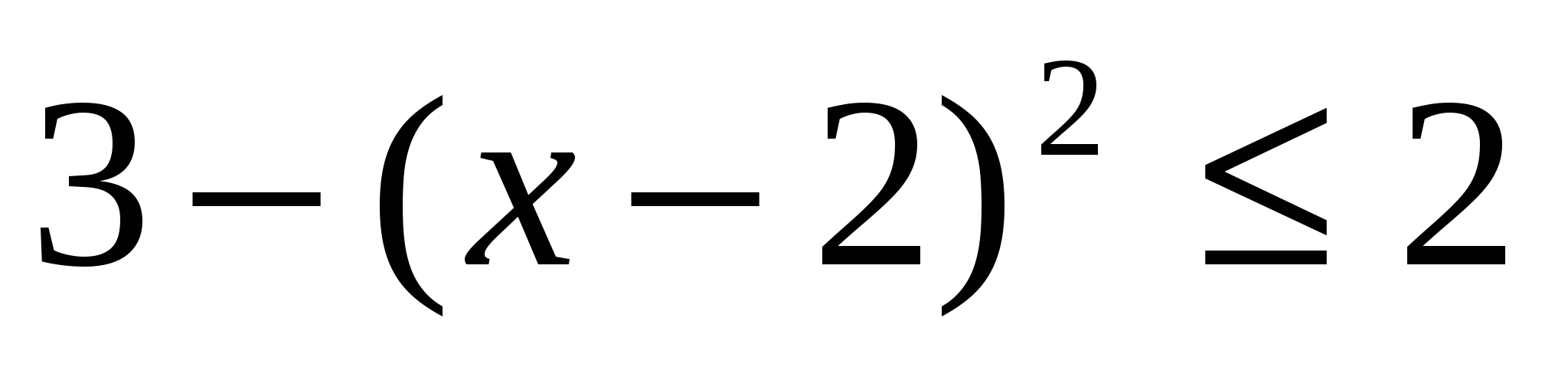 .
.
Левая часть уравнения больше правой, значит, данное уравнение не имеет корней.
Ответ: нет корней.
2)Решить уравнение: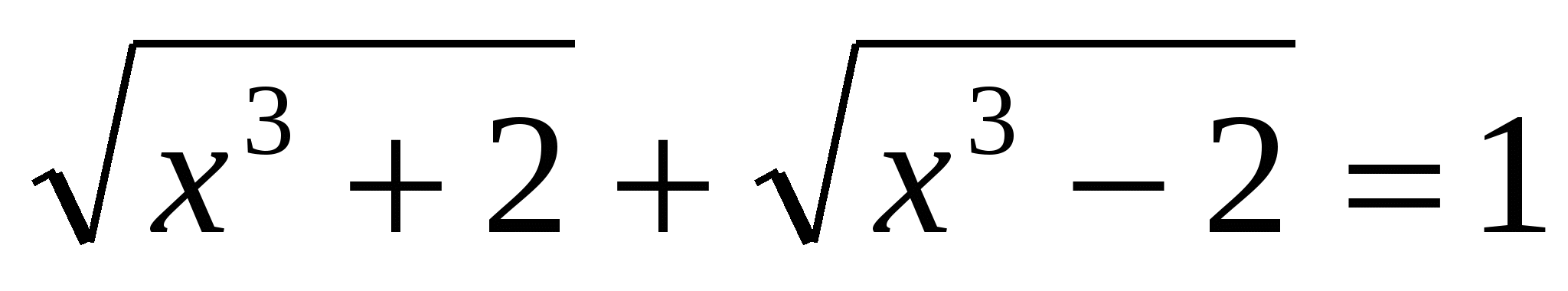 .
.
Решение: имеем стандартное иррациональное уравнение. Тем не менее, не будем спешить возводить в квадрат. Для начала найдем ОДЗ уравнения:
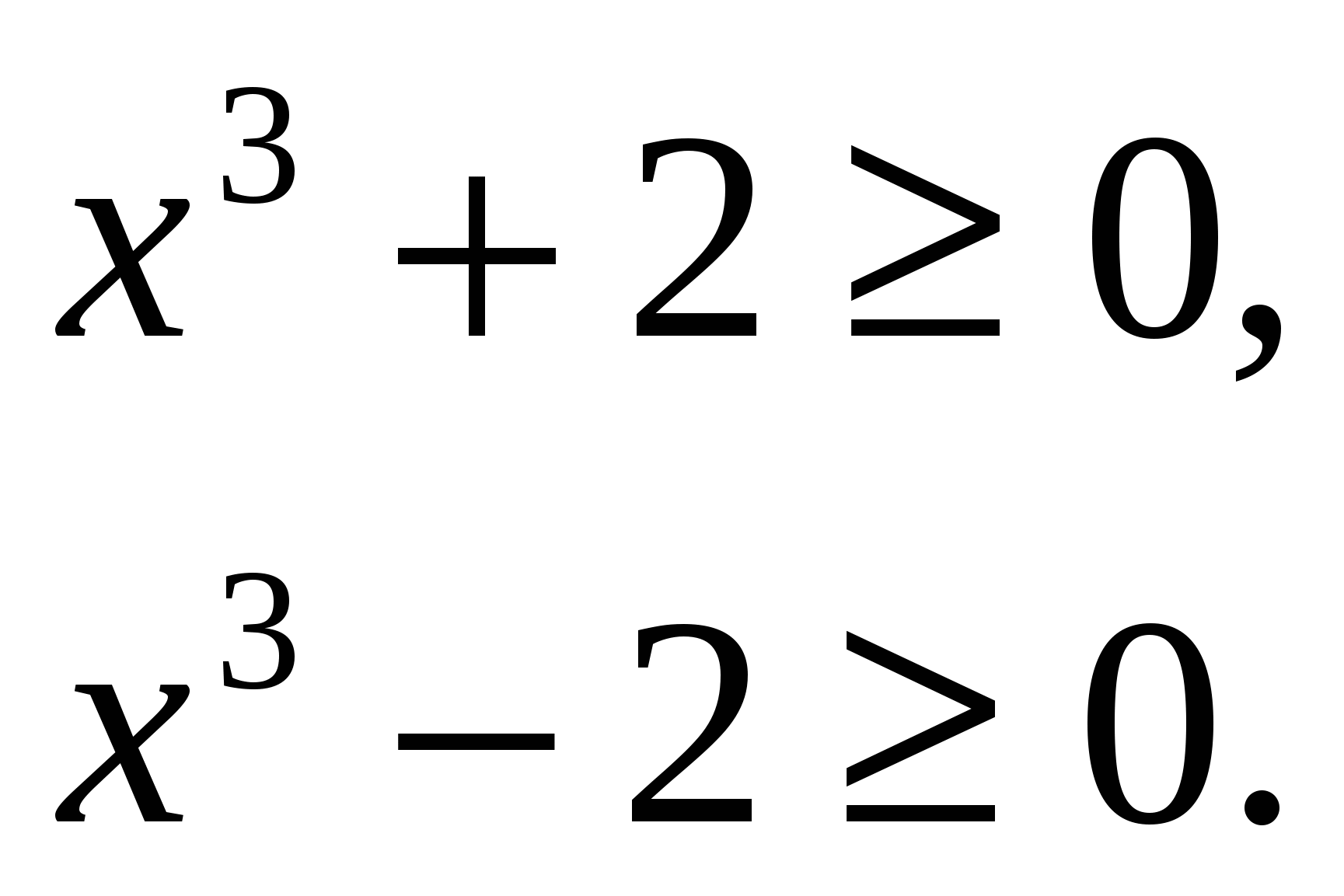
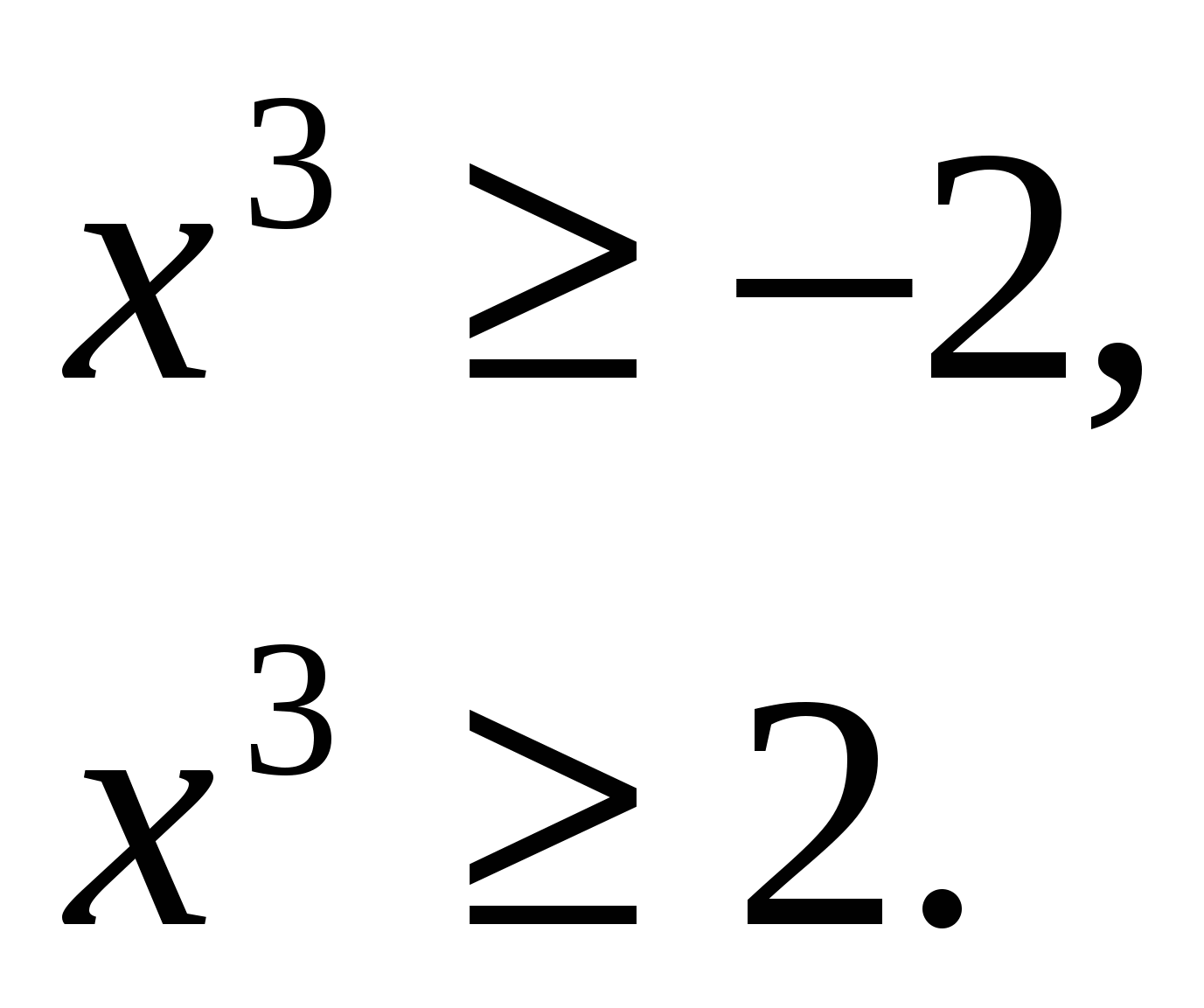
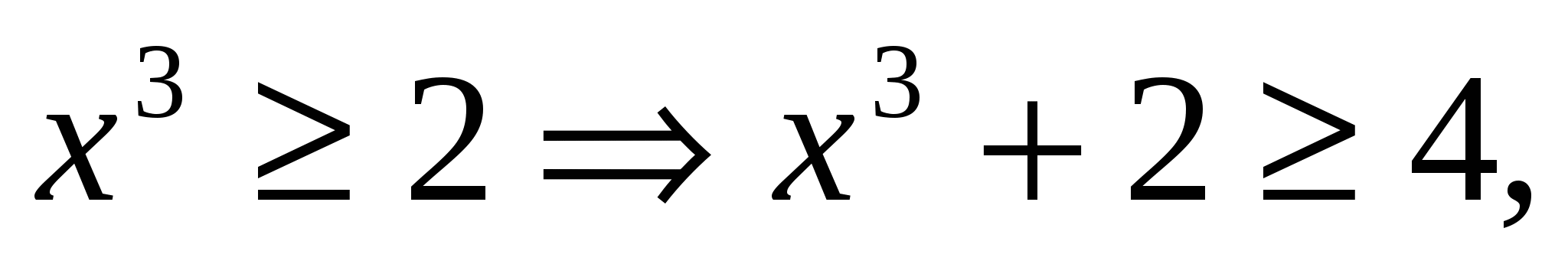 значит
значит 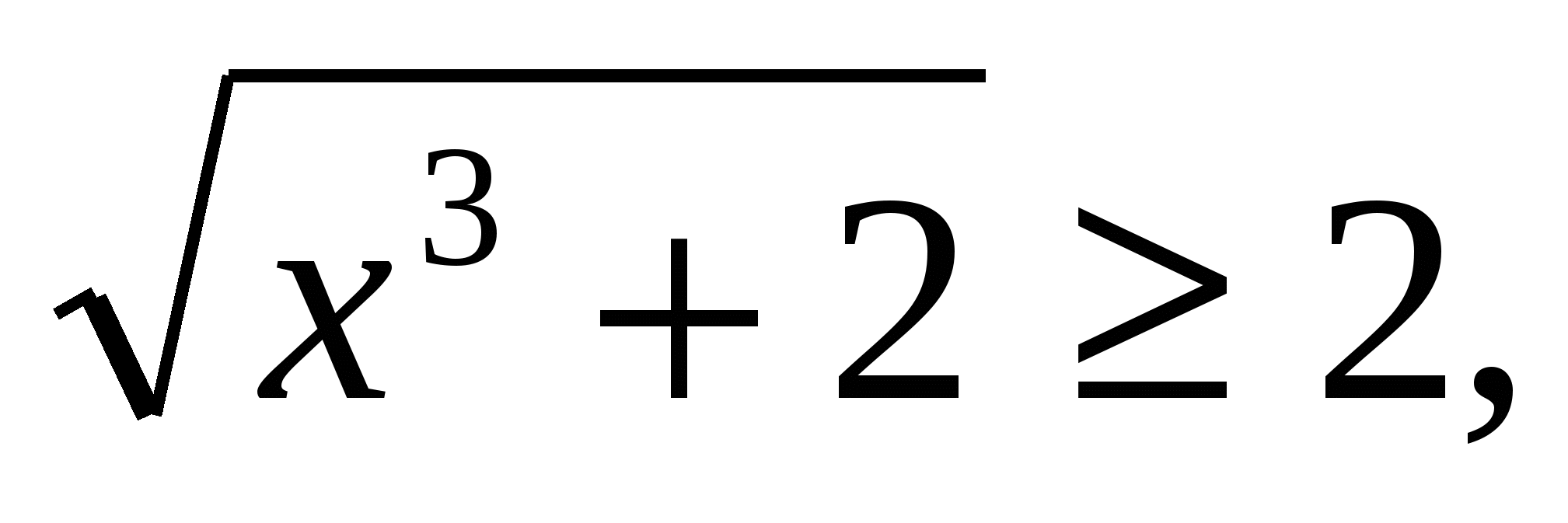 т.к.
т.к. 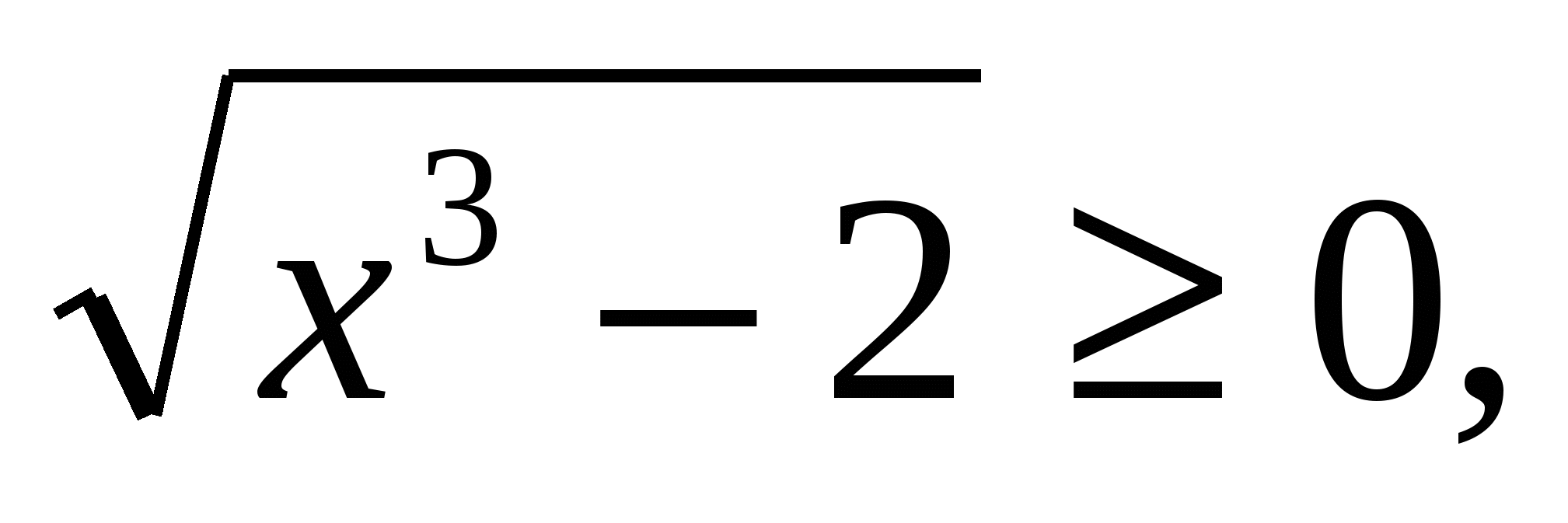 то левая часть уравнения больше 2 , а правая равна 1. Следовательно, данное уравнение не имеет корней.
то левая часть уравнения больше 2 , а правая равна 1. Следовательно, данное уравнение не имеет корней.
Ответ: нет корней.
3)Решить уравнение: 2cosx=cosx+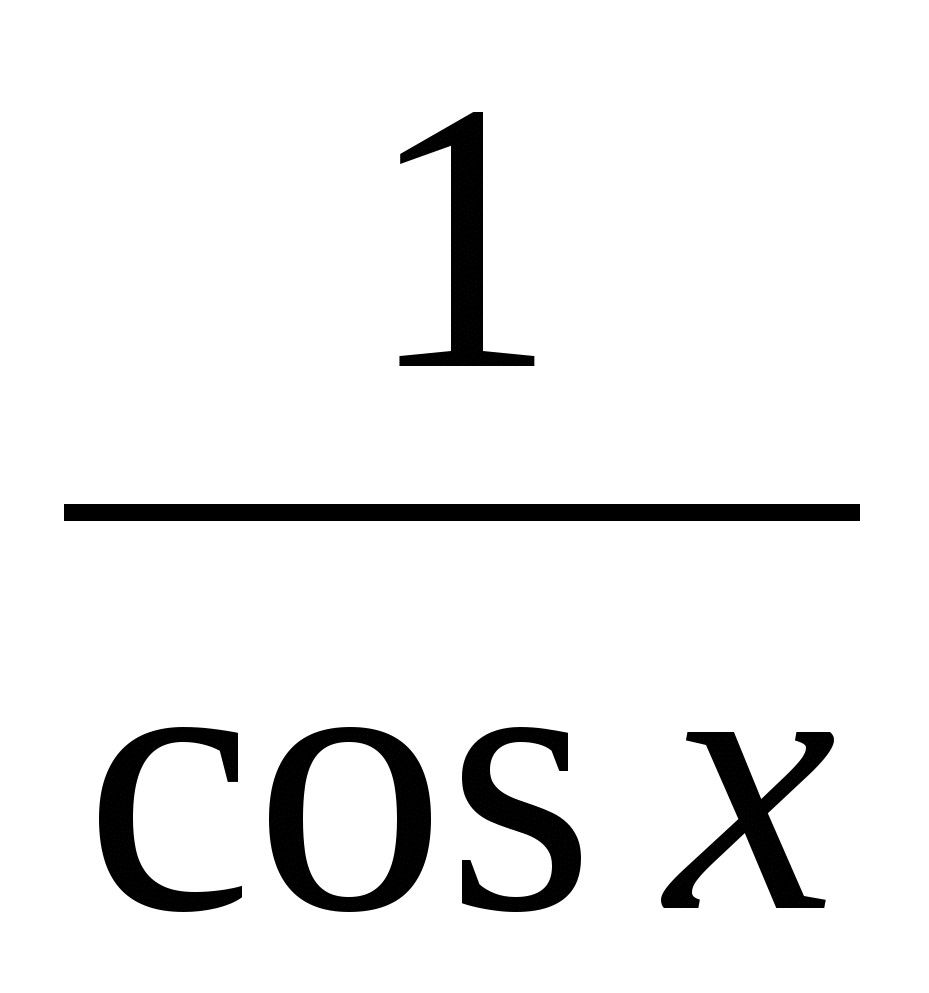 .
.
Решение: вновь оценим правую и левую части уравнения.
Т.к. 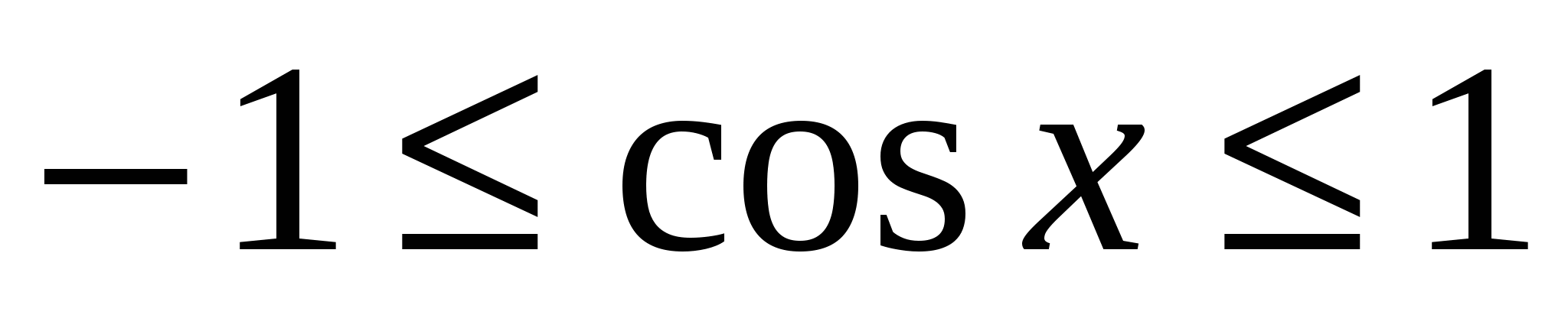 , то левая часть уравнения
, то левая часть уравнения ![]() .
.
Правая часть уравнения должна быть положительна, т.к. 2t>0, значит cosx>0. Используя неравенство Коши 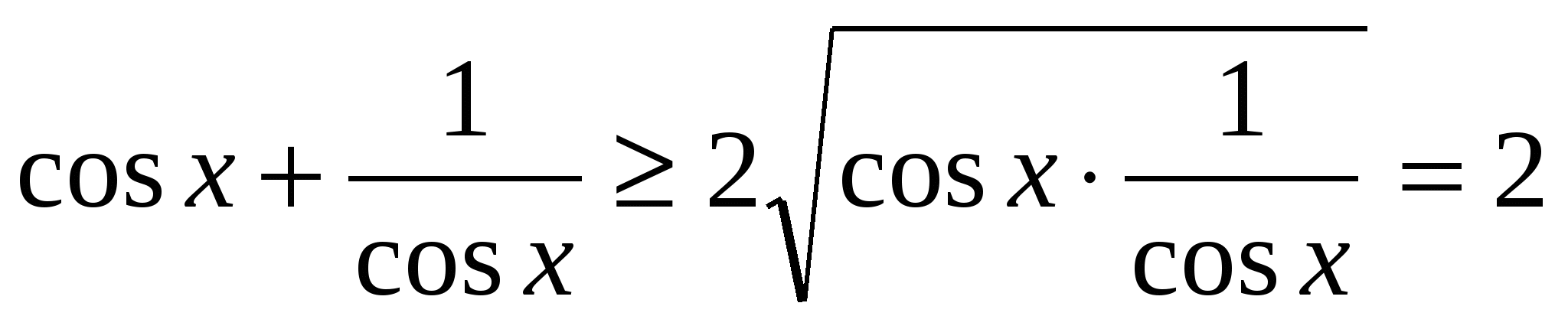 .
.
Тогда, если корень данного уравнения существует, то только в том случае, если правая и левая части уравнений равны 2.
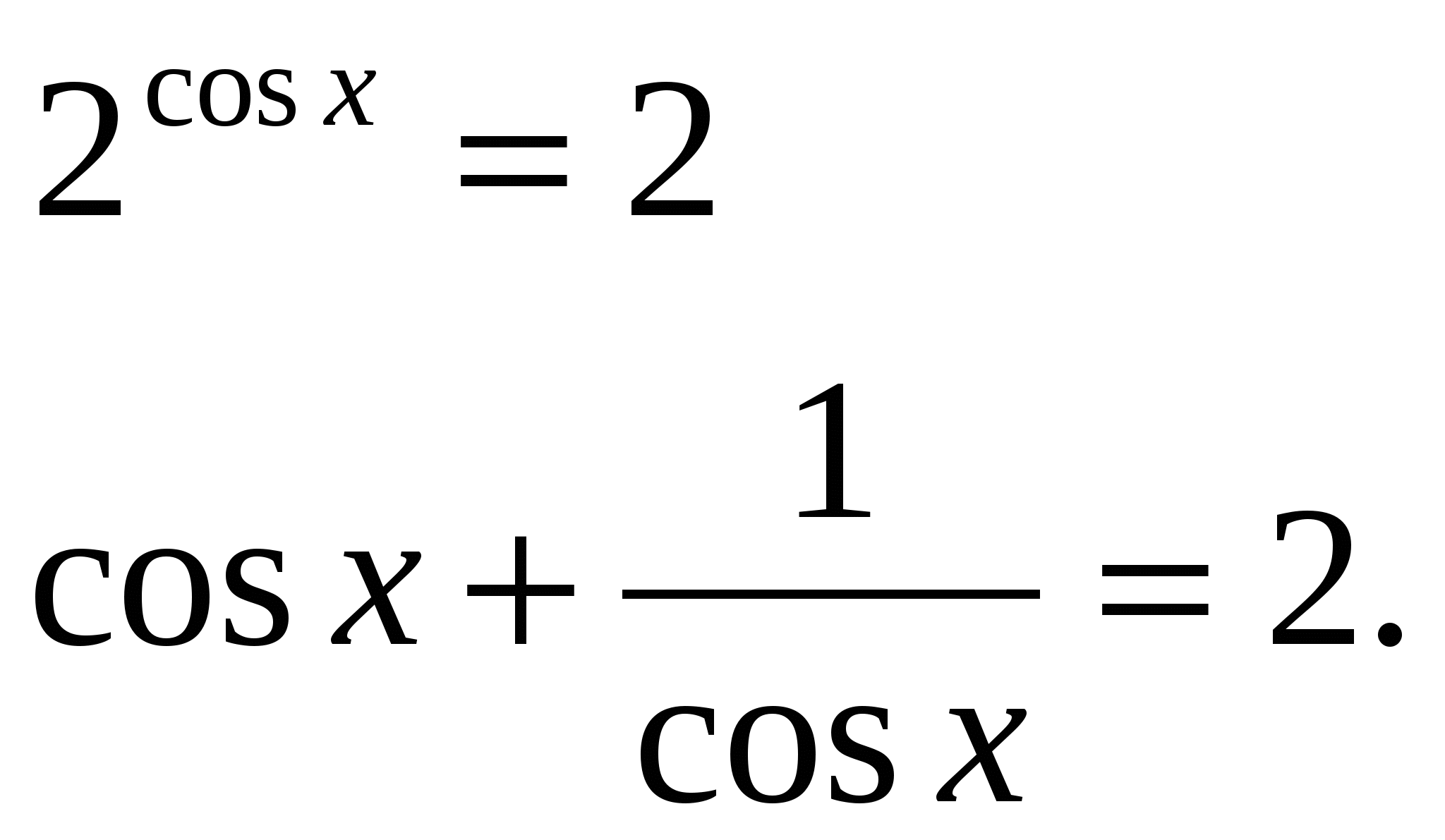
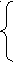
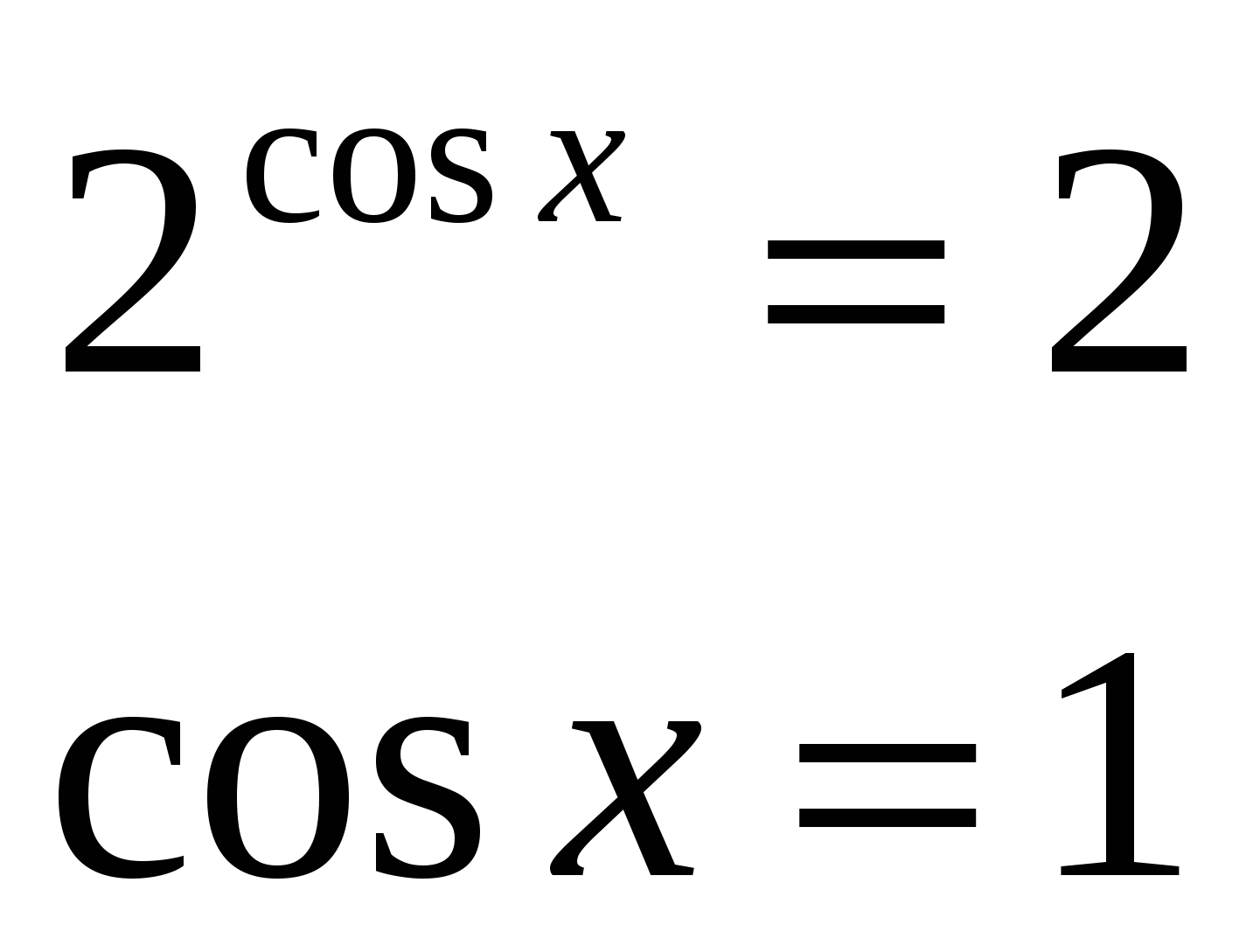
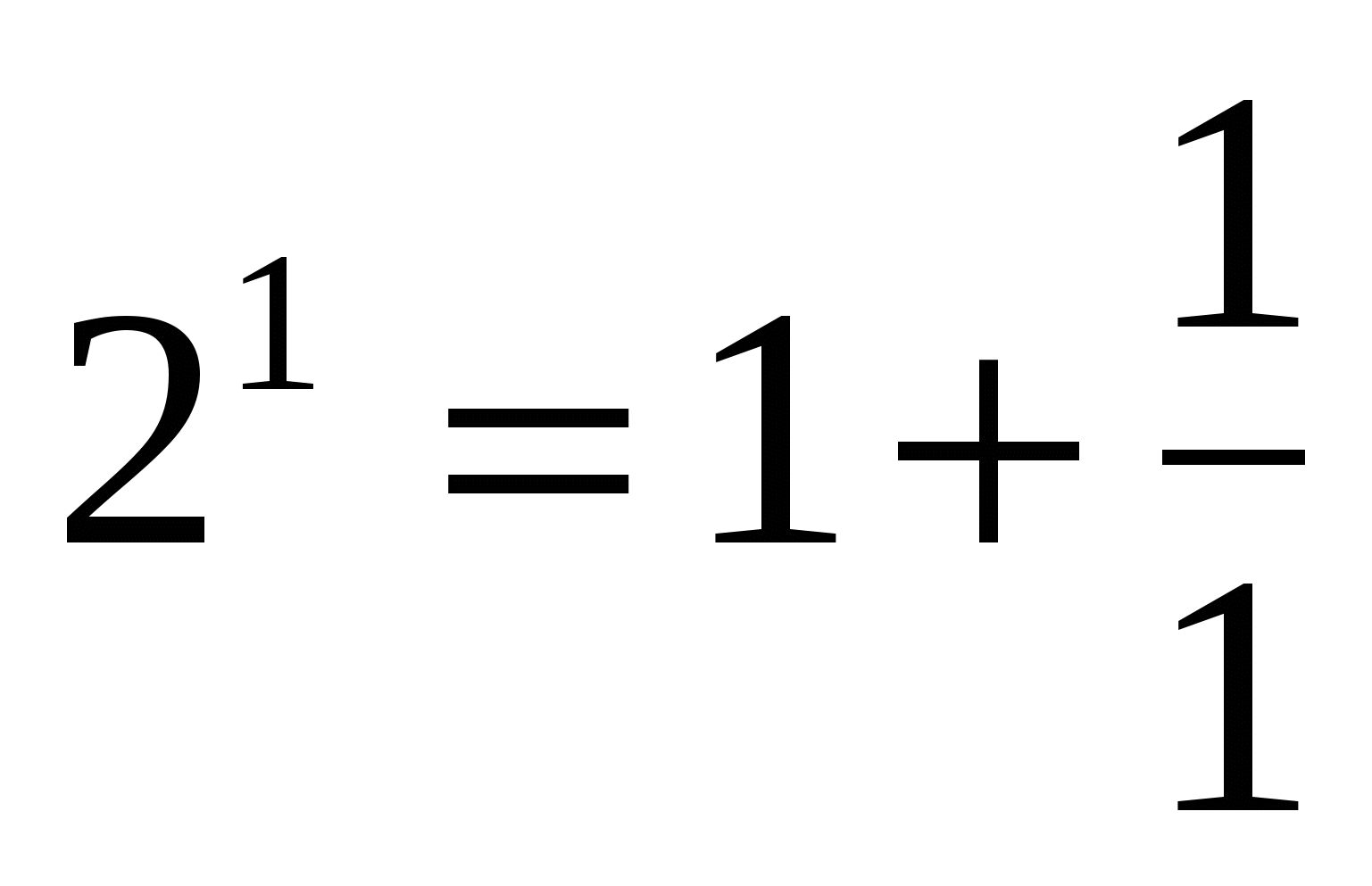
![]()
 х=2Пк, к
х=2Пк, к
Ответ: х=2Пк, к Z.
Z.
4) Решить уравнение: 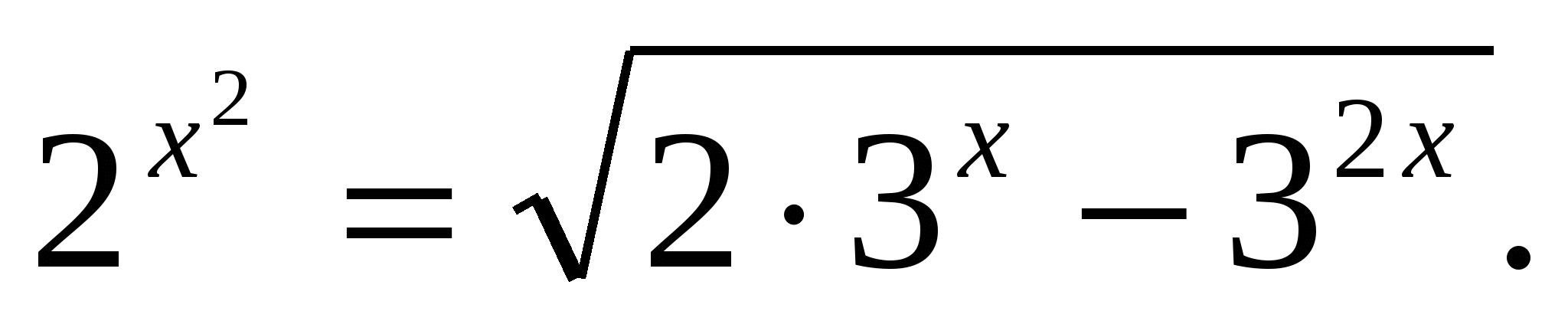
Решение: 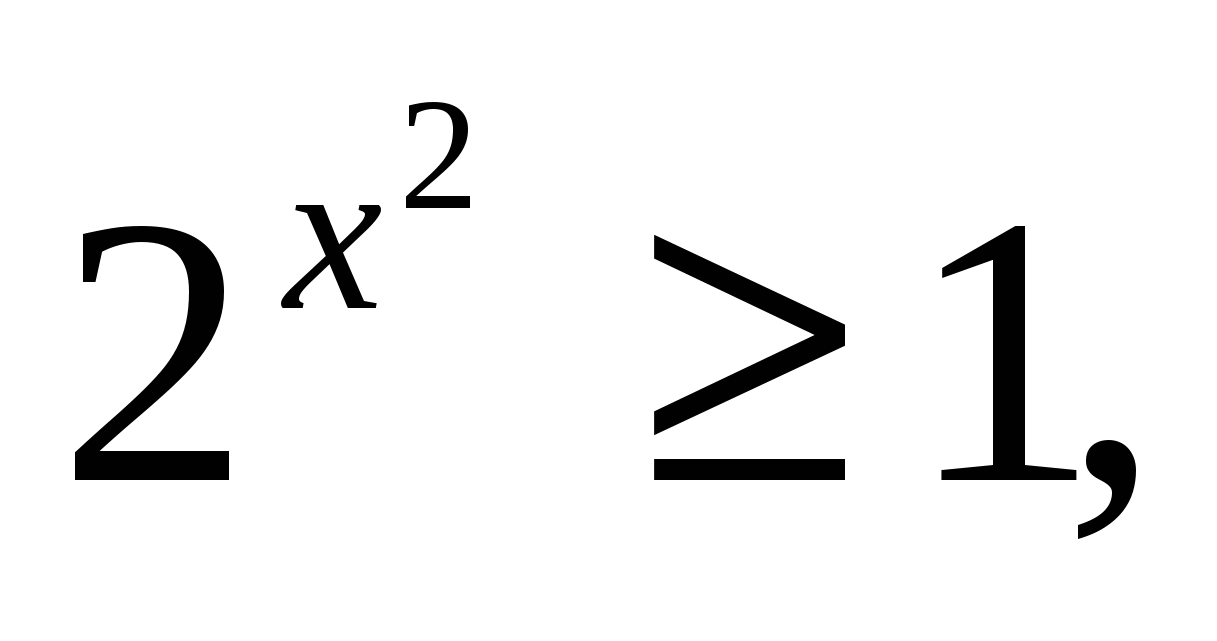 а
а 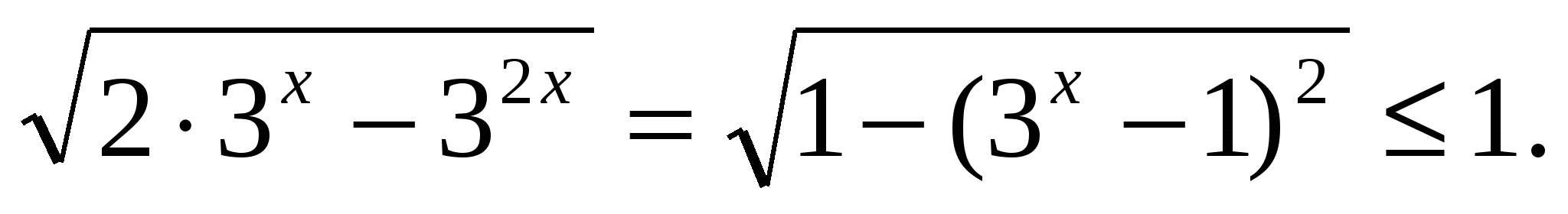 Решение этого уравнения равносильно системе:
Решение этого уравнения равносильно системе:
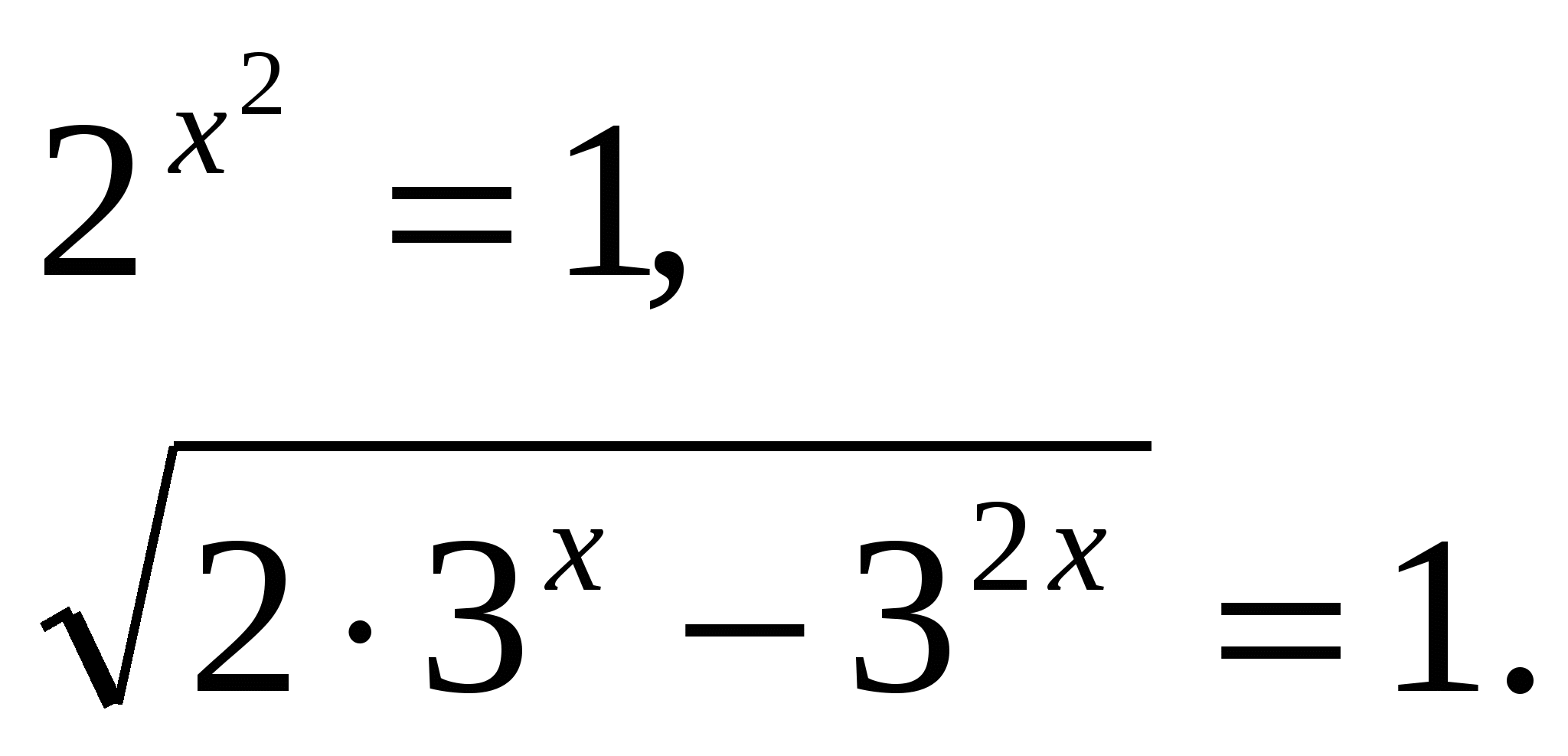
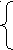
Из первого уравнения системы получаем х=0, проверим является ли х=0 решением второго уравнения системы: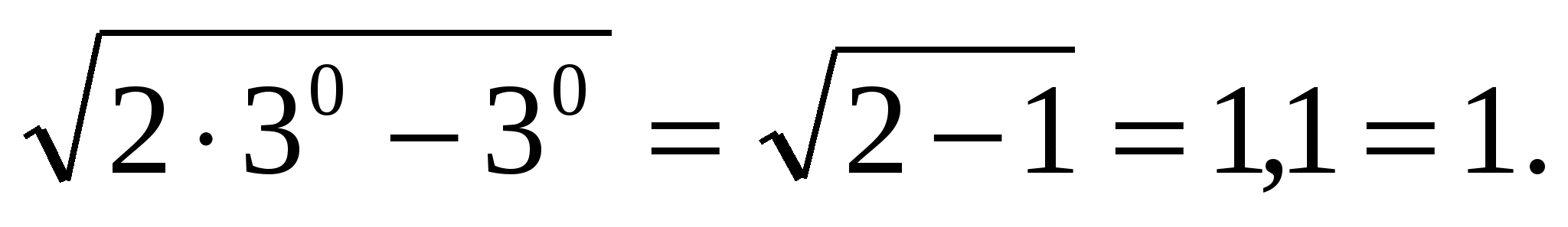 х=0 корень уравнения.
х=0 корень уравнения.
Ответ: х=0.
5) Решить уравнение: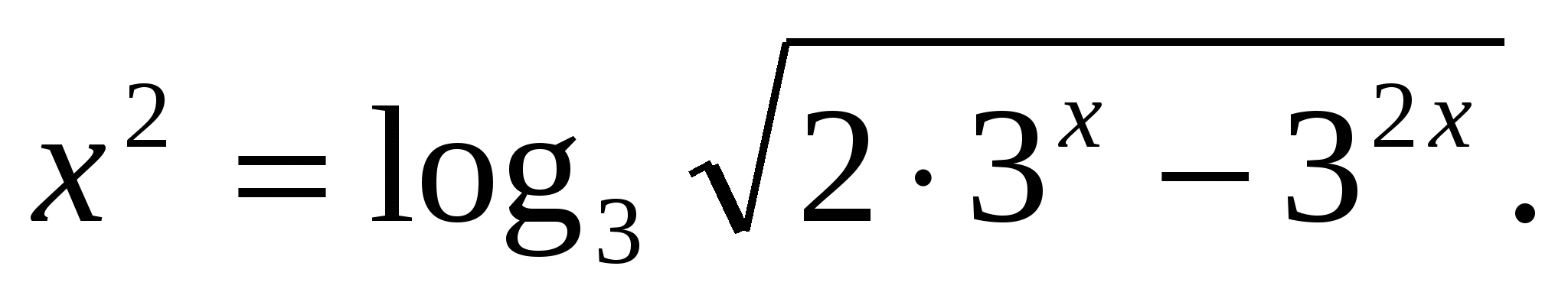
Решение этого уравнения аналогично предыдущему: очевидно х2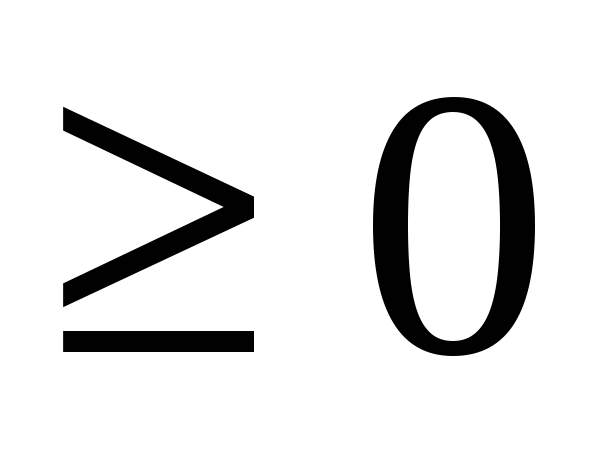 и log
и log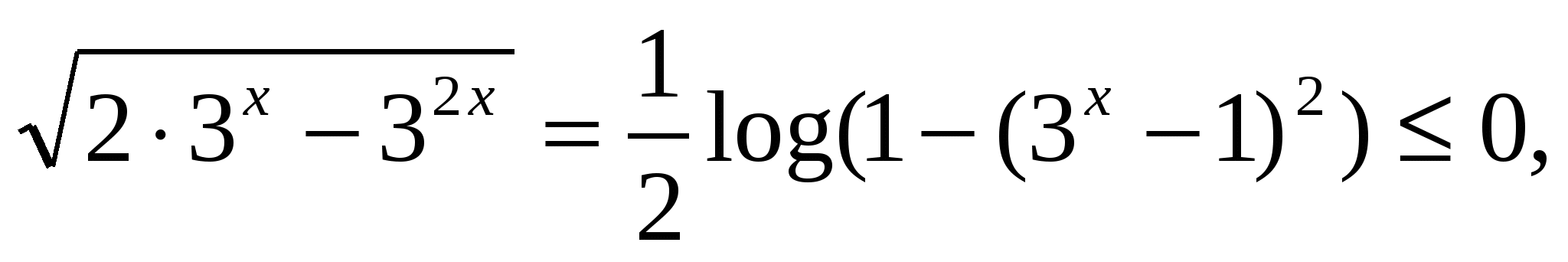 т.к. основание логарифма 3>1, а
т.к. основание логарифма 3>1, а
1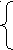 -(3х-1)2
-(3х-1)2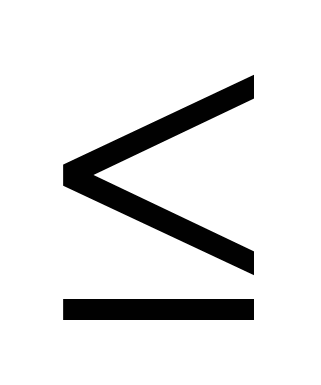 1, уравнение равносильно системе:
1, уравнение равносильно системе:
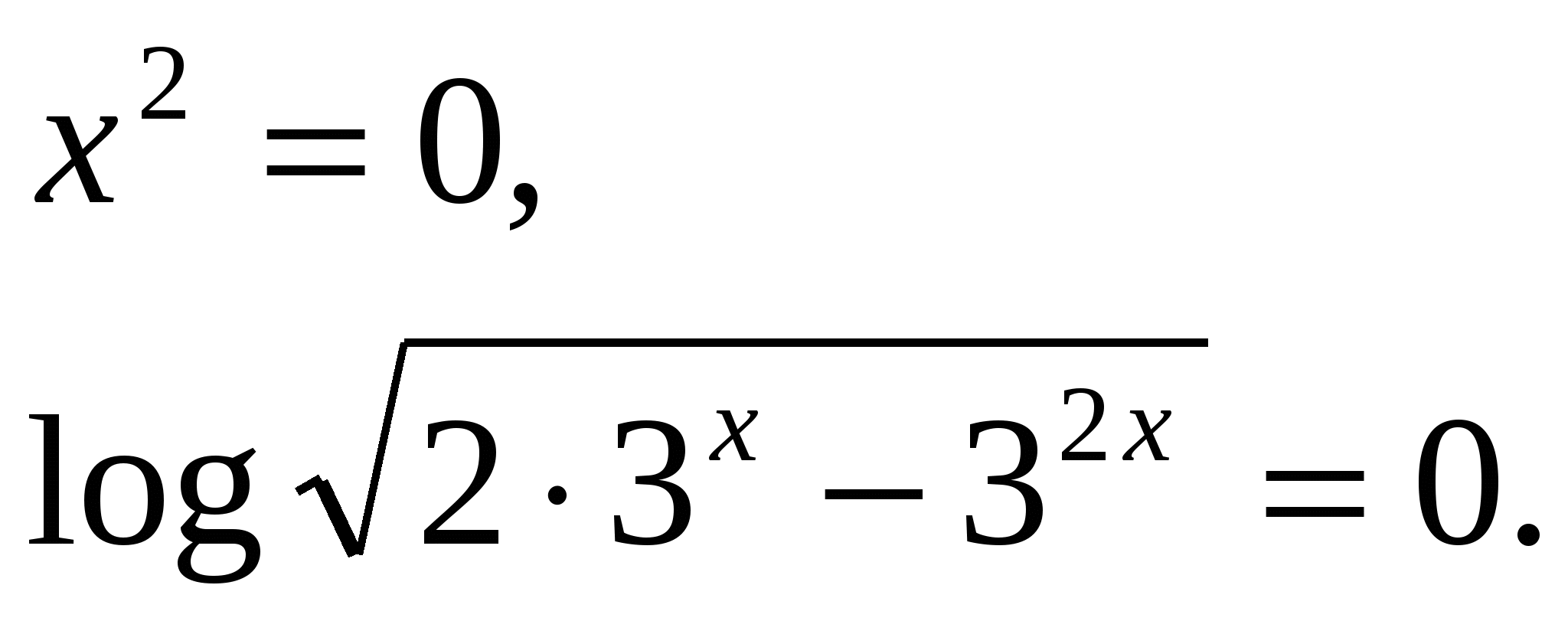
х=0- корень уравнения.
Ответ: х=о.
6) Найти целые корни уравнения: (6-х)(х-2)(х+3)(х+9)=24х2
Решение: это уравнение предлагалось на едином экзамене, рассмотрим решение этого уравнения двумя способами: с помощью оценки левой и правой частей уравнения, и второй способ- с помощью преобразований. Первый способ, мне так кажется, более прост и экономичен по времени его решения.
а) правя часть данного уравнения не отрицательна, значит
(6-х)(х-2)(х+3)(х+9)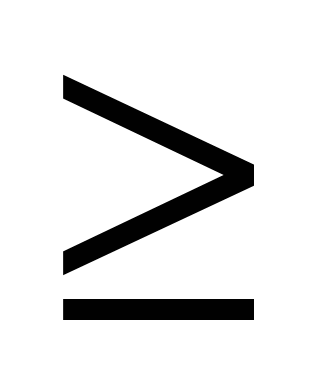 0, решим это неравенство методом интервалов:
0, решим это неравенство методом интервалов:
- + - + -

-9 -3 2 6  х
х

 Целые решения этого уравнения следует искать среди делителей свободного члена, равного 6 (-2) 3 9= -324.
Целые решения этого уравнения следует искать среди делителей свободного члена, равного 6 (-2) 3 9= -324.
Перечислим все целые значения являющиеся решением неравенства:
-9,-8,-7,-6,-5,-4,-3,2,3,4,5,6. Очевидно, что 6,2,-3,-9 не являются корнями уравнения, (т.к. при этих значениях левая часть уравнения равна нулю, а правая нет) числа -7,5,-8 не являются делителями числа -324. Проверим, являются ли решениями числа --6,-4,3,4.
х=-6, 12⋅ (-8)⋅ (-3) ⋅3 =864, 24 ⋅ 36=864, 864=864.
х=-4, 10⋅ (-6) ⋅(-1) ⋅5=300, 24⋅ 16=384, 300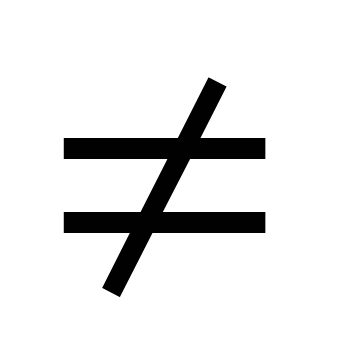 384.
384.
х=3, 3 ⋅ 1 6 ⋅12 =216, 24⋅ 9=216, 216=216.
х=4, 2 ⋅ 2⋅ 7 ⋅ 13=364, 24⋅ 16=384, 364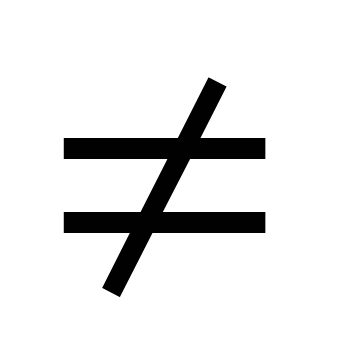 384.
384.
Итак, х=-6, х=3 целые корни уравнения.
Ответ: х=-6; х=3.
б) решим это же уравнение другим способом:
(6-х)(х-2)(х+3)(х+9)=24х2, выполним некоторые преобразования:
(6х+18-х2-3х)(х2 +7х-18)=24х2
(-х2+3х+18)(х2+7х-18)=24х2
очевидно, что х=о не является корнем уравнения, разделим обе части уравнения на х2
-х2(х-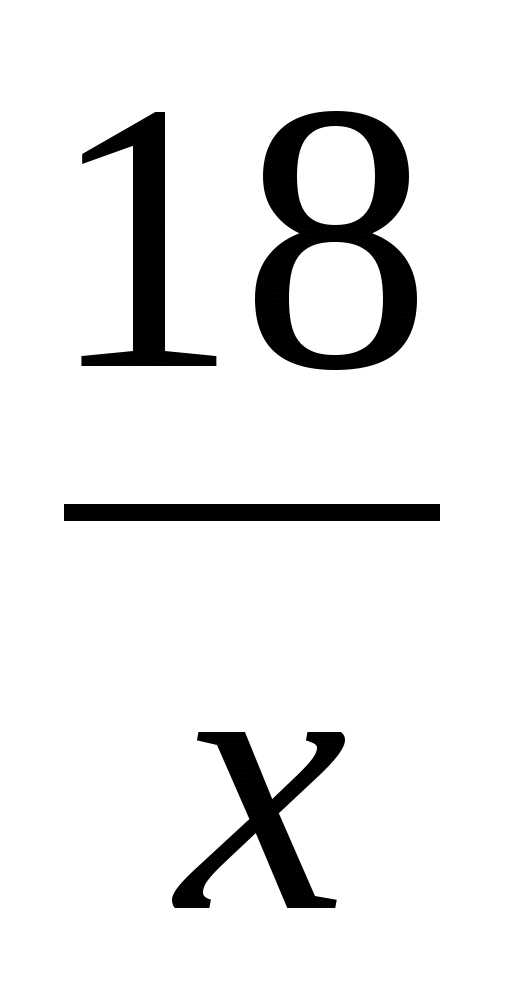 -3)(х-
-3)(х-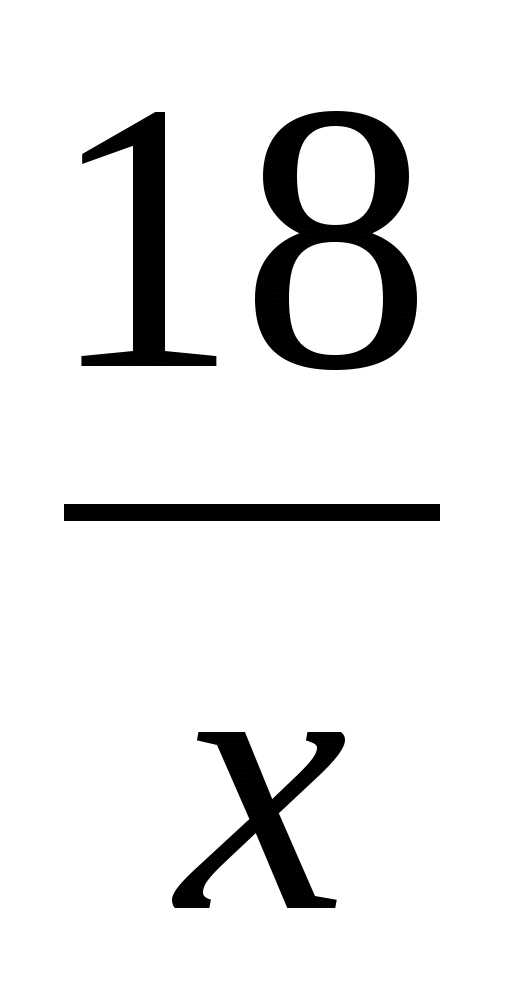 +7)=24х2,
+7)=24х2,
(х-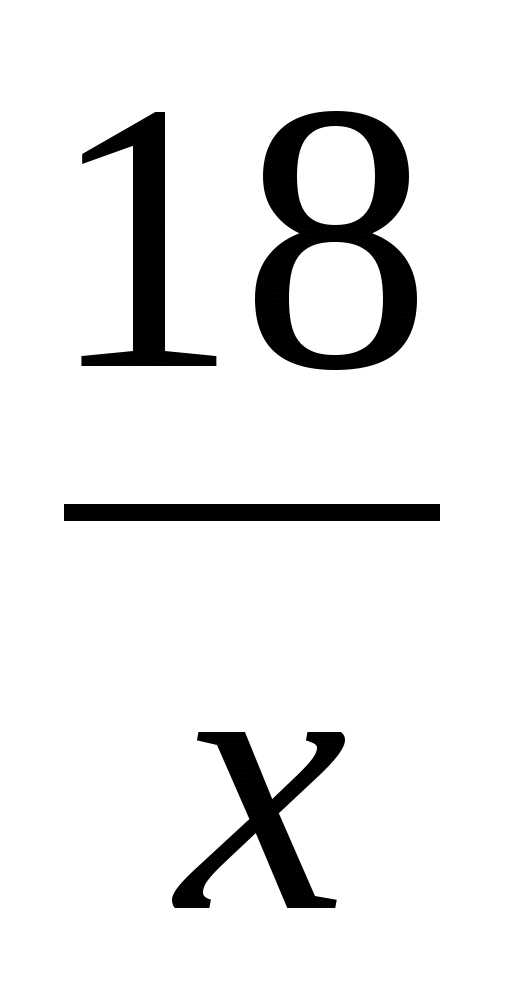 -3)(х-
-3)(х-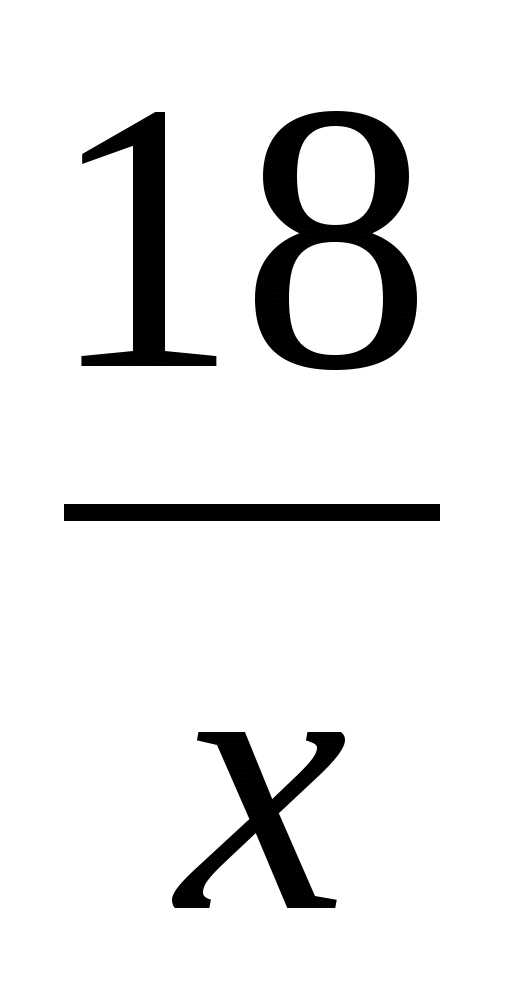 +7)=-24,
+7)=-24,
Пусть 
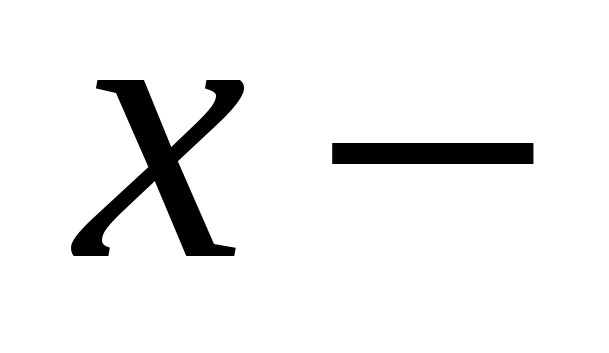
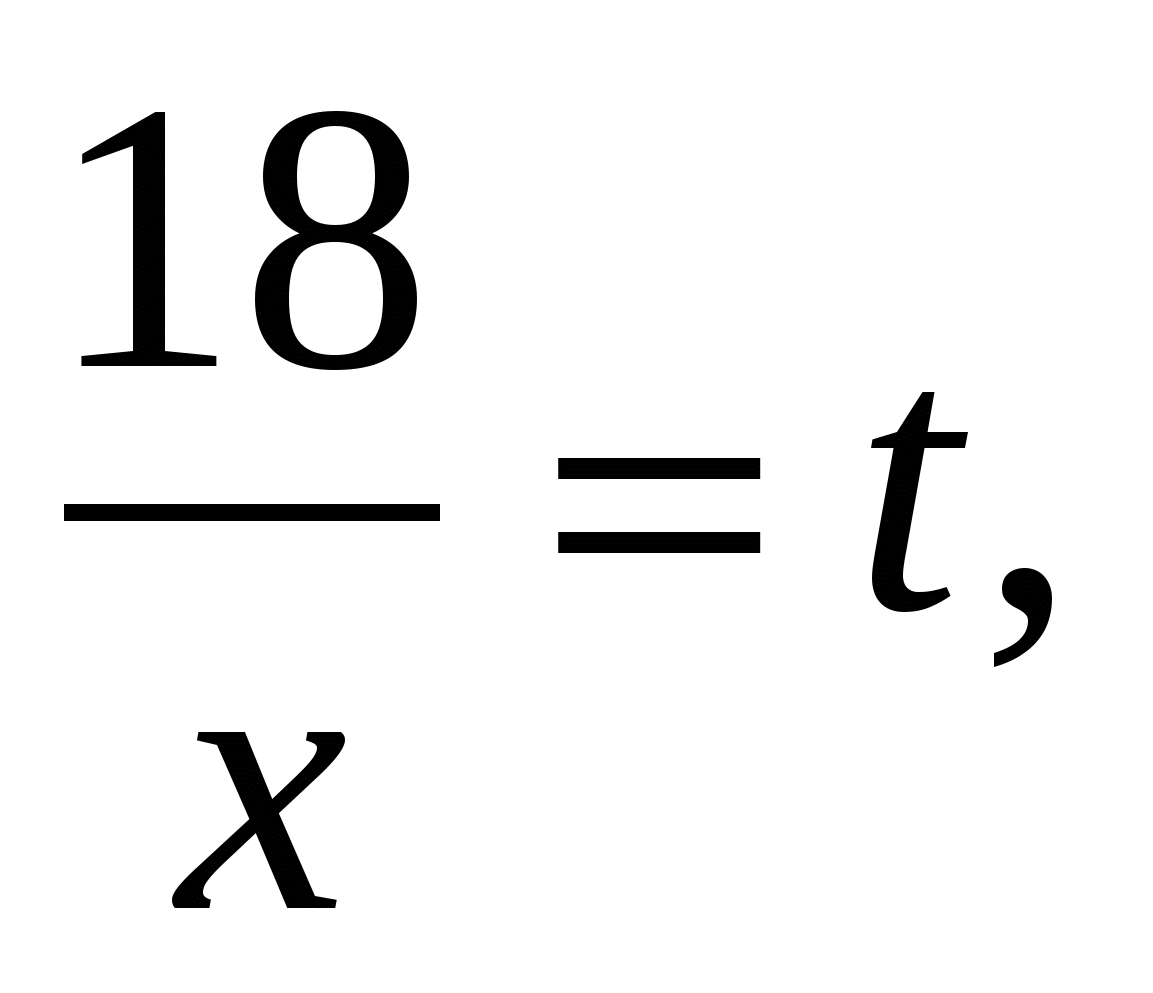 тогда (t-3)(t+7)=-24,
тогда (t-3)(t+7)=-24,
t2+4t-21=-24, t2+4t+3=0, t1=-1 ,t2=-3.
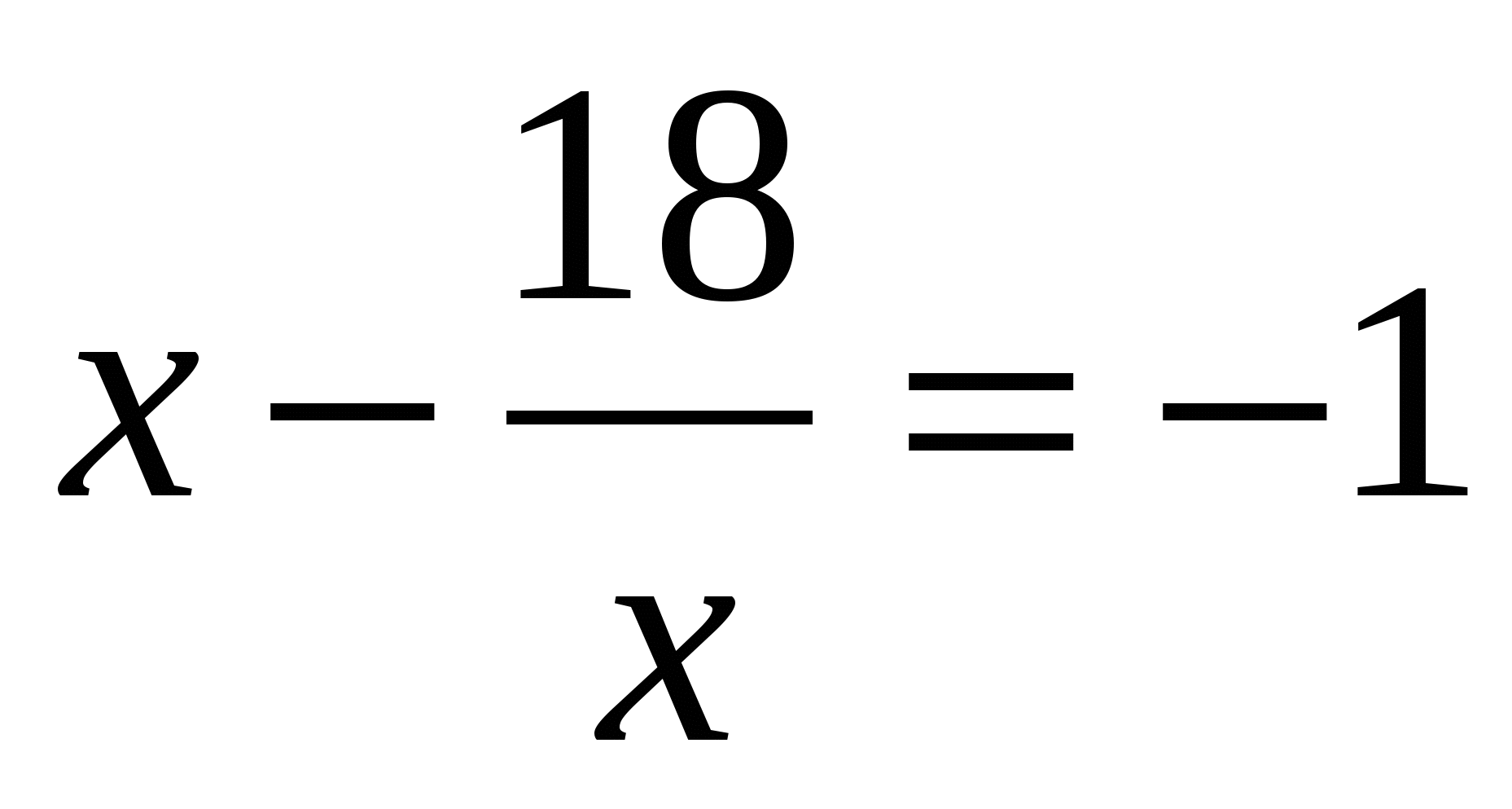 / х
/ х
х2+х-18=0 ,х1,2=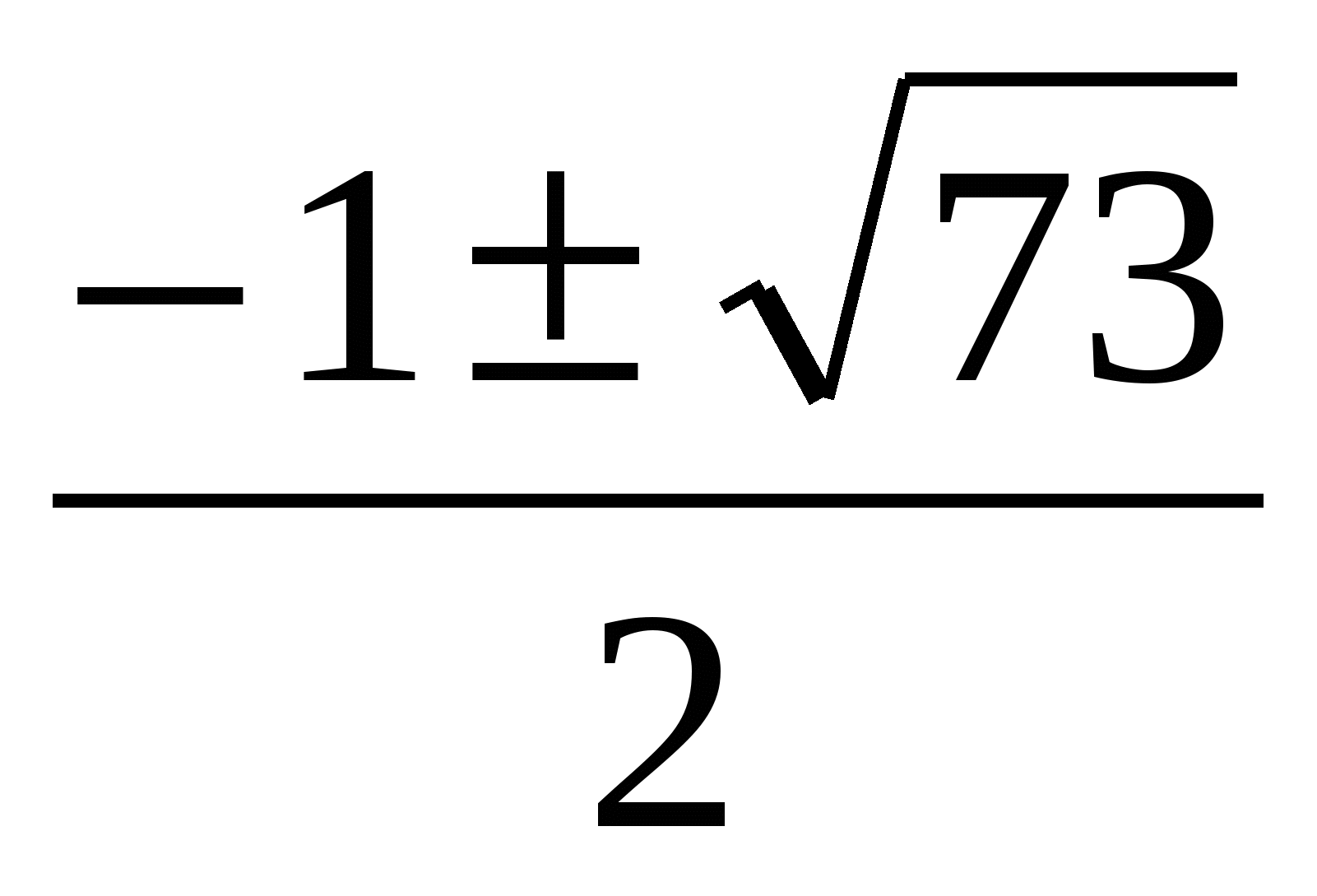 - не являются целыми решениями уравнения.
- не являются целыми решениями уравнения.
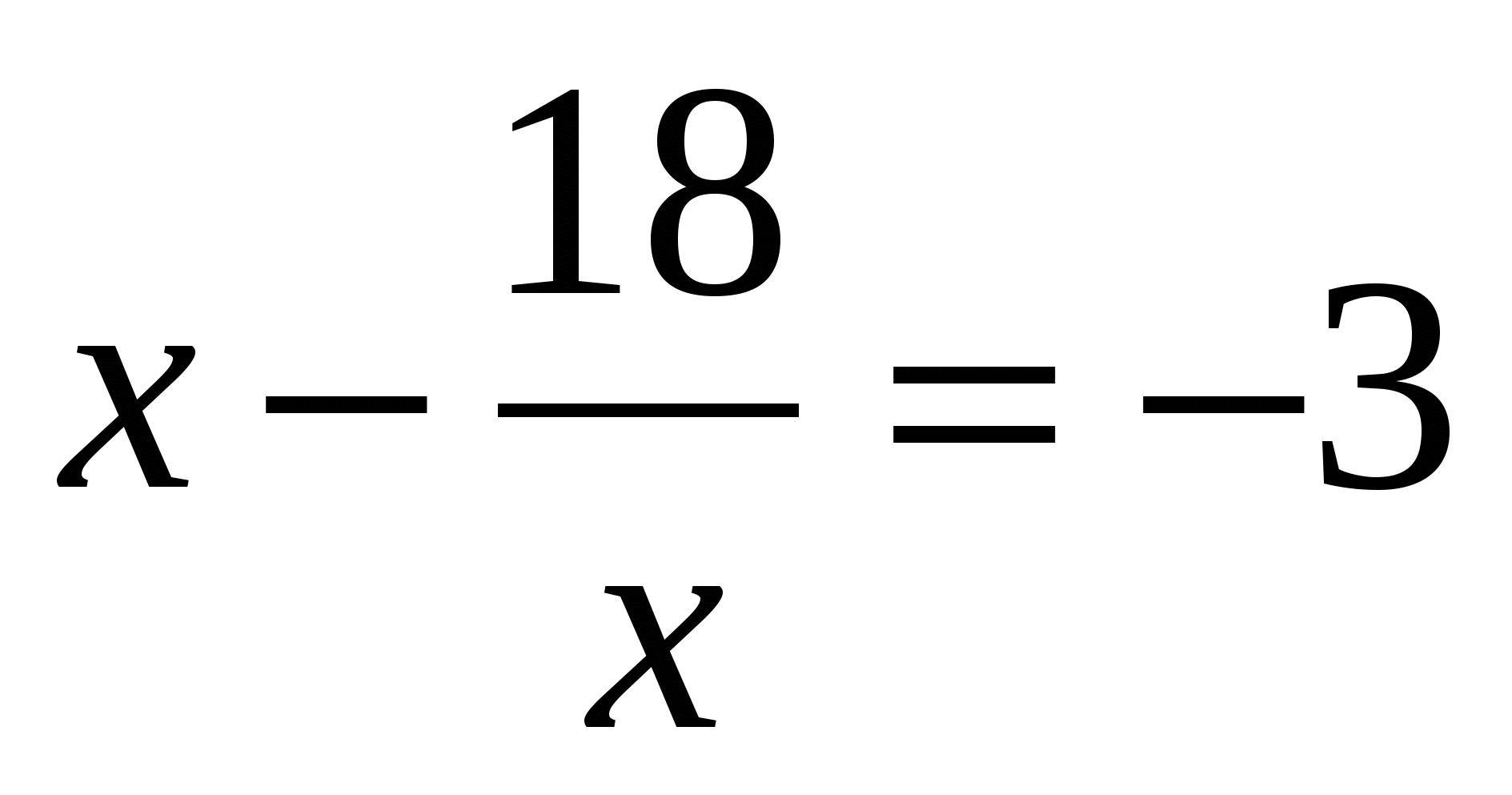
 /х
/х
х2+3х-18=0, х3=-6, х4=3.
Ответ: х=-6;х=3.
7)Решить уравнение: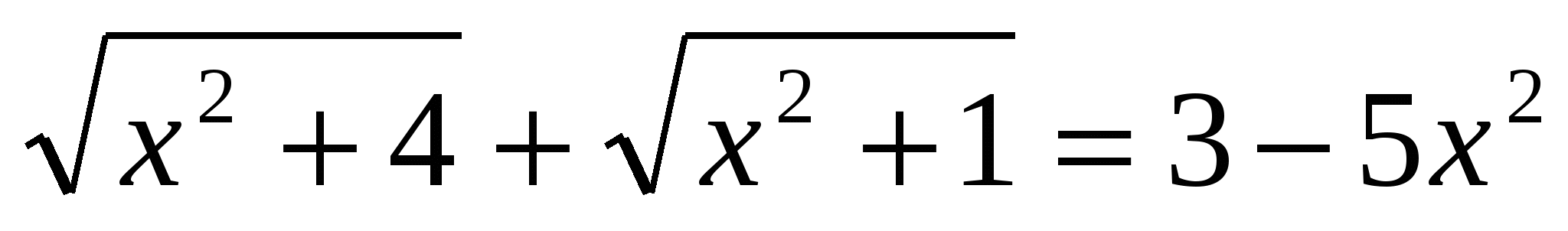
Решение: метод возведения в квадрат при решении этого уравнения приводит к рациональному уравнению восьмой степени, корни которого найти не легко. Заметим, что левая часть уравнения существует при любых действительных значениях переменной х, а правая не отрицательна при условии 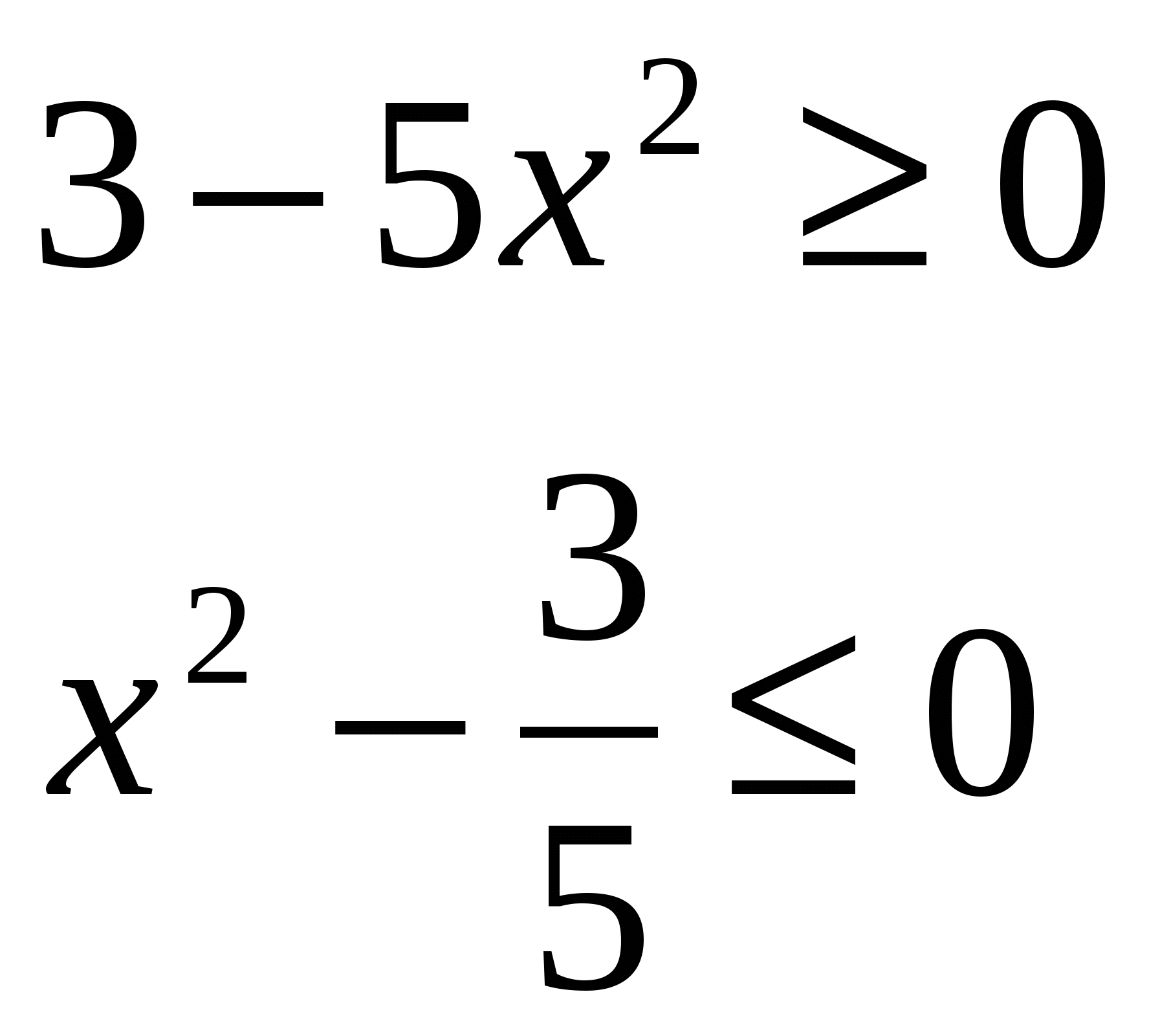
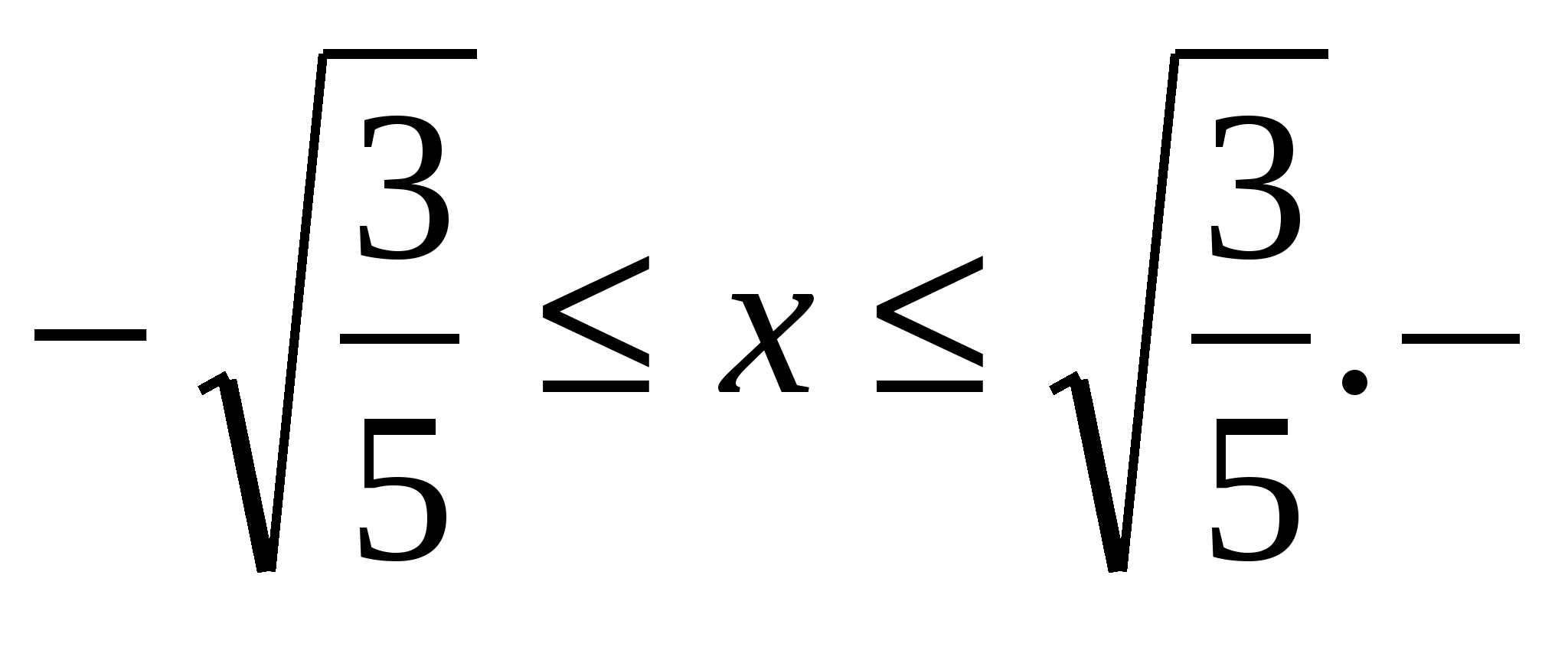
Заметим, что 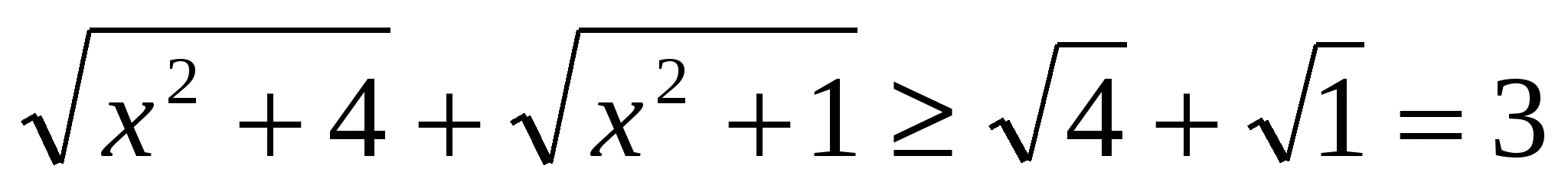 ,
,
в то время как 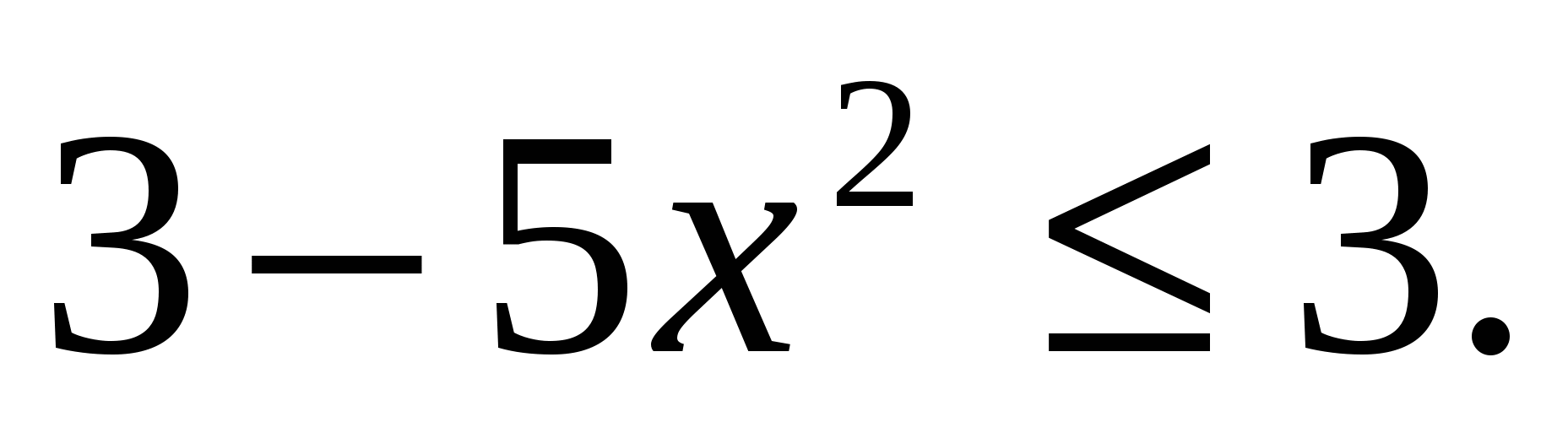 Следовательно, левая часть исходного уравнения может быть равна правой части, только если обе части уравнения равны 3.
Следовательно, левая часть исходного уравнения может быть равна правой части, только если обе части уравнения равны 3.
Значит х=0- единственный корень уравнения .
Ответ: х=0.
8)Решить уравнение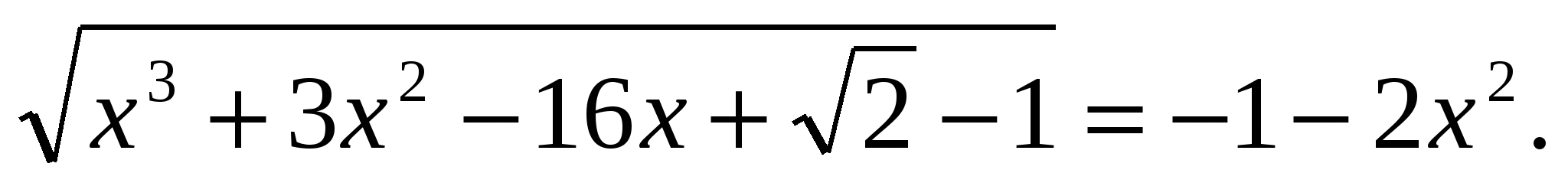
Решение: попытки найти корни, возводя обе части уравнения в квадрат, обречены на неудачу. Выпишем условие существования функции, стоящей в левой части уравнения 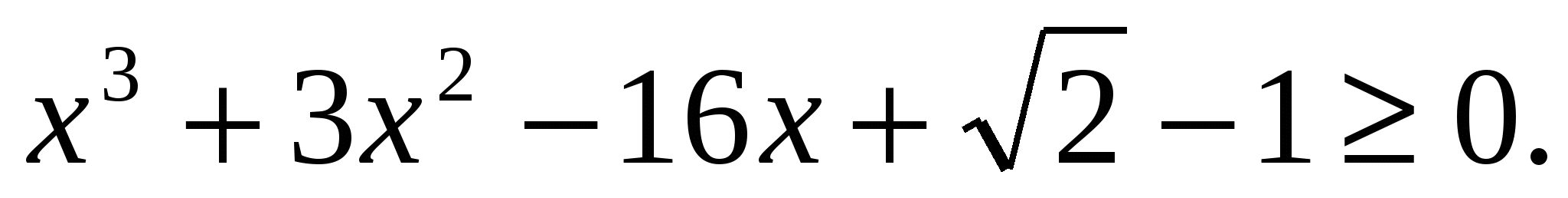 Решение этого неравенства, также представляется проблематичным. Проверим не отрицательность правой части -1-2х2>0 это неравенство решений не имеет, но тогда исходное уравнение не имеет корней, т.к. левая часть его неотрицательная функция.
Решение этого неравенства, также представляется проблематичным. Проверим не отрицательность правой части -1-2х2>0 это неравенство решений не имеет, но тогда исходное уравнение не имеет корней, т.к. левая часть его неотрицательная функция.
Ответ: нет корней.
9) Решить уравнение 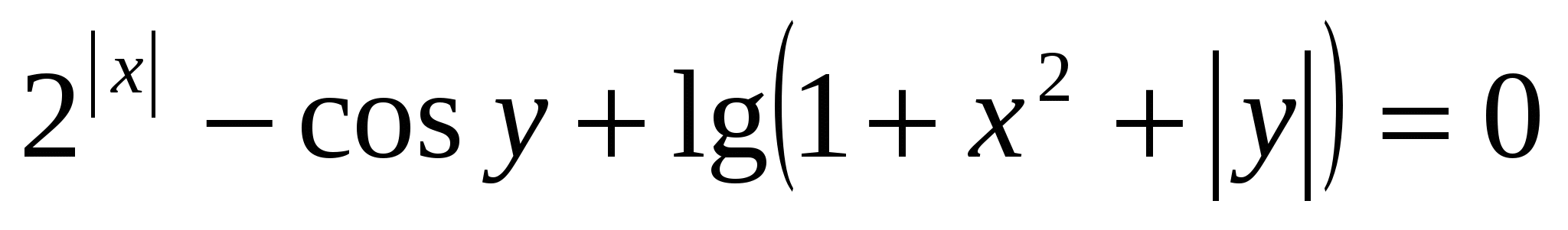
Решение: если для многих предыдущих уравнений можно было найти традиционный путь - решение с помощью привычных школьных рассуждений, правда, затратив при этом гораздо больше времени. А это уравнение лишает нас такого выбора. Обычно подобные задачи условно называют нестандартными. Уже «внешний вид» подобного уравнения подсказывает, что для решения надо придумать что-то нетрадиционное.
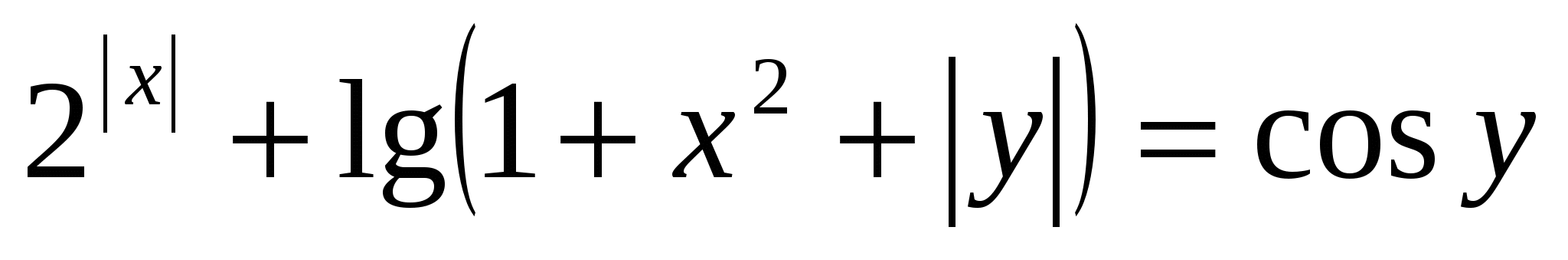
Оценим правую часть уравнения: 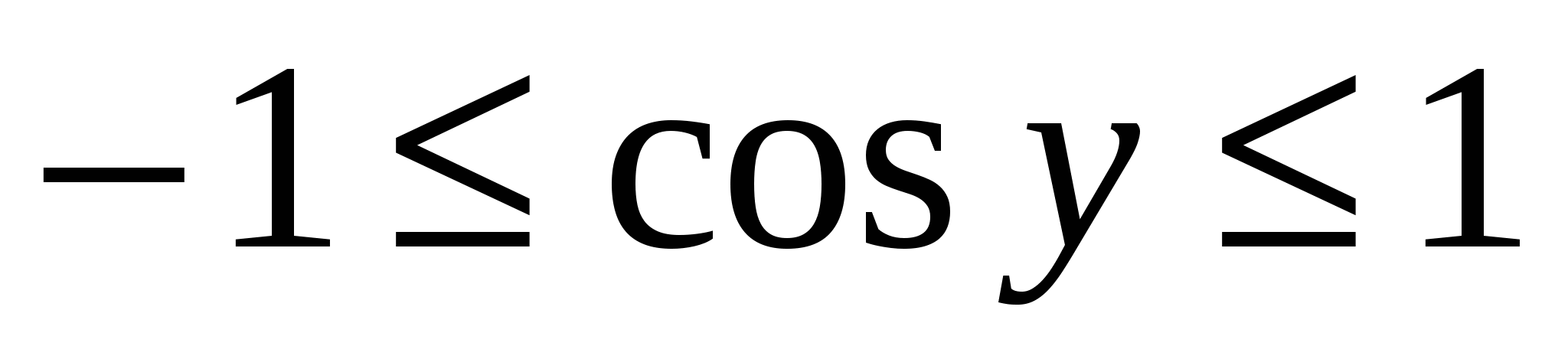 , оценим левую часть уравнения:
, оценим левую часть уравнения: 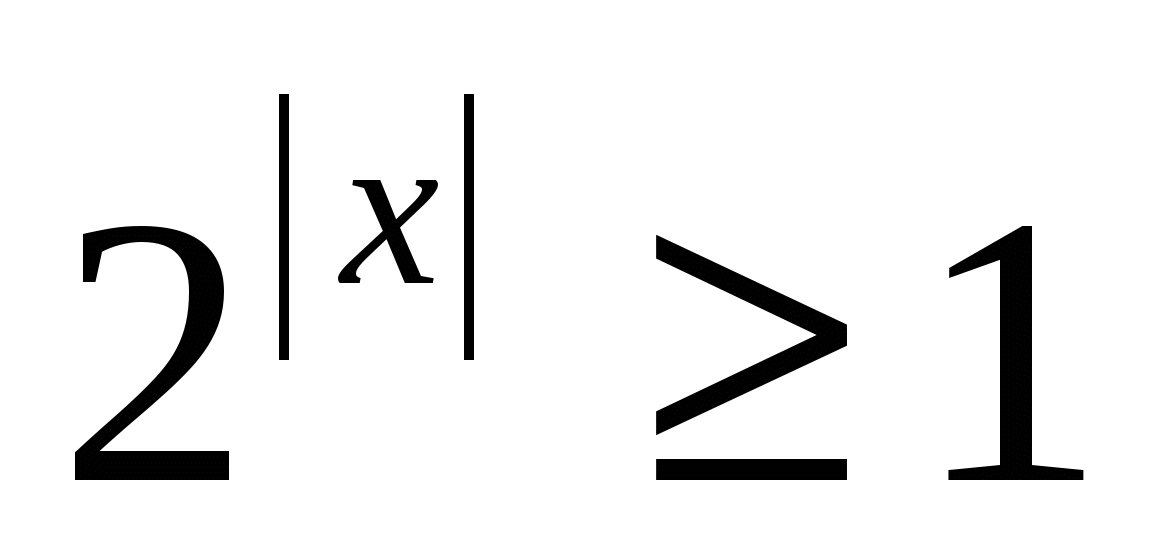 ,
, 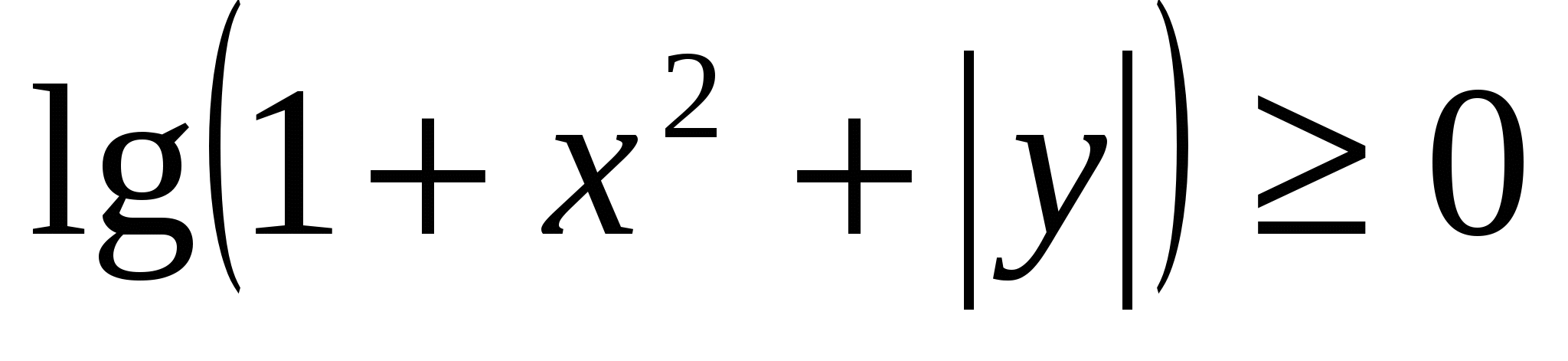 ,
, 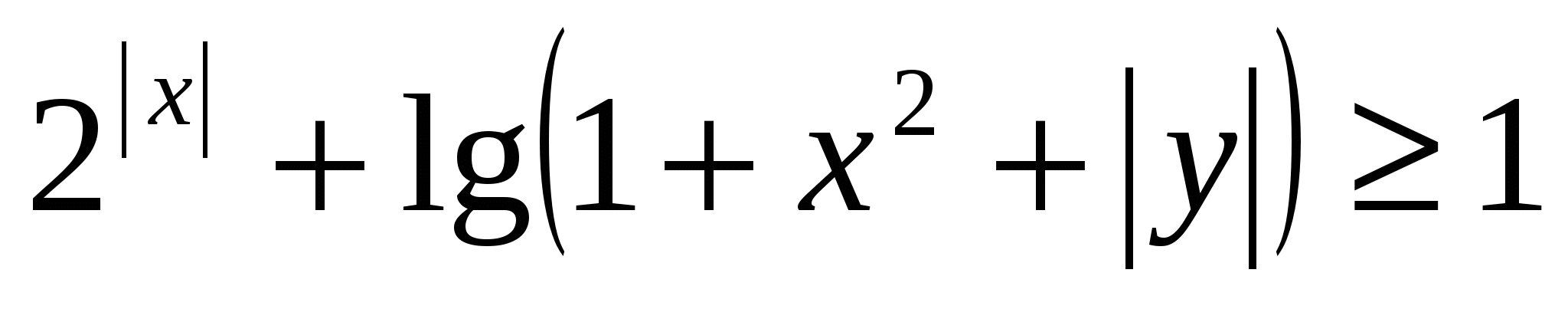 .
.
И сходное уравнение имеет корни лишь в том случае, если cosy=1,
сходное уравнение имеет корни лишь в том случае, если cosy=1,
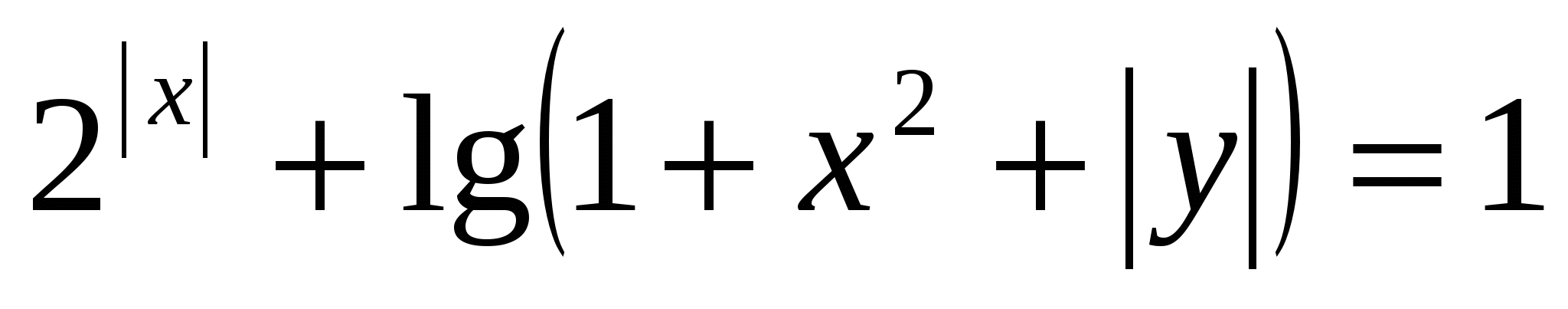
т огда cosy =1
огда cosy =1
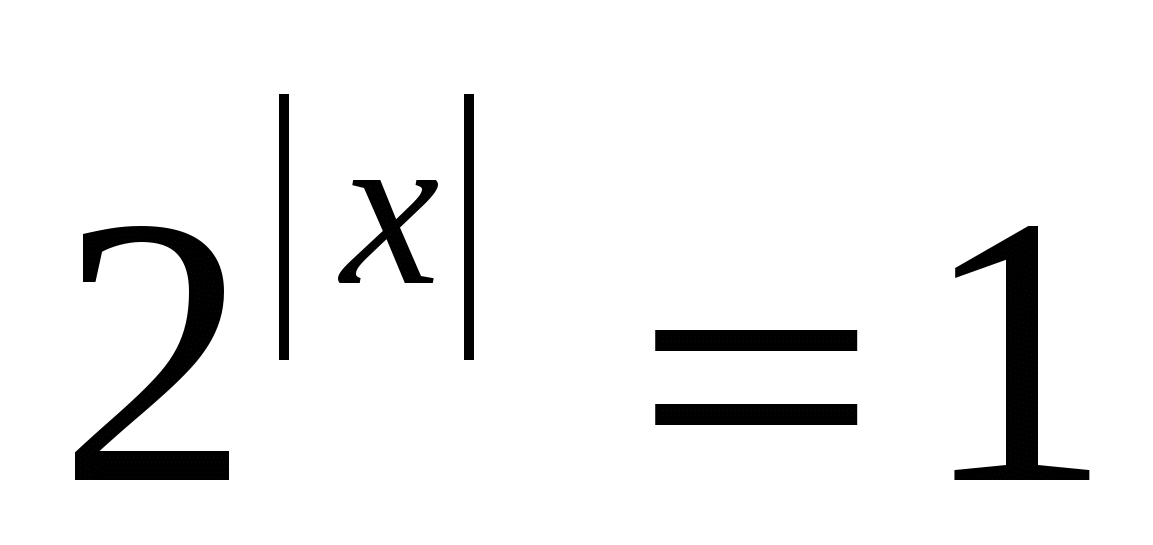
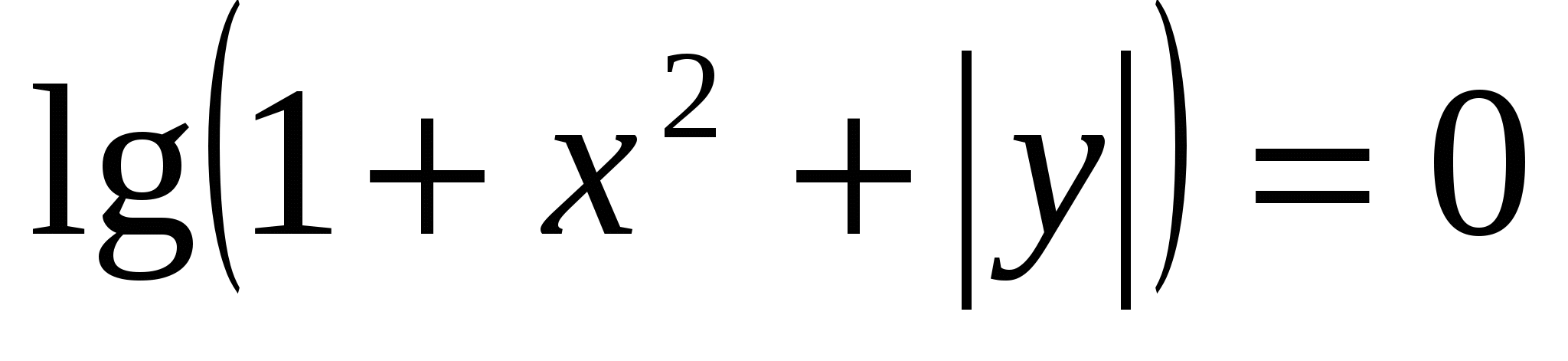 значит х=0, у=0.
значит х=0, у=0.
Ответ: (0;0).
Использование монотонности функций при решении уравнений.
С каждым уравнением связаны конструирующие их аналитические выражения. Последние в свою очередь могут задавать функции одной или нескольких переменных. Поэтому присутствие функций, а точнее их свойства, не могут не влиять на решения задач такого рода. Просто в одних случаях мы как бы негласно используем свойства функций, в других - явно ссылаемся на них. Порой «гласное» смещение акцентов в сторону свойств функций может оказать существенную пользу в поиске рациональных идей решения.
Очень часто мы встречаемся с такими уравнениями, в которых методом подбора легко определить корень, чаще всего один. Казалось бы, все просто, но ведь решить уравнение, это значит не только найти его корень, но и доказать, что он единственный. Столкнувшись с этим, многие начинают решать это уравнение стандартным способом, который может оказаться запутанным и сложным. Но если применить свойства монотонности функций, то можно многие подобные уравнения решать более рационально.
Основная идея такова: если f(x) монотонно возрастает, а g(x) монотонно убывает, то уравнение f(x)=g(x) имеет не более одного решения, причем если х=х0- решение этого уравнения, то при х >х0 (х входит в область определения обеих функций f(x) и g(x)) будет f(x)>g(x) , а при х<x0 будет f(x)<g(x).
Подтвердим сказанное примерами:
1)Решить уравнение:3х+4х=7х.
Решение: разделим обе части уравнения на 7х, ![]() очевидно, что х=1- корень уравнения и он единственный т.к. левая часть уравнения представляет собой монотонно убывающую функцию. Следовательно, каждое свое значение она принимает один раз.
очевидно, что х=1- корень уравнения и он единственный т.к. левая часть уравнения представляет собой монотонно убывающую функцию. Следовательно, каждое свое значение она принимает один раз.
Ответ: х=1.
2)Решить уравнение: 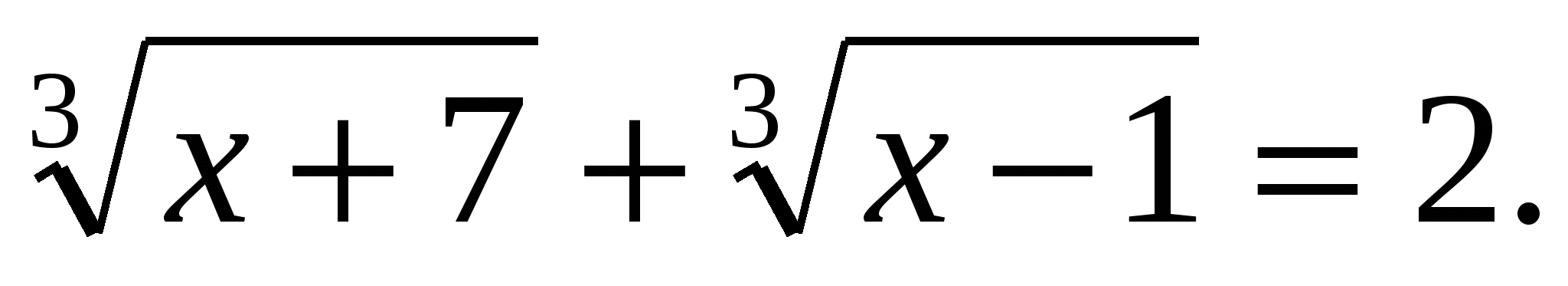
Решение: традиционный метод решения такого уравнения хорошо известен. Легко заметить, что х=1 корень. Левая часть уравнения задают возрастающую функцию, правя константу. Следовательно, данное уравнение может иметь не более одного корня.
Ответ: х=1.
3)Решить уравнение: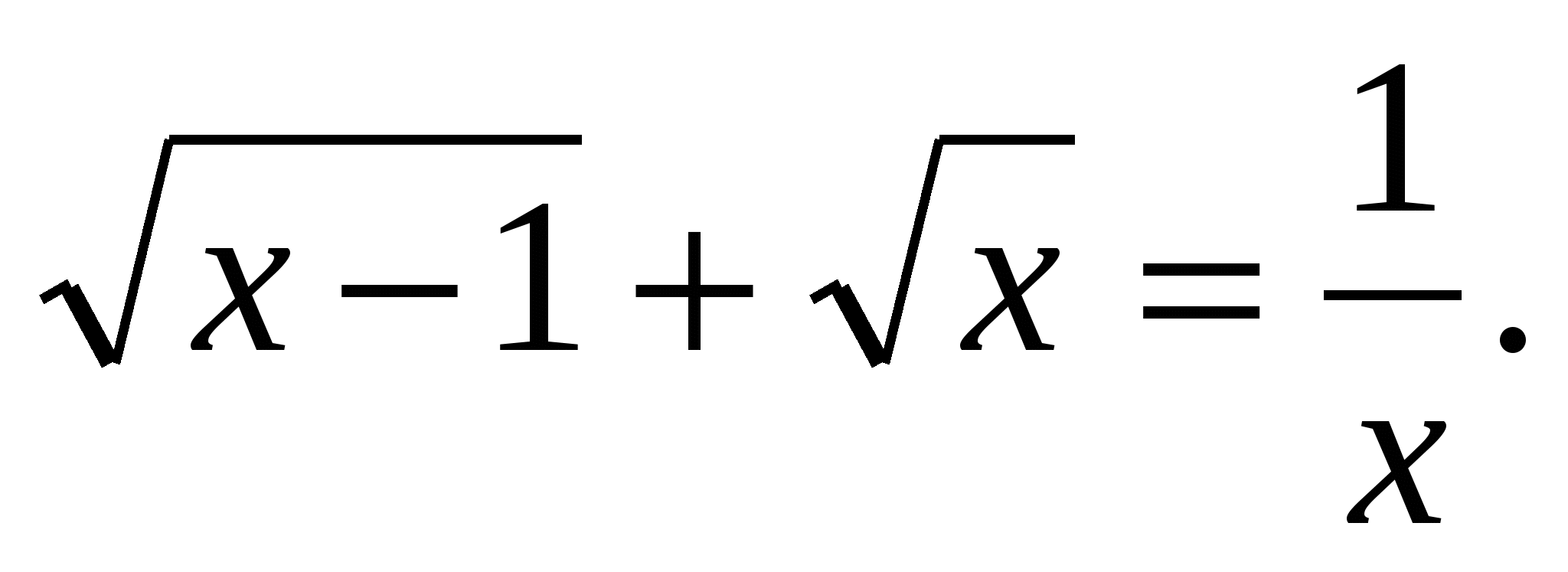
Решение: х=1, функция у=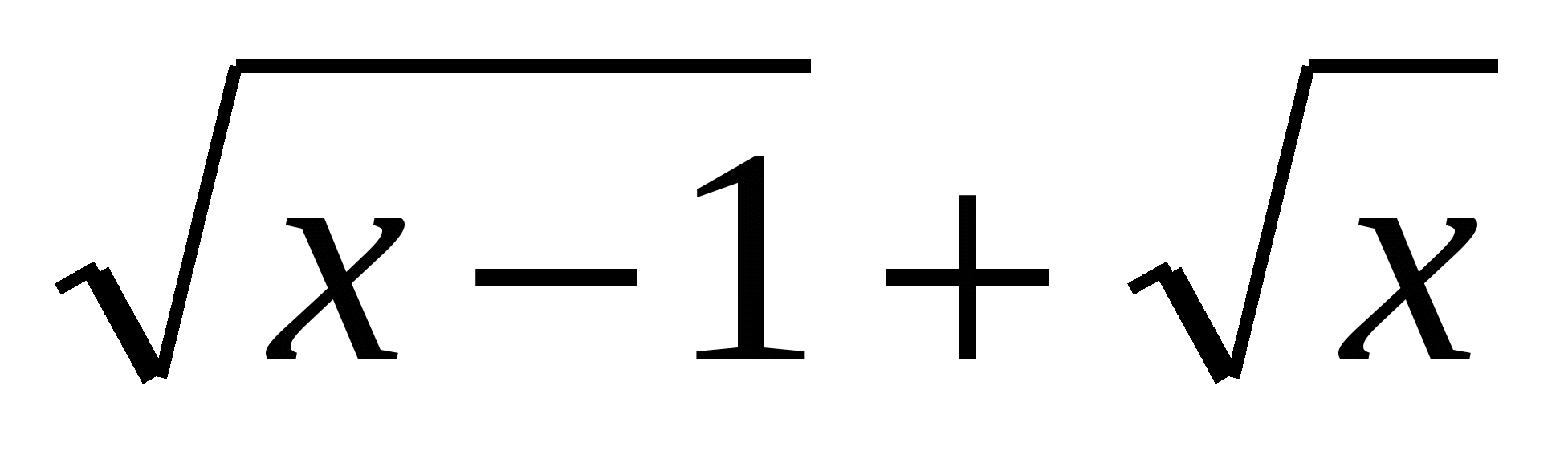 возрастает на множестве
возрастает на множестве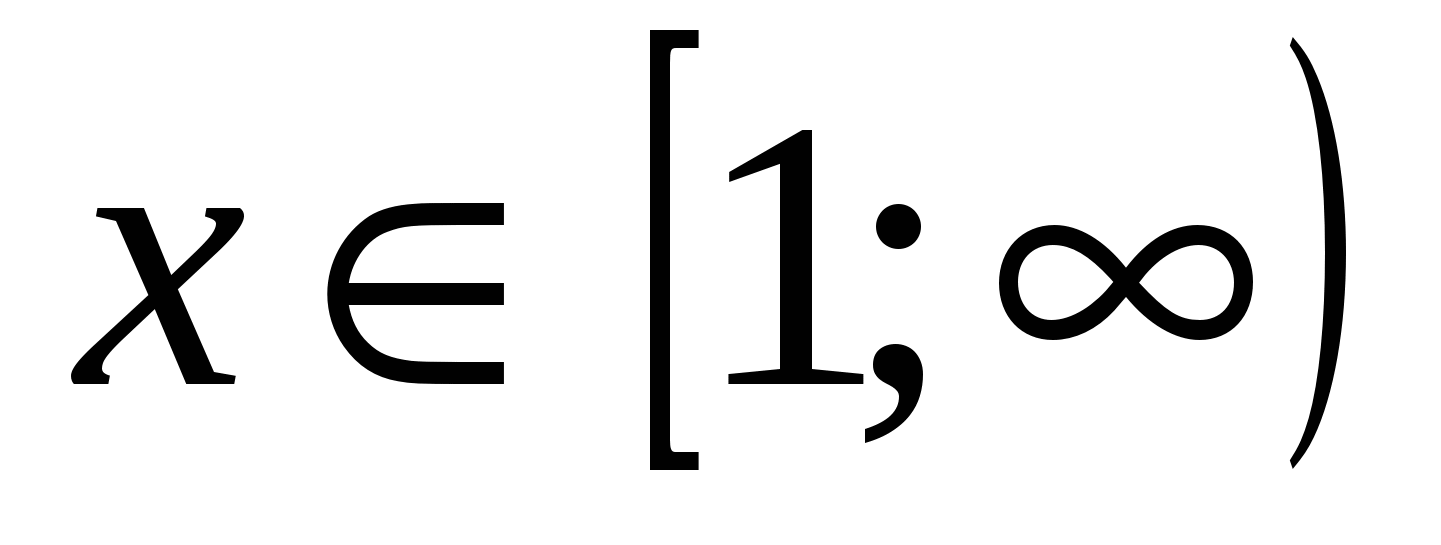
на этом же множестве у=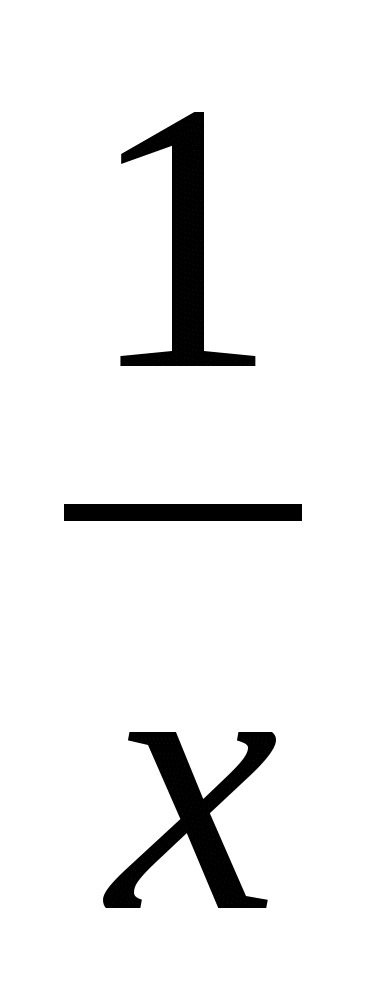 убывает. Поэтому х=1- единственный корень.
убывает. Поэтому х=1- единственный корень.
Ответ: х=1.
4)Решить уравнение: 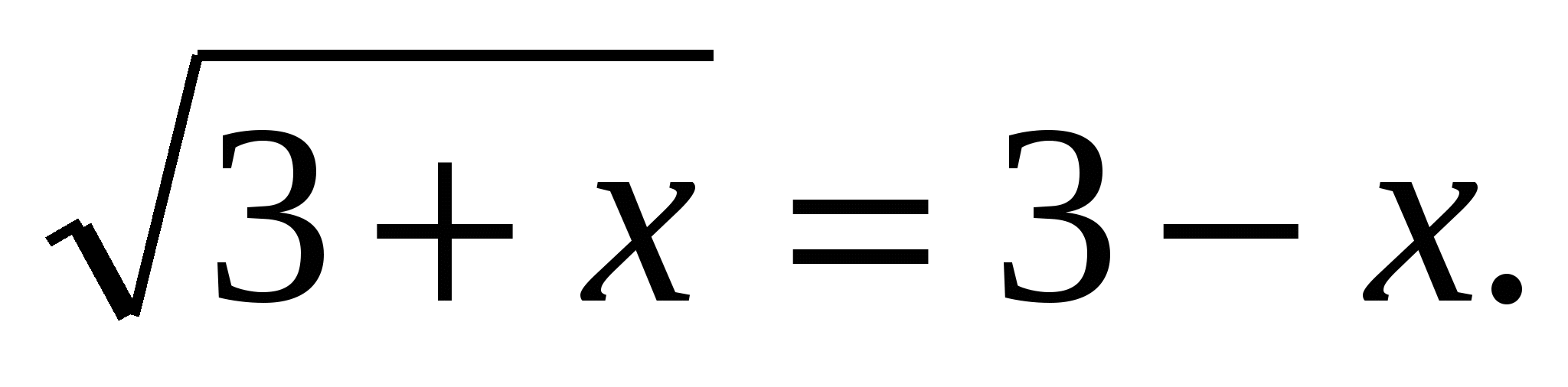
Решение: функция, расположенная в левой части уравнения, монотонно возрастающая на области орределения., а функция, стоящая в правой части, убывает. Следовательно, данное уравнение имеет не более одного корня. Значение корня легко подбирается х=1.
Ответ: х=1.
5) Решить уравнение: 3х-1=5-х.
Решение: х=2 единственный корень т.к. у=3х-1-монотонно возрастающая функция, а у=5-х - монотонно убывающая.
Ответ: х=2.
6)Решить уравнение: 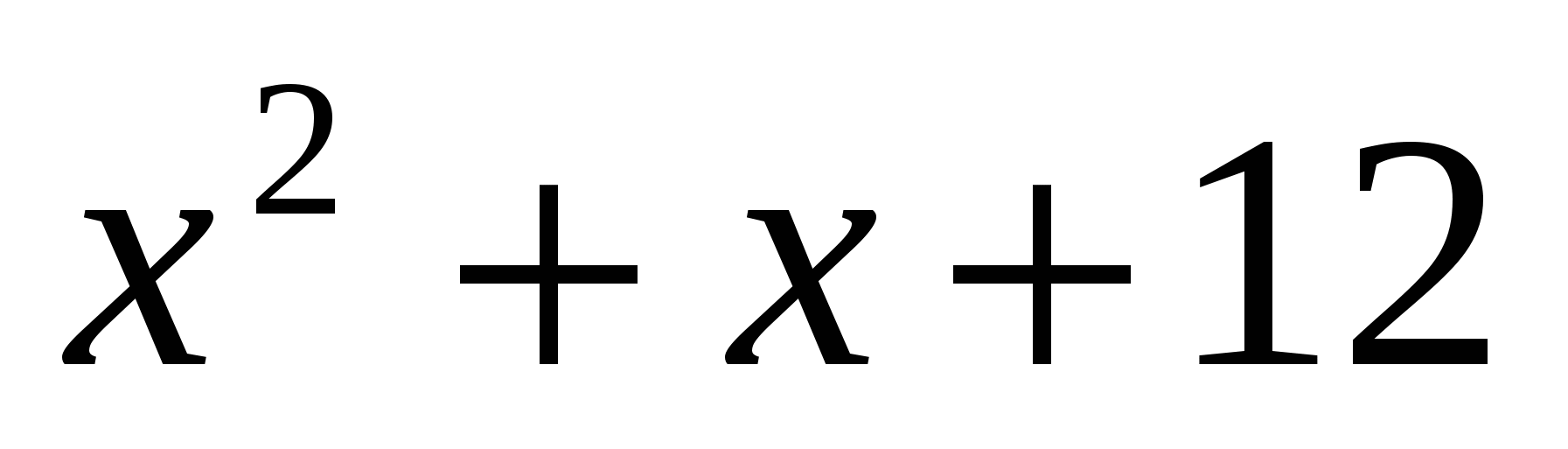
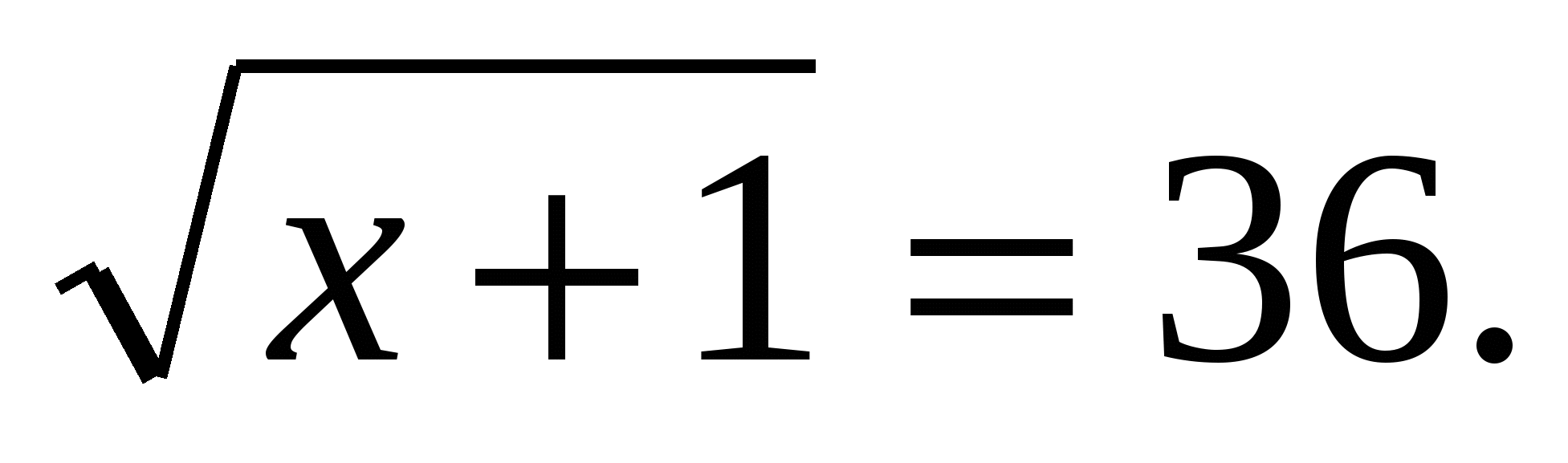
Решение: это уравнение легко «превратить» в рациональное четвертой степени. Поиск корней последнего затруднителен, и учащийся должен обладать высокой степенью изобретательности, чтобы справиться с этой задачей. Выберем путь менее традиционный: несложно обнаружить, что х=3 - корень уравнения. Область определения уравнения 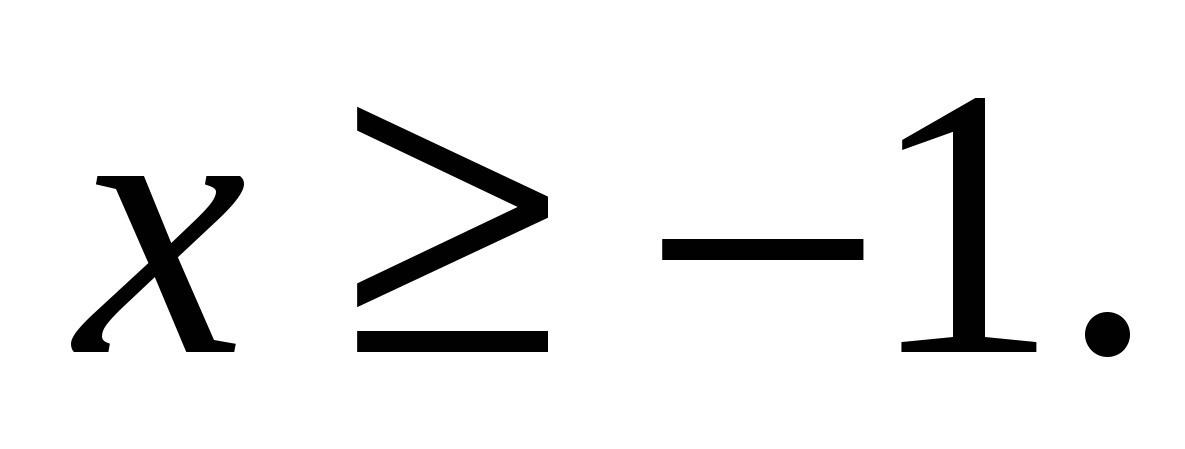 Но теперь, в отличии от ранее рассмотренных левая часть уравнения не задает монотонную функцию. Однако на промежутке
Но теперь, в отличии от ранее рассмотренных левая часть уравнения не задает монотонную функцию. Однако на промежутке 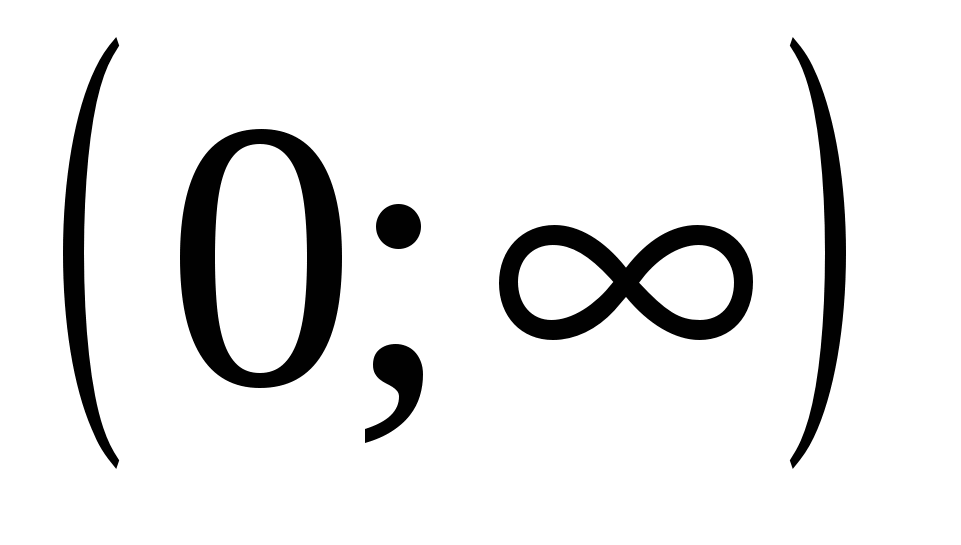 указанная функция возрастает и х=3 принадлежит этому промежутку. Значит, на промежутке
указанная функция возрастает и х=3 принадлежит этому промежутку. Значит, на промежутке 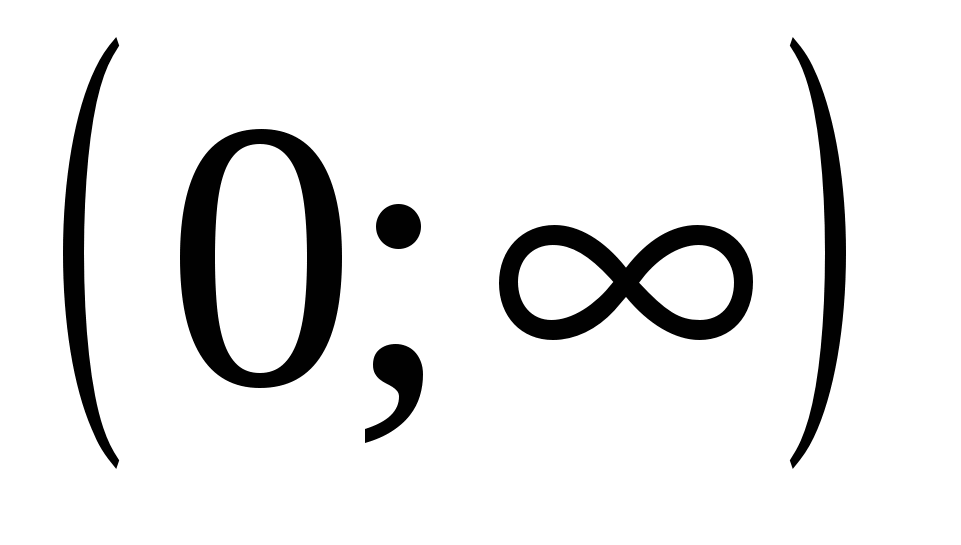 данное уравнение имеет единственный корень. Осталось исследовать поведение функции у=
данное уравнение имеет единственный корень. Осталось исследовать поведение функции у=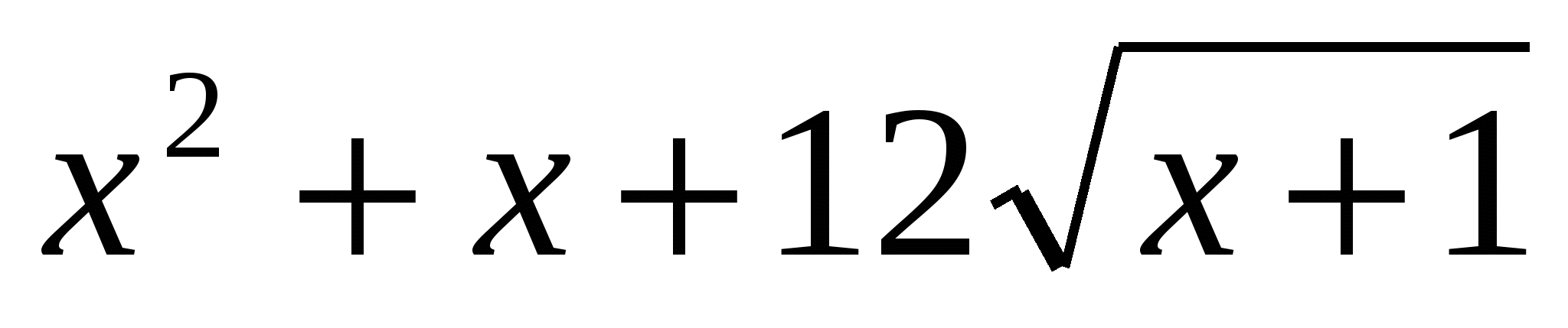 на отрезке
на отрезке 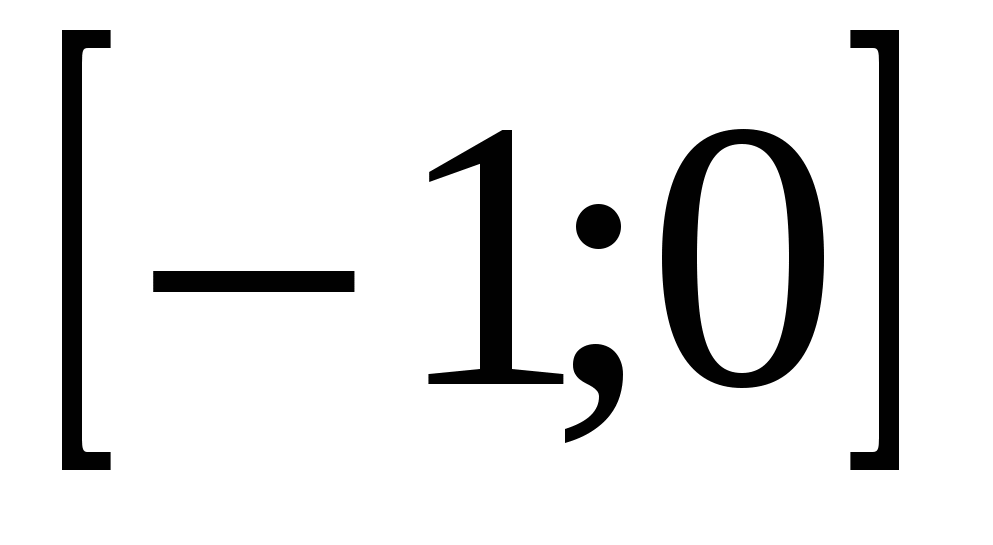 при
при 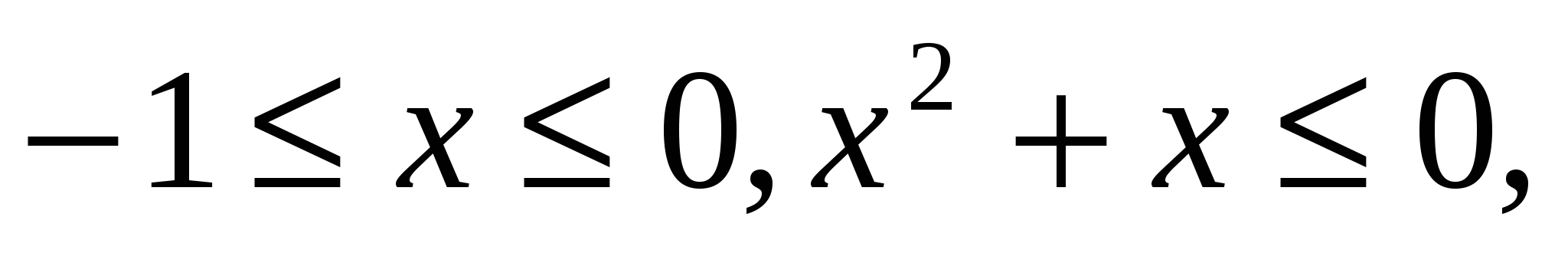
а 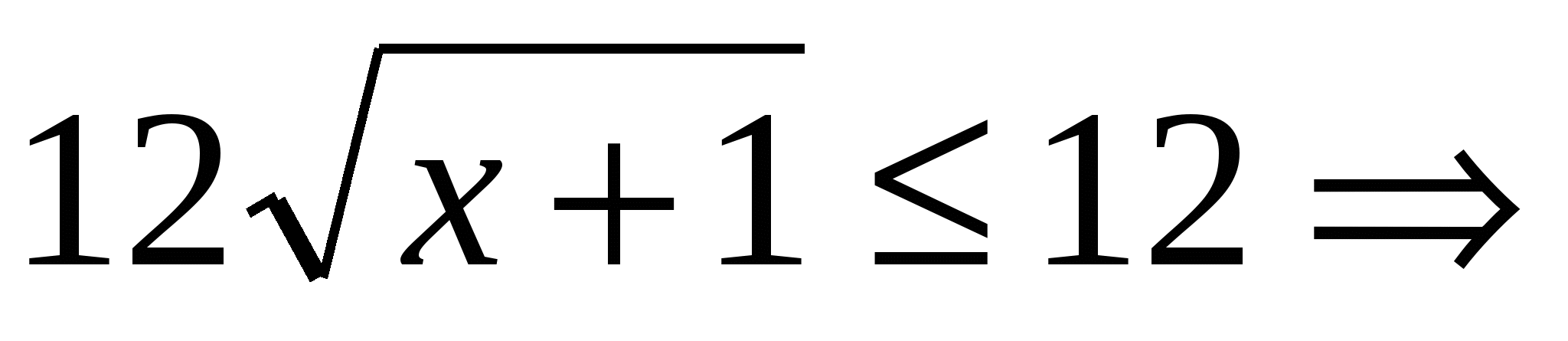 на отрезке
на отрезке 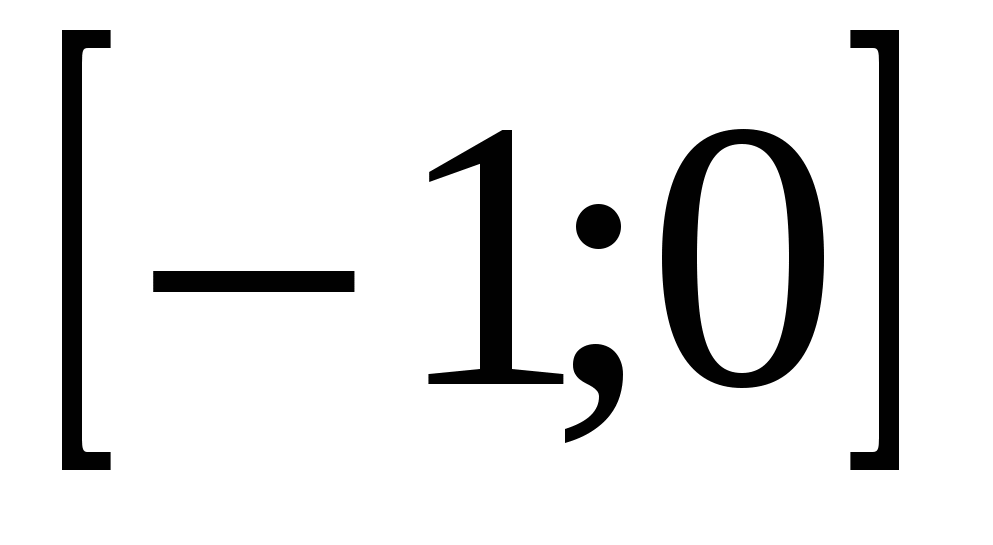 исходное уравнение корней не имеет.
исходное уравнение корней не имеет.
Ответ: х=3.
7)Решить уравнение:4 33х+1+4=5 29х .
.
Решение: казалось бы это уравнение нельзя решить тем же способом,
что и предыдущие. Но если произвести замену 3х=t, то основываясь на монотонности функций можно решить уравнение относительно t,а потом найти корень исходного уравнения.
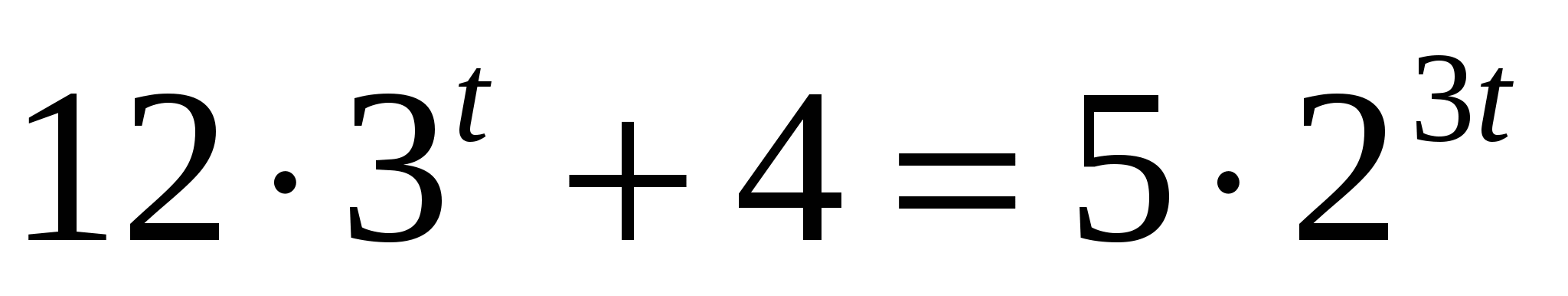 , t=1 является корнем. Проверим: 12 31+4=36+4=40 ,5 23=40, 40=40 t=1 корень, докажем что он единственный, для этого изменим вид уравнения.
, t=1 является корнем. Проверим: 12 31+4=36+4=40 ,5 23=40, 40=40 t=1 корень, докажем что он единственный, для этого изменим вид уравнения.
12 3t+4=5 23t/3t
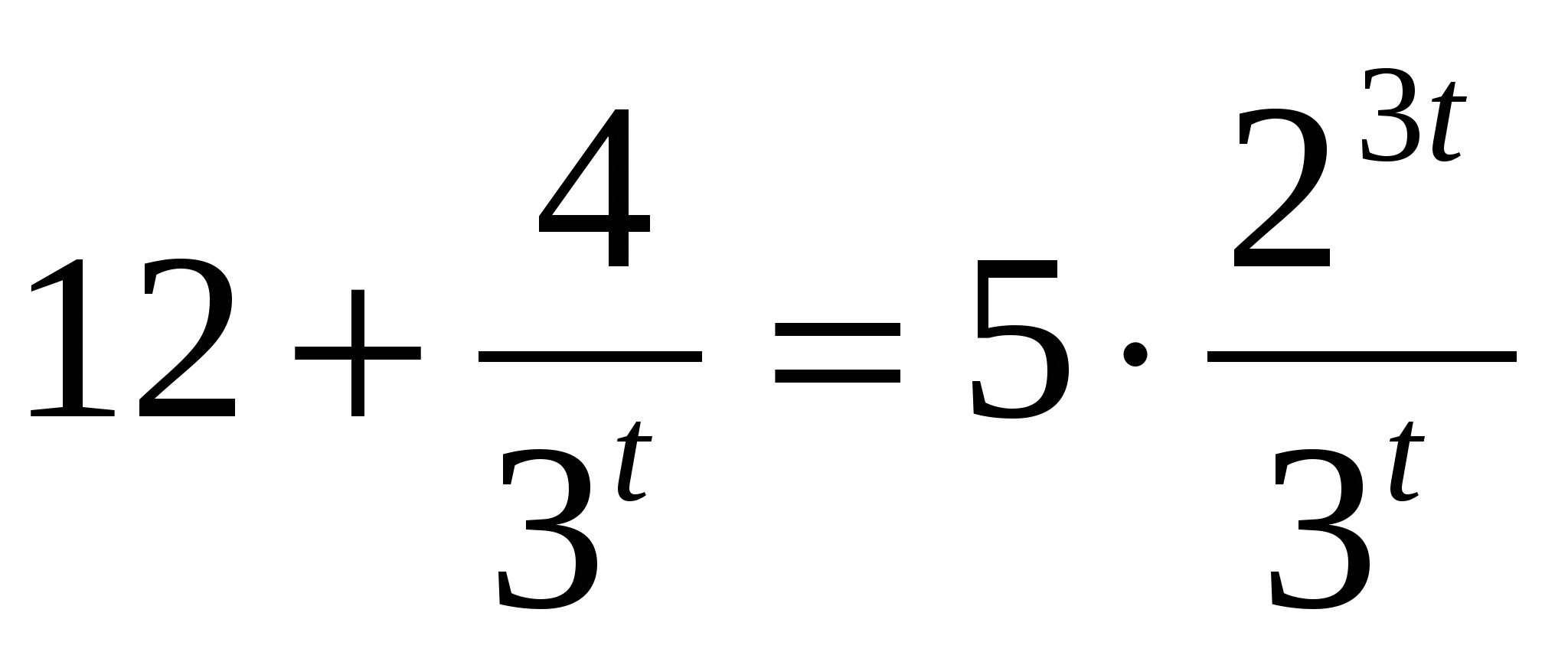 Функция у=5
Функция у=5 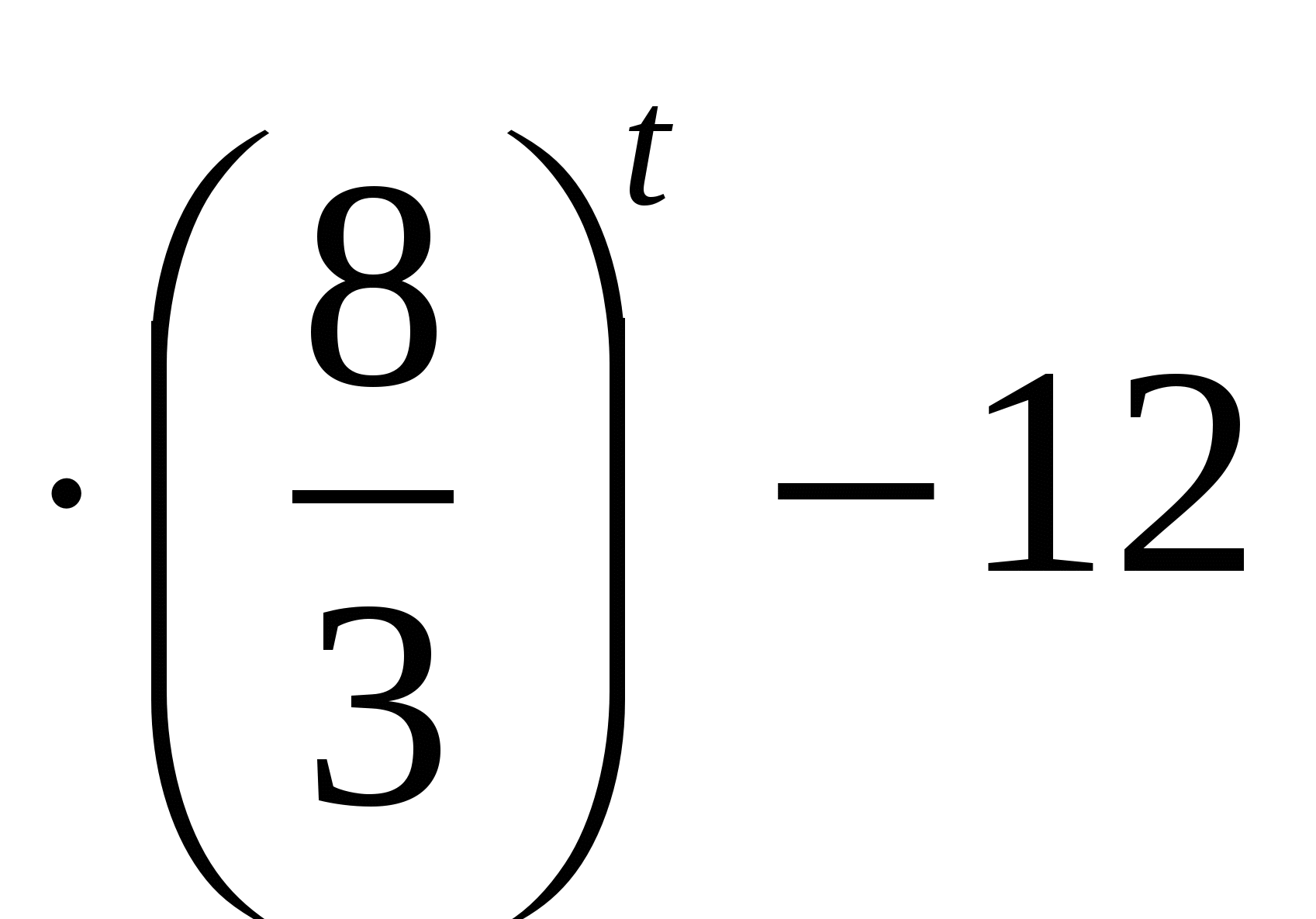 монотонно возрастающая, а у=
монотонно возрастающая, а у=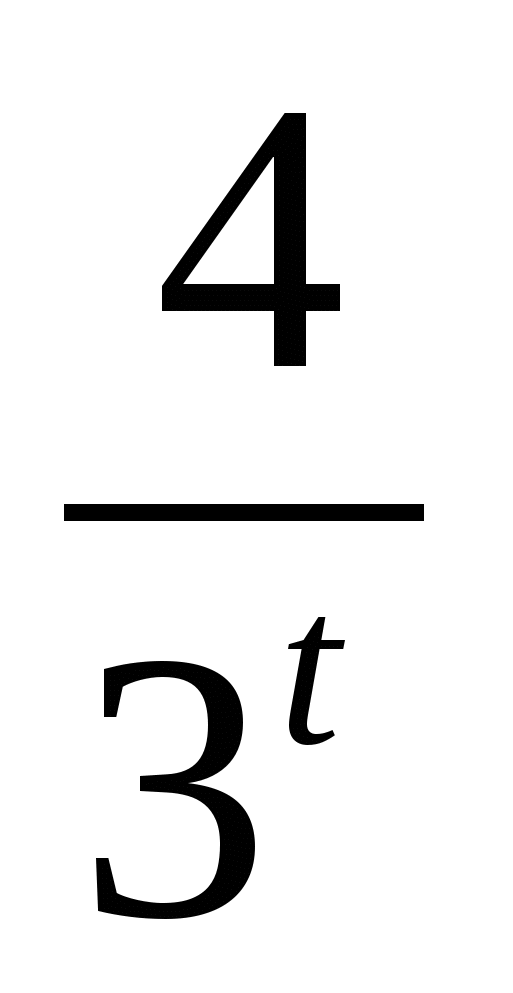 монотонно убывающая при любом t, следовательно, уравнение относительно t может иметь только один корень t =1, значит, исходное уравнение имеет только один корень х=
монотонно убывающая при любом t, следовательно, уравнение относительно t может иметь только один корень t =1, значит, исходное уравнение имеет только один корень х=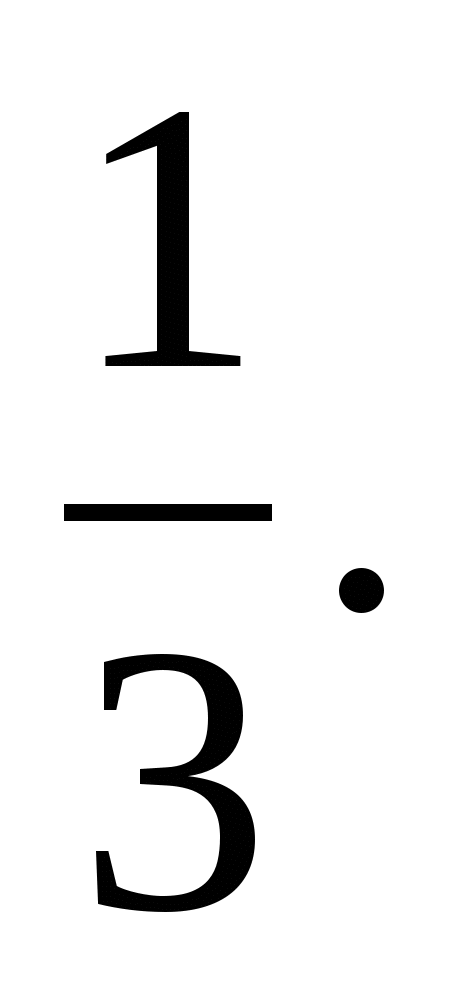
Ответ: х=![]()
Рассмотрим модификацию идеи: если f(x) монотонно возрастает, а g(x) монотонно убывает, то уравнение f(x)=g(x) имеет не более одного решения, она заключается в следующем: если f(x)- монотонная функция, то из равенства f(x)=f(у) следует, что х=у.
Используем эту идею при решении уравнений.
8)Решить уравнение log6-xlog2x=log7-xlog2(2x).
Решение: преобразуем уравнение: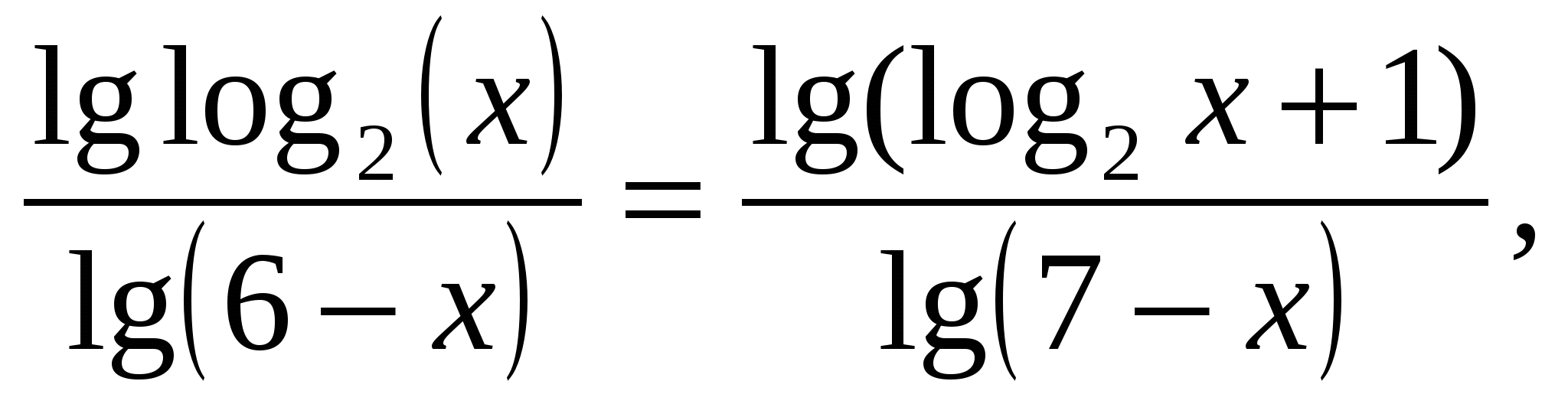
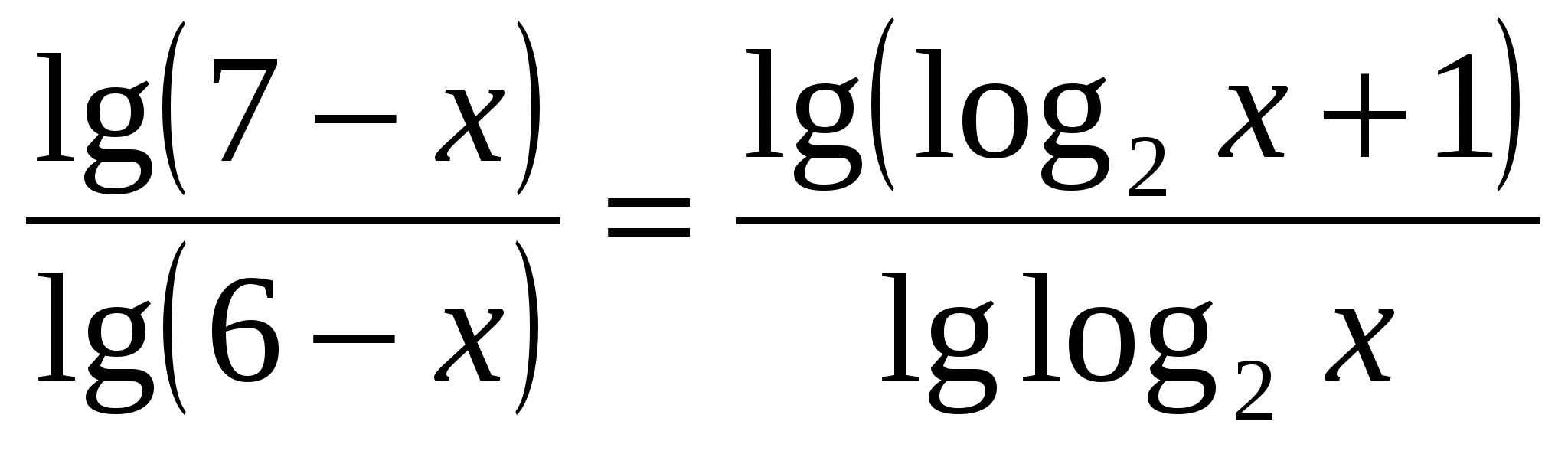
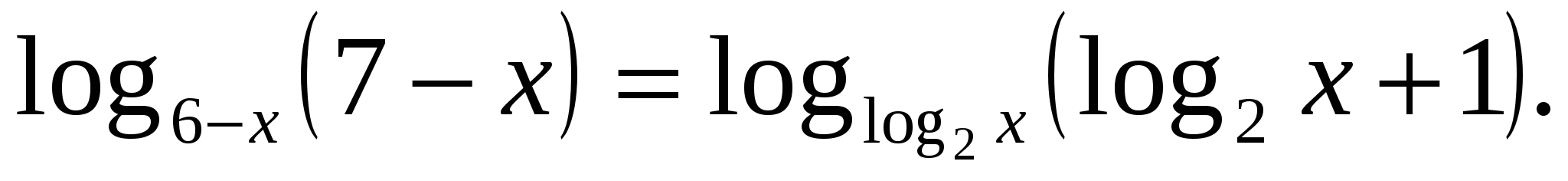
Рассмотрим функцию f(t)=logt(t+1). Докажем, что при t>1 эта функция монотонно убывает.
f(t)-1=logt(t+1)-1=logt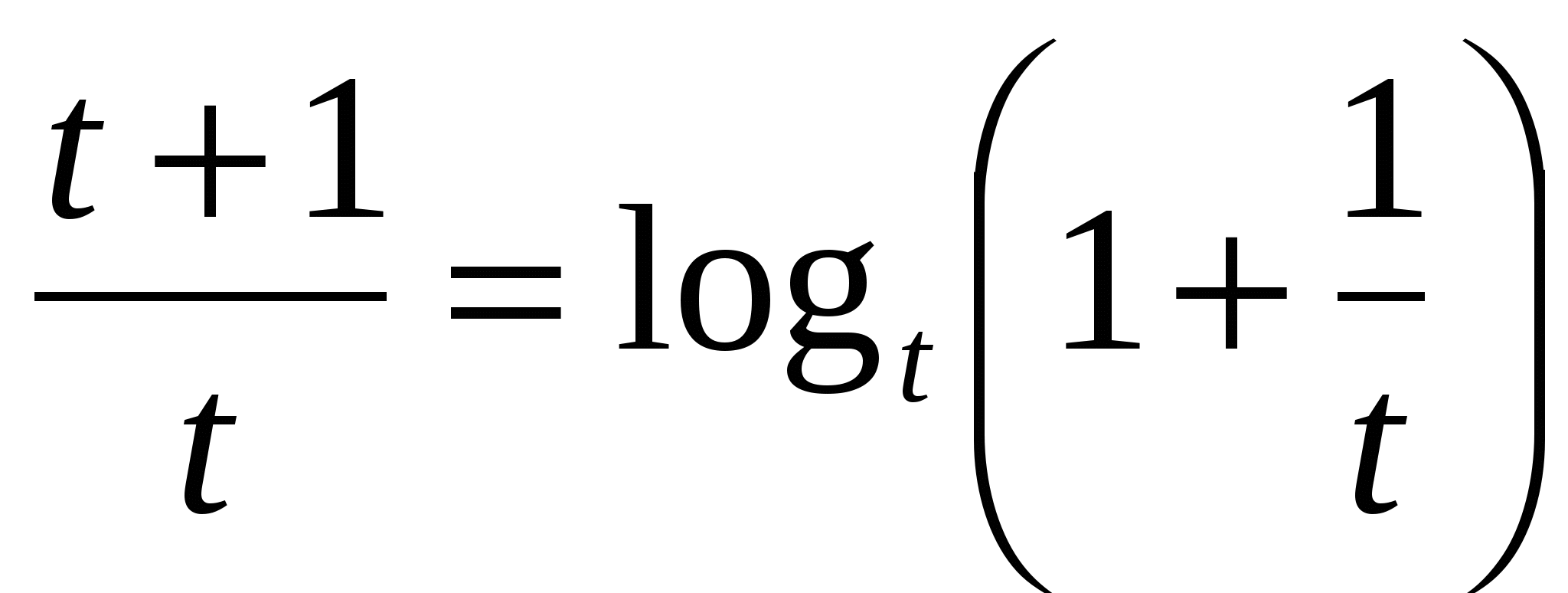 -получившаяся функция, очевидно, является убывающей( основание растет, под знаком логарифма функция убывает).
-получившаяся функция, очевидно, является убывающей( основание растет, под знаком логарифма функция убывает).
Наше уравнение имеет вид: f(6-x)=f(log2х), значит, log2х=6-х. Слева функция возрастающая, справа убывающая, следовательно, решение единственно, оно легко находится подбором: х=4. Ответ: х=4.
9) Решить уравнение 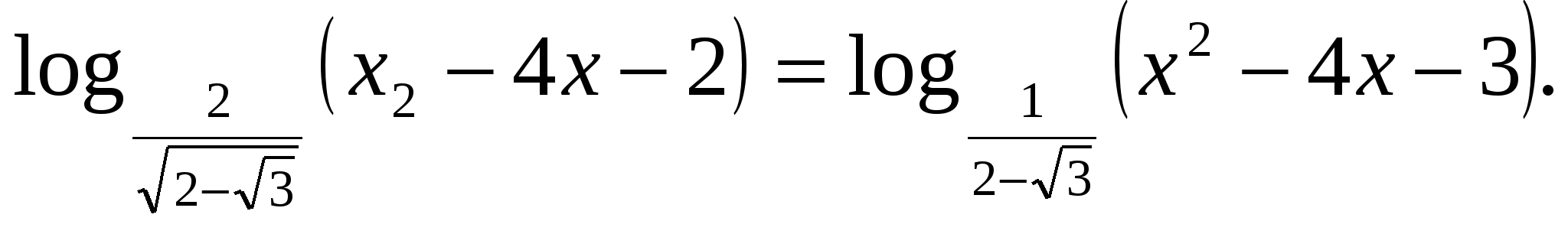
Решение: пусть х2-4х-2=t, t>0.
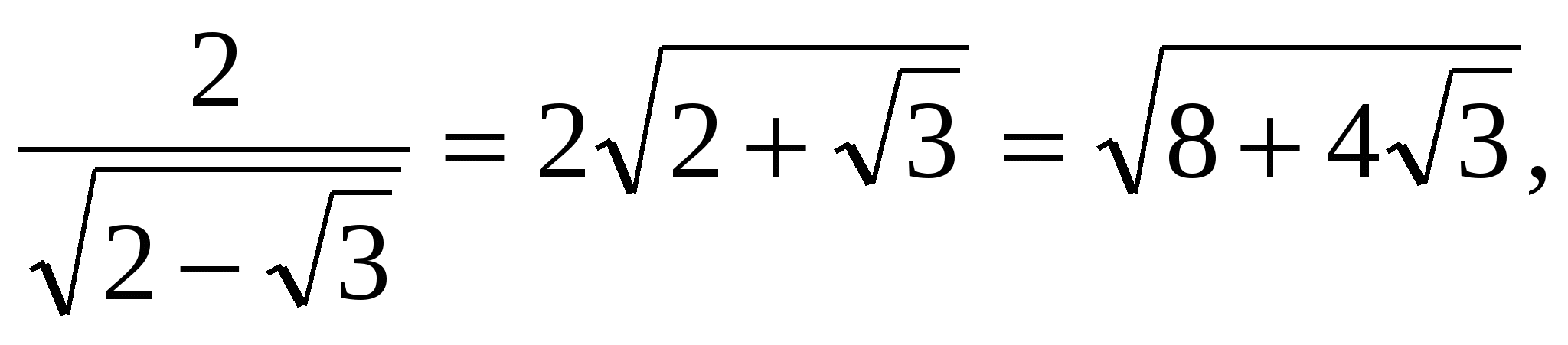
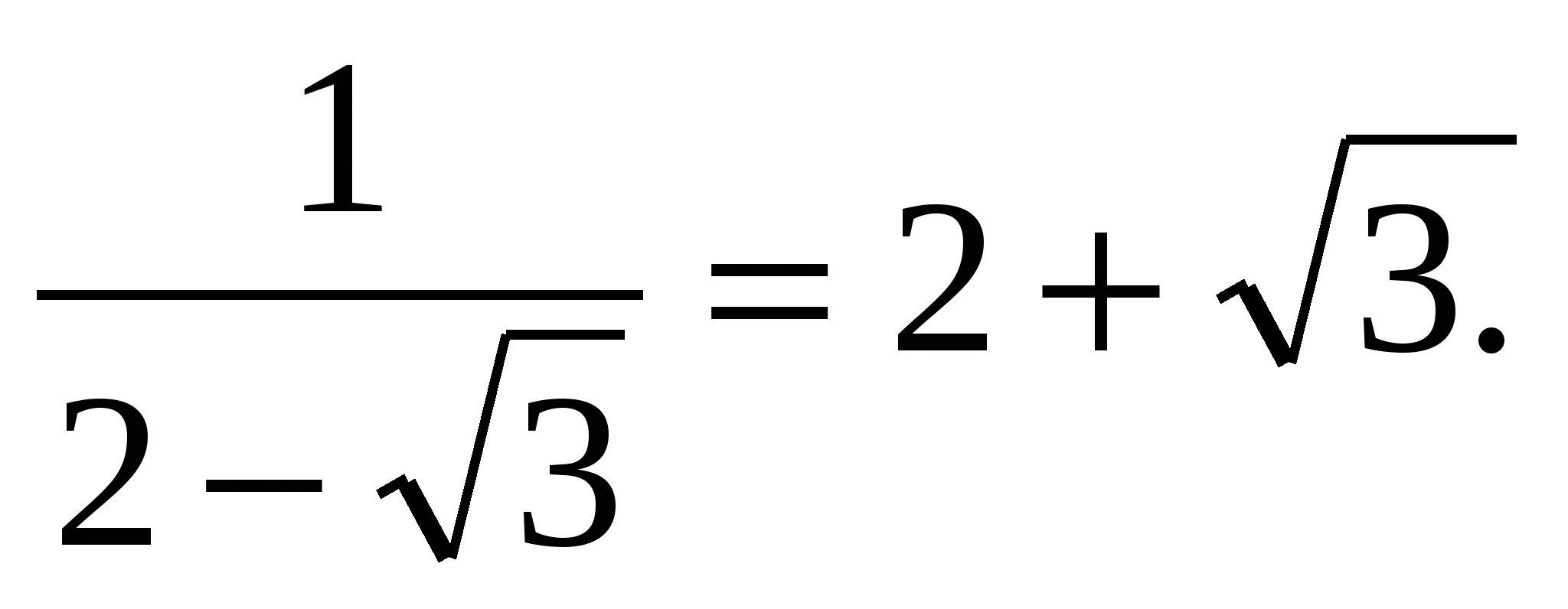
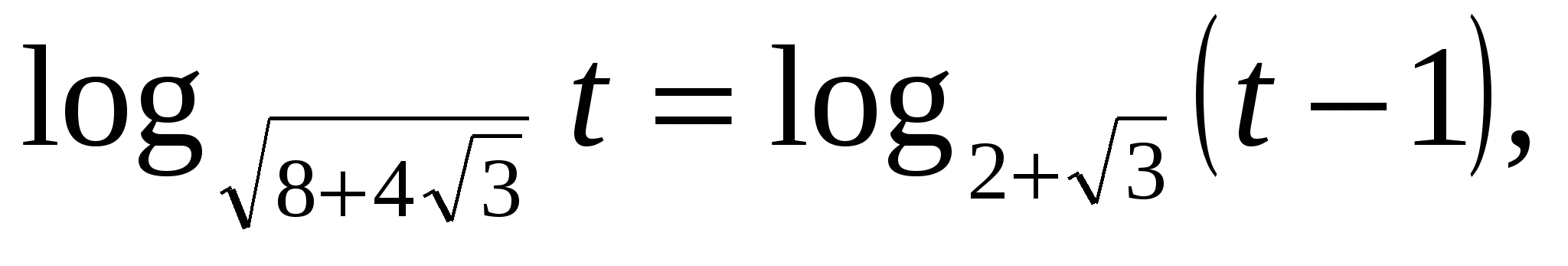
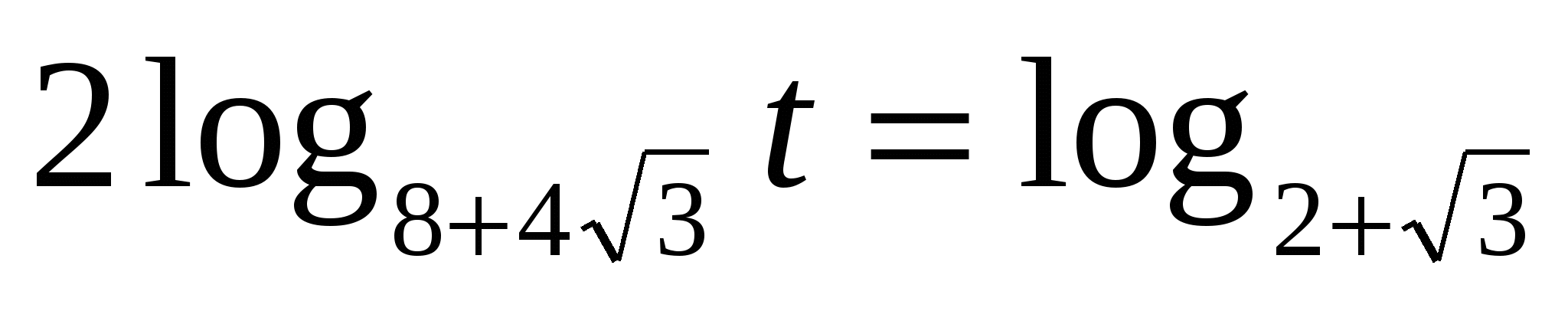 | : 2
| : 2
![]()
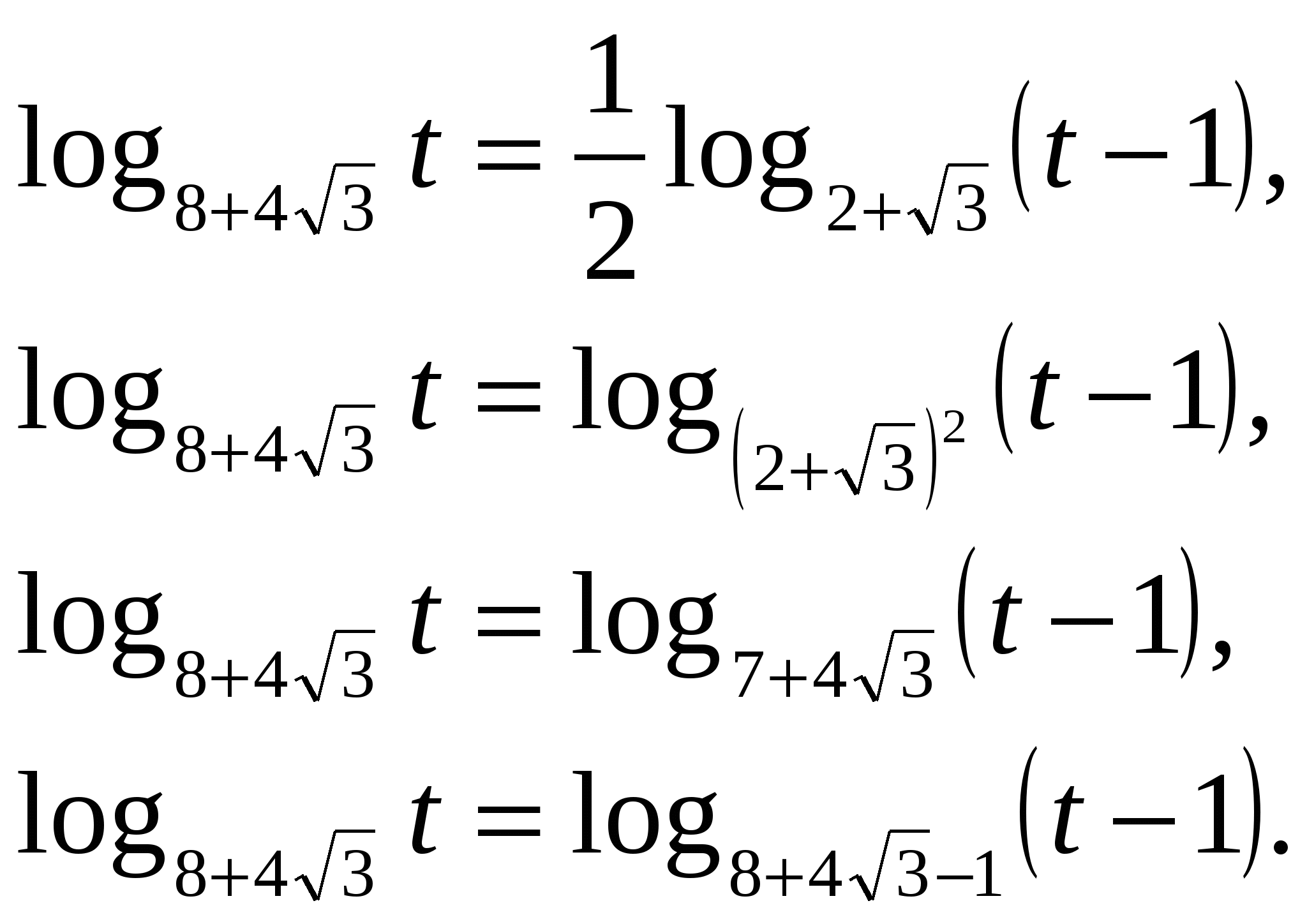
Пусть 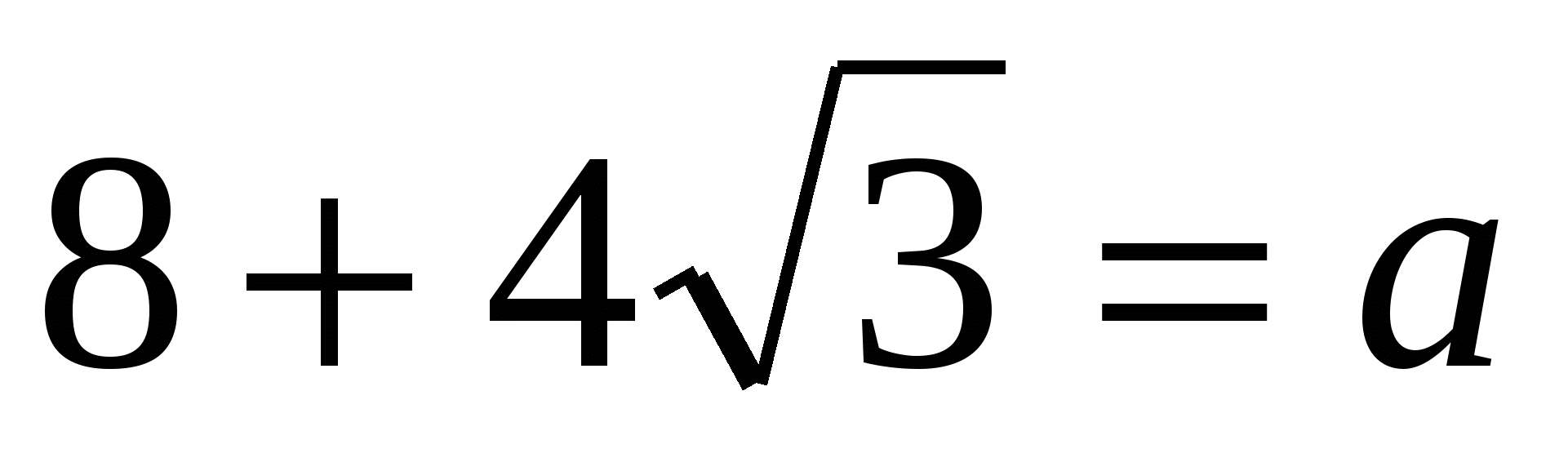 ,
, 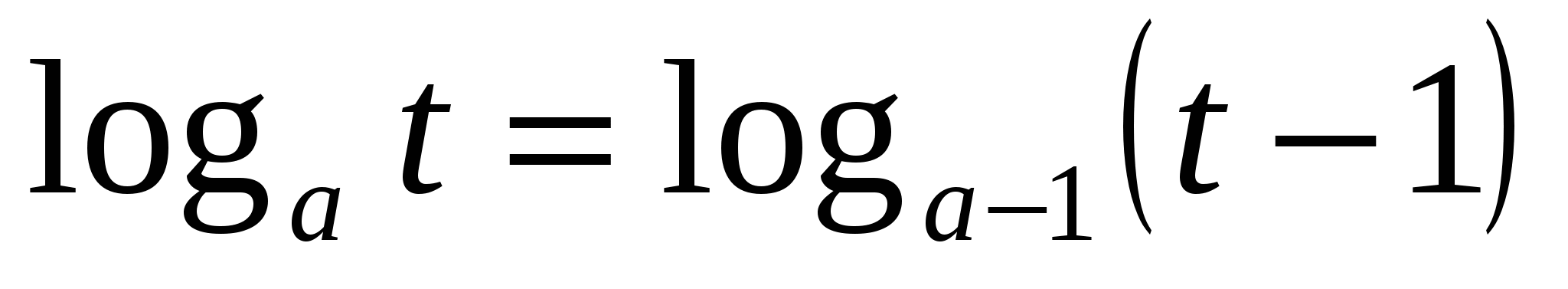
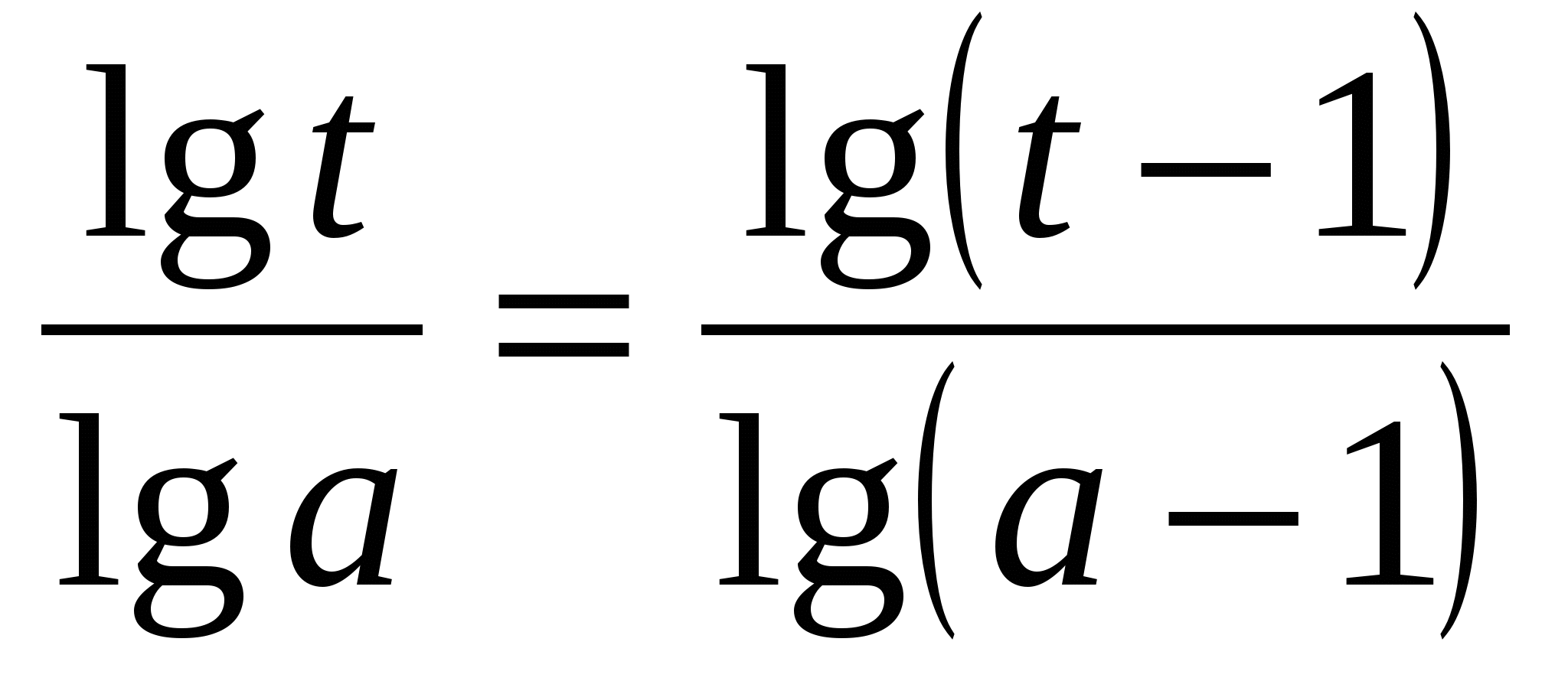 ,
, 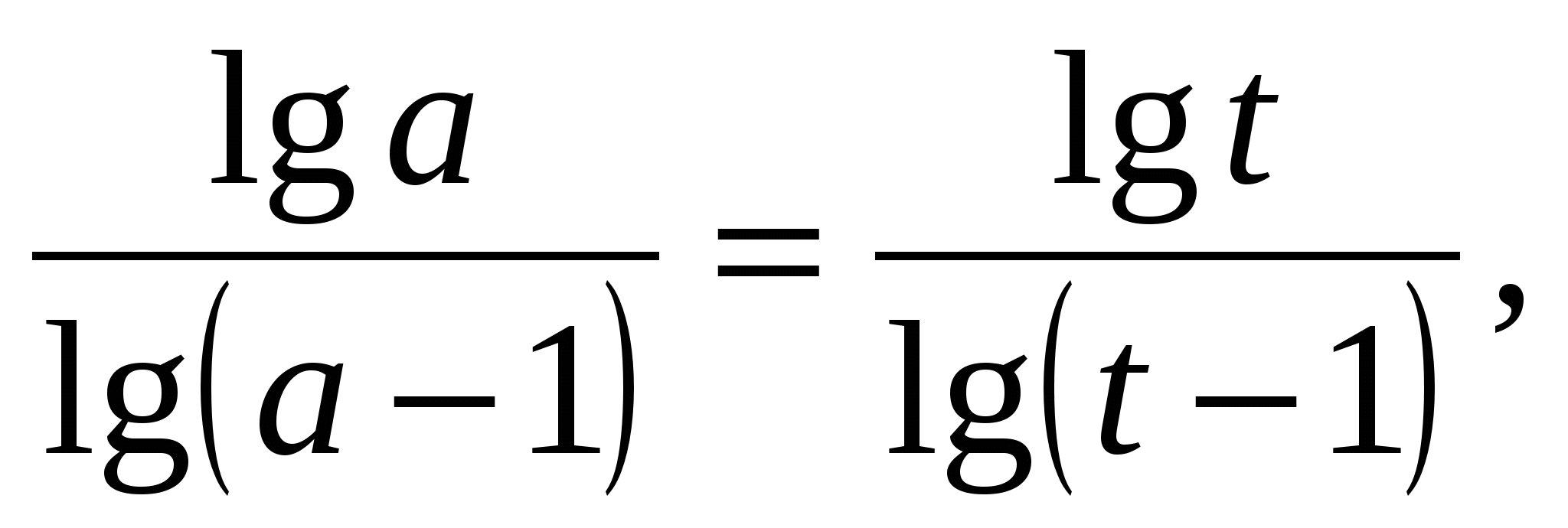
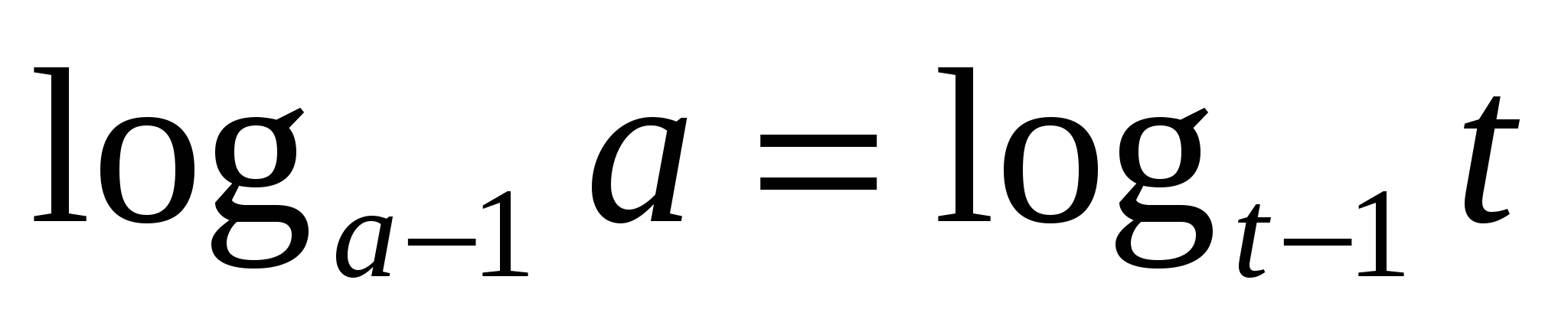 т.к. функция
т.к. функция 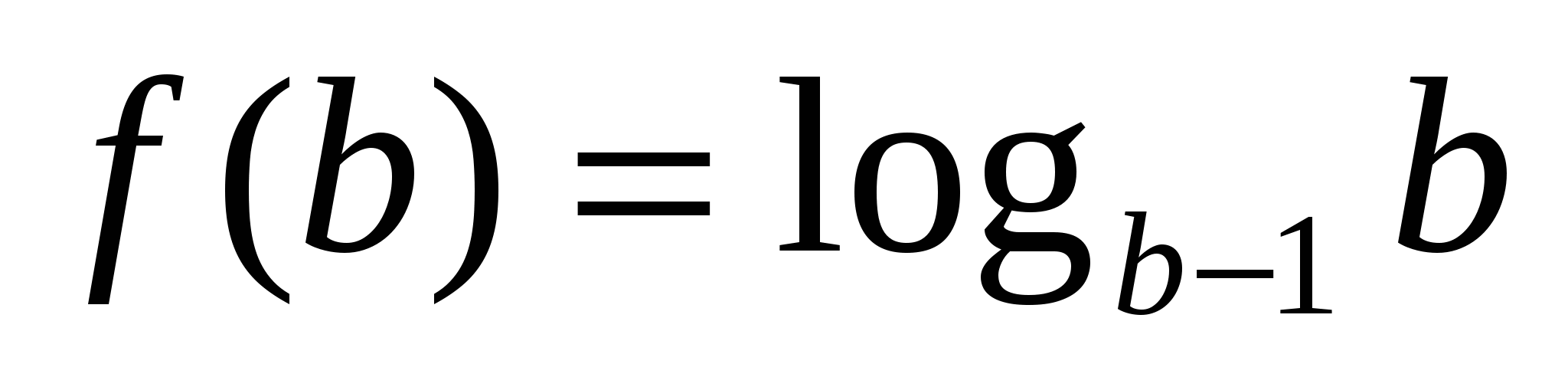 монотонна (это мы доказывали в предыдущем уравнении) то f(a)=f(t) равносильно a=t, т.е. получаем уравнение
монотонна (это мы доказывали в предыдущем уравнении) то f(a)=f(t) равносильно a=t, т.е. получаем уравнение
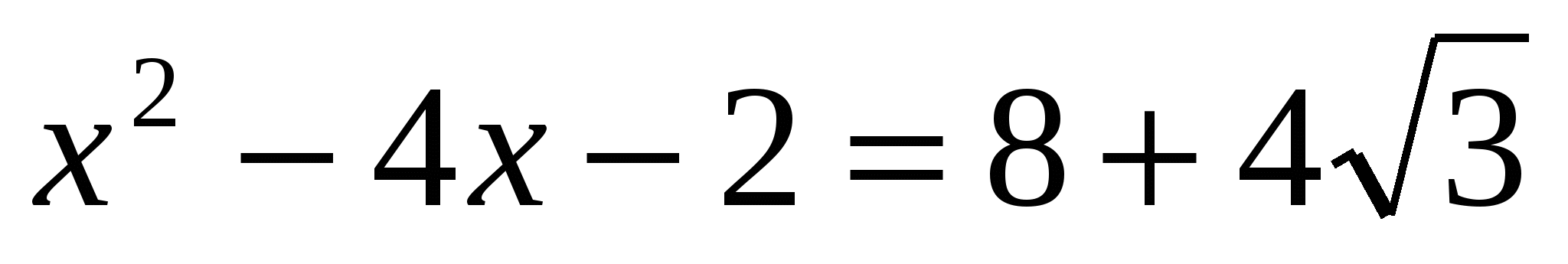
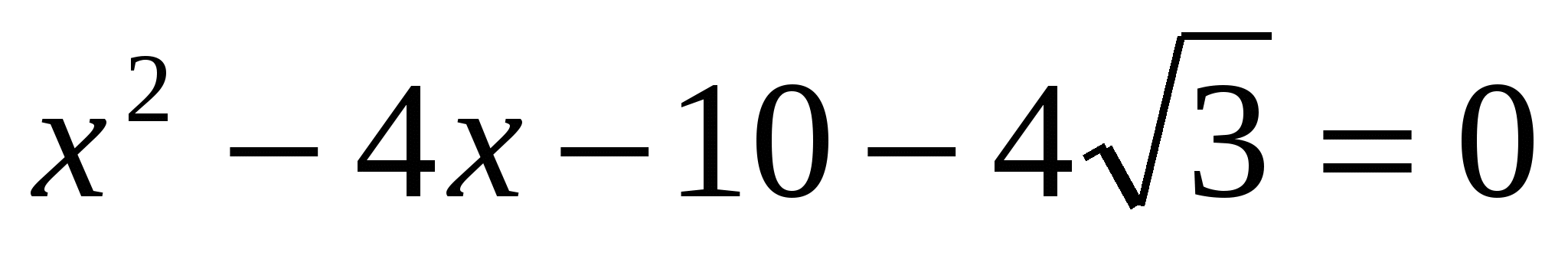
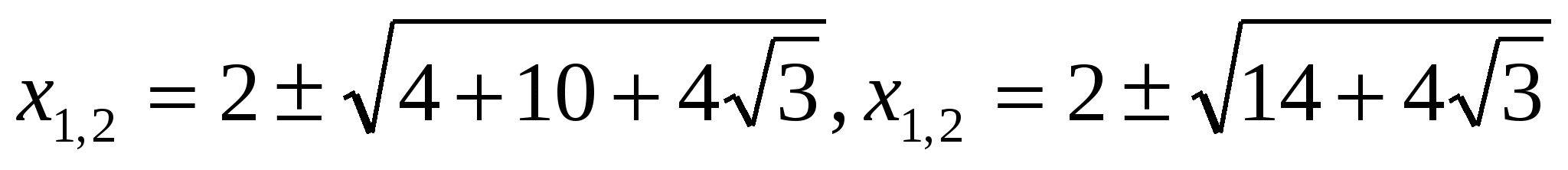 .
.
Ответ: 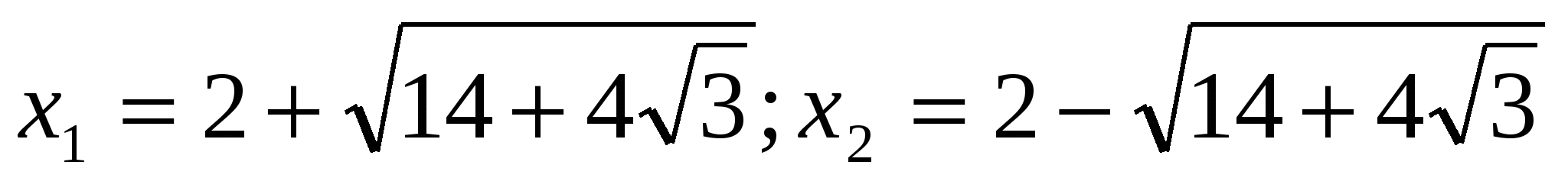 .
.
Использование эквивалентности при решении уравнений.
При решении уравнений вида f(f(x)) = x полезна бывает теорема: Если у=f(х) - монотонно возрастающая функция, то уравнения f(x)=x и f(f(x))=x эквивалентны.
Приведем несколько примеров использования этой теоремы.
1)Решить уравнение 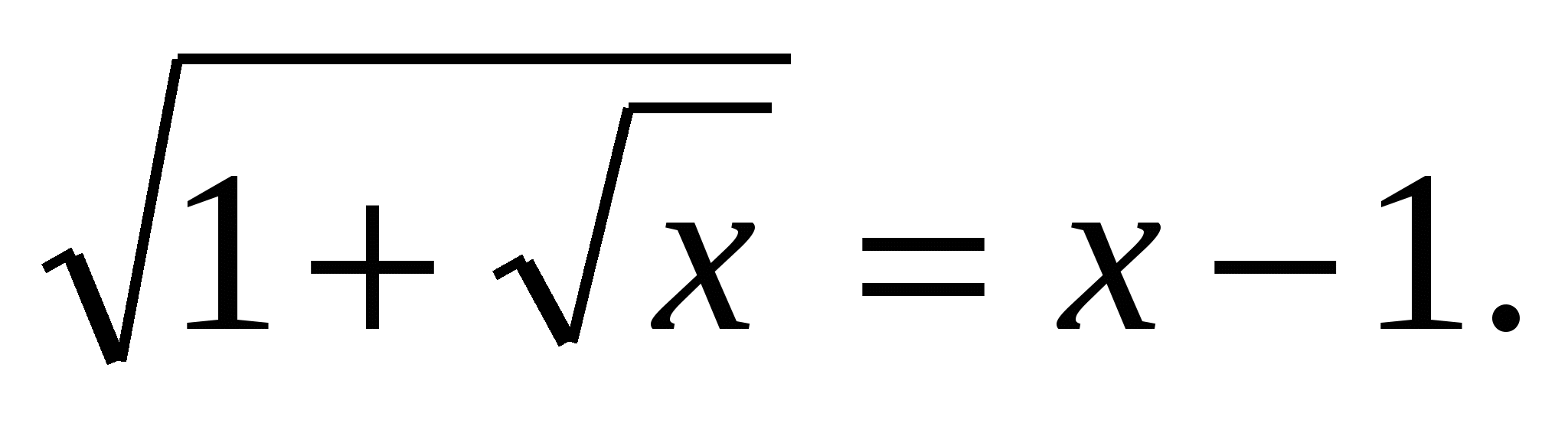
Решение: перепишем уравнение: 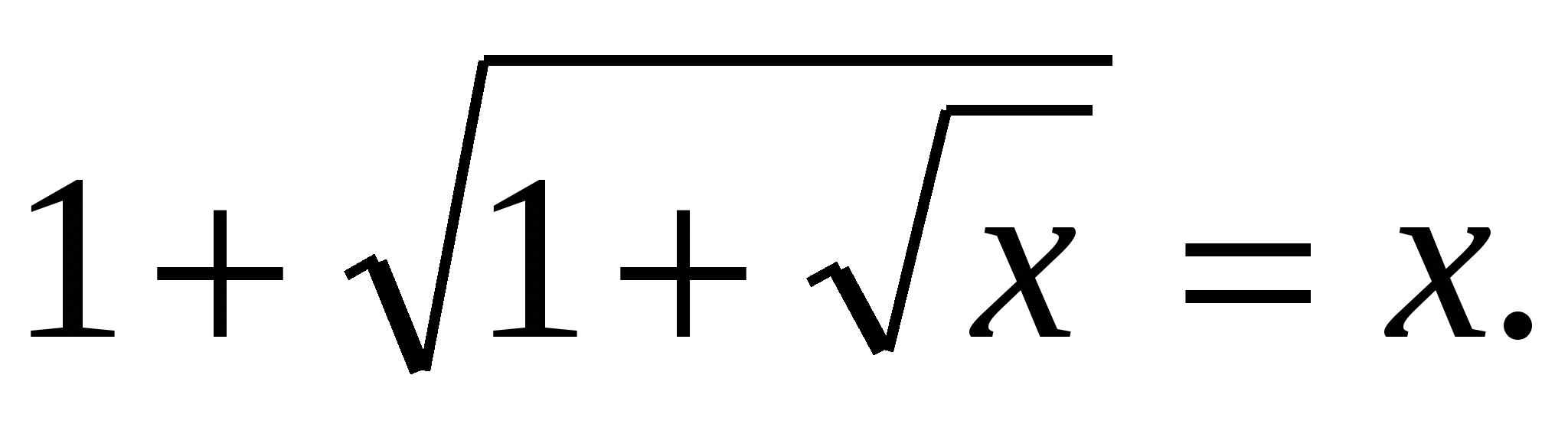 Рассмотрим функцию f(x)=1+
Рассмотрим функцию f(x)=1+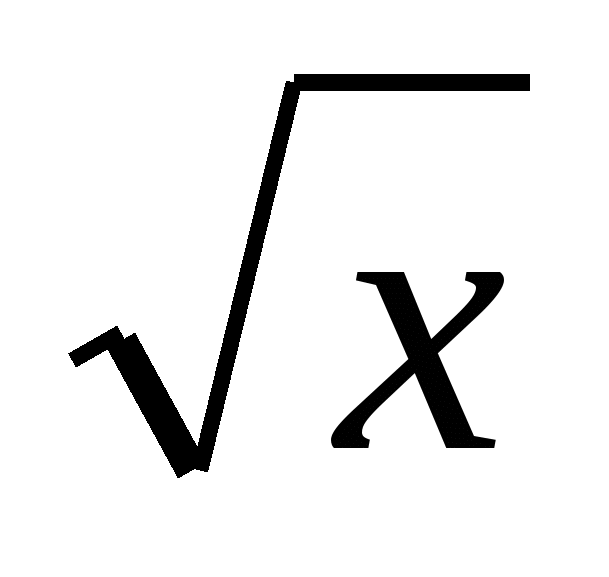 , эта функция монотонно возрастает. Имеем уравнение f(f(x))=x.
, эта функция монотонно возрастает. Имеем уравнение f(f(x))=x.
В соответствии с теоремой заменяем его эквивалентным уравнением f(x)=x или 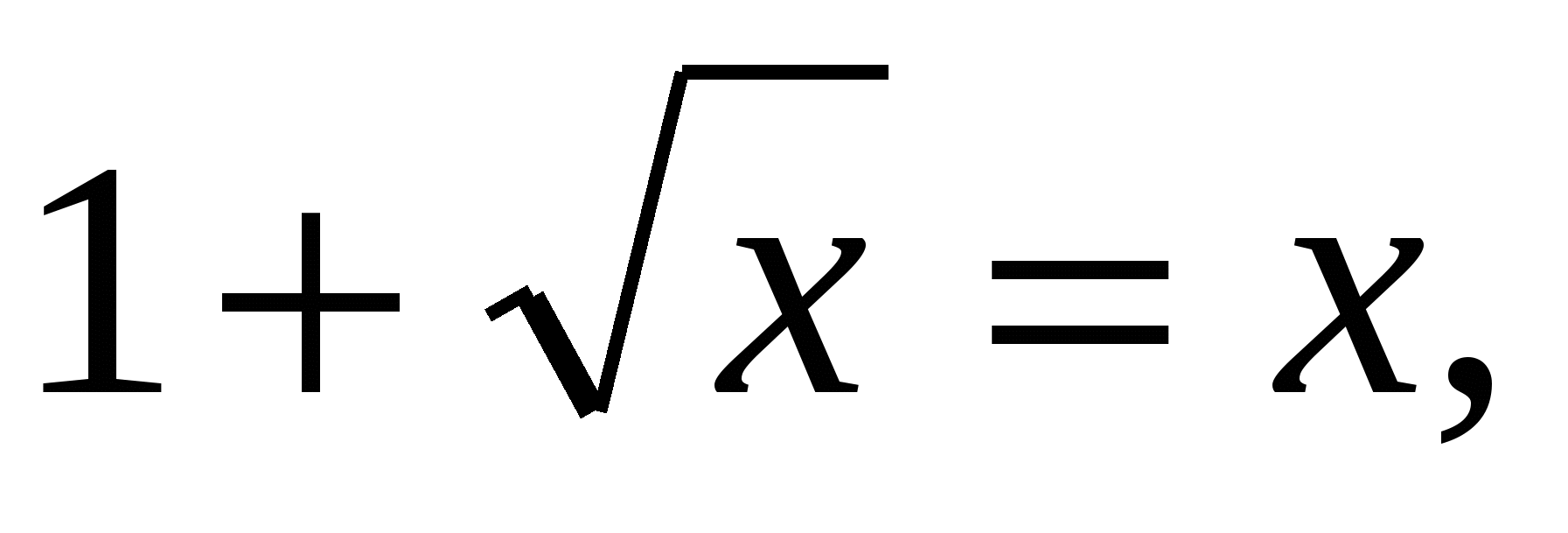
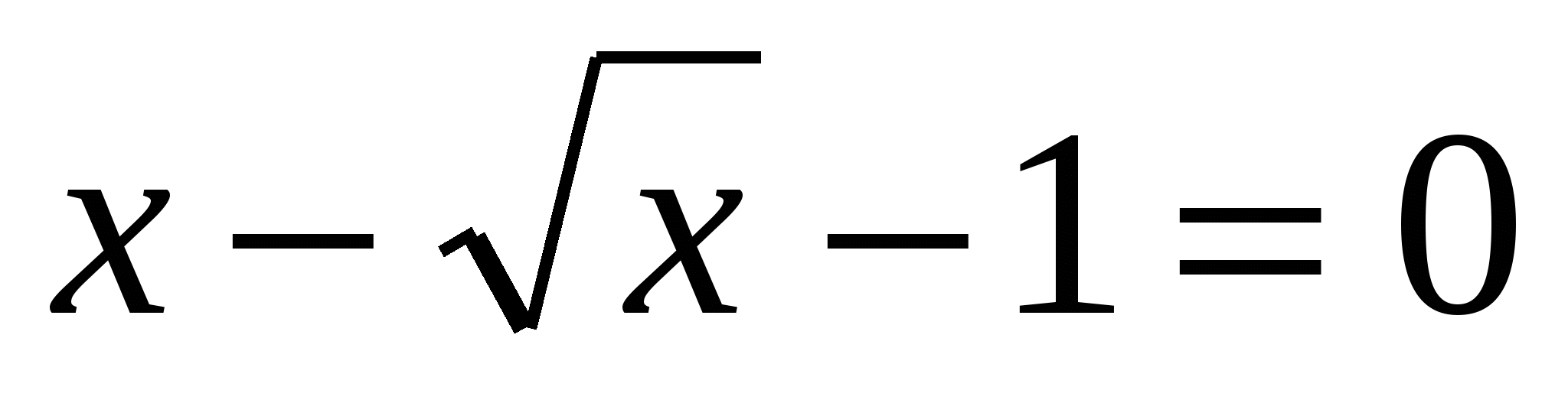 . Пусть
. Пусть 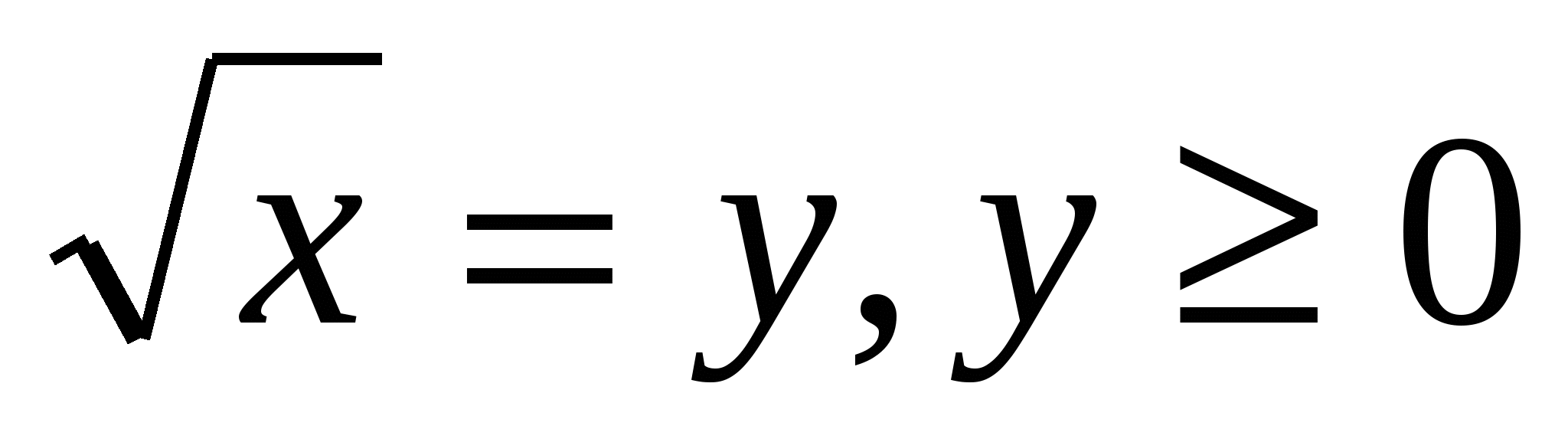 . Имеем у2-у-1=0,
. Имеем у2-у-1=0,
у1,2=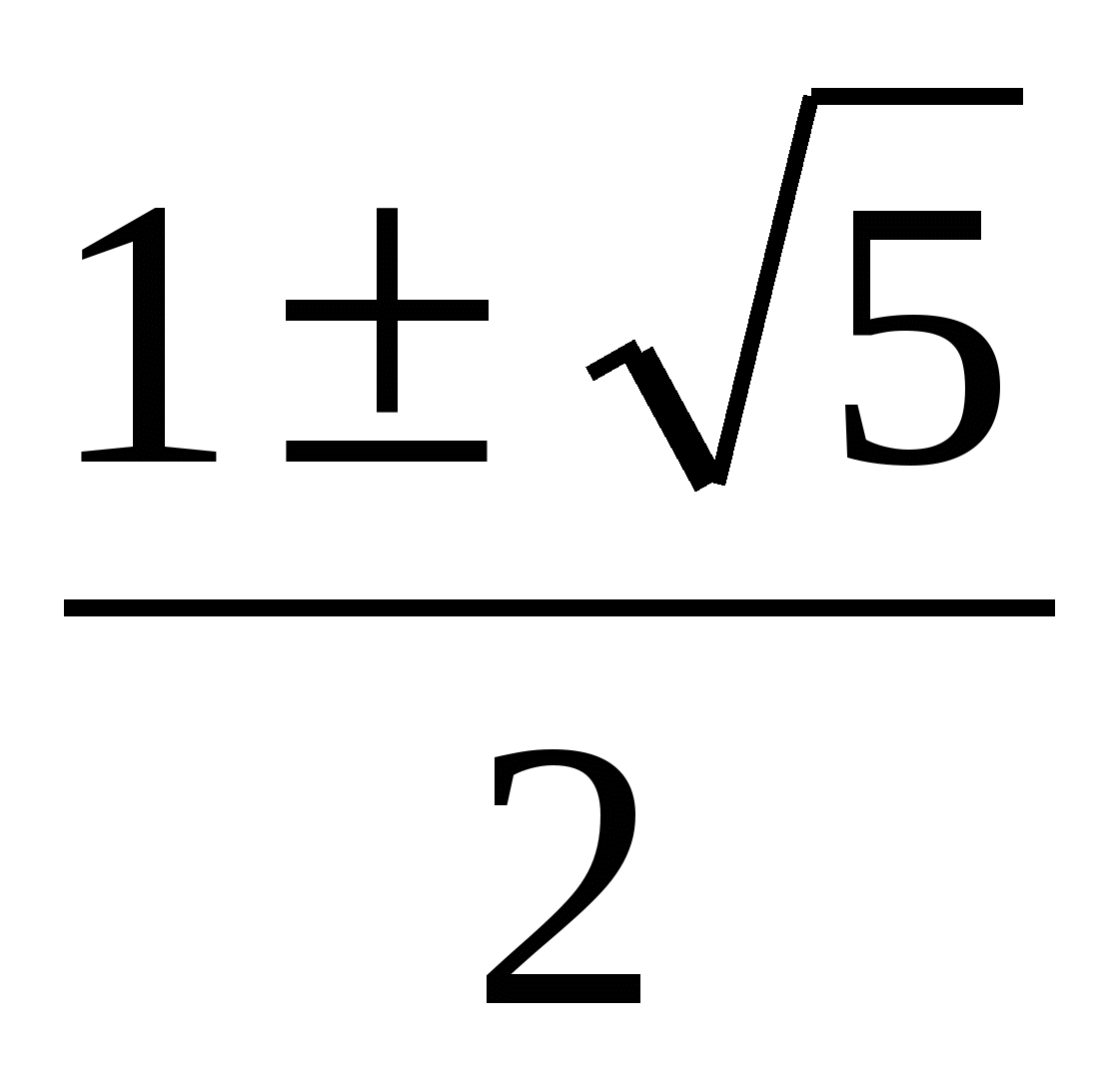 ; у1=
; у1=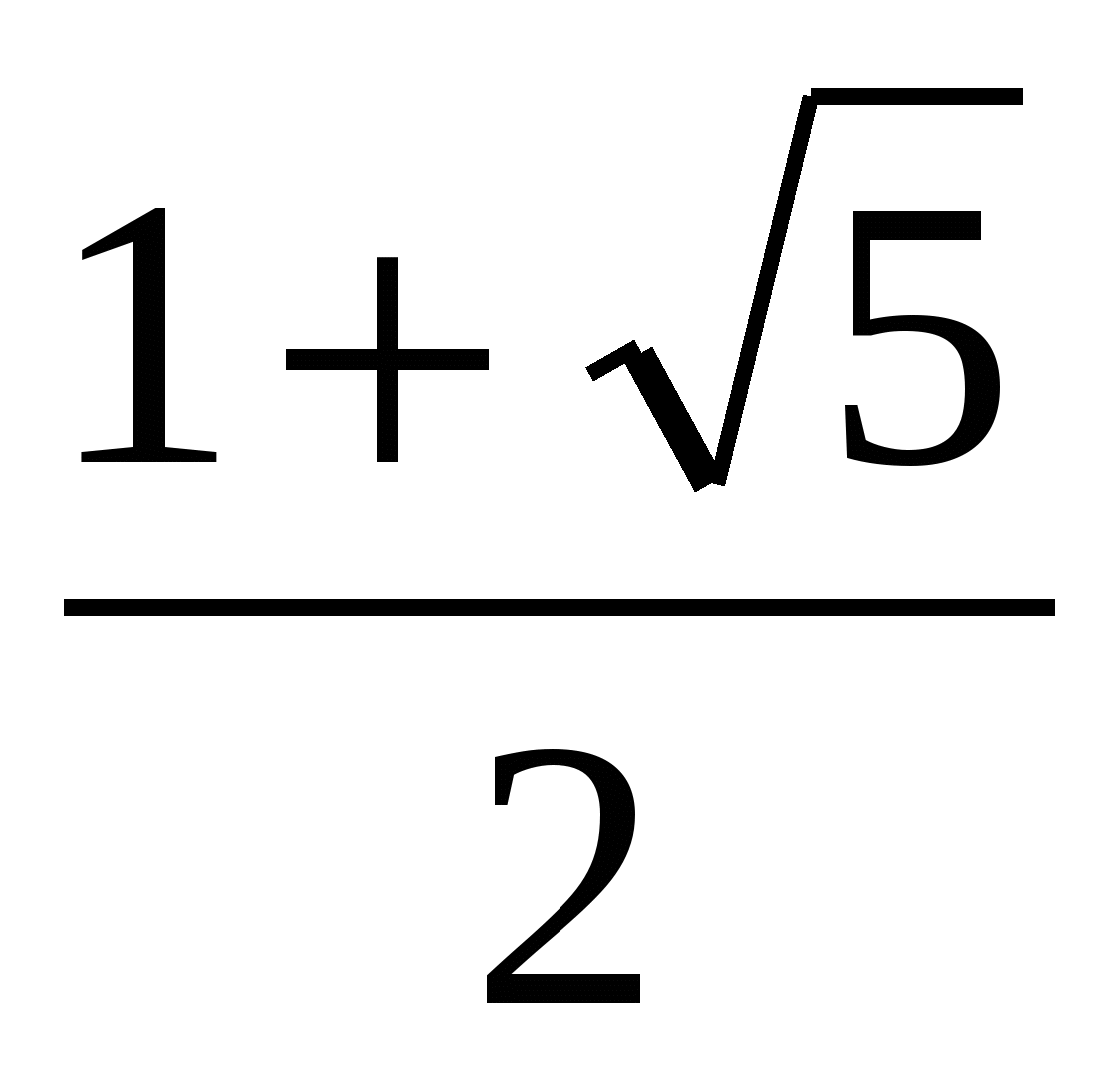 , у2=
, у2=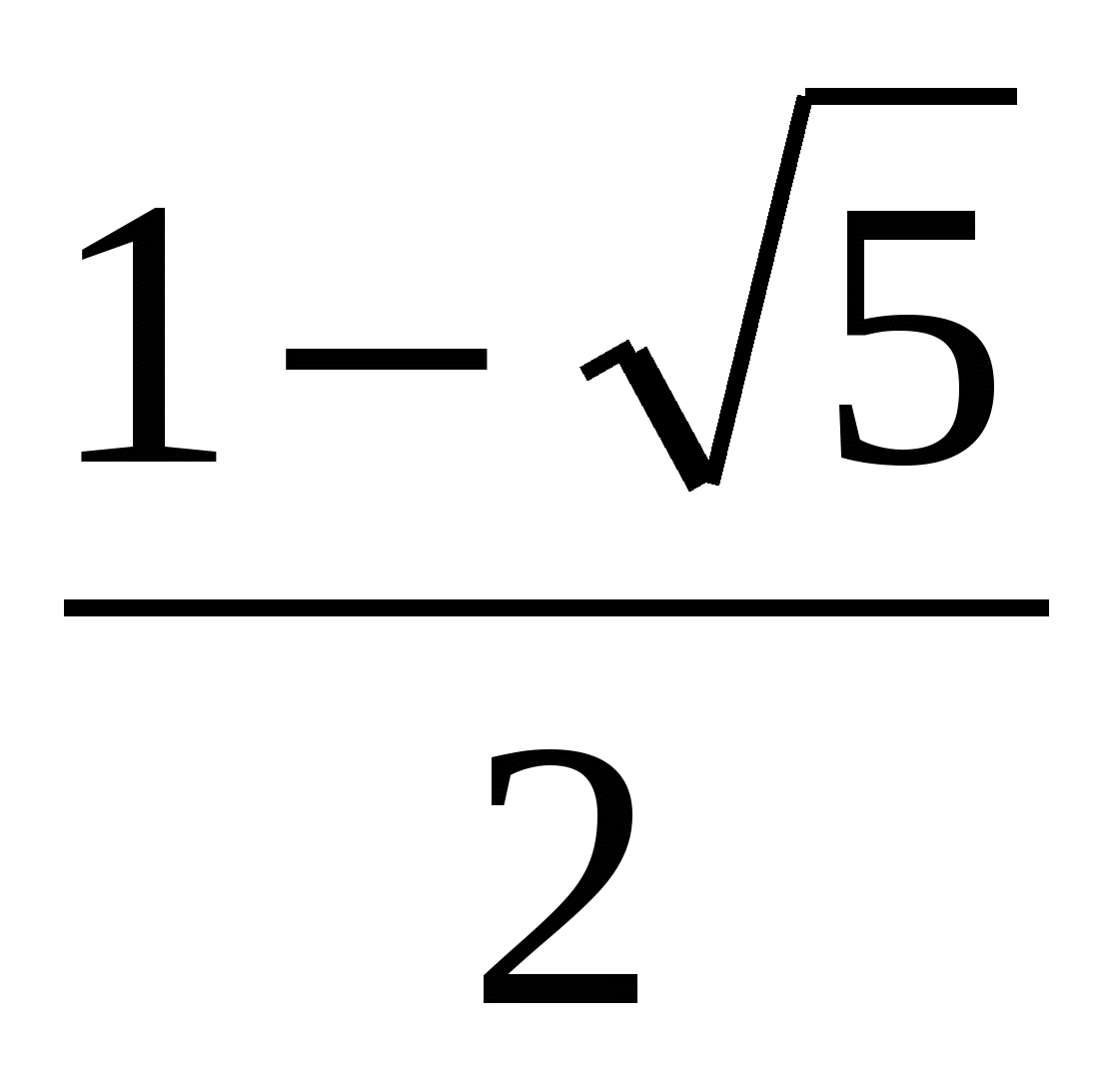 - не удовлетворяет условию
- не удовлетворяет условию 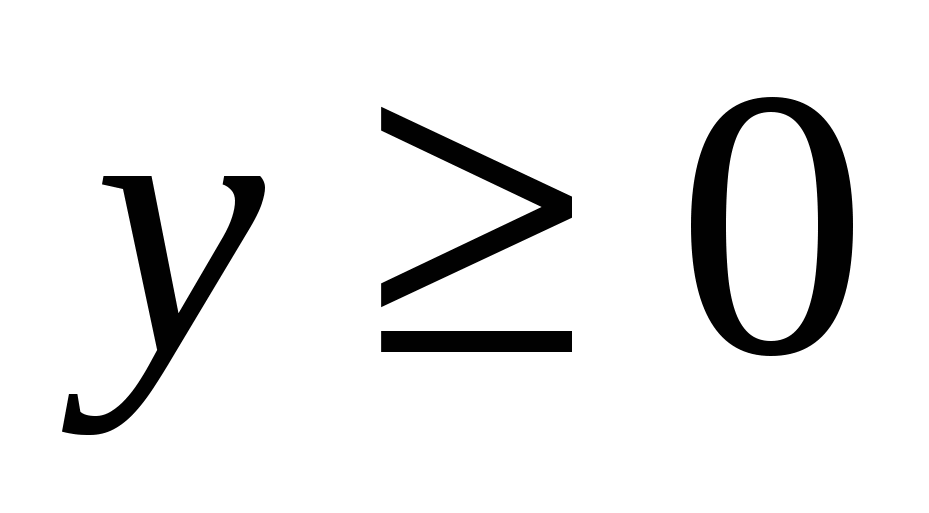 .
.
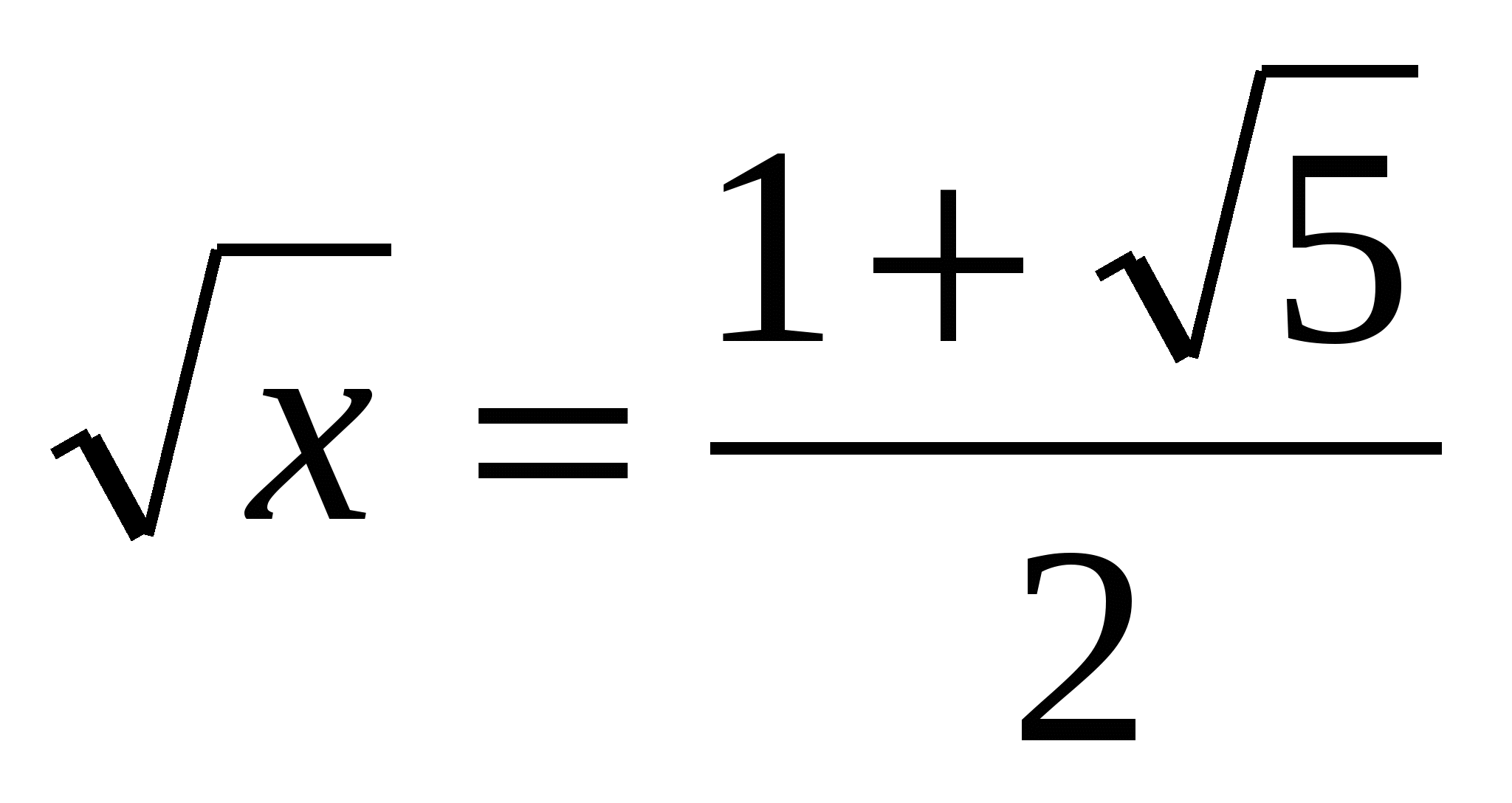 ,
, 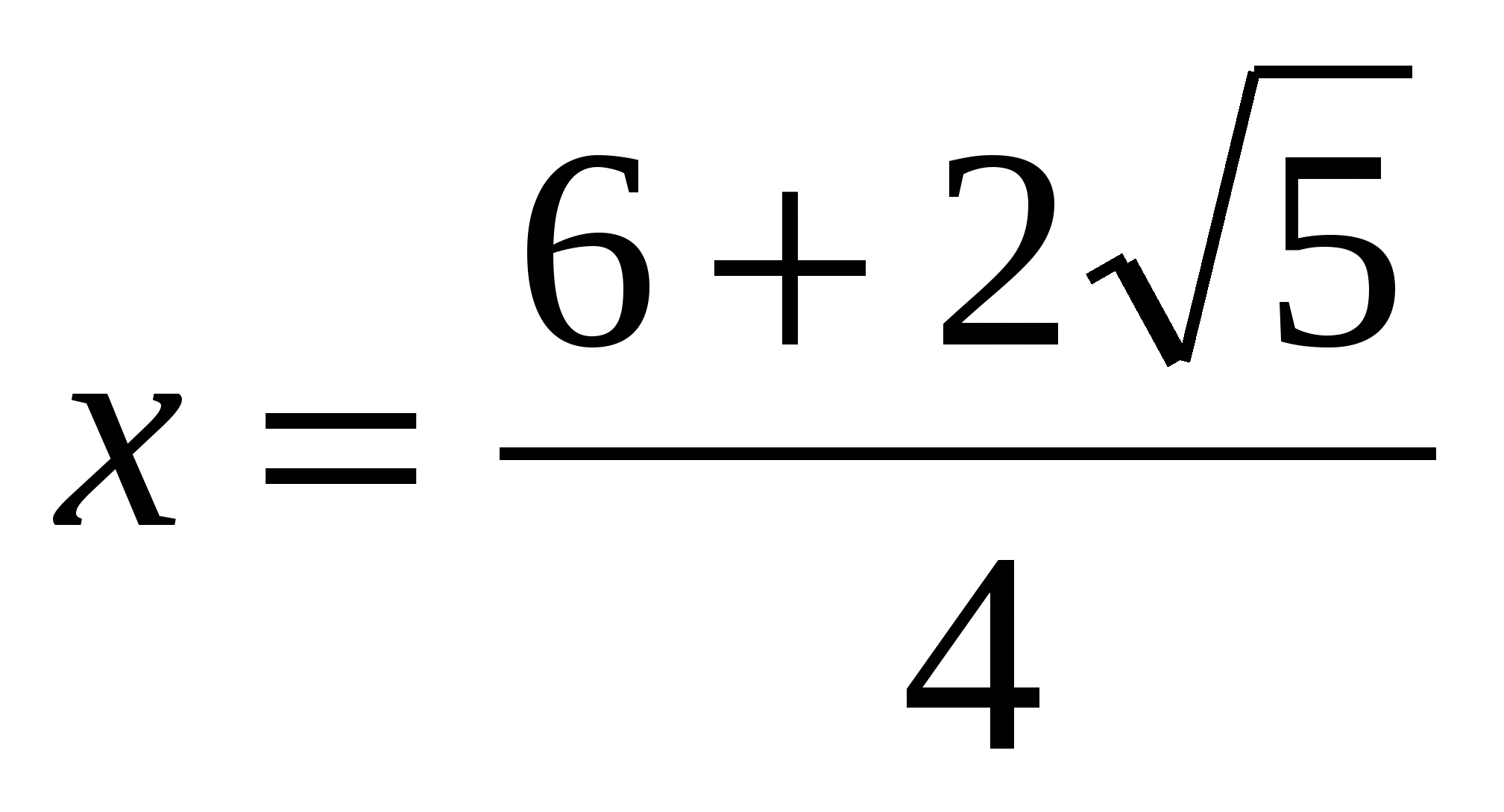 , х=
, х=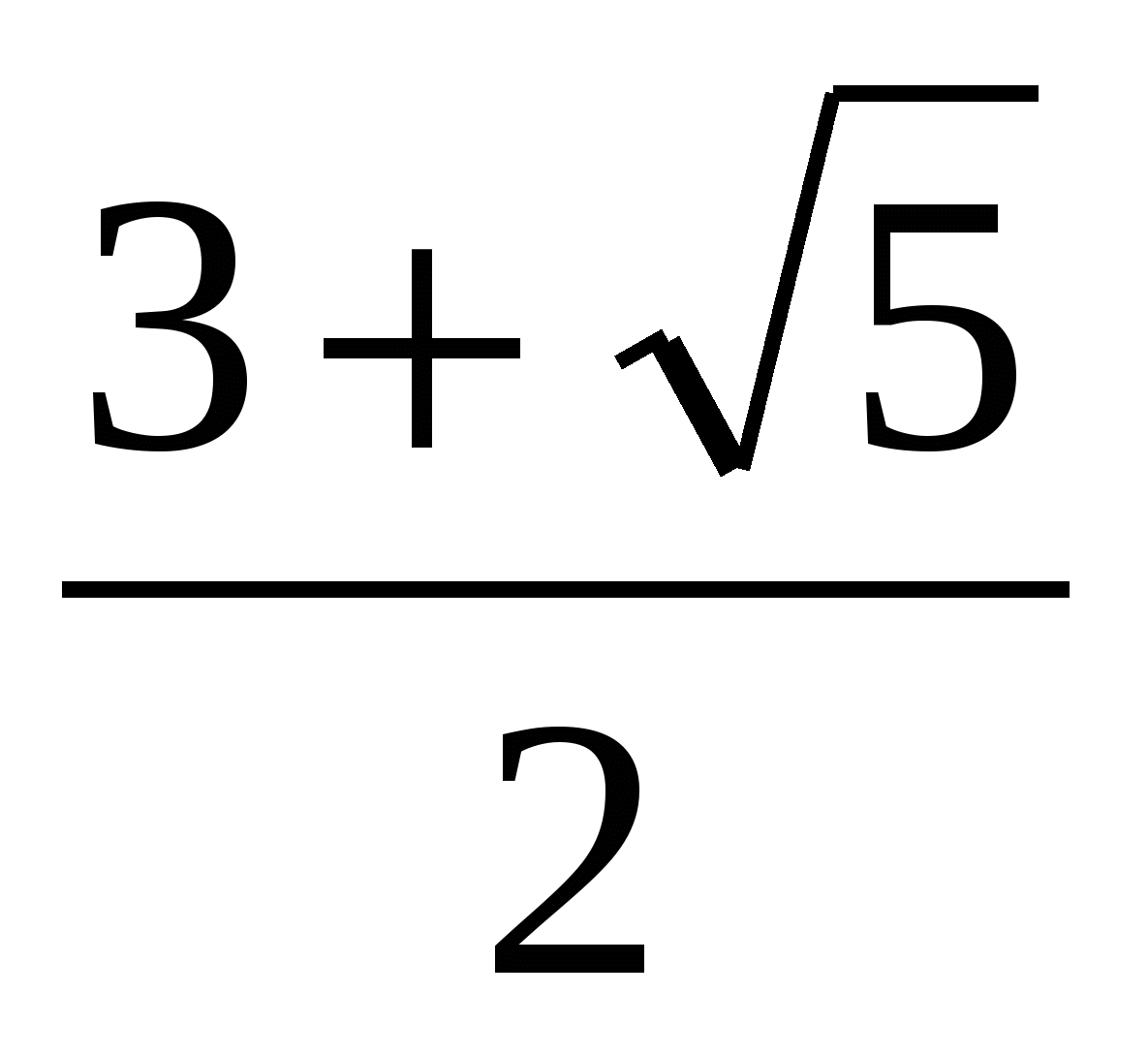 .
.
Ответ: х=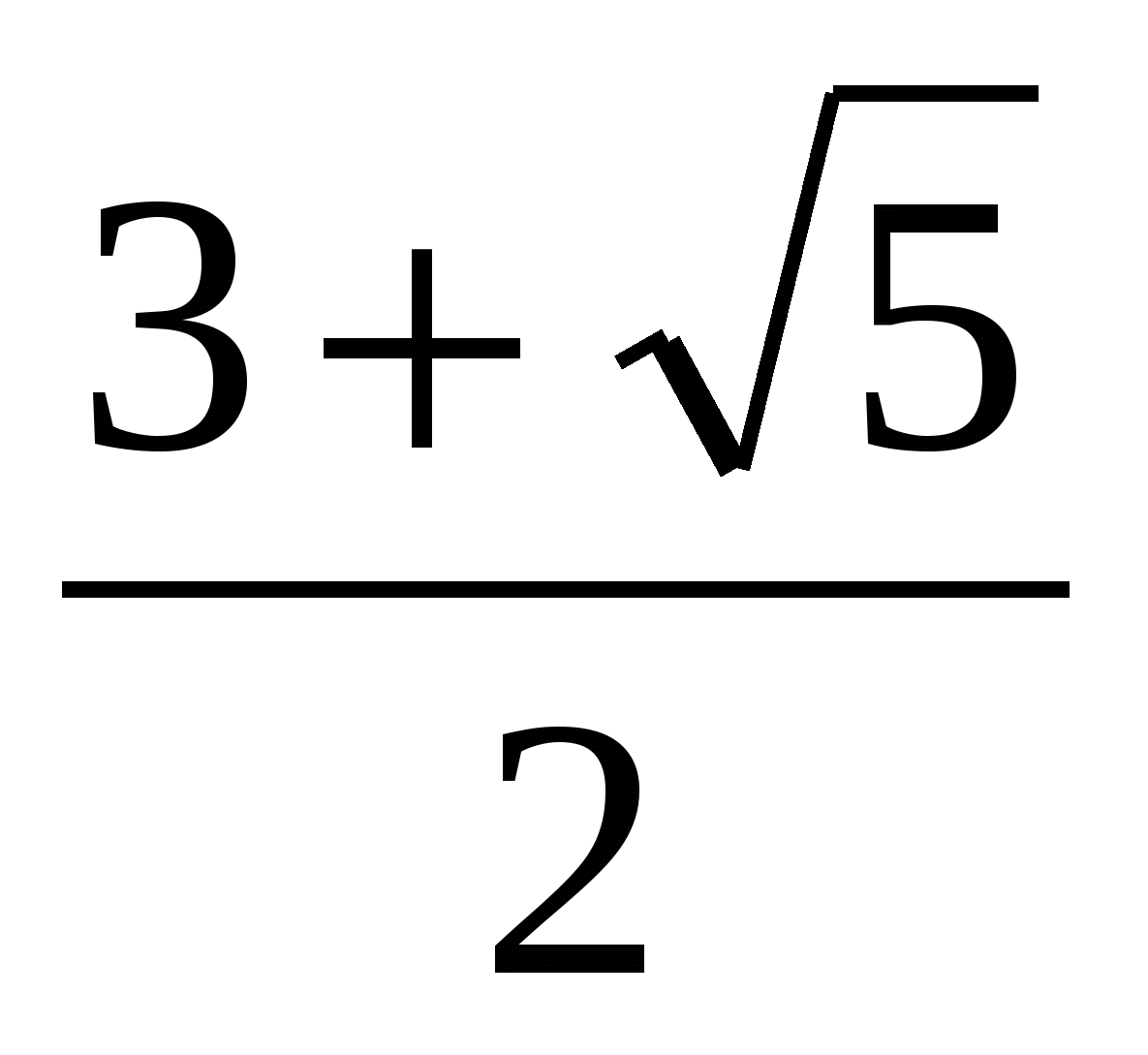 .
.
2)Решить уравнение 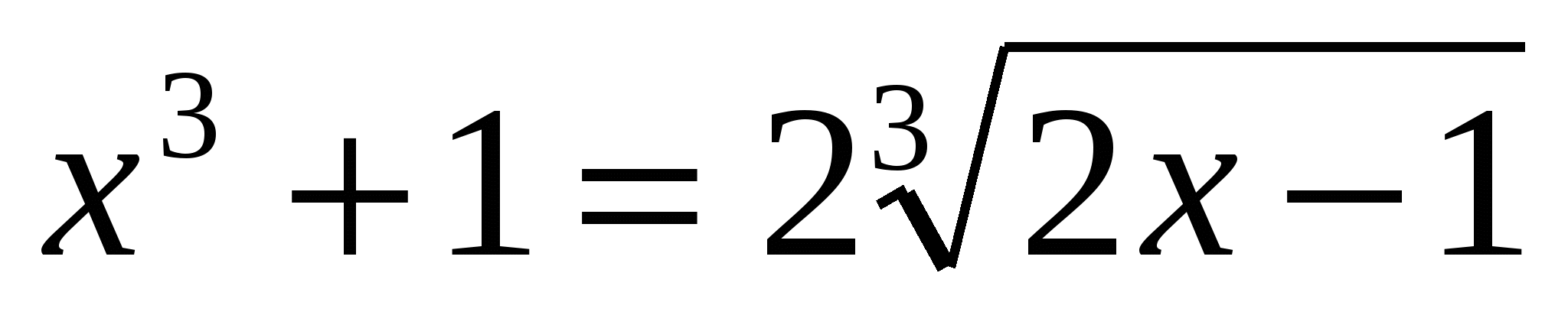 .
.
Решение: преобразуем уравнение 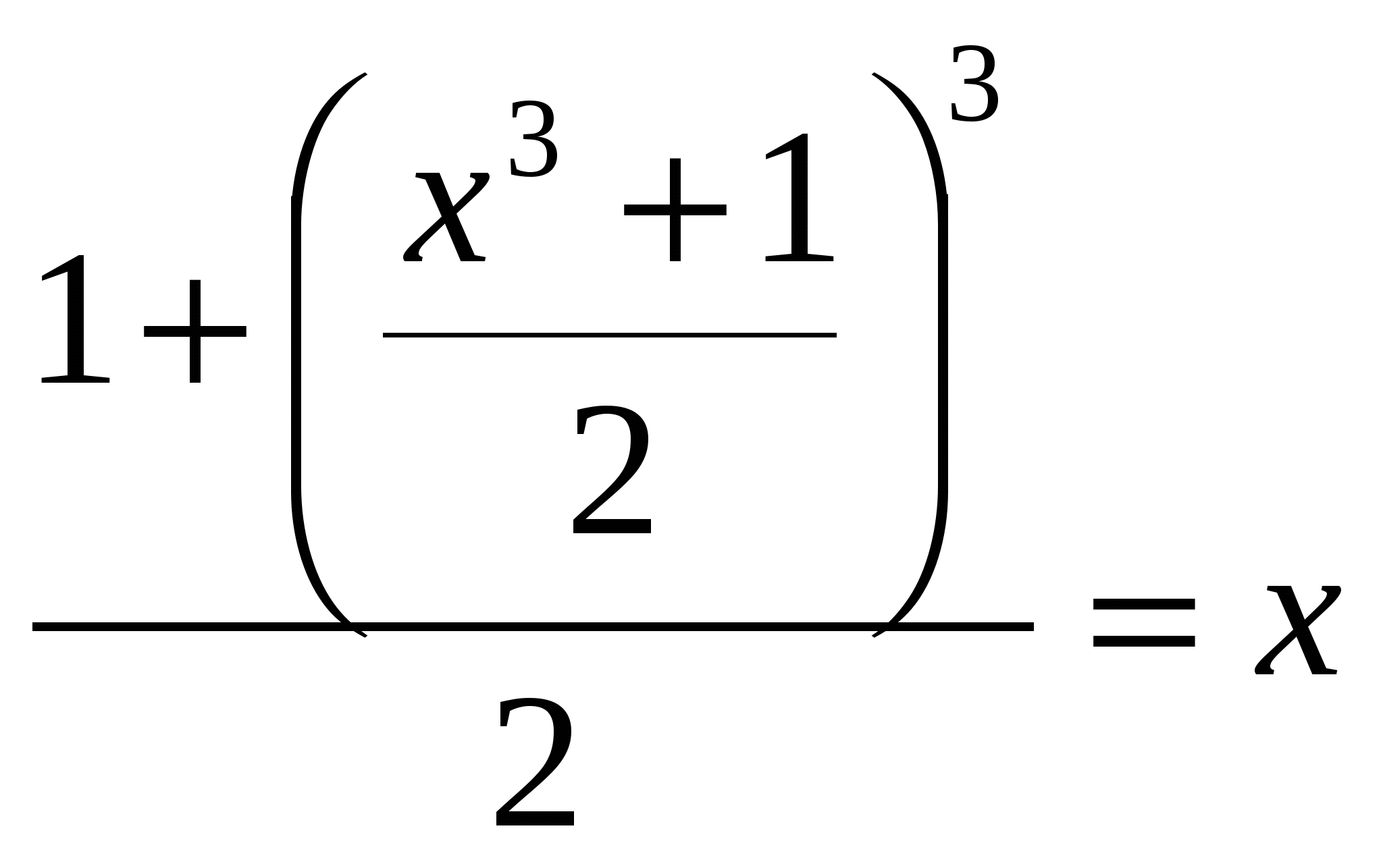 .
.
Данное уравнение имеет вид: f(f(x))=x, где f(x)=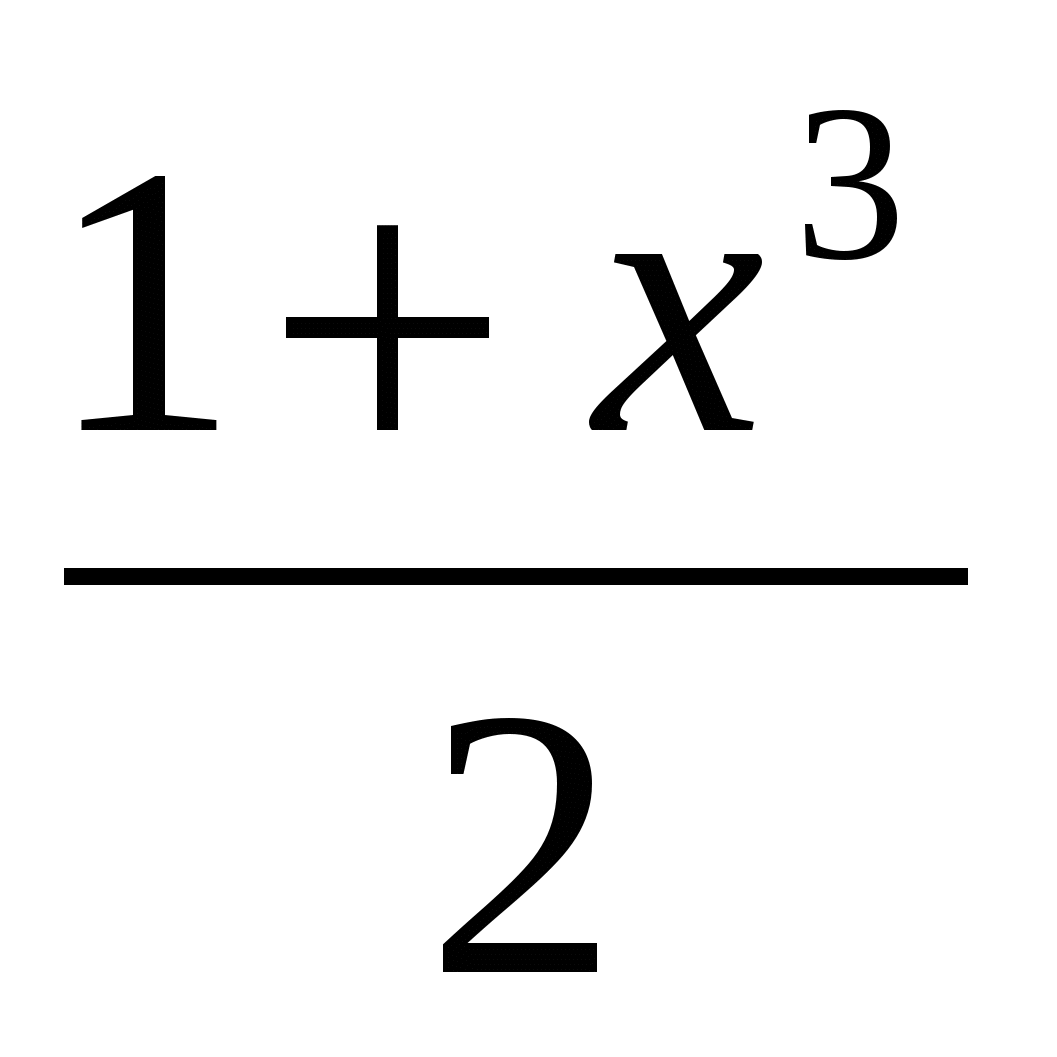 , эта функция монотонно возрастает. Согласно теореме имеем эквивалентное уравнение:
, эта функция монотонно возрастает. Согласно теореме имеем эквивалентное уравнение: 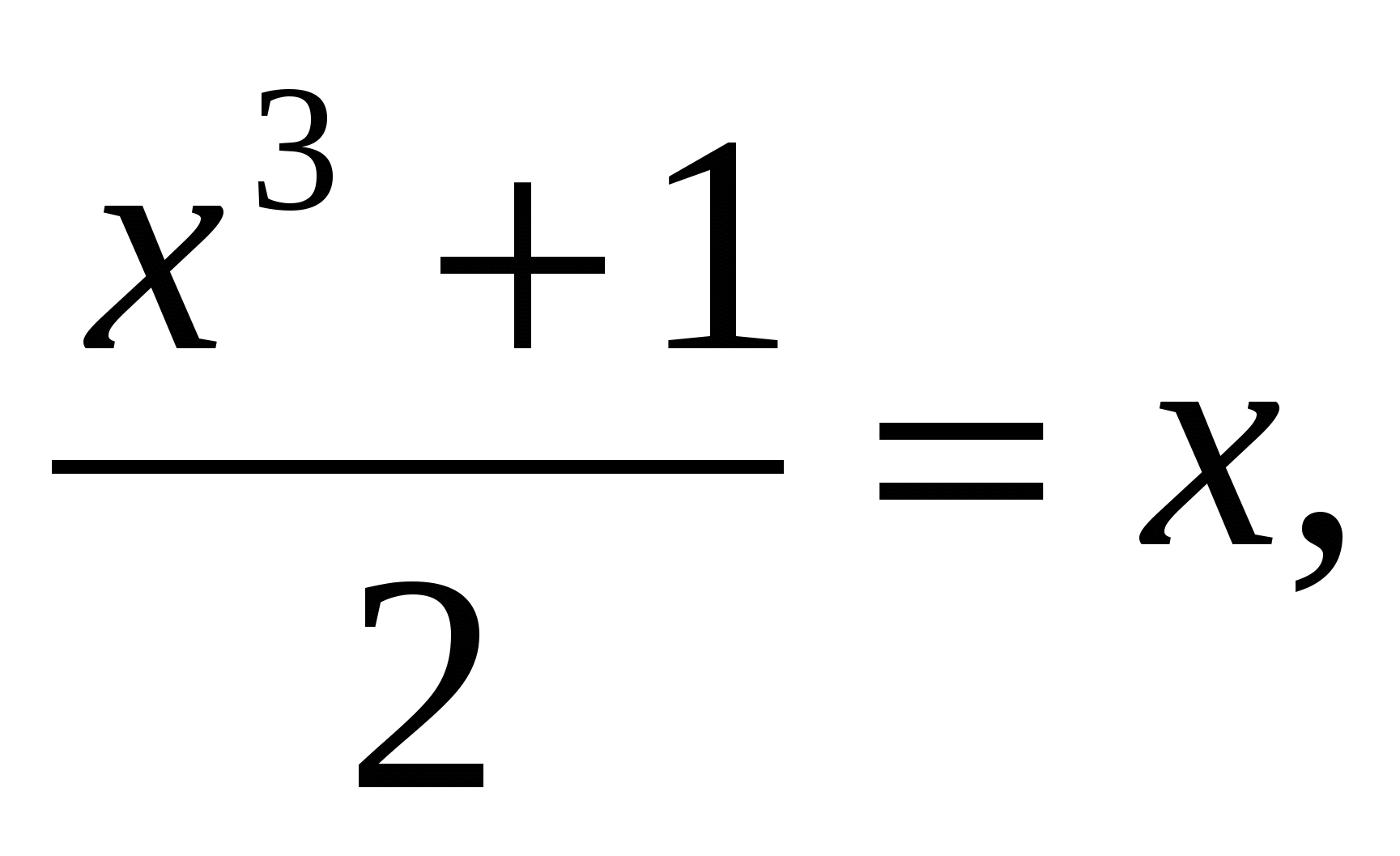 х3-2х+1=0, (х-1)(х2+х-1)=0. х1=1 или х2+х-1=0, х2,3=
х3-2х+1=0, (х-1)(х2+х-1)=0. х1=1 или х2+х-1=0, х2,3=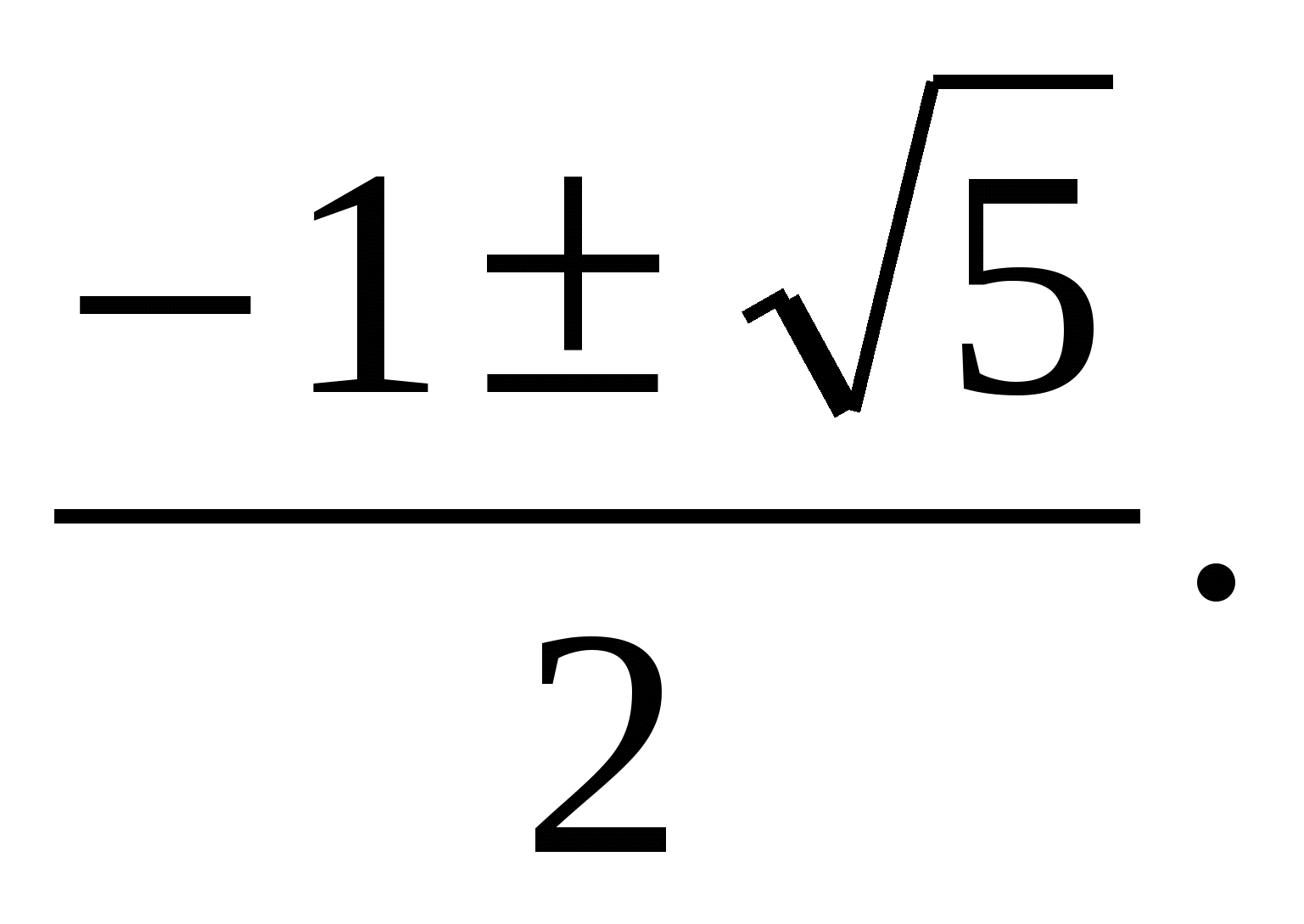
Ответ: х1=1, х2=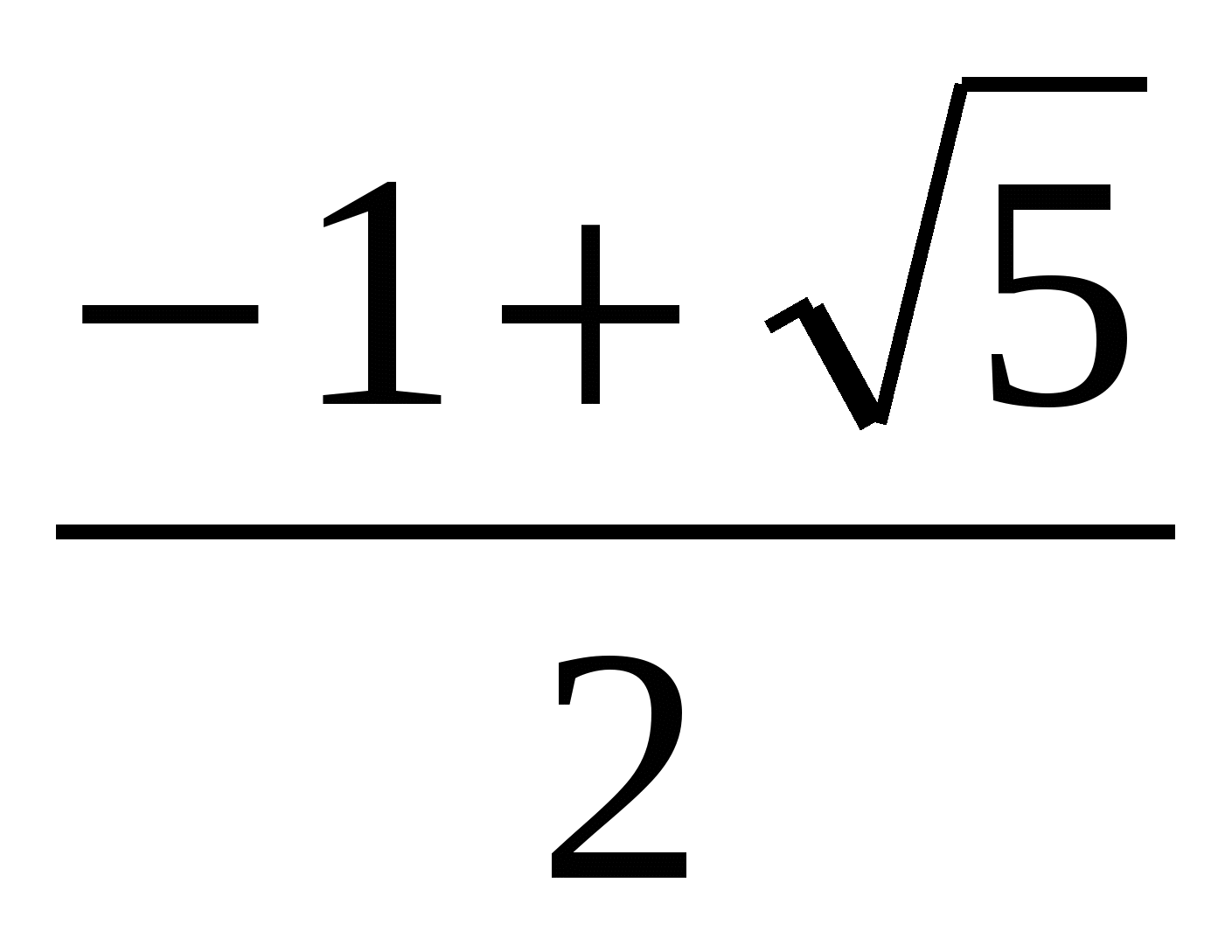 , х3=
, х3=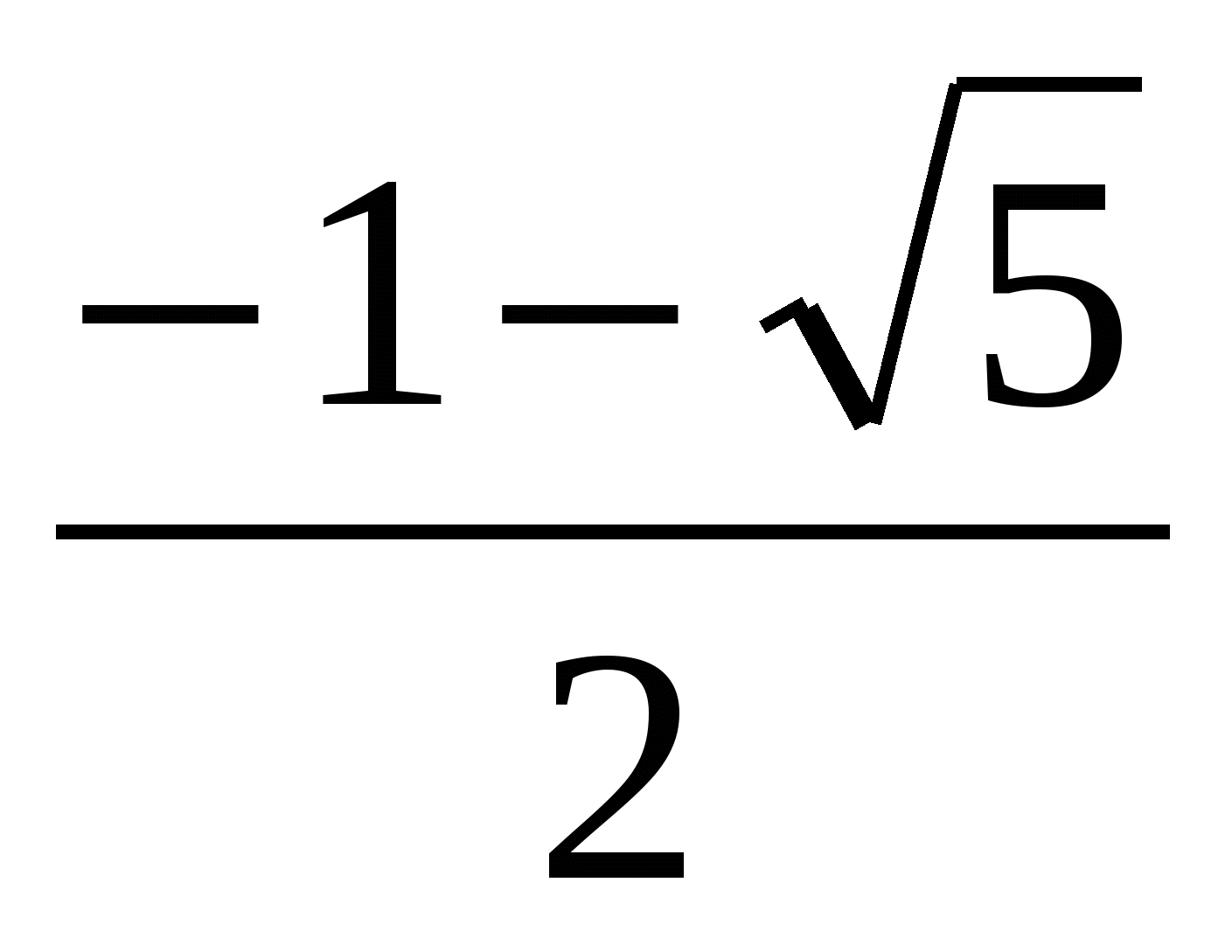
3)Решить уравнение 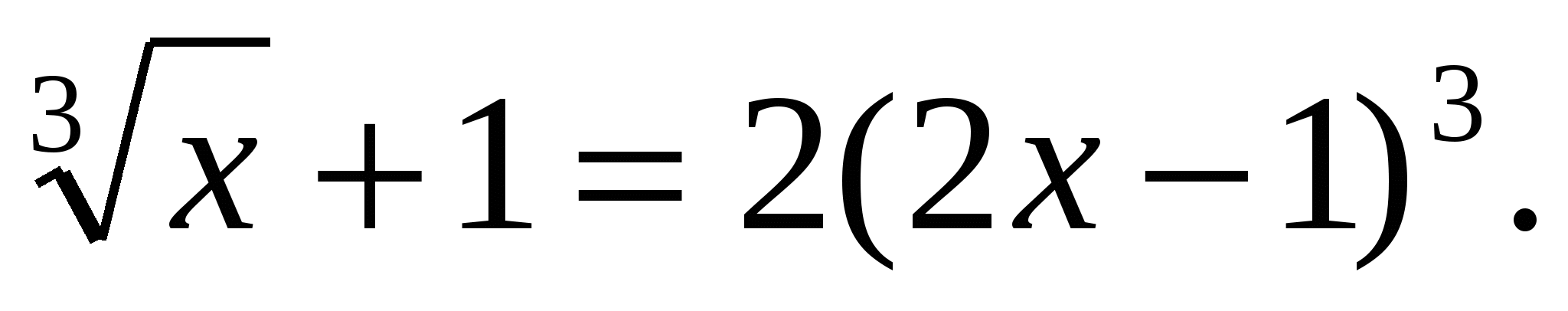
Решение: выполним некоторые преобразования 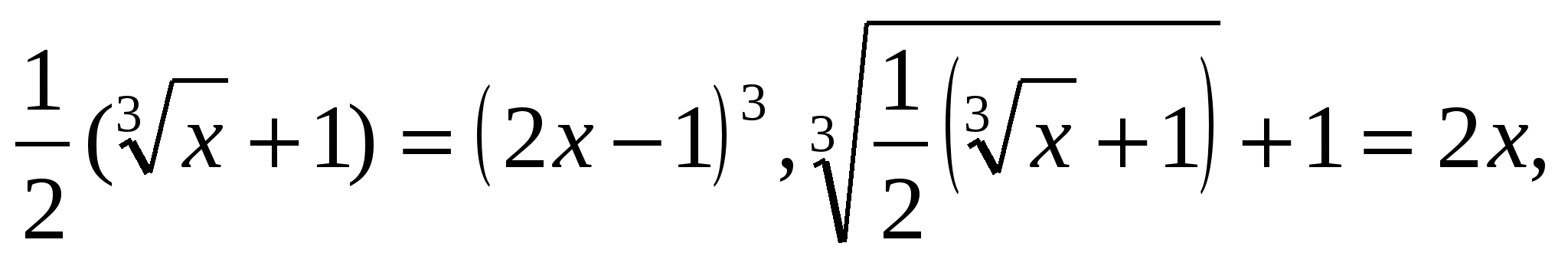 ,
, 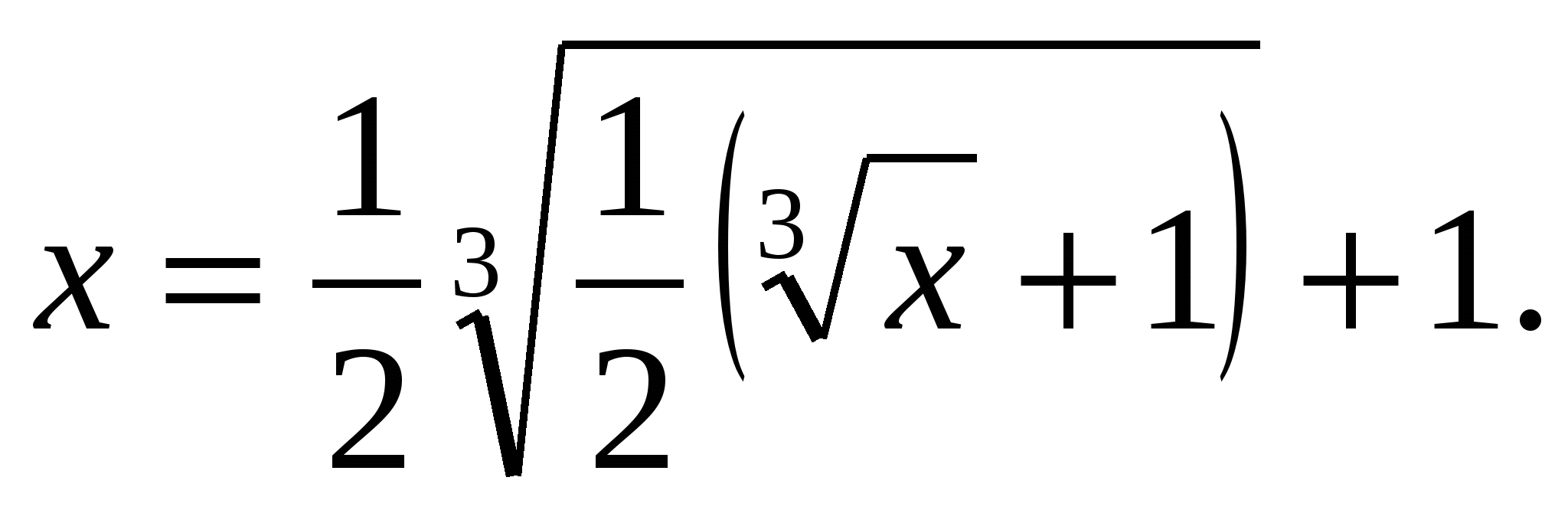 Это уравнение имеет вид x=f(f(х)), где f(х)=
Это уравнение имеет вид x=f(f(х)), где f(х)=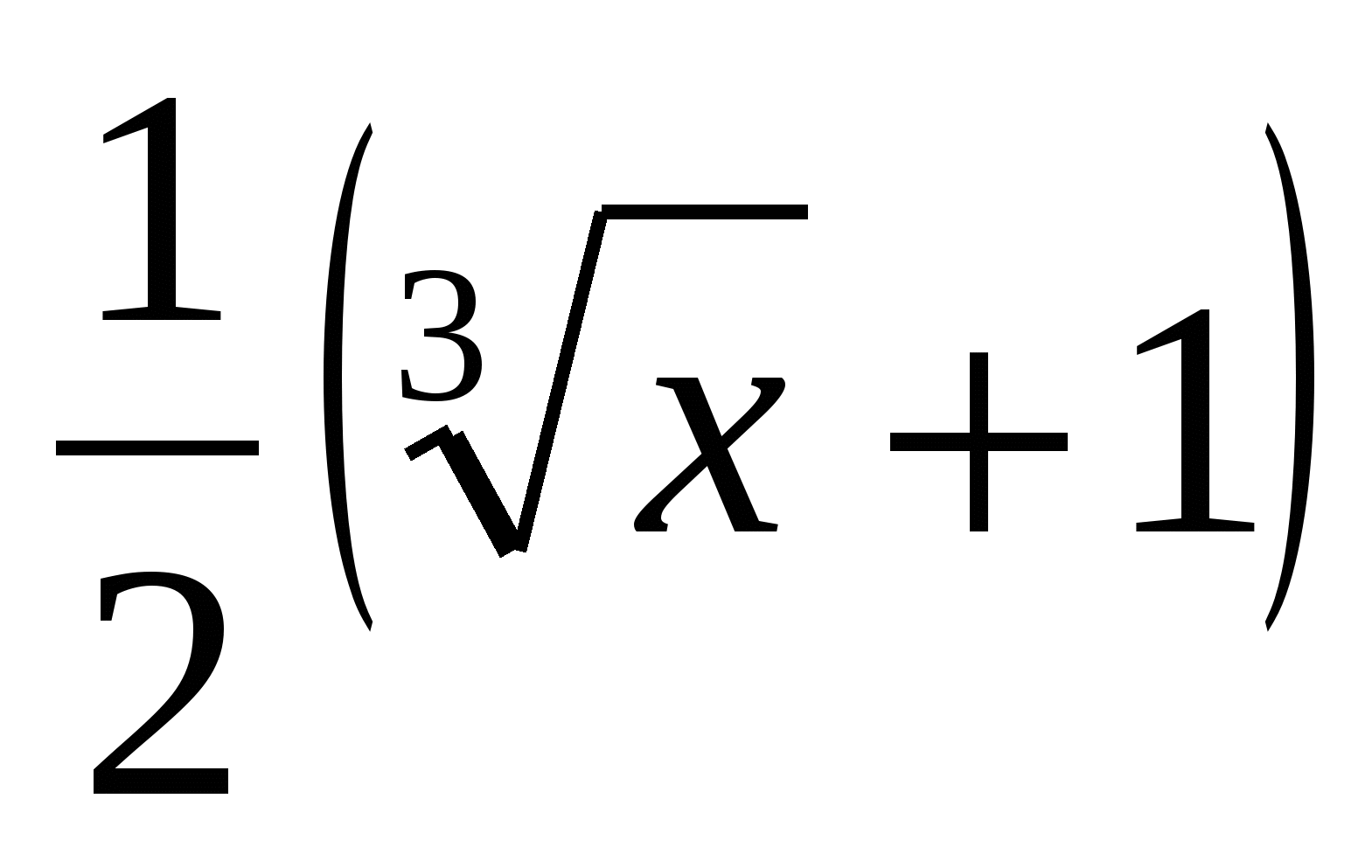 , f(х)- монотонно возрастает. Следовательно, уравнение эквивалентно
, f(х)- монотонно возрастает. Следовательно, уравнение эквивалентно 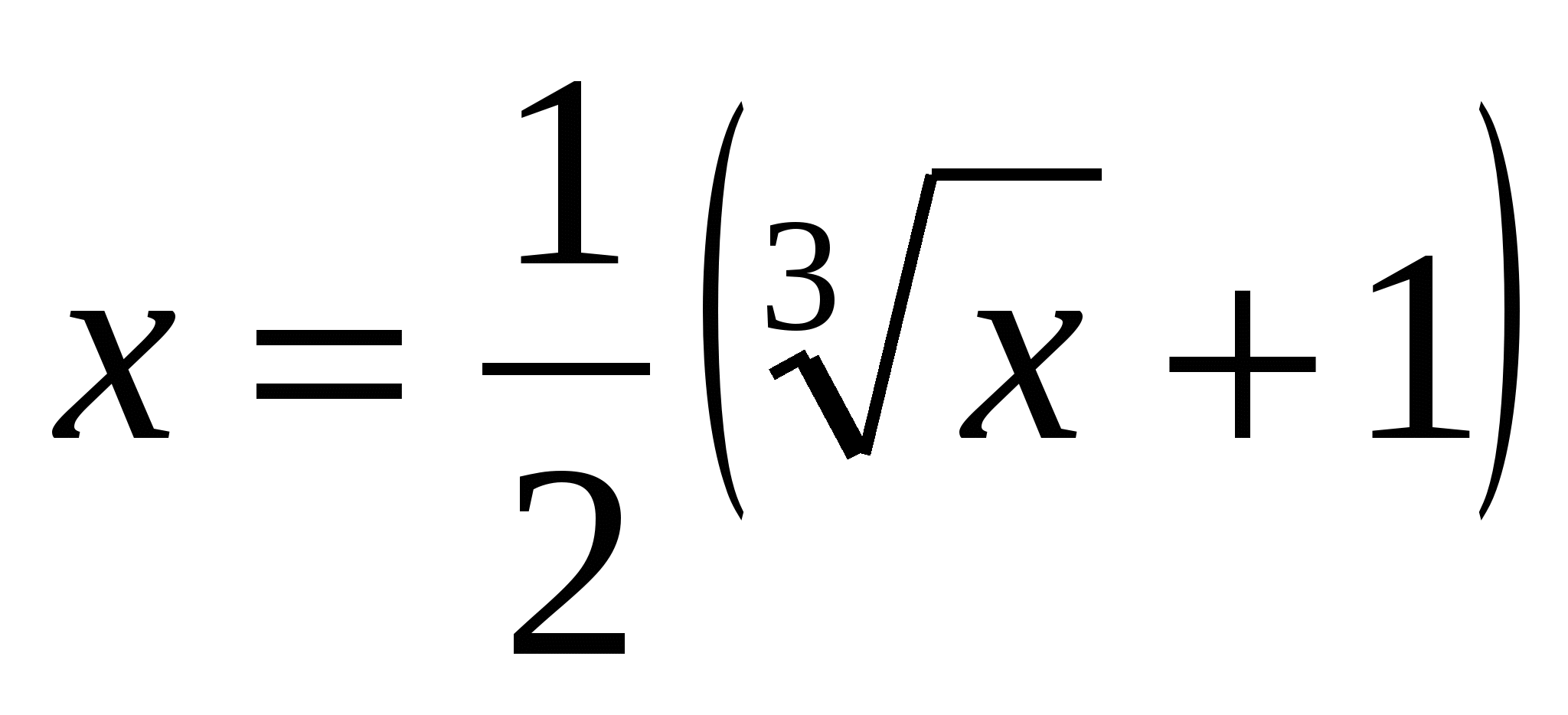 . Заменим
. Заменим 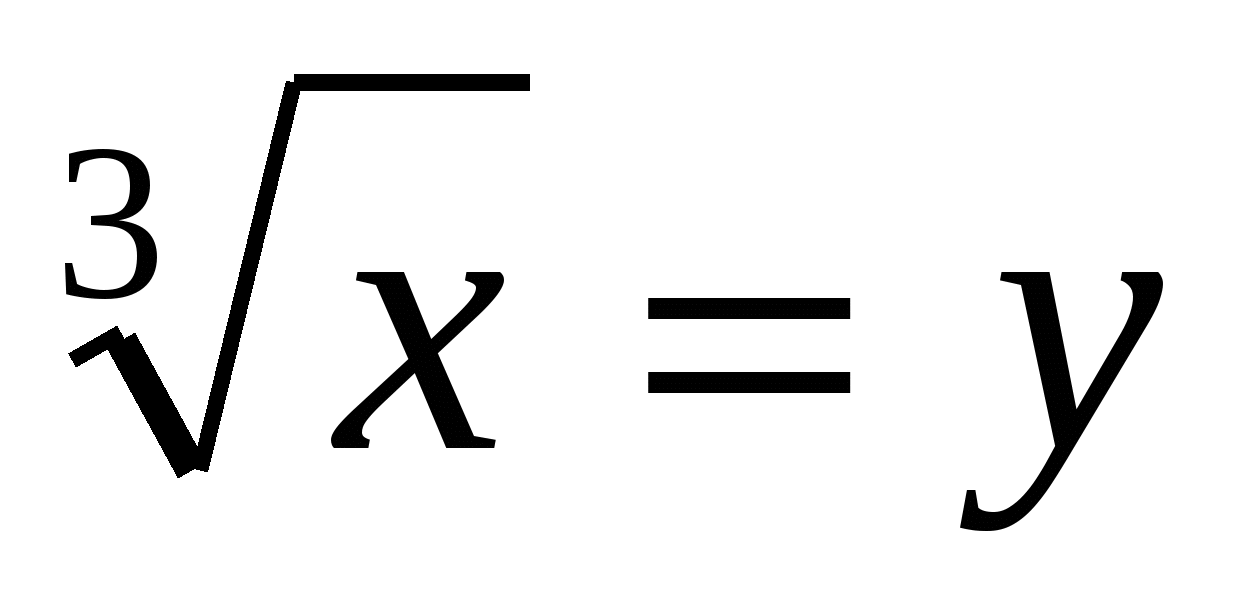 , получим 2у3-у-1=0. у3-у+у3-1=0,у(у2-1)+(у-1)(у2+у+1)=0,(у-1)(у2+1+у2+у+1)=0,(у-1)(2у2+у+1)=0
, получим 2у3-у-1=0. у3-у+у3-1=0,у(у2-1)+(у-1)(у2+у+1)=0,(у-1)(у2+1+у2+у+1)=0,(у-1)(2у2+у+1)=0
у=1, уравнение 2у2+у+1=0 не имеет корней.
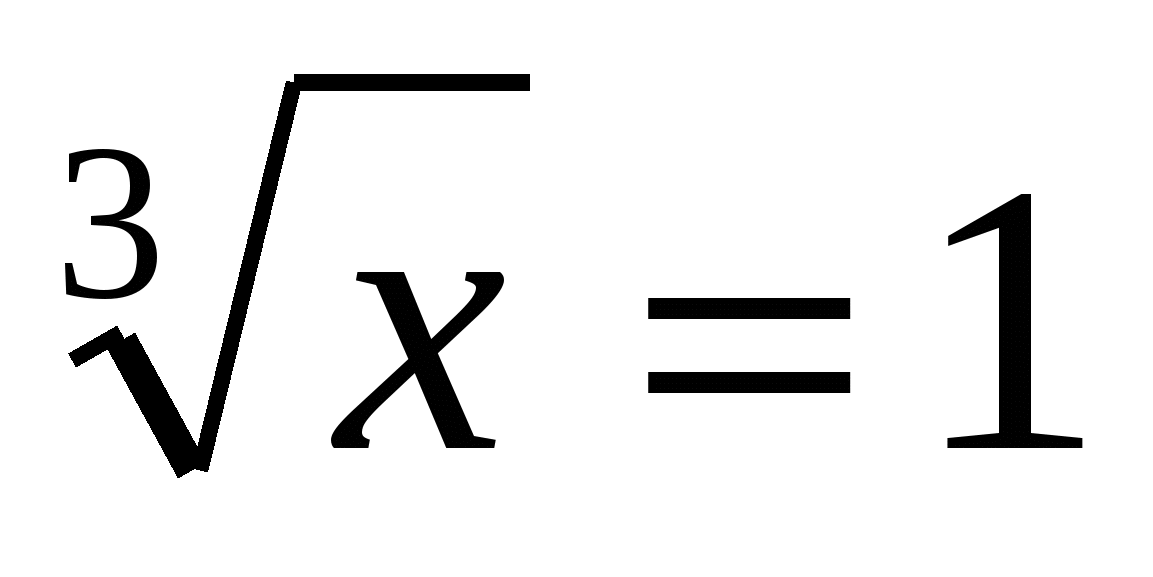 , х=1.
, х=1.
Ответ: х=1.
4)Решить уравнение ln(1+lnх)=x-1.
Решение: ln(1+lnx)+1=x, Это уравнение имеет вид x=f(f(x) , где f(x)=lnх+1. f(x)=1+lnx - монотонно возрастает при х > 0, следовательно, уравнение эквивалентно уравнению х=lnх+1, х-1=lnх.
Решим это уравнение графически: у=х-1 - графиком этой функции является прямая, проходящая через точки с координатами (0;-1), (1;0)
Функция у=lnx определена при х>0 . Очевидно, что х=1-корень уравнения, его единственность подтверждается графически.



Ответ: х=1.
Использование четности функции при решении уравнений.
1)Может ли при каком-нибудь значении а уравнение 2х8-3ах6+4х4-ах2=5 иметь пять корней?
Решение: рассмотрим функцию f(х)=2х8-3ах6+4х4-ах-5. Она определена при всех действительных х, является четной, т.к.f(x)=f(-x) и область определения симметрична относительно нуля.
График функции f(х) симметричен относительно оси ординат, то есть для любого х из области определения, -х из области определения и только х=0 симметричен сам себе. Тогда, если исходное уравнение имеет нечетное число корней (пять), то х=0 - корень уравнения. Проверкой убеждаемся, что х=0 не является корнем уравнения - 0=5. Значит, исходное уравнение не может иметь пять корней не при каких а.
Ответ: не при каких действительных а уравнение 2х8-3ах6+4х4-ах2=5 не может иметь пять корней.
2)Докажите, что уравнение 3х+3-х=ах4+2х2+2 имеет нечетное число корней.
имеет нечетное число корней.
Решение: рассмотрим функцию f(х)=3х+3-х-ах4-2х2-2. Она определена при всех действительных х, является четной. Согласно предыдущей задаче, если имеет нечетное число корней, то х=0 корень исходного уравнения. Проверим: 30+30=2, 0+0+2=2, 2=2. х=0 является корнем уравнения, значит, исходное уравнение имеет нечетное число корней.
Ответ: уравнение 3х+3-х =ах4+2х2+2 имеет нечетное число корней.
3)Найдите все действительные значения параметра а, при которых уравнение 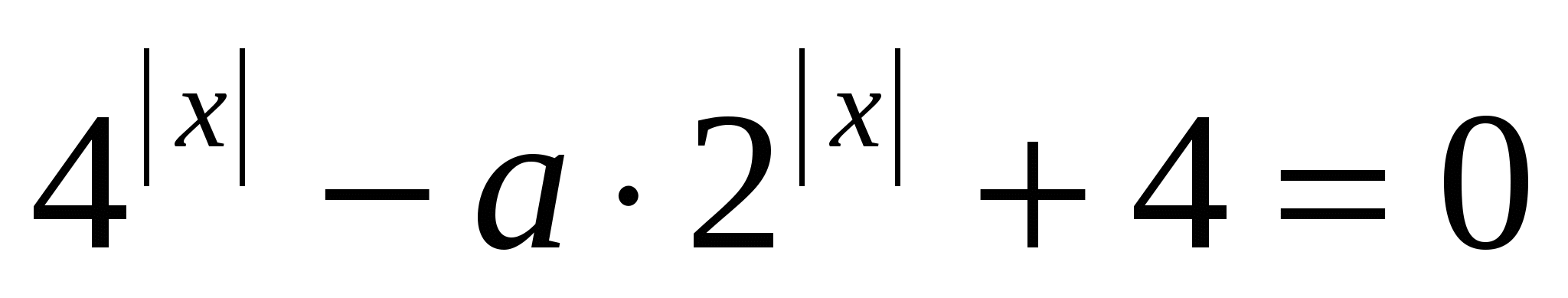 имеет единственное решение.
имеет единственное решение.
Решение: рассмотрим функцию f(х)=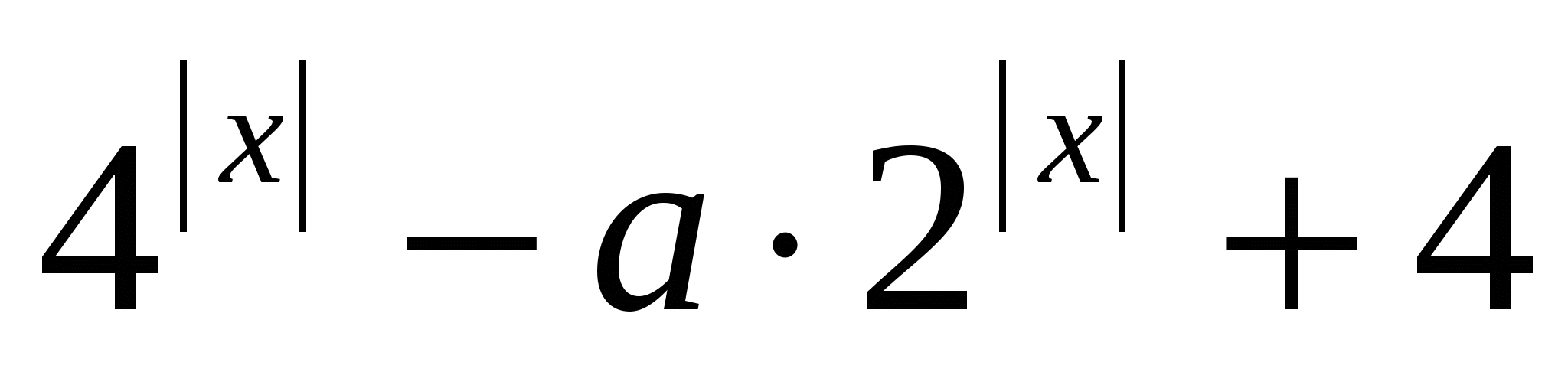 , определена при всех действительных х, четная, т.к. f(-х)=f(х) и область определения симметрична относительно нуля. График функции f(х) симметричен относительно оси ординат, х=0 симметричен сам себе. Таким образом, х=0 может являться либо единственным решением, либо одним из нескольких. Найдем f(0). f(0)=40-20а+4=5-а. f(0)=0, если а=5. Дабы исключить значения а, при которых уравнение f(х)=0 имеет два и более решений, сделаем проверку. Если а=5, то f(х)=0.
, определена при всех действительных х, четная, т.к. f(-х)=f(х) и область определения симметрична относительно нуля. График функции f(х) симметричен относительно оси ординат, х=0 симметричен сам себе. Таким образом, х=0 может являться либо единственным решением, либо одним из нескольких. Найдем f(0). f(0)=40-20а+4=5-а. f(0)=0, если а=5. Дабы исключить значения а, при которых уравнение f(х)=0 имеет два и более решений, сделаем проверку. Если а=5, то f(х)=0.
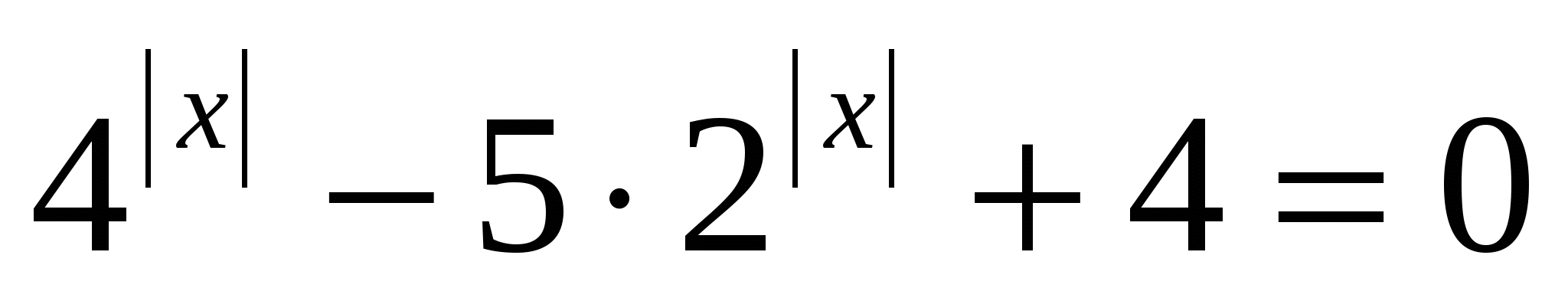 . Решая это уравнение с помощью замены
. Решая это уравнение с помощью замены 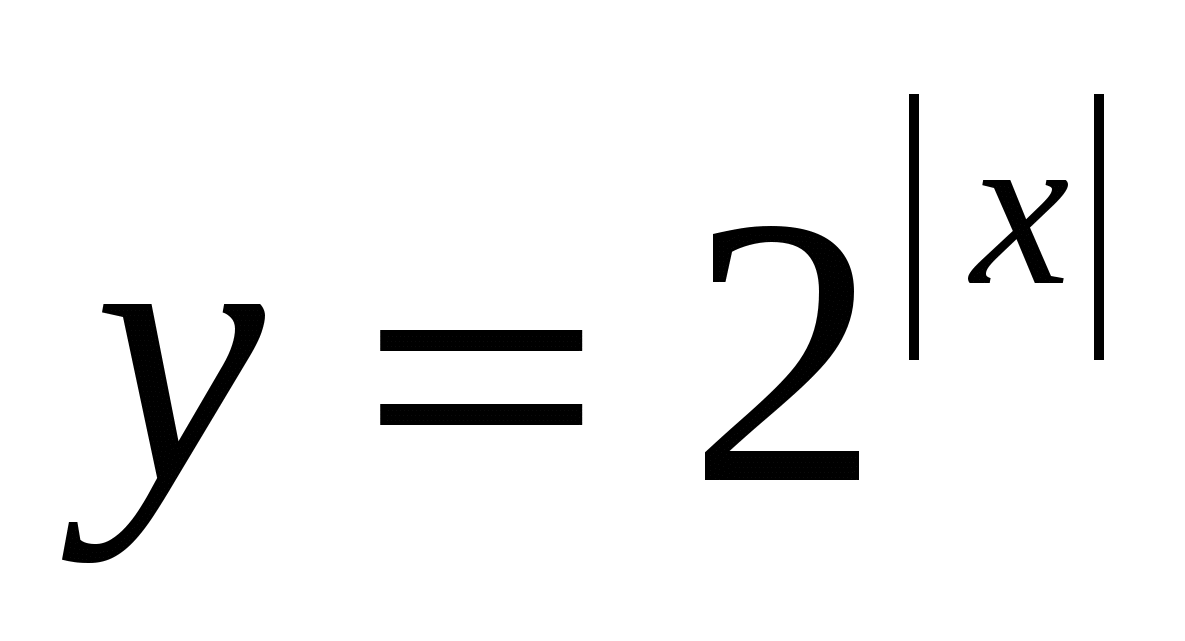 , получим
, получим 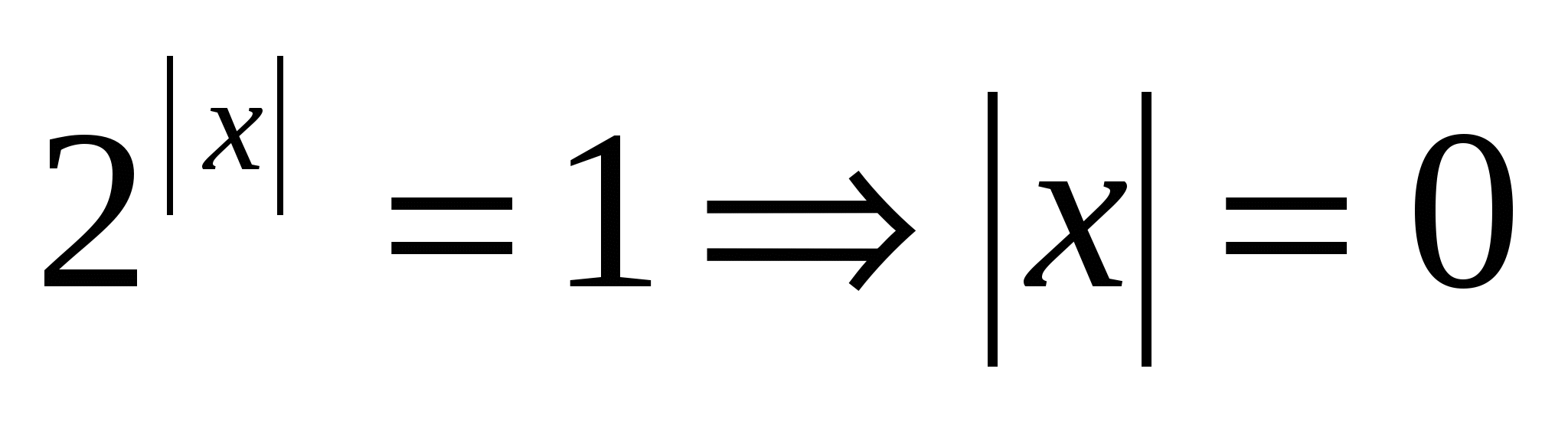 , х=0 или
, х=0 или 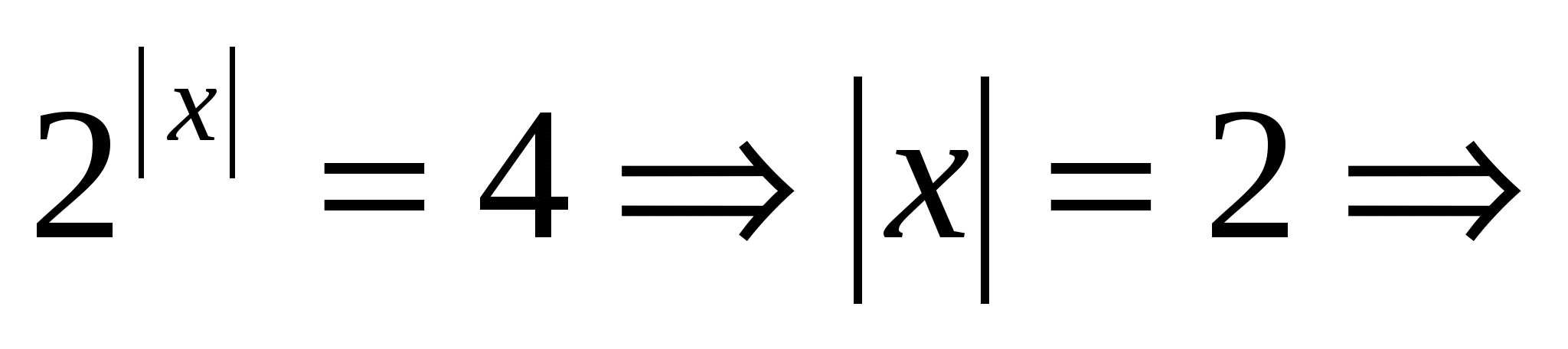 х=2;х=-2. То есть уравнение f(х)=0 имеет три решения, где х=0 - одно из них.
х=2;х=-2. То есть уравнение f(х)=0 имеет три решения, где х=0 - одно из них.
Ответ: нет таких действительных а.
4)Установите число корней уравнения 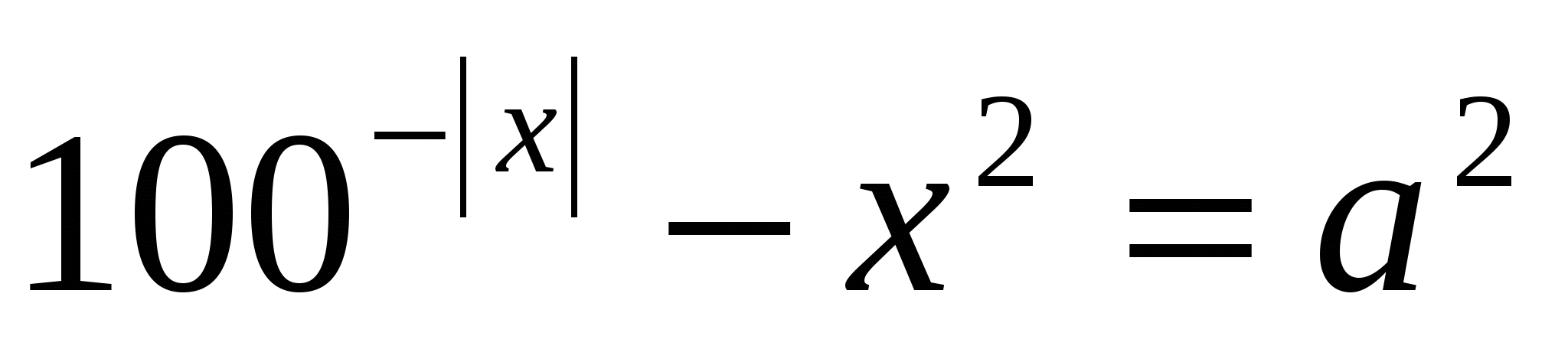 в зависимости от параметра а.
в зависимости от параметра а.
Решение: оценим левую часть уравнения 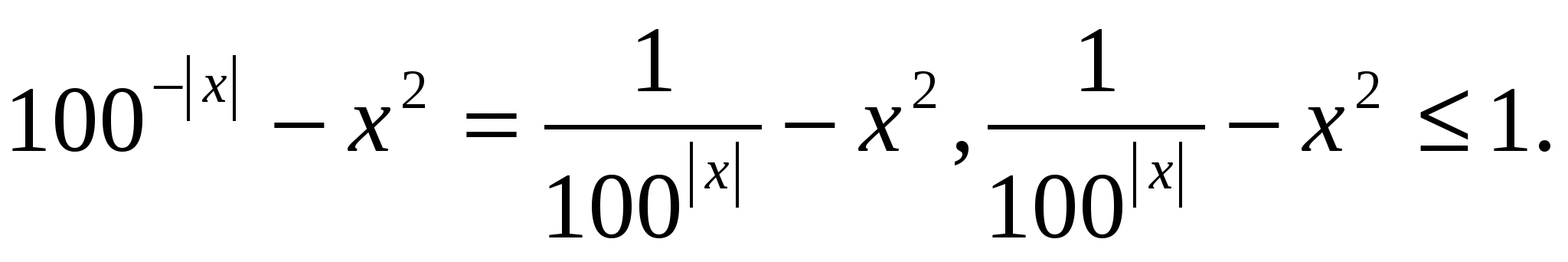 Правая часть уравнения а2 >0.Корни исходного уравнения существуют при условии
Правая часть уравнения а2 >0.Корни исходного уравнения существуют при условии 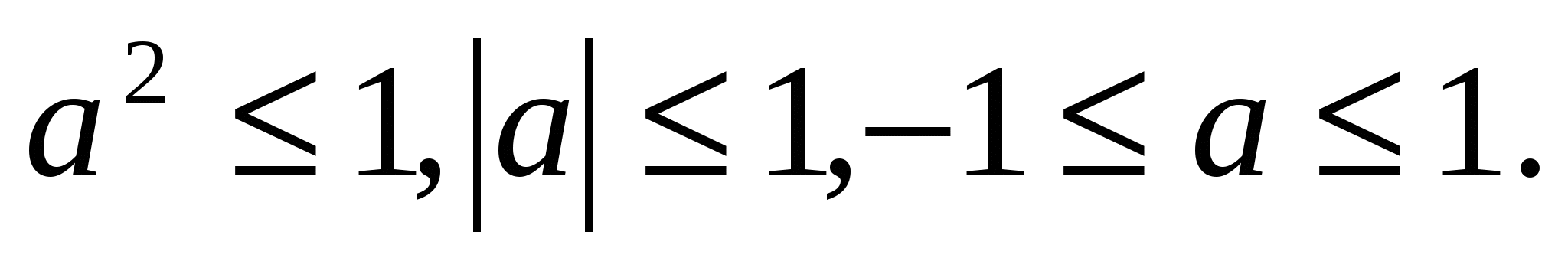 Рассмотрим функцию f(х)=
Рассмотрим функцию f(х)=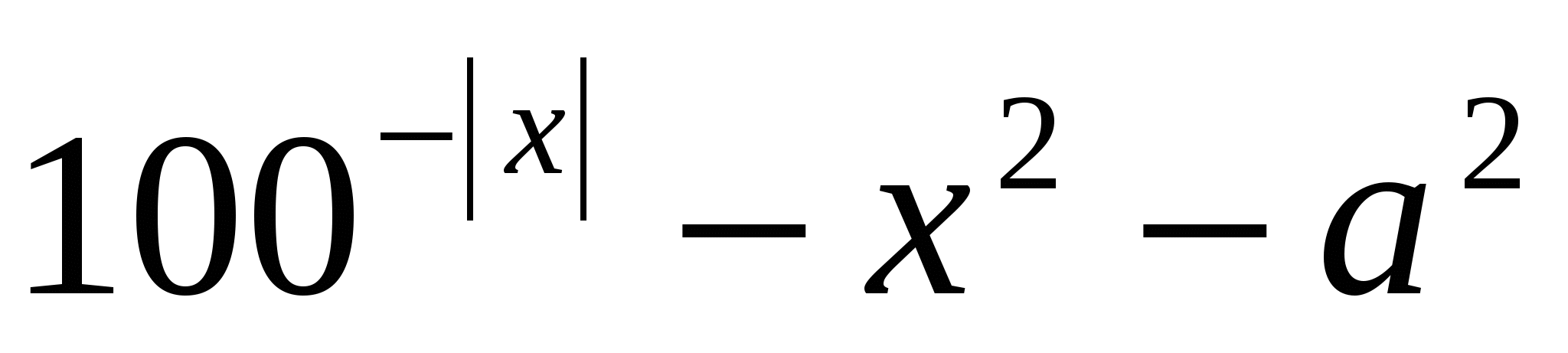 , она определена при х
, она определена при х R, является четной . При х
R, является четной . При х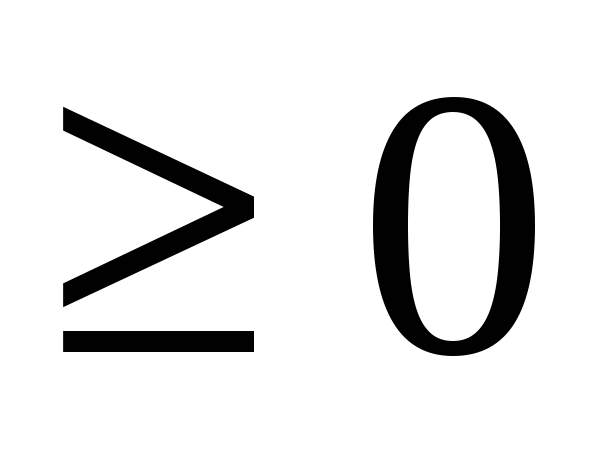 функция, расположенная в левой части исходного уравнения является монотонно убывающей а, справа константа , значит данное уравнение на этом промежутке имеет единственный корень. Если х=0, то 1000-02=а2, а2=1, а=1 или а=-1.Пользуясь четностью функции исходное уравнение имеет один корень при а =
функция, расположенная в левой части исходного уравнения является монотонно убывающей а, справа константа , значит данное уравнение на этом промежутке имеет единственный корень. Если х=0, то 1000-02=а2, а2=1, а=1 или а=-1.Пользуясь четностью функции исходное уравнение имеет один корень при а =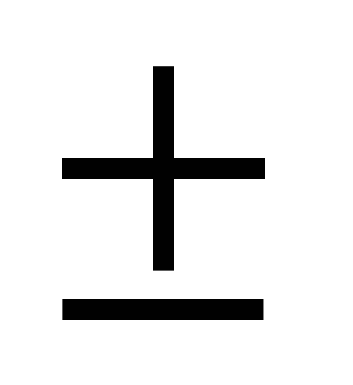 1 , два корня при
1 , два корня при 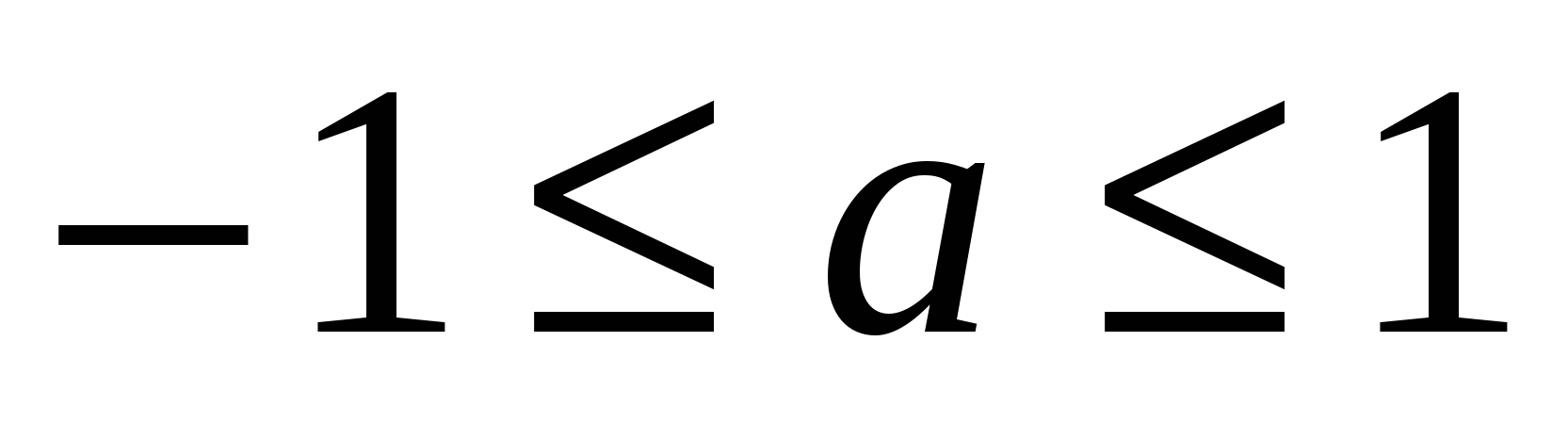 , нет корней при
, нет корней при 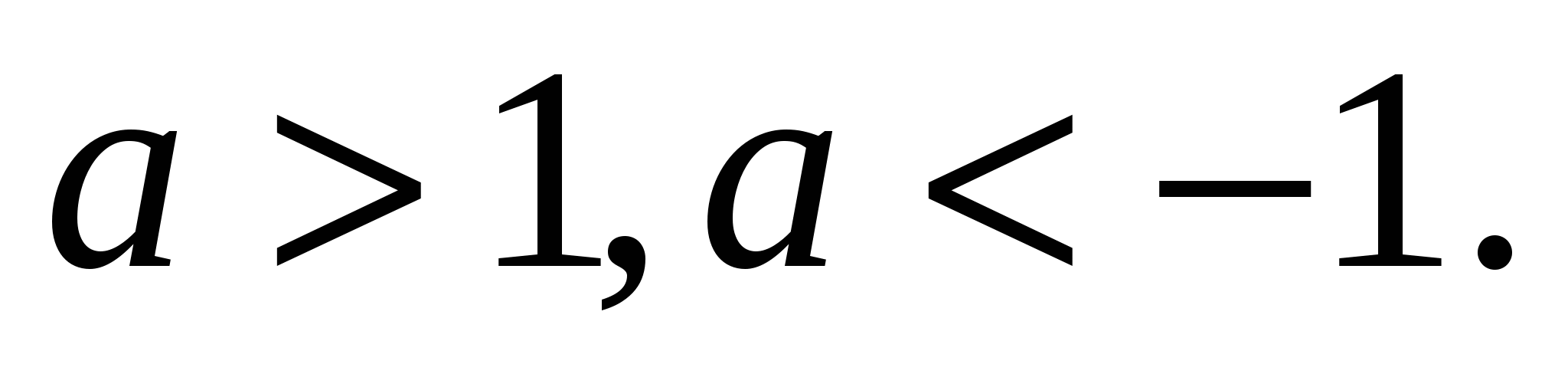
Ответ: если а =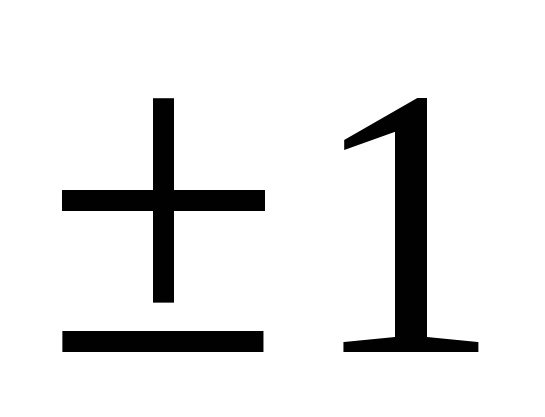 -один корень; если
-один корень; если 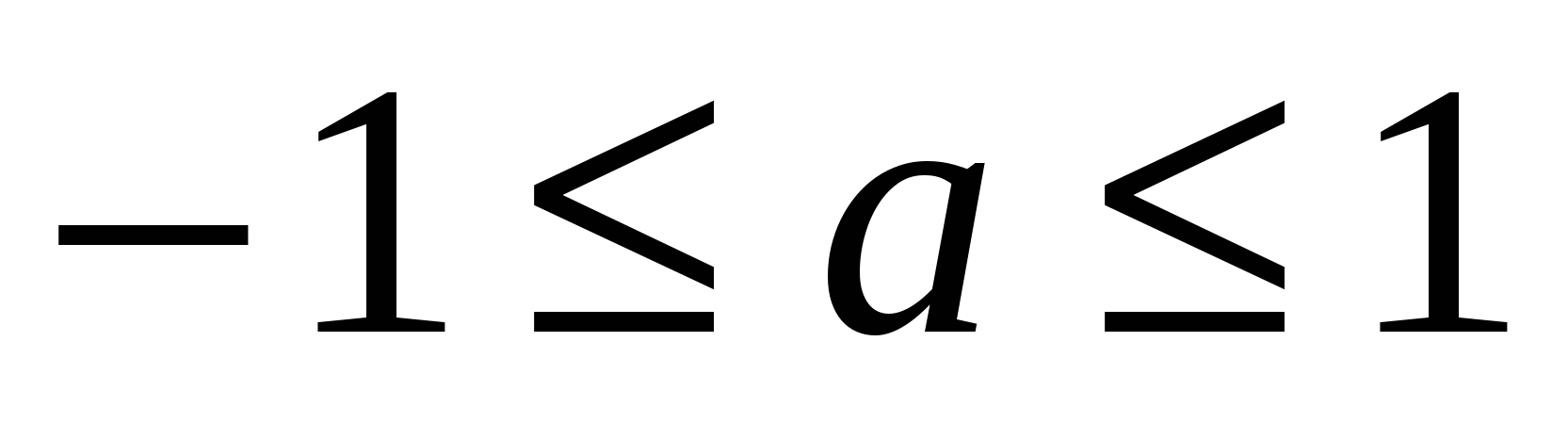 - два корня; если а<-1,a>1-нет корней.
- два корня; если а<-1,a>1-нет корней.
Использование векторов при решении уравнений.
![]()

При решении некоторых уравнений удобнее использовать скалярное произведение векторов, покажем на примерах преимущество этого метода, и в чем он заключается.
1)Решить уравнение 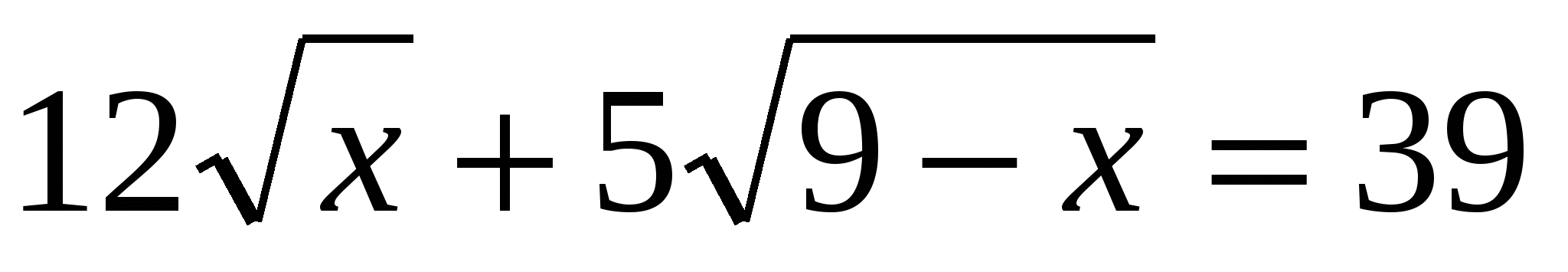
Решение: область определения этого уравнения: 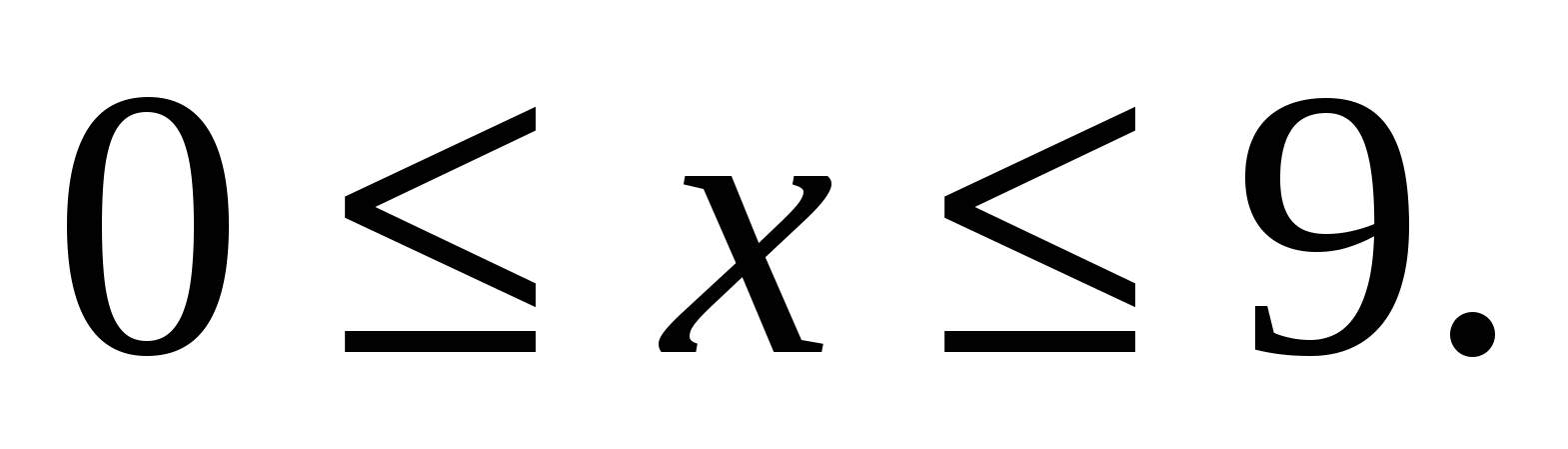 Решим его стандартным способом и покажем, насколько трудоемки вычисления, что даже обычным калькулятором не справиться.
Решим его стандартным способом и покажем, насколько трудоемки вычисления, что даже обычным калькулятором не справиться.
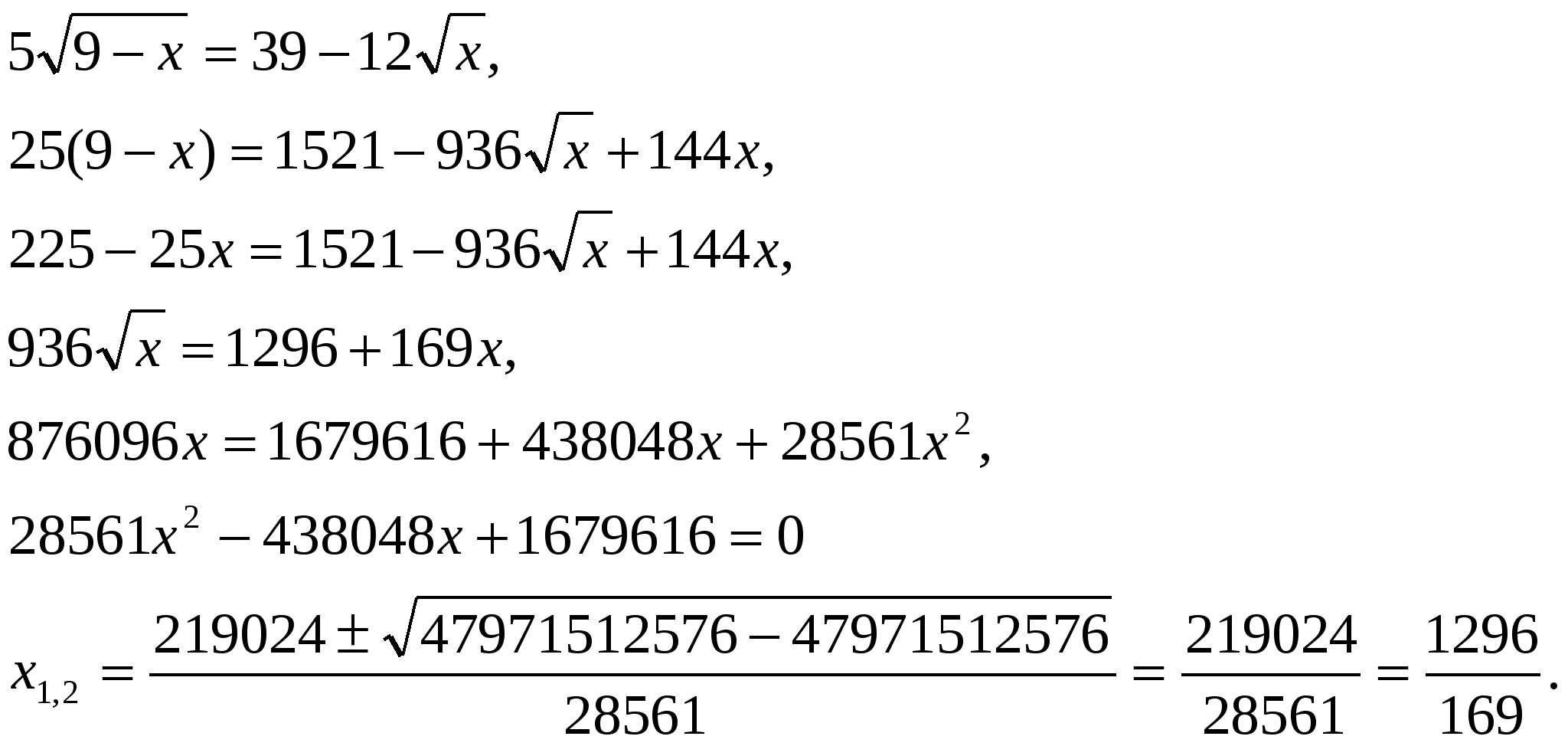
Проверка 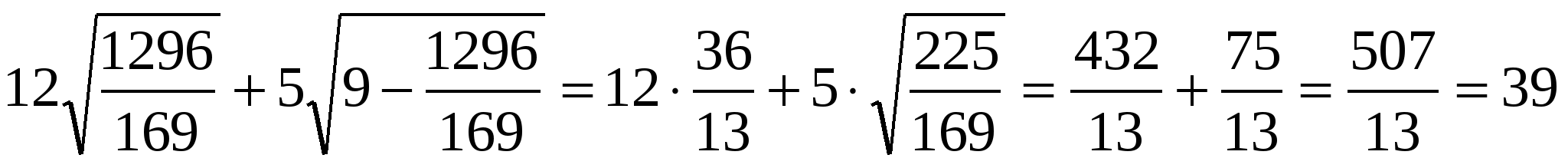 , 39=39.
, 39=39.
Ответ: х=![]()
Решим это уравнение другим способом: пусть 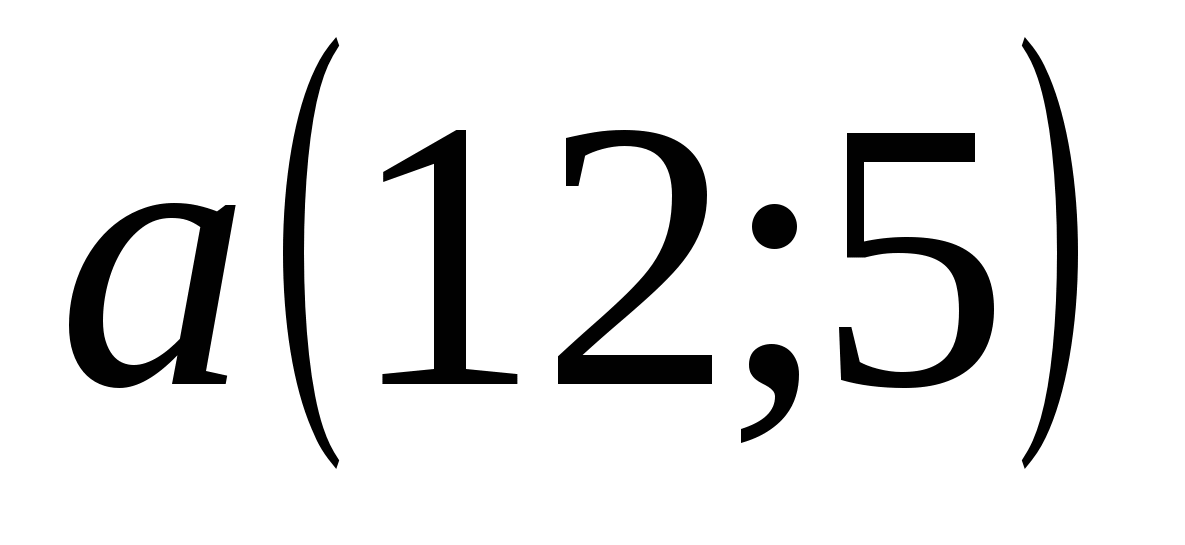
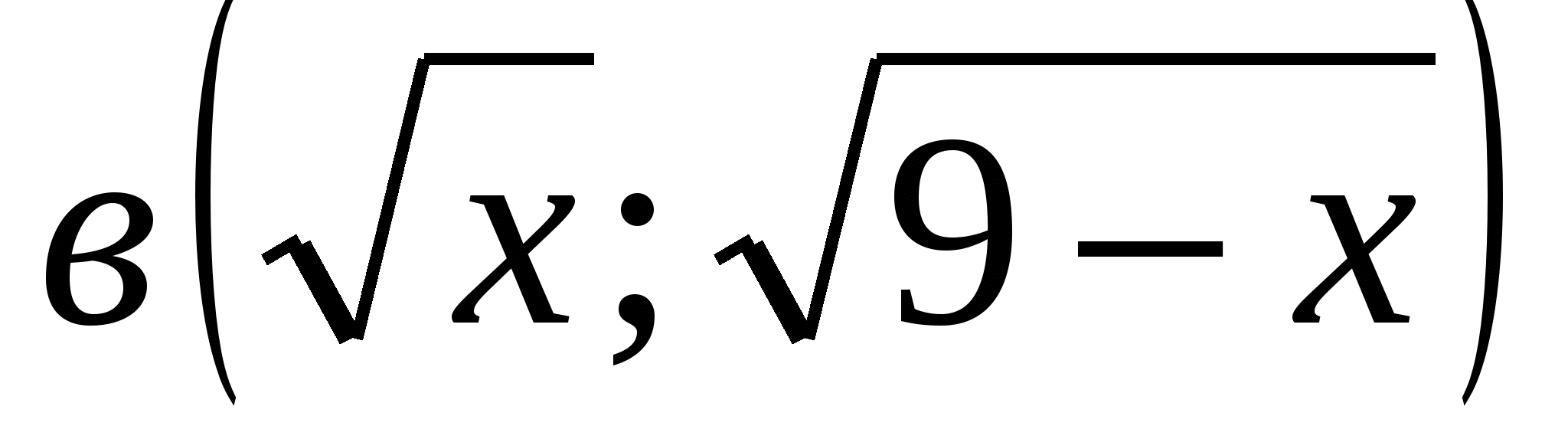 воспользуемся скалярным произведением векторов и их коллинеарностью.
воспользуемся скалярным произведением векторов и их коллинеарностью.
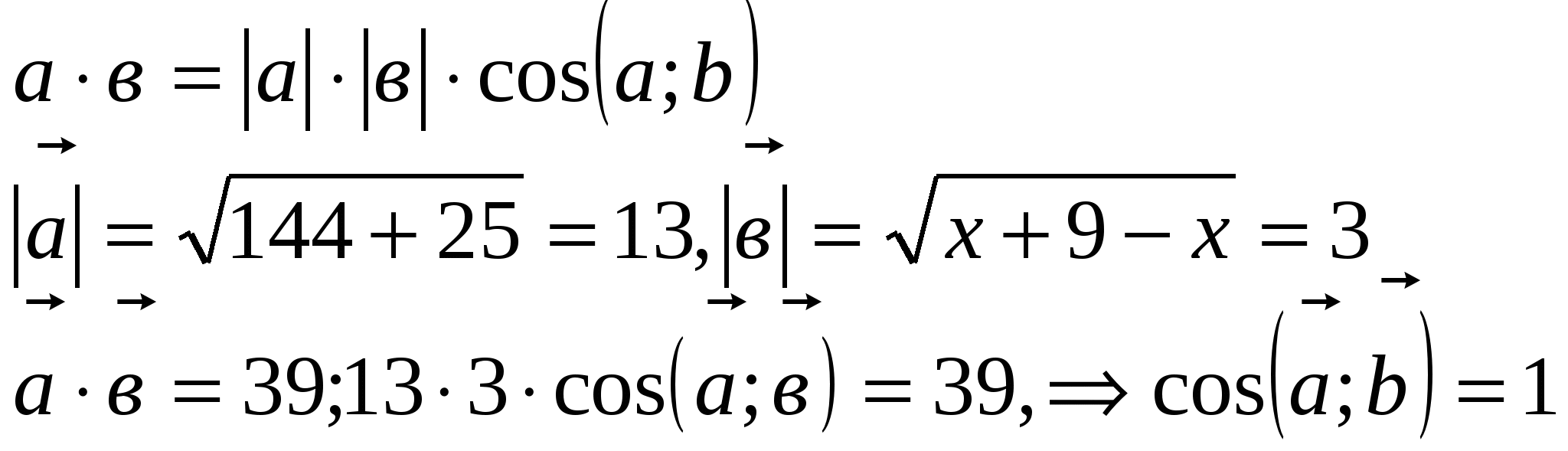
значит векторы 

 коллинеарные, тогда
коллинеарные, тогда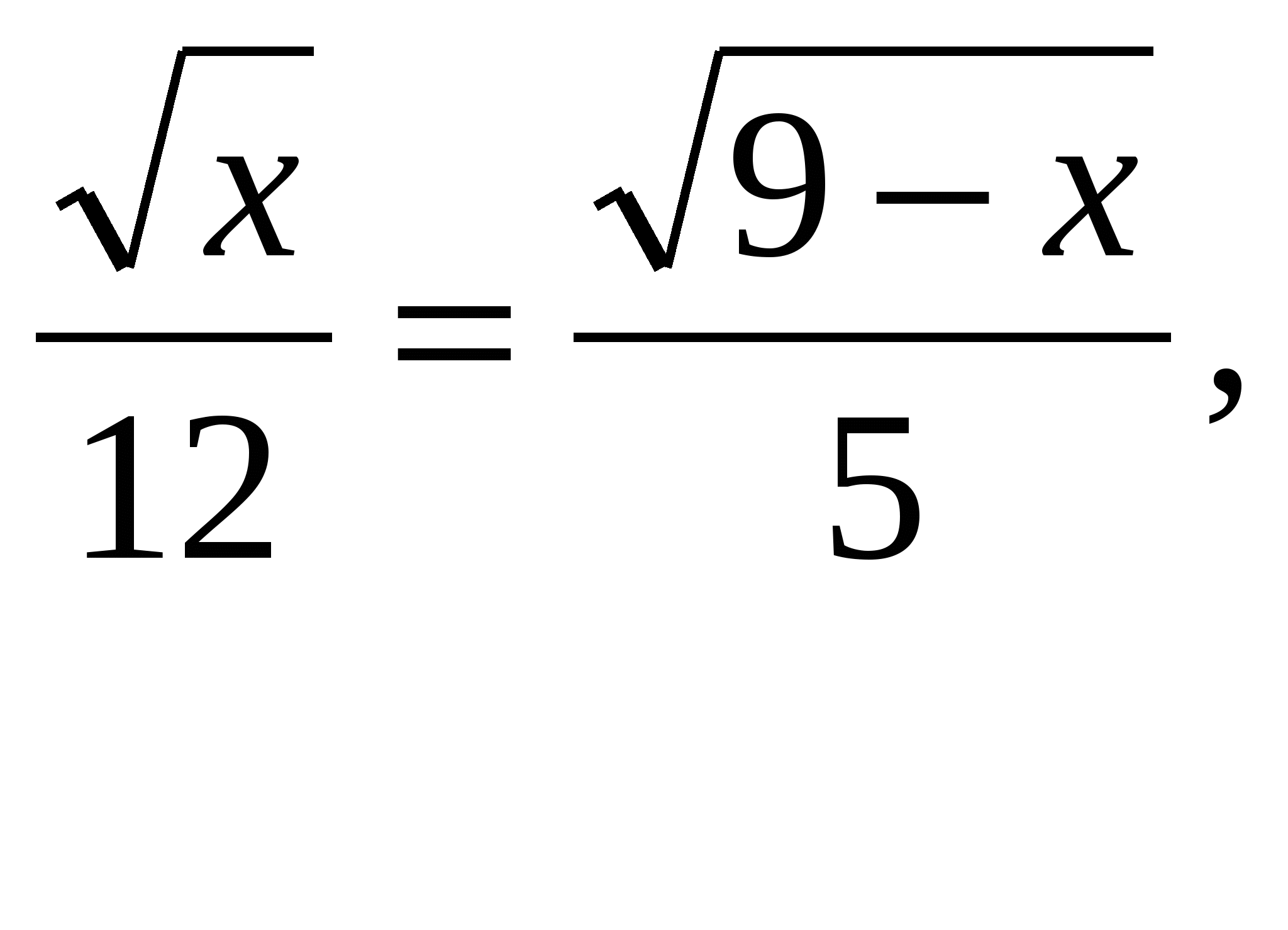
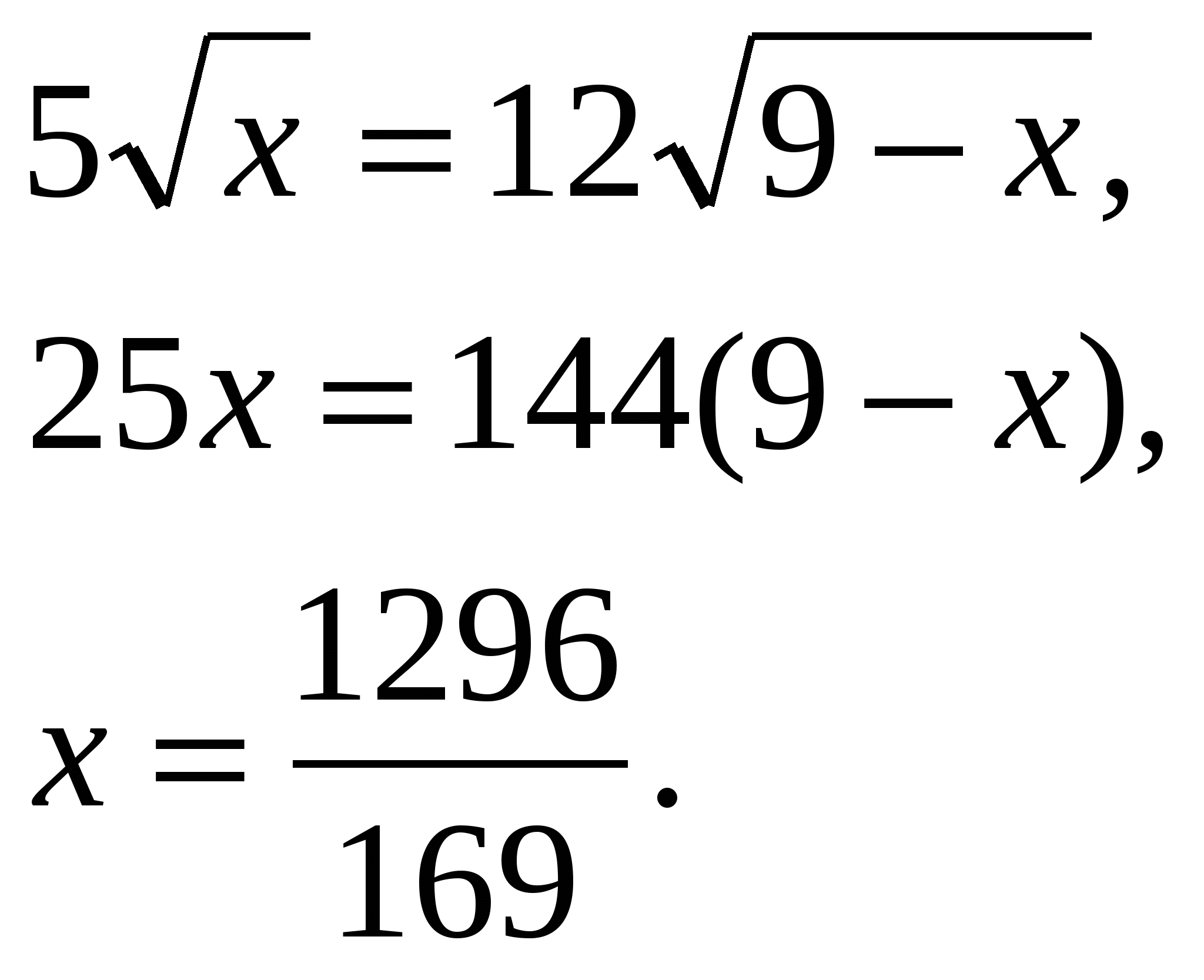
Ответ: х=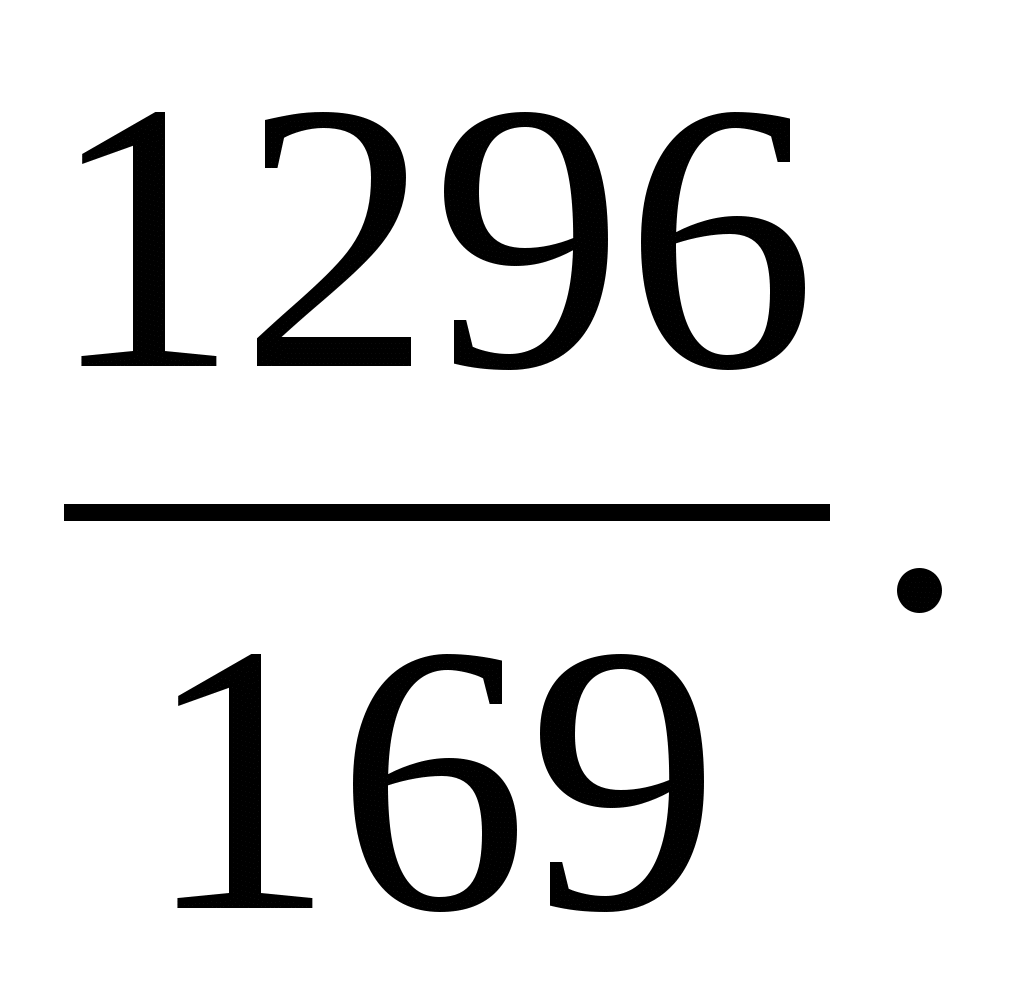
2)Решить уравнение 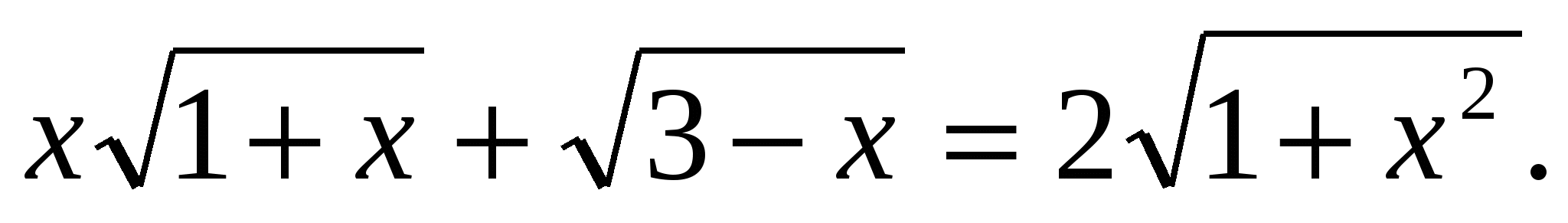
Решение: если решать это уравнение стандартным путем, возводя в квадрат обе части уравнения, причем дважды, то получим рациональное уравнение шестой степени, которое решить весьма сложно. Более рациональный способ решения этого уравнения - применение скалярного произведения векторов.
Область определения уравнения 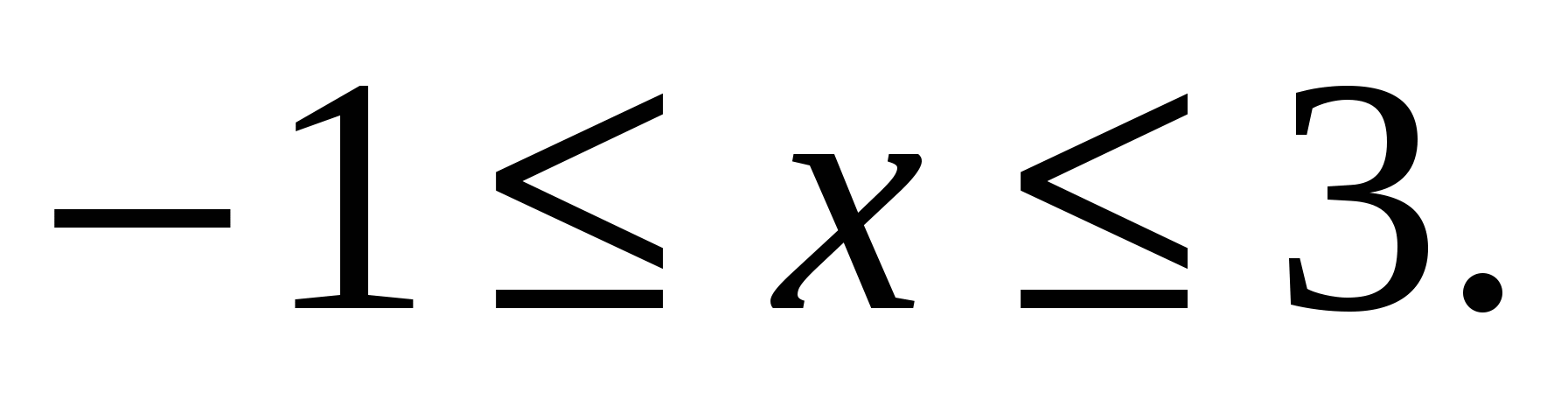

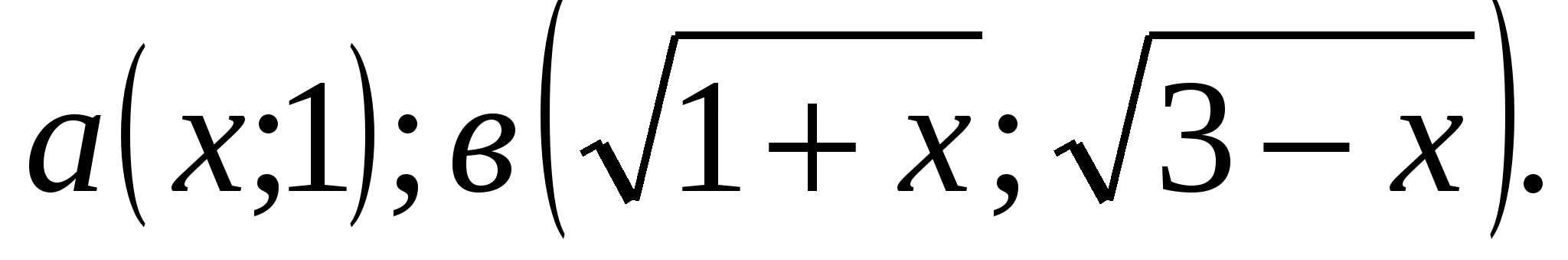
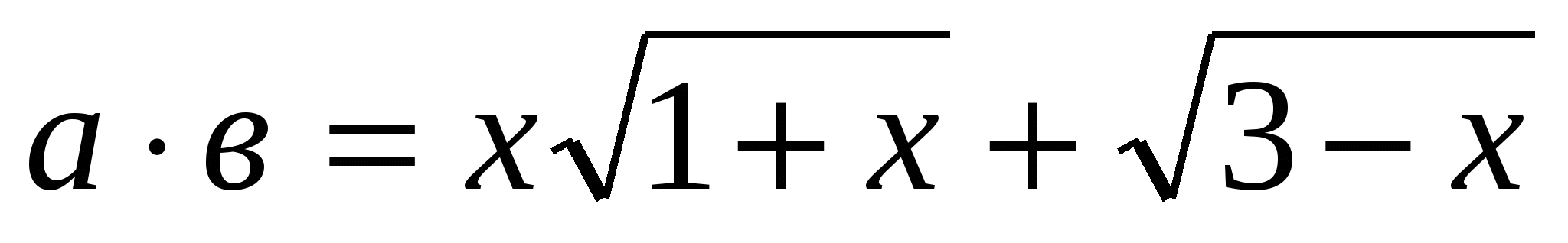
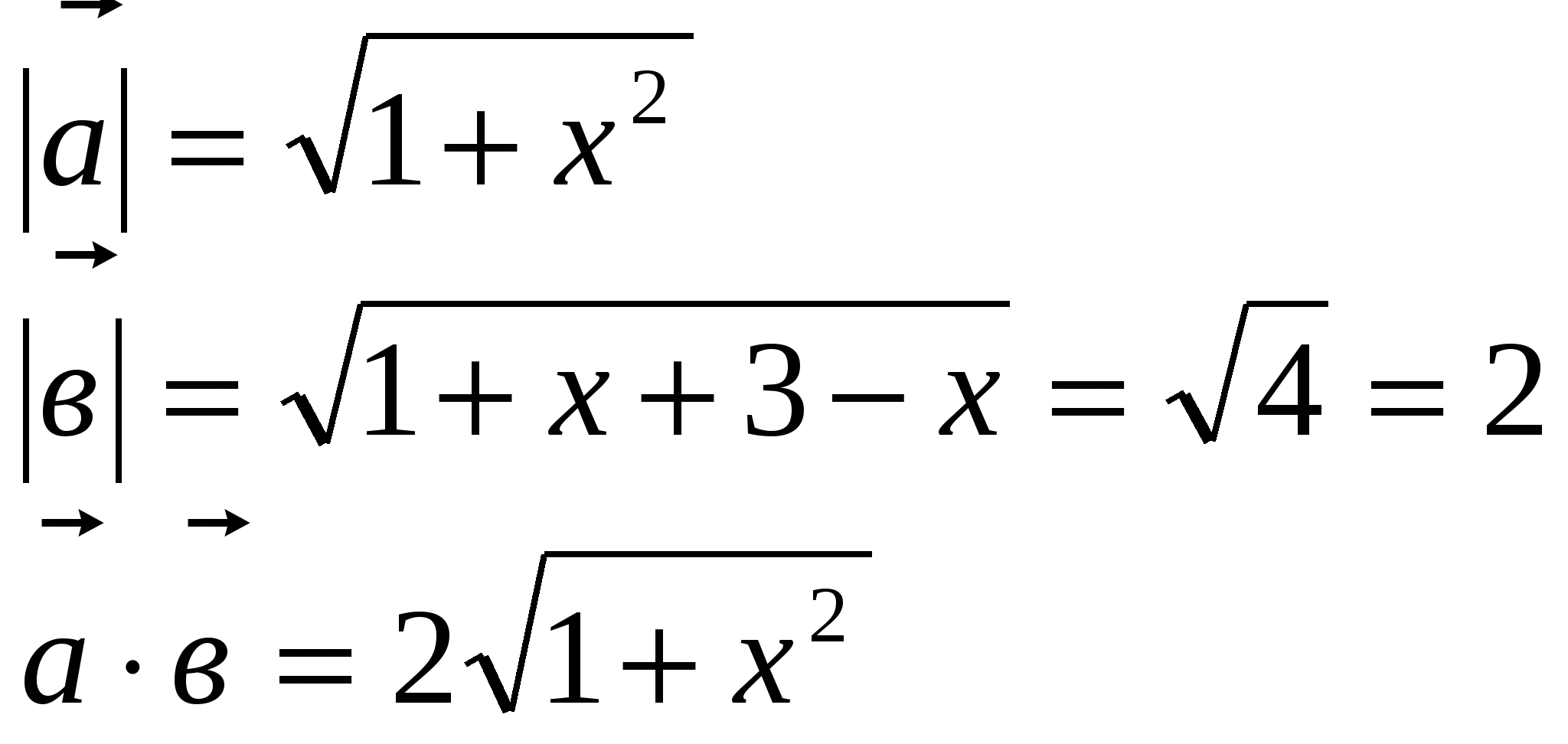
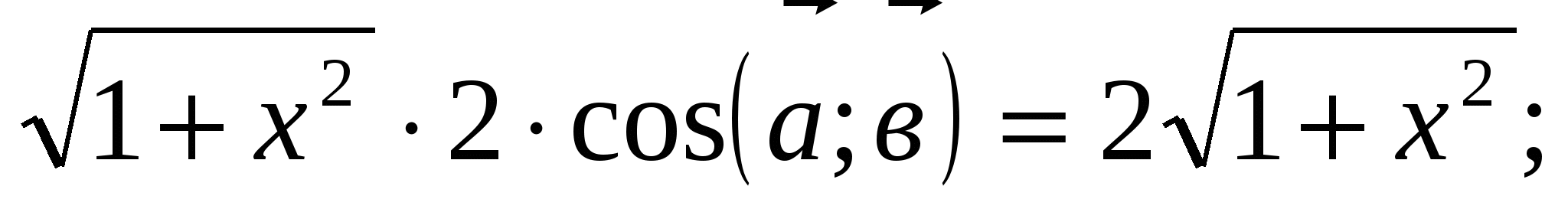
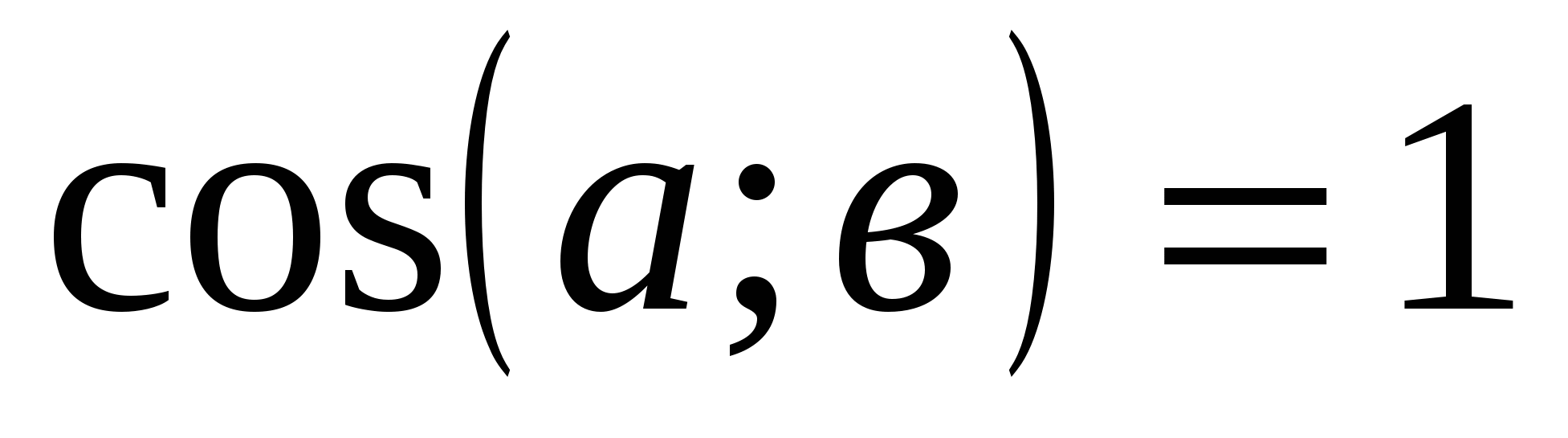
значит векторы  и
и  коллинеарные, тогда
коллинеарные, тогда
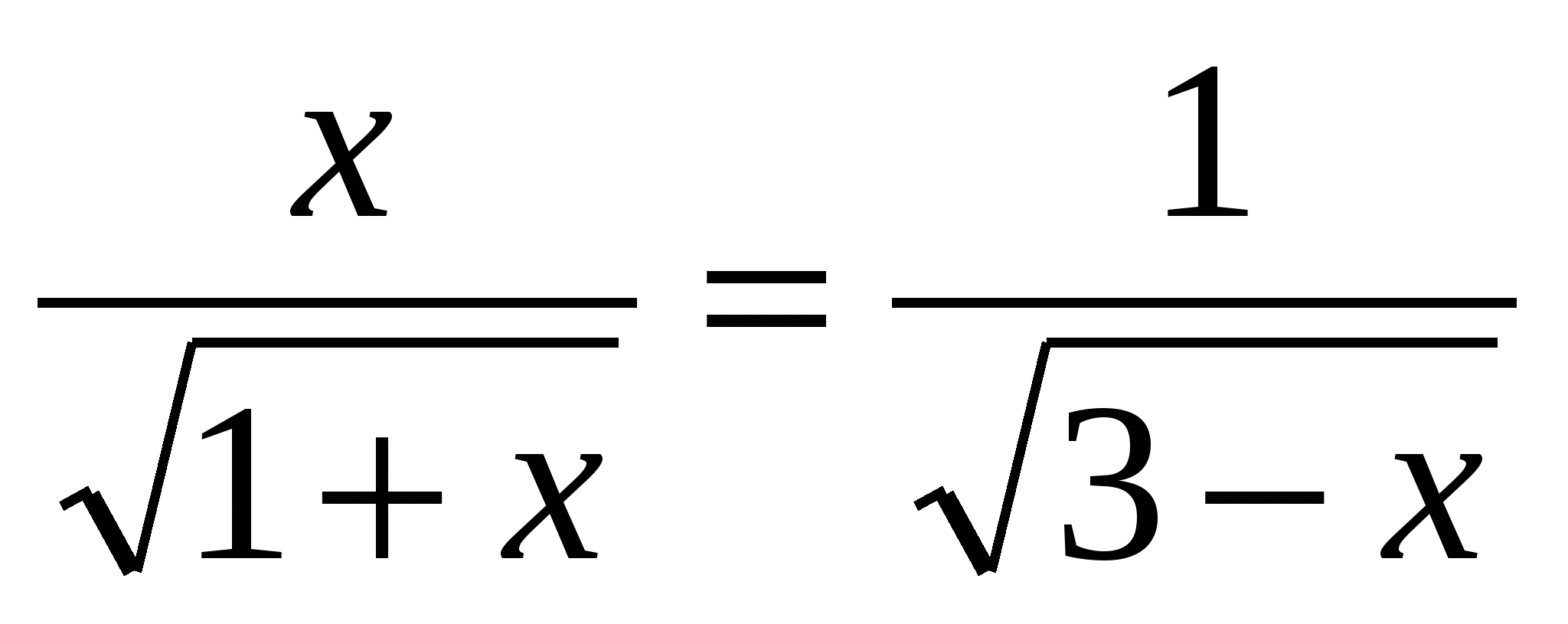 ;
; 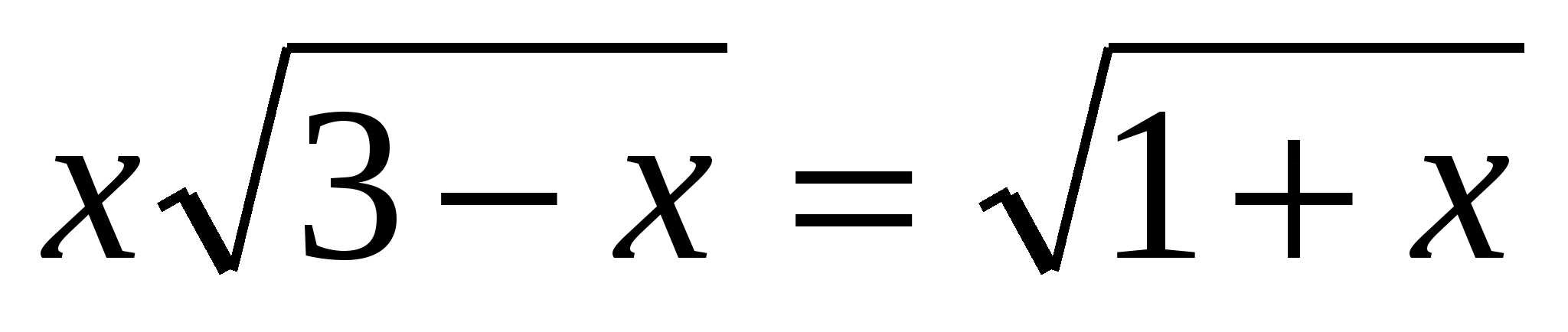 это уравнение равносильно системе
это уравнение равносильно системе
х 2(3-х)=1+х 3х2-х3-1-х=0
2(3-х)=1+х 3х2-х3-1-х=0
х 0 х3-3х2+х+1=0 х=1 - корень уравнения
0 х3-3х2+х+1=0 х=1 - корень уравнения
(х-1)(х2-2х-1)=0 х2-2х-1=0 х1=1+![]() х2=1-
х2=1-![]() - не удовлетворяет условию х
- не удовлетворяет условию х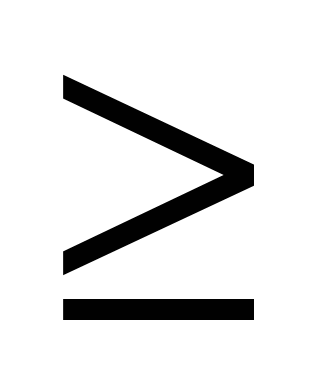 0. х=1 и х=1+
0. х=1 и х=1+ удовлетворяют области определения.
удовлетворяют области определения.
Ответ: х=1; х=1+ .
.
3)Решить уравнение 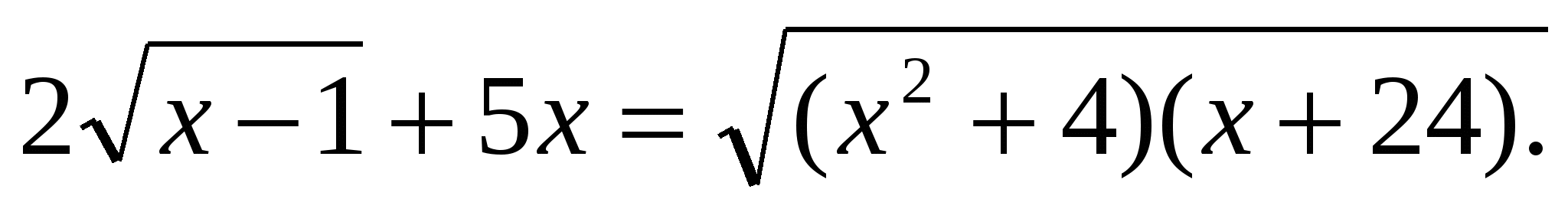
Решение: решим это уравнение тем же способом, каким решали предыдущее. Область определения уравнения х 1
1 
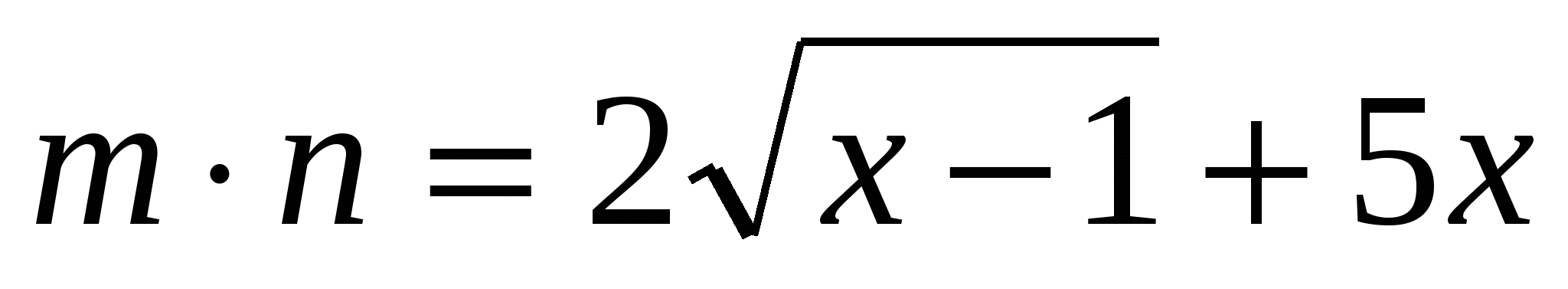
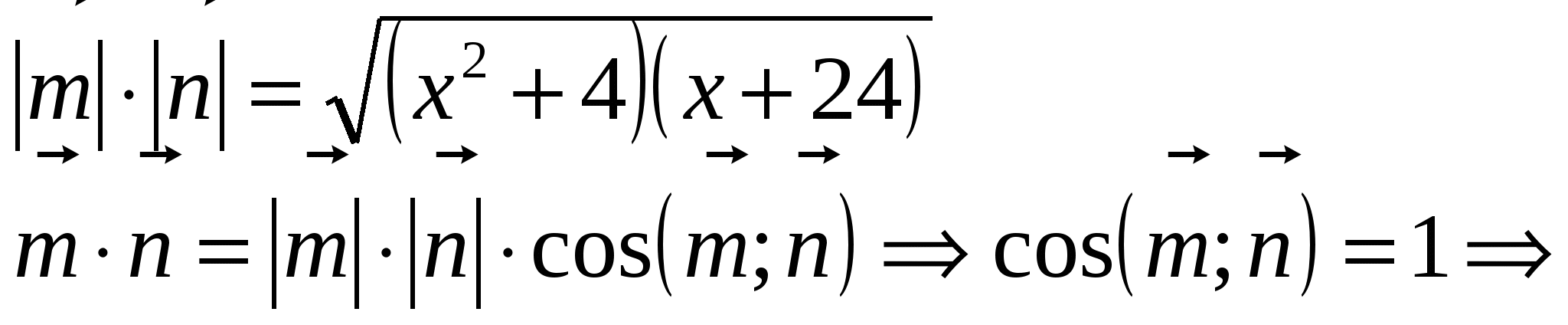 векторы
векторы  и
и  коллинеарные, значит
коллинеарные, значит 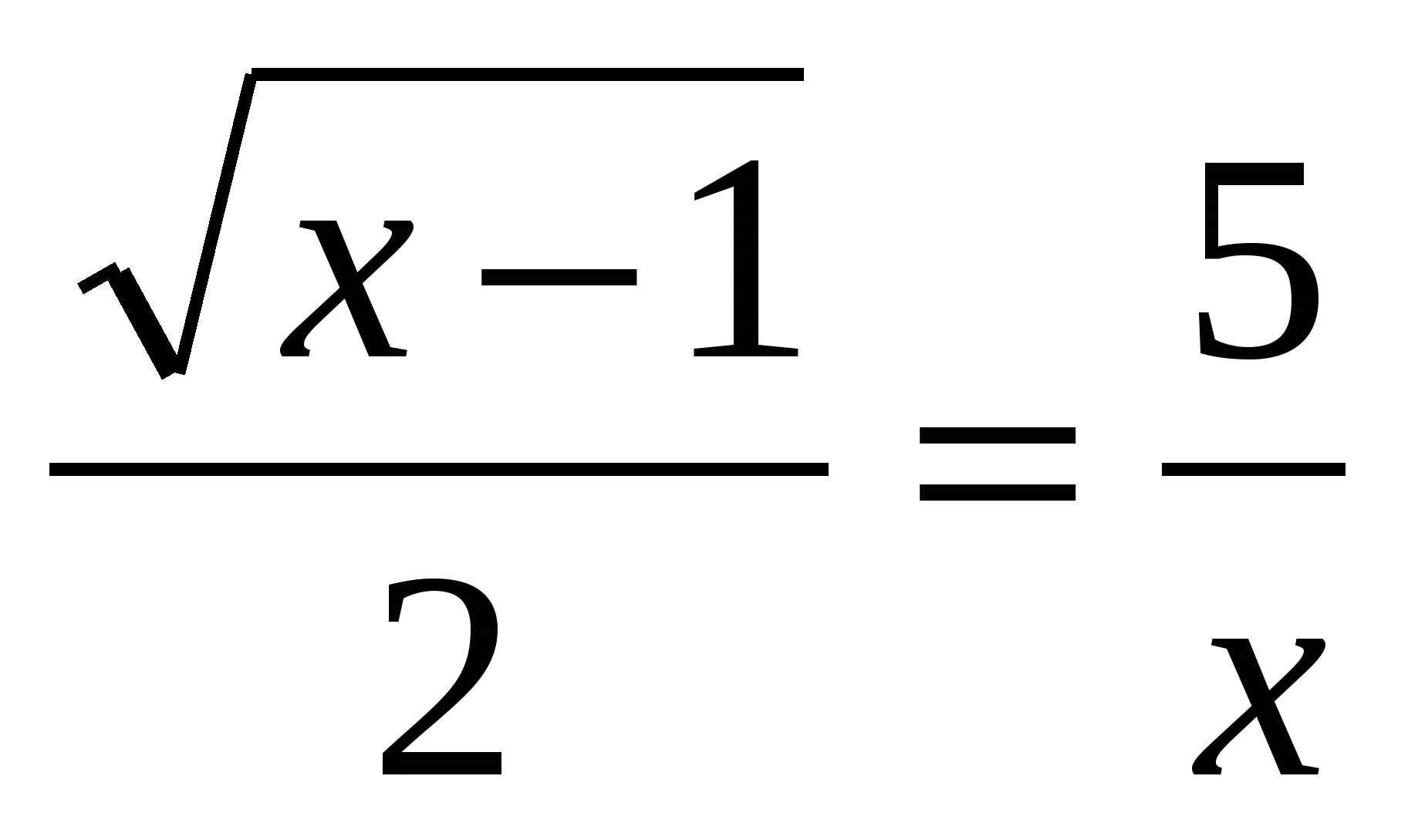
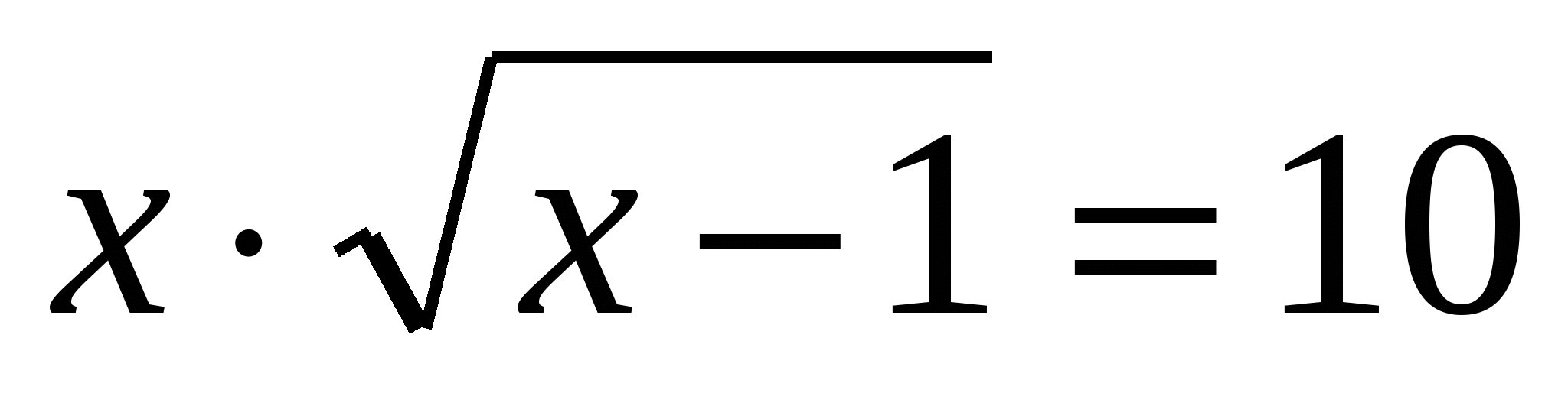
х2(х-1)=10, х3-х2-10=0 подбором находим корень х=5.
(х-5)(х2+4х+20)=0 уравнение х2+4х+20=0 корней не имеет.
х=5 - единственный корень .
Ответ: х=5.
3)Решить уравнение 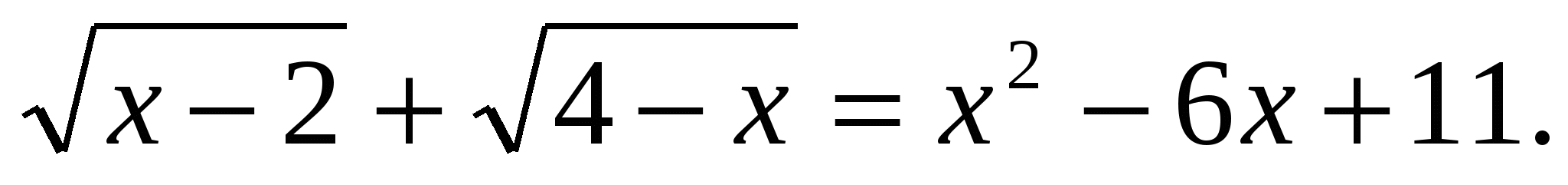
Решение: найдем область допустимых значений х этого уравнения
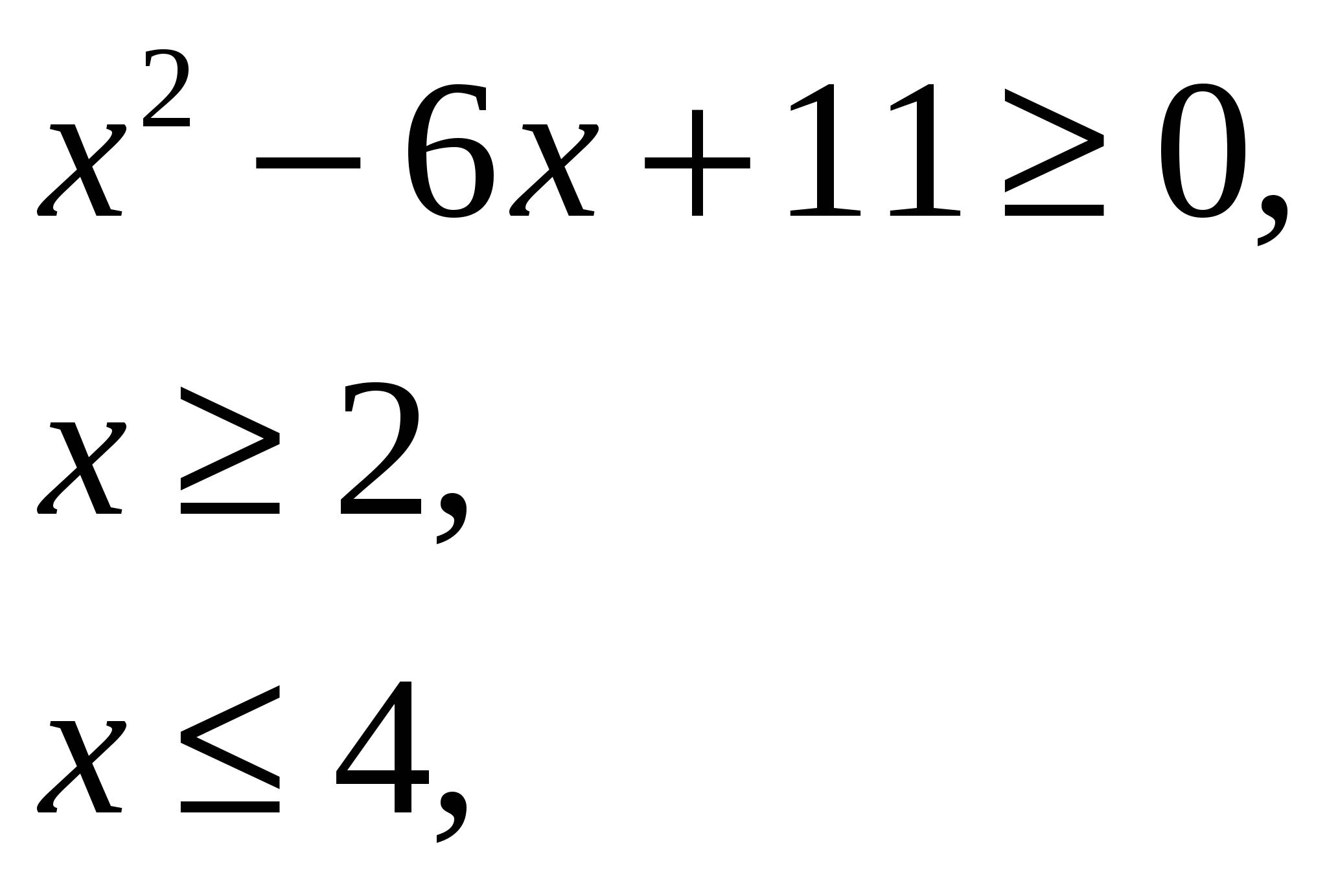
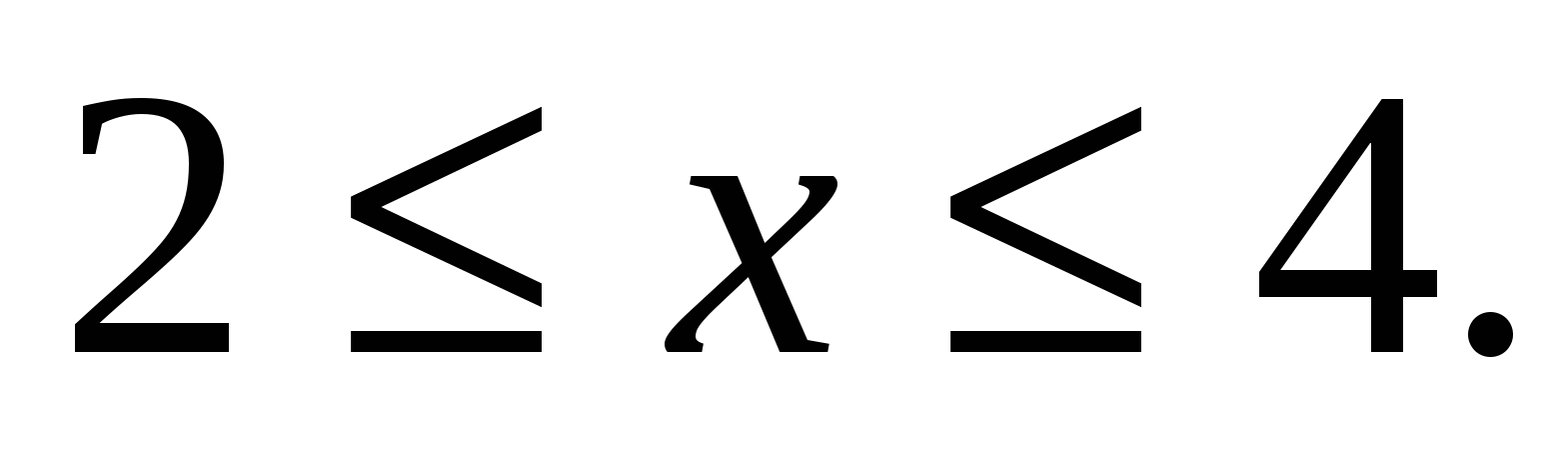
используем векторы для оценки левой части уравнения.
Пусть 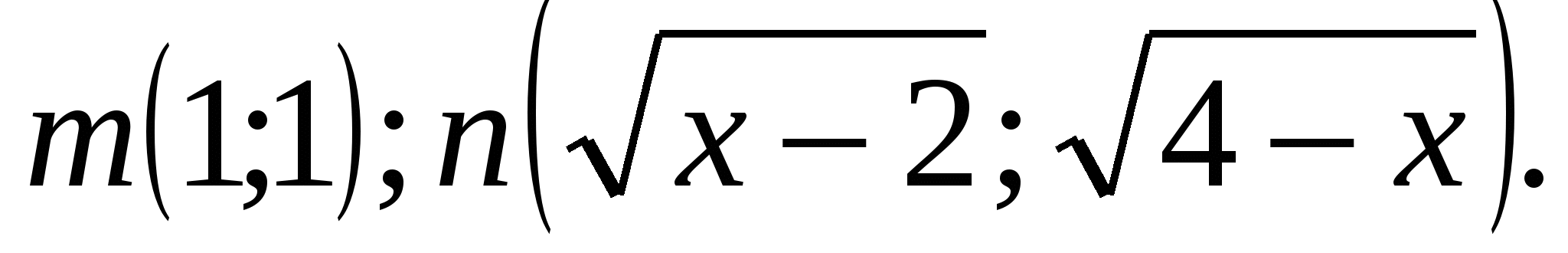
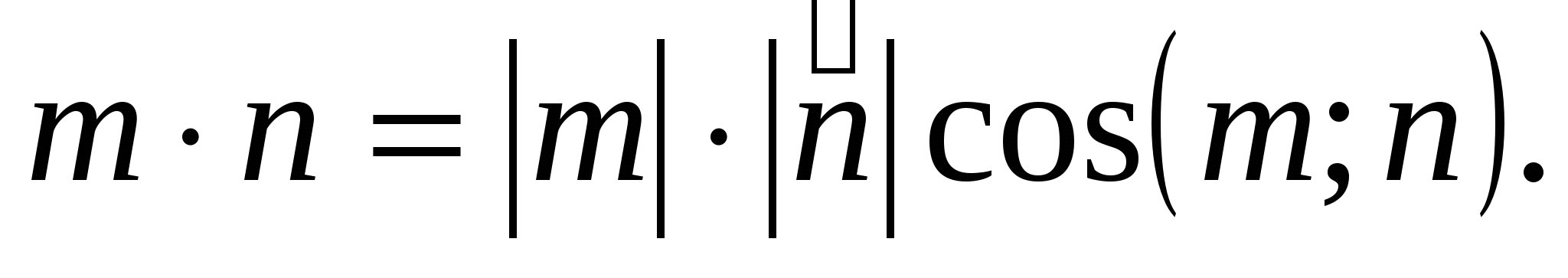
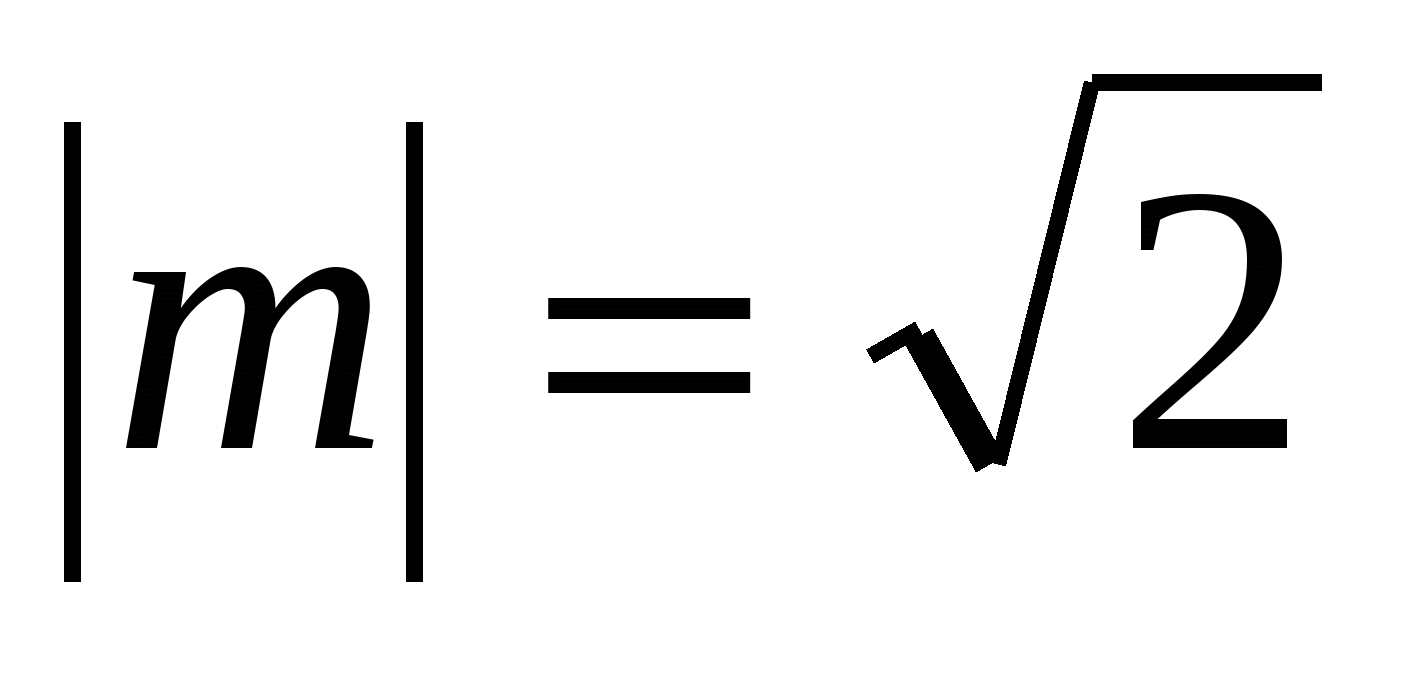
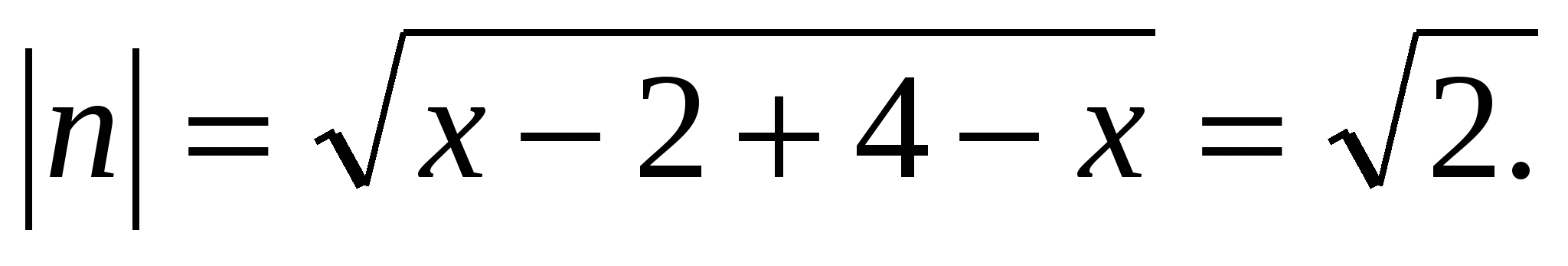 т.к.
т.к. 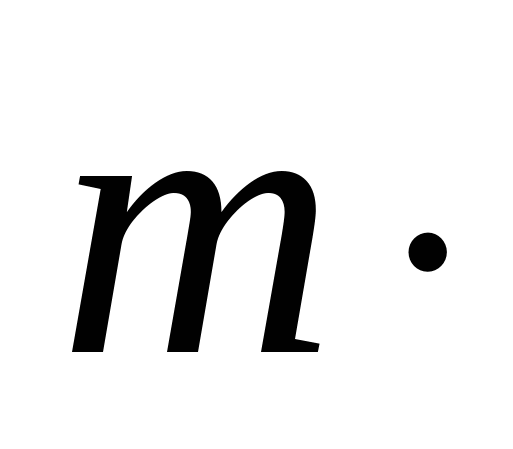
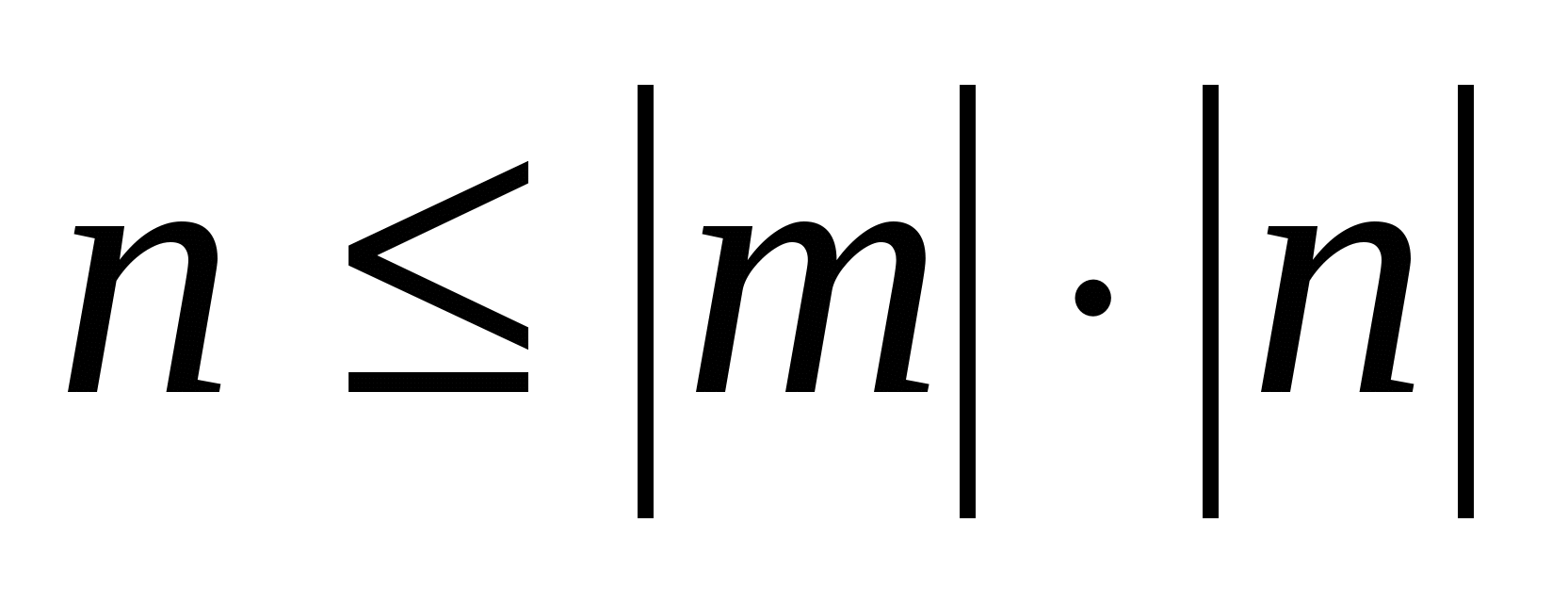 то
то 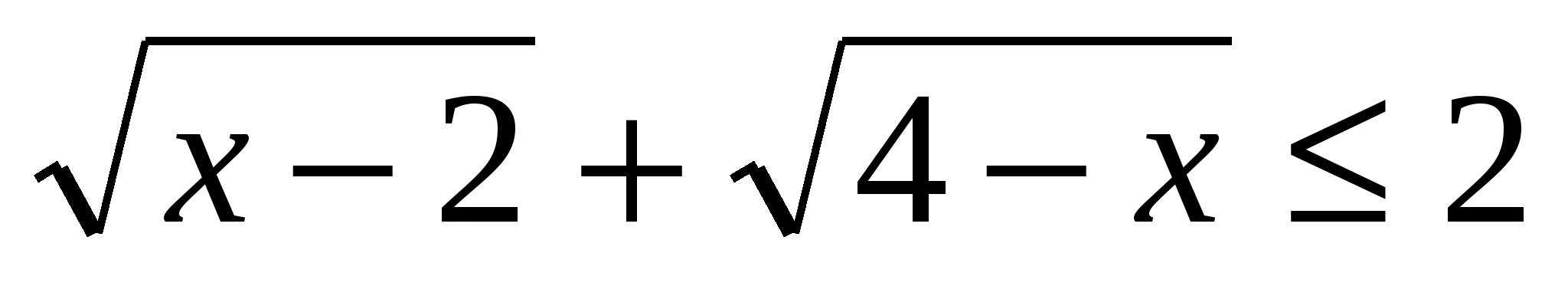 .
.
Оценим правую часть уравнения: х2-6х+11=(х-3)2+2, (х-3)2+2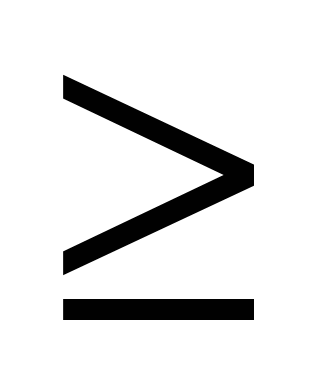 2.
2.
Значит ,если уравнение имеет корни, то они существуют при условии: если левая и правя части уравнения равны двум. Найдем такие значения х.
(х-3)2+2=2, х=3.
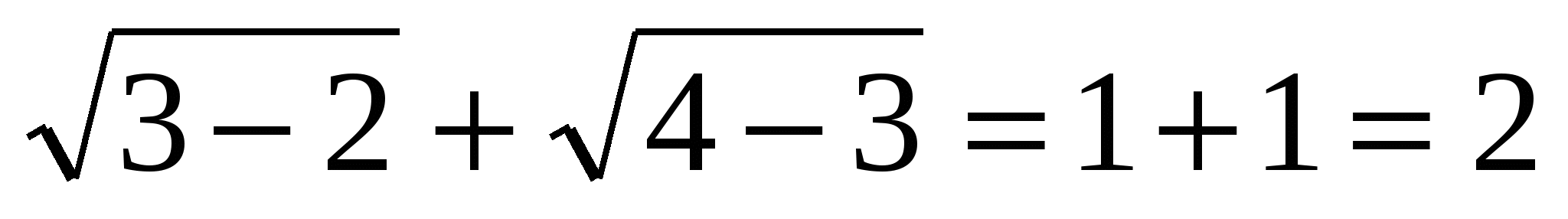 , 2=2, значит х=3 - единственный корень уравнения.
, 2=2, значит х=3 - единственный корень уравнения.
Ответ: х=3.
Использование неравенства между средним арифметическим и средним геометрическим положительных чисел при решении уравнений.
При решении некоторых уравнений удобно пользоваться неравенством между средним арифметическим и средним геометрическим положительных чисел 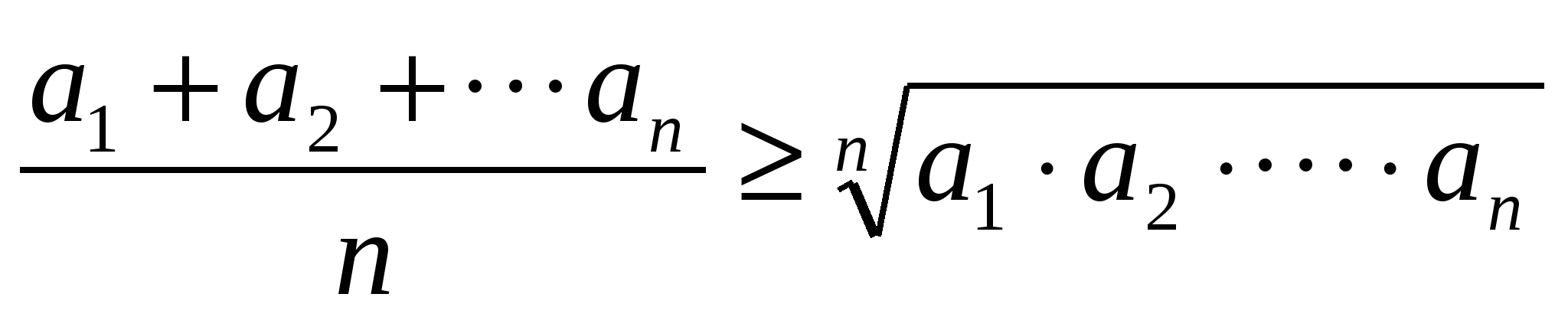 , где аi> 0; (1)равенство достигается при условии а1=а2=….=ап . (2)
, где аi> 0; (1)равенство достигается при условии а1=а2=….=ап . (2)
1)Решить уравнение 2х+4х+2564=3 16х.
Решение: попытки решить такое уравнение стандартным путем чаще всего заканчиваются неудачей, использование неравенства между средним арифметическим и средним геометрическим существенно облегчает задачу. Оценим левую часть уравнения:
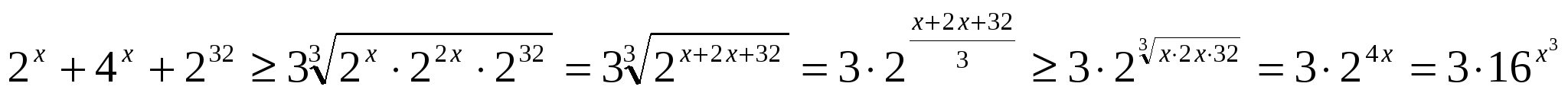
Левая часть уравнения не меньше 3 16х, а правая равна 3 16х. Равенство возможно только при условии 2х=4х=232, х=2.
Ответ: х=2.
2)Решить уравнение 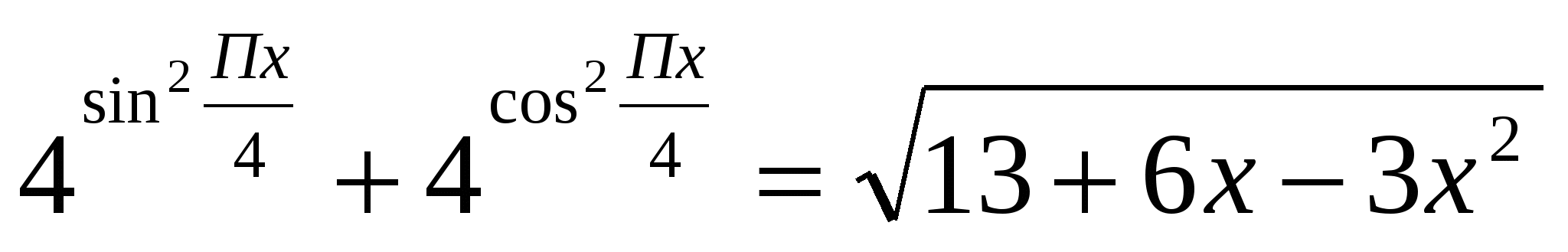 .
.
Решение: оценим правую часть уравнения. Рассмотрим функцию у=13+6х-3х2, графиком этой функции является парабола, ветви которой направлены вниз, наибольшее значение достигается при вершине параболы. Найдем координаты вершины параболы: х0=1, у0=13+6-3=16, значит 13+6х-3х2<16, тогда 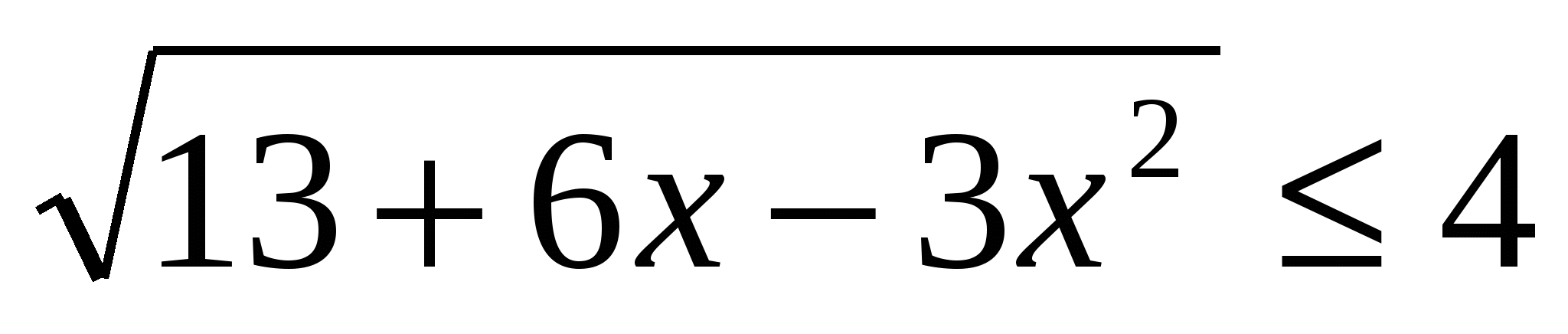 .
.
Оценим левую часть уравнения, используя неравенство (1) ![]() . Значит, исходное уравнение имеет корни в том случае, если левая и правая части уравнений одновременно равны 4.
. Значит, исходное уравнение имеет корни в том случае, если левая и правая части уравнений одновременно равны 4. 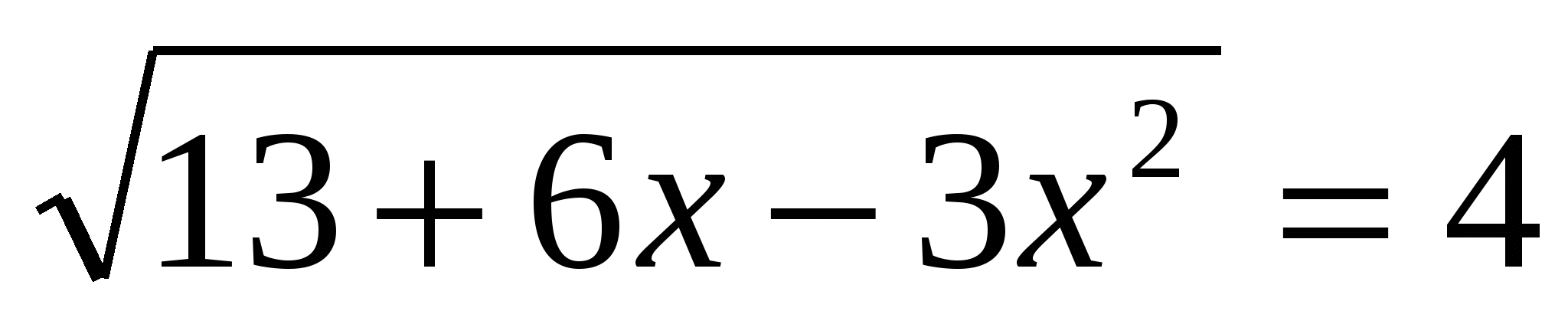 , х=1.
, х=1.
Проверим правую часть уравнения 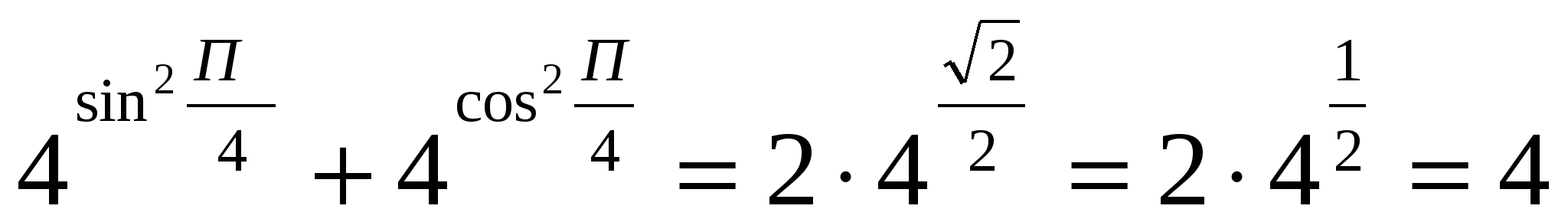 ,х=1- корень исходного уравнения.
,х=1- корень исходного уравнения.
Ответ: х=1.
3)Решить уравнение 
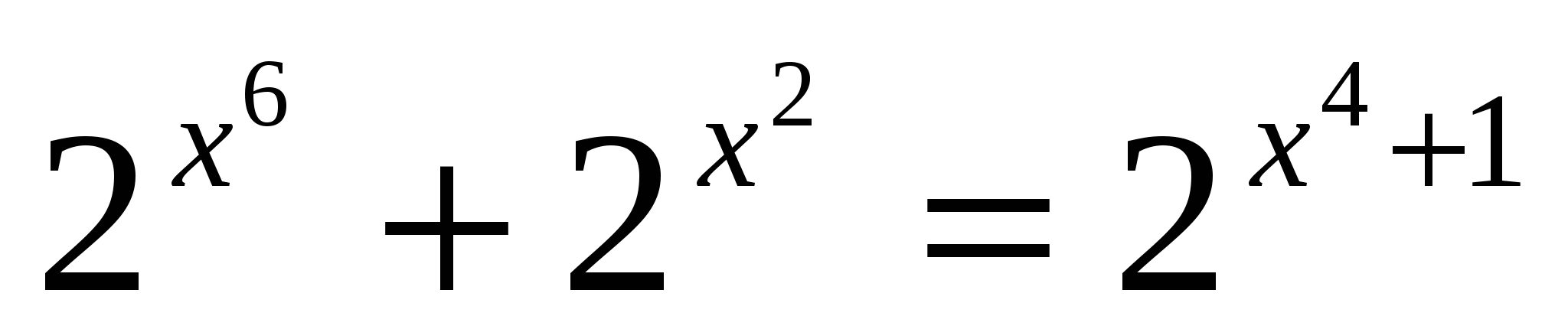 . Решение: оценим левую часть уравнения
. Решение: оценим левую часть уравнения 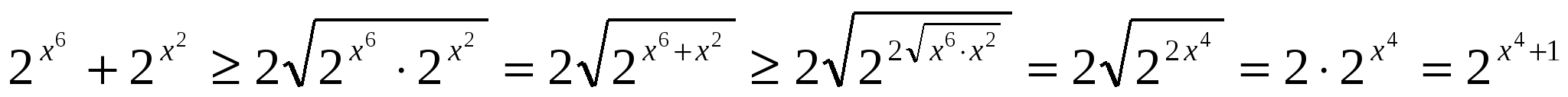 , что равно правой части уравнения. При этом равенство достигается, когда
, что равно правой части уравнения. При этом равенство достигается, когда 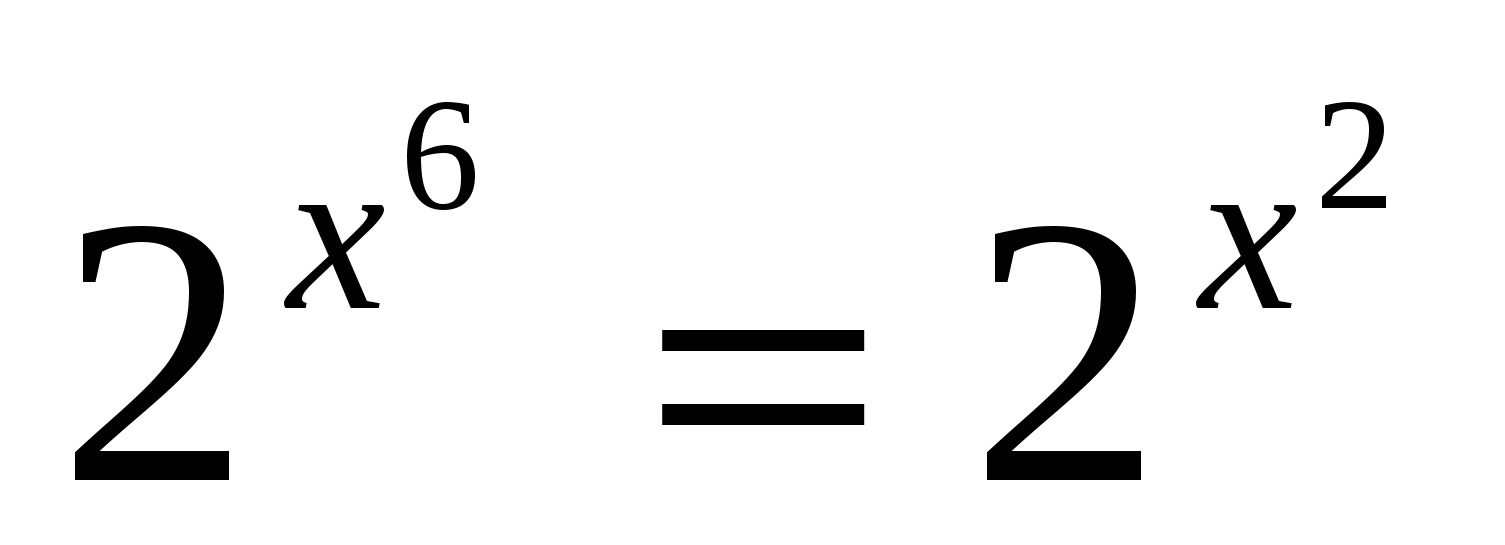 и х6=х2, что одно и то же. Последнее уравнение имеет , очевидно корни х=0 и х=1, х=-1.
и х6=х2, что одно и то же. Последнее уравнение имеет , очевидно корни х=0 и х=1, х=-1.
Ответ: х=0; х=1; х=-1.
4)Решить уравнение 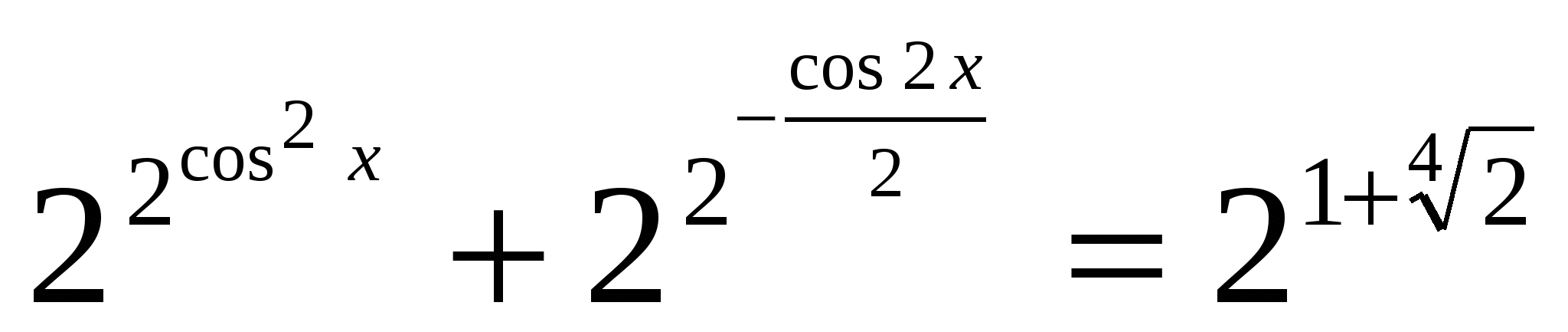 .
.
Решение: дважды применяя неравенство о среднем арифметическом и среднем геометрическом ( во второй раз в показателе степени), получаем цепочку равенств и неравенств
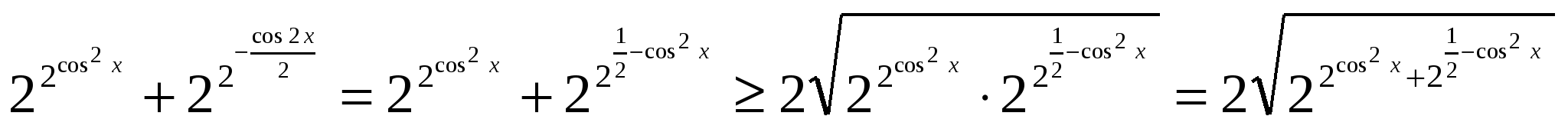 =
=
=
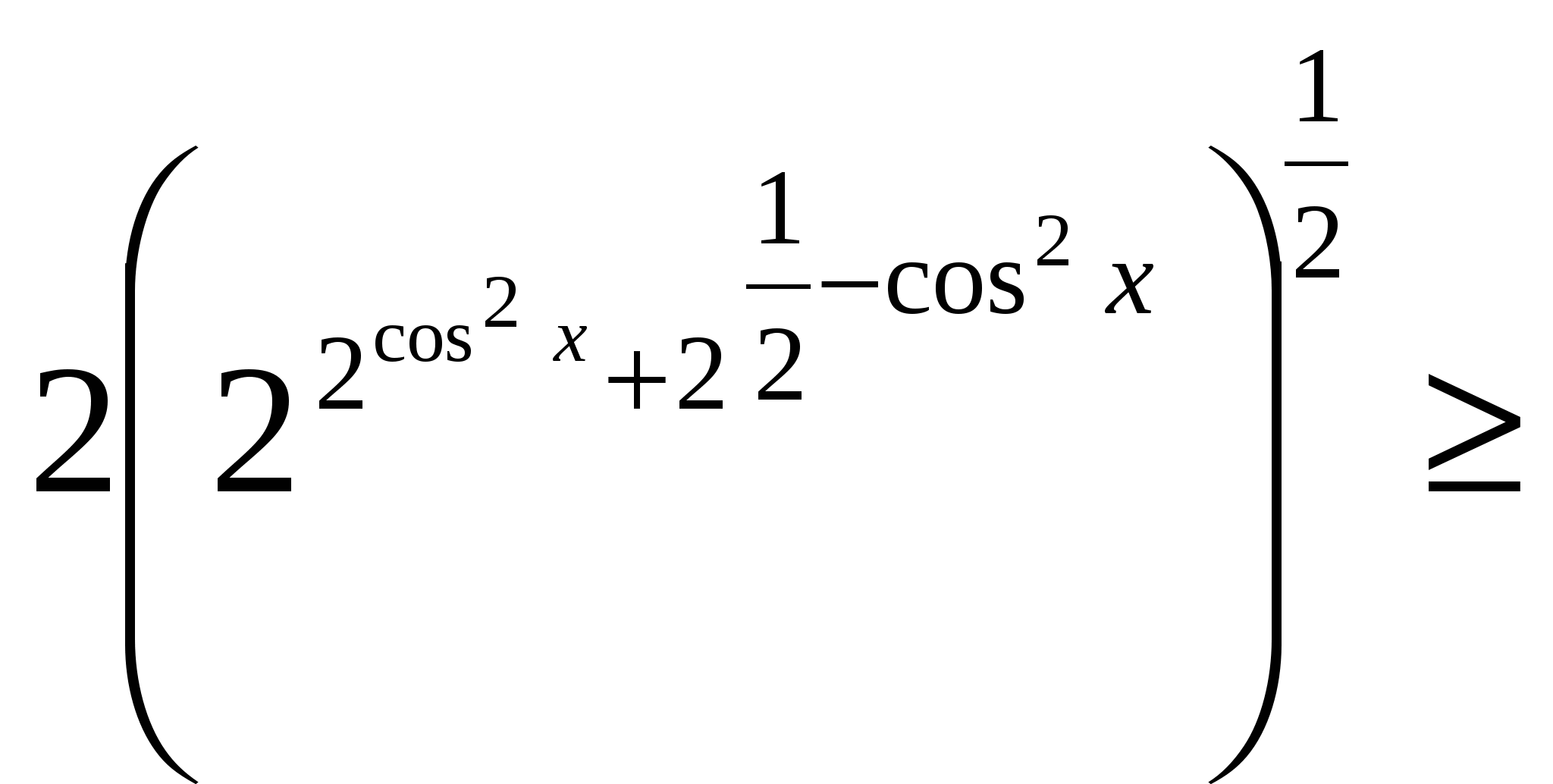
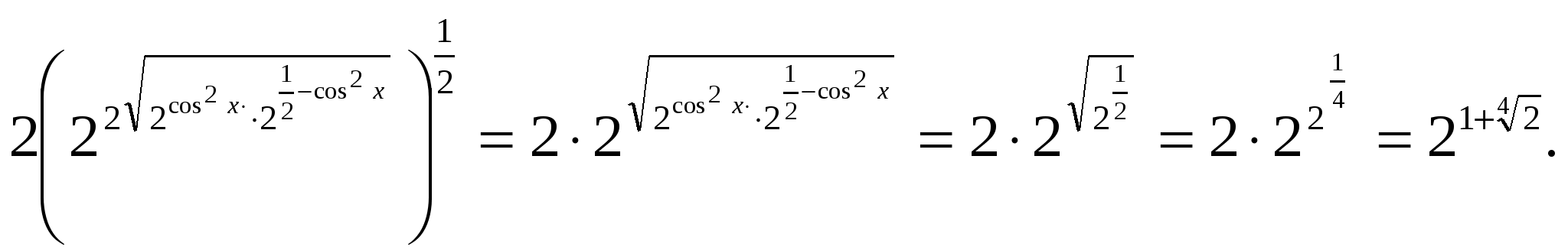
При этом равенство достигается при условии 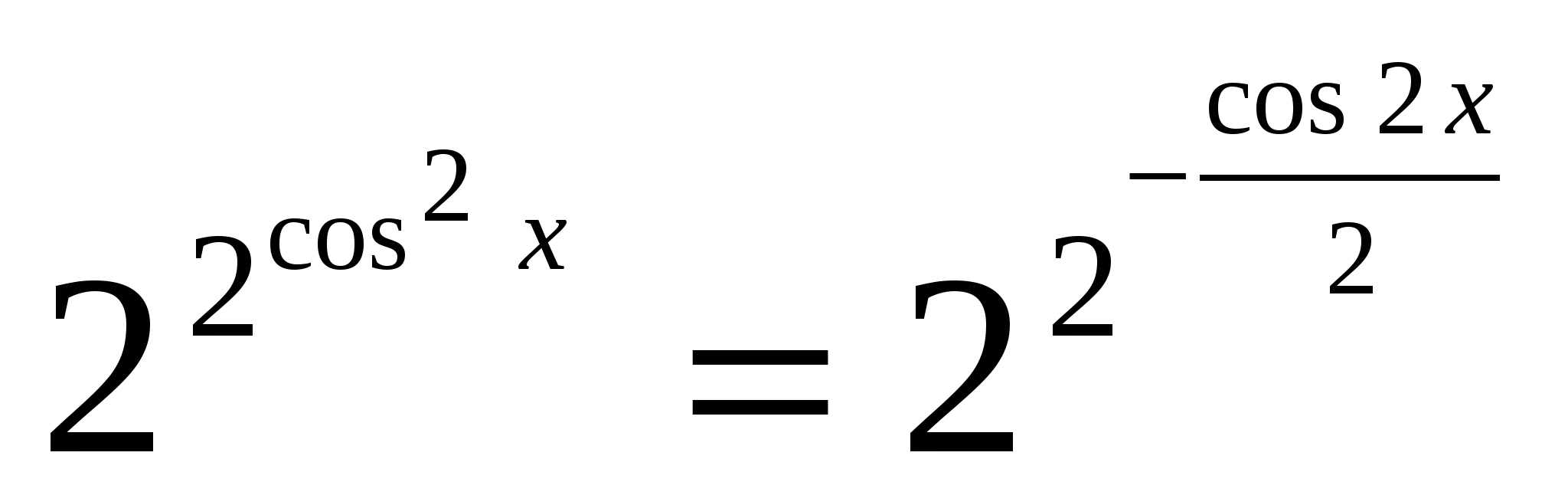 , тогда
, тогда 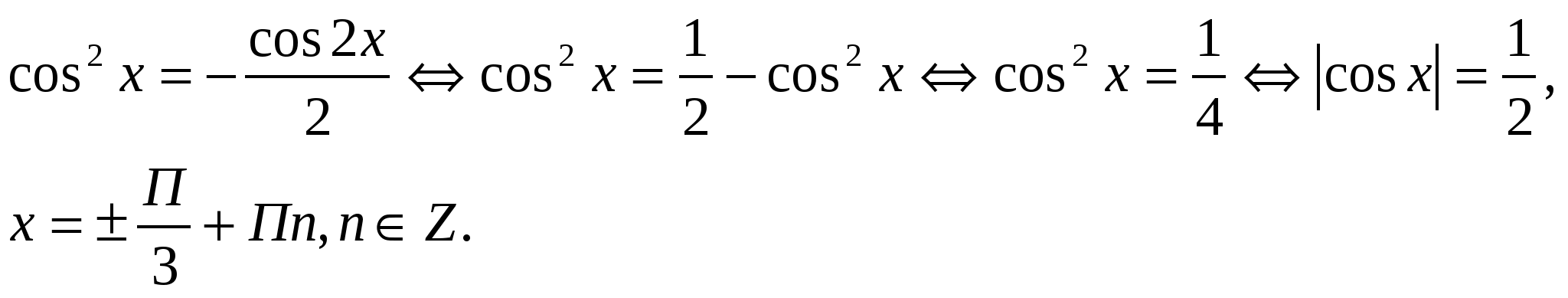
Ответ: 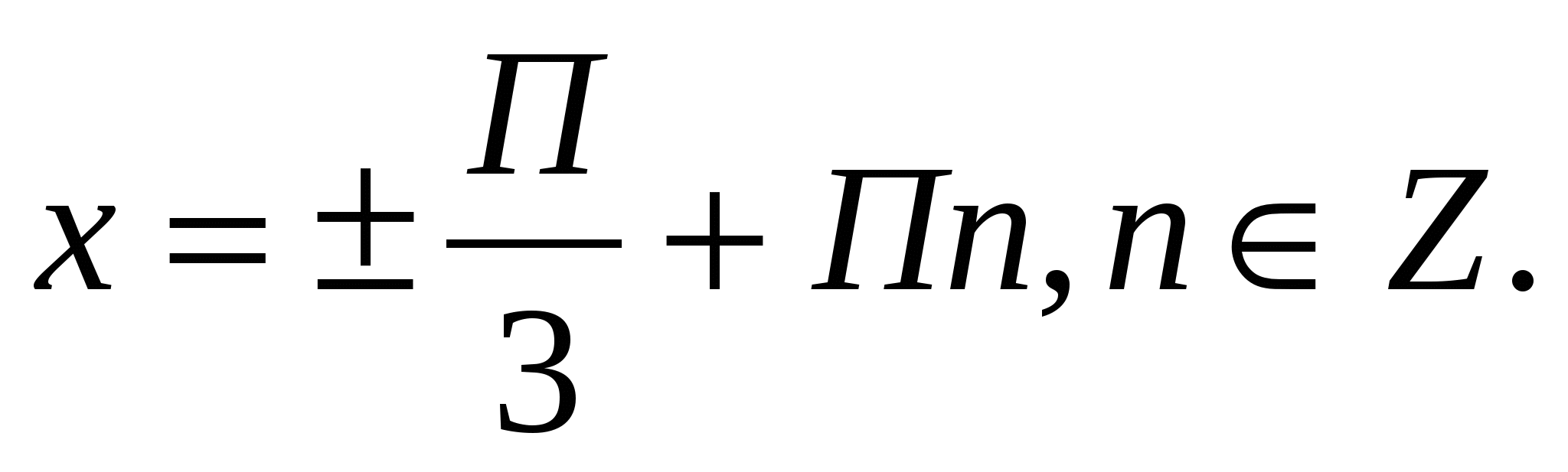
ЗАКЛЮЧЕНИЕ.
В этой работе собраны решения уравнений нетрадиционными методами, с помощью которых можно решать достаточно сложные задачи. Нестандартное решение заключается в том, чтобы путем логических рассуждений, основываясь на свойства функций, на неравенство между средним арифметическим и средним геометрическим, на скалярное произведение векторов, избежать громоздких математических преобразований, а иногда решить уравнение, которое нельзя решить стандартными способами. Несмотря на то, что выше были рассмотрены только уравнения, с помощью этих методов можно решать и другие задачи. К сожалению, нельзя привести четкой классификации по методам решения уравнений. Выбор метода решения предстоит сделать ученику на основе анализа исходных уравнений. Развивается умственная культура учащихся через систему задач. При решении уравнений нестандартными способами возникают вопросы, проявляется интерес к поиску нового способа решения. По окончании этой темы было проведено семинарское занятие, где ребята предлагали свои методы решения уравнений или систем уравнений. Работа на практическом занятии позволяет формировать у ученика важные для современного человека компетенции: умение самостоятельно приобретать необходимые знания, применять их на практике, умение грамотно работать с информацией, анализировать её и критически обрабатывать, умение занимать свою позицию в дискуссиях, наконец, умение сотрудничать и работать в коллективе
Опыт показывает, что в условиях современной школы актуально звучат слова:
« Скажи мне, и я забуду. Покажи мне, и я запомню. Дай мне действовать самому, и я научусь».
Список литературы.
-
Авдонин Н.И., Голубев В.К. 30 уроков репетитора по математике
-Н. Новгород, «Век»,1997г.,-304с.
-
Варианты тестов по математике вНф ГУВШЭ в 2000-2001гг.
Бляхман Л.Г.,Громов Е.М. и др. Н.Н.:2001-38с
3. Горнштейн П. И. Мерзляк. А.Г. Экзамен по математике и его подводные рифы-«Илекса», Харьков :Гимназия,1998г.,-237с. 4.Дорофеев Г.В., Муравин Г.К., Седова Е. А. Сборник заданий для подготовки и проведения письменного экзамена по математике (курс А) и алгебре и началам анализа (курс В) за курс средней школы.11класс.-М.:Дрофа ,2001.-192с.
5.Мерзляк А.Г., Полонский В.Б. Алгебраический тренажер-«Илекса»,
Харьков: Гимназия,1998г.,-320с.
6.Сенниковский Я.И. Приватный репетиторъ по математике- Н.Новгород:
АО «ИЛМА», 1995г.,-242с.
7.Черкасов О.Ю., Якушев А.Г. Математика: интенсивный курс подготовки к экзамену.- М.: 2001.-432с.
8.Шарыгин И.Ф., Голубев В.И. Факультативный курс по математике: Решение задач по математике 11класс.-М.:Просвещение,1991г.,-384с.
9.Газета «Математика», №25,36,48-Москва: Первое сентября
1 Игнатьева Г.А., Волкова В.О., Шишкина О.П. Дидактика развивающего обучения. Н.Новгород,1998.
2 П.И. Горнштейн, А.Г.Мерзляк, В.Б. Полонский, М.С. Якир. Экзамен по математике и его подводные рифы.-М.: Илекса,Харьков:Гимназия,1998.
3 Психология.Немов.


