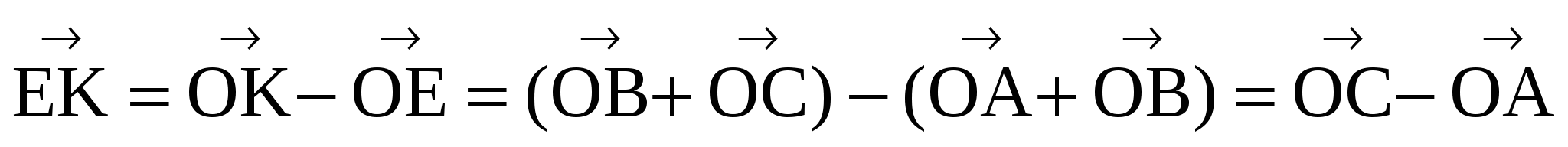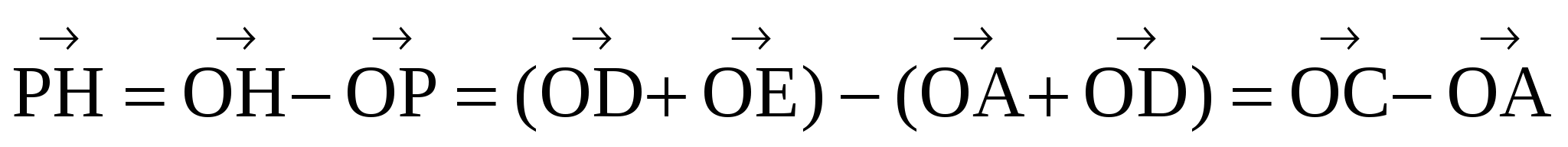- Преподавателю
- Математика
- Программа электива для 9 класса Методы решения геометрических задач
Программа электива для 9 класса Методы решения геометрических задач
| Раздел | Математика |
| Класс | 9 класс |
| Тип | Рабочие программы |
| Автор | Дюндикова Л.А. |
| Дата | 28.08.2015 |
| Формат | zip |
| Изображения | Есть |
Методы решения геометрических задач
При решении геометрических задач обычно используются три основных метода: геометрический - когда требуемое утверждение выводится с помощью логических рассуждений из ряда известных теорем; алгебраический - когда искомая геометрическая величина вычисляется на основании различных зависимостей между элементами геометрических фигур непосредственно или с помощью уравнений; комбинированный - когда на одних этапах решение ведется геометрическим методом, а на других - алгебраическим. Какой бы путь ни был выбран, успешность его использования зависит, естественно, от знания теорем и умения применять их.
В качестве основного метода решения геометрических задач, который стоит освоить и отработать в первую очередь, выступает алгебраический метод. Алгебраический метод, вернее основные его модификации, могут быть в достаточной степени алгоритмизированы. В качестве примера можно привести метод опорного элемента и метод вспомогательного параметра.
Метод опорного элемента является основным методом составления уравнений в геометрических задачах и заключается в следующем: один и тот же элемент (сторона, угол, площадь, радиус и т. д.) выражается через известные и неизвестные величины двумя разными способами, и полученные выражения приравниваются. Довольно часто в качестве опорного элемента выбирают площадь фигуры. Тогда говорят, что для составления уравнения используется метод площадей.
Если в задаче требуется найти отношение каких-либо величин, то, как правило, задача решается методом вспомогательного параметра. Это значит, что в начале решения мы объявляем какую-либо величину известной, обозначив ее, например, буквой а, затем выражаем через а те величины, отношение которых требуется найти. Когда составляется искомое отношение, вспомогательный параметр а сокращается. Метод вспомогательного параметра применяется в задачах, где геометрическая фигура определена с точностью до подобия.
Ставя во главу угла алгебраический метод, следует всегда помнить, что речь идет о геометрической задаче, поэтому работая над ней, следует искать геометрические особенности, учиться смотреть и видеть геометрическую суть.
Кроме вышеперечисленных методов можно назвать еще координатный метод, векторный метод, метод ключевых задач, метод дополнительных построений.
Необходимо научить школьников решению «базисных» (элементарных) задач, то есть тех, которые входят как составные элементы во многие другие задачи. Таковыми являются, например, задачи на отыскание основных элементов треугольника: медианы, высоты, биссектрисы, радиусов вписанной и описанной окружностей. Под элементарными мы будем понимать задачи в одно действие, сделанное на основании известной теоремы или формулы, причем конфигурация, в которой эта формула или теорема применяется, достаточно четко обозначена в условии задачи.
В теоретическую часть школьного курса геометрии включены в основном теоремы, работающие на сам курс, то есть необходимые для его дальнейшего развития. Многие теоремы в известном смысле прикладного характера, областью приложения которых являются задачи, а не теория, из курса исключены.
В связи с этим возникает необходимость в выделении некоторого количества задач, так называемых элементарных (базисных, опорных, ключевых), иллюстрирующих тот или иной часто встречающийся метод или прием решения задач, которые учащийся должен усвоить и освоить. Следует обращать внимание учащихся на «рабочие теоремы», то есть теоремы, которые, с одной стороны, активно используются при решении задач, но с другой стороны, как показывает опыт, либо не всегда рассматриваются при изучении геометрии, либо тщательно не отрабатываются.
Первым и важнейшим этапом решения геометрической задачи является построение чертежа. Нельзя научиться решать достаточно содержательные геометрические задачи, не выработав привычки делать «большой и красивый» чертеж, удовлетворяющий не только формально математическим требованиям, но и известным эстетическим критериям. После построения чертежа следует вспомнить все факты, относящиеся к данным и искомым элементам задачи, а также соотношения между ними.
Таким образом, умение решать геометрические задачи определяется четырьмя слагаемыми: 1) чертеж; 2) метод; 3) владение определенным объемом геометрических фактов и теорем; 4) наличие достаточно активно используемого запаса опорных задач.
Метод дополнительного построения
Характеристика метода. Довольно часто, когда в условии задачи фигурирует медиана треугольника, бывает полезным продлить ее за точку, лежащую на стороне треугольника, на отрезок, равный самой медиане. Полученная новая точка соединяется с вершиной (вершинами) исходного треугольника, в результате чего образуются равные треугольники. Равенство соответствующих элементов этих треугольников помогает найти неизвестную величину или доказать предложенное утверждение.
Пример задачи. Докажите, что треугольник является равнобедренным, если совпадают проведенные из одной и той же вершины медиана и биссектриса.
Метод введения вспомогательного элемента
Характеристика метода. Длину некоторого отрезка рассматриваемой в задаче фигуры полагают равной, например, x и затем находят искомую величину. При этом в одних случаях вспомогательная величина в процессе решения задачи "исчезает" (сокращается), а в других ее нужно определить через данные условия и поставить в полученное для искомой величины выражение.
Пример задачи. Найдите площадь выпуклого четырехугольника, диагонали которого перпендикулярны и равны d1 и d2.
Метод площадей
Характеристика метода. Из названия следует, что главным объектом данного метода является площадь. Для ряда фигур, например для треугольника, площадь довольно просто выражается через разнообразные комбинации элементов фигуры (треугольника). Поэтому весьма эффективным оказывается прием, когда сравниваются различные выражения для площади данной фигуры. В этом случае возникает уравнение, содержащее известные и искомые элементы фигуры, разрешая которое мы определяем неизвестное. Здесь и проявляется основная особенность метода площадей - из геометрической задачи он "делает" алгебраическую, сводя все к решению уравнения (а иногда системы уравнений).
Само сравнение выражений для площади фигуры может быть различным. Иногда площадь фигуры представляется в виде суммы площадей ее частей. В других случаях приравниваются выражения, основанные на различных формулах площади для одной и той же фигуры, что позволяет получить зависимость между ее элементами.
Суть метода площадей не ограничивается только описанным выше приемом. Иногда бывает полезно рассмотреть отношение площадей фигур, одна из которых (или обе) содержит в себе искомые элементы.
Пример задачи. Найти формулу для площади произвольного треугольника.
Метод восходящего анализа
Характеристика метода. Данный метод решения задач имеет ряд особенностей: 1) не требуется обратимости рассуждений (только при доказательстве, при решении задач обратимость имеет место), т.к. возможность обратного перехода проверяется на каждом шаге поиска решения; 2) учащиеся должны хорошо усвоить фразу: «Чтобы доказать… достаточно доказать…». Термин «достаточно» подходит больше, чем «надо», поскольку можно подобрать несколько различных утверждений, для каждого из которых искомое является следствием; 3) в общей схеме восходящего анализа не разъясняется, как получить утверждение, из которого следует искомое, такое утверждение подыскивается, исходя из конкретных условий задач.
Пример задачи. В плоскости даны четырёхугольник АВСD и т. О. Доказать, что точки, симметричные точке О относительно середин четырёхугольника, являются вершинами параллелограмма.
Пример оформления доказательства восходящим анализом.
В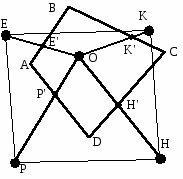 плоскости даны четырёхугольник АВСD и т. О. Доказать, что точки, симметричные точке О относительно середин четырёхугольника, являются вершинами параллелограмма.
плоскости даны четырёхугольник АВСD и т. О. Доказать, что точки, симметричные точке О относительно середин четырёхугольника, являются вершинами параллелограмма.
Дано: ABCD - четырёхугольник, т. О; AE'=BE';
BK'=CK'; CH'=ДH';
DP'=AP'; EE'=E'O; KK'=K'O; HH'=H'O; PP'=P'O
Доказать: EKHP - параллелограмм
Доказательство:
1) Движение от искомых:
1 - Чтобы доказать, что четырехугольник - параллелограмм, достаточно доказать, что противоположные стороны его равны и параллельны;
2 - Чтобы доказать, что противоположные стороны равны и параллельны, достаточно доказать, что 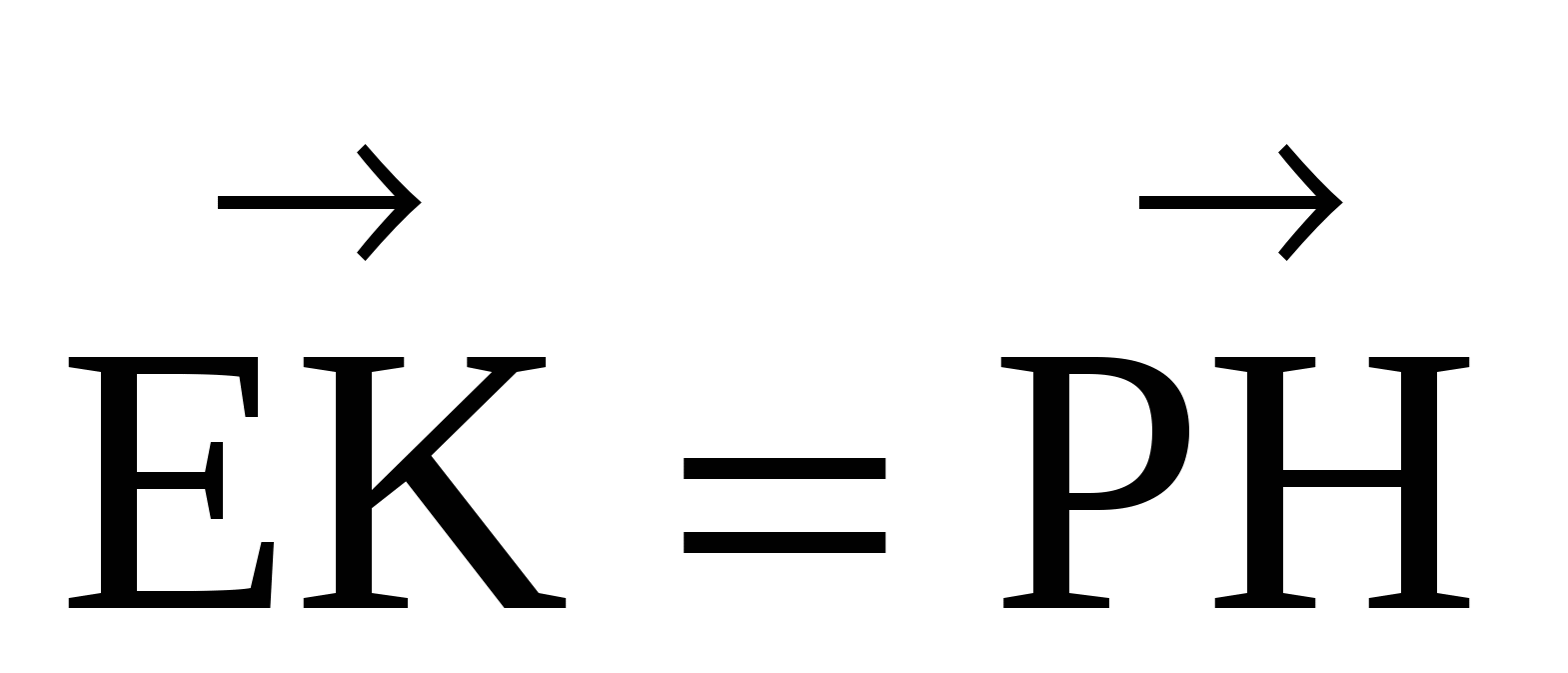
3 - А для этого достаточно выразить их через один вектор (метод вспомогательного параметра).
Заданные векторы удобно брать такие, которые связывают все данные векторы. Положение всех точек определяется векторами 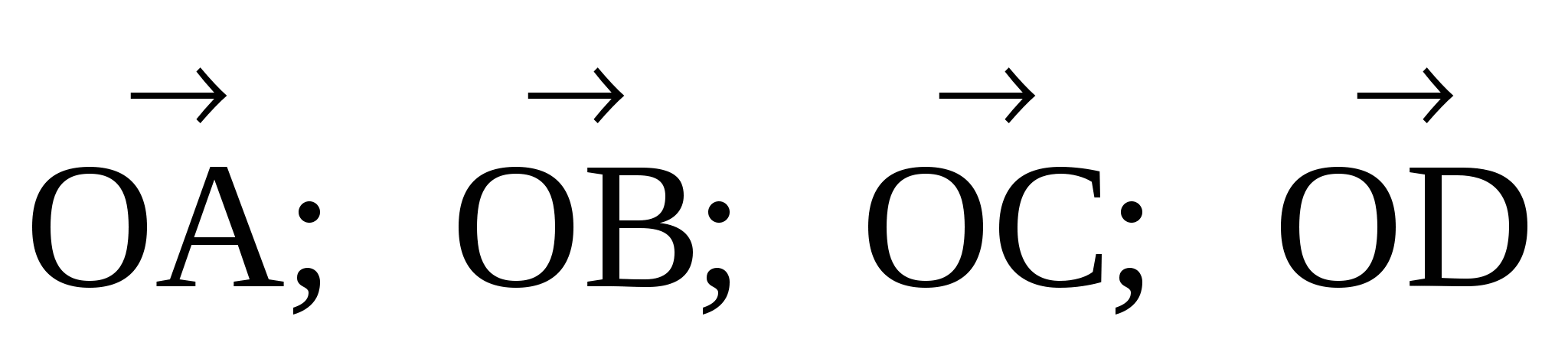 их считаем данными.
их считаем данными.
2) Движение от данных:
1 - (Е и О симметричны) => (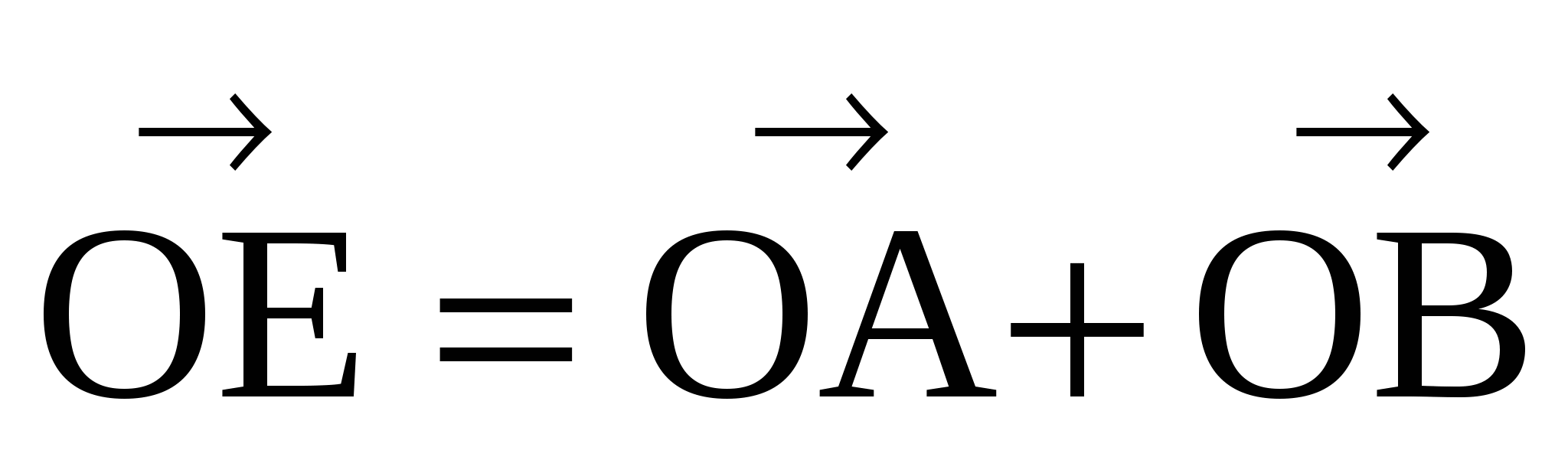 );
);
(Р и О симметричны) => (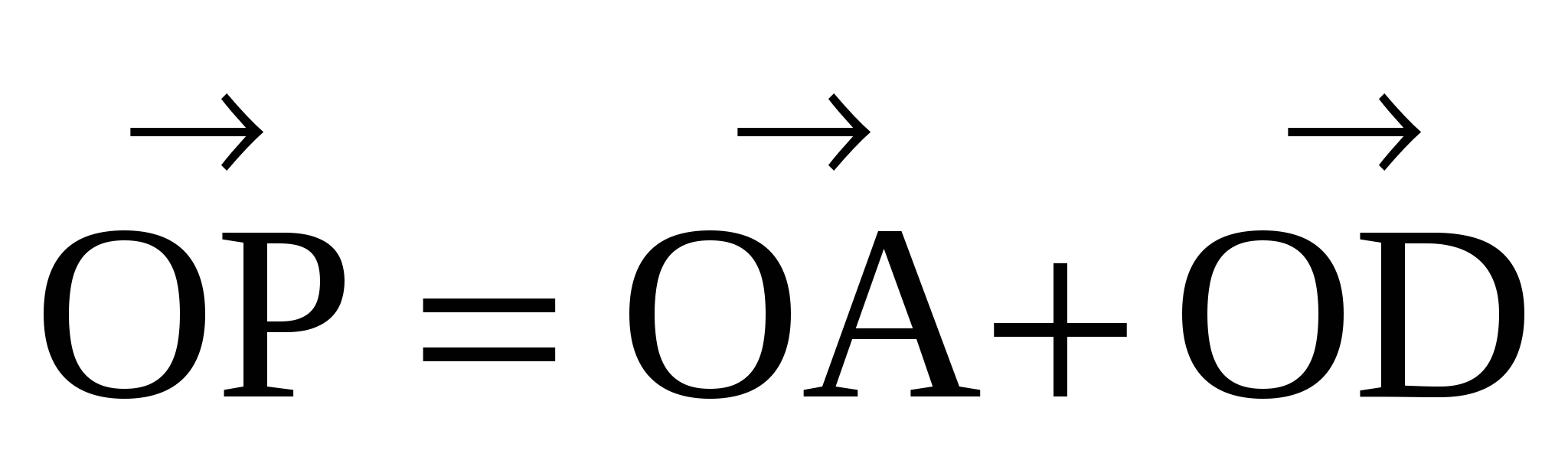 );
);
(Н и О симметричны) => (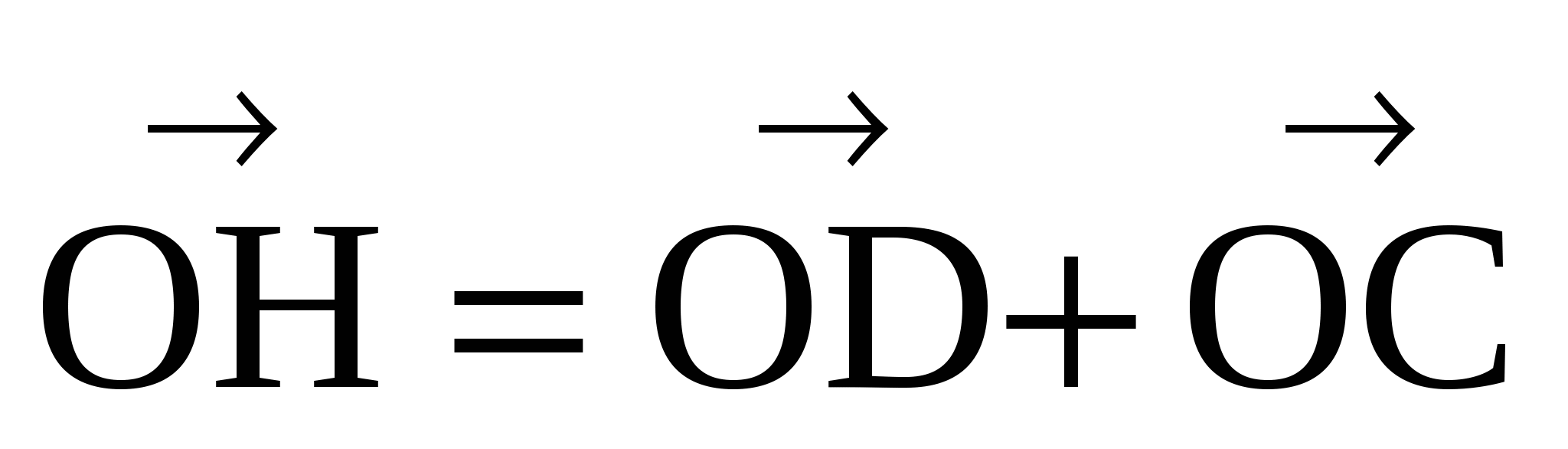 );
);
(К и О симметричны) => (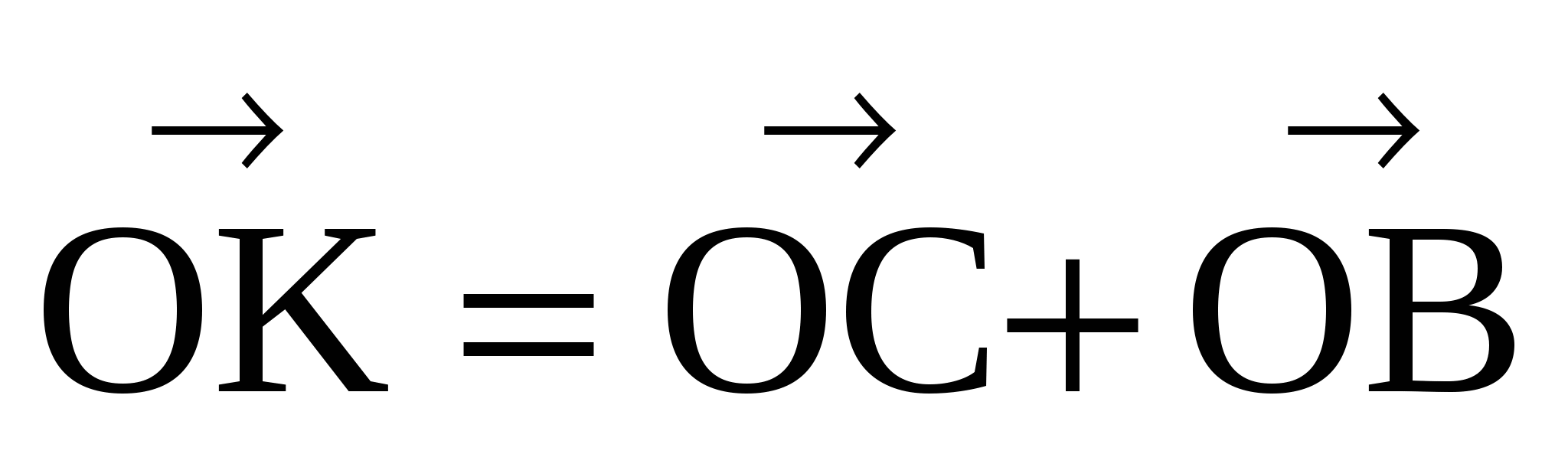 ).
).
Искомые и данные величины максимально сблизились, возникает догадка, ученик вспоминает нужную теорему. Главное условие закономерности при поиске решения задач методом "попеременного движения с двух сторон": "Вероятность вспоминания нужного определения, теоремы, правила, закона, способа решения задачи возрастает, если искомые и данные задачи сближены анализом и синтезом настолько, что в оставшийся интервал как раз укладывается данная теорема, целиком заполняя этот интервал".
Путь решения найден: