- Преподавателю
- Математика
- ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
| Раздел | Математика |
| Класс | - |
| Тип | Другие методич. материалы |
| Автор | Пастухова О.Л. |
| Дата | 26.02.2014 |
| Формат | docx |
| Изображения | Есть |
ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
1. УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА
-
Общие понятия.
Дифференциальным уравнением называется уравнение, которое, кроме независимых переменных и неизвестных функций этих переменных, содержит еще и производные неизвестных функций или их дифференциалы. Если функции, входящие в дифференциальное уравнение, зависят от одной независимой переменной, то уравнение называется обыкновенным дифференциальным уравнением. Если же в уравнение входят частные производные
неизвестных функций по нескольким независимым переменным, то уравнение называют дифференциальным уравнением с частными производными. В настоящей главе мы будем рассматривать лишь обыкновенные дифференциальные уравнения, и большая часть главы будет посвящена тому случаю, когда задано одно уравнение, содержащее одну неизвестную функцию.
Пусть x-независимая переменная и y-искомая функция этой переменной. Общий вид дифференциального уравнения будет
Ф(x, y, y', y", … , y(n)) = 0.
Наивысший порядок n производных неизвестной функции, входящих в уравнение, называется порядком дифференциального уравнения. В настоящем параграфе мы будем рассматривать одно обыкновенное дифференциальное уравнение первого порядка. Общий вид такого уравнения будет
Ф(x, y, y') = 0 (1)
или, в решенной относительно y форме,
y'=f (x, y). (2)
Пользуясь другим обозначением производной, можем записать это уравнение в виде
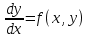 . (3)
. (3)
Если некоторая функция
y = φ(x) (4)
удовлетворяет дифференциальному уравнению (1) или (2), т. е. если это уравнение обращается в тождество относительно x при замене y и у' на φ(x) и φ'(х), то функция (4) называется решением этого дифференциального уравнения. Сама задача нахождения решений дифференциального уравнения называется обычно задачей интегрирования дифференциального уравнения.
В простейшем случае, когда правая часть уравнения (2) не содержит y, получается дифференциальное уравнение вида
y' = f (x) (5)
Нахождение его решений есть основная задача интегрального исчисления, и все множество этих решений дается формулой
y = 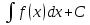 (6)
(6)
где C- произвольная постоянная. Таким образом, в этом простейшем случае имеется семейство решений дифференциального уравнения, содержащее произвольную постоянную. Как мы увидим, и в общем случае дифференциального уравнения первого порядка мы будем иметь семейство решений, содержащее произвольную постоянную:
y = φ (x, C) (7)
Такое семейство решений называется общим интегралом уравнения. Общий интеграл может выражаться в неявной форме или в форме, решенной относительно C:
φ (x, y, C) = 0 или (x, y) = C (71)
Придавая произвольной постоянной C различные численные значения, будем получать различные решения уравнения- так называемые частные решения уравнения.
Укажем геометрическую интерпретацию дифференциального уравнения и его решений. Если рассматривать х и у как координаты точек плоскости, то дифференциальное уравнение (2) определяет в каждой точке (x, y), где определена функция f (x, у), угловой коэффициент касательной у' к некоторой линии. Искомое решение (4) уравнения (2) есть такая кривая (в частном случае - прямая), которая в каждой своей точке имеет угловой коэффициент касательной y' определяемый равенством (2). Такая кривая называется интегральной кривой дифференциального уравнения. Иначе говоря, понятие решения уравнения (2) совпадает с понятием интегральной кривой (в частном случае - прямой) этого уравнения на плоскости XOY.
Общий интеграл (7) дает бесчисленное множество интегральных кривых или, точнее говоря, семейство кривых, зависящее от одной произвольной постоянной.
Положим, что функция f (x, у) однозначна и непрерывна в некоторой области В плоскости XOY. Пусть линия l соответствующая решению (7), принадлежит этой области, и функция φ (x) определена на некотором промежутке l изменения х. Говоря о решении (4), мы, согласно сказанному выше, считаем, что φ (х) непрерывна и имеет производную для x, принадлежащих l. Если к промежутку l принадлежит его левый конец, то производная φ'(х) есть производная справа, а на правом конце - производная слева. Из уравнения (3) и непрерывности f (x, у) непосредственно следует, что и производная φ'(х) решения непрерывна на l.
Во всем предыдущем мы считаем, естественно, что все функции однозначны. Из однозначности φ(х) следует, что прямые, параллельные оси ОУ, могут пересекать интегральную кривую не более чем в одной точке. Если мы перепишем уравнение (2), или (3), в виде
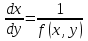 (31)
(31)
т. е. будем считать не у функцией от x, а x функцией от у, то прямые, параллельные оси ОХ, могут пересекать интегральные кривые не более чем в одной точке. Пусть интегральная кривая l уравнения (2) такова, что не только прямые, параллельные оси ОУ, но и прямые, параллельные оси ОХ, пересекают ее не более чем в одной точке, т. е. в уравнении у = φ(х) функция φ(х) имеет однозначную обратную функцию x=ψ(y). При этом l является и интегральной кривой дифференциального уравнения (31). В дальнейшем мы будем иметь дело главным образом с уравнением вида (2).
-
Определение решения по начальному условию. Теорема существования и единственности.
Простейшее уравнение (5) имеет бесчисленное множество решений, поскольку в формулу (6) входит произвольная постоянная. Но нетрудно показать, что мы получим вполне определенное решение уравнения (5), если поставим так называемое начальное условие, а именно потребуем, чтобы искомая функция у принимала заданное значение y0 при заданном значении x=x0.
Это начальное условие запишем в виде
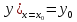 (8)
(8)
Действительно, пусть f(x) - непрерывная на некотором промежутке l функция и точка х = х0 принадлежит l. Заменяя в формуле (6) неопределенный интеграл определенным с переменным верхним пределом х и нижним пределом x0 вместо (6) получим
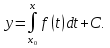
Первое слагаемое обращается ь нуль при x = x0, и чтобы удовлетворить условию (8), надо положить C=y0. Таким образом, уравнение (5) при начальном условии (8) имеет единственное решение
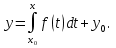
Отметим, что это решение имеет место во всем промежутке l.
Аналогично, если мы имеем общий интеграл (7) какого-либо уравнения (2), то для удовлетворения начальному условию (8) надо определить произвольную постоянную С из равенства
y0 = φ(x0, С). (9)
Обратимся теперь к геометрической интерпретации. Положим, что функция f (x, у) определена в некоторой области В плоскости XOY и в этой области однозначна и непрерывна. В каждой точке (x, у), принадлежащей В, из уравнения (2) определяется, как мы уже упоминали, угловой коэффициент y' касательной к искомой интегральной кривой. Через точку (х, у) проведем небольшой отрезок прямой, образующий с осью ОХ такой угол α, что tg α=y', и придадим этому отрезку какое-либо направление (переход к противоположному направлению не изменит tg α). Мы видим, что уравнение (2) равносильно определению в области В поля направлений т. е. в каждой точке области В уравнение (2) определяет некоторое направление. Интегральные кривые уравнения (2) суть кривые i, лежащие в области В и обладающие следующим свойством: в каждой точке (x, у) касательная к l имеет направление, определяемое указанным выше полем направлений. Начальное условие (8) сводится к требованию, чтобы интегральная кривая проходила через заданную точку (х0, y0), находящуюся в В. Приведем теперь геометрические соображения, из которых наглядно, но не строго логически, следует, что через заданную точку М0 (x0 , у0) проходит одна и только одна интегральная кривая.
РисунокРазобьем плоскость XOY прямыми (рис. 1), параллельными осям, на малые квадраты так, чтобы точка М0 лежала в вершине одного из этих квадратов (это - несущественно). Из точки М0 проводим в направлении возрастания x отрезок прямой М0М1 с угловым коэффициентом у' = f (x0 , у0) до ближайшего пересечения с одной из прямых сетки квадратов. Пусть (x1 , у1) - координаты точки М1. Из M1 проводим в направлении возрастания х отрезок прямой М1М2 с угловым коэффициентом 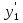 = f (x1 , у1) до ближайшего пересечения с одной из прямых сетки квадратов и т. д. Это построение можно выполнить и в направлении убывания х. Построенная таким образом ломаная линия и представляет приближенно для х, близких к x0, искомую интегральную кривую уравнения (2), проходящую через точку М0. тот факт, что через всякую точку М0 из В проходит одна я только одна интегральная кривая. Это утверждение справедливо и будет дальше доказано, если f (x, у) обладает кроме непрерывности еще некоторым свойством.
= f (x1 , у1) до ближайшего пересечения с одной из прямых сетки квадратов и т. д. Это построение можно выполнить и в направлении убывания х. Построенная таким образом ломаная линия и представляет приближенно для х, близких к x0, искомую интегральную кривую уравнения (2), проходящую через точку М0. тот факт, что через всякую точку М0 из В проходит одна я только одна интегральная кривая. Это утверждение справедливо и будет дальше доказано, если f (x, у) обладает кроме непрерывности еще некоторым свойством. 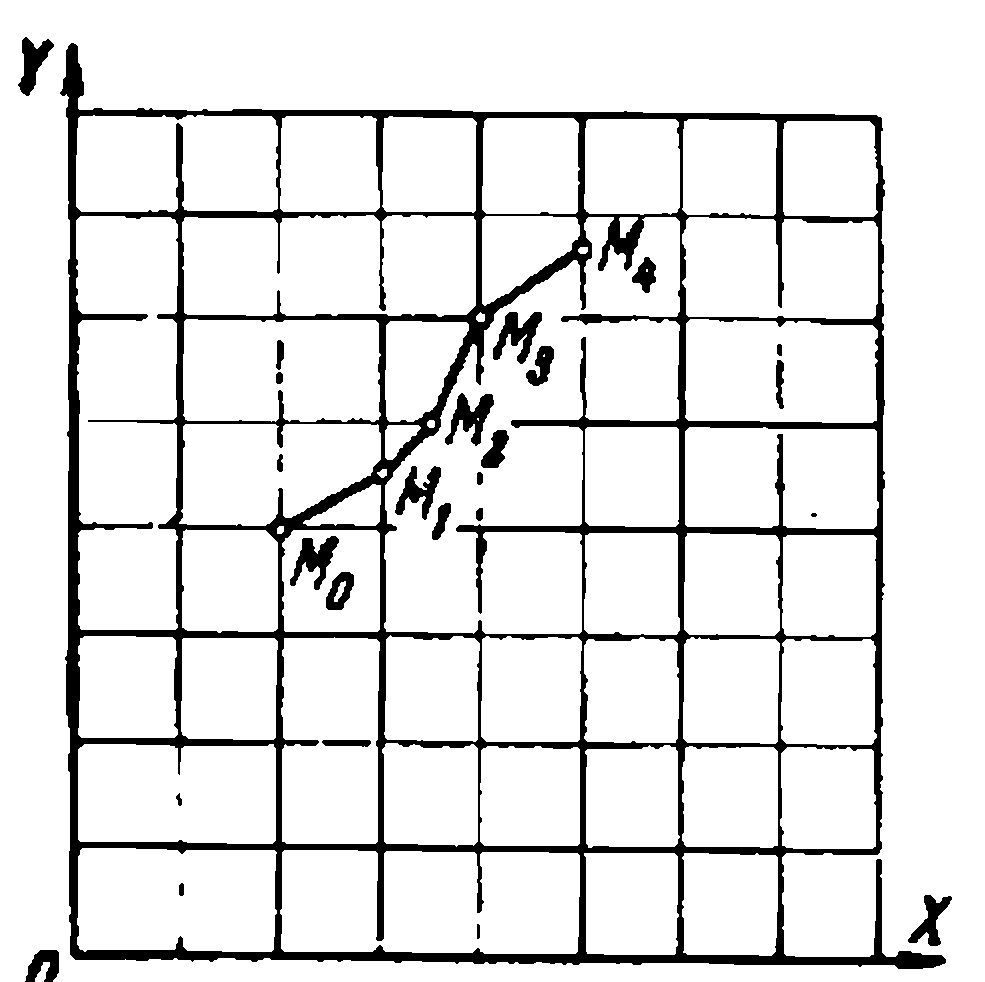
Положим для определенности, что B - открытая область, т. е. область, к которой мы не причисляем ее границы (В может быть и всей плоскостью). Имеет место следующая теорема.
Теорема А. Если f(x, у) непрерывна и имеет непрерывную частную производную по у в В, то через каждую точку, принадлежащую В, проходит одна и только одна интегральная кривая уравнения (2).
Теорема эта, которую мы пока примем без доказательства, называется обычно теоремой существования и единственности решения дифференциального уравнения (2) при заданном начальном условии.
В дальнейшем, для краткости, сформулированную теорему мы будем называть теоремой А. В конце следующей главы мы приведем доказательство этой теоремы и ряд дополнений к ней. Укажем, как надо понимать утверждение единственности решения при заданном начальном условии. Пусть y = φ1 (x) и y = φ2 (x) суть два решения уравнения (2), удовлетворяющие условию (8), причем первое определено на некотором промежутке l1, а второе на промежутке l2 изменения х, а точка x0 принадлежит этим промежуткам. При этом на общей части промежутков l1 и l2 должно иметь место тождество φ1 (x) φ2 (x). Предполагается, конечно, что интегральные кривые y = φ1 (x) и y = φ2 (x) не выходят из области В, где f (x, у) определена и удовлетворяет указанным в теореме условиям.
В следующих разделах мы укажем некоторые частные типы дифференциальных уравнений, интегрирование которых приводится к вычислению неопределенных интегралов или, как говорят, их интегрирование приводится к квадратурам. Отметим, что вычисление интеграла связано с вычислением площади, откуда и происходит термин «квадратура». При рассмотрении упомянутых частных типов мы приведем ряд примеров, на которых мы проиллюстрируем указанные выше соображения, связанные с теоремой А.


