- Преподавателю
- Математика
- Дидактические материалы по теме Комбинаторика
Дидактические материалы по теме Комбинаторика
| Раздел | Математика |
| Класс | - |
| Тип | Другие методич. материалы |
| Автор | Мелькис А.И. |
| Дата | 06.12.2014 |
| Формат | doc |
| Изображения | Есть |
Дидактические материалы
Комбинаторика
Составитель: Мелькис А.И.
Правило произведения
-
Выбор вариантов
С выбором возможных вариантов человек сталкивается в своей жизни очень часто: выбор способа передвижения к месту работы или учебы, распределение порядка выполнения намеченных дел, планирование свободного времени и т.п. А игра в шахматы? Делая очередной ход, вы анализируете множество различных продолжений и останавливаете свой выбор на том, которое вам кажется наиболее выгодным.
Общие законы комбинирования вариантов, формулы для подсчета их числа, правила их перебора составляют часть математики, которая называется комбинаторикой.
Толчком к развитию этой древней науки явилось появление новой вычислительной техники, которая предоставила возможность осуществлять переборы миллионов вариантов. С другой стороны, многие важные прикладные задачи при решении их простым перебором вариантов приводят к такому объему вычислений, которые в принципе нельзя реализовать на вычислительной машине. Это заставило искать новые алгоритмы целенаправленного перебора вариантов, совершенствовать методы подсчета или оценки их количества.
-
Составление таблиц
Представим себе группу из 5 мальчиков (Боря, Володя, Гриша, Дима и женя) и 4 девочек (Аня, Ира, Оля и Лена). Как удобнее всего перебрать все пары, состоящие из одного мальчика и одной девочки? Естественно составить таблицу, в строки которой выписать имена мальчиков, а в столбцы - имена девочек. Каждая клетка этой таблицы соответствует одной паре «мальчик - девочка», причем все возможные пары будут перебраны.
Мальчики
Девочки
А
И
О
Л
Б
БА
БИ
БО
БЛ
В
ВА
ВИ
ВО
ВЛ
Г
ГА
ГИ
ГО
ГЛ
Д
ДА
ДИ
ДО
ДЛ
Ж
ЖА
ЖИ
ЖО
ЖЛ
Прямоугольные таблицы используются очень часто: периодическая таблица элементов Д.И.Менделеева, таблица растворимости соединений, таблица Брадиса и т.д. Таблица позволяет удобно расположить пары элементов двух множеств. При этом количество таких пар подсчитать легко.
Из 5 мужских имен и 4 женских можно составить 5*4=20 пар имен.
Правило произведения
Пусть даны два конечных множества А и В. Пусть множество А содержит m элементов, а множество В - n элементов. Число различных пар, которые можно составить, взяв по одному элементу из каждого множества, равно произведению mn.
Пример
На 5 перекрестках зажжено 5 светофоров (каждый светофор находится в одном их 3-х положений - зажжен красный, зеленый или желтый свет). Сколькими способами можно это сделать, если считать, что светофоры работают друг от друга независимо?
Первый светофор можно зажечь тремя способами, второй тоже тремя, третий - тремя и т.д. общее число способов равно 3*3*3*3*3=35=243
3. Выбор представителей
Задача.
«В училище есть 3 группы первого курса. В первой - 20 человек, во второй и третьей - по 25. Нужно выбрать по одному представителю от каждой группы. Каким числом способов это можно сделать?»
1) (20*25*25=12500)
2) Сначала выберем одного представителя от каждой группы. Это можно сделать 20 способами (а в первой группе 20 человек). Затем выберем одного представителя от второй группы и составим пары (представитель первой группы, представитель второй группы). По правилу произведения таких пар будет20*25-500. Затем, к каждой паре подсоединяя представителя из третьей группы, мы как бы снова составляем «пару», первый элемент которой - одна из полученных 5000 пар, а второй элемент - один представитель третьей группы. Общее количество таких «пар» равно 500*25=12500.
Таким же рассуждением можно обобщить правило произведения для любого количества множеств.
4. Число слов
Многие задачи комбинаторики удобно рассматривать на следующей «языковой» модели. Исходное множество - это множество букв. Будем называть его алфавитом (можно, например, взять русский алфавит из 33 букв или латинский алфавит из 25 букв). Назовем словом произвольную (конечную) последовательность букв. Например, ВЕРА, АРБА, КААН, БРКС, ТТТТ - четырехбуквенные «слова», составленные из русского алфавита. Другой пример: номера автомашин обычно состоят из трехбуквенного «слова» и «слова», составленного из «цифрового алфавита» (ММЕ 273).
Пусть в алфавите 20 букв. Сколько можно составить двухбуквенных слов из этого алфавита? Двухбуквенное слово - это пара, на каждом месте которой стоит только одна из букв данного алфавита. Число таких пар можно сосчитать и с помощью таблицы: 20*20=400.
А как подсчитать число трехбуквенных слов? Трехбуквенные слова - это тройки, составленные из букв данного алфавита. Если в алфавите 20 букв, то число трехбуквенных слов равно 20*20*20=203=8000.
Если в алфавите число букв равно n, то в предыдущей формуле для числа k-буквенных слов надо заменить 20 на n и получить следующую формулу.
Число к-буквенных слов в алфавите из n букв равно nк.
Задача.
На рояле 88 клавиш. Сколькими способами можно последовательно извлечь 6 звуков?
Первый звук можно извлечь 88 способами (нажать любую клавишу). При добавлении второго звука число вариантов увеличивается в 88 раз т.е. два звука последовательно можно извлечь 882 способами, три звука - 883, четыре - 884 способами и т.д.
Ответ: 886.
5. Составление расписания
Пусть мы составляем последовательность элементов данного множества, например, выписываем в виде слова буквы данного алфавита, составляем числа из цифр, мелодии из нот и т.д. так подсчитывают число получаемых комбинаций в том случае, когда члены этой последовательности берутся независимо друг от друга. Однако часто встречаются задачи на подсчет числа комбинаций, в которых выбираемые элементы связаны друг с другом каким-то ограничениями, зависимостями. Важным примером такой задачи является задача о составлении расписания.
Задача
В классе 20 человек. Сколькими способами можно составить расписание дежурства на 6 дней недели так, чтобы каждый день дежурил один человек и никто не дежурил дважды?
Будем составлять список дежурных. На понедельник можно назначить дежурным любого из 20 человек. На вторник выбрать дежурным любого человека из 19 оставшихся. Таким образом, на 2 дня можно выбрать дежурных числом способов, равным 20*19=380.
Выбор первого дежурного накладывает ограничение - его нельзя выбирать во второй день.
Выбрав дежурных на первые два дня 0*19 способами, на третий можно выбрать любого из оставшихся 18 человек, т.е. число дежурных увеличится в 18 раз. Продолжая выбор дежурных, мы получим, сто на 6 дней можно выбрать дежурных числом способов, равным 20*19*18*17*16*15 (6 множителей). Задача решена.
Составление расписания дежурств можно иначе себе представить так: имеется 20 человек и 6 мест (дни недели). Нужно разместить на этих местах по одному человеку из 20 человек. Такие комбинации часто и называют -размещения.
В общем виде: пусть у нас есть п человек и к мест (к<=п). Каким числом способов можно разместить на этих местах (по одному на каждом месте) людей из данного множества?
На первое место - любой из п человек, на второе - любой из (п-1) оставшихся, на третье - любой из ( п-2) оставшихся и т.д. Число вариантов будет перемножаться. Общее число множителей равно к. Как4 записать произведение к последовательных целых чисел в убывающем порядке, самое большее из которых равно п? Это можно сделать так:
п*(п-1)*(п-2)*…*(п-к+1).
Формула для для числа размещений п объектов на к местах:
Апк=п*(п-1)*…(п-к+1).
6. Перестановки
В общем виде произведение целых чисел от 1 до п включительно обозначается п! (читается «п факториал»). Таким образом, 1!=1, 2»=2, 3!=1*2*3=6, 4!=1*2*3*4=24, 5!=1*2*3*4*5=120 и т.д.
В общем виде: п!=(п-1)!...
Перестановкой элементов данного множества называется расположение их в определенном порядке.
Примеры
-
Заданное множество состоит из букв А и В. Перестановок всего 2: АВ и ВА.
-
Заданное множество состоит из трех цифр: 1, 2 и 3. перестановок шесть: 123, 132, 213, 231, 312, 321.
-
Число перестановок из п элементов обозначается Рп.
Рп =п*(п-1)*…2*1=п!.
Контрольные вопросы
-
В чем состоит правило произведения?
-
Как подсчитать число слов в алфавите, состоящем из п букв?
-
Что такое размещение?
-
Что такое перестановка?
-
Как вычислить число перестановок п предметов?
Биномиальные коэффициенты
1. Число сочетаний
Наборы элементов данного множества без учета их порядка называют сочетанием (их можно было бы назвать подмножествами данного множества).
В общем случае число сочетаний из п элементов по к обозначается так:
Спк (це из п по к) равно
П*(п-1)*…*(п-к+1)
Спк = ------------------------------
к!
Сп1=1,
п-1 п*(п-1)*(п-2)
Сп2= ---------- Сп3= ----------------------
-
1*2*3
Задачи
-
Сколько различных результатов может быть в тираже «Спортлото 5 из 36»?
Из 36 номеров нужно выбрать 5 (без учета порядка). Число таких выборов равно:
36*35*34*33*32
С365= -------------------------- =376992
1*2*3*4*5
-
Вы заполнили карточку «Спортлото 5 из 36». Сколько возможно различных результатов тиражей, в которых будет ровно 3 из отмеченных вами номеров?
Сначала выберем из отмеченных 5 номеров те три, которые попадут в тираж. Это можно сделать числом способов, равным
5*4*3*2*1
С53= ----------------- =10
1*2*3
Оставшиеся в тираже два номера могут быть любыми из числа номеров, вами не отмеченных (их осталось 31). Эти два номера можно выбрать числом способов, равным
31*30
С312=------------ =465
1*2
Общее число способов находят, комбинируя все выборы первых трех и последних двух номеров по правилу произведения. Ответ: 465*10=4650.
-
В группе 20 человек. Каким числом способов можно выбрать из нее команду из трех человек и, кроме того, одного капитана?
Способ 1. Сначала выберем капитана (20 способов), а затем из оставшихся 19 человек выберем команду из трех человек
20*19*18
С193= -------------------- =969 способов.
1*2*3
Составляя комбинации по правилу произведения, получим ответ: 969*20=19380 способов.
Способ 2. Сначала выберем команду
20*19*18
С203=------------------- =1140 способов.
1*2*3
Затем из оставшихся 17 человек выберем капитана (17 способов). Комбинируя варианты, получим ответ: 1140*17=19380 способов
Способ 3. Сначала выберем четырех человек
20*19*18*17
С204=-------------------- =4845 способов,
1*2*3*4
а затем из четырех выбранных человек одного назначим капитаном (4 способа). Ответ: 4845*4=19380 способов.
2. Бином Ньютона
Коэффициенты Спк для подсчета числа сочетаний называются биномиальными коэффициентами, потому что они используются в формуле бином Ньютона. Бином Ньютона служит для возведения в степень суммы двух слагаемых (бином - это двучлен).
Пример
Возвести в степень (1+х)4
(1+х)4 =1+С41х + С42х2 + С43х3 + С44х4 =1+4х+6х2+4х3+х4
Формула в общем виде:
(1+х)п=1+Сп1х+Сп2х2+…+Спп-1+хп
3. Свойства биномиальных коэффициентов
Выпишем биномиальные коэффициенты Спк в виде треугольной таблицы. Для удобства допустим, что к принимает нулевое значение, полагаяСп0=1(это соглашение можно оправдать так: из к элементов 0 элементов можно выбрать одним способом - ничего не взяв). Таблицу построим следующим образом:
С00
С10 С10
С20 С21 С22
С30 С31 С32 С33
Подставляя вместо Спк их числовые значения , получим таблицу:
1
-
1
1 2 1
1 3 3 1
1 4 6 4 1
15 10 10 5 1
……………………….
В строчках таблицы стоят коэффициенты, участвующие в формуле бинома Ньютона для возведения в квадрат, куб, четвертую степень и т.д.
Построенная таблица известна в математике давно и называется треугольником Паскаля.
Способ образования строк треугольника Паскаля таков: каждое число равно сумме двух чисел, стоящих над ним.
Свойство 1.
Биномиальные коэффициенты, равноотстоящие от концов одной строки, равны между собой: Спк=Спп-к.
Свойство 2.
Сумма биномиальных коэффициентов, стоящих в одной строке, равна степени двойки:
1=1
1+ 1=2
1+2+ 1=22
1+3+3 1=23
…………………………….
В общем виде: Сп0+Сп1+…+Спп-1+Спп=2п.
Свойство 3
Биномиальные коэффициенты возрастают от первого до середины, а затем убывают до последнего.
Свойство 4.
Сп-1к-1+Сп-1к.
Контрольные вопросы
Что такое сочетание?
Какова формула для числа сочетаний?
Как стоится треугольник Паскаля
перечислите свойства биномиальных коэффициентов.
Вероятность
Классическое определение вероятности
Необходимость количественной оценки вероятных событий появилась давно и послужила толчком к созданию в 17 - 18 вв. новой математической дисциплины - теории вероятностей.
Начавшись с оценки вероятности выигрыша или проигрыша в азартных играх, теория вероятности постепенно пришла к решению трудных задач измерения надежности сложных устройств, эффективности работы различных систем, оценки качества больших партий изделий, задач долгосрочного планирования и многих других прикладных задач.
Простейшей ситуацией, в которой мы без колебаний приписываем событиям определенные числа, является подбрасывание вверх монеты. Здесь мы считаем, что вероятности выпадения герба или цифры (орла или решки) равны по 0,5.
Пример
1. Пусть бросается игральный кубик, и будем считать вероятностью выпадения каждого из чисел от 1 до 6 число 1/6. Как подсчитать вероятность выпадения числа, делящегося на 3?
Из всех возможных шести исходов благоприятными являются два: выпадение тройки и выпадение шестерки. Искомой вероятностью будет дробь 2/6 = 1/3.
-
Монета бросается три раза подряд. Какова вероятность того, что ровно два раза подряд выпадет герб и, следовательно, один раз цифра?
Обозначим исход одного бросания Г или Ц (герб или цифра). Возможные исходы трех бросаний получаются обычным способом: ГГГ, ГГЦ, ГЦГ, ГЦЦ, ЦГГ, ЦГЦ, ЦЦГ, ЦЦЦ. Все эти восемь исходов равновероятны. Из них благоприятными по условию являются ГГЦ, ГЦГ, ЦГГ.
Вероятностью события называют отношение числа благоприятных исходов к числу всех исходов.
Такое определение вероятности появилось самым первым, по-видимому, еще в 16 в., его обычно называют классическим определением вероятности. Оно предполагает, что некоторое испытание уже произошло и его результат можно разбить на некоторое (конечное0 число равновероятных исходов.
Применение комбинаторики к решению простейших вероятностных задач
1. С какой вероятностью можно угадать три номера в тираже «Спортлото 5 из 36»?
Общее число возможных результатов равно
36*35*34*33*32
С365= ------------------------- =376992.
1*2*3*4*5
Число благоприятных результатов равно 10*С312=4650. Искомая вероятность равна
4650/376992=775/62832.
2. В группе 20 человек, 5 из них должны быть выбраны дежурными. С какой вероятностью одному учащемуся не выпадет быть дежурным?
Общее число вариантов 5 из 20 равно С205. Для получения благоприятных вариантов надо выбирать 5 человек из 19 (из всех, кроме одного). Число таких вариантов равно С195. для нахождения вероятности не будем отдельно вычислять коэффициенты С205 и С195, а составим дробь и произведем сокращения. Р - искомая вероятность.
С195 19*18*17*16*15 1*2*3*4*5 15 3
Р=--------- =------------------------- * ------------------------- =- ----- =---- = 0,75
С205 1*2*3*4*5 20*19*18*17*16 20 4
-
Сохраним условие предыдущей задачи и найдем вероятность того, что вам выпадет быть дежурным.
Если вероятность не быть дежурным равна 0,75, то вероятность быть дежурным равна 0,25.
Повторные испытания
Ситуация, в которой подряд независимо друг от друга производятся одинаковые испытания, встречается очень часто, например бросание монеты или игральной кости, стрельба из одного орудия без учета результата произведенных выстрелов, параллельное
включение в сеть одинаковых предохранителей и т.п.
Пример с бросанием монеты. При каждом испытании есть два равновероятных исхода: Г (выпал герб) и Ц (выпала цифра). Допустим, что монету бросили подряд п раз. Сколько последовательностей исходов при этом можно получить? Последовательность результатов испытаний можно записать как слово в двухбуквенном алфавите, например ГЦЦГЦ. Число п-буквенных слов в таком алфавите равно 2п. Таким образом, общее число возможных вариантов при повторном бросании монеты будет иметь вид 2п.
Какова вероятность того, что при п-кратном бросании монеты все время будет выпадать герб? Ясно, что из всех возможных 2п вариантов благоприятным является один: ГГ…Г (Г-п раз). Искомая вероятность равна 1/2п. Например, при п=10 эта вероятность равна 1/1024<0,001.
Интуитивно ясно, что при повторных испытаниях будет получаться результат, стремящийся к нулю. Формула 1/2п дает точную оценку (в опыте с бросанием монеты) интересующей нас вероятности.
Вероятность того, что при бросаниях монеты ни разу не выпадет герб, т.е. все время будет выпадать цифра, тоже равна 333.
Возьмем п=3. Если нас интересует только то, сколько раз выпадет герб (или цифра), то возможные варианты будут такими: 1) три раза герб; 2) два раза герб; 3) один раз герб;
4) ни одного раза не выпал герб. Вероятность этих событий равны соответственно 1/8, 3/8, 3/8, 1/8. Проводя перебор вариантов для п=4, мы получим такой набор вероятностей: 1/16, 4/16, 6/16, 4/16, 1/16. В числителях стоят биноминальные коэффициенты. Составим таблицу:
1
1/2 1/2
1/4 2/4 1/4
1/8 3/8 3/8 1/8
1/16 4/16 6/16 4/16 1/16
Она получается из треугольника Паскаля делением каждой строки на соответствующую степень двойки, т.е. сумму чисел в этой строке, и представляет таблицу распределения вероятностей различных исходов при повторном бросании монеты.
Задачи
1. Какова вероятность того, что при четырех бросаниях монеты хотя бы один раз выпадет герб?
2. Какова вероятность того, что при четырех бросаниях монеты герб выпадет не менее двух раз?
3. Какова вероятность того, что при п бросаниях монеты хотя бы один раз выпадет герб? Запишите последовательность этих чисел в виде десятичных дробей с тремя десятичными знаками.
4. Сколько раз надо бросить монету, чтобы вероятность выпадения хотя бы одного герба была не меньше 0,999?
Задачи
Правило произведения
1. Номер автомашины состоит из 3 букв русского алфавита (33 буквы) и 4 цифр. Сколько существует различных номеров автомашин?
2. В лифте, останавливающемся на 7 этажах, едут 10 человек. Каждый из них независимо друг от друга может сойти на любом этаже. Сколько способов существует?
3. В алфавите 32 буквы, 10 из которых гласные. Сколько существует пятибуквенных слов, начинающихся с гласной буквы? («Слово» - это любая последовательность букв).
4. Сколько можно составить шестибуквенных «слов»из алфавита в 32 буквы таких, что никакие две одинаковые буквы не стояли бы рядом?
5. Алфавит состоит из трех букв. Каждое «слово» языка содержит любое число букв, но не более четырех. Сколько в этом языке существует фраз, содержащих ровно пять (непустых) слов?
6. В алфавите 22 согласные и 10 гласных букв. Сколько существует шестибуквенных «слов» с чередующимися гласными и согласными буквами? Сколько существует семизначных слов с теми же условиями?
7. Сколько существует шестизначных чисел, делящихся на 5?
8. В 12-ричной системе счисления имеется 12 цифр. Сколько в этой системе имеется 7-значных чисел?
9. Сколькими способами можно разложить семь разных монет в три кармана?
10. Флаги многих государств представляют собой полотнища, состоящие из трех горизонтальных полос различного цвета. Сколько таких трехцветных флагов можно составить, имея в распоряжении материал шести цветов?
11. Сколько можно составить пятизначных чисел, в десятичной записи которых хотя бы один раз встречается цифра 5?
12. На полке нужно поставить три пятитомных собрания сочинений так, чтобы все пять томов каждого из собраний сочинений стояли друг за другом, хотя и не обязательно в порядке следования номеров тома. Сколькими способами это можно сделать?
13. В двух колоннах по 15 человек стоят 15 мальчиков и 15 девочек. Сколькими способами их можно расставить так, чтобы все мальчики стояли в левой колонне (все девочки тогда окажутся в правой)?
14. Сколькими способами можно усадить 20 человек за круглым столом, считая способы одинаковыми, если их можно получить один из другого движением по кругу?
15. Сколько существует пятизначных чисел, делящихся на 5, в записи которых нет одинаковых цифр?
16. Сколькими способами можно расставить на шахматной доске 8 ладей так, чтобы они не били друг друга?
17. Сколькими способами можно расставить в ряд числа 1, 2, …, 100 так, чтобы числа 1, 2, 3 попали рядом и притом шли в порядке возрастания?
18. Сколько различных делителей имеет число 22*33*44*55?
19. Десять различных писем надо запечатать в конверты и наклеить на каждый конверт марок на 4 коп. Имеются марки трех сортов по 4 коп. и четырех сортов по 2 коп. (в неограниченном количестве). Сколькими способами можно наклеить марки на конверты?
Сочетания
1. Сколькими способами можно составить дозор из трех солдат и одного офицера, если всего есть 50 солдат 3 офицера?
2. на уроке спросили 5 учеников из 35 учеников класса. Каждый из опрошенных получил одну из четырех отметок: 2, 3, 4 или 5. Сколько разных записей могло появиться в журнале?
3. Сколькими способами на собрании, где присутствует 100 человек, можно выбрать 7 членов президиума, в число которых входить председатель или секретарь собрания или оба вместе?
4. В мешке лежат п различных пар ботинок. Сколькими способами можно выбрать из мешка 2к ботинок так, чтобы из них нельзя было составить ни одной пары?
5. Из мешка, содержащего m черных и n белых шаров, выкладывают подряд шары. Сколько разных последовательностей может получиться? (Шары одного цвета между собой неразличимы).
6. Замок в автоматической камере хранения открывается лишь после того, как набирается определенный набор четырех цифр. Пассажир забыл набранный номер, но помнил, что в нем все цифры были разные и шли они в порядке возрастания. Сколько комбинаций ему придется перебрать, чтобы открыть замок?
7. Сколько диагоналей можно провести в п-угольнике?
8. В классе 19 мальчиков и 11 девочек. Сколькими способами можно выбрать команду в 7 человек? Решите эту задачу двумя способами, в одном из них перебирая, сколько девочек может входить в команду (от 0 до 7).
9. мама каждый день выдает на десерт по одному фрукту. У нее есть три одинаковых яблока, 5 одинаковых груш, 2 одинаковых персика и 1 апельсин. Сколькими способами она может выдать эти фрукты в течение 11 дней?
10. Сколькими способами 20 одинаковых монет можно разложить в три кармана так, чтобы в каждом лежало не менее двух монет?
11. Из слова «рот» перестановками букв можно получить еще такие слова: «тор», «орт», «отр», «тро», «рто». Их называют анаграммами. Сколько анаграмм можно составить : 1) из слова «логарифм2; 2) из слова «реестр»?
Бином Ньютона
1. В выражении (х-1)*(х-2)*(х-3)*…*(х-100) раскрыты скобки и приведены подобные. Найдите коэффициент при х99.
2. Используя биномиальную формулу, раскройте скобки в выражении (х+у)6.
3.напишите первые три члена выражения (х+у)50.
Прикладные задачи
1. сколько различных сопротивлений можно получить, используя резисторы и их соединения, из следующего набора: R1=10, R2=100, R3=1000 Ом.
2. Сколько различных сопротивлений можно получить последовательным и параллельным соединениями резисторов из следующего набора: R1=1Ом, R2=2 Ом, R3=4 Ом, R4=8 Ом, R5=16 Ом.
3. Сколько различных сопротивлений можно получить различными соединениями трех одинаковых резисторов?
Вероятность
1. Из букв слова «уравнение» наугад выбирается одна буква. Какова вероятность, что: 1) эта буква будет гласной; 2) согласной; 3) эта буква будет «щ»?
2. В ящике имеется 4 белых и 7 черных шаров. Какова вероятность того, что наудачу вынутый шар окажется белым?
3. В ящике 90 стандартных и 10 нестандартных деталей. Какова вероятность того, что среди 10 наугад вынутых деталей бракованных не окажется?
4. военный летчик получил задание уничтожить три рядом расположенных склада боеприпасов противника. На борту самолета бомба. Вероятность попадания в первый склад 1,01, во второй - 0,008, в третий - 0,024. любое попадание в результате детонации вызывает взрыв и остальных складов. Какова вероятность того, что склады противника будут уничтожены?
5. В телевизоре 10 ламп. Для любой из ламп вероятность того, что она останется исправной в течение года, равна p. Какова вероятность того, что: 1) в течение года хотя бы одна лампа выйдет из строя; 2) в течение года выйдет из строя ровно 1 лампа; 3) ) в течение года выйдут из строя 2 лампы?
Контрольное задание
Вариант 1
-
В меню 4 закуски, 3 супа, 7 вторых и 2 десерта. Сколькими способами можно выбрать обед из четырех блюд?
-
Сколько есть четырехзначных чисел с разными цифрами?
-
В роте 3 офицера, 7 сержантов и 50 рядовых. Сколькими способами можно выбрать отряд из одного офицера, двух сержантов и пяти рядовых?
-
Вероятность попадания при одном выстреле равна 0,6. Какова вероятность ни разу не попасть в цель при трех выстрелах?
Вариант 2
-
Выбрано 10 согласных и 5 гласных. Сколько можно составить слов из 8 букв, в которых гласные и согласные буквы чередуются?
-
Сколькими способами можно выбрать 6 человек из 20 так, чтобы два данных человека не были выбраны вместе?
-
Сколькими способами можно переставить буквы в слове АБАКАН так, чтобы согласные шли в алфавитном порядке?
-
вероятность попадания при одном выстреле равна 0,8. Какова вероятность того, что при трех выстрелах будет не более одного промаха?
Вероятностью события А называется отношение числа исходов, благоприятствующих событию А, к общему числу несовместных, единственно возможных и равновозможных исходов.
Вероятность события А обозначается символом Р(А) или, в краткой записи, просто
буквой Р. Р=m/n
1. Из пяти карточек с буквам А, Б, В, Г, Д наудачу последовательно выбирают три и раскладывают в ряд. Какова вероятность получения слова ДВА?
(1/60)
2. Найти вероятность того, что при подбрасывании двух монет хотя бы на одной из них выпадет герб.
(3/4)
3. Найти вероятность того, что при бросании двух игральных костей сумма очков не превзойдет 5.
(5/18)
4. Бросаются три игральные кости. Какова вероятность того, что на всех костях выпадет одно и то же число?
(1/36)
5. Найти вероятность того, что наудачу выбранное двузначное число делится на 8.
(11/90)
6. Подсчитать вероятность того, что в наудачу выбранном телефонном номере, состоящем из 4 цифр, все цифры окажутся различными (телефонный номер может начинаться с цифры 0).
(0,504)
7. Из колоды в 36 карт наудачу вынули 3 карты. Какова вероятность того, что все вынутые карты оказались масти пик?
(1/85)
8. Из урны, содержащей 5 белых и 3 черных шара, наудачу вынули два шара. Что вероятнее: будут шары одинакового цвета или разного?
(Вероятнее, что шары будут разного цвета).
9. В лотерее 100 билетов, из них 40 выигрышных. Какова вероятность того, что из трех взятых билетов равно один окажется выигрышным?
(236/539)
10. Среди 20 деталей 4 нестандартных. Найти вероятность того, что из 6 наудачу взятых деталей окажется 4 стандартных и 2 нестандартных.
(91/323)
11. 10 человек случайным образом садятся за круглый стол. Найти вероятность того, что два определенных лица окажутся рядом.
(2/9)
12. На две наудачу выбранные клетки шахматной доски поставлены две ладьи. Какова вероятность того, что ладьи не бьют друг друга? (7/9)
Объединением событий А и В называется событие, состоящее в наступлении хотя бы одного из событий А и В.
Объединение событий А и В обозначается символом А+В.
Вероятность объединения несовместных событий А и В равна сумме вероятностей этих событий:
Р(А+В)=Р(А)+Р(В)
1. Два стрелка ведут стрельбу по мишени. Положим:
А1 - попадание в мишень первым стрелком;
А2 - попадание в мишень вторым стрелком.
Что представляет собой событие А1+А2?
(Попадание в мишень хотя бы одним стрелком (или первый попадет, а второй не попадет, или первый не попадет, а второй попадет, или попадут оба стрелка)).
Вероятность совмещения событий А и В равна произведению вероятности одного из них на условную вероятность другого, вычисленную в предположении, что первое событие произошло:
Р(А*В)=Р(А)*Р(В/А) или Р(А*В)=Р(В)*Р(А/В).
Пример 1. Студент пришел на экзамен, зная лишь 20 вопросов из 30. какова вероятность того, что студент ответит на каждый из двух вопросов, заданных ему экзаменатором? Рассмотрим события:
А - студент знает первый вопрос;
В - студент знает второй вопрос.
Р(А)=20/30=2/3. Если событие А произошло, то среди оставшихся 29 вопросов студент знает 19, следовательно, Р(В/А)=19/29. По теореме умножения Р(А*В)=Р(А)*Р(В/А)=2/3*19/29=38/87.
Пример 2. Имеются 2 колоды по 36 карт. Из каждой колоды наудачу выбрали по карте. Найти вероятность того, что обе карты оказались тузами.
Пусть
А - появление туза в первой колоде;
В - появление туза во второй колоде.
В каждой колоде 4 туза, поэтому Р(А)=Р(В)=4/36=1/9.
События А и В, очевидно, независимы, следовательно, по теореме умножения Р(А*В)=Р(А)*Р(В) =1/9*1/9=1/81.
1. Два самолета сбросили по одной бомбе на некоторый объект, который будет разрушен только в том случае, если в него попадут обе бомбы. Вероятность попадания в объект первой бомбы равна 0,8, второй - 0,65. найти вероятность разрушения объекта.
(0,52).
2. Из колоды в 36 карт последовательно вынули 3 карты (не возвращая их в колоду). Найти вероятность того, что первая и третья карты были красной масти, а вторая - черной.
(9/70).
3. Считая рождение мальчика и рождение девочки равновозможными, найти вероятность того, что наудачу выбранной семье, имеющей трех детей, все дети окажутся одного пола.
(1/4).
4. В одной урне 3 белых и 5 черных шаров, в другой - 5 белых и 2 черных шара. Из каждой урны наудачу взяли по шару. Какова вероятность появления шаров равного цвета?
(31/56).
5. Два игрока поочередно по одному разу бросили монету. Найти вероятность того, что у первого игрока герб выпал раньше, чем у второго.
(5/8).
6. Из 15 деталей, среди которых 8 - первого сорта, 5 - второго сорта и 2 - третьего сорта, наудачу взяли две детали. Найти вероятность того, что обе детали одного сорта.
(13/35).
7. В урне 10 шаров. Вероятность вытаскивания из урны двух белых шаров равна 2/15. Сколько в урне белых шаров?
(4).
Вероятность события, противоположного событию А, выражается формулой.:
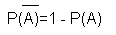
Два стрелка сделали по одному выстрелу в цель. Вероятности попадания стрелками в цель равны 0,6 и 0,8. Найти вероятность того, что хотя бы один стрелок попадет в цель. Пусть
А - попадание в цель первым стрелком;
В - попадание в цель вторым стрелком.
Найти вероятность противоположных событий, т.е. вероятности непопадания стрелками в цель:
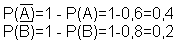
Вероятность непопадания в цель обоими стрелками находится по теореме умножения
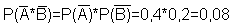
Попадание в цель хотя бы одним стрелком является событием, противоположным непопаданию в цель обоими стрелками, поэтому
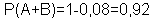
1. рабочий обслуживает 3 станка. Вероятность того, что в течение часа станок не потребует внимания рабочего, равна для первого станка 0,8, для второго - 0,5, для третьего - 0,6. Найти вероятность того, что в течение часа хотя бы один станок не потребует внимания рабочего.
(0,86).
2. Из урны, содержащей 2 белых и 3 черных шара, вынули 2 шара. Какова вероятность того, что хотя бы один из этих шаров белый?
(0,7).
3. Игральная кость брошена 4 раза. Что вероятнее, выпадет хотя бы один раз число 6 или нет?
(Вероятнее, что выпадет).
4. Два орудия ведут стрельбу по танку. Вероятность попадания в танк для первого орудия - 0,5, для второго - 0,4. Найти вероятность хотя бы одного попадания в танк, если из каждого орудия сделано по 3 выстрела.
(0,973).
5. Студент, разыскивая книгу, решил обойти 3 библиотеки. Для каждой библиотеки одинаково вероятно, есть в ее фонде эта книга или нет. Что вероятнее, достанет студент книгу или нет.
( Вероятнее, что достанет).
7. Сколько раз нужно подбросить монету, чтобы с вероятностью, большей 0,99, можно было бы ожидать хотя бы одного выпадения герба.
(7 или более раз).
Вероятность того, что при п испытаниях случайное событие с постоянной вероятностью Р произойдет ровно m раз, выражается формулой:
Рm,n=СnmРm(1-Р)n-m
Эта формула называется формулой Бернулли.
В семье 6 детей. Что при этом вероятнее: что мальчиков и девочек поровну или что мальчиков больше, чем девочек?
Сначала по формуле Бернулли найдем вероятность того, что мальчиков и девочек поровну, т.е. в семье 3 мальчика и 3 девочки:
6*5*4 1 5
Р3,6=С63(1/2)3(1-1/2)6-3= --------- * ---- = ----
1*2*3 26 16
Далее, мальчиков в семье будет больше, чем девочек, если их будет 4, 5 или 6.
6*5 1 15
Р4,6=С64(1/2)4(1-1/2)6-4= ----- * ---- = -----,
1*2 26 64
1 3
Р5,6=С65(1/2)5(1-1/2)6-5=6* ---- = ----,
26 32
1 1
Р6,6= ---- = -----.
26 64
(при нахождении Р6,6 пользуемся просто теоремой умножения; формула Бернулли применима и в этом случае, если условиться считать, что при любом n Сn0=1).
Вероятность того, что мальчиков больше, чем девочек, находим с помощью теоремы сложения:
15 3 11
Р= ----- + ----- = ----- .
64 32 32
Таким образом. Вероятнее, что мальчиков больше, чем девочек.
1. Из колоды в 36 карт 5 раз наудачу вынули одну карту, каждый раз возвращая ее в колоду. Найти вероятность того, что среди вынутых карт ровно 2 были масти пик.
(135/512).
2. Что вероятнее выиграть у равносильного противника в шахматы: 3 партии из 4 или 5 из 8?
(Вероятнее выиграть 3 партии из 4).
3. Батарея дала 6 выстрелов по объекту, вероятность попадания в который при каждом выстреле равна 1/3. найти вероятность разрушения объекта, если для этого требуется не меньше двух попаданий.
Указание. При решении задачи целесообразно сначала найти вероятность противоположного события.
(0,65).
Решение комбинаторных задач с помощью графов и способа умножения
В развитии детей большую роль играют задачи, формирующие комбинаторный стиль мышления. Комбинаторные задачи привлекательны тем, что легко могут быть оформлены в виде головоломок. Они вызывают у учащихся большой интерес. А так как способы их решения резко отличаются от обычных школьных, знакомство с ними способствует развитию математического мышления школьников.
Решение задач с помощью графов
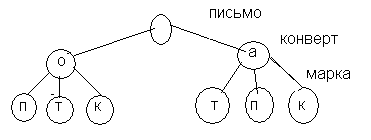
1. У Лены 2 конверта: обычный и авиа, и 3 марки: прямоугольная, квадратная и треугольная. Сколькими способами он может выбрать конверт и марку, чтобы отправить письмо?
Ответ: 6 вариантов.
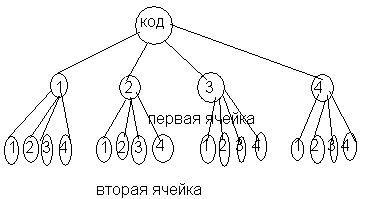
2. Ужасные грабители Кнопка и Скрепка решили украсть из сейфа золотой ключик Буратино. Для того, чтобы открыть замок входной двери, им нужно подобрать двузначный код. Причем известно, что дверь запирает Буратино, который знает пока еще только 4 цифры: 1, 2, 3, 4. Сколько вариантов придется перебрать Кнопке и Скрепке, чтобы проникнуть в дом?
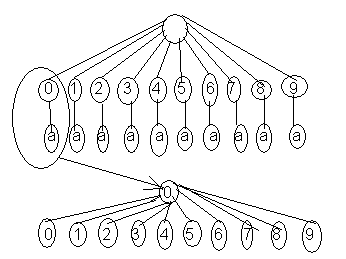
3. Проникнуть в дом - полдела. Кнопке и Скрепке нужно еще открыть сейф. Но сейф запирает папа Карло, а он знает все цифры. Сколько двузначных кодов нужно перебрать грабителям, чтобы открыть сейф?
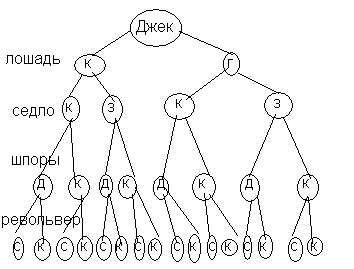
4.У ковбоя Джека две лошади: каурой и гнедой масти, два седла: красное и зеленое, две пары шпор: длинные и короткие, два револьвера: один марки «Кольт», другой - «Смит-и-Вессон». Сколькими способами Джек может экипироваться для конной прогулки по прериям?
5. Космический корабль «Циклоп» опустился на неизвестную планету Х звезды и У созвездия Центавр. Планета оказалась обитаема и разделена океанами на три материка. Каждый материк выдвинул трех представителей для того, чтобы лететь с кораблем на Землю. Представителей первого материка зовут Манн, Зан, Сан, второго - Пын, Фын, Шин, третьего - Хыр, Кыр, Дыр. Но на «Циклопе» не хватит анабиозных ванн для девяти человек. Он может взять только трех. Сколько способов у инопланетян составить делегацию на Землю?
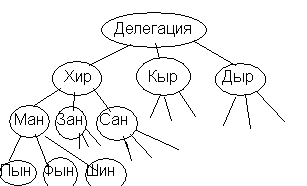
Можно решить эти задачи способом умножения.
Решение задач способом умножения
1. У Кролика две табуретки: красная и зеленая. К нему в гости пришли Вини-Пух и Пятачок. Сколькими способами он может рассадить гостей?
Решение: на красную табуретку может сесть или Пятачок или Пух. В любом случае на оставшуюся табуретку сядет второй гость, т.е. всего два способа.
2.В следующий раз к Кролику пришли три гостя: Вини-Пух, Пятачок и ослик Ив. Сколькими способами он может рассадить гостей на синей, красной и желтой табуретках?
Решение: на красную табуретку может сесть или Пух, или Пятачок, или Ив. Всего имеются три возможности. На синюю табуретку сядет один из двух оставшихся гостей. Ну а на желтую табуретку сядет тот гость, который не успел занять ни красную, ни синюю. Получается 3*2*1=6 способов.
3.Сколькими способами Кролик может рассадить пять гостей на пяти разноцветных табуретках?
Решение: 5*4*3*2*1=120 способов.
Произведение 1*2*3*4*5 обозначается 5! (факториал).
4. На борту космического корабля «Циклоп» три пилота и два инженера. Сколькими способами можно составить экипаж разведывательного катера из одного пилота и одного инженера?
Ответ: 6 способами.
5. В некотором городе у всех велосипедистов были трехзначные номера. Но велосипедисты попросили, чтобы в этих номерах не встречались цифры 0 8, потому что первая из них похожа на вытянутое колесо, ну а что для велосипедиста «восьмерка» колеса - знает каждый. Хватит ли им номеров, если в этом городе велосипеды имеют 710 человек?
Решение: для выбора цифры сотен номера имеется восемь возможностей, а именно 1, 2, 3, 4, 5, 6, 7, 9. Сколько же возможностей для выбора цифры десятков и единиц. Всего номеров будет: 8*8*8=512. Так что на всех обладателей велосипедов их не хватит.
6. Хвати ли номеров, если велосипедисты смягчат свои требования и согласятся на
цифру 0?
Ответ: хватит, номеров будет 9*9*9=729.
7. В пятом классе изучаются восемь предметов. В среду пять уроков, и все различны. Сколькими способами можно составить расписание на среду?
Ответ: 8*7*6*5*4=6720 способов.
8.Сколько всего автомобильных номеров можно составить из четырех цифр и трех букв?
Ответ: 10*10*10*10*32*32*32=327680000 номеров.
9. Сколько различных пятизначных чисел можно составить из цифр 0,1, 3, 4, 5?
Ответ: 1*2*3*4*2=48 чисел.
10. Андрей, Боря, Витя, Гриша, Дима и Женя решили покататься на карусели, сиденья которой изображали льва, тигра, слона, оленя, медведя и жирафа. Ребята заспорили, кому на какого зверя садиться, и решили перепробовать все способы. Сколько раз им пришлось для этого прокатиться на карусели?
Ответ: 6!=1*2*3*4*5*6=720 раз.
11. В городе проводится первенство по футболу между шестью командами. Сколько состоится матчей?
Решение: В матче «Мотор» - «Искра» неважно, какая команда будет первая, а какая вторая. А при методе подсчета 6*7=42 этот матч подсчитан дважды - и как встреча «Мотора» с «Искрой», и как игра «Искры» с «Мотором». Поэтому ответ вдвое больше, чем следует. В первенстве состоялся : 42/2=21 матч.
12. А сколькими способами можно зачеркнуть 5 номеров из 36, играя в «Спортлото»?
Решение: ответ 36*35*34*33*32=4523904 будет неверным, так как все равно, вычеркиваем мы сначала номер 13, а потом 3 или наоборот, т.е. вычеркивание номеров в порядке 13, 3, 6, 17, 10 дает тот же результат, что и вычеркивание в порядке 6, 17, 3, 10, 13. А так как 5 номеров можно переставлять друг с другом 5*4*3*2*1=120 способами, то верный ответ будет таким: 4523904/120=376992.
Литература:
1. М.И.Башмаков. Математика, Москва «Высшая школа» 1994.
2. Н.Я.Виленкин. Комбинаторика. М., 1965.
3. Н.Я.Виленкин. Популярная комбинаторика. М., 1975.
4. Н.Я.Виленкин, И.Я.Депман. За страницами учебника математики. М., 1989.
5. Оре Ойстин. Графы и их применения. М., 1965.
6. Ю.Г.Горст. «Начала теории вероятностей». Красноярск -1968.


