- Преподавателю
- Математика
- Урок «Арифметика последовательностей и рекуррентные соотношения»
Урок «Арифметика последовательностей и рекуррентные соотношения»
| Раздел | Математика |
| Класс | - |
| Тип | Конспекты |
| Автор | Крапивин А.А. |
| Дата | 12.06.2013 |
| Формат | doc |
| Изображения | Есть |
Арифметика последовательностей и рекуррентные соотношения
В школьном курсе математики знакомство с рекуррентными соотношениями происходит на примерах арифметической и геометрической прогрессий. Рассмотрение рекуррентных соотношений другого вида (например, числа Фибоначчи) часто входят в программы факультативов, а их решения, как правило, получают методом математической индукции, что требует определенного навыка в построении правильного индуктивного предположения. В настоящей заметке предложен подход к решению этих задач на основе построения арифметических последовательностей (формальные степенные ряды). Этот подход широко применяется во многих разделах математики, а применительно к рекуррентным соотношениям позволяет заменить рекуррентное соотношение уравнением в формальных степенных рядах. В частности, рекуррентные соотношения с постоянными коэффициентами приводят к линейному уравнению в формальных степенных рядах, которое решается стандартным образом с учетом специфики арифметики формальных степенных рядов.
-
Пусть
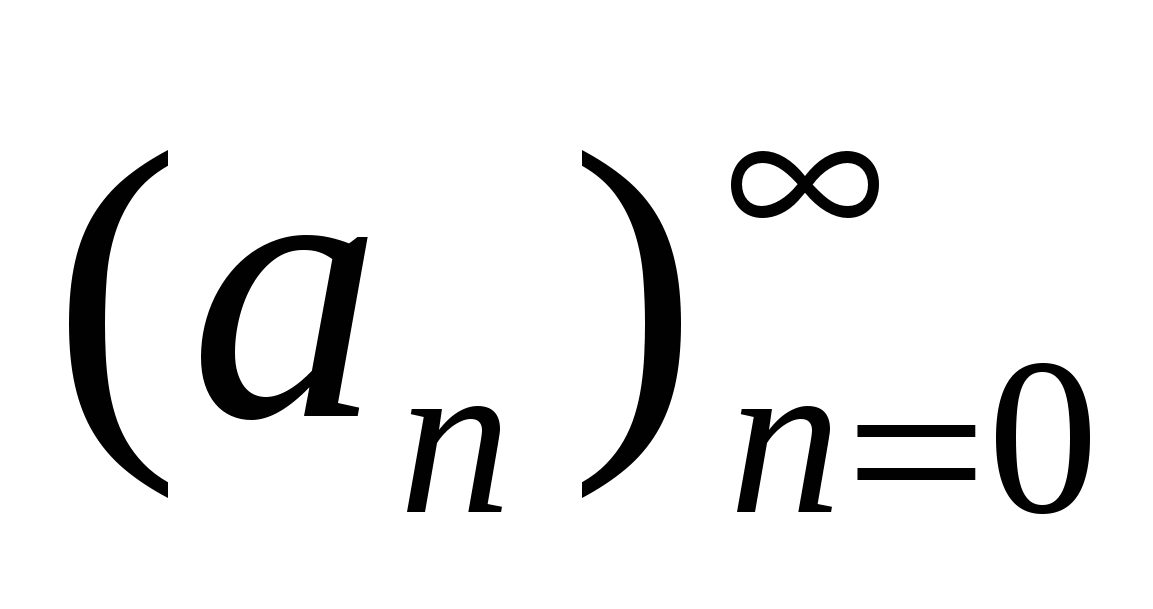 - последовательность элементов множества A (A = Z, Q, R, C). Будем записывать последовательность
- последовательность элементов множества A (A = Z, Q, R, C). Будем записывать последовательность 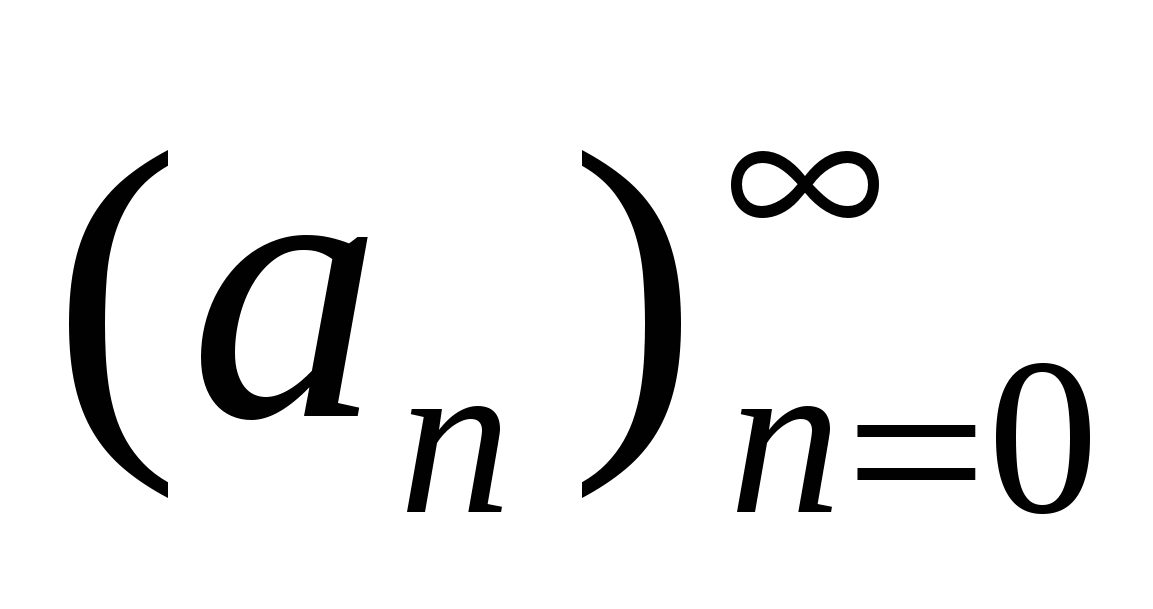 в виде
в виде
![]() , (1)
, (1)
где t - формальная переменная. Такая форма записи последовательности называется формальным степенным рядом. Конечную последовательность 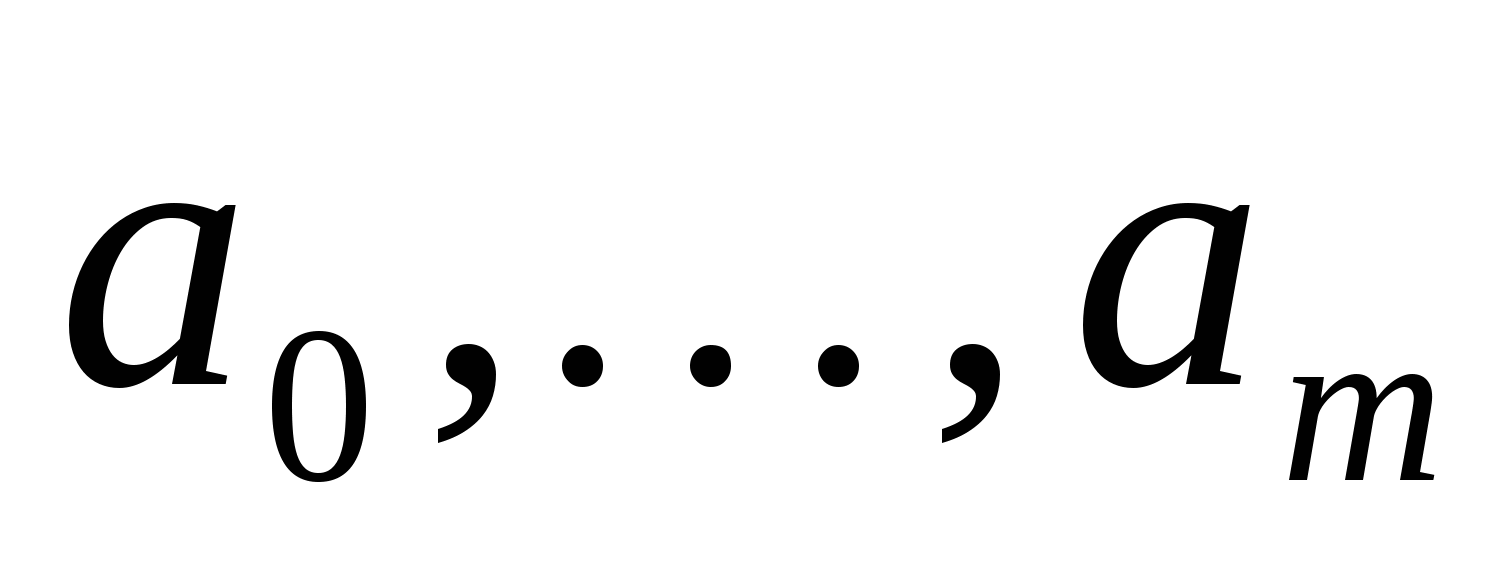 будем рассматривать как бесконечную последовательность, в которой
будем рассматривать как бесконечную последовательность, в которой 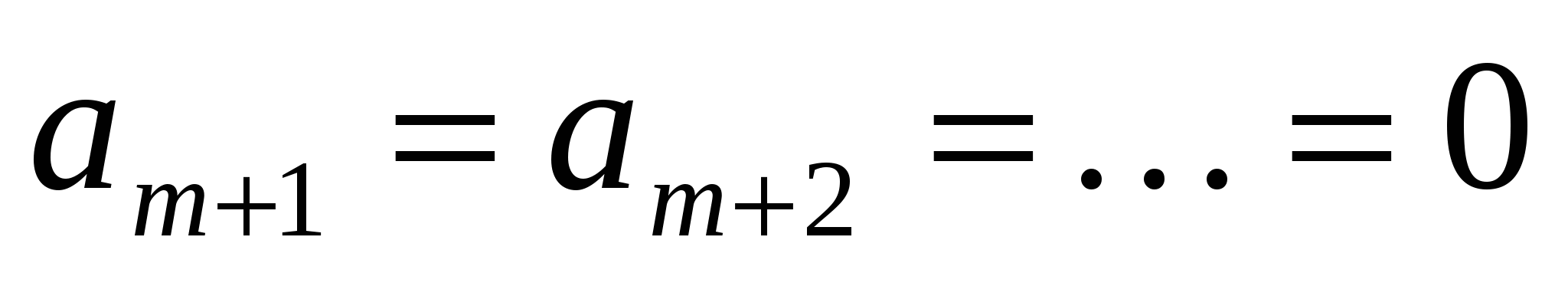 . Слагаемые вида
. Слагаемые вида ![]() часто будем опускать и записывать конечную последовательность
часто будем опускать и записывать конечную последовательность 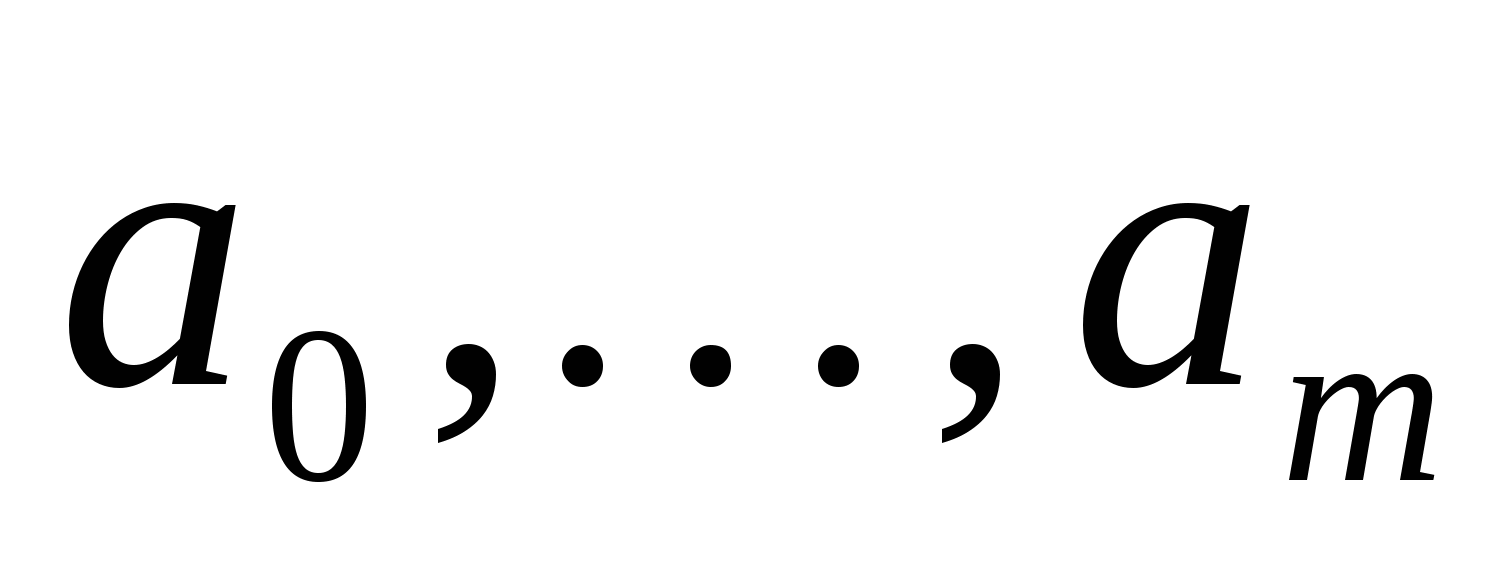 в виде
в виде 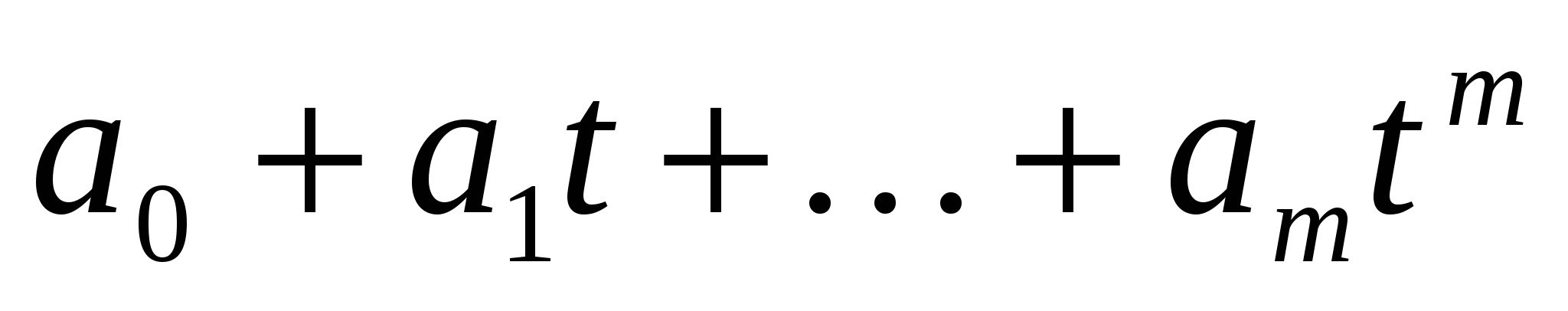 . Множество формальных степенных рядов с коэффициентами из
. Множество формальных степенных рядов с коэффициентами из  будем обозначать
будем обозначать 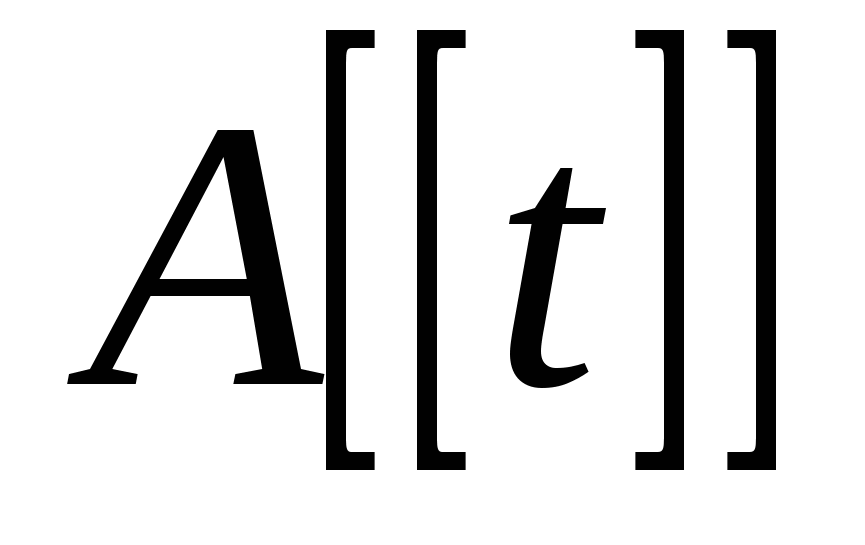 . Если
. Если 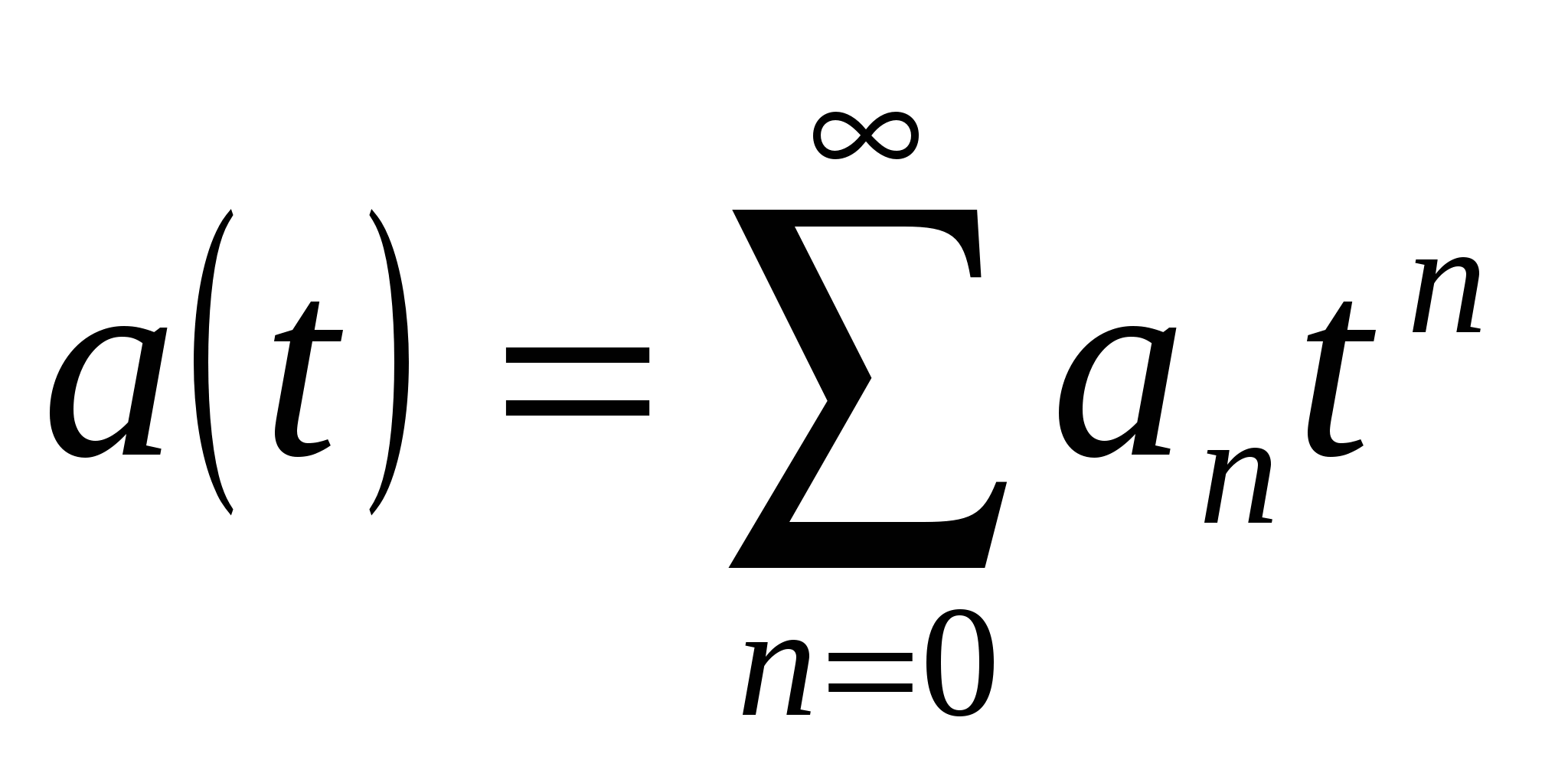 , то коэффициент
, то коэффициент ![]() называется свободным членом формального степенного ряда
называется свободным членом формального степенного ряда 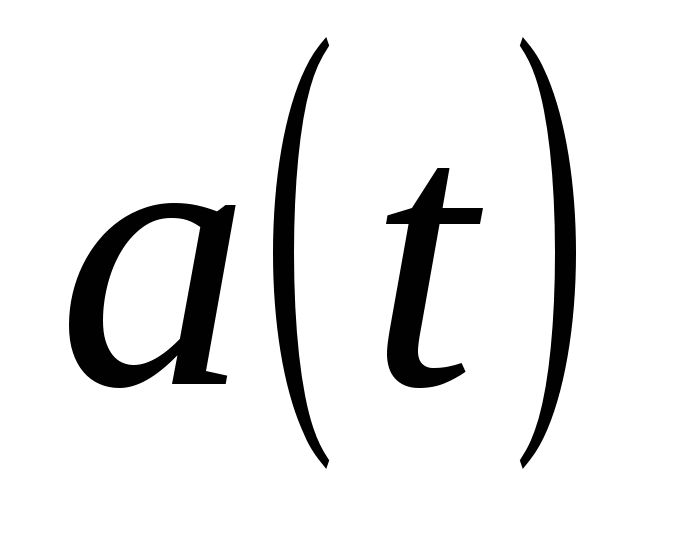 и будем обозначать
и будем обозначать 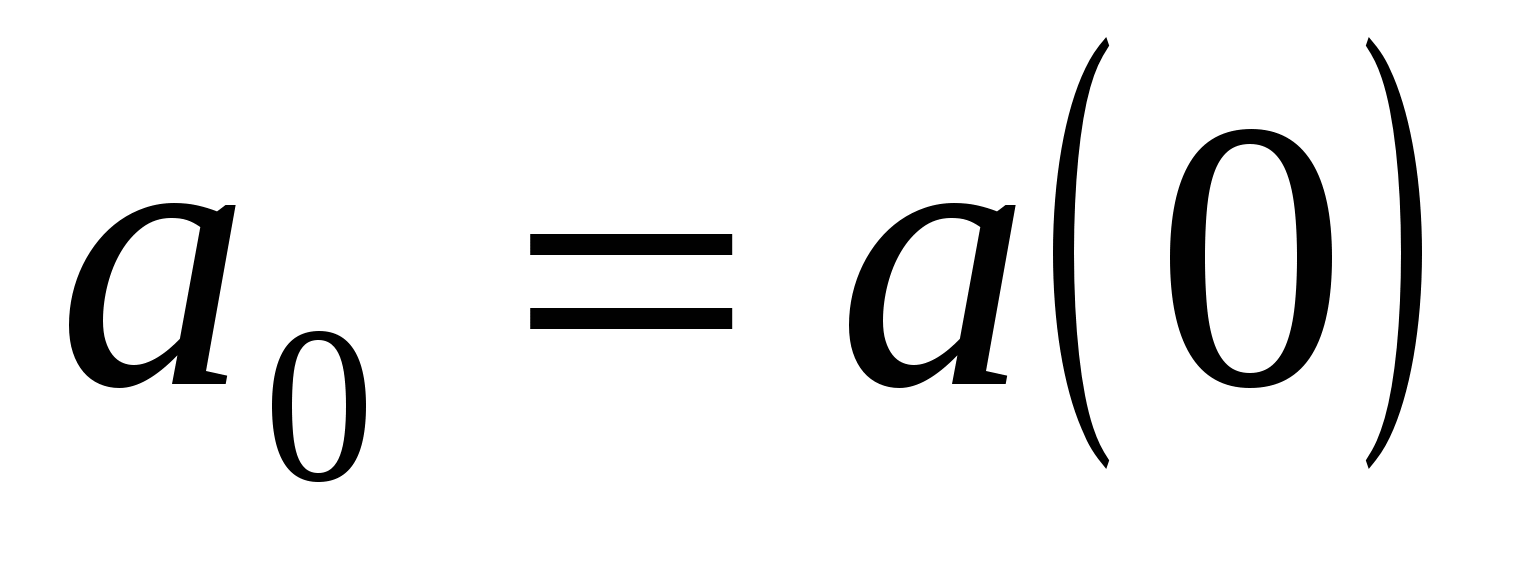 .
.
-
Введем на множестве формальных степенных рядов
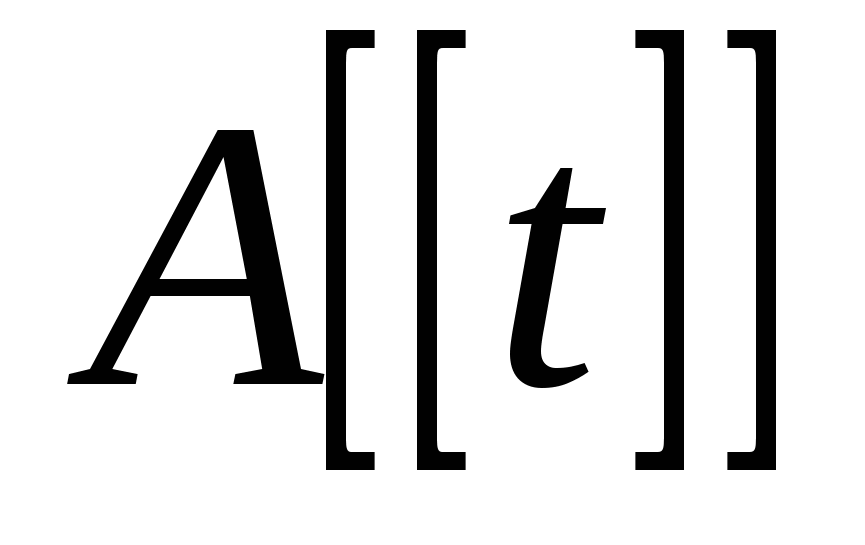 операции сложения и умножения.
операции сложения и умножения.
Если
![]() ,
, 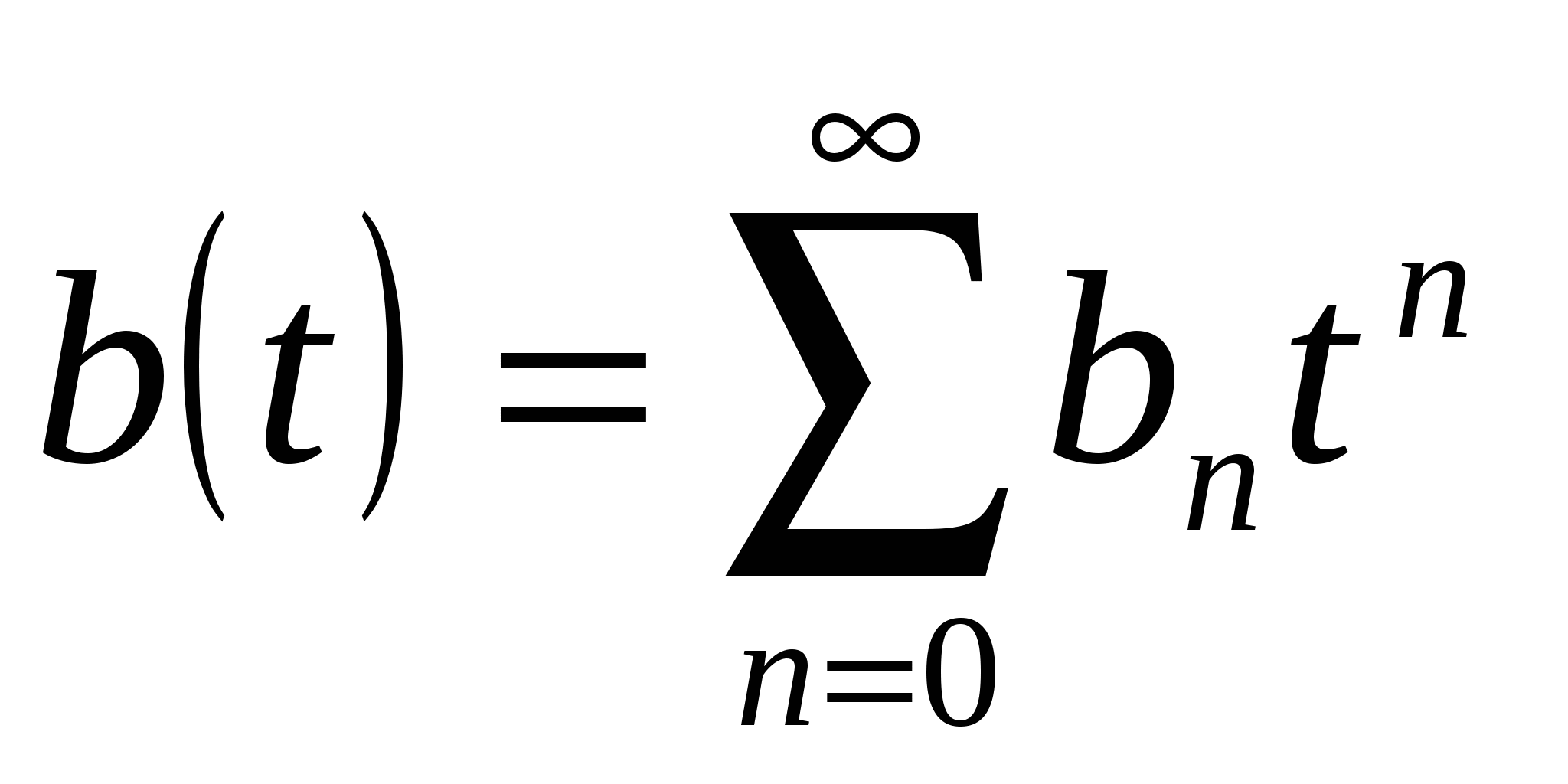 ,
,
то
![]() , (2)
, (2)
![]() , (3)
, (3)
где
![]() . (4)
. (4)
Непосредственно проверяется, что введенные операции обладают свойствами:
![]() , (5)
, (5)
![]() , (6)
, (6)
![]()
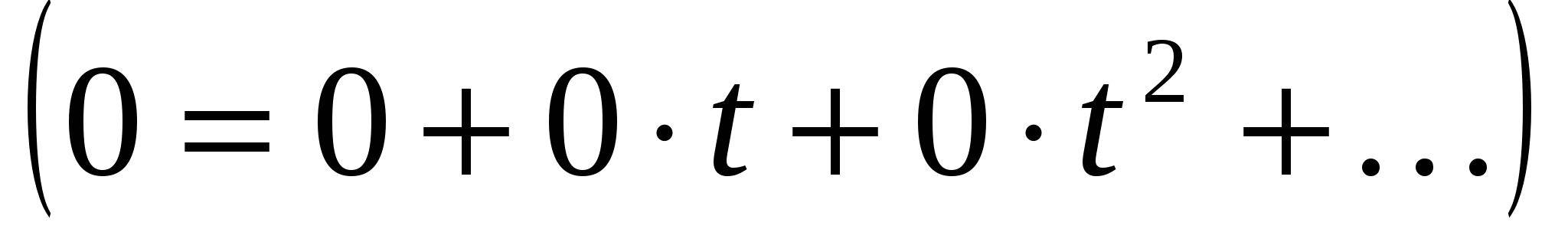 (7)
(7)
Если 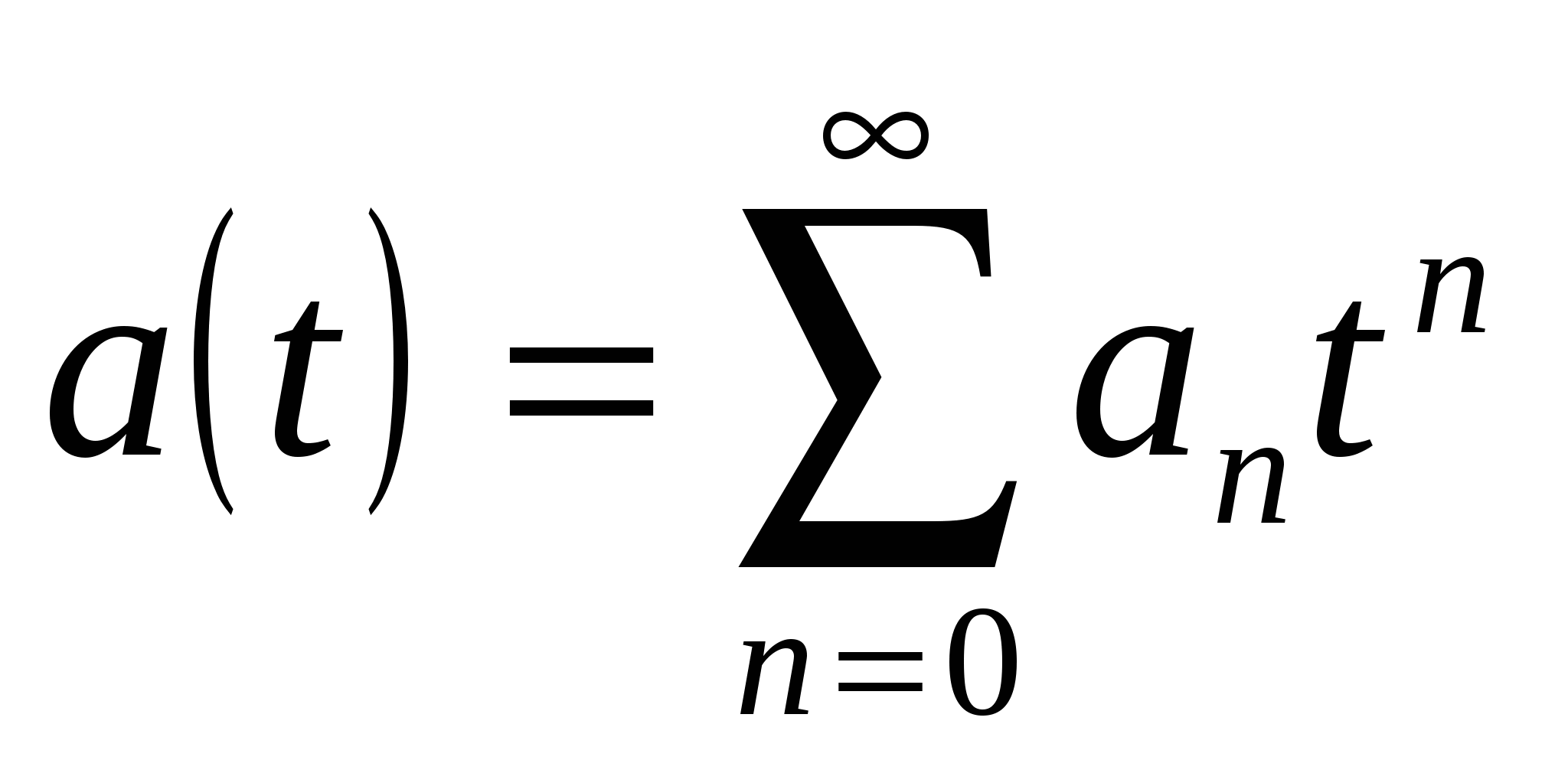 , то определим противоположный ряд
, то определим противоположный ряд 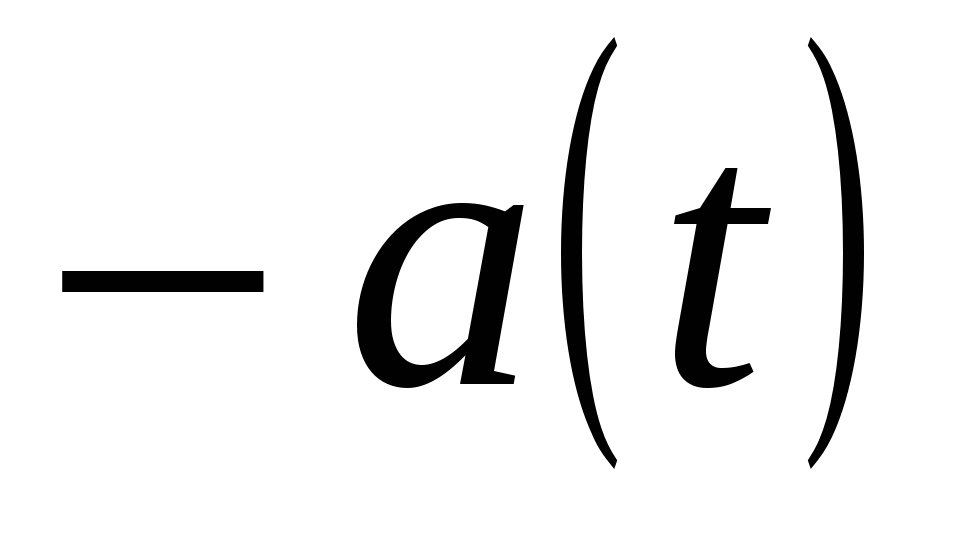 формулой
формулой
![]() . (8)
. (8)
Тогда
![]() . (9)
. (9)
Операция умножения в 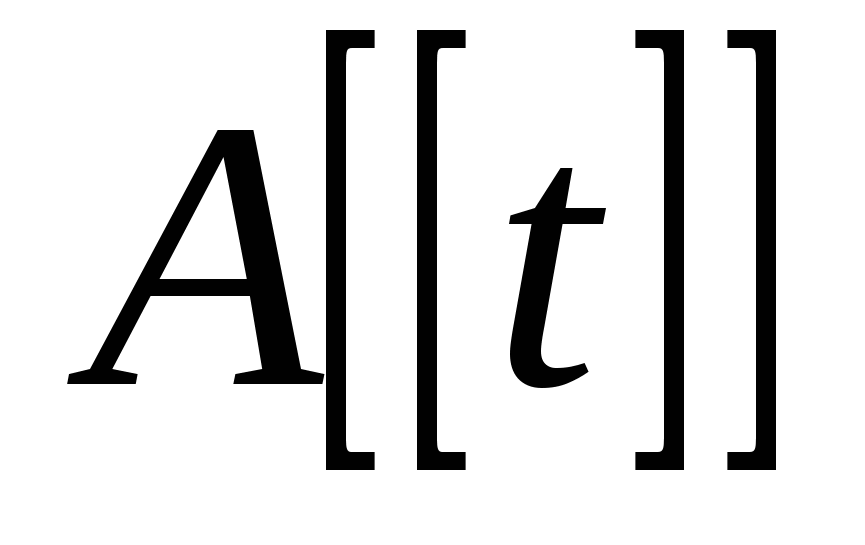 обладает свойствами:
обладает свойствами:
![]() , (10)
, (10)
![]() , (11)
, (11)
![]() (12)
(12)
![]()
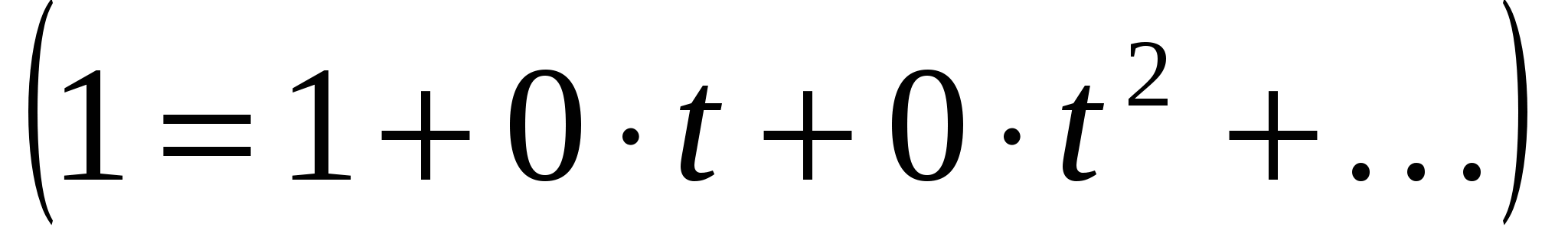 . (13)
. (13)
-
Определим для формального степенного ряда
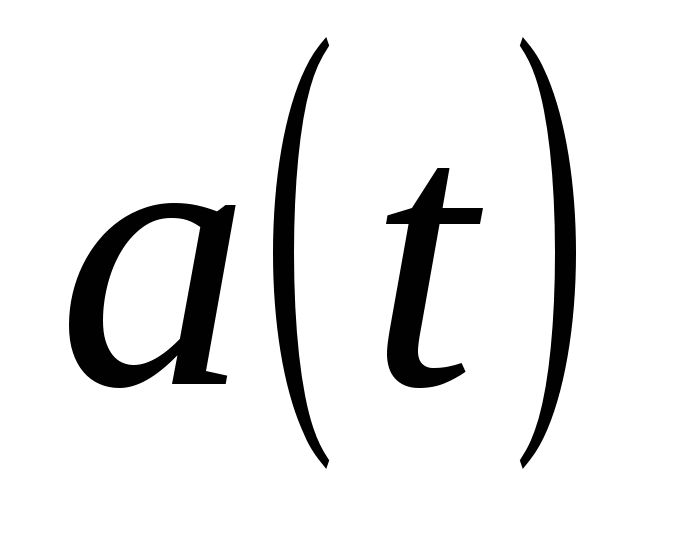 производную
производную 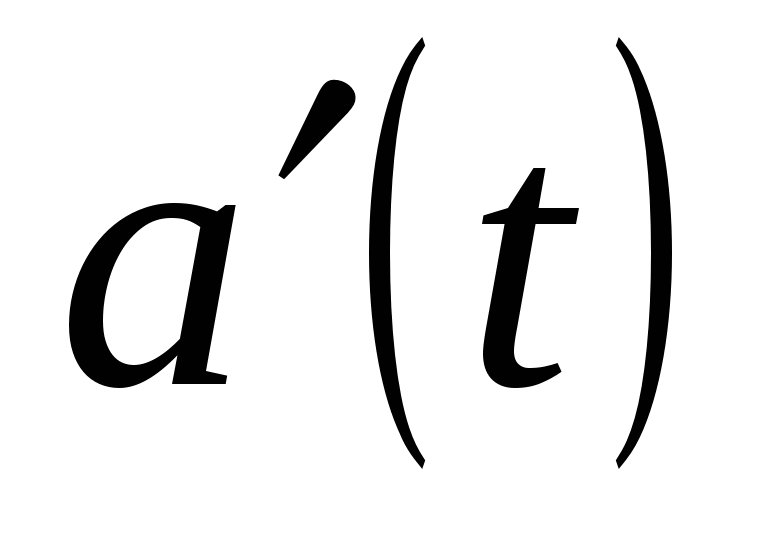 формулой
формулой
![]() (14)
(14)
Производная обладает свойствами:
![]() , (15)
, (15)
![]() . (16)
. (16)
Равенства (15), (16) непосредственно вытекают из определения (14).
Если 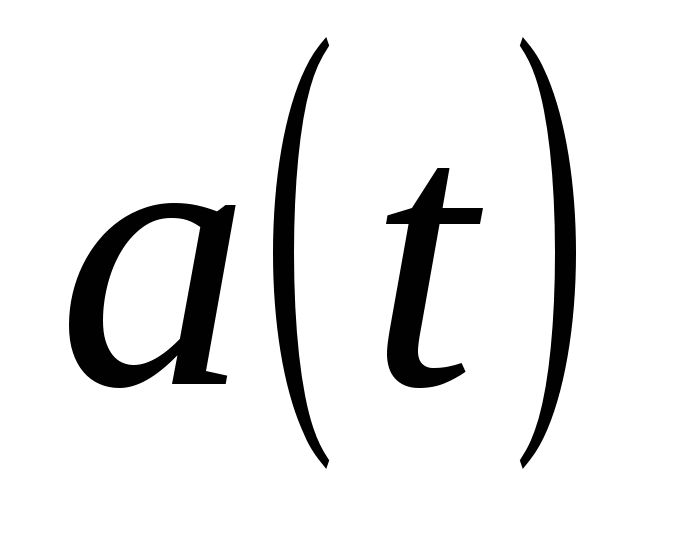 - произвольный формальный степенной ряд, а
- произвольный формальный степенной ряд, а 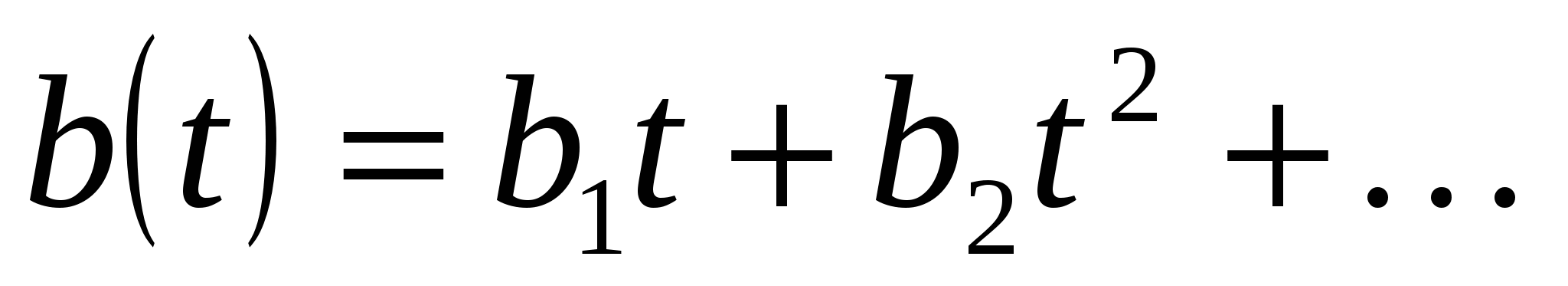 - формальный степенной ряд без свободного члена, т.е.
- формальный степенной ряд без свободного члена, т.е. 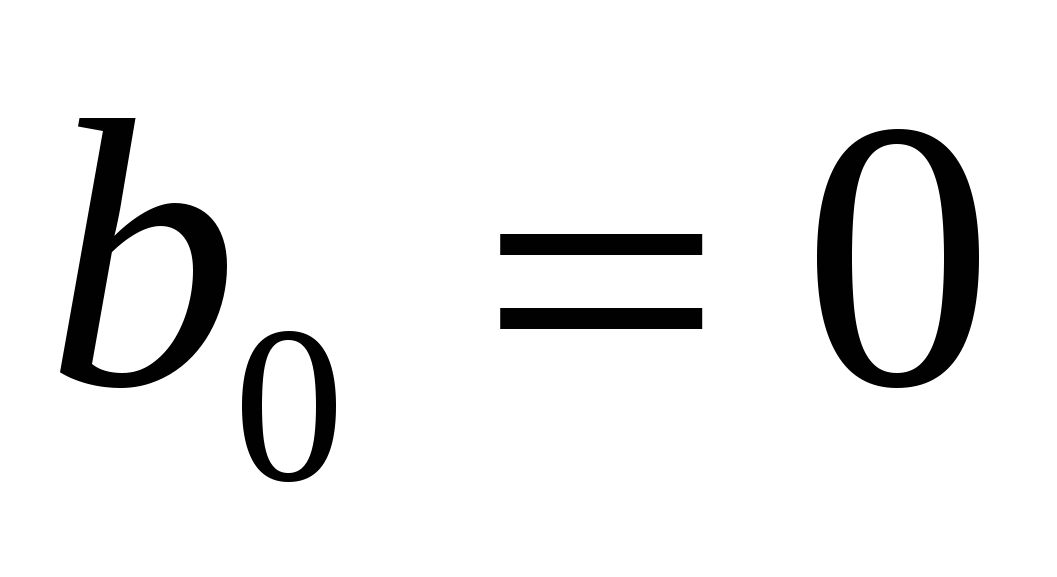 , то определена подстановка
, то определена подстановка
![]() . (17)
. (17)
-
Рассмотрим вопрос об обратимости формального степенного ряда. Формальный степенной ряд
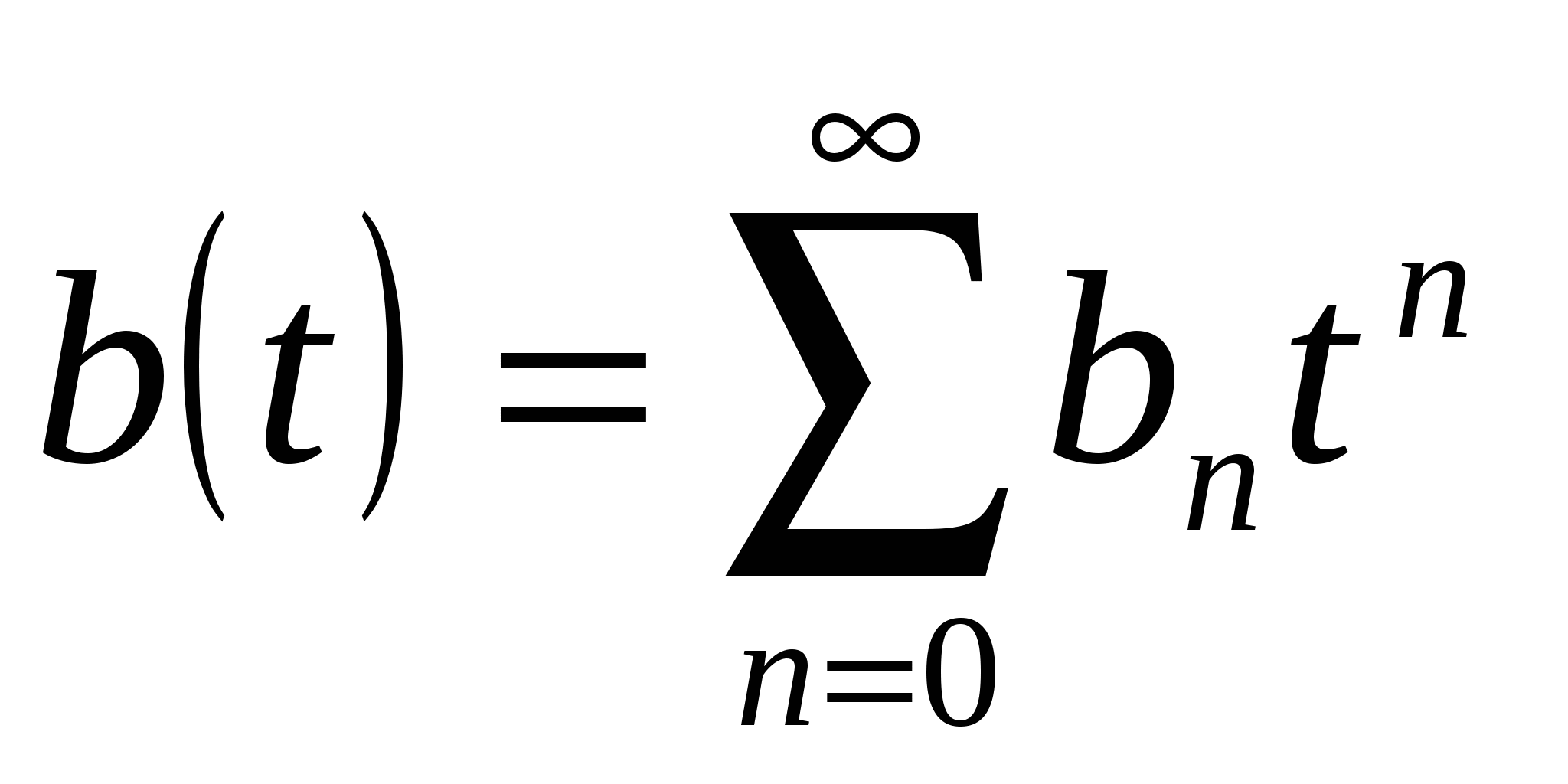 называется обратным к формальному степенному ряду
называется обратным к формальному степенному ряду 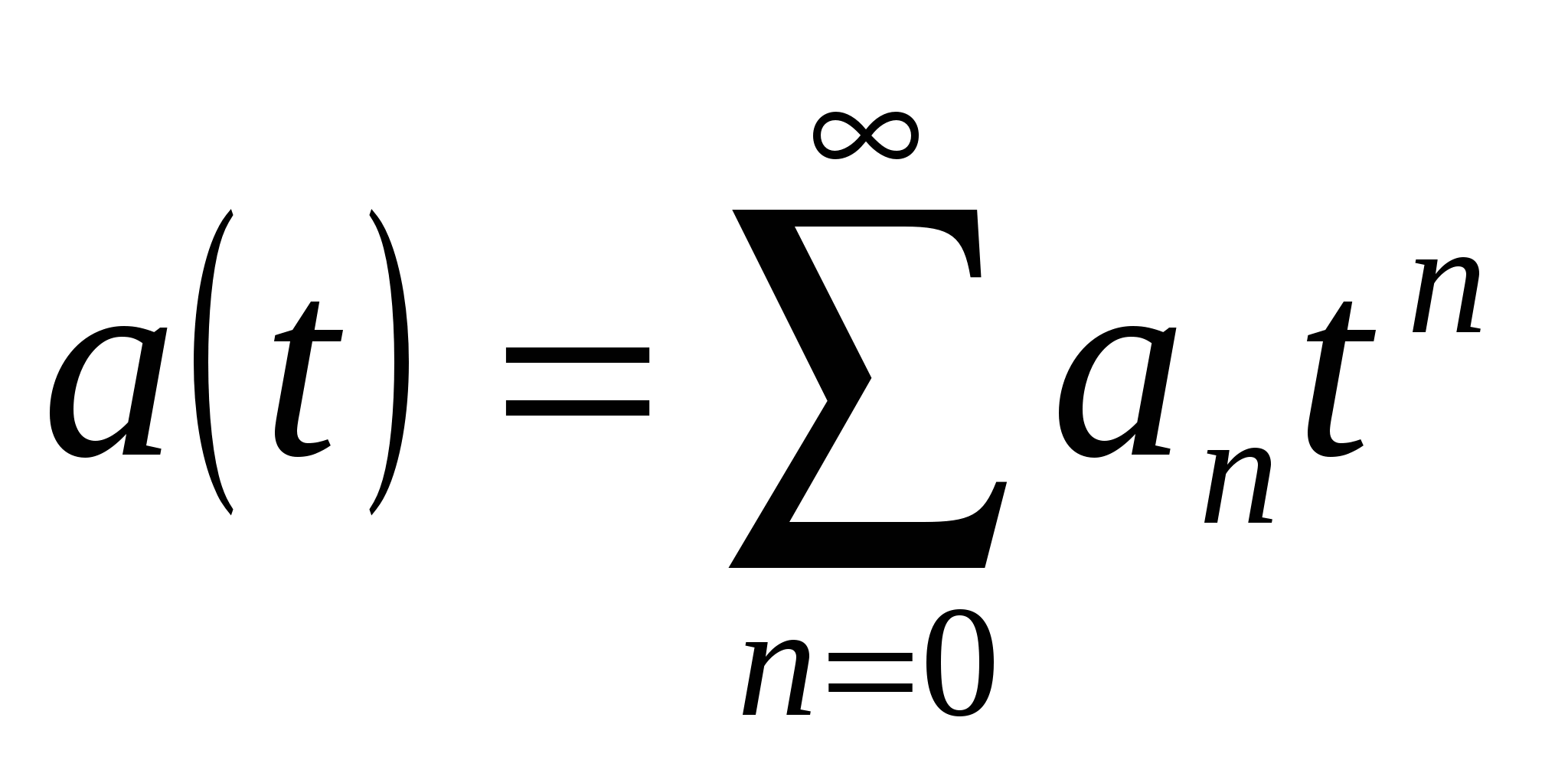 , если
, если
![]() . (18)
. (18)
Если обратный формальный степенной ряд существует, то он единственен и обозначается
![]() .
.
Примеры.
-
Пусть
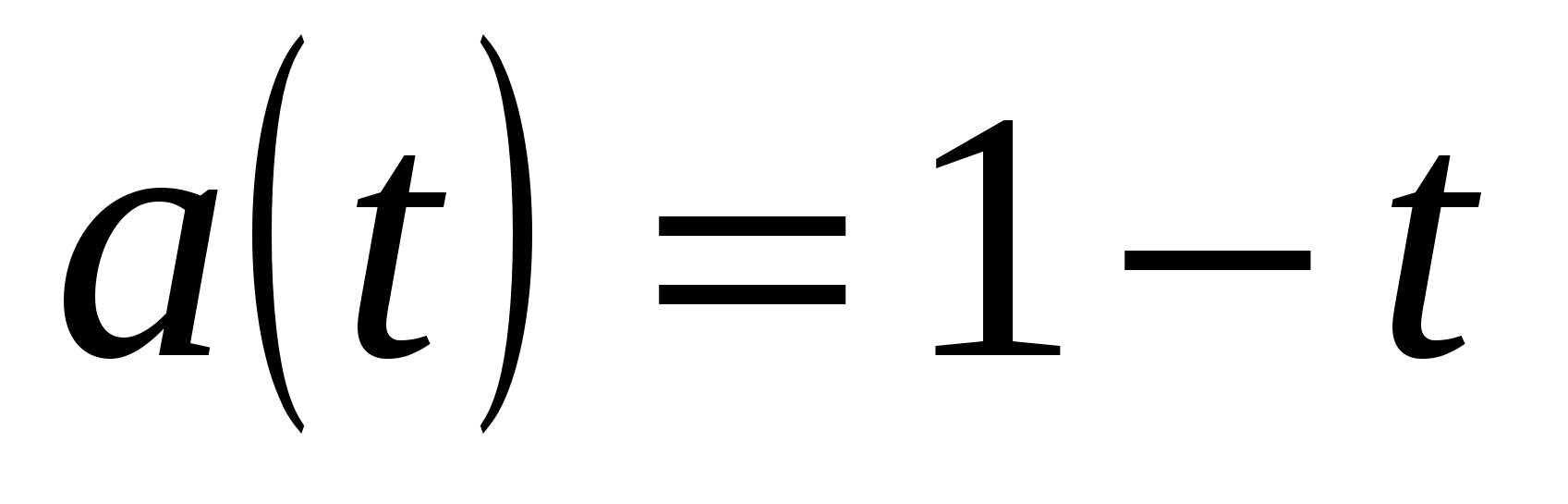 . Тогда
. Тогда
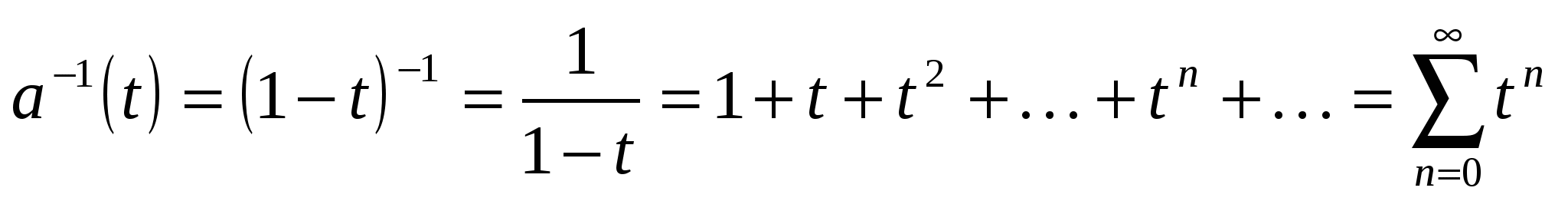
(сумма бесконечной геометрической прогрессии).
-
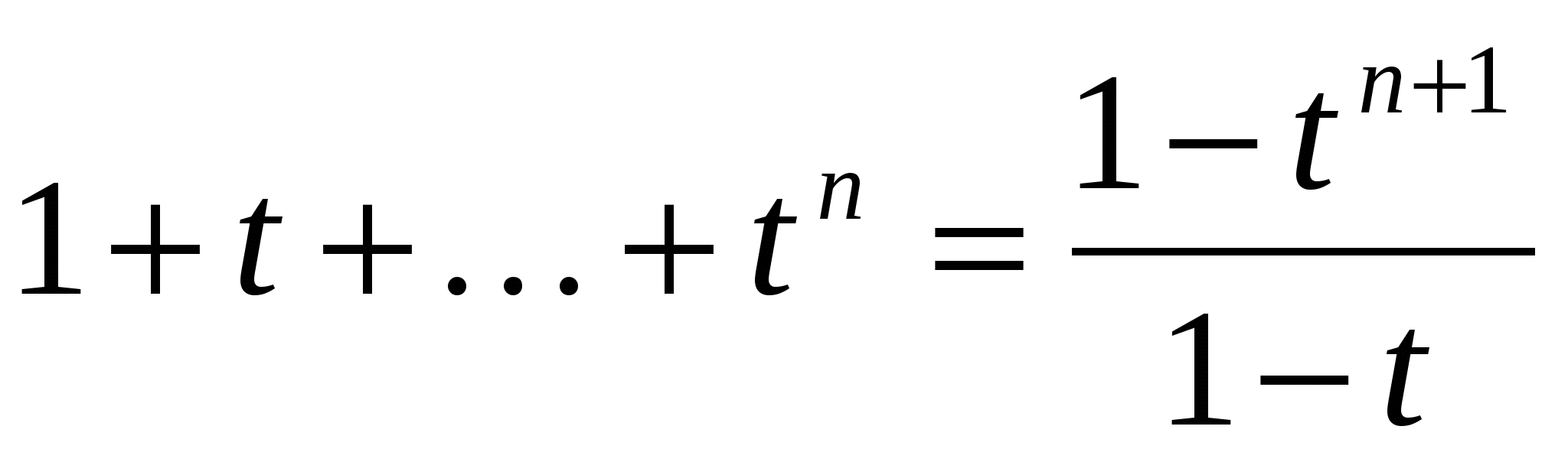 (сумма конечной геометрической прогрессии).
(сумма конечной геометрической прогрессии).
Следующая теорема дает критерий обратимости формального степенного ряда.
Теорема. Формальный степенной ряд 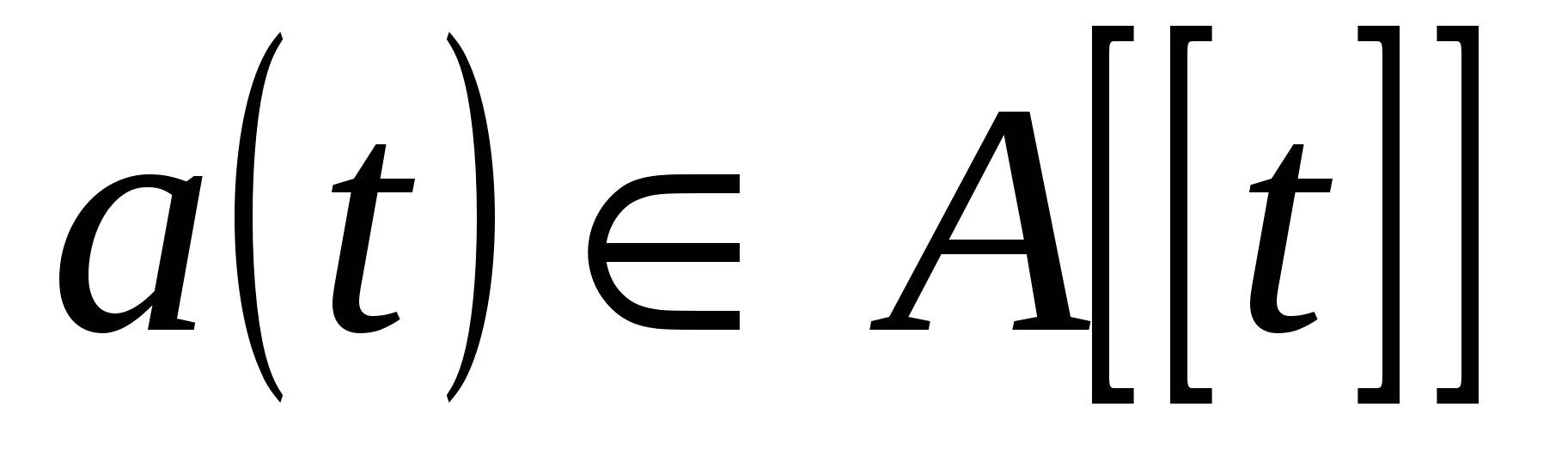 обратим тогда и только тогда, когда свободный член
обратим тогда и только тогда, когда свободный член 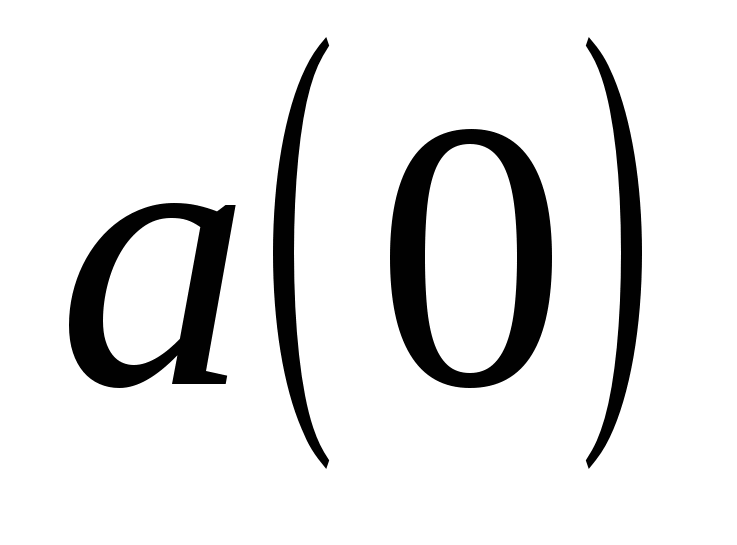 обратим в
обратим в  .
.
□ 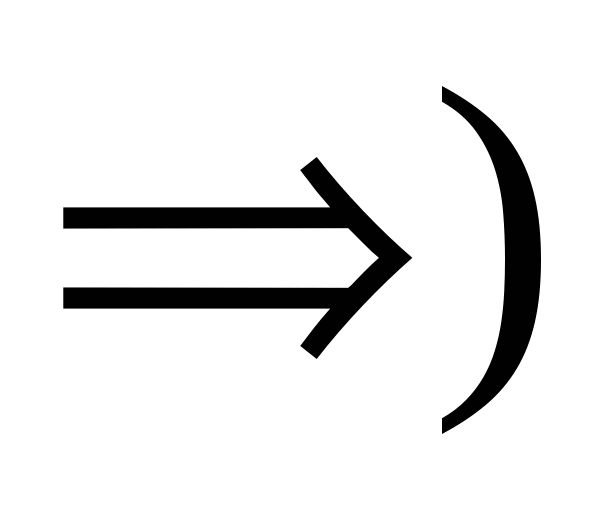 Если
Если 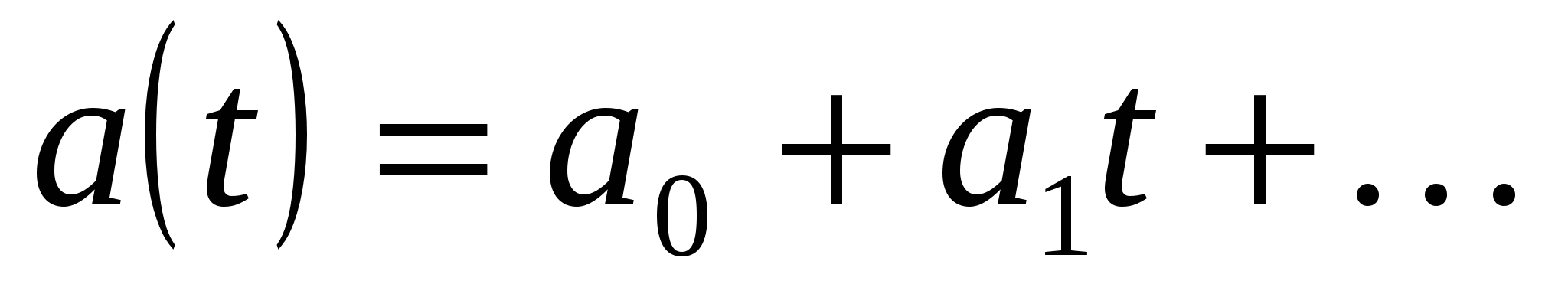 обратим в
обратим в 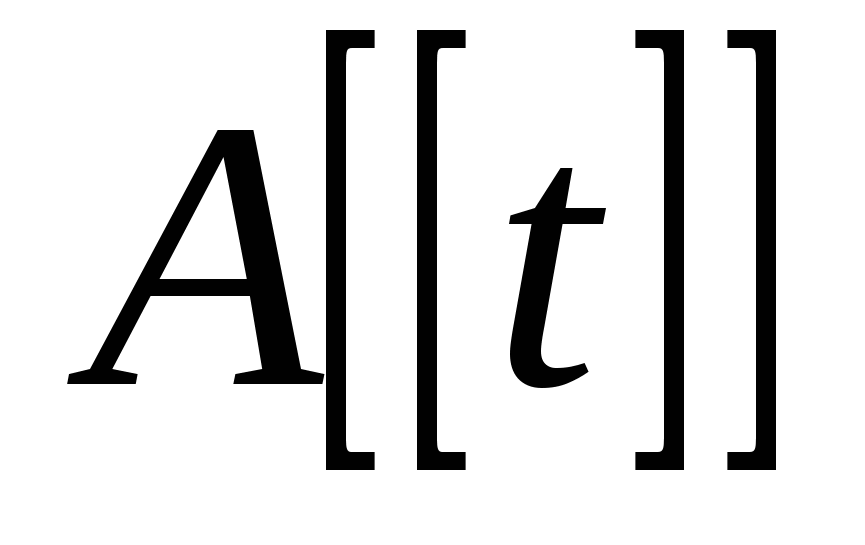 и
и 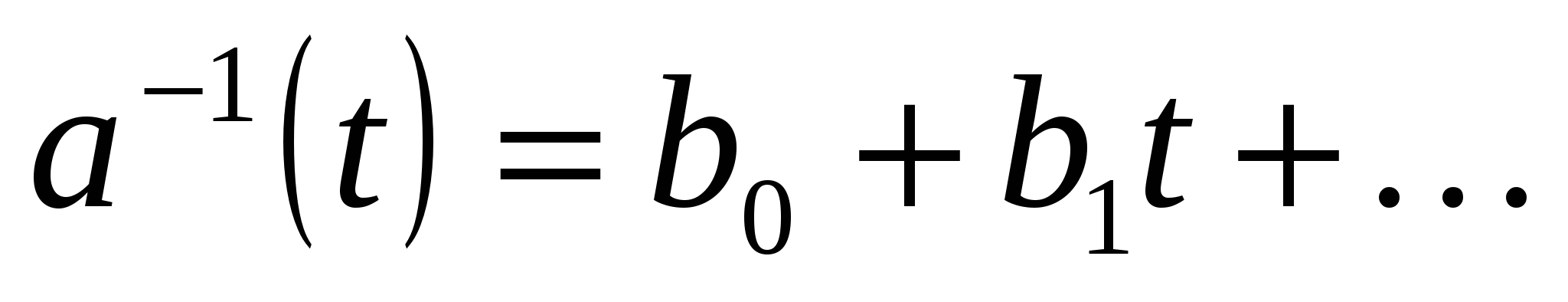 , то
, то 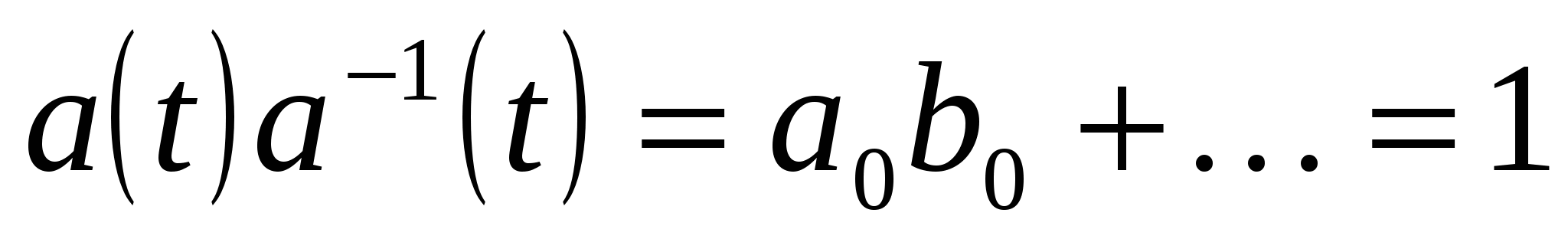 . В частности,
. В частности, 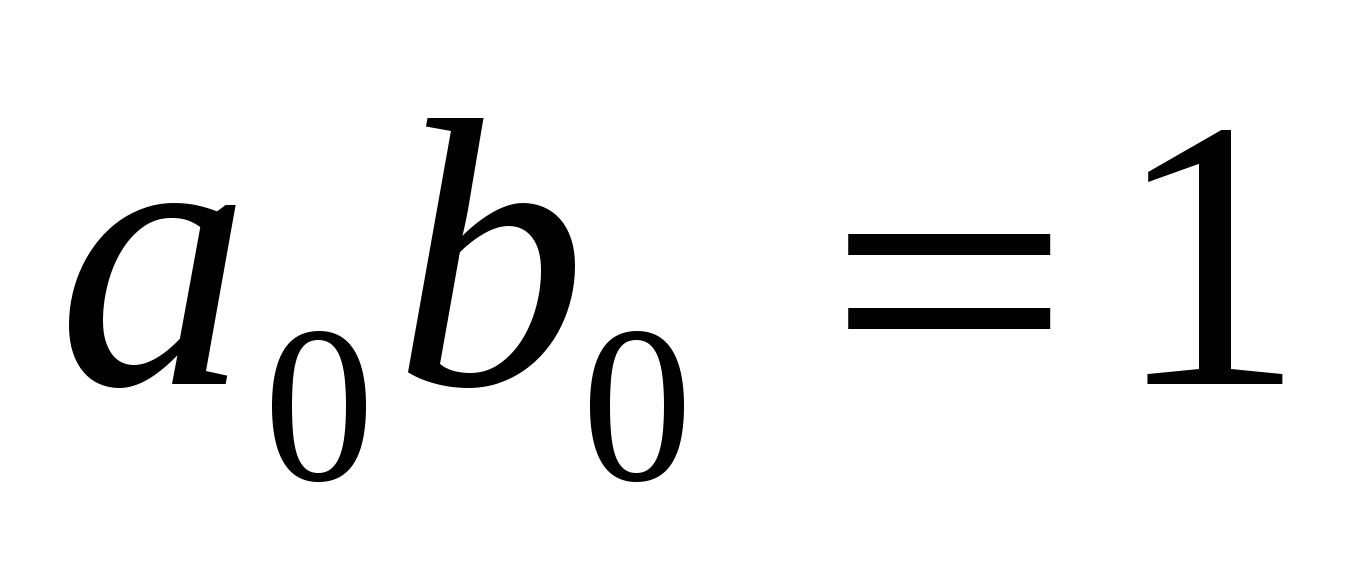 , т.е.
, т.е. 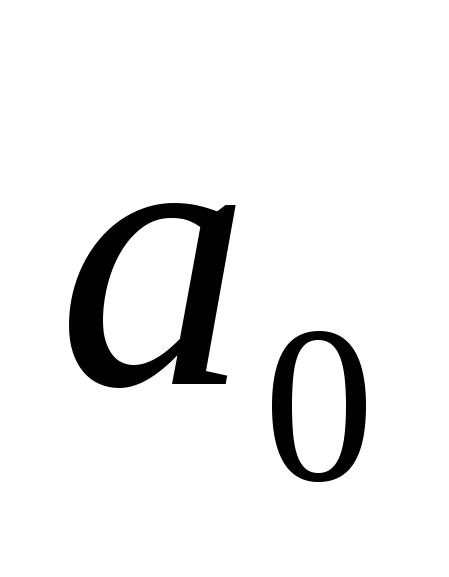 обратим в
обратим в  .
.
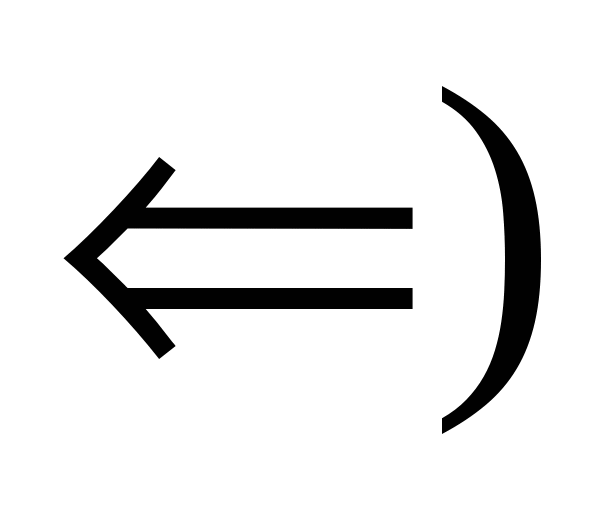 Пусть
Пусть 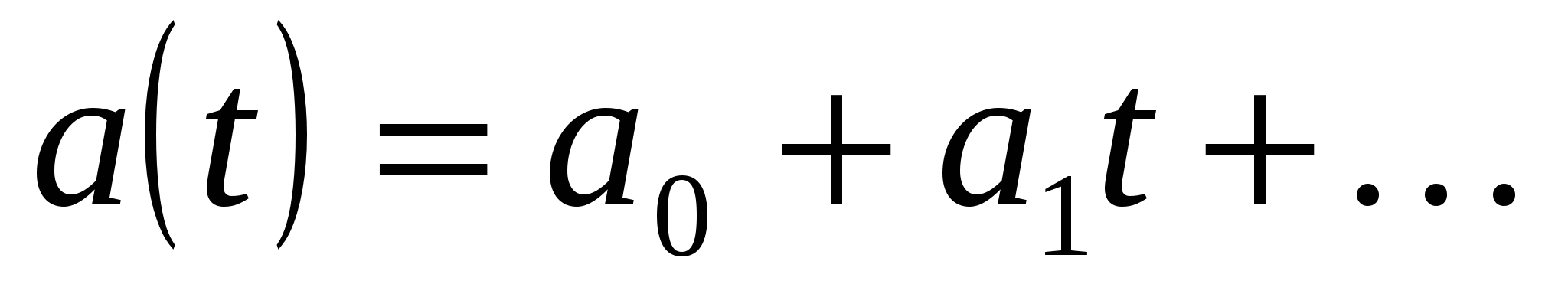 и
и 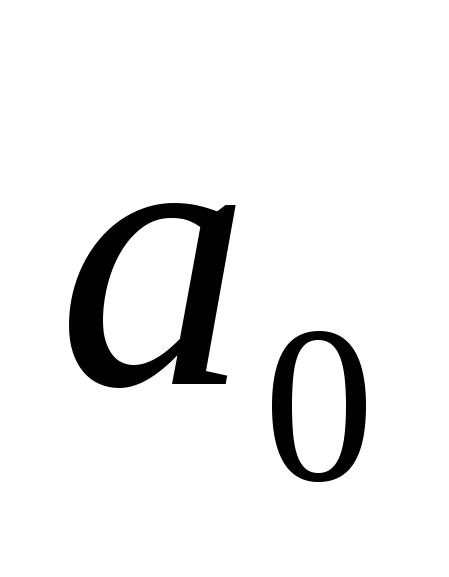 обратим в
обратим в  . Тогда
. Тогда
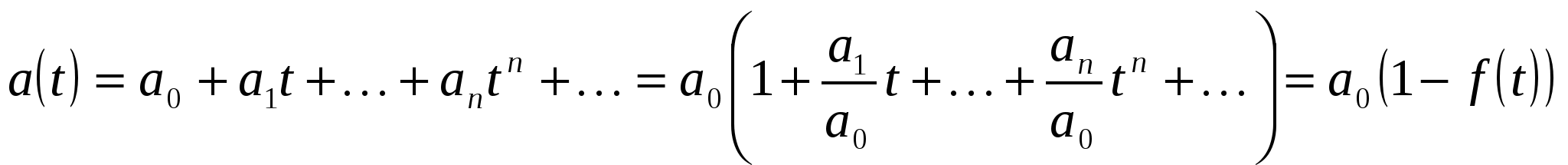 ,
,
где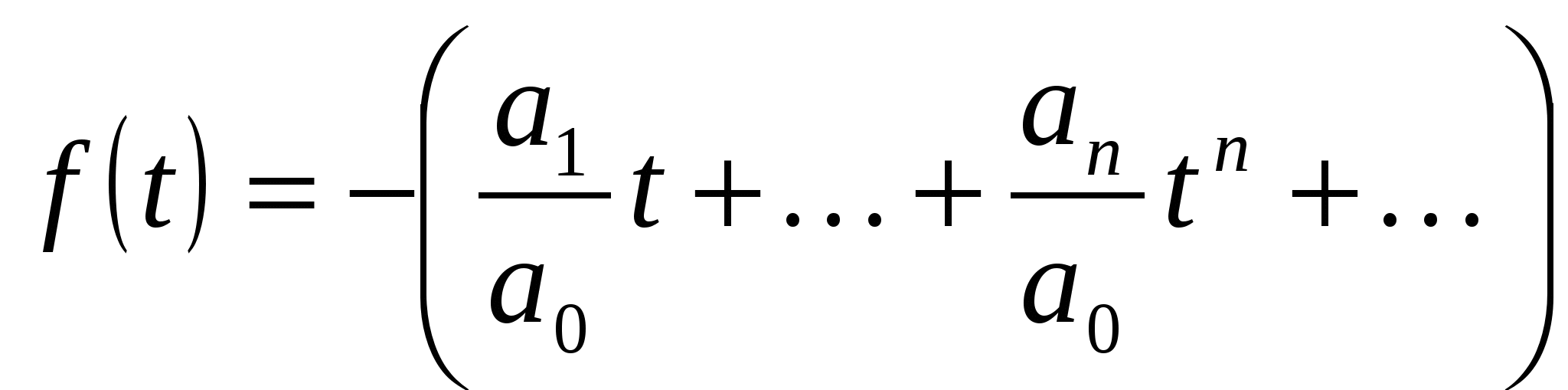 - формальный степенной ряд без свободного члена. Воспользуемся формулой бесконечной геометрической прогрессии с подстановкой
- формальный степенной ряд без свободного члена. Воспользуемся формулой бесконечной геометрической прогрессии с подстановкой 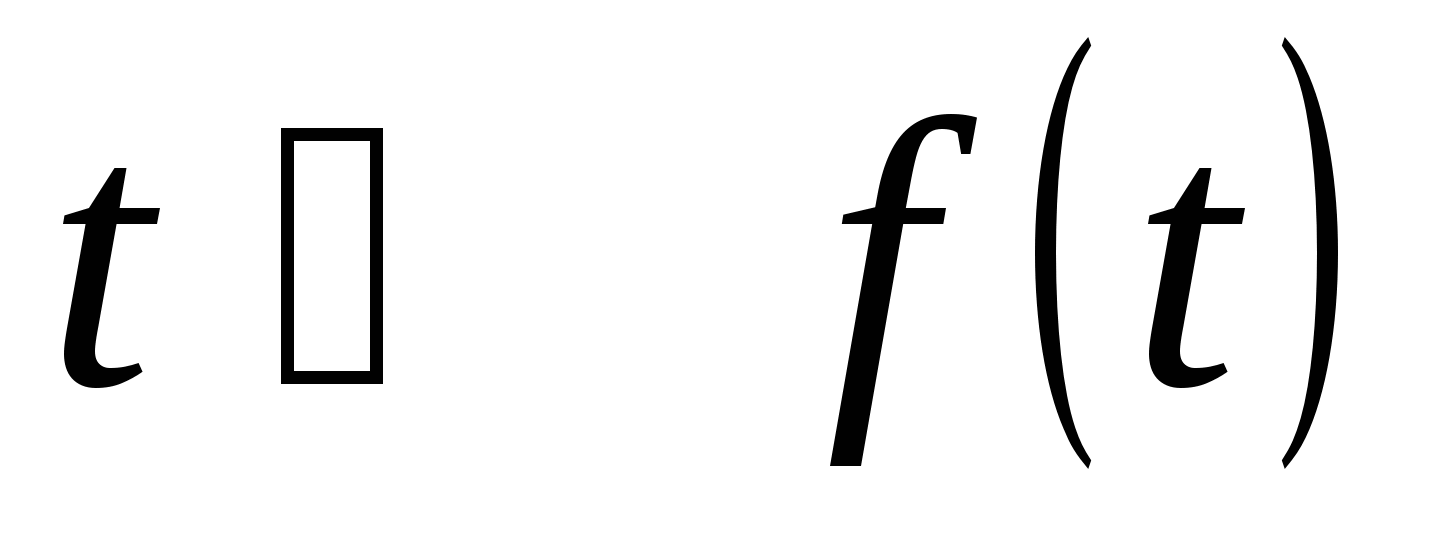 , т.е. определим
, т.е. определим
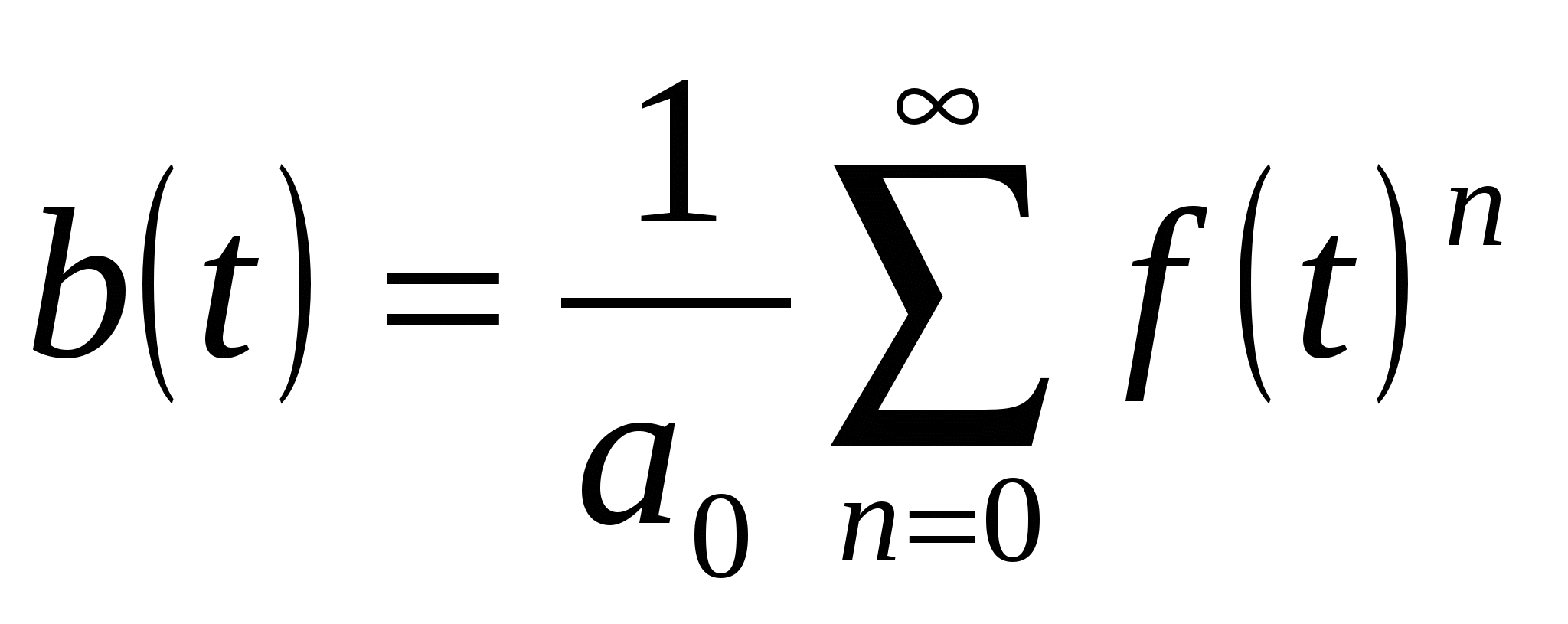 .
.
Непосредственная проверка приводит к равенству
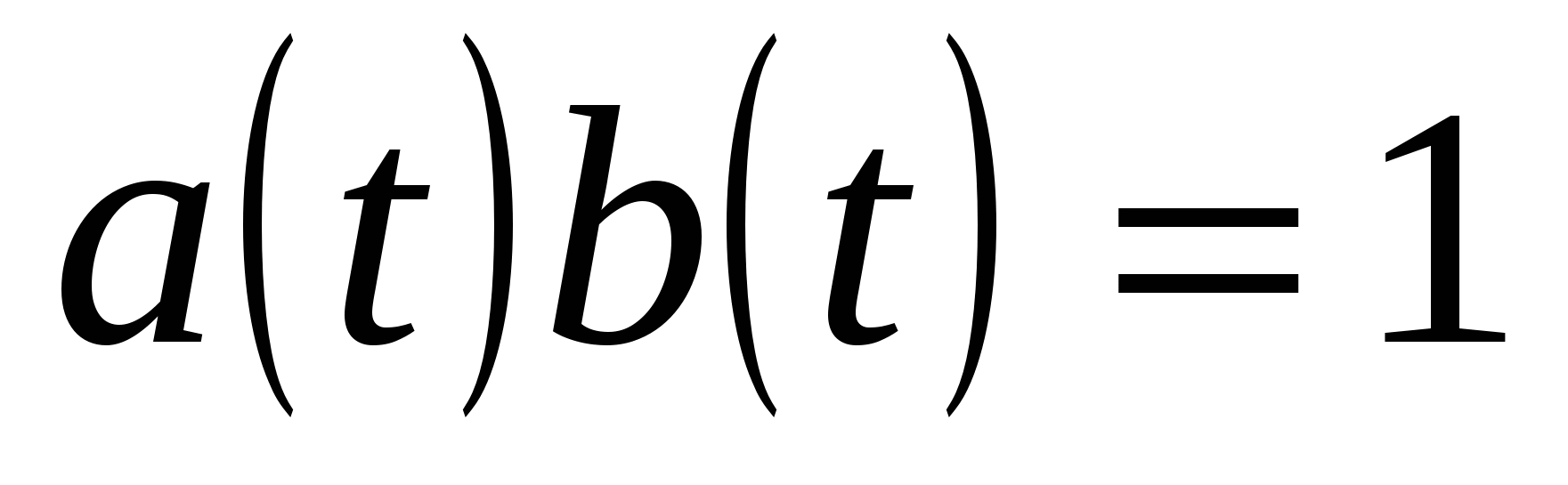 , т.е.
, т.е. 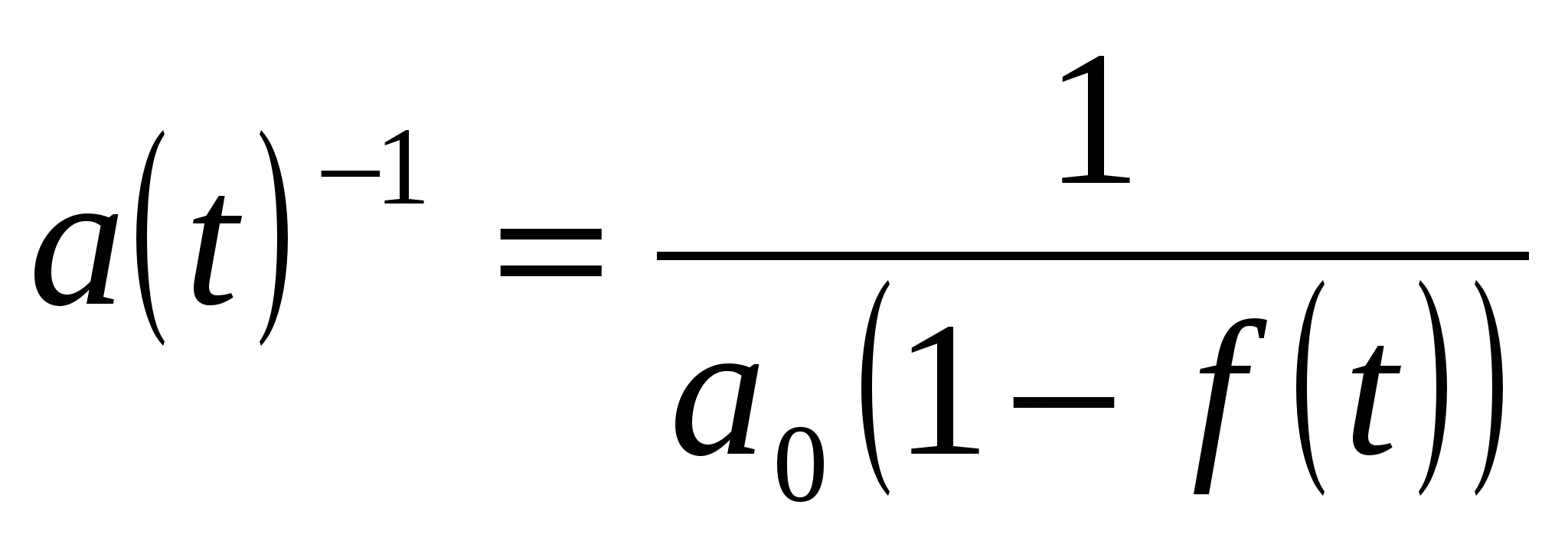 ■
■
-
В качестве приложения формальных степенных рядов рассмотрим рекуррентные соотношения с постоянными коэффициентами. Арифметика формальных степенных рядов позволяет в этом случае полностью решить вопрос вычисления таких последовательностей. В качестве примера рассмотрим числа Фибоначчи (см., например, [1]), т.е., последовательность
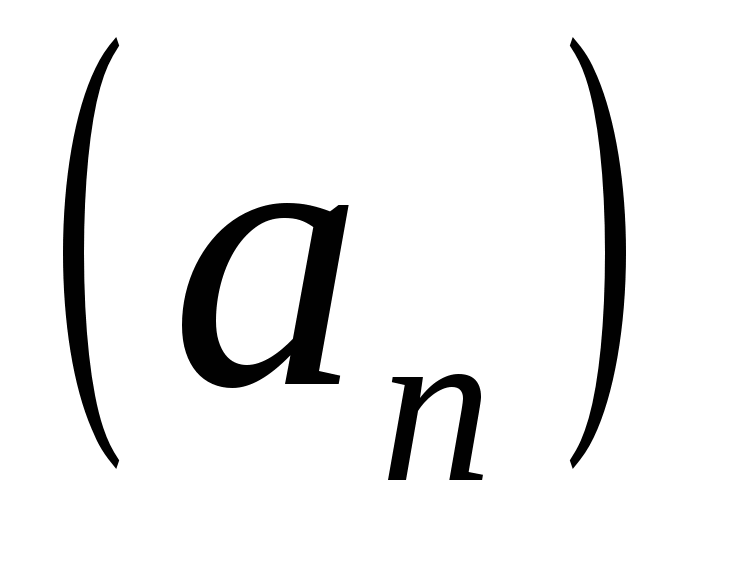 , заданную условиями:
, заданную условиями:
![]() ,
, 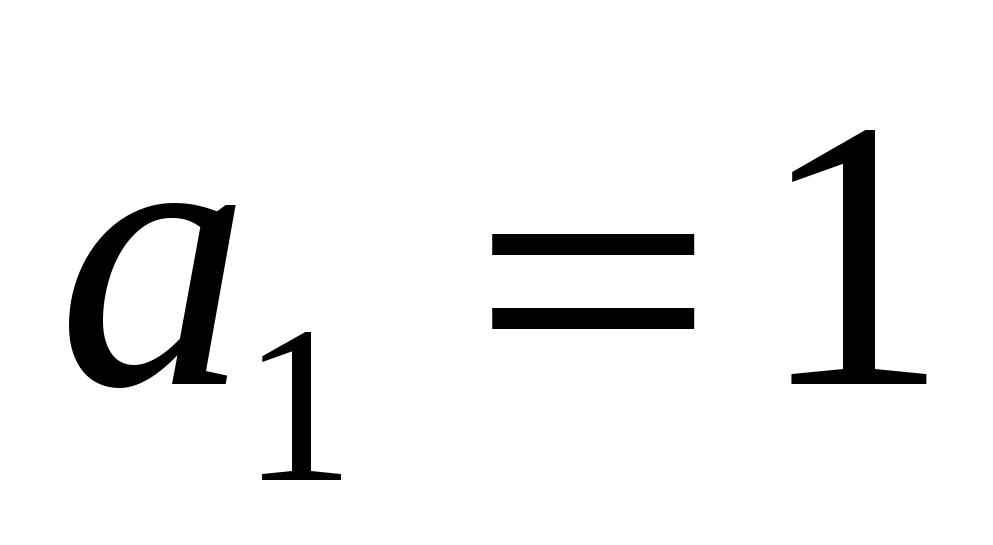 ,
, 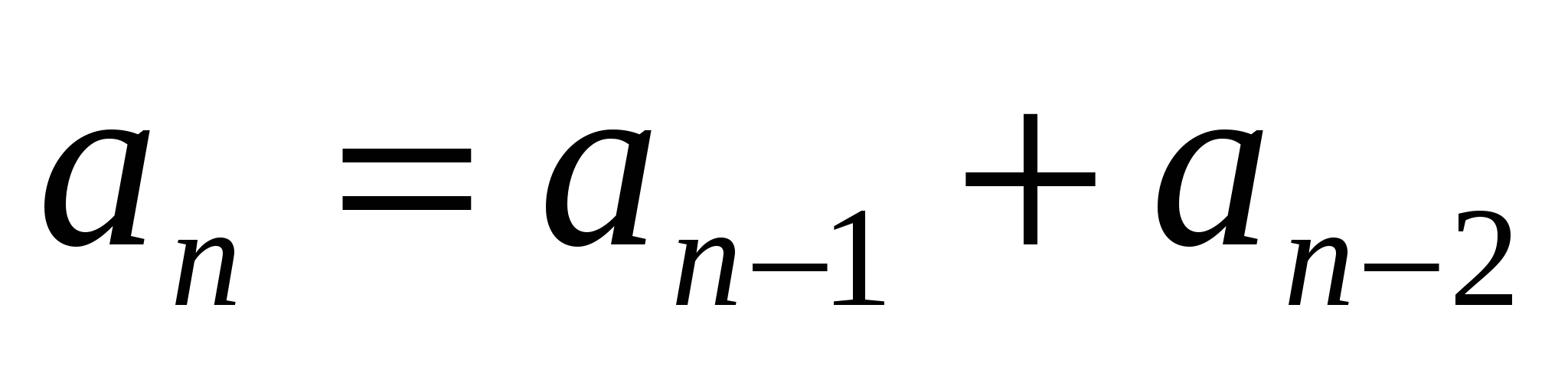
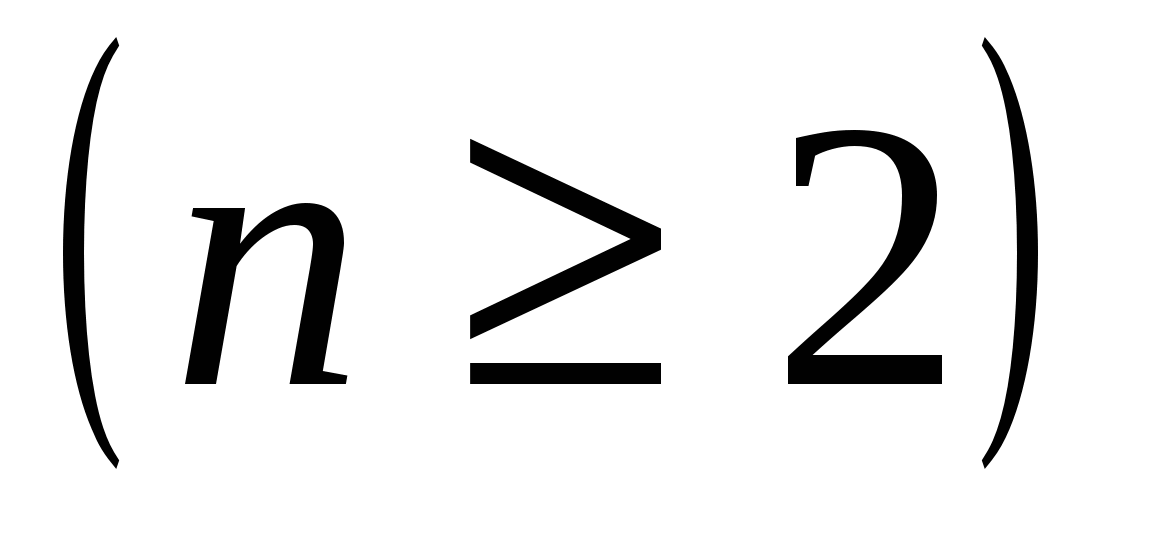 . (19)
. (19)
Пусть 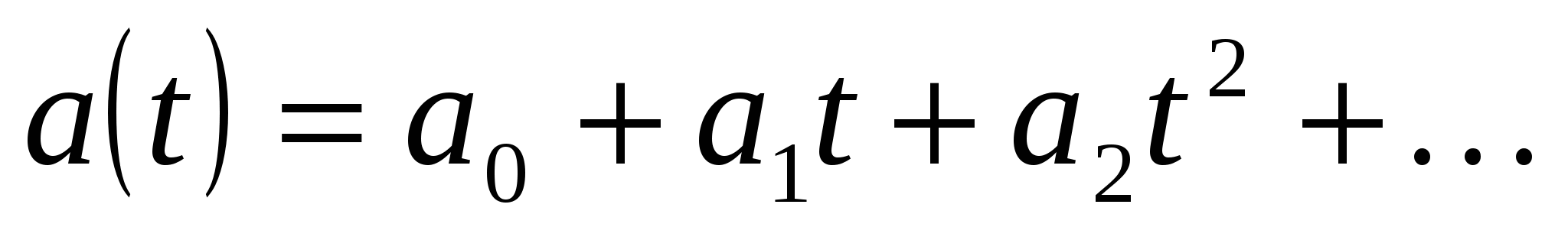 - соответствующий формальный степенной ряд. Из рекуррентного соотношения (19) следует равенство
- соответствующий формальный степенной ряд. Из рекуррентного соотношения (19) следует равенство
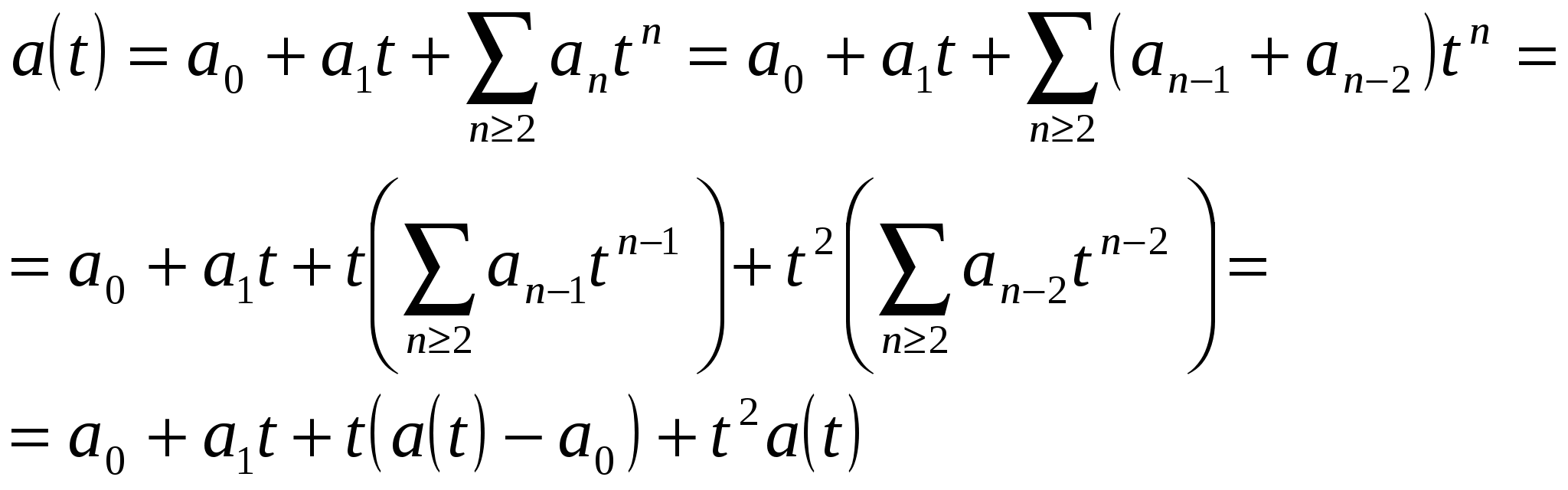
Учитывая начальные условия ![]() ,
, 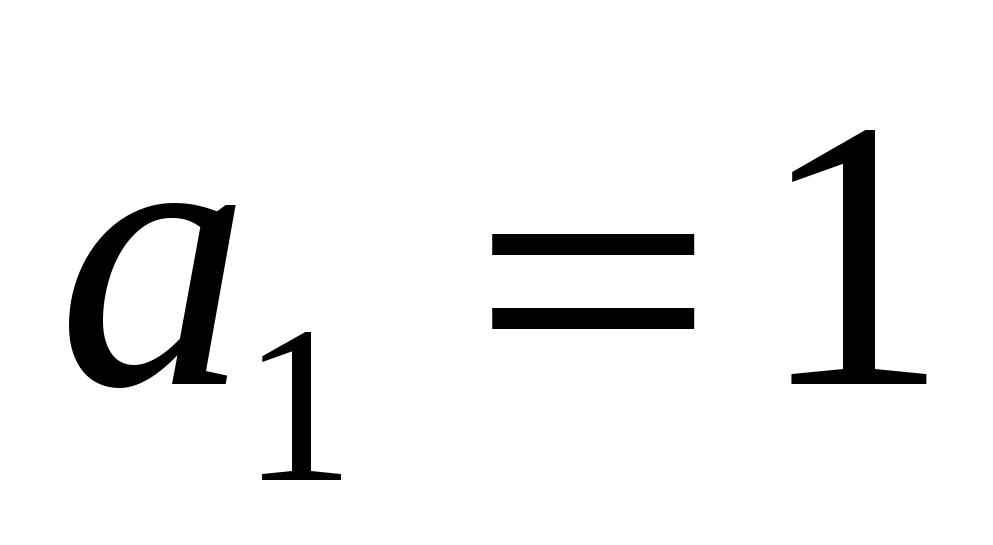 , получаем,
, получаем,
 , т.е.,
, т.е., 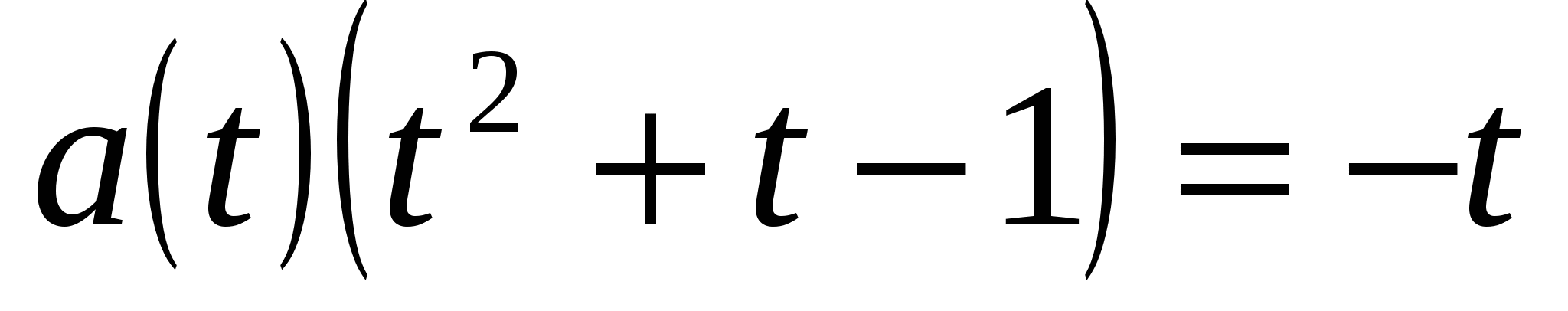 ,
, 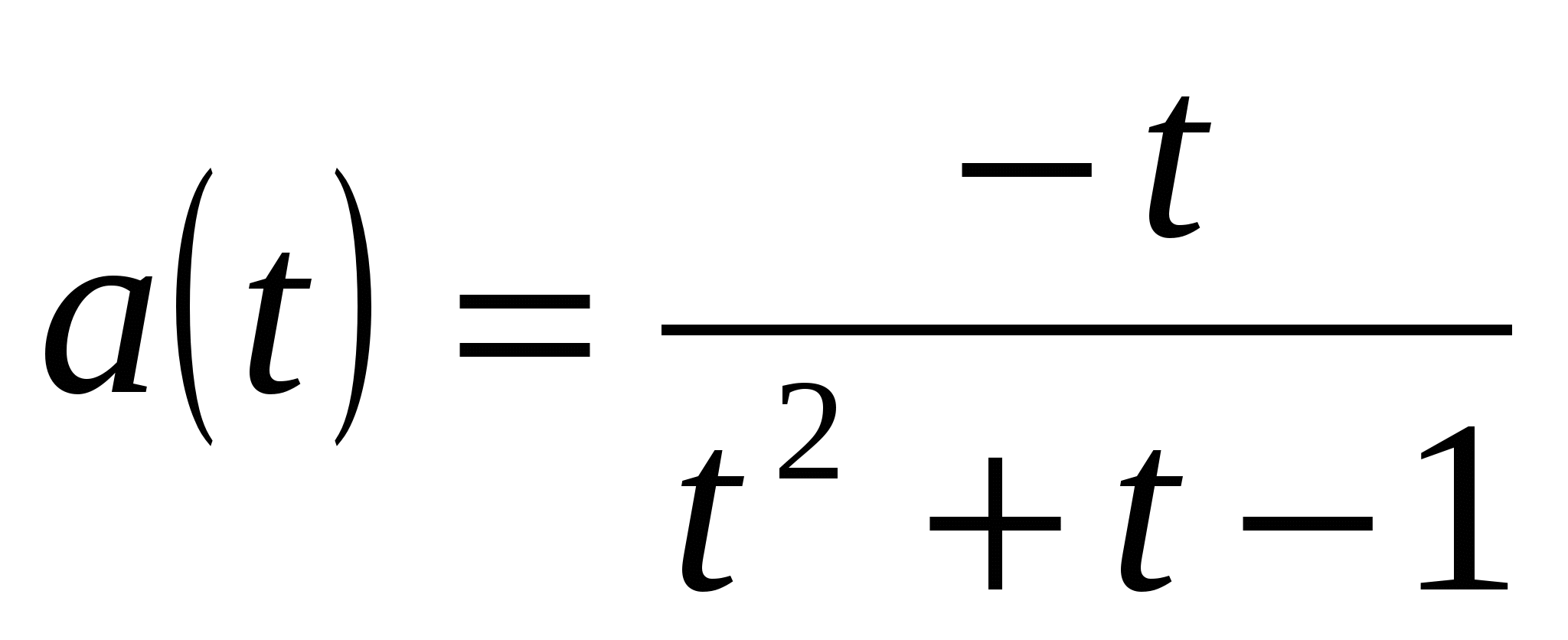 .
.
Таким образом, задача сводится к вычислению
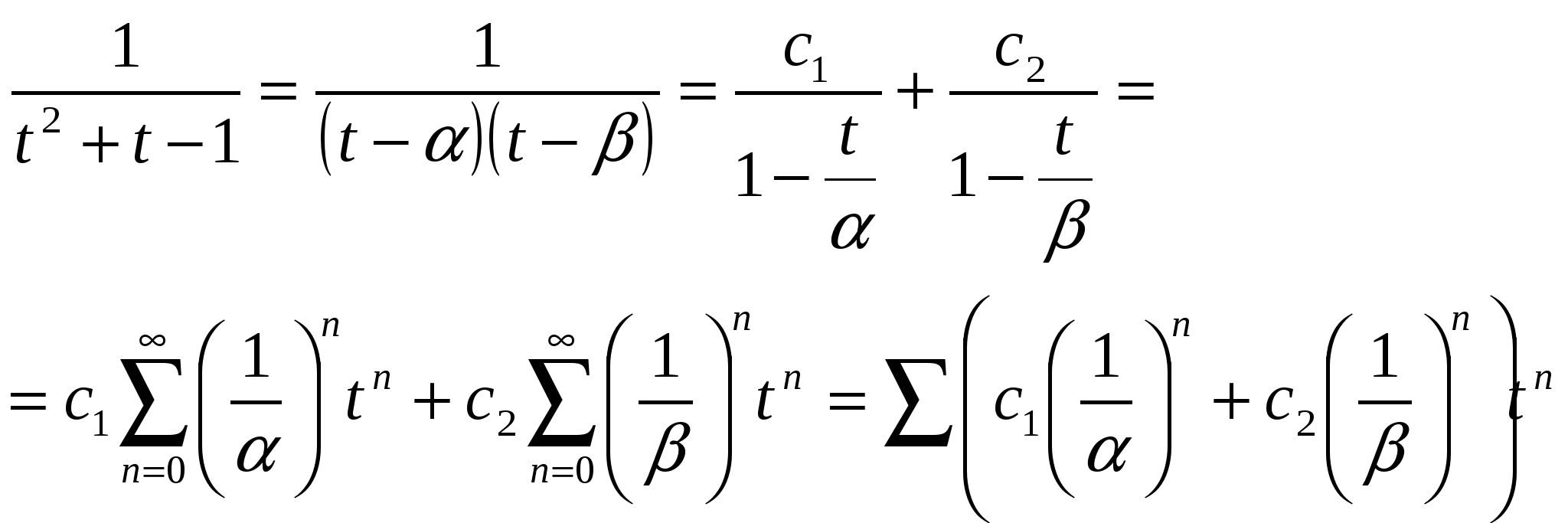
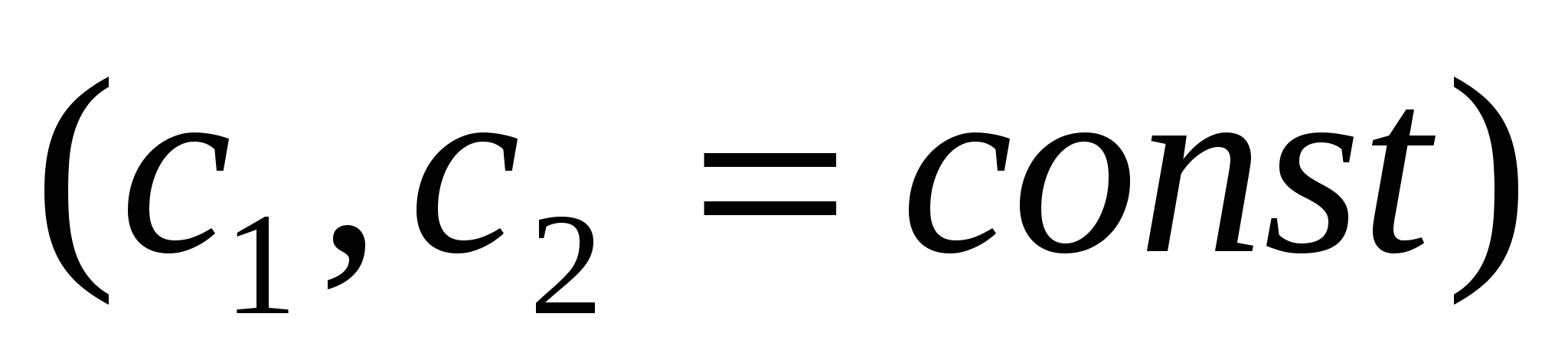 .
.
Следовательно,  , где
, где 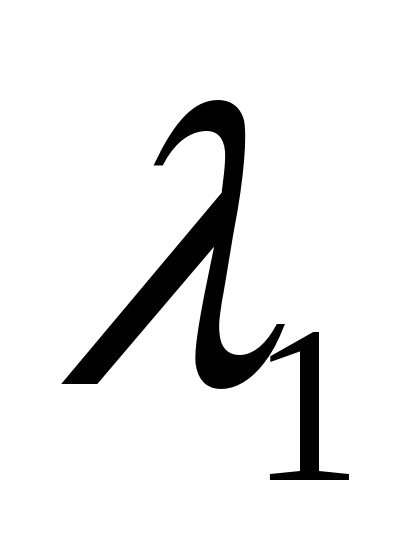 и
и 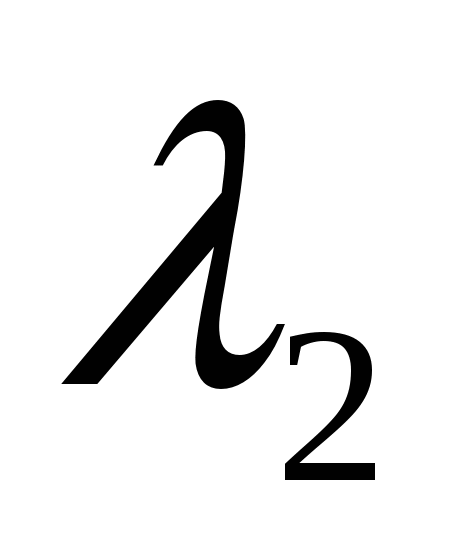 - корни уравнения
- корни уравнения ![]() , а
, а 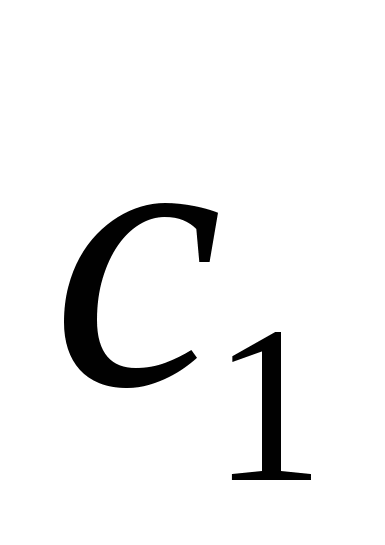 и
и 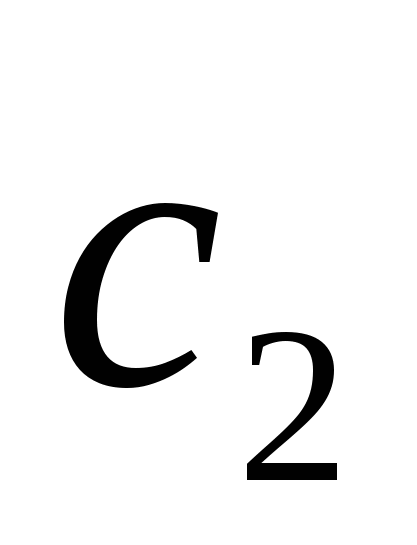 находим из начальных условий. Вычисляя - получаем:
находим из начальных условий. Вычисляя - получаем:
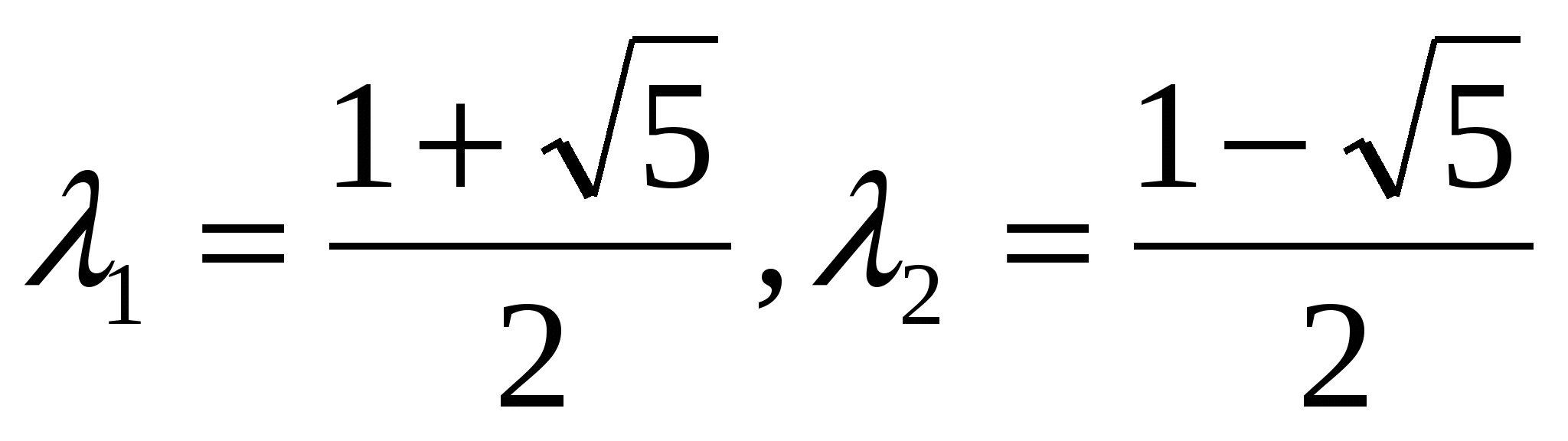 ;
; 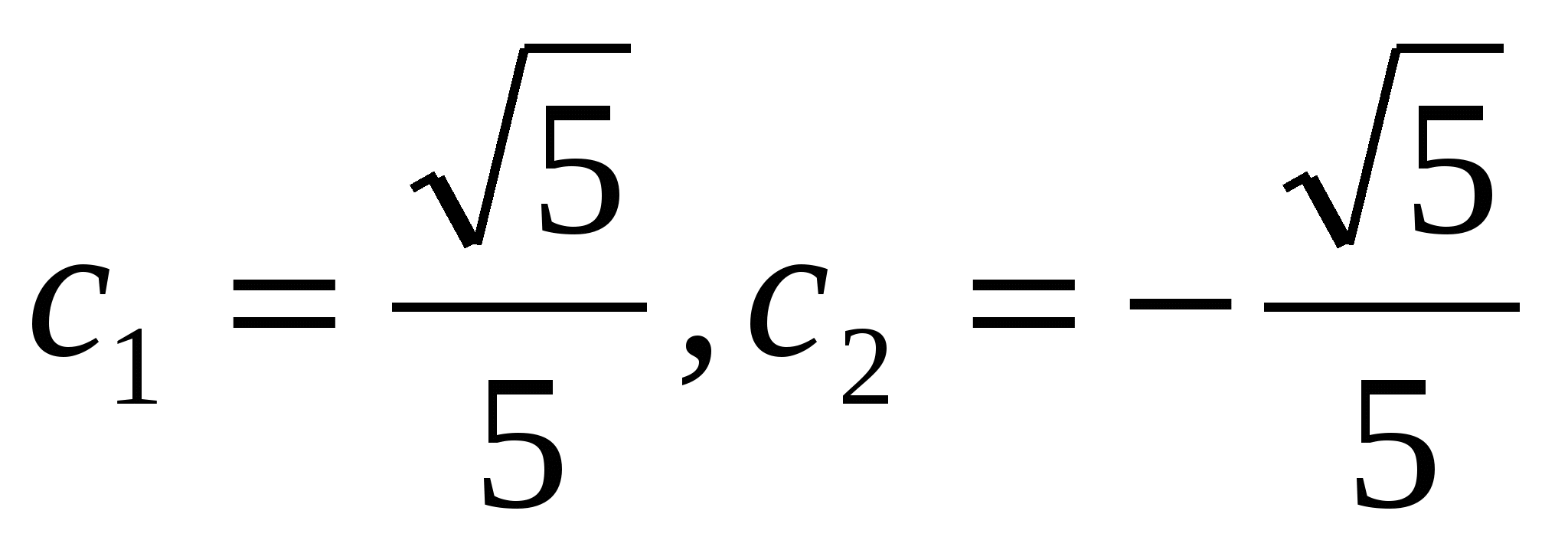 .
.
В итоге,
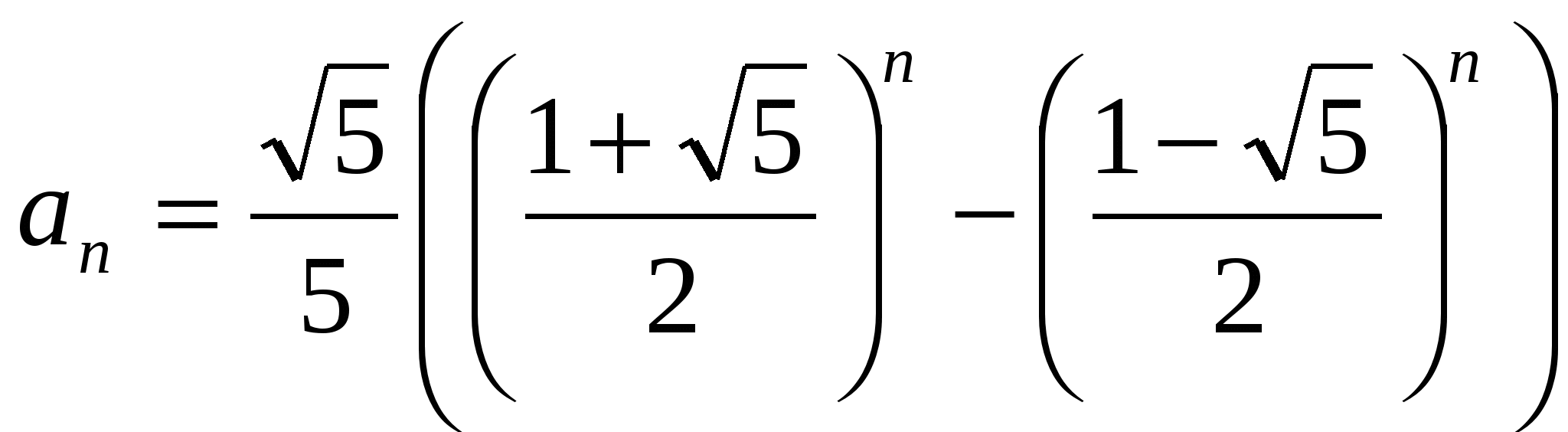 ,
, 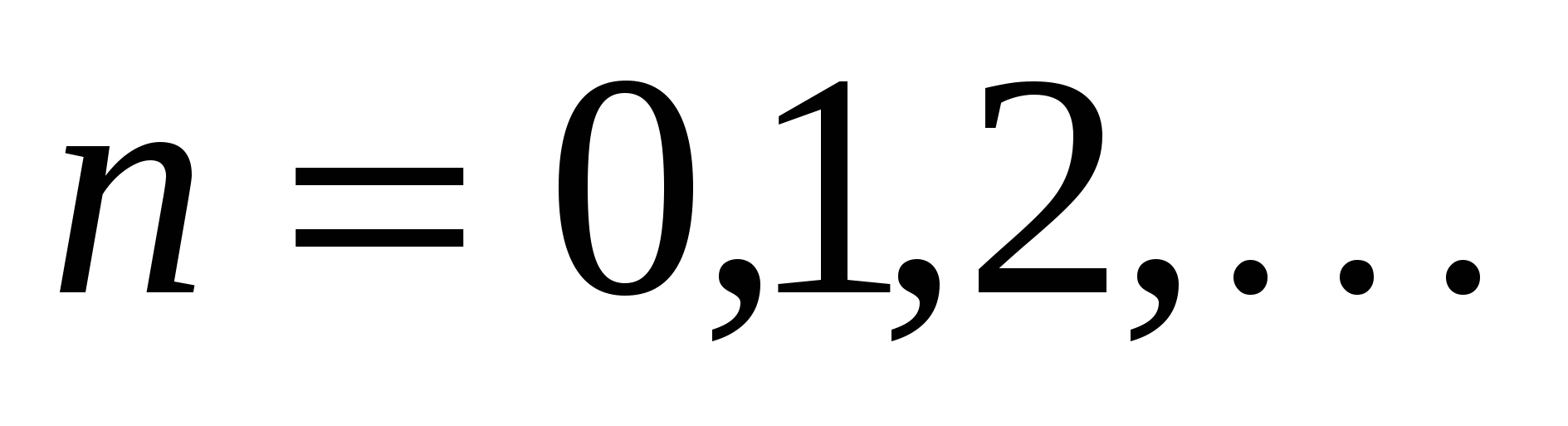
Итак, решение рекуррентного соотношения (19) сводится к решению линейного уравнения в R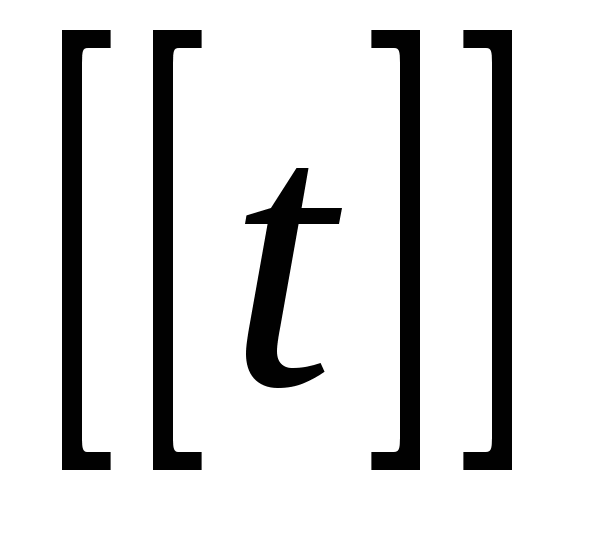 .
.
Этот подход непосредственно распространяется на рекуррентные соотношения с постоянными коэффициентами:
![]() ,
, 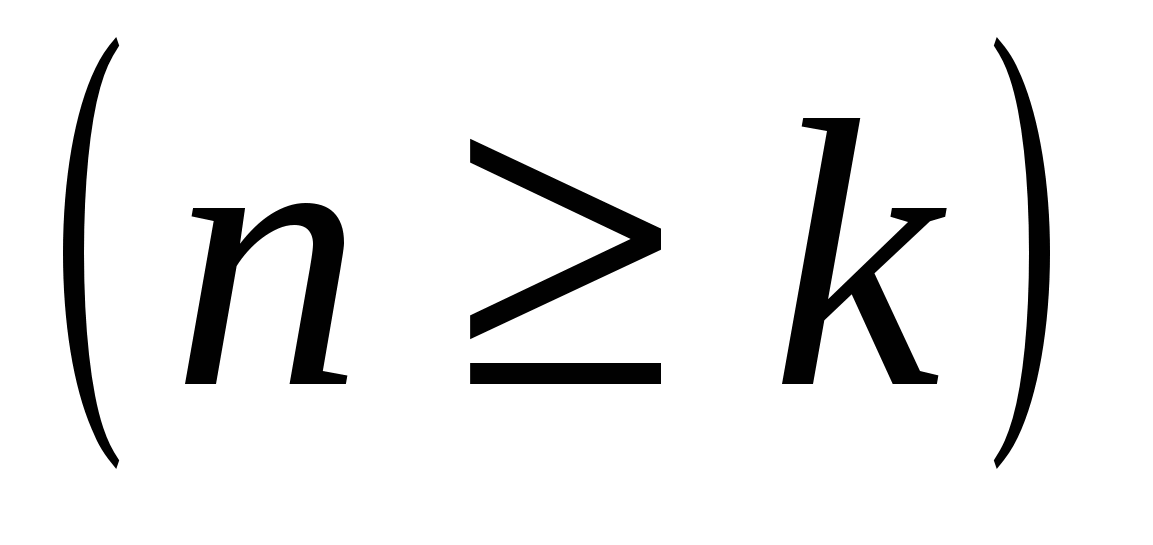 (20)
(20)
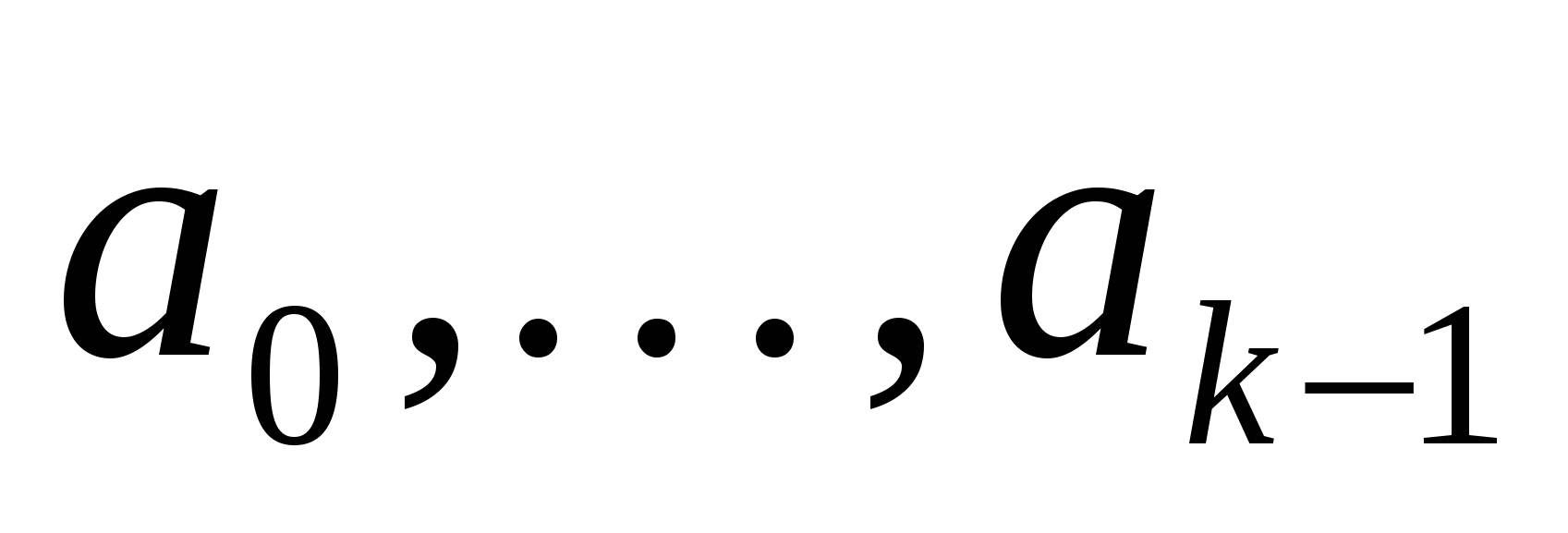 - заданные числа (начальные условия).
- заданные числа (начальные условия).
Характеристическим уравнением рекуррентного соотношения 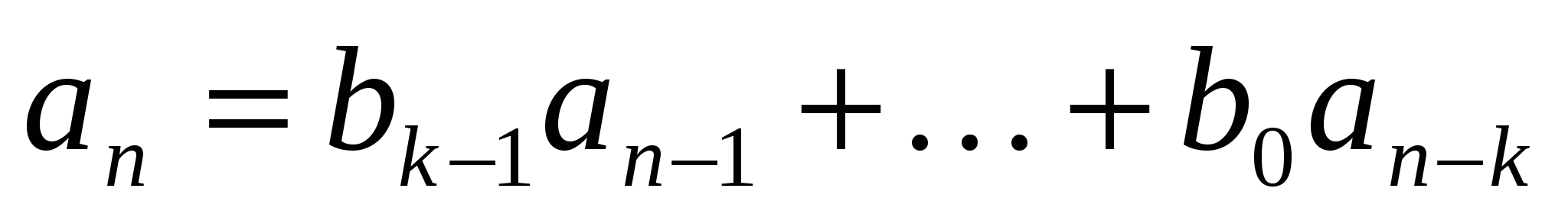 называется уравнение
называется уравнение
![]() (21)
(21)
Следующая теорема служит обобщением приведенного примера.
Теорема. Если характеристическое уравнение (21) рекуррентного соотношения (20) имеет простые корни 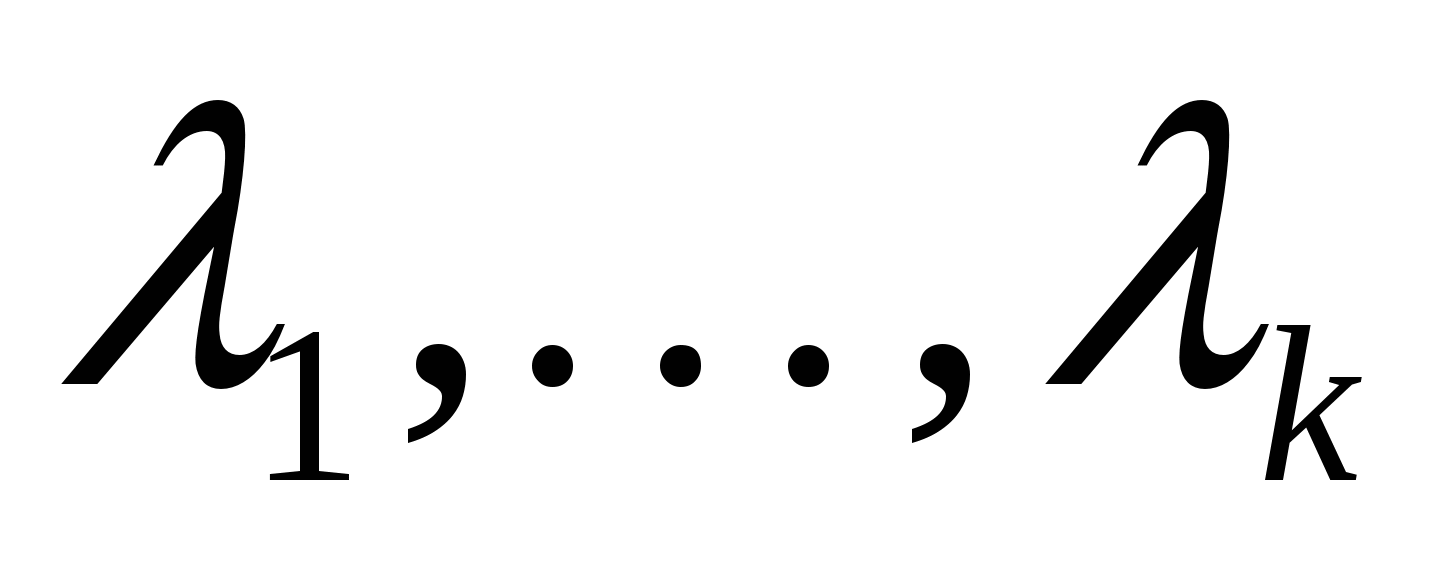 , то решения рекуррентного соотношения (20) имеют вид
, то решения рекуррентного соотношения (20) имеют вид
![]() , (22)
, (22)
где 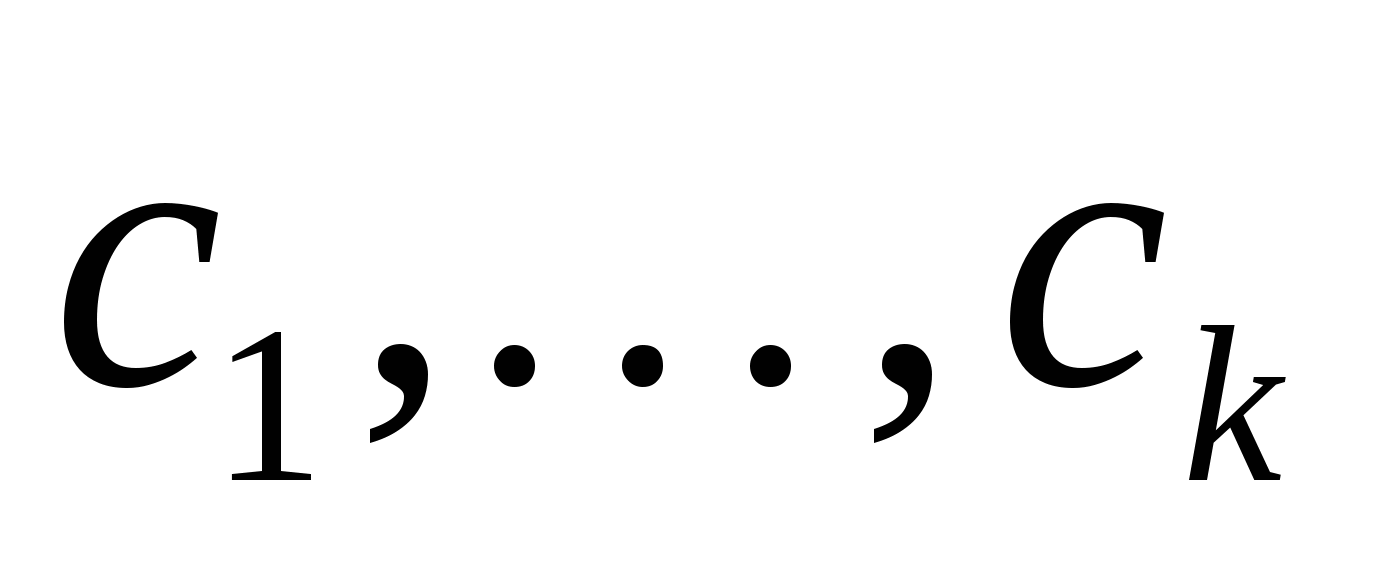 - постоянные коэффициенты. (Коэффициенты
- постоянные коэффициенты. (Коэффициенты 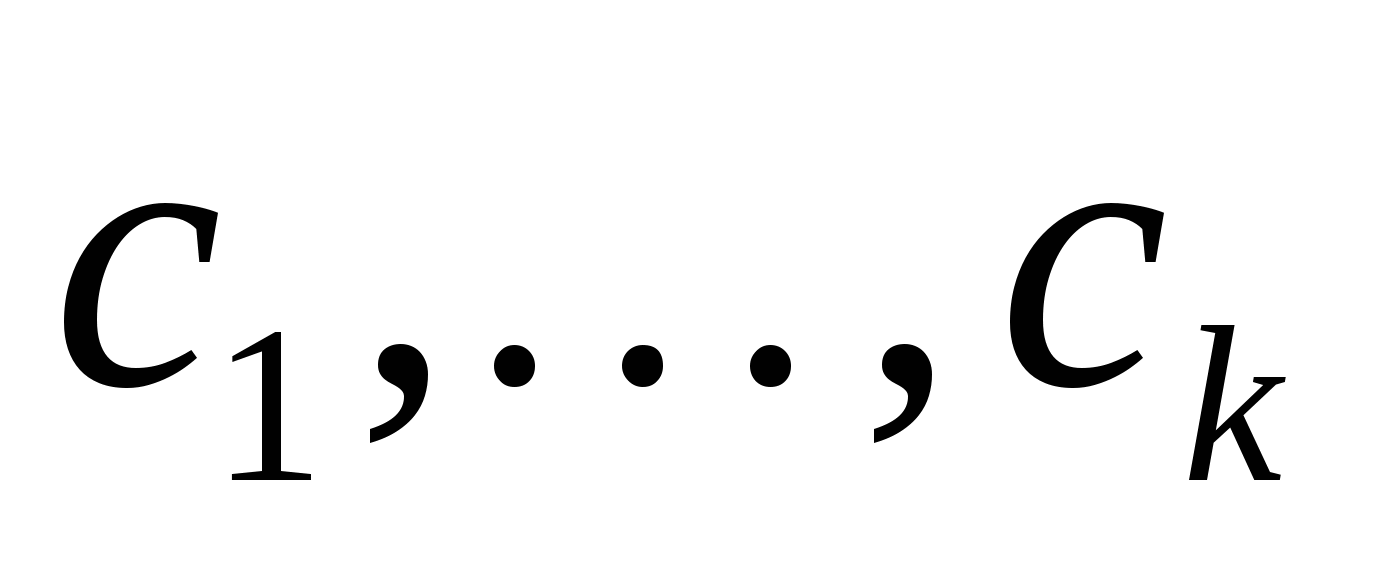 можно определить из начальных условий
можно определить из начальных условий 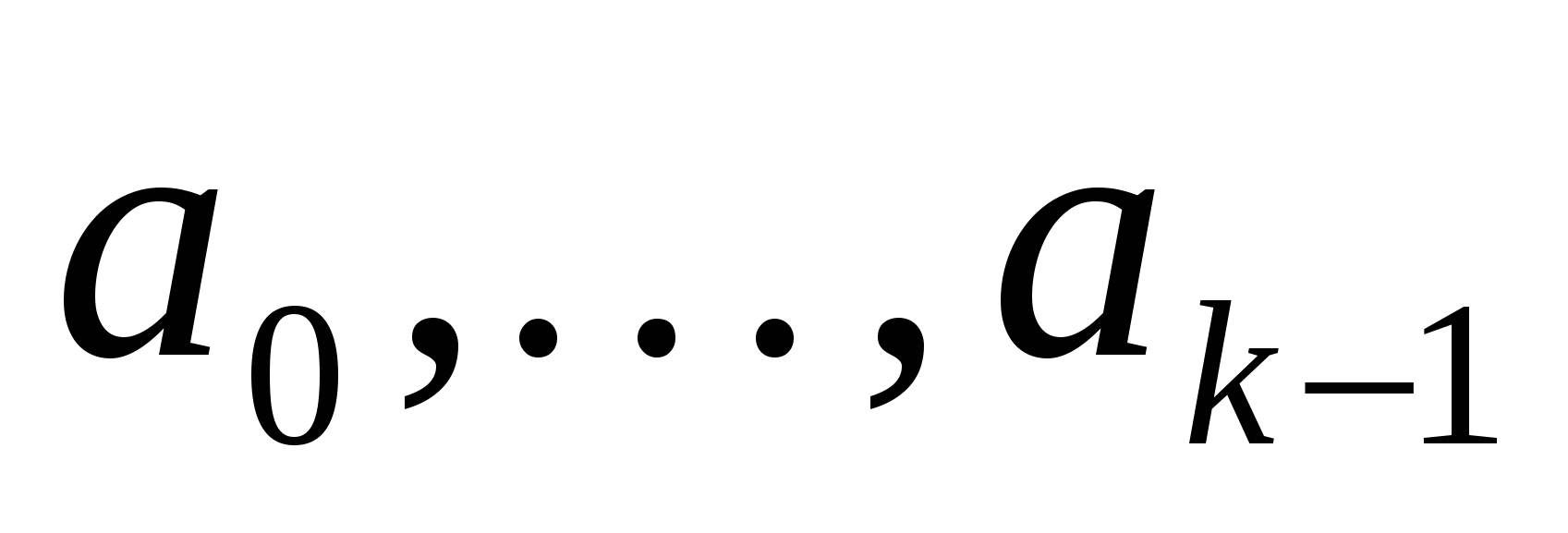 .)
.)
Таким образом, если характеристическое уравнение имеет простые корни, то решение рекуррентного соотношения (22) - сумма геометрических прогрессий со знаменателями 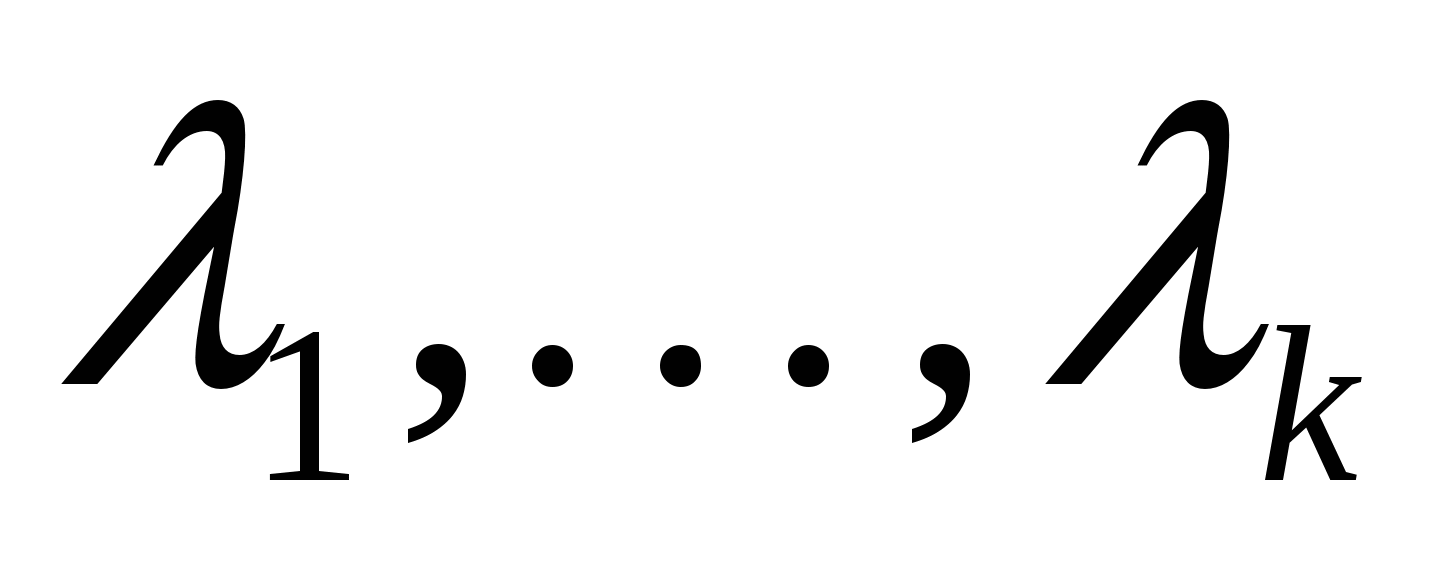 .
.
□ Пусть
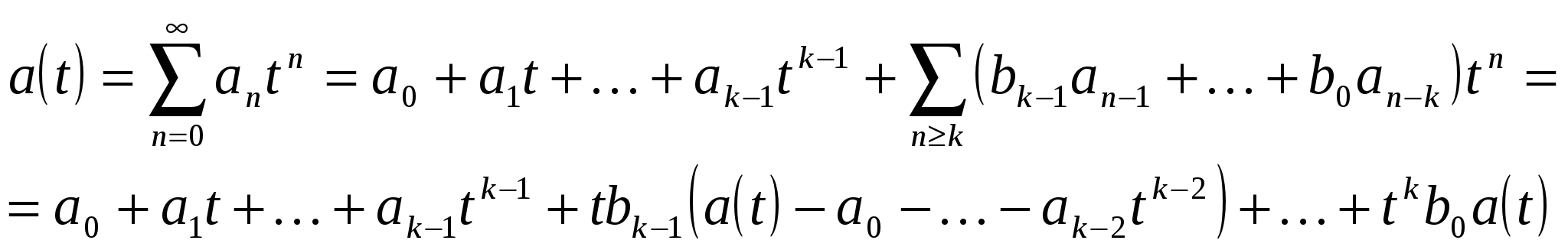
Итак, 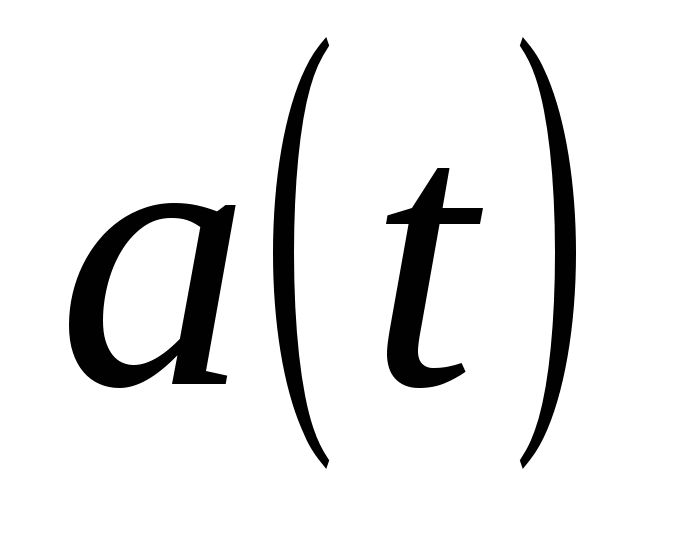 удовлетворяет линейному уравнению
удовлетворяет линейному уравнению
![]() , (23)
, (23)
где 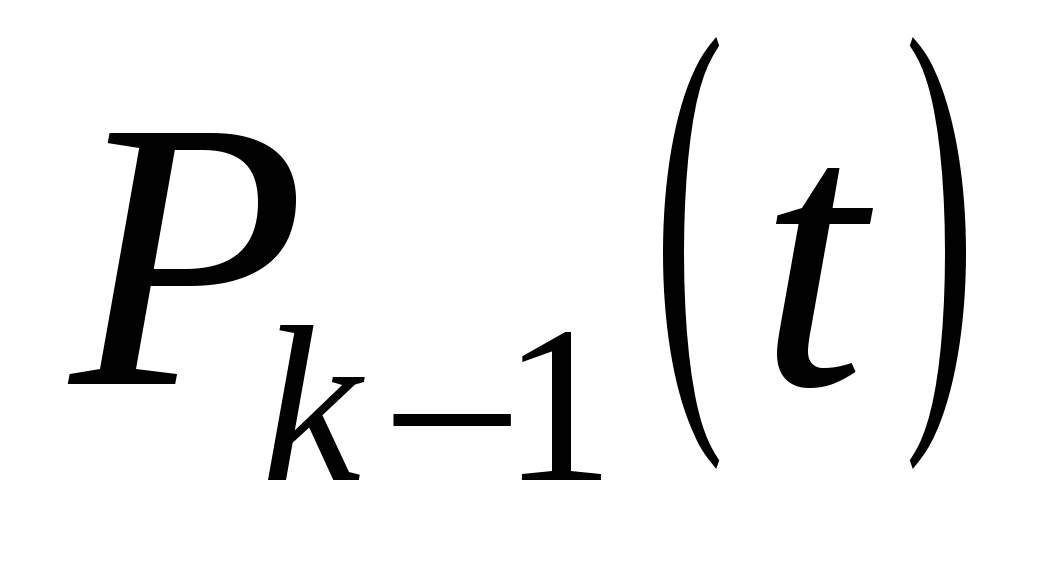 - многочлен степени
- многочлен степени 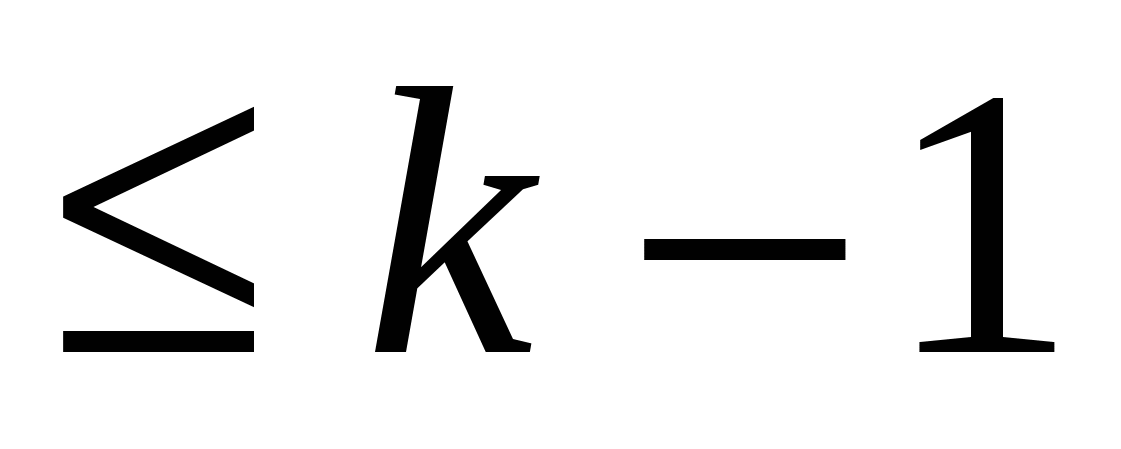 . Отсюда
. Отсюда
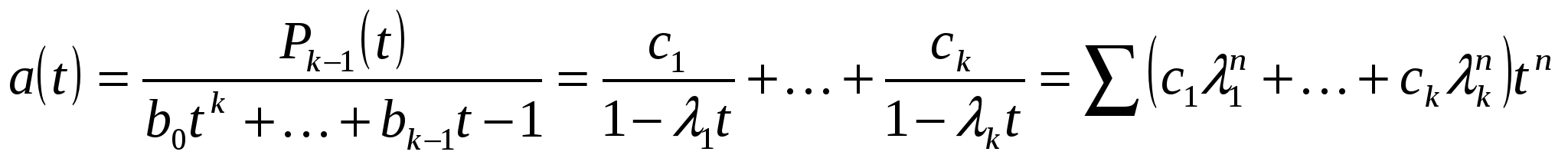 ,
,
где 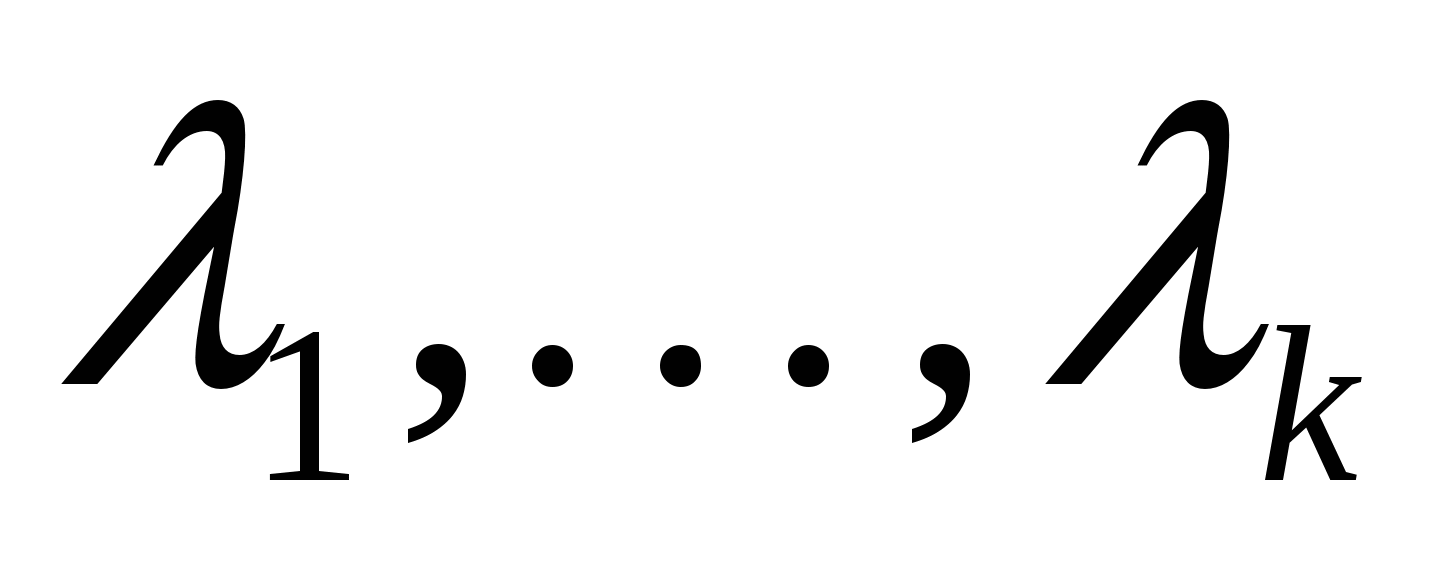 - корни характеристического уравнения, а
- корни характеристического уравнения, а 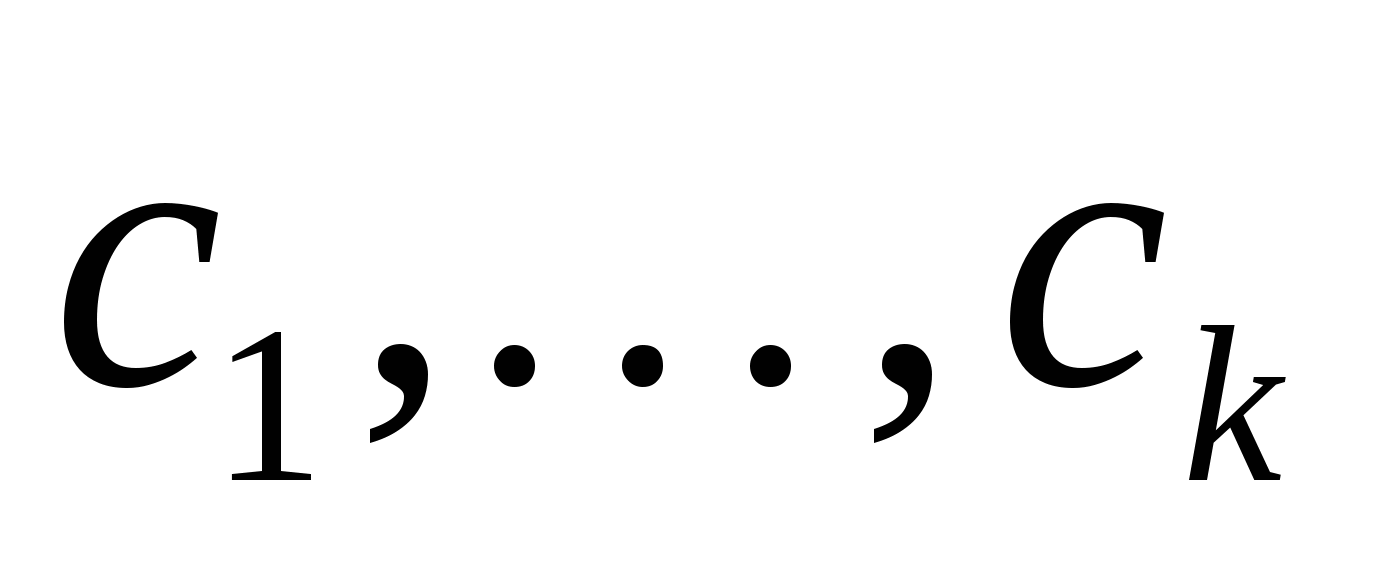 - постоянные коэффициенты. Следовательно,
- постоянные коэффициенты. Следовательно, 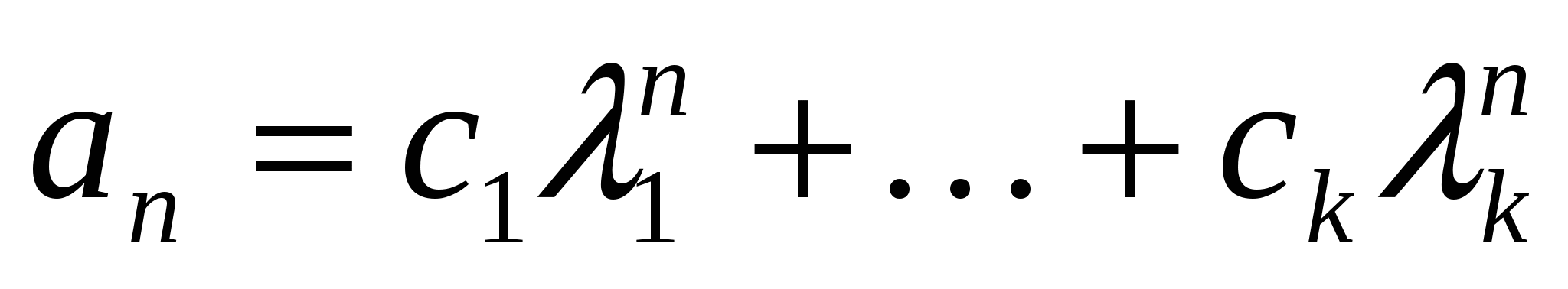 .■
.■
Если характеристическое уравнение рекуррентного соотношения (20) имеет корни 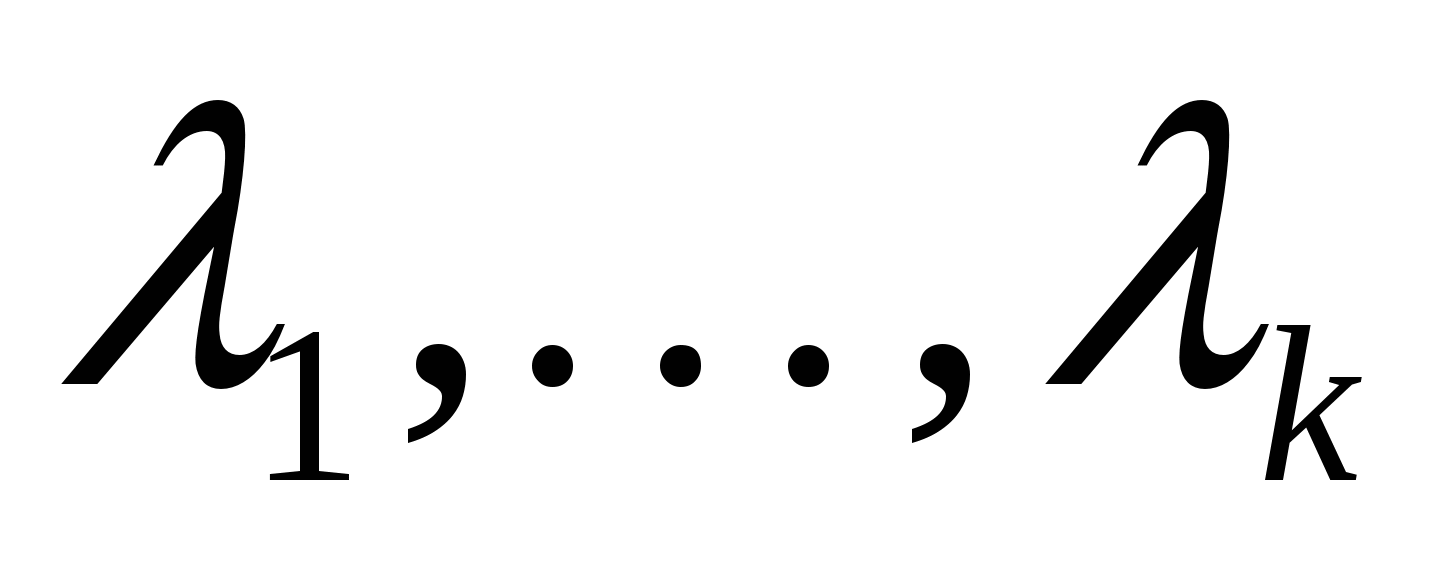 кратностей
кратностей 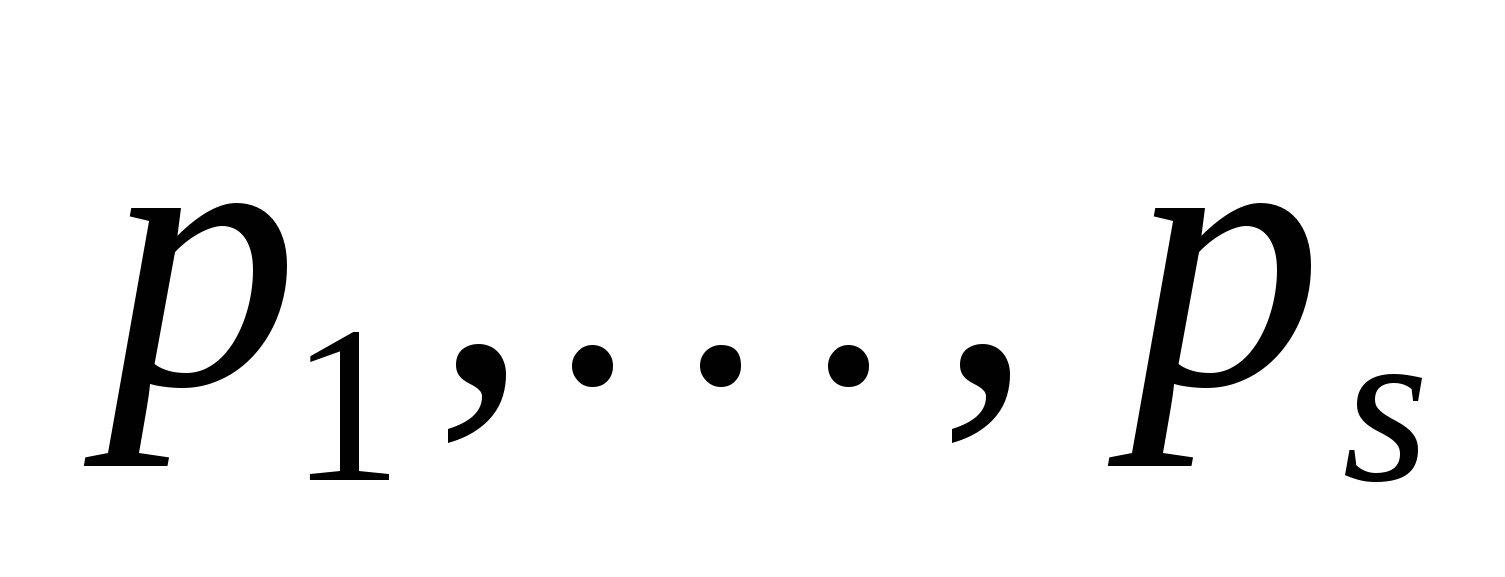 соответственно, то при решении линейного уравнения (23) нужно воспользоваться равенством
соответственно, то при решении линейного уравнения (23) нужно воспользоваться равенством
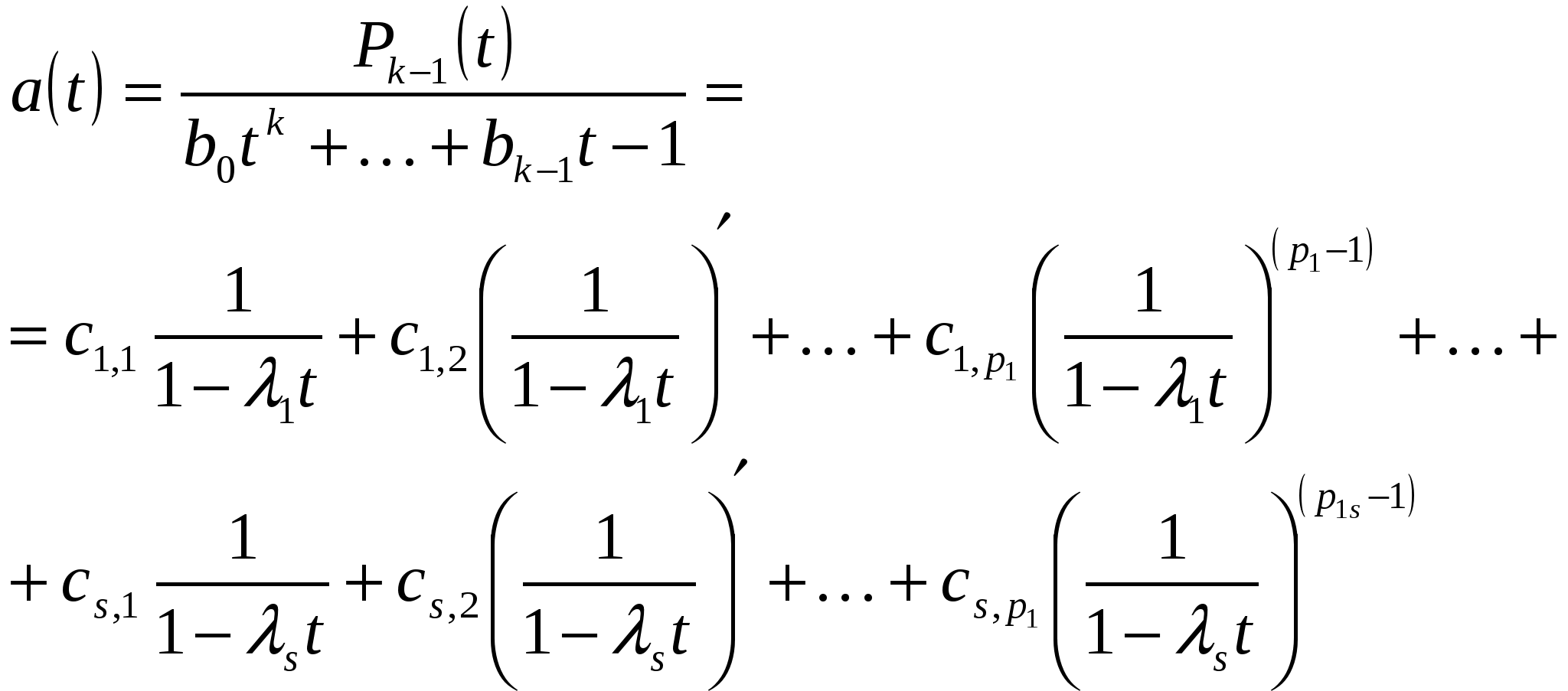
(при этом полагаем, что 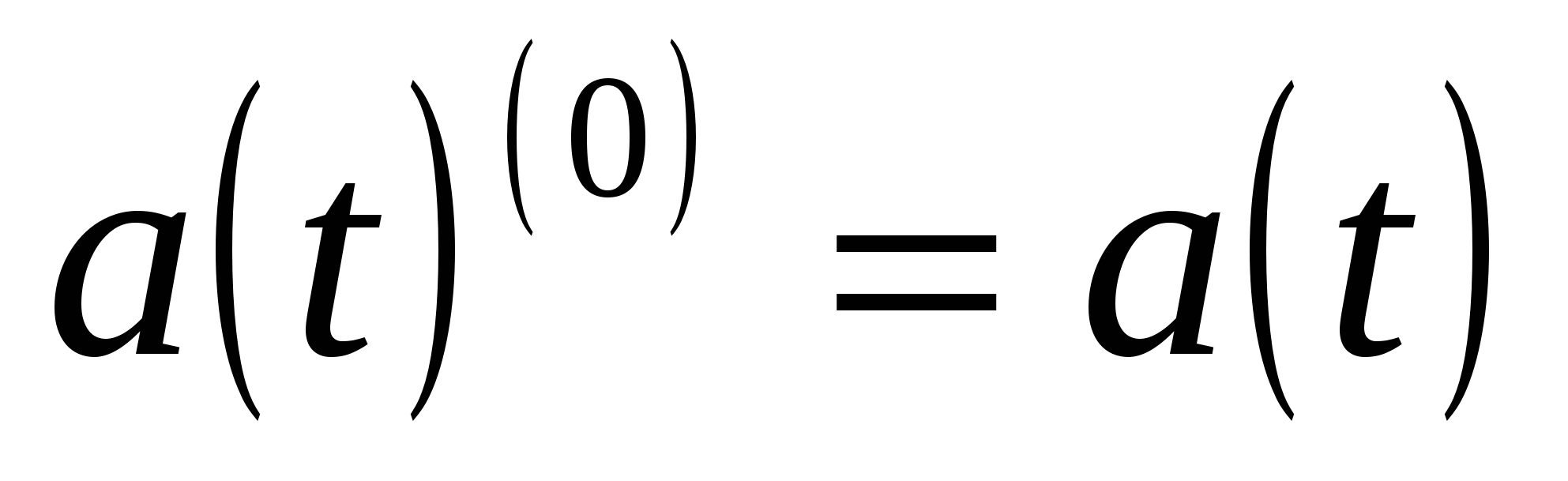 ).
).
Отсюда следует
Теорема. Если характеристическое уравнение (21) рекуррентного соотношения (20) имеет корни 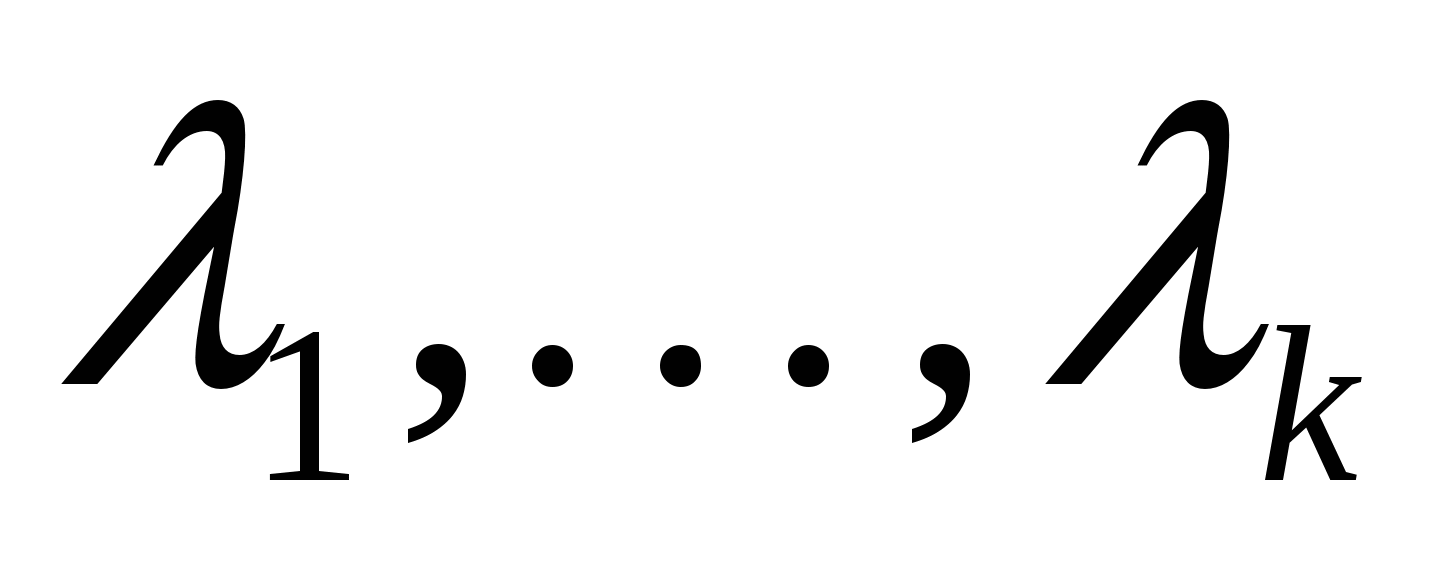 кратностей
кратностей 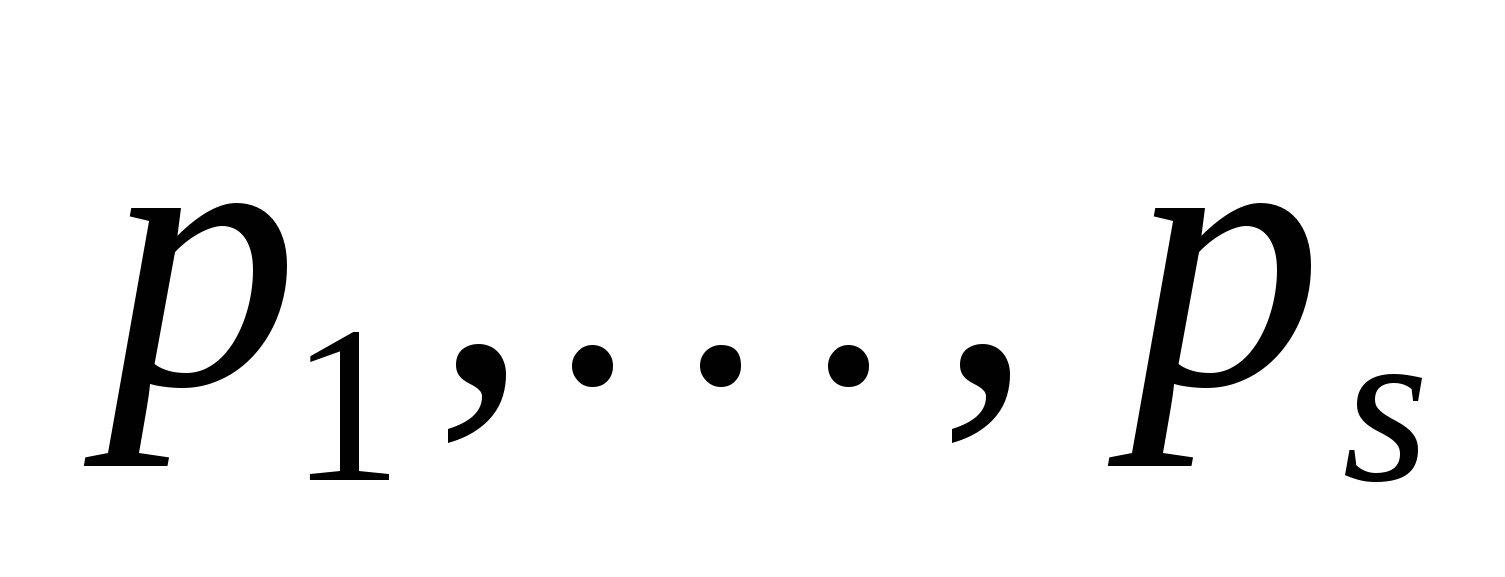 соответственно, то решение рекуррентного соотношения (20) есть сумма геометрических прогрессий и их производных до порядка
соответственно, то решение рекуррентного соотношения (20) есть сумма геометрических прогрессий и их производных до порядка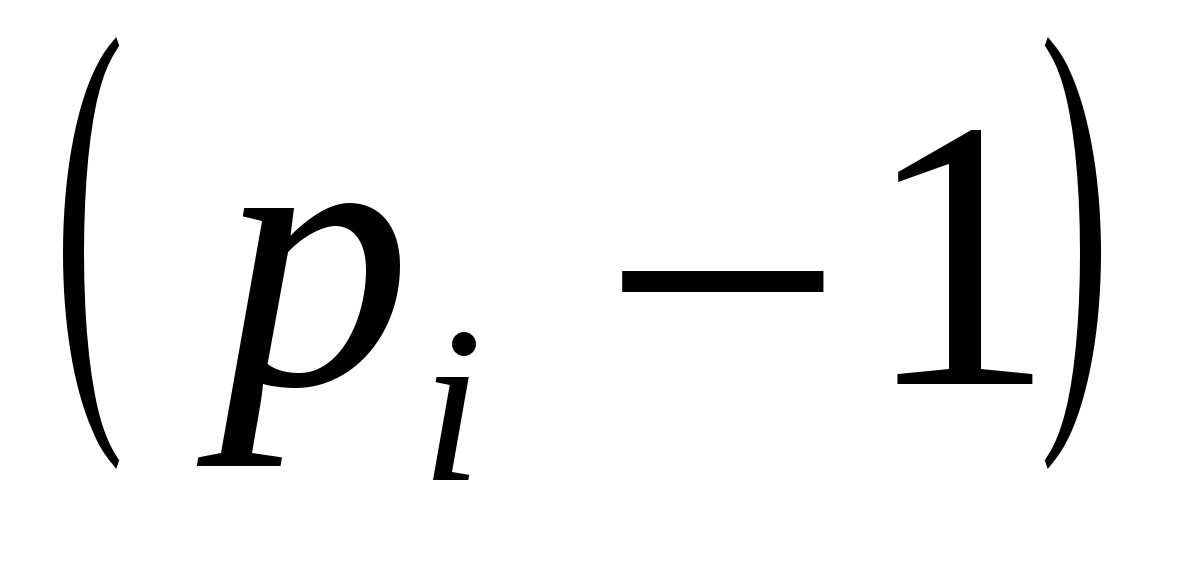
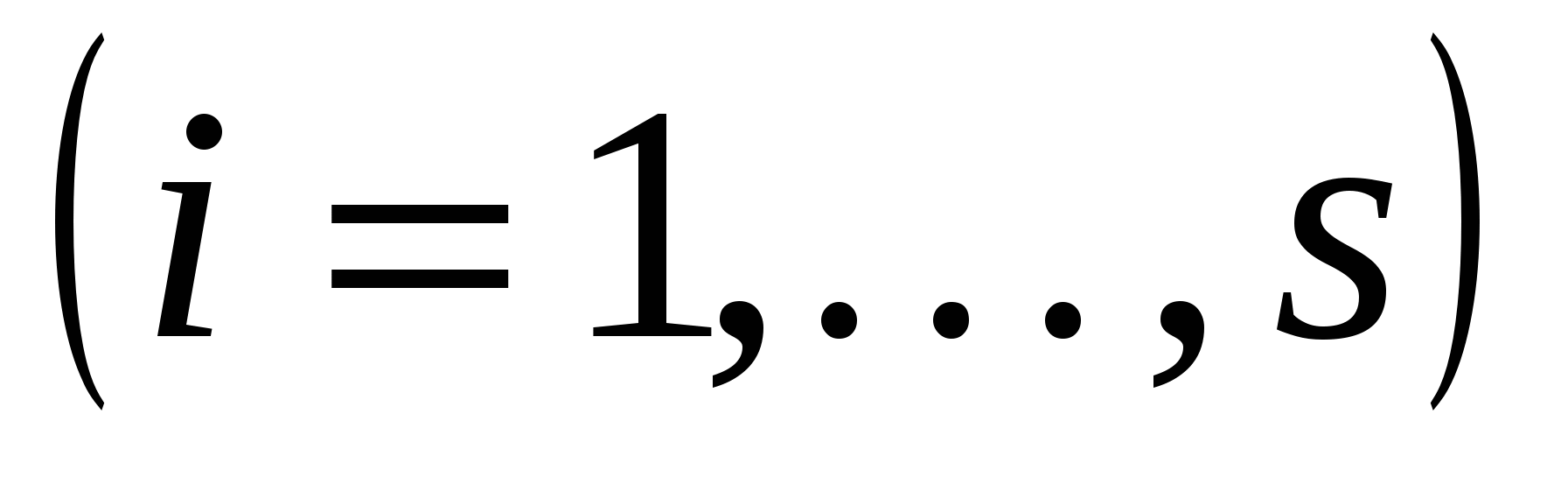 .
.
Литература.
-
Башмаков М.И., Беккер Б.М., Гольховой В.М. Задачи по математике, Алгебра и анализ, «Наука», Библиотечка «Квант», вып. 22, 1982г.
Крапивин Александр Александрович,
преподаватель математики ГОУ Пушкинский лицей №1500, к.ф-м.н.
Тел. (495)994-5848, 8(916)550-7075.


