- Преподавателю
- Математика
- Методическая разработка элективного курса
Методическая разработка элективного курса
| Раздел | Математика |
| Класс | - |
| Тип | Конспекты |
| Автор | Рагина Н.И. |
| Дата | 21.12.2014 |
| Формат | doc |
| Изображения | Есть |
«Средние величины и соотношения между ними»
Методическая разработка
элективного курса для 9 класса
Рагина Нина Ивановна-учитель
математики МБОУ СОШ №2
План:
1.Средние величины, их сущность и значение. Историческая справка
2.Определение средних величин
3.Доказательство теорем, связанных со средними величинами
4. Геометрическая интерпретация связи средних величин
5.Применение средних величин при решении некоторых
геометрических и алгебраических задач
6.Средние величины, используемые в математической статистике и
экономике
1.Средние величины, их сущность и значение. Историческая справка
Понятие средней величины знакомо каждому из нас, так как они имеют большое значение в повседневной жизни. С помощью среднего можно, например, определить:
а) среднее потребление витаминов в течение года;
б) средний возраст учителей в школе;
в) средний процент качества знаний и т.д.
В экономике средние - это важнейшие показатели товарооборота, запасов, цен, прибыли, рентабельности и других показателей работы отраслей народного хозяйства.
Почему средние так прочно вошли в нашу жизнь? Потому что ,средняя - это один из приемов обобщений. Важность средних величин для науки и экономики отмечалась в работах многих ученых. Весьма широко применял средние и относительные величины английский ученый Кинг (1648-1712) при анализе данных населения Англии (средний доход на семью, средний подушевой доход и др.) Не обошлось и без курьезов. Так английский ученый Петти (1623-1673) предлагал использовать в качестве меры стоимости - затраты на среднее дневное пропитание одного взрослого работника. И его не смущала абстрактность средней, то, что данные конкретного человека могут с ней не совпадать. В качестве еще одного яркого примера приведу рассказ Г. Успенского «Живые цифры». Там средний доход определялся сложением 1 млн. рублей миллионера Колотушкина и 1 гроша просвирни Кукушкиной и получалось, что он составлял 0,5 млн. рублей. Есть еще теория среднего человека» - это идеал человека, но в природе такого человека не существует.
Хотя средние - это обобщающие показатели, но они не всегда типичны и верны. Таким образом, средняя величина может быть как почти объективна, так и фиктивна, если она не рассчитана по однородной совокупности и теряет всякий смысл.
Школьникам средние знакомы как числовые величины. О них было известно еще более 2000 лет назад. Именно тогда стало известно неравенство, содержащееся в десятой книге «Начал» Евклида и гласящее: Среднее геометрическое двух неотрицательных чисел не больше среднего арифметического этих чисел. Доказательство основывалось на фундаментальном неравенстве, которое выражает неотрицательность квадрата любого числа
(l-m)2≥0( если(l-m)2=0 , то l=m);
l2+m2≥2lm, 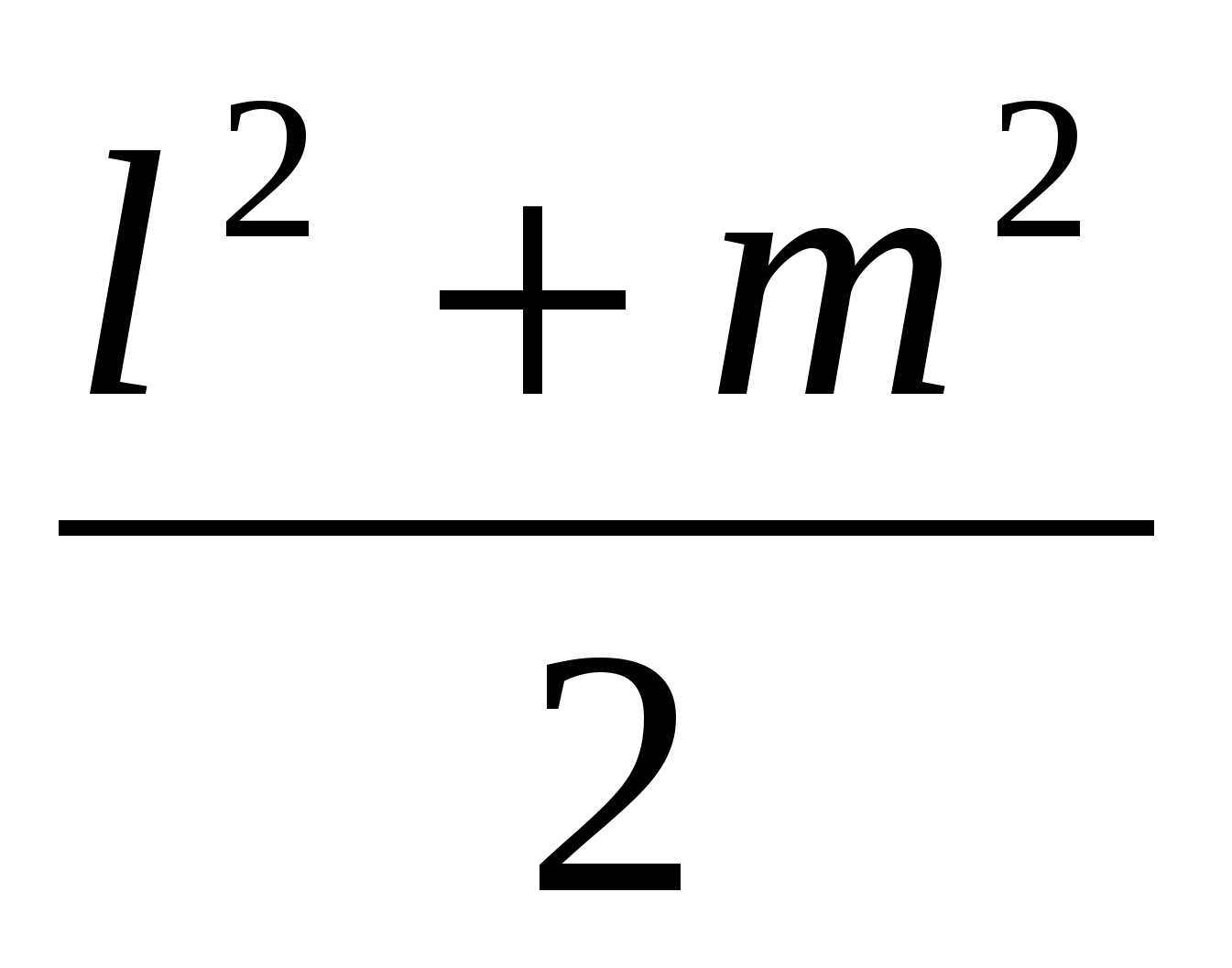 ≥lm; l2=a, m2=b, значит,
≥lm; l2=a, m2=b, значит, 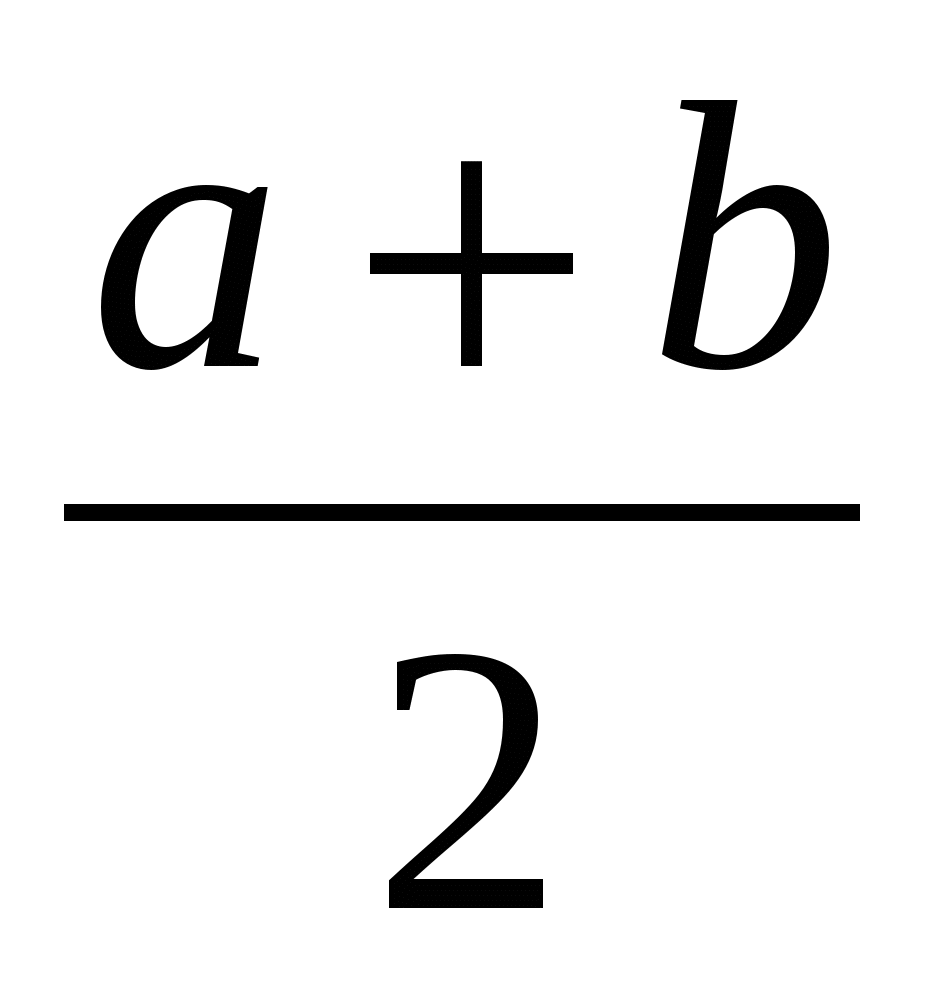 ≥
≥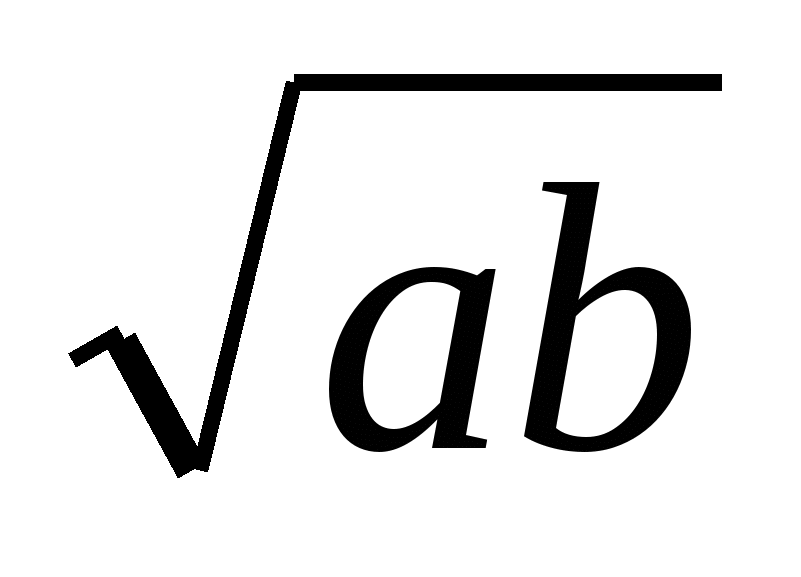
Обобщив для 3,4,…,п неотрицательных чисел Огюстен Луи Коши в 1821 году доказал, что 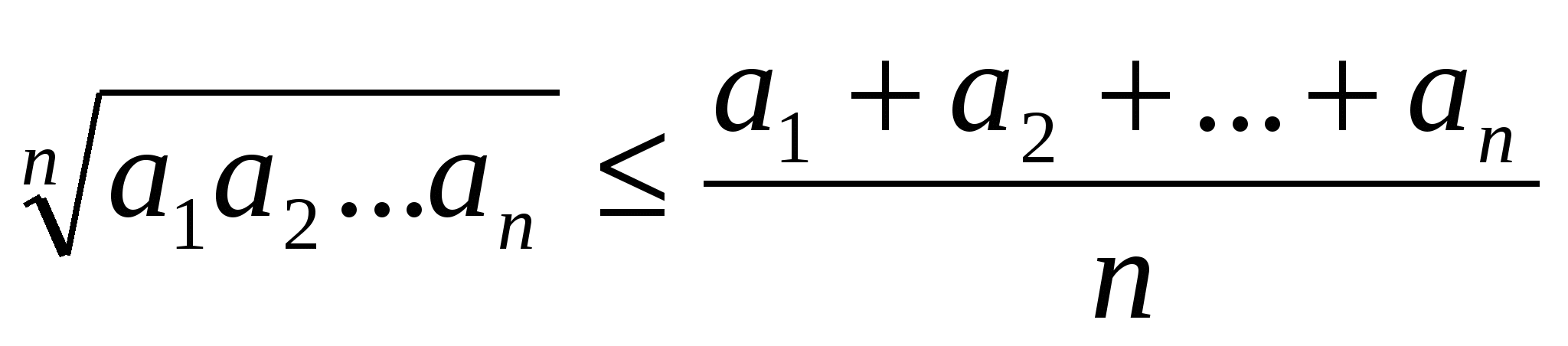 ;
;
Классическое доказательство основано на методе математической индукции
2.Определение средних величин
Общее определение средней величины:
Средней величиной действительных чисел называют число х, удовлетворяющее условию m < x < M, где
m- наименьшее среди этих чисел,
M - наибольшее.
Средняя одна, если эти числа равны.
Наиболее знакомы в школьной математике следующие средние величины:
Среднее- арифметическое:
Средним арифметическим действительных чисел а1 ,а2,…ап ; (п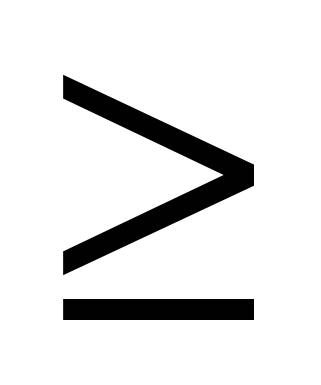 2) называется действительное число А=А(а1 ,а2,…ап)=
2) называется действительное число А=А(а1 ,а2,…ап)= 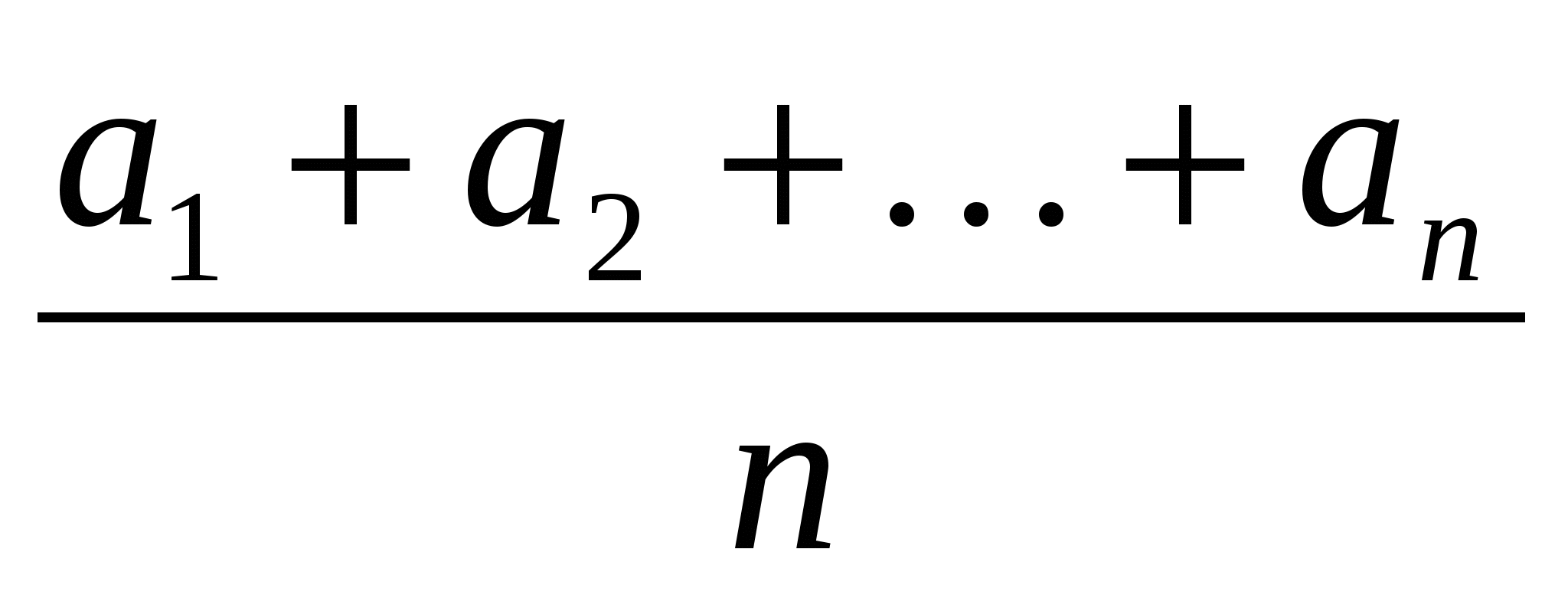
Пример: 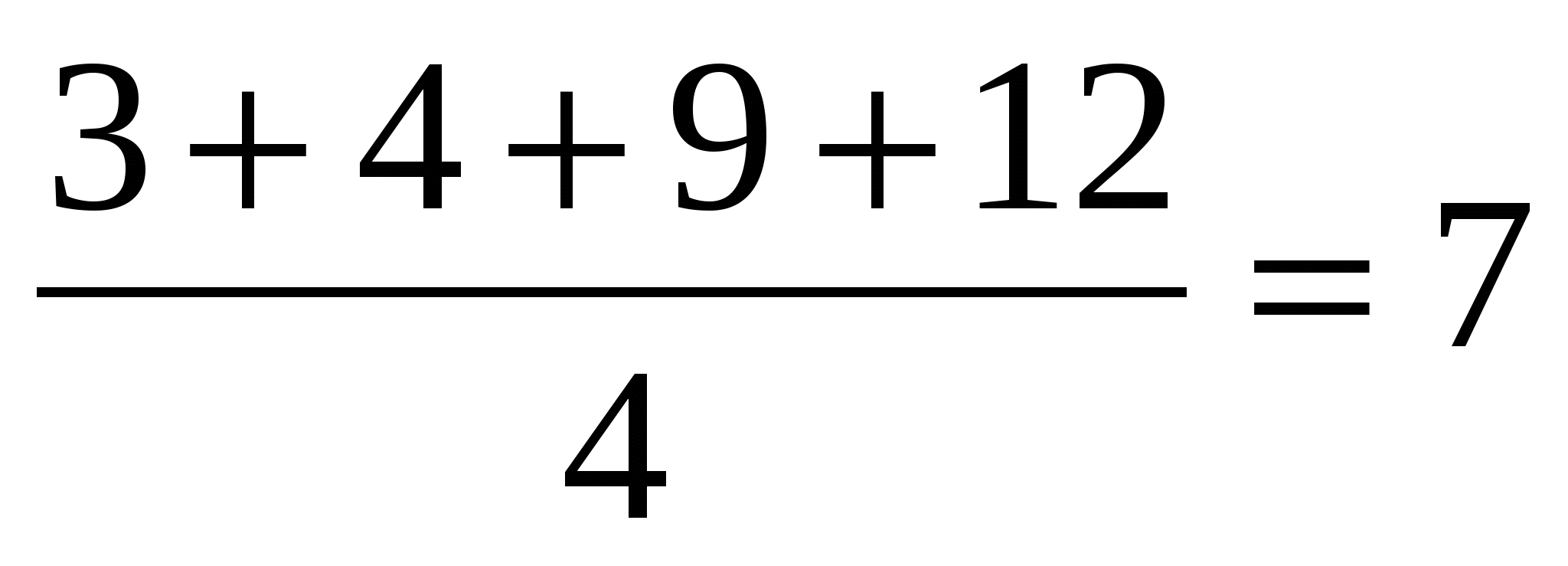
Среднее геометрическое:
Средним геометрическим действительных неотрицательных чисел
а1 ,а2,…ап ; (п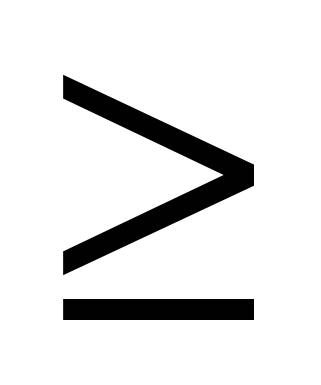 2)называют действительное неотрицательное число
2)называют действительное неотрицательное число
G = G(а1 ,а2,…ап)= 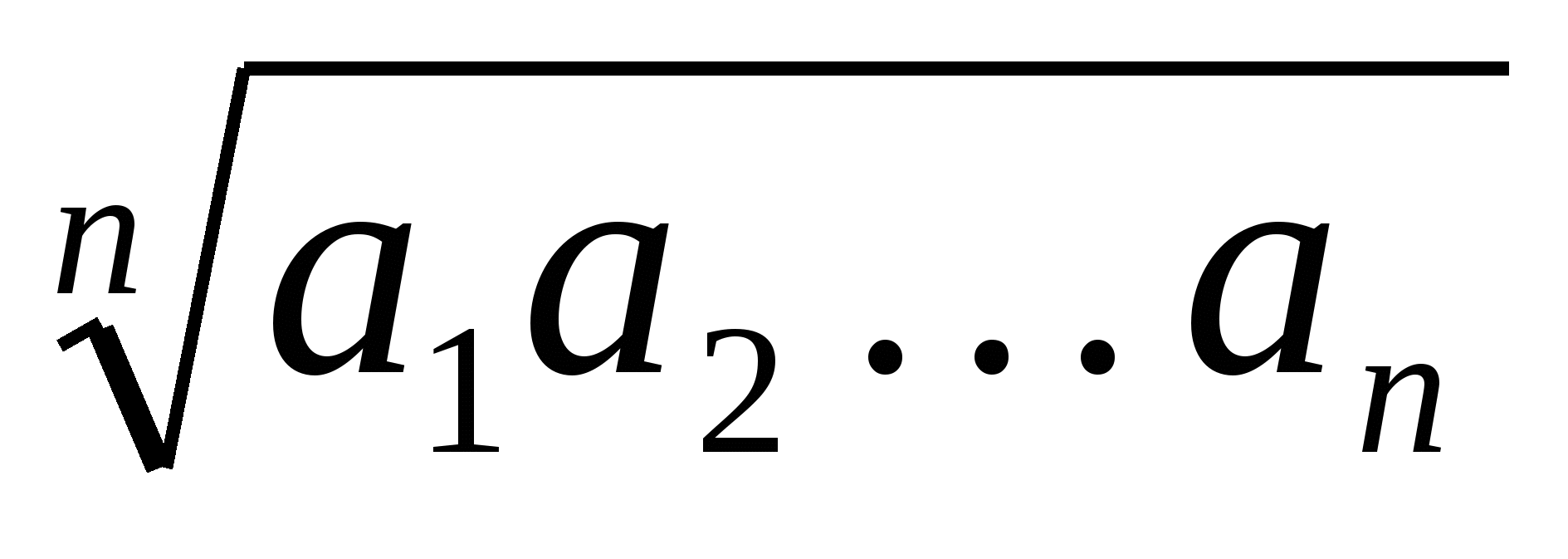 ;
;
Если a1=a2=…=an ,то G=a
Пример: 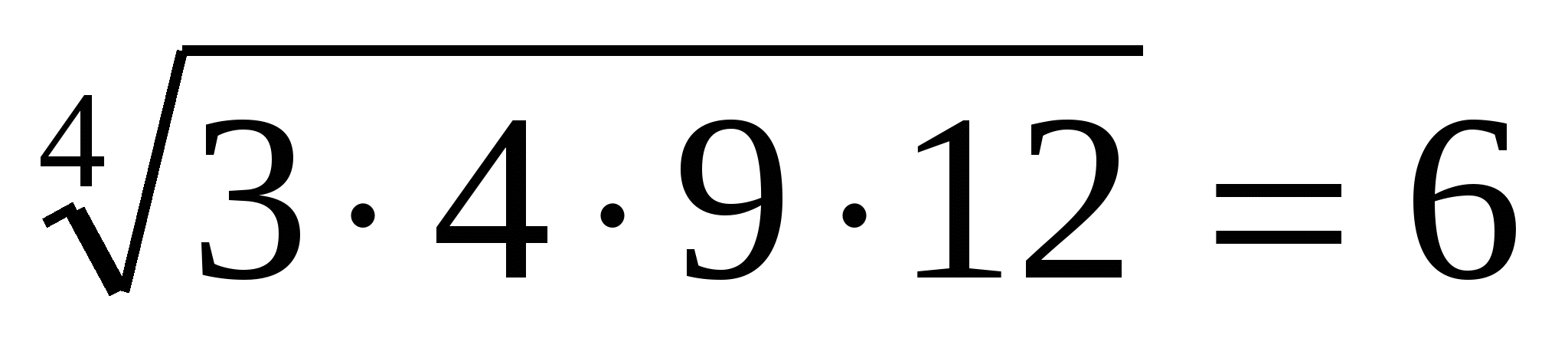 ;
;
Для двух положительных чисел равенство двух отношений  a:d=c:b, называют геометрической пропорцией, а числа с и d - средними членами пропорции.
a:d=c:b, называют геометрической пропорцией, а числа с и d - средними членами пропорции.
Если с = d = х, то а : х = х : в; х2=ав; х = √ав - среднее геометрическое (или среднее пропорциональное) положительных чисел а и в.
Если а = в, то х = а.
С помощью G(а; в), где а›0, в›0 можно определить:
а) длину высоты прямоугольного треугольника, опущенную из вершины прямого угла на гипотенузу;
б) по заданному отрезку строить отрезки длины √а и др.
Между средним арифметическим и средним геометрическим есть замечательное соотношение - неравенство Коши, о котором упоминалось выше. Однако, наиболее знакомо неравенство Коши для п=2 (реже п=3).
В школьном курсе математики среднее арифметическое и среднее геометрическое встречаются довольно часто, например:
а) каждый член (кроме первого и последнего) арифметической прогрессии является средним арифметическим равноотстоящих от него членов прогрессии;
б) каждый член (кроме первого и последнего) геометрической прогрессии является средним геометрическим равноотстоящих от него членов прогрессии;
в) свойство средней линии трапеции;
г) свойство высоты прямоугольного треугольника, опущенной на гипотенузу из вершины прямого угла.
Учителю на уроке желательно проиллюстрировать примеры и заодно повторить теорию.
Гораздо меньше известны в школьном курсе математики такие средние как среднее гармоническое и среднее квадратическое (квадратичное).
Средним гармоническим действительных положительных чисел
а1 ,а2,…ап ; (п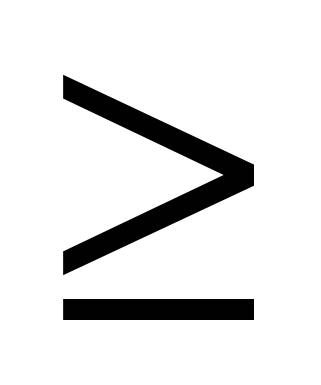 2) называют число Н = Н(а1 ,а2,…ап) =
2) называют число Н = Н(а1 ,а2,…ап) = 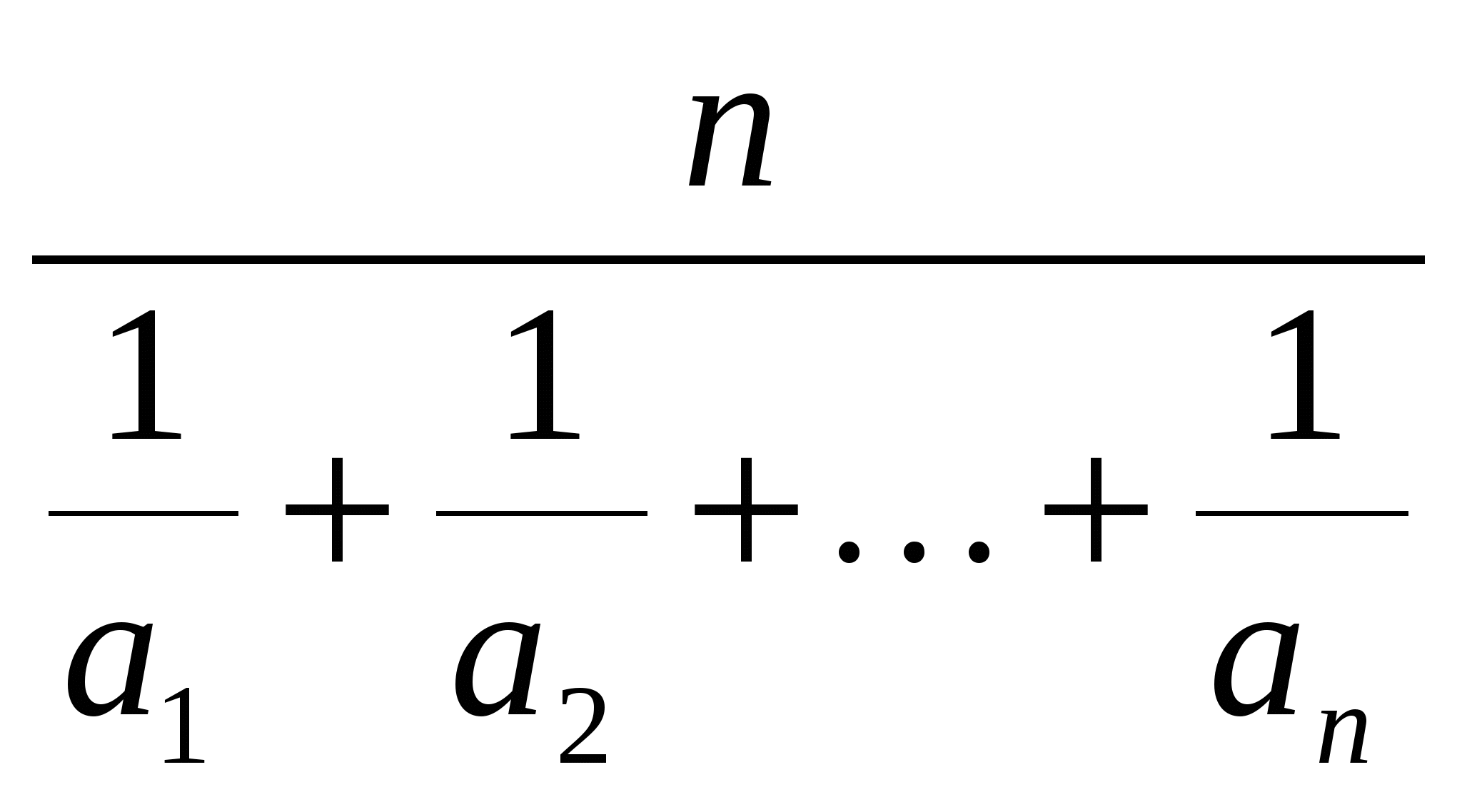 ;
;
Пример: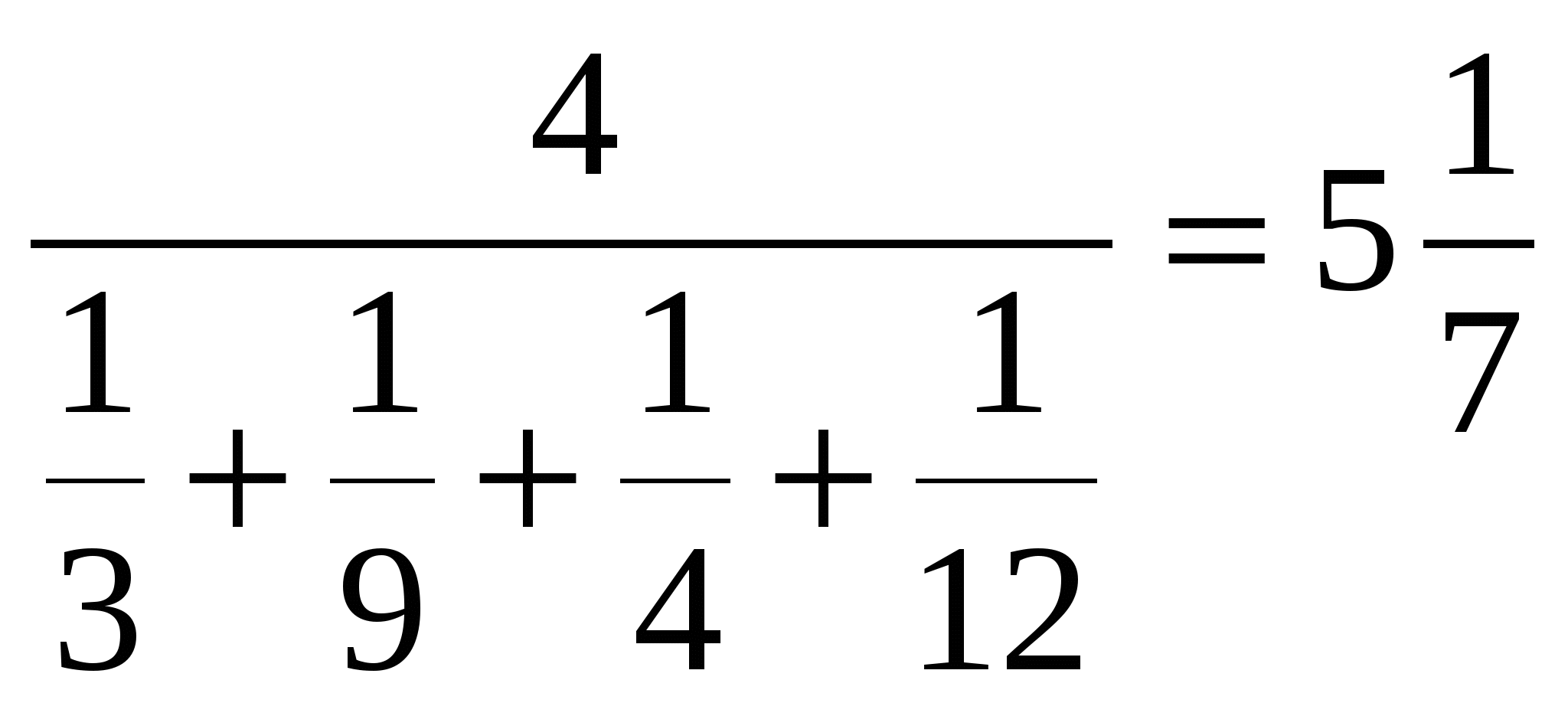 ;
;
Средним квадратичным действительных чисел а1 ,а2,…ап ; (п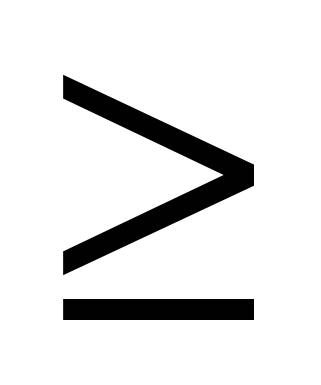 2) называют число Q = Q(а1 ,а2,…ап) =
2) называют число Q = Q(а1 ,а2,…ап) = 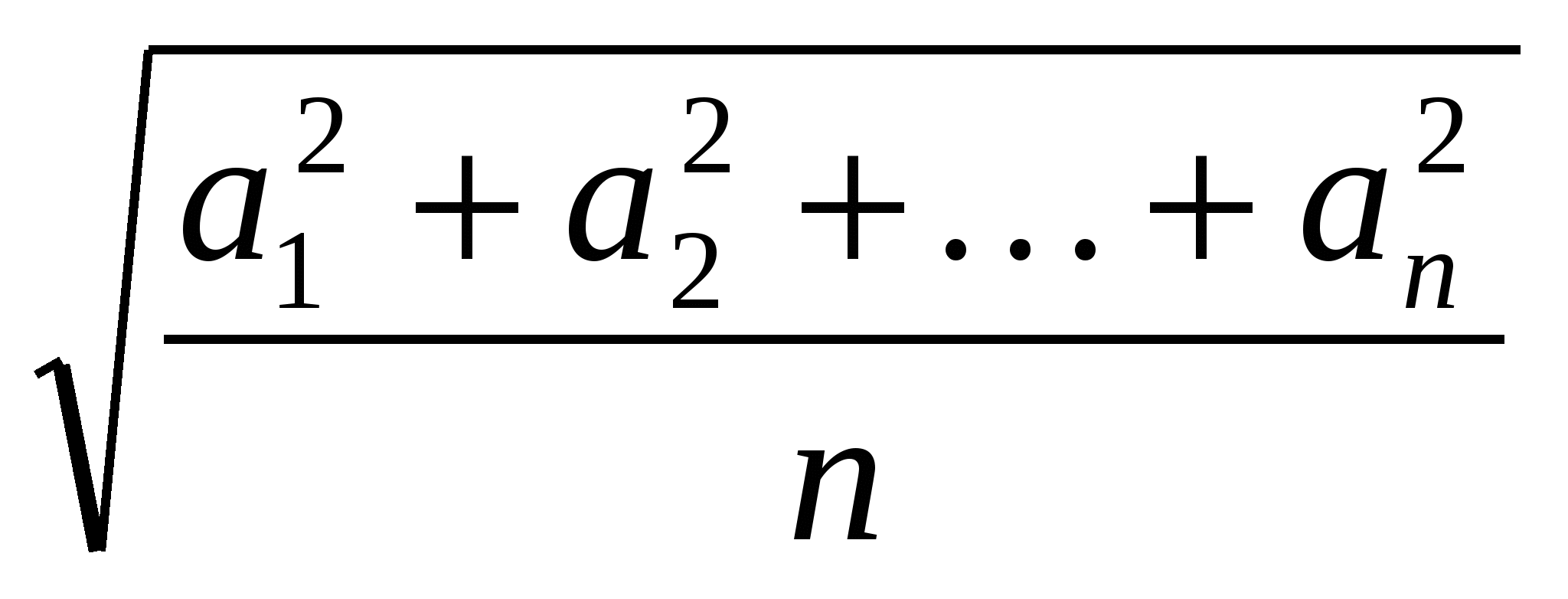 .
.
Пример: Q = 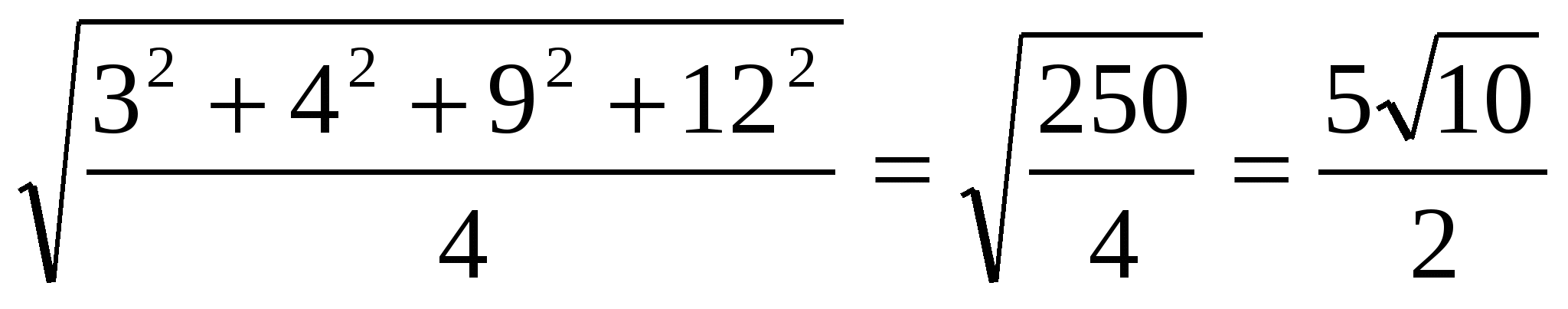 ;
;
Эти 2 средние присутствуют в школьном курсе как бы анонимно и даже, когда мы в задачах их явно используем, то чаще всего не называем. Однако, в учебнике алгебры за 8 класс под редакцией М.И Башмакова эти средние рассматриваются достаточно подробно на физических и геометрических задачах (беседа «Продолжим изучение средних величин» стр. 116-117)
Примеры:
1) Определить среднюю скорость туриста на всем пути, если он из пункта А
до пункта В шел со скоростью V1 км/ч, а обратно со скоростью V2 км/ч.
Решение:
Пусть S - расстояние между А и В. Vcр= 
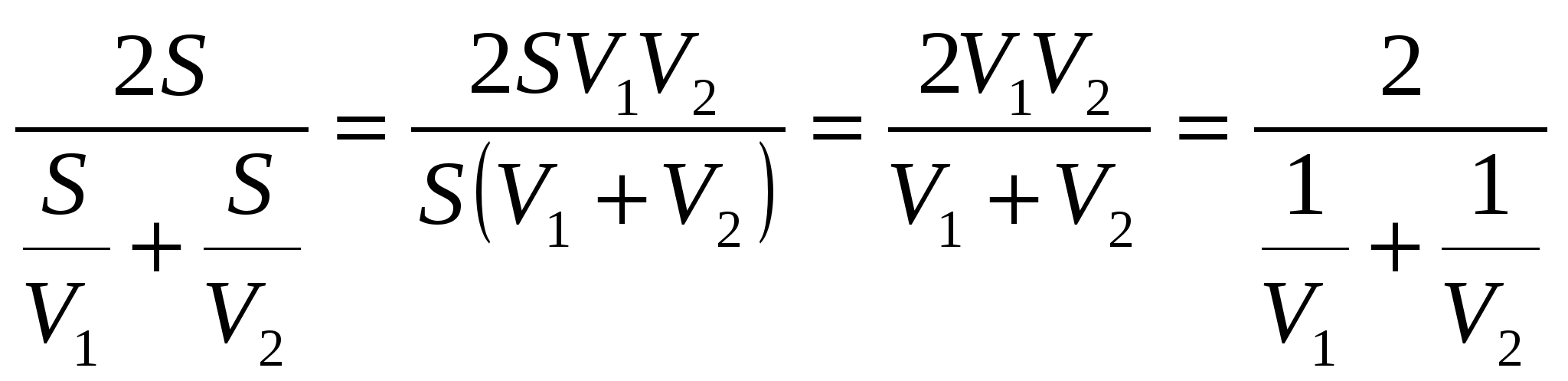 ;
;
Т.е. Vср = Н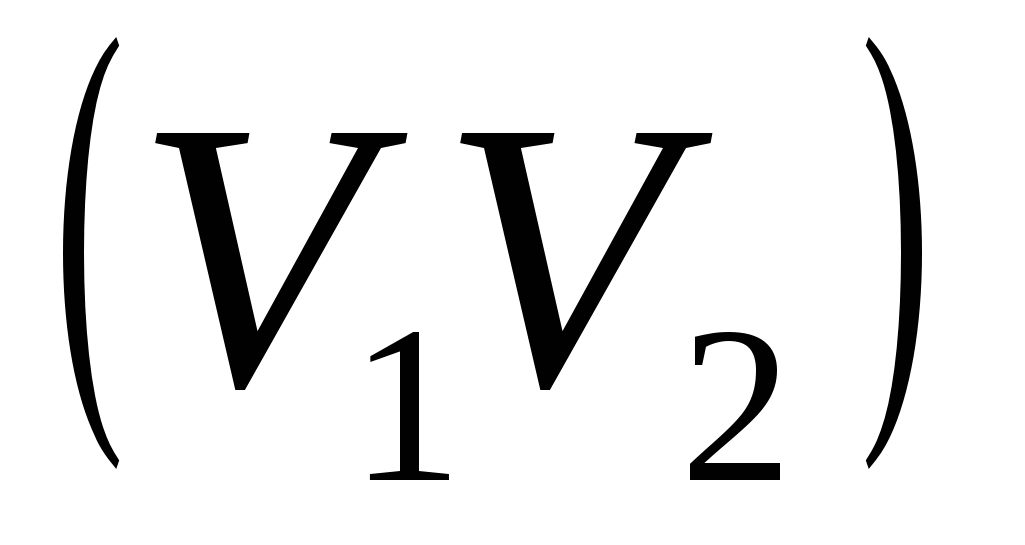 - среднее гармоническое.
- среднее гармоническое.
2) Определить общее сопротивление R параллельно соединенных проводников, если их сопротивления R1 и R2.
Решение:
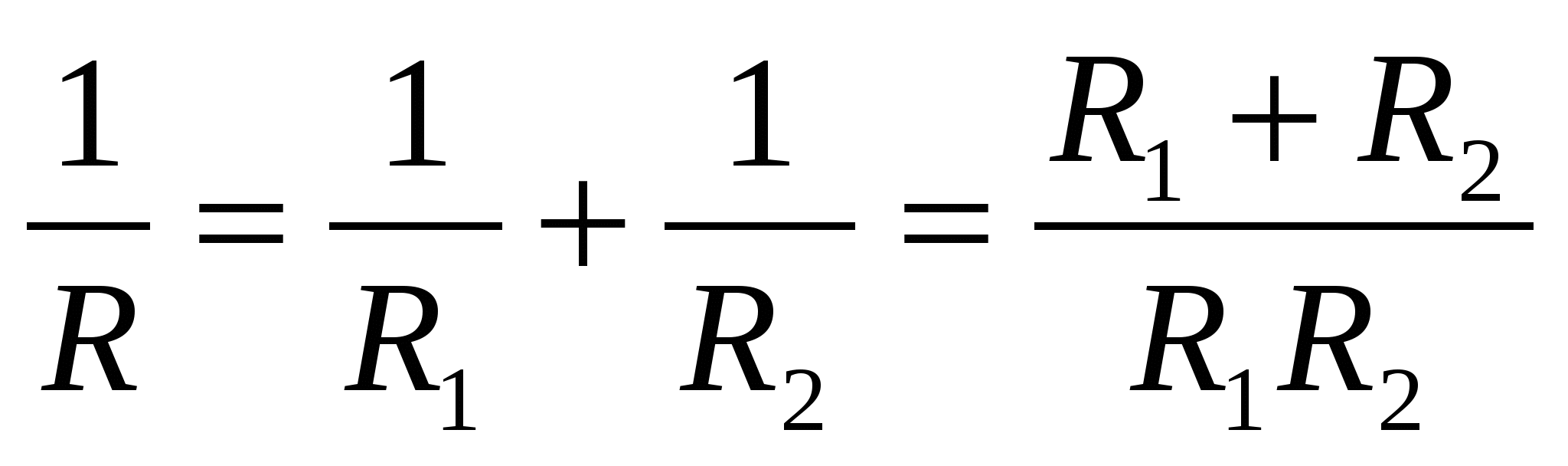 ;
; 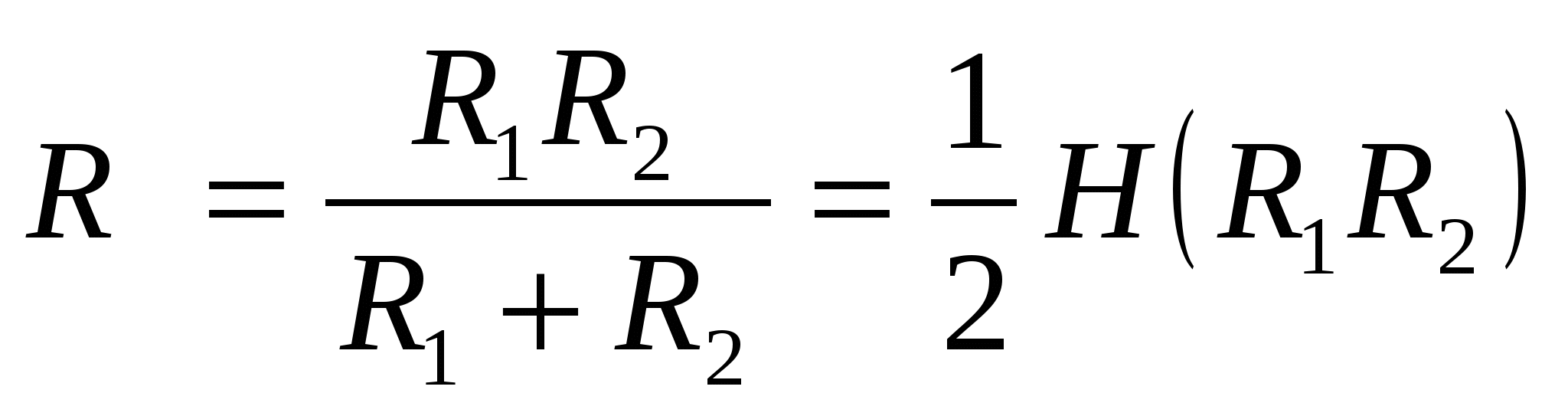 ;
;
Желательно дать учащимся два вида записи среднего гармонического, в частности при п=2:
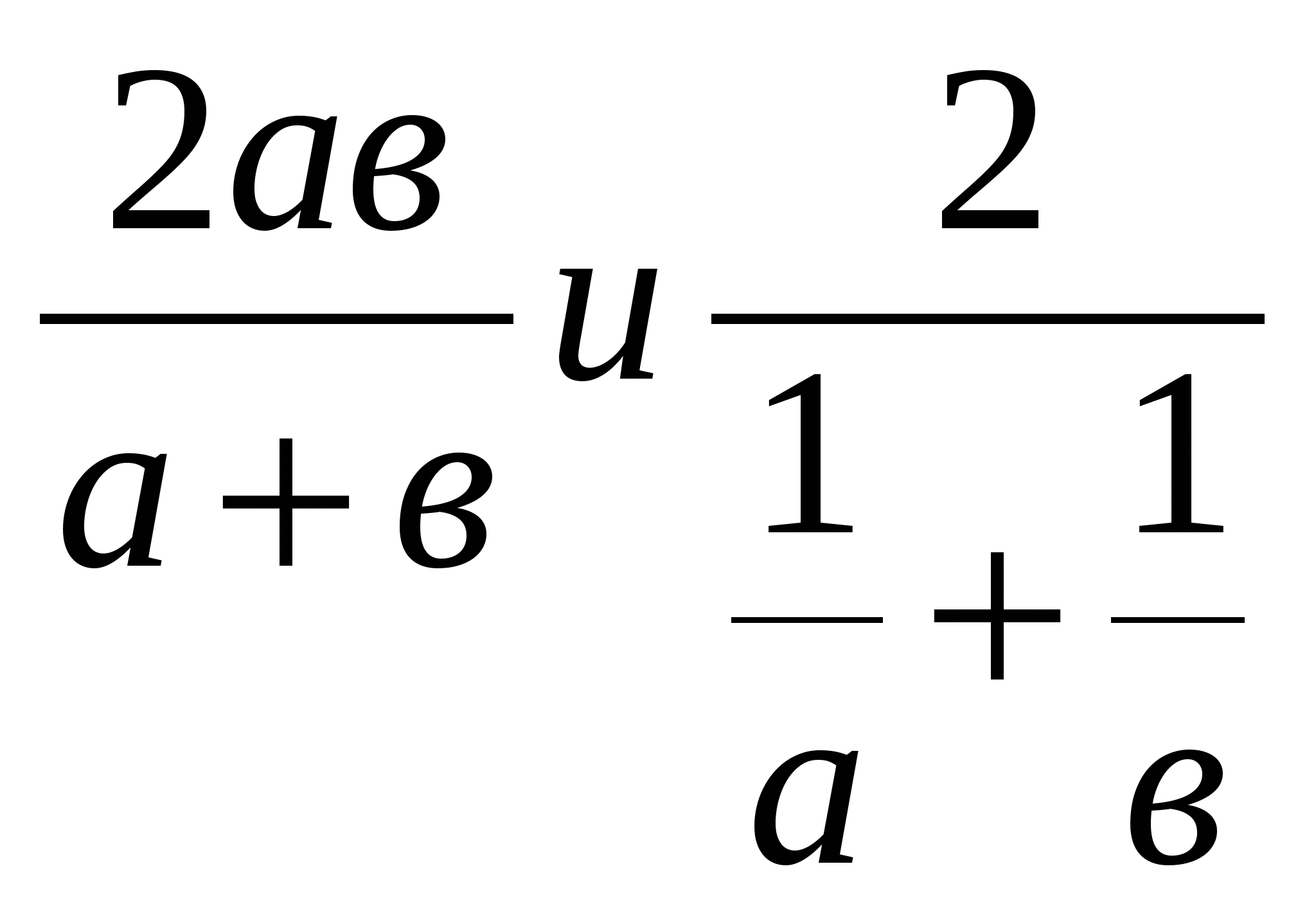 ;
;
3) Построить по заданным отрезкам а и в отрезок длины 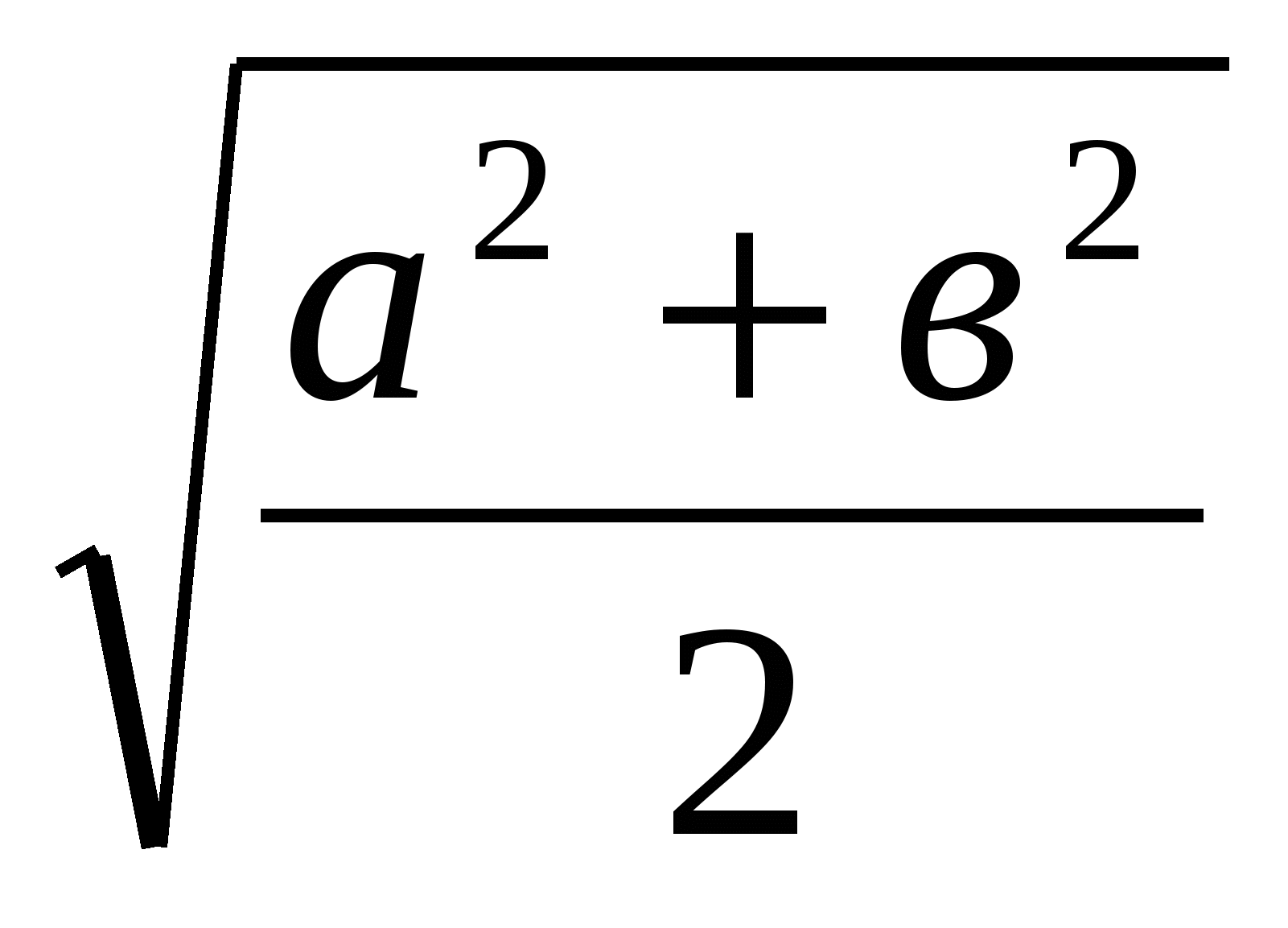 ;
;
4) Доказать, что в последовательности 1,1/2,1/3, …,1/п, (п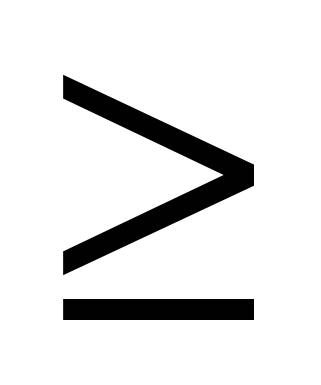 3) каждый член, кроме первого и последнего является средним гармоническим соседних с ним членов.
3) каждый член, кроме первого и последнего является средним гармоническим соседних с ним членов.
Решение: рассмотрим последовательность (ап), где а1=1, а2=1/2, …,ап=1/п, надо показать, что ак= Н(ак-1;ак+1)= 1/к .
Н(1/к-1;1/к+1) = 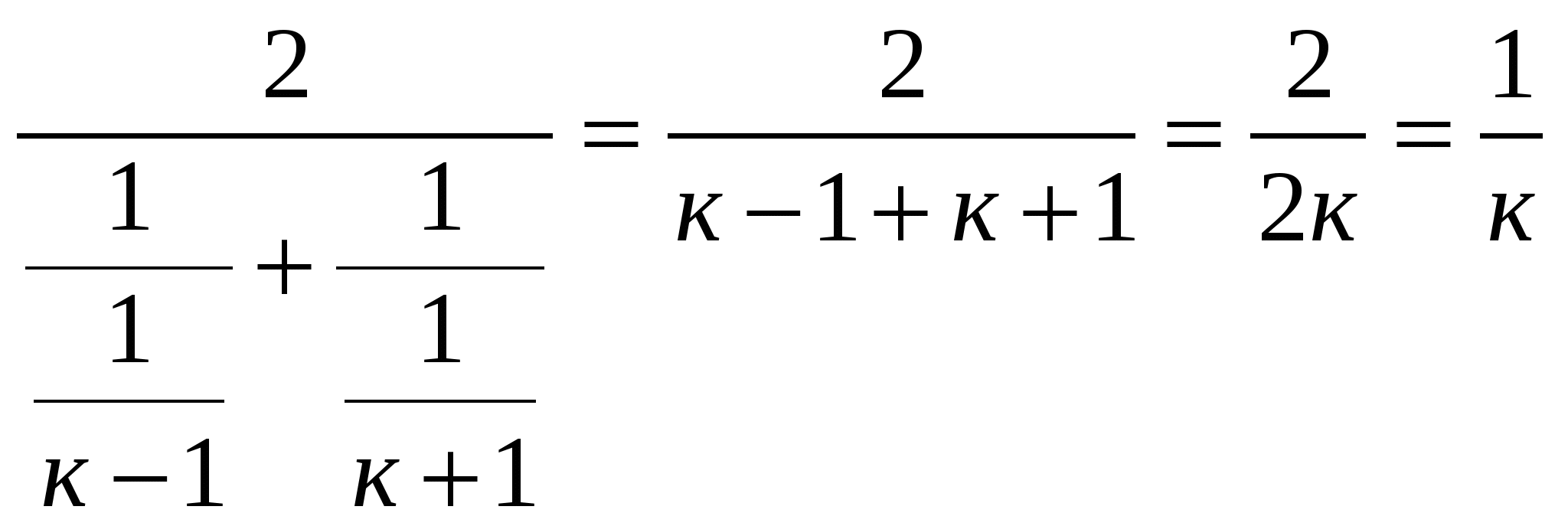 .
.
Последовательность 1,1/2,1/3, …,1/п, (п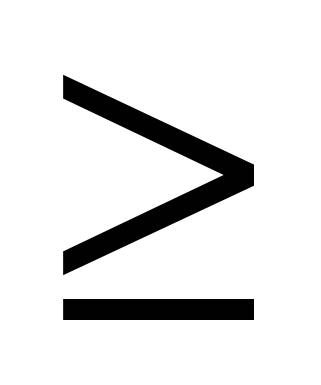 3) - пример гармонической последовательности ( каждый член, кроме первого и последнего - среднее гармоническое равноотстоящих от него членов).
3) - пример гармонической последовательности ( каждый член, кроме первого и последнего - среднее гармоническое равноотстоящих от него членов).
3.Доказательство теорем, связанных со средними величинами
В каком же соотношении находятся все средние величины?
Сравнивая результаты примеров, получаем:
А (3,4,9,12) = 7
G (3,4,9,12) = 6
Н (3,4,9,12) = 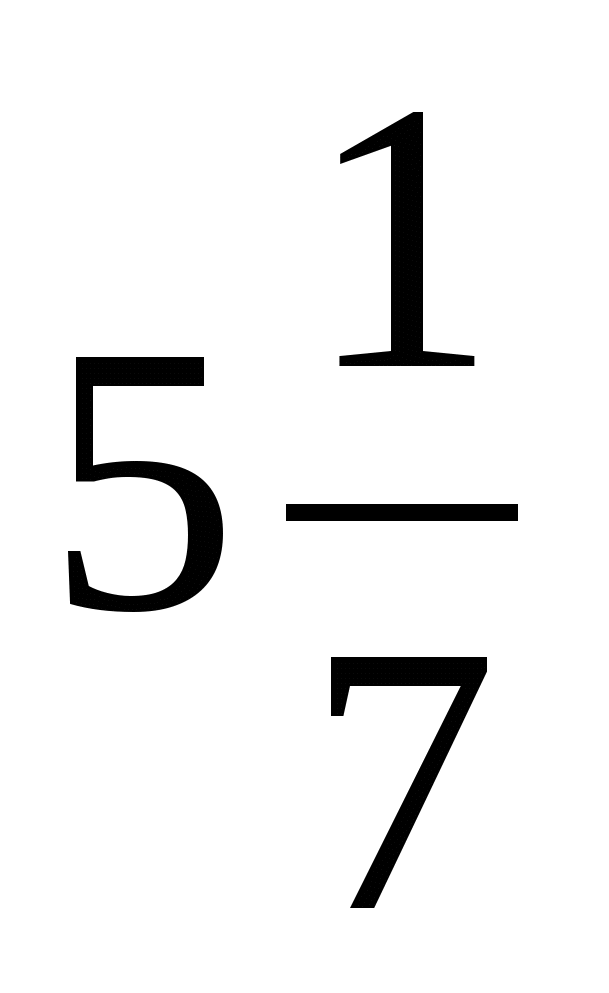
Q (3,4,9,12) = 2,5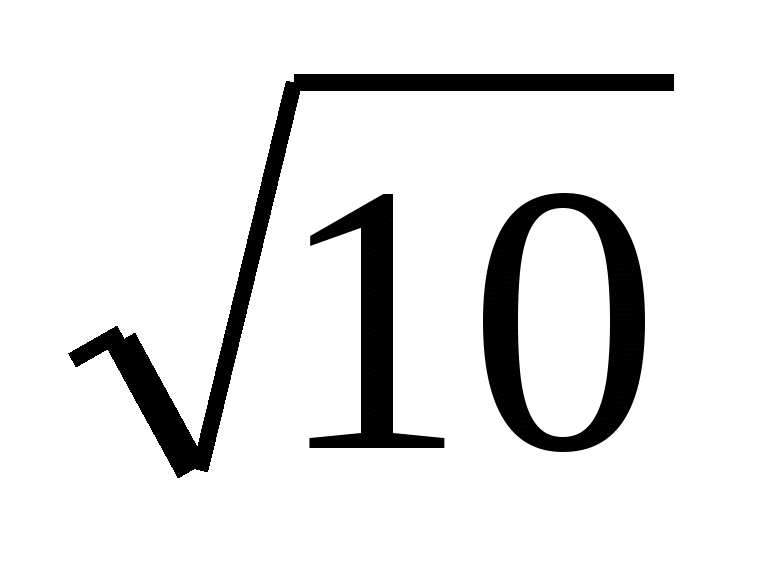
На основании числовых примеров выдвигаем гипотезу, что Н ![]() G
G  A
A  Q
Q
Желательно, чтобы учащиеся сами сформулировали теорему для любых
положительных чисел а и в:
Теорема 1:
Для любых положительных чисел а и в справедливы следующие соотношения:
min {а,в} Н(а.в)
Н(а.в)  G(а,в)
G(а,в)  А(а,в)
А(а,в)  Q(а,в)
Q(а,в)  max(а,в),
max(а,в),
где max(а,в) - наибольшее из чисел а и в,
min {а,в}- наименьшее из чисел а и в.
Доказательство:
1. Обоснование крайних соотношений достигается методом оценок заменить оба числа а и в соответственно на меньшее, точнее, на не большее) и на большее ( на не меньшее) в выражениях для среднего гармонического и среднего квадратического, а соотношение G(а,в)  А(а,в) уже было доказано.
А(а,в) уже было доказано.
2. Докажем, что Н(а.в)  G(а,в), т.е что
G(а,в), т.е что 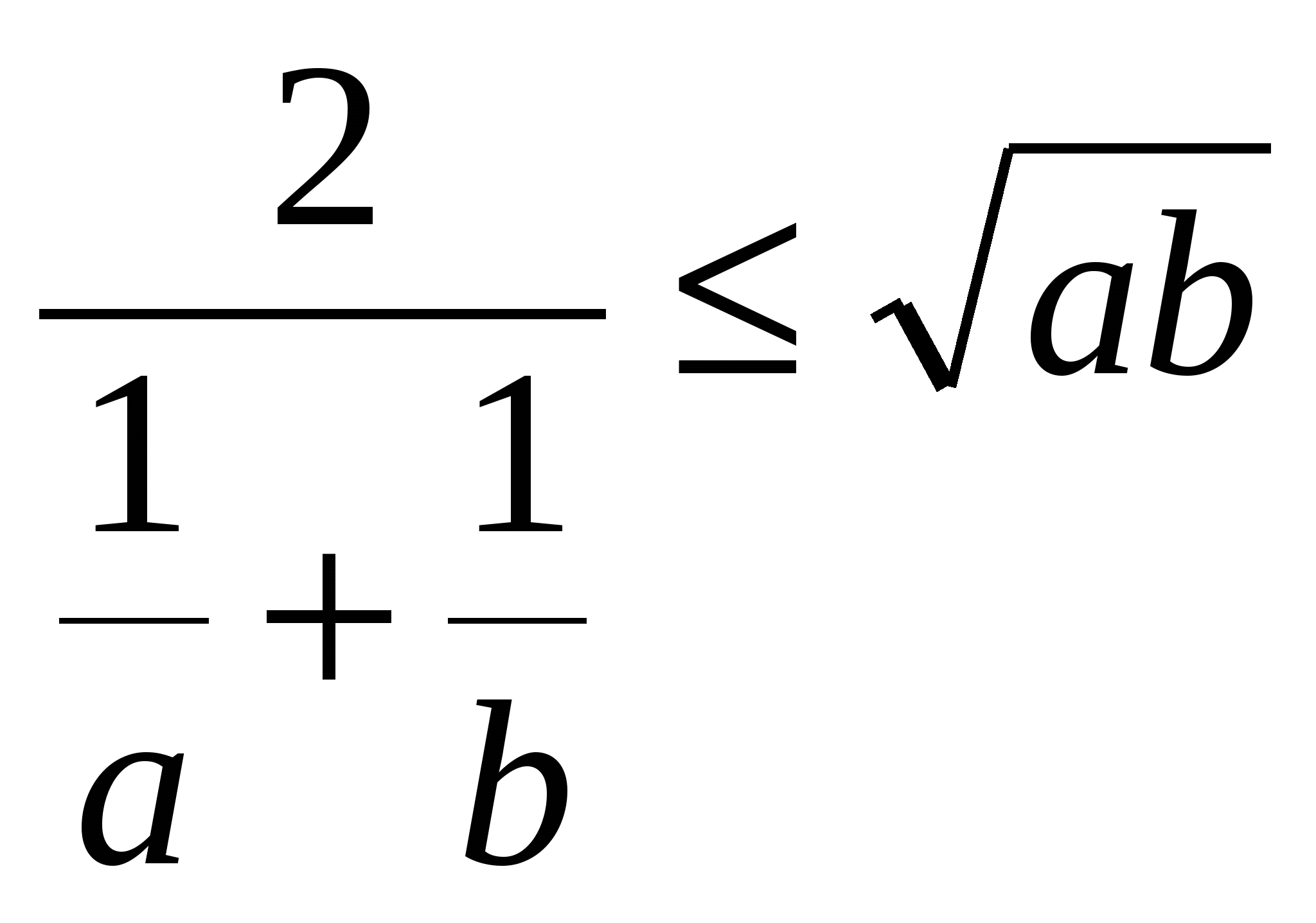 ;
;
Для чисел ![]() применим неравенство Коши:
применим неравенство Коши:
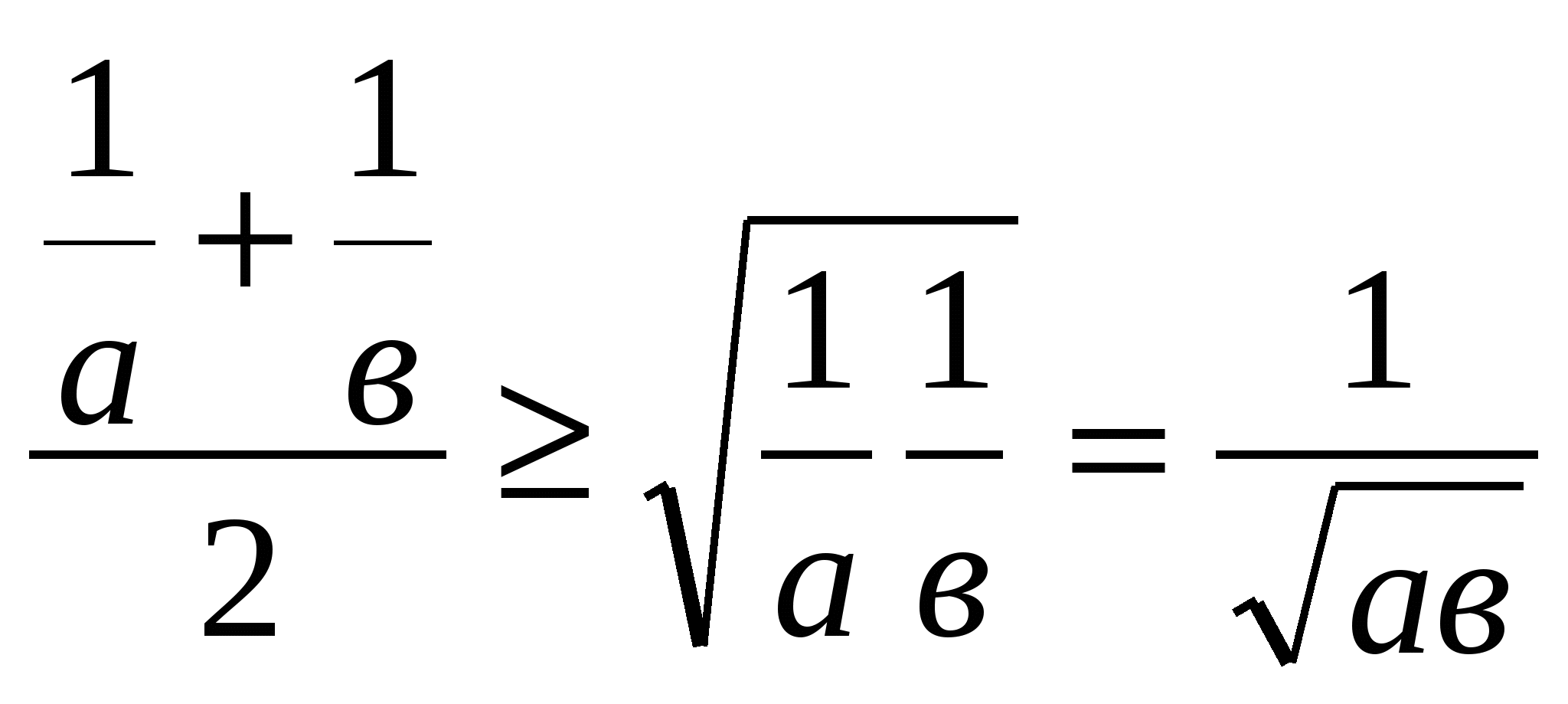 ; по свойству числовых неравенств а ›0, в ›0 и а ≥ в, то
; по свойству числовых неравенств а ›0, в ›0 и а ≥ в, то
1/а ![]() 1/в, значит,
1/в, значит, 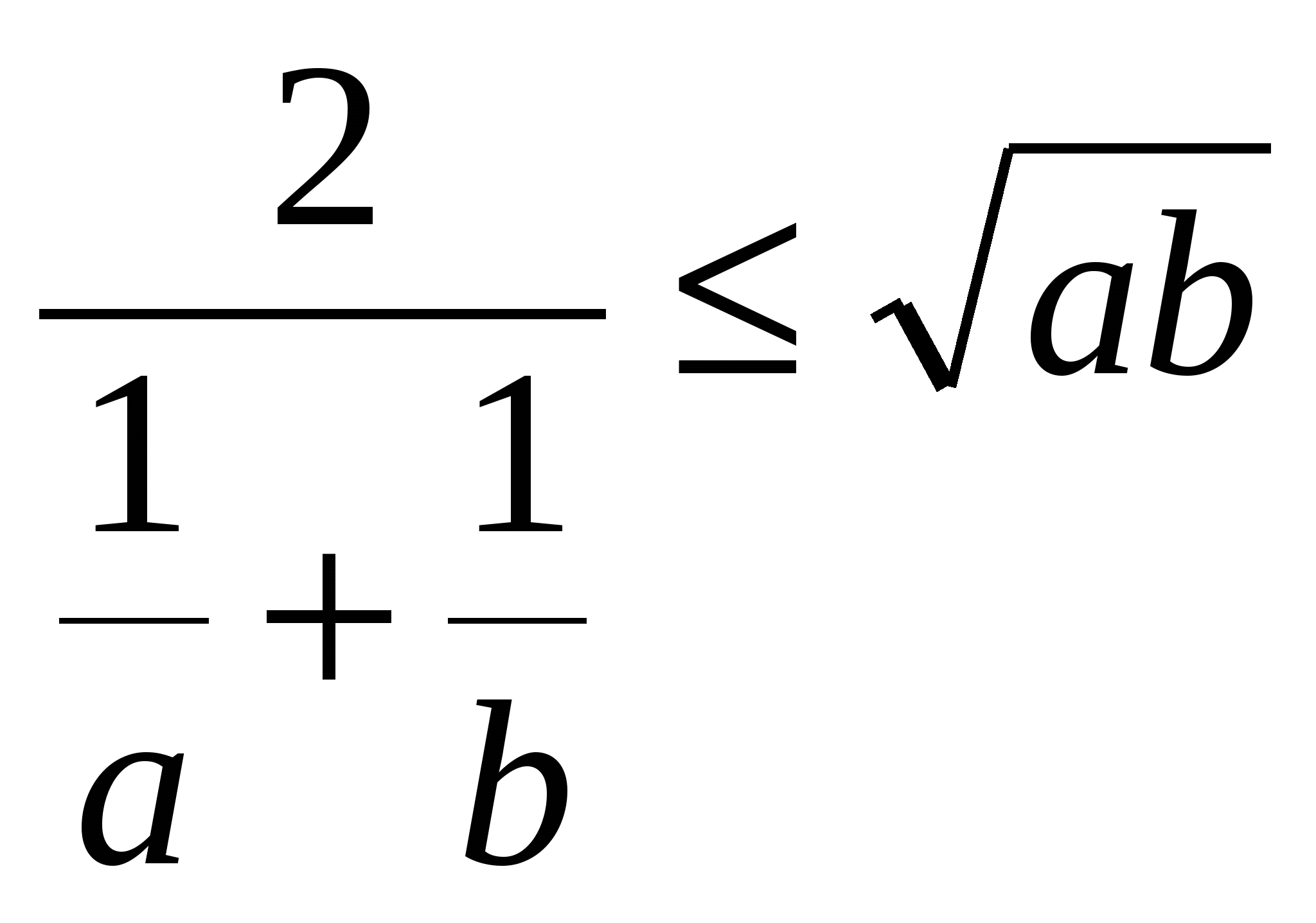 .
.
3. Докажем, что А(а,в)  Q(а,в), т.е
Q(а,в), т.е 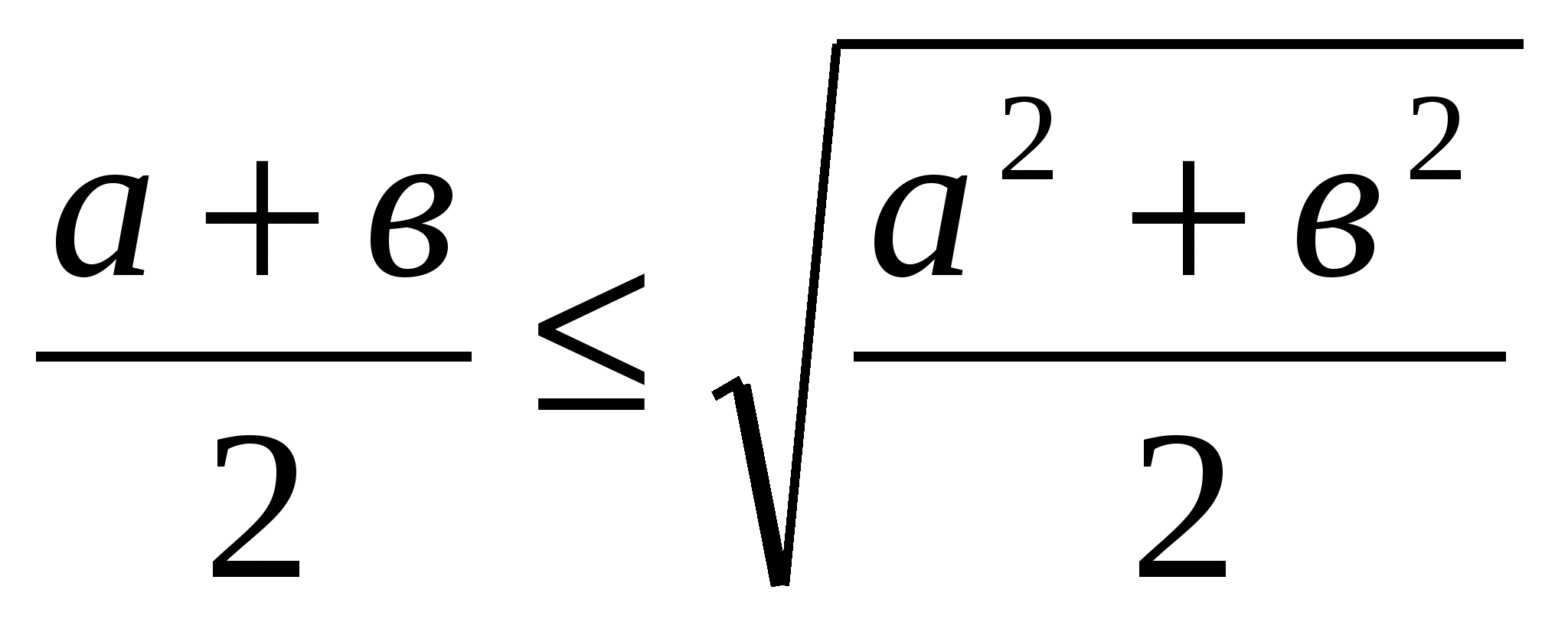 .
.
Перейдя к равносильному неравенству (а + в)2![]() 2(а2+ в2) и используя частный случай неравенства Коши - Буняковского:
2(а2+ в2) и используя частный случай неравенства Коши - Буняковского:
(1а+1в) 2  ((а2+в2)(12+12), значит,
((а2+в2)(12+12), значит, 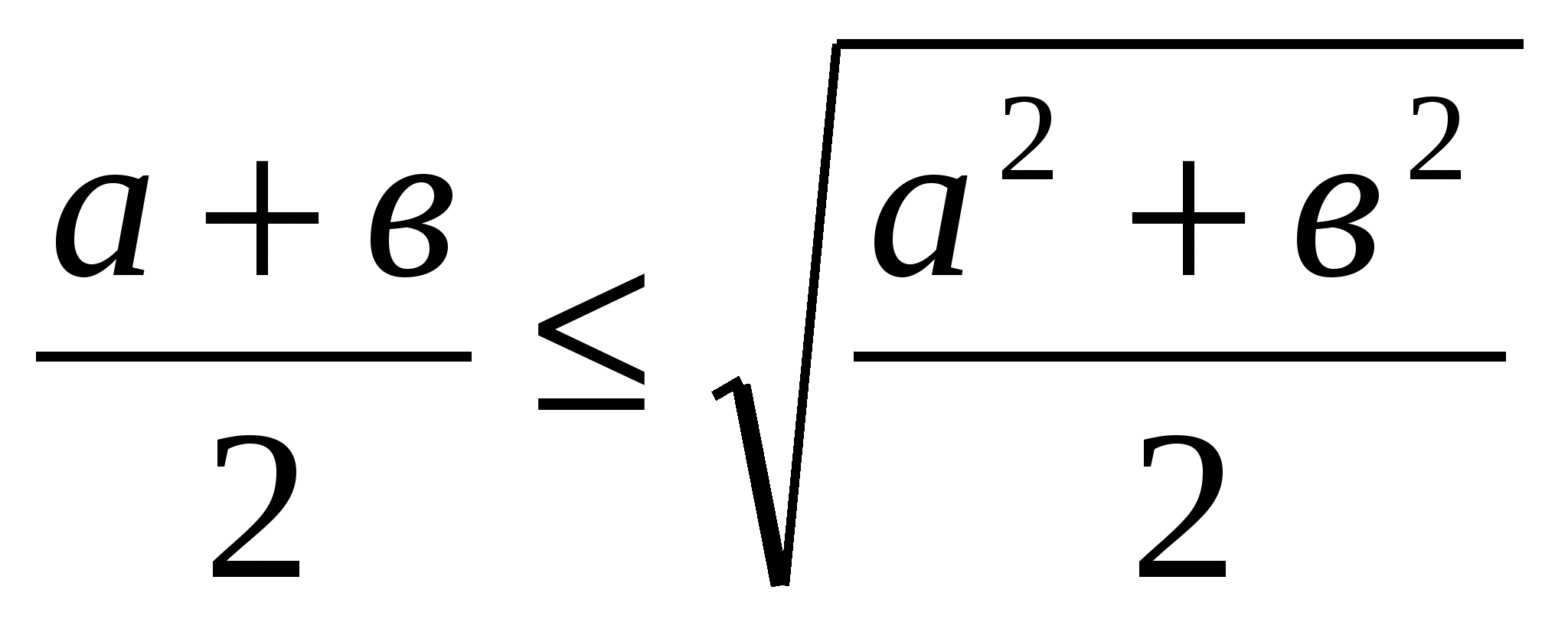 .
.
Теперь можно предложить ученикам сформулировать теорему для п положительных чисел:
Теорема 2: Для любого числа положительных чисел а1 ,а2,…ап ; (п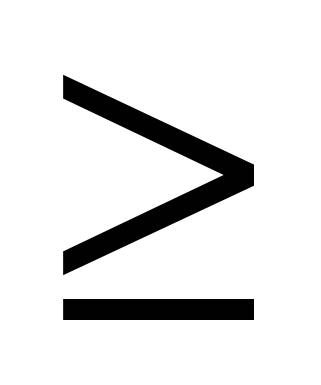 2)веры следующие соотношения:
2)веры следующие соотношения:
min { а1 ,а2,…ап ; } Н(а1 ,а2,…ап ; )
Н(а1 ,а2,…ап ; )  G(а1 ,а2,…ап ;)
G(а1 ,а2,…ап ;)  А(а1 ,а2,…ап ;)
А(а1 ,а2,…ап ;)  Q(а1 ,а2,…ап ;)
Q(а1 ,а2,…ап ;)  max {а1 ,а2,…ап ; }
max {а1 ,а2,…ап ; }
Доказательство аналогично случаю для двух чисел .
Применение теоремы можно рассмотреть на примерах.
1.Докажите, что для любых положительных чисел а, в, с справедливо неравенство:
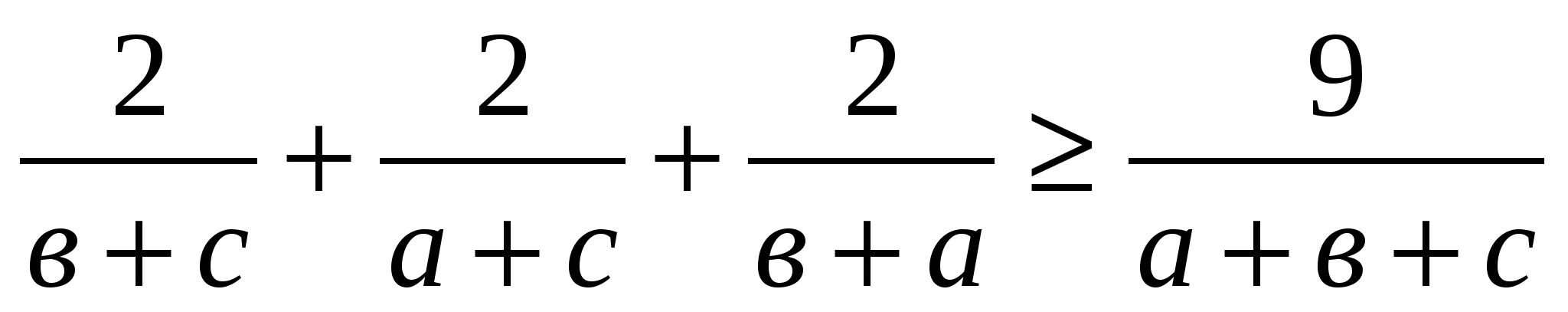
Доказательство:
Используя теорему 2: Н  А
А
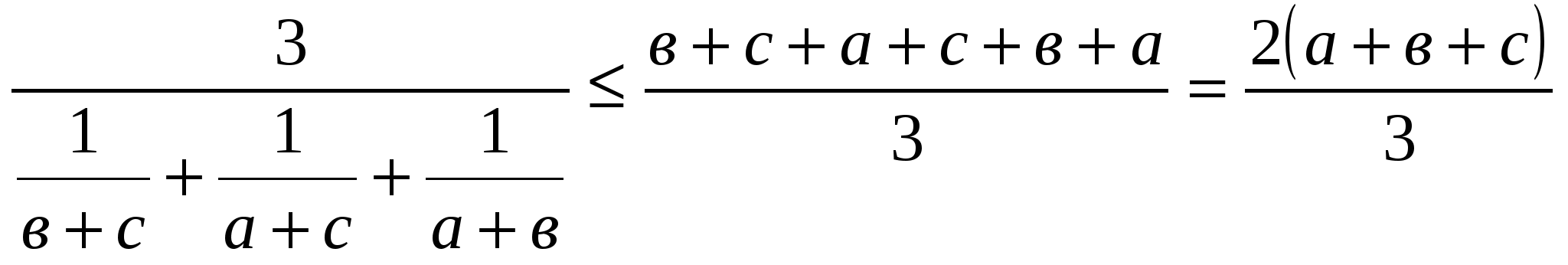
Имеем: 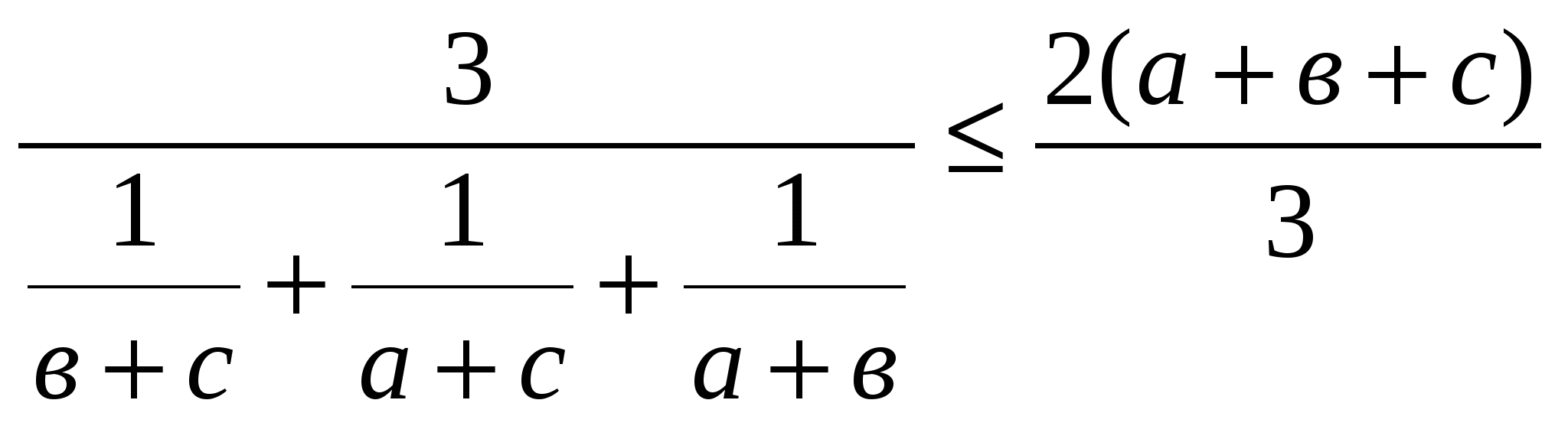 ; отсюда
; отсюда 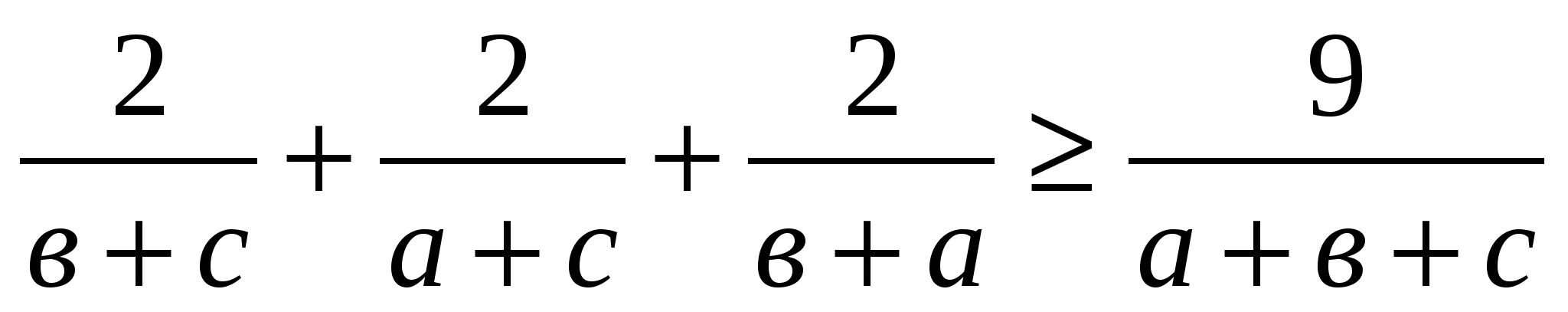 .
.
2.Доказать, что для любых положительных а и в , а≠в и nєN справедливо:
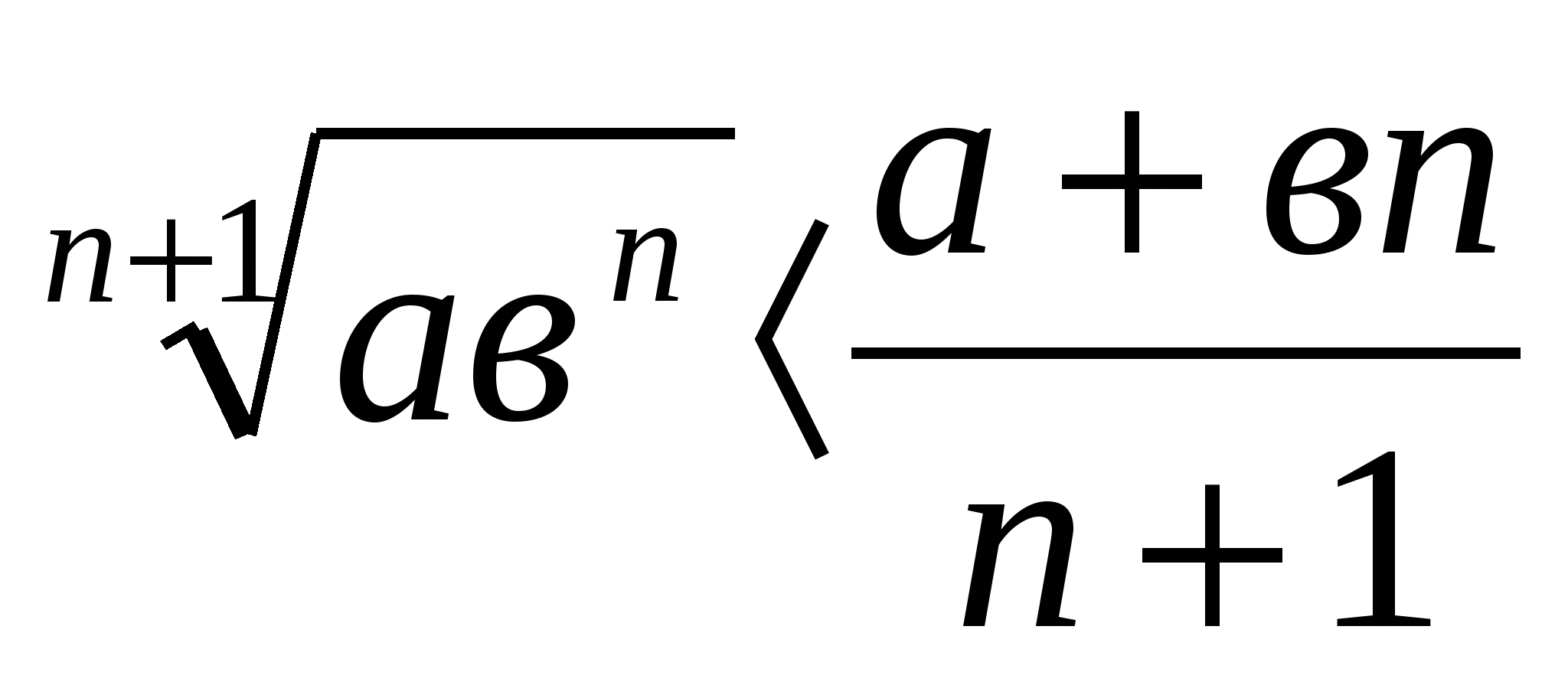 ;
;
Доказательство:
![]()
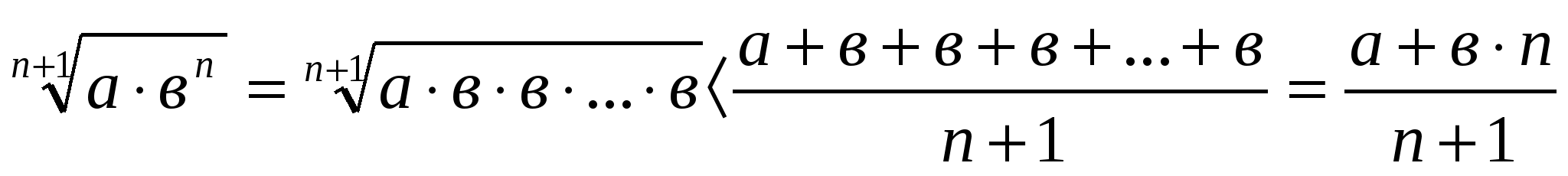 ;
;
3. Доказать, что последовательности (1+1/п)п и (1-1/п)п- возрастающие, а последовательность (1+1/п)п+1- убывающая.
Доказательство:
а) пусть а=1, в=1+1/п, тогда 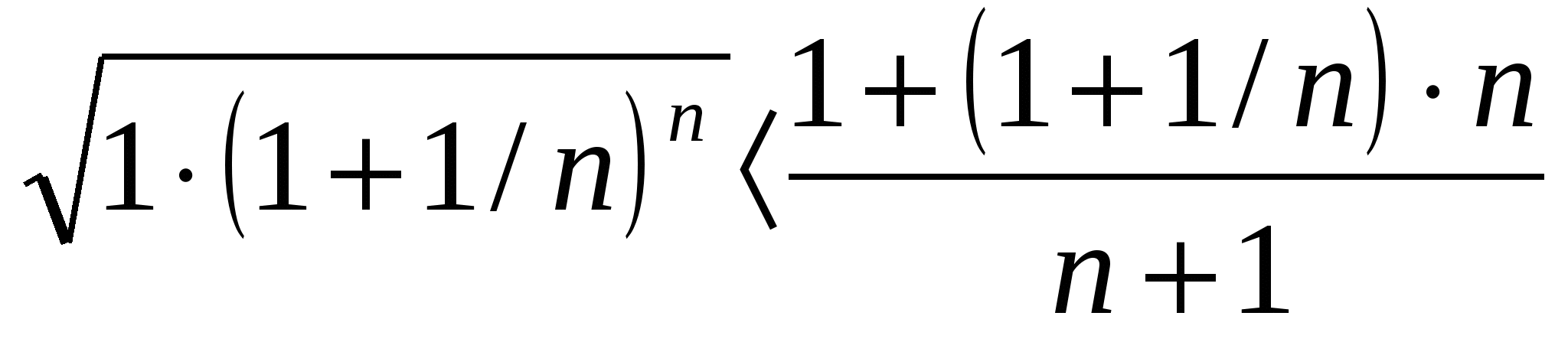 ( доказано выше),
( доказано выше),
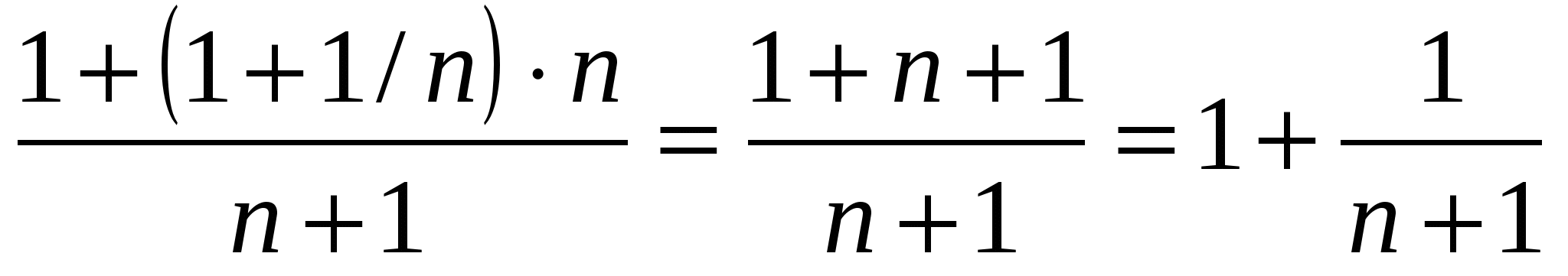 , т.е (1+1/п)п < (1+1/(п+1))п+1, значит, последовательность (1+1/п)п возрастает (по определению);
, т.е (1+1/п)п < (1+1/(п+1))п+1, значит, последовательность (1+1/п)п возрастает (по определению);
б) аналогично доказывается, что последовательность(1-1/п)п-возрастающая,
(можно предложить учащимся доказать самостоятельно);
в) 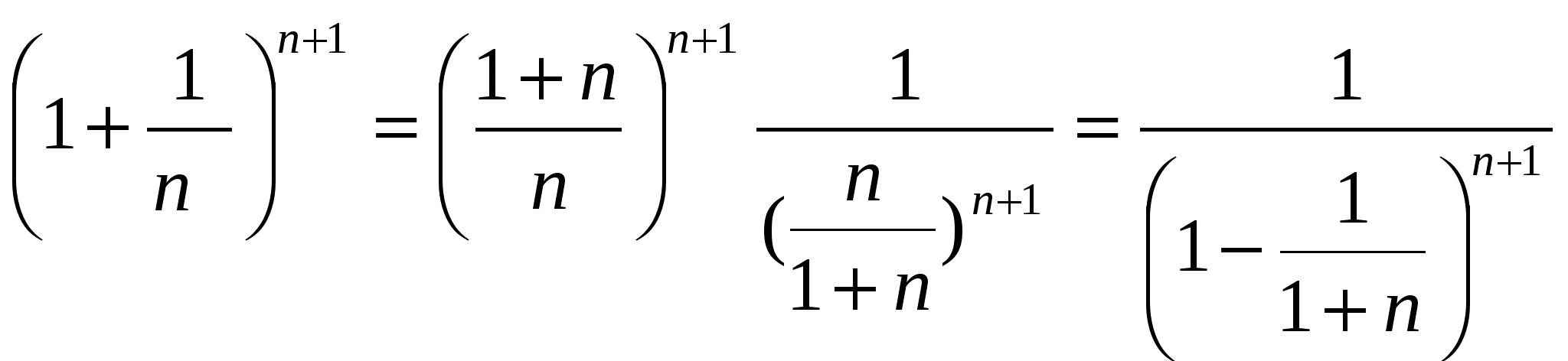 .
.
Последовательность ап=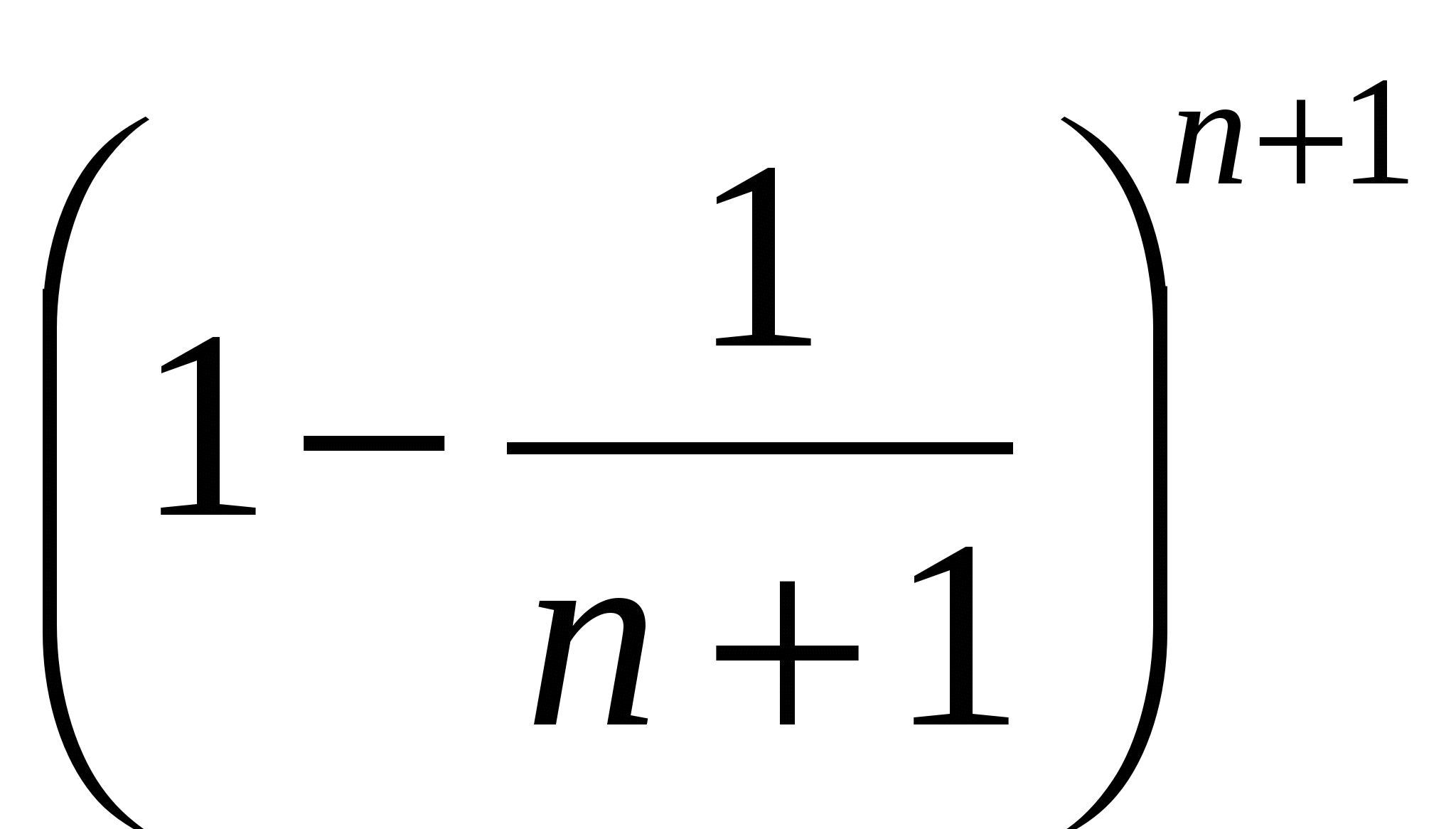 возрастает, значит, последовательность 1/ап - убывает.
возрастает, значит, последовательность 1/ап - убывает.
4. Геометрическая интерпретация связи средних величин
Геометрическая интерпретация неравенств, связывающих средние величины, очень важна. Достаточно показать ее для двух положительных чисел на примере трапеции.
Рассмотрим произвольную трапецию MNPK с основаниями а и в.
Проведем прямые, параллельные
основаниям трапеции так, что
1) Прямая НН 1 проходит через точку
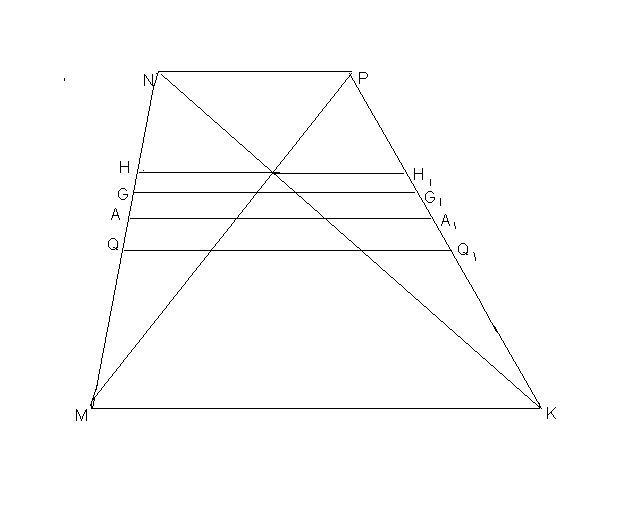 пересечения диагоналей трапеции,
пересечения диагоналей трапеции,
2) Прямая GG1 делит трапецию на две подобных трапеции,
3) Прямая АА1 проходит через середины боковых сторон трапеции,
4) Прямая НН 1 делит трапецию на две равновеликие трапеции.
1)
a) Пусть НН 1=х.
Треугольники MNK и HNO подобны (ученики самостоятельно доказывают)
MK:HO = NK:NO = b : HO ;
(NO+OK):NO =1+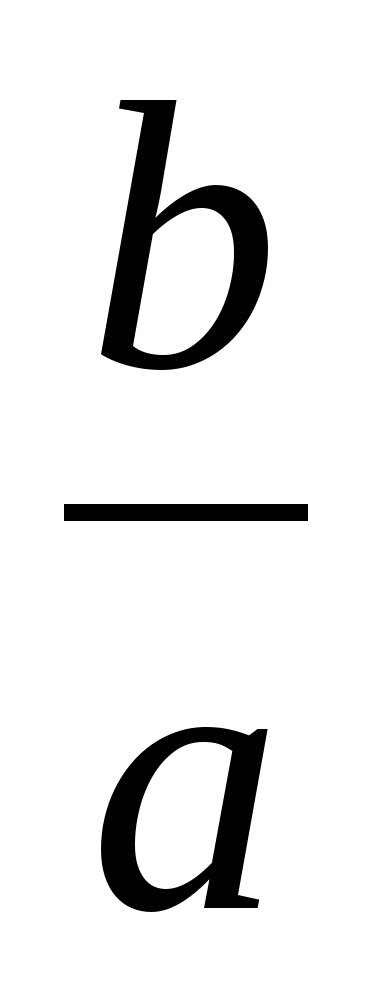 (из подобия треугольниковNOP и KOM)
(из подобия треугольниковNOP и KOM)
Отсюда: MK:HO = ( a+ b) : a; HO=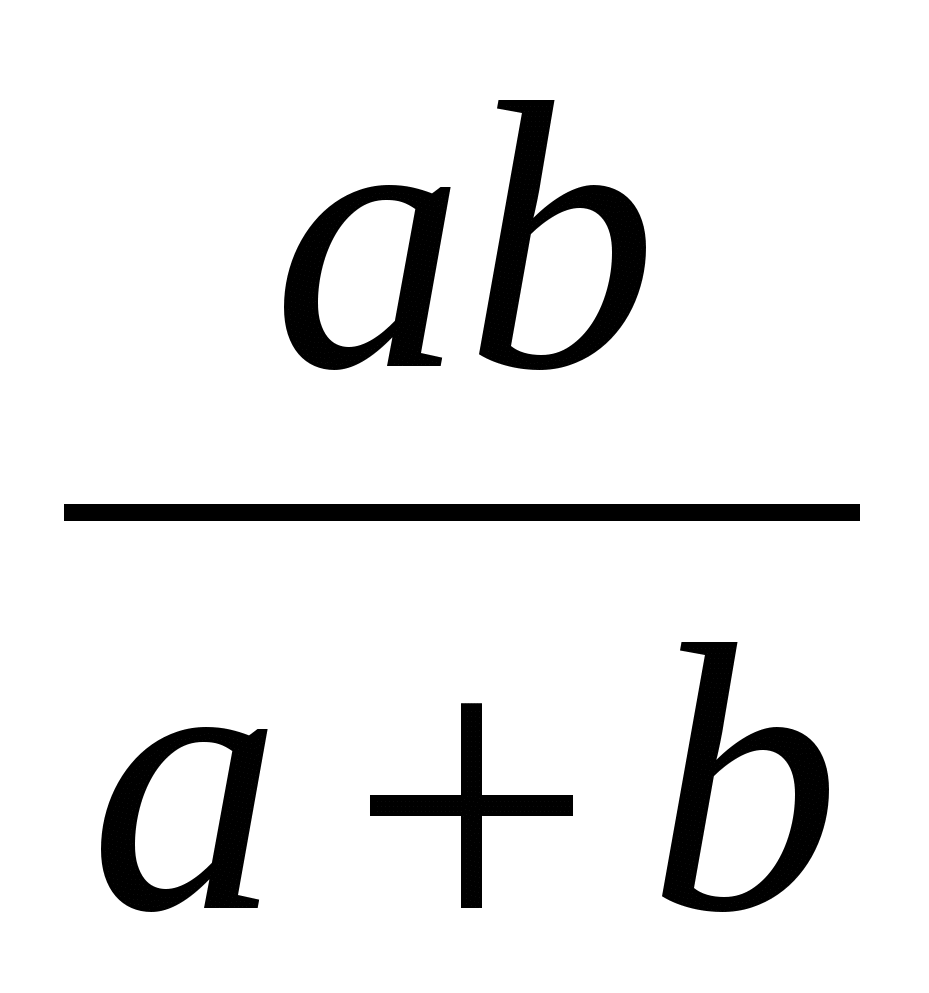 ;
;
б) Треугольники OH1K и NPK подобны,
значит, HP: OH1=(NO+OK):OK,
NP: OH1= ON:OK +1; т.е a: OH1= ![]() ;
;
в) OH+OH1 = 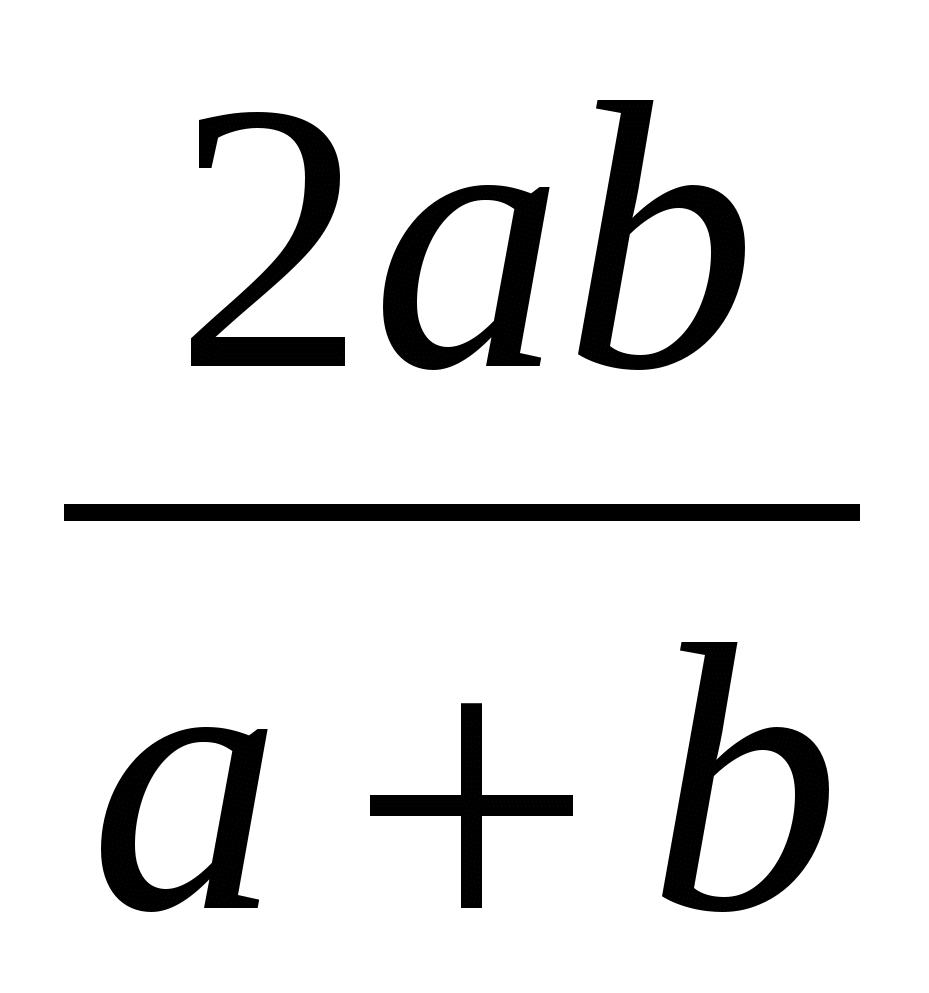 = H(a; b) НН 1 = H(a; b)
= H(a; b) НН 1 = H(a; b)
2) Пусть GG1= х
Из подобия трапеций GNPG! и MG G!K:
а : x = x : b; отсюда, х = 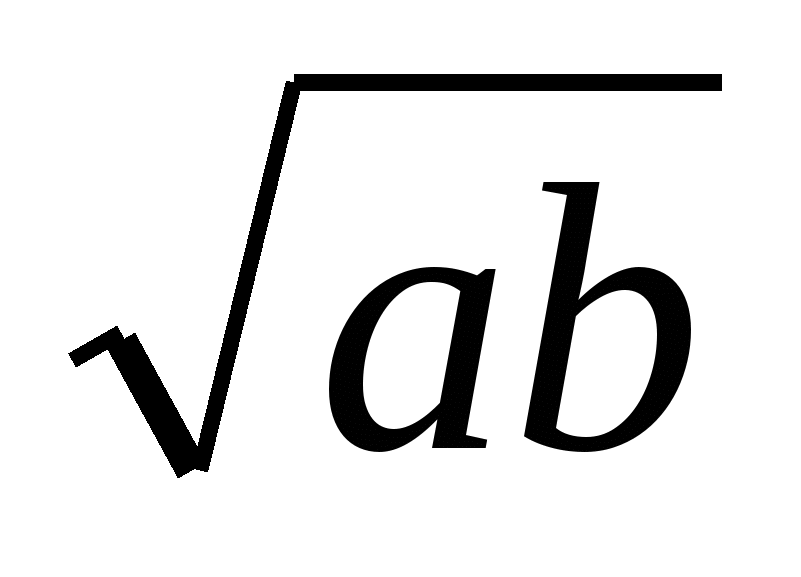 GG1 = G(a; b)
GG1 = G(a; b)
3) АА1 - средняя линия трапеции по определению, АА1=![]() , АА1=А(a;b)
, АА1=А(a;b)
4) Пусть QQ1= х, по условию:
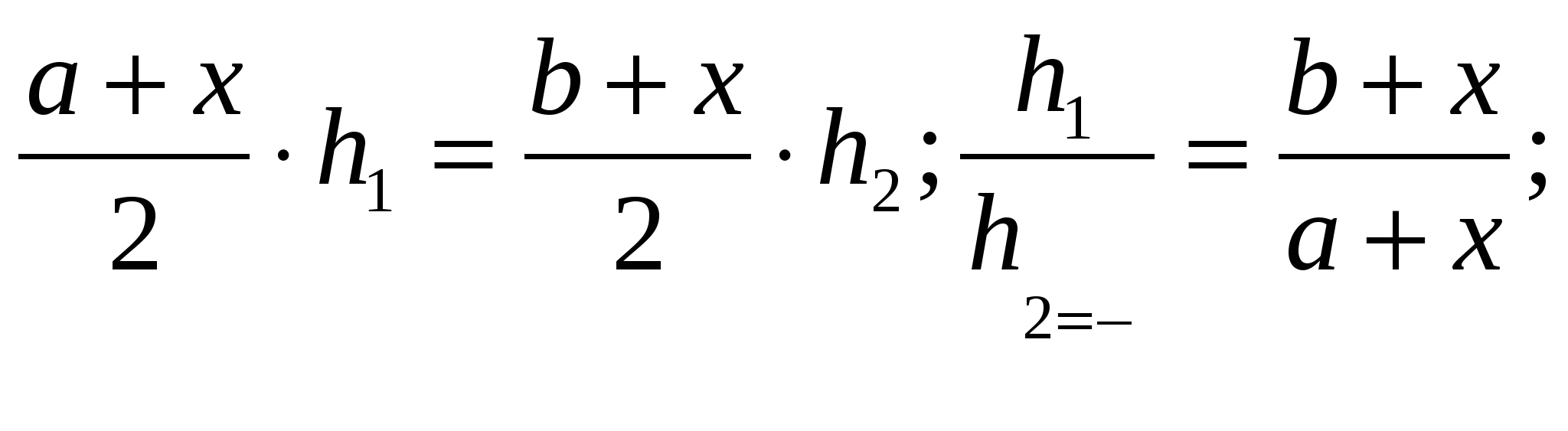 (1) , с другой стороны,
(1) , с другой стороны,
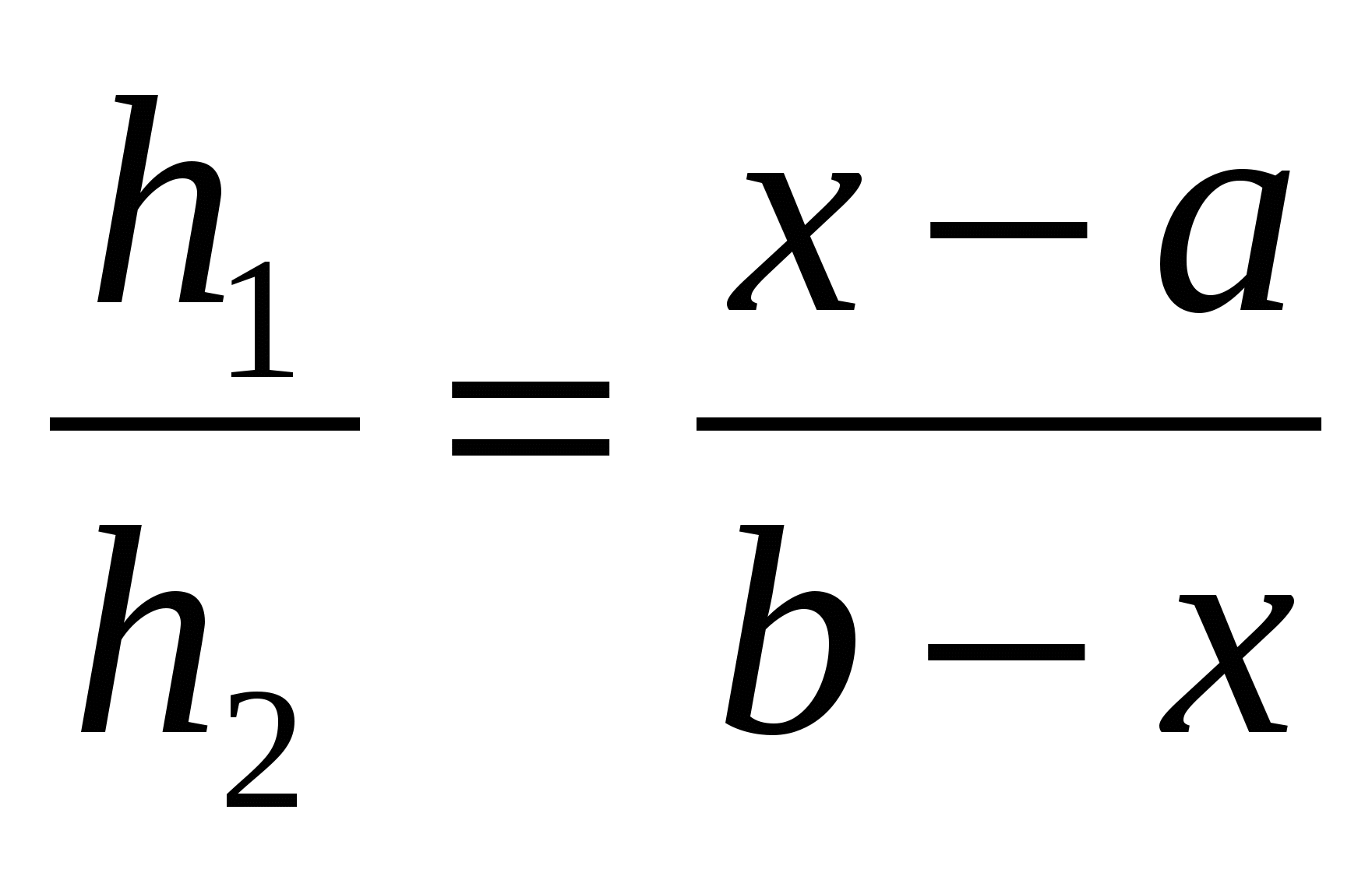 (2). Имеем:
(2). Имеем: 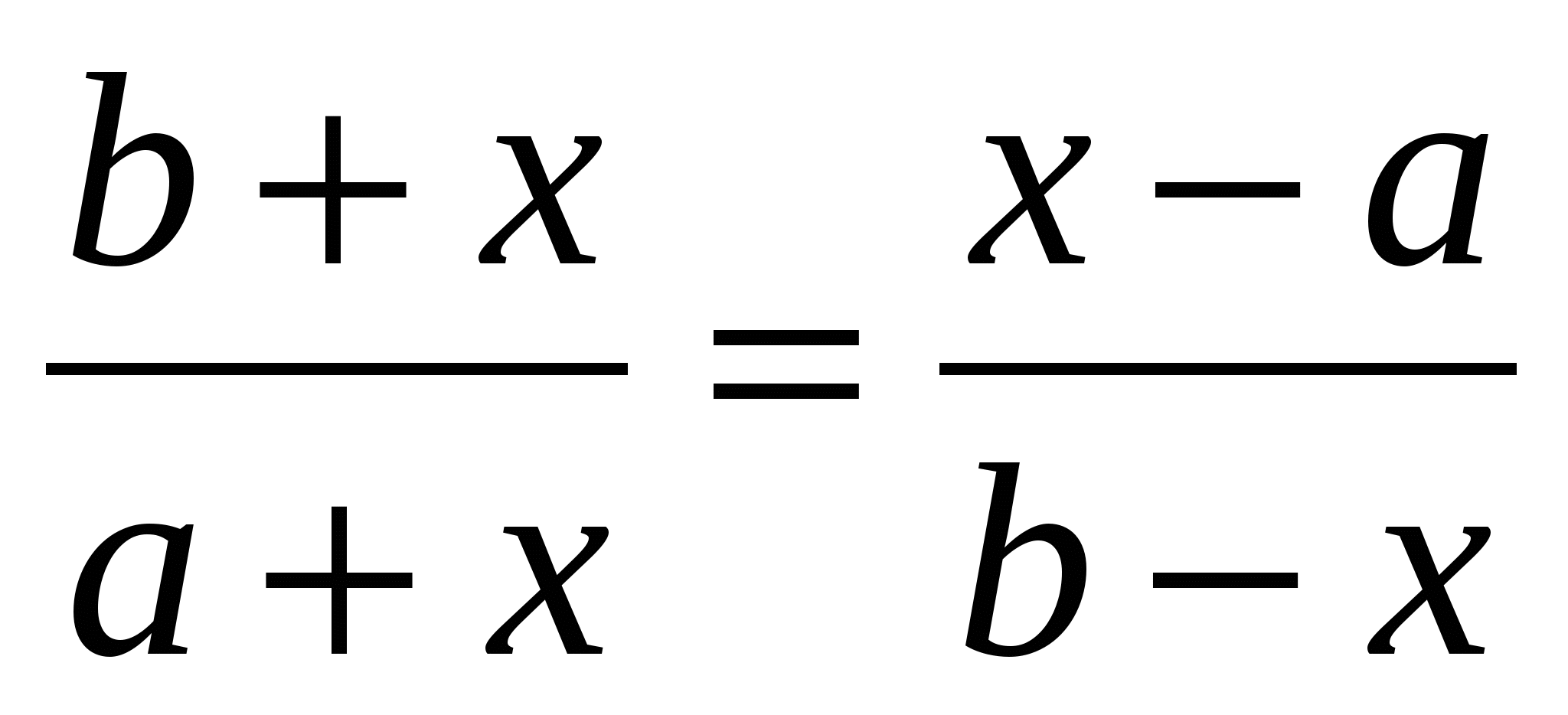 ;
;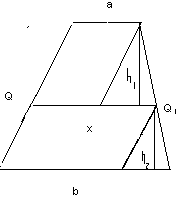
b2-x2=x2-a2, х2=![]() ; т.е QQ1=Q(a; b)
; т.е QQ1=Q(a; b)
Таким образом, мы доказали, что в трапеции есть все вышеупомянутые средние. Осталось доказать что,
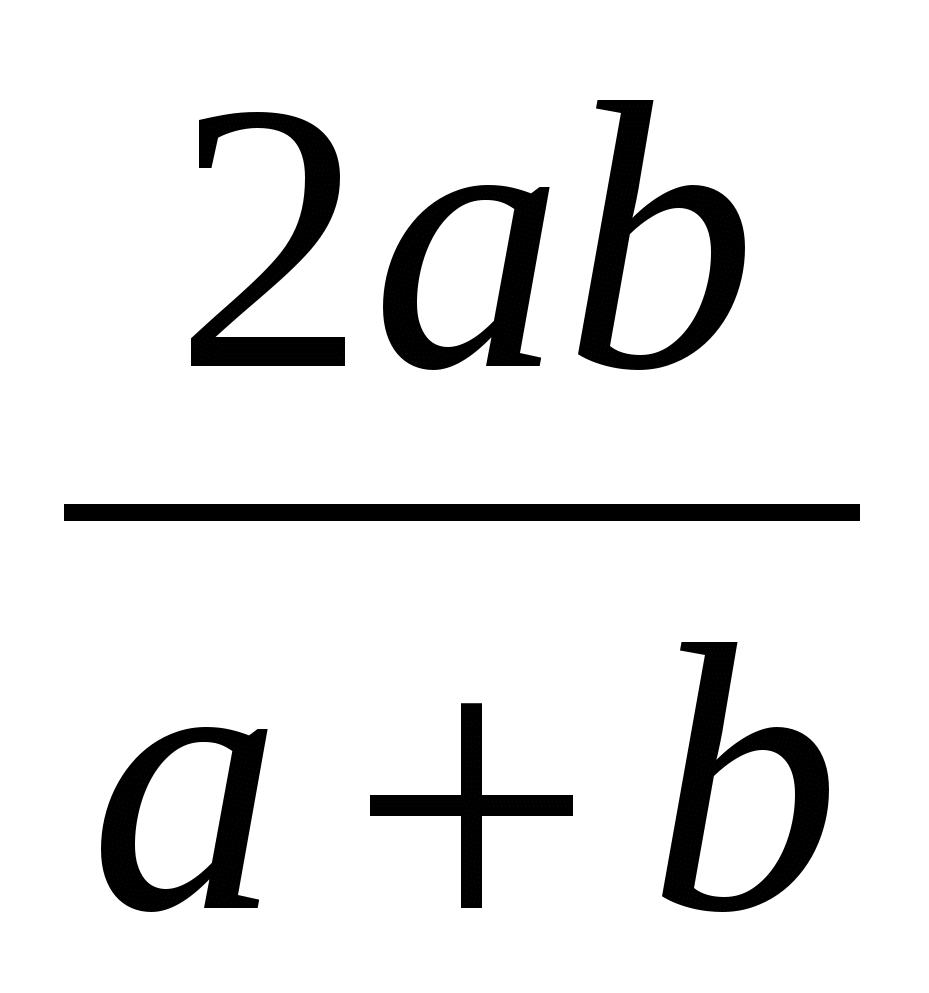

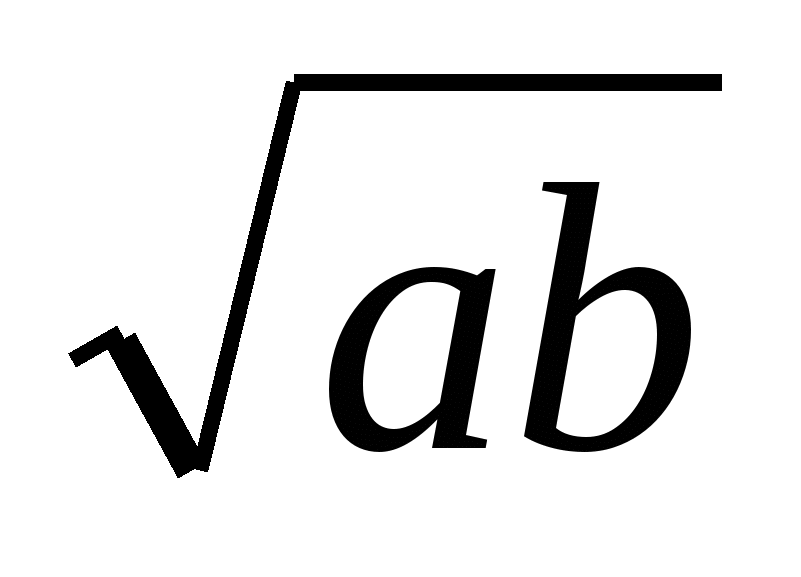

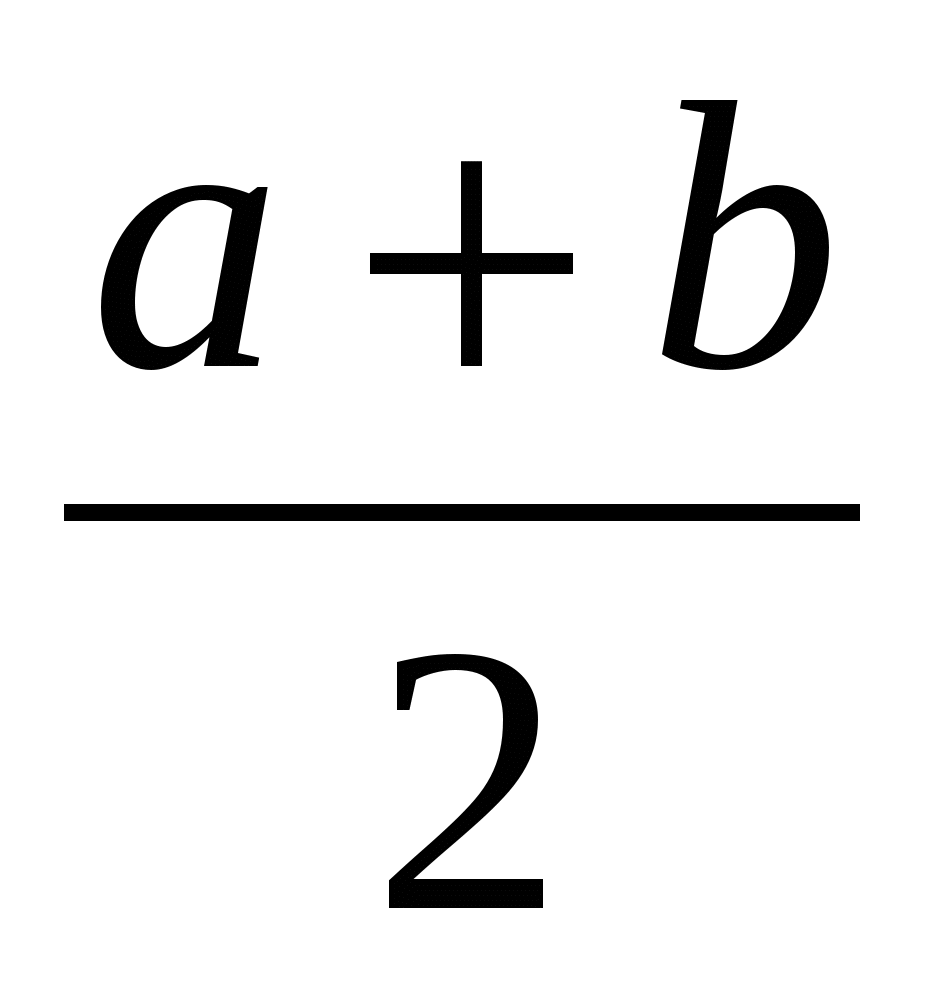

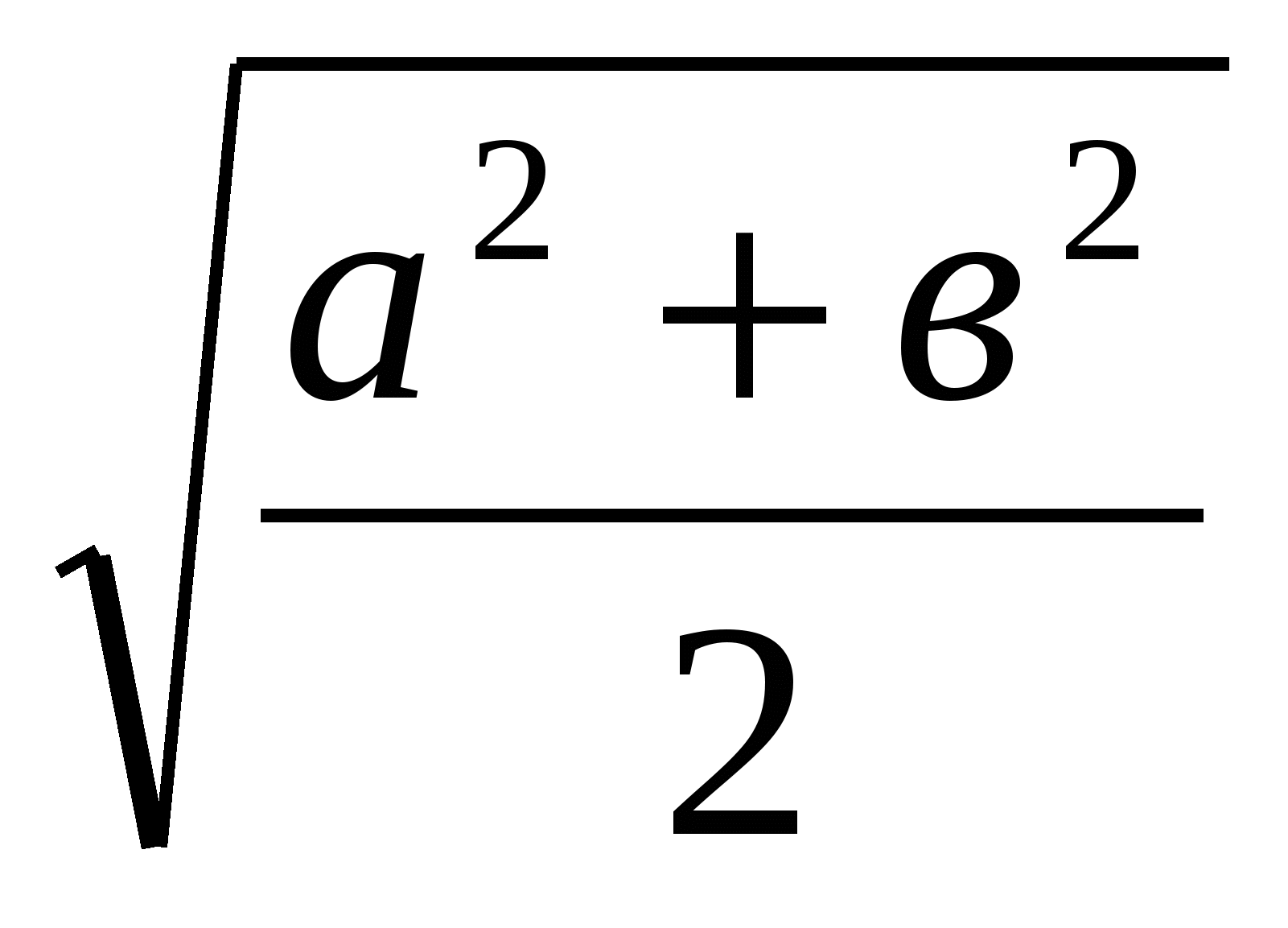 .
.
Можно привести такое доказательство:
a) NH:HM = a: b, a <b; 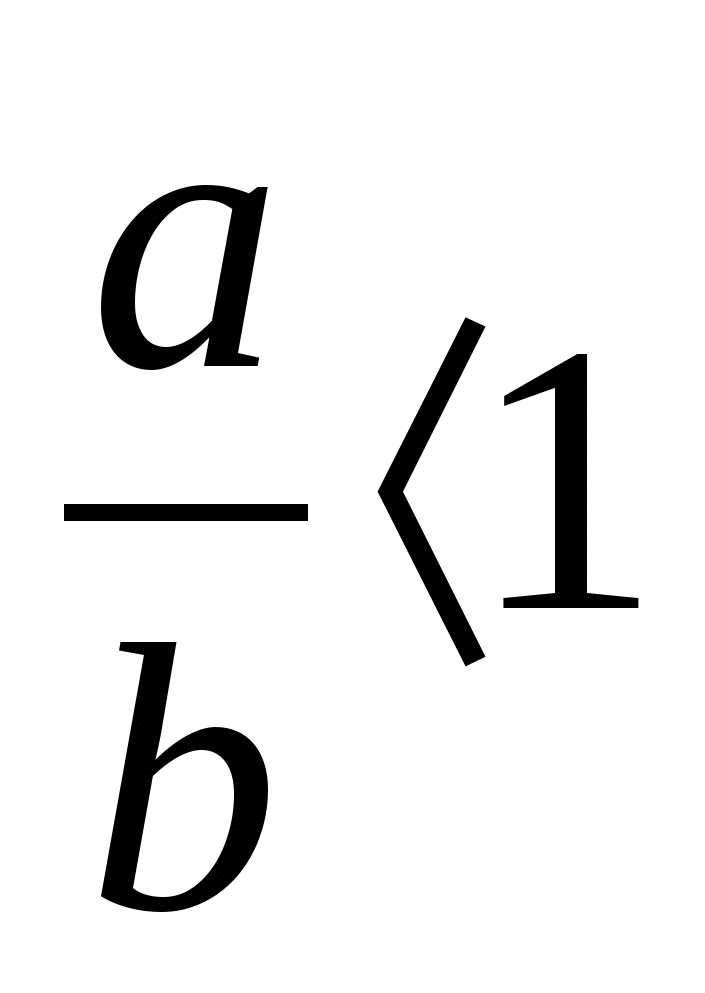 ;
;
NG:GM=a: GG1=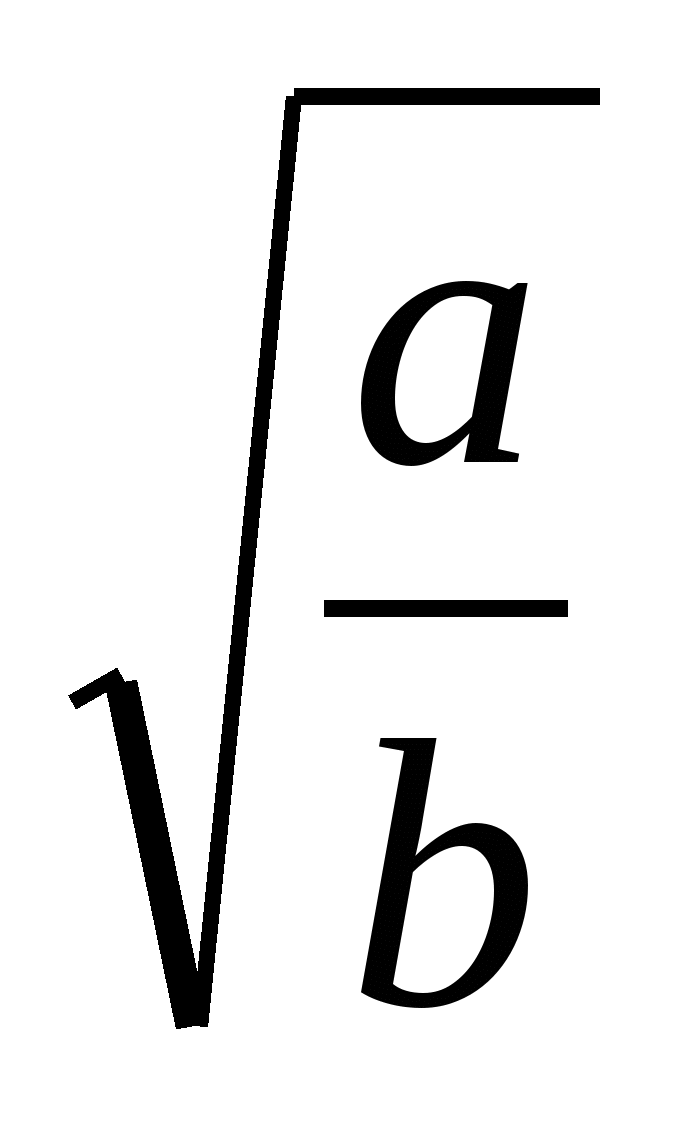 ; 1›
; 1› 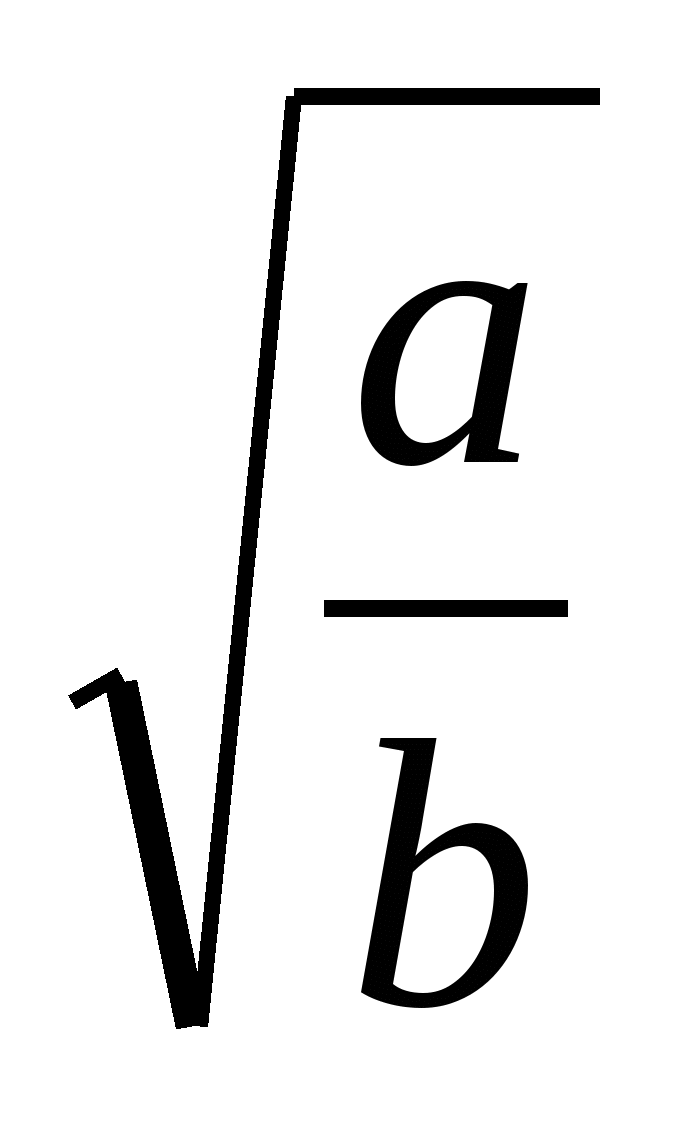 › , т.к
› , т.к 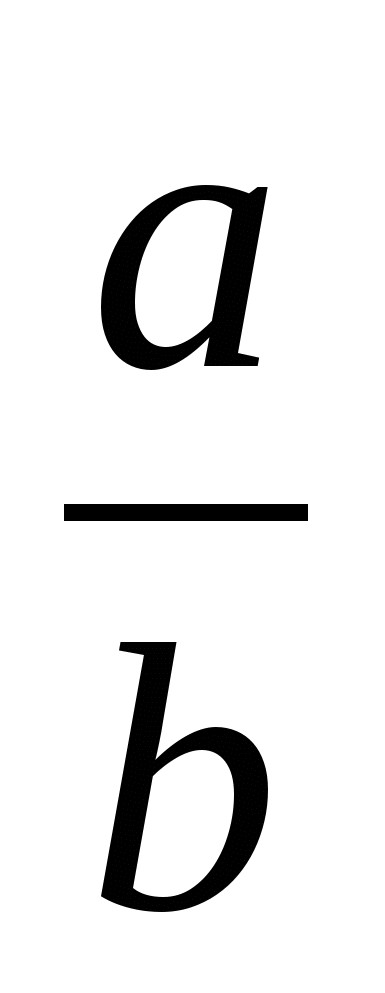 <1, значит, НН 1
<1, значит, НН 1  GG1,
GG1,
б) GG1<АА1, т.к АА1=1 , т.о НН 1  GG1
GG1  АА1,
АА1,
в) NQ:QM= h1:h2=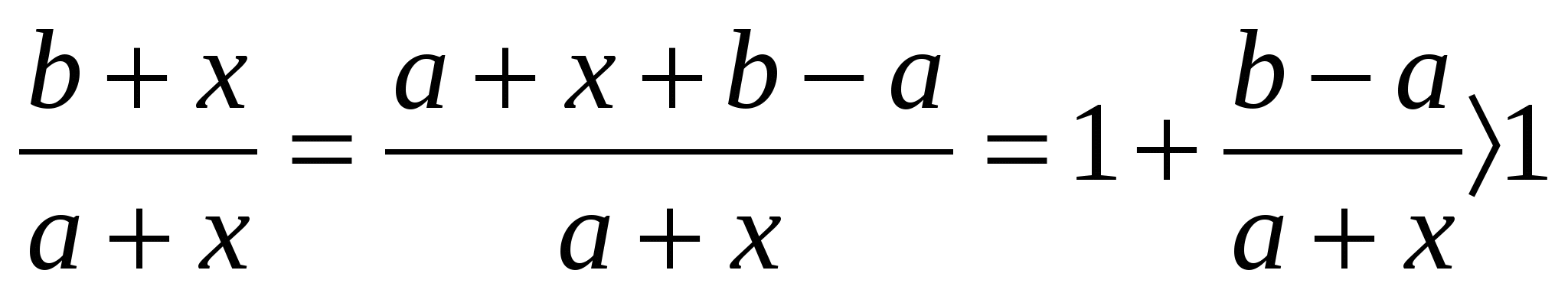 , т.о
, т.о
НН 1  GG1
GG1  АА1
АА1  QQ1, т.е
QQ1, т.е 
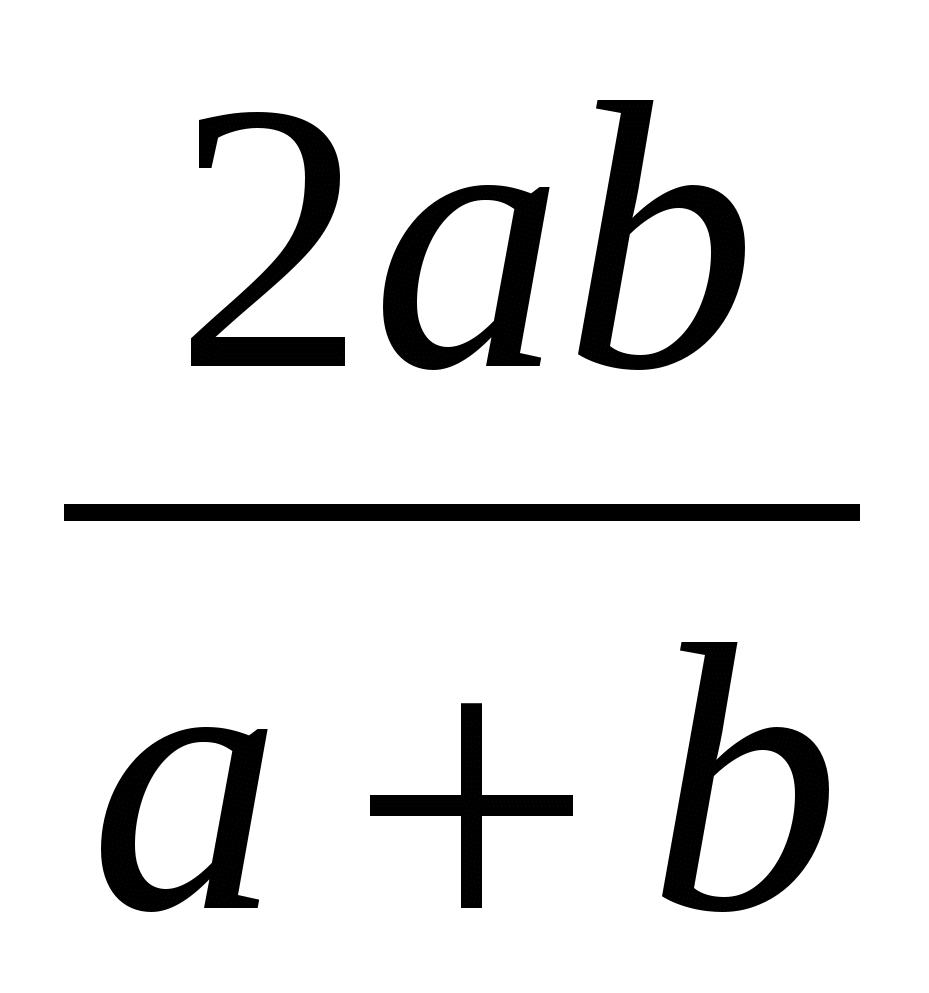

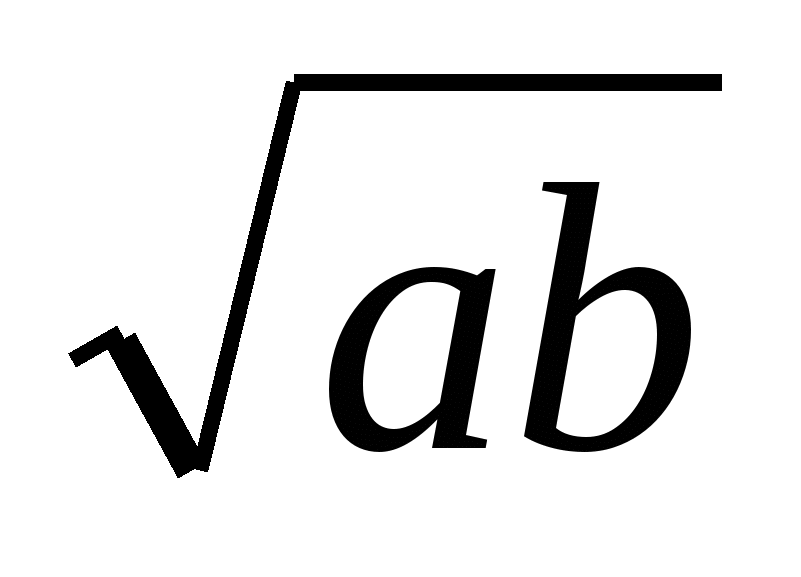

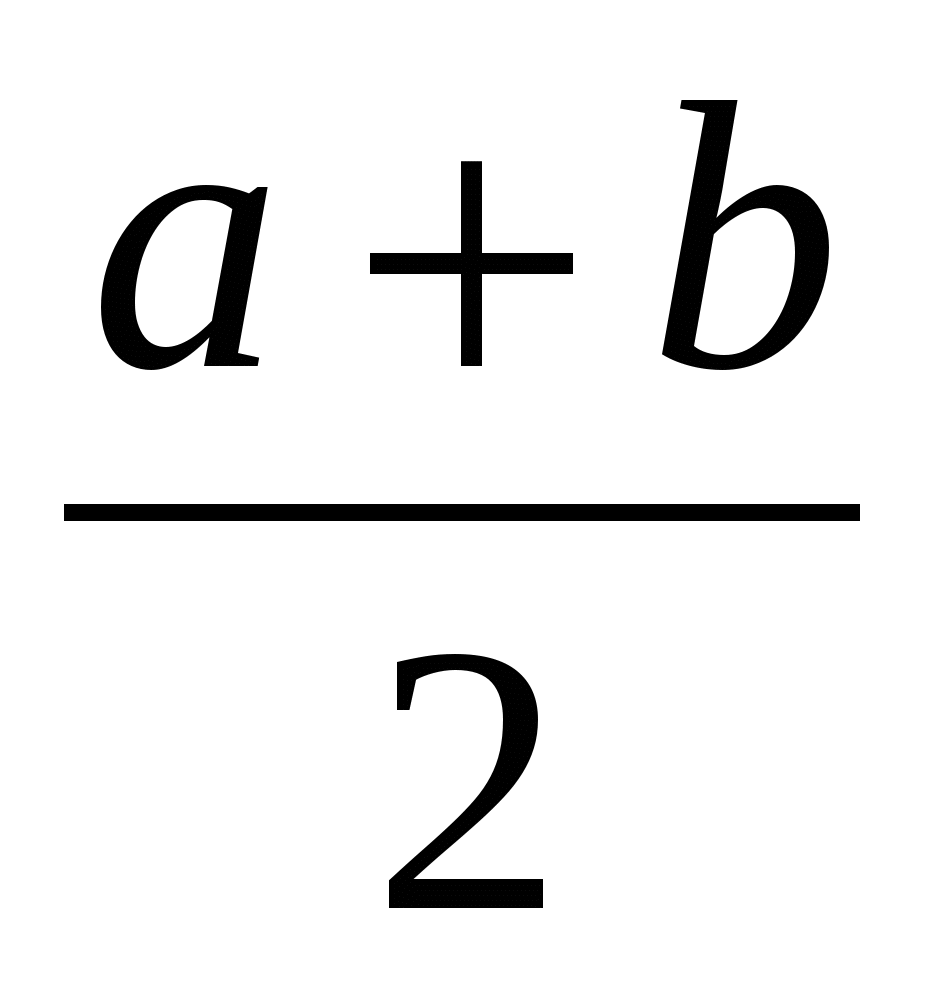

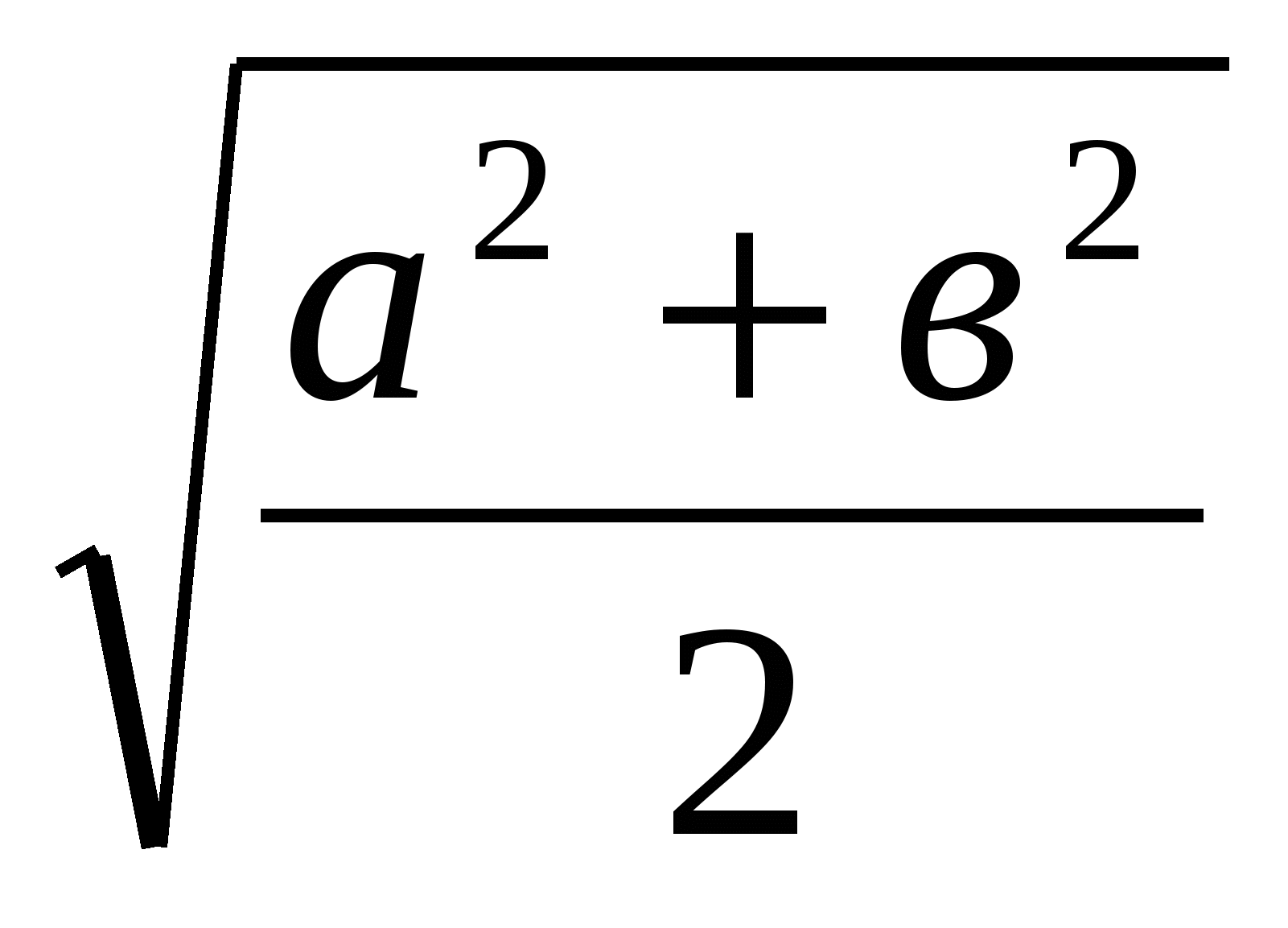 . (ч. т. д )
. (ч. т. д )
Равенство будет, когда а = b, тогда фигура- параллелограмм и доказательство неинтересно, но можно задать ученикам вопрос: какая фигура будет в случае равенства а и b.
Вторая интерпретация теоремы 1 связана с прямоугольным треугольником. Целесообразно привести и ее, с целью повторить геометрию и показать красоту математических заключений.
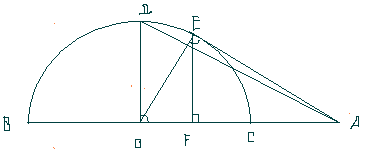
1. Возьмем полуокружность с центром в точке О и диаметром ВС.
2. Проведем  О Д
О Д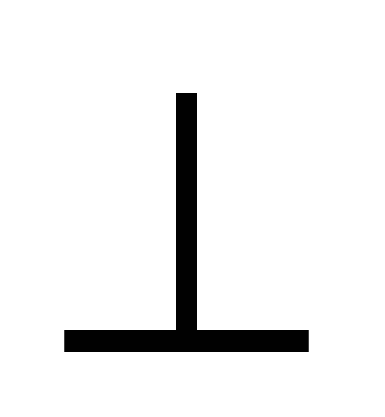 ВС.
ВС.
3. На продолжении ВС возьмем точку А произвольно и проведем АЕ - касательную к окружности.
4. Проведем ЕF 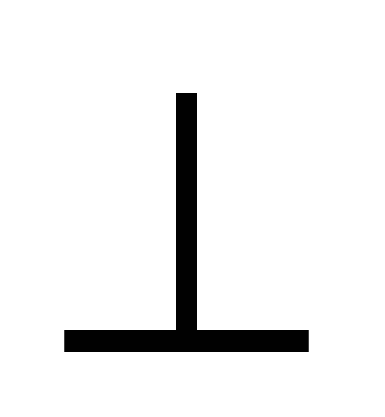 BC/
BC/
5. Пусть АВ=а1, АС=а2, (а1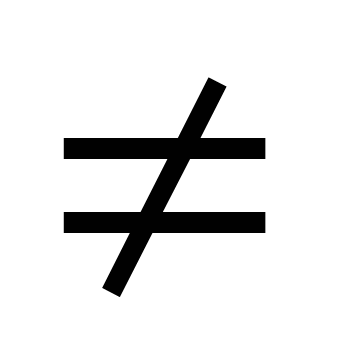 а2), тогда АО =
а2), тогда АО =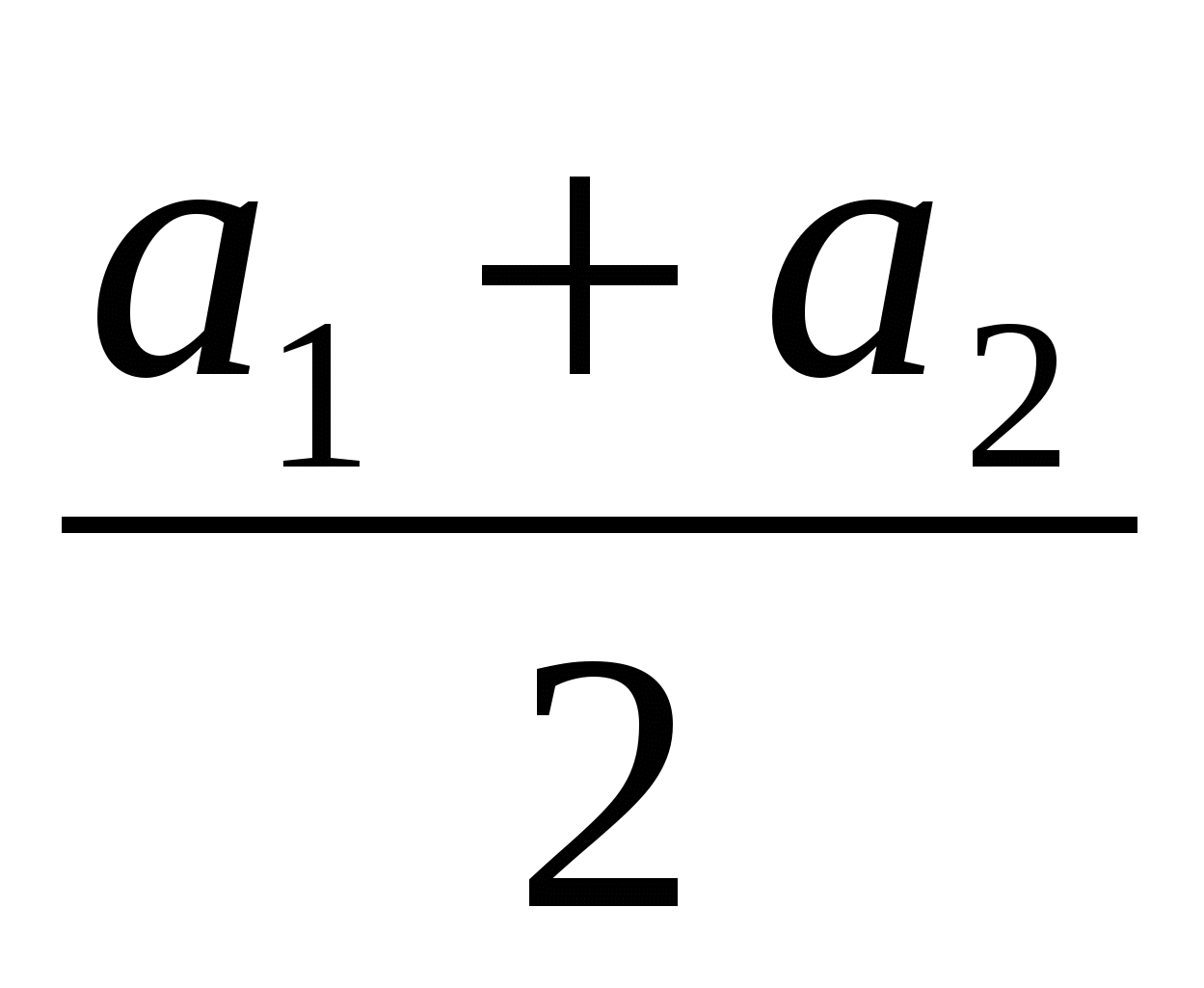 (ВС= а1 - а2,
(ВС= а1 - а2,
ОС = ½( а1 -а2), ОА = а2-½( а1 -а2) = 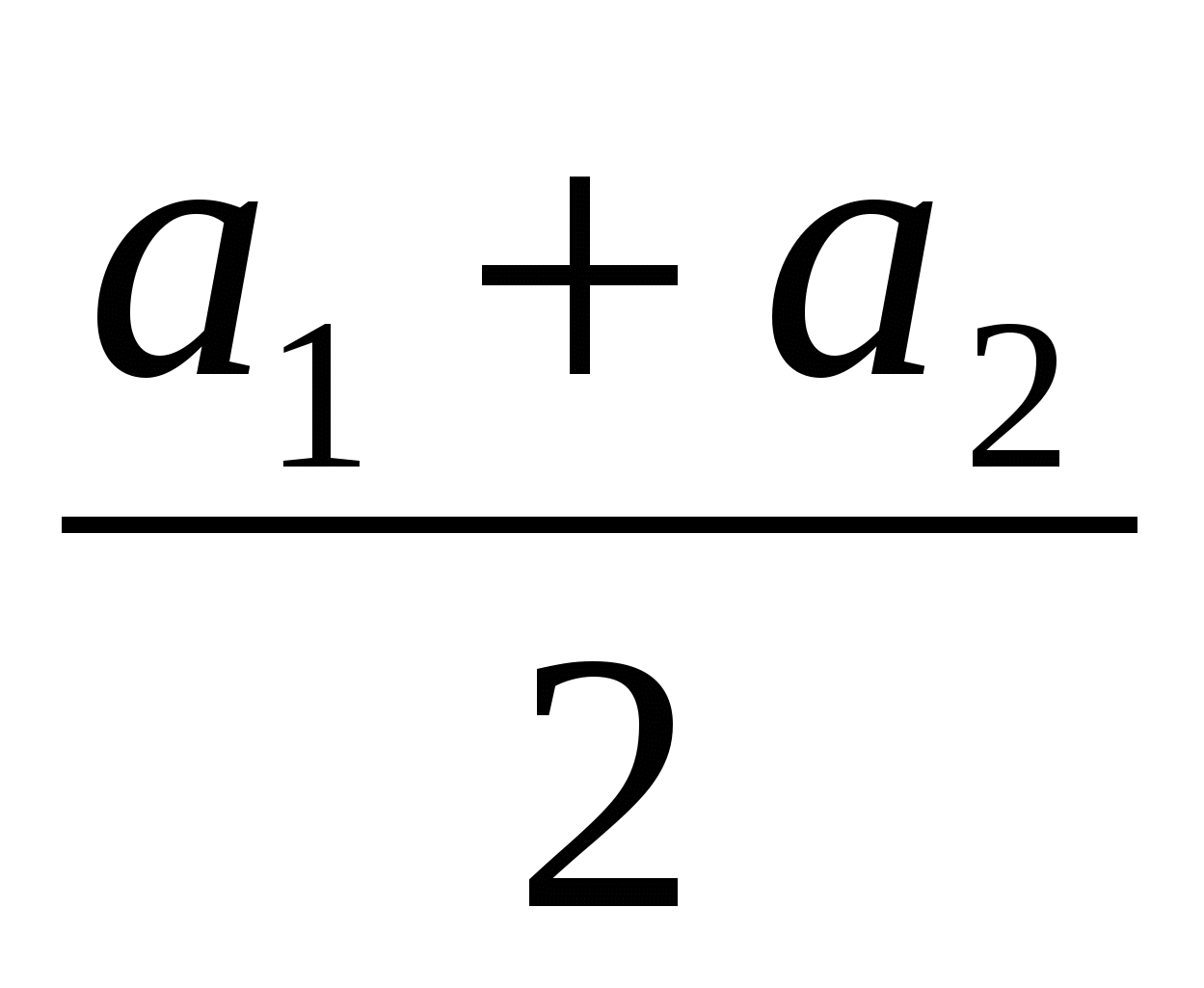
6. Из треугольника ОЕА: АЕ = 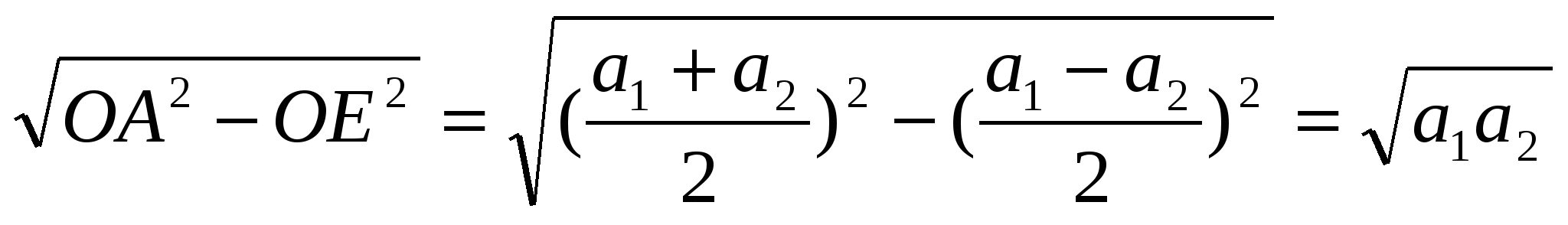
7. Из треугольника ОДА: АД =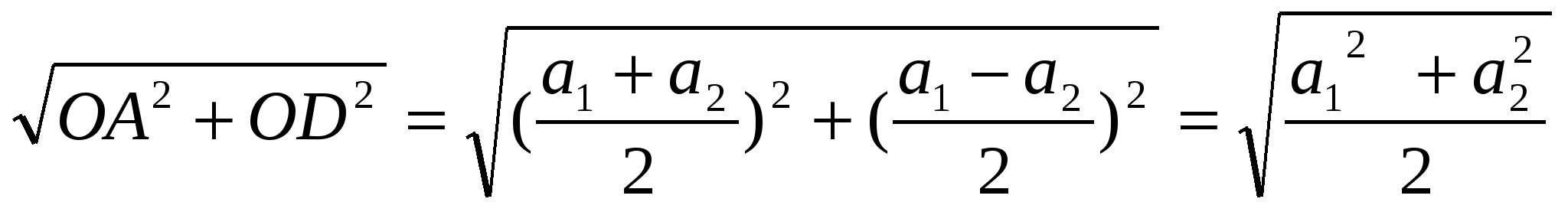
8. AF=AE2/OA, AF=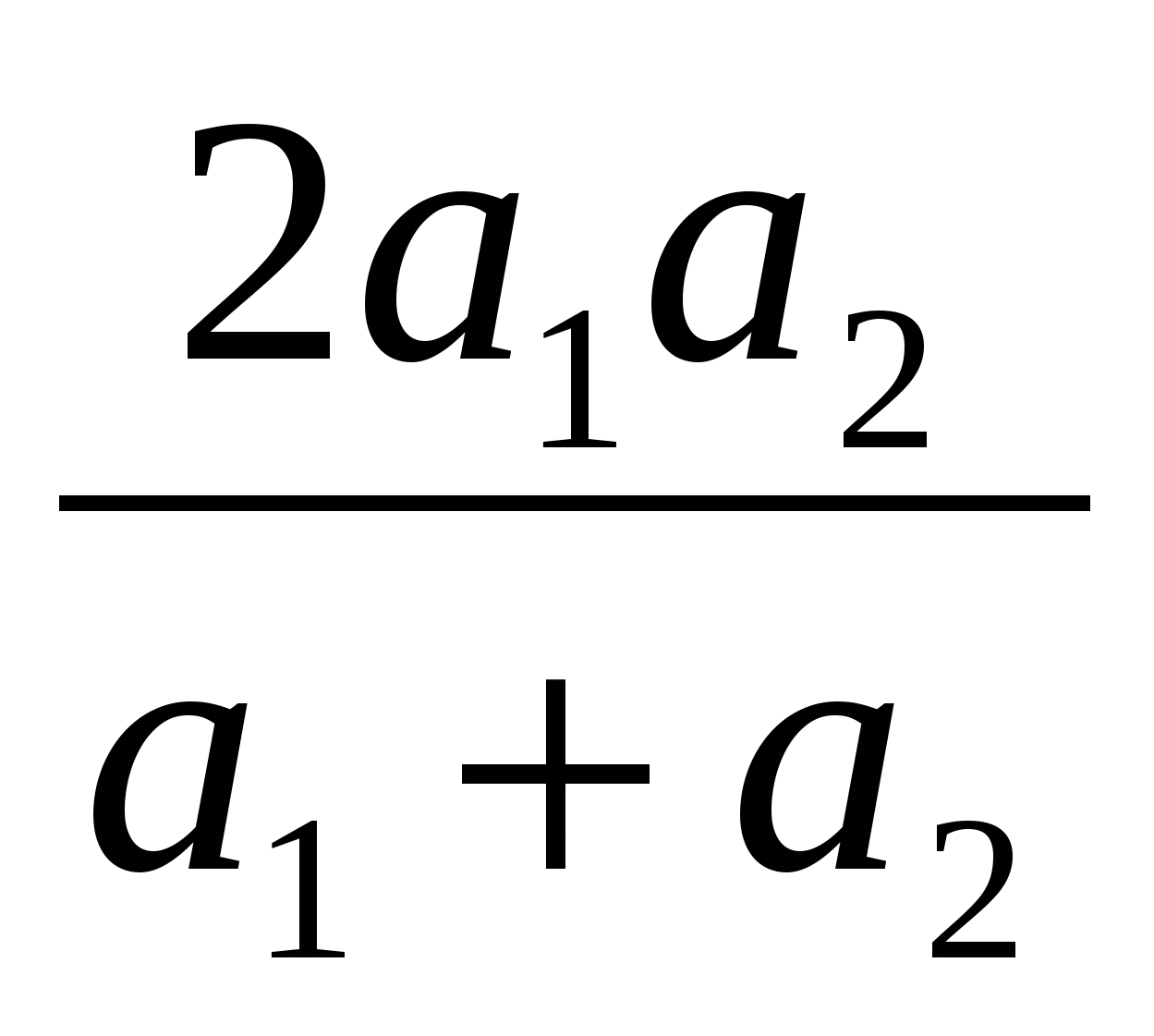 .
.
Таким образом, АЕ - среднее геометрическое полож. чисел а1 и а2
АО - Среднее- арифметическое полож. чисел а1 и а2
АД - Среднее квадратичное полож. чисел а1 и а2
АF - среднее гармоническое полож. чисел а1 и а2
Предложить учащимся самим доказать (исходя из чертежа), что
AF<AE<OA<AD, а равенство при ?.
Замечание: Средним геометрическим двух положительных чисел является также среднее геометрическое между их средним арифметическим и средним гармоническим. (Предложить сам-но в этом убедиться).
5.Применение средних величин при решении некоторых
геометрических и алгебраических задач
Есть много интересных геометрических интерпретаций частных случаев теоремы 1.
Пример 1.
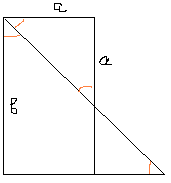
a2/2 +b2/2 ≥ ab ( и далее )
Пример 2.
Можно предложить задачи:
1) Окружности диаметров а и в касаются внешним образом. Доказать, что отрезок их общей внешней касательной, заключенный между точками касания, равен среднему геометрическому их диаметров.
2. Окружности диаметров а и в не имеют общих точек, а отрезок их общей внешней касательной, заключенный между точками, равен среднему арифметическому диаметров. Докажите, что расстояние между центрами окружностей равно среднему гармоническому диаметров.
3). Подумайте, как с помощью рисунка к задаче 1 доказать, что
Н(а; в) ![]() G(а; в)
G(а; в)
( найти расстояние от точки касания окружностей до внешней касательной, а треугольник с вершинами в трех точках касания - прямоугольный).
Пример3. Неравенство Коши и объемы.
Ниже пример доказательства неравенства Коши применительно для трех положительных чисел, которое приведено в журнале « Квант», кроме этого еще некоторые задачи и упражнения, опубликованные в 1975-2000г в этом же журнале.




Применение средних величин при решении уравнений, неравенств и других задач.
1) Решить уравнение:
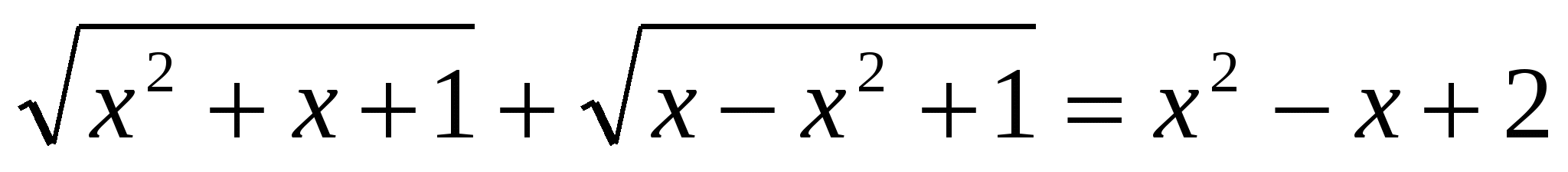 .
.
Решение:
Применим неравенство Коши к левой части уравнения:
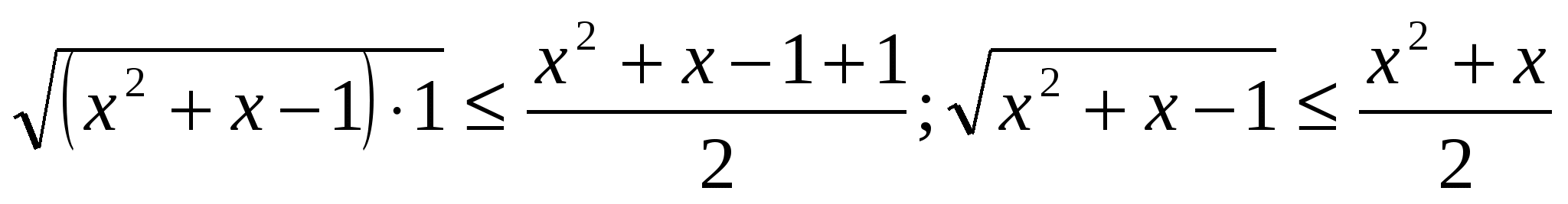 (1)
(1)
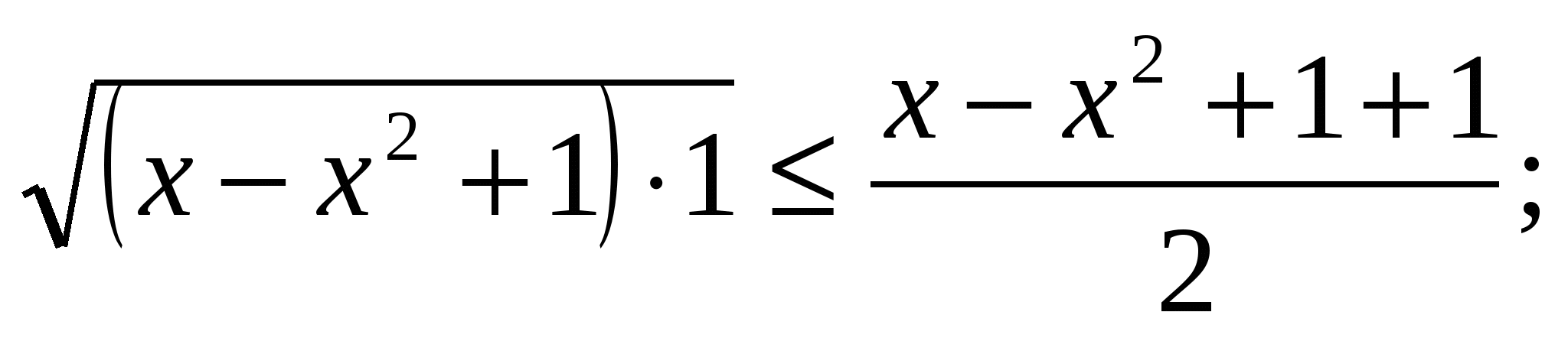
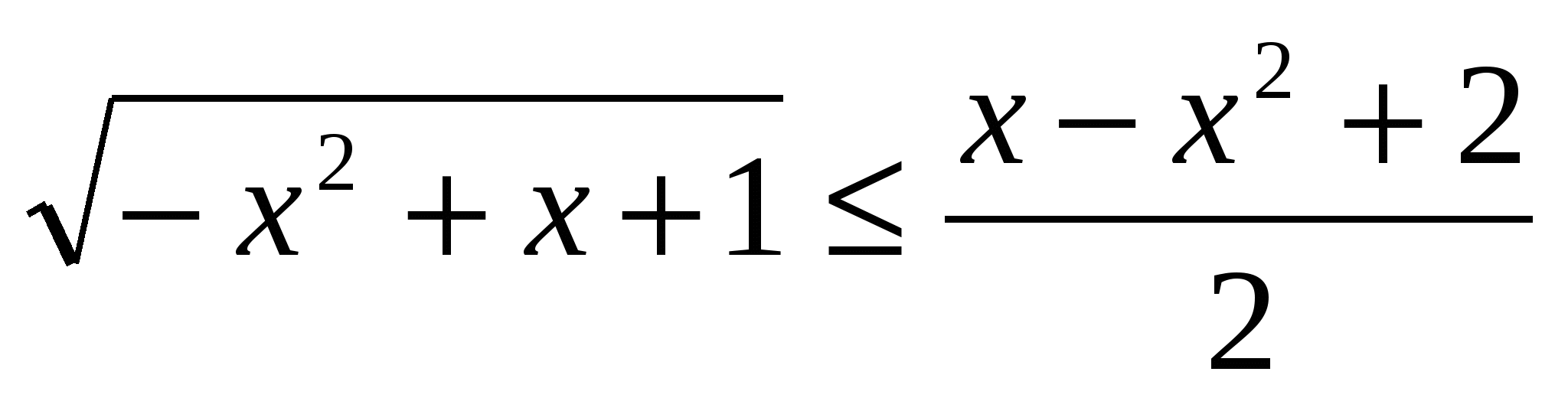
Сложив (1) и (2): 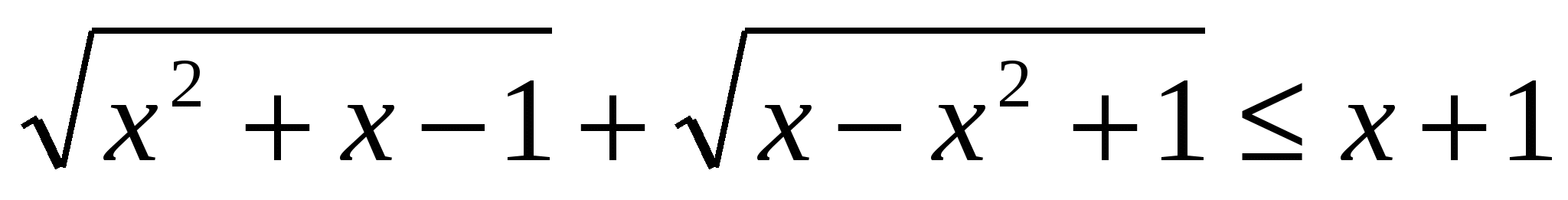 ;
;
Таким образом, х2-х+2 х+1; (х-1)2
х+1; (х-1)2 0; х=1 Ответ: х=1.
0; х=1 Ответ: х=1.
2) Решить уравнение:
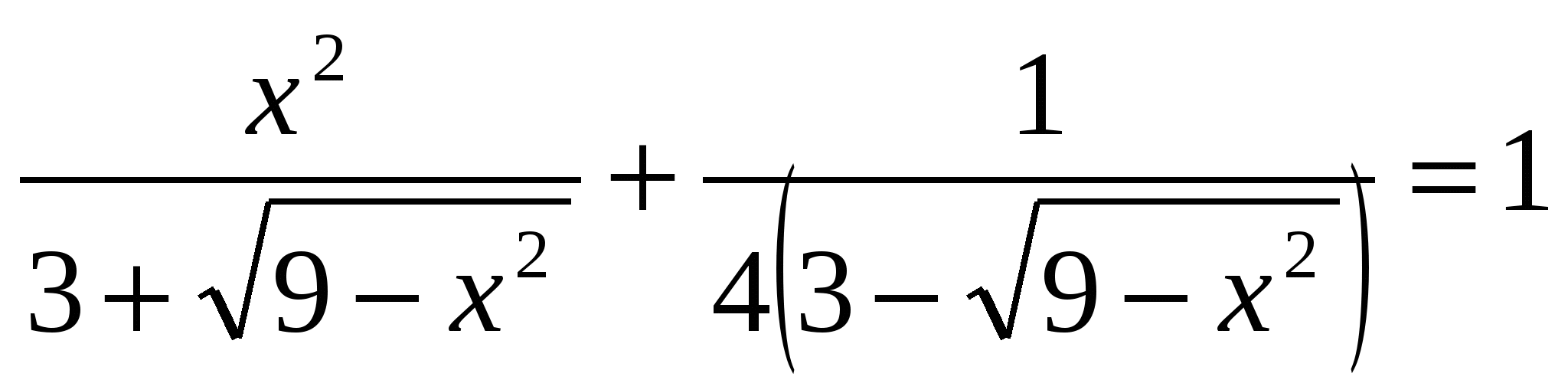 ;о.о.у:
;о.о.у: 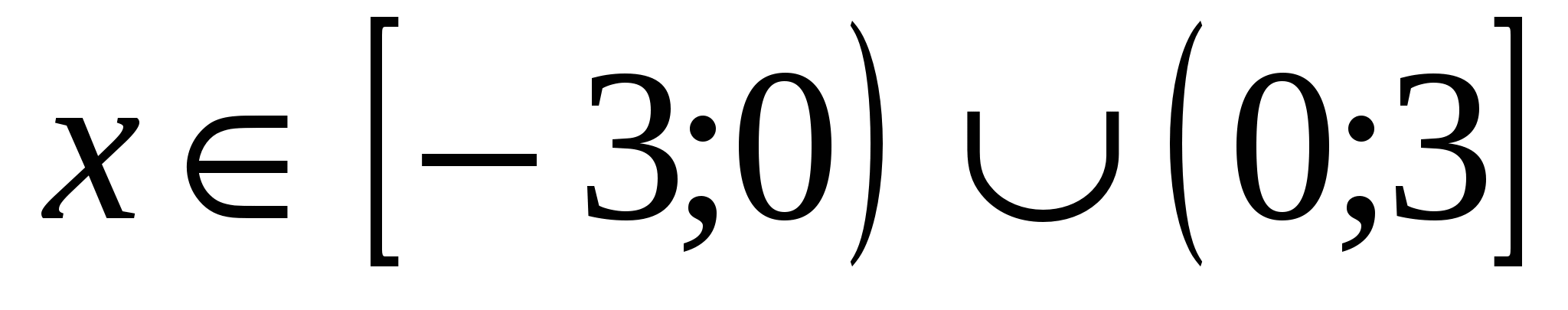
Решение:
Подстановка: 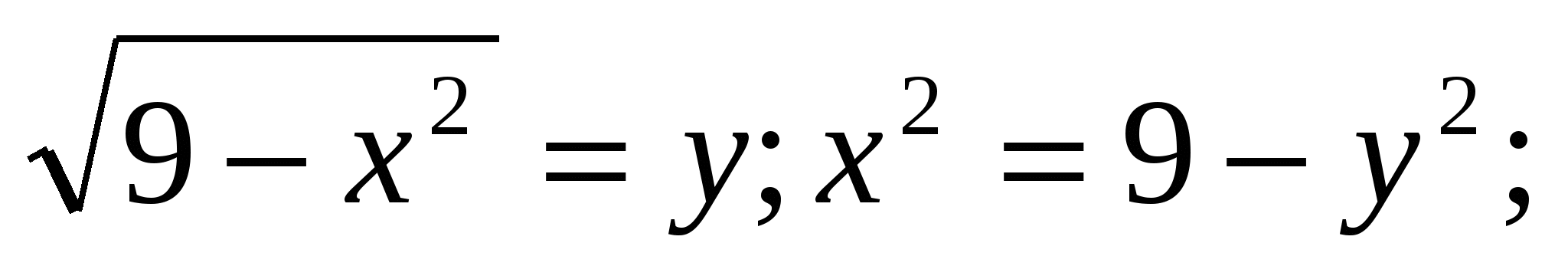
Уравнение принимает вид: 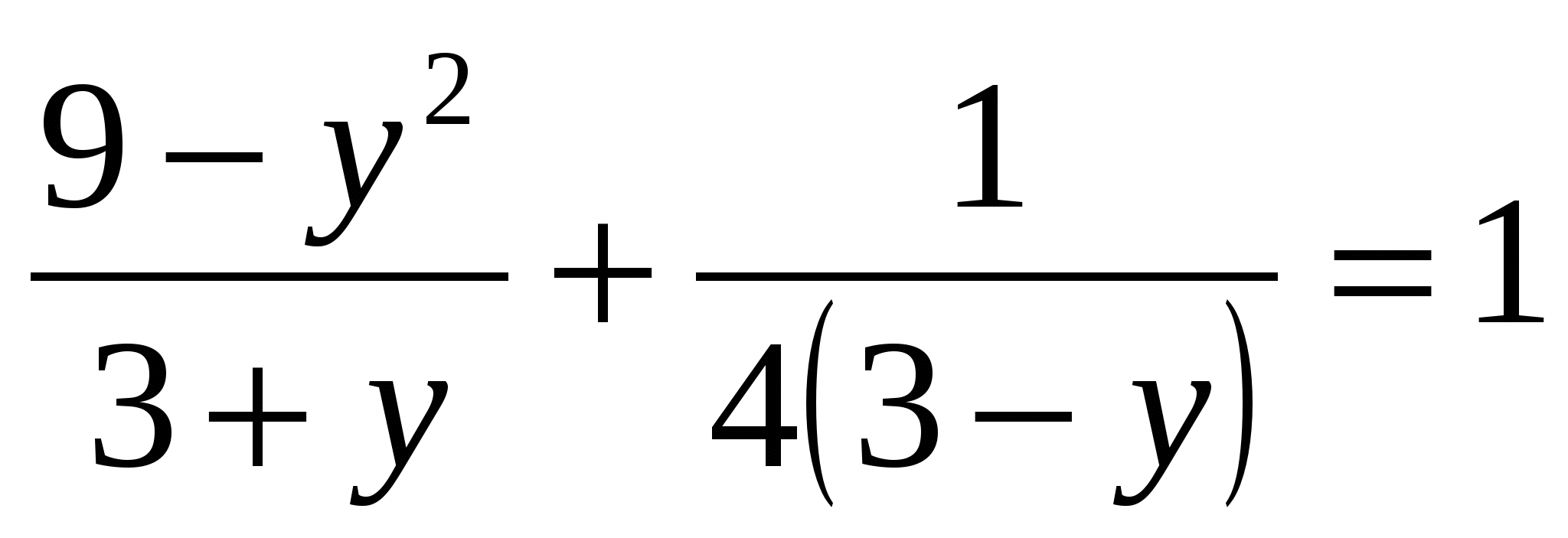 ;
;
Применим н. Коши: 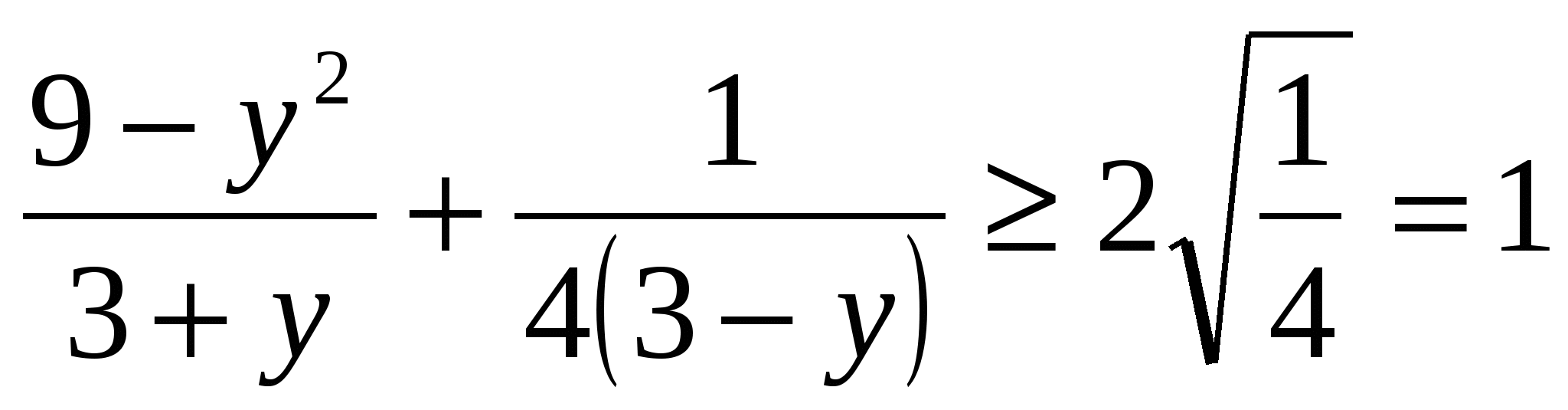 ; значит, слагаемые равны (т.к неравенство обратилось в равенство)
; значит, слагаемые равны (т.к неравенство обратилось в равенство)
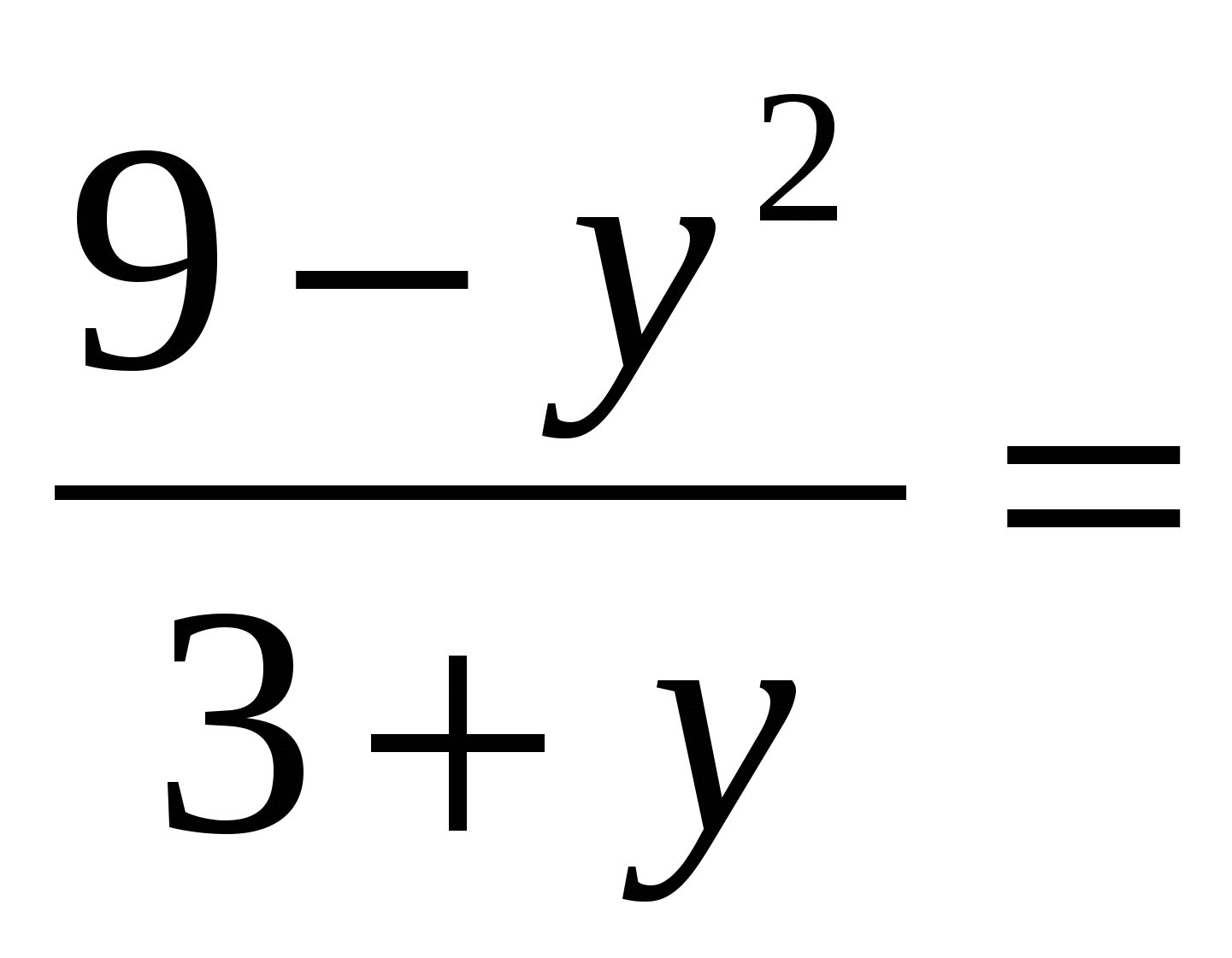
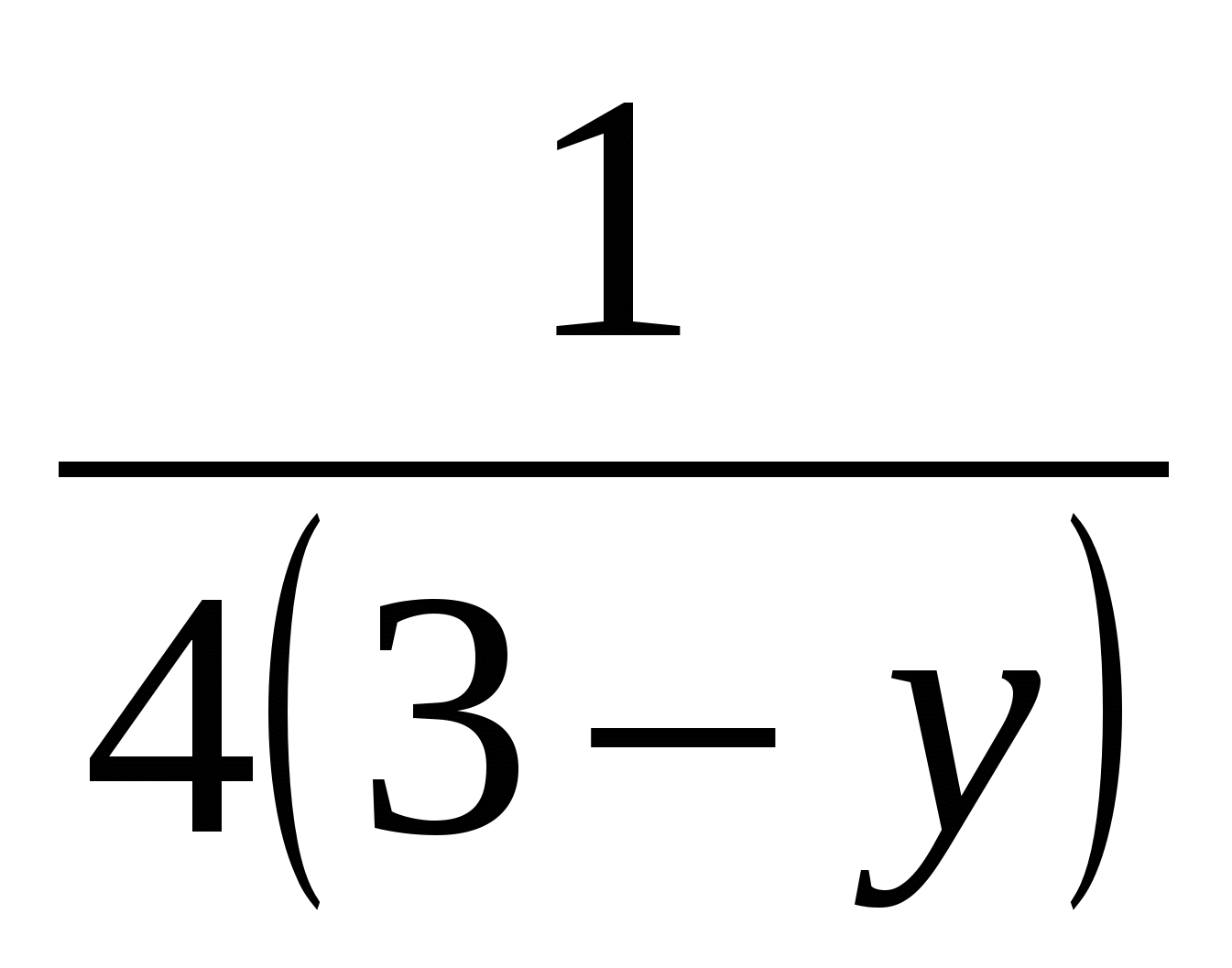 ; у≥0; у+3›0
; у≥0; у+3›0
3-у=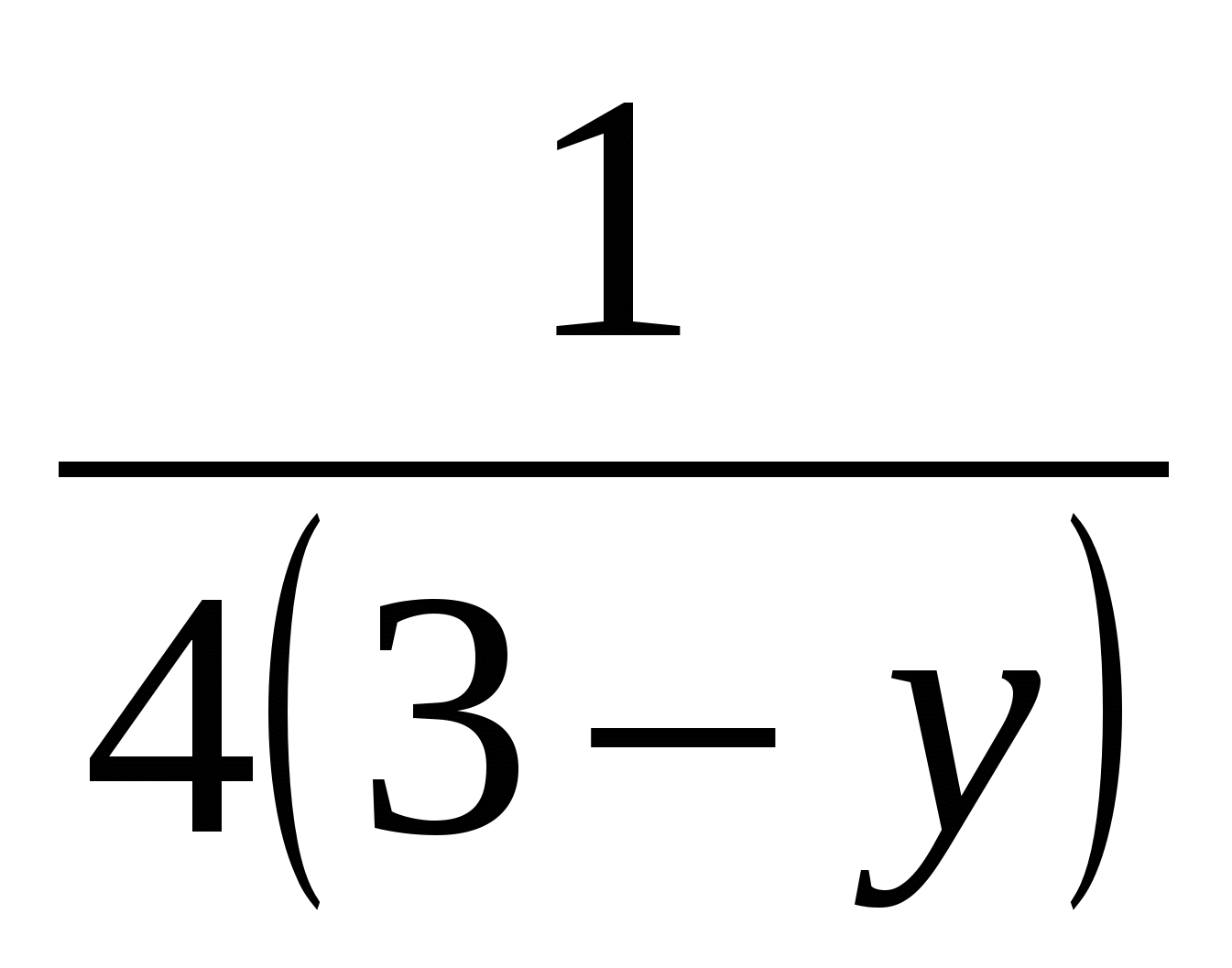 ; 4(3-у)2=1/4; 3-у=
; 4(3-у)2=1/4; 3-у=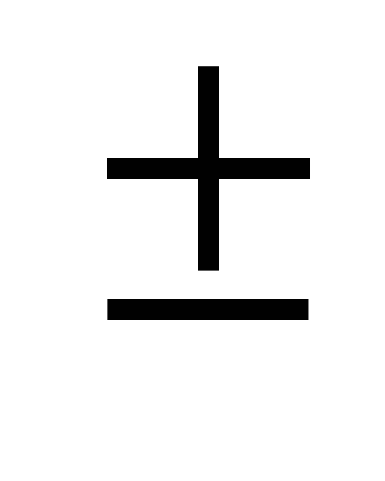 1/2; 1) у=5/22, , х =
1/2; 1) у=5/22, , х =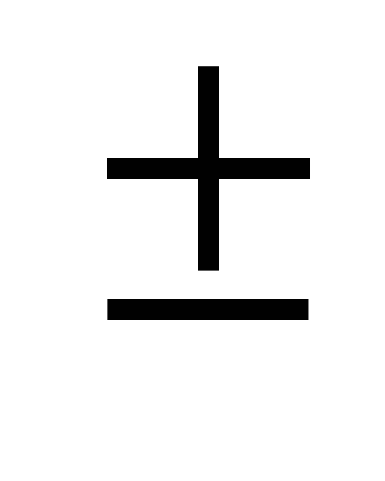
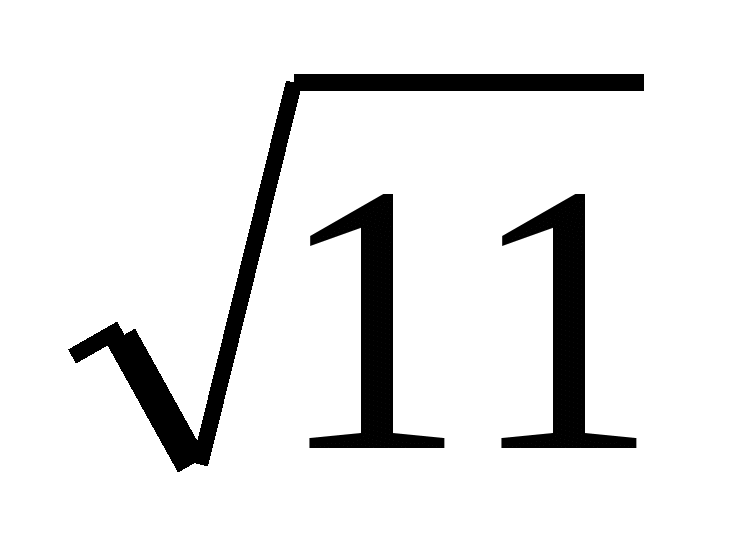 /2
/2
2) у=7/2, х2=-13/4- корней нет.
Ответ: х =![]()
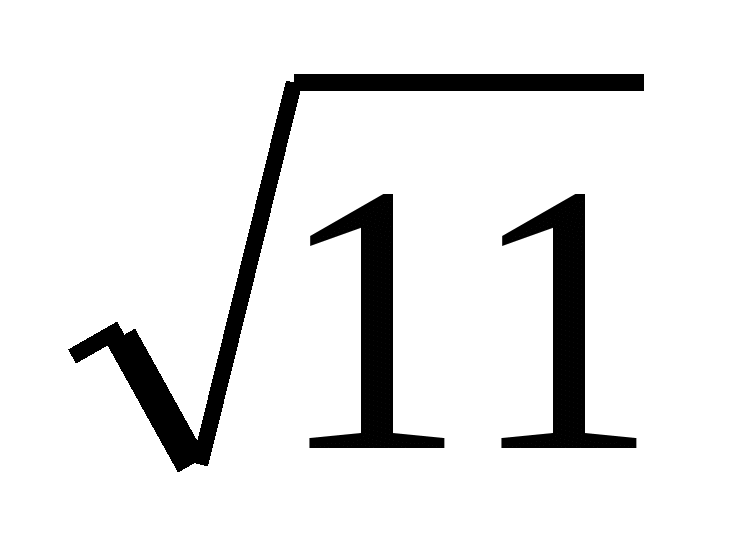 /2
/2
3) Решить уравнение:
2х4+2у4 = 4ху - 1. (*)
Решение:
Применяя н. Коши: 2х4+2у4≥2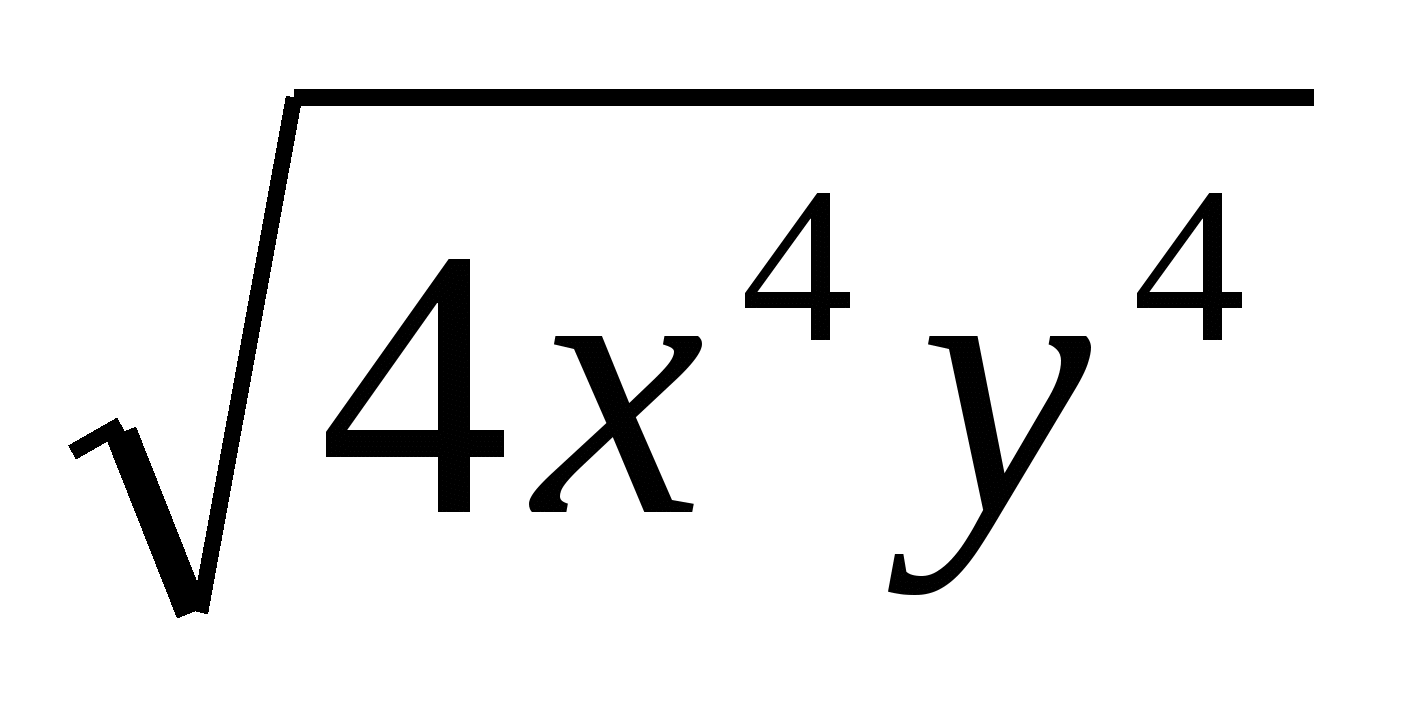 , 2х4+2у4≥4х2у2, (2ху-1)2
, 2х4+2у4≥4х2у2, (2ху-1)2 0,
0,
xy =1/2, у =1/2х.
Подставляя в уравнение (*) и решив его, получим: 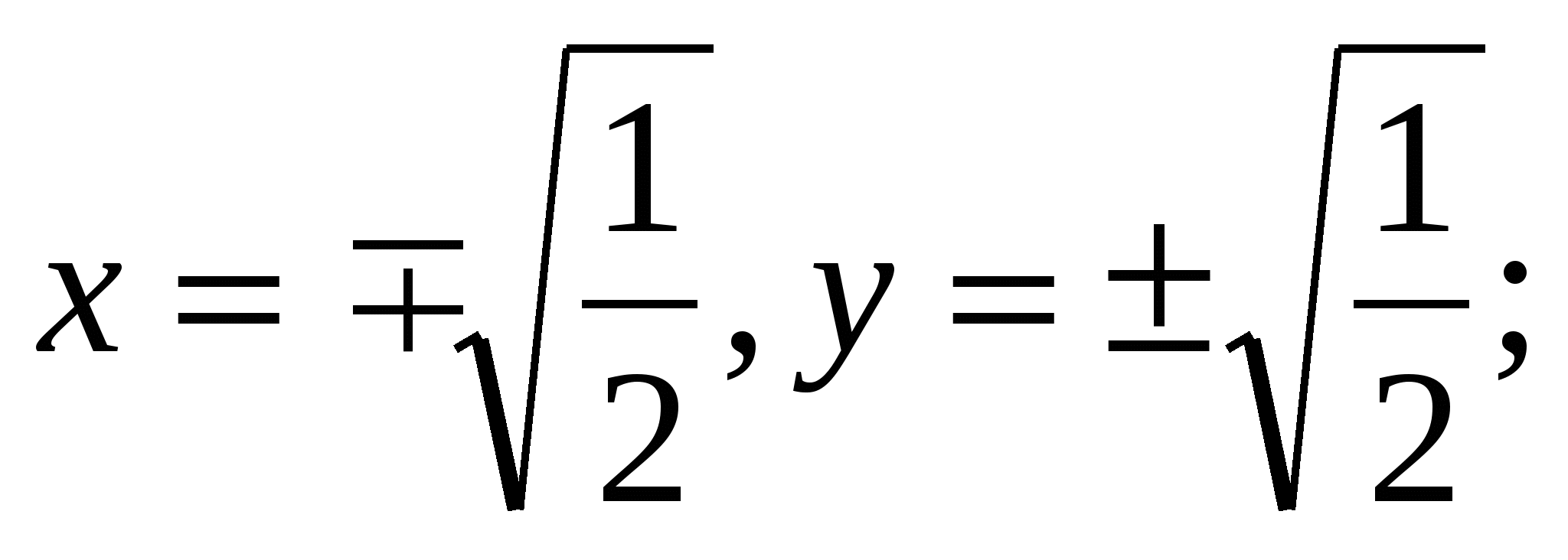
4) Решить уравнение:
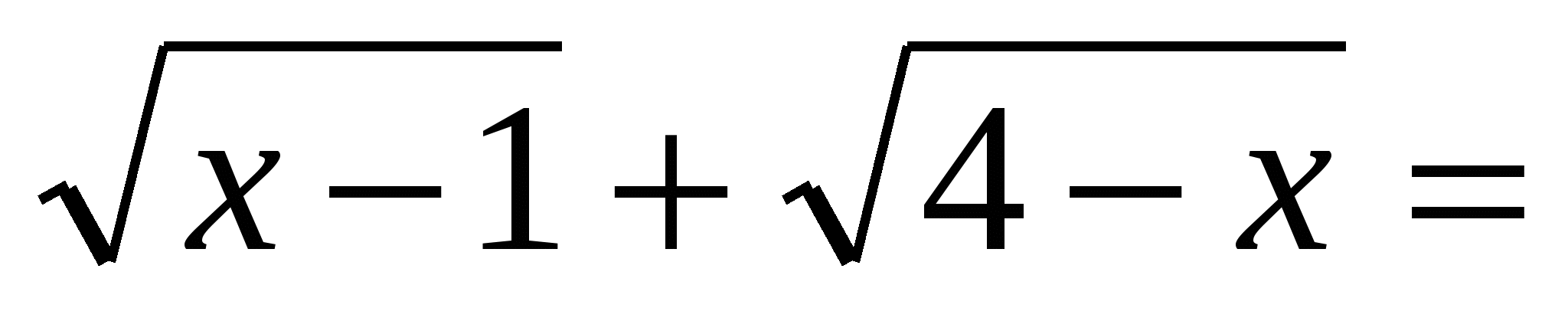 х2+6х+11.
х2+6х+11.
Решение:
Применяя н. Коши: 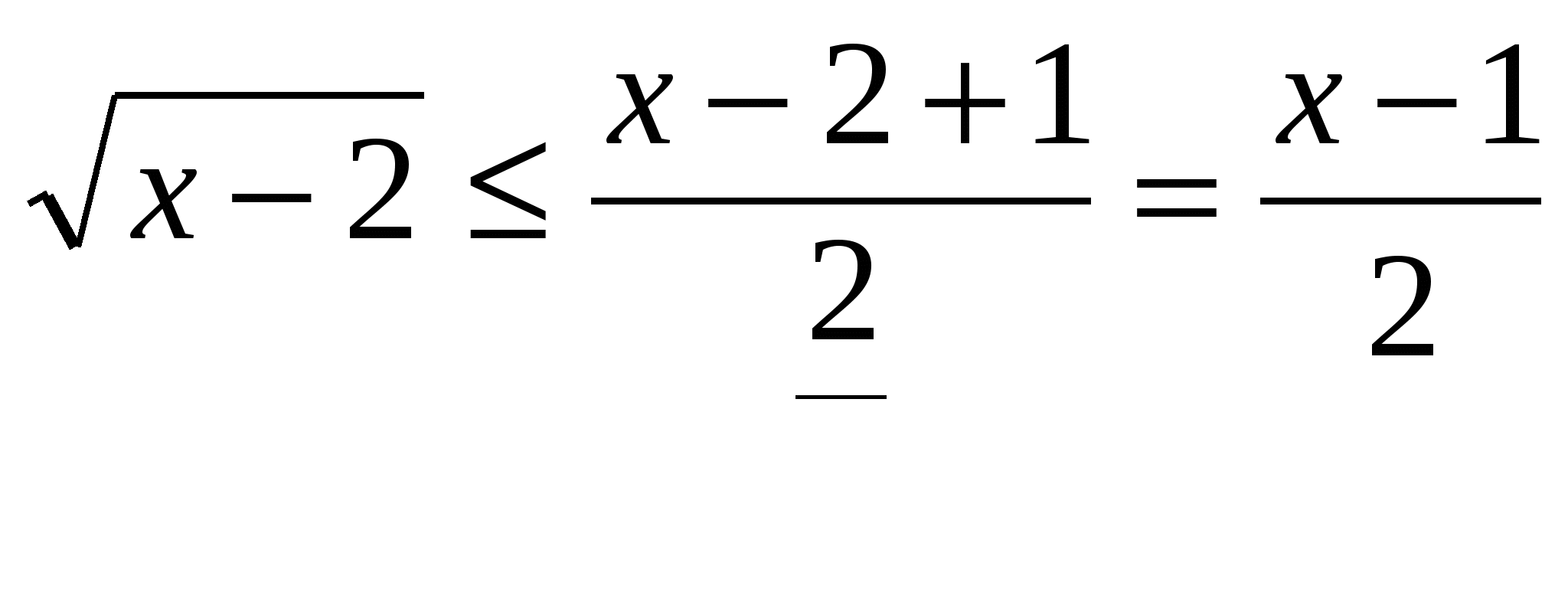 ,
,
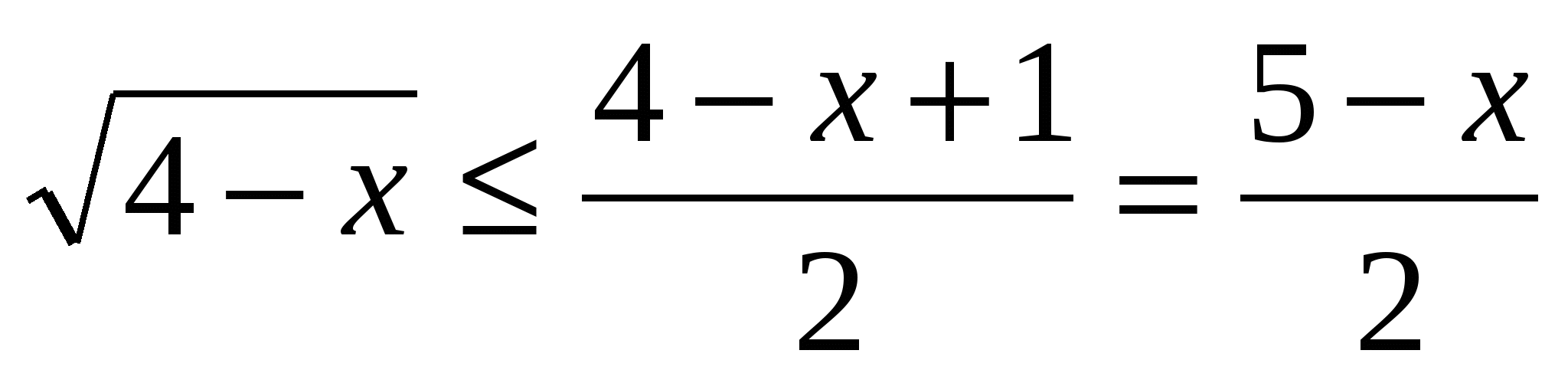 ,
,
Сложим обе части неравенств и получим, что 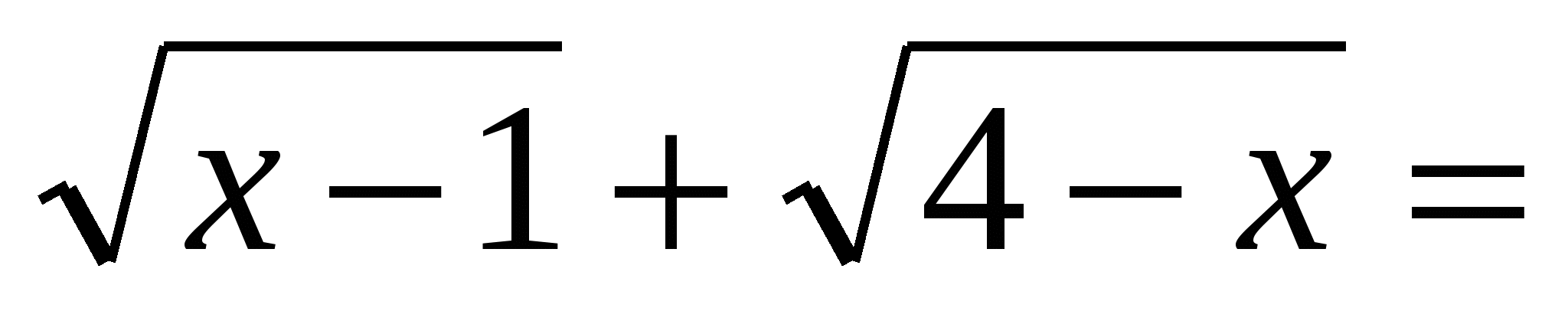 2.
2.
а х2+6х+11=(х-3)2+2 ≥2 ,
Значит, уравнение имеет решение только тогда, когда его левая и правая части равны 2. Легко заметить, что х=3.
5) Доказать, что log1719>log1920.
Доказательство:
Докажем, что 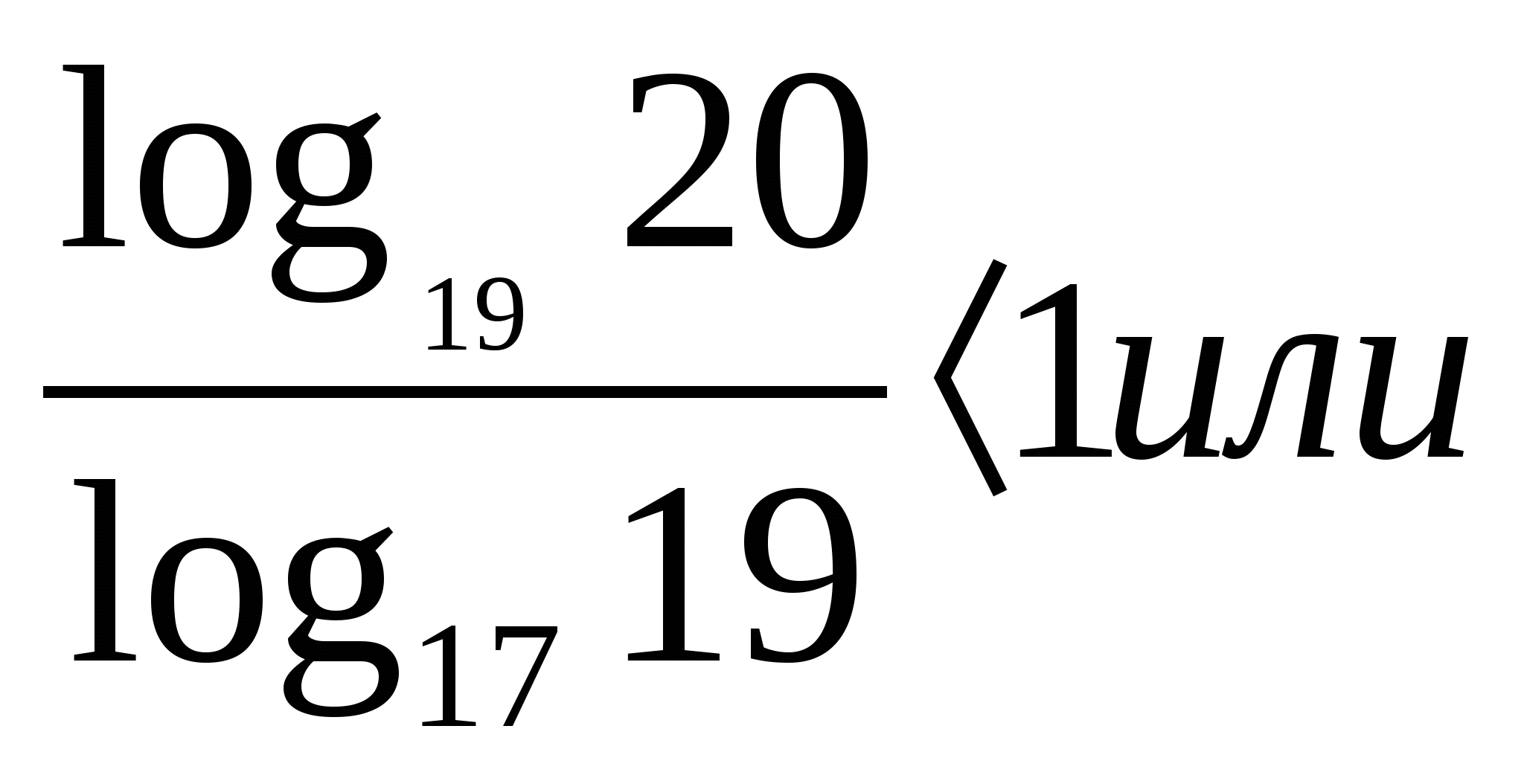 log1920·log1917<1.
log1920·log1917<1.
По н. Коши log1920·log1917
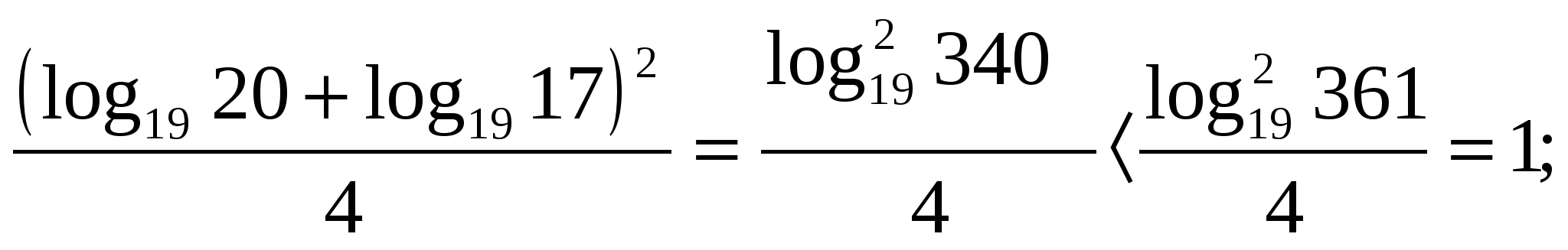
Т.е log1719>log1920.
6) Решить неравенство: ((sin2 ( x+ y )+ 2 sin(x + y)+2)log2(3x+3-x)  1.
1.
Решение:
Перепишем неравенство: (sin(x + y)+1)2+1≥1, 3x+3-x ≥ 2 (н. Коши), значит,
log2(3x+3-x) ≥1.
Таким образом, неравенство имеет решение только в случае равенства:
((sin2 ( x+ y )+ 2 sin(x + y)+2)log2 (3x+3-x) = 1, значит,
.sin(x + y)=-1, а 3х = 1.
Ответ:(0; -П/2+Пк; к є Z).
7) При каких х функция f(x)=(1+2х)4(1-2х)достигает
на отрезке[0; 1/2]наибольшего значения?
Решение:
f(x)=¼·(1+2х) (1+2х) (1+2х) (1+2х)(4-8х),
Найдем среднее арифметическое :
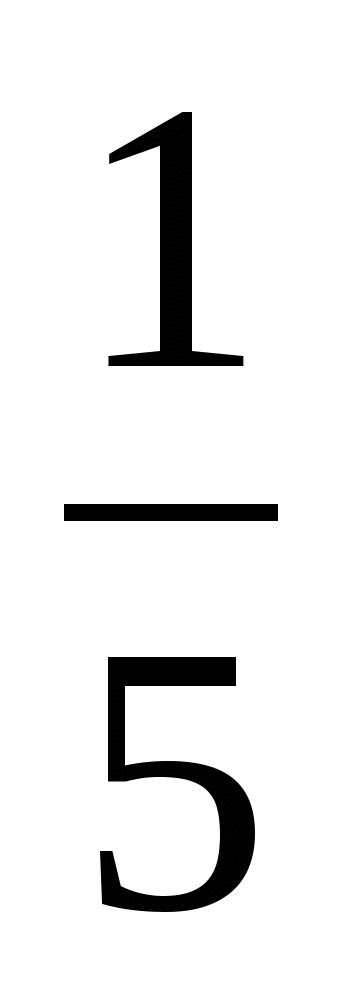 ((1+2х)+ (1+2х)+ (1+2х)+ (1+2х)+ (4-8х))=
((1+2х)+ (1+2х)+ (1+2х)+ (1+2х)+ (4-8х))=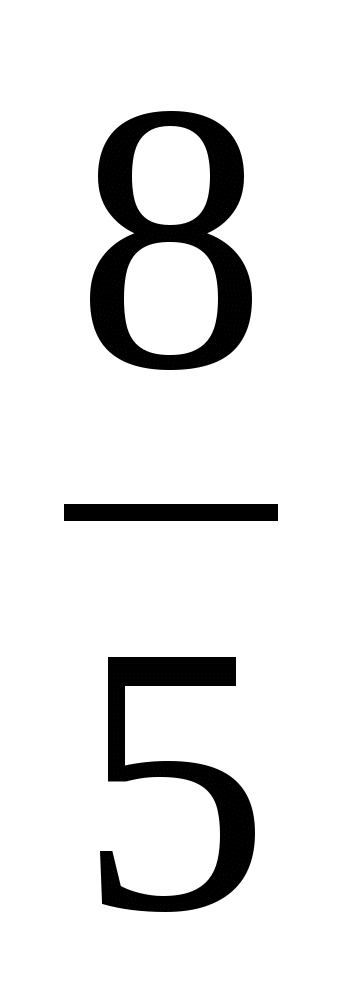 ,
,
f(x) 
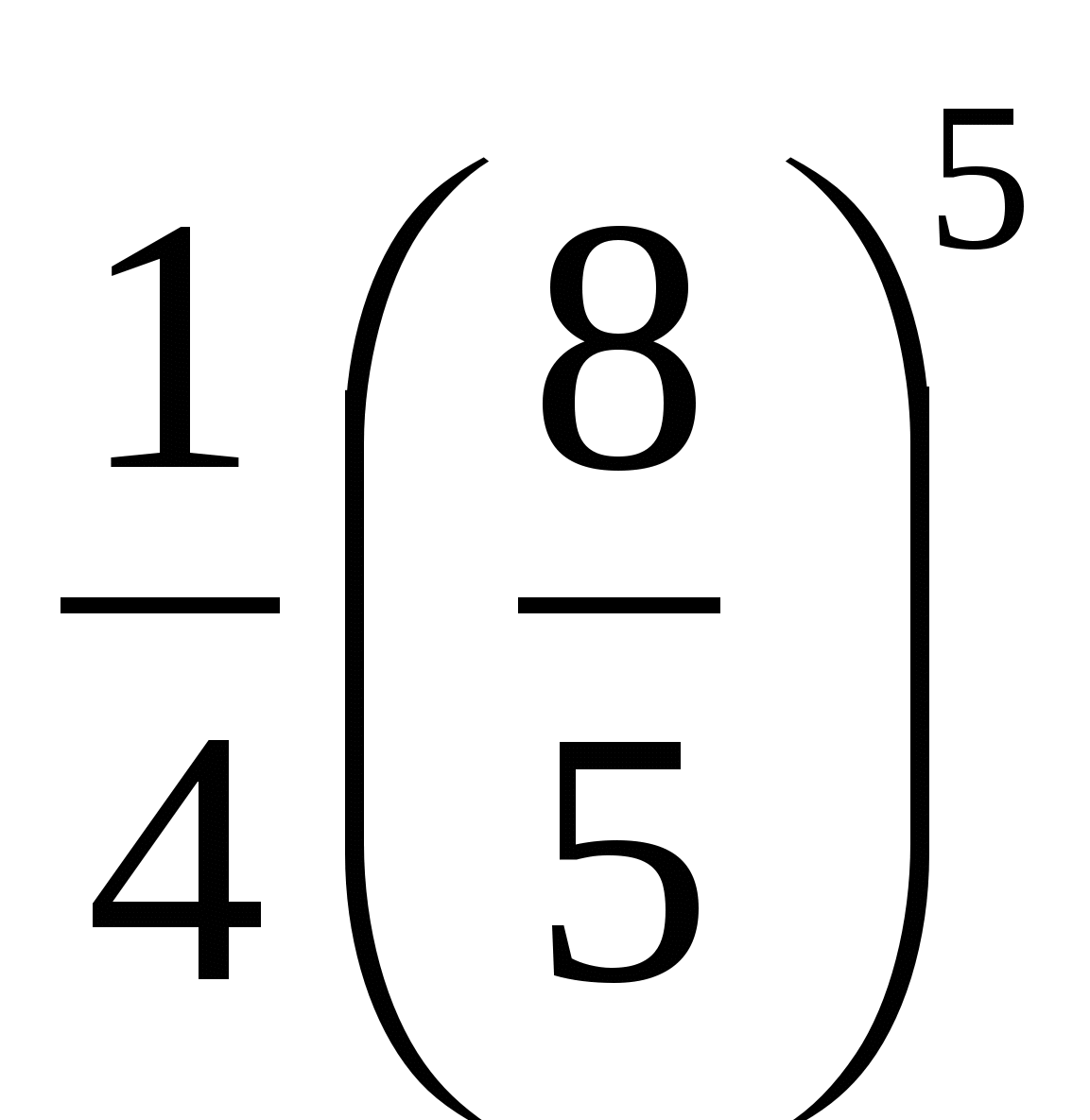 , значит,
, значит,
f(x) достигает своего наибольшего значения, когда(1+2х)= (4-8х), х = 0,3
8) Найти наибольшее и наименьшее значение функции f(x)=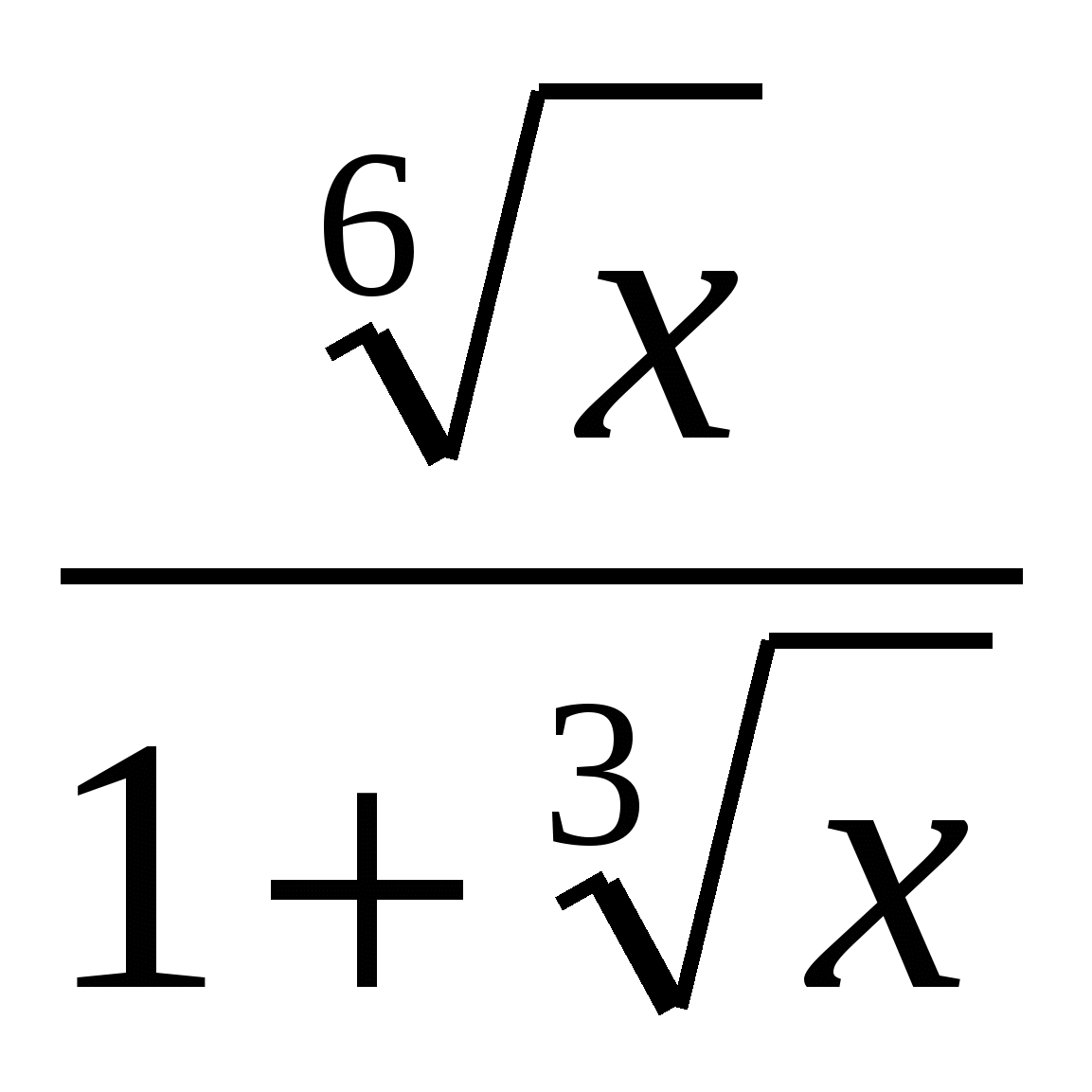 .
.
Решение:
Записать ![]() =
=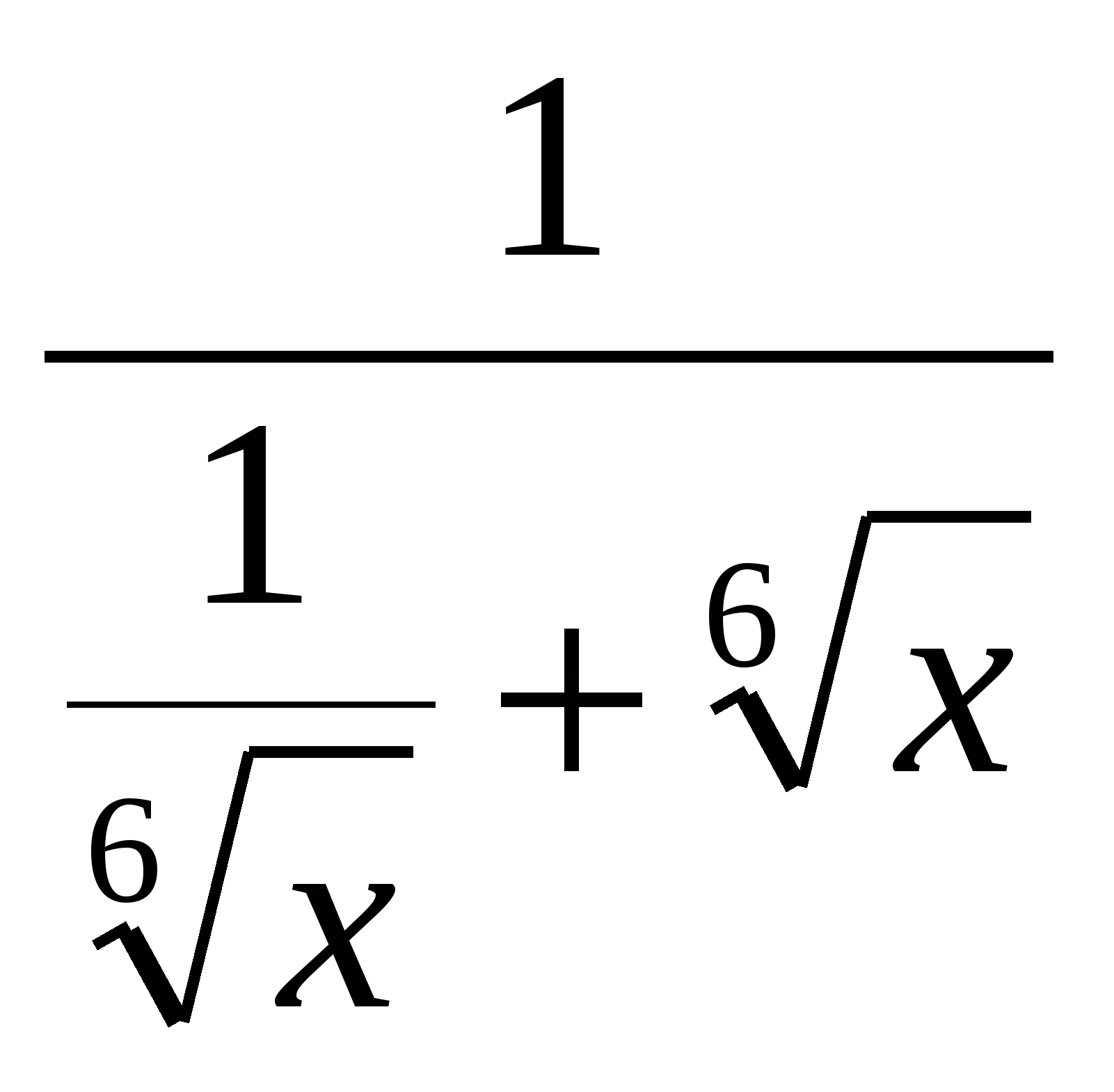 и применить н. Коши для знаменателя этой дроби.
и применить н. Коши для знаменателя этой дроби.
Ответ: наименьшее значение f(x) равно 0
наибольшее значение (x )равно ½.
Предложить ученикам решить самостоятельно или на усмотрение учителя такие задачи:
а)Найти наименьшее значение f(x)=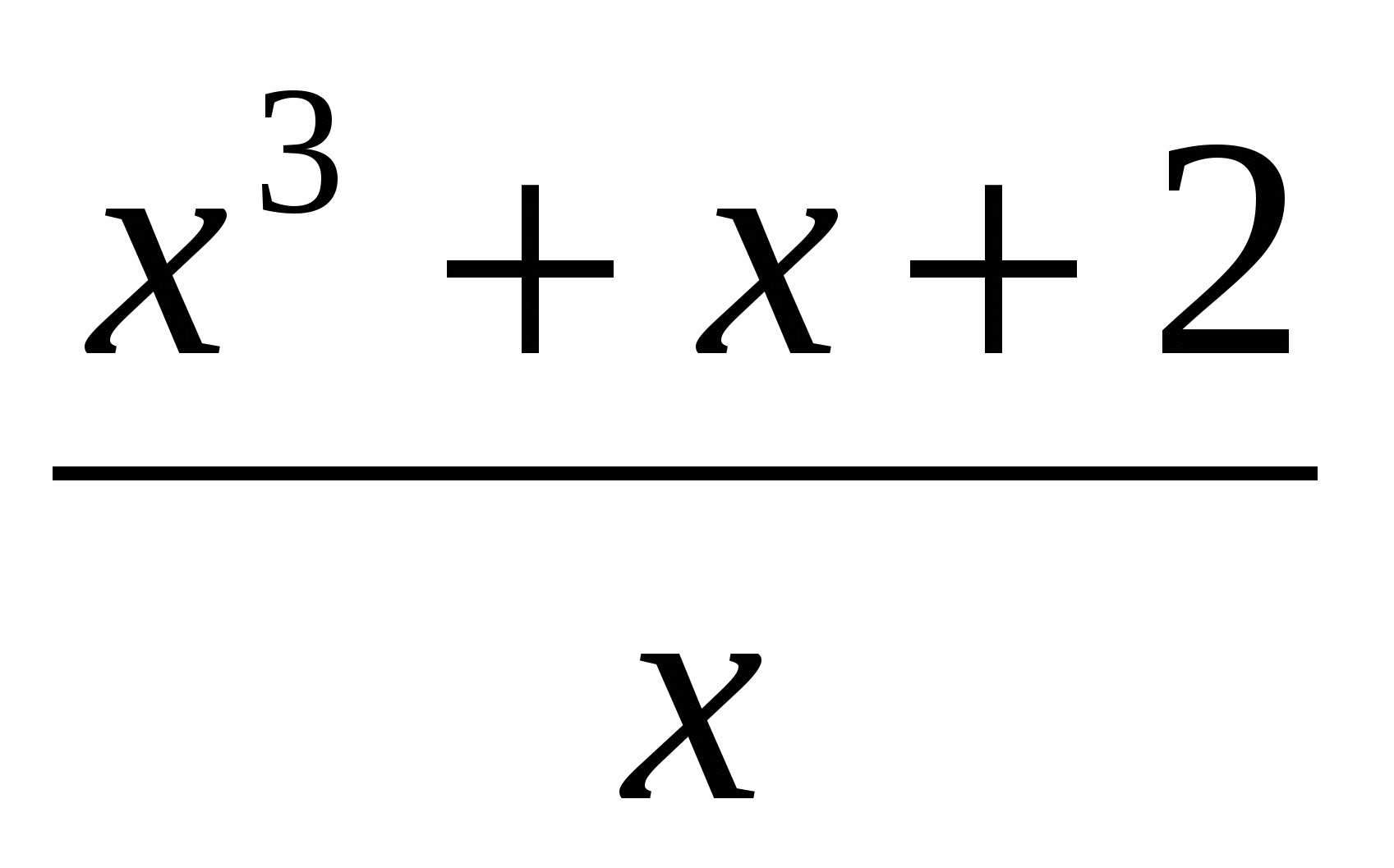 ; где х - положительное число;
; где х - положительное число;
б) Найти наибольшее значение f(x)=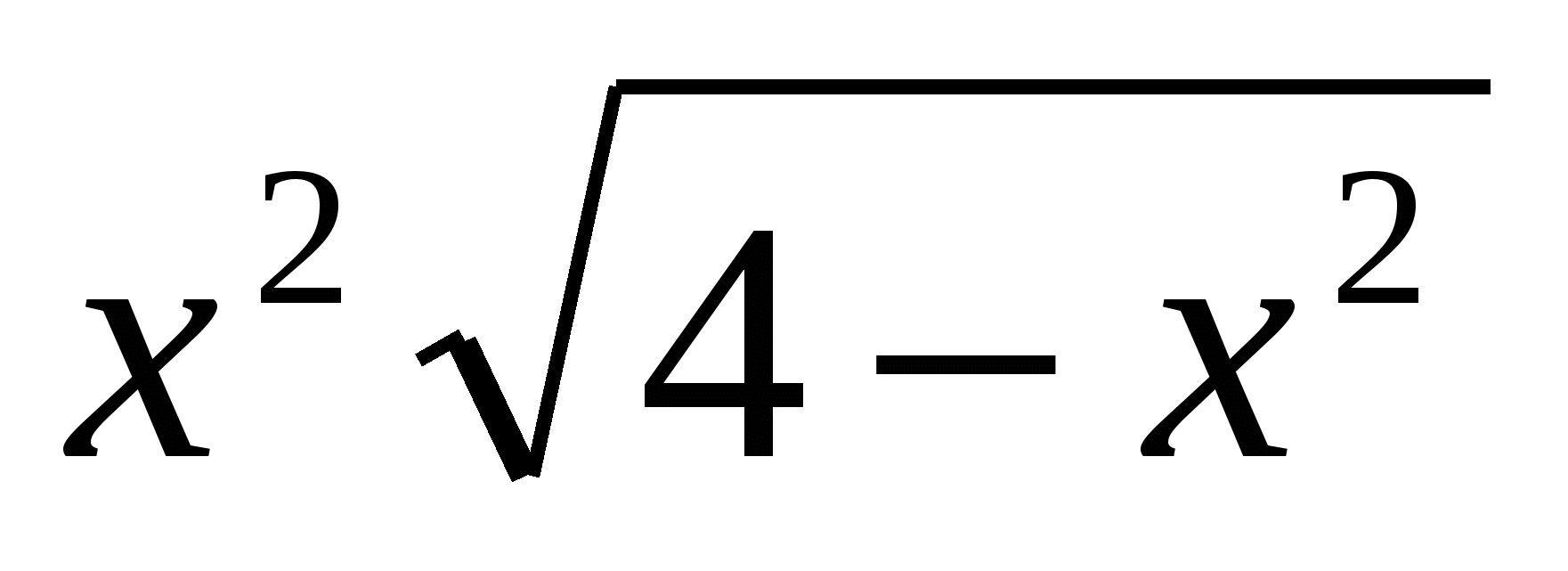 на отрезке [-2;2].
на отрезке [-2;2].
9)Доказать, что если А+В+С= π, то ( sin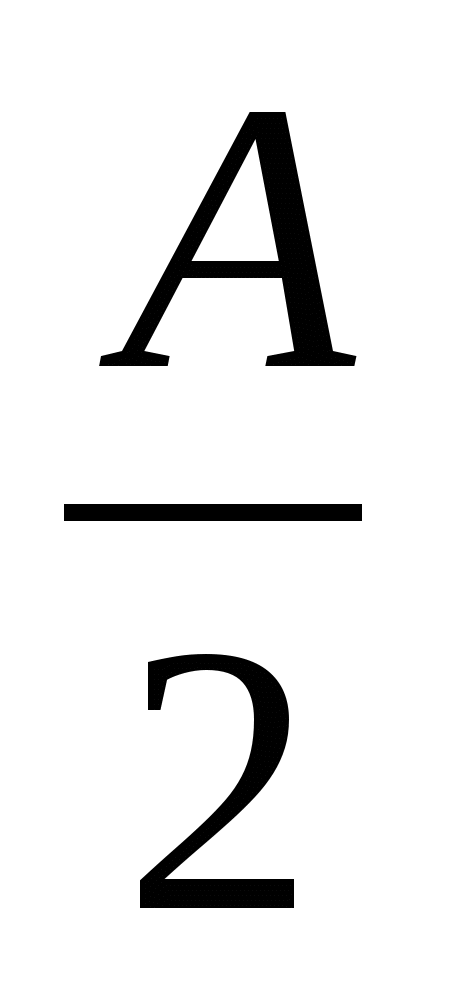 )-1 + ( sin
)-1 + ( sin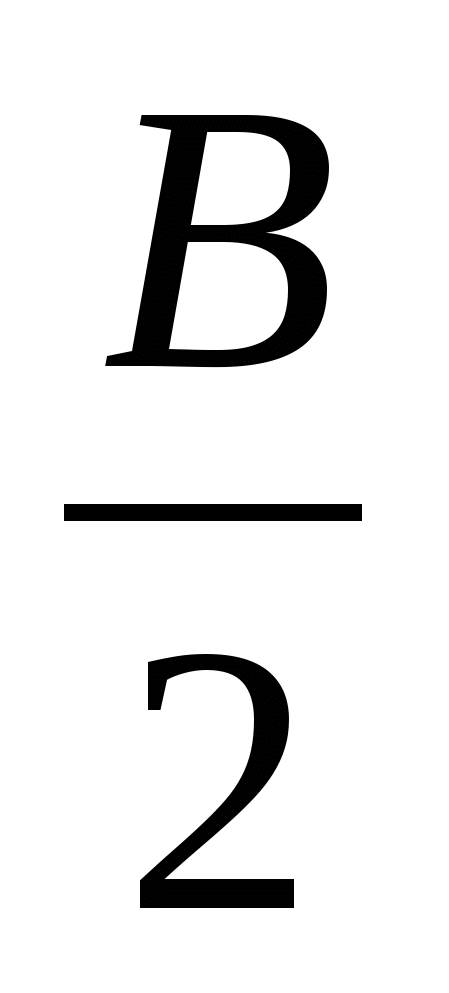 )-1 + (sin
)-1 + (sin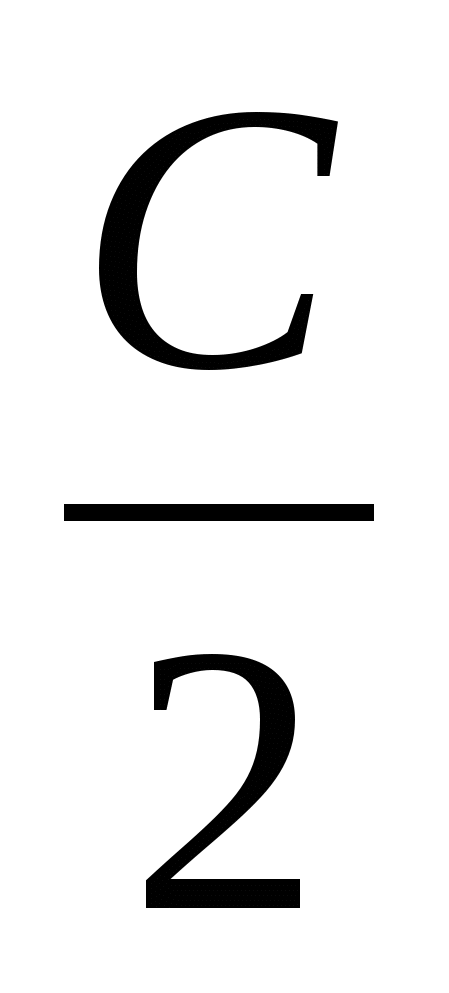 )-1
)-1 1
1
При доказательстве воспользоваться неравенством Коши для левой части, а произведение sin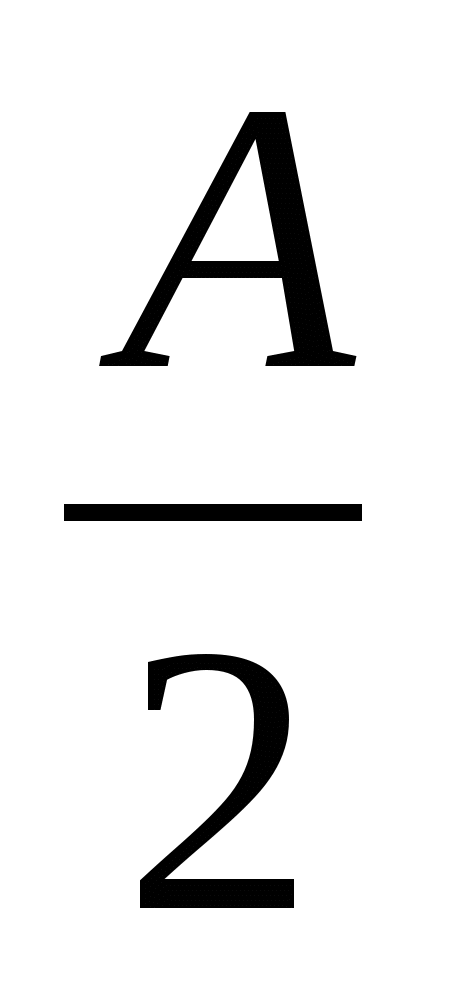 sin
sin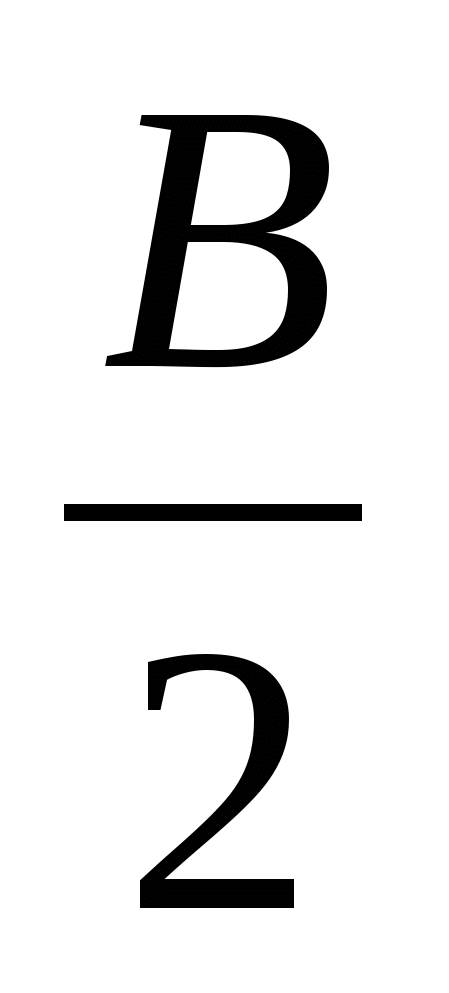 sin
sin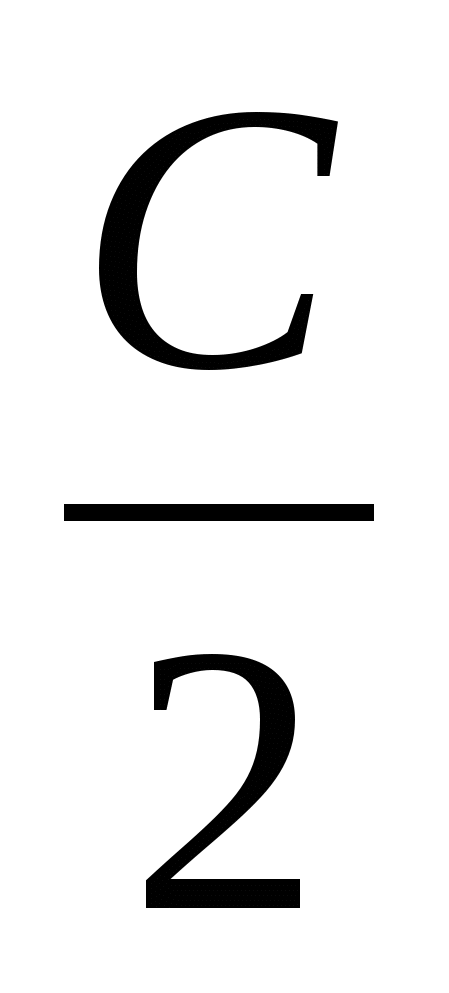 преобразовать и записать как
преобразовать и записать как
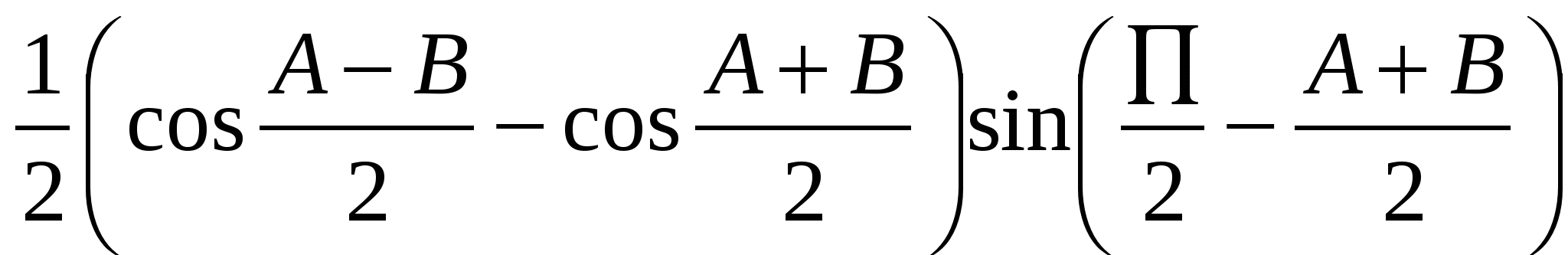 и т. д.
и т. д.
Аналогичные задания можно дать домой, например:
а) если А+В+С= π, то 8cosA cosB cosC 1;
1;
б) если А+В+С= π, то tg2A+ tg2B+ tg2C ≥ 9.
Очень хороша задача прикладного характера про дешевый ящик:
2 стенки ящика, имеющего форму прямоугольного параллелепипеда и объем 1м3, изготавливаются из одного материала , 4 другие из материала, который в 8 раз дешевле.
При каких размерах x, y, z ящика стоимость материалов, нужных для его изготовления, минимальна ?
Решение:
1) по условию xyz = 1;
2) пусть стоимость второго материала р рублей;
3) возможны случаи: а) стенки смежные,
б) стенки не смежные.
а) пусть стенки смежные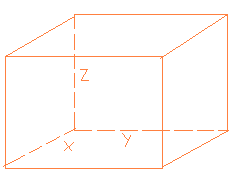
и стоимость 1м3 второго материала - Р рублей, тогда стоимость всего материала , необходимого для изготовления ящика:
S1 = 8p( xy + yz) + p( xy + yz + 2xz) = pxyz (9/z + 9/x +2/y) = p ((9/z + 9/x 2/y).
б) пусть стенки не смежные, тогда стоимость всего материала , необходимого для изготовления ящика:
S2 = 8p2xy + p( 2xz + 2yz)=2pxyz( 8/z + 1/y + 1/x) = 2p( 8/z + 1/y + 1/x).
Применим н. Коши:
(9/z + 9/x +2/y) ≥ 3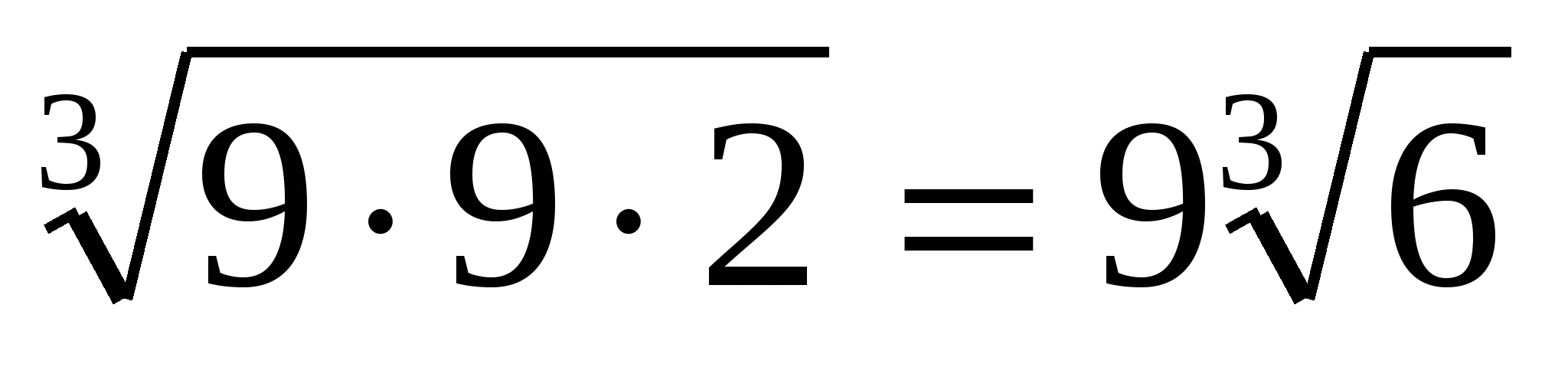 , S1 ≥ 9
, S1 ≥ 9 ![]() p ;
p ;
( 8/z + 1/y + 1/x) ≥ 3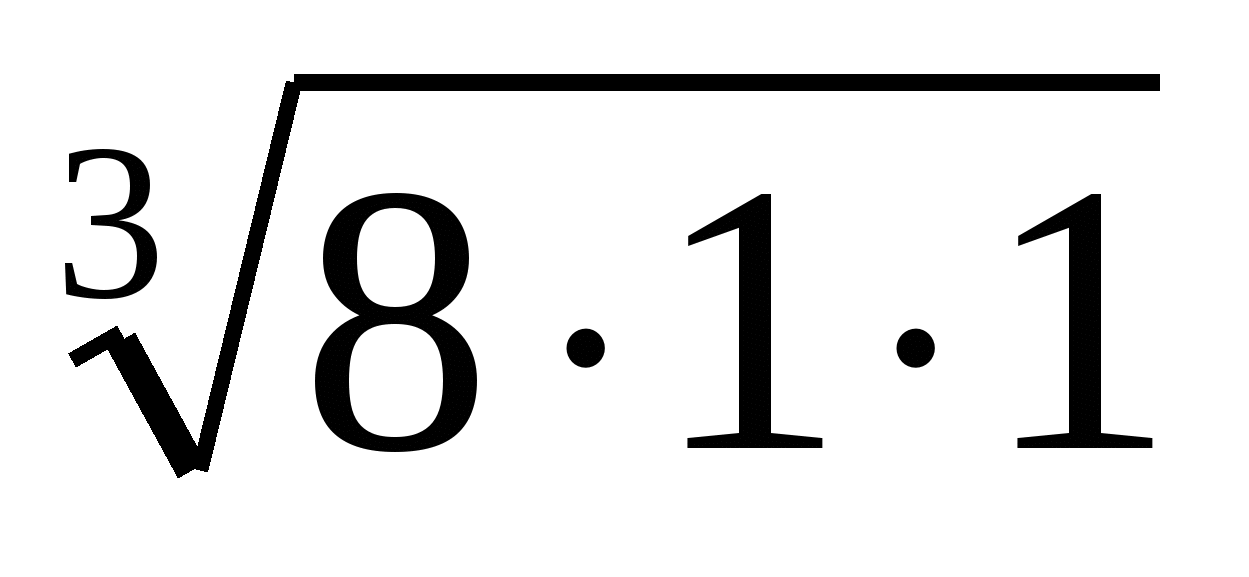 = 6, S2 ≥ 12p,
= 6, S2 ≥ 12p,
Но 9 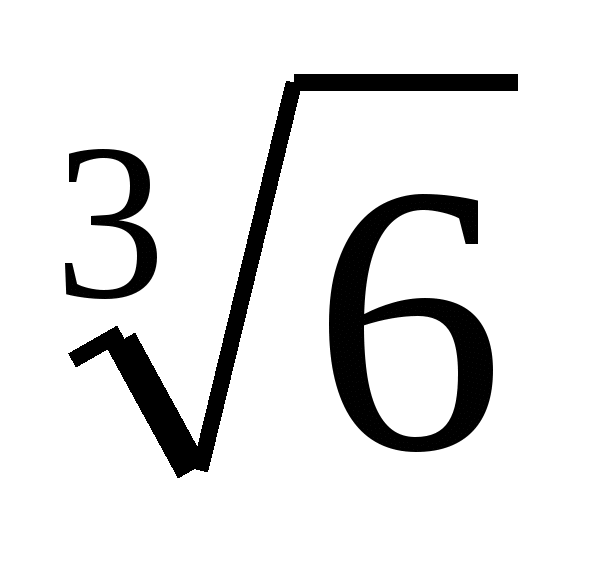 p ≥ 12p, значит, стоимость S2 будет минимальна тогда и только тогда, когда будет минимальна сумма ( 8/z + 1/y + 1/x), а это будет, когда в неравенстве Коши будет равенство, т. е:
p ≥ 12p, значит, стоимость S2 будет минимальна тогда и только тогда, когда будет минимальна сумма ( 8/z + 1/y + 1/x), а это будет, когда в неравенстве Коши будет равенство, т. е:
8/z = 1/y = 1/x, учитывая, что xyz=1, получаем: x=0,5; y=0,5; z=4.
Ответ: стоимость всего материала , необходимого для изготовления ящика минимальна, если его стенки имеют форму квадрата со стороной 0,5м, а расстояние между ними равно 4м.
На усмотрение учителя число примеров на применение средних величин(в основном, неравенства Коши) можно увеличить или уменьшить.
В математике существуют и другие средние величины, например, среднее арифметико-геометрическое Гаусса и среднее арифметико-гармоническое.
Есть способ введения понятия средней величины с помощью так называемого предельного перехода. Его суть - определить среднюю величину нового вида как предел последовательности, члены которой формируются с помощью уже введенных и изученных средних величин.
Пусть а>в, а>0, в>0, тогда образуем две последовательности:
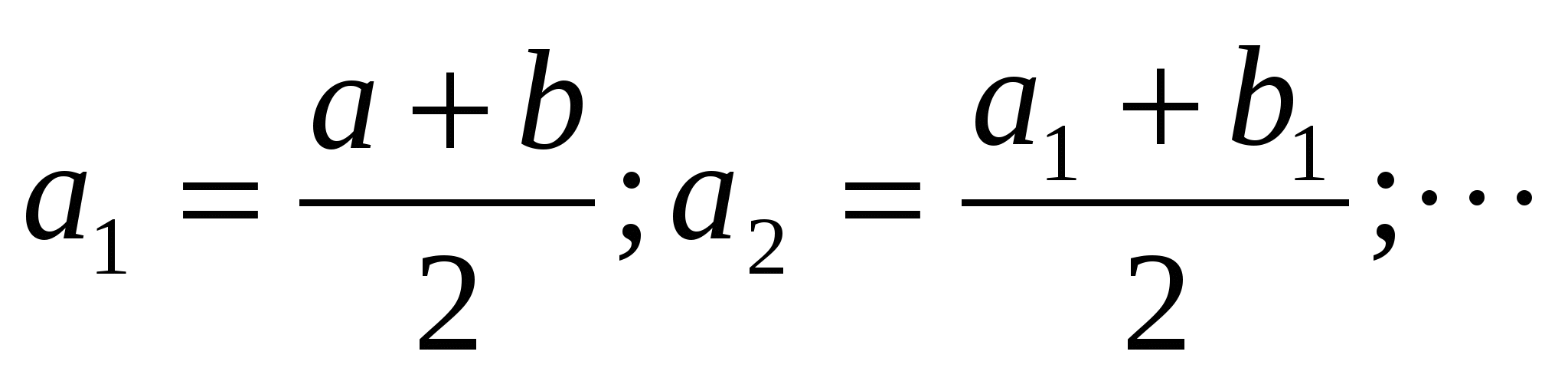
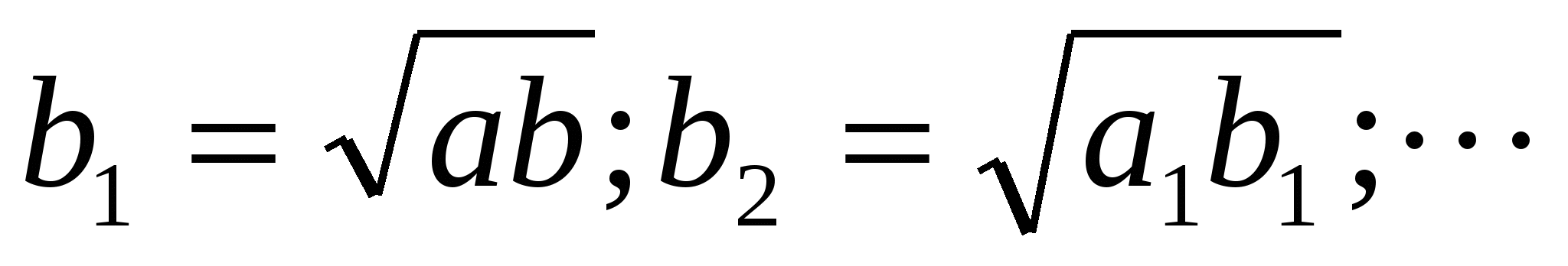
которые обладают следующими свойствами:
А) (ап)- убывающая и ограниченная снизу,
Б) (вп)-возрастающая и ограничена сверху
В) обе последовательности сходятся к конечным пределам и они совпадают.
Определение:
Общий предел последовательностей (ап) и (вп) называют средним арифметико-геометрическим чисел а и в.
Если повторить такое построение, но среднее геометрическое заменить на среднее гармоническое, то получим (ап ) и (вп), обладающие свойствами А-В, но общий предел равен 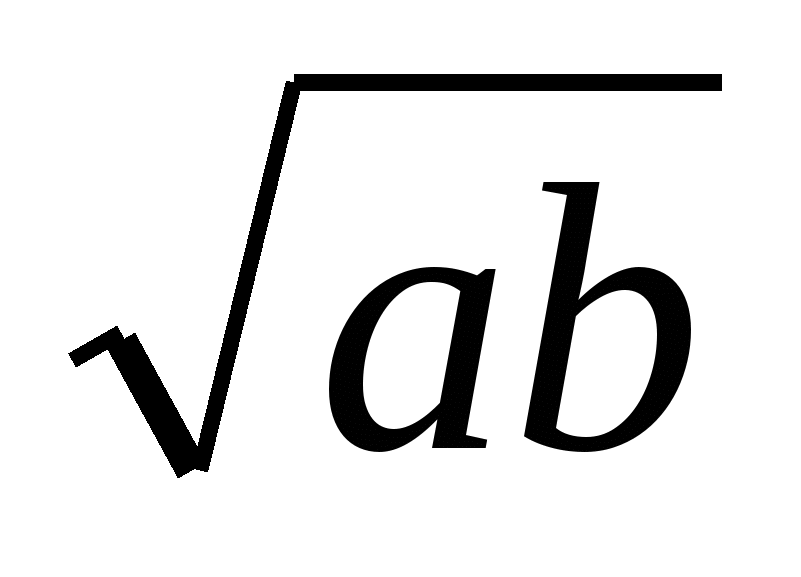 , то это арифметико-гармоническое.
, то это арифметико-гармоническое.
Есть еще симметрические средние величины, но их определение достаточно сложно для учеников и учитель должен сам решить давать в конкретном классе эти величины подробно или нет.
6.Средние величины, используемые в математической статистике и экономике
В практике статистической обработки материала возникают различные задачи, имеются особенности изучаемых явлений, и поэтому для их решения требуются различные сведения, которые получают, применяя средние величины.
Средняя, рассчитанная по совокупности в целом, называется в статистике общей средней. Средние, вычисленные для каждой группы, называются групповыми средними. Общая средняя отражает общие черты изучаемого явления, а групповая средняя дает характеристику размера явления, складывающуюся в конкретных условиях данной группы.
Например, статистическое изучение рождаемости и среднего количества детей в семье на территории бывшего СССР проводилось по регионам. Традиционно более высокая рождаемость была в Средней Азии и Закавказье по сравнению с центральными районами России. Среднее количество детей в семье, исчисленное по каждому региону - это групповые средние, а соответственно исчисленной по всей территории СССР - это общая средняя. Сравнительный анализ групповых и общих средних используется для характеристики социально-экономических типов изучаемого общественного явления.
Существуют две категории средних величин:
1. Степенные средние.
К ним относятся:
Средняя арифметическая
Средняя гармоническая
Средняя геометрическая
2. Структурные средние:
Мода
Медиана.
Выбор того или иного вида средней производится в зависимости от целей исследования, экономической сущности усредняемого характера имеющихся исходных данных.
Если учитель захочет дать более подробно материал по этой теме, то
источников достаточно.
25


