- Преподавателю
- Математика
- Задачи для подготовки к олимпиаде по математике
Задачи для подготовки к олимпиаде по математике
| Раздел | Математика |
| Класс | - |
| Тип | Другие методич. материалы |
| Автор | Проскокова А.В. |
| Дата | 06.11.2015 |
| Формат | docx |
| Изображения | Есть |
Задача № 1. На острове живут 7 синих, 9 зеленых и 11 красных хамелеонов. Когда 2 хамелеона разного цвета встречаются, они оба меняют свой цвет на третий ( синий и зеленый на красный и так далее). Возможно ли, что в какой-то момент все хамелеоны станут одного цвета?
Решение: Введем следующие обозначения: R- красные хамелеоны, G- зеленые, B- синие. Получим, что популяция красных равна 11+2 R-В- G.
Популяция синих равна 7+2В- R- G. Популяция зеленых равна 9+2G- R-В.
Всего хамелеонов 27. Значит для того, чтобы все стали красными нужно получить либо 16 красных к уже существующим 11. Будем считать, что должны происходить встречи только синих и зеленых, так как нам нужны только красные. За один шаг получается 2 красных хамелеона и расходуется по одному синему и зеленому, то есть требуется получить 8 пар красных и израсходовать по 8 синих и зеленых хамелеонов. Но не хватает синих (так как их всего 7) для полного перекрашивания в красный цвет.
Аналогично, чтобы получить 27 синих, нужно по 10 красных и зеленых (не хватает зеленых, так как их всего 9). Чтобы получит 27 зеленых, надо по 9 хамелеонов остальных цветов, тогда снова не хватает синих (их всего 7). То есть невозможно, что в какой-то момент все хамелеоны станут одного цвета.
Задача № 2 Может ли десятичная запись факториала натурального числа оканчиваться одиннадцатью нулями? Напомним, что n!=1 2
2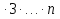
Решение: Пусть на конце числа m! стоят одиннадцать нулей. Это означает, что число m! Делится на 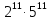 . Поскольку в числе m! Двойки встречаются в качестве сомножителей чаще, чем пятерки, нам необходимо найти такое число m! В разложении которого на простые множители будет встречаться 11 пятерок. Рассмотрим ряд чисел, имеющих в разложении на простые множители число 5.
. Поскольку в числе m! Двойки встречаются в качестве сомножителей чаще, чем пятерки, нам необходимо найти такое число m! В разложении которого на простые множители будет встречаться 11 пятерок. Рассмотрим ряд чисел, имеющих в разложении на простые множители число 5.
Это:5, 10, 15, 20, 25,30,35,40,45, 50,55,60,65…Нужно учитывать, что числа 25, 50, 75, … делятся на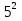 . В разложении числа 45! на простые множители присутствуют 10 пятерок, а в разложении числа 50!- присутствует 12 пятерок. Значит, числа m!, в разложении которого 11 пятерок не существует. Следовательно, десятичная запись факториала натурального числа оканчиваться одиннадцатью нулями не может.
. В разложении числа 45! на простые множители присутствуют 10 пятерок, а в разложении числа 50!- присутствует 12 пятерок. Значит, числа m!, в разложении которого 11 пятерок не существует. Следовательно, десятичная запись факториала натурального числа оканчиваться одиннадцатью нулями не может.
Задача № 3 Имеется шесть различных кошельков. Сколькими способами можно разложить в них двенадцать одинаковых монет, чтобы пустым остался максимум один кошелек?
Решение: Рассмотрим случай, когда пустых кошельков нет. Тогда в каждый кошелек мы должны положить по одной монете, тогда оставшиеся 6 монет мы должны разложить в 6 оставшихся кошельков. Каждому такому разложению составим картинку вида

Всего 6 кошельков+5 разделителей=11. Таким образом, число возможных разложений равно числу таких картинок. В данной картинке 11 клеточек из которых нужно выбрать ровно 5 клеточек (эти клеточки являются и «разделителями» уже содержимого кошелька и число способов из 11 элементов равно 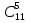 . Допустим, что один кошелек пустой, тогда в оставшиеся 5 нужно положить по одной монете и 7 монет распределить по пяти. И снова необходимо каждому такому разложению сопоставить диаграмму вида
. Допустим, что один кошелек пустой, тогда в оставшиеся 5 нужно положить по одной монете и 7 монет распределить по пяти. И снова необходимо каждому такому разложению сопоставить диаграмму вида

Число таких диаграмм равно числу выборов 4 элементов из 11, т.е. 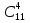 . Так как пустым может быть любой из 6 кошельков, тогда общее число таких возможностей равно
. Так как пустым может быть любой из 6 кошельков, тогда общее число таких возможностей равно 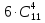 и, учитывая первый случай, получим
и, учитывая первый случай, получим
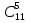 +
+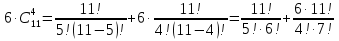 =2472.
=2472.
Задача № 4 Какое наименьшее значение может принять выражение
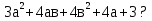
Решение: Преобразуем выражение, выделив в нем полные квадраты:
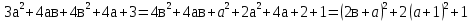
Выражение не может оказаться меньше 1, т.к. первые 2 слагаемых являются точными квадратами, и, следовательно, оба неотрицательны. При а=-1, и в=0,5, значение выражения равно 1. Ответ: наименьшее значение равно 1.
Задача № 5. Строительная компания строила дорогу из города А в город В. За первый 8-часовой рабочий день она построила 2 км. Ночью прошел дождь и смыл всю разметку, которая была нарисована на построенном участке дороги. На следующий день разметка была восстановлена, и на это ушла часть рабочего времени. Скорость восстановления разметки-6км/ч. В результате на второй день был построен более короткий участок дороги. Следующей ночью вся разметка опять была смыта дождем, и ее восстановление снова потребовало части рабочего времени. На каком максимальном расстоянии могли находиться города А и В, если известно, что дорога между ними в результате была построена, и во время строительства каждую ночь лил дождь?
Решение: Так как скорость восстановления равна 6км/ч, за восьмичасовой рабочий день можно восстановить 48км дорожной разметки. Пусть города находятся на некотором меньшем расстоянии, например (48-х)км. Начало рабочего дня всегда начинается с восстановления разметки, по времени восстановление никогда не будет занимать больше (48-х)/6=8-х/6 часов. Значит после восстановления разметки у рабочих есть еще минимум х/6 часов для строительства нового участка дороги. Если скорость строительства дороги U(не будем ее вычислять, хотя это возможно, раз нам дано, что за 1 рабочий день построено 2км дороги), то каждый день строится минимум
Uх/6км. Ну а раз каждый день строится как минимум некоторое определенное количество километров, в конце концов, дорога будет построена. Результат. Если расстояние между городами меньше 48км, то между ними будет построена дорога. Если расстояние между ними больше 48км, дорога никогда не будет построена, потому что рабочего дня не будет хватать даже на то, чтобы восстановить разметку на участке дороги между городами. Ответ:48.


