- Преподавателю
- Математика
- Методическая разработка по теме Многочлены
Методическая разработка по теме Многочлены
| Раздел | Математика |
| Класс | - |
| Тип | Конспекты |
| Автор | Горбачевская З.Ф. |
| Дата | 19.04.2015 |
| Формат | doc |
| Изображения | Есть |
Методическая разработка темы «Многочлены»
Многочлены
Под многочленом понимается выражение вида: а0хn + а1хn-1 + … + аn-1х + аn, где а0, а1, аn - произвольные действительные числа называемые коэффициентами многочлена, х - переменная, n - целое неотрицательное число.
Такая запись называется каноническим видом многочлена.
Если коэффициент а0 при хn отличен от нуля, то одночлен а0хn называют старшим членом многочлена, а0 - старшим коэффициентом, аn называют свободным членом многочлена.
Любое число, отличное от нуля, можно считать многочленом.
Если все коэффициенты многочлена равны нулю, то такой многочлен называется нулевым. Многочлен со старшим коэффициентом равным 1 называют приведенным.
Пусть P(х) = а0хn + а1хn-1 + … + аn, а0 ≠ 0, то число n называют степенью многочлена. Многочлены нулевой степени - это просто числа. Нулевые многочлены не имеют степени.
Два многочлена считаются равными, если их каноническая запись одинакова, то есть многочлены имеют одну и ту же степень и коэффициенты при одинаковых степенях неизвестных совпадают.
Если вместо переменной х в многочлен Р(х) подставить число с, то получится число, которое называется значением многочлена при х = с.
Значение любого многочлена при х = 0 равно его свободному члену, а сумма коэффициентов многочлена есть его значение в точке 1.
Корнем многочлена Р(х) называется такое число , что Р(a) = 0.
Упражнения
-
Выполните действия: (х3 + х - 1)(х2 + х + 1) - (х - 1)(х4 + х2 - 1).
-
Найдите свободные члены и суммы коэффициентов:
а) (х2 + х - 1)2005
б) (3х2 - 4х + 2)100
-
Докажите тождества:
а) (х - 1)(х + 1)(х2 + 1) = х4 - 1
б) (х - 1)(х + 1)(х2 - х + 1)(х2 + х + 1) = х6 - 1
-
Доказать, что (х + а)(х + 2а)(х + 3а)(х + 4а) + а4 - полный квадрат.
Деление многочленов
Определение: Многочлен Р(х) делится на многочлен Q(х) ≠ 0, если существует такой многочлен R(х), что выполняется равенство Р(х) = Q(х)∙R(х).
Свойства делимости многочленов
-
Если два многочлена делятся на Q(х), то и их сумма и разность также делятся на Q(х).
-
Если Р(х) делится на Q(х), то и любое произведение Р(х)∙N(х) делятся на Q(х).
-
Если Р(х) делится на Q(х), а Q(х) делится на N(х), то и Р(х) делится на N(х).
Теорема 1 (о делении с остатком)
Пусть Р(х) и В(х) - два произвольные многочлена, причем многочлен В(х) ≠ 0. Тогда существует единственная пара многочленов Q(х) и R(х) таких, что выполняется равенство Р(х) = В(х) Q(х) + R(х) и многочлен R(х) либо равен нулю, либо имеет меньшую степень, чем многочлен В(х)
Q(х) - называется неполным частным,
Р(х) - остаток.
При делении многочленов можно использовать деление «углом».
Пример 1. ![]()
 х4 - 11х2 + 3х + 1 х2 + х + 1
х4 - 11х2 + 3х + 1 х2 + х + 1

 х4 + х3 + х2 х2 - х - 11 - неполное частное
х4 + х3 + х2 х2 - х - 11 - неполное частное
 - х3 - 12х2 + 3х
- х3 - 12х2 + 3х
 - х3 - х2 - х
- х3 - х2 - х
-11х2 + 4х + 1
- 11х2 - 11х - 11
 15х + 12 - остаток
15х + 12 - остаток
х4 - 11х2 + 3х + 1 = (х2 + х + 1)(х2 - х - 11) + (15х + 12)
Пример 2. ![]()
 3х6 + 2х4 - 2х3 + х - 6 х4 + 2х + 2
3х6 + 2х4 - 2х3 + х - 6 х4 + 2х + 2

 3х6 + 6х3 + 6х2 3х2 + 2
3х6 + 6х3 + 6х2 3х2 + 2
 2х4 - 8х3 - 6х2
2х4 - 8х3 - 6х2
 2х4 + 4х + 4
2х4 + 4х + 4
8х3 - 6х2 - 3х - 10
3х6 + 2х4 + х - 6 = (х4 + 2х + 2)(3х2 + 2) - (8х3 + 6х2 + 3х + 10)
Пример 3. х4 - 10х3 + 35х2 - 50х + 24 = (х - 1)(х3 - 9х2 + 26х - 24)
Многочлен Р(х) делится на многочлен В(х) тогда и только тогда, когда существует многочлен Q(х) такой, что Р(х) = В(х) ∙ Q(х)
Пишут Р(х) ![]() В(х).
В(х).
Упражнения
-
Найти неполное частное и остаток от деления:
а) х2 - 2х + 1 на х - 1
б) х5 - 6х3 + 2х2 - 4 на х2 - х + 1
в) х4 + х2 + 1 на х + 5
г) х7 - 1 на х3 + х + 1
-
При каком значении k выполняется деление без остатка многочлена
х3 + 6х2 + kх + 12 на х + 4?
-
Делится ли многочлен х5 + 3х4 + 4х3 - 2х2 + 5 - 5 без остатка на х2 - 3х + 2?
Теорема Безу. Схема Горнера.
Число α называется корнем многочлена Р(х), если Р(α) = 0.
Теорема 2. Если многочлен Р(х) делится на х - α, то α является корнем многочлена Р(х).
Теорема 3 (теорема Безу). Остаток от деления многочлена Р(х) на двучлен х - α равен Р(α), т.е. значению этого многочлена при х = α.
Пример 1. Найдите остаток от деления многочлена х4 + 5х3 - 3х + 6 на х + 3
α = - 3 Р(-3) = (-3)4 + 5(-3)3 - 3 ∙ (-3) + 6 = -39. Ответ: - 39.
Пример 2. Докажите, не выполняя деление, что 3х5 + 4х4 - х2 - 18х делится на х + 2: α = -2 Р(-2) = 0. Т.к. остаток равен 0, то многочлен делится на х + 2.
Пример 3. Делится ли многочлен х100 - 3х + 2 на х2 - 1
х2 - 1 = (х + 1)(х - 1)
Для того, чтобы многочлен делился на х2 - 1, он должен делиться на х - 1 и на х + 1. Найдем остатки от деления
α = 1, Р(1) - 1100 - 3 + 2 = 0; Р(х)  х - 1
х - 1
α = -1, Р(-1) = (-1)100 + 3 + 2 = 6 Р(х)
= -1, Р(-1) = (-1)100 + 3 + 2 = 6 Р(х)  х + 1. Ответ: х100 - 3х + 2 не делится на х2 - 1
х + 1. Ответ: х100 - 3х + 2 не делится на х2 - 1
Пример 4. При каких а и в выполняется деление без остатка многочлена
х4 + 3х3 - 2х2 + ах + в на многочлен х2 - 3х + 2?
х2 - 3х + 2 = (х - 1)(х - 2)
α = 1 Р(1) = 2 + а + в
α = 2 Р(2) = 32 + 2а + в.
По условию остатки равны 0, получаем
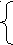 2 + а + в = 0 а = -30
2 + а + в = 0 а = -30
32 + 2а + в = 6 в = 28
Схема Горнера
Деление многочлена Р(х) = а0хn + а1хn - 1 + … + аn на двучлен х - α удобно выполнять по схеме Горнера
Р(х) = (х - α) ∙ Q(х) + вn, где Q(х) = в0хn - 1 + в1хn - 2 + … + вn - 1 вn -остаток от деления
а0
а1
а2
…
аn - 1
аn
α
в0 = а0
в1 = а1 + αв0
в2 = α2 + αв1
…
вn - 1 = аn - 1 + αвn - 2
вn = аn + αвn - 1
в1, в2 … заполняются так: берутстоящие над ней число первой строки и прибавляют к нему произведение α и предыдущего элемента второй строки:
Пример 1. Выполните деление многочлена
а) х3 + 4х2 - 24 на х - 2 α = 2
1
4
0
-24
2
1
6
12
0
х3 + 4х2 - 24 = (х - 2)(х2 + 6х + 12)
б) х4 - 5х3 + 2х2 + 3х - 7 на х - 2
1
-5
2
3
-7
2
1
-3
-4
-5
-17
х4 - 5х3 + 2х2 + 3х - 7 = (х - 2)(х3 - 3х2 - 4х - 5) - 17
в) 4х5 - 7х4 + 5х3 - 2х + 1 на х - 3
4
-7
5
0
-2
1
3
4
5
20
60
178
535
4х5 - 7х4 + 5х3 - 2х + 1 = (х - 3)(4х5 + 5х3 + 20х2 + 60х + 178) + 535
Пример 2.
Найти по схеме Горнера значение многочлена х5 - 2х4 - х3 + 2х + 5 при х = 7
1
-2
-1
0
2
5
7
1
5
34
238
1668
11667
Р(7) = 11667
Упражнения
-
Докажите, что
а) (3х5 + 4х4 - х2 - 18х)  (х + 2)
(х + 2)
б) (х9 + х8 + х7 + х6 + х5 + х4 + х3 + х2 + х + 1)  (х + 1)
(х + 1)
-
При каких а и в многочлен х4 - 2х3 - 13х2 + ах + в делится на х2 - 5х + 1
-
Найдите Р(-1) и Р(
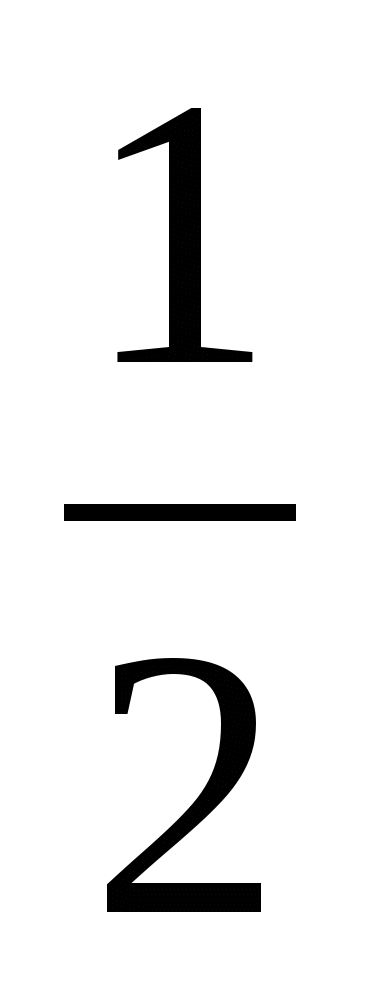 ), если Р(х) = 2х4 - 7х3 - 3х2 + 5х - 1
), если Р(х) = 2х4 - 7х3 - 3х2 + 5х - 1 -
Разделите 21 + у - 2у2 - у3 на у + 3, используя схему Горнера.
Многочлены с целыми коэффициентами.
Теорема Безу и ее следствия дают способ разложения многочлена на множители, если известны его корни. Как отыскать эти корни?
Для многочлена с целыми коэффициентами помогает решить эту задачу теорема Эйзенштейна:
Если Р(х) = а0хn + … + аn - многочлен с целыми коэффициентами, а х = 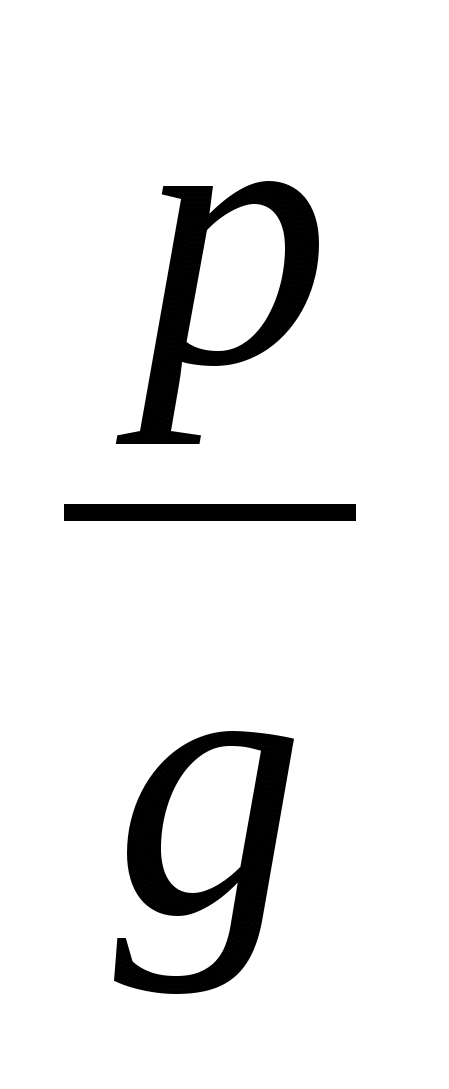 - его рациональный корень (дробь
- его рациональный корень (дробь 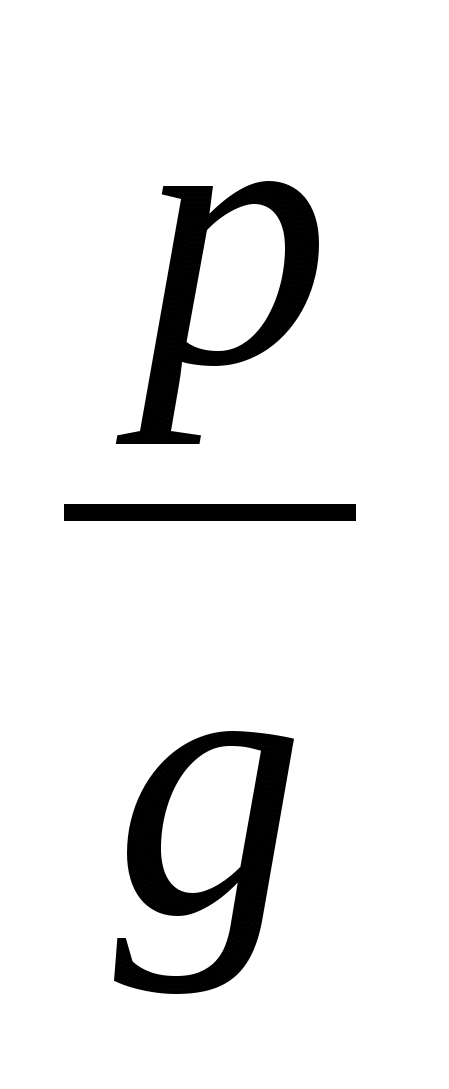 - несокращаемая, g > 0), то р является делителем старшего коэффициента а0.
- несокращаемая, g > 0), то р является делителем старшего коэффициента а0.
Следствие 1. Любой целый корень многочлена с целыми коэффициентами является делителем свободного члена.
Следствие 2. Если старший коэффициент многочлена с целыми коэффициентами равен 1, то все рациональные корни многочлена, если они существуют, целые.
Пример 1. Разложите на множители с целыми коэффициентами многочлен
Р(х) - 2х4 - 7х3 - 3х2 + 5х + 1.
Ищем сначала целые корни среди делителей свободного члена: ±1
Р(1) = 2 - 7 - 3 + 5 - 1 ≠ 0
Р(-1) = 2 + 7 - 3 - 5 - 1 = 0; х = -1 - корень многочлена.
Делим Р(х) на х + 1
2
-7
-3
5
-1
-1
2
-9
6
-1
0
Р(х) = (х + 1)(2х3 - 9х2 + 6х - 1)
Далее раскладываем на множители многочлен Q(х) = 2х3 - 9х2 + 6х - 1
Q(1) ≠ 0; Q(-1) ≠ 0, т.е. целых корней нет.
Тогда ищем дробные корни: ±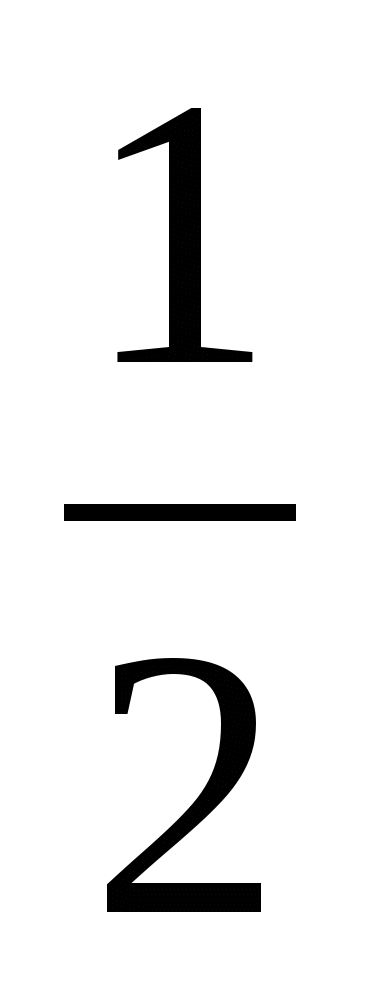
Q(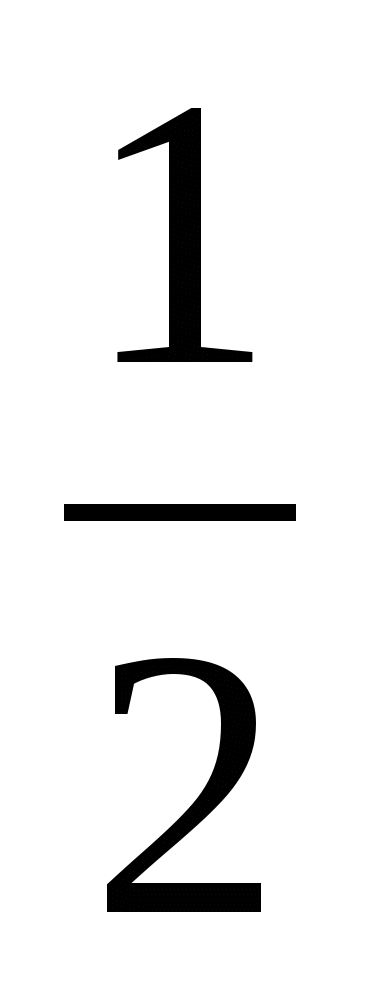 ) = 0
) = 0
2
-9
6
-1
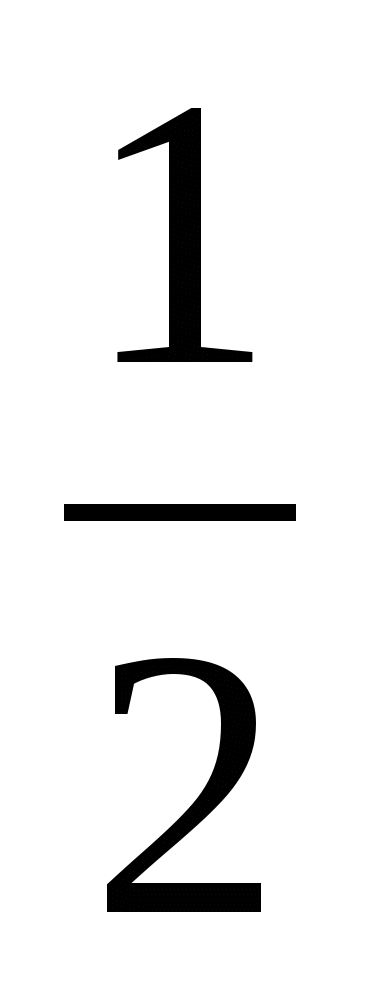
2
-8
2
0
Р(х) = (х + 1)(х - 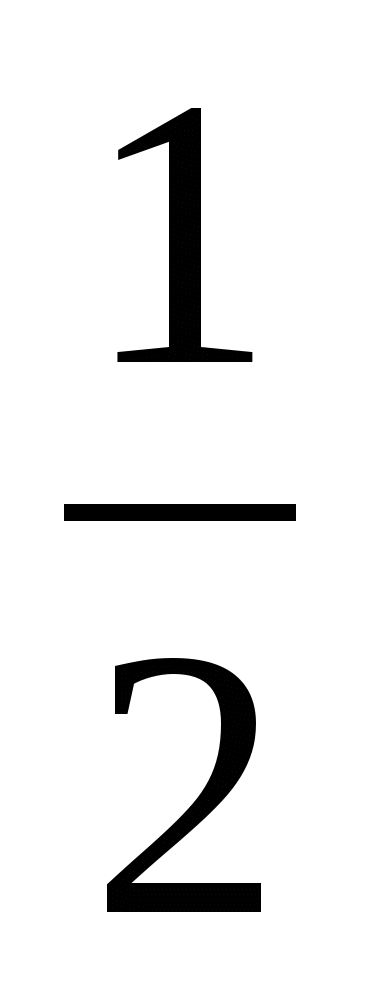 )(2х2 - 8х + 2) = (х + 1)(2х - 1)(х2 - 4х + 1)
)(2х2 - 8х + 2) = (х + 1)(2х - 1)(х2 - 4х + 1)
Для отыскания корней многочлена можно применять следующие свойства:
-
Многочлен с положительными коэффициентами не может иметь положительных корней.
-
Число 1 является корнем многочлена тогда и только тогда, когда сумма его коэффициентов равна 0.
-
Для того, чтобы число -1 являлось корнем многочлена необходимо и достаточно, чтобы сумма его коэффициентов, стоящих на четных местах, равнялась сумме коэффициентов, стоящих на нечетных местах.
Пример 2. Разложите на множители многочлен х4 + 2х3 - 2х2 - 6х + 5.
Т.к. сумма коэффициентов равна нулю, то х =1 является корнем многочлена
1
2
-2
-6
5
1
1
3
1
-5
0
Р(х) = (х - 1)(х3 + 3х2 + х - 5)
И снова сумма коэффициентов Q(х) = х3 + 3х2 + х - 5 равна нулю, значит х = 1 - корень
1
3
1
-5
1
1
4
5
0
Р(х) = (х - 1)2(х2 + 4х + 5)
Кратные корни
Может случиться, что Р(х) делится не только на х - α, но и на (х - α)k, где k > 1.
В этом случае говорят, что α является кратным членом многочлена Р(х).
Если многочлен Р(х) делится на (х - α)k и не делится на (х - α)k + 1, то α называют конем многочлена Р(х) кратным k.
Пример 1. Р(х) = х3 - х2 - 8х + 12 х = 2 является корнем многочлена.
Подставим вместо х = 2, получаем Q(2) = 0
Р(х) = (х - 2)2(х + 3). 2 не является корнем многочлена х + 3, т.е. многочлен делится на (х - 2)2, а не делится на (х - 2)3, т.е. 2 - корень многочлена второй кратности.
Упражнения
-
Разложите на множители:
а) х3 - х2 - 28х + 45
б) х3 - 6х2 - х + 30
в) х4 - 7х3 + 8х2 + 28х - 48
г) х3 - 2х2 - 5х + 6
-
Сократите дробь:
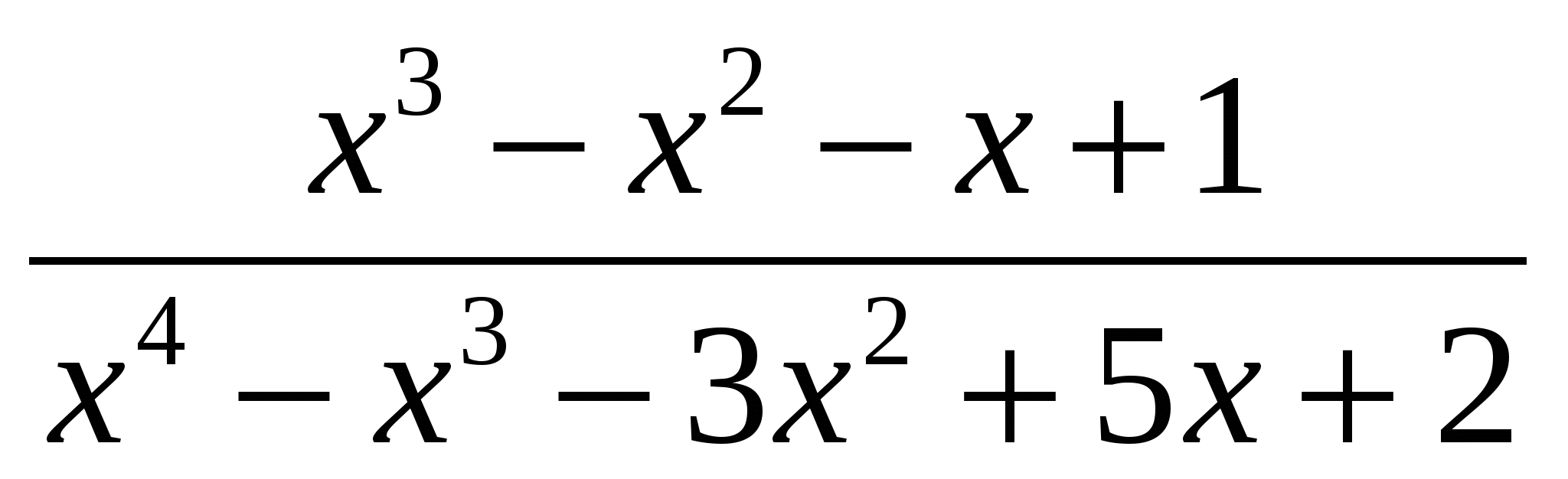
-
Какую кратность имеет корень:
а) х = 2 многочлена х5 - 5х4 + 7х3 - 2х2 + 4х - 8
б) х = 5 многочлена х5 - 15х4 + 76х3 - 140х2 + 75х - 125
Подстановка делителей свободного члена может оказаться очень утомительным занятием. Чтобы уменьшить число проверяемых корней полезно воспользоваться следующей теоремой:
Пусть Р(х) - приведенный многочлен с целыми коэффициентами, α - его целый корень. Тогда для любого целого числа k число Р(k) делится на α - k.
Отбор проводят так: сначала берут делители свободного члена. Пусть это будут числа α1, α2, … αn. После этого вычисляют Р(1). Если αm - корень многочлена Р(х), то αm - 1 должно быть делителем Р(1). Поэтому из чисел α1, α2, … αn выбирают те, для которых αm - 1 является делителем Р(1). После этого вычисляют Р(-1). Если и после этого осталось слишком много «претендентов», то вычисляют Р(2) и берут из оставшихся чисел, для которых αm - 2 - делители Р(2).
Пример 1.
Найти целые корни многочлена Р(х) = х4 + х 3 - 11х2 - 5х + 30.
Делители свободного члена: ±1; ±2; ±3; ±5; ±6; ±10; ±15; ±30. Р(1) = 16
Вычитаем из чисел единицу, получаем 0; -2; 1; -3; 2; -4; 4; -6; 5; -7; 9; -11; 14; -16; 29; -31.
Из них находим делители 16. Это -2; 1; 2; -4; 4; -16.
Получаем -1; 2; 3; -3; 5; -15 (среди них нужно искать корни).
Находим Р(-1) = 24.
К оставшимся числам прибавляем единицу, получаем 0; 3; 4; -2; 6; -14
Из них делители 24: 3; 4; -2; 6
Получаем: 2; 3; -3; 5
Р(2) = 16 + 8 - 44 - 10 + 30 = 0; х = 2 - корень многочлена
1
1
-11
-5
30
2
1
3
-5
-15
0
Р(х) = (х - 2)(х3 + 3х2 - 5х - 15)
Р(3) ≠ 0
Р(-3) = 0 х = -3 - корень
1
3
-5
-15
-3
1
0
-5
0
Р(х) = (х - 2)(х + 3)(х2 - 5)
Ответ: целые корни 2 и -3.
Пример 2.
Разложите многочлен на множители Р(х) = х4 - 7х3 + 8х2 + 28х - 48
±1; ±2; ±3; ±4; ±6; ±8; ±12; ±16; ±24; ±48 - делители свободного члена
Р(1) = 1 - 7 + 8 + 28 - 48 = -18
0; -2; 1; -3; 2; -4; 3; -5; 5; -7; 7; -9; 11; -13; 15; -17; 23; -25; 47; -49
Делители -18: -2; 1; -3; 2; 3; -9
Получаем -1; 2; -2; 3; 4; -8
Р(-1) = 1 + 7 + 8 - 28 - 48 = - 60
0; 3; -1; 4; 5; -7
Делители -60: 3; -1; 4; 5
Получаем 2; -2; 3; 4
Р(2) = 16 - 56 + 32 + 56 - 48 = 0 х = 2 - корень
1
-7
8
28
-48
2
1
-5
-2
24
0
Р(х) = (х - 2)(х3 - 5х2 - 2х + 24)
Р(-2) = -8 - 20 + 4 + 24 = 0 х = -2 - корень
1
-5
-2
24
-2
1
-7
12
0
Р(х) = (х - 2)(х + 2)(х2 - 7х + 12)
Р(3) = 0
1
-7
12
3
1
-4
0
Р(х) = (х - 2)(х + 2)(х - 3)(х - 4)
Самостоятельная работа
-
Разделите многочлены с остатком:
а) х4 - 4х3 + 6х2 - 7х + 2 на х2 - х + 2
б) 2х3 + 3х2 - 8 на х + 1
-
Найдите остаток от деления многочлена х5 - 17х + 1 на х + 2
-
Докажите, что многочлен (х + 1)6 - х6 - 2х - 1 делится на х(х + 1)(2х + 1)
-
Разложите многочлены на множители:
а) х5 - 2х4 - 4х3 + 4х2 - 5х + 6
б) х3 - 6х2 - х + 30
Ответы к самостоятельной работе
-
а) х4 - 4х3 + 6х2 - 7х + 2 = (х2 - х + 2)(х2 - 3х + 1)
б) 2х3 + 3х2 - 8 = (х + 1)(2х2 + х - 1) - 7
-
Остаток равен 3.
-
(х + 1)6 - х6 - 2х - 1
 х(х + 1)(2х + 1), т.к. Р(0) = 0, Р(-1) = 0, Р(-
х(х + 1)(2х + 1), т.к. Р(0) = 0, Р(-1) = 0, Р(-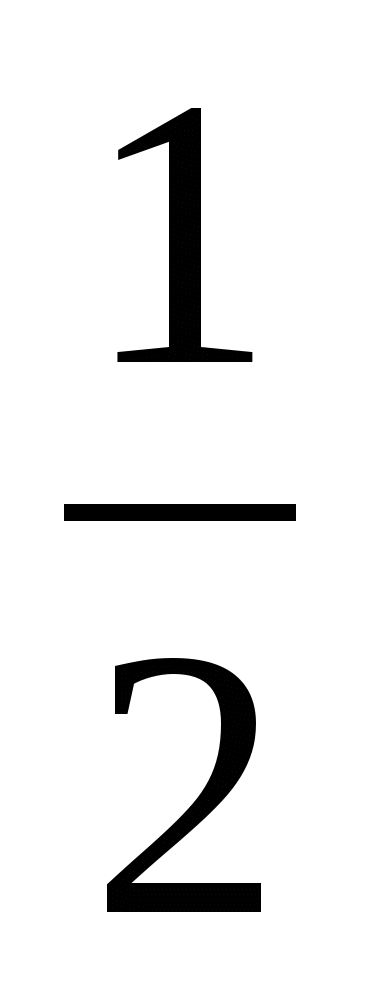 ) = 0
) = 0 -
а) х5 - 2х4 - 4х3 + 4х2 - 5х + 6 = (х - 1)(х + 2)(х - 3)(х2 + 1)
б) х3 - 6х2 - х + 30 = (х + 2)(х - 3)(х - 5)
Уравнения высших степеней.
Уравнение вида Р(х) = 0, где Р(х) - многочлен, степень которого выше второй.
Для решения таких уравнений используются два основных метода решения: разложения на множители и метод введения новой переменной.
Метод разложения на множители
Р(х) = 0
Р1(х) ∙ Р2(х) … Рn(х) = 0
Р1(х) = 0 или … Рn(х) = 0
Пример 1.
Решить уравнение: х3 + 4х2 - 24 = 0
Найдем хотя бы один целый корень уравнения
х = 2 - корень
(х - 2)(х2 + 6х + 12) = 0
х - 2 = 0 или х2 + 6х + 12 = 0 D < 0, корней нет. Ответ х = 2
Пример 2.
2х3 - 7х2 + 5х - 1 = 0
Делители свободного члена ±1
Р(1) ≠ 0, Р(-1) ≠ 0. целых корней нет.
Ищем рациональные корни : ± 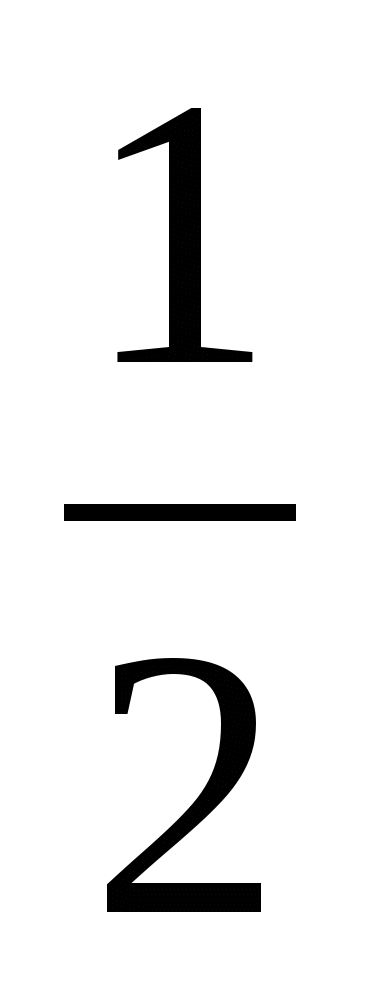
Р(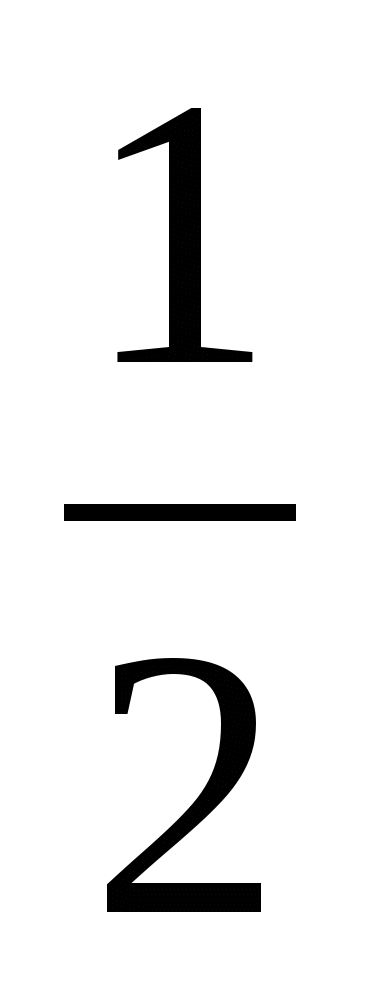 ) = 0 х =
) = 0 х = 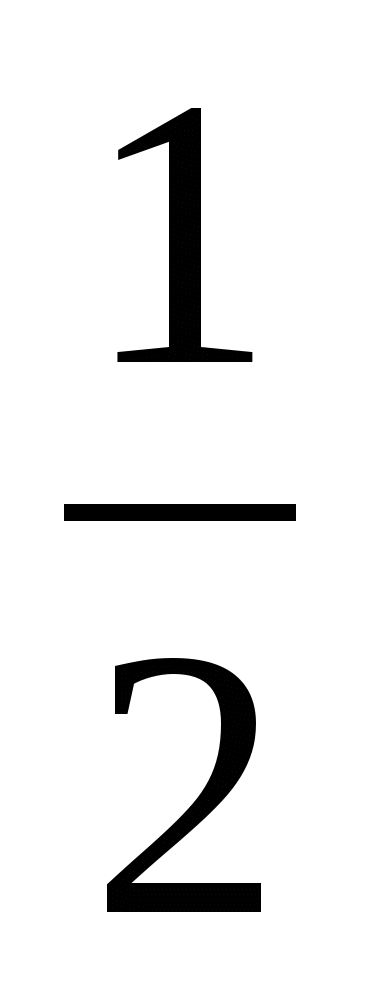 - корень
- корень
(х - 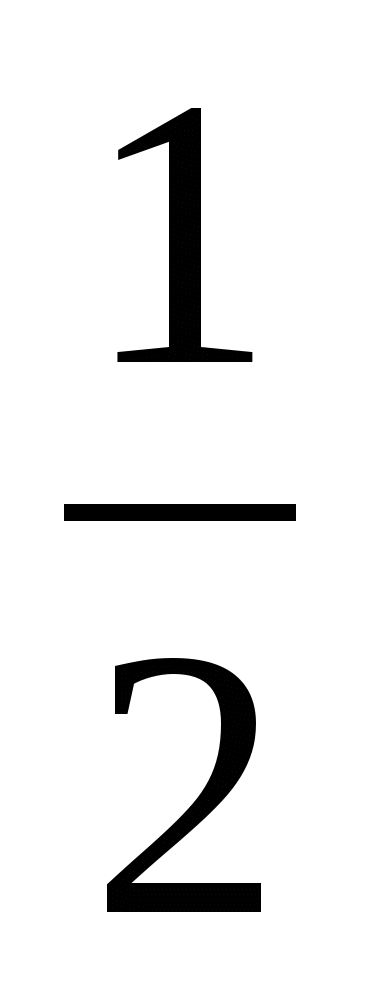 )(2х2 - 6х + 2) = 0
)(2х2 - 6х + 2) = 0
х1 = 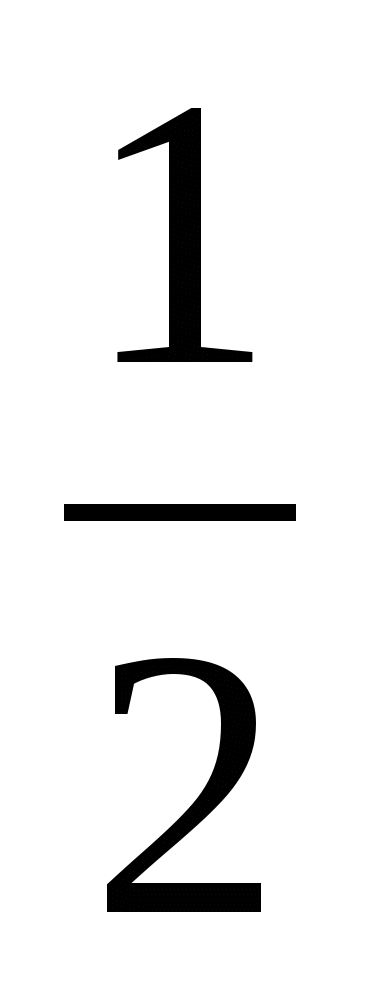 или х2 - 3х + 1 = 0
или х2 - 3х + 1 = 0
х2,3 = 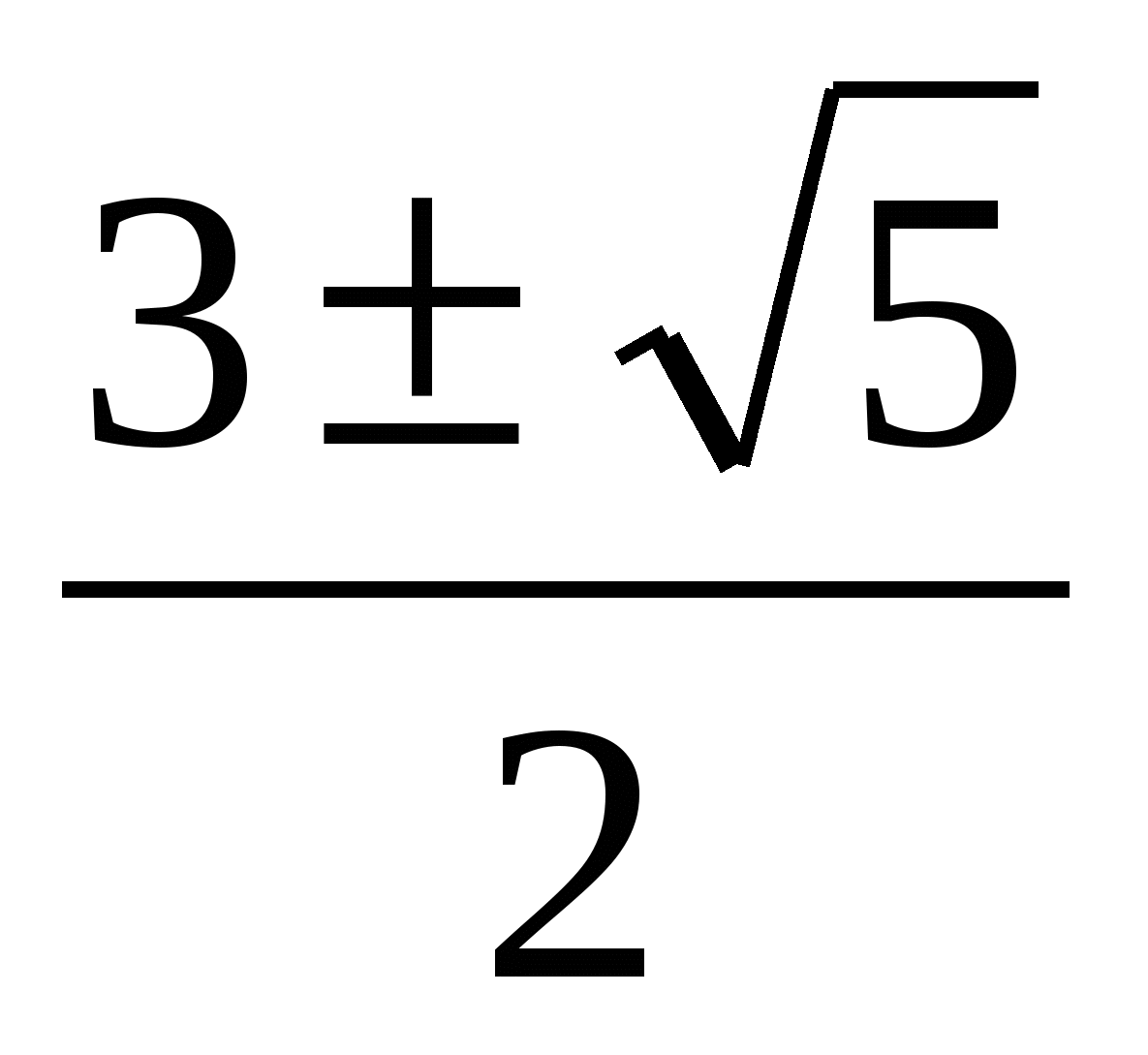 Ответ:
Ответ: 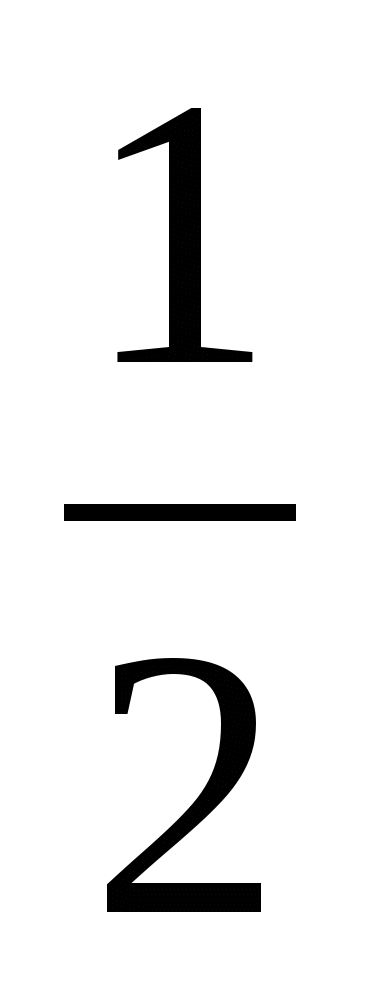 ;
; 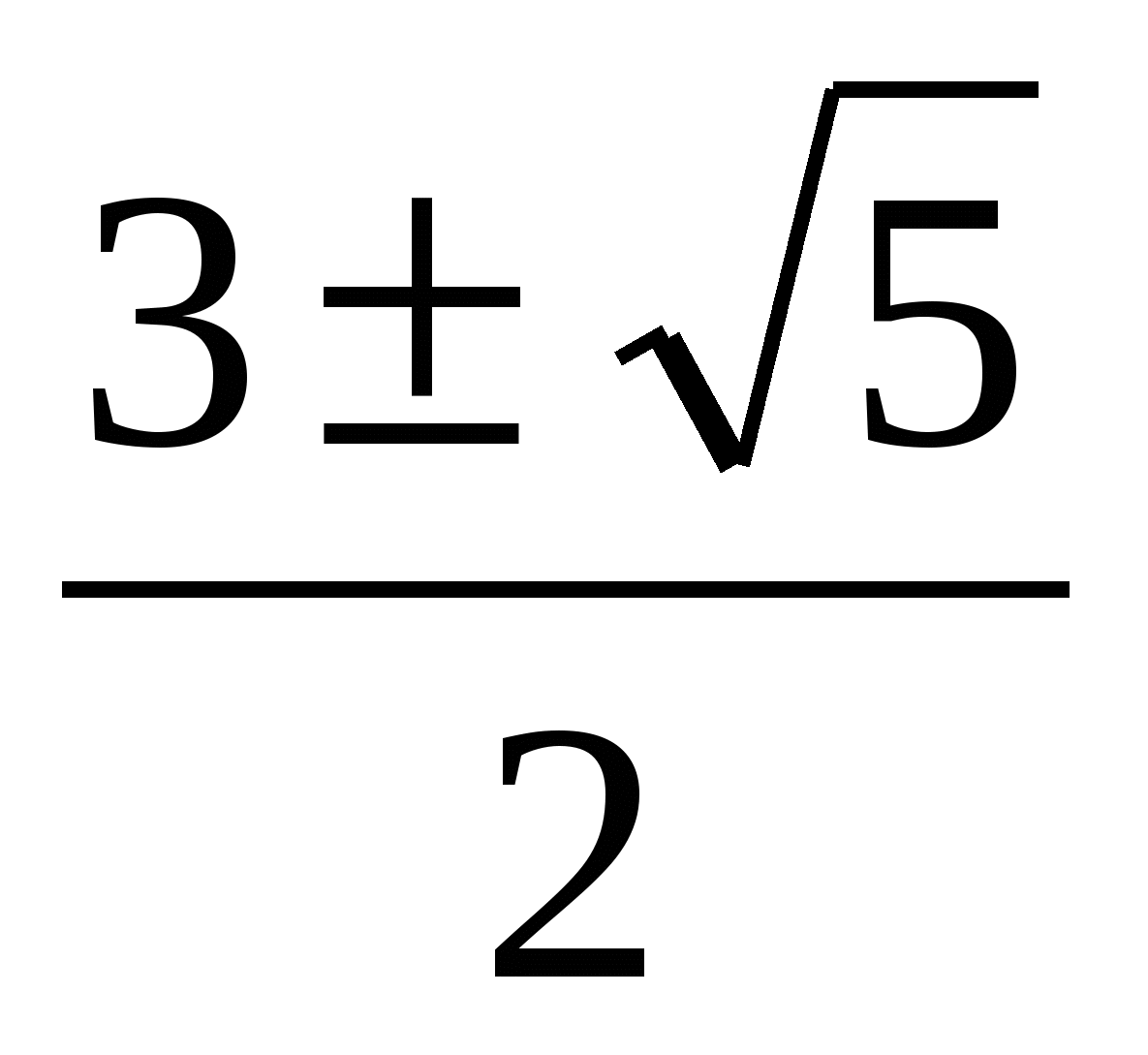
Пример 3.
2х4 - 5х3 + 5х2 - 2 = 0
Т.к. сумма коэффициентов равна 0, то число 1 - корень уравнения
2
-5
5
0
-2
1
2
-3
2
2
0
(х - 1)(х + 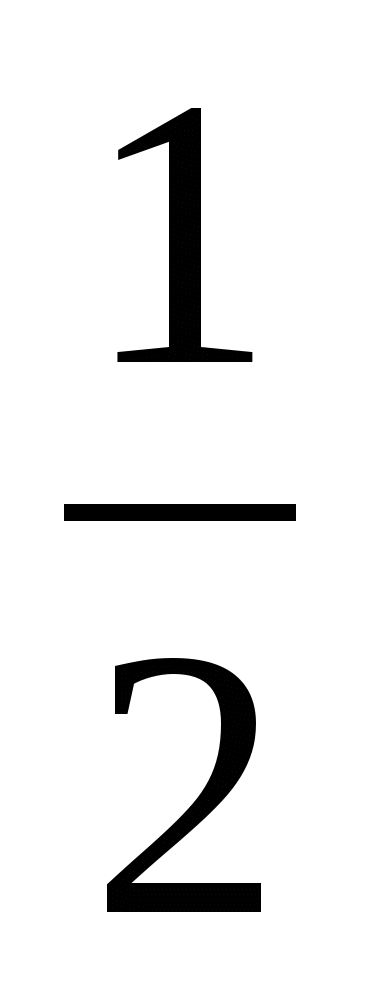 )(х2 - 2х + 2) = 0
)(х2 - 2х + 2) = 0
х1 = 1 или х2 = -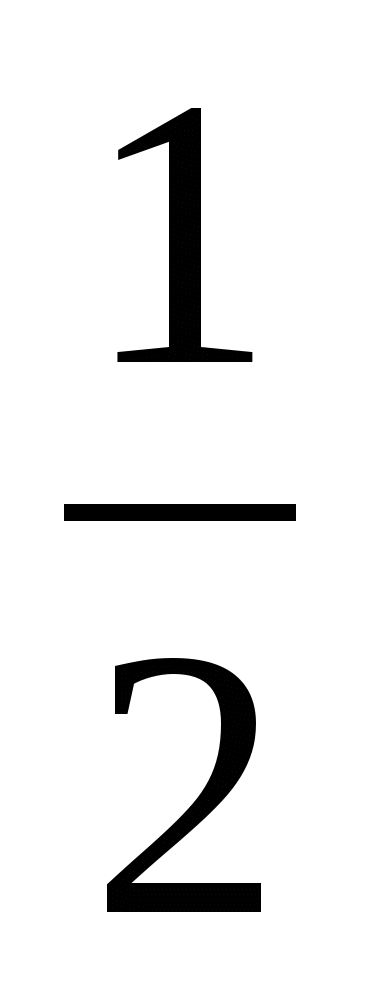 или х2 - 2х + 2 = 0 D < 0, корней нет. Ответ: 1; -
или х2 - 2х + 2 = 0 D < 0, корней нет. Ответ: 1; - 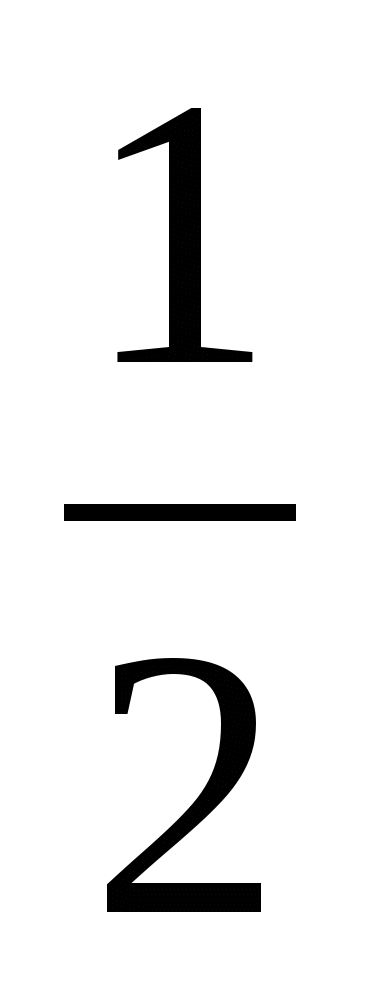
Пример 4.
х4 + х3 + 3х2 + 2х + 2 = 0
1 способ.
Т.к. все коэффициенты многочлена положительные, то многочлен не может иметь положительных корней. Т.к. многочлен приведенный, то все рациональные корни, если они существуют, целые.
Делители свободного члена ±1; ±2.
Значит, нужно проверить только -1 и -2. Р(-1) ≠ 0; Р(-2) ≠ 0. Значит уравнение корней не имеет.
2 способ.
Представим 3х2 как х2 + 2х2
(х4 + х3 + х2) + (2х2 + 2х + 2) = 0
х2(х2 + х + 1) + 2/х2 + х + 1) = 0
(х2 + х + 1)(х2 + 2) = 0
х2 + х + 1 = 0 или х2 + 2 = 0
D < 0, корней нет х2 ≠ -2, корней нет
Ответ: корней нет.
Многочлен P(х) = а0хn + а1хn-1 + … + аn называется возвратным, если его коэффициенты, одинаково удаленные от начала и от конца, равны между собой.
Тогда уравнение Р(х) = 0 называется возвратным, где Р(х) - возвратный многочлен.
Уравнение вида ах3 + вх2 + вх + а = 0 называют возвратным уравнением 3-й степени.
Уравнение вида ах4 + вх3 + сх2 + вх + а = 0 называют возвратным уравнением 4-й степени.
Пример 5. 2х3 + 7х2 + 7х + 2 = 0
Это возвратное уравнение 3-й степени, у него сумма коэффициентов, стоящих на четных местах, равна сумме коэффициентов, стоящих на нечетных местах. Значит число 1 является корнем уравнения
(х + 1)(2х2 + 5х + 2) = 0
х1 = -1; х2 = -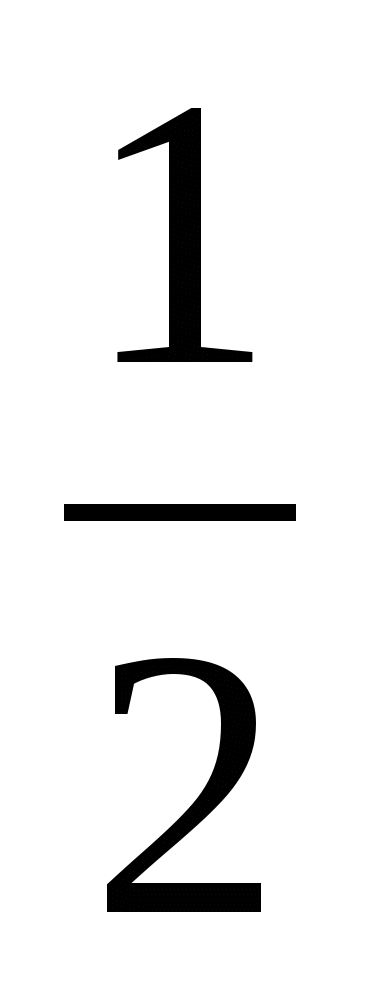 ; х3 = -2.
; х3 = -2.
Метод введения новой переменной
Пример 1. х4 - 2х2 - 15 = 0
Такое уравнение называют биквадратным.
х2 = t, t ≥ 0
t2 - 2 t - 15 = 0; t1 = -3; t2 = 5
-3 исключаем, получаем х2 = 5; х = ± .
.
Ответ: ±![]()
Пример 2 х(х - 1)(х - 2)(х - 3) = 24
(х2 - 3х)(х2 - 3х + 2) = 24
х2 - 3х = у; у(у + 2) = 24
у1 = 4; у2 = -6
х2 - 3х = 4 и х2 - 3х = -6
х1 = 4; х2 = -1 х2 - 3х + 6 = 0 корней нет.
Ответ: -1; 4.
Пример 3 (х2 + х + 1)2 - 3х2 - 3х - 7 = 0
(х2 + х + 1)2 - 3х2 - 3х - 3 - 4 = 0
(х2 + х + 1)2 - 3(х2 + х + 1) - 4 = 0
х2 + х + 1 = t
t2 - 3t - 4 = 0
t1 = -1; t2 = 4
х2 + х + 1 = -1 и х2 + х + 1 = 4
D < 0, корней нет х1,2 = 
Ответ: 
Пример 4. х4 + х3 - 4х2 + х + 1 = 0
Это возвратное уравнение 4-й степени, х = 0 не является его корнем; тогда разделим обе его части на х2
х2 + х - 4 + 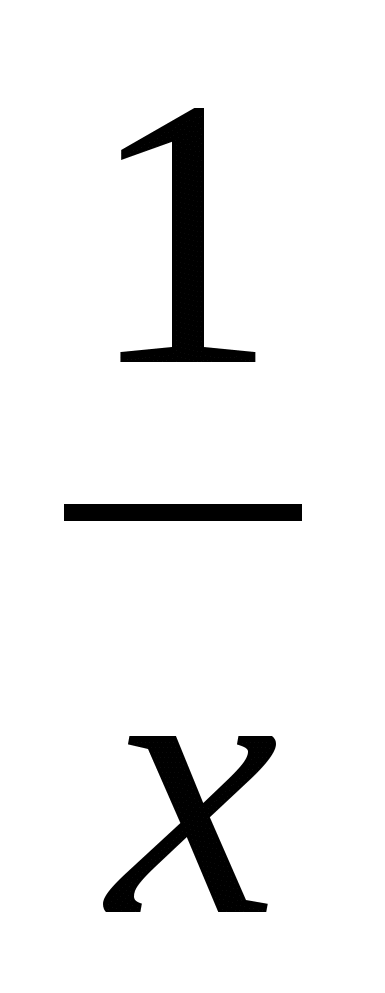 +
+ 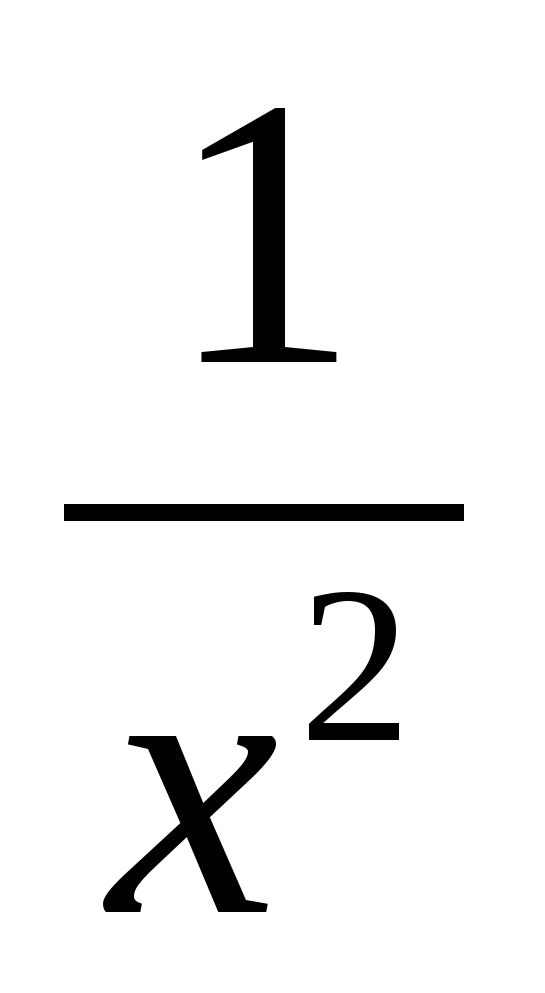 = 0
= 0
(х2 + 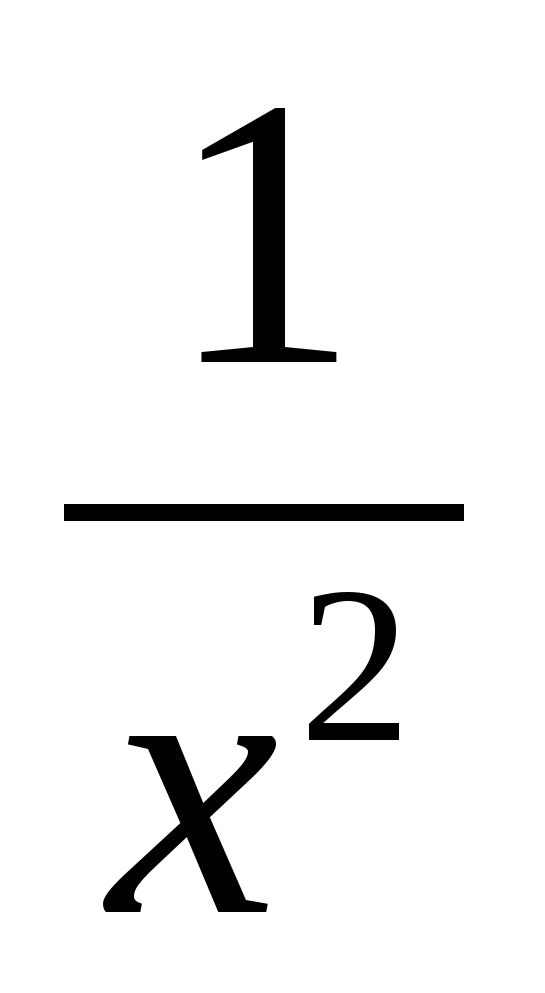 ) + (х +
) + (х + 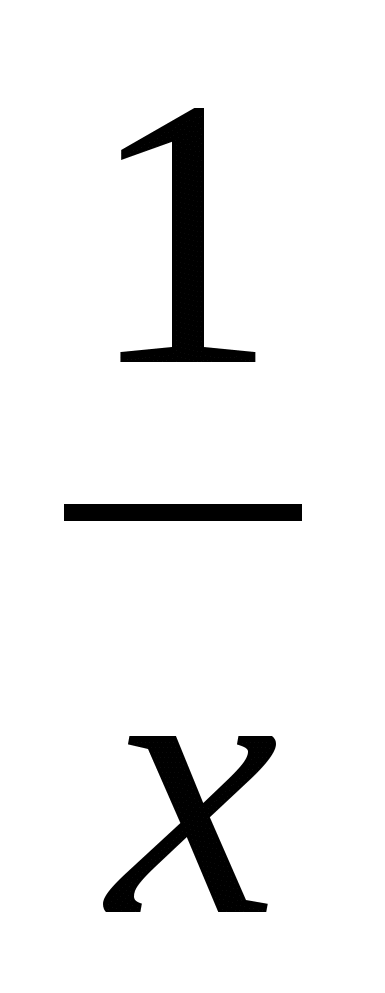 ) - 4 = 0
) - 4 = 0
х + 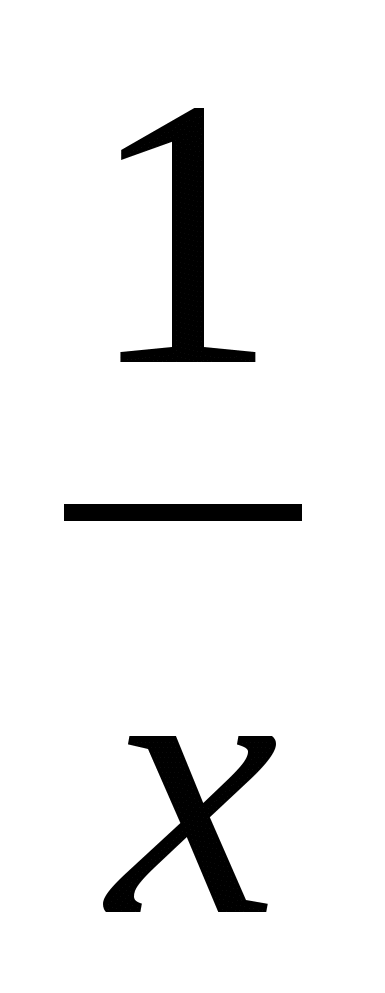 = у
= у
Возведем обе части в квадрат
х2 + 2 ∙ х ∙ 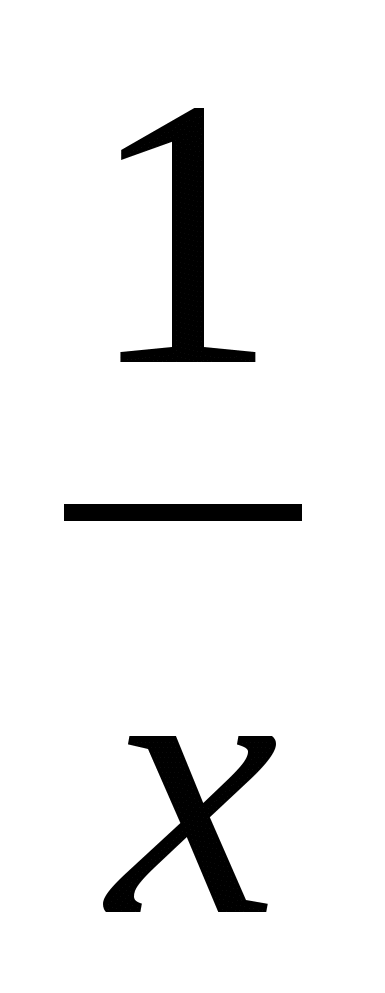 +
+ 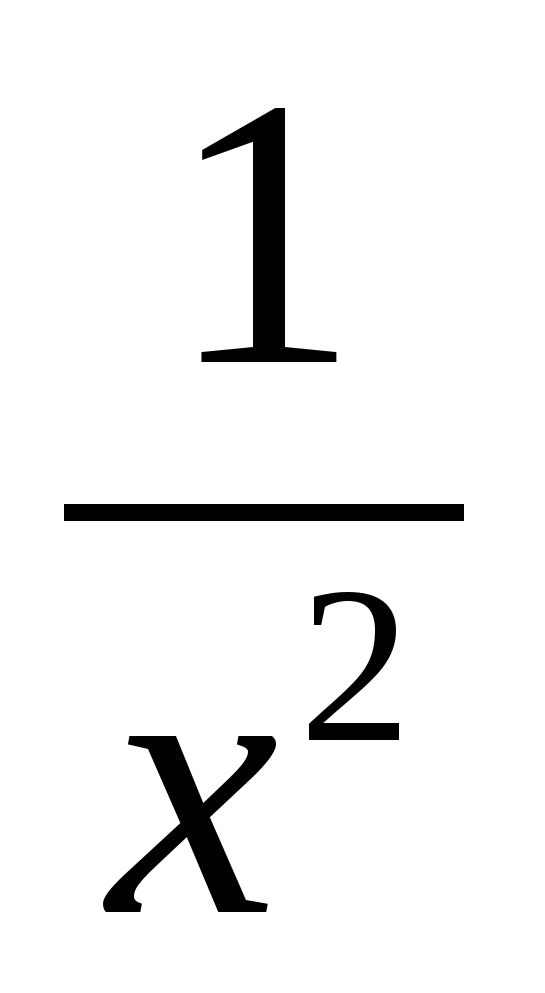 = у2, отсюда х2 +
= у2, отсюда х2 + 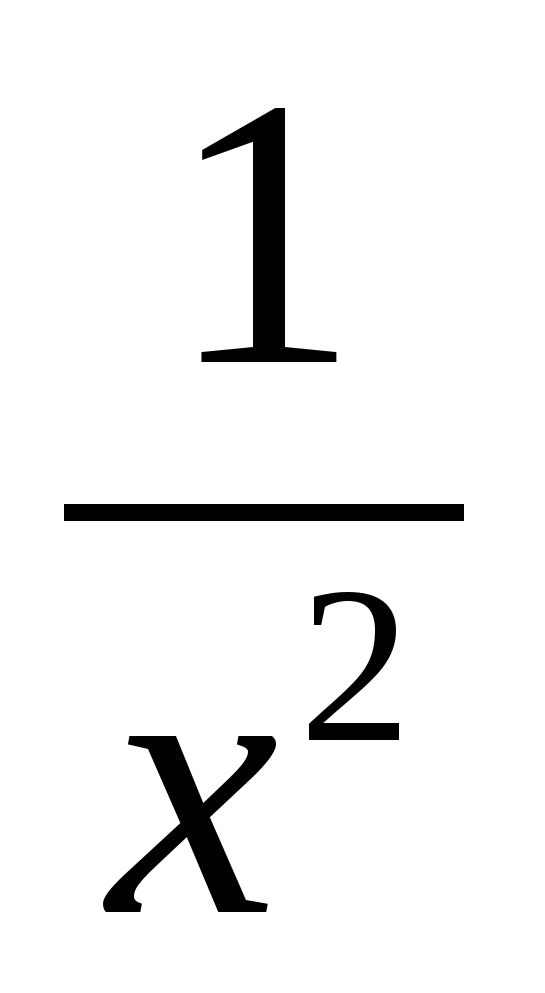 = у2 - 2
= у2 - 2
у2 - 2 + у - 4 = 0
у2 + у - 6 = 0, у1 = -3; у2 = 2
х + 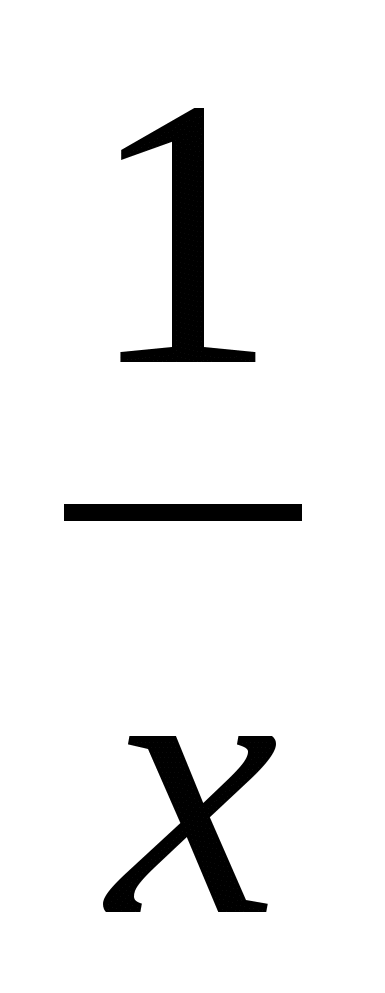 = -3 и х +
= -3 и х + 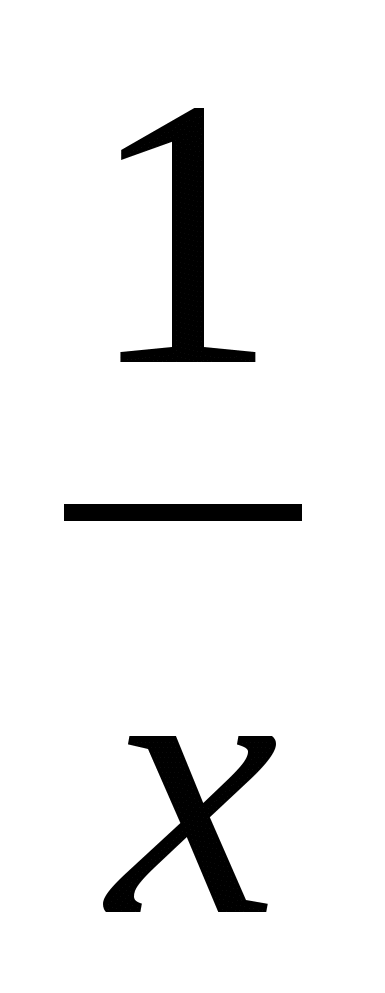 = 2
= 2
х1,2 = 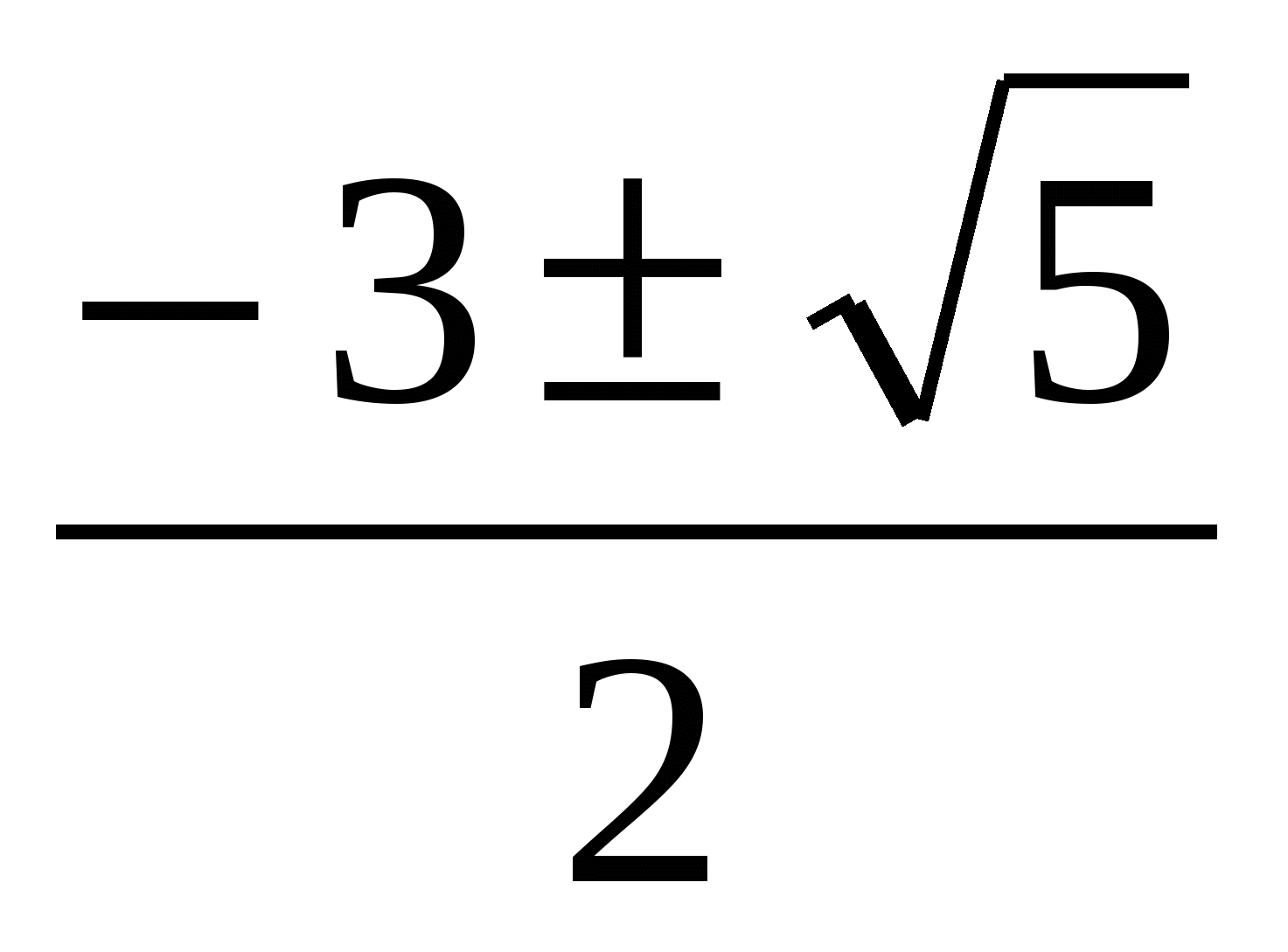 х3,4 = 1
х3,4 = 1
Ответ: 1; 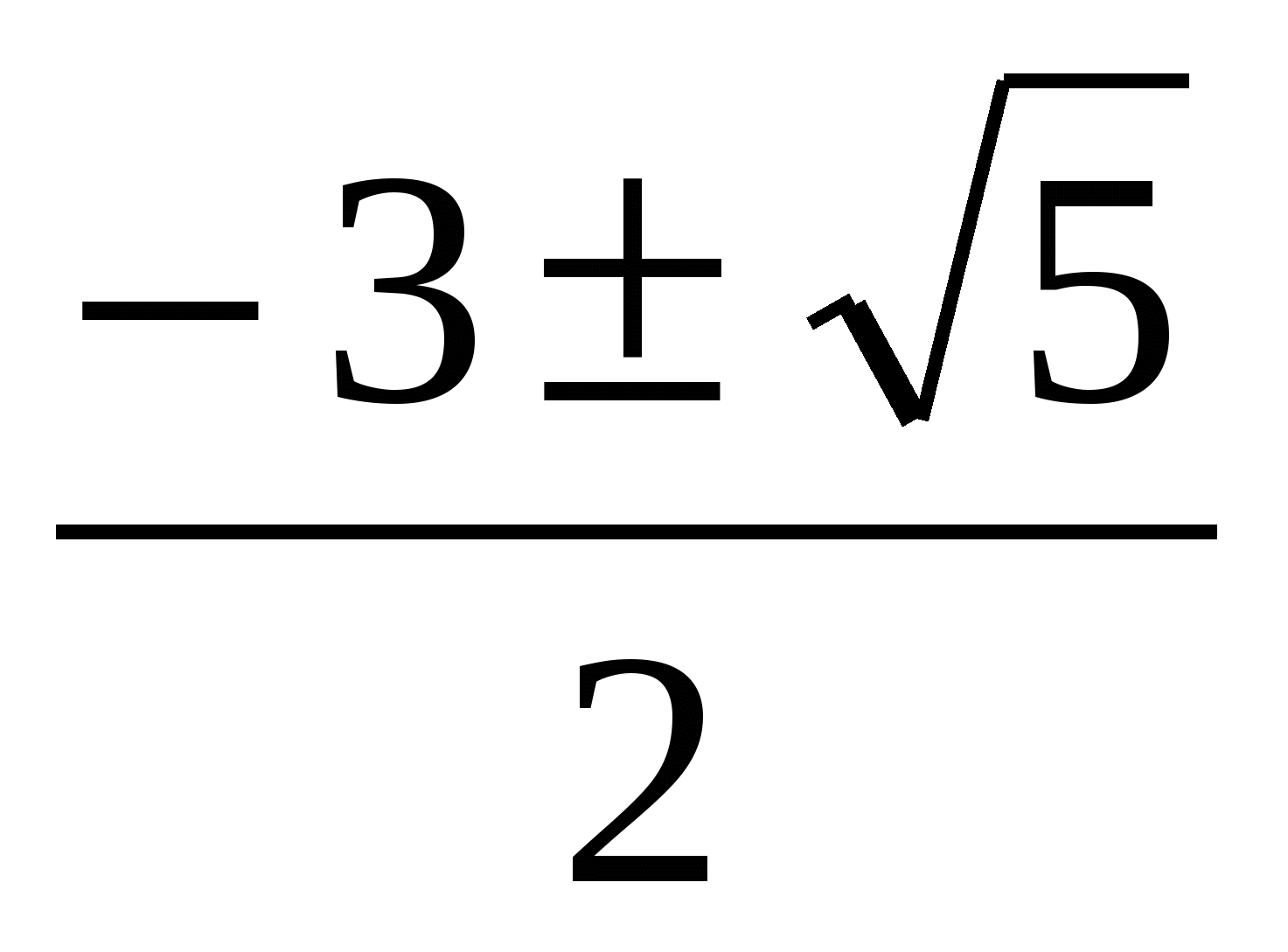 .
.
Пример 5. 6х4 - 35х3 + 62х2 - 35х + 6 = 0 / : х2
6х2 - 35х + 62 - 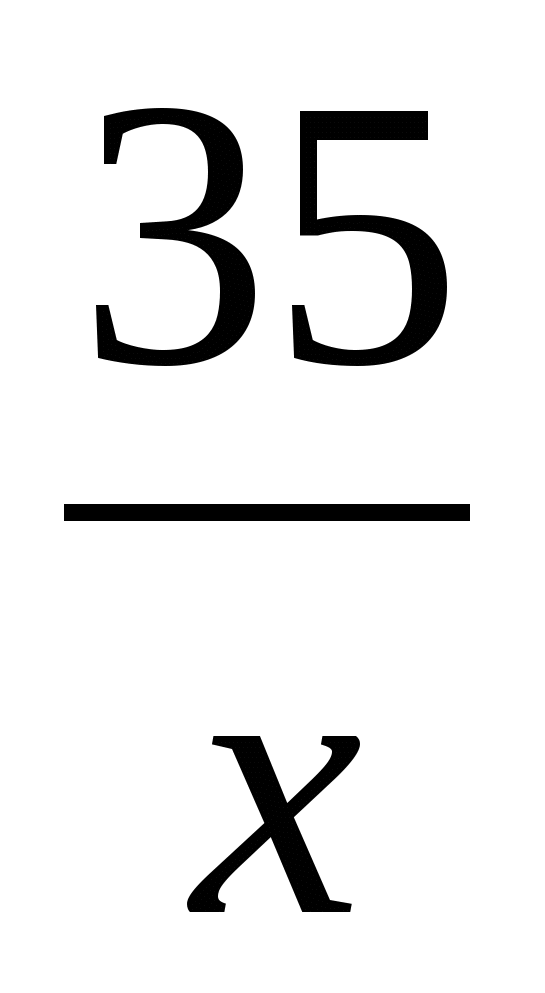 +
+  = 0
= 0
6(х2 + 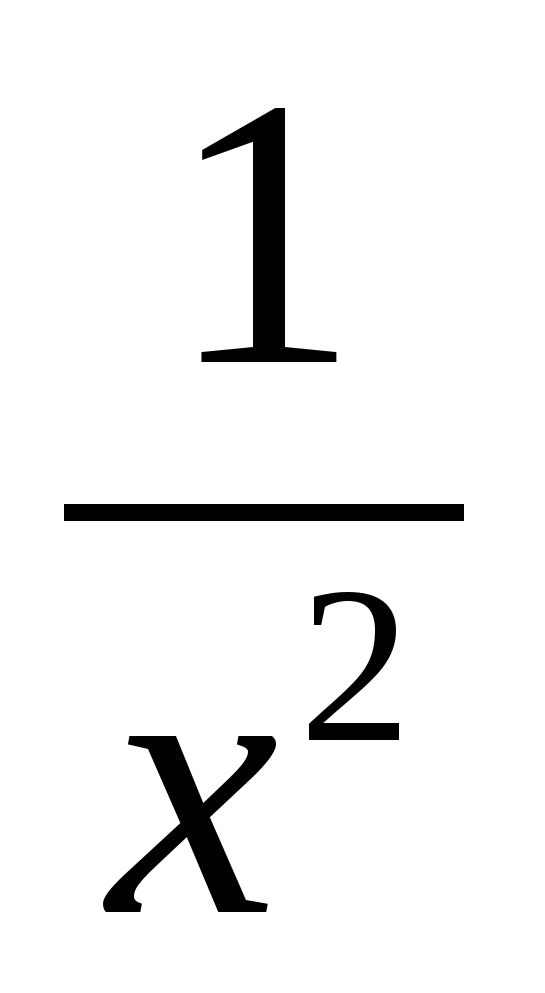 ) - 35(х +
) - 35(х + 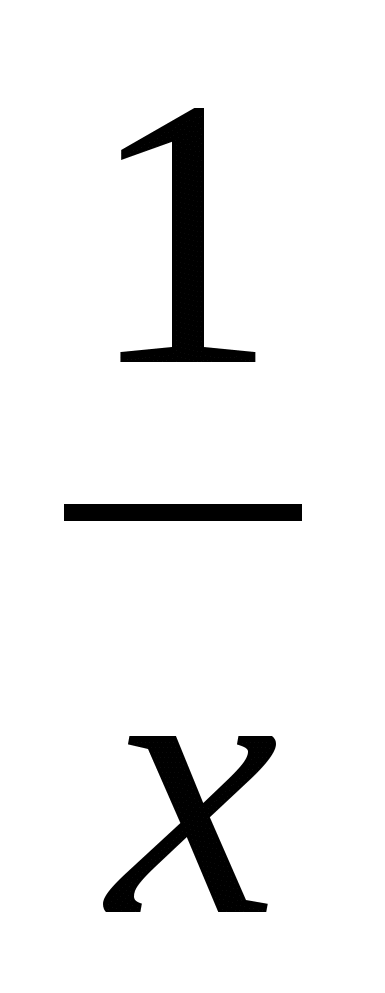 ) + 62 = 0
) + 62 = 0
х + 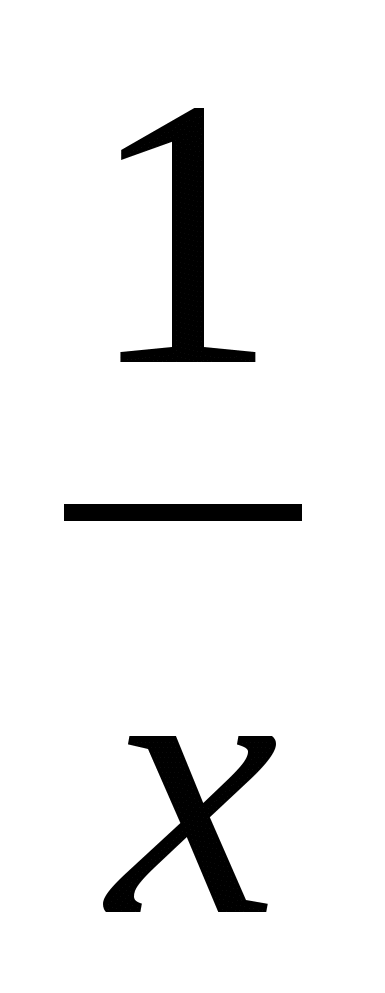 = у
= у
6(у2 - 2) - 35у + 62 = 0
6у2 - 35у + 50 = 0; у1 = 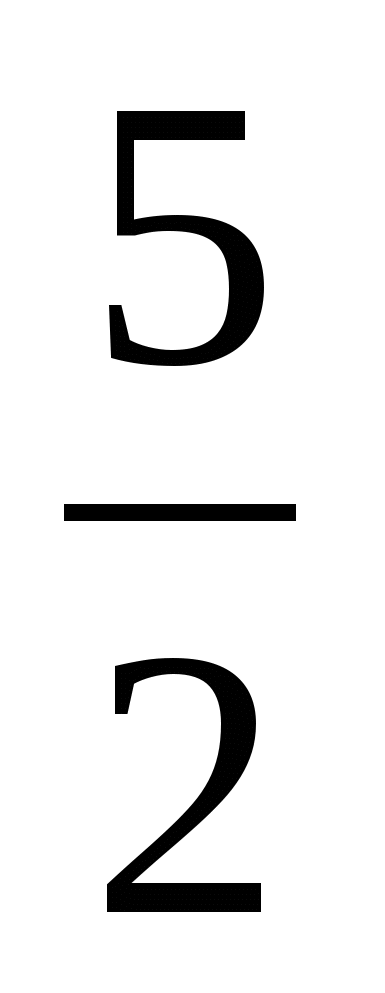 ; у2 =
; у2 = 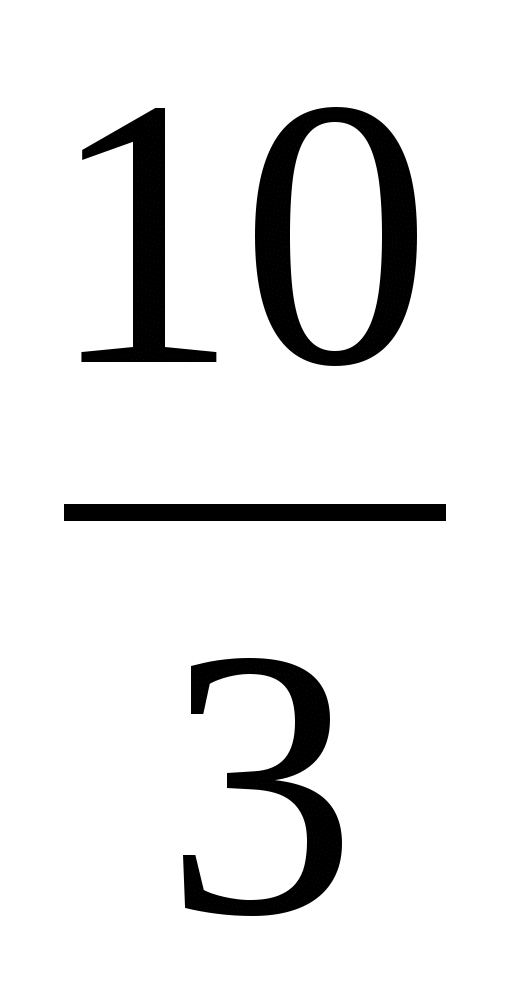
х + 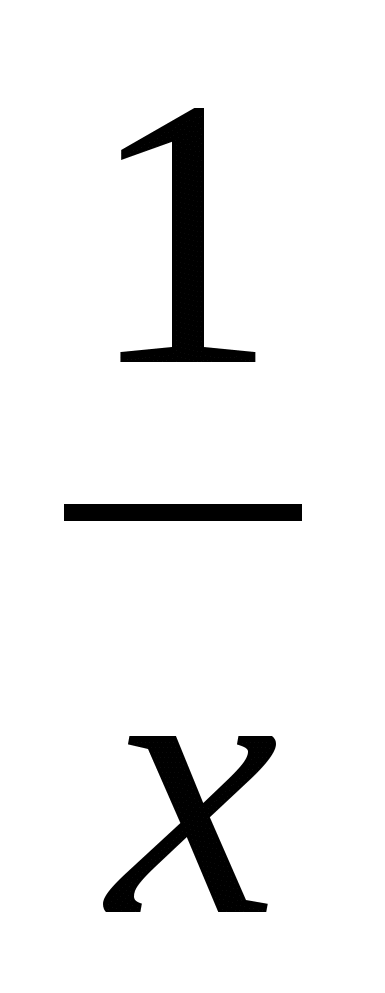 =
= 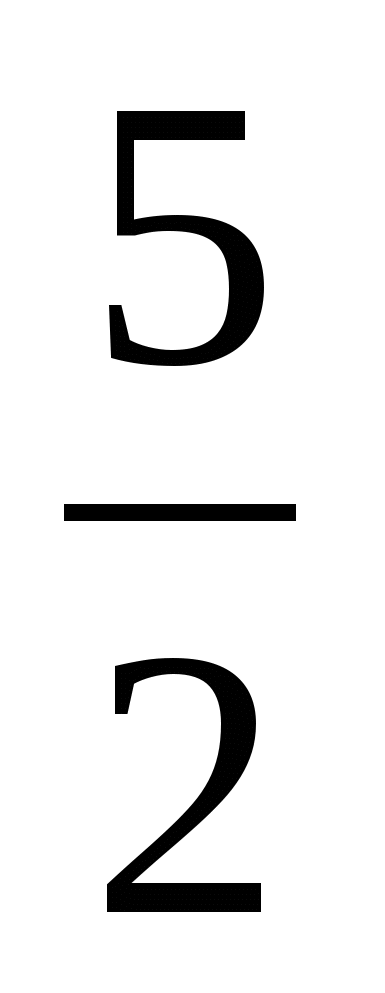 и х +
и х + 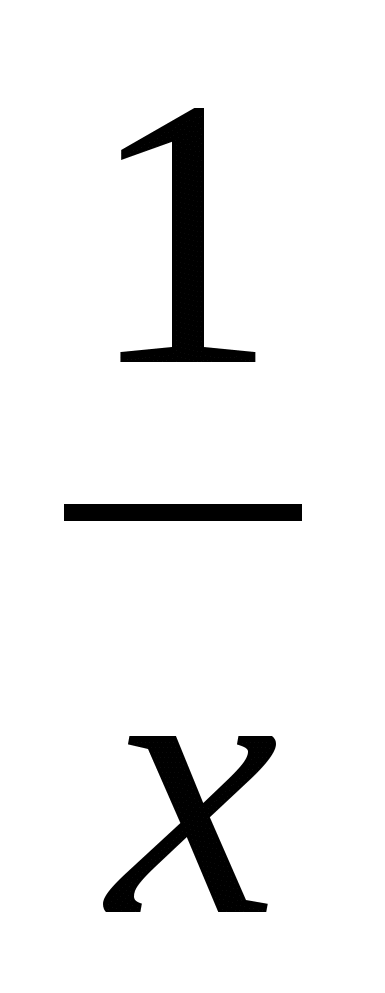 =
= 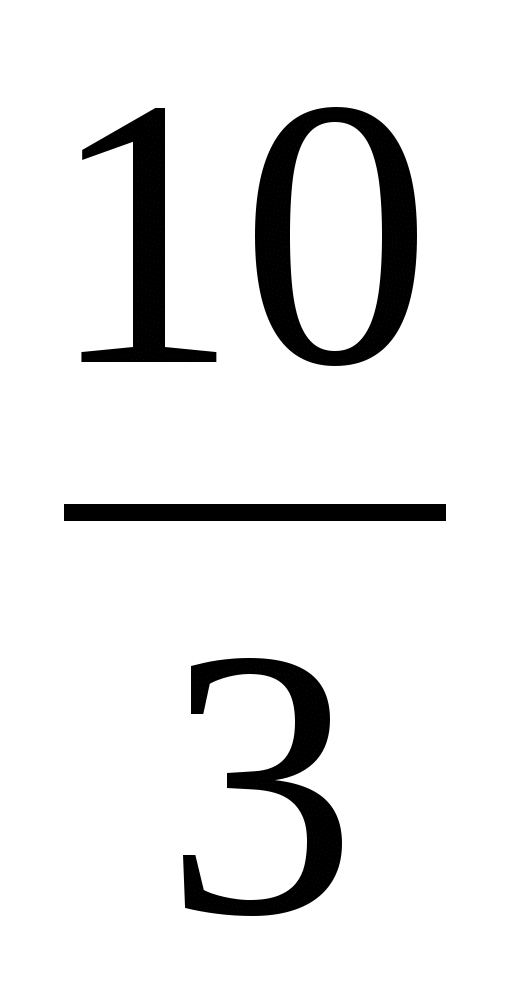
х1 = 2; х2 = 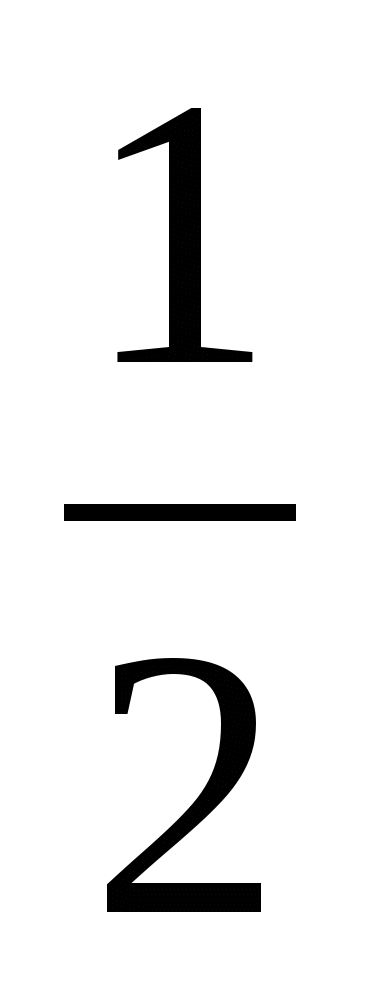 х3 = 3; х4 =
х3 = 3; х4 = ![]()
Ответ: 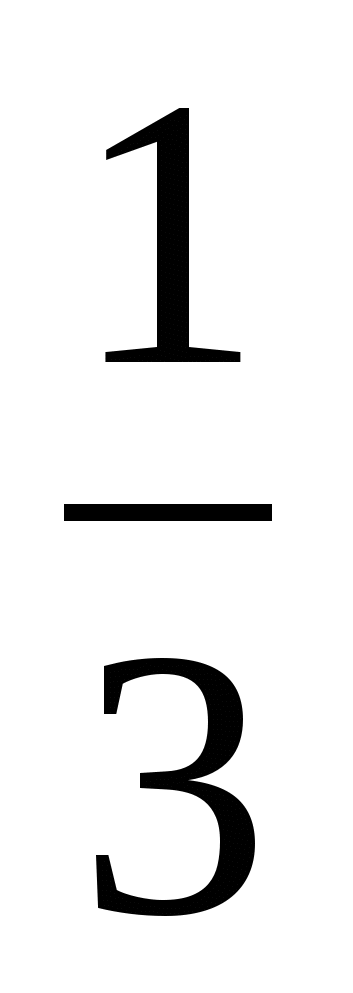 ;
; 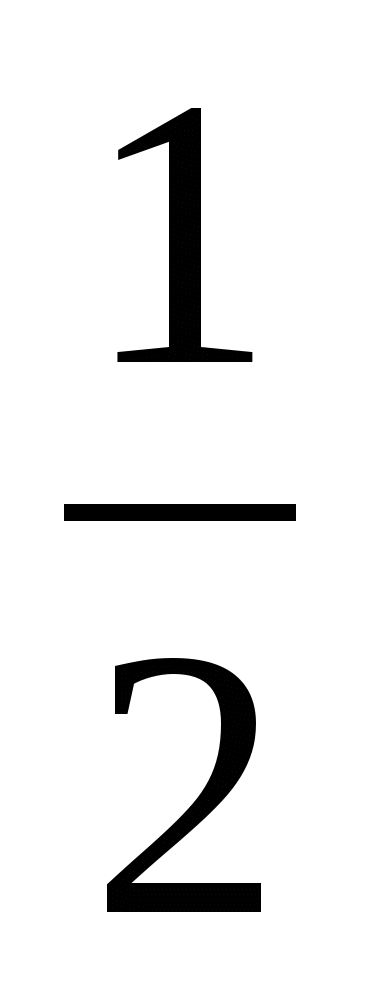 ; 2; 3.
; 2; 3.
Пример 6. 4х3 - 10х2 + 14х - 5 = 0 / ∙2
8х3 - 5 ∙ 4х2 + 14 ∙ 2х - 10 = 0
(2х)3 - 5(2х)2 + 14(2х) - 10 = 0
2х = у
у3 - 5у2 + 14у - 10 = 0
Сумма коэффициентов равна нулю, значит х = 1 - корень уравнения.
(у - 1)(у2 - 4у + 10) = 0
у1 = 1 или у2 - 4у + 10 = 0
D < 0, корней нет
2х = 1
х = 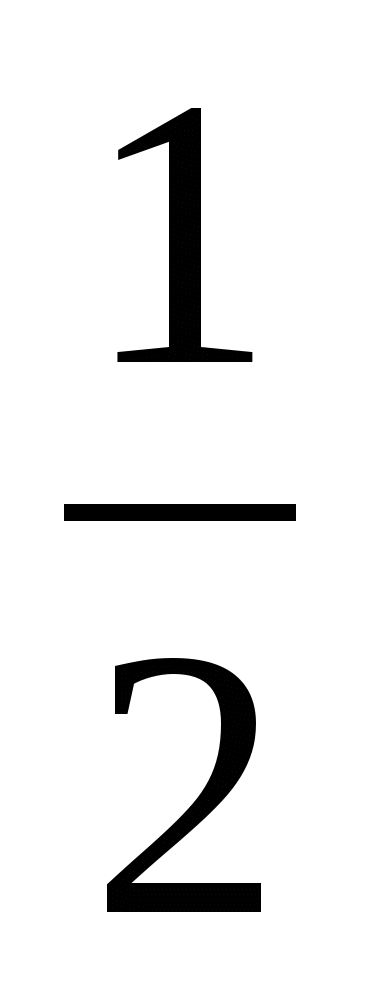
Ответ: 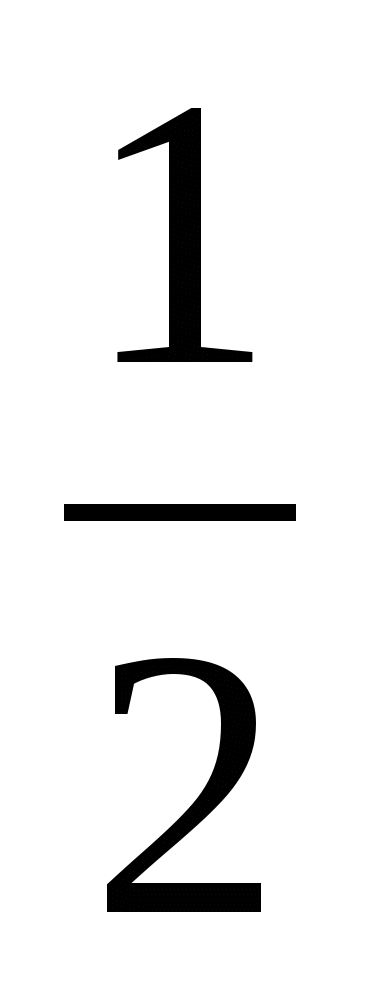
Упражнения
-
Решите уравнения:
а) х3 - 5х + 4 = 0
б) 8х3 - 4х + 1 = 0
в) 2х4 - 5х3 - х2 + 3х + 1 = 0
г) (х + 1)(х + 3)(х + 5)(х + 7) = 9
д) х4 - 2х3 - х2 - 2х + 1 = 0
е) х4 + х3 - 16х2 + 2х + 4 = 0
ж) 5х + ![]() = 2х2 +
= 2х2 + 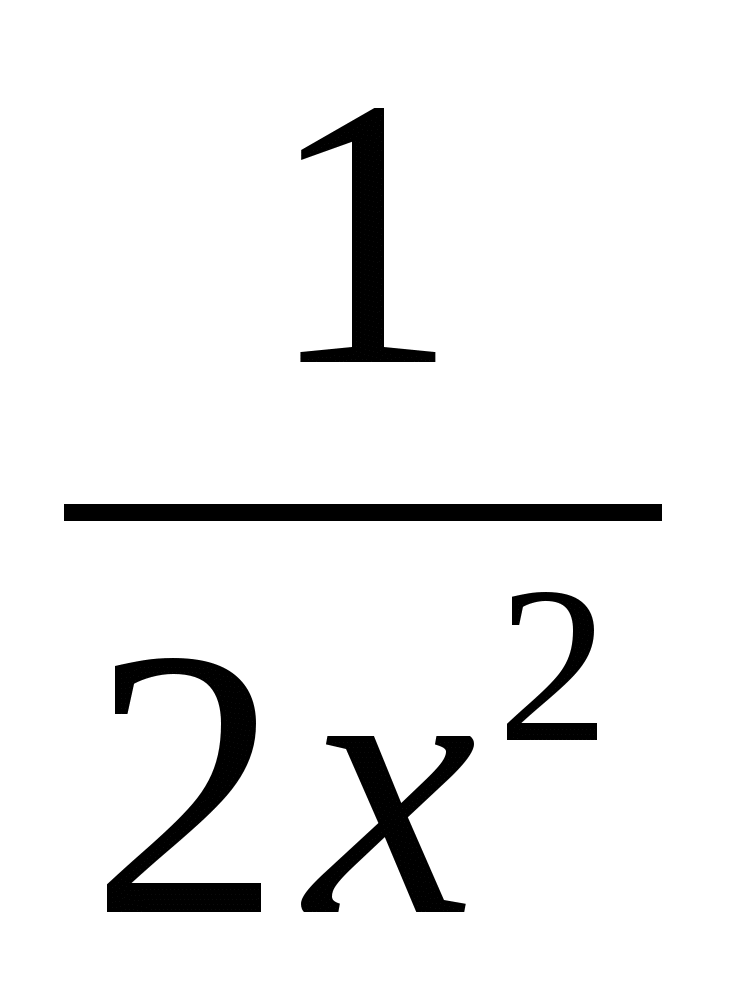 + 4
+ 4
-
Найдите а и решите уравнение
а) 6х3 - 2(а - 9)х2 - 3(а - 1)х + а = 0, если х = 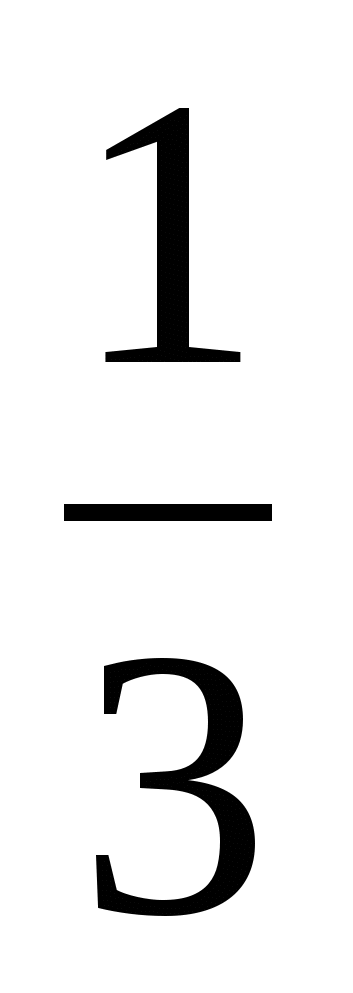 - корень уравнения
- корень уравнения
б) 2х3 - (а + 4)х2 + 2(а - 1)х + а = 0, х = 0,5
-
Многочлен Р(х) = 2х3 + х2 + ах + в при делении на х + 1 дает остаток 18,
а на х - 2 делится без остатка. Найти корни многочлена.
-
Многочлен Р(х) = х3 + ах2 + вх + с при делении на х + 1 и на х + 2 дает остаток 12, один из корней Р(х) равен 1. Найти остальные корни.
-
Решите уравнения
а) х4 + х3 - 4х2 + х + 1 = 0
б) 6х4 + 5х3 - 38х2 + 5х + 6 = 0
в) х3 - 3х2 - 3х + 1 = 0
г) 3х3 - 7х2 - 7х + 3 = 0
Контрольная работа по теме «Многочлены»
-
Разложите многочлен х4 + 2х3 - 13х2 - 38х - 24 на множители.
-
Решите уравнения:
а) х3 - 5х2 + 3х + 1 = 0
б) х4 - 7х3 + 14х2 - 7х + 1 = 0
-
При каких значениях а и в многочлен 2х4 + 3х3 - ах2 + вх - 3 делится без остатка на х + 3, а при делении на х - 2 дает остаток, равный 5?
-
Выполните деление с остатком х3 -3х + 2 на х - 2.
Ответы:
-
Р(х) = (х + 1)(х + 2)(х + 3)(х - 4)
-
а) 1; 2 ±
 б) 2 ±
б) 2 ± 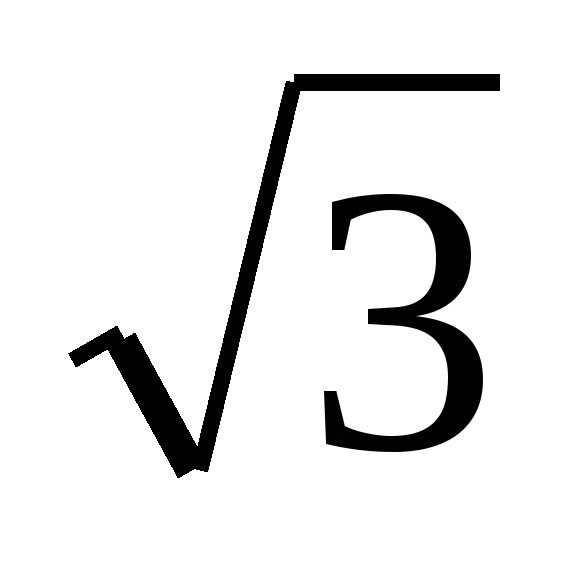 ;
; 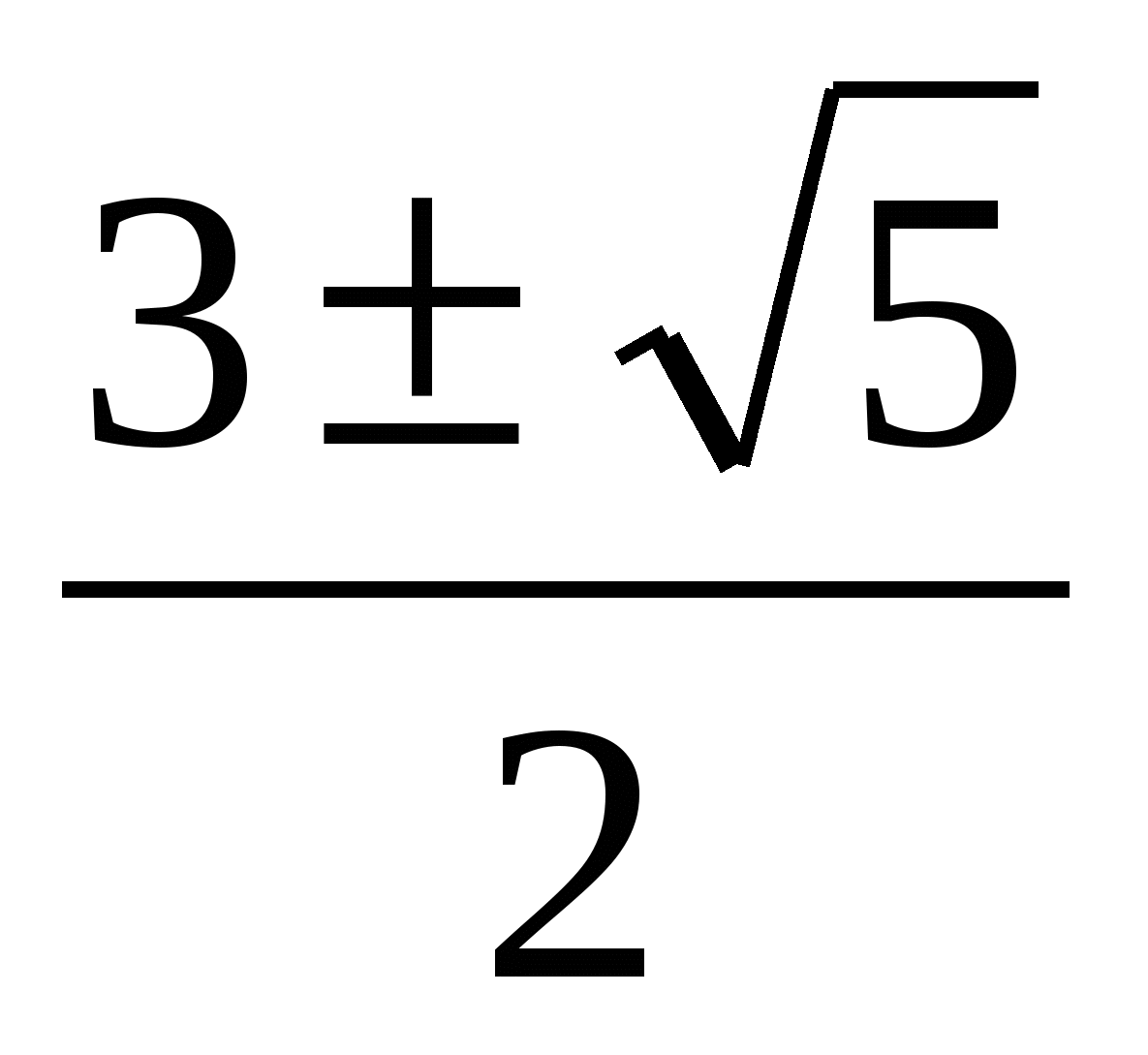
-
а = 10; в = -4.
-
х3 -3х + 2 = (х - 2)(х2 + 2х + 1) + 4.


